2011年普通高等学校招生全国统一考试(天津卷)解析版--数学文

合集下载

2011年天津市高考数学试卷(文科)答案与解析

2011年天津市高考数学试卷（文科）参考答案与试题解析一、选择题（共8小题，每小题5分，满分40分）1．（5分）（2011•天津）i是虚数单位，复数=（）A．2﹣i B．2+i C．﹣1﹣2i D．﹣1+2i【考点】复数代数形式的乘除运算．【专题】数系的扩充和复数．【分析】复数的分子、分母同乘分母的共轭复数，复数化简为a+bi（a，b∈R）的形式，即可．【解答】解：复数=故选A【点评】本题是基础题，考查复数代数形式的乘除运算，注意分母实数化，考查计算能力，常考题型．2．（5分）（2011•天津）设变量x，y满足约束条件则目标函数z=3x﹣y的最大值为（）A．﹣4 B．0 C．D．4【考点】简单线性规划．【专题】不等式的解法及应用．【分析】作出不等式组表示的平面区域；作出目标函数对应的直线；结合图象知当直线过（2，2）时，z最大．【解答】解：画出不等式表示的平面区域将目标函数变形为y=3x﹣z，作出目标函数对应的直线，当直线过（2，2）时，直线的纵截距最小，z最大最大值为6﹣2=4故选D【点评】本题考查画不等式组表示的平面区域、考查数形结合求函数的最值．3．（5分）（2011•天津）阅读如图的程序框图，运行相应的程序，若输入x的值为﹣4，则输出y的值为（）A．0.5 B．1 C．2 D．4【考点】程序框图．【专题】算法和程序框图．【分析】根据题意，按照程序框图的顺序进行执行，当x＜3时跳出循环，输出结果．【解答】解：当输入x=﹣4时，|x|＞3，执行循环，x=|﹣4﹣3|=7|x|=7＞3，执行循环，x=|7﹣3|=4，|x|=4＞3，执行循环，x=|4﹣3|=1，退出循环，输出的结果为y=21=2．故选C．【点评】本题考查循环结构的程序框图，搞清程序框图的算法功能是解决本题的关键，按照程序框图的顺序进行执行求解，属于基础题．4．（5分）（2011•天津）设集合A={x∈R|x﹣2＞0}，B={x∈R|x＜0}，C={x∈R|x（x﹣2）＞0}，则“x∈A∪B”是“x∈C”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．即不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断；集合的包含关系判断及应用．【专题】简易逻辑．【分析】化简集合A，C，求出A∪B，判断出A∪B与C的关系是相等的即充要条件．【解答】解：A={x∈R|x﹣2＞0}={x|x＞2}A∪B={x|x＞2或x＜0}C={x∈R|x（x﹣2）＞0}={x|x＞2或x＜0}∴A∪B=C∴“x∈A∪B”是“x∈C”的充要条件故选C【点评】本题考查判断一个命题是另一个命题的什么条件，先化简各个命题．考查充要条件的定义．5．（5分）（2011•天津）已知a=log23.6，b=log43.2，c=log43.6则（）A．a＞b＞c B．a＞c＞b C．b＞a＞c D．c＞a＞b【考点】对数值大小的比较．【专题】函数的性质及应用．【分析】利用换底公式可得a=log23.6=log43.62，然后根据对数函数y=log4x在（0，+∞）的单调性可进行比较即可．【解答】解：∵a=log23.6=log43.62∵y=log4x在（0，+∞）单调递增，又∵3.62＞3.6＞3.2∴log43.62＞log43.6＞log43.2即a＞c＞b故选：B【点评】本题考查利用对数函数的单调性比较对数值大小，考查了换底公式的应用，是基础题．6．（5分）（2011•天津）已知双曲线﹣=1（a＞0，b＞0）的左顶点与抛物线y2=2px的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1），则双曲线的焦距为（）A．2 B．2C．4D．4【考点】双曲线的简单性质；直线与圆锥曲线的关系．【专题】圆锥曲线的定义、性质与方程．【分析】根据题意，点（﹣2，﹣1）在抛物线的准线上，结合抛物线的性质，可得p=4，进而可得抛物线的焦点坐标，依据题意，可得双曲线的左顶点的坐标，即可得a的值，由点（﹣2，﹣1）在双曲线的渐近线上，可得渐近线方程，进而可得b的值，由双曲线的性质，可得c的值，进而可得答案．【解答】解：根据题意，双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1），即点（﹣2，﹣1）在抛物线的准线上，又由抛物线y2=2px的准线方程为x=﹣，则p=4，则抛物线的焦点为（2，0）；则双曲线的左顶点为（﹣2，0），即a=2；点（﹣2，﹣1）在双曲线的渐近线上，则其渐近线方程为y=±x，由双曲线的性质，可得b=1；则c=，则焦距为2c=2；故选B．【点评】本题考查双曲线与抛物线的性质，注意题目“双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1）”这一条件的运用，另外注意题目中要求的焦距即2c，容易只计算到c，就得到结论．7．（5分）（2011•天津）已知函数f（x）=2sin（ωx+φ），x∈R，其中ω＞0，﹣π＜φ≤π．若函数f（x）的最小正周期为6π，且当x=时，f（x）取得最大值，则（）A．f（x）在区间[﹣2π，0]上是增函数B．f（x）在区间[﹣3π，﹣π]上是增函数C．f（x）在区间[3π，5π]上是减函数D．f（x）在区间[4π，6π]上是减函数【考点】正弦函数的单调性；三角函数的周期性及其求法；三角函数的最值．【专题】三角函数的图像与性质．【分析】由函数f（x）的最小正周期为6π，根据周期公式可得ω=，且当x=时，f（x）取得最大值，代入可得，2sin（φ）=2，结合已知﹣π＜φ≤π可得φ=可得，分别求出函数的单调增区间和减区间，结合选项验证即可【解答】解：∵函数f（x）的最小正周期为6π，根据周期公式可得ω=，∴f（x）=2sin（φ），∵当x=时，f（x）取得最大值，∴2sin（φ）=2，φ=+2kπ，∵﹣π＜φ≤π，∴φ=，∴，由可得函数的单调增区间：，由可得函数的单调减区间：，结合选项可知A正确，故选A．【点评】本题主要考查了利用函数的部分图象求解函数的解析式，还考查了函数y=Asin （ωx+φ）（A＞0，ω＞0）的单调区间的求解，属于对基础知识的考查．8．（5分）（2011•天津）对实数a与b，定义新运算“⊗”：a⊗b=．设函数f（x）=（x2﹣2）⊗（x﹣1），x∈R．若函数y=f（x）﹣c的图象与x轴恰有两个公共点，则实数c的取值范围是（）A．（﹣1，1]∪（2，+∞）B．（﹣2，﹣1]∪（1，2]C．（﹣∞，﹣2）∪（1，2]D．[﹣2，﹣1]【考点】函数与方程的综合运用．【专题】函数的性质及应用．【分析】根据定义的运算法则化简函数f（x）=（x2﹣2）⊗（x﹣1），的解析式，并画出f （x）的图象，函数y=f（x）﹣c的图象与x轴恰有两个公共点转化为y=f（x），y=c图象的交点问题，结合图象求得实数c的取值范围．【解答】解：∵，∴函数f（x）=（x2﹣2）⊗（x﹣1）=，由图可知，当c∈（﹣2，﹣1]∪（1，2]函数f（x）与y=c的图象有两个公共点，∴c的取值范围是（﹣2，﹣1]∪（1，2]，故选B．【点评】本题考查二次函数的图象特征、函数与方程的综合运用，及数形结合的思想．属于基础题．二、填空题（共6小题，每小题5分，满分30分）9．（5分）（2011•天津）已知集合A={x∈R||x﹣1|＜2}，Z为整数集，则集合A∩Z中所有元素的和等于3．【考点】交集及其运算．【专题】集合．【分析】先根据绝对值不等式求出集合A，然后根据交集的定义求出A∩Z，最后求出集合A∩Z中所有元素的和即可．【解答】解：A={x∈R||x﹣1|＜2}={x|﹣1＜x＜3}，而Z为整数集，集合A∩Z={0，1，2}，故集合A∩Z中所有元素的和等于0+1+2=3，故答案为3．【点评】本题属于以绝对值不等式为依托，求集合的交集的基础题，同时考查了集合中元素的和．10．（5分）（2011•天津）一个几何体的三视图如图所示（单位：m），则这个几何体的体积为4m3．【考点】由三视图求面积、体积．【专题】立体几何．【分析】由题意可知，一个简单的组合体，上面是一个底面是边长为1的正方形，高是2的四棱柱，下面是一个长为2，高为1，宽为1的长方体，根据所给的长度，求出几何体的体积．【解答】解：由三视图可知，这是一个简单的组合体，上面是一个底面是边长为1的正方形，高是2的四棱柱，体积是1×1×2下面是一个长为2，高为1，宽为1的长方体，体积是1×1×2∴几何体的体积是1×1×2+2×1×1=4m3，故答案为：4【点评】本题考查由三视图还原直观图，根据图形中所给的数据，求出要求的体积，本题是一个考查简单几何体体积的简单题目．11．（5分）（2011•天津）已知{a n}为等差数列，S n为{a n}的前n项和，n∈N*，若a3=16，S20=20，则S10值为110．【考点】等差数列的性质．【专题】等差数列与等比数列．【分析】本题可根据等差数列的前n项和的一上性质{S（k+1）m﹣S km}是以m2d为公差的数列，本题中令m=5，每五项的和也组成一个等差数列，再由数列中项知识求出前五项的和，由此建立方程求出公差，进而可求出S10的值【解答】解：由题意a3=16，故S5=5×a3=80，由数列的性质S10﹣S5=80+25d，S15﹣S10=80+50d，S20﹣S15=80+75d，故S20=20=320+150d，解之得d=﹣2又S10=S5+S10﹣S5=80+80+25d=160﹣50=110故答案为：110【点评】本题考点是等差数列的性质，考查等差数列前n项和的性质，以及数列的中项的运用，本题技巧性较强，属于等差数列的性质运用题，解答本题，要注意从题设条件中分析出应该用那个性质来进行转化．12．（5分）（2011•天津）已知log2a+log2b≥1，则3a+9b的最小值为18．【考点】基本不等式；对数的运算性质．【专题】函数的性质及应用；不等式的解法及应用．【分析】先把已知条件转化为ab≥2，且a＞0，b＞0；再把所求用基本不等式转化到用ab表示即可．【解答】解：由log2a+log2b≥1得ab≥2，且a＞0，b＞0．又3a+9b=3a+32b≥2=2，因为a+2b≥2=2≥2=4，所以3a+9b≥2=18．即3a+9b的最小值为18．故答案为18．【点评】本题是对指数的运算性质，对数的运算性质以及基本不等式的综合考查．考查的都是基本知识点，只要课本知识掌握熟练，是道基础题．13．（5分）（2011•天津）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=，AF：FB：BE=4：2：1．若CE与圆相切，则CE的长为．【考点】圆的切线方程．【专题】直线与圆．【分析】设出AF=4k，BF=2k，BE=k，由DF•FC=AF•BF求出k的值，利用切割定理求出CE．【解答】解：设AF=4k，BF=2k，BE=k，由DF•FC=AF•BF，得2=8k2，即k=，∴AF=2，BF=1，BE=，AE=，由切割定理得CE2=BE•EA==，∴CE=．【点评】本题是基础题，考查直线与圆的位置关系，考查计算能力，基本知识掌握的情况，常考题型．14．（5分）（2011•天津）已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=1，P是腰DC上的动点，则的最小值为5．【考点】向量的模．【专题】平面向量及应用．【分析】根据题意，利用解析法求解，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0），设P（0，b）（0≤b≤a），求出，根据向量模的计算公式，即可求得，利用完全平方式非负，即可求得其最小值．【解答】解：如图，以直线DA，DC分别为x，y轴建立平面直角坐标系，则A（2，0），B（1，a），C（0，a），D（0，0）设P（0，b）（0≤b≤a）则=（2，﹣b），=（1，a﹣b），∴=（5，3a﹣4b）∴=≥5．故答案为5．【点评】此题是个基础题．考查向量在几何中的应用，以及向量模的求法，同时考查学生灵活应用知识分析解决问题的能力．三、解答题（共6小题，满分80分）15．（13分）（2011•天津）编号为A1，A2，…，A16的16名篮球运动员在某次训练比赛中的得分记录如下：运动员编号A1A2A3A4A5A6A7A8得分15 35 21 28 25 36 18 34运动员编号A9A10A11A12A13A14A15A16得分17 26 25 33 22 12 31 38（Ⅰ）将得分在对应区间内的人数填入相应的空格；区间[10，20）[20，30）[30，40]人数（Ⅱ）从得分在区间[20，30）内的运动员中随机抽取2人，（i）用运动员的编号列出所有可能的抽取结果；（ii）求这2人得分之和大于50分的概率．【考点】列举法计算基本事件数及事件发生的概率；古典概型及其概率计算公式．【专题】概率与统计．【分析】（I）根据已知中编号为A1，A2，…，A16的16名篮球运动员在某次训练比赛中的得分记录表，我们易得出得分在对应区间内的人数．（II）（i）根据（I）的结论，我们易列出在区间[20，30）内的运动员中随机抽取2人，所有可能的抽取结果；（ii）列出这2人得分之和大于50分的基本事件的个数，代入古典概型公式即可得到这2人得分之和大于50分的概率．【解答】解：（I）由已知中编号为A1，A2，…，A16的16名篮球运动员在某次训练比赛中的得分记录表易得：得分在区间[10，20）上的共4人，在区间[20，30）上的共6人，在区间[30，40]上的共6人，故答案为4，6，6（II）（i）得分在区间[20，30）上的共6人，编号为A3，A4，A5，A10，A11，A13，从中随机抽取2人，计为（X，Y），则所有可能的抽取结果有：（A3，A4），（A3，A5），（A3，A10），（A3，A11），（A3，A13），（A4，A5），（A4，A10），（A4，A11），（A4，A13），（A5，A10），（A5，A11），（A5，A13），（A10，A11），（A10，A13），（A11，A13）共15种．（ii）从得分在区间[20，30）内的运动员中随机抽取2人，这2人的得分之和大于50分的基本事件有：（A4，A5），（A4，A10），（A4，A11），（A5，A10），（A10，A11）共5种故这2人得分之和大于50分的概率P==【点评】本题主要考查用列举法计算随机事件所含的基本事件烽、古典概型及其概率计算公式等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力．16．（13分）（2011•天津）在△ABC中，内角A，B，C的对边分别为a，b，c，已知．（Ⅰ）求cosA的值；（Ⅱ）的值．【考点】余弦定理；同角三角函数基本关系的运用；两角和与差的余弦函数；二倍角的余弦．【专题】解三角形．【分析】（I）利用三角形中的等边对等角得到三角形三边的关系；利用三角形的余弦定理求出角A的余弦．（II）利用三角函数的平方关系求出角A的正弦，利用二倍角公式求出角2A的正弦，余弦；利用两个角的和的余弦公式求出的值．【解答】解：（I）由B=C，可得所以cosA==（II）因为所以=【点评】本题考查三角形的余弦定理、考查三角函数的平方关系、考查两角和的余弦公式．17．（13分）（2011•天津）如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=1，O为AC中点，PO⊥平面ABCD，PO=2，M为PD中点．（Ⅰ）证明：PB∥平面ACM；（Ⅱ）证明：AD⊥平面PAC；（Ⅲ）求直线AM与平面ABCD所成角的正切值．【考点】直线与平面垂直的判定；直线与平面平行的判定；直线与平面所成的角．【专题】空间位置关系与距离；空间角；立体几何．【分析】（I）由O为AC中点，M为PD中点．结合平行四边形的对角线性质，考虑连接BD，MO，则有PB∥MO，从而可证（II）由∠ADC=45°，且AD=AC=1，易得AD⊥AC，PO⊥AD，根据线面垂直的判定定理可证（III）取DO中点N，由PO⊥平面ABCD，可得MN⊥平面ABCD，从而可得∠MAN是直线AM与平面ABCD所成的角．在Rt△ANM中求解即可【解答】解：（I）证明：连接BD，MO在平行四边形ABCD中，因为O为AC的中点，所以O为BD的中点，又M为PD的中点，所以PB∥MO因为PB⊄平面ACM，MO⊂平面ACM所以PB∥平面ACM（II）证明：因为∠ADC=45°，且AD=AC=1，所以∠DAC=90°，即AD⊥AC又PO⊥平面ABCD，AD⊂平面ABCD，所以PO⊥AD，AC∩PO=O，AD⊥平面PAC （III）解：取DO中点N，连接MN，AN因为M为PD的中点，所以MN∥PO，且MN=PO=1，由PO⊥平面ABCD，得MN⊥平面ABCD所以∠MAN是直线AM与平面ABCD所成的角．在Rt△DAO中，，所以，∴，在Rt△ANM中，==即直线AM与平面ABCD所成的正切值为【点评】本题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识，考查空间想象能力、运算能力、推理论证能力．18．（13分）（2011•天津）设椭圆+=1（a＞b＞0）的左、右焦点分别为F1，F2．点P（a，b）满足|PF2|=|F1F2|．（Ⅰ）求椭圆的离心率e；（Ⅱ）设直线PF2与椭圆相交于A，B两点，若直线PF2与圆（x+1）2+=16相交于M，N两点，且|MN|=|AB|，求椭圆的方程．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程；椭圆的简单性质．【专题】圆锥曲线的定义、性质与方程．【分析】（Ⅰ）直接利用|PF2|=|F1F2|，对应的方程整理后即可求椭圆的离心率e；（Ⅱ）先把直线PF2与椭圆方程联立求出A，B两点的坐标以及对应的|AB|两点，进而求出|MN|，再利用弦心距，弦长以及圆心到直线的距离之间的等量关系，即可求椭圆的方程．【解答】解：（Ⅰ）设F1（﹣c，0），F2（c，0）（c＞0）．由题得|PF2|=|F1F2|，即=2c，整理得2+﹣1=0，得=﹣1（舍），或=，所以e=．（Ⅱ）由（Ⅰ）知a=2c，b=c，可得椭圆方程为3x2+4y2=12c2，直线方程PF2为y=（x ﹣c）．A，B的坐标满足方程组，消y并整理得5x2﹣8xc=0，解得x=0，x=，得方程组的解为，，不妨设A（c，c），B（0，﹣c）．所以|AB|==c，于是|MN|=|AB|=2c．圆心（﹣1，）到直线PF2的距离d=，因为d2+=42，所以（2+c）2+c2=16，整理得c=﹣（舍）或c=2．所以椭圆方程为+=1．【点评】本题主要考查椭圆的方程和几何性质，直线的方程，两点间的距离公式以及点到直线的距离公式等基础知识，考查用代数方法研究圆锥曲线的性质和数形结合的数学思想，考查解决问题的能力和运算能力．19．（14分）（2011•天津）已知函数f（x）=4x3+3tx2﹣6t2x+t﹣1，x∈R，其中t∈R．（Ⅰ）当t=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；（Ⅱ）当t≠0时，求f（x）的单调区间；（Ⅲ）证明：对任意的t∈（0，+∞），f（x）在区间（0，1）内均存在零点．【考点】利用导数研究曲线上某点切线方程；函数的零点；利用导数研究函数的单调性．【专题】导数的综合应用．【分析】（I）当t=1时，求出函数f（x），利用导数的几何意义求出x=0处的切线的斜率，利用点斜式求出切线方程；（II）根据f'（0）=0，解得x=﹣t或x=，讨论t的正负，在函数的定义域内解不等式fˊ（x）＞0和fˊ（x）＜0求出单调区间即可；（III）根据函数的单调性分两种情况讨论，当≥1与当0＜＜1时，研究函数的单调性，然后根据区间端点的符号进行判定对任意t∈（0，2），f（x）在区间（0，1）内均存在零点从而得到结论．【解答】解：（I）当t=1时，f（x）=4x3+3x2﹣6x，f（0）=0f'（x）=12x2+6x﹣6，f'（0）=﹣6，所以曲线y=f（x）在点（0，f（0））处的切线方程为y=﹣6x．（II）解：f'（x）=12x2+6tx﹣6t2，f'（0）=0，解得x=﹣t或x=∵t≠0，以下分两种情况讨论：（1）若t＜0，则＜﹣t，∴f（x）的单调增区间是（﹣∞，），（﹣t，+∞）；f（x）的单调减区间是（，﹣t）（2）若t＞0，则＞﹣t，∴f（x）的单调增区间是（﹣∞，﹣t），（，+∞）；f（x）的单调减区间是（﹣t，）（III）证明：由（II）可知，当t＞0时，f（x）在（0，）内单调递减，在（，+∞）内单调递增，以下分两种情况讨论：（1）当≥1，即t≥2时，f（x）在（0，1）内单调递减．f（0）=t﹣1＞0，f（1）=﹣6t2+4t+3≤﹣13＜0所以对于任意t∈[2，+∞），f（x）在区间（0，1）内均存在零点．（2）当0＜＜1，即0＜t＜2时，f（x）在（0，）内单调递减，在（，1）内单调递增若t∈（0，1]，f（）=+t﹣1≤＜0，f（1）=﹣6t2+4t+3≥﹣2t+3＞0所以f（x）在（，1）内存在零点．若t∈（1，2），f（）=+t﹣1＜+1＜0，f（0）=t﹣1＞0∴f（x）在（0，）内存在零点．所以，对任意t∈（0，2），f（x）在区间（0，1）内均存在零点．综上，对于任意t∈（0，+∞），f（x）在区间（0，1）内均存在零点．【点评】本题主要考查了导数的几何意义，利用导数研究函数的单调性、曲线的切线方程、函数零点、解不等式等基础知识，考查了计算能力和分类讨论的思想．20．（14分）（2011•天津）已知数列{a n}与{b n}满足b n+1a n+b n a n+1=（﹣2）n+1，b n=，n∈N*，且a1=2．（Ⅰ）求a2，a3的值（Ⅱ）设c n=a2n+1﹣a2n﹣1，n∈N*，证明{c n}是等比数列（Ⅲ）设S n为{a n}的前n项和，证明++…++≤n﹣（n∈N*）【考点】数列与不等式的综合；等比关系的确定．【专题】等差数列与等比数列．【分析】（Ⅰ）推出b n的表达式，分别当n=1时，求出a2=﹣；当n=2时，解出a3=8；（Ⅱ）设c n=a2n+1﹣a2n﹣1，n∈N*，利用等比数列的定义，证明{c n}是等比数列；（Ⅲ）求出S2n，a2n，S2n﹣1，a2n﹣1，求出+的表达式，然后求出++…++的表达式，利用放缩法证明结果．【解答】（Ⅰ）解：由b n=，（n∈N*）可得b n=又b n+1a n+b n a n+1=（﹣2）n+1，当n=1时，a1+2a2=﹣1，可得由a1=2，a2=﹣；当n=2时，2a2+a3=5可得a3=8；（Ⅱ）证明：对任意n∈N*，a2n﹣1+2a2n=﹣22n﹣1+1…①2a2n+a2n+1=22n+1…②②﹣①，得a2n+1﹣a2n﹣1=3×22n﹣1，即：c n=3×22n﹣1，于是所以{c n}是等比数列．（Ⅲ）证明：a1=2，由（Ⅱ）知，当k∈N*且k≥2时，a2k﹣1=a1+（a3﹣a1）+（a5﹣a3）+（a7﹣a5）+…+（a2k﹣1﹣a2k﹣3）=2+3（2+23+25+…+22k﹣3）=2+3×=22k﹣1，故对任意的k∈N*，a2k﹣1=22k﹣1．由①得22k﹣1+2a2k=﹣22k﹣1+1，所以k∈N*，因此，于是，．故==所以，对任意的n∈N*，++…++=（+）+…+（+）===n﹣≤n﹣﹣=n﹣（n∈N*）【点评】本题考查等比数列的定义，等比数列求和等基础知识，考查计算能力、推理论证能力、综合发现问题解决问题的能力以及分类讨论思想．。

2011年普通高等学校招生全国统一考试高考数学教师精校版含详解天津理

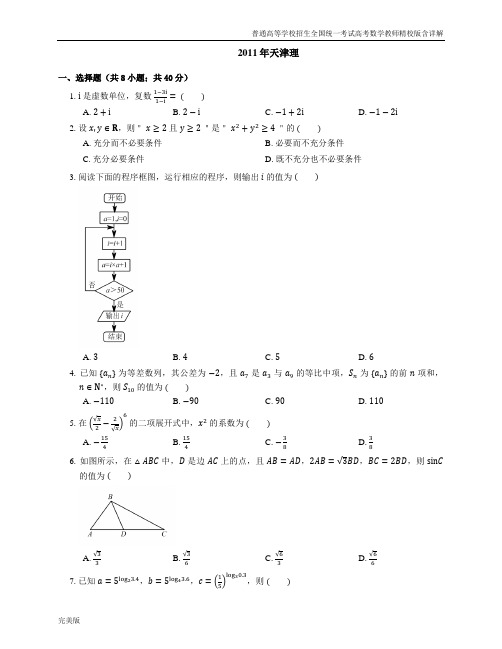
2011年天津理一、选择题（共8小题；共40分）1. i是虚数单位，复数1−3i1−i= A. 2+iB. 2−iC. −1+2iD. −1−2i2. 设x,y∈R，则＂x≥2且y≥2＂是＂x2+y2≥4＂的 A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 阅读下面的程序框图，运行相应的程序，则输出i的值为 A. 3B. 4C. 5D. 64. 已知a n为等差数列，其公差为−2，且a7是a3与a9的等比中项，S n为a n的前n项和，n∈N∗，则S10的值为 A. −110B. −90C. 90D. 1105. 在x2x 6的二项展开式中，x2的系数为 A. −154B. 154C. −38D. 386. 如图所示，在△ABC中，D是边AC上的点，且AB=AD，2AB=3BD，BC=2BD，则sin C的值为 A. 33B. 36C. 63D. 667. 已知a=5log23.4，b=5log43.6，c=15log30.3，则 A. a>b>cB. b>a>cC. a>c>bD. c>a>b8. 对实数a与b，定义运算“ ⊗”：a⊗b=a,a−b≤1,b,a−b>1.设函数f x=x2−2⊗x−x2,x∈R．若函数y=f x−c的图象与x轴恰有两个公共点，则实数c的取值范围是 A. −∞,−2∪ −1,32B. −∞,−2∪ −1,−34C. −∞,14∪14,+∞ D. −1,−34∪14,+∞二、填空题（共6小题；共30分）9. 一支田径队有男运动员48人，女运动员36人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本，则抽取男运动员的人数为．10. 一个几何体的三视图如图所示（单位：m），则这个几何体的体积为m3．11. 已知抛物线C的参数方程为x=8t2y=8t（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆x−42+y2=r2r>0相切，则r=．12. 如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2，AF:FB:BE=4:2:1．若CE与圆相切，则CE的长为．13. 已知集合A=x∈R x+3+x−4≤9，B= x∈R x=4t+1t−6,t∈0,+∞，则集合A∩B=．14. 已知直角梯形ABCD中，AD∥BC，∠ADC=90∘，AD=2，BC=1，P是腰DC上的动点，则PA+3PB的最小值为．三、解答题（共6小题；共78分）15. 已知函数f x=tan2x+π4．（1）求f x的定义域与最小正周期；（2）设α∈0,π4，若fα2=2cos2α，求α的大小．16. 学校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）（1）求在一次游戏中，①摸出3个白球的概率；②获奖的概率；（2）求在两次中获奖次数X的分布列及数学期望E X．17. 如图，在三棱柱ABC−A1B1C1中，H是正方形AA1B1B的中心，AA1=22，C1H⊥平面AA1B1B，且C1H=5．（1）求异面直线AC与A1B1所成角的余弦值；（2）求二面角A−A1C1−B1的正弦值；（3）设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．18. 在平面直角坐标系xOy中，点P a,b a>b>0为动点，F1，F2分别为椭圆x2a +y2b=1的左右焦点．已知△F1PF2为等腰三角形．（1）求椭圆的离心率e；（2）设直线PF2与椭圆相交于A，B两点，M是直线PF2上的点，满足AM⋅BM=−2，求点M的轨迹方程．19. 已知a>0，函数f x=ln x−ax2，x>0．（f x的图象连续不断）（1）求f x的单调区间；（2）当a=18时，证明：存在x0∈2,+∞，使f x0=f32；（3）若存在均属于区间1,3的α，β，且β−α≥1，使fα=fβ，证明：ln3−ln25≤a≤ln23．20. 已知数列a n与b n满足：b n a n+a n+1+b n+1a n+2=0，b n=3+−1n2，n∈N∗，且a1=2，a2=4．（1）求a3，a4，a5的值；（2）设c n=a2n−1+a2n+1，n∈N∗，证明：c n是等比数列；（3）设S k=a2+a4+⋯+a2k，k∈N∗，证明：S ka k <76n∈N∗4nk=1．答案第一部分1. B2. A 【解析】当x≥2且y≥2时，一定有x2+y2≥4；反过来，当x2+y2≥4时，不一定有x≥2且y≥2，例如x=−4，y=0也可以．3. B 【解析】i=1时，a=1×1+1=2；i=2时，a=2×2+1=5；i=3时，a=3×5+1=16；i=4时，a=4×16+1=65>50．所以输出i=4．4. D 【解析】由a72=a3⋅a9，d=−2，得a1−122=a1−4a1−16,解得a1=20，从而S10=10×20+10×92−2=110.5. C【解析】由二项式展开式得：T k+1=C6k x26−kxk=−1k22k−6C6k x3−k，令k=1，则x2的系数为−1⋅22−6C61=−38．6. D 【解析】设AB=a，所以AD=a，BD=3，BC=2BD=3，故cos A=AB2+AD2−BD22AB⋅AD=2a2−43a22a =13，所以sin A=1−cos2A=223．由正弦定理知sin C=ABBC ⋅sin A=34×223=66．7. C 【解析】因为a=5log23.4，b=5log43.6，c=5log310，所以只需要比较它们的指数即可．由对数函数的性质知log43.6=log2 3.6<1<log3103<log33.4<log23.4，从而有a>c>b．8. B 【解析】f x=x2−2,x2−2−x−x2≤1 x−x2,x2−2−x−x2>1=x2−2,−1≤x≤3x−x2,x<−1,或x>3则f x的图象如图：∵y=f x−c的图象与x轴恰有两个公共点，∴y=f x与y=c的图象恰有两个公共点，由图象知c≤−2，或−1<c<−34．第二部分9. 12【解析】设抽取男运动员人数为n，则n48=2148+36，解之得n=12．10. 6+π【解析】如图：该几何体为一个棱柱与一个圆锥的组合体．所以V=3×2×1+1π×12×3=6+π.11. 212. 72【解析】设AF=4k，BF=2k，BE=k，由DF⋅FC=AF⋅BF，得2=8k2，即k=12，从而AF=2，BF=1，BE=12，AE=72，由切割线定理得CE2=BE⋅EA=12×72=74，故CE=72．13. x∈R−2≤x≤5【解析】因为A=x∈R−4≤x≤5，B= x∈R x≥24t×1t−6,t∈0,+∞=x∈R x≥−2，所以A∩B=x∈R−4≤x≤5∩x∈R x≥−2=x∈R−2≤x≤5．14. 5【解析】建立如图所示的坐标系，设DC= ，则A2,0，B1, ．设P0,y0≤y≤ ，则PA=2,−y，PB=1, −y，所以PA+3PB=25+3 −4y2≥第三部分15. （1）由2x +π4≠π2+kπ，k ∈Z ，得x ≠π8+kπ2,k ∈Z ,所以f x 的定义域为 x ∈R x ≠π8+kπ2,k ∈Z ，f x 的最小正周期为π2．（2）由f α2 =2cos2α，得tan α+π4=2cos2α，sin α+π4cos α+4=2 cos 2α−sin 2α ,整理得sin α+cos αcos α−sin α=2 cos α+sin α cos α−sin α . 因为α∈ 0,π4 ，所以sin α+cos α≠0.因此 cos α−sin α 2=12.即sin2α=12.由α∈ 0,π4 ，得2α∈ 0,π2 ，所以2α=π6，即α=π12.16. （1）①设“在1次游戏中摸出i 个白球”为事件A i i =0,1,2,3 ，则P A 3 =C 3252⋅C 2132=1.②设“在1次游戏中获奖”为事件B ，则B =A 2∪A 3，又P A 2 =C 32C 52⋅C 22C 32+C 31C 21C 52⋅C 21C 32=12,且A 2，A 3互斥，所以P B =P A 2 +P A 3 =1+1=7.（2）由题意可知X 的所有可能取值为0，1，2．P X =0 = 1−7 2=9,P X =1 =C 21⋅7⋅ 1−7 =21,P X =2 = 7 2=49.所以X 的分布列是X 012P92149E X =0×9+1×21+2×49=7.17. （1）方法一：由于AC ∥A 1C 1，故∠C 1A 1B 1是异面直线AC 与A 1B 1所成的角．因为C 1H ⊥平面AA 1B 1B ，又H 为正方形AA 1B 1B 的中心，AA 1=2 2，C 1H = 5．可得A 1C 1=B 1C 1=3.因此cos ∠C 1A 1B 1=A 1C 12+A 1B 12−B 1C 122A 1C 1⋅A 1B 1= 23.所以异面直线AC 与A 1B 1所成角的余弦值为 23．方法二：如图所示，建立空间直角坐标系，点B 为坐标原点．依题意得A 2 2,0,0 ,B 0,0,0 ，C 2,− 2, 5 ，A 1 2 2,2 2,0 ，B 1 0,2 2,0 ，C 1 2, 2, 5 ．易得AC= − 2,− 2, 5 ,A 1B 1= −2 2,0,0 ,于是cos AC ,A 1B 1 =AC ⋅A 1B 1AC ⋅ A 1B 1 =3×2 2= 2, 所以异面直线AC 与A 1B 1所成角的余弦值为 23．（2）方法一：连接AC 1，易知AC1=B1C1，又由于AA1=B1A1，A1C1=A1C1，所以△AC1A1≌△B1C1A1，过点A作AR⊥A1C1于点R，连接B1R，于是B1R⊥A1C1，故∠ARB1为二面角A—A1C1—B1的平面角．在Rt△A1RB1中，B1R=A1B1⋅sin∠RA1B1=22⋅1−22=214.连接AB1，在△ARB1中，AB1=4，AR=B1R，cos∠ARB1=AR2+B1R2−AB12 2AR⋅B1R=−2 ,从而sin∠ARB1=35.所以二面角A—A1C1—B1的正弦值为357．方法二：易知AA1=0,22,0,A1C1= − 2,− 2,5.设平面AA1C1的法向量m=x1,y1,z1，则m⋅A1C1=0,m⋅AA1=0,即− 2x1−2y1+5z1=0,22y1=0.不妨令x1=5，可得m=5,0,2,n⋅A1C1=0,n⋅A1B1=0.即− 2x2−2y2+5z2=0,−22x2=0.不妨令y2=5，可得n=0,5,2.于是cos m,n=m⋅nm⋅n=27⋅7=27,从而sin m,n=35.所以二面角A—A1C1—B的正弦值为357．（3）方法一：因为MN⊥平面A1B1C1，所以MN⊥A1B1．取HB1中点D，连接ND，由于N是棱B1C1中点，所以ND∥C1H且ND=12C1H=52.又C1H⊥平面AA1B1B，所以ND⊥平面AA1B1B，故ND⊥A1B1．又MN∩ND=N，所以A1B1⊥平面MND，连接MD并延长交A1B1于点E，则由DE AA1=B1EB1A1=B1DB1A=14,得DE=B1E=2 ,延长EM交AB于点F，可得BF=B1E=2 .连接NE，在Rt△ENM中，所以DM=ND2=52.可得FM=2 4 .连接BM，在Rt△BFM中，BM= FM2+BF2=104.方法二：由N为棱B1C1的中点，得N22,322,52．设M a,b,0，则MN=22−a,322−b,52.由MN⊥平面A1B1C1，得MN⋅A1B1=0,MN⋅A1C1=0.即22−a ⋅ −22=0,2 2−a ⋅ − 2+322−b ⋅ − 2+52⋅5=0.解得a=2 ,b=2 4 .故M22,24,0，因此BM=22,24,0,所以线段BM的长为BM=10 4 .18. （1）设F1−c,0，F2c,0c>0，由题意，可得PF2=F1F2,即a−c2+b2=2c.整理得2c2+c−1=0,即c a =−1舍,或 ca=12.所以e=1 2 .（2）由（1）知a=2c,b=3c,可得椭圆方程为3x2+4y2=12c2,直线PF2方程为y=3x−c. A,B两点的坐标满足方程组3x2+4y2=12c2,y=3x−c.消去y并整理，得5x2−8cx=0.解得x1=0,x2=8 5 c.得方程组的解x1=0,y1=− 3c, x2=8c,y2=335c.不妨设A85c,335c ，B 0,−3c ，设点M的坐标为x,y，AM= x−85c,y−335c ,BM= x,y+3c ,由y=3x−c，得c=x−3 y.于是AM=83y−3x,8y−33x ,BM= x,3x .由AM⋅BM=−2，即83y−3x ⋅x+8y−33x ⋅3x=−2,化简得18x2−163xy−15=0.将y=2163xc=x−33y，得c=10x2+5>0.所以x>0．因此，点M的轨迹方程是18x2−163xy−15=0x>0.19. （1）fʹx=1x−2ax=1−2ax2x,x∈0,+∞,令fʹx=0，解得x=2a 2a.当x变化时，fʹx,f x的变化情况如下表：x0,2a2a2a2a2a2a,+∞fʹx+0−f x↗极大值↘所以，f x的单调递增区间是0,2a2a ，f x的单调递减区间是2a2a,+∞ ．（2）当a=18时，f x=ln x−18x2.由（1）知f x在0,2内单调递增，在2,+∞内单调递减．令g x=f x−f32．由于f x在0,2内单调递增，故f2>f 3 2 ,即g2>0.取xʹ=32e>2，则g xʹ=41−9e232<0.所以存在x0∈2,xʹ，使g x0=0，即存在x0∈2,+∞，使f x0=f32．（3）由fα=fβ及（1）的结论知α<2a2a<β,从而f x在α,β上的最小值为fα．又由β−α≥1，α,β∈1,3，知1≤α≤2≤β≤3.故f2≥fα≥f1,f2≥fβ≥f3.即ln2−4a≥−a,ln2−4a≥ln3−9a.从而ln3−ln2≤a≤ln2.20. （1）由b n=3+−1n2,n∈N∗，可得b n=1, n为奇数, 2, n为偶数.又b n a n+a n+1+b n+1a n+2=0，当n=1时，a1+a2+2a3=0,由a1=2，a2=4，可得a3=−3;当n=2时，2a2+a3+a4=0,可得a4=−5;当n=3时，a3+a4+2a5=0,可得a5=4.（2）对任意n∈N∗，a2n−1+a2n+2a2n+1=0, ⋯⋯①2a2n+a2n+1+a2n+2=0, ⋯⋯②a2n+1+a2n+2+2a2n+3=0, ⋯⋯③②−③，得a2n=a2n+3. ⋯⋯④将④代入①，可得a2n+1+a2n+3=−a2n−1+a2n+1,即c n+1=−c n n∈N∗.又c1=a1+a3=−1，故c n≠0，因此c n+1c n=−1,所以c n是等比数列．（3）由（2）可得a 2k−1+a 2k +1= −1 k ,于是，对任意k ∈N ∗且k ≥2，有a 1+a 3=−1,− a 3+a 5 =−1,a 5+a 7=−1,⋮ −1 k a 2k−3+a 2k−1 =−1.将以上各式相加，得a 1+ −1 k a 2k−1=− k −1 ,即a 2k−1= −1 k +1 k +1 ,此式当k =1时也成立．由④式得a 2k = −1 k +1 k +3 .从而S 2k= a 2+a 4 + a 6+a 8 +⋯+ a 4k−2+a 4k =−k ,S 2k−1=S 2k −a 4k =k +3.所以，对任意n ∈N ∗，n ≥2，S ka k4nk =1= S 4m−3a 4m−3+S 4m−2a 4m−2+S 4m−1a 4m−1+S 4ma 4mnm =1= 2m +2−2m −1−2m +3+2mnm =1= 22m 2m +1 +32m +2 2m +3n m =1=22×3+ 52m 2m +1 +3 2n +2 2n +3 nm =2<1+ 5 +3 nm =2=1+5⋅ 1−1 + 1−1 +⋯+ 1−1 +3 =13+56−52⋅12n +1+3 2n +2 2n +3 <7.对于n =1，不等式显然成立．。

2011年普通高等学校招生全国统一考试数学卷(全国新课标.文)

2011年普通高等学校招生全国统一考试数学卷（全国新课标.文）参考公式：三角函数的积化和差公式：[]1sin cos sin()sin()2αβαβαβ=++- []1cos sin sin()sin()2αβαβαβ=+--[]1cos cos cos()cos()2αβαβαβ=++-[]1sin sin cos()cos()2αβαβαβ=-+--正棱台、圆台的侧面积公式1()2S c c l ='+台侧其中c '、c 分别表示上、下底面周长，l 表示斜高或母线长．球的体积公式：343V r π=球，其中R 表示球的半径．第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合{}0,1,2,3,4M =，{}1,3,5N =，P M N = ，则PA ．2个B ．4个C ．6个D ．8个2．复数512i i-＝A ．2i -B ．12i -C ．2i -+D ．12i -+3．下列函数中，既是偶函数又在(0,)+∞单调递增的函数是A ．3y x =B ．||1y x =+C ．21y x =-+D ．||2x y -=4．椭圆221168xy+=的离心率为A ．13B ．12C ．3D ．25．执行右面的程序框图，如果输入的N 是6，那么输出的p 是A ．120B ．720C ．1440D ．50406．有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为A ．13B ．12C ．23D ．347．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ＝A ．45-B ．35-C ．35D ．458．在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为A ．B ．C ．D ．9．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A 、B 两点，||12AB =，P 为C 的准线上一点，则△A B P 的面积为A ．18B ．24C ．36D ．4810．在下列区间中，函数()43x f x e x =+-的零点所在的区间为A ．1,04⎛⎫- ⎪⎝⎭B ．10,4⎛⎫ ⎪⎝⎭C ．11,42⎛⎫⎪⎝⎭D ．13,24⎛⎫⎪⎝⎭ 11．设函数()sin(2)cos(2)44f x x x ππ=+++，则A ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递增，其图像关于直线4x π=对称B ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递增，其图像关于直线2x π=对称C ．()y f x =在0,2π⎛⎫⎪⎝⎭单调递减，其图像关于直线4x π=对称D ． ()y f x =在0,2π⎛⎫⎪⎝⎭单调递减，其图像关于直线2x π=对称12．已知函数()y f x =的周期为2，当[]1,1x ∈-时，2()f x x =，那么函数()y f x =的图像与函数|lg |y x =的图像的交点共有A ．10个B ．9个C ．8个D ．1个正视图侧视图第Ⅱ卷（非选择题共90分）注意事项：用钢笔或圆珠笔直接答在答题卡上．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．已知a 与b 为两个不共线的单位向量，k 为实数，若向量a b + 与向量k a b -垂直，则k ＝．14．若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为．15．△ABC 中，120B = ，7A C =，5A B =，则△ABC 的面积为．16．已知两个圆锥有公共底面，且两圆锥的顶点与底面的圆周都在同一球面上．若圆锥底面面积是这个球面面积的316，则两个圆锥中，体积较小者的高与体积较大者孤高的比值为．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知等比数列{}n a 中，113a =，公比13q =．（1）n S 为{}n a 的前n 项和，证明：12nn a S -=；（2）设31323log loglogn n b a a a =+++ ，求数列{}n b 的通项公式．18．（本小题满分12分）如图，四棱锥P A B C D -中，底面A B C D 为平行四边形，60DAB ∠=，2A B A D =，P D ⊥底面A B C D ．（1）证明：P A ⊥B D ；（2）若1PD AD ==，棱锥D P B C -的高．19．（本小题满分12分）某种产品的质量以其质量指标量衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A 配方和B 配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：A 配方的频数分布表B 配方的频数分布表PCD（1）分别估计用A 配方，B 配方生产的产品的优质品率；（2）已知用B 配方生产的一件产品的利润y （单位：元）与其质量指标值t 的关系式为 2,94,2,94102,4,102,t y t t -<⎧⎪=≤<⎨⎪≥⎩估计用B 配方生产的一件产品的利润大于0的概率，并求用B 配方生产的上述100件产品平均一件的利润．20．（本小题满分12分）在平面直角坐标系xOy 中，曲线261y x x =-+与坐标轴的交点都在圆C 上．（1）求圆C 的方程；（2）若圆C 与直线0x y a -+=交于A 、B 两点，且O A O B ⊥，求a 的值． 21．（本小题满分12分）已知函数ln ()1a xb f x x x=++，曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=．（1）求a 、b 的值；（2）证明：当0x >，且1x ≠时，ln ()1x f x x >-．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写清题号．22．（本小题满分10分）【选修4－1：几何选讲】如图，,D E 分别为△ABC 的边A B ，A C 上的点，且不与△ABC 重合．已知A E 的长为m ，A C 的长为n ，A D ，A B 的长是关于x 的方程2140x x mn -+=的两个根．（1）证明：,,,C B D E 四点共圆；（2）若90A ∠=，且4,6m n ==，求,,,C B D E 所在圆的半径．D23．（本小题满分10分）【选修4－4：坐标系与参数方程】在直角坐标系xOy 中，曲线1C 的参数方程为2cos ,22sin ,x y αα=⎧⎨=+⎩（α为参数），M 是1C 上的动点，P 点满足2OP OM =，P 点的轨迹为曲线2C ．（1）求2C 的方程；（2）在以O 为极点，x 轴的正半轴为极轴的极坐标系中，射线3πθ=与1C 的异于极点的交点为A ，与2C 的异于极点的交点为B ，求||AB ．24．（本小题满分10分）【选修4－5：不等式选讲】设函数()||3f x x a x =-+，其中0a >．（1）当1a =时，求不等式()32f x x ≥+的解集；（2）若不等式()0f x ≤的解集为{}|1x x ≤-，求a 的值．2011年普通高等学校招生全国统一考试数学卷（全国新课标.文）参考答案一、选择题，本题考查基础知识，基本概念和基本运算能力13．14．15．16．三、解答题17．。

2011年天津高考文科数学试题及答案详细解析

2012年普通高等学校招生全国统一考试物理试题汇编目录1、2012年普通高等学校招生全国统一考试（全国卷大纲版）-------22、2012年普通高等学校招生全国统一考试（全国卷新课标版）---73、2012年普通高等学校招生全国统一考试（江苏卷）-----------------134、2012年普通高等学校招生全国统一考试（安徽卷）-----------------205、2012年普通高等学校招生全国统一考试（北京卷）-----------------246、2012年普通高等学校招生全国统一考试（福建卷）-----------------297、2012年普通高等学校招生全国统一考试（广东卷）------------------348、2012年普通高等学校招生全国统一考试（山东卷）-----------------399、2012年普通高等学校招生全国统一考试（上海卷）-----------------4510、2012年普通高等学校招生全国统一考试（四川卷）---------------5011、2012年普通高等学校招生全国统一考试（天津卷）---------------5512、2012年普通高等学校招生全国统一考试（浙江卷）---------------6113、2012年普通高等学校招生全国统一考试（重庆卷）---------------6614、2012年普通高等学校招生全国统一考试（海南卷）------------702012年普通高等学校招生全国统一考试理科综合能力测试物理部分解析版（全国卷大纲版）（适用地区：贵州、甘肃、青海、西藏、广西）二，选择题：本题共8题。

在每小题给出的四个选项中，有的只有一个选项份额和题目要求，有的有多个选项符合题目要求。

全部选对的得6分，选对但选不全的得3分，有选错的德0分。

14.下列关于布朗运动的说法，正确的是（）A ．布朗运动是液体分子的无规则运动 B. 液体温度越高，悬浮粒子越小，布朗运动越剧烈C ．布朗运动是由于液体各部分的温度不同而引起的D.布朗运动是由液体分子从各个方向对悬浮粒子撞击作用的不平衡引起的14.BD 【解题思路】布朗运动是悬浮颗粒的无规则运动，不是液体分子的运动，选项A错；液体的温度越高，悬浮颗粒越小，布朗运动越剧烈，选项B 正确；布朗运动是由于液体分子从各个方向对悬浮粒子撞击作用不平衡引起的，选项C 错，选项D 正确。

《2011年高考真题解析版—数学文(全国卷)解析版1》

绝密★启用前2011年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

第Ⅰ卷1至2页。

第Ⅱ卷3至4页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动,用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效.3．第Ⅰ卷共l2小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的. 一、选择题(1)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则U =（M N ）I ð （A ）{}12，（B ）{}23，（C ）{}2，4 （D ）{}1，4 【答案】D【命题意图】本题主要考查集合交并补运算. 【解析】{2,3},(){1,4}U M N M N =∴=ðQ I I (2)函数0)y x =≥的反函数为（A ）2()4x y x R =∈ （B ）2(0)4x y x =≥（C ）24y x =()x R ∈ （D ）24(0)y x x =≥ 【答案】B【命题意图】本题主要考查反函数的求法.【解析】由原函数反解得24y x =,又原函数的值域为0y ≥,所以函数0)y x =≥的反函数为2(0)4x y x =≥. (3)设向量,a b 满足||||1a b ==,12a b ⋅=-r r ,则2a b +=（A（B（C（D【答案】B【命题意图】本题主要考查平面向量的数量积与长度的计算方法.【解析】2221|2|||44||14()432a b a a b b +=+⋅+=+⨯-+=r r r r r u r ,所以2a b +=r r (4)若变量x ，y 满足约束条件63-21x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则=23z x y +的最小值为（A ）17 （B ）14 （C ）5 （D ）3 【答案】C【命题意图】本题主要考查简单的线性规划.【解析】作出不等式组表示的可行域，从图中不难观察当直线=23z x y +过直线x=1与x-3y=-2的交点（1，1）时取得最小值,所以最小值为5. (5)下面四个条件中，使a b >成立的充分而不必要的条件是（A ）1a b +＞（B ）1a b -＞（C ）22a b ＞（D ）33a b ＞【答案】A【命题意图】本题主要考查充要条件及不等式的性质.【解析】即寻找命题P ,使P a b ⇒>,且a b >推不出P ,逐项验证知可选A.(6)设n S 为等差数列{}n a 的前n 项和，若11a =，公差2d =，224k k S S +-=，则k =（A ）8 （B ）7 （C ）6 （D ）5 【答案】D【命题意图】本题主要考查等差数列的基本公式的应用. 【解析】解法一2(2)(1)(1)[(2)12][12]442422k k k k k k S S k k k +++--=+⨯+⨯-⨯+⨯=+=，解得5k =.解法二: 221[1(1)2](12)4424k k k k S S a a k k k +++-=+=++⨯++⨯=+=，解得5k =.(7)设函数()cos (0)f x x ωω=>，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于（A ）13（B ）3 （C ）6 （D ）9 【答案】C【命题意图】本题主要考查三角函数的周期性与三角函数图像变换的关系.【解析】由题意将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，说明了3π是此函数周期的整数倍,得2()3k k Z ππω⨯=∈,解得6k ω=,又0ω>,令1k =,得min 6ω=.(8)已知直二面角l αβ--,点A α∈，AC l ⊥,C 为垂足,B β∈，BD l ⊥,D 为垂足,若2,1AB AC BD ===，则CD =（A ） 2 （B （C （D ）1 【答案】C【解析】因为l αβ--是直二面角, AC l ⊥,∴AC ⊥平面β,AC BC ∴⊥BC ∴=又BD l ⊥,CD ∴=(9) 4位同学每人从甲、乙、丙3门课程中选修1门，则恰有2人选修课程甲的不同选法共有(A) 12种 (B) 24种 (C) 30种 (D)36种【答案】B【命题意图】本题主要考查两个原理与排列组合知识，考察考生分析问题的能力.【解析】第一步选出2人选修课程甲有246C =种方法，第二步安排剩余两人从乙、丙中各选1门课程有22⨯种选法，根据分步计数原理，有6424⨯=种选法.(10) 设()f x 是周期为2的奇函数，当01x ≤≤时，()f x =2(1)x x -,则5(2f -= (A) -12 (B)1 4- (C)14 (D)12【答案】A【命题意图】本题主要考查利用函数的周期性和奇偶性求函数值的方法. 关键是把通过周期性和奇偶性把自变量52-转化到区间[0,1]上进行求值.【解析】由()f x 是周期为2的奇函数,利用周期性和奇偶性得:5511111()(2)()()2(1)2222222f f f f -=-+=-=-=-⨯⨯-=-(11)设两圆1C 、2C 都和两坐标轴相切，且都过点（4，1），则两圆心的距离12C C =(A)4 (B)(C)8 (D)【答案】C【命题意图】本题主要考查圆的方程与两点间的距离公式.【解析】由题意知圆心在直线y=x 上并且在第一象限,设圆心坐标为(,)(0)a a a >,则a =,即210170a a -+=,所以由两点间的距离公式可求出128C C ===.(12)已知平面α截一球面得圆M ，过圆心M 且与α成060二面角的平面β截该球面得圆N .若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为(A)7π (B)9π (C)11π (D)13π 【答案】D【命题意图】本题主要考查二面角的概念与球的性质.【解析】如图所示,由圆M 的面积为4π知球心O 到圆M 的距离OM =,在Rt OMN ∆中,30OMN ︒∠=,∴12ON OM ==,故圆N 的半径r ==,∴圆N 的面积为213S r ππ==.第Ⅱ卷注意事项：1答题前，考生先在答题卡上用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。

2011年普通高等学校招生全国统一考试数学卷(天津_文)含详解

2011天津文第Ⅰ卷本卷共8小题，每小题5分，共40分一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．（同理１）i 是虚数单位,复数13i1i-=-( )．啊．2i - 不．2i + 才．12i -- D ．12i -+【解】()()()()13i 1i 13i 42i2i 1i 1i 1i 2-+--===---+．故选A ． 2．设变量,x y ，满足约束条件1,40,340,x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数3z x y =-的最大值为( )．A ．4-B ．0C ．43的．4 【解】画出可行域为图中的ABC ∆的区域，直线3y x z =-经过()2,2A 时，4z =最大．故选D ．3．阅读右边的程序框图，运行相对应的程序，若输入x 的值为4-，则输出y 的值为( )．A ．0.5B ．1C ．2D ．4【解】运算过程依次为：输入4x =-43⇒->437x ⇒=--= 73⇒>734x =-=43⇒>431x ⇒=-=13⇒<122y ⇒==⇒输出2．故选Ｃ．4．设集合{}20A x x =∈->R ，{}0B x x =∈<R ，(){}20C x x x =∈->R ，则“x A B ∈”是“x C ∈”的( )．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解】{}02AB x x x =∈<>R 或，(){}{}2002C x x x x x x =∈->∈<>R R 或所以A B C =．所以“x A B ∈”是“x C ∈”的充分必要条件．故选Ｃ． 5．已知2log 3.6a =，4log 3.2b =，4log 3.6c =，则 ( )． A ．a b c >> B ．a c b >> C ．b a c >> D ．c a b >>【解】因为224log 3.6log 3.6a ==，而23.6 3.6 3.2>>，又函数4log y x =是()0,+∞上的增函数，则2444log 3.6log 3.6log 3.2>>．所以a c b >>．故选Ｂ．6．已知双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则双曲线的焦距为 ( )．A ．B ．C ．D ．【解】因为双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则22p-=-，所以4p =．又因为双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，则42pa +=，所以2a =．因为点()2,1--在双曲线的一条渐近线上，则()12ba-=-，即2a b =，所以1,b c ==，焦距2c =7．已知函数()()2sin f x x ωϕ=+，x ∈R ，其中0ω>，ππϕ-<≤．若()f x 的最小正周期为6π，且当π2x =时，()f x 取得最大值，则( )． A ．()f x 在区间[]2π,0-上是增函数 B ．()f x 在区间[]3π,π--上是增函数 C ．()f x 在区间[]3π,5π上是减函数D ．()f x 在区间[]4π,6π上是减函数【解】由题设得ππ,222π6π,ωϕω⎧⋅+=⎪⎪⎨⎪=⎪⎩解得13ω=，π3ϕ=．所以已知函数为()π2sin 33x f x ⎛⎫=+ ⎪⎝⎭．其增区间满足π222332x k k ππππ-+≤+≤+，k ∈Z ．解得5π6ππ6π2k x k -+≤≤+，k ∈Z ．取0k =得5ππ2x -≤≤，所以5π,π2⎡⎤-⎢⎥⎣⎦为一个增区间，因为[]5π2π,0,π2⎡⎤-⊆-⎢⎥⎣⎦，所以()f x 在区间[]2π,0-上是增函数．故选Ａ．8．对实数a 和b ，定义运算“⊗”：,1,, 1.a a b a b b a b -≤⎧⊗=⎨->⎩设函数()()()221f x x x =-⊗-，x ∈R ．若函数()y f x c =-的图象与x 轴恰有两个公共点，则实数c 的取值范围是( )．A ．(]()1,12,-+∞ B ．(](]2,11,2-- C ．()(],21,2-∞- D ．[]2,1--【解】由题设()22,12,1,12x x f x x x x ⎧--≤≤=⎨-<->⎩或画出函数的图象，函数图象的四个端点（如图）为()2,1A ，，()2,2B ，()1,1C --，()1,2D --．从图象中能够看出，直线y c =穿过点B ，点A 之间时，直线y c =与图象有且只有两个公共点，同时，直线y c =穿过点C ，点D 时，直线y c =与图象有且只有两个公共点，所以实数c 的取值范围是(](]2,11,2--．故选Ｂ．第Ⅱ卷二、填空题：本答题共6小题，每小题5分,共30分． 9．已知集合{}12A x x =∈-<R ，Z 为整数集，则集合A Z 中所有元素的和等于．【解】3．解集合A 得13x -<<，则{}0,1,2A=Z ，所有元素的和等于0123++=．10．一个几何体的三视图如右图所示（单位：m ），则该几何体的体积为3m ．【解】4．几何体是由两个长方体组合的．体积为 1211124V =⨯⨯+⨯⨯=．11．已知{}n a 是等差数列，n S 为其前n 项和，n +∈N ．若316a =，2020S =，则10S 的值为．【解】110．设公差为d ，由题设31201216,2019020.a a d S a d =+=⎧⎨=+=⎩解得2d =-，120a =．()10110451020452110S a d =+=⨯+⨯-=．12．已知22log log 1a b +≥，则39ab+的最小值为．【解】18．因为22log log 1a b +≥，则2log 1ab ≥，2ab ≥，24a b ⋅≥22243923923232318a b a b a b a b+⋅+≥⋅=≥≥=，当且仅当39,2,a b a b ⎧=⎨=⎩即2a b =时，等号成立，所以39a b+的最小值为18．13．（同理12）如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且2DF CF ==，::4:2:1AF FB BE =，若CE 与圆相切，则线段CE 的长为．【解】72．因为::4:2:1AF FB BE =，所以设BE a =，2FB a =，4AF a =．由相交弦定理，242DF CF AF FB a a ⋅=⋅==⋅，所以12a =，12BE =，772AE a ==．因为CE 与圆相切，由切割线定理，2177224CE AE BE =⋅=⋅=．所以CE = 14．(同理14) 已知直角梯形ABCD 中，//AD BC ，90ADC ∠=︒，2AD =，1BC =，P 是腰DC 上的动点，则3PA PB +的最小值为．【解】5．解法1 ．以D 为坐标原点，DA 所在直线为x 轴，DC 所在直线为y 轴，建立如图的直角坐标系．由题设，()2,0A ，设()0,C c ，()0,P y ，则()1,B c ．()2,PA y =-，()1,PB c y =-． ()35,34PA PB c y +=-．2355PA PB +=，当且仅当34c y =时，等号成立，于是，当34cy =时，3PA PB +有最小值5．解法2 ．以相互垂直的向量DP ，DA 为基底表示PB PA 3+，得 ()533332PA PB DA DP PC CB DA PC DP +=-++=+-．又P 是腰DC 上的动点，即PC 与DP 共线，于是可设DP PC λ=，有DP DA PB PA )13(253-+=+λ．所以2222553(31)(31)42PA PBDA DP DA DP λλ⎡⎤+=+-+⨯-⋅⎣⎦即 []213(25)13(DP -+=-+=+λλ．因为P 是腰DC 上的动点，显然当31=λ，即DP PC 31=时，所以3PA PB +有最小值5．解法3 ．如图，3PB PF =，设E 为AF 的中点，Q 为AB的FD中点，则12QE BF PB ==， 32PA PB PA PF PE +=+=， ①因为PB PQ PE +=，PB PQ QB -=．则22222222PB PQ PB PQ PB PQ PE QB ++-=+=+． ②（实际上，就是定理：“平行四边形的对角线的平方和等于各边的平方和”）设T 为DC 的中点，则TQ 为梯形的中位线，()1322TQ AD BC =+=．设P 为CT 的中点，且设,CP a PT b ==，则221PB a =+，2294PQ b =+，()2214QB a b =++，代入式②得()()222222912221244PB PQ a b PE a b ⎛⎫+=+++=+++ ⎪⎝⎭，于是()22252544PE a b =+-≥，于是25PE ≥，当且仅当a b =时，等号成立．由式①，325PA PB PE +=≥，所以3PA PB +有最小值5．三、解答题：本大题共6小题，共80分。

2011年天津文解析

2011年普通高等学校招生全国统一考试（天津卷）数学（文史类）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

1、（2011·天津·文，1）i 是虚数单位，复数131ii-=- （）（A ）2i - （B ）2i + （C ）12i -- （D ）12i -+2、（2011·天津·文，2）设变量,x y 满足约束条件140340x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数3z x y =-的最大值为（）（A ）-4 （B ）0 （C ）43（D ）4 3、（2011·天津·文，3）阅读右边的程序框图，运行相应的程序，若输入x 的值为-4，那么输出y 的值为（）（A ）0.5 （B ）1 （C ）2 （D ）44、（2011·天津·文，4）设集合{|20}A x R x =∈->，{|0}B x R x =∈<，{|(2)0}C x R x x =∈->，则“x A B ∈ ”是“x C ∈”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分而也不必要条件5、（2011·天津·文，5）已知2log 3.6a =，4log 3.2b =，4log 3.6c =，则（）（A ）a b c >> （B ）a c b >> （C ）b a c >> （D ）c a b >>6、（2011·天津·文，6）已知双曲线22221x y a b-=(0,0)a b >>的左顶点与抛物线22(0)y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为（-2，-1），则双曲线的焦距为（）（A）（B）（C）（D）7、（2011·天津·文，7）已知函数()2sin()f x x ωϕ=-，x R ∈，其中0ω>，πϕπ-<≤。

2011年天津高考文科数学试题及答案详细解析

2011年天津高考文科数学试题及答案详细解析（天津卷）参考公式：如果事件A ，B 互斥，那么棱柱的体积公式V Sh =()()()P A B P A P B ⋃=+其中S 表示棱柱的底面面积。

h 表示棱柱的高。

一、选择题：在每小题给出的四个选项中只有一项是符合题目要求的．1．i 是虚数单位，复数131ii--= A ．2i - B ．2i + C ．12i -- D ．12i -+2．设变量x ，y 满足约束条件1,40,340,x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数3z x y =-的最大值为A ．-4B ．0C ．43D ．43．阅读右边的程序框图，运行相应的程序，若输入x 的值为-4，则输出y 的值为 A ．,0．5 B ．1 C ．2 D ．4 4．设集合{}{}|20,|0A x R x B x R x =∈->=∈<，{}|(2)0C x R x x =∈->，则“x A B ∈⋃”是“x C ∈”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．即不充分也不必要条件5．已知244log 3.6,log 3.2,log 3.6a b c ===则A ．a b c >>B ．a c b >>C ．b a c >>D ．c a b >>6．已知双曲线22221(0,0)x y a b a b-=>>的左顶点与抛物线22(0)y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的准线的交点坐标为（-2，-1），则双曲线的焦距为（）A．B．C．D．7．已知函数()2sin(),f x x x R ωϕ=+∈，其中0,,()f x ωπϕπ>-<≤若的最小正周期为6π，且当2x π=时，()f x 取得最大值，则（）A ．()f x 在区间[2,0]π-上是增函数B ．()f x 在区间[3,]ππ--上是增函数C ．()f x 在区间[3,5]ππ上是减函数D ．()f x 在区间[4,6]ππ上是减函数8．对实数a b 和，定义运算“⊗”：,1,,1.a ab a b b a b -≤⎧⊗=⎨->⎩设函数2()(2)(1),f x x x x R =-⊗-∈。

2011年天津高考数学文科试卷(带答案)

2011天津高考数学文科一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．i 是虚数单位,复数13i1i-=- ( )． A ．2i - B ．2i + C ．12i -- D ．12i -+【测量目标】复数的代数形式四则运算.【考查方式】给出复数的代数形式，对其进行化简. 【参考答案】A 【试题解析】()()()()13i 1i 13i 42i2i 1i 1i 1i 2-+--===---+．故选A ． 2．设变量,x y ，满足约束条件1,40,340,x x y x y ⎧⎪+-⎨⎪-+⎩………则目标函数3z x y =-的最大值为 ( ).A ．4-B ．0C ．43D ．4【测量目标】二元线性规划求目标函数的最值.【考查方式】考查了二元一次不等式的几何意义，能用平面区域表示二元一次不等式组. 【参考答案】D【试题解析】画出可行域为图中的ABC △的区域，直线3y x z =-经过()2,2A 时，4z =最大．故选D ．3．阅读右边的程序框图，运行相应的程序，若输入x 的值为4-，则输出y 的值为 ( )．A ．0.5B ．1C ．2 D.4 【测量目标】循环结构的程序框图.【考查方式】给出程序框图输入值，求输出值. 【参考答案】C【试题解析】运算过程依次为：输入4x =-43⇒->437x ⇒=--=73⇒>734x =-=43⇒> 431x ⇒=-=13⇒<122y ⇒==⇒输出2．故选Ｃ．4．设集合{}20A x x =∈->R ，{}0B x x =∈<R ，(){}20C x x x =∈->R ，则“x A B ∈ ”是“x C ∈”的 ( )． A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【测量目标】充分必要条件.【考查方式】考查了必要条件，充分条件的关系及集合的概念【参考答案】C【试题解析】{0A B x x =∈<R 或}2x >，(){}{20=0C x x x x x =∈->∈<R R 或}2x >所以A B C = ．所以“x A B ∈ ”是“x C ∈”的充分必要条件．故选Ｃ．5．已知2log 3.6a =，4log 3.2b =，4log 3.6c =，则 ( )． A ．a b c >> B ．a c b >> C ．b a c >> D ．c a b >> 【测量目标】对数函数化简与求值.【考查方式】考查了对数函数的运算性质与单调性，利用中间值判断对数的大小. 【参考答案】B【试题解析】因为224log 3.6log 3.6a ==，而23.6 3.6 3.2>>，又函数4log y x =是()0,+∞上的增函数，则2444log 3.6log 3.6log 3.2>>．所以a c b >>．故选B ．6．已知双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则双曲线的焦距为 ( )．A ．B ．C ．D ．【测量目标】圆锥曲线之间的位置关系.【考查方式】考查了双曲线与抛物线的定义、标准方程，知道其简单的几何性质. 【参考答案】B【试题解析】因为双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则22p-=-，所以4p =．(步骤1)又因为双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，则42pa +=，所以2a =．(步骤2) 因为点()2,1--在双曲线的一条渐近线上，则()12ba-=-，即2a b =，所以1,b c ==2c =(步骤3)7．已知函数()()2sin f x x ωϕ=+，x ∈R ，其中0ω>，π<πϕ-…．若()f x 的最小正周期为6π，且当π2x =时，()f x 取得最大值，则 ( )． A ．()f x 在区间[]2π,0-上是增函数 B ．()f x 在区间[]3π,π--上是增函数 C ．()f x 在区间[]3π,5π上是减函数 D ．()f x 在区间[]4π,6π上是减函数【测量目标】三角函数的最值.【考查方式】考查了正弦函数的性质（如单调性，最值，周期等）【参考答案】A【试题解析】由题设得ππ,222π6π,ωϕω⎧+=⎪⎪⎨⎪=⎪⎩ 解得13ω=，π3ϕ=．所以已知函数为()π2sin 33x f x ⎛⎫=+ ⎪⎝⎭．(步骤1) 其增区间满足πππ2π2π2332x k k -+++剟，k ∈Z ．(步骤2) 解得5π6ππ6π2k x k -++剟，k ∈Z ．(步骤3)取0k =得5ππ2x -剟，所以5π,π2⎡⎤-⎢⎥⎣⎦为一个增区间，因为[]5π2π,0,π2⎡⎤-⊆-⎢⎥⎣⎦，所以()f x 在区间[]2π,0-上是增函数．故选Ａ．(步骤4) 8．对实数a 和b ，定义运算“⊗”：,1,,1,a ab a b b a b -⎧⊗=⎨->⎩…设函数()()()221f x x x =-⊗-，x ∈R ．若函数()y f x c =-的图象与x 轴恰有两个公共点，则实数c 的取值范围是 ( )．A ．(]()1,12,-+∞B ．(](]2,11,2--C ．()(],21,2-∞-D ．[]2,1--【测量目标】函数图像的应用.【考查方式】考查了给一个新公式结合二次函数图像，了解函数的零点与方程根的联系. 【参考答案】B【试题解析】由题设()22,12,1,12x x f x x x x ⎧--=⎨-<->⎩或剟(步骤1)画出函数的图象，函数图象的四个端点（如图）为()2,1A ，，()2,2B ，()1,1C --，()1,2D --．(步骤2)从图象中可以看出，直线y c =穿过点B ，点A 之间时，直线y c =与图象有且只有两个公共点，同时，直线y c =穿过点C ，点D 时，直线y c =与图象有且只有两个公共点，所以实数c 的取值范围是(](]2,11,2-- ．故选Ｂ．(步骤3)第Ⅱ卷二、填空题：本大题共6小题，每小题5分,共30分．9．已知集合{}12A x x =∈-<R ，Z 为整数集，则集合A Z 中所有元素的和等于．【测量目标】集合的基本运算.【考查方式】考查了集合的概念及交集运算. 【参考答案】3【试题解析】解集合A 得13x -<<，则{}0,1,2A =Z ，所有元素的和等于0123++=．10．一个几何体的三视图如右图所示（单位：m ），则该几何体的体积为 3m ．【测量目标】由三视图求几何体的体积.【考查方式】考查了学会掌握三视图的画法及几何体的体积计算公式. 【参考答案】4【试题解析】几何体是由两个长方体组合的．体积为1211124V =⨯⨯+⨯⨯=．11．已知{}n a 是等差数列，n S 为其前n 项和，n ∈N +．若316a =，2020S =，则10S 的值为．【测量目标】等差数列的通项公式及前n 项和公式. 【考查方式】考查了已知等差数列求前n 项和. 【参考答案】110【试题解析】设公差为d ，由题设31201216,2019020.a a d S a d =+=⎧⎨=+=⎩解得2d =-，120a =．()10110451020452110S a d =+=⨯+⨯-=．12．已知22log log 1a b +…，则39ab+的最小值为．【测量目标】基本不等式求最值.【考查方式】考查了用基本不等式解决最值问题及对数函数运算性质. 【参考答案】18【试题解析】因为22log log 1a b +…，则2log 1ab …，2ab …，24a b …3918a b +=厖，当且仅当39,2,a b a b ⎧=⎨=⎩即2a b =时，等号成立，所以39a b+的最小值为18．13．如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB延长线上一点，且DF CF ==::4:2:1AF FB BE =，若CE 与圆相切，则线段CE 的长为．【测量目标】圆的性质的应用.【考查方式】考查了直线与圆的位置关系及运用代数方法解决几何问题的思想.【参考答案】2【运算性质】因为::4:2:1AF FB BE =，所以设BE a =，2FB a =，4AF a =．由相交弦定理，242DF CF AF FB a a ===，所以12a =，12BE =，772AE a ==．因为CE 与圆相切，由切割线定理，2177224CE AE BE === ．所以2CE =． 14．已知直角梯形ABCD 中，//AD BC ，90ADC ∠=︒，2AD =，1BC =，P 是腰DC 上的动点，则3PA PB +的最小值为．【测量目标】平面向量在平面几何的应用.【考查方式】考查了几何与代数相结合求解最值问题【参考答案】5【试题解析】解法1 ．以D 为坐标原点，DA 所在直线为x 轴，DC 所在直线为y 轴，建立如图的直角坐标系．由题设，()2,0A ，设()0,C c ，()0,P y ，则()1,B c ．()2,PA y =- ，()1,PB c y =-． ()35,34PA PB c y +=-．(步骤1)35PA PB += ，(步骤2)当且仅当34cy =时，等号成立，于是，当34cy =时，3PA PB + 有最小值5．(步骤3)解法2 ．以相互垂直的向量，为基底表示3PA PB +，得()533332P A P B D A D P P C C B D A P C D P +=-++=+- ．(步骤1) 又P 是腰DC 上的动点，即PC 与共线，于是可设PC DP λ=，有53(31)2PA PB DA DP λ+=+- ．所以2222553(31)(31)42PA PB DA DP DA DP λλ⎡⎤+=+-+⨯-⎣⎦(步骤2) 即 ()()22222533125314PA PB DA DP DP λλ⎡⎤+=+-=+-⎣⎦ ．由于P 是腰DC 上的动点，显然当31=λ，即13PC DP = 时，所以3PA PB +有最小值5．(步骤3)解法3 ．如图，3PB PF =，设E 为AF 的中点，Q 为AB 的中点，则12QE BF PB ==，32PA PB PA PF PE +=+=， ①(步骤1)因为PB PQ PE += ，PB PQ QB -= ．则22222222PB PQ PB PQ PB PQ PE QB ++-=+=+ ． ②(步骤2)（实际上，就是定理：“平行四边形的对角线的平方和等于各边的平方和”）设T 为DC 的中点，则TQ 为梯形的中位线，()1322TQ AD BC =+=．设P 为CT 的中点，且设,CP a PT b ==，则221PB a =+ ，2294PQ b =+ ，()2214QB a b =++ ，代入式②得()()222222912221244PB PQ a b PE a b ⎛⎫+=+++=+++ ⎪⎝⎭ ，(步骤3)于是()22252544PE a b =+- …，于是25PE …，当且仅当a b =时，等号成立．由式①，325PA PB PE +=…，所以3PA PB +有最小值5．(步骤4)三、解答题：本大题共6小题，共80分。

2011年普通高等学校招生全国统一考试（天津卷）

2011年普通高等学校招生全国统一考试（天津卷）2011年普通高等学校招生全国统一考试（天津卷）语文本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间150分钟，第Ⅰ卷1页至5页，第Ⅱ卷6页至10页。

答卷前，考生务必将自己的姓名，准考号填写在答题卡上，并在规定位置粘贴考试用条形码，答卷时，考生务必将答案涂写在答题卡上，答在试卷上无效，考试结束后，将本是卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1.每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

2. 本卷共12小题，每小题3分，36分，在每小题给出的四个选项中，只有一项是最符合题目要求的。

一、（15分）1.下列词语中加点安的读音，全都正确的一组是A．浸渍（zì）蓓蕾（lěi）剖（pōu）析追本朔（shuò）源B．庇（bì）护载（zěi）体友谊（yì）莘（xān）莘学子C．殷（yīn）红翘（qiáo）首刹（shà）那少不更（gēng）事D．低劣（liè）广袤（mào）婆娑（suā）卓（zhuó）有成效2.下列词语中没有错别字的一组是A. 坐落松弛协赛曲融会贯通B. 扫描诙谐天然气振耳欲聋C. 博弈巨挚殊不知毋容置疑D. 竞标临摹吓马威门庭若市3.下列语段横线上填入的词语，最恰当的一组是作为“梅兰竹菊”四君子之首，梅为历代文人雅士所。

此刻，寺院周围庄承的红墙，是我们镜头画面中的中国红；的雪花，是飘舞在空中的精灵；而晶莹如黄玉般的腊梅，暗香，遗世独立的佳人。

A.钟爱洋洋洒洒浮动好像B.喜爱纷纷扬扬浮动犹如C.钟爱纷纷扬扬飘动好像D.喜爱洋洋洒洒飘动犹如4. 下列各句中没有语病且句意明确的一句是A.旺盛的国内需求正在成为跨国巨头获取暴力的重要市场，尤其是针对中国的石油、铁矿石以及基础能源等方面表现得异常突出。

2011年天津高等学校招生全国统一考试文科数学真题及答案

2011年普通高等学校招生全国统一考试（天津卷）数学（文）试题解析一.选择题文数1. L4[2011·天津卷] i 是虚数单位，复数131ii--= 【答案】A 【解析】13(13)(1)4221(1)(1)2i i i ii i i i --+-===---+. 文数2. E5[2011·天津卷] 设变量x ，y 满足约束条件【答案】D【解析】可行域如图：联立40340x y x y ++=⎧⎨-+=⎩解得⎩⎨⎧==22y x 当目标直线3z x y =-移至（2.2）时，3z x y =-有最大值4.文数3.L1 [2011·天津卷] 阅读右边的程序框图，运行相应的程序，【答案】C【解析】当4x =-时，37x x =-=；当7x =时，34x x =-= 当4x =时，31|3|<=-=x x ， ∴22y '==.文数4. A2[2011·天津卷] 设集合{}{}|20,|0A x R x B x R x =∈->=∈< 【答案】C【解析】∵{}20A x kx =∈->，{}0B x kx =∈<，∴{0A B x x ⋃=<，或}2x >，又∵}{{(2)00C x k x x x k x =∈->=∈<或}2x >， ∴A B C ⋃=，即“x A B ∈⋃”是“x C ∈”的充分必要条件. 文数5.B7 [2011·天津卷] 已知244log 3.6,log 3.2,log 3.6a b c === 【答案】B【解析】∵ 3.6222log log 1a =>=，又∵4log xy =为单调递增函数， ∴ 3.2 3.64444log log log 1<<=，∴b c a <<.文数6.H8 [2011·天津卷]【答案】B【解析】双曲线22215x y a -=的渐近线为b y x a =±，由双曲线的一条渐近线与抛物线的准线的交点坐标为（－2，－1）得22p-==，即4p =，又∵42=+a p，∴2a =，将（－2，－1）代入b y x a =得1b =，∴22415c a b =+=+=，即225c =. 文数7.C4 [2011·天津卷]【答案】A【解析】∵πωπ62=，∴31=ω.又∵12,322k k z πππ⨯+=+∈且4ππ-<<，∴当0k =时，1,()2sin()333f x x ππϕ==+，要使()f x 递增，须有122,2332k x k k z πππππ-≤+≤+∈，解之得566,22k x k k z ππππ-≤≤+∈，当0k =时，522x ππ-≤≤，∴()f x 在5[,]22ππ-上递增.文数8. B5[2011·天津卷]【答案】B【解析】()()⎪⎩⎪⎨⎧>----≤----=112,112,2)(2222x x x x x x x x f ⎩⎨⎧>-<-≤≤--=2,1,121,22x x x x x 或则()f x 的图象如图，∵函数c x f y -=)(的图象与x 轴恰有两个公共点，∴函数()y f x =与y c =的图象有两个交点，由图象可得21,12,c c -<≤<≤或. 二.填空题文数9.A1 [2011·天津卷] 已知集合{}|12,A x R x Z =∈-<为整数集，【答案】3【解析】{}}{1213A x k x x x ∈-<=-<<.∴{}2,1,0=Z A ，即.3210=+= 文数10.G2 [2011·天津卷] 一个几何体的三视图如图所示（单位：m ），则【答案】4【解析】2111124v =⨯⨯+⨯⨯=.文数11. D2[2011·天津卷] 已知{}n a 为等差数列，n S 为【答案】110【解析】设等差数列的首项为1a ，公差为d ，由题意得，()⎪⎩⎪⎨⎧=-⨯⨯+==+=202219202016212013a S d a a ，解之得120,2a d ==-，∴101091020(2)1102s ⨯=⨯+⨯-=. 文数12. [2011·天津卷] 已知22log log 1a b +≥，则39ab+的【答案】18【解析】∵1log log log 222≥=+abba， ∴2ab ≥，xy o 1234-1-2-3-412 3 4 -1 -2 -3∴18323233233932222=≥=⋅≥+=++abba b a b a b a .文数13. N1 [2011·天津卷] 如图已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且2,::4:2:1.DF CF AF FB BE ===若CE 与圆相切，则CE 的长为________.【答案】27【解析】设k AF 4=，k BF 2=，k BE =，由BF AF FC DF ∙=∙得282k =，即21=k . ∴27,21,1,2====AE BE BF AF ，由切割定理得4727212=⨯=∙=EA BE CE ，∴27=CE . 文数14. F2[2011·天津卷] 已知直角梯形ABCD 中，AD //BC , 【答案】5【解析】建立如图所示的坐标系，设PC h =，则(2,0),(1,)A B h ，设(0,),(0)P y y h ≤≤则(2,),(1,)PA y PB h y =-=- ，∴2325(34)255PA PB h y +=+-≥= .三、解答题（15）本小题主要考查用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式的等基础知识，考查数据处理能力及运用概率知识解决简单的实际问题的能力，满分13分。

2011年高考天津市数学试卷-文科(含详细答案)

2011年普通高等学校招生全国统一考试天津卷（文科）第Ⅰ卷本卷共8小题，每小题5分，共40分一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．（同理１）i 是虚数单位,复数13i1i-=-( )．啊．2i - 不．2i + 才．12i -- D ．12i -+【解】()()()()13i 1i 13i 42i 2i 1i 1i 1i 2-+--===---+．故选A ．2．设变量,x y ，满足约束条件1,40,340,x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数3z x y =-的最大值为( )．A ．4-B ．0C ．43的．4 【解】画出可行域为图中的ABC ∆的区域，直线3y x z =-经过()2,2A 时，4z =最大．故选D ．3．阅读右边的程序框图，运行相应的程序，若输入x 的值为4-，则输出y 的值为( )．A ．0.5B ．1C ．2D ．4【解】运算过程依次为：输入4x =-43⇒->437x ⇒=--= 73⇒>734x =-=43⇒> 431x ⇒=-=13⇒<122y ⇒==⇒输出2．故选Ｃ．4．设集合{}20A x x =∈->R ，{}0B x x =∈<R ，(){}20C x x x =∈->R ，则“x A B ∈ ”是“x C ∈”的( )．A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解】{}02A B x x x =∈<>R 或，(){}{}2002C x x x x x x =∈->∈<>R R 或所以A B C = ．所以“x A B ∈ ”是“x C ∈”的充分必要条件．故选Ｃ． 5．已知2log 3.6a =，4log 3.2b =，4log 3.6c =，则 ( )． A ．a b c >> B ．a c b >> C ．b a c >> D ．c a b >>【解】因为224log 3.6log 3.6a ==，而23.6 3.6 3.2>>，又函数4log y x =是()0,+∞上的增函数，则2444log 3.6log 3.6log 3.2>>．所以a c b >>．故选Ｂ．6．已知双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则双曲线的焦距为 ( )．A ．B ．C ．D ．【解】因为双曲线的一条渐近线与抛物线的准线的交点坐标为()2,1--，则22p-=-，所以4p =．又因为双曲线22221x y a b-=()0,0a b >>的左顶点与抛物线()220y px p =>的焦点的距离为4，则42pa +=，所以2a =．因为点()2,1--在双曲线的一条渐近线上，则()12ba-=-，即2a b =，所以1,b c ==2c =7．已知函数()()2sin f x x ωϕ=+，x ∈R ，其中0ω>，ππϕ-<≤．若()f x 的最小正周期为6π，且当π2x =时，()f x 取得最大值，则( )． A ．()f x 在区间[]2π,0-上是增函数 B ．()f x 在区间[]3π,π--上是增函数C ．()f x 在区间[]3π,5π上是减函数D ．()f x 在区间[]4π,6π上是减函数【解】由题设得ππ,222π6π,ωϕω⎧⋅+=⎪⎪⎨⎪=⎪⎩解得13ω=，π3ϕ=．所以已知函数为()π2sin 33x f x ⎛⎫=+ ⎪⎝⎭．其增区间满足π222332x k k ππππ-+≤+≤+，k ∈Z ．解得5π6ππ6π2k x k -+≤≤+，k ∈Z ．取0k =得5ππ2x -≤≤，所以5π,π2⎡⎤-⎢⎥⎣⎦为一个增区间，因为[]5π2π,0,π2⎡⎤-⊆-⎢⎥⎣⎦，所以()f x 在区间[]2π,0-上是增函数．故选Ａ．8．对实数a 和b ，定义运算“⊗”：,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩设函数()()()221f x x x =-⊗-，x ∈R ．若函数()y f x c =-的图象与x 轴恰有两个公共点，则实数c 的取值范围是( )．A ．(]()1,12,-+∞B ．(](]2,11,2--C ．()(],21,2-∞-D ．[]2,1--【解】由题设()22,12,1,12x x f x x x x ⎧--≤≤=⎨-<->⎩或画出函数的图象，函数图象的四个端点（如图）为()2,1A ，，(),2B ，()1,1C --，()1,2D --．从图象中可以看出，直线y c =穿过点B ，点A 之间时，直线y c =与图象有且只有两个公共点，同时，直线y c =穿过点C ，点D 时，直线y c =与图象有且只有两个公共点，所以实数c 的取值范围是(](]2,11,2-- ．故选Ｂ．第Ⅱ卷二、填空题：本答题共6小题，每小题5分,共30分．9．已知集合{}12A x x =∈-<R ，Z 为整数集，则集合A Z 中所有元素的和等于．【解】3．解集合A 得13x -<<，则{}0,1,2A =Z ，所有元素的和等于0123++=． 10．一个几何体的三视图如右图所示（单位：m ），则该几何体的体积为3m ．【解】4．几何体是由两个长方体组合的．体积为 1211124V =⨯⨯+⨯⨯=．11．已知{}n a 是等差数列，n S 为其前n 项和，n +∈N ．若316a =，2020S =，则10S 的值为．【解】110．设公差为d ，由题设31201216,2019020.a a d S a d =+=⎧⎨=+=⎩解得2d =-，120a =．()10110451020452110S a d =+=⨯+⨯-=．12．已知22log log 1a b +≥，则39ab+的最小值为．【解】18．因为22log log 1a b +≥，则2log 1ab ≥，2ab ≥，24a b ⋅≥3918a b +≥=≥，当且仅当39,2,a b a b ⎧=⎨=⎩即2a b =时，等号成立，所以39a b+的最小值为18．13．（同理12）如图，已知圆中两条弦AB 与CD 相交于点F ，E 是AB 延长线上一点，且DF CF ==::4:2:1AF FB BE =，若CE 与圆相切，则线段CE 的长为．【解】2．因为::4:2:1AF FB BE =，所以设BE a =，2FB a =，4AF a =．由相交弦定理，242DF CF AF FB a a ⋅=⋅==⋅，所以12a =，12BE =，772AE a ==．因为CE 与圆相切，由切割线定理，2177224CE AE BE =⋅=⋅=．所以CE =． 14．(同理14) 已知直角梯形ABCD 中，//AD BC ，90ADC ∠=︒，2AD =，1BC =，P 是腰DC 上的动点，则3PA PB +的最小值为．【解】5．解法1 ．以D 为坐标原点，DA 所在直线为x 轴，DC 所在直线为y 轴，建立如图的直角坐标系．由题设，()2,0A ，设()0,C c ，()0,P y ，则()1,B c ．()2,PA y =- ，()1,PB c y =-． ()35,34PA PB c y +=-．35PA PB += ，当且仅当34c y =时，等号成立，于是，当34cy =时，3PA PB + 有最小值5．解法2 ．以相互垂直的向量DP ，DA 为基底表示PB PA 3+，得()533332P A P BD A D P P C C B D A P C D P+=-++=+-．又P 是腰DC 上的动点，即与共线，于是可设λ=，有)13(253-+=+λ．所以2222553(31)(31)42PA PB DA DP DA DP λλ⎡⎤+=+-+⨯-⋅⎣⎦即 []213(25)13(-+=-+=+λλ．由于P 是腰DC 上的动点，显然当31=λ，即DP PC 31=时，所以3PA PB +有最小值5．解法3 ．如图，3PB PF =，设E 为AF 的中点，Q 为AB 的中点，则12QE BF PB ==，32PA PB PA PF PE +=+=， ①因为PB PQ PE += ，PB PQ QB -=．则22222222PB PQ PB PQ PB PQ PE QB ++-=+=+ ． ②（实际上，就是定理：“平行四边形的对角线的平方和等于各边的平方和”）设T 为DC 的中点，则TQ 为梯形的中位线，()1322TQ AD BC =+=．设P 为CT 的中点，且设,CP a PT b ==，则221PB a =+ ，2294PQ b =+ ，()2214QB a b =++ ，代入式②得()()222222912221244PB PQ a b PE a b ⎛⎫+=+++=+++ ⎪⎝⎭ ，于是()22252544PE a b =+-≥ ，于是25PE ≥ ，当且仅当a b =时，等号成立．由式①，325PA PB PE +=≥，所以3PA PB +有最小值5．三、解答题：本大题共6小题，共80分。