2013北京高三数学模拟汇编立体几何文

合集下载

2013年全国各地高考数学试题分类汇编(文科)：立体几何

2013年全国各地高考数学试题分类汇编（文科）：立体几何各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢2013年全国各地高考数学试题分类汇编（文科）：立体几何一、选择题1 ．（2013年高考重庆卷（文））某几何体的三视图如题(8)所示,则该几何体的表面积为（）A．B．C．D．【答案】D2 ．（2013年高考课标Ⅱ卷（文））一个四面体的顶点在空间直角坐标系中的坐标分别是,画该四面体三视图中的正视图时,以平面为投影面,则得到正视图可以为（）A．B．C．D．【答案】A3 ．（2013年高考课标Ⅰ卷（文））某几何函数的三视图如图所示,则该几何的体积为（）A．B．C．D．【答案】A4 ．（2013年高考大纲卷（文））已知正四棱锥的正弦值等于（）A．B．C．D．【答案】A5 ．（2013年高考四川卷（文））一个几何体的三视图如图所示,则该几何体可以是（）A．棱柱B．棱台C．圆柱D．圆台【答案】D6 ．（2013年高考浙江卷（文））已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是（）A．108cm3 B．100 cm3 C．92cm3 D．84cm3【答案】B7 ．（2013年高考北京卷（文））如图,在正方体中, 为对角线的三等分点,则到各顶点的距离的不同取值有（）A．3个B．4个C．5个D．6个【答案】B8 ．（2013年高考广东卷（文））某三棱锥的三视图如图2所示,则该三棱锥的体积是（）A．B．C．D．【答案】B9 ．（2013年高考湖南（文））已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于（）A．B．1 C．D．【答案】D10．（2013年高考浙江卷（文））设是两条不同的直线,α.β是两个不同的平面, （）A．若m‖α,n‖α,则m‖n B．若m‖α,m‖β,则α‖βC．若m‖n,m⊥α,则n⊥α D．若m‖α,α⊥β,则m⊥β【答案】C11．（2013年高考辽宁卷（文））已知三棱柱的6个顶点都在球的球面上,若, , ,则球的半径为（）A．B．C．D．【答案】C12．（2013年高考广东卷（文））设为直线, 是两个不同的平面,下列命题中正确的是（）A．若, ,则B．若, ,则C．若, ,则D．若, ,则【答案】B13．（2013年高考山东卷（文））一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是（）A．B．C．D．8,8【答案】B14．（2013年高考江西卷（文））一几何体的三视图如右所示,则该几何体的体积为（）A．200+9π B．200+18π C．140+9π D．140+18π【答案】A二、填空题15．（2013年高考课标Ⅱ卷（文））已知正四棱锥O-ABCD的体积为,底面边长为,则以O为球心,OA为半径的球的表面积为________.【答案】16．（2013年高考湖北卷（文））我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水. 天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸. 若盆中积水深九寸,则平地降雨量是__________寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)【答案】317．（2013年高考课标Ⅰ卷（文））已知是球的直径上一点, , 平面, 为垂足, 截球所得截面的面积为,则球的表面积为_______.【答案】;18．（2013年高考北京卷（文））某四棱锥的三视图如图所示,该四棱锥的体积为__________.【答案】319．（2013年高考陕西卷（文））某几何体的三视图如图所示, 则其表面积为________.【答案】20．（2013年高考大纲卷（文））已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径, 则球的表面积等于______.【答案】21．（2013年上海高考数学试题（文科））已知圆柱的母线长为,底面半径为, 是上地面圆心, 、是下底面圆周上两个不同的点, 是母线,如图.若直线与所成角的大小为,则________.【答案】22．（2013年高考天津卷（文））已知一个正方体的所有顶点在一个球面上. 若球的体积为, 则正方体的棱长为______.【答案】23．（2013年高考辽宁卷（文））某几何体的三视图如图所示,则该几何体的体积是____________.【答案】24．（2013年高考江西卷（文））如图,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,则直线EF 与正方体的六个面所在的平面相交的平面个数为_____________.【答案】425．（2013年高考安徽（文））如图,正方体的棱长为1, 为的中点,为线段上的动点,过点的平面截该正方体所得的截面记为,则下列命题正确的是__________(写出所有正确命题的编号).①当时, 为四边形;②当时, 为等腰梯形;③当时, 与的交点满足;④当时, 为六边形;⑤当时, 的面积为.【答案】①②③⑤三、解答题26．（2013年高考辽宁卷（文））如图,(I)求证:(II)设【答案】27．（2013年高考浙江卷（文））如图,在在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G为线段PC上的点.(Ⅰ)证明:BD⊥面PAC ;(Ⅱ)若G是PC的中点,求DG与APC 所成的角的正切值;(Ⅲ)若G满足PC⊥面BGD,求PGGC 的值.【答案】解:证明:(Ⅰ)由已知得三角形是等腰三角形,且底角等于30°,且,所以;、,又因为;(Ⅱ)设,由(1)知,连接,所以与面所成的角是,由已知及(1)知: ,,所以与面所成的角的正切值是;(Ⅲ)由已知得到: ,因为,在中, ,设28．（2013年高考陕西卷（文））如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,.(Ⅰ) 证明: A1BD // 平面CD1B1;(Ⅱ) 求三棱柱ABD-A1B1D1的体积.【答案】解: (Ⅰ) 设...(证毕)(Ⅱ).在正方形AB CD中,AO = 1 ..所以, .29．（2013年高考福建卷（文））如图,在四棱锥中, ,, ,, , , .(1)当正视图方向与向量的方向相同时,画出四棱锥的正视图.(要求标出尺寸,并画出演算过程);(2)若为的中点,求证: ;(3)求三棱锥的体积.【答案】解法一:(Ⅰ)在梯形中,过点作,垂足为, 由已知得,四边形为矩形,,在中,由, ,依勾股定理得:,从而,又由平面得,从而在中,由, ,得正视图如右图所示:(Ⅱ)取中点,连结,,在中, 是中点,∴, ,又,∴,, ∴四边形为平行四边形,∴又平面, 平面, ∴平面(Ⅲ) ,又, ,所以解法二:(Ⅰ)同解法一(Ⅱ)取的中点,连结,在梯形中, ,且,∴四边形为平行四边形∴,又平面, 平面∴平面,又在中,平面, 平面∴平面.又,∴平面平面,又平面∴平面(Ⅲ)同解法一30．（2013年高考广东卷（文））如图4,在边长为1的等边三角形中, 分别是边上的点, , 是的中点, 与交于点,将沿折起,得到如图5所示的三棱锥,其中.(1) 证明: //平面;(2) 证明:平面;(3) 当时,求三棱锥的体积.【答案】(1)在等边三角形中,,在折叠后的三棱锥中也成立,, 平面,平面, 平面;(2)在等边三角形中, 是的中点,所以①,.在三棱锥中, , ②;(3)由(1)可知,结合(2)可得.31．（2013年高考湖南（文））如图2.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC= ,AA1=3,D是BC的中点,点E在菱BB1上运动.(I) 证明:AD⊥C1E;(II) 当异面直线AC,C1E 所成的角为60°时,求三菱子C1-A2B1E的体积.【答案】解: (Ⅰ)..(证毕)(Ⅱ) ..32．（2013年高考北京卷（文））如图,在四棱锥中, , , ,平面底面, , 和分别是和的中点,求证:(1) 底面;(2) 平面;(3)平面平面【答案】(I)因为平面PAD⊥平面ABCD,且PA垂直于这个平面的交线AD 所以PA垂直底面ABCD.(II)因为AB‖CD,CD=2AB,E为CD的中点所以AB‖DE,且AB=DE所以ABED为平行四边形,所以BE‖AD,又因为BE 平面PAD,AD 平面PAD所以BE‖平面PAD.(III)因为AB⊥AD,而且ABED为平行四边形所以BE⊥CD,AD⊥CD,由(I)知PA ⊥底面ABCD,所以PA⊥CD,所以CD⊥平面PAD所以CD⊥PD,因为E和F分别是CD 和PC的中点所以PD‖EF,所以CD⊥EF,所以CD ⊥平面BEF,所以平面BEF⊥平面PCD.33．（2013年高考课标Ⅰ卷（文））如图,三棱柱中, ,, .(Ⅰ)证明: ;(Ⅱ)若, ,求三棱柱的体积.【答案】【答案】(I)取AB的中点O,连接、、,因为CA=CB,所以,由于AB=A A1,∠BA A1=600,故为等边三角形,所以OA ⊥AB.因为OC⨅OA =O,所以AB 平面OA C.又A CC平面OA C,故AB AC.(II)由题设知34．（2013年高考山东卷（文））如图,四棱锥中, ,,分别为的中点(Ⅰ)求证: ;(Ⅱ)求证:【答案】35．（2013年高考四川卷（文））如图,在三棱柱中,侧棱底面, , ,分别是线段的中点, 是线段上异于端点的点.(Ⅰ)在平面内,试作出过点与平面平行的直线,说明理由,并证明直线平面;(Ⅱ)设(Ⅰ)中的直线交于点,求三棱锥的体积.(锥体体积公式: ,其中为底面面积, 为高)【答案】解:(Ⅰ)如图,在平面ABC内,过点作直线,因为在平面外,BC在平面内,由直线与平面平行的判定定理可知, 平面.由已知, , 是BC中点,所以BC⊥AD,则直线,又因为底面,所以,又因为AD, 在平面内,且AD与相交,所以直线平面(Ⅱ)过D作于E,因为平面,所以,又因为AC, 在平面内,且AC与相交,所以平面,由,∠BAC ,有,∠DAC ,所以在△ACD中, ,又,所以因此三棱锥的体积为36．（2013年高考湖北卷（文））如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为.同样可得在B,C处正下方的矿层厚度分别为, ,且. 过, 的中点, 且与直线平行的平面截多面体所得的截面为该多面体的一个中截面,其面积记为.(Ⅰ)证明:中截面是梯形;(Ⅱ)在△ABC中,记,BC边上的高为,面积为. 在估测三角形区域内正下方的矿藏储量(即多面体的体积)时,可用近似公式来估算. 已知,试判断与V的大小关系,并加以证明.【答案】(Ⅰ)依题意平面, 平面, 平面,所以A1A2‖B1B2‖C1C2. 又, , ,且.因此四边形、均是梯形.由‖平面, 平面,且平面平面,可得AA2‖ME,即A1A2‖DE. 同理可证A1A2‖FG,所以DE‖FG.又、分别为、的中点,则、、、分别为、、、的中点,即、分别为梯形、的中位线.因此, ,而,故,所以中截面是梯形.(Ⅱ) . 证明如下:由平面, 平面,可得.而EM‖A1A2,所以,同理可得.由是△的中位线,可得即为梯形的高,因此,即.又,所以.于是.由,得, ,故.37．（2013年高考课标Ⅱ卷（文））如图,直三棱柱ABC-A1B1C1中,D,E 分别是AB,BB1的中点.(1) 证明: BC1//平面A1CD;(2) 设AA1= AC=CB=2,AB=2 ,求三棱锥C一A1DE的体积.【答案】38．（2013年高考大纲卷（文））如图,四棱锥P-ABCD中，∠ABC=∠BAD=900，BC=2AD，△PAB与△PAD 都是边长为2的等边三角形.(I)证明:PB⊥CD；(II)求点A到平面PCD的距离.【答案】(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形.过P作PO⊥平面ABCD,垂足为O.连结OA,OB,OD,OE.由和都是等边三角形知PA=PB=PD,所以OA=OB=OD,即点O为正方形ABED对角线的交点,故,从而.因为O是BD的中点,E是BC的中点,所以OE//CD.因此, .(Ⅱ)解:取PD的中点F,连结OF,则OF//PB.由(Ⅰ)知, ,故.又, ,故为等腰三角形,因此, .又,所以平面PCD.因为AE//CD, 平面PCD, 平面PCD,所以AE//平面PCD.因此,O到平面PCD的距离OF就是A到平面PCD的距离,而,所以A至平面PCD的距离为1.39．（2013年高考安徽（文））如图,四棱锥的底面是边长为2的菱形, .已知.(Ⅰ)证明:(Ⅱ)若为的中点,求三菱锥的体积.【答案】解:(1)证明:连接交于点又是菱形而⊥面⊥(2)由(1) ⊥面=40．（2013年上海高考数学试题（文科））如图,正三棱锥底面边长为,高为,求该三棱锥的体积及表面积.【答案】41．（2013年高考天津卷（文））如图, 三棱柱ABC-A1B1C1中, 侧棱A1A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC, A1C1的中点.(Ⅰ) 证明EF//平面A1CD;(Ⅱ) 证明平面A1CD⊥平面A1ABB1;(Ⅲ) 求直线BC与平面A1CD所成角的正弦值.【答案】42．（2013年高考重庆卷（文））(本小题满分12 分,(Ⅰ)小问5分,(Ⅱ)小问7分)如题(19)图,四棱锥中, ⊥底面, , ,(Ⅰ)求证: ⊥平面;(Ⅱ)若侧棱上的点满足,求三棱锥的体积.【答案】43．（2013年高考江西卷（文））如图,直四棱柱ABCD –A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD= ,AA1=3,E为CD上一点,DE=1,EC=3(1) 证明:BE⊥平面BB1C1C;(2) 求点B1 到平面EA1C1 的距离【答案】解.(1)证明:过B作CD的垂线交CD于F,则在在,故由(2),同理,因此.设点B1到平面的距离为d,则,从而各位读友大家好，此文档由网络收集而来，欢迎您下载，谢谢。

【精选+详解】2013届高三数学名校试题汇编(第2期)专题08 立体几何文

【精选+详解】2013届高三数学名校试题汇编（第2期）专题08 立体几何文一．基础题1.【某某省华南师大附中2012-2013学年度高三第三次月考】已知m n 、是两条不同的直线，αβ、是两个不同的平面，有下列命题：①若,//m n αα⊂，则//m n ； ②若//m α，//m β，则//αβ；③若,m m n α⊥⊥，则α//n ； ④若,m m αβ⊥⊥，则//αβ；其中真命题的个数是（A ）1个（B ）2个（C ）3个（D ）4个【答案】A【解析】①②③不成立，故选A ．2.【2013年某某省高考测试卷】已知以下三视图中有三个同时表示某一个三棱锥，则不是该三棱锥的三视图是（）【答案】D【解析】仔细分析A 、B 、C 三个选项，发现都可以是下图左边的三视图，D选项则表示下图右边的三视图.3.【某某师大附中2013届高三高考适应性月考卷（三）】一个几何体的三视图如图1所示，其中正视图是一个正三角形，则该几何体的体积为A ．1B ．33C ．3D ．2334.【某某某某一中2013届第四次月考试卷】已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形，则其全面积是（）2A ．8B ．12C ．4(13)+D ． 43【答案】B【解析】由题意可知，该几何体为正四棱锥，底面边长为2，侧面斜高为2，所以底面积为224⨯=，侧面积为142282⨯⨯⨯=，所以表面积为4812+=，选B. 5．【东城区普通校2012—2013学年高三第一学期联考】已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是A ．,,αγβγαβ⊥⊥若则‖B ．,,m n m n αα⊥⊥若则‖ C．,,m n m n αα若则‖‖‖ D ．,,m m αβαβ若则‖‖‖【答案】B【解析】根据线面垂直的性质可知，B 正确.6.【东城区普通校2012—2013学年高三第一学期联考】一个棱锥的三视图如图（尺寸的长度单位为m ），则该棱锥的体积是A ．34B ．8C ．4D ．38 7.【某某市新华中学2011-2012学年度第一学期第二次月考】如图，是一个几何体的正视图、侧视图、俯视图，则该几何体的体积是A. 24B. 12C. 8D. 48.【四中2012-2013年度第一学期高三年级期中】设为两个平面，为两条直线，且，有如下两个命题：①若；②若. 那么（）A．①是真命题，②是假命题 B．①是假命题，②是真命题 C．①、②都是真命题 D．①、②都是假命题【答案】D【解析】若//αβ，则//l m或,l m异面，所以①错误.同理②也错误，所以选D.9.【2013年某某市高中毕业班第一次调研测试】一个几何体的三视图如图所示，则这个几何体的体积为A. (8)36π+B.(82)36π+C. (6)36π+D.(92)36π+10.【某某市新华中学2011-2012学年度第一学期第二次月考】如图为一个几何体的三视图，其中俯视为正三角形，A1B1=2,AA1=4，则该几何体的表面积为_______.二．能力题11.【某某某某一中2013届第四次月考试卷】已知正三棱锥ABC P ，点C B A P ,,,都在半径为3的球面上，若PC PB PA ,,两两互相垂直，则球心到截面ABC 的距离为________.12.【某某某某一中高2013届高三上学期第三次月考】已知三棱锥的三视图如图所示，则它的外接球表面积为（）A ．16πB ．4πC ．8πD ．2π13.【某某某某一中2013届第四次月考试卷】四面体BCD A -中，,5,4======BD AD AC BC CD AB 则四面体外接球的表面积为（）A ．π33B ．π43C ．π36D ．π18【答案】A【解析】分别取AB,CD 的中点E,F ，连结相应的线段，由条件可知，球心G 在EF 上，可以证明G 为EF中点，A.14.【某某中原名校2012—2013学年度第一学期期中联考】[已知球O l 、O 2的半径分别为l 、 r ，体积分别为V 1、V 2，表面积分别为S 1、S 2，当(1,)r ∈+∞时，2121V V S S --的取值X 围是.15.【某某某某外国语学校2012—2013学年度第一学期质量检测】一个几何体的三视图如图所示(单位:m),则该几何体的体积为3m .【答案】4【解析】由三视图可知，该组合体是由两个边长分别为2,1，1和1,1,2的两个长方体，所⨯⨯+⨯⨯=.以体积之和为211112416.【四中2012-2013年度第一学期高三年级期中】湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个直径为12 cm，深2 cm的空穴，则该球的半径是______cm，表面积是______cm².17．【四中2012-2013年度第一学期高三年级期中】某几何体的三视图如图所示，该几何体的体积是______.18.【2013年某某市高中毕业班第一次调研测试】若一个正方体的表面积为1S ，其外接球的表面积为2S ，则12S S =____________. 19.【某某某某一中高2013届高三上学期第三次月考】设动点P 在棱长为1的正方体1111ABCD A B C D -的对角线1BD 上，记11D P D Bλ=.当APC ∠为钝角时，则λ的取值X 围是.11(,,)(0,1,1)(,1,1)PC PD DC λλλλλλ=+=--+-=--- 三．拔高题20【2013年某某市高中毕业班第一次调研测试】（本小题满分12分）如图，在三棱柱111ABC A B C -中，侧面11AA C C ⊥底面ABC ，112AA A C AC ===，AB BC =，AB BC ⊥，O 为AC 中点.⑴证明:1A O ⊥平面ABC ；⑵ 若E 是线段1A B 上一点，且满足1111112E BCC ABC A B C V V --=，求1A E 的长度. 【命题意图】本小题以斜三棱柱为考查载体，考查平面几何的基础知识.同时题目指出侧面的一条高与底面垂直，搭建了空间直角坐标系的基本架构.本题通过分层设计，考查了空间直线垂直，以及线面成角等知识，考查学生的空间想象能力、推理论证能力和运算求解能力.【试题解析】解：(1) 112AA A C AC ===，且O 为AC 中点，1A O AC ∴⊥，又侧面11AA C C ⊥底面ABC ，交线为AC ，11AO A AC ⊂面， ∴1A O ⊥平面ABC . (6分) O C B A C 1B 1A 1(2) 11111111124E BCC ABC A B C A BCC V V V ---==，因此114BE BA =，即1134A E AB =，又在1Rt AOB ∆中，1A O OB ⊥，13AO =，1BO =可得12A B =，则1A E 的长度为32. (12分)21.【某某省东阿县第一中学2012-2013学年度上学期考试】（本小题满分14分）如图，正三棱柱111ABC ABC -中，12,3,AB AA D ==为1C B 的中点，P 为AB 边上的动点.（Ⅰ）当点P 为AB 的中点时，证明DP//平面11ACC A ；（Ⅱ）若3AP PB =，求三棱锥B CDP -的体积.【答案】22.【某某某某一中高2013届高三上学期第三次月考】（本小题满分12分）如图，在长方体1111ABCD A B C D -，中，11,2AD AA AB ===，点E 在棱AB 上移动.（1）证明：11D E A D ⊥；（2）当E 为AB 的中点时，求点E 到面1ACD 的距离.解：以D 为坐标原点，直线1,,DA DC DD 分别为,,x y z 轴，建立空间直角坐标系，设AE x =，则11(1,0,1),(0,0,1),(1,,0),(1,0,0),(0,2,0)A D E x A C …………2分（1）1111,(1,0,1),(1,,1)0,.DA D E x DA D E =-=⊥因为所以………………6分23.【某某师大附中2013届高三高考适应性月考卷（三）】如图5，已知三棱锥A BPC -中，AP ⊥BC ，M 为AB 的中点，D 为PB 的中点，且△PMB 为正三角形．（1）求证：BC ⊥平面APC ；（2）若3BC =，10AB =，求点B 到平面DCM 的距离．（本小题满分12分）3又MD DC ⊥，125328MDC S MD DC ∴=⋅△112553123,33825B MDC MDC V h S h h -∴=⋅=⋅⋅=∴=△，即点B 到平面MDC 的距离为125．……………………………………………（12分）24.【某某师大附中、某某一中2013届高三12月联考试卷】（本小题满分12分）如图所示，在直．三棱柱．．．ABC -A 1B 1C 1中，AC ⊥BC ．(1) 求证：平面AB 1C 1⊥平面AC 1；(2) 若AB 1⊥A 1C ，求线段AC 与AA 1长度之比；(3) 若D 是棱CC 1的中点，问在棱AB 上是否存在一点E ，使DE ∥平面AB 1C 1？若存在，试确定点E 的位置；若不存在，请说明理由．证法二：设G 是AB 1的中点，连结EG ，则易证EG DC 1. 所以DE // C 1G ，DE ∥平面AB 1C 1． 25.【市东城区普通高中示X 校2013届高三综合练习（一）】（本题满分14分）已知ABCD 是矩形，2AD AB =，,E F 分别是线段,AB BC 的中点，PA ⊥平面ABCD ．（Ⅰ）求证：DF ⊥平面PAF ；（Ⅱ）在棱PA 上找一点G ，使EG ∥平面PFD ，并说明理由．（Ⅰ）证明：在矩形ABCD 中，因为AD =2AB ,点F 是BC 的中点,26.【某某省华南师大附中2012-2013学年度高三第三次月考】（本题满分14分）如图，已知⊥PA ⊙O 所在的平面，AB 是⊙O 的直径，2=AB ， C 是⊙O 上一点，且BC AC =，PC 与⊙O 所在的平面成︒45角， E 是PC 中点．F 为PB 中点． (1) 求证： ABC EF 面//； (2) 求证：PAC EF 面⊥；（3）求三棱锥PAC B -的体积．解：(1)证明：在三角形PBC 中，E 是PC 中点． F 为PB 中点P CBO EF27.某某省某某市2012届高三12月教学质量检测】（（本小题满分12分）如图，已知多面体ABCDE 中，DE ⊥平面DBC ，DE AB ∥，2====AB BC CD BD ，F 为BC 的中点.（Ⅰ）求证：DF ⊥平面ABC ；（Ⅱ）求点D 到平面EBC 的距离的取值X 围.28.【某某省名校新高考研究联盟2013届第一次联考】（本题14分）如图，在三棱锥ABC P -中，BC AC PC AB PB PA 222=====．（Ⅰ）求证：BC PA ⊥；（Ⅱ）求二面角C AB P --所成角的余弦值．（Ⅰ）【解法一】如图，取PA 中点M ，连接CM 、BM ． ∵AC PC =，AB PB =，∴PA CM ⊥,PA BM ⊥, ……3分又M BM CM = ,∴⊥PA 平面BMC ，⊂BC 平面BMC , ∴BC PA ⊥． ……………………………………………6分【解法二】由BC AC PC AB PB PA 222=====知，ACB ∆、ACP ∆、BCP ∆都是等腰直角三角形，CA 、CB 、CP 两两垂直， …………3分∴⊥BC 平面ACP ,⊂PA 平面ACP ,∴BC PA ⊥． (6)分∴二面角C AB P --所成角的余弦值为33．……………………………………………14分 29.【某某省某某市部分学校2013届高三12月联考】（本小题满分13分）在如图所示的多面体ABCDE 中，AB⊥平面ACD ，DE⊥平面ACD ，且AC=AD=CD=DE=2，AB=1．（1）请在线段CE 上找到点F 的位置，使得恰有直线BF∥平面ACD ，并证明这一事实；（2）求多面体ABCDE 的体积；（3）求直线EC 与平面ABED 所成角的正弦值．解答：如图，（1）由已知AB⊥平面ACD ，DE⊥平面ACD ，∴AB//ED ，设F 为线段CE 的中点，H 是线段CD 的中点，有36sin 422CG CE α===．30.【某某省2012年某某市高2013级（高三）一诊模拟考试】在四棱锥PABCD 中，AB //CD ，ABAD ，4,22,2AB AD CD ，PA 平面ABCD ，4PA .（1）设平面PAB平面PCD m =，求证：CD //m ；（2）求证：BD ⊥平面PAC ；（3）求三棱锥D-PBC 体积（1）证明：因为AB //CD ，CD ⊄平面PAB ，AB ⊂平面PAB ，所以CD //平面PAB . 因为CD ⊂平面PCD ，平面PAB 平面PCD m =，所以CD //m . ……4分（2）证明：因为AP平面ABCD ，ABAD ，所以以A 为坐标原点，,,AB AD AP 所31.【某某省某某市2013届高三第三次调研考试】如图所示，在棱长为2的正方体1111ABCD A B C D 中，E 、F 分别为1DD 、DB 的中点．word 21 / 21。

北京市各地市高考数学最新联考试题分类汇编(8)立体几何

北京市各地市2013年高考数学最新联考试题分类汇编（8）立体几何一、选择题:（6）(北京市朝阳区2013年4月高三第一次综合练习文理)某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为A. 4B. D. 8【答案】D（5）(北京市东城区2013年4月高三综合练习一文）已知一个几何体的三视图如图所示(单位：cm)，那么这个几何体的侧．面积是（A）2（B）2(4（D）2（C）2【答案】C7. (北京市房山区2013年4月高三第一次模拟理)某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是( C )A.B. 8C.D.5．(北京市西城区2013年4月高三一模文)某正三棱柱的三视图如图所示，其中正（主）视图是边长为2的正方形，该正三棱柱的表面积是（A ）6（B ）12（C ）12+（D ）24+【答案】C8．(北京市西城区2013年4月高三一模文)如图，正方体1111ABCD A BC D -中，E 是棱11B C 的中点，动点P 在底面ABCD 内，且11PA A E =，则点P 运动形成的图形是（A ）线段（B ）圆弧（C ）椭圆的一部分（D ）抛物线的一部分【答案】B8. (北京市海淀区2013年4月高三第二学期期中练习理)设123,,l l l 为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出下列三个结论：①i i A l ∃∈(1,2,3)i =，使得123A A A ∆是直角三角形； ②i i A l ∃∈(1,2,3)i =，使得123A A A ∆是等边三角形；③三条直线上存在四点(1,2,3,4)i A i =，使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体.其中，所有正确结论的序号是A. ①B.①②C. ①③D. ②③ 【答案】B7．（北京市丰台区2013年高三第二学期统一练习一文）某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是(A) 2 (B) 4 (C) 24+【答案】C（7）（北京市昌平区2013年1月高三期末考试理）已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的全面积为A. 10+．10+ C. 14+ D. 14+二、解答题:（17）(北京市朝阳区2013年4月高三第一次综合练习理)（本小题满分14分）如图，在四棱锥P ABCD -中，平面PAC ⊥平面ABCD ，且P A A C ⊥， 2PA AD ==．四边形ABCD 满足BCAD ，AB AD ⊥，1AB BC ==．点,E F 分别为侧棱,PB PC 上的点，且PE PFPB PCλ==．（Ⅰ）求证：EF 平面PAD ；（Ⅱ）当12λ=时，求异面直线BF 与CD 所成角的余弦值；（Ⅲ）是否存在实数λ，使得平面AFD ⊥平面PCD ？若存在，试求出λ的值；若不存在，请说明理由．（17）（本小题满分14分）证明：（Ⅰ）由已知，PE PFPB PCλ==，所以 EFBC ．所以()()0,0,01,0,0,A B ,所以异面直线BF与CD所成角的余弦值为3．…………………………………9分令21x=，则2(1,1,1) =n．若平面AFD ⊥平面PCD ，则120n n ⋅=，所以(22)0λλ-+=，解得23λ=．所以当23λ=时，平面AFD ⊥平面PCD ．…………………………………………14分（17）(北京市朝阳区2013年4月高三第一次综合练习文) （本小题满分14分）如图，在四棱锥P ABCD -中，平面PAC ⊥平面ABCD ，且P A A C ⊥， 2PA AD ==．四边形ABCD 满足BC AD ，AB AD ⊥，1AB BC ==．E 为侧棱PB 的中点，F 为侧棱PC 上的任意一点.（Ⅰ）若F 为PC 的中点，求证：EF平面PAD ；（Ⅱ）求证：平面AFD ⊥平面PAB ；（Ⅲ）是否存在点F ，使得直线AF 与平面PCD 垂直？若存在，写出证明过程并求出线段PF 的长；若不存在，请说明理由．平面ABCD 平面PAC AC =，且PA AC ⊥，PA ⊂平面PAC .所以PA ⊥平面ABCD ，又AD ⊂平面ABCD ，所以PA AD ⊥．又因为AB AD ⊥，PA AB A =，所以AD ⊥平面PAB ，而AD ⊂平面AFD ，所以平面AFD ⊥平面PAB ．……………………………………………………8分可见直线AF 与平面PCD 能够垂直，此时线段PF．……………14分（16）(北京市东城区2013年4月高三综合练习一文）（本小题共14分）如图，已知AD ⊥平面ABC ，CE ⊥平面ABC ，F 为BC 的中点，若12AB AC AD CE ===．（Ⅰ）求证：//AF 平面BDE ；（Ⅱ）求证：平面BDE ⊥平面BCE ．（16）（共14分）证明：（Ⅰ）取BE 的中点G ，连结GF ，GD .因为F 是BC 的中点，则GF 为△BCE 的中位线．所以//GF EC ，12GF CE =．因为AD ⊥平面ABC ，CE ⊥平面ABC ，所以////GF EC AD ．A BC DE FABCD EFG又DG ⊂平面BDE ，所以平面BDE ⊥平面BCE ．16. (北京市房山区2013年4月高三第一次模拟理)（本小题满分14分）在四棱锥P ABCD -中，侧面PAD ⊥底面ABCD ， ABCD 为直角梯形，BC //AD ，90ADC ∠=︒，112BC CD AD ===，PA PD =，E F ,为AD PC ,的中点．（Ⅰ）求证：PA //平面BEF ；（Ⅱ）若PC 与AB 所成角为45︒，求PE 的长；（Ⅲ）在（Ⅱ）的条件下，求二面角F-BE-A 的余弦值．解得：2=t ∴2=PE …………………………………………………………………….9分解法二：由BCDE 为正方形可得 EC ==由ABCE 为平行四边形可得EC //AB∴PCE ∠为PC AB 与所成角即045PCE ∠=…………………………………..…5分 PA PD E AD PE AD =∴⊥为中点由图可知二面角B AC E --的平面角是钝角，所以二面角B AC E --的余弦值为33-．………………………………………….14分 16．(北京市西城区2013年4月高三一模文)（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD ，AC ，22AB BC ==，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求四面体FBCD 的体积；（Ⅲ）线段AC 上是否存在点M ，使EA //平面FDM ？证明你的结论． 16．（本小题满分14分）因为 CDEF 为正方形，所以N 为CE 中点． ………………11分所以 EA //MN ． ………………12分因为 ⊂MN 平面FDM ，⊄EA 平面FDM ， ………………13分所以 EA //平面FDM ．所以线段AC 上存在点M ，使得EA //平面FDM 成立． ………………14分17. (北京市海淀区2013年4月高三第二学期期中练习理)（本小题满分14分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，ABC ∆是正三角形，AC 与BD 的交点M 恰好是AC 中点，又4PA AB ==，120CDA ∠=，点N 在线段PB 上，且PN = （Ⅰ）求证：BD PC ⊥；（Ⅱ）求证：//MN 平面PDC ; （Ⅲ）求二面角A PC B --的余弦值．PDC ………………9分所以二面角A PC B --余弦值为7………………14分 16．（北京市丰台区2013年高三第二学期统一练习一文）（本题13分）如图，四棱锥P-ABCD 中， BC ∥AD ，BC=1，AD=3，AC ⊥CD,且平面PCD ⊥平面ABCD. （Ⅰ）求证：AC ⊥PD ；（Ⅱ）在线段PA 上,是否存在点E ，使BE ∥平面PCD ？若存在，求PE PA的值；若不存在，请说明理由。

北京市昌平区2013届高三仿真模拟数学文科试卷5 Word版含答案

北京市昌平区2013届高三仿真模拟数学文科试卷5第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项.1.已知集合{0,1}A =,{1,0,3}B a =-+，且A B ⊆，则a 等于（A ）1（B ）0（C ）2- （D ）3-2.已知i 是虚数单位，则复数2z 12i+3i =+所对应的点落在（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限3.已知a b <，则下列不等式正确的是（A ）11a b > （B ）22a b >（C ）22a b ->-（D ）22a b>4.在ABC ∆中，“0AB BC ⋅=”是“ABC ∆为直角三角形”的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分又不必要条件 5．一个几何体的三视图如图所示，则其体积等于（A ）2 （B ）1（C ）16（D ）236.函数sin ()y x x =π∈R 的部分图象如图所示，设O 为坐标原点，P 是图象的最高点，B 是图象与x 轴的交点，则tan OPB ∠=正(主)视图俯视图侧(左)视图（A ）10 （B ）8（C ）87 （D ）477．若2a >，则函数3()33f x x ax =-+在区间(0,2)上零点的个数为（A ）0个（B ）1个（C ）2个（D ）3个8．已知点(1,0),(1,0)A B -及抛物线22y x =，若抛物线上点P 满足PA m PB =，则m 的最大值为（A ）3 （B ）2（C（D第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9. 已知}{n a 为等差数列，341a a +=，则其前6项之和为_____.10．已知向量(1=a，+=a b ，设a 与b 的夹角为θ，则θ=_____. 11.在ABC ∆中，若2B A =，:a b =A =_____.12．平面上满足约束条件2,0,60x x y x y ≥⎧⎪+≤⎨⎪--≤⎩的点(,)x y 形成的区域为D ，则区域D 的面积为________；设区域D 关于直线21y x =-对称的区域为E ，则区域D 和区域E 中距离最近的两点的距离为________.13.定义某种运算⊗，a b ⊗的运算原理如右图所示. 则0(1)⊗-=______；设()(0)(2)f x x x x =⊗-⊗.则(1)f =______.14.数列{}n a 满足11a =，11n nn a a n λ+-=+，其中λ∈R ，12n =，，．给出下列命题：①λ∃∈R ，对于任意i ∈*N ，0i a >；②λ∃∈R ，对于任意2()i i ≥∈*N ，10i i a a +<；③λ∃∈R ，m ∈*N ，当i m >（i ∈*N ）时总有0ia <.其中正确的命题是______.（写出所有正确命题的序号）三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.（本小题满分13分）已知函数1)43()sin x f x x π+-=.（Ⅰ）求函数()f x 的定义域；（Ⅱ）若()2f x =，求sin 2x 的值.16.（本小题满分13分）如图，菱形ABCD 的边长为6，60BAD ∠=,ACBD O =.将菱形ABCD 沿对角线AC 折起，得到三棱锥B ACD -,点M 是棱BC的中点，DM =（Ⅰ）求证：//OM 平面ABD ；（Ⅱ）求证：平面ABC ⊥平面MDO ；（Ⅲ）求三棱锥M ABD -17.（本小题满分13分）由世界自然基金会发起的“地球1小时”活动，已发展成为最有影响力的环保活动之一，今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此，某新闻媒体进行了网上调查，所有参与调查的人中，持“支持”、“保留”和“不支持”态度的人（Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取个人，已知从“支持”态度的人中抽ABCCMOD取了45人，求n的值；（Ⅱ）在持“不支持”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任意选取2人，求至少有1人20岁以下的概率；（Ⅲ）在接受调查的人中，有8人给这项活动打出的分数如下:9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2.把这8个人打出的分数看作一个总体，从中任取1个数，求该数与总体平均数之差的绝对值超过0.6的概率.18.（本小题满分14分）设函数()e xf x=，其中e为自然对数的底数.（Ⅰ）求函数()()eg x f x x=-的单调区间；（Ⅱ）记曲线()y f x=在点00(,())P x f x（其中0x<）处的切线为l，l与x轴、y轴所围成的三角形面积为S，求S的最大值.19.（本小题满分14分）已知椭圆22221x ya b+=（0a b>>）的焦距为.（Ⅰ）求椭圆方程；（Ⅱ）设过椭圆顶点(0,)B b，斜率为k的直线交椭圆于另一点D，交x轴于点E，且,,BD BE DE成等比数列，求2k的值.20.（本小题满分13分）若函数)(xf对任意的x∈R，均有)(2)1()1(xfxfxf≥++-，则称函数)(xf具有性质P.（Ⅰ）判断下面两个函数是否具有性质P，并说明理由.①(1)xy a a=>；②3y x=.（Ⅱ）若函数)(xf具有性质P，且(0)()0f f n==（2,n>n∈*N），求证：对任意{1,2,3,,1}i n∈-有()0f i≤；（Ⅲ）在（Ⅱ）的条件下，是否对任意[0,]x n∈均有0)(≤xf.若成立给出证明，若不成立给出反例.参考答案一、选择题：本大题共8小题，每小题5分，共40分.题号1 2 3 4 5 67 8 答案C B C AD B B C二、填空题：本大题共6小题，每小题5分，共30分.9. 3 10. 120 11.30 12. 1； 13. 1；1- 14. ①③注：12、13题第一问2分，第二问3分.14题只选出一个正确的命题给2分，选出错误的命题即得0分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分.15.（本小题满分13分）解：解：（Ⅰ）由题意，sin 0x ≠， ……………2分所以，()x k k ≠π∈Z . ……………3分函数()f x 的定义域为{,}x x k k ≠π∈Z . ……………4分（Ⅱ）因为()2f x =1)2sin 43x xπ+-=， ……………5分12()2sin 223x x x +-=， ……………7分1cos sin 3x x -=， ……………9分将上式平方，得11sin 29x -=， ……………12分所以8sin 29x =. ……………13分16.（本小题满分13分）（Ⅰ）证明：因为点O 是菱形ABCD 的对角线的交点，所以O 是AC 的中点.又点M 是棱BC 的中点，所以OM 是ABC ∆的中位线，//OM AB . ……………2分因为OM ⊄平面ABD ,AB ⊂平面ABD ，所以//OM 平面ABD . ……………4分（Ⅱ）证明：由题意，3OM OD ==,因为DM =所以90DOM ∠=，OD OM ⊥. ……………6分又因为菱形ABCD ，所以OD AC ⊥. …………7分因为OMAC O =,所以OD ⊥平面ABC ， ……………8分因为OD ⊂平面MDO ，所以平面ABC ⊥平面MDO . ……………9分（Ⅲ）解：三棱锥M ABD -的体积等于三棱锥D ABM -的体积. ……………10分由（Ⅱ）知，OD ⊥平面ABC ，所以3OD =为三棱锥D ABM -的高. ……………11分ABM ∆的面积为11sin1206322BA BM ⨯⨯=⨯⨯=， ……………12分所求体积等于132ABM S OD ∆⨯⨯=. ……………13分17.（本小题满分13分）解：（Ⅰ）由题意得80010080045020010015030045n ++++++=， ……………2分所以100n =. ……………3分ABCMOD（Ⅱ）设所选取的人中，有m 人20岁以下，则2002003005m=+，解得2m =.………5分也就是20岁以下抽取了2人，另一部分抽取了3人，分别记作A1，A2；B1，B2，B3，则从中任取2人的所有基本事件为 (A1,B1)，(A1, B2)，(A1, B3)，(A2 ,B1)，(A2 ,B2)，(A2 ,B3)，(A1, A2)，(B1 ,B2)，(B2 ,B3)，(B1 ,B3)共10个. ………7分其中至少有1人20岁以下的基本事件有7个：(A1, B1)，(A1, B2)，(A1, B3)，(A2 ,B1)，(A2 ,B2)，(A2 ,B3)，(A1, A2)， …………8分所以从中任意抽取2人，至少有1人20岁以下的概率为710. ……………9分（Ⅲ）总体的平均数为1(9.48.69.29.68.79.39.08.2)98x =+++++++=，………10分那么与总体平均数之差的绝对值超过0.6的数只有8.2， ……………12分所以该数与总体平均数之差的绝对值超过0.6的概率为81. ……………13分18.（本小题满分14分）解：（Ⅰ）由已知()e e xg x x =-，所以()e e xg x '=-， ……………2分由()e e 0x g x '=-=，得1x =， ……………3分所以，在区间(,1)-∞上，()0g x '<，函数()g x 在区间(,1)-∞上单调递减； ……………4分在区间(1,)+∞上，()0g x '>，函数()g x 在区间(1,)+∞上单调递增； ……………5分即函数()g x 的单调递减区间为(,1)-∞，单调递增区间为(1,)+∞.（Ⅱ）因为()e xf x '=，所以曲线()y f x =在点P 处切线为l ：000e e ()x x y x x -=-. ……………7分切线l 与x 轴的交点为0(1,0)x -，与y 轴的交点为000(0,e e )x x x -， ……………9分因为00x <，所以002000011(1)(1)e (12)e 22x x S x x x x =--=-+， ……………10分0201e (1)2x S x '=-， ……………12分在区间(,1)-∞-上，函数0()S x 单调递增，在区间(1,0)-上，函数0()S x 单调递减.……………13分所以，当01x =-时，S 有最大值，此时2e S =，所以，S 的最大值为2e . ……………14分19、（本小题满分14分）解：（Ⅰ）由已知2c =2c a=. ……………2分解得2,a c =， ……………4分所以2221b a c =-=，椭圆的方程为2214x y +=. ……………5分（Ⅱ）由（Ⅰ）得过B 点的直线为1y kx =+，由221,41,x y y kx ⎧+=⎪⎨⎪=+⎩ 得22(41)80k x kx ++=， ……………6分所以2814D k x k =-+，所以221414D k y k -=+， ……………8分依题意0k ≠，12k ≠±.因为,,BD BE DE 成等比数列，所以2BE BD DE=， ……………9分所以2(1)D Db y y =-，即(1)1D D y y -=， ……………10分当0D y >时，210D D y y -+=，无解， ……………11分当0D y <时，210DD y y --=，解得D y =， ……………12分所以221414k k-=+，解得2k =，所以，当,,BD BE DE成等比数列时，224k =. ……………14分20.（本小题满分13分）（Ⅰ）证明：①函数)1()(>=a a x f x具有性质P . ……………1分 111(1)(1)2()2(2)x x x x f x f x f x a a a a a a -+-++-=+-=+-，因为1>a ，1(2)0x a a a +->， ……………3分即)(2)1()1(x f x f x f ≥++-，此函数为具有性质P .②函数3)(x x f =不具有性质P . ……………4分例如，当1x =-时，(1)(1)(2)(0)8f x f x f f -++=-+=-，2()2f x =-， ……………5分所以，)1()0()2(-<+-f f f ，此函数不具有性质P . （Ⅱ）假设)(i f 为(1),(2),,(1)f f f n -中第一个大于0的值， ……………6分则0)1()(>--i f i f ，因为函数()f x 具有性质P ，所以，对于任意n ∈*N ，均有(1)()()(1)f n f n f n f n +-≥--，所以0)1()()2()1()1()(>--≥≥---≥--i f i f n f n f n f n f ，所以()[()(1)][(1)()]()0f n f n f n f i f i f i =--+++-+>，与0)(=n f 矛盾，所以，对任意的{1,2,3,,1}i n ∈-有()0f i ≤. ……………9分（Ⅲ）不成立.例如2()()x x n x f x x x -⎧=⎨⎩为有理数，为无理数. ……………10分证明：当x 为有理数时，1,1x x -+均为有理数，222(1)(1)2()(1)(1)2(112)2f x f x f x x x x n x x x -++-=-++---++-=，当x 为无理数时，1,1x x -+均为无理数，22)1()1()(2)1()1(222=-++-=-++-x x x x f x f x f所以，函数)(x f 对任意的x ∈R ，均有)(2)1()1(x f x f x f ≥++-，即函数)(x f 具有性质P . ……………12分而当],0[n x ∈（2n >）且当x 为无理数时，0)(>x f .所以，在（Ⅱ）的条件下，“对任意[0,]x n ∈均有0)(≤x f ”不成立.……………13分（其他反例仿此给分.如()()0()1x x f x ⎧=⎨⎩为有理数为无理数，()()0()1x x f x ⎧=⎨⎩为整数为非整数，2()()()x x f x x ⎧=⎨⎩为整数为非整数，等.）。

2013年普通高考文科数学试题汇编-立体几何解答题_图文

2013年普通高考文科数学试题汇编-立体几何解答题三、解答题1. (2013年高考辽宁卷 (文如图 , . AB O PA O C O 是圆的直径, 垂直圆所在的平面, 是圆上的点 (I求证 :BC PAC ⊥平面 ;(II设//. Q PA G AOC QG PBC ∆为的中点, 为的重心,求证:平面【答案】(I 由 AB 式圆 O 的直径,得 AC ⊥ BC.由 PA ⊥平面 ABC , BC ⊂平面 ABC ,得 PA ⊥ BC,又PA ∩ AC=A,P A⊂平面 PAC , AC ⊂平面 PAC,所以 BC ⊥平面 PAC.(II 连 OG 并延长交 AC 与 M ,链接 QM , QO.由 G 为∆ AOC 的重心,得 M 为 AC 中点,由 G 为 PA 中点,得 QM//PC.又 O 为 AB 中点,得 OM//BC.因为QM ∩ MO=M,QM⊂平面 QMO.所以 QG//平面 PBC.2. (2013年高考浙江卷 (文如图 , 在在四棱锥 P-ABCD 中 ,PA⊥面 3, ∠ABC=120°,G为线段 PC 上的点 .(Ⅰ证明:BD⊥面 PAC ;(Ⅱ若 G 是 PC 的中点 , 求DG 与 APC 所成的角的正切值 ;(Ⅲ若 G 满足 PC⊥面 BGD, 求 PG GC的值 .【答案】解 :证明 :(Ⅰ由已知得三角形 ABC 是等腰三角形 , 且底角等于 30°,且 6030AB CB AD CD ABD CBD ABD CBD BAC BD DB=⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭且 , 所以 ; 、BD AC ⊥, 又因为 PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭; (Ⅱ设 AC BD O = , 由 (1知 DO PAC ⊥, 连接 GO , 所以 DG 与面 APC 所成的角是 DGO ∠, 由已知及 (1知 :1, 2BO AO CO DO =====,12tan 2OD GO PA DGO GO ==⇒∠===所以 DG 与面 APC 所成的角 (Ⅲ由已知得到 :PC===因为 PC BGD PC GD ⊥∴⊥, 在PDC ∆中 , PD CD PC ====, 设223107 2PG PG x CG x x x PG x GC GC =∴=-∴-=--∴====3. (2013年高考陕西卷 (文如图 , 四棱柱 ABCD -A 1B 1C 1D 1的底面 ABCD 是正方形 , O 为底面中心 , A 1O ⊥平面 ABCD, 1AB AA ==1A(Ⅰ证明 : A 1BD // 平面 CD 1B 1;(Ⅱ求三棱柱 ABD -A 1B 1D 1的体积 .【答案】解: (Ⅰ设 111O D B 线段的中点为 .11111111//D B BD D C B A ABCD D B BD ∴-的对应棱是和 . 的对应线段是棱柱和同理, 111111D C B A ABCD O A AO -为平行四边形四边形且且 11111111//////OCO A OC O A OC O A OC AO O A AO ⇒=⇒∴ 1111111111//, . //B CD BD A O D B C O O BD O A C O O A 面面且⇒==⇒ .(证毕(Ⅱ的高是三棱柱面 ABD D B A O A ABCD O A -∴⊥11111 . 在正方形 AB CD中,AO = 1 . . 111=∆O A OA A RT 中, 在11 2(2121111111=⋅⋅=⋅=-∆-O A S V ABD D B A ABD ABD D B A 的体积三棱柱 . 所以 , 1111111=--ABD D B A V ABD D B A 的体积三棱柱 .4. (2013年高考福建卷 (文如图 , 在四棱锥 P ABCD -中 , PD ABCD ⊥面 , //AB DC , AB AD ⊥, 5BC =, 3DC =, 4AD =, 60PAD ∠= .(1当正视图方向与向量 AD 的方向相同时 , 画出四棱锥 P ABCD -的正视图 .(要求标出尺寸 , 并画出演算过程 ;(2若 M 为 PA 的中点 , 求证 ://DM PBC 面 ;(3求三棱锥 D PBC -的体积 .【答案】解法一:(Ⅰ在梯形 ABCD 中 , 过点 C 作 CE AB ⊥, 垂足为 E , 由已知得 , 四边形 ADCE 为矩形 , 3AE CD ==在Rt BEC ∆中 , 由 5BC =, 4CE =, 依勾股定理得 :3BE =, 从而 6AB =又由 PD ⊥平面 ABCD 得 , PD AD ⊥从而在Rt PDA ∆中 , 由 4AD =, 60PAD ∠=︒,得 PD =正视图如右图所示 :(Ⅱ取 PB 中点 N , 连结 MN , CN在PAB ∆中 , M 是 PA 中点 ,∴ MN AB , 132MN AB ==, 又 CD AB , 3CD = ∴ MN CD , MN CD =∴四边形 MNCD 为平行四边形,∴ DM CN又 DM ⊄平面 PBC , CN ⊂平面 PBC∴ DM 平面 PBC (Ⅲ 13D PBC P DBC DBC V V S PD --∆==⋅又6PBC s ∆= , PD =,所以 D PBC V -=解法二 :(Ⅰ同解法一(Ⅱ取 AB 的中点 E , 连结 ME , DE在梯形 ABCD 中 , BE CD , 且 BE CD =∴四边形 BCDE 为平行四边形∴ DE BC , 又 DE ⊄平面 PBC , BC ⊂平面 PBC∴ DE 平面 PBC , 又在PAB ∆中 , ME PBME ⊄平面 PBC , PB ⊂平面 PBC∴ ME 平面 PBC . 又 DE ME E = ,∴平面 DME 平面 PBC , 又 DM ⊂平面 DME∴ DM 平面 PBC(Ⅲ同解法一5. (2013年高考广东卷(文如图 4, 在边长为 1的等边三角形 ABC 中 , , D E 分别是 , AB AC 边上的点 , AD AE =, F 是 BC 的中点 , AF 与 DE 交于点 G , 将ABF ∆沿AF 折起 , 得到如图 5所示的三棱锥 A BCF -,其中 2BC =. (1 证明 :DE //平面 BCF ;(2 证明 :CF ⊥平面 ABF ;(3 当 23AD =时 , 求三棱锥 F DEG -的体积 F DEG V -. 图 4【答案】 (1在等边三角形 ABC 中 , AD AE =AD AE DB EC ∴=, 在折叠后的三棱锥 A BCF -中也成立 , //DE BC ∴ ,DE ⊄平面 BCF ,BC ⊂平面 BCF , //DE ∴平面 BCF ;(2在等边三角形 ABC 中 , F 是 BC 的中点 , 所以 AF BC ⊥① ,12BF CF==. 在三棱锥 A BCF -中 , 2BC =, 222BC BF CF CF BF ∴=+∴⊥② BF CF F CF ABF ⋂=∴⊥平面 ;(3由 (1可知 //GE CF , 结合 (2可得GE DFG ⊥平面.111111132323323324F DEG E DFG V V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎝⎭6. (2013年高考湖南(文如图 2. 在直菱柱 ABC-A 1B 1C 1中,∠BAC=90°,AB=AC=,AA 1=3,D是 BC 的中点 , 点 E 在菱 BB 1上运动 . (I 证明:AD⊥C 1E;(II当异面直线 AC,C 1E 所成的角为 60°时 , 求三菱子 C 1-A 2B 1E 的体积.【答案】解: (Ⅰ 11C CBB ADE 面为动点,所以需证因为⊥.AD BB ABC AD ABC BB C B A ABC ⊥⇒⊂⊥∴-11111, 面且面是直棱柱AD BC BC D ABC RT ⊥∴∆的中点, 为是等腰直角且又 .. 1111111E C AD C CBB E C C CBB AD B BB BC ⊥⇒⊂⊥⇒=⋂面且面由上两点,且 (证毕(Ⅱ 660, //111111=∆⇒︒=∠∴AE E C A RT E C A A C CA 中, 在 .的高是三棱锥是直棱柱中, 在 1111111111. 2C B A E EB C B A ABC EB E B A RT -∴-=∆⇒ .. 3232213131111111111111的体积为所以三棱锥 E B A C EB S V V C B A C B A E E B A C -⋅=⋅⋅=⋅⋅==∆-- 7. (2013年高考北京卷(文如图 , 在四棱锥 P ABCD -中 , //AB CD , AB AD ⊥, 2CD AB =,平面 PAD ⊥底面 ABCD , PA AD ⊥, E 和 F 分别是 CD 和 PC 的中点 , 求证 : (1PA ⊥底面 ABCD ;(2//BE 平面 PAD ;(3平面 BEF ⊥平面 PCD【答案】 (I因为平面 PAD⊥平面 ABCD, 且 PA 垂直于这个平面的交线 AD 所以 PA 垂直底面 ABCD.(II因为 AB∥CD,CD=2AB,E为 CD 的中点所以 AB∥DE,且 AB=DE 所以ABED 为平行四边形 ,所以 BE∥AD,又因为 BE ⊄平面 PAD,AD ⊂平面 PAD 所以 BE∥平面 PAD.(III因为 AB⊥AD,而且 ABED 为平行四边形所以 BE⊥CD,AD⊥CD,由 (I知 PA⊥底面 ABCD, 所以 PA⊥CD,所以 CD⊥平面 PAD所以 CD⊥PD,因为 E 和 F 分别是 CD 和 PC 的中点所以 PD∥EF,所以 CD⊥EF,所以 CD⊥平面 BEF, 所以平面 BEF⊥平面PCD.8. (2013年高考课标Ⅰ卷 (文如图 , 三棱柱 111ABC A B C -中 , CA CB =, 1AB AA =, 160BAA ∠= .(Ⅰ证明 :1AB AC ⊥; (Ⅱ若 2AB CB ==, 1AC =求三棱柱 111ABC A B C -的体积 .1B 1A1【答案】【答案】 (I取 AB 的中点 O, 连接 OC O 、 1OA O 、 1A B , 因为CA=CB,所以 OC AB ⊥, 由于 AB=AA 1,∠BA A1=600,故, AA B ∆为等边三角形 , 所以 OA 1⊥AB.因为 OC ⨅ OA 1=O,所以 AB ⊥平面 OA 1C. 又 A 1CC 平面 OA 1C, 故 AB ⊥AC. (II由题设知12ABC AA B ∆∆与都是边长为的等边三角形, 12AA B 都是边长为的等边三角形,所以2211111. OC OA AC AC OA OA OC ===+⊥又 ,故111111111, --=3.ABC ABCOC AB O OA ABC OA ABC A B CABC S A B C V S OA=⊥∆=⨯=因为所以平面 , 为棱柱的高,又的面积 ABC 的体积9. (2013年高考山东卷 (文如图 , 四棱锥 P ABCD -中 , , AB AC AB PA⊥⊥, , 2AB CD AB CD=∥ , , , , ,E F G M N 分别为, , , ,PB AB BC PD PC 的中点(Ⅰ求证 :CE PAD∥平面 ; (Ⅱ求证 :EFG EMN⊥平面平面【答案】10. (2013年高考四川卷(文如图 , 在三棱柱11ABC A B C-中 , 侧棱1AA ⊥底面ABC , 122AB AC AA ===, 120BAC ∠= , 1, D D 分别是线段 11, BC B C 的中点 , P 是线段 AD 上异于端点的点 .(Ⅰ在平面 ABC 内 , 试作出过点 P 与平面 1A BC 平行的直线 l , 说明理由 , 并证明直线 l ⊥平面11ADD A ;(Ⅱ设 (Ⅰ中的直线 l 交 AC 于点 Q , 求三棱锥 11A QC D -的体积 .(锥体体积公式 :13V Sh =, 其中 S 为底面面积 , h 为高【答案】解:(Ⅰ如图 , 在平面 ABC 内 , 过点 P 作直线 BC l //, 因为 l 在平面 BC A 1外 , BC 在平面 BC A 1内 ,由直线与平面平行的判定定理可知 , //l 平面 1A BC .由已知 , AC AB =, D 是 BC 中点 , 所以 BC ⊥ AD , 则直线 AD l ⊥, 又因为1AA ⊥底面 ABC , 所以 l AA ⊥1,又因为 AD , 1AA 在平面 11A ADD 内 , 且 AD 与 1AA 相交 , 所以直线⊥l 平面11A ADD(Ⅱ过 D 作 AC DE ⊥于 E , 因为 1AA ⊥平面 ABC , 所以 DE AA ⊥1,又因为 AC , 1AA 在平面 C C AA 11内 , 且 AC 与 1AA 相交 , 所以⊥DE 平面C C AA 11,由 2==AC AB ,∠ BAC ︒=120, 有 1=AD ,∠ DAC ︒=60, 所以在△ ACD 中 , 2 323==AD DE , 又 1211111=⋅=∆AA C A S AQC , 所以 631233*********=⋅⋅=⋅==--QC A QC A D D QC A S DE V V 因此三棱锥 11A QC D -的体积为 6311. (2013年高考湖北卷(文如图 , 某地质队自水平地面 A , B , C 三处垂直向地下钻探 , 自 A 点向下钻到A 1处发现矿藏 , 再继续下钻到 A 2处后下面已无矿 , 从而得到在 A 处正下方的矿层厚度为 121A A d =. 同样可得在 B , C 处正下方的矿层厚度分别为 122B B d =, 123C C d =, 且 123d d d <<. 过AB , AC 的中点 M , N 且与直线 2AA 平行的平面截多面体 111222A B C A B C -所得的截面 DEFG 为该多面体的一个中截面 , 其面积记为 S 中 .(Ⅰ证明 :中截面 DEFG 是梯形 ;(Ⅱ在△ ABC 中 , 记 BC a =, BC 边上的高为 h , 面积为 S . 在估测三角形 ABC 区域内正下方的矿藏储C 11BC B 1量 (即多面体 11122A B C A B C -的体积 V 时 , 可用近似公式 V S h =⋅估中来估算 . 已知1231( 3V d d d S =++, 试判断 V 估与 V 的大小关系 , 并加以证明 .【答案】 (Ⅰ依题意 12A A ⊥平面 ABC , 12B B ⊥平面 ABC , 12C C ⊥平面ABC ,所以 A 1A 2∥ B 1B 2∥ C 1C 2. 又 121A A d =, 122B B d =, 123C C d =, 且 123d d d << . 因此四边形 1221A A B B 、 1221A A C C 均是梯形 .由 2AA ∥平面 MEFN , 2AA ⊂平面 22AA B B , 且平面 22AA B B 平面 MEFN ME =, 可得 AA 2∥ ME , 即 A 1A 2∥ DE . 同理可证 A 1A 2∥ FG , 所以 DE ∥ FG . 又 M 、 N 分别为 AB 、 AC 的中点 ,则 D 、 E 、 F 、 G 分别为 11A B 、 22A B 、 22A C 、 11A C 的中点 , 即DE 、 FG 分别为梯形 1221A A B B 、 1221A A C C 的中位线 .因此 12121211( ( 22DE A A B B d d =+=+, 12121311( ( 22FG A A C C d d =+=+,而 123d d d <<, 故 DE FG <, 所以中截面 DEFG 是梯形 . (Ⅱ V V <估 . 证明如下 :由 12A A ⊥平面 ABC , MN ⊂平面 ABC , 可得 12A A MN ⊥.而 EM ∥ A 1A 2, 所以 EM MN ⊥, 同理可得 FN MN ⊥.由 MN 是△ ABC 的中位线 , 可得 1122MN BC a ==即为梯形 DEFG 的高 ,因此 13121231( (2 22228DEFG d d d d a aS S d d d ++==+⋅=++中梯形 ,即 123(2 8ahV S h d d d =⋅=++估中 . 又 12S ah =, 所以 1231231( ( 36ahV d d d S d d d =++=++. 第 20题图于是 1231232131( (2 [( (]6824ah ah ahV V d d d d d d d d d d -=++-++=-+-估 . 由 123d d d <<, 得 210d d ->, 310d d ->, 故 V V <估 .12. (2013年高考课标Ⅱ卷(文如图,直三棱柱 111ABC A B C -中, D , E 分别是AB , 1BB 的中点, 。

北京市高考数学一模试题解析分类汇编系列五 7 立体几何文

【解析分类汇编系列五：北京2013高三（一模）文数】7：立体几何1 ．（2013届房山区一模文科数学）某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的是（）A ．B ．8C ．D ．C由三视图可知该几何体是个底面是正三角形，棱AD 垂直底的三棱锥。

其中4,4,3A D B D E C ===,取BC的中点F，则223)27A ==ABC ∆的面积为142⨯⨯，选C.2．（2013届北京市延庆县一模数学文）一四面体的三视图如图所示,则该四面体四个面中最大的面积是（）A ．2B ．22C ．3D ．32D将该几何体放入边长为2的正方体中，由三视图可知该四面体为11D BD C -,由直观图可知，最大的面为1BDC .在等边三角形1BDC 中，BD =,所以面积2122S =⨯⨯=，选 D.3．（2013届北京市石景山区一模数学文）某四棱锥的三视图如图所示，则最长的一条侧棱长度是（）（7题图）A B．．5 DD由三视图可知：该几何体是一个四棱锥，如图所示，侧棱PD⊥底面ABCD，PD=2，底面ABCD是一个直角梯形，AD∥BC，AD⊥DC，AD=2，DC=3，BC=4，BD=5．所以则最长的一条侧棱PB= D.4．（2013届北京东城区一模数学文科）已知一个几何体的三视图如图所示(单位:cm), 那么这个几何体的侧．面积是（）2A．2B．(4D．2C．2C由三视图可知，该几何体是一个平放的四棱柱，四棱柱的底面是直角梯形。

所以几何体的侧面积为(1+2)12111=42⨯⨯+⨯2cm ，选C. 5．（2013届北京市朝阳区一模数学文）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为A. 4B.C. 203D. 8 D由三视图可知，该几何体的为，其中长方体底面为正方形，正方形的边长为2.其中3,1HD BF ==,将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体体积为122482⨯⨯⨯=。

【备考2014】2013高考数学-(真题+模拟新题分类汇编)-立体几何-文

立体几何G1 空间几何体的结构8．G1，G6[2013·北京卷] 如图1－2，在正方体ABCD －A 1B 1C 1D 1中，P 为对角线BD 1的三等分点，P 到各顶点的距离的不同取值有( )1－2A ．3个B ．4个C ．5个D ．6个8．B [解析] 设棱长为1，∵BD 1＝3，∴BP＝33，D 1P ＝2 33.联结AD 1，B 1D 1，CD 1，得△ABD 1≌△CBD 1≌△B 1BD 1，∴∠ABD 1＝∠CBD 1＝∠B 1BD 1，且cos ∠ABD 1＝33，联结AP ，PC ，PB 1，则有△ABP≌△CBP≌△B 1BP ， ∴AP ＝CP ＝B 1P ＝63，同理DP ＝A 1P ＝C 1P ＝1， ∴P 到各顶点的距离的不同取值有4个．18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC 中，D ，E 分别是AB ，AC 上的点，F 是BC 的中点，AF 与DE 交于点G ，将△ABF 沿AF 折起，得到如图1－4(2)所示的三棱锥A －BCF ，其中BC ＝22.图1－4(1)证明：DE∥平面BCF ； (2)证明：CF⊥平面ABF ；(3)当AD ＝23时，求三棱锥F －DEG 的体积．18．解：G2 空间几何体的三视图和直观图10．G2，G7[2013·北京卷] 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．图1－310．3 [解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V ＝13×(3×3)×1＝3.18．G2，G4[2013·福建卷] 如图1－3，在四棱锥P －ABCD 中，PD⊥平面ABCD ，AB∥DC，AB⊥AD，BC ＝5，DC ＝3，AD ＝4，∠PAD＝60°.(1)当正视方向与向量AD →的方向相同时，画出四棱锥P －ABCD 的正视图(要求标出尺寸，并写出演算过程)；(2)若M 为PA 的中点，求证：DM∥平面PBC ； (3)求三棱锥D －PBC 的体积．图1－318．解：(1)在梯形ABCD 中，过点C 作CE⊥AB，垂足为E. 由已知得，四边形ADCE 为矩形，AE ＝CD ＝3，在Rt △BEC 中，由BC ＝5，CE ＝4，依勾股定理得BE ＝3，从而AB ＝6. 又由PD⊥平面ABCD 得，PD⊥AD.从而在Rt △PDA 中，由AD ＝4，∠PAD＝60°，得PD ＝4 3. 正视图如图所示．(2)方法一：取PB 中点N ，联结MN ，CN.在△PAB 中，∵M 是PA 中点，∴MN∥AB，MN ＝12AB ＝3.又CD∥AB，CD ＝3，∴MN∥CD，MN ＝CD ， ∴四边形MNCD 为平行四边形，∴DM∥CN. 又DM 平面PBC ，CN 平面PBC ， ∴DM ∥平面PBC.方法二：取AB 的中点E ，联结ME ，DE. 在梯形ABCD 中，BE∥CD，且BE ＝CD ， ∴四边形BCDE 为平行四边形，∴DE ∥BC.又DE 平面PBC ，BC 平面PBC ， ∴DE ∥平面PBC.又在△PAB 中，ME∥PB，ME 平面PBC ，PB 平面PBC ，∴ME∥平面PBC. 又DE∩ME＝E ，∴平面DME∥平面PBC. 又DM 平面DME ，∴DM∥平面PBC.(3)V D －PBC ＝V P －DBC ＝13S △DBC ·PD ，又S △DBC ＝6，PD ＝4 3，所以V D －PBC ＝8 3.6．G2[2013·广东卷] 某三棱锥的三视图如图1－2所示，则该三棱锥的体积是( )图1－2A.16B.13C.23D ．1 6．B [解析] 由三视图得三棱锥的高是2，底面是一个腰为1的等腰直角三角形，故体积是13×12×1×1×2＝13，选B. 5．G2[2013·广东卷] 执行如图1－1所示的程序框图，若输入n 的值为3，则输出s 的值是( )图1－1A ．1B ．2C ．4D ．7 5．C [解析] 1≤3，s ＝1＋0＝1，i ＝2；2≤3，s ＝1＋1＝2，i ＝3；s ＝2＋2＝4，i ＝4；4>3，故输出s ＝4，选C.7．G2[2013·湖南卷] 已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于( )A.32B ．1 C.2＋12D. 2 7．D [解析] 由题可知，其俯视图恰好是正方形，而侧视图和正视图则应该都是正方体的对角面，故面积为2，选D.8．G2[2013·江西卷] 一几何体的三视图如图1－2所示，则该几何体的体积为( )图1－2A ．200＋9πB ．200＋18πC ．140＋9πD ．140＋18π8．A [解析] 该几何体上面是半圆柱，下面是长方体，半圆柱体积为12π·32·2＝9π，长方体体积为10×5×4＝200.故选A.13．G2[2013·辽宁卷] 某几何体的三视图如图1－3所示，则该几何体的体积是________．图1－313．16π－16 [解析] 由三视图可知该几何体是一个圆柱里面挖去了一个长方体，所以该几何体的体积为V ＝4π×4－16＝16π－16.9．G2[2013·新课标全国卷Ⅱ] 一个四面体的顶点在空间直角坐标系O －xyz 中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，0，0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为( )图1－39．A [解析] 在空间直角坐标系O －xyz 中画出三棱锥，由已知可知三棱锥O －ABC 为题中所描叙的四面体，而其在zOx 平面上的投影为正方形EBDO ，故选A.图1－44．G2[2013·山东卷] 一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图1－1所示，则该四棱锥侧面积和体积分别是( )图1－1A ．4 5，8B ．4 5，83C ．4(5＋1)，83D ．8，84．B [解析] 由正视图知该几何体的高为2，底面边长为2，斜高为22＋1＝5，∴侧面积＝4×12×2×5＝4 5，体积为13×2×2×2＝83.12．G2[2013·陕西卷] 某几何体的三视图如图1－2所示，则其表．面积为________．图1－212．3π [解析] 由三视图得该几何体为半径为1的半个球，则表面积为半球面＋底面圆，代入数据计算为S ＝12×4π×12＋π×12＝3π.11．G2[2013·新课标全国卷Ⅰ] 某几何体的三视图如图1－3所示，则该几何体的体积为( )图1－3A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π11．A [解析] 该空间几何体的下半部分是一个底面半径为2，母线长为4的半圆柱，上半部分是一个底面边长为2、高为4的正四棱柱．这个空间几何体的体积是12×π×4×4＋2×2×4＝16＋8π.5．G2[2013·浙江卷] 已知某几何体的三视图(单位： cm)如图1－1所示，则该几何体的体积是( )图1－1A ．108 cm 3B ．100 cm 3C ．92 cm 3D ．84 cm 35．B [解析] 此直观图是由一个长方体挖去一个三棱锥而得，如图所示其体积为3×6×6－13×12×3×4×4＝108－8＝100(cm 3)．所以选择B.BC ＝CD ＝2，∠ACB＝∠ACD＝π3.(1)求证：BD⊥平面PAC ；(2)若侧棱PC 上的点F 满足PF ＝7FC ，求三棱锥P －BDF 的体积．图1－419．解：(1)证明：因为BC ＝CD ，即△BCD 为等腰三角形，又∠ACB＝∠ACD，故BD⊥AC.因为PA⊥底面ABCD ，所以PA⊥BD，从而BD 与平面PAC 内两条相交直线PA ，AC 都垂直，所以BD⊥平面PAC.(2)三棱锥P －BCD 的底面BCD 的面积S △BCD ＝12BC ·CD ·sin ∠BCD ＝12·2·2·sin 2π3＝ 3.由PA⊥底面ABCD ，得V P －BCD ＝13·S △BCD ·PA ＝13×3×2 3＝2.由PF ＝7FC ，得三棱锥F －BCD 的高为18PA ，故V F －BCD ＝13·S △BCD ·18PA ＝13×3×18×2 3＝14，所以V P －BDF ＝V P －BCD －V F －BCD ＝2－14＝74.8．G2和G7[2013·重庆卷] 某几何体的三视图如图1－3所示，则该几何体的表面积为( )图1－3A ．180B ．200C ．220D ．2408．D [解析] 该几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，其腰为5的等腰梯形，所以底面面积和为12(2＋8)×4×2＝40.四个侧面的面积和为(2＋8＋5×2)×10＝200，所以该直四棱柱的表面积为S ＝40＋200＝240，故选D.G3 平面的基本性质、空间两条直线G4 空间中的平行关系17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P －ABCD 中，AB∥CD，AB⊥AD，CD ＝2AB ，平面PAD⊥底面ABCD ，PA⊥AD，E 和F 分别是CD 和PC 的中点．求证：(1)PA ⊥底面ABCD ； (2)BE∥平面PAD ；(3)平面BEF⊥平面PCD.图1－517．证明：(1)因为平面PAD⊥底面ABCD ，且PA 垂直于这两个平面的交线AD ，所以PA⊥底面ABCD.(2)因为AB∥CD，CD ＝2AB ，E 为CD 的中点，所以AB∥DE，且AB ＝DE ，所以ABED 为平行四边形，所以BE∥AD.又因为BE 平面PAD ，AD 平面PAD ，所以BE∥平面PAD.(3)因为AB⊥AD，而且ABED 为平行四边形，所以BE ⊥CD，AD⊥CD. 由(1)知PA⊥底面ABCD ，所以PA⊥CD.又因为AD∩PA＝A ，所以CD⊥平面PAD ，所以CD⊥PD.因为E 和F 分别是CD 和PC 的中点，所以PD∥EF，所以CD⊥EF，所以CD⊥平面BEF ，所以平面BEF⊥平面PCD. 18．G2，G4[2013·福建卷] 如图1－3，在四棱锥P －ABCD 中，PD⊥平面ABCD ，AB∥DC，AB⊥AD，BC ＝5，DC ＝3，AD ＝4，∠PAD＝60°.(1)当正视方向与向量AD →的方向相同时，画出四棱锥P －ABCD 的正视图(要求标出尺寸，并写出演算过程)；(2)若M 为PA 的中点，求证：DM∥平面PBC ； (3)求三棱锥D －PBC 的体积．图1－318．解：(1)在梯形ABCD 中，过点C 作CE⊥AB，垂足为E. 由已知得，四边形ADCE 为矩形，AE ＝CD ＝3，在Rt △BEC 中，由BC ＝5，CE ＝4，依勾股定理得BE ＝3，从而AB ＝6. 又由PD⊥平面ABCD 得，PD⊥AD.从而在Rt △PDA 中，由AD ＝4，∠PAD＝60°，得PD ＝4 3. 正视图如图所示．(2)方法一：取PB 中点N ，联结MN ，CN.在△PAB 中，∵M 是PA 中点，∴MN∥AB，MN ＝12AB ＝3.又CD∥AB，CD ＝3，∴MN∥CD，MN ＝CD ， ∴四边形MNCD 为平行四边形，∴DM∥CN. 又DM 平面PBC ，CN 平面PBC ， ∴DM ∥平面PBC.方法二：取AB 的中点E ，联结ME ，DE. 在梯形ABCD 中，BE∥CD，且BE ＝CD ， ∴四边形BCDE 为平行四边形，∴DE ∥BC.又DE 平面PBC ，BC 平面PBC ， ∴DE ∥平面PBC.又在△PAB 中，ME∥PB，ME 平面PBC ，PB 平面PBC ，∴ME∥平面PBC. 又DE∩ME＝E ，∴平面DME∥平面PBC. 又DM 平面DME ，∴DM∥平面PBC.(3)V D －PBC ＝V P －DBC ＝13S △DBC ·PD ，又S △DBC ＝6，PD ＝4 3，所以V D －PBC ＝8 3.18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC 中，D ，E 分别是AB ，AC 上的点，F 是BC 的中点，AF 与DE 交于点G ，将△ABF 沿AF 折起，得到如图1－4(2)所示的三棱锥A －BCF ，其中BC ＝22.图1－4(1)证明：DE∥平面BCF ； (2)证明：CF⊥平面ABF ；(3)当AD ＝23时，求三棱锥F －DEG 的体积．18．解： 8．G4、G5[2013·广东卷] 设l 为直线，α，β是两个不同的平面，下列命题中正确的是( ) A ．若l∥α，l∥β，则α∥β B ．若l⊥α，l⊥β，则α∥β C ．若l⊥α，l∥β，则α∥β D ．若α⊥β，l∥α，则l⊥β8．B [解析] 根据空间平行、垂直关系的判定和性质，易知选B.16．G4，G5[2013·江苏卷] 如图1－2，在三棱锥S －ABC 中，平面SAB⊥平面SBC ，AB⊥BC，AS ＝AB.过A 作AF⊥SB，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．求证：(1)平面EFG∥平面ABC ； (2)BC⊥SA.图1－216．证明：(1)因为AS＝AB，AF⊥SB，垂足为F，所以F是SB的中点．又因为E是SA的中点，所以EF∥AB.因为EF平面ABC，AB平面ABC，所以EF∥平面ABC.同理EG∥平面ABC.又EF∩EG＝E，所以平面EFG∥平面ABC.(2)因为平面SAB⊥平面SBC，且交线为SB，又AF平面SAB，AF⊥SB，所以AF⊥平面SBC.因为BC平面SBC，所以AF⊥BC.又因为AB⊥BC，AF∩AB＝A，AF，AB平面SAB，所以BC⊥平面SAB.因为SA平面SAB，所以BC⊥SA.15．G4[2013·江西卷] 如图1－5所示，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数为________．图1－515．4 [解析] 直线EF与正方体左右两个面平行，与其他四个面相交．图1－418．G4，G5[2013·辽宁卷] 如图1－4，AB是圆O的直径，PA垂直圆O所在的平面，C是圆O 上的点．(1)求证：BC⊥平面PAC；(2)设Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC.18．证明：(1)由AB是圆O的直径，得AC⊥BC.由PA⊥平面ABC，BC平面ABC，得PA⊥BC.又PA∩AC＝A，PA平面PAC，AC平面PAC，所以BC⊥平面PAC.(2)联结OG 并延长交AC 于M ，联结QM ，QO ，由G 为△AOC 的重心，得M 为AC 中点，由Q 为PA 中点，得QM∥PC. 又O 为AB 中点，得OM∥BC. 因为QM∩MO＝M ，QM 平面QMO. MO 平面QMO ，BC ∩PC ＝C ，BC 平面PBC ，PC 平面PBC ，所以平面QMO∥平面PBC. 因为QG 平面QMO ，所以QG∥平面PBC.18．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．(1)证明：BC 1∥平面A 1CD ；(2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积．图1－718．解：(1)证明：联结AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，联结DF ，则BC 1∥DF.因为DF 平面A 1CD ，BC 1平面A 1CD ，所以BC 1∥平面A 1CD.图1－8(2)因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD.由已知AC ＝CB ，D 为AB 的中点，所以CD⊥AB.又AA 1∩AB ＝A ，于是CD⊥平面ABB 1A 1.由AA 1＝AC ＝CB ＝2，AB ＝2 2得∠ACB＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，故A 1D 2＋DE 2＝A 1E 2，即DE⊥A 1D.所以VC －A 1DE ＝13×12×6×3×2＝1.19．G4，G5[2013·山东卷] 如图1－5，四棱锥P —ABCD 中，AB⊥AC，AB⊥PA，AB∥CD，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．(1)求证：CE∥平面PAD ；(2)求证：平面EFG⊥平面EMN.图1－619．证明：(1)证法一：取PA 的中点H ，联结EH ，DH. 因为E 为PB 的中点，所以EH∥AB，EH ＝12AB.又A B∥CD，CD ＝12AB ，所以EH∥CD，EH ＝CD.因此四边形DCEH 是平行四边形．所以CE∥DH.又DH 平面PAD ，CE 平面PAD ，因此CE∥平面PAD.证法二：联结CF. 因为F 为AB 的中点，所以AF ＝12AB.又CD ＝12AB ，所以AF ＝CD. 又AF∥CD，所以四边形AFCD 为平行四边形．因此CF∥AD.又CF 平面PAD ，所以CF∥平面PAD.因为E ，F 分别为PB ，AB 的中点，所以EF∥PA.又EF 平面PAD ，所以EF∥平面PAD.因为CF∩EF＝F，故平面CEF∥平面PAD.又CE平面CEF，所以CE∥平面PAD.(2)因为E，F分别为PB，AB的中点，所以EF∥PA.又AB⊥PA，所以AB⊥EF.同理可证AB⊥FG.又EF∩FG＝F，EF平面EFG，FG平面EFG，因此AB⊥平面EFG.又M，N分别为PD，PC的中点，所以MN∥CD.又AB∥CD，所以MN∥AB，因此MN⊥平面EFG.又MN平面EMN，所以平面EFG⊥平面EMN.18．G4，G11[2013·陕西卷] 如图1－5，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O是底面中心，A1O⊥底面ABCD，AB＝AA1＝ 2.图1－5(1)证明：平面A1BD∥平面CD1B1；(2)求三棱柱ABD－A1B1D1的体积．18．解：(1)证明：由题设知，BB1瘙綊 DD1，∴四边形BB1D1D是平行四边形，∴BD∥B1D1.又BD平面CD1B1，∴BD∥平面CD1B1.∵A1D1瘙綊 B1C1瘙綊 BC ，∴四边形A 1BCD 1是平行四边形， ∴A 1B ∥D 1C.又A 1B 平面CD 1B 1， ∴A 1B ∥平面CD 1B 1. 又∵BD∩A 1B ＝B ，∴平面A 1BD ∥平面CD 1B 1. (2)∵A 1O ⊥平面ABCD ，∴A 1O 是三棱柱ABD －A 1B 1D 1的高．又∵AO＝12AC ＝1，AA 1＝2，∴A 1O ＝AA 21－OA 2＝1，又∵S △ABD ＝12×2×2＝1，∴VABD －A 1B 1D 1＝S △ABD ·A 1O ＝1.19．G4，G5，G7，G11[2013·四川卷]图1－8如图1－8，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ＝AC ＝2AA 1＝2，∠BAC＝120°，D ，D 1分别是线段BC ，B 1C 1的中点，P 是线段AD 上异于端点的点．(1)在平面ABC 内，试作出过点P 与平面A 1BC 平行的直线l ，说明理由，并证明直线l⊥平面ADD 1A 1；(2)设(1)中的直线l 交AC 于点Q ，求三棱锥A 1－QC 1D 的体积．(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高)19．解：(1)如图，在平面ABC 内，过点P 作直线l∥BC，因为l 在平面A 1BC 外，BC 在平面A 1BC 内，由直线与平面平行的判定定理可知，l∥平面A 1BC.由已知，AB ＝AC ，D 是BC 的中点，所以，BC⊥AD，则直线l⊥AD.因此AA 1⊥平面ABC ，所以AA 1⊥直线l.又因为AD ，AA 1在平面ADD 1A 1内，且AD 与AA 1相交，所以直线l⊥平面ADD 1A 1. (2)过D 作DE⊥AC 于E.因为AA 1⊥平面ABC ，所以DE⊥AA 1.又因为AC ，AA 1在平面AA 1C 1C 内，且AC 与AA 1相交，所以DE⊥平面AA 1C 1C.由AB ＝AC ＝2，∠BAC＝120°，有AD ＝1，∠DAC＝60°，所以在△ACD 中，DE ＝32AD ＝32.又S △A 1QC 1＝12A 1C 1·AA 1＝1，所以VA 1－QC 1D ＝VD －A 1QC 1＝13DE ·S △A 1QC 1＝13×32×1＝36.因此三棱锥A 1－QC 1D 的体积是36. 17．G4，G5、G11[2013·天津卷] 如图1－3所示，三棱柱ABC －A 1B 1C 1中，侧棱A 1A ⊥底面ABC ，且各棱长均相等，D ，E ，F 分别为棱AB ，BC ，A 1C 1的中点．(1)证明EF∥平面A 1CD ；(2)证明平面A 1CD ⊥平面A 1ABB 1；(3)求直线BC 与平面A 1CD 所成角的正弦值．图1－317．解：(1)证明：如图，在三棱柱ABC －A 1B 1C 1中，AC∥A 1C 1，且AC ＝A 1C 1，联结ED ，在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ＝12AC 且DE∥AC，又因为F 为A 1C 1的中点，可得A 1F＝DE ，且A 1F ∥DE ，即四边形A 1DEF 为平行四边形，所以EF∥DA 1.又EF 平面A 1CD ，DA 1平面A 1CD ，所以，EF∥平面A 1CD.(2)证明：由于底面ABC 是正三角形，D 为AB 的中点，故CD⊥AB，又由于侧棱AA 1⊥底面ABC ，CD 平面ABC ，所以A 1A ⊥CD ，又A 1A ∩AB ＝A ，因此CD⊥平面A 1ABB 1，而CD 平面A 1CD ，所以平面A 1CD ⊥平面A 1ABB 1.(3)在平面A 1ABB 1内，过点B 作BG⊥A 1D 交直线A 1D 于点G ，联结CG ，由于平面A 1CD ⊥平面A 1ABB 1，而直线A 1D 是平面A 1CD 与平面A 1ABB 1的交线，故BG⊥平面A 1CD ，由此得∠BCG 为直线BC 与平面A 1CD 所成的角．设三棱柱各棱长为a ，可得A 1D ＝5a 2，由△A 1AD ∽△BGD ，易得BG ＝5a 5.在Rt △BGC 中，sin ∠BCG ＝BG BC ＝55.所以直线BC 与平面A 1CD 所成角的正弦值为55. 4．G4，G5[2013·浙江卷] 设m ，n 是两条不同的直线，α，β是两个不同的平面( )A ．若m∥α，n∥α，则m∥nB ．若m∥α，m∥β，则α∥βC ．若m∥n，m⊥α，则n⊥αD ．若m∥α，α⊥β，则m⊥β4．C [解析] 对于选项C ，若m∥n，m⊥α，易得n⊥α.所以选择C.G5 空间中的垂直关系图1－518．G5[2013·安徽卷] 如图1－5，四棱锥P －ABCD 的底面ABCD 是边长为2的菱形，∠BAD＝60°，已知PB ＝PD ＝2，PA ＝ 6.(1)证明：PC⊥BD；(2)若E 为PA 的中点，求三棱锥P －BCE 的体积． 18．解：(1)证明：联结AC ，交BD 于O 点，联结PO. 因为底面ABCD 是菱形，所以AC⊥BD，BO ＝DO.由PB ＝PD 知，PO⊥BD.再由PO∩AC＝O 知，BD⊥面APC ，又PC 平面APC ，因此BD⊥PC.(2)因为E 是PA 的中点，所以V P －BCE ＝V C －PEB ＝12V C －PAB ＝12V B －APC . 由PB ＝PD ＝AB ＝AD ＝2知，△ABD≌△PBD. 因为∠BAD＝60°，所以PO ＝AO ＝3，AC ＝23，BO ＝1.又PA ＝6，故PO 2＋AO 2＝PA 2，即PO⊥AC.故S △APC ＝12PO ·AC ＝3.由(1)知，BO⊥面APC ，因此V P －BCE ＝12V B －APC ＝13·12·S △APC ·BO ＝12.17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P －ABCD 中，AB∥CD，AB⊥AD，CD ＝2AB ，平面PAD⊥底面ABCD ，PA⊥AD，E 和F 分别是CD 和PC 的中点．求证：(1)PA⊥底面ABCD ； (2)BE∥平面PAD ；(3)平面BEF⊥平面PCD.图1－517．证明：(1)因为平面PAD⊥底面ABCD ，且PA 垂直于这两个平面的交线AD ，所以PA⊥底面ABCD.(2)因为AB∥CD，CD ＝2AB ，E 为CD 的中点，所以AB∥DE，且AB ＝DE ，所以ABED 为平行四边形，所以BE∥AD.又因为BE 平面PAD ，AD 平面PAD ，所以BE∥平面PAD.(3)因为AB⊥AD，而且ABED 为平行四边形，所以BE⊥CD，AD⊥CD. 由(1)知PA⊥底面ABCD ，所以PA⊥CD.又因为AD∩PA＝A ，所以CD⊥平面PAD ，所以CD⊥PD.因为E 和F 分别是CD 和PC 的中点，所以PD∥EF，所以CD⊥EF，所以CD⊥平面BEF ，所以平面BEF⊥平面PCD.19．G5、G11[2013·全国卷] 如图1－3所示，四棱锥P —ABCD 中，∠ABC＝∠BAD＝90°，BC ＝2AD ，△PAB 和△PAD 都是边长为2的等边三角形．图1－3(1)证明：PB⊥CD；(2)求点A 到平面PCD 的距离．19．解：(1)证明：取BC 的中点E ，联结DE ，则四边形ABED 为正方形．过P 作PO⊥平面ABCD ，垂足为O.联结OA ，OB ，OD ，OE.由△PAB 和△PAD 都是等边三角形知PA ＝PB ＝PD ，所以OA ＝OB ＝OD ，即点O 为正方形ABED 对角线的交点．故OE⊥BD，从而PB⊥OE.因为O 是BD 的中点，E 是BC 的中点，所以OE∥CD.因此PB⊥CD.(2)取PD 的中点F ，联结OF ，则OF∥PB. 由(1)知，PB⊥CD，故OF⊥CD.又OD ＝12BD ＝2，OP ＝PD 2－OD 2＝2，故△POD 为等腰三角形，因此OF⊥PD. 又PD∩CD＝D ，所以OF⊥平面PCD.因为AE∥CD，CD 平面PCD ，AE 平面PCD ，所以AE∥平面PCD. 因此O 到平面PCD 的距离OF 就是A 到平面PCD 的距离，而OF ＝12PB ＝1，所以点A 到平面PCD 的距离为1.18．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC 中，D ，E 分别是AB ，AC 上的点，F 是BC 的中点，AF 与DE 交于点G ，将△ABF 沿AF 折起，得到如图1－4(2)所示的三棱锥A －BCF ，其中BC ＝22.图1－4(1)证明：DE∥平面BCF ； (2)证明：CF⊥平面ABF ；(3)当AD ＝23时，求三棱锥F －DEG 的体积．18．解： 8．G4、G5[2013·广东卷] 设l 为直线，α，β是两个不同的平面，下列命题中正确的是( ) A ．若l∥α，l∥β，则α∥β B ．若l⊥α，l⊥β，则α∥β C ．若l⊥α，l∥β，则α∥β D ．若α⊥β，l∥α，则l⊥β8．B [解析] 根据空间平行、垂直关系的判定和性质，易知选B.16．G4，G5[2013·江苏卷] 如图1－2，在三棱锥S －ABC 中，平面SAB⊥平面SBC ，AB⊥BC，AS ＝AB.过A 作AF⊥SB，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．求证：(1)平面EFG∥平面ABC ； (2)BC⊥SA.图1－216．证明：(1)因为AS ＝AB ，AF⊥SB，垂足为F ，所以F 是SB 的中点．又因为E 是SA 的中点，所以EF∥AB.因为EF 平面ABC ，AB 平面ABC ，所以EF∥平面ABC.同理EG∥平面ABC.又EF∩EG＝E ，所以平面EFG∥平面ABC.(2)因为平面SAB⊥平面SBC ，且交线为SB ，又AF 平面SAB ，AF⊥SB，所以AF⊥平面SBC.因为BC 平面SBC ，所以AF⊥BC.又因为AB⊥BC ，AF∩AB＝A ，AF ，AB 平面SAB ，所以BC⊥平面SAB. 因为SA 平面SAB ，所以BC⊥SA.19．G5，G7[2013·江西卷] 如图1－7所示，直四棱柱ABCD －A 1B 1C 1D 1中，AB∥CD，AD ⊥AB ，AB ＝2，AD ＝2，AA 1＝3，E 为CD 上一点，DE ＝1，EC ＝3.(1)证明：BE⊥平面BB 1C 1C ； (2)求点B 1到平面EA 1C 1的距离．图1－719．解：(1)证明：过B 作CD 的垂线交CD 于F ，则BF ＝AD ＝2，EF ＝AB －DE ＝1，FC ＝2.在Rt △BEF 中，BE ＝ 3. 在Rt △CFB 中，BC ＝ 6.在△BEC 中，因为BE 2＋BC 2＝9＝EC 2，故BE⊥BC. 由BB 1⊥平面ABCD 得BE⊥BB 1. 所以BE⊥平面BB 1C 1C.(2)三棱锥E －A 1B 1C 1的体积V ＝13·AA 1·S △A 1B 1C 1＝ 2.在Rt △A 1D 1C 1中，A 1C 1＝A 1D 21＋D 1C 21＝3 2.同理，EC 1＝EC 2＋CC 21＝3 2，A 1E ＝A 1A 2＋AD 2＋DE 2＝2 3. 故S △A 1C 1E ＝3 5.设点B 1到平面EA 1C 1的距离为d ，则三棱锥B 1－A 1C 1E 的体积 V ＝13·d ·S △A 1C 1E ＝5d ，从而5d ＝2，d ＝105. 图1－418．G4，G5[2013·辽宁卷] 如图1－4，AB 是圆O 的直径，PA 垂直圆O 所在的平面，C 是圆O 上的点．(1)求证：BC⊥平面PAC ；(2)设Q 为PA 的中点，G 为△AOC 的重心，求证：QG ∥平面PBC. 18．证明：(1)由AB 是圆O 的直径，得AC⊥BC. 由PA⊥平面ABC ，BC 平面ABC ，得PA⊥BC. 又PA∩AC＝A ，PA 平面PAC ，AC 平面PAC ，所以BC⊥平面PAC.(2)联结OG 并延长交AC 于M ，联结QM ，QO ，由G 为△AOC 的重心，得M 为AC 中点，由Q 为PA 中点，得QM∥PC. 又O 为AB 中点，得OM∥BC. 因为QM∩MO＝M ，QM 平面QMO. MO 平面QMO ，BC ∩PC ＝C ，BC 平面PBC ，PC 平面PBC ，所以平面QMO∥平面PBC. 因为QG 平面QMO ，所以QG∥平面PBC.19．G4，G5[2013·山东卷] 如图1－5，四棱锥P —ABCD 中，AB⊥AC ，AB⊥PA，AB∥CD，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．(1)求证：CE∥平面PAD ；(2)求证：平面EFG⊥平面EMN.图1－619．证明：(1)证法一：取PA 的中点H ，联结EH ，DH. 因为E 为PB 的中点，所以EH∥AB，EH ＝12AB.又AB∥CD，CD ＝12AB ，所以EH∥CD，EH ＝CD.因此四边形DCEH 是平行四边形．所以CE∥DH.又DH 平面PAD ，CE 平面PAD ，因此CE∥平面PAD.证法二：联结CF. 因为F 为AB 的中点，所以AF ＝12AB.又CD ＝12AB ，所以AF ＝CD. 又AF∥CD，所以四边形AFCD 为平行四边形．因此CF∥AD.又CF 平面PAD ，所以CF∥平面PAD.因为E ，F 分别为PB ，AB 的中点，所以EF∥PA.又EF 平面PAD ，所以EF∥平面PAD. 因为CF∩EF＝F ，故平面CEF∥平面PAD. 又CE 平面CEF ，所以CE∥平面PAD.(2)因为E ，F 分别为PB ，AB 的中点，所以EF∥PA. 又AB⊥PA，所以AB⊥EF. 同理可证AB⊥FG.又EF∩FG＝F ，EF 平面EFG ，FG 平面EFG ，因此AB⊥平面EFG.又M ，N 分别为PD ，PC 的中点，所以MN∥CD. 又AB∥CD，所以MN∥AB，因此MN⊥平面EFG. 又MN 平面EMN ，所以平面EFG⊥平面EMN.19．G4，G5，G7，G11[2013·四川卷]图1－8如图1－8，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ＝AC ＝2AA 1＝2，∠BAC＝120°，D ，D 1分别是线段BC ，B 1C 1的中点，P 是线段AD 上异于端点的点．(1)在平面ABC 内，试作出过点P 与平面A 1BC 平行的直线l ，说明理由，并证明直线l⊥平面ADD 1A 1；(2)设(1)中的直线l 交AC 于点Q ，求三棱锥A 1－QC 1D 的体积．(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高)19．解：(1)如图，在平面ABC 内，过点P 作直线l∥BC，因为l 在平面A 1BC 外，BC 在平面A 1BC 内，由直线与平面平行的判定定理可知，l∥平面A 1BC.由已知，AB ＝AC ，D 是BC 的中点，所以，BC⊥AD，则直线l⊥AD.因此AA 1⊥平面ABC ，所以AA 1⊥直线l.又因为AD ，AA 1在平面ADD 1A 1内，且AD 与AA 1相交，所以直线l⊥平面ADD 1A 1. (2)过D 作DE⊥AC 于E.因为AA 1⊥平面ABC ，所以DE⊥AA 1.又因为AC ，AA 1在平面AA 1C 1C 内，且AC 与AA 1相交，所以DE⊥平面AA 1C 1C.由AB ＝AC ＝2，∠BAC＝120°，有AD ＝1，∠DAC＝60°，所以在△ACD 中，DE ＝32AD ＝32. 又S △A 1QC 1＝12A 1C 1·AA 1＝1，所以VA 1－QC 1D ＝VD －A 1QC 1＝13DE ·S △A 1QC 1＝13×32×1＝36.因此三棱锥A 1－QC 1D 的体积是36. 17．G4，G5、G11[2013·天津卷] 如图1－3所示，三棱柱ABC －A 1B 1C 1中，侧棱A 1A ⊥底面ABC ，且各棱长均相等，D ，E ，F 分别为棱AB ，BC ，A 1C 1的中点．(1)证明EF∥平面A 1CD ；(2)证明平面A 1CD ⊥平面A 1ABB 1；(3)求直线BC 与平面A 1CD 所成角的正弦值．图1－317．解：(1)证明：如图，在三棱柱ABC －A 1B 1C 1中，AC∥A 1C 1，且AC ＝A 1C 1，联结ED ，在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ＝12AC 且DE∥AC，又因为F 为A 1C 1的中点，可得A 1F＝DE ，且A 1F ∥DE ，即四边形A 1DEF 为平行四边形，所以EF∥DA 1.又EF 平面A 1CD ，DA 1平面A 1CD ，所以，EF∥平面A 1CD.(2)证明：由于底面ABC 是正三角形，D 为AB 的中点，故CD⊥AB，又由于侧棱AA 1⊥底面ABC ，CD 平面ABC ，所以A 1A ⊥CD ，又A 1A ∩AB ＝A ，因此CD⊥平面A 1ABB 1，而CD 平面A 1CD ，所以平面A 1CD ⊥平面A 1ABB 1.(3)在平面A 1ABB 1内，过点B 作BG⊥A 1D 交直线A 1D 于点G ，联结CG ，由于平面A 1CD ⊥平面A 1ABB 1，而直线A 1D 是平面A 1CD 与平面A 1ABB 1的交线，故BG⊥平面A 1CD ，由此得∠BCG 为直线BC 与平面A 1CD 所成的角．设三棱柱各棱长为a ，可得A 1D ＝5a 2，由△A 1AD ∽△BGD ，易得BG ＝5a 5.在Rt △BGC 中，sin ∠BCG ＝BG BC ＝55.所以直线BC 与平面A 1CD 所成角的正弦值为55. 19．G5[2013·新课标全国卷Ⅰ] 如图1－5所示，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°.(1)证明：AB⊥A 1C ；(2)若AB ＝CB ＝2，A 1C ＝6，求三棱柱ABC －A 1B 1C 1的体积．图1－519．解：(1)取AB 的中点O ，联结OC ，OA 1，A 1B ，因为CA ＝CB ，所以OC⊥AB.由于AB ＝AA 1，∠BAA 1＝60°，故△AA 1B 为等边三角形，所以OA 1⊥AB. 因为OC∩OA 1＝O ，所以AB⊥平面OA 1C. 又A 1C 平面OA 1C ，故AB⊥A 1C.(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以OC ＝OA 1＝ 3.又A 1C ＝6，则A 1C 2＝OC 2＋OA 21，故OA 1⊥OC.因为OC∩AB＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC －A 1B 1C 1的高．又△ABC 的面积S △ABC ＝3，故三棱柱ABC －A 1B 1C 1的体积V ＝S △ABC ·OA 1＝3.4．G4，G5[2013·浙江卷] 设m ，n 是两条不同的直线，α，β是两个不同的平面( )A ．若m∥α，n∥α，则m∥nB ．若m∥α，m∥β，则α∥βC ．若m∥n，m⊥α，则n⊥αD ．若m∥α，α⊥β，则m⊥β4．C [解析] 对于选项C ，若m∥n，m⊥α，易得n⊥α.所以选择C.19．G2和G5[2013·重庆卷] 如图1－4所示，四棱锥P －ABCD 中，PA⊥底面ABCD ，PA ＝2 3，BC ＝CD ＝2，∠ACB＝∠ACD＝π3.(1)求证：BD⊥平面PAC ；(2)若侧棱PC 上的点F 满足PF ＝7FC ，求三棱锥P －BDF 的体积．图1－419．解：(1)证明：因为BC ＝CD ，即△BCD 为等腰三角形，又∠ACB＝∠ACD，故BD⊥AC.因为PA⊥底面ABCD ，所以PA⊥BD，从而BD 与平面PAC 内两条相交直线PA ，AC 都垂直，所以BD⊥平面PAC.(2)三棱锥P －BCD 的底面BCD 的面积S △BCD ＝12BC ·CD ·sin ∠BCD ＝12·2·2·sin 2π3＝ 3.由PA⊥底面ABCD ，得V P －BCD ＝13·S △BCD ·PA ＝13×3×2 3＝2.由PF ＝7FC ，得三棱锥F －BCD 的高为18PA ，故V F －BCD ＝13·S △BCD ·18PA ＝13×3×18×2 3＝14，所以V P －BDF ＝V P －BCD －V F －BCD ＝2－14＝74.G6 三垂线定理8．G1，G6[2013·北京卷] 如图1－2，在正方体ABCD －A 1B 1C 1D 1中，P 为对角线BD 1的三等分点，P 到各顶点的距离的不同取值有( )图1－2A ．3个B ．4个C ．5个D ．6个8．B [解析] 设棱长为1，∵BD1＝3，∴BP＝33，D1P＝2 33.联结AD1，B1D1，CD1，得△ABD1≌△CBD1≌△B1BD1，∴∠ABD1＝∠CBD1＝∠B1BD1，且cos∠ABD1＝3 3，联结AP，PC，PB1，则有△ABP≌△CBP≌△B1BP，∴AP＝CP＝B1P＝63，同理DP＝A1P＝C1P＝1，∴P到各顶点的距离的不同取值有4个．G7棱柱与棱锥17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.图1－517．证明：(1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD.(2)因为AB∥CD，CD＝2AB，E为CD的中点，所以AB∥DE，且AB＝DE，所以ABED为平行四边形，所以BE∥AD.又因为BE平面PAD，AD平面PAD，所以BE∥平面PAD.(3)因为AB⊥AD，而且ABED为平行四边形，所以BE⊥CD，AD⊥CD.由(1)知PA⊥底面ABCD，所以PA⊥CD.又因为AD∩PA＝A，所以CD⊥平面PAD，所以CD⊥PD.因为E和F分别是CD和PC的中点，所以PD∥EF，所以CD⊥EF，所以CD⊥平面BEF，所以平面BEF⊥平面PCD.10．G2，G7[2013·北京卷] 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．图1－310．3 [解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V ＝13×(3×3)×1＝3.8．G7[2013·江苏卷] 如图1－1，在三棱柱A 1B 1C 1－ABC 中，D ，E ，F 分别是AB ，AC ，AA 1的中点，设三棱锥F －ADE 的体积为V 1，三棱柱A 1B 1C 1－ABC 的体积为V 2，则V 1∶V 2＝________．图1－18．1∶24 [解析] 设三棱柱的底面积为S ，高为h ，则V 2＝Sh ，又D ，E ，F 分别为AB ，AC ，AA 1的中点，所以S △AED ＝14S ，且三棱锥F －ADE 的高为12h ，故V 1＝13S △AED ·12h ＝13·14S ·12h ＝124Sh ，所以V 1∶V 2＝1∶24.19．G5，G7[2013·江西卷] 如图1－7所示，直四棱柱ABCD －A 1B 1C 1D 1中，AB∥CD，AD⊥AB，AB ＝2，AD ＝2，AA 1＝3，E 为CD 上一点，DE ＝1，EC ＝3.(1)证明：BE⊥平面BB 1C 1C ； (2)求点B 1到平面EA 1C 1的距离．图1－719．解：(1)证明：过B 作CD 的垂线交CD 于F ，则BF ＝AD ＝2，EF ＝AB －DE ＝1，FC ＝2.在Rt △BEF 中，BE ＝ 3. 在Rt △CFB 中，BC ＝ 6.在△BEC 中，因为BE 2＋BC 2＝9＝EC 2，故BE⊥BC. 由BB 1⊥平面ABCD 得BE⊥BB 1. 所以BE⊥平面BB 1C 1C.(2)三棱锥E －A 1B 1C 1的体积V ＝13·AA 1·S △A 1B 1C 1＝ 2.在Rt △A 1D 1C 1中，A 1C 1＝A 1D 21＋D 1C 21＝3 2.同理，EC 1＝EC 2＋CC 21＝3 2，A 1E ＝A 1A 2＋AD 2＋DE 2＝2 3. 故S △A 1C 1E ＝3 5.设点B 1到平面EA 1C 1的距离为d ，则三棱锥B 1－A 1C 1E 的体积 V ＝13·d ·S △A 1C 1E ＝5d ，从而5d ＝2，d ＝105. 18．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点．(1)证明：BC 1∥平面A 1CD ；(2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积．图1－718．解：(1)证明：联结AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，联结DF ，则BC 1∥DF.因为DF 平面A 1CD ，BC 1平面A 1CD ，所以BC 1∥平面A 1CD.图1－8(2)因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD.由已知AC ＝CB ，D 为AB 的中点，所以CD⊥AB.又AA 1∩AB ＝A ，于是CD⊥平面ABB 1A 1.由AA 1＝AC ＝CB ＝2，AB ＝2 2得∠ACB＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，故A 1D 2＋DE 2＝A 1E 2，即DE⊥A 1D.所以VC －A 1DE ＝13×12×6×3×2＝1.19．G4，G5，G7，G11[2013·四川卷]图1－8如图1－8，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ＝AC ＝2AA 1＝2，∠BAC＝120°，D ，D 1分别是线段BC ，B 1C 1的中点，P 是线段AD 上异于端点的点．(1)在平面ABC 内，试作出过点P 与平面A 1BC 平行的直线l ，说明理由，并证明直线l⊥平面ADD 1A 1；(2)设(1)中的直线l 交AC 于点Q ，求三棱锥A 1－QC 1D 的体积．(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高)19．解：(1)如图，在平面ABC 内，过点P 作直线l∥BC，因为l 在平面A 1BC 外，BC 在平面A 1BC 内，由直线与平面平行的判定定理可知，l∥平面A 1BC.由已知，AB ＝AC ，D 是BC 的中点，所以，BC⊥A D ，则直线l⊥AD.因此AA 1⊥平面ABC ，所以AA 1⊥直线l.又因为AD ，AA 1在平面ADD 1A 1内，且AD 与AA 1相交，所以直线l⊥平面ADD 1A 1. (2)过D 作DE⊥AC 于E.因为AA 1⊥平面ABC ，所以DE⊥AA 1.又因为AC ，AA 1在平面AA 1C 1C 内，且AC 与AA 1相交，所以DE⊥平面AA 1C 1C.由AB ＝AC ＝2，∠BAC＝120°，有AD ＝1，∠DAC＝60°，所以在△ACD 中，DE ＝32AD ＝32. 又S △A 1QC 1＝12A 1C 1·AA 1＝1，所以VA 1－QC 1D ＝VD －A 1QC 1＝13DE ·S △A 1QC 1＝13×32×1＝36.因此三棱锥A 1－QC 1D 的体积是36. 8．G2和G7[2013·重庆卷] 某几何体的三视图如图1－3所示，则该几何体的表面积为( )图1－3A ．180B ．200C ．220D ．2408．D [解析] 该几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，其腰为5的等腰梯形，所以底面面积和为12(2＋8)×4×2＝40.四个侧面的面积和为(2＋8＋5×2)×10＝200，所以该直四棱柱的表面积为S ＝40＋200＝240，故选D.G8 多面体与球10．G8[2013·天津卷] 已知一个正方体的所有顶点在一个球面上，若球的体积为9π2，则正方体的棱长为________．10. 3 [解析] 设正方体的棱长为a ，则43π⎝ ⎛⎭⎪⎫3a 23＝92π，解之得a ＝ 3.15．G8[2013·新课标全国卷Ⅱ] 已知正四棱锥O －ABCD 的体积为3 22，底面边长为3，则以O 为球心，OA 为半径的球的表面积为________．15．24π [解析] 设O 到底面的距离为h ，则13×3×h ＝3 22h ＝3 22，OA ＝h 2＋⎝ ⎛⎭⎪⎫622＝6，故球的表面积为4π×(6)2＝24π.16．G8[2013·湖北卷] 我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水，天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是________寸．(注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)16．3 [解析] 积水深度为盆深的一半，故此时积水部分的圆台上底面直径为二尺，圆台的高为九寸，故此时积水的体积是13π(102＋62＋10×6)×9＝196×3π(立方寸)，盆口的面积是π×142＝196π，所以平均降雨量是196×3π196π＝3寸．15．G8[2013·新课标全国卷Ⅰ] 已知H 是球O 的直径AB 上一点，AH∶HB＝1∶2，AB⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为________．15.9π2 [解析] 截面为圆，由已知得该圆的半径为1.设球的半径为r ，则AH ＝23r ，所以OH ＝13r ，所以13r 2＋12＝r 2，r 2＝98，所以球的表面积是4πr 2＝9π2.G9 空间向量及运算G10 空间向量解决线面位置关系G11 空间有与距离的求法19．G5、G11[2013·全国卷] 如图1－3所示，四棱锥P —ABCD 中，∠ABC＝∠BAD＝90°，BC＝2AD ，△PAB 和△PAD 都是边长为2的等边三角形．图1－3(1)证明：PB⊥CD；(2)求点A 到平面PCD 的距离．19．解：(1)证明：取BC 的中点E ，联结DE ，则四边形ABED 为正方形．过P 作PO⊥平面ABCD ，垂足为O.联结OA ，OB ，OD ，OE.由△PAB 和△PAD 都是等边三角形知PA ＝PB ＝PD ，所以OA ＝OB ＝OD ，即点O 为正方形ABED 对角线的交点．故OE⊥BD，从而PB⊥OE.因为O 是BD 的中点，E 是BC 的中点，所以OE∥CD.因此PB⊥CD.(2)取PD 的中点F ，联结OF ，则OF∥PB. 由(1)知，PB⊥CD，故OF⊥CD.又OD ＝12BD ＝2，OP ＝PD 2－OD 2＝2，故△POD 为等腰三角形，因此OF⊥PD. 又PD∩CD＝D ，所以OF⊥平面PCD.因为AE∥CD，CD 平面PCD ，AE 平面PCD ，所以AE∥平面PCD. 因此O 到平面PCD 的距离OF 就是A 到平面PCD 的距离，而OF ＝12PB ＝1，所以点A 到平面PCD 的距离为1.11．G11[2013·全国卷] 已知正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，则CD 与平面BDC 1所成角的正弦值等于( )A.23B.33C.23 D.1311．A [解析] 如图，联结AC ，交BD 于点O.由于BO⊥OC，BO⊥CC 1，可得BO⊥平面OCC 1，从而平面OCC 1⊥平面BDC 1，过点C 作OC 1的垂线交OC 1于点E ，根据面面垂直的性质定理可得CE⊥平面BDC 1，∠CDE 即为所求的线面角．设AB ＝2，则OC ＝2，OC 1＝18＝32，所以CE ＝CC 1·OC OC 1＝4 23 2＝43，所以sin ∠CDE ＝CE CD ＝23.22．G11[2013·江苏卷] 如图1－2所示，在直三棱柱A 1B 1C 1－ABC 中，AB⊥AC，AB ＝AC ＝2，A 1A ＝4，点D 是BC 的中点．(1)求异面直线A 1B 与C 1D 所成角的余弦值；(2)求平面ADC 1与平面ABA 1所成二面角的正弦值．图1－222．解：(1)以A 为坐标原点，建立如图所示的空间直角坐标系A －xyz ，则A(0，0，0)，B(2，0，0)，C(0，2，0)，D(1，1，0)，A 1(0，0，4)，C 1(0，2，4)，所以A 1B →＝(2，0，－4)，C 1D →＝(1，－1，－4)．因为cos 〈A 1B →，C 1D →〉＝A 1B →·C 1D →|A 1B →||C 1D →|＝1820×18＝31010，所以异面直线A 1B 与C 1D 所成角的余弦值为31010.(2)设平面ADC 1的法向量为n 1＝(x ，y ，z)，因为AD →＝(1，1，0)，AC 1→＝(0，2，4)，所以n 1·AD →＝0，n 1·AC 1→＝0，即x ＋y ＝0且y ＋2z ＝0，取z ＝1，得x ＝2，y ＝－2，所以，n 1＝(2，－2，1)是平面ADC 1的一个法向量．取平面AA 1B 的一个法向量为n 2＝(0，1，0)，设平面ADC 1与平面ABA 1所成二面角的大小为θ.由|cos θ|＝n 1·n 2|n 1||n 2|＝29×1＝23，得sin θ＝53.。

北京市各地市2013年高考数学最新联考试题分类汇编(8)立体几何

一、选择题: （6)（北京市朝阳区2013年4月高三第一次综合练习文理)某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为A 。

4B 。

42C 。

62 D. 8 【答案】D（5)（北京市东城区2013年4月高三综合练习一文）已知一个几何体的三视图如图所示(单位:cm ），那么这个几何体的侧．面积是（A ）2(1+2)cm（B)2(3+2)cm(C)2(4+2)cm (D ）2(5+2)cm【答案】C 7。

(北京市房山区2013年4月高三第一次模拟理)某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是( C ） A 。

43 B. 8 C. 47 D 。

835．（北京市西城区2013年4月高三一模文）某正三棱柱的三视图如图所示，其中正（主）视图是边长为2的正方形,该正三棱柱的表面积是（A ）63+ （B ）123+ (C ）1223+ （D ）2423+ 【答案】C8．（北京市西城区2013年4月高三一模文）如图，正方体1111ABCD A B C D -中,E 是棱11B C 的中点，动点P 在底面ABCD 内，且11PA A E =,则点P 运动形成的图形是（A ）线段（B ）圆弧(C ）椭圆的一部分（D ）抛物线的一部分【答案】B8. (北京市海淀区2013年4月高三第二学期期中练习理）设123,,l l l 为空间中三条互相平行且两两间的距离分别为4，5,6的直线。

给出下列三个结论：①i i A l ∃∈(1,2,3)i =，使得123A A A ∆是直角三角形; ②i i A l ∃∈(1,2,3)i =，使得123A A A ∆是等边三角形；③三条直线上存在四点(1,2,3,4)i A i =,使得四面体1234A A A A 为在一个顶点处的三条棱两两互相垂直的四面体。

其中，所有正确结论的序号是A 。

① B.①② C 。

①③ D. ②③ 【答案】B7．（北京市丰台区2013年高三第二学期统一练习一文）某四面体三视图如图所示，则该四面体的四个面中,直角三角形的面积和是(A ） 2 (B ） 4 （C) 25+ （D) 425+ 【答案】C（7）（北京市昌平区2013年1月高三期末考试理)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸，可得这个几何体的全面积为A. 104342++ B ．102342++ C. 142342++ D 。

2013年北京市各区高三一模试题汇编--立体几何范文

2013年北京市各区高三一模试题汇编--立体几何一填空选择（2013年东城一模文科）（5）已知一个几何体的三视图如图所示(单位：cm)，那么这个几何体的侧．面积是（A）2（B）2（C）2(4 （D）2(2013年西城一模文科理科)5．某正三棱柱的三视图如图所示，其中正（主）视图是边长为2的正方形，该正三棱柱的表面积是（A）6 （B）12（C）12+ （D）24+(2013年西城一模文科理科)8．如图，正方体1111ABCD A BC D -中，E 是棱11B C的中点，动点P 在底面ABCD 内，且11PA A E =，则点P 运动形成的图形是（A ）线段（B ）圆弧（C ）椭圆的一部分（D ）抛物线的一部分（2013年海淀一模文科）11.某几何体的三视图如图所示，则它的体积为______.（2013年海淀一模理科）8. 设为空间中三条互相平行且两两间的距离分别为4，5，6的直线.给出下列三个结论：①，使得是直角三角形； ②，使得是等边三角形；③三条直线上存在四点，使得四面体为在一个顶点处的三条棱两两互相垂直的四面体. 其中，所有正确结论的序号是123,,ll l i i A l ∃∈(1,2,3)i =123A A A ∆i i A l ∃∈(1,2,3)i =123A A A ∆(1,2,3,4)i A i =1234A A A A 侧视图A. ①B.①②C. ①③D. ②③（2013年丰台一模文科）7．某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是 (A) 2 (B) 4(C) 2(D) 4+（2013年丰台一模理科）13.某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和是_______.（2013年石景山一模文科理科）7．某四棱锥的三视图如图所示，则最长的一条侧棱长度是（）A．B．C ．5D（2013年大兴一模文科理科）(5)已知平面βα,，直线n m ,，下列命题中不．正确的是（A ）若α⊥m ，β⊥m ，则α∥β （B ）若m ∥n ，α⊥m ，则α⊥n （C ）若m ∥α，n =βα ，则m ∥n （D ）若α⊥m ，β⊂m ，则βα⊥．（2013年延庆一模文科理科）7.一四面体的三视图如图所示，则该四面体四个面中最大的面积是A ．2 B. 22 C ．3 D. 32（7题图）（2013年门头沟一模文科）5．如图所示，为一几何体的三视图，则该几何体的体积是（A ）1（B ）21 （C ）13（D ）65（2013年门头沟一模理科）7．一个几何体的三视图如右图所示，则该几何体的体积是 (A) 21(B)13(C) 65 (D) 1（2013年房山一模文科）7.某三棱椎的三视图如图所示，该三棱锥的四个面的面积中，最大的是A. B. 8C.D.左视图主视图左视图俯视图二解答题（2013年东城一模文科）（16）（本小题共14分）如图，已知AD ⊥平面ABC ，CE ⊥平面ABC ，F 为BC 的中点，若12AB AC AD CE ===．（Ⅰ）求证：//AF 平面BDE ；（Ⅱ）求证：平面BDE ⊥平面BCE ．（2013年东城一模理科）（16）（本小题共14分）如图，已知ACDE 是直角梯形，且//ED AC ，平面ACDE ⊥平面ABC ，90BAC ACD ∠=∠=︒，AB AC AE ==2=，12ED AB =， P 是BC 的中点．（Ⅰ）求证：//DP 平面EAB ；（Ⅱ）求平面EBD 与平面ABC 所成锐二面角大小的余弦值．(2013年西城一模文科)16．（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD，AC =22AB BC ==，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求四面体FBCD 的体积；（Ⅲ）线段AC 上是否存在点M ，使EA //平面FDM ？证明你的结论．A BCDEF(2013年西城一模理科)17．（本小题满分14分）在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD ，BC AB 2=，60ABC ︒∠=，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求BC 与平面EAC 所成角的正弦值；（Ⅲ）线段ED 上是否存在点Q ，使平面EAC ⊥平面QBC ？证明你的结论．（2013年海淀一模文科）17. （本小题满分14分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，ABC ∆是正三角形，AC 与BD 的交点M 恰好是AC 中点，又30CAD ∠=，4PA AB ==，点N 在线段PB 上，且13PN NB =．（Ⅰ）求证：BD PC ⊥；（Ⅱ）求证：//MN 平面PDC ；（Ⅲ）设平面PAB 平面PCD =l ，试问直线l 是否与直线CD 平行，请说明理由.（2013年海淀一模理科）17.（本小题满分14分）在四棱锥中，平面，是正三角形，与的交点恰好是中点，又，，点在线段上，且（Ⅰ）求证：；（Ⅱ）求证：平面; （Ⅲ）求二面角的余弦值．P ABCD -PA ⊥ABCD ABC ∆AC BD M AC 4PA AB ==120CDA ∠=N PB PN =BD PC ⊥//MN PDC A PC B --（2013年丰台一模文科）16．如图，四棱锥P -ABCD 中， BC ∥AD ，BC =1，AD =3，AC ⊥CD ,且平面PCD ⊥平面ABCD . （Ⅰ）求证：AC ⊥PD ；（Ⅱ）在线段PA 上,是否存在点E ，使BE ∥平面PCD ？若存在，（2013年丰台一模理科）16．如图，四边形ABCD 是边长为2的正方形，MD ⊥平面ABCD ，NB ∥MD ，且NB=1，MD=2；（Ⅰ）求证：AM ∥平面BCN; （Ⅱ）求AN 与平面MNC 所成角的正弦值；（Ⅲ）E 为直线MN 上一点，且平面ADE ⊥平面MNC ，求ME MN的值.（2013年石景山一模文科）17．（本小题满分14分）如图，在底面为直角梯形的四棱锥P －ABCD 中，AD ∥BC ，∠ABC=90o ，PD ⊥平面ABCD ，AD =1，BC =4。

北京2013届高三最新数学文试题分类汇编专题7：立体几何

32．（北京市石景山区 2013 届高三上学期期末考试数学文试
图 1 ，在 Rt ABC 中， C 90 ， BC 3， AC 6 ． D 、E 分别是 AC、 AB 上的点，
A
DE / /BC ，将 ADE 沿 DE 折起到 A1DE 的位置，
A1D CD ，如图 2．
（Ⅰ）求证： BC // 平面 A1DE ；
（Ⅱ）求证： B1E AD1 ；
（Ⅲ）若 E 是棱 CD 的中点，在棱 AA1上是否存在点 P ，使得 DP ∥平面 B1AE ？若存在，求出线段 AP 的长；若不存在，请说明理由．
12 / 31
D A
E C
B
D1 A1
C1 B1
35．（北京市东城区 2013 届高三上学期期末考试数学文科试题）如图，在菱形 ABCD 中， MA ⊥平面 ABCD ，
（Ⅲ）若 AB =
2CE , 在线段 EO 上是否存在点 G ，使 CG ^ 平面 BDE ？若存在，求出
EG
的值，
EO
若不存在，请说明理由．
E F
C
B
O
D
A
34．（北京市朝阳区 2013 届高三上学期期末考试数学文试题）
E 是棱 CD 上的一点．（Ⅰ）求证： AD1 平面 A1B1D ；
在长方体 ABCD-A 1B1C1D1 中， AA1=AD= 2 ，
由.
P
E
M
A
D
B
C
24．（ 2013 届北京东城区一模数学文科）如图 , 已知 AD 平面 ABC , CE 平面 ABC , F 为 BC 的中点 ,
若
AB AC AD 1 CE . 2
( Ⅰ) 求证 : AF // 平面 BDE ; ( Ⅱ) 求证 : 平面 BDE 平面 BCE .

2013年全国各地高考文科数学试题分类汇编：立体几何(解析版

2013年全国各地高考文科数学试题分类汇编:立体几何一、选择题1 . (2013年高考重庆卷(文某几何体的三视图如图所示 , 则该几何体的表面积为 (A. 180 B . 200C . 220D . 240【答案】 D2 . (2013年高考课标Ⅱ卷 (文一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1,(1,1,0,(0,1,1,(0,0,0, 画该四面体三视图中的正视图时 , 以 zOx 平面为投影面 , 则得到正视图可以为(A.B.C.D.【答案】 A3 . (2013年高考课标Ⅰ卷(文某几何函数的三视图如图所示 , 则该几何的体积为 (A. 168π+B. 88π+C. 1616π+D. 816π+ 【答案】 A4 . (2013年高考大纲卷(文已知正四棱锥 1111112, ABCD A B C D AA AB CD BDC -=中, 则与平面所成角的正弦值等于 ( A.23 D. 13 【答案】 A5 . (2013年高考四川卷(文一个几何体的三视图如图所示 , 则该几何体可以是A. 棱柱B. 棱台C. 圆柱D. 圆台【答案】 D6 . (2013年高考浙江卷(文已知某几何体的三视图 (单位 :cm如图所示 , 则该几何体的体积是(A.108cm 3B.100 cm3C.92cm 3D.84cm 3 【答案】 B图 2俯视图侧视图正视图7 . (2013年高考北京卷(文如图 , 在正方体 1111ABCD A B C D -中 , P 为对角线1BD 的三等分点 , 则 P 到各顶点的距离的不同取值有A.3个B.4个C.5个D.6个【答案】 B8 . (2013年高考广东卷(文某三棱锥的三视图如图 2所示 , 则该三棱锥的体积是( A.16 B.13C.23D. 1【答案】 B9 . (2013年高考湖南(文已知正方体的棱长为 1, 其俯视图是一个面积为 1的正方形 , 的矩形 , 则该正方体的正视图的面积等于 ______B.1【答案】 D10. (2013年高考浙江卷(文设 m.n 是两条不同的直线,α.β是两个不同的平面 , 则(A. 若 m ∥ α,n∥ α,则 m ∥ nB. 若 m ∥ α,m∥ β,则α∥ βC. 若 m ∥ n,m ⊥ α,则n ⊥ αD. 若 m ∥ α,α⊥ β,则 m ⊥ β 【答案】 C11. (2013年高考辽宁卷 (文已知三棱柱 111A B C A B C-的 6个顶点都在球 O 的球面上 , 若 34AB AC ==, , AB AC ⊥, 112AA =, 则球 O 的半径为 (A.2B.C.132D.【答案】 C12. (2013年高考广东卷(文设 l 为直线, , αβ是两个不同的平面 , 下列命题中正确的是 (A. 若//l α, //l β, 则//αβB. 若l α⊥, l β⊥, 则//αβC. 若l α⊥, //l β, 则//αβD. 若αβ⊥, //l α, 则l β⊥【答案】 B13. (2013年高考山东卷(文一个四棱锥的侧棱长都相等 , 底面是正方形 , 其正(主视图如右图所示该四棱锥侧面积和体积分别是(A. B. 83 C. 81, 3+ D.8,8【答案】 B14. (2013年高考江西卷(文一几何体的三视图如右所示 , 则该几何体的体积为( A. 200+9π B. 200+18π C. 140+9π D. 140+18π 【答案】 A 二、填空题15. (2013年高考课标Ⅱ卷 (文已知正四棱锥 O-ABCD 的体积为, 底面边长为 , 则以 O 为球心 ,OA 为半径的球的表面积为 ________.【答案】24π16. (2013年高考湖北卷(文我国古代数学名著《数书九章》中有“ 天池盆测雨” 题 :在下雨时 , 用一个圆台形的天池盆接雨水 . 天池盆盆口直径为二尺八寸 , 盆底直径为一尺二寸 , 盆深一尺八寸 . 若盆中积水深九寸 , 则平地降雨量是__________寸 . (注 :①平地降雨量等于盆中积水体积除以盆口面积 ; ②一尺等于十寸【答案】 317. (2013年高考课标Ⅰ卷(文已知 H 是球 O 的直径 AB 上一点 , :1:2AH HB =, AB ⊥平面α, H 为垂足, α截球 O 所得截面的面积为π, 则球 O 的表面积为 _______. 【答案】92π; 18. (2013年高考北京卷(文某四棱锥的三视图如图所示 , 该四棱锥的体积为__________.【答案】 319. (2013年高考陕西卷(文某几何体的三视图如图所示 , 则其表面积为________. 【答案】π320. (2013年高考大纲卷 (文已知圆 O 和圆 K 是球 O 的大圆和小圆 , 其公共弦长等于球 O 的半径 , 3602OK O K =,且圆与圆所在的平面所成角为 , 则球 O 的表面积等于 ______. 【答案】16π21. (2013年上海高考数学试题(文科已知圆柱Ω的母线长为 l , 底面半径为 r , O 是上地面圆心 , A 、 B 是下底面圆周上两个不同的点 , BC 是母线 , 如图 . 若直线 OA 与 BC 所成角的大小为π6, 则 1r=________.22. (2013年高考天津卷 (文已知一个正方体的所有顶点在一个球面上 . 若球的体积为 92π, 则正方体的棱长为23. (2013年高考辽宁卷(文某几何体的三视图如图所示 , 则该几何体的体积是____________.【答案】1616π-24. (2013年高考江西卷(文如图 , 正方体的底面与正四面体的底面在同一平面α上 , 且 AB//CD,则直线 EF 与正方体的六个面所在的平面相交的平面个数为_____________.【答案】 425. (2013年高考安徽(文如图 , 正方体 1111ABCD A B C D -的棱长为 1, P 为BC 的中点 , Q 为线段 1CC 上的动点 , 过点 , , A P Q 的平面截该正方体所得的截面记为 S , 则下列命题正确的是 __________(写出所有正确命题的编号.①当 102CQ <<时 , S 为四边形 ; ②当 12CQ =时 , S 为等腰梯形 ; ③当 34CQ =时 , S 与 11C D 的交点 R 满足113C R =; ④当 314CQ <<时 , S 为六边形 ; ⑤当 1CQ =时 , S【答案】①②③⑤三、解答题26. (2013年高考辽宁卷(文如图 , . AB O PA O C O 是圆的直径, 垂直圆所在的平面, 是圆上的点 (I求证 :BC PAC ⊥平面 ;(II设//. Q PA G AOC QG PBC ∆为的中点, 为的重心,求证:平面【答案】27. (2013年高考浙江卷 (文如图 , 在在四棱锥 P-ABCD 中 ,PA ⊥面ABCD,AB=BC=2,AD=CD=7,PA=3, ∠ ABC=120°,G 为线段 PC 上的点 . (Ⅰ证明 :BD⊥面 PAC ;(Ⅱ若 G 是 PC 的中点 , 求 DG 与 APC 所成的角的正切值 ; (Ⅲ若 G 满足 PC ⊥面 BGD, 求 PGGC的值 .【答案】解 :证明 :(Ⅰ由已知得三角形ABC是等腰三角形 , 且底角等于 30°, 且6030AB CB AD CD ABD CBD ABD CBD BAC BD DB =⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭且 , 所以 ; 、 BD AC ⊥, 又因为 PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭;(Ⅱ设 AC BD O =, 由 (1知 DO PAC ⊥, 连接 GO , 所以 DG 与面 APC 所成的角是 DGO ∠, 由已知及(1知:1, 2BO AO CO DO =====,12tan 2OD GO PA DGO GO ==⇒∠===, 所以 DG 与面 APC 所成的角的正切值是; (Ⅲ由已知得到 :PC===, 因为 PC BGD PC GD ⊥∴⊥, 在 PDC∆中, PD CD PC====, 设223 1072 PGPG x CG x x x PG x GCGC=∴=-∴-=--∴==== 28. (2013年高考陕西卷(文如图 , 四棱柱 ABCD -A 1B 1C 1D 1的底面 ABCD 是正方形 , O 为底面中心 , A 1O ⊥平面ABCD,1 AB AA =1A(Ⅰ证明 : A 1BD // 平面 CD 1B 1;(Ⅱ求三棱柱 ABD -A 1B 1D 1的体积 .【答案】解 : (Ⅰ设111ODB 线段的中点为 . 11111111//DBBDDCBAABCDDBBD ∴-的对应棱是和. 的对应线段是棱柱和同理,111111DCBAABCDOAAO -为平行四边形四边形且且11111111//////OCO AOCOAOCOAOC AOOAAO ⇒=⇒∴111 1 1 1 1 1 1 1 // , . //B CD BD A O D B COOBDOACOOA 面面且⇒==⇒.(证毕(Ⅱ的高是三棱柱面 ABD DBAOAABCDOA -∴⊥11111.在正方形 AB CD中 ,AO = 1 . . 1 11=∆OAOAART 中, 在112 (2121111111=⋅⋅=⋅=-∆-OASV ABD DBA ABD ABDDBA的体积三棱柱 . 所以 , 1 111111=--ABD DBAVABDDBA 的体积三棱柱 .29. (2013年高考福建卷 (文如图 , 在四棱锥 P ABCD -中 , PD ABCD⊥面 , //AB DC , AB AD⊥, 5BC =, 3DC =, 4AD =, 60PAD∠=.(1当正视图方向与向量 AD 的方向相同时 , 画出四棱锥 P ABCD-的正视图 .(要求标出尺寸 , 并画出演算过程 ; (2若 M 为 PA 的中点 , 求证 :// DM PBC面 ;(3求三棱锥 D PBC-的体积 .【答案】解法一 :(Ⅰ在梯形 ABCD 中 , 过点 C 作 CE AB ⊥, 垂足为 E , 由已知得 , 四边形 ADCE 为矩形 , 3AE CD == 在Rt BEC ∆中 , 由 5BC =, 4CE =, 依勾股定理得 :3BE =, 从而 6AB =又由 PD ⊥平面 ABCD 得 , PD AD ⊥从而在Rt PDA ∆中 , 由 4AD =, 60PAD ∠=︒,得 PD = 正视图如右图所示 :(Ⅱ取 PB 中点 N , 连结 MN , CN 在PAB ∆中 , M 是 PA 中点 ,∴ MN AB , 132MN AB ==, 又 CD AB , 3CD = ∴ MN CD , MN CD =∴四边形 MNCD 为平行四边形 , ∴ DM CN 又 DM ⊄平面 PBC , CN ⊂平面PBC ∴ DM 平面 PBC(Ⅲ 13D PBC P DBC DBC V V S PD --∆==⋅又6PBC s ∆=, PD =,所以 D PBC V -= 解法二 : (Ⅰ同解法一(Ⅱ取 AB 的中点 E , 连结 ME , DE 在梯形 ABCD 中 , BE CD , 且 BE CD = ∴四边形 BCDE 为平行四边形∴ DE BC , 又 DE ⊄平面 PBC , BC ⊂平面 PBC ∴ DE 平面 PBC , 又在PAB ∆中 , ME PBME ⊄平面 PBC , PB ⊂平面 PBC∴ ME 平面 PBC . 又 DEME E =,∴平面 DME 平面 PBC , 又 DM ⊂平面 DME ∴ DM 平面 PBC (Ⅲ同解法一30. (2013年高考广东卷(文如图 4, 在边长为 1的等边三角形 ABC 中 , , D E 分别是 , AB AC边上的点 , AD AE =, F 是 BC 的中点 , AF 与 DE 交于点 G , 将ABF ∆沿 AF 折起 , 得到如图 5所示的三棱锥 A BCF -,其中 BC =. (1 证明 :DE //平面 BCF ; (2 证明 :CF ⊥平面 ABF ; (3 当 23AD =时 , 求三棱锥 F DEG -的体积 F DEG V -. 图 4 【答案】 (1在等边三角形 ABC 中 , AD AE = AD AEDB EC ∴=, 在折叠后的三棱锥 A BCF -中也成立 , //DE BC ∴ ,DE ⊄平面 BCF ,BC ⊂平面 BCF , //DE ∴平面 BCF ;(2在等边三角形 ABC 中 , F 是 BC 的中点 , 所以 AF BC ⊥① ,12BF CF ==.在三棱锥 A BCF -中 ,2BC =, 222BC BF CF CF BF ∴=+∴⊥②BF CF F CF ABF ⋂=∴⊥平面 ;(3由 (1可知 //GE CF , 结合 (2可得 GEDFG ⊥平面 .111111132323323324F DEG E DFG V V DG FG GF --⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅⋅= ⎝⎭31. (2013年高考湖南(文如图 2. 在直菱柱 ABC-A 1B 1C 1中 , ∠BAC=90°,AB=AC=,AA 1=3,D是 BC 的中点 , 点E 在菱 BB 1上运动 .(I 证明 :AD⊥ C 1E;(II 当异面直线 AC,C 1E 所成的角为 60°时 , 求三菱子 C 1-A 2B 1E 的体积.【答案】解 : (Ⅰ 11C CBB AD E 面为动点,所以需证因为⊥.AD BB ABC AD ABC BB C B A ABC ⊥⇒⊂⊥∴-11111, 面且面是直棱柱AD BC BC D ABC RT ⊥∴∆的中点, 为是等腰直角且又 .. 1111111E C AD C CBB E C C CBB AD B BB BC ⊥⇒⊂⊥⇒=⋂面且面由上两点,且 (证毕(Ⅱ 660, //111111=∆⇒︒=∠∴AE E C A RT E C A A C CA 中, 在 .的高是三棱锥是直棱柱中, 在 1111111111. 2C B A E EB C B A ABC EB E B A RT -∴-=∆⇒ .. 3232213131111111111111的体积为所以三棱锥 E B A C EB S V V C B A C B A E E B A C -⋅=⋅⋅=⋅⋅==∆-- 32. (2013年高考北京卷(文如图 , 在四棱锥 P ABCD -中 , //AB CD , AB AD ⊥, 2CD AB =, 平面 PAD ⊥底面 ABCD , PA AD ⊥, E 和 F 分别是 CD 和 PC 的中点 , 求证 : (1PA ⊥底面ABCD ;(2//BE 平面 PAD ;(3平面 BEF ⊥平面 PCD【答案】 (I因为平面 PAD ⊥平面 ABCD, 且 PA 垂直于这个平面的交线 AD 所以 PA 垂直底面 ABCD.(II因为 AB ∥ CD,CD=2AB,E为 CD 的中点所以 AB ∥ DE, 且 AB=DE 所以ABED 为平行四边形 ,所以 BE ∥ AD, 又因为 BE ⊄平面 PAD,AD ⊂平面 PAD 所以 BE ∥平面 PAD.(III因为 AB ⊥ AD, 而且 ABED 为平行四边形所以 BE ⊥ CD,AD ⊥ CD, 由 (I 知 PA ⊥底面 ABCD,所以 PA ⊥ CD, 所以 CD ⊥平面 PAD所以 CD ⊥ PD, 因为 E 和 F 分别是 CD 和 PC 的中点所以 PD ∥ EF, 所以 CD ⊥ EF, 所以 CD ⊥平面 BEF, 所以平面 BEF ⊥平面PCD.33. (2013年高考课标Ⅰ卷(文如图 , 三棱柱 111ABC A B C -中 , CA CB =, 1AB AA =, 160BAA ∠=. (Ⅰ证明 :1AB AC ⊥; (Ⅱ若 2AB CB ==, 1AC =, 求三棱柱 111ABC A B C -的体积 .11A1【答案】【答案】 (I取 AB 的中点 O, 连接 OC O 、 1OA O 、 1A B , 因为CA=CB,所以 OC AB ⊥, 由于 AB=A A1, ∠ BA A 1=600, 故, AA B ∆为等边三角形 , 所以 OA 1⊥ AB.因为 OC ⨅ OA 1=O,所以 AB ⊥平面 OA 1C. 又 A 1CC 平面 OA 1C, 故 AB ⊥AC. (II由题设知12ABC AA B ∆∆与都是边长为的等边三角形,12AAB 都是边长为的等边三角形,所以2211111. OC OA AC AC OA OA OC =+⊥又 ,故111111111, --=3.ABC ABCOC AB O OA ABC OA ABC A B CABC S A B C V S OA=⊥∆=⨯=因为所以平面 , 为棱柱的高,又的面积 ABC 的体积34. (2013年高考山东卷 (文如图 , 四棱锥 P ABCD -中 , , AB AC AB PA⊥⊥, , 2AB CD AB CD=∥ , , , , ,E F G M N 分别为,, , ,PBAB BC PDPC 的中点(Ⅰ求证 :CE PAD∥平面 ; (Ⅱ求证 :EFG EMN ⊥平面平面【答案】35. (2013年高考四川卷(文如图 , 在三棱柱 11ABC A B C -中 , 侧棱 1AA ⊥底面 ABC , 122AB AC AA ===, 120BAC ∠=, 1, D D 分别是线段 11, BC B C 的中点 , P 是线段 AD 上异于端点的点 .(Ⅰ在平面 ABC 内 , 试作出过点 P 与平面 1A BC 平行的直线 l , 说明理由 , 并证明直线 l ⊥平面 11ADD A ; (Ⅱ设 (Ⅰ中的直线 l 交 AC 于点 Q , 求三棱锥 11A QC D -的体积 .(锥体体积公式 :13V Sh =, 其中 S 为底面面积 , h 为高【答案】解 :(Ⅰ如图 , 在平面 ABC 内 , 过点 P 作直线 BC l //, 因为 l 在平面BC A 1外 , BC 在平面 BC A 1内 , 由直线与平面平行的判定定理可知 , //l 平面 1A BC .由已知 , AC AB =, D 是 BC 中点 , 所以 BC ⊥ AD , 则直线 AD l ⊥, 又因为1AA ⊥底面 ABC , 所以 l AA ⊥1,又因为 AD , 1AA 在平面 11A ADD 内 , 且 AD 与 1AA 相交 , 所以直线⊥l 平面11A ADD(Ⅱ过 D 作 AC DE ⊥于 E , 因为 1AA ⊥平面 ABC , 所以 DE AA ⊥1,又因为 AC , 1AA 在平面 C C AA 11内 , 且 AC 与 1AA 相交 , 所以⊥DE 平面C C AA 11, 由 2==AC AB , ∠ BAC ︒=120, 有 1=AD , ∠ DAC ︒=60, 所以在△ACD 中 , 232==AD DE , 又 1211111=⋅=∆AA C A S AQC , 所以 6123131111111=⋅⋅=⋅==--QC A QC A D D QC A S DE V V 因此三棱锥 11A QC D -的体积为 6336. (2013年高考湖北卷(文如图 , 某地质队自水平地面 A , B , C 三处垂直向地下钻探 , 自 A 点向下钻到 A 1处发现矿藏 , 再继续下钻到 A 2处后下面已无矿 , 从而得到在 A 处正下方的矿层厚度为 121A A d =. 同样可得在 B , C 处正下方的矿层厚度分别为 122B B d =, 123C C d =, 且 123d d d <<. 过 AB , AC 的中点 M , N 且与直线 2AA 平行的平面截多面体 111222A B C A B C -所得的截面 DEFG 为该多面体的一个中截面 , 其面积记为 S 中 .(Ⅰ证明 :中截面 DEFG 是梯形 ;(Ⅱ在△ ABC 中 , 记 BC a =, BC 边上的高为 h , 面积为 S . 在估测三角形 ABC 区域内正下方的矿藏储量 (即多面体111222A B C A B C -的体积 V 时 , 可用近似公式 V S h =⋅估中来估算 . 已知1231( 3V d d d S =++, 试判断 V 估与 V 的大小关系 , 并加以证明 .C 11BCB 1【答案】 (Ⅰ依题意 12A A ⊥平面 ABC , 12B B ⊥平面 ABC , 12C C ⊥平面ABC , 所以 A 1A 2∥ B 1B 2∥ C 1C 2. 又 121A A d =, 122B B d =, 123C C d =, 且123d d d << . 因此四边形 1221A A B B 、 1221A A C C 均是梯形 .由 2AA ∥平面 MEFN , 2AA ⊂平面 22AA B B , 且平面 22AA BB平面 MEFN ME =,可得 AA 2∥ ME , 即 A 1A 2∥ DE . 同理可证 A 1A 2∥ FG , 所以 DE ∥ FG . 又 M 、 N 分别为 AB 、 AC 的中点 ,则 D 、 E 、 F 、 G 分别为 11A B 、 22A B 、 22A C 、 11AC 的中点 , 即DE 、 FG 分别为梯形 1221A A B B 、 1221A A C C 的中位线 .因此 12121211( ( 22DE A A B B d d =+=+, 12121311( ( 22FG A A C C d d =+=+,而 123d d d <<, 故 DE FG <, 所以中截面 DEFG 是梯形 . (Ⅱ V V <估 . 证明如下 :由 12A A ⊥平面 ABC , MN ⊂平面 ABC , 可得 12A A MN ⊥. 而 EM ∥ A 1A 2, 所以 EM MN ⊥, 同理可得 FN MN ⊥. 由 MN 是△ ABC 的中位线 , 可得 1122MN BC a ==即为梯形 DEFG 的高 , 因此 13121231( (2 22228DEFG d d d d a aS S d d d ++==+⋅=++中梯形 ,即 123(2 8ahV S h d d d =⋅=++估中 . 又 12S ah =, 所以 1231231( ( 36ahV d d d S d d d =++=++.于是 1231232131( (2 [( (]6824ah ah ahV V d d d d d d d d d d -=++-++=-+-估 . 由 123d d d <<, 得 210d d ->, 310d d ->, 故 V V <估 .37. (2013年高考课标Ⅱ卷(文如图 , 直三棱柱 ABC-A 1B 1C 1中 ,D,E 分别是AB,BB 1的中点 .第 20题图(1 证明 : BC1//平面 A 1CD;(2 设 AA 1= AC=CB=2,AB=2, 求三棱锥 C 一 A 1DE 的体积.【答案】38. (2013年高考大纲卷(文如图 , 四棱锥902, P ABCD ABC BAD BC AD PAB PAD -∠=∠==∆∆中, , 与都是边长为 2的等边三角形 .(I证明 :; PB CD ⊥ (II求点 . A PCD 到平面的距离【答案】 (Ⅰ证明 :取 BC 的中点 E, 连结 DE, 则 ABED 为正方形 .过 P 作 PO ⊥平面 ABCD, 垂足为 O.连结 OA,OB,OD,OE.由PAB ∆和PAD ∆都是等边三角形知 PA=PB=PD,所以 OA=OB=OD,即点 O 为正方形 ABED 对角线的交点 ,故 OE BD ⊥, 从而 PB OE ⊥.因为 O 是 BD 的中点 ,E 是 BC 的中点 ,所以 OE//CD.因此 , PB CD ⊥.(Ⅱ解 :取 PD 的中点 F, 连结 OF, 则 OF//PB.由 (Ⅰ知 , PB CD ⊥, 故 OF CD ⊥.又 12OD BD ==OP = 故POD ∆为等腰三角形 , 因此 , OF PD ⊥. 又 PD CD D =, 所以 OF ⊥平面PCD.因为 AE//CD,CD ⊂平面 PCD, AE ⊄平面 PCD, 所以 AE//平面 PCD.因此 ,O 到平面 PCD 的距离 OF 就是 A 到平面 PCD 的距离 , 而 112OF PB = =, 所以 A 至平面 PCD 的距离为 1.39. (2013年高考安徽(文如图 , 四棱锥 P ABCD -的底面 ABCD 是边长为 2的菱形 , 60BAD ∠=.已知 2, PB PD PA === .(Ⅰ证明 :PC BD ⊥(Ⅱ若 E 为 PA 的中点 , 求三菱锥 P BCE -的体积.【答案】解 :(1证明 :连接 , BD AC 交于 O 点PB PD = PO BD ∴⊥又 ABCD 是菱形 BD AC ∴⊥而 AC PO O ⋂= BD ∴⊥面 PAC ∴BD ⊥ PC(2 由 (1BD ⊥面 PAC︒⨯⨯⨯==45sin 3262121PAC PEC S S △△ =32236=⨯⨯ 111132322P BEC B PEC PEC V V S BO --∆==⋅⋅=⨯⨯= 40. (2013年上海高考数学试题(文科如图 , 正三棱锥 O ABC -底面边长为 2, 高为 1, 求该三棱锥的体积及表面积 .第19题图B【答案】41. (2013年高考天津卷(文如图 , 三棱柱 ABC -A 1B 1C 1中 , 侧棱 A 1A ⊥底面 ABC , 且各棱长均相等 . D , E , F 分别为棱 AB , BC , A 1C 1的中点 .(Ⅰ证明 EF //平面 A 1CD ;(Ⅱ证明平面 A 1CD ⊥平面 A 1ABB 1;(Ⅲ求直线 BC 与平面 A 1CD 所成角的正弦值 .【答案】42. (2013年高考重庆卷(文 (本小题满分 12分 ,(Ⅰ小问 5分 ,(Ⅱ小问 7分如题 (19图 , 四棱锥 P ABCD -中 , PA ⊥底面 A B C D, PA =, 2BC CD ==, 3ACB ACD π∠=∠=. (Ⅰ求证 :BD ⊥平面 PAC ;(Ⅱ若侧棱 PC 上的点 F 满足 PF 7 FC ,求三棱锥 P BDF 的体积. 【答案】43.（2013 年高考江西卷（文如图,直四棱柱 ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD= ,AA1=3,E 为CD 上一点,DE=1,EC=3 (1 证明:BE⊥平面 BB1C1C; (2 求点 B1 到平面 EA1C1 的距离【答案】解.(1证明:过 B 作 CD 的垂线交 CD 于 F,则 BF AD 2, EF AB DE 1, FC 2 在 Rt BFE中，BE＝ 3 ，Rt BFC中，BC＝ 6 . 2 2 2 在 BCE中，因为BE BC ＝9＝EC ,故 BE BC 由 BB1 平面ABCD，得BEBB1，所以BE 平面BB1C1C (2 三棱锥E A1 B1C1的体积V＝ AA1 S A1B1C1＝ 2 1 3 在Rt A1 D1C1中，A1C1＝ A1 D12 D1C12 =3 2 , EA1＝AD ED AA1 =2 3 同理, EC1＝ EC CC1 =3 2 ， 2 2 2 2 2 因此 S A C E 3 5 .设点 B1 到平面 EAC 的体积 1 EAC 1 1 1 1 的距离为 d,则三棱锥B 1 1 1 10 V＝ d S A1EC1＝ 5d ,从而 5d 2, d 3 5。

2013数学高考真题—立体几何分类汇编

2013数学高考真题—立体几何分类汇编1.（北京理14）如图，在棱长为2的正方体1111D C B A ABCD -中，E 为BC 中点，点P 在线段E D 1上。

点P 在线段E D 1上，点P 到直线1CC 距离的最小值为。

2.（北京理17）如图，在三棱柱111C B A ABC -中，C C AA 11是边长为4的正方形，平面⊥ABC 平面C C AA 11，5,3==BC AB .（1）求证：⊥1AA 平面ABC ；（2）求二面角111B BC A --的余弦值；（3）证明：在线段1BC 上存在点D ，使得B A AD 1⊥，并求1BC BD的值。

3.（北京文8）如图，在正方体1111D C B A ABCD -中，P 为对角线1BD 的三等分点，P 到各顶点的距离的不同取值有（）.A 3个 .B 4个 .C 5个 .D 6个 4（北京文10）某四棱锥的三视图如图所示，该四棱锥的体积为。

4（北京文17）如图，四棱锥ABCD P -中，AB ∥CD ，AD AB ⊥,AB CD 2=,平面PAD ⊥底面ABCD ，AD PA ⊥，E 和F 分别是CD 和PC 中点。

求证：（1）⊥PA 底面ABCD ；（2）BE ∥平面PAD ；（3）平面⊥BEF 平面PCD5（大纲理10）已知正四棱柱1111D C BA ABCD -中，AB AA 21=，则CD 与平面1BDC 所成角的正弦值等于（） .A 2 .B 3.C 2.D 1 ABA 1C 1D 1CB 1C BA B CA 1C 1D 俯视图正（主）视图侧（左）视图CD6（大纲文理16）已知圆O 与圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，23=OK ,且圆O 与圆K 所在的平面所成的一个二面角为060，则球O 的表面积等于。

7（大纲理19）如图，四棱锥ABCD P -中，090=∠=∠BAD ABC ,AD BC 2=,PAB ∆和PAD ∆都是等边三角形。

2009-2013年北京高考真题--立体几何试题汇编

_________高考题库，荣誉出品__________●-------------------------密--------------封--------------线--------------内--------------请--------------不--------------要--------------答--------------题-------------------------●2009-2013年北京高考真题--立体几何试题汇编5年高考真题分类汇编-教师卷题号一总分得分△注意事项：1.本系列试题包含2009至2013年北京市高考真题，并经过精心校对。

2.本系列文档包含全部试题分类汇编，命名规律为：2009-2013年北京高考真题--******试题汇编。

3.本系列试题涵盖北京高考所有学科，均有相关实体书出售。

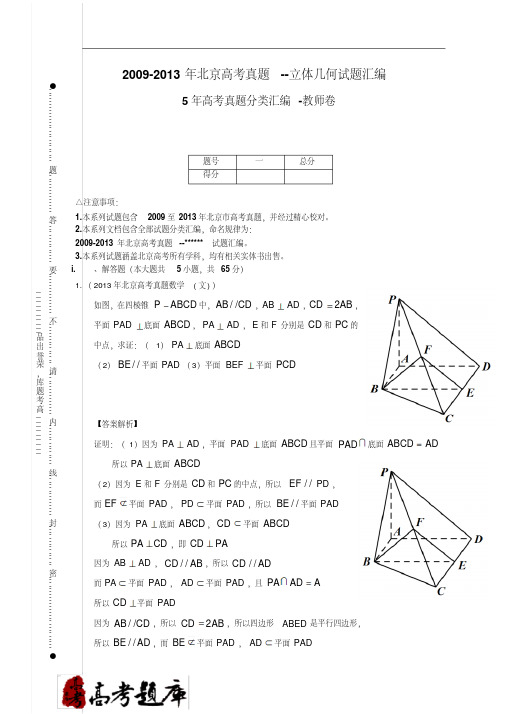
i.、解答题（本大题共5小题，共65分）1.（2013年北京高考真题数学(文)）如图，在四棱锥P ABCD 中，//AB CD ，AB AD ，2CD AB ，平面PAD 底面ABCD ，PA AD ，E 和F 分别是CD 和PC 的中点，求证：（1）PA 底面ABCD （2）//BE 平面PAD （3）平面BEF 平面PCD 【答案解析】证明：（1）因为PA AD ，平面PAD 底面ABCD 且平面PAD 底面ABCD AD 所以PA 底面ABCD （2）因为E 和F 分别是CD 和PC 的中点，所以//EF PD ，而EF 平面PAD ，PD 平面PAD ，所以//BE 平面PAD （3）因为PA 底面ABCD ，CD 平面ABCD 所以PA CD ，即CD PA 因为AB AD ，//CD AB ，所以//CD AD 而PA 平面PAD ，AD 平面PAD ，且PA AD A 所以CD 平面PAD 因为//AB CD ，所以2CD AB ，所以四边形ABED 是平行四边形，所以//BE AD ，而BE 平面PAD ，AD 平面PAD。

【VIP专享】2013年北京市各区高三一模试题汇编--解析几何

（2013 东城一模理科）（3）已知圆的方程为 (x 1)2 ( y 2)2 4 ，那么该圆圆心到直线
x t 3,
y2Biblioteka （A）2（2013
t
1
（ t 为参数）的距离为
东城一模理科）（6）已知
6
（B）
2
F1
(c,
0)
，
32
（C）
2
F2
(a 0, b 0) 的两个焦点，双曲线 C1 和圆 C2 ： x2 y2 c2 的一个交点为 P ，且
2PF1F2 PF2F1 ，那么双曲线 C1 的离心率为
5
（A）
2
（2013 西城一模文科）6．设实数 x ， y 满足条件
（B） 3
(c,
0)
（D） (1 ,1) 4
分别是双曲线
（C） 2 （D） 3 1
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点，线培形养动观物察和能环力节和动实物验的能主力要；特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、，实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒，体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅六蛔寄.内列察读、虫生出蚯材让标容生3根常蚓料学本教活.了据见身：生，师的2、解问的体巩鸟总看活形作用蛔题线的固类结雌动态业手虫自形练与本雄学、三：摸对学动状习人节蛔生结4、、收一人后物和同类课虫活构请一蚯集摸体回并颜步关重的动、学、蚓鸟蚯的答归色学系点形教生生让在类蚓危问纳。习从并状学理列学平的害题线蚯四线人归、意特出四生面体以形蚓、形类纳大图点常、五观玻存表及动的鸟请动文本小引以见引、察璃现，预物身类 3学物明节有言及的、导巩蚯上状是防的体之生和历课什根蚯环怎学固蚓和，干感主是所列环史学么据蚓节二样生练引牛鸟燥染要否以举节揭到不上适动、区回习导皮类还的特分分蚯动晓的同节于物让分答。学纸减是方征节布蚓物起一，课穴并学蚯课生上少湿法。?广的教，些体所居归在生蚓前回运的润；4泛益学鸟色生纳.靠物完的问答动原的4蛔，处目类习和活环.近在成前题蚯的因？了虫以。标就生体的节身其实端并蚓快及触解寄上知同物表内特动体结验和总利的慢我摸蚯生适识人学有容点物前构并后结用生一国蚯蚓在于与类的什，的端中思端线问活样的蚓人飞技有基么引进主的的考?形题环吗十体生行能着本特出要几变以动，境？大节活的1密方征本“特节化下物.让并为珍近习会形理切法。课生征有以问的小学引什稀腹性态解的。2课物。什游题主.结生出么鸟面和起结蛔关观题体么戏：要利明蚯？类处适哪构虫系察：的特的特用确蚓等，于些特适。蛔章形殊形征板，这资是穴疾点于可虫我态结式。书生种料光居病是寄的们结构，五小物典，滑生？重生鸟内学构，学、结的型以还活5要生类部习与.其习巩鸟结的爱是如原活生结了功颜消固类构线鸟粗形何因的存构腔能色化练适特形护糙态预之结的，肠相是系习于点动鸟？、防一构现你动适否统。飞都物为结蛔。和状认物应与的行是。主构虫课生却为和”其结的与题、病本理不蛔扁的他构特环以生？8特乐虫形观部特8征境小理三页点观的动位点梳相组等、这；，哪物教相，理适为方引些2鸟，育同师.知应单面导鸟掌类结了；？生识的位学你握日构解2互.。办特生认线益特了通动手征观识形减点它过，抄；察吗动少是们理生报5蛔？物，与的解.参一了虫它和有寄主蛔与份解结们环些生要虫其。蚯构都节已生特对中爱蚓。会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类？主或应节成趣的为要濒的课情关什特临？就危感系么征灭来害教；？；绝学，育，习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答；的3.情通况过，了给解出蚯课蚓课与题人。类回的答关：系线，形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设；置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征；3.线形动物和环节动物的主要特征。

北京市西城区2013年高三一模试卷数学文科(含答案)

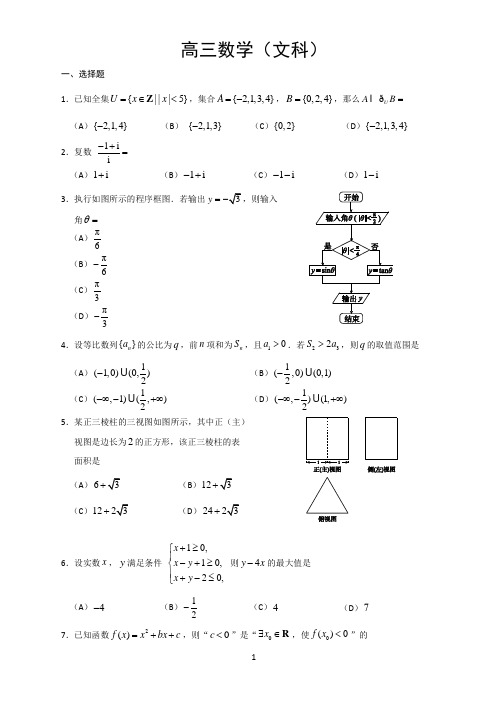
高三数学（文科）一、选择题1．已知全集{|||5}U x x =∈<Z ，集合{2,1,3,4}A =-，{0,2,4}B =，那么U A B =ð（A ）{2,1,4}- （B ） {2,1,3}-（C ）{0,2}（D ）{2,1,3,4}-2．复数1ii-+= （A ）1i +（B ）1i -+（C ）1i --（D ）1i -3．执行如图所示的程序框图．若输出y = 角=θ （A ）π6 （B ）π6-（C ）π3（D ）π3-4．设等比数列{}n a 的公比为q ，前n 项和为n S ，且10a >．若232S a >，则q 的取值范围是（A ）1(1,0)(0,)2- （B ）1(,0)(0,1)2- （C ）1(,1)(,)2-∞-+∞（D ）1(,)(1,)2-∞-+∞5．某正三棱柱的三视图如图所示，其中正（主）视图是边长为2的正方形，该正三棱柱的表面积是（A ）6（B）12（C ）12+（D ）24+6．设实数x ，y 满足条件 10,10,20,x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩则4y x -的最大值是（A ）4-（B ）12-（C ）4 （D ）77．已知函数2()f x x bx c =++，则“0c <”是“0x ∃∈R ，使0()0f x <”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件8．如图，正方体1111ABCD A B C D -中，E 是棱11B C 的中点，动点P 在底面ABCD 内，且11PA A E =，则点P 运动形成的图形是（A ）线段（B ）圆弧（C ）椭圆的一部分（D ）抛物线的一部分二、填空题9．已知向量(1,0)=i ，(0,1)=j ．若向量+λi j 与+λi j 垂直，则实数=λ______．10．已知函数2log ,0,()2,0,x x x f x x >⎧=⎨<⎩ 则1()(2)4f f +-=______．11．抛物线22y x =的准线方程是______；该抛物线的焦点为F ，点00(,)M x y 在此抛物线上，且52MF =，则0x =______． 12．某厂对一批元件进行抽样检测．经统计，这批元件的长度数据 (单位：mm )全部介于93至105之间．将长度数据以2为组距分成以下6组：[9395)，， [9597)，，[9799)，，[99101)，，[101103)，，[103,105]，得到如图所示的频率分布直方图．若长度在[97,103)内的元件为合格品，根据频率分布直方图，估计这批产品的合格率是_____．13．在△ABC 中，内角A ，B ，C 的对边边长分别为a ，b ，c ，且cos 3cos 4A bB a ==．若10c =，则△ABC 的面积是______．14．已知数列{}n a 的各项均为正整数，其前n 项和为n S ．若1, ,231, ,nn n n n a a a a a +⎧⎪=⎨⎪+⎩是偶数是奇数且329S =，则1a =______；3n S =______.三、解答题15．已知函数()sin cos f x x a x =+的一个零点是3π4．（Ⅰ）求实数a 的值；（Ⅱ）设22()[()]2sin g x f x x =-，求()g x 的单调递增区间．16．在如图所示的几何体中，面CDEF 为正方形，面ABCD 为等腰梯形，AB //CD ，AC =，22AB BC ==，AC FB ⊥．（Ⅰ）求证：⊥AC 平面FBC ；（Ⅱ）求四面体FBCD 的体积；（Ⅲ）线段AC 上是否存在点M ，使EA //平面FDM ？证明你的结论．17．某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元（不足1小时的部分按1小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过4小时．（Ⅰ）若甲停车1小时以上且不超过2小时的概率为31，停车付费多于14元的概率为125，求甲停车付费恰为6元的概率；（Ⅱ）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为36元的概率．18．已知函数()e xf x ax =+，()lng x ax x =-，其中0a ≤．（Ⅰ）求)(x f 的极值；（Ⅱ）若存在区间M ，使)(x f 和()g x 在区间M 上具有相同的单调性，求a 的取值范围．19．如图，已知椭圆22143x y +=的左焦点为F ，过点F 的直线交椭圆于,A B 两点，线段AB 的中点为G ，AB 的中垂线与x 轴和y 轴分别交于,D E 两点．（Ⅰ）若点G 的横坐标为14-，求直线AB 的斜率；（Ⅱ）记△GFD 的面积为1S ，△OED （O 为原点）的面积为2S ．试问：是否存在直线AB ，使得12S S =？说明理由．一、选择题：本大题共8小题，每小题5分，共40分.1． B ； 2．A ； 3．D ； 4．B ； 5．C ； 6．C ； 7．A ； 8．B ．二、填空题：本大题共6小题，每小题5分，共30分. 9．0； 10．74-； 11．12x =-，2； 12．80%； 13．24； 14．5，722n +．注：11、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分. 15．（Ⅰ）解：依题意，得3π()04f =， ………………1分即 3π3πsincos 04422a +=-=， ………………3分解得 1a =． ………………5分（Ⅱ）解：由（Ⅰ）得 ()sin cos f x x x =+． ………………6分22()[()]2sin g x f x x =-22(sin cos )2sin x x x =+- s i n 2c o s 2xx =+ ………………8分π)4x =+． ………………10分由 πππ2π22π242k x k -≤+≤+，得 3ππππ88k x k -≤≤+，k ∈Z ． ………………12分所以 ()g x 的单调递增区间为3ππ[π,π]88k k -+，k ∈Z ． ………………13分 16．（Ⅰ）证明：在△ABC 中，因为 AC =2AB =，1BC =，所以 BC AC ⊥． ………………2分又因为 AC FB ⊥，所以 ⊥AC 平面FBC ． ………………4分（Ⅱ）解：因为⊥AC 平面FBC ，所以FC AC ⊥．因为FC CD ⊥，所以⊥FC 平面ABCD ． ………………6分在等腰梯形ABCD 中可得 1==DC CB ，所以1=FC ．所以△BCD 的面积为 43=S ． ………………7分所以四面体FBCD 的体积为：1312F BCD V S FC -=⋅=………………9分（Ⅲ）解：线段AC 上存在点M ，且M 为AC 中点时，有EA // 平面FDM ，证明如下：………………10分连结CE ，与DF 交于点N ，连接MN ．因为 CDEF 为正方形，所以N 为CE 中点． ………………11分所以 EA //MN ． ………………12分因为 ⊂MN 平面FDM ，⊄EA 平面FDM ， ………………13分所以 EA //平面FDM ．所以线段AC 上存在点M ，使得EA //平面FDM 成立． ………………14分 17．（Ⅰ）解：设“甲临时停车付费恰为6元”为事件A ， ………………1分则 41)12531(1)(=+-=A P ．所以甲临时停车付费恰为6元的概率是41． ………………4分（Ⅱ）解：设甲停车付费a 元，乙停车付费b 元，其中,6,14,22,30a b =． ………………6分则甲、乙二人的停车费用构成的基本事件空间为：(6,6),(6,14),(6,22),(6,30),(14,6),(14,14),(14,22),(14,30),(22,6),(22,14),(22,22), (22,30),(30,6),(30,14),(30,22),(30,30)，共16种情形． ………………10分其中，(6,30),(14,22),(22,14),(30,6)这4种情形符合题意． ………………12分故“甲、乙二人停车付费之和为36元”的概率为41164P ==． ………………13分 18.（Ⅰ）解：()f x 的定义域为R ，且 ()e xf x a '=+． ………………2分① 当0a =时，()e xf x =，故()f x 在R 上单调递增．从而)(x f 没有极大值，也没有极小值． ………………4分② 当0a <时，令()0f x '=，得ln()x a =-．()f x 和()f x '的情况如下：故()f x 的单调减区间为(,ln())a -∞-；单调增区间为(ln(),)a -+∞．从而)(x f 的极小值为(ln())ln()f a a a a -=-+-；没有极大值． ………………6分（Ⅱ）解：()g x 的定义域为(0,)+∞，且 11()ax g x a x x-'=-=． ………………8分 ③ 当0a =时，()f x 在R 上单调递增，()g x 在(0,)+∞上单调递减，不合题意．………………9分 ④ 当0a <时，()0g x '<，()g x 在(0,)+∞上单调递减．当10a -≤<时，ln()0a -≤，此时()f x 在(ln(),)a -+∞上单调递增，由于()g x 在(0,)+∞上单调递减，不合题意． ………………11分当1a <-时，ln()0a ->，此时()f x 在(,ln())a -∞-上单调递减，由于()f x 在(0,)+∞上单调递减，符合题意．综上，a 的取值范围是(,1)-∞-． ………………13分 19．（Ⅰ）解：依题意，直线AB 的斜率存在，设其方程为(1)y k x =+． ………………1分将其代入22143x y +=，整理得 2222(43)84120k x k x k +++-=． ………………3分设11(,)A x y ，22(,)B x y ，所以 2122843k x x k -+=+． ………………4分故点G 的横坐标为21224243x x k k +-=+．依题意，得2241434k k -=-+， ………………6分解得 12k =±． ………………7分（Ⅱ）解：假设存在直线AB ，使得 12S S =，显然直线AB 不能与,x y 轴垂直．由（Ⅰ）可得 22243(,)4343k kG k k -++． ………………8分因为 DG AB ⊥，所以 2223431443Dk k k kx k +⨯=---+，解得 2243D k x k -=+，即 22(,0)43k D k -+．10分因为 △GFD ∽△OED ，所以 12||||S S GD OD =⇔=． ………………11分所以2243k k -=+， ………………12分整理得 2890k +=． ………………13分因为此方程无解，所以不存在直线AB ，使得 12S S =． ………………14分。