2021届高考数学模拟试卷汇编:立体几何(含答案解析)
2021年高考数学高考数学压轴题 立体几何多选题分类精编及解析

2021年高考数学高考数学压轴题 立体几何多选题分类精编及解析一、立体几何多选题1.已知正方体1111 ABCD A B C D -的棱长为2,M 为1DD 的中点,N 为正方形ABCD 所在平面内一动点,则下列命题正确的有( )A .若2MN =,则MN 的中点的轨迹所围成图形的面积为πB .若N 到直线1BB 与直线DC 的距离相等,则N 的轨迹为抛物线C .若1D N 与AB 所成的角为3π,则N 的轨迹为双曲线 D .若MN 与平面ABCD 所成的角为3π,则N 的轨迹为椭圆【答案】BC 【分析】对于A ,连接MN ,ND ,DP ,得到直角MDN △,且P 为斜边MN 的中点,所以1PD =,进而得到P 点的轨迹为球面的一部分,即可判断选项A 错误;对于B ,可知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,利用抛物线定义知B 正确;对于C ,建立空间直角坐标系,设(,,0)N x y ,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简可知N 的轨迹为双曲线;对于D ,MN 与平面ABCD 所成的角为3MND π∠=,3ND =,可知N 的轨迹是以D 为圆心,33为半径的圆周; 【详解】对于A ,如图所示,设P 为MN 的中点,连接MN ,ND ,DP ,由正方体性质知MDN △为直角三角形,且P 为MN 的中点,2MN =,根据直角三角形斜边上的中线为斜边的一半,知MDN △不管怎么变化,始终有1PD =,即P 点的轨迹与正方体的面围城的几何体是一个以D 为球心,1为半径的球的18,其面积214182S ππ=⨯⨯=,故A 错误;对于B ,由正方体性质知,1BB ⊥平面ABCD 由线面垂直的性质定理知1NB BB ⊥,即NB 是点N 到直线1BB 的距离,在平面ABCD 中,点N 到定点B 的距离与到定直线DC 的距离相等,所以点N 的轨迹是以点B 为焦点,直线DC 为准线的抛物线,故B 正确; 对于C ,如图以D 为直角坐标系原点,建立空间直角坐标系,(,,0)N x y ,1(0,0,2)D ,(0,2,0)A ,(2,2,0)B ,则1(,,2)D N x y =-,(0,2,0)AB =,利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅,化简整理得:2234y x -=,即221443y x -=,所以N 的轨迹为双曲线,故C 正确;对于D ,由正方体性质知,MN 与平面ABCD 所成的角为MND ∠,即3MND π∠=,在直角MDN △中,3ND =,即N 的轨迹是以D 3D 错误; 故选:BC 【点睛】关键点睛:本题考查立体几何与解析几何的综合,解题的关键是抓住解析几何几种特殊曲线的定义,考查学生的逻辑推理能力,转化与划归能力与运算求解能力,属于难题.2.在正三棱柱111ABC A B C -中,2AC =,11CC =,点D 为BC 中点,则以下结论正确的是( ) A .111122A D AB AC AA =+- B .三棱锥11D AB C -的体积为3C .1AB BC ⊥且1//AB 平面11AC DD .ABC 内到直线AC 、1BB 的距离相等的点的轨迹为抛物线的一部分 【答案】ABD 【分析】A .根据空间向量的加减运算进行计算并判断;B .根据1111D ABC A DB C V V --=,然后计算出对应三棱锥的高AD 和底面积11DB C S,由此求解出三棱锥的体积;C .先假设1AB BC ⊥,然后推出矛盾;取AB 中点E ,根据四点共面判断1AB //平面11AC D 是否成立;D .将问题转化为“ABC 内到直线AC 和点B 的距离相等的点”的轨迹,然后利用抛物线的定义进行判断. 【详解】A .()11111111222A D A A AD AD AA AB AC AA AB AC AA =+=-=+-=+-,故正确; B .1111D AB C A DB C V V --=,因为D 为BC 中点且AB AC =,所以AD BC ⊥, 又因为1BB ⊥平面ABC ,所以1BB AD ⊥且1BB BC B =,所以AD ⊥平面11DB C ,又因为36322AD BD BC ===,111111222DB C S BB B C =⨯⨯=, 所以1111111162333D AB C A DB C DB C V V AD S --==⨯⨯=⋅⋅=,故正确;C .假设1AB BC ⊥成立,又因为1BB ⊥平面ABC ,所以1BB BC ⊥且111BB AB B =,所以BC ⊥平面1ABB ,所以BC AB ⊥,显然与几何体为正三棱柱矛盾,所以1AB BC ⊥不成立;取AB 中点E ,连接11,,ED EA AB ,如下图所示:因为,D E 为,BC AB 中点,所以//DE AC ,且11//AC A C ,所以11//DE AC ,所以11,,,D E A C 四点共面,又因为1A E 与1AB 相交,所以1AB //平面11AC D 显然不成立,故错误;D .“ABC 内到直线AC 、1BB 的距离相等的点”即为“ABC 内到直线AC 和点B 的距离相等的点”,根据抛物线的定义可知满足要求的点的轨迹为抛物线的一部分,故正确; 故选:ABD. 【点睛】方法点睛:求解空间中三棱锥的体积的常用方法:(1)公式法:直接得到三棱锥的高和底面积,然后用公式进行计算;(2)等体积法:待求三棱锥的高和底面积不易求出,采用替换顶点位置的方法,使其求解高和底面积更容易,由此求解出三棱锥的体积.3.已知图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起,使得每个三角形所在的平面都与平面ABCD 垂直,再顺次连接EFGH ,得到一个如图2所示的多面体,则( )A .AEF 是正三角形B .平面AEF ⊥平面CGHC .直线CG 与平面AEF 2D .当2AB =时,多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ,连接OH 、OM ,证明出OH ⊥平面ABCD ,然后以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,求出EF ,可判断A 选项的正误,利用空间向量法可判断BC 选项的正误,利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ,连接OH 、OM , 在图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,则1122CH GH EH DH ===,O 为CD 的中点,OH CD ∴⊥,平面CDH ⊥平面ABCD ,平面CDH 平面ABCD CD =,OH ⊂平面CDH ,OH ∴⊥平面ABCD ,在图1中,设正方形EFGH 的边长为()220a a >,可得四边形ABCD 的边长为2a , 在图1中,ADE 和ABF 均为等腰直角三角形,可得45BAF DAE ∠=∠=, 90BAD ∴∠=,∴四边形ABCD 是边长为2a 的正方形,O 、M 分别为CD 、AB 的中点,则//OC BM 且OC BM =,且90OCB ∠=,所以,四边形OCBM 为矩形,所以,OM CD ⊥,以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项,由空间中两点间的距离公式可得2AE AF EF a ===,所以,AEF 是正三角形,A 选项正确;对于B 选项,设平面AEF 的法向量为()111,,m x y z =,(),0,AE a a =-,()0,,AF a a =,由111100m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩,取11z =,则11x =,11y =-,则()1,1,1m =-,设平面CGH 的法向量为()222,,n x y z =,(),0,CG a a =,()0,,CH a a =-,由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩,取21z =-,可得21x =,21y =-,则()1,1,1n =--,()22111110m n ⋅=+--⨯=≠,所以,平面AEF 与平面CGH 不垂直,B 选项错误;对于C 选项,6cos ,23CG m CG m a CG m⋅<>===⨯⋅, 设直线CG 与平面AEF 所成角为θ,则sin 6θ=,23cos 1sin θθ=-=,所以,sin tan 2cos θθθ==,C 选项正确; 对于D 选项,以ABCD 为底面,以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -,则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点,因为2AB =,即1a =,则1OH =,长方体1111ABCD A B C D -的体积为2214V =⨯=,11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△,因此,多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=, D 选项错误.故选:AC. 【点睛】方法点睛:计算线面角,一般有如下几种方法:(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin hlθ=(l 为斜线段长),进而可求得线面角; (3)建立空间直角坐标系,利用向量法求解,设a 为直线l 的方向向量,n 为平面的法向量,则线面角θ的正弦值为sin cos ,a n θ=<>.4.一副三角板由一块有一个内角为60°的直角三角形和一块等腰直角三角形组成,如图所示,090B F ∠=∠=,060,45,A D BC DE ∠=∠==,现将两块三角形板拼接在一起,得三棱锥F CAB -,取BC 中点O 与AC 中点M ,则下列判断中正确的是( )A .BC FM ⊥B .AC 与平面MOF 3C .平面MOF 与平面AFB 所成的二面角的平面角为45°D .设平面ABF 平面MOF l =,则有//l AB【答案】AD 【分析】证明BC ⊥面FOM 可判断A ;根据AC 与平面MOF 所成的角为060CMO ∠=判断B ;利用特殊位置判断C ;先证明//AB 面MOF ,由线面平行的性质定理可判断D ; 【详解】由三角形中位线定理以及等腰三角形的性质可得,,BC OF BC OM OM OF O ⊥⊥=,所以BC ⊥面FOM BC FM ⇒⊥,故A 正确;因为BC ⊥面FOM ,所以AC 与平面MOF 所成的角为060CMO ∠=,所以余弦值为12,故B 错误;对于C 选项可以考虑特殊位置法,由BC ⊥面FOM 得面ABC ⊥面FOM ,所以点F 在平面ABC 内的射影在直线OM 上,不妨设点F 平面ABC 内的射影为M ,过点M 作//BC MN ,连结NF .易证AB ⊥面MNF ,则l ⊥面MNF ,所以MFN ∠为平面MOF与平面AFB 所成的二面角的平面角,不妨设2AB =,因为060A,所以23BC =,则13,12OF BC OM ===,显然MFN ∠不等于45°,故C 错误. 设面MOF 与平面ABF 的交线为l ,又因为//,AB OM AB ⊄面MOF ,OM ⊂面MOF ,所以//AB 面MOF ,由线面平行的性质定理可得://l AB ,故D 正确; 故选:AD.【点睛】方法点睛:求直线与平面所成的角有两种方法:一是传统法,证明线面垂直找到直线与平面所成的角,利用平面几何知识解答;二是利用空间向量,求出直线的方向向量以及平面的方向向量,利用空间向量夹角余弦公式求解即可.5.如图,正方体1111ABCD A B C D -的棱长为3,线段11B D 上有两个动点,E F ,且1EF =,以下结论正确的有( )A .AC BE ⊥B .异面直线,AE BF 所成的角为定值C .点A 到平面BEF 的距离为定值D .三棱锥A BEF -的体积是定值 【答案】ACD 【详解】由AC BD ⊥,1AC DD ⊥可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确; 取特例,当E 与1D 重合时,F 是F ',AE 即1AD ,1AD 平行1BC ,异面直线,AE BF '所成的角是1C BF '∠,当F 与1B 重合时,E 是E ',BF 即1BB ,异面直线,AE BF '所成的角是1A AE '∠,可知1C BF '∠与1A AE '∠不相等,故异面直线,AE BF 所成的角不是定值,故B 错误;连结BD 交AC 于O ,又AC ⊥平面11D DBB ,点A 到平面11BDD B 的距离是2AO ,也即点A 到平面BEF 的距离是22,故C 正确; 2AO 为三棱锥A BEF -的高,又1111224BEFS =⨯⨯=△,故三棱锥A BEF -的体积为112234224⨯⨯=为定值,D 正确. 故选:ACD 【点睛】求空间中点到平面的距离常见方法为: (1)定义法:直接作平面的垂线,求垂线;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离; (3)向量法:计算斜线在平面的法向量上的投影即可.6.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥ B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 5 【答案】AC 【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN .取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F∠==22C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62D 错误.故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.7.(多选题)如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是( )A .113P AA D V -=B .点P 必在线段1BC 上C .1AP BC ⊥D .AP ∥平面11AC D 【答案】BD【分析】对于A ,1111111113326P AA D AA D V S CD -=⋅=⨯⨯⨯⨯=, 对于B,C,D ,如图以D 为坐标原点可建立空间直角坐标系,利用空间向量判即可.【详解】对于A ,因为点P 在平面11BCC B ,平面11BCC B ∥平面1AA D ,所以点P 到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长, 所以1111111113326P AA D AA D V S CD -=⋅=⨯⨯⨯⨯=,A 错误; 对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则11(1,0,0),(,1,),(1,1,0),(0,0,1),(1,1,1),(0,1,0)A P x z B D B C所以11(1,1,),(1,1,1),(1,0,1)AP x z BD BC =-=--=--, 因为1AP BD ⊥,所以1110AP BD x z ⋅=--+=,所以x z =,即(,1,)P x x ,所以(,0,)CP x x =,所以1CP xBC =-,即1,,B C P 三点共线, 所以点P 必在线段1B C 上,B 正确;对于C ,因为1(1,1,),(1,0,1)AP x x BC =-=-,所以111AP BC x x ⋅=-+=,所以1AP BC ⊥不成立,C 错误;对于D ,因为11(1,0,1),(0,1,1),(0,0,0)A C D ,所以11(1,0,1),(0,1,1)DA DC ==, 设平面11AC D 的法向量为(,,)n x y z =,则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩, 令1x =,则1,1z y =-=,所以(1,1,1)n =-,所以110AP n x x ⋅=-+-=,所以AP n ⊥,所以AP ∥平面11AC D ,D 正确,故选:BD【点睛】此题考查了空间线线垂直的判定,线面平行的判定,三棱锥的体积,考查空间想象能力,考查计算能力,属于较难题.8.(多选题)在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为△ABC 的重心,则111333PQ PA PB PC =++C .若0PA BC =,0PC AB =,则0PB AC =D .若四面体P ABC -各棱长都为2,M N ,分别为,PA BC 的中点,则1MN = 【答案】ABC【分析】作出四面体P ABC -直观图,在每个三角形中利用向量的线性运算可得. 【详解】对于A ,1233AD AC AB =+,32AD AC AB ∴=+,22AD AB AC AD ∴-=- , 2BD DC ∴=,3BD BD DC BC ∴=+=即3BD BC ∴=,故A 正确;对于B ,Q 为△ABC 的重心,则0QA QB QC ++=,33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++,故B 正确; 对于C ,若0PA BC =,0PC AB =,则0PA BC PC AB +=,()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+=0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=,0AC PB ∴=,故C 正确;对于D ,111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯= 2MN ∴=,故D 错误.故选:ABC【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量.(3)在立体几何中三角形法则、平行四边形法则仍然成立.9.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点B .平面1D MN 与BC 的交点是BC 的三点分点C .平面1D MN 与AD 的交点是AD 的三等分点D .平面1D MN 将正方体分成两部分的体积比为1∶1【答案】BC【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F ,连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=,连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==, NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF ,,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒,,,A B F ∴三点共线,取AB 中点S ,连MS , 则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴=== N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点,点Q 是线段AD 靠近点D 的三等分点,点H 是线段11B C 靠近点1C 的三等分点.做出线段BC 的另一个三等分点P ',做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体从而平面1D MN 将正方体分成两部分体积比为2∶1.故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.10.如果一个棱锥的底面是正方形,且顶点在底面内的射影是底面的中心,那么这样的棱锥叫正四棱锥.若一正四棱锥的体积为18,则该正四棱锥的侧面积最小时,以下结论正确的是( ).A .棱的高与底边长的比为22B .侧棱与底面所成的角为4πC .棱锥的高与底面边长的比为2D .侧棱与底面所成的角为3π 【答案】AB【分析】 设四棱锥S ABCD -的高为h ,底面边长为a ,由21183V a h ==得254h a =,然后可得侧面积为242108a a+,运用导数可求出当32a =时侧面积取得最小值,此时3h =,然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案.【详解】设四棱锥S ABCD -的高为h ,底面边长为a可得21183V a h ==,即254h a=所以其侧面积为1422⋅⋅==令()242108f a a a =+,则()23321084f a a a ⨯'=-令()233210840f a a a ⨯'=-=得a =当(a ∈时()0f a '<,()f a 单调递减当()a ∈+∞时()0f a '>,()f a 单调递增所以当a =时()f a 取得最小值,即四棱锥的侧面积最小此时3h =所以棱锥的高与底面边长的比为2,故A 正确,C 错误侧棱与底面所成的角为SAO ∠,由3h =,a =可得3AO = 所以4SAO π∠=,故B 正确,D 错误 故选:AB【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值,属于综合题.。
2021年全国新高考模拟数学试题分类-----立体几何
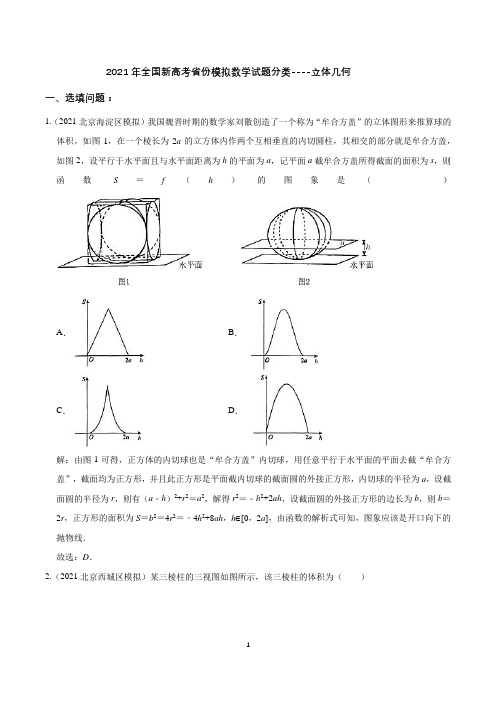
=(a﹣1,﹣1,c﹣1), =(1,1,0), =(0,1,1),
设平面DBC1的法向量 =(x,y,z),则 ,取x=1,得 =(1,﹣1,1),
∵B1E∥平面BDC1,∴ =a﹣1+1+c﹣1=0,解得a+c=1,
∴a2+c2=(a+c)2﹣2ac=1﹣2ac,ac≤( )2= ,设直线B1E与直线AB所成角为θ,
则 ,
故x2= , ,z2= ,
结合图像易得①②正确;
三组对棱长度分别为a=5,b=6,c=7,则x= ,y= ,z= ,
因为等腰四面体的体积是对应长方体体积减去四个小三棱锥的体积,
所以等腰四面体的体积xyz﹣ = =2 ,③正确;
三组对棱长度分别为a,b,c的“等腰四面体”的外接球直径2R= ≠ ,④错误.
故选:D.
2.(2021北京西城区模拟)某三棱柱的三视图如图所示,该三棱柱的体积为( )
A. B. C.8D.4
解:根据几何体的三视图转换为直观图为:该几何体为底面为等腰直角三角形,高为2的直三棱柱;
如图所示:
故 ,
故选:D.
3.(2021湖南模拟)如图,在平行四边形ABCD中,AB=1,AD=2,∠A=60°,沿对角线BD将△ABD折起到△PBD的位置,使得平面PBD⊥平面BCD,下列说法正确的有( )
A.平面PCD⊥平面PBD
B.三棱锥P﹣BCD四个面都是直角三角形
C.PD与BC所成角的余弦值为
D.过BC的平面与PD交于M,则△MBC面积的最小值为
解:△BCD中,CD=1,BC=2,∠A=60°,
所以BD= ,故BD2+CD2=BC2,所以BD⊥CD,
2021年高考数学真题模拟试题专项汇编之立体几何(文)(Word版,含解析)

(8)立体几何(文)——2021年高考数学真题模拟试题专项汇编1.【2021年新高考Ⅰ卷,3】已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为( ) A.2B.22C.4D.422.【2021年新高考Ⅱ卷,4】卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨道高度为36000km (轨道高度指卫星到地球表面的最短距离).把地球看成一个球心为O ,半径为6400km 的球,其上点A 的纬度是指OA 与赤道所在平面所成角的度数,地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为α.该卫星信号覆盖的地球表面面积22π(1cos )S r α=-(单位:2km ),则S 占地球表面积的百分比为( ) A.26%B.34%C.42%D.50%3.【2021年北京卷,4】某四面体的三视图如图所示,该四面体的表面积为( )33+ B.1213+3 4.【2021年浙江卷,4】某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A.32B.3C.322D.325.【2021年新高考Ⅱ卷,5】正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则四棱台的体积为( ) A.5623B.562C.282D.28236.【2021年浙江卷,6】如图,已知正方体1111ABCD A B C D -,,M N 分别是1A D ,1D B 的中点,则( )A.直线1A D 与直线1D B 垂直,直线//MN 平面ABCDB.直线1A D 与直线1D B 平行,直线MN ⊥平面11BDD BC.直线1A D 与直线1D B 相交,直线//MN 平面ABCDD.直线1A D 与直线1D B 异面,直线MN ⊥平面11BDD B7.【2021年北京卷,8】定义:24小时内降水在平地上积水厚度(mm )来判断降雨程度.其中小雨(10<mm ),中雨(10mm —25mm ),大雨(25mm —50mm ),暴雨(50mm —100mm ),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级( )A.小雨B.中雨C.大雨D.暴雨8.【2021年全国乙卷(文),10】在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为( ) A.π2B.π3C.π4D.π69.【2021年全国甲卷(文),14】已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为__________.10.【2021年上海卷,9】已知圆柱的底面半径为1,高为2,AB 为上底面圆的一条直径,点C 为下底底面圆周上的一个动点,点C 绕着下底底面旋转一周,则ABC △面积的取值范围为____________.11.【2021年全国乙卷(文),16】以图①为正视图,在图②③④③中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为___________(写出符合要求的一组答案即可).12.【2021年全国乙卷(文),18】如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.13.【2021年安徽怀宁模拟,18】如图,在三棱柱111ABC A B C -中,侧面11AAC C ⊥底面11,2,ABC AA AC AC AB BC ====,且AB BC ⊥,O 为AC 的中点.(1)求证:平面11A B O ⊥平面1BCA ;(2)若点E 在1BC 上,且//OE 平面1A AB ,求三棱锥1E A BC -的体积.14.【2021年广西桂林模拟(文),18】如图所示,在三棱锥A BCD -中,侧棱AB ⊥平面BCD ,F 为线段BD 中点,Q 为线段AB 中点,2π3BCD ∠=,3AB =,2BC CD ==.证明:(1)CF ⊥平面ABD ; (2)求点D 到平面QCF 的距离.15.【2021年全国甲卷(文),19】已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形.2AB BC ==,E ,F 分别为AC 和1CC 的中点,11BF A B ⊥,(1)求三棱锥F EBC -的体积;(2)已知D 为棱11A B 上的点,证明:BF DE ⊥.答案以及解析1.答案:B解析:本题考查圆锥的侧面展开图.设圆锥的底面半径为r ,母线长为l .由题意可得2ππr l =,所以222l r ==. 2.答案:C解析:由题意可知,6400cos 0.1536000640036000r r α==≈++,所以从同步卫星上可望见的地球的表面积222π(1cos )2π(10.15)S r r α=-≈-,此面积与地球表面积之比约为222π(10.15)100%42%4πr r -⨯≈.3.答案:A解析:画正方体,删点,剩下的4个点就是三棱锥的顶点,如图:1333311(11)2S +=⨯⨯⨯+=表. 4.答案:A解析:本题考查几何体的三视图.该几何体是高为1的四棱柱,其底面为三个全等的直角边为1的等腰直角三角形拼成的梯形,面积为32,故其体积是32. 5.答案:D解析:本题考查棱台的体积.将正四棱台1111A B C D ABCD -补成四棱锥P ABCD -,作PO ⊥底面ABCD 于点O ,交平面1111A B C D 于点1O ,则棱台1111A B C D ABCD -的体积1111P ABCD P A B C D V V V --=-.由题意,11112142PA PO A B PA PO AB ====,易知,4PA =,22AO =22224(22)22PO PA AO --=,所以12PO =,则1322(44)223P ABCD V -=⨯⨯⨯,1111142(22)23P A B C D V -=⨯⨯,所以棱台1111A B C D ABCD -的体积111132242282P ABCD P A B C D V V V --=-==.6.答案:A解析:本题考查空间的线线关系与线面关系.易知1A D ⊥平面1ABD ,故11A D D B ⊥,排除B ,C 项;连接1AD ,可知//MN AB ,所以//MN 平面ABCD ,A 项正确;因为AB 不垂直于平面11BDD B ,//MN AB ,所以直线MN 不垂直于平面11BDD B ,D 项错误.7.答案:B解析:由相似的性质可得,小圆锥的底面半径2002502r ==,故231π5015050π3V =⨯⨯⨯=⋅小圆锥,积水厚度3250π12.5π100V h S ⋅===⋅大小圆锥圆,属于中雨,故选B. 8.答案:D解析:本题考查立体几何中的线面关系及解三角形的应用.如图,记正方体的棱长为a ,则1111112AD C B A C B D a ====,所以1122B P PC a ==,221162BP B P B B a =+=.在1BC P 中,由余弦定理得22211113cos 22PB C B PC PBC PB C B +-∠==⋅,所以1π6PBC ∠=.又因为11//AD BC ,所以1PBC ∠即为直线PB 与1AD 所成的角,所以直线PB 与1AD 所成的角为π6.9.答案:39π解析:本题考查圆锥的体积与侧面积.由题可得圆锥的体积21π12π30π3V r h h ===,可得52h =,故圆锥的母线22132l r h +,所以圆锥的侧面积π39πS rl ==. 10.答案:5]解析:本题主要考查空间几何体.上顶面圆心记为O ,下底面圆心记为O ',连接OC ,过点C 作CM AB ⊥,垂足为点M ,则12ABCSAB CM =⨯⨯,根据题意,AB 为定值2,所以ABCS 的大小随着CM 长短的变化而变化.当点M 与点O 重合时,22125CM OC ==+=,取得最大值,此时12552ABCS =⨯⨯=.当点M 与点B 重合时,CM 取最小值2,此时12222ABCS=⨯⨯=.综上所述,ABCS 的取值范围为[2,5].11.答案:②⑤或③④解析:本题考查几何体的三视图.由高度可知,侧视图只能为②或③.当侧视图为②时,则该三棱锥的直观图如图1,平面PAC ⊥平面ABC ,2PA PC ==,5BA BC =2AC =,此时俯视图为⑤;当侧视图为③时,则该三棱锥的直观图如图2,PA ⊥平面ABC ,1PA =,5AC AB ==2BC =,此时俯视图为④.12.答案:(1)因为PD ⊥底面ABCD ,AM ⊂底面ABCD , 所以PD AM ⊥.又因为PB AM ⊥,PD PB P ⋂=,PB ,PD ⊂平面PBD , 所以AM ⊥平面PBD .因为AM ⊂平面PAM ,所以平面PAM ⊥平面PBD .(2)由PD ⊥底面ABCD ,所以PD 即为四棱锥P ABCD -的高,DPB 是直角三角形. 由题可知底面ABCD 是矩形,1PD DC ==,M 为BC 的中点,且PB AM ⊥.设2AD BC a ==,取CD 的中点为E ,CP 的中点为F ,连接MF ,AF , EF ,AE ,可得//MF PB ,//EF DP ,那么AM M F ⊥,AM F 为直角三角形,且12EF =,2144AE a =+,21AM a =+,222142AF EF AE a =++因为DPB 是直角三角形,所以根据勾股定理得224BP a =+,则2242a MF +=.由AM F 是直角三角形,可得222AM MF AF +=,解得22a =, 所以底面ABCD 的面积22S a ==,则四棱锥P ABCD -的体积11221333V S h =⋅⋅=⨯⨯-.13.答案:(1)1111,//,AB BC AB A B BC A B ⊥∴⊥,在1A AC 中,112AA AC AC ===,O 是AC 的中点,1AO AC ∴⊥,又平面11AAC C ⊥平面ABC ,平面11AAC C平面ABC AC =,1A O ∴⊥平面ABC .BC ⊂平面1,ABC AO BC ∴⊥. 111,A B AO ⊂平面111111,A B O A B AO A =,BC ∴⊥平面11A B O , 又BC ⊂平面1BCA ,∴平面1BCA ⊥平面11A B O .(2)如图,连接1B C ,设1B C 与1BC 交于点E ,连接1,OE AB , 易得1//OE AB ,1AB ⊂平面11,ABB A OE ⊄平面11ABB A ,//OE ∴平面11ABB A ,∴满足条件的E 为1BC 的中点.11111 1122E A BCC A BC B A CC V V V ---==三棱锥三棱锥三棱锥21133212346=⨯⨯⨯⨯=, 故三棱锥1E A BC -的体积为36.14.答案:(1)AB ⊥平面BCD ,CF ,BD ⊂平面BCD ,AB CF ∴⊥,AB BD ⊥.2BC CD ==,F 为BD 中点,CF BD ∴⊥.又CF AB ⊥,AB BD B =,AB ,BD ⊂平面ABD ,CF ∴⊥平面ABD .(2)在三棱锥Q DCF -中,设D 到平面QFC 距离为d . Q DCF D QCF V V --=,1133DCFQCFQB Sd S ∴⋅⋅=⋅⋅,DCFQCFQB S d S ⋅∴=.1112π322sin 2223DCFDCBSS ==⨯⨯⨯⨯=,2π44222cos 233BD =+-⨯⨯⨯.AB BD ⊥,3AB =,Q ,F 分别为AB ,BD 的中点.22912212ADAB BD QF ++∴====.QCF 中,π2cos 13CF ==,235422CQ ⎛⎫=+ ⎪⎝⎭,21QF =. 25211244cos 55212QCF +-∴∠==⨯⨯,21sin QCF ∴∠=. 152121122QCFS∴=⨯⨯=. 33372221d ∴==.15.答案:(1)如图,取BC 的中点为M ,连接EM .由已知易得//EM AB ,2AB BC ==,1CF =,112EM AB ==,11//AB A B , 由11BF A B ⊥得EM BF ⊥,又易得EM CF ⊥,BF CF F ⋂=,所以EM ⊥平面BCF , 故1111121132323F EBC E FBC V V BC CF EM --==⨯⨯⨯=⨯⨯⨯⨯=三棱锥三棱锥.(2)连接1A E ,1B M ,由(1)知11//EM A B , 所以ED 在平面11EMB A 内.在正方形11CC B B 中,由于F ,M 分别是1CC ,BC 的中点,所以1tan 2CF CBF BC ∠==,111tan 2BM BB M BB ∠==, 且这两个角都是锐角,所以1CBF BB M ∠=∠, 所以111190BHB BMB CBF BMB BB M ∠=∠+∠=∠+∠=︒, 所以1BF B M ⊥,又11BF A B ⊥,1111B M A B B ⋂=,所以BF ⊥平面11EMB A , 又DE ⊂平面11EMB A ,所以BF DE ⊥.。
2021年北京高三一模分类汇编立体几何(含解析)

2021北京高三一模数学汇编:立体几何一.选择题(共9小题)1.(2021•延庆区一模)某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是直角三角形,俯视图是直角梯形,则该四棱锥的体积是()A.1 B.2 C.3 D.42.(2021•西城区一模)某四棱锥的三视图如图所示,则该四棱锥的表面积为()A.12 B.C.16 D.3.(2021•东城区一模)某四棱锥的三视图如图所示,该四棱锥的体积为()A.B.9 C.D.274.(2021•怀柔区一模)某四棱柱的三视图如图所示,该几何体的体积为()A.2 B.4 C.6 D.85.(2021•石景山区一模)一几何体的直观图和主视图如图所示,下列给出的四个俯视图中正确的是()A.B.C.D.6.(2021•房山区一模)祖暅是我国南北朝时代伟大的科学家,他在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”.意思是,如果两个等高的几何体在同高处截得的截面面积恒等,那么这两个几何体的体积相等.此即祖暅原理.利用这个原理求球的体积时,需要构造一个满足条件的几何体,已知该几何体三视图如图所示,用一个与该几何体的下底面平行相距为h(0<h<2)的平面截该几何体,则截面面积为()A.4πB.4πh2C.π(2﹣h2)D.π(4﹣h2)7.(2021•朝阳区一模)某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,则该三棱锥最长的棱长为()A.2 B.C.D.8.(2021•门头沟区一模)某四棱锥的三视图如图所示,则此四棱锥最长的棱长为()A.2 B.C.4 D.9.(2021•丰台区一模)某三棱锥的三视图如图所示,该三棱锥中最长的棱长为()A.2 B.C.D.4二.填空题(共1小题)10.(2021•丰台区一模)如图,从长、宽、高分别为a,b,c的长方体AEBF﹣GCHD中截去部分几何体后,所得几何体为三棱锥A﹣BCD.下列四个结论中,所有正确结论的序号是.①三棱锥A﹣BCD的体积为;②三棱锥A﹣BCD的每个面都是锐角三角形;③三棱锥A﹣BCD中,二面角A﹣CD﹣B不会是直二面角;④三棱锥A﹣BCD中,三条侧棱与底面所成的角分别记为α,β,γ,则sin2α+sin2β+sin2γ≤2.三.解答题(共11小题)11.(2021•延庆区一模)如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是边长为2的正方形,侧面ADD1A1为矩形,且侧面ADD1A1⊥底面ABCD,AA1=4,E,M,N分别是BC,BB1,A1D的中点.(Ⅰ)求证:MN∥平面C1DE;(Ⅱ)求二面角D﹣C1E﹣B1的余弦值.12.(2021•西城区一模)如图,在正方体ABCD﹣A1B1C1D1中,E为DD1的中点.(Ⅰ)求证:BD∥平面ACE;(Ⅱ)求直线AD与平面ACE所成角的正弦值.13.(2021•东城区一模)如图,在长方体ABCD﹣A1B1C1D1中,四边形BCC1B1是边长为1的正方形,AB=2,M,N分别为AD,A1B1的中点.(Ⅰ)求证:MA1∥平面ANC;(Ⅱ)求直线CN与平面D1AC所成角的正弦值.14.(2021•海淀区一模)在如图所示的多面体中,AB∥CD,四边形ACFE为矩形,AB=AE=1,AD=CD=2.(Ⅰ)求证:平面ABE∥平面CDF;(Ⅱ)设平面BEF∩平面CDF=l,再从条件①、条件②、条件③这三个条件中选择若干个作为已知,使二面角B﹣l﹣C的大小确定,并求此二面角的余弦值.条件①:AB⊥AD;条件②:AE⊥平面ABCD;条件③:平面AED⊥平面ABCD.15.(2021•丰台区一模)如图,四棱锥P﹣ABCD中,底面ABCD是菱形,,M是棱PB上的点,O是AD 中点,且PO⊥底面ABCD,.(Ⅰ)求证:BC⊥OM;(Ⅱ)若,求二面角B﹣OM﹣C的余弦值.16.(2021•怀柔区一模)如图,在四棱柱ABCD﹣A1B1C1D1中,AB1⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2.(Ⅰ)求证:C1D∥平面ABB1A1;(Ⅱ)求证:AC⊥BC1;(Ⅲ)求二面角C1﹣BD﹣D1的余弦值.17.(2021•房山区一模)如图,在直三棱柱ABC﹣A1B1C1中,已知AB=BC=1,AC=,BB1=2,E为CC1上一点,且EC=.(Ⅰ)求证:平面ABE⊥平面B1BCC1;(Ⅱ)求直线A1C与平面ABE所成角的正弦值.18.(2021•石景山区一模)如图,在五面体ABCDEF中,面ABCD为正方形,面ABFE∩面CDEF=EF,AD⊥ED,CD ⊥EA.(Ⅰ)求证:CD∥平面ABFE;(Ⅱ)若EF=ED,CD=2EF=2,求平面ADE与平面BCF所成的锐二面角的大小.19.(2021•朝阳区一模)如图,在四棱锥P﹣ABCD中,O是AD边的中点,PO⊥底面ABCD,PO=1.在底面ABCD 中,BC∥AD,CD⊥AD,BC=CD=1,AD=2.(Ⅰ)求证:AB∥平面POC;(Ⅱ)求二面角B﹣AP﹣D的余弦值.20.(2021•门头沟区一模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,AB=PA,PA⊥底面ABCD,∠ABC=,E是PC上任一点,AC∩BD=O.(Ⅰ)求证:平面EBD⊥平面PAC;(Ⅱ)若E是PC的中点,求ED与平面EBC所成角的正弦值.21.(2021•平谷区一模)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,△PAB为正三角形,且侧面PAB⊥底面ABCD,PM=MD.(Ⅰ)求证:PB∥平面ACM;(Ⅱ)求二面角M﹣BC﹣D的余弦值.2021北京高三一模数学汇编:立体几何参考答案一.选择题(共9小题)1.【分析】由三视图还原原几何体,该几何体为四棱锥,底面ABCD为直角梯形,AD∥BC,AB⊥AD,PA⊥底面ABCD,且PA=AD=2,AB=BC=1,再由棱锥体积公式求解.【解答】解:由三视图还原原几何体如图,该几何体为四棱锥,底面ABCD为直角梯形,AB⊥AD,PA⊥底面ABCD,且PA=AD=2,则该几何体的体积为V=.故选:A.【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.2.【分析】由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,由此求出四棱锥的表面积.【解答】解:由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,画出四棱锥的直观图,如图所示:则该四棱锥的表面积为:S=S正方形ABCD+S△PAB+S△PAD+S△PBC+S△PCD=22+×2×3+×2×3.故选:D.【点评】本题考查了利用三视图求几何体表面积,是基础题.3.【分析】由三视图知该四棱锥底面为正方形,且一侧棱垂直于底面,结合图中数据求出四棱锥的体积.【解答】解:由三视图知该四棱锥是底面为正方形,且一侧棱垂直于底面,画出四棱锥的直观图,如图所示:则该四棱锥的体积为V=S正方形ABCD•PA=×36×3=9.故选:B.【点评】本题考查了利用三视图求几何体的体积,是基础题.4.【分析】首先把三视图转换为几何体的直观图,进一步求出几何体的体积.【解答】解:根据几何体的三视图转换为直观图为:该几何体为底面为直角梯形,高为2的直四棱柱;如图所示:故:V=.故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的体积公式的应用,主要考查学生的运算能力和数学思维能力,属于基础题.5.【分析】通过几何体结合三视图的画图方法,判断选项即可.【解答】解:几何体的俯视图,轮廓是矩形,所以C;几何体的上部的棱与正视图方向垂直,所以A不正确.故选:B.【点评】本题考查三视图的画法,几何体的结构特征,属于基础题.6.【分析】根据三视图知该几何体为一个圆柱挖去一个圆锥,得到截面为圆环,根据圆环面积公式计算即可.【解答】解:由已知得到几何体为一个圆柱挖去一个圆锥,底面半径为2,截面为圆环,设小圆半径为r,则=,所以r=h,所以截面圆环的面积为4π﹣πh2=π(3﹣h2);故选:D.【点评】本题考查了几何体得到三视图以及截面面积的计算问题,也考查了空间几何体的结构特征,是基础题.7.【分析】首先把三视图转换为几何体的直观图,进一步求出几何体的个各棱长,从而确定结果.【解答】解:根据几何体的三视图转换为直观图为:该几何体为三棱锥A﹣BCD;如图所示:所以:AB=BC=,CD=BD=7,AC=,故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,三棱锥的棱长的求法,主要考查学生的运算能力和数学思维能力,属于基础题.8.【分析】画出直观图,利用三视图的数据转化求解即可.【解答】解:根据直观图不难得出,PC是最长的棱长,长度为:.故选:D.【点评】本题考查三视图求解几何体的相关数据,最长棱长的求法,是基础题.9.【分析】首先把三视图转换为几何体的直观图,进一步求出最大棱长.【解答】解:根据几何体的三视图转换为直观图为:该几何体为三棱锥体;如图所示:最长的棱长为AB=.故选:C.【点评】本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的棱长的求法,主要考查学生的运算能力和数学思维能力,属于基础题.二.填空题(共1小题)10.【分析】求出三棱锥A﹣BCD的体积判断①;由余弦定理的推论判断②;利用空间向量判断③;直接证明sin2α+sin2β+sin2γ≤2判断④.【解答】解:对于①,长方体的体积为abc,三棱锥A﹣BCD的体积为abc﹣4×=,故①正确;对于②,三棱锥A﹣BCD的每一个面的三边长都可以用过一个顶点的三条侧棱表示,不妨以△ACD为例,AD2=a2+c2,AC2=b8+c2,CD2=a6+b2,∵AD2+AC5>CD2,AD2+CD3>AC2,AC2+CD3>AD2,∴△ACD一定是锐角三角形,同理可得△ABC,△BCD为锐角三角形,则三棱锥A﹣BCD的每个面都是锐角三角形,故②正确;对于③,如图,分别以FA、FD所在直线为x、y,则A(a,0,4),b,0),b,0),5,0),0,c),C(a,b,c),2,c),,,,设平面ACD的一个法向量为,由,取y=7,则,同理可得平面BCD的一个法向量为,,取a=b=,,可得二面角A﹣CD﹣B是直二面角;对于④,不妨设AB与底面所成角为α,AD与底面所成角为γ,由③可知,平面BCD的一个法向量为,,sinβ=,==.同理可得,,,则sin6α+sin2β+sin2γ,故④正确.故答案为:①②④.【点评】本题考查空间角与多面体体积的求法,考查空间想象能力与思维能力,考查运算求解能力,是中档题.三.解答题(共11小题)11.【分析】(Ⅰ)连结B1C,ME,利用中位线定理可证明四边形MNDE为平行四边形,从而得到MN∥ED,由线面平行的判定定理证明即可;(Ⅱ)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面的法向量,然后由向量的夹角公式求解即可.【解答】(Ⅰ)证明:连结B1C,ME,E分别为BB1,BC的中点,所以ME∥B5C,且,又因为N为A1D的中点,所以,由题设知A1B7∥DC且A1B1=DC,可得B3C∥A1D且B1C=A8D,故ME∥ND且ME=ND,因此四边形MNDE为平行四边形,所以MN∥ED,又MN⊄平面C1DE,ED⊂平面C1DE,所以MN∥平面C8DE;(Ⅱ)因为底面ABCD是正方形,所以CD⊥AD,又因为侧面ADD1A1⊥底面ABCD,且侧面ADD2A1∩底面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面ADD1A2,又DD1⊂平面ADD1A6,所以CD⊥DD1,又因为侧面ADD1A2为矩形,所以AD⊥DD1,以点D为坐标原点建立空间直角坐标系D﹣xyz如图所示,其中D(0,2,0),C1(7,2,4),4,0),2,3),所以,,因为CD⊥平面ADD1A4,所以DC⊥平面BCC1B1,故为平面C7EB1的一个法向量,设为平面DC1E面的法向量,则,即,令y=﹣2,可得,所以,因为二面角A﹣DE﹣B4的平面角是钝角,所以二面角A﹣DE﹣B1的余弦值.【点评】本题考查了立体几何的综合应用,涉及了线面平行的判定定理的应用,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.12.【分析】(Ⅰ)连接BD交AC于点O,连接OE,证明OE∥BD1.然后证明BD1∥平面ACE.(Ⅱ)不妨设正方体的棱长为2,建立空间直角坐标系A﹣xyz.求出平面ACE的法向量,利用空间向量的数量积求解直线AD与平面ACE所成角的正弦值即可.【解答】(Ⅰ)证明:连接BD交AC于点O,连接OE,在正方形ABCD中,OB=OD.因为E为DD1的中点,所以OE∥BD1.………………(7分)因为BD1⊄平面ACE,OE⊂平面ACE,所以BD1∥平面ACE. ………………(8分)(Ⅱ)解:不妨设正方体的棱长为2,建立如图所示的空间直角坐标系A﹣xyz.则A(0,5,0),2,7),2,0),6,1),所以,,. ………………(8分)设平面ACE的法向量为=(x,y,所以所以即令y=﹣1,则x=7,于是=(1,2)设直线AD与平面ACE所成角为θ,则.………………(13分)所以直线AD与平面ACE所成角的正弦值为.【点评】本题考查直线与平面平行的判定定理的应用,直线与平面所成角的求法,考查空间想象能力,转化思想以及计算能力,是中档题.13.【分析】(Ⅰ)取AC的中点O,连结OM,ON,先证明OM∥CD,OM=CD,再证明NA1∥CD,NA1=CD,从而证明MA1∥ON,利用线面平行的判定定理证明即可;(Ⅱ)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面D1AC的法向量,由向量的夹角公式求解即可.【解答】(Ⅰ)证明:取AC的中点O,连结OM,因为M是AD的中点,所以OM∥CD CD,在长方体ABCD﹣A6B1C1D5中,因为N是A1B1的中点,所以NA3∥CD,NA1=CD,所以NA1∥OM且NA1=OM,所以四边形NOMA3是平行四边形,所以MA1∥ON,又因为MA1⊄平面ANC,ON⊂平面ANC,所以MA8∥平面ANC;(Ⅱ)解:在长方体ABCD﹣A1B1C5D1中,以点B为坐标原点,则C(1,6,0),2,2),D1(1,7,1),1,6),所以,设平面D1AC的法向量为,则有,即,令y=1,则x=2,故,所以=,故直线CN与平面D1AC所成角的正弦值为.【点评】本题考查了线面平行的证明以及线面角的求解,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.14.【分析】(Ⅰ)利用线面平行的判定定理分别证明CF∥平面ABE,CD∥平面ABE,再利用面面垂直的判定定理,即可证明面面平行;(Ⅱ)若选①②:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.若选①②③:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.若选①③:建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,求出平面BEF和平面CDF的法向量,然后利用空间向量的夹角公式求解即可.【解答】解:(Ⅰ)证明:因为四边形ACFE为矩形,所以CF∥AE,又AE⊂平面ABE,CF⊄平面ABE,又因为AB∥CD,又AB⊂平面ABE,所以CD∥平面ABE,又CD∩CF=C,CD,所以平面ABE∥平面CDF;(Ⅱ)选择①②:因为AE⊥平面ABCD,AB,所以AE⊥AB,AE⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,6),0,1),4,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.选择①②③:因为AE⊥平面ABCD,AD⊂平面ABCD,因为平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,所以AB⊥平面ADE,又AE⊂平面ADE,所以AB⊥AE,又因为AB⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,3),0,1),7,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.选择①③:因为平面AED⊥平面ABCD,平面AED∩平面ABCD=AD,所以AB⊥平面ADE,又AE⊂平面ADE,所以AB⊥AE,在矩形ACFE中,AE⊥AC,又AC,AB⊂平面ABCD,所以AE⊥平面ABCD,又AD⊂平面ABCD,所以AE⊥AD,所以AB,AE,以点A为坐标原点建立空间直角坐标系如图所示,则B(1,0,5),0,1),4,1),所以,设平面BEF的法向量为,则,即,令x=1,则y=﹣1,故,因为AD⊥平面ABE,又平面ABE∥平面CDF,所以AD⊥平面CDF,取平面CDF的一个法向量为,所以,故二面角B﹣l﹣C的余弦值为.【点评】本题考查了立体几何的综合应用,涉及了面面平行的判定定理,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.15.【分析】(Ⅰ)推导出OB⊥AD,由AD∥BC,得OB⊥BC,由PO⊥底面ABCD,得OP⊥BC,从而BC⊥平面POB,由此能证明BC⊥OM.(Ⅱ)由PO⊥底面ABCD,OB⊥AD,建立空间直角坐标系O﹣xyz,利用向量法能求出二面角B﹣OM﹣C的余弦值.【解答】解:(Ⅰ)证明:在菱形ABCD中,,△ABD为等边三角形,∵O为AD的中点,∴OB⊥AD,∵AD∥BC,∴OB⊥BC,∵PO⊥底面ABCD,BC⊂平面ABCD,∴OP⊥BC,∵OP∩OB=O,OP,∴BC⊥平面POB,∵M是棱PB上的点,∴OM⊂平面POB,∴BC⊥OM.(Ⅱ)∵PO⊥底面ABCD,OB⊥AD,建立如图所示的空间直角坐标系O﹣xyz,设OA=1,则OP=OB=,O(0,0,6),0,0),,0),,2),0,),∴=(﹣7,,由PM=,得==(6,,),设=(x,y,由,令y=2,得),∵平面POB的法向量为=(1,5,∴cos<>==.由题知二面角B﹣OM﹣C为锐二面角,∴二面角B﹣OM﹣C的余弦值为.【点评】本题考查线线垂直的证明,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.16.【分析】(Ⅰ)证明C1D平行于平面ABB1A1内的直线AB1即可;(Ⅱ)证明AC垂直于平面C1BD内两条相交直线,得到AC⊥平面C1BD,从而得到AC⊥BC1;(Ⅲ)先求二面角两面的法向量,再用夹角公式计算二面角的余弦值即可.【解答】解:(Ⅰ)证明:因为B1C1∥BC、B6C1=BC,AD∥BC,所以B1C2∥AD、B1C1=AD,所以四边形B5C1DA为平行四边形,所以C1D∥AB4,AB1⊂平面ABB1A7,C1D⊄平面ABB1A4,所以C1D∥平面ABB1A2;(Ⅱ)证明:因为AB1⊥平面ABCD,由(Ⅰ)知C1D∥AB8,所以C1D⊥平面ABCD,又因为AC⊂平面ABCD,所以AC⊥C1D,因为ABCD是正方形,所以AC⊥BD,又因为C6D∩BD=D,所以AC⊥平面C1BD,因为C1B⊂平面C6BD,所以AC⊥BC1;(Ⅲ)因为AB1⊥平面ABCD,所以AB5⊥AD,AB1⊥AB,又因为ABCD是正方形,所以AB⊥AD,于是AD、AB1两两垂直,建立如图所示的空间直角坐标系,平面C4BD的法向量为==(1,1,=(﹣4,1,0),,﹣1,),设平面BDD6的法向量为=(x,y,则,令y=,则,,1),所以二面角C2﹣BD﹣D1的余弦值为==.【点评】本题考查了直线与平面位置关系,线面垂直的判定定理和性质,考查了二面角的计算问题,属于中档题.17.【分析】(Ⅰ)由BB1⊥平面ABC,知BB1⊥AB,由勾股定理的逆定理证AB⊥BC,再结合线面垂直的判定定理、面面垂直的判定定理,即可证明平面ABE⊥平面B1BCC1;(Ⅱ)以B为原点建立空间直角坐标系,求得平面ABE的法向量,设直线A1C与平面ABE所成角为θ,由sin θ=|cos<,>|,求出直线A1C与平面ABE所成角的正弦值.【解答】解:(Ⅰ)证明:由直三棱柱的性质知,BB1⊥平面ABC,∵AB⊂平面ABC,∴BB1⊥AB,∵AB=BC=4,AC=,∴AB⊥BC,又BB1∩BC=B,BB2、BC⊂平面B1BCC1,∴AB⊥平面B4BCC1,∵AB⊂平面ABE,∴平面ABE⊥平面B1BCC6.(Ⅱ)以B为原点,BA,BB1所在直线分别为x,y,z轴,则A(1,3,0),0,3),1,0),8,),A7(1,0,4),∴=(﹣1,6,=(1,0,=(5,1,),设平面ABE的法向量为=(x,y,则,即,令z=2,则x=0,∴=(3,2),设直线A1C与平面ABE所成角为θ,则sinθ=|cos<,>|=||=,故直线A1C与平面ABE所成角的正弦值为.【点评】本题考查空间中线与面的垂直关系、线面角的求法,熟练掌握线面、面面垂直的判定定理或性质定理,以及利用空间向量处理线面角的方法是解题的关键,考查逻辑推理能力和运算能力,属于中档题.18.【分析】(Ⅰ)证明CD∥AB,然后证明CD∥平面ABFE.(Ⅱ)以点D为坐标原点,DA,DC,DE分别为x,y,z轴,建立空间直角坐标系.求出平面ADE的法向量,平面BCF的法向量,利用空间向量的数量积求解平面ADE与平面BCF所成锐二面角的大小即可.【解答】(Ⅰ)证明:在五面体ABCDEF中,因为面ABCD是正方形,所以CD∥AB.又因为AB⊂平面ABFE,CD⊄平面ABFE,所以CD∥平面ABFE.(Ⅱ)解:因为面ABCD是正方形,所以CD⊥AD.又因为CD⊥AE.又AD∩AE=A,所以CD⊥平面ADE又因为DE⊂平面ADE,所以CD⊥DE.因为面ABCD是正方形,所以CD⊥AD.又因为AD⊥DE,所以以点D为坐标原点,DA,DE分别为x,y,如图建立空间直角坐标系.因为CD=2EF=2,EF=ED,7,0),0,7),2,0),4,0),0,5).由(Ⅰ)CD∥平面ABFE,CD⊂平面CDEF,平面CDEF∩平面ABFE=EF,所以CD∥EF.所以.可得F(2,1,1).由题意知平面ADE的法向量为设平面BCF的法向量为.由得令y=1,得z=3,所以设平面ADE与平面BCF所成锐二面角为θ.cosθ=.所以平面ADE与平面BCF所成锐二面角为【点评】本题考查直线与平面平行的判断定理的应用,二面角的平面角的求法,考查空间想象能力,转化思想以及计算能力,是中档题.19.【分析】(Ⅰ)先证明四边形ABCO是平行四边形,即可得到AB∥OC,由线面平行的判定定理证明即可;(Ⅱ)建立空间直角坐标系,然后求出所需点的坐标,利用待定系数法求出平面BAP的法向量,由向量的夹角公式求解即可.【解答】(Ⅰ)证明:在四边形ABCD中,因为BC∥AD,,O是AD的中点,则BC∥AO,所以四边形ABCO是平行四边形,所以AB∥OC,又因为AB⊄平面POC,CO⊂平面POC,所以AB∥平面POC;(Ⅱ)连结OB,因为PO⊥平面ABCD,PO⊥OD,又因为点O时AD的中点,且,所以BC=OD,因为BC∥AD,CD⊥AD,所以四边形OBCD是正方形,所以BO⊥AD,建立空间直角坐标系如图所示,则A(0,﹣2,B(1,0,C(3,1,D(0,3,P(0,0,所以,设平面BAP的法向量为,则,即,令y=1,故,因为OB⊥平面PAD,所以是平面PAD的一个法向量,所以=,由图可知,二面角B﹣AP﹣D为锐角,所以二面角B﹣AP﹣D的余弦值为.【点评】本题考查了立体几何的综合应用,涉及了线面平行的判定定理的应用,在求解空间角的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.20.【分析】(Ⅰ)证明PA⊥BD,BD⊥AC,推出BD⊥平面PAC,即可证明平面EBD⊥平面PAC.(Ⅱ)E是PC的中点,连结OE,OB,OC,OE两两垂直,建立如图所示的坐标系,求出平面EBC的法向量,直线DE的方向向量,利用空间向量的数量积求解ED与平面EBC所成角的正弦值即可.【解答】解:(Ⅰ)PA⊥平面ABCD⇒PA⊥BD,…………………………………(1分)底面ABCD菱形,可得BD⊥AC又PA∩AC=A,又PA⊥BD,BD⊥AC,PA⊂平面PAC,AC⊂平面PAC,…………………………………………(2分)BD⊂平面EBD,平面EBD⊥平面PAC(Ⅱ)若E是PC的中点,连结OE,……(6分)所以,OB,OE两两垂直,………(1分)不妨设AB=2,则…(6分)设平面EBC的法向量为=(x,y,,取x=1,则y=z=,=(1,,),直线DE的方向向量为=(,0,cos==.ED与平面EBC所成角的正弦值为:.【点评】本题考查直线与平面垂直的判断定理的应用,直线与平面所成角的求法,是中档题.21.【分析】(Ⅰ)连接BD交AC于H点,连接MH,推导出MH∥BP,从而PB∥平面ACM;(Ⅱ)取AB中点O,连接PO,证明PO⊥平面ABCD,以O为原点,分别以OB,OH,OP所在直线为x,y,z轴建立空间直角坐标系,分别求出平面MBC与平面ABCD的一个法向量,由两法向量所成角的余弦值可得二面角M ﹣BC﹣D的余弦值.【解答】证明:(Ⅰ)连接BD交AC于H点,连接MH,∵四边形ABCD是菱形,∴点H为BD的中点.又∵M为PD的中点,∴MH∥BP,又∵BP⊄平面ACM,MH⊂平面ACM,∴PB∥平面ACM;解:(Ⅱ)取AB中点O,连接PO,∵△PAB为正三角形,且侧面PAB⊥底面ABCD,以O为原点,分别以OB,OP所在直线为x,y,则B(1,0,6),2,0),1,),=(0,2,0),,1,),设平面MBC的一个法向量为,由,取z=,得,平面ABCD的一个法向量为,∴cos<>==.由图可知,二面角M﹣BC﹣D为锐角.【点评】本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.。
2021年高考数学立体几何全真模拟预测练习卷含答案

251.已知两平面α,β相交于直线a,直线b在β内与直线a相交于A点,直线c在平面α内与直线a平行,请用反证法论证b,c为异面直线.解析:这题规定用反证法,提出与结论相反的假定后,要注意分可能的几种情况讨论.证:用反证法.假设b,c共面,则b∥c或b,c相交.(1)若b∥c,∵c∥a, ∴a∥b这与b∩a=A的已知条件矛盾;(2)若b∩c=P,∵bβ,∴P∈β.又∵cα,∴P∈α. ∴P∈α∩β而α∩β=a.∴P∈a,这样c,a有了公共点P,这与a∥c的已知条件矛盾.综上所述,假设不成立,所以b、c为异面直线.说明本题如不指明用反证法,也可以考虑用平面直线的判定定理来证明.252.如图,在棱长为a的正方体ABCD—A1B1C1D1中,异面直线AA1和BD1的中点分别是E、F.(1)证明EF是AA1与BD1的公垂线段;(2)求异面直线AA1和BD1间的距离.解析:(1)连接ED 1、EB , 则显然ED 1=EB =25a 又F 为BD 1之中点. ∴ EF ⊥BD 1; 连接FA 1,FA.∵ F 为正方体的中心,∴ FA =FA 1,又E 为AA 1之中点, ∴ EF ⊥A 1A.故EF 为AA 1与BD 1的公垂线段. (2)在Rt ΔEFD 1中 EF =2121FD ED -=a a a 22434522=-. 故AA 1到BD 1间的距离是a 22.评析:今后学习了线面的位置关系之后,可以利用“转化”的思想求距离. 253. 如图所示,正三棱锥S —ABC 的侧棱与底面的边长相等,如果E 、F 分别为SC 、AB 的中点,求异面直线EF 与SA 所成的角.解析:计算EF 、SA 所成的角,可把SA 平移,使其角的顶点在EF 上.为此取SB 之中点G ,连GE 、GF 、BE 、AE ,由三角形中位线定理:GE =21BC ,GF =21SA ,且GF ∥SA ,所以∠GFE 就是EF 与SA 所成的角.若设此正三棱锥棱长为a ,那么GF =GE =21a,EA =EB =23a,EF =22)21(AB EA =22a ,因为ΔEGF 为等腰直角三角形.∠EFG =45°,所以EF 与SA 所成的角为45°. 说明 异面直线所成角的求法:利用定义构造角,可固定一条,平移另一条,或同时平移到某个特殊的位置,顶点选在特殊的位置上,通过证明所作的角就是所求的角或者补角,解三角形,可求.254. 在空间四边形ABCD 中,M 、N 、P 、Q 分别是四边上的点,且满足MBAM=NB CN =QD AQ =PDCP =k.(1)求证:M 、N 、P 、Q 共面.(2)当对角线AC =a,BD =b ,且MNPQ 是正方形时,求AC 、BD 所成的角及k 的值(用a,b 表示) 解析:(1)∵MBAM =QD AQ =k ∴ MQ ∥BD ,且MB AM AM +=1+k k∴BD MQ =AB AM =1+k k∴ MQ =1+k kBD 又NB CN =PDCP=k ∴ PN ∥BD ,且NB CN CN +=1+k k∴BD NP =CB CN =1+k k 从而NP =1+k kBD ∴ MQ ∥NP ,MQ ,NP 共面,从而M 、N 、P 、Q 四点共面. (2)∵MA BM =k 1,NC BN =k1∴MA BM =NC BN =k 1,MABM BM +=11+k ∴ MN ∥AC ,又NP ∥BD.∴ MN 与NP 所成的角等于AC 与BD 所成的角.∵ MNPQ 是正方形,∴∠MNP =90° ∴ AC 与BD 所成的角为90°, 又AC =a ,BD =b ,AC MN =BA BM =11+k ∴ MN =11+k a 又 MQ =11+k b,且MQ =MN , 1+k k b =11+k a ,即k =ba.说明:公理4是证明空间两直线平行的基本出发点.255.已知:直线a 和直线b 是异面直线,直线c ∥a ,直线b 与c 不相交,求证:b 、c 是异面直线.证:因为b,c 不相交,b 、c 的位置关系有b ∥c 或b 、c 异面两种可能. 假设b ∥c,∵ c ∥a,∴ a ∥b ,这与已知a,b 是异面直线矛盾. 所以b 与c 不能平行,又b 、c 不相交 所以b,c 是异面直线.256.分别和两条异面直线AB 、CD 同时相交的两条直线AC 、BD 一定是异面直线,为什么?证明:假设AC 、BD 不异面,则它们都在某个平面α内,这时A 、B 、C 、D 四点都在α上,由公理1知A、B 、C 、D α,这与已知AB 与CD 异面矛盾,所以AC 、BD 一定是异面直线.257. 如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( ) A.1715B.21C.178D.23解析:过A 点在平面ABB 1A 1内作AF ,使A 1F =D 1F 1,则ADF 1F 是平行四边形,∴FA ∥DF 1,再过E 1在平面ABB 1A 1内作E 1E ∥FA ,则∠BE 1E 即是BE 1与DF 1所成的角,由已知BE 1=DF 1=411B A ,ABCD —A 1B 1C 1D 1是正方体,∴ E 1E =417A 1B 1, 又DF 1=AF =E 1E ,DF 1=BE 1. ∴ E 1E =417A 1B 1,EB =21A 1B 1 在ΔBE 1E 中,cos ∠BE 1E =11221212BE E E BE BE E E ⋅⋅-+=1715.∴ 应选A.258. 在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( ) A.23B.1010C.53D.52解析:由图所示,AM 与CN 是异面直线,过N 作平行于AM 的平行线NP ,交AB 于P ,由定义可知∠PNC 就是AM 与CN 所成的角.因ΔPBC ,ΔPBN ,ΔCBN 皆为直角三角形,且BP =41,BN =21,BC =1,故PN 2=(41)2+(21)2=165,CN 2=(21)2+12=45,PC 2=(41)2+12=1617,在ΔPCN 中cos ∠PNC =CN PN PC CN PN ⋅-+2222,所以cos ∠PNC =52,因此应选D.259. 已知异面直线a 与b 所成的角为50°,P 为空间一定点,则过点P 且与a 、b 所成的角都是30°的直线有且仅有( )A.1条B.2条C.3条D.4条解析: 过P 点分别作直线a ′∥a,b ′∥b,则a ′与b ′的夹角为50°,由异面直线所成的角的定义可知,过P 点与a ′,b ′成30°角的条数,就是所求的条数.画图可知,过P点与a′、b′成30°角的直线只有两条.∴应选B.的直260. .若a、b为异面直线,P为空间一点,过P且与a、b所成角均为3线有( )A.二条B.二条或三条C.二条或四条D.二条、三条或四条解析:D。
2021年高考数学三轮专项模拟试卷 理(立体几何)(含解析)新人教A版(1)

立体几何本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部份,共150分,考试时刻120分钟.第Ⅰ卷一、选择题(本大题共8小题,每题5分,共40分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的)1.(2021·肇庆模拟)在△ABC中,已知|AB→|=|BC→|=|CA→|=2,那么向量AB→·BC→=( )A.2 B.-2C.2 3 D.-23【解析】向量AB→与BC→的夹角为2π3,那么AB→·BC→=2×2×cos23π=-2.【答案】B2.在正四面体P-ABC中,D,E,F别离是AB,BC,CA的中点,下面四个结论中不成立的( ) A.BC∥平面PDFB.DF⊥平面PAEC.平面PDE⊥平面ABCD.平面PAE⊥平面ABC【解析】假设平面PDF⊥平面ABC,那么极点P在底面的射影在DF上,又因为正四面体的极点在底面的射影是底面的中心,因此结论不成立,应选C.【答案】C3.(2021·济宁模拟)点M、N别离是正方体ABCD—A1B1C1D1的棱A1B1、A1D1的中点,用过A、M、N 和D、N、C1的两个截面截去正方体的两个角后取得的几何体如以下图1,那么该几何体的正(主)视图、侧(左)视图、俯视图依次为( )图1A.①②③B.②③④C.①③④D.②④③【解析】依照三视图的概念可知选B.【答案】 B4.(2021·枣庄模拟)设z =x +y ,其中实数x ,y 知足⎩⎪⎨⎪⎧x +2y ≥0,x -y ≤0,0≤y ≤k ,若z 的最大值为6,那么z 的最小值为( )A .-3B .-2C .-1D .0【解析】由z =x +y 得y =-x +z ,作出⎩⎪⎨⎪⎧x +2y ≥0,x -y ≤0,0≤y ≤k ,的区域BCO ,平移直线y =-x +z ,由图象可知当直线通过C 时,直线的截距最大,现在z =6,由⎩⎪⎨⎪⎧y =x ,y =-x +6,解得⎩⎪⎨⎪⎧x =3,y =3,因此k =3,解得B (-6,3),代入z =x +y 得最小值为z =-6+3=-3,选A. 【答案】 A5.(2021·课标全国卷Ⅰ)如图2,有一个水平放置的透明无盖的正方体容器,容器高8 cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm ,若是不计容器厚度,那么球的体积为( )图2 cm 3 cm 3 cm 3cm 3【解析】 如图,作出球的一个截面,那么MC =8-6=2(cm),BM =12AB =12×8=4(cm).设球的半径为R cm ,那么R 2=OM 2+MB 2=(R -2)2+42,∴R =5,∴V 球=43π×53=5003π(cm 3). 【答案】 A6.(2021·临汾模拟)已知平面α⊥平面β,α∩β=l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,那么以下四种位置关系中,不必然成立的是( )A .AB ∥m B .AC ⊥m C .AB ∥βD .AC ⊥β【解析】 因为m ∥α,m ∥β,α∩β=l ,因此m ∥l . 因为AB ∥l ,因此AB ∥m ,故A 必然正确.因为AC ⊥l ,m ∥l ,因此AC ⊥m ,从而B 必然正确. 因为AB ∥l ,l ⊂β,AB ⊄β. 因此AB ∥β.故C 也正确.因为AC ⊥l ,当点C 在平面α内时,AC ⊥β成立,当点C 不在平面α内时,AC ⊥β不成立,故D 不必然成立.【答案】 D7.在正三棱柱ABC —A 1B 1C 1中,D 是AC 的中点,AB 1⊥BC 1,那么平面DBC 1与平面CBC 1所成的角为( )A .30°B .45° C.60° D .90°【解析】 以A 为坐标原点,AC →,AA 1→的方向别离为y 轴和z 轴的正方向成立空间直角坐标系.设底面边长为2a ,侧棱长为2b , 则A (0,0,0),C (0,2a,0),D (0,a,0),B (3a ,a,0),C 1(0,2a,2b ),B 1(3a ,a,2b ).由AB 1→⊥BC 1→,得AB 1→·BC 1→=0,即2b 2=a 2. 设n 1=(x ,y ,z )为平面DBC 1的一个法向量, 则n 1·DB →=0,n 1·DC 1→=0.即⎩⎪⎨⎪⎧3ax =0,ay +2bz =0.又2b 2=a 2,令z =1,解得n 1=(0,-2,1).同理可求得平面CBC 1的一个法向量为n 2=(1,3,0).利用公式cos θ=|n 1·n 2||n 1||n 2|=22,得θ=45°.【答案】 B8.(2021·成都模拟)已知正四棱锥S —ABCD 中,SA =23,那么当该棱锥的体积最大时,它的高为( )A .1 C .2D .3【解析】如下图,设正四棱锥高为h,底面边长为a,那么22a=12-h2,即a2=2(12-h2),因此V =13×a 2×h =23h (12-h 2)=-23(h 3-12h ), 令f (h )=h 3-12h ,则f ′(h )=3h 2-12(h >0),令f ′(h )=0,则h =2,现在f (h )有最小值,V 有最大值. 【答案】 C 第Ⅱ卷二、填空题(本大题共7小题,每题5分,共35分,把答案填在题中横线上) 9.(2021·东营模拟)已知等比数列{a n },假设存在两项a m ,a n 使得a m ·a n =a 23,那么1m +4n的最小值为________.【解析】 由等比数列的性质知m +n =6,那么1m +4n =16⎝ ⎛⎭⎪⎫1m +4n (m +n )=16⎝⎛⎭⎪⎫5+4m n +n m ≥32,当且仅当4m n =nm,即m =2,n =4时等号成立. 【答案】 3210.已知函数f (x )=A sin ⎝⎛⎭⎪⎫ωx +π6(A >0,ω>0)的最小正周期为2,且f (0)=3,那么函数f (3)=________.【解析】 ω=2π2=π,由f (0)=A sin π6=3得A =23,因此f (x )=23sin ⎝ ⎛⎭⎪⎫πx +π6,因此f (3)=23sin ⎝⎛⎭⎪⎫3π+π6=- 3.【答案】 -311.设三棱柱的侧棱垂直于底面,所有棱的长都为a ,极点都在一个球面上,那么该球的表面积为________.【解析】 设球心为O ,正三棱柱上底面为△ABC ,中心为O ′,因为三棱柱所有棱的长都为a ,那么可知OO ′=a 2,O ′A =33a ,又由球的相关性质可知,球的半径R =OO ′2+O ′A 2=216a ,因此球的表面积为4πR 2=73πa 2.【答案】 73πa 212.(2021·南通模拟)关于直线m ,n 和平面α,β有以下四个命题:①若m ∥α,n ∥β,α∥β,那么m ∥n ; ②若m ∥n ,m ⊂α,n ⊥β,那么α⊥β; ③若α∩β=m ,m ∥n ,那么n ∥α且n ∥β; ④若m ⊥n ,α∩β=m ,那么n ⊥α或n ⊥β. 其中假命题的序号是________.【解析】 命题①m 与n 也可相交或异面,因此①是假命题;命题②由条件可得m ⊥β,又m ⊂α,故α⊥β,因此②是真命题;命题③也可取得n ⊂α或n ⊂β,因此③错;命题④由已知只能取得n 垂直α与β内的一条直线,无法判定n ⊥α或n ⊥β,因此命题④错.【答案】 ①③④13.(2021·陕西高考)某几何体的三视图如图3所示,那么其体积为________. 图3【解析】 原几何体可视为圆锥的一半,其底面半径为1,高为2, ∴其体积为13×π×12×2×12=π3.【答案】 π314.对大于或等于2的自然数m 的n 次方幂有如下分解方式: 22=1+3 23=3+5 32=1+3+5 33=7+9+1142=1+3+5+7 43=13+15+17+19 52=1+3+5+7+9 53=21+23+25+27+29依照上述分解规律,假设m 3(m ∈N *)的分解中最小的数是73,那么m 的值为________. 【解析】 由所给等式知,m 3分解中第1个数为数列3,5,7,…中第2+3+4+…+(m -1)+1项,即m 2-m2项,从而m 3分解中第1个数为m 2-m +1,由m 2-m +1=73得m =9.【答案】 915.(2021·南昌模拟)三棱锥S —ABC 中,∠SBA =∠SCA =90°,△ABC 是斜边AB =a 的等腰直角三角形,那么以下结论中:图4①异面直线SB与AC所成的角为90°.②直线SB ⊥平面ABC ; ③平面SBC ⊥平面SAC ; ④点C 到平面SAB 的距离是12a .其中正确结论的序号是________.【解析】 由题意知AC ⊥平面SBC ,故AC ⊥SB ,SB ⊥平面ABC ,平面SBC ⊥平面SAC ,①②③正确;取AB 的中点E ,连接CE ,可证得CE ⊥平面SAB ,故CE 的长度即为C 到平面SAB 的距离12a ,④正确.【答案】 ①②③④三、解答题(本大题共6小题,共75分,解许诺写出文字说明、证明进程或演算步骤) 16.(本小题总分值12分)(2021·深圳模拟)在△ABC 中,角A ,B ,C 所对边的边长别离是a ,b ,c .(1)假设c =2,C =π3且△ABC 的面积等于3,求cos(A +B )和a ,b 的值;(2)假设B 是钝角,且cos A =35,sin B =1213,求sin C 的值.【解】 (1)∵A +B +C =π,C =π3,∴A +B =π-C ,∴cos(A +B )=cos(π-C )=-cos C =-cos π3=-12.由余弦定理及已知条件得,a 2+b 2-ab =4, 又因为△ABC 的面积等于3,因此12ab sin C =3,得ab =4.联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4,解得a =2,b =2.(2)∵B 是钝角,且cos A =35,sin B =1213,∴sin A =1-cos 2A = 1-⎝ ⎛⎭⎪⎫352=45, cos B =-1-sin 2B =-1-⎝ ⎛⎭⎪⎫12132=-513, ∴sin C =sin[π-(A +B )]=sin(A +B )=sin A cos B +cos A sin B =45×⎝ ⎛⎭⎪⎫-513+35×1213=1665.17.(本小题总分值12分)(2021·青岛模拟)在如图5所示的多面体ABCDE 中,AB ⊥平面ACD ,DE ⊥平面ACD ,且AC =AD =CD =DE =2,AB =1.图5(1)请在线段CE 上找到点F 的位置,使得恰有直线BF ∥平面ACD ,并证明这一结论;(2)求多面体ABCDE 的体积.【解】 (1)如下图,由已知AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB ∥ED ,设F 为线段CE 的中点,H 是线段CD 的中点,连接BF 、FH 、AH ,那么FH 綊12ED ,又AB =12ED , ∴FH 綊AB ,∴四边形ABFH 是平行四边形,∴BF ∥AH ,又因为BF ⊄平面ACD ,AH ⊂平面ACD ,∴BF ∥平面ACD .(2)取AD 中点G ,连接CG .因为AB ⊥平面ACD ,∴CG ⊥AB ,又CG ⊥AD ,∴CG ⊥平面ABED ,即CG 为四棱锥C —ABED 的高,求得CG =3,∴V C —ABED =13·1+22·2·3= 3.18.(本小题总分值12分)(2021·黄冈模拟)如图6,三棱柱ABC —A 1B 1C 1的侧面AA 1B 1B 为正方形,侧面BB 1C 1C 为菱形,∠CBB 1=60°,AB ⊥B 1C .(1)求证:平面AA 1B 1B ⊥平面BB 1C 1C ;(2)假设AB =2,求三棱柱ABC —A 1B 1C 1的体积.图6【解】 (1)由侧面AA 1B 1B 为正方形,知AB ⊥BB 1.又AB ⊥B 1C ,BB 1∩B 1C =B 1,因此AB ⊥平面BB 1C 1C ,又AB ⊂平面AA 1B 1B ,因此平面AA 1B 1B ⊥平面BB 1C 1C .(2)由题意,CB =CB 1,设O 是BB 1的中点,连接CO ,那么CO ⊥BB 1.由(1)知,CO ⊥平面AA 1B 1B ,且CO =32BC =32AB = 3.连结AB 1,那么VC —ABB 1=13S △ABB 1·CO =16AB 2·CO =233. 因为VB 1—ABC =VC —ABB 1=13VABC —A 1B 1C 1=233, 故三棱柱ABC —A 1B 1C 1的体积VABC —A 1B 1C 1=2 3. 19.(本小题总分值13分)已知数列{a n }的前n 项和为S n ,且S n =2a n -2,数列{b n }知足b 1=1,且b n +1=b n +2.(1)求数列{a n },{b n }的通项公式;(2)设c n =1--1n 2a n -1+-1n 2b n ,求数列{c n }的前2n 项和T 2n .【解】 (1)当n =1,a 1=2;当n ≥2时,a n =S n -S n -1=2a n -2a n -1,∴a n =2a n -1.∴{a n }是等比数列,公比为2,首项a 1=2,∴a n =2n .由b n +1=b n +2,得{b n }是等差数列,公差为2.又首项b 1=1,∴b n =2n -1.(2)c n =⎩⎪⎨⎪⎧2n n 为奇数,-2n -1 n 为偶数,∴T 2n =2+23+…+22n -1-[3+7+…+(4n -1)]=22n +1-23-2n 2-n . 20.(本小题总分值13分)如图7所示,PA ⊥平面ABC ,点C 在以AB 为直径的⊙O 上,∠CBA =30°,PA =AB =2,点E 为线段PB 的中点,点M 在弧AB 上,且OM ∥AC .图7(1)求证:平面MOE ∥平面PAC .(2)求证:平面PAC ⊥平面PCB .(3)设二面角M —BP —C 的大小为θ,求cos θ的值.【解】 (1)因为点E 为线段PB 的中点,点O 为线段AB 的中点,因此OE ∥PA .因为OM∥AC,因为OE ⊂平面MOE ,OM ⊂平面MOE ,OE ∩OM =O ,因此平面MOE ∥平面PAC .(2)因为点C 在以AB 为直径的⊙O 上,因此∠ACB =90°,即BC ⊥AC .因为PA ⊥平面BAC ,BC ⊂平面ABC ,因此PA ⊥BC .因为AC ⊂平面PAC ,PA ⊂平面PAC ,PA ∩AC =A ,因此BC ⊥平面PAC .因为BC ⊂平面PCB ,因此平面PAC ⊥平面PCB .(3)如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,成立空间直角坐标系C —xyz .因为∠CBA =30°,PA =AB =2,因此CB =2cos 30°=3,AC =1.延长MO 交CB 于点D .因为OM ∥AC ,因此MD ⊥CB ,MD =1+12=32, CD =12CB =32. 因此P (1,0,2),C (0,0,0),B (0,3,0),M ⎝ ⎛⎭⎪⎪⎫32,32,0. 因此CP →=(1,0,2),CB →=(0,3,0).设平面PCB 的法向量m =(x ,y ,z ).因为⎩⎨⎧ m ·CP →=0,m ·CB →=0.因此⎩⎪⎨⎪⎧ x ,y ,z ·1,0,2=0,x ,y ,z ·0,3,0=0,即⎩⎪⎨⎪⎧ x +2z =0,3y =0.令z =1,那么x =-2,y =0.因此m =(-2,0,1).同理可求平面PMB 的一个法向量n =(1,3,1). 因此cos 〈m ,n 〉=m·n |m|·|n|=-15. 因为二面角M —BP —C 为锐二面角,因此cos θ=15. 图821.(本小题总分值13分)(2021·天津高考)如图8,四棱柱ABCD —A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ∥DC ,AB ⊥AD ,AD =CD =1,AA 1=AB =2,E 为棱AA 1的中点.(1)证明B 1C 1⊥CE ;(2)求二面角B 1CE C 1的正弦值;(3)设点M 在线段C 1E 上,且直线AM 与平面ADD 1A 1所成角的正弦值为26,求线段AM的长.【解】 如图,以点A 为原点,以AD ,AA 1,AB 所在直线为x 轴、y 轴、z 轴成立空间直角坐标系,依题意得A (0,0,0),B (0,0,2),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0).(1)证明:易患B 1C 1→=(1,0,-1),CE →=(-1,1-1),于是B 1C 1→·CE →=0,因此B 1C 1⊥CE .(2)B 1C →=(1,-2,-1).设平面B 1CE 的法向量m =(x ,y ,z ), 则⎩⎨⎧ m ·B 1C →=0,m ·CE →=0,即⎩⎪⎨⎪⎧x -2y -z =0,-x +y -z =0.消去x ,得y +2z =0, 不妨令z =1,可得一个法向量为m =(-3,-2,1).由(1)知,B 1C 1⊥CE ,又CC 1⊥B 1C 1,可得B 1C 1⊥平面CEC 1,故B 1C 1→=(1,0,-1)为平面CEC 1的一个法向量.于是cos 〈m ,B 1C 1→〉=m ·B 1C 1→|m ||B 1C 1→|=-414×2=-277,从而sin 〈m ,B 1C 1→〉=217. 因此二面角B 1—CE —C 1的正弦值为217. (3)AE →=(0,1,0),EC 1→=(1,1,1).设EM→=λEC1→=(λ,λ,λ),0≤λ≤1,有AM→=AE→+EM→=(λ,λ+1,λ).可取AB→=(0,0,2)为平面ADD1A1的一个法向量.设θ为直线AM与平面ADD1A1所成的角,那么sin θ=|cos〈AM→,AB→〉|=|AM→·AB→||AM→||AB→|=2λλ2+λ+12+λ2×2=λ3λ2+2λ+1,于是λ3λ2+2λ+1=26,解得λ=13(负值舍去),因此AM= 2.。
2021年高考数学专题分类汇编:立体几何(含答案)
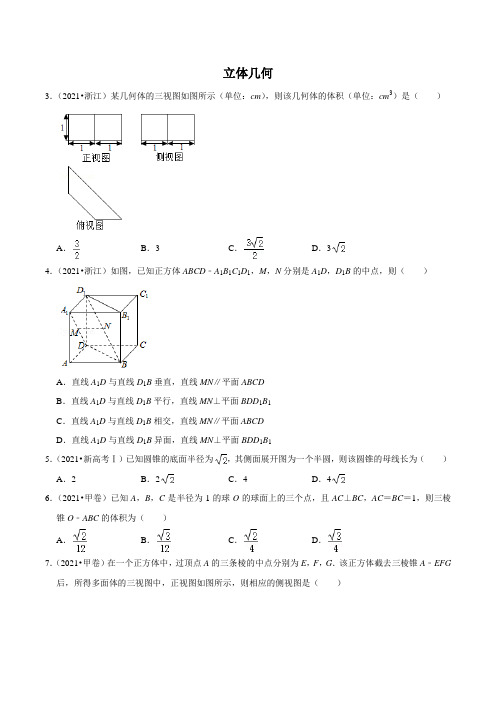
立体几何3.(2021•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.B.3C.D.34.(2021•浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN∥平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN∥平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B15.(2021•新高考Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.2C.4D.46.(2021•甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O﹣ABC的体积为()A.B.C.D.7.(2021•甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A﹣EFG 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A.B.C.D.8.(2021•乙卷)在正方体ABCD﹣A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为()A.B.C.D.18.(2021•甲卷)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为.19.(2021•甲卷)已知向量=(3,1),=(1,0),=+k.若⊥,则k=.20.(2021•乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为(写出符合要求的一组答案即可).21.(2021•上海)已知圆柱的底面半径为1,高为2,则圆柱的侧面积为.40.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC 和CC1的中点,BF⊥A1B1.(1)求三棱锥F﹣EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE.41.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC中点,且PB⊥AM.(1)求BC;(2)求二面角A﹣PM﹣B的正弦值.42.(2021•浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC =4,P A=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.(Ⅰ)证明:AB⊥PM;(Ⅱ)求直线AN与平面PDM所成角的正弦值.43.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC 和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?44.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1)证明:平面P AM⊥平面PBD;(2)若PD=DC=1,求四棱锥P﹣ABCD的体积.45.(2021•新高考Ⅰ)如图,在三棱锥A﹣BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E﹣BC﹣D的大小为45°,求三棱锥A﹣BCD的体积.46.(2021•上海)四棱锥P﹣ABCD,底面为正方形ABCD,边长为4,E为AB中点,PE⊥平面ABCD.(1)若△P AB为等边三角形,求四棱锥P﹣ABCD的体积;(2)若CD的中点为F,PF与平面ABCD所成角为45°,求PC与AD所成角的大小.答案解析3.(2021•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.B.3C.D.3【解答】解:由三视图还原原几何体如图,该几何体为直四棱柱,底面四边形ABCD为等腰梯形,其中AB∥CD,由三视图可知,延长AD与BC后相交于一点,且AD⊥BC,且AB=,CD=,AA1=1,等腰梯形的高为=,则该几何体的体积V==.故选:A.4.(2021•浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN∥平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN∥平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1【解答】解:连接AD1,如图:由正方体可知A1D⊥AD1,A1D⊥AB,∴A1D⊥平面ABD1,∴A1D⊥D1B,由题意知MN为△D1AB的中位线,∴MN∥AB,又∵AB⊂平面ABCD,MN⊄平面ABCD,∴MN∥平面ABCD.∴A对;由正方体可知A1D与平面BDD1相交于点D,D1B⊂平面BDD1,D∉D1B,∴直线A1D与直线D1B是异面直线,∴B、C错;∵MN∥AB,AB不与平面BDD1B1垂直,∴MN不与平面BDD1B1垂直,∴D错.故选:A.5.(2021•新高考Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.2C.4D.4【解答】解:由题意,设母线长为l,因为圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,则有,解得,所以该圆锥的母线长为.故选:B.6.(2021•甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O﹣ABC的体积为()A.B.C.D.【解答】解:因为AC⊥BC,AC=BC=1,所以底面ABC为等腰直角三角形,所以△ABC所在的截面圆的圆心O1为斜边AB的中点,所以OO1⊥平面ABC,在Rt△ABC中,AB=,则,在Rt△AOO1中,,故三棱锥O﹣ABC的体积为.故选:A.7.(2021•甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A﹣EFG 后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A.B.C.D.【解答】解:由题意,作出正方体,截去三棱锥A﹣EFG,根据正视图,可得A﹣EFG在正方体左侧面,如图,根据三视图的投影,可得相应的侧视图是D图形,故选:D.8.(2021•乙卷)在正方体ABCD﹣A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为()A.B.C.D.【解答】解∵AD1∥BC1,∴∠PBC1是直线PB与AD1所成的角(或所成角的补角),设正方体ABCD﹣A1B1C1D1的棱长为2,则PB1=PC1==,BC1==2,BP==,∴cos∠PBC1===,∴∠PBC1=,∴直线PB与AD1所成的角为.故选:D.19.(2021•甲卷)已知向量=(3,1),=(1,0),=+k.若⊥,则k=.【解答】解:因为向量=(3,1),=(1,0),=+k,由⊥,则=32+12+k•(3×1+1×0)=10+3k=0,解得k=.故答案为:.20.(2021•乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为②⑤或③④(写出符合要求的一组答案即可).【解答】解:观察正视图,推出正视图的长为2和高1,②③图形的高也为1,即可能为该三棱锥的侧视图,④⑤图形的长为2,即可能为该三棱锥的俯视图,当②为侧视图时,结合侧视图中的直线,可以确定该三棱锥的俯视图为⑤,当③为侧视图时,结合侧视图虚线,虚线所在的位置有立体图形的轮廓线,可以确定该三棱锥的俯视图为④.故答案为:②⑤或③④.21.(2021•上海)已知圆柱的底面半径为1,高为2,则圆柱的侧面积为4π.【解答】解:圆柱的底面半径为r=1,高为h=2,所以圆柱的侧面积为S侧=2πrh=2π×1×2=4π.故答案为:4π.40.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC 和CC1的中点,BF⊥A1B1.(1)求三棱锥F﹣EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE.【解答】解:(1)在直三棱柱ABC﹣A1B1C1中,BB1⊥A1B1,又BF⊥A1B1,BB1∩BF=B,BB1,BF⊂平面BCC1B1,∴A1B1⊥平面BCC1B1,∵AB∥A1B1,∴AB⊥平面BCC1B1,∴AB⊥BC,又AB=BC,故,∴,而侧面AA1B1B为正方形,∴,∴,即三棱锥F﹣EBC的体积为;(2)证明:如图,取BC中点G,连接EG,B1G,设B1G∩BF=H,∵点E是AC的中点,点G时BC的中点,∴EG∥AB,∴EG∥AB∥B1D,∴E、G、B1、D四点共面,由(1)可得AB⊥平面BCC1B1,∴EG⊥平面BCC1B1,∴BF⊥EG,∵,且这两个角都是锐角,∴∠CBF=∠BB1G,∴∠BHB1=∠BGB1+∠CBF=∠BGB1+∠BB1G=90°,∴BF⊥B1G,又EG∩B1G=G,EG,B1G⊂平面EGB1D,∴BF⊥平面EGB1D,又DE⊂平面EGB1D,∴BF⊥DE.41.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC中点,且PB⊥AM.(1)求BC;(2)求二面角A﹣PM﹣B的正弦值.【解答】解:(1)连结BD,因为PD⊥底面ABCD,且AM⊂平面ABCD,则AM⊥PD,又AM⊥PB,PB∩PD=P,PB,PD⊂平面PBD,所以AM⊥平面PBD,又BD⊂平面PBD,则AM⊥BD,所以∠ABD+∠ADB=90°,又∠ABD+∠MAB=90°,则有∠ADB=∠MAB,所以Rt△DAB∽Rt△ABM,则,所以,解得BC=;(2)因为DA,DC,DP两两垂直,故以点D位坐标原点建立空间直角坐标系如图所示,则,P(0,0,1),所以,,设平面AMP的法向量为,则有,即,令,则y=1,z=2,故,设平面BMP的法向量为,则有,即,令q=1,则r=1,故,所以=,设二面角A﹣PM﹣B的平面角为α,则sinα==,所以二面角A﹣PM﹣B的正弦值为.42.(2021•浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,P A=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.(Ⅰ)证明:AB⊥PM;(Ⅱ)求直线AN与平面PDM所成角的正弦值.【解答】(Ⅰ)证明:在平行四边形ABCD中,由已知可得,CD=AB=1,CM=BC=2,∠DCM=60°,∴由余弦定理可得,DM2=CD2+CM2﹣2CD×CM×cos60°=,则CD2+DM2=1+3=4=CM2,即CD⊥DM,又PD⊥DC,PD∩DM=D,∴CD⊥平面PDM,而PM⊂平面PDM,∴CD⊥PM,∵CD∥AB,∴AB⊥PM;(Ⅱ)解:由(Ⅰ)知,CD⊥平面PDM,又CD⊂平面ABCD,∴平面ABCD⊥平面PDM,且平面ABCD∩平面PDM=DM,∵PM⊥MD,且PM⊂平面PDM,∴PM⊥平面ABCD,连接AM,则PM⊥MA,在△ABM中,AB=1,BM=2,∠ABM=120°,可得,又P A=,在Rt△PMA中,求得PM=,取AD中点E,连接ME,则ME∥CD,可得ME、MD、MP两两互相垂直,以M为坐标原点,分别以MD、ME、MP为x、y、z轴建立空间直角坐标系,则A(,2,0),P(0,0,),C(),又N为PC的中点,∴N(),,平面PDM的一个法向量为,设直线AN与平面PDM所成角为θ,则sinθ=|cos<>|==.故直线AN与平面PDM所成角的正弦值为.43.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC 和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?【解答】(1)证明:连接AF,∵E,F分别为直三棱柱ABC﹣A1B1C1的棱AC和CC1的中点,且AB=BC=2,∴CF=1,BF=,∵BF⊥A1B1,AB∥A1B1,∴BF⊥AB∴AF===3,AC===,∴AC2=AB2+BC2,即BA⊥BC,故以B为原点,BA,BC,BB1所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(2,0,0),B(0,0,0),C(0,2,0),E(1,1,0),F(0,2,1),设B1D=m,则D(m,0,2),∴=(0,2,1),=(1﹣m,1,﹣2),∴•=0,即BF⊥DE.(2)解:∵AB⊥平面BB1C1C,∴平面BB1C1C的一个法向量为=(1,0,0),由(1)知,=(1﹣m,1,﹣2),=(﹣1,1,1),设平面DEF的法向量为=(x,y,z),则,即,令x=3,则y=m+1,z=2﹣m,∴=(3,m+1,2﹣m),∴cos<,>====,∴当m=时,面BB1C1C与面DFE所成的二面角的余弦值最大,此时正弦值最小,故当B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小.44.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1)证明:平面P AM⊥平面PBD;(2)若PD=DC=1,求四棱锥P﹣ABCD的体积.【解答】(1)证明:∵PD⊥底面ABCD,AM⊂平面ABCD,∴PD⊥AM,又∵PB⊥AM,PD∩PB=P,PB,PD⊂平面PBD.∴AM⊥平面PBD.∵AM⊂平面P AM,∴平面P AM⊥平面PBD;(2)解:由PD⊥底面ABCD,∴PD即为四棱锥P﹣ABCD的高,△DPB是直角三角形;∵ABCD底面是矩形,PD=DC=1,M为BC的中点,且PB⊥AM.设AD=BC=2a,取CP的中点为F.作EF⊥CD交于E,连接MF,AF,AE,可得MF∥PB,EF∥DP,那么AM⊥MF.且EF=.AE==,AM==,.∵△DPB是直角三角形,∴根据勾股定理:BP=,则MF=;由△AMF是直角三角形,可得AM2+MF2=AF2,解得a=.底面ABCD的面积S=,则四棱锥P﹣ABCD的体积V==.45.(2021•新高考Ⅰ)如图,在三棱锥A﹣BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E﹣BC﹣D的大小为45°,求三棱锥A﹣BCD的体积.【解答】解:(1)证明:因为AB=AD,O为BD的中点,所以AO⊥BD,又平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,所以AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD;(2)方法一:取OD的中点F,因为△OCD为正三角形,所以CF⊥OD,过O作OM∥CF与BC交于点M,则OM⊥OD,所以OM,OD,OA两两垂直,以点O为坐标原点,分别以OM,OD,OA为x轴,y轴,z轴建立空间直角坐标系如图所示,则B(0,﹣1,0),,D(0,1,0),设A(0,0,t),则,因为OA⊥平面BCD,故平面BCD的一个法向量为,设平面BCE的法向量为,又,所以由,得,令x=,则y=﹣1,,故,因为二面角E﹣BC﹣D的大小为45°,所以,解得t=1,所以OA=1,又,所以,故=.方法二:过E作EF⊥BD,交BD于点F,过F作FG⊥BC于点G,连结EG,由题意可知,EF∥AO,又AO⊥平面BCD所以EF⊥平面BCD,又BC⊂平面BCD,所以EF⊥BC,又BC⊥FG,FG∩EF=F所以BC⊥平面EFG,又EF⊂平面EFG,所以BC⊥EG,则∠EGF为二面角E﹣BC﹣D的平面角,即∠EGF=45°,又CD=DO=OB=OC=1,所以∠BOC=120°,则∠OCB=∠OBC=30°,故∠BCD=90°,所以FG∥CD,因为,则,所以,则,所以EF=GF=,则,所以.46.(2021•上海)四棱锥P﹣ABCD,底面为正方形ABCD,边长为4,E为AB中点,PE⊥平面ABCD.(1)若△P AB为等边三角形,求四棱锥P﹣ABCD的体积;(2)若CD的中点为F,PF与平面ABCD所成角为45°,求PC与AD所成角的大小.【解答】解:(1)∵△P AB为等边三角形,且E为AB中点,AB=4,∴PE=2,又PE⊥平面ABCD,∴四棱锥P﹣ABCD的体积V=PE•S正方形ABCD=×2×42=.(2)∵PE⊥平面ABCD,∴∠PFE为PF与平面ABCD所成角为45°,即∠PFE=45°,∴△PEF为等腰直角三角形,∵E,F分别为AB,CD的中点,∴PE=FE=4,∴PB==,∵AD∥BC,∴∠PCB或其补角即为PC与AD所成角,∵PE⊥平面ABCD,∴PE⊥BC,又BC⊥AB,PE∩AB=E,PE、AB⊂平面P AB,∴BC⊥平面P AB,∴BC⊥PB,在Rt△PBC中,tan∠PCB===,故PC与AD所成角的大小为arctan.。
2021年高考数学立体几何全真模拟预测练习卷含答案

191. 如图1所示,边长AC =3,BC =4,AB =5的三角形简易遮阳棚,其A 、B 是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30°角,试问:遮阳棚ABC 与地面成多大角度时,才能保证所遮影面ABD 面积最大?解析: 易知,ΔABC 为直角三角形,由C 点引AB 的垂线,垂足为Q ,则应有DQ 为CQ 在地面上的斜射影,且AB 垂直于平面CQD ,如图2所示.因太阳光与地面成30°角,所以∠CDQ =30°,又知在ΔCQD 中,CQ =512,由正弦定理,有︒30sin CQ =QCD QD ∠sin , 即 QD =56sin ∠QCD.为使面ABD 的面积最大,需QD 最大,这只有当∠QCD =90°时才可达到,从而∠CQD =60°.故当遮阳棚ABC 与地面成60°角时,才能保证所遮影面ABD 面积最大.192. 如图所示,已知三棱锥S —ABC 中,SA =SB =SC ,且AC 2+BC 2=AB 2,由此可推出怎样的结论?解析: 引SO ⊥平面ABC(O 为垂足),连结OC.∵SA =SB =SC ,∴OA =OB =OC ,∴O 是ΔABC 的外心,(结论1)又∵AC 2+BC 2=AB 2,∴ΔABC 是直角三角形,且AB 是斜边,故O 是斜边AB 的中点.因而SO 平面SAB(结论2)∴平面SAB ⊥平面ABC(结论3)193. 正三棱柱ABC —A 1B 1C 1中,各棱长均为2,M 为AA 1中点,N 为BC 的中点,则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.解析: (1)从侧面到N ,如图1,沿棱柱的侧棱AA 1剪开,并展开,则MN =22AN AM +=22)12(1++=10(2)从底面到N 点,沿棱柱的AC 、BC 剪开、展开,如图2.则MN =︒⋅-+120cos 222AN AM AN AM=21312)3(122⨯⨯⨯++=34+ ∵34+<10∴m in MN =34+.194. 已知二面角A —BC —D 为150°,ΔABC 是边长为a 的等边三角形,ΔBCD 是斜边为BC 的等腰直角三角形.求两个顶点A 和D 间的距离.解析:.取BC 的中点E ,连DE 和AE ,利用余弦定理AD =27a 195. .如图,ABCDEF 为正六边形,将此正六边形沿对角线AD 折叠.(1)求证:AD ⊥EC ,且与二面角F —AD —C 的大小无关;(2)FC 与FE 所成的角为30°时,求二面角F —AD —C 的余弦值.解析:(1)正六边形ABCDEF ,在折叠前有AD ⊥EC ,设AD 与EC 交于M ,折叠后即有AD ⊥ME ,AD ⊥MC.则AD ⊥平面EMC ,无论∠EMC 的大小如何,总有AD ⊥EC.(2)利用余弦定理,有cos ∠EMC =97196. 在直角BVC 的角顶点V ,作直角所在平面的斜线VA ,使二面角A —VB —C 与二面角A —VC —B 都等于45°,求二面角B —VA —C 的度数.解析:在VA 上取A ′作平面VCB 的垂线,垂足为O ,作OC ′⊥VC ,OB ′⊥VB ,连A ′C ′、A ′B ′,则∠A ′C ′O 和∠A ′B ′O 分别为二面角A-VC —B 与二面角A —VB —C 的平面角.易证VB ′OC ′为正方形.设VB ′=a ,可求得A ′B ′=a.VA ′=a.过B ′作B ′D ⊥VA ,连结C ′D.则∠B ′DC ′为二面角B —VA —C 的平面角.在Rt ΔB ′VA ′中,可求B ′D =36a ,又DE ⊥B ′C ′,B ′E =22a ,则在Rt ΔB ′DE 中可求得∠B ′DE =60°.二面角B —VA —C 为120°.197. 已知直线l 与平面α内交于一点O 的三条直线OA 、OB 、OC 成等角,求证:l ⊥α解析:若l 过O 点,在l 上任取一点P ,作PH ⊥α,垂足H ,则H 即在∠AOB 的平分线上,又在∠BOC 的平分线上,∴H 是它们的公共点,故H 与O 重合;若l 不过O 点,可作过O 的直线l ′,使l ′∥l 即可证明.198. 空间四边形ABCD 的各边与两条对角线的长都为1,点P 在AD 上移动,点Q 在CB 上移动,求点P 与点Q 的最短距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 26 页 2021年高考数学模拟试卷汇编:立体几何
1.(2020届安徽省“江南十校”高三综合素质检测)如图,在平面四边形ABCD 中,满足,AB BC CD AD ==,且10,8AB AD BD +==,沿着BD 把ABD 折起,使点A 到达点P 的位置,且使2PC =,则三棱锥P BCD -体积的最大值为( )
A .12
B .2
C .23
D .163 2.(2020届河南省六市高三第一次模拟)已知圆锥的高为33,若该圆锥的顶点与底面的圆周都在同一个球面上,则这个球的体积与圆锥的体积的比值为( ) A .
53 B .329 C .43 D .259
3.已知三棱锥P ABC -中,O 为AB 的中点,PO ⊥平面ABC ,90APB ∠=︒,2PA PB ==,则有下列四个结论:①若O 为ABC V 的外心,则2PC =;②ABC V 若为等边三角形,则⊥AP BC ;③当90ACB ∠=︒时,PC 与平面PAB 所成的角的范围为0,4π⎛⎤ ⎥⎝⎦
;④当4PC =时,M 为平面PBC 内一动点,若OM ∥平面PAC ,则M 在PBC V 内轨迹的长度为2.其中正确的个数是( ).
A .1
B .2
C .3
D .4 4.(2020届河南省濮阳市高三模拟)在四面体P ABC -中,ABC V 为正三角形,边长为6,6PA =,8PB =,10PC =,则四面体P ABC -的体积为( ) A .811B .10C .24 D .1635.(2020届河南省天一大联考“顶尖计划”高三二联)已知三棱锥D ABC -的外接球半径为2,且球心为线段BC 的中点,则三棱锥D ABC -的体积的最大值为( ) A .23 B .43 C .83 D .163 6.(2020届河南省天一大联考“顶尖计划”高三一联)已知四棱锥S ABCD -的底面为矩形,。
