数字信号处理(第三版)高西全丁玉美课后答案
数字信号处理第三版 第一章高西全丁玉美课后答案

第 1 章
时域离散信号和时域离散系统
解线性卷积也可用Z变换法, 以及离散傅里叶变换求解, 这是后面几章的内容。 下面通过例题说明。 设x(n)=R4(n), h(n)=R4(n), 求y(n)=x(n)*h(n)。 该题是两个短序列的线性卷积, 可以用图解法(列表法) 或者解析法求解。 表1.2.1给出了图解法(列表法), 用公 式可表示为 y(n)={…, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, …}
第 1 章
时域离散信号和时域离散系统
%以下为绘图部分 n=0: length(yn)-1; subplot(2, 1, 1); stem(n, yn, ′.′) xlabel(′n′); ylabel(′y(n)′) 程序运行结果如图1.3.2所示。 由图形可以看出, 5项滑 动平均滤波器对输入波形起平滑滤波作用, 将信号的第4、 8、 12、 16的序列值平滑去掉。
sin[ π(t − nT ) / T ] xa (t ) = xa (nt ) π(t − nT ) / T n = −∞
∑
∞
这是由时域离散信号理想恢复模拟信号的插值公式。
第 1 章
时域离散信号和时域离散系统
1.2 解线性卷积的方法 解线性卷积的方法
解线性卷积是数字信号处理中的重要运算。 解线性卷积有 三种方法, 即图解法(列表法)、 解析法和在计算机上用 MATLAB语言求解。 它们各有特点。 图解法(列表法)适合 于简单情况, 短序列的线性卷积, 因此考试中常用, 不容易 得到封闭解。 解析法适合于用公式表示序列的线性卷积, 得 到的是封闭解, 考试中会出现简单情况的解析法求解。 解析 法求解过程中, 关键问题是确定求和限, 求和限可以借助于 画图确定。 第三种方法适合于用计算机求解一些复杂的较难的 线性卷积, 实验中常用。
数字信号处理第三版西安电子(高西全丁美玉)2356课后答案

(1)
上式中指数函数的傅里叶变换不存在,引入奇异函数 函数,它的傅里叶变换可以
表示成:
(2)
(3)
式中
式中
上式推导过程中,指数序列的傅里叶变换仍然不存在,只有引入奇异函数函数,才能写出它的傅里叶变换表达式。
14.求以下序列的Z变换及收敛域:
(2) ;
(3) ;
(6)
解:
(2)
(3)
(6)
16.已知:
y(n)的波形如题8解图(二)所示.
(3)
y(n)对于m的非零区间为 。
①
②
③
最后写成统一表达式:
11.设系统由下面差分方程描述:
;
设系统是因果的,利用递推法求系统的单位取样响应。
解:
令:
归纳起来,结果为
12.有一连续信号 式中,
(1)求出 的周期。
(2)用采样间隔 对 进行采样,试写出采样信号 的表达式。
解:
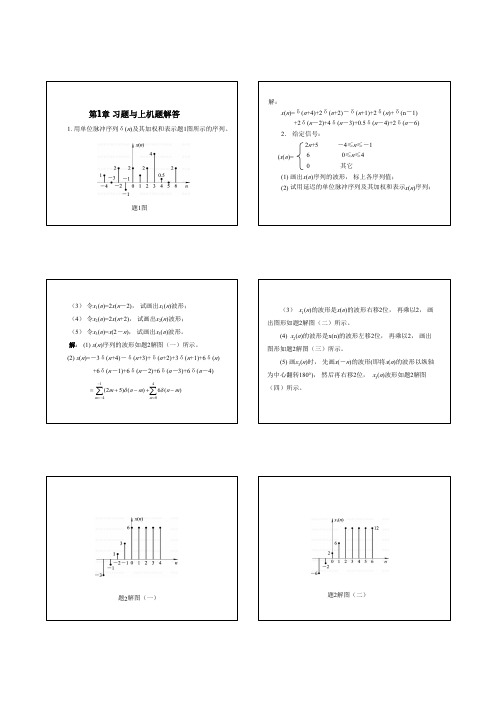
(1)x(n)的波形如题2解图(一)所示。
(2)
(3) 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4) 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画 时,先画x(-n)的波形,然后再右移2位, 波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
按照上式可以有两种级联型结构:
(a)
画出级联型结构如题2解图(二)(a)所示。
(b)
画出级联型结构如题2解图(二)(b)所示●。
3.设系统的系统函数为
,
试画出各种可能的级联型结构。
解:
由于系统函数的分子和分母各有两个因式,可以有两种级联型结构。
数字信号处理课后答案+第2章(高西全丁美玉第三版)

j k j k e 4 (e 4
n 0
3
~ (n)e x
j
2 kn 4
π 4
n 0
1
j kn e 2
1j k e 2源自j k e 4 )
2 cos(
π j k k) e 4
~ X ( k )以4为周期
证明输入x(n)=A cos(ω0n+j)的稳态响应为
y (n) A | H (e j0 ) | cos0 n j (0 )
解: 假设输入信号x(n)=ejω0n,系统单位脉冲响应为h(n), 则系统输出为
y ( n) h( n) x ( n) e j 0 n
(9)
x(n / 2) n 偶数 x9 (n) n 奇数 0
解:(1)
FT[ x(n n0 )]
n
x(n n0 )e jn
令n′=n-n0, 即n=n′+n0, 则
FT[ x(n n0 )]
(2)
FT[ x (n)]
n
x(n)e jn
令n′=-n, 则
FT[ x(n)]
n
x(n)e jn X (e j )
(4)
FT[x(n)*y(n)]=X(ejω)Y(ejω)
下面证明上式成立:
x ( n) y ( n)
m
x ( m) y ( n m)
FT[ x(n) y (n)]
n
x(n)e j2n X (e j2 )
数字信号处理课后答案+第5章(高西全丁美玉第三版)

题3解图(二)
4. 设系统的系统函数为
(1 + z −1 )(1 − 1.414 z −1 + z −2 ) H ( z) = 4 (1 − 0.5 z −1 )(1 + 0.9 z −1 + 0.81z − 2 )
试画出各种可能的级联型结构, 并指出哪一种最好。 解: 由于系统函数的分子和分母各有两个因式, 因 而可以有两种级联型结构。 H(z)=H1(z)H2(z) ①
Y ( z ) ab − (a + b) z −1 + z −2 H ( z) = = X ( z ) 1 − (a + b) z −1 − abz − 2
按照Masson公式画出直接型结构如题3解图(一)所示。
题3解图(一)
(2) 级联型结构。 将H(z)的分子和分母进行因式分解, 得到
(a − z −1 )(b − z −1 ) H ( z) = = H1 ( z) H 2 ( z) −1 −1 (1 − az )(1 − bz )
1 1 y (n) = x(n) + x(n − 1) + y (n − 1) + y (n − 2) 3 4
试画出系统的直接型结构。 解: 由差分方程得到滤波器的系统函数为
1 + z −1 H ( z) = 1 −1 1 − 2 1− z − z 3 4
画出其直接型结构如题2解图所示。
题2解图
1 −1 1+ z 3 H ( z) = 3 −1 1 − 2 1− z + z 4 8
(1) 按照系统函数H(z), 根据Masson公式, 画出直接型 结构如题1解图(一)所示。
数字信号处理课后答案+第3章(高西全丁美玉第三版)

k = 0, 1, ⋯, N − 1
(8) 解法一 直接计算:
1 jω 0 n x8 (n) = sin(ω0 n) ⋅ RN (n) = [e − e − jω 0 n ] R N ( n ) 2j
X 8 ( n) =
∑
n =0
N −1 kn x8 (n)WN
1 = [ e jω 0 n − e − jω 0 n ] e 2 j n =0
1− e
j(ω0 −
2π N k) 2π N −1 sin (ω0 − j(ω0 − k )( ) N 2 N 2 =e 2π sin (ω0 − k ) / 2 N
k = 0, 1, ⋯, N − 1
或
X 7 (k ) =
1 − e jω0 N
2π j(ω0 − k ) N 1− e
N −1
N −1
由于 所以
∑
n =0
N −1
n WN ( m + k )
N = 0
m= N −k m ≠ N − k , 0≤ m ≤ N − 1
DFT[X(n)]=Nx(N-k)
N −1 k =0
k=0, 1, …, N-1
5. 如果X(k)=DFT[x(n)], 证明DFT的初值定理
证: 由IDFT定义式
2π mn +θ ) N 2π mn +θ ) N ]
1 = [e 2j
j(
−e
− j(
2π = sin mn + θ N
n=0, 1, …, N-1
3. 已知长度为N=10的两个有限长序列:
1 0 ≤ n ≤ 4 x1 (n) = 0 5 ≤ n ≤ 9
数字信号处理课后答案+第4章(高西全丁美玉第三版)

令 y(n)=x1(n)+jx2(n) Y(k)=DFT[y(n)] 则
这样, 通过一次N点IFFT计算就完成了计算2N点DFT。 当然还要进行由Y(k)求X1(k)、 X2(k)和X(k)的运算(运算量相对
k=0, 1, …, N-1
⎧ ⎛n⎞ ⎪ x1 ⎜ 2 ⎟ ⎪ ⎝ ⎠ x (n) = ⎨ ⎪x ⎛ n −1 ⎞ ⎪ 2⎜ 2 ⎟ ⎠ ⎩ ⎝
n = 偶数 n = 奇数
在编程序实现时, 只要将存放x1(n)和x2(n)的两个数组的元 素分别依次放入存放x(n)的数组的偶数和奇数数组元素中 即可。
运算流图。 但画图占篇幅较大, 这里省略本题解答, 请 读者自己完成。
很少)。 (2) 与(1)相同, 设 x1(n)=x(2n) n=0, 1, …, N-1 x2(n)=x(2n+1) n=0, 1, …, N-1 X1(k)=DFT[x1(n)] X2(k)=DFT[x2(n)] 则应满足关系式
1 X 1 ( k ) = DFT[ x1 ( n)] = Yep ( k ) = [Y ( k ) + Y * ( N − k )] 2 1 jX 2 (k ) = DFT[ jx2 (n)] = Yep (k ) = [Y ( k ) − Y * ( N − k )] 2
4. 设x(n)是长度为2N的有限长实序列, X(k)为x(n)的 2N点DFT。 (1) 试设计用一次N点FFT完成计算X(k)的高效算法。 (2) 若已知X(k) ,试设计用一次N点IFFT实现求X(k)的 2N点IDFT运算。
x1(n)和x2(n)均为实序列, 所以根据DFT的共轭对称性, 可用
② 由X1(k)和X2(k)构成N点频域序列Y(k): Y(k)=X1(k)+jX2(k)=Yep(k)+Yop(k)
数字信号处理第三版课后答案

数字信号处理第三版课后答案西安电⼦(⾼西全丁美⽟第三版)数字信号处理课后答案1.2教材第⼀章习题解答1.⽤单位脉冲序列及其加权和表⽰题1图所⽰的序列。
解:2.给定信号:(1)画出序列的波形,标上各序列的值;(2)试⽤延迟单位脉冲序列及其加权和表⽰序列;(3)令,试画出波形;(4)令,试画出波形;(5)令,试画出波形。
解:(1)x(n)的波形如题2解图(⼀)所⽰。
(2)(3)的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(⼆)所⽰。
(4)的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所⽰。
(5)画时,先画x(-n)的波形,然后再右移2位,波形如题2解图(四)所⽰。
3.判断下⾯的序列是否是周期的,若是周期的,确定其周期。
(1),A是常数;(2)。
解:(1),这是有理数,因此是周期序列,周期是T=14;(2),这是⽆理数,因此是⾮周期序列。
5.设系统分别⽤下⾯的差分⽅程描述,与分别表⽰系统输⼊和输出,判断系统是否是线性⾮时变的。
(1);(3),为整常数;(5);(7)。
解:故该系统是时不变系统。
故该系统是线性系统。
(3)这是⼀个延时器,延时器是⼀个线性时不变系统,下⾯予以证明。
令输⼊为,输出为,因为故延时器是⼀个时不变系统。
⼜因为故延时器是线性系统。
(5)令:输⼊为,输出为,因为故系统是时不变系统。
⼜因为因此系统是⾮线性系统。
(7)令:输⼊为,输出为,因为故该系统是时变系统。
⼜因为故系统是线性系统。
6.给定下述系统的差分⽅程,试判断系统是否是因果稳定系统,并说明理由。
(1);(3);(5)。
(1)只要,该系统就是因果系统,因为输出只与n时刻的和n时刻以前的输⼊有关。
如果,则,因此系统是稳定系统。
(3)如果,,因此系统是稳定的。
系统是⾮因果的,因为输出还和x(n)的将来值有关.(5)系统是因果系统,因为系统的输出不取决于x(n)的未来值。
如果,则,因此系统是稳定的。
7.设线性时不变系统的单位脉冲响应和输⼊序列如题7图所⽰,要求画出输出输出的波形。
西安电子(高西全丁美玉第三版)数字信号处理课后答案第2章

这是时域卷积定理。
第2章 时域离散信号和系统的频域分析
(5) 若y(n)=x(n)h(n), 则
Y (e j ) 1 H (e j ) X (e j ) 2π
这是频域卷积定理或者称复卷积定理。
(6)
xe
(n)
1 2
[x(n)
滤波器是高通还是低通等滤波特性, 也可以通过分析极、 零点分布确定, 不必等画出幅度特性再确定。 一般在最靠近 单位圆的极点附近是滤波器的通带; 阻带在最靠近单位圆的 零点附近, 如果没有零点, 则离极点最远的地方是阻带。 参 见下节例2.4.1。
第2章 时域离散信号和系统的频域分析
2.4 例
[例2.4.1] 已知IIR数字滤波器的系统函数
c (Rx , Rx )
这两式分别是序列Z变换的正变换定义和它的逆Z变 换定义。
第2章 时域离散信号和系统的频域分析
(8)
x(n) 2 1
X (e j ) 2d
n
2π 2
x(n) y(n) 1
n
2π
c
X
(v)Y
(
1 v
)
dv v
max[Rx ,
H(z) 1 1 0.9z 1
试判断滤波器的类型(低通、 高通、 带通、 带阻)。 (某
解: 将系统函数写成下式:
H(z) 1 = z 1 0.9z 1 z 0.9
第2章 时域离散信号和系统的频域分析
系统的零点为z=0, 极点为z=0.9, 零点在z平面的原点, 不影响频率特性, 而惟一的极点在实轴的0.9处, 因此滤波 器的通带中心在ω=0处。 毫无疑问, 这是一个低通滤波器。
数字信号处理第三版高西全版课后习题答案

数字信号处理课后答案 高西全、丁美玉版教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理课后答案第6章(高西全丁美玉第三版)

Ha
(s)
(s2
2
7.2687 1016 Re[s1]s | s1 |2 )(s2 2
Re[s2
]s
|
s2
|2 )
7.2687 1016
(s2 1.6731104 s 4.7791108 )(s2 4.0394104 s 4.7790108 )
也可得到分母多项式形式, 请读者自己计算。 3. 设计一个巴特沃斯高通滤波器, 要求其通带截止频率
解: (1) 确定滤波器技术指标。 αp=0.2 dB, Ωp=2πfp=6π×103 rad/s αs=50 dB, Ωs=2πfs=24π×103 rad/s
λp=1,
s
Hale Waihona Puke s p4(4) 求阶数N和ε。
N arch k 1
arch s
k 1
100.1as 1 100.1ap 1 1456.65
sa (1) Ha (s) (s a)2 b2
Ha(s)的极点为 s1=-a+jb, s2=-a-jb
将Ha(s)部分分式展开(用待定系数法):
Ha (s)
sa (s a)2 b2
A1 s s1
A2 s s2
A1(s s2 ) A2 (s s1) (s a)2 b2
H (z)
2
Ak
k 1 1 es k T z 1
1
1/ 2 e(a jb)T
z
1
1
1/ 2 e(a jb)T
z
1
按照题目要求, 上面的H(z)表达式就可作为该题的答案。 但在工程实际中, 一般用无复数乘法器的二阶基本节结构 来实现。 由于两个极点共轭对称, 所以将H(z)的两项通分 并化简整理, 可得
数字信号处理课后解答+第6章(高西全丁美玉第三版)

b (2) Ha (s) = (s + a)2 + b2
Ha(s)的极点为 s1=-a+jb,
将Ha(s)部分分式展开:
s2=-a-jb
j
j
−
Ha (s)
=
s
−
2 (−a
−
jb)
+
s
2 − (−a +
jb)
套用教材(6.3.4)式, 得到
j
j
−
H(z) = −
2
+
2
1 − e(−a− jb)T z−1 1 − e(−a+ jb)T z−1
教材第6章习题与上机题解答
1. 设计一个巴特沃斯低通滤波器, 要求通带截止频率
fp=6 kHz,通带最大衰减αp=3 dB, 阻带截止频率fs=12kHz, 阻带最小衰减αs=25 dB。 求出滤波器归一化系统函数G(p)以 及实际滤波器的Ha(s)。 解: (1) 求阶数N。
N = lg ksp lg λsp
7π
7π
p4 = −ch0.5580sin
8
+ j ch0.5580 cos 8
= −0.4438 − j1.0715
(4) 将G(p)去归一化, 求得实际滤波器系统函数Ha(s):
Ha (s)
=
Q( p) |
p=
s
Ωp
=
Ω
4 p
4
=
Ω
4 p
4
∏ 1.7368 (s − Ωp pk ) 1.7368∏ (s − sk )
(1) Ha (s) = (s + a)2 + b2
b (2) Ha (s) = (s + a)2 + b2
数字信号处理课后答案+第2章(高西全丁美玉第三版)

上式中|H(ejω)|是ω的偶函数, 相位函数是ω的奇函数, |H(ejω)|=|H(e-jω)|, θ(ω)=-θ(-ω), 故
1 y (n) A H (e j0 ) e jj e j0 n e j (0 ) e jj e j0 n e j (0 ) 2 A H (e j0 ) cos(0 n j (0 ))
j
πk 4
π δ( k ) 2
5. 设题5图所示的序列x(n)的FT用X(ejω)表示, 不直接求出 X(ejω), 完成下列运算或工作:
题5图
j0 (1) X (e )
(2)
π
π
X (e j )d
(3) X (e jπ ) (4) 确定并画出傅里叶变换实部Re[X(ejω)]的时间序列 xa(n); (5) (6)
令n′=2n, 则
FT[ x(2n)]
n , n取偶数
x(n)e jn / 2
j n 1 n [ x(n) (1) x(n)]e 2 2 n
1
1 1 j n j n 1 x ( n )e 2 e jn x(n)e 2 2 n n
题4解图
或者
1 1 j πk j πk e 2 (e 2 1 j πk e 2 )
~ X (k )
n 0
1
π j kn e 2
1 e jπk
π j k 1 e 2
1 1 1 j πk j πk j πk e 4 (e 4 e 4 )
1 j πk e 4
证明输入x(n)=A cos(ω0n+j)的稳态响应为
数字信号处理课后答案全+第1章(高西全丁美玉第三版)
② 0≤n≤3时, y(n)= 1=n+1
m =0
∑
3
③ 4≤n≤7时, y(n)= 1=8-n
= −4
∑ m n
y(n)的波形如题8解图(一)所示。
(2) y(n) =2R4(n)*[δ(n)-δ(n-2)]=2R4(n)-2R4(n-2) =2[δ(n)+δ(n-1)-δ(n+4)-δ(n+5)]
(4) y(n)=x(n-n0) (5) y(n)=ex(n)
(4)假设n0>0, 系统是因果系统, 因为n时刻输出只 和n时刻以后的输入有关。 如果|x(n)|≤M, 则|y(n)|≤M, 因 此系统是稳定的。 (5) 系统是因果系统, 因为系统的输出不取决于x(n) 的未来值。 如果|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM, 因此 系统是稳定的。 7. 设线性时不变系统的单位脉冲响应h(n)和输入序列
−1 4
(3) x1(n)的波形是x(n)的波形右移2位, 再乘以2, 画 出图形如题2解图(二)所示。 (4) x2(n)的波形是x(n)的波形左移2位, 再乘以2, 画出 图形如题2解图(三)所示。 (5) 画x3(n)时, 先画x(-n)的波形(即将x(n)的波形以纵轴 为中心翻转180°), 然后再右移2位, x3(n)波形如题2解图 (四)所示。
先确定求和域。 由R4(m)和R5(n-m)确定y(n)对于m的 非零区间如下: 0≤m≤3 -4≤m≤n
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
n
最后结果为 0
n<0或n>7
y(n)=
n+1 0≤n≤3
数字信号处理课后答案+第3章(高西全丁美玉第三版)

j
2π mn N ,
0<m< N
2π x(n) = cos mn , 0 < m < N N
(7) (8) (9)
x(n)=ejω0nRN(n) x(n)=sin(ω0n)RN(n) x(n)=cos(ω0n)RN(N)
(10) x(n)=nRN(n) 解: (1)
H (k ) = ∑ ∑ x((n′ + lN )) N e
l =0 n′=0
m −1 N −1
−j
2π( n′+lN ) k rN
2π 2π −j n′k − j lk N −1 k r −1 − j 2π lk ′)e mN e m = X ∑ e m = ∑ ∑ x(n l =0 n′=0 r l =0 m −1
2. 已知下列X(k), 求x(n)=IDFT[X(k)]
N jθ 2e N − jθ X (k ) = e 2 0 k =m k = N −m 其它k
(1)
(2)
N jθ − j 2 e N − jθ X (k ) = j e 2 0
kn X (k ) = ∑ x(n)W N n =0 =0 N −1
所以
kn DFT[ X (n)] = ∑ X (n)W N n =0 N −1
N −1 mn kn = ∑ ∑ x(m)W N W N n =0 m =0
N −1
n = ∑ x ( m)∑ W N ( m + k ) m =0 n =0
解法二 由DFT共轭对称性可得同样结果。 因为
x9 (n) = cos(ω 0 n) ⋅ R N (n) = Re[ x 7 (n)]
数字信 处理 西安电子科技大学出版 高西全丁美玉 第三版 课后习题答案 全

=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
=2x(n)+x(n-1)+ x(n-2)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(n2 )+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
k nn0
如果|x(n)|≤M, 则
第 1 章 时域离散信号和时域离散系统
(4)假设n0>0, 系统是因果系统, 因为n时刻输出只和n时刻以后的输入 有关。 如果|x(n)|≤M, 则|y(n)|≤M,
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
9. 证明线性卷积服从交换律、 结合律和分配律, 即证明下面等式成立: (1) x(n)*h(n)=h(n)*x(n) (2) x(n)*(h1(n)*h2(n))=(x(n)*h1(n))*h2(n) (3) x(n)*(h1(n)+h2(n))=x(n)*h1(n)+x(n)*h2(n) 证明: (1) 因为
(2) 因为ω=
,
所以
1
8
=16π, 这是无理数, 因此是非周期序列。
2π
第 1 章 时域离散信号和时域离散系统
* 4. 对题1图给出的x(n)要
1
2
求:
1
2
(1) 画出x(-n)的波形;
第 1 章 时域离散信号和时域离散系统
解:(1) x(-n)的波形如题4 (2) 将x(n)与x(-n)的波形对应相加, 再除以2, 得到xe(n)。 毫无疑问, 这是 一个偶对称序列。 xe(n)的波形如题4解图(二)所示。 (3) 画出xo(n)的波形如题4解图(三)所示。
数字信号处理_西安电子(_高西全丁美玉)第三版_课后习题答案(全)1-7章[1]
![数字信号处理_西安电子(_高西全丁美玉)第三版_课后习题答案(全)1-7章[1]](https://img.taocdn.com/s3/m/9f0528cd2cc58bd63186bd71.png)
第 1 章
(6) y(n)=x(n2) 令输入为
时域离散信号和时域离散系统
x(n-n0)
输出为 y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n)
故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)] 故系统是线性系统。
解: (1) y(n)=x(n)*h(n)= R4(m)R5(n-m)
先确定求和域。 由R4(m)和R5(n-m)确定y(n)对于m的
0≤m≤3 -4≤m≤n
m
非零区间如下:
第 1 章
时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0 ② 0≤n≤3时, y(n)=
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
第 1 章
(5)y(n)=x2(n) (6)y(n)=x(n2) (7)y(n)= n
时域离散信号和时域离散系统
x(m) (8)y(n)=x(n)sin(ωn)
m 0
解: (1) 令输入为 x(n-n0)
输出为
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2) =y′(n)
数字信号处理第三版西安科大出版高西全丁玉美课后答桉第3和4章

1
N 1
X (k) 2
n0
N k0
第3章 离散傅里叶变换(DFT)及其快速算法
(FFT)
7)
(1) 长度为N的共轭对称序列xep(n)与反共轭对称序列
xop(n):
xep(n) xep(N n)
xop (n) xop (N n)
序列x(n)的共轭对称分量与共轭反对称分量:
xep (n)
所以
~xN (n)
x(n rN )
r
即 ~xN (n) 是x(n)的周期延拓序列, 由DFT与DFS的关系
可得出
xN (n) IDFT[ X (k)] ~xN (n)RN (n) x(n rN )RN (n) r
第3章 离散傅里叶变换(DFT)及其快速算法
(FFT)
xN(n)=IDFT[X(k)]为x(n)的周期延拓序列(以N为延拓周期) 的主值序列。 以后这一结论可以直接引用。
DFT[x(n m)N RN (n)] WNkm X (k)
5) 频域循环移位性质
DFT[WNnm x(n)] X ((k m)) N RN (k)
第3章
6) 循环卷积:
离散傅里叶变换(DFT)及其快速算法 (FFT)
L1
yc (n) h(m)x((n m))L RL (n)=h(n) L x(n)
(1)在h(n)的尾部加L-N个零点, 在x(n)的尾部加L-M
(2)计算L点的H(k)=FFT[h(n)]和L点的X(k)=FFT [x(n)];
(3) 计算Y(k)=H(k)X(k) (4) 计算Y(n)=IFFT[Y(k)], n=0,1,2,3,…,L-1。 但当h(n)和x(n)中任一个的长度很长或者无限长时, 需用 书上介绍的重叠相加法和重叠保留法。
数字信号处理第三版西安科大出版高西全丁玉美课后答案第7章

第6章
有限脉冲响应(FIR)数字滤波器的设计
2. 已知第一类线性相位FIR滤波器的单位脉冲响应长度 为16, 其16个频域幅度采样值中的前9个为: Hg(0)=12, Hg(1)=8.34, Hg(2)=3.79, Hg(3)~Hg(8)=0 根据第一类线性相位FIR滤波器幅度特性Hg(ω)的特点, 求 其余7个频域幅度采样值。 解: 因为N=16是偶数(情况2), 所以FIR滤波器幅度 特性Hg(ω)关于ω=π点奇对称, 即Hg(2π-ω)=-Hg(ω)。 其N点 采样关于k=N/2点奇对称, 即 Hg(N-k)=-Hg(k) k=1, 2, …, 15 综上所述, 可知其余7个频域幅度采样值: Hg(15)=-Hg(1)=-8.34, Hg(14)=-Hg(2)=-3.79, Hg(13)~Hg(9)=0
c | | ≤
(1) 求出理想低通滤波器的单位脉冲响应hd(n);
(2) 求出加矩形窗设计的低通FIR滤波器的单位脉冲响
应h(n)表达式, 确定α与N之间的关系; (3) 简述N取奇数或偶数对滤波特性的影响。 解: (1) 1 π 1 c j jn j j n hd (n) H d (e )e d e e d π c 2π 2π sin[c (n )] π(n )
1 j2 (e 0.9e j 2.1 0.9e j e j2 )e j2 10
1 (2.1 1.8 cos 2 cos 2)e j2 10
第6章
有限脉冲响应(FIR)数字滤波器的设计
幅度特性函数为
2.1 1.8 cos 2 cos 2 H g () 10 相位特性函数为
第6章
有限脉冲响应(FIR)数字滤波器的设计
(完整版)数字信号处理(第三版)高西全丁玉美课后答案

西安电子(咼西全丁美玉第二版)数字信号处理课后答案1.2 教材第一章习题解答解:x(n)(n 4)2 (n 2)0.5 (n 4) 2 (n(n 1) 2 (n) (n 1) 2 (n 2) 4 (n 3) 6)2n 5, 4 n 12.给定信号 :x(n)6,0 n 4 0,其它(1) 画出x(n)序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示 x(n)序列;(3) 令X 1(n) 2x(n 2),试画出捲(n)波形; (4) 令 X 2(n) 2x(n 2),试画出 X 2(n)波形; (5) 令 x 3(n) 2x(2 n),试画出 X 3(n)波形。
解:(1) x(n)的波形如 题2解图(一)所示。
(2)x(n) 3 (n 4) (n 3) (n 2) 3 (n 1) 6 (n)6 (n 1) 6 (n 2) 6 (n 3) 6 (n 4)(5)画X 3(n)时,先画x(-n)的波形,然后再右移 2位,X 3(n)波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
3(1) x(n) Acos( n -),A 是常数;1j (7n)(2) x(n) e 8。
1.用单位脉冲序列(n)及其加权和表示 题1图所示的序列。
(3) x, n)的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4) X 2 (n)的波形是x(n)的波形左移 2位,在乘以2,画出图形如 题2解图(三)所示。
解:3 2 14(1)W , ,这是有理数,因此是周期序列,周期是T=14 ;7 w 31 2(2)w , 16 ,这是无理数,因此是非周期序列。
8 w5.设系统分别用下面的差分方程描述,x(n)与y(n)分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)y(n) x(n) 2x(n 1) 3x(n 2);(3)y(n) x(n n°),n o为整常数;(5)y(n) x2(n);(7)y(n) nx(m)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安电子(高西全丁美玉第三版)数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w wππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =;(7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。
12121212()[()()]()()2((1)(1))3((2)(2))y n T ax n bx n ax n bx n ax n bx n ax n bx n =+=++-+-+-+-1111[()]()2(1)3(2)T ax n ax n ax n ax n =+-+- 2222[()]()2(1)3(2)T bx n bx n bx n bx n =+-+- 1212[()()][()][()]T ax n bx n aT x n bT x n +=+故该系统是线性系统。
(3)这是一个延时器,延时器是一个线性时不变系统,下面予以证明。
令输入为1()x n n -,输出为'10()()y n x n n n =--,因为'110()()()y n n x n n n y n -=--=故延时器是一个时不变系统。
又因为12102012[()()]()()[()][()]T ax n bx n ax n n bx n n aT x n bT x n +=-+-=+故延时器是线性系统。
(5) 2()()y n x n =令:输入为0()x n n -,输出为'20()()y n x n n =-,因为2'00()()()y n n x n n y n -=-=故系统是时不变系统。
又因为21212122212[()()](()())[()][()] ()()T ax n bx n ax n bx n aT x n bT x n ax n bx n +=+≠+=+ 因此系统是非线性系统。
(7) 0()()nm y n x m ==∑令:输入为0()x n n -,输出为'()()nm y n x m n==-∑,因为'00()()()n n m y n n x m y n -=-=≠∑故该系统是时变系统。
又因为1212120[()()](()())[()][()]nm T ax n bx n ax m bxm aT x n bT x n =+=+=+∑故系统是线性系统。
6. 给定下述系统的差分方程,试判断系统是否是因果稳定系统,并说明理由。
(1)11()()N k y n x n k N-==-∑;(3)00()()n n k n n y n x k +=-=∑;(5)()()x n y n e =。
解:(1)只要1N ≥,该系统就是因果系统,因为输出只与n 时刻的和n 时刻以前的输入有关。
如果()x n M ≤,则()y n M ≤,因此系统是稳定系统。
(3)如果()x n M ≤,00()()21n n k n n y n x k n M +=-≤≤+∑,因此系统是稳定的。
系统是非因果的,因为输出还和x(n)的将来值有关.(5)系统是因果系统,因为系统的输出不取决于x(n)的未来值。
如果()x n M ≤,则()()()x n x n My n eee=≤≤,因此系统是稳定的。
7. 设线性时不变系统的单位脉冲响应()h n 和输入序列()x n 如题7图所示,要求画出输出输出()y n 的波形。
解:解法(1):采用图解法()()()()()m y n x n h n x m h n m ∞==*=-∑图解法的过程如题7解图所示。
解法(2):采用解析法。
按照题7图写出x(n)和h(n)的表达式:()(2)(1)2(3)1()2()(1)(2)2x n n n n h n n n n δδδδδδ=-++-+-=+-+-因为()*()()()*()()x n n x n x n A n k A x nk δδ=-=-所以1()()*[2()(1)(2)]212()(1)(2)2y n x n n n n x n x n x n δδδ=+-+-=+-+-将x(n)的表达式代入上式,得到()2(2)(1)0.5()2(1)(2) 4.5(3)2(4)(5)y n n n n n n n n n δδδδδδδδ=-+-+-+-+-+-+-+-8. 设线性时不变系统的单位取样响应()h n 和输入()x n 分别有以下三种情况,分别求出输出()y n 。
(1)45()(),()()h n R n x n R n ==;(2)4()2(),()()(2)h n R n x n n n δδ==--;(3)5()0.5(),()nn h n u n x R n ==。
解:(1) 45()()*()()()m y n x n h n R m R n m ∞=-∞==-∑先确定求和域,由4()R m 和5()R n m -确定对于m 的非零区间如下:03,4m n m n ≤≤-≤≤根据非零区间,将n 分成四种情况求解: ①0,()0n y n <=②003,()11nm n y n n =≤≤==+∑③3447,()18m n n y n n =-≤≤==-∑④7,()0n y n <= 最后结果为0, 0,7()1, 038, 47n n y n n n n n <>⎧⎪=+≤≤⎨⎪-≤≤⎩y(n)的波形如题8解图(一)所示。
(2)444()2()*[()(2)]2()2(2) 2[()(1)(4)(5)]y n R n n n R n R n n n n n δδδδδδ=--=--=+-----y(n)的波形如题8解图(二)所示. (3)55()()*()()0.5()0.5()0.5()n mnmm m y n x n h n R m u n m R m u n m ∞∞--=-∞=-∞==-=-∑∑y(n)对于m 的非零区间为04,m m n ≤≤≤。
①0,()0n y n <=②11110.504,()0.50.50.5(10.5)0.520.510.5n nnmn n n nm n y n ------=-≤≤===--=--∑③54110.55,()0.50.50.5310.510.5nmn nm n y n ---=-≤===⨯-∑最后写成统一表达式:5()(20.5)()310.5(5)nny n R n u n =-+⨯-11. 设系统由下面差分方程描述:11()(1)()(1)22y n y n x n x n =-++-;设系统是因果的,利用递推法求系统的单位取样响应。
解:令:()()x n n δ=11()(1)()(1)22h n h n n n δδ=-++- 2110,(0)(1)(0)(1)122111,(1)(0)(1)(0)122112,(2)(1)22113,(3)(2)()22n h h n h h n h h n h h δδδδ==-++-===++=======归纳起来,结果为11()()(1)()2n h n u n n δ-=-+12. 有一连续信号()cos(2),a x t ft πϕ=+式中,20,2f H z πϕ==(1)求出()a x t 的周期。
(2)用采样间隔0.02T s =对()a x t 进行采样,试写出采样信号()a xt 的表达式。
(3)画出对应()a xt 的时域离散信号(序列) ()x n 的波形,并求出()x n 的周期。
————第二章————教材第二章习题解答1. 设()jwX e 和()jwY e 分别是()x n 和()y n 的傅里叶变换,试求下面序列的傅里叶变换: (1)0()x n n -; (2)()x n -; (3)()()x n y n ; (4)(2)x n 。
解:(1)00[()]()jw nn FT x n n x n n e∞-=-∞-=-∑令''00,n n n n n n =-=+,则'00()'0[()]()()jw n n jw n jwn FT x n n x n eeX e∞-+-=-∞-==∑(2)****[()]()[()]()jw njw n jwn n FT x n x n ex n eX e-∞∞-=-∞=-∞===∑∑(3)[()]()jw nn FT x n x n e∞-=-∞-=-∑令'n n =-,则'''[()]()()jw njwn FT x n x n eX e∞-=-∞-==∑(4) [()*()]()(j wj wF T x n y n X eY e= 证明: ()*()()(m x n y n x m y n m∞=-∞=-∑[()*()][()()]jw nn m FT x n y n x m y n m e∞∞-=-∞=-∞=-∑∑令k=n-m ,则[()*()][()()] ()() ()()jw kjw nk m jw kjw nk m jwjwF T x n y n x m y k eey k ex m eX e Y e∞∞--=-∞=-∞∞∞--=-∞=-∞===∑∑∑∑2. 已知001,()0,jww w X ew w π⎧<⎪=⎨<≤⎪⎩求()jwX e 的傅里叶反变换()x n 。
