希望杯第十至第十五届四年级题目

合集下载

第十五届小学四年级希望杯全国数学邀请赛试题及答案资料

精品文档
第十五届小学“希望杯”全国数学邀请赛
四年级第1试试题
2017年3月19日上午8：30至10：00
以下每题6分，共120分。
1、计算：19×75+23×25 = .
2、定义新运算：，，如：，b)b(aba20）4（1babb414a。则按从左到右的顺序计算：.321448114
abcabcabc最小是则是奇数，是三位数，若且.是33、的倍数，a
精品文档．
精品文档
9、下图是由12个面积为1的方格组成，则图中和阴影梯形面积相同的长方形有个。
10、某学习小组数学成绩的统计图如下，该小组的平均成绩是分。
11、今年，小军5岁，爸爸31岁，再过年，爸爸的年龄是小军的 3倍。
12、10个连续的自然数从小到大排列，若最后6个数的和比前4个数的和的2倍大15，则这10个数中最小的数是。
第15届“希望杯”数学邀请赛四年级1试参考答案
题号
1
2
3
4
5
6
7
8
9
10
答案
2000
21
102
15
9
4
336
13
10
90
题号
11
12
13
14
15
16
17
18
19
20
答案
8
6
40
15
五

144
6:13
118
15
；24
精品文档．
17、甲、乙两人分别从A，B两地同时出发，相向而行，甲到达A，B中点C时，乙距C点还有240米，乙到达C点时，甲已经超过C点360米，则两人在D点相遇时，CD的距离是米。

小学四年级希望杯历年数学竞赛试题与答案1_14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

9．甲、乙、丙、丁四个学习小组共有图书280本，班主任老师提议让四个组的书一样多，得到拥护，于是从甲调14本给乙，从乙调15本给丙，从丙调17本给丁，从丁调18本给甲。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

第十五届小学“希望杯”全国数学邀请赛试卷(四年级第1试)

2017年第十五届小学“希望杯”全国数学邀请赛试卷（四年级第1试）每小题10分，共120分1．（10分）计算：19×75+23×25＝．2．（10分）定义新运算：a△b＝（a+b）×b，a□b＝a×b+b，如：1△4＝（1+4）×4＝20，1□4＝1×4+4＝8，按从左到右的顺序计算：1△2□3＝．3．（10分）是三位数，若a是奇数，且是3的倍数，则最小是．4．（10分）三个连续自然数的乘积是120，它们的和是．5．（10分）已知x，y是大于0的自然数，且x+y＝150，若x是3的倍数，y是5的倍数，则（x，y）的不同取值有对．6．（10分）如果8×（2+1÷x）＝18，则x＝．7．（10分）观察以下的一列数：11，17，23，29，35，…若从第n个数开始，每个数都大于2017，则n＝．8．（10分）图中由20个方格组成，其中含有A的正方形有个．9．（10分）图中由12个面积为1的方格组成，则图中和阴影梯形面积相同的长方形有个．10．某学习小组数学成绩的统计图如图，该小组的平均成绩是分．11．今年，小军5岁，爸爸31岁，再过年，爸爸的年龄是小军的3倍．12．10个连续的自然数从小到大排列，若最后6个数的和比前4个数的和的2倍大15，则这10个数中最小的数是．13．如图，把一个边长是5cm的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向移动其中的4个长方形，则所得图形的周长是cm．14．在一个长方形内画三个圆，这个长方形最多可被分成部分．15．2017年3月19日是星期日，据此推算，2017年9月1日是星期．16．观察7＝5×1+2，12＝5×2+2，17＝5×3+2，这里7，12和17被叫做“3个相邻的被5除余2的数”，若有3个相邻的被5除余2的数的和等于336，则其中最小的数是．17．甲，乙两人分别从A，B两地同时出发，相向而行，甲到达A，B中点C 时，乙距C点还有240米，乙到达C点时，甲已经超过C点360米，则两人在D点相遇时，CD的距离是米．18．洋洋从家出发去学校，若每分钟走60米，则它6：53到达学校，若每分钟走75米，则她6：45到达学校，洋洋从家里出发的时刻是．19．袋子中有黑白两种颜色的棋子，黑子的个数是白子的个数的2倍，每次从袋中同时取出3个黑子和2个白子，某次取完后，白子剩下1个，黑子剩下31个，则袋中原有黑子个．20．有一笔钱，用来给四（1）班的学生每人买一个笔记本，若每本3元，则可多买6本；若每本5元，则差30元．若用完这笔钱，恰好给每人买一个笔记本，则共买笔记本个，其中3元的笔记本个．2017年第十五届小学“希望杯”全国数学邀请赛试卷（四年级第1试）参考答案与试题解析每小题10分，共120分1．（10分）计算：19×75+23×25＝2000 ．【分析】将75拆分成3×25，然后利用乘法的分配律，把后面的23加在一起，刚好是80×25【解答】解：19×75+23×25＝19×3×25+23×25＝57×25+23×25＝25×（57+23）＝25×80＝2000故答案是：2000【点评】本题考查了四则运算的巧算，本题突破点是：将75拆分成3×25，然后利用乘法的分配律求出答案2．（10分）定义新运算：a△b＝（a+b）×b，a□b＝a×b+b，如：1△4＝（1+4）×4＝20，1□4＝1×4+4＝8，按从左到右的顺序计算：1△2□3＝21 ．【分析】定义新运算需要理解题中给出的运算过程，△的运算是两数和再乘以第二个数的积运算．□的运算是两数的积与第二个数的和运算．【解答】解：依题意可知：a△b＝（a+b）×b得1△2＝（1+2）×2＝6a□b＝a×b+b得6□3＝3×6+3＝21故答案为：21【点评】本题的关键是找到新定义的符号的意义和运用．同时注意做题时的顺序是从左向右的顺序计算，那么代表他们是同级运算．问题解决．3．（10分）是三位数，若a是奇数，且是3的倍数，则最小是102 ．【分析】要使最小，那么百位数字最小是1，那么十位数字是0，这个数就为，然后根据能被3整除的数的特征确定c的最小值即可．【解答】解：要使最小，那么百位数字最小是1，那么十位数字是0，这个数就为，又因为是3的倍数，所以可得：1+0+c的和是3的倍数，所以，c最小是2，则，最小是102．故答案为：102．【点评】本题考查了能被3整除的数的特征的灵活应用，关键是确定百位和十位的数字．4．（10分）三个连续自然数的乘积是120，它们的和是15 ．【分析】首先把120分解质因数，把质因数分作三组，使各组数字相乘后的结果是三个连续的自然数，即可得解．【解答】解：120＝2×2×2×3×5＝（2×2）×（2×3）×5，2×2＝4，2×3＝6，5，即，三个连续自然数的乘积是120，这三个数是4、5、6，所以，和是：4+5+6＝15．故答案为：15．【点评】本题考查了灵活应用合数分解质因数来解决较复杂问题．5．（10分）已知x，y是大于0的自然数，且x+y＝150，若x是3的倍数，y是5的倍数，则（x，y）的不同取值有9 对．【分析】首先根据5的整除特性可知尾数是0或者5，那么150和5的倍数差依然是尾数是0或者5的数字枚举即可．【解答】解：根据5的整除特性可知尾数是0或者5．那么150减去这个数字尾数还是0或者5．可以找到尾数是0或者5的数字是3的倍数．30，60，90，120，15，45，75，105，135共9个数字满足条件．对应的数字就有9对．故答案为：9．【点评】本题是考察数的整除特性，关键在于找到尾数是0或5的数字是3的倍数，枚举即可解决问题．6．（10分）如果8×（2+1÷x）＝18，则x＝ 4 ．【分析】8×（2+1÷x）＝18运用逆推的方法，先用18除以8求出小括号里面算式的结果，再减去2得到差，求出1÷x的结果，再用1除以求出的差，即可得到x的值．【解答】解：8×（2+1÷x）＝182+1÷x＝18÷82+1÷x＝2.251÷x＝2.25﹣21÷x＝0.25x＝1÷0.25x＝4故答案为：4．【点评】解决本题根据加减法之间的互逆关系，以及乘除法之间的互逆关系，从结果向前推算，得出x的值．7．（10分）观察以下的一列数：11，17，23，29，35，…若从第n个数开始，每个数都大于2017，则n＝336 ．【分析】观察以下的一列数：11，17，23，29，35，…可以看出规律是相邻的数：后面的比前面的大6；求第n个数开始每个数都大于2017，则n＝．【解答】解：11＝5+6×117＝5+6×223＝5+6×329＝5+6×4…第n个数＝5+6×n所以有：5+6n＞20176n＞2012n＞335 (2)n＝336；故答案为：336．【点评】等差数列规律题，求第n项的数字．8．（10分）图中由20个方格组成，其中含有A的正方形有13 个．【分析】按题意，可以分类讨论，只有一个方格的正方形，含有四个方格的正方形，含有九个方格的正方形，含有16个方格的正方形，再数一下含有A的正方形即可得出结果．【解答】解：根据分析，①只有一个方格的正方形且含有A的有：1个；②含有4个方格且含有A的正方形有：4个；③含有9个方格且含有A的正方形有：6个；④含有16个方格且含有A的正方形有：2个；综上，含有A的正方形共有：1+4+6+2＝13个．故答案是：13【点评】本题考查了排列组合奇组合图形的计数，突破点是：分类讨论找到含有A的正方形，算出个数的总数．9．（10分）图中由12个面积为1的方格组成，则图中和阴影梯形面积相同的长方形有10 个．【分析】设小方格的边长是1，则梯形的上底是1，下底是2，高是2，根据梯形的面积公式，求出阴影部分的面积是3，长方形是有3个小方格拼成的，再分别找出横看和竖看各有多少个这样的长方形，再相加即可．【解答】解：设小方格的边长是1，则梯形的面积是：（1+2）×2÷2＝3×2÷2＝3也就是长方形的面积是3；1×1＝1，一个小方格的面积是1，那么长方形是有3个小方格拼成的，竖着看每列都是3个小方格，一共有4列，所以有4个长方形符合要求；横着看，每行前三个小方格可以组成1个面积是3的长方形，后3个小方格也可以组成面积是3的长方形，所以每行都有2个面积是3的长方形；横着一共是：3×2＝6（个）4+6＝10（个）答：图中和阴影梯形面积相同的长方形有 10个．故答案为：10．【点评】解决本题先设出方格的边长，得出阴影部分的面积，再找出与之面积相等的长方形的个数即可．10．某学习小组数学成绩的统计图如图，该小组的平均成绩是90 分．【分析】求出总分及相应的人数，即可求出相应的平均数．【解答】解：由题意，该小组的平均成绩是（85×6+89×3+95×5+98×1）÷（6+3+5+1）＝90，故答案为90．【点评】本题考查平均数问题，考查学生的计算能力，正确求出总分及相应的人数是关键．11．今年，小军5岁，爸爸31岁，再过8 年，爸爸的年龄是小军的3倍．【分析】根据“今年，小军5岁，爸爸31岁”求出父子的年龄差是（31﹣5）岁，由于此年龄差不会改变，倍数差是3﹣1＝2，所以利用差倍公式，求出当父亲年龄是儿子年龄的3倍时儿子的年龄，由此进一步解决问题．【解答】解：父子年龄差是：31﹣5＝26（岁），爸爸的年龄是小军的3倍时，小军的年龄是：26÷（3﹣1）＝26÷2＝13（岁），13﹣5＝8（年），答：再过8年，爸爸的年龄是小军的3倍．故答案为：8．【点评】解答此题的关键是根据两人的年龄差不会随着时间的改变而变化，利用差倍公式求出儿子相应的年龄，由此解决问题．差倍问题的关系式：数量差÷（倍数﹣1）＝1倍数（较小数），1倍数（较小数）×倍数＝几倍数（较大数）．12．10个连续的自然数从小到大排列，若最后6个数的和比前4个数的和的2倍大15，则这10个数中最小的数是 6 ．【分析】本题主要考察等差数列．【解答】解：设最小的数为x，则剩余自然数依次为x+1，x+2，…，x+9，由题可得2（4x+1+2+3）+15＝6x+4+5+6+7+8+9，化简后是8x+27＝6x+39∴x＝6，【点评】本题可以借助列方程，设最小的数为x，一一用x表示其他连续自然数，根据等量关系就可求解．13．如图，把一个边长是5cm的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向移动其中的4个长方形，则所得图形的周长是40 cm．【分析】本题考察图形边长的平移．【解答】解：画出移动后的图，所得图形的周长是5×2+（5+1×2+2×2+3×2+4×2+5）＝10+30＝40cm．【点评】本题主要抓住平移后的图形每条边边长为多少即可求解．14．在一个长方形内画三个圆，这个长方形最多可被分成15 部分．【分析】在一个长方形内画三个圆，要使这个长方形被分成的部分最多，就要使圆与圆，圆与长方形之间的交点尽量多，据此画图即可．【解答】解：画图如下：所以，这个长方形最多可被分成 15部分．故答案为：15．【点评】本题考查了图形的划分，关键是明确如何使交点尽量多．15．2017年3月19日是星期日，据此推算，2017年9月1日是星期五．【分析】先求3月19日到9月1日经过了多少天，再求这些天里有几周，还余几天，再根据余数判断．【解答】解：3月19日到3月31日共：31﹣19＝12（天）4、6月30天，5、7、8月31天，一共：30×2+31×3+12+1＝60+93+13＝166（天）166÷7＝23（周）…5（天）所以3月19日是星期日，9月1日是星期五．答：2017年9月1日是星期五．故答案为：五．【点评】解决这类问题先求出经过的天数，再求经过的天数里有几周还余几天，再根据余数推算．16．观察7＝5×1+2，12＝5×2+2，17＝5×3+2，这里7，12和17被叫做“3个相邻的被5除余2的数”，若有3个相邻的被5除余2的数的和等于336，则其中最小的数是107 ．【分析】本题主要考察等差数列中最小的项．【解答】解：因为这三个数都是被5除余2，所以这三个相邻的数是个等差数列，中间数是336÷3＝112，所以最小的是112﹣5＝107．【点评】本题主要找到每相邻两个数相差5就能解答．17．甲，乙两人分别从A，B两地同时出发，相向而行，甲到达A，B中点C 时，乙距C点还有240米，乙到达C点时，甲已经超过C点360米，则两人在D点相遇时，CD的距离是144 米．【分析】由题目中的已知条件，得出甲乙的速度比，进而又得出他们的路程比，这样求出甲到达中点后再与乙共行240米，甲行的路程即CD之间的距离．【解答】解：由题意知“甲走360米时乙正好走240米”，甲、乙的速度比是360：240＝3：2相同时间内，甲、乙的路程比等于他们的速度比即3：2甲乙共行240米，甲行的路程是240×3÷（2+3）＝144（米）故：CD的距离是144米．【点评】解此题的突破口就是能得出他们的速度比，之后就可轻松解答了．18．洋洋从家出发去学校，若每分钟走60米，则它6：53到达学校，若每分钟走75米，则她6：45到达学校，洋洋从家里出发的时刻是6：13 ．【分析】6时53分﹣6时45分＝8分钟，设从家到学校若每分钟走60米，x分钟到学校，则若每分钟走75米，x﹣8分钟到学校，因为从家到学校的距离一定，根据“速度×时间＝路程”列方程解答即可．【解答】解：设从家到学校若每分钟走60米，x分钟到学校，6时53分﹣6时45分＝8分钟60x＝（x﹣8）×7560x＝75x﹣60015x＝600x＝40；6时53分﹣40分＝6时13分；答：洋洋从家里出发的时刻是6：13．故答案为：6：13．【点评】此题考查列方程解应用题，本题关键是根据题意找出基本数量关系，设未知数为x，由此列方程解决问题．19．袋子中有黑白两种颜色的棋子，黑子的个数是白子的个数的2倍，每次从袋中同时取出3个黑子和2个白子，某次取完后，白子剩下1个，黑子剩下31个，则袋中原有黑子118 个．【分析】因黑子个数是白子个数的2倍，可假设黑子每次取的个数也是白子的2倍，即黑子每次2×2＝4个、白子每次取2个，则白子余1个时，黑子余2个．现每次黑子取少4﹣3＝1个了，则黑子多出来的数量，除以应取和实取的差，就是取的次数．据此解答．【解答】解：假设黑子每次取的个数也是白子的2倍，即黑子每次2×3＝6个、白子每次取3个，则：（31﹣1×2）÷（2×2﹣3）＝29÷1＝29（次）3×29+31＝87+31＝118（个）答：袋中原有黑子 118个．故答案为：118．【点评】本题的关键是根据黑子是白子个数的2倍，假设每次取黑子的个数是白子的2倍，与实际取黑子的差，及实际取与假设取应剩下黑子的差，进行解答．20．有一笔钱，用来给四（1）班的学生每人买一个笔记本，若每本3元，则可多买6本；若每本5元，则差30元．若用完这笔钱，恰好给每人买一个笔记本，则共买笔记本24 个，其中3元的笔记本15 个．【分析】若每本3元，则多3×6＝18元，则总人数为（18+30）÷（5﹣3）＝24人，总钱数有5×24﹣30＝90元，进而可得结论．【解答】解：由题意得若每本3元，则多3×6＝18元，则总人数为（18+30）÷（5﹣3）＝24人，总钱数有5×24﹣30＝90元，若钱用完刚好买24本，则3元的笔记本有（24×5﹣90）÷（5﹣3）＝15个，故答案为24，15．【点评】本题考查分配盈亏问题，考查学生的计算能力，属于中档题．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/4/22 16:51:11；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。

第十五届小学四年级“希望杯”全国数学邀请赛试题及答案

第十五届小学“希望杯”全国数学邀请赛四年级第1试试题以下每题6分，共120分。

1、计算：19×75+23×25 = .2、定义新运算：b b a b a ⨯+=*)(，b b a b a +⨯=⊗，如：2044141=⨯+=*）（，844141=+⨯=⊗。

则按从左到右的顺序计算：=⊗*321 .3、abc 是三位数，若a 是奇数，且abc 是3的倍数，则abc 最小是 .4、三个连续自然数的乘积是120，它们的和是 .5、已知x ，y 是大于0的自然数，且150=+y x 。

若x 是3的倍数，y 是5的倍数，则),(y x 的不同取值有对。

6、如果18128=÷+⨯）（x ，则=x .7、观察以下的一列数，依次是11，17，23，29，35，….若从第n 个数开始，每个数都大于2017，则=n .8、下图由20个方格组成，其中含有A 的正方形有个。

9、下图是由12个面积为1的方格组成，则图中和阴影梯形面积相同的长方形有个。

10、某学习小组数学成绩的统计图如下，该小组的平均成绩是分。

11、今年，小军5岁，爸爸31岁，再过年，爸爸的年龄是小军的3倍。

第8题第9题第10题12、10个连续的自然数从小到大排列，若最后6个数的和比前4个数的和的2倍大15，则这10个数中最小的数是。

13、把一个边长是5厘米的正方形纸片沿虚线分成5个长方形，然后按照箭头标记的方向和长度移动其中的4个长方形，则所得图形的周长是厘米。

14、在一个长方形内画三个圆，这个长方形最多可被分成部分。

15、2017年3月19日是星期日，据此推算，2017年9月1日是星期。

16、观察2=，2⨯12+5⨯17+=，这里，7，12和17被叫做“3个相邻的被535157+⨯2=，2除余2的数”，若有3个相邻的被5除余2的数的和等于336，则其中最小的数是.17、甲、乙两人分别从A，B两地同时出发，相向而行，甲到达A，B中点C时，乙距C点还有240米，乙到达C点时，甲已经超过C点360米，则两人在D点相遇时，CD的距离是米。

第十五届小学“希望杯”全国数学邀请赛四年级

第十五届小学“希望杯”全国数学邀请赛四年级第2试试题一、填空题（每小题5分，共60分）1．计算：110025411÷⨯÷=__________．【答案】16【解析】乘除混合运算；原式4441116=⨯÷=．2．有15个数，他们的平均数是17，加入1个数后，平均数变为20，则加入的数是__________．【答案】65【解析】平均数；原来15个数之和为1517255⨯=，加入一个数后和为1620320⨯=，则加入的数为32025565-=．3．若abc 和def 是两个三位数，且1a b =+，2b c =+，34abc def ⨯+=，则def =__________．【答案】964【解析】有余数的除法、最值问题；由题意得3a ⨯为一位数，a 与b 相差1，与c 相差3，则3a =，2b =，0c =，则32034964def =⨯+=．4．已知100a b +=，若a 除以3，余数是2，b 除以7，余数是5，则a b ⨯的最大值是__________．【答案】2491【解析】数论；和不变，差小积大．则要求a 与b 的差尽可能小即可，32a ÷=75b ÷= ，100a b +=，则53a =，47b =，53472491a b ⨯=⨯=．5．如图所示，两个完全相同的等腰三角形中各有一个正方形，图乙中的正方形面积为36平方厘米，则图甲中的正方形面积为__________平方厘米．【答案】32【解析】图形拼接与分割；根据正方形对角线性质及等腰三角形的性质作辅助线，如下图，将乙中等腰三角形平均分成4份，则三角形面积为362472÷⨯=（平方厘米），图甲将三角形平均分成了9个相同的小三角形，则正方形占4个，即甲图中三角形面积为729432÷⨯=（平方厘米）．甲乙6．边长为20的正方形的面积恰好等于边长为a 和边长为b 的两个正方形的面积的和，若a 和b 都是自然数，则a b +=__________．【答案】28【解析】平方数；222020400a b +=⨯=，又因为a 、b 为自然数，解得12a =，16b =，28a b +=．7．今年是2017年，年份的数字和是10，则本世纪内，数字和是10的所有年份的和是__________．【答案】18396【解析】数论；由题意得符合条件的四位数，千位为2，百位为0，十位和个位数字和为8即可，满足条件的有2008、2017、2026、2035、2044、2053、2062、2071、2080，即和为18396．8．在纸上画2个圆，最多可得到2个交点，画3个圆，最多可得到6个交点，那么如果在纸上画10个圆，最多可得到__________个交点．【答案】90【解析】枚举、归纳思想；由题得，2个圆最多有2个交点，3个圆最多有246+=个交点，4个圆最多有24612++=个交点，5个圆最多有246820+++=个交点，以此类推10个圆最多交点个数为 24681890+++++= 个点．9．小红带了面额50元，20元，10元的人民币各5张，6张，7张，她买的230元的商品，那么，有__________种付款方式．【答案】11【解析】枚举思想；10．甲、乙、丙三个数的和是2017，甲比乙的2倍少3，乙比丙的3倍多20，则甲是__________．【答案】1213【解析】和倍问题；由题得和为2017，则丙为(20172033)(133)196-⨯+÷+⨯=，乙：196320608⨯+=，甲：608231213⨯-=．11．篮球比赛中，三分线外投中一球可得3分，三分线内投中一球可得2分，罚篮投中一球得1分．某球队在一次比赛中共投进32个球，得65分，已知二分球的个数比三分球的个数的4倍多3个，则这个球队在比赛中罚篮共投中__________球．【答案】4【解析】列方程解应用题；解设三分球的有x 个，则二分球有(43)x +个，一分球有(3253295)x x --=-个，列方程：32(43)(295)165x x x +⨯++-⨯=，解得5x =，一分球有：29554-⨯=（个），即罚篮共投中4球．12．在下图的乘法算式中，A 、B 、C 、D 、E 、F 、G 、H 、I 分别表示彼此不同的一位数：则“FIGAA ”表示的五位数是__________．【答案】15744【解析】数字谜；突破口：ABC C ⨯为三位数、C C A ⨯=，则2C =，代入计算可知2C =，4A =，9B =，3D =，8E =，1F =，7G =，6H =，5I =则“FIGAA ”表示15744．二、解答题（每小题15分，共60分．）每题都要写出推算过程．13．甲、乙两人同时从A ，B 两地出发，相向而行，甲每分钟走70米，乙每分钟走60米，两人在距离中点80米的地方相遇，求A ，B 两地之间的距离．【答案】2080【解析】行程问题；由题意可知，甲比乙多走：802160⨯=（米），相遇时间：160(7060)16÷-=（分钟），则AB 两地相距16(7060)2080⨯+=（米）．14．老师给学生分水果，准备了两种水果，其中橘子的个数比苹果的个数的3倍多3个．每人分2个苹果，则余下6个苹果；每人分7个橘子，最后一人只能分得1个橘子．求学生的人数．【答案】27【解析】盈亏问题；解设学生人数为x 个，则苹果数为(26)x +个橘子数为7(1)1x -+个，则列方程：(26)337(1)1x x +⨯+=-+，解得27x =．15．两个相同的正方形重合在一起，将上层的正方形向右移动3厘米，再向下移动5厘米，得到如图所示的图形，已知阴影部分的面积是57平方厘米，求正方形的边长．【答案】9【解析】图形面积；设边长为a ，则35(3)57a a +⨯-=，则9a =．16．商店推出某新款手机的分期付款活动，有两种方案供选择．方案一：第一个月付款800元，以后每月付款200元；×AA G I F G HA F AE B D C CBA方案二：前一半的时间每月付款350元，后一半的时间每月付款150元．两种方案付款总数与时间都相同，求这款手机的价格．【答案】3000【解析】经济问题；解设时间为x 个月，则方案一：800(1)200x +-⨯，方案二：23502150x x ÷⨯+÷⨯，由题知付款总数与时间都相同，则800(1)20023502150x x x +-⨯=÷⨯+÷⨯，解得12x =，付款总数为800(1)2003000x +-⨯=元．。

全国四年级希望杯数学竞赛全部试题与规范标准答案

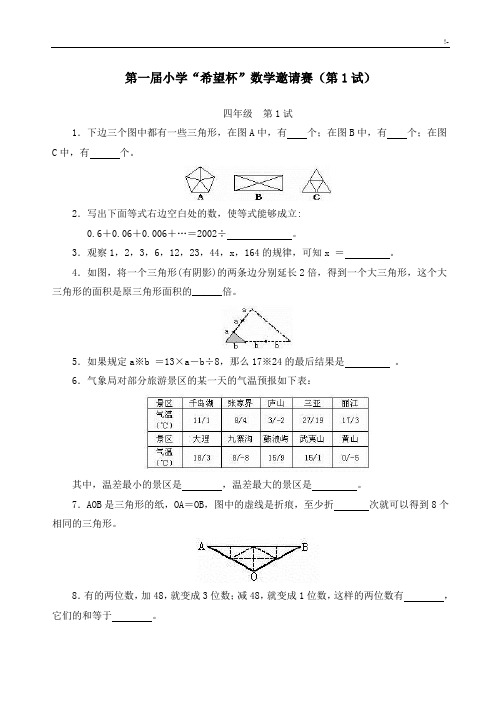
第一届小学“希望杯”数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处的数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)的两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

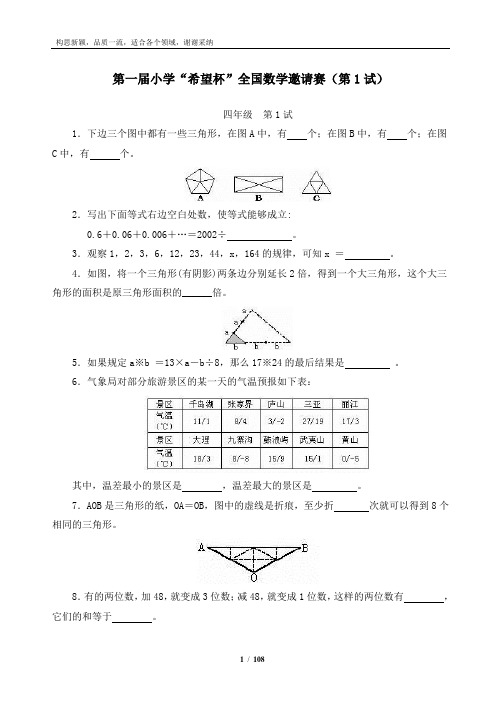
第一届小学“希望杯”全国数学邀请赛（第1试）四年级第1试1．下边三个图中都有一些三角形，在图A中，有个；在图B中，有个；在图C中，有个。

2．写出下面等式右边空白处数，使等式能够成立:0.6＋0.06＋0.006＋…＝2002÷。

3．观察1，2，3，6，12，23，44，x，164的规律，可知x ＝。

4．如图，将一个三角形(有阴影)两条边分别延长2倍，得到一个大三角形，这个大三角形的面积是原三角形面积的______倍。

5．如果规定a※b ＝13×a－b÷8，那么17※24的最后结果是。

6．气象局对部分旅游景区的某一天的气温预报如下表：其中，温差最小的景区是，温差最大的景区是。

7．AOB是三角形的纸，OA＝OB，图中的虚线是折痕，至少折次就可以得到8个相同的三角形。

8．有的两位数，加48，就变成3位数；减48，就变成1位数，这样的两位数有，它们的和等于。

这时四个组的书一样多。

这说明甲组原来有书本。

10．幼儿园老师给几组小朋友分苹果，每组分7个，少3个；每组分6个，则多4个，苹果有个，小朋友共组。

11．在 a＝20032003×2002和 b＝20022003×2003中，较大的数是，它比较小的数大。

12．小明的家离学校2千米，小光的家离学校3千米，小明和小光的家相距千米。

13．甲、乙、丙三人中只有1人会开汽车。

甲说：“我会开。

”乙说：“我不会开。

”丙说：“甲不会开。

”三人的话只有一句是真话。

会开车的是。

14．为了支援西部，1班班长小明和2班班长小光带了同样多的钱买了同一种书44本，钱全部用完，小明要了26本书，小光要了18本书。

回校后，小明补给小光28元。

小明、小光各带了元，每本书价元。

第十五届“希望杯”全国数学邀请赛四年级第2试真题及答案详解

第十五届小学希望杯全国数学邀请赛四年级第2试真题1. 计算：1100÷25×4÷11=_________2. 有15个数，它们的平均数是17，加入1个数后，平均数变成20，则加入的数是_________3. 若abc和def是两个三位数，且a=b+1, b=c+2, abc×3+4=def=,则def=4. 已知a+b=100，若a除以3，余数是2，b除以7，余数是5，则a×b的值最大是_________5. 如图所示，两个完全相同的等腰三角形中各有一个正方形，图乙中的正方形面积为36平方厘米，则图甲中的正方形面积为_________平方厘米6. 边长为20的正方形的面积恰好等于边长为a和边长为b的两个正方形的面积的和，若a和b 都是自然数，则a+b=_________7. 今年是2017年，年份的数字和是10，则本世纪内，数字和是10的所有年份的和是_________8. 在纸上画2个圆，最多可以得到2个交点，画3个圆，最多可得到6个交点。

那么，如果在纸上画10个圆，最多可得到________个交点9. 小红带了面额50元，20元，10元的人民币各5张，6张，7张，她买了230元的商品，那么有________种付款方式。

10. 甲、乙、丙的三个数的和是2017，甲比乙的2倍少3，乙比丙的3倍多20，则甲是________11. 篮球比赛中，三分线外投中1球得3分，三分线内投中1球得2分，罚篮投中1球得1分，某球队在一次比赛中共投进32球，得65分，已知2分球的个数比三分球的个数的4倍多3个，则这个球队在比赛中罚篮共投中________球12. 篮球比赛中，三分线外投中1球得3分，三分线内投中1球得2分，罚篮投中1球得1分，某球队在一次比赛中共投进32球，得65分，已知2分球的个数比三分球的个数的4倍多3个，则这个球队在比赛中罚篮共投中________球二、解答题（每小题15分，共60分.）每题都要写出推算过程.1313.甲、乙两人同时从A、B两地出发，相向而行，甲每分钟走70米，乙每分钟走60米，两人在距离中点80米的地方相遇，求A，B两地之间的距离14.老师给学生分水果，准备了两种水果，其中橘子的个数比苹果的个数的3倍多3个，每人分2个苹果，则余下6个苹果，每人分7个橘子，最后一人只能分得1个橘子，求学生的人数15. 两个相同的正方形重合在一起，将上层的正方形向右移动3厘米，再向下移动5厘米，得到图中的图形，已知阴影部分的面积是57平方厘米，求正方形的边长。

第十五届小学“希望杯”全国数学邀请赛培训题及答案四年级

第十五届（2017年）小学“希望杯”全国数学邀请赛四年级培训题1．计算：20172071207720172037201721112017⨯+⨯-⨯-⨯．2．计算：9999222233333334⨯+⨯．3．比较大小：20162018A =⨯，20172017B =⨯，20152019C =⨯．4．定义新运算⊗：a a b b b b ⊗⨯⨯⨯个=，求()()1423⊗⊗⊗．5．一个自然数，各个数位上的数字之和是74，这个数最小是多少？6．一个三位数被3除余1，被5除余3，被7除余5，这个数最大是多少？7．一个整除算式，被除数比商大126，除数是7，求被除数．8．一个三位教，它的各位数字之和是20，十位数字比个位数字大1，如果将百位数字与个位数字对调，得到的三位数比原三位数大198，求原数．9．在从1开始的n 个连续的自然数中，去掉其中的一个数，余下各数的和是2017，求去掉的数．10．若干个数的平均数是17，加入一个新数2017后，这组数的平均数变成21，原来共有多少个数？11．用2，0，1，7这四个数字可以组成多少个没有重复数字的四位偶数？12．已知a ，b ，c 是三个质数，且a b c <<，93a b c +⨯=，求a ，b ，c ．13．a ，b ，c 是彼此不同的非0自然数，若6a b c ++=，求四位奇数aabc 中最小的那个．14．a ，b ，c 是彼此不同的非0自然数，若6a b c ++=，求四位奇数aabc 中最大的那个．15．三位数abc 是质数，a ，b ，c 也是质数，cba 是偶数，ab 是5的倍数，求三位数abc ．16．求被7除，余数是3的最小的三位数．17．求被7除，余数是4的最大的四位数．18．将分别写有数字3，7，8的三张卡片排成三位数abc ，使它是43的倍数，求abc ．19．已知a ，b ，c 是不同的质数．且三位数abc 能同时可被3，7整除，求abc ．20．用写有2，3，5，7的四张纸片可以排成多少个小于1000的质数？21．四位数abbc 可被两位数ac 整除，若a c <，5a c +=，求b ．22．在下面的算式里加上一对括号，使算式成立．123456789100⨯⨯+⨯++++=23．在等号左边添上适必的运算符号、括号，使等式成立．99998a =24．从1至9的自然数中选择8个数填入下面的方框中，使得计算结果尽量大，那么这个结果最大是多少？()÷⨯+-⨯-+□□□□□□□□25．在下图的算式中，A ，B ，C ，D 代表0～9四个各不相同的数字，且A 是最小的质教，求四位数ABCD ．26．在如图的算式中，“希”、“望”、“杯”三个字分别代表0～9中三个不同的数字，求“希望杯”代表的数．27．a ，b ，c ，d ，e 都是自然数，且09c b a d e <<<<<≤，若如图的算式成立，求abc ．28．求2016920169201699999991999⨯+个个个末尾有多少个0？29．求201020112012201320142015234567+++++的末位数字．30．根据下面一列数的规律，求第2017数教．2，4，6，8，10，…．31．找规律，填数：1，1，2，3，5，8，13，21，（），（），（），…32．把数字1～12填到下图的圆圈中，使每个圆上的数字之和相等．33．同一平面内的2条直线最多有1个交点，3条直线最多有3个交点，10条直线最多有多少个交点？34．按班规律，写出上、下两条横线上应填的数．35．如图现察前面两个正方形中数之间的关系，根据规律求第三个正方形中“？”代表的数．36．正方体骰子上1和6相对，2和5相对，3和4相对，把它放在水平桌面上（如图6），将骰子向右翻滚90︒，然后在桌面上按逆时针方句旋转90︒，则完成一次变换（如图7），若骰子的初始位置为图6，那么完成23次变换后，朝上一面的数字是什么？37．有一串数字，任何相邻的4个数之和都是22，若从左边起第2，5，12个数分别是3，7，8，求第11个数．38．小伟和小明交流暑假中的活动情况，小伟说：“我参加了夏令营，外出一个星期，这七天的日期数之和是84．”小明说：“我假期到家住了七天，日期数的和再加月份数也是84．”那么，小伟出发的日期和小明回家的日期分别是几号？39．某个月中星期一多于星期二，而星期日多于星期六，那么这个月有多少天，这个月的5号是星期几？40．6位同学数学考试的平均成绩是93分，他们的成绩是互不相同的整数，且最高分是99分，最低分是75分，求按分数从高到低居第三位的同学的得分．41．为了表扬好人好事，需核实一件事，厂方找了A，B，C，D四人．A说：“是B做的．”B说：“是D做的．”C说：“是我做的．”D说：“B说的不对．”若这四人中只有一人说了实话，问：这件事是谁做的．42．晶晶家门牌号码满足：（1）若是4的倍教，则它就是60～69中的数；（2）若不是5的倍数，则它就是70～79中的数；（3）若不是8的倍数，则它就是80～89中的数．晶晶家的门牌号码？43．数一数，图中有多少个三角形？44．数一数，图中包含“☆”的长方形（包含正方形）有多少个？45．数一数，图中有多少个三角形？46．数一数，图中有多少个长方形（包含正方形）？47．数一数，在图12中的不同位置可以画出多少个图13所示的图形？（方向可以旋转）48．图14由10个相同的小正方形组成，请用三种方法把它分割成两个大小相等、形状相同的部分（沿图中的线分割）．49．将图中的〇分别涂成红色、黄色或绿色，要求有线段相连的两个相邻〇涂不同的颜色，共有多少种不同涂法？50．小聪学玩魔方，向小笨拜师学艺．小笨首先出了一道题考他．从下图的四个图形中，每个小正方形都标上了颜色．若要求一个正方体两个相对面上的颜色都一样，那么下列4个展开图有几个是正确的？51．从图中任意选择四个点，可组成多少个不同的正方形？（不同的点组成的正方形视为不同的正方形）52．有5根小木棒的长度分别为1cm ，1cm ，2cm ，3cm ，5cm ．从中任取3根，不同的长度和有几种？53．一个长方形的长和宽都是整数，且它的面积和周长恰好在数值上相等，那么长方形的长和宽分别是多少？（不需写过程）54．如图，已知100AD =，65BD =，75AC =，求BC ．55．如图，两个完全相同的等腰三角形中各有一个正方形，图甲中的正方形面积为48平方厘米，求图乙中的正方形面积．56．两个边长为8厘米的正方形如图20重叠，若图中阴影部分的面积为24厘米，那么所拼成的大长方形周长是多少厘米？57．图中的正六边形被分为12个相同的小三角形，每个小三角形的面积为1．问：图中面积等于3的梯形有多少个？58．图中有20个相同的小三角形，它们的面积都是1，问图中面积为3的梯形有多少个？59．图中的3个图中，网格小正方形的边长都是1，求各图中阴影部分的面积．60．如图，从边长是8的正方形上我掉两个边长是2的正方形和两个腰长是4的等腰直角三角形，求余下部分的面积．61．一张长方形纸片，长是10厘米，宽是7厘米．把它的右上角样下折叠，如图25所示，再把左下角往上折叠如图26所示，求未盖住部分（阴影部分）的面积．62．一个长方形，若长增加3，宽增加2，则面积增加33；若长增加1，宽增加3，则面积增加26，求原长方形私周长．63．如图，在长是12的线段上画两个正方形，已知两个正方形的面积的差是48，求其中大正方形的面积．64．如图，长方形边长是12，宽是6．把长分成三等份，宽分成两等份，再将长方形内某点与分割点连接，求阴影部分面积．65．在一条直路的一侧等距离地植了128棵树，路的两端都有树．若第3棵树和第7棵树相距20米，求这条路的长．66．有一个报时钟，每敲响一下，声音可持续．2秒且每两次敲响的时间间隔相同．如果敲响5下，那么从敲响第一下到最后一下持续声音结束，一共需要26秒．现在敲响10下，从敲响第一下到最后一下持续声音结束，一共需要多少秒？67．楠楠6岁时，爸爸36岁，再过多少年，爸爸的年龄是楠楠年龄的4倍？68．今年父亲的年龄是兄弟年龄和的2倍，是兄弟年龄差的8倍．父午三人年龄和是48岁，长兄和弟弟今年各几岁？69．今年，李林和爸爸的年龄的和是50岁，5年后，爸爸的年龄比李林年龄的3倍小4岁，爸爸比李林大几岁？70．妈妈像女儿这样大时，女儿才两岁，当女儿长到妈妈现在这样大时，妈妈86岁，求妈妈现在的年龄．71．两棵树上一共有25只鸟，先是左边树上的鸟有一半飞到了右边树上，然后右边树上的8只鸟又飞到了左边树上．这时左边树上的鸟比右边树上多3只，请问最开始左边树上有几只鸟？72．有甲、乙、两、丁四个书库．共有图书24000本．从甲书库调运1500本书到乙书库，然后从乙书库调运1800本书到丙书库，再从丙书库调运2200本书到丁书库，最后从丁书库调运1700本书到甲书库．此时，甲、乙、丙、丁书库的图书数量相等．求甲书库原来有图书多少本？73．小肯同学去肯德基用餐，先买了一份“豪华午餐”，吃完后又买了一个“脆皮甜筒”，一共花了180角．若以角计费，“豪华午餐”的价格末尾有个0，如果把0去掉，正好是“脆皮甜筒”价格的一半．两样各花了多少元？74．一辆油连桶重19千克．用了一半油以后．再连桶一称，共重12千克．求原来油和桶各重多少？75．小笨和小聪练习打字．两分钟内，小笨比小聪多打49个字．又比小聪的3倍多7个字．问：两分钟内．小聪和小笨分别打了多少字？76．小笨和小聪买了60包方便面，小聪比小笨每周少吃4包，二人恰好用了6周吃完了所有的方便面．求小笨每周吃多少包方便面？77．甲、乙、两三数之和为177，乙比丙的两倍少4，甲比丙的3倍多7，求甲、乙、丙三数．78．某单位请小王临时帮忙，规定12天报酬是人民币660元和一个MP4播放器．可是小王工作了七天后，因有急事不能继续，结果这个单位根据每天平均值给小王一个MP4播放器和人民币150元．问：一个MP4播放器价值多少元？79．小明今年得压岁钱1650元，比小亮的2倍少150元，求小亮今年得压岁钱多少元？80．麦当劳餐厅推出“夏日冰饮第二杯半价”活动，贝贝同学买了2杯“麦旋风”，共花了18元．那么一杯“麦旋风”原价多少元？81．小王对小李说：“你给我100元，我的钱是你的2倍．”小李对小王说:“你给我20元，我的钱是你的5倍．”原来两人各有多少钱？82．小明、小刚和小面为灾区儿童捐书，小明比小刚多捐了7本，小刚比小商多捐了13本，小明捐的本教是小面的3倍，求三人一共捐了多少本书？83．A，B，C，D四个数，每次去掉一个数，将其余下的三个数求平均数，这样计算了4次，得到下面四个数：23，26，30，33求A，B，C，D的平均数．84．有一群小朗友分一堆苹果．如果减少1人，每人可分得8个；如果增加2人，每人可分得6个．求实际有多少个小朋友？85．有一群小朋友分一堆苹果，如果每人分5个，就会剩下4个苹果，这时离开了3个小朋友，那么每人分6各还会剩4个．那么原来一共有多少个苹果？86．张丽正在读一本181页的故事书，可是她不小心把书合上了，只记得刚读宄的连续两页页码之和为81，如果张丽每天读30页，那么剩下的几天能读完？87．小华有8个练习本，小明有7个练习本，小强没有，他付了10元从小华和小明购买了一些后，三人有相同数量的练习本．若每个练习本的价格都相同，则小华应得几元钱？88．甲、乙、丙3人手机都使用了“畅聊卡”，并获得了赠送一个月基础话费的优惠，一个月后三人均超过了基础话费，甲付了70元，乙付了50元，丙付了30元．3人通话时长共计90小时，如果一个人通话90小时，要付350元，那么丙通话了多少小时？89．运1200吨水泥．甲、乙两个车队共同运榆需要运30次．若甲车队每次可比乙车队多运10吨，则甲车队独立运输需要运几次？90．一个牧民年初买了一头母羊．每年能生2只公丰，4只母羊，每只小母羊两年后，每年又可以生6只羊，其中2只公苹，4只母羊．这样从今年开始到第3年底、一共有多少只羊？91．小明家2013年初买了一头母羊．每年春天生2只公羊和3只母羊，每只小母羊从第三年头起，每年春天生2只公羊和3只母羊．那么从2013年开始到2017年夏天，小明家共有只羊？92．有一根木糙上有两种刻度，第一种相度将木棍分成10等份，第二种朝度将木棍分成12等份，如果沿每条刻度线将木棍锯断，请问木棍共被锯成多少段？93．和尚分馒头：100个和尚分100个馒头，大和尚每人分3个，小和尚每3个人分1个，刚好分完．大、小和尚各有多少人？94．3名肖学去参加数学竞赛，共10道题，答对一道题得10分，答错一道题扣3分．这3个同学都回答了所有的问题，小笨得了87分．小聪得了74分，香香得了9分，问，他们一共答对了几道题？95．今有鸡兔同笼，有33个头，有108只脚，求鸡和兔各多少只？96．两列火车同时从北京和沈阳相对开出，从北京开出的火车每小时行59千未，从沈阳开出的火车每小时行64千米，6小时后两车相遇．北京到沈阳的铁路线长多少千米？97．南京长江大桥是新中国第一座自己设计，建造的铁路、公路两用桥．清晨，一列长228米的火车，以每秒20米的速度通过南京长江大桥，共用了350秒．那么桥的全长是多少米？98．甲、乙两人分别从A、B两地同时以30千米/时、20千米/时速度相向而行，相遇后继续前行各自到达B、A两地后立即返回，到第二次相遇时相遇点，该点离第一次遇点40米，求A、B两地相距多少千米？99．红红和明明的家相距380米，两人两时从家中出发，在同一条笔直的路上行走，红红每分钟走65米，明明每分钟走55米，3分钟后两人相距多少米？100．甲、乙两地是一条电车线路两端的发车站，每隔一定时间两站同时发、出一辆电车，每辆电车每隔4分钟都会遇到一辆迎面开来的电车，上午10点时，小明、小强两人分别从甲、乙车站同时出发，相向而行，小明每5分钟遇到一辆迎面开来的电车，小强每6分钟遇到一辆迎面开来的电车，如果电车行软全程需42分钟，求小明和小强相遇的时刻？。

希望杯第十至第十五届四年级题目

最新第十五届小学“希望杯”全国数学邀请赛四年级第1试赛及答案

第十五届小学四年级希望杯全国数学邀请赛试题及答案资料

小学四年级希望杯历年数学竞赛试题与答案1_14届(最新全套完整版)

第十五届小学“希望杯”全国数学邀请赛试卷(四年级第1试)

第十五届小学四年级“希望杯”全国数学邀请赛试题及答案

第十五届小学“希望杯”全国数学邀请赛四年级

全国四年级希望杯数学竞赛全部试题与规范标准答案

小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第十五届“希望杯”全国数学邀请赛四年级第2试真题及答案详解

第十五届小学“希望杯”全国数学邀请赛培训题及答案 四年级

第十五届小学“希望杯”全国数学邀请赛培训题及答案四年级