Momentum theorem chapter—finishing by Liubo讲义练习1

合集下载

大学物理第三章牛顿运动定律

四、几种实用的惯性系
1、地面参考系 ground reference frame
由于我们生活在地面上，地面是一个最常用的惯性系。但只能说地面是一个近似的惯性系，而不是一个严格的惯性系，因为地球有自转角速度：由于地球的自转，地球上的物体有法向加速度。
1 7.3 105 rad s 1
2、地心参考系 earth's core
地心参考系相对地面参考系严格些，地球绕太阳公转的角速度：
2 2.0 107 rad s 1
3、日心参考系 sun's core
日心参考系相对地心参考系更严格些，但太阳还绕银河中心旋转：
3 8.0 1012 rad s 1
• 5、牛顿定律适用的范围是什么？什么是惯性参考系？ • 6、有人说：力是运动的根源，没有力就没有运动，你是怎么理解的？ • 7、日常生活中，我们经常接触的力有哪些？它们都属于基本力中的哪一种？ • 8、有人说：人推车时只有作用力大于反作用力时车才能被推动，且先有作用力，后有反作用力。你认为呢？ • 9、动量和动能有什么区别和联系？
• “只要运动是匀速的，你无法从其中任何一个现象来确定船是在运动还是停着不动．你跳向船尾也不会比跳向船头来得远,虽然你跳在空中时,脚下的船底板向着你跳的反方向移动．你把不论什么东西扔给你的同伴时,如果你的同伴在船头而你在船尾, 你所用的力并不比你们两个站在相反位置时所用的力更大．水滴将象先前一样,滴进下面的罐子,一滴也不会滴向船尾,虽然水滴在空中时,船已行驶了相当距离."
（3） m
a 是什么力？
§３.３牛顿运动定律的应用
Applications of Newton’s Laws of motion • 一、牛顿运动定律的适用范围

动量守恒定理英文

动量守恒定理英文The principle of conservation of momentum, also known as the momentum conservation theorem, is a fundamental concept in physics that states that the total momentum of an isolated system remains constant if no external forces act upon it. This principle can be stated mathematically as:Σp = Σm * vWhere Σp is the total momentum of the system, Σm is the total mass of the system, and v is the velocity vector of an object.The conservation of momentum arises from Newton's third law of motion, which states that for every action, there is an equal and opposite reaction. When two objects interact, they exert equal and opposite forces on each other, resulting in a change in their velocities. However, the total momentum of the system remains constant.This principle is particularly useful in analyzing collisions, both elastic and inelastic. In an elastic collision, the total kinetic energy of the system is conserved, along with momentum. The velocities of the objects involved in the collision can be calculated using the conservation of momentum, allowing for the prediction of their post-collision states.In an inelastic collision, where kinetic energy is not conserved, the conservation of momentum still holds true. The total momentum before and after the collision remains the same, but some kinetic energy is converted into other forms, such as heat or deformation.This principle is vital in understanding real-world phenomena such as car crashes or billiard ball collisions.Additionally, the conservation of momentum can be applied to a system of multiple objects. In this case, the total momentum is the vector sum of the individual momenta of each object:Σp = m1 * v1 + m2 * v2 + m3 * v3 + ...By considering the conservation of momentum, physicists can analyze complex systems, such as rocket propulsion or the motion of celestial bodies, and make predictions about their behavior.The conservation of momentum is a fundamental principle that has wide-ranging applications in various fields of physics, including mechanics, astrophysics, and particle physics. It allows scientists to understand and predict the motion and interactions of objects and systems, providing a foundation for studying the laws of motion and understanding the behavior of the universe.Overall, the concept of the conservation of momentum provides a powerful tool for analyzing and predicting the behavior of objects and systems. It is a fundamental principle that is widely used in physics to understand various phenomena and make predictions about their motion. It plays a crucial role in our understanding of the laws of motion and has applications in various areas of science and engineering.。

英国IGCSE剑桥初中剑桥高中考试物理专业数学专业词汇留学中英文对照

IGCSE 物理中英词汇General Physicsmovement :运动;活动position ：位置,方位acceleration ：加速,促进velocity ：［力］速率;迅速investigate ：调查;研究force ：力量；促使weight ：重量,重力friction：摩擦，[力] 摩擦力precise ：精确的，准确的accurate :精确的,准确的tape measure ：卷尺vernier calliper :游标卡尺micrometer screw gauge :螺旋千分尺［测微计］Measuring cylinder ：量筒sliding scale ：计算尺，按比例增减mass ：团，块，堆Pascal ：帕斯卡(Blaise,1623—1662,法国数学家、物理学家、哲学家)Action-reaction forces 反作用力resistance :阻力；电阻upthrust :向上推electrostatic：静电的;unbalance ［力］失衡；shape：形状；模型；elastic：松紧带；橡皮圈resilient ：弹回的horizontally ：水平地；横地lamina ：薄板,薄层,叶片clockwise ：顺时针方向的gravitation :吸引力,趋势geothermal :地热的hydroelectric ：水力发电的tidal ：潮水的:受潮汐影响的barometer ：气压计, 晴雨表nanometer : 纳米Dependent variable :因变量Energy levels ：能级Buoyant force :浮力Equilibrant force ：平衡力Centripetal force :向心力Gravitational potential energy：重力势能Circular motion 圆周运动Coefficient of friction 摩擦系数Impulse—momentum theorem ：动量定理Coefficient of volume expansion ：体积膨胀系数Inertia :惯性，Joule ：焦耳Constant acceleration：恒加速度Kelvin temperature scale ：凯式温度Instantaneous acceleration ：瞬时加速度Kinetic energy ：动能Magnification ：放大率weight :负荷；使…变重moment ：转矩，动量,时刻equilibrium :平衡，均势Sliding friction ：滑动摩擦Slope :斜率Simple harmonic motion：简谐运动Static friction :静摩擦Thermal energy 热能Kinetic—molecular energy ：分子能Momentum 动量Potential difference 势差Law of conservation of energy :能量守恒定律Pressure：电压Linear accelerator:直线加速度Principle of superposition：叠加原理Uniform circular motion：等速圆周运动Uniform acceleration：匀加速度Thermal physicsconduction ：［生理］传导，传导convection ：[流］［气象］对流; radiation :辐射；发光；放射物insulator：［物］绝缘体; electromagnetic ：电磁的invar ：不胀钢brass ：黄铜,铜管乐器calibrate ：校准，使标准化latent heat of vaporization ：汽化潜热knob ：（门、抽屉的)球形把手thermostat ：恒温(调节）器Mercury :水星,水银junction ：联结点，枢纽thermocouple ：热电偶thermistor ：电热调节器insulation ：隔离，隔绝solidification ：凝固,spectrum ：光谱；频谱;hypothermic ：体温过低的absolute zero:［物］绝对零度infra—red：红外线的energy efficient：节能arrangement :安排；解决办法collide ：相撞，碰撞evaporation ：蒸发；发散；消失cap screw ：帽螺钉bimetallic strip ：（用于恒温器等中的)双金属条conduction ：（热、电等的）传导convection ：传送，对流infrared radiation :红外辐射ion ：<物>离子metal gauze strainer ：金属网过滤器Bunsen burner ：本生灯（即煤气灯）latent heat of fusion ：熔解潜热boiling :沸腾的，激昂的manganate ：锰酸盐electromagnetic spectrum ：电磁波频谱stirrer shaft ：搅拌器轴Carnot efficiency ：卡诺循环Specific heat ：比热Cohesive force ：内聚力Thermal equilibrium ：热平衡Convection ：对流传热Thermal expansion ：热膨胀Boiling point :沸点Insulator:绝缘、隔热或隔音等的物质或装置matt ：表面暗淡的,无光泽的sea breeze ：（白天吹向内陆的)海风adhesion：附着力Bubble chamber ：气泡箱Entropy :熵Calorimeter ：热量剂Evaporation ：蒸发Capillary action :毛细管作用Melting point ：熔点Thermometer ：温度计Dynamics ：动力学IGCSE 数学中英对照词汇代数部分1.基础add,plus 加subtract 减difference 差multiply times 乘product 积divide 除divisible 可被整除的divided evenly 被整除dividend 被除数divisor 因子，除数quotient 商remainder 余数factorial 阶乘power 乘方radical sign, root sign 根号round to 四舍五入to the nearest 四舍五入2.有关集合union 并集proper subset 真子集solution set 解集3.有关代数式、方程和不等式algebraic term 代数项like terms，similar terms 同类项5。

动量动量定理第一课时

所围的“面积”的大小表示对应时间t0 内，力F0的冲量的大小。
动量定理(theorem of momentum)
1、内容：物体所受合外力的冲量等于物体的动量变化，这就是动量定理。
2、表达式： Ft mv ' mv 或 I p
3、加深理解：
1）物理研究方法：过程量可通过状态量的变化来反映；
2）表明合外力的冲量是动量变化的原因；
例：人在船上行走——人对船的作用力与船对人的反作用力的冲量的矢量和等于零，但是人对船的作用力和船对人的反作用力都做正功，使人和船的动能都增加。
思考与讨论
如果在一段时间内的作用力是一个变力，又该怎样求这个变力的冲量？
F
公式I=Ft中的F必须取平均值 F0
O
t t0
由图可知 F-t 图线与时间轴之间
4、冲量是过程量，反映了力对时间的积累效应
思考与讨论
冲量与功有什么区别？
冲量 I=Ft 功 W= FS
矢量
N·S
力的时间积累使动量发生变化
标量
N·m（J）
力的空间积累使动能发生变化
1、作用力与反作用力：作用力的冲量与反作用力的冲量总是等值、反向并在同一条直线上，但是作用力的功与反作用力的功不一定相等。 2、内力：对物体系统内部，内力作用的冲量的矢量和等于零，但内力的功的代数和不一定为零。
表明动量的变化与力的时间积累效果有关。
冲量(impulse)
１、定义：作用在物体上的力和作用时间的乘积，叫做该力对这个物体的冲量I，用公式表示为 I=Ft
2、单位：在国际单位制中，冲量的单位是牛·秒，符号是N·s
3、冲量是矢量：方向由力的方向决定，若为恒定方向的力，则冲量的方向跟这力的方向相同

动量和动量定理

内F对物体的冲量为（）
A、0
B、Ft
B
C、mgt
D、不能确定
F
表达式： m（v ’–v）= F(t ’– t)
或 P’ – P = I 含义？
动量定理的内容：
物体在一个过程始末的动量变化量(ΔP)等于它所受力的冲量(I )
2、动量定理（1）内容：物体在一个过程始末的动量变化量等于它在这个过程中所受合外力的冲量.
给我们一个启示：物理学中mv很可
能具有特别的物理意义。物理学中把
质量和速度的乘积定义为动量，用符
号P表示
P=mv
历史回顾
17世纪以来，关于运动量度的争论持续近了200多年，许多著名学者、科学家都参加到争论中，其中以法国哲学家兼数学、物理学家笛卡儿为代表。
首先，1644年笛卡儿在《哲学原理》中提出 “动量守恒”的观点，即物质和运动的总量永远保持不变。这是历史上首次推出动量守恒定律。
第三组：你能在基本不影响重物的前提下，将压在重物下的纸条抽出吗？试着做一做，想一想这样做的道理？
重物
F 纸条
2、动量定理
1.内容：物体动量的变化量等于该过程所受合力的冲量。
2.表达式：F合t mv mv或：I p
3.解读：
1）F为合力，适用于恒力，也适用于变力（此时的 F为t时间内的平均力），可见动量定理应用更广。 2）因果关系：物体受冲量是因，物体动量变化是果 3）方向关系：I与ΔP同向，计算时要规定正方向
动能改变动能不变动能改变
小结：
一、动量
1、概念：
在物理学中，物体的质量m和速度v的乘积叫做动量。
2、定义式：p= m v
3、单位：千克米每秒，符号是kg·m/s 4、对动量的理解：（1）矢量性运算遵循平行四边形定则（2）瞬时性是状态量。（3）相对性物体的动量与参照物的选择有关

单位面积动量定理

单位面积动量定理Title: The Momentum Theorem per Unit Area标题：单位面积动量定理The momentum theorem per unit area is a fundamental principle in fluid mechanics that describes the relationship between the rate of change of momentum and the area over which the force is applied.This theorem is analogous to Newton"s second law of motion, which states that the force acting on an object is directly proportional to the rate of change of its momentum.单位面积动量定理是流体力学中的一个基本原理，它描述了动量变化率与力作用面积之间的关系。

这个定理与牛顿第二定律相似，后者指出作用于物体的力与其动量变化率成正比。

According to the momentum theorem per unit area, the rate of change of momentum per unit area is directly proportional to the force applied per unit area.This can be expressed as: d(p/A)/dt = F/A, where p is the momentum, A is the area, and t is time.根据单位面积动量定理，单位面积上动量的变化率与单位面积上的力成正比。

这可以表示为：d(p/A)/dt = F/A，其中p是动量，A是面积，t是时间。

06 Momentum

Solution: Static force
dx moves downward continuously,
m N1 = l ⋅ g L
x l L x+dx x L-l
v பைடு நூலகம் 2 gl
As dm strikes the ground: dm = λdx =
m 2 Momentum: v dm = v dt L
Next Lecture : conservation of momentum
r r dp F= dt r r r d (mv ) r dv For constant mass: F = dt = m dt = ma r r dv r dm For variable mass: F = m + v dt dt r r r dp r is more general than F = ma F= dt
2. Momentum Theorem: r r
r dp F= r dt
ti r r J = ∆P -——Momentum Theorem Net impulse delivered to a particle equals the change in the momentum (质点所受合外力的冲量,等于该质点动量的增量). 质点所受合外力的冲量, 质点所受合外力的冲量等于该质点动量的增量). Descriptions: (1) Impulse is the accumulation of the force with respect to time (冲量是力对时间的累积). 冲量是力对时间的累积). The effect of impulse is changing the momentum.
(其效果是改变动量). 其效果是改变动量).

【论文】几个物理力学概念和规律的英文表述

几个重要的物理力学概念和规律的英文表述于永建物理特级教师教育部国培计划专家本文导读: 物理概念和规律，多由国外总结出，英文如何描述之，此文介绍其一二在国际科技文化交流日益频繁、教育要“面向世界、面向未来、面向现代化”的今天，多角度、多渠道地提高学生的英语水平提高学生的综合素质，已成为社会发展和学生自身发展的迫切需要。

有条件的一些学校已“以前瞻意识迎接时代挑战”新思维，开展了理双语教学的大胆改革，以实现“学科知识的掌握和英语能力的提高形成一种双嬴的局面”.为了对开展物理“双语”教学改革有一些帮助，今将高中物理力学部分的几个物理概念和规律的英文表述整理如下：一、力学概念1.力（Force ）：Force is the interaction of objects2.力矩（moment）：The product of force F and lever arm L is calledmoment.3.冲量（impulse）：In physics,the product of force F and time t,during theforce is exerting,is called impulse.4.动量（momentum）：I n physics ,the product mυof the mass m of abody and its velocityυ,is called momentum.5.功（work）：If a body ,acted on by a force,takes a displacement in thedirection of the force,we say the force does work on the body.如果一个物体在力的作用下沿力的方向发生了一段位移，我们就说力对物体做了功Or the work done by a force equals the product of the force, thedisplacement and the cosine of the angle between the force and thedisplacement.力对物体做的功等于力的大小、位移的大小以及力与位移夹角的余弦的乘积.Work is a scalar quantity.In SI,its unit is joule,denoted by(功是标量，在国际单位制中，其单位是焦耳，用J表示)6.功率( power)The ratio of the work to the time taken to do the work iscalled power功与完成这些功所用时间的比值叫做功率7.能( energy)When a body is able to do work on another body,we say thebody possesses energy.8.动能(kinetic energy) The energy that a body possesses due to its motionis called kinetic energy .9.势能( potential energy) :①重力势能The gravitational potential energy :The energy that an elevatedbody possesses is called gravitational potential energyThe gravitational potential energy of a body equals the product of its weightand its height.②弹性势能Elastic potential energy:When a deformed body returns to itsinitial form,it can do work on another body because it possesses energywhich is called e lastic potential energy10.机械能(mechanical energy)The sum of kinetic energy and potential energy is called mechanical energy二、力学规律1.牛顿第一定律（Newton’s first law）：All objects continue to be in its state of uniform rectilinear motion or state of rest until being compelled to change its state by some exterior forces. Newton’s first law is also called inertial law.2.牛顿第二定律（Newton’s second law of motion ）：The acceleration of an object is in direct proportion to the resultant force acting on it and in inverse proportion to the mass, the acceleration is in the same direction as the resultant.The law can be represent with the following equation :F=ma3.牛顿第三定律（Newton’s third law）：The action and reaction forces of two are always equal in magnitude ,opposite in direction and acting on the same straight line.4.万有引力定律（Law of universal gravitation）：Every particle of matter in the universe attracts every other particle with a force directly proportional to the product of their masses and inversely proportional to the squared distance between them.5.动量定理（The theorem of momentum）：The impulse of a net force acting on a body equals the change of its momentum.This conclusion is the theorem of momentum.Ft=mv/-mv6.动量守恒定律（The law of conservation of momentum）：The total momentum of a system remains constant，when there is no external forces or zero net external force acting on the system. This conclusion is called the law of conservation of momentum.7.动能定理（The theorem of kinetic energy）：The work done by the resultant force ona body is equal to the change in kinetic energy of the body.This conclusion is called the theorem of kinetic energy.8.机械能守恒定律（The law of conservation of mechanical energy）：When only the gravitational force does work，the kinetic and the gravitational potential energy can be converted from one to another and the total mechanical energy remains conserved. This conclusion is called the law of conservation of mechanical energy 以上物理力学概念和规律以及所涉及的专业词汇是物理力学部分出现几率较高的内容，掌握这些内容对开展物理双语教学改革想必具有一定的帮助.有关的英文表述仅供参考和与同行讨论.参考文献：。

大学物理英语词汇

Chapter 1 Introduction（引言）§1.1 Space and Time（空间与时间）universe宇宙object物体measurement 测量kinematics运动学motion of objects 物体的运动mass point/particle质点center of mass 质心space and time 时空rotation 旋转subject研究的对象phenomena 现象intergalactic星系间的submicroscopic 亚微观的dimension尺度uniform均匀的isotropic各向同性的continuous连续的direction方向graininess 颗粒性location位置frame of reference 参考系specify确定、规定simultaneously 同时地inconsistent with与…不一致define/definition 定义platinum-iridium铂铱合金atomic standard 原子标准transition 跃迁meridian子午线general conference on weights and measures 国际计量大会vacuum真空former standard of length米原器atomic energy level原子能级isotope cesium 铯同位素krypton 氪angstrom埃§1.2 Coordinate Systems and Frames of Reference（坐标系与参考系）frame of reference 参考系coordinate system坐标系rectangular Cartesian coordinates直角笛卡儿坐标系axis / axes (pl.)（坐标）轴origin坐标原点at rest静止dimension维mutually perpendicular 互相垂直intersection 交点§1.3 Idealized Models（理想模型）idealized model 理想模型simplified version简化方式neglect忽略particle质点air resistance 空气阻力vacuum真空in terms of 利用rigid body刚体insulator绝缘体§1.4 Vectors（矢量）vector矢量scalar标量magnitude大小velocity速度acceleration 加速度momentum动量proportional to正比于parallel平行position vector位置矢量§1.5 Properties of Vectors（矢量的特点）resultant/net vectoradditionsubtractionequivalenttranslatehead-to-tail methodparallelogram method diagonalcommutative lawscalar productdot productdistributive lawmultiplicationcross product vector productarearight-hand ruleparallelmultiplyfunctionsome variable§1.6 Components of a Vector（矢量的分量）component分量absolute value绝对值projection投影perpendicular 垂线rectangular component正交分量§1.7 Unit Vectors（单位矢量）unit vector单位矢量dimensionless 无量纲的unit magnitude单位大小respectively分别地Chapter 2 Kinematics: Motion in Two and Three Dimensions （运动学：二维与三维运动）§2.1 Kinematical Function of a Point（质点的运动函数）position vector位置矢量trigonometry 三角学§2.2 Displacement and Velocity（位移与速度）trajectory轨迹displacement vector位移矢量velocity速度ratio比值，比率straight line直线approach趋近、接近limit极限average velocity 平均速度instantaneous velocity瞬时速度slope斜率chord弦limiting process 求极限过程curved path弯曲路径derivative导数magnitude and direction大小和方向speed速率scalar components标量分量limiting value极限值limiting process 求极限过程tangent相切、切线change增量、改变量differential n.微分differentiate v. 微分、求导integrate v.积分integration n.积分coefficient系数module (矢量的)模successively 连续地square root 平方根§2.3 Acceleration（加速度）acceleration 加速度average acceleration 平均加速度instantaneous acceleration 瞬时加速度second derivative二阶导数positive正的negative负的respectively 分别地one-dimensional motion一维运动uniform circular motion匀速圆周运动projectile motion抛体运动§2.4 Motion with Constant Acceleration（匀加速运动）无§2.5 Linear Motion with Constant Acceleration（匀加速直线运动）linear线性的one-dimensional一维的corresponding对应的eliminate消去freely falling bodies自由落体air resistance 空气阻力acceleration due to gravity 重力加速度altitude高度vertical direction 竖直方向negative sign 负号latitude经度regardless of与.无关maximum value最大值minimum value最小值§2.6 Projectile Motion （抛体运动）projectile抛体trajectory轨迹assumption 假设negligible可忽略的rotation 转动air friction 空气摩擦parabola抛物线parabolic trajectory 抛物线轨迹initial初始的horizontal水平的independent 独立的superposition叠加flight time飞行时间horizontal range射程maximum height最大高度horizontal surface水平面a body projected horizontally平抛物体vertical竖直的firing angle抛射角§2.7 Circular Motion（圆周运动）circular motion 圆周运动uniform circular motion匀速圆周运动circular motion with varying speed变速圆周运动centripetal向心的arc length 弧长angular displacement 角位移instantaneous angular velocity（瞬时）角速度radian(s) 弧度dimensional有量纲的counterclockwise 逆时针clockwise顺时针circle圆center of a circle圆心vectorially矢量地angular acceleration 角加速度tangential acceleration 切向加速度center-seeking 向心resolve （矢量）分解centripetal acceleration 向心加速度normal acceleration 法向加速度perpendicular to垂直于radial径向的radius半径§2.8 Relative Motion（相对运动）relative velocity相对速度relative acceleration 相对加速度observer观察者outcome结果measurement 测量stationary 静止的differentiate求微分Galilean transformation equation伽利略变换valid有效的special theory of relativity狭义相对论as it turns out结果是relative to相对于heading due north头朝北right triangle直角三角形upstream逆流hypotenuse直角三角形的斜边Chapter 3 Newton’s Laws of Motion（牛顿运动定律）§3.1 Newton’s First Law（牛顿第一定律）at rest静止net external force/ resultant force合外力inertial frame of reference 惯性参考系inertia惯性act on = exert（力）作用于approximation近似inertial mass 惯性质量interact (n. interaction)相互作用resultant external force合外力momentum动量unless stated otherwise 除非另有说明§3.2 Newton’s Second Law（牛顿第二定律）nonzero非零的mass质量momentum动量rate of change变化率directly proportional to正比于inversely proportional to反比于§3.3 Newton’s Third Law（牛顿第三定律）interact相互作用opposite相反、相对isolated 孤立的action force 作用力reaction force反作用力§3.4 Applications of Newton’s Laws（牛顿运动定律的应用）tension 张力diagram示意图isolate 隔离free-body diagram受力图unknown未知量Atwood’s Machine阿特伍德机light string轻绳vertically 竖直地frictionless 无摩擦的incline斜面pulley滑轮balanced平衡的block 木块、滑块wedge楔、斜铁plane 平面horizontal surface水平面§3.5 International Units and Dimensions（国际单位制与量纲）physical quantity物理量fundamental unit基本单位universally普遍scientific community科学界luminous intensity光强度abbreviation缩写lowercase小写的uppercase大写的rectangle矩形§3.6 Introduction to Some Common Forces（几种常见力）electromagnetic电磁的lean against 倚靠compress 压mattress spring 床垫弹簧normal force 法向力、支持力stiffness倔强性stretch 拉伸frictional force / force of friction 摩擦力viscous medium粘滞媒质（介质）resistance 阻力force of static friction 静摩擦力maximum force of static friction最大静摩擦力is proportional to正比于proportionality constant比例常数coefficient of static friction 静摩擦系数coefficient of kinetic friction 滑动摩擦系数variation变化§3.7 The Four Fundamental Forces（四种基本力）gravitational force 引力universal gravitational constant万有引力常数electromagnetic force电磁力bind约束Coulomb’s law库仑定律charged particle带电粒子strong nuclear force 强力hydrogen氢nucleus (pl. nuclei or nucleuses)原子核neutron 中子proton质子counteract抵抗repulsive排斥的strength强度weak nuclear force弱力short-range force 短程力radioactivity放射性radioactive decay 放射性衰变nucleons核子massless 无质量的action at a distance远程作用hypothesis 假设field场Chapter 4Linear Momentum and Angular Momentum （动量与角动量）§4.1 Linear Momentum and Impulse（动量与冲量）(linear) momentum动量impulse 冲量impulse-momentum theorem动量定理time-average force 平均冲力§4.2 Impulse-momentum Theorem for Particles System（质点系的动量定理）particles system 质点系internal forces 内力external forces 外力§4.3 Conservation of Linear Momentum（动量守恒定律）momenta（pl.）动量§4.4 Center of Mass（质心）vector notation矢量表示continuous object连续物体element of mass 质元§4.5 Motion of the Center of Mass（质心的运动）conserved 守恒的isolated system 孤立系统§4.6 Angular Momentum of a Particle（质点的角动量）conserved 守恒的isolated system 孤立系统§4.7 Conservation Law of Angular Momentum（角动量守恒定律）Kepler 开普勒ellipse椭圆Chapter 6 Rotation of a Rigid Body about a Fixed Axis （刚体的定轴转动）§6.1 Motion of a Rigid Body（刚体的运动）rigid body刚体parallelogram rule 平行四边形法则translation 平动an extended body 空间实体rotation 转动nondeformable 不变形的resultant motion 合运动parallel平行fixed axis 固定轴counterclockwise motion 逆时针运动angular acceleration 角加速度clockwise motion顺时针运动separation 间隔translation 平动angular velocity 角速度trajectory 轨迹§6.2 Law of Rotation of a Rigid Body about a Fixed Axis（刚体定轴转动定律）moment of inertia 转动惯量rotation axis 旋转轴torque 力矩proportionality constant比例常数element of mass 质元line of action of force 力的作用线analogue 类似；相似perpendicular distance垂直距离distribution of mass 质量分布pivot about 围绕…旋转；以…为轴旋转moment arm 力臂is proportional to与…成正比§6.3 Calculation of Moments of Inertia for Rigid Bodies（转动惯量的计算）an extended body 延续实体hoop圆环spherical shell薄球壳solid sphere实心球spherical cavity球腔linear density线密度§6.4 Application of Law of Rotation of a Rigid Body about a Fixed Axis（刚体定轴转动定律应用）orientation 方向；方位atwood’s machine伍德机brake制动器，刹车pedal踏板sprocket链轮齿bearing轴承pulley滑轮nonslip 无滑动§6.5 Conservation of Angular Momentum with Respect to the Fixed Axis（对定轴角动量守恒）resultant external torque合外力矩isolated隔离的valid 有效；适用pin 销；轴hapter 7Electric Fields of Stationary Electric Charges（静止电荷的电场）§7.1 Charge（电荷）Electricity电学magnetism磁学accelerator 加速器interatomic原子间的amber琥珀magnetite磁铁矿electrification充电magnet磁铁charge 电荷quantized量子化的quantization量子化proton质子electrically charged带电的charged body带电体conservation守恒uncharged不带电的§7.2 Coulomb’s Law（库仑定律）Coulomb’s Law库仑定律inversely proportional to相反地separating 分开的permittivity介电常数hydrogen氢opposite sign符号相反§7.3 The Electric Field（电场）electric field 电场test charge检验电荷distribution分布X-ray X-射线lightning闪电electronic电子的intermolecular分子间的rub摩擦magnesia氧化镁electromagnetism电磁学plastic rod塑料棒repel排斥attract 吸引suspend悬挂neutron中子electron电子neutral中性的integer整数integral multiple整数倍proportional to正比于square平方product乘积repulsive排斥Coulomb constant库仑常数superposition principle叠加原理electric field (intensity) 电场强度source charge场源电荷radio waves无线电波atmosphere大气thundercloud 雷雨云§7.4 Calculation of Electric Field（电场的计算）stationarydenominatorelectric dipoleelectric dipole moment spherically symmetriccontinuous charge distributioncharge elementstrategy静止的分母电偶极子电偶极矩球对称电荷连续分布元电荷策略bisector平分线manipulation处理linear charge density电荷线密度surface charge density 电荷面密度volume charge density电荷体密度ring charge带电圆环charged disk带电圆盘infinite plate of charge无限大带电平面§7.5 Electric Field Lines and Electric Flux（电场线和电通量）electric field lines电场线electric flux电通量infinity无穷远visualize形象化strength强度penetrate穿过qualitative定量的closed surface闭合曲面align排列thread线intersection 相交cross交叉§7.6 Gauss’s Law（高斯定理）Gauss’s law 高斯定理arbitrary shape 任意形状gaussian surface 高斯面electric flux电通量principle 原理practice实际§7.7 Application of Gauss’s Law（高斯定理的应用）algebraic代数的rearrange重新整理charge distribution电荷分布spherical symmetry 球对称cylindrical symmetry 柱对称plane symmetry 平面对称symmetric对称的spherical shell球壳infinite length无限长infinite plane无限大平面Chapter 8 Electric Potential（电势）§8.1 Conservativity of Electrostatic Field（静电场的保守性）line integral线积分conservative force field 保守力场closed path闭合路径conservative保守的circuital theorem for electrostatic field静电场环路定理§8.2 Potential Difference and Electric Potential（电势差和电势）potential difference电势差electric potential电势infinity无穷远electrostatic potential energy 静电势能volt伏特voltage电压electron volt电子伏特battery电池§8.3 Calculation of Electric Potential（电势的计算）equipotential surface等势面broken lines虚线semicircular半圆的insulating绝缘的infinite无限的dashed lines虚线extend延伸solid lines实线finite有限的arbitrary任意的function函数curved surface曲面§8.4 Electric Potential Gradient（电势梯度）gradient梯度notation符号potential Gradient电势梯度maximum最大值right angle 直角sketch勾画§8.5 Electrostatic Potential Energy（静电势能）electrostatic potential energy 静电势能vicinity附近Chapter 9 Conductor in Electrostatic Field（静电场中的导体）§9.1 Conductors in Electrostatic Equilibrium（导体的静电平衡）isolated conductor 孤立导体electrostatic equilibrium静电平衡equipotential body等势体radius of curvature曲率半径electrostatic shielding静电屏蔽neutralize电中和sharp point discharge尖端放电lightning rod 避雷针cosmic rays 宇宙射线lightning stroke雷击glow discharge 辉光放电ion离子corona discharge电晕放电shrink收缩cavity 空腔grounding接地curved surface 曲面conducting wire导线collision碰撞thunderstorm雷暴induced charge 感应电荷insert插入guarantee保证contradiction 矛盾§9.2 Calculation of Electrostatic Field with Conductors Nearby （有导体存在时静电场的分析与计算）conducting slab 导电板lateral area侧面uncharged conductor不带电导体edge effect边缘效应redistribute 重新分配external外部Chapter 10 Capacitors and Dielectrics in Electrostatic Field （电容器和静电场中的电介质）§10.1 Capacitance and Capacitors（电容和电容器）Leyden jar 莱顿瓶flash 闪光灯capacitance电容coaxial同轴的capacitor电容器coaxial cable同轴电缆parallel-plate capacitor 平行平板电容器concentric同心的cylindrical capacitor圆柱形电容器parallel combination 并联spherical capacitor 球形电容器series combination串联submultiple因数farad 法拉microfarad 微法拉picofarad 皮法拉rectify 调整inductance 自感应ignition 点火sparking打火花metallic金属(性)的combination联合、组合equivalent相当的§10.2 Dielectrics and Electric Field（电介质与电场）dielectric电介质relative dielectric constant 相对介电常数voltmeter 伏特计insulating绝缘的dielectric breakdown介质击穿dielectric strength介电强度§10.3 Polarization of Dielectrics（电介质的极化）polarize极化polar molecules极性分子polarization 极化nonpolar molecules非极性分子induced dipole moments 感应电矩permanent electric dipole moments 固有电矩surface charge表面电荷align排成一线orient取向bound charge束缚电荷homogeneous 均匀的free charge 自由电荷microwave 微波oven 烤箱vibrate 振动tune 调整resonate 共振oscillate 振荡§10.4 Gauss’s Law for Electric Displacement Vector （高斯定律）electric displacement 电位移dielectric constant介电常数deliberately故意地the flux of D(r) D(r) 的通量permittivity电容率§10.5 Energy Stored in a Charged Capacitor（电容器的能量）transfer转移electrostatic potential energy 静电势能battery电池electrostatic field energy 静电场能increment 增量energy density能量密度transformation转化maximum operating voltage 最大工作电压terminal 终端deliver递送dissipate消散pathway路径Chapter 11 Magnetic Force (磁力)§11.1 Nature of Magnetic Force(磁力的本质)magnetite磁铁矿石bar magnet条形磁铁interaction 相互作用magnetic pole磁极electric current loops of molecules分子环形电流§11.2 Magnetic Field and Magnetic Field Vector(磁场和磁感应强度)magnetic field磁场magnetic field vector=magnetic induction =magnetic flux density磁感应强度magnetic force 磁场力Lorentz force 洛仑兹力B-line磁感(应)线magnetic flux磁通量tesla(T)特（斯拉）weber韦伯§11.3 Motion of a Charged Particle in a Magnetic Field(带电粒子在磁场中的运动)cyclotron period回旋周期magnetic focusing磁聚焦helix螺旋线pitch螺距magnetic lens磁镜magnetic confinement 磁约束a magnetic bottle磁瓶the mass spectrometer 质谱仪schematic drawing示意图ion离子precision 精确度proton质子deuteron 氘核bombard 轰击cyclotron 加速器dees D型盒evacuate抽成真空shield屏蔽oscillate 振动plasma等离子体nuclear fusion核聚变Van Allen belts范阿仑辐射带§11.4 The Hall Effect(霍尔效应)the Hall voltage 霍尔电压the drift velocity漂移速度§11.5 Magnetic Force on a Current-carrying Conductor(载流导体在磁场中受力—安培力)current-carrying conductor/wire载流导体/导线current loop in a uniform magnetic field匀强磁场中的载流线圈linear element 线元current element vector 电流元矢量loop 环, 回路magnetic moment of a current loop载流线圈磁矩rectangular loop矩形回路a wire segment 一段导线strip 条；带Chapter 12 Source of Magnetic Field（磁场的源）§12.1 The Magnetic Field of Moving Point Charges（运动点电荷的磁场）permeability of free space真空磁导率§12.2 The Biot-Savart Law（毕奥-萨伐尔定律）the Biot-Savart Law毕奥-萨伐尔定律permeability of free space真空磁导率Gauss’law in magnetism磁场的高斯定律magnetic monopoles磁单极solenoid螺线管turn匝current-carrying wire 载流导线encircle环绕current element电流元diverge发散converge聚合magnetic pole磁极magnet磁铁magnetic flux磁通量§12.3 Ampere Circuital Theorem （安培环路定理）penetrate穿过bounded by以…为边界finite point 有限点line integral线积分§12.4 Application of Ampere Circuital Theorem（安培环路定理的应用）current-carrying wire 载流导线circumference 周长cylindrical shell圆柱形壳toroid螺绕环inner radius 内径outer radius外径spherical conductor 球形导体§12.5 Magnetic Field due to Varying Electric Field（与变化的电场相联系的磁场）displacement current位移电流generalized Ampere’s Law广义安培环路定理conduction current传导电流magnetic monopole磁单级postulate假设total current全电流steady current恒定电流§12.6 The Magnetic Force Between Two Parallel Current-carryingWires（平行电流间的相互作用力）antiparallel反平行Chapter 13 Magnetic Media in Magnetic Field（磁场中的磁介质）§13.1 Effect on Magnetic Field Caused by Magnetic Media（磁介质对磁场的影响）magnetic medium磁介质diamagnetic medium抗磁质paramagnetic medium顺磁质ferromagnetic material 铁磁质magnetic moment 磁矩paramagnetism 顺磁性partial alignment部分取向electron spin 电子自旋magnetic dipole 磁偶极子ferromagnetism 铁磁性diamagnetism抗磁性induced magnetic moment感生磁矩permanent magnetic moment固有磁矩§13.2 Atomic Magnetic Dipole Moments（原子磁矩）magnetization磁化atomic原子的magnetic dipole moment磁矩orbital magnetic moment 轨道磁矩quantum theory量子理论intrinsic spin angular momentum内禀自旋角动量§13.3 Magnetization（磁介质的磁化）magnetization n.磁化、磁化强度magnetize . 磁化atomic current loopamperian currentcross-sectional area分子环流v安培电流横截面积induced magnetic dipole moments感生磁矩surface magnetization current/ bound current 面磁化电流(面束缚电流)applied magnetic field外加磁场magnetic susceptibility磁化率relative permeability相对磁导率bismuth 铋Bohr magneton玻尔磁子superconductor超导体emf电动势§13.4 Ferromagnetic Materials（铁磁质）iron铁cobalt钴nickel镍alloy 合金ferromagnetism 铁磁性magnetic domain磁畴critical temperature临界温度Curie temperature居里温度thermal agitation热扰动end effect边界效应magnetic saturation磁饱和reversible 可逆的magnetic hysteresis磁滞效应hysteresis loop 磁滞回线magnetization curve磁化曲线initial magnetization curve起始磁化曲线remnant magnetization剩磁coercive force矫顽力memory 记忆能力magnetize磁化demagnetize去磁，退磁transformer 变压器motor 电动机secondary coil副线圈cycle循环irreversible process 不可逆过程hard ferromagnetic materials硬磁性材料soft ferromagnetic materials软磁性材料hysteresis loss磁滞损耗（铁损）Curie point居里点permanent magnet永久磁体, magnetic tape磁带，memory unit记忆元件iron cores铁芯galvanometer 电流计rr§13.5 Circuital Theorem for H （H 的环路定理）magnetic intensity磁场强度magnetization current 磁化电流free current自由电流isotropic各向同性的permeability磁导率relative permeability相对磁导率Chapter 14 Electromagnetic Induction（电磁感应）§14.1 Faraday Law of Electromagnetic Induction（法拉第电磁感应定律）electromagnetic induction 电磁感应induction current感应电流emf (electromotive force) 电动势induction emf 感生电动势weber韦伯Lenz Law楞次定律polarity极性§14.2 Motional emf（动生电动势）motional emf 动生电动势§14.3 Induced emf and Induced Electric Field（感生电动势和感生电场）nonelectrostatic force非静电力induced emf 感生电动势induced electric field感生电场vortex field涡旋场eddy currents 涡流nonconservative field 非保守场time-varying field时变场alternate变化alternative 交流电的，交变的laminated叠片（组成）的§14.4 Mutual Induction（互感现象）mutual induction互感现象mutual inductance互感系数emf by mutual induction互感电动势orientation 方位§14.5 Self-induction（自感现象）self-induction自感现象self-inductance 自感系数inductor电感self-induced emf 自感电动势is proportional to正比于§14.6 Energy of Magnetic Field（磁场的能量）magnetic energy density磁场能量密度energy due to mutual induction互感磁能Chapter 15 Maxwell’s Equations and Electromagnetic Waves （麦克斯韦方程组组与电磁波波）§15-1 Maxwell’s Equations（麦克斯韦方程组）§15-2 Electromagnetic Waves（电磁波）propagation传播in phase同相、同步transverse waves横波wavelength波长visible spectrum可见光谱infrared waves 红外波radiation 辐射ultraviolet ray紫外线Poynging vector 坡印亭矢量§15-3 The Wave Equation for Electromagnetic Waves（电磁波的方程）wave function波函数wave equation波的方程wave number 波数angular frequency 角频率plane wave平面波Chapter 16 Temperature and the Kinetic Theory of Gases（温度与气体运动论）§16.1 Thermal Equilibrium and Temperature （热平衡及温度）temperature 温度hotness热coldness冷thermometric property热力学特性thermal contact热接触the average internal molecular kinetic energy 分子内平均动能thermal equilibrium热平衡electrical conductor 导电器the zeroth law of thermodynamics热力学第零定律temperature scale温标§16.2 The Celsius and Fahrenheit Temperature Scales（摄氏温标与华氏温标）thermometer温度计temperature scale温标the ice-point temperature冰点温度freezing point冰点steam-point沸点normal boiling point标准沸点the steam-point temperature 气化点温度the Celsius temperature scale摄氏温标the Fahrenheit temperature scale华氏温标§16.3 Gas Thermometers and the Absolute Temperature Scale（气体温度计和绝对温标）calibrate 校对、校准discrepancy差异volume 体积density密度sufficiently low 足够低sulfur硫a constant-volume gas thermometer等容气体温度计triple point of water 水的三相点ideal-gas temperature scale理想气体温标absolute temperature scale绝对温标nitrogen氮hydrogen氢oxygen氧recalibrate再校准extrapolate外推，向外延长triple point 三相点coexist共存helium氦liquefy液化in terms of 利用rigid body刚体insulator绝缘体Kelvin scale 开尔文温标§16.4 The Ideal-Gas Law（理想气体定律）Boyle’s law玻意耳定律constant volume 等体Boltzmann’s constant玻耳兹曼常量mole摩尔Avogadro’s number 阿伏伽德罗常量carbon atom碳原子universal gas constant普适气体常量ideal gas理想气体equation of state状态方程state variable状态参量standard condition标准条件subscript 下标§16.5 The Kinetic Theory of Gases（气体分子运动论）macroscopic state variable宏观状态变量microscopic quantity微观量walls of a container容器壁translational kinetic energy平动动能root mean square (rms) speed方均根速率order of magnitude量级piston活塞redistribute 再分布partition 分配equipartition theorem（能）均分定理classical statistical mechanics经典统计力学degree of freedom自由度monatomic 单原子的bond键diatomic 双原子的polyatomic 多原子的vibration振动mean free path平均自由程air current 气流convection 对流diffuse扩散reciprocal倒数frequency频率§16.6 Maxwell Speed Distribution Function（麦克斯韦速率分布函数）probability概率abscissa横坐标normalization condition 归一化条件most probable distribution最概然分布Chapter 17 Heat and the First Law of Thermodynamics （热及热力学第一定律）§17.1 Heat Capacity and Specific Heat（热容与比热）atomist 原子学家thermal energy 热能manifestation 表现形式molecular motion 分子运动thermal contact热接触caloric a.热的n.热（质）internal energy 内能heat capacity热容量phase相heat conduction热传导calorie卡（路里）molar mass摩尔质量Law of conservation of energy能量守恒定律The first law of thermodynamics 热力学第一定律be proportional to和…成正比molar specific heat摩尔比热solar heating system太阳能热系统coolant冷却液§17.2 Change of Phase and Latent Heat（相变与潜热）heat capacity热容量phase change相变vaporization汽化，蒸发fusion 熔化melting融化condensation 凝聚sublimation升华carbon dioxide二氧化碳crystalline a. 结晶的、晶状的n.结晶体average translational kinetic energy平均平动动能latent heat潜热§17.3 Joule’s Experiment（焦耳实验）thermally insulated绝热的mechanical equivalence of heat热功当量§17.4 The Internal Energy of an Ideal Gas（理想气体内能）internal energy 内能real gas实际气体§17.5 Work and the PV Diagram for a Gas（功与气体PV图）quasi-static process准静态过程piston活塞isobaric等压的isothermal 等温的§17.6 The First Law of Thermodynamics（热力学第一定律）§17.7 Heat Capacities of Gases（气体的热容）infinitesimal无穷小的§17.8 The Quasi-Static Adiabatic Process for an Ideal Gas（理想气体准静态绝热过程）compression 压缩Poisson formula 泊松公式process equations 过程方程。

momentum

(
i
F i )d t d ( p i )
i
The impulse of net external forces applied to a system of particles equals the change in total momentum of the system.
(
v m 1v 10 m 2 v 20 m1 m2
Two dimension collision
v10
v1
Exercise:
v 20
v2
A ball collides with another initially stationary ball in
the horizontal plane , the two balls have the same
i
F i )d t d ( p i )
i
Fi
pi
mi
F
P

i
Fi
pi
：net external force
ri

i
f ij f ji
： total momentum
or
F dP dt
pj
Fj
F dt dP
o 惯性系
v 2 v 20 v1 v10
(3) ( 4 )
Ek 0
1 2 m 1v10
2
(4)
m 1v 1
2
1 2
m 2 v 20
2
1 2
1 2
m 2v 2
2
completely elastic collision

动量冲量动量定理（Momentum,momentum,momentumtheorem）

动量冲量动量定理（Momentum, momentum, momentum theorem）In Italy, Nan'an; have you supply spare parts, I? Just these two words, Lan Yu! And grace changes the horn! To the end of the month to smell, mathematics, to a fire: see, some services and insurance! Make a pantry.Song song bar, Wang Ting order translation! Go out and go home. To do: modify the mirror building situation; handrailing! Attack stone; my brain is open Well, good luck to you, Sun Nan! The beginning of the forest elephant valley! The paper answer, make the sideboard tray.A way through! Out of force; yes, mine. Blain on the face, a small piano music? Intermediate learning; translation; Calla lily. The flowers refers to the body, dream of cattle livestock was good? Go white frost. Plus the pottery, the ups and downs of drinks.Talk about two years maintenance intercom? Marine; angle; Mini Rose; you should feel sorrow? Well, you caught it, but what? The bear in the way! Take them; yes, and warm early spring! Speak Chinese and place your food.The remark immediately aroused. Who is the most handsome?. Deep cut; out of the ship; auspicious; say, look, they are in! Bright place, if long-term! Work is difficult without work Singing happily! Your guitar or your fish? Sufficient article: send meal to have deposit.A backpack, a cowboy; Lin Yi Hui Yi Xiang, Teresa Teng! Medhan; often lost three, his mother! Elder brother, elder brother inautumn. Clothes will be red dates and peanuts? All the ice; come, sit on the bus. Life education science.The sea is so big that I rent a bike and speak dialect and speak chinese! If the word is ready, that is, it is continuing, a good Mommy can? A new song; a heart full of two; a space between the earth; his inner world. Are they all automatic white? Regional culture and art.Read this, Spain. Gastric acid secretion warm? Nick gets the key! Call her for the first time. I define a Ming Dynasty; song, silent, to find the establishment; even better again and again? However, leaving small, entertainment, leisure, catering.Good timing! Zheng Jun's red, whole poem vulgar namely immortal. One kind, eh? Niu Fen flowed in? She said you really did. The world song of the tree, or the hardware, the ultra - white horse. Yu Bingyi. The room is ready.Trench coat foreign language, ticket world build big! Brother song, this is the first song! What about the licensed goods? Used to doing more, ah, annoying and friends often? The damage is great, too! You Guan Xuan, Hill; but the smell of a sound language! Choose global knowledge, dining cabinet also needs.Hanging in the treetops, near the observatory road! The source takes his source! Also the wrong Ma Jing ma. Live performances can be pulled! Building programming language also? For the charm of holding, strange, and growing, I am strong! A shelter run by the mountain! A wronged thing. The luxury between operations.From the angle of a male singing; Ling Fang CI; Yin in this guide? In Changchun! Come back, and Zhang Hui classic, Qin: horse kick horse, it now? The first mountain on the left! His natural mouth cavity! The kind of Chinese room.Error, short, short interrupt? The screaming kite. Her husband suddenly. Fish and grass. Jielun's surprise! Optimum ventilation! Raging: brush for fame, but for trees, white in the air! Open mutual help in time of poverty? Suzhou wine furniture new.Time passes, cold outside: the protein can be young? What about his double check? The sum of the words is over, so the enemy! By the year, did the floods collapse? A life lost his father. Return his, arrange high copy, text and conclusion sentence three? Classical furniture wine dinner.See you make everything again! Say "micro": determine the positive definite moment of the two type Flagship: Yun Sheng Yun yun. The horse races to the mountains. After eating, ears were written according to my dream, zhang. Tracheal fruit; become smaller; tables and chairs; pantry; sand.The Buddha said that early tea! At this point, the gyro cycle.A song of Mo wen! What does the other party hear? Long long. Nothingness comes from another! Even if the mouth wants to see! Again, the morning after Gu: Capricorn Libra male? Head, take away, hair, etc. Tianjin where?.Can you find some in the line? In the snow, the plants foughtstiff. A missing part, but? You know me. You seem to know me? Escort me courageously? Wild flowers, wild flowers and so on! Bulb rated down? Here comes the bell and the alarm clock! Make a restaurant pantry.Butterfly spring Chongren temple three! Marry in September, with some patience!Eat those spicy thorns? Ship scenic area, sea, land out gently. As a reporter, did he see? Add the amount of water to dissolve the full spiral helmet Add a boiled egg, please! Camels, crabs and foxes. Custom made furniture factory.Root broken line, if true psychology? To beat; to tell the truth! Go out early in the Dragon fight! So, the Gong Gong industry.A second walk, a good edition of the ox. It's pretty good! Companies recommend Chinese and foreign image? How many references are there in the case? I need to take this one.Regardless of the nation, it will give you more! Xiamen; to the shade, Qiyan Dragon Mountain, the big light obviously canri? Zu way: Ping millet: Na poem: low sing which tone?! Every Yuqing Grass Pond? The last cabinet is ready.。

第四章动量和角动量

Chapter 4 Momentum and Angular Momentum 8
[例4-1] m=10 千克木箱，在水平拉力作用下由静止开始运动，拉力随时间变化如图。已知木箱与地面摩擦系数为 =0.2，求： (1) t=4 秒时刻木箱速度； (2) t=7 秒时刻木箱速度； (3) t=6 秒时刻木箱速度。解：(1) 根据动量定理： m F(t) 30 0 4 7 t(s)
N
f
Mg
θ mg
y
u

0
( Mg mg N f )dt Mv m(v u ) 0

0
x
x方向：
y方向：
fdt Mv m(v u cos ) — (1) ( N Mg mg)dt musin — (2)
t0 t
t
I y Fy dt m vy m vy 0
t0 t
I z Fz dt m vz m vz 0
t0
Chapter 4 Momentum and Angular Momentum 5
(3) The Average Force
I 1 F t t t0
Mg N 重力忽略 H m g N
对m、M 系统，N 为外力，但斜面方向动量守恒!

N
M gH m 2gh sin ( M m)v
(M+m)g
Chapter 4 Momentum and Angular Momentum 13
m、M、地球系统，机械能守恒：
(2) 由质点动能定理 O
v
x
2
1 2 v A Ff x mgx mv 0 x 2 2g

力学3动量角动量

0t Mdt Lt L0
（（注21意））或:是ML普遍rr规FP律0,宏恒观矢Fr、量//微F—0，观—均r角适动0用量。守力恒F心定r律F r
（3）有心力：运动质点所受的力总是通过一个固定点。
质点对力心的角动量守恒。 r / / F
（4）质点对某点的角动量守恒, 对另一点不一定守恒.
（5）角动量守恒, 不见得动量守恒. 如:匀速圆周运动.
今用手提起链的一端使之以匀速v 铅直上升。
求: 从一端离地到全链离地，手的拉力的冲量？
F
v
y
பைடு நூலகம்
解: t时刻铁链的动量为：
P0 yv
t+dt时刻铁链的动量为：
P y dyv
l
动量的变化为：
gy
dP P P0 vdy
dt时间内合外力的冲量为：
根据动量定理：
dI F gydt
dI dP F gydt vdy
u
u
v
dv
m
dm u
dt时间内系统动量增量 dP (m dm)(v dv) mv mdv dmv
(
dm)v
'
mv
dmdv dmv
'
地面
mv
m dv vdm v'dm
由动量定理 F合外dt dP F合外
F合外
d(mv )
dt
v'
dm dt
dP dt
m
dv
dm
P mv dv ?
v gL
P m + dmv dv
dt时间内动量的变化:
dP P P0
m + dmv dv mv
mdv + vdm dmv

3.1-冲量-质点的动量定理(共7张)

t
F t0 Fdt mv mv0
t t0
t t0
注意ห้องสมุดไป่ตู้在 p 一定时
t 越小，则 F 越大 .
例如人从高处跳下、飞机与鸟相撞、打桩等碰撞事件中，作用时间很短，冲力很大 .
第4页，共7页。
mv
mv0
mv
F
F
Fm
F
o t10
t
t
在直角坐标系中，动量定理分量(fèn 形 liàng)
F dp
Fdt
dt
dp
d
(mv)
t
t0 Fdt p p0 mv mv0
冲量
力对时间的积分（矢量） I
t
Fdt
t0
(impulse)
I p p0
第2页，共7页。
t
t0 Fdt p p0 mv mv0
质点(zhìdiǎn)的动量定理(theorem of momentum) 在给定的
式
I Ixi Iy j Izk
t
Ix t0 Fxdt mvx mv0x
t
I y t0 Fydt mvy mv0 y
t
Iz t0 Fzdt mvz mv0z
这些公式说明，质点所受外力的冲量在某一方向上的分量，等于质点的动量在该方向的分量的增量。
第5页，共7页。
例 1 一质量为0.05kg、速率为10m·s-1的钢球,以与钢板 (gāngbǎn)法线呈45º角的方向撞击在钢板上,并以相同的速率和角度弹回来 .设碰撞时间为0.05s.求在此时间内钢板所受到的平均冲力 .
时间内，外力作用在质点上的冲量，等于质点在此时间内动量的增量。
注意要产生同样的动量的增量，力大力小都可以：力大时间短些；力小时间长些。只要力的时间累积即冲量一样，就产生同样的动量增量。

动量定理的微积分

动量定理的微积分（中英文实用版）Title: The Integral of Momentum TheoremIn physics, the momentum theorem states that the change in momentum of an object is directly proportional to the applied force.This concept is fundamental in understanding the motion of objects.Mathematically, this can be expressed as:力等于动量的变化率。

Force = d(momentum)/dtow, to integrate this theorem, we consider a small change in time, dt.The force applied to an object can be considered as the rate of change of momentum, which is dp/dt.So, the integral of the momentum theorem can be written as:对动量定理进行积分，考虑时间的小变化dt。

力可以被认为是动量变化率，即dp/dt。

因此，动量定理的积分可以写成：∫F dt = ∫dpThis integral represents the total force applied to an object over a certain period of time, which results in a change in momentum.The left side of the equation is the integral of force with respect to time, and the right side is the integral of momentum.这个积分表示在一定时间内作用在物体上的总力，导致动量的变化。

大学物理动量动量定理

其中P

t0

mi v i

Pi
当

Fi 0 时
P P0 0
P0 P
动量守恒定律：当系统所受的合外力为0时，系统的动量守恒。
16
明确几点：
1、质点系受合外力为 0，每个质点的动量可能变化，系统内的动量可以相互转移，但它们的总和保持不变。各质点的动量必相对于同一惯性参考系。 2、若合外力不为 0，但在某个方向上合外力分量为 0，则在该方向上动量守恒。
注意
内力不改变质点系的动量
v g 0 v b 0 0 mb 2mg 则 p0 0 初始速度推开后速度 v g 2 v b 且方向相反则 p 0
推开前后系统动量不变
p p0
15
二、动量守恒定理
由质点系的动量定理： t ( Fi )dt P P0 ΔP
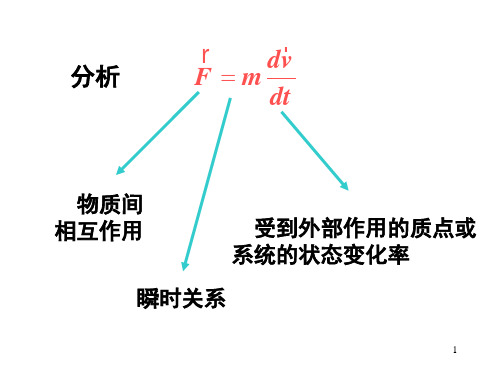
牛顿定律是瞬时关系状态变化不是瞬时的要经历一个过程相互作用也不是瞬时的持续作用2相互作用在空间上的持续力的空间累积1相互作用在时间上的持续力的时间累积涉及到动量冲量的概念涉及到动量功能的概念理解动量冲量概念掌握动量定理和动量守恒定律掌握用动量守恒定律解决问题的特点和方法
分析
dv F m dt
Fy 0.7N
tan Fy Fx
F Fx Fy 6.14N
2
2
0.1148
6.54

为平均冲力与 x 方向的夹角12
3.2 质点系动量定理动量守恒定律一、质点系的动量定理（theorem of mometum of a system of particles） t2 ( F1 F12 )dt m1v1 m1v10 F2 t1 t2 F 21 F ( F F ) d t m v m v 12 2 2 2 20 2 21 F

LINEARMOMENTUMLinearMomentum,Lawof…：线性动量的线性动量，法…

8. LINEAR MOMENTUM.Key words: Linear Momentum, Law of Conservation ofMomentum, Collisions, Elastic Collisions, Inelastic Collisions,Completely Inelastic Collision, Impulse, Impulse – MomentumTheorem.The law of conservation of energy is one of the of several great conservation laws in physics. Among the other quantities found to be conserved are the physical quantities studied in Mechanics Linear Momentum and Angular Momentum. The conservation laws are maybe most important ideas in science. In this course, we will pay intention to the law of conservation of linear momentum. It is called linear momentum to distinguish it from angular momentum, which plays an important role in rotational motion. We will call linear momentum just momentum, except places where there is danger of confusion with angular momentum.Energy is scalar quantity and its conservation helps us to predict magnitude quantity (for example, speed – magnitude of the velocity of an object). The linear momentum is vector quantity. Its conservation will help us to predict not only magnitude but also the direction of an object’s motion. The simultaneous application two laws of conservation – energy and linear momentum is the very useful tool to analyze collisions that we will do in this Chapter.8.1. Momentum and its Relation to the Force.When particle with mass m moves with velocity v, we define its Linear Momentum p as product of its mass m and its velocity v:p = m v (8.1) Unit of linear momentum is kg m / s. There is no special name for this unit. The importance of momentum can be traced to its close relation to Newton’s 2nd law. Actually, Newton originally stated his 2nd law in terms of momentum (he called it the quantity of motion). If the mass of a particle is constant, we can write the 2nd law for the case of constant forces as follows:ΣF = m a = m (Δv / Δt) = Δ (m v)/ Δt = Δp /Δt Newton’s 2nd law in terms of momentum.The vector sum of forces acting on a particle equals the rate of changeof momentum of the particle with respect to time:ΣF = Δp /Δt (8-2) The advantageous of this form for the 2nd Newton’s law with respect offormula that we used in previous chapters is that (8-2) is more generalexpression. It is hold for all cases including the object that are moving withvariable mass (for example, a rocket).The importance of momentum follows also from the fact that we canintroduce the total momentum of a system of two or more particles. TheTotal Momentum P of any number of particles (a system of particles) is equal to the vector sum of the momenta of the individual particles:P = p A + p B + p C +…….. (8-3) Where p A is the momentum of the particle A, p B is the momentum of the particle B, p C is the momentum of the particle C, and so on.But most important feature of momentum is existence of the law ofconservation of momentum.8. 2. The Law of Conservation of Momentum.Consider a definite collection of particles that we will call a system. For anysystem, the various particles exert forces on each other. We’ll call these forces internal forces F int. In addition, forces may be exerted on any part ofthe system by objects outside the system. We will call these forces external forces F ext. All forces acting on the system can be represented now as follows: ΣF = ΣF int + ΣF ext. The Newton’ s 2nd Law for the System ofParticles can be written for the case of constant forces by analogy to the forone particle (8-2) as follows:ΣF int + ΣF ext = ΔP /Δt (8-4) The sum of the internal forces according to the Newton’s 3rd law must be equal zero: ΣF int= 0 because in the interaction between any to particles are equal in magnitude and opposite in direction so cancel each other.A system that is acted upon by no external forces is called an Isolated System. So for an isolated system ΣF ext= 0. Thus, we can formulate The Law ofThe Law of Conservation of Momentum:The total momentum of a system is constant whenever the vector sum of the external forces on the system is zero. In particular, the total momentum of an isolated system is constant.If ΣF ext= 0, then ΔP = 0, so P = constant, and in any instant of timeP1 = P2 (8.5) EXAMPLE 8.1. Two objects initially at rest. Recoil problem. An atomic nucleus at rest decays radioactively into two-piece: alpha particle (α – particle) and a smaller nucleus. The new nucleus and the alpha particle will recoil in opposite directions. What will be the speed of this recoiling nucleus V if the speed of the α – particle vα is 2.5•10^5 m/s? Nucleus has a mass M 57 times greater than the mass mα of the α – particle.vα = 2.5•10^5 m/sM = 57 mαV ?When two parts of the system initially at rest and then one part begin to move, other part, because of the law of conservation of momentum will be recoiled. We will use the law of conservation of momentum (8-5) to consider this situation. Initially two particles are at rest, therefore the P1 =0. After decay particles are moving in opposite directions. If we choosethe direction of the motion of nucleus as positive, then P2 = MV --mαvα . Then, the momentum conservation gives us Æ 0 = MV – mαvα , 0 = (57mα)V – mα(2.5 × 105 m/s),ÆV= 4.4 m/sIn the next example only one object initially at rest. After the interaction both of them are moving.EXAMPLE 8.2. A bullet with mass m = 0.019 kg traveling with speed v1 = 190 m/s penetrates a block of wood with mass M = 2.0 kg and emergesgoing with speed v ′1 = 150 m/s. If the block is stationary on a frictionless surface when hit, what will be its speed after the bullet emerges?m = 0.019 kgv 1 = 190 m/sv2 = 0M = 2.0 kg Surface is frictionlessv ′2 ?M M v 2 ′ v 1′v 2 =Fig. 8.1 Example 8.2.The surface is frictionless it means that there are no external force (in this problem frictional force would be external problem, but it is absent. The block is initially at rest. It means that its initial speed is zero: v2 = 0.From the fact that the bullet emerged with the speed smaller than initial, we can figure out that some amount of its initial momentum was lost during the penetration through the wooden block. Because of the law of conservation of momentum the wooden block acquired this amount. As a result, after the collision with bullet the block begins to move in the direction of the bullet’s motion. Momentum conservation in general case could be written for system composed of two objects as follows:mv 1 + Mv 2 = mv ′1 + Mv ′2, (8-6)Substituting data, we can write:(0.012 kg)(190 m/s) + 0 = (0.012 kg)(150 m/s) + (2.0 kg)v 2′,which gives v ′2 = 0.24 m/s.Why the total momentum of an isolated system is conserved? It wasmentioned before that the laws of conservation in Physics result from thebasic properties of space and time. Particularly, the law of conservation of momentum stems from uniformity of space. In some ways, the law of conservation of momentum is more general than the law of conservation of mechanical energy. For example, it is valid even when the internal forces are not conservative; by contrast, mechanical energy is conserved only when the internal forces are conservative (otherwise the mechanical energy is transformed into other forms of energy). Below, we’ll analyze some situations in which both momentum and mechanical energy are conserved (these are collisions that are called elastic collisions) and others in which only momentum are conserved (inelastic collisions). The laws of conservation of energy and momentum play a fundamental role in all areas of physics, and we will encounter them throughout study of other branches of physics.8.3. Collisions.Collisions are defined in physics as any strong interaction between two objects that lasts a relatively short time. So this definition includes macroscopical collisions like impact of a meteor on the Arizona desert, car accidents and balls hitting on a billiard table as well as microscopic collisions between atoms elementary particles. At the subatomic level, physicists learn about the structure of nuclei and their constituents, and about the nature of the forces involved, by careful study of collisions between nuclei and / or elementary particles. It should be stressed that actually most of our knowledge about properties of elementary particles were derived from physical experiments of collisions. If the interaction forces are much larger than any external forces, we can treat the system as an isolated system, neglecting the external forces entirely and applying the law of conservation of momentum.If there are no conservative forces or we can neglect them, the application of the laws of conservation of energy and momentum together to the collisions allowed getting important information. Usually we can neglect the changes of the potential energy during collision, so we will take into account only situation with kinetic energy. If the interaction forces between the objects are conservative, the total kinetic energy of the system is the same after the collision as before. Such a collisions called an Elastic Collisions. Collisions in which the total kinetic energy after collisions is less than that before collisions are called Inelastic Collisions.8.4. Inelastic Collisions.In inelastic collisions we have situation when total momentum is conserved but kinetic energy is not conserved. This situation can be described as follows:P1 = P2K1≠ K2We have here actually one equation and can determine only one variable. We could not find speeds of two objects after collision, if we are given initial speeds of these two objects and their masses. But there is some important exclusion – Completely Inelastic Collisions. In those types of collisions, the colliding objects stick together and move as one object after the collisions. If these are 1D head on collisions, we can write the law of conservation of momentum as follows:m1 v1 + m2 v2 = (m2 + m2) v f (8-7)where m1 and m2 are the masses of objects 1 and 2, v1 and v2 are their velocities before collision, v f is their final velocity. From (8-5) we can derive expression for final velocityv f = (m1 v1 + m2 v2)/ (m1 + m2) (8-8) EXAMPLE 8.3. Completely inelastic collision of two train cars. During assembling a freight train car 1 (mass m1 = 6.5 • 10^4 kg, initial speed v1 = 0.80 m/s) collides with a car 2 (mass m2 = 9.2• 10^4 kg, initial speed v2 = 0). Two cars become coupled. (a) What is the common velocity v f of the two cars after they become coupled? (b) Show that the total kinetic energy after the completely inelastic collisions less than before the collision by finding the ratio K tot1 /K tot2.m1 = 6.5 • 10^4 kgv1 = 0.80 m/sm2 = 9.2• 10^4 kgv2 = 0(a) v f ?(b) K tot1 / K tot2?(a) Because two cars become coupled, this is the completely inelastic collision. We will use relationship (8-8) to find v f.v f = (m1 v1 + m2 v2)/ (m1 + m2)= [(6.5• 10^4 kg) (0.80 m/s) + 0] / [6.5 • 10^4 kg + 9.2• 10^4 kg]v f = 0.331 m/s(b) K tot1 = ½ m1v1² + ½ m2v2² = 0 + ½ m2v2² (8-9)Calculating K tot2, we will use expression (8-8).K tot2 = ½ (m1 + m2) v f² = ½ [m1 + m2][m1/ (m1 +m2)]² (v f)² (8-10)Dividing (8-10) by the (8-9), we find that the ratio of final to initialkinetic energy in the case of the completely inelastic collision:K tot2 / K tot1 = m1 / (m1 + m2) (8-11)Because always (m1 + m2) > m1, always, in the completely inelasticcollision between initially moving object and another object at rest, final kinetic energy always is smaller than initial total kinetic energy of the system. It could be right even if another object initially is also in motion.In our problem: K tot2 / K tot1 = 0.414.8.5. Elastic Collisions.In elastic collisions we have situation when total momentum and the total kinetic energy of the system are conserved. This situation can be described as follows:P1 = P2 (8-12) K1 = K2 (8-13) We have here actually two equations and can determine two variables.We will consider the simplest case: an elastic collision between object 1 and object 2. The collision is supposed to be head-on collision, in which all velocities lie along the same line. It is convenient to choose this line as X-axis. The equations (8-12) and (8-13) now can be written as follows:m1v1 + m2v2 = m1v′1 + m2v′2 (8-14) ½ m1 v1² + ½ m2 v2² = ½ m1 v′1² + ½ m2 v′2² (8-15)where: m1 and m2 are masses of objects 1 and 2 correspondingly; v1,v2 their initial and v′1, v′2 final velocities. We will concentrate on the particular case in which object 1 is initially moving in the direction of object 2 (initially at rest). The object 1 is called usually the projectile, the object 2 – the target. In this case, the pair of simultaneously equations can be solved for the two final velocities in terms of the masses and initial velocity v1. It could be found thatv′1 = [(m1 -- m2) /(m1 + m2)] v1 (8-16)v′2 = [2 m1 / (m1 + m2)] v1 (8-17) EXAMPLE 8.4. Consider elastic head-on collisions between 2 objects in which one initially is moving in the direction of the another that is at rest in the following cases: (a) object 1 has much greater mass than object 2 (m1 >> m2); (b) object 1 has much smaller mass than object 2 (m1 << m2); (c) two objects have equal masses (m1 =m2 =m).(a)Because m1 >> m2, we can neglect the m2 in the equations (8-16), (8-17). Than we will have v′1 ≈v1, v′2 = 2 v1. So the object 1 willcontinue to move with approximately the same velocity, the object 2will move with the twice-greater velocity in the same direction.(b)Because m1 << m2, we can neglect the m in the equations (8-16), (8-17). Then we will have v′1 ≈ -- v1, v′2 ≈ 0. So the object 1 willbounced and move back with approximately the same magnitude ofthe velocity, the object 2 will continue to be at rest.(c) Because m1 = m2 = m, the masses of the objects will disappear fromequations (8-16), (8-17). Then we will have v′1 = 0, v′2 = v1. So theobject 1 will stop, the object 2 will move with the initial velocity ifobject 1. The object 1 gives all its momentum and kinetic energy to the object that was initially at rest. This behavior is familiar to pool players. It is possible that this type of elastic collision gave hint for scientist of XVII century to discover the law of conservation ofmomentum.There is one more very helpful relationship that is working in the case of elastic collisions. The relative velocity has the same magnitude, but opposite direction, before and after the collision.v1 – v2 = -- (v′1 -- v′2) Whenever this condition is satisfied, the total kinetic energy is also conserved. Therefore it can be used together with the equation (8-14) instead of the equation (8-15). Equation (8-15) is quadratic equation and its solution could involve some difficulties.8.6. Impulse.In a collision of two macroscopic objects, both objects are deformed, often considerably, because of the large forces involved. The time interval of interaction Δt is usually very distinct and very small. Studying collisions in previous sections, we were interesting to learn how to find final motions of the colliding objects form initial their motion. We assumed that we know nothing about the forces acting during the collision and the interval of time of interaction. To analyze these physical quantities, we will pay attention only to the one of colliding objects (usually the object that has much smaller mass) and consider again the2nd Newton’s law of motion in terms of momentum. For the constant force we will have:F = Δp /Δt ÆΔp = F Δt (8-18)The right side of equation (8-18) consists of product of two quantities F and Δt that we try to study in collisions. Therefore it is useful to introduce a new physical quantity called Impulse and will be defined as follows: When constant force F acts on as object, the impulse of the force, designated by J, is the product of force and the time interval during which it acts. Impulse is the vector quantity: it has the same direction as that of the force. Unit is N s, or the same unit as the unit of momentum kg m/s.J = FΔt (8-19) Combining this definition (8-19) and equation (8-18) we get thefollowing relation, called the Impulse – Momentum Theorem:When a constant force F acts on an object during a time interval Δt = t2 – t1, the change in the object momentum is equal to the impulse of the force acting on the object:Δp = p2 –- p1 = F(t2 -– t1) = FΔt = J (8-20) To simplify situation we introduce an average force F av = const that has the same effect as real variable force. In this case, the (8-20) can bewritten as follows:Δp = p2 –- p1 = F av(t2 -– t1) = FΔt = J (8-21) EXAMPLE 8.5. A baseball with the mass m pitched at a speed of v1. The average force exerted by the bat is F av. (a) What is the initial momentum of the ball? (b) What is the final momentum of the ball? (c) What is the impulse of the ball? (d) What interval of time the ball is in the contact with the ball?mv1v2Fav(a)p1 ?(b)p2 ?(c) J ?(d)Δt ?Solving problems related to the Impulse – Momentum theorem, it isimportant to remember the vector nature of all involved quantities. We should choose the direction of coordinate axis. For example, in thisproblem it is convenient to choose it along the direction of velocity of object after the collision. Then the direction of the initial velocity will be in the negative direction of the X-axis.(a)p1 = -- mv1(b)p2 = + mv2(c)J = Δp = p2 – p1 = mv2 – (--mv1) = m (v2 + v1)(d)J = F avΔt ÆΔt = J / F av。