哈工程5系信号与系统03-05本科生试卷答案
哈尔滨工程大学信号与系统试卷与答案

第2页 共 4页y 1(t);4. 写出描述该系统的系统方程。
四、(12分)设一因果连续时间LTI 系统输入x (t)和输出y (t)关系为:y ''(t)+3y '(t)+2y (t)=x (t)1. 求该系统的系统函数H (s),画出其零极点图,并判别系统的稳定性;2. 确定此系统的冲激响应h (t);3. 求系统的幅频特性与相频特性表达式。
五、(8分)一个离散LTI 系统的单位样值响应为:h (n )=αnu (n )1. 试用时域卷积方法求该系统的单位阶跃响应g(n );2. 确定该系统的系统方程。
六、(24分)已知函数x (t)和y (t)分别为:∑∞-∞=-=n n t t x )4()(δ ,t t t y 6sin 4cos )(+=1. 求y (t)的指数傅立叶级数表示,说明其频带宽度;2. 求x (t)的傅立叶级数展开表达式,简略画出其幅度谱线图;3. 求x (t)的傅立叶变换表达式X (j ω),简略画出X (j ω);4. 求y (t)的傅立叶变换表达式Y (j ω),简略画出Y (j ω);5. 确定信号y (t)的奈奎斯特频率与奈奎斯特间隔。
6.确定信号s (t)=x (t)y (t)的频谱。
七、(16分)一个因果的离散时间LTI 系统描述如下:)()2(21)1(43)(n x n y n y n y =-+--其中x (n)为输入,y (n)为输出。
1. 试求该系统的系统函数H (z),画出H (z)的零、极点图;2. 求系统的单位样值响应h (n),并说明系统的稳定性;3. 用求和器、数乘器和延时器画出其结构框图;4. 如)(31)(,1)2(,2)1(n u n x y y n⎪⎭⎫⎝⎛==-=-,求y (n)。
第3页 共4页 第4页 共 4页八、(8分)假设x (t)的傅立叶变换X (j ω)=0,|ω| >ωm ,而信号g(t )可表示成)}sin (]cos )({[cos )()(ttt t x t t x t g c c c πωωω*-= 式中*记做卷积,而ωc >ωm 。
哈工程五系信号与系统03-05本科生试卷

哈尔滨工程大学试卷(2003)考试科目:通信原理一、填空(本题20分)1、某数字传输系统传送8进制信号,码元速率为3000B,则该系统的信息速率为。
2、随参信道传输媒质的特点是、、。
3、为提高发送信号功率效率,通常采用直接法从数字信号中提取位同步,其基本方法有,和锁相提取法。
4、在模拟调制系统中,门限效应是指解调器门限值时,急剧恶化的现象。
能产生门限效应的调制方式有,。
5、在数字通信中,可以通过观察眼图来定性地了解噪声和对系统性能的影响。
6、30/32路PCM时分复用系统的基群速率为,每帧bit。
7、在增量调制系统中,当模拟信号斜率陡变时,阶梯电压波形有可能跟不上信号的变化,形成很大失真的阶梯电压波形,这样的失真称为。
8、载波同步包括插入导频法和,对DSB信号若采用插入导频法提取载波,则插入的导频与调制端载波的是关系。
9、调制信道可以分为和。
π”现象,可以对基10、为了防止二进制移相键控信号在相干解调时出现“倒带数字信号先进行,然后作BPSK调制。
二、(本题10分)Hω如下设某数字基带传输系统的发送滤波器、信道及接收滤波器组成总特性()图,问:(1)若要以2/T S波特的速率进行数据传输,该系统是否存在码间干扰,判断的理论依据是什么?(2)若要以1/T S波特的速率进行数据传输,该系统是否存在码间干扰?S S()H ω三、(本题20分)某数据代码为1 0 1 1 0 0 0 0 1 1 1 0,(1)画出相应的单极性归零码,差分码,HDB 3码波形;(2)画出对应的2PSK 信号,2DPSK 信号波形(自行规定参考相位)。
四、(本题15分)已知话音信号的频率范围限制在0~4000Hz ,其双边带调制信号的时域表达式为()()cos m c S t m t t ω=,接收端采用相干解调,(1)画出接收端解调的原理框图;(2)当接收端的输入信噪比为20dB 时,计算解调的输出信噪比。
五、(本题15分)采用移频键控方式在有效带宽为2400Hz 的传输信道上传送二进制数字信息,已知2FSK 信号的两个载频f 1=980Hz,f 2=1580 Hz ,码元速率R B =300B ,传输信道输出端的信噪比为6dB,试求:(1)2FSK 信号的第一零点带宽;(2)采用包络检波法解调时系统的误码率; (3)采用同步检测法解调时系统的误码率;六、(本题15分)在模拟信号数字传输系统中,对模拟话音信号()m t 进行13折线A 律编码,已知编码器的输入信号范围为5V ±,输入抽样脉冲幅度为 3.984V -,最小量化间隔为1个单位。
哈工大信号与系统第三章术后作业答案张晔

fltnzlults因为是bniif.c EJ.siunwndttjErsincnwtsdt品奇这是咋求的求锯⻮信号ftkocnejnmtcniiffme则⼴哻f则fits品蕊ei哔世这是利⽤指数表示求三⻆函数形式下的⽐⼆ffctldt.FI ff aniiffmcoscnwtgdtiifl ttEjcoscnwtydttf奇㷒依然为奇则为0⼆if Ewscnwtdt2元ㄨ103kHz 6.128X 2X106t1间隔ME巺⼆㗟s不4112X1066.28106带亮13乺烈烈6nfzxi14三次诮波11批t 10⽐红__2.12Et E 4i 1lCniÈffme atdtfcne atdttffze.at dt其中ain⼆弦表ǏF试⻦扣与fun的傅⽴叶变换Fifn Filmfit Alum ut沙井控ult.int坷同样将fun表示⼀下⼆是cult ultt t Al ul ti Ultt则Fl funk Ftw ejwto詏们对于la 来说原因为三⻆以及余弦之积inn则n 01wtionjtoiw zuScilE 2对于⼼来说原⼆Sin 5元右侧的相当于则Sachi ii nl ócw 5元-01W 5到vivre怎么看出来的ht利⽤时域积分把原函看成积分原⽐⽐出⼀吐动deno 个吢砟⼼ólug201W e iwi nameÍjmjw⼆⽆以costing tisinihgznwilosciugtisin int器nomaunt jw求的傅⾥叶变换利⽤傅⾥叶变换的定义式求FlwkfofneiTltftltgeiwtdt.ttcu.int Fxi Eij w W2t恐器加⼀兜圜篮圝噬部⼆品ceiwte Mtice2N.ie可以应leine全部转化为⼼sin之形成三吉xzcoswth.zwszwtfw.zsinz.ru为了求得⽴叶级则要利⽤原tniiFocwilninw.F4从⽽cnet.to cnn.in代⼊上式中则代⼊到了覃⽴叶级数的公式中funÍcneimt⼀H求⼼的傅⾥叶交换则Rcntawhn HIM⼆舙⽅站1jhntl 然后求输⼊信号的得主叶交换在⼀个周期内P fltsejwtdt in哭⼏⼆T T teiwtdtiwlteiwt jeiwtsiEijiMn D 求fun的傅⽴叶级数90i hits dtf.li灬i1第⼀次分布积分⼜弄错了duty卡twsnwitdt ijtwscnw ndt lnwdwscnwnliw.co scnwtsi ǜǐ⼆声n.dz cost 哔_sinc 哔⼆前211叮n华⼆则no 时IAN则An 有加上n 为偶iq ⼥终900则⼈品㹷n 为奇彘流iiwiwiwj.ws对fun 进⾏傉⽴叶交他fun为奇函数外an sc.no求dni ǐǕsincnwmdt.lu 笇d n ⾔Ǖs in2巺七d t ⾔ǜ则所求即为flat fun 不⽤合求iii nt1111111iinnnniiii。
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
信号与系统参考答案
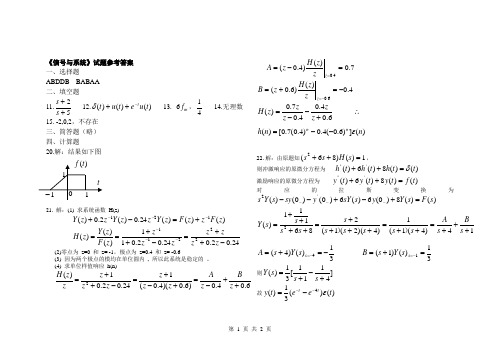
第 1 页 共 1 页《信号与系统》试题参考答案 一、选择题ABDDB BABAA 二、填空题 11.52++s s 12.)()()(t u e t u t t-++δ 13. m f 6,41 14.无理数15. -2,0,2,不存在三、简答题(略) 四、计算题20.解:结果如下图21. 解:(1) 求系统函数 H(z))()()(24.0)(2.0)(121z F z z F z Y z z Y z z Y ---+=-+ 24.02.024.02.011)()()(22211-++=-++==---z z zz z z z z F z Y z H (2)零点为 z=0 和 z= -1,极点为 z=0.4 和 z= -0.6(3) 因为两个极点的模均在单位圆内 , 所以此系统是稳定的 。
(4) 求单位样值响应 h(n)6.04.0)6.0)(4.0(124.02.01)(2++-=+-+=-++=z B z A z z z z z z z z H7.0)()4.0(4.0=-==z z z H z A4.0)()6.0(6.0-=+=-=z z z H z B6.04.04.07.0)(+--=z zz z z H ∴)(])6.0(4.0)4.0(7.0[)(n n h n n ε--=22.解:由原题知1)()86(2=++s H s s,则冲激响应的原微分方程为 )()(8)(6)('''t t h t h t h δ=++激励响应的原微分方程为 )()(8)(6)('''t f t y t y t y =++对应的拉斯变换为)()(8)0(6)(6)0()0()('2s F s Y y s sY y sy s Y s =+-+-----14)4(1(1)4)(2(1(286111)(2+++=++=++++=++++=s Bs A s s s s s s s s s s Y ))31)()4(4-=+=-=s s Y s A 31)()1(1=+=-=s s Y s B则]4111[31)(+-+=s s s Y 故)()(31)(4t e e t y tt ε---=111-)(t f t第 2 页 共 2 页23.答:(1))(2)(3)()(2s Y s sY s F s Y s--=231)()()(2++==s s s F s Y s H 对应微分方程为)()(2)(3)('"t f t y t y t y =++24.答:当0<t 时,0)(=t y当10<<t 时,⎰=⨯=t t d t y 0212)(τ 当21<<t 时,2)(=t y当32<<t 时,⎰--=+-=⨯=21)3(2)12(212)(t t t d t y τ 当3>t 时,0)(=t y注意:作题时各时段的图形。
哈尔滨工程大学试卷

2 a21 a22
BZ0
2 X Z0
j(2 BX )
j
X Z0
T
S 21
BZ 0
2 X Z0
j(2
BX )
A
1
(BZ0
X Z0
)2
(2
BX
)2
S21 2
4
21
arctg (
2 BX
BZ 0
X Z0
)
1 S11 1 S11
1.一特性阻抗为 Z0 300 的传输线,传送信号至天线,工作频率为 300MHz ,由 于传输线与天线不匹配,测得电压驻波比 3 ,第一个电压波腹点至输入端的距离 为 dmax1 0.2m 。试求传输线的输入阻抗 Zin 及输入导纳Yin 。 2.求一特性阻抗 Z0 200 ,输入阻抗 Z sc j100 ,工作频率为 500MHz 的均匀无 耗终端短路线的最短几何长度 l ?
波长数为 0.074 ,故终端短路线的最短几何长度 l 0.074 4.44cm 。
九、矩形波导的尺寸为 a 28.5mm, b 12.6mm ,波导中传输电磁波的工作频率为 15GHz 。试问波导中可能传输的波形有哪些?(20 分)
解:
第3页
C 20mm ,由矩形波导中导行波截止波长的表达式,即 f
c
2
m
2
n 2
a b
可得:
c (TE10 ) 57mm
c (TE01) 25.2mm
哈尔滨工程大学信号与系统试卷与答案

图2
6、已知连续时间系统系统函数 ,求冲激响应 的初值 和终值 。
7、求下列两个序列的卷积,并画出卷积结果的波形
二、(15分)已知系统, , ;若激励信号为 , 时,求系统的完全响应,并指出其零输入响应、零状态响应、自由响应、强迫响应各分量。
三、(12分)已知某离散时间LTI系统的单位脉冲响应为 ,该系统对输入信号 的输出响应为 ,求输入信号 。已知系统是因果的。
1.求系统函数 ,并画出系统的零极点图;
2.求单位样值响应 ,并说明系统的稳定性与因果性;
3.如果系统的输入为 ,求系统的输出响应 ;
4.求系统的频率响应,粗略绘出系统的幅频特性,并标注出 时的幅值。
四、(15分)如图3所示电路, ,零极点分布如,已知 ,输入信号 的频谱如图6所示,完成下列各题:
图5
图6
(1)画出 的频谱 。
(2)画出 的频谱
(3)求系统的输出信号 ,并求其频谱 。
六、(15分)某离散时间LTI系统由下列微分方程描述,已知系统是因果的。且初始松弛。
一、(28分)计算下列各小题,每题4分。
1、试判断连续时间系统 ,( 为激励, 为响应)是否为:(1)线性系统;(2)时不变系统;(3)因果系统;(4)稳定系统。(注:要求写明判别过程)
2、计算下列信号值:
(1) (2)
3、求图1两个信号的卷积,并画出卷积结果的波形
图1
4、已知某连续时间信号 的频带宽度为 ,如果对 进行均匀抽样,奈奎斯特间隔 和奈奎斯特频率 各是多少?如果抽样频率 小于奈奎斯特频率 ,则抽样后频谱会出现什么现象?
哈工程5系信号与系统第三章总结

信号与系统第三章总结3.1.1 LTI 系统对复指数信号的响应1.连续时间LTI 系统对复指数信号 的响应对于连续时间LTI 系统,当输入()st x t e =时输出为()()st y t H s e =其中H(s)是一个复振幅因子,它是复变量s 的函数,它与系统单位冲激响应h(t)的关系为 ()()st H s h e d ττ+∞--∞=⎰2.离散时间LTI 系统对复指数序列n z 的响应对于离散时间LTI 系统,当输入[]n x n z =时,输出[]()n y n H z z =其中H(z)是一个复振幅因子,它是复变量z 的函数,它与系统单位脉冲响应h[n]的关系为 ()[]k k H z h n z +∞-=-∞=∑3.系统的特征函数及特征值一个信号,若系统对该信号的输出响应仅是一个常数(可能是复数)乘以输入,则称该信号为系统的特征函数,而幅度因子称为系统的特征值。
复指数信号 是连续时间LTI 系统的特征函数;对某一给定的s 值,常数H(s)就是与特征函数 有关的特征值。
复指数序列nz 是离散时间LTI 系统的特征函数;对于某一给定的z 值,常数H(z)就是与特征函数n z 有关的特征值。
3.1.2连续时间周期信号的傅里叶级数表示1.周期信号如果存在某个正值T 是的x(t)满足()()x t x t T =+,对全部t则x(t)为周期信号。
x(t)的基波周期就是满足上式的最小非零正值T ,而02T πω=称为基波频率。
正弦信号和复指数信号是两个基本的周期信号00()cos(),()j t x t t x t eωωϕ=+= 2.复指数型傅里叶级数成谐波关系的复指数信号集: st e st e st e 20()0,1,2T jk t jk t k t e e k πωϕ===±±其线性组合: 也是周期的,基波周期 的两项基波频率为 ——基波分量或一次谐波分量的两项基波频率为 ——N 次谐波分量 上式中{k a }称为x(t)的复傅里叶系数,或称为x(t)的频谱系数,可由下式求出: 2011()()jk t jk t k T T T T a x t e dt x t e dt πω--==⎰⎰令k=0,可得到 ,即0a 等于x(t)一个周期的平均值,是x(t)的直流分量。
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …,cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π是正交的。
3.3实周期信号()f t 在区间(,)22T T -的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-不正交可得 2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
哈尔滨工程大学信号与系统试卷与答案

第2页 共 2页Figure 1 Figure 22. (12 points)series coefficients:X [k ] = -j δ[k - 2] + j δ[k +2] + 2δ[k - 3] + 2δ[k + 3], ω0 = π(2) Determine the discrete-time Fourier series (DTFS) coefficients of the periodic signals depicted in Fig.3.Figure 3 Figure 46. (10 points)Determine and draw sketches of the Fourier series and Fourier transform representation of the square wave depicted in Fig.47. (8 points)(1) Compute the discrete-time Fourier transform (DTFT) of the signal depicted in Fig.5.Figure 5 Figure 6(2) Draw the Fourier transform of a impulse-train sampled version of the continuous-time signal having the Fourier transform depicted in Fig.6 for (a) T = 1/2(s) and (b) T = 2(s), where T is sampling period.8. (6 points)Shown in Fig.7 is the frequency response H (j ω) of a continuous-time filter. For each of the input signals x (t ) below, determine the filtered output signal y (t ).(1) x (t ) = cos(2πt +θ) (2) x (t ) = cos(4πt +θ)第3页 共4页 第4页 共 4页Figure 79. (8 points)Find the inverse Fourier transform of the following spectra: (1) X (j ω) = 2δ(ω - 4) (2) X (e j ω) = 2cos(2ω)(3) X (j ω) = ⎩⎨⎧><πωπωω,0,cos 2(4) X (e j ω) = ⎩⎨⎧<<-otherw ise02 4,/,πωπωj e , on -π < ω < π10. (16 points)Consider a continuous-time LTI system for which the input x (t ) and output y (t ) are related by the differential equationy" (t ) - y' (t ) - 6y (t ) = x' (t ) + x (t )(1) Determine the frequency response H (j ω) of the system.(2) Determine the system function H (s) of the system. Sketch the pole-zero plot of H (s )(3) Determine the system impulse response h (t ) for each of the following cases:(a) The system is stable; (b) The system is causal.(4) Let x (t ) = e -2t u (t ). Find the output y (t ) of the causal system.11. (6 points)Consider a message signal m (t ) with the spectrum shown in Fig.8. The message bandwith ωm = 2π×103 rad/s. The signal is applied to a product modulator, together with a carrier wave A c cos(ωc t ), producing the modulated signal s (t ). The modulated signal is next applied to a synchronous demodulator (shown in Fig.9).(1) Determine the spectrum of the demodulator output when (a) the carrier frequency ωc = 2.5π×103 rad/s and (b) the carrier frequency ωc = 1.5π×103 rad/s.(2) What is the lowest carrier frequency for which each component of the modulated signal s (t ) is uniquely determined by m (t ).Figure 8 Figure 912. (6 points)(1) Draw a sketch of the spectrum ofx (t ) = cos(50πt )sin(700πt )Label the frequencies and complex amplitudes of each component.(2) Determine the minimum sampling frequency that can be used to sample x (t ) without aliasing for any of the components.。
《信号和系统》试题(卷)与答案解析

i go2012年度教学质量综合评估测验卷《信号与系统》试题注:1、开课学院:信息工程学院学院。
命题组:电子信息教研组2、考试时间:120分钟,所有答案均写在答题纸上。
3、适用班级:信息工程学院通信工程专业及电子类专业。
4、在答题前,请在所发两张答题纸上认真填写所要求填写的个人信息。
卷面题型及分值:总分一二三四五六七八九十100202060一、选择题(每小题2分,共10小题。
每一小题仅有一个选项是正确的。
共计20分)1、下列说法不正确的是( )。
A 、一般周期信号为功率信号。
B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
C 、ε(t )是功率信号;D 、e t 为能量信号2、下列关于冲激函数性质的表达式不正确的是()。
A 、B 、)()0()()(t f t t f δδ=()t aat δδ1)(=C 、D 、)(d )(t tεττδ=⎰∞-)()-(t t δδ=3、,属于其极点的是()。
)2)(1()2(2)(-++=s s s s s H A 、1 B 、2 C 、0 D 、-24、If f 1(t ) ←→F 1(jω), f 2(t ) ←→F 2(jω) Then[ ]A 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) *b F 2(jω) ]B 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) - b F 2(jω) ]C 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) + b F 2(jω) ]D 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) /b F 2(jω) ]5、下列说法不正确的是()。
A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当k→∞时,响应均趋于0。
B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。
哈尔滨工程大学试卷答案

= 6.72× 8 m 10
d.c
WCA =0 QCA =ΔECA = v CV (TA-TC ) =1500 J WBC =PB (VC-VB ) =-400 J ΔEBC = v CV (TC-TB ) =-1000 J QBC =ΔEBC + WBC =-1400 J
PD iza r F
CV
v0
Tri om
a / N dv 1 ,
0 I3 2r r [ I 1 ln I 2 ln ] 2 r 2r I 0 3 [ I 1 ln 2 I 2 ln 2] 2 I 0 3 ( I 1 I 2 ) ln 2 2
al
r 0 I 3 r I1 I [ d x 2 d x] 2 0 r x 2r x 0
F I3 [
0
r
0 I1 0 I 2 ]d x 2(r x) 2(2r x)
3、 (本题 11 分)
I Il d r 0 I l ln b vt 解:(1) Φ(t ) B d S 0 l d r 0 2r 2 a v t r 2 a vt S
(2)
4、 (本题 10 分) 0→v 0: 2v 0
nI
2 4
7、0 8、2.6108 m/s
12、1.51 13、
Do
dV 1
二、计算题(共 61 分)
1、 (本题 10 分) 解:其中 3/4 圆环在 D 处的场 AB 段在 D 处的磁感强度
ww w
2
cuC
11、150V
10、不变;变长;波长变长某一波长
1 2 1 BC 段在 D 处的磁感强度 B3 [ 0 I /(4b)] ( 2 I B1 、 B2 、 B3 方向相同,可知 D 处总的 B 为 B 0 4 B2 [ 0 I /(4b)] (
《信号与系统》试题及答案,DOC

2012年度教学质量综合评估测验卷《信号与系统》试题注:1、开课学院:信息工程学院学院。
命题组:电子信息教研组2、考试时间:120分钟,所有答案均写在答题纸上。
3、适用班级:信息工程学院通信工程专业及电子类专业。
4、在答题前,请在所发两张答题纸上认真填写所要求填写的个人3、)2)(1()(-+=s s s H ,属于其极点的是()。
A 、1B 、2C 、0D 、-2 4、If f 1(t )←→F 1(j ω),f 2(t )←→F 2(j ω)Then[] A 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)*b F 2(j ω)] B 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)-b F 2(j ω)]C、[a f1(t)+b f2(t)]←→[a F1(jω)+b F2(jω)]D、[a f1(t)+b f2(t)]←→[a F1(jω)/b F2(jω)]5、下列说法不正确的是()。
A、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当k→∞时,响应均趋于0。
67A、f(t)=cos(2t)+cos(4t)B、f(t)=sin(2t)+sin(4t)C、f(t)=sin2(4t)D、f(t)=cos2(4t)+sin(2t)8、已知某LTI连续系统当激励为)(t f时,系统的冲击响应为)(t h,零状态响应为)(t y zs ,零输入响应为)(t y zi ,全响应为)(1t y 。
若初始状态不变时,而激励为)(2t f 时,系统的全响应)(3t y 为()。
A 、)(2)(t y t y zs zi +B 、()2()zi y t f t +C 、)(4t y zsD 、)(4t y zi 9、设有一个离散反馈系统,其系统函数为:)1(2)(k z zz H --=,问若要使该系统稳定,常数应k 该满足的条件是()。
A 17、已知)21(2323)(22<<+-+=z z z z z X ,则=)(n x 。
哈工大信号与系统期末试题2005

(B)
H
(z)
=
1 + 4z −1 z −1 + 3
;
(C) y(n) + 4 y(n −1) = x(n) − 3x(n −1) ;
(D) H (z) = 3z +1 。
z+4
∑
E-1
x(n)
-4
3 ∑ y(n)
三、判断题(每题 1 分,共 10 分)
1. 线性时不变系统一定是因果系统。 2. 强迫响应是零状态响应的一部分。 3. sin(ω0t)u(t) 的傅立叶变换为 jπ[δ (ω + ω0 ) −δ (ω − ω0 )];
信号?其中 n 为整数。
(A) 能量,功率,周期,数字; (C) 能量,功率,周期,非周期,
(B) 功率,能量,抽样,非周期; (D) 功率,能量,数字,非周期。
2. 某连续时间系统的输入 r(t) 和输出 e(t) 满足 r(t) = e(t + 2) ,则该系统为
。
(A) 因果、时变、线性、稳定; (C) 非因果、时变、线性、稳定;
率范围为 fL ≤ f g ≤ fH ,则 fL 和 fH 分别为
。
(A) 998kHz,1002kHz;
(B) 997kHz,1003kHz;
(C) 1000kHz,1002kHz;
(D) 996kHz,1002kHz。
5. 如下图所示的方框图表示的系统,其系统函数或差分方程正确的是
.
(A) y(n) − 4 y(n −1) = 3x(n) ;
8. 稳定系统的自由响应一定是瞬态响应。
9. 在正弦信号激励下稳定系统的零状态响应都是稳态响应。
∞
10. 离散系统为因果稳定系统的充要条件是 ∑ h(n) < ∞ 。 n=0
大学考试试卷《信号与系统》及参考答案

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。
信号与系统考试题及答案

信号与系统考试题及答案第一题:问题描述:什么是信号与系统?答案:信号与系统是电子工程和通信工程中重要的基础学科。
信号是信息的传递载体,可以是电流、电压、声音、图像等形式。
系统是对信号进行处理、传输和控制的装置或网络。
信号与系统的研究内容包括信号的产生、变换、传输、处理和控制等。
第二题:问题描述:信号的分类有哪些?答案:信号可以根据多种特征进行分类。
按照时间域和频率域可以将信号分为连续时间信号和离散时间信号;按照信号的能量和功率可以分为能量信号和功率信号;按照信号的周期性可以分为周期信号和非周期信号;按照信号的波形可以分为正弦信号、方波信号、脉冲信号等。
第三题:问题描述:什么是线性时不变系统?答案:线性时不变系统是信号与系统领域中重要的概念。
线性表示系统满足叠加性原理,即输入信号的线性组合经过系统后,输出信号也是输入信号的线性组合。
时不变表示系统的性质不随时间变化而改变。
线性时不变系统具有许多重要的性质和特点,可以通过线性时不变系统对信号进行处理和分析。
第四题:问题描述:系统的冲激响应有什么作用?答案:系统的冲激响应是描述系统特性的重要参数。
当输入信号为单位冲激函数时,系统的输出即为系统的冲激响应。
通过分析冲激响应可以得到系统的频率响应、幅频特性、相频特性等,从而对系统的性能进行评估和优化。
冲激响应还可以用于系统的卷积运算和信号的滤波等应用。
第五题:问题描述:如何对信号进行采样?答案:信号采样是将连续时间信号转换为离散时间信号的过程。
常用的采样方法包括周期采样和非周期采样。
周期采样是将连续时间信号按照一定的时间间隔进行等间隔采样;非周期采样是在信号上选取一系列采样点,采样点之间的时间间隔可以不相等。
采样频率和采样定理是采样过程中需要考虑的重要因素。
第六题:问题描述:什么是离散傅里叶变换(DFT)?答案:离散傅里叶变换是对离散时间信号进行频域分析的重要工具。
通过计算离散傅里叶变换可以将离散时间信号转换为复数序列,该复数序列包含了信号的频率成分和相位信息。
通信信号分析与处理智慧树知到答案章节测试2023年哈尔滨工业大学

第一章测试1.概率是衡量一个事件发生可能性大小的数量指标,其值介于-1和1之间。
()A:对B:错答案:B2.随机试验E的可能结果称为样本,不可再分的事件称为基本事件,所有基本事件的集合称为样本空间。
()A:错B:对答案:B3.样本空间的完备性是指样本空间必须包含随机试验的所有可能的基本结果。
()A:错B:对答案:B4.对随机试验而言,样本空间给出它的所有可能的试验结果,事件描述了所关心的具体情况,而概率给出每一事件发生的概率,则(样本空间,事件,概率)称为概率空间。
()A:对B:错答案:B5.如果我们把某事件看成“结果”,把产生这个事件的条件看成是导致这个结果的可能的“原因”,则可以形象地把全概率公式看为“由结果推原因”;而贝叶斯公式则恰好相反,其作用在于“由原因推结果”。
()A:对B:错答案:B6.()表示事件发生的频繁程度,而()表示事件发生的可能性,如果试验次数足够多,那么()具有稳定性,且趋近于事件()。
上述内容的空格中依次填入()A:概率,频率,概率,频率B:概率,概率,频率,频率C:频率,频率,概率,概率D:频率,概率,频率,概率答案:D7.相应于概率对应的概率空间,条件概率对应()。
A:统计概率空间B:概率空间C:频率空间D:条件概率空间答案:D8.对于随机变量X和Y,存在()A:E[ E[X] ]=0B:E[XY]=E[X]E[Y]C:对于任意常数c和b,有E[cX+bY]=cE[X]+bE[Y]D:对于任意常数C, 有E[C]=0答案:C9.有许多随机变量,它们是由()的随机变量的综合影响所形成的,而其中每个因素作用都很小,这种随机变量往往服从或近似服从正态分布,或者说它的极限分布是正态分布。
A:大量的互不相关B:有限的互不相关C:有限的互相独立D:大量的互相独立答案:D10.下列说法错误的是()A:随机变量的数学期望是常数B:随机变量序列收敛性由弱到强:依分布收敛、依概率收敛、依概率1收敛、处处收敛C:两个随机变量的相关系数不能是负数。
信号与系统本科试题及答案

信号与系统本科试题及答案一、选择题(每题2分,共10分)1. 在信号与系统的分析中,下列哪一项不是连续时间信号的基本属性?A. 幅度B. 频率C. 相位D. 时间答案:D2. 一个线性时不变系统的最基本特点是:A. 输出唯一确定B. 系统参数随时间变化C. 对输入信号的响应是确定的D. 对任何复杂信号都能准确响应答案:C3. 下列哪个操作不会改变信号的频率内容?A. 时间平移B. 频率调制C. 振幅调制D. 时间缩放答案:A4. 对于一个理想的低通滤波器,其传递函数在频域中表现为:A. 低频信号通过,高频信号被阻挡B. 高频信号通过,低频信号被阻挡C. 所有信号都被阻挡D. 所有信号都通过答案:A5. 在信号与系统的分析中,卷积运算主要用于描述:A. 信号的能量分布B. 信号的频率分布C. 系统的冲激响应与输入信号之间的关系D. 信号的时域采样答案:C二、填空题(每题2分,共10分)6. 一个连续时间信号若满足 _________ 条件,则该信号是能量信号。
答案:信号的平方可积7. 采样定理指出,如果一个信号的频率内容完全位于低频带,那么该信号可以被其采样点的值唯一确定,采样频率应大于信号最高频率的_________ 倍。
答案:28. 拉普拉斯变换的一个重要性质是 _________ ,即线性时不变系统的输出是输入信号经过变换后乘以系统函数再进行逆变换的结果。
答案:线性9. 在离散时间信号处理中,离散傅里叶变换(DFT)可以用来计算信号的 _________ 表示。
答案:频谱10. 一个系统是因果系统的充分必要条件是其冲激响应 _________ 。
答案:在t=0之前为零三、简答题(每题10分,共20分)11. 简述信号的分类及其特点。
答案:信号可以分为连续时间信号和离散时间信号。
连续时间信号在整个时间轴上都有定义,如正弦波、指数信号等。
离散时间信号则在离散的时间点上有定义,如单位脉冲信号。
此外,信号还可以根据其是否可积、是否有界等属性进一步分类。
