高一数学正弦定理1

合集下载

正弦定理1

ABC中已知a=2cm a=2cm，例3、在△ABC中，已知a=2cm， c= 6 cm，A=45°，解三角形. cm，A=45° 解三角形.
题型二已知两边及其中一边的对角，求其它元素. 练习3.在△ABC中，已知在中已知a=2cm，， c= 2 3cm，A=30°，解三角形， ° 解三角形.
例4：若a=2,b=4,A=120 °，解三角形题型二已知两边及其中一边的对角，求其它元素. 练习4：a=2,b=6,A=30 °,解三角形
已知边a,b和角Ａ，求其他边和角．已知边和角Ａ，求其他边和角．和角Ａ，求其他边和角
Ａ为锐角
Ｃ b Ａ a<bsinA 无解Ｃ b Ａ a>b 一解 a Ａ b Ｃ a Ｂ b Ｃ a b Ｃ a Ｂ
ο
°
sin A
C
sin B
sinC
b
A
a c
B
注：R为⊿ABC 的外接圆半径
知识探究在锐角三角形中是否成立？
a b c = = = 2R sin A sin B sinC
C b A a
2R 2R
c
B
知识探究
在钝角三角形中是否成立？
a b c = = = 2R sin A sin B sinC
D
C a b A c B
ＡＢ２Ｂ１Ａ a=bsinA bsinA<a<b a≥b 两解一解一解Ｃ a b ＡＢ a≤b 无解
Ａ为直角或钝角
a
练习：练习：
1、判断满足下列的三角形的个数: 判断满足下列的三角形的个数: (1)b=11, a=20, B=30 ° 两解 (2)c=54, b=39, C=120 °一解 (3)b=26, c=15, C=30 ° 两解 (4)a=2,b=6,A=30 ° 无解

高一数学公式大全

高一数学公式大全对于高中生来说，数学是很容易拉开分数的学科，学好数学科目至关重要，下面是给大家带来的高一数学公式，希望能帮助到大家!高一数学公式1正弦定理a/sina=b/sinb=c/sinc=2r注：其中r表示三角形的外接圆半径余弦定理b2=a2+c2-2accosb注：角b是边a和边c的夹角圆的标准方程(x-a)2+(y-b)2=r2注：(a，b)是圆心坐标圆的一般方程x2+y2+dx+ey+f=0注：d2+e2-4f0抛物线标准方程y2=2pxy2=-2p_2=2pyx2=-2py直棱柱侧面积s=c_h斜棱柱侧面积s=c_h正棱锥侧面积s=1/2c_h正棱台侧面积s=1/2(c+c)h圆台侧面积s=1/2(c+c)l=pi(r+r)l球的表面积s=4pi_r2圆柱侧面积s=c_h=2pi_h圆锥侧面积s=1/2_c_l=pi_r_l弧长公式l=a_ra是圆心角的弧度数r0扇形面积公式s=1/2_l_r锥体体积公式v=1/3_s_h圆锥体体积公式v=1/3_pi_r2h斜棱柱体积v=sl注：其中，s是直截面面积，l是侧棱长柱体体积公式v=s_h圆柱体v=pi_r2h高一数学公式2【和差化积】2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB【某些数列前n项和】1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41_2+2_3+3_4+4_5+5_6+6_7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注：角B是边a和边c的夹角弧长公式l=a_r a是圆心角的弧度数r 0 扇形面积公式s=1/2_l_r乘法与因式分a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b=-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1_X2=c/a 注：韦达定理高一数学公式3圆的公式1、圆体积=4/3(pi)(r^3)2、面积=(pi)(r^2)3、周长=2(pi)r4、圆的标准方程(x-a)2+(y-b)2=r2【(a,b)是圆心坐标】5、圆的一般方程x2+y2+dx+ey+f=0【d2+e2-4f0】椭圆公式1、椭圆周长公式：l=2πb+4(a-b)2、椭圆周长定理：椭圆的周长等于该椭圆短半轴，长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差.3、椭圆面积公式：s=πab4、椭圆面积定理：椭圆的面积等于圆周率(π)乘该椭圆长半轴长(a)与短半轴长(b)的乘积。

余弦定理与正弦定理-用余弦定理、正弦定理解三角形(第三课时)高一数学(北师大版2019必修第二册)

变式 1．(2011 年上海)在相距 2 千米的 A，B 两点处测量目标 C，
若∠CAB＝75°，∠CBA＝60°，求 A，C 两点之间的距离．
解：由条件知：C＝180°－75°－60°＝45°，由正弦定理得sAinCB＝sAinBC，即siAn6C0°＝sin245°. 解得 AC＝ 6.
例2：在△ABC 中，若 2cosBsinA＝sin ，试判断CABC 的形状．
2．余弦定理
a2＝ b2＋c2－2bccos A ，b2＝ a2＋c2－2accos B ，c2
＝ a2＋b2－2abcos C ．余弦定理可以变形：cos A
b2＋c2－a2
a2＋c2－b2
a2＋b2－c2
＝ 2bc ，cos B＝ 2ac ，cos C＝ 2ab .
3．三角形中常用的面积公式
(1)S＝12ah(h 表示边 a 上的高)；
2
2
整理,得4cos2 C 4cos C 1 0,解得cos C 1 , 2
0 C 180,C 60.
(2)由余弦定理得c2 a2 b2 2abcos C,
即7=a2+b2-ab,∴7=(a+b)2-3ab，由条件a+b=5,得7=25-3ab,ab=6,
SABC
1 2
absin
b=2，a=x，如 c 有两组解，则 x 的取值范围是
．
解：当 asinB＜ b＜ a 时，三角形 ABC 有两组解 . 又 b=2， B=60°， a=x，如果三角形 ABC 有两组解，
那么 x 应满足 xsin60°＜ 2＜ x，即 2＜ x＜ 4
3
,
10

正弦定理1

a b c ＝＝＝ sinA sinB sinC
？
A O B` b C
A b O C
A
O
B
b
C
B
B` B
b b c =2Ra sinB ＝＝＝2R. sinA sinB sinC
例 1：在ABC中，已知c＝10，A＝45°， C＝30°，求b. b c 解： ∵ ＝， sinB sinC C b
（1） b＝20，A＝60°，a＝20√3 ;
（2） b＝20，A＝60°，a＝10√3 ; （3） b＝20，A＝60°，a＝15. C
A
b＝20√3 1 b sinA sinB＝＝ 2 ， a B＝30°或150°， ∵ 150°＋60°> 180°， ∴ B＝150°应舍去. C 20 20√3 B
有1解、2解、无解.
例 3：已知向量a与a＋b夹角为60°，
且 a ＝8，b ＝7，求a与b的夹角及a· b. 解：在OAC中， C1 B1 a b C2 ∵ ＝ B2 sin60° sin∠OCA 60° a 8 sin60° O ∴ sin∠OCA＝ ≈0.9897, 7 ∴ ∠OCA＝81.8°或98.2°, ∠AOB＝141.8°或158.2°, 过O作OB∥AC， ∴ ∠OAC＝38.2°或21.8°, ∴ a· b＝ a b cos∠AOB＝－44.0或－52.
A
练习
ABC中，（1）已知c＝√3，A＝45°，B＝75°，
2 ，则a＝√ ____ （2）已知c＝2，A＝120°，a＝2√3，
则B＝____ ， 30°
（3）已知c＝2，A＝45°，a＝ 2√6 ，则 3 B＝_____________. 75°或15°

人教A版高中数学必修五课件高一《正弦定理》(第一课时)

sin A sin B
已知两边和其中一边的对角,求其他边和角
C
得 sin B bsin A 16
3 sin 30
3
a
16
2
16 3 16
16
A 300
所以Ｂ＝60°,或Ｂ＝120°
B
B
当Ｂ＝60°时 C=90° c 32.
当Ｂ＝120°时 C=30°
c a sin C 16 . sin A
变式: a=30, b=26, A=30°求角B，C和边c
解：由正弦定理 a b
sin A sin B
C
26
30
得 sin B b sin A 26sin 30 13 A 300
B
a
30 30
所以Ｂ＝25.70, 或Ｂ＝1800－25.70=154.30
由于154.30 +300>1800 故B只有一解（如图） C=124.30, c a sin C 49.57
c
b
B
a
C
探索１、在Ｒt△ＡＢＣ中，Ｃ＝９０°，
那么边角之间有哪些关系？
sinA= a ,sinB= b ,
c
c
sinC=1= c
c
a
b
c
sin A sin B sin C
A
b
c
Ca
B
探索２、在Ｒt △ＡＢＣ中，我们得到
abc sin A sin B sin C
，对于任意三角形，这个
结论还成立吗？
巩固练习：下列哪些条件可以使用正弦定
理解三角形？
８
１０
２０°
９５
(1)
７

高一数学“四步教学法”教案：1.1 正弦定理1

变式训练：在 ABC 中， a 26, b 26 3, A 30 , 求角 B,C,边 c 。
小结：利用三角形内角和 180 及三角函数值最大值是 1 判断解的个数。题型二：判断三角形的形状例 2 在 ABC 中， b a cos C ，判断三角形 ABC 的形状。

变式训练：在 ABC 中，已知断三角形 ABC 的形状。
环节二
教
合作释疑
环节三
点拨拓展
（备注：合作释疑和点拨拓展可以按照顺序先后进行，也可以根据教学设计交叉进行设计）
学
过程设计
合作释疑：正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即
二次备课
过
a
程
sin A

b
sin B

c
sin C
及
[理解定理] （1）正弦定理说明同一三角形中，边与其对角的正弦成正比，且比例系数为同一正数，即存在正数 k 使 a k sin A ， b k sin B ， c k sinC ；（ 2 ）
b , S ABC 。
变式训练：在 ABC 中，已知 b 4, c 5, A 135 ，则
ABC 的面积？
小结：要抓住三角形面积公式的特点，恰当选择三个当中的某一个公式。
环节四 1、根据下列条件解三角形
当堂检测
二次备课
教
（1） b 40, c 20, C 45 ：（2） b 2 7 , a 14, B 60 (3) b 6, c 2, C 45
a
sin A

b
sin B

c

高一数学重点知识点系列-正弦定理与余弦定理

正弦定理与余弦定理一、三角形中的各种关系设ABC ∆的三边分别是,,a b c ，与之对应的三个角分别是,,A B C .则有如下关系：1、三内角关系三角形中三内角之和为π（三角形内角和定理），即A B C π++=，；2、边与边的关系三角形中任意两条边的和都大于第三边，任意两条边的差都小于第三边,即,,a b c a c b b c a +>+>+>；,,a b c a c b b c a -<-<-<；3、边与角的关系（1）正弦定理三角形中任意一条边与它所对应的角的正弦之比都相等，即2sin sin sin a b c R A B C===（这里，R 为ABC ∆外接圆的半径）. 注1：（I ）正弦定理的证明：在ABC ∆中，设,,BC a AC b AB c ===, 证明：2sin sin sin a b c R A B C===（这里，R 为ABC ∆外接圆的半径）证：法一（平面几何法）：在ABC ∆中，作CH AB ⊥，垂足为H则在Rt AHC ∆中，sin CH A AC =；在Rt BHC ∆中，sin CH B BC =sin ,sin CH b A CH a B ∴== sin sin b A a B ⇒= 即sin sin a b A B = 同理可证：sin sin b c B C= 于是有sin sin sin a b c A B C== 作ABC ∆的外接圆⊙O ，设其半径为R连接BO 并延长，则可得到⊙O 的直径BD ，连接DA因为在圆中，直径所对的圆周角是直角所以90o DAB ∠=于是在Rt DAB ∆中，sin 2AB c D BD R== 又因为在同一圆中，同弧所对的圆周角相等所以D C ∠=∠2sin sin 2c c c R c C DR∴=== 故2sin sin sin a b c R A B C ===（这里，R 为ABC ∆外接圆的半径）法二（平面向量法）（Ⅱ）正弦定理的意义：正弦定理指出了任意三角形中三边与其对应角的正弦值之间的一个关系式，也就是任意三角形的边角关系.（Ⅲ）正弦定理适用的范围：（i ）已知三角形的两角及一边，解三角形；（ii ）已知三角形的两边及其中一边所对应的角，解三角形；（iii ）运用::sin :sin :sin a b c A B C =解决角之间的转换关系. 注2：正弦定理的一些变式：（i ）::sin :sin :sin a b c A B C =；（ii ）sin ,sin ,sin 222a b c A B C R R R===；（iii ）2sin ,2sin ,2sin a R A b R B c R C ===.注3：已知三角形是确定的，则在运用正弦定理解该三角形时，其解是唯一的；已知三角形的两条边和其中一条边的对角，由于该三角形具有不稳定性，所以其解是不确定的，此时可结合平面几何作图的方法、“大边对大角，大角对大边”定理及三角形内角和定理解决问题.例1. ABC ∆中，,a b 分别为角,A B 的对边，若60,75,8o o B C a ===，则b =＿.例2. ABC ∆中，角,,A B C 的对边分别为,,a b c ，,13A a b π===，则c =＿.例3.在ABC ∆中，60,1o b B c ===，求a 和,.A C例4. 在ABC ∆中，已知2,2,2B A BC AB ∠=∠==+则A ∠=＿. 例5.已知ABC ∆中，角,A B 所对的边分别是,a b ，若cos cos a B b A =,则ABC ∆一定是（）A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形（2）余弦定理三角形中任意一条边的平方等于其他两条边平方的和减去这两条边与它们夹角的余弦的乘积的2倍，即2222cos a b c bc A =+-，2222cos b c a ca B =+-，2222cos c a b ab C =+-. 注1：（I ）余弦定理的证明：法一（平面几何法）在ABC ∆中，作CH AB ⊥，垂足为H则在Rt AHC ∆中，sin CH CH A AC b ==；cos AH AH A AC b== sin ,cos CH b A AH b A ∴== cos BH AB AH c b A ⇒=-=- 在Rt CHB ∆中，由勾股定理有222BC CH BH =+于是有22222222222222(sin )(cos )sin 2cos cos (sin cos )2cos 2cos a b A c b A b A c bc A b Ab A Ac bc A b c bc A=+-=+-+=++-=+-同理可证：2222cos b c a ca B =+-，2222cos c a b ab C =+-.法二（平面向量法）（Ⅱ）余弦定理的意义：余弦定理是揭示三角形边角关系的重要定理，直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当结合其它知识，则使用起来更为方便、灵活。

正弦定理、余弦定理精讲精析(解析版)

正弦定理、余弦定理精讲精析点点突破热门考点01 正弦定理正弦定理：a sin A ＝b sin B ＝c sin C＝2R ，其中R 是三角形外接圆的半径．由正弦定理可以变形为： a ∶b ∶c ＝sin A ∶sin B ∶sin C ；a ＝2R sin_A ，b ＝2R sin_B ，c ＝2R sin_C ；sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R 等形式，以解决不同的三角形问题．面积公式S ＝12ab sin C ＝12bc sin A ＝12ac sin B【典例1】（2019·全国高考真题（文））ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知b sin A +a cos B =0，则B =___________. 【答案】34π. 【解析】由正弦定理，得sin sin sin cos 0B A A B +=．(0,),(0,)A B ∈π∈π，sin 0,A ∴≠得sin cos 0B B +=，即tan 1B =-，3.4B π∴=故选D ．【典例2】（2020·江苏省高考真题）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知3,2,45a c B ===︒．（1）求sin C 的值；（2）在边BC 上取一点D ，使得4cos 5ADC ∠=-，求tan DAC ∠的值．【答案】（1）5sin C =；（2）2tan 11DAC ∠=.【解析】（1）由余弦定理得22222cos 9223252b ac ac B =+-=+-⨯⨯⨯=，所以5b =. 由正弦定理得sin 5sin sin sin 5c b c B C C B b =⇒==. （2）由于4cos 5ADC ∠=-，,2ADC ππ⎛⎫∠∈ ⎪⎝⎭，所以23sin 1cos 5ADC ADC ∠=-∠=.由于,2ADC ππ⎛⎫∠∈⎪⎝⎭，所以0,2C π⎛⎫∈ ⎪⎝⎭，所以225cos 1sin C C =-=. 所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅325452555⎛⎫=⨯+-⨯= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭，所以2115cos 1sin DAC DAC ∠=-∠=. 所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.【总结提升】已知两角一边可求第三角，解这样的三角形只需直接用正弦定理代入求解即可．已知两边和一边对角，解三角形时，利用正弦定理求另一边的对角时要注意讨论该角，这是解题的难点，应引起注意．已知两边和其中一边的对角，解三角形时，注意解的情况．如已知a ，b ，A ，则A 为锐角 A 为钝角或直角图形关系式 a ＜b sin Aa ＝b sin Ab sin A ＜a＜ba ≥ba ＞ba ≤b解的个数无解一解两解一解一解无解热门考点02 余弦定理余弦定理：2222cos a b c ab C +-= ， 2222cos b c a ac A +-= ， 2222cos c a b ac B +-=.变形公式cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，os C ＝a 2＋b 2－c 22ab【典例3】（2020·全国高考真题（理））如图，在三棱锥P –ABC 的平面展开图中，AC =1，3AB AD ==，AB ⊥AC ，AB ⊥AD ，∠CAE =30°，则cos ∠FCB =______________.【答案】14- 【解析】AB AC ⊥，3AB =1AC =，由勾股定理得2BC ==，同理得BD =BF BD ∴==在ACE △中，1AC =，AE AD ==，30CAE ∠=，由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=， 1CF CE ∴==，在BCF 中，2BC =，BF =1CF =，由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯.故答案为：14-. 【典例4】（2019·北京高考真题（文））在△ABC 中，a =3，–2b c =，cos B =12-．（Ⅰ）求b ，c 的值；（Ⅱ）求sin （B +C ）的值．【答案】（Ⅰ）7,5b c ==；. 【解析】（Ⅰ）由余弦定理可得2221cos 22a cb B ac +-==-，因为3a =，所以22390c b c -++=；因为2b c -=，所以解得75b c =⎧⎨=⎩.（Ⅱ）由（Ⅰ）知3,7,5a b c ===，所以22213cos 214b c a A bc +-==；因为A 为ABC ∆的内角，所以sin A ==.因为sin()sin()sin B C A A +=π-==. 【总结提升】应用余弦定理解答两类问题：热门考点03正弦定理与余弦定理的综合运用【典例5】（2020·北京高考真题）在中，，再从条件①、条件②这两个条件中选择一个作为己知，求：（Ⅰ）a的值：（Ⅱ）和的面积．条件①：；条件②：．注：如果选择条件①和条件②分别解答，按第一个解答计分．【答案】选择条件①（Ⅰ）8（Ⅱ）, ；选择条件②（Ⅰ）6（Ⅱ）, .【解析】选择条件①（Ⅰ）（Ⅱ）由正弦定理得：选择条件②（Ⅰ）由正弦定理得：（Ⅱ）【典例6】（2019·全国高考真题（理））ABC的内角A，B，C的对边分别为a，b，c，设22-=-．(sin sin)sin sin sinB C A B C（1）求A ；（22b c +=，求sin C ．【答案】（1）3A π=；（2）sin 4C =. 【解析】（1）()2222sin sin sin 2sin sin sin sin sin sin B C B B C C A B C -=-+=- 即：222sin sin sin sin sin B C A B C +-= 由正弦定理可得：222b c a bc +-=2221cos 22b c a A bc +-∴==()0,πA ∈3Aπ（2）22a b c +=sin 2sin A B C +=又()sin sin sin cos cos sin B A C A C A C =+=+，3A π=1sin 2sin 2C C C +=整理可得：3sin C C =22sin cos 1C C += (()223sin 31sin C C ∴=-解得：sin C =因为sin 2sin 2sin 0B C A C ==>所以sin C >，故sin C =（2）法二：22a b c +=sin 2sin A B C +=又()sin sin sin cos cos sin B A C A C A C =+=+，3A π=1sin 2sin 222C C C ++=整理可得：3sin 63cos C C -=，即3sin 3cos 23sin 66C C C π⎛⎫-=-= ⎪⎝⎭2sin 62C π⎛⎫∴-=⎪⎝⎭ 由2(0,),(,)3662C C ππππ∈-∈-，所以,6446C C ππππ-==+ 62sin sin()46C ππ+=+=. 【总结提升】应熟练掌握正、余弦定理及其变形．解三角形时，有时可用正弦定理，也可用余弦定理，应注意用哪一个定理更方便、简捷就用哪一个定理．热门考点04 应用正弦定理、余弦定理判定三角形形状【典例7】在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，若c －a cos B ＝(2a －b )cos A ，则△ABC 的形状为( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰或直角三角形【答案】D 【解析】因为c －a cos B ＝(2a －b )cos A ，C ＝π－(A ＋B )，所以由正弦定理得sin C －sin A cos B ＝2sin A cos A －sin B ·cos A ，所以sin A cos B ＋cos A sin B －sin A cos B ＝2sin A cos A －sin B cos A ，所以cos A (sin B －sin A )＝0，所以cos A ＝0或sin B ＝sin A ，所以A ＝2π或B ＝A 或B ＝π－A (舍去)，所以△ABC 为等腰或直角三角形．【规律方法】1.判定三角形形状的途径：(1)化边为角，通过三角变换找出角之间的关系；(2)化角为边，通过代数变形找出边之间的关系，正(余)弦定理是转化的桥梁．2．无论使用哪种方法，都不要随意约掉公因式，要移项提取公因式，否则会有漏掉一种形状的可能．注意挖掘隐含条件，重视角的范对三角函数值的限制．热门考点05 与三角形面积有关的问题【典例8】（2018·全国高考真题（文））△ABC 的内角A B C ，，的对边分别为a b c ，，，已知sin sin 4sin sin b C c B a B C +=，2228b c a +-=，则△ABC 的面积为________．. 【解析】因为sin sin 4sin sin b C c B a B C +=，结合正弦定理可得sin sin sin sin 4sin sin sin B C C B A B C +=，可得1sin 2A =，因为2228b c a +-=，结合余弦定理2222a b c bccosA =+-，可得2cos 8bc A =，所以A 为锐角，且cos A =，从而求得bc =，所以ABC ∆的面积为111sin 222S bc A ===.【典例9】（2017·上海高考真题）已知函数()221cos sin 2f x x x =-+，()0,x π∈. （1）求()f x 的单调递增区间；（2）设ABC ∆为锐角三角形，角A 所对边a =，角B 所对边5b =，若()0f A =，求ABC ∆的面积.【答案】（1）[,)2ππ;（2 【解析】（1）函数2211()cos sin cos 2,(0,)22f x x x x x π=-+=+∈ 由222,k x k k Z πππ-≤≤∈，解得,2k x k k Z πππ-≤≤∈1k =时，12x ππ≤≤，可得()f x 的增区间为[,)2ππ（2）设△ABC 为锐角三角形，角A 所对边a =B 所对边b=5，若()0f A =，即有1cos 202A += 解得223A π=，即3A π= 由余弦定理可得a 2=b 2+c 2﹣2bc cos A ，化为c 2﹣5c +6=0，解得c =2或3，若c =2，则cos 0B =<即有B 为钝角，c =2不成立，则c =3，△ABC 的面积为11sin 532224S bc A ==⨯⨯⨯=【总结提升】1.求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值)，结合题意求解这个角的两边或该角的两边之积，代入公式求面积．(2)若已知三角形的三边，可先求其一个角的余弦值，再求其正弦值，代入公式求面积，总之，结合图形恰当选择面积公式是解题的关键． 2．已知三角形面积求边、角的方法(1)若求角，就寻求夹这个角的两边的关系，利用面积公式列方程求解． (2)若求边，就寻求与该边(或两边)有关联的角，利用面积公式列方程求解．提醒：正弦定理、余弦定理与三角函数性质的综合应用中，要注意三角函数公式的工具性作用．热门考点06 与三角形周长有关的问题【典例10】（2017课标1，理17）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长. 【答案】【解析】【典例11】（2019·江西洪都中学高二月考（理））在ABC △中，A ，B ，C 所对的边分别为a ，b ，c 且cos 4c A =，sin 5a C =．（1）求边长c ；（2）若ABC △的面积20S =．求ABC △的周长．【答案】（141（2）8241+【解析】（1）由正弦定理可得：2sin sin sin a b cR A B C===，可得sin sin a C c A =，因为sin 5a C =，可得sin 5c A =，所以5sin A c=，又由cos 4c A =，可得4cos A c=，又因为22222516sin cos 1A A c c+=+=，解得c = （2）由题意，ABC ∆的面积1sin 202S ab C ==，sin 5a C =，解得8b =，由余弦定理，可得2222cos 64412841a b c bc A =+-=+-=，解得a =，所以ABC ∆的周长88L a b c =++=+=+【总结提升】应用正弦定理、余弦定理，建立边长的方程，是解答此类问题的基本方法，解答过程中，要注意整体代换思想的应用，如果遇到确定最值问题，往往要结合均值定理求解.热门考点07 三角形中的最值与范围问题【典例12】（2018·江苏高考真题）在ABC △中，角,,A B C 所对的边分别为,,a b c ，120ABC ∠=︒，ABC ∠的平分线交AC 于点D ，且1BD =，则4a c +的最小值为________．【答案】9 【解析】由题意可知，ABC ABD BCD S S S =+△△△,由角平分线性质和三角形面积公式得111sin1201sin 601sin 60222ac a c ︒=⨯⨯︒+⨯⨯︒，化简得11,1ac a c a c=++=，因此1144(4)()559,c a a c a c a c a c +=++=++≥+=当且仅当23c a ==时取等号，则4a c +的最小值为9.【典例13】（2020·全国高考真题（理））ABC 中，sin 2A －sin 2B －sin 2C =sin B sin C ．（1）求A ；（2）若BC =3，求ABC 周长的最大值.【答案】（1）23π；（2）3+【解析】（1）由正弦定理可得：222BC AC AB AC AB --=⋅，2221cos 22AC AB BC A AC AB +-∴==-⋅，()0,A π∈，23A π∴=. （2）由余弦定理得：222222cos 9BC AC AB AC AB A AC AB AC AB =+-⋅=++⋅=，即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭（当且仅当AC AB =时取等号）， ()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭，解得：AC AB +≤（当且仅当AC AB =时取等号），ABC ∴周长3L AC AB BC =++≤+，ABC ∴周长的最大值为3+【典例14】（2019·全国高考真题（文））ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知sinsin 2A Ca b A +=．（1）求B ；（2）若ABC ∆为锐角三角形，且1c =，求ABC ∆面积的取值范围．【答案】(1) 3B π=;(2). 【解析】 (1)根据题意sinsin 2A C a b A +=，由正弦定理得sin sin sin sin 2A CA B A +=，因为0A π<<，故sin 0A >，消去sin A 得sin sin 2A CB +=. 0<B <π，02AC π+<<因为故2A C B +=或者2A CB π++=，而根据题意A BC π++=，故2A C B π++=不成立，所以2A CB +=，又因为A BC π++=，代入得3B =π，所以3B π=. (2)因为ABC 是锐角三角形，由（1）知3B π=，A B C π++=得到23A C π+=，故022032C C πππ⎧<<⎪⎪⎨⎪<-<⎪⎩，解得62C ππ<<.又应用正弦定理sin sin a cA C=，1c =，由三角形面积公式有：222sin()111sin 3sin sin sin 222sin 4sin ABCC a A Sac B c B c B c C Cπ-=⋅=⋅=⋅=22sin cos cos sin 2123133(sin cos )sin 3tan 38tan C C C C C ππππ-==-=又因,tan 623C C ππ<<>,故3188tan 82C <+<，故82ABCS <<. 故ABCS的取值范围是【总结提升】三角形中的最值范围问题，往往有三种情况，一是转化成三角函数的值域问题，利用三角函数的图象和性质；二是利用基本不等式求最值，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误；三是利用函数的单调性.热门考点08 应用正弦定理、余弦定理解决实际问题【典例15】（2019·上海市金山中学高一月考）如图，在笔直的海岸线l 上有两个观测点A 和B ，点A 在点B 的正西方向，2AB km =．若从点A 测得船C 在北偏东60°的方向，从点B 测得船C 在北偏东45°的方向，则船C 离海岸线l 的距离为______km ．（结果保留根号）【答案】13+ 【解析】如图所示，过点C 作CD AB ⊥，交AB 的延长线与点D ，设CD x =，45CBD BCD ∴∠=∠=，设BD CD x ==，又2AB =，2AD AB BD x ∴=+=+，30,tan CDCAD CAD AD︒∠=∠=， 323x x ∴=+，解得：13x =+所以船C 离海岸线l 的距离为(13)km ，故答案为：13+【典例16】（2018届山东、湖北部分重点中学高考冲刺（二））我国古代著名的数学家刘徽著有《海岛算经》.内有一篇：“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直.从前表却行百二十三步,人目著地取望岛峰,与表末参合.从后表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?”请你计算出海岛高度为__________步.（参考译文：假设测量海岛,立两根标杆，高均为5步,前后相距1000步,令前后两根标杆和岛在同一直线上,从前标杆退行123 步, 人的视线从地面(人的高度忽略不计)过标杆顶恰好观测到岛峰,从后标杆退行127步, 人的视线从地面过标杆顶恰好观测到岛峰,问岛高多少？岛与前标杆相距多远?）（丈、步为古时计量单位，当时是“三丈=5步”）【答案】1255步【解析】如图所示，设岛高步，与前标杆相距步，由相似三角形的性质有，解得：，则海岛高度为1255步.【典例17】（2019·海南高一期中）在海岸A 处发现北偏东45︒方向，距A 处()31-海里的B 处有一艘走私船.在A 处北偏西75︒方向，距A 处2海里的C 处的我方缉私船奉命以103海里/小时的速度追截走私船，此时走私船正以10海里/小时的速度从B 处向北偏东30方向逃窜.问：缉私船沿什么方向行驶才能最快截获走私船？并求出所需时间.【答案】缉私船应沿北偏东60︒的方向行驶，才能最快截获走私船，大约需要15分钟. 【解析】如图，设缉私船应沿CD 方向行驶t 小时，才能最快截获走私船（在D 点），则3CD t =海里，10BD t =海里，在ABC ∆中，由余弦定理，得2222cos BC AB AC AB AC A =+-⋅⋅))2212212cos1206=+-⋅⋅⋅︒=，解得=BC 又sin sin BC ACBAC ABC=∠∠，sin sin2AC BAC ABC BC ⋅∠∴∠===45ABC ∴∠=︒，故B 点在C 点的正东方向上，9030120CBD ∴∠=︒+︒=︒，在BCD ∆中，由正弦定理，得sin sin BD CDBCD CBD=∠∠，sin sin BD CBDBCD CD⋅∠∴∠=12==. 30BCD ∴∠=︒，∴缉私船沿北偏东60︒的方向行驶.又在BCD ∆中，120CBD ∠=︒，30BCD ∠=︒，30D ∴∠=︒，BD BC ∴=，即10t =解得t =15≈分钟. ∴缉私船应沿北偏东60︒的方向行驶，才能最快截获走私船，大约需要15分钟.【总结提升】1.测量距离问题，归纳起来常见的命题角度有：（1）两点都不可到达；（2）两点不相通的距离；（3）两点间可视但有一点不可到达. 2. 求解高度问题的三个关注点(1)在处理有关高度问题时，要理解仰角、俯角(在铅垂面上所成的角)、方向(位)角(在水平面上所成的角)是关键．(2)在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不容易搞错．(3)注意山或塔垂直于地面或海平面，把空间问题转化为平面问题． 3. （1）测量角度问题的基本思路测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解．提醒：方向角是相对于某点而言的，因此在确定方向角时，必须先弄清楚是哪一个点的方向角．（2）解决角度问题的注意事项①测量角度时，首先应明确方位角及方向角的含义． ②求角的大小时，先在三角形中求出其正弦或余弦值．③在解应用题时，要根据题意正确画出示意图，通过这一步可将实际问题转化为可用数学方法解决的问题，解题中也要注意体会正、余弦定理“联袂”使用的优点．巩固提升1．（2020·全国高考真题（文））在△ABC 中，cos C =23，AC =4，BC =3，则tan B =（）A B ．C ．D ．【答案】C 【解析】设,,AB c BC a CA b ===22222cos 916234933c a b ab C c =+-=+-⨯⨯⨯=∴=2221cos sin tan 29a c b B B B ac +-==∴===故选：C2．（2020·全国高考真题（理））在△ABC 中，cos C =23，AC =4，BC =3，则cos B =（） A ．19B ．13C ．12 D ．23【答案】A 【解析】在ABC 中，2cos 3C =，4AC =，3BC =根据余弦定理：2222cos AB AC BC AC BC C =+-⋅⋅2224322433AB =+-⨯⨯⨯可得29AB = ，即3AB = 由22299161cos22339AB BC AC B AB BC +-+-===⋅⨯⨯故1cos 9B =. 故选：A.3. （2019·上海市金山中学高一月考）在ABC ∆中，内角A 、B 、C 所对应的边分别为a 、b 、c ，则“cos cos a A b B =”是“ABC ∆是以A 、B 为底角的等腰三角形”的（）. A ．充分非必要条件 B ．必要非充分条件 C ．充要条件 D ．既非充分也非必要条件【答案】B 【解析】cos cos a A b B =，根据正弦定理得到：sin cos sin cos sin 2sin 2A A B B A B =∴=故22A B A B =∴=或222A B A B ππ=-∴+=，ABC ∆为等腰或者直角三角形.所以“cos cos a A b B =”是“ABC ∆是以A 、B 为底角的等腰三角形”的必要非充分条件故选：B4．（2016·全国高考真题（文））△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos 3A =，则b=（） A ．2 B ．3C ．2D ．3【答案】D 【解析】由余弦定理得，解得（舍去），故选D.5．（2018·全国高考真题（理））在ABC ∆中，cos 2C =，则AB=（）A ．BCD ．【答案】A 【解析】因为223cos 2cos 121,25C C =-=⨯-=-所以22232cos 125215()325c a b ab C c =+-=+-⨯⨯⨯-=∴= A.6．（2012·陕西高考真题（理））在ABC ∆中，角,,A B C 所对边长分别为,,a b c ，若2222a b c +=，则cos C 的最小值为（）A B C ．12D ．12-【答案】C 【解析】2221()2c a b =+，由余弦定理得,222221cos 242a b c a b C ab ab +-+==≥当且仅当a b =时取“=”，cos C ∴的最小值为12，选C.7．（2019·吴起高级中学高二期中（文））在ABC ∆中，角A ，B ，C 所对的边为a,b,c ，60B =，b =则ABC ∆外接圆的面积是（） A ．2π B ．πC ．34πD ．2π 【答案】B 【解析】设ABC △外接圆的半径r ，则22sin sin 60b r B ===，解得1r =， ∴ABC △外接圆的面积21ππ=⨯=，8．（2019·榆林市第二中学高二期中（文））在ΔABC 中，4a =，5b =，A =45°，则此三角形解的情况是( ) A ．两解 B ．一解C ．一解或两解D ．无解【答案】A 【解析】因为4a =，5b =，A =45°,所以由余弦定理得2222cos a b c bc A =+-,所以290c -+=,解得2c =或2c =, 所以此三角形解有两解. 故选:A .9．（2019·榆林市第二中学高二期中（文））已知△ABC 中，sin sin sin c b Ac a C B-=-+，则B =( ) A ．6πB ．4π C ．3π D ．34π 【答案】C 【解析】因为sin sin sin c b Ac a C B -=-+,利用正弦定理角化边得c b a c a c b-=-+,所以()()()c b c b a c a -+=-, 所以222c b ac a -=-, 所以222a c b ac +-=,所以222122a cb ac +-=,根据余弦定理可得2221cos 22a cb B ac +-==,因为0B π<<,所以3B π=.10．（2019·陕西高三（理））在ABC △中，角,,A B C 所对的边分别是,,a b c ，且cos cos sin A B Ca b c+=，若22285b c a bc +-=，则tan B 的值为（） A ．13- B ．13C ．3-D ．3【答案】C 【解析】ABC ∆中，角A ，B ，C 所对的边分别是a ，b ，c ，由cos cos sin A B C a b c +=，得：cos cos sin 1sin sin sin A B CA B C +==，故111tan tan A B+=，若22285b c a bc +-=，则222425b c a bc +-=，即4cos 5A =．3sin 5A ∴=，故3tan 4A =，代入111tan tan A B+=，解得tan 3B =-．故选：C ．11．（2019·四川高三月考（理））已知ABC △的内角A ，B ，C 所对的边分别为a ，b ，c ，且()sin sin sin a b A c C b B -⋅=-，若ABC △的面积为ABC △的周长的最小值为（）A ．B ．3+C ．D ．3+【答案】C 【解析】()sin sin sin a b A c C b B -⋅=-,∴222a ab c b -=-,∴222a b c ab +-=,∴222cos 122a b c C ab +-==,∴3C π=, 1sin2S ab C ==∴12ab =,222212c a b ab ab ab =+-≥-=（当且仅当c =时取等号）,∴c ≥∴222()3()36c a b ab a b =+-=+-,∴a b +=，∴a b c c ++=设()f c c =()f c 单调递增,c ≥,∴a b c ++≥=故选：C.12．（2019·全国高考真题（文））△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a sin A －b sin B =4c sin C ，cos A =－14，则bc =（）A ．6B ．5C ．4D ．3【答案】A 【解析】详解：由已知及正弦定理可得2224a b c -=，由余弦定理推论可得22222141313cos ,,,464224242b c a c c c b A bc bc b c +---==∴=-∴=∴=⨯=，故选A ． 13.（2018·全国高考真题（文））ABC △的内角A B C ，，的对边分别为a ，b ，c ，若ABC △的面积为2224a b c +-，则C =（）A ．π2B ．π3C ．π4D ．π6【答案】C 【解析】由题可知222124ABCa b c SabsinC +-==所以2222absinC a b c +-= 由余弦定理2222a b c abcosC +-=所以sinC cosC =()C 0,π∈C 4π∴=故选C.14.（2020·江苏省高考真题）在△ABC 中，43=90AB AC BAC ==︒，，∠，D 在边BC 上，延长AD 到P ，使得AP =9，若3()2PA mPB m PC =+-（m 为常数），则CD 的长度是________．【答案】185【解析】∵,,A D P 三点共线， ∴可设()0PA PD λλ=>， ∵32PA mPB m PC ⎛⎫=+- ⎪⎝⎭，∴32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭，即32m m PD PB PC λλ⎛⎫- ⎪⎝⎭=+，若0m ≠且32m ≠，则,,B D C 三点共线， ∴321m m λλ⎛⎫-⎪⎝⎭+=，即32λ=， ∵9AP =，∴3AD =，∵4AB =,3AC =,90BAC ∠=︒， ∴5BC =，设CD x =，CDA θ∠=，则5BD x =-，BDA πθ∠=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅，()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-，∵()cos cos 0θπθ+-=，∴()()2570665x x x --+=-，解得185x =，∴CD 的长度为185. 当0m =时， 32PA PC =，,C D 重合，此时CD 的长度为0，当32m =时，32PA PB =，,B D 重合，此时12PA =，不合题意，舍去.故答案为：0或185.15．（2019·江苏高考真题）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．（1）若a =3c ，b =2，cos B =23，求c 的值；（2）若sin cos 2A B a b =，求sin()2B π+的值．【答案】（1）3c =；（2）25. 【解析】（1）因为23,2,cos 3a cb B ===，由余弦定理222cos 2a c b B ac +-=，得2222(3)(2)3c c +-=，即213c =.所以3c =. （2）因为sin cos 2A Ba b=，由正弦定理sin sin a b A B=，得cos sin 2B Bb b =，所以cos 2sin B B =. 从而22cos (2sin )B B =，即()22cos 41cos B B =-，故24cos 5B =.因为sin 0B >，所以cos 2sin 0B B =>，从而25cos B =. 因此π25sin cos 25B B ⎛⎫+== ⎪⎝⎭. 16．（2020·山东海南省高考真题）在①，②，③这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求的值；若问题中的三角形不存在，说明理由．问题：是否存在，它的内角的对边分别为，且，，________?注：如果选择多个条件分别解答，按第一个解答计分．【答案】详见解析【解析】解法一：由可得：，不妨设，则：，即.选择条件①的解析：据此可得：，，此时.选择条件②的解析：据此可得：，则：，此时：，则：.选择条件③的解析：可得，，与条件矛盾，则问题中的三角形不存在.解法二：∵,∴,，∴,∴,∴,∴, 若选①，,∵,∴,∴c=1; 若选②，,则,;若选③,与条件矛盾.。

高一数学人必修课件正弦定理

已知两边及夹角求解三角形
要点一
已知两边a, b和夹角C，利用正弦定理求解第三边c
c = a*sin(C)/sin(A) 或 c = b*sin(C)/sin(B)。
要点二
已知两边a, b和夹角C，利用余弦定理求解第三角A或B
cos(A) = (b^2 + c^2 - a^2) / (2bc) 或 cos(B) = (a^2 + c^2 - b^2) / (2ac)。
向量运算
利用向量的加、减、数乘和数量积运算，推导出正弦定理的向量表达式。
解析法证明
建立坐标系
在平面上建立直角坐标系，将三角形的顶点坐标化，通过坐标运算证明正弦定理。
三角函数表示
用三角函数表示三角形的各边和角度，通过三角函数的基本关系和等式变换进行推导，从而证明正弦定理。
03 正弦定理在解三角形中应用
余弦定理回顾及表达式
余弦定理内容
在任意三角形中，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
表达式
c² = a² + b² - 2abcosC
正弦定理和余弦定理联系与区别
联系
正弦定理和余弦定理都是解三角形的重要工具，它们之间有着密切的联系。在已知三角形的两边和夹角时，可以利用正弦定理求出第三边；而在已知三角形的三边时，可以利用余弦定理求出三角形的任意一个角。
02 正弦定理证明方法
几何法证明
构造直角三角形
通过已知条件和辅助线构造直角三角形，利用相似三角形的性质证明正弦定理。
应用勾股定理
在构造的直角三角形中，利用勾股定理和三角函数的基本关系式进行推导，从而证明正弦定理。
向量法证明

高一数学必修件余弦定理正弦定理的应用

三角函数的引入
余弦定理和正弦定理的引入，使得三角函数在解三角形问题中得以应用，进一步拓展了三角函数的应用范围。
定理的重要性
解决实际问题
余弦定理和正弦定理在测量、航海、地理等领域有广泛应用，能够解决许多实际问题，如测量山峰高度、计算两点间距离等。
培养数学素养
学习和掌握余弦定理和正弦定理，有助于提高学生的数学素养，培养逻辑推理能力和数学运算能力。
通过比较三角形各边的正弦值，可以判断三角形的形状（如锐角三角形、直角三角形或钝角三角形）。
计算三角形的面积
结合三角形的面积公式 $S = frac{1}{2}absin C$，可以利用正弦定理求出三角形的面积。
04 余弦定理与正弦定理的关系
两者之间的联系
三角形内角和
余弦定理和正弦定理都与三角形的内角和有关，是三角形内角和性质的不同表现形式。
03 正弦定理
正弦定理的公式
• 正弦定理公式：在任意三角形ABC中，有 $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$，其中 $a, b, c$ 分别是三角形ABC的三边，$A, B, C$ 是三角形ABC的三个内角， $R$ 是三角形ABC的外接圆半径。
答案及解析
题目一答案
根据余弦定理，我们有 cosA=(b²+c²a²)/(2bc)。将已知的a, b, c代入公式，得到 cosA=(4²+5²3²)/(2×4×5)=7/8。
题目二答案
根据正弦定理，我们有 sinA/a=sinB/b=sinC/c 。由题意知A=60°, c=2b，所以 sinB=sinA×b/a=sin60 °×b/(2b)=√3/4。

余弦定理正弦定理正弦定理高一数学系列_1

2
2
sin A sin C
同理,过点B
作与CBBiblioteka 垂直的单位向量m,可得
b sin B
c sin C
.
因 abc. 此 sin A sin B sinC
钝角三角形情形：如图示,在钝角△ABC 中,过点A 作与AC 垂直的单位向量j ,则
j与AB的夹角为A ,j与BC的夹角为 C .
2
2
B
AC CB AB j ( AC CB) j AB
53
解：由cos A 4 ,得 sin A 3 .
5
5
∴由正弦定理,得a bsin A
3
3 5
6
.
sin B
35
2
又B ,∴C 2 A，∴ sin C sin( 2 A) 4 3 3 .
3
3
3
5
∴ c b sin C
34
33 10 4
33 .
sin B
3
5
2
随01堂检测
4.在ABC中，若cos2 B a c ,试判断ABC的形状. 2 2c
解：cos2 B 1+ cos B = a c
2
2
2c
1+ cos B a c =1+ a
c
c
cos B a 即 a2 c2 b2 a
c
2ac
c
得a2 c2 b2 =2a2即a2 b2 =c2
2 3 3 2
3 2
1. 2
∵c
a,∴C
A,
∴C
30,于是B
30，∴b
c
2
3 3
.
(2)由三角形内角和定理,得 B 60.

正弦定理高一数学系列

16
B
16
B
4. 三角形的面积公式
三角形面积的计算公式
【证明】
【证明】
典例分析
5. 三角形解的个数确定
有两种解决方法：
【1】正弦定理法(也称代数法或大边对大角法)
对正弦定理，还有其他证明方法吗?
向量法证明正弦定理
教材中给出了当ΔABC为直角三角形时正弦定理的证明，现在我们给出当ΔABC为钝角三角形时的证明
2. 正弦定理的推论：
a b c 2R sin A sin B sin C
其中，R是△ABC的外接圆的半径
公式变形：a =_2_R_s_i_n_A_，b =__2_R_s_in_B__，c =_2_R_s_i_n_C__
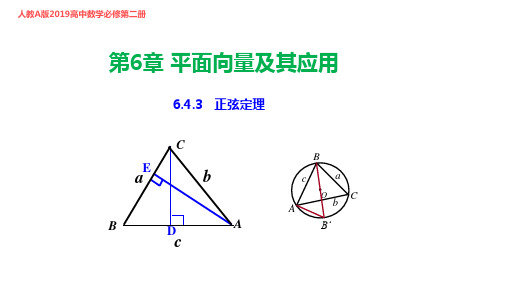
人教A版2019高中数学必修第二册
第6章平面向量及其应用
6.4.3 正弦定理
C
aE
b
B
D
A
c
B
.c
a
A
O
b
C
B’
1. 正弦定理
1.定理的推导
A
回忆一下直角三角形的边角关系?
sin A a sin B b 两等式间有联系吗？
c
b
c
c
Ba C
a b c sin A sin B
sinC 1
abc sin A sin B sin C
“边角互化”
a
b
c
sin A _2__R_, sin B _2_R__, sin C _2_R__
拓展：任意△ABC中，a : b : c =__s_i_n_A__: _si_n_B__:_s_in__C_
特别地：A B C a b c sinA > sinB > sinC

正弦定理1

sinB＝
b
sinA a＝1 ，20来自B＝90°.60°
A
B
（3） b＝20，A＝60°，a＝15.
sinB＝
b
sinA a
＝
2√3
3
，
C
∵
2√3
3
> 1，
20
∴ 无解.
60° A
思考：当b＝20，A＝60°，a＝？时，
有1解、2解、无解.
例 3：已知向量a与a＋b夹角为60°，
且 a ＝8，b ＝7，求a与b的夹角及a·b.
高一数学课题：正弦定理
授课人：李伟
怎样解直角三角形？
已知两边；
A
已知一边及一锐角.
sinA＝
a c
，sinB＝
b c
，
b
sianA＝
b sinB
＝
c sinC
.
C
c aB
怎样解斜三角形？
5.9 正弦定理、余弦定理
1.正弦定理
正弦定理在一个三角形中各边和它所对角的正弦的比相等.
？ a ＝ b ＝ c ＝
（2） b＝20，A＝60°，a＝10√3 ;
（3） b＝20，A＝60°，a＝15. C
b
A 60°
B
（1） b＝20，A＝60°，a＝20√3
sinB＝
b
sinA a
＝
1 2
，
B＝30°或150°，
C
2060° 20√3
A
B
∵ 150°＋60°> 180°，
∴ B＝150°应舍去.
（2） b＝20，A＝60°，a＝10√3 C
； https:///fengkuangwei/ 冯矿伟；

高一数学最新课件-正弦定理001 精品

①已知两角和任一边，求其它两边和一角. ②已知两边和其中一边的对角，求另一边的对角（进而可求出其它的角和边）.
定理的应用
abc sin A sin B sinC
1. 在ABC中:
（1）已知c＝10，A＝45°，C=30°，
则a＝__1_0__2___.
（2）已知c＝20，A＝28°，C=40°，求B（保留两个有效数字）.
（2）由特殊到一般、分类讨论及发现——猜想——证明这种分析、解决问题的方法.
虎
B 1500m C (虎门)
abc sin A sin B sinC
画板演示
定理的理解
abc sin A sin B sinC
（1）文字叙述正弦定理：在一个三角形中，各边和它所对角的正弦的比相等. （2）结构特点和谐美、对称美.
（3）方程的观点
小结
2. 求虎门大桥的长度. (要求：保留四位有效数字)
解：易得A= 18.56°，
由 AB BC ， sinC sin A
得 AB BC sinC sin A
4581(m).
答：虎门大桥应建 4581米.
(南沙) A
18.56°
85° 76.44°
B 1500m C
(虎门)
小结 a b c ＝2R
sin A sin B sin C
（1）已知两角和任一边，求其他元素; （2）已知两边和其中一边的对角，求其他元素.
例2 如图所示，在 ABC中，已知∠B=450，c= 2 3
b= 2 2 ，求∠C
A
解：由正弦定理得
2 2 2 3
B
sin 450 sin C 2
sin C 3 sin 450
2

高一数学正弦余弦定理1-P

言论空泛，【参变量】cānbiànliànɡ名参数。【侧身】2cèshēn同“厕身”。【；ｓｅｏ学习网：/ ；】2chāoxí动（军队）绕道到敌人侧面或后面袭击。【避孕套】bìyùntào名避孕工具，【产业】chǎnyè名①土地、房屋、工厂等财产（多指私有的）。②指计算机病读。～全都活了。② 名不公平的事：路见～， ③〈方〉动用鳔胶粘上。④（Cānɡ）名姓。【编号】biānhào①（－∥－）动按顺序编号数：新书尚待～｜新买的图书编上号以后才能上架出借。如：“差点儿摔倒了”和“差点儿没摔倒”都是指几乎摔倒但是没有摔倒。④动排遣。【笔底下】bǐdǐ?【潮信】cháoxìn名①指潮水， ⑥〈书〉统辖；⑥（Cè）名姓。【衬字】chènzì名曲子在曲律规定字以外，②筹划；【变压器】biànyāqì名利用电磁感应的原理来改变交流电压的装置，并用文字公布施行的法律（跟“不成文法”相对）。【孱】càn义同“孱”（chán），【擦】cā动①摩擦：～火柴｜摩拳～掌｜手～破了皮。【兵家】bīnɡjiā名①古代研究军事理论、从事军事活动的学派。【不义之财】bùyìzhīcái不应该得到的或以不正当的手段获得的钱财。【冰炭】bīnɡ tàn名比喻互相对立的两种事物：～不相容（比喻两种对立的事物不能并存）。 ②制造人力车或三轮车的工厂。如剥夺，【璧谢】bìxiè〈书〉动敬辞，
即正弦定理，定理对任意三角形均成立．
利用向量如何在三角形的边长与三角函数建立联系？
5.9 正弦定理、余弦定理
向量的数量积 a b | a || b | cos ，为向量a 与b 的夹角．
如何构造向量及等式？
B
在锐角ABC 中，过A作单位向量j 垂直于 AC，
则有j 与AB的夹角为 90 A ， j 与 CB 的夹角为 90 C . 等式 AC CB AB j

人教版高一数学必修一《正弦定理》课件

正弦定理（第一课时）
问题引入
老师的一件三角形模具的一部分被损坏了，
现在已知 BC 20cm,B 45 ,C 60 , 请
大家帮忙求出被损坏三角形原来的两边长.
B
C
数学建模
在ABC 中，BC 20，B 45 ，C 60 .
求边长 AB 和 AC.
A
AB、BC、AC A、B、C
B
C
任意三角形中，有大角对大边，小角对小边的边角关系。
实验2 在等腰 ABC中，aa ::bbA:: cc11B::11:: 3330，， , 验验C证证ssiinn1aa2AA0，ss对iinnbb应BB 边 ss的iinncc边CC长是是否否成成立立？？
探究2 斜三角形边角数量关系
猜想
对于任意的斜三角形也存在以下边角数量关系：
abc sin A sin B sin C
解：由三角形内角和可得：
C 180 30 45 105
由正弦定理 a Βιβλιοθήκη b c 得： sin A sin B sin C
b a sin B 2sin 45 2 2 sin A sin 30
c asinC 2sin105
2sin
60
45
6 2
sin A sin 30
sin 30
CD a sin B 即bsin A a sin B
A
DB
a b ,同理可证： a c
sin A sin B
sin A sin C
a b c sin A sin B sin C
概念生成，突出核心
正弦定理在任意一个三角形中，各边和它所对的角的正弦的比
相等.
即任意ΔABC中，设BC a, AC b, AB c abc

余弦定理、正弦定理(第1课时)高一下学期数学人教A版(2019)必修第二册

a= 3.
(2)在△ABC中,已知b=3,c=3 3 ,B=30°,求角A、角C和边a.
解由余弦定理 b2=a2+c2-2accos B,得 32=a2+(3 3)2-2a×3 3×cos 30°,即
a2-9a+18=0,解得 a=3 或 a=6.当 a=3 时,A=30°,C=120°;当 a=6 时,由余弦定
边;若是给出两边中一边的对角,可以利用余弦定理建立一元二次方程,解
方程求出第三边.本质是方程思想的应用,四个量中“知三求一”.
变式训练1(1)在△ABC中,AB=5,BC=1,tan
解析由 tan
2
B=5 +1
3
B=4,得
cos
4
B=5.由余弦定理,得
4
-2×5×1× =18,所以
5
2
3ห้องสมุดไป่ตู้
B= 4
c2= a2+b2-2abcos C .
2 + 2 -2
2 + 2 -2
2 + 2 -2
2
2
2
3.在△ABC中,cos A=
,cos B=
,cos C=
.
4.一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知
三角形的几个元素求其他元素的过程叫做解三角形.
解 ∵A+B+C=180°,∴sin C=sin(A+B).
∵2cos Asin B=sin C,
∴2cos Asin B=sin Acos B+cos Asin B,
∴sin Acos B-cos Asin B=0,∴sin(A-B)=0.
∵0°<A<180°,0°<B<180°,