用WinQSB 求解决策问题2
winQSB实例

winQSB实例附录:WinQSB用法简介WinQSB是Quantitative Systems for Business的缩写,WinQSB是一种教学软件,里面有大量的模型,对于非大型的问题一般都能计算,较小的问题还能演示中间的计算过程。
为此将WinQSB求解运筹学相关问题的使用方法简介如下。
内容包括:线性规划划及整数规划、目标规划、分配问题、运输问题、最短路问题、最小部分树问题、网络最大流问题、货郎担问题、计划评审技术、二人零和对策、决策分析。
1.winQSB求解线性规划及整数规划[例]求解线性规划问题:min40003000zxx,,1210020012000xx,,,12,30040020000xx,,,12st..,20010015000xx,,12,,xx,0,,12第1步:生成表格选择“程序,winQSB,Linear and Integer Programming,File,New Program”,生成对话框:问题题头(Problem Title):没有可不输入;变量数(Number of Variables):2;约束条件数(Number of Constraints):3;目标优化条件(Objective Criterion):最小(Minimization)数据输入格式(Data Entry Format):矩阵式电子表格式(Spreadsheet Matrix Form)变量类型(Default Variable Type):非负连续变量选择第1个单选按钮(Nonnegative continuous);非负整型变量选择第2个单选按钮(Nonnegative integer);二进制变量选择第3个按钮(Binary[0,1]);自由变量选择第4个按钮(Unsigned/unrestricted)。
第2步:输入数据单击“OK”,生成表格并输入数据如下:注:第1行为目标系数;2~4行为约束系数、约束符及右端项;第5行为变量下限;第6行为变量上限,第7行为变量类型。
WinQSB2.0 生产管理运筹学软件实例分析与求解

5.求解线性规划。启动程序开始→程序→WinQSB→Linear and Integer Programming。
6.学习例题点击File→Load Problem→lp.lpp,点击菜单栏Solve and Analyze或点击工具栏中的图标用单纯形法求解,观赏一下软件用单纯形法迭代步骤。用图解法求解,显示可行域,点击菜单栏Option →Change XY Ranges and Colors,改变X1、X2的取值区域(坐标轴的比例),单击颜色区域改变背景、可行域等8种颜色,满足你的个性选择。
系统提示要使线性规划问题有解,应该改变第二个约束条件。
(12)保存结果。求解后将结果显示在顶层窗口,点击File→Save As,系统以文本格式存储计算结果。
(13)将计算表格转换成Excel表格。在计算结果界面中点击File→Copy to Clipboard,系统将计算结果复制到剪贴板,再粘贴到Excel表格中即可。
(三)操作步骤:
1.将WinQSB文件复制到本地硬盘;在WinQSB文件夹中双击setup.exe。
2.指定安装WinQSB软件的目标目录(默认为C:\ WinQSB)。
3.安装过程需输入用户名和单位名称(任意输入),安装完毕之后,WinQSB菜单自动生成在系统程序中。
4.熟悉WinQSB软件子菜单内容及其功能,掌握操作命令。
表1-1初始单纯型表
(5)修改变量名和约束名。
系统默认变量名为X1,X2,…,Xn,约束名为C1,C2,…,Cm。默认名可以修改,点击菜单栏Edit后,下拉菜单有四个修改选项:修改标题名(Problem Name)、变量名(Variable Name)、约束名(Constraint Name)和目标函数准则(max或min)。由于WinQSB软件支持中文,读者可以输入中文名称。
winQSB 指南

1、启动线性规划(LP)和整数规划(ILP)程序。点击开始→程序→WinQSB →Linear and Integer Programming,显示线性规划和整数规划工作界面。
2、建立新问题或者打开磁盘中已有的文件。点击 File→New Problem 建立 一个新问题。输入本问题的文件名称 lp1(读者可以任意取名),决策变量个数 4 和约束条件个数 5,由于本问题是一个最大化问题,所以选择 Maximization,同 时可以确定数据的输入形式,一种为表单形式,一种为模型形式。如果我们选择
9、模型形式转换。点击菜单栏 Format→Switch to Normal Model Form,将表 2-9 电子表格转换成表 2-12 的模型形式,再点击一次转换成表 2-9 的电子表格。
10、写出对偶模型。点击菜单栏 Format→Switch to Dual Form,系统自动给 出线性规划的对偶模型,再点击一次给出原问题模型。
Entering Variable
Feasible Area
Feasible Solution
Infeasible
Infeasibility Analysis
Leaving Variable
Left-hand side
Lower or Upper Bound
Minimum
and
Maximum Allowable Cj
⎪⎪2 ⎨
x1
⎪
+ 3x2 ≥ x2 ≥ 2
−6
⎪⎩ x1, x2 ≥ 0
(4) max z = 3x1 + 9x2
7
⎧x1 + 3x2 ≤ 22
⎪ ⎪⎪ ⎨
−
x1 + x2
(七)网络计划的WinQSB求解电子教案

(七)网络计划的W i n Q S B求解实验七网络计划一、实验目的掌握WinQSB软件绘制计划网络图,计算时间参数,求关键路线。
二、实验内容和要求用WinQSB软件求解教材P184例1的网络计划问题。
具体题目:某项工程由11项作业组成(分别用代号A,B,……,J,K表示),其计划完成时间及作业间相互关系如表7-1所示,要求编制该项工程的网络计划并计算其时间参数。
表7-1三、实验操作步骤1、运行“PERT_CPM”,出现图1所示界面图12、运行file菜单下的new problem 命令,出现图2所示界面。
图2中各项目含义:图2Problem Type(问题类型)如下:Deterministic CPM:确定型关键路线法Probabilistic PERT:概率型网络计划技术Data Entry Format——选择数据输入是以矩阵或图形输入Select CPM Data Field——Normal Time 正常时间Crash Time 赶工时间Normal Cost 正常费用Crash Cost 赶工费用3、求例1,则①Problem Title后给文件命名,Number of Activities后给出作业数‘11’,Time Unit后给出时间单位‘day’,②Problem Type选择’Deterministic CPM’,③ Select CPM Data Field选’Normal Time’,④输入界面如图3所示,OK确定后出现输入矩阵如图4所示,图3图4图4中表格各项含义如下:Activity Number:作业编号,按1、2、3等依次对各项作业编号Activity Name:作业名称,可自行取名填入Immediate Predecessor:紧前工序,填入该项作业的紧前作业,可以填紧前作业的编号或名称,若有多项紧前作业,每项之间用西文状态下的逗号’,’隔开Normal Time:作业时间按表7-1填入后如图5所示图5按运行图标运行,得结果如图6所示图6图6中从左到右各列含义依次如下:1、作业编号2、作业名称3、该作业是否是关键路径上的关键作业,若是则为Yes,若不是则no4、作业时间5、作业最早可能开始时间6、作业最早可能完成时间7、作业最迟必须开始时间8、作业最迟必须完成时间9、作业总时差图6中最后两行给出了项目完成时间,本题为51,和关键路径的数量,本题为1。
winQSB用法

1.winQSB 求解线性规划及整数规划
[例]求解线性规划问题:
min z = 4000 x1 + 3000 x2 ⎧100 x1 + 200 x2 ≥ 12000 ⎪300 x + 400 x ≥ 20000 ⎪ 1 2 s.t. ⎨ ⎪200 x1 + 100 x2 ≥ 15000 ⎪ ⎩ x1 , x2 ≥ 0
第 2 步:修改目标要求,输入数据 从系统菜单选择“Edit�Goal Criteria and Names” ,弹出对话框:
选择第 3 个目标约束,将 Maximize 改为 Minimeze, “OK” ,输入数据,得:
第 3 步:求解 从菜单选择“Solve and Analyze�Solve the Problem” ,生成如下运行结果:
即:1�4�7�8,最短路长:8
6.winQSB 求解最小部分树问题
[例]求解最小部分树问题:
v2 2 2
3 5 3 2 2 v6 4 v7 v4 4 v5
v3
2
8 v8
v1 4
2
3
第 1 步:生成表格 选择“程序�winQSB�Network Modeling�File �New Program” ,弹出对话框:
问题类型(Problem Type) :分配问题(Assignment Problem)
优化条件(Objective Criterion) :最小(Minimization) 数据输入格式(Data Entry Format) :电子表格形式(Spreadsheet Matrix Form) 任务数(Number of Objects) :3 人员数(Number of Assignments) :3 第 2 步:输入数据 单击“OK” ,并输入数据:
WinQSB教程

实验一:线性规划
求解步骤: 1.启动线性规划和整数规划程序 2.建立新问题或者打开磁盘中已有的文件 3.输入数据 4.修改变量类型 5.修改变量名和约束名 6.求解 7.结果显实及分析 8.单纯形表 9.模型形式转变 10.写出对偶模型
(2)建立新问题或打开磁盘中已有的文件. 按照上图所示建立或打开一个LP问题; 点击“File”“Load Problem”打开磁盘中的LP问题数据文件 (LP程序自带后缀为“.LPP”的三个例题,供学习参考); 点击“File”“New Problem”建立新问题 出现如图6所示的问题选项输入界面.
将WinQSB的数据复制到Office文档:
先清空剪贴板,选中WinQSB表格中要复制的单元格, 点击Edit→Copy,然后粘贴到Excel或Word文档中.
将WinQSB的计算结果复制到Office文档: 问题求解后,先清空剪贴板,点击File → Copy to clipboard就将结果复制到Office文档. 保存计算结果: 问题求解后,点击File → Save as,系统以文本格式 (*.txt)保存结果,然后复制到Office文档.
Z 661.4285
第6行提示Alternate Solution Exists!!知原线性规 划问题有多重解。
41
实验一:线性规划
返回
Company Logo
实验一:线性规划
返回
Company Logo
WinQSB简介
可以用WinQSB软件做什么?
WinQSB是一种教学软件,里面有大量的 模型,对于非大型的问题一般都能计算,较小 的问题还能演示中间的计算过程。 WinQSB V2.0共有19个子系统(见表1), 分别用于解决运筹学不同方面的问题。
WinQSB教程-线性规划

Contents
0
WinQSB 软件简介
4
运输与指派问题
1
2 3
线性规划
5
6
网络模型
对偶理论
网络计划
整数规划
WinQSB简介
WinQSB软件是什么?可以用它做什么?
QSB是Quantitative Systems for Business的缩 写。该软件是由美籍华人Yih-Long Chang和 Kiran Desai共同开发,可广泛应用于解决管理 科学、决策科学、运筹学及生产管理等领域的 问题。该软件界面设计友好,使用者很容易学 会并用它来解决管理和商务问题,表格形式的 数据录入以及表格与图形的输出结果都给使用 者带来极大的方便。
实验一:线性规划相关问题分析求解
b. Lenny 需要确定每一个工作轮换的开始需要由多少个讲 西班牙语的全职操作人员、讲英语的全职工作人员和兼职 人员。Creative Chaos 咨询公司建议他使用线性规划, 使得在接听所有电话的前提下运作成本最小的方式处理这 个问题。 建立问题的数学模型:
2
3
Dynamic Programming
DP
动态规划
设备场地 布局
最短路问题、背包问 题、生产与存储
设备场地设计、功能 布局、线路均衡布局
Facility Location FLL and Layout
WinQSB的系统分类
序 号 程 序 启动程 序名称 内容 应用范围
4
Linear Programming and Integer linear Programming
实验一:线性规划相关问题分析求解
对于下面的分析,只考虑员工花费在接听电话上的劳 动成本。文书工作的成本由其他成本中心处理。 a. 为了接听所有的电话,呼叫中心工作日每两个小时 工作轮换期间讲西班牙语的操作人员和讲英语的工作 人员各需要多少?由于半个人是没有意义的,所以请 提供一个整数。
WinQSB的基本操作

– ②Edit菜单,如图9。
图9
– ③Format菜单,如图10 。
Font:选择显示字体〔为Windows 标准的字体对话框〕 Row height:调整电子表格行高。 Column weight:调整电子表格列宽。
图10
• Format->Number:选择数字的显示格式。选择此菜 单,弹出窗口如图11。
下图5所示。
①标题栏:显示了程序的名称。 ②菜单栏:共有两个菜单:File 和Help。 File菜单只有三个子菜单:
New Problem:创立新问题 Load Problem:装载问题 Exit:退出 Help菜单为帮助菜单〔略〕 ③工具栏:供给了执行菜单栏各 功能的快捷按钮。
④信息栏:把鼠标移动到工具栏 按钮上时,信息栏会给出相应的 说明信息。
打印 快速打印窗口 结果另存 复制到剪贴板
打印字体设置 打印设置
图16
退出
– Results菜单
– 如图17,主要是对问题进展各种不同的分析和
显示。
解概要
约束条件概要
目标函数灵敏度分析 右端项灵敏度分析
组合报表
不行行分析 无界分析
执行参数分析 显示参数分析 图形显示参数分析
最终单纯形表 猎取候补最优解
• 货郎担问题〔Traveling Salesman Problem〕 • 最近距离〔Nearest Neighbor Heuristic〕 • 最小本钱〔Cheapest Insertion Heuristic〕 • 双向沟通式〔Two-way Exchange Improvement Heuristic〕 • 分枝定界法〔Branch and Bound Method〕 • 活动数〔Number of Activities〕 • 时间单位〔Time Unit〕 • 确定型〔只有正常活动时间〕选择“Deterministic CPM”
用WinQSB 求解决策问题2

*** 用WinQSB 求解决策问题2
.决策树分析
例: 某公司需要决定建大厂还是建小厂来生产一种新产品,该产品的市场寿命为10年。
建大厂的投资为280万元,建小厂的投资为140万元。
估计10年内销售状况的概率分布是:需求高的概率为0.5,需求一般的概率为0.3,需求低的概率为0.2。
不同工厂规模和市场需求量的组合对应的年收益见表10-23。
试用决策树进行决策。
第1步:生成表格
在问题类型(Problem Type )中选择决策树分析(Decision Tree Analisis ),出现下面的表格。
图10.18
在表格中填写问题的题目(Problem Title ),以及决策树中点(或事件)的个数,其中包括终点的个数。
本例中有一个决策点,两个机会点,此外还有六个端点,总共有九个点。
第2步:输入数据
单击“OK ”并输入数据。
表10.27
在第一列中将九个点进行编号,在第二列中决策点标D,机会点及各分枝的端点标C,在第三列中,写出每一个点后面紧跟着的点的编号,第四列填写收益值,负值表示损失值,第五列填写机会分枝发生的概率。
第3步:求解
点击工具栏中的“Solve and Analyze”—“Solve the Problem”,得到下面的计算结果。
其结论是:选择建大厂,期望收益360万元。
表10.28
如果想画出本问题的决策树,可点击工具栏中的“Solve and Analyze” “Draw Decision Tree”或点击符号,就会出现下面的决策树图。
图10.19。
WinQSB2.0软件实例与求解答案分析
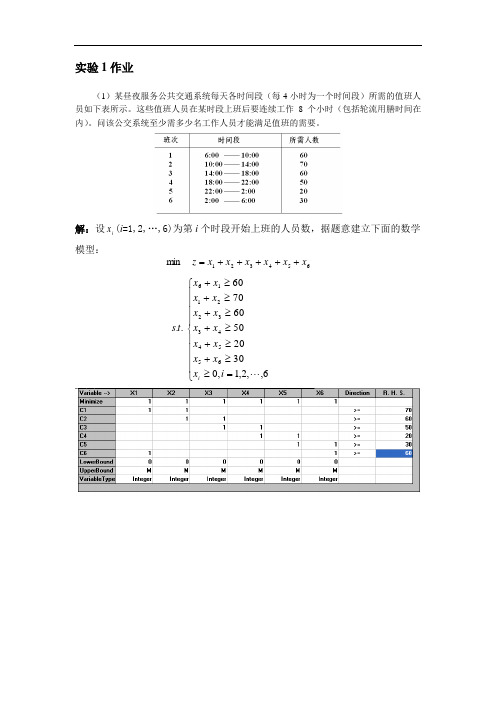
实验1作业(1)某昼夜服务公共交通系统每天各时间段(每4小时为一个时间段)所需的值班人员如下表所示。
这些值班人员在某时段上班后要连续工作8个小时(包括轮流用膳时间在内)。
问该公交系统至少需多少名工作人员才能满足值班的需要。
解:设ix(i=1,2,…,6)为第i个时段开始上班的人员数,据题意建立下面的数学模型:654321m in xxxxxxz+++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≥+≥+≥+≥+≥+≥+6,,2,1,0302050607060..655443322116ixxxxxxxxxxxxxt si(2)(任务分配问题)某车间有甲、乙两台机床,可用于加工三种工件。
假定这两台车床的可用台时数分别为800和900,三种工件的数量分别为400、600和500,且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。
问怎样分配车床的加工任务,才能既满足加工工件的要求,又使加工费用最低?解:设在甲车床上加工工件1、2、3的数量分别为321,,x x x ,在乙车床上加工工件1、2、3的数量分别为654,,x x x 。
建立以下线性规划模型:6543218121110913m in x x x x x x z +++++=⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤++≤++=+=+=+6,,2,1,09003.12.15.08001.14.0500600400 ..654321635241 i x x x x x x x x x x x x x t s i 车床类 型 单位工件所需加工台时数 单位工件的加工费用 可用台时数 工件1 工件2 工件3 工件1 工件2 工件3 甲 0.4 1.1 1.0 13 9 10 800 乙 0.5 1.2 1.3 11 12 8 900(3)(厂址选择问题)考虑A 、B 、C 三地,每地都出产一定数量的原料,也消耗一定数量的产品(见表9-15)。
已知制成每吨产品需3吨原料,各地之间的距离为:A-B :150km ,A-C :100km ,B-C :200km 。
winQSB教学-推荐下载

1.winQSB 求解线性规划[例]求解线性规划问题:1212121212min 400030001002001200030040020000..20010015000,0z x x x x x x s t x x x x =++≥⎧⎪+≥⎪⎨+≥⎪⎪≥⎩第1步:生成表格选择“程序→winQSB →Linear and Integer Programming →File →New Program ”,生成对话框:4问题题头(Problem Title ):没有可不输入;变量数(Number of Variables ):2;约束条件数(Number of Constraints ):3;目标优化条件(Objective Criterion ):最小(Minimization )数据输入格式(Data Entry Format ):矩阵式电子表格式(Spreadsheet Matrix Form )变量类型(Default Variable Type ):非负连续变量选择第1个单选按钮(Nonnegative continuous );非负整型变量选择第2个单选按钮(Nonnegative integer );二进制变量选择第3个按钮(Binary[0,1]);自由变量选择第4个按钮(Unsigned/unrestricted )。
第2步:输入数据单击“OK ”,生成表格并输入数据如下:注:第1行为目标系数;2~4行为约束系数、约束符及右端项;第5行为变量下限;第6行为变量上限,第7行为变量类型。
第3步:求解选择“Solve and Analyze”菜单,在二级菜单中:若选择“Solve and Display Steps”,显示单纯形法迭代步骤,选择“Simplex Iteration”直到最终单纯形表。
若选择“Solve the Problem”,生成如下运行结果:决策变量(Decision Variable):x1、x2最优解:x1=60,x2=30;目标系数:c1=4000,c2=3000;最优值:330000;其中x1贡献240000、x2贡献90000;检验数,或称缩减成本(Reduced Cost):0,0。
winQSB求解计划评审技术的例题

winQSB求解计划评审技术[例]某建筑公司从一所大学那里成功中标了一个新教学大楼建设项目,学校要求这个新教学大楼必须在一年内能够投入使用。
合同包括下面列出的一些条款:(1)若建筑公司在49周之内不能完成此建设任务,就要赔偿25万元。
(2)若此项目能在41周内完工,建筑公司就会获得18万元的额外奖金奖励。
完成这个建筑项目所需工序及各工序所需的时间(周)见表。
建筑公司希望能够按时完成该建设项目,以及可能会取得进度上的提前。
试问:如何对该项目进行管理?第1步:生成表格选择“程序→winQSB→PERT_CPM→File→New Program”,弹出对话框:活动数(Number of Activities):14时间单位(Time Unit):week(周)问题类型(Problem Type):确定型(只有正常活动时间)选择“Deterministic CPM”;概率型(包括正常活动时间、乐观时间和悲观时间)选择“Probabilistic PERT”数据输入格式(Data Entry Format):电子表格(Spreadsheet)数据范围(Select CPM Data Field):可选项(多选)有正常时间(Normal Time)、赶工时间(Crash Time)、正常成本(Normal Cost)、赶工成本(Crash Cost)、实际成本(Actual Cost)、完成的百分比(Percent Complete)第2步:输入数据单击“OK”,并输入数据:紧前活动(Immediate Predecessor):输入活动编号,多个紧前活动用逗号“,”分开。
第3步:求解从系统菜单选择“Solve and Analyze Solve Critical Path”,生成如下运行结果:运行结果中:关键线路(On Critical Path):“yes”为关键线路、“No”为非关键线路;最早开始时间(Earliest Start):表示紧前活动已完成,可以开始的时刻;最早完成时间(Earliest Finish):表示最早可以完成的时刻;最迟开始时间(Latest Start):表示不影响后续活动开始的最迟开始时刻;最迟完成时间(Latest Finish):表示在最迟开始时刻开始经过活动时间而完成的时刻;富余时间(Stack):富余时间为0的为关键线路。
用WinQSB 求解决策问题1

*** 用WinQSB 求解决策问题一、介绍如何使用WinQSB计算相关的决策问题。
WinQSB软件用于决策分析的子程序是“Decision Analisis”。
见图10.16。
图10.16主菜单的内容分别是:贝叶斯分析、支付表分析、二人零和博弈和决策树分析。
读者可根据需要按标题前的按钮。
计算机默认贝叶斯分析。
一.收益表分析例。
对下列收益矩阵的进行决策。
表10.23第1步:生成表格选择“程序→winQSB→Decision Analysis→File→New Program”图10.17问题类型((Problem Type):收益表分析(Payoff Table Analysis)自然状态数(Mumber of the States of Nature):3决策方案数(Number of Decision Alternatives):3 第2步:输入数据单击“OK”,并输入数据:表10.24第3步:求解从系统菜单选择“Solve and Analyze Solve Critical Path”,生成如下运行结果:表10.25即:悲观准则(Maximin):最优方案:3,决策值:10乐观准则(Maximax):最优方案:1,决策值:60乐观系数准则(Hurwicz):最优方案:1,决策值:27最小后悔值准则(Minimax Regret):最优方案:1,决策值:16等概率准则(Equal Likelibook):最优方案:1,决策值:21.33期望后悔值(Expected Regret):最优方案:1,决策值:10.7无信息期望值(Expected V alue without any Information):21.8完全信息期望值(Expected V alue with Perfect Information):32.5信息的价值(Expected V alue of Perfect Information):10.7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3步:求解 点击工具栏中的“Solve and Analyze”—“Solve the Problem”,得到下面 的计算结果。其结论是:选择建大厂,期望收益360万元。
表10.28
如果想画出本问题的决策树,可点击工具栏中的“Solve
and
Analyze”“Draw Decision Tree”或点击符号
,就会出现下面的决策树图。
图10.19
合对应的年收益见表10-23。试用决策树进行决策。
表10.26 (万元)
收
益
需求高 需求一般 需求
低
建大厂
100 60 -20
建小厂
状 态 方 案
25 45 55
第1步:生成表格 在问题类型(Problem Type)中选择决策树分析(Decision Tree Analisis),出现下面的表格。
*** 用WinQSB 求解决策问题2
.决策树分析
例: 某公司需要决定资为280万元,建小厂的投资为140万
元。估计10年内销售状况的概率分布是:需求高的概率为0.5,需求一
般的概率为0.3,需求低的概率为0.2。不同工厂规模和市场需求量的组
图10.18 在表格中填写问题的题目(Problem Title),以及决策树中点(或事 件)的个数,其中包括终点的个数。本例中有一个决策点,两个机会 点,此外还有六个端点,总共有九个点。 第2步:输入数据 单击“OK”并输入数据。
表10.27
在第一列中将九个点进行编号,在第二列中决策点标D,机会点及各 分枝的端点标C,在第三列中,写出每一个点后面紧跟着的点的编号, 第四列填写收益值,负值表示损失值,第五列填写机会分枝发生的概 率。
