反比例函数图象导学单
反比例函数的图像与性质导学案

5.2 反比例函数的图象与性质(一)学习目标1.会作反比例函数的图象。
2.能从函数图象中获取信息,指导反比例函数的主要性质。
回顾交流1、请举一个一次函数的例子 正比例函数的例子2、一次函数的图象是 作函数图像的一般步骤是3、下列关系是反比例函数的是 (1)圆的周长C 与圆的半径R ; (2)圆的面积S 与圆的半径R ;(3)汽车从A 地到B 地所需的时间t 与平均速度v ; (4)当电池的电压一定时,电阻R 与电流强度I 。
4、请举一个反比例函数的例子 反比例函数的图像是直线吗? 它会不会和坐标轴相交呢?为什么? 自学探究你能画出xy 4-=的图象吗?x -8 -4 -3 -2 -1 -0.5 0.5 1 2 3 4 8xy 4-=议一议(1)你认为作反比例函数图象时应注意哪些问题?(2)在连线时必须用 连接各点。
曲线的发展趋势是(3)观察x y 4=和xy 4-=的图象,它们有什么相同点和不同点? 总结:反比例函数图像的性质:反比例函数y = xk的图象是(1) 当 k>0 时,两支曲线分别位于第___、___象限, (2) 当 k<0 时,两支曲线分别位于第___、___象限. 练习巩固1.己知函数 的图象是双曲线,且y 随x 的增大而增大,则m=______;2.若M(2,2)和N(b,-1-n2)是反比例函数 图象上两点,则此函数的图象在第__________象限. 3.如果反比例函数xmy 41-=的图象位于第二、四象限,那么m 的范围为 . 4.所受压力为F (F 为常数且F ≠ 0) 的物体,所受压强P 与所受面积S 的图象大致为( )5.反比例函数 2k y x= (0≠k )的图象位于 ( )(A ) 第一、二象限 (B ) 第一、三象限 (C ) 第二、四象限 (D ) 第一、四象限 回顾总结本节课主要内容是反比例函数的图像,你能说出它的图像的特点吗?()2212--=m x m y x ky =反馈练习 1.反比例函数xy 4=的图象是________,过点(2-,____),其图象分布在_ __象限; 2.已知y 与x 成反比例,当1=y 时,4=x ,则当2=x 时,_____=y ;3.反比例函数和正比例函数的图象都经过点A(1-,2-),则这两个函数的解析式分别是_________和_________;4.某厂有煤1500吨,这些煤能用的天数y 与每天用煤的吨数x 之间的函数关系式为_______ 5.下列等式中,哪个等式表示y 是x 的反比例函数 ( ) (A ) k y x =(B ) 23y x = (C ) 121y x =+ (D ) 21xy -= 6.已知反比例函数的图象经过点(1,2),则它的图象也一定经过 ( ) (A ) (1-,2-) (B ) (1-,2) (C ) (1,2-) (D ) (2-,1)7.反比例函数 2k y x= (0≠k )的图象位于 ( )(A ) 第一、二象限 (B ) 第一、三象限 (C ) 第二、四象限 (D ) 第一、四象限 8.如图,反比例函数ky x=的图象经过点A ,则k 的值是 ( ) (A ) 2 (B ) 1.5 (C ) 3- (D ) 32-9.点A 为反比例函数图象上一点,它到原点的距离为5,到x 轴的距离为3,若点A 在第二象限内,则这个反比例函数的解析式为 ( ) (A ) 12y x =(B )12y x =- (C ) 112y x = (D ) 112y x=- 10.反比例函数my x=的图象分布在第二、四象限,则点(m ,2-m )在 ( ) (A ) 第一象限 (B ) 第二象限 (C ) 第三象限 (D ) 第四象限 11.若函数21(31)n n y n x --=-是反比例函数,且它的图象在二、四象限内,则n 的值是( )(A )0 (B ) 1 (C ) 0或1 (D ) 非上述答案 12.已知12y y y =+,其中1y 与1x成反比例且比例系数为1k ,2y 与2x 成正比例且比系数为2k ,若1-=x 时,0=y ,则1k 与2k 的关系为 ( ) (A ) 12k k =- (B ) 12k k ≠ (C ) 121k k =- (D ) 12k k = 提升能力已知正比例函数y kx =与反比例函数3y x=的图象都过A(m ,1)点.求: (1)正比例函数的解析式;(2)正比例函数与反比例函数的另一个交点的坐标.。
新北师大版九年级数学上册《反比例函数的图像》导学案

新北师大版九年级数学上册《反比例函数的图像》导学案1.作函数图象的一般步骤是:__列表,描点,连线__.2.反比例函数y =kx的图象是由__两支曲线__组成的.当k >0时,两支曲线分别位于第__一、三__象限内;当k <0时,两支曲线分别位于第__二、四__象限内.3.反比例函数的图象既是__轴对称__图形,又是__中心对称__图形,其对称轴为直线__y =x 或y =-x __,其对称中心为__原点__.知识点一:反比例函数的图象1.(2014·淮安)若反比例函数y =kx的图象经过点(5,-1),则双曲线位于( B )A .第一、三象限B .第二、四象限C .第一、四象限D .第二、三象限2.(2014·兰州)若反比例函数y =k -1x的图象位于第二、四象限,则k 的取值可以是( A )A .0B .1C .2D .以上都不是3.已知反比例函数y =m -1x的图象的一支位于第一象限,则常数m 的取值范围是__m>1__.4.画出反比例函数y =6x 和y =-6x的图象.解:略知识点二:根据图象确定反比例函数的表达式5.如图是我们学过的反比例函数,它的函数表达式可能是( B )A .y =x 2B .y =4xC .y =-3xD .y =12x,第5题图) ,第6题图)6.如图,已知OA =6,∠AOB =30°,则经过点A 的反比例函数的表达式为( B )A .y =-93xB .y =93xC .y =9xD .y =-9x7.(2014·怀化)已知点A(-2,4)在反比例函数y =kx(k ≠0)的图象上,则k 的值为__-8__.知识点三:利用反比例函数求点的坐标8.若反比例函数y =8x的图象经过点(-2,m ),则m 的值是( C )A.14 B .-14C .-4D .4 9.反比例函数y =-6x的图象是轴对称图形,它的对称轴有( B )A .1条B .2条C .3条D .4条10.反比例函数y =kx(k >0)的图象与经过原点的直线l 相交于A ,B 两点,已知A 点的坐标为(2,1),那么B 点的坐标为__(-2,-1)__.11.当x >0时,函数y =-5x的图象在( A )A .第四象限B .第三象限C .第二象限D .第一象限12.(易错题)已知函数y =(m +1)xm 2-5是反比例函数且图象位于第二、四象限内,则m 的值为( B )A .2B .-2C .±2D .-1213.(2014·聊城)如图,一次函数y 1=k 1x +b 的图象和反比例函数y 2=k 2x的图象交于A(1,2),B(-2,-1)两点,若y 1<y 2,则x 的取值范围是( D )A .x <1B .x <-2C .-2<x <0或x >1D .x <-2或0<x <114.已知一个函数图象与y =6x 的图象关于y 轴对称,则这个函数的表达式为__y =-6x__.15.如图,在平面直角坐标系xOy 中,正比例函数y =kx 的图象与反比例函数y =2x的图象有一个交点A (m ,2).(1)求m 的值;(2)求正比例函数y =kx 的表达式;(3)试判断点B (-2,-1)是否在反比例函数的图象上,并说明理由.解:(1)m =1(2)正比例函数y =kx 的表达式为y =2x (3)点B (-2,-1)在反比例函数图象上,∵当x =-2时,y =2-2=-1,∴点B (-2,-1)在双曲线y =2x上16.如图,一次函数y =kx +b 的图象与反比例函数y =mx的图象相交于A (-2,1),B (1,n )两点.(1)求反比例函数与一次函数的表达式;(2)根据图象写出当一次函数的值大于反比例函数的值时,x 的取值范围.解:(1)把A (-2,1)代入y =m x ,得m =-2.即反比例函数为y =-2x ,则n =-21=-2.即B (1,-2).把A (-2,1),B (1,-2)代入y =kx +b ,求得k =-1,b =-1.∴一次函数的表达式为y =-x -1 (2)x<-2或0<x<117.已知,反比例函数y =kx和一次函数y =2x -1,其中一次函数的图象经过点(k ,5).(1)试求反比例函数的表达式;(2)若点A 在第一象限,且同时在上述两函数的图象上,求A 点的坐标.解:(1)一次函数y =2x -1的图象经过点(k ,5),∴5=2k -1,解得k =3.所以反比例函数的表达式为y =3x (2)把y =3x 代入y =2x -1得3x =2x -1,解得x 1=-1(因为点A 在第一象限,故舍去),x 2=32.当x =32时,y =2,∴A 点坐标为(32,2)18.如图,点A (1,a )在反比例函数y =3x(x >0)的图象上,AB 垂直于x 轴,垂足为点B ,将△ABO 沿x 轴向右平移2个单位长度,得到Rt △DEF ,点D 落在反比例函数y =kx(x >0)的图象上.(1)求点A 的坐标; (2)求k 的值.解:(1)∵点A (1,a )在y =3x 的图象上,∴a =31=3.∴点A (1,3) (2)∵△ABO 向右平移2个单位长度,得到△DEF ,∴D (3,3).∵点D 在y =k x (x>0)的图象上,∴3=k3.∴k =9第2课时 反比例函数的性质1.反比例函数y =kx,当k >0时,图象的两个分支分别位于第__一、三__象限,在每个象限内,y 随x 的增大而__减小__;当k <0时,图象的两个分支分别位于第__二、四__象限,在每个象限内,y 随x 的增大而__增大__.2.过反比例函数y =kx图象上任意一点P (x ,y )作x 轴,y 轴的垂线,所得矩形的面积为__|k|__.知识点一:反比例函数图象的性质1.如果反比例函数y =kx(k ≠0),当x >0时,y 随x 的增大而增大,则反比例函数的图象经过( B )A .第一、三象限B .第二、四象限C .第一、四象限D .第二、三象限2.(2014·随州)关于反比例函数y =2x的图象,下列说法正确的是( D )A .图象经过点(1,1)B .两个分支分布在第二、四象限C .两个分支关于x 轴对称D .当x <0时,y 随x 的增大而减小3.(2014·天津)已知反比例函数y =10x,当1<x<2时,则y 的取值范围是( C )A .0<y <5B .1<y <2C .5<y <10D .y >104.点(2,y 1),(3,y 2)在函数y =-2x的图象上,则y 1__<__y 2.(填“>”“<”或“=”)5.已知反比例函数y =m -2x的图象上有两个点A (x 1,y 1),B (x 2,y 2)且0<x 1<x 2时,y 1>y 2,则m 的取值范围是__m>2__.6.反比例函数y =(2m -1)xm 2-2,当x >0时,y 随x 的增大而增大,求m 的值. 解:根据题意,m 2-2=-1,解得m =±1.∵当x>0时,y 随x 的增大而增大,∴2m-1<0.解得m<12.∴m =-1知识点二:反比例函数图象中比例系数k 的几何意义7.如图,正方形OABC ,正方形ADEF 的顶点A ,D ,C 在坐标轴上,顶点F 在AB 上,顶点B ,E 在函数y =1x(x >0)的图象上,则点E 的坐标是( A )A .(5+12,5-12)B .(3+52,3-52)C .(5-12,5+12)D .(3-52,3+52)8.(2014·黔东南)如图,正比例函数y =x 与反比例函数y =2x的图象相交于A ,B 两点,BC ⊥x 轴于点C ,则△ABC 的面积为( B )A .1B .2C .3D .4,第8题图) ,第9题图)9.如图,点A 在双曲线y =kx上,AB ⊥x 轴于点B ,△ABO 的面积是2,则k =__-4__.10.(2014·怀化)已知一次函数y =kx +b 的图象如图,那么正比例函数y =kx 和反比例函数y =kx在同一坐标系中的图象大致是( B )11.(2014·湘潭)如图,点A ,B 在双曲线y =4x上,分别经过A ,B 两点向坐标轴作垂线段,已知S 阴影=1,则S 1+S 2=( D )A .3B .4C .5D .612.(易错题)已知点A(1,y 1),B(2,y 2),C(-3,y 3)都在反比例函数y =6x的图象上,则y 1,y 2,y 3的大小关系是( D )A .y 3<y 1<y 2B .y 1<y 2<y 3C .y 2<y 1<y 3D .y 3<y 2<y 113.已知(x 1,y 1),(x 2,y 2)为反比例函数y =kx图象上的点,当x 1<x 2<0时,y 1<y 2,则k的一个值可为__-1(只要k<0即可)__.(只需写出符合条件的一个k 的值)14.如图,一次函数y =x +b 与反比例函数y =kx在第一象限的图象交于点B ,且点B的横坐标为1,过点B 作y 轴的垂线,C 为垂足,若S △BCO =32,求一次函数和反比例函数的表达式.解:∵一次函数y =x +b 过点B ,且点B 的横坐标为1,∴y =1+b ,即B (1,1+b ).∵BC ⊥y 轴,且S △BCO =32,∴12×OC ×BC =12×1×(b +1)=32,解得b =2.∴B (1,3),∴一次函数的表达式为y =x +2.又∵y =k x 过点B ,∴k =3.∴反比例函数的表达式为y =3x15.(2014·苏州)如图,已知函数y =kx(x>0)的图象经过点A ,B ,点A 的坐标为(1,2),过点A 作AC ∥y 轴,AC =1(点C 位于点A 的下方),过点C 作CD ∥x 轴,与函数的图象交于点D ,过点B 作BE ⊥CD ,垂足E 在线段CD 上,连接OC ,OD.(1)求△OCD 的面积;(2)当BE =12AC 时,求CE 的长.解:(1)y =kx(x>0)的图象经过点A (1,2),∴k =2,∵AC ∥y 轴,AC =1,∴点C 的坐标为(1,1).∵CD ∥x 轴,点D 在函数图象上,∴点D 的坐标为(2,1).∴S △OCD =12×1×1=12 (2)∵BE =12AC ,∴BE =12,∴B (43,32),∴CE =43-1=1316.(2014·遂宁)已知:如图,反比例函数y =kx的图象与一次函数y =x +b 的图象交于点A(1,4),点B(-4,n).(1)求一次函数和反比例函数的表达式; (2)求△OAB 的面积;(3)直接写出一次函数值大于反比例函数值的自变量x 的取值范围.解:(1)把点A (1,4)分别代入反比例函数y =kx ,一次函数y =x +b ,得k =1×4,1+b =4,解得k =4,b =3,反比例函数的表达式是y =4x,一次函数表达式是y =x +3 (2)当x =-4时,y =-1,B (-4,-1),当y =0时,x +3=0,x =-3,设直线AB 交x 轴于点C ,C (-3,0),S △AOB =S △AOC +S △BOC =12×3×4+12×3×1=152(3)∵B (-4,-1),A (1,4),∴根据图象可知:当x>1或-4<x<0时,一次函数值大于反比例函数值专题(十五) 反比例函数与不等式1.已知A (-1,y 1),B (2,y 2)两点在双曲线y =3+2mx上,且y 1>y 2,则m 的取值范围是( D )A .m <0B .m >0C .m >-32D .m <-322.(2014·黔西南)已知如图,一次函数y =ax +b 和反比例函数y =kx的图象相交于A ,B两点,不等式ax +b>kx的解集为( B )A .x <-3B .-3<x <0或x >1C .x <-3或x >1D .-3<x <13.(2014·南充)如图,一次函数y 1=kx +b 的图象与反比例函数y 2=mx的图象相交于点A(2,5)和点B ,与y 轴相交于点C(0,7).(1)求这两个函数的表达式; (2)当x 取何值时,y 1<y 2.解:(1)∵反比例函数y 2=m x 的图象过点A (2,5),∴5=m2,m =10,即反比例函数的表达式为y =10x,∵一次函数y 1=kx +b 的图象过点A (2,5)和C (0,7),∴b =7,k =-1,即一次函数表达式为y =-x +7(2)解方程组⎩⎪⎨⎪⎧y =-x +7,y =10x ,得⎩⎨⎧x 1=2,y 1=5,或⎩⎨⎧x 2=5,y 2=2,∴另一交点B 的坐标为(5,2),根据图象可知,当0<x<2或x>5时,y 1<y 24.(2014·巴中)如图,在平面直角坐标系xOy 中,已知四边形DOBC 是矩形,且D(0,4),B(6,0).若反比例函数y =k 1x(x>0)的图象经过线段OC 的中点A ,交DC 于点E ,交BC于点F.设直线EF 的表达式为y =k 2x +b.(1)求反比例函数和直线EF 的表达式; (2)求△OEF 的面积;(3)请结合图象直接写出不等式k 2x +b -k 1x>0的解集.解:(1)∵四边形DOBC 是矩形,且D (0,4),B (6,0),∴C 点坐标为(6,4),∵点A为线段OC 的中点,∴A 点坐标为(3,2),∴k 1=3×2=6,∴反比例函数表达式为y =6x,把x =6代入y =6x 得x =1,则F 点的坐标为(6,1),把y =4代入y =6x 得x =32,则E 点坐标为(32,4),把F (6,1),E (32,4)代入y =k 2x +b 得⎩⎪⎨⎪⎧6k 2+b =1,32k 2+b =4,解得⎩⎪⎨⎪⎧k 2=-23,b =5∴直线EF 的表达式为y =-23x +5 (2)△OEF 的面积=S 矩形BCDO -S △ODE -S △OBF -S △CEF =454 (3)不等式k 2x +b -k 1x >0的解集为32<x<65.(2014·德阳)已知一次函数y 1=x +m 的图象与反比例函数y 2=6x的图象交于A ,B 两点.已知当x>1时,y 1>y 2;当0<x<1时,y 1<y 2.(1)求一次函数的表达式;(2)已知反比例函数图象在第一象限上有一点C 到y 轴的距离为3,求△ABC 的面积. 解:(1)一次函数表达式为:y 1=x +5 (2)由题意得C (3,2),联立⎩⎪⎨⎪⎧y =x +5,y =6x解得⎩⎨⎧x 1=1,y 1=6,⎩⎨⎧x 2=-6,y 2=-1,∴B (-6,-1),作CD ∥x 轴交AB 于点D ,则点D 的坐标为(-3,2),CD =3-(-3)=6,∴S △ABC =S ADC +S △BDC =12×6×4+12×6×3=21专题(十六) 反比例函数与一次函数的综合一、反比例函数与正比例函数1.(2014·益阳)正比例函数y =6x 的图象与反比例函数y =6x的图象交点位于( D ) A .第一象限 B .第二象限C .第三象限D .第一、三象限2.已知直线y =kx (k >0)与双曲线y =3x交于点A (x 1,y 1),B (x 2,y 2)两点,则x 1y 2+x 2y 1的值为( A )A .-6B .-9C .0D .9二、反比例函数与一次函数3.(2014·咸宁)如图,双曲线y =m x与直线y =kx +b 交于点M ,N ,并且点M 的坐标为(1,3),点N 的纵坐标为-1,根据图象信息可得关于x 的方程m x=kx +b 的解为( A ) A .-3,1 B .-3,3C .-1,1D .-1,34.如图,在平面直角坐标系xOy 中,函数y =4x(x >0)的图象与一次函数y =kx -k 的图象的交点为A (m ,2).(1)求一次函数的表达式;(2)设一次函数y =kx -k 的图象与y 轴交于点B ,与x 轴交点为C ,若点P 是x 轴上一点,且满足△P AB 的面积是4,直接写出P 点的坐标.解:(1)将A (m ,2)代入y =4x(x>0)得,m =2,则A 点坐标为A (2,2),将A (2,2)代入y =kx -k 得2k -k =2,解得k =2,则一次函数表达式为y =2x -2 (2)∵一次函数y =2x -2与x 轴的交点为C (1,0),与y 轴的交点为B (0,-2),S △ABP =S △ACP +S △BPC ,∴12×2CP +12×2CP =4,解得CP =2,则P 点坐标为(3,0),(-1,0)5.(2014·广东)如图,已知A(-4,12),B(-1,2)是一次函数y =kx +b 与反比例函数y =m x(m ≠0,m<0)图象的两个交点,AC ⊥x 轴于点C ,BD ⊥y 轴于点D. (1)根据图象直接回答:在第二象限内,当x 取何值时,一次函数大于反比例函数的值?(2)求一次函数表达式及m 的值;(3)P 是线段AB 上的一点,连接PC ,PD ,若△PCA 和△PDB 面积相等时,求点P 坐标.解:(1)由图象可知,当-4<x<-1时,一次函数大于反比例函数的值 (2)y =kx +b 的图象过点(-4,12),(-1,2),则⎩⎪⎨⎪⎧-4k +b =12,-k +b =2,解得⎩⎨⎧k =12,b =52,一次函数的表达式为y =12x +52,反比例函数y =m x的图象过点(-1,2),m =-1×2=-2 (3)连接PC ,PD ,如图,设P (x ,12x +52).由△PCA 和△PDB 面积相等得12×12×(x +4)=12×1×(2-12x -52),得x =-52,y =12x +52=54,∴P 点坐标为(-52,54)。
《反比例函数的图象和性质》导学案

【探究二】
画出反比例函数 y 4 和 x
y 4的函数图象。 x
描点法
列
描
连
表
点
线
【探究三】
4 fx =
x -4 gx = x
y4 x
-15
-10
-5
反比例函数的图象是 由两支曲线组成的. 因此称反比例函数的 图象为双曲线;
1、这几个函数图
象有什么共同点?
谢 谢大家
10
2、函数图象分别
8
位于哪几个象限?
6 4
y4 x
3、y随的x变化 有怎样的变化?
2
5
10
15
-2
-4
-6 当k>0时,两支双曲线分别 -8 位于第一,三象限内;
当k<0时,两支双曲线分别 位于第二,四象限内;
猜想
反比例函数的图象性质见下表:
y= k
K>0
K<0
x
图 象
当k>0时,函Biblioteka 图象 当k<0时,函数图象• 4.若函数 y 2xm 是反比例函m=______
• 5.反比例函数 y= 4 ,经过点(1,_ _),
其中4叫比例 x
.
新知探究
1.自学:课本P56—58 2.探究 要求:完成下列探究问题 方法:独立画图,认真思考,交流想法 时间:15分钟
【探究一】
• 作出一次函数 y 4x 的图象,图象是什么形状
(2)若在每一象限内,y随x增大而增大,则k_>__4____.
3.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽 车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
17.1.2反比例函数的图像和性质 精品导学案

反比例函数的图像和性质(1)导学案学习目标1.会画反比例函数图象,理解反比例函数的图象和性质.2.感悟“数形结合”、“变化与对应”和“转化”的数学思想,并能应用数形结合和转化思想根据反比例函数的图象探究其性质.学习重点:1、反比函数的图像画法2、反比例函数的性质。
学习难学习难点:反比例函数的性质。
一、知识链接:(忆一忆)(注意:这里第1、2题要学生在上课前写在黑板上,可以多写几组,上课时,老师要稍微点一下。
为下面探究反比例函数的性质做一个铺垫。
3、4题问一下就可以了。
)1、函数做图的步骤是___________、_______________、____________。
2、正比例函数的性质填写下表:3、正比例函数的图像和性质是怎么得到的?是如何研究的?(经过哪几个步骤)4、反比例函数的表达式 ___________________________解析式中自变量x的取值能为0吗?为什么______________________、二、合作探究、展示交流1、做一做(展示)问题:反比例函数的图像是什么样的?画出下列函数图像①y=10/x y=8/x y=6/x(注意每两个小组做一个)做图应该注意的几点:(注意这里是学生在做图时思考的问题,教师在讲解时也要让学生进行口答)(1)列表时取值应注意什么?x的取值能为零吗?为什么?(2)连线时应该注意什么?(3)反比例函数图像还是直线吗?是什么?(4)图像和坐标轴有交点吗?为什么?(这里需要小组合作探究一下,从图像中和解析式中一起来考虑)2、议一议(这是小组合作的部分,要求小组成员合作完成)问题一:(1)观察前三个函数的解析式有什么共同点:(2)观察前三个函数图像有什么共同点:有哪些特征?你能填写下表吗?3)当取不同大于0的值时,上述结论是否适用于所有的反比例函数?(注意:这里需要教师用几何画板演示,还有要学生从解析式来分析所有的函数都符合这一规律)问题二:做出下列反比例函数的图像:④y=-6/x ⑤y=-8/x ⑥y=-10/x (注意每两个小组做一个)(4)观察后三个函数解析式有什么共同点:(5)观察后三个函数的图像有什么共同点:你能填写下表吗?(6)当取不同小于0的值时,上述结论是否适用于所有的反比例函数?问题三:(7)前三个函数解析式和后三个函数解析式有什么不同?(k的取值范围不同)前三个函数图象和后三个函数图象有什么不同?由什么决定的?(8)你能总结出反比例函数图像的性质吗?在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
26.1.2反比例函数的图像和性质导学单(2)

九 年级 数学 学科 土城子中学问题导学单 课 题
26.1.2反比例函数的图像和性质(2) 设计者
张晓梅 审核者 潘明玲 学习时间 学生姓名 阅读教材7------8页,回答下列问题:
1.已知反比例函数的图象经过点(2,3).
(1)求这个函数解析式。
(2)这个函数的图象位于哪些象限?y 随x 的增大如何变化?
(3)点B(1,6) ,(-221
,-25
2),D(2,5)是否在这个函数的图象上?
2、如图,是反比例函数y=x m 5 的图象 的一支,根据图象回答下列问题:
(1)图象的另一支位于哪个象限?常数m
的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a , b)和点B(/a , /b ).如果a >/a ,那么b 和/b 有怎样的大小关系?
o x y。
反比例函数复习(一)导学单

反比例函数复习一、考点分布(近十年成都中考分析)二、考点精析考点一:反比例函数的图象与性质1.已知反比例函数y =kx 的图象经过点P (-1,2),则这个函数的图象位于( )A.第二、三象限B. 第一、三象限C. 第三、四象限D. 第二、四象限2.已知A (x 1,3)、B (x 2,6)都在反比例函数y =−3x 的图象上,则下列关系式一定正确的是( )A.021<<x xB.210x x <<C.012<<x xD.120x x << 3.已知反比例函数xy 3=,下列结论不正确的是( ) A.其图象经过点(3,1) B.其图象分别位于第一、三象限 C.当0>x 时,y 随x 的增大而减小 D.当1>x 时,3>y4.已知反比例函数xk y 1-=(k 是常数,1≠k )的图象有一支在第二象限,那么k 的取值范围是 5.如图所示,已知直线)0(11≠=k x k y 与反比例函数)0(22≠=k xky 的图象交于M,N 两点.若点M 的坐标是(1,2),则点N 的坐标是( )A.(-1,-2)B. (-1,2)C. (1,-2)D. (-2,-1)考点二:反比例函数中k 的几何意义6.如图,过x 轴上任意一点P 作y 轴的平行线,分别与反比例函数)0(3>=x xy ,)0(6->=x x y 图象交于A 点和B 点,若C 为y 轴上任意一点,连接AC 、BC,则ABC ∆的面积为第5题图第6题图7.在平面直角坐标系中,点A 是x 轴上任意一点,BC 平行于x 轴,分别交)0(3>=x xy 、)0(<=x xky 的图象于B 、C 两点,若ABC ∆的面积为2,则k 的值为( ) A. -1 B. 1 C. 21-D. 21 考点三:反比例函数与一次函数的综合8.已知一次函数)0(1≠+=k b kx y 与反比例函数)(02≠=m xmy 的图象如图所示,则当21y y >时,自变量x 满足的条件是( )A.31<<xB.31≤≤xC.1>xD.3<x9.如图,直线)0(3≠-=k kx y 与坐标轴分别交于点C 、B ,与双曲线)0(2<-=x xy 交于点)1,(m A ,则AB 的长是( )A. 52B.13C. 32D. 26三、考点突破例1.如图,已知反比例函数)0(≠=m xmy 的图象经过点)(4,1,一次函数b x y +-=的图象经过反比例函数图象上的点Q(-4,n ).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x 轴、y 轴交于A 、B 两点,与反比例函数图象的另一个交点为P 点,连接OP 、OQ ,求OPQ ∆的面积.即学即练:如图10,一次函数)0(1≠+=a b ax y 的图象与反比例函数)为常数,(02≠=k k xky 的图象交于A 、B 两点,过点A 作x AC ⊥轴,垂足为C ,连接OA ,已知OC =2,23tan =∠AOC ,)2-(,m B . (1)求一次函数和反比例函数的解析式; (2)结合图象直接写出:当21y y >时,x 的取值范围第9题图第7题图第8题图图10。
初中数学九年级下册《反比例函数的图象和性质》导学案

26.1.2 反比例函数的图象和性质第1课时 反比例函数的图象和性质学习目标:1.能用描点法画出反比例函数的图象.2.掌握反比例函数的图象和性质,并会用性质解决问题. 学习重难点:重点:反比例函数的图象和性质难点:理解反比例函数的性质,并能灵活运用 学习过程: 一、温故知新 1.反比例函数的反比例函数的表达式是 ____________ _______;解析式中自变量x 的取值能为0吗? 为什么?_______________ _______。
2.一次函数和二次函数的图象分别是 ,它们性质分别是: 。
3. 画函数图象的一般步骤是(1) ;(2) ;(3) 。
二、新知导学1. 活动一:在直角坐标系中画出下列函数的图像: 画出反比例函数y=x 6 和 y=-x6的图象 画图时注意:(1)列表时取值应注意什么?(2)连线时应该注意什么?(3)x 的取值能为零吗?图像和坐标轴有交点吗?为什么?2.合作探究探讨1.观察右面图形想想下列问题: (1)反比例函数xky的图象是 由 组成的.(通常称为 )(2)当k =6时,两支曲线分别位于第 象限内,在每一象限内......,y 值随 。
(3)当k =-6时,两支曲线分别位于第 象限内,在每一象限内......,y 值随 。
(4)y=x 6和y=-x6的图象关于 对称。
归纳:反比例函数( )的图像和性质:6y=x6y=-xk>0k<0反比例函数的图像是 ;当k >0时,双曲线的两支分别位于___ ___象限,在每个象限内y 值随x 值的增大而______;当k <0时,双曲线的两支分别位于__ ____象限,在每个象限内y 值随x 值的增大而______. 3.典例分析例.设函数y=(m-2)4-m x .当m 取何值时,它是反比例函数?它的图象位于哪些象限内?在每个象限内,当x 的值增大时,对应的y 值是随着增大,还是随着减小?跟踪练习:1.(上海·中考)在平面直角坐标系中,反比例函数 图象的两支分别在( )(A )第一、三象限 (B )第二、四象限 (C )第一、二象限 (D )第三、四象限2.反比例函数xy 2=的图象是 ,当x <0时,图象在第 象限。
九年级数学下册《反比例函数的图象和性质》导学案

26.1.2反比例函数的图象和性质【学习目标】知识与技能:1、会用描点法画反比例函数的图象2、结合图象分析并掌握反比例函数的性质过程与方法:1、通过描点法作图,体现数形结合的数学思想2、通过观察反比例函数的图象,分析,探究反比例函数的性质,体现从特殊到一般、分类讨论的数学思想,培养学生的探究、归纳及概括能力。
情感态度与价值观:1、通过学习反比例函数的图象,感知其图象的美。
2、通过研究反比例函数图象的性质,体会数学研究的严谨性,推理论证的逻辑美。
【学习重点】画反比例函数图象,理解并掌握反比例函数的图象和性质。
【学习难点】通过观察、分析,归纳出反比例函数的性质,并能灵活应用【学法指导】自主、合作、探究x x x x几何画板进行展示,学生通过观察,回答图象的特征。
完成表格: 反比例函数的图象和性质图象形状图像性质 (位置、变化趋势)论、自主探究,完成学习任务【课堂练习,巩固内化】1、下列图象中是反比例函数图象的是( )2、函数 的图象在第________象限,在每一象限内,y 随x 的增大而_________.3、函数 的图象在第________象限,在每一象限内,y 随x 的增大而_________.4、函数 ,当x>0时,图象在第____象限,y 随x 的增大而_________.5、已知反比例函数 (1)若函数的图象位于第一三象限, 则m_____________; (2)若在每一象限内,y 随x 增大而增大, 则m_____________.6、若反比例函数 (k <0)的图象上有两点 A (x 1,y 1),B (x 2,y 2),且 x 1>x 2>0,则 y 1、y 2 的大小关系是( ).A .y 1>y 2B .y 1<y 2C .y 1=y 2D . 不能确定变式1:若反比例函数 (k <0)的图象上有两点 A (x 1,y 1),B (x 2,y 2),且 x 1>x 2,则 y 1、y 2 的大小关系是( ).A .y 1>y 2B .y 1<y 2C .y 1=y 2D . 不能确定变式2:若反比例函数 (k <0)的图象上有三点 A (x 1,y 1),B (x 2,学生独立思考完成,通过练习得到进一步的巩固20y x =30y x =-y x π=xky =xm y -=4xk y =xky =请同学们试着将你所学的反比例函数的知识绘制成美丽的图案。
5.21反比例函数的图像与性质导学案

课题:5.21反比例函数图像与性质创编 王军 审核 姓名 班级 学习目标:1.进一步熟悉画函数图象的主要步骤,会画反比例函数的图象。
2.体会函数三种表示方法的相互转换,对函数进行认识上的整合。
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质 学习重点:掌握反比例函数的画图学习难点:画反比例函数的图象;并从函数图象中获取信息,探索并研究反比例函数的主要性质. 学习过程 一、知识回顾:1,画一次函数的图像有那几个步骤? 3、画出反比例函数y=6的图象思考:1、列表时所选取的数值不同,图像的形状相同吗?2、连线时能否连成折线,为什么必须用光滑的曲线连接各点3、曲线的发展趋势如何?那么你在今后画图像时,应注意那些问题?画出反比例函数y=-6的图象三、【总结提升】1、请同学们观察y=x 6和y=-x6的图象,回答问题:(1)你能发现它们的共同特点吗?(2)每个函数的图象分别位于哪几个象限?(3)在每个象限内,y 随x 的变化如何变化?说说你的理由。
如果把“在每个象限内”这几个字去掉,你同意吗?为什么?(4)每个函数的双曲线会与坐标轴相交吗?为什么?(5)比例函数y=x 6与y=-x 6的图象有什么关系?你是如何得出的? 2、反比例函数y=x k(k 为常数且k ≠0)图象与性质:(1)反比例函数y=x k的图像是 ;(2)反比例函数y=xk(k 为常数且k ≠0)性质:k>0时,双曲线的两支分别位于第_________象限,在每个象限内______________________________________________.k<0时,双曲线的两支分别位于第_________象限,在每个象限内_____________________________________________.当堂检测:1.如果函数22(1)m y m x -=-是反比例函数,那么m 的值是_________ ;2.已知函数1k y x+=的图象两支分布在第二、四象限内,则k 的范围是_________ 3.双曲线ky x=经过点(2-,3),则_____=k ; 4.若函数21(31)nn y n x --=-是反比例函数,且它的图象在二、四象限内,则n 的值是5,画出y=3/x 与y=-3/x 的图像。
第五章《反比例函数的图象与性质》单元复习导学案

九年级上期数学第五章《反比例函数的图象与性质》单元复习导学案一、反比例函数的概念:1.什么叫反比例函数?答: 的函数,叫做反比例函数。
2.反比例函数的表达式有以下三种形式:① ;② ;③ 。
二、反比例函数的图象与性质:1.反比例函数的图象是 线,它的两个分支无限接近 ,但永远不能 。
2.当0k >时,双曲线的 分别位于第 、 象限,在 内,y 随x 的增大而减小,图象呈 趋势;当0k <时,双曲线的 分别位于第 、 象限,在 内,y 随x 的增大而增大,图象呈 趋势。
3.反比例函数的图象既是 对称图形,又是 对称图形,它的对称中心是 ;当0k >时,它的对称轴是直线 ;当0k <时,它的对称轴是直线 。
4.由反比例函数的表达式xy k =可以得到:过反比例函数图象上任意一点分别作x 轴、y 轴的垂线,与坐标轴所围成的矩形的面积一定等于 (如图1)。
5.在反比例函数ky x=(0k ≠)中,当||k 越大时,双曲线的弯曲程度(即曲率)越 ,图象越 原点;当||k 越小时,双曲线的弯曲程度(即曲率)越 ,图象越 原点。
三、学以至用:1. 判定下列函数是不是反比例函数。
若是,在括号内打“√”,若不是,在括号内打“×”? ①22y x -=( );②1y -=( ); ③213y x =+( ); ④21y x =-( );⑤2y =( );⑥y = ); ⑦ 1(2)y m x -=-( ); ⑧ 22a y x --=( )。
(注:本小题中的x 是自变量,a 、m 是常数)2. (1)若函数224(1)k k y k x --=+是反比例函数,则k = ;(2)若反比列函数1232)12(---=k kx k y 的图象经过二、四象限,则k = 。
3. 设有反比例函数1k y x-=,(1x ,1y )、(2x ,2y )为其图象上的两点,若120x x <<时,12y y >,则k 的取值范围为 。
人教九年级下册数学-反比例函数的图象和性质导学案

26.1.2 反比例函数的图象和性质第1课时 反比例函数的图象和性质学习目标:1.能用描点法画出反比例函数的图象.2.掌握反比例函数的图象和性质,并会用性质解决问题.学习重难点:重点:反比例函数的图象和性质难点:理解反比例函数的性质,并能灵活运用学习过程:一、温故知新1.反比例函数的反比例函数的表达式是 ____________ _______;解析式中自变量x 的取值能为0吗? 为什么?_______________ _______。
2.一次函数和二次函数的图象分别是 ,它们性质分别是: 。
3. 画函数图象的一般步骤是(1) ;(2) ;(3) 。
二、新知导学1. 活动一:在直角坐标系中画出下列函数的图像:画出反比例函数y=x 6 和 y=-x6 的图象 画图时注意:(1)列表时取值应注意什么?(2)连线时应该注意什么?(3)x 的取值能为零吗?图像和坐标轴有交点吗?为什么?2.合作探究探讨1.观察右面图形想想下列问题:(1)反比例函数x k y 的图象是 6y=x 6y=-xk>0 k<0由 组成的.(通常称为 )(2)当k =6时,两支曲线分别位于第 象限内,在每一象限内......,y 值随 。
(3)当k =-6时,两支曲线分别位于第 象限内,在每一象限内......,y 值随 。
(4)y=x 6和y=-x6的图象关于 对称。
归:反比例函数( )的图像和性质:反比例函数的图像是 ;当k >0时,双曲线的两支分别位于___ ___象限,在每个象限内y 值随x 值的增大而______;当k <0时,双曲线的两支分别位于__ ____象限,在每个象限内y 值随x 值的增大而______.3.典例分析例.设函数y=(m-2)4-m x .当m 取何值时,它是反比例函数?它的图象位于哪些象限内?在每个象限内,当x 的值增大时,对应的y 值是随着增大,还是随着减?跟踪练习: 1.(上海·中考)在平面直角坐标系中,反比例函数图象的两支分别在( ) (A )第一、三象限 (B )第二、四象限(C )第一、二象限 (D )第三、四象限2.反比例函数xy 2=的图象是 ,当x <0时,图象在第 象限。
北师大版-数学-九年级上册-6.2 反比例函数的图像与性质(第1课时) 导学案
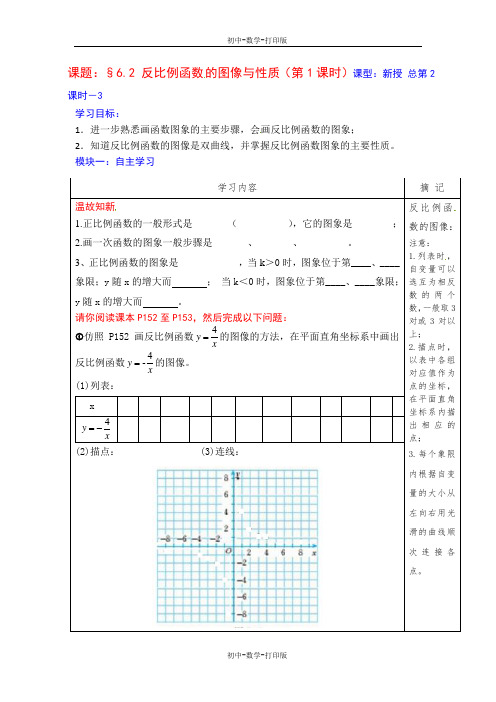
课题:§6.2 反比例函数的图像与性质(第1课时)课型:新授 总第2课时-3 学习目标:1.进一步熟悉画函数图象的主要步骤,会画反比例函数的图象;2.知道反比例函数的图像是双曲线,并掌握反比例函数图象的主要性质。
模块一:自主学习学习内容摘 记 温故知新1.正比例函数的一般形式是______ (__________),它的图象是________;2.画一次函数的图象一般步骤是_______、_______、_________。
3、正比例函数的图象是____________,当k >0时,图象位于第____、____象限;y 随x 的增大而 ; 当k <0时,图象位于第____、____象限;y 随x 的增大而 。
请你阅读课本P152至P153,然后完成以下问题: 仿照P152画反比例函数x y 4=的图像的方法,在平面直角坐标系中画出反比例函数x y 4-=的图像。
(1)列表: xx y 4-= (2)描点: (3)连线:反比例函数的图像: 注意:1.列表时,自变量可以选互为相反数的两个数,一般取3对或3对以上;2.描点时,以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点;3.每个象限内根据自变量的大小从左向右用光滑的曲线顺次连接各点。
模块二:交流研讨模块三:巩固内化研讨内容摘 记内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。
把你的修改意见在讲学稿上直接标注。
并按照组长的分工,每位同学选择一个内容向全组同学进行交流。
如有不同意见,直接提出或质疑。
内容二:判断下列函数的图像是否正确?若错误,请说明理由。
(1)x y 4=(2)xy 4= 内容三:观察x4y =和x4-y =的图象,回答下列问题。
(1)反比例函数是中心对称图形吗?如果是,请找出对称中心。
(2)反比例函数是轴对称图形吗?如果是,请找出对称轴。
(3)写出两个反比例函数的相同点和不同点;(4)反比例函数x4y =和x4-y =的图象分别在哪两个象限,由什么确定?注意:(1) 0x ≠;(2)连线时不能用折线,必须用光滑的曲线连接各点;(3)反比例函数的图像不是直线,不能用“两点法”作图; 图象是延伸的,不要画成有明确端点; (4)曲线的发展趋势是无限靠近坐标轴,但不和坐标轴相交。
新湘教版九年级上反比例函数图像性质导学案

新湘教版九年级上反⽐例函数图像性质导学案反⽐例函数学习⽬标1、理解并掌握反⽐例函数的概念;2、会根据实际问题中的条件确定反⽐例函数的解析式。
体验学习⼀、课前预学1、京沪线铁路全程为1463km ,则乘坐列车所⽤时间t (h )与该列车平均速度v (km/h )的关系式为_________________2、⼀个矩形草坪的⾯积为1000m 2,则草坪的长y (m )与宽x (m )的关系式为_________________ 3、在直流电路中,电压为220V ,则电流I (A )与电阻R (Ω)的关系式为_____________ 观察上述3个解析式,你发现了什么共同特征?归纳:如果两个变量y 与x 的关系可以表⽰成的形式,那么称y 是x 的反⽐例函数,其中x 是⾃变量,⾃变量x 的取值范围是;常数k (k ≠0)称为反⽐例函数的注意:反⽐例函数还可以记作为:三、新知应⽤问题⼀:下列关系式中y 是x 的反⽐例函数吗?如果是,⽐例系数是多少? (1)x y 4-= (2) xy 41-= (3)1--=x y(4)2011=xy (5)12+=x y (6)xy 12-=问题⼆:下列问题中,变量间的对应关系可以⽤怎样的函数表达式表⽰?并确定它们是否是反⽐例函数。
1、苹果每千克x 元,花10元钱可买y 千克的苹果;2、矩形的周长18㎝,较长的边y (㎝)随着较短的边x (㎝)的变化⽽变化;3、按每分钟xL 的速度向容积为150L 的⽔池中注⽔,注满⽔池需y min ;4、菱形ABCD 的⾯积为180㎡,那么对⾓线AC 的长y (m )随对⾓线BD 的长x (m )的变化⽽变化;问题三:若函数28)3(m x m y -+=是反⽐例函数,求m 。
四、课堂练习1.下列等式中,哪些是反⽐例函数(1)3x y =(2)x y 2-= (3)xy =21 (4)25+=x y(5)xy 23-= (6)31+=x y (7)y =x -42.当m 取什么值时,函数23)2(m x m y --=是反⽐例函数?五、课外作业1、写出下列问题中两个变量之间的函数关系式,并判断其是否为反⽐例函数. 如果是,指出⽐例系数k 的值.(1)底边为5cm 的三⾓形的⾯积y (cm 2)随底边上的⾼x (cm )的变化⽽变化;(2)某组有耕地⾯积200亩,⼈均占有耕地⾯积y (亩)随⼈⼝数量x (⼈)的变化⽽变化;2、下列哪些关系式中的y 是x 的反⽐例函数?如果是,⽐例系数是多少?(1)y =23 x ;(2)y =23x ;(3)xy +2=0;(4)xy =1;(5)x =23y .3、当_______=k 时,函数23)12(-+=k xk y 是反⽐例函数4、已知y 与x 成反⽐例,且当x =2时,y =3,求y 与x 之间的函数关系式?反⽐例函数的图像和性质(1)学习⽬标:1、会⽤描点法画反⽐例函数的图象;2、结合图象分析并掌握反⽐例函数的性质;体验学习:⼀、课前预学1、画函数图象的⼀般步骤是:。
北师大版九年级数学上精品导学案(可打印)6.1反比例函数导学单

九年级数学导学案班级:姓名: 【学习课题】§6.1 反比例函数【学习目标】1.理解反比例函数的概念,会求比例系数。
2.感受反比例函数是刻画世界数量关系的一种有效模型,能够列出实际问题中的反比例函数关系. 【学习重点】理解反比例函数的概念,会求比例系数。
【学习难点】正确列出实际问题中的反比例函数关系。
【学习过程】一、温故知新1、在某一变化过程中,不断变化的量叫,保持不变的量叫 .2、在某一变化过程中,如果一个变量(y)随着另一个变量(x)的变化而不断变化,那么x叫,y 叫 .3、一般地,在某个变化中,有两个变量x和y,如果给定一个x的值,相应地就确定了一个y的值,那么我们称y是x的 ,其中x叫 .4、函数的表示方法:、、。
5、若两个变量x,y的关系可以表示成 (k,b是常数,k≠0)的形式,则称y是x的一次函数(x为自变量,y为因变量).特别地,当常数b=0时,就成为: (k是常数,k≠0),称y是x的正比例函数。
6、一次函数与正比例函数之间的关系: 函数是特殊的函数.7、若每天背10个单词,那么所掌握的单词总y(个)与时间x(天)之间的关系函数式为。
8、小明原来掌握了150个单词,以后每天背10个单词,那么他所掌握单词总量y(个)与时间x(天)之间的关系式为。
9、九年级英语全册约有单词1200个,小明同学计划用x(天)全部掌握,那么平均每天需要记忆的单词量y(个)与时间x(天)之间的关系式为。
10、一个面积为6400㎡的长方形,那么花坛的长a(m)与宽b(m)之间的关系式为。
11、京沪高速公路长1262km,汽车沿京沪高速公路从上海驶往北京,汽车行完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的函数关系式为。
二、合作探究1、电流I、电阻R、电压U之间满足关系式 U=IR。
在照明电路中,正常电压U=220V。
(1)求I与R之间的函数关系式?(2)变量I是R的反比例函数吗?R(Ώ)20 60I(A) 2.22、在某一电路中,保持电压U(伏)不变,电流I(安)是电阻R(欧)的反比例函数,当电阻R=5欧时,电流I=2安。
