培优练习(附答案) -平面直角坐标系

合集下载

小学六年级小升初毕业语文培优试题(附答案解析)

小学六年级小升初毕业语文培优试题（附答案解析）书写展示。

请你将下面的句子抄写在横线上，要求规范、端正、整洁。

书香润泽童年，阅读丰富人生。

愿我们课余时间都能捧起书本，领略文字的魅力、汲取成长的力量。

_______________________下列加点的字注音完全正确的一项是（）A．档．（dàng）次给．（jǐ）予模．（mó）样惩．（chéng）罚B．潜．（qián）能歼．（jiān）灭造诣．（yì）膝．（qī）盖C．尽．（jǐng）管拖累．（lěi）亲戚．（qì）鲜血（xuè）D．躯壳．（qiào）称．（chēng）赞瞠．（chēng）目阿．（ē）谀下列各组词语没有错别字的一项是（）A．通宵达旦马踏飞燕完壁归赵弱不禁风B．别出新材守株侍兔吹毛求疵郑重其事C．阴谋鬼计谈笑风生无动于衷世外桃源D．断章取义德高望重根深蒂固如法炮制与诗句“遥望洞庭山水翠，白银盘里一青螺”运用的修辞手法相同的一项是（）A．留连戏蝶时时舞，自在娇莺恰恰啼。

B．谁道人生无再少？门前流水尚能西！C．可怜九月初三夜，露似真珠月似弓。

D．桃花潭水深千尺，不及汪伦送我情。

下列句子中，有语病的是哪一项？（）A．爷爷的菜园里种满了西红柿、桃子、青葱、大蒜等蔬菜。

B．忘不了家乡，忘不了家乡的小河，那是我成长的乐园。

C．春风化雨又一年，老王家的果园呈现出一派生机勃勃的景象。

D．在英勇的解放军面前，敌人只能落荒而逃。

下列句子中的标点符号使用不正确的一项是（）A．枣子必大了三四倍——要是真的干红枣也有那么大，那就妙极了！B．恐怕第三件事才是买各种玩意儿——风筝、空竹、口琴等。

C．“你过来，”名叫金百合的牛说：“我要让你在我的角上跳舞。

”D．我想：等革命胜利以后，一定要把它送到革命烈士纪念馆去，让我们的子子孙孙都来瞻仰它。

下列文学常识搭配有误的一项是（）A．《朝花夕拾》——鲁迅——现代B．《行路难》——李白——唐C．《饮湖上初晴后雨》——苏轼——宋D．《红楼梦》——曹雪芹——明下列句子的顺序排列最恰当的一项是（）①然后，它踩着哗哗流淌的江水，走到一块礁石上亲了又亲。

光的反射折射专题培优讲座(高难度选用)配套练习+考点分析+答案解析

1.如图所示，在竖直平面xOy内，人眼位于P（0,4）位置处，平面镜MN竖直放置其两端M、N的坐标分别为（3，1）和（3，0），某发光点S在该竖直平面y轴的右半部分某一区域内自由移动时，此人恰好都能通过平面镜看见S的像，则该区域的最大面积为（图中长度单位为：m）（）A．0.5m2 B．3.5m2C．4m2 D．4.5m2（考点：光的反射折射定理及应用）（答案:关键词：平面镜，最大面积重要知识：光的反射定律如图，连接MP、NP，根据光的反射定律，做出MP的入射光线AM，做出NP的入射光线BN，梯形ABNM是发光点S的移动范围．下底AB为2m，上底为1m，高为3m，根据梯形形面积公式得：×（1m+2m）×3m =4.5m2故选D．本题涉及到光的反射定律的作图，梯形面积的计算，把物理和数学结合起来，体现了学科间的综合)2.如图所示，在竖直平面xOy上，人眼位于坐标点（3，0）上，一块平面镜水平放置，介于坐标（0，3）和（﹣1，3）之间．今有一发光点P从坐标原点沿x轴负方向运动，此过程中P点在下列哪个区间运动时，人眼可以从平面镜中观察到P点的像（）A．0→﹣1区间B．﹣1→﹣3区间C．﹣3→﹣5区间D．﹣5→﹣∞区间（考点：光的反射折射定理及应用）（答案:关键词：平面镜，区间范围重要知识：平面镜成像的特点、原理、现象人眼位于坐标点（3，0）上，x坐标，x=3关于0对称点是﹣3，x=3关于﹣1对称点是﹣5，因为一块平面镜水平放置，所以发光点经过x轴[﹣3，﹣5]之间会被看到．故选C．若要看到物体在平面镜中的像，则需借助于边界光线，边界光线的公共部分即完整像的观察范围)3.如图，S为小电珠，它发出的光可看作由一点发出的。

S正对圆孔，到孔的距离为L，透过圆孔的光在后面的光屏上得到一个圆斑．若在孔上嵌一凸透镜，则光屏上立刻出现一个清晰的亮点，则该透镜的焦距、圆孔与光屏之间的距离可能为（）A．L2，L2 B．L2，L C．L，L D．L，2L（考点：光的反射折射定理及应用）（答案:关键词：小电珠，凸透镜重要知识：凸透镜成像规律及其探究实验由“光屏上立刻出现一个清晰的亮点”，可知亮点是发光点的等大的像，则根据凸透镜成像规律u=2f时，v=2f，可知L=2f，则该透镜的焦距f=L2，圆孔与光屏之间的距离即像距v=2f=L故选B．解答此题的关键是根据“光屏上立刻出现一个清晰的亮点”判断出此时物像等大)4.有一高度为H的田径运动员正在进行100米的比赛，在终点处，有一站在跑道旁边的摄影记者用照相机给他拍摄冲线运动，摄影记者使用的照相机的光圈（控制进光量的多少）是16，快门（曝光时间）是 s 160 ，得到照片后测得照片中人的高度为h ，胸前号码布上模糊部分的宽度是△L ，由以上数据可以知道运动员的（）A ．100m 成绩B ．冲线速度C ．100m 内的平均速度D ．人离照相机的距离（考点：光的反射折射定理及应用）（答案:关键词：运动员，速度重要知识：速度的计算A.100m 的成绩指的是总时间，运动员的运动过程是一个变速运动，故无法求得运动时间，故A 错误；B ．胸前号码上的模糊部分的宽度为△L ，即为两次曝光时运动员的底片上的位移，根据运动员底片上的高度和实际高度的比例即可求得两次曝光的实际位移为：x=△LH/h ，所以冲刺时的瞬时速度v=x/t=60△LH/h ，故B 正确；C.100m 内的平均速度等于总位移除以总时间，因无法求得时间，所以无法求出平均速度，故C 错误；D ．根据题目所给数据，求不出人离相机的距离，故D 错误；故选B ．运动员在整个比赛过程中速度是变化的，无法求得运动的总时间，但在冲刺阶段，非常短的时间内，可以用平均速度去代替瞬时速度)61.如图所示，一底面半径为R 的圆锥体，放在一焦距为f 的凸透镜的主光轴上，并使其对称轴与主光轴重合，顶和底面中心分别在焦点和2倍焦距处，圆锥体经透镜所成的像是（）A ．在透镜左侧，为圆锥面放大的虚像B ．在透镜右侧，为放大的圆锥形实像C ．在透镜右侧，为有限长圆柱形实像D ．在透镜右侧，为无限长圆柱形实像（考点：光的反射折射定理及应用）（答案:关键词：圆锥体，透镜重要知识：凸透镜成像规律及其探究实验由题意知，圆锥体的顶点和底面分别在焦点和2倍焦距处，其它部分在f 和2f 之间，所以可以成圆锥的实像，像在凸透镜的右侧，底面的像在右侧的2f 处，其它部分随着物距的减小，像增大，像距也增大，焦点处的顶点发出的光线经凸透镜将平行射出，所以顶点的像在无限远处，因此在透镜的右侧，成了一个无限圆柱体的实像．故选D．此题考查了学生对凸透镜成像特点的应用，要掌握成像特点与物距、像距之间的关系．)62.小明同学正对竖直的平面镜站立，小明的脸宽为18cm，小明两眼的距离为8cm，小明欲使自己无论闭上左眼还是右眼，都能用另一只眼睛从镜中看到自己的整个脸，则镜子的宽度至少为（）A．8cm B．10 cm C．13 cm D．26 cm（考点：光的反射折射定理及应用）（答案:关键词：平面镜，宽度重要知识：平面镜成像的特点、原理、现象如图所示，人的脸宽为AB等于18cm，两眼为C、D，CD=8cm，如果用左眼看完整的像需用PR之间的平面镜，如果用右眼看完整的像需用QS 之间的平面镜，所以无论闭上左眼或右眼都能看到完整的像需用PS之间的平面镜因PS=是梯形CDB′A′的中位线，则PS=(A′B′+CD)/2．因AB=A′B′=18cm．CD=8cm，所以PS=(18cm+8cm)/2=13cm.故选C．由平面镜成像特点确定了像的位置后，正确找出边界光线是解题的关键63.如图所示，一平面镜放在圆筒的中心处，平面镜正对筒壁上一点光源S，点光源发出一细光束垂直射向平面镜．平面镜从图示位置开始绕圆筒中心轴O匀速转动，在转动30°角时，点光源在镜中所成的像转过的角度θ1，照射到筒壁上的反射光斑转过的角度θ2，则（）A．θ1=30°，θ2=30°B．θ1=30°，θ2=60°C．θ1=60°，θ2=30°D．θ1=60°，θ2=60°（考点：光的反射折射定理及应用）（答案:关键词：平面镜，转过角度重要知识：光的反射定律如图所示，平面镜旋转30°，相当于入射角增大30°，则反射角和入射角的夹角为60°，即反射光线转过60°，所以，由左右两图的“虚像”的位置可知：点光源在镜中所成的像转过的角度为60°．故选D本题主要考查学生对光的反射定律的了解和掌握，通过画图解答，学生更容易理解，此题要求学生应具备一定的空间想象能力)64.有些电工仪表的刻度盘上有一个弧形缺口，缺口下面有一面镜子，它的作用是（）A．读数时使眼睛处于正确位置B．增加刻度盘的亮度C．检验仪表是否水平D．便于观察仪表的内部结构（考点：光的反射折射定理及应用）（答案:关键词：电工仪表，一面镜子重要知识：平面镜的应用仪表的指针比较细，容易产生误差，镜子对光线有反射作用，且光路是可逆的，读数时，眼睛看指针与镜子里的指针影像重叠，使得读数比较准确．故选A．本题主要考查的是平面镜在生活中的应用．)65.如图所示，两个平面镜相互垂直竖直放置，点光源在平面镜内成三个像，现让点光源S在水平面内沿圆周顺时针运动，则可以观察到镜子内的三个像（）A．全都做顺时针运动B．全都做逆时针运动C．一个顺时针运动，另外两个逆时针运动D．一个逆时针运动，另外两个顺时针运动（考点：光的反射折射定理及应用）（答案:关键词：平面镜，三个像重要知识：作光的反射光路图如图所示：现让点光源S在水平面内沿圆周顺时针运动，则镜子内的三个像中，S0、S′均做逆时针运动．S″是重合的像，相反了两次，应该做顺时针时针转动，故选项C正确．解答此题的关键是要明确平面镜成像的特点，像与物体是左右相反的)66.如图所示，在桌子边放一个三棱镜，在后面放上一支短蜡烛并点燃后我们只有蹲下身去才通过三棱镜看到烛焰，这是因为（）A．烛焰被三棱镜反射光所造成的B．光线通过三棱镜后会向下偏折C．这是烛焰光经三棱镜后成的实像D．以上说法都可能（考点：光的反射折射定理及应用）（答案:关键词：三棱镜，蜡烛重要知识：光的折射规律光先从空气斜射入玻璃，折射角小于入射角，光线会靠近法线；当光线从玻璃中射向空气时，折射角大于入射角，光线会远离法线．即光线通过三棱镜后会向下偏折．故选B．此题主要考查光的折射定律，根据折射定律判断折射光线与入射光线之间的关系)67.如图所示，凸透镜的下半部分被截去，其上半部分的高度为L．在其左焦点F 处放有高为L的发光物AB，在右焦点F'，处放有一平面镜MN．则关于AB通过凸透镜的成像情况，下列说法中正确的是（）A．成一个正立等大的虚像和一个正立放大的虚像B．成一个正立等大的虚像和一个倒立缩小的实像C．AB的上半部分成一个等大倒立的实像，下半部分不成像D．AB的下半部分成一个等大倒立的实像，上半部分不成像（考点：光的反射折射定理及应用）（答案:关键词：凸透镜，焦点重要知识：凸透镜成像的应用（1）如图（a）所示，取AB物体的中点P分析：从该点发光的光线，经凸透镜折射后，折射光线应为平行光，经平面镜反射后，反射光线仍为平行光．但所有这些光线的位置均在凸透镜光心以下，所以这些光线不可能直接会聚成像，也不可能通过凸透镜会聚成像．P点以上各点发出的光线，情况与P点相似，但反射光线的位置更要向下移．P点以下各点发出的光线，情况虽与P点也相似，但反射光线的位置向上移，这些平行光可经凸透镜第二次折射，折射光线应会聚在左侧焦平面上的某点处．（2）如图（b）所示，点Q发出的光线经凸透镜折射、平面镜反射、再经凸透镜折射后，在Q点正下方距主光轴相同距离的Q’处会聚成像，该像显然是倒立的、等大的．本题正确选项为D．故选D．本题可用作图法进行分析，取AB物体的中点P分析，P点以上各点发出的光线，P点以下各点发出的光线三种情况进行分析)68.如图所示，位于凸透镜主光轴上某发光点P发出红、黄、绿三色复光，当用与主光轴相垂直的毛玻璃屏从透镜附近沿轴方向向远移动时，在屏上将依次看到（）A．红、黄、绿亮点B．红、绿、黄亮点C．黄、红、绿亮点D．绿、黄、红亮点（考点：光的反射折射定理及应用）（答案:关键词：凸透镜，玻璃屏重要知识：凸透镜成像的应用凸透镜是玻璃制成的，同一个凸透镜，不同颜色的光波长不同，凸镜对其折射率不同．玻璃对绿光的折射率比红光大．也就是说，对于绿光的焦距比红光的小，绿黄红波长依此增大，折射率依此减小，所以在屏上将依次看到绿、黄、红亮点．故选D．根据不同颜色的光波长不同，凸镜对其折射率不同．绿黄红波长依此增大，折射率依此减小可作出选择)69.两平面镜AM、AN之间的夹角为90 °，凸透镜的主光轴恰好是该直角的角平分线，凸透镜的光心为O，A点恰好是凸透镜的焦点，光源S位于主光轴上，通过该系统，光源S所成的像为（）A．四个虚像，三个实像B．四个虚像，一个实像C．三个虚像，一个实像D．三个虚像，两个实像（考点：光的反射折射定理及应用）（答案:关键词：平面镜，凸透镜重要知识：平面镜成像的特点、原理、现象,凸透镜成像规律如图所示：①S通过两个平面镜成3个虚像，（因为其中两个重合了），分别是S1、S2、S3；②S1、S2分别在凸透镜的焦点处，则不能成像，只有S3在凸透镜的焦点以外，且通过凸透镜的光心，可以成一个实像S4；③S在凸透镜的焦点以内，由u＜f，成正立放大的虚像S′；综上分析，通过该系统，光源S所成的像有四个虚像，一个实像．故选B．注意区分光线经过凸透镜折射，是光线的实际会聚点，而平面镜是反射光线的反向延长线的会聚点)70.用普通照相机拍照时，要按被照物体距相机镜头的远近进行“调焦”，使用起来不太便捷．有一种“傻瓜”相机，只要把想拍摄的景物全部纳入取景器内，不论远处还是近处的物体，在照片上都比较清晰，从而使拍照的过程变得十分快捷．这种“傻瓜”相机不用“调焦”的奥秘是（）A．采用了长焦距的镜头，使远近不同的物体成像的位置相差不大B．采用了短焦距的镜头，使远近不同的物体成像的位置相差不大C．采用了长焦距的镜头，使远近不同的物体成像的位置相同D．采用了短焦距的镜头，使远近不同的物体成像的位置相同（考点：光的反射折射定理及应用）（答案:关键词：普通照相，调焦重要知识：生活中的透镜简易“傻瓜”照相机镜头的焦距不能改变，暗箱长度也不能改变．拍照时只要把景物全部纳入取景器内，无论物距如何变化，都能拍出比较清晰的照片，这主要是因为这种照相机的焦距小，物距都远大于2倍焦距，像距接近焦距，这样远近不同的物体成像的位置相差不大，所以不用调节．通过以上分析，只有选项B是正确的．故选B．本题主要考查学生对：凸透镜成像的应用的了解和掌握，以及物距远大于2倍焦距的时候，像距接近1倍焦距等知识点的理解和掌握)71.焦距为f1的凸透镜与焦距为f2的凹透镜的主光轴重合，光心间距为15cm．平行于主光轴的一束平行光通过两透镜后得到一束宽为d的平行光束，如图（a）所示，若将两透镜位置互换将得到一束宽度为4d的平行光束，由图（b）所示，则（）A．f1=30cm，f2=15cm B．f1=15cm，f2=15cmC．f1=30cm，f2=20cm D．f1=45cm，f2=30cm（考点：光的反射折射定理及应用）（答案:关键词：透镜；平行光束；宽度重要知识：凸透镜成像的应用设平行光束宽度为D，根据两个透镜焦点在透镜左侧重合，则有D：d=f1：f2①；由“焦距为f1的凸透镜与焦距为f2的凹透镜的主光轴重合，光心间为15cm”可得f1=15cm+f2 ②，由图（b）所示的两个透镜焦点在两透镜之间重合，则有D：4d=f2：f1 ③，由①②③解得：f1=30cm，f2=15cm．故选A.本题考查凹透镜对光的作用以及相似三角形对应边成比例的性质，属于一道跨学科的题目，综合性较强)72.如图所示，两平面镜OA和OB夹角为α，入射光线平行于OB镜且在两镜面间经12次反射后不再与镜面相遇．则两镜面之间的夹角α可能为（）A．13°B．14°C．15°D．16°（考点：光的反射折射定理及应用）（答案:关键词：两平面镜；入射光线；反射重要知识：平面镜成像的特点、原理、现象如图：反射一次反射角度较小α，第一次反射反射角90﹣α，第二次反射反射角90﹣2α…要想使光线反射12次，那么第六次反射光线不能垂直照在镜子A上（下面的那个图）要是垂直照在A上的话，根据光路可逆，要反射13次才能出去．第六次反射光线照在A上的入射角β，如果等于α，根据光路可逆原理，此后反射的光路和前六次的光路相同，最终会平行OA射出去．所以β可以等于αβ小于α反射12次也可以，只是最终光线射出时和OB成角小于α．α=β时根据三角形内角和是180,有α+6α+6β=180,α+6α+6α=180,13α=180解得：α=13.84β减小，α会变大，所以此时的α是最小值．如果反射6次后，在反射5次就射出镜子外的话，有α+6α+5β’=180α=β’时，刚好是平行OB射出．12α=180α=15，此时只能反射11次，所以α不能等于15．α的取值范围13.84＜α＜15故该角一定在大于13.8°与小于15°之间，所以B中的14°是正确的．故选B．此题主要考查了光的反射定律，结合平行线的性质和反射求解，此题体现了不同学科间是相互联系的特点)73.如果不慎在照相机的镜头上粘上一个灰尘颗粒（如图），那么拍摄的相片（）A．其上部将出现一个黑点B．其下部将出现一个黑点C．其上部和下部皆无黑点D．其上部和下部各出现一个黑点（考点：光的反射折射定理及应用）（答案:关键词：镜头上粘上一个灰尘颗粒重要知识：凸透镜成像规律及其探究实验当照相机的镜头上沾上一个黑点，还有另外的部分光线，经凸透镜折射会聚成像，像的大小不发生变化，折射光线减少，会聚成的像变暗故选C．本题主要考察凸透镜成实像时，无论遮住凸透镜的上部、下部、中间，都不能改变像的大小，但是像变暗，凸透镜遮住的越多，像越暗）74.如图所示，水平地面上有一不透光的边长为x的正方体物块．在正方体正左方有一点光源S，点光源和正方体物块的距离也为x．若在点光源S的上方距离为H处水平放置平面镜，H大小固定不变，平面镜足够大．不考虑其他光源的存在，那么在正方体的另一侧水平面上，将会由于点光源S发出的光线经平面镜反射而被照亮，现改变x的大小，当x增大到时，照亮区域将消失．（考点：光的反射折射定理及应用）（答案:关键词：点光源；平面镜；不透光正方体重要知识：光直线传播的应用本题考查了光的反射的应用，根据题意作出光路图，应用数学知识求解本题即可）75.无云的晴天，如果你在野外迷失了方向，可以在地平线上竖直立一根杆，地面上的OA是杆的影子，过了一段时间后，影子移到了OB位置，则AB箭头所指的方向为____方（选填“东”“南”“西”或“北”）．（考点：光的反射折射定理及应用）（答案:关键词：晴天；竖立一杆；影子重要知识：光沿直线传播的应用一天内，太阳从东方升起逐渐向西方移动，根据光的直线传播，影子会从西方逐渐向东方移动，所以OB在OA的东方，所以箭头所指的方向是东方．故答案为：东．根据太阳东升西落和光的直线传播，太阳在东方时，影子在西方，太阳在西方时，影子在东方即可解答．）76.某同学家的热水器的温度控制器未能正确安装，他从镜子里看到了如图所示的像，则此时显示的温度是_____，如果显示的温度是64℃，请在下面空格处画出通过镜子看到的数字的像_____．（考点：光的反射折射定理及应用）（答案:关键词：从镜子里看看到的像重要知识：平面镜成像的特点、原理、现象本题考查了镜面反射的原理与性质．解决此类题应认真观察，注意技巧）77.如图，AB表示一水平放置的平面镜，P1P2是水平放置的米尺（有刻度的一面朝着平面镜），MN是屏，三者互相平行．屏MN上的ab表示一条水平的缝（即a、b之间是透光的）．某人眼睛紧贴米尺上的小孔S（其位置见图），可通过平面镜看到米尺的一部分刻度．试在本题的图上用三角板作图求出可看到的部位，并在P1P2上把这部分涂以标志．（考点：光的反射折射定理及应用）（答案:关键词：通过平面镜看到米尺的一部分刻度重要知识：平面镜成像的相关作图（1）①分别作P1P2、Ma、bN对于AB的对称线P′1 P′2、M′a′、b′N′，则P′1 P′2就是P1P2对于平面镜AB的像，M′N′是MN对于平面镜AB的像．②连接S、a并延长，与P′1 P′2交于一点，并作该点对于AB的对称点，此对称点在P1P2上，是可看到部位的左端．③连接S、b′并延长，与P′1 P′2交于一点，作该点对于AB的对称点，此对称点也在P1P2上，是可看到部位的右端．上述顺序也可以是①③②．（2）①作S点对AB的对称点S′，S′就是S的像点．②连接S、a并延长，与AB交于C点③连接S′、C并延长，与P1P2交于一点，此点就是可看到部位的左端．④连接S′、b并延长，与P1P2交于一点，此点就是可看到部位的右端．上述顺序也可以是②①③④或①④②③．此题主要考查学生对平面镜成像的特点的理解和掌握,解答此题要结合几何知识,因此要注意学科间知识的渗透）78.如图所示，一宽为ab的平面镜，垂直纸面放置，平面镜可以绕其中心轴O 转动，MN为离平面镜一段距离的直线．人眼在ab与MN之间的某固定位置P点（图中没有标出），通过平面镜ab观察MN．转动平面镜，人眼可以通过平面镜观察到MN上不同的区域．当平面镜ab与直线MN平行时，人眼通过平面镜恰能观察到MN上从A点到B点的整个区域．（1）利用刻度尺等工具，确定人眼所在位置．（2）将平面镜ab绕O轴顺时针转过θ角，利用刻度尺等工具，画出人眼此时通过平面镜在MN上观察到的区域．（考点：光的反射折射定理及应用）（答案:关键词：眼睛能看到物体MN的AB部分重要知识：平面镜成像的特点、原理、现象（1）连接A与平面镜的左边缘并延长，连接B与平面镜的右边缘并延长，两条直线交与P1点，P1是眼睛的像的位置．根据平面镜成像特点，由点向平面镜作垂线并延长，根据物像到平面镜的距离相等，找出人眼睛的位置P．（2）当平面镜转动θ后，根据物像到平面镜的距离相等，作出人眼在转过θ角后的平面镜中的像P2．连接P2点和转动后的平面镜的两个边缘并延长，交与物体MN上，即为观察到的范围．熟练掌握眼睛通过平面镜观察到的范围的两种求解方法是解答本题的关键.)79.如图，凸透镜L的焦距为f，F为焦点，在离透镜1.5f处垂直主光轴放置一平面镜M，左侧焦点F的正上方有一点光源S，试通过作图确定在凸透镜右侧所成像点的位置，要求作出两条光路．（考点：光的反射折射定理及应用）（答案:关键词：凸透镜；点光源；像点重要知识：透镜的光路图；平面镜成像的相关作图因点光源S正好在凸透镜左侧焦点F的正上方，根据平面镜成像的特点可知点光源S关于平面镜的像点在2F上，连接像点与左边焦点F，与镜面的交点即为入射点，连接入射点与焦点即为点光源S的反射光线，并将其延长，经凸透镜折射后将平行主光轴射出，在过S作平行主光轴的光线经凸透镜折射后过右边焦点，两条直线的交点S′即为右侧所成像点的位置，如图所示：此题综合考查平面镜成像特点和凸透镜三条特殊光线，有一定难度，属于难题．)80.（1）根据入射光线和折射光线，在图甲中的实线框内画出适当的透镜；（2）据图乙中的入射光线作出这两条入射光线通过透镜后相应的折射光线；（3）请根据近视眼的成因和矫正方法，在图丙所示的方框内画出矫正所需的透镜并完成光路图；（4）如图丁所示，OO′为透镜的主光轴，AB是物体，A′B′是AB经过透镜所成的像．用作图方法找出透镜的位置，并在这个位置画出这个透镜．（考点：光的反射折射定理及应用）（答案:关键词：透镜；入射光线；折射光线；近视眼的矫正重要知识：透镜的光路图（1）前面入射光线是会聚的，经过透镜折射后，变为了平行光，由此可知该透镜对光线有发散作用，应该是凹透镜；后面平行光经过透镜折射后变得发散，由此可知该透镜对光线有发散作用，因此是凹透镜．如图所示：（2）平行于主光轴的光线经凸透镜折射后将过焦点，过焦点的光线经凸透镜折射后折射光线平行于主光轴；平行于主光轴的光线经凹透镜折射后折射光线反向延长通过焦点，过光心的光线其传播方向不变，如图所示：（3）近视眼是晶状体曲度变大，会聚能力增强，即折光能力增强，像呈在视网膜的前方，应佩戴发散透镜，使光线推迟会聚．如图所示：（4）连接A、A′，与主光轴相交于一点，即为凸透镜的光心．然后即可做出凸透镜，如下图所示：熟练掌握透镜对光线的会聚或者发散作用、透镜的特殊光线以及近视眼和远视眼的成因及矫正方法是解决此题的关键.）81.小孔成像是光的直线传播的实例．北宋科学家沈括也做过精彩的描述，他在《梦溪笔谈》中写道：“…若鸢飞空中，其影随鸢而移；或中间为窗隙所束，则影与鸢遂相违，鸢东则影西，鸢西则影东．又如窗隙中楼塔之影，中间为富所束，亦皆倒垂…”．（如图）。

浙教版九年级数学下册培优练习附答案：3.3 由三视图描述几何体

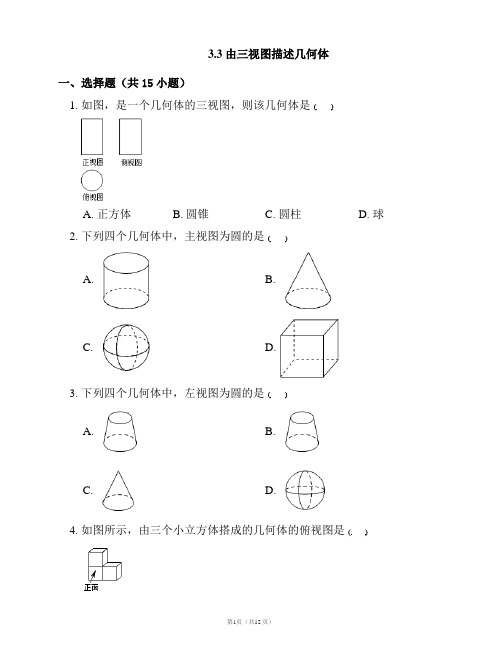
3.3 由三视图描述几何体一、选择题（共15小题）1. 如图，是一个几何体的三视图，则该几何体是A. 正方体B. 圆锥C. 圆柱D. 球2. 下列四个几何体中，主视图为圆的是A. B.C. D.3. 下列四个几何体中，左视图为圆的是A. B.C. D.4. 如图所示，由三个小立方体搭成的几何体的俯视图是A. B.C. D.5. 由个相同的立方体搭成的几何体如图所示，则它的主视图是A. B.C. D.6. 将一个长方体内部挖去一个圆柱（如图所示），它的主视图是A. B.C. D.7. 下图几何体的主视图是A. B.C. D.8. 与如图所示的三视图对应的几何体是A. B.C. D.9. 右图是由四个小正方体叠成的一个立体图形，那么它的俯视图是A. B.C. D.10. 在生活和生产实践中，我们经常需要运用三视图来描述物体的形状和大小小亮在观察左边的热水瓶时，得到的左视图是A. B.C. D.11. 在生活和生产实践中，我们经常需要运用三视图来描述物体的形状和大小．小亮在观察热水瓶的左边时，得到的左视图是A. B.C. D.12. 我国古代数学家利用“牟合方盖”（如图甲）找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体．图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是A. B.C. D.13. 一个几何体零件如图所示，则它的俯视图是A. B.C. D.14. 如图是由五个相同的小立方块搭成的几何体，则它的俯视图是A. B.C. D.15. 小明从正面观察下图所示的两个物体，看到的是A. B.C. D.二、填空题（共15小题）16. 写出一个三视图中主视图与俯视图完全相同的几何体的名称．17. 若一个几何体的三视图相同，则这个几何体是．18. 一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是．19. 主视图、左视图、俯视图都相同的几何体为（写出两个）．20. 如果一个几何体的视图之一是三角形，这个几何体可能是（写出个即可）．21. 一个几何体从正面、上面和左面看到的都是大小相同的圆，则这个几何体是22. 通常，主视图反映物体的和，俯视图反映物体的和，视图反映物体的高和宽．23. 已知一个几何体的三视图如图所示，则该几何体是．24. 如图，在一次数学活动课上，张明用个边长为的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小正方体，王亮所搭几何体表面积为．25. 用小立方块搭一个几何体，使得它从正面看与从上面看到的形状图如图所示．假设搭这样的几何体至少用个小立方块，至多用个小立方块，则．26. 如图，是由一些小立方块所搭几何体的三种视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个大正方体，至少还需要个小立方块．27. 小明把个棱长为分米的正方体摆在课桌上成如图形式，然后把露出的表面都涂上颜色，则被他涂上颜色部分的面积为平方分米．28. 如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图．则这个几何体可能是由个正方体搭成的．29. 如图是一个几何体从三个方面看到的形状图，若这个几何体的体积是，则它的表面积是．30. 边长为的个正方体，在地面上摆成如图所示的形式，如果把露出表面的部分都涂上颜色，那么被涂上颜色的总面积为．三、解答题（共5小题）31. 如图所示，分别从正面、左面、上面观察该立体图形，能得到什么平面图形?32. 如图是一些小正方体搭成的几何体俯视图，小正方形中的数字表示该位置的小正方体的个数，请画出它的主视图，左视图．33. 根据下面的俯视图，其搭建的每一正方体边长为，画出它的主视图和左视图，并求其表面积．34. 某学校设计了如图所示的一个雕塑，取名为"阶梯"．现在打算用油漆喷刷所有暴露面，经测量，每个小立方块的棱长为米．请计算需喷油漆的总面积是多少?35. 从正面、左面、上面观察如图所示的几何体，分别画出你所看到的几何体的形状图．答案1. C2. C3. D 【解析】答案 D4. A5. C6. A 【解析】解析：如图所示放置的几何体分为两部分，长方体的主视图是矩形，圆柱体的主视图也是矩形，但里面的圆柱体的轮廓线用虚线表示，并且外面的长方形比较大，里面的长方形比较小．答案：A7. C8. B9. B10. B11. B12. B13. C14. A15. C16. 正方体17. 球体或正方体18. 球体19. 球体、正方体20. 三棱柱、三棱锥、圆锥21. 球22. 长，高，长，宽，左23. 圆柱24. ，【解析】总共有小正方体个，所以王亮还需要个；几何体的表面积为．25.【解析】如图小正方形中的数字表示该位置小立方块的个数．最多有个，最少有个，所以，，故．26.【解析】由俯视图易得最底层有个小立方体，第二层有个小立方体，第三层有个小立方体，那么共有个几何体组成．若搭成一个大正方体，共需个小立方体，所以还需个小立方体．27.【解析】从物体的前面看有个小正方形，后面看有个小正方形，左面看有个小正方形，右面看有个小正方形，上面看有个小正方形，露出的表面共有（个）小正方形，则被他涂上颜色部分的面积为平方分米．28. 或或【解析】综合主视图和俯视图，这个几何体的底层有个小正方体，第二层最少有个，最多有个，第三层最少有个，最多有个，因此搭成这样的一个几何体至少需要小正方体木块的个数为：个，至多需要小正方体木块的个数为：个，即这个几何体可能是由或或个正方体搭成的．29.【解析】这个几何体的长是，宽是，体积是，设它的高为，则，解得．它的表面积是：．第11页（共12 页）30.【解析】侧面小正方形个数，从上向下看，上表面共有个小正方形，又每个小正方形的面积是，所以被涂上颜色的总面积为．31. 从正面看该立体图形得到三角形，从左面看该立体图形得到长方形，从上面看该立体图形得到长方形．32. 如图所示：33. 如图即为所求．表面积为．34. 画出雕塑"阶梯"的形状图，如图所示．每个小正方形的面积都是（平方米），所以喷漆总面积为（平方米）．答：需喷油漆的总面积为平方米．35.第12页（共12 页）。

人教统编版四年级语文下册第1单元培优合练测试卷(含答案)

人教统编版四年级语文下册第1单元培优合练时间：90分钟满分：100分班级：姓名：得分： .一、根据语境，看拼音写词语。

（6分）月明人静的夜里，偶尔有一两只灰色的biān fú（）掠过村庄的wū yán（），lí bɑ（）旁已经见不到飞舞的qīnɡ tínɡ（）。

伴随着纺织娘的催眠曲，人们进入了tián mì（）的mènɡ xiānɡ（）。

二、选择题。

（15分）1.下列加点字的读音有误的一项是（）A.稀疏．（shū）剥．莲蓬（bō）锐．利（ruì）B.附．近（fù）率．领（shuài）鸡冠．（ɡuān）C.闪烁．（shuò）绮．丽（yǐ）耍赖．（lài）D.倘．若（tǎnɡ）应和．（hè）老鹰．（yīnɡ）2.下列词语搭配不正确的一项是（）A.碧绿的藤叶奇幻的云彩B.暖和的晴天独特的风光C.迷人的风景鲜嫩的绿荫D.明洁的丝绸绮丽的朝霞3.下列诗句中,不属于描写乡村生活的一项是（）A.儿童急走追黄蝶，飞入菜花无处寻。

B.蓬头稚子学垂纶，侧坐莓苔草映身。

C.村北村南布谷忙，村前村后稻花香。

D.长安回望绣成堆，山顶千门次第开。

4.下面句子中的加点词可以用哪个词语替换？最恰当的一项是（）2022年6月5日，带着全国人民的期望和祝福，“神舟十四号”载人飞船迎来了问鼎苍穹的壮丽．．时刻。

A.雄壮B.辉煌C.美丽D.绚丽5.下面说法错误的一项是（）A.《宿新市徐公店》描写了初春农村的景色，表现出儿童们的顽皮和淘气。

B.《乡下人家》描绘了一个个自然、和谐的场景，展现了乡下人家朴实而充满诗意的乡村生活。

C.《天窗》抓住了孩子好动、爱玩的特点，利用丰富的想象，描写了乡村儿童从天窗中获得想象的乐趣。

D.《三月桃花水》描写了阳春三月的美丽景色，赞美了春天的美丽，抒发了作者对春天和大自然的热爱。

数学小学六年级小升初复习培优试题测试卷(附答案)

数学小学六年级小升初复习培优试题测试卷（附答案）一、选择题1．下列各式中（a 、b 均不为0），a 和b 成反比例关系的是（）。

A ．0.7a b =B ．1.28a b =C ．154a b =D ．3ab = 2．如果A 点用数对表示为（1，5），B 点用数对表示数（1，1），C 点用数对表示为（3，1），那么三角形ABC 一定是（）三角形。

A ．钝角B ．锐角C ．直角 3．光明村今年每百户拥有电脑96台，比去年增加了32台，今年比去年增加了百分之多少？正确的算式是（）．A ．32÷96×100%B ．32÷（96-32）×100%C ．96÷32×100%4．三角形的3个顶点A 、B 、C 用数对表示分别是（2，1）、（2，4）、（4，5），那么这个三角形定是（）三角形。

A ．锐角B ．直角C ．钝角D ．等腰5．学校电脑班有女生18人，比男生人数的13少2人，电脑班有多少男生？设男生有x 人，下列方程正确的是（）。

A ．18－13x ＝2 B ．13x －2＝18 C ．13x ＋2＝18 D ．（x ＋2）×13＝18 6．一个长方体，有两个相对的面是正方形。

它的长是8cm ，宽是5cm 。

这个长方体的表面积最少是（）2cm 。

A ．130B ．200C ．210D ．288 7．如图，表示福福骑车从家到图书馆看书然后返回家的过程中离家的距离与时间的变化关系。

下面说法错误的是（）。

A ．福福家到图书馆的距离是5千米B ．福福去图书馆的骑车速度是10千米/小时C ．福福在图书馆停留了2小时D ．福福从图书馆返回家用了0.5小时 8．有下列四个说法：①0的倒数是0；②《中学生作文》的单价一定，总价与订阅的数量成反比例关系；③周长相等的两个圆面积相等；④圆锥的高是圆柱的高的3倍，它们的体积一定相等，其中正确说法的个数是（）。

浙教版九年级数学下册培优练习附答案：3.2简单几何体的三视图

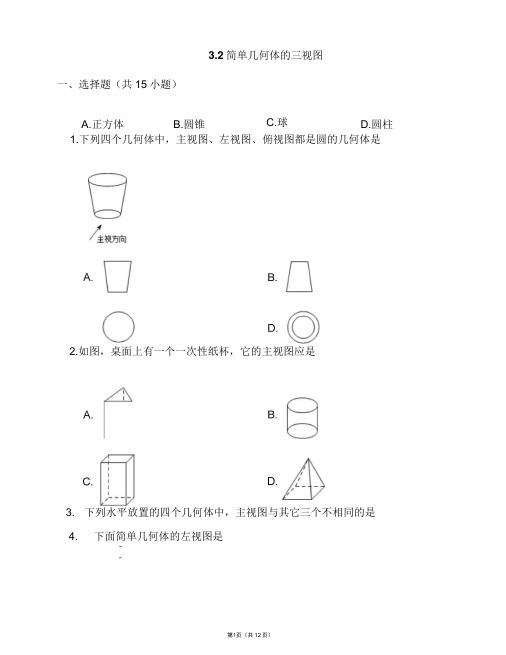
3.2简单几何体的三视图一、选择题（共15小题）A.正方体B.圆锥C.球D.圆柱1.下列四个几何体中，主视图、左视图、俯视图都是圆的几何体是2.如图，桌面上有一个一次性纸杯，它的主视图应是3. 下列水平放置的四个几何体中，主视图与其它三个不相同的是4. 下面简单几何体的左视图是! AA. Eb C. nnd5. 有。

个相同的立方体搭成的几何体如图所示，则它的主视图是6.下列四个立体图形中，主视图为圆的是.：■B. pp D. FPnD.B. D.A.B.C.B.8. 如图是一个由若干个棱长为|的正方体构成的几何体的三视图，则构成这个几何体的体积为■'.9. 如图几何体的主视图是A.C. Em10. 如图，由三个小立方体搭成的几何体的俯视图是11.如图所示的支架是由两个长方形构成的组合体，则它的主视图是主视圏左视囹俯视囹A.C.B.正面A. I —D.C. D.A. B.12.由、个相同的立方体搭成的几何体如图，则它的主视图是A.C.13. 有一篮球如图放置，其主视图为14. 由：个相同小立方体搭成的几何体如图所示，则它的主视图是兔视方向A.D.D.C.D.4觇力向B.A.C. D.15. 若干桶方便面摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆方便面共有■：.A. •-桶B.桶C 」桶 D. |】桶二、填空题（共15小题）16. _________________________________ 如图，由四个小正方体组成的几何体中，若每个小正方体的棱长都是 •，则该几何体俯视图的面积是 .17. 一个几何体，是由许多规格相同的小正方体堆积而成的，其主视图、左视图如图所示，要摆成这样的图形，至少需用 __________________________ 块小正方体.主视图18. 一个几何体的三视图如图所示（其中标注的长），则这个几何体的体积是 _______________ .ab—厂。

南京师范大学附中树人学校八年级数学上册第十二章《全等三角形》提高练习(培优练)

一、选择题1．如图，△ACB ≌△A′C B′，∠ACB ＝70°，∠ACB′＝100°，则∠BCA′度数是（）A ．40°B ．35C ．30°D ．45°A 解析：A【分析】根据已知ACB ≌A′CB′，得到∠A′CB′=∠ACB=70︒，再通过∠ACB′=100︒，继而利用角的和差求得∠BCB′=30︒，进而利用∠BCA′=∠A′CB′-∠BCB′得到结论．【详解】解：∵ACB ≌A′CB′，∴∠A′CB′=∠ACB=70︒，∵∠ACB′=100︒，∴∠BCB′=∠ACB′-∠ACB=30︒，∴∠BCA′=∠A′CB′-∠BCB′=40︒，故选：C ．【点睛】本题考查了全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．2．如图，,AD BC ⊥垂足为,D BF AC ⊥，垂足为,F AD 与BF 交于点,5,2E AD BD DC ===，则AE 的长为（）A ．2B ．5C ．3D ．7C解析：C【分析】先证明△ACD ≌△BED ，得到CD=ED=2，即可求出AE 的长度．【详解】解：∵AD BC ⊥，BF AC ⊥，∴90AFE BDE ADC ∠=∠=∠=︒，∵AEF BED ∠=∠，∴EAF EBD ∠=∠，∵5AD BD ==，∴△ACD ≌△BED ，∴CD=ED=2，∴523AE AD ED =-=-=；故选：C ．【点睛】本题考查了全等三角形的判定和性质，余角的性质，解题的关键是掌握全等三角形的判定和性质，从而进行解题．3．如图，BD 是四边形ABCD 的对角线， AD//BC ，AB AD <，分别过点A ，C 作AE BD ⊥，CF BD ⊥，垂足分别为点E ，F ，若BE DF =，则图中全等的三角形有( )A ．1对B ．2对C ．3对D ．4对C解析：C【分析】根据AD //BC 证得ADB CBD ∠=∠，由BE DF =得到BF=DE ，由此证明△ADE ≌△CBF ，得到AE=CF ，AD=CB ，由此证得△ABE ≌△CDF ，得到AB=CD ，由此利用SSS 证明△ABD ≌△CDB.【详解】解：∵AD //BC ，∴ADB CBD ∠=∠，BE DF =，BF DE ∴=，AE BD ⊥，CF BD ⊥，AED CFB ∠∠∴=90=，()ADE CBF ASA ∴≅，AE CF ∴=，AD CB =，∵∠AEB=∠CFD 90=，BE=DF ，()ABE CDF SAS ∴≅，AB CD ∴=，BD DB =，AB=CD ，AD CB =，()ABD CDB SSS ∴≅,则图中全等的三角形有：3对，故选:C .【点睛】此题考查三角形全等的判定定理：SSS 、SAS 、ASA 、AAS 、HL ，根据已知条件找到对应的边或角是解题的关键.4．如图，ABC 和DEF 中，∠A=∠D ，∠C=∠F ，要使ABC DEF ≅，还需增加的条件是（）A ．AB=EFB ．AC=DFC ．∠B=∠ED ．CB=DE B解析：B【分析】根据AAS 定理或ASA 定理即可得．【详解】在ABC 和DEF 中，,A C F D ∠∠∠=∠=，∴要使ABC DEF ≅，只需增加一组对应边相等即可，即需增加的条件是AB DE =或AC DF =或BC EF =，观察四个选项可知，只有选项B 符合，故选：B ．【点睛】本题考查了三角形全等的判定定理，熟练掌握三角形全等的判定定理是解题关键． 5．已知：如图，BD 为△ABC 的角平分线，且BD=BC ，E 为BD 延长线上的一点，BE=BA ，过E 作EF ⊥AB ，F 为垂足，下列结论：①△ABD ≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF 其中正确的是（）A ．①②③B ．①③④C ．①②④D ．①②③④D解析：D【分析】易证ABD EBC ∆∆≌，可得BCE BDA ∠=∠，AD=EC 可得①②正确；再根据角平分线的性质可求得DAE DCE ∠=∠ ，即③正确，根据③可判断④正确；【详解】∵ BD 为∠ABC 的角平分线，∴ ∠ABD=∠CBD ，∴在△ABD 和△EBD 中，BD=BC ，∠ABD=∠CDB ，BE=BA ，∴△ABD EBC ∆∆≌(SAS)，故①正确；∵ BD 平分∠ABC ，BD=BC ，BE=BA ，∴ ∠BCD=∠BDC=∠BAE=∠BEA ，∵△ABD ≌△EBC ，∴∠BCE=∠BDA ，∴∠BCE+∠BCD=∠BDA+∠BDC=180°，故②正确；∵∠BCE=∠BDA ，∠BCE=∠BCD+∠DCE ，∠BDA=∠DAE+∠BEA ，∠BCD=∠BEA ，∴∠DCE=∠DAE ，∴△ACE 是等腰三角形，∴AE=EC ，∵△ABD ≌△EBC ，∴AD=EC ，∴AD=AE=EC ，故③正确；作EG ⊥BC ，垂足为G ，如图所示：∵ E 是BD 上的点，∴EF=EG ，在△BEG 和△BEF 中BE BE EF EG=⎧⎨=⎩ ∴ △BEG ≌△BEF ，∴BG=BF ，在△CEG 和△AFE 中EF EG AE CE =⎧⎨=⎩∴△CEG ≌△AFE ，∴ AF=CG ，∴BA+BC=BF+FA+BG-CG=BF+BG=2BF ，故④正确；故选：D ．【点睛】本题考查了全等三角形的判定，全等三角形对应边、对应角相等的性质，本题中熟练求证三角形全等和熟练运用全等三角形对应边、对应角相等的性质是解题的关键； 6．如图，OB 平分∠MON ，A 为OB 的中点，AE ⊥ON ，EA=3，D 为OM 上的一个动点，C 是DA 延长线与BC 的交点，BC //OM ，则CD 的最小值是（）A ．6B ．8C ．10D ．12A解析：A【分析】根据两条平行线之间的距离可知当CD ⊥OM 时，CD 取最小值，先利用角平分线的性质得出AD =AE =3，利用全等三角形的判定和性质得出AC =AD =AE =3，进而解答即可．【详解】解：由题意得，当CD ⊥OM 时，CD 取最小值，∵OB 平分∠MON ，AE ⊥ON 于点E ，CD ⊥OM ，∴AD =AE =3，∵BC ∥OM ，∴∠DOA =∠B ，∵A 为OB 中点，∴AB =AO ，在△ADO 与△ABC 中B DOA AB AO BAC DAO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADO ≌△ABC (SAS ),∴AC =AD =3，∴336CD AC AD =+=+=，故选A ．【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离，关键是利用全等三角形的判定和性质得出AC =AD =AE =3．7．如图，在OAB 和OCD 中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ，下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠，其中正确的为（）A ．①②③B ．①②④C ．②③④D ．①②③④B解析：B【分析】由SAS 证明AOC BOD ≅得出OCA ODB ∠=∠，=AC BD ，①正确；由全等三角形的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，得出40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，由AAS 证明OCG ODH ≅（AAS ），得出OG=OH ，由角平分线的判定方法得出MO 平分BOC ∠，④正确；由AOB COD ∠=∠，得出当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM ，由AOC BOD ≅得出COM BOM ，由MO 平分BMC ∠得出∠=∠CMO BMO ，推出COM BOM ≅，得出OB=OC ，OA=OB ，所以OA=OC ，而OA OC >，故③错误；即可得出结论．【详解】∵40AOB COD ∠=∠=︒，∴AOB AOD COD AOD ∠+∠=∠+∠即AOC BOD ∠=∠在AOC △和BOD 中OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴AOC BOD ≅（SAS ）∴OCA ODB ∠=∠，=AC BD ，①正确；∴OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，∴40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，在OCG 和ODH 中OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OCG ODH ≅（AAS ），∴OG=OH∴MO 平分BOC ∠，④正确；∴AOB COD ∠=∠∴当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM∵AOC BOD ≅∴COM BOM ，∵MO 平分BMC ∠∴∠=∠CMO BMO ，在COM 和BOM 中 OCM BOM OM OMCMO BMO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴COM BOM ≅（ASA ）∴OB=OC ，∵OA=OB ，∴OA=OC ，与OA OC >矛盾，∴③错误；正确的有①②④；故选：B【点睛】本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．8．如图，点C，D在线段AB上，AC DB=，AE//BF，添加以下哪一个条件仍不能判定△AED≌△BFC（）A．ED CF=B．AE BF=C．E F∠=∠D．ED//CF A解析：A【分析】欲使△AED≌△BFC，已知AC=DB，AE∥BF，可证明全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可；【详解】∵ AC=BD，∴ AD=CE，∵ AE∥BF，∴∠A=∠E，A、如添加ED=CF，不能证明△AED≌△BFC，故该选项符合题意；B、如添加AE=BF，根据SAS，能证明△AED≌△BFC，故该选项不符合题意；C、如添加∠E=∠F，利用AAS即可证明△AED≌△BFC，故该选项不符合题意；D、如添加ED∥CF，得出∠EDC=∠FCE，利用ASA即可证明△AED≌△BFC，故该选项不符合题意；故选：A．【点睛】本题考查了全等三角形的判定定理的理解和掌握，此类添加条件题，要求学生应熟练掌握全等三角形的判定定理；9．在尺规作图作一个角的平分线时的两个三角形全等的依据是（）A．SAS B．AAS C．SSS D．HL C解析：C【分析】根据作图过程可知用到的三角形全等的判定方法是SSS．【详解】解：尺规作图-作一个角的角平分线的作法如下：①以O为圆心，任意长为半径画弧，交AO、BO于点F、E，②再分别以F、E为圆心，大于12EF长为半径画弧，两弧交于点M，③画射线OM，射线OM即为所求．由作图过程可得用到的三角形全等的判定方法是SSS ．故选：C ．【点睛】本题主要考查了基本作图以及全等三角形的判定，关键是掌握作一个角的平分线的基本作图方法．10．如图，要判定△ABD ≌△ACD ，已知AB ＝AC ，若再增加下列条件中的一个，仍不能说明全等，则这个条件是（）A ．CD ⊥AD ，BD ⊥ADB ．CD ＝BDC ．∠1＝∠2D ．∠CAD ＝∠B AD C解析：C【分析】在△ACD 和△ABD 中，AD=AD ，AB=AC ，由全等三角形判定定理对选项一一分析，排除不符合题意的选项即可．【详解】解：添加A 选项中条件可用HL 判定两个三角形全等，故选项A 不符合题意；添加B 选项中的条件可用SSS 判定两个三角形全等，故选项B 不符合题意；添加C 选项中的条件∠1＝∠2可得∠CDA=∠BDA ，结合已知条件不SS 判定两个三角形全等，故选项C 符合题意；添加D 选项中的条件可用SAS 判定两个三角形全等，故选项D 不符合题意．故选：C ．【点睛】本题考查了全等三角形的判定，判定三角形全等的方法：SSS 、SAS 、ASA 、AAS ，判断直角三角形全等的方法：“HL”．二、填空题11．如图，AOP BOP ∠=∠，PD OA ⊥，C 是OB 上的动点，连接PC ，若4PD =，则PC 的最小值为_________．4【分析】当PC 垂直于OB 时PC 最小根据角平分线的性质可求最小值【详解】解：当PC ⊥OB 时PC 最小∵PC ⊥OB ∴PC=PD=4故答案为：4【点睛】本题考查了垂线段最短和角平分线的性质能够根据垂线段最解析：4【分析】当PC 垂直于OB 时，PC 最小，根据角平分线的性质可求最小值．【详解】解：当PC ⊥OB 时，PC 最小，∵AOP BOP ∠=∠，PD OA ⊥，PC ⊥OB ，∴PC=PD=4，故答案为：4．【点睛】本题考查了垂线段最短和角平分线的性质，能够根据垂线段最短的性质判断出点C 的位置，并根据角平分线的性质得出PC=PD 是根关键．12．如图，∠ABC=∠DCB ，要使△ABC ≌△DCB ，还需要补充一个条件：___．（一个即可）AB=CD （或∠A=∠D 或∠ACB=∠DBC ）【分析】根据已知条件：两个三角形已经具备∠ABC=∠DCB 及公共边BC 再添加任意一组角或是AB=CD 即可【详解】∵∠ABC=∠DCBBC=CB ∴当AB=解析：AB=CD （或∠A=∠D 或∠ACB=∠DBC ）【分析】根据已知条件：两个三角形已经具备∠ABC=∠DCB 及公共边BC ，再添加任意一组角，或是AB=CD 即可．【详解】∵∠ABC=∠DCB ，BC=CB ，∴当AB=CD 时，利用SAS 证明△ABC ≌△DCB ；当∠A=∠D 时，利用AAS 证明△ABC ≌△DCB ；当∠ACB=∠DBC 时，利用ASA 证明△ABC ≌△DCB ，故答案为：AB=CD （或∠A=∠D 或∠ACB=∠DBC ）．此题考查添加一个条件证明两个三角形全等，熟记全等三角形的判定定理是解题的关键． 13．如图，在ABC 中，=6AB ，=4AC ，点D ，E 分别在边AB ，AC 上，2BD AE CE ===，//CE AB 交DE 的延长线于点F ，则CF 的长为_____________．4【分析】根据ASA 证明△ADE ≌△CFE 得CF=AD 再求出AD 的长即可【详解】解：∵AB=6BD=2∴AD=AB-BD=6-2=4∵∴∠BAC=∠FCE 在△ADE 和△CFE 中∴△ADE ≌△CFE ∴解析：4【分析】根据ASA 证明△ADE ≌△CFE 得CF=AD ，再求出AD 的长即可．【详解】解：∵AB=6，BD=2∴AD=AB-BD=6-2=4∵//CE AB∴∠BAC=∠FCE ，在△ADE 和△CFE 中BAC FCE AE CEAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CFE∴CF=AD=4．故答案为：4．【点睛】此题主要考查了全等三角形的判定与性质，证明△ADE ≌△CFE 是解答此题的关键． 14．如图，两根旗杆间相距22米，某人从点B 沿BA 走向点A ，一段时间后他到达点M ，此时他分别仰望旗杆的顶点C 和D ，两次视线的夹角为90°，且CM DM =．已知旗杆BD 的高为12米，该人的运动速度为2米/秒，则这个人运动到点M 所用时间是________秒．5【分析】根据题意证明利用证明根据全等三角形的性质得到米再利用时间=路程÷速度计算即可【详解】解：∵∴又∵∴∴在和中∴∴米（米）∵该人的运动速度他到达点M 时运动时间为s 故答案为5【点睛】本题解析：5【分析】根据题意证明C DMB ∠=∠，利用AAS 证明ACM BMD ≌，根据全等三角形的性质得到12BD AM ==米，再利用时间=路程÷速度计算即可．【详解】解：∵90CMD ∠=︒，∴90CMA DMB +=︒∠∠，又∵90CAM ∠=︒，∴90CMA C ︒∠+∠=，∴C DMB ∠=∠，在 Rt ACM △和Rt BMD △中， A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()Rt ACM Rt BMD AAS ≌，∴12BD AM ==米，221210BM =-=（米），∵该人的运动速度2m/s ，他到达点M 时，运动时间为5210=÷s ．故答案为5．【点睛】本题考查了全等三角形的应用；解答本题的关键是利用互余关系找三角形全等的条件，对应角相等，并巧妙地借助两个三角形全等，寻找所求线段与已知线段之间的等量关系．本题的关键是求得Rt ACM Rt BMD ≌．15．如图，在Rt ABC △中，90C ∠=︒，10AC =，5BC =，线段PQ AB =，P ，Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AD 上运动，当AQ =______时，ABC 和PQA △全等．5或10【分析】分两种情况：当AQ=5时当AQ=10时利用全等三角形的判定及性质定理得到结论【详解】分两种情况：当AQ=5时∵∴AQ=BC ∵AD ⊥AC ∴∠QAP=∠ACB=∵AB=PQ ∴≌△PQA （解析：5或10分两种情况：当AQ=5时，当AQ=10时，利用全等三角形的判定及性质定理得到结论．【详解】分两种情况：当AQ=5时，∵5BC =，∴AQ=BC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴ABC ≌△PQA （HL ）；当AQ=10时，∵10AC =，∴AQ=AC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴△ABC ≌△QPA ，故答案为：5或10．【点睛】此题考查全等三角形的判定及性质定理，运用分类思想，动点问题，熟记三角形的判定定理及性质定理是解题的关键．16．如图，在Rt ABC △中，90C ∠=︒，以顶点A 为圆心，任意长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交BC 于点D ．若3CD =，10AB =，则ABD △的面积是______．15【分析】如图过点D 作DE ⊥AB 于E 首先证明DE=CD=3再利用三角形的面积公式计算即可【详解】解：如图过点D 作DE ⊥AB 于E 由作图可知AD 平分∠CAB ∵CD ⊥ACDE ⊥AB ∴DE=CD=3∴S △ 解析：15【分析】如图，过点D 作DE ⊥AB 于E ．首先证明DE=CD=3，再利用三角形的面积公式计算即可．【详解】解：如图，过点D 作DE ⊥AB 于E ．由作图可知，AD 平分∠CAB ，∵CD ⊥AC ，DE ⊥AB ，∴DE=CD=3，∴S △ABD =12•AB•DE=12×10×3=15，故答案为15．【点睛】本题考查了作图-基本作图，角平分线的性质定理等知识，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题．17．如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，交BC 边于点D ，若12AB =，4CD =，则ABD △ 的面积为__________．24【分析】过D 作DE ⊥AB 垂足为E 根据角平分线定理可得DE=CD=4然后根据三角形的面积公式计算即可【详解】解：如图：过D 作DE ⊥AB 垂足为E ∵AD 平分交BC 边于点D ∴DE=CD=4∴的面积为AB解析：24【分析】过D 作DE ⊥AB 垂足为E ，根据角平分线定理可得DE=CD=4,然后根据三角形的面积公式计算即可．【详解】解：如图：过D 作DE ⊥AB 垂足为E ，∵90C ∠=︒，AD 平分BAC ∠，交BC 边于点D ，∴DE=CD=4，∴ABD △ 的面积为12AB·DE=12×12×4=24．故答案为：24．【点睛】本题主要考查了角平分线的性质定理，正确作出辅助线、构造角平分线定理所需条件成为解答本题的关键．18．如图，AD 为∠CAF 的角平分线，BD=CD ，∠DBC=∠DCB ，∠DCA=∠ABD ，过D 作DE ⊥AC 于E ，DF ⊥AB 交BA 的延长线于F ，则下列结论：①△CDE ≌△BDF ；②CE=AB+AE ；③∠DAF=∠CBD ．其中正确的结论有_____．（填序号）①②③【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF 再利用HL 证明Rt △CDE 和Rt △BDF 全等根据全等三角形对应边相等可得CE ＝AF 利用HL 证明Rt △ADE 和Rt △ADF 全等根据全等三解析：①②③．【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF ，再利用“HL”证明Rt △CDE 和Rt △BDF 全等，根据全等三角形对应边相等可得CE ＝AF ，利用“HL”证明Rt △ADE 和Rt △ADF 全等，根据全等三角形对应边相等可得AE ＝AF ，然后求出CE ＝AB ＋AE ；根据全等三角形对应角相等可得∠DBF ＝∠DCE ，利用“8字型”证明∠BDC ＝∠BAC ；根据三角形内角和定理及平角的性质，可得∠DAF ＝∠CBD ．【详解】解：如图∵AD 平分∠CAF ，DE ⊥AC ，DF ⊥AB ，∴DE ＝DF ，在Rt △CDE 和Rt △BDF 中，BD CD DE DF⎧⎨⎩＝＝ ∴Rt △CDE ≌Rt △BDF （HL ），故①正确；∴CE ＝BF ，在Rt △ADE 和Rt △ADF 中，AD AD DE DF＝＝⎧⎨⎩ ， ∴Rt △ADE ≌Rt △ADF （HL ），∴AE ＝AF ，∴CE ＝AB ＋AF ＝AB ＋AE ，故②正确；∵Rt △CDE ≌Rt △BDF ，∴∠DBF ＝∠DCE ，∵∠AOB ＝∠COD ，（设AC 交BD 于O ），∴∠BDC ＝∠BAC ，∵AD 平分∠FAE ，∴∠DAF ＝∠DAE∵BD ＝CD∴∠DBC ＝∠DCB∵∠BAC ＋∠DAF ＋∠DAE ＝180°，∠BDC ＋∠DBC ＋∠DCB ＝180°，∠BDC ＝∠BAC∴∠DAF ＋∠DAE ＝∠DBC ＋∠DCB∴∠DAF ＝∠CBD ，故③正确综上所述，正确的结论有①②③．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并准确识图判断出全等的三角形是解题的关键，难点在于需要二次证明三角形全等． 19．如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，BD 平分ABC ∠．若P 是BC 边上一动点，则DP 长的最小值为______．3【分析】过D 作DE ⊥BC 于EDE 即为DP 长的最小值由题意可以得到△BAD ≌△BED 从而得到DE 的长度【详解】解：如图过D作DE⊥BC于EDE即为DP长的最小值由题意知在△BAD和△BED 中∴△BA解析：3【分析】过D作DE⊥BC于E，DE即为DP 长的最小值，由题意可以得到△BAD≌△BED，从而得到DE的长度．【详解】解：如图，过D作DE⊥BC于E，DE即为DP 长的最小值，由题意知在△BAD和△BED中，A DEBABD EBD BD BD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△BED，∴ED=AD=3，故答案为3．【点睛】本题考查三角形全等的应用，熟练掌握三角形全等的判定和性质是解题关键．20．如图，△ABC中，∠C=90°，AC=40cm，BD平分∠ABC，DE⊥AB于E，AD：DC=5：3，则D到AB的距离为__________cm．15【分析】根据角平分线的性质可得DE=DC然后求出DC即得答案【详解】解：∵AC=40cmAD：DC=5：3∴DC=15cm∵BD平分∠ABCDE⊥AB∠C=90°∴DE=DC=15cm即D到AB解析：15【分析】根据角平分线的性质可得DE=DC，然后求出DC即得答案．【详解】解：∵AC=40cm，AD：DC=5：3，∴DC=15cm，∵BD 平分∠ABC ，DE ⊥AB ，∠C=90°，∴DE=DC=15cm ，即D 到AB 的距离为15cm ．故答案为：15．【点睛】本题考查了角平分线的性质，属于基础题目，熟练掌握角平分线的性质定理是解题关键．三、解答题21．如图，点A ，D ，B ，E 依次在同一条直线上，BC DF =，AD BE =，ABC EDF ∠=∠，求证：A E ∠=∠．解析：证明见解析．【分析】先根据已知条件得出AB ED =，再利用SAS 证明ABC EDF △≌△，最后根据全等三角形的性质即可得出答案．【详解】证明：∵AD BE =，∴AD DB BE DB +=+，∴AB ED =．在ABC 和EDF 中，AB ED ABC EDF BC DF =⎧⎪∠=∠⎨⎪=⎩，∴()ABC EDF SAS △≌△，∴A E ∠=∠．【点睛】本题考查了全等三角形的判定及性质，熟练掌握全等三角形的判定方法是解题的关键． 22．在ABC 中，AD 是ABC 的高，30B，52C ︒∠=（1）尺规作图：作ABC 的角平分线AE（2）求DAE ∠的大小．解析：（1）作图见解析；（2）11【分析】（1）以任意长度为半径，点A 为圆心画圆弧，分别交AB 、AC 于点M 、N ；再分别以点M 、N 为圆心，大于2MN 的长度为半径画圆弧并相交于点K ，连接AK ，AK 交BC 于点E ，即可得到答案；（2）结合题意，根据三角形内角和定理，得BAC ∠；再根据角平分线性质得EAC ∠；结合AD 是ABC 的高，根据直角三角形两锐角互余的性质计算得DAC ∠；最后通过DAE EAC DAC ∠=∠-∠的关系计算完成求解．【详解】（1）作图如下：AE 即为ABC 的角平分线；（2）∵30B ，52C ︒∠=∴180180305298BAC B C ∠=-∠-∠=--=∵AE 为BAC ∠的角平分线∴492BAC EAC ∠∠== ∵AD 是ABC 的高 ∴90ADC ∠=∴90905238DAC C ∠=-∠=-=∴493811DAE EAC DAC ∠=∠-∠=-=．【点睛】本题考查了角平分线、三角形内角和、直角三角形两锐角互余、三角形高的知识；解题的关键是熟练掌握角平分线、三角形内角和、直角三角形两锐角互余的性质，从而完成求解．23．如图，Rt △ABC 中，∠ACB=90°，D 是AB 上的一点，过D 作DE ⊥AB 交AC 于点E ，CE=DE ．连接CD 交BE 于点F ．（1）求证：BC=BD ；（2）若点D 为AB 的中点，求∠AED 的度数．解析：（1）见详解；（2）60°．【分析】（1）利用HL 直接证明Rt △DEB ≌Rt △CEB ，即可解决问题．（2）首先证明△ADE ≌△BDE ，进而证明∠AED=∠DEB=∠CEB ，即可解决问题．【详解】证明：（1）∵DE ⊥AB ，∠ACB=90°，∴△DEB 与△CEB 都是直角三角形，在△DEB 与△CEB 中，EB EB DE CE =⎧⎨=⎩， ∴Rt △DEB ≌Rt △CEB （HL ），∴BC=BD ．（2）∵DE ⊥AB ，∴∠ADE=∠BDE=90°；∵点D 为AB 的中点，∴AD=BD ；在△ADE 与△BDE 中，AD BD ADE BDE DE DE =⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△BDE （SAS ），∴∠AED=∠DEB ；∵△DEB ≌△CEB ，∴∠CEB=∠DEB ，∴∠AED=∠DEB=∠CEB ；∵∠AED+∠DEB+∠CEB=180°，∴∠AED=60°．【点睛】该命题以三角形为载体，以考查全等三角形的判定及其应用为核心构造而成；解题的关键是灵活运用全等三角形的判定及其性质，来分析、判断或推理．24．如图，已知AB ∥CD ，BE 平分∠ABC ，DE 平分∠ADC ，∠BAD =80°，试求：（1）∠EDC 的度数．（2）若∠BCD =n °，试求∠BED 的度数．（用含n 的式子表示）（3）类比探究：已知AB ∥CD ，BE 、DE 分别是∠ABC 、∠ADC 的n 等分线，ABE ∠=1ABC n ∠，1CDE ADC n∠=∠，∠BAD =α，∠BCD =β，请猜想∠BED = ．解析：（1）40︒；（2）1402BED n ∠=︒+︒；（3）1()αβ+n 【分析】（1）根据平行线的性质及角平分线的性质即可得解；（2）过点E 作EF ∥AB ，则EF ∥AB ∥CD ，由AB ∥CD ，BE 平分∠ABC ，推出12BEF ABE n ∠=∠=︒，利用EF ∥CD ，求得∠FED =∠EDC =40°，即可得到 1402BED n ∠=︒+︒；（3）过点E 作EF ∥AB ，则EF ∥AB ∥CD ，利用AB ∥CD 推出∠ABC =∠BCD =β，∠ADC =∠BAD =α，求得1ABE n β∠=，111FED CDE ADC BAD n n n α∠=∠=∠=∠=，利用EF ∥AB ，求出1BEF ABE n β∠=∠=，即可得到1()BED n αβ∠=+．【详解】解：（1）∵AB ∥CD ，∴∠ADC =∠BAD =80°，又∵DE 平分∠ADC ，∴1402EDC ADC ∠=∠=︒；（2）如图，过点E 作EF ∥AB ，则EF ∥AB ∥CD ，∵AB ∥CD ，∴∠ABC =∠BCD =n °，又∵BE 平分∠ABC ， ∴12ABE n ∠=︒， ∵EF ∥AB ， ∴12BEF ABE n ∠=∠=︒， ∵EF ∥CD ，∴∠FED =∠EDC =40°，∴1402BED n ∠=︒+︒．（3）1()αβ+n．如图，过点E 作EF ∥AB ，则EF ∥AB ∥CD ，∵AB ∥CD ，∴∠ABC =∠BCD =β，∠ADC =∠BAD =α，∴1ABE nβ∠=，111FED CDE ADC BAD n n n α∠=∠=∠=∠=， ∵EF ∥AB ， ∴1BEF ABE n β∠=∠=， ∴1()BED nαβ∠=+．故答案为：1()αβ+n ．【点睛】此题考查平行线的性质，角平分线的性质，熟记平行线的性质并正确引出辅助线解决问题是解题的关键．25．如图，在ACD △与BCE 中，AC BC =，CD CE =，ECD ACB ∠=∠．（1）求证：AD BE =；（2）若105ACD ∠=︒，32D ∠=︒，求B 的度数．解析：（1）见解析；（2）43°【分析】利用 SAS 证明≌ACD BCE 即可;由全等三角形的性质可知:B A ∠=∠ 再根据三角形内角和为180︒，可求出A ∠的度数，即可求出B ．【详解】（1）证明：∵ECD ACB ∠=∠．∴ECD ACE ACB ACE ∠+∠=∠+∠∴ACD BCE ∠=∠，在ACD △和BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴()ACD BCE SAS ≌∴AD BE =（2）∵105ACD ∠=︒，32D ∠=︒∴1801053243A ∠=︒-︒-︒=︒由（1）得≌ACD BCE∴43B A ∠=∠=︒．【点睛】本题考查了全等三角形的判定和性质，三角形的内角和定理，属于中考常考题型． 26．在平面直角坐标系中，点A 坐标(5,0)-，点B 坐标(0,5)，点 C 为x 轴正半轴上一动点，过点A 作AD BC ⊥交y 轴于点E ．（1）如图①，若点C 的坐标为(3,0)，求点E 的坐标；（2）如图②，若点C 在x 轴正半轴上运动，且5OC <，其它条件不变，连接DO ，求证：DO 平分ADC ∠；（3）若点C 在x 轴正半轴上运动，当OC CD AD +=时，则OBC ∠的度数为________．解析：（1）(0,3)E ；（2）见解析；（3）30OBC ∠=︒．【分析】（1）先根据AAS 判定△AOE ≌△BOC ，得出OE=OC ，再根据点C 的坐标为（3，0），得到OC=OE=3，进而得到点E 的坐标；（2）先过点O 作OM ⊥AD 于点M ，作ON ⊥BC 于点N ，根据△AOE ≌△BOC ，得到S △AOE =S △BOC ，且AE=BC ，再根据OM ⊥AE ，ON ⊥BC ，得出OM=ON ，进而得到OD 平分∠ADC ；（3）在DA 上截取DP=DC ，连接OP ，根据SAS 判定△OPD ≌△OCD ，再根据三角形外角性质以及三角形内角和定理，求得∠PAO=30°，进而得到∠OBC=30°．【详解】证明：（1）AD BC ⊥，AO BO ⊥，90AOE BDE BOC ∠∠∠∴===︒．又AEO BED ∠=∠，OAE OBC ∴∠=∠．(5,0)A -，(0,5)B ， 5OA OB ∴==．在AOE △和BOC 中OAE OBC OA OBAOE BOC ∠=∠⎧⎪=⎨⎪∠=∠⎩， (ASA)AOE BOC ∴≌，OE OC ∴=． C 点坐标(3,0)，3OE OC ∴==，(0,3)E ∴．（2）过O 作OM AD ⊥于M ，ON BC ⊥于N ，AOE BOC ≌，AOE BOC S S ∴=，AE BC =， 1122AE OM BC ON ∴⨯⨯=⨯⨯， OM ON ∴=，OM AD ⊥，ON BC ⊥，DO ∴平分ADC ∠．（3）如所示，在DA 上截取DP=DC ，连接OP ，∵∠PDO=∠CDO ，OD=OD ，∴△OPD ≌△OCD ，∴OC=OP ，∠OPD=∠OCD ，∵OC CD AD +=，∴OC=AD-CD∴AD-DP=OP ，即AP=OP ，∴∠PAO=∠POA ，∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB ，又∵∠PAO+∠OCD=90°，∴3∠PAO=90°，∴∠PAO=30°，∵OAP OBC ∠=∠∴∠OBC=∠PAO =30°．【点睛】本题属于三角形综合题，主要考查了全等三角形的判定与性质，角平分线的判定定理以及等腰直角三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，运用全等三角形的性质进行求解．27．如图，∠ACB 和∠ADB 都是直角，BC ＝BD ，E 是AB 上任意一点．（1）求证：△ABC ≌△ABD ．（2）求证：CE ＝DE ．解析：（1）见解析；（2）见解析．【分析】（1）利用“HL ”证明Rt △ACB ≌Rt △ADB 即可；（2）由Rt △ACB ≌Rt △ADB 得到∠CAB ＝∠DAB ，AC ＝AD ，然后利用“SAS ”可证明△ACE ≌△ADE ，从而得到CE ＝DE ．【详解】证明：（1）在Rt △ACB 和Rt △ADB 中，AB AB BC BD =⎧⎨=⎩， ∴Rt △ACB ≌Rt △ADB （HL ）；（2）∵Rt △ACB ≌Rt △ADB ，∴∠CAB ＝∠DAB ，AC ＝AD ，在△ACE 和△ADE 中，AC AD CAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△ADE （SAS ），∴CE ＝DE ．【点睛】此题考查全等三角形的判定及性质，根据图形的特点确定对应相等的条件，利用：SSS 、SAS 、ASA 、AAS 或HL 证明两个三角形全等由此解决问题是解题的关键．28．在学习了“等边对等角”定理后，某数学兴趣小组的同学继续探究了同一个三角形中边与角的数量关系，得到了一个正确的结论：“在同一个三角形中，较长的边所对的角较大”，简称：“在同一个三角形中，大边对大角”．即，如图：当 AB ＞AC 时，∠C ＞∠B ．该兴趣小组的同学在此基础上对等腰三角形“三线合一”性质的一般情况，继续进行了深入的探究，请你补充完整：（1）在△ABC 中，AD 是BC 边上的高线．①如图1，若AB =AC ，则∠BAD =∠CAD ；②如图2，若AB ≠AC ，当AB ＞AC 时，∠BAD ∠CAD ．（填“>”，“<”，“=”）证明：∵ AD 是BC 边上的高线，∴∠ADB =∠ADC =90°．∴ ∠BAD =90°-∠B ，∠CAD =90°-∠C ．∵AB ＞AC ，∴ （在同一个三角形中，大边对大角）．∴∠BAD ∠CAD ．（2）在△ABC 中，AD 是BC 边上的中线．①如图1，若AB =AC ，则∠BAD =∠CAD ；②如图3，若AB ≠AC ，当AB ＞AC 时，∠BAD ∠CAD ．（填“>”，“<”，“=”）证明：解析：（1）①见解析，②∠B<∠C ，>；（2）①见解析；②＜【分析】（1）①由HL 证明Rt △ABD ≌Rt △ACD 可得结论；②由AB ＞AC 得∠C ＞∠B 即可得出结论；（2）①由SSS 证明△ABD ≌△ACD 可得结论；②作辅助线证明△BDE CDA ≅∆，得BE CA =，∠BED CAD =∠，证得∠BAD BED <∠，即可得到结论．【详解】解：（1）①证明：∵AD 是BC 边上的高线∴∠ADB=∠ADC=90°，在Rt △ADB 和Rt △ADC 中AB AC AD AD =⎧⎨=⎩∴Rt △ABD ≌Rt △ACD∴∠BAD =∠CAD ；②证明：∵ AD 是BC 边上的高线，∴∠ADB =∠ADC =90°．∴ ∠BAD =90°-∠B ，∠CAD =90°-∠C ．∵AB ＞AC ， ∴∠B<∠C （在同一个三角形中，大边对大角）．∴∠BAD > ∠CAD ．故答案为：∠B<∠C ，>；（2）①证明：∵AD 是BC 边上的中线∴BD=CD在△ABD 和△ACD 中AB AC AD AD BD CD =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACD∴∠BAD=∠CAD②如图，延长AD 至点E ，使AD=ED ，连接BE ，∵AD 是△ABC 的BC 边上的中线，∴BD CD =在△BDE 和△CDA 中，BD CD BDE CDA ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE CDA ≅∆∴BE CA =，∠BED CAD =∠，又AB AC >，则AB BE >∴∠BAD BED <∠∴∠BAD CAD <∠．故答案为：＜．【点睛】此题主要考查了全等三角形的判定与性质，作出辅助线构造全等三角形是解答此题的关键．。

六年级小升初数学复习培优试题测试题(附答案解析)

六年级小升初数学复习培优试题测试题（附答案解析）一、选择题1．一个零件的高是4mm，在图纸上的高是2cm．这C幅图纸的比例尺是（）．A．1:5B．5:1C．1:2D．2:12．下图是用小方块拼搭而成的几何模型，如果把这个模型的表面全部涂上红色（包括底面），则四个面涂上红色的有（）块。

A．2 B．3 C．4 D．53．一块长方形绿地，长12 dm，宽是长的23，求这块长方形绿地的面积．正确的算式是( )．A．12×23B．12×（12×23）C．（12+23）×2 D．12×（1-23）4．一个三角形三内角的度数的比为2∶2∶3，这个三角形是（）。

A．锐角三角形B．直角三角形C．钝角三角形5．甲、乙两人练习赛跑，甲每秒跑7m，乙每秒跑6.5m，甲让乙先跑5m，设x秒后甲可追上乙，则下列四个方程中不正确的是（）A．7x=6.5x+5 B．7x+5=6.5x C．（7﹣6.5）x=5 D．6.5x=7x﹣56．下图是一个正方体的展开图。

写有数字“1”的面和写有（）的面是相对的。

A．数字“3”B．字母“A”C．字母“B”7．下面各句话中，表述错误的是（）。

A．三个奇数的和一定是奇数B．2020年的第一季度共有91天C．一个三角形的面积比与它等底等高的平行四边形的面积少50%D．在﹣1、0、3、﹣2、﹣0.1这几个数中，最小的数是﹣0.18．两个圆柱的底面周长相等，则它们的（）相等。

A．侧面积B．表面积C．底面积D．体积9．某通讯公司的手机收费按原标准每分钟降低了a元，再次下调了25%，现在的收费标准为每分钟b元，原收费标准是（）。

A．43b a-B．43ba C．43b a+D．34b a+10．用M ，N ，P ，Q 各代表四种简单几何图形（线段、等边三角形、正方形、圆）中的一种。

图1﹣图4是由M ，N ，P ，Q 中的两种图形组合而成的（组合用“&”表示）。

九年级数学圆的综合的专项培优练习题(含答案)附答案解析

九年级数学圆的综合的专项培优练习题(含答案)附答案解析一、圆的综合1．如图，△ABC 是⊙O 的内接三角形，点D 在BC uuu r 上，点E 在弦AB 上（E 不与A 重合），且四边形BDCE 为菱形．（1）求证：AC=CE ；（2）求证：BC 2﹣AC 2=AB•AC ；（3）已知⊙O 的半径为3．①若AB AC =53，求BC 的长； ②当AB AC为何值时，AB•AC 的值最大？【答案】（1）证明见解析；（2）证明见解析；（3）2；②32【解析】分析：（1）由菱形知∠D=∠BEC ，由∠A+∠D=∠BEC+∠AEC=180°可得∠A=∠AEC ，据此得证；（2）以点C 为圆心，CE 长为半径作⊙C ，与BC 交于点F ，于BC 延长线交于点G ，则CF=CG=AC=CE=CD ，证△BEF ∽△BGA 得BE BG BF BA =，即B F•BG=BE•AB ，将BF=BC-CF=BC-AC 、BG=BC+CG=BC+AC 代入可得；（3）①设AB=5k 、AC=3k ，由BC 2-AC 2=AB•AC 知6k ，连接ED 交BC 于点M ，Rt △DMC 中由DC=AC=3k 、MC=126k 求得22CD CM -3，可知OM=OD-3，在Rt △COM 中，由OM 2+MC 2=OC 2可得答案．②设OM=d ，则MD=3-d ，MC 2=OC 2-OM 2=9-d 2，继而知BC 2=（2MC ）2=36-4d 2、AC 2=DC 2=DM 2+CM 2=（3-d ）2+9-d 2，由（2）得AB•AC=BC 2-AC 2，据此得出关于d 的二次函数，利用二次函数的性质可得答案．详解：（1）∵四边形EBDC 为菱形，∴∠D=∠BEC ，∵四边形ABDC 是圆的内接四边形，∴∠A+∠D=180°，又∠BEC+∠AEC=180°，∴∠A=∠AEC ，∴AC=CE；（2）以点C为圆心，CE长为半径作⊙C，与BC交于点F，于BC延长线交于点G，则CF=CG，由（1）知AC=CE=CD，∴CF=CG=AC，∵四边形AEFG是⊙C的内接四边形，∴∠G+∠AEF=180°，又∵∠AEF+∠BEF=180°，∴∠G=∠BEF，∵∠EBF=∠GBA，∴△BEF∽△BGA，∴BE BGBF BA=，即BF•BG=BE•AB，∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC，BE=CE=AC，∴（BC﹣AC）（BC+AC）=AB•AC，即BC2﹣AC2=AB•AC；（3）设AB=5k、AC=3k，∵BC2﹣AC2=AB•AC，∴6k，连接ED交BC于点M，∵四边形BDCE是菱形，∴DE垂直平分BC，则点E、O、M、D共线，在Rt△DMC中，DC=AC=3k，MC=126k，∴223CD CM k-=，∴OM=OD﹣DM=33k，在Rt△COM中，由OM2+MC2=OC2得（33）2+6k）2=32，解得：k=33或k=0（舍），∴62；②设OM=d，则MD=3﹣d，MC2=OC2﹣OM2=9﹣d2，∴BC 2=（2MC ）2=36﹣4d 2，AC 2=DC 2=DM 2+CM 2=（3﹣d ）2+9﹣d 2，由（2）得AB•AC=BC 2﹣AC 2=﹣4d 2+6d+18=﹣4（d ﹣34）2+814， ∴当d=34，即OM=34时，AB•AC 最大，最大值为814， ∴DC 2=272， ∴AC=DC=362， ∴AB=964，此时32AB AC =．点睛：本题主要考查圆的综合问题，解题的关键是掌握圆的有关性质、圆内接四边形的性质及菱形的性质、相似三角形的判定与性质、二次函数的性质等知识点．2．已知AB ，CD 都是O e 的直径，连接DB ，过点C 的切线交DB 的延长线于点E ． ()1如图1，求证：AOD 2E 180∠∠+=o ；()2如图2，过点A 作AF EC ⊥交EC 的延长线于点F ，过点D 作DG AB ⊥，垂足为点G ，求证：DG CF =；()3如图3，在()2的条件下，当DG 3CE 4=时，在O e 外取一点H ，连接CH 、DH 分别交O e 于点M 、N ，且HDE HCE ∠∠=，点P 在HD 的延长线上，连接PO 并延长交CM 于点Q ，若PD 11=，DN 14=，MQ OB =，求线段HM 的长．【答案】（1）证明见解析（2）证明见解析（3）37【解析】【分析】（1）由∠D +∠E =90°，可得2∠D +2∠E =180°，只要证明∠AOD =2∠D 即可；（2）如图2中，作OR ⊥AF 于R ．只要证明△AOR ≌△ODG 即可；（3）如图3中，连接BC 、OM 、ON 、CN ，作BT ⊥CL 于T ，作NK ⊥CH 于K ，设CH 交DE于W ．解直角三角形分别求出KM ，KH 即可；【详解】()1证明：如图1中，O Q e 与CE 相切于点C ，OC CE ∴⊥，OCE 90∠∴=o ，D E 90∠∠∴+=o ，2D 2E 180∠∠∴+=o ，AOD COB ∠∠=Q ，BOC 2D ∠∠=，AOD 2D ∠∠=，AOD 2E 180∠∠∴+=o ．()2证明：如图2中，作OR AF ⊥于R ．OCF F ORF 90∠∠∠===o Q ，∴四边形OCFR 是矩形，AF//CD ∴，CF OR =，A AOD ∠∠∴=，在AOR V 和ODG V 中，A AOD ∠∠=Q ，ARO OGD 90∠∠==o ，OA DO =，AOR ∴V ≌ODG V ，OR DG ∴=，DG CF ∴=，()3解：如图3中，连接BC 、OM 、ON 、CN ，作BT CL ⊥于T ，作NK CH ⊥于K ，设CH 交DE 于W ．设DG 3m =，则CF 3m =，CE 4m =，OCF F BTE 90∠∠∠===o Q ，AF//OC//BT ∴，OA OB =Q ，CT CF 3m ∴==，ET m ∴=，CD Q 为直径，CBD CND 90CBE ∠∠∠∴===o ，E 90EBT CBT ∠∠∠∴=-=o ，tan E tan CBT ∠∠∴=，BT CT ET BT∴=， BT 3m m BT∴=， BT 3m(∴=负根已经舍弃)，3m tan E 3∠∴== E 60∠∴=o ，CWD HDE H ∠∠∠=+Q ，HDE HCE ∠∠=，H E 60∠∠∴==o ，MON 2HCN 60∠∠∴==o ，OM ON =Q ，OMN ∴V 是等边三角形，MN ON ∴=，QM OB OM ==Q ，MOQ MQO ∠∠∴=，MOQ PON 180MON 120∠∠∠+=-=o o Q ，MQO P 180H 120∠∠∠+=-=o o ， PON P ∠∠∴=，ON NP 141125∴==+=，CD 2ON 50∴==，MN ON 25==，在Rt CDN V 中，2222CN CD DN 501448=-=-=，在Rt CHN V 中，CN 48tan H 3HN HN∠===， HN 163∴=，在Rt KNH V 中，1KH HN 832==，3NK HN 24==，在Rt NMK V 中，2222MK MN NK 25247=-=-=，HM HK MK 837∴=+=+．【点睛】本题考查圆综合题、全等三角形的判定和性质、平行线的性质、勾股定理、等边三角形的判定和性质、锐角三角函数等知识，添加常用辅助线，构造全等三角形或直角三角形解题的关键.3．已知O e 的半径为5，弦AB 的长度为m ，点C 是弦AB 所对优弧上的一动点． ()1如图①，若m 5=，则C ∠的度数为______o ；()2如图②，若m 6=．①求C ∠的正切值；②若ABC V 为等腰三角形，求ABC V 面积．【答案】()130；()2C ∠①的正切值为34；ABC S 27=V ②或43225. 【解析】【分析】 ()1连接OA ，OB ，判断出AOB V 是等边三角形，即可得出结论；()2①先求出10AD =，再用勾股定理求出8BD =，进而求出tan ADB ∠，即可得出结论；②分三种情况，利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论．【详解】()1如图1，连接OB ，OA ，OB OC 5∴==，AB m 5==Q ，OB OC AB ∴==，AOB ∴V 是等边三角形，AOB 60∠∴=o ， 1ACB AOB 302∠∠∴==o ，故答案为30；()2①如图2，连接AO 并延长交O e 于D ，连接BD ，AD Q 为O e 的直径，AD 10∴=，ABD 90∠=o ，在Rt ABD V 中，AB m 6==，根据勾股定理得，BD 8=，AB 3tan ADB BD 4∠∴==， C ADB ∠∠=Q ，C ∠∴的正切值为34； ②Ⅰ、当AC BC =时，如图3，连接CO 并延长交AB 于E ，AC BC =Q ，AO BO =，CE ∴为AB 的垂直平分线，AE BE 3∴==，在Rt AEO V 中，OA 5=，根据勾股定理得，OE 4=，CE OE OC 9∴=+=，ABC 11S AB CE 692722∴=⨯=⨯⨯=V ； Ⅱ、当AC AB 6==时，如图4，连接OA 交BC 于F ，AC AB =Q ，OC OB =，AO ∴是BC 的垂直平分线，过点O 作OG AB ⊥于G ，1AOG AOB 2∠∠∴=，1AG AB 32==， AOB 2ACB ∠∠=Q ，ACF AOG ∠∠∴=，在Rt AOG V 中，AG 3sin AOG AC 5∠==， 3sin ACF 5∠∴=，在Rt ACF V 中，3sin ACF 5∠=， 318AF AC 55∴==，24CF 5∴=， ABC 111824432S AF BC 225525∴=⨯=⨯⨯=V ； Ⅲ、当BA BC 6==时，如图5，由对称性知，ABC 432S 25=V ．【点睛】圆的综合题，主要圆的性质，圆周角定理，垂径定理，等腰三角形的性质，三角形的面积公式，用分类讨论的思想解决问题是解本题的关键．4．如图，AB 为O e 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O e 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O e 的切线，理由见解析；（2）证明见解析.【解析】【分析】（1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE V V ∽即可解决问题.【详解】()1解：结论：DE 是O e 的切线．理由：连接OD ．CDB ADE ∠=∠Q ，ADC EDB ∴∠=∠，//CD AB Q ，CDA DAB ∴∠=∠，OA OD =Q ，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠，AB Q 是直径，90ADB ∴∠=o ，90ADB ODE ∴∠=∠=o ，DE OD ∴⊥，DE ∴是O e 的切线．()2//CD AB Q ，ADC DAB ∴∠=∠，CDB DBE ∠=∠，AC BD ∴=n n， AC BD ∴=，DCB DAB ∠=∠Q ，EDB DAB ∠=∠，EDB DCB ∴∠=∠，CDB ∴V ∽DBE V ，CD DB BD BE∴=， 2BD CD BE ∴=⋅，2AC CD BE ∴=⋅．【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.5．在⊙O 中，点C 是AB u u u r 上的一个动点(不与点A ，B 重合)，∠ACB=120°，点I 是∠ABC 的内心，CI 的延长线交⊙O 于点D ，连结AD,BD ．（1）求证：AD=BD．（2）猜想线段AB与DI的数量关系，并说明理由．（3）若⊙O的半径为2，点E，F是»AB的三等分点，当点C从点E运动到点F时，求点I 随之运动形成的路径长．【答案】（1）证明见解析；（2）AB=DI，理由见解析（3）23【解析】分析：（1）根据内心的定义可得CI平分∠ACB，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I 随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE是直径∴DE=4，∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，∴∠ADB=60°∴弧AB的度数为120°，∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.6．如图，AB是⊙O的直径，PA是⊙O的切线，点C在⊙O上，CB∥PO．（1）判断PC与⊙O的位置关系，并说明理由；（2）若AB=6，CB=4，求PC的长．【答案】（1）PC是⊙O的切线，理由见解析；（235 2【解析】试题分析：（1）要证PC是⊙O的切线，只要连接OC，再证∠PCO=90°即可．（2）可以连接AC，根据已知先证明△ACB∽△PCO，再根据勾股定理和相似三角形的性质求出PC的长．试题解析：（1）结论：PC是⊙O的切线．证明：连接OC∵CB∥PO∴∠POA=∠B，∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC，OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线．（2）连接AC∵AB是⊙O的直径∴∠ACB=90°（6分）由（1）知∠PCO=90°，∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴．点睛：本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．同时考查了勾股定理和相似三角形的性质．7．如图，在RtΔABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F.（1）求证：AE=BF；（2）连接EF，求证：∠FEB=∠GDA；（3）连接GF,若AE=2，EB=4，求ΔGFD的面积.【答案】（1）（2）见解析；（3）9【解析】分析：（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=12AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF ，BG ，由三角形AED 与三角形BFD 全等，得到ED =FD ，进而得到三角形DEF 为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE =BF =1，在直角三角形BEF 中，利用勾股定理求出EF 的长，利用锐角三角形函数定义求出DE 的长，利用两对角相等的三角形相似得到三角形AED 与三角形GEB 相似，由相似得比例，求出GE 的长，由GE +ED 求出GD 的长，根据三角形的面积公式计算即可．详解：（1）连接BD ．在Rt △ABC 中，∠ABC =90°，AB =BC ，∴∠A =∠C =45°． ∵AB 为圆O 的直径，∴∠ADB =90°，即BD ⊥AC ，∴AD =DC =BD =12AC ，∠CBD =∠C =45°，∴∠A =∠FBD ．∵DF ⊥DG ，∴∠FDG =90°，∴∠FDB +∠BDG =90°．∵∠EDA +∠BDG =90°，∴∠EDA =∠FDB ．在△AED 和△BFD 中，A FBD AD BD EDA FDB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED ≌△BFD （ASA ），∴AE =BF ；（2）连接EF ，BG ． ∵△AED ≌△BFD ，∴DE =DF ．∵∠EDF =90°，∴△EDF 是等腰直角三角形，∴∠DEF =45°． ∵∠G =∠A =45°，∴∠G =∠DEF ，∴GB ∥EF ，∴∠FEB =∠GBA ． ∵∠GBA =∠GDA ，∴∠FEB =∠GDA ；（3）∵AE =BF ，AE =2，∴BF =2．在Rt △EBF 中，∠EBF =90°，∴根据勾股定理得：EF 2=EB 2+BF 2．∵EB =4，BF =2，∴EF∵△DEF 为等腰直角三角形，∠EDF =90°，∴cos ∠DEF =DEEF． ∵EF=∴DE=2． ∵∠G =∠A ，∠GEB =∠AED ，∴△GEB ∽△AED ，∴GE AE =EBED，即GE •ED =AE •EB ，∴GE =8，即GE，则GD =GE +ED∴11192252S GD DF GD DE =⨯⨯=⨯⨯==．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．8．如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．【答案】(1) B（，2）．(2)证明见解析.【解析】试题分析：（1）在Rt△ABN中，求出AN、AB即可解决问题；（2）连接MC，NC．只要证明∠MCD=90°即可试题解析：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．考点：切线的判定；坐标与图形性质．9．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C ＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB＝90°,∴点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,除去点（2,2）,∴当PM⊥x轴时,点P纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆．10．.如图，△ABC中，∠ACB＝90°，∠A＝30°，AB＝6．D是线段AC上一个动点（不与点A重合），⊙D与AB相切，切点为E，⊙D交射线．．BC于．．DC于点F，过F作FG⊥EF交直线点G，设⊙D的半径为r．（1）求证AE＝EF；（2）当⊙D与直线BC相切时，求r的值；（3）当点G落在⊙D内部时，直接写出r的取值范围．【答案】(1)见解析,(2)r=3,(3)63 3r<<【解析】【分析】（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，即可求解；（2）如图2所示，连接DE，当圆与BC相切时，切点为F，∠A=30°，AB=6，则BF=3，AD=2r，由勾股定理，即可求解；（3）分点F在线段AC上、点F在线段AC的延长线上两种情况，分别求解即可．【详解】解：设圆的半径为r；（1）连接DE，则∠ADE=60°=∠DEF+∠DFE，而∠DEF=∠DFE，则∠DEF=∠DFE=30°=∠A，∴AE=EF；（2）如图2所示，连接DE，当圆与BC相切时，切点为F∠A=30°，AB=6，则BF=3，AD=2r，由勾股定理得：（3r）2+9=36，解得：3（3）①当点F 在线段AC 上时，如图3所示，连接DE 、DG ，333,3933FC r GC FC r =-==- ②当点F 在线段AC 的延长线上时，如图4所示，连接DE 、DG ，333,3339FC r GC FC r ===-两种情况下GC 符号相反，GC 2相同，由勾股定理得：DG 2=CD 2+CG 2，点G 在圆的内部，故：DG2＜r2，即：22(332)(339)2r r r +-<整理得：25113180r r -+<6335r <<【点睛】本题考查了圆的综合题：圆的切线垂直于过切点的半径；利用勾股定理计算线段的长．11．如图，⊙O 是△ABC 的外接圆，AB 是直径，过点O 作OD ⊥CB ，垂足为点D ，延长DO 交⊙O 于点E ，过点E 作PE ⊥AB ，垂足为点P ，作射线DP 交CA 的延长线于F 点，连接EF ，（1）求证：OD＝OP；（2）求证：FE是⊙O的切线．【答案】（1）证明见解析；（2）证明见解析．【解析】试题分析：（2）证明△POE≌△ADO可得DO=EO；（3）连接AE，BE，证出△APE≌△AFE即可得出结论．试题解析：（1）∵∠EPO=∠BDO=90°∠EOP=∠BODOE=OB∴△OPE≌△ODB∴OD="OP"（2）连接EA，EB∴∠1=∠EBC∵AB是直径∴∠AEB=∠C=90°∴∠2+∠3=90°∵∠3=∠DEB∵∠BDE=90°∴∠EBC+∠DEB=90°∴∠2=∠EBC=∠1∵∠C=90°∠BDE=90°∴CF∥OE∴∠ODP=∠AFP∵OD=OP∴∠ODP=∠OPD∵∠OPD=∠APF∴∠AFP=∠APF∴AF=AP 又AE=AE∴△APE≌△AFE∴∠AFE=∠APE=90°∴∠FED=90°∴FE是⊙O的切线考点：切线的判定．12．如图，点B在数轴上对应的数是﹣2，以原点O为原心、OB的长为半径作优弧AB，使点A在原点的左上方，且tan∠AOB＝3，点C为OB的中点，点D在数轴上对应的数为4．（1）S扇形AOB＝（大于半圆的扇形）；（2）点P是优弧AB上任意一点，则∠PDB的最大值为°（3）在（2）的条件下，当∠PDB最大，且∠AOP＜180°时，固定△OPD的形状和大小，以原点O为旋转中心，将△OPD顺时针旋转α（0°≤α≤360°）①连接CP，AD．在旋转过程中，CP与AD有何数量关系，并说明理由；②当PD∥AO时，求AD2的值；③直接写出在旋转过程中，点C到PD所在直线的距离d的取值范围．【答案】（1）103π（2）30（3）①AD＝2PC②20+83或20+83③1≤d≤3【解析】【分析】（1）利用扇形的面积公式计算即可．（2）如图1中，当PD与⊙O相切时，∠PDB的值最大．解直角三角形即可解决问题．（3）①结论：AD＝2PC．如图2中，连接AB，AC．证明△COP∽△AOD，即可解决问题．②分两种情形：如图3中，当PD∥OA时，设OD交⊙O于K，连接PK交OC于H．求出PC即可．如图④中，当PA∥OA时，作PK⊥OB于K，同法可得．③判断出PC的取值范围即可解决问题．【详解】（1）∵tan∠AOB＝3，∴∠AOB＝60°，∴S扇形AOB＝23002103603ππ⋅⋅=（大于半圆的扇形），（2）如图1中，当PD与⊙O相切时，∠PDB的值最大．∵PD是⊙O的切线，∴OP⊥PD，∴∠OPD ＝90°， ∵21sin 42OP PDO OD ∠=== ∴∠PDB ＝30°，同法当DP ′与⊙O 相切时，∠BDP ′＝30°，∴∠PDB 的最大值为30°．故答案为30．（3）①结论：AD ＝2PC ．理由：如图2中，连接AB ，AC ．∵OA ＝OB ，∠AOB ＝60°，∴△AOB 是等边三角形，∵BC ＝OC ，∴AC ⊥OB ，∵∠AOC ＝∠DOP ＝60°，∴∠COP ＝∠AOD ，∵2AO OD OC OP==， ∴△COP ∽△AOD ， ∴2AD AO PC OC==， ∴AD ＝2PC ． ②如图3中，当PD ∥OA 时，设OD 交⊙O 于K ，连接PK 交OC 于H ．∵OP ＝OK ，∠POK ＝60°，∴△OPK 是等边三角形，∵PD∥OA，∴∠AOP＝∠OPD＝90°，∴∠POH+∠AOC＝90°，∵∠AOC＝60°，∴∠POH＝30°，∴PH＝12OP＝1，OH＝3PH＝3，∴PC＝2222PH CH1(13)523+=++=+，∵AD＝2PC，∴AD2＝4（5+23）＝20+83．如图④中，当PA∥OA时，作PK⊥OB于K，同法可得：PC2＝12+（3﹣1）2＝5﹣23，AD2＝4PC2＝20﹣83．③由题意1≤PC≤3，∴在旋转过程中，点C到PD所在直线的距离d的取值范围为1≤d≤3．【点睛】本题属于圆综合题，考查了切线的性质，相似三角形的判定和性质，旋转变换，勾股定理，等边三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题．13．如图，已知AB是⊙O的直径，BC是弦，弦BD平分∠ABC交AC于F，弦DE⊥AB于H，交AC于G．①求证：AG＝GD；②当∠ABC满足什么条件时，△DFG是等边三角形？③若AB＝10，sin∠ABD＝35，求BC的长．【答案】（1）证明见解析；（2）当∠ABC＝60°时，△DFG是等边三角形．理由见解析；（3）BC 的长为145．【解析】【分析】（1）首先连接AD ，由DE ⊥AB ，AB 是O e 的直径，根据垂径定理，即可得到¶¶AD AE =，然后根据在同圆或等圆中，同弧或等弧所对的圆周角相等，证得∠ADE ＝∠ABD ，又由弦BD 平分∠ABC ，可得∠DBC ＝∠ABD ，根据等角对等边的性质，即可证得AG=GD ；（2）当∠ABC=60°时，△DFG 是等边三角形，根据半圆（或直径）所对的圆周角是直角与三角形的外角的性质，易求得∠DGF=∠DFG=60°，即可证得结论；（3）利用三角函数先求出tan ∠ABD 34=，cos ∠ABD ＝45，再求出DF 、BF ，然后即可求出BC.【详解】（1）证明：连接AD ，∵DE ⊥AB ，AB 是⊙O 的直径，∴¶¶AD AE =，∴∠ADE ＝∠ABD ，∵弦BD 平分∠ABC ，∴∠DBC ＝∠ABD ，∵∠DBC ＝∠DAC ，∴∠ADE ＝∠DAC ，∴AG ＝GD ；（2）解：当∠ABC ＝60°时，△DFG 是等边三角形．理由：∵弦BD 平分∠ABC ，∴∠DBC ＝∠ABD ＝30°，∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴∠CAB ＝90°﹣∠ABC ＝30°，∴∠DFG ＝∠FAB+∠DBA ＝60°，∵DE ⊥AB ，∴∠DGF ＝∠AGH ＝90°﹣∠CAB ＝60°，∴△DGF 是等边三角形；（3）解：∵AB 是⊙O 的直径，∴∠ADB ＝∠ACB ＝90°，∵∠DAC ＝∠DBC ＝∠ABD ，∵AB ＝10，sin ∠ABD ＝35， ∴在Rt △ABD 中，AD ＝AB•sin ∠ABD ＝6，∴BD8，∴tan ∠ABD ＝34AD BD ，cos ∠ABD ＝4=5BD AB ，在Rt △ADF 中，DF ＝AD•tan ∠DAF ＝AD•tan ∠ABD ＝6×34＝92， ∴BF ＝BD ﹣DF ＝8﹣92＝72， ∴在Rt △BCF 中，BC ＝BF•cos ∠DBC ＝BF•cos ∠ABD ＝72×45＝145． ∴BC 的长为：145．【点睛】此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识．此题综合性较强，难度较大，解题的关键是掌握数形结合思想与转化思想的应用，注意辅助线的作法．14．如图，AB 是半圆⊙O 的直径，点C 是半圆⊙O 上的点，连接AC ，BC ，点E 是AC 的中点，点F 是射线OE 上一点．（1）如图1，连接FA ，FC ，若∠AFC ＝2∠BAC ，求证：FA ⊥AB ；（2）如图2，过点C 作CD ⊥AB 于点D ，点G 是线段CD 上一点（不与点C 重合），连接FA ，FG ，FG 与AC 相交于点P ，且AF ＝FG ．①试猜想∠AFG 和∠B 的数量关系，并证明；②连接OG ，若OE ＝BD ，∠GOE ＝90°，⊙O 的半径为2，求EP 的长．【答案】（1）见解析；（2）①结论：∠GFA ＝2∠ABC ．理由见解析；②PE 3．【解析】【分析】（1）证明∠OFA ＝∠BAC ，由∠EAO +∠EOA ＝90°，推出∠OFA +∠AOE ＝90°，推出∠FAO ＝90°即可解决问题．（2）①结论：∠GFA＝2∠ABC．连接FC．由FC＝FG＝FA，以F为圆心FC为半径作⊙F．因为»»=，推出∠GFA＝2∠ACG，再证明∠ACG＝∠ABC．AG AG②图2﹣1中，连接AG，作FH⊥AG于H．想办法证明∠GFA＝120°，求出EF，OF，OG即可解决问题．【详解】（1）证明：连接OC．∵OA＝OC，EC＝EA，∴OF⊥AC，∴FC＝FA，∴∠OFA＝∠OFC，∵∠CFA＝2∠BAC，∴∠OFA＝∠BAC，∵∠OEA＝90°，∴∠EAO+∠EOA＝90°，∴∠OFA+∠AOE＝90°，∴∠FAO＝90°，∴AF⊥AB．（2）①解：结论：∠GFA＝2∠ABC．理由：连接FC．∵OF垂直平分线段AC，∴FG＝FA，∵FG＝FA，∴FC＝FG＝FA，以F为圆心FC为半径作⊙F．∵»»AG AG=，∴∠GFA＝2∠ACG，∵AB是⊙O的直径，∴∠ACB ＝90°，∵CD ⊥AB ，∴∠ABC +∠BCA ＝90°，∵∠BCD +∠ACD ＝90°，∴∠ABC ＝∠ACG ，∴∠GFA ＝2∠ABC ．②如图2﹣1中，连接AG ，作FH ⊥AG 于H ．∵BD ＝OE ，∠CDB ＝∠AEO ＝90°，∠B ＝∠AOE ，∴△CDB ≌△AEO （AAS ），∴CD ＝AE ，∵EC ＝EA ，∴AC ＝2CD ．∴∠BAC ＝30°，∠ABC ＝60°，∴∠GFA ＝120°，∵OA ＝OB ＝2，∴OE ＝1，AE ＝，BA ＝4，BD ＝OD ＝1， ∵∠GOE ＝∠AEO ＝90°，∴OG ∥AC ， 323DG OG ∴==, 22221AG DG AD ∴=+=， ∵FG ＝FA ，FH ⊥AG ，∴AH ＝HG 21∠AFH ＝60°， ∴AF ＝27sin 603AH ︒=，在Rt △AEF 中，EF 2213AF AE -=， ∴OF ＝OE +EF ＝43 ， ∵PE ∥OG ， ∴PE EF OG 0F=，∴1342333PE，∴PE＝36．【点睛】圆综合题，考查了垂径定理，勾股定理，圆周角定理，全等三角形的判定和性质，锐角三角函数，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.15．如图1，⊙O的直径AB=12，P是弦BC上一动点（与点B，C不重合），∠ABC=30°，过点P作PD⊥OP交⊙O于点D．（1）如图2，当PD∥AB时，求PD的长；（2）如图3，当弧DC=弧AC时，延长AB至点E，使BE=12AB，连接DE．①求证：DE是⊙O的切线；②求PC的长．【答案】（1）26；（2）①证明见解析；②33﹣3．【解析】试题分析：（1）根据题意首先得出半径长，再利用锐角三角三角函数关系得出OP，PD的长；（2）①首先得出△OBD是等边三角形，进而得出∠ODE=∠OFB=90°，求出答案即可；②首先求出CF的长，进而利用直角三角形的性质得出PF的长，进而得出答案．试题解析：（1）如图2，连接OD，∵OP⊥PD，PD∥AB，∴∠POB=90°，∵⊙O的直径AB=12，∴OB=OD=6，在Rt△POB中，∠ABC=30°，∴OP=OB•tan30°=6×=2，在Rt△POD中，PD===；（2）①如图3，连接OD，交CB于点F，连接BD，∵，∴∠DBC=∠ABC=30°，∴∠ABD=60°，∵OB=OD，∴△OBD是等边三角形，∴OD⊥FB，∵BE=AB，∴OB=BE，∴BF∥ED，∴∠ODE=∠OFB=90°，∴DE是⊙O的切线；②由①知，OD⊥BC，∴CF=FB=OB•cos30°=6×=3，在Rt△POD中，OF=DF，∴PF=DO=3（直角三角形斜边上的中线，等于斜边的一半），∴CP=CF﹣PF=3﹣3．考点：圆的综合题。

华南师大附中培优试题1

培优练习〔1〕2022－02－24 一、选择题： 1、函数)(1x fy -=的图象过〔1,0〕,那么)121(-=x f y 的反函数的图象一定过点〔〕A ．〔1,2〕B ．〔2,1〕C ．〔0,2〕D ．〔2,0〕 2、从P 点引三条射线PA,PB,PC,每两条射线夹角为60°,那么平面PAB 和平面PBC 所成二面角正弦值为〔〕A ．322 B ．36 C ．33 D ．23 3、x ,y 满足不等式组22224222+-++=⎪⎩⎪⎨⎧-≥≤+≤y x y x t y y x xy 则的最小值为〔〕A ．59 B ．2 C ．3D ．24、在斜三棱柱ABC －A 1B 1C 1中,A 0,B 0,分别为侧棱AA 1,BB 1上的点,且知BB 0:B 0B 1=3:2,过A 0,B 0,C 1的截面将三棱柱分成上下两个局部体积之比为2:1,那么 AA 0:A 0A 1= 〔〕 A ．2:3 B ．4:3 C ．3:2 D ．1:1 二、填空题：5、=-++∞→)(lim 2n n n n .6、某气象站天气预报准确率是80%,5次预报中至少有4次准确的概率是〔精确到0.01〕.7、设a,b 都是正实数,且2a+b=1,设2242b a ab T --=那么当a=______且b=_______时,T 的最大值为_______. 8、如图,矩形ABCD 中,3=DC ,AD=1,在DC 上截取DE=1,将△ADE 沿AE 翻折到D ′点,当D ′在平面ABC 上的射影落在AE 上时,四棱锥D ′—ABCE 的体积是________；当D ′在平面ABC 上的射影落在AC 上时,二面角D ′—AE —B 的平面角的余弦值是_________.三、解做题：〔过程要完整、表述要标准〕 9、〔本小题总分值12分〕是否存在常数c ,使得不等式yx yy x x c y x y y x x +++≤≤+++2222对任意正实数x 、y 恒成立？证实你的结论．10、〔本小题总分值12分〕甲乙两人独立解某一道数学题,该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92. 〔1〕求该题被乙独立解出的概率；〔2〕求解出该题的人数ξ的数学期望和方差. 11、〔本小题总分值14分〕),2(|2|lg )1()(2R a a a x a x x f ∈-≠++++=〔Ⅰ〕假设)(x f 能表示成一个奇函数)(x g 和一个偶函数)(x h 的和,求)(x g 和)(x h的解析式；〔Ⅱ〕假设)(x f 和)(x g 在区间])1(,(2+-∞a 上都是减函数,求a 的取值范〔Ⅲ〕在〔Ⅱ〕的条件下,比拟61)1(和f 的大小．12、〔本小题总分值12分〕定义域为[0,1]的函数f (x)同时满足：〔1〕对于任意x ∈[0,1],总有f (x)≥0；〔2〕f (1) =1；〔3〕假设01≥x ,02≥x ,121≤+x x ,那么有)()()(2121x f x f x x f +≥+. 〔Ⅰ〕试求f(0)的值；〔Ⅱ〕试求函数f(x)的最大值；〔Ⅲ〕试证实：满足上述条件的函数f(x)对一切实数x,都有f(x)≤2x . 13、〔本小题总分值16分〕在直角坐标平面内,两点A 〔-2,0〕及B 〔2,0〕,动点Q 到点A 的距离为6,线段BQ 的垂直平分线交AQ 于点P.〔Ⅰ〕证实|PA|+|PB|为常数,并写出点P 的轨迹T 的方程；〔Ⅱ〕过点B 的直线l 与曲线T 相交于M 、N 两点,线段MN 的中点R 与点S 〔-1,0〕的连线的纵截距为t,试求t 的取值范围.14、〔本小题总分值14分〕〔文科〕椭圆C 的中央在原点,焦点在x 轴上,一条经过点)5,3(-且方向向量为)5,2(-=V 的直线l 通过椭圆C 的右焦点F,且交椭圆C 于A 、B 两点,又.2FB AF =〔1〕求直线l 的方程；〔2〕求椭圆C 的方程.〔理科〕椭圆C 的中央在原点,焦点在x 轴上,一条经过点〔3,－5〕且方向向量为)5,2(-=V 的直线l 交椭圆C 于A 、B 两点,交x 轴于M 点,又MB AM 2=.〔1〕求直线l 方程；〔2〕求椭圆C 长轴长取值的范围.培优练习〔1〕答案一、选择题：AABA 二、填空题：5．;21 6．0.74; 7．41；21；2122-； 8．12262-；32- 三、9、〔此题总分值12分〕解：当y x =时,由不等式得32=c ……3分下面分两局部给出证实：⑴先证3222≤+++y x y y x x ,此不等式⇔)2)(2(2)2(3)2(3y x y x y x y y x x ++≤+++222y x xy +≤⇔,此式显然成立； ……7分⑵再证3222≥+++y x y y x x , 此不等式⇔)2)(2(2)2(3)2(3y x y x y x y y x x ++≥+++xy y x 222≥+⇔,此式显然成立． ……10分综上可知,存在常数32=c ,是对任意的整数x 、y ,题中的不等式成立．12分10、〔此题总分值12分〕解：〔1〕记甲、乙分别解出此题的事件记为A 、B.设甲独立解出此题的概率为P 1,乙为P 2. 〔2分〕那么P 〔A 〕=P 1=0.6, P(B)=P 2:48.08.06.0)()()2(44.08.04.02.06.0)()()()()1(08.02.04.0)()()0()2()7(8.032.04.092.06.06.092.0)1)(1(1)(1)(2222212121的概率分布为分即则ξξξ=⨯=⋅===⨯+⨯=+===⨯=⋅=====-+∴=-+=---=⋅-=+B P A P P B P A P B P A P P B P A P P P P P P P P P P P P B A P B A P)12(4.096.136.2)()(4.01728.00704.01568.048.0)4.12(44.0)4.11(08.0)4.10(22222分或利用=-=-==++=⋅-+⋅-+⋅-=ξξξξE E D D11、〔此题总分值14分〕解：〔Ⅰ〕设)()()(x h x g x f += ①,其中)(x g 是奇函数,)(x h 是偶函数, 那么有 )()()()()(x h x g x h x g x f +-=+-=- ② 联立①,②可得x a x g )1()(+=,|2|lg )(2++=a x x h 〔直接给出这两个函数也给分〕…3分〔Ⅱ〕函数x a x g )1()(+= 当且仅当 01<+a ,即1-<a 时才是减函数, ∴1-<a又4)1(|2|lg )21(|2|lg )1()(222+-++++=++++=a a a x a x a x x f ∴)(x f 的递减区间是 )21,(+--∞a ……5分由得21)1(2+-≤+a a ∴ ⎪⎩⎪⎨⎧+-≤+-<21)1(12a a a 解得123-<≤-a ∴a 取值范围是)1,23[-- ……8分〔Ⅲ〕)123(|2|lg 2|2|lg )1(1)1(-<≤-+++=++++=a a a a a f |2|lg )1(++a a 和在)1,23[--上为增函数 ……10分∴21lg 21|2)23(|lg )223()1(+=+-++-≥f 61101lg 312181lg 3121=⋅+>⋅+=∴61)1(>f 即61)1(大于f . ……14分12、〔此题总分值12分〕解：〔Ⅰ〕令021==x x ,依条件〔3〕可得f(0+0) ≥f(0)+f(0),即f(0) ≤0.又由条件〔1〕得f(0) ≥0,那么f(0)=0…………………… 3分〔Ⅱ〕任取1021≤<≤x x ,可知]1,0(12∈-x x那么)()(])[()(1121122x f x x f x x x f x f +-≥+-=…………… 5分即0)()()(1212≥-≥-x x f x f x f ,故)()(12x f x f ≥ 于是当0≤x ≤1时,有f(x)≤f(1)=1因此,当x=1时,f(x)有最大值为1,………………… 7分〔Ⅲ〕证实：研究①当]1,21(∈x 时,f(x) ≤1<2x ②当]21,0(∈x 时,首先,f(2x) ≥f(x)+f(x)=2f(x),∴)2(21)(x f x f ≤………………9分显然,当]21,21(2∈x 时, 21)1(21)212(21)21()(=⋅=⋅⋅≤≤f f f x f 成立.假设当]21,21(1k k x +∈时,有k x f 21)(≤成立,其中k ＝1,2,…那么当]21,21(12++∈k k x 时,111212121)21(21)212(21)21()(+++=⋅≤⋅=⋅⋅≤≤k k k k k f f f x f可知对于]21,21(1n n x +∈,总有n x f 21)(≤,其中n=1,2,…而对于任意]21,0(∈x ,存在正整数n,使得]21,21(1n n x +∈,此时x x f n 221)(≤≤………………… …11分③当x=0时,f(0)=0≤2x ………… ……12分综上可知,满足条件的函数f(x),对x ∈[0,1],总有f(x) ≤2x 成立.13、〔此题总分值16分〕解：〔Ⅰ〕连结PB.∵线段BQ 的垂直平分线与AQ 交于点P, ∴|PB|=|PQ|,又|AQ|=6,∴|PA|+|PB|=|PA|+|PQ|=|AQ|=6〔常数〕. …2分又|PA|+|PB|>|AB|,从而P 点的轨迹T 是中央在原点,以A 、B 为两个焦点,长轴在x 轴上的椭圆,其中,2a=6,2c=4,∴椭圆方程为15922=+y x …6分〔Ⅱ〕当直线l 与x 轴垂直时,MN 的中点为R 〔2,0〕直线RS 的纵截距t =0 …7分当直线l 与x 轴不垂直时,设其斜率为k, 点),(11y x M 、),(22y x N 、),(R R y x R .由⎪⎩⎪⎨⎧=+-=159)2(22y x x k y ,消去y 整理得： 0453636)95(2222=-+-+k x k x k …9分∴59362221+=+k k x x ,那么5918)2(21221+=+=k k x x x R 5910)25918()2(222+-=-+=-=k kk k k x k y R R直线RS 的方程为)1(527102++-=x k ky . 令x=0,可得直线RS 的纵截距527102+-=k kt . 如果k=0,那么t=0；如果k ≠0,那么kk t 52710+-=.∵156||5||27|527|≥+=+k k k k 当且仅当915±=k 时,等号成立. …14分 ∴9150≤<t 或0915<≤-t 综上可知,所求t 的取值范围是]915,915[-. …16分 14、〔此题总分值12分〕〔文〕解：〔1〕直线l 过点〔3,－5〕且方向向量为方程为则l V ),5,2(-= )1(25:5523--=+=--x y y x 化简为……………………………………〔4分〕〔2〕设直线),(),,(1)1(2522112222y x B y x A by a x x y 交于与椭圆=+--=, 由2122y y BF AF -=-=求得……………………………………………………〔7分〕将中代入222222152b a y a x b y x =++-=,整理得0)1(54)54(222222=-+-+a b y b y a b由韦达定理可知：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=+-=⋅-=+=+22222221222221254)1(5454y a b a b y y y a b b y y 〔9分〕由①2/②知 )1)(54(322222-+=a a b b ……………………………………〔12分〕又,34,12222⎪⎩⎪⎨⎧===-b a b a 故可求得因此所求椭圆方程为：13422=+y x …〔14分〕〔理〕解：〔1〕直线l 过点〔3,－5〕且方向向量为)5,2(-=V5523+=--∴y x l 方程为化简为：)1(25--=x y …………〔4分〕 ………………① ………………②〔2〕设直线1)1(252222=+--=by a x x y 和椭圆交于两点A 〔x 1,y 1〕,B 〔x 2,y 2〕,和x 轴交于M 〔1,0〕由2122y y MB AM -==知………………………………………………〔7分〕将0)1(54)54(152222222222222=-+-+=++-=a b y b y a b b a y a x b y x 中得代入…………………………………………①由韦达定理知：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=+-=⋅-=+=+22222221222221254)1(5454y a b a b y y y a b b y y 由②2/③ 知：32b 2=〔4b 2+5a 2〕〔a 2－1〕…………………………………………〔10分〕化为22229)1(54a a a b --=………………………………………………④对方程①求判别式,且由△>0即0)1()54(4)54(222222>-⋅+-=∆a b a b b化简为：54522>+b a ………………………………………………⑤ 12分由④式代入⑤可知：,91,59)1(5522222<<>--+a aa a a 求得又椭圆的焦点在x 轴上, 那么,22b a >由④知：.3411,31,49)1(5422222<<<<<--=a a a aa ab 求得结合因此所求椭圆长轴长2a 范围为〔).3142,2 14分………………② ………………③。

六年级数学下册计算题专项练习题附答案(培优)

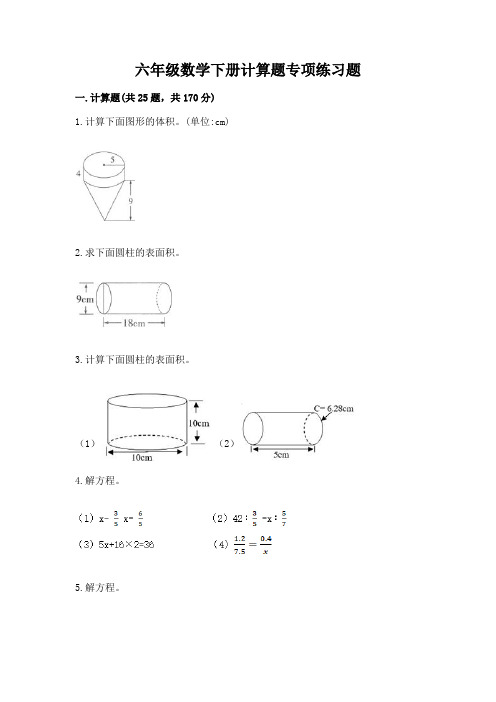
六年级数学下册计算题专项练习题一.计算题(共25题，共170分)1.计算下面图形的体积。

(单位:cm)2.求下面圆柱的表面积。

3.计算下面圆柱的表面积。

（1）（2）4.解方程。

5.解方程。

（1）42∶=x∶（2）4（x-9）=8 （3）x-60=180 6.解方程。

7.计算下列图形的体积。

（1）（2）8.计算下列圆柱的表面积。

（单位:cm）（1）（2）9.计算下面图柱的表面积是多少？（单位：cm）10.解比例。

11.求圆柱体的表面积和体积。

12.计算下面各圆锥的体积。

（1）底面周长9.42m，高是1.8m。

（2）底面直径是6dm，高是6dm。

13.求下图圆锥的体积。

14.看图列式并计算。

（1）看图列式计算。

（2）看图列式计算。

15.解比例。

16.求未知数x。

17.口算。

18.列式计算.（1）某机关精简后有工作人员75人，比原来少45人，精简了百分之几？（2）4.5的减去1.5，所得的差再除以2.1，商是多少？19.如图是一种钢制的配件（图中数据单位：cm）请计算它的表面积和体积。

20.求未知数x。

21.求未知数x。

22.求下列图形的体积。

（单位:dm）（1）（2）23.解方程。

24.直接写出答案。

25.如图是一种钢制的配件(图中数据单位：cm)，请计算它的表面积和体积。

( π 取3.14)参考答案一.计算题1.3.14×52×4+3.14×52×9×=549.5(cm3)2.3.14×（）2×2+3.14×9×18=635.85(cm2)3.（1）3.14×10×10=31.4×10=314（cm）3.14×（10÷2）×2=3.14×5×2=3.14×25×2=78.5×2=157（cm）314+157=471（cm）（2）6.28×5=31.4（cm）6.28÷3.14÷2=2÷2=1（cm）3.14×1×2=6.28（cm）31.4+6.28=37.68（cm）4.（1）3（2）50（3）（4）2.55.（1）50（2）11（3）8406.（1）0.7（2）8（3）2（4）6007.（1）3.14×3×8=3.14×9×8=28.26×8=226.08（cm）（2）4÷2=2（cm）3.14×2×4.5÷3=3.14×4×4.5÷3=12.56×1.5=18.84（cm）8.（1）2πr2+2πrh=2×3.14×（20÷2）2+2×3.14×（20÷2）×8=1130.4（cm2）（2）2πr2+2πrh=2×3.14×42+2×3.14×4×10=351.68（cm2）9.37.68平方厘米10.x=；x=1.5；x=1.5；x=11.表面积：3.14×5×2×8+3.14×52×2＝252.6+157＝409.6（平方厘米）体积：3.14×52×8＝3.14×25×8＝628（立方厘米）答：圆柱的表面积是409.6平方厘米，体积是628立方厘米。

中考数学一元二次方程培优练习(含答案)附答案解析

一、一元二次方程真题与模拟题分类汇编（难题易错题）1．解方程：(x+1)(x ﹣3)=﹣1．【答案】x 1=1+3，x 2=1﹣3【解析】试题分析：根据方程的特点，先化为一般式，然后利用配方法求解即可.试题解析：整理得：x 2﹣2x=2，配方得：x 2﹣2x+1=3，即（x ﹣1）2=3，解得：x 1=1+3，x 2=1﹣3．2． y 与x 的函数关系式为：y=1.7x （x≤m ）;或( x≥m) ；3．关于x 的一元二次方程ax 2+bx+1=0．（1）当b=a+2时，利用根的判别式判断方程根的情况；（2）若方程有两个相等的实数根，写出一组满足条件的a ，b 的值，并求此时方程的根．【答案】（1）方程有两个不相等的实数根；（2）b=-2，a=1时，x 1=x 2=﹣1．【解析】【详解】分析：（1）求出根的判别式24b ac ∆=-，判断其范围，即可判断方程根的情况.（2）方程有两个相等的实数根，则240b ac ∆=-=，写出一组满足条件的a ，b 的值即可.详解：（1）解：由题意：0a ≠．∵()22242440b ac a a a ∆=-=+-=+>， ∴原方程有两个不相等的实数根．（2）答案不唯一，满足240b ac -=（0a ≠）即可，例如：解：令1a =，2b =-，则原方程为2210x x -+=，解得：121x x ==．点睛：考查一元二次方程()200++=≠ax bx c a 根的判别式24b ac ∆=-，当240b ac ∆=->时，方程有两个不相等的实数根.当240b ac ∆=-=时，方程有两个相等的实数根.当240b ac ∆=-<时，方程没有实数根.4．淘宝网举办“双十一”购物活动许多商家都会利用这个契机进行打折让利的促销活动．甲网店销售的A 商品的成本为30元/件，网上标价为80元/件．（1）“双十一”购物活动当天，甲网店连续两次降价销售A 商品吸引顾客，问该店平均每次降价率为多少时，才能使A商品的售价为39.2元/件？（2）据媒体爆料，有一些淘宝商家在“双十一”购物活动当天先提高商品的网上标价后再推出促销活动，存在欺诈行为．“双十一”活动之前，乙网店销售A商品的成本、网上标价与甲网店一致，一周可售出1000件A商品．在“双十一”购物活动当天，乙网店先将A商品的网上标价提高a%，再推出五折促销活动，吸引了大量顾客，乙网店在“双十一”购物活动当天卖出的A商品数量相比原来一周增加了2a%，“双十一”活动当天乙网店的利润达到了3万元，求乙网店在“双十一”购物活动这天的网上标价．【答案】（1）平均每次降价率为30%，才能使这件A商品的售价为39.2元；（2）乙网店在“双十一”购物活动这天的网上标价为100元．【解析】【分析】（1）设平均每次降价率为x，才能使这件A商品的售价为39.2元，根据原标价及经过两次降价后的价格，即可得出关于x的一元二次方程，解之取其较小值即可得出结论；（2）根据总利润＝每件的利润×销售数量，即可得出关于a的一元二次方程，解之取其正值即可得出a的值，再将其代入80（1+a%）中即可求出结论．【详解】（1）设平均每次降价率为x，才能使这件A商品的售价为39.2元，根据题意得：80（1﹣x）2＝39.2，解得：x1＝0.3＝30%，x2＝1.7（不合题意，舍去）．答：平均每次降价率为30%，才能使这件A商品的售价为39.2元．（2）根据题意得：[0.5×80（1+a%）﹣30]×1000（1+2a%）＝30000，整理得：a2+75a﹣2500＝0，解得：a1＝25，a2＝﹣100（不合题意，舍去），∴80（1+a%）＝80×（1+25%）＝100．答：乙网店在“双十一”购物活动这天的网上标价为100元．【点睛】本题考查一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．5．为了让学生亲身感受合肥城市的变化，蜀山中学九（1）班组织学生进行“环巢湖一日研学游”活动，某旅行社推出了如下收费标准：（1）如果人数不超过30人，人均旅游费用为100元；（2）如果超过30人，则每超过1人，人均旅游费用降低2元，但人均旅游费用不能低于80元．该班实际共支付给旅行社3150元，问：共有多少名同学参加了研学游活动？【答案】共有35名同学参加了研学游活动．【解析】试题分析：由该班实际共支付给旅行社3150元，可以判断出参加的人数在30人以上，等量关系为：（100﹣在30人基础上降低的人数×2）×参加人数=3150，得到相关解后根据人均活动费用不得低于80元作答即可．试题解析：∵100×30=3000＜3150，∴该班参加研学游活动的学生数超过30人．设九（1）班共有x 人去旅游，则人均费用为[100﹣2（x ﹣30）]元，由题意得： x[100﹣2（x ﹣30）]=3150，整理得x 2﹣80x+1575=0，解得x 1=35，x 2=45，当x=35时，人均旅游费用为100﹣2（35﹣30）=90＞80，符合题意．当x=45时，人均旅游费用为100﹣2（45﹣30）=70＜80，不符合题意，应舍去．答：该班共有35名同学参加了研学旅游活动．考点：一元二次方程的应用．6．已知关于x 的方程x 2﹣（2k +1）x +4（k ﹣12）＝0．（1）求证：无论k 取何值，此方程总有实数根；（2）若等腰△ABC 的一边长a ＝3，另两边b 、c 恰好是这个方程的两个根，求k 值多少？【答案】（1）详见解析；（2）k ＝32或2．【解析】【分析】（1）计算判别式的值，利用完全平方公式得到△＝（2k ﹣3）2≥0，然后根据判别式的意义得到结论；（2）利用求根公式解方程得到x 1＝2k ﹣1，x 2＝2，再根据等腰三角形的性质得到2k ﹣1＝2或2k ﹣1＝3，然后分别解关于k 的方程即可．【详解】（1）∵△＝（2k +1）2﹣4×4（k ﹣12）＝4k 2﹣12k +9＝（2k ﹣3）2≥0， ∴该方程总有实数根；（2）()2k 12k 3x=2±＋﹣ ∴x 1＝2k ﹣1，x 2＝2， ∵a 、b 、c 为等腰三角形的三边，∴2k ﹣1＝2或2k ﹣1＝3，∴k ＝32或2．【点睛】本题考查了根的判别式以及等腰三角形的性质，分a 是等腰三角形的底和腰两种情况是解题的关键.7．已知：关于x 的一元二次方程221(1)204x m x m +++-=. （1）若此方程有两个实数根，求没m 的最小整数值；（2）若此方程的两个实数根为1x ，2x ，且满足22211221184x x x m x +=--，求m 的值. 【答案】（1）-4；（2）m=3【解析】【分析】（1）利用根的判别式的意义得到△≥0，然后解不等式得到m 的范围，再在此范围内找出最小整数值即可；（2）利用根与系数的关系得到12(1)x x m +=-+，212124x x m =-，然后解关于m 的一元二次方程，即可确定m 的值．【详解】解：（1）∵221(1)204x m x m +++-=有两个实数根， ∴221(1)41(2)04m m ∆=+-⨯⨯-≥，∴290m +≥， ∴92m ≥-； ∴m 的最小整数值为：4m =-；（2）由根与系数的关系得：12(1)x x m +=-+，212124x x m =-，由22212121184x x x x m ++=-得： ()22211121844m m m ⎛⎫⎡⎤-+--=- ⎪⎣⎦⎝⎭∴22150m m +-=，解得：3m =或5m =-； ∵92m ≥-， ∴3m =.【点睛】本题考查了根与系数的关系：若x 1，x 2是一元二次方程ax 2+bx+c=0（a≠0）的两根时，则12b x x a +=-，12c x x a=．也考查了根的判别式．解题的关键是熟练掌握根与系数的关系和根的判别式.8．解方程：（x 2+x ）2+（x 2+x ）＝6．【答案】x 1＝﹣2，x 2＝1【解析】【分析】设x2+x＝y，将原方程变形整理为y2+y﹣6＝0，求得y的值，然后再解一元二次方程即可．【详解】解：设x2+x＝y，则原方程变形为y2+y﹣6＝0，解得y1＝﹣3，y2＝2．①当y＝2时，x2+x＝2，即x2+x﹣2＝0，解得x1＝﹣2，x2＝1；②当y＝﹣3时，x2+x＝﹣3，即x2+x+3＝0，∵△＝12﹣4×1×3＝1﹣12＝﹣11＜0，∴此方程无解；∴原方程的解为x1＝﹣2，x2＝1．【点睛】本题考查了换元法和一元二次方程的解法，设出元化简原方程是解答本题的关键.9．阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发现：当a＞0，b＞0时：∵（a b-）2=a﹣2ab+b≥0∴a+b≥2ab，当且仅当a=b时取等号．请利用上述结论解决以下问题：（1）请直接写出答案：当x＞0时，x+1x的最小值为．当x＜0时，x+1x的最大值为；（2）若y=27101x xx+++，（x＞﹣1），求y的最小值；（3）如图，四边形ABCD的对角线AC、BD相交于点O，△AOB、△COD的面积分别为4和9，求四边形ABCD面积的最小值．【答案】（1）2；﹣2．（2）y的最小值为9；（3）四边形ABCD面积的最小值为25．【解析】【分析】（1）当x＞0时，按照公式a+b ab a=b时取等号）来计算即可；当x＜0时，﹣x＞0，1x-＞0，则也可以按公式a+b ab a=b时取等号）来计算；（2）将y 27101x x x ++=+的分子变形，分别除以分母，展开，将含x 的项用题中所给公式求得最小值，再加上常数即可；（3）设S △BOC =x ，已知S △AOB =4，S △COD =9，由三角形面积公式可知：S △BOC ：S △COD =S △AOB ：S △AOD ，用含x 的式子表示出S △AOD ，再表示出四边形的面积，根据题中所给公式求得最小值，加上常数即可．【详解】（1）当x ＞0时，x 1x +≥=2；当x ＜0时，﹣x ＞0，1x -＞0．∵﹣x 1x -≥=2，∴则x 1x +=-（﹣x 1x -）≤﹣2，∴当x ＞0时，x 1x +的最小值为 2．当x ＜0时，x 1x +的最大值为﹣2．故答案为：2，﹣2．（2）∵x ＞﹣1，∴x +1＞0，∴y 27101x x x ++=+()2(1)5141x x x ++++=+=（x +1）41x +++5=4+5=9，∴y 的最小值为9．（3）设S △BOC =x ，已知S △AOB =4，S △COD =9 则由等高三角形可知：S △BOC ：S △COD =S △AOB ：S △AOD ，∴x ：9=4：S △AOD ，∴S △AOD 36x =，∴四边形ABCD 面积=4+9+x 36x +≥=25．当且仅当x =6时，取等号，∴四边形ABCD 面积的最小值为25．【点睛】本题考查了配方法在最值问题中的应用．对不能直接应用公式的，需要正确变形才可以应用．10．元旦期间，某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.（1）求甲、乙两种苹果的进价分别是每千克多少元？（2）在（1）的情况下，超市平均每天可售出甲种苹果100千克和乙种苹果140千克，若将这两种苹果的售价各提高1元，则超市每天这两种苹果均少售出10千克，超市决定把这两种苹果的售价提高x 元，在不考虑其他因素的条件下，使超市销售这两种苹果共获利960元，求x 的值.【答案】（1）甲、乙两种苹果的进价分别为10元/千克,8元/千克；（2）x 的值为2或7.【解析】【分析】（1）根据题意列二元一次方程组即可求解,（2）根据题意列一元二次方程即可求解.【详解】（1）解：设甲、乙两种苹果的进价分别为a 元/千克, b 元/千克.由题得：()()18344282a b a b +=⎧⎨+++=⎩解之得：108a b =⎧⎨=⎩答：甲、乙两种苹果的进价分别为10元/千克,8元/千克（2）由题意得：()()()()410010214010960x x x x +-++-=解之得：12x =，27x =经检验，12x =，27x =均符合题意答：x 的值为2或7.【点睛】本题考查了二元一次方程组和一元二次方程的实际应用,中等难度,列方程是解题关键.。

数学小学六年级上册期末复习培优试题测试题(附答案解析)

数学小学六年级上册期末复习培优试题测试题（附答案解析）一、填空题1．填上合适的单位。

一个水杯的高是1( )，容积是700( )。

一辆卡车的质量是2.5( )，速度是每小时80( )。

2．在一个直径是10厘米的圆内画一个最大的正方形,这个正方形的面积是( )平方厘米。

3．比20米多15是( )米，20米比( )米少15。

4．杨叔叔骑自行车45分钟行了25千米，他每分钟行______千米，行1千米需要______分钟。

5．在一张长12厘米、宽8厘米的长方形纸片上剪半径为1厘米的圆片，最多可以剪( )个圆片．6．果园里有桃树、梨树和苹果树共有500棵，其中桃树占25，苹果树和梨树棵数的比是7∶3，果园里有桃树( )棵，苹果树比梨树多( )棵。

7．○×△＝36，○÷△＝4，○＝( )，△＝( )。

8．一只茶杯单价是一把茶壶的14，李阿姨的钱正好可以买4把茶壶和20只茶杯，一把茶壶可以替换( )只茶杯，李阿姨的钱可以买( )把茶壶。

9．0.6t∶250kg化成最简整数比是( )，比值是( )。

10．如图，用同样长的小木棒摆一摆，照这样摆下去，第6幅图需要______根这样的小木棒，第n幅图需要______根这样的小木棒。

11．以半圆为弧的扇形圆心角是（）。

A．90°B．180°C．360°12．下面算式中，得数最大的是（）。

A．2153⨯B．40.255⨯C．2257÷13．2∶3的前项加上4，要使比值不变，后项应乘（）。

A．3 B．4 C．6 D．9 14．下面几句话中，（）中的数可以改写成百分数。

A．一本练习的价钱为0.5元B．甲体重是乙体重的7 8C．一车煤重89100吨D．一段绸带长90100m15．大圆与小圆周长之比是3∶2，则它们的面积之比是（）。

A．1.5∶1 B．9∶4 C．3∶216．如果a×b＝1，那么（）。

A．a和b都是倒数B．a和b互为倒数C．a和b的倒数是117．如果甲数的60%等于乙数的75%（甲乙两数均不为0），那么甲数（）乙数。

小学一年级上册数学《解答题》专项练习附参考答案(培优)

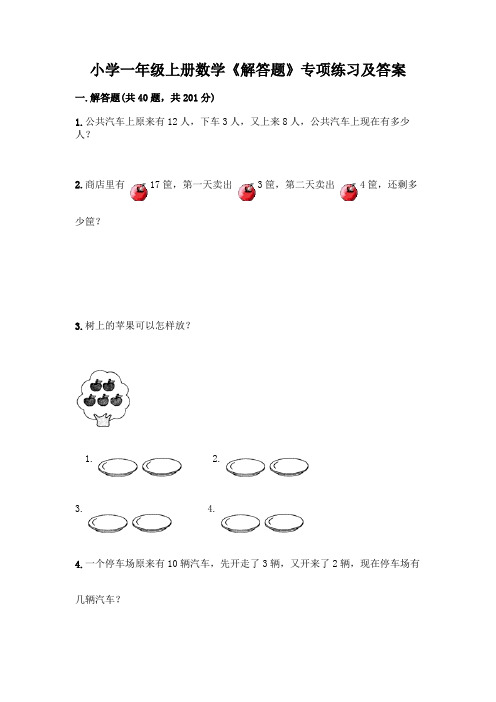
小学一年级上册数学《解答题》专项练习及答案一.解答题(共40题，共201分)1.公共汽车上原来有12人，下车3人，又上来8人，公共汽车上现在有多少人？2.商店里有17筐，第一天卖出3筐，第二天卖出4筐，还剩多少筐？3.树上的苹果可以怎样放？1. 2.3. 4.4.一个停车场原来有10辆汽车，先开走了3辆，又开来了2辆，现在停车场有几辆汽车？5.被减数和减数都是15，差是多少?6.（1）一共植了多少棵树？□○□○□＝□（棵）（2）请你再提出一个数学问题，并试着解答。

7.妈妈买了一些苹果，第一天吃了5个，第二天吃了8个，两天一共吃了多少个？8.小明买了一个文具盒和一枝自动笔，付给售货员15元钱，应找回多少钱？9.停车场开走了8辆小汽车，现在还有9辆，停车场原来有多少辆小汽车?10.停车场上原来有6辆小汽车，又开来8辆，停车场现在停了多少辆小汽车？11.小丽有2个玩具，小红有3个玩具，小华的玩具比小丽多2个，小华有几个玩具？12.盒子里的皮球取出9个, 还剩7个, 盒子里原来有几个皮球?13.悦悦排队买汉堡，这一队共5人，从后往前数，悦悦排第3，悦悦前面有几个人？14.提出数学问题并解决。

图中的小朋友正在办板报，有一个小朋友站在桌子上写字，其余的3个小朋友分别在下边写字、扶桌子、读板报内容．（1）站在桌子上的有1人，站在地上的有3人，一共有几人?（2）男生有2人，女生有2人，一共有几人?（3）扶桌子的有1人，写字的有2人，读板报内容的有1人，一共有几人?（4）站在地上的小朋友比站在桌子上的多几人?15.小红折了8只千纸鹤，姐姐比她多折4只，姐姐折了多少只千纸鹤？16.小猪妈妈给小猪哥哥7个苹果，给小猪弟弟8个苹果，这时隔壁的小猪花花过来玩，要使它们三个的苹果个数同样多，那么小猪哥哥和小猪弟弟各应给小猪花花几个苹果?17.小明吃掉了7块蛋糕，盘子里还剩下5块，原来盘子里一共有几块蛋糕？18.公交车上有14个人，到某站下去3个人，又上来2个人，车上现在有多少个人？19.小芳种了13株向日葵。

小学数学六年级上册期末模拟培优试题(附答案解析)

小学数学六年级上册期末模拟培优试题（附答案解析）一、填空题1．在下面的括号中填上适当的数或单位。

5.4公顷＝( )平方米 3.25时＝( )时( )分一台微波炉的容积约是16( )一个苹果的体积约是120( )2．张洋把一个由草绳编织成的圆形茶杯垫片沿直径剪开，得到两个近似的三角形，再将两个三角形拼成平行四边形（如下图）。

测得平行四边形的底是15.7厘米，圆形茶杯垫片的半径是( )厘米3．校合唱团有128人，男同学占整个合唱团的14，后来又增加了部分男同学，这时男同学占这个合唱团的25，现在合唱团一共有( )人。

4．一辆汽车行23千米用118升汽油。

那么行1千米用( )升油，1升油可行( )千米。

5．把一个圆形纸片沿半径分成若干偶数等份的扇形，然后再拼成一个近似的长方形，这个长方形的周长比圆形纸片的周长多6cm，这个圆形纸片的面积是________cm2。

6．一个三角形，三个角的度数比是3∶4∶2，那么最大的一个角是( )，这是一个( )三角形。

7．一只小狗的质量相当于3只小兔的质量，那么3只小狗和6只小兔的总质量相当于________只小狗的质量，或者相当于________只小兔的质量。

8．笔记本的单价是练习本的5倍。

买4本笔记本的钱可以买( )本练习本。

9．某班学生人数在40人到50人之间，男生和女生人数的比是5∶6，这个班有男生( )人，女生( )人。

10．根据上图的规律，第5个图形应画( )个三角形。

11．下图中，能正确表示圆心角的是（）。

A．B．C．12．已知1770.992316a b c ⨯=⨯=÷（a 、b 、c 均大于0）。

则下列排序正确的是（）。

A ．b ＞a ＞cB ．a ＞b ＞cC ．c ＞a ＞bD ．c ＞b ＞a13．把一个正方形看作“1”，平均分成10份，涂色部分不能表示（）。

A ．0.7B ．710C ．70%D ．714．如果把3∶5的后项加上15，要使比值不变，比的前项应该（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平面直角坐标系
一、平面直角坐标系中的点的特征 1、对于点p(x,y),
(1)在第一象限时，0>x ，0>y ； (2)在第二象限时，0<x ，0>y ； (3)在第三象限时，0<x ，0<y ； (4)在第四象限时，0>x ，0<y ； 2、对于点p(x,y), (1)在
x 轴上时，0=y ，x 可取任意数；(2)在y 轴上时，0=x ，y 可取任意数；
3、对于点p(x,y),
(1)若在第一、三象限的角平分线上时，y x =；
(2)若在第二、四象限的角平分线上时，横、纵坐标互为相反数，即0=+y x . 5、平行于
x 轴的直线上的点纵坐标相同，横坐标不同；平行于y 轴的直线上的点的横坐标相
同，纵坐标不同.
例1：（1）已知在平面直角坐标系中，点2(+m P ，)1+m 是
x 轴上的一点，则点P 的坐标
为 .
（2）若点b a M +(，)ab 在第二象限，则点a N (，)b 在第象限. （3）已知线段AB ∥x 轴,若点A 的坐标为（1，2），线段AB 的长为3，则点B 的坐标
为 .
分析：（1）
x 轴上的点纵坐标为0；（2）第二象限上的点横坐标为负数，纵坐标为正数；
（3）平行于x 轴上的点纵坐标相同.
练：1、已知1(M ，)2-，a N (，)b .若MN ∥x 轴,则=a ，=b ；若MN ∥y 轴,
则=a ，=b ；MN ⊥
x 轴,且MN ＝2，则N .
二、探索点的坐标规律
解决点的规律探索型问题应从最简单的情形入手，进而找出规律、解决问题.
例2：在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点，且规定，正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x 轴的正方形.边长为1的正方形
内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点，…，
则边长为8的正方形内部的整点的个数为（） A 、64 B 、49 C 、36 D 、25
分析：求出边长1，2，3，4，5，6，7的正方形的整点的个数，得到边长为1和2的正方形内部有1个整点，边长为3和4的正方形内部有9个整点，边长为5和6的正方形内部有25个整点，推出边长为7和8的正方形内部有49个整点，即可得出答案.
-1
-1
1
1O y x
1、在平面直角坐标系中，点1A （1，1），2A （2，4），3A （3，9），4A （4，16），…，用你发现的规律确定点9A 的坐标为 .
2、如图，将长方形ABCD 放置在平面直角坐标系中，A B ∥x 轴，且AB ＝4，AD ＝2，且A （2，1）. （1）求B ，C ，D 的坐标，并说明将长方形ABCD 进行怎样的平移使点C 移到点A 处；（2）y 轴上是否存在点P ，使△PAB 的面积等于长方形ABCD 面积的
4
3
，若存在，求出P 点坐标；若不存在，说明理由.
D
C
B
A y
x
4
3
2
165
4321O
参考答案
例1：（1）P(1，0) （2）第三象限（3）B （4，2）或（－2，2）练1：1≠a ， 2-=b ；1=a ，2-≠b ；（1，0）或（1，－4）例2：B
练2：（1）4A （2，0）；8A （4，0）；12A （6，0）；
（2）n A 4（n 2，0）；（3）向上. 例3：18.5 四、巩固练习
1、（9，81）. 提示：n A n (，2
n ）
2、（1）B （6，1），C （6，3），D （2，3），将长方形ABCD 先向左平移4个单位，再向下平移2个单位，
可使点C 移到点A.
（2）存在，理由如下：
设0(P ，a ），则12
1
-⋅=∆a AB S ABP ∴4
3
241421⨯⨯=-⨯⨯a
∴31=-a ，
∴4=a 或－2
故P （0，4）或（0，－2）。