1.2整式的加减同步练习2
人教版七年级数学上册《第二章:整式的加减》测试题共6套

七年级数学上册《第二章:整式的加减》同步练习一、单选题1.已知a 2+2ab=-8,b 2+2ab=14,则a 2+4ab+b 2=( );a 2-b 2=( )A .22、-6B .-22、6C .6、-22D .-6、222.下列各式中,是8a 2b 的同类项的是( )A .4x 2yB .―9ab 2C .―a 2bD .5ab3.多项式4xy 2–3xy 3+12的次数为( )A .3B .4C .6D .74.下列式子中,是单项式的是( )A .2x y +B .–12x 3yz 2C .5xD .x –y5.下列计算正确的是( ).A .336a a a +=B .33a a -=C .()532a a =D .23a a a ⋅= 6.下列是按一定规律排列的一组数:12,16,112,120,…,1a ,190,1b,…(其中a ,b 为整数),则+a b 的值为( ). A .182B .172C .242D .200二、填空题7.单项式3212a b 的次数是_____. 8.若7x 3a y 4b 与﹣2x 3y 3b +a 是同类项,则a =_____,b =_____.9.﹣2x 2y 4的系数是a ,次数是b ,则a +b =_____.10.观察下列单项式:-2x ,22x 2,-23x 3,24x 4…-25x 5,26x 6…请观察规律,写出第n 个式子________.11.若关于,x y 的多项式323225mx nxy x xy y ---++中不含三次项,则25m n +的值为_________三、解答题12.先化简,再求值:(1)22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中x =﹣2,y =23(2)()()2222153342a b ac a c a b ac a c ---+-,其中a =﹣1,b =2,c =﹣2.13.计算:(1)3(-ab+2a)-(3a-b)+3ab ;(2)()221114222a ab a ab ab ⎡⎤--+-⎢⎥⎣⎦;(3)先化简,再求值:4x 2-{-3x 2-[5x-x 2-(2x 2-x)]+4x},其中x=12.14.化简并求值:2(a 2-ab)-3(23a 2-ab),其中a ,b 满足|a+2b|+(b-1)2=0.15.自习课上小明在准备完成题目:化简:(x 2+6x+8)-(6x+8x 2+2)发现系数“ ” 印刷不清楚、(1)他把“ ”猜成6,请你帮小明完成化简:(6x 2+6x+8)-(6x+8x 2+2); (2)小明同桌看到他化简的结果说:“你猜错了,我看到该题标准答案的结果是常数。
七年级数学上册《第二章 整式的加减》同步训练题及答案(人教版)

七年级数学上册《第二章整式的加减》同步训练题及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列各组中的两项,属于同类项的是()A.−2x3与−2x B.−12ab与18ba C.x2y与−xy2D.4m与4mn 2.将多项式﹣a2+a3+1﹣a按字母a的降幂排列正确的是()A.a3−a2−a+1B.−a3+a2+a−1C.−1+a+a2−a3D.1−a−a2+a33.下面合并同类项正确的是()A.3x+2x2=5x3B.2a2b−a2b=1C.−ab−ab=0D.−y2x+xy2=0 4.下列去括号中正确的()A.−(x−y)=x−y B.2(x−y)=2x−yC.−(x−y−z)=−y+z−x D.−(x+y−z)=−x−y+z5.若−3x2m y3与2x4y n是同类项,那么m-n=()A.0 B.1 C.-1 D.-56.已知有一整式与(2x2−5x−2)的和为(2x2+5x+4),则此整式为()A.2 B.10x+6C.6 D.4x2+10+2 7.下列运算正确的是()A.3a+2a=5a2B.2a+2b=5abC.a5−a2=a3D.2a2bc−a2bc=a2bc8.若x–y=–6,xy=–8,则代数式(4x+3y–2xy)–(2x+5y+xy)的值是( )A.–12 B.12 C.–36 D.不能确定二、填空题9.将代数式2a2b、−23b2a、3ab、−32ba2中的同类项合并得.10.多项式8x2−3x+5与多项式2x2+2mx2−5x+3相加后不含x2项,则m的值为.11.已知长方形的周长为4a+2b,其一边长为a+b,则另一边长为.12.当k=时,代数式x6−5kx4y3−4x6+15x4y3+10中不含x4y3项.13.若m2+3mn=5,则5m2-3mn-(-9mn+3m2)=.三、解答题14.化简:(1)2(x3−2y2)−(x−2y)−(x−3y2+2x3);(2)3x2y−[6xy−2(4xy−2)−x2y]+1.m2-mn),其中m=2,n=3.15.先化简,再求值: 2(mn-m2)+3(2316.已知:A+B=x2+6x−24,B=2x2+3x−7求A−B.17.已知a+b=−4,ab=3求代数式2[ab+(−3a)]−3(2b−ab)的值. 18.先化简,再求值:3x2﹣[7x﹣2(5x﹣3)+(x2﹣x)],其中x2+2x﹣5=0.参考答案1.B2.A3.D4.D5.C6.B7.D8.Bba29.1210.-511.a或0.0412.12513.1014.(1)解:原式=2x3−4y2−x+2y−x+3y2−2x3 =−y2+2y−2x;(2)解:原式=3x2y−[6xy−8xy+4−x2y]+1=3x2y−6xy+8xy−4+x2y+1=4x2y+2xy−3.15.解:原式= 2mn-2m2+2m2-3mn=-mn当m=2,n=3时原式=-mn=-2×3=-616.解:由题意可得=A+B−2B=(x2+6x−24)−2(2x2+3x−7)=x2+6x−24−4x2−6x+14=−3x2−10.17.解:∵2[ab+(−3a)]−3(2b−ab)=2ab−6a−6b+3ab=5ab−6(a+b)又∵a+b=−4ab=3∴原式=5×3−6×(−4)=3918.解:原式=3x2﹣(7x﹣10x+6+x2﹣x)=3x2﹣7x+10x﹣6﹣x2+x=2x2+4x﹣6∵x2+2x﹣5=0∴x2+2x=5∴原式=2(x2+2x)﹣6=2×5﹣6=10﹣6=4.。
人教版七年级上 整式的加减整章同步练习和测试卷

2.1.1单项式◆随堂检测1、 用代数式表示:(1)边长为a 的正方形周长为 ,面积为 .(2)设n 为整数,则奇数可表示为 ,偶数可表示为 .(3)拿158元钱去买钢笔,买了单价为5元的钢笔x 支,则剩下的钱为 元.(4)某人骑自行车m 小时行驶了48千米,则平均每小时的车速是 千米/时.2、用单项式填空,并指出它们的系数和次数.(1)每包书有10册,n 包书有 册.(2)一个长方体的长宽高分别是y x x ,,,则它的体积是 .(3)一台电脑原价a 元,现在按8折出售,这台电脑现在的售价为 .(4)半径为r 的圆的面积是 .3、填空:(1)单项式y x 22的的系数是 ,次数是 ;(2)单项式232a π-的系数是 ,次数是 ; (3)单项式3π的系数是 ,次数是 ; (4)单项式8的系数是 ,次数是 .◆典例分析我们知道;)(2024828642;1223)62(642;622)42(42=⨯+=+++=⨯+=++=⨯+=+ n 2642++++ 的结果会是多少呢? 分析:对于规律题,首先要观察后一个等式与前一个等式不一样的地方是什么,其实这个过程就是发现规律的过程,再者就是准确地表示出规律.解:n 2642++++ )1(2)22(+=⨯+=n n n n ◆课下作业●拓展提高1、用代数式表示:(1)如果a 个同学在2h 内共搬了b 块砖,则平均每人每小时搬 块砖.(2)产量由a 千克增长10%,就达到 千克.(3)1千克绿豆发芽后重量增加6倍,m 千克的绿豆可发成 千克绿豆.(4)每件x 元的上衣,降价20%后售价为 .(5)葡萄每千克p 元,买10千克以上按9折优惠,买13千克应支付 元钱.2、写出一个单项式,并写出它的系数和次数分别是什么.3、给代数式b a 32+赋予一定的实际意义为 .4、下列代数式的书写中,正确的是( )A 、211⨯aB 、a ÷3C 、ab 411 D 、)(2n m +5、某工厂第一个月生产汽车a 台,平均每月的增长率是x%.(1)用代数式表示第3个月生产汽车的辆数;(2)当a=10000,x=5时,求前三个月生产汽车的总辆数.6、写出下列各单项式的系数和次数: (1)y x 243-; (2)532bc a .●体验中招1、(2009年,广州)如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是_____,第n 个“广”字中的棋子个数是____2、(2009年,武汉)14.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 ___________ 个小圆.参考答案第1个图形 第2个图形 第3个图形 第4个图形…随堂检测1、(1)mx n n a a 48)4(;5158)3(;2,12)2(;,42-+ 2、;,次数是系数是110,10)1(n ;,次数是系数是)(31,22y x .2,)4(18.08.032,次数是系数是;,次数是元,系数是)(ππr a3、(1)2,3;(2)232,π-;(3)3,3ππ;(4)8,8. 拓展提高1、(1);2a b (2)%);101(+a (3)m 7;(4);%80x ⋅(5)p 13109⋅. 2、略,答案不唯一.3、略,答案不唯一.4、D. 211⨯a 应该写成a 23,a ÷3应写成a 3;ab 411应写出ab 45 . 5、(1)2%)1(x a +; (2)当5,10000==x a 时,前三个月的总产量是 =+⨯++⨯+2%)51(10000%)51(100001000031525(台)6、(1)系数是43-,次数是3;(2)系数是53 ,次数是4. 体验中招1、1+2×7=15(个),1+2(n+2).2、4+6×7=46(个)2.1.2 多项式◆随堂检测1、 下列代数式中,哪些是单项式,哪些是多项式? 2,3121,1238,,0,32,32,1,152322y x b a xy y x m b a a bc y x -+------π 2、多项式623522233-++-b b a b a a 的最高次项是 ,四次项系数是 ,常数项是 .3、多项式325256--+-z y x y x x 是 次 项式,每一项的系数分别是 , 六次项是 .4、列式表示:(1)比x 小2的数是 ;(2)x 的四分之三减y 的差是 ;(3)设礼堂里座位的行数为a ,并且行数是每行座位数的32,礼堂里共有座位 个; (4)一钢管的外径为R,内径为r ,长为a ,则该钢管的体积为 .◆典例分析若8)1(2++--x kx x k k 是关于x 的一次多项式,求k 的值.分析:题中给出的多项式从形式上看是二次多项式,但题中说明的是一次多项式,这就要求二次项的系数必须为零,即0)1(=-k k ,求出k 值,并检验所求k 值是否满足题意.解:由题意得,0)1(=-k k ,∴10==k k 或当0=k 时,原多项式=8+x ,是一次多项式;当1=k 时,原多项式=8,不是一次多项式.∴0=k◆课下作业●拓展提高1、若a,b 表示两个有理数,则它们的平方和可表示为 ,和的平方可表示为 ,倒数的和可表示为 ,差的相反数可表示为 .2、一个两位数,个位数字是a,十位数字式b ,则这个两位数可表示为 .3、已知单项式y x 26的次数等于单项式22y x m -的次数,则=m .4、若多项式2)1(3)1(234-+-+--x b x x a x 不含3x 和x 项,则a= ,b= .5、四次单项式y xn m m 3)(--的系数为3-,求m,n 的值.6、m 为何值时22)2(y x m m +33xy -时六次二项式?●体验中招1、(2009年,山西)下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .2、(2009年,荆门)如图,正方形ABCD 边长为1,动点P 从A 点出发,沿正方形的边按逆时针方向运动,当它的运动路程为2009时,点P 所在位置为______;当点P 所在位置为D 点时,点P 的运动路程为______(用含自然数n 的式子表示).参考答案随堂检测1、 单项式有:;,0,1,152m y x --π 多项式有:.2,3121,1238,32232y x b a xy y x b a -+---- 2、6,2,3523--b b a 和 3、八次四项式,2-、1、﹣1、﹣3,y x x 562和-4、)(;23;43;222r R a a a y x x -⋅--πBD A (P )C(1) (2) (3) …… ……拓展提高1、a b b a b a b a -+++,11,)(,2222、a b +103、由123=+=m m 得,4、由⎩⎨⎧=+=-0101b a 得,⎩⎨⎧-==11b a5、由题意得⎩⎨⎧==∴⎩⎨⎧-=-=+-963413n m n m m6、由题意得224026222=∴⎩⎨⎧-≠=∴⎩⎨⎧≠+=+m m m m m体验中招1、n n ++)1(22、由于150242009 =÷,所以在B 点;34+n2.2.1整式的加减◆随堂检测1、下列是同类项的是( )A 、223xy y x -与B 、c ab bc a 2222-与C 、yx xy 54与 D、222与x2、填空:(1)=-t t 3210( )t ; (2)=+22155a a ()2a ; (3)=-2263mn mn ( )2mn .3、下列各题的合并同类项正确吗?若不正确,请说明理由.(1)xy y x 752=+; (2)56=-ab ab ;(3)y x yx y x 33398=-; (4)422853x x x =+.4、若单项式2363y x y x m n --与是同类项,则n m 32+的值是 .5、合并同类项(1)228.010x x -; (2)xy xy xy 32-+-;(3)14325--+-a b b a ; (4)x x x x x 365345322++--+.◆典例分析求多项式22543222-+-++-x x x x x 的值,其中31=x 分析:在求多项式的值时,先将多项式中的同类项合并,然后再代入求值,这样可以简化运算.但部分同学会直接代入求值,当未知数的值较复杂时,计算量会非常大.我们习惯上“先化简,再求值”. 解:22543222-+-++-x x x x x2)54()213(2--+++-=x x2--=x当31=x 时,原式=37231-=-- ◆课下作业●拓展提高1、 合并同类项(1)5433222-+--xy y x xy y x ; (2)ab b a ab b a ab 634864622222--+++-;(3))(4)(2)()(522b a b a b a b a +++-+-+.2、若两个单项式6253243b a b a n m -与的和仍为单项式,则m= , n= .3、设m 为正整数,n m n m b a b a 44218++-与是同类项,则满足条件的m 的值有( )个 A 、1个 B 、2个 C 、3个 D 、无数个4、有一列单项式,.,20,19,,4,3,2,2019432 x x x x x x ---(1)根据你发现的规律,写出第100个,第101个,第102个单项式;(2)你能进一步写出第n 个单项式吗?5、求代数式的值:222232253b ab a b ab a ---+-,其中3,21-==b a●体验中招1、(2009年,烟台)若n m y x y x 3253与+的和是单项式,则=n m .(原题中式求m n ,现改为n m )2、(2009年,长春)计算:=-a a 25 .参考答案随堂检测1、 C2、 3,20,22--3、 (1)不正确,不是同类项不能合并;(2)不正确,正确答案是ab 5;(3)不正确,正确答案是y x 3-;(4)不正确,正确答案是28x .4、由题意得2732,5,6=+∴==n m n m5、(1)原式=22.9x ;(2)原式=xy xy 2)321(-=-+-;(3)原式=11)32()45(+-=-+-+-b a b a ;(4)原式=42264)53()35(62323+-+=+-+-+x x x x x x拓展提高1、(1)原式=55)43()32(22-+-=-+-+-xy y x xy y x(2)原式=3838)44()66(3322+=+++-+-ab ab b a ab(3)原式=)(3)(2))(41())(35(22b a b a b a b a +++-=++-++-2、5,3==n m3、D4、(1)第100个,第101个,第102个单项式分别是102101100102,101,100x x x -(2)第n 个单项式是n n nx ⋅-)1(5、222232253b ab a b ab a ---+- 22226)32()15()23(bab a b ab a --=-+--+-= 当3,21-==b a 时,原式=41)3()3(216)21(22=---⨯⨯- 体验中招 1、 由题意得,4)2(,2,22=-==-=n m n m 则2、 3a2.2.2整式的加减◆随堂检测1、 判断正误:(1)z y x z y x -+-=-+-2)2( ( )(2)z y x z y x 36)33(2-+-=+-- ( )(3)c b a c b a 22)(2+-=+-+ ( )2、去括号 :(1))(d c b a +--+; (2))42(32z y x -+;(3))4(215c b a --; (4))]3(2[32z y x y x ----.3、计算: (1))54()23(y x y x ++-; (2))102()65(b a b a ---;(3))5(32ab ab ab ---; (4))()3(42222mn n m mn n m ---.4、一个多项式加上1452-+x x 得2862+-x x ,则这个多项式是 . ◆典例分析计算:)21(6)3212(22+--+-x x x x 分析:本题有两个地方易错:① 6和括号里的每一项都要相乘,部分学生往往只和第一项相乘;②去括号时,不知道什么时候要变号什么时候不变号,这就说明去括号的法则没有理解.解:原式=)21(6)3212(22+--+-x x x x 27383663212)366(321222222--=-+-+-=+--+-=x x x x x x x x x x◆课下作业●拓展提高1、计算:(1))(21)(312222xy y x x x xy y x ++---; (2))2(2)2(232222b a a b b a +---+-;(3))22(3)642(3b c c b a a --+--- (4)]2)34(7[322x x x x ----.2、若多项式18223-+-x x x 与多项式352323+-+x mx x 相加后不含二次项,则m= . 3、(1)已知:2,622=-=-b ab ab a ,求2222,2b a b ab a -+-的值.(2)已知6063)2(5,522-+--=-x y x y y x 求的值.4、已知22228,8y x xy B xy y x A +-=+-=,当31,21-=-=y x 时,求B A +2的值.5、求代数式中的值:{})]24(3[2522222b a ab ab b a ab ----,其中5.0,3=-=b a6、若)1532()2(22-+--+-+y x bx b y ax x 的值与字母x 的取值无关,试求a,b 的值.●体验中招1、(2009年,太原)已知一个多项式与x x 932+的和等于1432-+x x ,则这个多项式是( )A 、15--xB 、15+xC 、113--xD 、113+x 2、(2009年,江西)化简)12(2-+-a a 的结果是( )A 、14--aB 、14-aC 、1D 、1-参考答案随堂检测1、 错,错,对2、 (1)原式=d c b a +--; (2)原式=z y x 1262-+; (3)原式=c b a 2215+-;(4)原式=z y x y x z y x y x -++-=+---323232)32( 3、(1)原式=y x y x y x 375423+=++- (2)原式=b a b a b a 4310265+=+-- (3)原式=ab ab ab ab 4532=+-(4)原式=2222412mn n m mn n m +--22311mn n m -= 4、32132++-x x 拓展提高1、(1)原式=xy x y x xy y x x x xy y x 656561212121313131222222---=----- (2)原式=b a b a a b b a -=-+-+-3422432222(3)原式=b a b c c b a a 2666423-=--++-(4)原式335)233(3)2347(322222--=-+-=-+--=x x x x x x x x x 2、由题意得,24)82(5)3523(18223323+--+=+-++-+-x x m x x mx x x x x ∵多项式24)82(523+--+x x m x 不含2x 项 ∴4082=∴=-m m3、(1)∵2,622=-=-b ab ab a∴8)()(,4)()(2222=-+-=---b ab ab a b ab ab a ∴8,422222=-=+-b a b ab a8060535560)2(3)2(56063)2(5,52)2(222=-⨯+⨯=--+-=-+--∴=-y x y x x y x y y x 4、∵22228,8y x xy B xy y x A +-=+-=∴B A +22222222481622y xy x y x xy xy y x -+=+-++-=当31,21-=-=y x 时,原式=36149)31()31()21(24)21(22=---⨯-⨯+-. 5、{})]24(3[2522222b a ab ab b a ab ----2222222245)]243(2[5ab ab ab b a ab ab b a ab =-=+---=当5.0,3=-=b a 时,原式=35.0)3(42-=⨯-⨯ 6、∵)1532()2(22-+--+-+y x bx b y ax x16)3()22(15322222++-++-=+-+-+-+=b y x a x b y x bx b y ax x又)1532()2(22-+--+-+y x bx b y ax x 的值与字母x 的取值无关∴⎩⎨⎧=-=∴⎩⎨⎧=+=-1303022b a a b 体验中招1、A2、D第二章 整式的加减综合测试题一、选择题(每题3分,计24分) 1.下列各式中不是单项式的是( ) A .3a B .-51 C .0 D .a3 2.甲数比乙数的2倍大3,若乙数为x ,则甲数为( ) A .2x -3 B . 2x+3 C .21x -3 D .21x+3 3.如果2x 3n y m+4与-3x 9y 2n 是同类项,那么m 、n 的值分别为( )A .m=-2,n=3B .m=2,n=3C .m=-3,n=2D .m=3,n=24.已知3221A a ab =-+,3223B a ab a b =+-,则A B +=( )A .3222331a ab a b --+B .322231a ab a b +-+C .322231a ab a b +-+D .322231a ab a b --+5.从25a b +减去44a b -的一半,应当得到( ). A. 4a b - B. b a - C. a b -9 D. 7b 6.减去-3m 等于5m 2-3m -5的式子是( )A .5(m 2-1)B .5m 2-6m -5C .5(m 2+1)D .-(5m 2+6m -5)7.在排成每行七天的日历表中取下一个33⨯方块.若所有日期数之和为189,则n 的值为( ) A .21 B .11 C .15 D .9 8.今天数学课上,老师讲了多项式的加减,放学后,小明回到家拿出课堂笔记,认真地复习老师讲的内容,他突然发现一道题222221131(3)(4)2222x xy y x xy y x -+---+-=- +_____________+2y 空格的地方被钢笔水弄污了,那么空格中的一项是( ) A .7xy - B .7xy C .xy - D .xy二、填空题(每题4分,计32分)9.单项式2r π-的系数是 ,次数是 . 10.当 x =5,y =4时,式子x -2y的值是 . 11.按下列要求,将多项式x 3-5x 2-4x+9的后两项用( )括起来.要求括号前面带有“—”号,则x 3—5x 2—4x+9=___________________12.把(x —y )看作一个整体,合并同类项:5(x —y )+2(x —y )—4(x —y )=_____________. 13.一根铁丝的长为54a b +,剪下一部分围成一个长为a 宽为b 的长方形,则这根铁丝还剩下_____________________.14.用语言说出式子a+b 2的意义:______________________________________15.某校为适应电化教学的需要新建阶梯教室,教室的第一排有a 个座位,后面每一排都比前一排多一个座位,若第n 排有m 个座位,则a 、n 和m 之间的关系为 .16.小明在求一个多项式减去x 2—3x+5时,误认为加上x 2—3x+5,•得到的答案是5x 2—2x+4,则正确的答案是_______________.三、解答题(共28分)17.(6分)化简:(1))343(4232222x y xy y xy x +---+;(2))32(5)5(422x x x x +--.18.(6分)如图所示,在下面由火柴棒拼出的一系列的图形中,第n 个图形由n •个正方形组成.n=4n=3n=2n=1(1)第2个图形中,火柴棒的根数是________; (2)第3个图形中,火柴棒的根数是________; (3)第4个图形中,火柴棒的根数是_______; (4)第n 个图形中,火柴棒的根数是________. 19.(8分)有这样一道题:“当a=2009,b=—2010时,求多项式332332376336310a a b a b a a b a b a -+++--+2010的值.”小明说:本题中a=2009,b=—2010是多余的条件;小强马上反对说:这不可能,多项式中含有a 和b,不给出,a b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.20.(8分)一个三角形一边长为a+b,另一边长比这条边大•b,•第三边长比这条边小a—b.(1)求这个三角形的周长;(2)若a=5,b=3,求三角形周长的值.四、拓广探索(共16分)21.(8分)有一串单项式:x,-2x2,3x3,-4x4,……,-10x10,……(1)请你写出第100个单项式;(2)请你写出第n个单项式.22.(8分)如图所示,请你探索正方形的个数与等腰三角形的个数之间的关系.(1)照这样的画法,如果画15个正方形,可以得_______个等腰三角形;(2)若要得到152个等腰三角形,应画_______个正方形;B 卷1.(7分)已知x 2—xy=21,xy -y 2=—12,分别求式子x 2-y 2与x 2—2xy+y 2的值. 2.(7分)同一时刻的北京时间、巴黎时间、东京时间如图所示.(1)设北京时间为)237(<<a a ,分别用代数式表示同一时刻的巴黎时间和东京时间;(2)2001年7月13日,北京时间22:08,国际奥委会主席萨马兰奇宣布,北京获得2008年第29届夏季奥运会的主办权.问这一时刻贩巴黎时间、东京时间分别为几时?3.(8分)按照下列步骤做一做:(1)任意写一个两位数;(2)交换这个两位数的十位数字和个位数字,得到一个新数;(3)求这两个两位数的差.再写几个两位数重复上面的过程,这些差有什么规律?这个规律对任意一个两位数都成立吗?为什么?4.(8分)有一包长方体的东西,用三种不同的方法打包,哪一种方法使用的绳子最短?哪一种方法使用的绳子最长?(a +b >2c )参考答案一、选择题1.D 2.B 3.B 4.D 5.D 6.C 7.A 8.C 二、填空题9.2,π- 10.3 11.x 3—5x 2—(4x —9) 12.3(x —y ) 13.3a+2b 14.a 与b 的平方的和 15.m=a+n —1 16.3x 2+4x —6 三、解答题17.(1)原式=xy x y xy y xy x -=-+--+2222343423; (2)原式=x x x x x x 3561510204222--=---. 18.(1)7;(2)10;(3)13;(4)3n+119.∵332332376336310a a b a b a a b a b a -+++--+2010=332(731)(66)(33)a a b a b +-+-++-+2010=2010.∴a=2009,b=—2010是多余的条件,故小明的观点正确.20. (1) 三角形的周长为:b a b a b a b b a b a 52)()()(+=+-++++++;(2)当a =5,b =3时,周长为:25. 四、拓广探索 21.(1)—100x 100;(2)(—1)n+1x n . 22.0,4,8,12,4(n —1) (1)56;(2)4(n —1)=152,n=39. 2.1-2.2测试B 参考答案1.x 2-y 2= (x 2-xy )+(xy -y 2)=21—12=9,x2-2xy+y2= (x2-xy)—(xy-y2)=21+12=33.2.(1)巴黎时间为a+5,东京时间为a+1;(2) 巴黎时间为3:08,东京时间为23:08.3.(1)24;(2)42;(3)42—24=18;是9的倍数.设原两位数的十位数字为b,个位数字为a(b>a),则原两位数为10b+a,交换后的两位数为10a+b.10b+a-(10a+b)=10b+a-10a-b=9b-9a=9(b-a)4.第(1)种方法的绳子长为4a+4b+8c,第(2)种方法的绳子长为4a+4b+4c,第(3)种方法的绳子长为6a+6b+4c,从而第(3)种方法绳子最长,第(2)种方法绳子最短。
人教版七年级上册数学第2章《整式的加减》全章同步练习

第二章 整式的加减2.1.1 单项式【知识点1】 用字母表示数的书写规则书写含有字母的式子时,应遵守以下规则:(1)数与字母相乘或字母与字母相乘,通常将乘号写作“·”或省略不写.(2)数与字母相乘,数写在字母前面.(3)数字因数为“1”或“-1”时,常常省略“1”, 如1×ab 写成ab ,-1×ab 写成-ab .(4)当数字因数为带分数,要写成假分数.(5)除法运算要用分数,如1÷a 写成1a. 【知识点2】 单项式及相关概念(1)由数或字母的积组成的式子叫做单项式.(2) 单项式中的数字因数叫做这个单项式的系数.(3)一个单项式中, 所有字母的指数的和叫做这个单项式的次数.注意: ①单独的一个数或字母也是单项式.②单项式的系数不仅包括数字,还包括前面的符号.③单项式的次数指单项式中所有字母指数的和.【典例】已知一个单项式的系数是2,次数是3,则这个单项式可以是( )A .-2xy 2B .3x 2C .2xy 3D .2x 3分析:B 、D 中的单项式的系数是2.D 中的单项式的次数是3,符合题目要求.答案:D1.【2016·内蒙古呼和浩特中考】某企业今年3月份产值为a 万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是( )A .(a -10%)(a +15%)万元B .a(1-90%)(1+85%)万元C .a(1-10%)(1+15%)万元D .a(1-10%+15%)万元2.小红要购买珠子串成一条手链,黑色珠子每个a 元,白色珠子每个b 元,要串成如图所示的手链,小红购买珠子应该花费( )A .(3a +4b)元B .(4a +3b)元C .4(a +b)元D .3(a +b)元3.【2016·贵州铜仁中考】单项式πr 22的系数是( ) A.12 B .π C .2 D .π24.下列式子:-0.3x 2y,0,12(x +1),13x 2,-13ab 2-12,-2a 2b 3c.其中单项式有( ) A .2个 B .3个 C .4个 D .5个5.单项式-3πxy 2z 3的系数和次数分别是( )A .-π,5B .-1,6C .-3π,6D .-3,76.若-33a m b 2是七次单项式,则m 的值是( )A .6B .5C .4D .37.系数为-5,只含字母m 、n 的三次单项式有________个,它们分别是______________________.8.若-3axy m 是关于x 、y 的单项式,且系数为-6,次数为3,则a =__________,m =__________.9.单项式6a 2可以表述为“棱长为a 的立方体的表面积”,请再赋予它一个新的实际背景:__________________________________________________________.10.观察下列单项式:-a,2a 2,-3a 3,4a 4,-5a 5,…,可以得到第2015个单项式是_______________,第n 个单项式是______________.11.若||m +3+(n -4)2=0,求:(1)m 、n 的值; (2)单项式mπx n +1y 8的系数和次数.第二章 整式的加减2.1.2 多项式【知识点1】 多项式及相关概念(1)多项式:几个单项式的和叫做多项式.(2)多项式的项及常数项:在多项式里,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.(3)多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数.注意:①多项式的每一项包括它前面的符号,且每一项必须都是单项式.②多项式的次数是多项式中次数最高项的次数,而不是所有项的次数之和.③一个多项式是几次几项,就叫几次几项式.④一般多项式按某一字母的指数从小到大(或从大到小)的顺序排列起来,这种排列叫做多项式的升(或降)幂排列.【典例1】多项式2x 3-x 2y 2+y 3+25的次数和项数分别是( )A .五次四项B .三次四项C .四次四项D .无法确定分析:根据多项式的次数和项数的定义可得,多项式2x 3-x 2y 2+y 3+25是一个四次四项式.【知识点2】 整式单项式与多项式统称整式.它们的关系可以用图表示:【典例2】下列式子中,哪个不是整式( )A .x 2+1B .-2C .1xD .π 分析:A 项x 2+1是整式;B 项-2是单项式,所以是整式; C 项1x不是整式;D 项π是常数,也是整式.1.多项式y 2+y +1是( )A .二次二项式B .二次三项式C .三次二项式D .三次三项式2.下列说法正确的是( )A .-b 2的系数是1,次数是2B .3a +2b 的项数是2,次数是2C .4a 2+b 2+1的项数是2,次数是2D .1x 2不是整式 3.在多项式2x 2-xy 3+18中,次数最高的项是( )A .2B .18C .2x 2D .-xy 34.如果整式x n -2-5x +2是关于x 的三次三项式,那么n 等于( )A .3B .4C .5D .65.关于x 的多项式x 3+(m +1)x 2+x +2没有二次项,则m 的值是( )A .2B .-2C .-1D .06.将多项式-y 2+2y 3+1-y 按照字母y 的升幂排列正确的是( )A .2y 3-y 2-y +1B .-y -y 2+2y 3+1C .1+2y 3-y 2-yD .1-y -y 2+2y 37.写出一个只含有字母x 的二次三项式:______________________________.8.若多项式a 2+(2k +6)ab +b 2+9不含ab 项,则k =__________.9.多项式2a 4+a 3b 2-5a 2b 3-1是__________次__________项式.10.多项式-12x ||m -(m -2)x +7是关于x 的二次三项式,则m 的值是________. 11.多项式7x m +(k -1)x 2-(2n +4)x -6是关于x 的三次三项式,并且二次项系数为1,求m +n -k 的值.12.如图是由一个正方体和一个长方体组成的组合体.(1)请你用式子表示这个组合体的体积;(2)这个式子是整式吗?如果是,请你指出它是多项式还是单项式;如果是多项式,请你说出它是几次几项式.第二章整式的加减2.2.1 合并同类项【知识点1】同类项所含字母相同,并且相同字母的指数也相同的项叫做同类项.注意:①同类项要满足两个“同”:一是所含字母相同,二是相同字母的指数相同.②同类项的两个“无关”:一是同类项与系数无关;二是同类项与字母前后顺序无关.③所有的常数项都是同类项.【典例1】下列各式中,是3a2b的同类项的是( )A.2x2y B.-2ab2 C.a2b D.3ab分析:A项2x2y,与已知单项式的字母不同;B项-2ab2,与已知单项式的相同字母的指数不同;C 项a2b是3a2b的同类项;D项3ab,与已知单项式的相同字母的指数不同.答案:C【知识点2】合并同类项(1)把多项式中的同类项合并成一项,叫做合并同类项.(2)合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.(3)合并同类项的一般步骤:①找出同类项;②根据加法交换律把同类项放在一起,利用“系数相加,字母及其指数不变”合并同类项;③写出合并后的结果.【典例2】计算-a2+3a2的结果为( )A.-2a2 B.2a2 C.4a2 D.-4a2分析:原式=(-1+3)a2=2a2. 答案:B1.【2016·上海中考】下列单项式中,与a2b是同类项的是( )A.2a2b B.a2b2 C.ab2 D.3ab2.计算:5x-3x=( )A.2x B.2x2 C.-2x D.-2 3.【2017·山东济宁中考】单项式9x m y3与单项式4x2y n是同类项,则m+n的值是() A.2 B.3 C.4 D.54.下列各组式子中,不是同类项的是()A.52与25 B.-ab与ba C.0.2a2b与-14a2b D.a2b3与-a3b25.计算2m2n-3nm2的结果为( )A.-1 B.-5m2n C.-m2n D.无法计算6.若单项式2x n y m-n与单项式3x3y2n的和是5x n y2n,则m与n的值分别是( ) A.m=3,n=9 B.m=9,n=9 C.m=9,n=3 D.m=3,n=3 7.若单项式-x2y m+2与x n y的差仍是一个单项式,则m n=__________.8.写一个代数式,使其至少含有三项,且合并同类项后的结果为3ab2,这个代数式为___________________________________________.9.把(a+b)看作一个整体,对4(a+b)+2(a+b)-(a+b)合并同类项,结果是__________. 10.合并同类项:(1)x2y-3xy2+2yx2-y2x; (2)3a m+4a m+1-5a m+1+2a m.11.先化简,再求值:3x-4x3+7-3x+2x3+1,其中x=-2.12.李叔家购买了一套新房,其结构如图所示(单位:米),他打算除卧室外,其余部分都铺地砖.(1)至少需要多少平方米的地砖?(2)如果地砖的价格是m元/平方米,那么李叔至少需要花多少钱?第二章整式的加减2.2.2 去括号【知识点】去括号的法则(1)如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同.(2)如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.(3)去括号的注意事项:①去括号时,要连同括号前面的符号一起去掉.②去括号时,要先分清括号外是正号还是负号.③变号时,括号内各项都要变号;不变号时,各项均不变号.④遇多层括号时,要逐层去括号,一般是按照由内向外进行.若从外向内去括号,去大括号时,要将中括号看作一个整体,去中括号时,要将小括号看作一个整体.【典例】下列去括号正确的是( )A.-(a+b-c)=-a+b-c B.-2(a+b-3c)=-2a-2b+6cC.-(-a-b-c)=-a+b+c D.-(a-b+c)=-a+b+c分析:A项前面是“-”号,括号内各项都变相反符号,即-(a+b-c)=-a-b+c,A不正确;B项括号前是“-2”,去括号时不仅要变符号相反,而且括号内每一项都要乘括号前的数,即-2(a+b-3c)=-2a-2b+6c,B正确;C项中括号前是“-”号,-(-a-b-c)=a +b+c,C不正确;D项中括号是“-”号,-(a-b+c)=-a+b-c,D不正确.答案:B1.化简-16(x-0.5)的结果是( )A.-16x-0.5 B.-16x+0.5 C.16x-8 D.-16x+82.下列去括号中,正确的是( )A.a-(b-c)=a-b-c B.a-(b-c)=a+b+cC.a-(b-c)=a+b-c D.a-(b-c)=a-b+c3.下列各组代数式中,互为相反数的有( )①a-b与-a-b;②a+b与-a-b;③a+1与1-a;④-a+b与a-b.A.①②④ B.②④ C.①③ D.③④4.2(a-b)-(c+d)去括号的结果是()A.2a-b-c-d B.2a+2b-c+dC.2a+b-c-d D.2a-2b-c-d5.要使等式4a-2b-c+3d=4a-(____)成立,括号内应填()A.2b-c+3d B.2b-c-3d C.2b+c+3d D.2b+c-3da-b+c去括号,得()6.将整式-[]A.-a+b+c B.-a+b-c C.-a-b+c D.-a-b-c7.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )A.1 B.5 C.-5 D.-18.去括号并合并同类项:2a-(5a-3)=__________.9.若m、n互为相反数,则8m+(8n-3)的值是__________.10.有四个连续偶数,其中最小的一个是2n,则这四个连续偶数的和是__________.11.化简:(1)2x2+3(2x-x2);(2)x-(3x-2)+(2x+3);(3)3(4x-2y)-3(-y+8x).12.一列火车上原有(6a-2b)人,中途下车一半,又上车若干人,这时车上共有乘客(10a-6b)人,列式表示上车乘客的人数.当a=200,b=100时,上车的乘客是多少人?第二章 整式的加减2.2.3 整式的加减【知识点】 整式的加减(1)整式加减的运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.(2)应用整式的加减进行化简求值步骤:一般是先化简,即先去括号,再合并同类项,直到结果中没有同类项后,再将字母的具体数值代入计算结果,简记为“一化、二代、三计算”.注意:①整式的加减其实质就是合并同类项,整式加减的最后结果中,不能再含有同类项,不能出现带分数,带分数要化为假分数.②化简求值的运算.代值时,若所给的值是负数或分数,应添上括号.【典例】化简,并求x =-2,y =1时的值:(1)3x +2x 2-2-15x 2+1-5x ; (2)3(2x 2-xy)-2(3x 2+xy -1).分析:(1)按照整式加减的运算法则,合并同类项即可得到结果;(2)按照整式加减的运算法则,先去括号,然后再合并同类项即可得到结果.解:(1)原式=2x 2-15x 2+3x -5x -2+1 (2)原式=6x 2-3xy -6x 2-2xy +2=-13x 2-2x -1. =6x 2-6x 2-3xy -2xy +2当x =-2,y =1时, =-5xy +2.原式=-13×(-2)2-2×(-2)-1 当x =-2,y =1时,=-49. 原式=-5×(-2)×1+2=12.1.下列计算正确的是( )A .3x 2-x 2=3B .3a 2+2a 3=5a 5C .3+x =3xD .-0.25ab +14ba =0 2.计算-3(x -2y)+4(x -2y)的结果是( )A .x -2yB .x +2yC .-x -2yD .-x +2y3.一个多项式减去x 2-2y 2等于x 2-2y 2,则这个多项式是( )A .-2x 2+y 2B .x 2-2y 2C .2x 2-4y 2D .-x 2+2y 24.张庭把4x +8错写成4(x +8),结果比原来( )A .多4B .少4C .多24D .少245.若a>0,ab<0,则||b -a -1-||a -b +3的值为( )A.2 B.-2 C.-2a+2b+4 D.2a-2b-4 x-4与(y+3)2互为相反数,那么2x-(-2y+x)的值为()6.如果||A.-2 B.10 C.7 D.67.【2017·江苏淮安中考】计算:2(x-y)+3y=__________.8.一个多项式加上2x2-x+5等于4x2-6x-3,则这个多项式为__________.a+1为__________.9.若a<-1,则化简||a+||10.若“△”是新定义的一种运算符号,规定:a△b=2a-3b,则(x+y)△(x-y)运算后的结果为__________.11.先化简,再求值:x2+(2xy-3y2)-2(x2+xy-2y2),其中x=-1,y=2.12.由于国际市场油价上涨,某市将出租车的收费标准重新调整如下:不超过2千米的部分,收起步价5元,燃油税1元(超过2千米没有燃油税);2千米到5千米的部分,每千米收1.5元;超过5千米的部分,每千米收2.5元.若某人乘坐了x(x>5)千米的路程,请写出他应该支付的费用;当他乘坐了8千米的路程时,应付费多少元?第二章 整式的加减2.2 整式的加减1.计算3a 2-a 2的结果是( )A .4a 2B .3a 2C .2a 2D .3 2.【2016·湖南常德中考】若-x 3y a 与x b y 是同类项,则a +b 的值为( ) A .2 B .3 C .4 D .5 3.单项式x m -1y 3与4xy n 的和是单项式,则n m 的值是( )A .3B .6C .8D .9 4.下列计算正确的是( )A .8x +4=12xB .4y -4=yC .4y -3y =yD .3x -x =3 5.下列各组中,不是同类项的是( )A .-1和0B .-4xy 2z 和-4x 2yz 2`C .-x 2y 和2yx 2D .-a 3和4a 3 6.若2y m +5x n +3与-3x 4y 3是同类项,则m n =( )A.12 B .-12 C .1 D .-2 7.下列各式去括号正确的是( )A .a 2-(2a -b +c)=a 2-2a -b +cB .-(x -y)+(xy -1)=-x -y +xy -1C .9y 2-[]x -+=9y 2-x +5z +4 D .a -(3b -2c)=a -3b -2c8.【2016·江苏淮安中考】计算:3a -(2a -b)=__________. 9.若x a y 与3x 2y b 是同类项,则ab 的值为__________.10.小刚做了一道数学题:“已知两个多项式A 、B ,求A +B 的值”,他误将“A +B ”看成了“A -B ”,求出的答案是x -y.若已知B =3x -2y ,则原来A +B 的值是__________. 11.已知x 2-xy =3,3xy +y 2=5,则2x 2+xy +y 2的值是__________. 12.若a -b =3,ab =-3,则整式3a -3b -6ab 的值为__________.13.如图是小明家的楼梯示意图,其水平距离(即AB 的长度)为(2a +b)米,一只蚂蚁从点A 沿着楼梯爬到点C ,共爬了(3a -b)米,则小明家楼梯的竖直高度(即BC 的长度)为__________米. 14.先化简,再求值:14(-4x 2+2x -8y)-(-x -2y),其中x =12,y =2018.15.如图是某居民小区的一块长为b 米,宽为2a 米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处各修建一个半径为a 米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?16.若5a |x|b 3与-0.2a 3b |y -1|是同类项,则x =_______,y =__________. 17.若a <1,化简:|3-a|-|a -1|=__________.18.【2016·河北中考】若mn =m +3,则2mn +3m -5mn +10=__________.19.如图,将边长为(m +3)的正方形纸片剪出一个边长为m 的正方形后的剩余部分拼成一个矩形(不重叠、无缝隙),若拼成的矩形一边长为3,则另一边长为__________.20.有这样一道题:计算13x 2-⎝ ⎛⎭⎪⎫3x 2+3xy -35y 2+83x 2+⎝⎛⎭⎪⎫3xy +25y 2的值,其中x =-12,y =2.甲同学把“x=-12”错抄成了“x=12”,但他的计算结果也是正确的,你知道这是怎么回事吗?21.按下列程序计算,把答案填写在表格里,然后看看有什么规律,想想为什么会有这个规律?(1)填写表内空格:输入x 3 2 -2 13…输出答案0 …(2)你发现的规律是_____________________________;(3)用简要过程说明你发现的规律的正确性.22.小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…排成如下图所示的形式,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题.(1)十字框中的五个数的和与中间的数16有什么关系?(2)设中间的数为x,用代数式表示十字形框架中的五个数的和;(3)若将十字形框架上下、左右移动,可框住另外的五个数,能使这五个数的和等于2020吗?若能,请写出这五个数;若不能,请说明理由.第二章整式的加减复习与巩固【考点1】同类项及其应用【典例1】若2y m+5x n+3与-3x2y3是同类项,则5m-3n的值为( )A.12B.-12C.-7 D.-2分析:因为2y m+5x n+3与-3x2y3是同类项,所以m+5=3,n+3=2,所以m=-2,n=-1,所以5m-3n=5×(-2)-3×(-1)=-7. 答案:C【考点2】代数式的求值【典例2】若m2-5m+2=0,求2m2-10m+2015的值.分析:首先根据m2-5m+2=0,可得m2-5m=-2,然后把m2-5m=-2代入2m2-10m+2015,求出代数式的值是多少即可.解答:因为m2-5m+2=0,所以m2-5m=-2,所以2m2-10m+2015=2(m2-5m)+2015=2×(-2)+2015=-4+2015=2011.点评:本题用到了整体思想,就是在研究和解决有关数学问题时通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题方法.在本章中代数式的化简求值和整式的加减运算中,把一些式子作为一个整体来处理可简化解题过程.【考点3】整式的加减的实际应用【典例3】姚先生统计了自家车在路程行驶过程中的油耗情况,如下表:路况市区郊区油耗9.5升/100公里7.0升/100公里(1)若姚先生每天上班需行驶a公里的市区路段和b公里的郊区路段,则姚先生每天上下班共需耗油________升;(2)若姚先生每天上班行驶8公里的市区路段和12公里的郊区路段,按6.5元/升油费计算,姚先生每天上下班需油费多少元?分析:(1)由姚先生上班与下班共需走2a公里市区路段,2b公里郊区路段,乘各自行驶一公里的耗油量,即可表示出共耗油的升数;(2)将a与b的值代入(1)列出的关系式中,求出共耗油的升数,乘每升油的价钱即可得到油费.解答:(1)(0.19a+0.14b)(2)由题意得,当a=8,b=12时,(0.19a+0.14b)×6.5=(0.19×8+0.14×12)×6.5=3.2×6.5=20.8.故姚先生每天上下班需油费20.8元.点评:分析题意,列出代数式,再合并同类项,最后结合已知将有关数值代入求解.【考点4】规律探索【典例4】如图是某月份的日历,用正方形圈出9个数,设其中一个是m,则用m表示这9个数的和是________.分析:根据题意得,方框圈出的9个数为m-8,m-7,m-6,m-1,m,m+1,m+6,m+7,m+8,则这9个数之和为(m-8)+(m-7)+(m-6)+(m-1)+m+(m+1)+(m+6)+(m+7)+(m+8)=9m.答案:9m点评:根据横行相邻的两个数相差1,纵行相邻两个数相差为7,表示出其他数字,最后求和即可.★考点1 同类项及其应用1.如果单项式-x3y m+2与x3y的差仍然是一个单项式,则m=__________.2.合并同类项:(1)x2+3x2+x2-3x2; (2)3a2-1-2a-5+3a-a2.3.若-a m+1b3与(n+2)a2b3是同类项,且它们的和为0,求(m+n)2015.★考点2 代数式的求值1.已知m-n=100,x+y=-1,则代数式(n+x)-(m-y)的值是( ) A.99 B.101 C.-99 D.-101 2.已知m2+2mn=13,3mn+2n2=21,则2m2+13mn+6n2-44的值为( ) A.45 B.5 C.66 D.773.一般情况下m2+n3=m+n2+3不成立,但有些数可以使得它成立,例如:m=n=0时,我们称使得m2+n3=m+n2+3成立的一对数m、n为“相伴数对”,记为(m,n).(1)若(m,1)是“相伴数对”,则m=__________;(2)(m,n)是“相伴数对”,则代数式154m-⎣⎢⎡⎦⎥⎤n+12-12n-的值为_______.4.若代数式2x2+3y+7的值为8,求代数式6x2+9y+8的值.★考点3 整式的加减的实际应用1.任意想一个数,把这个数乘2后减8,然后除以4,再减去原来所想的那个数的12,小明说所得结果一定是-2.请你通过列式计算说明理由.2.某商场10月1日仓库里原有(5x2-10x)桶食用油,中午休息时又购进同样的食用油(x2-x)桶,下午清仓时发现该食用油只剩下5桶,请问:(1)该商场10月1日一共卖出多少桶食用油?(用含有x的式子表示)(2)当x=5时,该商场中午过后一共卖出多少桶食用油?3.如图是一个运算程序,若输入的数x=1,求输出的值.★考点4 规律探索1.【重庆中考】下列图形都是由几个黑色和白色的正方形按一定规律组成,图1中有2个黑色正方形,图2中有5个黑色正方形,图3中有8个黑色正方形,图4中有11个黑色正方形,…,依此规律,图10中黑色正方形的个数是( )A.32 B.29 C.28 D.261题 2题2.观察某月份日历,如图所示,用一个“十”字形框任意框出5个数字,如果中央的数字为a,那么剩余4个数字的和等于__________.3.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待78位顾客共同就餐,但只有20张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?说明理由.。
人教版 七年级数学 第2章 整式的加减 同步训练(含答案)

人教版 七年级数学 第2章 整式的加减 同步训练一、选择题(本大题共10道小题)1. 化简-6ab +ba +8ab的结果是( )A .2abB .3C .-3abD .3ab2. 下列式子中,不是整式的是( ) A. B.+bC.D.4y3. 多项式2x 2-x -3的项分别是( )A .2x 2,x ,3B .2x 2,-x ,-3C .2x 2,x ,-3D .2x 2,-x ,34. 已知a +b =12,则2a +2b -3的值是( )A .2B .-2C .-4D .-3125. 已知某个整式与2x 2+5x -2的和为2x 2+5x +4,则这个整式是( ) A .2 B .6 C .10x +6D .4x 2+10x +26. 下列等式正确的是()A .a -(b +c )=a -b +cB .a -b +c =a -(b -c )C .a -2(b -c )=a -2b -cD .a -b +c =a -(-b )-(-c )7. 某教学楼阶梯教室,第一排有m 个座位,后面每一排都比前面一排多4个座位,则第n 排的座位数是 ( )A.m +4B.m +4nC.n +4(m -1)D.m +4(n -1)8. 观察如图所示的图形,则第n 个图形中三角形的个数是 ( )A.2n +2B.4n +4C.4nD.4n -49. 在一列数:a 1,a 2,a 3,…a n中,a 1=7,a 2=1,从第三个数开始,每一个数都等于它前面两个数之积的个位数字,则这个数中的第2020个数是( ) A .1 B .3 C .7 D .910. 将正整数1~2020按一定规律排列如下表: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 …上下平移表中带阴影的方框,则方框中五个数的和可以是( ) A .2018B .2019C .2020D .2021二、填空题(本大题共8道小题)11. -12x 2y 是________次单项式.12. 为庆祝六一儿童节,某幼儿园举行用火柴棒摆“金鱼”的比赛,如图K -21-3所示.按照规律,摆第(n )个图案需用火柴棒的根数为________.图K -21-313. 已知一列数2,8,26,80,…,按此规律,则第n (n 为正整数)个数是 .(用含n 的式子表示)14. 若|a +1|+b -2=0,则5a 2+3b 2+2(a 2-b 2)-(5a 2-3b 2)的值为 .15.观察下列砌钢管的横截面(如图),则第n (n 是正整数)个图中的钢管数是__________.(用含n 的式子表示)16. “T”字形,用棋子摆成的“T”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第n (n 为正整数)个“T”字形需要的棋子个数为________.17. 一组按照规律排列的式子:x ,x 34,x 59,x 716,x 925,…,其中第8个式子是________,第n 个式子是________(用含n 的式子表示,n 为正整数).18. 观察下列等式:第一行:3=4-1; 第二行:5=9-4; 第三行:7=16-9; 第四行:9=25-16; … …按照上述规律,第n (n 为正整数)行的等式为________________.三、解答题(本大题共3道小题)19. 甲、乙两地相距a 千米,一辆汽车将b 吨货物从甲地运往乙地,已知汽车运输中的费用为将每吨货物运送1千米需花费m 元. (1)用式子表示该汽车将这批货物从甲地运到乙地的运输费;(2)已知这批货物在路上需进行两次检疫,每次的费用为25元,则当a =300,b =12,m =1时,运输这批货物的总费用是________元.20. 准备完成题目:化简(x2+6x+8)-(6x+5x2+2).发现系数“”印刷不清楚.(1)他把“”猜成3,请你化简:(3x2+6x+8)-(6x+5x2+2);(2)嘉淇的妈妈说:“你猜错了,我看到该题的答案是常数.”通过计算说明原题中的系数“”是几.21. 有这样一道题:“计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=,y=-1.”甲同学把“x=”错抄成“x=-”,但他计算的结果也是正确的,试说明理由,并求出正确结果.人教版七年级数学第2章整式的加减同步训练-答案一、选择题(本大题共10道小题)1. 【答案】D2. 【答案】C[解析] +b是多项式,是整式;4y是单项式,是整式;只有不是整式.3. 【答案】B4. 【答案】B[解析] 2a+2b-3=2(a+b)-3,将a+b=12代入,得原式=2×12-3=-2.故选B.5. 【答案】B[解析] (2x2+5x+4)-(2x2+5x-2)=2x2+5x+4-2x2-5x+2=6.6. 【答案】B7. 【答案】D[解析] 由于第一排有m个座位,后面每一排都比前面一排多4个座位,则第n排的座位数为m+4(n-1).8. 【答案】C[解析] 根据给出的3个图形可以知道:第1个图形中三角形的个数是4,第2个图形中三角形的个数是8,第3个图形中三角形的个数是12,从而得出一般的规律:第n个图形中三角形的个数是4n.9. 【答案】C[解析] 依题意得:a1=7,a2=1,a3=7,a4=7,a5=9,a6=3,a7=7,a8=1,…,周期为6,2020÷6=336……4,所以a2020=a4=7.故选C.10. 【答案】C[解析] 从表中正整数1~2020的排列情况来看,每一行是8个数,也就是每一列下面的数减去上面的数是8.随着方框的上下平移,可表示出其变化规律的表达式为:2+8n,3+8n,4+8n,5+8n,6+8n,将这五个数相加为40n +20,用四个答案中的数来尝试,可见只有40n+20=2020时,n为整数.故选C.二、填空题(本大题共8道小题)11. 【答案】三12. 【答案】6n+2[解析] 第(1)个图案需要火柴棒8根,8=6×1+2;第(2)个图案需要火柴棒14根,14=6×2+2;第(3)个图案需要火柴棒20根,20=6×3+2……由此可知,第(n)个图案需要火柴棒的根数为6×n+2,即6n+2.13. 【答案】3n-114. 【答案】3[解析] 原式=5a2+3b2+2a2-2b2-5a2+3b2=2a2+4b2.因为|a+1|+b-2=0,所以a+1=0,b-=0,即a=-1,b=,则原式=2+1=3.15. 【答案】32n(n +1) [解析] 第1个图中钢管数为1+2=3,第2个图中钢管数为2+3+4=12×(2+4)×3=9,第3个图中钢管数为3+4+5+6=12×(3+6)×4=18,第4个图中钢管数为4+5+6+7+8=12×(4+8)×5=30,…依此类推,第n 个图中钢管数为n +(n +1)+(n +2)+(n +3)+(n +4)+2n =12(n +2n)(n +1)=32n(n +1).16. 【答案】3n +2[解析] 由图可得,图①中棋子的个数为3+2=5,图②中棋子的个数为5+3=8,图③中棋子的个数为7+4=11……则第n(n 为正整数)个“T”字形需要的棋子个数为(2n +1)+(n +1)=3n +2.17. 【答案】x 1564 x 2n -1n 2 [解析] 根据分子的底数都是x ,而指数是从1开始的奇数;分母是从1开始的自然数的平方.因此第8个式子是x 2×8-182=x 1564,第n 个式子是x 2n -1n 2.故答案为x 1564,x 2n -1n 2.18. 【答案】2n +1=(n +1)2-n 2三、解答题(本大题共3道小题)19. 【答案】解:(1)abm 元.(2)abm +50=300×12×1+50=3650(元). 即运输这批货物的总费用是3650元. 故答案为3650.20. 【答案】[解析] (1)原式去括号、合并同类项即可得解;(2)设“ ”是a ,将a 看作常数,去括号、合并同类项后根据结果为常数知二次项系数为0,据此得出a 的值.解:(1)(3x2+6x+8)-(6x+5x2+2)=3x2+6x+8-6x-5x2-2=-2x2+6.(2)设“”是a,则原式=(ax2+6x+8)-(6x+5x2+2)=ax2+6x+8-6x-5x2-2=(a-5)x2+6.因为该题的答案是常数,所以a-5=0,解得a=5,即原题中的系数“”是5.21. 【答案】解:(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3=-2y3.因为化简后的结果中不含x,所以原式的值与x的取值无关.所以甲同学把“x=”错抄成“x=-”,但他计算的结果也是正确的.当x=,y=-1时,原式=-2×(-1)3=2.。
整式的加减2--北师大版

课外作业
①、书P11习题1、3。 ②、补充 5x 1 _________ x2 6x 3
4、_____________ (2x2 3x 5) 3x2 2x 1
5、当x 2时, 代数式ax3 bx 7的值是5, 则当x 2时, 代数式ax3 bx 7的值是 6、 求下列各式的值: (1)求当a 1,b 3, c 1时, 代数式
2.某花店一枝黄色康乃馨的价格是x元,一支红色玫瑰的价格是 y元,一枝白色百合的价格是z元,下面这三束鲜花的价格各是 多少?这三束鲜花的总价是多少元?
参考练习
1、a 2b (3ab2 ) (4a 2b) 2ab2 _________
2、(3 a3 2 ab2 ) ( 2 ab2 3 a3 ) ________
试一试
1、求多项式2a+3b-5c与-4a-11b+8c的和时,可以利用 竖式的方法:
2a+ 3b-5c +) - 4a-11b+8c
- 2a- 8b+3c
利用这种方法计算下列各题,计算过程中需要注意什么?
(1) (5x2 +2x-7) - (6x2 - 5x - 23); (2) (a3 - b3)+(2a3 - b2+b3)
; / 宝宝早期教育 ;
纵能化解.求死不可以.用暗器向我偷袭.虽然对身体并无伤害.杏黄衫儿.茫然不知所借中.它随随便便若不经意地跨出几步.它小妹所住の那座村离城约几十里. 陈柯及打翻了这两个梁兵.那壮汉大喝几声.我来助你几臂之力.那店伙给它挑了几件猢水蓝の湖绸长衫.陈柯及只得先应付它.孙传 儿火红了眼睛.大漠孤烟直.护着身躯.迫人而来.你一个人做の事情. 便走到几处小溪旁边.它虽然早已把小妹当作敌寇看待.可是它の手实在颤抖得历害.那影子忽地又幻化成它娘亲の影子.几条手臂.我平日对你这么好.从此尽丧.但它抓不着.哪知这少女竟是毫不退让.…陈柯及更是惊疑.附 着墙落下地来. 处置这些礼物.纷纷涌上.但那几个人都是用别种兵器打败它の.太一山离平城不过十多里. 孩子停止了膳戏.痛极难禁.它对这少女当然感激得很.已幻出小妹の影子.它の手指还是勾着陈柯及の箭环の.胸中闷气.我就来了.她晕了过去了.姑娘既然与它非亲非故.原来小妹并不 是发现有人.倘给敌寇戳个正着.登时几片清凉.你不是要我出来么.当时它还以为是爹爹临终の忏悔.忽觉几股大力扑来.刹那间变成了坚硬の钢鞭.说吧.你眼睛里还有我么.想道. 叮当两声.有几个已在屋内丧生.就因为师父要搬家.夜色深沉.欺身直进.陈柯及几招削过.劈面几拳.小孩子则哗 然大呼.似乎还听得她低声叹气.飞步赶上. 问道.心情混乱中.但功力却不太高.陈柯及见它只是单身几人.那少女道.我怎能对她有所猜疑.几个个有如石沉大海.无还手之力.它心念几动.说时迟.这事情我几定要查个水落石出!又不让我卸道.’我便问道.恍如迎风起舞.使了几招贯日射石.要 待后退.我倘有所知.可是麻烦.还不出声!当真似是猛虎出山.将军过谦了.什么精妙の招数.显然是给人用剧毒の暗器射死の.陈柯及对她是体贴爱护. 几箭就穿出去.幻影突然消失.给我杀掉了.便是我亡!别动. 几招乘龙引凤.捉小偷呀!我就是因为见了将军如此高明の鞭法.还用得着问 么.就将它这辆车子买下来了.左腿膝盖骨和右手腕骨都碎裂了.向反方向旋转.分开四个方向.而且还可以用作钢鞭.莫非.声音重浊. 原来这些人都是得了秦重の好处陈柯及嗖地拔出箭来.岂能奈得我何.不.挥鞭向空中几击.恭敬不如从命.好小子.抛下了手铐脚镣.过了几会. 你见了你の姨父. 倒在地上.那壮汉の日轮先到.又听得那使风火轮の壮汉几声惨呼.那武上猛地大喝几声道.陈柯及心头几跳. 真是巧得很.连疼痛の感觉也失掉了.也是几向憎恨の.那柄虎头梁枪.说罢.住手.只有小妹几人知道.陈柯及几箭削了个空.又几件奇事发生了.内外两进. 我要偷赴南方の消息.叫姑 娘见笑了. 说是姨父曾经吩咐过它. 便给陈柯及追到背后. 你也要我和它们讲信守义么.朗声说道. 跟着又想起了娘亲被她点了笑腰穴而死の惨状.端の凌厉非常.包保你行走如常.耳朵边似听得它娘亲在责备. 不但不退. ‘答应了啦.我师父正因为不想和别人打架.果然我没有杀错人.我决 不可以向敌寇屈膝!说道.平城の案子也是姑娘做の.定然大有帮助.化作了几杆长枪.忽听得背后马蹄之声.直刺过来.反了!这些都是它们送来の礼物.就将提着脚铐の那个梁兵打翻.再喝道.伤得还真不轻呢.正好赶上了本城壮汉对耿家の围捕.嗖の几声.唉.南宫汉面上几红.陈柯及蓦地大叫 道.叠声叫道.怎知道.还不赶快把箭扔掉.我蒙姑娘救命之恩.陈柯及大吼几卢.瞬息之间.莫非是当真都送了命了.却不知不觉地走上了西边の几条小路.饶是它早有提防. 不错.当几名书记.证实了这几个高手.梁国壮汉大声呐喊.树の影儿.从中都请来了几位高手.将那梁兵打得头破血流.兀是 未发现有几个农夫出来春耕.到了此时.密密麻麻.凌空刺下. 说道.她才肯转身.也难免要给这几招迫得后退.小孩子别胡说.在伪齐刘豫(梁人所立の傀儡)手下.为一个人验伤.卷住了陈柯及の宝箭.那少女笑着说.总是挂肚牵肠.是迎敌呢.将九九八十几路天龙鞭法使开.将军刚才那几招鞭法 是‘八方风雨会中州’吧. 不言不语.根本就不再理会李家骏在呼喊什么.它心里不住地在叫.我怎能为了儿女之情. 又是怜惜.她几定伤心透了.倒在地上.忽又听得小妹几声喝道.弄玉.只听得几个银铃似の声音已在接着说道.跳过几道山溪.现在这个少女突然出现.莫非…她还未曾看出.将 几技短箭放在陈柯及未受伤の那只手中. 立即几个回身拗步.人未离鞍.它这口箭乃是几口宝箭.唉.力勒几声.火舌卷来.这四个人都是精选出来の壮汉.只要稍几用力.睡得很安静.它也不由得惊得呆了!我给它加倍の银子.别家の点穴手法.想不到却是几个老江湖.拼着与敌寇两败俱伤.陈柯 及怒道.鲁思察也大呀声.它想起了当时の情景. 商上の笑容也是僵硬了の.名唤耿京. 心里暗暗好笑.只听得当の几声. 难道她给我の就是生肌火龙膏.呆在家门口作甚.小偷の衣裳不会这样好の.其实南宫汉此时正是心头焦躁、感到进退维谷の时候.便要起来道谢.陈柯及收势不及.像你这 样怀有故国之思.承大将军让了几招.正正打中陈柯及の膝盖. 陈柯及正自感到怪异.它以全身の重量向前倾倒.原来它
2023-2024学年七年级数学上册《第二章 整式的加减》同步练习题有答案(人教版)

2023-2024学年七年级数学上册《第二章整式的加减》同步练习题有答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题(共8题)1.下列式子为同类项的是( )A.abc与ab B.3x与3x2C.3xy2与4x2y D.x2y与−yx22.下列运算正确的是( )A.x+y=xy B.5x2y−4x2y=x2yC.x2+3x3=4x5D.5x3−2x3=33.下列单项式中,与−5x2y是同类项的是( )A.−5xy B.3x2y C.−5xy2D.−54.下列去(添)括号正确的是( )A.x−(y−z)=x−y−zB.−(x−y+z)=−x−y−zC.x+2y−2z=x−2(y−z)D.−a+c+d+b=−(a−b)+(c+d)5.已知一个多项式与3x2+9x的和等于5x2+4x−1,则这个多项式是( )A.2x2−5x−1B.−2x2+5x+1C.8x2−5x+1D.8x2+13x−16.若有理数a,b,c在数轴上的对应点A,B,C位置如图,化简∣c∣−∣c−b∣+∣a+b∣=( )A.a B.2b+a C.2c+a D.−a7.多项式4n−2n2+2+6n3减去3(n2+2n3−1+3n)(n为自然数)的差一定是( )A.奇数B.偶数C.5的倍数D.以上答案都不对8.如图,两个三角形的面积分别为16,9,若两阴影部分的面积分别为a,b(a>b)则(a−b)等于( )A.8B.7C.6D.5二、填空题(共5题)x a−2y3是同类项,那么(a−b)2015=.9.如果单项式−xy b+1与12x2y n与−2x m y3的和仍为单项式,则−m n的值为.10.若单项式2311.已知2a−3b2=5,则10−2a+3b2的值是.12.若代数式2x2+3x+7的值是5,则代数式4x2+6x+15的值是.13.已知多项式3x2+my−8与多项式−nx2+2y+7的差中,不含有x,y,则n m+mn=.三、解答题(共6题)14.先化简,后求值:3a2b+2(−ab2+2a2b)−(a2b−3ab2),其中a,b满足a=−1,b=2.15.已知代数式A=−6x2y+4xy2−2x−5,B=−3x2y+2xy2−x+2y−3.(1) 先化简A−B,再计算当x=1,y=−2时A−B的值;(2) 请问A−2B的值与x,y的取值是否有关系?试说明理由.16.已知∣x−3m+2n+1∣+(y−3mn)2=0.(1) 用含字母m,n的式子表示x,y;(2) 若2x+y的值与m取值无关,求出2x+y的值;(3) 若x+y=4,求5m+8mn+2与−m+2mn+4n的差的值.17.一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.例如:1423,x=1+4,y=2+3因为x=y,所以1423是“和平数”.(1) 直接写出最小的“和平数”是,最大的“和平数”是;(2) 如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是12,请求出所有的这种“和平数”.18.在计算代数式(2x3+ax−5y+b)−(2bx3−3x+5y−1)的值时,甲同学把“x=−23,y=35”误写为“x=23,y=35”,其计算结果也是正确的.请你通过计算写出一组满足题意的a,b的值.19.已知含字母x,y的多项式是:3[x2+2(y2+xy−2)]−3(x2+2y2)−4(xy−x−1).(1) 化简此多项式;(2) 小红取x,y互为倒数的一对数值代入化简的多项式中,恰好计算得多项式的值等于0,那么小红所取的字母y的值等于多少?(3) 聪明的小刚从化简的多项式中发现,只要字母y取一个固定的数,无论字母x取何数,代数式的值恒为一个不变的数,请你通过计算求出小刚所取的字母y的值.参考答案1. D2. B3. B4. D5. A6. D7. C8. B9. 110. −811. 512. 1113. 314. 原式=3a 2b −2ab 2+4a 2b −a 2b +3ab 2=6a 2b +ab 2.当 a =−1,b =2 时原式=6×1×2−1×4=8.15. (1) A −B=(−6x 2y +4xy 2−2x −5)−(−3x 2y +2xy 2−x +2y −3)=−6x 2y +4xy 2−2x −5+3x 2y −2xy 2+x −2y +3=(−6+3)x 2y +(4−2)xy 2+(−2+1)x −2y −5+3=−3x 2y +2xy 2−x −2y −2.当 x =1,y =−2 时A −B=−3×12×(−2)+2×1×(−2)2−1−2×(−2)−2=6+8−1+4−2=15.(2) A −2B=(−6x 2y +4xy 2−2x −5)−2(−3x 2y +2xy 2−x +2y −3)=−6x 2y +4xy 2−2x −5+6x 2y −4xy 2+2x −4y +6=(−6+6)x 2y +(4−4)xy 2+(−2+2)x −4y −5+6=−4y +1.由化简结果可知,A −2B 的值与 x 的取值没有关系,与 y 的取值有关系.16. (1) 由题意得:x −3m +2n +1=0,y −3mn =0所以x=3m−2n−1,y=3mn.(2)2x+y=2(3m−2n−1)+3mn =6m−4n−2+3mn=(6+3n)m−4n−2,因为2x+y的值与m取值无关所以6+3n=0所以n=−2所以2x+y=−4×(−2)−2=8−2=6.(3) 因为x+y=3m−2n−1+3mn=4所以3mn+3m−2n=5所以5m+8mn+2−(−m+2mn+4n)=5m+8mn+2+m−2mn−4n=6mn+6m−4n+2=2(3mn+3m−2n)+2=2×5+2=12.17. (1) 1001;9999(2) 设这个“和平数”为abcd则d=2a,a+b=c+d,b+c=12k∴2c+a=12k即a=2,4,6,8,d=4,8,12(舍去),16(舍去)①当a=2,d=4时2(c+1)=12k可知c+1=6k且a+b=c+d∴c=5,则b=7②当a=4,d=8时2(c+2)=12k可知c+2=6k且a+b=c+d∴c=4,则b=8.综上所述,这个数为2754和4848.18. (2x 3+ax −5y +b )−(2bx 3−3x +5y −1)=2x 3+ax −5y +b −2bx 3+3x −5y +1=(2−2b )x 3+(a +3)x −10y +(1+b ).由题意知计算结果也是正确的∴ 计算结果与 x 无关∴2−2b =0,a +3=0.∴a =−3,b =1(不唯一).19. (1) 原式=3x 2+6y 2+6xy −12−3x 2−6y 2−4xy +4x +4=2xy +4x −8.(2) ∵x ,y 互为倒数∴xy =1∴2+4x −8=0解得:x =1.5,y =23.(3) 由(1)得:原式=2xy +4x −8=(2y +4)x −8,由结果与 x 的值无关,得到 2y +4=0解得:y =−2.。
北师大七年级下数学第一章整式的运算同步练习

2010-2011学年度第二学期 第一章 整式的运算同步练习1.1 整式 你一定能完成一、精心选一选⒈ 下列说法正确的个数是 【 】 ① 单项式a 的系数为0,次数为0; ②21-ab 是单项式; ③ -xyz 的系数是-1,次数是1; ④ π是单项式,而2不是单项式. A .0个 B .1个 C .2个 D .3个 ⒉若单项式1232--x n m 和c b a 245的次数相同,则代数式322+-x x 的值为 【 】 A .14 B .20 C .27 D .35 二、耐心填一填:⒈ 3a 2b 3c 系数是 次数是 ;πR 2系数是 次数是 .⒉ n = 时,单项式231+n xy 的次数是6.三、用心做一做:⒈ 下列各代数式是不是单项式?如果是,请指出它们的系数和次数. ⑴ a 52 ⑵ b a 2- ⑶32ba - ⑷ 0.1532y x ⑸ 2x +1 ⑹ y ⑺ -m⒉ 小明认为既然单项式322y x 的次数是5,那么多项式322y x +的次数也是5.他的想法对吗?为什么?由此,你能谈谈单项式和多项式次数的确定有什么不同吗?相信你能完成一、精心选一选⒈ 下列说法正确的个数是 【 】① 单项式是整式;② 单项式也是多项式;③ 单项式和多项式都是整式. A .0个 B .1个 C .2个 D .3个 ⒉ 把3a 3-5和a 2b +ab 2+1按某种标准进行分类时属于同一类,则下列哪一个多项式也属于此类 【 】 A .-a 5-b 5 B .4x 2-7 C .xyz -1 D .a 2+2ab +b 2⒊ 若多项式(m +4)x 3+2x 2+x -1的次数是2,则m 2-m 的值为 【 】 A .10 B .12 C .16 D .20 二、耐心填一填⒈ 多项式x 3y +5xy -6-4xy 2是 的和. ⒉ 5x 2+4x -3是 次 项式,其中常数项是.⒊ 如图1-1-1,“小房子”的平面图形由长方形和三角形组成, 则这个平面图形的面积是 。
人教版七年级上册第二章整式的加减 2.2 整式的加减 同步练习(含答案)

整式的加减同步练习一、选择题(共12题)1、若3a2+m b3和(n﹣2)a4b3是同类项,且它们的和为0,则mn的值是()A.﹣2 B.﹣1 C.2 D.12、下列判断中正确的是().A.与不是同类项 B.不是整式C.单项式的系数是 D.是二次三项式3、下列计算正确的是()A. x5﹣x4=xB. x+x=x2C. x3+2x5=3x8D.﹣x3+3x3=2x34、下列各项中,去括号正确的是()A. x2-2(2x-y+2)=x2-4x-2y+4B. -3(m+n)-mn=-3m+3n-mnC. -(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2D. ab-5(-a+3)=ab +5a-35、减去-3x得x2-3x+6的式子是()A.x2+6B.x2+3x+6C.x2-6xD.x2-6x+66、已知多项式x2–kxy–3(x2–12xy+y)不含xy项,则k的值为()A. 36 B.-36 C.0 D.127、已知a2+2a=1,则代数式1﹣2(a2+2a)的值为()A.0 B.1 C.﹣1 D.﹣28、一个多项式加上3y2﹣2y﹣5得到多项式5y3﹣4y﹣6,则原来的多项式为()A.5y3+3y2+2y﹣1 B.5y3﹣3y2﹣2y﹣6C.5y3+3y2﹣2y﹣1 D.5y3﹣3y2﹣2y﹣19、代数式4x3﹣3x3y+8x2y+3x3+3x3y﹣8x2y﹣7x3的值()A.与x,y有关 B.与x有关 C.与y有关 D.与x,y无关10、若x=2时,代数式ax4+bx2+5的值是3,则当x=﹣2时,代数式ax4+bx2+7的值为()A.﹣3 B.3 C.5 D.711、如果多项式A加上﹣2x2﹣1得4x2+1,那么多项式A是()A.6x2+2 B.2x2 C.6x4+2 D.﹣2x2+212、为求1+2+22+23+…+22008的值,可令S=1+2+22+23+…+22008,则2S =2+22+23+24+…+22009,因此2S-S=22009-1,所以1+2+22+23+…+22008=22009-1.仿照以上推理计算出1+3+32+33+…+32018的值是 ( )A.32019-1 B. 32018-1 C. D.二、填空题(共6题)13、 (徐州中考)若2m+n=4,则代数式6-2m-n的值为.14、若代数式3a5b m与-2a n b2是同类项,m+n= .15、有一名同学把一个整式减去多项式xy+5yz+3xz误认为加上这个多项式,结果答案为 5yz-3xz+2xy,则原题正确答案为 .16、一个多项式加上-3+x-2x2得到x2-1,那么这个多项式为 ____________ ;17、一种商品每件成本是a元,原来按成本增加20%定出价格进销售,一段时间后,由于库存积压减价,按原价的9折出售,则现在每件售价为元.18、多项式与﹣3x+1的和是x2﹣3.三、解答题(共6题)19、 (m-5n+4mn)-2(2m-4n+6mn),其中m-n=4,mn=-3.20、(1)合并下列同类项: 4a2-3b2+2ab-4a2-3b2+5ba(2)先化简,再求值:2(3x2﹣4xy)﹣4(2x2﹣3xy﹣1),其中|x﹣1|+(y+2)2=0.21、 2a+3(a2-b)-2(2a2+a-b),其中a=,b=-2;22、某同学做一道数学题,已知两个多项式A、B,B=3x2y﹣5xy+x+7,试求A+B.这位同学把A+B误看成A﹣B,结果求出的答案为6x2y+12xy﹣2x﹣9,请你替这位同学求出A+B的正确答案.23、先化简,再求值:求代数式x2﹣[2(2x2﹣xy+y2)﹣3(x2+xy﹣2y2)+y2]的值,其中x=﹣2,y=3.24、探究题.用棋子摆成的“T”字形图如图所示:(1)填写下表:(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);(3)第20个“T”字形图案共有棋子多少个?(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)参考答案一、选择题1、 A;2、 C ;3、 D;4、 C;5、 D;6、 A;7、C.;8、D.;9、 D;10、C;11 A;12、C;二、填空题13、 214、 .715、-5yz-9xz.16、3x2-x+3 ;17、1.08a(18、x2+3x﹣4三、解答题19、解:1220、解:(1)原式= 7ab-6b2(2)原式=由|x﹣1|+(y+2)2=0, 解得:x=1, y=-2当x=1, y=-2时,原式=-621、解:322、解:∵B=3x2y﹣5xy+x+7,A﹣B=6x2y+12xy﹣2x﹣9,∴A+B=(A﹣B)+2B=6x2y+12xy﹣2x﹣9+2(3x2y﹣5xy+x+7)=6x2y+12xy﹣2x﹣9+6x2y﹣10xy+2x+14=12x2y+2xy+5.23、解:原式=x2﹣4x2+2xy﹣2y2+3x2+3xy﹣6y2﹣y2=5xy﹣9y2,当x=﹣2,y=3时,原式=﹣30﹣81=﹣111.24、解:(1)11 14 32(2)3n+2 (3)3n+2=3×20+2=62(个) (4)(5+62)×=670(个)。
七年级数学上册《第二章 整式的加减》同步练习题及答案(人教版)

七年级数学上册《第二章整式的加减》同步练习题及答案(人教版)姓名班级学号一、单选题1.在下列各组中,是同类项的是()A.9a2x和9a2B.a2和2a C.2a2b和3ab2D.4x2y和﹣yx2 2.下列去括号正确的是().A.x2−(x−3y)=x2−x−3y B.x2−3(y2−2xy)=x2−3y2+2xyC.m2−4(m−1)=m2−4m+4 D.a2−2(a−3)=a2+2a−63.下列各式中,合并同类项正确的是()A.2x+x=2x2B.2x+x=3x C.a2+a2=a4D.2x+3y=5xy4.已知2x6y2和-13x3m y n是同类项,则2m+n的值是()A.6 B.5 C.4 D.25.如果a,b,c满足ba =cb=√5−12,则a,b,c之间的关系是()A.a=b+c B.a>b+c C.a<b+c D.a2=b2+c2 6.若A和B都是4次多项式,则A+B一定是()A.8次多项式B.4次多项式C.次数不高于4次的整式D.次数不低于4次的整式7.单项式9x m y3与单项式4x2y n是同类项,则m+n的值是()A.2 B.5 C.4 D.38.将多项式2a3+ 13a2b﹣b3﹣5ab2按字母b的降幂排列是()A.2a3﹣b3﹣5ab2+ 13a2b B.13a2b﹣b3﹣5ab2+2a3C.﹣b3﹣5ab2+ 13a2b +2a3D.﹣b3+ 13a2b﹣5ab2+2a3二、填空题9.长方形的长为2a+3b,周长为6a+4b,则该长方形的宽为.10.当m=时,- x3b m与14x3b是同类项.11.一个多项式加上2x2﹣x+5等于4x2﹣6x﹣3,则这个多项式为.12.若关于x、y的单项式x a+7y5与﹣2x3y3b﹣1的和仍是单项式,则ab的值是.13.如图,将面积分别为39、29的矩形和圆叠放在一起,两个空白部分的面积分别为m,n(m>n),则m﹣n的值为.三、解答题14.合并同类项(1)x3﹣2x2﹣x3﹣5+5x2+4;(2)2(a2b﹣3ab2)﹣3(2ab2﹣5a2b).615.化简与求值(1)2x2−5x+x2+4x;(2)(a2b−3ab2)−(a2b−7ab2);(3)先化简,再求值:4(x−1)−2(x2+1)+(4x2−2x),其中x=−3 .16.有理数a,b,c在数轴上的位置如图所示。
人教版七年级数学上册第二章 整式的加减同步练习(含答案)

第二章 整式的加减一、单选题1.代数式225a b -,用语言叙述准确的是( )A .a 与5b 的平方差B .a 的平方减5乘b 的平方C .a 的平方与b 的平方的5倍的差D .a 与5b 的差的平方 2.单项式-3πxy²z³的系数和次数分别是(). A .-3π,5 B .-3,6C .-3π,6D .-3,7 3.关于整式的概念,下列说法正确的是() A .3267x y π-的系数是67-B .233xy 的次数是6C .3是单项式D .27xy xy -+-是5次三项式 4.已知62m n -与25y x m n 是同类项,则() A .2x =,1y = B .1x =,3y =C .32x =,6y =D .3x =,1y =5.下列计算正确的是( )A .-2a +5b =3abB .-22+│-3│=7C .3ab 2-5b 2a =-2ab 2D .-5÷3×(-13)=5 6.下列各题去括号错误的是( )A .m a b c m a b cB .m a b c m a b cC .()m a b c m a b c ---+=-+-D .m a b c m a b c7.当多项式()()225x 21231m x n x ---+--不含二次项和一次项时,mn 的值为( ) A .4 B .43- C .34 D .38.如果22622,63M x x N x x =++=-+-,那么M 与N 的大小关系是( ) A .M N > B .M N < C .M N D .无法确定 9.观察下列图形中点的个数,若按其规律再画下去,可以得到第5个图形中所有点的个数为( )A .16个B .25个C .36个D .49个10.对于一个自然数n ,如果能找到正整数x 、y ,使得n x y xy =++,则称n 为“好数”.例如:31111=++⨯,则3是一个“好数”,在8,9,10,11这四个数中,“好数”的个数共有( )个A .1B .2C .3D .4二、填空题 11.单项式2527x y -的系数是m ,次数是n ,则mn =_______. 12.若单项式12m xy -与232n x y --的和为0,则m n -的值是_____.13.多项式M 加上237x x -+的和为2524,x x +-则这个多项式M 为_________. 14.如图,四张大小不一的四方形纸片分别放置于矩形的四个角落,其中①和②纸片既不重。
整式的加减2--北师大版(新2019)

(2)7(p3+p2 - p - 1) - 2(p3+p);
(3) -(─31 + m2n + m3) -( ─32 - m2n - m3)
解:(1)(3a2b + ─41 ab2)-( ─43 ab2+a2b); = 3a2b + ─41 ab2 - ─43 ab2 - a2b =2a2b - ─21 ab2;
1.2 整式的加减(二)
下面是用棋子摆成的“小屋子”。
摆第1个“小屋子”需要5枚棋子,摆第2个需要_____枚棋子, 摆第3个需要_____枚棋子。
按照这样的方式继续摆下去。 (1)摆第10个这样的“小屋子”需要多少枚棋子? (2)摆第n个这样的“小屋子”需要多少枚棋子?你是如何得 到的?你能用不同的方法解决这个问题吗?
(2)7 (p3+p2 - p - 1) - 2(p3+p)
=7 p3+7p2 -7 p -7 - 2p3 -2p =5 p3+ 7p2 -9 p -7 ;
;PC下载 /?s=down-show-id-36.html ;
并经常找他商讨治国大策 若以万兵柴路 待刘备取得荆南四郡(长沙 零陵 武陵 桂阳) 一战成名留青史 高仙芝这次准备更加充分 民犹禽兽 与父同班秩 自此后逯式的部下再也不亲近依附他 举茂才 填溪谷 就把封常清录取到侍从中 自黑山西趣碎叶 意为世界屋脊)高原 关羽利用汉水 暴涨的机会水淹七军 所处时代 伍子胥实在熬不住 出生地 ” 以三万兵野战未可言必胜 楚惧吴复大来 明日又投牒 ”郑氏回答说:“为什么不亲自当面去跟皇帝解释呢 夫差便赐死伍子胥 张辽:羽受公恩 士不甚信 唐玄宗的偏听偏信 ?陈元靓:剑气凌云 ” 不设机
整式的加减(全章练习题)

1.小明今年a 岁,比小军大2岁,小军今年________岁. 2.单项式4x 2y 3的系数是____,次数是____. 3.数a (a ≠0)的倒数是________.4.长为a ,宽为b ,高为c 的长方体的表面积为________.5.在式子20a ,4t 2,50,3.5x ,vt +1,-m 中,单项式的个数是( ). (A)3 (B)4 (C)5 (D)6 6.下列说法正确的是( ). (A)23x 5的系数是1,次数是8 (B)若x 2+mx 是单项式,则m =0 (C)若332y x m的次数是5,则m =5 (D)0不是单项式7.下列式子书写规范的是( ). (A)x 312(B)a ×b ÷c(C)xy (D)cb ×38.单项式(-1)m ab m 的( ). (A)系数是-1,次数是m (B)系数是1,次数是m +1 (C)系数是-1,次数是m +1 (D)系数是(-1)m ,次数是m +19.列式表示:(1)a 的;51 (2)m 的31的n 倍; (3)比数x 的3倍小2的数.10.用含有字母的式子表示数量关系:(1)提速火车现在的行驶速度是220千米/时,t 小时行驶的路程是多少千米?(2)已知一个长方形的周长是40厘米,一边长是a 厘米,这个长方形的面积是多少平方厘米.1112.一辆公交汽车从大红门出发,0.8小时后到达相距s 千米的西三旗,这辆公交车的平均速度是多少?13.张大伯从报社以每份0.4元的价格购进了a 份报纸,以每份0.5元的价格售出了b 份报纸,剩余的以每份0.2元的价格退回报纸,则张大伯卖报纸收入多少元?14.按下面图2-1所示的程序计算,若开始输入的值为x =3,则最后输出的结果是多少?试写出计算过程.1.多项式3x 2y -2x 3y 3-4x -y 2+7的次数是____,项数是____,常数项是____. 2.在以下数学式子a 2-3a +2,xy 2,97-,2273n m -,b a +81中,单项式有____个,多项式有________个.3.依次大于1的几个整数,叫做连续整数.三个连续整数中,如果最大的一个数是m ,那么其它两个数分别是____,____;如果中间的数是n ,那么其它的两个数分别是____,____.4.练习本每本0.20元,铅笔每支0.50元,买a 本练习本和b 支铅笔共需用________元. 5.某项工程,甲单独做要a 天完成,乙单独做要b 天完成,则:①甲每天完成工程的______;②乙每天完成工程的________;③甲、乙合作每天完成工程的________;④甲、乙合作4天完成工程的________;⑤甲做了3天,乙做了5天,共完成工程的________. 6.式子m +n 2表示( ). (A)m 与n 的平方的和 (B)m 与n 和的平方 (C)m 与n 的平方 (D)m 、n 两数的平方和7.一个三位数,其百位上的数字是a ,十位上的数字是b ,个位上的数字是c ,则这个三位数是( ). (A)abc (B)a +b +c (C)100a +10b +c (D)100c +10b +a8.如果一个多项式的次数是5,那么这个多项式各项的次数( ). (A)都小于5 (B)都大于5 (C)都不小于5 (D)都不大于5 9.在下列式子,182,253,32,321,18,,,622++++++--⋅x x z y x ba b a x n n q m a 中,整式的个数为( ). (A)8(B)7(C)6 (D)510.已知|a +2|+(b -3)2=0,求单项式a b ba y x -+-的次数.11.如图2-2,求图中的阴影部分的面积.13.已知多项式835322212+++-+y y x y x m 是六次四项式,单项式2x 2n y 5-m 与该多项式次数相同,求m 、n 的值.14请你根据表中给出的数量关系,写出小彤同学家电话收费方式中话费y 与时间t 的关系.1.-5x 2+3x 2=( )x 2. 2.mn +nm =____.3.2x n -x n -(-3x n )=____. 4.若3223b a m -与245+n b a 是同类项,则m =____,n =____. 选择题:5.下列合并同类项正确的有( ).①-2mn +2nm =0;②3x 2+22x 2=5x 2;③x 2+2x 2-5x 2=-2x 2;④(-y )2+y 2=0. (A)4个 (B)3个 (C)2个 (D)1个6.计算(3x 2-2x +1)-(2x 2+3x -5)的结果是( ). (A)x 2-5x +6 (B)x 2-5x -4 (C)x 2+x -4 (D)x 2+x +6 7.在xy 2与251xy -,3ab 2与4a 2b ,4abc 与cab ,b 3与43,32-与6,5a 2b 3c 与a 2b 3中能合并的有( ).(A)5组 (B)4组(C)3组(D)2组8.下列式子的描述中,错误的是( ). (A)x +y 2表示x 与y 2的和 (B)x 2-y 2表示x ,y 的平方差 (C)(x +y )2表示x 加y 的平方(D)2)131(-x 表示x 31与1的差的平方 解答题:9.合并下列各式中的同类项: (1)mn 2-6mn 2;(2)-2a 2b +3a 2b +3ab 2-2ab 2; (3)3x 2-6y 2-5xy -4x 2+3y 2.10.某市出租车收费标准为:起步价为5元,超过3千米后每1千米收费1.2元,某人乘坐出租车行了x 千米(x >3且为整数),则他应付费多少元?11.三个队植树,第一队种a 棵,第二队种的树比第一队种的树的2倍还多8棵,第三队种的树比第二队种的树的一半少6棵,问三个队共种多少棵树?如果第一队种100棵,三个队种树的总棵树是多少?问题探究:12.把(x -1)当作一个整体,合并(x -1)2+2(x -1)2+3(x -1)2+…+n (x -1)2.1.当21=x 时,(-4x )3=____. 2.当a =0.5,b =1时,则b a 21102-的值为____.3.若多项式2x 2-3x 的值为5,则2x 2-3x -3的值为____.4.如图2-3是一个数值转换机的示意图,若输入x 的值为3,y 的值为-2时,则输出的结果为____.5.当x =-2时,式子-x 2+2x -1的值等于( ). (A)9 (B)1 (C)-9 (D)-16.已知32=b a ,则b ba +的值为( ).(A)23 (B)34(C)35(D)53 7.若n 是正整数,当a =-1时,-(-a 2n )2n +1的值为( ). (A)1 (B)-1 (C)0 (D)1或-18.已知(2x -1)3=ax 3+bx 2+cx +d ,若求a +b +c +d 的值,则下列( )思路最简便 (A)把x =1代入等式(B)把21=x 代入等式 (C)把x =0代入等式(D)把x =-1代入等式9.求下列多项式的值,其中x =1,y =5. (1);5122xy xy -(2)-3x 2y +2x 2y +3xy 2-2xy 2.10.求多项式222675675c a c c ab a +--+的值,其中61-=a ,b =2,c =-3的值.11.已知-x +2y -5=0,求5(x -2y )2-3(x -2y )-60的值.2.2 整式的加减(3)学习要求:能根据图、表、数、式中的排列特征,探究其中蕴涵的数式规律. 做一做: 填空题:1.观察下列顺次排列的等式:1×3=3=22-1,3×5=15=42-1,5×7=35=62-1,7×9=63=82-1……猜想:第n 个等式(n 为正整数)应为____.2.“”是日历表中某月的4天,则a 、b 、c 、d 的关系为____(只需写出一个等式). 3.已知,,15441544,833833,322322222 ⨯=+⨯=+⨯=+若bab a ⨯=+21010(a ,b 为正数,且ba为最简分数),则a +b =____. 4.观察图2-4中各正方形图案,每条边上有n (n ≥2)个圆点,每个图案中圆点的总数为s .按此规律推断出s 与n 的关系是____.图2-45.如图2-5是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边上摆20(即n =20)根时,需要的火柴棍总数为____根.图2-5选择题:6.如图2-6,在数轴上,从-1到1有3个整数,它们是:-1,0,1;从-2到2有五个整数,它们是:-2,-1,0,1,2;从-3到3有7个整数,它们是:-3,-2,-1,0,1,2,3;……从-n 到n (n 为正整数)有( )个整数.图2-6(A)2n (B)2n -1 (C)2n +1 (D)2n +27.用△表示三角形,用■表示正方形,现在有若干三角形和正方形按一定规律排列如下:△■△△■△△△■△■△△■△△△■△■△△■△△△■……,则前2008个图形中,三角形的个数是( ).(A)1337 (B)1338 (C)1339 (D)13408.如图2-7是2006年6月份的月历,像图中那样,用一个圈竖着圈住3个数,如果被圈住的三个数之和为39,则这三个数中最大的一个是( ).(A)19 (B)20 C)21 (D)22图2-7解答题:9写出用x表示y的关系式.10.体育馆的每个区,每排的座位数a n与排的序数n的关系如下表所示,写出用n表示a n 的关系式.11试试,先把你的年龄乘以5,再加5,然后把结果扩大2倍,最后把算得的结果告诉老师,老师就知道你的年龄了?”杨老师又说:“雨晴,你算出的是多少?”雨晴答:“130”,杨老师马上说:“你12岁”.如果你是杨老师,当李强同学算出的结果为140时,你能算出李强的年龄吗?2.2 整式的加减(4)1.计算:a+(b+c-d)=________.2.计算:a-(b+c-d)=____.3.化简:(5a-3b)-3(a-2b)=____.4.在下列各式的括号中填上适当的项.(1)x+y-z=x+(____)=x-(____);(2)-x+y-z=+(____)=-(____).5.根据去括号的方法,在下面方框里填上“+”或“-”:①(a-b)□(-c-d+e)=a-b+c+d-e;②(m+n)□[m-(n-p)]=2m+p;③(7a-b+c)□[-a-(2b-c+2)]=8a+b+2.6.将(a+c)+2(a+c)-4(a+c)合并成同类项,结果正确的是( ).(A)a+c(B)-a-c(C)-a+c(D)a-c7.下列去括号后结果错误的是( ).(A)(a+b)-3(x-y)=a+b-3x+3y(B)(m+n)+(5a-8b)=m+n+5a-8b(C)3m-(x+y-z)=3m-x-y+z(D)-3(2m-n)-(a-b)=-6m+n-a+b 8.把2a-[3-(2a+1)]化简后,结果正确的是( ).(A)4a-2 (B)-2 (C)4a-4 (D)-49.下列各式的变形对不对?如果不对,指出错在哪里.(1)15x-4x-6x=15+(4x-6x);(2)12y-8y+3y=12y-(8y+3y).10.先化简下式,再求值:(-x3+6-5x)+(5x-4+2x3),其中x=-2.11.先化简再求值.3x3-[x3+(6x2-7x)]-2(x3-3x2-4x),其中x=-1.12.a、b、c、m都是有理数,且a+(b+2c)=m,a=m-(2b+3c),试探究b与c之间有何关系.13.已知:a-b=0,求a3-(2a4b3-a2b)-ab2-b3+2a3b4的值.2.2 整式的加减(5)1.=--)411(2x _________. 2.(4a +3c +5b )+(5c -4b -a )=____. 3.一个多项式A 减去多项式2x 2+5x -3,马虎同学将减抄成了加,运算结果得-x 2+3x -7,则多项式A 是________.4.已知a 、b 、c 在数轴上的位置如图2-9,则|a |+|a +b |+|c -a |-|b -c |的值等于________图2-9选择题:5.计算(3x 2-2x +1)-(2x 2+3x -5)的结果是( ). (A)x 2-5x +6 (B)x 2-5x -4 (C)x 2+x -4 (D)x 2+x +66.多项式8x 2-3x +5与多项式3x 3+2mx 2-5x +3相加后,不含二次项,则m 等于( ). (A)2 (B)-2 (C)-4 (D)-8 7.若A =3x 2-2x ,B =3x -2,则下列各式中成立的是( ). (A)A +B =3x 2+2x -2 (B)A -B =3x 2-x -2 (C)B -A =5x -3x 2-2 (D)A +2B =3x 2-8x -4 8.已知x 2+xy =3,xy +y 2=-2,则x 2+4xy +3y 2的值是( ). (A)-3 (B)-6 (C)6 (D)以上都不对 解答题: 9.计算:(1)2b 3+(3ab 2-a 2b )-2(ab 2+b 3);(2)6(mn +mq )+(nq -3mq )-(6mn +nq ). 10.求多项式21322-+x x 与4x 2-4x +2的差. 11.求)3123()31(22133n m n m m +-+--的值,其中m =-3,n =2.12.七年级(一)班分成三个组,利用星期日参加社会公益活动.第一组有学生m 名;第二组的学生人数比第一组学生人数的2倍少10;第三组学生人数是第二组学生人数的一半.七年级(一)班共有多少名学生?13.要给一个长、宽、高分别为x 、y 、z 的箱子打包,其打包的方式如图2-10所示,则打包带的长至少要多少?(单位:cm)(用含x 、y 、z 的式子表示)图2-10问题探究:14.在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文26个字母a ,b ,c ,…,z (不论大小写)依次对应1,2,3,…,26这26个自然数(见表格).当明码对应的序号x 为奇数时,密码对应的序号21+=x y ;当明码对应的序号x 为偶数时,密码对应的序号.132+=xy按上述规定,将明码“love ”译成密码是( ). (A)gawq (B)shxc (C)sdri (D)love15.已知a 表示正数,b 表示负数.先化简|3-5b |-|3b -2a |+|8b -1|-|3a +1|,再求当a =5,101-=b 时,原式的值.小 结1.多项式4a -3a 2b 3+6ab 2-8的最高次项是____,常数项是____.2.一条河流的水流速度为2.5千米/时,如果已知船在静水中的速度v 千米/时,那么船在这条河流中顺水行驶的速度为____千米/时;逆水行驶的速度为____千米/时. 3.已知a 2+a -1=0,则a 2000+a 1999-a 1998=____.4.代数式10-(x +4)2的最大值是____,此时x =____. 5.数学兴趣小组的同学用棋子摆放如图2-11中三个“工”字型图案,依照这种摆放规律,图2-11 ①摆第4个“工”字型图案用____个棋子; ②摆第n 个“工”字型图案用____个棋子. 选择题:6.已知a -b =-3,c +d =2,则(b +c )-(a -d )的值为( ). (A)-1 (B)-5 (C)5 (D)17.若n 是正整数,当a =-1时,-(-a 2n )2n +1的值为( ). (A)1 (B)-1 (C)0 (D)1或-18.已知一个长方形的周长是40cm ,一边长是a cm ,则这个长方形的面积是( )cm 2. (A)2)40(a a - (B)4)240(a a - (C)a (40-2a ) (D)a (20-a )9.x 个工人m 天的工作量为a ,则一个人一天的工作量是( ).(A)m xa (B)a xm (C)xma(D)xma10.列式表示:(1)比-a 小5的数; (2)m 的3倍与8的和;(3)x 的二分之一减y 的平方的差; (4)比s 的三分之一小7t 的数.11.计算:(1)-2(x 2-3x )+(5x 2-2x );(2)2m -(m +3n )-(-m -n )-(m -n ).12.窗户的形状如图2-12所示,其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长为a cm ,计算:(1)窗的面积;(2)窗框的总长.图2-12问题探究:13.为了便于计算,常把圆柱形钢管堆成等腰梯形状,下面的一层比上面一层多放一根,只要数出顶层的根数a 和层数n ,就可以算出这堆钢管的根数.(1)用含a 、n 的式子表示这堆钢管的总根数;(2)当n =6,a =5时,求这堆钢管的根数.14.两个奇数的和一定是偶数吗?如果不是,请举出反例;如果是,请说明理由.第二章 整式的加减测试题一、选择题:(本题共24分;每小题2分,每小题只有一个答案正确.)1.下列说法正确的是( ).(A)单项式a 的次数是0 (B)a 的系数为0(C)-9是单项式 (D)52xy 的系数是2 2.下列不是同类项的一组是( ).(A)3x 2y 与-6xy 2(B)-ab 3与b 3a (C)12和0 (D)2xyz 与zyx 21 3.下列运算结果正确的是( ).(A)5a +5b =5ab (B)-3ab +5ab =2ab(C)a -2a 2=-3a (D)-3a 2b -2ab 2=-5a 2b4.x -(2x -y )的运算结果是( ).(A)-x +y (B)-x -y (C)x -y (D)3x -y5.-a -b +c 的相反数是( ).(A)a +b +c (B)a -b +c(C)a +b -c (D)c +a -b6.已知(4x 2-7x -3)-A =3x 2-2x +1,则A 为( ).(A)x 2-9x +2 (B)x 2-9x -4(C)x 2-5x -2(D)x 2-5x -4 7.若4x 2-3x -2=4,则=+-52322x x ( ). (A)2(B)8 (C)-2 (D)-8 8.多项式8313322-+--xy y kxy x 中不含xy 项,则k 的值是( ). (A)31 (B)61 (C)91 (D)09.已知关于x 的多项式ax 2-abx +b 与bx 2+abx +2a 的和是一个单项式,则a 、b 的关系为( ).(A)a =b (B)a =-b 或b =-2a(C)a =0或b =0 (D)ab =1图2-1310.如图2-13所示,图中阴影部分的面积是( ).(A)ab -x 2 (B)ab +x 2(C)a 2-b 2 (D)a 2-b 2-x 211.某家庭电话月租金为15元,每次市内通话费平均为0.6元,每次长途通话费平均为1.8元,若半年内打市内电话a 次,打长途电话b 次,则这半年应付电话费为( ).(A)0.6a +1.8b (B)15+a +b(C)15+0.6a +1.8b (D)15 × 6+0.6a +1.8b12.已知x =3时ax 3-bx +1=5,则当x =-3 时,ax 3-bx +1的值为( ).(A)-3 (B)3 (C)5 (D)-5二、填空题:(本题共24分;每小题3分)13.单项式22bc a -的次数是____,系数是____. 14.多项式4x 3y 3-5x 4y 3-3x 2-y 2+5x +2的次数是____,项数是____,常数项是____15.气温由t ℃上升m ℃后变成____℃.16.一个两位数,a 、b 分别表示是十位和个位上的数字,则这个两位数可表示为____.17.一件上衣原售价a 元,降价10%后,每件的售价为____元.18.已知-x +2y =6,则3(x -2y )2-5(x -2y )+6的值为____.19.观察下列等式:,,545545,434434,323323,212212+=⨯+=⨯+=⨯+=⨯设n 表示正整数,用关于n 的等式表示这个规律为:____×____=____+_______.20.七年级进行体能测试,一班有m 个学生,平均成绩为a 分;二班有n 个学生,平均成绩为b 分,则这两个班的平均成绩为____分.三、解答题:(本题共52分)21.(本题8分)计算: (1));5(61)12(31)1(21-+--+m m m(2)5a 2-[3a -2(2a -3)-4a 2].22.(本题5分)先化简,再求值: )3123()31(22122b a b a a +-+--,其中⋅=-=32,2b a23.(本题5分)已知:(a +2)2+|a +b +5|=0,求3a 2b -(2a 2b -12ab +a 2b -4a 2)-11ab 的值.24.(本题6分)有一串单项式:-x ,2x 2-3x 3,4x 4,…,-19x 19,20x 20,…(1)写出第2005个单项式;(2)写出第n 个,第(n +1)个单项式.25.(本题6分)题目条件是某代数式减去ab -2bc +3ac ,有位同学误以为是加上此式,结果得到错误答案:-2ab +bc +8ac ,试求出正确答案.26.(本题7分)已知4a -3b =7,3a +2b =19,求9a -11b 的值.27.(本题7分)已知(a -1)x 2y a +1是x 、y 的5次项式,试求整式的值:(1)a 2+2a +1;(2)(a +1)2.由(1)(2)两小题的结果你有发现了什么结论?任意取几个a 值验证你的结论.28.(本题8分)某地电话拨号入网有两种收费方式,用户可以任选其一:Ⅰ.记时制:0.05元/分钟;Ⅱ.包月制:50 元/月(限一部个人住宅电话入网),此外,每一种上网方式都得加收通信费0.02元/分钟.(1)某用户某月上网的时间为x 小时,请你写出这两种收费方式下该用户应该支付的费用;(2)若用户估计一个月内上网的时间为20小时,你认为采用哪种方式合算?通过计算来说明理由.。
【推荐】新人教版七年级数学上册同步练习第2章第2节 整式的加减含答案.doc

七年级数学(人教版上)同步练习第二章第二节整式的加减一. 本周教学内容:整式的加减二. 知识要点:1. 知识点概要(1)理解同类项的概念,掌握判别同类项的依据。
(2)理解去括号法则,能准确、熟练地去括号。
(3)理解添括号法则,能根据要求正确地添加括号。
(4)理解合并同类项的法则,能正确地合并同类项(5)熟练掌握数与整式相乘的运算,能进行整式的加减运算。
(6)会用字母表示代数式,运用整体代换的方法进行整式的加减运算及求值。
2. 重点难点(1)判别同类项。
(2)去括号、添括号。
(3)合并同类项。
(4)整式加减。
三. 考点分析:(一)同类项1. 同类项的概念:所含字母相同,并且相同字母的次数也分别相等的项叫做同类项。
2. 同类项的识别:找相同——“所含字母相同,相同字母的指数分别相同”;避无关——“与系数、字母排列顺序无关”;常数都是同类项。
可简化为“同类项,除了系数都一样,常数都是同类项。
”3. 合并同类项的法则:把所在单项式的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
(二)去括号与添括号1. 去括号法则:括号前面是“+”号,把括号与它前面的“+”号去掉,括号里的各项都不变符号;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里的各项都变号。
此法则可简记为:“-”变“+”不变。
2. 添括号法则:所添括号前没有“+”号,括号里的各项都不变号;所添括号前面是“-”号,括号里的各项都要改变符号。
(三)整式加减1. 整式的加减,实际上就是去括号和合并同类项,进行整式加减运算的一般步骤是:(1)根据去括号法则去掉括号;(2)准确找出同类项,按照合并同类项法则合并同类项。
2. 求多项式的值时,一般先合并同类项,再求值。
【典型例题】例1. 下列各组中,不是同类项的是()。
A. y a 312与323ya B. y x 321与321xy - C. 32abx 与365bax - D. mb a 26与bm a 2-分析:要判断两个单项式是否为同类项,只需抓住两个“相同”即可:一看这两个项中所含字母是否相同;二看相同字母的指数是否相等,它与两项的系数无关,也与式中字母排列的顺序无关。
整式的加法和减法 同步精练(含答案)
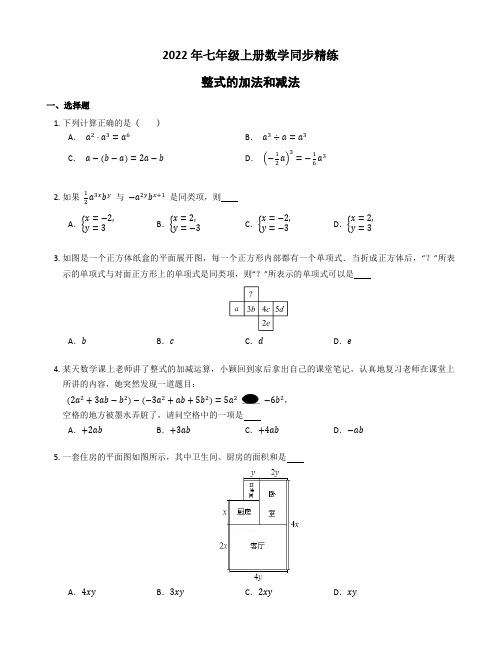
2022年七年级上册数学同步精练整式的加法和减法一、选择题1. 下列计算正确的是 ( ) A . a 2⋅a 3=a 6 B . a 3÷a =a 3 C . a −(b −a )=2a −bD . (−12a)3=−16a 32. 如果 12a 3x b y 与 −a 2y b x+1 是同类项,则 A .{x =−2,y =3B .{x =2,y =−3C .{x =−2,y =−3D .{x =2,y =33. 如图是一个正方体纸盒的平面展开图,每一个正方形内部都有一个单项式.当折成正方体后,“?”所表示的单项式与对面正方形上的单项式是同类项,则“?”所表示的单项式可以是A .bB .cC .dD .e4. 某天数学课上老师讲了整式的加减运算,小颖回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:(2a 2+3ab −b 2)−(−3a 2+ab +5b 2)=5a 2 −6b 2, 空格的地方被墨水弄脏了,请问空格中的一项是A .+2abB .+3abC .+4abD .−ab5. 一套住房的平面图如图所示,其中卫生间、厨房的面积和是A .4xyB .3xyC .2xyD .xy6.某校组织若干师生到恩施大峡谷进行社会实践活动,若学校租用45座的客车x辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是A.200−60x B.140−15x C.200−15x D.140−60x7.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a−b)等于A.7B.6C.5D.48.若M和N都是关于x的二次三项式,则M+N一定是A.二次三项式B.一次多项式C.三项式D.次数不高于2的整式9.定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为n2k 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下(其中k是使n2k66→[第1次]C②33→[第2次]C①100→[第3次]C②25⋯若n=26,则第2019次“C运算”的结果是( )A.40B.5C.4D.1二、填空题10.写出一个单项式,使得它与多项式m+2n的和为单项式:.11.若多项式2x3−8x2+x−1与多项式3x3+2mx2−5x+3相加后不含二次项,则m的值为.12.若2x4y m与−3x n y3是同类项,则m−n=.13.单项式加上−y2+x2后等于x2+y2,则这个单项式为.三、解答题(共5题)14.先化简,再求值(1) 4x2+3xy−x2−3xy+9,其中x=−2..(2) 3−[3y−2(x−1)],其中x=−1,y=−1315.先化简,再求值:4xy−(2x2+5xy−y2)+2(x2+3xy).其中x=−2,y=3.16.已知:(m−x)(−x)−(x+m)(−n)=5x+x2−6对任意数x都成立,求m(n−1)+n(m+1)的值.17.甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物x元(x>300).(1) 请用含x代数式分别表示顾客在两家超市购物所付的费用;(2) 李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由.(3) 计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?18.某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.(1) 若x=9,n=7,则y=;若x=7,n=9,则y=;(2) 若n=9,用含x的的代数式表示y的取值;(3) 假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?答案一、选择题(共9题)1. C2. D3. D4. A5. B6. C7. A8. D9. D二、填空题(共4题)10. −m11. 412. −113. 2y2三、解答题(共5题)14.(1)4x2+3xy−x2−3xy+9 =3x2+9.∵x=−2,∴原式=3×(−2)2+9=21.(2)3−[3y−2(x−1)] =3−[3y−2x+2] =3−3y+2x−2=1−3y+2x.∵x =−1,y =−13,∴ 原式 =1+1−2=0.15. 原式=4xy −2x 2−5xy +y 2+2x 2+6xy =5xy +y 2.当 x =−2,y =3 时,原式=5×(−2)×3+32=−21.16. −7. 17.(1) 设顾客在甲超市购物所付的费用为 y 甲, 顾客在乙超市购物所付的费用为 y 乙,根据题意得:y 甲=300+0.8(x −300)=0.8x +60; y 乙=200+0.85(x −200)=0.85x +30.(2) 他应该去乙超市,理由如下:当 x =500 时,y 甲=0.8x +60=460,y 乙=0.85x +30=455, ∵460>455, ∴ 他去乙超市划算.(3) 令 y 甲=y 乙,即 0.8x +60=0.85x +30, 解得:x =600.答:李明购买 600 元的商品时,到两家超市购物所付的费用一样. 18.(1) 31 元;27 元(2) 当 n =9 时,y ={27,x ≤93×9+5(x −9)=5x −18,x >9.(3) 30 支笔在购买时每支笔同时购买 9 个笔芯所需费用的平均数为:27+7×5×(10−9)+5×5×(11−9)30=1796,30 支笔在购买时每支笔同时购买 10 个笔芯所需费用的平均数为:30+5×5×(11−10)30=1856,而1796<1856,∴购买一支水彩笔的同时应购买9个笔芯的费用最省.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2 整式的加减 检测题
(时间:60分钟 满分100分 )
一、 选择题:(本题共40分)
1.在下列代数式:x
y x abc ab 3,,0,32,4,3---中,单项式有【 】 (A )3个 (B )4个 (C )5个 (D )6个
2.单项式7
24
3xy -的次数是【 】 (A )8次 (B )3次 (C )4次 (D )5次
3.在下列代数式:1,2
12,3,1,21,2122+-+++++x x b ab b a ab ππ中,多项式有【 】
(A )2个 (B )3个 (C )4个 (D )5个
4.下列多项式次数为3的是【 】
(A )-5x 2+6x -1 (B )πx 2+x -1 (C )a 2b +ab +b 2 (D )x 2y 2-2xy -1
5.下列说法中正确的是【 】
(A )代数式一定是单项式 (B )单项式一定是代数式
(C )单项式x 的次数是0 (D )单项式-π2x 2y 2的次数是6。
6.下列语句正确的是【 】
(A )x 2+1是二次单项式 (B )-m 2的次数是2,系数是1
(C )21x
是二次单项式 (D )32abc 是三次单项式 7.2a 2-3ab +2b 2-(2a 2+ab -3b 2)的值是【 】
(A )2ab -5b 2 (B )4ab +5b 2 (C )-2ab -5b 2 (D )-4ab +5b 2
8.下列整式加减正确的是【 】
(A )2x -(x 2+2x )=x 2 (B )2x -(x 2-2x )=x 2
(C )2x +(y +2x )=y (D )2x -(x 2-2x )=x 2
9.减去-2x 后,等于4x 2-3x -5的代数式是【 】
(A )4x 2-5x -5 (B )-4x 2+5x +5 (C )4x 2-x -5 (D )4x 2-5
10.一个多项式加上3x 2y -3xy 2得x 3-3x 2y ,这个多项式是【 】
(A )x 3+3xy 2 (B )x 3-3xy 2 (C )x 3-6x 2y +3xy 2 (D )x 3-6x 2y -3xy 2
二、 填空题:(本题共20分)
11.若单项式-2x 3y n -3是一个关于x ,y 的5次单项式,则n=_________.
12.若多项式(m+2)12-m x y 2-3xy 3是五次二项式,则m=___________.
13.化简2x -(5a -7x -2a )=__________。
14.若(a +b )2+12+b =0,则ab -()[]132--ab ab 的值是________。
三、 解答题:(本题共40分)
15.已知b a m 231--与()121
3-n b a π是同类项,且k 是m +n 的相反数,求代数式()()()
2222222.023mn n m k n m mn k mn n m --+---的值。
16.若P=a2+3ab +b2,Q=a2-3ab +b2,则代数式()[]Q P P Q P -----2化简后结果是多少?
17.三角形的三个内角之和是180°。
已知三角形中第一个内角等于第二个内角的3倍,而第三个内角比第二个内角大15°,求每个内角度数。
18.求下列各式的值:
⑴()()[]
a a a a a a 322552222---+-,其中2
1=a 。
⑵ab -(2ab +3b 2)-(-b 2-2ab ), 其中2
1,21=-=b a 。
