如何讲好时域取样定理
时域采样定理

电子信息工程学系实验报告课程名称:数字信号处理实验项目名称; 时域采样定理 实验时间:2013.05.08班级: 通信102 姓名: 学号:0107052一、实 验 目 的:熟悉并加深采样定理的理解,了解采样信号的频谱和模拟信号频谱之间的关系。
二、实 验 环 境:计算机、MATLAB 软件。
三、实验内容和步骤1.给定模拟信号如下:)()sin()(0t u t Ae t atax Ω=- 假设式中128.444=A ,250=α,s rad /2500π=Ω,将这些参数代入式中,对)(t x a 进行傅立叶变换,得到)(Ωj X a ,并可画出它的幅频特性f jf X a ~)(;根据该曲线可以选择采样频率。
2.按照选定的采样频率对模拟信号进行采样,得到时域离散信号)(n x :)()sin()()(0nT u nT Ae nT x n x anT a Ω==-这里给定采样频率如下:s f =1 kHz 、300 Hz 、200 Hz 。
分别用这些采样频率形成时域离散信号,按顺序分别用)(1n x 、)(2n x 、)(3n x 表示。
选择观测时间50=p T ms 。
3.计算)(n x 的傅立叶变换()j X e ω:100()[()]sin()i i n anT j j n i n X e FT x n Ae nT e ωω---===Ω∑ (5)式中,=i 1,2,3,分别对应三种采样频率的情况⎪⎭⎫ ⎝⎛===s T s T s T 2001,3001,10001321。
采样点数以下式计算: p i iT n T =(6)式中,ω是连续变量。
为用计算机进行数值计算,改用下式计算:100()[()]sin()i kk n j j n anT M i n X eDFT x n Ae nT e ωω---===Ω∑ (7)式中,2k k Mπω=,k =0,1,2,3,…,M -1;M=64。
时域抽样定理

时域抽样定理时域抽样定理是数字信号处理中的基本理论之一,它对于理解信号采样和重构有着重要的意义。
本文将详细介绍时域抽样定理的原理、条件和应用。
1. 定理原理时域抽样定理,又称为奈奎斯特采样定理(Nyquist Sampling Theorem),是由哈里·奈奎斯特(Harry Nyquist)于20世纪20年代提出的。
该定理指出:在连续时间信号中,如果信号的最高频率为fs,则采样频率必须大于2fs才能保证采样后的离散信号能完美地重构出原始信号。
2. 定理条件奈奎斯特采样定理的成立需要满足以下两个条件:2.1 带宽限制条件信号的带宽必须是有限的。
即信号的频谱必须在一定范围内有限制,不允许有无限大的频率成分存在。
如果信号的带宽无限大,那么无论采样频率多高,也无法在离散信号中准确地表示原始信号。
2.2 采样频率条件采样频率必须大于信号最高频率的两倍。
只有在这种条件下,才能够完美地重构出原始信号。
如果采样频率低于信号最高频率的两倍,将会出现混叠效应,导致重构的信号与原始信号存在偏差。
3. 定理应用奈奎斯特采样定理在实际应用中有着广泛的应用,尤其是在信号处理和通信领域。
3.1 数字音频和视频在数字音频和视频领域,奈奎斯特采样定理的应用非常重要。
通过在一定的采样频率下对模拟音频或视频信号进行抽样,可以得到离散的数字信号。
这些离散的信号可以通过数学算法来进行处理和压缩,从而实现高保真度的音频和视频传输。
3.2 通信系统在通信系统中,奈奎斯特采样定理被广泛应用于调制和解调过程中。
发送端将模拟信号进行抽样和量化,将其转换为数字信号后进行传输。
接收端通过接收到的数字信号进行解调和重构,实现原始模拟信号的恢复。
3.3 图像处理在图像处理领域,奈奎斯特采样定理可以用于图像的采集和重构。
通过在一定的采样频率下对图像进行抽样,可以得到离散的像素值。
这些像素值可以用于图像的处理、压缩和重构,从而实现高质量的图像处理效果。
简述时域取样定理

简述时域取样定理时域取样定理是数字信号处理中的基本原理之一,它指出,要准确地对连续时间信号进行数字化处理,就需要按照一定的采样频率对信号进行取样。
这个定理在实际应用中具有重要的指导意义。
在生活中,我们经常会遇到需要将连续时间信号转换成数字信号的情况,比如说我们使用手机录音、数码相机拍照、CD音乐录制等等。
在这些过程中,都需要将连续的声音信号转换成数字化的信号,才能够被相应的设备处理和储存。
而时域取样定理正是为了保证这一过程的准确和可靠性而存在的。
时域取样定理的核心观点是,对于任意一个连续时间信号,只要其频谱没有超过采样频率的一半,那么通过一定的采样频率对信号进行取样,就能够完全还原原始信号的信息。
换句话说,只要我们的采样频率足够高,就能够保证数字信号中包含了足够多的信息,以使我们能够准确地还原原始信号。
那么,为什么要限制频谱不能超过采样频率的一半呢?这是因为信号在取样时,会产生一个称为混叠的现象。
混叠是指原始信号的高频成分在采样过程中被错误地表示成低频成分。
这种错误表示会导致原始信号的信息丢失和失真。
为了避免这种失真,我们需要保证在采样时,信号的频谱不会超过采样频率的一半,从而保证了取样信号的可靠性。
这个定理的发现与数学家奈奎斯特(Nyquist)息息相关。
奈奎斯特把上述观点扩展到了一个更一般的形式,提出了奈奎斯特定理。
奈奎斯特定理规定,要完全还原一个连续时间信号,我们需要以不低于信号最高频率的两倍的采样频率进行取样。
也就是说,如果一个信号的最高频率为f,我们就需要以不低于2f的采样频率对信号进行取样,才能够准确还原原始信号的信息。
总结起来,时域取样定理是数字信号处理中非常重要的理论基础。
它告诉我们,在对连续时间信号进行数字化处理时,一定要按照一定的采样频率进行取样,以保证信号的准确性和可靠性。
同时,我们还需要遵循奈奎斯特定理,确保采样频率不低于信号最高频率的两倍。
只有这样,我们才能够在数字信号处理中获得准确、清晰的结果。
时域取样定理简述

时域取样定理简述一、什么是时域取样定理时域取样定理(Nyquist-Shannon采样定理)是指在信号的离散化表示中,为了能够完美地重构出原始信号,取样频率必须大于信号频谱中最高频率的二倍。
也就是说,采样频率必须足够高,才能确保取样后的离散信号不损失原始信号的信息。
二、为什么要进行时域取样在信号处理与通信领域,我们常常需要对连续信号进行离散化处理。
离散化后的信号更易于存储、处理和传输。
而时域取样是指根据一定的规则,在时间轴上等间隔采集连续信号的采样值。
通过对连续信号进行时域取样,我们可以将连续信号转化为一组离散采样值,从而方便后续的数字信号处理。
三、取样频率的选择根据时域取样定理,取样频率必须大于信号频谱中最高频率的二倍。
这是为了避免混叠现象的发生,即采样频率不足以恢复原始信号。
在实际应用中,我们通常会选择取样频率略高于最高频率的二倍,以确保完整采样信号的重构。
这样,就能够对原始信号进行逆取样,从离散信号中恢复出原始连续信号。
四、时域取样的数学表示对于原始信号x(t)和采样频率为f_s的离散化信号x_s(n),二者之间的关系可以通过数学公式表示:x_s(n) = x(t) * s(n) = x(nT_s)其中,x(t)表示原始信号,s(t)为采样脉冲(如理想脉冲),x_s(n)为离散化信号,n为采样点的索引,T_s为采样周期。
当我们得到离散化信号x_s(n)后,可以通过插值或滤波等方法进行信号重构,从而恢复出原始信号x(t)。
1. 插值法插值法是一种简单有效的信号重构方法。
常用的插值法有线性插值、最近邻插值和三次样条插值等。
其中,三次样条插值在重构低频信号时效果更好,但计算复杂度较高。
2. 滤波法滤波法是另一种常用的信号重构方法。
通过设计合适的滤波器,可以滤除离散化信号中的混叠分量,从而恢复出原始信号。
在滤波法中,常用的滤波器有低通滤波器和带通滤波器。
低通滤波器用于滤除混叠频率,带通滤波器用于滤除采样频率之外的频率分量。
实验四 时域采样定理

实验内容和步骤1、 给定模拟信号如下:)()sin()(0t u t Ae t ata x Ω=-假设式中128.444=A ,250=α,s rad /2500π=Ω,将这些参数代入式中,对)(t x a 进行傅立叶变换,得到)(Ωj X a ,并可画出它的幅频特性f jf X a ~)(;根据该曲线可以选择采样频率。
这里给定采样频率如下:f=1 kHz ,300 Hz ,200 Hz 。
分别用这些采样频率形成时域离散信号x(n),打印三种采样频率的幅度曲线|X(ej ω)|~ω,k=0,1,2,3,…,M-1;M=64。
Matlab 编程如下:%用1000Hz 采样频率 clear all;T1=1/1000; n=0:64/(1000*T1); A=444.128; a=50*sqrt(2.0);w0=50*sqrt(2.0)*pi; xn1=A*exp(-a*n*T1).*sin(w0*n*T1); Xk1=fft(xn1,1024); subplot(322);stem(n,xn1,'.'); grid onxlabel('n');ylabel('x(n)');title('1000Hz 采样 x(n)'); k=0:1023;wk=2*k/1024;subplot(321);plot(wk,abs(Xk1));grid on;xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');title('FT[x(n)]');%用300Hz 采样频率 T2=1/300; n2=0:64/(1000*T2);A=444.128; a=50*sqrt(2.0);w0=50*sqrt(2.0)*pi; xn2=A*exp(-a*n2*T2).*sin(w0*n2*T2); Xk2=fft(xn2,1024);subplot(324);stem(n2,xn2,'.');grid on ;title(' 300Hz 采样 x(n2)');xlabel('n');ylabel('x(n2)'); k=0:1023;wk=2*k/1024;subplot(323);plot(wk,abs(Xk 2));gridon ;title('(a)FT[x(n2)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|'); %用200Hz 采样频率 T3=1/200; n3=0:64/(1000*T3); A=444.128;a=50*sqrt(2.0);w0=50*sqrt(2.0)*pi;xn3=A*exp(-a*n3*T3).*sin(w0*n3*T3);Xk3=fft(xn3,1024); subplot(326);stem(n3,xn3,'.');grid on ;title('200Hz 采样 x(n3)');xlabel('n');ylabel('x(n3)');k=0:1023;wk=2*k/1024; subplot(325);plot(wk,abs(Xk3));grid on ;title('(a)FT[x(n3)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');2.按照选定的采样频率对模拟信号进行采样,得到时域离散信号)(n x :)()sin()()(0nT u nT Ae nT x n x anTa Ω==-这里给定采样频率如下:50=A ,250=α,s rad /2500π=Ωs f =1 kHz ,300 Hz ,200 Hz 。
数字信号处理实验三时域及频域采样定理
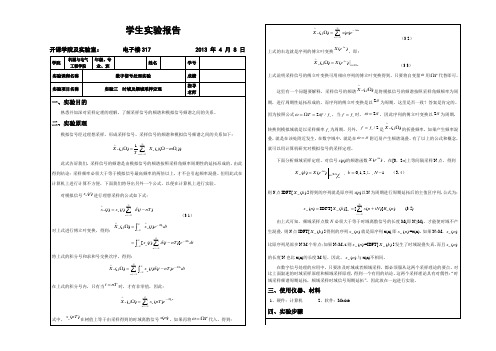
Xk1=fft(x1,length(n1)); %采样序列x1(n)的FFT变换
Xk2=fft(x2,length(n2)); %采样序列x2(n)的FFT变换
Xk3=fft(x3,length(n3)); %采样序列x3(n)的FFT变换
k1=0:length(Xk1)-1;
fk1=k1/Tp; %x1(n)的频谱的横坐标的取值
这里给定采样频率如下: ,300Hz,200Hz。分别用这些采样频率形成时域离散信号,按顺序分别用 、 、 表示。选择观测时间 。
3.计算 的傅立叶变换 :
(3.6)
式中, ,分别对应三种采样频率的情况 。采样点数用下式计算:
(3.7)
(3.6)式中, 是连续变量。为用计算机进行数值计算,改用下式计算:
下面分析频域采样定理。对信号x(n)的频谱函数 ,在[0,2π]上等间隔采样N点,得到
(3.4)
则N点IDFT[ ]得到的序列就是原序列x(n)以N为周期进行周期延拓后的主值区序列,公式为:
(3.5)
由上式可知,频域采样点数N必须大于等于时域离散信号的长度M(即N≥M),才能使时域不产生混叠,则N点IDFT[ ]得到的序列 就是原序列x(n),即 =x(n)。如果N>M, 比原序列尾部多N-M个零点;如果N<M,z则 =IDFT[ ]发生了时域混叠失真,而且 的长度N也比x(n)的长度M短,因此。 与x(n)不相同。
时域采样定理的内容

时域采样定理的内容时域采样定理是指将连续时间信号转换为离散时间信号的过程。
在数字信号处理中,时域采样定理是非常重要的基础知识,因为它涉及到信号的采样频率和采样周期的选择,对于数字信号的重构和处理有着至关重要的作用。
时域采样定理的基本原理是:一个连续时间信号可以通过对其进行一定的采样,将其转换为一个离散时间信号。
采样频率是指每秒钟采样的次数,采样周期是指两次采样之间的时间间隔。
根据时域采样定理的要求,如果采样频率大于信号最高频率的两倍,那么就可以完全恢复原来的连续时间信号,否则就会出现采样失真的情况。
时域采样定理是数字信号处理中的重要概念,它为我们提供了一种将连续时间信号转换为离散时间信号的方法,从而使得信号可以在计算机等数字设备中进行处理。
在数字信号处理过程中,时域采样定理的应用非常广泛,包括音频处理、图像处理、视频处理等领域。
在音频处理中,时域采样定理被广泛应用于音频编码和解码过程中。
通常情况下,采样频率要高于音频信号的最高频率,以确保信号在采样过程中不会失真。
在音频编码和解码的过程中,我们需要对音频信号进行采样,并将其转换为数字信号,然后对数字信号进行压缩和解压缩,最终得到高质量的音频信号。
在图像处理中,时域采样定理被应用于数字图像的采样和重构过程中。
通过将连续时间图像转换为离散时间图像,我们可以在计算机上对图像进行处理和编辑,从而实现图像的增强和修复等功能。
在数字图像采样和重构的过程中,采样频率和采样周期的选择非常重要,它们直接影响图像的质量和精度。
在视频处理中,时域采样定理被广泛应用于数字视频的采样和重构过程中。
与图像处理类似,数字视频的采样和重构也需要考虑采样频率和采样周期的选择,以确保视频信号在处理过程中不会失真。
通过数字视频的采样和重构,我们可以实现视频的编辑、剪辑、压缩和解压缩等功能。
时域采样定理在数字信号处理中扮演着非常重要的角色,它为我们提供了一种将连续时间信号转换为离散时间信号的方法。
时域采样定理

时域采样定理简介时域采样定理是一种重要的信号处理理论,它指出:对于一个连续时间的信号,如果以足够高的频率对其进行采样,那么原始信号可以完全通过采样信号进行恢复。
时域采样定理为我们提供了对连续时间信号进行数字化处理的基础。
定理表述时域采样定理最常见的表述是由Shannon在1949年提出的。
它可以表述为:对于一个带宽受限的连续时间信号x(t),如果其最高频率为B,那么我们至少需要以2B的频率对其进行采样,才能够完全还原原始信号。
数学上可以用以下公式表示时域采样定理:$$ x(t) = \\sum_{n=-\\infty}^{\\infty} x(nT_s) \\cdot\\text{sinc}\\left(\\frac{t-nT_s}{T_s}\\right) $$在这个公式中,T s是采样周期,x(nT s)是采样信号,$\\text{sinc}(x)$是sinc函数,其定义为$\\text{sinc}(x) = \\frac{\\sin(\\pi x)}{\\pi x}$。
采样频率根据时域采样定理,我们需要以足够高的频率来对信号进行采样。
采样频率的选择由信号的带宽决定。
带宽是信号中存在的最高频率分量。
为了满足时域采样定理,我们需要采用Nyquist采样频率,即至少为信号带宽的两倍。
这样可以确保采样频率足够高,能够捕捉到信号中所有的频率分量。
采样误差在实际应用中,由于多种因素的影响,我们很难达到理想的采样条件。
采样误差是指由于采样频率不足或其他因素引起的信号失真。
当采样频率在Nyquist采样频率的一定范围内时,信号的恢复误差是可以接受的。
但是一旦采样频率低于Nyquist采样频率的两倍,就会出现采样失真,这将导致信号无法完全还原。
为了减小采样误差,我们可以采用过采样的方式。
过采样即采样频率大于Nyquist采样频率的两倍。
这样可以增加采样点的数量,提高还原信号的精度。
应用领域时域采样定理在许多领域有着广泛的应用。
时域采样定理频带为F的连续信号 f

答:1)原则上仅需在圆柱弹性元件上下表面各贴一片应变片 R1 和 R2(见图),并与两阻值和应变片阻值相同的固定电阻组成电桥。 没有力、弯矩作用时,R1=R2=R,电桥输出电压 U0 为零。 2)测拉力时,由于受拉,Δ R1=Δ R2,测弯矩时,由于受弯,Δ R1`=Δ R2`。测定拉力的电桥如图 b,R1 和 R2 组成电桥的相对 臂。测定弯矩的电桥如图 c,R1 和 R2 组成相邻臂。测拉力的电桥输出电压 U0
简化电路,设 (2)当半桥双臂各并联一片时:
时,计算得:
பைடு நூலகம்
,所以不能提高灵敏度。
简化电路,设 18
时,计算得:
,所以也不能提高灵敏度。 如果电桥激励电压是
用电阻应变片接成全桥 ,测量某一构件的应变,已知其变化规律为 。求此电桥输出信号的频谱。
R U i (t ) 解:U0(t)= R
,
R R =Kε (t)
时域采样定理 频带为 F 的连续信号 f(t)可用一系列离散的采样值 f(t1),f(t1±Δt),f(t1± 2Δt),...来表示,只要这些采样点的时间间隔 Δt≤1/2F, 便可根据各采样值完全恢复原来的信号 f(t)。 这是时域采样定理的一种表述方式。 时域采样定理的另一种表述方式是: 当时间信号函数 f(t)的最高频率分量为 fM 时,f(t)的值可由一系列采样间隔小于或等于 1/2fM 的采样值来确定,即采样点的重复频率 f≥2fM。图为模拟信号和采样样本的示意图。 时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。 频域采样定理 对于时间上受限制的连续信号 f(t)(即当│t│>T 时,f(t)=0,这里 T=T2-T1 是信号的持续时间) ,若其频谱为 F(ω), 则可在频域上用一系列离散的采样值 来表示,只要这些采样点的频率间隔 ω≦π / tm 。 连续信号在时间(或空间)上以某种方式变化着,而采样过程则是在时间(或空间)上,以 T 为单位间隔来测量连续信号的值。T 称为采样间隔。在实际中,如果信号是时间的函数,通常他们的采样间隔都很小,一般在毫秒、微秒的量级。采样过程产生一系列 的数字,称为样本。样本代表了原来地信号。每一个样本都对应着测量这一样本的特定时间点,而采样间隔的倒数,1/T 即为采样频 率,fs,其单位为样本/秒,即赫兹(hertz)。 如果不能满足上述采样条件,采样后信号的频率就会重叠,即高于采样频率一半的频率 成分将被重建成低于采样频率一半的信号。这种频谱的重叠导致的失真称为混叠,而重建出来的信号称为原信号的混叠替身,因为 这两个信号有同样的样本值。 一个频率正好是采样频率一半的弦波信号,通常会混叠成另一相同频率的波弦信号,但它的相位和幅度改变了 以下两种措施可避免混叠的发生: 提高采样频率,使之达到最高信号频率的两倍以上; 引入低通滤波器或提高低通滤波器的参数;该低通滤波器通常称为抗混叠滤波器 抗混叠滤波器可限制信号的带宽,使之满足采样定理的条件。从理论上来说,这是可行的,但是在实际情况中是不可能做到的。因 为滤波器不可能完全滤除奈奎斯特频率之上的信号,所以,采样定理要求的带宽之外总有一些“小的”能量。不过抗混叠滤波器可使 这些能量足够小,以至可忽略不计。 15 圆柱形弹性元件,在拉、弯联合作用下,如题图 4-1a,应变片应如何布片和正确接电桥才能测定拉力 p 和弯矩 M,并能消除拉 力和弯矩间的相互干扰?
请说明时域采样定理的内容

请说明时域采样定理的内容时域采样定理是信号处理领域的基本理论,用来描述在某一特定采样频率下,时间域上的信号能够被采样、存储、处理。
时域采样定理又称为贝尔定理,它对于数字信号处理有很重要的意义,它指出了采样、傅里叶变换等技术的依据,因此,它也是数字信号处理的基石之一。
时域采样定理的内容核心很简单,它的基本共识如下:如果一个信号以载波周期T,频率为F的周期波形到达,则可以在每个周期最后采样一次,并将原信号恢复其原貌。
这一定理的公式可以用下面的式子来描述:F = 1/T根据这一定理,我们可以认为,如果一个信号以一定频率传播,那么它所拥有的采样频率应该是该信号传播频率的两倍。
如果你想采样这样一个信号,那么可以采用原始信号的两倍频率进行采样,这样就能够保证采样不会错过任何一个波形的信息点,从而能够最大限度地完整地恢复原信号。
时域采样定理还可以用于解决信号含有亚调制问题,即信号传播时已经存在多个高频信号,如果将这些信号直接降低频率采样,就会丢失一些信号信息。
解决这个问题,需要采用时域采样定理,将原始频率变换至在采样频率下即可被抽取出来,从而避免出现丢失信息的现象。
另外,由于时域采样定理的存在,各种数字信号处理的工具和算法也得到了发展。
有史以来,存在许多信号处理的基础理论和算法,其中最早的就是时域采样定理,它为信号处理的研究提供了有用的思路,让我们进一步了解信号处理所需要的技术。
今天,时域采样定理依然是信号处理领域的一个基础理论,也是信号处理工具和算法开发的基础。
它可以应用于探测噪声、降低噪声,以及领域有关的数字信号处理分析、构建、变换等方面,它为信号处理技术的发展提供了坚实的基础。
总而言之,时域采样定理是信号处理领域的基本理论,它指出了采样、傅里叶变换等技术的依据,并且它的存在促进了各种数字信号处理的工具和算法的发展,为信号处理技术的提高提供了支持和帮助。
请说明时域采样定理的内容

请说明时域采样定理的内容时域采样定理是一个重要的数字信号处理原理,它允许一个数字信号以较低的采样速率,能够捕捉其在时域上的特征。
简要地说,这个定理指出,可以通过采样一个信号的有限子集,来恢复其原始的信号。
通常,这个定理对于许多数字信号处理技术被广泛应用。
时域采样定理的最早提出者是埃米尔格罗斯曼,1948年在他的文章中提出了这个定理。
他认为,该定理可以用来描述在信号处理领域通常发现的现象。
他的论文被广泛的用于数字信号处理任务,当时的技术已经发展得足够先进,可以让他对数字信号处理原理的理解变得更加深刻。
时域采样定理指出,任何在某种时间帧内进行采样的二进制信号,它的频率必须低于采样速率的一半,才能够被准确地采样和复原。
这条定理通常被称为“半量规则”,也被称为“贝尔定律”,它被广泛应用在数字信号处理领域中。
时域采样定理的另一个重要特性是,在采样过程中,会产生一些信号失真,是以采样频率的增加而增加的。
这就意味着,如果要采样一个更高频率的信号,就必须增加采样频率,来保证信号处理的质量和准确性。
引入的失真可能会影响信号的准确性,尤其是在信号处理过程中。
时域采样定理在数字信号处理技术中发挥着重要作用。
它可以用来采样和处理多种信号,包括声音、视频、图像和电信信号等。
它可以用来采样测试采样精度,以及用于信号处理系统中的过程控制。
在电子系统中,采样和处理信号可以提供一个可靠、有效的信号处理方法,而且它可以节省大量的时间和资源。
时域采样定理的重要性在于,它可以帮助我们了解和控制信号的特性,进而有助于更好地实现相应的信号处理任务。
它还可以作为一种技术平台,来实现多种信号处理任务,其中包括图像处理、低功耗处理、音频处理、模糊控制、机器学习等。
它同样可以用来处理和优化硬件系统,以最小的功耗实现最高的效率。
时域采样定理是一个重要的数字信号处理原理,可以用于处理各种不同类型的信号,并有助于提高信号处理任务的效率。
它的采样可以用来测试采样的精度,并可以用于分析和优化信号性能,以达到最佳的效果。
简述奈奎斯特时域采样定理的内容

简述奈奎斯特时域采样定理的内容
采样定理是美国电信工程师h.奈奎斯特在年提出的,在数字信号处理领域中,采样定理是连续时间信号(通常称为“模拟信号”)和离散时间信号(通常称为“数字信号”)之间的基本桥梁。
该定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。
1、采样过程所应遵循的规律,又称取样定理、抽样定理。
采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。
2、在展开演示/数字信号的切换过程中,当取样频率fs.max大于信号中最低频率fmax的2倍时(fs.max\ue2fmax),取样之后的数字信号完备地留存了完整信号中的信息,通常实际应用领域中确保取样频率为信号最低频率的2.56~4倍。
取样定理又称奈奎斯特定理。
3、如果对信号的其它约束是已知的,则当不满足采样率标准时,完美重建仍然是可能的。
在某些情况下(当不满足采样率标准时),利用附加的约束允许近似重建。
这些重建的保真度可以使用bochner定理来验证和量化。
如何讲好时域取样定理

如何讲好时域取样定理作者:刘建宝,秦昕昕,欧阳华来源:《教育教学论坛》2013年第18期摘要:时域取样定理是“信号与系统”和“数字信号处理”等课程的重要内容,但是,目前高等院校普遍使用的国内外经典教材对这部分内容论述不够清晰,没有证明连续时间信号与离散时间信号频谱的关系,尤其是引入了理想冲激取样过程,物理意义不明确,影响了学生理解。
本文对时域取样定理进行了深入的思考,提出了两种讲解思路,教学实践表明,对增强学生对该内容的理解,提高授课质量,有较强的针对性。
关键词:时域取样定理;理想冲激取样;课程改革中图分类号:G642.4 文献标志码:A 文章编号:1674-9324(2013)18-0188-03How to Explain the Sampling Theorem in Time LogicallyLiu Jianbao,Qin Xinxin,Ouyang HuaNaval University of Engineering,Wuhan,ChinaAbstract:The sampling theorem in time is very important in the courses of Signals and Systems and Digital Signal Processing.But it has not been explained logically in the books which have been used widely in colleges and universities,and the relationship between the spectrum in frequency domain of continuous-time signal and that of discrete-time signal has not been proved, especially the physical meanings of impulse-train sampling are illogical.So some students have difficult in comprehending the sampling theorem.Two methods have been used in teaching practices which are proposed in this paper,the efficiency testifies that the methods are beneficial to improve teaching effect.Keywords:sampling theorem in time;impulse-train sampling;teaching reform一、引言“信号与系统”和“数字信号处理”课程是自动化、电子信息通信及计算机等专业本科生重要的基础课,其基本的分析方法和系统原理广泛应用于信号与信息处理、通信及电路与系统、计算机处理等领域,是一门理论性和应用性极强的课程,也是电子、信息、自动化等专业的必修课程之一,其教学质量的好坏将涉及到能否为后续专业课程打好基础的问题。
时域取样定理

时域取样定理时域取样定理是信号处理中的一项重要定理,它描述了如何从连续时间信号中获取离散时间信号的方法。
该定理在通信、音频处理、图像处理等领域有着广泛的应用。
时域取样定理的核心思想是将连续时间信号转换为离散时间信号,使得信号在时间上变得离散化。
具体而言,时域取样定理规定了在连续时间信号中按一定时间间隔取样时,为了使得取样后的离散时间信号能够完全还原原始信号,取样频率必须满足一定的条件。
在数学上,时域取样定理可以用下面的方式描述:如果一个信号的频率范围为[-B, B],那么为了完全还原原始信号,取样频率必须大于2B。
换句话说,取样频率必须大于信号频率的两倍。
为了更好地理解时域取样定理,我们可以通过一个简单的例子来说明。
假设有一个连续时间信号,它的频率范围为[-100Hz, 100Hz],我们想要对这个信号进行取样。
根据时域取样定理,取样频率必须大于2*100Hz=200Hz。
如果取样频率为250Hz,那么取样后的离散时间信号可以完全还原原始信号;但如果取样频率为150Hz,那么取样后的离散时间信号将无法完全还原原始信号,从而导致信号失真。
时域取样定理的应用非常广泛。
在通信领域,由于信号在传输过程中需要经过模数转换和数模转换等操作,采用时域取样定理可以方便地将连续时间信号转换为数字信号,从而进行数字信号处理和传输。
在音频处理领域,时域取样定理可以用来将模拟音频信号转换为数字音频信号,实现音频的录制、编辑和播放等功能。
在图像处理领域,时域取样定理可以将连续时间图像转换为离散时间图像,为图像的压缩和处理提供基础。
除了应用领域广泛外,时域取样定理也有着一些实际应用中需要注意的问题。
首先,取样频率必须满足大于信号频率的两倍,但并不意味着取样频率越高越好。
过高的取样频率可能会导致浪费存储空间和计算资源。
其次,如果信号的频率范围超过了取样频率的一半,那么会出现混叠现象,即高频信号被错误地表示为低频信号。
为了避免混叠现象,我们需要在进行取样之前对信号进行低通滤波,将超过取样频率一半的频率成分去除。
4_17 连续时间信号时域抽样定理

4. 信号时域抽样理论分析
X(j)
1
6 8
8
6
-28 -24 -0
0
0 24 28
f
fm=28 kHz
X(ejW)
1/T
-32 -28 -24 -0 -6 - -8 -4 0 4 8 6 0 24 28
36 f
fsam=8 kHz
信号时域抽样理论分析
X(j
0
m
sam
X(ej
1 T
sam m
0
m sam
X(j
1
sam 2 B
m m+B
0
m-B m
m 1000k rad/s, B 8k rad/s
4. 信号时域抽样理论分析
窄带高频信号的抽样
中心频率24kHz,带宽8kHz。 解调后语音信号
fsam=56kHz 抽样后的频谱。 解调后语音信号
下,信号x(t)可以用等间隔T的抽样值唯一表示。 抽样间隔T需满足:
T π m 1 (2 fm)
fsam 2fm (或ωsam 2ωm)
fsam= 2fm 为最小抽样频率,称为Nyquist Rate。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
4. 信号时域抽样理论分析
sam 2m
1
m
0 m
X (e jT )
X [ j( sam )]
1 X ( j)
T
X [ j( sam )]
...
...
sam m 0 m sam
4. 信号时域抽样理论分析
离散序列x[k]频谱与抽样间隔T之间的关系
实验二_时域采样和频域采样.

一、实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。
要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。
二、实验原理及方法1、时域采样定理的要点:a)对模拟信号)(t x a 以间隔T 进行时域等间隔理想采样,形成的采样信号的频谱)(ˆΩj X 是原模拟信号频谱()aX j Ω以采样角频率s Ω(T s /2π=Ω)为周期进行周期延拓。
公式为:)](ˆ[)(ˆt x FT j X a a=Ω )(1∑∞-∞=Ω-Ω=n s a jn j X T b)采样频率s Ω必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频谱不产生频谱混叠。
利用计算机计算上式并不方便,下面我们导出另外一个公式,以便用计算机上进行实验。
理想采样信号)(ˆt xa 和模拟信号)(t x a 之间的关系为: ∑∞-∞=-=n a a nT t t x t x)()()(ˆδ 对上式进行傅立叶变换,得到:dt e nT t t x j X t j n a a Ω-∞∞-∞-∞=⎰∑-=Ω])()([)(ˆδ dt e nT t t x t j n a Ω-∞-∞=∞∞-∑⎰-)()( δ=在上式的积分号内只有当nT t =时,才有非零值,因此:∑∞-∞=Ω-=Ωn nT j aae nT xj X )()(ˆ上式中,在数值上)(nT x a =)(n x ,再将T Ω=ω代入,得到:∑∞-∞=-=Ωn nj aen x j X ω)()(ˆ上式的右边就是序列的傅立叶变换)(ωj e X ,即 T j a e X j X Ω==Ωωω)()(ˆ 上式说明理想采样信号的傅立叶变换可用相应的采样序列的傅立叶变换得到,只要将自变量ω用T Ω代替即可。
2、频域采样定理的要点:a)对信号x(n)的频谱函数X(ej ω)在[0,2π]上等间隔采样N 点,得到2()() , 0,1,2,,1j N k NX k X e k N ωπω===-则N 点IDFT[()N X k ]得到的序列就是原序列x(n)以N 为周期进行周期延拓后的主值区序列,公式为:()IDFT[()][()]()N N N N i x n X k x n iN R n ∞=-∞==+∑b)由上式可知,频域采样点数N 必须大于等于时域离散信号的长度M(即N ≥M),才能使时域不产生混叠,则N 点IDFT[()N X k ]得到的序列()N x n 就是原序列x(n),即()N x n =x(n)。
时域采样定理频带为F的连续信号 f

时、频域采样定理的验证
实验二时、频域采样定理的验证
实验目的
掌握时域采样定理,频域采样定理。
掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;掌握频域采样会引起时域周期化,以及频域采样定理及其对频域采样点数选择的指导作用。
实验内容
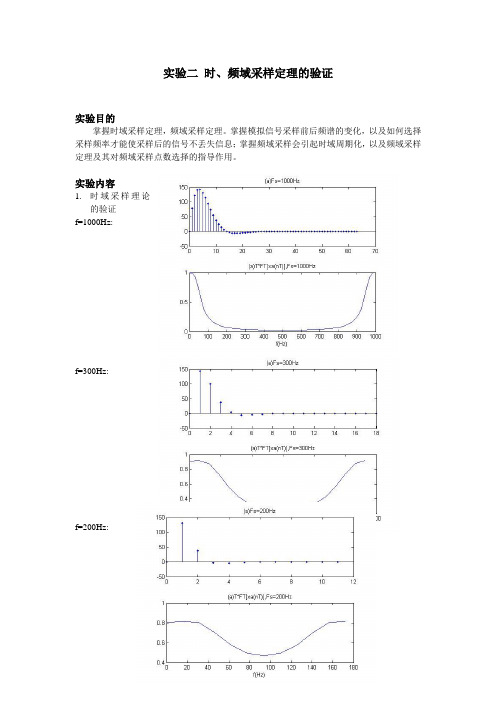
1.时域采样理论
的验证
f=1000Hz:
f=300Hz:
f=200Hz:
2.频域采样理论的验证
实验小结
通过本次实验,我巩固了信号在matlab中的运算表示方法、图形输出函数(plot、stem),同时会用软件求fft和ifft,由此验证了时域采样定理,频域采样定理。
通过观察不同平率的模拟信号采样,采样频率如果过低会导致丢失信息;通过频域采样发现它会引起时域周期化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
But i t h a s no t be e n e x p l a i n e d l o g i c a l l y i n t h e b oo k s whi c h h a v e be e n us e d wi d e l y i n c o l l e g e s a n d u n i ve r s i t i e s , a nd t he r e l a io t n s h i p
b e t we e n t h e s p e c t r um i n f r e q ue n c y d o ma in o f c o n t i n uo u s —t i me s i g na l a nd t h a t o f d i s c r e t e —t i me s i g na l ha s no t b e e n p r ov e d, e s pe c i a l l y t he p h y s i c l a me a n i n g s o f i mp u l s e —t r a i n s a mp l i ng a r e i l l o g i c a 1 . S o s o me s t u de nt s h a ve d i ic f u l t i n c o mp r e h e n d i n g t h e s a mp l i ng t he or e m. Tw o me  ̄o d s h a ve be e n u s e d i n t e a c h i ng pr a c t i c e s whi c h a r e p r o p o s e d i n t h i s pa p e r , t he e ic f i e nc y t e s if t i e s t ha t t h e me t ho d s a r e be ne ic f i a l t o i mp r o ve t e a c ing h e fe c t .
关键 词 : 时域取 样 定理 ; 理 想冲 激取 样 ; 课 程 改 革 中图分 类 号 : G 6 4 2 . 4 文 献标 志码 : A
文章 编号 : 1 6 7 4 — 9 3 2 4 ( 2 0 1 3o w t o Ex p l a i n t h e S a mp l i n g T h e o r e m i n T i me L o g i c a l l y
K e y wo r d s: s a mp h n g t h e o r e m i n t i me ; mp i u l s e — t r i a n s m p a l i n g ; t e a c in h g r e f o r m
一
、
引言
教材主要有吴大正 主编 的《 信号与线性系统分析》 口 1 、 奥本
“ 信号与系统” 和“ 数字信号处理” 课程是 自动化 、 电子 信息通信及计算机等专业本科生重要 的基础课 , 其基本的 分析方法和系统原理广泛应用于信号与信息处理、 通信及 电路与系统 、 计算机处 理等领域 , 是一 门理论性和应用性 极强的课程 , 也是电子 、 信息 、 自动化等专业的必修课程之 其教学质量的好坏将涉及到能否为后续专业课 程打好 基础的问题 。N y q u i s t 时域取样定理是“ 信号与系统” 和“ 数 字信号处理” 等课程的重要 内容 , 是联系连续时间信号和
’
L i u J i a n b a o , Q i n X i n x i n , O u y a n g Hu a
Na v l a U n i v e r s i t y o f En g i n e e r i n g, Wu h a n, C h i n a
Ab s t r a c t : Th e s a mp l i n g t he o r e m i n t i me i s v e r y i mp o r t a n t i n t h e c o ur s e s o f S i g n a l s a nd S y s t e ms a n d Di g i t a l S i g l 1 a 1 Pr o c e s s i ng .
【 高教研究】
如何讲好 时域取样 定理
刘建宝 , 秦 昕昕 , 欧 阳华
( 海军工程大学 , 湖北 武汉 4 3 0 0 3 3 )
摘要 : 时域 取 样 定理 是 “ 信 号与 系统” 和“ 数 字信 号 处理 ” 等课 程 的重要 内容 , 但是 , 目前 高等 院校普 遍 使 用 的 国 内外 经
一
,
离散时间信号的纽带 , 如何有效地增强学生对该 内容的理 解, 提高教学质量 , 值得广大高等院校教师进行深入思考
和教 学实 践 。
二、 现 状 目前 , 高等院校开设“ 信号与系统” 课程所使用的经典
典教 材 对这 部 分 内容论 述 不够 清晰 ,没有证 明连续 时 间信 号与 离散 时 间信 号频 谱 的关 系,尤其 是 引入 了理 想冲激 取 样过
程, 物理意义不明确 , 影响了学生理解。 本文对时域取样定理进行 了深入的思考, 提 出了两种讲解思路 , 教学实践表明, 对增 强 学 生对该 内容 的 理解 , 提 高授课 质 量 , 有较 强 的针 对性 。
