九年级数学下册新课结束综合测试卷课件新沪科版
2023年沪科版初中数学九年级(下)期末综合测试卷及答案(共四套)
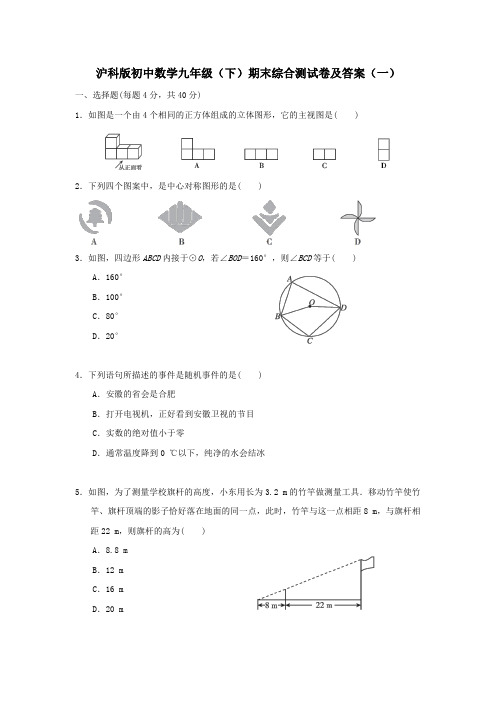
沪科版初中数学九年级(下)期末综合测试卷及答案(一)一、选择题(每题4分,共40分)1.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()2.下列四个图案中,是中心对称图形的是()3.如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD等于() A.160°B.100°C.80°D.20°4.下列语句所描述的事件是随机事件的是()A.安徽的省会是合肥B.打开电视机,正好看到安徽卫视的节目C.实数的绝对值小于零D.通常温度降到0℃以下,纯净的水会结冰5.如图,为了测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为()A.8.8mB.12mC.16mD.20m6.如图是以△ABC 的边AB 为直径的半圆O ,点C 恰好在半圆上,过点C 作CD ⊥AB 于点D .已知cos∠ACD =35,BC =4,则AC 的长为()A.1B.203C.3D.1637.一个不透明的袋内装有标号分别为1,2,3,4的4个小球(小球除标号外其余均相同).从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字.则组成的两位数是3的倍数的概率为()A.14B.516C.716D.128.如图,这是一个长方体纸盒的表面展开图,纸片厚度不计.根据图中数据,可得这个盒子的容积为()A.6B.8C.10D.159.如图,AB 为⊙O 的直径,C 为⊙O 上一点,弦AD 平分∠BAC ,交BC 于点E ,AB =6,AD =5,则AE 的长为()A.2.5B.2.8C.3D.3.210.如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线l ,与⊙O 过点A 的切线交于点B ,且∠APB =60°,设OP =x ,则△PAB 的面积y 关于x 的函数图象大致是()二、填空题(每题5分,共20分)11.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是________.12.小明家的客厅有一张直径为1.2米,高为0.8米的圆桌BC ,在距地面2米的A 处有一盏灯,圆桌的影子为DE ,依据题意建立如图所示的平面直角坐标系,其中D 点坐标为(2,0),则点E 的坐标是________.13.如图,矩形ABCD 中,AB =3,BC =2,E 为BC 的中点,AF =1,以EF 为直径的半圆与DE交于点G ,则劣弧GE ︵的长为________.14.抛物线y =-x 2-2x +3与x 轴交于A ,B 两点,若一个半径为5的圆也经过点A ,B ,则该圆的圆心坐标为______________.三、(每题8分,共16分)15.如图是由5个大小相同的小正方体搭成的几何体,其中每个小正方体的棱长为1cm.(1)直接写出这个几何体的表面积:__________;(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.16.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.(1)请分别作出如图所示的两个三角形的最小覆盖圆;(要求:尺规作图,保留作图痕迹,不写作法)(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论.(不要求证明)四、(每题8分,共16分)17.如图,在8×8的小正方形网格中,△ABC三顶点的坐标分别为A(2,3),B(2,1),C(5,1),把△ABC绕着点A顺时针旋转90°得到△AEF,点B的对应点为E,点C的对应点为F.(1)在图中画出△AEF;(2)点C的运动路径长为____________;(3)直接写出线段BC扫过的面积:________.18.一个不透明的袋中装有20个只有颜色不同的球,其中有5个黄球,8个黑球,7个红球.(1)求从袋中摸出1个球是黄球的概率;(2)现从袋中取出若干个黑球,搅匀袋中的球,使从袋中摸出1个球是黑球的概率是13.求从袋中取出黑球的个数.五、(每题10分,共20分)19.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.20.如图,已知直线l :y =3x ,点A 1的坐标为(1,0),过点A 1作x 轴的垂线交直线l 于点B 1,以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2;过点A 2作x 轴的垂线交直线l 于点B 2,以原点O 为圆心,OB 2长为半径画弧交x 轴于点A 3,…,按此方法进行下去.求:(1)点B 1的坐标和∠A 1OB 1的度数;(2)弦A 4B 3的弦心距.六、(12分)21.在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中剩余的小球搅匀后,再从袋中摸出另一个小球.(1)请你列出摸出小球上的数可能出现的所有结果;(2)规定:如果摸出的两个小球上的数都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?七、(12分)22.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连接AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若OC=2,求DE的长;(3)在∠A从15°增大到30°的过程中,请直接写出弦AD在圆内扫过的面积.八、(14分)23.如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.(1)请判断直线PA与⊙O的位置关系,并说明理由;(2)求证:AG2=AF·AB;(3)若⊙O的直径为10,AC=25,AB=45,求△AFG的面积.答案一、1.A 2.D 3.B 4.B 5.B6.D点拨:∵AB 为直径,∴∠ACB =90°,∴∠ACD +∠BCD =90°.∵CD ⊥AB ,∴∠BCD +∠B =90°,∴∠B =∠ACD ,∵cos∠ACD =35,∴cos B =35,易知tan B =43,∵BC =4,∴tan B =AC BC =AC 4=43,∴AC =163.7.B 8.A9.B点拨:连接BD ,∵AD 平分∠BAC ,∴∠CAE =∠DAB ,∴CD ︵=BD ︵.∵AB 是⊙O 的直径,∴∠ACE =∠ADB =90°,∴△ACE ∽△ADB ,∴AC AD =AE AB ,即AC 5=AE6.设AC =5x ,则AE =6x ,∴DE =5-6x .连接OD 交BC 于点F ,则DO ⊥BC ,∴OD ∥AC ,易知OF =12AC =52x ,∴DF =OD -OF =3-52x ,易得△ACE ∽△DFE ,∴AC DF =AE DE ,即5x 3-52x =6x5-6x ,解得x =715(x =0舍去),则AE =6x =2.8.10.D二、11.41512.(4,0)13.54π点拨:如图,连接OG ,DF ,根据勾股定理分别求出DF 、EF ,证明Rt△DAF ≌Rt△FBE ,求出∠DFE =90°,进而推出∠GOE=90°,最后根据弧长公式计算即可.14.(-1,1)或(-1,-1)点拨:不妨设点A 在点B 的左侧.∵抛物线y =-x 2-2x +3与x 轴交于A ,B 两点,∴A (-3,0),B (1,0),∴圆心在直线x =-1上,设圆心坐标为(-1,m ),由题意得22+m 2=(5)2,解得m =±1,∴圆心坐标为(-1,1)或(-1,-1).三、15.解:(1)22cm 2(2)如图所示:16.解:(1)如图所示.(2)若三角形为锐角三角形,则其最小覆盖圆为三角形的外接圆;若三角形为直角三角形或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.四、17.解:(1)如图所示,△AEF 即为所求.(2)132π点拨:易知AC =22+32=13,∠CAF =90°,∴点C 的运动路径长为90·π·13180=132π.(3)94π点拨:线段BC 扫过的面积为S 扇形CAF -S 扇形BAE =90·π·(13)2360-90·π·22360=134π-π=94π.18.解:(1)20个球里面有5个黄球,故P (摸出1个球是黄球)=520=14.(2)设从袋中取出x (0<x <8,且x 为整数)个黑球,则此时袋中总共还有(20-x )个球,黑球剩(8-x )个.因为从袋中摸出1个球是黑球的概率是13,所以8-x 20-x =13,解得x =2.经检验,x =2是所列方程的解,且符合实际.所以从袋中取出了2个黑球.五、19.解:该几何体的形状是直四棱柱.由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm.∴菱形的边长为52cm,∴棱柱的侧面积S =52×8×4=80(cm 2).20.解:(1)设B 1的坐标为(1,m ).∵B 1在直线l 上,∴3=m ,∴B 1(1,3).∴A 1B 1=3,OA 1=1,∴tan∠A 1OB 1=A 1B 1OA 1=3,∴∠A 1OB 1=60°.(2)如图,作OH ⊥A 4B 3于H .由题意可得OA 2=2,OA 3=4,OA 4=8.∵OA 4=OB 3,OH ⊥A 4B 3,∴∠A 4OH =12∠A 4OB 3=30°,∴OH =OA 4·cos30°=8×32=4 3.∴弦A 4B 3的弦心距为43.六、21.解:(1)可能出现的所有结果如下表-1-212-1(-1,-2)(-1,1)(-1,2)-2(-2,-1)(-2,1)(-2,2)1(1,-1)(1,-2)(1,2)2(2,-1)(2,-2)(2,1)(2)∵x 2-3x +2=0,∴(x -1)(x -2)=0,∴x 1=1,x 2=2.∵共有12种等可能的结果,其中摸出的两个小球上的数都是方程x 2-3x +2=0的根的结果有2种,摸出的两个小球上的数都不是方程x 2-3x +2=0的根的结果有2种,∴P (小明赢)=212=16,P (小亮赢)=212=16,∴游戏规则公平.七、22.(1)证明:如图,连接OD ,则OD ⊥DE ,∴∠ODA +∠EDC =90°.∵OA =OD ,∴∠OAD =∠ODA ,又∵OA ⊥OB ,∴∠OAD +∠OCA =90°,∴∠OCA =∠EDC .又∵∠OCA =∠ECD ,∴∠ECD =∠EDC .(2)解:由(1)知,∠ECD =∠EDC ,∴ED =EC .设ED =x ,则OE =OC +CE =2+x .在Rt△ODE 中,∵OD 2+DE 2=OE 2,OD =OA =8,∴82+x 2=(2+x )2,解得x =15,∴DE 的长为15.(3)解:弦AD 在圆内扫过的面积为16π3+163-16.点拨:如图,连接OD ′,过点O 作OH ⊥AD ′于点H ,延长AO 交⊙O 于点M ,过点D 作DN ⊥AM 于点N .设弦AD 在圆内扫过的面积为S ,则S =S 扇形AOD -S △OAD -S 弓形ABD ′,由题意知,∠OAH =30°,∴在Rt△OAH 中,∠AOH =60°,AH =32OA =43,OH =12OA =4,∴AD ′=2AH =83,∠AOD ′=120°,∴S 弓形ABD ′=S 扇形AOD ′-S △OAD ′=120π×82360-12×83×4=64π3-163.在Rt△ODN 中,∠DON =2∠OAD =30°,∴DN =12OD =4,∴S△OAD =12OA ·DN =12×8×4=16.∵∠AOD =180°-∠DON =150°,∴S 扇形AOD =150π×82360=80π3,∴S =S 扇形AOD -S △OAD -S 弓形ABD ′=80π3-16-=16π3+163-16,∴弦AD 在圆内扫过的面积为16π3+163-16.八、23.(1)解:PA 与⊙O 相切.理由如下:连接CD .∵AD 为⊙O 的直径,∴∠ACD =90°.∴∠D +∠CAD =90°.∵∠B =∠D ,∠PAC =∠B ,∴∠PAC =∠D .∴∠PAC +∠CAD =90°,即DA ⊥PA .∴PA 与⊙O 相切.(2)证明:连接BG .∵AD 为⊙O 的直径,CG ⊥AD ,∴AC ︵=AG ︵.∴∠AGF =∠ABG .∵∠GAF =∠BAG ,∴△AGF ∽△ABG .∴AG ∶AB =AF ∶AG .∴AG 2=AF ·AB .(3)解:连接BD .∵AD 是⊙O 的直径,∴∠ABD =90°.∵AG 2=AF ·AB ,AG =AC =25,AB =45,∴AF =AG 2AB= 5.∵CG ⊥AD ,∴∠AEF =∠ABD =90°.又∵∠EAF =∠BAD ,∴△AEF ∽△ABD .∴AE AB =AF AD ,即AE 45=510,解得AE =2.∴EF =AF 2-AE 2=1.∵EG =AG 2-AE 2=4,∴FG =EG -EF =4-1=3.∴S △AFG =12FG ·AE =12×3×2=3.沪科版初中数学九年级(下)期末综合测试卷及答案(二)一、选择题(每题4分,共40分)1.下列图形中,是中心对称图形但不是轴对称图形的是()2.如图所示的四个几何体中,左视图是矩形的个数是()A.1B.2C.3D.43.下列所给的事件中,是必然事件的是()A.一个标准大气压下,水加热到100℃时会沸腾B.买一注福利彩票会中奖C.连续4次抛掷质地均匀的硬币,4次均正面朝上D.2021年的春节假期屯溪区将下雪4.如图,点A 、C 、B 在⊙O 上,已知∠AOB =∠ACB =α,则α的值为()A.135°B.120°C.110°D.100°5.从-1、2、3、-6这四个数中任取两数,分别记为m 、n ,那么点(m ,n )在函数y =6x的图象上的概率是()A.12B.13C.14D.186.《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:今有勾八步,股十五步,问勾中容圆,径几何?其意思:今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆(内切圆)的直径是多少?此问题中,该内切圆的直径是()A.5步B.6步C.8步D.10步7.一个几何体的三视图如图所示,那么这个几何体的侧面积是()A.16πB.24πC.32πD.48π8.已知圆锥的底面半径为4cm,母线长为6cm,则它的侧面展开图的面积等于()A.24cm 2B.48cm 2C.24πcm 2D.12πcm 29.如图,在△ABC 中,CA =CB ,∠ACB =90°,以AB 的中点D 为圆心,作圆心角为90°的扇形EDF ,点C 恰好在EF ︵上,设∠BDF =α(0°<α<90°).当α由小到大变化时,图中阴影部分的面积()A.由小变大B.由大变小C.不变D.先由小变大,后由大变小10.如图,已知⊙O 的半径为1,锐角三角形ABC 内接于⊙O ,BD ⊥AC 于点D ,OM ⊥AB 于点M ,则sin∠CBD 的值等于()A.OM 的长B.2OM 的长C.CD 的长D.2CD 的长二、填空题(每题5分,共20分)11.如图,AB 为⊙O 的直径,CD ⊥AB ,若AB =10,CD =8,则圆心O 到弦CD 的距离为________.12.小颖妈妈经营的玩具店某次进了一箱黑、白两种颜色的球共3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球有________个.13.如图,高为6m 的电线杆的顶上有一盏路灯,电线杆的底部为A ,身高1.5m 的男孩站在与点A 相距6m 的点B 处,若男孩以6m 为半径绕电线杆走一圈,则他在路灯下的影子BC 扫过的面积为________m 2.14.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm 2.三、解答题(15题10分,19,20题每题14分,21题16分,其余每题12分,共90分)15.如图,在正方形网格中,△ABC 为格点三角形(即三角形的顶点都在格点上).(1)把△ABC 沿BA 方向平移后,点A 移动到点A 1,在网格中画出平移后得到的△A 1B 1C 1;(2)把△A 1B 1C 1绕点A 1按逆时针方向旋转90°,在网格中画出旋转后的△A 1B 2C 2;(3)如果网格中小正方形的边长为1,求点B 经过(1)(2)变换的路径总长.16.如图是某个几何体的三视图.(1)写出这个几何体的名称;(2)根据图中的有关数据,求这个几何体的表面积.17.如图,A ,B 是⊙O 上的两点,∠AOB =120°,C 是AB ︵的中点,连接AB .(1)求证:AB 平分∠OAC ;(2)延长OA 至点P 使得OA =AP ,连接PC ,若⊙O 的半径为1,求PC 的长.18.在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果.节目组规定:每位选手至少获得两位评委的“通过”才能晋级.(1)请用树状图列举出选手A 获得三位评委评定的各种可能的结果;(2)求选手A 晋级的概率.19.如图所示,文华在广场上游玩时,他由路灯A 走向路灯B ,当他走到P 点时,发现他身后的影子的顶部刚好接触路灯A 的底部,当他再向前走12m 到达Q 点时,发现他身前的影子的顶部刚好接触到路灯B 的底部,已知文华的身高为1.6m,两个路灯的高度都是9.6m,且AP =QB =x m.(1)求两个路灯之间的距离;(2)当文华走到路灯B 时,他在路灯A 下的影子长是多少?20.如图,AB 为半圆O 的直径,AC 是⊙O 的一条弦,D 为BC ︵的中点,作DE ⊥AC ,交AC 的延长线于点E ,交AB 的延长线于点F ,连接DA .(1)求证:EF 为半圆O 的切线;(2)若DA=DF=63,求阴影区域的面积.(结果保留根号和π)21.如图,在矩形ABCD中,AD=a cm,AB=b cm(a>b>4),半径为2cm的⊙O在矩形内且与AB,AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).(1)如图①,点P沿着A→B→C→D的方向匀速移动,全程共移动了______cm.(用含a,b的代数式表示)(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离.(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),PD与⊙O1恰好相切?请说明理由.答案一、1.B 2.B3.A4.B5.B6.B点拨:如图,在Rt△ABC 中,AC =8,BC =15,∠C =90°,∴AB =AC 2+BC 2=17,∴S △ABC =12AC ·BC =12×8×15=60,设内切圆的圆心为O ,分别连接圆心和三个切点及OA 、OB 、OC ,设内切圆的半径为r ,则S △ABC =S △AOB +S △BOC +S △AOC =12×r ×(AB +BC +AC )=20r ,∴20r =60,解得r =3,∴内切圆的直径为6步,故选B.7.B点拨:由三视图知该几何体是圆柱,其底面直径是4,高是6,故这个几何体的侧面积是π×4×6=24π.8.C 9.C10.A点拨:如图,连接OA ,OB .∵OA =OB ,OM ⊥AB ,∴∠BOM =∠AOM =12∠AOB .∵∠C =12∠AOB ,∴∠BOM =∠C .∵BD ⊥AC ,OM ⊥AB ,∴∠CBD +∠C =90°,∠OBM +∠BOM =90°,∴∠CBD =∠OBM .∵sin∠OBM =OMOB=OM ,∴sin∠CBD =OM ,即sin∠CBD 的值等于OM 的长.二、11.312.210013.28π14.200点拨:由三视图可知立体图形由上下两个长方体构成,上面长方体长4mm,宽2mm,高4mm,下面长方体长8mm,宽6mm,高2mm,去掉重合部分,立体图形表面积为6×8×2+8×2×2+6×2×2+4×4×2+4×2×2=200(mm 2).三、15.解:(1)如图.(2)如图.(3)如图,点B 经过的路径为线段BB 1和B 1B 2︵,∴点B 经过的路径总长为32+32+90π·2180=32+2π2.16.解:(1)直三棱柱.(2)表面积为12×3×4×2+15×3+15×4+15×5=192.17.(1)证明:如图,连接OC .∵∠AOB =120°,C 是AB ︵的中点,∴∠AOC =∠BOC =60°.又∵OA =OB =OC ,∴△OAC 和△OBC 都是等边三角形,∴OA =AC =OB =BC ,∴四边形AOBC 是菱形,∴AB 平分∠OAC .(2)解:由(1)知△OAC 是等边三角形,∴∠AOC =∠OCA =∠OAC =60°.∵OA =AC ,OA =AP ,∴AP =AC ,∴∠APC =∠ACP =12∠OAC =30°,∴∠OCP =∠OCA +∠ACP =60°+30°=90°.∴在Rt△OPC 中,PC =OC tan∠APC =1tan30°=133= 3.18.解:(1)画树状图如图:(2)由(1)可知共有8种等可能的结果,其中晋级的有4种结果,所以P (选手A 晋级)=48=12.19.解:(1)由题意可知,PQ =12m,AB =(12+2x )m.易知1.69.6=AP AB ,即1.69.6=x 12+2x,解得x =3.∴AB =18m,即两个路灯之间的距离为18m.(2)设当文华走到路灯B 时,他在路灯A 下的影子长是a m,则 1.69.6=a a +18,解得a =3.6.∴他在路灯A 下的影子长是3.6m.20.(1)证明:如图,连接OD ,∵D 为BC ︵的中点,∴CD ︵=DB ︵.∴∠EAD =∠DAO .∵OA=OD,∴∠DAO=∠ODA.∴∠ODA=∠EAD.∴OD∥AE.∵DE⊥AC,∴DE⊥OD.∴EF是半圆O的切线.(2)解:如图,连接OC,CD.∵DA=DF,∴∠DAF=∠F.又由(1)知∠CAD=∠DAF,∴∠F=∠DAF=∠CAD.∵∠EAF+∠F=90°,∴3∠F=90°.∴∠F=30°.∴∠BAC=60°.又∵OC=OA,∴△OAC为等边三角形.∴∠AOC=60°.由(1)知OD⊥EF,∴∠DOF=90°-∠F=60°.在Rt△DOF中,DF=63,∴OD=DF·tan30°=63×33=6.在Rt△AED中,DA=63,∠CAD=30°,∴DE=12DA=33,EA=DA·cos30°=9.∵∠COD=180°-∠AOC-∠DOF=60°,OC=OD,∴△COD 是等边三角形.∴∠DCO =60°=∠AOC .∴CD ∥AB .∴S △ACD =S △COD .∴S 阴影=S △AED -S 扇形COD =12×9×33-60π·62360=2732-6π.21.解:(1)(a +2b )(2)在整个运动过程中,点P 移动的距离为(a +2b )cm,圆心O 移动的距离为2(a -4)cm.由题意,得a +2b =2(a -4).①∵点P 移动2s 到达B 点,即点P 用2s 移动了b cm,点P 继续移动3s,到达BC 的中点,即点P 用3s 移动了12a cm,∴b 2=12a3.②=24,=8.∵点P 移动的速度与⊙O 移动的速度相等,∴⊙O 移动的速度为b2=4(cm/s).∴在这5s 时间内圆心O 移动的距离为5×4=20(cm).(3)存在这种情形.理由如下:设点P 移动的速度为v 1cm/s,⊙O 移动的速度为v 2cm/s,∴v 1v 2=a +2b 2(a -4)=20+2×102×(20-4)=54.如图,作直线OO 1,设直线OO 1与AB 交于点E ,与CD 交于点F ,⊙O 1与AD 相切于点G ,连接O 1G ,则O 1G ⊥AD .若PD 与⊙O 1相切,设切点为H ,连接O 1H ,则O 1H ⊥DP ,O 1G =O 1H ,易得Rt△DO 1G ≌Rt△DO 1H ,∴∠ADB =∠BDP .∵BC ∥AD ,∴∠ADB =∠CBD .∴∠BDP =∠CBD ,∴BP =DP ,设BP =x cm,则DP =x cm,PC =(20-x )cm,在Rt△PCD 中,由勾股定理,可得PC 2+CD 2=PD 2,即(20-x )2+102=x 2,解得x =252.∴此时点P 移动的距离为10+252=452(cm),易知EF ∥AD ,∴△BEO 1∽△BAD ,∴EO 1AD =BE BA ,即EO 120=10-210,∴EO 1=16cm,∴OO 1=14cm.(i )当⊙O 首次到达⊙O 1的位置时,⊙O 移动的距离为14cm,此时点P 与⊙O 移动的速度比为45214=4528,∵4528≠54,∴此时PD 与⊙O 1不可能相切.(ii )当⊙O 在返回途中到达⊙O 1的位置时,⊙O 移动的距离为2×(20-4)-14=18(cm),此时点P 与⊙O 移动的速度比为45218=4536=54,∴此时PD 与⊙O 1恰好相切.沪科版初中数学九年级(下)期末综合测试卷及答案(三)一、选择题(每题4分,共40分)1.下列图形中,是中心对称图形的是()2.如图是一个由4个相同的正方体组成的立体图形,它的主视图是()3.下列语句所描述的事件是随机事件的是()A.安徽的省会是合肥B.打开电视机,正好看到安徽卫视的节目C.实数的绝对值小于零D.通常温度降到0℃以下,纯净的水会结冰4.如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD等于() A.160°B.100°C.80°D.20°5.如图,为了测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为()A.8.8m B.12m C.16m D.20m6.如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D.已知cos∠ACD=35,BC=4,则AC的长为()A.1B.203C.3D.1637.九(4)班第三学习小组共有8名学生,其中女生3名,男生5名,如果从中随机选择1名学生参加学校举行的国学经典演讲比赛,那么选到女生的概率是()A.58B.35C.38D.148.如图,空心卷筒纸的高度为12cm,外径(直径)为10cm,内径为4cm,在比例尺为14的三视图中,其主视图的面积是()A.21π4cm2B.21π16cm2C.30cm2D.7.5cm29.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为()A.2.5B.2.8C.3D.3.210.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O 过点A的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是()二、填空题(每题5分,共20分)11.如图,AB为⊙O的直径,CD⊥AB,若AB=10,CD=8,则圆心O到弦CD 的距离为________.12.小颖妈妈经营的玩具店某次进了一箱黑、白两种颜色的球共3000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球有________个.13.如图,高为6m的电线杆的顶上有一盏路灯,电线杆的底部为A,身高1.5m 的男孩站在与点A相距6m的点B处,若男孩以6m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为________m2.14.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm2.三、解答题(15题10分,19,20题每题14分,21题16分,其余每题12分,共90分)15.如图,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;(3)如果网格中小正方形的边长为1,求点B经过(1)(2)变换的路径总长.16.如图是某个几何体的三视图.(1)说出这个几何体的名称;(2)根据图中的有关数据,求这个几何体的表面积.17.如图,△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB,垂足为D,BC=2,AC=4,sin∠BAC=1.3(1)求证:△ACD∽△ECB;(2)求⊙O的面积.18.在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果.节目组规定:每位选手至少获得两位评委的“通过”才能晋级.(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;(2)求选手A晋级的概率.19.如图所示,文华在广场上游玩时,他由路灯A走向路灯B,当他走到P点时,发现他身后的影子的顶部刚好接触路灯A的底部,当他再向前走12m到达Q点时,发现他身前的影子的顶部刚好接触到路灯B的底部,已知文华的身高为1.6m,两个路灯的高度都是9.6m,且AP=QB=x m.(1)求两个路灯之间的距离;(2)当文华走到路灯B时,他在路灯A下的影子长是多少?20.如图,AB为半圆O的直径,AC是⊙O的一条弦,D为BC︵的中点,作DE ⊥AC,交AC的延长线于点E,交AB的延长线于点F,连接DA.(1)求证:EF为半圆O的切线;(2)若DA=DF=63,求阴影区域的面积.(结果保留根号和π)21.如图,在矩形ABCD中,AD=a cm,AB=b cm(a>b>4),半径为2cm的⊙O 在矩形内且与AB,AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).(1)如图①,点P沿着A→B→C→D的方向匀速移动,全程共移动了______cm.(用含a,b的代数式表示)(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离.(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),PD与⊙O1恰好相切?请说明理由.答案一、1.A2.A3.B4.B 5.B6.D点拨:∵AB为直径,∴∠ACB=90°,∴∠ACD+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠B=∠ACD,∵cos∠ACD=35,∴cos B=3 5,易知tan B=43,∵BC=4,∴tan B=ACBC=AC4=43,∴AC=163.7.C8.D点拨:12×14=3(cm),10×14=2.5(cm),3×2.5=7.5(cm2),即其主视图的面积是7.5cm2.9.B点拨:连接BD,∵AD平分∠BAC,∴∠CAE=∠DAB,∴CD︵=BD︵.∵AB是⊙O的直径,∴∠ACE=∠ADB=90°,∴△ACE∽△ADB,∴ACAD=AE AB,即AC5=AE6.设AC=5x,则AE=6x,∴DE=5-6x.连接OD交BC于点F,则DO ⊥BC ,∴OD ∥AC ,易知OF =12AC =52x ,∴DF =OD -OF =3-52x ,易得△ACE ∽△DFE ,∴AC DF =AEDE ,即5x 3-52x =6x 5-6x,解得x =715(x =0舍去),则AE =6x =2.8.10.D 二、11.312.210013.28π14.200点拨:由三视图可知立体图形由上下两个长方体构成,上面长方体长4mm ,宽2mm ,高4mm ,下面长方体长8mm ,宽6mm ,高2mm ,去掉重合部分,立体图形表面积为6×8×2+8×2×2+6×2×2+4×4×2+4×2×2=200(mm 2).三、15.解:(1)如图.(2)如图.(3)如图,点B 经过的路径为线段BB 1和B 1B 2︵,∴点B 经过的路径总长为32+32+90π·2180=32+2π2.16.解:(1)直三棱柱.(2)表面积为12×3×4×2+15×3+15×4+15×5=192.17.(1)证明:∵∠CAD 和∠CEB 都为BC ︵所对的圆周角,∴∠CAD =∠CEB .∵CD ⊥AB ,∴∠CDA =90°,∵CE 为⊙O 的直径,∴∠CBE =90°,∴∠CDA =∠CBE ,∴△ACD ∽△ECB .(2)解:在Rt △ACD 中,sin ∠BAC =CD AC =13,∵AC =4,∴CD =13AC =43.∵△ACD ∽△ECB ,∴AC EC =CD CB ,即4EC =432,∴EC =6,∴⊙O 的半径为3,∴⊙O 的面积为9π.点拨:解题的关键是利用三角形相似的判定证得三角形相似,第(1)题的结论可以作为第(2)题的条件.18.解:(1)画树状图如图:(2)由(1)可知共有8种等可能的结果,其中晋级的有4种情况,所以P (A 晋级)=48=12.19.解:(1)由题意可知,PQ =12m ,AB =(12+2x )m.易知1.69.6=AP AB ,即1.69.6=x 12+2x ,解得x =3.∴AB =18m.即两个路灯之间的距离为18m.(2)设当文华走到路灯B 时,他在路灯A 下的影子长是a m ,则1.69.6=a a +18,解得a =3.6.∴他在路灯A 下的影子长是3.6m.20.(1)证明:如图,连接OD ,∵D 为BC ︵的中点,∴CD ︵=DB ︵.∴∠EAD =∠DAO .∵OA =OD ,∴∠DAO =∠ODA .∴∠ODA =∠EAD .∴OD ∥AE .∵DE ⊥AC ,∴DE ⊥OD .∴EF 是半圆O 的切线.(2)解:如图,连接OC ,CD .∵DA =DF ,∴∠DAF =∠F .又由(1)知∠CAD =∠DAF ,∴∠F =∠DAF =∠CAD .∵∠EAF +∠F =90°,∴3∠F =90°.∴∠F =30°.∴∠BAC =60°.又∵OC =OA ,∴△OAC 为等边三角形.∴∠AOC =60°.由(1)知OD ⊥EF ,∴∠DOF =90°-∠F =60°.在Rt △DOF 中,DF =63,∴OD =DF ·tan 30°=63×33=6.在Rt △AED 中,DA =63,∠CAD =30°,∴DE =12DA =33,EA =DA ·cos 30°=9.∵∠COD =180°-∠AOC -∠DOF =60°,OC =OD ,∴△COD 是等边三角形.∴∠DCO =60°=∠AOC .∴CD ∥AB .∴S △ACD =S △COD .∴S 阴影=S △AED -S 扇形COD =12×9×33-60π·62360=2732-6π.21.解:(1)(a +2b )(2)∵在整个运动过程中,点P 移动的距离为(a +2b )cm ,圆心O 移动的距离为2(a -4)cm.由题意,得a +2b =2(a -4).①∵点P 移动2s 到达B 点,即点P 用2s 移动了b cm ,点P 继续移动3s ,到达BC 的中点,即点P 用3s 移动了12a cm ,∴b 2=12a 3.②=24,=8.∵点P 移动的速度与⊙O 移动的速度相等,∴⊙O 移动的速度为b2=4(cm/s).∴在这5s 时间内圆心O 移动的距离为5×4=20(cm).(3)存在这种情形.理由如下:设点P 移动的速度为v 1cm/s ,⊙O 移动的速度为v 2cm/s ,由题意,得v1v 2=a +2b 2(a -4)=20+2×102×(20-4)=54.如图,作直线OO 1,设直线OO 1与AB 交于点E ,与CD 交于点F ,⊙O 1与AD 相切于点G ,连接O 1G ,则O 1G ⊥AD .若PD 与⊙O 1相切,设切点为H ,连接O 1H ,则O 1H ⊥DP ,O 1G =O 1H ,易得Rt△DO1G≌Rt△DO1H,∴∠ADB=∠BDP.∵BC∥AD,∴∠ADB=∠CBD.∴∠BDP=∠CBD,∴BP=DP,设BP=x cm,则DP=x cm,PC=(20-x)cm,在Rt△PCD中,由勾股定理,可得PC2+CD2=PD2,即(20-x)2+102=x2,解得x=25 2.∴此时点P移动的距离为10+252=452(cm),易知EF∥AD,∴△BEO1∽△BAD,∴EO1AD=BEBA,即EO120=10-210,∴EO1=16cm,∴OO1=14cm.(i)当⊙O首次到达⊙O1的位置时,⊙O移动的距离为14cm,此时点P与⊙O移动的速度比为45214=4528,∵4528≠54,∴此时PD与⊙O1不可能相切.(ii)当⊙O在返回途中到达⊙O1的位置时,⊙O移动的距离为2×(20-4)-14=18(cm),此时点P 与⊙O 移动的速度比为45218=4536=54,∴此时PD 与⊙O 1恰好相切.沪科版初中数学九年级(下)期末综合测试卷及答案(四)一、选择题(本大题共10小题,每小题4分,满分40分)题号12345678910答案CADCDBACDB1.下列图形中,既是轴对称图形又是中心对称图形的是2.如图,将正方体沿相对的棱的中点切割去其四分之一,则剩余部分的主视图是3.如图,AB 是☉O 的弦,OC ⊥AB ,交☉O 于点C ,连接OA ,OB ,BC ,若∠ABC=20°,则∠AOB 的度数是A.40°B.50°C.70°D.80°4.(包头中考)下列事件中,属于不可能事件的是A.某个数的绝对值大于0B.某个数的相反数等于它本身C.任意一个五边形的外角和等于540°D.长分别为3,4,6的三条线段能围成一个三角形5.如图,正方形的边长都相等,其中阴影部分面积相等的有A.(1)(2)(3)(4)B.(2)(3)(4)C.(1)(2)(3)D.(1)(3)(4)6.将分别标有-10,-2,2,4,5数字的五个小球装在一个不透明的口袋中,这些球除数字外无其他差别.随机摸出一球,把小球上的数字作为点的横坐标;不放回,再随机摸出一球,把小球上的数字作为点的纵坐标.则两次摸出的球上的数字组成的点的坐标恰好在反比例函数y=20的图象上的概率是A.425B.15C.14D.127.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC,△COB,弓形BmC 的面积分别为S1,S2,S3,则它们之间的关系是A.S2<S1<S3B.S3<S2<S1C.S1<S3<S2D.S1<S2<S38.从一个半径为10的圆形纸片上裁出一个最大的正六边形,此正六边形的边心距是A.52B.102C.53D.1039.如图,在Rt△ABC中,∠C=90°,以BC为直径的☉O交AB于点D,E是AC的中点,连接DE.下列结论:①DE是☉O的切线;②∠CED+2∠B=180°;③若AD=16,DE=10,则BC=15.其中正确的结论是A.①②B.①③C.②③D.①②③第9题图第10题图10.如图,线段AB=4,C为线段AB上的一个动点,以AC,BC为边作等边△ACD和等边△BCE,☉O外接于△CDE,则☉O半径的最小值为。
2023年沪科版初中数学九年级(下)期末综合测试卷及答案
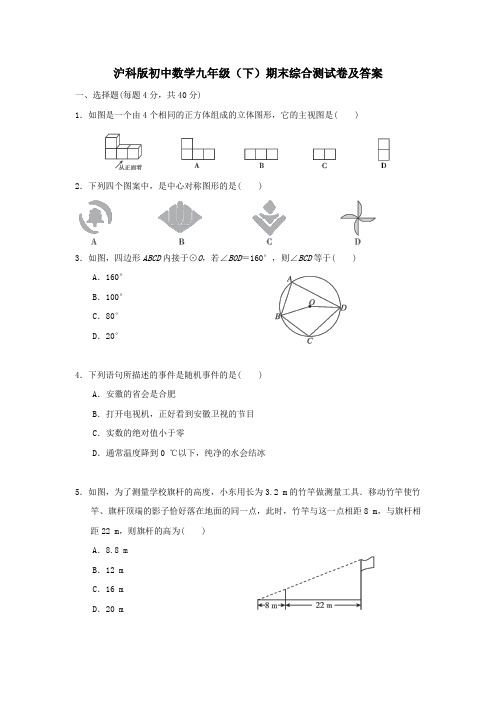
沪科版初中数学九年级(下)期末综合测试卷及答案一、选择题(每题4分,共40分)1.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )2.下列四个图案中,是中心对称图形的是( )3.如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD等于( ) A.160°B.100°C.80°D.20°4.下列语句所描述的事件是随机事件的是( )A.安徽的省会是合肥B.打开电视机,正好看到安徽卫视的节目C.实数的绝对值小于零D.通常温度降到0 ℃以下,纯净的水会结冰5.如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为( )A.8.8 mB.12 mC.16 mD.20 m6.如图是以△ABC 的边AB 为直径的半圆O ,点C 恰好在半圆上,过点C 作CD ⊥AB 于点D .已知cos ∠ACD =35,BC =4,则AC 的长为( )A .1B .203C .3D .1637.一个不透明的袋内装有标号分别为1,2,3,4的4个小球(小球除标号外其余均相同).从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字.则组成的两位数是3的倍数的概率为( ) A .14B .516C .716D .128.如图,这是一个长方体纸盒的表面展开图,纸片厚度不计.根据图中数据,可得这个盒子的容积为( )A .6B .8C .10D .159.如图,AB 为⊙O 的直径,C 为⊙O 上一点,弦AD 平分∠BAC ,交BC 于点E ,AB =6,AD =5,则AE 的长为( ) A .2.5 B .2.8 C .3 D .3.210.如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线l ,与⊙O 过点A 的切线交于点B ,且∠APB =60°,设OP =x ,则△PAB 的面积y 关于x 的函数图象大致是( )二、填空题(每题5分,共20分)11.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是________.12.小明家的客厅有一张直径为1.2米,高为0.8米的圆桌BC ,在距地面2米的A 处有一盏灯,圆桌的影子为DE ,依据题意建立如图所示的平面直角坐标系,其中D 点坐标为(2,0),则点E 的坐标是________.13.如图,矩形ABCD 中,AB =3,BC =2,E 为BC 的中点,AF =1,以EF 为直径的半圆与DE交于点G ,则劣弧GE ︵的长为________.14.抛物线y =-x 2-2x +3与x 轴交于A ,B 两点,若一个半径为5的圆也经过点A ,B ,则该圆的圆心坐标为______________.三、(每题8分,共16分)15.如图是由5个大小相同的小正方体搭成的几何体,其中每个小正方体的棱长为1 cm.(1)直接写出这个几何体的表面积:__________;(2)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.16.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.(1)请分别作出如图所示的两个三角形的最小覆盖圆;(要求:尺规作图,保留作图痕迹,不写作法)(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论.(不要求证明)四、(每题8分,共16分)17.如图,在8×8的小正方形网格中,△ABC三顶点的坐标分别为A(2,3),B(2,1),C(5,1),把△ABC绕着点A顺时针旋转90°得到△AEF,点B的对应点为E,点C的对应点为F.(1)在图中画出△AEF;(2)点C的运动路径长为____________;(3)直接写出线段BC扫过的面积:________.18.一个不透明的袋中装有20个只有颜色不同的球,其中有5个黄球,8个黑球,7个红球. (1)求从袋中摸出1个球是黄球的概率;(2)现从袋中取出若干个黑球,搅匀袋中的球,使从袋中摸出1个球是黑球的概率是13.求从袋中取出黑球的个数.五、(每题10分,共20分)19.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.20.如图,已知直线l :y =3x ,点A 1的坐标为(1,0),过点A 1作x 轴的垂线交直线l 于点B 1,以原点O 为圆心,OB 1长为半径画弧交x 轴于点A 2;过点A 2作x 轴的垂线交直线l 于点B 2,以原点O 为圆心,OB 2长为半径画弧交x 轴于点A 3,…,按此方法进行下去.求:(1)点B 1的坐标和∠A 1OB 1的度数;(2)弦A4B3的弦心距.六、(12分)21.在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有-1、-2、1、2,从袋中任意摸出一个小球(不放回),将袋中剩余的小球搅匀后,再从袋中摸出另一个小球.(1)请你列出摸出小球上的数可能出现的所有结果;(2)规定:如果摸出的两个小球上的数都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?七、(12分)22.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连接AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若OC=2,求DE的长;(3)在∠A从15°增大到30°的过程中,请直接写出弦AD在圆内扫过的面积.八、(14分)23.如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.(1)请判断直线PA与⊙O的位置关系,并说明理由;(2)求证:AG2=AF·AB;(3)若⊙O的直径为10,AC=2 5,AB=4 5,求△AFG的面积.答案一、 1.A 2.D 3.B 4.B 5.B6.D 点拨:∵AB 为直径,∴∠ACB =90°,∴∠ACD +∠BCD =90°.∵CD ⊥AB ,∴∠BCD +∠B =90°,∴∠B =∠ACD ,∵cos ∠ACD =35,∴cos B =35,易知tan B =43,∵BC =4,∴tan B =AC BC =AC 4=43,∴AC =163.7.B 8.A9.B 点拨:连接BD ,∵AD 平分∠BAC ,∴∠CAE =∠DAB ,∴CD ︵=BD ︵.∵AB 是⊙O 的直径,∴∠ACE =∠ADB =90°,∴△ACE ∽△ADB ,∴AC AD =AE AB ,即AC 5=AE6.设AC =5x ,则AE =6x ,∴DE =5-6x .连接OD 交BC 于点F ,则DO ⊥BC ,∴OD ∥AC ,易知OF =12AC =52x ,∴DF =OD -OF =3-52x ,易得△ACE ∽△DFE , ∴AC DF =AE DE ,即5x 3-52x=6x 5-6x, 解得x =715(x =0舍去),则AE =6x =2.8. 10.D二、11.41512.(4,0) 13.54π 点拨:如图,连接OG ,DF ,根据勾股定理分别求出DF 、EF ,证明Rt △DAF ≌Rt △FBE ,求出∠DFE =90°,进而推出∠GOE=90°,最后根据弧长公式计算即可. 14.(-1,1)或(-1,-1)点拨:不妨设点A 在点B 的左侧.∵抛物线y =-x 2-2x +3与x 轴交于A ,B 两点, ∴A (-3,0),B (1,0), ∴圆心在直线x =-1上,设圆心坐标为(-1,m ),由题意得22+m 2=(5)2,解得m =±1, ∴圆心坐标为(-1,1)或(-1,-1). 三、15.解:(1)22 cm 2(2)如图所示:16.解:(1)如图所示.(2)若三角形为锐角三角形,则其最小覆盖圆为三角形的外接圆;若三角形为直角三角形或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.四、17.解:(1)如图所示,△AEF 即为所求.(2)132π 点拨:易知AC = 22+32= 13,∠CAF =90°, ∴点C 的运动路径长为90·π· 13180=132π.(3)94π 点拨:线段BC 扫过的面积为S 扇形CAF -S 扇形BAE =90·π·( 13)2360-90·π·22360=134π-π=94π. 18.解:(1)20个球里面有5个黄球,故P (摸出1个球是黄球)=520=14.(2)设从袋中取出x (0<x <8,且x 为整数)个黑球,则此时袋中总共还有(20-x )个球,黑球剩(8-x )个.因为从袋中摸出1个球是黑球的概率是13,所以8-x 20-x =13,解得x =2.经检验,x =2是所列方程的解,且符合实际.所以从袋中取出了2个黑球. 五、19.解:该几何体的形状是直四棱柱.由三视图知,棱柱底面菱形的对角线长分别为4 cm ,3 cm. ∴菱形的边长为52 cm ,∴棱柱的侧面积S =52×8×4=80(cm 2).20.解:(1)设B 1的坐标为(1,m ).∵B 1在直线l 上,∴3=m ,∴B 1(1,3). ∴A 1B 1=3,OA 1=1,∴tan ∠A 1OB 1=A 1B 1OA 1=3,∴∠A 1OB 1=60°. (2)如图,作OH ⊥A 4B 3于H .由题意可得OA 2=2,OA 3=4,OA 4=8. ∵OA 4=OB 3,OH ⊥A 4B 3, ∴∠A 4OH =12∠A 4OB 3=30°,∴OH =OA 4·cos30°=8×32=4 3. ∴弦A 4B 3的弦心距为4 3. 六、21.解:(1)可能出现的所有结果如下表-1 -2 1 2 -1 (-1,-2)(-1,1) (-1,2) -2 (-2,-1) (-2,1)(-2,2) 1 (1,-1) (1,-2) (1,2) 2(2,-1)(2,-2)(2,1)(2)∵x 2-3x +2=0,∴(x -1)(x -2)=0,∴x 1=1,x 2=2.∵共有12种等可能的结果,其中摸出的两个小球上的数都是方程x 2-3x +2=0的根的结果有2种,摸出的两个小球上的数都不是方程x 2-3x +2=0的根的结果有2种, ∴P (小明赢)=212=16,P (小亮赢)=212=16,∴游戏规则公平.七、22.(1)证明:如图,连接OD ,则OD ⊥DE ,∴∠ODA +∠EDC =90°.∵OA =OD ,∴∠OAD =∠ODA ,又∵OA ⊥OB ,∴∠OAD +∠OCA =90°,∴∠OCA =∠EDC .又∵∠OCA =∠ECD ,∴∠ECD =∠EDC .(2)解:由(1)知,∠ECD =∠EDC ,∴ED =EC .设ED =x ,则OE =OC +CE =2+x .在Rt △ODE 中,∵OD 2+DE 2=OE 2,OD =OA =8,∴82+x 2=(2+x )2,解得x =15,∴DE 的长为15.(3)解:弦AD 在圆内扫过的面积为16π3+16 3-16. 点拨:如图,连接OD ′,过点O 作OH ⊥AD ′于点H ,延长AO 交⊙O 于点M ,过点D 作DN ⊥AM 于点N .设弦AD 在圆内扫过的面积为S ,则S =S 扇形AOD -S △OAD -S 弓形ABD ′,由题意知,∠OAH =30°,∴在Rt △OAH 中,∠AOH =60°,AH =32OA =4 3,OH =12OA =4, ∴AD ′=2AH =8 3,∠AOD ′=120°,∴S 弓形ABD ′=S 扇形AOD ′-S △OAD ′=120π×82360-12×8 3×4=64π3-16 3. 在Rt △ODN 中,∠DON =2∠OAD =30°,∴DN =12OD =4, ∴S △OAD =12OA ·DN =12×8×4=16. ∵∠AOD =180°-∠DON =150°,∴S 扇形AOD =150π×82360=80π3, ∴S =S 扇形AOD -S △OAD -S 弓形ABD ′=80π3-16-⎝ ⎛⎭⎪⎫64π3-16 3=16π3+16 3-16, ∴弦AD 在圆内扫过的面积为16π3+16 3-16. 八、23.(1)解:PA 与⊙O 相切.理由如下:连接CD .∵AD 为⊙O 的直径,∴∠ACD =90°.∴∠D +∠CAD =90°.∵∠B =∠D ,∠PAC =∠B ,∴∠PAC =∠D .∴∠PAC +∠CAD =90°,即DA ⊥PA .∴PA 与⊙O 相切.(2)证明:连接BG .∵AD 为⊙O 的直径,CG ⊥AD ,∴AC ︵=AG ︵.∴∠AGF =∠ABG .∵∠GAF =∠BAG ,∴△AGF ∽△ABG .∴AG ∶AB =AF ∶AG . ∴AG 2=AF ·AB .(3)解:连接BD .∵AD 是⊙O 的直径,∴∠ABD =90°. ∵AG 2=AF ·AB ,AG =AC =2 5,AB =4 5,∴AF =AG 2AB = 5. ∵CG ⊥AD ,∴∠AEF =∠ABD =90°.又∵∠EAF =∠BAD ,∴△AEF ∽△ABD .∴AE AB =AF AD ,即AE 4 5=510,解得AE =2.∴EF =AF 2-AE 2=1. ∵EG =AG 2-AE 2=4,∴FG =EG -EF =4-1=3.∴S △AFG =12FG ·AE =12×3×2=3.。
秋九年级数学沪科版下册课件:期末检测卷(共35张PPT)

•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 7:59:44 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
