函数图像
经典数学函数图像大全
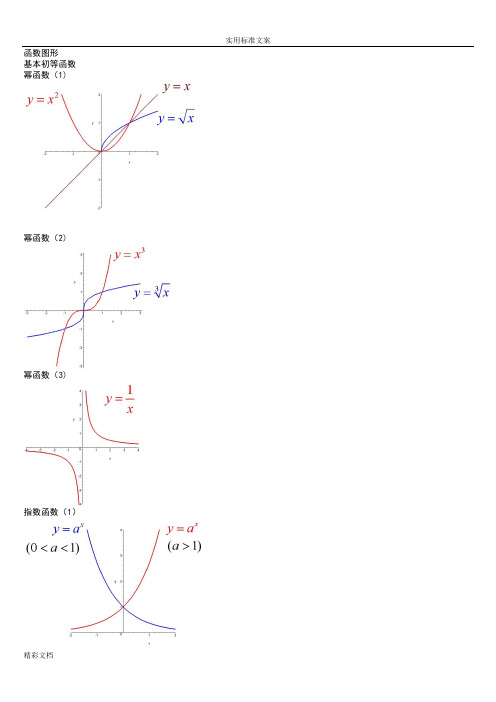
函数图形 基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质) 极限的性质 (4) (局部有界性) 极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx 等价于xarcsinx等价于xtanx等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线实用标准文案精彩文档y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2) 数列的夹逼性 (1) 数列的夹逼性 (2)。
经典数学函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
经典数学函数图像大全

. 函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)双曲函数(3)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)反双曲函数(5).y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x|取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2) limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)。
函数图像ppt课件

03
描点法
根据函数表达式,在坐标 系中逐个描出对应的点(x, y),然后用平滑的曲线将 这些点连接起来。
计算法
利用数学软件或计算器, 输入函数表达式,自动生 成函数图像。
表格法
根据函数表达式和已知数 据,制作表格,然后在坐 标系中根据表格数据绘制 出函数图像。
函数图像的观察与分析
观察图像形状
通过观察函数的图像,可以初 步判断函数的类型(如一次函 数、二次函数、三角函数等)
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
06
复合函数的图像
复合函数的定义与性质
总结词
理解复合函数的定义与性质是绘制和分 析其图像的基础。
VS
详细描述
复合函数是由两个或多个函数的组合而成 的函数。它具有一些特殊的性质,如复合 函数的导数、极限等。了解这些性质有助 于更好地绘制和分析复合函数的图像。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
03
二次函数的图像
二次函数的定义与性质
总结词
二次函数的定义、性质和 表达式
二次函数的定义
二次函数是指形式为 y=ax^2+bx+c(其中a、 b、c为常数,且a≠0)的 函数。
二次函数的性质
二次函数具有开口方向、 顶点、对称轴等性质,这 些性质决定了函数图像的 形状和位置。
复合函数图像的绘制
总结词
掌握绘制复合函数图像的方法是理解其性质 和应用的必要手段。
详细描述
绘制复合函数图像需要使用数学软件或绘图 工具,如Matlab、GeoGebra等。在绘制 过程中,需要注意函数的定义域、值域以及 函数的单调性、奇偶性等性质。
数学函数图像大全

8.其它公式(推导出来的 )
$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$ $1-sin(a)=(sin(a/2)-cos(a/2))^2$
$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$ 4.积化和差公式 (上面公式反过来就得到了) $sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$ $cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$ $sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$
y=sin(1/x) (4) y = [1/x](1)
y = [1/x](2)
y=21/x y=21/x (2) y=xsin(1/x)
考研数学函数图像大全
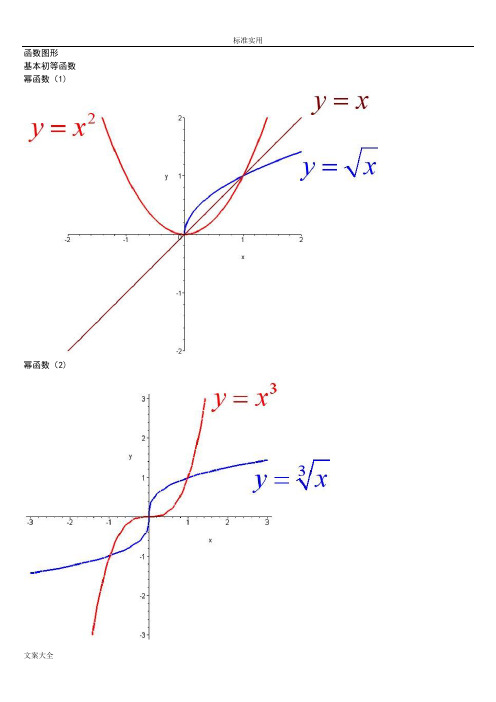
基本初等函数
幂函数(1)
幂函数(2)
幂函数(3)
指数函数(1)
指数函数(2)
指数函数(3)
对数函数(1)
对数函数(2)
三角函数(1)
三角函数(2)
三角函数(3)
三角函数(4)
三角函数(5)
反三角函数(1)
反三角函数(2)
反三角函数(3)
反三角函数(4)
反三角函数(5)
反三角函数(6)
反三角函数(7)
反三角函数(8)
双曲函数(1)
双曲函数(2)
双曲函数(3)
双曲函数(4)
双曲函数(5)
双曲函数(6)
Байду номын сангаас双曲函数(7)
反双曲函数(1)
反双曲函数(2)
反双曲函数(3)
反双曲函数(4)
反双曲函数(5)
反双曲函数(6)
y=sin(1/x) (1)
y=sin(1/x) (2)
y=sin(1/x) (3)
y=sin(1/x) (4)
精品函数图形基本初等函数幂函数1幂函数2精品精品幂函数3指数函数1指数函数2精品精品指数函数3对数函数1精品精品对数函数2三角函数1精品精品三角函数2三角函数3精品精品三角函数4三角函数5精品精品反三角函数1反三角函数2精品精品反三角函数3反三角函数4精品精品反三角函数5反三角函数6精品精品反三角函数7反三角函数8精品精品双曲函数1双曲函数2精品精品双曲函数3双曲函数4精品精品双曲函数5双曲函数6精品精品双曲函数7反双曲函数1精品精品反双曲函数2反双曲函数3精品精品反双曲函数4反双曲函数5精品精品反双曲函数6ysin1x精品精品ysin1x精品精品ysin1x精品精品
常用函数图像
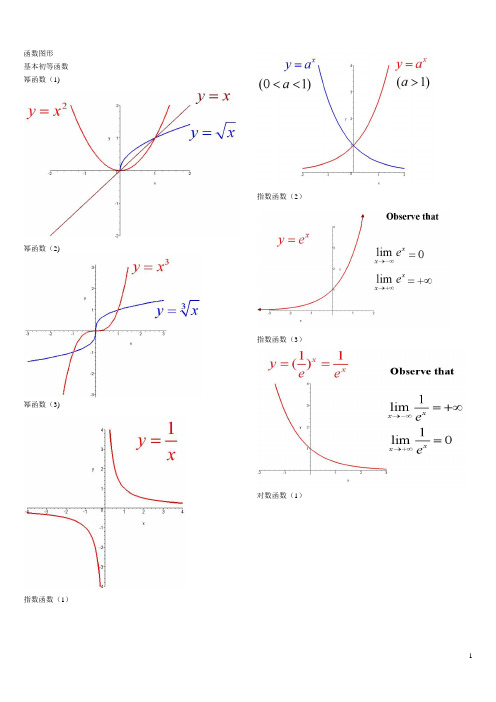
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)三角函数(3)对数函数(2)三角函数(4)三角函数(1)三角函数(5)三角函数(2)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4)y = [1/x](1) y = [1/x](2) y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x) y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)等价无穷小 (x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本) ^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了。
经典数学函数图像(大全)

经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线,其一般形式为 y = mx + b,其中 m是斜率,b 是 y 轴截距。
当 m > 0 时,直线向上倾斜;当 m < 0 时,直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线,其一般形式为 y = ax^2 + bx + c,其中 a、b、c 是常数。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线,余弦函数图像与正弦函数图像相似,但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线,其一般形式为 y = a^x,其中 a 是底数,x 是指数。
当 a > 1 时,曲线上升;当 0 < a < 1 时,曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线,其一般形式为 y =log_a(x),其中 a 是底数,x 是真数。
当 a > 1 时,曲线上升;当0 < a < 1 时,曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线,而双曲正切函数图像是一条周期性振荡的曲线。
7. 幂函数图像幂函数图像是一条上升或下降的曲线,其一般形式为 y = x^n,其中 n 是指数。
当 n > 0 时,曲线上升;当 n < 0 时,曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线,其一般形式为 y = k/x,其中 k是常数。
当 k > 0 时,曲线位于第一和第三象限;当 k < 0 时,曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数,包括反正弦函数、反余弦函数和反正切函数。
经典数学函数图像大全-数学函数图像-函数图像 全
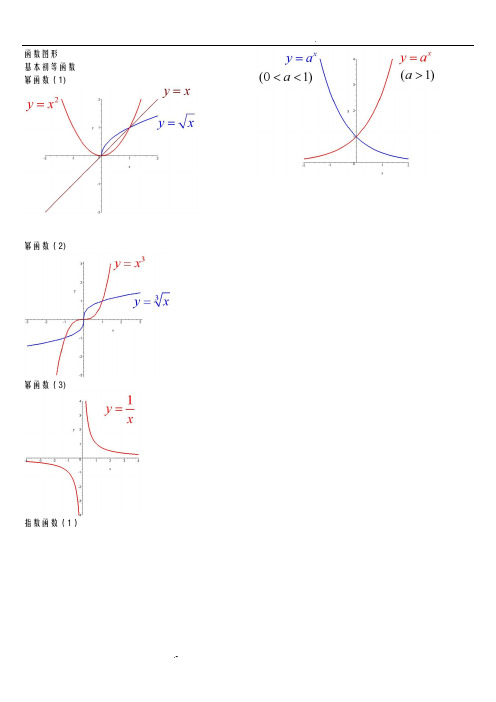
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2) y=xsin(1/x) y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性) 极限的性质(2) (局部保号性)极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
经典数学函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(5)反三角函数(6)反三角函数(7)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y = [1/x](2) y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2 sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
经典数学函数图像大全-数学函数图像
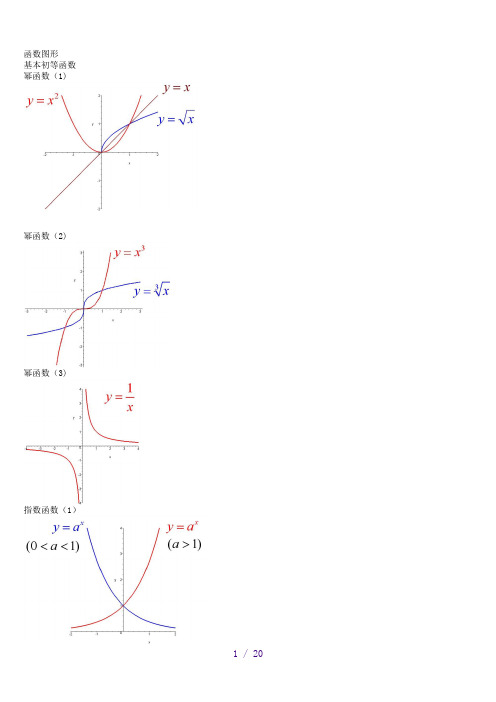
基本初等函数
幂函数(1)
幂函数(2)
幂函数(3)
指数函数(1)
指数函数(2)
指数函数(3)
对数函数(1)
对数函数(2)
三角函数(1)
三角函数(2)
三角函数(3)
三角函数(4)
三角函数(5)
反三角函数(1)
反三角函数(2)
反三角函数(3)
反三角函数(4)
反三角函数(5)
反三角函数(6)
反三角函数(7)
y = [1/x](1)
y = [1/x](2)
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x)
y=e1/x
y=sinx (x->∞)
绝对值函数 y = |x|
符号函数 y = sgnx
取整函数 y= [x]
极限的几何解释 (1)
极限的几何解释 (2)
极限的几何解释 (3)
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
y=sinx/x (x->∞)
夹逼定理(1)
夹逼定理(2)
数列的夹逼性 (1)
数列的夹逼性 (2)
(注:文档可能无法思考全面,请浏览后下载,供参考。可复制、编制,期待你的好评与关注)
极限的性质 (1) (局部保号性)
极限的性质 (2) (局部保号性)
极限的性质 (3) (不等式性质)
极限的性质 (4) (局部有界性)
极限的性质 (5) (局部有界性)
两个重要极限
y=sinx/x (1)
y=sinx/x (2)
limsinx/x的一般形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课标高考总复习(文)
RJ· A版· 数学
考纲要求
新课标高考总复习(文)
考情分析
从近两年的高考试题来看,图象 的辨识与对称性以及利用图象研究 函数的性质、方程、不等式的解是 会利用函数 高考的热点,多以选择题、填空题 的图象研究函 的形式出现,属中低档题,主要考 数的有关性质. 查基本初等函数的图象的应用以及 数形结合思想,如2011年全国课标 卷、山东卷、北京卷等.
(x)的图象是否具有对称性?其对称轴(中心)是什么?若f(a+x)=-f(b-x)
RJ· A版· 数学
新课标高考总复习(文)
自主检测
A.②①③④
C.④①③②
B.②③①④
D.④③①②
RJ· A版· 数学
新课标高考总复习(文)
解析:第一个图象过点 (0,0),与 ④对应; k - 第二个图象为反比例函数图象,表达式为 y= , ③y= x 1恰好符 x 合, ∴第二个图象对应 ③; 第三个图象为指数函数图象,表达式为 y= ax,且 a>1, ①y= 2x恰 好符合, ∴第三个图象对应 ①; 第四个图象为对数函数图象,表达式为 y= logax,且 a>1, ②y= log2x恰好符合, ∴第四个图象对应 ②. ∴四个函数图象与函数序号的对应顺序为 ④③①②.选 D.
RJ· A版· 数学
3.函数图象的应用
新课标高考总复习(文)
(1) 函数图象形象地显示了函数的性质,为研究数量关系提供了 “形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重 视数形结合解题的思想方法. (2)对于给定的函数的图象,要能从图象的左右、上下分布范围、 变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、 周期性,注意图象与函数解析式中参数的关系.
新课标高考总复习(文)
考点 3 用图 1.函数图象形象地显示了函数的性质( 如单调性、奇偶性、最 值等),为研究数量关系问题提供了“形”的直观性,因此常用函 数的图象研究函数的性质. 2.有些不等式问题常转化为两函数图象的上、下关系来解. 3.方程解的个数常转化为两熟悉的函数图象的交点个数问题 来求解.
RJ· A版· 数学
新课标高考总复习(文)
6.函数f(x)与g(x)的定义域为[m,n],它们的图象如图所示,则不 等式f(x)g(x)<0的解集是________.
答案:[m,a)∪(a,b)∪(c,d)
RJ· A版· 数学
新课标高考总复习(文)
(对应学生用书P38)
考点1
作图象
画函数图象的一般方法有: (1) 直接法:当函数表达式 ( 或变形后的表达式 ) 是熟悉的基本函数
+ +1
的图象,再向下平移一个单位得到 y= 2x 1- 1的图象,如图 (2).,可见原函数可由 y=- 向左平移 3个单位再 x x+ 3 x+ 3
向上平移 1个单位而得,如图 (3). (4)首先作出 y= log2x的图象 C1,然后将 C1向左平移 1个单位,得到 y = log2(x+ 1)的图象 C2,再把 C2在 x轴下方的图象作关于 x轴对称的图 象,即为所求图象 C3: y= |log2(x+ 1)|.如图 (4)(实线部分 ).
RJ· A版· 数学
新课标高考总复习(文)
x 例 2 (2011 年山东高考)函数 y=2 -2sinx 的图象大致是(
)
RJ· A版· 数学
新课标高考总复习(文)
【解析】 当 x=0 时,y=0,即图象过(0,0),排除 A, 1 1 y′= -2cosx,令 y′>0,得 cosx< , 2 4 x 此不等式的解集由无数个区间并成, 故函数 y=2-2sinx 有无 数个增区间,故选 C.
(3)作出y=log2x的图象,再向下平移一个单位,最后将x轴下方的 图象作关于x轴对称的图象,即得所求图象,如图(3)实线部分.
RJ· A版· 数学
考点 2 识图、辨图
新课标高考总复习(文)
对于给定函数的图象,要能从图象的左右、上下分布范围、 变化趋势、对称性等方面来获取图中所提供的信息,解决这类问 题的常用方法有:(1)定性分析法,也就是通过对问题进行定性的 分析,从而得出图象的上升(或下降)的趋势,利用这一特征来分析 解决问题;(2)定量计算法,也就是通过定量的计算来分析解决问 题;(3)函数模型法,也就是由所提供的图象特征,联想相关函数 模型,利用这一函数模型来分析解决问题.
变为原来的A倍,横坐标不变而得到; ② y=f(ax)(a>0)的图象,可将 y =f(x)的图象上所有点的横坐标 1 变为原来的 倍,纵坐标不变而得到. a
RJ· A版· 数学
新课标高考总复习(文)
问题探究1:函数y=f(2x-1)的图象与y=f(2x)的图象有何关系?
1 提示:函数y=f(2x-1)的图象是由函数y=f(2x)的图象向右平移 个 2 单位得到的.
RJ· A版· 数学
例1 作出下列函数的图象.
+
新课标高考总复习(文)
(1)y=x2-2|x |-1;(2)y=2x 1-1; x+2 (3)y= ;(4)y=|log2(x +1)|. x+3
【分析】 先将原函数式化简、变形、讨论性质,然后利用描点
法,图象变换法作图.
RJ· A版· 数学
【解】
新课标高考总复习(文)
且函数为偶函数,先用描点法作
2 x - 2x- 1, x≥0 (1)y= 2 x + 2x- 1, x<0
出 [0,+ ∞)上的图象,再根据对称性作出 (- ∞, 0)上的图象.得图象 如图(1). (2)y= 2x 1- 1的图象可由 y= 2x的图象向左平移 1个单位,得 y= 2x
RJ· A版· 数学
新课标高考总复习(文)
RJ· A版· 数学
新课标高考总复习(文)
作出下列函数的图象: 2x-1 1 |x| (1)y=( ) ;(2)y= ;(3)y=|log2x -1|. 2 x-1
RJ· A版· 数学
新课标高考总复习(文)
1 1 解:(1)作出y=( )x的图象,保留 y=( )x图象中x≥0的部分,加上 y 2 2 1 1 =( )x的图象中 x>0部分关于 y轴的对称部分,即得 y=( )|x|的图象,如图 2 2 (1)实线部分.
RJ· A版· 数学
新课标高考总复习(文)
例 3 (1)(2011 年高考新课标卷)已知函数 y=f(x)的周期为 2, 当 x∈[-1,1]时 f(x)=x2,那么函数 y=f(x)的图象与函数 y=|lgx|的 图象的交点共有( A.10 个 C.8 个 ) B.9 个 D.1 个
(2)直线 y=1 与曲线 y=x2-|x|+a 有四个交点, 则 a 的取值范 围是________. 【解析】 (1)观察图象可知,共有 10 个交点.
数.所以 f(x)的图象关于y轴对称.
答案:D
RJ· A版· 数学
新课标高考总复习(文)
3.已知图①中的图象对应的函数为y=f(x),则图②的图象对应的 函数为( ) B.y=| f(x)| D.y=-f(|x|) A.y=f(|x|) C.y=f(-|x|)
答案:C
RJ· A版· 数学
新课标高考总复习(文)
与坐标轴的交点等),描点,连线.
RJ· A版· 数学
2.利用图象变换作图 (1)平移变换
新课标高考总复习(文)
RJ· A版· 数学
(2)对称变换
新课标高考总复习(文)
RJ· A版· 数学
(3)伸缩变换 ①y=A
新课标高考总复习(文)
f(x)(A>0)的图象,可将 y=f(x)的图象上所有点的纵坐标
RJ· A版· 数学
x2-x+a,x≥0, (2)y= 2 x +x+a,x<0,
新课标高考总复习(文)
作出图象,如图所示.
1 此曲线与 y 轴交于(0,a)点,最小值为 a-4,要使 y=1 与其 1 5 有四个交点,只需 a-4<1<a,∴1<a<4.
【答案】 (1)A 5 (2)1<a< 4
.∴y= x+ 1.
当 x>0时,设解析式为 y= a(x- 2)2- 1, 1 ∵图象过点 (4,0), ∴0= a(4- 2)2- 1,得 a= . 4 综上:函数 f(x)在 [- 1,+ ∞)上的解析式为 x+ 1,- 1≤x≤0 f(x)=1 . 2 x- 2 - 1, x>0 4 x+1,-1≤x≤0 答案: f(x)=1 2 x - 2 - 1, x>0 4
答案:D
RJ· A版· 数学
2.(2010年重庆高考)函数 A.关于原点对称 C.关于x轴对称
新课标高考总复习(文)
)
4x+1 f(x)= x 的图象( 2 B.关于直线y =x对称 D.关于y 轴对称
解析:
f(x) = 2x + 2 - x ,因为 f( - x) =
f(x) ,所以
f(x) 为偶函
RJ· A版· 数学
新课标高考总复习(文)
(对应学生用书P37) 知识梳理 1.利用描点法作函数图象
其基本步骤是列表、描点、连线,首先:(1)确定函数的定义域;
(2)化简函数解析式; (3)讨论函数的性质(奇偶性、单调性、周期性、对 称性等);其次:列表(尤其注意特殊点、零点、最大值点、最小值点、
1 x 1 x 4.为了得到函数y=3×( ) 的图象,可以把函数y=( ) 的图象向 3 3 ________平移________个单位长度. 1 x 1 x-1 1 x 解析:y=3×( ) =( ) ,则只需把y=( ) 的图象向右平移1个单 3 3 3 位长度.
答案:右 1
RJ· A版· 数学
