广东省珠海市八年级数学上册 第十四章 一次函数 一次函数单元测试卷(无答案) 人教新课标版
人教版八年级数学上册第十四章一次函数单元测试题

第十四章一次函数单元检测题 (考试时间为120分钟,满分120分)姓名学号得分_____________一、填空题(每题3分,共30分)1、已知一个一次函数的图象过点(-1,3),则这个一次函数的解析式可以是__________________; (只需写出一个解析式即可,不必考虑所有情况).2、若点P 1(–1,4)和P 2(1,b )关于y 轴对称,则b = ;3、直线x y 312-=与x 轴交点的坐标是________;4、若一次函数y =mx -(m -2)过点(0,2),则m = ;5、函数y =x 的取值范围是 ;6、如果直线b ax y +=经过一、二、四象限,那么ab ____0 (“<”、“>”或“=”);7、下列三个函数y=-2x+1,y=-41x —3,y=(32-)x+2的共同点是___________________; 8、函数y = -x +3的图象与x 轴,y 轴围成的三角形面积为_________________;9、某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米n 元水费收费;用水超过10立方米的,超过部分加倍收费.某职工某月缴水费18n 元,则该职工这个月实际用水为___________;10、有边长为a 的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2、3、4…的等边三角形(如图).根据图形推断每个等边三角形卡片总数S 与边长n 的关系式 ;二、选择题(每题3分,共30分)11、函数y =x-2x+2的自变量x 的取值范围是( ) A.x ≥-2 B.x ≤-2 C..x >-2 D.x <-212、一根弹簧原长10cm ,它所挂的重量不超过10kg ,并且挂重1kg 就伸长1.5cm ,写出挂重后弹簧长度y (cm )与挂重x (kg )之间的函数关系式是( ) A.y =1.5(x +10)(0≤x ≤10) B.y =1.5x +10 (0≤x ) C.y =1.5x +10 (0≤x ≤10) D.y =1.5(x -10) (0≤x ≤10)13、无论m 为何实数,直线m x y 2+=与4+-=x y 的交点不可能在( )A.第一象限B.第二象限C.第三象限D.第四象限 14、某兴趣小组做实验,将一个装满水的啤酒瓶倒置(如图), 并设法使瓶里的水从瓶中匀速流出.那么该倒置啤酒瓶内水面高度h 随水流出的时间t 变化的图象大致是 ( )A. B. C. D. 15、已知函数122y x =-+,当-1<x ≤1时,y 的取值范围是( ) A.5322y -<≤ B.3522y << C.3522y <≤ D.3522y ≤<16、某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A 地后,宣传8分钟;然后下坡到B 地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A 地仍要宣传8分钟,那么他们从B 地返回学校用的时间是( ) A.45.2分钟 B.48分钟 C.46分钟 D.33分钟17、下列函数中,①y =πx ②y=2x-1 ③y=1/x ④y=2-3x ⑤y=x 2-1中,是正比例函数的有( ) A.4个 B.3个 C.2个 D.1个 18、函数31-=x y 中自变量的取值不可以是( ) A 、4 B 、3 C 、2 D 、119、将函数y=x+2的图象向上平移3个单位,这时函数的解析式为( ): A. y=x+5 B. y=3x+5 C. y=-3x+5 D. y=x-1 20、下列函数关系y 中,变量y 与x 成正比例函数关系的是( ) A.y=x 2 B.y=32x C.y=x-3 D.y=x5- 三、解答题:21、观察图,先填空,然后回答问题:(1)由上而下第n 行,白球有_______个;黑球有_______个.(2)若第n 行白球与黑球的总数记作y , 则请你用含n 的代数式表示y ,并指出其中n 的取值范围(10分)22、已知,直线y =2x +4与直线y =-2x -1.(1) 求两直线与y 轴交点A 、B 的坐标;(2) 求两直线交点C 的坐标; (3) 求△ABC 的面积(12分)23、 旅客乘车按规定可以免费携带一定重量的行李.如果所带行李超过了规定的重量,就要按超重的千克收取超重行李费.已知旅客所付行李费y (元)可以看成他们携带的行李质量x (千克)的一次函数为561-=x y .画出这个函数的图象,并求旅客最多可以免费携带多少千克的行李。
一次函数单元测试题(含答案)

第十四章 一次函数测试题(时间:90分钟 总分120分)一、相信你一定能填对!(每小题3分,共30分) 1.下列函数中,自变量x 的取值范围是x ≥2的是( )A .y=2x -B .y=2x - C .y=24x - D .y=2x +·2x -2.下面哪个点在函数y=12x+1的图象上( ) A .(2,1) B .(-2,1) C .(2,0) D .(-2,0) 3.下列函数中,y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 4.一次函数y=-5x+3的图象经过的象限是( ) A .一、二、三 B .二、三、四 C .一、二、四 D .一、三、四5.若函数y=(2m+1)x 2+(1-2m )x (m 为常数)是正比例函数,则m 的值为( )A .m>12B .m=12C .m<12D .m=-126.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限,则k 的取值范围是( ) A .k>3 B .0<k ≤3 C .0≤k<3 D .0<k<37.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A .y=-x-2 B .y=-x-6 C .y=-x+10 D .y=-x-1⑧.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y (升)与行驶时间t (时)的函数关系用图象表示应为下图中的( )9.李老师骑自行车上班,最初以某一速度匀速行进,•中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y•(千米)与行进时间t (小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )10.一次函数y=kx+b 的图象经过点(2,-1)和(0,3),•那么这个一次函数的解析式为( ) A .y=-2x+3 B .y=-3x+2 C .y=3x-2 D .y=12x-3 二、你能填得又快又对吗?(每小题3分,共30分)11.已知自变量为x 的函数y=mx+2-m 是正比例函数,则m=________,•该函数的解析式为_________. 12.若点(1,3)在正比例函数y=kx 的图象上,则此函数的解析式为________.13.已知一次函数y=kx+b 的图象经过点A (1,3)和B (-1,-1),则此函数的解析式为_________. 14.若解方程x+2=3x-2得x=2,则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方.15.已知一次函数y=-x+a 与y=x+b 的图象相交于点(m ,8),则a+b=_________.16.若一次函数y=kx+b 交于y•轴的负半轴,•且y•的值随x•的增大而减少,•则k____0,b______0.(填“>”、“<”或“=”)17.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组30220x y x y --=⎧⎨-+=⎩的解是________.18.已知一次函数y=-3x+1的图象经过点(a ,1)和点(-2,b ),则a=________,b=______.19.如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9,则k 的值为_____.20.如图,一次函数y=kx+b 的图象经过A 、B 两点,与x 轴交于点C ,则此一次函数的解析式为__________,△AOC 的面积为_________.三、认真解答,一定要细心哟!(共60分) 21.(14分)根据下列条件,确定函数关系式: (1)y 与x 成正比,且当x=9时,y=16;(2)y=kx+b 的图象经过点(3,2)和点(-2,1).22.(12分)一次函数y=kx+b 的图象如图所示:xy1234-2-1CA-14321O(1)求出该一次函数的表达式; (2)当x=10时,y 的值是多少? (3)当y=12时,•x 的值是多少?566-2xy1234-2-15-14321O23.(12分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题: (1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?24.(10分)如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y (元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y 与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?25.(12分)已知雅美服装厂现有A 种布料70米,B 种布料52米,•现计划用这两种布料生产M 、N 两种型号的时装共80套.已知做一套M 型号的时装需用A 种布料1.•1米,B 种布料0.4米,可获利50元;做一套N 型号的时装需用A 种布料0.6米,B 种布料0.•9米,可获利45元.设生产M 型号的时装套数为x ,用这批布料生产两种型号的时装所获得的总利润为y 元. ①求y (元)与x (套)的函数关系式,并求出自变量的取值范围; ②当M 型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?答案:1.D 2.D 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.A 11.2;y=2x 12.y=3x 13.y=2x+1 14.<2 15.1616.<;< 17.58xy=-⎧⎨=-⎩18.0;7 19.±6 20.y=x+2;421.①y=169x;②y=15x+7522.y=x-2;y=8;x=1423.①5元;②0.5元;③45千克24.①当0<t≤3时,y=2.4;当t>3时,y=t-0.6.②2.4元;6.4元25.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A种布料[1.1x+0.•6(80-x)]米,共用B种布料[0.4x+0.9(80-x)]米,∴解之得40≤x≤44,而x为整数,∴x=40,41,42,43,44,∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);②∵y随x的增大而增大,∴当x=44时,y最大=3820,即生产M型号的时装44套时,该厂所获利润最大,最大利润是3820元.。
八年级数学一次函数单元测试题

八年级数学一次函数单元测试题又到了单元检测的时刻了,教师们要如何准备测试题呢?下面是店铺带来的关于八年级数学一次函数单元测试题的内容,希望会给大家带来帮助!八年级数学一次函数单元测试题::1、请你写出一个经过点(1,1)的函数解析式 .2、在函数中,当自变量满足时,图象在第一象限.3、中国电信宣布,从某天起,县城和农村电话收费标准一样,在县内通话3分钟内的收费是0.2元,每超1分钟加收0.1元,则电话费(元)与通话时间 ( 分,为正整数)的函数关系是 ;4、老师给出一个函数,甲、乙、丙各正确指出了这个函数的一个性质:甲:函数的图象经过第一象限; 乙:函数的图象经过第三象限;丙:在每个象限内,y随x的增大而减小.请你根据他们的叙述构造满足上述性质的一个函数:5、一个函数的图象经过点(1,2),且y随x的增大而增大而这个函数的解析式是(只需写一个)6、如果点A(—2,a)在函数y= x+3的图象上,那么a的值等于A、—7B、3C、—1D、47、小明、小强两人进行百米赛跑,小明比小强跑得快,如果两人同时跑,小明肯定赢,现在小明让小强先跑若干米,图中的射线a、b 分别表示两人跑的路程与小明追赶时间的关系,根据图象判断:小明的速度比小强的速度每秒快A、1米B、1.5米C、2米D、2.5米8、某日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水立方米,水费为元,则与的函数关系用图象表示正确的是9、如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量()A 小于3吨B 大于3吨C 小于4吨D 大于4吨10、如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( )A、1个B、2个C、3个D、4个11、某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元 . 小彬经常来该店租碟,若每月租碟数量为x张.(1)写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间的函数关系式:(2)写出会员卡租碟方式应付金额y2(元)与租碟数量x(张)之间的函数关系式:(3)小彬选取哪种租碟方式更合算?12、某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:x(元) 15 20 30 …y(件) 25 20 10 …若日销售量y是销售价x的一次函数.(1)求出日销售量y(件)与销售价x(元)的函数关系式:(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?13、图9是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:(1)汽车在前9分钟内的平均速度是(2)汽车在中途停了多长时间?(3)当16≤t≤30时,求S与t的函数关系式.14、如图15—1和15—2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.(1)如图15—1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;(2)如图15—2,在Rt△ABC向下平移的过程中,请你求出y与x 的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?15、在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。
最新-广东省珠海市八年级数学上册 第十四章 一次函数

广东省珠海市八年级数学上册 第十四章 一次函数 一次函数单元测试卷人教新课标版3.若函数y = -2x m +2+n -5是正比例函数,则m 的值是 ,n 的值为________.4.一次函数2y x =-+的图象与x 轴的交点坐标是_________,与y 轴的交点坐标是__________. 5、在函数y=51x -中,自变量x 的取值范围是____________。
6、函数x 的取值范围是____________。
7.若直线y =kx +b 平行于直线y =5x +3,且与y 轴相交于点(0,2),则k =______,b =______. 8、直线421-=x y 向下平移2个单位得到_________________ 9.已知直线4+=x y 与x 轴,y 轴围成一个三角形,则这个三角形面积为 . 10.如下图,直线y=kx+b 交坐标轴于A 、B 两点,则不等式kx+b>0的解集是_________ 11.根据下图所示的程序计算函数值,若输入的x 值为21-,则输出的结果为 .12.如图,已知函数y=ax+b 和y=kx 的图象交于点P ,则根据图象可得关于x ,y 的二元一次方程组,.y ax b y kx =+⎧⎨=⎩的解是________.二、选择题(每题4分,共20分)13、下列函数中,一次函数是( ) A .B.C.8y x =D.11y x =+ 14、下图中表示y 是x 函数的图象是( )15、汽车由南京驶往相距300千米的上海,当它的平均速度是100千米/时,下面哪个图形表示汽车距上海的路程s (千米)与行驶时间t (小时)的函数关系?( )(A ) (B ) (C ) (D )16、已知函数y=kx (k ≠0)中,y 随x 的增大而增大,那么一次函数y=kx-k 的图象经过( ) A .一,二,三象限 B .一,二,四象限 C .一,三,四象限 D .二,三,四象限17、一次函数y 1=kx+b 与y 2=x+a 的图象如图测所示,则下列结论: ①k<0;②a>0; ③当x<3时,y 1<y 2中,正确的个数是( )A .0个B .1个C .2个D .3个三、解答题(共70分)(8分)18、已知一次函数图象经过(3,4)和(-1,-8)两点,求此一次函数的解析式;(10分)19、已知y 与x 成正比,且当1x =时,4y =-.(1)求y 与x 之间的函数关系式;(2)若点(a ,2)在这个函数图象上,求a .(10分) 20、、已知函数(21)y m x m =-+(1)若此函数是正比例函数,求m 的值;(2)若这个函数是一次函数,且y 随着x 的增大而减小,求m 的取值范围.(12分)21、某汽车的油缸盛油10升,已知汽车平均耗油量为0.1 L/km(1)写出油缸中的剩油量y (升)与汽车行驶路程x (千米)之间的函数关系式;(2) 求出自变量的取值范围; (3)画出(1)中的函数图象。
初二上册数学一次函数单元测试题及答案(K12教育文档)

(直打版)初二上册数学一次函数单元测试题及答案(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)初二上册数学一次函数单元测试题及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)初二上册数学一次函数单元测试题及答案(word版可编辑修改)的全部内容。
初二上册数学一次函数单元测试题一、填空题(每小题5分,共25分)1、若函数28y m x-=-是正比例函数,则常数m的值是。
(3)m2、已知一次函数2=-,请你补充一个条件 ,使y随x的增大而减小。
y kx3、从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是 .4、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,某市居民每月交水费y(元)与水量x(吨)的函数关系如图所示,请你通过观察函数图象,回答自来水公司收费标准:若用水不超过5吨,水费为元/吨;若用水超过5吨,超过部分的水费为元/吨。
5、学校阅览室有能坐4 人的方桌,如果多于4 人,就把方桌拼成一行,2张方桌拼成一行能坐6 人,如图所示,请你结合这个规律,填写下表:拼成一行的桌子1234……n人数468……二、选择题(每小题5分,共25分,每小题只有一个正确答案)6、下列各曲线中不能表示y是x的函数的是………………………………………( )A. B. C. D.7、若点A(2,4)在函数2=-的图象上,则下列各点在此函数图象上的是()y kxA .(0,—2)B .(错误!,0)C .(8,20)D .(错误!,错误!)8、右图是温度计的示意图,左边的刻度表示摄氏温度,右边的刻度表示华氏温度,华氏温度y (°F )与摄氏温度(°C )x 之间的函数关系式为………( )A .9325y x =+ B .40y x =+C .5329y x =+D .5319y x =+9、“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟先到了终点。
八年级数学《一次函数》单元综合测试卷

10
20
30
40
50 t /万
1 1 千米/分 B.2 千米/分 C.1 千米/分 D. 千米/分 2 3
二、仔细填一填(每题 4 分,共 40 分) 11.已知函数 y=4-2x 的图象经过(1,a),则 a 的值是_____________. 1 是正比例函数,则 m=_____________. 13.在一次函数 y=2x-2 的图像上,与 x 轴的距离等于 1 的点的坐标是 14.当 x=________时,函数 y=2x-4 与 y=3x-3 有相同的函数值. 15.写出一次函数 y=-2x+3 的图象上的一个点的坐标是:____________. 16.如果一次函数 y=kx+b 的图象如图所示,那么 k______0,b______0. 17.把直线 y=-2x 沿 y 轴向上平移 2 个单位长度,所得直线的函数关系式为___________. 18.一长方形的长比宽多 2 厘米,则这长方形的面积 S(厘米 2)与长 x(厘米)的函数关系式是 19.一次函数 y=-2x+4 的图象与 x 轴、y 轴所围成的三角形面积是________. 20. 正方形 A1B1C1O,A2B2C2C1,A3B3C3C2 按如图所示的方式放置.点 A1,A2,A3 和点 C1,C2,C3 分别在直线 x 轴上,已知点 B1(1,1),B2(3,2), 则 B3 的坐标是_______. 三、灵活地运用 21. (本题 6 分)已知一次函数 y=kx+b 的图像如图所示,求其函数关系式。 22. (本题 10 分)一次函数 y=kx+4 的图象经过点(-3,-2). (1)求这个函数表达式; (2)画出该函数的图象. (3)判断(-5,3)是否在此函数的图象上;
(完整版)八年级数学第十四章一次函数单元测试题(含答案),推荐文档

.下面哪个点在函数y=的图象上(1
2
.( D 9.李老师骑自行车上班,最初以某一速度匀速行进, 中途由于自行车发生故障,停下
修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y (千米)与行进时间时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是(
25.(12分)已知雅美服装厂现有A种布料70米,B种布料52米, 现计划用这两种布
料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1. 1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料
0. 9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时
装所获得的总利润为y元.
①求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
②当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?。
(word完整版)初二上册数学一次函数单元测试题及,文档
初二上册数学一次函数单元测试题一、填空题〔每题 5 分,共 25 分〕1、假设函数y (3m)x m28是正比率函数,那么常数 m 的值是。
2、一次函数y kx 2 ,请你补充一个条件,使 y 随x的增大而减小。
3、从 A 地向 B 地打长途,准时收费,3 分钟内收费 2.4 元,今后每高出 1 分钟加收 1元,假设通话 t 分钟〔t3〕,那么需付费 y〔元〕与〔t分钟〕之间的函数关系式是。
4、某市自来水公司为了激励市民节约用水,采用分段收费标准,某市居民每个月交水费 y〔元〕与水量 x〔吨〕的函数关系以以下图,请你经过观察函数图象,答复自来水公司收费标准:假设用水不高出 5 吨,水费为元/吨;假设用水高出 5 吨,高出局部的水费为元/吨。
5、学检阅览室有能坐 4 人的方桌,若是多于 4 人,就把方桌拼成一行,2 张方桌拼成一行能坐 6 人,以以下图,请你结合这个规律,填写下表:拼成一行的桌子数1234n 人数468二、选择题〔每题 5 分,共 25 分,每题只有一个正确答案〕6、以下各曲线中不能够表示 y 是 x 的函数的是〔〕A .B .C .D .7、假设点 A 〔2,4〕在函数 ykx2 的图象上,那么以下各点在此函数图象上的是〔〕311A .〔0,-2〕B .〔2,0〕C .〔8,20〕D .〔2,2〕8、右图是温度计的表示图,左边的刻度表示摄氏温度,右边的刻度表示华°°〕氏温度,华氏温度 y 〔 F 〕与摄氏温度〔 C 〕x 之间的函数关系式为 〔A .9B .y5 x 32yx 40C . y5x 32D . y5x 31999、“龟兔赛跑〞表达了这样的故事:当先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是赶快追赶,但为时已晚,乌龟先到了终点。
用 S 1、S 2 分别表示乌龟和兔子所行的行程,t 为时间,那么以以下图象中与故事相切合的是 〔〕A .B .C .D .10、如图 OA 、AB 分别表示甲、乙两名同学运动的一次函数图象,图中 s 和 t 分别表示运动行程和时间,甲的速度比乙快,以下说法:①射线 AB 表示甲的行程与时间的函数关系;②甲的速度比乙快 1.5 米/秒;③甲让乙先跑 12米;④8 秒钟后,甲高出了乙,其中正确的说法是 〔 〕A .①②B .②③④C .②③D .①③④三、解答题 〔此大题总分值 50 分〕212、〔8 分〕画出函数y2x 6 的图象,利用图象:〔1〕求方程2x60 的解;〔2〕求不等式 2x 6 >0的解;〔3〕假设 1 y 3 ,求 x 的取值范围。
广东省珠海市八年级数学上册 第十四章 一次函数 一次函数复习题(无答案) 人教新课标版

广东省珠海市八年级数学上册 第十四章 一次函数 一次函数复习题人教新课标版4、一次函数y=kx+b 的图像过一、二、四象限,则k________0,b________0.5、若函数y=(a -3)x+a 2-9是正比例函数,则a=________,图像过________象限. 6、直线421-=x y 可以由直线121+=x y 向 平移 个单位得到。
7、方程3x-9=0的解是_______,则函数y=3x-9与x 轴交于点_______.8、如果34x y x +=-在实数范围内有意义,那么x 的取值范围是 _______ 。
9、已知y 与4x -1成正比例,且当x=3时,y=6,写出y 与x 的函数关系式 。
10、直线b kx y +=1与152+-=x y 平行,且经过(2,1),则解析式y 1= __ 。
11、.某市市内电话费y (元)与通话时间t (分钟)之间的 函数关系图象如图所示,则通话7分钟需付电话费 _____ 元。
12、若正比例函数mx y =的图像经过点A (1x ,1y )和点B (2x ,2y ),当1x <2x 时1y >2y , 则m 的取值范围是 . 二、选择题:13.下列函数中,一次函数是( ) A .B.C.8y x =D.11y x =+ 14.下图中表示y 是x 函数的图象是( )15.如图,直线y=kx+b 交坐标轴于A 、B 两点,则不等式kx+b>0的解集是( )A .x>-2B .x>3C .x<-2D .x<316、 已知某函数(12)y m x =+中,函数值y 随自变量x 的增大而减小,那么m 取值范围( ) (A )21-≤m (B) 21-≥m (C) 21-<m (D) 21->m17、一次函数y=-2x+3的图像不经过的象限是( ).(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限18、有一游泳池注满水,现按一定速度将水排尽,然后进行清洗,再按相同速度注满清水,使用 一段时间后,又按相同的速度将水排尽,则游泳池的存水量为h(米)随时间t(小时)变化的大致图象是( )19、汽车由南京驶往相距300千米的上海,当它的平均速度是100千米/时,下面哪个图形表示汽车距上海的路程s (千米)与行驶时间t (小时)的函数关系?( ) (A ) (B ) (C ) (D ) 三、解答题:20、已知一次函数图象经过(3,5)和(-4,-9)两点, (1)求此一次函数;(2)若点(m,2)在函数图象上,求m 的值.21、如图,l A 、l B 分别表示A 步行与B 骑车在同一路上行驶的路程S 与时间t 的关系。
广东省珠海市八年级数学上册 第十四章 一次函数 14.1.3函数的图象随堂练习(1)(无答案) 人教新课标版
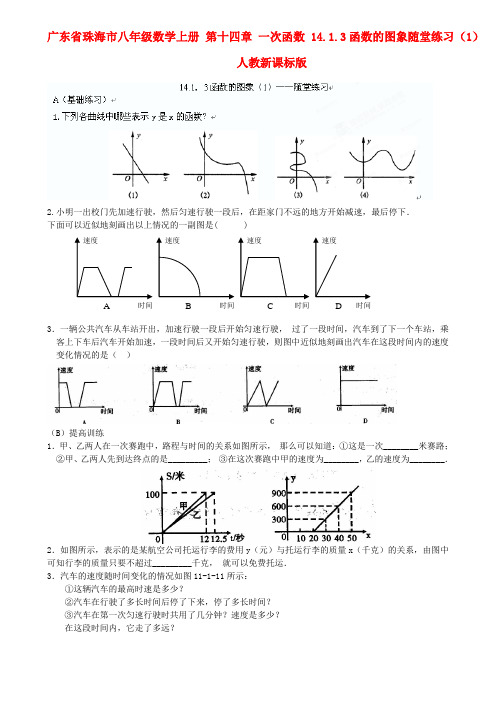
广东省珠海市八年级数学上册 第十四章 一次函数 14.1.3函数的图象随堂练习(1)人教新课标版2.小明一出校门先加速行驶,然后匀速行驶一段后,在距家门不远的地方开始减速,最后停下.3.一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,•过了一段时间,汽车到了下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,则图中近似地刻画出汽车在这段时间内的速度变化情况的是( )(B )提高训练1.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,•那么可以知道:①这是一次________米赛路;②甲、乙两人先到达终点的是_________;•③在这次赛跑中甲的速度为________,乙的速度为________.2.如图所示,表示的是某航空公司托运行李的费用y (元)与托运行李的质量x (千克)的关系,由图中可知行李的质量只要不超过_________千克,•就可以免费托运. 3.汽车的速度随时间变化的情况如图11-1-11所示: ①这辆汽车的最高时速是多少?②汽车在行驶了多长时间后停了下来,停了多长时间?③汽车在第一次匀速行驶时共用了几分钟?速度是多少? 在这段时间内,它走了多远?BCDA图6(C )拓展提升1.如图5所示,OA 、BA 分别表示甲、乙两名学生运动的路程 与时间的关系图象,图中s 和t 分别表示运动路程和时间, 根据图象判断快者的速度比慢者的速度每秒快( ) A.2.5m B.2m C. 1.5m D.1m14.1.3函数的图象(1)——课后作业A (基础练习)1、如图所示,分别给出了变量x 与y 之间的对应关系,y 不是x 的函数的图象是( )2.某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时装产品150件,未装箱的产品数量为y ,•生产时间为t ,那么y 与t 的大致图象只能是图中的( )3、张大伯去散步,从家走了20min ,到离家900m 的阅报亭看了10min 报纸后,用了10min 返回到家,如图表示张大伯离家时间与距离之间的关系是( )4.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是( ).))))(B )提高训练1.甲、乙两同学从A 地出发,骑自行车在同一条路上行驶到B 地,他们离出发地的距离s (千米)和行驶时间t(小时)之间的函数关系的图象如图7所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发0.5小时;(4) 相遇后,甲的速度小于乙的速度;(5)甲乙两人同时到达目的地.其中符合图象的描述的说法有_______.(填序号)2.甲、乙两人赛跑,路程s 与时间t 的关系如图8所示,那么可以知道:(1)这是一次________m 赛跑;(2)甲、乙两人中先到达终点的是____;(3)乙在这次赛跑中的速度为____m/s.3.如图,反映了小明从家到超市的时间与距离之间关系的一幅图.(1)图中反映了哪两个变量之间的关系?超市离家多远?(2)小明到达超市用了多少时间?小明往返花了多少时间?(3)小明离家出发后20分钟到30分钟内可能在哪里?(4)小明从家到超市时的平均速度是多少?返回时的平均速度是多少?(C )拓展提升1、如图10是小陈同学骑自行车上学的路程与时间的关系图象,请你根据图象描述他上学路上的情况.(新知预习)1.对于一个函数,如果把自变量x和函数y•的每对对应值分别作为点的________坐标与_________坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的_________.2.一种豆子每千克售2元,写出豆子的总售价y(元)与所售豆子的数量x(千克)之间的函数关系式,画出这个函数的图象.小红是这样解答的:y(元)与x(千克)之间的函数关系式为y=2x.列表得:在平面直角坐标系中,描出以下各点(1,),(2,),(3,),…,用平滑的曲线连结描出各点的坐标,即得到y=2x的图象(画坐标系表示)。
广东省珠海市八年级数学上册 第十四章 一次函数 14.3.1一次函数与一元一次方程随堂练习(无答案)

广东省珠海市八年级数学上册第十四章一次函数 14.3.1一次函数与一元一次方程随堂练习人教新课标版2.某种拖拉机的油箱可储油40L,加满油并开始工作后,•油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.(1)求y与x的函数解析式;(2)一箱油可供拖拉机工作几小时?(C)拓展提升1、已知关于x的方程mx+n=0的解是x=-2,则直线y=m x+n与x•轴的交点坐标是________.2.已知直线y=kx+b与直线y=3x-1交于y轴同一点,则b的值是().A.1 B.-1 C.13D.-1314.3.1一次函数与一元一次方程——课后作业(A)基础练习1.直线y=3x+9与x轴的交点是().A.(0,-3) B.(-3,0) C.(0,3) D.(0,-3)2.直线y=kx+3与x轴的交点是(1,0),则k的值是().A.3 B.2 C.-2 D.-33.方程3x+2=8的解是__________,则函数y=3x+2在自变量x等于_____•时的函数值是8.4.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a•的值是______.(B)巩固训练1.看图填空:(1)当y=0时,x=_______;(2)直线对应的函数表达式是_________.2.已知直线y=2x+8与x轴和y轴的交点的坐标分别是_______、_______.•与两条坐标轴围成的三角形的面积是__________.3.2008年夏天,某省由于持续高温和连日无雨,水库蓄水量普遍下降.下图是某水库的蓄水量V(万立方米)与干旱时间t(天)之间的关系图,回答下列问题:(1)该水库原蓄水量是_________万立方米,持续干旱10•天后,•水库的蓄水量为_____万立方米.(2)若水库的蓄水量小于400万立方米时,将发生严重干旱警报,请问:•持续干旱_______天后,将发生严重干旱警报;(3)按此规律,持续干旱______天时,水库将干涸?(写出解答过程)(C)拓展提升1.已知一次函数y=ax+b(a,b是常数),x与y的部分对应值如下表:x -2 -1 0 1 2 3y 6 4 2 0 -2 -4求方程ax+b=0的解.小明先用待定系数法求出函数y=ax+b的解析式是_______,再画函数y=______的图象,该图象与x轴交于点_____,所以方程ax+b=0的解是_______.你还有更好的方法吗?说出来和大家分享.(新知预习)a )的形式,1、由于任何一元一次不等式都可转化为ax+b>0或ax+b<0(a,b是常数,0所以解一元一次不等式可以看作:当一次函数值大(小)于0时,求_______________2、已知函数y=2x-4,当x______时,y<0;3、对于函数y=-x+3,当x_____ 时,y>0;当x______时,y<0。
广东省珠海市八年级数学上册 第十四章 一次函数 14.3.2一次函数与一元一次不等式随堂练习(无答案
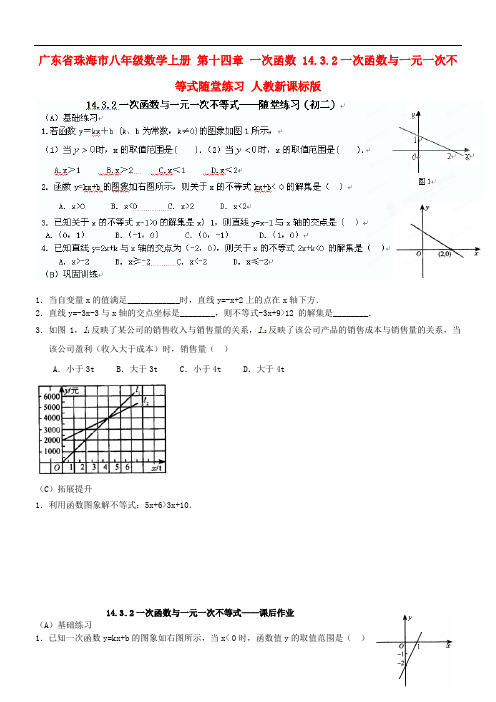
广东省珠海市八年级数学上册第十四章一次函数 14.3.2一次函数与一元一次不等式随堂练习人教新课标版1.当自变量x的值满足____________时,直线y=-x+2上的点在x轴下方.2.直线y=-3x-3与x轴的交点坐标是________,则不等式-3x+9>12•的解集是________.3.如图1,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量()A.小于3t B.大于3t C.小于4t D.大于4t(C)拓展提升1.利用函数图象解不等式:5x+6>3x+10.14.3.2一次函数与一元一次不等式——课后作业(A)基础练习1.已知一次函数y=kx+b的图象如右图所示,当x< 0时,函数值y的取值范围是()A .y>0B .y<0C .-2<y<0D .y<-22.函数y=kx+b 的图象如右图所示,则关于x 的不等式kx+b< 0的解集是( )A .x>0B .x<0C .x>1D .x<13.已知关于x 的不等式kx-2>0(k ≠0)的解集是x>3,则直线y=-kx+2与x•轴的交点是__________.(B )巩固训练1、作出函数x y 33-=的图象,并根据图象回答下列问题:(1)y 的值随x 的增大而 ;(2)图象与x 轴的交点坐标是 ;与y 轴的交点坐标是 ;(3)当x 时,y ≥0 ; (4)函数x y 33-=的图象与坐标轴所围成的三角形的面积是________________.2.育英中学需要添置某种教学仪器,方案1:到商家购买,每件需要8元;方案2:学校自己制作,每件4元,另外需要制作工具租用费120元.设需要仪器x 件,方案1与方案2的费用分别为y 1,y 2(元).(1)写出y 1的函数表达式是_____________,y 2的函数表达式是_____________.(2)在图2所示的直角坐标系中,画出两个函数的图象.(3)•观察图象发现制作仪器_______•件时,•两种方案的费用相同;•制作仪器______件时,方案1费用少;制作仪器_____件时,方案2的 费用少,和你的同学交流,你是怎样发现的.(4)瞬间决策:学校需制作仪器56件,采用方案________便宜.(C )拓展提升1.在同一坐标系中画出一次函数y 1=-x+1与y 2=2x-2的图象,并根据图象回答下列问题:(1)写出直线y 1=-x+1与y 2=2x-2的交点P 的坐标.(2)直接写出:当x 取何值时y 1>y 2;y 1<y 2(新知预习) O X Y OXY1、方程组y ax by mx n=+⎧⎨=+⎩的解是函数y=ax+b与函数y=mx+n的图象的________坐标,画出两个一次函数的图象,找出它们的交点,得到相应的二元一次方程组的解.2.方程组157x yx y+=⎧⎨-=⎩解为________,则直线y=-x+15和y=x-7的交点坐标是________.•。
广东省珠海市八年级数学上册 第十四章 一次函数 14.3.2一次函数与二元一次方程(组)随堂练习(无答案) 人
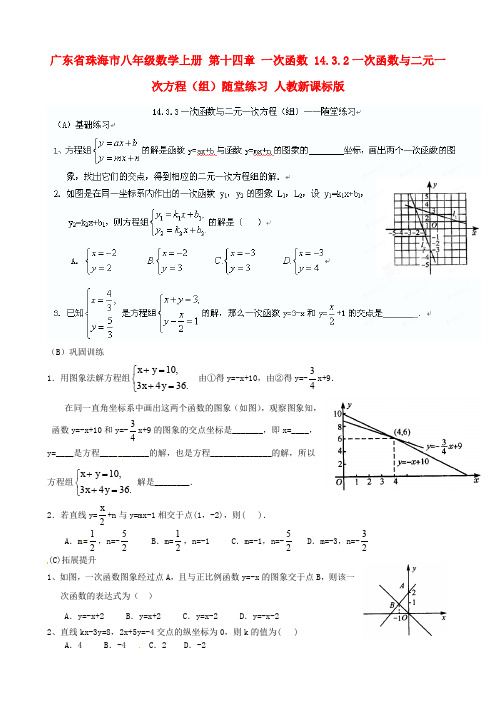
广东省珠海市八年级数学上册 第十四章 一次函数 14.3.2一次函数与二元一次方程(组)随堂练习 人教新课标版(B )巩固训练1.用图象法解方程组10,3436.x y x y +=⎧⎨+=⎩ 由①得y=-x+10,由②得y=-34x+9.在同一直角坐标系中画出这两个函数的图象(如图),观察图象知,•函数y=-x+10和y=-34x+9的图象的交点坐标是_______,即x=____,y=____是方程___________的解,也是方程______________的解,所以方程组10,3436.x y x y +=⎧⎨+=⎩解是________. 2.若直线y=2x +n 与y=mx-1相交于点(1,-2),则( ). A .m =12,n=-52 B .m=12,n=-1 C .m=-1,n=-52 D .m=-3,n=-32 (C)拓展提升1、如图,一次函数图象经过点A ,且与正比例函数y=-x 的图象交于点B ,则该一次函数的表达式为( )A .y=-x+2B .y=x+2C .y=x-2D .y=-x-22、直线kx-3y=8,2x+5y=-4交点的纵坐标为0,则k 的值为( )A .4B .-4C .2D .-214.3.3一次函数与二元一次方程(组)——课后作业(A )基础练习1.若一次函数y ax b =+和y cx d =+在同一坐标系内的图象的交点坐标是(2,-3),则方程组⎩⎨⎧+=+=d cx y b ax y 的解是( )A .23x y =⎧⎨=⎩B .23x y =⎧⎨=-⎩C .32x y =-⎧⎨=⎩D .23x y =-⎧⎨=⎩2.如果直线y=3x+6与y=2x-4交点坐标为(a ,b ),则x a y b=⎧⎨=⎩是方程组_______的解( •)A .3624y x y x -=⎧⎨+=-⎩B .3624y x y x -=⎧⎨-=⎩C .3634x y x y -=⎧⎨-=⎩D .3624x y x y -=-⎧⎨-=-⎩3.如图,已知函数y=ax+b 和y=kx 的图象交于点P ,则根据图象可得关于x ,y 的二元一次方程,.y ax b y kx =+⎧⎨=⎩的解是________. (B )巩固训练1.解方程组157x y x y +=⎧⎨-=⎩解为________,则直线y=-x+15和y=x-7的交点坐标是________.•2.一次函数y=3x+7的图象与y 轴的交点在二元一次方程 -2x+•by=•18•上,则b=_______.3、如图,已知直线1:23l y x =+,直线2:5l y x =-+,直线1l 、2l 分别交x 轴于B 、C 两点,1l 、2l 相交于点A 。
广东省珠海市八年级数学上册 第十四章 一次函数 14.2.2 一次函数图像随堂练习(2)(无答案) 人教新课标版
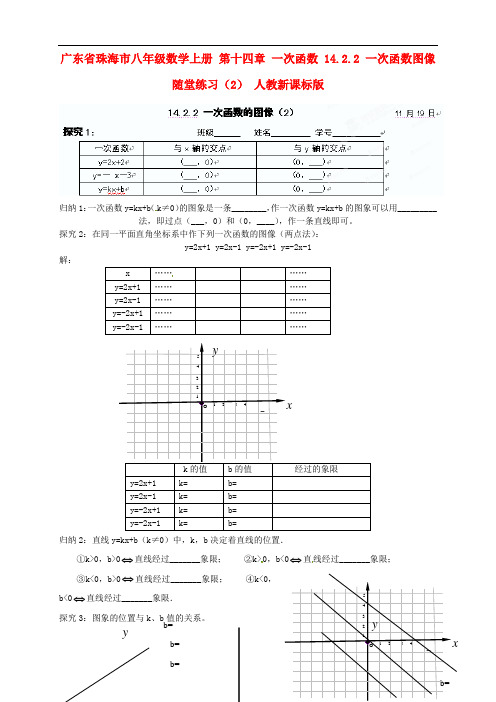
y b=______b=______b=______b=______广东省珠海市八年级数学上册 第十四章 一次函数 14.2.2 一次函数图像随堂练习(2) 人教新课标版归纳1:一次函数y=kx+b (k ≠0)的图象是一条________,作一次函数y=kx+b 的图象可以用_________法,即过点(___,0)和(0,____),作一条直线即可。
探究2:在同一平面直角坐标系中作下列一次函数的图像(两点法):y=2x+1 y=2x-1 y=-2x+1 y=-2x-1解:x …… …… y=2x+1 …… …… y=2x-1………… y=-2x+1 …… …… y=-2x-1 …………k 的值b 的值 经过的象限y=2x+1 k= b= y=2x-1 k= b= y=-2x+1 k= b= y=-2x-1k=b=归纳2:直线y=kx+b (k ≠0)中,k ,b 决定着直线的位置.①k>0,b>0⇔直线经过_______象限; ②k>0,b<0⇔直线经过_______象限;③k<0,b>0⇔直线经过_______象限; ④k<0,b<0⇔直线经过_______象限. 探究3:图象的位置与k 、b 值的关系。
543 2 1 -5 x4 3 2 1O y543 21 -5 x4 3 2 1O yb=______b=______K_______0(填>,<,=) K_______0(填>,<,=)归纳3:直线y=kx+b 的图象与y 轴交点的纵坐标就是______(k/b )的值.14.2.2 一次函数的图像(2)——随堂练习 11月19日 A 1.在直角坐标系中,画一次函数y=-3x+3的图象时,通常过点______和_____画一条直线. 2.直线y=2x-3 ,其中k=___,b=____,直线经过_______象限,y 随x 的增大而________.与x 轴的交点是(__,___),与y 轴的交点是(___,___).B 1.观察一次函数y=kx+b 图象判断常数k 与b 的取值范围(填>、<、=)。
广东省珠海市八年级数学上册 第十四章 一次函数 14.2.2 一次函数图象随堂练习(3)(无答案)

__________ ∴y=________________ ∴解得:2.一次函数的解析式的假设:(1)过的原点的直线——函数解析式可以设为__________。
(2)一次函数图象与直线y=3x 平行,则此一次函数解析式可以设为________。
(提示:若两条直线平行,则k 值相等)(3)已知一次函数图象与y 轴的交点是(0,5),则此一次函数解析式可以设为__________。
B.1.已知一次函数图象经过(-2,-1),(1,8)两点,求其解析式.解:设一次函数的解析式为__________.∵直线过点( , )( , )2、如右图,直线 l 是一次函数y=kx+b 的图象.(1)试确一次函数的解析式。
解:∵直线与y 轴的交点是(__ ,__)∴b=______。
则此直线的解析式可以设为__________.又∵过点(___,___),代入得:________________解得k=__________, ∴直线 l 的解析式是________________.(2)当x=30时,y=_____。
(3)当y=30时, x=_____。
C. 1.已知y-2与x+1成正比例,且x=-2时y=-1,求y 与x 之间的函数关系式。
2.在弹性限度内,弹簧的长度y (厘米)是能挂物体质量x (千克)的一次函数,一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米,写出y•与x 之间的关系式。
(只列式,不计算)14.2.2 函数图象(3)(待定系数法)——课后作业A1、根据条件确定一次函数的表达式:y 是x 的正比例函数,则可设此函数关系为___________,当x=2时,y=6,求y l 24o y x与x 之间的关系式为________________.2、已知,一次函数的图象与直线y=2x+1平行,则此一次函数解析式可以设为__________,且这条直线过点(-1,1),则它的解析式是_________.B1、某物体沿一个斜坡下滑,它的速度 v (米/秒)与其下滑时间 t (秒)的关系如右图所示:(1)请写出 v 与 t 的关系式; (2)下滑3秒时物体的速度是多少?2、函数 y=kx+b 的图象如图所示,求k ,b 的值及函数表达式。
广东省珠海市八年级数学上册 第十四章 一次函数 14.2.2 一次函数图象随堂练习(1)(无答案
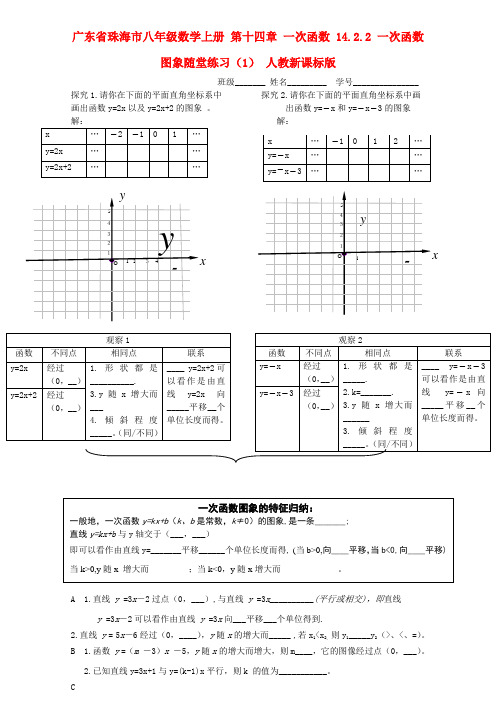
广东省珠海市八年级数学上册 第十四章 一次函数 14.2.2 一次函数图象随堂练习(1) 人教新课标版班级_______ 姓名_________ 学号_______________ 探究1.请你在下面的平面直角坐标系中 探究2.请你在下面的平面直角坐标系中画 画出函数y=2x 以及y=2x+2的图象 。
出函数y=-x 和y=-x -3的图象 解:A 1.直线 y =3x -2过点(0,___),与直线 y =3x__________(平行或相交),即直线y =3x -2可以看作由直线 y =3x 向___平移___个单位得到.2.直线 y = 5x -6经过(0,____),y 随x 的增大而_____ ,若x 1<x 2, 则y 1_____y 2(>、<、=)。
B 1.函数 y =(m -3)x -5,y 随x 的增大而增大,则m____,它的图像经过点(0,___)。
2.已知直线y=3x+1与y=(k-1)x 平行,则k 的值为___________。
Cxx如图,点A (-3,4)在一次函数y=-3x-5的图象上,图象与y 轴的交点为B ,•那么△AOB 的面积是多少?14.2.1课后作业 A .1.直线y=kx+b 经过(0,___),它可以看作由直线y=kx 平移│b │个单位长度得到,当b>0时,向______平移,•当b<0时,向________平移. 2.一次函数y=kx+b ,当k>0时,y 随x 的增大而_____,当k<0•时,y•随x•的增大而______. 3.直线y=-2x+1,其中,k_____0, y 随x 的增大而_____,图像经过点(0,___),它可以看作由直线y=-2x 向________平移______个单位长度得到. B.1.点P 1(x 1,y 1),P 2(x 2,y 2)是一次函数y=-4x+3图象上的两个点,且x 1<x 2,则y 1与y 2的大小关系是( ) A .y 1>y 2 B .y 1>y 2>0 C .y 1<y 2 D .y 1=y 2 2.直线y=3x 向上平移1个单位得到直线_____,直线y=-x-2向下平移5个单位得到直线_____ 3.当k_______时,函数y=(k-2)x+12,y 随x 的增大而减小. 4.在同一直角坐标系中(如图1),画出函数1y =x+1与2y =-4x-4的图象. C1.(1)在直角坐标系中作直线y=-12x+2的图象,写出它与两坐标轴的交点A 、B 的坐标. (2)求出这条直线与坐标轴围成的三角形的面积AOBS.预习教材P116例31.一次函数y=kx+b (k ≠0)的图象是一条________。
八年级数学上册一次函数单元测试题(含答案)-

八年级数学上册一次函数单元测试题(含答案)-(时间:90分钟 总分120分)一、相信你一定能填对!(每小题3分,共30分) 1.下列函数中,自变量x 的取值范围是x ≥2的是( )A ...D .2.下面哪个点在函数y=12x+1的图象上( ) A .(2,1) B .(-2,1) C .(2,0) D .(-2,0) 3.下列函数中,y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 4.一次函数y=-5x+3的图象经过的象限是( ) A .一、二、三 B .二、三、四 C .一、二、四 D .一、三、四5.若函数y=(2m+1)x 2+(1-2m )x (m 为常数)是正比例函数,则m 的值为( ) A .m>12 B .m=12 C .m<12 D .m=-126.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限,则k 的取值范围是( ) A .k>3 B .0<k ≤3 C .0≤k<3 D .0<k<37.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A .y=-x-2 B .y=-x-6 C .y=-x+10 D .y=-x-18.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量y (升)与行驶时间t (时)的函数关系用图象表示应为下图中的( )9.李老师骑自行车上班,最初以某一速度匀速行进,•中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y•(千米)与行进时间t (小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )10.一次函数y=kx+b 的图象经过点(2,-1)和(0,3),•那么这个一次函数的解析式为( ) A .y=-2x+3 B .y=-3x+2 C .y=3x-2 D .y=12x-3 二、你能填得又快又对吗?(每小题3分,共30分)11.已知自变量为x 的函数y=mx+2-m 是正比例函数,则m=________,•该函数的解析式为_________. 12.若点(1,3)在正比例函数y=kx 的图象上,则此函数的解析式为________.13.已知一次函数y=kx+b 的图象经过点A (1,3)和B (-1,-1),则此函数的解析式为_________. 14.若解方程x+2=3x-2得x=2,则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方. 15.已知一次函数y=-x+a 与y=x+b 的图象相交于点(m,8),则a+b=_________.16.若一次函数y=kx+b 交于y•轴的负半轴,•且y•的值随x•的增大而减少,•则k____0,b______0.(填“>”、“<”或“=”)17.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组30220x y x y --=⎧⎨-+=⎩的解是________.18.已知一次函数y=-3x+1的图象经过点(a,1)和点(-2,b ),则a=________,b=______.19.如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9,则k 的值为_____.20.如图,一次函数y=kx+b 的图象经过A 、B 两点,与x 轴交于点C,则此一次函数的解析式为__________,△AOC 的面积为_________.三、认真解答,一定要细心哟!(共60分) 21.(14分)根据下列条件,确定函数关系式: (1)y 与x 成正比,且当x=9时,y=16;(2)y=kx+b 的图象经过点(3,2)和点(-2,1).22.(12分)一次函数y=kx+b 的图象如图所示:(1)求出该一次函数的表达式; (2)当x=10时,y 的值是多少? (3)当y=12时,•x 的值是多少?23.(12分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?24.(10分)如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y (元)与通话时间t (分钟)之间的函数关系的图象.(1)写出y 与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?25.(12分)已知雅美服装厂现有A 种布料70米,B 种布料52米,•现计划用这两种布料生产M 、N 两种型号的时装共80套.已知做一套M 型号的时装需用A 种布料1.•1米,B 种布料0.4米,可获利50元;做一套N 型号的时装需用A 种布料0.6米,B 种布料0.•9米,可获利45元.设生产M 型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y 元. ①求y (元)与x (套)的函数关系式,并求出自变量的取值范围; ②当M 型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?答案:1.D 2.D 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.A 11.2;y=2x 12.y=3x 13.y=2x+1 14.<2 15.1616.<;< 17.58xy=-⎧⎨=-⎩18.0;7 19.±6 20.y=x+2;421.①y=169x;②y=15x+7522.y=x-2;y=8;x=1423.①5元;②0.5元;③45千克24.①当0<t≤3时,y=2.4;当t>3时,y=t-0.6.②2.4元;6.4元25.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A种布料[1.1x+0.•6(80-x)]米,共用B种布料[0.4x+0.9(80-x)]米,∴解之得40≤x≤44,而x为整数,∴x=40,41,42,43,44,∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);②∵y随x的增大而增大,∴当x=44时,y最大=3820,即生产M型号的时装44套时,该厂所获利润最大,最大利润是3820元.。
八年级数学上册一次函数单元测试题(含答案)-

八年级数学上册一次函数单元测试题(含答案)-(时间:90分钟 总分120分)一、相信你一定能填对!(每小题3分;共30分) 1.下列函数中;自变量x 的取值范围是x ≥2的是( )A ...D .2.下面哪个点在函数y=12x+1的图象上( ) A .(2;1) B .(-2;1) C .(2;0) D .(-2;0) 3.下列函数中;y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 4.一次函数y=-5x+3的图象经过的象限是( ) A .一、二、三 B .二、三、四 C .一、二、四 D .一、三、四5.若函数y=(2m+1)x 2+(1-2m )x (m 为常数)是正比例函数;则m 的值为( )A .m>12B .m=12C .m<12D .m=-126.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限;则k 的取值范围是( ) A .k>3 B .0<k ≤3 C .0≤k<3 D .0<k<37.已知一次函数的图象与直线y=-x+1平行;且过点(8;2);那么此一次函数的解析式为( ) A .y=-x-2 B .y=-x-6 C .y=-x+10 D .y=-x-18.汽车开始行驶时;油箱内有油40升;如果每小时耗油5升;则油箱内余油量y (升)与行驶时间t (时)的函数关系用图象表示应为下图中的( )9.李老师骑自行车上班;最初以某一速度匀速行进;•中途由于自行车发生故障;停下修车耽误了几分钟;为了按时到校;李老师加快了速度;仍保持匀速行进;如果准时到校.在课堂上;李老师请学生画出他行进的路程y•(千米)与行进时间t (小时)的函数图象的示意图;同学们画出的图象如图所示;你认为正确的是( )10.一次函数y=kx+b 的图象经过点(2;-1)和(0;3);•那么这个一次函数的解析式为( ) A .y=-2x+3 B .y=-3x+2 C .y=3x-2 D .y=12x-3 二、你能填得又快又对吗?(每小题3分;共30分)11.已知自变量为x 的函数y=mx+2-m 是正比例函数;则m=________;•该函数的解析式为_________. 12.若点(1;3)在正比例函数y=kx 的图象上;则此函数的解析式为________.13.已知一次函数y=kx+b 的图象经过点A (1;3)和B (-1;-1);则此函数的解析式为_________. 14.若解方程x+2=3x-2得x=2;则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方.15.已知一次函数y=-x+a 与y=x+b 的图象相交于点(m ;8);则a+b=_________.16.若一次函数y=kx+b 交于y•轴的负半轴;•且y•的值随x•的增大而减少;•则k____0;b______0.(填“>”、“<”或“=”)17.已知直线y=x-3与y=2x+2的交点为(-5;-8);则方程组30220x y x y --=⎧⎨-+=⎩的解是________.18.已知一次函数y=-3x+1的图象经过点(a ;1)和点(-2;b );则a=________;b=______.19.如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9;则k 的值为_____.20.如图;一次函数y=kx+b 的图象经过A 、B 两点;与x 轴交于点C ;则此一次函数的解析式为__________;△AOC 的面积为_________.三、认真解答;一定要细心哟!(共60分) 21.(14分)根据下列条件;确定函数关系式: (1)y 与x 成正比;且当x=9时;y=16;(2)y=kx+b 的图象经过点(3;2)和点(-2;1).22.(12分)一次函数y=kx+b 的图象如图所示:(1)求出该一次函数的表达式; (2)当x=10时;y 的值是多少? (3)当y=12时;•x 的值是多少?23.(12分)一农民带了若干千克自产的土豆进城出售;为了方便;他带了一些零钱备用;按市场价售出一些后;又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示;结合图象回答下列问题: (1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完;这时他手中的钱(含备用零钱)是26元;问他一共带了多少千克土豆?24.(10分)如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y (元)与通话时间t (分钟)之间的函数关系的图象.(1)写出y 与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?25.(12分)已知雅美服装厂现有A 种布料70米;B 种布料52米;•现计划用这两种布料生产M 、N 两种型号的时装共80套.已知做一套M 型号的时装需用A 种布料1.•1米;B 种布料0.4米;可获利50元;做一套N 型号的时装需用A 种布料0.6米;B 种布料0.•9米;可获利45元.设生产M 型号的时装套数为x ;用这批布料生产两种型号的时装所获得的总利润为y 元. ①求y (元)与x (套)的函数关系式;并求出自变量的取值范围; ②当M 型号的时装为多少套时;能使该厂所获利润最大?最大利润是多?答案:1.D 2.D 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.A 11.2;y=2x 12.y=3x 13.y=2x+1 14.<2 15.1616.<;< 17.58xy=-⎧⎨=-⎩18.0;7 19.±6 20.y=x+2;421.①y=169x;②y=15x+7522.y=x-2;y=8;x=1423.①5元;②0.5元;③45千克24.①当0<t≤3时;y=2.4;当t>3时;y=t-0.6.②2.4元;6.4元25.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A种布料[1.1x+0.•6(80-x)]米;共用B种布料[0.4x+0.9(80-x)]米;∴解之得40≤x≤44;而x为整数;∴x=40;41;42;43;44;∴y与x的函数关系式是y=5x+3600(x=40;41;42;43;44);②∵y随x的增大而增大;∴当x=44时;y最大=3820;即生产M型号的时装44套时;该厂所获利润最大;最大利润是3820元.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省珠海市八年级数学上册 第十四章 一次函数 一次函数单元测试卷
人教新课标版
3.若函数y = -2x m +2
+n -5是正比例函数,则m 的值是 ,n 的值为________.
4.一次函数2y x =-+的图象与x 轴的交点坐标是_________,与y 轴的交点坐标是__________. 5、在函数y=
5
1
x -中,自变量x 的取值范围是____________。
6、函数x 的取值范围是____________。
7.若直线y =kx +b 平行于直线y =5x +3,且与y 轴相交于点(0,2),则k =______,b =______. 8、直线42
1
-=
x y 向下平移2个单位得到_________________ 9.已知直线4+=x y 与x 轴,y 轴围成一个三角形,则这个三角形面积为 . 10.如下图,直线y=kx+b 交坐标轴于A 、B 两点,则不等式kx+b>0的解集是_________ 11.根据下图所示的程序计算函数值,若输入的x 值为2
1
-
,则输出的结果为 .
12.如图,已知函数y=ax+b 和y=kx 的图象交于点P ,则根据图象可得关于x ,y 的二元一次方程组
,
.y ax b y kx =+⎧⎨
=⎩
的解是________.
二、选择题(每题4分,共20分)
13、下列函数中,一次函数是( ) A .
B.
C.8y x =
D.11
y x =+ 14、下图中表示y 是x 函数的图象是( )
15、汽车由南京驶往相距300千米的上海,当它的平均速度是100千米/时,下面哪个图形表示汽车距上海的路程s (千米)与行驶时间t (小时)的函数关系?( )
(A ) (B ) (C ) (D )
16、已知函数y=kx (k ≠0)中,y 随x 的增大而增大,那么一次函数y=kx-k 的图象经过( ) A .一,二,三象限 B .一,二,四象限 C .一,三,四象限 D .二,三,四象限
17、一次函数y 1=kx+b 与y 2=x+a 的图象如图测所示,则下列结论: ①k<0;②a>0; ③当x<3时,y 1<y 2中,正确的个数是( )
A .0个
B .1个
C .2个
D .3个
三、解答题(共70分)
(8分)18、已知一次函数图象经过(3,4)和(-1,-8)两点,求此一次函数的解析式;
(10分)19、已知y 与x 成正比,且当1x =时,4y =-.
(1)求y 与x 之间的函数关系式;(2)若点(a ,2)在这个函数图象上,求a .
(10分) 20、、已知函数(21)y m x m =-+
(1)若此函数是正比例函数,求m 的值;
(2)若这个函数是一次函数,且y 随着x 的增大而减小,求m 的取值范围.
(12分)21、某汽车的油缸盛油10升,已知汽车平均耗油量为0.1 L/km
(1)写出油缸中的剩油量y (升)与汽车行驶路程x (千米)之间的函数关系式;
(2) 求出自变量的取值范围; (3)画出(1)中的函数图象。
(15分)22、、如图,l A、l B分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
(1、2、3空每空3分,4为6分)
(1)B出发时与A相距千米。
(2)走了一段路后,自行车发生故障,进行
修理,所用的时间是小时。
(3)B出发后 _____ 小时与A相遇。
(4)求出A行走的路程S与时间t的函数关系式。
(15分)23、图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y(元)与通话时间t(分钟)之间的关系图像.(1为3分,2为8分,3为4分)
(1)从图像知,通话2分钟需付的电话费是元.(2)求出该图像的解析式(写出求解过程).
(3)通话6分钟需付多少电话费?
6
时)
l A。
