《数字逻辑电路(A)》复习题逻辑代数基础
数字逻辑复习题

一、填空题:1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
15、数字逻辑中的有与, 或, 非基本逻辑运算。
16、逻辑函数有四种表示方法,它们分别是真值表、逻辑图、逻辑表达式和卡诺图。
二、判断正误题2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
(对)4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
数字逻辑电路总复习
128
16
4 2 1
二、常用逻辑关系及运算
1. 三种基本逻辑运算:与 、或、非 2. 四种复合逻辑运算: 与非 、或非、与或非、异或 真值表 函数式 逻辑符号
三、逻辑代数的公式和定理
是推演、变换和化简逻辑函数的依据,有些与普通代数相 同,有些则完全不同,要认真加以区别。这些定理中,摩根定 理最为常用。
第一章 逻辑代数基础
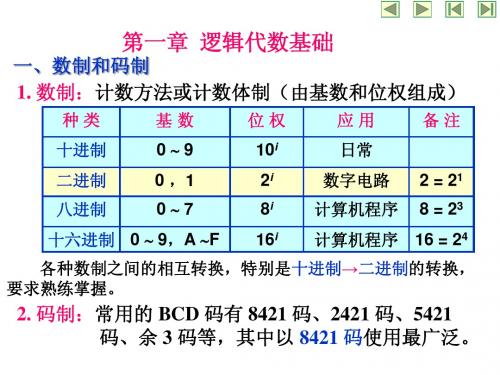
一、数制和码制 1. 数制:计数方法或计数体制(由基数和位权组成)
种类 十进制
二进制 八进制
基数 09
0 ,1 07
位权 10i
2i 8i
应用 日常
数字电路 计算机程序
备注
2 = 21 8 = 23
十六进制 0 9,A F
16i
计算机程序
16 = 24
各种数制之间的相互转换,特别是十进制→二进制的转换, 要求熟练掌握。
逻辑代数的基本公式 1. 关于常量与变量关系公式
A 0 A (1) A1 A (1’) A 1 1 (2) A 0 0 (2’)
2. 若干定律 交换律:
A B B A (3) A B B A (3’)
( A B) C A ( B C )
2. 码制:常用的 BCD 码有 8421 码、2421 码、5421 码、余 3 码等,其中以 8421 码使用最广泛。
1.十进制数到N进制数的转换 整数部分:除以N看余数 小数部分:乘以N看向整数的进位 2. N进制数转换为十进制数:方法:按权展开 3.基本逻辑和复合逻辑: (1)异或逻辑:特点:相同为0、相异为1 逻辑函数表达式:P = AB=AB+AB (2)同或逻辑:特点:相同为1、相异为0 逻辑函数表达式:P = A⊙ B =AB+AB 异或逻辑与同或逻辑是互非关系:
数字逻辑10套题

《数字逻辑电路》试题一一、填空题1.()10=()2=()8=()16。
2.()2=()10。
3.()10=( ) 8421-BCD。
4.A⊕0= 。
5.大体门电路包括、、。
6.A⊙B= 。
7.N各逻辑变量组成某个逻辑函数,那么其完整的真值表应有种不同的组合。
8.数字逻辑电路包括两类,别离是电路和电路。
9.JK触发器的特性方程是。
10.任何时刻,电路的输出,不仅与该时刻电路的输入有关,而且还与电途经去的输入有关的电路,称为电路。
11.F(A,B,C,D)=CD,它包括了个最小项。
12.A(A+B)= 。
13.F=AB+AC,这种形式的逻辑函数表达式称为。
14.F=A·B·A·C这种形式的逻辑函数表达式称为。
15.有18个信息需用二进制代码来表示它们,那么最少需要位二进制。
16.与将JK触发器作成T’(翻转)触发器,应使其J= , K= 。
17.设计一个25进制计数器,最少需要个触发器。
二、选择题1.已知字符T的ASCII码值的十进制数表示为84,若是将最高位设置为奇校验位,那么字符T的ASCⅡ码值设置奇校验位后,它的二进制表示为( )A 01001101B 11001101C 01101011 D2. 以下个数中最大的是()A (.0101) 2B 16C 10 C 83. 在一个逻辑电路中,有两个输入信号X、Y和一个输出信号V。
当且仅当X=一、Y=0时,V=0,那么V的逻辑表达式为()A X+YB X·YC X·YD X+Y4. A·A·B·B·C=( )A ABC C 1D 05. A+BC+AB+A=( )A AB AC 1D 06. F(A,B,C)=ABC+ABC+ABC=( )A ∑m(0,2,4)B ∑m(3,5,7)C ∑m(1,3,5)D ∑m(4,5,7)7. A⊕B=( )A AB+ AB B AB + ABC A BD A B8. 对正逻辑而言,某电路是与门,那么对负逻辑而言是()A 与门B 与非门C 或非门D 或门触发器在同步工作时,假设现态Q n=0,要求抵达次态Q n+1=1,那么应使JK=( )A 00B 01C 1XD X110.图(1)中要求输出F=B,那么A应为( )A 0B 1 A =1 FC B BD B 图(1)三、化简以下函数表达式一、代数化简:Y=(AB+A B+A B)(A+B+D+A B D)二、Y=AB+A B+A B3、卡诺图化简:F=(A,B,C,D)=∑m(0,1,2,3,4,6,8,9,10,11,12,14)四、芯片的应用1.别离用74138和74153实现逻辑函数表达式F=AB+BC+AC2.用1.用与非门设计一个组合电路,用来检测并行输入的四位二进制数B4B3B2B1当其值大于或等于5时,输出F=1,反之F=0。
数电 逻辑代数基础练习题

数字电子技术
第 1 章 逻辑代数基础
单项选择题
20、当变量 A、B、C 取值为101 时,下列三变量函数最小项中等于
1 的是
( )。
A m1
×
B m3
×
C m5
√
D m7
×
分析提示
将 ABC = 101 代入各最小项: m 1AB C1010 m3ABC 1010 m5ABC1011 m 7AB 1C 010
第 30 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
30、函数 Y = ABC + ABC + ABC + ABC 的最简化简结果为 ( ) 。
须先变换成同一进制,再比较大小、相等关系。
如统一表示成十进制数:
( 101111 ) 2 = ( 47 ) 10 ( 3A ) 16= ( 58 ) 10
( 55 ) 8= ( 45 ) 10 ( 01010110 ) 8421BCD= ( 56 ) 10
第2页
数字电子技术
第 1 章 逻辑代数基础
8
6
9
3
3
3
5
3
6
第4页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
7、常用的BCD码有8421码、2421码、余3码等,其中既是有权码
又是自补码的是
( )。
A 8421码 C 余3码
×
B 2421码
√
×
D 余3循环码
×
分析提示
2421码代码中从左至右每一位的权分别为 2、4、2、1,为有 权码; 2421码代码中 0和9、 1和8、 2和7、 3和6、 4和5 互 补, 为自补码。
2018-2019-1《数字逻辑电路》复习题

一. 单项选择题1、要使JK 触发器在时钟作用下的次态与现态相反,J\K 端取值应为( )。
A. J=K=0B. J=0,K=1C. J=1,K=0D. J=K=1 2、已知74LS138译码器的输入三个使能端均有效时,地址码(A2为高位,A0为低位)A2A1A0=111,则输出Y0-Y7是( )。
A . 10111111 B .11011111 C .11101111 D .11111110 3、下列触发器中,克服了空翻现象的有( )。
A.边沿D 触发器B.钟控RS 触发器C.基本RS 触发器D.钟控JK 触发器 4、电平异步时序逻辑电路,不允许两个或两个以上输入信号( )。
A.同时为1 B. 同时为0 C. 同时改变 D.同时出现 5、边沿D 触发器是时钟脉冲CP 的( )触发的。
A .下降沿B .上升沿C .高电平D .低电平6、某计数器的状态转换图如下,其计数的容量为( )A .5 B. 6 C .7 D. 87、组合电路通常由( )组成。
A .逻辑门电路B .触发器C .计数器 8、在何种输入情况下,“与非”运算的结果式逻辑“0”( ) A .全部输入是“0” B .任意输入是“0” C .仅一输入是“0”D .全部输入是“1” 9、最大项和最小项的关系是( )A .i i m M =B .=i i m MC .1i i m M ⋅=D .无关系 10、在四变量卡诺图中,逻辑上不相邻的一组最小项为( )。
A. m1与m3B.m4与m6C. m5与m13D. m2与m8 11、下列集成电路芯片中,( )属于时序逻辑电路。
A .译码器B .寄存器C .编码器D .选择器 12、设计一个9进制同步计数器,至少需要( )个触发器。
A .4B .5C .6D .1813、若4位异步二进制减法计数器当前的状态是1110,下一个输入时钟脉冲后,其内容变为( )。
A .1100B .1101C .1110D .111114、函数F(A,B,C)=AB+BC+AC 的最小项表达式为( )。
数字逻辑电路复习题

数字逻辑电路复习题1、数制与编码(-21)10 =( )10补(78.8)16=( )10(0.375)10=( )2(65634.21)8=( )16(121.02)16=( )4(49)10 =( )2=( )16(-1011)2 =( )反码=( )补码四位二进制数1111的典型二进制格林码为( )2、化简逻辑函数F (A 、B 、C 、D )=∏M (0、2、5、7、8、10、13、15)。
3、说明同步时序逻辑电路的分析步骤。
4、说明什么是组合逻辑电路。
5、说明什么是Moore 型时序逻辑电路。
6、完成下列代码之间的转换:(1)(0101 1011 1101 0111.0111)8421BCD =( )10;(2)(359.25)10=( )余3;(3)(1010001110010101)余3=( )8421BCD 。
7、试写出下列二进制数的典型Gray 码:101010,10111011。
8、用逻辑代数公理和定理证明:①C B A ⊕⊕=A ⊙B ⊙C②)B A (⊕⊙B A AB = ③C AB C B A C B A ABC A ++=⋅ ④C A C B B A C A C B B A ++=++ ⑤1B A B A B A AB =+++9、将下列函数转化成为最小项表达式和最大项表达式①F (A 、B 、C 、D )=)D C )(C B A )(B A )(C B A (++++++②F (A 、B 、C )=C A C B A BC A C AB +++③F (A 、B 、C 、D )=)B AC )(C B (D D BC ++++④F (A 、B 、C 、D )=ABCD D C B A D B A B C +++10、利用卡诺图化简逻辑函数F (A 、B 、C 、D )=4m (10,11,12,13,14,15)∑ 11、将下列函数简化,并用“与非”门和“或非”门实现该电路并判断有无竞争冒险现象,并予以消除。
数字逻辑电路考试复习

作业题 P70 题1.11(b)、(d)、(f) 题1.12 ⑴、⑶ P71 题1.13 ⑵ 题1.14 ⑵、⑷ 题1.15 ⑶、⑹
(1-5)
作业题 P71 题1.16(a) P72 题1.17 画出[题1.4] ⑴中函数的逻 辑图
(1-6)
作业题 P135 题2.2 P136 题2.3(a)
Y1 A B 0 A B
Y2 A B
Y3 AB 0 (AB 2-10)
作业题 P139 题2.13 P140 题2.15 P141 题2.16
(2-11)
一、填空题 1、使用(三态门 )可以实现总线结构;使用(OC )门可 实现“线与”逻辑。 2、TTL门输入端口为 “与” 逻辑关系时,多余的 输入端可(悬空 )处理;TTL门输入端口为 “或” 逻 辑关系时,多余的输入端应接(低)电平;CMOS门输 入端口为“与”逻辑关系时,多余的输入端应接(高 ) 电平,具有“或”逻辑端口的CMOS门多余的输入端 应接( 低)电平;即CMOS门的输入端不允许( 悬空)。 3、TTL与非门的电路结构由(输入级)、(中间放大级) 和(输出级 )三部分组成。
5、8个输入的编码器,按二进制编码,其输出的编码 有( 3 ) 位。 6、3个输入的译码器,最多可译码出( 8 ) 路输出。
(3-19)
二、单项选择题 1、在二进制译码器中,若输入有4位代码,则输出有 ( D )信号。 A、 2 个 B、 4个 C、 8个 D、16个 2、若在编码器中有50个编码对象,则要求输出二进 制代码位数为( B )位。 A、5 B 、6 C、10 D、50 3、在在大多数情况下,对于译码器而言( A )。 A、其输入端数目少于输出端数目 B、其输入端数目多于输出端数目 C、其输入端数目与输出端数目几乎相同
逻辑代数基础试题及答案

逻辑代数基础试题及答案1. 逻辑代数中,与运算的符号是什么?答案:与运算的符号是“∧”。
2. 逻辑代数中,或运算的符号是什么?答案:或运算的符号是“∨”。
3. 逻辑代数中,非运算的符号是什么?答案:非运算的符号是“¬”。
4. 逻辑代数中,异或运算的符号是什么?答案:异或运算的符号是“⊕”。
5. 逻辑代数中,同或运算的符号是什么?答案:同或运算的符号是“≡”。
6. 逻辑代数中,如何表示变量A和变量B的与运算?答案:变量A和变量B的与运算表示为“A∧B”。
7. 逻辑代数中,如何表示变量A和变量B的或运算?答案:变量A和变量B的或运算表示为“A∨B”。
8. 逻辑代数中,如何表示变量A的非运算?答案:变量A的非运算表示为“¬A”。
9. 逻辑代数中,如何表示变量A和变量B的异或运算?答案:变量A和变量B的异或运算表示为“A⊕B”。
10. 逻辑代数中,如何表示变量A和变量B的同或运算?答案:变量A和变量B的同或运算表示为“A≡B”。
11. 在逻辑代数中,德摩根定律是什么?答案:德摩根定律包括两个部分,即(¬A)∨(¬B) = ¬(A∧B)和 (¬A)∧(¬B) = ¬(A∨B)。
12. 逻辑代数中,如何证明A∧(A∨B) = A?答案:根据分配律,A∧(A∨B) = (A∧A)∨(A∧B)。
由于A∧A = A,所以表达式简化为A∨(A∧B)。
由于A∨A = A,最终表达式简化为A。
13. 逻辑代数中,如何证明A∨(¬A∧B) = A∨B?答案:根据分配律,A∨(¬A∧B) = (A∨¬A)∧(A∨B)。
由于A∨¬ A = 1(真),表达式简化为1∧(A∨B)。
由于任何变量与1的与运算结果都是该变量本身,最终表达式简化为A∨B。
14. 逻辑代数中,如何证明A∧(¬A∨B) = ¬A∨B?答案:根据分配律,A∧(¬A∨B) = (A∧¬A)∨(A∧B)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个变量取值组合?
A. n
B. 2n
C. n2
D. 2n
4. 逻辑函数的表示方法中具有唯一性的是
。
A .真值表
B. 表 达 式
C.逻辑图 D.卡诺图
5.F=A+BD+CDE+D= 。(加一个盈余项AD)
A.
B.
C. D.
6.逻辑函数F= = 。
A. B
B. A
C.
D.
7.求一个逻辑函数F的对偶式,可将F中的 。
A.全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输
入是1
10.在何种输入情况下,“或非”运算的结果是逻辑0。
A.全部输入是0
B.全部输入是1 C.任一输入为0,其他输入为
1 D.任一输入为1
二、判断题(正确打√,错误的打×) 1. 逻辑变量的取值,1比0大。( × )。
2. 异或函数与同或函数在逻辑上互为反函数。( √ )。 3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。( × )。 4.因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。( × ) 5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。( √) 6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相 等。( × ) 7.逻辑函数两次求反则还原,逻辑函数的对偶式再作对偶变换也还 原为它本身。( √ ) 8. 因为逻辑表达式A+B +AB=A+B+AB成立,所以A+B= A+B成 立。( × )
4.可使公式的推导和记忆减少一半,有时可利于将或与表达式化简。
四、思考题 1.都有输入、输出变量,都有运算符号,且有形式上相似的某些定理,
但逻辑代数的取值只能有0和1两种,而普通代数不限,且仅有逻辑含 义,无数值大小,运算符号所代表的意义也不同。 2.通常从真值表容易写出标准最小项表达式,从逻辑图易于逐级推导得 逻辑表达式,从与或表达式或最小项表达式易于列出真值表。 3.因为真值表具有唯一性。
逻辑代数基础
一、选择题(多项选择)
1. 以下表达式中符合逻辑运算法则的是 。
A .C · C = C 2 B . 1 + 1 =1 0
.C0< 1 D.A+11=
2. 逻辑变量的取值1和0可以表示:
。
A.开关的闭合、断开 B.电位的高、低 C.真与假
D. 电流
的有、无
3. 当逻辑函数有n个变量时,共有
三、填空题
1. 逻辑代数又称为 代数。最基本的逻辑关系有 、 、
三种。常用的几种复合逻辑运算为 、 、 、 、
。
2. 逻辑函数的常用表示方法有 、 、 。
3. 逻辑代数中与普通代数相似的定律有 、 、 。摩根定律
又称为 。
4. 逻辑代数的三个重要规则是
、
、
。
5.逻辑函数F=+B+D的反函数= A(C+) 。
第二章答案
一、选择题 1. D 2. ABCD 3. D 4. AD 5. AC 6. A 7. ACD 8. C 9. D 10. BCD
二、判断题 1.× 2.√ 3.√ 4.× 5.√ 6.× 7.√ 8.× 三、填空题 1.布尔 与 或 非 与非 或非 与或非 同或 异或 2.逻辑表达式 真值表 逻辑图 3.交换律 分配律 结合律 反演定律 4.代入规则 对偶规则 反演规则 5.A(C+) 6.A+BC+0 7.(A+B)(+C)(B+C)=(A+B)(+C) 8.1 9.0 10.
A .“·”换成“+”,“+”换成“·”
B.原变量换成 反变量,反变量换 成原变量
C. 变 量 不 变
D.常数中“0” 换成“1”,“1” 换成“0”
E. 常 数 不 变
8.A+BC= 。
A .A+B
B. A + C
C.( A+B)(A+C) D.B+C
9.在何种输入情况下,“与非”运算的结果是逻辑0。 D
6.逻辑函数F=A(B+C)·1的对偶函数是 A+BC+0 。
7.添加项公式AB+C+BC=AB+C的对偶式为
。
8.逻辑函数F=+A+B+C+D=
。
9.逻辑函数F== 。
10.已知函数的对偶式为+,则它的原函数为 。
四、思考题 1. 逻辑代数与普通代数有何异同? 2. 逻辑函数的三种表示方法如何相互转换? 3. 为什么说逻辑等式都可以用真值表证明? 4. 对偶规则有什么用处?
