最值问题之将军饮马
初二数学:最值问题最常考的一种:将军饮马

初二数学:最值问题最常考的一种:将军饮马!一、知识点回顾最值问题其实考察的知识点还是比较简单的:①两点之间直线最短②点到直线的距离垂线段最短③圆外一点到圆上最短距离与最长距离④几何转化为解析式求最大最小值今天我们要讲的是两点之间直线最短类型中最常考的一种:将军饮马!二、模型讲解首先我们来了解一下到底什么是将军饮马模型?传说有一个将军牵着一匹马在A点,他们目标是要去B地,但由于马渴了,要先去L这条河喝一下水,问在哪个点喝水能使得马和将军走的路最少?这个点我们应该怎么找?为什么这么确定的P点到A点和到B点的距离之和是最短?因为点A与A’关于L对称,也就是说L垂直平分AA’。
那在L上任意一点到A与到A’的距离都是相等的,那么A到直线一点的距离转换为A’到直线上的距离,又由两点之间线段最短,可以得到A’B即为最小值。
刚刚我们给的是一条边,两个点,求两点之间的最短距离;现在把条件换一下,换成一个点两条边我们应该怎么办?如图:现题目变成这样,在OA、OB上分别取两点M、N,连接MN,MC,NC,要求这三条线段之和最小。
如何定确定 M、N这两点?总结将军饮马最主要用到的就是中垂线定理,也就是垂直平分线的一点到两端点的距离相等。
下面我们一起来看一看具体的题目。
三、真题演练四、整体总结将军饮马模型是最值问题中出现频率较高的一种,而且在平时的考试中也经常会出现,因此掌握好将军饮马模型对我们解决最值问题还是有很大的帮助。
将军饮马的本质是中垂线上的一点到两端点的距离相等。
微信热文精选:早安心语:一路感恩,且行且珍惜英语口语:抠门英文怎么说善解人意,是因为这些星座喜欢你24种碱性食物越吃越年轻!爆笑,熊孩子到底有多可怕呢?(有视频)。
将军饮马系列---最值问题

实用标准“将军饮马”系列最值问题1. 两点之间,线段最短.2. 点到直线的距离,垂线段最短.3. 三角形两边之和大于第三边,两边之差小鱼第三边.-知识讲解古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦.有一天,有位将军不远千里专程前来向海伦求教一个百思不得其解的问题: 饮马,然后再到B 地军营视察,显然有许多走法.问怎样走路线最短呢?精通数理的海伦稍加思索, 作了完善的回答.这个问题后来被人们称作“将军饮马”问题.F 面我们来看看数学家是怎样解决的.海伦发现这是一个求折线和最短的数学问题. 根据公理:连接两点的所有线中,线段最短.若A 、B 在河流的异侧,直接连接 AB , AB 与I 的交点即为所求.若A 、B 在河流的同侧,根据两点间线段最短,那么显然要把折线变成直线再解.4. A B 分别为同一圆心0半径不等的两个圆上的一点,如图,将军从A 出发到河边海伦解决本问题时,是利用作对称点把折线问题转化成直线现在人们把凡是用对称点来实现解题的思想方法叫对称原理,即轴对称思想轴对称及其性质:把一个图形沿某一条直线折叠, 如果直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形.这条直线就是它的对称轴. 这时我们就说这个图形关于这条直线 (或轴)对称.如等腰 ABC 是轴对称图形.把一个图形沿着某一条直线折叠, 如果它能够与另一个图形重合, 那么就是说这两个图形关于这条 直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.如下图,ABC 与 A'B'C'关于直线I 对称,I 叫做对称轴.A 和A , B 和B' , C 和C'是对称点.轴对称的两个图形有如下性质:① 关于某条直线对称的两个图形是全等形; ② 对称轴是任何一对对应点所连线的垂直平分线;③两个图形关于某条直线对称,如果他们的对应线段或延长线相交,那么交点在对称轴上.线段垂直平分线:垂直平分线上点到线段两个端点的距离相等;到线段两个端点距离相等的点在线段的垂直平分线上.AP-aP^A B实用标准当已知条件出现了等腰三角形、角平分线、高,或者求几条折线段的最小值等情况, 对称变换,以“补齐”图形,集中条件。
最值模型之将军饮马11个常考模型(模型精讲)

最值模型之将军饮马(11个常考模型)模型背景【模型来历】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.【考点】两点之间线段最短,垂线段最短;三角形两边三边关系;轴对称;平行四边形--平移;【解题思路】学会化归,移花接木,化折为直【核心思想】共线与垂线段最短。
模型精讲一.两动一定型(2种模型):两定点到直线上一动点的距离和最小。
1如图1-1在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小.【证明】图1-2。
PA+PB的最小值即为线段AB的长度理由:在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP'中,AP´+BP´>AB,即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时,PA+PB最小.反思:解决本题很简单,但却点明了将军饮马的解题思路。
1.1如图1-3,如图,定点A和定点B在定直线l的同侧要求:在直线l上找一点P,使得PA+PB值最小 。
作法:图1-41.作A关于直线CD对称点A'。
2.连A'B。
3.交点P就是要求点。
连线长A'B就是PA+PB最小值。
【证明】:图1-5在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP'中,AP´+BP´>AB,即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时,PA+PB最小.二.造桥选址,移花接木。
1已知:如图2-1,直线a∥b,A、B分别为a上方和b下方的定点,(直线AB不与a垂直)要求:在a、b之间求作垂线段PQ,使得AP+PQ+BQ最小。
中考重难点易错专题 最值模型之将军饮马11个常考模型(模型精讲)

最值模型之将军饮马(11个常考模型)模型背景【模型来历】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.【考点】两点之间线段最短,垂线段最短;三角形两边三边关系;轴对称;平行四边形--平移;【解题思路】学会化归,移花接木,化折为直【核心思想】共线与垂线段最短。
模型精讲一.两动一定型(2种模型):两定点到直线上一动点的距离和最小。
1如图1-1在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小.【证明】图1-2。
PA+PB的最小值即为线段AB的长度理由:在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP'中,AP´+BP´>AB,即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时,PA+PB最小.反思:解决本题很简单,但却点明了将军饮马的解题思路。
1.1如图1-3,如图,定点A和定点B在定直线l的同侧要求:在直线l上找一点P,使得PA+PB值最小 。
作法:图1-41.作A关于直线CD对称点A'。
2.连A'B。
3.交点P就是要求点。
连线长A'B就是PA+PB最小值。
【证明】:图1-5在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP'中,AP´+BP´>AB,即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时,PA+PB最小.二.造桥选址,移花接木。
1已知:如图2-1,直线a∥b,A、B分别为a上方和b下方的定点,(直线AB不与a垂直)要求:在a、b之间求作垂线段PQ,使得AP+PQ+BQ最小。
最值系列之将军饮马(一)

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
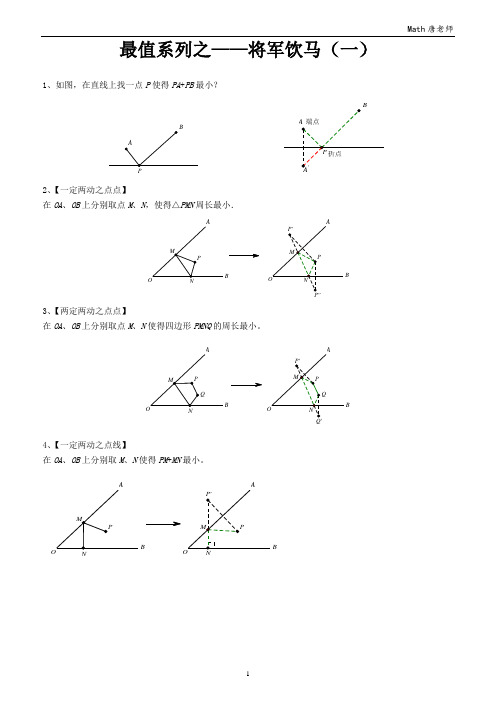
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?【问题分析】这个问题的难点在于P A+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB (折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.P''A当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
初中数学最值问题01专题-将军饮马模型与最值问题(含答案)

初中数学最值问题专题1 将军饮马模型与最值问题【模型导入】 什么是将军饮马?“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【模型描述】如图,将军在图中点A 处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?【模型抽象】如图,在直线上找一点P 使得P A +PB 最小?这个问题的难点在于P A +PB 是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段. 【模型解析】作点A 关于直线的对称点A ’,连接P A ’,则P A ’=P A ,所以P A +PB =P A ’+PB 当A ’、P 、B 三点共线的时候,P A ’+PB =A ’B ,此时为最小值(两点之间线段最短)B 将军军营河P【模型展示】【模型】一、两定一动之点点在OA 、OB 上分别取点M 、N ,使得△PMN 周长最小.此处M 、N 均为折点,分别作点P 关于OA (折点M 所在直线)、OB (折点N 所在直线)的对称点,化折线段PM +MN +NP 为P ’M +MN +NP ’’,当P ’、M 、N 、P ’’共线时,△PMN 周长最小.【例题】如图,点P 是∠AOB 内任意一点,∠AOB =30°,OP =8,点M 和点N 分别是射线OA 和射线OB 上的动点,则△PMN 周长的最小值为___________.BBP OBAMNP''A【模型】二、两定两动之点点在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。
考虑PQ 是条定线段,故只需考虑PM +MN +NQ 最小值即可,类似,分别作点P 、Q 关于OA 、OB 对称,化折线段PM +MN +NQ 为P ’M +MN +NQ ’,当P ’、M 、N 、Q ’共线时,四边形PMNQ 的周长最小。
初中数学最值系列之将军饮马

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?【问题分析】这个问题的难点在于PA+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.P''A当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
最值问题----将军饮马(二)

----之将军饮马(二)
什么是将军饮马?
【问题描述】: 如图,将军在图中点A处,现在他要带马去河 边喝水,之后返回军营,问:将军怎么走能使得路程最短?
【问题简化】: 如图,在直线上找一点P使得PA+PB最小?
【问题分析】:这个问题的难点在于PA+PB是一段折线段,通过观察图形很难得出结 果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段 最短”等,所以此处,需转化问题,将折线段变为直线段.
因为M、N皆为动点, 所以过点C作AB的垂线, 可得最小值.
08 菱形、矩中的将军饮马。
【问题描述】:如图,在菱形ABCD中,AC为6倍根号2,BD=6,E是BC的中点,P、M 分别是AC、AB上的动点,连接PE、PM,则PE+PM的最小值是____________.
【问题解析】:此处P为 折点,作点M关于AC的对 称点M',恰好在AD上, 化折线EP+PM为EP+PM'.
本节课你的收获是什么?
【问题解析】:对称点并不一 定总是在已知图形上.
07角分线系列之点到点。
【问题描述】:如图,在Rt△ABC中,∠ACB=90°,AC=6.AB=12,AD平分∠ACB,点 F是AC的中点,点E是AD上的动点,则CE+EF的最小值为________.
【问题解析】:此处E 点为折点,可作点C关 于AD的对称,对称点C' 在AB上且在AB中点, 化折线段CE+EF为 C'E+EF,当C'、E、F 共线时得最小值,C'E为 CB的一半.
【问题解析】:M点为折点,作B点关于AD的对称点,即C点,连接CN,即为所求的 最小值.过点C作AB垂线,利用勾股定理求得CN的长为2倍根号7.
最值系列之将军饮马

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?【问题简化】如图,在直线上找一点P使得PA+PB最小?【问题分析】这个问题的难点在于PA+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接PA’,则PA’=PA,所以PA+PB=PA’+PB当A’、P、B三点共线的时候,PA’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
初中数学几何最值问题(将军饮马、将军过河、费马点、隐圆、瓜豆、胡不归、阿氏圆)
1、如图,在直线上找一点P使得PA+PB最小?2、【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B3、【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
BB4、【一定两动之点线】在OA、OB上分别取M、N使得PM+MN最小。
BB【将军过桥】1.已知将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?2.已知A 、B 两点,MN 长度为定值,求确定M 、N 位置使得AM +MN +NB 值最小?军营河1.如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________.x2.如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CDEFM几何图形中的将军饮马正方形中的将军饮马1. 如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值是___________.NMD CBA2.如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .(2,2)B .5(2,5)2C .8(3,8)3D .(3,3)3.如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( )PDCBAA .4B .5C .6D .7三角形中的将军饮马1.如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________.A BCDMN2. 如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为( )E AFCDBA .3B .4C .33D .233. 如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( )NMDCBAA .3B .2C .23D .44.如图,△ABC 中,∠BAC =75°,∠ACB =60°,AC =4,则△ABC 的面积为_;点D ,点E ,点F 分别为BC ,AB ,AC 上的动点,连接DE ,EF ,FD ,则△DEF 的周长最小值为 .矩形、菱形中的将军饮马1. 如图,在菱形ABCD 中,AC=BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是( )EPDCBAMA .6 B.C.D .4.52.如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( )A .4(0,)3B .5(0,)3C .(0,2)D .10(0,)33.如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和PA +PB的最小值为( )DCBAPA. B.C.D4.如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )H FGEDCB AA.B. C. D.特殊角的对称1. 如图,∠AOB =60°,点P 是∠AOB 内的定点且OPM 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )ABMOPNABC .6D .32. 如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .x3. 如图,已知正比例函数y =kx (k >0)的图像与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图像上的两个动点,则AM +MP +PN 的最小值为____________.求两线段差的最大值问题基本图形解析:在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A-P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
最值系列之将军饮马 - 解析

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?P【问题分析】这个问题的难点在于P A+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB 上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.AP''当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
中考专题系列之最值——将军饮马

中考专题系列之最值——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?【问题分析】这个问题的难点在于P A+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.P''A当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
2020中考数学复习 最值问题-将军饮马问题 (51张PPT)

04、特殊角的对称 ----60°角的对称
【分析】
此处M、N均为折点,分别作点P关于OB、OA的对 称点P'、P'',化△PMN周长为P'N+NM+MP''.
4、60°、30°、20°角中的将军饮马
02、将军饮马模型系列 ————“一定两动”之点到点
在OA、OB上分别取点M、N,使得△PMN周长最小。
此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线) 的对称点,化折线段PM+MN+NP为P'M+MN+NP'',当P'、M、N、P''共线时,△PMN 周长最小。
03、几何图形中的将军饮马 ----菱形和矩形中的“将军饮马”
【面积与折点】 如图,在矩形ABCD中,AB=6,AD=3,动点P满足△APB的面积是矩形
ABCD面积的三分之一,则点P到A、B两点距离之和PA+PB的最小值为_________.
03、几何图形中的将军饮马 ----菱形和矩形中的“将军饮马”
【将军过双桥】
已知将军在图中点A处,现要过 两条河去往B点的军营,桥必须 垂直于河岸建造,问:桥建在何 处能使路程最短?
05、将军过桥
【分析】考虑PQ、MN均为定值,所以路程最短等价于 AP+QM+NB最小,对于这彼此分离的三段,可以通过平 移使其连接到一起.AP平移至A'Q,NB平移至MB',化 AP+QM+NB为A'Q+QM+MB'.
最值问题----将军饮马(三)

----之将军饮马(三)
什么是将军饮马?
【问题描述】: 如图,将军在图中点A处,现在他要带马去河 边喝水,之后返回军营,问:将军怎么走能使得路程最短?
【问题简化】: 如图,在直线上找一点P使得PA+PB最小?
【问题分析】:这个问题的难点在于PA+PB是一段折线段,通过观察图形很难得出结 果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段 最短”等,所以此处,需转化问题,将折线段变为直线段.
【问题解决】作点A关于直线的 对称点A',连接PA',则PA'=PA, 所以PA+PB=PA'+PB.
当A'、P、B三点共线的时 候,PA'+PB=A'B,此时为最小 值(两点之间线段最短)
09 将军饮马(面积与折点)。
【问题描述】:如图,在矩形ABCD中,AB=6,AD=3,动点P满足△APB的面积是矩形 ABCD面积的三分之一,则点P到A、B两点距离之和PA+PB的最小值为_________.
【解析】:此处点P为折点, 作点M关于OA的对称对称点 M'如图所示,连接PM',化 PM+PN为PM'+PN.
当M'、P、N共线时,得最 小值,又∠M'ON=60°且 ON=2OM',可得∠OM'N=90°, 故P点坐标可求。
13 将军饮马( 20°角的对称)。
【问题描述】:如图,已知正比例函数y=kx(k>0)的图像与x轴相交所成的锐角为 70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图 像上的两个动点,则AM+MP+PN的最小值为___________ .
中考数学二次函数压轴题突破最值问题之将军饮马

O
N
P''
此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N
所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、
N、P’’共线时,△PMN周长最小.
【例题】如图,点 P 是∠AOB 内任意一点,∠AOB=30°,OP=8,点 M 和点 N 分别是射线 OA 和射线 OB 上的动点,则△PMN 周长的最小值为___________.
形 PMNQ 的周长最小。
【一定两动之点线】
在OA、OB上分别取M、N使得PM+MN最小。
A
A
P'
M P
M
P
O
N
B
ON
B
此处 M 点为折点,作点 P 关于 OA 对称的点 P’,将折线段 PM+MN 转化为 P’M+MN ,即 过点 P’作 OB 垂线分别交 OA、OB 于点 M、N,得 PM+MN 最小值(点到直线的连线中, 垂线段最短)
二次中物函理 数压轴题突破 ——最值问题之将军饮马
中物理
将军饮马(一)
1 一、什么是将军饮马?
【问题引入】 “白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人 李颀《古从军行》里的一句诗。而由此却引申出一系 列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】 如图,将军在图中点A处,现在他要带马去河边喝水,之后返 回军营,问:将军怎么走能使得路程最短?
当A’、P、B三点共线的时候,PA’+PB=A’B, 此时为最小值(两点之间线段最短)
【思路概述】
作端点(点A或点B)关于折点(上图P点)所在直线的对称,
最值系列之将军饮马

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?【问题分析】这个问题的难点在于P A+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.P''A当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
1最值系列之将军饮马

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?A B将军军营河【问题简化】如图,在直线上找一点P使得P A+PB最小?二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.例题:如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA 和射线OB上的动点,则△PMN周长的最小值为___________.【两定两动之点点】在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。
BB考虑PQ 是条定线段,故只需考虑PM +MN +NQ 最小值即可,类似,分别作点P 、Q 关于OA 、OB 对称,化折线段PM +MN +NQ 为P ’M +MN +NQ ’,当P ’、M 、N 、Q ’共线时,四边形PMNQ 的周长最小。
【一定两动之点线】在OA 、OB 上分别取M 、N 使得PM +MN 最小。
BB此处M 点为折点,作点P 关于OA 对称的点P ’,将折线段PM +MN 转化为P ’M +MN ,即过点P ’作OB 垂线分别交OA 、OB 于点M 、N ,得PM +MN 最小值(点到直线的连线中,垂线段最短)三、几何图形中的将军饮马1.正方形中的将军饮马(1)如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值是___________NMDCBA POBAM N(2).如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为(3).如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB上的动点,则PC +PD 的最小值为2.三角形中的将军饮马(1).如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________.(2).如图,在Rt △ABD 中,AB =6,∠BAD =30°,∠D =90°,N 为AB 上一点且BN =2AN , M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________.PDCBAABCDM NN M D BA3.角分线系列之点点如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为4.角分线系列之点线(2)如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是5.矩形、菱形中的将军饮马如图,在菱形ABCD 中,AC=BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是EPDCBAM6.折点在边上如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( )E AFCDBNM D C BA7.折点与面积如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和P A +PB 的最小值为( )8.全等与对称如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为9.60°角的对称如图,∠AOB =60°,点P 是∠AOB 内的定点且OPM 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( ).10.30°角的对称如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .DCBAPH FGEDCB AABMOP Nx11.20°角的对称如图,已知正比例函数y=kx(k>0)的图像与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图像上的两个动点,则AM+MP+PN 的最小值为____________.12.将军过桥已知将军在图中点A处,现要过河去往B点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN长度恒定,只要求AM+NB最小值即可.问题在于AM、NB彼此分离,所以首先通过平移,使AM与NB连在一起,将AM向下平移使得M、N重合,此时A点落在A’位置.问题化为求A’N+NB最小值,显然,当共线时,值最小,并得出桥应建的位置.【用几何变换将若干段原本彼此分离线段组合到一起】【将军过两个桥】已知将军在图中点A 处,现要过两条河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?军营B考虑PQ 、MN 均为定值,所以路程最短等价于AP +QM +NB 最小,对于这彼此分离的三段,可以通过平移使其连接到一起.BAP 平移至A ’Q ,NB 平移至MB ’,化AP +QM +NB 为A ’Q +QM +MB ’.B当A ’、Q 、M 、B ’共线时,A ’Q +QM +MB ’取到最小值,再依次确定P 、N 位置.【将军遛马】如图,将军在A点处,现在将军要带马去河边喝水,并沿着河岸走一段路,再返回军营,问怎么走路程最短?【问题简化】已知A、B两点,MN长度为定值,求确定M、N位置使得AM+MN+NB值最小?军营河【分析】考虑MN为定值,故只要AM+BN值最小即可.将AM平移使M、N重合,AM=A’N,将AM+BN转化为A’N+NB.构造点A关于MN的对称点A’’,连接A’’B,可依次确定N、M位置,可得路线.(1).如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点A、C在坐标轴上,点D 的坐标为(6,4),E为CD的中点,点P、Q为BC边上两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐示应为______________.x(2).如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CDEFM。
1最值系列之将军饮马

最值系列之——将军饮马一、什么是将军饮马?【问题引入】“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【问题描述】如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?军营B将军河【问题简化】如图,在直线上找一点P使得P A+PB最小?【问题分析】这个问题的难点在于P A+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.【问题解决】作点A关于直线的对称点A’,连接P A’,则P A’=P A,所以P A+PB=P A’+PB当A’、P、B三点共线的时候,P A’+PB=A’B,此时为最小值(两点之间线段最短)【思路概述】作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B B此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P’M+MN+NP’’,当P’、M、N、P’’共线时,△PMN周长最小.【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________.P O B AMN【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P’、P’’,化PM+PN+MN为P’N+MN+P’’M.P''A当P’、N、M、P’’共线时,得△PMN周长的最小值,即线段P’P’’长,连接OP’、OP’’,可得△OP’P’’为等边三角形,所以P’P’’=OP’=OP=8.A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最值问题之将军饮马学生姓名:年级:
科目: .
任课教师:日期:
时段: .
将军饮马问题
模型1两定一动
例:如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点
则DN+MN的最小值为()
A:6 B:8 C:2 D:10
解析:第一步—找:找定点、动点、动点所在的直线
第二步—作:作定点关于动点所在直线的对称点(从对称性入手)
第三步—连:连接对称点与另一个点
第四步—求:求解(一般勾股定理求解)
模型2一定两动
例:如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,则BM+MN的最小值为()
A.10 B.8 C.5 D.6
解析:第一步—找:找定点、动点、动点所在的直线
第二步—作:作定点关于动点所在直线的对称点(从对称性入手)
第三步—连:连接对称点与另一个点
第四步—造:构造垂直
第五步—求:求解(一般等积法或相似求解)
模型3求四边形的周长最小值
例:如图,当四边形PABN的周长最小时,a= .
解析:本题要求四边形周长最小值。
因为AB、PN是定长,问题转化为求PA+NB的最小值,跟模型1类似,所以我们需要平移确定交点,转换成模型1去讲解
模型4 一定点、两定直线
例:点P是∠MON内的一点,分别在OM,ON上作点A,B,使△PAB的周长最小?
解析:第一步:分别画点P关于直线OM、ON的对称点P1、P2
第二步:联结P1P2,交OM、ON于点A、点B
跟踪练习
1.如图:点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP=32,则△PMN的周长的最小值为.
2.已知,A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=1,且MN=4,P为直线上的动点,|PA﹣PB|的最大值为.
3.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标
PA-的值最大的点,Q是y轴上使得QA十QB 系如图所示.若P是x轴上使得PB
的值最小的点,则OQ
OP•=.
4.如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.
5.如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15°,点D、E分别为AM、AB的动点,则BD+DE的最小值是
6.五边形ABCDE 中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC 、DE 上分别找一点M 、N ,使得△AMN 的周长最小,则△AMN 周长的最小值为 。
7.如图,平面直角坐标系中,分别以点A (2,3),点B (3,4)为圆心,1、3为半径作⊙A 、⊙B,M,N 分别是⊙A ,⊙B 上的动点,P 为x 轴上的动点,则PM+PN 的最小值为( )
A 、4-25
B 、 1-17
C 、6-22
D 、17
8.如图,∠MON=30°,A 在OM 上,OA=2,D 在ON 上,OD=4,C 在OM 上的任意一点,B 是ON 上的任意一点,则折线ABCD 的最短长度为 .
9.如图1,等边△ABC的边长为6,AD,BE是两条边上的高,点O为其交点.
P,N分别是BE,BC上的动点.
(1)当PN+PD的长度取得最小值时,求BP的长度;
(2)如图2,若点Q在线段BO上,BQ=1,求QN+NP+PD的最小值.
10.如图,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、E.F分别是边AB、BC、AC上的动点则DE+EF+FD的最小值为( )
A. 4.8
B. 6
C. 10
D. 无法确定
课堂检测测试题成绩
教学需要加快()保持()放慢()
课堂反馈◇非常满意◇满意◇一般◇差。
