多元凸函数的判定

合集下载

多元凸函数判据

多元凸函数判据是数学中的一个重要概念，它在优化理论、机器学习等领域有着广泛的应用。

下面我将简要介绍多元凸函数判据的基本概念和性质。

首先，我们需要了解什么是多元函数。

在n个变量中的实值函数就是n元函数。

在数学上，多元函数是一个集合，其中的元素是一个二元有序数组，代表一个变量和该变量对应的函数值。

凸函数是一种特殊的函数，它在定义域的某个子集上是凸的。

对于多元函数，如果它在定义域的某个子集上的所有点处的导数都存在，且满足一定的条件（如对所有的点都成立），则这个多元函数被称为凸函数。

多元凸函数判据是一种判断多元函数是否为凸函数的准则。

它的基本思想是利用函数的几何性质来判断函数的导数性质。

在多元函数的几何学习中，我们知道函数的局部性态常常反映了全局的性质，因此可以通过研究局部性质来判断全局性质。

多元凸函数判据的主要内容包括：1. 定义域和值域：多元凸函数的定义域是一个凸集，值域是一个凸集。

这意味着函数的定义域和值域都满足一定的凸性条件。

2. 梯度：多元函数的梯度是一个向量场，它描述了函数在某一点处的变化趋势。

如果一个多元函数的梯度在某个子集上是存在的，且具有某些特定的性质（如线性或恒等性），则这个多元函数被称为是可微分的。

3. 拉格朗日函数：在多元函数中，拉格朗日函数是一个非常重要的工具。

它可以用来表示多元函数的泛函关系，并且可以借助它来推导函数的性质。

综上所述，多元凸函数判据是数学中的一个重要概念，它提供了一种判断多元函数是否为凸函数的简便方法。

通过定义域、梯度、拉格朗日函数等概念和性质的研究，我们可以更深入地了解多元函数的性质，为解决实际问题提供更有价值的工具和方法。

函数的凹凸性定义

函数的凹凸性定义函数的凹凸性是描述函数曲线在图像上的弯曲程度和凸出程度的性质。

在数学中，凹（concave）和凸（convex）是两个相对的概念，用于描述一条曲线或曲面的形状。

具体来说，凹函数表示曲线向下弯曲，凸函数表示曲线向上弯曲。

凹凸性在优化问题和最优化理论中具有重要的应用。

在函数的凹凸性中，凸函数有许多优良的性质，例如在最优化问题中，任何凸函数的局部极小值就是全局极小值，这为优化问题的求解提供了有效的方法。

一元函数的凹凸性：凹凸性的定义可以通过一元函数的二阶导数来描述。

对于一个二次可导的一元函数f(x)，函数的凹凸性可以通过函数的二阶导数f''(x)的符号来判定。

若f''(x)>0，则函数f(x)在区间内上凸，在该区间内的任意两个点x1和x2，有f(x1)<f(x2)；若f''(x)<0，则函数f(x)在区间内下凸，在该区间内的任意两个点x1和x2，有f(x1)>f(x2)；若f''(x)=0，则函数f(x)在该点的凹凸性无定义，需要通过其他方法来判定。

总结起来，根据函数的二阶导数的符号，可以确定函数的凹凸性。

当f''(x)大于零时，函数是凸的；当f''(x)小于零时，函数是凹的。

多元函数的凹凸性：对于多元函数 f(x1, x2, ..., xn)，凹凸性的定义和判定需要通过二阶偏导数来描述。

定义：对于定义在凸集上的连续可微函数，如果对于集合上的任意两点x和y，有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y)，其中0≤λ≤1，则函数f(x)是凸函数。

根据多元函数的定义和凸函数的性质，可以确定一个多元函数的凹凸性：1. 凸函数：如果多元函数的 Hessian 矩阵（二阶偏导数矩阵）是半正定的，则函数是凸的。

即，对于函数的 Hessian 矩阵 H，如果对于任意的向量 v，有v^THv ≥ 0，则函数是凸的。

凸函数三元函数

凸函数三元函数
我们要证明一个三元函数是凸函数，首先需要了解凸函数的定义。

凸函数的定义：对于一个定义在某个开集上的函数f，如果对于该集合中的任意两点x1和x2，以及任意λ∈(0,1)，都有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)，那么我们称f为凸函数。

现在，我们假设有一个三元函数f(x,y,z)，我们要证明它是凸函数。

我们可以按照以下步骤进行：
第一步，假设有两个点A(x1,y1,z1)和B(x2,y2,z2)在函数的定义域内。

第二步，根据凸函数的定义，我们需要找到一个λ∈(0,1)，使得f(λA+(1-λ)B)≤λf(A)+(1-λ)f(B)。

第三步，根据凸函数的性质，如果一个函数在某一点的一阶导数大于0，那么该函数在该点是凸的。

因此，我们可以计算f的一阶偏导数，并检查其是否大于0。

如果所有的偏导数都大于0，那么函数是凸的。

第四步，通过计算一阶偏导数，我们可以得到一个不等式系统。

如果这个不
等式系统对于所有的x, y, z都成立，那么我们可以说f是一个凸函数。

综上所述，为了证明一个三元函数是凸函数，我们需要证明对于所有的x, y, z，该函数的一阶偏导数都大于0。

凸函数的性质及判定

2008年9月第28卷第5期天水师范学院学报J our nal of Ti ans h ui N or m al U ni ve r si t yS e p．，2008V01．28N o．5凸函数的性质及判定刘开生，王贵军(天水师范学院数学与统计学院，甘肃天水741001)摘要：给出了凸函数的一些重要性质及判定定理，研究了函数的凸性与函数奇偶性、单调性之问的关系。

关t词：凸函数；性质；关系中图分类号：0174．6文献标识码：A文章编号：1671—1351(2008)05—0012—021预备知识文献【1】中给出凸函数的定义如下：设触)为定义在区间I上的函数，若对任意两点菇I，X2和实数O<A<I，总军￡“A戈l+(1一A)z2)≤。

讹1)+(1一A批2)，则镌触)为定义在I上的凸函数。

若锹从，+(10k：)≥讹1)+(1_A掀2)，则镌舷)为定义在I上的凹函数。

其次，文献还给出了判别触)为I上的凸函数的四个等价命题；同时也给出了利用二阶导数判别厂0)为I上凸(凹)函数的判断命题。

定理1．1设，b)为定义在区间I上的可导函数。

则下述命题等价(1)．肭为I上的凸函数；(2)厂0)为I上的增函数；(3)对I上任意两点名，，互：有m2)≥触，)矿@t)02．略t)；(4)．尸@)≥0，茗∈I．定理1．2f11设M为定义在区间I上的二阶可导函数，则在I上触)为凸(凹)函数的充要条件是厂0)≥O(尸G)≤0)，茗∈I定理1．掣l若触)为区间I上的凸函数．则慨。

，戈：∈I，欹华)≤世屿监2主要结果及其证明定理2．1勘∞石@)均为【a，b】上的凸函数，贝岍G)坼仁)也是【a'b】上的凸函数。

定理2．2蝴∽为【a，bl上的凸函数，j}为正常数，则坼)也为【a，b】上的凸函数。

注2．1：定理2．1和定理2．2利用文献f11中所给的定义可直接证明。

定理2．3设u吡)为[a，hi I-I拘凸函数，g(∞在【a，bl t-单调递增，且也为[a，b】上的凸函数，则复合函数的讧))也是【a，b】上的凸函数。

多元凸函数的性质及其应用

收稿日期:2008-06-30
第16卷第4期
2008年12月
北京石油化工学院学报
Journal of Beijing Institute of
Petro-chemical Technology
Vol.16 No.4
Dec.2008
多元凸函数的性质及其应用
游煦
别它的凸性。这在实际应用中有一定的意义。
关键词多元凸函数;梯度向量;Hesse矩阵;半正定阵;二次函数
中图法分类号 O174
凸分析是近几十年形成和发展起来的一个
新数学分支。它在数学规划、控制论、多元统计
等领域都有广泛的应用。文献[1-3]给出了一
些判别多元函数凸性的充分必要条件,但是这
ence[1,3],we can get some necessary and sufficient conditions for judging the convexity of func-
tion of many variables by directional derivative and limit.Furthermore,we obtain the method of
(北京石油化工学院数理系,北京102617)
摘要从多元凸函数的定义及文献中已有的性质出发,利用方向导数和极限等数学工具,
给出了一个判别多元函数凸性的充分必要条件,进一步利用函数f(x)的Hesse矩阵Hf(x)的半正
定性来判定函数的凸性。特别地,对于二次函数f(x)=12xTAx+bTx直接利用矩阵A的正定性可以判
t≤
f(x2)-f(x1), (5)
令t※0+,式(5)左端得到f(x)在点x1处沿方

凸函数判定方法的研究

凸函数判定方法的研究鸡冠山九年一贯制学校张岩2013年12月15日目录摘要 (ii)关键词 (ii)Abstract (ii)Key words (ii)前言 (iii)一、凸函数的基本理论 (1)1、预备知识 (1)2、凸函数的概念及性质 (2)二、凸函数的判定方法 (4)（一）一元函数凸性的判定方法 (4)1、利用作图判断函数凸性 (4)2、其它判定方法 (5)（二）多元函数凸性的判定方法 (8)1、多元凸函数的有关概念 (8)2、多元函数凸性的判定方法 (9)三、凸函数几个其他判定方法 (12)四、总结 (14)参考文献 (14)致谢 (15)凸函数判定方法的研究摘要:凸函数是一类非常重要的函数，借助它的凸性可以科学准确地描述函数图像，而且可以用于不等式的证明。

同时，凸函数也是优化问题中重要的研究对象，研究的内容非常丰富，研究的结果已在许多领域得到广泛的应用，因此凸函数及其性质以及凸性判定的充要条件的研究就显得尤为重要。

本文首先给出了凸函数的一些基本概念和结论，然后针对一元和多元函数，对凸函数的判定做了研究和讨论，本文最后也给出几种新的判定凸函数的方法。

关键词：凸函数；梯度；Hesse 矩阵；泰勒定理Abstract: Convex function is a kind of very important functions, with the help of its convexity we can accurately describe the graph of functions and it can also be used to prove the inequalities. As the significant object in optimization problems, the contents about convex functions we study are very abundant, the results obtained so far has been applied to many fields. Therefore, the topic we concern about is deserved to be discussed. In this paper, we firstly present some basic definitions and properties of convex functions, then aiming at the univariate function and multi-variable functions we give several criterions for determining the convexity of functions. Finally, some new principles are also given.Key words：Convex function; Gradient; Hesse matrix; Taylor Theorem前言提起凸函数,人们都会想起它的许多良好性质和在数学中的重要作用。

第三节凸函数

f(x1+ λ (x2-x1))= f(x1) + λ▽f(x1)T(x2-x1)+o(λ) (1) 而由于f(x)是D上的凸函数，又有
f(x1+ λ (x2-x1))=f(λ x2+ (1-λ )x1)
≤ λ f(x2) + (1-λ ) f(x1)
(2)
两式联立，有
λ f(x2) + (1-λ ) f(x1) ≥ f(x1) + λ▽f(x1)T(x2-x1)+o(λ)
f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)
则称f(x)是定义集D上的凸函数。
定义2 严格凸函数 f[λx1+(1-λ)x2]＜λf(x1)+(1-λ)f(x2)
则称f(x)是定义集D上的凸函数。注：将上述定义中的不等式反向，可以得到
凹函数的定义。
凸函数的几何性质
对一元函数f(x),在几何上λf(x1)+(1-λ)f(x2) （0≤α≤1)表示连接(x1，f(x1))， (x2，f(x2))的线段。
• 性质3 设D是内部非空的凸集，f(x)是定义在D上的凸函数，则f(x)在D的内部连续。
注意：凸函数在定义域的边界有可能不连续。例如，设f(x)的定义域是区间[1,4] x2,1<x<4
f(x)=
2,x=1 f(x)是区间[1,4]上的凸函数，但显然在边界点x=1处不连续。
三、凸函数的判定
其中，x=λx1+(1-λ)x2 , 0≤λ≤1
(x2-xf1()x_ )
_
由于D是凸集，故x∈D,由已知条件，当然▽2
f(也x_ )是半正
定矩阵。于是有

函数凹凸性的应用

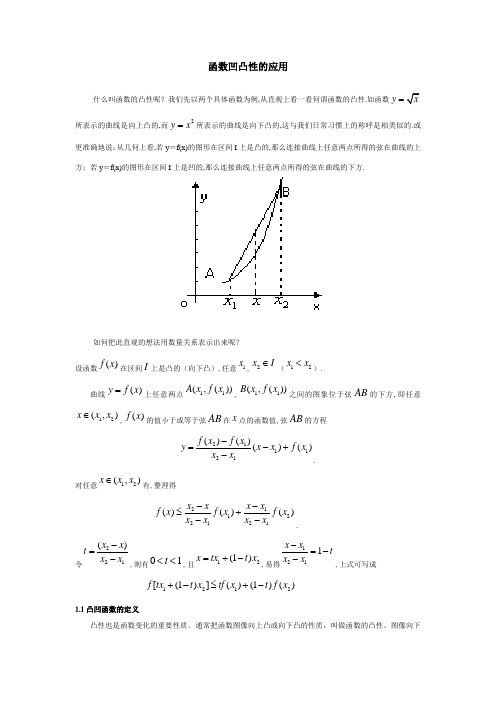
函数凹凸性的应用什么叫函数的凸性呢？我们先以两个具体函数为例,从直观上看一看何谓函数的凸性.如函数y =所表示的曲线是向上凸的,而2y x =所表示的曲线是向下凸的,这与我们日常习惯上的称呼是相类似的.或更准确地说：从几何上看,若y ＝f(x)的图形在区间I 上是凸的,那么连接曲线上任意两点所得的弦在曲线的上方；若y ＝f(x)的图形在区间I 上是凹的,那么连接曲线上任意两点所得的弦在曲线的下方.如何把此直观的想法用数量关系表示出来呢？设函数()f x 在区间I上是凸的（向下凸）,任意1x ,2x I∈（12x x <）.曲线()y f x =上任意两点11(,())A x f x ,11(,())B x f x 之间的图象位于弦AB的下方,即任意12(,)x x x ∈,()f x 的值小于或等于弦AB 在x 点的函数值,弦AB 的方程211121()()()()f x f x y x x f x x x -=-+-.对任意12(,)x x x ∈有,整理得21122121()()()x x x x f x f x f x x x x x --≤+--.令221()x x t x x -=-,则有01t <<,且12(1)x tx t x =+-,易得1211x x tx x -=--,上式可写成1212[(1)]()(1)()f tx t x tf x t f x +-≤+-1.1凸凹函数的定义凸性也是函数变化的重要性质。

通常把函数图像向上凸或向下凸的性质，叫做函数的凸性。

图像向下凸的函数叫做凸函数，图像向上凸的函数叫做凹函数。

设[]()()()()()211212:,,,0,1,11f I R I f ff x x x x x x λλλλλ→∀∈∀∈+-≤+-若不等式成立，（1）则称f为I 上的凸函数。

若()120,1,,x x λ∀∈≠()()()()()121211f ff x x x x λλλλ+-+-不等式（2）则称f 为I 上的严格凸函数。

函数凹凸性的性质判定及应用

函数凹凸性的判定性质及应用曹阳数学计算机科学学院摘要：函数的凹凸性在数学研究中具有重要的意义。

本文从凸函数的多种定义入手，引出凹凸函数的性质，介绍了凹凸函数的性质及判定定理。

在此基础上，将一元函数的凹凸性进行推广，推广到二元函数上，讨论了二元函数凹凸性的性质，判定方法及其应用。

一元到二元，即增加了一个变量，那么对于ｎ元的情况是否有相似的函数存在呢？本文层层深入，将二元函数进行再次推广，至ｎ元的情形，给出ｎ元凹凸函数的定义，判定方法及性质。

本文主要讨论了一元，二元，多元凹凸函数的定义，性质，及判定方法，并介绍了它们应用。

关键词：凹凸性；一元函数；二元函数；多元函数；判别法；应用；Convex function of Judge Properties and Applications Abstract: The function of convexity in mathematical research is of great significance. In this paper, the definition of convex function of a variety of start, leads to uneven nature of the function, describes the properties of convex functions and decision theorem. On this basis, the concave and convex functions of one variable to promote, promote to the binary function, discusses the uneven nature of the nature of the binary function, determine the method and its application. One to a binary, an increase of a variable, then for n-whether it is a similar function exist? This layers of depth, the binary function tore-promote, to the case of n-given definition of n-convex function, determine the methods and properties. This article focuses on one element, binary, multiple convex function definition, nature, and judging methods, and describes their application.Keywords: Convexity; One Function; Binary function; Multiple functions; Criterion; Applications;1.引言凸函数是数学中一类极其重要的函数，它在最优化，运筹与控制理论，模具设计等方面具有重要的理论和实践意义。

凸函数的几个等价定义讲解

本科生毕业论文题目凸函数的几个等价定义系别班级姓名学号答辩时间年月学院目录摘要 (4)1凸函数的定义 (6)2凸函数的等价定义和性质 (6)2.1凸函数的等价定义 (6)2.2凸函数的性质 (7)3凸函数等价定义和性质的应用举例 (10)3.1一些集合上的凸函数举例 (10)3.2运用凸函数等价定义证明不等式 (11)总结 (16)参考文献 (17)谢辞 (18)凸函数的几个等价定义摘要凸函数是一类重要的函数，它的概念最早见于Jensen在1905年的著述中。

它在纯粹数学和应用数学的众多领域中具有广泛的应用，现已成为数学规划、对策论、数理经济学、变分学和最优控制等学科的理论基础和有力工具。

为了理论上的突破，加强它们在实践中的应用，产生了广义凸函数。

本文主要归纳了凸函数的几个常见定义和性质以及它们在不等式证明等几个方面的应用。

关键词：凸函数；等价性；不等式Several equivalent of convex function definedAbstractConvex function is a kind of important function, it is the concept of the earliest Jensen in 1905 in the works. It in pure mathematics and applied mathematics of many fields has wide application, it has become the mathematical programming, the game theory and mathematical economics, variational learn and optimal control subjects such as theoretical basis and powerful tools. In order to theoretical breakthrough, strengthen them in practical application, produced the generalized convex function. This paper mainly summarizes the convex function of several common definition and characteristics and their inequation and so on several aspects in the application. [Key wards]Convex functions; Equivalence; Inequality.凸函数是一种性质特殊的函数，在许多数学分支中，经常可以看到有关的应用，例如在数学分析、函数论、泛函分析、最优化理论等当中。

函数的凸性及其判别的充要条件

! ! , ?" ,"存在 ,"% = 6 E : 4 ’: : ! 4 ? ?$#
@ 4 @ 并且由 ! "式知 ,"存在 # ! "" 类似地可得到 :’ ! @ @ $ ,"* :’ ! ," :4 !
不减的 $ 为了证明函数的凸性 # 只要证明对 4, ’ 0, 0 # # # ! # " 有 , , , ’ , , , 5 /1
关键词 " 连续 % 可微 % 凸函数 % 充要条件中图分类号 "Y " # ’ & !K ’ """ 文献标志码 "(" 文章编号 "’ ) & ’*+ ’ # # , # # & # "*# # , N*# "
’" 引言
凸函数是一类特殊的函数 $ 利用凸函数的性质可以证明数学中的许多著名的不等式 $ 如詹森 " # 不等式 & 赫尔德 " # 不等式等 $ 凸函 S 1 2 4 7 2 0 8 = > 7 D 数的不同形式的定义在不同的场合使用各有方便之处 $ 在同济大学编写的 ’ 高等数学( 教材中! 给出 :" 在" 内是凸函数的定义 $ ,# /! 1# 定义 ’K 若 :" 在" 内连续! 并且对 ’) ,# /! 1# 有) , /! 1# 4, ’! ,5 "
’ 设 :! ,"在 ! /# 1"内可微 # ,"为 "" 定理 "6 :! @ ! 内的凸函数 8: ! 在! 内是单调不减 /# 1" ," /# 1" 的# 进而 # 若:! 在! 内二阶可导 # 则:! 在 ," /# 1" ," ; ! # " 内是凸函数 ! " /1 8: , & # 证明 % 定理 , 的后一结果是前一个结果的直接推论 # 因而 # 只要证明定理的前一部分 $ 由 :! ,"在 ! /# 1"内可微及 :! ,"是 ! /# 1"内

凸函数与严格凸函数的几个新判别准则

凸函数与严格凸函数的几个新判别准则凸函数是数学中一类非常重要的函数形式，它在优化理论、经济学、物理学等领域都有广泛的应用。

而严格凸函数则是凸函数中的一种特殊情况，具有更严格的性质。

在本文中，我们将讨论凸函数和严格凸函数的定义，并介绍凸函数与严格凸函数的几个新判别准则。

首先，我们来回顾一下凸函数的定义。

对于定义在实数集合上的函数f(x)，如果对于任意的x1和x2以及任意的t∈[0,1]，都有如下的不等式成立，那么f(x)是一个凸函数：f(tx1+(1-t)x2) ≤ tf(x1) + (1-t)f(x2)凸函数的定义可以解释为，对于函数上的任意两个点，连接这两个点的线段上的所有点的函数值都不大于这条线段的两个端点的函数值的加权平均。

也就是说，凸函数图像上的任意两点之间的线段上的所有点都位于图像的下方或者位于图像上。

接下来，我们来介绍凸函数的两个基本性质：1.凸函数的定义域必须是一个凸集。

这意味着，对于定义在一维空间上的凸函数，它的定义域必须是一个区间，对于定义在多维空间上的凸函数，它的定义域必须是一个凸集合。

2.凸函数的一阶导数是单调递增的。

这意味着，对于凸函数f(x)，它的导数f'(x)在定义域上必须是单调递增的，也就是说，对于任意的x1<x2，在x1和x2之间的任意一点x，都有f'(x1)≤f'(x)≤f'(x2)。

不过，仅仅通过这两个性质来判断一个函数是否是凸函数可能不够严格，因为它们仅仅是凸函数的充要条件而不是必要条件。

为此，我们引入了更严格的严格凸函数的定义。

对于定义在实数集合上的函数f(x)，如果对于任意的x1和x2(x1≠x2)，都有如下的不等式成立，那么f(x)是一个严格凸函数：f(tx1+(1-t)x2) < tf(x1) + (1-t)f(x2)严格凸函数的定义要求连接函数上任意两点的线段上的所有内点的函数值都严格小于连接这两个点的线段的两个端点的函数值的加权平均。

凸函数简介——精选推荐

凸函数简介凸函数简介凸函数凸函数是⼀个定义在某个向量空间的凸⼦集C（区间）上的实值函数f，⽽且对于凸⼦集C中任意两个向量x1,x2,f((x1+x2)/2)≤(f(x1)+f(x2))/2。

于是容易得出对于任意(0,1)中有理数p,f(px1+(1-p)x2)≤pf(x1)+(1-p)f(x2)。

如果f连续，那么p可以改成任意(0,1)中实数。

若这⾥凸集C即某个区间I,那么就是：设f为定义在区间Ｉ上的函数，若对Ｉ上的任意两点Ｘ１，Ｘ２和任意的实数λ∈（０，１），总有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则f称为Ｉ上的凸函数。

判定⽅法可利⽤定义法、已知结论法以及函数的⼆阶导数对于实数集上的凸函数，⼀般的判别⽅法是求它的⼆阶导数，如果其⼆阶导数在区间上恒⼤于等于0，就称为凸函数。

（向下凸）如果其⼆阶导数在区间上恒⼤于0，就称为严格凸函数。

性质定义在某个开区间C内的凸函数f在C内连续，且在除可数个点之外的所有点可微。

如果C是闭区间，那么f有可能在C的端点不连续。

⼀元可微函数在某个区间上是凸的，当且仅当它的导数在该区间上单调递减。

⼀元连续可微函数在区间上是凸的，当且仅当函数位于所有它的切线的上⽅：对于区间内的所有x和y，都有f(y) ≥ f(x) + f '(x) (y x)。

特别地，如果f '(c) = 0，那么c是f(x)的最⼩值。

⼀元⼆阶可微的函数在区间上是凸的，当且仅当它的⼆阶导数是⾮负的；这可以⽤来判断某个函数是不是凸函数。

如果它的⼆阶导数是正数，那么函数就是严格凸的，但反过来不成⽴。

例如，f(x) = x4的⼆阶导数是f "(x) = 12 x2，当x = 0时为零，但x4是严格凸的。

更⼀般地，多元⼆次可微的连续函数在凸集上是凸的，当且仅当它的⿊塞矩阵在凸集的内部是正定的。

凸函数的任何极⼩值也是最⼩值。

严格凸函数最多有⼀个最⼩值。

对于凸函数f，⽔平⼦集{x | f(x) < a}和{x | f(x) ≤ a}（a ∈ R）是凸集。

(完整word版)多元凸函数的判定

多元凸函数的判定1 引言凸函数是一类基本函数，具有非常好的分析学性质,在极值研究、不等式证明、数学规划、逼近论、变分学、最优控制理论、对策论等领域有着广泛的应用。

人们对一元凸函数性质和判定方法已经有了丰富的研究，但随着凸函数应用范围的不断扩展,多元凸函数越来越多的被研究. 一元函数凸性的判定方法也被推广到多元函数,文献[4］将凸函数与导函数之间的关系推广,给出了用梯度判定多元函数凸性的方法,文献［5］将凸函数与二阶导数之间的关系推广,给出了用黑塞矩阵判定多元函数凸性的方法。

而多元函数的梯度与黑塞矩阵在计算中往往比较繁琐，本文将着力研究多元函数凸性判定方法的改进，使凸函数判定的计算更加简洁，应用更加方便. 2 定义及引理本节主要介绍本文用到的定义及引理。

定义2。

1[2]设n R D ⊂，如果D 中的任意两点的连线也在D 内，则称D 为n R 中的凸集。

即对任意21,P P ，数)1,0(∈λ，总有D P P ∈-+21)1(λλ。

定义2。

2［1］设n R D ⊂为非空凸集，f 为定义在D 上的函数,若对任意)1,0(,,21∈∈λD P P ，总有)()1()())1((2121P f P f P P f λλλλ-+≤-+, (1)则称f 为D 上的凸函数. 反之，如果总有)()1()())1((2121P f P f P P f λλλλ-+≥-+，（2）则f 为D 上的凹函数.若上述(1)、（2）中的不等式改为严格不等式，则相应的函数称为严格凸函数和严格凹函数。

定义]2[3.2 )(P f 是定义在n R D ⊂上的多元函数，若在点),,,(210n x x x P ⋅⋅⋅存在对所有自变量的偏导数，则称向量))(,),(),((00021P f P f P f nx x x ⋅⋅⋅为函数)(P f 在点0P 的梯度,记作)).(,),(),(()()(0000021P f P f P f P gradf P f n x x x ⋅⋅⋅==∇定义]2[4.2 )(P f 是定义在n R D ⊂上的多元函数，且在点),,,(210n x x x P ⋅⋅⋅具有二阶连续偏导数，记⎪⎪⎪⎪⎪⎭⎫⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=)()()()()()()()()()(0000000000212221212111P f P f P f P f P f P f P f P f P f P H n n n n n n x x x x x x x x x x x x x x x x x x f 它称为)(P f 在0P 的黑赛矩阵。

确定多元凸函数的一个充分条件

确定多元凸函数的一个充分条件多元凸函数，亦称为多元可凸函数，是一种在n维空间中定义的凸函数，它在n维空间内具有以下性质：1）它在每个数轴上是单调递增的，比如说它在x轴和y轴上都是单调递增的；2）它的局部最优解是全局最优解，局部最优解即所有x和y变量取出了一组值时函数得到的极大值，也是函数取极大值的唯一解；3）它同时必须满足变量的约束条件；4）在n维空间的所有可能的输入值中，它的输出值是共轭变函数的极小值。

综上所述，多元凸函数的一个充分条件就是满足在n维空间中，它的单调性，局部最优解是全局最优解，满足变量的约束条件以及在n维空间的所有可能的输入值中，它的输出值是共轭变函数的极小值。

有了这些条件的满足，多元凸函数才能展示其优越的性能，并能够被广泛应用在多种面向。

多元凸函数在非线性优化中有着广泛的应用，它的计算也变得比较容易，性能更为优良，所以受到了很多科学家和工程师的关注。

其应用从简单的数值模型到复杂的深度学习模型，比如说线性模型，神经网络模型，支持向量机，决策树，k最近邻等等都是多元凸函数的重要应用。

而在学术领域，多元凸函数也有很多应用，它可用于描述多个变量之间的可视化关系，从而获得对数据的更好的理解，从而找到新的研究视角，进行有价值的思考与讨论。

综上所述，一个多元凸函数的充分条件包括：在n维空间，它的单调性、局部最优解为全局最优解、满足变量的约束条件以及在n维空间的所有可能的输入值中，它的输出值是共轭变函数的极小值。

多元凸函数的计算性能更优良，被广泛应用在多种面向，从数值模型到深度学习模型，在学术领域也有很多应用，可用于描述多个变量之间的可视化关系，从而获得对数据的更好的理解。

函数的单调性与凹凸性的判别法

x
由 f ( x) 0，可知 f ( x) f ( ).
故
f
(x) x

0，即
f (x) x
在 [0,a] 上单调减少。
3. 求函数f ( x) x2ex在[0,)上的最大值。
解： f ( x) 2xex x2ex xex (2 x)
x1 x2，对任一 (0,1)，总有： f ((1 )x1 x2 ) (1 ) f ( x1) f ( x2 )
则称函数 f ( x) 在 I 内是凸的(convex)；若有：
f ((1 )x1 x2 ) (1 ) f ( x1) f ( x2 )
x ln(1 x ) x ln(1 x) x.
1 x
1 x
1 x
2. 设 f ( x) 在 [0,a] 上二次可导，且 f (0) 0, f ( x) 0，证明 f ( x) 在 [0,a] 上单调减少；
x
证明：f ( x) 在上二次可导，故由 Lagrange 定理，
1 x 1 x x 0 时，f ( x) 0，f ( x 在 (0,) 上严格单调上升，于是有：
f ( x) f (0), 即 x ln(1 x).
当 1 x 0 时, f ( x) 0，f ( x) 在 (1,0) 内严格单调
下降，也有：
f ( x) f (0), 即 x ln(1 x).
2. 带Lagrange余项的Taylor公式：
f (x)
f ( x0 )
f ( x0 )( x x0 )
f
( x0 ) ( x 2!

x0 )2

多元二次函数凹凸性的判别方法

多元二次函数凹凸性的判别方法一、凹凸性的定义对于一个函数$f(x)$，如果定义域中的任意两点$x_1$和$x_2$以及介于其之间的任意一点$x$都满足以下条件：1.如果对于$x_1<x<x_2$，有$f(x)>f(x_1)$和$f(x)>f(x_2)$，则称函数在该区间上是上凹的（凹上的）；2.如果对于$x_1<x<x_2$，有$f(x)<f(x_1)$和$f(x)<f(x_2)$，则称函数在该区间上是下凹的（凹下的）；3. 如果对于$x_1 < x < x_2$，有$f(x) \geq f(x_1)$和$f(x) \geq f(x_2)$，则称函数在该区间上是上凸的（凸上的）；4. 如果对于$x_1 < x < x_2$，有$f(x) \leq f(x_1)$和$f(x) \leq f(x_2)$，则称函数在该区间上是下凸的（凸下的）。

二、二元二次函数与二次型的关系考虑一个二元二次函数$f(x, y) = ax^2 + by^2 + 2cxy + dx + ey + f$，其中$a \neq 0$和$b \neq 0$（否则$f(x, y)$不是二次函数）。

将它的二次项$ax^2 + by^2 + 2cxy$写成矩阵形式，有：$\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} a & c \\ c & b \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$其中$\begin{bmatrix} a & c \\ c & b \end{bmatrix}$就是二次型的矩阵，记为$A$，$\begin{bmatrix} x & y \end{bmatrix}$和$\begin{bmatrix} x \\ y \end{bmatrix}$是行向量和列向量，它们分别表示点$(x, y)$。

多元函数对变量对凸

多元函数对变量对凸
在数学中，多元函数是指具有多个自变量的函数。

而对凸则是
指函数的图像在定义域内的任意两点连线上方的部分都在函数的图
像上方。

多元函数对变量对凸的概念是指在多元函数中，如果函数
对每一个变量都是凸的，那么这个多元函数就是对变量对凸的。

对变量对凸的概念在优化问题中具有重要意义。

在实际问题中，经常需要优化多元函数，找到使函数取得最大或最小值的变量取值。

而对变量对凸的函数在优化问题中通常具有良好的性质，可以更容
易地找到全局最优解。

具体地，一个二元函数 f(x, y) 对变量对凸的定义如下：对于
任意的 x1, x2 和 y，以及0 <= λ <= 1，有：
f(λx1 + (1-λ)x2, y) <= λf(x1, y) + (1-λ)f(x2, y)。

这个定义表明，对于固定的 y，函数 f(x, y) 对变量 x 是凸的。

同样地，可以定义对于变量 y 的凸性。

多元函数对变量对凸的性质使得在优化问题中可以应用诸如凸
优化的方法来求解。

凸优化问题有着良好的性质，可以利用凸性质来保证得到的解是全局最优解。

总之，多元函数对变量对凸是数学中重要的概念，它在优化问题中具有重要的应用价值。

对于对变量对凸的函数，我们可以更容易地找到最优解，这对于解决实际问题具有重要的意义。

判断函数凸凹性的五种方法

判断函数凸凹性的五种方法判断函数的凸性和凹性可以通过以下几种方法：1. 通过二阶导数（对于一元函数）对于一元函数f(x)，其凸性和凹性可以通过其二阶导数f′′(x)来判断：●如果f′′(x)≥0对于所有x在函数的定义域内都成立，并且至少在某个子区间内f′′(x)>0，则函数f(x)在该定义域内是凸的。

●如果f′′(x)≤0对于所有x在函数的定义域内都成立，并且至少在某个子区间内f′′(x)<0，则函数f(x)在该定义域内是凹的。

注意：如果f′′(x)在定义域内恒等于0，则函数是线性的，既是凸的又是凹的。

2. 通过一阶导数（对于一元函数，但较不直观）虽然不如二阶导数直观，但也可以通过分析一阶导数f′(x)的单调性来判断函数的凸凹性。

不过，这种方法通常需要更多的分析和技巧，并且不如二阶导数方法直接。

3. 通过定义（对于一元或多元函数）●凸函数：对于定义域内的任意两点x1,x2（对于多元函数，则是任意两个点x1,x2）和任意实数0≤λ≤1，如果都有●f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)●（对于多元函数，则是类似的向量不等式），则称f是凸函数。

●凹函数：与凸函数相反，将上述不等式中的“≤”替换为“≥”，则称f是凹函数。

4. 利用Hessian矩阵（对于多元函数）对于多元函数f(x)，其Hessian矩阵是一个由二阶偏导数组成的矩阵。

函数的凸凹性可以通过检查Hessian矩阵的正定性或负定性来判断：●如果Hessian矩阵在函数的定义域内处处半正定（即所有特征值非负），则函数是凸的。

●如果Hessian矩阵在函数的定义域内处处半负定（即所有特征值非正），则函数是凹的。

5. 图形判断（直观方法）通过观察函数的图形，也可以直观地判断其凸凹性。

凸函数的图形在其上任意两点之间的连线总是位于图形之上，而凹函数的图形则在其上任意两点之间的连线之下。

注意●在判断函数的凸凹性时，需要注意函数的定义域。