人教A版高中必修二试题四川省成都市新都一中高级第三期周练01学生版.docx

合集下载

人教A版高中必修二试题四川省成都市新都一中高级第三期周练01学生版

四川省成都市新都一中高2015级第三期周练01第I 卷（选择题）一、选择题（本大题共12哥个小题，每小题5分，12个小题共计60分）1．过点()1,2，且与直线220x y ++=垂直的直线方程为A .20x y -=B .230x y -+=C .240x y +-=D .250x y +-=2．已知{}n a 是首项为2且公差不为0的等差数列，若136,,a a a 成等比数列，则{}n a 的前9项和等于（） A ．26B ．30C ．36D ．403．某棱锥的三视图（单位：cm ）如图所示，则该棱锥的体积等于（）A ．310cmB ．320cmC ．330cmD ．340cm4．过两直线l 1：x －3y ＋4＝0和l 2：2x ＋y ＋5＝0的交点和原点的直线方程为（）A ．19x －9y ＝0B ．9x ＋19y ＝0C ．19x －3y ＝0D ．3x ＋19y ＝05．如果AC ＜0且BC ＜0，那么直线Ax ＋By －C ＝0不通过A .第一象限B .第二象限C .第三象限D .第四象限6．下列说法错误的是（）A ．若直线//a 平面α，直线//b 平面α，则直线a 不一定平行于直线bB ．若平面α不垂直于平面β，则α内一定不存在直线垂直于平面βC ．若平面α⊥平面β，则α内一定不存在直线平行于平面βD ．若平面α⊥平面v ，平面β⊥平面v ，l αβ=I ，则l 一定垂直于平面v7．若数列{}n a 是等差数列，首项10a >，201520160a a +>，201520160a a ⋅<，则使前n 项和n S 取得最大值的自然数n 是（）A ．1007B ．1008C ．2015D ．20168．已知点(1,2)-和在直线:10l ax y -+=(0)a ≠的同侧，则直线l 倾斜角的取值范围是（） A ．(,)43ππB ．3(0,)(,)34πππU C ．35(,)46ππD ．23(,)34ππ 9．不等式组20,240,320x y x y x y +-≥⎧⎪+-≤⎨⎪+-≥⎩表示的平面区域的面积为（）A ．2B ．4C ．6D ．810．设,x y 满足约束条件1210,0y x y x x y ≤+⎧⎪≥-⎨⎪≥≥⎩，则目标函数(0,0)z abx y a b =+>>的最大值为11，则a b +的最小值为（）A ．2B ．4C ．6D ．811．当方程22220x y kx y k ++++=表示圆取得最大面积时，直线()12y k x =-+的倾斜角为（） A ．34πB ．4πC ．2πD ．0 12．在棱长为3的正方体1111ABCD A B C D -中，P 在线段1BD 上，且112BP PD =，M 为线段11B C 上的动点，则三棱锥M PBC -的体积为（）A ．1B ．32C ．92D ．与M 点的位置有关第II 卷（非选择题）二、填空题（本大题共计4个小题，每小题4分，共计16分）13．数列{}n a满足()111n a n N a *+==∈，记2n n b a =，则数列{}1n n b b +前n 项和n S = ． 14．若,x y 满足约束条件20210220x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩，则3z x y =+的最大值为 .15．直线1l ：310ax y ++=，2l ：()2110x a y +++=，若12∥l l ，则a = ．16．已知圆222430x y x y +--+=关于直线()300,0ax by a b +-=>>对称，则12a b +的最小值为．三、解答题（本大题共计6个小题，满分74分）17．某企业准备投资1200万元兴办一所中学，对当地教育市场进行调查后，得到了如下的数据表格（以学段硬件建设（万元）配备教师数教师年薪（万元）初中26/班 2/班 2/人高中 54/班 3/班 2/人因生源和环境等因素，全校总班级至少20个班，至多30个班.（Ⅰ）请用数学关系式表示上述的限制条件；（设开设初中班x 个，高中班y 个）（Ⅱ）若每开设一个初、高中班，可分别获得年利润2万元、3万元，请你合理规划办学规模使年利润最大，最大为多少？18．已知实数x ，y 满足2040250x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩求：（1）z ＝x ＋2y －4的最大值；（2）z ＝x 2＋y 2－10y ＋25的最小值；（3）z ＝211y x ++的取值范围．19．如图，已知点A （﹣3，0），B （3，0），M 是线段AB 上的任意一点，在AB 的同侧分别作正方形AMCD 、MBEF ，⊙P 和⊙Q 是两个正方形的外接圆，它们交于点M ，N ．（1）证明：直线MN 恒过一定点S ，并求S 的坐标；（2）过A 作⊙Q 的割线，交⊙Q 于G 、H 两点，求|AH |•|AG |的取值范围．20．如图，在四棱锥P ABCD -中，AB ⊥平面BCP ，//CD AB ，2AB BC CP BP ====，1CD =.（1）求点B 到平面DCP 的距离；（2）点M 为线段AB 上一点（含端点），设直线MP 与平面DCP 所成角为α，求sinα的取值范围.21．如图，四边形ABCD 中，//AB CD ，30ABD ∠=o ，2223AB CD AD ===，DE ⊥面ABCD ，//EF BD ，且23EF BD =. （1）求证：//FB 面ACE ；（2）若CF 与面ABCD 所成角的正切为24，求三棱锥F ABC -的体积.22．已知数列{}n a 的前n 项和n S 满足：(1)n n n S t S a =-+（t 为常数，且0t ≠，1t ≠）．（1）求{}n a 的通项公式；（2）设2n n n n b a S a =+⋅，若数列{}n b 为等比数列，求t 的值；（3）在满足条件（2）的情形下，设41n n c a =+，数列{}n c 的前n 项和为n T ，若不等式12274nk n n T ≥-+-对任意的*n N ∈恒成立，求实数k 的取值范围．。

四川省成都市新都第一中学2018-2019学年高一下学期人教必修2物理试题

成都市新都一中2018-2019学年度人教版必修2高一物理试题一．本题共15小题；每小题4分，共60分。

在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。

全部选对的得4分，选不全的得2分，有选错或不答的得0分.1.关于万有引力常量，下列说法正确的是A. 万有引力常量等于两个质量均为1的物体相距1时的相互引力B. 牛顿发现万有引力定律时，给出了万有引力常量的值C. 万有引力常量的测出，证明了万有引力的存在D. 通过万有引力常量的测定，使卡文迪许算出了地球的质量【答案】ACD【解析】【详解】根据可知，万有引力常量等于两个质量均为1的物体相距1时的相互引力，选项A正确；牛顿发现万有引力定律时，并没有给出万有引力常量的值，后来卡文迪许由扭秤实验测出了引力常量，选项B错误；万有引力常量的测出，证明了万有引力的存在，选项C正确；通过万有引力常量的测定，使卡文迪许算出了地球的质量，被称为第一个测量地球质量的人，选项D正确；故选ACD.2.做匀速圆周运动的物体A. 速度不变B. 加速度不变C. 角速度不变D. 速率不变【答案】CD【解析】【详解】做匀速圆周运动的物体，速度的大小不变，即速率不变，方向不断变化，即速度不断变化；加速度大小不变，方向不断变化，即加速度不断变化；角速度不变；故选CD.3.关于第一宇宙速度，下列说法正确的是A. 它是人造地球卫星绕地球作匀速圆周运动的最大速度B. 它是人造地球卫星在圆形轨道上的最小运行速度C. 它是能使卫星绕地球运行的最小发射速度D. 它是人造卫星绕地球作椭圆轨道运行时在近地点的速度【答案】AC【解析】【详解】第一宇宙速度是绕地球做圆周运动的近地卫星的速度，根据可知，是人造地球卫星绕地球作匀速圆周运动的最大速度，它是能使卫星绕地球运行的最小发射速度；故选AC.4.有关运动的合成，以下说法正确的是A. 两个直线运动的合运动一定是直线运动B. 两个不在一直线上的匀速直线运动的合运动一定是直线运动C. 两个匀加速直线运动的合运动一定是匀加速直线运动D. 匀加速直线运动和匀速直线运动的合运动一定是直线运动【答案】B【解析】【详解】两个直线运动的合运动不一定是直线运动，例如平抛运动，选项A错误；两个不在一直线上的匀速直线运动的合运动一定是直线运动，选项B正确；两个匀加速直线运动的合运动，若合加速度和合初速度方向不共线，则合运动是曲线运动，选项C错误；匀加速直线运动和匀速直线运动的合运动不一定是直线运动，例如平抛运动，选项D错误；故选B.5. 关于向心力的下列说法中正确的是A. 向心力不改变做圆周运动物体速度的大小B. 做匀速圆周运动的物体，其向心力是不变的C. 做圆周运动的物体，所受合力一定等于向心力D. 做匀速圆周运动的物体，一定是所受的合外力充当向心力【答案】AD【解析】A、向心力总是指向圆心，而速度总是沿着切线方向，故向心力一定垂直于速度，不改变速度的大小，故A正确；B、做匀速圆周运动的物体所受的合力总是指向圆心，方向不断变化，是变力，故B错误；C、物体做变速圆周运动时，合力不总是指向圆心，故合力不一定等于向心力，向心力为合力的一个分力，故C错误；D、做匀速圆周运动的物体所受的合力总是指向圆心，提供向心力，故D正确。

高中数学人教a版必修2试题及答案

高中数学人教a版必修2试题及答案一、选择题（每题3分，共30分）1. 若函数\( f(x) = \frac{1}{x} \)在点x=2处的导数为\( f'(2) \)，则\( f'(2) \)的值为：A. 0.5B. -0.5C. 2D. -22. 已知数列\( \{a_n\} \)是等差数列，且\( a_1 = 3 \)，\( a_4 =10 \)，则\( a_7 \)的值为：A. 17B. 15C. 13D. 113. 设函数\( g(x) = x^3 - 3x + 1 \)，若\( g(2) = 3 \)，则\( g(-2) \)的值为：A. -3B. 3C. -1D. 14. 圆的方程为\( (x-2)^2 + (y-3)^2 = 9 \)，该圆的半径为：A. 3B. 6C. 9D. 125. 向量\( \vec{a} = (1, 2) \)和向量\( \vec{b} = (3, 4) \)，则\( \vec{a} \cdot \vec{b} \)的值为：A. 5B. 8C. 11D. 146. 函数\( h(x) = x^2 - 4x + 3 \)的顶点坐标为：A. (2, -1)B. (4, -1)C. (2, 1)D. (4, 1)7. 已知集合A={1, 2, 3}，集合B={2, 3, 4}，则A∩B的元素个数为：A. 1B. 2C. 3D. 48. 直线\( y = 2x + 1 \)与直线\( y = -x + 4 \)的交点坐标为：A. (1, 3)B. (3, 1)C. (-1, 3)D. (3, -1)9. 函数\( f(x) = \sin(x) \)的周期为：A. \( \pi \)B. \( 2\pi \)C. \( \frac{\pi}{2} \)D. \( \frac{2\pi}{3} \)10. 若\( \lim_{x \to 0} \frac{\sin(2x)}{x} = 2 \)，则\( \lim_{x \to 0} \frac{\sin(3x)}{x} \)的值为：A. 3B. 6C. 9D. 12二、填空题（每题4分，共20分）1. 若\( \cos(\theta) = \frac{1}{3} \)，则\( \sin(\theta) \)的值为______。

人教A版高中必修二试题期中考试试题.doc

数学期中考试试题时间： 120分钟一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在答题卷相应的表格中（本大题共12个小题，每小题5分，共60分） 1．sin330︒等于（）A ．32- B ．12-C ．12D ．322. 已知542cos ,532si n-=θ=θ，则角θ终边所在象限是（） A. 第三象限 B. 第四象限 C. 第三或第四象限 D. 以上都不对3. 已知sin αcos α = 18,则cos α－sin α的值等于（）A ．±34 B ．±23 C ．23 D ．－234．用单位立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值与最大值分别为（）A ．9与13B ．7与10C ．10与16D ．10与15 5. 已知函数f (x)=sin(x-2π）（x ∈ R ），下面结论错误的是（） A. 函数的最小正周期为2π B. 函数在区间[]π,0上是增函数 C. 函数的图像关于直线x=0对称 D. 函数是奇函数6．如图，一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是( )．A ．324 B . 334 C. 63 D . 387.下列命题为真命题的是（）A. 平行于同一平面的两条直线平行；B.与某一平面成等角的两条直线平行；主视图俯视图俯视图主视图左视图C. 垂直于同一平面的两条直线平行；D.垂直于同一直线的两条直线平行。

8. 若圆柱、圆锥的底面直径和高都等于球的直径，则圆柱、圆锥、球的体积的比为（） A ．1:2:3 B ．2：3：4 C ．3:2:4 D ．3:1:2 9. 已知x 2si n )x (tan f =，则)1(-f 的值是（）A. 1B. 1-C.21D. 0 10. 正方体ABCD- A ’B ’C ’D ’中，二面角D ’-AB-D 的大小是（）A. 30°B.45°C. 60°D. 90°11. 函数)si n(ϕω+=x A y 在一个周期内的图象如下，此函数的解析式为A.)322sin(2π+=x y B.)32sin(2π+=x y C.)32sin(2π-=x yD.)32sin(2π-=x y12．底面是正三角形，且每个侧面是等腰三角形的三棱锥是A. 一定是正三棱锥B. 一定是正四面体C. 不是斜三棱锥D. 可能是斜三棱锥二、填空题：请把答案填在答题卷中横线上（本大题共4个小题，每小题4分，共16分）。

2023年四川省成都市新都第一中学高一数学第二学期期末监测试题含解析

2022-2023学年高一下数学期末模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本大题共10小题，每小题5分，共50分。

在每个小题给出的四个选项中，恰有一项是符合题目要求的1．已知1sin63πα⎛⎫+=⎪⎝⎭，则2cos23πα⎛⎫-⎪⎝⎭的值等于（）A．59-B．79-C．59D．792．三条线段的长分别为5，6，8，则用这三条线段A．能组成直角三角形B．能组成锐角三角形C．能组成钝角三角形D．不能组成三角形3．下列命题中正确的是（）A．相等的角终边必相同B．终边相同的角必相等C．终边落在第一象限的角必是锐角D．不相等的角其终边必不相同4．把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是()A．对立事件B．互斥但不对立事件C．不可能事件D．必然事件5．执行如图所示的程序框图，输出S的值为（）A ．－32B ．32C ．－12D ．126．已知幂函数()f x 过点(2,2)，则(9)f 的值为( ) A ．13B ．1C ．3D ．67．某林区改变植树计划，第一年植树增长率，以后每年的植树增长率都是前一年植树增长率的，若成活率为，经过年后，林区的树木量是原来的树木量的多少倍？（） A ．B ．C ．D ．8．过正方形ABCD 的顶点A ，作PA ⊥平面ABCD ，若PA BA =，则平面ABP 和平面CDP 所成的锐二面角的大小是A ．30B ．45︒C ．60︒D ．90︒9．在等差数列{}n a 中，265,1a a =-=，则10a 等于( ) A ．5B ．6C ．7D ．810．直线3y kx =+与圆22(3)(2)4x y -+-=相交于M ，N 两点，若||23MN ≥．则k 的取值范围是（）A ．3,04⎡⎤-⎢⎥⎣⎦B ．30,4⎡⎤⎢⎥⎣⎦C ．3,03⎡⎤-⎢⎥⎣⎦D ．2,03⎡⎤-⎢⎥⎣⎦二、填空题：本大题共6小题，每小题5分，共30分。

高一数学人教A版必修二模块测试题(含答案)

高一数学人教A 版必修二模块测试一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知直线x －3y －2＝0，则该直线的倾斜角为( ) A ．30° B ．60° C ．120°D ．150°2．过点A (4，a )和B (5，b )的直线与y ＝x ＋m 平行，则|AB |的值为( ) A ．6 B. 2 C ．2D ．不确定3．在空间直角坐标系中已知点P (0,0，3)和点C (－1,2,0)，则在y 轴上到P 和C 的距离相等的点M 坐标是( )A ．(0,1,0) B.⎝ ⎛⎭⎪⎫0，－12，0 C.⎝ ⎛⎭⎪⎫0，12，0 D ．(0,2,0)4．若直线(1＋a )x ＋y ＋1＝0与圆x 2＋y 2－2x ＝0相切，则a 的值为( ) A ．1或－1 B ．2或－2 C ．1D ．－15．如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( )A.433πB.12πC.33πD.36π6．在空间给出下面四个命题(其中m，n为不同的两条直线，α，β为不同的两个平面)①m⊥α，n∥α⇒m⊥n②m∥n，n∥α⇒m∥α③m∥n，n⊥β，m∥α⇒α⊥β④m∩n＝A，m∥α，m∥β，n∥α，n∥β⇒α∥β其中正确的命题个数有()A．1个B．2个C．3个D．4个7．直线l将圆x2＋y2－2x－4y＝0平分，且与直线x＋2y＝0垂直，则直线l 的方程是()A．2x－y＝0 B．2x－y－2＝0C．x＋2y－3＝0 D．x－2y＋3＝08．若点A(－3，－4)，B(6,3)到直线l：ax＋y＋1＝0的距离相等，则实数a的值为()A.79B．－13C.79或13D．－79或－139．点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD＝AD，则PA与BD所成角的度数为()A．30°B．45°C．60°D．90°10．在四面体A－BCD中，棱AB，AC，AD两两互相垂直，则顶点A在底面BCD上的投影H为△BCD的()A．垂心B．重心C．外心D．内心11．圆x2＋y2＋2x＋4y－3＝0上到直线x＋y＋1＝0的距离为2的点共有()A．1个B．2个C．3个D．4个12．将边长为a的正方形ABCD沿对角线AC折起，使得BD＝a，则三棱锥D －ABC的体积为()A.212a3 B.a312C.24a3 D.a36二、填空题(本大题共4小题，每小题4分，共16分．请把正确答案填在题中横线上)13．如下图所示，Rt△A′B′C′为水平放置的△ABC的直观图，其中A′C′⊥B′C′，B′O′＝O′C′＝1，则△ABC的面积为________．14．已知A(0,8)，B(－4,0)，C(m，－4)三点共线，则实数m的值是________．15．直线y＝2x＋3被圆x2＋y2－6x－8y＝0所截得的弦长等于________．16．已知正四棱锥O－ABCD的体积为322，底面边长为3，则以O为球心，OA为半径的球的表面积为________．三、解答题(本大题共6小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)(2015·河源市高二(上)期中)轴截面为正三角形的圆锥内有一个内切球，若圆锥的底面半径为2，求球的体积．18．(本小题满分12分)(2015·福建八县一中联考)已知直线l：kx－y＋1－2k＝0(k∈R)．(1)证明：直线l过定点；(2)若直线l交x轴正半轴于点A，交y轴正半轴于点B，O为坐标原点，且|OA|＝|OB|，求k的值．19．(本小题满分12分)(2015·西安一中期末)已知正方体ABCD－A1B1C1D1，O 是底面ABCD对角线的交点．求证：(1)C1O∥平面AB1D1；(2)A1C⊥平面AB1D1.20．(本小题满分12分)求圆心在直线y＝－2x上，并且经过点A(0,1)，与直线x＋y＝1相切的圆的标准方程．21．(本小题满分13分)如图所示，在四棱锥V－ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD.(1)求证：AB⊥平面VAD；(2)求平面VAD与平面VDB所成的二面角的大小．22.(本小题满分13分)如图，设P是圆x2＋y2＝25上的动点，点D是P在x轴上的投影，M为PD上一点，且|MD|＝45|PD|.(1)当P在圆上运动时，求点M的轨迹C的方程；(2)求过点(3,0)且斜率为45的直线被C所截线段的长度．高一数学人教A 版必修二模块测试(参考答案含题目)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知直线x －3y －2＝0，则该直线的倾斜角为( ) A ．30° B ．60° C ．120°D ．150°解析：直线x －3y －2＝0的斜率k ＝33，故倾斜角为30°，选A. 答案： A2．过点A (4，a )和B (5，b )的直线与y ＝x ＋m 平行，则|AB |的值为( ) A ．6 B. 2 C ．2D ．不确定解析：由k AB ＝b －a5－4＝1，得b －a ＝1，即|AB |＝(5－4)2＋(b －a )2＝ 2.故选B. 答案： B3．在空间直角坐标系中已知点P (0,0，3)和点C (－1,2,0)，则在y 轴上到P 和C 的距离相等的点M 坐标是( )A ．(0,1,0) B.⎝ ⎛⎭⎪⎫0，－12，0 C.⎝ ⎛⎭⎪⎫0，12，0 D ．(0,2,0)解析：设M (0，y,0)，则|MP |＝|MC |，所以y 2＋(3)2＝(－1)2＋(2－y )2，解得y ＝12，故选C.答案： C4．若直线(1＋a )x ＋y ＋1＝0与圆x 2＋y 2－2x ＝0相切，则a 的值为( ) A ．1或－1B ．2或－2C ．1D ．－1解析：圆x 2＋y 2－2x ＝0的圆心(1,0)，半径为1，依题意得|1＋a ＋0＋1|(1＋a )2＋1＝1，即|a ＋2|＝(a ＋1)2＋1，平方整理得a ＝－1，故选D. 答案： D5．如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( )A.433πB.12πC.33πD.36π解析：由题意知，该几何体为沿轴截面切开的半个圆锥，圆锥的半径为1，高为3，故所求体积为12×13×π×12×3＝36π，选D.答案： D6．在空间给出下面四个命题(其中m ，n 为不同的两条直线，α，β为不同的两个平面)①m ⊥α，n ∥α⇒m ⊥n ②m ∥n ，n ∥α⇒m ∥α ③m ∥n ，n ⊥β，m ∥α⇒α⊥β ④m ∩n ＝A ，m ∥α，m ∥β，n ∥α，n ∥β⇒α∥β其中正确的命题个数有( ) A ．1个 B ．2个 C ．3个D ．4个解析： ②中m 也可能在平面α内，②错，①③④正确，故选C. 答案： C7．直线l 将圆x 2＋y 2－2x －4y ＝0平分，且与直线x ＋2y ＝0垂直，则直线l 的方程是( )A．2x－y＝0 B．2x－y－2＝0C．x＋2y－3＝0 D．x－2y＋3＝0解析：依题意知直线l过圆心(1,2)，斜率k＝2，所以l的方程为y－2＝2(x －1)，即2x－y＝0，故选A.答案： A8．若点A(－3，－4)，B(6,3)到直线l：ax＋y＋1＝0的距离相等，则实数a的值为()A.79B．－13C.79或13D．－79或－13解析：由|－3a－4＋1|a2＋12＝|6a＋3＋1|a2＋12，解得a＝－79或－13，故选D.答案： D9．点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD＝AD，则PA与BD所成角的度数为()A．30°B．45°C．60°D．90°解析：利用正方体求解，如图所示：PA与BD所成的角，即为PA与PQ所成的角，因为△APQ为等边三角形，所以∠APQ＝60°，故PA与BD所成角为60°，选C.答案： C10．在四面体A－BCD中，棱AB，AC，AD两两互相垂直，则顶点A在底面BCD上的投影H为△BCD的()A．垂心B．重心C．外心D．内心解析：因为AB⊥AC，AB⊥AD，AC∩AD＝A，因为AB ⊥平面ACD ，所以AB ⊥CD . 因为AH ⊥平面BCD ，所以AH ⊥CD ，AB ∩AH ＝A ，所以CD ⊥平面ABH ，所以CD ⊥BH . 同理可证CH ⊥BD ，DH ⊥BC ，则H 是△BCD 的垂心．故选A. 答案： A11．圆x 2＋y 2＋2x ＋4y －3＝0上到直线x ＋y ＋1＝0的距离为2的点共有( )A ．1个B ．2个C ．3个D ．4个解析：圆x 2＋y 2＋2x ＋4y －3＝0的圆心坐标是(－1，－2)，半径是22，圆心到直线x ＋y ＋1＝0的距离为2，∴过圆心平行于直线x ＋y ＋1＝0的直线与圆有两个交点，另一条与直线x ＋y ＋1＝0的距离为2的平行线与圆相切，只有一个交点，共有3个交点，故选C.答案： C12．将边长为a 的正方形ABCD 沿对角线AC 折起，使得BD ＝a ，则三棱锥D －ABC 的体积为( )A.212a 3 B.a 312 C.24a 3D.a 36解析：取AC 的中点O ，如图，则BO ＝DO ＝22a ，又BD ＝a ，所以BO ⊥DO ，又DO ⊥AC ，所以DO ⊥平面ACB ， V D －ABC ＝13S △ABC ·DO＝13×12×a 2×22a ＝212a 3.故选A. 答案： A二、填空题(本大题共4小题，每小题4分，共16分．请把正确答案填在题中横线上)13．如下图所示，Rt △A ′B ′C ′为水平放置的△ABC 的直观图，其中A ′C ′⊥B ′C ′，B ′O ′＝O ′C ′＝1，则△ABC 的面积为________．解析：由直观图画法规则将△A ′B ′C ′还原为△ABC ，如图所示，则有BO ＝OC ＝1，AO ＝2 2.故S △ABC ＝12BC ·AO ＝12×2×22＝2 2.答案： 2 214．已知A (0,8)，B (－4,0)，C (m ，－4)三点共线，则实数m 的值是________．解析： k AB ＝8－00＋4＝2，k BC ＝0＋4－4－m∵k AB ＝k BC ，∴m ＝－6. 答案：－615．直线y ＝2x ＋3被圆x 2＋y 2－6x －8y ＝0所截得的弦长等于________．解析：先求弦心距，再求弦长．圆的方程可化为(x －3)2＋(y －4)2＝25，故圆心为(3,4)，半径r ＝5. 又直线方程为2x －y ＋3＝0，所以圆心到直线的距离为d ＝|2×3－4＋3|4＋1＝5，所以弦长为2r 2－d 2＝2×25－5＝220＝4 5. 答案： 4 516．已知正四棱锥O －ABCD 的体积为322，底面边长为3，则以O 为球心，OA 为半径的球的表面积为________．解析：本题先求出正四棱锥的高h ，然后求出侧棱的长，再运用球的表面积公式求解．V 四棱锥O －ABCD ＝13×3×3h ＝322，得h ＝322，∴OA 2＝h 2＋⎝ ⎛⎭⎪⎫AC 22＝184＋64＝6. ∴S 球＝4πOA 2＝24π.答案： 24π三、解答题(本大题共6小题，共74分．解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)(2015·河源市高二(上)期中)轴截面为正三角形的圆锥内有一个内切球，若圆锥的底面半径为2，求球的体积．解析：如图所示，作出轴截面，因为△ABC 是正三角形，所以CD ＝12AC ＝2，所以AC ＝4，AD ＝32×4＝23，因为Rt △AOE ∽Rt △ACD ，所以OE AO ＝CD AC .设OE ＝R ，则AO ＝23－R ，所以R 23－R＝12，所以R ＝233. 所以V 球＝43πR 3＝43π·⎝ ⎛⎭⎪⎫2333＝323π27. 所以球的体积等于323π27. 18．(本小题满分12分)(2015·福建八县一中联考)已知直线l ：kx －y ＋1－2k ＝0(k ∈R )．(1)证明：直线l 过定点；(2)若直线l 交x 轴正半轴于点A ，交y 轴正半轴于点B ，O 为坐标原点，且|OA |＝|OB |，求k 的值．解析： (1)证明：法一：直线l 的方程可化为y －1＝k (x －2)，故无论k 取何值，直线l 总过定点(2,1)．法二：设直线过定点(x 0，y 0)，则kx 0－y 0＋1－2k ＝0对任意k ∈R 恒成立，即(x 0－2)k －y 0＋1＝0恒成立，所以⎩⎨⎧x 0－2＝0，－y 0＋1＝0解得x 0＝2，y 0＝1，故直线l 总过定点(2,1)．(2)因为直线l 的方程为y ＝kx －2k ＋1，则直线l 在y 轴上的截距为1－2k ，在x 轴上的截距为2－1k ，依题意1－2k ＝2－1k ＞0，解得k ＝－1或k ＝12(经检验，不合题意)所以所求k ＝－1.19．(本小题满分12分)(2015·西安一中期末)已知正方体ABCD －A 1B 1C 1D 1，O 是底面ABCD 对角线的交点．求证：(1)C 1O ∥平面AB 1D 1；(2)A 1C ⊥平面AB 1D 1.证明： (1)连接A 1C 1，设A 1C 1∩B 1D 1＝O 1，连接AO 1，因为ABCD －A 1B 1C 1D 1是正方体，所以A 1ACC 1是平行四边形，D 1B 1∩AB 1＝B 1，所以A 1C 1∥AC ，且A 1C 1＝AC ，又O 1，O 分别是A 1C 1，AC 的中点，所以O 1C 1∥AO 且O 1C 1＝AO ，所以AOC 1O 1是平行四边形，所以C 1O ∥AO 1，AO 1⊂平面AB 1D 1，C 1O ⊄平面AB 1D 1，所以C 1O ∥平面AB 1D 1，(2)因为CC 1⊥平面A 1B 1C 1D 1，所以CC 1⊥B 1D 1，又因为A 1C 1⊥B 1D 1，所以B 1D 1⊥平面A 1C 1C ，即A 1C ⊥B 1D 1，同理可证A 1C ⊥AB 1，又D 1B 1∩AB 1＝B 1，所以A 1C ⊥平面AB 1D 1.20．(本小题满分12分)求圆心在直线y ＝－2x 上，并且经过点A (0,1)，与直线x ＋y ＝1相切的圆的标准方程．解析：因为圆心在直线y ＝－2x 上，设圆心坐标为(a ，－2a )，则圆的方程为(x －a )2＋(y ＋2a )2＝r 2，圆经过点A (0,1)且和直线x ＋y ＝1相切，所以有⎩⎨⎧ a 2＋(2a ＋1)2＝r 2，|a －2a －1|2＝r ，解得a ＝－13，r ＝23，所以圆的方程为⎝ ⎛⎭⎪⎫x ＋132＋⎝ ⎛⎭⎪⎫y －232＝29. 21．(本小题满分13分)如图所示，在四棱锥V －ABCD 中，底面ABCD 是正方形，侧面VAD 是正三角形，平面VAD ⊥底面ABCD .(1)求证：AB ⊥平面VAD ；(2)求平面VAD 与平面VDB 所成的二面角的大小．解析： (1) 证明：∵底面ABCD 是正方形，∴AB ⊥AD .∵平面VAD ⊥底面ABCD ，平面VAD ∩底面ABCD ＝AD ，AB ⊥AD ，AB ⊂底面ABCD ，∴AB ⊥平面VAD .(2)取VD 的中点E ，连接AE ，BE .∵△VAD 是正三角形，∴AE ⊥VD ，AE ＝32AD .∵AB ⊥平面VAD ，VD ⊂平面VAD ，∴AB ⊥VD .又AB ∩AE ＝A ，∴VD ⊥平面ABE .∵BE ⊂底面ABE ，∴VD ⊥BE .∴∠ABE 就是平面VAD 与平面VDB 所成的二面角的平面角．在Rt △BAE 中，tan ∠BEA ＝BA AE ＝AD 32AD＝233. ∴平面VAD 与平面VDB 所成的二面角的正切值为233.22.(本小题满分13分)如图，设P 是圆x 2＋y 2＝25上的动点，点D 是P 在x 轴上的投影，M 为PD 上一点，且|MD |＝45|PD |.(1)当P 在圆上运动时，求点M 的轨迹C 的方程；(2)求过点(3,0)且斜率为45的直线被C 所截线段的长度．解析： (1)设M 的坐标为(x ，y )，P 的坐标为(x p ，y p )由已知得⎩⎪⎨⎪⎧ x p ＝x y p ＝5y 4，∵P 在圆上，∴x 2＋⎝ ⎛⎭⎪⎫54y 2＝25，即C 的方程为x 225＋y 216＝1.(2)过点(3,0)且斜率为45的直线方程为y ＝45(x －3)，设直线与C 的交点为A (x 1，y 1)，B (x 2，y 2) 将直线方程y ＝45(x －3)代入C 的方程，得x 225＋(x －3)225＝1整理得x 2－3x －8＝0 ∴x 1＝3－412，x 2＝3＋412∴线段AB 的长度为 |AB |＝(x 1－x 2)2＋(y 1－y 2)2 ＝ ⎝ ⎛⎭⎪⎫1＋1625(x 1－x 2)2＝ 4125×41＝415.。

人教A版高中必修二试题成都树德中学高级第三学期期中试题(文科)

H GFED CBA QCDBAP高中数学学习材料（灿若寒星精心整理制作）成都树德中学高2011级第三学期期中数学试题（文科）命题人：杨世卿审题人：陈杰一、选择题：本大题共12小题，每小题5分，共60分。

每小题仅有一个正确答案。

1．以下角：①异面直线所成角；②直线和平面所成角；③二面角的平面角；可能为钝角的有（）A ．0个B ．1个C ．2个D ．3个2. 一种冰激凌机的模型上半部分是半球，下半部分是圆锥，其三视图如图所示，则该型号蛋糕的表面积S 是（）A ．π115B ．π110C ．π105D ．π1003. 一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则这个平面图形的面积是（） A. 12＋22 B ．1＋22C ．1＋2D ．2＋2 4.已知两不同直线n m ,与三不同平面γβα,,，下列条件能推出α∥β的是（） A ．γα⊥且γβ⊥ B ． α⊂m ，β⊂n ，n m // C ．α⊥m 且β⊥m D ．α⊂m ,α⊂n ,β//m , β//n 5.下面四个说法中，正确的个数．．．．．为（）①三点确定一个平面；②ABC ∆在平面α外，其三边延长线分别和α交于R Q P ,,,则R Q P ,,一定共线； ③一个角的两边所在直线分别平行于另一个角的两边所在直线，则这两角相等； ④在三维空间中，三个平面最多把空间分成八部分。

A ．1 B ．2 C ．3 D ．4 6. 在正三棱柱(底面是正三角形，侧棱和底面垂直)111C B A ABC -中，12BB AB =,则异面直线1AB 与B C 1成角的大小为（） A ．60° B ．90° C ．105° D ．75° 7. 如图，空间四边形ABCD 的对角线BD AC ,相等，顺次连接各边中点H G F E ,,,,则四边形EFGH 一定是（）A ．矩形B ．正方形C ．菱形D ．空间四边形 8．,,PA PB PC 是从点P 引出的三条射线，两两夹角为60，则直线PC 和平面PAB 所成角的余弦值为（）A ．12B ．22C ．33D ．639．异面直线b a ,所成角为3π，直线a c ⊥，且c 也与b 异面，则直线b 与c 所成的角的范围为（） A ．]2,6[ππ B ．]2,3[ππ C ．]3,6[ππ D ．]32,3[ππ10. 有一个长方体容器1111D C B A ABCD -,装的水占恰好占其容积的一半；α表示水平的桌面,容器一边BC 紧贴桌面，沿BC 将其翻转使之略微倾斜，最后水面(阴影部分)与其各侧棱的交点分别是EFGH （如图），则下列对翻转后水形成的几何体形状说法正确．．的是（） A ．棱台 B ．棱柱C ．棱锥D ．和容器尺寸有关，不能确定11. 如图，矩形ABCD 的长2=AB ，宽x AD =，若⊥PA 平面ABCD ，矩形的边CD 上至少有一个．．．．．点Q ,使得BQ PQ ⊥，则x 的范围是（） A ．10≤<x B ．20≤<x C ．21≤<x D ．1≥x12.我们知道，在平面直角坐标系中，方程1=+bya x 表示的图形是一条直线，具有特定性质：“在x 轴，y 轴上的截距分别为b a ,”；类比到空间直角坐标系中，方程122=++z yx 表示的点集对应的图形也具有某特定性质，设此图形为α，则坐标原点到α的距离是（）A ．3B ．2C ．5D ．36二、填空题：本大题共四小题，每小题4分，共16分。

人教A版高中必修二试题四川省成都市新都一中高级高二部分班级10月考.doc

四川省成都市新都一中高2014级高二部分班级10月考数学本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。

两卷共4页，满分150分，考试时间120分钟. 考试结束后，参考公式：锥体的体积公式13V Sh=其中S 为底面积，h 为高球体的体积公式：343V R π=；球体的表面积公式：24S R π= 一、选择题1．三个互不重合的平面能把空间分成n 部分，则n 所有可能值为（）A ．4、6、8B ．4、6、7、8C ．4、6、7D ．4、5、7、8 2．某四棱锥的三视图如图所示,该四棱锥的表面积是A ．B ．16+C ．48D ．16+3．已知a ＝(λ＋1,0,2)，b ＝(6,2μ－1,2λ)，若a ∥b ，则λ与μ的值可以是 ( )A ．2，12B ．－13，12C ．－3,2D ．2,24．(2012·上海模拟)若m 、n 是两条不同的直线，α、β是两个不同的平面，则下列命题不．正确的是( ) A ．若α∥β，m ⊥α，则m ⊥β B ．若m ∥n ，m ⊥α，则n ⊥α C ．若m ∥α，m ⊥β，则α⊥βD ．若α∩β＝m ，且n 与α、β所成的角相等，则m ⊥n解析：容易判定选项A 、B 、C 都正确，对于选项D ，当直线m 与n 平行时，直线n 与两平面α、β所成的角也相等，均为0°，故D 不正确．答案：D5．如图，在正方体ABCD A 1B 1C 1D 1中，P 为BD 1的中点，则△PAC 在该正方体各个面上的射影可能是( )侧(左)视图俯视图A ．①④B ．②③C ．②④D ．①②解析：△PAC 在正方体的左右、前后侧面上的射影为④，上下侧面上的射影为①，选A. 答案：A6．已知a ＝(2，－1,3)，b ＝(－1,4，－2)，c ＝(7,5，λ)，若a ，b ，c 三向量共面，则实数λ等于( )A.627B.637C.607D.657解析：∵a 、b 、c 三向量共面，所以存在实数m 、n ，使得c ＝ma ＋nb . 即⎩⎪⎨⎪⎧7＝2m －n 5＝－m ＋4n λ＝3m －2n∴λ＝657. 答案：D7．(2011年高考辽宁卷)已知球的直径SC ＝4，A ，B 是该球球面上的两点，AB ＝2，∠ASC ＝∠BSC ＝45°，则棱锥S ABC 的体积为( )A.33 B.233 C.433 D.533解析：如图所示，由题意知，在棱锥S ABC 中，△SAC ，△SBC 都是等腰直角三角形，其中AB ＝2，SC ＝4，SA ＝AC ＝SB ＝BC ＝2 2.取SC 的中点D ，易证SC 垂直于平面ABD ，因此棱锥S ABC的体积为两个棱锥S ABD 和C ABD 的体积和，所以棱锥S ABC 的体积V ＝13SC ·S △ADB ＝13×4×3＝433.答案：C8．已知矩形ABCD ，AB=1，BC=2。

人教A版高中必修二试题成都七中-高一年级下期.docx

成都七中2014-2015学年度高一年级下期高2017届期末考试数学模拟试卷（三）一．选择题（每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求．）11. 已知等比数列{a n }中，a 2＞a 3＝1，则使不等式⎝⎛⎭⎪⎫a 1－1a 1＋⎝⎛⎭⎪⎫a 2－1a 2＋⎝⎛⎭⎪⎫a 3－1a 3＋…＋⎝⎛⎭⎪⎫a n －1an≥0成立的最大自然数n 是（）A.2B.5C.8D.1012.在等差数列{a n }中，a 3＋a 4＋a 5＝84，a 9＝73. 对任意m ∈N *，将数列{a n }中落入区间(9m,92m)内的项的个数记为b m ，设数列{b m }的前m 项和S m ，那么9mm S 的最小值为（）A.19 B. 89C.1D.8 二、填空题(每小题4分，共16分，把答案填在题中的横线上.)13. 直线l 过点A (2，1)，B (m ，2)(m ∈R )，其倾斜角为α，若344ππα<<，则m 的取值范围是________；16.下列说法正确的是_____________ ①若正数y x ,满足230x y +-=，则2x yxy+的最小值为3； ②已知)2,0(,∈y x ，且1=xy ，则y x -+-4422的最小值是72416+；③设数列{}n a 的前n 项和为n S .已知11a =,2121233n n S a n n n +=---，则数列{}n a 的通项公式2*,n a n n N =∈；④若数列{}n a 和{}n b 满足()()*∈=N n a a a nb n 221Λ.又{}na 为等比数列，且满足.6,2231b ba +==设()*∈-=N n b a c nn n 11．记数列{}n c 的前n 项和为n S ，对任意*∈N n ，均有n k S S ≥，则正整数k =3. 三.解答题（17-21每小题12分，22题14分，共74分.解答应写出文字说明，证明过程或演算步骤.）2017届高一下期末考试数学模拟试卷（三）参考答案一、选择题1. B2.D3.B4.D5.B6. A7. B8.D9.A 10.C 11.B 12.B 二、填空题13. (1,3)； 14.13 ； 15. 2 ； 16.①②③17. (1)2222221cos 6022cos b ac a bc ac c A A a b c bc A⎧=⎪+=+⇒=⇒=⎨⎪=+-⎩o . 6分(2)sin sin sin sin b B B Bc C⋅=，又2b ac =，有2sin sin sin B A C =，则 . 12分18. (1) 1cos()5cos()3cos()3cos()5αβαβαβαβ⎧+=⎪⎪⇒-=+⎨⎪-=⎪⎩14sin sin 2cos cos tan tan 2αβαβαβ⇒=⇒=19.方程22(1)40ax a x -++<的两根为2,2a，1o 当01a <<，即22a >，解为22x a <<；…4分2o 当1a >，即22a <，解为22x a <<； …8分3o 当1a =，即22a=，无解；… 11分综上，写成集合形式…12分20.(1) 12122=cos()||p p p p p αβ⋅-u u r u u ru u r u u r u u r 在方向上的投影为 3分 (2) 21212|2|=5+4cos()9|2|3p p p p αβ-≤⇒≤u u r u u r u u r u u r++，当cos()1αβ-=，即当2()k k Z αβπ-=∈时，12max |2|3p p =u u r u u r+， 7分(3) 12()(cos())1()23n nn n n a p p a λλαβλπαβ⎧=⋅=-⎪⇒=⎨-=⎪⎩u u ru u r， 9分12111()()()222n n S λλλ=+++L ， ,2,211(1())122(20)(1())121,2220=0n n n n n S λλλλλλλλλλλλ=⎧⎪=⎧⎪-⎪⎪⎪=≠≠=⎨⎨-⎪⎪-≠⎪⎪-⎩⎪⎩且， 12分21. （1）解：()cos 23sin 22sin(2)6f x x x x π=+=+ … 2分[0,]2x π∴∈ 72666x πππ∴≤+≤1sin(2)126x π∴-≤+≤ …3分()f x ∴的值域为[1,2]- … 4分（2）Q 6()5f θ=∴3sin(2)65πθ+= 又Q 263ππθ<<， ∴32262πππθ<+<∴ 4cos(2)65πθ+=- …5分∴cos 2cos[(2)]66ππθθ=+- …7分=cos(2)cos sin(2)sin 6666ππππθθ+++=4331552-⋅+⋅ =343- …8分22.(1)证明： 2324n n n S a =-⋅+ ① 当2n ≥时，1112324n n n S a ---=-⋅+ ②①-②得：112232n n n n a a a --=--⋅即11232n n n a a --=+⋅，等式两边同除2n得：113222n n n n a a --=+ ∴数列{}2n na是等差数列 …4分（2）Q 1112324S a =-⋅+，∴12a =由（1）113(1)222n n a a n =+-=312n - ∴3122nn n a -=⋅∴4(34)2n n S n -=- …6分12(4)(4)...(4)n n T S S S =-+-++-=12(314)2(324)2...(34)2n n ⋅-+⋅-++⋅-错位相减易求14(146)2n n T n =-- …8分（3）11(35)231322222n n n n n C n n -++=-+⋅⋅⋅=(35)(31)(32)2nn n n +-⋅+⋅ …9分 =2(32)(31)(31)(32)2nn n n n +---⋅+⋅=111(31)2(32)2n nn n ---+ …10分易求n Q =011(311)2(32)2nn -⨯-+=112(32)2nn -+ …12分显然{}n Q 单增，又1(32)2nn +>0， ∴112n Q Q ≤<即2152n Q ≤<…14分。

四川省成都市新都一中2024_2025学年高一数学上学期期中试题

四川省成都市新都一中2024-2025学年高一数学上学期期中试题考试时间：120分钟满分：150分第Ⅰ卷选择题（满分 60分）一、选择题（每题5分，共60分） 1．已知幂函数21()m f x x-=的图象经过点（2，8），则实数m 的值是（）A ．1-B ．12C ．2D ．32．已知集合{}2log 1A x x =<，集合{}|11B x x =-≤≤，则A B =（）A ．[1,1]-B ．[1,2)-C ．(]0,1D ．(),2∞-3．函数()1lg(2)f x x x =-++的定义域为（）A ．(2,1)-B ．[2,1]-C ．(2,)-+∞D ．(2,1]-4．函数11y x =-+在区间[]1,2上的最大值为（） A ．13-B ．12-C ．1-D ．不存在5．已知函数1()3()3x xf x =-，则()f x （）A ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数6．已知39log 2a =，1314b ⎛⎫= ⎪⎝⎭，13log 6c =，则a ，b ，c 的大小关系为（）A ．a b c >>B ．b a c >>C ．c b a >>D ．c a b >> 7．函数在上单调递减，且为奇函数．若，则满意的x的取值范围是 A.B.C.D.8．函数1xy x =+的图象是（） A ．B ．C ．D ．9．已知为了抗击新型冠状病毒肺炎保障师生平安，我校确定每天对教室进行消毒工作，已知药物释放过程中，室内空气中的含药量y（3/mg m ）与时间t （h ）成正比（102t <<）；药物释放完毕后，y 与t 的函数关系式为1()4t a y -=（a 为常数，12t ≥），据测定，当空气中每立方米的含药量降低到0.5（3/mg m ）以下时，学生方可进教室，则学校应支配工作人员至少提前( )分钟进行消毒工作 A ．30 B ．40 C ．60 D ．9010．函数2()ln(43)f x x x =+-的单调递减区间是（）A ．32⎛⎤-∞ ⎥⎝⎦，B ．3,42⎡⎫⎪⎢⎣⎭C ．3,2⎡⎫+∞⎪⎢⎣⎭D ．31,2⎛⎤- ⎥⎝⎦11．已知函数的定义域为R ，且对随意的12,x x 且12x x ≠都有()()()12120f x f x x x ⎡⎤-->⎣⎦成立，若()()2211f x f m m +>--对x ∈R 恒成立，则实数m 的取值范围是（）A ．()1,2-B ．[]1,2-C ．(,1)(2,)-∞-+∞D ．(][),12,-∞-⋃+∞12．已知定义在R 上的奇函数()f x 满意()()20f x f x +--=，且当[]0,1x ∈时，()()2log 1f x x =+，则下列结论正确的是（）①()f x 的图象关于直线1x =对称；②()f x 是周期函数，且2是其一个周期；③16132f f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭；④关于x 的方程()0f x t -=（01t <<）在区间()2,7-上的全部实根之和是12. A ．①④B ．①②④C ．③④D ．①②③第Ⅱ卷非选择题（满分 90分）二、填空题（每题5分，共20分）13．24432(3)(3)log 6427π-+-+-=__________14．已知函数831x y a-=-（0a >，且1a ≠）的图像恒过定点(,)A m n ，则log m n =_______15．已知3()4f x ax bx =+-,若(2)6f =,则(2)f -=________16．若平面直角坐标系内两点P ，Q 满意条件：，Q 都在函数的图象上；，Q 关于原点对称，则称点对是函数的图象上的一个“友好点对”已知函数且，若此函数的“友好点对”有且只有一对，则实数a 的取值范围是________三、解答题（共70分）17．（本小题满分10分）设全集U =R ，集合{}1A x x =≤，20x B xx ⎧⎫-=<⎨⎬⎩⎭．求：（1）A B ；（2）()UA B ．18．（本小题满分12分）已知幂函数()213()322mf x m m x +=--+在(0,)+∞上为增函数．（1）求()f x 解析式；（2）若函数2()(21)1y f x a x a =-++-在区间(2,3)上为单调函数，求实数a 的取值范围．19．（本小题满分12分）已知函数是定义在上的奇函数，满意，当时，有．求实数a ，b 的值；求函数在区间上的解析式，并利用定义证明函数在上的单调性．20．（本小题满分12分）已知定义在R 上的函数满意对随意且不恒为0．求和的值；试推断的奇偶性，并加以证明；若时为增函数，求满意不等式的x 的取值集合．21．（本小题满分12分）习近平总书记指出：“我们既要绿水青山，也要金山银山．”新能源汽车环保、节能，以电代油，削减排放，既符合我国的国情，也代表了世界汽车产业发展的方向．十九大指出中国的电动汽车革命早已绽开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的支配，2024年某企业支配引进新能源汽车生产设备看，通过市场分析，全年需投入固定成本3000万元，每生产x （百辆）需另投入成本y （万元），且210100,040100005014500,40x x x y x x x ⎧+<<⎪=⎨+-≥⎪⎩.由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完.（1）求出2024年的利润S （万元）关于年产量x 的函数关系式；（利润=销售额—成本）（2）当2024年产量为多少辆时，企业所获利润最大？并求出最大利润.22．（本小题满分12分）在函数定义域内，若存在区间，使得函数值域为[,]m p n p ++，则称此函数为“p 档类正方形函数”，已知函数，当时，求函数的值域；若函数的最大值是1，求实数k 的值；当时，是否存在，使得函数为“1档类正方形函数”？若存在，求出实数k 的取值范围；若不存在，请说明理由．答案1．【答案】C【解析】因为幂函数21()m f x x -=的图象经过点（2，8），所以2128m -=，解得2m =.2．【答案】C【解析】因为{}{}2log 102A x x x x =<=<<，{}|11B x x =-≤≤，所以{}(]010,1A B x x ⋂=<≤=. 3．【答案】D【解析】函数()lg(2)f x x =+有意义等价于102120x x x -≥⎧⇔-<≤⎨+>⎩，所以定义域为(2,1]-，4．【答案】A【解析】因为函数1y x =-在()0,∞+上单调递增，11y x =-+是由1y x =-向左平移一个单调后得到的函数，所以11y x =-+在()1,-+∞上单调递增，则11y x =-+在区间[]1,2上单调递增，所以最大值为max 11213y =-=-+. 5．【答案】A【解析】函数()133xxf x ⎛⎫=- ⎪⎝⎭的定义域为R ，()()111333,333xxx xxx f x f x --⎡⎤⎛⎫⎛⎫⎛⎫-=-=-+=--=-⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦即函数()f x 是奇函数，又1y 3,3xxy ⎛⎫==- ⎪⎝⎭在R 都是单调递增函数，故函数()f x 在R 上是增函数．6．【答案】A 7．【答案】D解：为奇函数，，．在上单调递减，由，得，即．8．【答案】C【解析】由题意，函数可化简得：1111x y x x -==+++ 则可将反比例函数1y x-=的图象由左平移一个单位，再向上平移一个单位，即可得到函数1xy x =+的图象，答案为选项C. 9．【答案】C【解析】依据图像：函数过点1,12⎛⎫ ⎪⎝⎭，故()1212,0211(),42t x t y f t t -⎧<<⎪⎪==⎨⎪≥⎪⎩，当12t ≥时，取()1211()42t f t -==，解得1t =小时60=分钟.10．【答案】B【解析】由2430x x +->得2340x x --<，解得：14x -<<，2()ln(43)f x x x =+-由ln y t =和234t x x =-++复合而成，ln y t =在定义域内单调递增，234t x x =-++对称轴为32x =，开口向下，所以234t x x =-++在31,2⎛⎫- ⎪⎝⎭单调递增，在3,42⎡⎫⎪⎢⎣⎭单调递减，所以2()ln(43)f x x x =+-的单调减区间为3,42⎡⎫⎪⎢⎣⎭，11．【答案】A【解析】由()()()12120f x f x x x -->⎡⎤⎣⎦，则函数()f x 在R 上为增函数，由()()2211f x f m m +>--对x ∈R 恒成立，故22min 1(1)m m x --<+，即211m m --<解得-1<m<2，12．【答案】A【解析】由()()20f x f x +--=可知()f x 的图象关于直线1x =对称，①正确；因为()f x 是奇函数，所以()()()2f x f x f x +=-=-，所以()()()42f x f x f x +=-+=，所以()f x 是周期函数，其一个周期为4，但不能说明2是()f x 的周期，故②错误；由()f x 的周期性和对称性可得1644243333f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.又当[]0,1x ∈时，()()2log 1f x x =+，所以()f x 在[]0,1x ∈时单调递增，所以1223f f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，即16132f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭，③错误；又[]0,1x ∈时，()()2log 1f x x =+，则可画出()f x 在区间[]2,8-上对应的函数图象改变趋势，如图.易得()0f x t -=（01t <<）即()f x t =（01t <<）在区间()2,7-上的根分别关于1，5对称，故零点之和为()21512⨯+=，④正确. 13．【答案】1【解析】依据指数幂运算及对数的性质,化简可得240432(3)(3)log 6427π-+-+-()2633231log 23=-++-31691=++-=.14．【答案】13【解析】令x ﹣8＝0，解得x ＝8，则y ＝3﹣1＝2，即恒过定点A （8，2）， ∴m ＝8，n ＝2，∴log m n ＝81log 23=. 15．【答案】．14-解：∵3()4f x ax bx =+-33()()4()()48f x f x ax bx a x b x ∴+-=+-+-+⨯--=- ∴()()8f x f x +-=-∵(2)6f =(2)14f ∴-=-16．【答案】解：当时，函数关于原点对称的函数为，即，，若此函数的“友好点对”有且只有一对，则等价为函数，与，，只有一个交点，作出两个函数的图象如图：若，则，与，，只有一个交点，满意条件，当时，，若，要使两个函数只有一个交点，则满意，即得，得或，，，综上或，即实数a 的取值范围是，故答案为：．17．【解析】（1）{}{}111A x x x x =≤=-≤≤，{}2002x B xx x x ⎧⎫-=<=<<⎨⎬⎩⎭，因此，{}01A B x x ⋂=<≤；（2）全集U =R ，{1UA x x ∴=<-或}1x >，因此，(){1U A B x x ⋃=<-或}0x >.18．【解析】（1）∵幂函数解析式为213()(322)mf x m m x+=--+，∴23221m m --+=，即23210m m +-=，解得1m =-或13，当1m =-时，2()f x x -=在(0,)+∞上为减函数，不合题意，舍去；当13m =时，2()f x x =在(0,)+∞上为增函数，符合题意，∴2()f x x =．（2）22(21)1y x a x a =-++-在区间(2,3)上为单调函数，函数对称轴为212a x +=，∴有2122a +≤或2132a +≥，解得32a ≤或52a ≥， ∴实数a 的取值范围为3{|2a a ≤或5}3a ≥．19．【解析】解：函数是定义在上的奇函数，，即，，又因为，所以，即，所以，综上可知，，由可知当时，，当时，，且函数是奇函数，当时，函数的解析式为，任取，，且，则，，，且，，，，于是，即，故在区间上是单调增函数20.【答案】解：令，得，，令，得，，是偶函数：令，则，是偶函数．由式得式，由得，函数是偶函数，则不等式等价为，时为增函数，不等式等价为，平方得，即，即，即满意不等式的x 取值集合为．21．【解析】（1）由题意，当040x <<时，25100101003000S x x x =⨯---2104003000x x =-+-；当40x ≥时，51005014100001000050030001500S x x x x x ⎛⎫=⨯--+-=-+ ⎪⎝⎭；所以2104003000,040100001500,40x x x S x x x ⎧-+-<<⎪=⎨⎛⎫-+≥ ⎪⎪⎝⎭⎩；（2）当040x <<时，210(20)1000S x =--+，当且仅当20x 时，max ()1000L x =；当40x ≥时，1000010000()1500150021300L x x x x x ⎛⎫=-+≤-⋅= ⎪⎝⎭ (当且仅当10000x x=，即100x =时，“=”成立) 因为10001300<，所以，当100x =时，即2020年生产100百辆时，该企业获得利润最大，且最大利润为1300万元.22．解：时，，因为，所以，所以函数的值域为．设，，则，若，则函数无最大值，即无最大值，不合题意；故，因此最大值在时取到，且，所以，解得或，由，所以．因为时，设，设真数为，此时对称轴，所以当时，为增函数，且，即在上为增函数所以，，即方程在上有两个不同实根，即，设，所以即方程有两个大于1的不等实根，因为，所以解得，由，得．即存在，使得函数为“1档类正方形函数”，且．。

人教A版高中数学必修第二册测试题(含答案)

人教A版高中数学必修第二册测试题（含答案）一、单选题1．设D为所在平面内一点，且，则（）A．B．C．D．2．若复数为纯虚数，则实数（）A．B．0C．5D．3．已知四边形为平行四边形，其中，则顶点的坐标为（）A．B．C．D．4．如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30,35)，[35,40)，[40,45)的上网人数呈现递减的等差数列分布，则年龄在[35,40)的网民出现的频率为( )A．0.04B．0.06C．0.2D．0.35．某三棱锥的三视图如右图所示，该三棱锥的体积为A．B．C．D．6．如果一个三位数的十位上的数字比个位和百位上的数字都大，则称这个三位数为“凸数”（如132），现从集合中任取3个互不相同的数字，组成一个三位数，则这个三位数是“凸数”的概率为（）A．B．C．D．7．下列说法正确的个数是（）①一组数据的标准差越大，则说明这组数据越集中；②曲线与曲线的焦距相等；③在频率分布直方图中，估计的中位数左边和右边的直方图的面积相等；④已知椭圆，过点作直线，当直线斜率为时，M刚好是直线被椭圆截得的弦AB的中点.A．1B．2C．3D．48．在中，一定成立的等式是（）A．B．C．D．9．从高二某班级中抽出三名学生．设事件甲为“三名学生全不是男生”，事件乙为“三名学生全是男生”，事件丙为“三名学生至少有一名是男生”，则（）A．甲与丙互斥B．任何两个均互斥C．乙与丙互斥D．任何两个均不互斥10．已知是平面，是直线，则下列命题不正确的是（）A．若则B．若则C．若则D．若，则11．某中学的高一、高二、高三共有学生1350人，其中高一500人，高三比高二少50人，为了解该校学生健康状况，现采用分层抽样方法进行调查，在抽取的样本中有高一学生120人，则该样本中的高二学生人数为( )A．80B．96C．108D．110二、填空题12．在复变函数相关领域中，欧拉公式为（这里是虚数单位），当时，可以得到，这个公式被誉为数学中最令人着迷的公式，根据欧拉公式，则______．13．玲玲和倩倩是一对好朋友，她俩都想去观看某明星的演唱会，可手里只有一张票，怎么办呢？玲玲对倩倩说：“我向空中抛2枚同样的一元硬币，如果落地后一正一反，就我去；如果落地后两面一样，就你去！”你认为这个游戏公平吗？答：________．14．气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22℃.现有甲、乙、丙三地连续5天的日平均温度的记录数据：（记录数据都是正整数）①甲地5个数据的中位数为24，众数为22；②乙地5个数据的中位数为27，总体均值为24；③丙地5个数据中有一个数据是32，总体均值为26，总体方差为10.8.则肯定进入夏季的地区有_____．15．已知水平放置的△ABC按“斜二测画法”得到如图所示的直观图，其中B′O′=C′O′=2，∠B'A'C'=90°，则原△ABC的面积为______．三、解答题16．在中，角所对的边分别为已知.（1）求A的大小；（2）如果，求的面积.17．宜宾市创建全国文明城市期间，一单位有甲、乙、丙三个志愿小组，其中甲组4人，乙组8人，丙组12人，现用分层抽样方法从这三个组中选出6人组成宣传小组.（1）应从甲组、乙组、丙组中各抽取多少人？（2）记选出6人分别为，现从这6人中抽取2人进入某小区进行创文宣传；①试用所给的字母列举出所有可能的抽取结果；②设事件是“抽取2人来自同一志愿小组”，求事件发生的概率. 18．某公司有名员工，根据男女员工人数比例，用分层随机抽样的方法从中抽取了人，调查他们的通勤时间（上下班途中花费的总时间，单位：分钟），将数据按照，，，分成组，并整理得到如下频率分布直方图：（I）从总体中随机抽取人，估计其通勤时间小于分钟的概率；（Ⅱ）求样本数据的中位数的估计值；（Ⅲ）已知样本中通勤时间大于或等于分钟的人都是男员工，通勤时间小于分钟的人中有一半是男员工，求该公司男员工的人数.19．如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC⊥CB，点M和N分别是B1C1和BC的中点．（1）求证：MB∥平面AC1N；（2）求证：AC⊥MB．20．设，复数，其中为虚数单位.（1）当为何值时，复数是虚数？（2）当为何值时，复数是纯虚数？（3）当为何值时，复数所对应的点在复平面内位于第四象限？21．如图，已知正方体内接于球O，且球的半径为，P，Q分别是，上的动点.（1）求正方体的棱长；（2）求的最小值；（3）若平面与平面所成二面角的大小为，平面与平面所成二面角的大小为，试求的最小值，及此时P点的位置.参考答案1．D2．A3．D4．C5．A6．D7．B8．C9．A10．D11．C12．413．公平14．①③15．816．（1）；（2）17．（1）甲组1人，乙组2人，丙组3人；（2）①，；②.18．（Ⅰ）；（Ⅱ）；（Ⅲ）.19．（1）见解析；（2）见解析20．（1）且；（2）；（3）. 21．（1）2（2）（3），点P位于BC的中点。

人教A版高中必修二试题四川省成都市新都一中高级测试题.doc

四川省成都市新都一中高2014级数学测试题时间：120分钟总分：150分一、选择题：本大题共12小题，每小题5分，共60分． 1．已知a 、b 、c 为三条不重合的直线，下面有三个结论： ①若a ⊥b ，a ⊥c ，则b ∥c ；②若a ⊥b ，a ⊥c 则b ⊥c ；③若a ∥b ，b ⊥c ，则a ⊥c .其中正确的个数为( )A ．0个B ．1个C ．2个D ．3个 [答案] B[解析] b 、c ⊂平面α，a ⊥α满足①②的条件，当b 与c 相交但不垂直时，①、②错；③正确．2．下列命题中不正确的是( )A ．若a ⊂α，b ⊂α，l ∩α＝A ，l ∩b ＝B ，则l ⊂α B ．若a ∥c ，b ∥c ，则a ∥bC ．若a ⊄α，b ⊂α，a ∥b ，则a ∥αD ．若一直线上有两点在已知平面外，则直线上所有点在平面外 [答案] D[解析] 当直线与平面相交时，直线与平面有且仅有一个公共点，除公共点外的其它点都在平面外．3．一个正方体的展开图如图所示，A 、B 、C 、D 为原正方体的顶点，则在原来的正方体中( )A ．AB ∥CD B ．AB 与CD 相交C ．AB ⊥CD D ．AB 与CD 所成的角为60° [答案] D[解析] 正方体的直观图如图，显然AB 与CD 异面，排除A 、B ，CD ∥BE ，△ABE 为正三角形，∴AB 与CD 所成的角为60°.4．下列命题中错误的是( )A ．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC ．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l ，那么直线l ⊥平面γD ．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β [答案] D[解析] 当平面α与β垂直时，设交线为l ，则在α内与l 平行的直线与β平行，∴A 真；假设在α内存在直线与β垂直，则由二平面垂直的判定定理知，α⊥β，故B 真；在l 上任取一点P 且P ∉γ，过P 作γ的垂线，垂足为Q ，∵α⊥γ，则Q 必在α与γ的交线l 1上，同理，Q 必在β与γ的交线l 2上，∴Q 是l 1与l 2的交点，∵l 1⊂α，l 2⊂β，∴Q 是α与β的一个公共点，∴Q ∈l ，∴l ⊥γ，∴C 真，易知D 假．5．下图是一几何体的三视图(单位：cm)，则这个几何体的体积为( )A ．1cm 3B ．3cm 3C ．2cm 3D ．6cm 3[答案] B[解析] 由三视图知，该几何体是一个横放的棱柱，棱柱的高为3，棱柱的底面是一个等腰三角形，其底为2，高为1，∴体积V ＝(12×2×1)×3＝3(cm 3)．6．如图，一个空间几何体的主视图、左视图都是周长为4，一个内角为60°的菱形，俯视图是圆及一点，那么这个几何体的表面积为( )A.π2 B ．π C.3π2 D ．2π [答案] B 我以我的荣誉发誓：决不给予或接受他人任何形式的帮助！姓名：[解析] 由三视图知，该几何体是两个同底的圆锥构成的组合体．圆锥的母线长为1，底半径为12，∴表面积S ＝2×(π×12×1)＝π.7．在空间四边形ABCD 中，AB →·CD →＋AC →·DB →＋AD →·BC →的值为( )A ．0 B.32C ．1D ．无法确定[答案] A[解析] 如图，AB →·CD →＋AC →·DB →＋AD →·BC →＝AB →·(AD →－AC →)＋AC →·(AB →－AD →)＋AD →·(AC →－AB →)＝AB →·AD →－AB →·AC →＋AC →·AB →－AC →·AD →＋AD →·AC →－AD →·AB →＝0. 8．斜二测画法中，边长为a 的正方形的直观图的面积为( )A ．a 2B.22a 2C.12a 2D.24a 2[答案] D[解析] S ＝a ·(a 2·sin45°)＝24a 2，故选D.9已知空间三点A (0,2,3)，B (－2,1,6)，C (1，－1,5)．若|a |＝3，且a 分别与AB →，AC →垂直，则向量a 为( )A ．(1,1,1)B ．(－1，－1，－1)C ．(1,1,1)或(－1，－1，－1)D ．(1，－1,1)或(－1,1，－1) [答案] C[解析] 设a ＝(x ，y ，z )，由条件知AB →＝(－2，－1,3)，AC →＝(1，－3,2)，∵a ⊥AB →，a ⊥AC →，|a |＝3，∴⎩⎪⎨⎪⎧－2x －y ＋3z ＝0x －3y ＋2z ＝0x 2＋y 2＋z 2＝3，将选项代入检验知选C.10．已知直线m 、n 和平面α、β，若α⊥β，α∩β＝m ，n ⊂α，要使n ⊥β，则应增加的条件是( )A ．m ∥nB ．n ⊥mC ．n ∥αD ．n ⊥α [答案] B[解析] 根据面面垂直的性质定理知，需增加条件n ⊥m .11.如图所示，在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，将△ABD 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A －BCD ，则在三棱锥A －BCD 中，下列命题正确的是( )A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABC [答案] D[解析] 在平面图形中CD ⊥BD ，折起后仍有CD ⊥BD ，由于平面ABD ⊥平面BCD ，故CD ⊥平面ABD ，CD ⊥AB .又AB ⊥AD ，故AB ⊥平面ADC .所以平面ABC ⊥平面ADC .12．球O 的球面上有四点S 、A 、B 、C ，其中O 、A 、B 、C 四点共面，△ABC 是边长为2的正三角形，平面SAB ⊥平面ABC ，则棱锥S －ABC 的体积的最大值为( )A ．1 B.13 C. 3 D.33[答案] D[解析] ∵O 、A 、B 、C 四点共面，∴△ABC 的外接圆为球大圆，∵△ABC 边长为2，∴球半径OA ＝23×(32×2)＝233，设AB 的中点为E ，则OE ＝13×(32×2)＝33，棱锥S －ABC的底面积S ＝34×22＝3为定值，欲使其体积最大，应有S 到平面ABC 的距离取最大值，又平面SAB ⊥平面ABC ，∴S 在平面ABC 上的射影落在直线AB 上，又SO ＝233为定值，∴S到平面ABC 的距离的最大值为2332－332＝1，∴V ＝13×3×1＝33.二、填空题（每小题4分，共16分）13已知a ＝(－2,1,3)，b ＝(－1,2,1)，若a ⊥(a －λb )，则实数λ的值为 2 14．(2011～2012·南通市调研)已知直线l ⊥平面α，直线m ⊂平面β，给出下列命题：①α∥β⇒l ⊥m ；②α⊥β⇒l ∥m ；③l ∥m ⇒α⊥β；④l ⊥m ⇒α∥β.其中正确命题的序号是________．[答案] ①③⎭⎬⎫⎭⎪⎬⎪⎫[解析] l ⊥α α∥β⇒l ⊥β m ⊂β⇒l ⊥m ，故①真；⎭⎬⎫⎭⎪⎬⎪⎫l ⊥αα⊥β⇒l ∥β或l ⊂β m ⊂β⇒/ l ∥m ，故②假；⎭⎬⎫⎭⎪⎬⎪⎫l ⊥αl ∥m⇒m ⊥α m ⊂β⇒α⊥β，故③真；⎭⎬⎫⎭⎪⎬⎪⎫l ⊥αl ⊥m⇒m ∥α或m ⊂α m ⊂β⇒/ α∥β，故④假．15．在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝2AB ，若E ，F 分别为线段A 1D 1，CC 1的中点，则直线EF 与平面ABB 1A 1所成角的余弦值为________．[答案] 63[解析] 解法一：以A 为坐标原点，AB 、AD 、AA 1分别为x 轴、y 轴、z 轴建立空间直角坐标系如图，设AB ＝1，则AD ＝AA 1＝2，∴F (1,2,1)，E (0,1,2)，∴EF →＝(1,1，－1)，平面ABB 1A 1的一个法向量n ＝(0,1,0)，则cos 〈n ，EF →〉＝n ·EF →|n |·|EF →|＝33，设EF 与平面ABB 1A 1所成角为θ，则sin θ＝33， ∴cos θ＝63. 解法二：取BB 1的中点M ，取FM 的中点N ，则EA 1綊FN ，∴四边形A 1EFN 为平行四边形，∴A 1N ∥EF ，∵EA 1⊥平面ABB 1A 1，∴MN ⊥平面ABB 1A 1，∴∠NA 1M 为直线EF 与平面ABB 1A 1所成的角，在Rt △A 1MN 中，A 1M ＝2，MN ＝1，∴A 1N ＝3，∴cos ∠NA 1M ＝A 1M A 1N ＝63，∴直线EF 与平面ABB 1A 1所成角的余弦值为63. 16．如图所示的几何体中，四边形ABCD 是矩形，平面ABCD ⊥平面ABE ，已知AB ＝2，AE ＝BE ＝3，且当规定主(正)视图方向垂直平面ABCD 时，该几何体的左(侧)视图的面积为22.若M 、N 分别是线段DE 、CE 上的动点，则AM ＋MN ＋NB 的最小值为________．[答案] 3[解析] 取AB 中点F ，∵AE ＝BE ＝3，∴EF ⊥AB ，∵平面ABCD ⊥平面ABE ，∴EF ⊥平面ABCD ，易求EF ＝2，左视图的面积S ＝12AD ·EF ＝22AD ＝22，∴AD＝1，∴∠AED ＝∠BEC ＝30°，∠DEC ＝60°，将四棱锥E －ABCD 的侧面AED 、DEC 、CEB 展开铺平如图，则AB 2＝AE 2＋BE 2－2AE ·BE ·cos120°＝3＋3－2×3×(－12)＝9，∴AB ＝3，∴AM ＋MN ＋BN 的最小值为3.三、解答题：本大题共6小题，共74分．解答应写出必要的文字说明，证明过程或演算步骤17．(本小题满分12分)如图，四棱锥P －ABCD 的底面ABCD 为直角梯形，其中BA ⊥AD ，CD ⊥AD ，CD ＝AD ＝2AB ，PA ⊥底面ABCD ，E 是PC 的中点．(1)求证：BE ∥平面PAD ；(2)若AP ＝2AB ，求证：BE ⊥平面PCD .[解析] (1)取PD 的中点F ，连结AF ，FE ，又∵E 是PC 的中点，∴在△PDC 中，EF ∥DC ，且EF ＝DC2，由条件知AB ∥DC ，且AB ＝DC2，∴EF 綊AB ，∴四边形ABEF 为平行四边形，∴BE ∥AF ，又AF ⊂平面PAD ，BE ⊄平面PAD ，∴BE ∥平面PAD . (2)由(1)FE ∥DC ，BE ∥AF ，又∵DC ⊥AD ，DC ⊥PA ，∴DC ⊥平面PAD ，∴DC ⊥AF ，DC ⊥PD ，∴EF ⊥AF ，在Rt △PAD 中，∵AD ＝AP ，F 为PD 的中点，∴AF ⊥PD ，又AF ⊥EF 且PD ∩EF ＝F ，∴AF ⊥平面PDC ，又BE ∥AF ，∴BE ⊥平面PDC .18．如图，在四棱锥P －ABCD 中，底面ABCD 为直角梯形，AD ∥BC ，∠ADC ＝90°，BC ＝12AD ，PA ＝PD ，Q 为AD 的中点． (1)求证：AD ⊥平面PBQ ；(2)若点M 在棱PC 上，设PM ＝tMC ，试确定t 的值，使得PA ∥平面BMQ .[解析] (1)证明：AD ∥BC ，BC ＝12AD ，Q 为AD 的中点，∴四边形BCDQ 为平行四边形，∴CD ∥BQ .∵∠ADC ＝90°，∴∠AQB ＝90°，即QB ⊥AD . ∵PA ＝PD ，Q 为AD 的中点，∴PQ ⊥AD . ∵PQ ∩BQ ＝Q ，∴AD ⊥平面PBQ .(2)解：当t ＝1时，PA ∥平面BMQ ，连接AC ，交BQ 于N ，连接MN .∵BC 綊12AD ，∴四边形BCQA 为平行四边形，且N 为AC 中点． ∵点M 是线段PC 的中点，∴MN ∥PA .∵MN ⊂平面BMQ ，PA ⊄平面BMQ ，∴PA ∥平面BMQ .19．如图，已知四棱锥P －ABCD ，侧面PAD 为边长等于2的正三角形，底面ABCD 为菱形，∠DAB ＝60°.(1)证明：∠PBC ＝90°；(2)若PB ＝3，求直线AB 与平面PBC 所成角的正弦值．[解析] (1)取AD 中点O ，连OP 、OB ，由已知得：OP ⊥AD ，OB ⊥AD ，又OP ∩OB ＝O ，∴AD ⊥平面POB ，∵BC ∥AD ，∴BC ⊥平面POB ，∵PB ⊂平面POB ， ∴BC ⊥PB ，即∠PBC ＝90°.(2)如图，以O 为坐标原点，建立空间直角坐标系O －xyz ，则A (1,0,0)，B (0，3，0)，C (－1，3，0)，由PO ＝BO ＝3，PB ＝3，得∠POB ＝120°，∴∠POz＝30°，∴P (0，－32，32)，则AB →＝(－1，3，0)，BC →＝(－1,0,0)，PB →＝(0，332，－32)，设平面PBC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－x ＝0332y －32z ＝0，取z ＝3，则n ＝(0,1，3)，设直线AB 与平面PBC 所成的角为θ，则sin θ＝|cos 〈AB →，n 〉|＝34.20．如图所示，直角梯形ACDE 与等腰直角△ABC 所在平面互相垂直，F 为BC 的中点，∠BAC ＝∠ACD ＝90°，AE ∥CD ，DC ＝AC ＝2AE ＝2.(1)求证：AF ∥平面BDE ；(2)求二面角B －DE －C 的余弦值．[解析] (1)取BD 的中点P ，连接EP 、FP ，则PF 綊12DC ，又∵EA 綊12DC ，∴EA 綊PF ，∴四边形AFPE 是平行四边形，∴AF ∥EP ，又∵EP ⊂平面BDE ，AF ⊄平面BDE ， ∴AF ∥平面BDE .(2)以CA 、CD 所在直线分别作为x 轴，z 轴，以过C 点和AB 平行的直线作为y 轴，建立如图所示坐标系．由DC ＝AC ＝2AE ＝2可得：A (2,0,0)，B (2,2,0)，E (2,0,1)，D (0,0,2)，则AB →＝(0,2,0)，BE →＝(0，－2,1)，BD →＝(－2，－2,2)．∵平面ACDE ⊥平面ABC ，平面ACDE ∩平面ABC ＝AC ，AB ⊥AC ，∴AB ⊥平面ACDE . ∴AB →＝(0,2,0)是平面CDE 的一个法向量，设平面BDE 的一个法向量n ＝(x ，y ，z )，则n ⊥BE →，n ⊥BD →，∴⎩⎪⎨⎪⎧n ·BE →＝0n ·BD →＝0，即⎩⎪⎨⎪⎧－2y ＋z ＝0－2x －2y ＋2z ＝0，整理得，⎩⎪⎨⎪⎧2y －z ＝0x ＋y －z ＝0，令y ＝1，得z ＝2，x ＝1，所以n ＝(1,1,2)是平面CDE 的一个法向量，则cos 〈AB →，n 〉＝AB →·n |AB →||n |＝1×22×12＋12＋22＝66. 可知二面角B －DE －C 的平面角θ∈(0，π2)，所以其余弦值为66. 21．一个四棱锥的三视图如图所示． (1)求证：PA ⊥BD ；(2)在线段PD 上是否存在一点Q ，使二面角Q －AC －D 的平面角为30°？若存在，求|DQ ||DP |的值；若不存在，说明理由．[解析] (1)由三视图可知P －ABCD 为四棱锥，底面ABCD 为正方形，且PA ＝PB ＝PC ＝PD ，连接AC 、BD 交于点O ，连接PO .因为BD ⊥AC ，BD ⊥PO ，所以BD ⊥平面PAC ，即BD ⊥PA .(2)由三视图可知，BC ＝2，PA ＝22，假设存在这样的点Q ，因为AC ⊥OQ ，AC ⊥OD ，所以∠DOQ 为二面角Q －AC －D 的平面角，在△POD 中，PD ＝22，OD ＝2，则∠PDO ＝60°，在△DQO 中，∠PDO ＝60°，且∠QOD ＝30°.所以DP ⊥OQ .所以OD ＝2，QD ＝22.所以DQ DP ＝14.22．(本小题满分12分)如图(1)所示，在直角梯形ABCP 中，BC ∥AP ，AB ⊥BC ，CD ⊥AP ，AD ＝DC ＝PD ＝2，E 、F 、G 分别为线段PC 、PD 、BC 的中点，现将△PDC 折起，使平面PDC ⊥平面ABCD (图(2))．(1)求证：AP ∥平面EFG ；(2)若点Q 是线段PB 的中点，求证：PC ⊥平面ADQ ； (3)求三棱锥C －EFG 的体积．[解析] (1)证明：∵E 、F 分别是PC ，PD 的中点， ∴EF ∥CD ∥AB .又EF ⊄平面PAB ，AB ⊂平面PAB ，∴EF ∥平面PAB . 同理，EG ∥平面PAB ，∴平面EFG ∥平面PAB . 又∵AP ⊂平面PAB ，∴AP ∥平面EFG . (2)解：连接DE ，EQ ，∵E 、Q 分别是PC 、PB 的中点，∴EQ ∥BC ∥AD .∵平面PDC ⊥平面ABCD ，PD ⊥DC ，∴PD ⊥平面ABCD . ∴PD ⊥AD ，又AD ⊥DC ，∴AD ⊥平面PDC ，∴AD ⊥PC . 在△PDC 中，PD ＝CD ，E 是PC 的中点，∴DE ⊥PC ，∴PC ⊥平面ADEQ ，即PC ⊥平面ADQ .(3)V C －EFG ＝V G －CEF ＝13S △CEF ·GC ＝13×12×1=16。

人教A版高中必修二试题四川省成都市实验外国语学校—高二上学期10月月考试题

高中数学学习材料（灿若寒星精心整理制作）四川省成都市实验外国语学校2013—2014学年高二上学期10月月考数学试题一、选择题（每题5分，共50分） 1. 三视图均相同的几何体有（）A ．球B ．正方体C ．正四面体D ．以上都对2.体积相等的球和正方体，它们的表面积的大小关系是（）A.S S >球正方体B.=S S 球正方体C.S S <球正方体D.不能确定3.直线12:370,:20l x y l kx y +-=--=与x 轴、y 轴围成的四边形有外接圆，则k 的值等于（）A.3-B.3C.6-D. 64.在0,0a b >>的条件下，三个结论：① 2,2ab a ba b +≤+ ②2222a b a b ++≤， ③22b a a b a b+≥+，其中正确个数的是（） A.0 B.1 C.2 D.35.如果1238,,,...,a a a a 是各项都大于零的等差数列，公差0d ≠，则（） A.1845a a a a > B.1845a a a a < C.1845a a a a +>+ D. 1845a a a a =6.下列判断中正确的是（）A.ABC ∆中，07,14,30a b A ===有两解；B.0,30,25,150ABC a b A ∆===中有一解；C.06,9,45ABC a b A ∆===中，有两解； D.09,10,60ABC b c B ∆===中，无解；7.甲、乙两人同时从寝室到教室，甲一半路程步行，一半路程跑步。

乙一半时间步行，一半时间跑步，如果两人步行速度和跑步速度均相同，则（）A.甲先到教室；B.乙先到教室C.两人同时到教室D.谁先到教室不确定8.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能是（）A.1B.2C.212- D.212+ 9.已知正三棱柱111ABC A B C -的棱长相等，E 是11A B 的中点，F 是11B C 的中点，则异面直线AE 和BF 所成角的余弦值是（）A.710B.23C.750D.1210.设实数0,,,bc ca ababc a b c≠成等差数列，则下列不等式一定成立的是（）A.||||b ac ≤B.2||b ac ≥ C.222a b c ≤≤ D.||||||2a c b +≤二．填空题（每题5分，共25分）11.若不等式组5002x y y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的面积区域是一个三角形，则a 的取值范围是 .12.下列命题（,m n 是两条直线，α是平面） ①若m //,//,n αα则//m n ； ②若//,//,m n n α则//m α；③若//m α，则m 平行于α内的所有直线； ④若m 平行于α内的的无数条直线，则//m α；以上正确的命题有个.13. 如图，E ，F 分别是正方体1AC 的面11ADD A 和面11BCC B 的中心，则四边形1BFD E 在该正方体的面上的正投影（投射线垂直于投影面的投影）可能是．（把所有可能图形的序号都填上）错误！未找到引用源。

人教A版高中必修二试题四川省成都市届高二期中测试(理数)

高中数学学习材料金戈铁骑整理制作郫县一中第三学期期中考试参考答案数学（理工类）一、选择题答案：二、填空题：本大题共4小题,每小题4分,共16分．13. 12580x y -+= 或 1x =； 14. 122⎡⎤⎢⎥⎣⎦， 15 33 16. ②③④三、解答题：本大题共6小题,满分74分．17. 解：由24020x y x y -+=⎧⎨+-=⎩得1l 与2l 的交点为（0，2）， ……………3分又∵3:3450l x y -+=的斜率为34，∴l 的斜率为43-， ………………6分由点斜式得所求直线l 的方程为42(0)3y x -=--， ………………9分即4360x y +-=为所求直线l 的方程 ………………12分 18.解:由2100x y y -+=⎧⎨=⎩∴A （－1，0） ………… 2 分又K AB =2011(1)-=-- ∵x 轴为∠A 的平分线，故K AC =－1 ………… 4分∴AC 边的方程为：y =－(x +1) …………6分∵BC 边上的高的方程为：x －2y +1=0 ………… 8分∴K BC =－2∴BC 边的方程为：y －2=－2（x －1）即：2x +y －4=0 ………… 10分由24010x y x y +-=⎧⎨++=⎩解得C （5，－6） …………12分 19. 解设圆心坐标为(3,)y y ， ………… 2分则圆心到y x =的距离为|3|2||2y y d y -== ………… 4分又因为圆C 与y 轴相切，则|3|r y = ………… 6分由题意知222(2)(7)3y y+= …………8分 1y ∴=± …………10分题号1 2 3 4 5 6 7 8 9 10 11 12 答案Ｃ C ＢＢＢＤＤＢ D ＢＢ A当1y =时，圆心为（3，1），则圆C 的方程为22(3)(1)9x y -+-= …………11分当1y =-时，圆心为（-3，-1），则圆C 的方程为22(3)(1)9x y +++= ……12分20.解:(1)直线方程()():21174l m x m y m +++=+,可以改写为()2740m x y x y +-++-=,所以直线必经过直线27040x y x y +-=+-=和的交点.由方程组270,40x y x y +-=⎧⎨+-=⎩解得3,1x y =⎧⎨=⎩即两直线的交点为A (3,1). ……3分又因为点()3,1A 与圆心()1,2C 的距离55d =<,所以该点在C 内,故不论m 取什么实数,直线l 与圆C 恒相交. ……6分(2)连接AC ,过A 作AC 的垂线,此时的直线与圆C 相交于B 、D .BD 为直线被圆所截得的最短弦长.此时,5,5,225545AC BC BD ===-=所以. 即最短弦长为45. ……9分又直线AC 的斜率12AC k =-,所以直线BD 的斜率为 2.此时直线方程为:()123,250.y x x y -=---=即 ……12分21．解：（Ⅰ）由题意，得2333a cc a⎧=⎪⎪⎨⎪=⎪⎩，………… 2分解得1,3a c ==， ∴2222b c a =-=，∴所求双曲线C 的方程为2212y x -=. ………… 4分（Ⅱ）设A 、B 两点的坐标分别为()()1122,,,x y x y ，线段AB 的中点为()00,M x y ，22012x y m y x -+=⎧⎪⎨-=⎪⎩得22220x mx m ---=（判别式0∆>）, ………… 7分 ∴12000,22x x x m y x m m +===+=, ………… 10分 ∵点()00,M x y 在圆225x y +=上，∴()2225m m +=，∴1m =±. ………… 12分 22.解答：（Ⅰ）设P （x ，y ），由椭圆定义可知，点P 的轨迹C 是以(03)(03)-，，，为焦点，长半轴为2的椭圆．它的短半轴222(3)1b =-=，故曲线C 的方程为2214y x +=． ········································································· 3分（Ⅱ）设1122()()A x y B x y ，，，，其坐标满足2214 1.y x y kx ⎧+=⎪⎨⎪=+⎩，消去y 并整理得22(4)230k x kx ++-=，判别式0∆>，故1212222344k x x x x k k +=-=-++，． ·································································· 6分若OA OB ⊥，即12120x x y y +=．而2121212()1y y k x x k x x =+++，于是22121222233210444k k x x y y k k k +=---+=+++，化简得2410k -+=，所以12k =±． ···································································· 9分（Ⅲ）2222221122()OA OB x y x y -=+-+ 22221212()4(11)x x x x =-+--+ 12123()()x x x x =--+ 1226()4k x x k -=+．·································································· 12分因为A 在第一象限，故10x >．由12234x x k =-+知20x <，从而120x x ->．又0k >，故220OA OB ->，即在题设条件下，恒有OA OB >． ································································· 14分。

人教A版高中必修二试题四川省成都市新都一中高级第三期周练01教师版含详解.docx

四川省成都市新都一中高2015级第三期周练01第I 卷（选择题）一、选择题（本大题共12哥个小题，每小题5分，12个小题共计60分） 1．过点()1,2，且与直线220x y ++=垂直的直线方程为A .20x y -=B .230x y -+=C .240x y +-=D .250x y +-= 【答案】A【解析】因为220x y ++=的斜率为12-，所以过点()1,2，且与直线220x y ++=垂直的直线的斜率为2，因此过点()1,2，且与直线220x y ++=垂直的直线的方程为()221,y x -=-既是20x y -=，故选A . 考点：1、直线垂直的性质；2、点斜式求直线方程.2．已知{}n a 是首项为2且公差不为0的等差数列，若136,,a a a 成等比数列，则{}n a 的前9项和等于（）A ．26B ．30C ．36D ．40 【答案】C【解析】设等差数列公差为d ，则由已知)52(2)22(2d d +⋅=+，解得21=d ，所以{}n a 的前9项和为362128929=⨯⨯+⨯. 考点：等差数列、等比中项．3．某棱锥的三视图（单位：cm ）如图所示，则该棱锥的体积等于（）A ．310cmB ．320cmC ．330cmD ．340cm【答案】B【解析】由三视图可知，该几何体为如下图所示的四棱锥P ABCD -，所以其体积1543203V =⨯⨯⨯=，故选B .考点：1.三视图；2.多面体的体积.4．过两直线l 1：x －3y ＋4＝0和l 2：2x ＋y ＋5＝0的交点和原点的直线方程为（）A ．19x －9y ＝0B ．9x ＋19y ＝0C ．19x －3y ＝ 0D ．3x ＋19y ＝0 【答案】D【解析】由题意得，联立方程组，可解得交点坐标为193(,)77-，所以过原点的直线的斜率为3037191907-=---，所以直线的方程为319y x =-，即13190x y +=，故选D ．考点：两条直线的交点；直线的方程．5．如果AC ＜0且BC ＜0，那么直线Ax ＋By －C ＝0不通过 A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】AABDC【解析】由直线0,1Ax By Ax By C C C +-=+=，0,0,0,0A B AC BC C C<<<<，即直线在坐标轴上的截距都小于零，必不过第一象限.考点:直线的截距式方程的应用. 6．下列说法错误的是（）A ．若直线//a 平面α，直线//b 平面α，则直线a 不一定平行于直线bB ．若平面α不垂直于平面β，则α内一定不存在直线垂直于平面βC ．若平面α⊥平面β，则α内一定不存在直线平行于平面βD ．若平面α⊥平面v ，平面β⊥平面v ，l αβ=I ，则l 一定垂直于平面v【答案】C【解析】若直线//a 平面α，直线//b 平面α，则a 与b 相交、平行或异面，故a 不一定平行于b ，所以A 正确；若平面α不垂直于平面β，则由平面与平面垂直的判定定理知α内一定不存在直线垂直于β，故B 正确；若平面α⊥平面β，则α内一定也存在直线平行于β，故C 错误；若平面α垂直于平面v ，平面β垂直于平面v ，l αβ=I ，则由平面与平面垂直的性质得l 一定垂直于平面v ，故D 正确；故选：C ．考点：空间中直线与直线之间的位置关系.7．若数列{}n a 是等差数列，首项10a >，201520160a a +>，201520160a a ⋅<，则使前n 项和n S 取得最大值的自然数n 是（）A ．1007B ．1008C ．2015D ．2016 【答案】C【解析】由题意可知0,020162015<>a a ，因此n 的最大值为2015，故选C . 考点：等差数列的性质．8．已知点(1,2)-和在直线:10l ax y -+=(0)a ≠的同侧，则直线l 倾斜角的取值范围是（） A ．(,)43ππ B ．3(0,)(,)34πππU C ．35(,)46ππ D ．23(,)34ππ 【答案】D【解析】因为点(1,2)-和在直线:10l ax y -+=(0)a ≠的同侧，所以(21)(01)03a a --+-+>，即(1)(0a a ++<，所以1a <<-，又直线l 的斜率k a =，即1k <<-，所以倾斜角的范围为23(,)34ππ，故选D . 考点：1.直线的倾斜角与斜率；2.线性规划.9．不等式组20,240,320x y x y x y +-≥⎧⎪+-≤⎨⎪+-≥⎩表示的平面区域的面积为（）A ．2B ．4C ．6D ．8 【答案】B【解析】其平面区域如图所示，面积为4)]2(2[)24(21=--⨯-⨯=S ，故选B . 考点：线性规划．10．设,x y 满足约束条件1210,0y x y x x y ≤+⎧⎪≥-⎨⎪≥≥⎩，则目标函数(0,0)z abx y a b =+>>的最大值为11，则a b +的最小值为（）A ．2B ．4C ．6D ．8 【答案】B【解析】在直角坐标系中作出可行域，如下图所示，因为0,0a b >>，所以目标函数z abx y =+取得最大值时的最优解为(2,3)B ，所以1123ab =⨯+，即4ab =，所以24a b ab +≥=，当且仅当2a b ==时取等号，故选B .考点：1.线性规划；2.基本不等式.11．当方程22220x y kx y k ++++=表示圆取得最大面积时，直线()12y k x =-+的倾斜角为（）A ．34π B ．4π C ．2πD ．0 【答案】A【解析】方程22220x y kx y k ++++=可化为：()22231124k x y k ⎛⎫+++=- ⎪⎝⎭ ①，若表示圆，则满足条件：23104k ->，即2403k ≤< ②．根据题意若圆的面积最大，则半径最大，由①知，22314r k =-，根据②，可得max 1r =，即0k =．此时直线()12y k x =-+为2y x =-+，倾斜角为34π，选A ．考点：1.圆的标准方程；2.直线的倾斜角．12．在棱长为3的正方体1111ABCD A B C D -中，P 在线段1BD 上，且112BP PD =，M 为线段11B C 上的动点，则三棱锥M PBC -的体积为（）A ．1B ．32 C ．92D ．与M 点的位置有关【答案】B【解析】三棱锥M PBC -的高为点M 到平面PBC的距离，即2h =，底面三角形PBC 的底为 3BC =，高为P 到BC的距离232⨯=所以三棱锥M PBC -的体积11333222V =⨯⨯=，故选B . 考点：1.正方体的性质；2.多面体的体积.第II 卷（非选择题）二、填空题（本大题共计4个小题，每小题4分，共计16分） 13．数列{}n a满足()111n a n N a *+==∈，记2n n b a =，则数列{}1n n b b +前n 项和n S = ．【答案】21nn +11n a +=得221112n n a a +-=，且2111a =，所以数列21n a ⎧⎫⎨⎬⎩⎭构成以1为首项，2为公差的等差数列，所以211(1)221n n n a =+-⨯=-，从而得到2121n a n =-，则121n b n =-，11111()(21)(21)22121n n b b n n n n +==--+-+，所以111111(1)2335212121n nS n n n =-+-++-=-++L . 考点：裂项相消法求和．【名师点睛】1．裂项相消法求和是历年高考的重点，命题角度凸显灵活多变，在解题中要善于利用裂项相消的基本思想，变换数列a n 的通项公式，达到求解目的．归纳起来常见的命题角度有：（1）形如a n ＝1n n+k （）型；（2）形如a n型；（3）形如a n ＝12n-12n+1•型；（4）形如a n ＝21n n+2g 型．2．裂项相消法求和时要注意：（1）抵消后并不一定只剩下第一项和最后一项，也有可能前面剩两项，后面也剩两项；（2）将通项裂项后，有时需要调整前面的系数，使裂开的两项之差和系数之积与原通项相等．如：若{a n }是等差数列，则1a n a n ＋1＝1d ⎝ ⎛⎭⎪⎫1a n －1a n ＋1，1a n a n ＋2＝12d ⎝ ⎛⎭⎪⎫1a n －1a n ＋2. 14．若,x y 满足约束条件20210220x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩，则3z x y =+的最大值为 .【答案】4【解析】在坐标系内作出可行域如下图所示的三角形区域，由图可知，目标函数3z x y =+取得最大值时的最优解为(1,1)B ，此时max 3114z =⨯+=. 考点：线性规划.15．直线1l ：310ax y ++=，2l ：()2110x a y +++=，若12∥l l ，则a = ．【答案】3-【解析】试题分析：因为直线1:310l ax y ++=与直线()2:2110l x a y +++=平行，所以1a ≠-，且231a a --=+，解得2a =或3a =-当2a =时，两直线平行，故舍去，则3a =-，故答案为3-.考点：两直线平行的性质.16．已知圆222430x y x y +--+=关于直线()300,0ax by a b +-=>>对称，则12a b+的最小值为．【答案】3【解析】由题设直线()300,0ax by a b +-=>>过圆心)2,1(C ，即32=+b a ，因3)45(31)225(31)21)(2(3121=+≥++=++=+b a a b b a b a b a ，故应填3. 考点：直线与圆的标准方程和基本不等式的运用．【易错点晴】本题考查的是直线与圆的位置关系、基本不等式的运用等知识和方法的综合运用.解答时先依据题设条件将问题圆222430x y x y +--+=关于直线()300,0ax by a b +-=>>对称进行等价转化直线()300,0ax by a b +-=>>过圆心)2,1(C .这是解答本题的一个重要的环节.从而为求12a b+的最小值提供条件.运用这一条件时，要对所求表达式和条件进行巧妙变形，这是解答本题的难点，因此要引起足够的重视.三、解答题（本大题共计6个小题，满分74分）17．某企业准备投资1200万元兴办一所中学，对当地教育市场进行调查后，得到了如下的数据表格（以班级为单位）：学段硬件建设（万元）配备教师数教师年薪（万元）初中 26 / 班 2 / 班 2 / 人高中54 / 班3 / 班2 / 人因生源和环境等因素，全校总班级至少20个班，至多30个班. （Ⅰ）请用数学关系式表示上述的限制条件；（设开设初中班x 个，高中班y 个）（Ⅱ）若每开设一个初、高中班，可分别获得年利润2万元、3万元，请你合理规划办学规模使年利润最大，最大为多少？【解析】（Ⅰ）设开设初中班x 个，高中班y 个，根据题意，线性约束条件为⎪⎪⎩⎪⎪⎨⎧∈≥∈≥≤⨯+⨯++≤+≤**,0,01200232254263020N y y N x x y x y x y x 即20302400,0,x y x y x x N y y N **≤+≤⎧⎪+≤⎪⎨≥∈⎪⎪≥∈⎩（Ⅱ）设年利润为z 万元，则目标函数为23z x y =+ 由（Ⅰ）作出可行域如图由方程组30240x y x y +=⎧⎨+=⎩ 得交点M （20，10）作直线:230l x y += ，平移l ，当l 过点M （20，10），z 取最大值70. ∴开设20个初中班，10个高中班时，年利润最大，最大利润为70万元. 考点：简单线性规划问题（用平面区域表示二元一次不等式组）.18．已知实数x ，y 满足2040250x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩求：（1）z ＝x ＋2y －4的最大值；（2）z ＝x 2＋y 2－10y ＋25的最小值；（3）z ＝211y x ++的取值范围．【解析】作出可行域如图所示，并求出顶点的坐标A （1，3）、B （3，1）、C （7，9）．（5分）（1）易知可行域内各点均在直线x ＋2y －4＝0的上方，故x ＋2y －4＞0，将点C （7，9）代入z 得最大值为21．（2）z ＝x 2＋y 2－10y ＋25＝x 2＋（y －5）2表示可行域内任一点（x ，y ）到定点M （0，5）的距离的平方，过M 作直线AC 的垂线，易知垂足N 在线段AC 上，故z 的最小值是|MN |2＝92．（3）z ＝2×()121y x ⎛⎫-- ⎪⎝⎭--表示可行域内任一点（x ，y ）与定点Q 11,2⎛⎫-- ⎪⎝⎭连线的斜率的两倍，因此k QA ＝74，k QB ＝38，故z 的范围为37,42⎡⎤⎢⎥⎣⎦考点：简单线性规划19．如图，已知点A （﹣3，0），B （3，0），M 是线段AB 上的任意一点，在AB 的同侧分别作正方形AMCD 、MBEF ，⊙P 和⊙Q 是两个正方形的外接圆，它们交于点M ，N ．（1）证明：直线MN 恒过一定点S ，并求S 的坐标；（2）过A 作⊙Q 的割线，交⊙Q 于G 、H 两点，求|AH |•|AG |的取值范围．【解析】（1）设点M （m ，0），其中m ∈（﹣3，3），则C （m ，m ＋3），F （m ，3﹣m ），P （，），Q （，）；易知⊙P 的方程为：＋＝，即x 2＋y 2﹣（m ﹣3）x ﹣（m ＋3）y ﹣3m ＝0；① ⊙Q 的方程为：＋＝，即x 2＋y 2﹣（3＋m ）x ﹣（3﹣m ）y ＋3m ＝0；②①﹣②得，公共弦MN 所在的直线方程为6x ﹣2my ﹣6m ＝0，整理得3x ﹣m （3＋y ）＝0，所以MN 恒过定点S （0，3）；（2）过点Q 作QT ⊥GH 于T ，则|TH |＝|TG |，从而|AH |•|AG |＝（|AT |﹣|TH |）•（|AT |＋|TG |）＝|AT |2﹣|TH |2＝（|AQ |2﹣|QT |2）﹣（|HQ |2﹣|QT |2）＝|AQ |2﹣|HQ |2＝＋﹣＝6m ＋18；由于m ∈（﹣3，3），|AH |•|AG |∈（0，36），即|AH |•|AG |的取值范围是（0，36）．【点评】本题考查了直线与圆的方程的应用问题，也考查了直线恒过的定点的应用问题以及垂径定理与切割线定理的应用问题，是综合性题目．20．如图，在四棱锥P ABCD -中，AB ⊥平面BCP ，//CD AB ，2AB BC CP BP ====，1CD =. （1）求点B 到平面DCP 的距离；（2）点M 为线段AB 上一点（含端点），设直线MP 与平面DCP 所成角为α，求sin α的取值范围. 【解析】（1）过点B 作BF PC ⊥，由平面DCP ⊥平面BCP 可知，BF 即点B 到面DCP 的距离，在正PBC ∆中，3BF =，即点B 到平面DCP 的距离为3.（2）∵//CD AB ，所以点M 到平面DCP 的距离即点B 到平面DCP 的距离，而[2,22]MP ∈，所以63sin [,]BF MP α=∈. 考点：1.线面垂直的判定与性质；2.直线与平面所成的角.【名师点睛】本题考查线面垂直的判定与性质、直线与平面所成的角，属中档题；文科立体几何解答题主要考查线面位置关系的证明及几何体体积的计算，空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系，其中推理论证的关键是结合空间想象能力进行推理，要防止步骤不完整或考虑不全致推理片面，该类题目难度不大，以中档题为主.21．如图，四边形ABCD 中，//AB CD ，30ABD ∠=o，2223AB CD AD ===，DE ⊥面ABCD ，//EF BD ，且23EF BD =. （1）求证：//FB 面ACE ；（2）若CF 与面ABCD 所成角的正切为24，求三棱锥F ABC -的体积. 【解析】（1）证明：设AC 交BD 于O ，连接EO ，在ABD ∆中，由余弦定理可得：3DB =.∴222AD BD AB +=，∴AD DB ⊥， ∵//AB CD ，∴AOB ∆∽COD ∆.∴2BO AB DO CD ==，∴23BO BD EF ==，又//EF BD ，∴四边形BOEF 为平行四边形. ∴//EO FB .又∵EO ⊂面ACE ，FB ⊄面ACE ， ∴//FB 面ACE .（2）过F 作//FM ED ，交DB 于M ，连接CM ， ∵ED ⊥平面ABCD ，∴FM ⊥平面ABCD ， ∴FCM ∠为FC 与面ABCD 所成的角，易知2DM EF ==在DCM ∆中，由余弦定理可得1CM =∴2tan 4FM FCM CM ∠==，∴24FM =.∵//DC AB ， ∴11333322ABC ABD S S DA DB ∆∆==•=⨯⨯= ∴11332633248F ABC F ABD ADB V V S FM --∆==•=⨯⨯=. 考点：（1）线面平行的判定；（2）几何体的体积.22．已知数列{}n a 的前n 项和n S 满足：(1)n n n S t S a =-+（t 为常数，且0t ≠，1t ≠）．（1）求{}n a 的通项公式；（2）设2n n n n b a S a =+⋅，若数列{}n b 为等比数列，求t 的值；（3）在满足条件（2）的情形下，设41n n c a =+，数列{}n c 的前n 项和为n T ，若不等式12274nkn n T ≥-+-对任意的*n N ∈恒成立，求实数k 的取值范围．【解析】（1）当1n =时，111(1)S t S a =-+，得1a t =．当2n ≥时，由(1)n n n S t S a =-+，即(1)n n t S ta t -=-+，① 得11(1)n n t S ta t ---=-+，②①-②，得1(1)n n n t a ta ta --=-+，即1n n a ta -=，∴（2n ≥）， ∴{}n a 是等比数列，且公比是t ，∴nn a t =．（2）由（1若数列{}n b 为等比数列，则有2213b b b =⋅，而212b t =，32(21)b t t =+，423(21)b t t t =++，故23242(21)(2)(21)t t t t t t ⎡⎤+=⋅++⎣⎦，解得代入n b ，得，知{}n b 为等比数列，∴∴当4n ≤时，1n nd d +>，当5n ≥时，1n nd d +<，，∴45d d <，考点：由n S 与n a 关系求通项，数列单调性【方法点睛】给出n S 与n a 的递推关系求n a ，常用思路是：一是利用1(2)n n n S S a n --=≥转化为n a 的递推关系，再求其通项公式；二是转化为n S 的递推关系，先求出n S 与n 之间的关系，再求n a 应用关系式11,1,2n n n s n a s s n -=⎧=⎨-≥⎩时，一定要注意分1,2n n =≥ 两种情况，在求出结果后，看看这两种情况能否整合在一起.。

人教A版高中必修二试题四川省成都市实验外国语学校—高二上学期10月月考试题.doc

四川省成都市实验外国语学校2013—2014学年高二上学期10月月考数学试题一、选择题（每题5分，共50分） 1. 三视图均相同的几何体有（）A ．球B ．正方体C ．正四面体D ．以上都对2.体积相等的球和正方体，它们的表面积的大小关系是（）A.S S >球正方体B.=S S 球正方体C.S S <球正方体D.不能确定3.直线12:370,:20l x y l kx y +-=--=与x 轴、y 轴围成的四边形有外接圆，则k 的值等于（）A.3-B.3C.6-D. 64.在0,0a b >>的条件下，三个结论：① 2,2ab a ba b +≤+ ②2222a b a b ++≤， ③22b a a b a b+≥+，其中正确个数的是（） A.0 B.1 C.2 D.35.如果1238,,,...,a a a a 是各项都大于零的等差数列，公差0d ≠，则（） A.1845a a a a > B.1845a a a a < C.1845a a a a +>+ D. 1845a a a a =6.下列判断中正确的是（）A.ABC ∆中，07,14,30a b A ===有两解；B.0,30,25,150ABC a b A ∆===中有一解； C.06,9,45ABC a b A ∆===中，有两解； D.09,10,60ABC b c B ∆===中，无解；7.甲、乙两人同时从寝室到教室，甲一半路程步行，一半路程跑步。

乙一半时间步行，一半时间跑步，如果两人步行速度和跑步速度均相同，则（）A.甲先到教室；B.乙先到教室C.两人同时到教室D.谁先到教室不确定8.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能是（）A.1B.2C.212- D.212+ 9.已知正三棱柱111ABC A B C -的棱长相等，E 是11A B 的中点，F 是11B C 的中点，则异面直线AE 和BF 所成角的余弦值是（）A.710B.23C.750D.1210.设实数0,,,bc ca ababc a b c≠成等差数列，则下列不等式一定成立的是（）A.||||b ac ≤B.2||b ac ≥ C.222a b c ≤≤ D.||||||2a c b +≤二．填空题（每题5分，共25分）11.若不等式组5002x y y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的面积区域是一个三角形，则a 的取值范围是 .12.下列命题（,m n 是两条直线，α是平面） ①若m //,//,n αα则//m n ； ②若//,//,m n n α则//m α；③若//m α，则m 平行于α内的所有直线；④若m 平行于α内的的无数条直线，则//m α；以上正确的命题有个.13. 如图，E ，F 分别是正方体1AC 的面11ADD A 和面11BCC B 的中心，则四边形1BFD E 在该正方体的面上的正投影（投射线垂直于投影面的投影）可能是．（把所有可能图形的序号都填上）错误!未找到引用源。

人教版高一英语必修二单元测试题全套带答案

人教版高一英语必修二单元测试题全套带答案Unit 1 单元测试题第二部分：阅读理解（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的四个选项（A、B、C和D）中，选出最佳选项。

AInsects (昆虫) are a very healthy food. They have almost as much protein (蛋白质) as meat from a pig or cow and are low in fat. Eating insects is also very good for the environment since they need less land and water than larger animals.Marcel Dicke, who studies insects, explained in a talk how insects also produce more meat from the food they eat. For example, imagine a farmer feeds a cow 10 pounds of food. Those 10 pounds of food produce about 1 pound of meat for people to eat. However, imagine the farmer gives a certain number of insects 10 pounds of food. Those 10 pounds of food produce 9 pounds of meat for people to eat!Eating more insects can also help people in poor areas. Many people can raise and sell insects, which can provide jobs and food.But insects will not replace (替代) animal meat very quickly. First, people in some countries would have to change how they think about eating insects. Many people in North America and Europe eat a lot of meat like beef and pork. But they do not traditionally eat insects. In fact, for many people in the west, eating insects sounds crazy! They believe insects are dirty and dangerous. Insects make them feel uncomfortable.Some people are trying to deal with this problem. For example, David George Gordon wrote a book named “The Eat-A-B ug Cookbook”, which tries to show people that insects can be delicious. Other insect experts travel around telling people about the benefits (好处) of eating insects. But they still have a lot of work to do.21. Eating insects _____.A. is not healthyB. makes people put on fatC. helps protect large animalsD. is environmentally friendly22. The example of Marcel Dicke is given to show _____.A. the high cost of food productionB. it’s quite easy for farmers to raise insectsC. raising insects is a good choice for farmersD. the different ways of feeding cows and insects23. The long way eating insects has to go mainly results from _____.A. their terrible tasteB. people’s old beliefsC. family traditionsD. eating methods24. We can infer from David and other insect experts that _____.A. people can make a lot of money from insectsB. insects should be better protectedC. people should eat more insectsD. it’s dangerous to eat insectsBKhan Academy is a website providing a free education for any person. The website includes more than 4,000 short teaching videos about many different subjects. Every month, over 7 million people go to the Khan Academy website to watch its videos.Khan Academy began with one man named Salman Khan. As a young man, Khan got a degree from Harvard Business School and began to work in business.In 2006, Khan used the Internet to help his young cousins, who lived far away, with their mathematics schoolwork. He drew numbers and pictures on the website to teach them. After a time, he put his videos onto the website YouTube, where his cousins could watch them any time they wanted. But Khan noticed that other people were also watching his videos on YouTube.By 2009, the number of people watching his videos on YouTube was getting very large. Khan decided to make the videos his job instead. So he officially began Khan Academy, providing videos on mathematics and other school subjects.People did not have to pay to watch the videos. But they could give Khan money if they wanted to support (支持) his work. Some people did give Khan small amounts of money, but he was still having a hard time. Later, a woman told Khan that Bill Gates uses Khan Academy for his kids. After that, the Bill and Melinda Gates Foundation began giving money to Khan Academy. In 2010Google gave the website money too, wanting Khan to translate his videos into the world’s most common languages. Today, people can see Khan’s videos in many different languages.Some people think that Khan Academy will be the way more and more people learn in the future. Teachers can use it in their classrooms. Khan believes that Khan Academy will never, and should never, replace a school. But he believes teachers and students can use it to make schools better.25. What can one get from Khan Academy?A. Video-making methods.B. Free learning information.C. Any help with the schoolwork.D. A good number of beautiful pictures.26. Salman Khan started Khan Academy _____.A. in 2006B. as a studentC. to satisfy the needs of learnersD. under the influence of his cousins27. What does Salman Khan think of Khan Academy?A. It will play an active role in school teaching.B. It can replace teachers in classrooms.C. It can replace a teaching school.D. It’s the future of education.CThe Tower of London, not a single tower but a large group, was built to guard London.Besides William and Henry VIII, the tower’s history has other famous names in British history. In 1389 a clerk of works (现场监工员) named Geoffrey Chaucer — author of The Canterbury Tales—oversaw (监督) the building of the Tower Wharf. In 1671 Colonel Blood tried to steal the crown jewels (皇冠上镶的宝石) after overpowering the elderly Jewel House keeper. (Blood was caught but later pardoned.) Today the jewels remain in the tower as they have since Blood’s day.For six centuries this place was also home to a group of animals from elephants to big cats. It stopped being used as an animals’ home in 1835 and its animals were moved to the London Zoo.Today visitors can walk the walls, visit guard towers and see the crown jewels. Guards at the tower, popularly known as beefeaters, not only guard the tower but also give interesting tours that are among the most popular parts of any visit.How to Get ThereTrains and the Dockland Light Railway stop near the tower. Buses 15, 42, 78 and 100 reach the tower, and riverboats stop at Tower Pier. Taxis, bicycles, and foot power are also good ways to reach the tower. Driving is a less attractive choice because of the expensive parking. When to GoThe tower is open all year round, except during the Christmas holidays (December 24 to 26) and January 1. School holidays and summertime are the busiest times.How to VisitAs expected at a place that has seen so much history, there is enough of interest at the Tower of London to keep visitors busy for days. Stop at the Welcome Center for visitor information on everything from the crown jewels to family fun activities.28. The underlined sentence in Paragraph 2 shows _____.A. the tower was built by famous peopleB. some famous people caused trouble thereC. there were many famous people in British historyD. there were many interesting stories connected to the tower29. Beefeaters at the tower _____.A. have two rolesB. like to eat beefC. seem very seriousD. often joke with visitors30. According to the text, the Tower of London is _____.A. easy to reachB. full of parked carsC. busy all year roundD. a perfect place for a one-day tourDQuite a few years ago, as I celebrated my 25th birthday with a party, I was surprised to receive an unusual present. The gift-giver smiled widely and said loudly, “It’s a nice, strong plant, so e ven you can’t kill it.”I was well known in my circle of friends as an “anti-gardener” — how was I going to care for this piece of greenery?For four years the plant received little care. I felt guilty (内疚的) just looking at it!As a non-gardener, my offer s to look after friends’ houses were met with laughter: “We appreciate (感激) the offer but, really, we don’t want to come home to a dead garden!” It didn’t occur to (想到) them that I just had no interest in having a garden. It was a choice, not a failing.So me time later my husband accepted a job in Belgium. Because I couldn’t throw away a gift, I decided to ask my neighbor to care for my plant.Our lovely house in Belgium had a beautiful garden. Slowly gardening became a part of my daily life, teaching me to slow down and to be happy in the silence of the garden. It was with regret that I left that garden to return to Sydney some months later.Back home life soon went back to normal. Then one day, it occurred to me that I could start my own little garden. So, I went to collect my unwanted plant from my neighbor. I took the plant home, watered it and watched as its leaves turned from a lifeless yellow to a rich green within weeks. Many years on, I still don’t know the name of my first plant, but I do know that as it grows, so do I. It symbolises a change in me when I stopped listening to the voices around me and started to believe in myself.31. When the author received a plant as a birthday gift, she felt _____.A. funnyB. guiltyC.excited D. displeased32. What did the author’s friends think of her?A. Her anti-gardening was a weakness.B. She was bored with gardening.C. She was a good housekeeper.D. Her dead garden was ugly.33. How did the author deal with the plant before moving away?A. She threw it away.B. She asked for help.C. She left it in the house.D. She gave it to a neighbor as a gift.34. The author’s stay in Belgium made her _____.A. miss her days back in SydneyB. feel sorry for her first plantC. fall in love with gardeningD. become strangely silent35. What does the author want to tell us from her experience?A. We should try to be perfect.B. Don’t be afraid of making mistakes.C. We should learn to make clear choices.D. Don’t refuse something you’ve never tried.第二节（共5小题；每小题2分，满分10分）根据短文内容，从短文后的选项中选出能填入空白处的最佳选项。

人教A版高中必修二试题四川省成都市届高二期中测试(理数).docx

郫县一中第三学期期中考试参考答案数学（理工类）一、选择题答案：二、填空题：本大题共4小题,每小题4分,共16分．13. 12580x y -+= 或 1x =； 14. 122⎡⎤⎢⎥⎣⎦，15 16. ②③④三、解答题：本大题共6小题,满分74分．17. 解：由24020x y x y -+=⎧⎨+-=⎩得1l 与2l 的交点为（0，2）， ……………3分又∵3:3450l x y -+=的斜率为34，∴l 的斜率为43-， ………………6分由点斜式得所求直线l 的方程为42(0)3y x -=--， ………………9分即4360x y +-=为所求直线l 的方程 ………………12分 18.解:由2100x y y -+=⎧⎨=⎩∴A （－1，0） ………… 2 分又K AB =2011(1)-=--∵x 轴为∠A 的平分线，故K AC =－1 ………… 4分 ∴AC 边的方程为：y =－(x +1) …………6分∵BC 边上的高的方程为：x －2y +1=0 ………… 8分 ∴K BC =－2∴BC 边的方程为：y －2=－2（x －1）即：2x +y －4=0 ………… 10分由24010x y x y +-=⎧⎨++=⎩解得C （5，－6） …………12分19. 解设圆心坐标为(3,)y y ， ………… 2分则圆心到y x =的距离为|d y = ………… 4分又因为圆C 与y 轴相切，则|3|r y = ………… 6分由题意知222)3y y += …………8分1y ∴=± …………10分当1y =时，圆心为（3，1），则圆C 的方程为22(3)(1)9x y -+-= …………11分当1y =-时，圆心为（-3，-1），则圆C 的方程为22(3)(1)9x y +++= ……12分20.解:(1)直线方程()():21174l m x m y m +++=+,可以改写为()2740m x y x y +-++-=,所以直线必经过直线27040x y x y +-=+-=和的交点.由方程组270,40x y x y +-=⎧⎨+-=⎩解得3,1x y =⎧⎨=⎩即两直线的交点为A (3,1). ……3分又因为点()3,1A 与圆心()1,2C的距离5d =<,所以该点在C 内,故不论m 取什么实数,直线l 与圆C 恒相交. ……6分(2)连接AC ,过A 作AC 的垂线,此时的直线与圆C 相交于B 、D .BD 为直线被圆所截得的最短弦长.此时,5,AC BC BD ====所以即最短弦长为……9分又直线AC 的斜率12AC k =-,所以直线BD 的斜率为 2.此时直线方程为:()123,250.y x x y -=---=即 ……12分21．解：（Ⅰ）由题意，得23a cc a⎧=⎪⎪⎨⎪=⎪⎩，………… 2分解得1,a c ==∴2222b c a =-=，∴所求双曲线C 的方程为2212y x -=. ………… 4分（Ⅱ）设A 、B 两点的坐标分别为()()1122,,,x y x y ，线段AB 的中点为()00,M x y ，22012x y m y x -+=⎧⎪⎨-=⎪⎩得22220x mx m ---=（判别式0∆>）, ………… 7分 ∴12000,22x x x m y x m m +===+=, ………… 10分 ∵点()00,M x y 在圆225x y +=上，∴()2225m m +=，∴1m =±. ………… 12分22.解答：（Ⅰ）设P （x ，y ），由椭圆定义可知，点P 的轨迹C是以(0(0，为焦点，& 鑫达捷致力于精品文档精心制作仅供参考 &鑫达捷长半轴为2的椭圆．它的短半轴1b ==，故曲线C 的方程为2214y x +=． ······················· 3分（Ⅱ）设1122()()A x y B x y ，，，，其坐标满足2214 1.y x y kx ⎧+=⎪⎨⎪=+⎩，消去y 并整理得22(4)230k x kx ++-=，判别式0∆>，故1212222344k x x x x k k +=-=-++，． ····················· 6分若OA OB ⊥u u u r u u u r ，即12120x x y y +=．而2121212()1y y k x x k x x =+++，于是22121222233210444k k x x y y k k k +=---+=+++，化简得2410k -+=，所以12k =±． ······················ 9分（Ⅲ）2222221122()OA OB x y x y -=+-+u u u u r u u u u r22221212()4(11)x x x x =-+--+ 12123()()x x x x =--+ 1226()4k x x k -=+． ····················· 12分因为A 在第一象限，故10x >．由12234x x k =-+知20x <，从而120x x ->．又0k >，故220OA OB ->u u u u r u u u u r ，即在题设条件下，恒有OA OB >u u u u r u u u u r ． ····················· 14分。

四川省成都市新都一中必修二综合测试：第一章空间几何体 Word版含答案

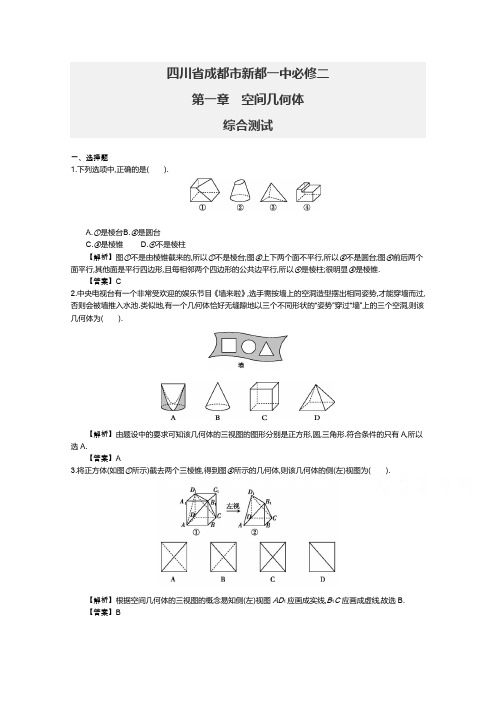
四川省成都市新都一中必修二第一章空间几何体综合测试一、选择题1.下列选项中,正确的是().A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱【解析】图①不是由棱锥截来的,所以①不是棱台;图②上下两个面不平行,所以②不是圆台;图④前后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以④是棱柱;很明显③是棱锥.【答案】C2.中央电视台有一个非常受欢迎的娱乐节目《墙来啦》,选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为().【解析】由题设中的要求可知该几何体的三视图的图形分别是正方形,圆,三角形.符合条件的只有A,所以选A.【答案】A3.将正方体(如图①所示)截去两个三棱锥,得到图②所示的几何体,则该几何体的侧(左)视图为().【解析】根据空间几何体的三视图的概念易知侧(左)视图AD1应画成实线,B1C应画成虚线,故选B.【答案】B4.如图,△O'A'B'是水平放置的△OAB 的直观图,则△OAB 的面积是( ).A.6B.3√2C.6√2D.12【解析】由水平放置的平面图形的斜二测画法的规则可知,△OAB 为直角三角形且直角边OB=2O'B'=4,OA=O'A'=6,因此S △OAB =12×4×6=12.【答案】D5.一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( ).A.8+π3B.8+23πC.8+83πD.8+163π【解析】此几何体为组合体,下部是正方体,上面是球的14,并且半径为1,所以此几何体的体积V=2×2×2+14×43π×13=8+π3,故选A .【答案】A6.如图,在底面边长为1,高为2的正四棱柱ABCD-A 1B 1C 1D 1中,点P 是平面A 1B 1C 1D 1内一点,则三棱锥P-BCD 的正(主)视图与侧(左)视图的面积之和为( ).A .1B .2C .3D .4【解析】设点P 在平面A 1ADD 1的射影为点P',在平面C 1CDD 1的射影为点P″,如图.。

人教A版高中必修二试题四川省成都市新都一中高级第三期周练01学生版.docx