(参考)基于运动学原理的仿真机器人运动预测模型研究
机器人运动学建模技术的工作原理

机器人运动学建模技术的工作原理机器人运动学建模技术为机器人的运动控制提供了基础,它是机器人技术中的一个重要组成部分。
机器人运动学建模技术主要利用数学方法和计算机软件对机器人系统进行建模和分析,从而优化机器人的运动控制。
一、机器人运动学基础机器人运动学是研究机器人运动规律和控制的一门学科,它主要包括前向运动学和逆向运动学两部分。
前向运动学是指已知机器人各关节的角度或位置,求出机器人末端执行器的位置和姿态;逆向运动学是指已知机器人末端执行器的位置和姿态,求出各个关节的角度或位置。
机器人运动学基础理论是机器人运动学建模技术的基础。
二、机器人运动学建模方法机器人运动学建模方法主要有基于DH方法的运动链式模型、基于坐标变换的运动学模型、基于位移向量法的运动学模型等。
1. 基于DH方法的运动链式模型DH方法是一种对机器人进行建模的方法,它可以将机器人运动链建立起来,并对每个关节的运动方向、长度和角度进行描述。
采用DH方法将机器人建模,可以有效地简化机器人的运动学分析,为机器人控制系统的设计提供了便利。
DH方法的建模步骤主要包括:(1)确定机器人的坐标系,建立虚拟的世界坐标系和机器人坐标系。
(2)确定机器人各关节的运动轴线,按照DH表示法,规定机器人关节的自由度和约束等条件。
(3)建立机器人的运动链,确定机器人各个部分间的运动关系,并计算出相应的转移矩阵。
通过建立DH方法的运动链模型,可以对机器人进行运动学分析,从而实现机器人的优化运动控制和精确位置控制。
2. 基于坐标变换的运动学模型坐标变换方法是一种常用的机器人建模方法,它可以对机器人的运动轨迹和姿态进行描述,并规定了机器人坐标系的变换规律。
坐标变换方法将机器人建模为一系列坐标系的变换,通过坐标系的变换,可以精确地描述机器人的运动轨迹和姿态。
(1)确定机器人的起始坐标系和目标坐标系,这些坐标系对应机器人的关节和工具末端。
(2)对机器人的各个部分和运动轨迹进行坐标系的变换,得到机器人的运动关系和姿态变化。
机器人运动学与动力学建模与分析

机器人运动学与动力学建模与分析摘要:机器人运动学与动力学建模与分析是机器人研究领域的重要内容。
本文将从机器人运动学和动力学的基本概念入手,介绍机器人的运动规划和控制方法,重点讨论了机器人建模和分析的方法。
通过对机器人运动规划和控制的研究,可以提高机器人的精准度和效率,为实现自主化、智能化的机器人应用提供理论基础。
1.引言随着科技的飞速发展,人工智能、机器学习等领域的成果不断涌现,智能化、自主化的机器人应用已逐渐深入到生产、生活、科研等各个领域。
机器人技术的研究与开发已成为当今世界科技竞争的焦点之一。
在这一背景下,对于机器人运动规划和控制方法的研究显得尤为重要。
本篇文章将围绕机器人运动学建模、姿态描述、动力学建模、运动规划方法和运动控制方法等方面进行深入探讨,以期为机器人领域的研究提供一定的理论参考。
2.机械臂运动学建模2.1旋转关节2.1.1旋转关节坐标系为了便于分析机器人运动,首先需要建立旋转关节的坐标系。
旋转关节坐标系主要包括基座坐标系、关节坐标系和末端执行器坐标系。
基座坐标系固定于机器人基座,用于描述机器人基座的相对位置和姿态;关节坐标系随关节转动而变化,用于描述关节的转动状态;末端执行器坐标系与末端执行器相连,用于描述末端执行器的位置和姿态。
2.1.2旋转关节角度表示旋转关节的角度表示采用旋转矩阵进行描述。
旋转矩阵包括三个旋转分量:绕x轴旋转的θx,绕y轴旋转的θy,以及绕z轴旋转的θz。
旋转矩阵可以表示为:R = [cos(θz) cos(θy) sin(θz) sin(θy),sin(θz) cos(θy) + cos(θz) sin(θy),cos(θz) sin(θy) + sin(θz) cos(θy)]2.1.3旋转关节正逆解正解:给定末端执行器的位姿,求解旋转关节的角度。
逆解:给定旋转关节的角度,求解末端执行器的位姿。
2.2 平移关节平移关节主要用于实现机器人在三维空间中的平移运动。
基于模型预测控制的四足机器人运动稳定策略

03
基于模型预测控制的运动稳定策略
模型预测控制的基本原理
基于模型预测控制(MPC)的四足机器人运动稳定策略是 一种先进的控制方法,它通过建立机器人的运动模型,对 机器人的未来行为进行预测和控制。
MPC的基本原理是利用预测模型对系统的未来行为进行预 测,并根据预测结果对当前的控制输入进行调整,以实现 系统的最优控制。
MPC的优势在于其对复杂系统的建模和控制能力,能够有 效地提高系统的稳定性和性能。
基于模型的四足机器人控制器设计
基于模型的四足机器人控制器设 计是实现机器人运动稳定的关键
步骤之一。
控制器需要利用机器人的运动学 和动力学模型,设计合适的控制 策略,以保证机器人在各种环境
下的稳定行走。
控制器设计需要考虑机器人的步 态、速度、负载等因素,以及环 境中的障碍物和地形变化等不确
搭建四足机器人实验平台,对 所提出的基于模型预测控制的 运动稳定策略进行实验验证和 性能评估。通过对比实验结果 ,证明所提出策略的有效性和 优越性。
02
四足机器人概述
四足机器人的结构与特点
01
四足机器人是一种仿生机器人,具有与生物四足行走相似的运 动模式和结构特点。
02
四足机器人通常由腿部机构、身体机构、传感器和控制系统等
需要进一步优化算法性能
虽然该研究已经取得了一定的成果,但仍有优化的空间。未来可以对算法的性能进行进一 步优化,以提高四足机器人的运动性能和稳定性。
06
参考文献与附录
参考文献
[请在此处插入参考 文献]
[请在此处插入参考 文献]
[请在此处插入参考 文献]
[请在此处插入参考 文献]
[请在此处插入参考 文献]
组成,具有较高的灵活性和稳定性。
机器人的动力学建模与运动控制方法研究

机器人的动力学建模与运动控制方法研究机器人是一种能够执行自主任务的智能化机械人。
在工业制造、航天、医疗和娱乐等领域中,它们被广泛应用,成为人们生产和生活的重要组成部分。
为了实现机器人的智能化运动,动力学建模与运动控制方法研究成为关键技术。
本文将介绍机器人的动力学建模方法以及运动控制方法的研究进展。
一、机器人的动力学建模方法机器人的动力学建模方法是机器人运动控制研究的基础。
动力学建模的目的是建立机器人系统的数学模型,目的在于描述机器人的运动学、动力学特性,为控制器的设计提供基础。
1. 基于欧拉-拉格朗日方程的动力学建模方法欧拉-拉格朗日(Euler-Lagrange)方程是描述运动系统的一种数学方法。
将机器人建模为一个刚体系统,利用欧拉-拉格朗日方程可以通过推导机器人的运动学和动力学性质来建立机器人的数学模型。
这种方法在机器人动力学建模中应用广泛。
相比传统的牛顿-欧拉(Newton-Euler)方法,欧拉-拉格朗日方程具有表达力强、形式简洁的优点。
2. 基于Newton-Euler方程的动力学建模方法Newton-Euler方程是另一种常用于机器人动力学建模的数学方法。
该方法结合了牛顿第二定律和欧拉运动方程,能完整地描述机器人的运动学和动力学特性。
该方法在机器人元件参数较为复杂的情况下,具有精度更高的特点。
二、机器人的运动控制方法机器人的运动控制方法是指通过对机器人动力学建模的数学模型进行控制来实现机器人的复杂运动。
其中包括力控制、位置控制、移动控制、路径控制等。
目前,常见的机器人运动控制方法主要有以下几种:1. PID控制方法PID控制方法是机器人运动控制中常用的一种控制方法。
通过对机器人位置、速度和加速度等参数进行控制,以实现机器人的位置或速度控制。
该方法简单易行,控制精度较高。
2. 轨迹跟踪控制方法轨迹跟踪控制方法是以机器人执行的轨迹作为控制目标,采用控制算法,实现机器人在期望轨迹上的精确运动。
机器人的运动学和动力学模型

机器人的运动学和动力学模型机器人的运动学和动力学是研究机器人运动和力学性质的重要内容。
运动学是研究机器人姿态、位移和速度之间关系的学科,动力学则是研究机器人运动过程中力的产生和作用的学科。
机器人的运动学和动力学模型可以帮助我们理解机器人的运动方式和受力情况,进而指导机器人的控制算法设计和路径规划。
一、机器人运动学模型机器人运动学模型是描述机器人运动方式和位置关系的数学表达。
机器人的运动状态可以用关节角度或末端执行器的位姿来表示。
机器人的运动学模型分为正运动学和逆运动学两种。
1. 正运动学模型正运动学模型是通过机器人关节角度或末端执行器的位姿来确定机器人的位置。
对于串联机器人,可以使用连续旋转和平移变换矩阵来描述机械臂的位置关系。
对于并联机器人,由于存在并联关节,正运动学模型比较复杂,通常需要使用迭代方法求解。
正运动学模型的求解可以通过以下几个步骤:(1) 坐标系建立:确定机器人的基坐标系和各个关节的局部坐标系。
(2) 运动方程描述:根据机器人的结构和连杆长度等参数,建立各个关节的运动方程。
(3) 正运动学求解:根据关节的角度输入,通过迭代计算,求解机器人的末端执行器的位姿。
正运动学模型的求解可以用于机器人路径规划和目标定位。
2. 逆运动学模型逆运动学模型是通过机器人末端执行器的位姿来确定机器人的关节角度。
逆运动学问题在机器人的路径规划和目标定位等任务中起着重要作用。
逆运动学求解的难点在于解的存在性和唯一性。
由于机器人的复杂结构,可能存在多个关节角度组合可以满足末端执行器的位姿要求。
解决逆运动学问题的方法有解析法和数值法两种。
解析法通常是通过代数或几何方法,直接求解关节角度,但是解析法只适用于简单的机器人结构和运动方式。
数值法是通过迭代计算的方式,根据当前位置不断改变关节角度,直到满足末端执行器的位姿要求。
数值法可以用于复杂的机器人结构和运动方式,但是求解时间较长。
二、机器人动力学模型机器人动力学模型是描述机器人运动时受到的力和力矩的模型。
机器人控制系统的建模与仿真方法研究

机器人控制系统的建模与仿真方法研究随着科技的不断进步,机器人技术的发展迅猛,机器人在各个领域的应用越来越广泛。
为了实现高效、稳定的机器人行为控制,建立准确的控制系统模型和进行仿真研究是至关重要的。
本文旨在探讨机器人控制系统的建模与仿真方法,介绍常用的建模方法,并分析仿真模型的建立及其应用。
一、机器人控制系统的建模方法1. 几何模型法几何模型法是一种常用的机器人控制系统建模方法。
该方法通过描述机器人的几何形状、关节结构和运动轨迹,建立机器人系统的几何模型。
常用的几何模型包括DH法、SDH法和Bishop法等。
其中,DH法是最经典的一种方法,通过参数化建立机器人的运动学模型,用于描述关节变量和坐标系之间的关系,从而实现机器人的运动规划和控制。
2. 动力学模型法动力学模型法是一种更加复杂而全面的机器人建模方法。
该方法基于牛顿运动定律和动力学原理,综合考虑机器人的质量、惯性、关节力矩和外力等因素,建立机器人系统的动力学模型。
动力学模型法可以更准确地描述机器人的运动和力学特性,对于复杂的机器人控制任务具有重要意义。
3. 状态空间模型法状态空间模型法是一种抽象程度较高、数学表达简洁的机器人控制系统建模方法。
该方法通过描述机器人系统的状态以及状态之间的转移规律,以矩阵的形式进行表示。
状态空间模型法适用于系统动态特性较强、多输入多输出的机器人系统,能够方便地进行控制器设计和系统分析。
二、机器人控制系统的仿真方法1. MATLAB/Simulink仿真MATLAB/Simulink是一种广泛应用于机器人控制系统仿真的工具。
Simulink提供了丰富的模块库和仿真环境,可以方便地构建机器人系统的仿真模型,并进行系统的可视化、实时仿真和参数调整。
通过Simulink,我们可以对机器人的运动学和动力学模型进行建模,并通过调整控制参数来优化机器人的控制性能。
2. 三维虚拟仿真三维虚拟仿真是一种直观、真实的机器人控制系统仿真方法。
基于MATLAB仿真的机器人运动学建模及控制技术研究

基于MATLAB仿真的机器人运动学建模及控制技术研究机器人的普及与应用越来越广泛,成为了工业自动化的重要组成部分。
但是,如何对机器人进行运动学建模与控制是机器人研究的重要问题之一。
近年来,由于计算机技术的发展,基于MATLAB仿真的机器人运动学建模及控制技术研究得到了广泛应用。
本文将对此方面的研究进行探讨。
一、机器人运动学建模机器人的运动学建模是指利用几何学和代数学知识来描述机器人的运动规律,从而实现机器人的运动控制。
根据机器人的类型,可以采用不同的方法进行运动学建模。
1、串联机器人的运动学建模串联机器人指的是由各种关节通过齿轮、链条等联接的机器人。
其运动学建模主要是研究各关节的角度、速度、加速度等变量与末端执行器之间的关系,从而实现机器人的控制。
这种建模的方法主要基于牛顿-欧拉方法,可以通过MATLAB中的符号化计算实现。
首先,需要对各个关节进行标号,并定义每个关节和基座之间的距离和角度。
然后,可以运用牛顿-欧拉方法来用关节运动学参数表示末端执行器的位置和姿态变量。
最后,通过控制关节运动学参数来控制机器人的运动。
2、并联机器人的运动学建模并联机器人由多个平台和机械臂组成,并联机器人可以同时控制多个执行器,从而实现更高效的工作。
并联机器人的运动学建模主要是研究机器人末端执行器的位置和姿态变量与各个执行器之间的关系。
建模方法主要包括支点变换法和雅可比矩阵法。
其中支点变换法是将并联机器人转化为串联机器人的形式,然后用串联机器人的运动学进行建模。
而雅可比矩阵法则是运用雅可比矩阵来建立机器人末端执行器的运动学模型,从而实现机器人的控制。
二、机器人运动控制机器人运动控制是指根据机器人的运动学模型,利用控制算法控制机器人的运动状态和轨迹。
在控制机器人的运动过程中,主要的控制方法包括开环控制、PID 控制和反馈控制等。
1、开环控制开环控制是一种简单的控制方法,即在机器人刚开始运动时就预设好机器人的运动轨迹和速度。
机器人控制中的动力学建模与仿真

机器人控制中的动力学建模与仿真机器人在现代社会的发展中起到了越来越重要的作用,无论是在制造业、医疗领域还是日常生活中,机器人都扮演着重要的角色。
与此同时,机器人控制技术也在不断进步,为机器人的精确运动和协调操作提供了重要保障。
而机器人控制中的动力学建模与仿真则是控制技术的关键环节,本文将探讨这一话题。
动力学建模是机器人控制中必不可少的一环,它涉及到机器人运动学、力学和控制理论等多个学科的知识。
首先,机器人的运动学描述了机器人的几何特征和位置关系,可以用来计算机器人的位姿和轨迹规划。
其次,机器人的力学研究了机器人的运动行为,包括力、力矩和能量等物理量的计算与分析,可以为控制系统提供运动规律。
最后,控制理论围绕着机器人的姿态调整、路径跟踪和力矩控制等问题展开研究,旨在实现机器人的精确控制和稳定运动。
在动力学建模的过程中,需要考虑到机器人的力学特性、控制器的反馈信号以及外界环境对机器人的影响等因素。
以机械臂为例,我们可以通过分析机械臂的质量分布、惯性力矩和摩擦系数等参数,建立机械臂的动力学模型。
同时,我们还可以引入传感器来实时测量机械臂的关节角度、位置和速度等信息,以供控制器进行反馈控制。
此外,外界环境的力学性质也需要纳入考虑范围,例如重力、摩擦力和碰撞力等,这些力将对机器人的运动产生重要影响。
一旦完成了动力学建模,我们就可以进行仿真实验,以验证模型的准确性和可行性。
仿真实验可以通过计算机程序来模拟机器人的运动行为,通过对不同输入信号的控制,可以观察机器人的响应和性能。
仿真实验的好处在于可以提前发现潜在问题,并优化控制算法,减少实际实验的时间和成本。
广泛使用的并联机器人就是一个很好的例子,通过动力学建模和仿真实验的过程,设计人员可以在模拟环境中不断调整参数,获得最优的控制效果。
然而,动力学建模与仿真并非一蹴而就的过程,它需要建立在坚实的理论基础之上。
在进行建模时,需要对机器人的力学特性和控制系统的原理有充分的了解,并运用数学、物理、计算机科学等多学科知识进行综合分析。
机器人建模与仿真算法

机器人建模与仿真算法引言机器人建模与仿真是现代机器人技术中的核心内容之一。
借助建模与仿真技术,可以实现对机器人的动力学、运动控制、感知系统等进行全面的分析与验证,从而为机器人的开发与应用奠定坚实的基础。
本文将从机器人建模与仿真的基本原理开始,介绍常用的机器人建模方法和仿真算法,并讨论目前该领域中的研究进展和应用前景。
一、机器人建模方法1. 几何建模法几何建模法是机器人建模中最基础的方法之一。
该方法通过对机器人的几何结构进行建模,来描述机器人在空间中的位置、姿态等信息。
常用的几何建模方法有欧拉角表示法、四元数表示法和转移矩阵表示法等。
这些方法主要应用于描述机器人的位姿和运动学关系。
2. 动力学建模法动力学建模法是机器人建模中的另一重要方法。
该方法通过运动学和动力学的方程来描述机器人的运动和力学行为。
机器人的运动学可以通过关节坐标和连接关系来描述,而动力学则进一步研究机器人的力学特性和运动学关系之间的关系。
常用的动力学建模方法有拉格朗日方程法、牛顿-欧拉方程法等。
3. 变分原理建模法变分原理建模法是机器人建模中较为复杂的方法之一,也是研究机器人动力学的重要手段。
该方法利用变分原理,将机器人的动力学方程转化为能量最小化的问题,从而求解出机器人的轨迹和运动规律。
常用的变分原理建模方法有哈密顿原理、哈密顿-雅可比原理等。
二、机器人仿真算法1. 刚体仿真算法刚体仿真算法是机器人建模与仿真中常用的算法之一。
该算法基于刚体动力学理论,通过对机器人的质量、转动惯量等物理特性进行建模,模拟机器人在力和力矩作用下的运动行为。
常用的刚体仿真算法有欧拉方法、中点法、龙格-库塔方法等。
2. 运动学仿真算法运动学仿真算法是机器人建模与仿真中的另一重要算法。
该算法基于机器人的运动学方程,模拟机器人的运动轨迹和关节角度等运动特性。
常用的运动学仿真算法有正向运动学算法、逆向运动学算法等。
3. 动力学仿真算法动力学仿真算法是机器人建模与仿真中复杂但重要的算法之一。
机器人运动学分析与仿真实现

机器人运动学分析与仿真实现在当今科技飞速发展的时代,机器人技术的应用越来越广泛,从工业生产中的自动化装配线,到医疗领域的手术机器人,再到家庭服务中的智能机器人,机器人已经逐渐融入到我们生活的方方面面。
而机器人运动学作为机器人技术的重要基础,对于机器人的设计、控制和应用具有至关重要的意义。
本文将对机器人运动学进行分析,并探讨其仿真实现的方法和过程。
一、机器人运动学的基本概念机器人运动学主要研究机器人各关节的运动与机器人末端执行器位姿之间的关系。
简单来说,就是如何通过控制机器人的关节角度或位移,来实现期望的末端执行器的位置和姿态。
机器人运动学可以分为正运动学和逆运动学两个方面。
正运动学是已知机器人各关节的参数(如关节角度、长度等),求解末端执行器在空间中的位置和姿态。
这就好比我们知道了一个人的各个肢体的长度和关节的转动角度,就能推算出他的手能够到达的位置。
逆运动学则是已知末端执行器的期望位置和姿态,求解各关节应有的参数值。
这相当于我们给定了一个目标位置,需要反过来计算出各个肢体应该如何运动才能达到这个目标。
二、机器人运动学模型的建立为了进行机器人运动学的分析,首先需要建立机器人的运动学模型。
常见的机器人模型有串联机器人和并联机器人。
串联机器人是由一系列关节依次连接而成,每个关节只有一个自由度;并联机器人则是由多个支链并行连接到动平台和静平台之间,具有多个自由度。
在建立模型时,需要确定机器人的连杆参数,包括连杆长度、连杆扭转角、关节偏移量和关节转角等。
这些参数通常可以通过机器人的机械结构设计图纸或实际测量得到。
以一个简单的平面两关节机器人为例,我们可以将其看作是两个连杆通过关节连接在一起。
设第一个连杆的长度为$l_1$,第二个连杆的长度为$l_2$,关节 1 的转角为$\theta_1$,关节 2 的转角为$\theta_2$。
通过三角函数的关系,可以得到末端执行器在平面坐标系中的位置坐标$(x, y)$与关节角度$\theta_1$ 和$\theta_2$ 之间的关系。
基于运动学模型的足球机器人运动免疫预测控制

1 足 球 机 器 人 运 动 学 模 型
在 足 球 机器 人 中 , 轮式 移 动 结 构 得 到 了广 泛 的
控制法 、 模糊控制 等方法 J 。但 是足球机器人运 动控制系统的模型在实际系统中存在控制参数难 以
调整 、 制 系统存 在 噪声 影 响等 问题 , 些控 制方 法 控 这
的适应 性 。
有 的两 轮 足球 机器 人运 动 学方 程 大多 是高 阶 的非 线
性系统 , 根据高阶运动学方程设计的控制器 易受系
统 固有 奇异 点 的影 响 , 奇 异 点 可 能 导致 系 统 出 现 该 极 限环 , 使得 机 器 人 围着 目标 点 作 圆 周 运 动 J 因 3。 此, 此类 高 阶系 统 的控制 难 以精 确 。近 年来 , 多控 许 制方 法 在 足 球 机 器 人 路 径 跟 踪 得 到 了应 用 , PD 如 I
的抗干扰能力 , 对模型误差具有较强的鲁棒性 等优 良性 质 ; 因此 , 更符 合不 易建 立 精确 数学 模 型 而且 比
较 复 杂 的工 业 生产 过程 的实 际要 求 。近年发 展起 来 的免疫 算法 是模 仿 了免 疫 系 统 的克 隆 选 择 , 阴性 选 择等 制 中 , 也得 到 了广泛 应 用 。本 文在 机器 人无 侧 向移 动 的条 件下 , 以左右 轮 的驱 动力 为输 人量 , 立两 轮 足球 机 建
来分 别对 平 动和 转 动建立 相 应 的数学 模 型 。 设 两轮机 器 人 的质 量 为 , 为 机 器 人 左 右 两 轮 的间距 分别 为 左右 轮 的驱 动力 ,。P 分 别 为 P 、:
行 平 动和 转 动控 制 。该算 法利 用 克隆选 择 算法 实现 预测控 制 的滚 动优 化 , 免 了求 带 约 束 目标 函数 的 避 最 优解 及 逆矩 阵 的复 杂推 导 , 提高 了运 算速 度 , 真 仿 结 果表 明 , 该方 法 对 机 器 人 平 动 和 移 动控 制 能 达 到 理 想 的控 制效 果 , 外 部 干 扰及 建 模 误 差 具 有 很 好 对
基于MATLAB的机器人正运动学分析与仿真

基于MATLAB的机器人正运动学分析与仿真机器人正运动学是研究机器人的位置、速度和加速度等参数与关节输入之间的关系的一门学科。
它是机器人控制中的重要环节,可以用于描述机器人的位置和方向,以实现准确的运动控制。
MATLAB作为一种强大的数学建模和仿真工具,被广泛应用于机器人正运动学的分析与仿真。
首先,机器人正运动学的分析就是要通过数学方法,推导出机械臂的运动方程。
MATLAB提供了丰富的数学工具箱,可以方便地进行符号计算和数值计算。
比如可以使用符号计算工具箱中的符号变量、方程求解函数等,来推导出机械臂各关节的位置、速度和加速度的表达式。
同时,MATLAB还可以使用数值计算工具箱中的数值求解函数,来求解非线性方程组,解决复杂的运动学问题。
其次,机器人正运动学的仿真是为了验证分析结果的正确性,以及探究机械臂的运动规律。
MATLAB提供了强大的图形界面工具,可以直观地展示机器人的运动过程。
比如可以使用绘图函数来绘制机器人的坐标系变换图,显示机械臂各关节的位置和方向。
同时,还可以使用动画函数来模拟机器人的运动过程,使得机器人在三维空间中实现真实的运动效果。
此外,MATLAB还可以使用仿真工具箱中的物理建模模块,对机器人进行动力学仿真,分析机械臂的工作空间、负载能力等性能指标。
最后,基于MATLAB的机器人正运动学分析与仿真,还可以应用于机器人轨迹规划和路径优化。
通过MATLAB的优化工具箱,可以对机器人的运动轨迹进行求解,找到满足特定要求的最佳路径。
同时,还可以使用MATLAB的控制工具箱,设计机器人的控制器,实现对机械臂的精确控制。
总之,基于MATLAB的机器人正运动学分析与仿真,能够方便、快捷地推导出机械臂的运动方程,并验证运动规律的正确性。
同时,还可以使用MATLAB的图形界面工具和仿真工具箱,进行机器人的可视化展示和动力学仿真。
此外,还可以应用MATLAB的优化工具箱和控制工具箱,实现机器人的轨迹规划和精确控制。
基于MATLAB和RobotStudio的6-DOF机器人运动学分析与仿真

基于MATLAB和RobotStudio的6-DOF机器人运动学分析与仿真郝建豹;宋春华【摘要】Aiming at the working difficulties of ship cabin,cabinet and other narrow space,a 6 degrees of freedom(6-DOF)robot was developed.First analyzes the mechanical structure of the robot,the robot D-H and robot coordinate form of forward and inverse kinematics equation was established based on the theory of D-H coordinates,followed by the application of MATLAB kinematics of the robot simulation,the results show that the robot kinematics and inverse kinematics equations exactly;finally a virtual prototype is designed,and the movement of the welding case is analyzed by RobotStudio simulation.In order to further verify the performance of the designed robot,it is compared with the general 6-DOF robot.The results show that the feasibility of the new robot,and provides a theoretical basis for the design of industrial robots to adapt to the cabinet and so on narrow space.%针对船体密封舱、箱柜等狭窄空间普遍存在的机器人难以工作问题,提出了一种新型6-DOF(degrees of freedom)机器人.首先分析了该机器人的机械结构,基于D-H坐标理论建立了机器人D-H坐标表格以及机器人正、逆运动学方程,其次应用MATLAB对机器人的运动学进行了仿真,结果表明所得的机器人正、逆运动学方程完全正确;最后设计了虚拟样机,利用RobotStudio 仿真分析了机器人箱体焊接的优点;为进一步验证设计的机器人运动性能,与通用6-DOF机器人做了对比分析.研究结果表明新型机器人运动的可行性,为设计适应箱柜等狭窄空间的工业机器人提供了理论依据.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)002【总页数】4页(P238-241)【关键词】6-DOF机器人;正逆运动学;MATLAB仿真;RobotStudio【作者】郝建豹;宋春华【作者单位】广东交通职业技术学院机电工程系,广东广州510800;广东交通职业技术学院机电工程系,广东广州510800【正文语种】中文【中图分类】TH161 引言随着工业自动化的发展,业界希望工业机器人能够像人类的手臂一样能够高效、灵活、优美自然的运动,6-DOF机器人是工业机器人应用最为广泛的一种类型[1]。
基于人机工效学的人体建模和运动仿真_陈萌

收稿日期:20000525基金项目:国家自然科学基金项目(59905009)作者简介:陈萌(1973-),男(汉),硕士研究生陈 萌文章编号:1003-8728(2001)04-0597-03基于人机工效学的人体建模和运动仿真陈 萌,陈立平(华中理工大学机械科学及工程学院,武汉 430074)摘 要:基于人机工效学的人体建模和运动仿真是虚拟现实技术中的研究热点之一。
为使设计人员早在设初期就可评估人体工程因素和装配设计中的人体工学问题,本文介绍了人体模型的树层次结构及相关术语概念,根据反向运动学原理分析了虚拟人在完成抓取/释放、坐立、下蹲等仿真过程中部件关联属性的特点和运行机理,最后讨论了在实现RU L A 姿势分析、N O IS H 提升分析和千卡(Kca l )能量消耗方面的劳工模型及其运动仿真的具体运用。
关 键 词:人机工效学;主控臂;部件关联;反向运动学;运动仿真中图分类号:T P11 文献标识码:A人体建模与仿真在虚拟现实研究领域中是实现虚拟设计和完成可视化仿真的重要基础。
为使设计人员在设计早期就能对人体工程因素进行评估,解决装配设计中的工人装配可达性问题;或将虚拟人体置于实际操作间,评判机床与其它设备的装配或空间布局是否会对虚拟人的正常操作带来负面影响;或是高效优化制造工艺流程并在“每小时工作量”等式中仿真人的能力极限,以及进行装配作业安全性分析、操作力量估测、体力消耗预测等人体工学问题方面,人体建模方法的选择和运动仿真关键技术的研究就显得尤为重要。
1 人体建模及相关术语概念在一个工作单元(w o rk cell)里,人体模型就是指一名劳工,它用设备单元(w o rker dev ice )来描述。
这个劳工单元和其它所有可进行编程操作的设备一样,从某种意义上说是由许多更小的部件(头、手、脚等)以特定方式依附在一起的树层次结构。
通过编程可以指定这些组件完成预期的运动。
为实现逼真感很强的运动仿真,此树层次结构建立得非常复杂。
高冗余度仿生机器人的运动学研究

机电信息工程高冗余度仿生机器人的运动学研究赵淑萍刘桐青(山东协和学院,山东济南250107)摘要:本文从技术和仿生2个层面解决救援技术限制的难题,增加我国救援装备的种类;从实践与理论2个方面探究仿生类救援装置的应用,有效将仿生类机械运用到灾难救援,减少人员的伤亡,间接降低国家的损失。
关键词:仿生机械1设计优势(1)模块化设计,可以根据任务灵活组装模块。
(2)采用设计的新型和壳地形适应性强,运动灵活,单由度高。
(3)通过特定的养输送可以为受困人员提供生养,维持生征,延长效。
(4)通过控制算法,深入,进入狭小空间的搜救;利用复合视觉进行微光!视距搜索,保护受困人员实例。
(5)质量轻便,单个模块仅重650g。
2研究的过程及实施2.1机械设计部分求行动灵活,关节自由度高,对关节部分提出设计灵活的要求。
(1)连接结构设计。
对已有技术,万向节结构具有运动灵活;正2.4按键与显示模块在系统中设计增加了4个独立按键,一个为开启测,另外3个为误差微。
OLED显示屏显示测量的人、环境数据。
3件设计软件按照模块化进行设计,分成DS18B20温度采集程序模块,@1x90614温度采集程序模块、按键控制程序、OLED显示程序、报 ,莫块构个.C文件,数个:。
4调试与结本文先用水银温度计测量水中温度,同时用DS18B20测量水表,测测量水表面温度,记录这3个 ,接着改变水温,分别再3种仪器测量对应的,经过多次测量得结构具有能力强的特点。
假设取其二者结合,设计出一款利用正交结构逼近万向节的连接式。
利用SolidWorks进行建模分析,建模图见图1,设计是将相连正交结构两轴逼近为0,理论设计中该结构可以与万向节功能,其三维具有一定角度限制,为一个,见图2。
其中A为关节连杆长度,实际圆锥夹角为42arctan,此范围可以做任意三维空间运动,超出槡2范围以其中~'周为主要运动,另~'轴为辅助运动,小围三。
过,理论设计和仿真结果一致。
实验四 机器人运动仿真

实验四机器人运动仿真在当今科技飞速发展的时代,机器人技术日益成熟,机器人运动仿真成为了研究和开发机器人系统的重要手段。
通过对机器人运动的仿真,可以在实际制造和部署之前,对机器人的性能、行为和任务完成能力进行评估和优化,从而降低成本、提高效率,并减少潜在的风险。
机器人运动仿真是基于计算机技术和数学模型,模拟机器人在不同环境和任务中的运动情况。
它涉及到多个学科领域的知识,如机械工程、控制工程、计算机科学和数学等。
首先,要进行机器人运动仿真,需要建立机器人的数学模型。
这包括对机器人的几何结构、关节类型和运动范围等进行精确的描述。
常见的机器人模型有串联机器人和并联机器人。
串联机器人由一系列依次连接的关节和连杆组成,其运动学分析相对较为复杂;而并联机器人则具有多个并行的运动链,具有较高的刚度和精度。
在建立数学模型之后,需要选择合适的仿真软件或工具。
市面上有许多专业的机器人仿真软件,如 RobotStudio、MATLAB Robotics Toolbox 等。
这些软件提供了丰富的功能和接口,可以方便地进行机器人的建模、编程和仿真分析。
以一个简单的工业机器人为例,假设它需要在生产线上完成物料搬运的任务。
在仿真过程中,我们需要设定机器人的起始位置、目标位置以及运动路径。
通过输入相关的参数,如关节速度、加速度和运动时间等,软件可以计算出机器人的运动轨迹,并以直观的方式展示出来。
在仿真过程中,还可以对机器人与环境的交互进行模拟。
例如,考虑机器人在搬运物料时与周围设备、障碍物的碰撞情况。
通过碰撞检测算法,可以及时发现潜在的碰撞风险,并对机器人的运动路径进行调整和优化,以确保其安全可靠地完成任务。
此外,机器人的控制系统也是仿真的重要组成部分。
控制系统决定了机器人如何响应输入指令,并实现精确的运动控制。
在仿真中,可以对不同的控制算法进行测试和比较,如 PID 控制、模糊控制和自适应控制等,以选择最适合实际应用的控制策略。
轮腿式移动机器人运动学分析与仿真

科技信息0科教前沿02010年第23期000c∞(“巩+蚴-sin(O+Ol+蚴如∞(肌口I+蚴+fleos(O+Oi)+LcosO+以sin(O+Ol+80cos(O+Ol+母0拓in(口+pI删+llsin(O+01)+LsinO+rOO1由于在此过程中前臂末端与参考坐标系在z方向上相对速度为零.所以町得Prz=12(oJ+Ol+的sin(“岛+∞+f1∞+矾)sin(O+01)+/xosin0=0(4)若台阶高度车体速度和转角0,,巩的变化规律已知,则可以由式(4)得到车体转角0的运动规律,进而由式(3)推导出质心位置在这一阶段的运动规律。
2.2逆运动学分析轮腿式移动机器人在越障过程中可以通过调节其相应的运动可控馈,对心以一定的越障行为翻越障碍。
为了实现机器人平稳越障。
减轻震动,保证移动载体的稳定性,就要求在越障过程中,机器人要通过控制其可变的结构保持机体重心以低缓的方式平稳上升以越过障碍。
机器人通过安装在其机体上的外部传感器可以感知地形障碍的特征及大致参数。
当获知运动前方待翻越的地形障碍特征要素后,便可以规划相应平缓的机器人重心越障轨迹。
为了控制机器人以一定的位姿跟踪该莺心连续轨迹,需要根据此条件下所要求的车体质心的速度和方位来确定驱动轮的转速,以使得机器人顺利平稳的翻越障碍。
为此进行相应控制变鼍的逆向求解。
设机器人移动平台质心的佗置和方位角为(R只,0)T,速度为(%%铆7;后轮中心坐标系B的速度为(y两'I,。
∥)7,根据刚体运动原理,有…一『y毋1一『b1V=y—xePo=ly匠l+to×Ic(5)【埘J【0J由式(5)可得驱动轮的速度:[cosO-sinO0]『L—幽1『oo颤y—J6)-sinO(V:-∽)]G萨IsinOcosO0K—雠l=lsino(P厂讪)+co咧PI_戗)l(6)【001儿∞J【∞J由于驱动轮做纯滚动,则驱动轮转速为:ta口=cosO(Vf-tob)-sinO(V:..cac).∽由于在越障过程中前臂和地形发生作用时.前臂的末端与地形障碍保持接触的运动约束限制,此时前臂与地面的接触点在其自身坐标系的z方向上相对参考坐标系的速度为零.则有转角速度都是未知的,同时限于篇幅,所以仅以晚做匀速运动,求0。
机器人仿真研究及运动学动力学分析

机器人仿真研究及运动学动力学分析一、概述随着科技的不断进步和创新,机器人技术已成为现代工程领域的研究热点。
机器人仿真研究及运动学动力学分析作为机器人技术的重要组成部分,对于提高机器人的运动性能、优化机器人的设计以及推动机器人技术的实际应用具有重要意义。
本文旨在深入探讨机器人仿真研究的基本原理和方法,以及运动学和动力学分析在机器人技术中的应用,以期为相关领域的研究者和工程师提供有益的参考和启示。
机器人仿真研究是通过建立数学模型和仿真环境,对机器人的运动行为、感知能力、决策过程等进行模拟和分析的过程。
通过仿真研究,可以预测机器人在实际环境中的表现,评估其性能,发现潜在的问题,进而对机器人进行优化和改进。
同时,仿真研究还可以为机器人的设计和开发提供有效的手段,降低开发成本,缩短开发周期。
运动学和动力学分析是机器人仿真的两个核心方面。
运动学主要研究机器人的几何位置和姿态随时间的变化规律,而不涉及力和力矩的作用。
动力学则更关注机器人在运动过程中所受的力和力矩,以及这些力和力矩如何影响机器人的运动状态。
通过对机器人进行运动学和动力学分析,可以深入了解机器人的运动特性和性能表现,为机器人的优化和控制提供理论支持。
本文将首先介绍机器人仿真研究的基本原理和方法,包括常用的仿真软件、建模方法以及仿真实验的设计和实施。
重点阐述运动学和动力学分析在机器人仿真中的应用,包括机器人运动学模型的建立和分析、动力学模型的建立和分析、以及基于运动学和动力学分析的机器人优化和控制方法。
对机器人仿真研究及运动学动力学分析的发展趋势和前景进行展望,以期为相关领域的研究者和工程师提供有益的参考和启示。
1. 机器人仿真研究的重要性仿真研究可以大幅降低研发成本。
在机器人设计的初期阶段,通过仿真软件模拟机器人的运动状态、工作环境以及与其他系统的交互,工程师可以在虚拟环境中测试和优化设计方案,避免在实际制造和测试过程中出现不必要的损失和浪费。
仿真研究有助于提高机器人的性能和安全性。
基于Coppeliasim与MATLAB的机器人建模与运动仿真
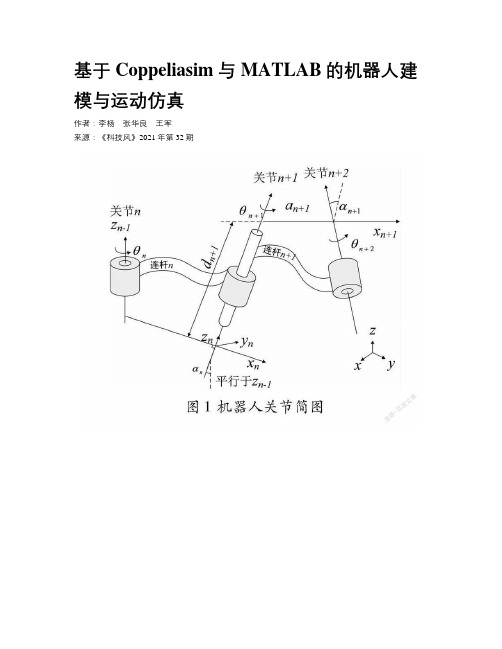
基于Coppeliasim与MATLAB的机器人建模与运动仿真作者:李杨张华良王军来源:《科技风》2021年第32期摘要:针对目前机器人模型构建烦琐,仿真过程复杂的问题,提出了基于Coppeliasim与MATLAB相结合实现对所研究机器人的建模与运动仿真。
首先使用3D建模软件SolidWorks 将模型导出,然后采用D-H参数建模法进行分析,得出机器人运动学模型表达式。
最后使用LuaSocket通信方式实现机器人与MATLAB中控制程序之间的通信连接。
目的是实现机器人复杂的运动学建模与运动仿真。
该方法研究了机器人关节运动和控制程序,分析了二者联合仿真的实用性。
以络石XB7机器人为代表,叙述机器人的3D模型仿真技术。
仿真结果表明机器人能够准确按照控制程序进行运动,验证本仿真方法的真实有效性。
关键词:机器人;Coppeliasim仿真;LuaSocket;D-H模型中图分类号:TP-242 文献标识码:A随着机器人建模与仿真在工业技术领域占有比重越来越大,在机器人设计与制造过程中,能够提前解决机器人运行中出现的问题,并避免在实操中呈现的各种安全隐患问题也变得尤为重要。
根据不同的仿真目标选择仿真工具成为开发机器人的关键。
L Pitonakova等人提出了V-REP,Gazebo和ARGOS机器人模拟器的功能和性能比较。
2019年11月,V-REP被重新命名为Coppeliasim,Coppeliasim在V-REP的基础上重写计算例程、碰撞处理检测、最短路径计算、超频树、近似传感器模拟以及点云方面,显著提高了运行速度。
但Coppeliasim仿真运动过程只能根据脚本执行,可操作性能差。
祁若龙等人指出MATLAB在机器人仿真领域应用广泛,但是MATLAB仿真在三维空间构型能力差,不能完整清晰的各个连杆与末端问的姿态。
本文针对以上的不足,提出了结合Coppeliasim与MATLAB通过LuaSocket通信使用控制器对机械臂控制,并得到机器人运动的关节角以及运动轨迹曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%
引言
仿真足球机器人比赛是足球机器人比赛中的实验平台, 实
能根据小球当前的运动轨迹找出小球将要经过的某一点, 并且 能 预 测 出 该 进 攻 队 员 到 达 这 个 点 所 需 的 周 期 数 (以 下 简 称 拍 数) , 然后比较进攻队员需要的拍数和球到达需要的拍数, 如果 相同, 那么机器人就可以让它预先就朝着这个点前进, 最终将 (( ) ) 。 在该点碰到球。 (如图 %
素的桔黄色高尔夫球。球应该各向同性, 即对于任何方向的运 动表现应一致。从球的运动中看出, 该平台中将球定位成一个 完全的弹性体, 球在运动过程中如果碰到障碍物上, 那么该碰 撞过程符合完全弹性碰撞的规律, 并且球的入射方向和出射方 向关于碰撞面的法线方向完全对称,且碰撞前后速度大小不 变。这里的障碍物包括墙面和机器人的侧面, 但不包括机器人 的 正 前 面 和 正 背 面 。 机 器 人 主 动 碰 撞 球 的 情 况 详 见 下 面 0$0 节。正常情况下, 球保持静止或以一定的初速度作匀减速直线 运动。这里必须考虑到平台的摩擦力作用, 由物理学公式可知 因 !"!#$, ! 是摩擦力, ! 是动摩擦因数, $ 是接触面间正压力, 此匀减速运动的加速度公式为:
F
物的足球机器人因为控制难度大, 实时性要求高和硬件的一系 列问题等, 现在还很难做出很有技术性的动作。先进的控制方 法、 队形和战术战略在仿真足球机器人比赛中远先于实物足球 机器人得到应用和检验。要让足球机器人实现战术策略, 首先 要有好的运动控制。 类似人类足球比赛中, 如果一个球员, 虽然 他有很好的配合思想, 但是他永远接不到从本方队友那里踢过 来的球, 那他绝不能算是一个好队员。 如果队中球员个个如此, 那么这个球队就永远不可能赢球。足球机器人比赛更是这样, 试想如果防守机器人不能准确地到达它应该站的防守位置, 那 再好的防守策略也只能是纸上谈兵。
"2 ! 01&01/ 03&03/"2
(; (/ < =,>/-<>-)
(& )
从这个关系出发, 很容易就能找到了碰撞点, 对于球撞到 计算机工程与应用 !""#$%&
4?
障碍物然后反弹的碰撞点, 这也是适用的。计算从碰撞点开始 到当 前 点 平 均 速 度 , 假 设 可 以 利 用 的 有 到 当 前 为 止 的 ! 拍 数 则可以利用以下关系: 据, 由此预测未来 " 拍的位置,
8-,9:4846 %%;2%%
运动学模型
预测方法 文献标识码 > 中图分类号 ?@!=
(!""# ) 文章编号 %""!+&<<%+ %&+""=&+"<
!"#$% &’ ()*$+,"+&- .&$*/ +- "0* !+1#)&!&" 234*$ &- 5+-*13"+,4 60*&)%
!0+ 73&8+- 9+ :*+0#3 :3-; <+’*+ =3- >+3-’*-; (A0B’:6,0/6 4C D4,B960: 87-0/70 , E4:6310260:/ @4.F6073/-7’. G/-;0:2-6F , H-I’/ )%"")!)
4 ’()*+,’,- %%./%% 中预测模型的建立
根据上面提出的这些运动模型, 建立了相应的预测模型。
4$%
球的预测模型
由前面运动模型知道, 球在被机器人撞击后, 以一定的初
速度开始做匀减速直线运动, 且加速度大小为常值。从这样的 理想角度出发,直接利用当前球和前两拍球的 位 置 , 0 个数据 逐差, 得出当前速度和当前加速度, 再利用匀加速直线运动公 式, 直接就可以计算出未来有限拍后的球的位置, 这种方法从 理论上说是完全正确的, 但运用到 实 际 ’()*+,’,- %%./%% 的 平 台中就很不合适, 预测出来的值和实际值比较, 偏差值已经超 出了允许的误差范围。究其原因, 是 因 为 ’()*+,’,- %%./%% 的 平台发回的全是截取后的整型数据,这就造成如果只用一、 两 拍内球走的距离作为运动的初速度, 结果就可能导致出错。要 得到尽可能准确的初速度,应该利用尽可能多的球的历史位 置, 求出多拍位移的平均值, 作为递推的初速度。 新的方法又产 生了新的问题,并不仅仅是多记录一些历史数据就可以解决 的, 关键是要确定这些数据中哪些是有效的, 因为比赛过程中 球不停地被机器人撞来撞去, 必须要从记录的历史数据中找到 可以利用的有效值, 即找出球在当前位置前的最近一次被某个 机器人的碰撞点。通过对实验测试的数据分析, 可以得出如果 球不被机器人撞击, 则球任意两拍走的位移之间, 满足一定的 关系如下:
平台。要对球和机器人进行预测, 首先应该搞清楚平台中的运 动学模型是怎样建立的, 即机器人和球它们本身的运动规律是 怎样的。结合对平台的技术测试, 分析如下:
0$%
球的运动学模型
%%./%% 规 则 中 指 出 比 赛 中 的 足 球 应 采 用 一 个 半 径 为 # 像
!
., . -(, (% "., /.-(, /(%
, /(。
%"&! ’ ("&!#$ ’ ("&!#() ’ ("&!)
(% )
0$!
机器人的运动学模型
机器人是 %" 像素 1%" 像素的正方形小车,机器人有唯一
的一个正面, 平台每个周期返回机器人的质心坐标以及正面的 朝向角。如图 ! 所示, * 是小车左右轮之间的距离, + 是小车转 弯的半径, , 是小车前进方向速度, " 是小车转弯的角速度,
’$!
机器人的预测模型
要精确预测机器人到达某点需要多少拍, 必须要能够精确
! ! ’ "#$%& ("(! ) ! ) (! ) ("(! ) ! ) - % *’./0 ’ $ # ! $ !
’$)
实验分析结果
在机器人足球仿真 %% 对 %% 平台上实际应用后, 发现预测
的精确程度相当高。 下面是一个关于预测机器人到达某点需要 多少拍的例子, 实验结果中机器人到达某点实际需要的拍数和 (* ) 预测所需要的拍数比较如图 # 所示。
0$0
关于机器人和球之间碰撞的运动模型
球在场上的运动都是由机器人碰撞产生的, 要想让球到达
某个指定点, 即驱动球按一定的方向运动, 必须要知道球的初
0
仿真平台中的运动学模型
国 际 比 赛 中 ’()*+,’,-%%.%% 比 赛 采 用 的 是 哈 工 大 的 仿 真
始速度和被撞后速度之间的关系。平台中球被视为弹性体, 碰 撞时间很短, 碰撞过程中摩擦力与瞬间的冲撞作用力相比可以 可以看成碰撞过程在碰撞方向上满足 忽略不计, 如图 0 所示, 动量守恒和能量守恒定理。关系式如下: (: ) % ., ! 9 % (, ! 5 % ., /! 9 % (, /! . (% . (% ! ! ! ! 其中, . 为机器人的质量, ( 为小球的质量, , ( 和 , /( 分 别为小球的碰前和碰后速度, 其中 , (% 和 , /(% 分别是 , ( 和 , /( 在碰撞方向上的投影, , (! 和 , /(! 分别为 , ( 和 , /( 在垂直于碰 撞方向上的投影, ,. 为机器人的碰前速度, , /. 为 机 器 人 的 碰 就得出了 后 速 度 。 解 出 , /(% 后 将 , / (% 与 , (! 进 行 矢 量 合 成 ,
图!
机器人的运动学模型
可以看出,通过控制左轮速和右轮速就能控制小车的运 动。当左轮速和右轮速一致时, 机器人走直线; 如 + 为无穷大, 机器人作圆周运动, 圆心在机器人右侧; 如 , * 小于 , * 大于 , +, 机器人作圆周运动, 圆心在机器人左侧。实际比赛中, 机器 , +, 人的左右轮速每个周期都可能设定完全不同的值,可以发现, 机器人每个周期内的位移只与这个周期所设定的轮速有关, 因 此每个周期内机器人的运动可以视为是一个瞬时圆周运动中 的一小段圆弧, 在此基础上可以进行有效的预测。
! ’ ("(! ) ! ) (! ) ("(! ) ! ) #+%& - % *’012 ’ + ! %
#
其中 ! 代表球的运动方向角, #$ 和 #+ 分 别 是 球 在 $ 和 + 方向上的位移, * 代表球的加速度。 除此之外, 还要考虑的就是, 如果预测的拍数比较多, 会出 现预测出的球的坐标超出边界以外或者对应预测点的球的最 而这是不可能的, 需要分别进行相应处理。处 终速度已小于 " , 理方法此处略。
?84")3,": D4/2-J0:-/K 630 :0’.+6-,0 B0:C4:,’/70 4C ,46-4/ 74/6:4. ’770B60J -/ 630 26:’60KF 4C 8-,9:4846, B:0J-76-4/ 4C 630 ,46-4/ 4C 630 :4(46 ’/J 630 (’.. -2 ’ /07022’:F ’/J 0CC076-;0 1’F 64 -,B:4;0 630 B0:C4:,’/70 4C 630 60’, -/ 630 ,’673$L’20J 4/ 630 M-/0,’6-72 ,4J0.2 4C 630 (’.. ’/J 630 :4(46 -/ 630 B.’6C4:, 4C 8-,9:4846 %%;2%% -/6:4J970J ’/J ’/’.FN0J, ’ ;’.-J ’/J B:’76-7’. ,0634J 64 B:0J-76 630 ,46-4/ 4C 630 :4(46 ’/J 630 (’.. -2 B96 C4:1’:J, 630 ;’.-J-6F 4C 13-73 3’2 (00/ B:4;0J -/ 630 0OB0:-,0/62$ 5*%@&)$4: 8-,9:4846%%;2%% , P-/0,’6-72 ,4J0., @:0J-76-4/ ,0634J
