1-1线性空间与线性变换
线性空间与线性变换

线性空间与线性变换线性空间是线性代数的一个重要概念,扮演着理解线性变换的基础角色。
本文将介绍线性空间的定义、性质以及线性变换的概念和特性。
一、线性空间的定义与性质线性空间,也被称为向量空间,是指一个集合,其中包含一些向量,满足特定的性质。
具体而言,线性空间需要满足以下几个条件:1. 封闭性:对于线性空间中的任意两个向量,它们的线性组合也属于该空间。
即,如果向量a和向量b属于线性空间V,那么对于任意标量α和β,αa + βb也属于V。
2. 加法封闭性:线性空间中的向量满足加法封闭性,即对于任意的向量a和b,它们的和a + b也属于该空间。
3. 数乘封闭性:线性空间中的向量满足数乘封闭性,即对于任意的向量a和标量α,它们的积αa也属于该空间。
4. 满足加法和数乘的运算性质:线性空间中的向量满足加法和数乘的交换律、结合律和分配律。
线性空间的性质还包括零向量、负向量和线性相关性。
零向量表示线性空间中存在一个使其与任何向量相加得到自身的向量,负向量表示线性空间中的向量存在一个加法逆元。
线性相关性指的是线性空间中存在一组向量线性组合为零向量的关系。
二、线性变换的定义和性质线性变换是指在两个线性空间之间的映射,它保持了向量空间中的线性结构。
具体而言,线性变换需要满足以下几个条件:1. 保持加法运算:对于线性变换T,对任意的向量a和b,有T(a +b) = T(a) + T(b)。
2. 保持数乘运算:对于线性变换T和标量α,有T(αa) = αT(a)。
线性变换的性质还包括零变换、恒等变换和可逆性。
零变换表示线性变换将所有向量映射为零向量。
恒等变换表示线性变换将每个向量映射为其本身。
可逆性表示存在一个逆变换,使得两个线性变换进行复合后得到恒等变换。
三、线性空间与线性变换的关系线性空间和线性变换密切相关,线性变换本质上是线性空间之间的映射,它将一个线性空间中的向量映射到另一个线性空间中。
线性变换保持了向量空间的线性结构,在线性代数中起到了重要的作用。
第1章 线性空间与线性变换-1

矩阵分析简明教程
事实上, a, b R a b ab R; R, a R a a R . 所以对定义的加法与数乘运算封闭. 下面一一验证八条线性运算规律: (1) a b ab ba b a; (2)(a b) c (ab) c (ab)c a(bc) a (b c); (3) R中存在零元素 1, 对于a R , 有
2
矩阵分析简明教程
例1 数域 F上的n维向量全体,按n维向量加法与n维 向量的数量乘法构成数域 F上的线性空间 F n 。 例2 数域 F 上 m n 阶矩阵全体,按矩阵的加法 和数乘,构成 F 上的线性空间 F mn 。 例3 数域 F上一元多项式全体按照多项式的加法以 及数与多项式的乘法构成 F 上的一线性空间 F[ x] 。
矩阵分析简明教程
第一章 线性空间与线性变换
矩阵分析简明教程
§1.1、线性空间的基本概念
线性空间是线性代数最基本的概念之一, 是矩阵论中极其重要的概念之一。它是向 量空间在元素和线性运算上的推广和抽象。
线性空间中的元素可以是向量、矩阵、多 项式、函数等,线性运算可以是我们熟悉 的一般运算,也可以是各种特殊的运算。
数的加法和数与函数的乘法构成线性空间 C[a, b]
矩阵分析简明教程
例6 齐次线性方程组 Ax 的所有解的集合构成数 域 R 上的线性空间 N ( A) ,称为 Ax 的解空间, 或矩阵 A 的核空间或零空间,即
N ( A) { x Rn | Ax , A Rmn} Ker( A)
向量个数 n 称为线性空间V 的维数,记为 dimV n
矩阵分析引论--第一章 线性空间与线性变换-线性空间的概念、 基变换与坐标变换

复数集的一个非空子集,含非零数,对和、差、 积、商(除数不为零)运算封闭.
• 性质:
必包含0与1; 有理数域是最小的数域.
目录 上页 下页 返回 结束
第一章第一二节 线性空间的概念、基变换与坐标变换
2、线性空间
定义1-1(线性空间) 设V是一非空集合,P是一数域,若
(1)在V上定义了一个二元运算(称为加法, a与b 的和记为a+b), 且 a , b V,有 a b V ;
(2)在P与V的元素之间还定义了一种运算(称为
数乘, k与a的数乘记为ka),
且 a V ,k P, 有 ka V ;
目录 上页 下页 返回 结束
第一章第一二节 线性空间的概念、基变换与坐标变换
(3)加法与数乘满足以下八条规则:
(ⅰ) a b b a; (ⅱ) (a b ) a (b );
第一章第一二节 线性空间的概念、基变换与坐标变换
第一节 线性空间的概念
一、线性代数回顾
★ n维向量:有序数组 ★ 线性运算:加法、数乘 ★ 运算律(八条) ★ 向量关系:线性相关、线性无关 ★ 向量空间 ★ 子空间 ★基
目录 上页 下页 返回 结束
第一章第一二节 线性空间的概念、基变换与坐标变换
(ⅲ) a 0 a;
(ⅳ) a (a ) 0;
(ⅴ) 1a a;
(ⅵ) k(la ) (kl)a;
(ⅶ) (k l)a ka la ;(ⅷ) k(a b ) ka kb .
则称集合V为数域P上的线性空间或向量空间.
目录 上页 下页 返回 结束
第一章第一二节 线性空间的概念、基变换与坐标变换
又若向量 b k1a1 k2a2 knan , 则b 也称为向量 a1,a2,,an 的线性组合,或称 b 可以由向量 a1,a2,,an 线性表示.
第1章 线性空间与线性变换
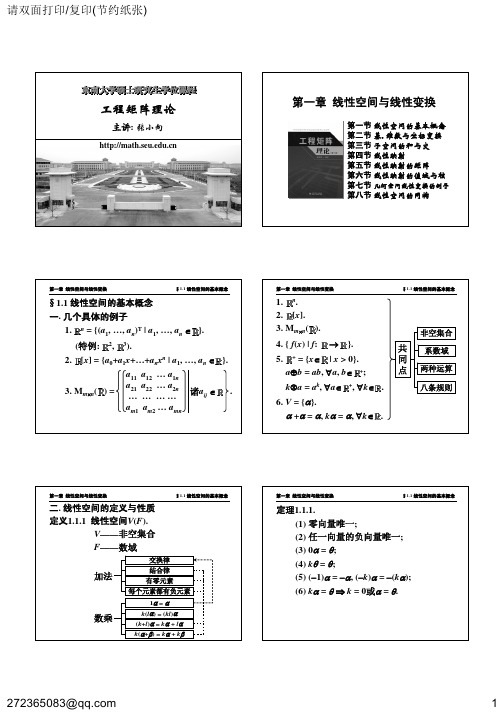
请双面打印/复印(节约纸张)工程矩阵理论主讲: 张小向第一章 线性空间与线性变换第一节 线性空间的基本概念 第二节 基, 维数与坐标变换 第三节 子空间的和与交 第四节 线性映射 第五节 线性映射的矩阵 第六节 线性映射的值域与核 第七节 几何空间线性变换的例子 第八节 线性空间的同构第一章 线性空间与线性变换§1.1 线性空间的基本概念第一章 线性空间与线性变换§1.1 线性空间的基本概念§1.1 线性空间的基本概念 一. 几个具体的例子 1.n= {(a1, …, an)T | a1, …, an ∈ }.2, 3).1. n. 2. [x]. 3. Mm×n( ). 4. { f(x) | f: → }. 5. = {x∈ | x > 0}. a⊕b = ab, ∀a, b∈ +; k⊗a = ak, ∀a∈ 6. V = {α}.+, +非空集合(特例: 2. [x] ={a0+a1x+…+anxn a11 a21 … am1| a1, …, an ∈ }. .3. Mm×n( ) =a12 … a1n a22 … a2n 诸aij ∈ … …… am2 … amn共 同 点系数域 两种运算 八条规则∀k∈ .α +α = α, kα = α, ∀k∈ .第一章 线性空间与线性变换§1.1 线性空间的基本概念第一章 线性空间与线性变换§1.1 线性空间的基本概念二. 线性空间的定义与性质 定义1.1.1 线性空间V(F). V——非空集合 F——数域 加法交换律 结合律 有零元素 每个元素都有负元素 1α = α k(lα) = (kl)α (k+l)α = kα + lα k(α+β) = kα + kβ定理1.1.1. (1) 零向量唯一; (2) 任一向量的负向量唯一; (3) 0α = θ; (4) kθ = θ; (5) (−1)α = −α, (−k)α = −(kα); (6) kα = θ ⇒ k = 0或α = θ.数乘272365083@1请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.1 线性空间的基本概念第一章 线性空间与线性变换§1.1 线性空间的基本概念三. 线性组合, 线性表示 1. 设α1, …, αk ∈V(F), x1, …, xk ∈F, 则称 x1α1 + … + xkαk 为α1, …, αk的一个线性组合. 2. 设α1, …, αk, β ∈ V(F). 若∃ x1, …, xk ∈ F s.t. β = x1α1 +…+ xkαk 则称β能由向量组α1, …, αk线性表示. 3. 若β1, …, βl都能由α1, …, αk线性表示,则称向量组β1, …, βl能由α1, …, αk线性表 示.四. 形式矩阵 设α1, …, αk , β1, …, βk ∈V(F). 1. 若α1 = β1, …, αk = βk , 则记(α1, …, αk) = (β1, …, βk). 2. 规定 (α1, …, αk) + (β1, …, βk) = (α1+β1, …, αk+βk). 3. 若a ∈F, 则规定 a(α1, …, αk) = (aα1, …, aαk).第一章 线性空间与线性变换§1.1 线性空间的基本概念第一章 线性空间与线性变换§1.1 线性空间的基本概念4. 若x1, …, xk ∈F, 则记 x1α1 +…+ xkαk = (α1, …, αk) x1 . xk 5. 若A = (A1, …, As) ∈ Mk×s(F), 则规定 (α1, …, αk)A = ((α1, …, αk)A1, …, (α1, …, αk)As). …注: 设α1, …, αk , β1, …, βk ∈V(F). a, b ∈ F, A, B ∈ Mk×s(F), C ∈ Ms×t(F). 记α = (α1, …, αk), β = (β1, …, βk), 则可以验证下列等式成立: ① a(α + β) = aα + aβ, ② (a+b)α = aα + bα, ③ a(bα) = (ab)α. ④ (α + β)A = αA + βA, ⑤ α(A+B) = αA + αB, ⑥ (αA)C = α(AC), ⑦ (aα)A = a(αA) = α(aA).第一章 线性空间与线性变换§1.1 线性空间的基本概念第一章 线性空间与线性变换§1.1 线性空间的基本概念五. 线性空间的子空间 定义1.1.2 子空间, W ≤ V(F) 定理1.1.2. 设∅ ≠ W ⊆ V(F), 则 W ≤ V(F) ⇔ W关于的加法和数乘封闭. 注: V(F)的两个平凡的子空间. {θ}, V(F)六. 由子集合{α1, α2, …, αk}生成的子空间 {α1, α2, …, αk}——生成系, 生成元集i=1 k∑ xiαi —— α1, α2, …, αk的一个线性组合 组合系数 W = { ∑ xiαi | ∀xi∈ F}.k记为L[α1, α2, …, αk]或span{α1, α2, …, αk}.i=1272365083@2请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.2 基, 维数与坐标变换第一章 线性空间与线性变换§1.2 基, 维数与坐标变换§1.2 基, 维数与坐标变换 一. 向量组的线性相关性 定义1.2.1 线性相关, 线性无关. 定理1.2.1 设(I) α1, α2, …, αs线性无关, 且能由 (II) β1, β2, …, βt线性表示, 则s ≤ t. 推论1 设(I)与(II)都线性无关, 且等价, 则s = t. 推论2 设(I)能由(II)线性表示, 且s > t, 则(I)必线性相关.二. 基、维数 定义1.2.2 基, 维数. 例子. 1. n. 2. [x], [x]n = {a0+a1x+…+an−1xn−1 | …}. 3. Mm×n( ). 4. { f(x) | f: → }. 5. = {x∈ | x > 0}. a⊕b = ab, ∀a, b∈ +; k⊗a = ak, ∀a∈ +, ∀k∈ . 6. V = {θ}.+第一章 线性空间与线性变换§1.2 基, 维数与坐标变换第一章 线性空间与线性变换§1.2 基, 维数与坐标变换定理1.2.2 若dimV = n, 则V中任意 n 个线性无 关的向量都构成V的一组基. 定理1.2.3 若W ≤ V, dimV = n, α1, …, αr 为W 的一组基, 则∃αr+1, …, αn∈ V 使得 α1, …, αr, αr+1, …, αn构成V的一组 基.三. 坐标 定义1.2.3 设α1, …, αn为V的一组基, ξ ∈ V. 若ξ = x1α1 + … + xnαn, 则称有序数组(x1, …, xn)为ξ在基 α1, …, αn下的坐标, (x1, …, xn)T称为ξ的坐标向量.第一章 线性空间与线性变换§1.2 基, 维数与坐标变换第一章 线性空间与线性变换§1.2 基, 维数与坐标变换定理1.2.4 设α1, …, αn为V的一组基, (β1, …, βr) = (α1, …, αn)x11 … x1r x11 … x1r xn1 … xnr … …四. 坐标变换 V的两组基 , P, 可逆X=xn1 … xnr,p11 … p1n (β1, …, βn) = (α1, …, αn) … … … , pn1 … pnn 称P为从基α1, …, αn到β1, …, βn的过渡矩 阵.…则β1, …, βr线性无关 ⇔ 秩(X) = r.272365083@…3请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.2 基, 维数与坐标变换第一章 线性空间与线性变换§1.3 子空间的和与交四. 坐标变换 V的两组基 P, 可逆§1.3 子空间的和与交 一. 基本概念与结论 定义1.3.1 设V1, V2 ≤ V. V1与V2的和: V1 + V2 = {α1 + α2 | α1∈V1, α2∈V2}. V1与V2的交: V1∩V2 = {α∈V | α∈V1且α∈V2}. 定理1.3.1 V1, V2 ≤ V ⇒ V1 + V2, V1∩V2 ≤ V.p11 … p1n (β1, …, βn) = (α1, …, αn) … … … , pn1 … pnnξ = (α1, …, αn)X = (β1, …, βn)Y,(α1, …, αn)PY ⇒ X = PY, Y = P−1X. ——坐标变换公式 =第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交注: ① 子空间V1∩V2与集合V1∩V2是一致的. ② 一般情况下, V1+V2 ≠ V1∪V2. 例如V =3,zOV1 = xOy平面, V2 = yOz平面, V1+V2 = V, V1∩V2 = y轴.定理1.3.2 (维数定理) 设V1, V2是V的两个有限维子空间, 则 dimV1 + dimV2 = dim(V1+V2) + dim(V1∩V2). 证明: (关键步骤) y(1) 取V1∩V2的一组基α1, …, αr ; (2) 把α1, …, αr扩充成V1的一组基 α1, …, αr, βr+1, …, βs ; (3) 把α1, …, αr扩充成V2的一组基 α1, …, αr, γr+1, …, γt ; (4) 验证α1, …, αr, βr+1, …, βs, γr+1, …, γt 线性无关(从而构成V1+V2的一组基).x③ V1+V2 = V1∪V2 的充分必要条件是 V1⊆V2 或 V2⊆V1.第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交k1α1+…+krαr+kr+1βr+1+…+ksβs+lr+1γr+1+…+ltγt = 0 ⇒ lr+1γr+1+…+ltγt = −k1α1−…−krαr−kr+1βr+1−…−ksβs ∈ V1∩V2 ⇒ ∃l1, …, lr s.t. lr+1γr+1+…+ltγt = l1α1+…+lrαr i.e. l1α1+…+lrαr −lr+1γr+1−…−ltγt = 0 ⇒ l1 = … = lr = lr+1 = … = lt = 0 ⇒ k1α1+…+krαr+kr+1βr+1+…+ksβs = 0 ⇒ k1 = … = kr = kr+1 = … = ks = 0dimV1 + dimV2 = dim(V1+V2) + dim(V1∩V2) 例1(1) V = 3, V1 = xOy平面, V2 = yOz平面, V1+V2 = V, V1∩V2 = y轴, dimV1 = dimV2 = 2, dim(V1+V2) = 3, dim(V1∩V2) = 1. zOyx272365083@4请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交例1(2) V = V2 =2×2,V1 =x y z tx = y ≤ V,例1(3) V = V2 =2×2,V1 =x −x y −yx, y ∈ ≤ V,≤ V,x y z tx + y + z = 0 ≤ V,x y z tx y x yx, y ∈0 0V1+V2 = ______. V1∩V2 =x=y且x+y+z=0 ,则 0 0 , 构成V1的一组基, 1 −11 0 0 1 , 构成V2的一组基, 1 0 0 11 −1dimV1 = dimV2 = 3, dim(V1∩V2) = 2, 故dim(V1+V2) = 3 + 3 − 2 = 4 = dimV, 可见V1+V2 = V.故dimV1 = dimV2 = 2.x −x y −y ∈V2 ⇔ x = y. x −x 故V1∩V2 = x −x x ∈.第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交可见1 −1 构成V1∩V2的一组基, 1 −1dim(V1∩V2) = 1. 故dim(V1+V2) = dimV1 + dimV2 − dim(V1∩V2) = 2 + 2 − 1 = 3. 事实上,1 0 0 1 1 −1 0 0 , , 1 0 , 0 1 线性相关, 0 0 1 −1二. 子空间的直和 定义1.3.2 设V1, V2 ≤ V. 若对于∀α∈V1+V2, ∃| α1∈V1, α2∈V2, s.t. α = α1 + α2, 则称V1 + V2为V1与V2的直和, 记为V1⊕V2.其中任意3个都线性无关, 因而构成V1+V2的 一组基.α = α1 + α2, α1∈V1, α2∈V2 ⇒ α = β1 + β2, β1∈V1, β2∈V2 α1 = β1, α2 = β2.第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交定理1.3.3 设V1, V2 ≤ V, 则下列条件等价: (1) V1 + V2是直和; (2) V1 + V2中0分解式唯一, 即 0 = α1+α2 (αi∈Vi) ⇒ α1 = α2 = 0; (3) V1∩V2 = {0}; 当dimV1, dimV2 < ∞时, 上述条件还等价于 (4) dim(V1+V2) = dimV1 + dimV2.定理1.3.4 设V1 ≤ V, dimV = n, dimV1 = r, 则存在V的n−r维子空间V2使得 V = V1⊕V2. 定义1.3.3 设V1, …, Vs ≤ V, 则V1, …, Vs的和 V1 + … + Vs = {α1 +…+ αs | αi∈Vi}. 若对于∀α ∈ V1 + … + Vs , ∃| αi∈Vi (i = 1, …, s) s.t. α = α1 + … + αs , 则称V1 +…+ Vs为V1, …, Vs的直和, 记为V1⊕…⊕Vs .272365083@5请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.3 子空间的和与交定理1.3.5 设Vi ≤ V (i = 1, …, s), 则TFAE: (1) V1 + … + Vs是直和; (2) V1 + … + Vs中0分解式唯一; (3) Vk∩Σi≠kVi = {0}, k = 1, …, s; 当dimVi < ∞ (i = 1, …, s)时, 上述条件还等价于 (4) Σ dimVi = dim( Σ Vi).i=1 i=1 s s例2. 设A2 = A ∈ Fn×n, V1 = {X ∈ Fn | AX = 0}, V2 = {X∈Fn | AX = X}. 证明: Fn = V1⊕V2. 证明: (1) 容易验证V1, V2 ≤ Fn. (2) ∀α∈Fn, 有α = (α − Aα) + Aα, A(α − Aα) = Aα − A2α = 0, A(Aα) = A2α = Aα. 可见α ∈ V1+V2. 这就证明了Fn ⊆ V1+V2. 又因为V1+V2 ⊆ Fn, 所以Fn = V1+V2.第一章 线性空间与线性变换§1.3 子空间的和与交第一章 线性空间与线性变换§1.4 线性映射例2. 设A2 = A ∈ Fn×n, V1 = {X ∈ Fn | AX = 0}, V2 = {X∈Fn | AX = X}. 证明: Fn = V1⊕V2. 证明: (1) 容易验证V1, V2 ≤ (2) Fn = V1+V2. (3) 若α∈V1∩V2, 则α = Aα = 0. Fn. 可见V1∩V2 ⊆ {0}. 又因为{0} ⊆ V1∩V2, 所以V1∩V2 = {0}. 综上所述, Fn = V1⊕V2.§1.4 线性映射 一. 映射 定义1.4.1 像 原像 • • • 映射 • • • • • • 满射 • •第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射• • 单射 注:• • •• • • 双射• • •f:→; a → |a| ;a→ √a2(∀a∈ ) (∀a∈ )g: →f = g —— ∀a∈ , f(a) = g(a) 一般地, 若映射f, g: A → B满足 f(a) = g(a) (∀a∈A) 则称映射f与g相等, 记为f = g.• • •• • •• •• • •不是映射不是映射272365083@6请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射• • • f • • •• • •• • • g • • • gf• • •注① 映射的复合运算满足结合律: f: A → B, g: B → C, h: C → D (hg)f = h(gf). A B f b• g C c• h D d•• • •a•[(hg)f](a) = (hg)[f(a)] = (hg)(b) = h[g(b)] = h{g[f(a)]} = h[(gf)(a)] = [h(gf)](a)f: A → B与g: B → C的乘积 gf: A → C定义为 ( gf )(a) = g[ f(a)] (∀a∈A).第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射注② 1A: A → A, f: A → B, 1B: B → B f⋅1A = f, A a• 1A A a• f 1B⋅f = f. B b• 1B B b• • • • 双射f • • • • • • • • •f的逆映射( f⋅1A)(a) = f [1A(a)] = f(a) (1B⋅f )(a) = 1B[ f(a)] = f(a)若映射f: A → B, g: B → A满足 gf = 1A, fg = 1B, 则称g为f 的逆映射, 记为g = f −1. 注① g = f −1 ⇒ f = g−1. 注② f: A → B有逆映射⇔ f: A → B为双射.第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射注② f: A → B有逆映射⇔ f: A → B为双射.证明: (⇒) 设f: A → B有逆映射g: B → A, 则 (1) ∀x, y ∈ A, 由 f(x) = f(y)可得 x = 1A(x) = gf(x) = gf(y) = 1A(y) = y. 可见 f: A → B为单射. (2) ∀b ∈ B, ∃a = g(b) ∈ A s.t. f(a) = f[g(b)] = fg(b) = 1B(b) = b. 可见 f: A → B为满射. 所以 f: A → B为双射.注② f: A → B有逆映射⇔ f: A → B为双射.证明: (⇐) 设 f: A → B为双射, 则 ∀b ∈ B, ∃| a ∈ A s.t. f(a) = b. 令g(b) = a, 可得 映射g: B → A. 而且 (1) ∀b ∈ B, 有 fg(b) = f[g(b)] = f(a) = b. 这就是说, fg = 1B. (2) ∀a ∈ A, 令b = f(a) ∈ B, 按g的定义, gf(a) = g[ f(a)] = g(b) = a. 这就是说, gf = 1A, 可见 f: A → B有逆映射g: B → A.272365083@7请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射例1. 设A为数域F上的n阶方阵, Fn = {(a1, …, an)T | a1, …, an∈F}. 映射f: Fn→ Fn定义为 f(x) = Ax. 证明下列条件等价: (1) f: Fn→ Fn为单射; (2) f: Fn→ Fn为满射; (3) A可逆.证明: (1)⇒(3) 假设A不可逆, 则|A| = 0, 故r(A) < n, 因而Ax = 0有非零解, 即存在x ≠ 0使得Ax = 0, 于是f(x) = Ax = 0 = A0 = f(0). 这与“f: F n→ F n为单射”矛盾. 所以A可逆. (3)⇒(1) 对于任意的x, y ∈ F n, 若f(x) = f(y), 即Ax = Ay, 因为A可逆, 所以x = A−1Ax = A−1Ay = y. 可见 f: F n→ F n为单射.第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射证明: (2)⇒(3) 因为f: F n→ F n是满射, 所以存在n阶方阵B = (ξ1, …, ξn)使得 AB = (Aξ1, …, Aξn) = ( f(ξ1), ..., f(ξn)) = (e1, …, en) = I. 从而|A|×|B| = |AB| = |I| = 1, 故|A| ≠ 0, 因而A可逆. (3)⇒(2) 对于任意的y ∈ F n, 令x = A−1y, 则x ∈ F n, 而且f(x) = Ax = AA−1y = y. 可见f: F n→ F n为满射.二. 线性映射与线性变换 定义1.4.2 设U, V为数域F上的线性空间. 若映射 f: V → U保持加法和数乘, 即 f(α+β) = f(α) + f(β), f(kα) = kf(α), ∀α, β ∈ V, k ∈ F, 则称 f 为线性映射. 特别地, 当U = V时, 称线性映射 f: V → V为V上的线性变换. 注① f(kα+lβ) = kf(α) + lf(β), ∀α, β ∈ V, k ∈ F.第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射注② Hom(V, U) = { f: V → U | f为线性映射}. 注③ 若 f ∈ Hom(V, U), 则 f(0V) = 0U; f(−α) = −f(α); f(x1α1+…+xsαs) = x1 f(α1) +…+ xs f(αs); α1, …, αs线性相关 ⇒ f(α1), …, f(αs)线性相关. 注④ 若 f: V → U 满足 f(α) = 0, ∀α∈V, 则 f ∈ Hom(V, U), 称为零映射, 记为0.注⑤ 若 f: V → V 满足 f(α) = α, ∀α∈V, 则 f ∈ Hom(V, V), 称为V上的恒等变换, 记为 I 或 IdV . 注⑥ 对于 f ∈ Hom(V, U), 可以把 ( f(α1), …, f(αs))记为f(α1, …, αs). 相应地, 可以把 f(x1α1+…+xsαs) = x1 f(α1) +…+ xs f(αs) 改写成 ( α1, ), …, f(α f((α1, …, αs)X) = f(f(α1…, αs)X. s))X272365083@8请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.4 线性映射三. 线性映射的运算 定义1.4.3 (1) 线性运算 设 f, g ∈ Hom(V, U), k ∈ F. 定义 ( f + g)(α) = f(α) + g(α), (kf )(α) = kf(α), ∀α∈V. (2) 复合运算 设 f∈Hom(V, U), g∈Hom(U, W). 定义 (gf )(α) = g[ f(α)], ∀α∈V.注: 对于V上的线性变换 f 及正整数s, 定义 f 0 = I, f 1 = f, f 2 = ff, …, f s = ff s−1. 定理1.4.1(1) 设 f, g ∈ Hom(V, U), k ∈ F, 则 f + g, kf ∈ Hom(V, U). (2) 设 f∈Hom(V, U), g∈Hom(U, W), 则 gf∈ Hom(V, W). 证明: (2) (gf )(kα+lβ) = g[ f(kα+lβ)] = g[kf(α) + lf(β)] = kg[ f(α)] + lg[ f(β)] = k(gf )(α) + l(gf )(β).第一章 线性空间与线性变换§1.4 线性映射第一章 线性空间与线性变换§1.5 线性映射的矩阵定理1.4.2 设 f ∈ Hom(V, U). 若 f 可逆, 则 f −1 ∈ Hom(U, V). 证明: ∀ξ, η ∈ U, k, l ∈ F, 令α = f −1(ξ ), β = f −1(η)∈ V, 则 f [ f −1(kξ + lη)] = kξ + lη = kf(α) + lf(β) = f(kα + lβ), 故 f −1(kξ + lη) = kα + lβ = kf −1(ξ ) + lf −1(η).§1.5 线性映射的矩阵 一. 线性映射在给定的基偶下的矩阵 设α1, …, αn为V的一组基, β1, …, βs为U的一组基, f ∈ Hom(V, U), 则存在A = (aij)s×n使得 ( f(α1), …, f(αn)) = (β1, …, βs)a11 … a1n as1 … asn,简记为 f(α1, …, αn) = (β1, …, βs)A. 称为 f 在基偶{α1, …, αn}与{β1, …, βs}下 的矩阵表示. A —— f 在基偶…下的矩阵.……第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵特别地, 设α1, …, αn为V的一组基, f ∈ Hom(V, V), 则存在A = (aij)n×n使得 ( f(α1), …, f(αn)) = (α1, …, αn)a11 … a1n an1 … ann注① 零映射在任意基偶下的矩阵都是O; 恒等变换在任一组基下的矩阵都是I. 注② 设α1, …, αn为V的一组基, ,…简记为 f(α1, …, αn) = (α1, …, αn)A. 称为 f 在基{α1, …, αn}下的矩阵表示. A —— f 在基{α1, …, αn}下的矩阵.…β1, …, βs为U的一组基, f(α1, …, αn) = (β1, …, βs)A. 若ξ = x1α1 + … + xnαn = (α1, …, αn)X, 则 f(ξ) = f(x1α1 + … + xnαn) = x1 f(α1) + … + xn f(αn) = ( f(α1), …, f(αn))X = f(α1, …, αn)X = (β1, …, βs)AX.272365083@9请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵例2. 在 [x]n中, D[p(x)] = p′(x), D(1, x, x2, …, xn−2, xn−1)0 0 0 . 0 … 0 1 0 … 0 0 0 2 … 0 … 2, …, xn−2, xn−1) 0 0 0 = (1, x, x n−2 0 0 0 … 0 0 0 0 … 0 … … …例3. D: [x]n → D(1, x, x2,[x]n−1, D[p(x)] = p′(x), …, xn−2, xn−1)0 0 0 . …0 1 0 … 0 0 0 2 … 0 = (1, x, x2, …, xn−2) 0 0 0 … … … ……n−1…0 0 0 … 0 n−1n−2例4. 设A ∈F s×n, f: F n → F s, f(X) = AX. f(e1, …, en) = (Ae1, …, Aen) = AIn = A = IsA = (ε1, …, εs)A.第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵二. 线性映射在两对基偶下的矩阵间的联系 定理1.5.1 设 f ∈ Hom(V, U), 其中 V的一组基α1, …, αn到另一组基 β1, …, βn的过渡矩阵为P; U的一组基ξ1, …, ξs到另一组基 η1, …, ηs的过渡矩阵为Q. 若 f(α1, …, αn) = (ξ1, …, ξs)A, f(β1, …, βn) = (η1, …, ηs)B, 则B = Q−1AP.证明: (β1, …, βn) = (α1, …, αn)P (η1, …, ηs) = (ξ1, …, ξs)Q f(α1, …, αn) = (ξ1, …, ξs)A f(β1, …, βn) = (η1, …, ηs)B⇒(ξ1, …, ξs)AP = f(α1, …, αn)P = f((α1, …, αn)P) = f(β1, …, βn) = (η1, …, ηs)B = (ξ1, …, ξs)QB ⇒ AP = QB ⇒ B = Q−1AP.第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵定理1.5.2 设 f ∈ Hom(V, V), 其中 V的一组基α1, …, αn到另一组基 β1, …, βn的过渡矩阵为P. 若 f(α1, …, αn) = (α1, …, αn)A, f(β1, …, βn) = (β1, …, βn)B, 则B = P−1AP.三. 线性变换运算的矩阵 设V的一组基为α1, …, αn , 线性变换 f: V→V在这组基下的矩阵记为 [ f ]. 定理1.5.3 设 f, g ∈ Hom(V, V), k ∈ F, 则 (1) [ f + g] = [ f ] + [g]. (2) [kf ] = k[ f ]. (3) [ fg] = [ f ][g]. (4) f 可逆⇒[ f −1] = [ f ]−1.272365083@10请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵证明: (1)( f + g)(α1, …, αn) = (( f + g)(α1), …, ( f + g)(αn)) = ( f(α1)+g(α1), …, f(αn)+g(αn)) = ( f(α1), …, f(αn)) + (g(α1), …, g(αn)) = f(α1, …, αn) + g(α1, …, αn) = (α1, …, αn)[ f ] + (α1, …, αn)[g] = (α1, …, αn){[ f ]+[g]}.证明: (2)(kf )(α1, …, αn) = ((kf )(α1), …, (kf )(αn)) = (kf(α1), …, kf(αn)) = k( f(α1), …, f(αn)) = kf(α1, …, αn) = k{(α1, …, αn)[ f ]} = (α1, …, αn){k[ f ]}.第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵证明: (3)( fg)(α1, …, αn) = (( fg)(α1), …, ( fg)(αn)) = ( f(g(α1)), …, f(g(αn))) = f(g(α1), …, g(αn)) = f(g(α1, …, αn)) = f((α1, …, αn)[g]) = f(α1, …, αn)[g] = ((α1, …, αn)[ f ])[g] = (α1, …, αn)([ f ][g]).证明: (4) 设[ f −1] = B, 即 f −1(α1, …, αn) = (α1, …, αn)B, 则(α1, …, αn) = ( ff −1)(α1, …, αn) = f( f −1(α1, …, αn)) = f((α1, …, αn)B) = f(α1, …, αn)B = ((α1, …, αn)[ f ])B = (α1, …, αn)([ f ]B), 由此可得[ f ]B = I, 因而[ f −1] = B = [ f ]−1.第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵例5. 设dimV = n, f ∈ Hom(V, V), f 2 = I. 证明: [ f ]相似于 Ir O (0 ≤ r ≤ n). O −In−r证明: 令V1 = {α∈V | f(α) = α}, V2 = {α∈V | f(α) = −α}, 则V1, V2 ≤ V 且V1∩V2 = {0}. 1 1 ∀α∈V, 令β = −(α +f(α)), γ = −(α −f(α)), 2 2 则由f 2 = I 可得 f(β) = β, f(γ) = γ, 故β ∈V1, γ ∈V2, α = β + γ ∈V1 + V2. 可见V1 + V2 ⊆ V ⊆ V1 + V2.因而V = V1 + V2 = V1⊕V2 . 设V1的一组基为α1, …, αr , V2的一组基为βr+1, …, βn , f 在V的基α1, …, αr , βr+1, …, βn下的矩阵为 Ir O . O −In−r 由定理1.5.2可知, [ f ]相似于 Ir O . O −In−r272365083@11请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.5 线性映射的矩阵四. 不变子空间 定义1.5.1 设 f ∈ Hom(V, V), W ≤ V. 若∀α∈W, 有 f(α)∈W, 则称W为V的关于 f 的不变子空间, 简称为 f 的不变子空间. 此时, 定义 f |W: W → W; α → f(α), 则 f |W ∈ Hom(W, W), 称为f 在W上 的限制.例如: ① 例5中, f ∈ Hom(V, V), f 2 = I, 则 V1 = {α∈V | f(α) = α}, V2 = {α∈V | f(α) = −α} 都是 f 的不变子空间. ② ∀ f ∈ Hom(V, V), {0}和V都是 f 的不变子空间.第一章 线性空间与线性变换§1.5 线性映射的矩阵第一章 线性空间与线性变换§1.6 线性映射的值域与核注: 设dimV = n, f ∈ Hom(V, V), V = U⊕W, 其中U, W都是 f 的不变子空间, U的一组基为α1, …, αr , W的一组基为βr+1, …, βn , 则 f |U(βi) = 0, i = r+1, …, n, f |W(αi) = 0, i = 1, …, r. 设 f |U在U的基α1, …, αr下的矩阵为A, f |W在W的基βr+1, …, βn下的矩阵为B, 则 f 在V的基α1, …, αr , βr+1, …, βn下的矩 A O 阵为 O B .§1.6 线性映射的值域与核 一. 定义 设 f ∈ Hom(V, U), 则称 f(V) = { f(α) |α∈V}为 f 的值域, 记为R( f ); 称K( f ) = {α∈V | f(α) = 0}为 f 的核. VK( f )U f → f(V) 0U第一章 线性空间与线性变换§1.6 线性映射的值域与核第一章 线性空间与线性变换§1.6 线性映射的值域与核二. 性质 定理1.6.1 设 f ∈ Hom(V, U), 则 (1) R( f ) ≤ U. (2) K( f ) ≤ V. (3) 当U = V时, R( f )和K( f )都是 f 的不变子空间. VK( f )U f → f(V) 0U例1. 设A ∈ Fs×n, f: Fn→ Fs定义为 f(X) = AX. 则R( f ) = {AX | X ∈ Fn} ≤ Fs, 这是A的列空间, 也称为A的值域, 记为R(A); K( f ) = {X ∈ Fn | AX = 0}, 这是AX = 0的解空间, 也称为A的核, 记为K(A).272365083@12请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.6 线性映射的值域与核第一章 线性空间与线性变换§1.6 线性映射的值域与核定理1.6.2 设 f ∈ Hom(V, U), dimV < ∞, 则 dimR( f ) + dimK( f ) = dimV. VK( f )U f → f(V) 0U ...... ...证明: 设α1, …, αk为K( f )的一组基, α1, …, αk, αk+1, …, αn为V的一组基, 则R( f ) = span{ f(αi) | i = 1, …, n} = span{ f(αi) | i = k+1, …, n}. 若ck+1 f(αk+1) + … + cn f(αn) = 0, 则 f(ck+1αk+1 + … + cnαn) = 0, 即ck+1αk+1 + … + cnαn ∈ K( f ), 故存在c1, …, ck使得 ck+1αk+1 + … + cnαn = c1α1 + … + ckαk , 即c1α1 + … + ckαk − ck+1αk+1 − … − cnαn = 0, 由此可得ck+1 = … = cn = 0. 可见 f(αk+1), …, f(αn) 线性无关, 故dimR( f ) + dimK( f ) = dimV.第一章 线性空间与线性变换§1.6 线性映射的值域与核第一章 线性空间与线性变换§1.6 线性映射的值域与核例2. 设A = 1 1 , f(X) = AX, ∀X∈ 2×2. (1) 分别求R( f )及K( f )的一组基, (2) R( f ) + K( f )是否为直和. 解: 取 2×2的一组基E11, E12, E21, E22. 则R( f ) = span{ f(E11), f(E12), f(E21), f(E22)}, 其中 f(E11) = f(E21) = E11 + E21, f(E12) = f(E22) = E12 + E22, 且E11 + E21, E12 + E22线性无关, 因此, E11 + E21, E12 + E22构成R( f )的一组 基.1 1设X = x1 x2 , 则 3 4 AX ⇔ x1 + x3 = x2 + x4 = 0 ⇔ X = x1(E11 − E21) + x2(E12 − E22). 又因为E11 − E21, E12 − E22线性无关, 可见E11 − E21, E12 − E22构成K( f )的一组基. (E11 + E21, E12 + E22, E11 − E21, E12 − E22)1 0 1 0x x= (E11, E12, E21, E22) 0 1 0 1 ,1 0 −1 0 0 1 0 −1第一章 线性空间与线性变换§1.6 线性映射的值域与核第一章 线性空间与线性变换§1.6 线性映射的值域与核(E11 + E21, E12 + E22, E11 − E21, E12 − E22)1 = (E11, E12, E21, E22) 0 1 0 1 0 1 0 0 其中r 0 1 −1 1 = 4. 1 0 0 0 1 0 −1 0 1 0 1 1 0 −1 0 0 1 , 0 −1故E11 + E21, E12 + E22, E11 − E21, E12 − E22线性 无关, 因而R( f ) + K( f )为直和.事实上, 若B ∈ R( f ) ∩ K( f ), 则存在X∈ 2×2 使得B = AX, 而且AB = O. 于是可得 2AX = A2X = A(AX) = AB = O, 故B = AX = O. 可见R( f ) ∩ K( f ) = {O}, 因此R( f ) + K( f )为直和.272365083@13请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.6 线性映射的值域与核第一章 线性空间与线性变换§1.6 线性映射的值域与核例3. 设A = 0 0 , f(X) = AX, ∀X∈ 2×2. (1) 分别求R( f )及K( f )的一组基, (2) R( f ) + K( f )是否为直和. 解: 取 2×2的一组基E11, E12, E21, E22. 则R( f ) = span{ f(E11), f(E12), f(E21), f(E22)}, 其中 f(E11) = f(E12) = O, f(E21) = E11, f(E22) = E12, 且 E11, E12 线性无关, 因此, E11, E12构成R( f )的一组基.0 1设X = x1 x2 , 则 3 4 AX ⇔ x3 = x4 = 0 ⇔ X = x1E11 + x2E12. 又因为E11, E12 线性无关, 可见E11, E12构成K( f )的一组基. 因为R( f ) = span{E11, E12} = K( f ), 因此R( f ) + K( f )不是直和.x x第一章 线性空间与线性变换§1.7 几何空间线性变换的例子第一章 线性空间与线性变换§1.7 几何空间线性变换的例子§1.7 几何空间线性变换的例子 一. 辐射相似变换 f:3二. 平行于某矢量的投影变换 对于任意的OP ∈P e23,e3→3OP → kOP (k > 0).设OP = x1e1 + x2e2 + x3e3, 令 f(OP) = x1e1 + x2e2, 则 f ∈ Hom(3, 3),e3 P O e1 1 0 0 0 0 0 e2O e1f在3的任意一组基下的矩阵都是kI.OP − f(OP) // e3,→ 0<k<1 压缩→ k>1 放大f 在e1, e2, e3下的矩阵为 0 1 0 , R( f ) = span{e1, e2}, K( f ) = span{e3}.第一章 线性空间与线性变换§1.7 几何空间线性变换的例子第一章 线性空间与线性变换§1.7 几何空间线性变换的例子三. 平行于某一方向的压缩(或延伸) 对于任意的OP ∈3,四. 平行于某一方向的推移 对于任意的OP ∈P e23,e3e3P e2设OP = x1e1 + x2e2 + x3e3,f(OP) = x1e1 + x2e2 + ax3e3, O (a > 0).e13, 3),设OP = x1e1 + x2e2 + x3e3,O e1f(OP) = (x1+ax2)e1 + x2e2 + x3e3, (a ≠ 0). 则 f ∈ Hom(3, 3),则 f ∈ Hom(OP − f(OP) // e3,1 0 0 0 0 a→OP − f(OP) // e1, f 在e1, e2, e3下的矩阵为 0 1 0 .0 0 1 1 a 0f 在e1, e2, e3下的矩阵为 0 1 0 .272365083@14请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.7 几何空间线性变换的例子第一章 线性空间与线性变换§1.7 几何空间线性变换的例子五. 旋转变换 见下一章. 六. 镜像变换 见下一章.平面上的例子:0 • 7 • 5 7 0 • 7 • 5 6• 0 5 x 7 0 y5 0 1 0 −0.2 1 0 5 x 7 0 y • 5 −1第一章 线性空间与线性变换§1.7 几何空间线性变换的例子第一章 线性空间与线性变换§1.7 几何空间线性变换的例子平面上的例子:平面上的例子:β αAβ = 0.5β2 0 A = 0 0.5β αcosφ sinφ B = −sinφ cosφ π/6Aα = 2 α第一章 线性空间与线性变换§1.7 几何空间线性变换的例子第一章 线性空间与线性变换§1.8 线性空间的同构平面上的例子: Cβ = β§1.8 线性空间的同构 一. 定义 设V, U都是数域F上的线性空间. 若∃双射σ∈ Hom(V, U), 则称V与U同构, 记为V ≅ U. 并且称σ为V到U的一个同构映射.βCα = − αα0 C = −1 1 0272365083@15请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.8 线性空间的同构第一章 线性空间与线性变换§1.8 线性空间的同构→二. 性质 定理1.8.1 设σ为线性空间V到U的同构映射, 则中向量α1, …, αk线性无关 ⇔ σ(α1), …, σ(αk)线性无关. 证明: (⇒) 设α1, …, αk线性无关, 则 c1σ(α1) + … + ckσ(αk) = 0 ⇒ σ(c1α1 + … + ckαk) = 0 = σ(0) ⇒ c1α1 + … + ckαk = 0 ⇒ c1 = … = ck = 0. 可见σ(α1), …, σ(αk)线性无关.→→第一章 线性空间与线性变换§1.8 线性空间的同构第一章 线性空间与线性变换§1.8 线性空间的同构二. 性质 定理1.8.1 设σ为线性空间V到U的同构映射, 则中向量α1, …, αk线性无关 ⇔ σ(α1), …, σ(αk)线性无关. 证明: (⇐) 设σ(α1), …, σ(αk)线性无关, 则 c1α1 + … + ckαk = 0 ⇒ c1σ(α1) + … + ckσ(αk) = σ(c1α1 + … + ckαk) = σ(0) = 0 ⇒ c1 = … = ck = 0. 可见α1, …, αk线性无关.三. 判定 定理1.8.2 设V与U是数域F上的有限维线性空 间, 则V ≅ U ⇔ dimV = dimU. 证明: (⇒) 设σ为V到U的一个同构映射, 则R(σ) = U, K(σ) = {0}. 故dimV = dimR(σ) + dimK(σ) = dimU.第一章 线性空间与线性变换§1.8 线性空间的同构第一章 线性空间与线性变换§1.8 线性空间的同构(⇐) 设dimV = dimU = n, α1, …, αn为V的一组基, ξ1, …, ξn为U的一组基. 对于任意的α = a1α1 + … + anαn ∈ V, 令σ(α) = a1ξ1 + … + anξn, 则 (1) σ : V → U为单射. 事实上, … (2) σ : V → U为单射. 事实上, … (3) σ ∈ Hom(V, U). 事实上, … 故V ≅ U.(1) σ : V → U为单射. 事实上, 若α = a1α1 +…+ anαn, β = b1α1 +…+ bnαn, 且σ(α) = σ(β), 则 a1ξ1 + … + anξn = b1ξ1 + … + bnξn, 故(a1−b1)ξ1 + … + (an−bn)ξn = 0, 由此可得 a1−b1 = … = an−bn = 0, 即(a1, …, an) = (b1, …, bn), 因而α = a1α1 +…+ anαn = b1α1 +…+ bnαn = β.272365083@16请双面打印/复印(节约纸张)第一章 线性空间与线性变换§1.8 线性空间的同构第一章 线性空间与线性变换§1.8 线性空间的同构(2) σ : V → U为满射. 事实上, ∀ξ∈U, 设ξ = a1ξ1 + … + anξn, 于是令α = a1α1 +…+ anαn, 则α ∈ V 且σ(α) = a1ξ1 + … + anξn = ξ.(3) σ ∈ Hom(V, U). 事实上, ∀α = a1α1 +…+ anαn, β = b1α1 +…+ bnαn, k, l ∈ F, 有 σ(kα + lβ) = σ((ka1+ lb1)α1 +…+ (kan+ lbn)αn) = (ka1+ lb1)ξ1 + … + (kan+ lbn)ξn = k(a1ξ1 +…+ anξn) + l(b1ξ1 +…+ bnξn) = kσ(α) + lσ(β).第一章 线性空间与线性变换§1.8 线性空间的同构第一章 线性空间与线性变换§1.8 线性空间的同构四. 例子 1. [x]n = {a0+…+an−1xn−1 | a0, …, an−1x∈ }. dim [x]n = n = dim 事实上, 容易验证n,2. dimM2×3( ) = 6, 故M2×3( ) ≅ 事实上, 容易验证6.故 [x]n ≅n;n.σ : M2×3( ) →a11 a12 a13 a21 a22 a236;σ : [x]n →a0+…+an−1xn−1 → 为同构映射.a0 an−1 …a11 a12 a → a13 21 a22 a23为同构映射.第一章 线性空间与线性变换§1.8 线性空间的同构3.= {x∈ | x > 0}. a⊕b = ab, ∀a, b∈ +; k⊗a = ak, ∀a∈ +, ∀k∈ . dim + = 1, 故 + ≅ . 事实上, 容易验证 → ; x → logax++为同构映射.272365083@17。
第1章 线性空间与线性变换讲义

a + b = ( x 1 + y1 , x 2 + y 2 , , x n + y n ) T
定义数乘:
ka = ( kx1 , kx 2 , , kx n ) T ,
R n 是数域 R 上的线性空间。 C n 是数域 C 上的线性空间。
4
例2 实数域 R上的全体 m×n 矩阵,对矩阵的加法 和数乘运算构成 R上的线性空间,记作 Rm×n
定义:设 V 是一个非空集合,F 为数域,a, b, g V, 对于任意的a, b V, 总有唯一的元素 g V
与之对应,称 g 为a 与b 的和,记作 g =a +b,且
(1) a + b = b + a ;
( 2 ) (a + b ) + g = a + ( b + g );
( 3) 存在零元素: b V , a V , a + b = a, 称 b 为零元素, 并记 b 为 0 ; ( 4) 存在负元素 a V , b V, a + b = 0; 称 b 为 a 的负元素, 并记 b 为 - a ;
(1) a , b W , 则a + b W (2) a W , k F , 则 ka W
则称W 是V 的子空间。
21
例1. 实数域上 n 维向量的集合
W = { ( 0, x 2 , , x n ) T | x 2 , , x n R }
则 W是 R n 的 子 空 间 。
则 P 称为由基 a 1 , a 2 , , a n 到基 b 1 , b 2 , , b n 的 转移矩阵(或过渡矩阵),其中
p11 p21 P= p n1 p12 p22 pn 2 p1n p2 n pnn
线性空间与线性变换

线性空间与线性变换线性空间和线性变换是线性代数中的重要概念,在数学和物理等领域有着广泛的应用。
本文将介绍线性空间和线性变换的概念、性质以及它们之间的关系。
一、线性空间的定义和性质线性空间是指具有加法运算和数乘运算的集合,满足以下条件:1. 加法运算闭合性:对于任意两个向量u和v,它们的和u+v仍然属于该集合。
2. 加法交换律:对于任意两个向量u和v,有u+v = v+u。
3. 加法结合律:对于任意三个向量u、v和w,有(u+v)+w =u+(v+w)。
4. 存在零向量:存在一个特殊的向量0,使得对于任意向量v,有v+0 = v。
5. 对于任意向量v,存在其负向量-u,使得v+(-u) = 0。
6. 数乘运算闭合性:对于任意标量c和向量v,它们的乘积cv仍然属于该集合。
7. 数乘结合律:对于任意标量c和d以及向量v,有(c+d)v = cv+dv。
8. 数乘分配律1:对于任意标量c以及向量u和v,有c(u+v) =cu+cv。
9. 数乘分配律2:对于任意标量c和d以及向量v,有(cd)v = c(dv)。
线性空间的例子包括n维向量空间和函数空间等。
它们满足上述定义中的所有条件。
二、线性变换的定义和性质线性变换是指将一个线性空间映射到另一个线性空间的映射,满足以下条件:1. 对于任意向量v和w以及标量c,线性变换T满足T(v+w) =T(v)+T(w)和T(cv) = cT(v)。
2. 线性变换T保持向量的线性组合关系,即对于任意向量v1、v2、...、vn和标量c1、c2、...、cn,有T(c1v1+c2v2+...+cnvn) =c1T(v1)+c2T(v2)+...+cnT(vn)。
3. 线性变换T将零向量映射为目标线性空间的零向量。
线性变换的例子包括平移、旋转和缩放等。
它们保持向量空间的线性结构和线性关系。
三、线性空间与线性变换的关系线性空间和线性变换之间存在着密切的联系。
给定一个线性空间V,定义一个线性变换T:V→W,其中W是另一个线性空间。
1-1 线性空间

2. 线性空间的基与坐标
(a) 基与坐标 给定数域K上的线性空间 上的线性空间V, 中的r个 给定数域 上的线性空间 ,x1,x2,…,xr是V中的 个 中的 向量。如果满足: 线性无关; 向量。如果满足:1. x1,x2,…,xr线性无关;2. V中 中 任意一个向量都可以由 一个向量都可以由x 线性表出, 任意一个向量都可以由 1,x2,…,xr线性表出,则称 x1,x2,…,xr是V的一组基(base),并称 i为基向量。 的一组基 的一组 ,并称x 基向量。 线性空间的维数就是基中所含基向量个数。 线性空间的维数就是基中所含基向量个数。 维线性空间V的一组基 坐标系。 称n维线性空间 的一组基 1,x2,…,xn为坐标系。 维线性空间 的一组基x 对任意x∈ , 对任意 ∈V,在该组基下的线性表示为 x = ξ1 x1 + ξ 2 x2 + L + ξ n xn , 在该坐标系下的坐标 则称ξ1,ξ2,…,ξn是x在该坐标系下的坐标 在该坐标系下的 (coordinate)或分量,记为 ξ1,ξ2,…,ξn)T。 或分量,记为(
第一章
线性空间与线性变换
1.1 线性空间 1.2 线性变换及其矩阵表示 1.3 常见特殊矩阵
1.1 线性空间
1. 线性空间及其性质 2. 线性空间的基与坐标 3. 线性子空间
1. 线性空间及其性质
(a) 集合 集合(set):是指一些对象的总体。 :是指一些对象的总体。 集合 元素(element):这些对象称为集合的元素。 这些对象称为集合的元素。 元素 这些对象称为集合的元素 整数集; 整数集; 线性方程组的解集; 线性方程组的解集; 由某个平面上所有的点构成的点集。 由某个平面上所有的点构成的点集。 表示集合, 是 的元素 用S表示集合,a是S的元素 a ∈ S 表示集合 a不是 的元素 a ∉ S 不是S的元素 不是
《矩阵分析》(第3版)史荣昌,魏丰.第一章课后习题答案

第1章 线性空间和线性变换(详解)1-1 证:用iiE 表示n 阶矩阵中除第i 行,第i 列的元素为1外,其余元素全为0的矩阵.用ij E (,1,2,,1)i j i n <=-表示n 阶矩阵中除第i 行,第j 列元素与第j 行第i 列元素为1外,其余元素全为0的矩阵.显然,iiE ,ijE 都是对称矩阵,iiE 有(1)2n n -个.不难证明iiE ,ijE 是线性无关的,且任何一个对称矩阵都可用这n+(1)2n n -=(1)2n n +个矩阵线性表示,此即对称矩阵组成(1)2n n +维线性空间.同样可证所有n 阶反对称矩阵组成的线性空间的维数为(1)2n n -.评注:欲证一个集合在加法与数乘两种运算下是一个(1)2n n +维线性空间,只需找出(1)2n n +个向量线性无关,并且集合中任何一个向量都可以用这(1)2n n +个向量线性表示即可.1-2解: 11223344x x x x ααααα=+++令解出1234,,,x x x x 即可.1-3 解:方法一 设11223344x x x x =+++A EE E E即123412111111100311100000x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦故12341231211203x x x x x x x x x x +++++⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦于是12341231,2x x x x x x x +++=++=1210,3x x x +==解之得12343,3,2,1x x x x ==-==-即A 在1234,,,E E E E 下的坐标为(3,3,2,1)T--.方法二 应用同构的概念,22R ⨯是一个四维空间,并且可将矩阵A 看做(1,2,0,3)T,1234,,,E E E E 可看做(1,1,1,1),(1,1,1,0),(1,1,0,0),(1,0,0,0)T T T T .于是有1111110003111020100311000001021000300011⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦因此A 在1234,,,E E E E 下的坐标为(3,3,2,1)T--.1-4 解:证:设112233440k k k k αααα+++=即1234123412313412411111110110110110k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦+++++⎡⎤==⎢⎥++++⎣⎦于是12341230,0k k k k k k k +++=++= 1341240,0k k k k k k ++=++=解之得12340k k k k ====故1234,,,αααα线性无关. 设123412341231341241111111011011011a b x x x x c d x x x x x x x x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦+++++⎡⎤=⎢⎥++++⎣⎦于是12341230,0x x x x x x x +++=++= 1341240,0x x x x x x ++=++=解之得122,x b c d a x a c =++-=-34,x a d x a b =-=-1234,,,x x x x 即为所求坐标.1-5 解:方法一 (用线性空间理论计算)32312233410()121,,,021,1,(1),(1)p x x x x x y y x x x y y ⎡⎤⎢⎥⎢⎥⎡⎤=+=⎣⎦⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎡⎤=---⎣⎦⎢⎥⎢⎥⎣⎦又由于23231,1,(1),(1)111101231,,,00130001x x x x x x ⎡⎤---⎣⎦⎡⎤⎢⎥-⎢⎥⎡⎤=⎣⎦⎢⎥-⎢⎥⎣⎦于是()p x 在基231,1,(1),(1)x x x ---下的坐标为11234111113012306001306000122y y y y -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦方法二 将3()12p x x =+根据幂级数公式按1x -展开可得32323()12(1)(1)(1)(1)(1)(1)(1)2!3!36(1)6(1)2(1)p x x p p p p x x x x x x =+''''''=+-+-+-=+-+-+- 因此()p x 在基231,1,(1),(1)x x x ---下的坐标为[]3,6,6,2T.评注:按照向量坐标定义计算,第二种方法比第一种方法更简单一些.1-6 解:①设[][]12341234,,,,,,=ββββααααP将1234,,,αααα与1234,,,ββββ代入上式得20561001133611001121011010130011⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦P 故过渡矩阵1100120561100133601101121001110131122223514221915223112822-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤---⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦P②设1212343410(,,,)10y y y y ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ξββββ将1234,,,ββββ坐标代入上式后整理得11234792056181336027112111310130227y y y y -⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦评注:只需将,i i αβ代入过渡矩阵的定义[][]12341234,,,,,,=ββββααααP 计算出P .1-7 解:因为12121212{,}{,}{,,,}span span span +=ααββααββ由于秩1212{,,,}3span =ααββ,且121,,ααβ是向量1212,,,ααββ的一个极大线性无关组,所以和空间的维数是3,基为121,,ααβ. 方法一 设1212{,}{,}span span ∈ξααββ,于是由交空间定义可知123411212111011030117k k k k -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥+++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦解之得1222122,4,3(k l k l l l l =-==-为任意数)于是11222[5,2,3,4]T k k l =+=-ξαα(很显然1122l l ββ=+ξ)所以交空间的维数为1,基为[5,2,3,4]T-.方法二 不难知12121212{,}{,},{,}{,}span span span span ''==ααααββββ其中2213[2,2,0,1],[,2,1,0]3TT ''=--=-αβ.又12{,}span 'αα也是线性方程组 13423422x x x x x x =-⎧⎨=-⎩ 的解空间.12{,}span 'ββ是线性方程组13423413232x x x x x x ⎧=-+⎪⎨⎪=-⎩ 的解空间,所以所求的交空间就是线性方程组1342341342342213232x x x x x x x x x x x x =-⎧⎪=-⎪⎪⎨=-+⎪⎪=-⎪⎩ 的解空间,容易求出其基础解系为[5,2,3,4]T-,所以交空间的维数为1,基为[5,2,3,4]T -.评注:本题有几个知识点是很重要的.12(1){,,,}n span ααα的基底就是12,,,nααα的极大线性无关组.维数等于秩12{,,,}n ααα.1212(2){,}{,}span span +ααββ1212{,,,}span =ααββ.(3)方法一的思路,求交1212{,}{,}span span ααββ就是求向量ξ,既可由12,αα线性表示,又可由12,ββ线性表示的那部分向量.(4)方法二是借用“两个齐次线性方程组解空间的交空间就是联立方程组的解空间”,将本题已知条件改造为齐次线性方程组来求解.1-8解:(1):解出方程组1234123420510640x x x x x x x x ---=⎧⎨---=⎩(Ⅰ)的基础解系,即是1V 的基, 解出方程组123420x x x x -++=(Ⅱ)的基础解系,即是2V 的基;(2): 解出方程组1234123412342051064020x x x x x x x x x x x x ---=⎧⎪---=⎨⎪-++=⎩的基础解系,即为12V V ⋂的基;(3):设{}{}1121,,,,,k l V span V span ααββ==,则11,,,,,k l ααββ的极大无关组即是12V V +的基. 1-9解:仿上题解.1-10解: 仿上题解.1-11 证:设210121()()()0k k l l l l --++++=ξξξξA AA①用1k -A从左侧成①式两端,由()0k=ξA 可得10()0k l -=ξA因为1()0k -≠ξA,所以00l =,代入①可得21121()()()0k k l l l --+++=ξξξA AA②用2k -A从左侧乘②式两端,由()0k=ξA可得00l =,继续下去,可得210k l l -===,于是21,(),(),,()k -ξξξξA AA线性无关.1-12 解:由1-11可知,n 个向量210,(),(),,()n -≠ξξξξAAA线性无关,它是V 的一个基.又由21212121[,(),(),,()][(),(),,()][(),(),,(),0]000010000100[,(),(),,()]0000010n n n n n n----⨯==⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ξξξξξξξξξξξξξξA A A AA A A A AAA AA 所以A 在21,(),(),,()n -ξξξξA AA下矩阵表示为n 阶矩阵000100001000000010⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦评注:n 维线性空间V 中任何一组n 个线性无关的向量组都可以构成V 的一个基,因此21,(),(),,()n -ξξξξA AA是V 的一个基.1-13证: 设()()()111,,,,,,,,,,,r s m r s A A ξξξββααα==设11,,,,,,r r s ξξξξξ是的极大无关组,则可以证明11,,,,,,r r s ααααα是的极大无关组.1-14 解:(1)由题意知123123[,,][,,]=ααααααA A123123111[,,][,,]011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦βββααα设A在基123,,βββ下的矩阵表示是B ,则11111123111011103011001215001244346238--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=---⎢⎥⎢⎥⎣⎦B P AP (2)由于0A ≠,故0=AX 只有零解,所以A的核是零空间.由维数定理可知A 的值域是线性空间3R .1-15解:已知()()2323,,,,A αααααα=11A(1) 求得式()()2323,,,,P εεεααα=11中的过渡矩阵P ,则1B P AP -=即为所求;(2)仿教材例1.5.1.(见<矩阵分析>史荣昌编著.北京理工大学出版社.) 1-16解:设()23,,A ααα=1,则{}23(),,;()R A span N A ααα=1就是齐次方程组0Ax = 的解空间. 1-17证:由矩阵的乘法定义知AB BA 与的主对角线上元素相等,故知AB BA 与的迹相等;再由1-18 题可证. 1-18证:对k 用数学归纳法证。
《矩阵分析》(第3版)史荣昌,魏丰.第一章课后知识题目解析

第1章 线性空间和线性变换(详解)1-1 证:用ii E 表示n 阶矩阵中除第i 行,第i 列的元素为1外,其余元素全为0的矩阵.用ij E (,1,2,,1)i j i n <=-表示n 阶矩阵中除第i 行,第j 列元素与第j 行第i 列元素为1外,其余元素全为0的矩阵.显然,ii E ,ij E 都是对称矩阵,ii E 有(1)2n n -个.不难证明ii E ,ij E 是线性无关的,且任何一个对称矩阵都可用这n+(1)2n n -=(1)2n n +个矩阵线性表示,此即对称矩阵组成(1)2n n +维线性空间. 同样可证所有n 阶反对称矩阵组成的线性空间的维数为(1)2n n -.评注:欲证一个集合在加法与数乘两种运算下是一个(1)2n n +维线性空间,只需找出(1)2n n +个向量线性无关,并且集合中任何一个向量都可以用这(1)2n n +个向量线性表示即可.1-2解: 11223344x x x x ααααα=+++令 解出1234,,,x x x x 即可.1-3 解:方法一 设11223344x x x x =+++A E E E E即123412111111100311100000x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦故 12341231211203x x x x x x x x x x +++++⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦于是12341231,2x x x x x x x +++=++=1210,3x x x +==解之得12343,3,2,1x x x x ==-==-即A 在1234,,,E E E E 下的坐标为(3,3,2,1)T--.方法二 应用同构的概念,22R ⨯是一个四维空间,并且可将矩阵A 看做(1,2,0,3)T,1234,,,E E E E 可看做(1,1,1,1),(1,1,1,0),(1,1,0,0),(1,0,0,0)T T T T .于是有1111110003111020100311000001021000300011⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦因此A 在1234,,,E E E E 下的坐标为(3,3,2,1)T--.1-4 解:证:设112233440k k k k αααα+++=即1234123412313412411111110110110110k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦+++++⎡⎤==⎢⎥++++⎣⎦于是12341230,0k k k k k k k +++=++= 1341240,0k k k k k k ++=++=解之得12340k k k k ====故1234,,,αααα线性无关. 设123412341231341241111111011011011a b x x x x c d x x x x x x x x x x x x x ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦+++++⎡⎤=⎢⎥++++⎣⎦于是12341230,0x x x x x x x +++=++= 1341240,0x x x x x x ++=++=解之得122,x b c d a x a c =++-=-34,x a d x a b =-=-1234,,,x x x x 即为所求坐标.1-5 解:方法一 (用线性空间理论计算)32312233410()121,,,021,1,(1),(1)p x x x x x y y x x x y y ⎡⎤⎢⎥⎢⎥⎡⎤=+=⎣⎦⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎡⎤=---⎣⎦⎢⎥⎢⎥⎣⎦又由于23231,1,(1),(1)111101231,,,00130001x x x x x x ⎡⎤---⎣⎦⎡⎤⎢⎥-⎢⎥⎡⎤=⎣⎦⎢⎥-⎢⎥⎣⎦于是()p x 在基231,1,(1),(1)x x x ---下的坐标为11234111113012306001306000122y y y y -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦方法二 将3()12p x x =+根据幂级数公式按1x -展开可得32323()12(1)(1)(1)(1)(1)(1)(1)2!3!36(1)6(1)2(1)p x x p p p p x x x x x x =+''''''=+-+-+-=+-+-+- 因此()p x 在基231,1,(1),(1)x x x ---下的坐标为[]3,6,6,2T.评注:按照向量坐标定义计算,第二种方法比第一种方法更简单一些.1-6 解:①设[][]12341234,,,,,,=ββββααααP将1234,,,αααα与1234,,,ββββ代入上式得20561001133611001121011010130011⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦P 故过渡矩阵1100120561100133601101121001110131122223514221915223112822-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤---⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦P②设1212343410(,,,)10y y y y ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ξββββ将1234,,,ββββ坐标代入上式后整理得11234792056181336027112111310130227y y y y -⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦评注:只需将,i i αβ代入过渡矩阵的定义[][]12341234,,,,,,=ββββααααP 计算出P .1-7 解:因为12121212{,}{,}{,,,}span span span +=ααββααββ由于秩1212{,,,}3span =ααββ,且121,,ααβ是向量1212,,,ααββ的一个极大线性无关组,所以和空间的维数是3,基为121,,ααβ. 方法一 设1212{,}{,}span span ∈ξααββ,于是由交空间定义可知123411212111011030117k k k k -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥+++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦解之得1222122,4,3(k l k l l l l =-==-为任意数)于是11222[5,2,3,4]T k k l =+=-ξαα(很显然1122l l ββ=+ξ)所以交空间的维数为1,基为[5,2,3,4]T-.方法二 不难知12121212{,}{,},{,}{,}span span span span ''==ααααββββ其中2213[2,2,0,1],[,2,1,0]3TT ''=--=-αβ.又12{,}span 'αα也是线性方程组 13423422x x x x x x =-⎧⎨=-⎩ 的解空间.12{,}span 'ββ是线性方程组13423413232x x x x x x ⎧=-+⎪⎨⎪=-⎩ 的解空间,所以所求的交空间就是线性方程组1342341342342213232x x x x x x x x x x x x =-⎧⎪=-⎪⎪⎨=-+⎪⎪=-⎪⎩ 的解空间,容易求出其基础解系为[5,2,3,4]T-,所以交空间的维数为1,基为[5,2,3,4]T -.评注:本题有几个知识点是很重要的.12(1){,,,}n span ααα的基底就是12,,,nααα的极大线性无关组.维数等于秩12{,,,}n ααα.1212(2){,}{,}span span +ααββ1212{,,,}span =ααββ.(3)方法一的思路,求交1212{,}{,}span span ααββ就是求向量ξ,既可由12,αα线性表示,又可由12,ββ线性表示的那部分向量.(4)方法二是借用“两个齐次线性方程组解空间的交空间就是联立方程组的解空间”,将本题已知条件改造为齐次线性方程组来求解.1-8解:(1):解出方程组1234123420510640x x x x x x x x ---=⎧⎨---=⎩(Ⅰ)的基础解系,即是1V 的基,解出方程组123420x x x x -++=(Ⅱ)的基础解系,即是2V 的基; (2): 解出方程组1234123412342051064020x x x x x x x x x x x x ---=⎧⎪---=⎨⎪-++=⎩的基础解系,即为12V V ⋂的基;(3):设{}{}1121,,,,,k l V span V span ααββ==,则11,,,,,k l ααββ的极大无关组即是12V V +的基. 1-9解:仿上题解.1-10解: 仿上题解.1-11 证:设210121()()()0k k l l l l --++++=ξξξξA AA①用1k -A从左侧成①式两端,由()0k=ξA 可得10()0k l -=ξA因为1()0k -≠ξA,所以00l =,代入①可得21121()()()0k k l l l --+++=ξξξA AA②用2k -A从左侧乘②式两端,由()0k=ξA可得00l =,继续下去,可得210k l l -===,于是21,(),(),,()k -ξξξξA AA线性无关.1-12 解:由1-11可知,n 个向量210,(),(),,()n -≠ξξξξAAA线性无关,它是V 的一个基.又由21212121[,(),(),,()][(),(),,()][(),(),,(),0]000010000100[,(),(),,()]0000010n n n n n n----⨯==⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ξξξξξξξξξξξξξξA A A AA A A A AAA AA 所以A在21,(),(),,()n -ξξξξA AA 下矩阵表示为n 阶矩阵0000100001000000010⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦评注:n 维线性空间V 中任何一组n 个线性无关的向量组都可以构成V 的一个基,因此21,(),(),,()n -ξξξξA AA是V 的一个基.1-13证: 设()()()111,,,,,,,,,,,r s m r s A A ξξξββααα==设11,,,,,,r r s ξξξξξ是的极大无关组,则可以证明11,,,,,,r r s ααααα是的极大无关组.1-14 解:(1)由题意知123123[,,][,,]=ααααααA A123123111[,,][,,]011001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦βββααα设A在基123,,βββ下的矩阵表示是B ,则11111123111011103011001215001244346238--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=---⎢⎥⎢⎥⎣⎦B P AP (2)由于0A ≠,故0=AX 只有零解,所以A的核是零空间.由维数定理可知A的值域是线性空间3R .1-15解:已知()()2323,,,,A αααααα=11A(1) 求得式()()2323,,,,P εεεααα=11中的过渡矩阵P ,则1B P AP -=即为所求; (2)仿教材例1.5.1.(见<矩阵分析>史荣昌编著.北京理工大学出版社.) 1-16解:设()23,,A ααα=1,则{}23(),,;()R A span N A ααα=1就是齐次方程组0Ax = 的解空间. 1-17证:由矩阵的乘法定义知AB BA 与的主对角线上元素相等,故知AB BA 与的迹相等;再由1-18 题可证.1-18证:对k 用数学归纳法证。
线性空间与线性变换

线性空间与线性变换线性空间(也称为向量空间)是线性代数的基本概念之一。
它是指由向量集合组成的集合,满足特定的运算规则。
线性空间中的向量可以是实数域上的实向量,也可以是复数域上的复向量。
线性空间的定义涵盖了许多重要的数学概念和定理,在各个领域中都有广泛的应用。
一、线性空间的定义线性空间的定义遵循以下几个基本条件:1. 封闭性:对于线性空间V中任意向量u和v,它们的线性组合也属于V。
即对于任意的标量a和b,有a*u + b*v∈V。
2. 加法结合性:对于线性空间V中任意向量u、v和w,有(u+v)+w = u+(v+w)。
3. 加法交换性:对于线性空间V中任意向量u和v,有u+v = v+u。
4. 零向量存在性:存在一个特殊的向量0,满足对于线性空间V中任意向量u,有u+0 = u。
5. 加法逆元存在性:对于线性空间V中任意向量u,存在一个向量-v,使得u+(-v) = 0。
6. 数量乘法结合性:对于线性空间V中任意的标量a、b和向量u,有(a*b)*u = a*(b*u)。
7. 标量乘法分配律:对于线性空间V中任意的标量a和向量u、v,有a*(u+v) = a*u + a*v。
8. 向量乘法分配律:对于线性空间V中任意的标量a和b,以及向量u,有(a+b)*u = a*u + b*u。
二、线性变换的定义与性质线性变换是一种将一个线性空间映射到另一个线性空间的函数。
线性变换也被称为线性映射或线性算子。
线性变换保持线性空间的线性结构,即对于线性空间V中任意的向量u和v,以及标量a和b,有以下性质:1. 线性变换将零向量映射到零向量,即T(0) = 0,其中T表示线性变换。
2. 线性变换保持向量的线性组合,即对于线性空间V中任意的向量u和v,以及标量a和b,有T(a*u + b*v) = a*T(u) + b*T(v)。
3. 线性变换的像空间是一个线性空间,即对于线性空间V中的线性变换T,其像空间W也是一个线性空间。
线性空间与线性变换解析

线性空间与线性变换解析线性空间和线性变换是线性代数中重要的概念。
线性空间是指具备了特定性质的向量集合,而线性变换是将一个向量空间映射到另一个向量空间的映射关系。
通过分析线性空间与线性变换的特点和性质,可以深入理解线性代数的基本概念与应用。
一、线性空间的定义与性质1.1 线性空间的定义线性空间,也称为向量空间,是指一个非空集合V及其上的两种运算:加法和标量乘法,满足以下八个条件:(1)加法交换律:对于任意的u和v,u+v=v+u;(2)加法结合律:对于任意的u、v和w,(u+v)+w = u+(v+w);(3)零向量存在:存在一个向量0,使得对于任意的u,u+0=u;(4)负向量存在:对于任意的u,存在一个向量-v,使得u+(-v)=0;(5)标量乘法结合律:对于任意的标量a和b,以及向量u,(ab)u=a(bu);(6)分配律1:对于任意的标量a和向量u、v,a(u+v)=au+av;(7)分配律2:对于任意的标量a和b,以及向量u,(a+b)u=au+bu;(8)单位元存在:对于任意的向量u,1u=u。
1.2 线性空间的基本性质(1)线性空间中的向量可以进行加法和标量乘法运算;(2)线性空间中的向量满足向量加法的封闭性和标量乘法的封闭性;(3)线性空间中的向量满足加法交换律、加法结合律和分配律;(4)线性空间中存在唯一的零向量和负向量;(5)线性空间中存在多个基向量,它们可以线性组合得到任意向量;(6)线性空间中的向量存在唯一的零向量和唯一的负向量。
二、线性变换的定义与性质2.1 线性变换的定义线性变换,也称为线性映射,是指将一个向量空间V映射为另一个向量空间W的一种映射关系。
若对于任意的向量u和v,以及任意的标量a和b,满足以下两个条件,则称该映射关系为线性变换:(1)保持加法运算:T(u+v) = T(u) + T(v);(2)保持标量乘法:T(au) = aT(u)。
2.2 线性变换的基本性质(1)线性变换保持零向量:T(0) = 0;(2)线性变换保持向量的加法和标量乘法运算;(3)线性变换保持向量的线性组合关系;(4)线性变换将线性无关向量映射为线性无关向量;(5)线性变换的核和像是向量空间。
01_矩阵论_第一章线性空间与线性变换

则有
1 0 0 1 0 0 0 0 A a11 0 0 a12 0 0 a21 1 0 a22 0 1
因此 R22 中任何一个向量都可写成向量组
1 0 0 1 0 0 0 0 E11 0 0 , E12 0 0 , E21 1 0 , E22 0 1
Pn [ x] { ai xi | ai R}
i 0 n 1
在通常多项式加法和数乘多项式运算下构成线性 空间 Pn[x]。 值得指出的是次数等于 n 1 的多项式集合
V { ai x | ai R, an1 0}
i i [a, b] = {f (x) | f (x) 是区间 [a, b] 上 实连续函数 } ,对于函数的加法与数乘运算构成 实数域上的线性空间。
定义 1.3 设 1, 2, …, n 是线性空间 Vn(F) 的一组基,若 V,
xi i (1 2
i 1 n
x1 x2 n ) x n
(1.1)
则称数 x1, x2, …, xn 是 在基 {1, 2, …, n} 下 的坐标,(1.1) 式中向量 (x1, x2, …, xn)T 为 的坐 标向量,也简称为坐标。
从上述线性空间例子中可以看到,许多常见 的研究对象都可以在线性空间中作为向量来研究。 另外应理解加法和数乘分别是 V 中的一个二元运 算和数域 F 和 V 中元素间的运算,要求运算满足 定义 1.1 中的八条性质,它们已不再局限在数的 加法、乘法的概念中。
一个数学例子 取集合为正实数集合 R+,F 为实数域 R,加 法“”和数乘“”如下定义 :a, bR+,ab = ab, :kR(i.e. F ),aR+,k a = ak。 在此运算下,R+ 是 R 上的一个线性空间,其中 加法零元素是 R+ 中的数 1,R+ 中元素 a 的负元素 是 a1。
矩阵理论课件 第一章 线性空间与线性变换

a1n
a2n
ann
前述关系可以表示为 AT 或 T T A
则称矩阵 A 为基 到基 的过渡矩阵(唯一且可逆)
定义2 (坐标变换)
设x V L(P) ,向量 x 在 基 和基 下的
坐标之间的关系,称之为坐标变换。
坐标变换与过渡矩阵的关系:
设 x k1x1 k2 x2 kn xn 和 x t1 y1 t2 y2 tn yn
和 W W1 W2 为直和,记为 W W1 W2 。
例6 设 R4的3个子空间:
① V1 (a, b, 0, 0)T a, b R ② V2 (0,0,c, 0)T c R ③ V3 (0,d,e, 0)T d,e R
容易验证V1 是V2直和, V1 V3不,V是2 直 V和3。
事实上 不妨设简单基为 (III )e1, e2 , , en ( x1, x2 , , xn ) (e1, e2 , , en )C1 ( y1, y2 , , yn ) (e1, e2 , , en )C2
( x1, x2 , , xn )C11C2
C C11C2
例4 设线性空间P3[t] 的两个基为: (I ) f1(t) 1, f2(t) 1 t, f3(t) 1 t t 2,
表示,不妨记
y1 a11x1 a21x2
y2
a12 x1
a22 x2
yn a1n x1 a2n x2
称上述关系为两组基的基变换。
an1xn an2 xn
ann xn
x1
y1
a11 a12
若记
x2
,
y2
A
a21
a22
xn
yn
an1 an2
Matrix1-1

Pn [x] = { p(x) ai xi :aiR } i0 运算:多项式的加法和数乘
C[a,b] = { f (x):f (x) 为 [a,b] 上连续(实)函数 }
运算:函数的加法和数乘 (还有C1[a,b]等 ) 不一样的线性空间:V=R+,F=R,a b = ab, a = a
2 坐标变换公式
已知
➢ 空间中两组基:{1, 2 ,...,n} 1,2, , n,
满足: (12...n ) (12...n )Cnn
1
2
3
➢ (12...n )X; (12...n )Y
讨论X和Y的关系
定理1.4 X=CY 或 Y=C-1X
例题11(P6)
例题 已知空间R22中两组基(I){Eij}
线性空间?
例子:次数为n-1的实多项式集合:
{
n1
p(x) ai xi
:aiR,且 an-1不为零 };
i0
平面上不过原点的直线;
空间中不过原点的直线或平面。
不是线性空间的例子与判别
例子:次数为n-1的实多项式集合:
{
n1
p(x) ai xi
:aiR,且 an-1不为零 };
i0
平面上不过原点的直线;
x2,…,xn 是 在基{i}下的坐标。i1
要点: 坐标与基有关 坐标的表达形式
例1:求 的坐标。
R22中向量
3 4
1 5
在基{ Eij }下
例2 设空间P4[x]的两组基为: { 1,x,x2,x3 } 和 { 1,(x – 1)1,(x – 1)2,(x – 1)3 } 求 f (x) = 2+3x+4x2+x3 在这两组基下的坐标。
第一章 线性空间与线性变换

xi ∈ P
(1.1.4)
称 x = (x1 , x2 ,L, xn ) T 是向量 α 在基 S 下的坐标, 且 x ∈ P.n
定理1 定理1.1.2 在 n 维线性空间 Vn 中,任一向量 在一个基下的坐标唯一.
V 这说明,当线性空间 Vn 的基 S 取定后, n 中任一
个向量的坐标是确定的,即假设 S = {α 1 ,α 2 ,L,α n }
定义1 定义1.2.2 如果 V1 + V2 中任一向量只能唯 一的表示成子空间 V1 的一个向量和子空间 V2 中的一个向量的和,则称 V1 + V2 是 V1 ,V2 • 的直和,记为 V1 ⊕ V2(或 V 1 + V 2 ).
S 是线性无关向量组;
V
中任一向量都是 S 中向量的线性组合.
V
α 称 S 是 V 的一个基(底), 1 ,α 2 ,L ,α n 称为V 的基
向量, S 中向量的个数 n ,称为线性空间 数,记为 dim(V ) = n。
的维
维数是 n 的线性空间 V 称为 n 维线性空间, 记为Vn . 假如 V 中存在任意多个线性无关的向量 时,称 V 为无限维线性空间. 如果 注: 定义1.1.3描述的基在线性空间中不唯一.
图1.2.1
图1.2.2
由于零子空间不含线性无关的向量,因此 没有基,它的维数规定为零。而对于 V 的其它 的子空间,由于它的线性无关的向量个数不可 能比整个线性空间线性无关的向量个数多,所 以子空间的维数比原空间的维数小,即
dim(W ) ≤ dim(V )
下面讨论子空间的生成问题。
设 S = {α 1 ,α 2 ,L,α m } 是数域 P上的线性空间 V 中的一 个向量组,在 P 中任取 m 个数 k1 , k 2 , L, k m , 做 S 中向 量的线性组合
第1章线性空间与线性变换讲义.ppt

12
a b A= c d = aE11 + bE12 + cE 21 + dE 22
例2 设
1 0 0 a1 = 2 , a 2 = 1 , a 3 = 0 3 2 1
例2. 设A为m×n 矩阵,向量的集合
N ( A) = { x | Ax = 0, x R n }
则N ( A) 是 R n 的子空间, 并称为A的零空间( 或核空间 ) 。
22
, a , , a V , 例3. 设V 是数域F上的线性空间,a 1 2 m
W = { x1a1 + x 2a 2 + + x ma m | x1 , x 2 , , x m F }
( 2 ) a W , k F ,则 k a W
则称W 是V 的子空间。
21
( 1 ) a , b W ,则 a + b W
例1. 实数域上 n 维向量的集合
W = { ( 0, x 2 , , x n ) T | x 2 , , x n R }
则W是 R n 的子空间。
1 m1 n
a , , a , b , , b V
若 向量组 { ,2 , ,m } 与 { ,2 , ,n } 等价 1 1
则W 1= W 2
a aa b bb
定义: 设W1, W2 是线性空间V 的子空间,称集合
{ a + b | a W , b W } 1 2
为W1与 W2 的和,记作 W1+ W2 称集合
是 R 3 中的两组基,求由基 a 1 , a 2 , a 3 到基 b 1 , b 2 , b 3 的转移矩阵P ;
第一章 线性空间与线性变换

an 2 收敛
n 1
线性空间的基本概念及其性质
基本概念:线性组合;线性表示;线性相关;线性无关; 向量组的极大线性无关组;向量组的秩。
❖ 基本性质:
(1) 含有零向量的向量组一定线性相关; (2) 整体无关则部分无关;部分相关则整体相关; (3) 如果含有向量多的向量组可以由含有向量少的向量组线
于是同可一得向量在13不24同的 基x1下10坐标11不同x2,
1 0 那1 它1们
有什么关系x呢3 ?10
1 1
x4
1 1
1 0
解得
x1
7, 3
x2
4 3
,
x3
1, 3
x4
2 3
同样可解出在第二组基下的坐标为
y1 1, y2 1, y3 1, y4 4
基变换与坐标变换
设
1,
2
,
,
(旧的)与
例4 在4维线性空间 R22 中,向量组
0 1 1 0 1 1 1 1 1 1, 1 1, 0 1, 1 0
与向量组
1 0 1 1 1 1 1 1 0 0, 0 0 , 1 0 , 1 1
是其两组基,求向量 坐标。
A
1 3
2 4
在这两组基下的
解:设向量A在第一组基下的坐标为 ( x1, x2, x3, x4 )T
子空间的交与和
❖ 两个子空间的交: V1 V2 : V1 & V2 ❖ 两个子空间的和: V1 V2 z x y : xV1, y V2
❖ 子空间交与和的性质
若V1和V2都是V的子空间,则V1∩V2和V1+V2也是V的子空 间.
V1∩V2 = V2∩V1,V1+V2=V2+V1 (V1∩V2)∩V3=V1∩(V2∩V3),(V1+V2)+V3=V1+(V2+V3) dimV1+dimV2=dim(V1+V2)+ dim(V1∩V2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明
1. 凡满足以上八条规律的加法及乘数运算, 称为线性运算. 2 . 判别线性空间的方法:一个集合,对于定 义的加法和数乘运算不封闭,或者运算不 满足八条性质的任一条,则此集合就不能 构成线性空间.
Department of Mathematics
Department of Mathematics
说明:
1)若数集F中任意两个数作某一运算的结果仍在F 中,则说数集F对这个运算是封闭的. 2)数域的等价定义:如果一个包含0,1在内的数 集F 对于加法,减法,乘法与除法(除数不为0) 是封闭的,则称集 F 为一个数域.
Department of Mathematics
Department of Mathematics
线性空间既是代数学的基本概念,也是矩阵论 的基本概念之一,本章首先介绍这一概念。学习过 这一部分内容的同学可以将本章作为对所学知识的 回顾和延伸。 在解析几何和线性代数中,我们已经学习过平 面与空间的向量,线性空间是解析几何中向量概念 的抽象化。 在线性代数中,学习过向量的线性相关性,现 在我们应用它来研究线性空间。
∴ R m × n 是一个线性空间 .
Department of Mathematics
例2 数域 F 上次数小于 n 的多项式的全体 ,
记作 P [ x ]n , 即 : P [ x ] = {a n −1 x n −1 + a n − 2 x n − 2 + 构成向量空间 . + a1 x + a 0 a i ∈ F }
则有
x ± y = (a ± c ) + (b ± d ) 2 ∈ Q( 2), x ⋅ y = (ac + 2bd ) + (ad + bc ) 2 ∈ Q( 2)
设 a + b 2 ≠ 0,
Department of Mathematics
于是 a − b 2 也不为0.
(否则,若 a − b 2 = 0, 则 a = b 2, a = 2 ∈ Q, 于是有 b 或 a = 0, b = 0 ⇒ a + b 2 = 0. 矛盾)
(2) 一个集合,如果定义的加法和乘数运算不 是 通常的实数间的加乘运算,则必需检验是否满足 八条线性运算规律. 例5. 正实数的全体,记作 R + ,在其中定义加法 及乘数运算为
a ⊕ b = ab, λ a = a λ , (λ ∈ R, a , b ∈ R + ).
验证 R + 对上述加法与乘数运算构成线性空间.
= (a1 + a2 )cos x + (b1 + b2 )sin x
= A sin( x + B )∈ S [ x ].
λs1 = λA1 sin( x + B1 ) = (λA1 )sin( x + B1 ) ∈ S [ x ]
∴ S [ x ] 是一个线性空间.
Department of Mathematics
( 2)(a ⊕ b ) ⊕ c = (ab ) ⊕ c = (ab )c = a ⊕ (b ⊕ c );
( 3) R +中存在零元素 1, 对任何 a ∈ R + , 有
a ⊕ 1 = a ⋅ 1 = a;
(4) ∀a ∈ R + , 有负元素 a −1 ∈ R + , 使
Department of Mathematics
λ
(λα ) = ⋅ 0 = 0.
λ
1
1
λ(λα ) = ⋅Fra bibliotekλ ⋅ α = α .
λ
∴ α = 0.
同理可证:若 α ≠ 0 则有 λ = 0.
Department of Mathematics
练习:
证明:数域F 上的线性空间V若含有一个非零 向量,则V一定含有无穷多个向量 证:设 α ∈ V , 且α ≠ 0
= 0+γ =γ.
向量 α 的负元素记为 − α .
Department of Mathematics
3. 0α = 0;
(− 1)α = −α ; λ 0 = 0.
证明 ∵α + 0α = 1α + 0α = (1 + 0 )α = 1α = α ,
∴ 0α = 0.
∵α + (− 1)α = 1α + (− 1)α = [1 + (− 1)]α = 0α = 0,
= λx
如果上述的两种运算满足以下八条运算规律, 那么 V 就称为数域 F 上的线性空间.记为: V (F )
Department of Mathematics
八条运算规律: 设x, y, z∈V ;λ , μ∈F
(1) x + y = y + x; ( 2) ( x + y ) + z = x + ( y + z );
对于通常的多项式加法 , 数乘 , 多项式的乘法
通常的多项式加法、数乘多项式的乘法两种运 算满足线性运算规律. 例3 数域F上n次的多项式的全体 , 记作Q[ x ]n ,即 :
Q[ x ] = {a n x n +
Department of Mathematics
+ a1 x + a0 a0 , a1 ,
而任意一个有理数可表成两个整数的商,
∴ Q ⊆ P.
Department of Mathematics
§1.2 线 性 空 间
一,线性空间的定义和举例 定义1 设V是一个非空集合, 为一数域.如果对于 F 任意两个元素 x, y ∈V ,总有唯一的一个元素 z 与之 对应,称为 x 与 y 的和,记作 z = x + y 若对于任一数 λ ∈F 与任一元素 x ∈ V ,总有唯 一的一个元素 ω ∈ V 与之对应,称为 λ 与 x 的积, 记作 ω
c + d 2 (c + d 2)(a − b 2) = a + b 2 (a + b 2)(a − b 2) ac − 2bd ad − bc = 2 + 2 2 ∈ Q. 2 2 a − 2b a − 2b Gauss数域 ∴ Q ( 2)为数域.
类似可证 Q ( i ) = a + bi a , b ∈ Q , i = −1 是数域.
第 一 章
线性空间与线性映射
Department of Mathematics
教学内容和基本要求
1,理解线性空间的概念,掌握基变换与坐标变换的公式; 2, 掌握子空间与维数定理,理解子空间的相关性质; 3, 理解线性变换的概念,掌握线性变换的矩阵示表示, 了解线性空间同构的含义. 重点: 线性空间的概念;子空间的维数定理;基变换与 坐标变换. 难点: 基变换与坐标变换
Department of Mathematics
§1.1
数 域
一,数域的定义 设F 是至少包含两个数的数集,如果F 中 定义: 任意两个数的和、差、积、商(除数不为0)仍是 F中的数,则称F为一个数域. 常见数域: 复数域 C ;实数域 R ;有理数域 Q ; (注意:自然数集N及整数集Z都不是数域.)
(8) λ (a ⊕ b ) = λ (ab ) = (ab ) = a λ b λ
λ
= a λ ⊕ b λ = λ a ⊕ λ b.
所以 R + 对所定义的运算构成线性空间.
Department of Mathematics
例6. n 个有序实数组成的数组的全体
S = ⎧x = (x ,x , ⎨ 1 2 ⎩
例1.证明:数集 是一个数域.
Q( 2 ) = a + b 2 | a,b ∈ Q
{
}
∵ 证: 0 = 0 + 0 2, 1 = 1 + 0 2, ∴ 0,1 ∈ Q( 2)
又对 ∀x , y ∈ Q( 2), 设 x = a + b 2, y = c + d 2,
a , b, c , d ∈ Q ,
n
,x )
n
T
x1 , x 2 ,
, xn ∈ R⎫ ⎬ ⎭
对于通常的有序数组的加法及如下定义的乘法
λ ( x1 , , xn ) = (0,
T
,0 ) 不构成线性空间.
解答: S n 对运算封闭.
但1 x = O , 不满足第五条运算规律 .
由于所定义的运算不是 线性运算 , 所以 S n不是 线性空间 .
Department of Mathematics
证明:
∀a , b ∈ R + , ⇒ a ⊕ b = ab ∈ R + ; ∀λ ∈ R , a ∈ R + , ⇒ λ a = a λ ∈ R + .
所以对定义的加法与乘数运算封闭. 下面一一验证八条线性运算规律:
(1) a ⊕ b = ab = ba = b ⊕ a;
∴ (− 1)α = −α .
λ 0 = λ [α + (− 1)α ] = λα + (− λ )α
= [λ + (− λ )]α = 0α
= 0.
Department of Mathematics
4.如果 λα = 0,则 λ = 0 或 证明 假设 λ ≠ 0 , 那么 又
1 1
. α =0
a ⊕ a − 1 = a ⋅ a − 1 = 1;
( 5 ) 1 a = a 1 = a;
( 6) λ
(μ a ) = λ a = (a
μ
μ λ
)
= a λμ = (λμ ) a;
(7) ( λ ⊕ μ ) a = a λ + μ = a λ a μ = a λ ⊕ a μ = λ a ⊕ μ a;
