工程力学第八章 剪切与挤压
同济大学工程力学剪切力
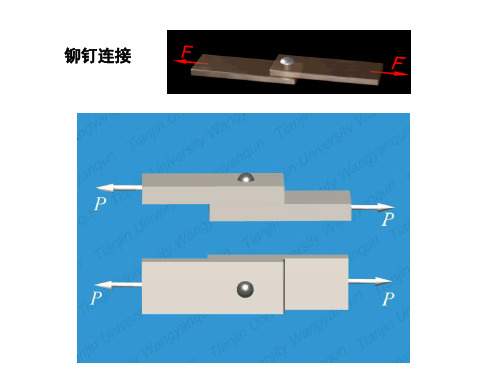
§3-3 挤压的实用计算
F
F
实际的挤压面是半个
圆柱面,而在实用计算中
用其直径平面Abs来代替
Fbs
实用计算中,名义挤压应
Fbs 力公式
挤压力不是内力,而是外力
bs
Fbs Abs
Abs d ——挤压面的计算面积
挤压的实用计算
试:校核接头的强度
解:1. 接头受力分析
当各铆钉的材料与直径均相同,且外力作用线在 铆钉群剪切面上的投影通过铆钉群剪切面形心时, 通 常即认为各铆钉剪切面上的剪力相等
F/4
m
F/n
m
m
F/4
m
F/n
2. 强度校核
剪切强度:
FS
F 4
4FS πd 2
F πd 2
99.5
MPa
[
]
挤压强度:
矩 m = 1600 Nm,轴的直径 d = 50 mm,键的许用切应力为[ ]= 80 M Pa ,许用挤压应力为[ bs]= 240M Pa,试设计键的长度。
解:键的受力分析如图
h
m2
F
FS
Fbs
2m d
2 1600 0.05
64kN
h
L
AQ
b
F m
d
切应力和挤压应力的强度条件
变形特点:构件沿两力作用线之间的某一截面产生相 对错动或错动趋势。
铆钉连接
F F
F
m
m
F
剪切面
双剪切
连接的破坏形式一般有:
测试题-剪切与挤压 - 答案

工程力学练习题(四)剪切与挤压1.如图2-2-1所示,一个剪切面上的内力为()。
A.F B.2F C.F/2图2-2-1(C)2.校核图2-2-2所示结构中铆钉的剪切强度,剪切面积是()。
A.πd2/4 B.dt C.2dt D.πd2(A)图2-2-2图2-2-3 3.在图2-2-3所示结构中,拉杆的剪切面形状是(),面积是()。
A.圆B.矩形C.外方内圆D.圆柱面E.a2 F.a2-πd2/4 G.πd2/4 H.πdb(D)(H)4.在图2-2-3所示结构中,拉杆的挤压面形状是(),面积是()。
A.圆B.矩形C.外方内圆D.圆柱面E.a2 F.a2-πd2/4 G.πd2/4 H.πd(C)(F)5.图2-2-6所示连接结构,铆钉为钢质,被连接件为铜质。
(1)该连接为结构。
(2)剪切破坏发生在上。
(3)挤压破坏发生在上。
A.单剪切B.双剪切C.被连接件之一D.铆钉图2-2-6(A)(D)(C)6.挤压变形为构件变形。
A.轴向压缩B.局部互压C.全表面(B)7.剪切破坏发生在上;挤压破坏发生在上。
A.受剪构件B.受剪构件周围物体C.受剪构件和周围物体中强度较弱者(A)(C)8.在校核材料的剪切和挤压强度时,当其中有一个超过许用值时,强度就()。
A.不够B.足够C.无法判断(A)计算题:1.图2-2-9中已知F=100kN,挂钩连接部分的厚度δ=15mm。
销钉直径d=30mm,销钉材料的许用切应力[]τ=60MPa,许用挤压应力jyσ⎡⎤⎣⎦=180MPa,试校核销钉强度。
若强度不够,应选用多大直径的销钉?图2-2-9参考答案:解:由截面法可得销钉每个剪切面上的剪力为F Q =F /2=100/2=50kNA=d×2δ取销钉中间段:挤压面上的挤压力为F jy =F=100kN,挤压面面积:jy 销钉剪切面面积:A=πd2/4,由剪切强度条件公式 τ=A F Q ,代入已知得: τ=43014.3500002⨯=70.77MPa > [τ] 所以销钉的剪切强度不够。
工程力学下题库

工程力学题库一、填空题(每空1分,共57分)(难度A)第八章轴向拉伸和压缩1. "强度"是构件在外力作用下____________ 的能力。
2. 通常,各种工程材料的许用切应力[T不大于其____________ 切应力。
3. 在材料力学中,对可变形固体的性质所作的基本假设是假设、___________________ 设和 ______________ 假设。
4. 衡量材料强度的两个重要指标是_______________ 和_____________________ 。
5. 由于铸铁等脆性材料的很低,因此,不宜作为承拉零件的材料。
6. 在圆轴的台肩或切槽等部位,常增设_____________________ 结构,以减小应力集中。
7. 消除或改善是提高构件疲劳强度的主要措施。
第九章剪切与扭转1. 应用扭转强度条件,可以解决_______________________ 、 _____________________ 和_____________ _____ —等三类强度计算问题。
2. 在计算梁的内力时,当梁的长度大于横截面尺寸____________ 倍以上时,可将剪力略去不计。
3. 若两构件在弹性范围内切应变相同,则切变模量G值较大者的切应力较______________ 。
4. 衡量梁弯曲变形的基本参数是___________________ 和________________________ 。
5. 圆轴扭转变形时的大小是___________________________________ 用来度量的。
6. 受剪切构件的剪切面总是___________ 于外力作用线。
7. 提高圆轴扭转强度的主要措施:______________________ 和__________________ 。
8. 如图所示拉杆头为正方形,杆体是直径为d圆柱形。
1. 作用在梁上的载荷通常可以简化为以下三种类型:___________ 、2. 按照支座对梁的约束情况,通常将支座简化为三种形式:______3. 根据梁的支承情况,一般可把梁简化为以下三种基本形式:____4. ___________________________ 对梁的变形有两种假设:、______________________________________ 。
《工程力学》剪切与挤压的实用计算

《工程力学》剪切与挤压的实用计算剪切和挤压是工程力学中两个非常重要的概念。
在工程实践中,往往需要对结构承受的剪切和挤压力进行计算,并通过计算结果来评估结构的稳定性和安全性。
本文将分别介绍剪切和挤压的概念和公式,并通过实例说明如何进行实用计算。
剪切是指力在结构内部沿着切面作用,导致结构内部产生剪应力和剪应变。
剪应力是垂直于切面方向的力与切面面积之比。
在工程实践中,常见的剪切力作用包括轴向力、剪力和扭矩。
对于轴向力和剪力,其剪应力可以通过下式计算:τ=F/A其中,τ为剪应力,F为作用力的大小,A为剪切面积。
对于扭矩作用,其剪应力的计算则需要考虑到截面形状和应力分布的不均匀性。
常见的情况是圆形截面的轴向受拉时的剪应力分布。
在这种情况下,剪应力的最大值出现在截面外圆周,可以通过下式进行计算:τ=T*r/I其中,τ为剪应力,T为扭矩的大小,r为截面距离外圆周的距离,I为截面的惯性矩。
挤压是指力在结构内部沿着压力方向作用,导致结构内部产生压应力和压应变。
挤压力作用常见于柱子或支撑结构的承重部分。
在计算挤压力时,首先需要确定结构的截面形状和尺寸。
然后可以通过下式计算挤压应力:σ=F/A其中,σ为挤压应力,F为挤压力的大小,A为截面积。
在实际工程中,剪切和挤压的计算往往需要考虑到结构的复杂性和非线性等因素。
此时,可以通过使用数值计算方法或专业软件进行计算,来得到更准确的结果。
此外,还需要根据结构的特点和工程要求,对计算结果进行适当的修正和调整。
举个例子来说明剪切和挤压的实用计算。
假设有一根圆柱形的支撑柱,柱子的直径为10cm,高度为2m。
假设柱子受到的挤压力为5000N。
1.根据柱子的直径计算出柱子的截面积:A = π * r^2 = π * (5cm)^2 = 78.54cm^22.将挤压力代入公式,计算出挤压应力:σ = F / A = 5000N / 78.54cm^2 = 63.73N/cm^2通过这个例子可以看出,挤压力的计算相对简单,只需要确定结构的截面形状和尺寸,并代入公式即可。
工程力学上课课件:剪切与挤压共31页文档

60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
剪的圆孔最小直d和最大厚度t 。
解 1)确定圆孔的最小直径。 冲剪的孔径等于冲头的直径,冲头
冲头
工作时需满足抗压强度条件,即
凸模
FN 4F
A d2
d
4F
4401030
4403m 4 m
故取最小直径为35mm。
t t
F 工件
d
d
2)求钢板得最大厚度。钢板剪切面上的剪力FQ=F, 剪切面的面积为dt。为能冲断圆孔,需满足下列条件
(2)若铆钉按图示排列,所需板宽b为多少?
F
F
解: 可能造成的破坏:
(1)因铆钉被剪断而使铆接被破坏; (2)铆钉和板在钉孔之间相互挤压过大,而使铆接被破坏; (3)因板有钉孔,在截面被削弱处被拉断。
可采用假设的计算方法: 假定每个铆钉所受的力都是一样的。
(1)铆钉剪切计算
F/2n
F/n
Q
F/2n
如图,上钢板孔左侧与铆钉上部左侧,下钢板右侧与铆钉 下部右侧相互挤压。
发生挤压的接触面称为挤压面。挤压面上的压力称为挤
压力,用Fjy表示。相应的应力称为挤压应力,用jy表示。
jy
F jy A jy
必须指出,挤压与压缩不同。挤压力作用在构件的表面, 挤压应力也只分布在挤压面附近区域,且挤压变形情况比较 复杂。当挤压应力较大时,挤压面附近区域将发生显著的塑 性变形而被压溃,此时发生挤压破坏。
三、剪应变 剪切胡克定律
构件在发生剪切变形时,截面沿外力的方向产生相对错 动。在构件受剪部位的某处取一小立方体——单元体,在剪 力的作用下,单元体将变成平行六面体,其左右两截面发生
《工程力学》练习题

《工程力学》练习题第一章绪论1. 强度是指构件在外力作用下抵抗_破坏_的能力,刚度是指构件在外力作用下抵抗_变形_的能力,稳定性是指构件在外力作用下保持_平衡_的能力。
2. 静力学研究的对象是刚体,刚体可以看成是由质点系组成的不变形固体。
材料力学研究的对象是变形固体。
(√)3. 变形固体四种基本变形,即拉压变形、剪切与挤压变形、扭转变形及弯曲变形。
(√)4. 在材料力学对变形固体假设中,最小条件假设是指在外力的作用下,变形固体所产生的变形较小,在强度校核计算中采用初始状态的尺寸进行计算。
(√)5. 材料力学对变形固体的假设中,同向异性假设是指变形固体在不同方位显示出的力学性能的差异性。
但在实际中仍然按各向同性计算。
(√)第二章静力学的基本概念和受力分析1. 刚体是指在力的的作用下,大小和形状不变的物体。
2. 力使物体产生的两种效应是___内_____效应和_ _外___效应。
3、力是矢量,其三要要素是(大小)、方向及作用点的位置。
4、等效力系是指(作用效果)相同的两个力系。
5、非自由体必受空间物体的作用,空间物体对非自由体的作用称为约束。
约束是力的作用,空间物体对非自由体的作用力称为(约束反力),而产生运动或运动的趋势的力称为主动力。
6、物体的平衡状态是静止状态。
(X)7、物体的平衡状态是匀速直线运动态。
(X)8.作用力与反作用力是一组平衡力系。
(X )9、作用在刚体上的二力,若此两力大小相等、方向相反并同时作用在同一直线上,若此刚体为杆件则称为而二力杆件。
(√)10、作用在刚体上的力,可以沿其作用线滑移到刚体上的任意位置而不会改变力对刚体的作用效应。
(√)11、作用在刚体上的力,不能沿其作用线滑移到刚体上的任意位置。
主要是滑移后会改变力对刚体的作用效应。
(X )12、作用在刚体上的三个非平行力,若刚体处于平衡时,此三力必汇交。
(√)13、两物体间相互作用时相互间必存在一对力,该对力称为作用力与反作用力。
剪切及挤压应力计算

剪切及挤压应力计算剪切应力是物体内部的应力状态之一,指物体内部各部分相对于其它部分的平动趋势。
挤压应力则是指物体受到外部挤压力作用后内部产生的应力。
剪切及挤压应力计算需要考虑物体的形状、尺寸以及施加力的方向和大小。
对于剪切应力的计算,可以通过剪切力与剪切面积之比来求得。
假设一个物体受到平行于其中一平面的剪切力作用,剪切力的大小为F,剪切面的积为A。
剪切应力可以表示为τ=F/A。
其中τ表示剪切应力。
如果物体的形状不规则,可以将其划分为多个小面元,然后求和计算得到总的剪切应力。
对于挤压应力的计算,可以通过挤压力与挤压面积之比来求得。
假设一个物体受到垂直于其中一平面的挤压力作用,挤压力的大小为P,挤压面的积为A。
挤压应力可以表示为σ=P/A。
其中σ表示挤压应力。
如果物体的形状不规则,可以将其划分为多个小面元,然后求和计算得到总的挤压应力。
剪切应力和挤压应力的计算都需要明确给定施加力的方向和大小,以及物体的面积。
对于规则形状的物体,可以通过几何方法直接计算得到。
对于不规则形状的物体,需要采用数值方法进行近似计算。
除了这种简单情况外,对于复杂的物体形状和受力情况,需要运用工程力学的知识,通过应力分析、协调方程等方法来进行计算。
在这种情况下,需要考虑物体的几何形状、材料的性质、受力的位置和大小等因素,以得到更精确的剪切应力和挤压应力的计算结果。
最后,需要注意的是,剪切应力和挤压应力是物体内部的应力状态,其大小与物体的尺寸和形状有关。
在工程设计中,需要根据所需的应力状态来选择合适的材料和设计结构,以保证物体在受力情况下不会发生破坏或变形。
总之,剪切应力和挤压应力的计算是工程力学中重要的内容之一,需要综合运用几何学、力学、材料学等知识,通过适当的数值计算或工程分析方法来进行。
这样可以为工程设计提供可靠的理论基础,以保证物体的强度和稳定性。
剪切与挤压(工程力学课件)

解得
考虑生产实际情况,圆整取最小直径为35mm。
剪切
解: (2)确定钢板的最大厚度t。
解得
挤压
挤压
1. 挤压的基本概念
➢ 连接件在发生剪切变形的同时,在传力的接触面上,由于局部受到压力 作用,致使接触面处的局部区域产生塑性变形,这种现象称为挤压。
构件上产生挤压变形的接触面称 为挤压面。挤压面上的压力称为 挤压力,用Fjy表示。一般情况下, 挤压面垂直于挤压力的作用线。 挤压面为下半个圆周面
d h
挤压
4.计算实例
例: 如图7.7所示拉杆,用四 个直径相同的铆钉固定在格板 上,拉杆与铆钉的材料相同, 试校核铆钉与拉杆的强度。已 知载荷F=80kN,板宽b= 80mm,板厚t=10mm,铆钉直 径d=16mm,许用切应力[τ]= 100MPa,许用挤压应力[σjy]= 100MPa,许用拉应力[σ]= 160MPa。
jy
F jy A jy
35.7 103 80 5
89.3MPa [ jy ]
所以键的剪切和挤压强度均满足要求。
可以看出:键的剪切强度一般有较大的储备,而挤压强度的储 备较少,因此工程上通常对键只作挤压强度计算。
剪切与挤压的工程实例与计算
例二:图示拖车挂钩用插销联接,已知挂钩厚度=10mm, [] =100MPa, [jy]=200MPa,拉力F=56kN,试设计插销的直径d。
剪切
2.剪切的实用计算——剪力
剪切面
Q
F
Q
Q
剪切
剪切面
F
Q
将螺栓从剪切面截开,由力的平衡,有:
Q为剪切内力,即剪应力在剪切面上的合力,我们称之为剪力
剪切
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
FC AC
F dh
为充分利用材料,切
应力和挤压应力应满足
C 2
F 2 4F
dh
d2
d 8h
目录
例8-1 螺栓接头如图所示。已知 F = 40 KN,螺栓的许用应力
[ ] 130MPa,[C ] 300MPa,钢板 的许用拉应力[ ] 160MPa ,试计算螺
栓所需的直径,并校核钢板的强度。
第八章 剪切挤压实用计算
第一节 剪切与挤压 第二节 剪切与挤压的强度计算
本章重点
剪切与挤压接件:结构中,起连接作用的构件。特点,几何尺寸小, 受力复杂。连接件通常产生剪切和挤压基本变形。 连接件实例
铆钉连接
螺栓连接 销轴连接
目录
平键连接
焊接连接
榫连接
目录
2.剪切受力特点:一对力作用线非常靠近。 3.剪切变形特点:受剪面发生错动。
面时,有效挤压面积即为接触面面积;当
接触面为圆柱面时,有效挤压面的面积为
圆柱的直径面面积。
目录
挤压强度条件:
C
FC AC
C
C 可由实验方法确定
钢材,[C]=(1.7~2)
目录
FQ F
A lb
C
FC AC
F cb
目录
FQ 4F A d2
A
可由实验方法确定
断
FQ断 A
F断 2A
[ ] 断
n
剪切器
钢材,[ ]=(0.6~0.8)
目录
二、挤压的实用计算
由图可见,挤压力FC等于F。
假设应力在有效挤压面积AC上均匀分布。
挤压应力计算公式
C
FC AC
FC
有效挤压面是指接触面在垂直于总挤
FC 压力作用线平面上的投影。当接触面为平
取螺栓直径为: d =14mm
目录
取螺栓直径为: d =14mm (3)钢板强度校核。
盖板厚度累加大于主板厚度,因此 只需校核主板强度。
主板被一个螺栓孔削弱,削弱处净截面积为
A (100 14) 18mm2 1 548mm2
F A
1
40 103 548 106
Pa
25.8MPa
结论:键安全
目录
例8-3 图示螺钉受拉力F作用。已知材料的剪切许用应力[τ] 和许用应力[σ]之间的关系为:[τ] = 0.6[σ]。试求螺钉直径d 与钉头高度h的合理比值。
解: 螺钉头受剪面面积 A dh
剪力 FQ=F
令 F [ ] dh
h F
d[ ]
螺杆受拉 FN=F
解:(1)螺栓的剪切强度计算。 螺栓有两个剪切面,
FQ=F/2=20 kN
FQ AQ
20 103
d2
[ ]
4
d 14mm
目录
(2)螺栓的挤压强度计算
挤压力FC 40kN,有效挤压面积 AC 18d
bs
FC AC
40 103 18d 103
[
bs ]
d 7.4mm
[ ]
结论:钢板安全。
目录
例8-2 一齿轮用平键与传动轴联结,如图所示。已知轴径
d 70mm ,键的许用应力 [ ] 60MPa, [bs ] 100MPa
轴传递的最大转矩 M e 2kN m。试校核键的强度。
解:(1)外力分析。
F
2Me d
22103 70103
令
4F
d2
[ ]
d2 4F
[ ]
h F F
d[ ] d0.6[ ]
h d
F
d 20.6[ ]
F[ ] 4F0.6[ ]
1 2.4
0.42
一、剪切实用计算
小结
FQ
A
A:剪切面面积
二、挤压的实用计算
C
FC AC
C
AC:有效挤压面面积
讨论题
1、如何判别受剪面和挤压面? 2、计算挤压面是曲面还是平面? 3、剪切、挤压的实用计算方法有工程实际意义吗? 4、同时给出剪切、挤压许用应力,如何设计截面或确定载荷?
N57.1kN
(2)剪切面和挤压面分析。
剪切面面积 AQ bl 挤压面面积为 AC hl 2
目录
(3)剪切强度和挤压强度校核。
FQ 57.1103 MPa 28.6MPa[]
AQ 20100
bs
FC AC
257.1103 12100
MPa
95.2MPa [bs]
受剪面:一对力之间的面。挤压面:互相压紧的面。 构件受剪切的同时,接触面上产生挤压现象。
目录
判别以下连接件的受剪面和挤压面:
目录
第二节 剪切与挤压的强度计算
一、剪切实用计算
由截面法可求得:FQ=F
假设切应力在剪切面(m-m截面)
均匀分布:
切应力计算公式: FQ
A
切应力强度条件: FQ
