高中数学 3.3.2函数的极值与导数教案 新人教A版选修1-1
高二数学3.3.2函数的极值与导数学案新人教A版选修1-1

?基础梳理
1.极值的概念.
如果函数 y = f ( x) 在点 x= a 的函数值 f ( a) 比它在点 x= a 附近其他点的函数值 都小,f ′ ( a)
=0,而且在点 x= a 附近的左侧 f ′(x ) < 0,右侧 f ′(x) > 0,则把点 a 叫做 y = f ( x) 的极小值
a 的取值范围是 ________ .
解析: f ′(x) = x2+ 2x+ a,∵ f ( x ) 在 R 上没有极值点,∴Δ= 4- 4a≤0,∴ a≥ 1.
答案: a≥1 4.求函数 f ( x) =- x( x -2) 2 的极值.
解析: 函数 f ( x ) 的定义域为 R. f ( x) =- x( x2- 4x + 4) =- x3+ 4x2- 4x, ∴ f ′ ( x) =- 3x2+ 8x - 4=- ( x - 2)(3 x- 2) ,
1
a=- ,
解得
2
b=- 2. 即 f ′(x ) = 3x2- x- 2= (3 x + 2)( x - 1) .函数 f ′ ( x) ,f ( x) 的变化情况见下表:
2
2
所以函数 f ( x ) 的递增区间是 -∞,- 3 与 (1 ,+∞ ) ,递减区间是 - 3, 1 .
1. f ′(x 0) = 0 是函数 y =f ( x) 在 x = x0 处有极值点的 ( C) A.充分不必要条件 B .充要条件
点, f ( a) 叫做函数 y = f ( x) 的极小值;如果函数 y= f ( x ) 在点 x= b 的函数值 f ( b) 比它在点 x = b
附近其他点的函数值都大, f ′( b) = 0,而且在点 x= b 附近的左侧 f ′(x) > 0,右侧 f ′(x ) < 0,
2019-2020学年人教A版选修1-1 3.3.2函数的极值与导数 教案

§3.3.2函数的极值与导数一、教学目标知识与技能:理解极大值、极小值的概念;能够运用判别极大值、极小值的方法来求函数的极值;掌握求可导函数的极值的步骤;过程与方法:多让学生举命题的例子,培养他们的辨析能力;以及培养他们的分析问题和解决问题的能力;情感、态度与价值观:通过学生的参与,激发学生学习数学的兴趣。
二、教学重点难点教学重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤.教学难点:对极大、极小值概念的理解及求可导函数的极值的步骤.三、教学过程:函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的.通过研究函数的这些性质,我们可以对数量的变化规律有一个基本的了解.我们以导数为工具,对研究函数的增减及极值和最值带来很大方便.四、学情分析我们的学生属于平行分班,学生已有的知识和实验水平有差距。
需要教师指导并借助动画给予直观的认识。
五、教学方法发现式、启发式新授课教学基本环节:预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备1.学生的学习准备:2.教师的教学准备:多媒体课件制作,课前预习学案,课内探究学案,课后延伸拓展学案。
七、课时安排:1课时八、教学过程(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑,使教学具有了针对性。
提问(二)情景导入、展示目标。
设计意图:步步导入,吸引学生的注意力,明确学习目标。
1、有关概念(1).极大值:一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点(2).极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0).就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点(3).极大值与极小值统称为极值在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值请注意以下几点:(ⅰ)极值是一个局部概念由定义,极值只是某个点的函数值与它附近点的函数值比较是大或小;并不意味着它在函数的整个的定义域内最大或最小。
高中数学 3.3.2函数的极值与导数学案 新人教A版选修1-1 学案

河北省唐山市开滦第二中学高中数学 3.3.2函数的极值与导数学案 新人教A 版选修1-1【学习目标】1.理解极大值、极小值的概念;2.能够运用判别极大值、极小值的方法来求函数的极值;3.掌握求可导函数的极值的步骤. 【重点难点】 求可导函数的极值的步骤 【学习内容】 学习过程 一、课前准备复习1:设函数y=f(x) 在某个区间内有导数,如果在这个区间内0y '>,那么函数y=f(x) 在这个区间内为 函数;如果在这个区间内0y '<,那么函数y=f(x) 在为这个区间内的 函数.复习2:用导数求函数单调区间的步骤:①求函数f (x )的导数()f x '. ②令 解不等式,得x 的范围就是递增区间.③令 解不等式,得x 的范围,就是递减区间 .二、新课导学 ※ 学习探究 探究任务一:问题1:如下图,函数()y f x =在,,,,,,,a b c d e f g h 等点的函数值与这些点附近的函数值有什么关系?()y f x =在这些点的导数值是多少?在这些点附近,()y f x =的导数的符号有什么规律?看出,函数()y f x =在点x a =的函数值()f a 比它在点x a =附近其它点的函数值都 ,()f a '= ;且在点x a =附近的左侧()f x ' 0,右侧()f x ' 0. 类似地,函数()y f x =在点x b =的函数值()f b 比它在点x b =附近其它点的函数值都 ,()f b '= ;而且在点x b =附近的左侧()f x ' 0,右侧()f x '0. 新知:我们把点a 叫做函数()y f x =的极小值点,()f a 叫做函数()y f x =的极小值;点b 叫做函数()y f x =的极大值点,()f b 叫做函数()y f x =的极大值.极大值点、极小值点统称为极值点,极大值、极小值统称为极值.极值反映了函数在某一点附近的 ,刻画的是函数的 .试试:(1)函数的极值 (填“是”,“不是”)唯一的. (2) 一个函数的极大值是否一定大于极小值.(3)函数的极值点一定出现在区间的 (内,外)部,区间的端点 (能,不能)成为极值点.反思:极值点与导数为0的点的关系:导数为0的点是否一定是极值点.比如:函数3()f x x =在x=0处的导数为 ,但它 (是或不是)极值点.即:导数为0是点为极值点的 条件.※ 典型例题例1 求函数31443y x x =-+的极值.变式1:已知函数32()f x ax bx cx =++在点0x 处取得极大值5,其导函数()y f x '=的图象经过点(1,0),(2,0),如图所示,求 (1) 0x 的值(2)a ,b ,c 的值.o12 y小结:求可导函数f(x)的极值的步骤:变式2:已知函数32()3911f x x x x=--+.(1)写出函数的递减区间;(2)讨论函数的极大值和极小值,如有,试写出极值;(3)画出它的大致图象.※动手试试练1. 求下列函数的极值:(1)2()62f x x x=--;(2)3()27f x x x=-;(3)3()612f x x x=+-;(4)3()3f x x x=-. 练2. 下图是导函数()y f x'=的图象,试找出函数()y f x=的极值点,并指出哪些是极大值点,哪些是极小值点.三、总结提升※学习小结1. 求可导函数f(x)的极值的步骤;2. 由导函数图象画出原函数图象;由原函数图象画导函数图象.※知识拓展函数在某点处不可导,但有可能是该函数的极值点.由些可见:“有极值但不一定可导”课后作业1. 函数232y x x=--的极值情况是()A.有极大值,没有极小值B.有极小值,没有极大值C.既有极大值又有极小值D.既无极大值也极小值2. 三次函数当1x=时,有极大值4;当3x=时,有极小值0,且函数过原点,则此函数是()A.3269y x x x=++ B.3269y x x x=-+C.3269y x x x=-- D.3269y x x x=+-3. 函数322()f x x ax bx a=--+在1x=时有极值10,则a、b的值为()A.3,3a b==-或4,11a b=-=B .4,1a b =-=或4,11a b =-=C .1,5a b =-=D .以上都不正确4. 函数32()39f x x ax x =++-在3x =-时有极值10,则a 的值为5. 函数32()3(0)f x x ax a a =-+>的极大值为正数,极小值为负数,则a 的取值范围为6.如图是导函数()y f x '=的图象,在标记的点中,在哪一点处(1)导函数()y f x '=有极大值? (2)导函数()y f x '=有极小值?(3)函数()y f x =有极大值?(4)导函数()y f x =有极小值?7. 求下列函数的极值: (1)2()62f x x x =++;(2)3()48f x x x =-.8.已知函数2()()f x x x c =-在2x =处有极大值,求c 的值.。
高二数学,人教A版选修1-1, 3.3.2,函数的极值与导数 ,课件

思考辨析 判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打 “×”. (1)导数为0的点一定是极值点. ( ) (2)函数的极大值一定大于极小值. ( ) (3)在定义域上的单调函数一定没有极值. ( ) (4)对于任意函数,极值点处的导数值一定等于0. ( ) (5)三次函数f(x)=x3+ax2+bx+c最多有两个极值. ( ) 答案:(1)× (2)× (3)√ (4)× (5)√
(3,+∞) + 单调 递增↗
所以函数在 x=-1 处取得极大值 f(3)=-6.
14 f(-1)= ,在 3
x=3 处取得极小值
探究一
探究二
探究三
思维辨析
(2)函数定义域为 R,f'(x)=
5������ ������2 +1
'=
-5(������+1)(������-1) (������2 +1)
2
,
令 f'(x)=0 得 x=-1 或 x=1. 当 x 变化时,f'(x),f(x)的变化情况如下表: x (-∞,-1) -1 (-1,1) 1 f'(x) 0 + 0 单调 单调 f(x) 极小值 极大值 递减↘ 递增↗
5 2 5 2
(1,+∞) 单调 递减↘
所以函数在 x=-1 处取得极小值 f(-1)=- ,在 x=1 处取得极大值 f(1)= .
π 所以函数在 x= 处取得极大值 6 5π √3 5π 小值 f =- + . 6 2 12
1 2
π 6
5π 6
+ 单调
5������ ,������ 6
递增↗
【数学】3.3.2《函数的极值、最值与导数》教案(新人教A版选修1-1)

§3.3.2-3函数的极值与最大(小)值与导数【成功细节】叶枝谈导数的计算的方法本节主要研究函数的极值、最值与函数导数之间的关系,导数作为研究函数的一种重要工具,在学习时应引起充分重视,这部分知识点不多,但涉及的题型比较多,在学习过程中我认为应该注意以下几个方面的问题:(1)理解函数极值的概念,函数极值刻画的是函数的局部性质,而函数的最值刻画的是函数的整体性质;(2)注意比较极值与最值的概念以及它们之间的联系,可导函数在极值点两侧导函数的符号相反,极大值不一定是最大值,极大值可能小于极小值,连续可导函数闭区间上的最值就是端点值与极值中的最大值、最小值等结论要熟练准确记忆;(3)可导函数有极值是该点处的导数值等于零的充分不必要条件,如函数3y x =,为R 上的增函数,不存在极值点,但0|0x y ='=;(4)若函数不可导,也可能存在极值,如()||f x x =在0x =处不可导,但0x =是函数的一个极小值;(5)要熟练掌握求解函数极值与最值的方法.如本题主要考查函数在闭区间上的最值的概念以及求解方法,解题时,我先利用导数求解函数()f x 在这个区间内的极值,因为22()3123(4)f x x x '=-=-,由()0f x '=求得2x =,或2x =-,而(2)82488f =-+=-,(2)824824f -=-++=,再求出函数在闭区间上的端点值,(3)273690f -=-+=,(3)2736817f =-+=,所以函数在闭区间上的最大值等于(2)24M f =-=,最小值(2)8m f ==-,所以24(8)32M m -=--=.【高效预习】(核心栏目)“要养成学生阅读书籍的习惯就非教他们预习不可”。
——叶圣陶【精读·细化】1.用10分钟的时间详细阅读教材93~96页,理解函数极小值与极大值的概念,可导函数的导数在极值点两侧的符号同号还是异号?在函数图象上是如何体现的?函数在某点有极值与该点处的导数【领会·感悟】1.函数在某点处的导数值等于零,该点不一定是函数的极值点,必须检验函数在该点两侧的符号是否相异.如函数3()f x x =,虽(2007年江苏13题)已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,则M m -=__.2007年江苏省文科状元叶枝【学习细节】(核心栏目)A .基础知识导数的计算知识点1 函数极值与导数【情景引入】如图为表示高台跳水运动员的高度h 随时间t 变化的函数2() 4.9 6.510h t t t =-++的图象,我们发现,t a =时,高台跳水运动员距水面高度最大.那么,函数()h t 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?【探究】如图,放大t a =附近函数()h t 的图像,可以看出()h a ';在t a =,当t a <时,函数()h t 单调递增,()0h t '>;当t a >时,函数()h t 单调递减,()0h t '<;这就说明,在t a =附近,函数值先增(t a <,()0h t '>)后减(t a >,()0h t '<).这样,当t 在a 的附近从小到大经过a 时,()h t '先正后负,且()h t '连续变化,于是有()0h a '=.【关注·思考】2.阅读教材第96—98页,理解最小值和最大值的概念?这些概念与极大值或极小值有什么关系?细节提示:最值刻画的是函数在某个闭区间上的一个整体性质,而极值缺某点【提升·解决】2.最值的求解可以把所有的极值点和端点处的函数值求解出来,然后相互比较即可.【思考】 对于一般的函数()y f x =,是否也有这样的性质呢?【想一想】如图,函数()y f x =在,a b 处的函数值与这两个点附近的函数值有什么关系?()y f x =在这两个点处的导数值是多少?在这两个点附近,()y f x =的导数的符号有什么规律?【探究】 由函数图象可知,函数()y f x =在点x a =的函数值()f a 比它在点x a =附近其他点的函数值都小,()0f a '=;而且在点x a =附近左侧,()0f x '<,在点x a =附近右侧,()0f x '>.函数()y f x =在点x b =的函数值()f b 比它在点x b =附近其他点的函数值都大,()0f b '=;而且在点x b =附近左侧,()0f x '>,在点x b =附近右侧,()0f x '<.我们把图中的点a 叫做函数()y f x =的极小值点,()f a 叫做函数()y f x =的极小值;点b 叫做函数()y f x =的极大值点,()f b 叫做函数()y f x =的极大值.【总结】设函数()y f x =在点0x 附近有定义,如果对0x 附近的所有的点,都有0()()f x f x <,则称0()f x 是函数()y f x =的一个极大值,记作y 极大值=0()f x ;如果对0x 附近的所有的点,都有0()()f x f x >,则称0()f x 是函数()y f x =的一个极小值,记作y 极小值=0()f x .极大值与极小值统称为极值(extreme value ). 【想一想】如图为函数()y f x =的图象,,,,,x c d e f g =是否为函数的极值点?如果是,请分析原因,如果不是,是说明理由.【探究】由函数图象可知,函数()y f x =在点,,x c e g =的函数值(),(),()f c f e f g 比它在点,,x c e g =附近其他点的函数值都小,()()()0f c f e f g '''===;而且在这些点附近左侧,()0f x '<,在这些点附近右侧,()0f x '>,由极值的定义可知这些点为函数()y f x =的极小值点,对应的函数值(),(),()f c f e f g 为函数()y f x =的极小值;函数()y f x =在点,,x d f h =的函数值(),(),()f d f f f h 比它在点,,x g f h =附近其他点的函数值都大,()()()0f d f f f h '''====;而且在这些点附近左侧,()0f x '>,在这些点附近右侧,()0f x '<.由极值的定义可知这些点为函数()y f x =的极大值点,对应的函数值(),(),()f d f f f h 为函数()y f x =的极大值.【提示】 对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号。
人教新课标A版高二数学《选修1-1》3.3.2 函数的极值与导数

3 4
.
当x变化时,f(x),f′(x)的变化情况如下表:
x
(-∞,0)
0 0 不是 极值
3;∞) 4
f′(x)
f (x )
↘
↘
0
27 256
+ ↗
3 ) 4
由上表可知,函数f(x)在区间(-∞,0)上是减函数,在区间(0,
第三章 导数及其应用
§3.3 导数在研究函数中的应用
3.3.2 函数的极值与导数
1.了解函数极值的概念,会从几何的角度直观理 解函数的极值与导数的关系,并会灵活应用. 2.结合函数的图象,了解函数在某点处取得极值 的必要条件和充分条件.
3.会用导数求最高次幂不超过三次的多项式函数
的极大值、极小值.
题目类型一、求已知函数的极值 【技法点拨】 求函数极值的步骤 求定义域 确定函数f(x)的定义域 求导函数f′(x)
求导数
求方程的根 列表
求f′(x)在定义域内的所有根 用f′(x)=0的根将定义域分 成若干区间,列表 由各个区间内f′(x)的符号, 判断极值情况
求极值
【典例训练】(建议教师以第2题为例题重点讲解)
极值点时,函数f(x)在该区间内的极大值点与极小
值点是交替出现的.
2.极值点与导数为零的点的辨析
(1)可导函数的极值点是导数为零的点,但是导数
为零的点不一定是极值点,即“点x0是可导函数
f(x)的极值点”是“f′(x0)=0”的充分不必要条件; (2)可导函数f(x)在点x0处取得极值的充要条件是 f′(x0)=0,且在x0左侧和右侧f′(x)的符号不同. (3)如果在x0的两侧f′(x)的符号相同,则x0不是f(x) 的极值点.
人教版选修1-1 3.3.2 函数的极值与导数 导学案

3. 3. 2 《函数的极值与导数》导学案制作人侯海燕审核高二数学组 2016.03.08 【学习目标】1.了解函数极值的概念,会从几何直观理解函数极值与导数的关系,并会灵活应用.2.掌握函数极值的判定及求法.3.掌握函数在某一点取得极值的条件.【学习重点】掌握函数极值的判定及求法.【学习难点】掌握函数在某一点取得极值的条件【预习导航】函数的极值反映的是函数在某点附近的性质,是局部性质.函数极值可以在函数图象上“眼见为实”,通过研究极值初步体会函数的导数的作用【问题探究】1.极值点与极值(1)极小值点与极小值 如图,函数y =f (x )在点x =a 的函数值f (a )比它在点x =a 附近其他点的函数值都小,f ′(a )=0;而且在点x =a 附近的左侧,右侧,则把点a叫做函数y =f (x )的极小值点,f (a )叫做函数y =f (x )的极小值.2.求函数y =f (x )的极值的方法解方程f ′(x )=0,当f ′(x 0)=0时:(1)如果在x 0附近的左侧f ′(x )>0,右侧f ′(x )<0,那么f (x 0)是.(2)如果在x 0附近的左侧f ′(x )<0,右侧f ′(x )>0,那么f (x 0)是.引言 “横看成岭侧成峰,远近高低各不同”,说的是庐山的高低起伏,错落有致,在群山中,各个山峰的顶端,虽然不一定是群山的最高处,但它却是其附近的最高点.那么每个山峰附近的走势如何?与导数有什么关系?探究活动一:探究点一函数的极值与导数的关系问题1如图观察,函数y =f (x )在d 、e 、f 、g 、h 、i 等点处的函数值与这些点附近的函数值有什么关系?y =f (x )在这些点处的导数值是多少?在这些点附近,y =f (x )的导数的符号有什么规律?问题2函数的极大值一定大于极小值吗?在区间内可导函数的极大值和极小值是唯一的吗?一般地,求函数的极值的方法是:(小组讨论总结)【思考】求函数31()443f x x x =-+的极值探究活动二:若某点处的导数值为零,那么,此点一定是极值点吗?举例说明问题:思考函数f (x )的定义域为开区间(a ,b ),导函数f ′(x )在(a ,b )内的图象 如图所示,则函数f (x )在开区间(a ,b )内有个极小值点.【当堂检测】求函数3()612f x x x =+-的极值【总结概括】 本节课的收获:【课后作业】必做题:1.教材第96页练习1,22. 教材第98页习题3.3 A 组第3,4,5题.选做题:同步练习册课后作业提升习题.。
高中数学 3.3.2函数的极值与导数课件 新人教A版选修1-1

精选ppt
7
题型三 函数极值的应用
例 3 当 a 为何值时,方程 x3-3x2-a=0 恰有一个实根、两个不等实根、三个不等实 根?有没有可能无实根?
精选ppt
5
题型二 已知函数的极值求参数的
值
例 2 已知 f(x)=ax3+bx2+cx(a≠0)在 x=±1 处取得极值,且 f(1)=-1. (1)试求常数 a、b、c 的值; (2)试判断 x=±1 是函数的极大值还是极小值,并说明理由.
解析:(1)易得 f′(x)=3ax2+2bx+c,
∵x=±1 是函数的极值点,
3.3.2 函数的极值与导数
精选ppt
1
精选ppt
2
题型一 求函数的极值
例 1 求函数 f(x)=x3-12x 的极值.
解析:易知函数的定义域为 R,且 f′(x)=3x2-12=3(x+2)(x-2).
令 f′(x)=0,得 x=-2 或 x=2.
当 x 变化时,f′(x),f(x)的变化情况如下表所示:
∴x=±1 是方程 3ax2+2bx+c=0 的两根.
-23ba=0,
由根与系数的关系知:
3ca=-1,
又 f(1)=-1,∴a+b+c=-1.
联立上述三式,解得,a=12,b=0,c=-32.
(2)由(1)得,f′(x)=32x2-32=32(x+1)(x-1),
当 x<-1 或 x>1 时,f′(x)>0;当-1<x<1 时,f′(x)<0.
(新课标)高中数学《3.3.2-函数的极值与导数》课件-新人教A版选修1-1

规律方法 已知函数极值情况,逆向应用确定函数的解析式, 进而研究函数性质时注意两点: (1)常根据极值点处导数为 0 和极值两个条件列方程组,利用待 定系数法求解. (2)因为导数值等于零不是此点为极值点的充要条件,所以利用 待定系数法求解后必须验证根的合理性.
第18页,共29页。
第22页,共29页。
如图(1),此时曲线 f(x)与 x 轴恰有两个交点,即方程 f(x)=0 恰 好有两个实数根,所以 a+2=0,a=-2.(10 分) 如图(2),当极小值等于 0 时,有极大值大于 0,此时曲线 f(x) 与 x 轴恰有两个交点,即方程 f(x)=0 恰好有两个实数根,所以 a-2=0,a=2.综上,当 a=2,或 a=-2 时方程恰有两个实数 根.(12 分)
第8页,共29页。
2.极值点与导数的关系 (1)可导函数的极值点一定是导数为 0 的点,但导数为 0 的点不 一定是函数的极值点. (2)导数为 0 的点可能是函数的极值点,如 y=x2,y′(0)=0,x =0 是极小值.导数为 0 的点也可能不是函数的极值点,如 y =x3,y′(0)=0,x=0 不是极值点.
第23页,共29页。
【题后反思】 用求导的方法确定方程根的个数是一种很有效的 方法,它是通过函数的变化情况,运用数形结合的思想来确定 函数的图象与 x 轴的交点个数.
第24页,共29页。
【变式 3】 设函数 f(x)=x3-6x+5,x∈R. (1)求函数 f(x)的单调区间和极值; (2)若关于 x 的方程 f(x)=a 有三个不同的实数根,求实数 a 的取 值范围. 解 (1)f′(x)=3x2-6,令 f′(x)=0, 解得 x=- 2或 x= 2. 因为当 x> 2或 x<- 2时,f′(x)>0; 当- 2<x< 2时,f′(x)<0, 所以 f(x)的单调递增区间为(-∞,- 2),( 2,+∞); 单调递减区间为(- 2, 2).
高二数学人教A版选修1-1第三章3.3.2函数的极值与导数导学案(含答案)
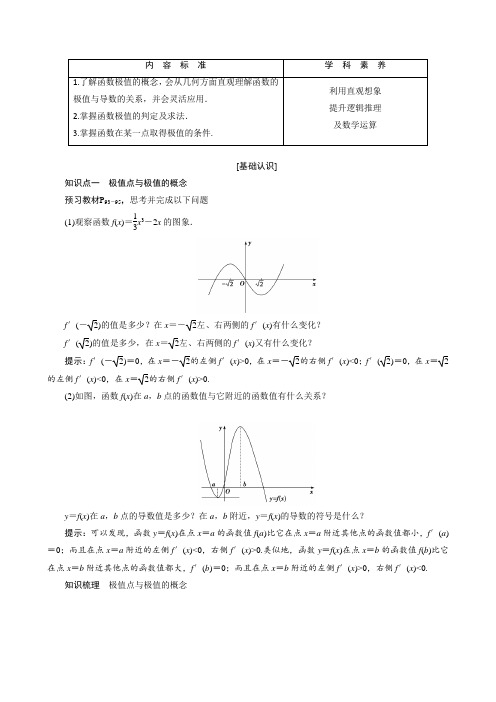
内 容 标 准学 科素 养 1.了解函数极值的概念,会从几何方面直观理解函数的极值与导数的关系,并会灵活应用. 2.掌握函数极值的判定及求法. 3.掌握函数在某一点取得极值的条件.利用直观想象 提升逻辑推理 及数学运算[基础认识]知识点一 极值点与极值的概念 预习教材P 93-95,思考并完成以下问题 (1)观察函数f (x )=13x 3-2x 的图象.f ′(-2)的值是多少?在x =-2左、右两侧的f ′(x )有什么变化? f ′(2)的值是多少,在x =2左、右两侧的f ′(x )又有什么变化?提示:f ′(-2)=0,在x =-2的左侧f ′(x )>0,在x =-2的右侧f ′(x )<0;f ′(2)=0,在x =2的左侧f ′(x )<0,在x =2的右侧f ′(x )>0.(2)如图,函数f (x )在a ,b 点的函数值与它附近的函数值有什么关系?y =f (x )在a ,b 点的导数值是多少?在a ,b 附近,y =f (x )的导数的符号是什么?提示:可以发现,函数y =f (x )在点x =a 的函数值f (a )比它在点x =a 附近其他点的函数值都小,f ′(a )=0;而且在点x =a 附近的左侧f ′(x )<0,右侧f ′(x )>0.类似地,函数y =f (x )在点x =b 的函数值f (b )比它在点x =b 附近其他点的函数值都大,f ′(b )=0;而且在点x =b 附近的左侧f ′(x )>0,右侧f ′(x )<0.知识梳理 极值点与极值的概念(1)极小值点与极小值如图,函数y =f (x )在点x =a 的函数值f (a )比它在点x =a 附近其他点的函数值都小,f ′(a )=0;而且在点x =a 附近的左侧f ′(x )<0,右侧f ′(x )>0,则把点a 叫做函数y =f (x )的极小值点,f (a )叫做函数y =f (x )的极小值.(2)极大值点与极大值如(1)中图,函数y =f (x )在点x =b 的函数值f (b )比它在点x =b 附近其他点的函数值都大,f ′(b )=0;而且在点x =b 的左侧f ′(x )>0,右侧f ′(x )<0,则把点b 叫做函数y =f (x )的极大值点,f (b )叫做函数y =f (x )的极大值.极大值点、极小值点统称为极值点,极大值和极小值统称为极值.知识点二 求函数y =f (x )的极值的方法 知识梳理 解方程f ′(x )=0,当f ′(x 0)=0时:(1)如果在x 0附近的左侧f ′(x )>0,右侧f ′(x )<0,那么f (x 0)是________. (2)如果在x 0附近的左侧f ′(x )<0,右侧f ′(x )>0,那么f (x 0)是________. 提示:(1)极大值 (2)极小值[自我检测]1.函数f (x )的定义域为R ,导函数f ′(x )的图象如图所示,则函数f (x )( )A .无极大值点,有四个极小值点B .有三个极大值点,两个极小值点C .有两个极大值点,两个极小值点D .有四个极大值点,无极小值点 答案:C2.已知函数f (x )=x +1x ,则f (x )( )A .有极大值2,极小值-2B .有极大值-2,极小值2C .无极大值,但有极小值-2D .有极大值2,无极小值 答案:B探究一极值与极值点的判断与求解[教材P98习题3.3A组4题]如图是导函数y=f′(x)的图象,在标记的点中,在哪一点处:(1)导函数y=f′(x)有极大值?(2)导函数y=f′(x)有极小值?(3)函数y=f(x)有极大值?(4)函数y=f(x)有极小值?解析:(1)点x2处f′(x)有极大值.(2)点x1、x4处f′(x)有极小值.(3)点x3处f(x)有极大值.(4)点x5处f(x)有极小值.[例1](1)已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x)()A.在(-∞,0)上为减函数B.在x=0处取极小值C.在(4,+∞)上为减函数D.在x=2处取极大值[解析]由导函数的图象可知:当x∈(-∞,0)∪(2,4)时,f′(x)>0,当x∈(0,2)∪(4,+∞)时,f′(x)<0,因此f(x)在(-∞,0),(2,4)上为增函数,在(0,2),(4,+∞)上为减函数,所以在x=0处取得极大值,在x =2处取得极小值,在x=4处取得极大值,故选C.[答案] C(2)求下列函数的极值:①f(x)=2x3+3x2-12x+1;②f(x)=x2-2ln x.[解析]①函数f(x)=2x3+3x2-12x+1的定义域为R,f′(x)=6x2+6x-12=6(x+2)(x-1),解方程6(x+2)(x-1)=0,得x1=-2,x2=1.当x变化时,f′(x)与f(x)的变化情况如下表:x (-∞,-2)-2 (-2,1) 1 (1,+∞)f ′(x ) +0 - 0 + f (x )极大值21极小值-6所以当x 当x =1时,f (x )取极小值-6.②函数f (x )=x 2-2ln x 的定义域为(0,+∞), f ′(x )=2x -2x =2(x +1)(x -1)x ,解方程2(x +1)(x -1)x =0,得x 1=1,x 2=-1(舍去).当x 变化时,f ′(x )与f (x )的变化情况如下表:x (0,1) 1 (1,+∞)f ′(x ) -0 + f (x )极小值1因此当x =1时,f (方法技巧 1.通过导函数值的正负确定函数单调性,然后进一步明确导函数图象与x 轴交点的横坐标是极大值点还是极小值点.2.求可导函数f (x )的极值的步骤 (1)确定函数的定义域,求导数f ′(x ). (2)求f (x )的拐点,即求方程f ′(x )=0的根.(3)利用f ′(x )与f (x )随x 的变化情况表,根据极值点左右两侧单调性的变化情况求极值.特别提醒:在判断f ′(x )的符号时,借助图象也可判断f ′(x )各因式的符号,还可用特殊值法判断. 跟踪探究 1.如图为y =f (x )的导函数的图象,则下列判断正确的是( )①f (x )在(-3,-1)上为增函数;②x =-1是f (x )的极小值点;③f (x )在(2,4)上为减函数,在(-1,2)上为增函数;④x =2是f (x )的极小值点.A .①②③B .②③C .③④D .①③④解析:由f ′(x )的图象知,-3<x <-1时,f ′(x )<0;f ′(-1)=0; -1<x <2时,f ′(x )>0;f ′(2)=0;2<x <4时,f ′(x )<0故f (x )在(-3,-1)和(2,4)上是减函数,在(-1,2)上是增函数,f (-1)是极小值,f (2)是极大值,所以②③正确,故选B.答案:B2.判断下列函数有无极值,如果有极值,请求出极值;如果没有极值,请说明理由. (1)y =13x 3+4;(2)y =e xx (x >0).解析:(1)f ′(x )=x 2. 令f ′(x )=0,解得x =0.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,0)0 (0,+∞)f ′(x ) + 0 + f (x )单调递增无极值单调递增(2)y ′=e x ·x -e x x 2=e x (x -1)x 2,令y ′=0,得x =1.当x 变化时,f ′(x ),f (x )的变化情况如下表:x (0,1) 1 (1,+∞)f ′(x ) - 0 + f (x )单调递减极小值单调递增探究二 利用函数极值确定参数的值[教材P 110复习参考题A 组7题]已知函数f (x )=x (x -c )2在x =2处有极大值,求c 的值.解析:∵f (x )=x 3-2cx 2+c 2x , ∴f ′(x )=3x 2-4cx +c 2.∴f ′(2)=0,即3×4-8c +c 2=0,得c =2,或c =6. 但c =2时,f (2)是极小值,不合题意,舍去,所以c =6.[例2] (1)已知函数f (x )=x 3+3ax 2+bx +a 2在x =-1处有极值0,则a =________,b =________. (2)若函数f (x )=13x 3-x 2+ax -1有极值点,则a 的取值范围为________.[解析] (1)∵f ′(x )=3x 2+6ax +b ,且函数f (x )在x =-1处有极值0,∴⎩⎪⎨⎪⎧f ′(-1)=0,f (-1)=0, 即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0,解得⎩⎪⎨⎪⎧ a =1,b =3或⎩⎪⎨⎪⎧a =2,b =9.当a =1,b =3时,f ′(x )=3x 2+6x +3=3(x +1)2≥0,此时函数f (x )在R 上为增函数,无极值,故舍去.当a =2,b =9时,f ′(x )=3x 2+12x +9=3(x +1)(x +3). 当x ∈(-∞,-3)时,f ′(x )>0, 此时f (x )为增函数;当x ∈(-3,-1)时,f ′(x )<0, 此时f (x )为减函数;当x ∈(-1,+∞)时,f ′(x )>0, 此时f (x )为增函数.故f (x )在x =-1处取得极小值, ∴a =2,b =9.(2)∵f ′(x )=x 2-2x +a ,由题意得方程x 2-2x +a =0有两个不同的实数根, ∴Δ=4-4a >0,解得a <1. [答案] (1)2 9 (2)(-∞,1)方法技巧 已知函数极值的情况,逆向应用确定函数的解析式时,应注意以下两点: (1)根据极值点处导数为0和极值两个条件列方程组,利用待定系数法求解.(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.跟踪探究 3.已知函数f (x )=ax 3+bx 2+cx (a ≠0)在x =±1处取得极值,且f (1)=-1. (1)求常数a ,b ,c 的值;(2)判断x =±1是函数的极大值点还是极小值点,试说明理由,并求出极值. 解析:(1)f ′(x )=3ax 2+2bx +c , ∵x =±1是函数f (x )的极值点,∴x =±1是方程f ′(x )=3ax 2+2bx +c =0的两根, 由根与系数的关系,得⎩⎨⎧-2b3a=0, ①c3a =-1, ②又f (1)=-1,∴a +b +c =-1.③ 由①②③解得a =12,b =0,c =-32.(2)由(1)知f (x )=12x 3-32x ,∴f ′(x )=32x 2-32=32(x -1)(x +1),当x <-1或x >1时,f ′(x )>0, 当-1<x <1时,f ′(x )<0,∴函数f (x )在(-∞,-1)和(1,+∞)上是增函数, 在(-1,1)上是减函数,∴当x =-1时,函数取得极大值f (-1)=1, 当x =1时,函数取得极小值f (1)=-1. 探究三 函数极值的综合应用[例3] 已知函数f (x )=x 3-3ax -1(a ≠0).若函数f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图象有三个不同的交点,求m 的取值范围.[解析] 因为f (x )在x =-1处取得极值且f ′(x )=3x 2-3a , 所以f ′(-1)=3×(-1)2-3a =0, 所以a =1,所以f (x )=x 3-3x -1,f ′(x )=3x 2-3, 由f ′(x )=0,解得x 1=-1,x 2=1. 当x <-1时,f ′(x )>0; 当-1<x <1时,f ′(x )<0; 当x >1时,f ′(x )>0.所以f (x )的单调增区间为(-∞,-1),(1,+∞);单调减区间为(-1,1), f (x )在x =-1处取得极大值f (-1)=1, 在x =1处取得极小值f (1)=-3. 作出f (x )的大致图象如图所示.因为直线y =m 与函数y =f (x )的图象有三个不同的交点,结合f (x )的图象可知,m 的取值范围是(-3,1). 方法技巧 利用导数可以判断函数的单调性,研究函数的极值情况,并能在此基础上画出函数的大致图象,从直观上判断函数图象与x 轴的交点或两个函数图象的交点的个数,从而为研究方程根的个数问题提供了方便.延伸探究 若本例“三个不同的交点”改为“两个不同的交点”,结果如何?改为“一个交点”呢? 解析:由本例解析可知当m =-3或m =1时,直线y =m 与y =f (x )的图象有两个不同的交点;当m <-3或m >1时,直线y =m 与y =f (x )的图象只有一个交点.跟踪探究 4.已知函数f (x )=x 3-6x 2+9x +3,若函数y =f (x )的图象与y =13f ′(x )+5x +m 的图象有三个不同的交点,求实数m 的取值范围.解析:由f (x )=x 3-6x 2+9x +3, 可得f ′(x )=3x 2-12x +9,∴13f ′(x )+5x +m =13(3x 2-12x +9)+5x +m =x 2+x +3+m ,则由题意可得x 3-6x 2+9x +3=x 2+x +3+m 有三个不相等的实根,即g (x )=x 3-7x 2+8x -m 的图象与x 轴有三个不同的交点.∵g ′(x )=3x 2-14x +8 =(3x -2)(x -4),∴令g ′(x )=0,得x =23或x =4.当x 变化时,g (x ),g ′(x )的变化情况如下表:则函数g (x )的极大值为g ⎝⎛⎭⎫23=6827-m ,极小值为g (4)=-16-m . ∵由y =f (x )的图象与y =13f ′(x )+5x +m 的图象有三个不同交点,得⎩⎪⎨⎪⎧g ⎝⎛⎭⎫23=6827-m >0,g (4)=-16-m <0, 解得-16<m <6827.即m 的取值范围为⎝⎛⎭⎫-16,6827.[课后小结](1)在极值的定义中,取得极值的点称为极值点,极值点指的是自变量的值,极值指的是函数值. (2)函数的极值是函数的局部性质.可导函数f (x )在点x =x 0处取得极值的充要条件是f ′(x 0)=0且在x =x 0两侧f ′(x )符号相反.(3)利用函数的极值可以确定参数的值,解决一些方程的解和图象的交点问题.[素养培优]1.误把导函数的零点当作函数的极值点求函数f (x )=x 4-x 3的极值,并说明是极小值还是极大值.易错分析 本题易错将导数为零的点都认为是极值点,其实不然,导数为零仅是零点是极值点的必要不充分条件,错解中还有一个误区就是认为极大值一定大于极小值.事实上,极值仅描述函数在该点附近的局部特征,极大值未必一定大于极小值.考查逻辑推理及数学运算.自我纠正 f ′(x )=4x 3-3x 2,令f ′(x )=0, 即4x 3-3x 2=0时,得x 1=0,x 2=34.当x 变化时,f (x ),f ′(x )的变化情况如下表:由上表可知函数f (x )在区间(-∞,0)上是减函数,在区间⎝⎛⎭⎫0,34上还是减函数,所以x =0不是函数的极值点,而函数f (x )在区间⎝⎛⎭⎫0,34上是减函数,在区间⎝⎛⎭⎫34,+∞上是增函数,所以函数f (x )在x =34处取得极小值,极小值为-27256.2.误把切点当作函数的极值点已知函数f (x )=ax 4+bx 2+c 的图象经过点(0,1),且在x =1处的切线方程是y =x -2,求f (x )的解析式. 易错分析 本题错在将切点当做极值点,得到f ′(1)=0的错误结论.其实,虽然切点和极值点都与导数有关,但它们却是两个完全不同的概念,不能混为一谈.考查逻辑推理及数学运算的学科素养.自我纠正 f ′(1)表示函数f (x )的图象在点(1,-1)处的切线斜率,应有f ′(1)=1,再联立f (0)=1,f (1)=-1便可得到正确答案:a =52,b =-92,c =1,因此f (x )=52x 4-92x 2+1.。
高中数学 3.3.2函数的极值与导数教案 新人教A版选修1-1

3.3.2函数的极值与导数教学重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤. 教学难点:对极大、极小值概念的理解及求可导函数的极值的步骤. 教学过程: 创设情景观察图3.3-8,我们发现,t a =时,高台跳水运动员距水面高度最大.那么,函数()h t 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?放大t a =附近函数()h t 的图像,如图3.3-9.可以看出()h a ';在t a =,当t a <时,函数()h t 单调递增,()0h t '>;当t a >时,函数()h t 单调递减,()0h t '<;这就说明,在t a =附近,函数值先增(t a <,()0h t '>)后减(t a >,()0h t '<).这样,当t 在a 的附近从小到大经过a 时,()h t '先正后负,且()h t '连续变化,于是有()0h a '=.对于一般的函数()y f x =,是否也有这样的性质呢?附:对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号 新课讲授 一、导入新课观察下图中P 点附近图像从左到右的变化趋势、P 点的函数值以及点P 位置的特点xo函数图像在P 点附近从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),在P 点附近,P 点的位置最高,函数值最大 二、学生活动学生感性认识运动员的运动过程,体会函数极值的定义. 三、数学建构极值点的定义:观察右图可以看出,函数在x =0的函数值比它附近所有 各点的函数值都大,我们说f (0)是函数的一个极大值;函数在x =2的函数值比它附近所有各点的函数值都小,我们说f (2)是函数的一个极小值。
人教版高中数学选修(1-1)-3.3《函数的极值与导数》教学设计

3.3.2 函数的极值与导数(周雪敏)一、教学目标1.核心素养通过学习函数的极值与导数,形成基本的数学抽象、逻辑推理和数学运算能力,并依据运算法则解决数学问题.2.学习目标(1)理解函数极值的概念.(2)理解函数极值与导数的关系.(3)掌握求函数极值的方法,并能应用极值解决求参数值、参数取值范围、判断函数零点的个数等问题.3.学习重点极大、极小值的概念和判别方法,以及求可导函数的极值的步骤.4.学习难点函数在某一点取得极值的必要条件与充分条件.二、教学设计(一)课前设计1.预习任务任务1在群山之中,各个山峰的顶端,虽然不一定是群山之中的最高处,但它却是其附近点的最高点.同样,各个谷底虽然不一定是群山之中的最低处,但它却是其附近点的最低点.假设如图是群山中各个山峰的一部分图像,观察如图中P 点附近图像从左到右的变化趋势,P 点的函数值以及点P 位置各有什么特点.想一想:图中P 点,Q 点的函数值与其附近的函数值有何关系?任务2预习教材P93—P96,完成P96相应练习题,并找出疑惑之处.2.预习自测1.已知0)(0='x f ,则下列结论中正确的是( )A.0x 一定是极值点B.如果在0x 附近的左侧0)(0>'x f ,右侧0)(0<'x f ,那么)(0x f 是极大值C.如果在0x 附近的左侧0)(0>'x f ,右侧0)(0<'x f ,那么)(0x f 是极小值D.如果在0x 附近的左侧0)(0<'x f ,右侧0)(0>'x f ,那么)(0x f 是极大值 解:B 直接根据极值概念判断,也可画出图象进行分析 .2.函数23bx ax y +=取得极大值和极小值时的x 的值分别为0和31,则( ) A.02=-b a B.02=-b a C.02=+b a D.02=+b a解:D bx ax y 232+=',据题意,0和31是方程0232=+bx ax 的两根,∴3132=-a b ,∴02=+b a . 3.若函数m x x y ++-=236的极大值为13,则实数=m .解:19- x x y 1232+-=',由0='y ,得0=x 或4=x ,容易得出当4=x 时函数取得极大值,所以1342643=+⨯+-m ,解得19-=m .4.若kx x y +=3在R 上无极值,则k 的取值范围为 .解:),0[+∞ k x y +='23,∵kx x y +=3在R 上无极值,∴0≥'y 恒成立,∴),0[+∞∈k .(二)课堂设计1.知识回顾⑴常见函数的导数公式及导数的四则运算法则.⑵函数的导数与函数的单调性的关系.⑶用导数求函数单调区间的步骤.2.问题探究问题探究一 函数极值的概念 ●活动一 探求新知如图观察,函数)(x f y =在d 、e 、f 、g 、h 、i 等点处的函数值与这些点附近的函数值有什么关系?如:以d 、e 两点为例,函数)(x f y =在点d x =处的函数值)(d f 比它在点d x =附近其他点的函数值都小;函数)(x f y =在点e x =处的函数值)(e f 比它在e x =附近其他点的函数值都大.探究:)(x f y =在这些点处的导数值是多少?在这些点附近,y =f(x)的导数的符号有什么规。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
甘肃省金昌市第一中学2014年高中数学 3.3.2函数的极值与导数教案 新
人教A 版选修
1-1
教学重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤. 教学难点:对极大、极小值概念的理解及求可导函数的极值的步骤. 教学过程: 创设情景
观察图3.3-8,我们发现,t a =时,高台跳水运动员距水面高度最大.那么,函数()h t 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?
放大t a =附近函数()h t 的图像,如图3.3-9.可以看出()h a ';在t a =,当t a <时,函数()h t 单调递增,()0h t '>;当t a >时,函数()h t 单调递减,()0h t '<;这就说明,在t a =附近,函数值先增(t a <,()0h t '>)后减(t a >,()0h t '<).这样,当t 在a 的附近从小到大经过a 时,
()h t '先正后负,且()h t '连续变化,于是有()0h a '=.
对于一般的函数()y f x =,是否也有这样的性质呢?
附:对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号 新课讲授 一、导入新课
观察下图中P 点附近图像从左到右的变化趋势、P 点的函数值以及点P 位置的特点
o
函数图像在P 点附近从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),
在P 点附近,P 点的位置最高,函数值最大 二、学生活动
学生感性认识运动员的运动过程,体会函数极值的定义. 三、数学建构
极值点的定义:
观察右图可以看出,函数在x =0的函数值比它附近所有 各点的函数值都大,我们说f (0)是函数的一个极大值;函数在x =2的函数值比它附近所有各点的函数值都小,我们说
f (2)是函数的一个极小值。
一般地,设函数)(x f y =在0x x =及其附近有定义,如果)(0x f 的值比0x 附近所有各点的函数值都大,我们说 f (0x )是函数
)(x f y =的一个极大值;如果)(0x f 的值比0x 附近所有各点的函数
值都小,我们说f (0x )是函数)(x f y =的一个极小值。
极大值与极小值统称极值。
取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值。
请注意以下几点:(让同学讨论)
(ⅰ)极值是一个局部概念。
由定义可知极值只是某个点的函数值与它附近点的函数值比较是
最大或最小。
并不意味着它在函数的整个的定义域内最大或最小。
(ⅱ)函数的极值不是唯一的。
即一个函数在某区间上或定义域内极大值或极小值可以不止一
个。
(ⅲ)极大值与极小值之间无确定的大小关系。
即一个函数的极大值未必大于极小值,如下图
所示,x 是极大值点,4x 是极小值点,而)(4x f >)(1x f 。
(ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。
而使函数取得最大
极值点与导数的关系:
复习可导函数在定义域上的单调性与导函数值的相互关系,引导学生寻找函数极值点与导数之间的关系.
由上图可以看出,在函数取得极值处,如果曲线有切线的话,则切线是水平的,从而有0)(='x f 。
但反过来不一定。
若寻找函数极值点,可否只由)(x f '=0求得即可?
探索:x =0是否是函数)(x f =x 3
的极值点?(展示此函数的图形)
在0=x 处,曲线的切线是水平的,即)(x f '=0,但这点的函数值既不比它附近的点的函数值大,
也不比它附近的点的函数值小,故不是极值点。
如果0x 使0)(0='x f ,那么0x 在什么情况下是的极值点呢?
观察下左图所示,若0x 是)(x f 的极大值点,则0x 两侧附近点的函数值必须小于)(0x f 。
因此,0x 的左侧附近)(x f 只能是增函数,即0)(>'x f ,0x 的右侧附近)(x f 只能是减函数,即0)(<'x f ,同理,如下右图所示,若0x 是极小值点,则在0x 的左侧附近)(x f 只能是减函数,即0)(<'x f ,在0x 的右侧附近)(x f 只能是增函数,即0)(>'x f ,
的关系):
若0x 满足0)(0='x f ,且在0x 的两侧)(x f 的导数异号,则0x 是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在0x 两侧满足“左正右负”,则0x 是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在0x 两侧满足“左负右正”,则0x 是)(x f 的极小值点,)(0x f 是极小值。
结论:0x 左右侧导数异号
0 是函数f(x)的极值点)(0x f '=0
反过来是否成立?各是什么条件?
点是极值点的充分不必要条件是在这点两侧的导数异号;点是极值点的必要不充分条件是在这点的导数为0. 学生活动
函数y =f (x )的导数y /与函数值和极值之间的关系为(D )
A 、导数y /由负变正,则函数y 由减变为增,且有极大值
B 、导数y /由负变正,则函数y 由增变为减,且有极大值
C 、导数y /由正变负,则函数y 由增变为减,且有极小值
D 、导数y /由正变负,则函数y 由增变为减,且有极大值四、数学应用
例1.(课本例4)求()3
1443
f x x x =
-+的极值 解: 因为()3
1443
f x x x =
-+,所以 ()'
2
4(2)(2)f x x x x =-=-+。
()'0,2,2f x x x ===-
下面分两种情况讨论: (1)当()'
f
x >0,即2x >,或2x <-时;
3,3-==b a (2)当()'
f
x <0,即22x -<<时.
当x 变化时, ()'
f
x ,()f x 的变化情况如下表:
x
(),2-∞
-2 (-2,2) 2 ()2,+∞
y '
+ 0 -
0 +
y
↗
极大值
283
↘
极小值43
-
↗
因此,当2x =-时,()f x 有极大值,并且极大值为28(2)3
f -=; 当2x =时,()f x 有极小值,并且极小值为4(2)3
f =-。
函数()3
1443
f x x x =-+的图像如图所示。
课堂训练:求下列函数的极值
让学生讨论总结求可导函数的极值的基本步骤与方法:
一般地,如果函数)(x f y =在某个区间有导数,可以用下面方法求它的极值:
① 确定函数的定义域; ② 求导数)(x f '; ③ 求方程)(x f '=0的根,这些根也称为可能极值点;
④ 检查)(x f '在方程)(x f '=0的根的左右两侧的符号,确定极值点。
(最好通过列表法) 强调:要想知道 x0是极大值点还是极小值点就必须判断 f '(x0)=0左右侧导数的符号 例题2(案例分析) 函数
223)(a bx ax x x f +--= 在 x=1 时有极值10,则a ,b 的值为(C )
A 、 或
B 、 或
x
x y +=11)(16128223++=x x x y -)(11,4=-=b a 1,4=-=b a 11,4=-=b a 11
,4=-=b a
C 、
D 、 以上都不对
略解:由题设条件得: 解之得
通过验证,都合要求,故应选择A
上述解法错误,正确答案选C ,注意代入检验 注意:f /(x 0)=0是函数取得极值的必要不充分条件 练习: 庖丁解牛篇(感受高考)
1、(2006年天津卷)函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( A ) A .1个 B .2个 C .3个 D . 4个
注意:数形结合以及原函数与导函数图像的区别 2、已知函数32
()f x ax bx cx =++在点0x
5,其导函数'()y f x =的图象经过点(1,0)
,(2,0).求:
(Ⅰ)0x 的值; (Ⅱ),,a b c 的值. 答案 (Ⅰ)0x =1; (Ⅱ)2,9,12a b c ==-=
例3求y =(x 2-1)3+1的极值
解:y ′=6x (x 2-1)2=6x (x +1)2(x -1)2 令y ′=0解得x 1=-1,x 2=0,x 3=1
当x 变化时,y ′,y 的变化情况如下表
x
()
,1-∞- -1 (-1,0) 0 (0,1) 1
()1,+∞
y '
- 0 - 0 + 0 + y
↘
无极值
↘
极小值0
↗
无极值
↗
∴当x =0时,y 有极小值且y 极小值=0
⎩⎨⎧==0)1(10)1(/f f ⎩⎨⎧=--=+--∴0231012b a a b a ⎩⎨⎧⎩⎨⎧=-=-==11433b a b a 或。
