关于相关回归和时间序列分析__时间序列 by 幽梦幺
时间序列分析和自回归模型的基础原理

时间序列分析和自回归模型的基础原理时间序列分析是一种用来研究一系列按照时间顺序排列的数据的统计方法。
它的目的是通过分析过去的数据来预测未来的趋势。
时间序列分析在经济学、金融学、气象学等领域都有广泛的应用。
本文将介绍时间序列分析的基本概念和自回归模型的基础原理。
时间序列是指按照时间顺序排列的一系列数据观测值。
比如,我们可以记录每天的气温变化、每月的销售额、每年的人口增长率等等。
时间序列分析的目标是探索数据背后的规律,以便作出准确的预测。
时间序列分析的基本原理之一是趋势分析,它用来描述数据的长期趋势。
趋势分析的方法包括移动平均法和指数平滑法。
移动平均法是通过计算一定时间段内观测值的平均值来平滑数据,以便观察数据的长期趋势。
指数平滑法则增加了对新数据的权重,以使得较新的观测值对预测结果的影响更大。
另一个重要的时间序列分析方法是季节性分析,它用来描述数据的季节性变化。
季节性分析的方法包括季节性指数法和周期性波动法。
季节性指数法是通过计算不同季节的平均值与总体平均值的比值来衡量数据的季节性变化。
周期性波动法则是通过拟合周期性函数来描述数据的季节性变化。
自回归模型是时间序列分析中常用的模型之一。
自回归模型基于观测值之间的自相关性来进行预测。
自回归模型的基本原理是当前观测值可以通过过去观测值的线性组合来表示。
自回归模型的阶数表示过去观测值的个数,它决定了模型的复杂程度。
自回归模型可以用来分析数据的趋势、季节性和随机性。
自回归模型的建立过程包括模型的选择、参数的估计和模型的验证。
模型的选择通常需要根据数据的性质和特点来确定。
参数的估计可以使用最小二乘法、极大似然估计法等方法。
模型的验证是用来评估模型的拟合效果和预测准确度的。
时间序列分析和自回归模型的基础原理为我们提供了一种有效的方式来理解和预测时间序列数据。
通过对数据的趋势、季节性和自相关性的分析,我们能够做出准确的预测,并做出相应的决策。
时间序列分析和自回归模型的应用范围广泛,可以帮助我们在经济、金融、气象等领域做出更好的决策。
回归分析与时间序列分析

回归分析与时间序列分析回归分析和时间序列分析是统计学中两个重要的分析方法。
两者在不同的背景和目的下使用,可以互相补充,帮助我们更好地理解和预测数据的变化趋势。
一、回归分析回归分析是一种用来研究因变量和自变量之间关系的统计方法。
它通过寻找一条最佳拟合曲线来描述自变量对因变量的影响程度。
回归分析可分为简单线性回归和多元线性回归两种。
简单线性回归是当只有一个自变量和一个因变量时的回归分析。
在该方法中,我们假设自变量和因变量之间存在线性关系,并通过计算最小二乘法来确定拟合直线的斜率和截距。
此外,还可以通过回归系数来评估自变量与因变量之间的相关性强度。
多元线性回归是当存在多个自变量和一个因变量时的回归分析。
与简单线性回归相比,多元线性回归考虑了多个自变量对因变量的影响。
通过最小二乘法,我们可以估计每个自变量对因变量的贡献,并且可以检验自变量的组合是否对因变量有显著影响。
二、时间序列分析时间序列分析是一种用来分析时间相关数据的统计方法。
它通过观察数据在时间上的变化来预测未来的趋势和模式。
时间序列可以分为平稳和非平稳两种类型。
平稳时间序列是指时间序列的均值和方差在时间上保持不变。
我们可以使用自相关函数(ACF)和偏自相关函数(PACF)来帮助我们识别数据的自相关性,并建立相应的时间序列模型,例如自回归移动平均模型(ARMA)。
非平稳时间序列是指时间序列的均值和方差在时间上发生变化。
我们可以使用差分操作来将非平稳时间序列转化为平稳时间序列,然后应用平稳时间序列的方法进行分析。
常见的非平稳时间序列模型有自回归积分移动平均模型(ARIMA)和季节性自回归积分移动平均模型(SARIMA)。
三、回归分析与时间序列分析的应用回归分析和时间序列分析都广泛应用于各个领域的研究和实践中。
在经济学领域,回归分析和时间序列分析可以帮助我们分析经济指标之间的关系,预测经济趋势,并制定相应的政策措施。
在市场营销领域,回归分析和时间序列分析可以帮助我们理解消费者行为、市场需求和产品销售趋势,从而优化营销策略。
Matlab中的回归分析与时间序列预测

Matlab中的回归分析与时间序列预测引言:在现代数据分析中,回归分析和时间序列预测是两个重要且广泛应用的领域。
Matlab作为一款功能强大的数学软件,在回归分析和时间序列预测方面提供了丰富的工具和函数,使得实现这些分析变得更加简单和高效。
本文将介绍Matlab中回归分析和时间序列预测的相关知识和方法,并结合实例进行说明。
一、回归分析回归分析是通过寻找自变量与因变量之间的关系,来推测未来观测值的一种分析方法。
在Matlab中,可以通过使用regress函数进行回归分析。
该函数可以拟合线性回归模型,并返回各个回归系数的估计值以及回归模型的统计信息。
下面我们以一个简单的例子来说明如何使用Matlab进行回归分析。
实例1:房价预测假设我们有一组数据,其中包含了房屋的面积和对应的售价。
我们希望通过房屋的面积来预测未来房价。
首先,我们需要导入数据并进行预处理。
```matlabdata = load('house_data.csv'); % 导入数据X = data(:, 1); % 提取面积作为自变量y = data(:, 2); % 提取房价作为因变量```接下来,我们可以使用regress函数进行回归分析,并得到回归系数的估计值。
```matlab[B, BINT, R, RINT, STATS] = regress(y, [ones(size(X)) X]); % 回归分析```其中,B为回归系数的估计值,BINT为回归系数的置信区间,R为残差,RINT为残差的置信区间,STATS为回归模型的统计信息。
我们可以打印出回归系数的估计值,以及回归模型的统计信息。
```matlabdisp('回归系数的估计值:');disp(B);disp('回归模型的统计信息:');disp(STATS);```运行以上代码,我们可以得到回归模型的结果。
通过回归系数的估计值,我们可以得到回归方程为y = B(1) + B(2) * X,其中B(1)为截距,B(2)为斜率。
时间序列预测与回归分析模型

时间序列预测与回归分析模型时间序列预测是一种基于时间数据的分析方法,用于预测未来的数值、趋势和季节性。
时间序列预测的基本原理是根据历史数据的观察和模式,构建一个数学模型来预测未来的数值。
该方法广泛应用于金融市场预测、经济趋势分析、气象预报等领域。
时间序列预测的主要优点是可以捕捉到数据中的趋势和季节性,对于周期性变化较为准确。
然而,时间序列预测的一个主要缺点是需要大量的历史数据来进行建模和预测,对于短期数据或变异性较大的数据不太适用。
回归分析是一种用于推断变量之间关系的统计方法。
回归分析的基本原理是通过建立一个数学模型,来描述自变量和因变量之间的关系,并用该模型来预测未来的数值。
回归分析的应用领域非常广泛,包括经济学、社会学、医学等领域。
回归分析的主要优点是可以利用更多的变量进行建模,对于多变量关系的推断更为准确。
然而,回归分析的一个主要缺点是对于数据中存在的非线性关系的拟合不够准确,需要对数据进行转换或引入更高阶的变量。
时间序列预测和回归分析在应用中常常被同时使用。
例如,在金融市场预测中,可以使用时间序列预测方法来预测未来的股价趋势,然后使用回归分析方法来推断股价与其他变量(如利率、通胀率等)之间的关系。
这种结合使用的方法可以更全面地分析和预测数据。
总之,时间序列预测和回归分析是两种不同的统计建模方法,用于预测未来的趋势和推断变量之间的关系。
时间序列预测主要适用于具有周期性和趋势性的数据,需要较长时间的历史数据支持。
而回归分析可以更好地处理多变量关系,但对于非线性关系的拟合可能不够准确。
在实际应用中,可以根据数据的特点和分析目的选择合适的方法,或者结合两种方法来进行更全面和准确的分析。
时间序列预测与回归分析模型

时间序列预测与回归分析模型
时间序列预测与回归分析模型是统计学中用于预测或描述随时间变化的变量或事件的基本技术。
时间序列预测通常涉及预测未来其中一时刻变量和事件的发展情况。
它也可以提供对事件发展趋势和结果的有用指导。
时间序列预测模型是预测未来的一种有效方法,其中采用数学预测技术和数据分析方法来预测以前发生的或未发生的事件。
时间序列模型有很多种,但它们都具有共同的目标,即从已知的历史数据中寻找可预测的规律以及拟合未来的变量。
一般来说,这些模型分为两类:统计模型和机器学习模型。
统计模型是基于时间序列数据建立的简单的数学模型,它们可以解释过去的变量和变化以及估计未来的趋势。
机器学习模型是基于历史数据的复杂机器学习模型,它们可以自动识别时间序列上的模式,并预测未来的变化趋势。
时间序列预测模型也可以应用于回归分析,即使用统计技术来研究两变量之间的关系,以推断出一个变量影响另一个变量的大小和方向。
最常见的时间序列回归模型包括线性回归模型、自回归模型(AR)、移动平均模型(MA)和自回归移动平均模型(ARMA)。
线性回归模型是最简单的回归模型,它用一条直线来拟合数据。
相关分析、回归分析、时间序列分析

1.2 相关分析类型和运用
1.2.1 皮尔逊相关(Pearson)直线相关
1. 定义: Pearson相关 (积差相关)是英国统计学家皮尔逊于20世纪初提出的一 种计算相关的方法。是一种运用较为普遍的计算相关系数的方法,也 是揭示两个变量线性相关方向和程度最常用和最基本的方法。
1.2.3 肯得尔相关(Kendall)等级相关
分析两个变量之间的相关,也可以用Kendall等级相关分析法。用一 个统计量来衡量以一个变量的等级为标准时,另一个变量的等级与它 不一致的情况。
不仅可以对两个变量作等级相关分析,还可以对多个变量作等级相关 分析。
Kendall等级相关系数也在-1与1之间变动。当 =0时,表示两变
(Pi P )(Qi Q ) (Pi P )2 (Qi Q )2
1.2 相关分析类型和运用 1.2.2 斯皮尔曼相关(Spearman)秩相关
4. Spearman相关系数ρ的假设检验: (1)当n≤50时,查“rs界值表” (2)当n>50时,用 t 检验
t检验法
1.2 相关分析类型和运用
1.1 认识相关关系 1.1.4 研究相关关系的工具:
1.1 认识相关关系 1.1.4 研究相关关系的工具:
散点图
(a)完全正相 (b)完全负相关 (c)无相关关系 关
(d)非线性关系 (e)正相关
(f)负相关
对不同类型的变量应采用不同的相关系数来度量。
双变量关系强度测量的主要指标 定类
定序
定类
Classical Statistical Analysis Method I
Correlation analysis,analysis of regression,analysis of time series
相关回归分析以及时间序列分析
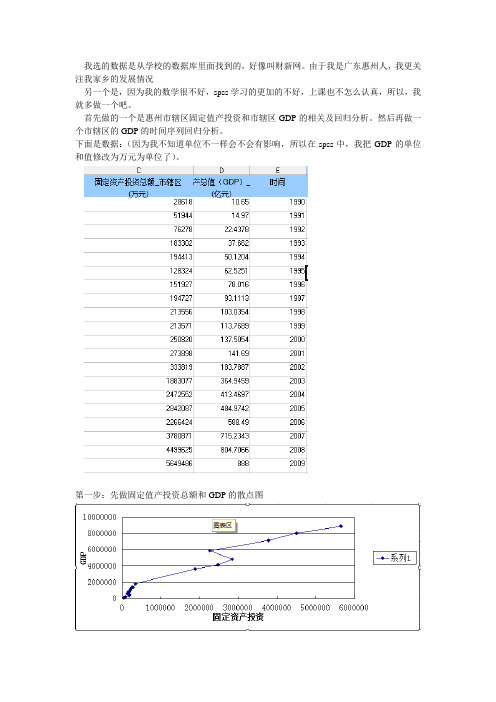
我选的数据是从学校的数据库里面找到的,好像叫财新网。
由于我是广东惠州人,我更关注我家乡的发展情况另一个是,因为我的数学很不好,spss学习的更加的不好,上课也不怎么认真,所以,我就多做一个吧。
首先做的一个是惠州市辖区固定值产投资和市辖区GDP的相关及回归分析。
然后再做一个市辖区的GDP的时间序列回归分析。
下面是数据:(因为我不知道单位不一样会不会有影响,所以在spss中,我把GDP的单位和值修改为万元为单位了)。
第一步:先做固定值产投资总额和GDP的散点图从图像中,我们是可以看到,这两者之间是有相关关系的。
当然,目前还不知道是线性的还是非线性的。
上面的情况中,只有06年的固定资产投资总额是出现了异常的。
由于数据有限,加能力有限,所以,就做一个简单相关分析。
我个人的认为是,GDP的会受到固定资产投资总额的影响,即前者是因变量,后者是自变量,而且从图上来看,两者大致呈直线分布。
可以看出GDP和固定资产投资总额的相关系数为0.980,对相关系数检验双侧的p值小于0.01,所以可以认为GDP和固定资产投资总额之间有非常密切的关系,而且随着固定资产投资总额的增加,GDP也会增加。
下面做回归分析。
从第二张表中可以看出,R的值与相关分析中的是一样的,都是0.980.从第三张表中可以看到,F值为444.008,P值小于0.05,说明该模型是有意义的,由于只有一个自变量,等价于说回归系数是有统计意义的。
从第四张表中,(这是最重要的一张了)可以看到,常量a=579259.759,b=1.616;所以大概可以得到回归方程为下面来验证一下这个方程的准确性如何。
我用2002年的数据来计算,得到的当年GDP大约为193亿,实际约为183亿,误差为10亿。
用2005年的数据得到的GDP大约为517亿,而时间为484亿,有33亿的误差,是否有特殊异常值导致了误差比较大呢?我把2006年的数据剔除了(老师你说不能剔除异常数据,但是我高中学的书上都是说某些异常数据是要剔除掉的)。
时间序列分析模型与回归分析模型算法说明

时间序列分析模型与回归分析模型算法说明本次模型采用时间序列分析模型与回归分析模型进行组合训练,以此来对经济指标进行时间序列预测发现其自身的规律性,据此预测未来一段时间内经济数据的变化。
同时采用回归分析对经济指标间的相关性进行分析,确定指标间的函数变动,探究指标之间的联系。
一、回归分析线性回归和逻辑回归通常是人们学习预测模型的第一个算法。
由于这二者的知名度很大,许多分析人员以为它们就是回归的唯一形式了。
而了解更多的学者会知道它们是所有回归模型的主要两种形式。
事实是有很多种回归形式,每种回归都有其特定的适用场合。
在这篇文章中,我将以简单的形式介绍7 中最常见的回归模型。
通过这篇文章,我希望能够帮助大家对回归有更广泛和全面的认识,而不是仅仅知道使用线性回归和逻辑回归来解决实际问题。
1. 什么是回归分析?回归分析是一种预测建模技术的方法,研究因变量(目标)和自变量(预测器)之前的关系。
这一技术被用在预测、时间序列模型和寻找变量之间因果关系。
例如研究驾驶员鲁莽驾驶与交通事故发生频率之间的关系,就可以通过回归分析来解决。
回归分析是进行数据建模、分析的重要工具。
下面这张图反映的是使用一条曲线来拟合离散数据点。
其中,所有离散数据点与拟合曲线对应位置的差值之和是被最小化了的,更多细节我们会慢慢介绍。
2. 为什么使用回归分析?如上面所说,回归分析能估计两个或者多个变量之间的关系。
下面我们通过一个简单的例子来理解:比如说,你想根据当前的经济状况来估计一家公司的销售额增长。
你有最近的公司数据,数据表明销售增长大约是经济增长的2.5 倍。
利用这种洞察力,我们就可以根据当前和过去的信息预测公司未来的销售情况。
使用回归模型有很多好处,例如:揭示了因变量和自变量之间的显著关系揭示了多个自变量对一个因变量的影响程度大小回归分析还允许我们比较在不同尺度上测量的变量的影响,例如价格变化的影响和促销活动的数量的影响。
这样的好处是可以帮助市场研究者/ 数据分析家/ 数据科学家评估选择最佳的变量集,用于建立预测模型。
时间序列回归

SARIMAX模型
01
SARIMAX模型是SARIMA模型的扩展,在SARIMA的基础 上引入外部解释变量(X)。
02
SARIMAX模型允许在预测时间序列时考虑外部因素的影响, 提高了模型的预测精度和解释能力。
03
在选择合适的SARIMAX模型时,需要确定外部解释变量的影 响方式和滞后阶数,以使模型能够更好地拟合和预测时间序列
气象预测
用于预测气温、降雨量、风速等气象指标。
时间序列回归的基本假设
线性关系
因变量与自变量之间存在线性关系,即它们 之间的关系可以用直线或曲线表示。
无自相关性
误差项之间没有自相关性,即误差项之间相 互独立。
平稳性
时间序列数据没有明显的趋势和季节性变化, 即数据的统计特性不随时间而变化。
同方差性
误差项的方差恒定,即方差不随时间而变化。
非线性趋势
对于非线性时间序列数据,可以使用 非线性回归模型来预测未来趋势,例 如指数回归、多项式回归等。
预测季节性变化
季节性自回归积分滑动平均模型(SARIMA)
适用于具有季节性特征的时间序列数据,通过季节性自回归和积分滑动平均来捕捉季节性变化规律,预测未来季 节性变化。
循环神经网络(RNN)
对于具有周期性特征的时间序列数据,可以使用循环神经网络进行预测,能够捕捉时间序列中的长期依赖关系。
时间序列回归
• 时间序列回归简介 • 时间序列回归模型 • 时间序列回归的参数估计与优化 • 时间序列回归的评估与诊断 • 时间序列回归的预测与决策 • 时间序列回归的案例分析
目录
01
时间序列回归简介
定义与概念
定义
时间序列回归是一种统计方法,用于 分析时间序列数据中两个或多个变量 之间的关系。它基于历史数据预测未 来的趋势和变化。
回归-时间序列判别分析

所以我们可以得到回归方程
Y=1.588X1+0.563X2+4.407
所以我们就可以根据x1、x2的值来预测 销量y。
由上面的回归方程我们可以看到x2的 系数靠近0,也就是说其实销量Y的值跟x2 的线性关系不是那么明显的,即说明这个 回归方程式可以改进的,其实我们可以从y 跟x2的散点图在x2=6.5的时候是有一定的 弯曲的,所以我们对模型进行改进
牙膏销售量与销售价格、广告费用等数据
首先在spss中导入数据,由于差价是根据厂家自己定 价和其他厂家平均价决定的,所有灵活性更好,将差价作 为x1,将广告费作为x2,销量作为y。在spss中画出y与x1 的散点图。以便我们观察y与x1的关系。
由图中我们大致可以看出差价x1与销量y是线性关系。 画出y与x2的散点图,
1 1 n
( x0 x )2
n
,
( xi x )2
i 1
yˆ0 ˆet1 (n 2) 2
1 1 n
( x0 x )2
n
]
( xi x )2
i 1
用最小二乘法寻找参数 0,1 的估计值,使离差平方和达极小
n
n
Q(ˆ0, ˆ1)
i 1
( yi
ˆ0
ˆ1xi )2
min 0 ,1
回归分析 时间序列
判别分析
回归分析
是由一个(或一组)非随机变量来估计或预测某 一个随机变量的观测值时,所建立的数学模型和 所进行的统计分析,称为回归分析。如果这个模 型是线性的,就称为线性回归分析。研究两个变 量间的相关关系的回归分析,称为一元回归分析 。
一元线性回归模型
在一元回归分析里,我们要考察的是随机变
x2:人均国有经济单位职工工资
关于时间序列分析

关于时间序列分析时间序列分析是一种用于分析时间序列数据的统计方法。
时间序列数据是按照时间顺序排列的观测结果,可以是连续的或离散的。
时间序列分析是一种重要的技术,可以用于很多领域,例如经济学、金融学、气象学等。
它可以揭示时间序列数据的变化规律、趋势和季节性,为预测未来发展趋势提供依据。
时间序列分析的目标是研究时间序列数据的内在结构,以便进行预测和解释。
其核心是确定数据中的趋势、周期和随机成分。
趋势表示时间序列的长期变化趋势,周期表示时间序列的短期变化趋势,随机成分表示时间序列的无规律波动。
时间序列分析包括多种方法和技术,其中最常用的有平滑法和回归分析。
平滑法通过移动平均、指数平滑等方法消除数据中的波动,以便更好地观察趋势。
回归分析则通过建立数学模型,以自变量对因变量的影响程度来解释时间序列数据。
平滑法在时间序列分析中有多种实现方式。
移动平均是一种常见的平滑方法,它通过计算一定时间窗口内的平均值来平滑时间序列数据。
指数平滑是另一种常见的平滑方法,它给予近期数据更大的权重,以反映出时间序列的变化趋势。
回归分析是一种常用的时间序列分析方法。
它通过建立数学模型来描述自变量与因变量之间的关系,并用于预测未来值。
回归分析可以分为线性回归和非线性回归两种。
线性回归假设自变量和因变量之间存在线性关系,而非线性回归则放宽了这一假设。
时间序列分析还包括一些其他技术,例如自相关分析和谱分析。
自相关分析用于分析时间序列数据中的自相关性,即随着时间的推移,观测值之间的关联程度。
谱分析则用于分析时间序列数据中的周期性和频率特征。
时间序列分析在实际应用中具有广泛的价值。
在经济学领域,它可以用于预测股票价格、通货膨胀率等变量的未来走势。
在气象学领域,它可以用于预测气温、降雨量等变量的未来变化。
在金融学领域,它可以用于分析股票价格、汇率等金融指标的波动规律。
总之,时间序列分析是一种重要的统计方法,可以用于分析时间序列数据的变化规律和趋势。
时间序列回归分析

时间序列回归分析是一种先进的统计方法,它将时间序列数据与其他变量的数据相结合,通过回归分析的方法对未来的数据进行预测和分析,为决策者提供重要的参考依据。
在现代经济学、金融学、工程学等领域中得到了广泛的应用,成为这些领域中的重要工具之一。
一、的核心思想的核心思想是将时间序列数据与其他变量的数据相结合,通过回归分析的方法,建立起一种数学模型,用于预测未来的数据变化趋势。
这种方法能够有效地检验各种特征的变化趋势和规律性,从而为决策者提供更加准确的信息和分析结果。
二、的流程分为三个步骤:数据的收集和准备、模型的建立和参数的估计、模型的检验和预测。
第一步,数据的收集和准备。
在进行之前,需要收集并准备好相应的数据,包括时间序列数据和其他相关的变量数据。
这些数据应该是完整、准确和可靠的,以确保建立出来的模型能够反映出实际的情况。
第二步,模型的建立和参数的估计。
在确定好数据集之后,需要选择合适的建模方法,并利用计算机软件进行参数的估计。
根据不同的数据特征,可以选择线性回归、非线性回归、ARIMA模型等建模方法。
在进行参数估计之前,需要对数据进行平稳性的检验,以确保数据满足建模的基本要求。
第三步,模型的检验和预测。
在进行模型的检验和预测之前,需要对建立好的模型进行各种统计检验,包括残差检验、OLS检验、平稳性检验等。
通过这些检验还可以对模型进行修正和改进,提高预测的准确度和可靠性。
最后,可以利用建立好的模型进行未来数据的预测,为决策者提供参考依据。
三、的应用领域能够广泛应用于经济学、金融学、工程学等多个领域,具有重要的应用价值。
在经济学中,有助于预测经济增长率、通货膨胀率、利率等经济指标的变化趋势,提供重要的经济预测依据。
在金融学中,可以帮助分析股票、债券、外汇等金融资产的价格趋势,对投资决策提供有力支持。
在工程学中,可以用于预测机器故障的发生时间、生产效率的提高等,提高工业生产的效能和经济效益。
四、总结作为先进的统计方法,能够帮助决策者更加准确地预测未来发展趋势,提高决策的准确性和可靠性。
时间序列分析基本知识讲解

时间序列分析基本知识讲解时间序列分析是指对一系列按照时间顺序排列的数据进行分析、建模和预测的方法。
它在许多领域都有广泛的应用,如经济学、金融学、气象学等。
时间序列数据的特点是具有时间依赖性和序列自相关性,即当前的观测值与前面的观测值之间存在一定的关联。
时间序列分析的基本目的是通过观察过去的数据模式,来预测未来的值或者了解数据的发展趋势。
在进行时间序列分析时,我们通常关注以下几个方面的内容:1. 趋势分析:时间序列数据中的趋势是指长期内数据值的增长或下降趋势。
趋势的存在可能是持续性的,也可能是周期性的。
常见的趋势分析方法包括移动平均法、指数平滑法等。
2. 季节性分析:时间序列数据中的季节性是指每年或每个周期内数据值呈现出的周期性规律。
季节性可以是固定的,也可以是随机的。
常用的季节性分析方法有季节性指数法、周期性指数法等。
3. 周期性分析:时间序列数据中的周期性是指数据值在一段时间内出现的循环规律。
周期性往往是由于外部因素引起的,如经济周期、自然环境等。
周期性分析常用的方法有傅里叶分析、自相关函数等。
4. 随机性分析:时间序列数据中的随机性是指数据值的不可预测性和不规律性。
随机性分析可以用来寻找数据中的异常值、离群点等。
常用的随机性分析方法有自回归滑动平均模型(ARMA)、随机游走模型等。
时间序列分析的基本步骤包括收集数据、可视化数据、数据预处理、建立模型、模型检验和评估模型的预测能力等。
常用的时间序列模型有自回归移动平均模型(ARMA)、自回归整合移动平均模型(ARIMA)、季节性自回归整合移动平均模型(SARIMA)等。
总之,时间序列分析是研究时间序列数据的变化规律和趋势的一种方法。
通过对时间序列数据的分析,我们可以预测未来的趋势和变化,辅助决策制定和问题解决。
在实际应用中,时间序列分析与其他统计方法和机器学习方法结合,可以提高分析预测的准确性和可靠性。
时间序列分析是研究时间序列数据的内在规律和趋势的一种方法。
时间序列分析基础

时间序列分析基础时间序列分析是统计学中重要的一个分支,它研究的是一组按时间顺序排列的数据。
通过对时间序列数据的分析,可以揭示数据背后的规律和趋势,帮助我们进行有效的预测和决策。
本文将介绍时间序列分析的基础知识,包括时间序列的特点、常用模型和分析方法。
时间序列的特点时间序列具有以下几个特点:趋势性(Trend):时间序列数据通常会呈现出长期趋势的变化,反映了数据在长期内的整体变化趋势。
季节性(Seasonality):某些时间序列数据会呈现周期性变动,这种周期性通常是与季节或周期相关的。
循环性(Cyclic):除了季节性变动外,时间序列数据还可能存在长短不一的周期性波动。
随机性(Irregularity):时间序列中还会存在一些随机波动或噪声,这些波动无法被趋势、季节性和循环性等因素所解释。
常用时间序列模型在时间序列分析中,常用的模型包括:平稳时间序列模型:平稳时间序列不会随着时间发生明显的波动,可以使用自回归移动平均模型(ARMA)进行建模。
自回归模型(AR):自回归模型假设当前观测值与过去若干个观测值相关。
移动平均模型(MA):移动平均模型假设当前观测值与过去若干个噪声项相关。
自回归移动平均模型(ARMA):ARMA模型将AR和MA结合在一起,适用于既有自相关又有滞后相关的序列。
自回归积分移动平均模型(ARIMA):ARIMA模型在ARMA基础上引入了差分操作,适用于非平稳时间序列。
时间序列分析方法进行时间序列分析时,一般包括以下几个步骤:数据收集:首先需要获取要分析的时间序列数据,可以是经济指标、股票价格、气象数据等。
可视化:通过绘制时序图、自相关图和偏自相关图等对数据进行可视化,观察其趋势和周期性。
平稳性检验:对时间序列数据进行单位根检验(ADF检验)、差分运算等操作,确保数据是平稳的。
模型拟合:根据数据特点选择合适的模型进行拟合,并通过最大似然估计等方法确定模型参数。
诊断检验:对拟合好的模型进行残差检验、残差自相关检验等,确保模型符合假设前提。
会计数据分析实践中的时间序列法与回归分析

会计数据分析实践中的时间序列法与回归分析在会计领域,数据分析是一项重要的活动,它帮助会计人员理解和解释财务数据,并为业务决策提供依据。
在这个过程中,时间序列法和回归分析是常用的工具和技术。
本文将介绍会计数据分析实践中的时间序列法和回归分析,并探讨它们的应用。
时间序列法是指基于一系列按时间顺序排列的数据样本,通过分析数据之间的关系来预测未来的趋势。
在会计数据分析中,时间序列法通常用于预测财务指标的变化,如销售额、利润等。
它可以帮助会计人员了解过去的变化趋势,并预测未来可能的变化。
时间序列法有多种模型,其中最常用的是移动平均法和指数平滑法。
移动平均法可以平滑数据,减少随机波动,揭示出数据的长期趋势;指数平滑法则更加注重最近的数据,认为最新的数据权重更高,因此更能反映出未来的趋势。
这两种方法都可以用来预测未来的财务指标,会计人员可以根据实际情况选择适合的方法。
回归分析是一种统计分析方法,用来研究两个或多个变量之间的关系。
在会计数据分析中,回归分析常用于研究某个财务指标与其他变量之间的关系。
例如,研究销售额与广告投入之间的关系,或者利润与成本之间的关系。
回归分析可以帮助会计人员确定影响财务指标的主要因素,并量化它们的影响程度。
在进行回归分析时,会计人员需要收集相关的数据,并建立一个数学模型来描述变量之间的关系。
通过分析模型的参数,他们可以得出结论,并进行预测。
在实践中,时间序列法和回归分析可以结合使用,以提高预测的准确性。
例如,会计人员可以先使用时间序列法对财务指标进行预测,然后使用回归分析来研究该指标与其他变量之间的关系,并进一步修正预测结果。
除了预测,时间序列法和回归分析还可以用于数据的比较和分析。
例如,会计人员可以使用时间序列法来分析过去几年的销售额变化,并进行季节性调整,以了解销售额在不同季节的表现。
他们还可以使用回归分析来比较不同公司或不同地区的财务指标,并找出差异的原因。
总之,时间序列法和回归分析在会计数据分析实践中起着重要的作用。
回归分析中的序列相关问题处理技巧(十)

回归分析是统计学中非常重要的一种数据分析方法,它可以用来探讨自变量和因变量之间的关系,以及预测未来的结果。
然而,在实际的回归分析中,经常会遇到序列相关的问题,这些问题会对回归分析的结果产生一定的影响。
本文将就回归分析中的序列相关问题进行深入探讨,并介绍处理这些问题的技巧。
序列相关是指时间序列数据中的观测值之间存在相关性。
在回归分析中,如果样本数据是时间序列数据,那么就很可能存在序列相关的问题。
序列相关可能会导致回归分析中的标准误差被低估,从而导致对系数估计的显著性判断出现偏误。
因此,处理序列相关问题是回归分析中非常重要的一步。
首先,我们来看一下序列相关的检验方法。
通常情况下,我们可以使用Durbin-Watson检验来检验序列相关的存在。
Durbin-Watson检验的原假设是残差之间不存在序列相关,如果p值小于显著性水平(通常取),则拒绝原假设,认为残差存在序列相关。
在检验出序列相关存在之后,我们需要对序列相关进行处理。
一种常见的处理方法是使用差分变换。
差分变换可以减弱序列相关的影响,使得残差之间更加独立。
通常情况下,我们可以对时间序列数据进行一阶差分,即将当前观测值减去前一个观测值,得到新的序列,然后再进行回归分析。
通过差分变换,我们可以有效地处理序列相关问题,提高回归分析的准确性。
除了差分变换之外,我们还可以使用ARIMA模型来处理序列相关。
ARIMA模型是一种常用的时间序列分析方法,它可以很好地建模序列相关的结构,并进行预测。
在回归分析中,我们可以使用ARIMA模型对残差进行建模,然后将建模结果作为新的解释变量加入回归方程中。
通过这种方法,我们可以更好地控制序列相关的影响,提高回归分析的效果。
此外,我们还可以使用异方差-自相关一致性(HAC)标准误差来处理序列相关问题。
HAC标准误差是一种修正的标准误差估计方法,它考虑了残差之间的序列相关性,从而可以更准确地估计回归系数的标准误差。
在实际应用中,使用HAC标准误差可以有效地处理序列相关问题,提高回归分析的准确性。
python_时间序列分类逻辑回归_概述及解释说明

python 时间序列分类逻辑回归概述及解释说明1. 引言1.1 概述本文旨在探讨Python中时间序列分类逻辑回归的概念、方法和应用。
时间序列分类是指对于一系列按照时间顺序排列的数据样本,通过建立适当的模型来预测其所属类别或标签。
而逻辑回归算法则是一种常用的分类算法,它基于线性回归模型,并通过使用逻辑函数来进行分类。
1.2 文章结构本文由5个主要部分组成,包括引言、Python时间序列分类逻辑回归概述、解释说明Python时间序列分类逻辑回归的步骤和方法、示例与应用场景分析以及结论与展望。
在引言部分,我们将首先介绍文章背景和目的,然后给出整篇文章的结构和安排。
1.3 目的本文旨在介绍Python中时间序列数据的分类问题以及如何运用逻辑回归算法进行相关建模。
我们将详细阐述该方法中涉及到的数据预处理步骤、特征工程技巧以及时间序列分类逻辑回归建模过程。
通过学习本文,读者将能够了解如何在Python中处理时间序列数据,并运用逻辑回归算法进行精确的分类。
此外,我们还将提供示例数据集介绍和实际应用案例分析,以便读者更好地理解该方法的实际应用与效果。
在结论部分,我们将总结本文的主要观点和结论,并对未来时间序列分类逻辑回归的发展方向和挑战进行展望。
2. Python时间序列分类逻辑回归概述:2.1 时间序列分类问题简介时间序列分类是一种机器学习任务,旨在根据给定的时间序列数据,对其进行分类或标记。
与传统的分类算法不同,时间序列分类需要考虑数据的时序特征和动态变化。
在时间序列分类中,我们需要解决可能存在的两个主要挑战:首先,时间序列数据通常具有高维度和长尺度;其次,时序数据可能会受到噪声、趋势和季节性等因素的影响。
2.2 逻辑回归算法简介逻辑回归是一种常用的二元分类算法。
它通过拟合一个Sigmoid函数曲线来建模离散目标变量的概率分布。
逻辑回归可用于探索输入特征与输出标签之间的关系,并做出预测。
在逻辑回归中,我们首先将连续型特征进行线性加权组合,并将结果输入到Sigmoid函数中。
分析时间序列和回归分析

分析时间序列和回归分析时间序列和回归分析是统计学中常用的数据分析方法。
时间序列分析适用于研究随时间变化的数据,而回归分析则用于探究变量之间的关系。
本文将分析时间序列和回归分析的基本原理、应用场景以及其在实践中的价值。
时间序列分析是一种研究时间上有规律的数据变动的统计方法。
在时间序列分析中,时间是一种重要的因素,数据点的顺序对结果有影响。
时间序列数据可以分为两种类型:离散时间序列和连续时间序列。
离散时间序列的观测点是在不同的时间点上进行的,如每日销售量或每年的GDP增长率。
而连续时间序列是在一段连续的时间范围内观测到的数据,如每天的温度变化曲线或股票每分钟的价格变动。
时间序列分析可以通过对数据的图形化展示和数学模型的建立来揭示数据的规律和趋势。
常见的时间序列分析方法包括平滑方法、分解方法和预测方法。
平滑方法使用移动平均或指数平均来消除随机波动,使得趋势更加明显。
分解方法将时间序列分解为趋势、季节性和随机成分,以便更好地理解各个组成部分的变化规律。
预测方法利用历史数据进行模型拟合,并预测未来的数值。
回归分析是一种用于研究两个或多个变量之间相互关系的统计方法。
它通过建立回归方程来描述变量之间的函数关系。
回归方程可以用来预测因变量的值,或者探究自变量对因变量的影响程度。
回归分析可以分为线性回归和非线性回归两种。
线性回归是回归分析中最常用的方法之一。
它基于因变量与自变量之间的线性关系进行建模。
线性回归方程的形式为Y = β0+ β1X1 +β2X2 + ... + βnXn,其中Y是因变量,X1、X2等是自变量,β0、β1、β2等是回归系数。
线性回归分析可以用于预测因变量的值,并且可以通过回归系数的显著性检验来评估自变量的影响程度。
非线性回归是回归分析中另一种常用的方法。
它适用于因变量与自变量之间的非线性关系。
非线性回归方程的形式不再是直线,而是曲线或其他形式。
非线性回归的建模过程需要选择适当的曲线形式,并通过参数估计的方法进行拟合。
回归分析与时间序列介绍 共13页

20
40
60
80
100
120
140
Y=a 0 + a1X
N
误差: yi a0 a1xi2最小 i1
目标:寻求变量之间的关系
1 线性回归分析2[4]
最小二乘法:
N
yi a0 a1xi2最小
i1
a 0iN 1yia 0a 1xi 2 2iN 1yia ˆ0a ˆ1xi 0
2季 5.3437 5.5326 5.6585 5.5326 5.8631 5.9655
3季 4.8479 4.7456 4.6748 4.9896 4.9974 5.2021
4季 6.4219 6.4092 6.6455 6.6423 6.7761 6.8941
线性回归计算长期趋势:
T=5789.8+21.8X
Y`=Y-长期趋势 Y`=Y-T 将Y`按周期(t)取平均
Ci
t n
n/t1
y`ij*t
j0
找周期方法: 1.估计 2.遍历 3.看频谱
不规则趋势:
不规则趋势=Y-长期趋势-周期趋势 I=Y-T-C
2.4 时间序列分解示例[6]
某城市居民用煤量:
1季 1991年 6.8784 1992年 6.8154 1993年 6.6344 1994年 7.1302 2019年 7.4135 2019年 7.4765
500
400
300
200
100
0 0
20
40
60
Y=a 0 + a1 X
aˆ1
(x x) ( y (x x)2
y)
aˆ0 y b x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下面摘录《数据分析与SPSS应用》一书关于相关回归和时间序列分析一些概念解释。
数据变量间主要存在二类关系:
一类是函数关系,一类是相关关系。
前者是变量间有确定关系,即一个变量的值能够在其他变量取值确定的情况下,按某种函数关系唯一确定;后者是变量间虽然具有的联系,并非确定关系,如价格与销量量,价格高了,销售量可能会上去,但无法确定销售量是多少。
通过散点图来观察,如果点都集中在一条直线附近,是线性相关,如果在一条曲线附近,则为非线性相关。
如果一个变量因另一个变量的增加而增加,减少而减少,则二个变量间存在正相关关系,反之则为负相关关系。
极端的相关是完全相关和零相关。
如某地区购买自行车多少与购买大蒜多少无关,是为零相关。
按我的理解,相关分析就是推断变量与变量之间关系的密切程度,回归就是在相关的基础上,找出变量间的拟合模型,从而进一步推测出未来的趋势和变量。
而时间序列则是以时间的作为观察的序列,来推断变量间的关系的一种模型。
以自带文件Trends chapter 13.sav为例,说明一下如何应用这三种分析工具。
3.时间序列
因为R的似合度分别为0.05,0.064,0.199和0.039,都比较低,方程的效果不太好,如果要预测数值还是选择时间序列比较合适,因为从刚才Sequence的图也可以观察到,数据是以后的时间来波动的变化关系。
选择Analyze->Time Series->Exponential Smoothing,出现图25
图25
把hstarts选入Variables选项,并在Model选择Winters(注意,三种不同的模型的选择:简单指数平滑适用于不包含长期趋势和季节成分的数据;Holt方法适合于包含长期趋势但不包含季节成分的数据;Winters方法适合于包含季节成分(以及长期趋势)的数据。
EXCEL中只有简单的指数回归,与这里的绝不相同,从这里也可以看到专业分析软件的优势更具体更仔细),又按Save键,如图26
图26
Predict Case选项中选择Predict through,并在Year栏填入1976,month填入6,这样就可以得到1976年1-6月份的预测值(注意,此处与上面的回归不同,不需要增加6个ID,不然结果会显示有缺失值)。
返回,按Parameters键,如图27
图27
分别把Alpha(截距项的平滑系数),Gamma(趋势项的平滑系数)和Delta(季节指数的平滑系数),设为从0到1之间以步长0.05搜索最优的参数值,其它选项采用默认值。
返回按OK,出现结果如图28:
图28
从图可看到平滑指数分别是Alpha=0.75,Gamma=0,Delta=0,而更重要的是,可以直接得到预测值,如图29:
图29
除了Fit一项的预测外,可以得到1976年1-6月的预测结果。
同时,可以通过FIT 1的预测情况与上面三次曲线回归方程比较,采用平均绝对误差、均方根误差和平均绝对百分误差的结果选择更佳的答案。
