MATLAB与概率统计
14MATLAB在概率统计中的应用

(2) (X,Y)落在x+y=1,x=0,y=0所围成的区域内的概率。
程序:
>> syms x y
>> f=exp(-x-y);
>> P_XY=int(int(f,y,0,1),x,0,1)
>> P_G=int(int(f,y,0,1-x),x,0,1)
运行结果显示如下:
P_XY= exp(-2)-2*exp(-1)+1
0.1 0.08 0.06 0.04 0.02
0 0
5
10
15
20
25
30
图 2-1
4.指数分布 例4-10 >>x = 0:0.1:10; >>y = exppdf(x,2); >>plot(x,y)
0.正态分布 例4-16 >> x=-3:0.2:3; >> y=normpdf(x,0,1); >> plot(x,y)
k 1
k 1
的和为随机变量X的数学期望,记为E(X),即
E(X) xkpk (1) k1
说明: (1)E的 X 求 E (X 法 ) x : kpk k1
(2)数学期望 存在性的判断:
看 级 数 xk pk是 否 绝 对 收 敛 。 k 1 即 xk pk是 否 收 敛 ? k1
例1:某厂产品的次品率为0.2 ,每生产一件
解:设h为车门高度,X为身高,求满足条件 P{X>h}0.01的h,即P{X<h}0.99。
程序:
>> h=norminv(0.99,175,6)
结果:
h= 188.9581
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用
Matlab提供了丰富的概率分布函数,可以帮助学生更好地理解不同的概率分布。
学生可以使用Matlab生成正态分布、二项分布、泊松分布等不同的概率分布,并画出相应的概率密度函数、累积分布函数等图形。
通过实际的计算和绘图,学生可以更直观地看到不同概率分布的特点,加深对概率分布的理解。
Matlab提供了各种统计函数,可以方便地进行数据的描述性统计和推断性统计。
学生可以使用Matlab计算样本的平均值、方差等描述性统计量,还可以使用Matlab进行假设检验、置信区间估计等推断性统计。
通过实际的计算和分析,学生可以更好地掌握统计学中的概念和方法。
Matlab还可以进行模拟实验,帮助学生理解概率和统计的原理。
学生可以使用Matlab 模拟抛硬币的实验,验证概率的定义和性质。
学生还可以使用Matlab模拟中心极限定理,观察样本均值的分布趋于正态分布的情况。
通过实际的模拟实验,学生可以更深入地理解抽样分布和极限定理等重要概念。
Matlab还可以用于数据的可视化。
学生可以使用Matlab绘制直方图、散点图、箱线图等图形,展示数据的分布和变化。
通过可视化的方式,学生可以更好地理解数据的特点和规律,并能够更直观地展示和解释统计分析的结果。
Matlab在《概率论与数理统计》教学中具有广泛的应用价值。
通过利用Matlab进行计算、模拟和可视化等任务,可以帮助学生更好地理解概率和统计的概念和方法,提高学习效果。
在教学中合理地使用Matlab可以有效地促进学生对概率论与数理统计的学习和理解。
第六章 MATLAB在概率统计中的应用

第六章MATLAB在概率统计中的应用概率统计的应用十分广泛,这不仅与概率的简洁直观有着密切的联系,还与实际问题中的众多现象的随机性、不确定性有着密切的联系。
概率统计几乎遍及所有科学技术领域以及工农业生产和国民经济的各个部门中。
例如,使用概率的方法可以进行天气预报、地震预测、产品的抽样检查、计算产品使用的平均寿命、置信估计等等。
有时也可通过概率统计的方法对实际问题进行仿真模拟。
随着概率统计方法的使用面的增加也出现的众多概率统计软件,例如SAS软件、R软件等等。
早期的MATLAB中有关概率统计的具体程序并不多见,但随着MATLAB版本的提高,也陆续引进的众多概率统计程序。
其中主要包括统计变量的数字特征、常用统计分布、常用随机数的产生、参数估计、区间估计、假设检验、方差分析和回归诊断及统计图的绘制等方面的各个程序。
6.1统计量的数字特征6.1.1简单数学期望和平均值Mean平均值函数对于一些服从特殊分布的随机变量而言直接利用数组的点乘和求和函数来获得数学期望值。
例如:X-202Pk0.40.30.3数学期望值E(X)的值可以通过下述方法获得>>x=[-202];>>Pk=[0.40.30.3]>>sum(x.*Pk)6.1.2数据的比较在给定的一组数据中,还常要对它们进行最大、最下、中值的查找或对它们排序等操作。
在MATLAB中提供了这些函数。
Max求随机变量的最大值元素Nanmax求随机变量的忽略nan的最大值运算Min求随机变量的最小值元素Median求随机变量的中值Sort对随机变量由小到大排序Sortrows对随机矩阵按首行进行行排序Range求随机变量的值范围,即最大值与最小值的差。
6.1.3方差和标准差Var(x)方差函数Std(x)标准差函数6.1.4偏斜度和峰度Skewness 随机分布的偏斜度函数Kurtosis 随机分布的峰度函数6.1.5协方差和相关系数Cov Corrcoef6.2常用的统计分布量6.2.1期望和方差(书292)6.2.3概率密度函数Y=pdf(name,X,A,B,C)6.2.4概率值函数6.2.5随机生成函数6.3参数估计利用样本对总体进行统计推断,主要有两大类,一类是参数估计,另一类是检验函数估计。
matlab在概率统计中的应用

matlab在概率统计中的应用
MATLAB在概率统计领域的应用广泛,由于它能精准地模拟出连续变化的数据,因此互联网公司和研究人员也在利用它进行统计分析。
MATLAB是一种在概率统计领域非常有效的分析工具,它可以帮助研究人员和
公司更准确、更快速地了解随机变量的分布、变化趋势等,为研究和决策提供依据。
MATLAB具有方便快捷的数据分析功能,可以进行概率统计领域的数值模拟和
数据挖掘,可以快速生成分析报告、表格摘要和图形展示等。
通过MATLAB,企业
可以迅速获取有效的市场数据,进行统计比较,对在市场上的表现、产品卖点进行准确的定位,提供准确的决策依据。
在投资策略的制定也可以采用这种方式,精准评估投资风险和收益,在避免各种不可靠未知因素造成投资损失的同时,做出更全面、明智的投资决定。
此外,MATLAB还能模拟出各种复杂的随机事件,可以精准预测和模拟不同的
概率统计模型,鉴于互联网公司每天面临的许多难以预测的情况,MATLAB的应用
可以帮助公司提前进行风险应对,更好地把握未来发展趋势。
总之,MATLAB在概率统计领域具有广泛的应用,可以帮助企业更充分地利用
数据,进行更准确、更可靠的数据分析和决策,提高营销策略及投资质量。
matlab软件在概率论与数理统计教学中的辅助应用

matlab软件在概率论与数理统计教学中的辅助应用1. 引言随着数学软件的快速发展,越来越多的数学教师开始使用软件来辅助他们的教学工作。
Matlab是一种强大的数学软件,可以用于概率论和数学统计的教学。
本文将介绍Matlab在教授概率论和数学统计时的优点和应用。
2. Matlab在概率论中的应用概率论是研究随机事件的规律性和不确定性的数学分支。
Matlab 可以用来计算概率分布、描述随机变量和随机过程等。
例如,考虑一个随机变量X服从正态分布,均值为mu,标准差为sigma。
在Matlab 中,可以用以下代码计算其概率密度函数:x = -5:0.1:5;y = normpdf(x,mu,sigma);plot(x,y)这将绘制出X的概率密度函数的图表。
同样,我们可以使用Matlab计算其他随机变量的概率分布函数。
另外,在概率论中,经常需要进行随机变量之间的相关性分析。
Matlab提供了很多函数,如cov、corr等,可以计算两个或多个随机变量之间的协方差和相关系数。
这有助于分析随机变量之间的关系和作出更明智的决策。
3. Matlab在数理统计中的应用数理统计是从样本中推断总体参数的一种方法。
Matlab可以用来计算样本的描述性统计、推断统计等。
例如,我们可以用以下代码计算一个样本的均值、方差和标准差:data = [2 3 4 5 6 7];mean_data = mean(data)var_data = var(data)std_data = std(data)这将输出样本的均值、方差和标准差。
此外,Matlab还提供了t检验、方差分析和线性回归等重要的推断统计函数,可以用于验证假设和识别关键变量。
4. 优点使用Matlab进行概率论和数学统计的教学有以下优点:4.1 可视化Matlab提供了一种直观的方式来可视化统计分析结果。
教师可以向学生展示图表、图形和实时数据,以便他们更好地理解概念和方法。
Matlab中的概率统计分析

Matlab中的概率统计分析概率统计分析是一门重要的统计学分支,可应用于各行各业。
在数据科学领域中,通过概率统计分析,我们可以对数据集进行探索性分析、建模以及预测。
Matlab作为一种流行的科学计算软件,提供了丰富的工具和函数来进行概率统计分析。
本文将介绍一些常见的概率统计分析方法以及它们在Matlab中的应用。
一、描述统计分析描述统计分析是通过对数据进行总结和可视化,来了解数据的分布和特征。
Matlab提供了多种函数和工具来进行描述统计分析。
例如,我们可以使用`mean`函数来计算数据的均值,使用`std`函数计算标准差。
此外,还可以通过`histogram`函数绘制直方图、通过`boxplot`函数绘制箱线图等。
二、概率分布及参数估计在概率统计分析中,概率分布是描述随机变量的函数。
在Matlab中,我们可以使用各种内置的概率分布函数,如正态分布、二项分布、泊松分布等。
这些函数可以用来计算随机变量在给定参数下的概率密度函数、累积分布函数等。
参数估计是概率统计分析的重要内容之一。
根据已有的样本数据,我们可以通过最大似然估计等方法来估计概率分布的参数。
在Matlab中,可以使用`fitdist`函数进行参数估计。
该函数可以根据给定的数据和概率分布类型,自动计算出最佳的参数估计结果。
三、假设检验假设检验用于验证关于总体参数的假设,并对观察到的样本数据进行统计推断。
Matlab提供了一系列的函数来进行假设检验。
例如,`ttest`函数可以用于t检验,`chi2gof`函数可以用于卡方检验等。
四、参数估计的抽样分布参数估计的抽样分布是概率统计分析中的重要概念之一。
通过对参数估计结果进行大量次数的模拟重复,可以得到参数估计的分布情况。
在Matlab中,通过使用`random`函数,我们可以生成服从特定概率分布的随机数。
结合循环语句,可以进行大量次数的模拟实验,进而得到参数估计的抽样分布。
五、相关性分析相关性分析用于研究两个或多个变量之间的相关关系。
概率论与数理统计MATLAB上机实验报告

《概率论与数理统计》MATLAB上机实验实验报告一、实验目的1、熟悉matlab的操作。
了解用matlab解决概率相关问题的方法。
2、增强动手能力,通过完成实验内容增强自己动手能力。
二、实验内容1、列出常见分布的概率密度及分布函数的命令,并操作。
概率密度函数分布函数(累积分布函数) 正态分布normpdf(x,mu,sigma) cd f(‘Normal’,x, mu,sigma);均匀分布(连续)unifpdf(x,a,b) cdf(‘Uniform’,x,a,b);均匀分布(离散)unidpdf(x,n) cdf(‘Discrete Uniform’,x,n);指数分布exppdf(x,a) cdf(‘Exponential’,x,a);几何分布geopdf(x,p) cdf(‘Geometric’,x,p);二项分布binopdf(x,n,p) cdf(‘Binomial’,x,n,p);泊松分布poisspdf(x,n) cdf(‘Poisson’,x,n);2、掷硬币150次,其中正面出现的概率为0.5,这150次中正面出现的次数记为X(1) 试计算X=45的概率和X≤45 的概率;(2) 绘制分布函数图形和概率分布律图形。
答:(1)P(x=45)=pd =3.0945e-07P(x<=45)=cd =5.2943e-07(2)3、用Matlab软件生成服从二项分布的随机数,并验证泊松定理。
用matlab依次生成(n=300,p=0.5),(n=3000,p=0.05),(n=30000,p=0.005)的二项分布随机数,以及参数λ=150的泊松分布,并作出图线如下。
由此可以见得,随着n的增大,二项分布与泊松分布的概率密度函数几乎重合。
因此当n足够大时,可以认为泊松分布与二项分布一致。
4、 设22221),(y x e y x f +−=π是一个二维随机变量的联合概率密度函数,画出这一函数的联合概率密度图像。
Matlab在概率统计中的应用

p = 0.6000 0.8000 0.9000 0.4000 0.6000 0.7000 0.9000 0.3000 0.7000 0.5000 pci =0.2624 0.4439 0.5550 0.1216 0.2624 0.34750.5550 0.0667 0.3475 0.1871
0.8784 0.9748 0.9975 0.7376 0.8784 0.9333 0.9975 0.6525 0.9333 0.8129
0.1667
9.6667
0.1389 0.3000
w =[ 0.0667 0.1667 0.2333 0.0333 0.2000] var(x,w) ans = 2.2225 11.3819 0.0623
样本标准差
1 n s ( xi x)2 n 1 i 1
MATLAB的标准差函数为std
例如
std(x) ans = 1.8708 std(x,1) ans = 1.7078
3.4059
0.4082
3.1091
0.3727
std(x,0,1) ans = 1.8708 30,2) ans = 3.4641 4.1633 4.5826 2.0817 2.5166 3.0000
例如 在漂白工艺中要考察温度对针制品断裂强力的影响,
在70℃与80℃下分别作了7次和9次测试,其测试数据如
下(单位:公斤)
70 ℃ 20.5 18.8 20.9 21.5 19.5 21.6 21.8
80℃
17.7
19.2
20.3 20
18.6
19
19.1
20
18.1
根据以往经验知两种温度下的断裂强力都服从正态分布, 其方差相等且相互独立。试问两种温度下的平均断裂强力 有无显著变化? 解 H0 μ1=μ2 H1 μ1≠μ2
matlab概率统计函数

matlab概率统计函数Matlab是一种流行的科学计算软件,其中包含了丰富的概率统计函数,可以用来进行统计分析、建模和预测等工作。
本文将介绍一些常用的Matlab概率统计函数及其应用。
1. normpdf函数:该函数用来计算正态分布的概率密度函数值。
对于给定的均值和标准差,可以使用该函数计算某个特定值的概率密度。
例如,可以使用normpdf函数计算身高在某个范围内的概率密度。
2. normcdf函数:该函数用来计算正态分布的累积分布函数值。
对于给定的均值和标准差,可以使用该函数计算某个特定值以下的累积概率。
例如,可以使用normcdf函数计算身高小于某个数值的累积概率。
3. binopdf函数:该函数用来计算二项分布的概率密度函数值。
对于给定的试验次数和成功概率,可以使用该函数计算在指定次数内出现特定成功次数的概率。
例如,可以使用binopdf函数计算在10次抛硬币试验中出现5次正面朝上的概率。
4. binocdf函数:该函数用来计算二项分布的累积分布函数值。
对于给定的试验次数和成功概率,可以使用该函数计算在指定次数内出现不超过特定成功次数的累积概率。
例如,可以使用binocdf函数计算在10次抛硬币试验中不超过5次正面朝上的累积概率。
5. poisspdf函数:该函数用来计算泊松分布的概率密度函数值。
对于给定的平均发生率,可以使用该函数计算在指定时间内发生特定次数的概率。
例如,可以使用poisspdf函数计算在一小时内发生3次事故的概率。
6. poisscdf函数:该函数用来计算泊松分布的累积分布函数值。
对于给定的平均发生率,可以使用该函数计算在指定时间内发生不超过特定次数的累积概率。
例如,可以使用poisscdf函数计算在一小时内不超过3次事故的累积概率。
7. hist函数:该函数用来绘制直方图。
通过将数据分成若干个区间,该函数可以显示每个区间的频数或频率。
例如,可以使用hist函数绘制一组数据的身高分布直方图。
matlab概率统计

MATLAB概率统计1. 概述概率统计是数学中的一个重要分支,用于研究随机现象的规律性和不确定性。
MATLAB作为一种强大的数值计算和数据可视化工具,提供了丰富的函数和工具箱,使得概率统计分析变得简单而高效。
本文将介绍MATLAB中常用的概率统计函数和方法,并结合实例进行详细说明。
2. 概率分布2.1 常见概率分布函数在概率统计中,常见的概率分布函数有正态分布、均匀分布、二项分布等。
MATLAB 提供了相应的函数来生成这些概率分布。
•正态分布:normrnd函数用于生成服从正态分布的随机数。
x = normrnd(mu, sigma, [m, n]);其中,mu表示均值,sigma表示标准差,[m, n]表示生成随机数矩阵的大小。
•均匀分布:unifrnd函数用于生成服从均匀分布的随机数。
x = unifrnd(a, b, [m, n]);其中,a和b表示均匀分布区间的上下界。
•二项分布:binornd函数用于生成服从二项分布的随机数。
x = binornd(n, p, [m, n]);其中,n表示试验次数,p表示成功的概率。
2.2 概率密度函数和累积分布函数除了生成随机数,MATLAB还提供了计算概率密度函数(PDF)和累积分布函数(CDF)的函数。
•概率密度函数:对于连续型随机变量,可以使用normpdf、unifpdf等函数计算其概率密度函数值。
y = normpdf(x, mu, sigma);其中,x表示自变量的取值,mu和sigma表示正态分布的均值和标准差。
•累积分布函数:使用normcdf、unifcdf等函数可以计算连续型随机变量的累积分布函数值。
y = normcdf(x, mu, sigma);其中,参数的含义同上。
对于离散型随机变量,可以使用相应的离散型概率分布函数来计算其概率质量函数(PMF)和累积分布函数(CDF)。
3. 统计描述3.1 均值与方差均值和方差是统计学中常用的描述统计量,MATLAB提供了相应的函数来计算均值和方差。
第7章 MATLAB在概率统计中的应用

第7章MA TLAB在概率统计中的应用一、统计量的数字特征(一)简单的数学期望和几种均值●mean(x) 平均值函数当x 为向量时,得到它的元素平均值;当x 为矩阵时,得到一列向量,每一行值为矩阵行元素的平均值,举例1:求矩阵A的平均值。
D=[74.001 74.005 74.003 74.001 74.00 73.998 74.006 74.02]Mean(d)举例2:设随机变量x的分布规律如下表,求E(x)和E(3x2+5)的值E(x)的值●E(x)的值:x=[-2 0 2],pk=[0.4 0.3 0.3]sum(x.*pk)●E(3x2+5)的值。
x=[-2 0 2],pk=[0.4 0.3 0.3]z=3*x.^2+5sum(z.*pk)(二)数据比较⏹max 最大值⏹min 最小值⏹median 中值⏹sort 由小到大排序(三)求和与积⏹ sum 求向量或矩阵的元素累和 ⏹prod : 求当前元素与所有前面元素的积举例:下面的程序用来求向量各元素的之和prod=1 varx=[2 3 4] for x=varx prod=prod*x end(四)方差和标准差为了反映随机变量与其均值的偏离程度 方差表示为标准差表示为: 样本方差为: 样本标准差为: ●方差函数Var①Var(x) x 为向量,返回向量的样本方差;x 为矩阵,则返回矩阵各列的方差。
②Var(x,1) 返回向量(矩阵x )的简单方差(即置前因子为n1的方差)③Var(x,w) 返回向量(矩阵)x 即以w 为权的方差。
● Std 标准差函数Std(x) 返回向量或矩阵x 的样本标准差(置前因子为11 n )Std(x,1) 返回向量或矩阵x 的标准差(置前因子为n1)举例: d=[74.001 74.005 74.003 74.001 74.00 73.998 74.006 74.02]mean(d)var(d,1) %方差 var(d) %样本方差 std(d,1) %标准差 std(d) %样本标准差(五)协方差和相关系数⏹cov(x):x 为向量,返回向量的方差,x 为矩阵时返回矩阵的协方差矩阵,其中协方差矩阵的对角元素是x 矩阵的列向量的方差值。
Matlab在《概率论与数理统计》教学中的应用

Matlab在《概率论与数理统计》教学中的应用概率论是《概率论与数理统计》课程中的重要部分,Matlab可以帮助学生更好地理解和应用概率论。
1. 随机数生成与概率计算Matlab可以生成符合不同分布的随机数,如正态分布、均匀分布等,并进行概率计算和统计推断。
以正态分布为例,使用命令“normrnd(mu,sigma,m,n)”可以生成一个mu为均值,sigma为标准差的n行m列的正态分布随机数矩阵。
使用函数“normpdf(x,mu,sigma)”可以计算正态分布的概率密度函数在x处的取值,使用函数“normcdf(x,mu,sigma)”可以计算正态分布的累积分布函数在x处的取值。
这些功能可以帮助学生更好地理解正态分布的概念和相关理论。
2. 离散随机变量的概率分布1. 数据描述与可视化Matlab可以帮助学生更好地进行数据描述和可视化。
使用命令“mean(x)”可以计算数据的平均值,使用命令“std(x)”可以计算数据的标准差,使用命令“hist(x)”可以绘制数据的直方图。
这些功能可以帮助学生更好地理解数据的基本特征和数据分布情况。
2. 参数估计与假设检验Matlab可以帮助学生完成参数估计和假设检验。
以t检验为例,使用命令“ttest(x,y)”可以进行两样本t检验,使用命令“ttest(x,m)”可以进行单样本t检验。
这些功能可以帮助学生更好地进行参数估计和假设检验的计算和分析。
结语综上所述,Matlab是一款重要的数学软件工具,在《概率论与数理统计》课程教学中发挥着重要的作用。
通过Matlab,学生可以更好地理解和应用概率论和数理统计的理论知识,提高他们的数据分析和计算能力。
matlab在概率统计教学中的应用浅析

matlab在概率统计教学中的应用浅析随着科学技术的进步,高等教育中的统计学教学更加注重实际应用,要求学生从实际问题出发,使用适当的计算机工具分析问题,研究数据,推理出结论,这就使Matlab在统计教学中有了越来越重要的地位。
Matlab是一个专为优化计算设计的编程软件,它采用高级数学语言,具有出色的图像生成能力,可以提供卓越的性能和更加高效的模拟,它的应用可以追溯到几乎所有的计算机领域。
Matlab在概率统计方面的应用主要体现在两个方面:第一是分析概率分布,如正态分布,离散分布等;第二是做概率统计模拟、数据挖掘、建模分析等。
Matlab可以帮助学生学习和掌握建模过程,更好地理解随机变量的变化,利用统计分布特性分析现象,更准确地估计和预测结果。
例如学习正态分布时,Matlab可以绘制正态曲线,分析曲线的的平均数、方差、标准偏差、区间估计等;通过Matlab 程序可以快速求解复杂的概率模型中的统计特征; Matlab可以用来实现模拟实验,研究事件发生概率;可以研究多类概率变量之间的关联关系,并利用概率统计方法做出预测结论;利用Matlab绘制图表,可以更加直观地理解概率统计结果。
Matlab在统计学教学中的应用还有几个特点:首先,Matlab可以提供真实数据,有助于学生理解统计的概念;其次,Matlab还可以构建复杂的模型,有助于学生更深入地理解概率统计;最后,Matlab 的图像表示可以更清楚地展示概率统计的结果,有助于学生学会统计方法的分析和判断。
从上面可以看出,Matlab在概率统计教学中的应用非常有效和重要,可以大大加快学习进程,提高学生的统计学能力,提升他们分析和解决实际问题的能力。
但是,matlab也有一些不足之处,例如使用matlab程序可能会比较复杂,需要学习相关的语法和编程技巧,这可能会增加学生的负担。
因此,对于教师来说,在使用matlab教学的同时,还需要重视学生的能力和技能培养,充分发挥matlab在概率统计教学中的最佳作用。
matlab在概率统计教学中的应用浅析

matlab在概率统计教学中的应用浅析概率统计是统计分析的一个重要组成部分,它的目的是帮助人们更好地理解和应用数据,更好地处理实际问题。
数字技术的出现丰富了概率统计的教学资源,其中一种技术是Matlab,它为概率统计的教学提供了极大的帮助。
本文结合实际案例,分析Matlab在概率统计教学中的应用。
首先,Matlab在概率统计教学中具有实时反馈、细枝末节分析和可视化等优势。
现代概率统计往往采用服从特定分布的随机变量来表示现实环境中的情况,例如随机变量对象和方法、概率密度函数和累积分布函数、几何分布或指数分布中的参数估计等,而这些计算过程在Matlab中可以轻松实现,它提供的算法代码能够节省大量的时间,实时地进行计算,并能够有效地分析和提取信息,而且还可以使用Matlab的可视化工具,将计算结果表现得更加直观和清晰。
其次,Matlab拥有强大的计算能力,能够有效解决概率统计中的复杂问题,这有利于提高概率统计的教学质量。
Matlab提供的多种统计分析方法,包括参数估计、检验、贝叶斯重新标定等,可以更好地描述某一现实场景,从而更加全面地对比分析概率统计的各个方面,从而推动概率统计教学内容的变革和拓展。
此外,Matlab可以使用事件计算机模拟实验,从而更好地提高概率统计教学的实践效果。
Matlab可以模拟实验仿真,帮助学生分析、理解概率统计概念,使学生更具体地体验概率统计的运用,从而更好地掌握概率统计的知识。
最后,Matlab还为概率统计教学提供了一种可行的、有效的教学方法,能够更好地满足学生的学习需求。
Matlab可以让教师和学生以更直观、更高效的方式学习概率统计,从而提高学生的学习效果,使学生能够更好地掌握概率统计相关知识。
综上所述,Matlab在概率统计教学中具有重要的应用价值,它可以有效提高概率统计教学的质量,同时可以更有效地满足学生的学习需求。
随着经济的发展和技术的进步,概率统计在现代社会中已经发挥着重要的作用,因此,在概率统计教学中运用Matlab可以更好地实现概率统计在社会发展中的应用价值。
概率统计在MATLAB中的实现方法解析

概率统计在MATLAB中的实现方法解析概率统计是一门研究随机现象的规律性和不确定性的学科,广泛应用于各个领域。
而MATLAB是一种强大的科学计算软件,可以在概率统计领域中提供很多实用的工具和方法。
本文将探讨概率统计在MATLAB中的实现方法,帮助读者更好地理解和应用于实践。
一、概率分布的生成和拟合在概率统计中,对于一些已知的概率分布,我们常常需要生成符合该分布的随机数,或者通过已有的样本数据对分布进行拟合。
在MATLAB中,可以使用一些函数来实现这些操作。
首先,对于已知的概率分布,例如正态分布(高斯分布),可以使用normrnd()函数生成符合该分布的随机数。
该函数的输入参数包括均值和标准差,输出为符合正态分布的随机数。
例如,我们可以生成100个符合均值为0,标准差为1的正态分布随机数:```MATLABx = normrnd(0, 1, 100, 1);```对于已有的样本数据,我们可以使用fitdist()函数对数据进行概率分布的拟合。
该函数可以自动选择合适的分布类型,并给出对应的参数估计值。
例如,我们有一组样本数据x,需要对其进行正态分布的拟合:```MATLABdist = fitdist(x, 'Normal');```通过fitdist()函数返回的dist对象,我们可以获取该分布的参数估计值、置信区间等信息。
二、假设检验和置信区间估计假设检验和置信区间估计是概率统计中常用的分析方法,用于判断样本数据是否符合某个假设、计算参数估计的可信度等。
在MATLAB中,可以使用一些函数来实现假设检验和置信区间估计。
对于假设检验,MATLAB提供了ttest2()和chi2gof()等函数,用于分别进行两样本t检验和卡方检验。
例如,我们有两组样本数据x和y,需要进行两样本t检验:```MATLAB[h, p] = ttest2(x, y);```通过ttest2()函数返回的h值可以判断是否拒绝原假设,p值则表示检验结果的显著性。
使用Matlab进行概率统计分析的方法

使用Matlab进行概率统计分析的方法概率统计是一门研究随机现象的规律性的数学学科,广泛应用于各个领域。
而Matlab作为一种高效的数值计算工具,也可以用来进行概率统计分析。
本文将介绍使用Matlab进行概率统计分析的一些常用方法和技巧。
一、概率统计的基本概念在介绍使用Matlab进行概率统计分析方法之前,首先需要了解一些基本概念。
概率是表示事件发生可能性的数值,通常用概率分布来描述。
而统计是通过收集、整理和分析数据来研究问题的一种方法,通过统计推断可以得到总体的一些特征。
二、Matlab中的概率统计函数在Matlab中,有许多内置的概率统计函数,可以直接调用来进行分析。
常用的概率统计函数有:1. 随机数生成函数:可以用来生成服从不同概率分布的随机数,如正态分布、均匀分布等。
2. 描述统计函数:可以用来计算数据的统计特征,如均值、方差、标准差等。
3. 概率分布函数:可以用来计算不同概率分布的概率密度函数、累积分布函数、分位点等。
4. 线性回归和非线性回归函数:可以用来拟合数据并进行回归分析。
5. 假设检验函数:可以用来进行参数估计和假设检验,如t检验、方差分析等。
这些函数可以通过Matlab的帮助文档来查找具体的使用方法和示例。
三、随机数生成和分布拟合随机数生成是概率统计分析的基础,Matlab提供了多种随机数生成函数。
例如,可以使用rand函数生成服从均匀分布的随机数,使用randn函数生成服从标准正态分布的随机数。
通过设置不同的参数,可以生成不同分布的随机数。
分布拟合是将实际数据与理论概率分布进行对比的方法,可以帮助我们判断数据是否符合某种分布。
Matlab提供了fitdist函数用于对数据进行分布拟合,可以根据数据自动选择合适的概率分布进行拟合,并返回相应的参数估计结果。
通过对数据拟合后的分布进行分析,可以更好地了解数据的性质。
四、描述统计和数据可视化描述统计是在数据收集和整理之后,对数据进行总结和分析的过程。
matlab在概率统计教学中的应用浅析

matlab在概率统计教学中的应用浅析概率统计作为一种计算技术,广泛应用于多个领域,其计算量大,涉及范围广泛,使用传统统计学工具有较大困难。
Matlab作为一种强大的计算工具,能够以高效的方式完成复杂的计算,为概率统计的教学及应用提供了有力的支撑。
本文从概率统计的理论基础、Matlab 的计算特性及课程设计实例三个角度,阐述Matlab在概率统计教学中的应用。
一、概率统计教学中需要考虑的问题在概率统计教学中,学生需要学习大量的理论知识和实践技能,这部分知识运算量大,容易出错;在实际的概率统计实践中,学生需要处理复杂的实际问题,需要具备较强的数据处理能力和抽象思维能力;最后,教学中的概率统计课程也要求老师能够明确实践性的把控,对学生的答案、思路和解决问题的方式等都有较高的要求。
二、Matlab在概率统计教学中的优势Matlab作为一种高级计算工具,具有诸多优势,可以有效完成复杂的计算,为概率统计教学打下坚实的基础。
首先,Matlab具有强大的计算能力,能够快速处理复杂数据,可以轻松完成概率统计中大量的计算工作,可以提高学习效率;其次,Matlab的模块化编程也能有效的帮助学生解决实际问题,学生可以快速地完成复杂的计算,帮助促进了学生的实践能力;最后,Matlab 的调试功能也很好,可以帮助用户解决一般的编程问题,从而更好的完成编程任务。
三、Matlab在概率统计教学中的应用Matlab在概率统计教学中的应用十分广泛,这里我们以一个实际的课程设计为例,来讨论Matlab在概率统计教学中的应用。
以独立样本t检验课程为例,学生通过使用Matlab可以完成以下几个任务:一是熟悉独立样本t检验的理论基础;二是建立独立样本t检验的计算模型;三是运用Matlab进行t检验的实际计算,并且求出t值;四是推理出t值是否显著,最后得出结论。
除此之外,学生完成这个实验之后,也可以使用Matlab生成报表,帮助他们理解当前实验过程中的问题,进而更好的解决实际概率统计问题。
完整版Matlab概率论及数理统计
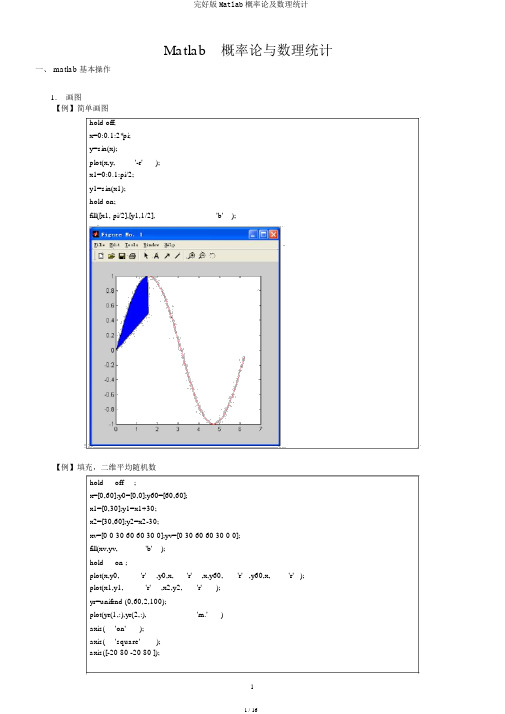
Matlab概率论与数理统计一、 matlab 基本操作1.画图【例】简单画图hold off;x=0:0.1:2*pi;y=sin(x);plot(x,y,'-r');x1=0:0.1:pi/2;y1=sin(x1);hold on;fill([x1, pi/2],[y1,1/2],'b' );【例】填充,二维平均随机数hold off;x=[0,60];y0=[0,0];y60=[60,60];x1=[0,30];y1=x1+30;x2=[30,60];y2=x2-30;xv=[0 0 30 60 60 30 0];yv=[0 30 60 60 30 0 0];fill(xv,yv,'b');hold on ;plot(x,y0,'r',y0,x,'r',x,y60,'r' ,y60,x,'r' );plot(x1,y1,'r',x2,y2,'r');yr=unifrnd (0,60,2,100);plot(yr(1,:),yr(2,:),'m.')axis('on');axis('square');2.排列组合C=nchoosek(n,k) :C C n k,例 nchoosek(5,2)=10, nchoosek(6,3)=20.prod(n1:n2) :从 n1 到 n2 的连乘【例】最少有两个人寿辰相同的概率n!C N nN !( N n)!N(N1)(N n1)公式计算 p 111N nN n N n365 364 (365rs1)365364365rs 1 1365rs1365365365rs=[20,25,30,35,40,45,50];%每班的人数p1=ones(1,length(rs));p2=ones(1,length(rs));%用连乘公式计算for i=1:length(rs)p1(i)=prod(365-rs(i)+1:365)/365^rs(i);end%用公式计算(改进)for i=1:length(rs)for k=365-rs(i)+1:365p2(i)=p2(i)*(k/365);end ;endp1(i)=exp(sum(log(365-rs(i)+1:365))-rs(i)*log(365));endp_r1=1-p1;p_r2=1-p2;Rs =[20253035404550 ]P_r=[0.4114 0.5687 0.7063 0.8144 0.8912 0.9410 0.9704]二、随机数的生成3.平均分布随机数rand(m,n); 产生 m 行 n 列的 (0,1) 平均分布的随机数rand(n); 产生 n 行 n 列的 (0,1)平均分布的随机数【练习】生成(a,b)上的平均分布4.正态分布随机数randn(m,n); 产生 m 行 n 列的标准正态分布的随机数【练习】生成N(nu,sigma.^2) 上的正态分布5.其他分布随机数函数名调用形式注释Unidrnd unid rnd (N,m,n)平均分布(失散)随机数binornd bino rnd (N,P,m,n)参数为 N, p的二项分布随机数Poissrnd poiss rnd (Lambda,m,n)参数为 Lambda的泊松分布随机数geornd geornd (P,m,n)参数为 p 的几何分布随机数hygernd hygernd (M,K,N,m,n)参数为 M, K, N 的超几何分布随机数Normrnd normrnd (MU,SIGMA,m,n)参数为 MU, SIGMA的正态分布随机数,SIGMA是标准差Unifrnd unif rnd ( A,B,m,n)[A,B] 上平均分布 ( 连续 ) 随机数Exprnd exprnd (MU,m,n)参数为 MU的指数分布随机数chi2rnd chi2 rnd(N,m,n)自由度为 N 的卡方分布随机数Trnd t rnd(N,m,n)自由度为 N 的 t分布随机数Frnd f rnd(N1, N2,m,n)第一自由度为N1, 第二自由度为 N2 的 F 分布随机数gamrnd gamrnd(A, B,m,n)参数为 A, B的分布随机数betarnd betarnd(A, B,m,n)参数为 A, B的分布随机数lognrnd lognrnd(MU, SIGMA,m,n)参数为 MU, SIGMA的对数正态分布随机数nbinrnd nbinrnd(R, P,m,n)参数为 R,P 的负二项式分布随机数ncfrnd ncfrnd(N1, N2, delta,m,n)参数为 N1, N2, delta 的非中心 F 分布随机数nctrnd nctrnd(N, delta,m,n)参数为 N,delta的非中心 t 分布随机数ncx2rnd ncx2rnd(N, delta,m,n)参数为 N,delta的非中心卡方分布随机数raylrnd raylrnd(B,m,n)参数为 B 的瑞利分布随机数weibrnd weibrnd(A, B,m,n)参数为 A, B的韦伯分布随机数三、一维随机变量的概率分布1.失散型随机变量的分布率(1)0-1 分布(2)平均分布(3) 二项分布: binopdf(x,n,p) ,若X ~ B(n, p),则P{ X k} C n k p k (1p) n k,x=0:9;n=9;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')y=[ 0.0404, 0.1556, 0.2668, 0.2668, 0.1715, 0.0735, 0.0210, 0.0039, 0.0004, 0.0000 ]‘当 n 较大时二项分布近似为正态分布x=0:100;n=100;p=0.3;y= binopdf(x,n,p);plot(x,y,'b-',x,y,'r*')(4) 泊松分布: piosspdf(x, lambda) ,若X ~k e ( ) ,则 P{ X k}k !x=0:9; lambda = 3;y= poisspdf (x,lambda);plot(x,y,'b-',x,y,'r*')y=[ 0.0498, 0.1494, 0.2240, 0.2240, 0.1680, 0.1008, 0.0504, 0.0216, 0.0081, 0.0027 ](5) 几何分布: geopdf (x, p),则P{ X k} p(1p) k 1y= geopdf(x,p);plot(x,y,'b-',x,y,'r*')y=[ 0.3000, 0.2100, 0.1470, 0.1029, 0.0720, 0.0504, 0.0353, 0.0247, 0.0173, 0.0121 ]C M k C N n k Mx=0:10;N=20;M=8;n=4;y= hygepdf(x,N,M,n);plot(x,y,'b-',x,y,'r*')y=[ 0.1022, 0.3633, 0.3814, 0.1387, 0.0144, 0, 0, 0, 0, 0, 0 ]2.概率密度函数1a x b(1)平均分布: unifpdf(x,a,b) ,f ( x)b a0其他a=0;b=1;x=a:0.1:b;y= unifpdf (x,a,b);112(2)正态分布: normpdf(x,mu,sigma) ,f ( x)e2 2 ( x)2x=-10:0.1:12;mu=1;sigma=4;y= normpdf(x,mu,sigma);rn=10000;z= normrnd (mu,sigma,1,rn); %产生 10000 个正态分布的随机数d=0.5;a=-10:d:12;b=(hist(z,a)/rn)/d;% 以 a 为横轴,求出 10000 个正态分布的随机数的频率plot(x,y,'b-',a,b,'r.')(3) 指数分布: exppdf(x,mu) ,f (x)1 e1xa x by= exppdf(x,mu); plot(x,y,'b-',x,y,'r*')1n1(4)2分布: chi2pdf(x,n) , f (x; n)2n 2x2( n 2)hold on x=0:0.1:30;n=4;y= chi2pdf(x,n);plot(x,y,'b');%blue n=6;y= chi2pdf(x,n);plot(x,y,'r');%redn=8;y= chi2pdf(x,n);plot(x,y,'c');%cyan n=10;y= chi2pdf(x,n);plot(x,y,'k');%black legend('n=4', 'n=6', 'n=8', 'n=10');(( n 1) 2) x 2(5) t 分布: tpdf(x,n) , f (x; n)(n 2)1nnhold on x=-10:0.1:10;n=2;y= tpdf(x,n);plot(x,y,'b');%blue e 2n 1 2x 0x 0n=20;y= tpdf(x,n);plot(x,y,'k');%black legend('n=2', 'n=6', 'n=10', 'n=20');n1n1 2n1n222(6) F 分布: fpdf(x,n1,n2) ,f ( x; n1, n2)(( n1n2 ) 2) n1x 21n1x x 0 (n1 2)(n2 2) n2n20x 0hold onx=0:0.1:10;n1=2; n2=6;y= fpdf(x,n1,n2);plot(x,y,'b');%bluen1=6; n2=10;y= fpdf(x,n1,n2);plot(x,y,'r');%redn1=10; n2=6;y= fpdf(x,n1,n2);plot(x,y,'c');%cyann1=10; n2=10;y= fpdf(x,n1,n2);plot(x,y,'k');%blacklegend(' n1=2; n2=6', ' n1=6; n2=10', ' n1=10; n2=6', ' n1=10; n2=10');3.分布函数 F (x) P{ X x}【例】求正态分布的累积概率值设 X ~ N(3,22),求P{2X 5},P{ 4 X 10},P{ X 2}, P{X3} ,4.逆分布函数,临界值y F (x) P{ X x} , x F 1 ( y) , x 称之为临界值【例】求标准正态分布的累积概率值y=0:0.01:1;x=norminv(y,0,1);【例】求2 (9) 分布的累积概率值hold offy=[0.025,0.975];x=chi2inv(y,9);n=9;x0=0:0.1:30;y0=chi2pdf(x0,n);plot(x0,y0,'r');x1=0:0.1:x(1);y1=chi2pdf(x1,n);x2=x(2):0.1:30;y2=chi2pdf(x2,n);hold onfill([x1, x(1)],[y1,0],'b');fill([x(2),x2],[0,y2],'b');5. 数字特色函数名调用形式注释sort sort(x),sort(A)排序 ,x 是向量, A 是矩阵,按各列排序sortrows sortrows(A) A 是矩阵,按各行排序mean mean(x)向量 x 的样本均值var var(x)向量 x 的样本方差std std(x)向量 x 的样本标准差median median(x)向量 x 的样本中位数geomean geomean(x)向量 x 的样本几何平均值harmmean harmmean(x)向量 x 的样本调停平均值skewness skewness(x)向量 x 的样本偏度max max(x)向量 x 的最大值min min(x)向量 x 的最小值cov cov(x), cov(x,y)向量 x 的方差,向量x,y 的协方差矩阵corrcoef corrcoef(x,y)向量 x,y 的相关系数矩阵【练习】二项分布、泊松分布、正态分布( 1)对n10, p 0.2 二项分布,画出 b(n, p) 的分布律点和折线;( 2)对np ,画出泊松分布( ) 的分布律点和折线;( 3)对np,2np(1 p) ,画出正态分布N ( , 2 )的密度函数曲线;( 4)调整 n, p ,观察折线与曲线的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N,P的二项随机数据函数binornd格式R = binornd(N,P) %N、P为二项分布的两个参数,返回服从参数为N、P的二项分布的随机数,N、P大小相同。
R = binornd(N,P,m) %m指定随机数的个数,与R同维数。
R = binornd(N,P,m,n) %m,n分别表示R的行数和列数例4-1>> R=binornd(10,0.5)R =3>> R=binornd(10,0.5,1,6)R =8 1 3 7 6 4>> R=binornd(10,0.5,[1,10])R =6 8 4 67 5 3 5 6 2>> R=binornd(10,0.5,[2,3])R =7 5 86 5 6>>n = 10:10:60;>>r1 = binornd(n,1./n)r1 =2 1 0 1 1 2>>r2 = binornd(n,1./n,[1 6])r2 =0 1 2 1 3 14.1.2 正态分布的随机数据的产生命令参数为μ、σ的正态分布的随机数据函数normrnd格式R = normrnd(MU,SIGMA) %返回均值为MU,标准差为SIGMA的正态分布的随机数据,R可以是向量或矩阵。
R = normrnd(MU,SIGMA,m) %m指定随机数的个数,与R同维数。
R = normrnd(MU,SIGMA,m,n) %m,n分别表示R的行数和列数例4-2>>n1 = normrnd(1:6,1./(1:6))n1 =2.1650 2.31343.02504.0879 4.8607 6.2827>>n2 = normrnd(0,1,[1 5])n2 =0.0591 1.7971 0.2641 0.8717 -1.4462>>n3 = normrnd([1 2 3;4 5 6],0.1,2,3) %mu为均值矩阵n3 =0.9299 1.9361 2.96404.12465.0577 5.9864>> R=normrnd(10,0.5,[2,3]) %mu为10,sigma为0.5的2行3列个正态随机数R =9.7837 10.0627 9.42689.1672 10.1438 10.59554.1.3 常见分布的随机数产生常见分布的随机数的使用格式与上面相同表4-1 随机数产生函数表4.1.4 通用函数求各分布的随机数据命令求指定分布的随机数函数random格式y = random('name',A1,A2,A3,m,n) %name的取值见表4-2;A1,A2,A3为分布的参数;m,n指定随机数的行和列例4-3 产生12(3行4列)个均值为2,标准差为0.3的正态分布随机数>> y=random('norm',2,0.3,3,4)y =2.3567 2.0524 1.8235 2.03421.9887 1.94402.6550 2.32002.0982 2.2177 1.9591 2.01784.2 随机变量的概率密度计算4.2.1 通用函数计算概率密度函数值命令通用函数计算概率密度函数值函数pdf格式Y=pdf(name,K,A)Y=pdf(name,K,A,B)Y=pdf(name,K,A,B,C)说明返回在X=K处、参数为A、B、C的概率密度值,对于不同的分布,参数个数是不同;name为分布函数名,其取值如表4-2。
表4-2 常见分布函数表例如二项分布:设一次试验,事件A发生的概率为p,那么,在n次独立重复试验中,事件A恰好发生K次的概率P_K为:P_K=P{X=K}=pdf('bino',K,n,p) 例4-4 计算正态分布N(0,1)的随机变量X在点0.6578的密度函数值。
解:>> pdf('norm',0.6578,0,1)ans =0.3213例4-5 自由度为8的卡方分布,在点2.18处的密度函数值。
解:>> pdf('chi2',2.18,8)ans =0.03634.2.2 专用函数计算概率密度函数值命令二项分布的概率值函数binopdf格式binopdf (k, n, p) %等同于)p,n,K',p —每次试验事件A发生的概(pdf'obin率;K—事件A发生K次;n—试验总次数命令泊松分布的概率值函数poisspdf格式poisspdf(k, Lambda) %等同于)'poispdf'(Lam da,K,s命令正态分布的概率值函数normpdf(K,mu,sigma) %计算参数为μ=mu,σ=sigma的正态分布密度函数在K处的值专用函数计算概率密度函数列表如表4-3。
表4-3 专用函数计算概率密度函数表例4-6 绘制卡方分布密度函数在自由度分别为1、5、15的图形>> x=0:0.1:30;>> y1=chi2pdf(x,1); plot(x,y1,':')>> hold on>> y2=chi2pdf(x,5);plot(x,y2,'+')>> y3=chi2pdf(x,15);plot(x,y3,'o')>> axis([0,30,0,0.2]) %指定显示的图形区域则图形为图4-1。
4.2.3 常见分布的密度函数作图1.二项分布例4-7>>x = 0:10;>>y = binopdf(x,10,0.5); >>plot(x,y,'+')2.卡方分布 例4-8>> x = 0:0.2:15; >>y = chi2pdf(x,4); >>plot(x,y)0.00.0.10.0.20.00.0.10.图4-23.非中心卡方分布 例4-9>>x = (0:0.1:10)';>>p1 = ncx2pdf(x,4,2); >>p = chi2pdf(x,4); >>plot(x,p,'--',x,p1,'-')4.指数分布 例4-10>>x = 0:0.1:10; >>y = exppdf(x,2); >>plot(x,y)0.00.0.10.0.0.0.0.0.图4-35.F 分布 例4-11>>x = 0:0.01:10; >>y = fpdf(x,5,3); >>plot(x,y)6.非中心F 分布 例4-12图4-1>>x = (0.01:0.1:10.01)'; >>p1 = ncfpdf(x,5,20,10); >>p = fpdf(x,5,20); >>plot(x,p,'--',x,p1,'-')0.0.0.0.0.0.0.0.图4-47.Γ分布 例4-13>>x = gaminv((0.005:0.01:0.995),100,10); >>y = gampdf(x,100,10); >>y1 = normpdf(x,1000,100); >>plot(x,y,'-',x,y1,'-.')8.对数正态分布 例4-14>>x = (10:1000:125010)';>>y = lognpdf(x,log(20000),1.0); >>plot(x,y)>>set(gca,'xtick',[0 30000 60000 90000 120000])>>set(gca,'xticklabel',str2mat('0','$30,000','$60,000',… '$90,000','$120,000'))x 10-300.1.2.3.x 10-5图4-59.负二项分布 例4-15>>x = (0:10);>>y = nbinpdf(x,3,0.5); >>plot(x,y,'+')10.正态分布例4-16>> x=-3:0.2:3;>> y=normpdf(x,0,1); >> plot(x,y)0.050.10.150.20.0.0.0.图4-611.泊松分布 例4-17>>x = 0:15;>>y = poisspdf(x,5); >>plot(x,y,'+')12.瑞利分布 例4-18>>x = [0:0.01:2]; >>p = raylpdf(x,0.5); >>plot(x,p)0.00.0.10.0.1.图4-713.T 分布 例4-19>>x = -5:0.1:5; >>y = tpdf(x,5);>>z = normpdf(x,0,1); >>plot(x,y,'-',x,z,'-.')14.威布尔分布 例4-20>> t=0:0.1:3;>> y=weibpdf(t,2,2); >> plot(y)0.0.0.0.0.1.图4-84.3 随机变量的累积概率值(分布函数值)4.3.1 通用函数计算累积概率值命令 通用函数cdf 用来计算随机变量K X ≤的概率之和(累积概率值) 函数 cdf格式 )A ,K ,e nam (cdf '')B ,A ,K ,e nam (cdf '' )C ,B ,A ,K ,e nam (cdf ''说明 返回以name 为分布、随机变量X ≤K 的概率之和的累积概率值,name 的取值见表4-1 常见分布函数表例4-21 求标准正态分布随机变量X 落在区间(-∞,0.4)内的概率(该值就是概率统计教材中的附表:标准正态数值表)。
