四个经典的算法案例
常用算法举例范文

常用算法举例范文在计算机科学中,算法是解决问题的一系列有序步骤,它能够帮助我们解决各种各样的问题。
以下是一些常用的算法及其举例:1.排序算法:-冒泡排序:通过比较相邻元素并交换位置来将最大的元素逐渐移动到数组的末尾。
-快速排序:选择一个基准元素,将数组分为两部分,左边的元素小于基准,右边的元素大于基准,然后递归地对两部分进行快速排序。
-归并排序:将数组划分为两个子数组,对每个子数组分别进行归并排序,然后将两个有序子数组合并成一个有序数组。
2.查找算法:-二分查找:对于有序数组,通过与中间元素进行比较,将查找范围缩小一半,直到找到目标元素或确定不存在。
-哈希查找:通过将关键字映射到数组的索引位置来进行查找,可以在常数时间内找到目标元素。
3.图算法:-广度优先(BFS):从起始节点开始,逐层遍历图中的节点,直到找到目标节点。
-深度优先(DFS):从起始节点开始,沿着一条路径一直向下,直到找到目标节点或无法继续为止。
4.动态规划算法:-背包问题:给定一组物品和一个容量限制,选择一些物品放入背包中,使得总价值最大。
-最长公共子序列(LCS):给定两个字符串,找到它们的最长公共子序列的长度。
5.数学算法:-欧几里得算法:计算两个整数的最大公约数。
-快速幂算法:计算一个数的幂运算,通过将指数进行二进制拆分来减少计算次数。
6.字符串处理算法:-KMP算法:通过利用已匹配字符的信息来避免不必要的回溯,实现高效的字符串匹配。
- Boyer-Moore算法:利用模式串中的信息来进行快速的字符串匹配。
7.图像处理算法:-图像平滑算法:通过对图像进行滤波处理,去除图像中的噪声,使其更加平滑。
-图像边缘检测算法:通过检测图像中的边缘信息,突出物体的轮廓。
8.机器学习算法:-K均值聚类算法:将数据集划分为K个簇,使得同一个簇内的数据点之间的距离最小化。
-支持向量机(SVM):将数据集映射到高维空间,并通过找到最优的超平面来实现分类。
回溯算法原理和几个常用的算法实例

回溯算法原理和几个常用的算法实例回溯算法是一种基于深度优先的算法,用于解决在一组可能的解中找到满足特定条件的解的问题。
其核心思想是按照特定的顺序逐步构造解空间,并通过剪枝策略来避免不必要的。
回溯算法的实现通常通过递归函数来进行,每次递归都尝试一种可能的选择,并在达到目标条件或无法继续时进行回溯。
下面介绍几个常用的回溯算法实例:1.八皇后问题:八皇后问题是一个经典的回溯问题,要求在一个8×8的棋盘上放置8个皇后,使得每个皇后都不能相互攻击。
即每行、每列和对角线上都不能有两个皇后。
通过在每一列中逐行选择合适的位置,并进行剪枝,可以找到所有满足条件的解。
2.0-1背包问题:0-1背包问题是一个经典的组合优化问题,要求在一组物品中选择一些物品放入背包,使得其总重量不超过背包容量,同时价值最大化。
该问题可以通过回溯算法进行求解,每次选择放入或不放入当前物品,并根据剩余物品和背包容量进行递归。
3.数独问题:数独问题是一个经典的逻辑推理问题,要求在一个9×9的网格中填入数字1-9,使得每行、每列和每个3×3的子网格中都没有重复数字。
该问题可以通过回溯算法进行求解,每次选择一个空格,并依次尝试1-9的数字,然后递归地进行。
4.字符串的全排列:给定一个字符串,要求输出其所有可能的排列。
例如,对于字符串"abc",其所有可能的排列为"abc"、"acb"、"bac"、"bca"、"cab"和"cba"。
可以通过回溯算法进行求解,每次选择一个字符,并递归地求解剩余字符的全排列。
回溯算法的时间复杂度通常比较高,因为其需要遍历所有可能的解空间。
但是通过合理的剪枝策略,可以减少的次数,提高算法效率。
在实际应用中,可以根据具体问题的特点来设计合适的剪枝策略,从而降低算法的时间复杂度。
算法解决实际问题实例

算法解决实际问题实例算法是计算机科学中的核心概念,它是一套定义了在解决问题时需要遵循的规则和步骤的总称。
算法的应用范围广泛,不仅局限于计算机领域,也包括了其他领域,如数学、物理学、经济学等。
本文将从实际问题的角度出发,介绍几个运用算法解决的实例。
第一个实例是旅行推荐系统。
对于喜爱周游世界的旅行者来说,他们在规划旅行路线时常常会面临以下问题:如何合理安排旅行的目的地,使得既能满足游客对景点的兴趣,又能合理安排时间和交通路线?这个问题通常可以通过图算法来解决。
首先,将每个景点作为图的一个节点,各节点之间的距离作为图的边。
然后,根据用户的兴趣偏好,给每个节点打分。
接下来,通过图搜索算法(如最短路径算法)找出一个或多个满足用户要求的旅行路线。
第二个实例是社交网络中的好友推荐。
随着社交网络的快速发展,人们面临了一个新的问题:如何在广大的网络中找到真正的朋友,而不只是浮于表面的社交关系?这个问题可以通过图算法和机器学习算法来解决。
首先,通过图算法建立社交网络的图模型。
然后,根据用户的行为和社交关系,使用机器学习算法预测用户之间的友谊强度。
最后,根据这一预测结果,推荐给用户潜在的好友。
第三个实例是电商平台的推荐系统。
在电商平台上,为了提高用户的购物体验和销售量,经常会使用推荐系统来推荐给用户可能感兴趣的商品。
推荐系统的核心是通过算法分析用户的历史行为和兴趣,根据这些信息给用户推荐相关的商品。
其中,常用的算法包括协同过滤算法、内容过滤算法和深度学习算法等。
通过这些算法,电商平台可以提高用户购买的满意度,从而提高用户黏性和销售额。
除了上述实际问题,算法还有很多其他的应用。
例如,医疗领域中的疾病诊断和药物设计、金融领域中的股票预测和风险控制、交通领域中的交通流优化和路径规划等。
这些问题都可以通过算法来解决,提高工作效率和精确度。
算法的应用不仅仅局限于计算机领域,也能够为其他科学和工程领域提供帮助。
通过合理地运用算法,可以解决实际问题,提高工作效率和解决方案的可行性。
经典算法实例范文

经典算法实例范文算法是一系列解决问题的步骤或规则,是计算机科学中非常重要的概念。
经典算法是指在计算机科学领域被广泛应用并被证明相对高效的算法。
本文将介绍几个经典算法的实例。
一、排序算法排序算法是最基本、最常用的算法之一、下面将介绍两个经典的排序算法。
1.冒泡排序冒泡排序是一种简单的排序算法,它的基本思路是多次遍历数组,每次将相邻的两个元素逐个比较,如果顺序不对则交换位置。
这样一次遍历后,最大的元素会被移到最后。
重复n-1次遍历,就可以完成排序。
冒泡排序的时间复杂度是O(n^2)。
2.快速排序快速排序是一种高效的排序算法,它的基本思路是选择一个基准元素,通过一趟排序将待排序的序列分成两个独立的部分,其中一部分的所有元素都小于基准,另一部分的所有元素都大于等于基准。
然后对这两个部分分别进行递归排序,最后合并两个部分得到有序序列。
快速排序的时间复杂度是 O(nlogn)。
二、查找算法查找算法是在给定的数据集合中一些特定元素的算法。
下面将介绍两个常用的查找算法。
1.二分查找二分查找也称为折半查找,是一种在有序数组中查找一些特定元素的算法。
它的基本思路是首先确定数组中间位置的元素,然后将要查找的元素与中间元素进行比较,如果相等则返回位置,如果小于则在左部分继续查找,如果大于则在右部分继续查找。
二分查找的时间复杂度是 O(logn)。
2.哈希查找哈希查找是通过哈希函数将关键字映射到哈希表中的位置,然后根据映射位置在哈希表中查找关键字。
哈希查找的时间复杂度是O(1)。
三、图算法图是由节点和边组成的一种数据结构,图算法主要用于解决与图相关的问题。
下面将介绍两个常用的图算法。
1.广度优先广度优先是一种用于图的遍历和的算法。
它的基本思路是从图的其中一顶点出发,遍历所有与之相邻的顶点,然后再依次遍历这些相邻顶点的相邻顶点,以此类推,直到访问完所有顶点,或者找到目标顶点。
广度优先使用队列来实现,时间复杂度是O(,V,+,E,),其中,V,表示图的顶点数,E,表示图的边数。
高中数学之算法案例

算法案例(讲义)➢ 知识点睛典型算法举例: 1. 辗转相除法①方法概述:两数相除,较大数除以较小数,得商和余数,继而较小数除以余数,重复操作,直至除尽,此时除数即为最大公约数.②原理:在a =bq +r 中,除数b 和余数r 能被同一个数整除,那么被除数a 也能被这个数整除.或者说,除数与余数的最大公约数,就是被除数与除数的最大公约数. 2. 秦九韶算法把一个n 次多项式改写成如下形式:1110121102312101210()()(())((()))n n n n n n n n n n n n n n n f x a x a x a x a a x a x a x a a x a x a x a x a a x a x a x a x a ----------=++++=++++=+++++==+++++……………… 记0n v a =,11n n v a x a -=+,…,10n n v v x a -=+.求多项式的值时,首先计算最内层括号内一次多项式的值,即v 1,然后由内向外逐层计算. 3. 进位制①k 进制:若k 是一个大于1的整数,那么以k 为基数的k 进制数可以表示为一串数字连写在一起的形式.110()n n k a a a a -…11011000n n n n a a a a N a k a a a k --∈<<<≤(,,…,,,,,…,,)②进位制数相互转化:k 进制转十进制,计算k 进制数a 的右数第i 位数字i a 与1i k -的乘积1i i a k -⋅,再将其累加,重复操作求和.十进制数转k 进制数(除k 取余法): 如右图,十进制数化为二进制数, 89=1011001(2).➢ 精讲精练1. 用“辗转相除法”求下列数的最大公约数:(1)459和357的最大公约数是____________;余数2222222012511224489(2)三个数324243135,,的最大公约数是____________.2. 用秦九韶算法求多项式的值:(1)计算多项式x x x x x x x f 876543)(23456+++++=在1.0=x 时的值时,需要做乘法和加法的次数分别是_______,_______;(2)求多项式23456()1235879653f x x x x x x x =+-++++在x =-4的值时,4v 的值为_______;(3)计算多项式5432()853261f x x x x x x =+++++,当2x =时的值为________. 3. 完成下列进制的转化:(3)(10)10202____=; (10)__________(8)101=;1231(5)=_____________(7).4. 三位七进制的数表示的最大的十进制的数是( )A .322B .402C .342D .3655. 在下列各数中,最小的数是( )A .)9(85B .)6(210C .)4(1000D .(2)1111116. 已知三个数12(16),25(7),33(4),按照从小到大的顺序排列为________________.7. 已知()175r =(10)125,则r =________.8. 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 的值分别为14,18,则输出的a 的值为( ) A .0B .2C .4D .149. 如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n ,x 的值分别为3,2,则输出v 的值为( ) A .35B .20C .18D .910.下面是把二进制数(2)11111化为十进制数的一个程序框图,判断框内应填入的条件是()A.5i>?B.4i≤?C.4i>?D.5i≤?11.执行如图所示的程序框图后,输出的值为4,则P的取值范围是()A.715816P<≤B.1516P>C.3748P<≤D.715816P<≤12.设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=________.13. 已知函数232 1 01 012 1x x y x x x x x -<⎧⎪=+<⎨⎪+⎩≤≥()()(),写出求该函数的函数值的算法,并画出程序框图.14. 设计一算法,求使20063212222>++++n Λ成立的最小正整数n 的值.15.设计算法计算:1112131415167S=++++++,画出程序框图.【参考答案】1. (1)51;(2)272. (1)6;5;(2)220;(3)3813. 101 145 3624. C5. D6. (4)(16)(7)331225<<7. 88. B9. C 10. C 11. C 12. 495 13. 略 14. 略 15. 略算法案例(随堂测试)1. 372和684的最大公约数是( )A .36B .186C .12D .5892. 用秦九韶算法计算多项式65432()3567983512f x x x x x x x =+++-++在x =-4时的值时,v 2的值为( )A .-57B .-22C .34D .743. 1234(8)=________(10);300=________(5);300=_______(6).4. 设计一个算法,输入正整数n ,输出111123n++++….【参考答案】1. C2. C3. 668;2 200;1 2204. 略算法案例(习题)➢ 巩固练习5. 求下列数的最大公约数:(1)1 443与999的最大公约数是_____________;(2)319,377,116的最大公约数是___________.6. 用秦九韶算法求n 次多项式1110()n n n n f x a x a x a x a --=++++…,当x =x 0时,0()f x 需要算乘法、加法的次数分别为( ) A .n 2,nB .2n ,nC .n ,2nD .n ,n7.已知532=++++,运用秦九韶算法计算x=3时的值时,v3的值为()()231f x x x x xA.27 B.11 C.109 D.368.用秦九韶算法求多项式765432=++++++在x=3时的值为________.()765432f x x x x x x x x9.把21化为二进制数,则此数为()A.10011(2)B.10110(2)C.10101(2)D.11001(2)10.一个k进制的三位数与某六进制的二位数等值,则k不可能是()A.3 B.4 C.5 D.711.下列各数中,最小的数是()A.75B.210(6)C.111111(2)D.85(9)12.若a=33(10),b=52(6),c=11111(2),则三个数的大小关系是()A.c>b>a B.b>c>a C.c>a>b D.a>b>c13.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7B.12C.17D.34第9题图第10题图14.如图是一个算法的程序框图,该算法所输出的结果是()A.11112310++++…B.11113519++++…C.111124620++++…D.231011112222++++…15.某程序框图如图所示,若输出的S=57,则判断框内为()A.k>4?B.k>5?C.k>6?D.k>7?11第11题图 第12题图16. 执行如图所示的程序框图,若输入k 的值为8,则判断框图可填入的条件是( )A .S ≤34?B .S ≤56?C .S ≤1112? D .S ≤1524?17. 设计一个算法,输入两个数,输出两个数中较大的一个.18.已知函数21111131x x y x x x x ⎧-<-⎪=+-⎨⎪+>≤≤()()(),试画出求函数值的程序框图.19. 对任意给定的正整数n ,写出一个求13+23+33+…+n 3的算法程序框图.20.设计算法求111112233499100++++⨯⨯⨯⨯…的值,要求画出程序框图.【参考答案】1.(1)111 (2)292.D3.D4.213245.C6.D7.C8.D9.C10.C11.A12.C13.略14.略15.略16.略12。
常见的随机算法、近似算法和启发式算法的案例

常见的随机算法、近似算法和启发式算法的案例常见的随机算法、近似算法和启发式算法的案例有:
随机算法:
1. 随机洗牌算法:用于打乱一组数据的顺序,常用于实现随机排列或游戏中的洗牌操作。
2. 蒙特卡洛算法:通过随机采样的方法,来估计一个问题的解或某个数值的概率分布,例如蒙特卡洛模拟的方法用于计算圆周率π的值。
近似算法:
1. 近似最近邻算法:快速搜索给定查询点最近邻的点,而不需要对所有数据点进行完全搜索,例如kd树算法。
2. 近似最小覆盖问题的算法:在给定一组区域的情况下,选择尽可能少的区域来覆盖所有点,例如贪心算法。
启发式算法:
1. 蚁群算法:模拟蚂蚁在寻找食物时的行为,通过信息素的释放和感知,来寻找全局最优解,常用于求解旅行商问题。
2. 遗传算法:基于生物进化理论,通过模拟自然选择、基因交叉、变异等操作,来搜索优化问题的解空间,例如用于解决旅行商问题或优化函数的最优解。
常见算法及其运算实例分析

常见算法及其运算实例分析算法是计算机科学中最重要的一部分。
算法既是计算机科学的基础,又是计算机编程的核心。
了解算法,可以让我们更深入地理解计算机的运行原理,以及如何利用计算机处理各种问题。
本文将为大家介绍几个常见的算法及其运算实例分析。
一、递归算法递归算法是一种函数调用自身的算法。
递归算法具有简单、直观、可理解等优点。
但同时也存在着栈溢出、时间复杂度高等问题。
递归算法通常包含有一些关键参数,如递归的次数和递归深度等,这些参数的变化对于程序的运行和结果都有着重要的影响。
实例:斐波那契数列我们可以通过递归算法来实现斐波那契数列。
斐波那契数列的定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2)。
通过递归算法,可以很容易地实现斐波那契数列。
我们只需要以递归方式调用F函数即可,代码如下:```def F(n):if n==0:return 0elif n==1:return 1else:return F(n-1)+F(n-2)```二、分治算法分治算法是将问题分解成若干个子问题,然后递归地分别解决每个子问题,最终合并成一个整体的算法。
分治算法通常解决的问题都具备“可分解性”和“合并性”的特征。
实例:二分查找二分查找可以用分治算法来实现。
二分查找的思想是将数组分成两个区间,分别判断目标值是否在每个区间中。
如果目标值存在于某个区间中,则继续在该区间中进行查找;否则在另一个区间中进行查找。
通过分治算法,我们可以将二分查找优化成O(log n)的时间复杂度。
代码如下:```def binary_search(arr, left, right, target):if left > right:return -1mid = (left + right) // 2if arr[mid] == target:return midelif arr[mid] < target:return binary_search(arr, mid+1, right, target)else:return binary_search(arr, left, mid-1, target)```三、贪心算法贪心算法可以理解为通过每步选择中的局部最优解,从而达到全局最优的解决方案。
分披萨算法题

分披萨算法题全文共四篇示例,供读者参考第一篇示例:分披萨算法题是一种经典的计算机算法题目,常常用来测试程序员的逻辑思维和编程能力。
分披萨算法题的形式通常是这样的:给定一个整数n,表示有n个朋友要一起分享一份披萨,现在要将披萨平均分配给这些朋友,问你最少需要切割几刀才能完成这个任务?这个问题实际上是一个数学问题,要想解答这个问题,我们首先要了解一下披萨的切割规则。
假设我们现在有n个朋友要一起分享一份披萨,首先我们切成n等份,然后每个人都可以选择任意一块披萨,接着再切割,然后让每个人再次选择。
这样一直切下去,直到每个人都只剩下一小块披萨,这样就完成了任务。
接下来我们讨论一下如何计算需要切几刀才能完成任务。
假设现在有n个朋友,我们要如何切割披萨才能让每个人都得到一块披萨呢?我们可以通过观察发现,第一刀切的时候,我们需要切n刀,也就是每个人都会得到一块披萨;第二刀切的时候,我们需要切n/2刀,也就是每两个人会得到一块披萨;第三刀切的时候,我们需要切n/4刀,也就是每四个人会得到一块披萨。
以此类推,我们可以发现,如果我们总共切x刀,那么最终每个人得到一块披萨,满足2^x >= n即可,其中^表示幂运算。
现在我们已经知道了需要切几刀才能完成任务,接下来我们来编写算法求解这个问题。
我们可以通过编写一个递归函数来实现这个算法,函数的思路是这样的:首先检查n是否为1,如果是,则返回0;如果不是,则调用递归函数计算n/2,再加上1的结果即可。
下面是这个算法的Python实现:```pythondef divide_pizza(n):if n == 1:return 0return divide_pizza(n // 2) + 1n = 8result = divide_pizza(n)print(result)```以上代码中,我们首先定义了一个名为divide_pizza的函数,接受一个整数n作为参数。
如果n等于1,则返回0,否则递归调用divide_pizza函数计算n/2,再加上1,最终返回结果。
五大经典算法以及案例

五大经典算法以及案例
1. 排序算法:使用冒泡排序算法对一个包含10个随机整数的数组进行排序。
案例:
给定数组:[4, 9, 2, 5, 1, 8, 3, 7, 6, 10]
排序后的数组:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
2. 查找算法:使用二分查找算法在一个有序整数数组中查找目标值。
案例:
给定有序数组:[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
目标值:11
查找结果:目标值在数组中的位置为5。
3. 图遍历算法:使用深度优先搜索算法遍历一个无向图。
案例:
给定无向图的邻接矩阵表示:
[0, 1, 1, 0, 0]
[1, 0, 0, 1, 1]
[1, 0, 0, 0, 1]
[0, 1, 0, 0, 0]
[0, 1, 1, 0, 0]
从节点1开始进行深度优先搜索的遍历结果:1 -> 2 -> 4 -> 3 -> 5
4. 动态规划算法:使用动态规划算法求解斐波那契数列的第n项。
案例:
求解斐波那契数列的第10项:
斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55
第10项为55。
5. 贪心算法:使用贪心算法解决背包问题。
案例:
给定背包容量为10,物品列表如下:
物品1:重量4,价值8
物品2:重量3,价值5
物品3:重量1,价值2
物品4:重量5,价值12
通过贪心算法选择物品装入背包的方案:
选择物品2,物品3,物品4装入背包,总重量为9,总价值为19。
穷举法算法案例

穷举法算法案例穷举法,又称为暴力搜索或者暴力破解,是一种简单直接的算法,它通过尝试所有可能的情况来寻找问题的解。
虽然在某些情况下效率不高,但在一些小规模问题或者需要精确解的情况下,穷举法仍然是一个有效的解决方案。
下面我们将通过几个案例来了解穷举法的具体应用。
案例一,寻找素数。
素数是指除了1和自身外没有其他因数的自然数,例如2、3、5、7等。
我们可以通过穷举法来寻找一定范围内的所有素数。
具体做法是从2开始,依次判断每个数是否能被2到该数平方根之间的所有数整除,如果不能则该数是素数。
这种方法虽然效率不高,但对于小范围内的素数搜索是可行的。
案例二,密码破解。
在密码学中,穷举法常常被用来破解简单的密码,例如暴力破解4位数字密码。
假设密码由0-9的数字组成,那么一共有10000种可能的密码组合。
通过穷举法,我们可以依次尝试每一种组合,直到找到正确的密码。
当然,对于更复杂的密码,穷举法可能需要花费更长的时间,但在一些情况下仍然是有效的。
案例三,旅行推销员问题。
旅行推销员问题是一个经典的组合优化问题,假设有n个城市,推销员需要从某个城市出发,经过每个城市一次,最终回到出发的城市,要求找到一条最短的路径。
穷举法可以用来解决这个问题,具体做法是列举出所有可能的路径,计算它们的长度,最终找到最短的路径。
虽然对于大规模的问题来说,穷举法并不是最优的解决方案,但在小规模问题上仍然是可行的。
总结。
穷举法作为一种简单直接的算法,在一些情况下仍然具有一定的应用价值。
然而,需要注意的是,穷举法在处理大规模问题时可能会面临效率低下的问题,因此在实际应用中需要根据具体情况选择合适的算法。
希望通过上述案例的介绍,能够让大家对穷举法有一个更加深入的了解。
数据挖掘十大算法案例

数据挖掘十大算法案例
以下是数据挖掘十大算法案例:
- C4.5:机器学习算法中的一个分类决策树算法,是决策树核心算法ID3的改进算法。
- The k-means algorithm:即K-Means算法。
- Support vector machines:支持向量机。
- The Apriori algorithm:Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。
- 最大期望(EM)算法。
- PageRank:网页排名算法。
- AdaBoost:一种迭代的学习算法。
- kNN:K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
- Naive Bayes:朴素贝叶斯算法。
这些算法在数据挖掘和机器学习领域中得到了广泛的应用,并且每个算法都有其独特的特点和应用场景。
在实际应用中,需要根据具体的问题和数据特点选择合适的算法,以获得最佳的效果。
常用算法举例范文

常用算法举例范文在计算机科学领域中,有许多常用的算法可以解决各种问题。
下面是一些常见的算法举例:1.排序算法排序算法用于将一组元素按照特定的顺序进行排列。
常见的排序算法包括冒泡排序、选择排序、插入排序、归并排序、快速排序等。
-冒泡排序:比较相邻的两个元素,如果前面的元素大于后面的元素,则交换它们的位置,重复这一过程直到整个序列有序。
-选择排序:每次从未排序的部分选取最小(或最大)的元素,将其放到已排序部分的末尾,重复这一过程直到整个序列有序。
-插入排序:将待排序元素逐个插入到已排序部分的适当位置,从而得到一个新的有序序列。
-归并排序:将两个有序的子序列合并成一个有序序列,逐渐缩小规模,直到整个序列有序。
-快速排序:通过一趟排序将待排序序列分割成两部分,其中一部分的所有元素都小于另一部分的所有元素,再分别对这两部分递归地进行快速排序。
2.算法算法用于在给定的数据集中查找特定元素或满足特定条件的元素。
常见的算法包括线性、二分、深度优先(DFS)、广度优先(BFS)等。
-线性:从头到尾依次检查每个元素,直到找到目标元素或遍历完整个数据集。
-二分:对于已排序的数据集,每次将数据集一分为二,并确定目标元素在哪个子集中,重复这一过程直到找到目标元素。
-DFS:通过递归或栈的方式进行,先访问节点的子节点,再依次访问其他没有被访问过的节点,直到遍历完整个图或找到目标节点。
-BFS:通过队列的方式进行,先访问当前节点的相邻节点,再依次访问这些相邻节点的相邻节点,直到遍历完整个图或找到目标节点。
3.图算法图算法用于解决与图相关的问题,例如寻找最短路径、最小生成树等。
常见的图算法包括Dijkstra算法、Bellman-Ford算法、Prim算法、Kruskal算法等。
- Dijkstra算法:用于寻找带权重的图中两个节点之间的最短路径,通过动态规划的方式逐步求解出最短路径。
- Bellman-Ford算法:用于寻找带权重的图中单源最短路径,可以处理负权重的情况,通过迭代更新节点的距离来求解最短路径。
算法案例(完整版)

例2 已知10b1(2)=a02(3),求数字a, b的值.
10b1(2)=1×23+b×2+1=2b+9. a02(3)=a×32+2=9a+2. 所以2b+9=9a+2,即9a-2b=7.
故a=1,b=1.
小 结
1. k进制数使用0~(k-1)共k个数字, 但左侧第一个数位上的数字(首位数字) 不为0. 2.用 an an-1 a2 a1(k ) 表示k 进制数,其中k称为基数,十进制数不标 注基数. 3. 把k进制数化为十进制数的一般算式 是: an an-1 a2 a1(k )
第一步,输入a和n的值. 第二步,令b=0,i=1. i-1 b 第三步, = b + ai ´ 2 , i=i+1. 第四步,判断i>n 是否成立.若是,则输 出b的值;否则,返回第三步.
同样地,把k进制数 a = an an-1 a2 a1(k )
化为十进制数b的算法和程序框图如何设 计? 第一步,输入a,k和n的值. 第二步,令b=0,i=1.
“更相减损术”在中国古代数学专著《 九章算术》中记述为:
可半者半之,不可半者,副置分母、 子之数,以少减多,更相减损,求其等 也,以等数约之.
例1 分别用辗转相除法和更相减损 术求168与93的最大公约数. 辗转相除法:168=93×1+75,
93=75×1+18, 75=18×4+3, 18=3×6.
a=rnrn-1„r1r0(2)
知识探究(二):十进制化k进制的算法
思考1:根据上面的分析,将十进制数a化 为二进制数的算法步骤如何设计? 第一步,输入十进制数a的值. 第二步,求出a除以2所得的商q,余数r. 第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.
回溯算法原理和几个常用的算法实例

回溯算法原理和几个常用的算法实例回溯算法是一种通过不断尝试和回退的方式来进行问题求解的算法。
它的基本思想是在过程中,当发现当前的选择并不符合要求时,就进行回退,尝试其他的选择,直到找到符合要求的解或者遍历完所有可能的选择。
回溯算法通常用于问题求解中的和排列组合问题,比如求解八皇后问题、0-1背包问题、数独等。
下面将介绍几个常用的回溯算法实例。
1.八皇后问题:八皇后问题是指在一个8×8的国际象棋棋盘上,放置八个皇后,使得任意两个皇后都不在同一行、同一列或同一斜线上。
可以通过递归的方式依次尝试每一行的位置,并判断当前位置是否满足条件。
如果满足条件,则进入下一行尝试;否则回溯到上一行,并尝试其他的位置,直到找到解或遍历完所有的可能。
2.0-1背包问题:0-1背包问题是指在给定一组物品和一个容量为C的背包,每个物品都有自己的重量和价值,求解在不超过背包容量时,如何选择物品使得背包中物品的总价值最大。
可以通过递归的方式依次考察每个物品,并判断是否选择当前物品放入背包。
如果放入当前物品,则背包容量减小,继续递归考察下一个物品;如果不放入当前物品,则直接递归考察下一个物品。
直到遍历完所有物品或背包容量为0时,返回当前总价值。
3.数独问题:数独是一种通过填充数字的方式使得每一行、每一列和每一个九宫格内的数字都满足一定条件的谜题。
可以通过递归的方式依次尝试填充每一个空格,并判断当前填充是否符合条件。
如果符合条件,则继续递归填充下一个空格;如果不符合条件,则回溯到上一个空格,并尝试其他的数字,直到找到解或遍历完所有的可能。
回溯算法的时间复杂度一般较高,通常为指数级别。
因此,在实际应用中,可以结合剪枝等优化策略来提高算法的效率。
此外,回溯算法也可以通过非递归的方式进行实现,使用栈来存储当前的状态,从而避免递归带来的额外开销。
总之,回溯算法是一种非常有效的问题求解方法,通过不断尝试和回退,可以在复杂的空间中找到符合要求的解。
简单的算法举例

简单的算法举例一、冒泡排序算法冒泡排序是一种基础的排序算法,通过比较相邻的元素并交换位置来进行排序。
它重复地遍历要排序的列表,比较每对相邻的元素,如果顺序不对就进行交换,直到整个列表排序完成。
二、选择排序算法选择排序算法是一种简单直观的排序算法,它将列表分为已排序和未排序两部分,每次从未排序的部分中选择最小(或最大)的元素,并将其放到已排序的部分的末尾。
三、插入排序算法插入排序算法是一种简单直观的排序算法,它将列表分为已排序和未排序两部分,每次从未排序的部分中选择一个元素插入到已排序的部分的合适位置。
四、归并排序算法归并排序算法是一种分治算法,它将列表递归地分成较小的部分,然后将这些部分按照顺序合并成一个有序的列表。
五、快速排序算法快速排序算法是一种分治算法,它通过选择一个基准元素将列表分成两部分,一部分小于基准元素,一部分大于基准元素,然后递归地对这两部分进行排序。
六、堆排序算法堆排序算法是一种利用堆这种数据结构进行排序的算法,它将列表看成一个完全二叉树,并将其调整为一个大顶堆或小顶堆,然后依次取出堆顶元素进行排序。
七、计数排序算法计数排序算法是一种非比较排序算法,它通过统计每个元素出现的次数,然后根据次数重新排列元素,从而实现排序。
八、桶排序算法桶排序算法是一种非比较排序算法,它将列表划分为若干个桶,然后将元素分配到相应的桶中,再对每个桶中的元素进行排序,最后将所有桶中的元素合并起来。
九、基数排序算法基数排序算法是一种非比较排序算法,它通过将元素按照各个位上的数字进行排序,先按照个位排序,再按照十位排序,依次类推,最终实现排序。
十、二分查找算法二分查找算法是一种在有序列表中查找特定元素的算法,它通过不断缩小查找范围,将查找时间复杂度从线性降低到对数级别。
c语言十大算法案例

c语言十大算法案例C语言是一种广泛应用于编程的高级语言,具有简单、灵活、高效等特点。
在C语言中,有许多经典的算法案例,这些算法案例不仅有助于提高编程能力,还能帮助我们理解计算机科学的基本原理。
下面列举了十个C语言的经典算法案例。
1. 冒泡排序算法:冒泡排序是一种简单但效率较低的排序算法,它通过多次比较和交换相邻元素的方式将最大或最小的元素逐步移动到数组的一端。
2. 快速排序算法:快速排序是一种常用的排序算法,它通过选择一个基准元素,将数组分成两个子数组,然后对子数组进行递归排序。
3. 二分查找算法:二分查找是一种高效的查找算法,它通过将查找范围缩小一半来快速定位目标元素。
4. 链表反转算法:链表反转是一种常见的操作,它可以将链表中的节点顺序逆转。
5. 汉诺塔算法:汉诺塔是一种经典的递归问题,它通过将圆盘从一个柱子移动到另一个柱子来演示递归的思想。
6. 最大公约数算法:最大公约数是指能够同时被两个或多个整数整除的最大正整数,求最大公约数的算法有多种,如辗转相除法和欧几里德算法。
7. 斐波那契数列算法:斐波那契数列是一个数列,其中每个数字都是前两个数字之和,求斐波那契数列的算法有多种,如递归和循环。
8. 图的深度优先搜索算法:深度优先搜索是一种用于遍历图的算法,它通过递归的方式依次访问图中的每个节点。
9. 图的广度优先搜索算法:广度优先搜索也是一种用于遍历图的算法,它通过队列的方式依次访问图中的每个节点。
10. 最短路径算法:最短路径算法用于找到图中两个节点之间的最短路径,常用的最短路径算法有迪杰斯特拉算法和弗洛伊德算法。
这些算法案例涵盖了排序、查找、链表操作、递归、图算法等多个方面,是C语言学习中不可或缺的部分。
通过学习和理解这些经典算法案例,我们可以提高自己的编程能力,并在解决实际问题时能够选择合适的算法。
希望本文能够对读者有所帮助,激发他们对C 语言算法的兴趣,并在编程的道路上不断进步。
10个经典的算法问题与解决方案

10个经典的算法问题与解决方案算法问题是计算机科学中非常重要的一部分,对于准备面试或提升自己的技能都是很有帮助的。
下面列举了10个经典的算法问题及其解决方案:1.两数之和(Two Sum)问题描述:给定一个整数数组和一个目标值,找出数组中和为目标值的两个数。
解决方案:使用哈希表记录每个数字的索引,然后遍历数组,查找目标值减当前数的差是否存在于哈希表中。
2.盛最多水的容器(Container With Most Water)问题描述:给定一个非负整数数组,数组中的每个表示一条柱子的高度,找出两个柱子,使得它们与x轴构成的容器可以容纳最多的水。
解决方案:维护两个指针,分别指向数组的开始和结尾,计算当前指针所指的两条柱子之间的面积,并更新最大面积。
然后移动指向较小柱子的指针,重复计算直到两个指针相遇。
3.三数之和(3Sum)问题描述:给定一个整数数组,找出数组中所有不重复的三个数,使得它们的和为0。
解决方案:首先对数组进行排序,然后固定一个数字,使用双指针在剩余的数字中寻找另外两个数使得它们的和为相反数。
4.最大子序和(Maximum Subarray)问题描述:给定一个整数数组,找到一个具有最大和的连续子数组(子数组最少包含一个元素)。
解决方案:使用动态规划的思想,从数组的第一个元素开始依次计算以当前位置结尾的子数组的最大和,并保存最大值。
5.二分查找(Binary Search)问题描述:给定一个排序的整数数组和一个目标值,使用二分查找算法确定目标值是否存在于数组中,并返回其索引。
解决方案:通过比较目标值与数组的中间元素来确定目标值是在左半部分还是右半部分,并更新搜索范围进行下一轮查找。
6.背包问题(Knapsack Problem)问题描述:给定一组物品和一个背包,每个物品都有自己的重量和价值,在不超过背包容量的情况下,找到一个组合使得总价值最大化。
解决方案:使用动态规划的思想,定义一个二维数组表示背包容量和物品数量,从左上角开始计算每个格子可以放置的最大价值。
四个经典的算法案例
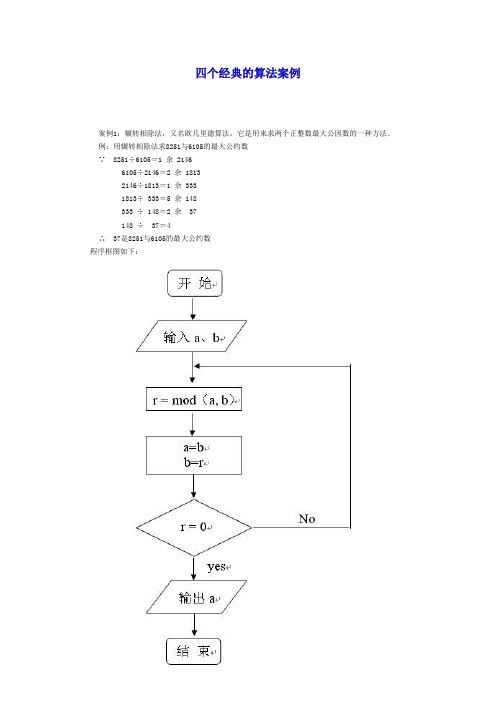
四个经典的算法案例案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数∵ 8251÷6105=1 余 21466105÷2146=2 余 18132146÷1813=1 余 3331813÷ 333=5 余 148333 ÷ 148=2 余 37148 ÷ 37=4∴ 37是8251与6105的最大公约数程序框图如下:其中 r = mod(a, b) r表示a÷b的余数案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7于是令 V0=5则 V1=2V0―5=2×5―5=5V2=V1X―4=5×5―4=21V3=V2X+3=21×5+3=108V4=V3X―6=108×5―6=534V5=V4X+7=534×5+7=2677∴ f(5) = 2677秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程框图如下:其中:t = GET a│i│ t表示a右数第i位利用上面的算法,把2进制数110011化为十进制的数即:1×20+1×21+0×22+0×23+1×24+1×25= 51以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本语句描述它。
四大算法应用实例

四大算法应用实例第一章:排序算法的应用实例排序算法是计算机科学中的一项基本技术,应用广泛。
下面具体介绍几个排序算法的应用实例:1.冒泡排序冒泡排序是一种简单直观的排序算法,它的应用场景十分广泛。
例如,对于一家超市而言,每天都会有大量的商品入库,给这些商品按照价格进行排序就需要用到冒泡排序算法。
此外,冒泡排序还可以用于诸如学生成绩排序、奖金排序等多种场景。
2.快速排序快速排序也是常用的一种排序算法,快速排序的优点在于其速度非常快。
在实际的应用场景中,快速排序可以用于分流,例如在一家餐厅中,依据年龄进行招聘时,可以利用快排将符合条件的线索分流到不同的部门,这样可以提高筛选速度,从而提高招聘效率。
3.归并排序归并排序也是一种较为常用的排序算法之一,它能够很好地解决大规模数据的排序问题。
因此归并排序在大数据领域得到了广泛的应用,例如银行的金融系统中,对于大量的交易记录数据按照不同的规则进行归类和排序时,可以使用归并排序算法。
1.广度优先搜索广度优先搜索是一种使用队列的搜索算法,其基本思想是从起点开始,依次遍历其相邻节点,直到找到目标节点或者所有节点遍历完毕。
广度优先搜索的应用场景很多,例如在社交网络中,我们需要查找与某个人有关系的所有人的信息,这个时候就可以使用广度优先搜索算法。
2.二分搜索二分搜索也是一种非常常用的搜索算法,可以大大提高搜索效率。
其基本思想是将有序序列分成两半,根据目标元素与中间元素的大小关系,选择继续在前半段或者后半段搜索,逐步缩小搜索区间,直到找到目标元素或者确定其不存在于序列中。
二分搜索的应用场景很多,例如在查找某个数字在一个大数组中出现的位置时,可以采用二分搜索算法。
1.最短路径算法最短路径算法是一种用于寻找图中两个节点之间最短路径的算法,其应用场景很多,例如在导航软件中,我们需要计算从起点到终点的最短路径,这时便可以使用最短路径算法。
2.最小生成树算法最小生成树算法是用于寻找图中任意两点之间最小权重的一棵生成树的算法,其应用场景也很广泛。
算法设计案例

算法设计案例算法设计案例是指在计算机科学中,通过编写程序来解决特定问题的过程。
这些问题可以是数学问题、数据处理问题、图形问题等等。
下面是一些常见的算法设计案例:1. 排序算法:排序算法是计算机科学中最基本的算法之一。
常见的排序算法有冒泡排序、插入排序、选择排序、快速排序、归并排序等等。
这些算法的目的是将一组数据按照一定的规则进行排序,以便更方便地进行后续的处理。
2. 图形算法:图形算法是指在计算机图形学中用来处理图形的算法。
常见的图形算法有线段裁剪、多边形填充、三角形剖分等等。
这些算法的目的是将图形进行处理,以便更好地显示在屏幕上。
3. 搜索算法:搜索算法是指在计算机科学中用来搜索特定数据的算法。
常见的搜索算法有深度优先搜索、广度优先搜索、A*搜索等等。
这些算法的目的是在大量数据中找到特定的数据,以便更好地进行后续的处理。
4. 数据压缩算法:数据压缩算法是指在计算机科学中用来压缩数据的算法。
常见的数据压缩算法有哈夫曼编码、LZW编码等等。
这些算法的目的是将大量数据进行压缩,以便更好地存储和传输。
5. 加密算法:加密算法是指在计算机科学中用来加密数据的算法。
常见的加密算法有DES、AES、RSA等等。
这些算法的目的是将数据进行加密,以便更好地保护数据的安全性。
6. 数据挖掘算法:数据挖掘算法是指在计算机科学中用来挖掘数据的算法。
常见的数据挖掘算法有聚类分析、关联规则挖掘、分类算法等等。
这些算法的目的是从大量数据中挖掘出有用的信息,以便更好地进行决策。
7. 机器学习算法:机器学习算法是指在计算机科学中用来训练机器学习模型的算法。
常见的机器学习算法有线性回归、逻辑回归、决策树、支持向量机等等。
这些算法的目的是通过训练机器学习模型来预测未来的数据。
8. 神经网络算法:神经网络算法是指在计算机科学中用来训练神经网络的算法。
常见的神经网络算法有前馈神经网络、循环神经网络、卷积神经网络等等。
这些算法的目的是通过训练神经网络来实现人工智能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四个经典的算法案例
案例1:辗转相除法,又名欧几里德算法,它是用来求两个正整数最大公因数的一种方法。
例:用辗转相除法求8251与6105的最大公约数
∵ 8251÷6105=1 余 2146
6105÷2146=2 余 1813
2146÷1813=1 余 333
1813÷ 333=5 余 148
333 ÷ 148=2 余 37
148 ÷ 37=4
∴ 37是8251与6105的最大公约数
程序框图如下:
其中 r = mod(a, b) r表示a÷b的余数
案例2:秦九韶算法,它是中国南宋时期数学家秦九韶提出的,用来解决多项式的求值问题,在西方被称作霍纳算法。
首先看一道例题:求多项式f(x)=2x5―5x4―4x3+3x2―6x+7当x=5时的值。
根据秦九韶算法:
f(x)可表示为f(x)=({[(2x―5)x―4]x+3}x―6)x+7
于是令 V0=5
则 V1=2V0―5=2×5―5=5
V2=V1X―4=5×5―4=21
V3=V2X+3=21×5+3=108
V4=V3X―6=108×5―6=534
V5=V4X+7=534×5+7=2677
∴ f(5) = 2677
秦九韶算法只用到乘法、加法两个简单运算,不需要乘方运算,它是多项式求值的简化算法。
下面看程序框图,其中a0、a1、a2、a3、a4、a5是f (x) 从右向左的系数。
案例3:排序:是一种基本并且常用的算法,排序的算法很多,可以参阅课本,这里不再叙述。
案例4:进位制
例:画程序框图,表示把k进制数a(共有n位),转化为十进制数b的过程
框图如下:
其中:t = GET a│i│ t表示a右数第i位
利用上面的算法,把2进制数110011化为十进制的数
即:1×20+1×21+0×22+0×23+1×24+1×25= 51
以上是四个经典算法,大家可以从中体会算法的基本思想和算法的基本结构,并尝试用算法的基本
语句描述它。
