最新人教版高中数学必修5第一章《应用举例》自我小测
最新人教版高中数学必修5第一章《应用举例(二)》自我检测
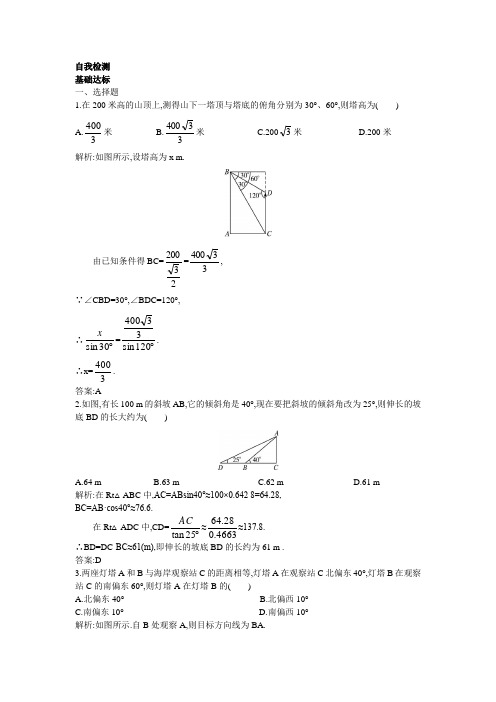
自我检测 基础达标 一、选择题1.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( ) A.3400米 B.33400米 C.2003米 D.200米 解析:如图所示,设塔高为x m.由已知条件得BC=23200=33400,∵∠CBD=30°,∠BDC=120°,∴︒30sin x =︒120sin 33400. ∴x=3400. 答案:A2.如图,有长100 m 的斜坡AB,它的倾斜角是40°,现在要把斜坡的倾斜角改为25°,则伸长的坡底BD 的长大约为( )A.64 mB.63 mC.62 mD.61 m 解析:在Rt △ABC 中,AC=ABsin40°≈100×0.642 8=64.28, BC=AB·cos40°≈76.6. 在Rt △ADC 中,CD=︒25tan AC ≈4663.028.64≈137.8.∴BD=DC-BC≈61(m),即伸长的坡底BD 的长约为61 m . 答案:D3.两座灯塔A 和B 与海岸观察站C 的距离相等,灯塔A 在观察站C 北偏东40°,灯塔B 在观察站C 的南偏东60°,则灯塔A 在灯塔B 的( ) A.北偏东40° B.北偏西10° C.南偏东10° D.南偏西10° 解析:如图所示.自B 处观察A,则目标方向线为BA.由已知可得A 在灯塔B 的北偏西10°. 答案:B4.如图,在山脚A 处测得山顶S 的仰角为45°,沿倾斜角为15°的斜坡向上走100米到B,又测得S 的仰角为75°,则山高为__________________米.( )A.50B.502C.503D.506 解析:在△ABS 中,由条件得∠BAS=30°,∠SBA=120°. 由正弦定理得︒120sin SA =︒30sin 100,∴SA=1003.在Rt △ADS 中,SD=sin45°×SA=22×1003=506. 答案:D5.某人先向正东方向走了x km,然后他向右转150°,向新的方向走了3 km,结果他离出发点恰好为3 km,那么x 的值为( )A.3B.23C.23或3D.3 解析:画出示意图后,由余弦定理有(3)2=x 2+32-2·x·3·cos30°, 解得x=23或x=3.答案:C6.在一座20 m 高的观测台顶测得对面一水塔塔顶的仰角为60°,塔底的俯角为45°,那么这座水塔的高是( ) A.20(1+33) m B.20(1+3) m C.10(6+2) m D.20(6+2) m 解析:h=20+20·tan60°=20(1+3).答案:B7.一船自西向东航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船航行的速度为________________海里/时.( ) A.2617 B.346 C.2217 D.342 解析:如图所示,由题意知∠APM=75°,∠APN=45°,∠ANP=45°,在△MPN 中,︒45sin 68=)4575sin(︒+︒MN ,∴MN=346(海里),这只船航行的速度为4634=2617(海里/时). 答案:A8.如图,B 、C 、D 三点在地面同一直线上,DC=a,从C 、D 两点测得A 点的仰角分别为β、α(α<β),则A 点离地面的高AB 等于()A.)sin(sin sin αββα-a B.)cos(sin sin αββα-aC.)sin(cos sin αββα-a D.)cos(cos cos αββα-a解析:tanα=BC a AB +,tanβ=BCAB,联立两式解得AB=αββαtan tan tan tan -a=ααβββαβαcos sin cos sin cos cos sin sin -a -αβαββαsin cos cos sin sin sin -a =)sin(sin sin αββα-a . 答案:A 二、填空题9.有一长为1 km 的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要加长______km..解析:如图,AC=ABsin20°=sin20°,BC=AB·cos20°=cos20°,DC=︒10tan AC=2cos 210°.∴DB=DC-BC=1. 答案:110.外国船只除特许外,不得进入离我国海岸线d 海里以内的区域,如图所示,设A 及B 是我们的观测站,A 与B 之间的距离为s 海里,海岸线是过A 、B 的直线,一外国船只在P 点,在A 站测得∠BAP=α,同时在B 站测得∠ABP=β,则α与β满足的三角不等式为_____________时,就应当向此未经特许的外国船只发出警告,命令其退出我国海域.解析:在△ABC 中,)sin(βαπ--s =βsin AP .AP=)sin(sin βαβ+∙s .在Rt △APM 中,h=sinα·AP=sinα·)sin(sin βαβ+∙s =)sin(sin sin βαβα+∙s . 答案:d≥)sin(sin sin βαβα+∙s三、解答题11.一舰艇在海上巡逻,沿岸自西向东航行,在A 处见岸边一灯塔C 在船的北偏东60°,一小时后在B 处见灯塔在船的北偏东30°.若舰艇每小时航行30海里.当舰艇至D 点处,可见灯塔在船的西北方向,求舰艇从A 到D 的航行距离.解法一:在△ABC 中, ∠CAB=30°,∠ABC=90°+30°=120°, ∴∠ACB=180°-120°-30°=30°. ∵AB=30×1=30,∴BC=AB=30. 在△BDC 中,∠CBD=90°-30°=60°, ∴∠BCD=180°-60°-45°=75°. 由正弦定理有︒45sin BC =︒75sin BD.∴BD=2sin75°·BC=302·sin75°≈40.98. ∴AD=AB+DB=30+40.98=70.98(海里). 解法二:在△ACD 中,易知AC=303,∠ACD=180°-30°-45°=105°, 由正弦定理,得︒105sin AD =︒45sin AC,∴AD=2×303sin105° =306sin105°≈70.98(海里).答:A 、D 两地相距约70.98海里.12.如图,在一个山坡上的一点A,测得山顶上一个微波塔顶端C 对于山坡的坡度的斜度为20°,向山顶前进80米后的B 点,又测得斜度为40°,设塔高为60米,求此山对于地面的倾角θ的余弦值.解:在△ABC 中,∠BAC=20°,∠ABC=180°-40°=140°,AB=80, ∴∠ACB=20°. 由正弦定理,得︒20sin 80=︒20sin BC,∴BC=80.在△BDC 中,∠BDC=90°+θ,∠DBC=40°, ∴由正弦定理,得︒40sin 60=)90sin(80θ+︒.∴cosθ=68sin40°≈0.857.答:此山对于地面的倾角θ的余弦值约为0.857.更上一层1.在海岸A 处,发现北偏东45°方向,距A 为(3-1)海里的B 处有一艘走私船,在A 处北偏西75°方向,距A 为2海里的C 处的缉私船奉命以103海里/时的速度追截走私船,此时走私船正以10海里/时的速度从B 处向北偏东30°方向逃窜,问缉私船沿什么方向可最快追上走私船?并求出所需要的时间.解:如图所示,设缉私船追上走私船的时间为t h,则有CD=103t,BD=10t,在△ABC 中,∵AB=3-1,AC=2,∠BAC=45°+75°=120°.∴BC=︒-∙∙-+-120cos )13(222)13(22=6. 根据正弦定理可得sin ∠ABC=BC AC ︒∙120sin =22.∴∠ABC=45°,而∠CBD=90°+30°=120°. 又sin ∠BCD=CD CBD BD ∠∙sin =21.∴∠BCD=30°,∠BDC=30°. ∴BD=BC=6,则有10t=6,t=106=0.245(h)=14.7(min). ∴缉私船沿北偏东60°方向,需14.7 min 能追上走私船.2.在一大河边上高a m 处的A 点,测得对岸一铁塔顶点M 的仰角为θ,而在河中铁塔倒影的俯角为φ,求铁塔的高度.解:如图所示,设直线A′M′在河面上,点N 是塔顶点M 在水中的倒影,M′是MN 与A′M′的交点,由于塔顶点M 与它在河中的倒影关于河面对称,故MN ⊥A′M′,且MM′=M′N. 由点A 向MN 作垂线,设垂足为B,且设AB=x, 则由题设条件知∠MAB=θ,∠BAN=φ. 于是在Rt △ABM 中,MB=xtanθ, 由于A′A=a,且MM′=M′N,∴由BN-MB=2a,可得xtanφ-xtanθ=2a. ∴x=θϕαtan tan 2-.∴MB=xtanθ=θϕθαtan tan tan 2-.∴BN=xtanφ=θϕϕαtan tan tan 2-.∴塔高M′M=2BNMB + =)sin()sin(θϕϕθ-+a .。
高中数学:1.2《应用举例》试题(新人教必修5).

第1题. 如图,一艘船以32.2n mile/h 的速度向正北航行.在A处看灯塔S在船的北偏东20 的方向,30 min 后航行到B处,在B处看灯塔在船的北偏东65 的方向,已知距离此灯塔6.5n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?答案:在A B S △中,32.20.516.1A B =⨯=n mile ,115A B S ∠=þ, 根据正弦定理,()sin sin 6520A S AB A B S=∠-,()sin sin 16.1sin 115sin 6520AB B AS AB ABS ⨯==⨯∠⨯=⨯⨯-S 到直线A B 的距离是sin 2016.1sin 115sin 207.06d AS =⨯=⨯⨯≈(cm ).所以这艘船可以继续沿正北方向航行.南第2题. 如图,在山脚A 测得出山顶P 的仰角为a ,沿倾斜角为β的斜坡向上走a 米到B ,在B 处测得山顶P 的仰角为γ,求证:山高()()sin sin sin -a a h a γβγ-=.答案:在A B P △中,180+ABP γβ∠=- , ()()()180- 180-180+ =-BPA ABPαβαβγβγα∠=--∠=---.在A B P △中,根据正弦定理,()()()()s i n s i n s i n -s i n 180+αs i n -s i n -A PA B A B PA P BAPAP αγαγβγβγα=∠∠=-⨯=所以山高为()()sin sin -sin sin -h AP ααγβαγα==.第3题. 测山上石油钻井的井架B C 的高,从山脚A 测得65.3A C =m ,塔顶B 的仰角α是2525'.已知山坡的倾斜角是1738' ,求井架的高B C .答案:在A B C △中,65.3A C =m ,=25251738747BAC αβ'''∠=--=,90=9017387222ABC β''∠=--=,根据正弦定理,sin sin A C B C A B CB A C=∠∠()sin 65.3sin 7479.3m sin sin 7222AC BAC BC ABC'∠==≈'∠井架的高约为9.3m .(6739)第4题. 如图,货轮在海上以35n mile / h 的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148的方向航行.为了确定船位,在B 点观察灯塔A 的方位角是126,航行半小时后到达C点,观察灯塔A 的方位角是78.求货轮到达C点时与灯塔A 的距离AβαDBC(精确到1 n mile ).答案:在A B C △中,B C =350.517.5⨯=n mile ,14812612ABC ∠=-= ,()78180148110ACB ∠=+-=,1801101258BAC ∠=--= ,根据正弦定理,sin sin A C B C A B CB A C=∠∠,sin 17.5sin 12 4.29sin sin 58BC ABC AC BAC∠==≈∠(nmile ). 货轮到达C点时与灯塔的距离是约4.29n mile .第5题. 轮船A 和轮船B 在中午12时离开海港C ,两艘轮船的航行方向之间的夹角为120 ,轮船A 的航行速度是25 n mile/h ,轮船B 的航行速度是15 n mile/h ,下午2时两船之间的距离是多少?答案:70 n mile .第6题. 如图,已知一艘船从30 n mile/h 的速度往北偏东10 的A 岛行驶,计划到达A 岛后停留10 min 后继续驶往B 岛,B 岛在A 岛的北偏西60的方向上.船到达C处时是上午10时整,此时测得B 岛在北偏西30 的方向,经过20 min 到达D处,测得B 岛在北偏西45的方向,如果一切正常的话,此船何时能到达B 岛?答案:在BC D △中, 30104B C D ∠=+=304560BCA20 min1801804510125BDC ADB ∠=-∠=--=,130103C D =⨯=(n mile ), 根据正弦定理,sin sin C D BD C BDBC D=∠∠,()10sin 40sin 18040125BD =∠--,10sin 40sin 15BD ⨯=.在ABD △中,451055ADB ∠=+=,1806010110BAD ∠=--=, 1801105515ABD ∠=--=.根据正弦定理, s i n s i n s i n A DB DA BA B DB A D A D B ==∠∠∠,就是sin 15sin 110sin 55A DB D A B ==,sin 1510sin 40 6.84sin 70sin 110BD AD ==≈(n mile ). sin 5510sin 40sin 5521.65sin 110sin 15sin 70BD AB ==≈(n mile).如果这一切正常,此船从C开始到B所需要的时间为:6.8421.65206010306086.983030A D A B+++⨯+≈+⨯≈(min )即约1小时26分59秒.所以此船约在11时27分到达B岛.第7题. 一架飞机在海拔8000m 的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是2739和,计算这个海岛的宽度.答案:约5821.71m .第8题. 一架飞机从A 地飞到B 到,两地相距700km .飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成21 角的方向飞行,飞行到中途,再沿与原来的飞行方向成35 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km 远了多少?答案:在A B C △中,700A B =km ,1802135124ACB ∠=--= , 根据正弦定理,700sin 124sin 35sin 21A CBC ==,700sin 35sin 124AC =,700sin 21sin 124BC =,700sin 35700sin 21786.89sin 124sin 124AC BC +=+≈(km ),所以路程比原来远了约86.89km .第9题. 为测量某塔的高度,在A ,B 两点进行测量的数据如图所示,求塔的高度.B答案:在21.418.6 2.8ABT ATB ∠=-=△中,,9018.6ABT ∠=+ ,15A B =(m ).根据正弦定理,sin 2.8cos 18.6A B A T =,15cos18.6sin 2.8AT ⨯=.塔的高度为15cos18.6tan 21.4tan 21.4114.05sin 2.8AT =≈(m ).第10题. A ,B 两地相距2558m ,从A ,B 两处发出的 两束探照灯光照射在上方一架飞机的机身上(如图),飞机离 两个探照灯的距离是多少?飞机的高度是多少?答案:飞机离A 处控照灯的距离是4801.53m , 飞机离B 处探照灯的距离是4704.21m , 飞机的高度是约4574.23m .第11题. 一架飞以326km/h 的速度,沿北偏东75的航向从城市A 出发向城市B 飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C ,问收到命令时飞机应该沿什么航向飞行,此时离城市C 的距离是多少?答案:A E =3261897.860⨯=km ,在AC D △中,根据余弦定理:AC ==101.235=根据正弦定理:sin sin AD AC AC DAD C=∠∠,sin 57sin 66sin 0.5144101.235AD ADCACD AC∠∠==≈,30.96ACD ∠≈,13330.96102.04ACB ∠≈-=.在A B C △中,根据余弦定理:AB ==245.93≈,222cos 2AB AC BCBAC AB AC+-∠=222245.93101.2352042245.93101.235+-=⨯⨯0.5847≈,54.21BAC ∠=.在A C E △中,根据余弦定理:CE ==90.75≈,222cos 2AE EC ACAEC AE EC+-∠=.22297.890.75101.2350.4254297.890.75+-≈≈⨯⨯,64.82AEC ∠=,()180180757564.8210.18AEC -∠--=-=.所以,飞机应该以南偏西10.18 的方向飞行,飞行距离约90.75km .第12题. 飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20250m ,速度为1000km/h ,飞行员先看到山顶的俯角为1830' ,经过150s 后又看到山顶的俯角为81 ,求山顶的海拔高度(精确到1m ).答案:飞行在150秒内飞行的距离是150100010003600d =⨯⨯m ,根据正弦定理,()sin 18.5sin 8118.5dx =-,这里x 是飞机看到山顶的俯角为81时飞机与山顶的距离.飞机与山顶的海拔的差是: ()sin 18.5tan 81tan 8114721.64sin 8118.5d x =≈-(m),CDBAE山顶的海拔是2025014721.645528-≈m .第13题. 一个人在建筑物的正西A 点,测得建筑物顶的仰角是α,这个人再从A 点向南走到B 点,再测得建筑物顶的仰角是β,设A ,B 间的距离是a ..答案:设建筑物的同度是h ,建筑物的底部是C , 则tan tan h h AC BC αβ==,.A B C △是直角三角形,B C 是斜边,所以222tan tan b h a αβ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,222211tan tan a h βα⎡⎤⎛⎫⎛⎫=-⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦, 222222tan tan tan tan a h αβαβ=-2222222sin sin sin cos cos sin a αβαβαβ=-()()222sin sin sin sin a αβαβαβ=--.所以,h =αABDCβah。
最新人教版高中数学必修5第一章《应用举例》例题与探究

典题精讲例1 在一次夏令营活动中,同学们在相距10海里的A 、B 两个小岛上活动结束后,有人提出到隔海相望的未知的C 岛上体验生活,为合理安排时间,他们需了解C 岛与B 岛或A 岛的距离.为此他们测得从A 岛望C 岛和B 岛成60°的视角,从B 岛望C 岛和A 岛成75°的视角,那么B 岛和C 岛之间的距离是多少海里?思路分析:根据题意不难将题意中所述的数据反映在图形上,结合图形分析不难得到结果. 解:如图1-2-3,在△ABC 中,由题意,知∠CAB=60°,∠ABC=75°,图1-2-3∴∠ACB=45°. 由正弦定理︒=︒60sin 45sin BC AB ,得BC=65海里. 绿色通道:根据题目的叙述正确画出示意图,然后在相应三角形中应用正弦定理就可以达到目的,真正把数学融入实际生活.变式训练 如图1-2-4所示,为了测量河对岸A 、B 两点间的距离,在这一岸定一基线CD ,现已测出CD=a 和∠ACD=α,∠BCD=β,∠BDC=γ,∠ADC=δ,试求AB 的长.图1-2-4思路分析:对于AB ,可以在△ABC 中求解,也可以在△ABD 中求解,若在△ABC 中,需求出AC 、BC ,再利用余弦定理求解.而AC 可在△ACD 内利用正弦定理求解,BC 可在△BCD 内利用正弦定理求解.解:在△ACD 中,已知CD=a ,∠ACD=α,∠ADC=δ,由正弦定理,得 AC=)sin(sin )](180sin[sin δαδδδ+=+-︒a a a . 在△BCD 中,由正弦定理,得BC=)sin(sin )](180sin[sin γβγγβγ+=+-︒a a . 在△ABC 中,已经求得AC 和BC ,又因为∠ACB=α-β,所以用余弦定理.就可以求得AB=)cos(222βα-∙∙-+BC AC BC AC .例2 如图1-2-5所示,一辆汽车在一条水平的公路上向正东行驶,到A 处时测得公路南侧远处一山顶D 在东偏南15°的方向上,行驶5 km 后到达B 处,测得此山顶在东偏南25°的方向上,仰角为8°,求此山的高度CD.图1-2-5思路分析:本题主要问题可能会出现在题目中所述的角度不能正确的分辨上,从而导致出错.只要能正确根据题目的叙述,将问题转化为一个数学问题,从而容易将问题解决. 要测出高CD ,只要测出高所在的直角三角形的另一条直角边或斜边的长即可.解:根据已知条件,可以计算出BC 的长.在△ABC 中,∠A=15°,∠C=25°-15°=10°, 根据正弦定理,CAB A BC sin sin =, 得BC=︒︒=10sin 15sin 5sin sin C A AB ≈7.452 4 km. ∴CD=BC×tan ∠DBC≈BC×tan8°≈1 047 m.答:山的高度约为1 047米.绿色通道:此类问题主要容易错在角度的具体位置找不对,另外在具体问题中有时可能不知道采用什么定理以及在哪些三角形中应用相应定理去解决问题,这些都要根据具体题目的已知条件具体分析.变式训练 如图1-2-6所示,为了测量上海东方明珠塔的高度,测量人员站在A 处测得塔尖的仰角为75.5°,前进38.5 m 后,在B 处测得塔尖的仰角为80°,试计算塔的高度.图1-2-6思路分析:由于CD 难以直接求解,我们可借助解直角三角形求解,只要能计算出BC 的长,则在Rt △BCD 中,可得塔高CD ,而BC 的长可在△ABC 中利用正弦定理求得.解:∵∠CAD=75.5°,∠CBD=80°,∴∠ACB=4.5°.在△ABC 中,由BACBC ACB AB ∠=∠sin sin , 得BC=︒︒⨯=∠∠5.4sin 5.75sin 5.38sin sin ACB BAC AB ≈477 m. ∴CD=BC·sin80°≈470 m,即塔的高度为470 m.例3 如图1-2-7所示,自动卸货汽车的车箱采用液压结构,设计时需要计算油泵顶杆BC 的长度.已知车箱的最大仰角为60°,油泵支点B 与车箱支点A 之间的距离为1.95 m ,AB 与水平线之间的夹角为6°20′,AC 长为1.40 m ,计算BC 的长.(保留三个有效数字)图1-2-7思路分析:求油泵顶杆BC 的长度也就是在△ABC 内,求边长BC 的问题,而根据已知条件,AC=1.40 m ,AB=1.95 m ,∠BAC=60°+6°20′=66°20′.相当于已知△ABC 的两边和它们的夹角,所以求解BC 可根据余弦定理.解:由余弦定理,得BC 2=AB 2+AC 2-2AB·ACcosA=1.952+1.402-2×1.95×1.40×cos66°20′=3.571.∴BC≈1.89 m.答:油泵顶杆BC 约长1.89 m.绿色通道:此题虽为解三角形问题的简单应用,但关键是把未知边所处的三角形找到,在转换过程中应注意“仰角”这一概念的意义,并排除题目中非数学因素的干扰,将数量关系从题目中准确地提炼出来.变式训练1 如图1-2-8所示,在某点B 处测得建筑物AE 的顶端A 的仰角为θ,沿BE 方向前进30 m ,至点C 处测得顶端A 的仰角为2θ,再继续前进310 m 至D 点,测得顶端A 的仰角为4θ,求θ的大小和建筑物AE 的高.图1-2-8思路分析:根据已知,结合图形,可以分析各边角的关系,最后会发现各已知聚集在△ACD 中,通过正弦定理可列出关于θ的方程,求出θ后,可求出AD,再在Rt △ADE 中,求AE.当然也可以通过方程求解.解法一:(用正弦定理求解)由已知,得在△ACD 中,AC=BC=30,AD=DC=310,∠ADC=180°-4θ, ∴)4180sin(302sin 310θθ-︒=. ∵sin 4θ=2sin 2θcos 2θ,∴cos 2θ=23,得2θ=30°.∴θ=15°. ∴在Rt △ADE 中,AD=310,∠ADE=4θ=60°,∴ AE= ADsin60°=15.解法二:(设方程来求解)设DE=x ,AE=h,在Rt △ACE 中,(103+x)2+h 2=302,在Rt △ADE 中,x 2+h 2=(310)2,两式相减,得x=35,h=15.∴在Rt △ACE 中,tan 2θ=33310=+x h. ∴2θ=30°,θ=15.解法三:(用倍角公式求解)设建筑物高为AE=x ,由题意,得∠BAC=θ,∠CAD=2θ, ∴AC=BC=30 m,AD=CD=310m.在Rt △ACE 中,sin 2θ=30x , ① 在Rt △ADE 中,sin 4θ=310x, ②②÷①,得cos 2θ=23.∴2θ=30°.∴θ=15°.AE=ADsin60°=15. 答:所求角θ为15°,建筑物高度为15 m.变式训练2 如图1-2-9,在海岸A 处发现北偏东45°方向,距A 处(13-)海里的B 处有一艘走私船.在A 处北偏西75°方向,距A 处2海里的C 处的我方缉私船,奉命以310海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B 处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.图1-2-9解:设缉私船应沿CD 方向行驶t 小时,才能最快截获(在D 点)走私船,则CD=310t 海里,BD=10t 海里.∵BC 2=AB 2+AC 2-2AB·AC·cosA=(3-1)2+22-2(3-1)·2cos120°=6,∴BC=6. ∵ABCAC A BC ∠=sin sin , ∴sin ∠ABC=226120sin 2sin =︒=∙BC A AC . ∴∠ABC=45°.∴B 点在C 点的正东方向上.∴∠CBD=90°+30°=120°. ∵CBDCD BCD BD ∠=∠sin sin ,∴sin ∠BCD=21310120sin 10sin =︒∙=∠∙tt CD CBD BD . ∴∠BCD=30°.∴缉私船的方向为北偏东60°.由∠CBD=120°,∠BCD=30°,得∠D=30°.∴BD=BC ,即10t=6.∴t=106小时≈15分钟. 答:缉私船沿北偏东60°的方向行驶,才能最快截获走私船,需时约15分钟.例 4 在某海滨城市附近海面上有一台风,据监测,当前台风中心位于城市O 的东偏南θ(cos θ=102)方向300 km 的海面P 处,并以20 km/h 的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km/h 的速度不断增大,问几小时后该城市开始受到台风的侵袭?受影响达多少小时?思路分析:设t 小时后台风中心在Q ,此时城市O 受到台风影响,即此时O 在台风侵袭的圆形区域内,注意台风在行进过程中,其半径在不断的增大,连结OQ ,把问题放到△OPQ 中,利用正弦、余弦定理解三角形即可.解:如图1-2-10,设在t 小时后台风中心在Q 点,此时台风侵袭的圆形区域半径为(10t+60) km. 若在此刻城市O 受到台风的影响,则OQ≤10t+60.图1-2-10由余弦定理,知OQ 2=PQ 2+PO 2-2PQ·POcos ∠OPQ.由PO=300,PQ=20t,cos ∠OPQ=cos (θ-45°)=cos θcos45°+sin θsin45° =54221021221022=⨯-+⨯, ∴OQ 2=(20t)2+3002-2×20t×300×54=202t 2-9 600t+3002.∴202t 2-9 600t+3002≤(10t+60)2.整理,得t 2-36t+288≤0.解得12≤t≤24.∴12小时后该城市开始受到台风的侵袭,受影响达12小时.绿色通道:本题关键是从示意图中抽象出三角形,建立数学模型,利用正弦、余弦定理解三角形,得到数学模型的解.变式训练 上例中,如果台风侵袭的圆形区域半径不变,那么该城市还会不会受到侵袭?如果会,几小时后受侵袭?如果不会,请说明理由.思路分析:假设该城市会受到侵袭,当台风到达Q 点时刚好侵袭该城市,仿例4构造△OPQ.则OQ=60,OP=300,∠OPQ=θ-45°,解三角形进行判断,若三角形有解,则会受到侵袭;无解,则不会受到侵袭.此问题还可以采用不等式的思想来解决,即OQ≤60时会受到侵袭.解不等式看是否有解.解:在△OPQ 中,∠OPQ=θ-45°,而cos θ=102, ∴sin θ=1027. ∵sin (θ-45°)=sin θcos45°-cos θsin45°=22(sin θ-cos θ)=53102622=⨯, 则OP·sin (θ-45°)=300×53=180.于是OQ=60<OP·sin (θ-45°),这样的三角形不存在.∴该城市不会受到台风的侵袭.问题探究问题 两千多年前,我国汉代的天文学家把商高的“测天量地”方法推广到计算太阳的高度.现在我们知道太阳离地球有1 460万千米之遥,可是古代人又能怎样测算呢?导思:把太阳看作一个固定不动的点,选择一根长度已知的标杆,某一时刻找到太阳直射的一个点,再在不同的两个地方把标杆竖起,测量其影子的长度,根据三角形计算就能估算出太阳的高度.探究:那时人们认为天是圆的,地是方的,太阳挂在天空中特定的地方,它的高度是可以测量的.于是,天文学家根据一根已知长度的标竿在不同地方的太阳的影子的长度不同来计算太阳的高度.汉代天文学家把这种计算方法称为“垂差术”.如图1-2-11,设太阳O 垂直照射到地面的C 点,高度为h ,标竿长为p ,在地方A 的影长为m ,在地方B 的影长为n ,A 到C 的距离为d ,则有图1-2-11 (1)mm d p h +=; (2)n AB n d p h ++=.解方程组,消去d ,得太阳离地面的高度h=mn AB p -∙+p. 请你们一起研究这个问题:这种测量方法的几何原理是什么?这种方法测量高度准不准,有什么局限性?你能结合本章知识来解决本题高度问题吗?。
高中数学必修5:1.2应用举例( 人教版高中数学必修5第一章解三角形 )

分析
在△AOP中,OA
OP tan 30
3h
在△BOP中,OB
OP tan 45
h
在△ABO中,AB2 OA2 OB2 2OAOB cos60
即 400 4h2 3h2
解得 h 400 4 3
题型四 求角度问题
例4 如图,在海岸A处发现北偏东45o方向,距A处 ( 3 1) 海里的B处有 一艘走私船. 在A处北偏西75o方向,距A处2海里的C处的我方缉私船,奉 命以 10 3 海里/时的速度追截走私船,此时走私船正以10海里/时的速度, 从B处向北偏东30o方向逃窜. 问:缉私船沿什么方向行驶才能最快截获走 私船?并求出所需时间.
2. 方位角:指以观测者为中心,从正北方向线顺时针旋转到目标方向线所 形成的水平角.如图所示的θ1、θ2即表示点A和点B的方位角.故方位角的范 围是[0o,360o).
测量中的有关概念、名词、术语
3. 方向角:以观测者为中心,指北或指南的方向线与目标方向线所成的小 于90°的水平角,它是方位角的另一种表示形式. 如图,左图中表示北偏 东30°,右图中表示南偏西60°.
6. 坡角、坡比:坡面与水平面的夹角称为坡角,坡面的竖直高度与水平宽 度的比称为坡比.
解三角形应用题
解三角形应用题时,通常都要根据题意,从实际问题中抽象出一个或几 个三角形,然后通过解三角形,得到实际问题的解,求解的关键是将实 际问题转化为解三角形问题.
题型一 测量一个不可到达点的距离
例1 海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角, 从B岛望C岛和A岛成75°的视角,则B,C间的距离是( )
ABC 45
题型四 求角度问题
分析 设缉私船应沿CD方向行驶 t 小时,才能最快 截获(在D点)走私船,则CD=10 3t ,BD=10t.
人教新课标A版高中数学必修5 第一章解三角形 1.2应用举例 同步测试(I)卷

C .
D .
10. (2分) 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在 , 两点进行测量, , , , 在同一个铅垂平面内. 海底探测仪测得
, 两点的距离为 海里,求 的面积( )平方海里。
A .
B .
C .
D .
11. (2分) (2017·赣州模拟) 如图所示,为了测量A,B处岛屿的距离,小明在D处观测,A,B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A,B两处岛屿间的距离为( )
17. (1分) (2017·邯郸模拟) 在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式,利用三角形的三条边长求三角形面积.若三角形的三边长为a,b,c,其面积S= ,这里p= (a+b+c),已知在△ABC中,BC=6,AB=2AC,其面积取最大值时sinA=________.
18. (1分) (2020·金堂模拟) 小王同学骑电动自行车以 的速度沿着正北方向的公路行驶,在点 处望见电视塔 在电动车的北偏东 方向上, 后到点 处望见电视塔在电动车的北偏东 方向上,则电动车在点 时与电视塔 的距离是________ .
A .
B .
C .
D .
5. (2分) 在 中,内角 的对边分别是 若 , 则 =( )
A .
B .
C .
D .
6. (2分) (2020·淮南模拟) 已知双曲线 的左右焦点分别为 、 ,过点 的直线交双曲线右支于 、 两点,若 是等腰三角形,且 .则 的周长为( )
A .
B .
C .
D .
7. (2分) A在塔底D的正西面,在A处测得塔顶C的仰角为45°,B在塔底D的南偏东60°处,在塔顶C处测得到B的俯角为30°,AB间距84米,则塔高为( )
人教版高中数学必修五练习第一章 1.2应用举例(一)

§1.2 应用举例(一)一、基础过关1.已知两灯塔A 和B 与海洋观测站C 的距离都等于a km ,灯塔A 在观测站C 的北偏东20°方向上,灯塔B 在观测站C 的南偏东40°方向上,则灯塔A 与灯塔B 的距离为( ) A .a km B.3a km C.2a kmD .2a km2.海上有A 、B 两个小岛相距10 n mile ,从A 岛望C 岛和B 岛成60°的视角,从B 岛望C 岛和A 岛成75°的视角,则B 、C 间的距离是( )A .10 3 n mile B.1063 n mileC .5 2 n mileD .5 6 n mile3.如图,为测一树的高度,在地面上选取A 、B 两点,从A 、B 两点分别测得望树尖的仰角为30°,45°,且A 、B 两点之间的距离为60 m ,则树的高度为( )A .(30+303) mB .(30+153) mC .(15+303) mD .(15+33) m4.如图,一货轮航行到M 处,测得灯塔S 在货轮的北偏东15°的方向上,与灯塔S 相距20海里,随后货轮按北偏西30°的方向航行30分钟后到达N 处,又测得灯塔在货轮的东北方向,则货轮的速度为( )A .20(6+2) 海里/小时B .20(6-2) 海里/小时C .20(6+3) 海里/小时D .20(6-3) 海里/小时5.如图,A 、N 两点之间的距离为________.6.如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,则塔高AB为________.7.要测量对岸两点A、B之间的距离,选取相距 3 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°,求A、B之间的距离.二、能力提升8.台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的持续时间为() A.0.5小时B.1小时C.1.5小时D.2小时9.太湖中有一小岛,沿太湖有一条正南方向的公路,一辆汽车测得小岛在公路的南偏西15°的方向上,汽车行驶1 km后,又测得小岛在南偏西75°的方向上,则小岛到公路的距离是________ km.10.江岸边有一炮台高30 m,江中有两条船,由炮台顶部测得俯角分别为45°和30°,而且两条船与炮台底部连成30°角,求两条船之间的距离.三、探究与拓展11.在海岸A处,发现北偏东45°的方向,距离A (3-1) n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 3 n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船?答案1.B 2.D 3.A 4.B 5.403 6.s ·tan θsin βsin (α+β)7.解 如图所示,在△ACD 中,∠ACD =120°, ∠CAD =∠ADC =30°, ∴AC =CD = 3 (km).在△BCD 中,∠BCD =45°,∠BDC =75°,∠CBD =60°. ∴BC =3sin 75°sin 60°=6+22(km).△ABC 中,由余弦定理,得 AB 2=(3)2+⎝⎛⎭⎪⎫6+222-23×6+22×cos 75°=3+2+3-3=5, ∴AB = 5 (km).∴A 、B 之间的距离为 5 km. 8.B 9.3610.解 如图所示∠CBD =30°,∠ADB =30°,∠ACB =45°. ∵AB =30 (m),∴BC =30 (m),BD =30tan 30°=30 3 (m). 在△BCD 中,CD 2=BC 2+BD 2-2BC ·BD ·cos 30°=900, ∴CD =30 (m),即两船相距30 m.11.解 如图所示,设缉私船用t h 在D 处追上走私船, 则有CD =103t ,BD =10t ,在△ABC 中,BC 2=AB 2+AC 2-2AB ·AC ·cos ∠BAC =(3-1)2+22-2×(3-1)×2×cos 120°=6, ∴BC = 6 (n mile),且sin ∠ABC =AC BC ·sin ∠BAC =26×32=22.∴∠ABC =45°,∴BC 与正北方向垂直.∵∠CBD =90°+30°=120°, 在△BCD 中,由正弦定理得 sin ∠BCD =BD ·sin ∠CBD CD=10t sin 120°103t =12,∴∠BCD =30°.即缉私船沿北偏东60°方向能最快追上走私船.。
人教A版高中数学必修五《1.2应用举例》练习题.docx

& 鑫达捷致力于精品文档 精心制作仅供参考 &鑫达捷 §1.2应用举例(练习)一.知识与技能目标1.能够运用正弦定理、余弦定理等知识和方法解决一些有关测量的实际问题;2.三角形的面积及有关恒等式.二.课内检测1. 某人向正东方向走x km 后,向右转150o ,然后朝新方向走3kmkm ,则x 等于( ).A. CD .32.在200米的山上顶,测得山下一塔顶与塔底的俯角分别为30,60o o ,则塔高为( )米.A .2003 BC .4003D3. 在∆ABC 中,60A ∠=︒,16AC =,面积为BC 的长度为( ).A .25B .51 C..494. 从200米高的山顶A 处测得地面上某两个景点B 、C 的俯角分别是30º和45º,且∠BAC =45º,则这两个景点B 、C 之间的距离 .5. 一货轮航行到M 处,测得灯塔S 在货轮的北偏东15°相距20里处,随后货轮按北偏西30°的方向航行,半小时后,又测得灯塔在货轮的北偏东45︒,则货轮的速度 .6. 已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m1-),n =(cos A ,sin A ). 若m ⊥n ,且a cos B +b cos A =c sin C ,求角B .三.课外作业1. 3.5米长的棒斜靠在石堤旁,棒的一端在离堤足1.2米地面上,另一端在沿堤上2.8米的地方,求堤对地面的倾斜角.2. 为测某塔AB 的高度,在一幢与塔AB 相距20m 的楼的楼顶处测得塔顶A 的仰角为030,测得塔基B 的俯角为45°,则塔AB 的高度为多少m ?3. 两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东030,灯塔B 在观察站C 南偏东60°,则A 、B 之间的距离为多少?4. 某观测站C 在目标A 的南偏西25o 方向,从A 出发有一条南偏东35o 走向的公路,在C 处测得与C 相距31km 的公路上有一人正沿着此公路向A 走去,走20km 到达D ,此时测得CD 距离为21km ,求此人在D 处距A 还有多远?5. 在某点B 处测得建筑物AE 的顶端A 的仰角为θ,沿BE 方向前进30m ,至点C 处测得顶端A 的仰角为2θ,再继续前进至D 点,测得顶端A 的仰角为4θ,求θ的大小和建筑物AE 的高.6. 如图,在四边形ABCD 中,AC 平分∠DAB ,∠ABC =060,AC =7,AD =6,S △ADCAB 的长.B C。
人教A版高中数学必修五同步练测:1.2应用举例.docx

高中数学学习材料马鸣风萧萧*整理制作1.2 应用举例(人教实验A 版必修5)建议用时 实际用时满分 实际得分45分钟100分一、选择题(本大题共5小题,每小题4分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某人朝正东方向走了x km 后,向左转150︒后,再向前走了3 km ,结果他离出发点恰好是3km ,那么x =( )A . B.2C.或 2D.2.一飞机沿水平方向飞行,在位置A 处测得正前下方地面目标C 的俯角为30°,向前飞行了10 000米,到达位置B 时测得正前下方地面目标C 的俯角为75°,这时飞机与地面目标C 的距离为( )米. A.2 000 B.2 500 C.5 000 D.7 5003.在ABCD 中,已知AB =1,AD =2,1AB AD ⋅=,则||AC =( )A. B. C. D.24.把一根30厘米长的木条锯成两段,分别作为钝角三角形ABC 的两边AB 和BC ,且∠ABC =120︒,当AB =( )厘米时,才能使第三条边AC 最短. A.13 B.14C.15D.165.如图所示,已知两座灯塔A 和 B 与海洋观察站C 的距离都等于 a km ,灯塔A 在观察站C 的北偏东 20°方向上,灯塔B 在观察站C 的南偏东40°方向上,则灯塔A 与灯塔B 的距离为( )A.a kmB.3a kmC.2a kmD.2a km二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)6.一只船自西向东航行,上午10时到达灯塔P 的南偏西75°、距灯塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船航行的速度为 .7.为了测河宽,在一岸边选定两点A 和B ,望对岸的标识物C ,测得∠CAB =45°,∠CBA =75°, AB =120米,则河宽 米.8.某人在草地上散步,看到他的正西方向有两根相距 6米的标杆,当他向正北方向步行3分钟后,看到一根标杆在其南偏西45°方向上,另一根标杆在其南偏西30°方向上,此人步行的速度是 米/分 . 9.江岸边有一炮台高30米,江中有两条船,由炮台顶部测得两船的俯角分别为45°和30°,而且两条船与炮台底部连线成30°角,则两条船相距 米. 三、解答题(共60分,解答应写出文字说明,证明过程或演算步骤)10.(14分)某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A 处获悉后,立即测出该渔船在方位角为45°、距离A 为10 n mile 的C 处,并测得渔船正沿方位角为105°的方向,以 9 n mile /h 的速度向某小岛B 靠拢,我海军舰艇立即以21 n mile /h 的速度前去营救,试问我海军舰艇应按照怎样的航向前进?并求出靠近渔船所用的时间.11.(14分)如图,在海岸A处发现北偏东45°方向,距A处( 3 -1)海里的B处有一艘走私船.在A 处北偏西75°方向,距A处2海里的C处的我方缉私船,奉命以10 3 海里/时的速度追截走私船,此时走私船正以10海里/时的速度,从B处向北偏东30°方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间. 12 .(16分)某海轮以30海里/时的速度航行,在A 点测得海面上油井P在南偏东︒60,向北航行40分钟后到达B点,测得油井P在南偏东30°方向上,海轮改为北偏东︒60的航向再行驶80分钟到达C点,求P、C间的距离.13.(16分)用同样高度的两个测角仪AB和CD同时望见气球E在它们的正西方向的上空,分别测得气球的仰角是α和β,已知B、D间的距离为a,测角仪的高度是b,求气球的高度.1.2 应用举例(人教实验A版必修5)答题纸得分:一、选择题题号 1 2 3 4 5答案二、填空题6. 7. 8. 9.三、解答题10.11.12.13.1.2 应用举例(人教实验A版必修5)参考答案1.C 解析:由余弦定理知3=x 2326x cos 30︒,解得x =3或23.故选C . 2.C 解析:设这时飞机与地面目标C 的距离为x 米,由正弦定理得10 000sin 45sin 30x ︒︒=,得x =5 000,故选C .3.B 解析:由||||cos 1AB AD AB AD A ⋅=⋅=,得cos A =12,即∠A =60︒,故∠B =120︒.由余弦定理知AC 2=12+22-4cos 120︒=7, 故||AC =7.故选B .4.C 解析:在△ABC 中,设AB = x (0<x <30)厘米 ,由余弦定理,得 AC 2=x22)30(x -+-2x (30-x )cos 120︒ =900-30x +x 2=(x 15+675,所以当AB =15厘米时,第三条边AC 最短.故选C .5. B 解析:易知∠ACB =120°,在△ABC 中,由余弦定理得2=AC 2+BC 2-2AC •BC cos 120°=22-22×(-)=32,∴ AB =. 6.1726 海里/时 解析:如图,由题意知∠MPN =75°+45°=120°, ∠PNM =45°. 在△PMN 中,由正弦定理,得sin120sin 45MN PM︒︒=, ∴ MN =68×3222=346(海里).又由M 到N 所用的时间为 14-10=4(小时),∴ 船的航行速度v =3464=1726(海里/时). 7. (60+203) 解析:把AB 看成河岸,要求的河宽就是C 到AB 的距离,也就是△ABC 的边AB 上的高.在△ABC 中,由正弦定理,得BC =120sin 45sin 60︒︒=406(米).则河宽为h =BC sin 75︒=406×426+=(60203)()+米. 8.(3+ 解析:如图所示,A 、B 两点的距离为6米,当此人沿正北方向走到C 点时,测得∠BCO =︒45,∠ACO =︒30,∴ ∠BCA =∠BCO -∠ACO =︒45-︒30=︒15.由题意,易知∠BAC =︒120,∠ABC =︒45.在△ABC 中,由正弦定理,得ABC AC ∠sin =BCAAB∠sin ,即AC = BCA ABC AB ∠∠⋅sin sin =︒︒⨯15sin 45sin 6=36+6.在Rt △AOC 中,有OC = AC ·cos ︒30= (36+6)×23= 9+33. 设此人步行速度为x 米/分,则x =3339+=(3+. 9.30 解析:设炮台顶部位置为A ,炮底为O ,两船位置分别为B 、C .在Rt △AOB 中,BO ==30米.在Rt △AOC 中,CO =303米. 在△BOC 中,由余弦定理,得BC 22230(303)230303cos30900=+-⨯⨯︒=,所以 BC =30米.10. 分析:设我海军舰艇从A 处靠近渔船所用的时间为 h ,则利用余弦定理建立方程来解决较好,因为如图中的∠1,∠2可以求出,而AC 已知,BC 、AB 均可用表示,故可看成是一个已知两边和其夹角求第三边的问题. 解:设我海军舰艇从A 处靠近渔船所用的时间为x h ,则AB =21 n mile ,=9 n mile ,=10 n mile ,∠ACB =∠1+∠2=45°+(180°-105°)=120°, 根据余弦定理,可得=+-2AC ·BC ·cos 120°得 (21=+(9-2×10×9cos 120°, 即36-9-10=0,解得=23 ,=-512 (舍去).∴ AB =21=14,=9=6.再由余弦定理可得:cos ∠BAC ===0.928 6, ∴∠BAC =21°47′,45°+21°47′=66°47′. 而我海军舰艇方位角为66°47′,23小时即40分钟.答:我海军舰艇应沿66°47′的方位角方向航行,靠近渔船则需要40分钟. 11. 解:设缉私船应沿CD 方向行驶t 小时,才能最快截获(在D 点)走私船, 则CD =103t 海里,BD =10t 海里. ∵=+-2AB ·AC ·cos A=+-2( 3 -1)·2cos 120°=6, ∴ BC = 6 .∵=, ∴ ===22, ∴ ∠ABC =45°,∴ B 点在C 点的正东方向上, ∴ ∠CBD =90°+30°=120°. ∵=,∴ sin ∠BCD ===12,∴ ∠BCD =30°,∴ ∠DCE =90°-30°=60°. 由∠CBD =120°,∠BCD =30°,得∠D =30°, ∴ BD =BC ,即10t = 6 , ∴ t =610(小时)≈15(分钟). 故缉私船沿北偏东60°的方向行驶才能最快截获走私船,约需15分钟. 12.解:如图,在△ABP 中,AB = 30×6040= 20,∠APB =︒30,∠BAP =︒120. 由正弦定理,得BPA AB ∠sin =BAPBP∠sin ,即2120=23BP ,解得BP =320.在△BPC 中,BC = 30×6080= 40, 由已知∠PBC =︒90,∴ PC ==+22BC PB 2240)320(+=720(海里).∴ P 、C 间的距离为720海里.13. 分析:在Rt △EGA 中求解EG ,只有角α一个条件,需要再有一边长被确定,而△EAC 中有较多已知条件,故可在△EAC 中考虑EA 边长的求解,而在△EAC 中有角β,∠EAC =180°-α两角与AC =BD =a 一边,故可以利用正弦定理求解EA . 解:在△ACE 中,AC =BD =a ,∠ACE =β,∠AEC =α-β, 根据正弦定理,得AE = 在Rt △AEG 中,EG ==, ∴ EF =EG +b =+b , 答:气球的高度是+b .。
最新人教版高中数学必修5第一章《应用举例》同步测控 2

1.2 应用举例5分钟训练(预习类训练,可用于课前)1.某人向正东方向走了x km 后向右转了150°,然后沿新方向走了3 km,结果离出发点恰好3 km,那么x 的值是_________________________.解析:由题意,作出示意图,由余弦定理列出关于x 的方程,解方程即可. 法一:如图,由题意可知,AB=x ,AC=3,BC=3,∠ABC=30°,由余弦定理,知AC 2=AB 2+BC 2-2AB·BC·cos ∠ABC. 3=x 2+9-2×3xcos30°. 整理,得x 2-33x+6=0, 解得x=32或x=3法二:先求A,由正弦定理,得sinA=330sin 3sin ︒=AC B BC =23.∵BC >AC ,∴A >B ,B=30°. ∴A 有两解,即A=60°或120°.当A=60°时,∠ACB=90°,∴x=3239=+. 当A=120°时,∠ACB=30°,∴x=AC=3. 答案:32或32.如图1-2-1,在河岸AC 测量河的宽度BC,测量下列四组数据,较适宜的是( )图1-2-1解析:在河的一岸测量河的宽度,关键是选准基线,在本题中AC 即可看作基线,在△ABC 中,能够测量到的边角为b 和α. 故应选D. 答案:DA.a 和cB.c 和bC.c 和βD.b 和α3.如图1-2-2,为了测量隧道口AB 的长度,给定下列四组数据,测量时应当用数据( )图1-2-2A.α,a,bB.α,β,aC.a,b,γD.α,β,b解析:选择点C,则在△ABC 中,a,b 可以测得,角γ也可测得,而α,β角是无法测得的. 答案:C4.有一长为10 m 的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长______________________m.( ) A.5 B.10 C.210 D.310解析:如图,设将坡底加长到B′时,倾斜角为30°,在△ABB′中,利用正弦定理可求得BB′的长度. 在△ABB′中,∠B′=30°,∠BAB′=75°-30°=45°,AB=10 m.由正弦定理,得BB′=21221030sin 45sin ⨯=︒︒AB =210.∴坡底要延伸210 m 时,斜坡的倾斜角将变为30°.故应选C. 答案:C10分钟训练(强化类训练,可用于课中)1.已知△ABC 的三边长分别为a-2,a,a+2,且它的最大角的正弦值为23,则这个三角形的面积是( ) A.415 B.4315 C.432 D.4335 解析:先判断出a+2所对角最大,设为α,则sinα=23. ∴cosα=±21. 当cosα=21时,由(a+2)2=a 2+(a-2)2-2a(a-2)·cosα,解得a=0,不合题意.当cosα=-21时,由(a+2)2=a 2+(a-2)2-2a(a-2)·cosα,解得a=5或a=0(舍去).∴S=21(a-2)·a·sinα=21×3×5×23=4315. 答案:B2.在△ABC 中,AB=7,AC=6,M 是BC 的中点,AM=4,则BC 等于( ) A.21 B.106 C.69 D.154 答案:解法一:由平行四边形对角线的平方和等于四条边的平方和,得 4AM 2+BC 2=2(AB 2+AC 2),∴BC=106164)3949(2=⨯-+.解法二:如图,设BC=2x,在△ABM 与△ACM 中,分别用余弦定理得 72=42+x 2-2×4x·cos ∠AMB , 62=42+x 2-2×4x·cos(π-∠AMB), 由以上两式得72+62=2(42+x 2), 解得x=2106,∴BC=2x=106. 答案:B3.△ABC 中,若已知三边为连续正整数,最大角是钝角,(1)求最大角;(2)求以此最大角为内角,夹此角的两边之和为4的平行四边形的最大面积. 解:(1)设a=k-1,b=k,c=k+1,(k ∈N *且k >1)∵C 是钝角,∴cosC=ab c b a 2222-+=)1(24--k k <0⇒1<k <4,∵k ∈N *,∴k=2或3.当k=2时,a=1,b=2,c=3不能构成三角形; 当k=3时,a=2,b=3,c=4,cosC=-41⇒∠C≈104°. (2)设平行四边形相邻两边为x,y,则S=xysinC=x(4-x)·415=-415(x-2)2+15.∴当x=2时,S max =15.4.如图1-2-3,为了测量上海东方明珠塔的高度,测量人员站在A 处测得塔尖的仰角为75.5°,前进38.5 m 后,在B 处测得塔尖的仰角为80°,试计算塔的高度.图1-2-3 解:∵∠CAD=75.5°,∠CBD=80°,∴∠ACB=4.5°.在△ABC 中,由BAC BC ACB AB ∠=∠sin sin ,∴BC=︒︒⨯=∠∠5.4sin 5.75sin 5.38sin sin ACB BAC AB ≈475.∴CD=BCsin80°≈468 m.∴塔的高度为468 m.5.如图1-2-4,甲船在A 处,乙船在A 处的南偏东45°方向,距A 有9海里,并以20海里/时的速度沿南偏西15°方向行驶,若甲船以28海里/时的速度行驶,应沿什么方向,用多少小时能最快追上乙船?(精确到度)图1-2-4解:假设用t 小时,甲船在C 处追上乙船,在△ABC 中, AC=28t,BC=20t,∠ABC=180°-45°-15°=120°. 由余弦定理,得AC 2=AB 2+BC 2-2AB·BC·cos ∠ABC , (28t)2=81+(20t)2-2×9×20t×(-21), 整理,得128t 2-60t-27=0, 即(4t-3)(32t+9)=0. ∴t=43. ∴AC=28×43=21, BC=20×43=15.由正弦定理,得sin ∠BAC=1435212315sin =⨯=∠ACABCBC , 又∠ABC=120°,∴∠BAC 为锐角,∠BAC=38°. ∴45°-38°=7°. ∴甲船应沿南偏东7°方向用43小时最快追上乙船. 30分钟训练(巩固类训练,可用于课后)1.从A 处望B 处的仰角为α,从B 处望A 处的俯角为β,则α、β的关系是( ) A.α>β B.α=β C.α+β=90° D.α+β=180°解析:要正确理解仰角、俯角的含义,准确地找出仰角、俯角的确切位置,如图,在A 处望B 处的仰角α与从B 处望A 处的俯角β是内错角(根据水平线平行),即α=β.答案:B2.如图1-2-5,它是曲柄连杆装置示意图,连杆AC=l,曲柄AB=r,曲柄AB 和曲轴BC 的夹角为α. (1)求连杆AC 和曲轴BC 间的夹角β的正弦值. (2)当α取什么值时,β最大? (3)求滑块C 的位移x.图1-2-5解:(1)在△ABC 中,由正弦定理,知sinβ=lrsinα. (2)由(1)知sinβ=lrsinα,当sinα=1时,sinβ最大. ∵0≤β≤2π,∴当sinβ最大时,β最大,即sinα=1时,α=2π,此时β最大. (3)在△ABC 中,由余弦定理:BC 2=AB 2+AC 2-2AB·AC·cos ∠BAC ,∴BC 2=r 2+l 2-2rlcos(π-α-β)=r 2+l 2+2rlcos(α+β).∴BC=)cos(222βα+++rl l r .∴位移x=r+l-BC=)cos(222βα+++rl l r .3.如图1-2-6,某炮兵阵地位于A 点,两观察所分别位于C 、D 两点.已知△ACD 为正三角形,且DC=3 km,当目标出现在B 时,测得∠CDB=45°,∠BCD=75°,求炮兵阵地与目标的距离是多少?(精确到0.01 km)图1-2-6解:由B=180°-∠BCD-∠CDB=60°, 在△BCD 中,由正弦定理,得BD=︒︒60sin 75sin CD =21(26+).在△ABD 中,∠ADB=45°+60°=105°,由余弦定理,得AB 2=AD 2+BD 2-2AD·BD·cos105°=3+41(26+)2+2×3×21(26+)×41(26-)=5+32,∴AB=325+≈2.91.∴炮兵阵地与目标的距离是2.91 km.4.如图1-2-7,在斜度一定的山坡上一点A 测得山顶上一建筑物顶端C 对于山坡的斜度为α,向山顶前进a m 到达B 点,从B 点测得斜度为β,设建筑物的高为h m,山坡对于地平面的倾斜角为θ,求证:cosθ=)sin(sin sin αββα-h a.图1-2-7证明:在△ABC 中,由正弦定理可知ACB a CBA AC ∠=∠sin sin ,即)sin(βπ-AC =)sin(αβ-a,∴AC=)sin(αβ-a sinβ.在△ADC 中,由正弦定理可知CDAACh ∠=sin sin α,又∠CDA=90°+θ, ∴θαββαcos )sin(sin sin -=a h . 整理,得cosθ=)sin(sin sin αββα-h a .5.地面上有一旗杆OP,如图1-2-8,为了测得它的高度,在地面上选一基线AB,测得AB=20 m,在A 处测得点P 的仰角为30°,在B 处测得点 P 的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度.(答案精确到个位数字)图1-2-8解:设旗杆的高度为h,由题意知∠OAP=30°,∠OBP=45°,在Rt △AOP 中,OA=OPcot30°=3h ,在Rt △BOP 中,OB=OPcot45°=h,在△AOB 中,由余弦定理,得 AB 2=OA 2+OB 2-2OA·OB·cos60°, 即202=(3h)2+h 2-32h×h×21,∴h 2=34400-≈176.4.∴h≈13(m).∴旗杆的高度为13 m.6.如图1-2-9,测量人员沿直线MNP 的方向测量,测得AB 的仰角分别是∠AMB=30°,∠ANB=45°,∠APB=60°,且MN=PN=500 m,求塔高AB.图1-2-9解:设AB=h ,∵AB ⊥MB ,AB ⊥NB ,AB ⊥PB, 又∠AMB=30°,∠ANB=45°,∠APB=60°, ∴MB=3h ,NB=h ,PB=33h. 在△MPB 中,cos ∠PMB=hh h MB MP BP MB MP 31000231310002222222⨯⨯-+=∙-+, 在△MNB 中,cos ∠PMB=hh h MB MN BN MB MN 3500235002222222⨯⨯-+=∙-+. ∴hh h h 31000250032003810002222+=+,整理,得h=6250(m). ∴塔高AB 为6250 m.7.如图1-2-10所示,a 是海面上一条南北方向的海防警戒线,在a 上点A 处有一个水声监测点,另两个监测点B 、C 分别在A 的正东方20 km 处和54 km 处.某时刻,监测点A 收到发自静止目标P 的一个声波,8 s 、28 s 后监测点B 、C 相继收到这一信号,在当时的气象条件下,声波在水中的传播速率是1.5 km/s.图1-2-10(1)设A 到P 的距离为x km,用x 表示B 、C 到P 的距离,并求x 的值. (2)求静止目标P 到海防警戒线a 的距离(精确到0.01 km). 解:(1)由题意PA-PB=1.5×8=12 km,PC-PB=1.5×20=30 km , ∴PB=x-12,PC=x+18.在△PAB 中,AB=20,由余弦定理,得cos ∠PAB=x x x x x AB PA PB AB PA 5323202)12(202222222+=⨯--+=∙-+.同理,可得cos ∠PAC=xx372-. 又cos ∠PAB=cos ∠PAC ,∴x x 5323+=xx372-,解得x=7132km.(2)如图,由题意作PD ⊥a,垂足为D,在Rt △PDA 中,PD=PAcos ∠APD=PAcos ∠PAB=x·xx 5323+≈17.71 km. ∴静止目标P 到海防警戒线a 的距离约为17.71 km.8.如图1-2-11,一辆汽车从O 点出发,沿海岸一条直线公路以100千米/时的速度向东匀速行驶,汽车开动时,在O 点南偏东方向距O 点500千米且与海岸距离为300千米的海上M 处有一快艇,与汽车同时出发,要把一件重要的物品递送给这辆汽车的司机,问快艇至少必须以多大的速度行驶,才能把物品递送到司机手中,并求快艇以最小速度行驶时方向与OM 所成的角.图1-2-11解:设快艇从M 处以v 千米/时的速度出发,沿MN 方向航行,t 小时后与汽车相遇.在△MON 中,MO=500,ON=100t ,MN=vt. 设∠MON=α,由题意知sinα=53,则cosα=54,由余弦定理知 MN 2=OM 2+ON 2-2OM·ON·cosα,即v 2t 2=5002+1002t 2-2×500×100t×54,整理,得v 2=(500×t1-80)2+3 600, 当t 1=50080,即t=425时,v min 2=3 600,∴v min =60,即快艇至少必须以60千米/时的速度行驶,此时MN=60×425=15×25,MQ=300, 设∠MNO=β,则sinβ=2515300⨯=54.∴α+β=90°,即MN 与OM 垂直.9.如图1-2-12,隔河看两目标A 、B,但不能到达,在岸边选取相距3 km 的C 、D 两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A ,B ,C ,D 在同一平面内),求两目标A 、B 之间的距离.图1-2-12解:在△ACD 中,∠ADC=30°,∠ACD=120°, ∴∠CAD=30°.∴AC=CD=3.在△BDC 中,∠CBD=180°-(45°+75°)=60°, 由正弦定理,得BC=︒︒60sin 75sin 3=226+.由余弦定理,得AB 2=AC 2+BC 2-2AC·BC·cos ∠BCA =(3)2+(226+)2-32×226+cos75°=5, ∴AB=5(km).∴两目标A ,B 之间的距离为5 km.10.在湖面上高h 米处,测得天空中一朵云的仰角为α,测得云在湖中之影的俯角为β,试证明云距湖面的高度为h)sin()sin(βαβα-+.解:如图,设湖面上高h 米处为A,测得云C 的仰角为α,测得C 在湖中之影D 的俯角为β,CD 与湖面交于M,过A 的水平线交CD 于E.设云高CM=x ,则CE=x-h ,DE=x+h ,AE=αtan hx -, 又AE=βtan hx +, ∴αtan h x -=βtan hx +. 整理,得x=αβαβtan tan tan tan -+h=h )sin()sin(βαβα-+.快乐时光忏 悔某人(到教堂):“神父,我……我有罪。
最新人教版高中数学必修5第一章《应用举例》同步测控1

1.2 应用举例5分钟训练(预习类训练,可用于课前)1.在△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3 ,则a ∶b ∶c 等于( ) A.1∶3∶2 B.1∶2∶3 C.2∶3∶1 D.3∶2∶1 解析:由已知得A=30°,B=60°,C=90°,根据正弦定理可知有CcB b A a sin sin sin ==, a ∶b ∶c=sin30°∶sin60°∶sin90°=1∶3∶2.答案:A2.从A 处望B 处的仰角为α,从B 处望A 处的俯角为β,则α、β 的关系为( ) A.α>β B.α+β=90° C.α=β D.α+β=180° 解析:由仰角、俯角的定义可知α=β. 答案:C3.在△ABC 中,a=2,b=3,c=4,则cosC=___________,其形状是___________.解析:由余弦定理得cosC=413224322222222-=⨯⨯-+=-+ab c b a <0,C 是钝角,故其形状是钝角三角形. 答案:41-钝角三角形 4.在△ABC 中,∠A ∶∠B=1∶2,a ∶b=1∶3,则∠A=___________,∠B=___________, ∠C=___________. 解析:由已知及正弦定理得31sin sin ==B A b a ,又B=2A , ∴A A A A A A cos 21cos sin 2sin 2sin sin 31===,cosA=23,A=6π,B=3π,C=2π.答案:6π 3π 2π10分钟训练(强化类训练,可用于课中)1.若三角形的三个角的比是1∶2∶3,最大的边是20,则这个三角形的面积为( ) A.350 B.1003 C.253 D.100 解析:由已知得A=30°,B=60°,C=90°,根据正弦定理可知有CcB b A a sin sin sin ==,a ∶b ∶c=sin30°∶sin60°∶sin90°=1∶3∶2,最小边为10. 答案:A2.边长为5、7、8的三角形的最大角与最小角的和是( )A.90°B.120°C.135°D.150°解析:本题只要先确定边长为7这边所对的内角,然后由三角形内角和定理,从而可求得最大角与最小角的和.设边长为7的边对应的角为B ,则cosB=21852785222=⨯⨯-+,∴B=60°. ∴A+C=120°.答案:B3.如右图,为测量障碍物两侧A 、B 间的距离,用a 、b 分别表示角A 、B 的对边,则下列给定四组数据中,测量时应当测的数据为( )A.a ,b ,∠AB.a ,∠A ,∠BC.b ,∠A ,∠BD.a ,b ,∠C 解析:由正余弦定理及生活实际容易得知. 答案:D4.甲船在岛B 的正南方A 处,AB=10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B 出发以每小时6千米的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间是( )A.7150分钟 B.715分钟 C.21.5分钟 D.2.15分钟 解析:AC 2=(10-4t)2+(6t)2-2×(10-4t)×6t×cos120°=28t 2-20t+100=28(t-145)2+7725故当t=145小时,即t=145×60=7150分钟时,甲乙两船距离最近. 答案:A5.已知一个平行四边形的两条邻边的长分别为2、3,且其中的一个内角为30°,则这个平行四边形的面积为___________. 解析:本题可以围绕着平行四边形的面积公式来考虑,或者连结其对角线将原平行四边形分成两个全等的三角形,从而由三角形的面积公式来求得结果,S=2×3sin30°=3. 答案:36.一树干被台风吹断折成与地面成30°角,树干底部与树尖着地处相距20米,求树干原来的高度.解析:根据题意画出如图示意图,问题转化到Rt △ABC 中,BC=20,B=30°,tan30°=BC AC ,AC=BCtan30°=20×332033=,∴AB=2AC, AC+AB=3AC=320(米).答案:即树干原来的高度为320米. 30分钟训练(巩固类训练,可用于课后)1.某人朝正东方向走了x km 后,向右转150°,再向前走了3 km ,结果他离出发点恰好为3 km ,那么x 的值是( )A.3B.23C.3或23D.3 解析:由题意画出示意图,设出发点为A ,则由已知可得AB=x 千米,BC=3千米,∠ABC=180 °-150°=30° . AC=3,∴CABBCAC ∠=︒sin 30sin .∴CAB ∠=sin 3213,∴sin ∠CAB=23. ∴∠CAB=60°或∠CAB=120°.当∠CAB=60°时,∠ACB=180°-30°-60°=90°.x=32千米;当∠CAB=120°,∠ACB=180°-120°-30°=30°.∴x=AC=3千米.答案:C2.如右图,B 、C 、D 三点在地面同一直线上,DC=a ,从C 、D 两点测得A 点的仰角分别是β、α(α<β),则A 点离地面的高AB 等于( )A.)cos(sin sin αββα-a B.)sin(sin sin αββα-aC.)sin(cos sin αββα-a D.)cos(cos cos αββα-a解析:在Rt △ABC 与Rt △ADC 中, tan β=BC AB ,tan α=BDAB,BC=ABcot β, BD=ABcot α,DC=BD-BC=AB(cot α-cot β)=a , AB=)sin(sin sin cos cot αββαβα-=-a a .答案:B3.(2006高考全国卷Ⅰ,文12)用长度分别为2、3、4、5、6(单位:cm )的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( ) A.58cm 2 B.106cm 2 C.553cm 2 D.20 cm 2 解析:用2、5连接,3、4连接各为一边,第三边长为6组成三角形,此三角形面积最大,面积为106cm 2.答案:B4.如右图,已知|F 1|=20 N ,|F 2|=30 N,|F 3|=40 N ,三力互成120°的角,求合力的大小.解:如下图,F 1、F 2的合力的大小|F|2=|F 1|2+ |F 2|2-2|F 1||F 2|cos60°=700 N.∴F≈26.46 N ,合力的大小为|F 3|-|F|=13.54 N.5.甲、乙两人去测大河两岸A 、B 两点的距离(如右图).当他们到达A 处时才发觉只带了测角仪,甲转身要回去拿工具.乙看见A 处那根24米长的电杆,忙说:“不用去了,能测出来.”甲用疑惑的目光望着乙.你能帮甲想一个办法吗?解:在A 点测得∠CAB ,在C 点测得∠BCA , 然后可求得∠B=180-(∠CAB+∠BCA ), 根据正弦定理∵)sin()180sin(sin sin C A AC C A AC B AC C AB +=--︒==∴AB=)sin(sin C A C+×AC, 带入实验数据即可求得A 、B 两点的距离. 解:在△ABC 中,∠B=152°-122°=30°,∠C=180°-152°+32°=60°,∠A=180°-30°-60°=90°,BC=235, ∴AC=43530sin 235=︒. 所以货轮与灯塔间的距离为354海里.6.如右图,货轮在海上以35海里/小时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B 点处观测到灯塔A 的方位角为122°.半小时后,货轮到达C 点处,观测到灯塔A 的方位角为32°.求此时货轮与灯塔之间的距离.7.在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边长. 求证:Ac b Ab c C B cos cos cos cos --=. 证法一:由正弦定理得AC C A AB B A AC R B R A B R C R A c b A b c cos sin )sin(cos sin )sin(cos sin 2sin 2cos sin 2sin 2cos cos -+-+=--=--CBC A B A cos cos cos sin cos sin ==.证法二:由余弦定理得C B abc a b ac b c a b c a b c b c a bc a c b c b bc a c b b c A c b A b c cos cos 222222cos cos 222222222222222222=-+-+=-+-+=-+⨯--+⨯-=--. 8.甲船在A 点发现乙船在北偏东60°的B 处,乙船以每小时a 海里的速度向北行驶,已知甲船的速度是3a 海里/小时,甲船沿着什么方向前进,才能最快与乙船相遇? 解:设甲船在C 处追上乙船,并设所用的时间为t 时,由已知得∠ABC=120°,BC=at ,AC=at 3. 由正弦定理得BACBC ABC AC ∠=∠sin sin即BACatat ∠=︒sin 120sin 3, ∴sin ∠BAC=21,即∠BAC=30°. ∴甲船沿着北偏东30°方向前进,才能最快与乙船相遇.9.在山坡上有一棵垂直的大树.试一试:不用爬树怎样可测出大树的高度.解:在山坡上有一棵垂直的大树,通过“标准步”及简易测角工具,计算出大树的高度,具体步骤为:(1)把每一步跨度基本相同的跨步方式称为标准步,每个人可用“标准步”走若干步(例如20步),反复几次,量出每次所走距离,并计算几次走动中每步的平均距离就能获得自己的“标准步”.(2)可用量角器加指针作为简易测角工具.具体操作步骤:从大树底部A 向下跨a 步“标准步”到了B ,用简易测角工具测得∠ABP=α,再向上跨了b 步“标准步”到了C(a >b),测得∠ACP=β,该同学测出自己眼睛至脚底的高度大约是h cm ,每步“标准步”跨度约为l cm,∴PA=)sin(cos sin 2)(sin sin 2222αβαβαββ--+-ab a b这样就可知这棵大树的高度,PD=PA·l+h.10.在一个正三角形中画一条分割线(可以是直线、折线或曲线),把这个正三角形的面积两等分.(1)试设想各种画分割线的方法,并比较各条分割线的长短;(2)在你所画出的所有分割线中,哪一种最短?这是不是所有可能的分割线中最短的?证明你的结论. 解:(1)图1、图2是容易想到的两种分法,分别计算分割线的长度(设正三角形的边长为1),得AD=23≈0.866 0(图1);DE=22≈0.707 1(图2).图3这种分割线是否一定比图2的分割线长?答案是肯定的,以下证明这一点.如图3,设AD=m,AE=n, 则21mnsin60°=2143⨯,得mn=21. 于是DE 2=m 2+n 2-2mncos60°=m 2+ n 2-mn≥2mn -mn=mn=21. 当且仅当m=n=22时等号成立,这说明DE min =22. 图4的情形一般被认为不可能是最短的,但计算验证一下又何妨?图4设AD=AE=AF=m ,由条件得:2×21m 2sin30°=83,故m 2=43. 于是DF 2=2m 2-2m 2cos30°=(23-)m 2=4332-. 因此,分割线的长为DF+EF=2DF=332-≈0.681 3<0.707 1. 这是一个令人咋舌的结论,用圆弧来分割是否会最短呢? 如图5,不难计算=123π≈0.673 4.图5(2)图5中为最短的分割线,证明如下:如图6,将六个全等的正三角形拼成一个正六边形,六段分割线形成一个封闭的图形.问题转化为:给定面积,画一个周长最短的封闭图形,显然圆的周长最短.图6。
高中数学必修五第一章小测试题.doc

B.l hC.1.5hD.2hA.0.5 h 必修五第一章小测(7.23) 一、 正弦定理1 (12广东文科数学)在AABC 中,若ZA = 60\ ZB = 45°, BC = 3近,则AC =V3A. 4 巧B. 2 也C.的D. 22. AABC 中,若 c = 2a cos %,则 AABC 的形状为()A.直角三角形B.等腰三角形C.等边三角形D.锐角三角形3.在 AABC 中,已知sinA = 2 sinBcosC,则 AABC —定是.( )A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形.5在厶 ABC 中,已知 b = 3, c = 3 羽,/LB = 30°,则 a= ______________ . 二、 余弦定理1在中,三个角A 、B 、C 的对边边长分别为a=3, b = 4, c = 6,则be cos A + ca cos B + ab cos c 的值为 ________2. 在Z\ABC 中,若 a?=沪+bc + c?,贝!JA = ___________ 。
3. 利用余弦定理说明△ ABC 的内角C 为锐角,则有6/2+Z?2>C 24.A ABC 中,己知(a+B+c )0+c-a ) = bc ,则A 的度数等于() A. 120-B . 60。
c. ISO' D . 30-三、 正弦定理与余弦定理综合 1. AABC 的内角A 、B 、C 的对边分别a ,b,c 若c =迈,b =品,B ,贝皿等于A.品B. 2C.屈D. V23.在ZXABC 中,A = 120°,a = V21,^ABC = A /3 ,求b,c 的值 四、 应用 1.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30。
、60。
,则塔高为.....( )A.B. 400舲米 c. 200jl 米 D. 200 米332. 台风中心从A 地以20 km/h 的速度向东北方向移动,离台风中心30 km 内的地区为危险区, 城市 B 在 4 的正东40 km 处,B 城市处于危险区内的时间 为()7 . 数列{a”}满足:(Zj第二章小测一、数列1.在数列1,123,5,&兀,21,34,55中,兀等于()A. 11B. 12C. 13D. 14二、等差数列1.已知{dn}是等差数列,且°2+。
高中数学 1.1.2 应用举例试题 新人教A版必修5

1.2应用举例一、选择题:本题共8个小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.【题文】已知A,B两地的距离为5 km,B,C两地的距离为10 km,经测量可知,120ABC∠=︒,则A,C两地的距离为( )A. 5 kmB.55 kmC. 75 kmD.57 km2.【题文】如图,一艘轮船以每小时60海里的速度自A沿南偏东35︒的方向直线航行,30分钟后到达B处,在C处有一座灯塔,轮船在A处观察灯塔,其方向是南偏东65︒,在B处观察灯塔,其方向是北偏东70︒,那么B,C间的距离是( )A.152海里B.153海里C.303海里D.302海里3.【题文】为了测量一建筑物的高度,某人在地面上选取共线的三点A,B,C,分别测得此建筑物的仰角为30︒,45︒,60︒,且AB=BC=30 m,如图所示,则建筑物的高度为( )A.56B. 106C. 156D. 6m4.【题文】如图,巡航艇在海上以60km/h的速度沿南偏东40︒的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东70︒,航行1h2到达C处,观测灯塔A的方向是北偏东65︒,则巡航艇到达C处时,与灯塔A的距离是( )A.10kmB. 102kmC. 15kmD. 152km5.【题文】如图所示,在一条水平直线上选取三点A ,B ,C 进行测量,测得AB =25 m ,BC =60 m ,水深AD =40 m ,BE =100 m ,CF=55 m ,则DEF ∠的余弦值为 ( )A.1665B.1965 C.1657 D. 17576.【题文】一架直升飞机在600 m 的高空中,测得地面上一座塔的塔顶与塔底的俯角分别是30︒和60︒,则塔高为 ( )A.400mB.4003mC.2003mD.200m7.【题文】若锐角△ABC 的面积为34,6AB AC ==,则BC =( ) A .4 B .25.26.78.【题文】△ABC 的三内角,,A B C 所对边的长分别是c b a ,,,若sin sin 3sin B A a cC -+=,则角B 的大小为( ) A .π6 B .5π6 C .π3 D .2π3二、填空题:本题共3小题.9.【题文】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a =5,b =3,sin C =2sin A ,则△ABC 的面积为 .10.【题文】两船同时从A 港出发,甲船以每小时20海里的速度向北偏东80︒的方向航行,乙船以每小时12海里的速度向北偏西40︒方向航行,一小时后,两船相距 海里.11.【题文】如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小.若12m AB =,20m AC =,45BCM ∠=︒,则tan θ的最大值是 .(仰角θ为AP 与平面ABC 所成角)三、解答题:解答应写出文字说明,证明过程或演算步骤.12.【题文】如图所示,在山顶上有一座塔,在山底测得塔顶的仰角∠CAB =45°,沿倾斜角为30°的斜坡走1 000米至S 点,又测得塔顶的仰角∠DSB =75°,求塔高BD .13.【题文】如图,渔船甲位于岛屿A 的南偏西60︒方向的B 处,且与岛屿A 相距18海里,渔船乙以15海里/小时的速度从岛屿A 出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2 h 追上,此时到达C 处.(1)求渔船甲的速度; (2)求sin α的值.14.【题文】在△ABC 中,内角A 、B 、C 的对边分别为,,a b c ,且()2213a b c ab--=-.(1)求角C ; (2)若3,2c b ==,求B 及△ABC 的面积.人教A 版数学 必修五 第一章 1.2应用举例 参考答案与解析1. 【答案】D【解析】在△ABC 中,AB =5 km ,BC =10km ,120ABC ∠=︒,根据余弦定理得,222o 5102510cos 120km AC AC =+-⨯⨯⨯⇒=.故选D.考点:利用余弦定理测量距离. 【题型】选择题 【难度】较易2. 【答案】A【解析】易知在△ABC 中,=30AB 海里,=303570105,45CAB ABC ACB ∠︒∠=︒+︒=︒∴∠=︒,,根据正弦定理得=sin 30sin 45BC AB︒︒,解得BC =(海里).考点:利用正弦定理测量距离. 【题型】选择题 【难度】较易3. 【答案】C【解析】设建筑物的高度为m h ,由题图知,2m PA h =,m PB =,m PC =,所以在△PBA 和中△PBC 中,分别由余弦定理的推论,得222cos=2302PBA h ∠⨯⨯①,22243023cos =2302h h PBC h+-∠⨯⨯②,因为180PBA PBC ︒∠+∠=,所以cos cos =0PBA PBC ∠+∠③.由①②③,解得156156h h ==-或(舍去),即建筑物的高度为306m . 考点:利用余弦定理测量高度. 【题型】选择题 【难度】一般4. 【答案】D【解析】在△ABC 中,()1=60=30km 2BC ⨯,o o o =7040=30ABC ∠-,=4065=105ACB ∠︒+︒︒,则()=18030105=45A ︒-︒+︒︒,由正弦定理,得()=152km AC .考点:利用正弦定理测量距离. 【题型】选择题 【难度】一般5. 【答案】 A【解析】 如图所示,作DM ∥AC 交BE 于N ,交CF 于M .)222215855298m DF MF DM =+=+=, ()2222256065m DE DN EN =+=+=,()()2222456075m EF BE FC BC =-+=+=,在△DEF 中,根据余弦定理的推论得,2222226575529816cos ==22657565DE EF DF DEF DE EF +-+-⨯∠=⨯⨯⨯.考点:利用余弦定理测量角度.【题型】选择题 【难度】一般6. 【答案】A 【解析】如图所示:在Rt△ACD 中可得tan 30CD AC︒=,3tan 3060020033CD AC BE =⋅︒=⨯==, 在△ABE 中,由正弦定理,o o=200sin 30sin 60AB BEAB =⇒,∴()600200400m DE BC ==-=. 考点:利用正弦定理测量高度. 【题型】选择题 【难度】较易7. 【答案】D【解析】三角形面积113sin 46sin 63,sin 222S AB AC A A A =⋅⋅=⨯⨯==,由于△ABC 为锐角三角形,所以1cos 2A =,由余弦定理可求得BC =,故选D.考点:三角形面积公式的应用. 【题型】选择题 【难度】一般8. 【答案】B【解析】222sin sin sin B A b a c a b C c --=⇒=⇒+-=2225πcos 0π26c a b B B B ac +-⇒==<<∴=Q ,,故选B.考点:正、余弦定理综合. 【题型】选择题 【难度】一般9. 【答案】3【解析】由正弦定理得2c a ==4cos5B ==,因此3113sin ,sin 3.5225B S ac B ====考点:正、余弦定理及三角形面积公式的应用. 【题型】填空题 【难度】一般10. 【答案】28【解析】如图,△ABC 中,20124080120AB AC CAB ︒︒==∠=+=︒,,, 由余弦定理得222201222012cos 120784BC ︒=+-⨯⨯⋅=,∴28BC =(海里).考点:利用余弦定理测量距离. 【题型】填空题 【难度】一般11. 【答案】53【解析】如图,过P 作PO BC ⊥于点O ,连接AO ,则PAO θ∠=,设OC x =,则OP x =,在直角△ABC 中,由勾股定理,得BC =16,所以4cos 5BCA ∠=.在△AOC 中,由余弦定理,得224400220324005AO x x x x =+-⨯⨯=-+, 从而22tan 324002049525OPAOx x x θ===-+⎛⎫-+ ⎪⎝⎭,当2045x =,即25x =时,tan θ取得最大值,为53.考点:利用余弦定理测量角度. 【题型】填空题 【难度】一般12. 【答案】500米【解析】∵∠SAB =∠CAB −∠CAS =45°−30°=15°, ∠SBA =∠ABC −∠SBC =45°−15°=30°,∴在△ABS 中,sin 15sin 30BS AS =︒︒,∴sin 15500sin 30AS BS ⋅︒==︒(米). ∴BD =BS ·sin 75°=500500=(米). 考点:利用正弦定理求高度.【题型】解答题【难度】较易13. 【答案】(1)21海里/小时 (2【解析】(1)依题意得,120BAC ∠=︒,18AB =,15230AC =⨯=,BCA α∠=. 在△ABC 中,由余弦定理,得222222cos 18302BC AB AC AB AC BAC =+-⋅⋅∠=+-1830cos1201764⨯⨯⨯︒=, 所以BC =42,所以渔船甲的速度为212BC =海里/小时. (2)在△ABC 中,18AB =,120BAC ∠=︒,BC =42,BCA α∠=, 由正弦定理,得sin sin 120AB BC α=︒,即18sin 1202sin 4214AB BC α⨯⋅︒===. 考点:利用正、余弦定理求距离、角度.【题型】解答题【难度】一般14. 【答案】(1)2π3C = (2)π4B =【解析】(1)由已知条件化简可得()223a b c ab --=-,变形可得222a b c ab +-=-, 由余弦定理的推论可得,2221cos 22a b c C ab +-==-, ()2π0,π,3C C ∈∴=Q .(2)2π3c b C ===Q ,∴由正弦定理可得sin sin b C B c ===又π,,4b c B C B <∴<∴=Q ,在△ABC 中, ()1sin sin sin cos cos sin 222A B C B C B C ⎛⎫=+=+=-+= ⎪⎝⎭. 11sin 22ABC S bc A ∆∴===. 考点:正、余弦定理综合应用.【题型】解答题【难度】一般。
人教新课标A版高中数学必修5 第一章解三角形 1.2应用举例 同步测试(I)卷

人教新课标A版高中数学必修5 第一章解三角形 1.2应用举例同步测试(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共30分)1. (2分) (2019高一下·佛山月考) 在中,已知三个内角为满足,则().A .B .C .D .2. (2分) (2018高一下·新乡期末) 在中,若,则是()A . 锐角三角形B . 钝角三角形C . 直角三角形D . 形状不确定3. (2分)在中a=1,b=3,C=60,则c=()A .B . 7C .D . 134. (2分) (2018高一下·江津期末) 一船以每小时 km的速度向东行驶,船在A处看到一灯塔B在北偏东60°,行驶4小时后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为()A . 60kmB . kmC . kmD . 30km5. (2分) (2018高二下·南宁月考) 在中,分别为角的对边长,,则三角形的形状为()A . 等腰直角三角形B . 等腰三角形或直角三角形C . 正三角形D . 直角三角形6. (2分)在△ABC中,b=4,c=3,BC边上的中线,则a=()A .B .C .D .7. (2分) (2018高二上·哈尔滨期中) 已知抛物线的顶点在坐标原点,焦点,为抛物线上的任一点,过点作圆的切线,切点分别为,,则四边形的面积最小值为()A .B .C .D .8. (2分) (2019高二上·四川期中) 在圆内,过点的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为A .B .C .D .9. (2分) (2016高一下·惠阳期中) 在△ABC中,∠A= ,AB=2,且△ABC的面积为,则边AC的长为()A . 1B .C . 2D . 310. (2分)一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 海里,则灯塔S在B处的()A . 北偏东75°B . 北偏东75°或东偏南75°C . 东偏南75°D . 以上方位都不对11. (2分)蓝军和红军进行军事演练,蓝军在距离的军事基地和,测得红军的两支精锐部队分别在处和处,且,,,,如图所示,则红军这两支精锐部队间的距离是()A .B .C .D .12. (2分) (2016高一下·老河口期中) 如图所示,为了测量某湖泊两侧A、B间的距离,李宁同学首先选定了与A、B不共线的一点C,然后给出了三种测量方案:(△ABC的角A、B、C所对的边分别记为a、b、c):①测量A、C、b;②测量a、b、C;③测量A、B、a;则一定能确定A、B间距离的所有方案的序号为()A . ①②B . ②③C . ①③D . ①②③13. (2分)如右图所示,在山脚A处测得该山峰仰角为θ,对着山峰在平坦地面上前进600 m后测得仰角为原来的2倍,继续在平坦地面上前进200 m后,测得山峰的仰角为原来的4倍,则该山峰的高度为()A . 200 mB . 300 mC . 400 mD . 100 m14. (2分)如图,在高为20m的楼顶A处观察前下方一座横跨河流的桥BC,测得桥两端B,C的俯角分别为60°,45°,则桥的长度为()A . mB . 10 mC . 20﹣ mD . 20﹣10 m15. (2分) (2019高一下·三水月考) 将一根长为的铁管折成一个的角,然后将、两端用木条封上,从而构成三角形在不同的折法中,面积的最大值为()A .B .C .D .二、填空题 (共5题;共5分)16. (1分)一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶2小时后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为________ km.17. (1分) (2017高一下·泰州期末) 若△ABC的面积为,BC=2,则的取值范围是________.18. (1分) (2016高三上·遵义期中) 某中学举行升旗仪式,在坡度为15°的看台E点和看台的坡脚A点,分别测得旗杆顶部的仰角分别为30°和60°,量的看台坡脚A点到E点在水平线上的射影B点的距离为10cm,则旗杆的高CD的长是________ m.19. (1分)(2017·闵行模拟) 地球的半径为R,在北纬45°东经30°有一座城市A,在北纬45°西经60°有一座城市B,则坐飞机从A城市飞到B城市的最短距离是________.(飞机的飞行高度忽略不计)20. (1分) (2016高二上·上杭期中) 一船以每小时12海里的速度向东航行,在A处看到一个灯塔B在北偏东60°,行驶4小时后,到达C处,看到这个灯塔B在北偏东15°,这时船与灯塔相距为________海里.三、解答题 (共3题;共15分)21. (5分)一艘海轮从A处出发,以40海里/时的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,求B,C两点间的距离.22. (5分) (2016高二上·福州期中) 某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观测点A,B(假设A,B,C,D在同一水平面上),且AB=80米,当航模在C 处时,测得∠ABC=105°和∠BAC=30°,经过20秒后,航模直线航行到D 处,测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)23. (5分) (2018高一下·雅安期中) 已知a,b,c分别为三个内角A,B,C所对的边长,且.(1)求角C的值;(2)若c=4,a+b=7,求. .的值.四、综合题 (共2题;共20分)24. (10分)(2016·江苏) 在△ABC中,AC=6, ,(1)求AB的长;(2)求cos(A﹣)的值.25. (10分)如图,有一块形状为等腰直角三角形的薄板,腰AC的长为a米(a为常数),现在斜边AB选一点D,将△ACD沿CD折起.翻扣在地面上,做成一个遮阳棚,如图(2),设△BCD的面积为S,点A到直线CD的距离为d,实践证明,遮阳效果y与S,d的乘积Sd成正比,比例系数为k,(k为常数,且k>0)(1)设∠ACD=θ,试将S表示为θ的函数(2)当点D在何处时,遮阳效果最佳(即y取得最大值)参考答案一、单选题 (共15题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题;共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共3题;共15分) 21-1、22-1、23-1、23-2、四、综合题 (共2题;共20分) 24-1、24-2、25-1、25-2、。
高中数学第一章解三角形1.2应用举例一限时练新人教A版必修5

1.2 应用举例(一)一、选择题1.如图,在河岸AC测量河的宽度BC,测量下列四组数据,较适宜的是( )A.a,c,αB.b,c,αC.c,a,βD.b,α,β2.三角形的一边长为14,这条边所对的角为60°,另两边之比为8∶5,则这个三角形的面积为( )A.403B.203C.402D.20 23.如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A-C-B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走(结果精确到0.1km,参考数据:2≈1.41,3≈1.73)( )A.3.4kmB.2.3kmC.5.1kmD.3.2km4.如图所示,为了测定河的宽度,在一岸边选定两点A、B,望对岸标记物C,测得∠CAB=30°,∠CBA =75°,AB =120m ,则河的宽度为( )A .230mB .240mC .50mD .60m5.海上有A 、B 两个小岛相距10nmile ,从A 岛望C 岛和B 岛成60°的视角,从B 岛望C 岛和A 岛成75°的视角,则B 、C 间的距离是( )A .103nmileB.1063nmile C .52nmileD .56nmile 二、填空题 6.一船以每小时15km 的速度向东航行,船在A 处看到一个灯塔B 在北偏东60°,行驶4h 后,船到达C 处,看到这个灯塔在北偏东15°,这时船与灯塔间的距离为________km.7.要测量对岸两点A 、B 之间的距离,选取相距3km 的C 、D 两点,并测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°,则A 、B 之间的距离为________km.8.某人在M 汽车站的北偏西20°的方向上的A 处,观察到点C 处有一辆汽车沿公路向M 站行驶.公路的走向是M 站的北偏东40°.开始时,汽车到A 的距离为31千米,汽车前进20千米后,到A 的距离缩短了10千米.则汽车到达M 汽车站还需行驶________km.三、解答题9.如图所示,一架飞机从A 地飞到B 地,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成21°角的方向飞行,飞行到中途,再沿与原来的飞行方向成35°夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km 远了多少?10.如图所示,一艘船以32.2nmile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5nmile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?11.如图,一人在C 地看到建筑物A 在正北方向,另一建筑物B 在北偏西45°方向,此人向北偏西75°方向前进30km 到达D 处,看到A 在他的北偏东45°方向,B 在北偏东75°方向,试求这两座建筑物之间的距离.答案精析1.D2.A3.A4.D5.D6.3027.58.159.解 在△ABC 中,AB =700 km ,∠ACB =180°-21°-35°=124°,根据正弦定理,700sin 124°=AC sin 35°=BCsin 21°, AC =700×sin 35°sin 124°,BC =700×sin 21°sin 124°, AC +BC =700×sin 35°sin 124°+700×sin 21°sin 124°≈786.89 (km),786.89-700=86.89(km).所以飞机的飞行路程比原来路程远了大约86.89 km.10.解 在△ABS 中,AB =32.2×0.5=16.1 n mile ,∠ABS =115°,根据正弦定理,AS sin ∠ABS =ABsin(65°-20°), AS =AB ×sin ∠ABS sin(65°-20°)=AB ×sin ∠ABS × 2 =16.1×sin 115°×2, S 到直线AB 的距离d =AS ×sin 20°=16.1×sin 115°×2×sin 20°≈7.1(n mile)>6.5(n mile). 所以这艘船可以继续沿正北方向航行.11.解 依题意得,CD =30 (km),∠ADB =∠BCD =30°=∠BDC ,∠DBC =120°,∠ADC =60°,∠DAC =45°.在△BDC 中,由正弦定理得BC =DC sin ∠BDCsin ∠DBC =30sin 30°sin 120°=10(km).在△ADC 中,由正弦定理得AC =DC sin ∠ADCsin ∠DAC =30sin 60°sin 45°=35(km). 在△ABC 中,由余弦定理得AB 2=AC 2+BC 2-2AC ·BC ·cos ∠ACB =(35)2+(10)2-2×35×10cos 45°=25. 所以AB =5(km),故这两座建筑物之间的距离为5 km.。
高中数学 第一章 解三角形 1.2 应用举例单元检测 新人教A版必修5-新人教A版高二必修5数学试题

应用举例(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.某次测量中,A 在B 的北偏东55°,则B 在A 的( )A .北偏西35°B .北偏东55°C .南偏西35°D .南偏西55°2.在△ABC 中,AB =3,AC =1,∠B =30°,则△ABC 的面积等于( ) A.32 B.34 C.32或 3 D.32或343.在一座20 m 高的观测台台顶测得对面一水塔塔顶仰角为60°,塔底俯角为45°,那么这座塔的高为( )A .20⎝ ⎛⎭⎪⎫1+33 m B .20(1+3) m C .10(6+2) m D .20(6+2) m 4.某人向正东方向走了x km 后向右转了150°,然后沿新方向走了3 km ,结果离出发点恰好为 3 km ,那么x 的值为( ) A. 3 B .2 3 C .23或 3 D .35.在△ABC 中,若cos B =14,sin C sin A =2,且S △ABC =154,则b 等于( )A .4B .3C .2D .16.有一长为10 m 的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长的长度(单位:m)是( )A .5B .10C .10 2D .10 3 7.如图所示,为测一树的高度,在地面上选取A ,B 两点,从A ,B 两点分别测得树尖的仰角为30°,45°,且A ,B 两点之间的距离为60 m ,则树的高度为( )A .(30+303) mB .(30+153) mC .(15+303) mD .(15+33) m 8.解放军某部举行实弹演习,其中炮兵阵地位于地面A 处,两观测点分别位于地面C 处和D 处,已知CD =6 000 m ,∠ACD =45°,∠ADC =75°,目标出现于地面B 处时,测得∠BCD =30°,∠BDC =15°,则炮兵阵地到目标B 的距离是( )A .5 000 mB .6 000 mC .1 00042 mD .1 00055 m9.如图所示,位于A 处的信息中心获悉:在其正东方向相距40 n mile 的B 处有一艘渔船遇险,在原地等待救援.信息中心立即把消息告知在其南偏西30°,相距20 n mile C 处的乙船,乙船立即沿直线CB 前往救援,则sin ∠ACB =( )A.217B.2114C.57D.51410.如图,甲船以每小时302海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于A 1处时,乙船位于甲船的北偏西105°方向的B 1处,此时两船相距20海里,当甲船航行20分钟到达A 2处时,乙船航行到甲船的北偏西120°方向的B 2处,此时两船相距102海里,则乙船每小时航行( )A .102海里B .202海里C .30海里D .302海里11.从某电视塔的正东方向的A 处,测得塔顶的仰角为60°,从电视塔的西偏南30°的B 处,测得塔顶的仰角为45°,若A ,B 间的距离为35 m ,则此电视塔的高度为( )A .521 mB .626 mC .821 mD .1021 m 12.如图,在四边形ABCD 中,已知∠B =∠C =120°,AB =4,BC =CD =2,则该四边形的面积等于( )A. 3 B .5 3C .6 3D .7 3 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案13.一蜘蛛沿东北方向爬行x cm 捕捉到一只小虫,然后向右转105°,爬行10 cm 捕捉到另一只小虫,这时它向右转135°爬行回它的出发点,那么x =________.14.一架飞机在海拔8 000 m 的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是30°和45°,则这个海岛的宽度为________.15.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足cos A 2=255,AB →·AC→=3,则△ABC的面积为________.16.某小区的绿化地有一个三角形的花圃区,若该三角形的三个顶点分别用A,B,C 表示,其对边分别为a,b,c,且满足(2b-c)cos A-a cos C=0,则在A处望B处和C处所成的视角为________.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°,若此军舰不改变航行的方向继续前进,问此军舰有没有触礁的危险?18.(本小题满分12分)在△ABC中,a+b=10,cos C是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.19.(本小题满分12分)某地电信局信号转播塔建在一山坡上,如图所示,施工人员欲在山坡上A,B两点处测量与地面垂直的塔CD的高,由A,B两地测得塔顶C的仰角分别为60°和45°,又知AB 的长为40 m,斜坡与水平面成30°角,则该转播塔的高度是多少米?20.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且cos C =15. (1)求sin ⎝⎛⎭⎪⎫C +π4的值;(2)若CA →·CB →=1,a +b =37,求边c 的值及△ABC 的面积.21.(本小题满分12分)如图,一辆汽车从A 市出发沿海岸一条笔直公路以每小时100 km 的速度向东匀速行驶,汽车开动时,在A 市南偏东方向距A 市500 km 且与海岸距离为300 km 的海上B 处有一快艇与汽车同时出发,要把一份稿件交送给这辆汽车的司机.(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与AB 所成的角.22.(本小题满分12分)某棚户区改造建筑用地区域近似为半径为R 的圆面,其平面示意图如图所示.该圆面的内接四边形ABCD 是原棚户建筑用地,测量可知AB =AD =40 km ,BC =60 km ,CD =20 km.请计算原棚户区建筑用地ABCD 的面积及圆面的半径R 的值.参考答案与解析1.【解析】选D.如图,A 在B 的北偏东55°,则B 在A 的南偏西55°. 2.【解析】选D.由余弦定理得, 1=3+BC 2-2×3×BC ×cos 30°, 即BC 2-3BC +2=0, 所以BC =2或BC =1,所以S △ABC =12×3×2×sin 30°=32或S △ABC =12×3×1×sin 30°=34.3.【解析】选B.如图所示,AB 为观测台,CD 为水塔,AM 为水平线.依题意,AB =20,∠DAM =45°,∠CAM =60°,所以MD =20,AM =20,CM =203,CD =20(1+3) m.4.【解析】选C.如图AB =x km ,BC =3 km ,AC = 3 km ,∠ABC =180°-150°=30°,所以AC 2=AB 2+BC 2-2AB ·BC ·cos 30° 即3=x 2+9-2×x ×3×32, 所以x 2-33x +6=0, 解得x =23或x = 3. 5.【解析】选C.因为c a =sin Csin A=2,所以c =2a .因为cos B =14所以sin B =154,又因为S △ABC =12ac sin B =a 2×154=154,所以a 2=1,即a =1,c =2, 所以b 2=a 2+c 2-2ac cos B =1+4-2×2×14=4,所以b =2.6.【解析】选C.如图,设将坡底加长到B ′时,倾斜角为30°,在△ABB ′中,利用正弦定理可求得BB ′的长度.在△ABB ′中,∠B ′=30°,∠BAB ′=75°-30°=45°,AB =10 m ,由正弦定理,得 BB ′=AB sin 45°sin 30°=10×2212=102(m).所以坡底延伸10 2 m 时,斜坡的倾斜角将变为30°. 7.【解析】选A.由正弦定理可得60sin (45°-30°)=PBsin 30°,PB =60×12sin 15°=30sin 15°,h =PB sin 45°=(30+303) m.8.【解析】选C.在△ACD 中,易求得∠CAD =60°.又因为CD =6 000,∠ACD =45°,由正弦定理有:AD =CD sin 45°sin 60°=23CD ;同理,在△BCD 中,易求得∠CBD =135°. 由正弦定理得,BD =CD sin 30°sin 135°=22CD ;又在△ABD 中,易知∠ADB =90°, 所以AB =AD 2+BD 2= 23+12CD =426CD =1 00042(m). 9.【解析】选A.在△ABC 中,AB =40,AC =20,∠BAC =120°,由余弦定理,得BC =207,由正弦定理,得sin ∠ACB =ABBC ·sin ∠BAC =217. 10.[导学号99570019] 【解析】选D.如图,连接A 1B 2,在△A 1A 2B 2中,易知∠A 1A 2B 2=60°,又易求得A 1A 2=302×13=102=A 2B 2,所以△A 1A 2B 2为正三角形,所以A 1B 2=10 2. 在△A 1B 1B 2中,易知∠B 1A 1B 2=45°, 所以B 1B 22=400+200-2×20×102×22=200, 所以B 1B 2=102,所以乙船每小时航行302海里. 11.【解析】选A.如图,在△AOC 中,OC =OA tan 60°⇒OA =33OC ,又在△BOC 中,OB =OC ,在△AOB 中,AB =35 m ,∠AOB =180°-30°=150°,由余弦定理,得AB 2=AO 2+BO 2-2AO ·BO cos ∠AOB ,即352=13OC 2+OC 2+OC 2⇒OC =521 m ,故选A.12.【解析】选B.连接BD (图略),在△BCD 中,由余弦定理可得BD 2=22+22-2×2×2·cos 120°=12,即BD =2 3.因为BC =CD , 所以∠CBD =30°.所以∠ABD =90°,即△ABD 为直角三角形. 故S 四边形ABCD =S △BCD +S △ABD=12×2×2×sin 120°+12×4×2 3 =3+43=5 3. 13. 【解析】如图所示,设蜘蛛原来在O 点,先爬行到A 点,再爬行到B 点,易知在△AOB 中,AB =10 cm ,∠OAB =75°,∠ABO =45°,则∠AOB =60°,由正弦定理知:x =AB ·sin ∠ABO sin ∠AOB =10×sin 45°sin 60°=1063cm.【答案】1063 cm14.【解析】如图所示,飞机位于海平面的B 点上方8 000 m 的A 处,测得海岛两侧海岸CD 的俯角分别为∠EAD =30°,∠EAC =45°,所以∠ACD =135°,∠ADC =30°,AB =8 000 m ,AB ⊥CD ,所以AD =2AB =16 000 m , 由正弦定理得CD sin 15°=ADsin 135°.所以CD =16 000×6-2422=8 000(3-1) m.【答案】8 000(3-1) m15.【解析】因为cos A =2cos 2A 2-1=35,所以sin A =45.又AB →·AC →=3,则bc cos A =3,所以bc =5.因此,△ABC 的面积S =12bc sin A =2.【答案】216.【解析】在△ABC 中,(2b -c )cos A -a cos C =0,结合正弦定理得2sin B cos A -sin C cos A -sin A cos C =0,即2sin B cos A -sin(A +C )=0,即2sin B cos A -sin B =0.又因为A ,B ∈(0,π),所以sin B ≠0,所以cos A =12,所以A =π3,即在A 处望B 处和C 处所成的视角为π3.【答案】π317.【解】过点B 作BD ⊥AE 于点D ,由已知,AC =8,∠ABD =75°,在△ABD 中,AD =BD ·tan 75°;在△CBD 中,CD =BD ·tan60°,而AD -CD =AC ,所以BD (tan 75°-tan 60°)=8.BD =8tan 75°-tan 60°=4>3.8,所以该军舰没有触礁危险.18.【解】因为2x 2-3x -2=0的根为x 1=2,x 2=-12,cos C 是方程2x 2-3x -2=0的一个根,所以cos C =-12,由余弦定理可得:c 2=a 2+b 2-2ab ·⎝ ⎛⎭⎪⎫-12=(a +b )2-ab ,所以c 2=100-a (10-a )=(a -5)2+75,当a =5时,c 最小且c =75=53,此时a +b +c =10+53,所以△ABC 周长的最小值为10+5 3.19. 【解】如图,根据题意可得,∠ABC =45°-30°=15°,∠DAC =60°-30°=30°, 所以∠BAC =150°, ∠ACB =15°. 所以AC =AB =40 m.在△ADC 中,∠BDC =120°,由正弦定理得, AC sin 120°=CDsin 30°,所以CD =40sin 30°sin 120°=4033(m),即转播塔的高度是4033m.20.【解】(1)由sin 2C +cos 2C =1,cos C =15,C ∈(0,π),得sin C =265.则sin ⎝ ⎛⎭⎪⎫C +π4=sin C cos π4+cos C sin π4=265×22+15×22=43+210.(2)因为CA →·CB →=|CA →||CB →|cos C =1,则ab =5. 又a +b =37.所以a 2+b 2=(a +b )2-2ab =27. 所以c 2=a 2+b 2-2ab cos C =25,则c =5. 所以S △ABC =12ab sin C = 6.21.【解】(1)如图,设快艇以v km/h 的速度从B 处出发,沿BC 方向,t h 后与汽车在C 处相遇,在△ABC 中,AB =500,AC =100t ,BC =vt ,BD 为AC 边上的高,BD =300.设∠BAC =α,则sin α=35,cos α=45. 由余弦定理,得BC 2=AC 2+AB 2-2AB ·AC cos α,所以v 2t 2=(100t )2+5002-2×500×100t ·45. 整理,得v 2=250 000t 2-80 000t+10 000 =250 000⎣⎢⎡⎦⎥⎤1t 2-825·1t +⎝ ⎛⎭⎪⎫4252+10 000-10 000×1625 =250 000⎝ ⎛⎭⎪⎫1t -4252+3 600. 当1t =425,即t =254时,v 2min =3 600,v min =60(km/h), 即快艇至少以60 km/h 的速度行驶才能把稿件送到司机手中.(2)当v =60 km/h 时,在△ABC 中, AB =500,AC =100×254=625,BC =60×254=375,由余弦定理,得cos ∠ABC =AB 2+BC 2-AC 22AB ·BC=0,所以∠ABC =90°,故快艇应向垂直于AB 的方向向北偏东方向行驶.22. 【解】因为四边形ABCD 内接于圆,所以∠ABC +∠ADC =180°.连接AC ,在△ABC ,△ACD 中,由余弦定理得AC 2=402+602-4 800cos ∠ABC =402+202- 1 600cos(180°-∠ABC ),所以cos ∠ABC =12,又因为∠ABC ∈(0°,180°),所以∠ABC =60°.过A 作AE ⊥BC ,交BC 于点E ,过A 作AF ⊥CD ,交CD 的延长线于点F , S 四边形ABCD =12BC ·AE +12CD · AF =12×60×40sin 60°+12×20×40sin(180°-120°)=8003(km 2).在△ABC 中,由余弦定理得AC 2=402+602-2×40×60cos 60°⇒AC =207(km), 又由正弦定理得2R =AC sin ∠ABC =40213⇒R =20213(km).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自我小测
夯基达标
1.有一长为10 m 的斜坡,它的倾斜角是75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延伸( )
A.5 m
B.10 m
C.m 210
D.m 310 1解析:如图,在△ABC 中,
设BC =x m,
由正弦定理可知︒
=︒30sin 10
45sin x ,
∴21030sin 45sin 10=︒
︒
=
x . 答案:C
2.江岸边有一炮台高30 m,江中有两条船,由炮台顶部测得俯角分别为45°和30°,而且两条船与炮台底部连线成30°角,两条船相距是( )
A.20 m
B.m 30
C.30 m
D.m 330 2 解析:如图,设CD 为炮台,A 、B 为两条船,由题意知CD =30 m,
∠CBD =45°,∠CAD =30°,∠ACB =30°. 在Rt △ACD 中,33060tan 30=︒=AC , 同理BC =30tan45°=30,
在△ABC 中,
AB 2=AC 2+BC 2-2AC ·BC ·cos ∠ACB
90030cos 30330230)330(22=︒⋅⨯⨯-+=. ∴AB =30(m). 答案:C
3.在锐角三角形ABC 中,若C =2B ,则
b
c
的取值范围是( ) A.)3,2( B.)2,3( C.(0,2) D.)2,2( 3 解析:∵C =2B , ∴
B B
B B
C b c cos 2sin 2sin sin sin ===, ∵C =2B ,△ABC 为锐角三角形, ∴0°<B <45°. ∴
1cos 2
2
<<B . ∴2cos 22<<B . 答案:D
4.从200 m 高的山顶看,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( ) A.
m 3400 B.m 33
400 C.
m 3
3
200 D.m 3200 4解析:由山顶看塔底的俯角为60°,可知山脚与塔底的水平距离为
3
200
,又山顶看塔顶的俯角为30°,设塔高为x m ,则33
3
200200⨯
=-x ,所以m 3400=x . 答案:A
5.某地电信局信号转播塔建在一山坡上,如图所示,施工人员欲在山坡上A 、B 两点处测量与地面垂直的塔CD 的高,由A 、B 两地测得塔顶C 的仰角分别为60°和45°,又知AB 的长为40米,斜坡与水平面成30°角,则该转播塔的高度是___________米.
5 解析:根据题意可得,∠ABC =45°-30°=15°,∠D AC =60°-30°=30°, ∴∠BAC =150°,∠ACB =15°. ∴AC =AB =40米. 在△ADC 中,∠BDC =120°, 由正弦定理,得
︒
=︒30sin 120sin CD
AC ,
∴3
3
40120sin 30sin 40=
︒︒=
CD . 答案:
3
340 能力提升
6.已知两灯塔A 、B 与观测点C 的距离都等于a km,灯塔A 在观测点C 的北偏东20°,灯塔B 在观测点C 的南偏东40°,则灯塔A 与B 的距离为___________ km. 6解析:如图,在△ABC 中,C A =CB =a km,
∠ACB =180°-20°-40°=120°, ∴由余弦定理可得
AB 2=AC 2+BC 2-2AC ·BC ·cos ∠ACB =a 2+a 2-2a ×a ×cos120°=3a 2. ∴km 3a AB =.
答案:a 3
7.一船以24 km/h 的速度向正北方向航行,在点A 处望见灯塔S 在船的北偏东30°方向上,15 mi n 后到点B 处望见灯塔在船的北偏东65°方向上,则船在点B 时与灯塔S 的距离是__________ km.(精确到0.1 km)
7解析:如图,由条件知,)km (660
15
24=⨯
=AB .
在△ABS 中,∠BAS =30°,AB =6,∠ABS =180°-65°=115°, ∴∠ASB =35°.
由正弦定理,得︒=︒35sin 30sin AB
BS ,
∴2.535sin 30sin 6≈︒
︒
=
BS . 答案:5.2
8.如图,在一个山坡上的一点A ,测得山顶上一个微波塔顶端C 对于山坡的坡度的斜度为20°,向山顶前进80米后的B 点,又测得斜度为40°,设塔高为60米,求此山对于地面的倾角θ的余弦值.
8解:在△ABC 中,∠BAC =20°,∠ABC =180°-40°=140°,AB =80, ∴∠ACB =20°. 由正弦定理,得︒
=︒20sin 20sin 80BC
,
∴BC =80.
在△BDC 中,CD =60,∠BDC =90°+θ,∠D BC =40°, ∴由正弦定理,得
)
90sin(80
40sin 60θ+︒=︒.
9.如图,当甲船位于A 处时获悉,在其正东方向相距20海里的B 处有一艘渔船遇险等待营救,甲船立即前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C 处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B 处救援(角度精确到1°)?
10.(2009辽宁高考,理17)如图,A ,B ,C ,D 都在同一个与水平面垂直的平面内,B ,D 为两岛上的两座灯塔的塔顶.测量船于水面A 处测得B 点和D 点的仰角分别为75°,30°,于水面C 处测得B 点和D 点的仰角均为60°,AC =0.1 km.试探究图中B,D 间距离与另外哪两点间距离相等,然后求B ,D 的距离(计算结果精确到0.01 km,449.26,414.12≈≈). 拓展探究
11.在△ABC 中,已知B b a C A sin )()sin (sin 2222-=-,其外接圆半径为2,求∠C 及三角形面积的最大值.
参考答案
∴857.040sin 6
8
cos ≈︒=
θ. ∴此山对于地面的倾角θ的余弦值约为0.857. 9 解:在△ABC 中,AB =20,AC =10,∠BAC =120°,
由余弦定理,知BC 2=AB 2+AC 2-2AB ·AC ·cos120°=202+102-2×20×10×(2
1
-)=700, ∴710=BC .
由正弦定理
BAC
BC
ACB AB ∠=∠sin sin ,
∴7
21120sin 7
1020sin sin =
︒⋅=
∠⋅=∠BAC BC
AB ACB .
∴∠ACB ≈41°.
∴乙船应沿北偏东30°+41°=71°的方向沿直线前往B 处救援. 10解:在△ACD 中,∠D AC =30°,∠ADC =60°-∠D AC =30°
,
所以CD =AC =0.1.
又∠BCD =180°-60°-60°=60°,
故CB 是△C AD 底边AD 的中垂线,所以BD =BA . 在△ABC 中,
ABC
AC
BCA AB ∠=∠sin sin ,
即206
2315sin 60sin +=︒︒=
AC AB ,
因此,km 33.020
6
23≈+=
BD .
故B ,D 的距离约为0.33 km.
11 解:设△ABC 的外接圆半径为R ,则2=R .
由
正
弦
定
理
,
得
R
b B R
c C R a A 2sin ,2sin ,2sin ===
,代
入
B b a
C A s i n )()s i n (
s i n 2222
-=-,得a 2-c 2=ab -b 2,即a 2+b 2-c 2=ab ,
∴2
1
22cos 222==-+=
ab ab ab c b a C . ∵0<C <π,
∴3
π=C . B A C ab S sin sin 32sin 2
1
==
B B s i n
)3
π
2s i n (32⋅-= B B B s i n )s i n 2
1c o s 23(
32⋅+= B B B 2
s i n 3c o s s i n 3+⋅= )2c o s 1(2
32s i n 23B B -+=
23
2c o s 232s i n 23+
-=
B B 2
3
)6π2s i n (3+
-=
B , ∴2
3
3max =
S ,当且仅当3π==B A 时成立.。
