2017年秋季学期新版青岛版九年级数学上学期3.5、三角形的内切圆课件
合集下载
三角形的内切圆ppt课件

(A)
1
A. rl
2
1
B. πrl
2
C.rl
D.πrl
2.已知O是△ABC的内心,∠BAC=70°,P为平面上一点,点O恰好又是△BCP的外心,则
∠BPC的度数为( C )
A.50°
°
C.62.5°
D.65°
3.已知一个直角三角形的两条直角边长分别是6和8,则此直角三角形的内切圆半径
r=_______.
如果AB=4,AC=5,AD=1,那么BC的长为_______.
7
4.(8分·推理能力、几何直观)如图,点E是△ABC的内心,AE的延长线和△ABC的外接
圆相交于点D,BC与AD相交于点F.求证:DE=DB.
【证明】如图,连接BE,
∵点E是△ABC的内心,
∴AE是∠BAC的平分线,BE是∠ABC的平分线,
3.5
三角形的内切圆
1111
课时学习目标
1.理解三角形内切圆的概念,掌握三角形内切
圆的性质,能准确辨析内心和外心的不同
2.掌握画三角形的内切圆的方法,能借助三角
形内切圆的性质解决有关几何问题
素养目标达成
抽象能力、几何直观
几何直观、推理能力、模型观念
基础主干落实
新知要点
1.三角形内切圆的有关概念
相切
∴∠BAD=∠CAD,∠ABE=∠CBE.
∵∠CAD=∠CBD,∴∠DBE=∠CBD+∠CBE=∠CAD+∠ABE=∠BAD+∠ABE=
∠BED,∴DE=DB.
本课结束
内心
与三角形各边都______的圆叫做三角形的内切圆,其圆心叫做三角形的______.
2.三角形内心的性质
九年级数学上册 3.5 三角形的内切圆课件 (新版)青岛版.pptx
(5)直角三角形 的内切圆的半径为r 与 各边长
ra、=b、ac的关系ab是b c 12
谢谢同学们的 参入配合!
13
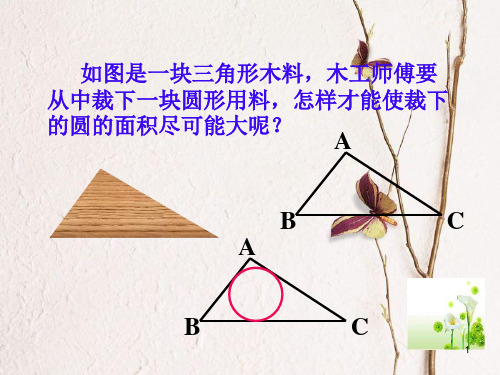
如图是一块三角形木料,木工师傅要 从中裁下一块圆形用料,怎样才能使裁下 的圆的面积尽可能大呢?
A
B
C
A
B
C
1
3.5 三角形的内切圆
2
【学习目标】
1.了解三角形的内切圆相关的概念 2.能利用三角形内心的性质进行证明 和计算 (重点、难点)
【教学重点,难点】
能利用三角形内心的性质进行证明和 计算
3
活动一:思考、操作
∠ABC、∠ACB
C 3.内心在三角形内
部.
8
探讨1: 设△ABC 的内切圆的半径为r,△ABC 的
各边长之和为C,△ABC 的面积S,我们会有什
么结论?
A
D
•
F
1
O
S = rC
B
r
2
(C为三角形周长,r为内切圆半径)
E直角三角形的两直角边分别是a,b,斜边为
c 则其内切圆的半径r为:
A
A
O B
B
C
4
三角形 内切圆 作法:
1、作∠B、∠C的平分线 BM和CN,交点为I。
2.过点I作ID⊥BC,垂足为D。 A
3.以I为圆心,ID为
半径作⊙I. ⊙I就是所求的圆。
NM I
B
D
C
5
定义:和三角形各边都相切的圆叫做三角形的
内切圆,内切圆的圆心叫做三角形的内心,这个 三角形叫做圆的外切三角形。
性质: 1.三角形的内心到三角形各边的距离相等;
2.三角形的内心在三角形的角平分线上;内心
ra、=b、ac的关系ab是b c 12
谢谢同学们的 参入配合!
13
如图是一块三角形木料,木工师傅要 从中裁下一块圆形用料,怎样才能使裁下 的圆的面积尽可能大呢?
A
B
C
A
B
C
1
3.5 三角形的内切圆
2
【学习目标】
1.了解三角形的内切圆相关的概念 2.能利用三角形内心的性质进行证明 和计算 (重点、难点)
【教学重点,难点】
能利用三角形内心的性质进行证明和 计算
3
活动一:思考、操作
∠ABC、∠ACB
C 3.内心在三角形内
部.
8
探讨1: 设△ABC 的内切圆的半径为r,△ABC 的
各边长之和为C,△ABC 的面积S,我们会有什
么结论?
A
D
•
F
1
O
S = rC
B
r
2
(C为三角形周长,r为内切圆半径)
E直角三角形的两直角边分别是a,b,斜边为
c 则其内切圆的半径r为:
A
A
O B
B
C
4
三角形 内切圆 作法:
1、作∠B、∠C的平分线 BM和CN,交点为I。
2.过点I作ID⊥BC,垂足为D。 A
3.以I为圆心,ID为
半径作⊙I. ⊙I就是所求的圆。
NM I
B
D
C
5
定义:和三角形各边都相切的圆叫做三角形的
内切圆,内切圆的圆心叫做三角形的内心,这个 三角形叫做圆的外切三角形。
性质: 1.三角形的内心到三角形各边的距离相等;
2.三角形的内心在三角形的角平分线上;内心
青岛版九年级数学上册课件【全册】

青岛版九年级数学上册课件【全 册】目录
0002页 0035页 0093页 0162页 0221页 0262页 0277页 0290页 0304页 0336页 0358页 0404页 0424页 0442页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一元二次方程的应用
青岛版九年级数学上册课件【全册 】
2.2 30°,45°,60°角的三角比
青岛版九年级数学上册课件【全册 】
2.3 用计算器求锐角三角比
青岛版九年级数学上册课件【全册 】
第1章 图形的相似
青岛版九年级数学上册课件【全册 】
1.1 相似多边形
青岛版九年级数学上册课件【全册 】
1.2 怎样判定三角形相似
青岛版九年级数学上册课件【全册 】
1.3 相似三角形的性质
青岛版九年级数学上册课件【全册 】
1.4 图形的位似
青岛版九年级数学上册课件【全册 】
第2章 解直角三角形
青岛版九年级数学上册课件【全册 】
பைடு நூலகம்2.1 锐角三角比
0002页 0035页 0093页 0162页 0221页 0262页 0277页 0290页 0304页 0336页 0358页 0404页 0424页 0442页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一元二次方程的应用
青岛版九年级数学上册课件【全册 】
2.2 30°,45°,60°角的三角比
青岛版九年级数学上册课件【全册 】
2.3 用计算器求锐角三角比
青岛版九年级数学上册课件【全册 】
第1章 图形的相似
青岛版九年级数学上册课件【全册 】
1.1 相似多边形
青岛版九年级数学上册课件【全册 】
1.2 怎样判定三角形相似
青岛版九年级数学上册课件【全册 】
1.3 相似三角形的性质
青岛版九年级数学上册课件【全册 】
1.4 图形的位似
青岛版九年级数学上册课件【全册 】
第2章 解直角三角形
青岛版九年级数学上册课件【全册 】
பைடு நூலகம்2.1 锐角三角比
最新青岛版九年级数学上册全册完整课件

册全册完 整课件
1.1 相似多边形
最新青岛版九年级数学上册全册完 整课件
1.2 怎样判定三角形相似
最新青岛版九年级数学上册全册完 整课件
1.3 相似三角形的性质
最新青岛版九年级数学上册全册完 整课件
2.2 30°,45°,60°角的三角比
最新青岛版九年级数学上册全册完 整课件
2.3 用计算器求锐角三角比
最新青岛版九年级数学上册全册完 整课件
最新青岛版九年级数学上册全册 完整课件目录
0002页 0035页 0085页 0154页 0190页 0192页 0204页 0206页 0236页 0238页 0280页 0310页 0339页 0373页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一元二次方程的应用
最新青岛版九年级数学上册全册完 整课件
1.4 图形的位似
最新青岛版九年级数学上册全册完 整课件
第2章 解直角三角形
最新青岛版九年级数学上册全册完 整课件
2.1 锐角三角比
1.1 相似多边形
最新青岛版九年级数学上册全册完 整课件
1.2 怎样判定三角形相似
最新青岛版九年级数学上册全册完 整课件
1.3 相似三角形的性质
最新青岛版九年级数学上册全册完 整课件
2.2 30°,45°,60°角的三角比
最新青岛版九年级数学上册全册完 整课件
2.3 用计算器求锐角三角比
最新青岛版九年级数学上册全册完 整课件
最新青岛版九年级数学上册全册 完整课件目录
0002页 0035页 0085页 0154页 0190页 0192页 0204页 0206页 0236页 0238页 0280页 0310页 0339页 0373页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一元二次方程的应用
最新青岛版九年级数学上册全册完 整课件
1.4 图形的位似
最新青岛版九年级数学上册全册完 整课件
第2章 解直角三角形
最新青岛版九年级数学上册全册完 整课件
2.1 锐角三角比
青岛版九年级上册3.5 三角形的内切圆(共12张PPT)

11
小
结
1.掌握三角形内切圆的概念;
2.会画三角形的内切圆;
3.会处理与三角形内切圆相关的题目.
12
A.三角形的内心到三角形三个顶点的距离相等 B.三角形的内心不一定在三角形的内部 C.等边三角形的内心,外心重合 D.一个圆一定有唯一一个外切三角形
10
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,
则它的内切圆与外接圆半径分别为( C )
A.1.5,2.5 C.1,2.5 B .2,5 D.2,2.5
2.如图2,⊙O是△A BC的内切圆,D,E,F是切点, 点,∠A=50°,∠C=60°,• 则∠DOE=( B ) A.70° B.110° C.120° D. 140°
8
3.如图,△ABC中,∠A=45°,I是内心,则∠BIC=( A.112.5° B.112° C.125°
A)
D.55°
9
4.下列命题正确的是( C )
3.5
三角形的内切圆
1
1.掌握三角形内切圆的概念;
2.会画三角形的内切圆; 3.会处理与三角形内切圆相关的题目.
2
(1)任意作一个∠AOB,如果在 ∠AOB内作圆,使其与两边OA,OB都 相切,满足条件的圆是否可以作出?
B C
圆心都在 ∠AOB的平分 线上
O
A
3
(2)任意作一个△ABC,如果在△ABC内作圆,使其
与各边都相切,满足上述条件的圆是否可以作出?如果
可以作出,能作出几个?圆心位置有什么特征?
4
Байду номын сангаас
(3)怎样用尺规作一个圆,使它与△ABC的各边都相 切呢? A 已知:⊿ABC.
求作:⊙I,使它与⊿ABC各边都相切. 作法
青岛版九年级数学上册全套精美课件

青岛版九年级数学上册全套精美课 件
2.5 解直角三角形的应用
青岛版九年级数学上册全套精美课 件
第3章 对圆的进一步认识
青岛版九年级数学上册全套精美课 件
3.1 圆的对称性
青岛版九年级数学上册全套精美课 件
3.2 确定圆的条件
青岛版九年级数学上册全套精美课 件
3.3 圆周角
青岛版九年级数学上册全套精美课 件
青岛版九年级数学上册全套精美课 件
2.2 30°,45°,60°角的三角比
青岛版九年级数学上册全套精美课 件
2.3 用计算器求锐角三角比
青岛版九年级数学上册全套精美课 件
2.4 解直角三角形
第1章 图形的相似
青岛版九年级数学上册全套精美课 件
1.1 相似多边形
青岛版九年级数学上册全套精美课 件
1.2 怎样判定三角形相似
青岛版九年级数学上册全套精美课 件
1.3 相似三角形的性质
青岛版九年级数学上册全套精美 课件目录
0002页 0037页 0097页 0158页 0207页 0231页 0268页 0298页 0300页 0329页 0356页 0401页 0415页 0451页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一二次方程的应用
青岛版九年级数学上册全套精美课 件
1.4 图形的位似
青岛版九年级数学上册全套精美课 件
第2章 解直角三角形
2.5 解直角三角形的应用
青岛版九年级数学上册全套精美课 件
第3章 对圆的进一步认识
青岛版九年级数学上册全套精美课 件
3.1 圆的对称性
青岛版九年级数学上册全套精美课 件
3.2 确定圆的条件
青岛版九年级数学上册全套精美课 件
3.3 圆周角
青岛版九年级数学上册全套精美课 件
青岛版九年级数学上册全套精美课 件
2.2 30°,45°,60°角的三角比
青岛版九年级数学上册全套精美课 件
2.3 用计算器求锐角三角比
青岛版九年级数学上册全套精美课 件
2.4 解直角三角形
第1章 图形的相似
青岛版九年级数学上册全套精美课 件
1.1 相似多边形
青岛版九年级数学上册全套精美课 件
1.2 怎样判定三角形相似
青岛版九年级数学上册全套精美课 件
1.3 相似三角形的性质
青岛版九年级数学上册全套精美 课件目录
0002页 0037页 0097页 0158页 0207页 0231页 0268页 0298页 0300页 0329页 0356页 0401页 0415页 0451页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一二次方程的应用
青岛版九年级数学上册全套精美课 件
1.4 图形的位似
青岛版九年级数学上册全套精美课 件
第2章 解直角三角形
青岛版九年级上4.5 三角形的内切圆

●
I
B
C
老师提示: 多边形的边与圆的位置关系称为切.
例题赏析
4
如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数
老师提示:若点I是外心呢?
挑战自我
5
1,已知△ABC的三边长分别为a,b,c,它的内切圆 A 半径为r,你会求△ABC的面积吗?
F I ●
●
E
B
┓
C
2,已知Rt△ABC的两直角边分别为a,b,你会求它的 A 内切圆半径吗?
九年级数学(上)第四章: 对圆的进一步认识
4.5 三角形的内切圆
做一做
1
三角形与圆的位置关系
• 从一块三角形材料中,能否剪下一个圆,使其与各边都 A A 相切?
I
● ●
I ●
●
B
┓
老师提示: 假设符合条件的圆已作出,则它的圆心到三边的距离 相等.因此,圆心在这个三角形三个角的平分线上,半径 为圆心到三边的距离
C
B
┓
C
想一想
2
三角形与圆的位置关系
• 这样的圆可以作出几个?为什么?. ∵直线BE和CF只有一个交点I, 并且点I到△ABC三边的距离相 等(为什么?),
A
F
I ●
●
E
B
┓
C
∴因此和△ABC三边都相切的圆可以作出一个, 并且只能作一个.
议一议
3
三角形与圆的位置关系
• 这圆叫做三角形的内切圆.这个 三角形叫做圆的外切三角形. • 内切圆的圆心是三角形三 条角平分线的交点,叫做三 角形的内心.
A A A
●
B
C
九级数学上册(青岛版)课件:3.5 三角形的内切圆 (共11张PPT)

OB相切,满足上述条件的圆是否 可以作出?如果可以作,能作多 少个?所作出的圆的圆心 O 的位 置有什么特征?为什么? 能作无数个 圆心0在∠ABC的平分线上。
精选 最新精品中小学课件 4
2.任意作一个△ABC,在△ABC内 作圆,使其与各边都相切,满足上述 条件的圆是否可以作出?如果可以作,
A
O
8
1.已知△ABC的三边长分别为a,b,c,它的内切圆 A 半径为r,你会求△ABC的面积吗?
1 s= (a b c)r 2
+ +
O●
●
B
┓
C
2.已知Rt△ABC的两直角边分别为a,b,你会求它的 内切圆半径吗? A
┐ B
精选 最新精品中小学课件
●
C
9
已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、
3.5 三角形的内切圆
精选
最新精品中小学课件
1
A
B
C
精选
最新精品中小学课件
2
学习目标:
1、了解三角形的内切圆、三角形的内心、圆的外 切三角形的概念。
2、会利用基本作图作三角形的内切圆。
3、了解三角形内心的性质,并会进行有关的计算。
精选
最新精品中小学课件
3
1 .任意作一个∠ ABC ,如果在
∠ABC内作圆,使其与两边OA、
AB的长分别为a、b、c,求其内切圆O的半径长.
A b-r b-r c r
b-r+a-r=c
F a-r a-r B
b
E r
.
O r
r=
a+b-c
2
C r Da
精选
最新精品中小学课件
精选 最新精品中小学课件 4
2.任意作一个△ABC,在△ABC内 作圆,使其与各边都相切,满足上述 条件的圆是否可以作出?如果可以作,
A
O
8
1.已知△ABC的三边长分别为a,b,c,它的内切圆 A 半径为r,你会求△ABC的面积吗?
1 s= (a b c)r 2
+ +
O●
●
B
┓
C
2.已知Rt△ABC的两直角边分别为a,b,你会求它的 内切圆半径吗? A
┐ B
精选 最新精品中小学课件
●
C
9
已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、
3.5 三角形的内切圆
精选
最新精品中小学课件
1
A
B
C
精选
最新精品中小学课件
2
学习目标:
1、了解三角形的内切圆、三角形的内心、圆的外 切三角形的概念。
2、会利用基本作图作三角形的内切圆。
3、了解三角形内心的性质,并会进行有关的计算。
精选
最新精品中小学课件
3
1 .任意作一个∠ ABC ,如果在
∠ABC内作圆,使其与两边OA、
AB的长分别为a、b、c,求其内切圆O的半径长.
A b-r b-r c r
b-r+a-r=c
F a-r a-r B
b
E r
.
O r
r=
a+b-c
2
C r Da
精选
最新精品中小学课件
青岛版数学九上3.5《三角形的内切圆》ppt-课件2

PPT教程: /powerpoint/
资料下载:/ziliao/
范文下载:-/fanwen/
试卷下载:/shiti/
教案下载:/jiaoan/
PPT论坛:
PPT课件:/kejian/
随堂练习
三角形与圆的“切”关系
分别作出直角三角形,钝角三角形的内切圆,并说明与 它们内心的位置情况?
老师提示: 先确定圆心和半径,尺规作图要保留作图痕迹.
A
A
●
┐
B
C
●
B
C
挑战自我
1,已知△ABC的三边长分别为a,b,c,它的内切圆
半径为r,你会求△ABC的面积吗?
A
F
E
I
●●
B
┓
C
2,已知Rt△ABC的两直角边分别为a,b,你会求它的
NIM
2.过点I作ID⊥BC,垂足为D. B
D
C
3.以I为圆心,ID为半径作
⊙I,⊙I就是所求的圆.
想一想
三角形与圆的位置关系
这样的圆可以作出几个?为什么?
∵直线BE和CF只有一个交点I, 并且点I到△ABC三边的距离相
F
等(为什么?),
B
A
E I ●●
┓
C
∴因此和△ABC三边都相切的圆可以作出一个, 并且只能作一个.
A
O
B
C
直角三角形的两直角边分别是5cm,12cm 则 其内切圆的半径为______。
A
12 O
C
B
5
小结:
名称
外心: 三角形 外接圆 的圆心
确定方法
图形
A
性质
三角形三边
1.OA=OB=OC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以AB为直径的⊙O交AC于点D,过点D的切线交BC于点E.
(1)求证: DE 1 BC 2 5 (2)若tanC= ,DE=2,求AD的长. 2
【解析】(1)连接BD,
∵AB为直径,∠ABC=90°, ∴BE切⊙O于点B,因为DE切⊙O于点D, 所以DE=BE, ∴∠EBD=∠EDB,
∵∠ADB=90°,
6.三角形的内心一定在三角形的内部( 对 )
A
【例题】
例 如图,在△ABC中,点O是内心, O
(1)若∠ABC=50°, ∠ACB=70°,
则∠BOC的度数________. 120°
B
C
(2)若∠A=80°,则∠BOC=_______. 130° (3)若∠BOC=110°,则∠A=______. 40°
∴△BAD∽△DAE,∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC, 又∵∠CAF=∠CDF, ∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°, 故DE是⊙O的切线.
3.(衡阳·中考)如图,在Rt△ABC中,∠ABC=90°,
【跟踪训练】
直角三角形的三边长与其内切圆半径间的关系 D 1.已知:如图,⊙O是Rt△ABC的内切圆,
A
∠C是直角, AC=3,BC=4.
求⊙O的半径r B
●
O
┓
┗ F
E
C A
3 45 r 1. 2
abc r . 2
B
c
●
O C
b
a
斜三角形的三边长及面积与其内切圆半径间的关系
2.已知:如图,△ABC的面积S=4cm2,
∴∠EBD+∠C=90°,∠BDE+∠CDE=90°, ∴∠C=∠EDC, ∴DE=CE, 1 DE BC 2
DE (2) 因为DE=2,
1 BC 2
AB BC
所以BC=4,在Rt△ABC中,tanC= 所以AB=BC·
5 2
=2 5
AB2 BC 2 (2 5 ) 2 4 2 =6
周长等于10cm. 求内切圆⊙O的半径r. B
A D O ●
┓
F
E
C
1 S r a b c . 2
4 r . 5
2S r . abc
3.如图,某乡镇在进入镇区的道路交叉口的三角地处建 造了一座镇标雕塑,以树立起文明古镇的形象.已知雕塑 中心M到道路三边AC、BC、AB的距离相等,AC⊥BC, BC=30m,AC=40m.求镇标雕塑 中心M离道路三边的距离有多远?
3.5
三角形的内切圆
1.使学生了解画三角形的内切圆的方法,了解三角形的 内切圆、圆的外切三角形、三角形内心的概念. 2.应用类比的数学思想方法研究内切圆,逐步培养学生 的研究问题能力. 3.激发学生动手、动脑主动参与课堂教学活动的热情.
圆和直线的位置关系 r o r o l (1)直线l和⊙O相离 (2)直线l和⊙O相切 (3)直线l和⊙O相交 d l d>r d=r
A 镇 商 业 区
.M D
F
C
E 镇工业区
B
提示: AC⊥BC,BC=30m,AC=40m,得AB=50m.由
a b c 30 40 50 r 10 m . 2 2
答:中心M离道路三边的距离有10m远.
1.设△ABC的边BC=8,AC=11,AB=15,内切
圆I和BC、AC、AB分别相切于点D、E、F. 求AE、CD、BF的长. 【解析】设 AE=x,BF=y,CD=z B x+y=15, 则 y+z=8, x+z=11, x=9, F
d
r
o d l
d<r
【探究一】
从一块三角形材料中,能否剪下一个圆,使其与各边都相切? A A
N
I ●
● ●
M
B
┓
C
B
┓ D
C
右上图就是所求圆的作法:
(1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D. (3)以I为圆心,ID为半径作⊙I,则⊙I就是所求作的内切 圆.
三角形. 三角形的内心是三角形三条角平分线的交点.
【探究二】
分别作出锐角三角形,直角三角形,钝角三角形的内切圆,Leabharlann 并说明它们内心的位置情况. A
A
● ●
A
B
C
B
┐ C
●
B
C
【跟踪训练】
判断题:
1.三角形的内心到三角形各个顶点的距离相等( 错 )
2.三角形的外心到三角形各边的距离相等 ( 错 ) 3.等边三角形的内心和外心重合( 对 ) 4.菱形一定有内切圆( 对 ) 5.矩形一定有内切圆( 错 )
AD AB AB AC
在Rt△ABC中,AC=
又因为△ABD∽△ACB,所以
10 所以AD= 3
,即
AD 2 5
2 5 6
本节课学习了以下内容: 1.作三角形的内切圆.
2.了解三角形的内切圆,三角形的内心概念.
奔向理想人生的征途是漫长的,但是只要坚强不 屈地向前奋进,理想就一定会实现。
A
x y
I.
x
E
z
C
y
D z
解得
y=6, z=2.
答: AE 、CD 、BF的长分别是9、2、6.
2.(黄冈·中考)如图,点P为△ABC的内心,延长AP交 △ABC的外接圆于D,在AC延长线上有一点E,满足AD2= AB·AE,求证:DE是⊙O的切线. A B P· D
·O
C
E
证明:连接DC,DO并延长交⊙O于F,连接AF. ∵AD2=AB· AE,∠BAD=∠DAE,
这样的圆可以作出几个呢?为什么? ∵直线BE和CF只有一个交点I,
A F I ●
●
并且点I到△ABC三边的距离相
等(为什么?) 因此和△ABC三边都相切的圆可 B
E
以作出一个,并且只能作一个.
┓
C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内
切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切
