菁华学校2009届高考数学二轮直通车夯实训练(21)
菁华学校高考数学二轮直通车夯实训练(2)

菁华学校2009届高考数学二轮直通车夯实训练(2)1. 设集合{1,2}M =,则满足条件{1,2,3,4}MN =的集合N 的个数( )A .1B 3C .4D .8 2. 已知命题“若p 则q ”为真,则下列命题中一定为真的是( )A .若p ⌝则q ⌝B .若q ⌝则p ⌝C .若q 则pD .若q ⌝则p3. 若π02α-<<,则点(cos ,sin )Q αα位于( ) A .第一象限B .第二象限C .第三象限D .第四象限4. 在等差数列{}n a 中,已知5710a a +=,n S 是数列{}n a 的前n 项和,则11S =( )A .45B .50C .55D .605. 如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积( )A .3π2B .2πC .3πD .4π6、如果U ={x |x 是小于9的正整数},}6,5,4,3{},4,3,2,1{==B A ,那么B C A C U U ⋂= ________.7、已知a 、b 为常数,若2410)(,34)(22++=+++=x x b ax f x x x f , 则5a -b =.8、函数212)32()(++-=x x x f 的值域是 . 9、已知集合},4221|{},1,1{1Z x x N M x ∈<<=-=+,则N M ⋂= . 10、若不等式组⎪⎩⎪⎨⎧≤≤≥≥+-2005x a y y x 表示的平面区域是一个三角形,则a 的取值范围是 .11、已知函数)(x f y =的图象在点))1(,1(f M 处的切线方程是221+=x y ,则)1()1('f f += .12、函数)1,0(1≠>=-a a a y x的图象恒过定点A ,若点A 在直线)0(01>=-+mn ny mx 上,则nm 11+的最小值为 . 13、函数3x y =与2)21(-=x y 的图象在区间]2,23[内的交点个数为 .14、 已知11)(22+++-==x x x x x f y ,则)1(i f -= .15、已知p 是r 的充分条件而不是必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件,现有下列命题: ①s 是q 的充要条件;②p 是q 的充分条件而不是必要条件; ③r 是q 的必要条件而不是充分条件; ④p ⌝是s ⌝的必要条件而不是充分条件; ⑤r 是s 的充分条件而不是必要条件.则其中正确命题的序号是 .16、已知函数bax x x f +=2)((a ,b 为常数)且方程f (x )-x +12=0有两个实根为x 1=3, x 2=4.(1)求函数f (x )的解析式; (2)设k >1,解关于x 的不等式;xkx k x f --+<2)1()(.17、设.2)(ln )()(2)(--==--=epqe e g x x f x f x q px x g ,且,其中(e 为自然对数的底数) (1)求p 与q 的关系; (2)若)(x g 在其定义域内为单调函数,求p 的取值范围.18、已知数列}2{1n n a ⋅-的前n 项和96n S n =-.(1) 求数列{n a }的通项公式; (2)设2(3log )3n n a b n =⋅-,求数列{1nb }的前n 项和.19、已知曲线Γ上任意一点P 到两个定点()1F 和)2F 的距离之和为4.(1)求曲线Γ的方程;(2)设过()0,2-的直线l 与曲线Γ交于C 、D 两点,且0OC OD ⋅=(O 为坐标原点),求直线l 的方程.20、如图,四棱锥ABCD S -的底面是正方形,⊥SA 底面ABCD ,E 是SC 上一点(1)求证:平面⊥EBD 平面SAC ;(2)设4=SA ,2=AB ,求点A 到平面SBD 的距离;夯实训练(2)参考答案1、C2、B3、D4、C5、A 1、{7,8} 2、2 3、[0,2] 4、{-1} 5、75<≤a6、37、48、09、1323i- 10、①②④ 11、(1)将4,321==x x 分别代入0122=+-+x bax x 得 ).2(2)(,2184169392≠-=⎩⎨⎧=-=⎪⎪⎩⎪⎪⎨⎧-=+-=+x x x x f b a ba ba 所以解得 (2)不等式即为02)1(,2)1(222<-++---+<-xk x k x x k x k x x 可化为.即.0))(1)(2(>---k x x x 研究三根的大小分3类:①当).,2(),1(,21+∞⋃∈<<k x k 解集为;②当);,2()2,1(0)1()2(,22+∞⋃∈>--=x x x k 解集为不等式为时 ③),()2,1(,2+∞⋃∈>k x k 解集为时当. 12、(1)由题意:,ln 2)(x x q px x g --= 又2)(--=eqpe e g 22--=--e q qe e q pe ,0)1)((=+-∴e e q p而01≠+ee q p =∴ED CB A S(2)由(1)知:,ln 2)(x xqpx x g --= 恒成立或满足在只需为单调函数在要使令0)(0)(:),0()(,),0()(,2)(22)(2222'≤≥+∞+∞+-=+-=-+=x h x h x h x g p x px x h x px px x x p p x g ① 当p =0时,h (x )=-2x02)(0)(02'<-=∴<∴>x xx g x h x )(x g ∴在(0,+ ∞)单调递减, 0=∴p 符合题意 ② 当p >0时p x px x h +-=2)(2为开口向上的抛物线, 其对称轴为px 1=∈(0,+∞) p p x h 1)(min -=∴01≥-∴pp 即1≥p 时0)(,0)('≥≥x g x h )(x g ∴在(0,+ ∞)单调递增, 1≥∴p 符合题意③ 当p <0时p x px x h +-=2)(2为开口向下的抛物线 其对称轴为∉=px 1(0,+∞) 只需h (x )≤0,即p ≤0时h (x )≤0在(0,+∞)恒成立0)('<x g )(x g ∴在(0,+ ∞)单调递减, 0<∴p 符合题意综上①②③可得,p ≥1或p ≤018、解:(1)1n =时,011123,3a S a ⋅==∴=;当11232,26,2n n n n n n n a S S a ----≥⋅=-=-∴=时. 23(1)3(2)2n n n a n -=⎧⎪∴=⎨-≥⎪⎩通项公式(2) 设{1nb }的前n 项和为n T ,当1n =时,1211113log 13,3b T b =-=∴==;2n ≥时,223(3log )(1)32n n b n n n -=⋅-=⋅+⋅,∴1n b 1(1)n n =+ ∴n T =1211111132334n b b b +++=++++⨯⨯1(1)n n +=5161n -+5161n T n ∴=-+19、解:(1)根据椭圆的定义,可知动点M 的轨迹为椭圆,其中2a =,c =1b ==. 所以动点M 的轨迹方程为2214x y +=.(2)当直线l 的斜率不存在时,不满足题意.当直线l 的斜率存在时,设直线l 的方程为2y kx =-,设11(,)C x y ,22(,)D x y , ∵0OC OD ⋅=,∴12120x x y y +=. ∵112y kx =-,222y kx =-, ∴21212122()4y y k x x k x x =⋅-++. ∴ 21212(1)2()40k x x k x x +-++=.………… ①由方程组221,4 2.x y y kx ⎧+=⎪⎨⎪=-⎩得()221416120k x kx +-+=.则1221614k x x k +=+,1221214x x k⋅=+, 代入①,得()222121612401414k k k k k +⋅-⋅+=++. 即24k =,解得,2k =或2k =-.所以,直线l 的方程是22y x =-或22y x =--20、(1)证明: ⊥SA 底面ABCD BD SA ⊥∴且AC BD ⊥ ∴SAC 平面⊥BD∴平面⊥EBD 平面SAC(2)解:因为ABD -S SBD -A V V =,且232221S SBD ⨯⨯=∆, 可求得点A 到平面SBD 的距离为34。
09届第二轮复习高三数学试题

2009届箴言中学高三数学二轮试题(文科 )一、选择题:本大题共 10小题,每小题 5分,共50分•在每小题给出的四个选项中,只有一项 是符合题目要求的.• 1、设A 、B 是两个集合,定义 A-B 二{x|x 代且x -一 B },若M 二{x||x 1匡2}, N ={x | x =\si n 二 |,» 三 R },则 M - N=() A • [- 3, 1] B • [ -3, 0) C . [0, 1] D . [- 3, 0] 2、 函数f(x)=1 log 2x 与g(x)=2i 在同一直角坐标系下的图象大致是 () 3、 已知正方体 满足条件PD 1 A.圆 ABCD --ABC 1D 1中,M 为AB 中点,棱长为 = 3PM ,则动点 B.椭圆 2, P 在底面ABCD 上形成的轨迹是 C 双曲线 P 是底面 ABCD 上的动点,且 () D.抛物线 4、 如图,平面内的两条相交直线 界)。
设 OP =mOR nOP 2 , I 、II 、 III 、W(不包含边 A . m >0, n >0 B . m > 0, n V 0 C . m V 0, n >0 D . m V 0, n V0 等差数列{a n }中,a 3 - 8,a 7=20 , 若数列{ 1 }的前n 项和a n a n 1A 、14B 、15C 、16D 、18 5. 且点P 落在第III 部分,则实数 m , n 满足( OP 1和OP 2将该平面分割成四个部分 4 一,则n 的值为() 25 2 2方程(a 1)x -2ax-3=0的两根捲, () X 2满足x 2〈 x ( 1 - x 2)且0< X 1,则实数a 的取值范围 弓一3 乜丨 2,丿 从集合{1,2,3,…,9}中任取三个数排成一列,则这三个数成等差数列的概率是 2 4 2 4・、 B 、 C 、 D 、63 63 21 21 8•已知双曲线x 2 -y 2二a 2(a 0)的左、右顶点分别为 A 、B ,双曲线在第一象限的图象上有 一点 P , PAB = •, PBA =2 , APB 二『,贝U () A 、tan 二 1 tan :tan = 0 C 、tan 二"tan : 2tan = 0二、填空题:本大题共 5小题,每小题 A. 1, .3 B. 1 ,3,二 C. D. B 、 C 、 9.设偶函数f (x)对任意x • R ,都有 tan J 1 ta n ——ta n = 0 tan :" tan - -2tan = 05分,共25分.把答案填在题中横线上. 1 f(x 3) ,且当 [-3,-2]时,f(x) = 2x ,f(x)则 f (113.5) =2 210.在平面直线坐标系 xOy 中,△ ABC 的顶点A(-6,0)和C(6,0),顶点B 在双曲线—丄 =1的25 11左支上,则sin A-sinC =sin B11.定义在(-1,1)上的函数f(x)=_5x ・sin x,如果f (1-a) • f (1-a 2) . 0 ,则实数a 的取值 范围为 12. (X-2)(X-1)5的展开式中x 2项的系数为 ______________x +2y <6-,目标函数z =| 2x — y +1|的最小值是 .x _0,y _02 214.已知椭圆 笃•打邛(a .b .0)的右焦点为F(c,0)过F 作与x 轴垂直的直线与椭圆相交于点 P ,过点P 的椭圆的切线I 与x 轴相交于点 A ,则点A 的坐标为 ______________ .15. 已知集合P ={x 1 Ex 兰6,X W N},对它的非空子集 A,先将A 中的每个元素k 分别乘以k36(-1),再求和(如 A={1,3,6},可求得和为(-1) 1・(-1) 3,(-1) 6=2),则对M 的所有非空子集,这些和的总和是 ____________ .三、解答题:本大题共 6个小题,共75分.解答应写出文字说明,证明过程或演算步骤 •16. (本小题满分12分)△ ABC 中,3tan Atan B -tan A -tan B =、_3 . (I )求/ C 的大小;(n)设角A , B , C 的对边依次为a,b,c ,若c =2,且△ ABC 是锐角三角形,求 a 2 b 2的取 值范围.17. (本小题满分12分)如图,四棱锥 P - ABCD 中,底面 ABCD 是边长为 2的正方形,PB _ BC, PD _ CD ,且PA=2, E 为PD 中点.(1)求证:PA_平面ABCD ;(2 )求二面角E - AC -D 的大小;(3)在线段BC 上是否存在点2距离为 空 ?若存在,确定点 F 的位置;若不存在,请说明理由513•约束条件:丿2x +y 兰 6B C18. (本小题满分12 分)a *(1 )记q n (n • N ),试比较c n 与c n 」勺大小;n +12 a4(2)是否存在实数 ‘使得当x 「时,f(x) = -x 4X -0对任意n ・N 恒成立?n +1若存在,求出最大的实数■;若不存在,说明理由.佃.(本小题满分12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响 •已知某学生选修甲而不选修乙和丙的概率为 0.08,选修甲和乙而不选修丙的概率是 0.12,至少选修一门的概 率是0.88,用■表示该学生选修的课程门数和没有选修的课程门数的乘积(I )记“函数f(X^X^ X 为R 上的偶函数”为事件 A ,求事件A 的概率;定义为,X 2 , I I I ,X n 的“倒平均数”为1平均数”为—(n N *),已知数列{a n }前n 项的“倒(n)求芒=2的概率20.(本小题满分13分)2 2已知椭圆x_ - X_ =1(a b .0)的右准线h : X = 2与x轴相交于点D ,右焦点F到上顶点的距a b离为2,点C(m,0)是线段OF上的一个动点•(I)求椭圆的方程;(n )是否存在过点F且与x轴不垂直的直线|与椭圆交于A、B两点,使得(CA - CB) _ BA,并说明理由•21 .(本小题满分14分) 已知正数数列{a n}的前n项和为S n,且a;• a;• a;•…,a;二S:.2(1)求证:a n 2S n - a n ;(2)求数列{a n}的通项公式;(3)若b n 3n- (-1)nj■ 2an.( ■为非零常数,n・N*),问是否存在整数入,使得对任意n N*,都有b n 1■ b n.2 21 62 2 2 a b [sin A • si n (_A 二 f]A2 216 2 2 16 1 1 16 8a 1 2」b 2 [sin 2 A -sin 2C][ (1-cos2A) (1-cos2C)] ______ 8(cos2A :;cos2C) 33 22 3 32^ -8 [cos 2A -^-)cos 2A ;;(」3)sin2A] =13 3 3 2 2 3即 20 :: a 2 b 2<8°3BC _ AB ,又 BC _ PB , ••• BC _ 平面 PAB ,二 BC _ PA .同理可证 CD _ PA ,•- PA_ 平面 ABCD .(2)解:设 M 为AD 中点,连结 EM ,又E 为PD 中点, 可得EM // PA ,从而EM _底面ABCD . 过M 作AC 的垂线MN ,垂足为N ,连结EN . 由三垂线定理有 EN _ AC ,• ENM 为二面角E - AC - D 的平面角.V2EMl在 Rt EMN 中,可求得 EM = 1, MN, • tan ^ENM2 .2MN1 ::-si n(A< <) 12 6J? 8sin(2A ')3 36匸仲二: 6 , 65二17.解法(1)证明:•••底面 ABCD 为正方形, 参考答案1.B2.D3.A4.B5.C6.D7.B8.C9. 0.210.11. 1 ::: a ::: 、. 2 12. 25 13.0214.(—,0) 15.96c16.解:(1)依题意:tan A 亠tan B1 -tan Atan B=7.3,即 tan(A B) - _ 3,又 0 ::: A • B :::二,C —A_B I ,3(2)由三角形是锐角三角形可得即二 ”A.二。
菁华学校高考数学二轮直通车夯实训练(18)

菁华学校高考数学二轮直通车夯实训练(18)1. 原命题:“设a 、b 、c R ∈,若22ac bc >则a b >”的逆命题、否命题、逆否命题真命题共有: 个。
2. 已知函数)x (f 满足)x (f 1)x (f 1)1x (f ,2)1(f -+=+=,则f(3)的值为________________, )2007(f )3(f )2(f )1(f ⋅⋅⋅⋅ 的值为_____________.3 已知两点(2,0),(0,2)A B -,点C 是圆0222=-+x y x 上任意一点,则ABC ∆面积的最小值是4. 设a ,b ,c 是空间的三条直线,下面给出四个命题:①若b a ⊥,c ⊥b ,则c a //;②若a 、b 是异面直线,b 、c 是异面直线,则a 、c 也是异面直线;③若a 和b 相交,b 和c 相交,则a 和c 也相交;④若a 和b 共面,b 和c 共面,则a 和c 也共面.其中真命题的个数是________个5. 右图的矩形,长为5,宽为2。
在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗。
则我们可以估计出阴影部分的面积约为 .6、不等式0121>+-x x 的解集是______. 7. 如果实数+∈R b a ,,且b a >,那么b 、ab 和)(21b a +由大到小的顺序是 . 8. ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c 成等比数列,且2c a =,则cos B = .9、若不等式x 2+ax +1≥0对于一切x ∈(0,12)成立,则a 的取值范围是_____。
10.数列{}n a 的前n 项和记为()11,1,211n n n S a a S n +==+≥(Ⅰ)求{}n a 的通项公式;(Ⅱ)等差数列{}n b 的各项为正,其前n 项和为n T ,且315T =,又112233,,a b a b a b +++成等比数列,求n T11.为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.(1) 求第四小组的频率和参加这次测试的学生人数;(2) 在这次测试中,学生跳绳次数的中位数落在第几小组内?(3) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?夯实训练(18)参考答案1.12.21-,3 3. 23- 4.0 5. 523 6.⎪⎭⎫ ⎝⎛-21,1 7. b ab )b a (21>>+ 8. 34 9、52a ≥- 9. 分析:(Ⅰ)运用公式a n =⎩⎨⎧--11n nS S S .2,1≥=n n 求a n . (Ⅱ)注意等差数列与等比数列之间的相互关系.解析:(Ⅰ)由121n n a S +=+可得()1212n n a S n -=+≥,两式相减得()112,32n n n n n a a a a a n ++-==≥, 又21213a S =+= ∴213a a =故{}n a 是首项为1,公比为3得等比数列∴13n n a -=(Ⅱ)设{}n b 的公比为d 频率组距 次数49.5 74.5 99.5 124.5 149.5由315T =得,可得12315b b b ++=,可得25b =故可设135,5b d b d =-=+, 又1231,3,9a a a ===由题意可得()()()2515953d d -+++=+解得10,221-==d d∵等差数列{}n b 的各项为正,∴0d >, ∴2d =∴()213222n n n T n n n -=+⨯=+ 10. 分析:解题涉及知识为所有频率和为1,=频数频率样本容量,中位数的定义等. 解析:(1) 第四小组的频率=1-(0.1+0.3+0.4)=0.2,因为第一小组的频数为5,第一小组的频率为0.1,所以参加这次测试的学生人数为5÷0.1=50(人).(2) 0.3⨯50=15,0.4⨯50=20,0.2⨯50=10,则第一、第二、第三、第四小组的频数分别为5,15,20,10.所以学生跳绳次数的中位数落在第三小组内.(3) 跳绳成绩的优秀率为(0.4+0.2)⨯100%=60%. 评析:本题考查学生对频率分布直方图的分析推理能力. 频率组距 次数49.5 74.5 99.5 124.5 149.5。
江苏省菁华学校2009届高考数学二轮直通车夯实训练(8)
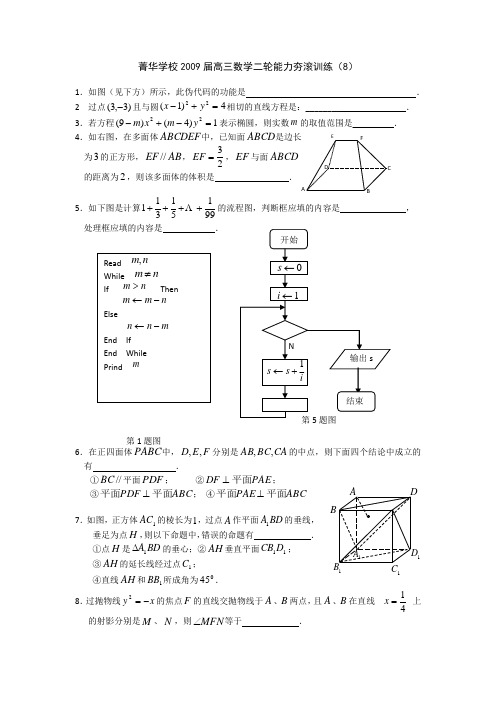
菁华学校2009届高三数学二轮能力夯滚训练(8)1.如图(见下方)所示,此伪代码的功能是 . 2 过点)3,3(-且与圆4)1(22=+-y x 相切的直线方程是:________ . 3.若方程1)4()9(22=-+-y m x m 表示椭圆,则实数m 的取值范围是_______ __. 4.如右图,在多面体ABCDEF 中,已知面ABCD 是边长 为3的正方形,AB EF //,23=EF ,EF 与面ABCD 的距离为2,则该多面体的体积是 .5.如下图是计算99151311++++的流程图,判断框应填的内容是 , 处理框应填的内容是 .6.在正四面体PABC 中,F E D ,,分别是CA BC AB ,,的中点,则下面四个结论中成立的有 .①//BC 平面PDF ; ②PAE DF 平面⊥; ③ABC PDF 平面平面⊥; ④ABC PAE 平面平面⊥7.如图,正方体1AC 的棱长为1,过点A 作平面BD A 1的垂线,垂足为点H ,则以下命题中,错误的命题有 . ①点H 是BD A 1∆的垂心;②AH 垂直平面11D CB ; ③AH 的延长线经过点1C ; ④直线AH 和1BB 所成角为045.8.过抛物线x y -=2的焦点F 的直线交抛物线于A 、B 两点,且A 、B 在直线41=x 上的射影分别是M 、N ,则MFN ∠等于 .BCFEAD第1题图111B9.一个多面体的直观图、主视图、左视图、俯视图如图所示,M 、N 分别为B A 1、11C B 的中点.(1) 求证://MN 平面11A ACC ; (2) 求证: MN 平面BC A 1.10、若椭圆ax 2+by 2=1与直线x +y =1交于A 、B 两点,M 为AB 的中点,直线OM (O 为原点)的斜率为22,且OA ⊥OB ,求椭圆的方程.1A主视图 左视图俯视图夯实训练(8)参考答案1.求m 、n 的最大公约数; 2. 3=x 或021125=++y x ;3. )9,213()213,4(⋃∈m ; 4. 215. 5.99>i , 2+←i i ; 6.①②④ ; 7. ④ ; 8. 090. 提示:由抛物线的定义得: BN BF AM AF ==,∴MFX AMF AFM ∠=∠=∠, NFX BNF BFN ∠=∠=∠ ∴090=∠MFN .9. 解:由题意可知,这个几何体是直三棱柱,且1,CC BC AC BC AC ==⊥ (1) 连结11,AB AC .由直三棱柱的性质得:1111C B A AA 平面⊥ ∴111B A AA ⊥∴四边形11A ABB 为矩形. ∴1AB 过B A 1的中点M .∴在11C AB ∆中,由中位线性质得:1//AC MN , 又∵111A ACC AC 平面⊂,11A ACC MN 平面⊄, ∴11//A ACC MN 平面.(2)∵11A ACC BC 平面⊥, 又∵111A ACC AC 平面⊂∴1AC BC ⊥而在正方形11A ACC 中,有11AC C A ⊥又∵C C A BC =⋂1, ∴BC A AC 11平面⊥. 又∵1//AC MN ∴BC A MN 1平面⊥.10、解:设A (x 1,y 1),B (x 2,y 2),M (221x x +,221y y +).x +y =1,ax 2+by 2=1,∴221x x +=b a b +,221y y +=1-221x x +=ba a+. ∴M (b a b +,ba a+). ∵k OM =22,∴b =2a . ①∵OA ⊥OB ,∴11x y ·22x y=-1. ∴x 1x 2+y 1y 2=0. ∵x 1x 2=ba b +-1,y 1y 2=(1-x 1)(1-x 2), ∴y 1y 2=1-(x 1+x 2)+x 1x 2=1-b a b +2+b a b +-1=ba a +-1.11由 ∴(a +b )x 2-2bx +b -1=0.∴b a b +-1+ba a +-1=0. ∴a +b =2. ②由①②得a =2(2-1),b =22(2-1). ∴所求方程为2(2-1)x 2+22(2-1)y 2=1.评述:直线与椭圆相交的问题,通常采取设而不求,即设出A (x 1,y 1),B (x 2,y 2),但不是真的求出x 1、y 1、x 2、y 2,而是借助于一元二次方程根与系数的关系来解决问题.由OA ⊥OB 得x 1x 2+y 1y 2=0是解决本题的关键.。
2009届高三年第二次模拟考试数学参考答案理科2009.05.24

仙游一中 2009届高三年第二次模拟考试2009.05.24现代中学数学参考答案 (理科)一、选择题:1. C2. A3. D4. D5. A6. B 7.A 8. C 9.C 10. A 二、填空题:11.x y 3±= 12. 2 . 13. ③ ④ 14. 49 15.三、解答题:16.解: (Ⅰ)∵222a cb ac +-=,∴2221cos 22a cb B ac +-==, …………3分 又∵0B π<<, ∴3B π=. …………6分(Ⅱ)6sin cos2m n A A ⋅=--223112sin 6sin 12(sin )22A A A =--=--,…10分 ∵203A π<<,∴0sin 1A <≤.∴当sin 1A =时,取得最小值为5-……13分 17.解:(1)设甲选手答对一个问题的正确率为1P ,则211(1)9P -= 故甲选手答对一个问题的正确率123P = 3分 (Ⅱ)选手甲答了3道题目进入决赛的概率为32()3=8274分选手甲答了4道题目进入决赛的概率为233218()3327C ⋅= 5分选手甲答了5道题目进入决赛的概率为23242116()()3381C = 6分选手甲可以进入决赛的概率88166427278181P =++= 8分 (Ⅲ)ξ可取3,4,5则有33211(3)()()333P ξ==+= 9分22223321212110(4)()()33333327P C C ξ==⋅⋅+⋅⋅= 10分222222442121218(5)()()()()33333327P C C ξ==+= 11分因此有(直接列表也给分)故3453272727E ξ=⋅+⋅+⋅= 13分 18.解:由三视图知,该多面体是底面为直角三角形的直三棱柱,ADE BCF AB BC -==且4,BF =2DE CF CBF π==∠=(1)证明:连续取BE ,易见BE 通过点M ,连接CE 。
09届第二轮复习高三数学试题(4)

2009届箴言中学高三数学二轮试题(文科)、选择题(本大题共8小题,每小题5分,共40分)设集合A珂-1,0,1},集合B -{0,1,2,3,},定义A BA*B中元素个数是A. 7已知全集UB . 10=R,集合A ={y y =-2%, x EC. 25R , B ={y y二{(x, y) x A B, y A B},则( )D. 52=x3— 3x,x • R,则Ap| eu B =()5.8.1 f< x;0 \ (B W xJ * f[a1 3a8 a15 =120,则2a g -印。
的值为( )B 22C 24> 2,命题q : x w Z ;如果"p且q ”与"非()x -1, x )Z(D){x(A 丫一等差数列CaJ中,A 20已知命题p: x -1条件的x为(A (x x^ 3或w—1,致}Z (B ){x-1 w x w 3,x^z}C 1—1, 0,1, 2,3D :0,1,2?在正整数数列中,由1开始依次按如下规则将某些数染成红色. 先染1 ,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染此后最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1, 2, 4, 5, 7, 9, 10, 12, 14, 16, 17,….则在这个红色子数列中,由1开始的第2003个数是()A 3844B 3943C 3945如图,设A、B、C、D为球0上四点,若AB、AC、AD两两互相垂直,且AB=AC = .6 , AD=2,则A、D两点间的球面距离为()D -8同时为假命题, 则满足JIA32nC —3已知点A、B、C不共线,A CB A且有D 二T TAB BCC如图,在平面直角坐标系xOy中,P x,y对应到另一个平面直角坐标系BC CA CA AB一=:r——,则有( v3 \3-2)l t吕(B )BC|c|cA AB<I BC'DA 1,0、B 1,1、C 0,1,映射f将xOy平面上的点uO'v上的点P,2xy,x2-y2,则当点P沿着折线9.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中a,b •「1,2,3,4,5,6二若a 二b 或a 二b -1,就称甲乙 心有灵犀”•现任意找两人 玩这个游戏,则他们心有灵犀”的概率为 _______________ . 10.直线3x ・4y-15=0被圆x 2y 2 25截得的弦AB 的长为 __________ 。
09届第二轮复习高三数学试题(3)

2009届箴言中学高三数学二轮试题(文科)一、选择题:本小题共 10小题,每小题5分,共50分,在每小题所给的四个选项中,只有一项是符合题目要求的。
1 •设条件p : x一1 0 ;条件q : (x 1)(x 1) 0 ,则q 是p 的()条件x 1A.充分不必要B.必要不充分C.充要D.既不充分也不必1 2•二项式(2x 43)n的展开式中含有非零常数项,则正整数 n 的最小值为( )3x 3A • 7B • 12C . 14D • 53 •对于一个有限数列p ( P 1, P 2, , P n ) , p 的蔡查罗和(蔡查罗为一数学家)定义为 1—(S s 2 ,其中 S kP 1 P 2P n (1 k n),若一个 99 项的数列n(P 1, P 2, , p 99)的蔡查罗和为1000,那么100项数列(1,P 1, P 2, , P 99)的蔡查罗和为()A . 991B . 992C . 993D . 99924.对于使 x 2xM成立的所有常数 M 中,我们把 2M 的最小值1叫做 x 2x 的上确界, 若 a,b R ,且ab 1,则1 -的上确界为 ( )2a b991A .-B一C.—D . -42245 •古代“五行”学说认为:“物质分金,木,土,水,火五种属性,金克木,木克土,土克水, 水克火,火克金”将五种不同属性的物质任意排成一列, 则属性相克的两种物质不能相邻的排 法数为 ( )、填空题:本小题共 5小题,每小题5分,共25分,将答案填在题中相应的横线上。
外接球的半径 R 为 ( ) A . 5、、2 22B . 5C .5.2D . 4 28 •椭圆C 1:x ay1的左准线为 l ,左、 右焦点分别为 F 1、F 2,抛物线C 2的准线为1,焦点ABCD 中,三组对棱棱长分别相等且依次为 7 .在四面体 则此四面体ABCD 的 OF 1 OGP ,线段PF 2的中点为 G ,O 是坐标原点,则的PF 1PF 21 1C .--D . 一22为F 2, C 1与C 2的一个交点为 值为()A . 1B . 1B • 10C . 156 .已知平面内的四边形 边形ABCD A •梯形 r 曰 定是 ABCD 和该平面内任一点( )B .菱形D . 20juu2 jujjP 满足:AP CP uuuu uujirBP 2 DP 2,那么四C .矩形D .正方形 34、 ,41、5,9. 若 x x 1 a 。
菁华学校高考数学二轮直通车夯实训练(10)

菁华学校2009届高三数学二轮能力夯实训练(10)1、在平面直角坐标系xOy 中,已知ABC ∆顶点(4,0)A -和(4,0)C ,顶点B 在椭圆221259x y +=上,则sin sin sin A C B += ; 2 已知(){}(){}Φ==--+-=++08)5(7,43)3(,y m x y x m y x m y x ,则直线()y x m ++343+=m 与坐标轴围成的三角形面积是 ;3、设F 为抛物线24y x =的焦点,A B C ,,为该抛物线上三点,若FA FB FC 0++=,则FA FB FC ++=____________;4的竹竿时,它在水平地面上的射影为1m ,同时,照射地面上一圆球时,如图所示,其影子的长度AB 等于则该球的体积为_________;5、定义某种运算⊗,S a b =⊗的计算原理如图,则式子5324⊗+⊗的结果为______ ;6、已知抛物线23y x =-+上存在关于直线0x y +=对称的相异两点A 、B ,则|AB|等于________;7、设椭圆22221(0)x y a b a b+=>>的离心率为1e 2=,右焦点为(0)F c ,,方程20ax bx c +-=的两个实根分别为1x 和2x ,则点12()P x x ,与圆222x y +=的位置关系为_______________;8、若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为_____________;9、P 为双曲线221916x y -=的右支上一点,M 、N 分别是圆22(5)4x y ++=和22(5)x y -+1=上的点,则PM PN -的最大值为______________;10、在直角坐标系xOy 中,以O 为圆心的圆与直线4x =相切. 第4题图 第5题图 主视图 俯视图左视图(1)求圆O 的方程;(2)圆O 与x 轴相交于A B ,两点,圆内的动点P 使PA PO PB ,,成等比数列,求PA PB 的取值范围.11、如图所示,等腰△ABC 的底边AB =3CD =,点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF AB ⊥.现沿EF 将△BEF 折起到△PEF 的位置,使PE AE ⊥。
菁华学校高考数学二轮直通车夯实训练(12)

菁华学校高考数学二轮直通车夯实训练(12)1、如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有()f n 对异面直线,则(4)f = ;()f n =(答案用数字或n 的解析式表示)2、在抽查某产品尺寸过程中,将其尺寸分成若干组,[,]a b 是其中的一组,已知该组的频率为m ,该组上的直方图的高为h ,则||a b -等于_______3、某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人,乙班50人. 现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是 分4、已知椭圆)0(2222〉〉+b a by a x 及内部面积为,ab S π=1B 、2B 是短轴的两个顶点,点P 是椭圆及内部的点, 21B PB ∆为锐角三角形的概率为__________5、 定义{}N x M x x N M ∉∈=-且,则集合)(N M M --=_________6、若*∈〉〉N n c b a ,,且ca n cb b a -≥-+-11恒成立,则n 的最大值是__________7、图l 是某县参加年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为1A 、2A 、…、m A (如2A表示身高(单位:cm )在[150,155)内的学生人数).图2是统计图l 中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm (含160cm ,不含180cm )的学生人数,那么在流程图中的判断框内应填写的条件是________________8、从1,2,……5这五个数字中,随机抽取3个不同的数,则和为偶数的概率为_____9、将一骰子连续抛掷三次,它落地时向上的点数依次..成等差数列的概率为________________________10、设有关于x 的一元二次方程2220x ax b ++=. (Ⅰ)若a 是从0123,,,四个数中任取的一个数,b 是从012,,三个数中任取的一个数,求上述方程有实根的概率.(Ⅱ)若a 是从区间[03],任取的一个数,b 是从区间[02],任取的一个数,求上述方程有实根的概率.11、已知函数)(x f 是),(+∞-∞上的增函数,对命题b a +若")()(,0b f a f +≥则)"()(b f a f -+-≥写出其逆命题,判断其真假并证明你的结论夯实训练(12)参考答案1、(1)2n n +;8;n(n-2); 解析:(1)2n n +;(4)428f =⨯=;()(2)f n n n =⋅- 2、m h3、解析:某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人,乙班50人. 现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是409050818590⨯+⨯=分 4、ab a -; 5、 N M 6、答案4提示:因,,*∈N nc b a 所以c a n c b b a -≥-+-11同解于n c b c a b a c a ≥--+--又42≥--+--+=--+-+--+-=--+--cb b a b ac b c b c b b a b a c b b a c b c a b a c a 所以4≤n 7、i<8; 853; 9、112 10、 解:设事件A 为“方程2220a ax b ++=有实根”.当0a >,0b >时,方程2220x ax b ++=有实根的充要条件为a b ≥.(Ⅰ)基本事件共12个:(00)(01)(02)(10)(11)(12)(20)(21)(22)(30)(31)(32),,,,,,,,,,,,,,,,,,,,,,,.其中第一个数表示a 的取值,第二个数表示b 的取值.事件A 中包含9个基本事件,事件A 发生的概率为93()124P A ==. (Ⅱ)试验的全部结束所构成的区域为{}()|0302a b a b ,,≤≤≤≤.构成事件A 的区域为{}()|0302a b a b a b ,,,≤≤≤≤≥. 所以所求的概率为2132222323⨯-⨯==⨯. 11、 逆命题为“)()(b f a f +若)()(b f a f -+-≥b a +则0≥”是真命题证明:假设0<+b a 则a b b a -<-<,由于函数)(x f 是),(+∞-∞上的增函数,则)()(),()(a f b f b f a f -<-<, 所以)()(b f a f +<)(a f -+)(b f -这与条件矛盾,故假设不成立,命题为真命题。
菁华学校2009年第二学期高二数学期中复习综合卷

菁华学校2009年第二学期高二数学期中复习综合卷(一)一、 填空题 1.dx x x x 2234253+-⎰的值为 2.曲线x y 1-=在点⎪⎭⎫ ⎝⎛-2,21处的切线方程为 3.函数()13++=x ax x f 有极值的充要条件是4.利用数学归纳法证明“*),12(312)()2)(1(N n n n n n n n ∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时,从“k n =”变到“1+=k n ”时,左边应增乘的因式是5. 复数54)31()22(i i -+等于6. 若55ln ,33ln ,22ln ===c b a ,则a,b,c 的大小关系为 7. 若函数2)(3-+=ax x x f 在区间),1(+∞内是增函数,则实数a 的取值范围是8. 已知复数z 满足211=-++z z ,则复数z 在复平面上对应点所表示图形是9. 由直线y=x-4,曲线x y 2=以及x 轴所围成的图形面积为10. 复数z 满足i z i 34)21(+=+,那么z= 。
11. 设函数ax x x f m +=)(的导数12)(/+=x x f ,则数列⎭⎬⎫⎩⎨⎧)(1n f (*N n ∈)的前n 项和为12. 观察⋅⋅⋅=++++++=++++=++=;710987654;576543,3432;112222,你得到的一般性结论是13. 已知(0)x ∈+,∞,观察下列几式:12x x+≥,22443,22x x x x x +=++ ≥类比有1()n a x n n x*++∈N ≥,则a = 14. 设a ∈R ,若函数3ax y e x =+,x ∈R 有大于零的极值点,则 a 的取值范围二.解答题15. 设点P 在曲线2x y =上,从原点向A (2,4)移动,如果直线OP ,曲线2x y =及直线x=2所围成的面积分别记为1S 、2S 。
(Ⅰ)当21S S =时,求点P 的坐标;(Ⅱ)当21S S +有最小值时,求点P 的坐标和最小值16.已知向量i =(1,0),j =(0,1),函数)0()(23≠++=a c bx ax x f 的图象在y 轴上的截距为1,在x =2处切线的方向向量为bj i c a 12)(--,并且函数当1=x 时取得极值。
菁华学校高考数学二轮直通车夯实训练(26)

1 / 2高考数学二轮直通车夯实训练(26)1.=++-ii i 1)21)(1( 2 已知单位向量,a b 它们的夹角为3π,则b a -2=3.(),()f x g x 都是奇函数且()()()2F x af x bg x =++在[)0,+∞上有最大值8,则在(,0)-∞上()F x 有最小值4. 如果直线y = x+a 与圆x 2+y 2=1有公共点,则实数a 的取值范围是 。
5.已知命题p :不等式|x |+|x -1|>a 的解集为R ,命题q :f (x )=-(5-2a )x是减函数,若p ,q 中有且仅有一个为真命题,则实数a 的取值范围是 .6. F 1、F 2是双曲线1201622=-y x 的焦点,点P 在双曲线上,若点P 到焦点F 1的距离等于9,则点P 到焦点F 2的距离等于 。
7.等差数列{}n a 中,1570,3.a a a >=它的前n 项和为n S ,若n S 取得最大值,则n= .8 、已知向量(46)(35)OA OB ==,,,,且OC OA AC OB ⊥,∥,则向量OC =___。
9、若直线1y kx =+与圆221x y +=相交于P Q ,两点,且120POQ ∠=(其中O 为原点),则k 的值为_____.10、一动圆圆心在抛物线x y 42=上,过点(0,1)且恒与定直线L 相切,则相线L 的方程为11.已知向量,a b 满足||1a b ==,且||3||(0)ka b a kb k +=->,令()f k a b =⋅, (Ⅰ)求()f k a b =⋅(用k 表示); (Ⅱ)当0k >时,21()22f k x tx ≥--对任意的[1,1]t ∈-恒成立,求实数x 的取值范围。
12.如图,在直四棱柱1111ABCD A B C D -中,已知122DC DD AD AB ===,AD DC AB DC ⊥,∥. (1)求证:11D C AC ⊥;(2)设E 是DC 上一点,试确定E 的位置,使1D E ∥平面1A BD ,并说明理由.BCD A1A1D1C 1B2 / 2夯实训练(26)参考答案1、2-i2、33、-44、[2,2]-5、[)2,16、177、7或88、24721⎛⎫-⎪⎝⎭, 9、3-3 10、1y =- 11、[]12,21);0(41)(2--∈>+=x k kk k f 12、(1)证明:在直四棱柱1111ABCD A B C D -中,连结1C D ,1DC DD =,∴四边形11DCC D 是正方形. 11DC D C ∴⊥.又AD DC ⊥,11AD DD DC DD D =⊥,⊥,AD ∴⊥平面11DCC D ,而1D C ⊂平面11DCC D ,1AD D C ∴⊥.1AD DC ⊂,平面1ADC ,且AD DC D =⊥,1D C ∴⊥平面1ADC , 又1AC ⊂平面1ADC ,1D C AC ∴1⊥. (2)连结1AD ,连结AE , 设11AD A D M =,BDAE N =,连结MN ,平面1AD E 平面1A BD MN =,要使1D E ∥平面1A BD ,须使1MN D E ∥, 又M 是1AD 的中点. N ∴是AE 的中点. 又易知ABN EDN △≌△, AB DE ∴=.即E 是DC 的中点.综上所述,当E 是DC 的中点时,可使1D E ∥平面1A BD .BCD A1A 1D 1C 1B BCD A1A 1D 1C 1B ME。
菁华学校2009年第二学期高二数学期中复习综合卷

菁华学校2009年第二学期高二数学期中复习综合卷(一)一、 填空题 1.dx x x x 2234253+-⎰的值为 2.曲线x y 1-=在点⎪⎭⎫ ⎝⎛-2,21处的切线方程为 3.函数()13++=x ax x f 有极值的充要条件是4.利用数学归纳法证明“*),12(312)()2)(1(N n n n n n n n ∈-⨯⋅⋅⋅⨯⨯⨯=+⋅⋅⋅++ ”时,从“k n =”变到“1+=k n ”时,左边应增乘的因式是5. 复数54)31()22(i i -+等于6. 若55ln ,33ln ,22ln ===c b a ,则a,b,c 的大小关系为 7. 若函数2)(3-+=ax x x f 在区间),1(+∞内是增函数,则实数a 的取值范围是8. 已知复数z 满足211=-++z z ,则复数z 在复平面上对应点所表示图形是9. 由直线y=x-4,曲线x y 2=以及x 轴所围成的图形面积为10. 复数z 满足i z i 34)21(+=+,那么z= 。
11. 设函数ax x x f m +=)(的导数12)(/+=x x f ,则数列⎭⎬⎫⎩⎨⎧)(1n f (*N n ∈)的前n 项和为12. 观察⋅⋅⋅=++++++=++++=++=;710987654;576543,3432;112222,你得到的一般性结论是13. 已知(0)x ∈+,∞,观察下列几式:12x x +≥,22443,22x x x x x +=++≥类比有1()n a x n n x*++∈N ≥,则a = 14. 设a ∈R ,若函数3ax y e x =+,x ∈R 有大于零的极值点,则 a 的取值范围二.解答题15. 设点P 在曲线2x y =上,从原点向A (2,4)移动,如果直线OP ,曲线2x y =及直线x=2所围成的面积分别记为1S 、2S 。
(Ⅰ)当21S S =时,求点P 的坐标;(Ⅱ)当21S S +有最小值时,求点P 的坐标和最小值16.已知向量i =(1,0),j =(0,1),函数)0()(23≠++=a c bx ax x f 的图象在y 轴上的截距为1,在x =2处切线的方向向量为bj i c a 12)(--,并且函数当1=x 时取得极值。
菁华学校高考数学二轮直通车夯实训练(22)

高考数学二轮直通车夯实训练(22)1、若函数113xy -=的值域是 .2、设111,,a b c 为非零实数,不等式:21110a x b x c ++>和22220a x b x c ++>的解集分别为集合,M N 那么:“222111a b c a b c ==”是“M N =”的 条件 3、把函数y =cos x -3si nx 的图象向左平移m 个单位(m >0)所得的图象关于y 轴对称,则m 的最小值是4、已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是5、设12,F F 为椭圆22221(0)x y a b a b+=>>的焦点,过1F 且垂直于x 轴的直线与椭圆交于A,B 两点,若△2ABF 为锐角三角形,则该椭圆离心率e 的取值范围是 . 6、黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第n 个图案中有白色地面砖 块。
7、下列命题中正确命题的序号为①若,,a b c R ∈,且a b >,则 22ac bc > ② 若,a b R ∈且0a b ⋅≠则2a bb a+≥ ③2020正视图20侧视图10 1020俯视图第1个 第2个 第3个若,a b R ∈且a b >,则()n na b n N +>∈ ④ 若,,a b c d >> 则a b d c> 8、设O 为坐标原点,曲线x 2+y 2+2x -6y +1=0上有两点P 、Q ,满足关于直线x +my +4=0对称,又满足OP ·OQ =0.(1)求m 的值; (2)求直线PQ 的方程.9、设函数2()ln(23)f x x x =++(Ⅰ)讨论()f x 的单调性; (Ⅱ)求()f x 在区间3144⎡⎤-⎢⎥⎣⎦,的最大值和最小值.10、已知向量m =(a +c ,a -b ),(sin ,sin sin )n B A C =-,m ∥n ,其中A 、B 、C 为△ABC 的内角, a 、b 、c 分别是角A 、B 、C 所对的边.(1)求角C 的大小; (2)求sin sin A B +的取值范围.11、设)0(3)(2≠-+=a x ax x f . (1)当2=a 时,解不等式0)(>x xf ;(2)当[]2,1,0-∈>x a 时,)(x f 的值至少有一个是正数,求a 的取值范围.夯实训练(22)参考答案1、(0,1)(1,)+∞ 2、既不充分又必要条件 3、32π 4、38000cm 35211<<e 6、n 2+4n+1 7、③8、解:(1)曲线方程为(x +1)2+(y -3)2=9表示圆心为(-1,3),半径为3的圆.∵点P 、Q 在圆上且关于直线x +my +4=0对称, ∴圆心(-1,3)在直线上.代入得m =-1. (2)∵直线PQ 与直线y =x +4垂直,∴设P (x 1,y 1)、Q (x 2,y 2),PQ 方程为y =-x +b .将直线y =-x +b 代入圆方程,得2x 2+2(4-b )x +b 2-6b +1=0.Δ=4(4-b )2-4×2×(b 2-6b +1)>0,得2-32<b <2+32. 由韦达定理得x 1+x 2=-(4-b ),x 1·x 2=2162+-b b .y 1·y 2=b 2-b (x 1+x 2)+x 1·x 2=2162+-b b +4b .∵OP ·OQ =0,∴x 1x 2+y 1y 2=0, 即b 2-6b +1+4b =0.解得b =1∈(2-32,2+32). ∴所求的直线方程为y =-x +1.i<89.解:()f x 的定义域为32⎛⎫-+ ⎪⎝⎭,∞. (Ⅰ)224622(21)(1)()2232323x x x x f x x x x x ++++'=+==+++. 当312x -<<-时,()0f x '>;当112x -<<-时,()0f x '<;当12x >-时,()0f x '>.从而,()f x 分别在区间312⎛⎫-- ⎪⎝⎭,,12⎛⎫-+ ⎪⎝⎭,∞单调增加,在区间112⎛⎫-- ⎪⎝⎭,单调减少. (Ⅱ)由(Ⅰ)知()f x 在区间3144⎡⎤-⎢⎥⎣⎦,的最小值为11ln 224f ⎛⎫-=+ ⎪⎝⎭.又31397131149ln ln ln 1ln 442162167226f f ⎛⎫⎛⎫⎛⎫--=+--=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0<.所以()f x 在区间3144⎡⎤-⎢⎥⎣⎦,的最大值为117ln 4162f ⎛⎫=+ ⎪⎝⎭.10. (1)∵m ∥n , ∴(a +c )(sin A -sin C )= (a -b )(sin B )∴(a +c )(a -c )=(a -b )b ,即222ab a b c =+-∴2221cos 22a b c C ab +-==,∴3C π=. (2) ∵2sin sin sin sin()3A B A A π+=+- 31sin sin 3)26A A A A π=+=+ ∵5(,)666A πππ+∈,∴1sin()(,1]62A π+∈, ∴3sin sin 3]A B +∈ 11.(1)当2=a 时,不等式0)(>x xf ,即2(23)0x x x +->, 即(23)(1)0x x x +-> , ∴ 原不等式的解集为:),1()0,23(+∞- (2)当]2,1[,0-∈>x a 时,)(x f 的值至少有一个是正数的充要条件是0)2(0)1(>>-f f 或,解得414>>a a 或,即a 的取值范围是 ),41(+∞。
菁华学校2009届高考数学二轮直通车夯实训练(17)

菁华学校2009届高考数学二轮直通车夯实训练(17)1、某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图 如图所示,若130-140分数段的人数为90人,则90-100分数段的人数为2 一个算法的程序框图如右图所示,若该程序输出的结果为54,则判断框中应填入的条件是 . 3.0000sin168sin72sin102sin198+= .4.已知i , j 为互相垂直的单位向量,a = i – 2j , b = i + λj ,且a 与b 的夹角为锐角,则实数λ的取值范围是 .5.已知函数()f x ,对任意实数,m n 满足()()(),f m n f m f n +=⋅且 (1)(0f a a =≠则()f n = ()n N +∈.6.符号[]x 表示不超过x 的最大整数,如[][]208.1,3-=-=π,定义函数{}[]x x x -=, 那么下列命题中正确的序号是 .(1)函数{}x 的定义域为R ,值域为[]1,0; (2)方程{}21=x ,有无数解; (3)函数{}x 是周期函数; (4)函数{}x 是增函数. 7.曲线)4cos()4sin(2ππ-+=x x y 和直线21=y 在y 轴右侧的交点按横坐标从小到大依次记为P 1,P 2,P 3,…,则|P 2P 4|等于 ____________8. 已知双曲线12222=-by a x )0,0(>>b a 的离心率e ∈,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为θ,则θ的取值范围是 . 9.定义运算()()a ab a b b a b ≤⎧*=⎨>⎩,例如,121*=,则函数2()(1)f x x x =*-的最大值为 .10.某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务(每人被安排是等可能的,每天只安排一人). (Ⅰ)共有多少种安排方法?(Ⅱ)其中甲、乙两人都被安排的概率是多少? (Ⅲ)甲、乙两人中至少有一人被安排的概率是多少?11.设函数)(),0(2)(1)2sin(x f y x f x =<<-=++ϕπϕ的图象的一条对称轴是直线.8π=x(1)求ϕ; (2)求函数)(x f y =的递减区间; (3)试说明)(x f y =的图象可由xy 2sin 2=的图象作怎样变换得到。
菁华学校高考数学二轮直通车夯实训练(24)

菁华学校高考数学二轮直通车夯实训练(24)1.若全焦U={1,2,3,4},A={1,2,3},B={2,3},则C U (A ∩B)=2已知数列{a n }是等差数列,且a 3+a 11=50,又a 4=13,则a 2等于3.设a ,b 是两个非零向量,若8a-kb 与-ka+b 共线,则实数k =4.已知函数y =f (x )的图象和y =sin(x +4π)的图象关于点P (4π,0)对称,则f (x )= 5.某种细胞开始时有2个,一小时后分裂成4个并死去1个,两小时后分裂成6个并死去1个,三个小时后分裂成10个并死去1个,……按照这种规律进行下去,100小时后细胞的存活数是 .6. 已知3(,),sin ,25παπα∈=则tan()4πα+=______。
7.在AB C ∆中, 若22A cos A sin =+, 则)4A tan(π-的值为 ______. 8. 棱长为3的正三棱柱内接于球O 中,则球O 的表面积为 。
9、设f (x )= 1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩ 则不等式()2f x >的解集为______。
10、在数列{a n }中,若a 1=1,a n +1=2a n +3 (n ≥1),则该数列的通项a n =____。
11.已知数列{a n }的首项a 1=1,其前n 项和为S n ,且对任意正整数n ,有n ,a n ,S n 成等差数列(1)求证:数列{S n +n +2}成等比数列.(2)求数列{a n }的通项公式.12.已知f (x )=ax 3+bx 2+cx +d (a ≠0)是定义在R 上的函数,其图象交x 轴于A 、B 、C 三点,若点B 的坐标为(2,0)且f (x )在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性(1)求实数c 的值;(2)在函数f (x )图象上是否存在一点M (x 0,y 0),使f (x )在点M 的切线斜率为3b ?若存在,求出点M 的坐标;不存在说明理由夯滚训练(24)参考答案1、{1,4}2、53、±224、-cos(x -4π) 5、2100+1 6、177、3 8、可求得.23,333311==⨯=OO AO 设该球的半径为R ,则AO =R 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菁华学校2009届高考数学二轮直通车夯实训练(21)
1.已知全集U=R ,集合)(},02
1
|
{},1|{N M C x x x N x x M U 则≥-+=≥==________ 2直线052)3(057)3()1(2=-+-=-+-++y x m m y m x m 与直线垂直的充要条件是___ 3.已知向量||,13||,3||,120则与=+= 等于___________
4.如果过点(0,1)斜率为k 的直线l 与圆04my kx y x 22=-+++ 交于M 、N 两点, 且M 、N 关于直线x+y=0对称,那么直线l 的斜率k=_____________;
此时,不等式组⎪⎩
⎪
⎨⎧≥≤-≥+-0y 0,my kx ,
01y kx 表示的平面区域的面积是_____________.
5.面积为S 的△ABC ,D 是BC 的中点,向△ABC 内部投一点,那么点落在△ABD 内的概率为_________
6.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的侧面积...为_________
7.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁—18岁的男生体重(kg ),得到频率分布直方图如右图: 根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是_____________
8、设数列{}n a 的通项公式为+=2n a n λ()n n *
∈N 且{}n a 满足1a <2a <3a <…<n a <
1+n a <…,则实数λ的取值范围是 .
9.设函数)}()
(1
{,12)()(*N n n f x x f ax x x f m
∈+='+=则数列
的导函数的前n 项和是
____________
10.如图,1111D C B A ABCD -是正四棱柱侧棱长为1,底面边长为2,E 是棱BC 的中点。
(1)求证://1BD 平面DE C 1; (2)求三棱锥BC D D 1-的体积.
11.已知数列}{n a 是等比数列,e a =4,如果72,a a 是关于
x 的方程:
)2(,012e k kx ex >=++两个实根,
(e 是自然对数的底数) (1) 求}{n a 的通项公式;
(2) 设:n n a b ln = ,n S 是数列}{n b 的前n 项的和,当:n S n =时,求n 的值; (3) 对于(2)中的}{n b ,设:21++=n n n n b b b c ,而 n T 是数列}{n c 的前n 项和,求n T 的
最大值,及相应的n 的值。
A 1
C
夯实训练(21)参考答案
1.{x |x ≤2} 2.23-==m m 或 3.4 4.1 ,4
1 5.
12 6.12
π 7.40 8.λ>-3 9、1+n n 10. (1)证明:连接D 1C 交DC 1于F ,连结EF
∵正四棱柱,∴四边形DCC 1D 1为矩形,∴F 为D 1C 中点. 在△CD 1B 中,∵E 为BC 中点,∴EF//D 1B.
又∵D 1B ⊄面C 1DE ,EF ⊂面C 1DE ,∴//1BD 平面DE C 1.
(2)连结BD ,D BC D BC D D V V --=11,∵正四棱柱,∴D 1D ⊥面DBC. ∵DC=BC=2,∴2222
1
=⨯⨯=
∆BCD S .
3212313111=⨯⨯=⋅⋅=
∆-D D S V BCD DBC D .∴三棱锥BC D D 1-的体积为3
2. 11.解:(1)由于 72,a a 是已知方程的两根,所以,有:,172e a a =
即: e
q qa a 1
611=, 而:e a =4,得 e q a =31 两式联立得:,3
-=e q 所以,n n n e q a a 31344--==
故 得数列}{n a 的通项公式为: n n e a 313-=
(2)n e a b n n n 313ln ln 313-===-,所以,数列}{n b 是等差数列,由前n 项和公式得: n n
n S n =-+=
2
)31310(,得 2323=-n ,所以有: 7=n
(3)由于 n b n 313-= 得: ......0654321>>>>>>>b b b b b b 又因为
21++=n n n n b b b c ,所以有:0,043223211>=>=b b b c b b b c , 而05433<=b b b c 0,076556544<=>=b b b c b b b c 且 当:5>n 时,都有 0<n c ,但是,83-=c
104=c 即:43c c < 所以,只有当:4=n 时,n T 的值最大,此时31010828280(max)=+-+=n T。
