高一数学必修1集合与函数概念单元测试题
高一数学试卷第一单元

必修一第一章集合与函数概念一、选择题1.设全集U ={x ,y |x ∈R ,y ∈R },集合M =⎭⎬⎫⎩⎨⎧1=2-3-|),(x y y x , P ={x ,y |y ≠x +1},那么C U M ∪P 等于. A .∅B .{2,3}C .2,3D .{x ,y |y =x +1}2.若A ={a ,b },B ⊆A ,则集合B 中元素的个数是. A .0B .1C .2D .0或1或23.函数y =fx 的图象与直线x =1的公共点数目是. A .1B .0C .0或1D .1或24.设函数fx =2x +3,gx +2=fx ,则gx 的表达式是. A .2x +1B .2x -1C .2x -3D .2x +75.已知函数fx =ax 3+bx 2+cx +d 的图象如图所示,则.A .b ∈-∞,0B .b ∈0,1C .b ∈1,2D .b ∈2,+∞6.设函数fx =⎩⎨⎧00++2 x c x c bx x ,,≤,若f -4=f 0,f -2=-2,则关于x 的方程fx =x 的解的个数为.A .1B .2C .3D .47.设集合A ={x |0≤x ≤6},B ={y |0≤y ≤2},下列从A 到B 的对应法则f 不是映射的是.A .f :x →y =21xB .f :x →y =31xC .f :x →y =41xD .f :x →y =61x8.有下面四个命题:①偶函数的图象一定与y 轴相交; ②奇函数的图象一定通过原点; ③偶函数的图象关于y 轴对称;④既是奇函数,又是偶函数的函数一定是fx =0x ∈R . 其中正确命题的个数是.第5题>A.1 B.2 C.3 D.49.函数y=x2-6x+10在区间2,4上是.A.递减函数B.递增函数C.先递减再递增D.先递增再递减10.二次函数y=x2+bx+c的图象的对称轴是x=2,则有.A.f1<f2<f4 B.f2<f1<f4C.f2<f4<f1 D.f4<f2<f1二、填空题11.集合{3,x,x2-2x}中,x应满足的条件是.12.若集合A={x|x2+a-1x+b=0}中,仅有一个元素a,则a=___,b=___.13.建造一个容积为8 m3,深为2 m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为元.14.已知fx+1=x2-2x,则fx=;fx-2=.15.y=2a-1x+5是减函数,求a的取值范围.16.设fx是R上的奇函数,且当x∈0,+∞时,fx=x1+x3,那么当x∈-∞,0时,fx=.三、解答题17.已知集合A={x∈R|ax2-3x+2=0},其中a为常数,且a∈R.①若A是空集,求a的范围;②若A中只有一个元素,求a的值;③若A中至多只有一个元素,求a的范围.18.已知M ={2,a ,b },N ={2a ,2,b 2},且M =N ,求a ,b 的值. 19.证明fx =x 3在R 上是增函数.20.判断下列函数的奇偶性: 1fx =3x 4+21x ;2fx =x -1xx-+11; 3fx =1-x +x -1;4fx =12-x +21x -.第一章集合与函数概念参考答案一、选择题 1.B解析:集合M 是由直线y =x +1上除去点2,3之后,其余点组成的集合.集合P 是坐标平面上不在直线y =x +1上的点组成的集合,那么M P 就是坐标平面上不含点2,3的所有点组成的集合.因此C U M P 就是点2,3的集合.C U M P ={2,3}.故选B . 2.D解析:∵A 的子集有∅,{a },{b },{a ,b }.∴集合B 可能是∅,{a },{b },{a ,b }中的某一个,∴选D .3.C解析:由函数的定义知,函数y =fx 的图象与直线x =1是有可能没有交点的,如果有交点,那么对于x =1仅有一个函数值.4.B解析:∵gx +2=2x +3=2x +2-1,∴gx =2x -1. 5.A解析:要善于从函数的图象中分析出函数的特点. 解法1:设fx =ax x -1x -2=ax 3-3ax 2+2ax ,比较系数得b =-3a ,c =2a ,d =0.由fx 的图象可以知道f 3>0,所以f 3=3a 3-13-2=6a >0,即a >0,所以b <0.所以正确答案为A .解法2:分别将x =0,x =1,x =2代入fx =ax 3+bx 2+cx +d 中,求得d =0,a = -31b ,c =-32b .∴fx =b -31x 3+x 2-32x =-3bx x -232-41. 由函数图象可知,当x ∈-∞,0时,fx <0,又x -232-41>0,∴b <0. x ∈0,1时,fx >0,又x -232-41>0,∴b <0. x ∈1,2时,fx <0,又x -232-41<0,∴b <0. 第5题x ∈2,+∞时,fx >0,又x -232-41>0,∴b <0. 故b ∈-∞,0. 6.C解:由f -4=f 0,f -2=-2,得22422b b c ⎧-=-⎪⎨⎪-+=-⎩,∴42b c =⎧⎨=⎩. ∴fx =⎩⎨⎧)0 ( 2)0 (2+4+2x ,x ,x x 由⎩⎨⎧得x =-1或x =-2;由得x =2.综上,方程fx =x 的解的个数是3个. 7.A解:在集合A 中取元素6,在f :x →y =21x 作用下应得象3,但3不在集合B = {y |0≤y ≤2}中,所以答案选A .8.A提示:①不对;②不对,因为偶函数或奇函数的定义域可能不包含0;③正确;④不对,既是奇函数又是偶函数的函数还可以为fx =0,x ∈-a ,a .所以答案选A .9.C解析:本题可以作出函数y =x 2-6x +10的图象,根据图象可知函数在2,4上是先递减再递增.答案选C .10.B解析:∵对称轴x =2,∴f 1=f 3.∵y 在〔2,+∞〕上单调递增, ∴f 4>f 3>f 2,于是f 2<f 1<f 4.∴答案选B . 二、填空题11.x ≠3且x ≠0且x ≠-1.解析:根据构成集合的元素的互异性,x 满足⎪⎩⎪⎨⎧ 解得x ≠3且x ≠0且x ≠-1. 12.a =31,b =91.x >0 x =2 ≤ > x ≤0 x 2+4x +2=x x ≠3,x 2-2x ≠3, x 2-2x ≠x .解析:由题意知,方程x 2+a -1x +b =0的两根相等且x =a ,则△=a -12-4b =0①,将x =a 代入原方程得a 2+a -1a +b =0②,由①②解得a =31,b =91.13.1760元.解析:设水池底面的长为x m,水池的总造价为y 元,由已知得水池底面面积为4 m 2.,水池底面的宽为x4m .池底的造价y 1=120×4=480.池壁的造价y 2=2×2x +2×2×x 4×80=4x +x16×80. 水池的总造价为y =y 1+y 2=480+4x +x16×80, 即y =480+320x +x4=480+320⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛4+22x -x . 当x =x2,即x =2时,y 有最小值为480+320×4=1760元.14.fx =x 2-4x +3,fx -2=x 2-8x +15.解析:令x +1=t ,则x =t -1,因此ft =t -12-2t -1=t 2-4t +3,即fx =x 2-4x +3.∴fx -2=x -22-4x -2+3=x 2-8x +15.15.-∞,21.解析:由y =2a -1x +5是减函数,知2a -1<0,a <21.16.x 1-x 3.解析:任取x ∈-∞,0,有-x ∈0,+∞, ∴f -x =-x 1+-x 3=-x 1-x 3,∵fx 是奇函数,∴f -x =-fx .∴fx =-f -x =x 1-x 3,即当x ∈-∞,0时,fx 的表达式为x 1-x 3.三、解答题17.解:①∵A 是空集,∴方程ax 2-3x +2=0无实数根. ∴⎩⎨⎧∆,a a 08-9=,0解得a >89.②∵A 中只有一个元素,≠ <∴方程ax 2-3x +2=0只有一个实数根.当a =0时,方程化为-3x +2=0,只有一个实数根x =32;当a ≠0时,令Δ=9-8a =0,得a =89,这时一元二次方程ax 2-3x +2=0有两个相等的实数根,即A 中只有一个元素.由以上可知a =0,或a =89时,A 中只有一个元素.③若A 中至多只有一个元素,则包括两种情形:A 中有且仅有一个元素;A 是空集.由①②的结果可得a =0,或a ≥89.18.解:根据集合中元素的互异性,有⎩⎨⎧==⎩⎨⎧==ab b a b b a a 2222或解得或或再根据集合中元素的互异性,得或19.证明:设x 1,x 2∈R 且x 1<x 2,则fx 1-fx 2=31x -32x =x 1-x 221x +x 1x 2+22x . 又21x +x 1x 2+22x =x 1+21x 22+4322x . 由x 1<x 2得x 1-x 2<0,且x 1+21x 2与x 2不会同时为0, 否则x 1=x 2=0与x 1<x 2矛盾,所以21x +x 1x 2+22x >0.因此fx 1-fx 2<0,即fx 1<fx 2,fx =x 3在R 上是增函数.20.解:1∵函数定义域为{x |x ∈R ,且x ≠0},f -x =3-x 4+21)(-x =3x 4+21x =fx ,∴fx =3x 4+21x 是偶函数. 2由xx-+11≥0⇔⎩⎨⎧≠01--1+1x x x ))((解得-1≤x <1. a =0 b =1 a =0 b =0a =41b =21 a =0b =1 a =41 b =21≥0∴函数定义域为x ∈-1,1,不关于原点对称,∴fx =x -1xx-11+为非奇非偶函数. 3fx =1-x +x -1定义域为x =1, ∴函数为fx =0x =1,定义域不关于原点对称, ∴fx =1-x +x -1为非奇非偶函数. 4fx =1-2x +2-1x 定义域为≥ -10≥1-22x x x ∈{±1},∴函数变形为fx =0x =±1,∴fx =1-2x +2-1x 既是奇函数又是偶函数.。
高一数学人教版必修一第一章《集合与函数概念》单元测试题(含答案)

三、解答题 :每小题 12 分,共 60 分
16、设 A { x Z || x | 6} , B 1,2,3 , C
3,4,5,6 ,求:
(题目有错漏,需修改,要么改为① A { x Z x 6} ,要么改为② C { 3,4,5} )
( 1) A (B C ) ;( 2) A C A (B C )
的元素 ( 1,2) 对应的 B 中的元素为(
A)
(A ) ( 3,1)
( B) (1,3)
( C) ( 1, 3)
(D ) (3,1)
5、下列各组函数 f ( x)与 g (x) 的图象相同的是( D )
(A ) f ( x) x, g( x) ( x ) 2
(B ) f ( x) x2 , g(x) (x 1) 2
第一章 《集合与函数概念》单元测试题
姓名:
班别:
学号:
一、选择题:每小题 4 分,共 40 分
1、在“①高一数学课本中的难题;②所有的正三角形;
2
③方程 x 2 0 的实数解”中,能够
表示成集合的是 ( A )
(A )② ( C )②③
( B)③ ( D)①②③
2、若 A x | 0 x 2 , B x |1 x 2 ,则 A B ( D )
元?
解: 设每天从报社买进 x 份,每月所获的利润为 f( x),则
① 当每天购入少于或等于 250 份的报纸的时候,全部都卖光了,则
f( x) =( 1-0.9) *30*x
故 f ( x)在 x
x 0 的值域为
,2
综上得, f ( x)的值域为 2,
,2
19、中山市的一家报刊摊点,从报社买进《南方都市报》的价格是每份
高中数学必修一第一章《集合与函数概念》单元测试题(含答案)
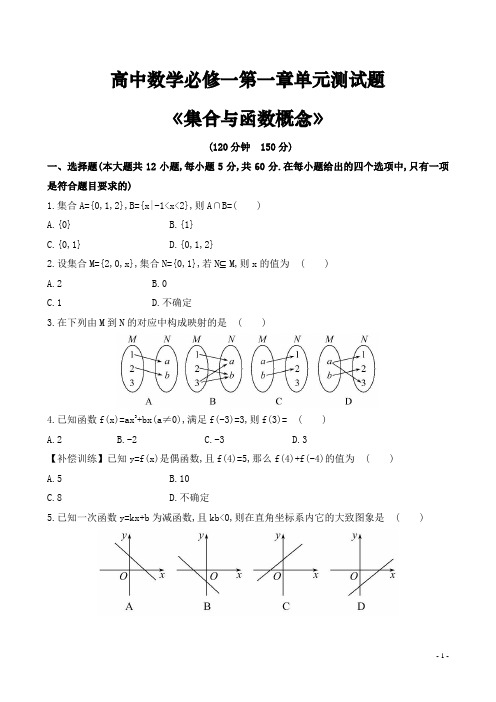
高中数学必修一第一章单元测试题《集合与函数概念》(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={0,1,2},B={x|-1<x<2},则A∩B=( )A.{0}B.{1}C.{0,1}D.{0,1,2}2.设集合M={2,0,x},集合N={0,1},若N⊆M,则x的值为( )A.2B.0C.1D.不确定3.在下列由M到N的对应中构成映射的是( )4.已知函数f(x)=ax3+bx(a≠0),满足f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( )A.5B.10C.8D.不确定5.已知一次函数y=kx+b为减函数,且kb<0,则在直角坐标系内它的大致图象是( )6.若f(x)=则f的值为( )A.-B.C.D.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+18.下列四个图形中,不是以x为自变量的函数的图象是( )9.已知集合A={x|x2+x+1=0},若A∩R=∅,则实数m的取值范围是( )A.m<4B.m>4C.0<m<4D.0≤m<410.函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( )A.(-∞,0]和(-∞,1]B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a ※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个12.设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知集合A={x|1≤x<2},B={x|x<a},若A∩B=A,则实数a的取值范围是.14.已知a是实数,若集合{x|ax=1}是任何集合的子集,则a的值是.15.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-⎧⎨⎩≤≤≤≤16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.(1)分别求A∩B,(B)∪A.R(2)已知C={x|a<x<a+1},若C⊆B,求实数a取值构成的集合.18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.20.(12分)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并用定义证明.21.(12分)(2015·葫芦岛高一检测)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.22.(12分)定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.高中数学必修一第一章单元测试题《集合与函数概念》参考答案(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={0,1,2},B={x|-1<x<2},则A∩B=( )A.{0}B.{1}C.{0,1}D.{0,1,2}【解析】选C.因为A={0,1,2},B={x|-1<x<2},所以A∩B={0,1}.2.(2015·天津高一检测)设集合M={2,0,x},集合N={0,1},若N⊆M,则x的值为( ) A.2 B.0C.1D.不确定【解析】选C.因为N⊆M,所以集合N中元素均在集合M中,所以x=1.3.在下列由M到N的对应中构成映射的是( )【解析】选C.选项A中,集合M中的数3在集合N中没有数与之对应,不满足映射的定义;选项B中,集合M中的数3在集合N中有两个数a,b与之对应;选项D中,集合M中的数a在集合N中有两个数1,3与之对应,不满足映射的定义.4.已知函数f(x)=ax3+bx(a≠0),满足f(-3)=3,则f(3)= ( )A.2B.-2C.-3D.3【解析】选 C.方法一:f(-3)=a(-3)3+b(-3)=-33a-3b=-(33a+3b)=3,所以33a+3b=-3.f(3)=33a+3b=-3.方法二:显然函数f(x)=ax3+bx为奇函数,故f(3)=-f(-3)=-3.【补偿训练】已知y=f(x)是偶函数,且f(4)=5,那么f(4)+f(-4)的值为( )A.5B.10C.8D.不确定【解析】选B.因为f(x)是偶函数,所以f(-4)=f(4)=5,所以f(4)+f(-4)=10.5.已知一次函数y=kx+b为减函数,且kb<0,则在直角坐标系内它的大致图象是( )【解析】选A.选项A图象为减函数,k<0,且在y轴上的截距为正,故b>0,满足条件,而B,C,D 均不满足条件.6.若f(x)=则f的值为( )A.-B.C.D.【解析】选C.因为<1,所以应代入f(x)=1-x2,即f=1-=.7.若f(g(x))=6x+3,且g(x)=2x+1,则f(x)= ( )A.3B.3xC.6x+3D.6x+1【解析】选B.由f(g(x))=f(2x+1)=6x+3=3(2x+1),知f(x)=3x.8.(2015·西城区高一检测)下列四个图形中,不是以x为自变量的函数的图象是( )【解析】选C.由函数定义知,定义域内的每一个x都有唯一函数值与之对应,A,B,D选项中的图象都符合;C项中对于大于零的x而言,有两个不同的值与之对应,不符合函数定义.9.已知集合A={x|x2+x+1=0},若A∩R=∅,则实数m的取值范围是( )A.m<4B.m>4C.0<m<4D.0≤m<4【解析】选D.因为A∩R=∅,所以A=∅,即方程x2+x+1=0无解,所以Δ=()2-4<0,所以m<4.又因为m≥0,所以0≤m<4.10.(2015·赣州高一检测)函数f(x)=|x|和g(x)=x(2-x)的单调递增区间分别是( ) A.(-∞,0]和(-∞,1] B.(-∞,0]和[1,+∞)C.[0,+∞)和(-∞,1]D.[0,+∞)和[1,+∞)【解析】选C.函数f(x)=|x|的单调递增区间为[0,+∞),函数g(x)=x(2-x)=-(x-1)2+1的单调递增区间为(-∞,1].11.对于任意两个正整数m,n,定义某种运算“※”如下:当m,n都为正偶数或正奇数时,m※n=m+n;当m,n中一个为正偶数,另一个为正奇数时,m※n=mn.则在此定义下,集合M={(a,b)|a ※b=12,a∈N*,b∈N*}中的元素个数是( )A.10个B.15个C.16个D.18个【解析】选B.若a,b同奇偶,有12=1+11=2+10=3+9=4+8=5+7=6+6,前面的每种可以交换位置,最后一种只有1个点(6,6),这时有2×5+1=11;若a,b一奇一偶,有12=1×12=3×4,每种可以交换位置,这时有2×2=4,所以共有11+4=15个.12.(2015·西安高一检测)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则使<0的x的取值范围为( )A.(-1,0)∪(1,+∞)B.(-∞,-1)∪(0,1)C.(-∞,-1)∪(1,+∞)D.(-1,0)∪(0,1)【解析】选D.由f(x)为奇函数,可知=<0.而f(1)=0,则f(-1)=-f(1)=0.又f(x)在(0,+∞)上为增函数,所以当0<x<1时,f(x)<0=f(1),此时<0;又因为f(x)为奇函数,所以f(x)在(-∞,0)上为增函数,所以当-1<x<0时,f(x)>0=f(-1),此时<0,即所求x的取值范围为(-1,0)∪(0,1).二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.(2015·开封高一检测)已知集合A={x|1≤x<2},B={x|x<a},若A∩B=A,则实数a的取值范围是.【解析】因为A∩B=A,所以A B,所以a≥2.答案:a≥214.已知a是实数,若集合{x|ax=1}是任何集合的子集,则a的值是.【解析】若集合{x|ax=1}是任何集合的子集,则它是空集,即方程ax=1无解,所以a=0.答案:015.已知f(x)为偶函数,则f(x)=x1,1x0, ______,0x 1.+-⎧⎨⎩≤≤≤≤【解析】当x∈[0,1]时,-x∈[-1,0],f(-x)=-x+1,又因为f(x)为偶函数,所以f(x)=f(-x)=1-x.答案:1-x16.定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)f(b)≤0;②f(a)+f(b)≤f(-a)+f(-b);③f(b)f(-b)≤0;④f(a)+f(b)≥f(-a)+f(-b).其中正确的是.(把你认为正确的不等式的序号全写上).【解析】若a+b≤0,则a≤-b,b≤-a,又因为f(x)为R上递减的奇函数,所以f(a)≥f(-b),f(b)≥f(-a),所以f(a)+f(b)≥f(-a)+ f(-b),④正确;又因为f(-b)=-f(b),所以f(b)f(-b)=-f(b)f(b)≤0,③正确.其余错误.答案:③④三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.B)∪A.(1)分别求A∩B,(R(2)已知C={x|a<x<a+1},若C⊆B,求实数a取值构成的集合.【解析】(1)A∩B={x|3≤x<6}.因为B={x|x≤2或x≥9},RB)∪A={x|x≤2或3≤x<6或x≥9}.所以(R(2)因为C⊆B,如图所示:所以解得2≤a≤8,所以所求集合为{a|2≤a≤8}.18.(12分)已知函数f(x)=.(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.【解析】(1)因为f(x)=,所以f(3)==-,所以点(3,14)不在f(x)的图象上.(2)f(4)==-3.(3)令=2,即x+2=2x-12,解得x=14.19.(12分)若函数f(x)=x2+4x+a的定义域和值域均为[-2,b](b>-2),求实数a,b的值.【解析】因为函数f(x)的对称轴方程为x=-2,所以函数f(x)在定义域[-2,b](b>-2)上单调递增,所以函数f(x)的最小值为f(-2)=a-4=-2,所以a=2.函数f(x)的最大值为f(b)=b2+4b+2=b.所以b2+3b+2=0,解得b=-1或b=-2(舍去),所以b=-1.20.(12分)(2015·烟台高一检测)已知函数f(x)=ax+b,且f(1)=2,f(2)=-1.(1)求f(m+1)的值.(2)判断函数f(x)的单调性,并用定义证明.【解析】(1)由f(1)=2,f(2)=-1,得a+b=2,2a+b=-1,即a=-3,b=5,故f(x)=-3x+5,f(m+1)=-3(m+1)+5=-3m+2.(2)函数f(x)在R上单调递减,证明如下:任取x1<x2(x1,x2∈R),则f(x2)-f(x1)=(-3x2+5)-(-3x1+5)=3x1-3x2=3(x1-x2),因为x1<x2,所以f(x2)-f(x1)<0,即f(x2)<f(x1),所以函数f(x)在R上单调递减.【拓展延伸】定义法证明函数单调性时常用变形技巧(1)因式分解:当原函数是多项式函数时,作差后的变形通常进行因式分解.(2)通分:当原函数是分式函数时,作差后往往进行通分,然后对分子进行因式分解.(3)配方:当原函数是二次函数时,作差后可考虑配方,便于判断符号.21.(12分)(2015·葫芦岛高一检测)已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.(1)判断f(x)的奇偶性.(2)求证:f(x)为R上的减函数.(3)求f(x)在区间[-3,3]上的值域.【解析】(1)取x=y=0,则f(0+0)=2f(0),所以f(0)=0.取y=-x,则f(x-x)=f(x)+f(-x),所以f(-x)=-f(x)对任意x∈R恒成立,所以f(x)为奇函数.(2)任取x1,x2∈(-∞,+∞),且x1<x2,则x2-x1>0,f(x2)+f(-x1)=f(x2-x1)<0,所以f(x2)<-f(-x1),又f(x)为奇函数,所以f(x1)>f(x2),所以f(x)是R上的减函数.(3)由(2)知f(x)在R上为减函数,所以对任意x∈[-3,3],恒有f(3)≤f(x)≤f(-3),因为f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=-2×3=-6,所以f(-3)=-f(3)=6,所以f(x)在[-3,3]上的值域为[-6,6].22.(12分)定义在(-1,1)上的函数f(x)满足:①对任意x,y∈(-1,1),都有f(x)+f(y)=f;②f(x)在(-1,1)上是单调递减函数,f=-1.(1)求f(0)的值.(2)求证:f(x)为奇函数.(3)解不等式f(2x-1)<1.【解题指南】(1)结合已知等式利用赋值法求解.(2)利用赋值法并结合奇偶性定义判断.(3)结合(2)的结论及已知条件得f=1,再利用奇偶性和单调性脱去符号“f”,转化为一次不等式求解.【解析】(1)令x=y=0,得2f(0)=f(0),所以f(0)=0.(2)令y=-x,得f(x)+f(-x)=f(0)=0,即f(x)=-f(-x),所以f(x)为奇函数.(3)因为f=-1,f(x)为奇函数,所以f=1,所以不等式f(2x-1)<1等价于f(2x-1)<f,又因为f(x)在(-1,1)上是减函数,所以2x-1>-,-1<2x-1<1,解得<x<1.所以不等式的解集为.【误区警示】解答本题(3)时易忽视函数定义域而得出解集为的错误.。
高一数学必修1集合与函数概念单元测试题.doc

D. M= {x I x<-l, 或一 1<兀<(), 或 x>()=, N= {ylyHO}
6. 已知 A 、B 两地相距 150 千米,某人开汽车以 60 千米 / 小时的速度从 A 地到达 B 地, B 地停留 1 小时后再以 50 T 米/ 小时的速度返冋 A 地,把汽车离开 A 地的距离 x 表示 为时
C. { ax2+bx+c=O la, b, cGR} D. { ax2-^-bx+c=O I d, b, cWR,且 aHO}
2. 图中阴影部分所表示的集合是 (
)
A.BA [Cu(AUC)]
B.(AUB) U(BUC)
3. 设集合 P 二{ 立方后等于白身的数 }, 那么集合 P 的真子集个数是
16. (12 分) 集合 A={(x,y)*2 + inx — y + 2 = 0 } ,集合 B={(x,y) 卜一 y+ 1 = 0,且 05 兀 52}, 又 AC/H0, 求实数 m 的取值范围 .
17. (12 分) 已知砂
2 xe ( 一 8,1) 心 1,+8) '求两的值
18. (12 分) 如图,用长为 1 的铁丝弯成卜 - 部为矩形,上部为半圆形的框 架,
A. 3
B. 4
C. 7
4. 设 P 二{ 质数 } , Q= { 偶数 }, 贝 1JPPQ等于
A. C.(AUC ) n( CuB)
B. 2
C. {2}
D. [Cu(ACC)] UB
D. 8 D. N
1 f(x)= 』x_2 + J1 —兀启意义 ;
2 函数是其定义域到值域的映射; 3 函数 y=2x(xwN) 的图象是一直线 ;
高一数学必修1《集合与函数概念》测试卷(含答案)

高一数学必修1《集合与函数概念》测试卷(含答案)第一章(一)《集合与函数概念》测试卷考试时间:120分钟满分:150分一.选择题(本大题共12小题,每小题5分,共60分)1.下列叙述正确的是()A.函数的值域就是其定义中的数集BB.函数y=f(x)的图像与直线x=m至少有一个交点C.函数是一种特殊的映射D.映射是一种特殊的函数2.如果A={x|x>-1},则下列结论正确的是()A.XXXB.{}⊆AC.{}∈AD.∅∈A3.设f(x)=(2a-1)x+b在R上是减函数,则有()A.a≥1/2B.a≤1/2C.a>1/2D.a<1/24.定义在R上的偶函数f(x),对任意x1,x2∈[0,+∞)(x1≠x2),有|x1-x2|<π/2,则有()A.f(3)<f(-2)<f(1)B.f(1)<f(-2)<f(3)C.f(-2)<f(1)<f(3)D.f(3)<f(1)<f(-2)5.若奇函数f(x)在区间[1,3]上为增函数,且有最小值,则它在区间[-3,-1]上()A.是减函数,有最小值0B.是增函数,有最小值0C.是减函数,有最大值0D.是增函数,有最大值06.设f:x→x是集合A到集合B的映射,若A={-2,0,2},则AB等于()A.{}B.{2}C.{0,2}D.{-2,0}7.定义两种运算:a⊕b=ab,a⊗b=a²+b²,则函数f(x⊗3-3)为()A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数8.若函数f(x)是定义域在R上的偶函数,在(-∞,0)上是减函数,且f(-2)=1/4,则使f(x)<1/4的x的取值范围为()A.(-2,2)B.(-2,0)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-2]∪[2,+∞)9.函数f(x)=x+(x|x|)的图像是()10.设f(x)是定义域在R上的奇函数,f(x+2)=-f(x),当|x|<1时,f(x)=x,则f(7.5)的值为()A.-0.5B.0.5C.-5.5D.7.511.已知f(-2x+1)=x²+1,且-1/2≤x≤1/2,则f(x)的值域为()A.[1,5/4]B.[1/4,5/4]C.[0,5/4]D.[1/4,2]12.设f(x)是定义在R上的奇函数,且f(x)在[-2,2]上单调递增,则f(x)在(-∞,-2)∪(2,+∞)上()A.单调递减B.单调不增也不减C.单调递增D.无法确定第一章(一)《集合与函数概念》测试卷考试时间:120分钟满分:150分一、选择题(本大题共12小题,每小题5分,共60分)1.下列叙述正确的是()A。
新课标高一数学必修1第一章集合与函数概念单元测试题及答案

数学必修一单元测试题集合与函数概念一、选择题1.集合},{b a 的子集有 ( )A .2个B .3个C .4个D .5个2. 设集合{}|43A x x =-<<,{}|2B x x =≤,则A B = ( )A .(4,3)-B .(4,2]-C .(,2]-∞D .(,3)-∞3.已知()5412-+=-x x x f ,则()x f 的表达式是( )A .x x 62+B .782++x xC .322-+x xD .1062-+x x4.下列对应关系:( )①{1,4,9},{3,2,1,1,2,3},A B ==---f :x x →的平方根②,,A R B R ==f :x x →的倒数③,,A R B R ==f :22x x →-④{}{}1,0,1,1,0,1,A B f =-=-:A 中的数平方其中是A 到B 的映射的是A .①③B .②④C .③④D .②③5.下列四个函数:①3y x =-;②211y x =+;③2210y x x =+-;④(0)1(0)xx y x x⎧-≤⎪=⎨->⎪⎩.其中值域为R 的函数有 ( )A .1个B .2个C .3个D .4个6. 已知函数212x y x ⎧+=⎨-⎩ (0)(0)x x ≤>,使函数值为5的x 的值是()A .-2B .2或52- C . 2或-2 D .2或-2或52-7.下列函数中,定义域为[0,∞)的函数是 ( )A .x y =B .22x y -=C .13+=x yD .2)1(-=x y8.若R y x ∈,,且)()()(y f x f y x f +=+,则函数)(x f ( )A . 0)0(=f 且)(x f 为奇函数B .0)0(=f 且)(x f 为偶函数C .)(x f 为增函数且为奇函数D .)(x f 为增函数且为偶函数9(A ) (B) (C ) (D)10.若*,x R n N ∈∈,规定:(1)(2)(1)n x x x x x n H =++⋅⋅⋅⋅⋅+-,例如:( ) 44(4)(3)(2)(1)24H -=-⋅-⋅-⋅-=,则52()x f x x H -=⋅的奇偶性为A .是奇函数不是偶函数B .是偶函数不是奇函数C .既是奇函数又是偶函数D .既不是奇函数又不是偶函数二、填空题11.若{}{}0,1,2,3,|3,A B x x a a A ===∈,则AB = .12.已知集合M={(x ,y )|x +y =2},N={(x ,y )|x -y =4},那么集合M ∩N = .13.函数()1,3,x f x x +⎧=⎨-+⎩1,1,x x ≤>则()()4f f = .14.某班50名学生参加跳远、铅球两项测试,成绩及格人数分别为40人和31人,两项测试均不及格的人数是4人,两项测试都及格的有 人.15.已知函数f(x)满足f(xy)=f(x)+f(y),且f(2)=p,f(3)=q ,那么f(36)= .三、解答题16.已知集合A={}71<≤x x ,B={x|2<x<10},C={x|x<a },全集为实数集R .(Ⅰ)求A ∪B ,(C R A)∩B ;(Ⅱ)如果A ∩C ≠φ,求a 的取值范围.17.集合A ={x |x 2-ax +a 2-19=0},B ={x |x 2-5x +6=0},C ={x |x 2+2x -8=0}.(Ⅰ)若A =B,求a 的值;(Ⅱ)若∅A ∩B ,A ∩C =∅,求a 的值. x y 0 x y 0 x y 0 x y 018.已知方程02=++q px x 的两个不相等实根为βα,.集合},{βα=A , =B {2,4,5,6},=C {1,2,3,4},A ∩C =A ,A ∩B =φ,求q p ,的值?19.已知函数2()21f x x =-.(Ⅰ)用定义证明()f x 是偶函数;(Ⅱ)用定义证明()f x 在(,0]-∞上是减函数;(Ⅲ)作出函数()f x 的图像,并写出函数()f x 当[1,2]x ∈-时的最大值与最小值. yox20.设函数1)(2++=bx ax x f (0≠a 、R b ∈),若0)1(=-f ,且对任意实数x (R x ∈)不等式)(x f ≥0恒成立.(Ⅰ)求实数a 、b 的值;(Ⅱ)当∈x [-2,2]时,kx x f x g -=)()(是单调函数,求实数k 的取值范围.2010级高一数学必修一单元测试题(一)参考答案一、选择题 CBACB AAACB二、填空题 11. {}0,3 12. {(3,-1)} 13. 0 14. 25 15. 2()p q +三、解答题16.解:(Ⅰ)A ∪B={x|1≤x<10}(C R A)∩B={x|x<1或x ≥7}∩{x|2<x<10}={x|7≤x<10}(Ⅱ)当a >1时满足A ∩C ≠φ17.解: 由已知,得B ={2,3},C ={2,-4}(Ⅰ)∵A =B 于是2,3是一元二次方程x 2-ax +a 2-19=0的两个根, 由韦达定理知:⎩⎨⎧-=⨯=+1932322a a 解之得a =5. (Ⅱ)由A ∩B ∅A ⇒∩≠B Φ,又A ∩C =∅,得3∈A ,2∉A ,-4∉A ,由3∈A ,得32-3a +a 2-19=0,解得a =5或a =-2当a =5时,A ={x |x 2-5x +6=0}={2,3},与2∉A 矛盾; 当a =-2时,A ={x |x 2+2x -15=0}={3,-5},符合题意.∴a =-2.18.解:由A ∩C=A 知A ⊆C又},{βα=A ,则C ∈α,C ∈β. 而A ∩B =φ,故B ∉α,B ∉β 显然即属于C 又不属于B 的元素只有1和3.不仿设α=1,β=3. 对于方程02=++q px x的两根βα, 应用韦达定理可得3,4=-=q p .19.(Ⅰ)证明:函数()f x 的定义域为R ,对于任意的x R ∈,都有22()2()121()f x x x f x -=--=-=,∴()f x 是偶函数.(Ⅱ)证明:在区间(,0]-∞上任取12,x x ,且12x x <,则有 22221212121212()()(21)(21)2()2()()f x f x x x x x x x x x -=---=-=-⋅+, ∵12,(,0]x x ∈-∞,12x x <,∴12120,x x x x -<0,+<即1212()()0x x x x -⋅+>∴12()()0f x f x ->,即()f x 在(,0]-∞上是减函数. (Ⅲ)解:最大值为(2)7f =,最小值为(0)1f =-.20.解:(Ⅰ)∵0)1(=-f ∴01=+-b a∵任意实数x 均有)(x f ≥0成立∴⎩⎨⎧≤-=∆>0402a b a 解得:1=a ,2=b(Ⅱ)由(1)知12)(2++=x x x f ∴1)2()()(2+-+=-=x k x kx x f x g 的对称轴为22-=k x ∵当∈x [-2,2]时,)(x g 是单调函数 ∴222-≤-k 或222≥-k ∴实数k 的取值范围是),6[]2,(+∞--∞ .21.解:(Ⅰ)令1==n m 得 )1()1()1(f f f +=所以0)1(=f0)21(1)21()2()212()1(=+-=+=⨯=f f f f f 所以1)21(=f (Ⅱ)证明:任取210x x <<,则112>x x 因为当1>x 时,0)(<x f ,所以0)(12<x x f 所以)()()()()(11211212x f x x f x f x x x f x f <+=⋅= 所以)(x f 在()+∞,0上是减函数.。
人教版高一数学必修一第一章单元检测试题及答案

高一数学第一章集合与函数概念单元检测试题一、选择题:共12题每题5分共60分1.已知函数的图象如下图所示,则函数的图象为2.下列各组函数为相等函数的是A. B.C. D.==3.函数的定义域为若对于任意的当时,都有则称函数在上为非减函数.设函数的上为非减函数,且满足以下三个条件:①②③=则等于A. B. C. D.4.设函数,则的最小值为A. B. C. D.5.函数f(x)=x2-4x+6(x∈[1,5))的值域是A.(3,11]B.[2,11)C.[3,11)D.(2,11]6.若函数在区间上单调,则实数的取值范围为A. B.C. D.7.定义运算:a*b=,如1*2=1,则函数f(x)=2x*2-x的值域为A.RB.(0,+∞)C.(0,1]D.[1,+∞)8.已知集合E={x|2-x≥0},若F⊆E,则集合F可以是A.{x|x<1}B.{x|x>2}C.{x|x>3}D.{x|1<x<3}9.已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f()的x的取值范围是() A.(,) B.[,) C.(,) D.[,)10.某部队练习发射炮弹,炮弹的高度与时间(秒)的函数关系式是,则炮弹在发射几秒后最高呢?A. B. C. D.11.已知,且,则等于A. B. C. D.12.已知集合和集合,则两个集合间的关系是A. B. C. D.M,P互不包含试卷第2页,总4页二、填空题:共4题每题5分共20分13.已知函数f(x)=a﹣x2(1≤x≤2)与的图象上存在关于轴对称的点,则实数的取值范围是A. C.14.设集合M={x|0≤x≤2},N={y|0≤y≤2}.给出下列四个图,其中能构成从集合M到集合N 的函数关系的是.15.给出下列二次函数,将其图象画在同一平面直角坐标系中,则图象的开口按从小到大的顺序排列为.(1)f(x)=-x2;(2)f(x)=(x+5)2;(3)f(x)=x2-6;(4)f(x)=-5(x-8)2+9.16.若函数的图像关于y轴对称,则的单调减区间为 .三、解答题:共6题共70分17.(本题10分)如果对函数f(x)定义域内任意的x1,x2都有|f(x1)-f(x2)|≤|x1-x2|成立,就称函数f(x)是定义域上的“平缓函数”.(1)判断函数f(x)=x2-x,x∈[0,1]是否为“平缓函数”;(2)若函数f(x)是闭区间[0,1]上的“平缓函数”,且f(0)=f(1),证明:对任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤成立.(注:可参考绝对值的基本性质①|ab|≤|a||b|,②|a+b|≤|a|+|b|)18.(本题12分)记函数的定义域为集合,集合.(1)求和;(2) 若,求实数的取值范围.19.(本题12分)设全集U={x|0<x<9,且x∈Z},集合S={1,3,5},T={3,6},求:(1)S∩T;(2).20.(本题12分)已知函数f(x)=.(1)用定义证明f(x)在区间[1,+∞)上是增函数;(2)求该函数在区间[2,4]上的最大值与最小值.21.(本题12分)定义在非零实数集上的函数对任意非零实数满足:,且当时.(Ⅰ)求及的值;(Ⅱ)求证:是偶函数;(Ⅲ)解不等式:.22.(本题12分)(1)证明:函数f(x )=在(-∞,0)上是减函数;(2)证明:函数f(x)=x3+x在R上是增函数.试卷第4页,总4页参考答案1.B【解析】本试题主要考查函数的图象.根据题意,由于函数图象可知,函数在y 轴右侧图象在x 轴上方,在y轴左侧的图象在x轴的下方,而函数在x>0时图象保持不变,因此排除C,D,对于选项A,由于在时偶函数,故在y轴左侧的图象与y轴右侧的图象关于y轴对称,故选B.【备注】无2.C【解析】本题主要考查相等函数、函数的定义域、值域与对应关系.A.因为这两个函数的值域不同,所以这两个函数不是相等函数;B.这两个函数的定义域不同,所以这两个函数不是相等函数;C.这两个函数的定义域、值域与对应关系均相同,所以这两个函数为相等函数;D.这两个函数的定义域不同,所以这两个函数不是相等函数.【备注】无3.D【解析】本题主要考查新定义问题、函数的性质及其综合应用.由题意,令x=0,由=可得由可得令则=同理=====令则==同理====. 非减函数的性质:当时,都有.因为所以所以=.【备注】无4.A【解析】本题主要考查分段函数的最值问题.由题意,函数的图象如图所示:红色图象即为所求解的函数的图象,可知最小值为0.【备注】无5.B【解析】f(x)=x2-4x+6=(x-2)2+2.∵f(x)图象的对称轴是直线x=2,∴f(x)在[1,2]上单调递减,在(2,5)上单调递增,∴f(x)的值域是[2,11).故选B.【备注】无6.C【解析】本题主要考查二次函数.依题意,函数在区间上单调,则函数的对称轴或,得或,故选C.【备注】无7.C【解析】本题主要考查在新型定义的前提下函数值域的求解.根据题目定义知f(x)=2x*2-x=,结合图象知其值域为(0,1].故选C.【备注】无8.A【解析】由题意知E={x|2-x≥0}={x|x≤2},F⊆E,观察选项知应选A.【备注】无9.A【解析】偶函数f(x)在区间[0,+∞)上单调递增,所以函数f(x)在区间(-∞,0]上单调递减.由于f(x)是偶函数,所以f(-x)=f(x),则f(-)= f().由f(2x-1)<f()得①或②,解①得≤x<,解②得<x<.综上可得<x<,故x的取值范围是(,).【备注】无10.C【解析】本题主要考查二次函数.依题意,根据二次函数得性质,函数的开口向下,对称轴为,故炮弹在发射后最高,故选C.【备注】无11.B【解析】本题主要考查函数的解析式与求值.因为,设,则,所以,因为,所以,解得,故选B.【备注】无12.D【解析】无【备注】无13.D【解析】本题主要考查二次函数的图像与性质,考查了逻辑推理能力与计算能力.因为函数f(x)=a ﹣x2(1≤x ≤2)与的图象上存在关于轴对称的点,所以函数f(x)=a﹣x2(1≤x≤2)与的图象上存在交点,所以有解,令,则,求解可得,故答案为D.【备注】无14.④【解析】图①中函数的定义域是[0,1];图②中函数的定义域是[-1,2];图③中对任意的x∈(0,2],其对应的y值不唯一.故①②③均不能构成从集合M到集合N 的函数,图④满足题意.【备注】无15.(4)(3)(2)(1)【解析】因为二次函数y=ax2+bx+c(a≠0)的图象在同一平面直角坐标系中|a|越小,图象开口越大,又|-|<||<||<|-5|,所以图象开口按从小到大的顺序排列为(4)(3)(2)(1).【备注】无16.【解析】本题考查函数的图象. 若函数的图像关于y轴对称,则a=0,,所以f(x)的单调减区间为.【备注】无17.(1)对任意的x1,x2∈[0,1],有-1≤x1+x2-1≤1,即|x1+x2-1|≤1.从而|f(x1)-f(x2)|=|(-x 1)-(-x2)|=|x1-x2||x1+x2-1|≤|x1-x2|,所以函数f(x )=x2-x,x∈[0,1]是“平缓函数”.(2)当|x1-x2|<时,由已知,得|f(x1)-f(x2)|≤|x1-x2|<;当|x1-x2|≥时,因为x1,x2∈[0,1],不妨设0≤x1<x2≤1,所以x2-x1≥.因为f(0)=f(1),所以|f(x1)-f(x2)|=|f(x 1)-f(0)+f(1)-f(x2)|≤|f(x1)-f(0)|+|f(1)-f (x2)|≤|x1-0|+|1-x2|=x1-x2+1≤-+1=.所以对任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤成立.【解析】无 【备注】无18.由条件可得{|2}A x x =>, (1)={|23}x x <≤,{|3}A B x x ⋃=≥-;(2) {|}C x x p =>,由可得2p ≥.【解析】本题考查函数的定义域与集合的运算.(1)先求出函数的定义域,再进行运算即可;(2)利用数轴进行分析即可得出结论.【备注】与不等式有关的集合运算或集合之间的关系问题通常可以借助数轴进行求解.19.U ={1,2,3,4,5,6,7,8} (1)S ∩T ={3} (2)S ∪T ={1,3,5,6}={2,4,7,8}【解析】本题主要考查集合的基本运算.(1)由交集的定义求解;(2)由并集与补集的定义求解. 【备注】无20.(1)任取x 1,x 2∈[1,+∞),且x 1<x 2,则f(x 1)-f(x 2)=-=.∵1≤x 1<x 2,∴x 1-x 2<0,(x 1+1)(x 2+1)>0, ∴f(x 1)-f(x 2)<0,即f(x 1)<f(x 2), ∴函数f(x)在区间[1,+∞)上是增函数. (2)由(1)知函数f(x)在区间[2,4]上是增函数, ∴f(x)max =f(4)==, f(x)min =f(2)==.【解析】无 【备注】无21.(1)f (1)=0,f (-1)=0;(2)f (-x )=f (x )+f (-1)=f (x )∴f (-x )=f (x ),所以函数是偶函数;(3)据题意可知,f(2)+f(x2-1/2)=f(2x2-1)≤0∴-1≤2x2-1<0或0<2x2-1≤1∴0≤x2<1/2或<x2≤1,所以不等式的解集为【解析】本题主要考查特殊函数的性质的判断与应用以及一元二次不等式的解法.(1)分别令x=1与x=—1即可求出结果;(2)利用函数奇偶性的定义即可证明;(3)根据题意与f(1)=0,f(-1)=0,原不等式可化为-1≤2x2-1<0或0<2x2-1≤1然后求解即可.【备注】无22.(1)设x1,x2是(-∞,0)上的任意两个实数,且x1<x2,则f (x1)-f(x2)=-.因为x1,x2∈(-∞,0),所以x1x2>0,又因为x1<x2,所以x2-x1>0,则>0.于是f(x1)-f(x2)>0,即f(x1)>f(x2).因此函数f(x )=在(-∞,0)上是减函数.(2)设x1,x2是R上的任意两个实数,且x1<x2,则x2-x1>0,而f(x2)-f(x1)=(+x2)-(+x1)=(x 2-x1)(+x2x1+)+(x2-x 1)=(x2-x1)(+x2x1++1)=(x2-x1)[(x2+)2++1].因为(x2+)2++1>0,x2-x1>0,所以f(x2)-f(x1)>0,即f(x2)>f(x1).因此函数f(x)=x3+x在R上是增函数.【解析】用定义证明函数f(x)在给定区间D上的单调性的一般步骤:①取值——任取x1,x2∈D,且x1<x2;②作差——f(x1)-f(x2);③变形——通过因式分解、配方、通分、有理化等方法,向有利于判断差值的符号的方向变形;④定号——判断f(x1)-f(x2)的正负;⑤下结论——指出函数f(x)在给定区间D上的单调性.【备注】无。
新课标高一数学必修1第一章集合与函数概念单元测试题

集合与函数概念单元测试题一、选择题(40)1.集合{,,}a b c 的真子集有 ( )A .6个B .7个C .8个D .9个2. 设集合{}|43A x x =-<<,{}|2B x x =≤,则A ∩B= ( )A .(4,3)-B .(4,2]-C .(,2]-∞D .(,3)-∞3.已知()5412-+=-x x x f ,则()x f 的表达式是( )A .x x 62+B .782++x xC .322-+x xD .1062-+x x 4.下列四个函数:①3y x =-;②211y x =+;③2210y x x =+-;④(0)1(0)x x y x x⎧-≤⎪=⎨->⎪⎩. 其中值域为R 的函数有 ( )A .1个B .2个C .3个D .4个5、已知函数212x y x ⎧+=⎨-⎩(0)(0)x x ≤>,使函数值为5的x 的值是( ) A .-2 B .2或52- C . 2或-2 D .2或-2或52- 6.下列函数中,定义域为[0,+∞)的函数是 ( )A .x y =B .22x y -=C .13+=x yD .2)1(-=x y7.若R y x ∈,,且)()()(y f x f y x f +=+,则函数)(x f ( )A . 0)0(=f 且)(x f 为奇函数B .0)0(=f 且)(x f 为偶函数C .)(x f 为增函数且为奇函数D .)(x f 为增函数且为偶函数8(A ) (B) (C ) (D)二、填空题(30)9.若函数 f (x )=(k-2)x 2+(k-1)x +3是偶函数,则f (x )的递减区间是10.若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A ∪B= .11.已知集合M={(x ,y )|x +y =2},N={(x ,y )|x -y =4},那么集合M ∩N = .12.函数()1,3,x f x x +⎧=⎨-+⎩ 1,1,x x ≤>则()()4f f = . 13.已知函数f(x)满足f(xy)=f(x)+f(y),且f(2)=p,f(3)=q ,那么f(36)= .14.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围是 .三、解答题15.(14)已知集合A={}71<≤x x ,B={x|2<x<10},C={x|x<a },全集为实数集R .(Ⅰ)求A ∪B ,(C R A)∩B ;(Ⅱ)如果A ∩C ≠φ,求a 的取值范围.16.(16)已知函数2()21f x x =-.(Ⅰ)用定义证明()f x 是偶函数;(Ⅱ)用定义证明()f x 在(,0]-∞上是减函数;(Ⅲ)作出函数()f x 的图像,并写出函数()f x 当[1,2]x ∈-时的最大值与最小值.。
人教版高一数学必修一第一章单元检测试题及参考答案

高一数学第一章集合与函数概念单元检测试题一、选择题:共12题每题5分共60分1.已知函数的图象如下图所示,则函数的图象为2.下列各组函数为相等函数的是A. B.C. D.==3.函数的定义域为若对于任意的当时,都有则称函数在上为非减函数.设函数的上为非减函数,且满足以下三个条件:①②③=则等于A. B. C. D.4.设函数,则的最小值为A. B.C. D.5.函数f(x)=x2-4x+6(x∈[1,5))的值域是A.(3,11]B.[2,11)C.[3,11)D.(2,11]6.若函数在区间上单调,则实数的取值范围为A. B.C. D.7.定义运算:a*b=,如1*2=1,则函数f(x)=2x*2-x的值域为A.RB.(0,+∞)C.(0,1]D.[1,+∞)8.已知集合E={x|2-x≥0},若F?E,则集合F可以是A.{x|x<1}B.{x|x>2}C.{x|x>3}D.{x|1<x<3}9.已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f()的x的取值范围是() A.(,) B.[,) C.(,) D.[,)10.某部队练习发射炮弹,炮弹的高度与时间(秒)的函数关系式是,则炮弹在发射几秒后最高呢?A. B. C. D.11.已知,且,则等于A. B. C. D.12.已知集合和集合,则两个集合间的关系是A. B. C. D.M,P互不包含二、填空题:共4题每题5分共20分13.已知函数f(x)=a﹣x2(1≤x≤2)与的图象上存在关于轴对称的点,则实数的取值范围是A. C.14.设集合M={x|0≤x≤2},N={y|0≤y≤2}.给出下列四个图,其中能构成从集合M到集合N 的函数关系的是.?15.给出下列二次函数,将其图象画在同一平面直角坐标系中,则图象的开口按从小到大的顺序排列为.?(1)f(x)=-x2;(2)f(x)=(x+5)2;(3)f(x)=x2-6;(4)f(x)=-5(x-8)2+9.16.若函数的图像关于y轴对称,则的单调减区间为.三、解答题:共6题共70分17.(本题10分)如果对函数f(x)定义域内任意的x1,x2都有|f(x1)-f(x2)|≤|x1-x2|成立,就称函数f(x)是定义域上的“平缓函数”.(1)判断函数f(x)=x2-x,x∈[0,1]是否为“平缓函数”;(2)若函数f(x)是闭区间[0,1]上的“平缓函数”,且f(0)=f(1),证明:对任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤成立.(注:可参考绝对值的基本性质①|ab|≤|a||b|,②|a+b|≤|a|+|b|)18.(本题12分)记函数的定义域为集合,集合.(1)求和;(2)若,求实数的取值范围. 19.(本题12分)设全集U={x|0<x<9,且x∈Z},集合S={1,3,5},T={3,6},求:(1)S∩T;(2).20.(本题12分)已知函数f(x)=.(1)用定义证明f(x)在区间[1,+∞)上是增函数;(2)求该函数在区间[2,4]上的最大值与最小值.21.(本题12分)定义在非零实数集上的函数对任意非零实数满足:,且当时.(Ⅰ)求及的值;(Ⅱ)求证:是偶函数;(Ⅲ)解不等式:.22.(本题12分)(1)证明:函数f(x)=在(-∞,0)上是减函数;(2)证明:函数f(x)=x3+x在R上是增函数.参考答案1.B【解析】本试题主要考查函数的图象.根据题意,由于函数图象可知,函数在y轴右侧图象在x 轴上方,在y轴左侧的图象在x轴的下方,而函数在x>0时图象保持不变,因此排除C,D,对于选项A,由于在时偶函数,故在y轴左侧的图象与y轴右侧的图象关于y轴对称,故选B.【备注】无2.C【解析】本题主要考查相等函数、函数的定义域、值域与对应关系.A.因为这两个函数的值域不同,所以这两个函数不是相等函数;B.这两个函数的定义域不同,所以这两个函数不是相等函数;C.这两个函数的定义域、值域与对应关系均相同,所以这两个函数为相等函数;D.这两个函数的定义域不同,所以这两个函数不是相等函数.【备注】无3.D【解析】本题主要考查新定义问题、函数的性质及其综合应用.由题意,令x=0,由=可得由可得令则=同理=====令则==同理====.非减函数的性质:当时,都有.因为所以所以=. 【备注】无4.A【解析】本题主要考查分段函数的最值问题.由题意,函数的图象如图所示:红色图象即为所求解的函数的图象,可知最小值为0.【备注】无5.B【解析】f(x)=x2-4x+6=(x-2)2+2.∵f(x)图象的对称轴是直线x=2,∴f(x)在[1,2]上单调递减,在(2,5)上单调递增,∴f(x)的值域是[2,11).故选B.【备注】无6.C【解析】本题主要考查二次函数.依题意,函数在区间上单调,则函数的对称轴或,得或,故选C.【备注】无7.C【解析】本题主要考查在新型定义的前提下函数值域的求解.根据题目定义知f(x)=2x*2-x=,结合图象知其值域为(0,1].故选C.【备注】无8.A【解析】由题意知E={x|2-x≥0}={x|x≤2},F?E,观察选项知应选A.【备注】无9.A【解析】偶函数f(x)在区间[0,+∞)上单调递增,所以函数f(x)在区间(-∞,0]上单调递减.由于f(x)是偶函数,所以f(-x)=f(x),则f(-)=f().由f(2x-1)<f()得①或②,解①得≤x<,解②得<x<.综上可得<x<,故x的取值范围是(,).【备注】无10.C【解析】本题主要考查二次函数.依题意,根据二次函数得性质,函数的开口向下,对称轴为,故炮弹在发射后最高,故选C.【备注】无11.B【解析】本题主要考查函数的解析式与求值.因为,设,则,所以,因为,所以,解得,故选B.【备注】无12.D【解析】无【备注】无13.D【解析】本题主要考查二次函数的图像与性质,考查了逻辑推理能力与计算能力.因为函数f(x)=a ﹣x2(1≤x≤2)与的图象上存在关于轴对称的点,所以函数f(x)=a﹣x2(1≤x≤2)与的图象上存在交点,所以有解,令,则,求解可得,故答案为D. 【备注】无14.④【解析】图①中函数的定义域是[0,1];图②中函数的定义域是[-1,2];图③中对任意的x∈(0,2],其对应的y值不唯一.故①②③均不能构成从集合M到集合N的函数,图④满足题意.【备注】无15.(4)(3)(2)(1)【解析】因为二次函数y=ax2+bx+c(a≠0)的图象在同一平面直角坐标系中|a|越小,图象开口越大,又|-|<||<||<|-5|,所以图象开口按从小到大的顺序排列为(4)(3)(2)(1).【备注】无16.【解析】本题考查函数的图象.若函数的图像关于y轴对称,则a=0,,所以f(x)的单调减区间为.【备注】无17.(1)对任意的x1,x2∈[0,1],有-1≤x1+x2-1≤1,即|x1+x2-1|≤1.从而|f(x1)-f(x2)|=|(-x1)-(-x2)|=|x1-x2||x1+x2-1|≤|x1-x2|,所以函数f(x)=x2-x,x∈[0,1]是“平缓函数”.(2)当|x1-x2|<时,由已知,得|f(x1)-f(x2)|≤|x1-x2|<;当|x1-x2|≥时,因为x1,x2∈[0,1],不妨设0≤x1<x2≤1,所以x2-x1≥.因为f(0)=f(1),所以|f(x1)-f(x2)|=|f(x1)-f(0)+f(1)-f(x2)|≤|f(x1)-f(0)|+|f(1)-f(x2)|≤|x1-0|+|1-x2|=x1-x2+1≤-+1=.所以对任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤成立.【解析】无【备注】无18.由条件可得{|2}A x x =>, (1)={|23}x x <≤,{|3}A B x x ⋃=≥-;(2){|}C x x p =>,由可得2p ≥.【解析】本题考查函数的定义域与集合的运算.(1)先求出函数的定义域,再进行运算即可;(2)利用数轴进行分析即可得出结论.【备注】与不等式有关的集合运算或集合之间的关系问题通常可以借助数轴进行求解. 19.U ={1,2,3,4,5,6,7,8} (1)S ∩T ={3} (2)S ∪T ={1,3,5,6}={2,4,7,8}【解析】本题主要考查集合的基本运算.(1)由交集的定义求解;(2)由并集与补集的定义求解. 【备注】无20.(1)任取x 1,x 2∈[1,+∞),且x 1<x 2,则 f(x 1)-f(x 2)=-=.∵1≤x 1<x 2,∴x 1-x 2<0,(x 1+1)(x 2+1)>0, ∴f(x 1)-f(x 2)<0,即f(x 1)<f(x 2), ∴函数f(x)在区间[1,+∞)上是增函数. (2)由(1)知函数f(x)在区间[2,4]上是增函数, ∴f(x)max =f(4)==, f(x)min =f(2)==.【解析】无 【备注】无 21.(1)f (1)=0,f (-1)=0;(2)f (-x )=f (x )+f (-1)=f (x )∴f (-x )=f (x ),所以函数是偶函数;(3)据题意可知,f (2)+f (x 2-1/2)=f (2x 2-1)≤0∴-1≤2x 2-1<0或0<2x 2-1≤1∴0≤x 2<1/2或<x 2≤1,所以不等式的解集为【解析】本题主要考查特殊函数的性质的判断与应用以及一元二次不等式的解法.(1)分别令x =1与x=—1即可求出结果;(2)利用函数奇偶性的定义即可证明;(3)根据题意与f (1)=0,f (-1)=0,原不等式可化为-1≤2x 2-1<0或0<2x 2-1≤1然后求解即可. 【备注】无22.(1)设x 1,x 2是(-∞,0)上的任意两个实数,且x 1<x 2,则f (x 1)-f (x 2)=-.因为x1,x2∈(-∞,0),所以x1x2>0,又因为x1<x2,所以x2-x1>0,则>0.于是f(x1)-f(x2)>0,即f(x1)>f(x2).因此函数f(x)=在(-∞,0)上是减函数.(2)设x1,x2是R上的任意两个实数,且x1<x2,则x2-x1>0,而f(x2)-f(x1)=(+x2)-(+x1)=(x2-x1)(+x2x1+)+(x2-x1)=(x2-x1)(+x2x1++1)=(x2-x1)[(x2+)2++1].因为(x2+)2++1>0,x2-x1>0,所以f(x2)-f(x1)>0,即f(x2)>f(x1).因此函数f(x)=x3+x在R上是增函数.【解析】用定义证明函数f(x)在给定区间D上的单调性的一般步骤:①取值——任取x1,x2∈D,且x1<x2;②作差——f(x1)-f(x2);③变形——通过因式分解、配方、通分、有理化等方法,向有利于判断差值的符号的方向变形;④定号——判断f(x1)-f(x2)的正负;⑤下结论——指出函数f(x)在给定区间D上的单调性.【备注】无。
高一数学必修一集合与函数的概念单元测试题附答案解析

高一数学必修一 集合与函数的概念单元测试 附答案解析(时间:120分钟 满分:150分)一、选择题(本大题共12个小题.每小题5分.共60分.在每小题给出的四个选项中.只有一项是符合题目要求的)1.设集合M ={x |x 2+2x =0.x ∈R }.N ={x |x 2-2x =0.x ∈R }.则M ∪N =( ) A .{0} B .{0,2} C .{-2,0} D .{-2,0,2}2.设f :x →|x |是集合A 到集合B 的映射.若A ={-2,0,2}.则A ∩B =( ) A .{0} B .{2} C .{0,2} D .{-2,0}3.f (x )是定义在R 上的奇函数.f (-3)=2.则下列各点在函数f (x )图象上的是( ) A .(3.-2) B .(3,2) C .(-3.-2) D .(2.-3)4.已知集合A ={0,1,2}.则集合B ={x -y |x ∈A .y ∈A }中元素的个数是( ) A .1 B .3 C .5 D .95.若函数f (x )满足f (3x +2)=9x +8.则f (x )的解析式是( )A .f (x )=9x +8B .f (x )=3x +2C .f (x )=-3x -4D .f (x )=3x +2或f (x )=-3x -46.设f (x )=⎩⎨⎧x +3 x >10,f x +5 x ≤10,则f (5)的值为( )A .16B .18C .21D .247.设T ={(x .y )|ax +y -3=0}.S ={(x .y )|x -y -b =0}.若S ∩T ={(2,1)}.则a .b 的值为( )A .a =1.b =-1B .a =-1.b =1C .a =1.b =1D .a =-1.b =-18.已知函数f (x )的定义域为(-1,0).则函数f (2x +1)的定义域为( ) A .(-1,1) B.⎝ ⎛⎭⎪⎫-1,-12 C .(-1,0) D.⎝ ⎛⎭⎪⎫12,19.已知A ={0,1}.B ={-1,0,1}.f 是从A 到B 映射的对应关系.则满足f (0)>f (1)的映射有( ) A .3个 B .4个 C .5个D .6个10.定义在R 上的偶函数f (x )满足:对任意的x 1.x 2∈(-∞.0](x 1≠x 2).有(x 2-x 1)[f (x 2)-f (x 1)]>0.则当n ∈N *时.有( )A .f (-n )<f (n -1)<f (n +1)B .f (n -1)<f (-n )<f (n +1)C .f (n +1)<f (-n )<f (n -1)D .f (n +1)<f (n -1)<f (-n ) 11.函数f (x )是定义在R 上的奇函数.下列说法:①f (0)=0; ②若f (x )在[0.+∞)上有最小值为-1.则f (x )在(-∞.0]上有最大值为1;③若f (x )在[1.+∞)上为增函数.则f (x )在(-∞.-1]上为减函数;④若x >0时.f (x )=x 2-2x .则x <0时.f (x )=-x 2-2x .其中正确说法的个数是( )A .1个B .2个C .3个D .4个12.f (x )满足对任意的实数a .b 都有f (a +b )=f (a )·f (b )且f (1)=2.则f 2f 1+f 4f 3+f 6f 5+…+f 2014f 2013=( )A .1006B .2014C .2012D .1007二、填空题(本大题共4小题.每小题5分.共20分.把答案填在题中横线上)13.函数y =x +1x 的定义域为________.14.f (x )=⎩⎨⎧x 2+1x ≤0,-2x x >0,若f (x )=10.则x =________.15.若函数f (x )=(x +a )(bx +2a )(常数a .b ∈R )是偶函数.且它的值域为(-∞.4].则该函数的解析式f (x )=________.16.在一定范围内.某种产品的购买量y 吨与单价x 元之间满足一次函数关系.如果购买1000吨.每吨为800元.购买2000吨.每吨为700元.那么客户购买400吨.单价应该是________元.三、解答题(本大题共6小题.共70分.解答应写出必要的文字说明、证明过程或演算步骤) 17.(本小题满分10分)已知集合A ={x |2≤x ≤8}.B ={x |1<x <6}.C ={x |x >a }.U =R . (1)求A ∪B .(∁U A )∩B ;(2)若A ∩C ≠∅.求a 的取值范围.18.(本小题满分12分)设函数f (x )=1+x 21-x 2.(1)求f (x )的定义域; (2)判断f (x )的奇偶性; (3)求证:f ⎝ ⎛⎭⎪⎫1x +f (x )=0.19.(本小题满分12分)已知y =f (x )是定义在R 上的偶函数.当x ≥0时.f (x )=x 2-2x . (1)求当x <0时.f (x )的解析式;(2)作出函数f (x )的图象.并指出其单调区间.20.(本小题满分12分)已知函数f (x )=2x +1x +1. (1)判断函数在区间[1.+∞)上的单调性.并用定义证明你的结论. (2)求该函数在区间[1,4]上的最大值与最小值.21.(本小题满分12分)已知函数f (x )的定义域为(0.+∞).且f (x )为增函数.f (x ·y )=f (x )+f (y ).(1)求证:f ⎝ ⎛⎭⎪⎫x y =f (x )-f (y );(2)若f(3)=1.且f(a)>f(a-1)+2.求a的取值范围.22.(本小题满分12分)某商场经销一批进价为每件30元的商品.在市场试销中发现.此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系:x 30404550y 6030150(1)在所给的坐标图纸中.根据表中提供的数据.描出实数对(x.y)的对应点.并确定y与x的一个函数关系式.(2)设经营此商品的日销售利润为P元.根据上述关系.写出P关于x的函数关系式.并指出销售单价x为多少元时.才能获得最大日销售利润?1.解析 M ={x |x (x +2)=0..x ∈R }={0.-2}.N ={x |x (x -2)=0.x ∈R }={0,2}.所以M ∪N ={-2,0,2}.答案 D2. 解析 依题意.得B ={0,2}.∴A ∩B ={0,2}.答案 C3. 解析 ∵f (x )是奇函数.∴f (-3)=-f (3).又f (-3)=2.∴f (3)=-2.∴点(3.-2)在函数f (x )的图象上.答案 A4. 解析 逐个列举可得.x =0.y =0,1,2时.x -y =0.-1.-2;x =1.y =0,1,2时.x -y =1,0.-1;x =2.y =0,1,2时.x -y =2,1,0.根据集合中元素的互异性可知集合B 的元素为-2.-1,0,1,2.共5个.答案 C5. 解析 ∵f (3x +2)=9x +8=3(3x +2)+2.∴f (x )=3x +2.答案 B6. 解析 f (5)=f (5+5)=f (10)=f (15)=15+3=18.答案 B7. 解析 依题意可得方程组⎩⎨⎧2a +1-3=0,2-1-b =0,⇒⎩⎨⎧a =1,b =1.答案 C8. 解析 由-1<2x +1<0.解得-1<x <-12.故函数f (2x +1)的定义域为⎝⎛⎭⎪⎫-1,-12.答案 B9. 解析 当f (0)=1时.f (1)的值为0或-1都能满足f (0)>f (1);当f (0)=0时.只有f (1)=-1满足f (0)>f (1);当f (0)=-1时.没有f (1)的值满足f (0)>f (1).故有3个.答案 A10.解析 由题设知.f (x )在(-∞.0]上是增函数.又f (x )为偶函数.∴f (x )在[0.+∞)上为减函数. ∴f (n +1)<f (n )<f (n -1). 又f (-n )=f (n ).∴f (n +1)<f (-n )<f (n -1). 答案 C11. 解析 ①f (0)=0正确;②也正确;③不正确.奇函数在对称区间上具有相同的单调性;④正确. 答案 C12. 解析 因为对任意的实数a .b 都有f (a +b )=f (a )·f (b )且f (1)=2.由f (2)=f (1)·f (1).得f (2)f (1)=f (1)=2. 由f (4)=f (3)·f (1).得f (4)f (3)=f (1)=2. ……由f (2014)=f (2013)·f (1). 得f (2014)f (2013)=f (1)=2.∴f (2)f (1)+f (4)f (3)+f (6)f (5)+…+f (2014)f (2013)=1007×2=2014. 答案 B13. 解析 由⎩⎨⎧x +1≥1,x ≠0得函数的定义域为{x |x ≥-1.且x ≠0}.答案 {x |x ≥-1.且x ≠0}14. 解析 当x ≤0时.x 2+1=10.∴x 2=9.∴x =-3.当x >0时.-2x =10.x =-5(不合题意.舍去). ∴x =-3. 答案 -315. 解析 f (x )=(x +a )(bx +2a )=bx 2+(2a +ab )x +2a 2为偶函数.则2a +ab =0.∴a =0.或b =-2.又f (x )的值域为(-∞.4].∴a ≠0.b =-2.∴2a 2=4. ∴f (x )=-2x 2+4. 答案 -2x 2+416. 解析 设一次函数y =ax +b (a ≠0).把⎩⎨⎧x =800,y =1000,和⎩⎨⎧x =700,y =2000,代入求得⎩⎨⎧a =-10,b =9000.∴y =-10x +9000.于是当y =400时.x =860.答案 86017. 解 (1)A ∪B ={x |2≤x ≤8}∪{x |1<x <6}={x |1<x ≤8}. ∁U A ={x |x <2.或x >8}. ∴(∁U A )∩B ={x |1<x <2}. (2)∵A ∩C ≠∅.∴a <8.18. 解 (1)由解析式知.函数应满足1-x 2≠0.即x ≠±1.∴函数f (x )的定义域为{x ∈R |x ≠±1}. (2)由(1)知定义域关于原点对称. f (-x )=1+(-x )21-(-x )2=1+x 21-x 2=f (x ).∴f (x )为偶函数.(3)证明:∵f ⎝ ⎛⎭⎪⎫1x =1+⎝ ⎛⎭⎪⎫1x 21-⎝ ⎛⎭⎪⎫1x 2=x 2+1x 2-1.f (x )=1+x 21-x 2.∴f ⎝ ⎛⎭⎪⎫1x +f (x )=x 2+1x 2-1+1+x 21-x 2=x 2+1x 2-1-x 2+1x 2-1=0. 19. 解 (1)当x <0时.-x >0.∴f (-x )=(-x )2-2(-x )=x 2+2x . 又f (x )是定义在R 上的偶函数. ∴f (-x )=f (x ). ∴当x <0时.f (x )=x 2+2x .(2)由(1)知.f (x )=⎩⎨⎧x 2-2x (x ≥0),x 2+2x (x <0).作出f (x )的图象如图所示:由图得函数f (x )的递减区间是(-∞.-1].[0,1].f (x )的递增区间是[-1,0].[1.+∞).20. 解 (1)函数f (x )在[1.+∞)上是增函数.证明如下:任取x 1.x 2∈[1.+∞).且x 1<x 2.f (x 1)-f (x 2)=2x 1+1x 1+1-2x 2+1x 2+1=x 1-x 2(x 1+1)(x 2+1). ∵x 1-x 2<0.(x 1+1)(x 2+1)>0. 所以f (x 1)-f (x 2)<0.即f (x 1)<f (x 2). 所以函数f (x )在[1.+∞)上是增函数.(2)由(1)知函数f (x )在[1,4]上是增函数.最大值f (4)=95.最小值f (1)=32.21. 解 (1)证明:∵f (x )=f ⎝ ⎛⎭⎪⎫xy·y =f ⎝ ⎛⎭⎪⎫x y +f (y ).(y ≠0)∴f ⎝ ⎛⎭⎪⎫x y =f (x )-f (y ).(2)∵f (3)=1.∴f (9)=f (3·3)=f (3)+f (3)=2. ∴f (a )>f (a -1)+2=f (a -1)+f (9)=f [9(a -1)].又f (x )在定义域(0.+∞)上为增函数.∴⎩⎨⎧a >0,a -1>0,a >9(a -1),∴1<a <98.22. 解 (1)由题表作出(30,60).(40,30).(45,15).(50,0)的对应点.它们近似地分布在一条直线上.如图所示.设它们共线于直线y =kx +b .则⎩⎨⎧50k +b =0,45k +b =15,⇒⎩⎨⎧k =-3,b =150.∴y =-3x +150(0≤x ≤50.且x ∈N *).经检验(30,60).(40,30)也在此直线上. ∴所求函数解析式为y =-3x +150(0≤x ≤50.且x ∈N *).(2)依题意P =y (x -30)=(-3x +150)(x -30)=-3(x -40)2+300.∴当x =40时.P 有最大值300.故销售单价为40元时.才能获得最大日销售利润.。
高一数学必修一集合与函数概念单元测试题

高一数学必修一集合与函数概念单元测试题班级 姓名 得分一、选择题(每小题只有唯一正确的答案,每小题5分,共60分。
)1.集合},{b a 的子集有 ( )A .2个B .3个C .4个D .5个2.设集合{}|43A x x =-<<,{}|2B x x =≤,则A B =I ( )A .(4,3)-B .(4,2]-C .(,2]-∞D .(,3)-∞3.已知()5412-+=-x x x f ,则()x f 的表达式是( )A .x x 62+B .782++x xC .322-+x xD .1062-+x x4.下列对应关系:①{1,4,9},{3,2,1,1,2,3},A B ==---f :x x →的平方根②,,A R B R ==f :x x →的倒数; ③,,A R B R ==f :22x x →-;④{}{}1,0,1,1,0,1,A B f =-=-:A 中的数平方。
其中是A 到B 的映射的是 ( )A .①③B .②④C .③④D .②③5.下列四个函数:①3y x =-;②211y x =+;③2210y x x =+-;④(0)1(0)x x y x x⎧-≤⎪=⎨->⎪⎩. 其中值域为R 的函数有 ( )A .1个B .2个C .3个D .4个6.已知函数212x y x⎧+=⎨-⎩ (0)(0)x x ≤>,使函数值为5的x 的值是( ) A .-2 B .2或52- C . 2或-2 D .2或-2或52- 7.下列函数中,定义域为[0,∞)的函数是 ( )A .x y =B .22x y -=C .13+=x yD .2)1(-=x y8.若R y x ∈,,且)()()(y f x f y x f +=+,则函数)(x f ( )A . 0)0(=f 且)(x f 为奇函数B .0)0(=f 且)(x f 为偶函数C .)(x f 为增函数且为奇函数D .)(x f 为增函数且为偶函数9)A10.已知函数f (x )的定义域为(0,1),则函数f (2x +1)的定义域为( )A .(0,1)B .(0,2)C .(0,3) D.⎪⎭⎫ ⎝⎛-0,21 11.函数y =x 2-2x +3,-1≤x ≤2的值域是( )A .RB .[]6,3C . [)+∞,2D .[]6,212.设()x f 是R 上的偶函数,且在[0,+∞)上单调递增,则()()()2,3,--f f f π的大小顺序是( )A .()()()32f f f π->>-B .()()()23f f f π->->C . ()()()23f f f π->>-D . ()()()32f f f π>->-二、填空题(本大题共4小题,每小题5分,共20分)13.若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B =I .14.函数()1,3,x f x x +⎧=⎨-+⎩ 1,1,x x ≤>则()()4f f = . 15.某班50名学生参加跳远、铅球两项测试,成绩及格人数分别为40人和31人,两项测试均不及格的人数是4人,两项测试都及格的有 人.16.已知函数()x f 满足()()()y f x f xy f +=,且()()33,22=-=f f ,那么()=36f .三、解答题(本大题6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)17.(10分)已知方程20x mx n ++=的两个不相等实根为βα,.集合},{βα=A , =B {2,4,5,6},=C {1,2,3,4},A ∩C =A ,A ∩B =φ,求,m n 的值?18.(12分)已知集合A={}71<≤x x ,B={x|2<x<10},C={x|x<a },全集为实数集R .(1)求A ∪B ,(C R A)∩B ; (2)如果A ∩C ≠φ,求a 的取值范围.。
高一数学必修1集合与函数概念单元测试题

“显示文本”不能横跨多行!新课标数学必修1第一章集合与函数概念测试题时间:2021.03.04 创作:欧阳地一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分)。
1.用描述法表示一元二次方程的全体,应是()A.{x|ax2+bx+c=0,a,b,c∈R}B.{x|ax2+bx+c=0,a,b,c∈R,且a≠0}C.{ax2+bx+c=0|a,b,c∈R}D.{ax2+bx+c=0|a,b,c∈R,且a≠0}2.图中阴影部分所表示的集合是()A.B∩[C U(A∪C)]B.(A∪B) ∪(B∪C)C.(A∪C)∩(C U B)D.[C U(A∩C)]∪B3.设集合P={立方后等于自身的数},那么集合P的真子集个数是()A.3 B.4 C.7 4.设P={质数},Q={偶数},则P∩Q等于()A .B .2C .{2} 5.设函数x y 111+=的定义域为M ,值域为N ,那么()A .M={x |x ≠0},N={y |y ≠0}B .M={x |x <0且x ≠-1,或x >0},N={y |y <0,或0<y <1,或y >1}C .M={x |x ≠0},N={y |y ∈R }D .M={x |x <-1,或-1<x <0,或x >0=,N={y |y ≠0}6.已知A 、B 两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离x 表示为时间t (小时)的函数表达式是( )A .x =60tB .x =60t +50tC .x =⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD .x =⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t7.已知g (x )=1-2x,f [g (x )]=)0(122≠-x x x ,则f (21)等于( ) A .1B .3C .15D .308.函数y=x x ++-1912是( )A .奇函数B .偶函数C .既是奇函数又是偶函数 D .非奇非偶数9.下列四个命题(1)f(x)=x x -+-12有意义;(2)函数是其定义域到值域的映射;(3)函数y=2x(x N ∈)的图象是一直线;(4)函数y=⎪⎩⎪⎨⎧<-≥0,0,22x x x x 的图象是抛物线,其中正确的命题个数是( ) A .1 B .2 C .3 D .410.设函数f (x )是(-∞,+∞)上的减函数,又若a ∈R ,则 ( )A .f (a )>f (2a )B .f (a 2)<f (a)C .f (a 2+a )<f (a )D .f (a 2+1)<f (a )二、填空题:请把答案填在题中横线上(每小题6分,共24分).11.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围是.12.函数f (x )的定义域为[a ,b ],且b >-a >0,则F (x )= f (x)-f (-x)的定义域是.13.若函数 f (x )=(K-2)x 2+(K-1)x +3是偶函数,则f (x )的递减区间是.14.已知x ∈[0,1],则函数y =x x --+12的值域是.三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).15.(12分)已知,全集U={x |-5≤x ≤3},A={x |-5≤x <-1},B={x |-1≤x <1},求C U A ,C U B ,(C U A)∩(C U B),(C U A)∪(C U B),C U (A ∩B),C U (A ∪B),并指出其中相关的集合.16.(12分)集合A={(x,y )022=+-+y mx x },集合B={(x,y )01=+-y x ,且02≤≤x },又A φ≠⋂B ,求实数m 的取值范围.17.(12分)已知f (x )=⎪⎩⎪⎨⎧+++-333322x x x x ),1()1,(+∞∈-∞∈x x ,求f [f (0)]的值.18.(12分)如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框架,若半圆半径为x ,求此框架围成的面积y 与x 的函数式y =f (x ),并写出它的定义域.19.(14分)已知f (x)是R 上的偶函数,且在(0,+ ∞)上单调递增,并且 f (x)<0对一切R x ∈成立,试判断)(1x f -在(-∞,0)上的单调性,并证明你的结论. 20.(14分)指出函数x x x f 1)(+=在(][)0,1,1,--∞-上的单调性,并证明之. 参考答案(5)一、DACCB DCBA D二、11.{211≤≤-k k }; 12.[a ,-a ]; 13.[0,+∞]; 14.[3,12-] ;三、15. 解: C U A={x |-1≤x ≤3};C U B={x |-5≤x <-1或1≤x ≤3};(C U A)∩(C U B)= {x |1≤x ≤3};(C U A)∪(C U B)= {x |-5≤x ≤3}=U ;C U (A ∩B)=U ;C U (A ∪B)= {x |1≤x ≤3}.相等集合有(C U A)∩(C U B)= C U (A ∪B);(C U A)∪(C U B)= C U (A ∩B).16. 解:由A ⋂B φ≠知方程组,,2001202y x y x y mx x 消去内有解在≤≤⎩⎨⎧=+-+-+得x 2+(m -1)x =0 在0≤x 2≤内有解, 04)1(2≥--=∆m 即m ≥3或m ≤-1.若m ≥3,则x 1+x 2=1-m <0,x 1x 2=1,所以方程只有负根. 若m ≤-1,x 1+x 2=1-m >0,x 1x 2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即至少有一根在[0,2]内.因此{m ∞-<m ≤-1}.17.解: ∵ 0∈(-1,∞), ∴f (0)=32,又 32>1, ∴f (32)=(32)3+(32)-3=2+21=25,即f [f (0)]=25.18.解:AB=2x , CD =πx ,于是AD=221xx π--, 因此,y =2x ·221x x π--+22x π,即y =-lx x ++224π. 由⎪⎩⎪⎨⎧>-->022102x x x π,得0<x <,21+π函数的定义域为(0,21+π).19.解:设x 1<x 2<0, 则-x 1 > -x 2 >0, ∴f (-x 1)>f (-x 2),∵f(x )为偶函数,∴f (x 1)>f (x 2) 又0)()()()()(1)(1)(x f 1(x) f 11221122>-=-=⎥⎦⎤⎢⎣⎡---x f x f x f x f x f x f(∵f (x 1)<0,f (x 2)<0)∴,)(x f 1)(x f 121->- ∴(x) f 1-是(∞,0)上的单调递减函数.20.解:任取x 1,x 2∈(]1,-∞-且x 1<x 22112112212121111)()(x x x x x x x x x x x f x f -=-⎪⎪⎭⎫⎝⎛+-⎪⎪⎭⎫ ⎝⎛+=--由x 1<x 2≤—1知x 1x 2>1, ∴01121>-x x , 即)()(12x f x f >∴f(x)在(]1,-∞-上是增函数;当1≤x 1< x 2<0时,有0< x 1x 2<1,得01121<-x x ∴)()(21x f x f >∴f(x)在[)0,1-上是减函数. 再利用奇偶性,给出),1(],1,0(+∞单调性,证明略.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章集合与函数概念测试题
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案
的代号填在题后的括号内(每小题5分,共50分)。
1.用描述法表示一元二次方程的全体,应是
( )
A .{x |ax 2+bx +c =0,a ,b ,c ∈R }
B .{x |ax 2+bx +c =0,a ,b ,c ∈R ,且a ≠0}
C .{ax 2+bx +c =0|a ,b ,c ∈R }
D .{ax 2+bx +c =0|a ,b ,c ∈R ,且a ≠0}
2.图中阴影部分所表示的集合是( )
A.B ∩[C U (A ∪C)]
B.(A ∪B) ∪(B ∪C)
C.(A ∪C)∩(C U B)
D.[C U (A ∩C)]∪B
3.设集合P={立方后等于自身的数},那么集合P 的真子集个数是
( )
A .3
B .4
C .7
D .8
4.设P={质数},Q={偶数},则P ∩Q 等于
( )
A .
B .2
C .{2}
D .N 5.设函数x y 111
+=的定义域为M ,值域为N ,那么
( )
A .M={x |x ≠0},N={y |y ≠0}
B .M={x |x <0且x ≠-1,或x >0},N={y |y <0,或0<y <1,或y >1}
C .M={x |x ≠0},N={y |y ∈R }
D .M={x |x <-1,或-1<x <0,或x >0=,N={y |y ≠0}
6.已知A 、B 两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,
在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离x 表示为时间t (小时)的函数表达式是
( ) A .x =60t B .x =60t +50t
C .x =⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t t
D .x =⎪
⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t 7.已知g (x )=1-2x ,f [g (x )]=)0(122
≠-x x
x ,则f (21)等于 ( )
A .1
B .3
C .15
D .30 8.函数y=x
x ++-1912是( ) A .奇函数 B .偶函数 C .既是奇函数又是偶函数 D .非奇非偶数
9.下列四个命题
(1)f(x)=x x -+-12有意义;
(2)函数是其定义域到值域的映射;
(3)函数y=2x(x N ∈)的图象是一直线;
(4)函数y=⎪⎩⎪⎨⎧<-≥0
,0,22x x x x 的图象是抛物线,其中正确的命题个数是 ( )
A .1
B .2
C .3
D .4
10.设函数f (x )是(-∞,+∞)上的减函数,又若a ∈R ,则
( )
A .f (a )>f (2a )
B .f (a 2)<f (a)
C .f (a 2+a )<f (a )
D .f (a 2+1)<f (a )
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范
围是 .
12.函数f (x )的定义域为[a ,b ],且b >-a >0,则F (x )= f (x)-f (-x)的定义域是 .
13.若函数 f (x )=(K-2)x 2+(K-1)x +3是偶函数,则f (x )的递减区间是 .
14.已知x ∈[0,1],则函数y =x x --+12的值域是 .
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知,全集U={x |-5≤x ≤3},
A={x |-5≤x <-1},B={x |-1≤x <1},求C U A ,
C U B ,(C U A)∩(C U B),(C U A)∪(C U B),
C U (A ∩B),C U (A ∪B),并指出其中相关的集合.
16.(12分)集合A={(x,y )022=+-+y mx x },集合B={(x,y )01=+-y x ,且
02≤≤x },又A φ≠⋂B ,求实数m 的取值范围.
17.(12分)已知f (x )=⎪⎩⎪⎨⎧+++-333322x
x x x ),1()1,(+∞∈-∞∈x x ,求f [f (0)]的值.
18.(12分)如图,用长为1的铁丝弯成下部为矩形,上部为半圆形的框
架,若半圆半径为x ,求此框架围成的面积y 与x 的函数式y =f (x ),
并写出它的定义域.
19.(14分)已知f (x)是R 上的偶函数,且在(0,+ ∞)上单调递增,并且f (x)<0对一切R
x ∈成立,试判断)(1x f -
在(-∞,0)上的单调性,并证明你的结论.
20.(14分)指出函数x
x x f 1)(+
=在(][)0,1,1,--∞-上的单调性,并证明之.
参考答案(5)
一、DACCB DCBA D
二、11.{2
11≤≤-k k }; 12.[a ,-a ]; 13.[0,+∞]; 14.[3,12-] ; 三、15. 解: C U A={x |-1≤x ≤3};C U B={x |-5≤x <-1或1≤x ≤3};
(C U A)∩(C U B)= {x |1≤x ≤3};(C U A)∪(C U B)= {x |-5≤x ≤3}=U ;
C U (A ∩B)=U ;C U (A ∪B)= {x |1≤x ≤3}.
相等集合有(C U A)∩(C U B)= C U (A ∪B);(C U A)∪(C U B)= C U (A ∩B).
16. 解:由A ⋂B φ≠知方程组,,200
1202y x y x y mx x 消去内有解在≤≤⎩⎨⎧=+-+-+
得x 2+(m -1)x =0 在0≤x 2≤内有解, 04)1(2≥--=∆m 即m ≥3或m ≤-1. 若m ≥3,则x 1+x 2=1-m <0,x 1x 2=1,所以方程只有负根.
若m ≤-1,x 1+x 2=1-m >0,x 1x 2=1,所以方程有两正根,且两根均为1或两根一个大于1,一个小于1,即
至少有一根在[0,2]内.
因此{m ∞-<m ≤-1}.
17.解: ∵ 0∈(-1,∞), ∴f (0)=32,又 32>1,
∴ f (32)=(32)3+(32)-3=2+21=25,即f [f (0)]=2
5. 18.解:AB=2x , CD =πx ,于是AD=221x x π--, 因此,y =2x · 2
21x x π--+22
x π, 即y =-lx x ++224
π. 由⎪⎩
⎪⎨⎧>-->022102x x x π,得0<x <,21+π 函数的定义域为(0,2
1+π). 19.解:设x 1<x 2<0, 则 - x 1 > - x 2 >0, ∴f (-x 1)>f (-x 2), ∵f (x )为偶函数, ∴f (x 1)>f (x 2) 又0)
()()()()(1)(1)(x f 1(x) f 11221122>-=-=⎥⎦⎤⎢⎣⎡---x f x f x f x f x f x f
(∵f (x 1)<0,f (x 2)<0)∴,)
(x f 1)(x f 121->- ∴(x)
f 1-是(∞,0)上的单调递减函数. 20.解:任取x 1,x 2∈(]1,-∞- 且x 1<x 2 2112112212121111)()(x x x x x x x x x x x f x f -=-⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+=--
由x 1<x 2≤—1知x 1x 2>1, ∴0112
1>-x x , 即)()(12x f x f > ∴f(x)在(]1,-∞-上是增函数;当1≤x 1< x 2<0时,有0< x 1x 2<1,得0112
1<-x x ∴)()(21x f x f >∴f(x)在[)0,1-上是减函数. 再利用奇偶性,给出),1(],1,0(+∞单调性,证明略.。
