2012年从化数学中考一模试卷(已排版)

合集下载

2012年中考模拟数学试题s

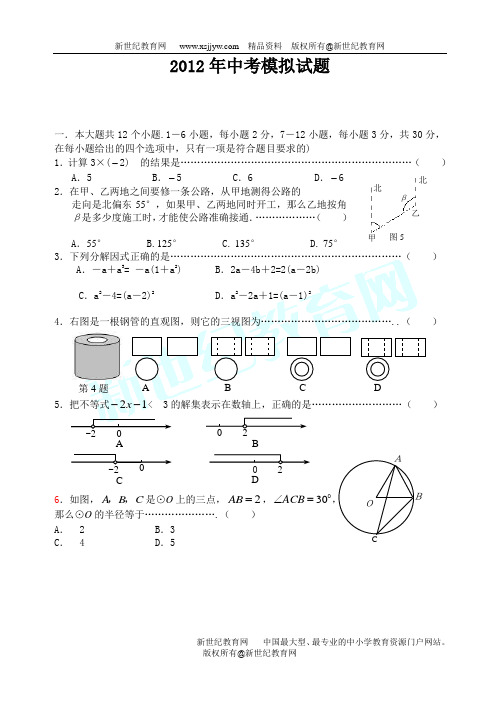
北β北图5甲乙2012年中考模拟试题一．本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．计算3×(-2) 的结果是……………………………………………………………（）A ．5B ．-5C ．6D ．-6 2．在甲、乙两地之间要修一条公路，从甲地测得公路的走向是北偏东55°，如果甲、乙两地同时开工，那么乙地按角β是多少度施工时，才能使公路准确接通．………………（）A ．55° B.125° C. 135° D. 75°3．下列分解因式正确的是……………………………………………………………（）A ．－a ＋a 3= －a(1＋a 2) B ．2a －4b ＋2=2(a －2b)C ．a 2－4=(a －2)2D ．a 2－2a ＋1=(a －1)24．右图是一根钢管的直观图，则它的三视图为…………………………………..（）5．把不等式12--x < 3的解集表示在数轴上，正确的是………………………（）6．如图，A B C ，，是⊙O 上的三点，2AB =，30ACB ∠= 那么⊙O 的半径等于………………….（） A ． 2 B ．3C ． 4D ．5AB DC 2 0 第4题第12题7. 某射击小组有20人，教练根据他们某次射击的数据绘制成如下图所示的统计图. 则这组数据的众数和中位数分别是………………………………………….（） A ．7、7 B ． 8、 7.5C ．7、 7.5D ． 8、88．如图，水平地面上有一面积为230cm π的扇形AOB ，半径OA=6cm ，且OA与地面垂直.在没有滑动的情况下，将扇形向右滚动至OB 与地面垂直为止，则O 点移动的距离为……………………………………………………………………………（）A. 20cmB.24cmC.10cm πD.30cm π 9．如图，是二次函数y=ax 2+bx+c 图象的一部分，其对称轴为直线x =1，若其与x 轴一交点为A （3，0），则由图象可知，方程 ax 2+bx+c =0的另一个解是……..（） A ．-2 B ．-1 C ．-1.5 D ．-2.510. 在△ABC 中，已知AB=5，AC=3，BC=4，则下列结论中正确的是………………（）A.sinA=45B.cosB=35C.tanA=34D.tanB=4311.如图2（a ），在直角梯形ABCD ，90B ∠=，DC AB ∥，动点P 从B 点出发，由B C D A →→→沿边运动，设点P 运动的路程为x ，ABP △的面积为y ，如果关于x 的函数y 的图象如图2（b ），则ABC △的面积为（）Ａ．10 Ｂ．Ｃ．18 Ｄ．12．如图，在△ABC 中，AB = AC ，AB = 8，BC = 12ACA ．64π-B ．1632π-C ．16π-D ．16π-数学试卷第2页 (共10页)第7题图2（a ）卷Ⅱ（非选择题，共90分）二．填空题（本大题共6个小题，每小题3分，共18分，把答案写在题中横线上）13的结果是．14．一把大遮阳伞，伞面撑开时可近似地看成是圆锥形，如图，它的母线长是2. 5米，底面半径为2米，则做这把遮阳伞需用布料的面积是平方米（接缝不计）。

2012春中考模拟题

绝密★启用前2012年广州市初中毕业生学业考试综合训练数学本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分．考试用时120分钟．第一部分（选择题共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1.下列计算正确的是（）A. 632a a a =• B.()()2222b a b a b a -=-+ C.()6223b a ab = D. 325=-a a2.将叶片图案旋转180°后，得到的图形是（）A ．B ．C ．D ．3.方程组⎩⎨⎧=+=-422y x y x 的解是（）A ．⎩⎨⎧==21y xB ．⎩⎨⎧==13y xC ．⎩⎨⎧-==2y xD ．⎩⎨⎧==02y x4.当x 为满足什么条件时，分式21+-x x 无意义（） A ．x =1 B ．x =－1 C ．x =2 D ．x =－2 5. 长方体的主视图与左视图如图所示（单位：cm ），则这个长方体的体积是（）A ．24cm 3B ．12cm 3C ．8cm 3D ．4cm 36.在一个不透明的口袋中，装有5个红球3个白球，它们除颜色外都相同，从中任意摸出一个球，摸到红球的概率为（）A ．15 B ．13 C ．58 D ．387.如图，DE 是△ABC 的中位线，若BC 的长是3cm ，则DE 的长是（）A ．1.5cmB ．2cmC ．3cmD ．6cm第5题图左视图主视图2342E A BCD8.实数a在数轴上的位置如图所示，则22(4)(11)a a -+- 化简后为（） A ． 7 B ．－7 C ． 2a －15 D ．无法确定9. 抛物线221y x x =-+的顶点坐标是（）A ．（1，0）B ．（－1，0）C ．（－2，1）D ．（2，－1） 10. 如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB ，垂足为D.若AC=5，BC=2，则sin ∠ACD 的值为( ) A.53 B.255 C. 52 D. 23第二部分（非选择题共120分）二、填空题（本大题共6小题，每小题3分，满分18分．） 11. —12的倒数是 12．因式分解：224a a -= ．13．不等式23x x >-的解集为．14．圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为 15．二次函数y=2x ²-6与x 轴的交点是___________________． 16．观察下列图形（每幅图中最小．．的三角形都是全等的），请写出第n 个图中最小．．的三角形的个数有个．三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）17．（本小题满分9分）解方程：2311-=+x x 18．（本小题满分9分）如图：在四边形ABCD 中，AD ∥BC ，AB =CD ，E 是BC 上一点，DE =AB 。

从化数学一模试卷初中答案

一、选择题（每题5分，共20分）1. 若a、b、c是等差数列，且a+b+c=9，则a²+b²+c²的值为（）A. 27B. 36C. 45D. 54答案：D解析：由等差数列的性质可知，a+b+c=3(a+d)，所以a+d=3。

又因为a²+b²+c²=(a+b+c)²-2(ab+bc+ac)，代入a+b+c=9，得a²+b²+c²=81-2(ab+bc+ac)。

由于a、b、c是等差数列，所以ab+bc+ac=3a²，代入上式得a²+b²+c²=81-6a²。

由a+d=3，得a=3-d，代入上式得a²+b²+c²=81-6(3-d)²。

因为a、b、c是等差数列，所以b=3，c=3+2d。

代入上式得a²+b²+c²=81-6(3-d)²=27。

2. 已知二次函数y=ax²+bx+c的图象与x轴交于点A(-2,0)、B(3,0)，且顶点坐标为C(1,4)，则该函数的解析式为（）A. y=2x²-4x+4B. y=2x²-4x-4C. y=2x²+4x+4D. y=2x²+4x-4答案：A解析：由题意可知，二次函数的图象与x轴交于点A(-2,0)、B(3,0)，所以函数的解析式可以表示为y=a(x+2)(x-3)。

又因为顶点坐标为C(1,4)，所以顶点坐标满足函数解析式，即4=a(1+2)(1-3)。

解得a=-1。

所以函数的解析式为y=-1(x+2)(x-3)，即y=2x²-4x+4。

3. 在直角坐标系中，点P(2,3)关于直线y=x的对称点为（）A. (3,2)B. (2,3)C. (-3,-2)D. (-2,-3)答案：A解析：点P(2,3)关于直线y=x的对称点，横坐标与纵坐标互换，即对称点为(3,2)。

2012年从化一摸试题及参考答案

2012年从化市初三数学一摸试题第一部分选择题（共30分）一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求）1．3-的值等于（ * ）． A ．3 B ．－3 C ．±3 D ．3 2．若分式21-x 有意义，则x 的取值范围是（ * ）． A ． 2x > B ．2≤xC ．x =2D ．2x ≠3．在下列运算中，计算正确的是 ( * )．A ． 725)(x x =B ． 222)(y x y x -=- C ． 10313x x x=÷ D ． 633x x x =+4．化简a a 12-+a a 1+的结果是（ * ）．A ．2a a + B ．1-a C ．1+a D ．15．菱形具有而矩形不一定具有的性质是（ * ）． A ．对角线相等 B ．对角线互相垂直 C ．对角线互相平分 D ．对角互补 6．将抛物线2y x =-向左平移2个单位后，得到的抛物线的解析式是（ * ）． A ．22y x =-+ B ．2(2)y x =-+ C ．2(2)y x =-- D ．22y x =--7．不等式组的解集在数轴上表示如图1所示，则该不等式组可能为（ * ）．A ．{12x x >-≤ B ．{12x x ≥-< C ．{12x x ≥-≤ D ．{12x x <-≥8．两个大小不同的球在水平面上靠在一起，组成如图2所示的几何体，则该几何体的左视图是（ * ）．A ．两个外离的圆B ．两个外切的圆C ．两个相交的圆D ．两个内切的圆9．已知正比例函数y kx =（0k ≠）的函数值y 随x 的增大而增大，则一次函数y kx k =+的图象大致是（ * ）．水平面主视方向图2图110．在平面直角坐标系中，对于平面内任一点()a b ，，若规定以下三种变换：①),(),(b a b a -=△； ②),(),(b a b a --=O ； ③),(),(b a b a -=Ω 按照以上变换有：)2,1())2,1((-=O △那么))4,3((ΩO 等于（ * ）． A ．（3，4） B ．（3，－4） C ．（－3, 4）D ．（－3，－4）第二部分非选择题（共120分）二、填空题（本大题共6小题，每小题3分，共18分．）11．在初三基础测试中，从化某中学的小明的6科成绩分别为语文120分，英语127分，数学123分，物理83分，化学80分，政治83分，则他的成绩的众数为 * 分．12．已知圆柱的底面半径为2cm ，高为5cm ，则圆柱的侧面积是 * cm 2 ．（结果保留π） 13．点（1，2）在反比例函数1ky x-=的图象上，则k 的值是 * ． 14．分解因式：a ax 42-= *15. 如图3，△ABC 中，DE ∥BC ，DE 分别交边AB 、AC 于D 、E 两点，若AD ：AB ＝１：3，则△ADE 与四边形DBCE 的面积比为 * ．16．如图4，已知正方形ABCD 的边长为3，E 为CD 边上一点，1=DE ．以点A 为中心，把△ADE 顺时针旋转090，得△E AB '，连接E E '，则E E '的长等于 * ．三、解答题（本大题共9小题，共102 分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分9分）解方程：451+=x x18. （本小题满分9分）先化简，再求值：22()()(2)3a b a b a b a ++-+-，其中32,32+=-=b a图 4图319. （本小题满分10分）如图5，已知,AB CD B C =∠=∠，AC 和BD 相交于点O ， E 是AD 的中点,连结OE ．（1）求证：△AOB≌△DOC；（2）求AEO ∠的度数．20．（本小题满分10分）如图6，矩形ABCD 的对角线AC 、BD 相交与点O,DE ∥AC,CE ∥BD. （1）求证：四边形OCED 是菱形；（2）若∠DOA=60°，AC 的长为8cm,求菱形OCED 的面积．21．(本小题满分12分)为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率。

2012年数学综合测试(一)理科答案(发排稿)

2012年广州市普通高中毕业班综合测试（一）数学（理科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．二、填空题：本大题查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．第13题仅填对1个，则给3分．9 10．2,23⎡⎤⎢⎥⎣⎦11．3 12．[]1,2 13．35，10 14． 15三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）（本小题主要考查两角和的正切、诱导公式、同角三角函数的基本关系和两角差的余弦等知识，考查化归与转化的数学思想方法，以及运算求解能力）（1）解：9f π⎛⎫⎪⎝⎭tan 34ππ⎛⎫=+ ⎪⎝⎭……………………………………………………………………………1分tantan 341tan tan34ππ+=ππ-…………………………………………………………………………3分 2==-………………………………………………………………………4分（2）解：因为3tan 3444f ααπππ⎛⎫⎛⎫+=++⎪ ⎪⎝⎭⎝⎭………………………………………………………………5分()tan α=+π……………………………………………………………………6分tan 2α==．……………………………………………………………………7分所以sin 2cos αα=，即sin 2cos αα=． ① 因为22sin cos 1αα+=， ②由①、②解得21cos 5α=．………………………………………………………………………………9分因为3,2απ⎛⎫∈π ⎪⎝⎭，所以cos α=，sin α=10分所以cos 4απ⎛⎫-⎪⎝⎭cos cos sin sin 44ααππ=+ ………………………………………………………11分525210⎛⎫=-+-⨯=- ⎪ ⎪⎝⎭．……………………………………12分17．（本小题满分12分）（本小题主要考查统计、方差、随机变量的分布列、均值（数学期望）等知识，考查或然与必然的数学思想方法，以及数据处理能力、运算求解能力和应用意识）（1）解：依题意，得11(87899696)(87909395)44a ⨯+++=⨯++++，……………………………1分解得3a =.…………………………………………………………………………………………………2分（2）解：根据已知条件，可以求得两组同学数学成绩的平均分都为92x =.……………………………3分所以乙组四名同学数学成绩的方差为()()()()222221879293929392959294s ⎡⎤=-+-+-+-=⎣⎦. ……………………………5分（3）解：分别从甲、乙两组同学中各随机选取一名同学，共有4416⨯=种可能的结果．……………6分这两名同学成绩之差的绝对值X 的所有情况如下表：所以X 的所有可能取值为0，1，2，3，4，6，8，9.…………………………………………………8分由表可得1(0)16P X ==，2(1)16P X ==，1(2)16P X ==，4(3)16P X ==， 2(4)16P X ==，3(6)16P X ==，1(8)16P X ==，2(9)16P X ==.所以随机变量X 随机变量X 的数学期望为121423012346161616161616EX =⨯+⨯+⨯+⨯+⨯+⨯12891616+⨯+⨯…………………………11分 6817164==.…………………………………………………………………………………………12分 ……………………10分18．（本小题满分14分）（本小题主要考查空间线面关系、直线与平面所成角、空间向量及坐标运算等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力）（1）证明1：因为平面⊥PAC 平面ABC ，平面PAC 平面ABC AC =， PD ⊂平面PAC ，AC PD ⊥，所以PD ⊥平面ABC ．…………………………………………………………………………………1分记AC 边上的中点为E ，在△ABC 中，AB BC =，所以AC BE ⊥．因为AB BC ==4=AC，所以BE ==3分因为PD ⊥AC ，所以△PCD为直角三角形．因为PD =，3CD =，所以PC ===4分连接BD ，在Rt△BDE 中，因为BE =，1DE =，所以BD ===5分因为PD ⊥平面ABC ，BD ⊂平面ABC ，所以PD ⊥BD ．在Rt△PBD 中，因为PD =，BD，所以PB ===．…………………………………………………6分在PBC ∆中，因为BC =PB =PC =所以222BC PB PC +=．所以PBC ∆为直角三角形．………………………………………………………………………………7分证明2：因为平面⊥PAC 平面ABC ，平面PAC I 平面ABC AC =， PD ⊂平面PAC ，AC PD ⊥，所以PD ⊥平面ABC ．…………………………………………………………………………………1分记AC 边上的中点为E ，在△ABC 中，因为AB BC=，所以AC BE ⊥．因为AB BC ==4=AC，所以BE ==3分连接BD ，在Rt △BDE 中，因为90BED ∠=o，BE =，1DE =，所以BD ===4分在△BCD 中，因为3CD =，BC =，BD ，所以222BC BD CD +=，所以BC BD ⊥．……………………………………………………………5分因为PD ⊥平面ABC ，BC ⊂平面ABC ，所以BC PD ⊥．…………………………………………………………………………………………6分因为BD PD D =，所以BC ⊥平面PBD ．因为PB ⊂平面PBD ，所以BC PB ⊥．所以PBC ∆为直角三角形．………………………………………………………………………………7分BPACDE（2）解法1：过点A 作平面PBC 的垂线，垂足为H ，连PH ，则APH ∠为直线AP 与平面PBC 所成的角．…………………………………………………………8分由（1）知，△ABC的面积12ABC S AC BE ∆=⨯⨯=．…………………………………………9分因为PD =，所以13P ABC ABC V S PD -∆=⨯⨯13=⨯=10分由（1）知PBC ∆为直角三角形，BC，PB =所以△PBC的面积11322PBC S BC PB ∆=⨯⨯==．……………………………………11分因为三棱锥A PBC -与三棱锥P ABC -的体积相等，即A PBC P ABC V V --=，即1333AH ⨯⨯=所以3AH =．……………………………………………………………12分在Rt △PAD中，因为PD =，1AD =，所以2AP ===．………………………………………………………13分因为3sin 2AH APH AP ∠=== 所以直线AP 与平面PBC14分解法2：过点D 作DM AP ∥，设DMPC M =，则DM 与平面PBC 所成的角等于AP 与平面PBC 所成的角．……………………………………8分由（1）知BC PD ⊥，BC PB ⊥，且PD PB P =，所以BC ⊥平面PBD ．因为BC ⊂平面PBC ，所以平面PBC ⊥平面PBD ．过点D 作DN PB ⊥于点N ，连接MN ，则DN ⊥平面PBC ．所以DMN ∠为直线DM 与平面PBC 所成的角．……10分在Rt△PAD 中，因为PD =，1AD =，所以2AP ===．………………………………………………………11分因为DM AP ∥，所以DM CD AP CA =，即324DM =，所以32DM =．………………………………12分由（1）知BD=，PB=PD ，所以PD BD DN PB ⨯===13分 BP A CDM N因为2sin 32DN DMN DE ∠===所以直线AP 与平面PBC14分解法3：延长CB 至点G ，使得BG BC =，连接AG 、PG ，……………………………………8分在△PCG中，PB BG BC === 所以90CPG ∠=o，即CP PG ⊥．在△PAC中，因为PC =2PA =，4AC =，所以222PA PC AC +=，所以CP PA ⊥．因为PA PG P =I ，所以CP ⊥平面PAG ．…………………………………………………………………………………9分过点A 作AK PG ⊥于点K ，因为AK ⊂平面PAG ，所以CP AK ⊥．因为PG CP P =I ，所以AK ⊥平面PCG ．所以APK ∠为直线AP 与平面PBC 所成的角．……………………………………………………11分由（1）知，BC PB ⊥，所以PG PC ==．在△CAG 中，点E 、B 分别为边CA 、CG 的中点，所以2AG BE ==12分在△PAG 中，2PA =，AG =PG =所以222PA AG PG +=，即PA AG ⊥．……………………………………………………………13分因为sin AG APK PG ∠===．所以直线AP 与平面PBC 所成角的正弦值为3．…………………………………………………14分解法4：以点E 为坐标原点，以EB ，EC 所在的直线分别为x 轴，y 轴建立如图的空间直角坐标系E xyz -，…………………………………………………………………………………………………8分BPACDEGK则()0,2,0A -，)B，()0,2,0C，(0,P -．于是(AP =，(2,1,PB =，(0,3,PC =设平面PBC 的法向量为(),,x y z =n ，则0,0.PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,30.y y +==⎪⎩ 取1y =，则z =x =所以平面PBC 的一个法向量为=n ．……………………………………………………12分设直线AP 与平面PBC 所成的角为θ，则sin cos 3AP AP AP θ⋅=<>===⋅n ,n n．所以直线AP 与平面PBC 所成角的正弦值为3．…………………………………………………14分若第（1）、（2）问都用向量法求解，给分如下：（1）以点E 为坐标原点，以EB ，EC 所在的直线分别为x 轴，y 轴建立如图的空间直角坐标系E xyz -，…………………………………………………………………………………………………1分则)B，()0,2,0C ，(0,P -．于是(BP =-，()2,0BC =．因为()()2,1,32,2,00BP BC =---=，所以BP BC ⊥．所以BP BC ⊥．所以PBC ∆为直角三角形．………………………………………………………………………………7分（2）由（1）可得，()0,2,0A -．于是(AP =，(2,1,PB =，(0,3,PC =．设平面PBC 的法向量为(),,x y z =n ，AA则0,0.PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n即0,30.y y +==⎪⎩ 取1y =，则z =x =所以平面PBC的一个法向量为=n ．……………………………………………………12分设直线AP 与平面PBC所成的角为θ，则sin cos AP AP AP θ⋅=<>===⋅n ,n n．所以直线AP 与平面PBC 14分 19．（本小题满分14分）（本小题主要考查等比数列的通项、裂项求和等知识，考查化归与转化的数学思想方法，以及抽象概括能力、运算求解能力和创新意识）（1）解：设等比数列{}n a 的公比为q ，依题意，有45323224,22.a a a a a +⎧=⎪⎨⎪=⎩即3452322,2.a a a a a =+⎧⎪⎨=⎪⎩……………………………………………………………………2分所以234111222112,2.a q a q a q a q a q ⎧=+⎪⎨=⎪⎩………………………………………………………………………………3分由于10a ≠，0q ≠，解之得11,21.2a q ⎧=⎪⎪⎨⎪=⎪⎩或11,21.a q ⎧=⎪⎨⎪=-⎩……………………………………………………5分又10,0a q >>，所以111,22a q ==，…………………………………………………………………6分所以数列{}n a 的通项公式为12nn a ⎛⎫= ⎪⎝⎭（*n ∈N ）．…………………………………………………7分（2）解：由（1），得()()252123n n n b a n n +=⋅++()()25121232n n n n +=⋅++．………………………………8分所以21121232n n b n n ⎛⎫=-⋅⎪++⎝⎭ 111(21)2(23)2n nn n -=-++．…………………………………………………………………10分所以12n n S b b b =+++L()()211111113525272212232n n n n -⎡⎤⎛⎫⎛⎫=-+-++-⎢⎥⎪ ⎪⋅⋅⋅++⎝⎭⎝⎭⎣⎦L ()113232nn =-+．故数列{}n b 的前n 项和()113232n nS n =-+．………………………………………………………14分 20．（本小题满分14分）（本小题主要考查椭圆与双曲线的方程、直线与圆锥曲线的位置关系、函数最值等知识，考查数形结合、化归与转化、函数与方程的数学思想方法，以及推理论证能力和运算求解能力）（1）解：依题意可得(1,0)A -，(1,0)B ．…………………………………………………………………1分设双曲线C 的方程为2221y x b-=()0b >，=2b =．所以双曲线C 的方程为2214y x -=．……………………………………………………………………3分（2）证法1：设点11(,)P x y 、22(,)T x y （0i x >，0i y >，1,2i =），直线AP 的斜率为k （0k >），则直线AP 的方程为(1)y k x =+，………………………………………………………………………4分联立方程组()221,1.4y k x y x ⎧=+⎪⎨+=⎪⎩………………………………………………………………………………5分整理，得()22224240k x k x k +++-=，解得1x =-或2244k x k -=+．所以22244k x k -=+．…………………………………………………………6分同理可得，21244k x k+=-．…………………………………………………………………………………7分所以121x x ⋅=．……………………………………………………………………………………………8分证法2：设点11(,)P x y 、22(,)T x y （0i x >，0i y >，1,2i =），则111AP y k x =+，221AT y k x =+．…………………………………………………………………………4分因为APAT k k =，所以121211y y x x =++，即()()2212221211y y x x =++．……………………………………5分因为点P 和点T 分别在双曲线和椭圆上，所以221114y x -=，222214y x +=．即()221141y x =-，()222241y x =-．…………………………………………………………………6分所以()()()()22122212414111x x x x --=++，即12121111x x x x --=++．……………………………………………………7分所以121x x ⋅=．……………………………………………………………………………………………8分证法3：设点11(,)P x y ，直线AP 的方程为11(1)1y y x x =++，………………………………………4分联立方程组()11221,11.4y y x x y x ⎧=+⎪+⎪⎨⎪+=⎪⎩…………………………………………………………………………5分整理，得222222111114(1)24(1)0x y x y x y x ⎡⎤++++-+=⎣⎦，解得1x =-或221122114(1)4(1)x y x x y +-=++．…………………………………………………………………6分将221144y x =-代入221122114(1)4(1)x y x x y +-=++，得11x x =，即211x x =．所以121x x ⋅=．…………………………………………………………………………………………8分（3）解：设点11(,)P x y 、22(,)T x y （0i x >，0i y >，1,2i =），则()111,PA x y =---，()111,PB x y =--．因为15PA PB ⋅≤，所以()()21111115x x y ---+≤，即221116x y +≤．…………………………9分因为点P 在双曲线上，则221114y x -=，所以22114416x x +-≤，即214x ≤．因为点P 是双曲线在第一象限内的一点，所以112x <≤．…………………………………………10分因为1221||||||2S AB y y ==，21111||||||22S OB y y ==，所以()()22222222122121121441544S S y y x x x x -=-=---=--．……………………………11分由（2）知，121x x ⋅=，即211x x =．设21t x =，则14t <≤，221245S S t t-=--．设()45t t f t =--，则()()()222241t t f t t t -+'=-+=，当12t <<时，()0f t '>，当24t <≤时，()0f t '<，所以函数()f t 在()1,2上单调递增，在(]2,4上单调递减．因为()21f =，()()140f f ==，所以当4t =，即12x =时，()()2212min40S S f -==．……………………………………………12分当2t =，即1x ()()2212max21S S f -==．………………………………………………13分所以2212S S -的取值范围为[]0,1．……………………………………………………………………14分说明：由()222212121254541S S x x x x -=-+≤-=，得()2212max1S S -=，给1分．21．（本小题满分14分）（本小题主要考查函数、导数、不等式、数学归纳法、二项式定理等知识，考查数形结合、化归与转化、分类与讨论的数学思想方法，以及运算求解能力）（1）证明：设11()()()1xx f x g x e x ϕ=-=--，所以1()1xx e ϕ'=-．………………………………………………………………………………………1分当0x <时，1()0x ϕ'<，当0x =时，1()0x ϕ'=，当0x >时，1()0x ϕ'>．即函数1()x ϕ在(,0)-∞上单调递减，在(0,)+∞上单调递增，在0x =处取得唯一极小值，………2分因为1(0)0ϕ=，所以对任意实数x 均有 11()(0)0x ϕϕ=≥．即1()()0f x g x -≥，所以()f x 1()g x ≥．………………………………………………………………………………………3分（2）解：当0x >时，()f x >()n g x ．………………………………………………………………………4分用数学归纳法证明如下：①当1n =时，由（1）知()f x 1()g x >．②假设当n k =（*k ∈N ）时，对任意0x >均有()f x >()k g x ，…………………………………5分令()()()k k x f x g x ϕ=-，11()()()k k x f x g x ϕ++=-，因为对任意的正实数x ，()()11()()()k kk x f x g x f x g x ϕ++'''=-=-，由归纳假设知，1()()()0k k x f x g x ϕ+'=->．…………………………………………………………6分即11()()()k k x f x g x ϕ++=-在(0,)+∞上为增函数，亦即11()(0)k k x ϕϕ++>，因为1(0)0k ϕ+=，所以1()0k x ϕ+>．从而对任意0x >，有1()()0k f x g x +->．即对任意0x >，有1()()k f x g x +>．这就是说，当1n k =+时，对任意0x >，也有()f x >1()k g x +．由①、②知，当0x >时，都有()f x >()n g x ．………………………………………………………8分（3）证明1：先证对任意正整数n ，()1e n g <．由（2）知，当0x >时，对任意正整数n ，都有()f x >()n g x ．令1x =，得()()11=e n g f <．所以()1e n g <．……………………………………………………………………………………………9分再证对任意正整数n ，()1232222112341nn g n ⎛⎫⎛⎫⎛⎫⎛⎫+++++≤ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭111112!3!!n =+++++．要证明上式，只需证明对任意正整数n ，不等式211!nn n ⎛⎫≤ ⎪+⎝⎭成立．即要证明对任意正整数n ，不等式1!2nn n +⎛⎫≤ ⎪⎝⎭（*）成立．……………………………………10分以下分别用数学归纳法和基本不等式法证明不等式（*）：方法1（数学归纳法）：①当1n =时，1111!2+⎛⎫≤ ⎪⎝⎭成立，所以不等式（*）成立．②假设当n k =（*k ∈N ）时，不等式（*）成立，即1!2kk k +⎛⎫≤ ⎪⎝⎭．………………………………………………………………………………………11分则()()()1111!1!1222k k k k k k k k +++⎛⎫⎛⎫+=+≤+= ⎪ ⎪⎝⎭⎝⎭．因为111101111112211121C C C2111112k k k k k k k k k k k k k k k k ++++++++++⎛⎫⎪+⎛⎫⎛⎫⎛⎫⎝⎭==+=+++≥ ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭+⎛⎫⎪⎝⎭，…12分所以()11121!222k k k k k ++++⎛⎫⎛⎫+≤≤ ⎪⎪⎝⎭⎝⎭．……………………………………………………………13分这说明当1n k =+时，不等式（*）也成立．由①、②知，对任意正整数n ，不等式（*）都成立．综上可知，对任意正整数n ，不等式()123222211e 2341nn g n ⎛⎫⎛⎫⎛⎫⎛⎫+++++≤< ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭成立． ……………………………………14分方法2（基本不等式法）：12n +≤，……………………………………………………………………………………11分 12n +≤， ……，12n +≤，将以上n 个不等式相乘，得1!2nn n +⎛⎫≤ ⎪⎝⎭．……………………………………………………………13分所以对任意正整数n ，不等式（*）都成立．综上可知，对任意正整数n ，不等式()123222211e 2341nn g n ⎛⎫⎛⎫⎛⎫⎛⎫+++++≤< ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭成立． ……………………………………14分。

从化数学一模试卷初中生

一、选择题（每题3分，共30分）1. 下列各数中，绝对值最小的是（）A. -3B. 2C. 0D. -22. 下列代数式中，正确的是（）A. 3a + 2b = 3(a + b)B. 2(x + y) = 2x + 2yC. 3x - 2y = 2x - 3yD. 4x + 5y = 2(2x + 5y)3. 已知等腰三角形底边长为8，腰长为10，则该三角形的面积是（）A. 32B. 40C. 48D. 644. 下列函数中，有最小值的是（）A. y = x^2B. y = -x^2C. y = x^2 + 1D. y = -x^2 + 15. 一个长方形的长是a，宽是b，则该长方形的周长是（）A. 2a + 2bB. 2a - 2bC. 2a / bD. 2b / a6. 下列图形中，对称轴最多的图形是（）A. 正方形B. 等腰三角形C. 圆D. 长方形7. 已知一个数是2的3次方，则该数的因数个数是（）A. 1B. 2C. 3D. 48. 下列数中，能被3整除的是（）A. 123B. 124C. 125D. 1269. 在直角坐标系中，点A(2, 3)关于x轴的对称点是（）A. (2, -3)B. (-2, 3)C. (2, -3)D. (-2, -3)10. 下列方程中，解为x = 2的是（）A. 2x + 3 = 7B. 2x - 3 = 7C. 2x + 3 = 5D. 2x - 3 = 5二、填空题（每题3分，共30分）11. 计算：(-2) × 3 + 4 × (-5) = ______12. 简化：2a + 3b - 2a + 4b = ______13. 已知等腰三角形的底边长为6，腰长为8，则该三角形的周长是 ______14. 函数y = 2x - 3的图像是一条直线，其斜率是 ______15. 下列数中，能被5整除的是 ______16. 在直角坐标系中，点B(3, -2)关于原点的对称点是 ______17. 方程2x - 3 = 7的解是 ______18. 简化：a^2 - a^2 + a^2 = ______19. 计算下列分式的值：2/3 ÷ 4/5 = ______20. 已知长方形的长是12，宽是5，则该长方形的面积是 ______三、解答题（每题10分，共30分）21. 解方程：3x - 2 = 5x + 422. 解不等式：2x - 3 > 523. 已知一个数的3倍加上4等于24，求这个数。

2012年广州华侨中学中考一模

2012初三第一次模拟考数学科问卷本试卷粉选择题和非选择题两部分，共三大题25小题，满分150分。

考试时间为120分钟。

注意事项：1.答卷前，考生务必在答题卷上用黑色字迹的钢笔或签字笔填写自己的学校、班别、姓名和学号。

2.选择题每小题选出答案后，请把答案填写在答题卷的答题栏内，不能答在试卷上。

3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图。

答案必须写在答题卷各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域，不准使用铅笔、圆珠笔或涂改液，不按以上要求作答的答案无效。

4.考生必须保持答题卡的整洁。

第一部分：选择题（共30分）一、选择题（本大题共10小题，每小题3分，满分30分） 1.下列各数中，最小的数是（）A.-1B.-2C.0D.1 2.数据26000用科学计数法表示为n106.2⨯，则n 的值是（） A.2 B.3 C.4 D.53.如图1，在□ABCD 中，AD=3cm,AB=2cm,则□ABCD 的周长等于（）A.10cmB.6cmC.5cmD.4cm 4.如果点A 在直线1-=x y 上，则A 点的坐标可以是（）A.(-1,0)B.(0,1)C.(1,-1)D.(1,0)5.小明从正面观察如图所示的圆柱体，则主视图是下列选项中的（）A B C D 6.方程组⎩⎨⎧=+=-332y x y x 的解是（）A.⎩⎨⎧==21y xB.⎩⎨⎧==32y xC.⎩⎨⎧==11y xD.⎩⎨⎧==12y x7.从1,2,3,4,5,6,7,8,9这九个自然数中任取一个，是2的倍数的概率为1p ，是3的倍数的概率为2p ，则：（）A. 1p <2pB.1p >2pC.1p =2pD.不能确定 8.对于抛物线3)5(22+-=x y ，下列说法正确的是（）A.开口向下，顶点坐标（5，3）B. 开口向上，顶点坐标（5，3）C.开口向下，顶点坐标（-5，3）D. 开口向上，顶点坐标（-5，3） 9.如图2，已知⊙o 是正方形ABCD 的外接圆，点E 是⊙o 上任意一点，则 BEC ∠的度数为（）A.45 B.30 C.60 D.9010.如图3，一个点在第一个象限的x 轴，y 轴上运动，且每秒移动一个单位，在第一秒钟，它从原点运用到（0，1），然后接着按图中箭头所示的方向运动[即（0,0）→（0,1）→（1,1）→（1,0）→…]，那么第35秒时该点所在位置的坐标是（） A.(4,0) B.(0,5) C.(5,0) D.(5,5)第二部分非选择题（共120分）二、填空题（本大题共6小题，每小题3分，满分18分） 11.分解因式m m 43-= . 12.方程213=-x 的解是 . 13.方程0432=-+x x 的两个实数根为21x x 、，则=+21x x . 14.一组数据2,2,3,3,5,众数是，中位数是 .15.在半径是20cm 的圆中，90的圆心角所对的弧长为 cm.(精确到0.1cm) 16.小刚和小明在太阳光下行走，小刚身高1.70m ，他的影长为3.40m ，小刚比小明高30cm,此刻小明的影长是 cm.三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤） 17.（本小题满分9分）解不等式2123xx +≤-。

2012年中考一模数学试题及答案(1)

2012年中考一模试题数学试卷（一）*考试时间120分钟试卷满分150分一、选择题（下列各题的备选答案中，只有一个答案是正确的，将正确答案的序号填在题后的括号内，每小题3分，共24分） 1．sin30°的值为（） A ．21 B ．23 C ．33 D ．222． △ABC 中，∠A ＝50°，∠B ＝60°，则∠C ＝（）A ．50°B ．60°C ．70°D ．80°3．如图，直线l 1、l 2、l 3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（） A ．一处． B ．两处 C ．三处． D ．四处． 4．点P （－2，1）关于x 轴对称的点的坐标是（）A ．（－2，－1）B ．（2，－1）C ．（1，－2）D ．（2，1）5．若x ＝3是方程x 2－3mx ＋6m ＝0的一个根，则m 的值为（）A ．1B ． 2C ．3D ．4 6．现有A 、B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A 立方体朝上的数字为x 、小明掷B 立方体朝上的数字为y 来确定点P （x y ，），那么它们各掷一次所确定的点P 落在已知抛物线24y x x =-+上的概率为（）A.118 B.112 C.19 D.167．右图是由几个小立方块搭成的几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，那么这个几何体的主视图是（）A ．B ．C ．D ．2 138．某超级市场失窃，大量的商品在夜间被罪犯用汽车运走。

三个嫌疑犯被警察局传讯，警察局已经掌握了以下事实：（１）罪犯不在A 、B 、C 三人之外；（２）C 作案时总得有A 作从犯；（３）B 不会开车。

在此案中能肯定的作案对象是（）A ．嫌疑犯AB ．嫌疑犯BC ．嫌疑犯CD ．嫌疑犯A 和C二、填空题（每小题3分，共24分）9．据中新社报道：2010年我国粮食产量将达到540000000000千克，用科学记数法表示这个粮食产量为______千克.10．用一个半径为6㎝的半圆围成一个圆锥的侧面，则这个圆锥的侧面积为㎝2.（结果保留π）11．△ABC 中，AB ＝6，AC ＝4，∠A ＝45°，则△ABC 的面积为．12．若一次函数的图象经过反比例函数4y x=-图象上的两点（1，m ）和（n ，2），则这个一次函数的解析式是 .13．某品牌的牛奶由于质量问题，在市场上受到严重冲击，该乳业公司为了挽回市场，加大了产品质量的管理力度，并采取了“买二赠一”的促销手段，一袋鲜奶售价1.4元，一箱牛奶18袋，如果要买一箱牛奶，应该付款元.14．通过平移把点A(2，－3)移到点A ’(4，－2)，按同样的平移方式，点B(3，1)移到点B′, 则点B′的坐标是 ________15．如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°。

2012中考数学模拟题(包含答案)

ＡＢＣＤ绝密★启用前2012年广州市初中毕业生学业考试综合训练数学本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分．考试用时120分钟．第一部分（选择题共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的．） 1、2的倒数是（） A 、12 B 、－12C 、2D 、－2 2、不等式x ＜2在数轴上表示正确的是（）3．下列命题中，属于假命题的是（） A 、三角形两边之差小于第三边 B 、三角形的外角和是360°C 、三角形的一条中线能将三角形分成面积相等的两部分D 、等边三角形即是轴对称图形，又是中心对称图形 4、方程组125x y x y +=⎧⎨-=⎩，的解是（）A ．12.x y =-⎧⎨=⎩， B ．23.x y =-⎧⎨=⎩， C ．21.x y =⎧⎨=⎩， D ．21.x y =⎧⎨=-⎩，5、在一个晴朗的上午，皮皮拿着一块正方形术板在阳光下做投影实验，正方形木板在地面上形成的投影不可能是（）6．如图，水平放置的下列几何体，主视图不是．．长方形的是（）7．如图，梯形ABCD 中，AD ∥BC ，EF 是梯形的中位线，对角线AC 交EF 于G ，若BC =10，EF =8，则GF 的长等于（）A 、2B 、3C 、4D 、5B ．D ．A ．C ． GF E D CBAＢ．Ｃ．D．8．将一个正方体沿某些棱展开后，能够得到的平面图形是（）9、已知x＜1）A、x－1 B、x＋1 C、－x－1 D、1－x10．已知圆锥的母线长为5，高为4，则该圆锥的侧面积为（）A．20π B．15π C．12π D．30π第二部分（非选择题共120分）二、填空题（本大题共6小题，每小题3分，满分18分．）11．如图，已知a b∥，1=50∠︒，则2∠= °．12．计算0)2(-=_________．13．使11+x在实数范围内有意义的x的取值范围是．14、如图，已知Rt△ABC中，斜边BC上的高AD＝4，cosB＝54，则AC＝_________．15、袋子中装有3个红球和5个白球，这些球除颜色外均相同．在看不到球的条件下，随机从袋中摸出一个球，则摸出白球的概率是__________．16．如图，小红作出了面积为1的正△ABC，然后分别取△ABC三边的中点A1，B1，C1，作出了正△A1B1C1，用同样的方法，作出了正△A2B2C2，……，由此可得，正△A8B8C8的面积是．三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）17．（本小题满分9分）因式分解：aax42-．18．（本小题满分9分）某教师为了对学生零花钱的使用进行教育指导，对全班50名学生每人一周内的零花钱数额进行了调查统计，并绘制了统计表及如图所示的统计图．请根据图表中的信息回答以下问题．（1）求a的值；（2）求这50名学生每人一周内的零花钱数额的众数和平均数．C1B第16题图第14题图AB CD第19题图19．（本小题满分10分）如图，已知平行四边形ABCD ．（1）用直尺和圆规作出ADC ∠的平分线DE ，交AB 于点E ，（保留作图痕迹，不要求写作法）；（2）求证：AD AE =．20．（本小题满分10分）先化简，再求值：22(3)(2)(2)2x x x x +++--，其中13x =-．21．（本小题满分12分）某企业2009年盈利1500万元，2011年克服全球金融危机的不利影响，仍实现盈利2160万元．从2009年到2011年，如果该企业每年盈利的年增长率相同，求：（1）该企业2010年盈利多少万元？（2）若该企业盈利的年增长率继续保持不变，预计2012年盈利多少万元？22．（本小题满分12分）如图，已知一次函数1y x m =+（m 为常数）的图象与反比例函数 2k y x=（k 为常数，0k ≠）的图象相交于点 A （1，3）．（1）求这两个函数的解析式及其图象的另一交点B 的坐标；（2）观察图象，写出使函数值12y y ≥的自变量x 的取值范围．23．（本小题满分12分）如图，在⊙O 中，直径AB 垂直于弦CD ，垂足为E ，连接AC ，将△ACE 沿AC 翻折得到△ACF ，直线FC 与直线AB 相交于点G ．（1）直线FC 与⊙O 有何位置关系？并说明理由；（2）若2OB BG ==，求CD 的长．A F24．（本小题满分14分）如图1，在边长为5的正方形ABCD 中，点E 、F 分别是BC 、DC 边上的点，且AE EF ⊥，2BE =.（1）求EC ∶CF 的值；（2）延长EF 交正方形外角平分线CP P 于点（如图2），试判断AE EP 与的大小关系，并说明理由；（3）在图2的AB 边上是否存在一点M ，使得四边形DMEP 是平行四边形？若存在，请给予证明；若不存在，请说明理由．25．（本小题满分14分）如图，抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A （－4，0）、B （2，0），与y 轴交于点C ，顶点为D ．E （1，2）为线段BC 的中点，BC 的垂直平分线与x 轴、y 轴分别交于F 、G ．（1）求抛物线的函数解析式，并写出顶点D 的坐标；（2）在直线EF 上求一点H ，使△CDH 的周长最小，并求出最小周长；（3）若点K 在x 轴上方的抛物线上运动，当K 运动到什么位置时，△EFK 的面积最大？并求出最大面积．图1 A D CB E 图2B C E D A F P F2012年广州市初中毕业生学业考试综合训练参考答案17．(2)(2)a x x +-18．（1）a 的值：10（人）；（2）这50名学生每人一周内的零花钱数额的众数：15元，平均数：12元 19．略20．原式＝6x ＋5，当13x =-时，原式＝3．21．（1）该企业2010年盈利1800万元；（2）预计2012年盈利2592万元22．解：（1）由题意，得31m =+，解得2m =，所以一次函数的解析式为12y x =+．由题意，得31k =，解得3k =，所以反比例函数的解析式为23y x =．由题意，得32x x+=，解得1213x x ==-，．当23x =-时，121y y ==-，所以交点(31)B --，．（2）由图象可知，当30x -<≤或1x ≥时，函数值12y y ≥．23．解：（1）直线FC与⊙O 相切．理由如下：连接OC ．∵OA OC =，∴12∠=∠，由翻折得，13∠=∠，90F AEC ∠=∠=︒． ∴23∠=∠． ∴OC ∥AF ． ∴90OCG F ∠=∠=︒． ∴直线FC 与⊙O 相切．（2）在Rt △OCG 中，1cos 22OC OC COG OG OB ∠===， ∴60COG ∠=︒．……6分在Rt △OCE 中，sin602CE OC =⋅︒=⨯……8分 ∵直径AB 垂直于弦CD ， ∴2CD CE ==．……9分24．解：（1）AE EF ⊥2390∴∠+∠=° 四边形ABCD 为正方形90B C ∴∠=∠=° 1390∴∠+∠=°12∠=∠ （3）90DAM ABE DA AB ∠=∠==°，A D1DAM ABE ∴△≌△DM AE ∴=AE EP =DM PE ∴=∴四边形DMEP 是平行四边形．解法②：在AB 边上存在一点M ，使四边形DMEP 是平行四边形证明：在AB 边上取一点M ，使AM BE =，连接ME 、MD 、DP ． 90AD BA DAM ABE =∠=∠=，°Rt Rt DAM ABE ∴△≌△14DM AE ∴=∠=∠，1590∠+∠=° 4590∴∠+∠=°AE DM ∴⊥ AE EP ⊥ DM EP ∴⊥∴四边形DMEP 为平行四边形（备注：此小题若有其他的证明方法，只要证出判定平行四边形的一个条件，即可得分）25．（1）由题意，得 ⎩⎨⎧=++=+-,0424,04416b a b a 解得21-=a ，b =－1．所以抛物线的解析式为4212+--=x x y ，顶点D 的坐标为（－1，29）．（2）设抛物线的对称轴与x 轴交于点M ．因为EF 垂直平分BC ，即C 关于直线EG 的对称点为B ，连结BD 交于EF 于一点，则这一点为所求点H ，使DH + CH 最小，即最小为DH + CH = DH + HB = BD =132322=+DM BM ．而 25)429(122=-+=CD ． ∴ △CDH 的周长最小值为CD + DR + CH =21335+．设直线BD 的解析式为y = k 1x + b ，则 ⎪⎩⎪⎨⎧=+-=+,29,021111b k b k 解得 231-=k ，b 1 = 3．所以直线BD 的解析式为y =23-x + 3．由于BC = 25，CE = BC ∕2 =5，Rt △CEG ∽△COB ，得 CE : CO = CG : CB ，所以 CG = 2.5，GO = 1.5．G （0，1.5）．同理可得直线EF 解析式为y =21x +23．联立直线BD 与EF 的方程，解得使△CDH 的周长最小的点H （43，815）．（3）设K （t ，4212+--t t ），x F ＜t ＜x E ．过K 作x 轴的垂线交EF 于N ．则 KN = y K －y N =4212+--t t －（21t +23）=2523212+--t t ．所以 S △EFK = S △KFN + S △KNE =21KN （t + 3）+21KN （1－t ）= 2KN = －t 2－3t + 5 =－（t +23）2 +429．B CED A F P5 41M即当t =－23时，△EFK 的面积最大，最大面积为429，此时K （－23，835）．。

2012年广东省初中毕业生学业考试数学模拟试卷(一)

2012年广东省初中毕业生学业考试数学模拟试卷(一)(时间：100分钟，满分120分)一、选择题(本大题共5小题，每小题3分，共15分；在每小题给出的四个选项中，只有一个是正确的)1．－4的倒数是( D ) A ．4 B ．－4 C.14 D ．－142．一种细菌的半径是0.000 045米，该数字用科学记数法表示正确的是( C )A ．4.5×105B ．45×106C ．4.5×10－5D ．4.5×10－43．函数y ＝－xx －1中自变量x 的取值范围是( D )A ．x ≥0B ．x <0且x ≠1C ．x <0D ．x ≥0且x ≠14．方程组⎩⎪⎨⎪⎧x ＋y ＝3x －y ＝－1的解是( A )A.⎩⎪⎨⎪⎧ x ＝1y ＝2B.⎩⎪⎨⎪⎧ x ＝1y ＝－2 C.⎩⎪⎨⎪⎧x ＝2y ＝1 D.⎩⎪⎨⎪⎧x ＝0y ＝－1 5．下列各图是选自历届世博会会徽中的图案，其中是中心对称图形的是( C )A. B.C. D.二、填空题(本大题共5小题，每小题4分，共20分)6．因式分解：ab 2－2ab ＋a ＝a (b －1)2.7．如果点P (4，－5)和点Q (a ，b )关于y 轴对称，则a 的值为－4. 8．一组数据1,6，x,5,9的平均数是5，那么这组数据的中位数是5. 9．双曲线y ＝2k －1x 的图象经过第二、四象限，则k 的取值范围是k <12.10．如图1－1，观察每一个图中黑色正六边形的排列规律，则第10个图中黑色正六边形有100个．图1－1三、解答题(本大题共5小题，每小题6分，共30分) 11．计算：(－2 011)0＋⎝⎛⎭⎫22－1＋||2－2－2cos60°. 解：原式＝1＋2＋2－2－1＝212．先化简，再求值：x －y x ÷⎝⎛⎭⎫x －2xy －y 2x ，其中x ＝2，y ＝－1.解：原式＝x －y x ·x x 2－2xy ＋y 2＝1x －y ，当x ＝2，y ＝－1时，原式＝1x －y ＝13. 13．如图1－2，在边长为1个单位长度的小正方形组成的网格中，△ABC 与△DFE 关于点O 成中心对称，△ABC 与△DFE 的顶点均在格点上，请按要求完成下列各题．(1)在图中画出点O 的位置；(2)将△ABC 先向右平移4个单位长度，再向下平移2个单位长度，得到△A 1B 1C 1，请画出△A 1B 1C 1；(3)在网格中画出格点M ，使A 1M 平分∠B 1A 1C 1.图1－2解：(1)如图D58，图中点O 为所求．图D58(2)如图D58，图中△A 1B 1C 1为所求． (3)如图D58，图中点M 为所求．14．如图1－3，已知二次函数y ＝－12x 2＋bx ＋c 的图象经过A (2,0)，B (0，－6)两点．(1)求这个二次函数的解析式；(2)设该二次函数的对称轴与x 轴交于点C ，连接BA 、BC ，求△ABC 的面积．图1－3解：(1)把A (2,0)，B (0，－6)代入y ＝－12x 2＋bx ＋c ，得⎩⎪⎨⎪⎧ －2＋2b ＋c ＝0c ＝－6，解得⎩⎪⎨⎪⎧b ＝4c ＝－6. ∴这个二次函数的解析式为y ＝－12x 2＋4x －6.(2)∵该抛物线对称轴为直线x ＝－42×⎝⎛⎭⎫－12＝4，∴点C 的坐标为(4,0)，∴AC ＝OC －OA ＝4－2＝2， ∴S △ABC ＝12×AC ×OB ＝12×2×6＝6.15．某市为缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯长AB ＝6 m ，∠ABC ＝45°，后考虑到安全因素，将楼梯脚B 移到CB 延长线上点D 处，使∠ADC ＝30°(如图1－4所示)．(1)求调整后楼梯AD 的长； (2)求BD 的长(结果保留根号)．图1－4解：(1)已知AB ＝6 m ，∠ABC ＝45°， ∴AC ＝BC ＝AB ·sin45°＝6×22＝3 2， ∵∠ADC ＝30°，∴AD ＝2AC ＝6 2. 答：调整后楼梯AD 的长为6 2m. (2)CD ＝AD ·cos30°＝6 2×32＝3 6， ∴BD ＝CD －BC ＝3 6－3 2. 答：BD 的长为(3 6－3 2)m.四、解答题(本大题共4小题，每小题7分，共28分)16．从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率： (1)抽取1名，恰好是女生；(2)抽取2名，恰好是1名男生和1名女生．解：(1)抽取1名，恰好是女生的概率是25.(2)分别用男1、男2、男3、女1、女2表示这五位同学，从中任意抽取2名，所有可能出现的结果有：(男1，男2)，(男1，男3)，(男1，女1)，(男1，女2)，(男2，男3)，(男2，女1)，(男2，女2)，(男3，女1)，(男3，女2)，(女1，女2)，共10种，它们出现的可能性相同．所有结果中，满足抽取2名，恰好是1名男生和1名女生(记为事件A )的结果共6种，所以P (A )＝610＝35.17．如图1－5，P 是矩形ABCD 下方一点，将△PCD 绕P 点顺时针旋转60°后恰好D 点与A 点重合，得到△PEA ，连接EB ，问△ABE 是什么特殊三角形？请说明理由．图1－5解：△ABE 是等边三角形，理由如下： △PCD 绕点P 顺时针旋转60°得到△PEA ，PD 的对应边是P A 、CD 的对就边是EA ，线段PD 旋转到P A ，旋转的角度是60°，即∠APD 为60°， ∴△P AD 是等边三角形， ∴∠DAP ＝∠PDA ＝60°， ∴∠PDC ＝∠P AE ＝30°，∠DAE ＝30°， ∴∠P AB ＝30°，即∠BAE ＝60°，又∵CD ＝AB ＝EA ，∴△ABE 是等边三角形．18．绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨，桃子12吨．现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售，已知一辆甲种货车可装枇杷4吨和桃子1吨，一辆乙种货车可装枇杷和桃子各2吨．(1)王灿有几种方案安排甲、乙两种货车可一次性地将水果运到销售地？(2)若甲种货车每辆要付运输费300元，乙种货车每辆要付运输费240元，则果农王灿应选择哪种方案，使运输费最少？最少运费是多少？解：(1)设安排甲种货车x 辆，则安排乙种货车(8－x )辆，依题意得⎩⎪⎨⎪⎧4x ＋2(8－x )≥20x ＋2(8－x )≥12，解此不等式组得2≤x ≤4. ∵x 是正整数，∴x 可取的值为2,3,4.因此安排甲、乙两种货车有三种方案：甲种货车乙种货车方案一 2辆 6辆方案二 3辆 5辆方案三4辆4辆(2)方案一所需运费为300×2＋240×6＝2 040元；方案二所需运费为300×3＋240×5＝2 100元；方案三所需运费为300×4＋240×4＝2 160元．∴王灿应选择方案一运费最少，最少运费是2 040元． 19．已知：如图1－6，在Rt △ABC 中，∠C ＝90°，∠BAC 的角平分线AD 交BC 边于D .(1)以AB 边上一点O 为圆心，过A 、D 两点作⊙O (不写作法，保留作图痕迹)，再判断直线BC 与⊙O 的位置关系，并说明理由；(2)若(1)中的⊙O 与AB 边的另一个交点为E ，AB ＝6，BD ＝2 3，求线段BD 、BE 与劣弧DE 所围成的图形面积(结果保留根号和π)．图1－6解：(1)如图D59(需保留线段AD 中垂线的痕迹)．图D59直线BC 与⊙O 相切．理由如下：连接OD ，∵OA ＝OD ，∴∠OAD ＝∠ODA . ∵AD 平分∠BAC ，∴∠OAD ＝∠DAC . ∴∠ODA ＝∠DAC . ∴OD ∥AC . ∵∠C ＝90°，∴∠ODB ＝90°，即OD ⊥BC . 又∵直线BC 过半径OD 的外端， ∴BC 为⊙O 的切线． (2)设OA ＝OD ＝r ，在Rt △BDO 中，OD 2＋BD 2＝OB 2， ∴r 2＋(2 3)2＝(6－r )2，解得r ＝2. ∵tan ∠BOD ＝BDOD ＝3，∴∠BOD ＝60°.∴S 扇形ODE ＝60π·22360＝23π.∴所求图形面积为S △BOD －S 扇形ODE ＝2 3－23π.五、解答题(本大题共3小题，每小题9分，共27分) 20．对于任何实数，我们规定符号⎪⎪⎪ a c⎪⎪⎪b d 的意义是⎪⎪⎪ a c⎪⎪⎪b d ＝ad －bc . (1)按照这个规定请你计算⎪⎪⎪ 57⎪⎪⎪68的值； (2)按照这个规定请你计算：当x 2－3x ＋1＝0时，⎪⎪⎪⎪⎪⎪x ＋1x －23xx －1的值．解：(1)⎪⎪⎪ 57⎪⎪⎪68＝5×8－6×7＝－2. (2)⎪⎪⎪ x ＋1x －2⎪⎪⎪3x x －1＝()x ＋1()x －1－3x ()x －2 ＝x 2－1－3x 2＋6x ＝－2x 2＋6x －1. 又∵x 2－3x ＋1＝0， ∴x 2－3x ＝－1，原式＝－2(x 2－3x )－1＝－2×(－1)－1＝1. 21．如图1－7(1)，将菱形纸片AB (E )CD (F )沿对角线BD (EF )剪开，得到△ABD 和△ECF ，固定△ABD ，并把△ABD 与△ECF 叠放在一起．(1)操作：如图1－7(2)，将△ECF 的顶点F 固定在△ABD 的BD 边上的中点处，△ECF 绕点F 在BD 边上方左右旋转，设旋转时FC 交BA 于点H (H 点不与B 点重合)，FE 交DA 于点G (G 点不与D 点重合)．求证：BH ·GD ＝BF 2.(2)操作：如图1－7(3)，△ECF 的顶点F 在△ABD 的BD 边上滑动(F 点不与B 、D 点重合)，且CF 始终经过点A ，过点A 作AG ∥CE ，交FE 于点G ，连接DG .探究：FD ＋DG ＝________.请予以证明．图1－7(1)证明：∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开，∴∠B＝∠D，∵将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，∴BF＝DF，∵∠HFG＝∠B，∴∠GFD＝∠BHF，∴△BFH∽△DGF，∴BFDG＝BHDF，∴BH·GD＝BF2.(2)证明：∵AG∥CE，∴∠F AG＝∠C，∵∠CFE＝∠CEF，∴∠AGF＝∠CFE，∴AF＝AG，∵∠BAD＝∠C，∴∠BAF＝∠DAG，△ABF≌△ADG，∴FB＝DG，∴FD＋DG＝BD.22．如图1－8，已知二次函数y＝x2－2mx＋4m－8.(1)当x≤2时，函数值y随x的增大而减小，求m的取值范围；(2)以抛物线y＝x2－2mx＋4m－8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M、N两点在抛物线上)，请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由；(3)若抛物线y＝x2－2mx＋4m－8与x轴交点的横坐标均为整数，求整数m的值．图1－8解：(1)∵y＝(x－m)2＋4m－8－m2，∴由题意得，m≥2.(2)如图D60，根据抛物线和正三角形的对称性，可知MN⊥y轴，设抛物线的对称轴与MN交于点B，则AB＝3BN.设N(a，b)，∴BN＝a－m(m<a)，又AB＝y B－y A＝b－(4m－8－m2)＝a2－2ma＋4m－8－(4m－8－m2)＝a2－2ma＋m2＝(a－m)2，∴(a－m)2＝3(a－m)，∴a －m ＝3，∴BN ＝3，AB ＝3，∴S △AMN ＝12AB ·2BN ＝12×3×2×3＝3 3.∴△AMN 的面积是与m 无关的定值．图D60(3)令y ＝0，即x 2－2mx ＋4m －8＝0时，有： x ＝2m ±2m 2－4m ＋82＝m ±(m －2)2＋4，由题意，(m －2)2＋4为完全平方数，令(m －2)2＋4＝n 2，即(n ＋m －2)(n －m ＋2)＝4 ∵m 、n 为整数，∴⎩⎪⎨⎪⎧ n ＋m －2＝2n －m ＋2＝2或⎩⎪⎨⎪⎧n ＋m －2＝－2n －m ＋2＝－2，解得⎩⎪⎨⎪⎧ m ＝2n ＝2或⎩⎪⎨⎪⎧m ＝2n ＝－2，综合得m ＝2.2012年广东省初中毕业生学业考试数学模拟试卷(二)(时间：100分钟，满分120分)一、选择题(本大题共5小题，每小题3分，共15分；在每小题给出的四个选项中，只有一个是正确的)1．－3的绝对值是( A ) A ．3 B ．－3 C.13 D ．－132．5月31日，参观上海世博会的游客约为505 000人.505 000用科学记数法表示为( D )A ．505×103B ．5.05×103C ．5.05×104D ．5.05×105 3．下列计算正确的是( C ) A ．a 4＋a 2＝a 6 B ．2a ·4a ＝8a C ．a 5÷a 2＝a 3 D ．(a 2)3＝a 5 4．不等式组⎩⎪⎨⎪⎧2x －1<x 15x ≤1的解集在数轴上表示正确的是( C )5．一个几何体的三视图如图2－1所示．那么这个几何体是( C )图2－1二、填空题(本大题共5小题，每小题4分，共20分) 6．若x 、y 为实数，且x ＋3＋|y －2|＝0，则x ＋y ＝－1.7．如图2－2，菱形ABCD 中，对角线AC 、BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为24，则OH 的长等于3.图2－28．如图2－3，抛物线y ＝－x 2＋2x ＋m (m ＜0)与x 轴相交于点A (x 1,0)、B (x 2,0)，点A 在点B 的左侧．当x ＝x 2－2时，y ＜0(填“＞”，“＝”或“＜”号)．图2－39．如图2－4，从⊙O 外一点A 引圆的切线AB ，切点为B ，连接AO 并延长交圆于点C ，连接BC .若∠A ＝26°，则∠ACB 的度数为32度．图2－410．有一数值转换器，原理如图2－5所示，若开始输入x 的值是5，可发现第一次输出的结果是8，第二次输出的结果是4，…，请你探索第2011次输出的结果是1.图2－5三、解答题(本大题共5小题，每小题6分，共30分) 11．计算：12－⎝⎛⎭⎫－12－1－tan 60°＋3－8＋||3－2. 解：原式＝2 3＋2－3－2＋2－3＝2. 12．解方程：x ＋4x (x －1)＝3x －1.解：方程两边同乘最简公分母x (x －1)，得x ＋4＝3x ，解得x ＝2. 经检验：x ＝2是原方程的根． ∴原方程的解为x ＝2. 13．先化简，再求值：⎝ ⎛⎭⎪⎫a －1a 2－4a ＋4－a ＋2a 2－2a ÷⎝⎛⎭⎫4a －1，其中a ＝2－ 3. 解：原式＝⎣⎢⎡⎦⎥⎤a －1(a －2)2－a ＋2a (a －2)÷4－a a＝a (a －1)－(a －2)(a ＋2)a (a －2)2·a4－a＝1(a －2)2. 当a ＝2－3时，原式＝13.14．省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表(单位：环)：第一次第二次第三次第四次第五次第六次甲 10 8 9 8 10 9 乙107101098(1)根据表格中的数据，计算出甲的平均成绩是______环，乙的平均成绩是______环； (2)分别计算甲、乙六次测试成绩的方差；(3)根据(1)、(2)计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由． ⎩⎨⎧⎭⎬⎫计算方差的公式：s 2＝1n [(x 1－x )2＋(x 2－x )2＋…＋(x n －x )2]解：(1)9 9(2)s 2甲＝16[(10－9)2＋(8－9)2＋(9－9)2＋(8－9)2＋(10－9)2＋(9－9)2]＝16(1＋1＋0＋1＋1＋0)＝23.s 2乙＝16[(10－9)2＋(7－9)2＋(10－9)2＋(10－9)2＋(9－9)2＋(8－9)2]＝16(1＋4＋1＋1＋0＋1)＝43. (3)推荐甲参加全国比赛更合适，理由如下：两人的平均成绩相等，说明实力相当；但甲的六次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适．15．“六一”儿童节前，某玩具商店根据市场调查，用2 500元购进一批儿童玩具，上市后很快脱销，接着又用4 500元购进第二批这种玩具，所购数量是第一批数量的1.5倍，但每套进价多了10元．(1)求第一批玩具每套的进价是多少元？(2)如果这两批玩具每套售价相同，且全部售完后总利润不低于25%，那么每套售价至少是多少元？解：设第一批玩具每套的进价是x 元，则第二批每套进价是(x ＋10)元，由题意得：2 500x ×1.5＝4 500x ＋10，解得x ＝50，经检验x ＝50是分式方程的解．故第一批玩具每套的进价是50元． (2)设每套售价至少是y 元， 2 50050×(1＋1.5)＝125(套)． 125y －2 500－4 500≥(2 500＋4 500)×25%， y ≥70，那么每套售价至少是70元．四、解答题(本大题共4小题，每小题7分，共28分)16．日本福岛出现核电站事故后，我国国家海洋局高度关注事态发展，紧急调集海上巡逻的海检船，在相关海域进行现场监测与海水采样，针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估．如图2－6，上午9时，海检船位于A 处，观测到某港口城市P 位于海检船的北偏西67.5°方向，海检船以21海里/时的速度向正北方向行驶，下午2时海检船到达B 处，这时观察到城市P 位于海检船的南偏西36.9°方向，求此时海检船所在B 处与城市P 的距离？⎝⎛参考数据：sin 36.90≈35，tan 36.90≈34，⎭⎫sin 67.50≈1213，tan 67.50≈125图2－6解：如图D61，过点P 作PC ⊥AB ，垂足为C ，设PC ＝x 海里，在Rt △APC 中，∵tan ∠A ＝PC AC， ∴AC ＝PC tan67.5°＝5x12.图D61在Rt △PCB 中，∵tan ∠B ＝PC BC， ∴BC ＝x tan36.9°＝4x3.∵AC ＋BC ＝AB ＝21×5， ∴5x 12＋4x3＝21×5，解得 x ＝60. ∵sin ∠B ＝PCPB，∴PB ＝PC sin ∠B ＝60sin36.9°＝60×53＝100(海里)．∴海检船所在B 处与城市P 的距离为100海里．17．2011年6月4日，李娜获得法网公开赛的冠军，圆了中国人的网球梦，也在国内掀起一股网球热．某市准备为青少年举行一次网球知识讲座，小明和妹妹都是网球球迷，要求爸爸去买门票，但爸爸只买回一张门票，那么谁去就成了问题，小明想到一个办法：他拿出一个装有质地、大小相同的2x 个红球与3x 个白球的袋子，让爸爸摸出一个球，如果摸出的是红球，妹妹去听讲座，如果摸出的是白球，小明去听讲座．(1)爸爸说这个办法不公平，请你用概率的知识解释原因；(2)若爸爸从袋中取出3个白球，再用小明提出的办法来确定谁去听讲座，请问摸球的结果是对小明有利还是对妹妹有利，说明理由．解：(1)∵红球有2x 个，白球有3x 个，∴P (红球)＝2x 2x ＋3x ＝25，P (白球)＝3x 2x ＋3x ＝35，∴P (红球)< P (白球)， ∴这个办法不公平．(2)取出3个白球后，红球有2x 个，白球有(3x －3)个， ∴P (红球)＝2x5x －3，P (白球)＝3x －35x －3，x 为正整数，∴P (红球)－ P (白球) ＝3－x5x －3.①当x <3时，则P (红球)> P (白球)， ∴对小妹有利．②当x ＝3时，则P (红球)＝ P (白球)， ∴对小妹、小明是公平的．③当x >3时，则P (红球)< P (白球)， ∴对小明有利．18．如图2－7，在⊙O 中，AB 为直径，AC 为弦，过点C 作CD ⊥AB 与点D ，将△ACD 沿AC 翻折，点D 落在点E 处，AE 交⊙O 于点F ，连接OC 、FC .(1)求证：CE 是⊙O 的切线；(2)若FC ∥AB ，求证：四边形AOCF 是菱形．图2－7解：(1)由翻折可知，∠F AC ＝∠OAC, ∠E ＝∠ADC ＝90°， ∵OA ＝OC ，∴∠OAC ＝∠OCA ， ∴∠F AC ＝∠OCA ， ∴OC ∥AE ， ∴∠OCE ＝90°，即OC ⊥CE . ∴CE 是⊙O 的切线．(2)∵FC ∥AB ，OC ∥AF ，∴四边形AOCF 是平行四边形． ∵OA ＝OC ，∴▱AOCF 是菱形．19．如图2－8，已知反比例函数y ＝kx 的图象经过第二象限内的点A (－1，m )，AB ⊥x轴于点B ，△AOB 的面积为2.若直线y ＝ax ＋b 经过点A ，并且经过反比例函数y ＝kx 的图象上另一点C (n ，－2)．(1)求直线y ＝ax ＋b 的解析式；(2)设直线y ＝ax ＋b 与x 轴交于点M ，求AM 的长．图2－8解：(1)∵点A (－1，m )在第二象限内， ∴AB ＝m ，OB ＝1，∴S △ABO ＝12AB ·BO ＝2.即12m ×1＝2，解得m ＝4，∴A (－1,4)． ∵点A (－1,4)在反比例函数y ＝kx 的图象上，∴4＝k－1，解得k ＝－4，∴反比例函数为y ＝－4x.又∵反比例函数y ＝－4x 的图象经过C (n ，－2)，∴－2＝－4n ，解得n ＝2，∴C (2，－2)．∵直线y ＝ax ＋b 过点A (－1,4)，C (2，－2)，∴⎩⎪⎨⎪⎧ 4＝－a ＋b －2＝2a ＋b ，解方程组得⎩⎪⎨⎪⎧a ＝－2b ＝2. ∴直线y ＝ax ＋b 的解析式为y ＝－2x ＋2. (2)当y ＝0时，即－2x ＋2＝0，解得x ＝1，即点M (1,0)．在Rt △ABM 中，∵AB ＝4，BM ＝BO ＋OM ＝1＋1＝2，由勾股定理得AM ＝2 5.五、解答题(本大题共3小题，每小题9分，共27分)20．为鼓励学生参加体育锻炼，学校计划拿出不超过3 200元的资金购买一批篮球和排球，已知篮球和排球的单价比为3∶2，单价和为160元．(1)篮球和排球的单价分别是多少元？(2)若要求购买的篮球和排球的总数量是36个，且购买的排球数少于11个，有哪几种购买方案？解：(1)设篮球的单价为x 元，则排球的单价为23x 元，据题意得x ＋23x ＝160，解得x ＝96. 故23x ＝23×96＝64. 所以篮球和排球的单价分别是96元、64元．(2)设购买的篮球数量为n 个，则购买的排球数量为(36－n )个．由题意得：⎩⎪⎨⎪⎧36－n <1196n ＋64(36－n )≤3 200，解得25＜n ≤28.而n 是整数，所以其取值为26,27,28，对应36－n 的值为10,9,8，所以共有三种购买方案：①购买篮球26个，排球10个； ②购买篮球27个，排球9个； ③购买篮球28个，排球8个．21．已知：如图2－9，在△ABC 中，BC ＝AC ，以BC 为直径的⊙O 与边AB 相交于点D ，DE ⊥AC ，垂足为点E .(1)求证：点D 是AB 的中点；(2)判断DE 与⊙O 的位置关系，并证明你的结论；(3)若⊙O 的直径为18，cos B ＝13，求DE 的长．图2－9(1)证明：如图D62，连接CD ，则CD ⊥AB ，图D62又∵AC ＝BC ，∴AD ＝BD , 即点D 是AB 的中点． (2)解：DE 是⊙O 的切线．理由是：连接OD ，则DO 是△ABC 的中位线， ∴DO ∥AC . 又∵DE ⊥AC ， ∴DE ⊥DO ，又∵OD 是⊙O 的半径， ∴DE 是⊙O 的切线．(3)∵AC ＝BC ，∴∠B ＝∠A ， ∴cos ∠B ＝cos ∠A ＝13.∵cos ∠B ＝BD BC ＝13，BC ＝18，∴BD ＝6，∴AD ＝6. ∵cos ∠A ＝AE AD ＝13，∴AE ＝2.在Rt △AED 中，DE ＝AD 2－AE 2＝4 2.22．如图2－10，已知二次函数y ＝－x 2＋bx ＋c 的图象经过A (－2，－1)，B (0,7)两点．图2－10(1)求该抛物线的解析式及对称轴； (2)当x 为何值时，y ＞0?(3)在x 轴上方作平行于x 轴的直线l ，与抛物线交于C 、D 两点(点C 在对称轴的左侧)，过点C 、D 作x 轴的垂线，垂足分别为F 、E .当矩形CDEF 为正方形时，求C 点的坐标．解：(1)把A (－2，－1)，B (0,7)两点的坐标代入 y ＝－x 2＋bx ＋c ，得⎩⎪⎨⎪⎧ －4－2b ＋c ＝－1c ＝7，解得⎩⎪⎨⎪⎧b ＝2c ＝7. 所以，该抛物线的解析式为y ＝－x 2＋2x ＋7，又因为y ＝－x 2＋2x ＋7＝－(x －1)2＋8，所以对称轴为直线x ＝1.(2)当函数值y＝0时，－x2＋2x＋7＝0的解为x＝1±2 2，结合图象，容易知道1－2 2<x<1＋2 2时，y>0. (3)当矩形CDEF为正方形时，设C点的坐标为(m，n)，则n＝－m2＋2m＋7，即CF＝－m2＋2m＋7.因为C、D两点的纵坐标相等，所以C、D两点关于对称轴x＝1对称，设点D的横坐标为p，则1－m＝p－1，所以p＝2－m，所以CD＝(2－m)－m＝2－2m.因为CD＝CF，所以2－2m＝－m2＋2m＋7，整理，得m2－4m－5＝0，解得m＝－1或5.因为点C在对称轴的左侧，所以m只能取－1.当m＝－1时，n＝－m2＋2m＋7＝－(－1)2＋2×(－1)＋7＝4.于是，点C的坐标为(－1,4)．。

2012年从化中考数序模拟试卷

5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。

我们只说喜欢，就算喜欢也是偷偷摸摸的。

”6.方茴说：“我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。

”7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。

8.这些孩子都很活泼与好动，即便吃饭时也都不太老实，不少人抱着陶碗从自家出来，凑到了一起。

9.石村周围草木丰茂，猛兽众多，可守着大山，村人的食物相对来说却算不上丰盛，只是一些粗麦饼、野果以及孩子们碗中少量的肉食。

2012年从化市初三综合测试数学试卷班别____________姓名____________________学号__________成绩____________一、选择题（本大题共10小题，每小题3分，共30分．）1．3-的值等于（）．A．3 B．－3 C．±3 D．32．若分式21-x有意义，则x的取值范围是（）．A．2x> B．2≤x C．x=2 D．2x≠3．在下列运算中，计算正确的是 ( )．A．725)(xx= B．222)(yxyx-=-C．10313xxx=÷ D．633xxx=+4．化简aa12-+aa1+的结果是（）．A．2aa+ B．1-a C．1+a D．15．菱形具有而矩形不一定具有的性质是（）．A．对角线相等 B．对角线互相垂直 C．对角线互相平分 D．对角互补6．将抛物线2y x=-向左平移2个单位后，得到的抛物线的解析式是（）．A．22y x=-+ B．2(2)y x=-+ C．2(2)y x=-- D．22y x=--7．不等式组的解集在数轴上表示如图1所示，则该不等式组可能为（）．A．{12x x>-≤ B．{12x x≥-<C．{12x x≥-≤D．{12x x<-≥8．两个大小不同的球在水平面上靠在一起，组成如图2所示的几何体，则该几何体的左视图是（）．A．两个外离的圆B．两个外切的圆C．两个相交的圆D．两个内切的圆9．已知正比例函数y kx=（0k≠）的函数值y随x的增大而增大，则一次函数y kx k=+的图象大致是（）．水平面主视方向5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。