大学物理3.电势.ppt
合集下载
大学物理-电势
Va E dl a E dl
讨论
a
a
1)电势零点的选择(参考点)
任意 视分析问题方便而定
参考点不同电势不同
10
通常：
理论计算有限带电体电势时选无限远为参考点
实际应用中或研究电路问题时取大地、仪器外 壳等
2)电势的量纲
SI制：单位 V (伏特)
量纲
V
W q
L2 MT
3I
1
3)电势是一个长程物理量
b b
a
f dl q E dl Wa Wb
a
a
b E dl
Wa
Wb
a
q
q 与试验电荷无关
根据静电场 Wa Wb 的环路定理 q q
E dl Va Vb
a
称 a b两点电势差
若选b点的势能为参考零点 则
a点的电势：
势能零点
势能零点
VA VB
11
rB rA
E
dr
Q 4πε0
rB dr rA r 2
()
4πε0 rA rB
（2）r R
VA VB
rB rA
E
dr
0
o A B A dr B
R
drrA r
r
rB
20
（3）r R 令 rB V 0
Q 1 1
VA VB
（4）r R
()
4πε0
rA R
q
x2 R2
x
R，VP
q 4πε0 x
V
dl
q
q
4πε0 R
4πε0 x2 R2
R
r
xo x
Px
o
x
大学物理第三章电势
2 π AR + 3 λ e E3 = 6 πε 0 r
方向沿径向向外
18
（2）选距离轴线的距离为 l ( l > R ) 处为电势 零点，计算圆柱体内、 零点，计算圆柱体内、外各点的电势分 布。 注意： 求各点电势（电势分布） 注意： 求各点电势（电势分布）时，要分 区域讨论，分区方式与场强相同。 区域讨论，分区方式与场强相同。 电势零点位置选择： 电势零点位置选择： “无限长”柱状带电 无限长” 对 体产生的电场， 体产生的电场，绝对不 能选无穷远处为电势零 点，只能选其它任一点 为电势零点。 为电势零点。
qo =∫ ⋅
5
静电场的保守性（静电场环路定理） 二、 静电场的保守性（静电场环路定理）
L2
∫
L
E ⋅ dl = 0
a
.
qo
L1
b
.
在静电场中，场强沿任意闭合路径的线积 在静电场中， 分等于零。 对任何静电场， 分等于零。即：对任何静电场，电场强度的 线积分都只取决于起点和终点的位置， 线积分都只取决于起点和终点的位置，而与连 接起点和终点间的路径无关。 接起点和终点间的路径无关。
15
例2（1197）一半径为R的“无限长”圆柱形带 1197）一半径为 的 无限长” 电体， 电体，其电荷体密度为 ρ = A r ( r ≤ R ) 式中A为常数 为常数。 式中 为常数。在此圆柱体外再罩一半 径为R 无限长” 径为 1 、线电荷密度为 λ e 的“无限长”圆 试求： 筒，试求： 圆柱体内、 （1）圆柱体内、外各点的电场强度分布 （2）选距离轴线的距离为 l ( l > R ) 处为电势零点，计算圆柱体内、 处为电势零点，计算圆柱体内、 外各点的电势分布。 外各点的电势分布。 （3）柱表面与柱壳之间的电势差。 柱表面与柱壳之间的电势差。
大学物理静电场3(电势)ppt课件
最新课件
9
单个点电荷的场的电势 U q
2）电势叠加原理（标量叠加）
q
Up Edl
Eidl
1
4
0r r1 r2
p
p
P Ei dl
qi
q2
4 0ri
或对连续分布带电体
U p
dq
4 0r
q
最新课件
dq
r
p
r3
ri
q3
qi
p
Up=?
10
Ua
i
qi
40ri
一个点电荷系的电场中,任一点的电势等于每一个点电 荷单独存在时在该点所产生电势的代数和。——电势 叠加原理
电势叠加原理 习题最指新课导件 P65 16
34
形状如图所示的绝缘细线，其上均匀分布着
正电荷。已知电荷线密度为λ，两段直线长 均为a，半圆环的半径为a。求环心O点的电 势？
电势叠加原理
求电势能和电力
习题指导P65 17
最新课件
35
３．有一边长为a的正方形平面，在其中垂线上距 中心O点a/2处，有一电量为q的正点电荷，如图所 示，则通过该平面的电场强度通量为：
b
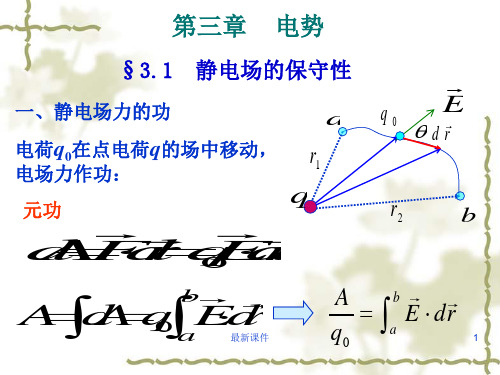
W a W bA a bq 0 aE d r
二、电势差：
移动单位正电荷从电场中a 点到b点，静电力所做 的功，为静电场中两点的电势差:
U abU aU ba bEdr最 新W 课q 件aW qb 描只述与电电场场的有性关质6
➢某点 (a点) 的电势：
首先设定电势0点（b点）：
Ua
b
Edr
积分与路径无关
最新课件
4
对任何静电场，电场强度的线积分都只取决于起 点和终点的位置而与积分路径无关－－静电场的
大学物理课件电势梯度
大学物理课件-电势梯度
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量，表示为▽Φ。
公式
▽Φ = -E，其中E是电场强度矢量，Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向，即电场线方向。
计算方法
在标量场中，梯度的方向可以通过求导数的方法得到，即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0， 其中▽表示哈密顿算子，E表示电场强 度矢量，ρ表示电荷密度，ε0表示真 空电容率。
计算步骤
时，需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词：非线性关系 总结词：方向判断
详细描述：在复杂电场中，电势梯度与电场强度 之间的关系可能变得非线性。例如，在点电荷产 生的电场中，电势梯度随距离的增加而减小，但 仍然与电场强度成正比。
详细描述：在复杂电场中，判断电势梯度的方向 需要考虑电场线的分布和方向。通常，电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量，表示电势在空间中的变化率，没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度，计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量，可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定，即电势降低的方向。
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量，表示为▽Φ。
公式
▽Φ = -E，其中E是电场强度矢量，Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向，即电场线方向。
计算方法
在标量场中，梯度的方向可以通过求导数的方法得到，即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0， 其中▽表示哈密顿算子，E表示电场强 度矢量，ρ表示电荷密度，ε0表示真 空电容率。
计算步骤
时，需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词：非线性关系 总结词：方向判断
详细描述：在复杂电场中，电势梯度与电场强度 之间的关系可能变得非线性。例如，在点电荷产 生的电场中，电势梯度随距离的增加而减小，但 仍然与电场强度成正比。
详细描述：在复杂电场中，判断电势梯度的方向 需要考虑电场线的分布和方向。通常，电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量，表示电势在空间中的变化率，没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度，计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量，可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定，即电势降低的方向。
《大学物理》第三章电势S
i
" p"
或： d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面（只知道总电量）”
在球心处的电势？ • 如果用“路径积分法”，本题应如何解？
例计算均匀带电q 的园环轴线上任一点的电势。 解： 用“电势叠加法” y （以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0） dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大，就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则：E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向（由点 a到点b′） 则：E dl a b 0 , a b
" p"
或： d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面（只知道总电量）”
在球心处的电势？ • 如果用“路径积分法”，本题应如何解？
例计算均匀带电q 的园环轴线上任一点的电势。 解： 用“电势叠加法” y （以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0） dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大，就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则：E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向（由点 a到点b′） 则：E dl a b 0 , a b
大学物理电势ppt课件
大学物理电势ppt课件目录•电势基本概念与性质•点电荷与连续分布电荷电势•导体与绝缘体在电场中电势特性•电势能、电势差及等势面•电场力做功与路径无关性讨论•总结回顾与拓展延伸01电势基本概念与性质电势定义及物理意义电势定义描述电场中某点电势能的性质，反映单位正电荷在该点所具有的电势能。
物理意义表示电场中某点对电荷的吸引或排斥能力，是标量，具有相对性。
电势单位与量纲单位伏特（V）量纲ML^2T^-2A^-1（质量、长度、时间和电流的强度量纲的组合）电势与电场关系电场强度与电势梯度关系电场强度等于电势梯度的负值。
电场线与等势面关系电场线总是垂直于等势面，且指向电势降低的方向。
多个点电荷在某点产生的电势等于各点电荷单独存在时在该点产生电势的代数和。
连续分布电荷电势叠加连续分布电荷在某点产生的电势等于电荷分布区域内各点电荷元在该点产生电势的代数和。
点电荷电势叠加电势叠加原理VS02点电荷与连续分布电荷电势描述点电荷间相互作用力，是电势计算的基础。
库仑定律单位正电荷在电场中某点具有的电势能。
电势定义$V =frac{kQ}{r}$，其中$k$为静电力常量，$Q$为场源电荷量，$r$为到场源电荷的距离。
点电荷电势公式点电荷电势计算连续分布电荷电势求解方法叠加原理对于多个点电荷或连续分布电荷产生的电势，可应用叠加原理进行求解。
积分方法对于连续分布电荷，需采用积分方法计算电势，如线积分、面积分或体积分。
常见连续分布电荷均匀带电直线、均匀带电平面、均匀带电球体等。
均匀带电直线电势通过高斯定理和积分方法求解，结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势利用高斯定理和叠加原理，可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势采用高斯定理和积分方法，可得到球体内外任意一点的电势表达式。
典型连续分布电荷电势实例分析030201电荷分布对电势影响电荷分布形状不同形状的电荷分布产生的电势分布不同，如点电荷、线电荷、面电荷和体电荷等。
电势及其梯度
q E= 2 4πε 0 r
1
cosθ dl = dr
q o
r
c
θ
r E
a b rb 1 qq qq0 1 1 0 − ∴W = ∫ dW = ∫ 2 dr = a ra 4πε 4πε 0 ra rb 0 r
温州大学物理与电子信息学院
电势和电势差
结论：在点电荷的电场中， 结论：在点电荷的电场中，电场力对试验电荷所 做的功， 做的功 ， 只与试验电荷所带电量以及起点和终点 位置有关，而与所经历的路径无关． 位置有关，而与所经历的路径无关． 问题：任何带电体系产生的电场的结果如何？ 问题：任何带电体系产生的电场的结果如何？ r r r Q E = E1 + E 2 + L r r r r r r r ∴W = ∫ F ⋅ dl = q0 ∫ E ⋅ dl = q0 ∫ ( E1 + E2 + L) ⋅ dl r r r r = q0 ∫ E1 ⋅ dl + q0 ∫ E2 ⋅ dl + L
ρR 2 r Up = − ln < 0 2εo R
P r o o
温州大学物理与电子信息学院
定义法求电势
R
r ρ r r r < R E= 2ε o
r≥R
r
.
p
ρR 2 r Up = − ln 2εo R < 0
R
r ρR 2 ˆ = λ r E= r ˆ 2πεor 2εor
r<R
r= 0处， U= Umax= ρ R 2 处 2εo ε
温州大学物理与电子信息学院
电势梯度概念 等势面 定义:电势相等的曲面 定义:
U1
+q
3感生电动势(大学物理 - 电磁感应部分)
沿 E感 线作半径为 r
的环路，分割导体
元 dl， 在 dl 上产生的感生
R o
h E感 r
dl
电动势为： d i E 感dl cos
i di E 感dl cos
由上题结果，圆形区 域内部的感生电场：
E感
R dB
2 dt
o
RrBiblioteka 例2：圆形均匀分布的磁场半径为 R，
磁场随时间均匀增 加，
dB k dt
在磁场中放置一长
为 L 的导体棒，求
棒中的感生电动势。
R
o B
L
E感 作用在导体棒上，
使导体棒上产生一个 向右的感生电动势，
感生电场 E感
由变化的磁场激发
电力线为闭合曲线 dB 0 dt
静电场为散场
E感
感生电场为有旋场
静电场E
感生电场E感
为保守场作功与路径无关 为非保守场作功与路径有关
电 场
E dl 0
的
性
静电场为有源场
质
E
dS
q
0
i
E感
dl
d m
dt
感生电场为无源场 E感 d S 0
d dt
s B
dS
如果回路面积不变则有：
i E感 d l sddBt d S
五、感生电场的计算与举例
1. 要求环路上各点的 E感大小相等，方向
与路径方向一致；
2.要求磁场均匀变化 dB 常量 , dt
且 d B // d S ; dt
的环路，分割导体
元 dl， 在 dl 上产生的感生
R o
h E感 r
dl
电动势为： d i E 感dl cos
i di E 感dl cos
由上题结果，圆形区 域内部的感生电场：
E感
R dB
2 dt
o
RrBiblioteka 例2：圆形均匀分布的磁场半径为 R，
磁场随时间均匀增 加，
dB k dt
在磁场中放置一长
为 L 的导体棒，求
棒中的感生电动势。
R
o B
L
E感 作用在导体棒上，
使导体棒上产生一个 向右的感生电动势，
感生电场 E感
由变化的磁场激发
电力线为闭合曲线 dB 0 dt
静电场为散场
E感
感生电场为有旋场
静电场E
感生电场E感
为保守场作功与路径无关 为非保守场作功与路径有关
电 场
E dl 0
的
性
静电场为有源场
质
E
dS
q
0
i
E感
dl
d m
dt
感生电场为无源场 E感 d S 0
d dt
s B
dS
如果回路面积不变则有：
i E感 d l sddBt d S
五、感生电场的计算与举例
1. 要求环路上各点的 E感大小相等，方向
与路径方向一致；
2.要求磁场均匀变化 dB 常量 , dt
且 d B // d S ; dt
大学物理电动势的计算课件
常见的能量转换情势
常见的能量转换情势包括机械能转换为电能、化学能转换为电能、太阳能转换为电能等。 这些转换都离不开电动势的作用。
04
实验：测量电动势
实验目的
掌握电动势的测量原 理和方法。
培养实验操作和数据 处理能力。
了解不同电源的电动 势和内阻。
实验原理
01
电动势是电源将其他情势的能 转化为电能的本领，单位为伏 特（V）。
02
电源的电动势等于电源没有接 入电路时两极间的电压。
03
通过测量电源在不同负载下的 端电压和电流，可以计算电动 势和内阻。
实验步骤与数据记录
2. 将电源、电压表、电流表 、可调电阻按照电路图连接
。
1. 准备实验器材：电源、电 压表、电流表、可调电阻、
导线等。
01
载下的电流和电压值。
大学物理电动势的计算课件
目录
• 电动势的基本概念 • 电动势的计算方法 • 电动势的应用 • 实验：测量电动势 • 习题与解答
01
电动势的基本概念
电动势的定义
电动势是衡量非静电力做功能力的物 理量，表示非静电力把单位正电荷从 负极经电源内部移到正极所做的功。
在电路中，电动势的大小等于非静电 力所做的功与电荷量的比值，即 $E = frac{W}{q}$。
解析2
对于进阶习题部分，难度有所提升。除了考察交变电动势的瞬时值的表达式外，还涉及 到了一些物理量的计算和推导。例如通过瞬时值的表达式求出最大值和角速度，进而得
到周期。
THANK YOU
基础习题
• 题目2： 一矩形线圈在匀强磁场 中匀速转动产生的感应电动势e = evwtsinwt，则下列判断正确 的是 ()
基础习题
常见的能量转换情势包括机械能转换为电能、化学能转换为电能、太阳能转换为电能等。 这些转换都离不开电动势的作用。
04
实验：测量电动势
实验目的
掌握电动势的测量原 理和方法。
培养实验操作和数据 处理能力。
了解不同电源的电动 势和内阻。
实验原理
01
电动势是电源将其他情势的能 转化为电能的本领，单位为伏 特（V）。
02
电源的电动势等于电源没有接 入电路时两极间的电压。
03
通过测量电源在不同负载下的 端电压和电流，可以计算电动 势和内阻。
实验步骤与数据记录
2. 将电源、电压表、电流表 、可调电阻按照电路图连接
。
1. 准备实验器材：电源、电 压表、电流表、可调电阻、
导线等。
01
载下的电流和电压值。
大学物理电动势的计算课件
目录
• 电动势的基本概念 • 电动势的计算方法 • 电动势的应用 • 实验：测量电动势 • 习题与解答
01
电动势的基本概念
电动势的定义
电动势是衡量非静电力做功能力的物 理量，表示非静电力把单位正电荷从 负极经电源内部移到正极所做的功。
在电路中，电动势的大小等于非静电 力所做的功与电荷量的比值，即 $E = frac{W}{q}$。
解析2
对于进阶习题部分，难度有所提升。除了考察交变电动势的瞬时值的表达式外，还涉及 到了一些物理量的计算和推导。例如通过瞬时值的表达式求出最大值和角速度，进而得
到周期。
THANK YOU
基础习题
• 题目2： 一矩形线圈在匀强磁场 中匀速转动产生的感应电动势e = evwtsinwt，则下列判断正确 的是 ()
基础习题
大学物理第三章电势
电势零点
8
P
电荷分布在有限空间， 取无穷远为 U= 0 点。
电位零点的选取： 电荷分布在无限空间， 取有限远点为U= 0 点。 一般工程上， 选大地或设备外壳为U=0点。
9
解题技巧：当场源带电体是球状带电体和柱状带 电体时，无论电势零点取在什么位置， 积分路径都应沿径向向外。此时，
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点（即:令Uc = 0）时，
电势零点
P
E cos dl
即：电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo
5
二、 静电场的保守性（静电场环路定理）
L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中，场强沿任意闭合路径的线积 分等于零。即：对任何静电场，电场强度的 线积分都只取决于起点和终点的位置，而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时，静电场力
8
P
电荷分布在有限空间， 取无穷远为 U= 0 点。
电位零点的选取： 电荷分布在无限空间， 取有限远点为U= 0 点。 一般工程上， 选大地或设备外壳为U=0点。
9
解题技巧：当场源带电体是球状带电体和柱状带 电体时，无论电势零点取在什么位置， 积分路径都应沿径向向外。此时，
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点（即:令Uc = 0）时，
电势零点
P
E cos dl
即：电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo
5
二、 静电场的保守性（静电场环路定理）
L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中，场强沿任意闭合路径的线积 分等于零。即：对任何静电场，电场强度的 线积分都只取决于起点和终点的位置，而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时，静电场力
(大学物理ppt)第 2 章 电势
ra
静电力作功与具体路径无关，只取决于检验电
荷的始末位置。 定义 电势差
rb A a b E dl ra q0
二、电势差和电势
2.电势
b a E dl ra d E dl
rb
即 若
称为电势零点 rb 则：电场中 a 点的电势 a r E dl
r rb 时， b 0,
a
通常
rb 时，b 0,
电势
a
ra
E dl
二、电势差和电势 电势
Biblioteka r E dl上式表明，电场中某点的电势大小，等于把单 位正电荷从该点经任意路径移到无限远处电场力 所作的功的大小。 电 势 单 位 ： 焦 尔 / 库 仑 ， 称 为 伏 特 ， 简 称 伏
A dA q0 Edr
L ra rb
q0q 1 1 ( ) 40 ra rb
一、静电场环路定理
2.静电场的保守性
在点电荷电场中，电场力对检验电荷所作的
功，只取决于检验电荷 q0 及其始末位置，与连 接始末位置的具体路径无关。这个性质称为静电 场的保守性。
一、静电场环路定理
二、电势差和电势
3.单个点电荷在空间的电势
点电荷在空间任意一点的电势 E dl
r
q
r
p
r
q dr 2 40 r
1
E
1 q 40 r
q e 2 r 40 r 1
积分路径沿位矢方向
二、电势差和电势
1 q 40 r
在正电荷的电场中，各点的电势均为正 值，离电荷越远的点，电势越低； 在负电荷的电场中 ，各点的电势均为负 值，离电荷越远的点，电势越高。
静电力作功与具体路径无关，只取决于检验电
荷的始末位置。 定义 电势差
rb A a b E dl ra q0
二、电势差和电势
2.电势
b a E dl ra d E dl
rb
即 若
称为电势零点 rb 则：电场中 a 点的电势 a r E dl
r rb 时， b 0,
a
通常
rb 时，b 0,
电势
a
ra
E dl
二、电势差和电势 电势
Biblioteka r E dl上式表明，电场中某点的电势大小，等于把单 位正电荷从该点经任意路径移到无限远处电场力 所作的功的大小。 电 势 单 位 ： 焦 尔 / 库 仑 ， 称 为 伏 特 ， 简 称 伏
A dA q0 Edr
L ra rb
q0q 1 1 ( ) 40 ra rb
一、静电场环路定理
2.静电场的保守性
在点电荷电场中，电场力对检验电荷所作的
功，只取决于检验电荷 q0 及其始末位置，与连 接始末位置的具体路径无关。这个性质称为静电 场的保守性。
一、静电场环路定理
二、电势差和电势
3.单个点电荷在空间的电势
点电荷在空间任意一点的电势 E dl
r
q
r
p
r
q dr 2 40 r
1
E
1 q 40 r
q e 2 r 40 r 1
积分路径沿位矢方向
二、电势差和电势
1 q 40 r
在正电荷的电场中，各点的电势均为正 值，离电荷越远的点，电势越低； 在负电荷的电场中 ，各点的电势均为负 值，离电荷越远的点，电势越高。
《大学物理》电势能、电势、梯度 (3)
r
ε ε A
=
=q 0E .dl
= q 0E .d
q
4π
q
0
o
rb ra
cosφq
r= 4π
dr r2
q
o
0
r
2d r
q
dr φ dl
b
r b dl φφ
ra q 0 E a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功
8 8
Wa = A a = q 0 a E .dl
(
或：Wa=A ab
=q 0
b
a E
.
dl
其中b为零势能点 )
dA =F. d l =q 0E .dl
r
=q 0E .dl cosφ
q
φ dl b
r b dl φφ
ra q 0 E
a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功
dr
设点电荷 q、试验电荷 qo r
dA =F. d l =q 0E .dl
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
1、点电荷对试验电荷作功 设点电荷 q、试验电荷 qo
dA =F. d l =q 0E .dl
q
b r b dl φφ
ra q 0 E
a
2-1-5
一、场强环流定理
当带电体在静电场中移动时，静电场力
对带电体要作功，这说明静电场具有能量。
清华大学大学物理经典课件——电势
电磁学（第三册）
第3章 电势
陈信义编
1
目录
§3.1 静电场的保守性 §3.2 电势差和电势 §3.3 电势叠加原理 §3.4 电势梯度 §3.5 电荷在外场中的静电势能 §3.6 电荷系的静电能 §3.7 静电场的能量 补充：静电场环路定理的微分形式
【演示实验】高压带电操作、电容器储能
2
§3.1 静电场的保守性
电场线 等势面
23
电场线
等势面
平行板电容器
24
人心脏的等电势 线，类似于电偶 极子。
25
二、场强和电势的关系
静电场中某点的电场强度，等于该点电 势的负梯度
EU
U xiUy jUz k
证明见力学§4.8由势能求保守力。 电势梯度矢量：U
静电场强等于负电势梯度矢量。
26
U 的基本特征：U 垂直于过该点的等势 面，方向是电势升高最快的方向。
i
U(p)p 0E drp 0E idr U i(p)
p
ip
i
15
1、点电荷体系
U(p)in14qi0ri
qj dqqi
p ri
2、连续分布的电荷体系
p
dq
r U(p)电荷 体4系 dq0r
16
【例】均匀带电圆环轴线上的电势
q
dq
r
R
O
x
p
U(
p)
dq
40r
1 4
0r
q
dq
q q
40r 40 R2x2
7
二、电势 选 p0 点为电势零点：Up0 0，则 p点电势
p0
U ( p) E dr p
—把单位正电荷自该点移到电势零点，电 场力作的功。
第3章 电势
陈信义编
1
目录
§3.1 静电场的保守性 §3.2 电势差和电势 §3.3 电势叠加原理 §3.4 电势梯度 §3.5 电荷在外场中的静电势能 §3.6 电荷系的静电能 §3.7 静电场的能量 补充：静电场环路定理的微分形式
【演示实验】高压带电操作、电容器储能
2
§3.1 静电场的保守性
电场线 等势面
23
电场线
等势面
平行板电容器
24
人心脏的等电势 线，类似于电偶 极子。
25
二、场强和电势的关系
静电场中某点的电场强度，等于该点电 势的负梯度
EU
U xiUy jUz k
证明见力学§4.8由势能求保守力。 电势梯度矢量：U
静电场强等于负电势梯度矢量。
26
U 的基本特征：U 垂直于过该点的等势 面，方向是电势升高最快的方向。
i
U(p)p 0E drp 0E idr U i(p)
p
ip
i
15
1、点电荷体系
U(p)in14qi0ri
qj dqqi
p ri
2、连续分布的电荷体系
p
dq
r U(p)电荷 体4系 dq0r
16
【例】均匀带电圆环轴线上的电势
q
dq
r
R
O
x
p
U(
p)
dq
40r
1 4
0r
q
dq
q q
40r 40 R2x2
7
二、电势 选 p0 点为电势零点：Up0 0，则 p点电势
p0
U ( p) E dr p
—把单位正电荷自该点移到电势零点，电 场力作的功。
大学物理 真空中静电场之三 (电势)
P
Q dr 2 40 r ?
P
Q
o
R
Q dr 2 4 0 r r
Q 4 0 r 1
r
图示
U
0
R
r
例2
计算电量为 Q 的带电球面球心的电势
求：球心处的电势 解：(用迭加原理） • 在球面上任取一电荷元
dq
o
Q R
• 电荷元在球心的电势为
球面上电荷在球心的总电势
Qx (R x )
2 3 2 2
dx
Q 40 R x
2 2
结果同上
作 业
习题P322-323
7-22,7-26,7-27,7-29
p
正电荷产生的电势为正，负电荷产生的电势为负,对吗？
2.电势迭加原理 内容:
U U i
i
标量迭加 3.电势迭加原理的应用(两种情况）
1) 电荷系产生的电势
1 qi U U i 4 0 ri i
a
ri
2) 连续分布的带电体的电势 方法一:利用迭加原理
dq
Q
P
U
dU
1.电势零点的选择(参考点)
Ua
1) 任意
2) 一般情况下: U = 0
a
E dl
3) 对无限大带电体产生的电势
2.电势差的单位--------V(伏特) 3.电场力的功和电势差的关系
U有限远处 = 0
Aab q (U a U b ) q E dl
Q ra r rdl cos
rdr
a
dl
1 Qq 1 qQ r dl rdr 2 3 4 0 r r 40 r
Q dr 2 40 r ?
P
Q
o
R
Q dr 2 4 0 r r
Q 4 0 r 1
r
图示
U
0
R
r
例2
计算电量为 Q 的带电球面球心的电势
求：球心处的电势 解：(用迭加原理） • 在球面上任取一电荷元
dq
o
Q R
• 电荷元在球心的电势为
球面上电荷在球心的总电势
Qx (R x )
2 3 2 2
dx
Q 40 R x
2 2
结果同上
作 业
习题P322-323
7-22,7-26,7-27,7-29
p
正电荷产生的电势为正，负电荷产生的电势为负,对吗？
2.电势迭加原理 内容:
U U i
i
标量迭加 3.电势迭加原理的应用(两种情况）
1) 电荷系产生的电势
1 qi U U i 4 0 ri i
a
ri
2) 连续分布的带电体的电势 方法一:利用迭加原理
dq
Q
P
U
dU
1.电势零点的选择(参考点)
Ua
1) 任意
2) 一般情况下: U = 0
a
E dl
3) 对无限大带电体产生的电势
2.电势差的单位--------V(伏特) 3.电场力的功和电势差的关系
U有限远处 = 0
Aab q (U a U b ) q E dl
Q ra r rdl cos
rdr
a
dl
1 Qq 1 qQ r dl rdr 2 3 4 0 r r 40 r
大学物理(下)03静电场3
大学物理（ 大学物理（下）
§11.3 电 势
静电场—电势 静电场 电势
1
§11.3 电 势
§11.3.1 §11.3.2 §11.3.3 §11.3.4 小结 电场力的功 电势能 电势 电势的计算
静电场—电势 静电场 电势
返回
2
§11.3
§11.3.1 电场力的功
1、在点电荷的电场中 、
电
+q
势
静电场—电势 静电场 电势
12
r+ ⋅ r− ≅ r
2
r− − r+ ≅ l cosθ
3. 连续带电体的电势 连续带电体的电势: (1). 电势积分法 电势积分法:
r dU
P
dq
UP = ∫
∞
dq 4πε0r
Q
Q
(2). 场强积分法 场强积分法:
UP = ∫
P
v v E ⋅ dL
特点： 计算场强对称分布带电体的电势方便。 特点： 计算场强对称分布带电体的电势方便。
W = qU
静电场—电势 静电场 电势
返回
9
§11.3.4 电势的计算
1、 点电荷的电势 、
UP
r ∞ r = ∫ E ⋅ dl
P
q
r
P
r dl
r 设 dr = d l
U
r E
∞
=
=
∫r
∞
E dr
∞
∫r 4πε 0
q 4πε0r
q
dr 2 r
q>0
r
o
=
q<0
静电场—电势 静电场 电势
10
2、电荷系的电势 、
(1). 当 P点 r > R2 ： P = U1 1
§11.3 电 势
静电场—电势 静电场 电势
1
§11.3 电 势
§11.3.1 §11.3.2 §11.3.3 §11.3.4 小结 电场力的功 电势能 电势 电势的计算
静电场—电势 静电场 电势
返回
2
§11.3
§11.3.1 电场力的功
1、在点电荷的电场中 、
电
+q
势
静电场—电势 静电场 电势
12
r+ ⋅ r− ≅ r
2
r− − r+ ≅ l cosθ
3. 连续带电体的电势 连续带电体的电势: (1). 电势积分法 电势积分法:
r dU
P
dq
UP = ∫
∞
dq 4πε0r
Q
Q
(2). 场强积分法 场强积分法:
UP = ∫
P
v v E ⋅ dL
特点： 计算场强对称分布带电体的电势方便。 特点： 计算场强对称分布带电体的电势方便。
W = qU
静电场—电势 静电场 电势
返回
9
§11.3.4 电势的计算
1、 点电荷的电势 、
UP
r ∞ r = ∫ E ⋅ dl
P
q
r
P
r dl
r 设 dr = d l
U
r E
∞
=
=
∫r
∞
E dr
∞
∫r 4πε 0
q 4πε0r
q
dr 2 r
q>0
r
o
=
q<0
静电场—电势 静电场 电势
10
2、电荷系的电势 、
(1). 当 P点 r > R2 ： P = U1 1
大学物理学第11章电势
38
例1 求电矩为 p=ql 的电偶极子在均匀外电场 E 中的电势能
l A
-q
B +q
θ
E
讨论:
39
§11.7 静电场的能量 电场能量密度
电场总能量
积分遍及整个空间
注意：电场能量存在于场强所在的全部空间
40
例2 在真空中一个均匀带电球体,半径为R,总电量为q,试利用电 场 能量公式求此带电系统的静电能。 思路分析： （1）确定电场分布；
R
（2）确定能量密度； （3）从电场能量定义出发求电场能量；
41
++
+
+
+R + +
+
+
+ +r
+ +
+ +
+ +
o +
+ dr +
+
+
+ + +
+++ +
42
期末复习.doc
解：思路分析：
+++ +
+R
o
+
（1）确定电势零点——无穷远处；
q+ （2）用高斯定律确定电场分布；
+ +
+
+ ++
+
+ + （3）确定电势分布；
10
++ +
+
+R
+
o
+ +++
例1 求电矩为 p=ql 的电偶极子在均匀外电场 E 中的电势能
l A
-q
B +q
θ
E
讨论:
39
§11.7 静电场的能量 电场能量密度
电场总能量
积分遍及整个空间
注意：电场能量存在于场强所在的全部空间
40
例2 在真空中一个均匀带电球体,半径为R,总电量为q,试利用电 场 能量公式求此带电系统的静电能。 思路分析： （1）确定电场分布；
R
（2）确定能量密度； （3）从电场能量定义出发求电场能量；
41
++
+
+
+R + +
+
+
+ +r
+ +
+ +
+ +
o +
+ dr +
+
+
+ + +
+++ +
42
期末复习.doc
解：思路分析：
+++ +
+R
o
+
（1）确定电势零点——无穷远处；
q+ （2）用高斯定律确定电场分布；
+ +
+
+ ++
+
+ + （3）确定电势分布；
10
++ +
+
+R
+
o
+ +++
大学物理第23章_电势
电场力做正功,电势能减少
U Ua Ub 0
Vab
V
Va
Vb
Ua
Ub q
因为q<0，所以电势增大
沿着电场线方向，电势降低。
VP VQ
P dl
Q
VP VQ
P
dl Q
思考（1）把电荷 +q 从P点移动到Q点，电场力 是作正功还是负功？P，Q两点哪点的电势高？
（2）如果移动的是负电荷呢？
Va
Ua q
已知电场分布可计算电势
电势差
Br r
ò VA - VB = E ?dl
A
记住！
A、B 两点间的电势差=将单位正电荷从A点 经任意路径移到B点的过程中电场力所做的功。
如何求电场中某点的电势？
设无穷远处电势为零
VA VA V VA
E dl
A
物理意义是什么？
将单位正电荷在电场中从A点经任意路径到达无 穷远处，静电场力所做的功。
电场力所作的功如何用电势差表示出来？
AAB q0 (VA VB )
沿着电场线方向，电势降低。A点电势高，B点
电势低。
对于正电荷：高电势 低电势
B
A 电场力做正功还是负功？
电势能如何变化？
负电荷呢？
例题 23-1 一负电荷（如电子）被放置在图中负极板附近的b 点。如果电子可以自由移动，问：电子的电势能是增加还是减 小？电势将如何变化？ 负电荷受力方向与电场方向相反， 在b点释放的电子将朝正极板运动。
例题23-4 一半径为 r0、总电荷为Q的带电导体球，试确定 距离球心为 r处的电势（a）r > r0，（b）r =r0，(c) r < r0。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
选 U 0 时
U内
q
4 0R
恒量
q1
U外 4 0r r (含点电荷)
由叠加原理：r RA :
U1
qA
4 0RA
qB
4 0RB
RA r RB :
U2
qA
4 0r
qB
4 0RB
r RB :
U3
qA qB
4 0r
[例七]在与面电荷密度的无限大均匀带电平板相距a处
有一点电荷q，求点电荷至平板垂线中点处的电势Up
q
o
aP 2
a
解一： 点电荷q在P处电势：
x
U1
q
4 0
q0qdr
4 0r 2
q
r r'
q0 E
dl
dr
A
dA
L
rb q0qdr
ra 4 0r 2
q0q
4 0
(
1 ra
1 rb
)
rb
可见静电力做功只与检验 电荷起点，终点的位置有关，
b 与所通过的路径无关。
闭合路径： ra rb
A0
推广到任意点电荷系和连续带电体
在点电荷系q1 , q2, …qn 的电场中移动 q0，电场力作功：
2.零势点要统一
1.场〈强1〉积确分定法（E由分定布义求）
〈2〉选零势点和积分路径
〈3〉由电势定义
零势点 零势点
Ua E dl E cos dl 计算 Ua
a
a
〈4〉讨论和总结
Q
E
U
E
dr
注意： ➢ 选取零势点：遵守上述原则。
➢ 若路径上各段 E 的表达式不同，应分段积分。
[例一] 点电荷 q 场中的电势分布
q
4 0R
Rr
1 r
oRr
[例三]无限大均匀带电平面 场中电势分布.Leabharlann 电场分布a o a
x
Ex
0
0
( a x a ) ( x a , x a )
电荷无限分布，在有限远处选零势点.令Uo 0 ， 沿 x 轴方向积分。
x a
区域：
U
a
x
Exdx
0
a
Exdx
0
(
0
)a a 0
3. 遵从叠加原理 ： U Ui （零势点相同）
即点电荷系场中任一点的电势等于各点电荷
单独存在时在该点产生的电势的代数和。
▲五. 电势的计算（两种基本方法）
场强积分法（由定义求） 叠加法 注意：选取零势点的原则 1.使场中电势分布有确定值
一般:场源电荷有限分布:选 U 0 场源电荷无限分布:不选U 0（为什么？） 许多实际问题中选 U地球 0
梯度意义: U 沿 n方向的变化率
梯度表示:
U
def
dU
n
grad
U
算符：
i
j
k
dn
x y z
2.
电势与场强的关系
q0： U1 U2
dA q0E dr q0E dn
U1
U2 n
dn
dA q0U1 q0U2 q0 dU
大小 E dU
U E
P
dr
r
E
方向
dn
E //( n )
〈2〉选零势点，写出 dq 在场点的电势 dU dV
〈3〉由叠加原理： U dU 或 U dU
〈4〉讨论和总结
Q dQ dU U dU
dq
r
[例四] 求均匀带电
R
圆环轴线上
oxPx
的电势分布
dq
解：在圆环上取点电荷dq ,
r R oxPx
令 U 0 dU dq
4 0r
U
x a
区域：
U
a
x
Exdx
0
a
Exdx
0
(
0
)a a 0
a x a 区域：
a o a
U
a 0
a o a a 0
x
U
0
Exdx
x
( 0
)(x )
x 0
x a 区域：
U
x
a
Exdx
x
0
Exdx
a
0
( 0
)( a
)
a 0
U — x 曲线如图
2. 叠加法
dl
〈1〉将带电体划分为典型电荷 dq dq dS
o
q
r
P
E
解：
E
qr
4 0 r
3
U
令 U 0
1 r
o
r
沿径向积分
U
P
E dl
r
qr dr
4 r3
0
qdr
r
4
r2
q
4
r
0
0
[例二] 均匀带电球面场中电势分布（q ，R ）
q
o
r
P
R
E
由高斯定理
E
0qr
4 0 r 3
(r R) (r R)
E
令 U 0 沿径向积分
o
1 r2
Rr
电场强度等于电势的负梯度
dU
E U n
负号表示电场强度和
dn 电势梯度方向相反.
UP
Po
E dl
E
U
dU
n
dn
三、用电势梯度法计算场强
E
U
dU
nˆ
dn
E
U
(
U
i
U
j
U
k)
x y z
特点：电势是标量,可以较方便的求出, 然后再微分求场强.
电势小结
一.静电场环路定理
1.表达： E dl 0
电势
§ 8.4 环路定理 电势
一. 静电力的功
ra
a
L
r
q0 E
q
r
dl
dr
rb
场源电荷： q
E
检验电荷： q0
r
dqr皆0A:为adlF点电Ldlr荷cbqo40sqr0rdd3llr
dl
dr
q0qrdr
4 0r 3 rdr
b
(
dr
dl ,
dr dl dr )
ra
a
L
dA
F dl
U外
P
E外dr
r
qr dr
4 0r 3
q1
4 0r r
U外
q
4 0r
1 r
U内
E
dr
R
E内
dr
E外
d r
P'
P'
R
R
qr dr
4 0r3
q
4 0R
恒量
均匀带电球面内电势与球面处电 势相等，
球面外电势与电量集中于球心的 点电荷情况相同。
q
o P
r
P
R
E
E
1 r2
o
U
dU
q 0
dq
4 0r
q
4 0( R2
x2
1
)2
可进一步由U电势分布求电qx场i强度分布
E x i 4 R2 x2 3 2 0
[例五]已知：RA, RB , qA, qB
求： U1, U 2 , U3
带电球面的电势分布：
球面内：U q 4 0R
RB
qB
qA
o RA 1
2 3
球面外：U q 4 0r
静电场是有势场（无旋场）。
三. 电势能 W
由 A保 EP W
b
A静电力 q0 E dl (Wb Wa ) Wa Wb
a
令 Wb 0 定义 b 为零势点 零 势 点
得： Wa q0 E dl
a
q0 在场中某点的电势能等于将 q0 由该点移到零
势点过程中电场力做的功。
零势点
二. 环路定理
由静电力做功只与检验电荷起点、终点的位置有关，
与所通过的路径无关
——
静电力是保守力
A LF dl Lq0E dl 0
静电场中任意闭合路径
静电场环路定理：LE dl 0
路径上各点的总场强
静电场强沿任意闭合路径的线积分为零，反映 了静电场是保守力场。
凡保守力都有与其相关的势能，
L
2. 意义：静场电，场 是是 有保 势守 场力 。
二.基本量 1.定义： 电势能：
电 势：
电势差：
零势点
Wa q0 E dl
a
零势点
Ua E dl
a
b
Uab Ua Ub E dl
a
2.性质：* 电势是标量函数 * 电势遵从叠加原理 （零势点相同时） * 电势具有相对性（与零势点有关） 电势差具有绝对性（与零势点无关）
性质 (1) 电场线与等势面处处正交
证明：将电荷从等势面上作位移 dl
dA q0E dl
q0Edl cos
0
电场力做功为零
E
而 q0,E,dl 0 / 2 E dl
(2)等势面的疏密反映电场的强弱
dl
E d
U U
U E d C
E d
d
(3)电场线的方向指向电势降落的方向
a 2
无限大带电平板在P处电势：
U2
Pa
Exdx
20
a 2
UP
U1
U2
q
2 0a
a 4 0
对不对？
qP
o