立几 平行与垂直
高中数学专项提升——立体几何中平行与垂直证明
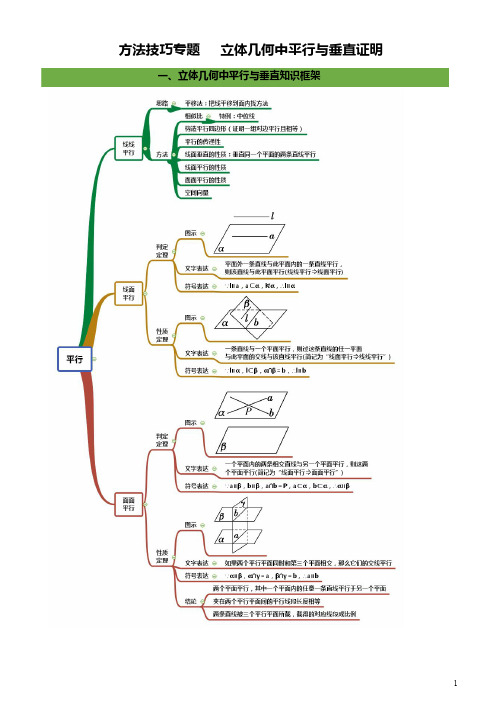
方法技巧专题立体几何中平行与垂直证明一、立体几何中平行与垂直知识框架cc∥∥b a ba ∥⇒二、立体几何中的向量方法【一】“平行关系”常见证明方法1.1直线与直线平行的证明1.1.1利用某些平面图形的特性:如平行四边形的对边互相平行等1.1.2利用三角形中位线性质1.1.3利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
1.1.4利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
1.1.5利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.1.1.6利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
1.1.7利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
1.1.8利用定义:在同一个平面内且两条直线没有公共点1.2直线与平面平行的证明1.2.1利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
αbaabαβb a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒b∥a b a αα⊂⊄α∥a ⇒αab1.2.2利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
βαaβαα∥⊂a β∥a ⇒1.2.3利用定义:直线在平面外,且直线与平面没有公共点1.3平面与平面平行的证明1.3.1利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
ααββ////∩⊂⊂ba Pb a b a =αβ//⇒αβbaP1.3.2利用某些空间几何体的特性:如正方体的上下底面互相平行等1.3.3利用定义:两个平面没有公共点1.例题【例1】如图,已知菱形ABCD ,其边长为2,60BAD ∠=,ABD ∆绕着BD 顺时针旋转120得到PBD∆,M 是PC 的中点.(1)求证://PA 平面MBD ;(2)求直线AD 与平面PBD 所成角的正弦值.证明(1)连结AC 交BD 于点O ,连结OM在菱形ABCD 中,O 为AC 中点, M 为PC 的中点∴OM 为∆APC 的中位线,∴OM ∥AP---------------(利用1.1.2中位线性质)又 OM ⊂面MBD ,且PA ⊄面MBD∴//PA 平面MBD----------------(利用1.2.1直线与平面平行的判定定理)【例2】已知四棱锥P-ABCD ,底面ABCD 是60=∠A 、边长为a 的菱形,又ABCD PD 底⊥,且PD=CD ,点M 、N 分别是棱AD 、PC 的中点.证明:DN//平面PMB 。
立几概念公式

基本公式·立几1.证明直线与直线的平行的思考途径(1)转化为判定共面二直线无交点; (2)转化为二直线同与第三条直线平行; (3)转化为线面平行; (4)转化为线面垂直; (5)转化为面面平行2.证明直线与平面的平行的思考途径(1)转化为直线与平面无公共点; (2)转化为线线平行; (3)转化为面面平行3.证明平面与平面平行的思考途径(1)转化为判定二平面无公共点; (2)转化为线面平行; (3)转化为线面垂直4.证明直线与直线的垂直的思考途径(1)转化为相交垂直; (2)转化为线面垂直;(3)转化为线与另一线的射影垂直; (4)转化为线与形成射影的斜线垂直5.证明直线与平面垂直的思考途径(1)转化为该直线与平面内任一直线垂直; (2)转化为该直线与平面内相交二直线垂直; (3)转化为该直线与平面的一条垂线平行; (4)转化为该直线垂直于另一个平行平面6.证明平面与平面的垂直的思考途径(1)转化为判断二面角是直二面角; (2)转化为线面垂直; (3) 转化为两平面的法向量垂直7 空间数乘向量分配律:λ(a+b )=λa +λb.8 平面向量加法的平行四边形法则向空间的推广始点相同且不在同一个平面内的三个向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对9 共线向量定理:对空间任意两个向量),0(,,≠b b a a ∥b ⇔存在实数λ使a=λb .P A B、、三点共线⇔||AP AB ⇔AP t AB=⇔(1)O P t O A tO B=-+||AB CD ⇔AB、C D共线且A B C D 、不共线⇔AB tCD =且A B C D 、不共线10 共面向量定理:向量p与两个不共线的向量a 、b 共面⇔存在实数对,x y ,使p xa yb =+ .推论 空间一点P 位于平面MAB 内的⇔存在有序实数对,x y ,使M P x M A y M B =+,或对空间任一定点O ,有序实数对,x y ,使O P O M x M A y M B =++11 对空间任一点O 和不共线的三点A 、B 、C ,满足O P xO A y O B z O C =++(x y z k ++=),则当1k =时,对于空间任一点O ,总有P 、A 、B 、C 四点共面;当1k ≠时,若O ∈平面ABC ,则P 、A 、B 、C 四点共面;若O ∉平面ABC ,则P 、A 、B 、C 四点不共面.CA B 、、、D 四点共面⇔AD与AB、A C共面⇔A D x AB y A C=+⇔(1)O D x y O A xO B yO C=--++(O ∉平面ABC )12 空间向量基本定理: 如果三个向量a 、b 、c不共面,那么对空间任一向量b ,存在一个唯一的有序实数组x ,y ,z ,使p=x a +y b +z c .推论 设O 、A 、B 、C 是不共面的四点,则对空间任一点P ,都存在唯一的三个有序实数x ,y ,z ,使O P x O A y O B z O C =++13 射影公式:已知向量AB=a 和轴l ,e是l 上与l 同方向的单位向量A 点在l 上的射影A ',作B 点在l 上的射影B ',则||cos ,A B AB a e a e ''=<>=⋅14.空间的线线平行或垂直:设111(,,)a x y z =r,222(,,)b x y z =r,则 a b r r P ⇔(0)a b b λ=≠r r r r⇔121212x x y y z zλλλ=⎧⎪=⎨⎪=⎩;a b⊥r r⇔a b ⋅=r r ⇔121212x x y y z z ++=15 夹角公式:设a =123(,,)a a a ,b=123(,,)b b b ,则cos ,a b <>=推论 2222222112233123123()()()a b a b a b a a a b b b ++≤++++,此即三维柯西不等式16 正棱锥的侧面与底面所成的角为θ,则cos S S θ=底面侧面特别对于正四面体每两个面所成的角为θ,有1cos 3θ=17.异面直线所成角:cos |cos ,|a b θ=r r=||||||a b a b ⋅=⋅r r r r (其中θ(090θ<≤oo)为异面直线a b ,所成角,,a b r r分别表示异面直线a b ,的方向向量)18 直线A B 与平面所成角: sin ||||AB m arc AB m β⋅= (m为平面α的法向量) 19 若A B C ∆所在平面β与过A B 的平面α成的角θ,另两边A C ,B C 与平面α成的角分别是1θ、2θ,A B 、为A B C ∆的两个内角,则2222212sin sin (sin sin )sin A B θθθ+=+特别地,当90ACB ∠= 时,有22212sin sin sin θθθ+=20 若A B C ∆所在平面β与过A B 的平面α成的角θ,另两边A C,B C 与平面α成的角分别是1θ、2θ,''A B 、为A B O ∆的两个内角,则222'2'212tan tan (sin sin )tan A B θθθ+=+特别地,当90AOB ∠= 时,有22212sin sin sin θθθ+=21 二面角l αβ--的平面角(根据具体图形确定是锐角或是钝角)cos ||||m n arc m n θ⋅= 或cos ||||m n arc m n π⋅-(m ,n 为平面α,β的法向量)22 三余弦定理设AC 是α内的任一条直线,AD 是α的一条斜线AB 在α内的射影,且BD ⊥AD ,垂足为D ,设AB 与α(AD)所成的角为1θ, AD 与AC 所成的角为2θ, AB 与AC 所成的角为θ.则1cos cos cos θθθ=23 三射线定理若夹在平面角为ϕ的二面角间的线段与二面角的两个半平面所成的角是1θ,2θ,与二面角的棱所成的角是θ,则有22221212sin sin sin sin 2sin sin cos ϕθθθθθϕ=+- ;1212||180()θθϕθθ-≤≤-+ (当且仅当90θ= 时等号成立)24 点Q 到直线l 距离:h =点P 在直线l 上,a为直线l 的方向向量, b=P Q )25 异面直线间的距离||||C D n d n ⋅=(12,l l 是两异面直线,其公垂向量为n ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离)26 点B 到平面α的距离:||||A B n d n ⋅= (n 为平面α的法向量,A α∈,A B 是α的一条斜线段)27 异面直线上两点距离公式1:d='E AA F ϕ=--)公式2: d =公式3:d=(两条异面直线a 、b 所成的角为θ,其公垂线段'AA 的长度为a 、b 上分别取两点E 、F ,'A E m =,A F n =,E F d =)长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、,夹角分别为123θθθ、、,则有2222123l l l l =++222123c o s c o s c o s 1θθθ⇔++=222123s i n s i n s i n 2θθθ⇔++=(立体几何中长方体对角线长的公式是其特例)29 面积射影定理 'cos SS =(平面多边形及其射影的面积分别是S 、'S ,它们所在平面所成锐二面角的为θ)30 斜棱柱的直截面:已知斜棱柱的侧棱长是l ,侧面积和体积分别是S 斜棱柱侧和V 斜棱柱,它的直截面的周长和面积分别是1c 和1S ,则①1S c l=斜棱柱侧;②1V S l =斜棱柱31.棱锥的平行截面的性质如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥的体积与原棱锥的体积的比等于顶点到截面距离与棱锥高的立方比;相应小棱锥的的侧面积与原棱锥的的侧面积的比等于顶点到截面距离与棱锥高的平方比.32 球的组合体(1)球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长 (2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长,(3) 球与正四面体的组合体: 棱长为a 12(3的14),外接球的半径(的34)基本公式·排列组合二项式定理1组合恒等式: (1) 1!22!33!!(1)!1n n n +⋅+⋅++⋅=+- (2)11mm n n n C C m--=;(3)14205312-=+++=+++n n n n n n nC C C C C C (4)121++++=++++r n r n r r r r r r C C C C C (5)321232-=++++n n n n n n n nC C C C (6)rm r n r m n r m n r m C C C C C C C +-=+++0110 排列数与组合数的关系:mmn nA m C =⋅!3.单条件排列(以下各条的大前提是从n 个元素中取m 个元素的排列) (1)“在位”与“不在位”①某(特)元必在某位有11--m n A 种;②某(特)元不在某位有11---m n m n A A (补集思想)1111---=m n n A A (着眼位置)11111----+=m n m mn A A A (着眼元素)种(2)紧贴与插空(即相邻与不相邻)①定位紧贴:)(n m k k ≤≤个元在固定位的排列有k m k n k k A A --种②浮动紧贴:n 个元素的全排列把k 个元排在一起的排法有k k k n k n A A 11+-+-种 注:此类问题常用捆绑法;③插空:两组元素分别有k 、h 个(1+≤h k ),把它们合在一起来作全排列,k 个的一组互不能挨近的所有排列数有k h h h A A 1+种(3)两组元素各相同的插空m 个大球n 个小球排成一列,小球必分开,当1+>m n 时,无解;当1+≤m n 时,有nm n nn m C AA11++=种排法(4)两组相同元素的排列:两组元素有m 个和n 个,各组元素分别相同的排列数为nnm C +4.分配问题(1)(平均分组有归属问题)将相异的mn 个物件等分给m 个人,各得n 件,其分配方法数共有nn nn nn mn nn mn nmn n mn C C C C C N )!()!(22=⋅⋅⋅⋅⋅=--(2)(平均分组无归属问题)将相异的mn 个物体等分为无记号或无顺序的m 堆,其分配方法数共有nnnn nn mn nn mn nmn n m mn m C C C C C N )!(!)!(!...22=⋅⋅⋅⋅=--(3)(非平均分组有归属问题)将相异的) 12m P(P=n +n ++n 个物体分给m 个人,物件必须被分完,分别得到1n ,2n ,...,m n 件,且1n ,2n ,...,m n 这m 个数彼此不相等,则其分配方法数共有!!! (212)11m n nn n p n p m p m C C C N mm=⋅⋅=-(4)(非完全平均分组有归属问题)将相异的) 12m P(P=n +n ++n 个物体分给m 个人,物件必须被分完,分别得到1n ,2n ,…,m n 件,且1n ,2n ,…,m n 这m 个数中分别有a 、b 、c 、…个相等,则其分配方法数有!...!!!...211c b a m C C C N mm nn n n p n p ⋅⋅=-12!!!!...!(!!!...)m p m n n n a b c =(5)(非平均分组无归属问题)将相异的) 12m P(P=n +n ++n 个物体分为任意的1n ,2n ,…,m n 件无记号的m 堆,且1n ,2n ,…,m n 这m 个数彼此不相等,则其分配方法数有!21m p N =(6)(非完全平均分组无归属问题)将相异的) 12m P(P=n +n ++n 个物体分为任意的1n ,2n ,…,m n 件无记号的m 堆,且1n ,2n ,…,m n 这m 个数中分别有a 、b 、c 、…个相等,则其分配方法数有!...)!!(!!...!!21c b a n n n p Nm =(7)(限定分组有归属问题)将相异的p (2m p n n n = 1+++)个物体分给甲、乙、丙,……等m 个人,物体必须被分完,如果指定甲得1n 件,乙得2n 件,丙得3n 件,…时,则无论1n ,2n ,…,m n 等m 个数是否全相异或不全相异其分配方法数恒有!!...!!...21211m nn n n p n p n n n p C C C N mm =⋅=-5. (1) 不定方程2n x x x m = 1+++(,n m N *∈)的正整数解有11m n C --个(2) 方程2n x x x m = 1+++(,n m N *∈)的非负整数解有 11n m n C +--个6 2012()()n n n f x ax b a a x a x a x =+=++++ 的展开式的系数关系:012(1)n a a a a f ++++= ; 012(1)(1)nn a a a a f -+++-=- ; 0a f =7 n 次独立重复试验中某事件恰好发生k 次的概率:()(1).k k n k n n P k C P P -=-。
方法技巧专题05立体几何中平行与垂直证明

方法技巧专题05立体几何中平行与垂直证明平行与垂直证明是立体几何中的重要内容之一,本文将介绍一些方法和技巧用于解决平行与垂直的证明问题。
一、平行性的证明方法:1.公共光线法:如果两条直线分别与第三条直线相交,在相交点处的两个对应的内角相等,则这两条直线是平行的。
例如,如果直线AB和CD都与直线EF相交,在交点F处的∠AFC=∠DFB,则AB,CD。
2.反证法:假设AB和CD不平行,然后通过构造形式,证明得到矛盾。
例如,如果直线AB和CD不平行,则可以证明存在一条直线EF与这两条直线分别相交于F和G,且所形成的内角∠FAG=π/2-∠DAF≠π/2,则与直线EF平行,这是与已知条件矛盾的,所以AB,CD。
3.平行线性质法:利用平行线的性质来证明其他线段平行。
例如,根据平行线的交角性质可证明,如果一条直线与一对平行线之一形成等于直角的角,则与另一条平行线也形成等于直角的角。
二、垂直性的证明方法:1.垂直线性质法:利用垂直线的性质来证明其他线段垂直。
例如,如果直线AB与直线CD相交于点E,且∠AED=∠BEC=π/2,则直线AB垂直于直线CD。
2.垂直线段法:如果两条线段的斜率之积为-1,则这两条线段垂直。
例如,如果直线AB和直线CD的斜率之积为-1,则AB⊥CD。
3.反证法:假设AB和CD不垂直,然后通过构造形式,证明得到矛盾。
例如,如果直线AB和CD不垂直,则可以证明存在一条直线EF与这两条直线相交于点G,且所形成的两个内角∠GAC和∠GDB之和小于π/2,这与直线EF垂直的性质矛盾,所以AB⊥CD。
综上所述,平行与垂直证明可以通过公共光线法、反证法、平行线性质法、垂直线性质法、垂直线段法等方法和技巧来解决。
在实际问题中,可以根据已知条件选择合适的方法和技巧,灵活运用来解决平行与垂直的证明问题。
第十一讲 立体几何(一) 平行与垂直.

第十一讲立体几何(一)平行与垂直【内容要点】垂直与平行是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解线面平行与垂直、面面平行与垂直的判定与性质,并能利用它们解决一些问题.直线与平面是立体几何的核心内容,主要包括:三条公理、三个推论、三线平行公理(公理4)、三垂线定理及其逆定理、三种位置关系(直线与直线、直线与平面、平面与平面)。
其中“平行问题”与“垂直问题”是两类重要的证明问题。
【例题剖析】例1. 如图,已知平面α∥β∥γ,A,C∈α,B,D∈γ,异面直线AB和CD分别与β交于E和G,连结AD和BC分别交β于F,H.(2)判断四边形EFGH是哪一类四边形;(3)若AC=BD=a,求四边形EFGH的周长.需经过分别与AB(或CD)共面的直线(例如AD)进行过渡,再利用平面几何知识达到论证的目标。
(2)在(1)的基础上,不难判断EFGH四边形的类型。
(3)利用(1)、(2)的结果再进一步进行探索。
解:(1)由AB,AD确定的平面,与平行平面β和γ的交线分别为(2)面CBD分别交β,γ于HG和BD.由于β∥γ,所以HG∥BD.同理EH∥AC.故EFGH为平行四边形。
评述此问题的最终解决都是利用平面几何的有关知识进行的,这里利用了辅助平面ABD和ADC是关键所在,本题也是利用线面、面面、线线平行的互相转化这一基本思想得到最后结果的.例2. 正方形ABCD和正方形ABEF所在平面互相垂直,点M,N分别在对角线AC和BF上,且AM=FN 求证:MN∥平面BEC分析:证线面平行⇐线线平行,需找出面BEC中与MN平行的直线。
证明(一):作NK∥AB交BE于K,作MH∥AB交BC于H∴MH∥NK∵ABCD与ABEF是两个有公共边AB的正方形∴它们是全等正方形∵AM=FN ∴CM=BN又∠HCM=∠KBN,∠HMC=∠KNB∴△HCM≌△KBN ∴MH=NK∴MHKN是平行四边形∴MN∥HK∵HK⊂平面BEC MN⊄平面BEC∴MN∥平面BEC证明(二):分析:利用面面平行⇒线面平行过N作NP∥BE,连MP,∵NP∥AF∴FN/FB=AP/AB∵AM=FN,AC=BF∴FN/FB=AM/AC ∴AP/AB=AM/AC∴MP∥BC ∴平面MNP∥平面BCE∴MN∥平面BCE解题中经常需要作互相平行的直线,为了使作直线的位置符合要求,构造成平行四边形,利用平行四边形对边这一关系是作平行线的依据之一。
(完整版)立体几何中平行与垂直证明方法归纳

c c ∥∥b a ba ∥⇒本文档系统总结归纳了立体几何中平行与垂直证明方法,特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。
是一份不可多得的好资料。
一、“平行关系”常见证明方法(一)直线与直线平行的证明1) 利用某些平面图形的特性:如平行四边形的对边互相平行 2) 利用三角形中位线性质3) 利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
4)利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
5) 利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.6) 利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
abαβba a =⋂⊂βαβα∥ba ∥⇒b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒αab7) 利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
8) 利用定义:在同一个平面内且两条直线没有公共点(二)直线与平面平行的证明1) 利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
2) 利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
3) 利用定义:直线在平面外,且直线与平面没有公共点(三)平面与平面平行的证明常见证明方法:1) 利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
αbaβαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaPb∥a b a αα⊂⊄α∥a ⇒2)利用某些空间几何体的特性:如正方体的上下底面互相平行等3)利用定义:两个平面没有公共点二、“垂直关系”常见证明方法(一)直线与直线垂直的证明1)利用某些平面图形的特性:如直角三角形的两条直角边互相垂直等。
探索立体几何中的平行与垂直关系

探索立体几何中的平行与垂直关系在立体几何中,平行与垂直是两种基本的关系。
平行是指两条直线或两个平面在空间中永远不相交,而垂直则是指两条直线或一个直线与一个平面之间的相互垂直关系。
这两种关系在几何学中有着广泛的应用和研究价值。
本文将探索立体几何中的平行与垂直关系,并讨论它们的性质和特点。
1. 平行关系在空间中,两条直线或两个平面如果永远不相交,我们就称它们为平行关系。
平行关系具有以下性质:- 平行关系是相对的:两个物体的平行关系与观察者的视角有关。
对于一个观察者来说,两条直线可能是平行的,而对于另一个观察者来说,这两条直线可能不平行。
- 平行关系保持不变:平行关系在空间中是始终保持不变的,无论两个物体在空间中如何移动、旋转或缩放,它们之间的平行关系都不会发生改变。
- 平行线的性质:如果一条直线与另外两条直线平行,那么这两条直线也是平行的。
此外,如果两条直线分别与第三条直线平行,则这两条直线也是平行的。
- 平行面的性质:如果两个平面相交于一条直线,并且与另外一个平面平行,那么这两个平面也是平行的。
同样,如果两个平面分别与第三个平面平行,则这两个平面也是平行的。
2. 垂直关系垂直关系是指在空间中,两条直线或一个直线与一个平面之间的相互垂直关系。
垂直关系具有以下性质:- 垂直关系是相对的:两个物体的垂直关系也与观察者的视角有关。
对于一个观察者来说,两条直线或一个直线与一个平面可能是垂直的,而对于另一个观察者来说,它们可能不垂直。
- 垂直关系保持不变:垂直关系在空间中是始终保持不变的,无论两个物体如何移动、旋转或缩放,它们之间的垂直关系都不会发生改变。
- 垂直线的性质:如果一条直线与另外两条直线垂直,那么这两条直线也是垂直的。
此外,如果两条直线分别与第三条直线垂直,则这两条直线也是垂直的。
- 垂直面的性质:如果一个平面与另外两个平面相交于一条直线,并且与另外一个平面垂直,那么这两个平面也是垂直的。
同样,如果两个平面分别与第三个平面垂直,则这两个平面也是垂直的。
专题20立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨:证明直线与平面的平行与垂直问题,一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
直线与平面的平行有两种方法:一是在面内找线;二是通过面面平行转化。
直线与平面垂直关键是找两条相交直线例1、(2019南通、泰州、扬州一调)如图,在四棱锥PABCD中,M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形,DA=DP.求证:(1)MN〃平面PBC;MD丄平面PAB.【证明】(1)在四棱锥P-ABCD中,M, N分别为棱PA, PD的中点,所以MN〃AD.(2分)又底面ABCD是矩形,所以BC〃AD.所以MN〃BC.(4分)又BC U平面PBC,MN Q平面PBC,所以MN〃平面PBC. (6分)(2)因为底面ABCD是矩形,所以AB丄AD.又侧面PAD丄底面ABCD,侧面PAD n底面ABCD=AD, AB U底面ABCD,所以AB丄侧面PAD.(8分)又MD U侧面PAD,所以AB丄MD.(10分)因为DA=DP,又M为AP的中点,从而MD丄PA. (12分)又PA,AB在平面PAB内,PA n AB=A,所以MD丄平面PAB.(14分)例2、(2019扬州期末)如图所示,在三棱柱ABCA1B1C1中,四边形AA1B1B为矩形,平面AA1B1B丄平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.(1)求证:EF〃平面ABC;(2)求证:BB]丄AC.规范解答(1)在三棱柱ABCA1B1C1中,四边形AA1B1B,四边形BB1C1C均为平行四边形,E, F分别是侧面AA1B1B, BB1C1C对角线的交点,所以E, F分别是AB1,CB1的中点,所以EF〃AC.(4分)因为EF Q平面ABC, AC U平面ABC,所以EF〃平面ABC.(8分)(2)因为四边形AA1B1B为矩形,所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.(12分)因为AC U平面ABC,所以BB1丄AC.(14分)例3、(2019南京、盐城二模)如图,在三棱柱ABCA1B1C1中,AB=AC, A1C丄BC], AB]丄BC1,D, E 分别是AB1和BC的中点.求证:(1)DE〃平面ACC1A1;(2)AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B,在三棱柱ABCA1B1C1中,AA1#BB1且AA1=BB1,所以四边形AA1B1B是平行四边形.又因为D是AB1的中点,所以D也是BA1的中点.(2分)在厶BA1C中,D和E分别是BA1和BC的中点,所以DE〃A]C.又因为DE G平面ACC1A1,A1C U平面ACC1A1,所以DE〃平面ACC1A1.(6分)(2)由(1)知DE〃A]C,因为A1C丄BC” 所以BC]丄DE.(8 分)又因为BC]丄AB1,AB1H DE=D,AB1,DE U平面ADE,所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.(10分)在厶ABC中,AB=AC,E是BC的中点,所以AE丄BC.(12分)因为AE丄BC1,AE丄BC,BC1H BC=B,BC1,BC U平面BCC1B1,所以AE丄平面BCC1B1. (14 分)例4、(2019苏锡常镇调研)如图,三棱锥DABC中,已知AC丄BC,AC丄DC,BC=DC,E,F 分别为BD,CD 的中点.求证:(1)EF〃平面ABC;(2)BD丄平面ACE.所以EF 〃平面ABC.(6分)(2)因为AC丄BC,AC丄DC,BC H DC = C,BC,DC U平面BCD所以AC丄平面BCD,(8分)因为BD U平面BCD,所以AC丄BD,(10分)因为DC=BC,E为BD的中点,所以CE丄BD,(12分)因为AC n CE = C, AC,CE U平面ACE,所以BD丄平面ACE.(14分)例5、(2019苏州三市、苏北四市二调)如图,在直三棱柱ABCA1B1C1中,侧面BCC1B1为正方形,A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证:(1) DE〃平面ABB1A1;(2) BC]丄平面A1B1C.规范解答(1)因为三棱柱ABCA1B1C1为直三棱柱,所以侧面ACC1A1为平行四边形.又A1C 与AC1 交于点D,所以D为AC]的中点,同理,E为BC]的中点•所以DE〃AB.(3分)又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].(6分)(2)因为三棱柱ABCA]B]C]为直三棱柱,所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.(8分)又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1,所以A]B]丄平面BCC]B].(10 分)又因为BC]U平面BCC]B1,所以A]B丄BC].(12分)又因为侧面BCC]B1为正方形,所以BC]丄BQ.又A1B1n B1C=B1,A1B1,B1C U平面A1B1C, 所以BC1丄平面A1B1C.(14分)例6、(2017苏北四市一模)如图,在正三棱柱ABCA1B1C1中,已知D, E分别为BC, B1C1的中点,点F 在棱CC1上,且EF丄CD.求证:(1)直线A1E〃平面ADC1;⑴证法1连结ED,因为D, E分别为BC, B1C1的中点,所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形,(2分)所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形,所以A]E〃AD.(4分)又因为AE G平面ADC, AD U平面ADC,所以直线AE〃平面ADC.(7分)1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点,所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形,所以N是CE的中点.(2分)因为A1ACC1为平行四边形,所以M是A1C的中点,(4分)所以MN//A\E.又因为A]E G平面ADC,MN U平面ADC,,所以直线Af〃平面ADC、.(7分)(2)在正三棱柱ABCA1B1C1中,BB]丄平面ABC.又AD U平面ABC,所以AD丄BB、.又A ABC是正三角形,且D为BC的中点,所以AD丄BC.(9分)又BB,,BC U 平面BBCC,,BB1A BC=B,所以AD丄平面B,BCC,,又EF U平面BBCC,所以AD丄EF.(11分)又EF丄CD,CD,AD U平面ADC,,C,D A AD=D,所以直线EF丄平面ADC,.(14分)题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题,一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理,切记不可缺条件。
完整版)立体几何中平行与垂直证明方法归纳

完整版)立体几何中平行与垂直证明方法归纳本文系统总结了立体几何中平行与垂直证明方法,适合高三总复时学生构建知识网络、探求解题思路、归纳梳理解题方法。
以下是常见证明方法:一、“平行关系”常见证明方法一)直线与直线平行的证明1.利用平行四边形的对边互相平行的特性;2.利用三角形中位线性质;3.利用空间平行线的传递性(即公理4);4.利用直线与平面平行的性质定理;5.利用平面与平面平行的性质定理;6.利用直线与平面垂直的性质定理;7.利用平面内直线与直线垂直的性质;8.利用定义:在同一个平面内且两条直线没有公共点。
二)直线与平面平行的证明1.利用直线与平面平行的判定定理;2.利用平面与平面平行的性质推论;3.利用定义:直线在平面外,且直线与平面没有公共点。
三)平面与平面平行的证明1.利用平面与平面平行的判定定理;2.利用某些空间几何体的特性;3.利用定义:两个平面没有公共点。
二、“垂直关系”常见证明方法一)直线与直线垂直的证明1.利用直角三角形的两条直角边互相垂直的特性;2.看夹角:两条共(异)面直线的夹角为90°,则两直线互相垂直;3.利用直线与平面垂直的性质:如果一条直线与一个平面垂直,则这条直线垂直于此平面内的所有直线。
1.利用空间几何体的特性:例如长方体侧棱垂直于底面。
2.观察直线与平面所成角度:若直线与平面所成角为90度,则该直线垂直于平面。
3.利用直线与平面垂直的判定定理:若一条直线与一个平面内的两条相交直线垂直,则该直线垂直于此平面。
4.利用平面与平面垂直的性质定理:若两个平面互相垂直,则在这两个平面内分别作垂直于交线的直线,则这两条直线互相垂直。
5.利用常用结论:例如若一条直线平行于一个平面的垂线,则该直线也垂直于此平面。
易错点12 立体几何中的平行与垂直(解析版)

易错点12 立体几何中的垂直与平行在立体几何中,点、线、面之间的位置关系,特别是线面、面面的平行和垂直关系,是高中立体几何的理论基础,是高考命题的热点与重点之一,一般考查形式为小题(位置关系基本定理判定)或解答题(平行、垂直位置关系的证明),难度不大。
立体几何中平行与垂直的易错点易错点1:线面平行的判定定理和性质定理在应用时都是三个条件,但这三个条件易混为一谈;面面平行的判定定理易把条件错误地记为"一个平面内的两条相交直线与另一个平面内的两条相交直线分别平行"而导致证明过程跨步太大。
易错点2:有关线面平行的证明问题中,对定理的理解不够准确,往往忽视",//,"a a b b αα⊄⊂三个条件中的某一个。
易错点3:线面平行的判定定理和性质定理在应用时都是三个条件,但这三个条件易混为一谈;面面平行的判定定理易把条件错误地记为"一个平面内的两条相交直线与另一个平面内的两条相交直线分别平行"而导致证明过程跨步太大;题组一:基本性质定理 1.(2021年浙江卷)已知正方形1111ABCD A B C D -,,M N 分别是11,A D D B 的中点,则( ). A .直线1A D 与直线1D B 垂直,直线//MN 平面ABCD B .直线1A D 与直线1D B 平行,直线MN ⊥平面11BDD B C .直线1A D 与直线1D B 相交,直线//MN 平面ABCDD .直线1A D 与直线1D B 平行,直线MN ⊥平面11BDD B【答案】A【解析】如图,连结1AD ,//,MN AB ∴//MN 平面ABCD ,1,AB A D ⊥11A D AD ⊥,1A D ∴⊥平面1AD B ,11A D D B ∴⊥2.(2021新高考1卷多选题)在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[]0,1λ∈,[]0,1μ∈,则A .当1λ=时,1AB P △的周长为定值 B .当1μ=时,三棱锥1P A BC -的体积为定值 C .当12λ=时,有且仅有一个点P ,使得1A P BP ⊥ D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P【答案】BD【解析】由点P 满足1BP BC BB λμ=+,可知点P 在正方形11BCC B 内.A 选项,当1λ=时,可知点P 在线段1CC (包括端点)上运动.1AB P △中,1AB =AP =1B P =1L AB AP B P =++不为定值,所以选项A 错误;B 选项,当1μ=时,可知点P 在线段11BC (包括端点)上运动.由图可知,线段11B C //平面1A BC ,即点P 到平面1A BC 的距离处处相等,1A BC △的面积是定值,所以三棱锥1P A BC -的体积为定值,所以选项B 正确;BCC 1B 1PABC A 1B 1C 1PABCA 1B 1C 1PC 选项,当12λ=时,分别取线段BC ,11B C 中点为D ,1D ,可知点P 在线段1DD (包括端点)上运动.很显然若点P 与D 或1D 重合时,均满足题意,所以选项C 错误.D 选项,当12μ=时,分别取线段1BB ,1CC 中点为M ,N ,可知点P 在线段MN (包括端点)上运动.此时,有且只有点P 与N 点重合时,满足题意. 所以选项D 正确.因此,答案为BD.3.(2019全国Ⅲ理8)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则( )A .BM =EN ,且直线BM 、EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM 、EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线 【答案】B【解析】 如图所示,联结,.因为点为正方形的中心,为正三角形,平面平面,是线段的中点,所以平面,平面,因为是中边上的中线,是中边上的中线,直线,是相交直线,设,则,ABCA 1B 1C 1D D 1PAB C A 1B 1C 1MNP A BCA 1B 1C 1MN(P)BE BD N ABCD ECD △ECD ⊥ABCD M ED BM ⊂BDE EN ⊂BDE BM BDE △DE EN BDE △BD BM EN DE a =2BD a =, 所以,, 所以.故选B .4.(2019全国Ⅱ理7)设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线 D .α,β垂直于同一平面 【解析】 对于A ,内有无数条直线与平行,则与相交或,排除; 对于B ,内有两条相交直线与平行,则;对于C ,,平行于同一条直线,则与相交或,排除; 对于D ,,垂直于同一平面,则与相交或,排除.故选B .题组二:线面平行5. (2021天津卷)如图,在棱长为2的正方体1111ABCD A B C D -中,E 为棱BC 的中点,F 为棱CD 的中点.(1)求证:1//D F 平面11A EC ;【解析】(1)以A 为原点,1,,AB AD AA 分别为,,x y z 轴,建立如图空间直角坐标系, 则()0,0,0A ,()10,0,2A ,()2,0,0B ,()2,2,0C ,()0,2,0D ,()12,2,2C ,()10,2,2D , 因为E 为棱BC 的中点,F 为棱CD 的中点,所以()2,1,0E ,()1,2,0F , 所以()11,0,2D F =-,()112,2,0A C =,()12,1,2A E =-, 设平面11A EC 的一个法向量为()111,,m x y z =,则11111111222020m x y m AC E x y A z ⎧⋅+=⎪⎨⋅+-=⎪==⎩,令12x =,则()2,2,1m =-, 因为1220m D F ⋅-==,所以1D F m ⊥, 因为1D F ⊄平面11A EC ,所以1//D F 平面11A EC ;6.(2017新课标Ⅱ)如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面三角形ABCD ,12AB BC AD ==,90BAD ABC ∠=∠=,E 是PD 的中点. (1) 证明:直线CE ∥平面PAB ;BE ==BM=EN a ==BM EN ≠αβαββα∥αββα∥αβαββα∥αβαββα∥【解析】(1)取PA的中点F,连结EF,BF.因为E是PD的中点,所以EF AD∥,12EF AD=.由90BAD ABC∠=∠=得BC AD∥,又12BC AD=,所以EF BC∥,四边形BCEF是平行四边形,CE BF∥,又BF⊂平面PAB,CE⊄平面PAB,故CE∥平面PAB.7.(2019全国Ⅰ理18)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;【解析】(1)连结B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=B1C.又因为N为A1D的中点,所以ND=A1D.由题设知A1B1DC,可得B1C A1D,故ME ND,因此四边形MNDE为平行四边形,MN∥ED.又MN平面EDC1,所以MN∥平面C1DE.题组三线线垂直8.(2021全国甲卷理)已知直三棱柱111CBAABC-中,侧面BBAA11为正方形,FEBCAB,,2==分别为AC和1CC的中点,D为棱11BA上的点,11BABF⊥.(1)证明:DEBF⊥;【解析】(1)因为E F,是直三棱柱111ABC A B C-中AC和1CC的中点,且2AB BC==,所以15CF BF==,,连结AF,由11BF A B⊥且11//AB A B,则BF AB⊥,于是3AF=,所以,22AC=,由222AB BC AC+=,则BA BC⊥,故如图右图所示,建立空间直角B xyz-坐标系:EMDCBAP1212===⊄于是(2,0,0)(0,0,0)(0,2,2)(1,1,0)(0,2,1)A B C E F ,,,,, 设1B D m =,则(,0,2)D m .于是,(0,2,1)BF =,(1,1,2)DE m =-- 由BF⃗⃗⃗⃗⃗ ⋅DE ⃗⃗⃗⃗⃗ =0可得BF ⊥DE ;9.(2021全国甲卷理)已知直三棱柱ABC −A 1B 1C 1中,侧面AA 1B 1B 为正方形.AB =BC =2,E ,F 分别为AC 和CC 1的中点,BF ⊥A 1B 1. (1)略(2)已知D 为棱A 1B 1上的点,证明:BF ⊥DE . 【解析】(2)取BC 中点M ,连接EM ,1MB ,1EA , 因为,E F 分别为1AC CC ,的中点,所以//EM AB ,因为11//A B AB ,所以11//EM A B ,所以11,,,E M B A 四点共面, 因为侧面11AA B B 为正方形,所以1BB AB =,又AB BC =,所以1BB BC =,所以侧面11BB C C 为正方形, 又F 为1CC 中点,M 为BC 中点,由平面几何知识可知1BF B M ⊥, 又11A B BF ⊥,1111B MA B B =,所以BF ⊥平面11EMB A ,而DE ⊆平面11EMB A ,所以BF DE ⊥.10.(2021新高考1卷)如图,在三棱锥A BCD -中,平面ABD ⊥平面BCD ,AB AD =,O 为BD 的中点.(1)证明:OA CD ⊥;【解析】(1)因为在ABD △中,AB AD =,O 为BD 中点,所以AO BD ⊥, 因为平面ABD ⊥平面BCD ,且平面ABD 平面=BCD BD ,AO ⊂平面ABD ,AO BD ⊥,所以AO ⊥平面BCD ,又因为CD ⊂面BCD ,所以AO CD ⊥.11.(2021浙江卷)如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,120ABC ∠=︒,1AB =,4BC =,PA =M ,N 分别为BC ,PC 的中点,PD DC ⊥,PM MD ⊥.(1)证明:AB PM ⊥;(2)求直线AN 与平面PDM 所成角的正弦值.【解析】(1)因为ABCD 是平行四边形,∠ABC =120°,AB =1,所以60DCB ∠=︒,AB ∥DC ,DC =AB =1.因为M 为BC 中点,BC =4,所以CM =2.在DCM △中,由余弦定理得22212cos601422132DM DC CM DC CM =+-⋅⋅︒=+-⨯⨯⨯=所以DM =90CDM ∠=︒,所以DM DC ⊥,因为PD DC PDMD D PD PDM MD PDM ⊥=⊂⊂,,面,面,所以DC PDM ⊥面,所以DC PM ⊥.因为PM MD ⊥,DC MD D DC ABCD MD ABCD =⊂⊂,面,面,所以PM ABCD ⊥面,所以AB PM ⊥.题组四:线面垂直 12.(2016全国II )如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将ΔDEF 沿EF折到ΔD EF '的位置,OD '=(I )证明:D H '⊥平面ABCD ;【解析】(I )证明:∵54AE CF ==,∴AE CF AD CD =,∴EF AC ∥. ∵四边形ABCD 为菱形,∴AC BD ⊥,∴EF BD ⊥, ∴EF DH ⊥,∴EF D H '⊥.∵6AC =,∴3AO =;又5AB =,AO OB ⊥,∴4OB =,∴1AEOH OD AO =⋅=,∴3DH D H '==, ∴222'OD OH D H '=+,∴'D H OH ⊥.又∵OHEF H =,∴'D H ⊥面ABCD .13.(2018全国卷Ⅱ)如图,在三棱锥-P ABC中,==AB BC PA PB PC ===4AC =,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;【解析】(1)因为4AP CP AC ===,O 为AC 的中点,所以OP AC ⊥,且OP =连结OB.因为AB BC AC ==,所以ABC △为等腰直角三角形, 且OB AC ⊥,122OB AC ==.由222OP OB PB +=知PO OB ⊥. 由⊥OP OB ,⊥OP AC 知PO ⊥平面ABC .14.(2019全国Ⅱ理17)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;【解析】 (1)由已知得,平面,平面,O MPCBA11B C ⊥11ABB A BE ⊂11ABB A故.又,所以平面.题组五:面面垂直15.(2021新高考2卷)在四棱锥Q ABCD-中,底面ABCD是正方形,若2AD=,QD QA==,3QC=,(1)证明:平面QAD⊥平面ABCD;【解析】(1)证明:取AD的中点M,连接,QM CM,QD QA=,∴QM AD⊥2QM==,CM3QC=,222QC QM CM∴=+,∴QM CM⊥又,AD CM⊂平面ABCD,AD CM M⋂=所以QM⊥平面ABCD,又QM⊂平面QAD,所以平面QAD⊥平面ABCD.16(2019全国Ⅲ理19)图1是由矩形ADEB、R t△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;11B C⊥BE1BE EC⊥BE⊥11EB CAB CDQMHAB CDQ【解析】 (1)由已知得AD BE ,CG BE ,所以AD CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB BE ,AB BC ,故AB 平面BCGE . 又因为AB 平面ABC ,所以平面ABC 平面BCGE . 17.(2018全国卷Ⅰ)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥. (1)证明:平面PEF ⊥平面ABFD ;【解析】(1)由已知可得,BF ⊥PF ,BF ⊥EF ,所以BF ⊥平面PEF .又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD .18.(2018全国卷Ⅲ)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC 平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为CD 上异于C ,D 的点,且DC 为直径,所以 DM ⊥CM . 又BC CM =C ,所以DM ⊥平面BMC .而DM 平面AMD ,故平面AMD ⊥平面BMC .1.已知平面α,直线m ,n 满足m α⊄,n α⊂,则“m ∥n ”是“m ∥α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【解析】若m α⊄,n α⊂,m ∥n ,由线面平行的判定定理知m ∥α.若m ∥α,m α⊄,n α⊂,不一定推出m ∥n ,直线m 与n 可能异面,故“m ∥n ”是“m ∥α”的充分不必要条件.故选A .⊥⊥⊥⊂⊥PFE D CBAMD CBA⊂⊂2.若,l m 是两条不同的直线,m 垂直于平面α ,则“l m ⊥ ”是“l ∥α”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【解析】由“m α⊥且l m ⊥”推出“l α⊂或l α∥”,但由“m α⊥且l α∥”可推出“l m ⊥”,所以“l m ⊥”是“l α∥”的必要而不充分条件,故选B .3.如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.证明:PB ∥平面AEC ;【解析】连接BD 交AC 于点O ,连结EO .因为ABCD 为矩形,所以O 为BD 的中点.又E 为PD 的中点,所以EO ∥PB .EO ⊂平面AEC ,PB ⊄平面AEC ,所以PB ∥平面AEC .4.如图,直三棱柱中,分别是的中点, (Ⅰ)证明://平面;【解析】(Ⅰ)连结,交于点O ,连结DO ,则O 为的中点,因为D 为AB 的中点,所以OD ∥,又因为OD 平面,平面,所以 //平面;5.如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.证明:PB ∥平面AEC ;【解析】(Ⅰ)连接BD 交AC 于点O ,连结EO .因为ABCD 为矩形,所以O 为BD 的中点.又E 为PD 的中点,所以EO ∥PB .EO ⊂平面AEC,PB ⊄平面AEC ,所以PB ∥平面AEC .6.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,AD BC ,111ABC A B C -,D E 1,ABBB 1AA AC CB AB ===1BC 1A CDA 11AC 1A C 1AC 1BC⊂1A CD 1BC ⊄1A CD 1BC 1A CD=3AB AD AC ==,4PA BC ==,M 为线段AD 上一点,2AM MD =, N 为PC 的中点.证明MN 平面PAB ;【解析】由已知得232==AD AM ,取BP 的中点T ,连接TN AT ,. 由N 为PC 中点知BC TN //,221==BC TN . 又BC AD //,故TN 平行且等于AM ,四边形AMNT 为平行四边形,于是AT MN //. 因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB .7.如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,1BAA ∠=60°.证明1AB A C ⊥;【解析】取AB 中点E ,连结CE ,,,∵AB =,=,∴是正三角形,∴⊥AB , ∵CA =CB , ∴CE ⊥AB ,∵=E ,∴AB ⊥面, ∴AB ⊥;8.如图,在四棱锥P ABCD -中,AB ∥CD ,且90BAP CDP ∠=∠=. 证明:平面PAB ⊥平面PAD ;B D1A B 1A E 1AA 1BAA ∠0601BAA ∆1A E 1CE A E ⋂1CEA 1A C D CB A P【解析】由已知90BAP CDP ∠=∠=︒,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD ,从而AB ⊥平面PAD .又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .9.如图,四面体ABCD 中,ABC ∆是正三角形,ACD ∆是直角三角形,ABD CBD ∠=∠,AB BD =.证明:平面ACD ⊥平面ABC ;【解析】由题设可得,ABD CBD ∆≅∆,从而AD DC =.又ACD ∆是直角三角形,所以0=90ACD ∠取AC 的中点O ,连接DO ,BO ,则DO AC ⊥,DO AO =.又由于ABC ∆是正三角形,故BO AC ⊥.所以DOB ∠为二面角D AC B --的平面角.在Rt AOB ∆中,222BO AO AB +=.又AB BD =,所以222222BO DO BO AO AB BD +=+==,故90DOB ∠=.所以平面ACD ⊥平面ABC .10.如图,四边形ABCD 为菱形,120ABC ∠=,,E F 是平面ABCD 同一侧的两点,BE⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC .证明:平面AEC ⊥平面AFC ;【解析】连接BD ,设BD AC G ,连接,,EG FG EF . 在菱形ABCD 中,不妨设1GB ,由120∠=ABC ,可得3AGGC , 由⊥BE 平面ABCD ,AB BC 可知,AE EC ,又∵⊥AE EC ,∴3EG,⊥EG AC , 在Rt EBG ∆中,可得2BE ,故22DF.在Rt FDG ∆中,可得62FG . 在直角梯形BDFE 中,由2BD ,2BE ,22DF ,可得322EF , ∴222EG FG EF +=,∴EG ⊥FG ,∵AC ∩FG =G ,∴EG ⊥平面AFC ,∵EG ⊂面AEC ,∴平面AFC ⊥平面AEC .ABC DE。
立体几何基础平行与垂直的性质与判定

立体几何基础平行与垂直的性质与判定立体几何基础——平行与垂直的性质与判定立体几何是数学中的一个重要分支,它研究的对象是在三维空间内的图形和物体。
在立体几何中,平行和垂直是两个基本概念,它们在判断和解决几何问题时起着重要的作用。
本文将介绍平行与垂直的性质和判定方法,帮助读者更好地理解立体几何的基础知识。
一、平行的性质与判定平行是指在同一平面内,两条直线永不相交的性质。
在立体几何中,我们常用平行性质来推导和证明定理。
以下是一些与平行相关的性质和判定方法。
1. 平行线性质:(1)平行线上的对应角相等:如果两条平行线被一条横截线所交,那么对应的角都是相等的。
(2)平行线上的内错角互补:如果两条平行线被一条横截线所交,那么内错角互补,即相互补充的角和为180度。
(3)平行线上的同旁内角相等:如果两条平行线被一条横截线所交,那么同旁内角相等,即相邻的内角相等。
2. 判定平行线的方法:(1)两条线段平行的充要条件是斜率相等:如果两条线段的斜率相等,那么它们是平行的。
(2)两个向量平行的充要条件是比值相等:如果两个向量的坐标分量比值相等,那么它们是平行的。
(3)两条直线互相垂直的充要条件是斜率乘积为-1:如果两条直线的斜率乘积为-1,那么它们互相垂直。
二、垂直的性质与判定垂直是指两条直线或线段在交点处互相成直角的性质。
垂直的性质在几何证明中经常被用到,下面是关于垂直的一些性质和判定方法。
1. 垂直线性质:(1)垂直线上的对应角互补:如果两条垂直线被一条横截线所交,那么对应的角互补,即相互补充的角和为90度。
(2)垂直线上的内角相等:如果两条垂直线被一条横截线所交,那么内角相等,即相邻的内角相等。
2. 判定垂直线的方法:(1)两条线段垂直的充要条件是斜率乘积为-1:如果两条线段的斜率乘积为-1,那么它们是垂直的。
(2)两个向量垂直的充要条件是内积为0:如果两个向量的内积为0,那么它们是垂直的。
三、平行和垂直在实际中的应用平行和垂直的性质在日常生活和工程实践中有广泛的应用。
立体几何中的平行与垂直

立体几何中的平行与垂直1线面平行(1)定义直线与平面无交点.(2)判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.(3)性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.2 面面平行(1)定义α∩β=∅⟹α|| β.(2)判定定理如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行.(3)面面平行的性质(1) a⊂αα||β}⇒a||β (面面平行⇒线面平行)(2)α || βα∩γ=aβ∩ γ=b}⇒ a || b (面面平行⇒线线平行)(3) 夹在两个平行平面间的平行线段相等.3 线面垂直(1)定义若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面.符号表述:若任意a⊂α都有l⊥a,则 l⊥α.(2)判定定理如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.(3)性质定理垂直同一平面的两直线平行4 面面垂直(1) 定义若二面角α−l−β的平面角为90∘,则 α⊥β;(2) 判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.(3) 性质定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.【例1】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是()A.CC1与B1E是异面直线 B.AC⊥平面ABB1A1C.AE,B1C1为异面直线,且AE⊥B1C1 D.A1C1∥平面AB1E练习.1.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为()A.直线BE与直线CF共面 B.直线BE与直线AF是异面直线C.平面BCE⊥平面PAD D.面PAD与面PBC的交线与BC平行【例2】如图1,在△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F.将△ABD沿BD折起,得到三棱锥A1﹣BCD,如图2所示.(Ⅰ)若M是A1C的中点,求证:DM∥平面A1EF;(Ⅱ)若平面A1BD⊥平面BCD,试判断直线A1B与直线CD能否垂直?并说明理由.练习 2.如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE (Ⅰ)求证:AE⊥BE(Ⅱ)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.【例3】.如图,已知菱形AECD的对角线AC,DE交于点F,点E为的AB中点.将三角形ADE 沿线段DE折起到PDE的位置,如图2所示.(Ⅰ)求证:DE⊥平面PCF;(Ⅱ)证明:平面PBC⊥平面PCF;(Ⅲ)在线段PD,BC上是否分别存在点M,N,使得平面CFM∥平面PEN?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.练习3 .如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.(1)求证:PE⊥BD;(2)过点D作DM⊥BC交BC于点M,点N为PB中点,若PE∥平面DMN,的值.求DEDC立体几何中的平行与垂直1线面平行(1)定义直线与平面无交点.(2)判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.(3)性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.2 面面平行(1)定义α∩β=∅⟹α|| β.(2)判定定理如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行.(3)面面平行的性质(1) a⊂αα||β}⇒a||β (面面平行⇒线面平行)(2)α || βα∩γ=aβ∩ γ=b}⇒ a || b (面面平行⇒线线平行)(3) 夹在两个平行平面间的平行线段相等.3 线面垂直(1)定义若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面.符号表述:若任意a⊂α都有l⊥a,则 l⊥α.(2)判定定理如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.(3)性质定理垂直同一平面的两直线平行4 面面垂直(1) 定义若二面角α−l−β的平面角为90∘,则 α⊥β;(2) 判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.(3) 性质定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.【例1】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是()A.CC1与B1E是异面直线 B.AC⊥平面ABB1A1C.AE,B1C1为异面直线,且AE⊥B1C1 D.A1C1∥平面AB1E解析 A不正确,因为CC1与B1E在同一个侧面中,故不是异面直线;B不正确,由题意知,上底面ABC是一个正三角形,故不可能存在AC⊥平面ABB1A1;C正确,因为AE,B1C1为在两个平行平面中且不平行的两条直线,故它们是异面直线;D不正确,因为A1C1所在的平面与平面AB1E相交,且A1C1与交线有公共点,故A1C1∥平面AB1E 不正确;故选:C.练习.1.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为()A.直线BE与直线CF共面 B.直线BE与直线AF是异面直线C.平面BCE⊥平面PAD D.面PAD与面PBC的交线与BC平行答案 C解析画出几何体的图形,如图,由题意可知,A,直线BE与直线CF共面,正确,因为E,F是PA与PD的中点,可知EF∥AD,所以EF∥BC,直线BE与直线CF是共面直线;B,直线BE与直线AF异面;满足异面直线的定义,正确.C,因为△PAB是等腰三角形,BE与PA的关系不能确定,所以平面BCE⊥平面PAD,不正确.D,∵AD∥BC,∴AD∥平面PBC,∴面PAD与面PBC的交线与BC平行,正确.故选:C.【例2】如图1,在△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F.将△ABD沿BD折起,得到三棱锥A1﹣BCD,如图2所示.(Ⅰ)若M是A1C的中点,求证:DM∥平面A1EF;(Ⅱ)若平面A1BD⊥平面BCD,试判断直线A1B与直线CD能否垂直?并说明理由.证明:(Ⅰ)取FC中点N.在图1中,由D,N分别为AC,FC中点,所以DN∥EF.在图2中,由M,N分别为A1C,FC中点,所以MN∥A1F,所以平面DMN∥平面A1EF,(5分)所以DM∥平面A1EF.解:(Ⅱ)直线A1B与直线CD不可能垂直.因为平面A1BD⊥平面BCD,EF⊂平面BCD,EF⊥BD,所以EF⊥平面A1BD,(8分)所以A1B⊥EF.假设有A1B⊥CD,注意到CD与EF是平面BCD内的两条相交直线,则有A1B⊥平面BCD.(1)(10分)又因为平面A1BD⊥平面BCD,A1E⊂平面A1BD,A1E⊥BD,所以A1E⊥平面BCD.(2)而(1),(2)同时成立,这显然与“过一点和已知平面垂直的直线只有一条”相矛盾,所以直线A1B与直线CD不可能垂直.练习 2.如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE (Ⅰ)求证:AE⊥BE(Ⅱ)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.证明:(Ⅰ)∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,∵AE⊂平面ABE,∴AE⊥BC,又∵BF⊥平面ACE,AE⊂平面ACE,∴AE⊥BF,∵BC∩BF=B,∴AE⊥平面BCE,又BE⊂平面BCE,∴AE⊥BE.(6分)解:(Ⅱ)在三角形ABE中过M点作MG∥AE交BE于G点,CE,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,则由比例关系得CN=13∵MG∥AE MG⊄平面ADE,AE⊂平面ADE,∴MG∥平面ADE,同理,GN∥平面ADE,∴平面MGN∥平面ADE,又MN⊂平面MGN,∴MN∥平面ADE,∴N点为线段CE上靠近C点的一个三等分点.(12分)【例3】.如图,已知菱形AECD的对角线AC,DE交于点F,点E为的AB中点.将三角形ADE 沿线段DE折起到PDE的位置,如图2所示.(Ⅰ)求证:DE ⊥平面PCF ;(Ⅱ)证明:平面PBC ⊥平面PCF ;(Ⅲ)在线段PD ,BC 上是否分别存在点M ,N ,使得平面CFM ∥平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.【解答】证明:(Ⅰ)折叠前,因为四边形AECD 为菱形,所以AC ⊥DE ;所以折叠后,DE ⊥PF ,DE ⊥CF ,又PF∩CF=F,PF ,CF ⊂平面PCF ,所以DE ⊥平面PCF(Ⅱ)因为四边形AECD 为菱形,所以DC ∥AE ,DC=AE .又点E 为AB 的中点,所以DC ∥EB ,DC=EB .所以四边形DEBC 为平行四边形.所以CB ∥DE .又由(Ⅰ)得,DE ⊥平面PCF ,所以CB ⊥平面PCF .因为CB ⊂平面PBC ,所以平面PBC ⊥平面PCF .解:(Ⅲ)存在满足条件的点M ,N ,且M ,N 分别是PD 和BC 的中点.如图,分别取PD 和BC 的中点M ,N .连接EN ,PN ,MF ,CM .因为四边形DEBC 为平行四边形,所以EF ∥CN ,EF =12BC =CN .所以四边形ENCF 为平行四边形.所以FC ∥EN .在△PDE 中,M ,F 分别为PD ,DE 中点,所以MF ∥PE .又EN ,PE ⊂平面PEN ,PE∩EN=E,MF ,CF ⊂平面CFM ,所以平面CFM ∥平面PEN .练习3 .如图,直角三角形ABC 中,A=60°,沿斜边AC 上的高BD ,将△ABD 折起到△PBD 的位置,点E 在线段CD 上.(1)求证:PE ⊥BD ;(2)过点D 作DM ⊥BC 交BC 于点M ,点N 为PB 中点,若PE ∥平面DMN ,求DE DC 的值.解析 (1)∵BD 是AC 边上的高,∴BD ⊥CD ,BD ⊥PD ,又PD∩CD=D,∴BD ⊥平面PCD ,又PE ⊂平面PCD 中,∴BD ⊥PE ,即PE ⊥BD ;(2)如图所示,连接BE ,交DM 与点F ,∵PE ∥平面DMN ,∴PE ∥NF ,又点N 为PB 中点,∴点F 为BE 的中点;∴DF=12BE=EF ;又∠BCD=90°﹣60°=30°,∴△DEF 是等边三角形,设DE=a ,则BD=√3a ,DC=√3BD=3a ;∴DE DC =a 3a =13.。
立体几何中的平行与垂直关系

立体几何中的平行与垂直关系在立体几何中,平行和垂直关系是非常基本且重要的概念。
通过理解和应用这些关系,我们可以更好地解决与立体图形相关的问题。
本文将介绍平行和垂直关系的定义和性质,并通过实例进行说明,以帮助读者更好地理解和运用这些概念。
一、平行关系在立体几何中,当两个线、面或者空间图形之间的相对位置满足特定条件时,我们可以说它们是平行的。
具体而言,以下是平行关系的定义和性质:1. 定义:如果两条直线在同一平面内,且在平面内没有交点,那么这两条直线被称为平行线。
用简单的符号表示为"//"。
2. 性质:平行线具有以下重要性质:a) 平行线之间的距离始终相等。
也就是说,如果有一条直线与一组平行线相交,那么从这条直线到任意一条平行线的距离都相等。
b) 平行线夹角与其对应的第三条平行线夹角相等。
也就是说,如果有两组平行线相交,那么相交的两对对应线之间的夹角相等。
二、垂直关系垂直关系是平行关系的一种特殊情况。
当两条直线、面或者空间图形之间的相对位置形成直角时,我们可以说它们是垂直的。
具体而言,以下是垂直关系的定义和性质:1. 定义:如果两条直线或者平面相交时,相交的两条直线或者平面的交角为90°,那么它们被称为垂直的。
2. 性质:垂直关系具有以下重要性质:a) 垂直线之间的夹角是直角,即为90°。
b) 垂直平面之间的夹角也是直角。
通过理解和应用平行和垂直关系,我们可以在解决立体几何问题时更加便捷和准确。
以下是一些实例,用以说明如何运用平行和垂直关系:实例1:矩形的性质考虑一个矩形ABCD,其中AB平行于CD,AD平行于BC。
根据平行关系的性质,我们可以得出以下结论:a) AB和CD之间的距离相等。
b) AD和BC之间的距离相等。
c) AB和CD之间的夹角以及AD和BC之间的夹角都是直角。
d) 矩形的对角线AC和BD相交于O,而OA和OC以及OB和OD之间的夹角也都是直角。
推导立体几何中的平行与垂直关系

推导立体几何中的平行与垂直关系在立体几何中,平行和垂直关系是两个重要的几何概念。
本文将通过推导的方式来探讨平行和垂直之间的关系,从而更深入地理解它们在空间中的性质和应用。
1. 平行线的推导在立体几何中,平行线是指在同一个平面内永不相交的两条直线。
我们可以通过以下的推导过程来证明平行线之间的关系。
(省略推导过程,只列出结论)结论1:如果两条直线分别与一条第三条直线相交,并且这两个交点的两组内角互补或对顶角相等,那么这两条直线是平行的。
结论2:如果两条直线被一组平行线截断,并且这两组截断线的对应角互等,那么这两条直线是平行的。
结论3:如果两条直线被同一平面平行于第三条直线截断,并且截断线上的对应角互等,那么这两条直线是平行的。
2. 垂直关系的推导垂直关系是指两条线段、两个平面或两个立体体素之间的相互垂直性。
下面是垂直关系的推导过程。
结论4:如果两条线段的斜率相乘为-1,则它们是垂直的。
结论5:如果两个平面的法向量垂直,则这两个平面是垂直的。
结论6:如果两个立体体素的对应面之间的相交线段互相垂直,则这两个立体体素是垂直的。
通过上述的推导过程,我们可以明确平行线和垂直关系在立体几何中的性质和判定条件。
这些性质和条件在实际问题中有着广泛的应用,例如在建筑设计、空间规划和工程测量等领域。
总结起来,平行和垂直关系是立体几何中的重要概念。
通过推导我们可以得出平行线的判定条件和垂直关系的性质,从而更好地理解它们在空间中的应用。
对于解决实际问题和深入学习几何学来说,这些知识将会帮助我们更好地理解和应用平行和垂直的性质。
在实践中,我们可以通过几何题目的解答来进一步巩固对平行和垂直关系的理解。
通过本文的学习,相信读者对于立体几何中的平行和垂直关系有了更深入的认识。
在以后的学习和工作中,我们可以灵活运用这些概念和推导方法,更好地解决与立体几何相关的问题。
立体几何作为数学的一个重要分支,在应用中有着广泛的价值和意义。
因此,深入理解并掌握平行和垂直关系是我们学习立体几何的关键。
初二立体几何的平行与垂直关系

初二立体几何的平行与垂直关系立体几何是数学中的一个重要分支,它研究的是三维空间中的几何形状和其性质。
在立体几何中,平行与垂直关系是一个基础概念,对于我们理解立体图形的性质和应用具有重要意义。
本文将详细介绍初二阶段立体几何中的平行与垂直关系,帮助读者更好地理解和掌握相关知识。
一、平行关系1. 平行的定义在平面几何中,我们知道两条直线如果永不相交,那么它们是平行的。
类似地,在立体几何中,两个平面如果永不相交,那么它们也是平行的。
两个平行的平面可以近似地理解为平行于地面的两个水平板,它们之间的距离始终保持不变。
2. 平行关系的表示方法在数学中,平行关系可以用符号“||”表示。
例如,平面ABCD || 平面EFGH表示平面ABCD与平面EFGH是平行的。
3. 平行关系的性质平行关系具有以下性质:(1)平行关系具有传递性。
即如果平面A || 平面B,平面B || 平面C,则可得出平面A || 平面C。
(2)两个平行面之间的任意两条相交直线都是平行的。
这个性质在立体几何的证明中常常被使用。
二、垂直关系1. 垂直的定义在平面几何中,如果两条直线相交且交角为90度,那么我们称这两条直线为垂直线。
类似地,在立体几何中,两个平面如果相交且交线与两平面的交角都为90度,那么我们称这两个平面为垂直平面。
2. 垂直关系的表示方法在数学中,垂直关系可以用符号“⊥”表示。
例如,线段AB ⊥线段CD表示线段AB与线段CD是垂直的。
3. 垂直关系的性质垂直关系具有以下性质:(1)垂直关系具有对称性。
即如果线段AB ⊥线段CD,则可得到线段CD ⊥线段AB。
(2)在平行平面中,与同一条直线垂直的两条直线是平行的。
三、平行和垂直关系的应用平行和垂直关系在生活中和其他学科中有广泛的应用。
1. 建筑设计中,平行和垂直关系是设计师在设计房间平面图时必须要考虑的因素。
合理利用平行和垂直线,可以使房间具备更好的功能性和美观性。
2. 制图学中,平行和垂直线的运用对于绘制准确的图形至关重要。
立体几何中的平行与垂直判定

立体几何中的平行与垂直判定立体几何是研究三维空间中的几何关系和性质的一门学科,平行与垂直判定是其中重要的一部分。
在解题过程中,准确判定两个线、面或空间立体之间的平行与垂直关系至关重要。
本文将介绍几种常用的判定方法,并通过具体例子进行说明。
一、平面与平面的判定在立体几何中,平面与平面间的平行与垂直关系是经常需要判断的。
下面将介绍两种常用的判定方法。
1. 垂直判定两个平面互相垂直的条件是它们的法向量垂直。
设平面1的法向量为n1(x1, y1, z1),平面2的法向量为n2(x2, y2, z2),则平面1和平面2垂直的条件可以表示为:n1·n2 = 0(向量的点积为0)例如,假设平面1过点A(1, 2, 3),其法向量为n1(2, -1, 3);平面2过点B(4, -1, 2),其法向量为n2(1, 2, -1)。
我们可以计算两个法向量的点积:n1·n2 = (2, -1, 3)·(1, 2, -1) = 2×1 + (-1)×2 + 3×(-1) = 0因此,平面1和平面2是垂直的。
2. 平行判定两个平面互相平行的条件是它们的法向量平行。
设平面1的法向量为n1(x1, y1, z1),平面2的法向量为n2(x2, y2, z2),则平面1和平面2平行的条件可以表示为:n1 = k·n2(k为非零实数)例如,假设平面1过点A(1, 2, 3),其法向量为n1(2, -1, 3);平面2过点B(4, -1, 2),其法向量为n2(1, 2, -1)。
我们可以通过判断两个法向量的比例关系来确定其是否平行。
在本例中,两个法向量的各个分量之间的比例并不相等,因此平面1和平面2不是平行的。
二、直线与直线的判定在立体几何中,直线与直线的平行与垂直关系也经常需要判断。
下面将介绍两种常用的判定方法。
1. 垂直判定两条直线互相垂直的条件是它们的方向向量垂直。
立体几何平行与垂直的判定与性质

• 平行与垂直的基本概念 • 平行线的判定 • 垂直线的判定 • 平行与垂直的性质 • 立体几何平行与垂直的应用
目录
01
平行与垂直的基本概念
平行的定义
总结词
在立体几何中,如果两条直线在同一平面内,且永远不会相交,则这两条直线 被称为平行的。
详细描述
在平面几何中,两条平行线被定义为在同一平面内,且永远不会相交的两条直 线。这个定义在立体几何中同样适用。在三维空间中,两条平行线可能位于不 同的平面,但它们永远不会在任何平面上相交。
在三维建模软件中,平行和垂直关系 也是构建复杂几何体的基础。通过设 定平行或垂直的约束条件,可以确保 模型的准确性和一致性。
实际生活中的平行与垂直应用
在城市规划和建筑设计中,平行和垂直的应用同样广泛。例如,确定道路、建筑 物的位置和方向时,需要利用平行和垂直关系来确保规划的科学性和合理性。
在机械设计和制造中,平行和垂直关系也是非常重要的。例如,在制造精密仪器 或机械设备时,需要确保各个部件之间的平行和垂直关系,以保证设备的准确性 和稳定性。
总结词
平行和垂直是两种互为对立的几何关系,它 们在三维空间中共同构成了直线之间的基本 关系。
详细描述
平行和垂直是直线之间最重要的两种关系。 在三维空间中,除了平行和垂直之外,直线 之间还可以是斜交的。平行和垂直的对立关 系使得它们在解决几何问题时具有重要的作 用。例如,在建筑设计和工程实践中,垂直 关系常常用于确定物体的位置和方向,而平 行关系则常常用于确定物体的尺寸和比例。
详细描述
在立体几何中,如果两条直线被第三条直线所截,并且内错角相等,则这两条直 线平行。这是因为内错角相等说明两条直线在同一平面内,并且没有交点,因此 它们是平行的。
立体几何平行与垂直定理总结

(2)范围: [0,180] (3)求法: 方法一:定义法。
m
Pl n
步骤 1:作出二面角的平面角(三垂线定理),并证明。
步骤 2:解三角形,求出二面角的平面角。
方法二:截面法。
步骤 1:如图,若平面 POA 同时垂直于平面和 ,则交线(射线)AP 和 AO 的
夹角就是二面角。 步骤 2:解三角形,求出二面角。
直线。
P l且P l
αPl
4 平行于同一条直线的两条直线平行
由公理1,2得到三个推论 推论1 经过一条直线和这条直线外 一点,有且只有一个平面 推论2 经过两条相交直线,有且只 有一个平面 推论3 经过两条平行直线,有且只 有一个平面
(一):线线平行:
方法一:用线面平行实现。
l //
m
l
//
l
方法二:用面面平行实现。
l
m
//
l
l
//
β α
l
方法三:用平面法向量实现。
n
l
n 若 为 平 面 的 一 个 法 向 量 , n l 且 α
l ,则 l // 。
(三)面面平行: 方法一:用线线平行实现。
l // l'
β
m // l, m
m'
且相交
//
l', m' 且相交
θ
O
步骤 2:解三角形,求出线面角。
n 方法二:向量法( 为平面 的一个法向量)。
n AP
sin cos n, AP n AP 方法三:等体积法求高.
(一) 二面角及其平面角
(1)定义:在棱 l 上取一点 P,两个半平面内分别作 l 的垂线(射线)m、n,则
专题11 立体几何 11.3平行与垂直证明 题型归纳讲义-2022届高三数学一轮复习(解析版)

所以 EF∥BC.
又因为 EF⊄平面 PBC,BC⊂平面 PBC,
△PAD 是正三角形,平面 PAD⊥平面 PBD.
(Ⅰ)求证:PA⊥BD;
(Ⅱ)设二面角 P﹣BD﹣A 的大小为α,直线 PA 与平面 PBC 所成角的大小为β,求 cos
(α+β)的值.
【解答】(Ⅰ)证明:∵∠BAD=45°,AD=1,�� = 2,
∴由余弦定理,得:
BD=
1 + 2 − 2 × 1 × 2 × ���45° =1,…(2 分)
性质定理
行,则过这条直线的任一
∵l∥α,
平面与此平面的交线与
l⊂β,α∩β
该直线平行(简记为“线面
=b,∴l∥b
平行⇒线线平行”)
2.平面与平面平行的判定定理和性质定理
文字语言
判定定理
图形语言
符号语言
一个平面内的两条相交
∵a∥β,b
直线与另一个平面平行,
∥β,a∩b
则这两个平面平行(简记
=P,a⊂α,
⊥AC,
所以 PA⊥面 ABC,
因为 BC⊂平面 ABC,
所以 PA⊥BC.
又因为 AB⊥BC,且 PA∩AB=A,
所以 BC⊥面 PAB.
….(9 分)
(Ⅲ)解:当点 F 是线段 AB 中点时,过点 D,E,F 的平面内的任一条直线都与平面 PBC
平行.
取 AB 中点 F,连 EF,连 DF.
由(Ⅰ)可知 DE∥平面 PBC.
��
理由.
【解答】(Ⅰ)证明:取 AB 中点 O,连接 EO,DO.
因为 EA=EB,所以 EO⊥AB. …(2 分)
立体几何平行与垂直所有概念、公理、定理汇总

立体几何的概念、公理、定理(一)立体几何三公理公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.,A a A a公理3:经过不在同一直线上的三点,有且只有一个平面。
A、B、C不在同一直线上有且只有一个平面α,使A∈α,B∈α,C∈α推论1:经过一条直线和这条直线外的一点,有且只有一个平面。
A a 有且只有一个平面,使推论2:经过两条相交直线,有且只有一个平面。
a∩b=A有且只有一个平面,使推论3:经过两条平行直线,有且只有一个平面。
a∥b=A有且只有一个平面,使(二)空间直线公理4 :平行于同一条直线的两条直线互相平行。
a∥bb∥c等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
cbaaA∈a,B∈aA∈,B∈aA∈aababcba//a c////////AB A BAC A C///BAC B A CA∈PP(三)直线和平面直线和平面平行的判定定理:如果平面外一条直线和 这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
定理 :如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直这个平面。
定理:一条直线垂直于两个平行平面中的一个平面, 它也垂直于另一个平面。
直线与平面垂直的性质定理:如果两条直线同垂直于一个平面, 那么这两条直线平行。
射影定理:从平面外一点向这个平面所引的垂线段和斜线段中, (1)射影相等的两条斜线段相等,射影较长的斜线段也较长; (2)相等的斜线段的射影相等,较长的斜线段的射影也较长; (3)垂线段比任何一条斜线段都短。
立体几何中的平行与垂直判定(续续)

立体几何中的平行与垂直判定(续续)立体几何中的平行与垂直判定几何学是研究形状、大小、相对位置以及属性的数学分支。
在几何学中,平行和垂直是基本的概念。
本文将继续探讨立体几何中的平行和垂直判定方法。
一、平行线的判定在平面几何中,两条直线平行的条件有多种,常用的方法包括以下几种:1. 关于同一直线的垂直线是平行线的判定方法。
如果两条直线分别与一条第三线相交,且分别垂直于第三线,那么这两条直线是平行的。
2. 使用平行线的性质进行判定。
根据平行线的定义,如果两条直线分别与第三条直线相交,并且对应角相等(即同位角相等),那么这两条直线是平行的。
3. 利用平行线的等夹判定。
如果两条直线分别与一条第三线相交,并且所成的内错角、内对角、锐角以及钝角都相等,那么这两条直线是平行的。
二、垂直线的判定与平行线类似,在立体几何中判定两条直线垂直的方法也有多种,常用的方法如下:1. 利用垂直线的性质进行判定。
如果两条直线分别与一条第三线相交,且所成的对应角互补(即和为90度),那么这两条直线是垂直的。
2. 使用垂直线的等角判定。
如果两条直线分别与一条第三线相交,并且所成的对顶角、邻补角以及对应角都相等,那么这两条直线是垂直的。
3. 关于同一点的垂直线是垂直线的判定方法。
如果两条直线分别通过一点,并且与第三条直线相交,且分别垂直于第三条直线,那么这两条直线是垂直的。
三、平行面的判定除了判定平行线和垂直线外,在立体几何中判定平行面也非常重要。
常用的平行面判定方法包括:1. 平面法向量的平行判定。
如果两个平面的法向量平行,那么这两个平面是平行的。
2. 利用两个平面上的垂线进行判定。
如果两个平面上各自的垂线相交,并且与第三个平面相交的直线垂直于第三个平面,那么这两个平面是平行的。
3. 使用平行面的性质进行判定。
如果两个平面分别与一条直线相交,并且对应角互补(即和为180度),那么这两个平面是平行的。
综上所述,平行与垂直的判定方法在立体几何中非常重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线、平面平行的判定及其性质一、选择题1、若两个平面互相平行,则分别在这两个平行平面内的直线( )A.平行B.异面C.相交D.平行或异面2、下列结论中,正确的有( )①若aα,则a∥α②a∥平面α,bα则a∥b③平面α∥平面β,aα,bβ,则a∥b ④平面α∥β,点P∈α,a∥β,且P∈a,则aαA.1个B.2个C.3个D.4个3、在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是( )A.平行B.相交C.在内D.不能确定4、a,b是两条异面直线,A是不在a,b上的点,则下列结论成立的是( )A.过A有且只有一个平面平行于a,bB.过A至少有一个平面平行于a,bC.过A有无数个平面平行于a,bD.过A且平行a,b的平面可能不存在5、已知直线a与直线b垂直,a平行于平面α,则b与α的位置关系是( )A.b∥αB.bαC.b与α相交D.以上都有可能6、下列命题中正确的命题的个数为( )①直线l平行于平面α内的无数条直线,则l∥α; ②若直线a在平面α外,则a∥α;③若直线a∥b,直线bα,则a∥α; ④若直线a∥b,b平面α,那么直线a就平行于平面α内的无数条直线.A.1B.2C.3D.47、下列命题正确的个数是( )(1)若直线l上有无数个点不在α内,则l∥α(2)若直线l与平面α平行,l与平面α内的任意一直线平行(3)两条平行线中的一条直线与平面平行,那么另一条也与这个平面平行(4)若一直线a和平面α内一直线b平行,则a∥αA.0个B.1个C.2个D.3个8、已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题中真命题是( ):①若m⊥α,m⊥β,则α∥β; ②若α⊥γ,β⊥γ,则α∥β;③若mα,nβ,m∥n,则α∥β; ④若m、n是异面直线,mα,m∥β,nβ,n∥α,则α∥β.A.①和②B.①和③C.③和④D.①和④9、长方体ABCD-A1B1C1D1中,E为AA1中点,F为BB1中点,与EF平行的长方体的面有()A.1个B.2个C.3个D.4个10、对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α、β都垂直于γ;②存在平面γ,使α、β都平行于γ;③α内有不共线的三点到β的距离相等;④存在异面直线l,M,使得l∥α,l∥β,M∥α,M∥β. 其中可以判断两个平面α与β平行的条件有()A.1个B.2个C.3个D.4个二、填空题1、在棱长为a的正方体ABCD—A1B1C1D1中,M、N分别是棱A1B1、B1C1的中点,P是棱AD上一点,AP= ,过P、M、N的平面与棱CD交于Q,则PQ=_________. 答案:2、如果空间中若干点在同一平面内的射影在一条直线上,那么这些点在空间的位置是__________.共线或在与已知平面垂直的平面内3、若直线a和b都与平面α平行,则a和b的位置关系是__________. 相交或平行或异面4、正方体ABCD-A1B1C1D1中,E为DD1中点,则BD1与过点A,C,E的平面的位置关系是_________. 平行三、解答题1、如图,直线AC,DF被三个平行平面α、β、γ所截.①是否一定有AD∥BE∥CF;②求证:.2、如图,ABCD是平行四边形,S是平面ABCD外一点,M为SC的中点.求证:SA∥平面MDB.证明:连结AC交BD于N,因为ABCD是平行四边形,所以N是AC的中点.又因为M是SC的中点,所以MN∥SA.因为MN平面MDB,所以SA∥平面MDB.3、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点,P是正方形ABCD的中心,求证:MN∥平面PB1C.第三章直线、平面垂直的判定及其性质一、选择题1、二面角指的是( )A.两个平面相交所组成的角B.经过同一条直线的两个平面所组成的图形C.一条直线出发的两个半平面组成的图形D.两个平面所夹的不大于90°的角参考答案与解析:解析:根据二面角的定义讨论,故选C.答案:C主要考察知识点:空间直线和平面2、α、β、γ、ω是四个不同平面,若α⊥γ,β⊥γ,α⊥ω,β⊥ω,则( )A.α∥β且γ∥ωB.α∥β或γ∥ωC.这四个平面中可能任意两个都不平行D.这四个平面中至多有一对平面平行参考答案与解析:解析:若α∩β=a.∵α⊥γ,β⊥γ,∴α⊥γ.同理a⊥ω.∴γ∥ω;若α∥β,则γ与ω相交或平行,∴α∥β或γ∥ω.答案:B主要考察知识点:空间直线和平面3、已知直线m、n与平面α、β,给出下列三个命题:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是( )A.0B.1C.2D.3参考答案与解析:解析:①m∥α,n∥α不一定有m∥α.②③正确.答案:C主要考察知识点:空间直线和平面4、如图2-3-15,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )图2-3-15A.平面PAB与平面PBC、平面PAD都垂直B.它们两两都垂直C.平面PAB与平面PBC垂直、与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直参考答案与解析:思路解析:∵PA⊥平面ABCD,∴PA⊥BC.又∵BC⊥AB,PA∩AB=A,∴PC⊥平面PAB,从而平面PBC⊥平面PAB.由AD⊥PA,AD⊥AB,PA∩AB=A得AD⊥平面PAB.∵AD平面PAD,∴平面PAD⊥平面PAB.答案:A主要考察知识点:空间直线和平面5、如图2-3-16,等边三角形ABC的边长为1,BC边上的高为AD,若沿AD折成直二面角,则A到BC的距离是……()图2-3-16A.1B.C.D.参考答案与解析:思路解析:折叠后BD=DC=,且∠BDC为二面角的平面角,∠BDC=90°,∴BC=.取BC中点E,连结DE,则DE⊥BC,进一步易证AE⊥BC,AE的长为所求距离.∵AD=,DE=BC=,∴AE=.答案:C主要考察知识点:空间直线和平面6、下列命题正确的是( )A.垂直于同一条直线的两直线平行B.垂直于同一条直线的两直线垂直C.垂直于同一个平面的两直线平行D.垂直于同一条直线的一条直线和平面平行参考答案与解析:思路解析:在空间中垂直于同一直线的两条直线,可能平行相交,也可能异面,所以A,B错,垂直于同一直线的直线和平面的位置关系可以是直线在平面内,直线和平面平行,所以D错.答案:C主要考察知识点:空间直线和平面7、空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是( )A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交参考答案与解析:解析:取BD中点E,连结AE、CE.∵AB=AD=BC=CD,∴AE⊥BD,CE⊥BD.∴BD⊥平面AEC.又AC面AEC,∴BD⊥AC.答案:C主要考察知识点:空间直线和平面8、线段AB的长等于它在平面α内射影长的2倍,则AB所在直线与平面α所成的角为()A.30°B.45°C.60°D.120°参考答案与解析:解析:由直角三角形的边角关系,可知直线与平面α所成的角为60°.答案:C主要考察知识点:空间直线和平面9、设α,β为两个不重合的平面,l,M,n为两两不重合的直线,给出下列四个命题:①若α∥β,,则l∥β;②若,,M∥β,n∥β,则α∥β;③若l∥α,l⊥β,则α⊥β;④若,,且l⊥M,l⊥n,则l⊥α.其中正确命题的序号是()A.①③④B.①②③C.①③D.②④参考答案与解析:解析:由面面平行的判定定理,知②错误;由线面垂直的判定定理知④错误.答案:C主要考察知识点:空间直线和平面10、下列说法中正确的是()①过平面外一点有且只有一条直线和已知平面垂直②过直线外一点有且只有一个平面和已知直线垂直③过平面外一点可作无数条直线与已知平面平行④过直线外一点只可作一条直线与已知直线垂直A.①②③B.①②③④C.②③D.②③④参考答案与解析:解析:由线面垂直的性质及线面平行的性质,知①②③正确;④错,过直线外一点作平面与直线垂直,则平面内的所有直线都与该直线垂直.答案:A主要考察知识点:空间直线和平面二、填空题【共4道小题】1、α、β是两个不同的平面,m、n是平面α、β外的两条不同直线,给出四个结论:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______.参考答案与解析:解析:假设①③④为条件,即m⊥n,n⊥β,m⊥α成立,如图.过m上一点P作PB∥N,则PB ⊥m,PB⊥β,设垂足为B.又设m⊥α,垂足为A,过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC,l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB,∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来,如果②③④成立,与上面证法类似可得①成立.答案:②③④①或①③④②.主要考察知识点:空间直线和平面2、α、β是两个不同的平面,m、n是平面α、β外的两条不同直线,给出四个结论:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______.参考答案与解析:解析:假设①③④为条件,即m⊥n,n⊥β,m⊥α成立,如图.过m上一点P作PB∥N,则PB ⊥m,PB⊥β,设垂足为B.又设m⊥α,垂足为A,过PA、PB的平面与α、β的交线l交于点C.∵l⊥PA,l⊥PB,∴l⊥平面PAB.∴l⊥AC,l⊥BC.∴∠ACB是二面角α-l-β的平面角.由m⊥n,显然PA⊥PB,∴∠ACB=90°,∴α⊥β.由①③④②成立.反过来,如果②③④成立,与上面证法类似可得①成立.答案:②③④①或①③④②.主要考察知识点:空间直线和平面3、设三棱锥P ABC的顶点P在平面ABC上的射影是H,给出下列命题:①若PA⊥BC,PB⊥AC,则H是△ABC的垂心;②若PA、PB、PC两两互相垂直,则H是△ABC的垂心;③若∠ABC=90°,H是AC的中点,则PA=PB=PC;④若PA=PB=PC,则H是△ABC的外心.请把正确命题的序号填在横线上:______________.参考答案与解析:解析:①若P A⊥BC,PB⊥AC,则H为垂心.②∵PA⊥PB,PA⊥PC,∴PA⊥面PBC.∴PA⊥BC.又PH⊥面ABC,∴PH⊥BC.∴BC⊥面PAH.∴AH⊥BC.同理BH⊥AC,∴H为垂心.③∵H为AC中点,∠ABC=90°,∴AH=BH=CH.又PH⊥面ABC,由勾股定理知PA=PB=PC.④∵PA=PB=PC,又PH⊥面ABC,同③可知 AH=BH=CH,∴H为外心.答案:①②③④主要考察知识点:空间直线和平面4、如图,P是二面角α-AB-β的棱AB上一点,分别在α、β上引射线PM、PN,截PM=PN,如果∠BPM=∠BPN=45°,∠MPN=60°,则二面角α-AB-β的大小是___________.参考答案与解析:解析:过M在α内作MO⊥AB于点O,连结NO,设PM=PN=a,又∠BPM=∠B PN=45°,∴△OPM≌△OPN.∴ON⊥AB.∴∠MON为所求二面角的平面角.连结MN,∵∠MPN=60°,∴MN=a.又,∴MO2+NO2=MN2.∴∠MON=90°.答案:90°主要考察知识点:空间直线和平面三、解答题【共3道小题】1、如图,在正方体ABCD—A1B1C1D1中,EF⊥A1D,EF⊥AC,求证:EF∥BD1.参考答案与解析:解析:要证明EF∥BD1,可构造与它们都垂直的一个平面.由于A1D,AC均为各面的对角线,通过对角线的平行性可构造垂直关系.证明:连结A1C1,由于AC∥A1C1,EF⊥AC,∴EF⊥A1C1.又EF⊥A1D,A1D∩A1C1=A1,∴EF⊥平面A1C1D. ①∵BB1⊥平面A1B1C1D1,A1C1平面A1B1C1D1,∴BB1⊥A1C1.又A1B1C1D1为正方体,∴A1C1⊥B1D1.∵BB1∩B1D1=B1,∴A1C1⊥平面BB1D1D.而BD1平面BB1D1D,∴BD1⊥A1C1.同理,DC1⊥BD1,DC1∩A1C1=C1,∴BD1⊥平面A1C1D. ②由①②可知EF∥BD1.主要考察知识点:空间直线和平面2、在长江汽车渡口,马力不足或装货较重的汽车上岸时,采用沿着坡面斜着成S形的方法向上开,这是为什么?你能从数学的角度进行解释吗?参考答案与解析:答案:在汽车马力恒定的情况下,行驶单位路程内,垂直上升高度愈大,汽车愈费“力”,当“力”所不及时,就会发生危险.日常经验告诉我们,走S形可减少这种危险,从数学的角度看,可作如下解释.图2-3-22如图,AB表示笔直向上行走的路线(AB⊥CA),α表示它与水平面所成的交角,CB表示斜着向上行走的路线,β表示它与水平面所成的夹角,它们所达到的高度都是BD.现在的问题就是要研究α和β这两个角哪个大,越大越费力.在Rt△BAD中,sinα=.①在Rt△BCD中,s inβ=.②比较①与②,因为AB、CB分别是直角三角形ABC的直角边和斜边,也就是说AB<CB,所以>.又因为α、β都是锐角,所以α>β.因此汽车沿着CB方向斜着向上开要省力.山区修筑的公路,采取盘山而上的方法,也是这个道理.主要考察知识点:空间直线和平面3、如图,在四面体ABCD中,△ABD、△ACD、△BCD、△ABC都全等,且,BC=2,求以BC 为棱、以面BCD和面BCA为面的二面角的大小.参考答案与解析:解:取BC的中点E,连结AE、DE,∵AB=AC,∴AE⊥BC.又∵△ABD≌△ACD,AB=AC,∴DB=DC.∴DE⊥BC.∴∠AE D为二面角A-BC-D的平面角.又∵△ABC≌△DBC,且△ABC为以BC为底的等腰三角形,故△DBC也是以BC为底的等腰三角形,∴.又△ABD≌△BDC,∴AD=BC=2.在Rt△DEB中,,BE=1,∴,同理.在△AE D中,∵AE=DE=,AD=2,∴AD2=AE2+DE2.∴∠AE D=90°.∴以面BCD和面BCA为面的二面角的大小为90°. 主要考察知识点:空间直线和平面。
