信号分析与处理课后习题答案
信号分析与处理答案第二版完整版

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。
(1)解当激励为时,响应为,即:由于方程简单,可利用迭代法求解:,,…,由此可归纳出的表达式:利用阶跃响应和冲激响应的关系,可以求得阶跃响应:(2)解 (a)求冲激响应,当时,。
特征方程,解得特征根为。
所以:…(2.1.2.1)通过原方程迭代知,,,代入式(2.1.2.1)中得:解得,代入式(2.1.2.1):…(2.1.2.2)可验证满足式(2.1.2.2),所以:(b)求阶跃响应通解为特解形式为,,代入原方程有,即完全解为通过原方程迭代之,,由此可得解得,。
所以阶跃响应为:(3)解(4)解当t>0时,原方程变为:。
…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程,比较两边的系数得:阶跃响应:求下列离散序列的卷积和。
(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。
当时:当时:当时:当时:当时:(7) ,解参见右图:当时:当时:当时:当时:当时:(8) ,解参见右图当时:当时:当时:当时:(9) ,解(10),解或写作:求下列连续信号的卷积。
(1) ,解参见右图:当时:当时:当时:当时:当时:当时:(2) 和如图2.3.2所示解当时:当时:当时:当时:当时:(3) ,解(4) ,解(5) ,解参见右图。
当时:当时:当时:当时:(6) ,解(7) ,解(8) ,解(9) ,解试求题图示系统的总冲激响应表达式。
解已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;解,,(2) ;,解,,,,可定出(3) ;,解,,,可定出某一阶电路如题图所示,电路达到稳定状态后,开关S 于时闭合,试求输出响应。
解由于电容器二端的电压在t=0时不会发生突变,所以。
信号分析与处理 第二版 (赵光宙 着)_课后习题参考答案

om
课后答案网
=
⎡ 1 ⎤ A2 1 lim ⎢ sin(2ω 0T + 2θ ) − sin(−2ω 0T + 2θ ) + 2T ⎥ 2 T →∞ ⎣ 2ω 0 2ω 0 ⎦
=∞
P = lim 1 T →∞ 2T
2
∫
T
−T
2 x2 (t )dt
kh
=
=
(3) x3 (t ) = sin 2t + sin 2π t
= lim ∫ (sin 2 2t + 2sin 2t sin 2π t + sin 2 2π t )dt
T →∞ −T
T
w
.k w
= lim [ 2T −
T →∞
T ⎡1 − cos 4t α = 2t cos(α + β ) − cos(α − β ) 1 − cos 4π t ⎤ dt = lim ∫ ⎢ + + ⎥ T →∞ −T β = 2π t 2 2 2 ⎣ ⎦ T ⎡ cos 4t cos(α + β ) − cos(α − β ) cos 4π t ⎤ dt = lim ∫ ⎢1 − + − T →∞ −T 2 2 2 ⎥ ⎣ ⎦
w
= A2 lim ∫
cos(2ω 0t + 2θ ) + 1 dt −T 2
T
.c
w = lim ∫ A2 cos(ω 0 + θ )dt
om
.c
−t
om
da
(4) (5) (6) (7)
w .c
不是周期信号 不是周期信号 不是周期信号 不是周期信号
2π 3 7m (2) 是周期信号, T = =7 4 (3) 是周期信号, T = 2
信号分析与处理课后答案_赵光宙

信号分析与处理课后答案一、信号分析基础1.1 什么是信号?信号是一种随时间变化的物理量或信息。
根据信号的特点,可以分为连续信号和离散信号。
连续信号是指在任意时间点上都能够取到值的信号,通常用连续函数来表示。
离散信号是指只在某些离散时间点上能够取到值的信号,通常用序列来表示。
1.2 信号处理的基本任务信号处理的基本任务包括信号的获取、表示、转换、分析和处理。
其中,信号的获取是指从外部获取信号的过程,信号的表示是指将信号用数学方法表示出来,信号的转换是指将信号从一种形式转换为另一种形式,信号的分析是指对信号进行频域、时域等方面的分析,信号的处理是指对信号进行滤波、降噪、压缩等处理操作。
二、离散信号的表示与运算2.1 离散信号的表示离散信号可以用序列表示。
序列是一系列按固定顺序排列的数值,通常用形如{x(n)}的表示方法。
2.2 离散信号的运算离散信号的运算包括加法、减法、乘法和除法等。
对于两个离散信号x(n)和y(n),它们的加法可以写作z(n) = x(n) + y(n),减法可以写作z(n) = x(n) - y(n),乘法可以写作z(n) = x(n) * y(n),除法可以写作z(n) = x(n) / y(n)。
三、信号的时域分析3.1 信号的时域表示信号的时域表示是指将信号用时间序列表示出来。
在时域分析中,常用的表示方法包括离散时间信号和连续时间信号。
离散时间信号可以用序列表示,连续时间信号可以用连续函数表示。
3.2 信号的时域分析方法信号的时域分析方法包括时域表示、自相关函数和相关函数等。
时域表示是指将信号在时域上的特征表达出来,自相关函数是指信号与其自身的乘积在不同时间点上的累加,相关函数是指两个信号在不同时间点上的乘积的累加。
四、信号的频域分析4.1 信号的频域表示信号的频域表示是指将信号在频域上的特征表达出来。
常用的频域表示方法包括傅里叶变换、频谱分析和功率谱分析等。
4.2 傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法。
信号分析与处理-杨西侠-课后答案二三五章
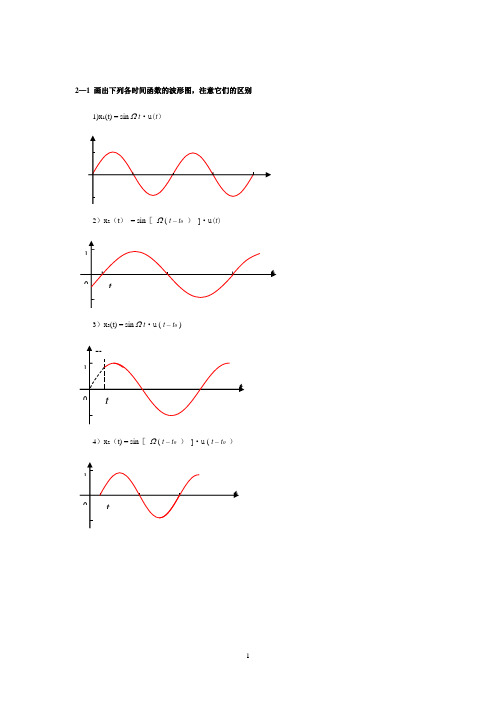
2—1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t ) = sin [ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )4)x 2(t) = sin [ Ω ( t – t 0 ) ]·u ( t – t 0 )-2-2 已知波形图如图2—76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x (t/2 )(5)x (-t)(6)x (—t-2)(7)x ( -t/2—2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(tt xδ(t) dt = x(—t0)(2)⎰+∞∞--)(tt xδ(t) dt = x(t0)x (-t-2)(3)⎰+∞∞--)(0t t δ u(t —2t ) dt = u (2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u (-t 0)(5)()⎰+∞∞--+tetδ(t+2) dt = e 2—2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7)()()[]⎰+∞∞-Ω---dt t t t e t j 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1—t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02—4 求下列各函数x 1(t )与x 2(t ) 之卷积,x 1(t )* x 2(t)(1) x 1(t ) = u(t ), x 2(t ) = e—at· u(t) ( a>0 )x 1(t)* x 2(t) =⎰+∞∞---ττττd t u eu a )()( =⎰-ta d e 0ττ =)1(1at e a--x 1(t )* x 2(t ) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos [Ω(t+1)+4π]u (t+1) – cos[Ω(t —1)+4π]u(t —1)(3) x 1(t) = u (t) – u(t-1) , x 2(t) = u(t ) – u (t —2)x 1(t )* x 2(t ) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t 〈0时,x 1(t )* x 2(t) = 0当 0<t 〈1时,x 1(t)* x 2(t ) =td τ⎰= t当 1<t <2时,x 1(t)* x 2(t ) =21d τ⎰= 1当 2<t<3时,x 1(t )* x 2(t ) = 12t d τ-⎰=3-t当 3〈t 时,x 1(t )* x 2(t) = 0(4) x 1(t) = u (t —1) , x 2(t) = sin t · u(t)x 1(t )* x 2(t ) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos (t-1)2—5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t )在一个周期( 0<t<T )的波形 (1) x(t)是偶函数,只含有偶次谐波分量f (t ) = f(—t ), f (t ) = f (t ±T/2)(2) x (t)是偶函数,只含有奇次谐波分量 f (t ) = f (-t ), f (t) = —f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(—t)(4) x(t)是奇函数,只含有奇次谐波分量f(t)= —f(—t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(—t), f(t) = f(t±T/2)(6)x(t)是奇函数,含有偶次和奇次谐波分量f(t)= —f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
信号分析与处理 第二版 (赵光宙 着)_课后习题参考答案

= lim ∫ (sin 2 2t + 2sin 2t sin 2π t + sin 2 2π t )dt
T →∞ −T
T
w
.k w
= lim [ 2T −
T →∞
T ⎡1 − cos 4t α = 2t cos(α + β ) − cos(α − β ) 1 − cos 4π t ⎤ dt = lim ∫ ⎢ + + ⎥ T →∞ −T β = 2π t 2 2 2 ⎣ ⎦ T ⎡ cos 4t cos(α + β ) − cos(α − β ) cos 4π t ⎤ dt = lim ∫ ⎢1 − + − T →∞ −T 2 2 2 ⎥ ⎣ ⎦
kh
=∞
da
= lim [ 2T −
sin 4T sin(2 + 2π )T sin(2 − 2π )T sin 4π T ⎤ + − − 4 2 + 2π 2 − 2π 4 ⎥ ⎦
w
sin(2 − 2π )T sin(2 − 2π )T sin 4π T sin 4π T ⎤ − − − 4 − 4π 4 − 4π 8 8 ⎥ ⎦
(4) x1 [n] = ( ) u[n] 解:
1 2
j (π / 2 n +π / 8 )
π
4
n)
w .c
(1) P∞ = 0, E ∞ = 1 / 4
(2) P∞ = 1, E ∞ = ∞ (5) P∞ = 1, E ∞ = ∞
(3) P∞ = 1 / 2, E ∞ = ∞
kh
da
(4) P∞ = 0, E ∞ = 4 / 3
2
kh
(6)
信号分析与处理答案(苪坤生 潘孟贤 丁志中 第二版)习题答案

第二章习题参考解答2.1 求下列系统的阶跃响应和冲激响应。
(1) )()1(31)(n x n y n y =--解 当激励为)(n δ时,响应为)(n h ,即:)()1(31)(n n h n h δ+-=由于方程简单,可利用迭代法求解:1)0()1(31)0(=+-=δh h ,31)0(31)1()0(31)1(==+=h h h δ,231)1(31)2()1(31)2(⎪⎭⎫ ⎝⎛==+=h h h δ…,由此可归纳出)(n h 的表达式:)()31()(n n h n ε=利用阶跃响应和冲激响应的关系,可以求得阶跃响应:)(])31(2123[311)31(1)31()()(10n k h n s n n k nk nk ε-=--===+=-∞=∑∑(2) )()2(41)(n x n y n y =--解 (a)求冲激响应)()2(41)(n n h n h δ=--,当0>n 时,0)2(41)(=--n h n h 。
特征方程0412=-λ,解得特征根为21,2121-==λλ。
所以: n n C C n h )21()21()(21-+= …(2.1.2.1)通过原方程迭代知,1)0()2(41)0(=+-=δh h ,0)1()1(41)1(=+-=δh h ,代入式(2.1.2.1)中得:121=+C C0212121=-C C 解得2121==C C , 代入式(2.1.2.1):0,)21(21)21(21)(>-+=n n h n n …(2.1.2.2)可验证)0(h 满足式(2.1.2.2),所以:)(])21()21[(21)(n n h n n ε-+=(b)求阶跃响应通解为 n n c C C n s )21()21()(21-+=特解形式为 K n s p =)(,K n s p =-)2(,代入原方程有 141=-K K , 即34=K完全解为34)21()21()()()(21+-+=+=n n p c C C n s n s n s通过原方程迭代之1)0(=s ,1)1(=s ,由此可得13421=++C C134212121=+-C C 解得211-=C ,612=C 。
信号分析与处理 第二版 (赵光宙 著)_khdaw

A2 1 ⎞ ⎛ 1 lim ⎜ − ⎟=0 2T T →∞ 2 2T ⎠ ⎝ 2Te
aw
T
答
案
网
(3) x3 (t ) = sin 2t + sin 2πt
(4) x 4 (t ) = e sin 2t
w
w
T →∞
若侵犯了您的版权利益,敬请来信通知我们! ℡
kh
da
⎡ 1 ⎤ A2 = lim ⎢ sin(2ω 0t + 2θ ) + t ⎥ 2 T →∞ ⎣ 2ω 0 ⎦ −T
kh
=∞
da
= lim [ 2T −
sin 4T sin(2 + 2π )T sin(2 − 2π )T sin 4π T ⎤ + − − 4 2 + 2π 2 − 2π 4 ⎥ ⎦
w
sin(2 − 2π )T sin(2 − 2π )T sin 4π T sin 4π T ⎤ − − − 4 − 4π 4 − 4π 8 8 ⎥ ⎦
(2) f 2 (t ) = sin ωt u (t − t 0 )
w
w
′ ( t ) 和 x2 ′ (t ) 的波形并写出相应的表达式。 (10)分别画出 x1
若侵犯了您的版权利益,敬请来信通知我们! ℡
.c
om
⎡ sin 4t sin(2 + 2π )t sin(2 − 2π )t sin 4π t ⎤ = lim ⎢t − + − − T →∞ 8 (2 + 2π )2 (2 − 2π )2 8π ⎥ ⎣ ⎦ 0T + 2θ ) − sin(−2ω 0T + 2θ ) A2 + lim 2 T →∞ 4ω 0T
信号分析与处理第二版(赵光宙着)_课后习题参考答案.

习题一 (P7)1. 指出题图1-1所示各信号是连续时间信号?还是离散时间信号。
题图 1-1解:1345(),(),(),()x t x t x t x t 是连续时间信号 26(),()x t x t 是离散时间信号。
2. 判断下列各信号是否是周期信号,如果是周期信号,求出它的基波周期。
(1) )4/3cos(2)(π+=t t x (2) )27/8cos()(+=n n x π(3) (4))1()(−=t j et x π)8/()(π−=n j en x (5) (6) []∑∞=−−−−=)31()3()(m m n m n n x δδ)(2cos )(t u t t x ×=π(7) )4/cos()4/cos()(πn n n x ×=(8) )6/2/sin(2)8/sin()4/cos(2)(ππππ+−+=n n n n x分析:(1) 离散时间复指数信号的周期性:为了使为周期性的,周期,就必须有,因此有。
nj eΩ0>N n j N n j e eΩ+Ω=)(1=Ωn j e N Ω必须为π2的整数倍,即必须有一个整数m,满足m N π2=Ω所以N m=Ωπ2 因此,若π2Ω为一有理数,为周期性的,否则,不为周期性的。
nj e Ω所以,周期信号基波频率为:nj e Ωm N Ω=π2 ,基波周期为:Ω=π2m N 。
(2) 连续时间信号的周期性:(略)k hd a w.c o mk hd aw.co mwww.k hd a w .c o m课后答案网答案:(1) 是周期信号,32π=T (2) 是周期信号,747==mT(3) 是周期信号,2=T(4) 不是周期信号 (5) 不是周期信号 (6) 不是周期信号 (7) 不是周期信号(8) 是周期信号,16=T3.试判断下列信号是能量信号还是功率信号。
(1) (2)tAe t x −=)(10≥t )cos()(02θω+=t A t x(3)tt t x π2sin 2sin )(3+= (4)t e t x t2sin )(4−=解:(1)1()0tx t Aet −=≥222201lim lim 2TTtt T T w A e dt A e −−→∞→∞⎡⎤==⎢⎥−⎣⎦∫()22221lim 1lim 122TT T T A A e e −→∞→∞⎛⎞=−=−−⎜⎟−⎝⎠22A =2222011limlim 0222Tt T T T A P A e dt TTe−→∞→∞⎛⎞==−−⎜⎟⎝⎠∫12T =1()x t ∴为能量信号(2)20()cos()x t A t ωθ=+w =∞ 22A P =20lim cos()TTT w A ωθ−→∞=+∫dt20cos(22)1lim 2TT T t A dt ωθ−→∞++=∫2001lim sin(22)22TT TA t t ωθω→∞−⎡⎤=+⎢⎥⎣⎦+ k hd a w.c o mk hd aw.co mwww.k hd a w .c o m课后答案网2000011lim sin(22)sin(22)2222T A T T ωθωθωω→∞⎡⎤=+−−+⎢⎥⎣⎦T +=∞ 221lim()2T TT P x T−→∞=∫t dt0020011sin(22)sin(22)22lim 122T T T A T ωθωθωω→∞⎡⎤+−−+⎢⎥⎢⎥=+⎢⎥⎢⎥⎣⎦2000sin(22)sin(22)lim24T T T A Tωθωω→∞+−−+=+θ 22A =2()x t ∴为功率信号(3)3()sin 2sin 2x t t t π=+2lim (sin 2sin 2)TTT w t π−→∞=+∫t dt dt22lim(sin 22sin 2sin 2sin 2)TTT t t t t ππ−→∞=++∫21cos 4cos()cos()1cos 4lim 2222TT T t t t dt t ααβαβπβπ−→∞=−+−−−⎡⎤=++⎢⎥=⎣⎦∫ cos 4cos()cos()cos 4lim 1222T T T t t dt αβαβπ−→∞+−−⎡⎤=−+−⎢⎥⎣⎦∫ sin 4sin(22)sin(22)sin 4lim 8(22)2(22)28TT T t t t t πππππ→∞t π−⎡⎤+−=−+−−⎢⎥+−⎣⎦ [sin 4sin(4)sin(22)sin(22)lim 2884444T T T T T Tππππ→∞−++=−+++++ sin(22)sin(22)sin 4sin 4444488T T T T πππππ−−⎤−−−−⎥−−⎦π [sin 4sin(22)sin(22)sin 4lim 2422224T T T T T ππππ→∞+−⎤=−+−−⎥+−⎦T π =∞k hd a w.c o mk hd aw.co mwww.k hd a w .c o m课后答案网231lim()2TTT P x T −→∞=∫t dt[sin 4sin(22)sin(22)sin 4lim 18(22)2(22)28T T T T T T T ππππ→∞⎤+−=−+−−⎥+−⎦T T π =13()x t ∴为功率信号(4)4()sin 2tx t e −=t tdt2lim sin 2Tt T t w e −−→∞=∫12cos 4lim 2TtTT te d −−→∞−=∫t 22lim lim cos 42tTT t T TT t e dt e tdt −−−−→∞→∞=−∫∫ 22lim lim cos 44Tt T t TT T Te e t −−−→∞→∞−⎡⎤=−⎢⎥−⎣⎦∫dt 222lim lim cos 444T T T tT T T e e e t −−−→∞→∞⎛⎞=+−⎜⎟−⎝⎠∫dt 22211cos 4cos 4sin 452TTtt t TTetdt e t e t −−−−−⎡⎤=−+⎢⎥⎣⎦∫∵222211lim lim cos 4sin 44452TT T t tT T T e e w e t −−−→∞→∞e t −⎛⎞⎡⎤∴=+−−+⎜⎟⎢⎥−⎣⎦⎝⎠222222111lim lim cos 4sin 4cos 4sin 444522T T T T T TT T e e e T e T e T e −−−→∞→∞⎛⎞⎡⎤=+−−+++⎜⎟⎢⎥−⎣⎦⎝⎠T 2222221111lim cos 4sin 4cos 4sin 444105105T T T T T T T e e e T e T e T e T −−−→∞⎛⎞=++−−−⎜⎟−⎝⎠221cos 4sin 41cos 4sin 4lim lim 41054105T TT T T T T T e e −→∞→∞⎡⎤⎡=−+−+−−⎢⎥⎢⎣⎦⎣⎤⎥⎦ 0=+∞221cos 4sin 41cos 4sin 4limlim 2410524105T T T T e T T e T P TT−→∞→∞⎡⎤⎡=−+−+−−⎢⎥⎢⎣⎦⎣T ⎤⎥⎦0=+∞4()x t ∴既非功率信号,也非能量信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号分析与处理课后习题答案第五章 快速傅里叶变换1.如果一台通用计算机的速度为平均每次复乘需要50us ,每次复加需要10us ,用来就散N=1024点的DFT ,问:(1)直接计算需要多少时间?用FFT 计算呢?(2)照这样计算,用FFT 计算快速卷积对信号进行处理是,估计可实现实时处理的信号最高频率? 解:分析:直接利用DFT 计算:复乘次数为N 2,复加次数为N(N-1);利用FFT 计算:复乘次数为20.5log N N ,复加次数为2log N N ;(1) 直接DFT 计算:复乘所需时间2215010245052.4288T N us us s =⨯=⨯=复加所需时间2(1)101024(10241)1010.47552T N N us us s =-⨯=-⨯= 所以总时间1262.90432DFT T T T s =+=FFT 计算:复乘所需时间3220.5log 500.51024log 1024500.256T N N us us s =⨯=⨯⨯⨯= 复加所需时间422log 101024log 1024100.1024T N N us us s =⨯=⨯⨯= 所以总时间为340.3584FFT T T T s =+= (2) 假设计算两个N 长序列1()x n 和2()x n 的卷积计算过程为如下:第一步:求1()X k ,2()X k ;所需时间为2FFT T ⨯第二步:计算12()()()X k X k X k =•,共需要N 次复乘运算所需时间为501024500.0512To N us us s =⨯=⨯=第三步:计算(())IFFT X k ,所需时间为FFT T所以总时间为230.35840.0512 1.1264FFT T T To s s s =⨯+=⨯+= 容许计算信号频率为N/T=911.3Hz2.设x(n)是长度为2N 的有限长实序列,()X k 为x(n)的2N 点得DFT 。
(1)试设计用一次N 点FFT 完成计算()X k 的高效算法;(2)若已知()X k ,试设计用一次N 点IFFT 实现x(n)的2N 点IDFT 运算。
解:本题的解题思路就是DIT-FFT 思想。
(1) 分析2N 点的FFT ,如下在始于分别抽取偶数点和奇数点x(n)得到两个N 长的实序列x1(n)和x2(n);X1(n) = x(2n), n = 0,1,…, N-1 X2(n) = x(2n+1), n = 0,1,…, N-1根据DIT-FFT 的思想,只要球的x1(n)和x2(n)的N 电DFT ,再经过简单的一级蝶形运算就可得到x(n)的2N 点的DFT 。
因为x1(n)和x2(n)均为实序列,所以根据DFT 的共轭对称性,可以用一次N 点FFT 求得X1(k)和X2(k)。
具体方法如下: 令 y(n) = x1(n) + jx2(n)Y(k) = DFT[y(n)], k = 0,1,…, N-1则 X1(k) = DFT[x1(n)] = Y ep (k) = 0.5[Y(k)+Y*(N-k)] X2(k) = DFT[jx2(n)] = Y op (k) = 0.5[Y(k)-Y*(N-k)] 2N 点得DFT[x(n)] = X(k)可由X1(k)和X2(k)得到122122()()(),0,1,,1()()(),,1,,21kN kN X k X k W X k k N X k X k W X k k N N N ⎧=+=-⎪⎨=-=+-⎪⎩ 这样,通过一次N 点FFT 计算就完成了计算2N 点DFT 。
当然由Y(k)求x1(k)和X2(k)需要相对小的额外计算量。
(2) 分析2N 点的IFFT 变换,如下与(1)相同,设X1(n),x2(n),X1(k),X2(k); n,k = 0,1,…, N-1 则应满足关系式122122()()(),0,1,,1()()()kN k N X k X k W X k k N X k N X k W X k ⎧=+=-⎪⎨+=-⎪⎩由上式可解出122()0.5[()()]()0.5[()()]kN X k X k X k N X k X k X k N W -=++=-+由以上分析可得出计算过程如下:○1由X(k)计算出X1(k)和X2(k),即 122()0.5[()()]()0.5[()()]kNX k X k X k N X k X k X k N W-=++=-+○2由X1(k)和X2(k)构成N 点频域序列Y(k) Y(k) = X 1(k) +jX 2(k) = Y ep (k) + Y op (k)其中Yep(k) = X1(k),Yop(k) = jX2(k),进行N 点IFFT 得到()[()]Re[()]Im[()],0,1,,1y n IFFT Y k y n j y n n N ====-由DFT 的共轭对称性知12Re[()]0.5[()*()][()]()Im[()]0.5[()*()][()]()ep op y n y n y n IDFT Y k x n y n y n y n IDFT Y k jx n =+===-==○3由x1(n)和x2(n)合成x(n) 1(),2()12(),2nx n x n n x n ⎧=⎪⎪=⎨-⎪=⎪⎩偶奇3.请给出16点时域抽选输入倒序、输出顺序基2-FFT 完整计算流图,注意P N W 及其p 值得确定。
解:第6章 无限长冲激响应(IIR )数字滤波器1.设系统的差分方程为()3(1)2(2)()5(1)y n y n y n x n x n +-+-=+-请画出该系统的直接型、级联型和并联型结构。
解:(1)直接-I 型结构:(2)直接-II 型结构:(3)级联型结构:111211()15115()*()132112Y z z z H z X z z z z z------++===++++-1(4)并联型结构 1134()121H z z z ---=+++2 设系统的系统函数为()()()()()11211211 3.17410.21 1.45z z z H z z zz ------++-=-++试画出该系统的级联型结构。
解:11211211 3.174()10.21 1.45z z z H z z z z ------++-=*-++3 设计一个模拟巴特沃斯低通滤波器,要求通带截止频率3p fkHz =,通带最大衰减3p dBα=,阻带截止频率12s f kHz =,阻带最小衰减50s dB α=。
求系统函数()H s 。
解:(1)求阶数N 。
lg lg sp spk N λ=-0.0032sp k ==≈332121042310s sp p πλπΩ⨯⨯===Ω⨯⨯ 带入N 的计算公式得:lg 0.0032 4.14lg 4N =-=,所以取N =5(2)求归一化系统函数()a H p 。
由阶数N =5直接查表可得到5阶巴特沃斯归一化低通滤波器系统函数()a H p 为:()543213.2361 5.2361 5.2361 3.23611a H p p p p p p =+++++(3)去归一化,由归一化系统函数()a H p 得到实际滤波器系统函数()H s 。
32310/c p rad s πΩ=Ω=⨯⨯,因此()()554233243.2361 5.2361 5.2361 3.23611ca sp cc c c c H s H p s s s s s =Ω=Ω=+Ω+Ω+Ω+Ω+带入c Ω的值即可。
4设计一个模拟切比雪夫低通滤波器,要求通带截止频率3p f kHz =,通带最大衰减3p dB α=,阻带截止频率12s f kHz =,阻带最小衰减50s dB α=。
求系统函数()H s 。
解:(1)确定滤波器技术指标:3p dB α=,32610/p p f rad s ππΩ==⨯50s dB α=,322410/s s f rad s ππΩ==⨯ 1p λ=,4ss pλΩ==Ω (2)求阶数N 和ε()()1s Arch k N Arch λ-=1316.978k -=≈ ()()316.978 3.12684Arch N Arch ==,为满足指标要求,取4N =0.9976ε==(3)求归一化系统函数()a H p :()()()1111127.9808a NNN kk k k H p p p p p ε-====⋅--∏∏其中,极点k p 可由下式求出:()()()()2121sin cos ,1,2,3,422k k k p ch jch k N Nππξξ--⎛⎫⎛⎫=-+=⎪ ⎪⎝⎭⎝⎭1111=0.220840.9976Arsh Arsh N ξε⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭()()10.2208sin 0.2208cos 0.39210.946588p ch jch j ππ⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭()()2330.2208sin 0.2208cos 0.94650.392188p ch jch j ππ⎛⎫⎛⎫=-+=-+⎪ ⎪⎝⎭⎝⎭()()3550.2208sin 0.2208cos 0.94650.392188p ch jch j ππ⎛⎫⎛⎫=-+=--⎪ ⎪⎝⎭⎝⎭()()4770.2208sin 0.2208cos 0.39210.946588p ch jch j ππ⎛⎫⎛⎫=-+=--⎪ ⎪⎝⎭⎝⎭(4)将()a H p 去归一化,求得实际滤波器系统函数()H s 。
()()()()4444117.98087.9808pa s p ppp k k k k H s H p s p s s =Ω===ΩΩ==-Ω-∏∏其中3610,1,2,3,4k p k k s p p k π=Ω=⨯=。
因为**4132,p p p p ==,所以**4132,s s s s ==。
将两对共轭极点对应的因子相乘,得到分母为二阶因子的形式,其系数全为实数。
带入即可得到相应结果。
5 模拟滤波器的系统函数为()2132H s s s =-+,试分别采用冲激响应不变法和双线性变换法将其转换成数字滤波器()H z 。
解:(1)冲激响应不变法(设抽样间隔为s T ) 可以求出()H s 的极点为:121,2s s ==所以()11112Ni i i A H s s s s s =-==+---∑()1121111111i s s s Nis T i T T A H z e z e z e z -=--=--=+--∑(2)双线性变换法(设抽样间隔为s T )()()()()()()112112111122122212121213211462484621s z s T z s s ssssssH z H s z z T z T z T T T z T T z z T---=+-------==⎛⎫⎛⎫---+ ⎪ ⎪++⎝⎭⎝⎭-++-+++=+6 假设某模拟滤波器系统函数()H s 是一个低通滤波器,并且有()()11z s z H z H s +=-=,数字滤波器()H z 的通带中心位于下面哪种情况?说明原因。
