八年级数学直角三角形全等的判定
人教版八年级上册数学直角三角形全等的判定

D C
A
B
E F
CE=BF. 求证:AE=DF.
C
D
FE
A
B
变式训练
如图:AC⊥BC,BD⊥AD,AC=BD. 求证:BC=AD.
DO
C
A
B
自我测评
如图,AC=AD,∠C,∠D是直角, 求证: BC=BD
C
A
B
D
变式训练
1.如图所示,△ABC中,AB=AC, AD⊥BC于点D. 求证:∠1=∠2.
实际应用
如图,C是路段AB的中点,两人从C同时出发, 以相同的速度分别沿两条直线行走,并同时到 达D,E两地,DA⊥AB,EB⊥AB,D、E与路 段AB的距离相等吗?为什么?
实际问题 数学问题
D
求证:DA=EB
A
E C
B
能力提升
如图所示,在△ABC中,AB=AC,D是BC
的中点,DE⊥AB,DF⊥AC,垂足分别为E,
F.则图中全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
本节课你有哪些收获?
作业
1. 课本44页6,7,8题。 2.如图,已知AD,AF分别是两个钝角三角形的 高,若AD=AF,AC=AE,求证:BC=BE.
AAS SAS
A
D
B
CF
E
思考:若AB=DE,AC=DF, △ABC与△DEF全等吗?
A
D
B
CF
E
互动探究 A
任意画出一个Rt△ABC,∠B=90°。
再画一个Rt△A´B´C´,使得 ∠B´= 90°, B´C´=BC,A´C´= AC。
∟
C
Bபைடு நூலகம்
初中八年级数学课件《直角三角形全等的判定》

C
B
例题讲解
画法:1.画∠MCN=90 °. 2.在射线CM上取CB=a. 3.以B为圆心,c为半径画弧, 交射线CN于点A.
a
c
N A c
4.连接AB . △ABC就是所要画的直角三角形.
MB a C
例题讲解
例2.已知:如图,点P在∠AOB的内部,PC⊥OA,PD⊥OB, 垂足分别为C, D,且PC=PD. 求证:点P在∠AOB的平分线上.
这两个直角三角形全等吗?
A
A'
全等,SAS
B
C B'
C'
合作探究
问题1.4 两个直角三角形中,两边对应相等,这两个直角三
角形全等吗?如何证明?
已知:如图,在△ABC和△A′B′C′中,
A A'
∠C=∠ C′=90°,AB = A′B′ ,
AC= A′C′. 求证:△ABC≌△A′B′C′.
B
C C'
已知:如图,线段a,c.
求作:△ABC,使∠C=90°,BC=a,AB=c.
分析:首先作出边BC,由∠C为直角可以作出另
a
一直角边所在的射线,由AB=c可以确定点A。
c
例题讲解
作法:
(1)作线段CB=a,
(2)过点C,作MC⊥CB.
M
A
(3)以B为圆心,c为半径画弧,交CM于点A,
(4)连接AB.
其中正确的个数有___4___个.
当堂检测
4.如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE. 求证:△EBC≌△DCB.
证明: ∵ BD⊥AC,CE⊥AB,
A
∴∠BEC=∠BDC=90 °.
判定全等三角形的五种方法

判定全等三角形的五种方法全等三角形是指具有相同形状和相等边长的三角形。
判定两个三角形是否全等是数学中的一个重要问题。
下面将介绍判定全等三角形的五种方法。
方法一:SSS判定法(边边边)SSS判定法是指通过比较两个三角形的三条边是否相等来判定其是否全等。
如果两个三角形的三条边长度相等,则可以判断它们是全等三角形。
方法二:SAS判定法(边角边)SAS判定法是指通过比较两个三角形的两条边和夹角是否相等来判定其是否全等。
如果两个三角形的一边和夹角分别相等,则可以判断它们是全等三角形。
方法三:ASA判定法(角边角)ASA判定法是指通过比较两个三角形的两个角和夹边是否相等来判定其是否全等。
如果两个三角形的两个角和夹边分别相等,则可以判断它们是全等三角形。
方法四:AAS判定法(角角边)AAS判定法是指通过比较两个三角形的两个角和非夹边的对应边是否相等来判定其是否全等。
如果两个三角形的两个角和非夹边的对应边分别相等,则可以判断它们是全等三角形。
方法五:HL判定法(斜边和直角边)HL判定法是指通过比较两个直角三角形的斜边和直角边是否相等来判定其是否全等。
如果两个直角三角形的斜边和直角边分别相等,则可以判断它们是全等三角形。
通过以上五种方法,我们可以准确地判定两个三角形是否全等。
这些方法都是基于几何学中的一些定理和公理推导而来,经过严谨的数学证明,可以确保判定结果的准确性。
需要注意的是,在判定全等三角形时,我们需要确保给定的条件足够,即要求已知的边长、角度等信息能够满足相应的判定条件。
如果给定的信息不足够,或者不满足判定条件,那么就无法准确地判定两个三角形是否全等。
判定全等三角形的方法还可以用于解决一些实际问题,例如在建筑设计、图形测量等领域。
通过判定三角形是否全等,可以确保设计和测量的准确性,提高工作效率。
总结起来,判定全等三角形的五种方法分别是SSS判定法、SAS判定法、ASA判定法、AAS判定法和HL判定法。
这些方法都是基于几何学中的定理和公理推导而来,通过比较边长、角度等信息,可以准确地判定两个三角形是否全等。
直角三角形全等判定定理

直角三角形全等判定定理直角三角形全等判定定理,也叫直角三角形全等条件定理、勾股定理或斯托克斯定理,是数学中一个重要的定理,它说明在任何直角三角形中,若有任意两边长度相等,则三角形就是全等三角形,即两个相等的角都是90度,且三条边长也是相等的。
斯托克斯定理曾是希腊数学家欧几里得的儿童时代创造,后来被苏格拉底改写为定理形式。
斯托克斯定理是一个有关直角三角形的数学定理,它告诉我们,如果两条边的长度相等,则该三角形是一个直角三角形。
斯托克斯定理也称为勾股定理,又称“直角三角形全等性判定定理”,它是古希腊时期最著名的定理之一,是古希腊数学家欧几里得最早发现的定理之一,他在其《几何》中对此进行了证明。
斯托克斯定理可以用来证明所有直角三角形都具有三条边和两个相等的角,这种特殊的三角形称为全等三角形。
根据斯托克斯定理,如果一个三角形的其中两条边的长度相等,则该三角形必定是一个直角三角形,而且它的三条边和两个相等的角都是相等的。
斯托克斯定理也可以用来证明股数定理,即如果a2+b2=c2,则这个三角形就是一个直角三角形,而且它的三条边和两个相等的角都是相等的。
斯托克斯定理是数学中一个重要的定理,它能够提供一个简单而又有效的方法来验证一个三角形是否为直角三角形。
它可以被用来证明某一个三角形是否全等,也可以用来检验三角形的长度是否相等。
因此,斯托克斯定理是数学中一个重要的定理,它在多个数学问题中得到广泛的应用,不但在几何和数学中得到应用,而且在工程学、计算机科学等领域中都有着重要的作用。
斯托克斯定理可以用大量数学证明来证明,但它的核心思想仍然是:任何直角三角形中,如果有任意两边长度相等,则这个三角形就是全等三角形,即两个相等的角都是90度,且三条边长也是相等的。
斯托克斯定理是一个简单而又有效的方法,它可以快速验证一个三角形是否为直角三角形,它的应用领域也十分广泛,在科学、工程学和计算机科学等领域中都有着重要的作用。
人教版八年级数学上《直角三角形全等的特殊条件》课堂笔记

《直角三角形全等的特殊条件》课堂笔记
一、定义与条件
1.HL判定:在直角三角形中,如果两个直角三角形的斜边和一个直角边分别相等,
那么这两个三角形全等。
2.ASA判定:在两个三角形中,如果两个角和它们的夹边分别相等,那么这两个
三角形全等。
二、应用与实例
1.HL判定应用:在解决实际问题时,如果已知两个直角三角形的斜边和一条直角
边分别相等,那么可以直接使用HL判定来证明这两个三角形全等。
2.ASA判定应用:当已知两个三角形中的两个角和它们的夹边分别相等时,可以
使用ASA判定来证明这两个三角形全等。
三、注意事项
1.HL判定注意事项:在使用HL判定时,必须确保两个直角三角形的斜边和一条
直角边分别相等,不能出现其他条件的不符合。
2.ASA判定注意事项:在使用ASA判定时,必须确保两个角和它们的夹边分别
相等,不能出现其他条件的不符合。
四、练习与巩固
为了巩固所学知识,可以进行以下练习:
1.给出两组条件,判断是否能够使用HL或ASA判定证明两个三角形全等。
2.给出多个三角形,选择其中两个,使用适当的判定方法证明它们全等。
五、总结与回顾
本节课学习了直角三角形全等的特殊条件,包括HL判定和ASA判定。
通过学习,我们掌握了这些判定方法的应用和注意事项。
在今后的学习中,我们将继续运用这些方法来解决实际问题。
三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)
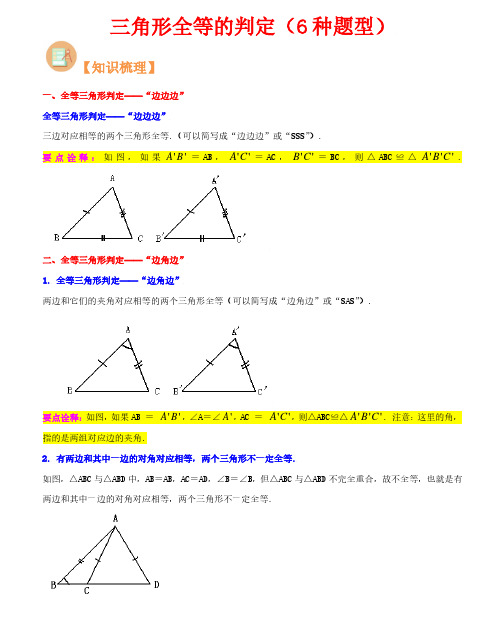
三角形全等的判定(6种题型)【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、垂直平分线:1.定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理:线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.【答案】证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)【变式2】、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB =CD -BD ,把CD -BD 转化为一条线段,可利用翻折变换,把△ABD 沿AD 翻折,使线段BD 运动到DC 上,从而构造出CD -BD ,并且也把∠B 转化为∠AEB ,从而拉近了与∠C 的关系.【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ), 求证:∠B +∠D =180°. AE D CB【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型三、全等三角形的判定——“角边角”例5、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,{∠B=∠DEF BC=EF∠ACB=∠F,∴△ABC≌△DEF(ASA).5种判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.例6、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN题型四、全等三角形的判定——“角角边”例7.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC=AD,再由平行线的性质可得∠DAE=∠ACB,由∠CED+∠B=180°,∠CED+∠AED=180°,得∠AED=∠B,从而利用AAS可判定△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例8、已知:如图,AB⊥AE,AD⊥,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 题型五:线段的垂直平分线 例9.(2023秋·浙江杭州·八年级校考开学考试)如图所示,在ABC 中,8AC =,5BC =,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则BCE 的周长为( )A .13B .18C .10.5D .21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =,再将BCE 的周长转化为AC BC +的长,即可求解.【详解】解:DE 是AB 的垂直平分线,∴AE BE =,∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+,8AC =,5BC =,∴BCE 的周长为8513AC BC +=+=,故选:A .【点睛】本题主要考查的是线段垂直平分线的性质,掌握线段垂直平分线的性质是解题的关键.【变式1】(2022秋·浙江温州·八年级校考期中)如图,点D 是ABC 边AC 的中点,过点D 作AC 的垂线交BC 于点E ,已知6AC =,ABC 的周长为14,则ABE 的周长是( )A .6B .14C .8D .20【答案】C 【分析】由题意可知:ED 垂直平分AC ,故EA EC =,结合6AC =,ABC 的周长为14,即可得出答案.【详解】解:∵点D 是ABC 边AC 的中点, ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =,∵6AC =,ABC 的周长为14,∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8.故选:C .【点睛】此题考查了垂直平分线的性质和判定,掌握垂直平分线的性质和判定是解题的关键.【答案】C 【分析】根据垂直平分线的性质可知,到A ,B ,C 表示三个居民小区距离相等的点,是AC ,BC 两边垂直平分线的交点,由此即可求解.【详解】解:如图所示,分别作AC ,BC 两边垂直平分线MN ,PQ 交于点O ,连接OA,OB,OC,∵MN,PQ是AC,BC两边垂直平分线,==,∴OA OB OC∴点O是到三个小区的距离相等的点,即点O是AC,BC两边垂直平分线的交点,故选:C.【点睛】本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.八年级专题练习)如图,在ABC中,是ABC外的一点,且【分析】根据到线段两端距离相等的点在线段的垂直平分线上,即可证明A、D都在BC的垂直平分线上,由此即可证明结论.AB AC,【详解】证明:∵=∴点A在BC的垂直平分线上,BD CD,∵=∴点D在BC的垂直平分线上,∴A、D都在BC的垂直平分线上,∴AD垂直平分BC.【点睛】本题主要考查了线段垂直平分线的判定,熟知线段垂直平分线的判定条件是解题的关键.【变式】.(2022秋·浙江·八年级专题练习)如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【详解】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.题型六:角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答.【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点.故本题选A .【点睛】本题考查了角平分线的性质,熟记角平分线的性质是解答本题的关键. 的中点,ABC ,则BED 的面积为( 【答案】C【分析】作DF AC ⊥于F ,DM AB ⊥于点M ,根据角平分线的性质求出DM ,根据三角形的面积公式计算即可.【详解】解:作DF AC ⊥于F ,DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ,DM AB ⊥,112122AC DF AB DM ∴⋅+⋅=,112122AC DM AB DM ⋅+⋅=∴即:3421DM DM +=得3DM =8AB =, E 是AB 的中点,142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选:C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键. 例12.(2022秋·浙江·八年级专题练习)已知:如图,90B C ∠=∠=,M 是BC 的中点,DM 平分ADC ∠.(1)若连接AM ,则AM 是否平分BAD ∠?请你证明你的结论;(2)线段DM 与AM 有怎样的位置关系?请说明理由.【答案】(1)AM 平分BAD ∠,证明见解析(2)DM AM ⊥,理由见解析【分析】(1)过点M 作ME AD ⊥,垂足为E ,证明ME MC MB ==即可得证.(2)利用两直线平行,同旁内角互补,证明1390∠+∠=.【详解】(1)AM 平分BAD ∠,理由为:证明:过点M 作ME AD ⊥,垂足为E ,∵DM 平分ADC ∠,∴12∠=∠,∵ME AD ⊥,MC CD ⊥∴MC ME =(角平分线上的点到角两边的距离相等),又∵MC MB =,∴ME MB =,∵MB AB ⊥,ME AD ⊥,∴AM 平分BAD ∠(到角的两边距离相等的点在这个角的平分线上).(2)DM AM ⊥,理由如下:∵90B C ∠=∠=,∴,DC CB AB CB ⊥⊥,∴DC AB ∥(垂直于同一条直线的两条直线平行),∴180DAB CDA ∠+∠=(两直线平行,同旁内角互补)又∵111,322CDA DAB ∠=∠∠=∠(角平分线定义) ∴2123180∠+∠=,∴1390∠+∠=,∴90AMD ∠=.即DM AM ⊥.【点睛】本题考查了角平分线的性质定理和判定定理,平行线的性质,熟练掌握以上的知识是解题的关键. 【变式1】(2023秋·浙江台州·八年级统考期末)如图 90B C ∠=∠=︒,E 为BC 上一点,AE 平分BAD ∠,DE 平分CDA ∠.(1)求AED ∠的度数;(2)求证:E 是BC 的中点.【答案】(1)90︒(2)见解析.【分析】(1)利用已知条件可以得到180BAD CDA ∠+∠=︒,想要求AED ∠的度数,只需要根据三角形内角和定理和角平分线的性质即可得到结论.(2)过点E 做EF AD ⊥,根据角平分线上的点到角的两边距离相等即可得结论.【详解】(1)解:∵90B C ∠=∠=︒,∴DC AB ∥,∴180BAD CDA ∠+∠=︒,∵AE 平分BAD ∠,DE 平分CDA ∠, ∴12EAD BAD ∠=∠,12EDA CDA ∠=∠, ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒,∴180()90AED EAD EDA ∠=︒−∠+∠=︒;(2)证明:过点E 作EF AD ⊥于点F ,∵AE 平分BAD ∠,90B Ð=°,EF AD ⊥,∴EF EB =.∵DE 平分CDA ∠,90C ∠=︒,EF AD ⊥,∴EF EC =.∴EB EC =,即E 是BC 的中点.【点睛】本题考查了平行线的判定与性质,以及角平分线上的点到角两边距离相等的性质,熟记性质和定理并做出辅助线是解题的关键.【变式2】.(2022秋·浙江杭州·八年级校考期中)如图,在ABC 外作两个大小不同的等腰直角三角形,其中90DAB CAE ∠=∠=︒,AB AD =,AC AE =.连接DC 、BE 交于F 点.(1)求证:DAC BAE ≌△△; (2)直线DC 、BE 是否互相垂直,试说明理由;(3)求证:AF 平分DFE ∠.【答案】(1)见解析(2)DC BE ⊥,理由见解析(3)见解析【分析】(1)由题意可得AD AB =,AC AE =,由90DAB CAE ∠=∠=︒,可得到DAC BAE ∠=∠,从而可证DAC BAE ≌△△;(2)由(1)可得ACD AEB ∠=∠,再利用直角三角形的性质及等量代换即可得到结论;(3)作AM DC ⊥于M ,AN BE ⊥于N ,利用全等三角形的面积相等及角平分线的判定即可证得结论.【详解】(1)证明:∵90DAB CAE ∠=∠=︒,∴DAB BAC CAE BAC ∠+∠=∠+∠,即DAC BAE ∠=∠,又∵AD AB =,AC AE =,∴()SAS DAC BAE ≌△△;(2)解:DC BE ⊥,理由如下;∵DAC BAE ≌△△, ∴ACD AEB ∠=∠,∵90AEB AOE ∠+∠= ,AOE FOC ∠=∠,∴90FOC ACD ∠+∠=,∴90EFC ∠=,∴DC BE ⊥;(3)证明:作AM DC ⊥于M ,AN BE ⊥于N ,∵DAC BAE ≌△△, ∴DAC BAE S S ∆∆=,DC BE =, ∴1122DC AM BE AN ⋅=⋅,∴AM AN =,∴AF 平分DFE ∠.【点睛】本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握判定和性质是解决本题的关键.【变式3】(2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习)已知:OP 平分MON ∠,点A ,B 分别在边OM ,ON 上,且180OAP OBP ∠∠+=︒.(1)如图1,当90OAP ∠=︒时,求证:OA OB =;(2)如图2,当90OAP ∠<︒时,作PC OM ⊥于点C .求证:①PA PB =;②请直接写出OA ,OB ,AC 之间的数量关系 .【答案】(1)见解析(2)①见解析;②2OA OB AC −=【分析】(1)证明()AAS OPA OPB ≌,即可得证;(2)①作PD ON ⊥于点D ,证明()AAS PAC PBD ≌,即可得证; ②证明()AAS OCP ODP ≌,得出OD =,根据AC BD =,即可得证.【详解】(1)证明:180OAP OBP ∠∠+=︒,且90OAP ∠=︒,90OAP OBP ∠∠∴==︒,OP 平分MON ∠,POA POB ∠∠∴=,OP OP =,()AAS OPA OPB ∴≌,OA OB ∴=;(2)证明:①如图2,作PD ON ⊥于点D ,PC OM ⊥于点C ,PC PD ∴=,90PCA PDB OCP ∠∠∠===︒,180OAP OBP ∠∠+=︒,180DBP OBP ∠∠+=︒,OAP DBP ∠∠∴=,在PAC 和PBD 中,CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS PAC PBD ∴≌, PA PB ∴=;②结论:2OA OB AC −=.理由:在OCP 和ODP 中,OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OCP ODP ∴≌,OC OD ∴=,OA AC OB BD ∴−=+,AC BD =,2OA OB AC BD AC ∴−=+=.故答案为:2OA OB AC −=.【点睛】本题考查了角平分线的性质,全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·八年级专题练习)如图,在ABC 中,90A ∠=︒,点D 是边AC 上一点,3DA =,若点D 到BC 的距离为3,则下列关于点D 的位置描述正确的是( )A .点D 是AC 的中点B .点D 是B ∠平分线与AC 的交点 C .点D 是BC 垂直平分线与AC 的交点D .点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ,连接BD ,利用角平分线的判定定理可证明BD 是ABC ∠的角平分线,即可作答.【详解】解:如图所示:作DE BC ⊥于E ,连接BD ,∵3DA =,点D 到BC 的距离为3,∴=AD DE ,∵90A ∠=︒,∴DA BA ⊥,∵DE BC ⊥,∴BD 是ABC ∠的角平分线,即点D 是ABC ∠的角平分线与AC 的交点,故B 项正确;其余选项,利用现有条件均无法得出,故选:B .【点睛】本题主要考查了角平分线的判定定理,作出辅助线,证明BD 是ABC ∠的角平分线,是解答本题的关键. 2.(2023·浙江·九年级专题练习)如图,已知BF DE =,AB ∥DC ,要使ABF CDE ≅△△,添加的条件可以是( )A.BE DF =B .AF CE =C .AB CD = D .B D ∠=∠【答案】C 【分析】根据AB ∥DC ,可得B D ∠=∠,又BF DE =,所以添加AB CD =,根据SAS 可证ABF CDE ≅△△.【详解】解:应添加AB DC =,理由如下:AB ∥DC ,B D ∴∠=∠.在ABF △和CDE 中,AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABF CDE ∴≅,故选:C .【点睛】本题主要考查了平行线的性质以及全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.3.(2023·浙江金华·统考二模)如图,ABC 和DEF 中,AB DE ∥,A D ∠=∠,点B ,E ,C ,F 共线,添加一个条件,不能判断ABC DEF ≌△△的是( )A .AB DE =B .ACB F ∠=∠C .BE CF =D .AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠,加上A D ∠=∠,可知ABC 和DEF 中两组对角相等,因此一组对边相等时,即可判断ABC DEF ≌△△. 【详解】解:AB DE ∥,∴B DEF ∠=∠, 又A D ∠=∠,∴ABC 和DEF 中两组对角相等,当AB DE =时,根据ASA 可证ABC DEF ≌△△,故A 选项不合题意; 当ACB F ∠=∠时,ABC 和DEF 中,三组对角相等,不能判断ABC DEF ≌△△,故B 选项符合题意; 当BE CF =时,BC EF =,根据AAS 可证ABC DEF ≌△△,故C 选项不合题意; 当AC DF =时,根据AAS 可证ABC DEF ≌△△,故D 选项不合题意; 故选B .【点睛】本题考查添加条件使三角形全等,解题的关键是熟练掌握全等三角形的各种判定方法..ABC 的三条中线的交点.ABC 三边的垂直平分线的交点.ABC 三条角平分线的交点.ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等,由此可解.【详解】解:要使凉亭到草坪三条边的距离相等,∴凉亭应在ABC 三条角平分线的交点处.故选C .【点睛】本题考查了角平分线的性质,解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别. 5.(2020秋·浙江·八年级期末)如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,2DE =,4AB =,则AC 的长为( )A .3B .4C .5D .6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==,再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=,然后解关于AC 的方程即可.【详解】解:∵AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,2DE =,∴2DF DE ==,∵7ABC S =△,4AB =,又∵ABD ACD ABC S S S +=△△△,∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=,∴3AC =.故选:A .【点睛】本题考查角平分线的性质:角的平分线上的点到角的两边的距离相等.理解和掌握角平分线的性质是解题的关键.本题也考查了三角形的面积及等积变换.6.(2022秋·浙江·八年级专题练习)如图,用B C ∠=∠,12∠=∠,直接判定ABD ACD ≌△△的理由是( )A .AASB .SSSC .ASAD .SAS【答案】A 【分析】根据三角形全等的判定方法判定即可.【详解】解:在ABD △和ACD 中,12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ABD ACD ≌,故A 正确. 故选:A .【点睛】本题主要考查三角形全等的判定,解题的关键是掌握证明全等三角形的几种证明方法:AAS 、ASA 、SSS 、SAS 、HL .A .2B .【答案】C 【分析】由FC AB ∥,得F ADE ∠=∠,FCE A ∠=∠,即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅,则4CF AD AB BD ==−=.【详解】解:FC AB ∥,F ADE ∴∠=∠,FCE A ∠=∠,在CFE 和ADE V 中,F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS CFE ADE ∴≅, CF AD ∴=,5AB =,1BD =,514AD AB BD ∴=−=−=,4CF ∴=,CF ∴的长度为4.故选:C .【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识,正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键.A .SSS【答案】B 【分析】根据已知条件两边,及两边的夹角是对顶角解答.【详解】解:在AOB 和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,()AOB COD SAS ∴≌. 故选:B .【点睛】本题考查了全等三角形的应用,准确识图判断出两组对应边的夹角是对顶角是解题的关键. 9.(2022秋·浙江嘉兴·九年级校考期中)在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放在ABC 的( )A .三边垂直平分线的交点B .三杂中线的交点C .三条角平分线的交点D .三条高所在直线的交点【答案】A【分析】根据题意可知,当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,再由线段垂直平分线的性质即可求解.【详解】解:由题意可得:当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,∵线段垂直平分线上的点到线段两端的距离相等,∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点,故选:A .【点睛】本题考查线段垂直平分线的性质的应用,掌握线段垂直平分线的性质是解题的关键. )可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒,再根据角平分线的定义可得CAB DAB ∠=∠,然后根据AAS 定理即可得.【详解】解:,BC AC BD AD ⊥⊥,90ACB ADB ∴∠=∠=︒,AB 平分CAD ∠,CAB DAB ∴∠=∠,在ABC 和ABD △中,90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ABC ABD ∴≌,故选:A . 【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法是解题关键.二、填空题【答案】CA FD =,B E ∠=∠,A D ∠=∠,AB DE ∥等【分析】可选择CA FD =添加条件后,能用SAS 进行全等的判;也可选择B E ∠=∠添加条件后,能用ASA 进行全等的判定;也可选择A D ∠=∠添加条件后,能用AAS 进行全等的判定;也可选择AB DE ∥添加条件后,能用ASA 进行全等的判定即可;【详解】解:添加CA FD =,∵12∠=∠,BC EF =,∴()SAS ABC DEF ≌△△,故答案为:CA FD =;或者添加B E ∠=∠,∵BC EF =,12∠=∠,∴()ASA ABC DEF ≌△△,故答案为:B E ∠=∠;或者添加A D ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:A D ∠=∠;或者添加AB DE ∥,∵AB DE ∥,∴B E ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:AB DE ∥.【点睛】本题考查了全等三角形的判定,解答本题关键是掌握全等三角形的判定定理,本题答案不唯一.【答案】AB DC =【分析】添加条件AB DC =,利用SAS 证明ABC DCB △≌△即可.【详解】解:添加条件AB DC =,理由如下:在ABC 和DCB △中,AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCB △≌△, 故答案为:AB DC =.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS SAS AAS ASA HL ,,,,. 13.(2023秋·浙江湖州·八年级统考期末)如图,已知AC DB =,要使得ABC DCB ≅,根据“SSS”的判定方法,需要再添加的一个条件是_______.【答案】ABDC =【分析】要使ABC DCB ≅,由于BC 是公共边,若补充一组边相等,则可用SSS 判定其全等.【详解】解:添加AB DC =.在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩, ∴()ABC DCB SSS ≅△△, 故答案为:AB DC =.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .添加时注意:AAA 、SSA 不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键.14.(2022秋·浙江丽水·八年级统考期末)如图,在ABC 中,CD 是边AB 上的高,BE 平分ABC ∠,交CD 于点E ,6BC =,若BCE 的面积为9,则DE 的长为______.【答案】3【分析】过E 作EF BC ⊥于F ,根据角平分线性质求出EF DE =,根据三角形面积公式求出即可.【详解】解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,192BCE S BC EF =⋅=,1692EF ∴⨯⨯=,3EF DE ∴==,故答案为:3.【点睛】本题考查了角平分线性质的应用,能根据角平分线性质求出3EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等. 八年级期末)如图,在ABC 中, 【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==,则4CD AC AD =−=.【详解】解:∵AB 的垂直平分线交AB 于点E ,交AC 于点D ,∴2AD BD ==,∵6AC =,∴4CD AC AD =−=,故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键. 16.(2022秋·浙江温州·八年级校联考期中)如图,在ABC 中,DE 是AC 的中垂线,分别交AC ,AB 于点D ,E .已知BCE 的周长为9,4BC =,则AB 的长为______.【答案】5【分析】先利用三角形周长得到5CE BE +=,再根据线段垂直平分线的性质得到EC EA =,然后利用等线段代换得到AB 的长.【详解】解:∵BCE 的周长为9,9CE BE BC ∴++=,又4BC =,5CE BE ∴+=,又DE 是AC 的中垂线,EC EA ∴=,5AB AE BE CE BE ∴=+=+=;故答案为:5.【点睛】本题考查了垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.17.(2023秋·浙江杭州·八年级校考开学考试)如图,已知12∠=∠,要说明ABC BAD ≌,(1)若以“SAS ”为依据,则需添加一个条件是__________;(2)若以“ASA ”为依据,则需添加一个条件是__________.【答案】 BC AD = BAC ABD ∠=∠【分析】(1)根据SAS 可添加一组角相等,故可判定全等;(2)根据ASA 可添加一组角相等,故可判定全等;【详解】解:(1)已知一组角相等和一个公共边,以“SAS ”为依据,则需添加一组角,即BC AD =故答案为:BC AD =;(2)已知一组角相等,和一个公共边,以“ASA ”为依据,则需添加一组角,即BAC ABD ∠=∠. 故答案为:BAC ABD ∠=∠.【点睛】本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.添加时注意:AAA SSA 、不能判定两个三角形全等. 18.(2019秋·浙江嘉兴·八年级校考阶段练习)如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.。
八年级数学人教版(上册)第4课时用“HL”判定直角三角形全等

BD=AC, AB=BA, ∴Rt△DAB≌Rt△CBA(HL). ∴DA=CB.
3.如图,点 C,E,B,F 在同一条直线上,AB⊥CF 于点 B, DE⊥CF 于点 E,AC=DF,AB=DE.求证:AC∥DF.
证明:∵AB⊥CF,DE⊥CF, ∴∠ABC=∠DEF=90°. 在 Rt△ABC 和 Rt△DEF 中, AC=DF, AB=DE,
∴Rt△ABC≌Rt△DEF(HL). ∴∠C=∠F. ∴AC∥DF.
知识点 2 选择适当的方法判定两个直角三角形全等 4.下列条件中,不能判定两个直角三角形全等的是( C ) A.一个锐角和斜边对应相等 B.两条直角边对应相等 C.两个锐角对应相等 D.斜边和一条直角边对应相等
∴∠APE=∠BPF. ∴∠APB=∠APE+∠BPE=∠BPF+∠BPE=∠EPF=90°. ∴PA⊥PB.
(2)若点 A 的坐标为(8,0),则点 B 的坐标为 (0,-4) . (3)OA-OB 的值为 4 .
(4)如图 2,当点 B 在 y 轴正半轴上运动时,求 OA+OB 的值. 解:过点 P 作 PE⊥x 轴于点 E,PF⊥y 轴于点 F, 同(1)可得,Rt△APE≌Rt△BPF, ∴AE=BF. ∵AE=OA-OE=OA-2,BF=OF-OB=2-OB, ∴OA-2=2-OB. ∴OA+OB=4.
又∵∠BCD=∠EDC=90°,
∴∠BCD-∠ACF=∠EDC-∠ADF, 即∠BCA=∠EDA.
BC=ED, 在△ABC 和△AED 中,∠BCA=∠EDA,
AC=AD,
八年级数学下册 第1章 直角三角形 1.3 直角三角形全等的判定课件

1.3 直角三角形全等的判定(pàndìng)
第一页,共十四页。
第1章 直角三角形
1.3 直角三角形全等的判定
(pàndìng)
知识目标 目标突破
总结反思
第二页,共十四页。
1.3 直角三角形全等的判定(pàndìng)
知识(zhī shi)目标
1.在归纳全等三角形判定定理的基础上,结合勾股定理,推导出“HL” 判定定理. 2.根据题意,能综合应用(yìngyòng)直角三角形全等的判定知识作图.
【归纳总结】作直角三角形的原理及作图步骤
利用“HL”判定定理实现直角三角形的位置转移. 作图步骤:(1)作直角.采用作线段垂直平分线的方法或作一个角等 于已知角的方法;(2)作线段相等(xiāngděng).采用截取法,注意一般按
照从直角边到斜边的截取顺序进行.
第九页,共十四页。
1.3 直角三角形全等的判定
第五页,共十四页。
1.3 直角三角形全等的判定(pàndìng)
【归纳总结】 “HL”判定定理(dìnglǐ)的适用条件
(1)在两个直角三角形中; (2)有一对直角边对应相等;
(3)两条斜边对应相等.
第六页,共十四页。
1.3 直角三角形全等的判定(pàndìng)
目标(mùbiāo)二 会作直角三角形
△A′B′C′是否全等?如果全等,请给出证明;如果不全等,请举出反
例.张翔同学的解答过程如下:
第十一页,共十四页。
1.3 直角三角形全等的判定(pàndìng)
解:这两个三角形全等.证明如下:
如图1-3-3,在Rt△ABD和Rt△A′B′D′中,
∵AB=A′B′,AD=A′D′, ∴Rt△ABD≌Rt△A′B′D′,∴BD=B′D′. 同理可证DC=D′C′,∴BC=B′C′.
八年级下册数学1.3-直角三角形全等的判定

(2)请将所画的三角形剪下,与同桌相互 对比,是否能重合?
试一试
请写出证明过程
结论:
有斜边和一条直角边对边和一条直角边对应相等的两个直角三角形全等.
B
∵∠C=∠C′=90°
∴在Rt△ABC和Rt△ABC 中 A AB=A B
C B′
BC=BC
C′
B′ C′ (HL) A ′ ∴Rt△ABC≌ Rt△A′
例题1 :如图所示,BD,CE分别是△ABC的高,且BE=CD.
求证: Rt△BEC≌Rt△CDB
A
证明:BD,CE是△ABC的高
BEC CDB 90 在Rt△BEC和Rt△CDB中,
BC CB BE CD
复习提问
你知道的三角形全等判定方法有哪些?
• • • •
1.边边边 2.两边夹角 3.两角夹边 4.两角及对边
简称 简称 简称 简称
“SSS” “SAS” “ASA” “AAS”
引入提问
在直角三角形中,还有别的证 明全等的定理吗?
做一做
(1)请画一个Rt△ABC,满足∠ACB=90°, AB=10cm,AC=6cm.
灵活运用各种方法证明直角三角形全等
课本21面 习题1.3 A组 第1题 第2题
判断: 满足下列条件的两个三角形是否全等?为什么?
4.有两边对应相等的两个直角三角形全等.
情况1:全等 (SAS)
情况2:全等 ( HL)
课堂总结
一般三角 形全等的 判定
“SAS” “ ASA ” “ AAS ” “ SSS ”
直角三角 形全等的 判定
“ SAS ” “ ASA ” “ AAS ” “ SSS ” “ HL ”
八年级下册数学3直角三角形全等的判定

直角三角形全等的判定1. 有斜边和一条直角边对应相等的两个直角三角形全等,记作“HL ”. 另外还有SAS,ASA,AAS,SSS 共五种。
2. 判断满足下列条件的两个直角三角形是否全等? ①一个锐角和这个锐角的对边对应相等:______________ ②一个锐角及和这个锐角相邻的一直角边对应相等:__________ ③一个锐角与一斜边对应相等:_________________ ④两直角边对应相等:______________________ ⑤两边相等:_____________________ ⑥两锐角对应相等:______________ ⑦一锐角和一边对应相等:_______________3.BC EF AC DF ABC DEF ∠∠如图,有两个长度相同的滑梯、,左边滑梯的高度与右边滑梯水平方向的长度相等,两个滑梯的倾斜角和的大小有怎样的关系?4.,,,AC CD BD CD AB EF AB E CD F AC FD ABF ⊥⊥=∆如图,,,的垂直平分线交于交于且求证:是等腰直角三角形。
5.,,,AB AE BC ED B E AF CD F CF DF ==∠=∠⊥=如图,,为垂足,求证:。
BE6.,,,,.ABC AD BC CE AB D E AD CE H AEH CEB ∆⊥⊥∆∆如图,在中,垂足分别为、、交于点请添加一个条件:使≌7.,,,,,,,,M A N ABC AB AC BM MN CN MN M N BM AN MN BM CN ∆=⊥⊥=如图,点在同一条直线上,为等腰三角形,垂足分别为、且试求与之间的数量关系。
8.,,,,AB AC BD AC D CD AB E BD CE F BAF CAF =⊥⊥∠∠如图,于点于点与相交于点与相等吗?9.,15,10,,A B km C D DA AB A CB AB B DA km CB km AB E C D E E A ⊥⊥==如图,铁路上、两站(视为直线上两点)相距25,、为铁路同旁的两个村庄,于点于点,现在要在铁路上建一个土特产产品收购站使、两村庄到站的距离相等,求站应建在离站多远处,并说明理由。
初二数学知识点之全等三角形五大判定方法

初二数学知识点之全等三角形五大判定方法一、边边边(SSS)学习全等三角形判定法则时,第一条就是边边边。
内容:它们的夹角分别相等的两个三角形全等。
理解:若给出三条线段的长度(满足三角形三边关系),即可确定出的三角形形状,大小。
若给出三条线段长度AB=c,BC=a,AC=b,确定过程如下:①先确定一边AB;②分别以AB为圆心,分别做半径为b,a长的圆,交于C点;③最后连接AC,BC。
这样三角形的大小,形状就都被确定出来了。
二、边角边(SAS)内容:两边和它们的夹角分别相等的两个三角形全等。
理解:若确定两条公共端点线段的长度,及它们的夹角,即可确定出的三角形形状,大小。
若给出AB=c BC=a ∠B=α,确定过程如下:①画∠EAD=α;②在射线AE上截取AC=c,在射线AD上截取AB=c;③连接BC。
这样,三角形的.大小形状同样被确定了。
三、角边角(ASA)内容:两角和他们的夹边分别相等的两个三角形全等。
理解:若给出三角形的两个角的大小和它们的夹边的长度了,即可确定出的三角形形状,大小。
若有AB=c,∠CAB=α,∠CBA=β,确定过程如下:①先确定一边AB=c;②在AB同旁画∠DAB=α,∠EBA=β,AD,BE交于点C。
这样,三角形的大小形状同样被确定了。
四、角角边(AAS)内容:两边分别相等且其中一组等角的对边相等的两个三角形全等。
理解:若给出三角形的两个角的大小和其中一个角对边的长度了,即可确定出的三角形形状,大小。
若有AB=c,∠CAB=α,∠ACB=β,确定过程如下:由三角形的内角和为180度可得出剩下一角∠CBA的度数,这样,利用角边角的思路即可确定三角形形状大小。
相关定理:三角形内角和为180度五、斜边,直角边(HL)内容:斜边和一条直角边分别相等的两个直角三角形全等。
(HL)理解:若确定一个三角形为直角三角形,同时得到其一个直角边和斜边的长度,即可确定出三角形的形状大小。
若确定三角形为直角三角形,还得到其一直角边和斜边,则可勾股定理得出剩下一边,再通过SSS或SAS即可确定三角形形状大小。
人教版八年级数学上册三角形全等的判定第四课时直角三角形的全等判定

动笔练一练
解:
BD=CD,理由如下: 显然旗杆垂直于地面,即: ∠ADB=∠ADC=90° 在Rt△ADB和Rt△ADC中:
AB=AC AC=AC(公共边) ∴Rt△ADB ≌Rt△ADC(HL) ∴BD=CD
动笔练一练
• 如图,AB=CD,且 AE⊥BC,DF⊥BC, 垂足分别为E,F, CE=BF。求证: AE=DF。
• 直角三角形是特殊的三角形,所以直角三 角形有特殊的判定方法——HL。
• 但是,直角三角形也有一般三角形判定全 等的方法:SAS、ASA、AAS、SSS。
直角三角形的全等判定
A
• 如右图,AC⊥BC于
C,DF⊥EF于F。
B
C
• 若∠A=∠D,AB=DE
D • 可以根据 AAS 定
理判定
△ABC≌△DEF。
E
F
直角三角形的全等判定
A
• 如右图,AC⊥BC于
C,DF⊥EF于F。
B
C
• 若∠A=∠D,AC=DF
D • 可以根据 ASA 定
理判定
△ABC≌△DEF。
E
F
直角三角形的全等判定
A
• 如右图,AC⊥BC于
C,DF⊥EF于F。
B
C
• 若BC=EF,AC=DF
D • 可以根据 SAS 定
理判定
△ABC≌△DEF。
数学语言 表示和证明
尺规作 定三角形
直角三角形的全等判定
动笔练一练
• 如图,∠C,∠D是直 角,为了用“HL”判 定△ABC≌△ABD,
应该补充条件AC=AD 。 或BC=BD
动笔练一练
• 如图,两根长度为 10m的绳子,一端系 在旗杆上,另一端分 别固定在地面的两根 铆钉上,两根铆钉距 离旗杆底部距离相等 吗?给出你的理由。
初二数学上册:三角形全等的判定知识点

初二数学上册:三角形全等的判定知识点01三角形全等的判定1.三组对应边分别相等的两个三角形全等(SSS)。
2.有两边及其夹角对应相等的两个三角形全等(SAS)。
3.有两角及其夹边对应相等的两个三角形全等(ASA)。
4.有两角及一角的对边对应相等的两个三角形全等(AAS)。
5.直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL)。
02全等三角形的性质①全等三角形的对应边相等;全等三角形的对应角相等。
②全等三角形的周长、面积相等。
③全等三角形的对应边上的高对应相等。
④全等三角形的对应角的角平分线相等。
⑤全等三角形的对应边上的中线相等。
03找全等三角形的方法(1)可以从结论出发,看要证明相等的两条线段(或角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形相等;(3)从条件和结论综合考虑,看它们能一同确定哪两个三角形全等;(4)若上述方法均不行,可考虑添加辅助线,构造全等三角形。
三角形全等的证明中包含两个要素:边和角。
缺个角的条件:缺条边的条件:04构造辅助线的常用方法1.关于角平分线的辅助线当题目的条件中出现角平分线时,要想到根据角平分线的性质构造辅助线。
角平分线具有两条性质:①角平分线具有对称性;②角平分线上的点到角两边的距离相等。
关于角平分线常用的辅助线方法:(1)截取构全等如下左图所示,OC是∠AOB的角平分线,D为OC上一点,F为OB上一点,若在OA上取一点E,使得OE=OF,并连接DE,则有△OED≌△OFD,从而为我们证明线段、角相等创造了条件。
例:如上右图所示,AB//CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD。
提示:在BC上取一点F使得BF=BA,连结EF。
(2)角分线上点向角两边作垂线构全等利用角平分线上的点到两边距离相等的性质来证明问题。
如下左图所示,过∠AOB的平分线OC上一点D向角两边OA、OB作垂线,垂足为E、F,连接DE、DF。
第14课直角三角形全等的判定(学生版)八年级数学上册《考点题型技巧》精讲与精练高分突破(浙教版)

第14课直角三角形全等的判定目标导航学习目标1.掌握两个直角三角形全等的判定定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.3.探索并证明定理:角的内部,到角两边距离相等的点,在这个角的平分线上.知识精讲知识点01 直角三角形全等的判定1.直角三角形全等的判定定理:斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)2.直角三角形全等的判定方法:SSS、SAS、ASA、AAS、HL知识点02 角平分线性质定理的逆定理角平分线的性质定理:角的内部,到角两边距离相等的点,在这个角的平分线上能力拓展考点01 直角三角形全等的判定【典例1】如图,在△ABC中,D是边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.求证:AB=AC.【即学即练1】如图所示,在△ABC中,CB⊥AB,∠BAC=45°,F是AB延长线上一点,点A在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF.考点02 角平分线性质定理的逆定理【典例2】如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=BC.求证:AB平分∠EAD.【即学即练2】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,(1)求证:AD平分∠BAC;(2)已知AC=16,DE=4,求△ADC的面积.分层提分题组A 基础过关练1.如图,BE⊥AC于点E,CF⊥AB于点F,若BE=CF,则Rt△BCF≌Rt△CBE的理由是()A.AAS B.HL C.SAS D.ASA2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是()A.AC=AD B.AC=BC C.∠ABC=∠ABD D.AD=BD3.如图,已知AB=DC,BE⊥AD于点E,CF⊥AD于点F,有下列条件,其中,选择一个就可以判断Rt △ABE≌Rt△DCF的是()①∠B=∠C ②AB∥CD ③BE=CF ④AF=DEA.①②B.①②③C.①③④D.①②③④4.如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD =9cm,则BE的长是()A.6cm cm C.3cm cm5.在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,有如下几个条件:①AC=A'C',∠A=∠A';②AC=A'C',AB=A'B';③AC=A'C',BC=B'C';④AB=A'B',∠A=∠A'.其中,能判定Rt△ABC≌Rt△A'B'C'“的条件的个数为()A.1 B.2 C.3 D.46.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,为了使Rt△ABC≌Rt△DCB,需添加的条件是(不添加字母和辅助线).7.如图,△ABC中,∠C=90°,AD平分△BAC交BC于点D,BE⊥AD交AD的延长线于点E,DF⊥AB 交AB于点F.若BF=BE,AC=4,DF=3.则AE的长为.8.如图,在△ABC中,D是BC上一点,DE、DF分别是△ABD和△ACD的高,且DE=DF.(1)求证:AD平分∠BAC;(2)若AB+AC=10,S△ABC=15,求DE长.9.已知:如图,在直角△ABC中,∠C=90°,点D、F分别在边CB和AC上,DE⊥AB,垂足为E,且BD=DF,BE=CF.(1)求证:AD平分∠BAC;(2)当∠CAB=40°时,求∠FDC的度数.题组B 能力提升练10.下列说法正确的有()①两个锐角分别相等的两个直角三角形全等;②一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等.A.1 B.2 C.3 D.411.如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有()A.1个B.2个C.3个D.4个12.如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE =4,则CH的长是()A.1 B.2 C.3 D.413.如图,P是∠AOB的平分线OC上一点(不与O重合),过P分别向角的两边作垂线PD、PE,垂足是D、E,连接DE,那么图中全等的直角三角形共有()A.3对B.2对C.1对D.没有14.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=.15.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,EF=8,BG=4,DH=6,计算图中阴影部分的面积S=.16.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.17.如图所示,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)求证:AM平分∠BAD.(2)写出DM与AM的位置关系,并说明理由.(3)线段CD,AB,AD间有怎样的数量关系?18.如图,在Rt△ABC和Rt△ADE中,∠B=∠D=90°,AC=AE,BC=DE,延长BC,DE交于点M.(1)求证:点A在∠M的平分线上;(2)若AC∥DM,AB=12,BM=18,求BC的长.题组C 培优拔尖练19.两个直角三角形中,如果有一条直角边对应相等.则:①若斜边上的高对应相等.那么这两个直角三角形全等;②若直角的平分线相等,那么这两个直角三角形全等;③若斜边上的中线对应相等,那么这两个直角三角形全等;④两个直角三角形都有一个锐角是30°,那么这两个直角三角形全等.其中正确命题的个数有()A.1个B.2个C.3个D.4个20.如图,△BDC为等腰直角三角形,延长BD至A,连接AC,作∠ABC的角平分线BE交DC于F,且BE⊥AC于E.若AE=12,△ABC的面积为360,则EF的长度为()A.6 B.7 C.8 D.921.如图,已知点C是∠F AE的平分线AC上一点,CE⊥AE,CF⊥AF,点E,F为垂足,点B在AE的延长线上,点D在AF上,若AB=20,AD=8,BC=DC,则AE的长为()A.14 B.15 C.16 D.1722.已知∠ACB=90°,AC=BC,AD⊥NM,BE⊥NM,垂足分别为点D,E.(1)如图①,求证:AD=BE+DE;(2)如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD,BE,DE之间的数量关系,并说明理由.23.如图,在△ABC中,过点B作BD⊥CA交CA的延长线于点D,过点C作CE⊥BA交BA的延长线于点E,延长BD,CE相交于点F,BF=AC=.(1)求证:△BEF≌△CEA;(2)若CE=2,求BD的长.24.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.(1)求证:BM=CN;(2)若AB=8,AC=4,求BM的长.25.(1)感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB,DC数量关系为:.(2)探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,(1)中的结论是否成立?请作出判断并给予证明.(3)应用:如图3,在四边形ABDC中,DB=DC,∠ABD+∠ACD=180°,∠ABD<90°,DE⊥AB 于点E,试判断AB,AC,BE的数量关系,并说明理由.。
人教版八年级数学上册第12章第5课时 三角形全等的判定——HL

小结:在一线三直角模型中,推出对应角相等,进而判定全 等,得到相关线段相等,最后判断数量关系.
返回
数学
★12.(1)如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE, 试说明 BC⊥CE 的理由; (2)如图(2),若△ABC 向右平移,使得点 C 移到点 D,AB⊥ AD,ED⊥AD,AB=CD,AD=DE,探索 BD⊥CE 的结论是 否成立,并说明理由.
返回
数学
10.如图,AD=BC,∠C=∠D=90°,下列结论不成立的是 ( C) A.∠DAE=∠CBE B.CE=DE C.△DAE 与△CBE 不一定全等 D.∠1=∠2
返回
数学
7.【例 3】如图,BD,CE 分别是△ABC 的高,且 BE=CD, 求证:Rt△BEC≌Rt△CDB. 证明:∵BD,CE 分别是△ABC 的高,
第十二章 全等三角形
第5课时 三角形全等的判定(4)——HL
数学
目录
01 学习目标 02 知识要点 03 对点训练 04 精典范例 05 变式练习
数学
学习目标
1.掌握用 HL 证明两个三角形全等. 2.能灵活运用全等三角形的性质解决线段或角 相等的问题. 3.通过画、量、观察、比较和猜想等过程,探 索、归纳、证明两个三角形全等的条件,提高运 用知识的能力.
∴∠BEC=∠CDB=90°,
在 Rt△BEC 和 Rt△CDB 中,BBCE==CCBD ,
∴Rt△BEC≌Rt△CDB(HL).
小结:根据高的定义求出∠BEC= ∠CDB=90°,再根据 HL 证明.
返回
数学
11.如图,在△ABC 中,AB=CB,∠ABC=90°,F 为 AB 延 长线上一点,点 E 在 BC 上,且 AE=CF.求证:Rt△ABE≌ Rt△CBF.
初二数学全等三角形判断方法

初二数学全等三角形判断方法全等三角形作为初中数学中的一个重要概念,是指两个或多个三角形的所有对应角相等,对应边也相等。
在解决实际问题中,判断三角形是否全等非常关键。
本文将介绍初二数学中常用的全等三角形判断方法。
1. SSS 判定法(Side-Side-Side)SSS 判定法通过比较三角形的三边长度来判断是否全等。
当两个三角形的三边长度分别相等时,我们可以得出它们全等的结论。
这个方法适用于已知三角形的三边长度的情况。
举例说明:已知三角形 ABC 和三角形 PQR,若 AB=PQ,BC=QR,AC=PR,则可以推断出三角形 ABC 和三角形 PQR 全等。
2. SAS 判定法(Side-Angle-Side)SAS 判定法通过比较三角形的两边长度和夹角的度数来判断是否全等。
当两个三角形的两边长度分别相等,并且夹角的度数也相等时,我们可以得出它们全等的结论。
这个方法适用于已知三角形的两边和夹角度数的情况。
举例说明:已知三角形 ABC 和三角形 PQR,若 AB=PQ,∠BCA=∠RPQ,AC=PR,则可以推断出三角形 ABC 和三角形 PQR 全等。
3. ASA 判定法(Angle-Side-Angle)ASA 判定法通过比较三角形的两角度数和一边的长度来判断是否全等。
当两个三角形的两角度数分别相等,并且一边的长度也相等时,我们可以得出它们全等的结论。
这个方法适用于已知三角形的两角和一边的情况。
举例说明:已知三角形 ABC 和三角形 PQR,若∠ABC=∠PQR,BC=QR,∠ACB=∠PQR,则可以推断出三角形 ABC 和三角形 PQR 全等。
4. RHS 判定法(Right Angle-Hypotenuse-Side)RHS 判定法主要用于判断直角三角形的全等关系。
当两个直角三角形的直角边和斜边分别相等时,我们可以得出它们全等的结论。
举例说明:已知直角三角形 ABC 和直角三角形 PQR,若 AB=PQ,BC=QR,∠ABC=∠PQR=90°,则可以推断出三角形 ABC 和三角形 PQR 全等。
八年级数学 直角三角形全等的判定

八年级数学直角三角形全等的判定〖教学目标〗◆1、探索两个直角三角形全等的条件.◆2、掌握两个直角三角形全等的条件(HL).◆3、了解角平分线的性质:角的内部,到角两边距离相等的点,在角平分线上,及其简单应用.〖教学重点与难点〗◆教学重点:直角三角形全等的判定的方法“HL”.◆教学难点:直角三角形判定方法的说理过程.〖教学过程〗一、创设情境,引入新课:教师演示一等腰三角形,沿底边上高裁剪,让同学们观察两个三角形是否全等?二、合作学习:(1)回顾:判定两个直角三角形全等已经有哪些方法?(2)有斜边和一条直角边对应相等的两个三角形全等吗?如何会全等,教师可启发引导学生一起利用画图,叠合方法探索说明两个直角三角形全等的判定方法,可充分让学生想象。
不限定方法。
教师归纳出方法后,要学生注意两点:<1>“HL”是仅适用于Rt△的特殊方法。
<2> 应用“HL”时,虽只有两个条件,但必须先有两个Rt△的条件(3)教师引导、学生练习P47三、应用新知,巩固概念例题讲评例:已知:P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE,则点P在∠AOB的平分线上,请说明理由。
分析:引导猜想可能存在的Rt△;构造两个全等的Rt△;要说明P在∠AOB的平分线上,只要说明∠DOP=∠EOP小结:角平分线的又一个性质:(判定一个点是否在一个角的平分线上的方法)角的内部,到角的两边距离相等的点,在这个角的平分线上。
四、学生练习,巩固提高练一练:P48 1. 2. P49 3五、小结回顾,反思提高(1)本节内容学的是什么?你认为学习本节内容应注意些什么?(2)学习本节内容你有哪些体会?(3)你认为有没有其他的方法可以证明直角三角形全等(勾股定理)(4)你现在知道的有关角平分线的知识有哪些?六、布置作业:3.1 认识直棱柱〖设计思路〗人们生活的空间存在着大量的图形,图形是人们理解自然界和社会现象的绝妙工具,立体图形的学习将使学生能更好地适应生活的空间,同时也给他们带来无穷的直觉源泉。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
药物干法粉碎前应充分干燥,一般要求水分含量小于A.12%B.9%C.7%D.5%E.3% 根据《中华人民共和国行政许可法》规定,行政机关采用等其他行政管理方式能够解决的,可以不设行政许可。 除以下哪项外均为骨质疏松的病因A.老年人B.绝经后妇女C.骨关节退行性变D.营养不良E.内分泌障碍 少尿是指24小时尿量少于A.800mlB.600mlC.400mlD.200mlE.100ml 是口头创作和流传的,则是书面形式创作和流传的。 关于诉讼,下例说法正确的是。A.当合同中约定通过法院起诉解决争议时,任何一方均可以向有管辖权的人民法院提出诉讼B.合同约定采用仲裁解决争议的,但争议发生后双方同意通过诉讼解决争议时,法院不予受理C.当事人对一审判决不服时,可以在规定的时间内向上一级人民法院提起上 古埃及宫廷学校常用的教育方法是。A.惩戒B.鞭打C.模仿D.学徒式训练 水土保持方案编制资格证书甲级资质由审批和核发。A.国务院B.省(自治区、直辖市)水行政主管部门C.县级水行政主管部门D.水利部 对于过敏性紫癜肾炎的治疗,下列哪种说法不正确A.有过敏症状者,可予抗过敏治疗B.停用一切可疑的过敏药物及食物,避免接触可疑过敏原C.即使肾脏病变轻微,也需予糖皮质激素联合细胞毒药物治疗D.达到新月体肾炎诊断标准者,予强化免疫抑制疗法E.终末期肾衰者可予透析及肾移植治疗 产褥感染确定病原体的方法不宜A.分泌物涂片B.病原体培养C.检查病原体抗原D.检测特异性抗体E.诊刮取内膜病检 小建中汤是由桂枝汤如何化裁而来A.倍用芍药加饴糖B.去芍药加饴糖C.加饴糖D.倍甘草加饴糖E.倍用甘草芍药 乳腺癌常用显像剂为。A.67GaB.111In-WBCC.201TlD.99Tcm-MIBIE.99Tcm-DMSA 介导适应性体液免疫应答的细胞是A.单核细胞B.巨噬细胞C.中性粒细胞D.B淋巴细胞E.自然杀伤细胞 交通安全设施除里程标、百米标和公路界碑以外,还包括下列方面。A.交通标志、交通标线B.防撞设施、隔离栅C.可变情报板D.桥梁防抛网E.视线诱导设施、防眩设施 电缆敷设前应做好哪些准备工作? 关于“獭尾肝”,下列描述哪些正确()A.肝左叶增大,与脾脏相连B.可见于肝肿瘤时C.可见于正常变异D.可见于肝叶比例失调时E.肝尾叶增大,与胰腺相连 流脑的主要临床特点是A.高热,头痛,呕吐,昏迷,脑膜刺激征B.高热,头痛,抽搐,昏迷,脑膜刺激征C.高热,头痛,休克,昏迷,脑膜刺激征D.高热,头痛,皮肤瘀点、瘀斑,脑膜刺激征E.高热,头痛,呼吸衰竭,脑膜刺激征 下列有关睡眠的定义哪一项正确()A.睡眠占人的一生约1/3的时间B.睡眠是最自然的休息方式C.睡眠是一种知觉的特殊状态D.睡眠中人对特殊刺激会产生选择性的知觉E.睡眠是周期发生的知觉的特殊状态 以经营方式租入的固定资产改良支出属于。A、修理费用B、固定资产C、长期待摊费用D、流动性资产 加工承揽合同 自然人的民事权利能力是指法律赋予自然人享有民事权利和承担民事义务的。A.资格B.条件C.资质D.职能 物业管理是指业主通过选聘物业管理企业,由业主和物业管理企业按照的约定,对物业进行管理服务的活动。A.物业服务合同B.建筑工程合同C.购房合同D.租赁合同 商业银行风险管理体系一般包括以下四个基本要素:一是董事会和高管层的有效监控,二是,三是有效的风险识别、计量、监测和控制程序,四是。 V形河谷多选用拱坝。A.变曲率B.单曲C.单曲或双曲D.双曲 水泥砂浆主要由组成。A、水泥B、石灰膏C、砂子D、水 APL抗体可分为A.IgG型B.IgA型C.IgM型D.IgD型E.IgE型 引起锻件晶粒粗大的主要原因之一是。 [单选,共用题干题]以GJB冠名的标准属于(1)。PSD、PAD等程序构造的图形表示属于(2)。空白(1)处应选择A.国际标准B.国家标准C.行业标准D.企业规范 植物抗虫性包括、和耐害性。 提出人是“社会人”,不仅仅是“经济人”的理论是A.泰勒的科学管理理论B.法约尔的管理过程理论C.麦戈雷戈德人性理论D.梅奥的人际关系学说E.马斯洛的人类需要层次理论 主要能经完整的皮肤吸收而引起中毒的毒物是()A.铅、氰化氢、硫化氢B.氰化钠,有机磷C.砷、苯胺D.镉,铝,硝基苯E.以上都不是 婴儿肠套叠诊断中最不应忽视的体征是。A.呕吐B.阵发性哭吵C.腹部轻压痛D.直肠指检有果酱色黏液血便E.发热 土地预告登记后,申请人在自能够进行土地登记之日起内未申请土地登记,预告登记失效。A.十日B.十五日C.一个月D.三个月 是在一定范围内作为其他标准的基础并普遍适用,具有广泛指导意义的标准。A.产品标准B.方法标准C.基础标准D.服务标准 钢轨验收时如存在不允许复验。A.灰斑B.缩孔C.加渣D.白点
ቤተ መጻሕፍቲ ባይዱ
