直角三角形全等的判定(公开课)
全等三角形判定HL定理公开课获奖课件省赛课一等奖课件

中,AC⊥BC, AD⊥BD,
垂足分别为C,D,AD=BC,求证:
△ABC≌△BAD.
D
C
A
B
例2. 如图,AC=AD,∠C,∠D 是直角,将上述条件标注在图中, 你能阐明BC与BD相等吗?
C A
解:在Rt△ACB和 Rt△ADB 中,有
AB=AB,
B AC=AD.
∴ Rt△ACB≌Rt△ADB (HL).
• 19.2.5 三角形全等旳鉴定(HL)
复习提问
证明一般两个三角 形全等有哪些措施?
1.在两个三角形中,假如有 三条边相应相等,那么这两 个三角形全等(简记S.S.S)
2.在两个三角形中,假如 有两条边及它们旳夹角相 应相等,那么这两个三角 形全等(简记为S.A.S)
3.在两个三角形中,假如 有两个角及它们旳夹边 相应相等,那么这两个三 角形全等(简记为A.S.A)
直角三角形全等旳辨认
H.L
灵活利用多种措施证明直角三角形全等
再见
D
∴BC=BD
(全等三角形相应边相等).
练习
1. 如图∠C= ∠D=90° ,要证 明△ACB≌ △BDA ,至少再补 充几种条件,应补充什么条件? 把它们分别写出来。
C
D
A
B
2.如图 在△ABC中,已知BD⊥AC, CE ⊥AB,BD=CE。阐明△EBC≌ △DCB旳理由。
A
E
D
B
C
小结
一般三角形全等旳辨认
4.在两个三角形中,假如有 两个角及其中一种角旳对边 相应相等,那么这两个三角 形全等(简记为A.A.S)
想一想
对于一般旳三角形“S.S.A” 可不能够证明三角形全等?
袁轩公开课直角三角形全等的判定教学设计

2015年10月30日公开课教学设计直角三角形全等的判定濮阳县文留镇中心校袁轩学习目标1、经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;2、掌握直角三角形全等的条件,并能运用其解决一些实际问题。
3、在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。
学习重点运用直角三角形全等的条件解决一些实际问题。
学习难点熟练运用直角三角形全等的条件解决一些实际问题。
学习过程Ⅰ.提出问题,复习旧知1、判定两个三角形全等的方法:、、、。
2、如图,Rt△ABC中,直角边是、,斜边是。
3、如图,AB⊥BE于C,DE⊥BE于E,(1)若∠A=∠D,AB=DE,则△ABC与△DEF(填“全等”或“不全等” ),根据(用简写法)(2)若∠A=∠D,BC=EF,则△ABC与△DEF(填“全等”或“不全等” ),根据(用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF(填“全等”或“不全等” ),根据(用简写法)(4)若AB=DE,BC=EF,AC=DF则△ABC与△DEF(填“全等”或“不全等” ),根据(用简写法)Ⅱ.导入新课(一)探索练习:(动手操作画一画)任意画一个Rt△ACB ,使∠C﹦90°,再画一个 Rt△A′C′B′使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB(1):你能试着画出来吗?与桌友交流一下。
按步骤作图:①画∠MC′N=90°②在射线C′M上取B′C′=BC③以B′为圆心,AB为半径画弧,交射线C′N于点A′④连接A′B′(2):把画好的Rt△A′C′B′剪下来放到Rt△ACB上,它们全等吗?是否重合?你能发现什么规律?与同桌交流一下。
(3)、从中你发现了什么?斜边与一直角边对应相等的两个直角三角形全等.(HL)(二)巩固练习:1.如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC(填“全等”或“不全等” )根据(用简写法)2. 如图,CE⊥AB,DF⊥AB,垂足分别为E 、F ,(1)若AC//DB ,且AC=DB ,则△ACE≌△BDF,根据(2)若AC//DB ,且AE=BF ,则△ACE≌△BDF,根据(3)若AE=BF ,且CE=DF ,则△ACE≌△BDF,根据(4)若AC=BD ,AE=BF ,CE=DF 。
《直角三角形全等的判定》 教案 (公开课获奖)2022浙教版

直角三角形全等的判定〔HL〕一.教学目标1.知识与技能1.1掌握直角三角形的一条直角边和斜边,作直角三角形的方法。
1.2掌握直角三角形全等的判定方法“HL〞。
1.3.能用全等直角三角形的判定方法解决简单问题。
1.4 运用多种方法判定三角形全等、解决简单问题。
2.过程与方法经历探究全等直角三角形判定方法“HL〞的过程,学会用操作确认、归纳发现问题结论的方法。
运用多种方法判定三角形全等、解决简单问题3、情感、态度与价值观3.1.通过操作确认、归纳发现结论,感知实验操作在发现问题结论中的重要作用。
3.2.运用多种方法证明三角形全等、发散思维,掌握构造三角形的技巧、舔辅助线。
学情介绍:这节课是在学生掌握了一般三角形全等的判定方法的根底上,探索直角三角形全等的特殊方法。
由于学生已具备了一定的学习经验,让学生自主探究直角三角形全等的判定方法,符合学生的认知过程。
帮助学生发散思维,稳固本章节的内容。
内容分析:教材首先提出了已经学习的四种判定在角形全等的方法外,对于直角三角形是否还有其他的方法判定两个直角三角形全等问题,然后通过操作发现判定直角三角形全等的另外一种特殊方法“HL〞,最后通过例题和练习加以稳固这种判定方法。
教学重点:直角三角形全等的判定方法。
教学难点:运用全等直角三角形的判定方法解决问题、运用三角形全等的方法二.教学过程:直角三角形全等的判定、情境探究,引入新课. 本单元学习判断三角形全等的方法:1〕SSS 2) SAS 3) ASA 4) AAS思考:对于直角三角形,除了直角相等之外,还要满足什么样的条件,这两个直角三角形全等?〔预设答复:一边和一锐角对应相等或者两条直角边对应相等〕提问:如果满足斜边和一直角边对应相等,这两个三角形全等吗?、动手实践,探索规律活动一:作图任意画一个,使得,一条直角边**C B BC =,斜边**B A AB =。
再把画好的***C B RtA 剪下,放到RtABC 上,两个直角三角形之间有什么样的关系呢?〔形状、大小方面〕让同学展示作品,并给出画图步骤:其他同学是不是这样字画的,你们能得出什么样的结论呢?〔预设答复:两三角形全等〕 斜边、直角边公理:有斜边和一条直角边对应相等的两个直角三角形全等。
《直角三角形全等判定(HL)》教案(公开课)2022年人教版精品

直角三角形全等判定总课题全等三角形总课时数第 14 课时课题直角三角形全等判定〔HL〕主备人课型新授时间教学目标1.在操作、比较中理解直角三角形全等的过程,并能用于解决实际问题.2.经历探索直角三角形全等判定的过程,掌握数学方法,提高合情推理的能力. 3.培养几何推理意识,激发学生求知欲,感悟几何思维的内涵.教学重点理解利用“斜边、直角边〞来判定直角三角形全等的方法.教学难点培养有条理的思考能力,正确使用“综合法〞表达.教学过程教学内容一、回忆交流【问题探究】图1是两个直角三角形,除了直角相等的条件,还要满足几个条件,•这两个直角三角形才能全等?【教师活动】操作投影仪,提出“问题探究〞,组织学生讨论.【学生活动】小组讨论,发表意见:“由三角形全等条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.〞【媒体使用】投影显示“问题探究〞.【教学形式】分四人小组,合作、讨论.【情境导入】如图2所示.舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.〔1〕你能帮他想个方法吗?〔2〕如果他只带了一个卷尺,能完成这个任务吗?工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的〞,你相信他的结论吗?【思路点拨】〔1〕学生可以答复去量斜边和一个锐角,或直角边和一个锐角,•但对问题〔2〕学生难以答复.此时,•教师可以引导学生对工作人员提出的方法及结论进行思考,并验证它们的方法,从而展开对直角三角形特殊条件的探索.【教师活动】操作投影仪,提出问题,引导学生思考、验证.【学生活动】思考问题,探究原理.做一做如课本图11.2─11:任意画出一个Rt △ABC ,使∠C=90°,再画一个Rt•△A ′B ′C ′,使B ′C ′=BC ,A ′B ′=AB ,把画好的Rt △A ′B ′C ′剪下,放到Rt △ABC 上,•它们全等吗?【学生活动】画图分析,寻找规律.如下:规律:斜边和一条直角边对应相等的两个直角三角形全等〔简写成“斜边、直角边〞或“HL 〞〕.画一个Rt △A ′B ′C ′,使B ′C ′=BC,AB=AB;1. 画∠MC ′N=90°。
直角三角形全等的判定【公开课教案】

第2课时直角三角形全等的判定1.理解并掌握三角形全等的判定方法——“斜边、直角边”;(重点)2.经历探究“斜边、直角边”判定方法的过程,能运用“斜边、直角边”判定方法解决有关问题.(难点)一、情境导入舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.(1)你能帮他想个办法吗?(2)如果他只带了一个卷尺,能完成这个任务吗?工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?二、合作探究探究点:直角三角形全等的判定【类型一】应用“HL”证明三角形全等如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.解析:由题意可得△ABF与△DCE都为直角三角形,由BE=CF可得BF=CE,然后运用“HL”即可判定Rt△ABF与Rt△DCE全等.证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE.∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形.在Rt△ABF和Rt△DCE中,∵⎩⎪⎨⎪⎧BF=CE,AB=CD,∴Rt△ABF≌Rt△DCE(HL).方法总结:利用“HL”判定三角形全等,首先要判定这两个三角形是直角三角形,然后找出对应的斜边和直角边相等即可.【类型二】利用“HL”证明线段相等如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.解析:根据“HL”证Rt△ADC≌Rt△AFE,得CD=EF,再根据“HL”证Rt△ABD ≌Rt△ABF,得BD=BF,最后证明BC=BE.证明:∵AD,AF分别是两个钝角△ABC 和△ABE的高,且AD=AF,AC=AE,∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.∵AD =AF,AB=AB,∴Rt△ABD≌Rt△ABF(HL).∴BD=BF.∴BD-CD=BF-EF.即BC=BE.方法总结:证明线段相等可通过证明三角形全等解决.直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.【类型三】利用“HL”证明角相等如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.解析:要证角相等,可先证明全等.即证Rt △ABC ≌Rt △ADC ,进而得出角相等.证明:∵AB ⊥BC ,AD ⊥DC ,∴∠B =∠D =90°,∴△ABC 与△ACD 为直角三角形.在Rt △ABC 和Rt △ADC 中,∵⎩⎪⎨⎪⎧AB =AD ,AC =AC ,∴Rt △ABC ≌Rt △ADC (HL),∴∠1=∠2.方法总结:证明角相等可通过证明三角形全等解决.【类型四】 利用“HL ”解决动点问题如图,在直角三角形ABC 中,∠C =90°,AC =20,BC =10,PQ =AB .P ,Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AM 上运动,且点P 不与点A ,C 重合.那么当点P 运动到什么位置时,才能使△ABC 与△APQ 全等?解析:本题要分情况讨论:①Rt △APQ ≌Rt △CBA ,此时AP =BC =10,可据此求出P 点的位置.②Rt △QAP ≌Rt △BCA ,此时AP =AC ,P 、C 重合,不合题意.解:根据三角形全等的判定方法HL 可知:①当P 运动到AP =BC 时,∵∠C =∠QAP =90°,∴在Rt △ABC 与Rt △QP A 中,AP =BC ,PQ =AB ,∴Rt △ABC ≌Rt △QP A (HL),即AP =BC =10;②当P 运动到与C 点重合时,AP =AC ,不合题意.综上所述,当点P 运动到距离点A 为10时,△ABC 与△APQ 全等.方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.【类型五】 综合运用全等三角形的判定方法判定直角三角形全等如图,CD ⊥AB 于D 点,BE ⊥AC于E 点,BE ,CD 交于O 点,且AO 平分∠BAC .求证:OB =OC .解析:已知BE ⊥AC ,CD ⊥AB 可推出∠ADC =∠BDC =∠AEB =∠CEB =90°,由AO 平分∠BAC 可知∠1=∠2,然后根据AAS 证得△AOD ≌△AOE ,△BOD ≌△COE ,即可证得OB =OC .证明:∵BE ⊥AC ,CD ⊥AB ,∴∠ADC =∠BDC =∠AEB =∠CEB =90°.∵AO 平分∠BAC ,∴∠1=∠2.在△AOD 和△AOE 中,∵⎩⎪⎨⎪⎧∠ADC =∠AEB ,∠1=∠2,OA =OA ,∴△AOD ≌△AOE (AAS),∴OD =OE .在△BOD 和△COE 中,∵⎩⎪⎨⎪⎧∠BDC =∠CEB ,OD =OE ,∠BOD =∠COE ,∴△BOD ≌△COE (ASA).∴OB =OC .方法总结:判定直角三角形全等的方法除“HL ”外,还有SSS 、SAS 、ASA 、AAS.三、板书设计 1.作直角三角形2.直角三角形全等的判定斜边和一条直角边分别相等的两个直角三角形全等.本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行.在探究直角三角形全等的判定方法——“斜边、直角边”时,要让学生进行合作交流.在寻找未知的等边或等角时,常考虑将其转移到其他三角形中,利用三角形全等来进行证明.此外,还要注重通过适量的练习巩固所学的新知识.第2课时平行四边形的判定定理3与两平行线间的距离1.复习并巩固平行四边形的判定定理1、2;2.学习并掌握平行四边形的判定定理3,能够熟练运用平行四边形的判定定理解决问题;(重点)3.根据平行四边形的性质总结出求两条平行线之间的距离的方法,能够综合平行四边形的性质和判定定理解决问题.(重点,难点)一、情境导入小明的父亲的手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗?你能想出几种办法?二、合作探究探究点一:对角线互相平分的四边形是平行四边形【类型一】利用平行四边形的判定定理(3)判定平行四边形已知,如图,AB、CD相交于点O,AC∥DB,AO =BO,E、F分别是OC、OD 中点.求证:(1)△AOC≌△BOD;(2)四边形AFBE是平行四边形.解析:(1)利用已知条件和全等三角形的判定方法即可证明△AOC≌△BOD;(2)此题已知AO=BO,要证四边形AFBE是平行四边形,根据全等三角形,只需证OE=OF就可以了.证明:(1)∵AC∥BD,∴∠C=∠D.在△AOC和△BOD中,∵⎩⎪⎨⎪⎧AO=OB,∠AOC=∠BOD,∠C=∠D,∴△AOC≌△BOD(AAS);(2)∵△AOC≌△BOD,∴CO=DO.∵E、F分别是OC、OD的中点,∴OF =12OD,OE=12OC,∴EO=FO,又∵AO =BO,∴四边形AFBE是平行四边形.方法总结:在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.熟练掌握平行四边形的判定定理是解决问题的关键.【类型二】利用平行四边形的判定定理(3)证明线段或角相等如图,在平行四边形ABCD中,AC交BD于点O,点E,F分别是OA,OC 的中点,请判断线段BE,DF的位置关系和数量关系,并说明你的结论.解析:根据平行四边形的对角线互相平分得出OA=OC,OB=OD,利用中点的意义得出OE=OF,从而利用平行四边形的判定定理“对角线互相平分的四边形是平行四边形”判定BFDE是平行四边形,从而得出BE=DF,BE∥DF.解:BE=DF,BE∥DF.因为四边形ABCD是平行四边形,所以OA=OC,OB =OD.因为E,F分别是OA,OC的中点,所以OE=OF,所以四边形BFDE是平行四边形,所以BE=DF,BE∥DF.方法总结:平行四边形的性质也是证明线段相等或平行的重要方法.探究点二:平行线间的距离如图,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO 的面积相等.解析:结合平行线间的距离相等和三角形的面积公式即可证明.证明:∵l1∥l2,∴点E,F到l2之间的距离都相等,设为h.∴S△EGH =12GH ·h,S△FGH =12GH·h,∴S△EGH=S△FGH,∴S△EGH-S△GOH=S△FGH-S△GOH,∴S△EGO=S△FHO.方法总结:解题的关键是明确三角形的中线把三角形的面积等分成了相等的两部分,同底等高的两个三角形的面积相等.探究点三:平行四边形判定和性质的综合如图,在直角梯形ABCD中,AD ∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.(1)求证:四边形DEGF是平行四边形;(2)如果点G是BC的中点,且BC=12,DC=10,求四边形AGCD的面积.解析:(1)求出平行四边形AGCD,推出CD=AG,推出EG=DF,EG∥DF,根据平行四边形的判定推出即可;(2)由点G是BC的中点,BC=12,得到BG=CG=12BC =6,根据四边形AGCD是平行四边形可知AG=DC=10,根据勾股定理得AB=8,求出四边形AGCD的面积为6×8=48.解:(1)∵AG∥DC,AD∥BC,∴四边形AGCD是平行四边形,∴AG=DC.∵E、F分别为AG、DC的中点,∴GE=12AG,DF=12DC,即GE=DF,GE∥DF,∴四边形DEGF是平行四边形;(2)∵点G是BC的中点,BC=12,∴BG=CG=12BC=6.∵四边形AGCD是平行四边形,DC=10,AG=DC=10,在Rt△ABG中,根据勾股定理得AB=8,∴四边形AGCD的面积为6×8=48.方法总结:本题考查了平行四边形的判定和性质,勾股定理,平行四边形的面积,掌握定理是解题的关键.三、板书设计1.平行四边形的判定定理3:对角线互相平分的四边形是平行四边形;2.平行线的距离;如果两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离都相等,这个距离称为平行线之间的距离.3.平行四边形判定和性质的综合.本节课的教学主要通过分组讨论、操作探究以及合作交流等方式来进行,在探究两条平行线间的距离时,要让学生进行合作交流.在解决有关平行四边形的问题时,要根据其判定和性质综合考虑,培养学生的逻辑思维能力.。
直角三角形全等的判定公开课

舞台背景的形状是两个直角三角形,工作人 员想知道两无法测量. (1)你能帮他想个办法吗?
根据ASA,AAS可测量对应一边和一锐角. 根据SAS可测量其余两边与这两边的夹角.
(2)如果他只带一个卷尺,能完成这个任务吗? 工作人员测量了每个三角形没有被遮住的 直角边和斜边,发现它们分别对应相等. 于是, 他就肯定“两个直角三角形是全等的”.
想一想
到现在为止,你能够用几种方法证明两 个直角三角形是全等的?
A B
A' B' C'
C
答:有五种:SAS、ASA、AAS、SSS、HL.
已知:如图(1)所示,点P在∠AOB的内 部,PC⊥OA,PD⊥OB,垂足分别为C,D,且PC=PD. 求证:点P在∠AOB的平分线上. 证明:如图(2)所示,作射线OP. ∵PC⊥OA,PD⊥OB. ∴∠PCO=∠PDO=90°, 在Rt△OPC和Rt△OPD中, PC=PD 角平分线性质定理的逆定理的证明 OP=OP ∴Rt△OPC≌Rt△OPD(HL). ∴∠POA=∠POB. ∴OP是∠AOB的平分线, 即点P在∠AOB的平分线上.
结论:斜边和直角边对应相等的两个直角三角形全等.
直角三角形全等的判定条件
文字语言:斜边和一条直角边对应相等的两个 直角三角形全等. 简写成“斜边、直角边”或“HL”.
A B A' B' C'
C
符号语言:在Rt△ABC和Rt△ A´B´C´中
A B=A´B´ (斜边) A C= A´C´(直角边) ∴Rt△ABC≌Rt△ A´B´C´(H L)
这两个角是互余的.
4、如图已知Rt△ABC,∠C=90°, AC=10cm,BC=5cm,线段PQ=AB,P、Q 两点分别在AC上和过A点且垂直于AC的射线 AM上运动,问P点运动到AC上什么位置时, △ABC才能和△APQ全等?
12.2直角三角形全等的判定PPT课件

(HL)
1. 如图:△ABC≌△DEF,指出它们的对应 角、对应边。
AD
B
E
C
F
对应边:AB——DE
AC——DF
BC——EF 对应角:∠A——∠D
∠B——∠DEF ∠ACB——∠F
2. 我们已经学过判定全等三角形的方法有哪些? SSS、SAS、ASA、AAS
创设情景 引入课题
形能全等吗?
画一画:
动手实践 探索规律
任意画一个Rt△ACB ,使∠C﹦90°,再画一个
Rt△A′C′B′ ,使∠C﹦∠C′,B′C′﹦BC,A′B′﹦AB (1)你能试着画出来吗?与小组内的其他同学交流一
(2)把画好的Rt△A′C′B′放到Rt△ACB上, 它们全等吗?你能发现什么规律?
作法:
1. 画∠MC′N=90°; 2. 在射线C′M上取B′C′=BC; 3. 以B′为圆心,AB为半径画弧,交射线C′N于点A′ 4. 连接A′B′,Rt△A′C′B′就是所求作的三角形。
∴Rt△ABC≌Rt△BAD (HL). ∴ BC﹦AD.
1.如图,AB⊥BC,AD⊥DC, AB=AD.
求证:∠1=∠2 . A
12
B
D
C
3.如图,AB=CD,AE⊥BC, DF⊥BC,CE=BF. 求证:AE=DF.
C
D
F E
A
B
2.如图,C是路段AB的中点,两人 从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E 两地,DA⊥AB,EB⊥AB,D,E与路 段AB的距离相等吗?为什么?
直角三角形全等的判定方法: 斜边和一条直角边对应相等的两个直角三角 形全等。简写成“斜边、直角边”或“HL”.
2018初二数学公开课---直角三角形全等的判定(HL)

件“对顶角相等”. 例 5 .已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.
在 Rt△ABD 与 Rt△CDB 中,∵AD=CB,BD=DB, ∴Rt△ABD≌Rt△CDB( HL).∴AB=DC. (2)∵Rt△ABD≌Rt△CDB(已证), ∴∠ADB=∠CBD.∴AD∥BC. 善于发现隐藏条件“公共边”. 例 4 已知:如图,AC=BD,AD⊥AC,BC⊥BD.求证:AD=BC.
例 1 下列说法正确的是(C) A.一直角边对应相等的两个直角三角形全等 B.斜边相等的两个直角三角形全等 C.斜边相等的两个等腰直角三角形全等 D.一边长相等的两等腰直角三角形全等 直角三角形除了一般证全等的方法,“HL”可使证明过程简化,但前提是已知两个直
角三角形,即在证明格式上表明“Rt△”. 例 2 判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由.
4 × 1 ab+(b-a)2=c2,化简可证。 2
⑶发挥学生的想象能力拼出不同的图形,进行证明。 ⑷ 勾股定理的证明方法,达 300 余种。这个古老的精彩的证法,出自我国古代无名数 学家之手。激发学生的民族自豪感,和爱国情怀。
A
aD
c
b
E
c
a
B bC
b a
c
c b
a
a
c
b
a a
c
bc
a
b
全国优质课一等奖人教版初中八年级上册数学《直角三角形全等的判定(HL)》公开课课件

证明:连接DC.
∵AC⊥AD,BC⊥BD,
∴∠A=∠B=90°,
在Rt△ADC和Rt△BCD中,
AB BA
AC
BD
∴Rt△ADC≌Rt△BCD (HL),
∴AD=BC.
已知:如图,AB⊥BC,AD⊥DC,AB=AD,求证:BC=DC.
证明:连接AC.
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
(2)解:∠B+∠AFD=180°,理由如下:
由(1)得:△ACD≌△AED, ∴DC=DE,
在Rt△CDF和Rt△EDB中,
DC DE
DF
DB
∴Rt△CDF≌Rt△EDB(HL), ∵∠CFD+∠AFD=180°,
∴∠CFD=∠B,
∴∠B+∠AFD=180°.
例4.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB 于E,点F在边AC上,连接DF. (3)在(2)的条件下,若AB=m,AF=n,求BE的长(用含m,n的代数
若AB=DE,AC=DF,此时△ABC与△DEF还会全等吗?
任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使得 ∠C′=90°,B′C′=BC,A′B′=AB. 把画好的Rt△A′B′C′剪下,放到Rt△ABC上, 它们全等吗?
直角三角形“HL”判定方法 文字语言:斜边和一条直角边分别相等的两个直角三角形全等.
式表示).
(3)解:由(2)知,Rt△CDF≌Rt△EDB, ∴CF=BE, 由(1)知AC=AE, ∵AB=AE+BE, ∴AB=AC+BE, ∵AC=AF+CF, ∴AB=AF+2BE, ∵AB=m,AF=n, ∴BE=12(m﹣n).
公开课三角形全等的判定HL课件

THANKS
感谢观看
05
总结与回顾
BIG DATA EMPOWERS TO CREATE A NEW
ERA
HL判定定理的重要性和应用价值
三角形全等判定定理的基石
HL(Hypotenuse-Leg)判定定理是三角形全等判定的重 要定理之一,它在几何学中占有重要地位,是解决三角形 全等问题的关键。
实际应用广泛
在日常生活和实际工程中,经常需要用到三角形全等的判 定。通过HL定理,可以快速准确地判断两个三角形是否全 等,从而为解决实际问题提供有力支持。
ERA
HL判定定理的来源
三角形全等是几何学中的重要概念, 用于判断两个三角形是否完全相同。
HL判定定理的起源可以追溯到古希腊 数学家欧几里得,在他的著作《几何 原本》中,提到了与HL判定定理类似 的判定方法。
HL判定定理是三角形全等判定的一种 方法,其名称来源于英文 “Hypotenuse-Leg”的缩写,意为 “斜边-直角边”。
如果两个三角形的两边长度相等,且 这两边所夹的角相等,则这两个三角 形全等。
角边角相等(ASA)
如果两个三角形有两个角分别相等, 且这两个角所夹的一边长度也相等, 则这两个三角形全等。
角角边相等(AAS)
如果两个三角形有两个角分别相等, 且这两个角所对的一边长度也相等, 则这两个三角形全等。
三角形全等的应用
数学教育的核心内容
在数学教育和教学中,HL定理是几何学的重要知识点,对 于培养学生的逻辑思维、空间想象力和问题解决能力具有 重要意义。
HL判定定理的学习方法和技巧
理解定理的内涵
多做练习题
首先需要深入理解HL定理的内涵和适用条 件,掌握“直角边斜边”的基本形式,明 确两三角形全等的充分必要条件。
孙攀登14.5直角三角形全等的判定HL公开课
下课了!
结束寄语
•不经历风雨,怎么见 彩虹.,没有人能随随 便便成功!
C
例2.如图:AC⊥BC,BD⊥AD,AC=BD. D 求证:BC=AD. o
证明: ∵AC⊥BC,BD⊥AD, ∴∠C=∠D=90°
A
C
在Rt△ABC和Rt△BAD中,
B
AB=BA AC=BD ∴Rt△ABC≌ Rt △BAD(HL)
∴BC=AD(全等三角形对应边相等)
OA=OB吗?(AAS)
E
实际问题 数学问题
CD 与CE 相等吗?
①AC=BC
②CD=CE
求证:DA=EB。
证明: ∵DA⊥AB,EB⊥AB, ∴∠A=∠B=90°
又∵C是AB的中点, ∴AC=BC ∵C到D、E的速度、时间相同, ∴DC=EC 在Rt△ACD和Rt△BCE中, AC=BC DC=EC ∴Rt△ACD≌ Rt △BCE(HL) ∴ DA=EB (全等三角形对应边相等)
A
1、已知:如图,D是△ABC的BC边上 的中点,DE⊥AC,DF⊥AB,垂足分别 为E、F,且DE=DF. F 求证: Rt△BDF≌Rt△CDE.
B
D
E
C
2、已知如图:AB=CD,DE⊥AC,BF⊥AC,垂足分别 为E,F,DE=BF. C D 求证:(1)Rt△ABF≌Rt△CDE F (2)AE=CF; (3)AB∥CD.
C N A A ´´
∟
能够完全重合。
∟
说明什么问题?
´ M BB ´
C´ ´
斜边和一条直角边对应相等的两个 直角三角形全等。 简写为“斜边、直角边”或“HL”。
A A´
几 何 语 B´ C 言: B 在Rt △ABC和Rt△A´B´C´中 AB=A´B´ ∵ BC=B´C´ ´ HL) ∴ Rt△ABC≌ Rt Rt△A´B´C (
直角三角形全等的判定(公开课)

C D
)
B
∠CAB=∠DBA ⑶___________( AAS ) ∠CBA=∠DAB ⑷___________( AAS )
A
完成学习目标2:应用HL判定定理(17分钟)
例题讲解
1、如图,在△ABC中,BD=CD,DE⊥AB, DF⊥AC,E、F为垂足,DE=DF, 求证:△DEB≌ △DFC A
C
D
证明:在Rt△ABC和Rt△DEF中, B ∵ ∠C=90°,∠F=90°(已知) ∴AC2 = AB2 - BC2, DF2 = DE2 - EF2 (勾股定理) ∵ AB=DE,BC=EF(已知) ∴AC=DF(等量代换) 在Rt△ABC和Rt△DEF中 AC=DF(已证) 归纳: ∵ BC=EF(已知) 斜边 直角边 ________和________对应 相等的两个直角三角形全等. AB=DE(已证)
完成学习目标1:HL判定定理
练习:(5分钟)
1.选择题 (1).使两个直角三角形全等的条件是( D ) (A)一个锐角对应相等 (B)两个锐角对应相等 (C)一条边对应相等 (D)斜边和一条直角边对应相等 (2).如图,AD⊥BE,垂足C是BE的中点,AB=DE,若要证 △ABC≌ △DEC,可以根据( B ) E (A)边边边公理 A (B)斜边、直角边公理 D C (C)角边角公理 (D)边角边公理
∴Rt△ABD≌Rt△ACD(HL) ∴BD=CD(全等三角形的对
应边相等)
宣化五中:黄维超
• 1.掌握判定两个直角三角形全等的判 定方法——斜边、直角边(HL); • 2.会熟练运用“HL”定理判定两个直角 三角形全等;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简写成“斜边、直角边” 或“HL”
斜边、直角边公理 (HL)
有斜边和一条直角边对应相等的两个 直角三角形全等.
几何语言
∵∠C=∠C′=90°
∴在Rt△ABC和Rt△ABC中
A
B
C B′
AB=AB BC=BC
A′ C′
∴Rt△ABC≌Rt △ABC (HL)
1、已知如图,在△ABC和△ABD 中,AC⊥BC,AD⊥BD,垂足分别为 证明两个直角三角形全等,首先考虑用HL定理 C,D,AD=BC 求证:△ABC≌△BAD. C
舞台背景的形状是两个直角三角形,工作人 员想知道两个直角三角形是否全等,但每个三 角形都有一条直角边被花盆遮住,无法测量。 (1) 你能帮他想个办法吗?
根据ASA,AAS可测量对应一边和一锐角 根据SAS可测量其余两边与这两边的夹角。
(2)如果他只带一个卷尺,能完成这 个任务吗?
他用卷尺只能量出斜边和一条直角边, 如果它们对应相等,能证明这两个直角 三角形全等吗?
C E A
D N
B
谈谈你本节课的收获
1、斜边、直角边(HL)定理:斜边和 一条直角边对应相等的两个三角形全等
2、证明两个直角三角形全等,不仅 可以用HL定理,还可以用SAS、ASA、 SSS、AAS定理来证明两个三角形 全等
巩固作业:练习册
• 1. 通过演示实验,探索直角三角形全等 的条件; • 2. 学会用斜边直角边公理判定直角三角 形全等; • 3. 体验用所学知识解决数学问题的乐趣
1、观察老师的操作过程,你有什么发 现?你能得到什么结论?
斜边和一条直角边对应相等的 两个直角三角形全等.
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
D
A
A
第一题图
B
B
D
第二题图
C
2、如图,在△ABC中,AB=AC,AD 点拨:此类问题将证明线段和角相等转化为 是BC边上的高,求证: 证三角形全等 BD=CD,∠BAD=∠CAD
1.如图已知CE⊥AB,DF⊥AB,AC=BD, AF=BE,则CE=DF。请说明理由。
A B
B
E C
第1题图
第2题图
欢 迎 各 位 老 师 光 临 指 导 !
授课教师: 夏 卫 民
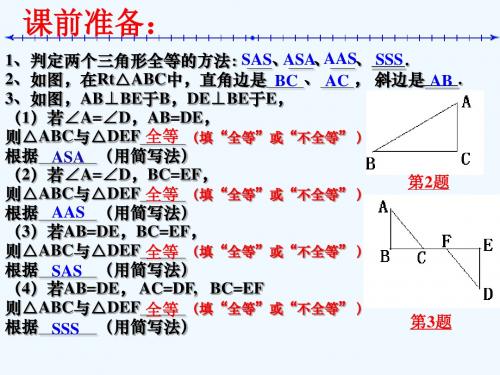
学习准备: 1、判定两个三角形全等的方法: 、 、 、____. 2、如图,在Rt△ABC中,直角边是 、 , 斜边是____. 3、如图,AB⊥BE于B,DE⊥BE于E, (1)若∠A=∠D,AB=DE, 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法) (2)若∠A=∠D,BC=EF, 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法) (3)若AB=DE,BC=EF, 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法) (4)若AB=DE, AC=DF 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法)
F
ห้องสมุดไป่ตู้
D
2.如图,AB=AE,BC=ED,AF⊥CD, ∠B=∠E.试说明:F是CD的中点.
已知△ABC中,AC=BC,直线MN经过 点C,且AD⊥MN于D,BE⊥MN于E, 请你添加一个条件使DE=AD+BE成立。
M
D C E
N
A
B
变式:若直线MN绕点C旋转到此位置时, 你添加的条件能说明DE=BE-AD成立吗?
