二级倒立摆数学模型的建立
二级倒立摆系统的最优控制

∞
ut
+
B
+
1 /S
x
C
y
A
R-1BT
P
五、仿真分析
将某二级倒立摆系统模型各参数代入式1-8,得出系数矩阵 设, 写出Matlab程序如下:
A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1; 0,-2.57163,0.164291,-16.6674,0.0124145,0.005; 0,29.9499,-15.1957,40.3167,-0.204856,0.17380; 0,29.9499,65.4455,-49.3949,0.463474,-0.59148]; B=[0;0;0;8.64636;-20.9146;25.9146]; C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0]; %求开环特征值 r1=eig(A) %加入最优反馈器 q1=100;q2=10;q3=5000;q4=0;q5=0;q6=0; Q=[q1 0 0 0 0 0;0 q2 0 0 0 0;0 0 q3 0 0 0;0 0 0 q4 0 0;0 0 0 0 q5 0;0 0 0 0 0 q6];R=1; %求最优增益矩阵、黎卡提方程的解、闭环特征值 [K,P,r2]=lqr(A,B,Q,R) Ac=[(A-B*K)];Bc=[B];Cc=[C];Dc=[D]; T=0:0.02:20;U=zeros(size(T)); x0=[0;-0.05;0.1;0;0;0]; [Y,X]=lsim(Ac,Bc,Cc,Dc,U,T,x0); %绘制下摆偏离垂直方向的角度变化曲线 figure(1);plot(T,Y(:,1)); xlabel('Time/sec');ylabel('01/rad');grid; %绘制上下摆角度之差的曲线 figure(2);plot(T,Y(:,2)); xlabel('Time/sec');ylabel('02-01/rad');grid; %绘制小车位移曲线 figure(3);plot(T,Y(:,3)) xlabel('Time/sec');ylabel('x(小车)/m');grid;
二级倒立摆的数学模型推导

二级倒立摆的数学模型推导一、二级倒立摆系统的结构二级倒立摆系统的结构如图1如示,机械部分主要有小车、下摆、上摆、导轨、皮带轮、传动皮带等,控制对象由小车、下摆、上摆组成,电气部分由电机、晶体管直流功率放大器、传感器以及保护电路组成。
图1 二级倒立摆结构示意图二、二级倒立摆的数学模型 (一)假设条件为了简化二级倒立摆的数学模型,作如下假设:1. 小车与导轨间的摩擦力与小车速度成正比;电机摩擦转矩与电机转矩成正比;上、下摆连接处摩擦力矩与二摆相对角速度成正比;下摆与小车连接处摩擦力矩与下摆相对角速度成正比。
2. 整个对象系统除皮带外视为刚体。
3. 皮带伸长忽略不计且传递作用力的延迟忽略不计。
4. 电路系统的传递延迟及功率放大器的非线性忽略不计。
5. 电机电感忽略不计。
6. 检测电位器设为线性的,即设检测信号分别为与r 、1θ、21θθ-成正比的电信号,且假设标定完全准确。
(二)系统参数说明推导中各符号的意义如下:0M :小车、皮带、电机转子、皮带轮归算到小车运动上的等效质量; 1M :下摆质量; 2M :上摆质量;1J :下摆转动惯量; 2J :上摆转动惯量;r :小车位移;1θ:下摆角位移;2θ:上摆角位移;1L :下摆全长(轴心到轴心); 1l :下摆质心与小车——下摆连接轴心距离; 2l :上摆质心与上摆——下摆连接轴心距离;'0F :小车与导轨间摩擦力,电机机械摩擦转矩,皮带轮摩擦转矩归算到小车运动上的等效摩擦系数,由下式定义等效摩擦力:'00f F r =⋅1F :下摆与小车摩擦力矩的等效摩擦系数,由下式定义等效摩擦力矩:111T F θ=⋅2F :上、下摆间摩擦力矩的等效摩擦系数,由下式定义等效摩擦力矩:2221()T F θθ=⋅-P :电机提供的控制力;U :电机外加电压即功率放大器输出电压; E :电机反电势; I :电机电流;R :电机等效电阻;i R :功率放大器等效输出电阻;d :皮带轮直径;θ:电机转速(/rad s );n 电机转速(转/分);K :功率放大器电压增益 ;e K :电势系数; t K :转矩系数;e :功率放大器的输入电压;参阅相关资料后,对各参数的取如下值:0M =1.328kg ,1M =0.220kg ,2M =0.187kg ,1J =0.004962kg m ⋅,2J =0.004822kg m ⋅,1L =0.490m ,1l =0.304m ,2l =0.226m ,'0F =22.947kg/s ,1F =0.00705/kg m s ⋅,2F =0.00264/kg m s ⋅,R =8.550Ω,i R =1.252Ω,d =0.130m ,K =8.000,t K =0.946/N m A ⋅(三)数学模型推导 此处少图3-2(P7)图3-2中,'i i f f =(1,2)i =小车在y 方向上无运动,小车受导轨垂直方向力示标出,推导中iy f ,ir f (1,2)i =分别表示i f 在y ,r 方向的分力。
平面两级倒立摆的建模
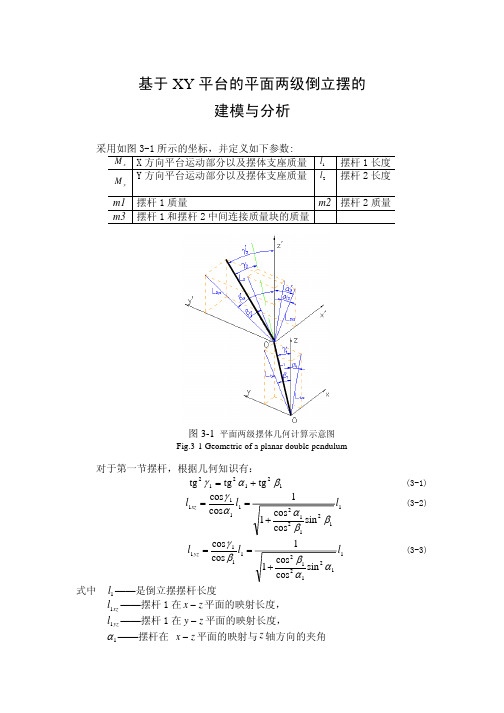
采用如图 3-1 所示的坐标,并定义如下参数:
M x X 方向平台运动部分以及摆体支座质量 l1 摆杆 1 长度
Y 方向平台运动部分以及摆体支座质量
My
l2
摆杆 2 长度
m1 摆杆 1 质量
m2 摆杆 2 质量
m3 摆杆 1 和摆杆 2 中间连接质量块的质量
(3-1) (3-2)
(3-3)
β1 ——摆杆在 y − z 平面的映射与 z 轴方向的夹角 γ 1 ——摆杆与 z 轴方向的夹角 γ 2 ——摆杆与 z 轴方向的夹角 在摆杆垂直向上的方向上,如果偏角α1, β1 << 1 ,则可以近似的认为
l1xz ≈ l1yz ≈ l1
因此,摆杆绕 X 轴和 Y 轴的转动惯量可以表示为:
⋅2
y1
⋅
⋅ y2
+
1 2
m1
⋅
2
+
1 2
m2
⋅2
z1 +
⋅2
⋅ z2
1 2
+
⋅2 ⋅2
J1 ⋅ (α1 + β1 )
1 2
J2
⋅
⋅
(α 2
2
+
⋅
β2
2
)
⎪ ⎪⎪⎩Tm3
=
1 2
m3
⋅
⋅2
x3 +
1 2
m3
⋅
⋅2
y3 +
1 2
m3
⋅
⋅2
z3
式中 x1 ——摆杆 1 中心点的 X 坐标;
y1 ——摆杆 1 中心点的 Y 坐标;
由拉各朗日方程:
直线二级倒立摆系统MATLAB模型的建立与仿真

直线二级倒立摆系统模型的建立与仿真1 引言倒立摆是一个高阶次、非线性、快速、多变量、强藕合、不稳定的系统。
在控制理论发展过程中,倒立摆常常被做为典型的被控对象来验证某一理论的正确性,以及在实际应用中的可行性,通过对倒立摆引入一个适当的控制方法使之成为一个稳定系统,来检验控制方法对不稳定性、非线性和快速性系统的处理能力。
该控制方法在军工、航天、机器人等领域和一般工业过程中都有广泛应用。
本文主要讨论二级倒立摆系统模型的建立和仿真。
2二级倒立摆系统数学模型直线二级倒立摆系统是由直线运动模块和两级倒立摆组件组成。
主要包括导轨、小车和各级摆杆、编码器等元件。
由驱动电机给小车施加一个控制力,迫使小车在导轨上左右移动。
而小车的位移和各级摆杆角度由编码器测得。
倒立摆的控制目标是使倒立摆的摆杆能在有限长的导轨上快速的达到竖直向上的稳定状态,以实现系统的动态平衡,并且小车位移和摆杆角度的振荡幅度较小,系统具有一定的抗干扰能力。
系统简化后的直线二级倒立摆系统物理结构图如图2.1所示。
图1.二级倒立摆系统模型系统模型建立所用的各参数如下:应用Lagrange 方程建立的数学模型为012221221211121221222212212222cos (,)cos()cos cos()1121111121111m +m +m (m l +m L )cos m l H (m l +m L )cos J m l m L m l L m l m l L J m l θθθθθθθθθθ⎡⎤⎢⎥=++-⎢⎥⎢⎥-+⎣⎦.1011...1221212122.11222cos (,,,)0(0(112222222f m l +m L sin m l H f f m l L sin f m l L sin f f θθθθθθθθθθθθθ⎡⎤-•⎢⎥⎢⎥=--•+⎢⎥⎢⎥-•+-⎢⎥⎣⎦111()-)-) 312(,)h θθ= [0 11211()sin m l m L g θ+ 212sin m l g θ] T0h =[1 0 0]T()1121212121312022(,)(,,,),x x H H h h u θθθθθθθθθθθθ⎡⎤⎡⎤⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦3 倒立摆PID控制器系统PID控制是比例积分微分控制的简称。
直线二级倒立摆建模与matlab仿真LQR
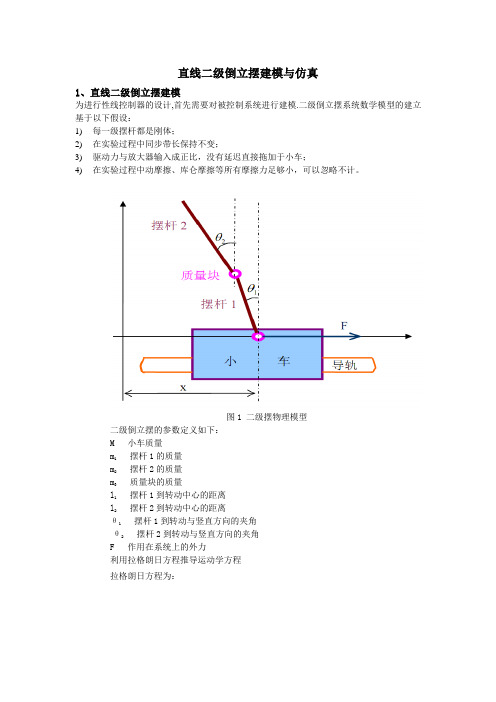
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
二级倒立摆系统的控制与仿真

二级倒立摆系统的控制与仿真一、引言在计算机参与的具有联系受控对象的控制系统中,有必要对联系控制系统设计数字控制器的必要,一般对于联系的控制对象设计数字控制器的方法有:第一种是应用联系系统理论得到的联系控制规律,再将控制规律离散化,用控制器实现,第二种是将联系的控制对象离散化,用离散控制理论设计控制器参数,数字再设计就是根据连续系统及相应的控制规律如何重新设计对应的离散系统与相应的离散控制规律。
我们采用的是最优等价准则、双线性变换法、平均增益法进行数字再设计。
二、LQR控制器设计(1) 二级倒立摆系统的状态空间模型设线性定常系统为x’=A*x(t)+B*u(t),y=C*x(t)其初始条件为x(t)=x0;其中:A=[0,1,0,0;40,0,0,0;0,0,0,1;-6,0,0,0];B=[0;-2;0;0.8];C=[1,0,0,0;0,0,1,0](2) 系统的能控性判定n=size(A); Tc=ctrb(A,B); nc=rank(Tc)n=6 6 nc=6从运行结果可知,系统的阶次为6,能控性矩阵的秩也为6,因此系统是能控的。
(3) 系统的能观性判定To=obsv(A,C);no=rank(To)no=6从运行结果可知,能观性矩阵的秩为6,与系统的阶次相等,因此系统是能观测的。
(4) LQR控制设计基于一级倒立摆系统具有能控性和能观性,因此可采用LQR进行控制,经大量反复试验和仿真,选取R=0.2,Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];F=lqr(A,B,Q,R)得到:F =2.2361 106.6465 -155.4620 5.1719 4.9639 -24.5330三、仿真曲线采用LQR控制方式,设初始状态为x(0)=[1,-1,0,0]’,在相同采样周期T下应用数字再设计方法对一级倒立摆系统进行仿真,其中F(T)分别取为:1. F(T)=F1(T)=F2. F(T)=F2(T)=F[I+(A+BF)T/2]3. F(T)=F3(T)=F[I-(A+BF)/2]-1(1) T=0.013s,øc=e(A+BF)T时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[G,H]=c2d(A-B*F,B,T); %%离散一的函数p0=eig(G),x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(G,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%响应曲线plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p0 =0.8647 + 0.0473i0.8647 - 0.0473i0.9224 + 0.0618i0.9224 - 0.0618i0.9932 + 0.0066i0.9932 - 0.0066i图1 øc=e(A+BF)T(2) T=0.013s,øc=ø +ΓF1(T)时系统的极点、状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0,0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;[Ad,B]=c2d(A,B,T); %%离散二的函数Ad=Ad-B*F;p1=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')p1 =0.8349 + 0.0388i0.8349 - 0.0388i0.9247 + 0.0561i0.9247 - 0.0561i0.9932 + 0.0066i0.9932 - 0.0066i图2 øc=ø +ΓF1(T)(3) T=0.013s,øc=ø+ΓF2(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P2=(A-B*F)*T/2; %%离散3的函数F2=F*(eye(size(P2))+P2)[Add,B]=c2d(A,B,T);Ad=[Add-B*F2];p2=eig(Ad)x0=[1 -1 0.5 0 0 0]';[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F2 =1.7236 90.8365 -126.5481 4.0012 4.5195 -19.9211 p2 =0.8676 + 0.0465i0.8676 - 0.0465i0.9224 + 0.0627i0.9224 - 0.0627i0.9932 + 0.0066i0.9932 - 0.0066i图3 øc=ø+ΓF2(T)(4) T=0.013s,øc=ø+ΓF3(T)时系统的极点、F(T)值和状态x1、x2、x3的离散仿真曲线A=[0,0,0,1,0,0;0,0,0,0,1,0;0,0,0,0,0,1;0,0,0,0,0,0;0,77.0642,-21.1927,0,0, 0;0,-38.5321,37.8186,0,0,0];B=[0;0;0;1;5.7012;-0.0728];C=[1,0,0,0,0,0;0,1,0,0,0,0;0,0,1,0,0,0];D=[0;0;0];Q=[1 0 0 0 0 0;0 64 0 0 0 0;0 0 256 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0;0 0 0 0 0 0];R=0.2;F=lqr(A,B,Q,R)T=0.013;P3=(A-B*F)*T/2; %%离散4的函数F3=F*(eye(size(P3))-P3)^-1[Add,B]=c2d(A,B,T);Ad=[Add-B*F3];p3=eig(Ad),[y,x,t]=dinitial(Ad,B,C,D,x0);t=0:0.1:(t-1)/10;subplot(3,1,1),x1=[1 0 0 0 0 0]*x'; %%显示程序plot(t,x1);grid;title('状态变量x1的响应曲线')subplot(3,1,2),x2=[0 1 0 0 0 0]*x';plot(t,x2);grid;title('状态变量x2的响应曲线')subplot(3,1,3),x3=[0 0 1 0 0 0]*x';plot(t,x3);grid;title('状态变量x3的响应曲线')F3 =1.7779 92.1683 -129.2365 4.1238 4.5459 -20.3464 p3 =0.8655 + 0.0476i0.8655 - 0.0476i0.9222 + 0.0622i0.9222 - 0.0622i0.9932 + 0.0066i0.9932 - 0.0066i图4 øc=ø+ΓF3(T)由上面的1-4图我们可以知道:F(T)分别取F1(T),F2(T),F3(T)构成的闭环离散系统时仿真曲线基本一致,相应情况的闭环极点也基本相同,而取F(T)=F3(T)时,从系统的极点看,用øc=ø+ΓF3(T)代替øc=e(A+BF)T 构成闭环系统的精确度相当好。
现代控制理论-大作业-倒立摆

摘要倒立摆系统是一个复杂的、高度非线性的、不稳定的高阶系统,是学习和研究现代控制理论最适宜的实验装置。
倒立摆的控制是控制理论应用的一个典型X例,一个稳定的倒立摆系统对于证实状态空间理论的实用性是非常有用的。
本文主要研究的是二级倒立摆的极点配置方法,首先用Lagrange 方程建立了二级倒立摆的数学模型,然后对二级倒立摆系统的稳定性进展了分析和研究,并给出了系统能控能观性的判别。
基于现代控制理论中的极点配置理论,根据超调量和调整时间来配置极点,求出反应矩阵并利用Simulink对其进展仿真,得到二级倒立摆的变化曲线,实现了对闭环系统的稳定控制。
关键词:二级倒立摆;极点配置;Simulink目录12 数学模型的建立和分析 (2)2.1 数学建模的方法 (2)2.2 二级倒立摆的结构和工作原理 (2)2.3 拉格朗日运动方程 (3) (4)3 二级倒立摆系统性能分析 (12)3.1 稳定性分析 (12)3.2 能控性能观性分析 (13)4 状态反应极点配置 (14)4.1 二级倒立摆的最优极点配置1 (14)4.2 二级倒立摆最优极点配置2 (16)5. 二级倒立摆matlab仿真 (18)5.1 Simulink搭建开环系统 (18)5.2 开环系统Simulink仿真结果 (19)5.3 Simulink搭建极点配置后的闭环系统 (20) (21)5.4.1 第一组极点配置仿真结果 (21)5.4.2 第二组极点配置仿真结果 (23) (25) (26)附录一 (26)1.绪论倒立摆最初诞生于麻省理工学院,仅有一级摆杆,另一端铰接于可以在直线导轨上自由滑动的小车上。
后来在此根底上,人们又进展拓展,设计出了直线二级倒立摆、环型倒立摆、平面倒立摆、柔性连接倒立摆、多级倒立摆等实验设备。
在控制理论的开展过程中,为验证某一理论在实际应用中的可行性需要按其理论设计的控制器去控制一个典型对象来验证。
倒立摆系统作为一个实验装置,形象直观,结构简单,本钱低廉;作为一个控制对象,他又相当复杂,同时就其本身而言,是一个高阶次、不稳定、多变量、非线性、强耦合系统,只有采取行之有效的控制方法才能使之稳定,因此倒立摆装置被公认为是自动控制理论中的典型实验设备。
二级倒立摆数学模型的建立与仿真培训资料

二级倒立摆数学模型的建立与仿真二级倒立摆数学模型的建立与仿真专业:控制工程姓名:淡丹学号:1406073摘要本文用分析力学中牛顿力学法及拉格朗日方程建立了二级倒立摆的数学模型。
根据已经建立的倒立摆数学模型,对其进行了可控性,可观测性及稳定性的分析与研究,并对状态反馈及状态观测器进行了仿真模拟,分析研究。
并通过分析比较得出,加状态观测器并不影响系统的输出的结论。
关键词:倒立摆状态空间极点配置状态反馈ABSTRACTNewtonian mechanics analysis method and the Lagrange equation of a mathematical model of double inverted pendulum has been used in this paper. According to the established mathematical model of inverted pendulum on the controllability, observability and stability of the analysis and research, and the state observer and state feedback is carried on the simulation ,analysis and research. And through the analysis and comparison of results, plus state observer does not affect the conclusions of the output of the system.KEY WORDS: inverted pendulum state space pole allocation state feedback一、二级倒立摆系统的组成二级倒立摆主要由以下四部分组成:1.在有限长的轨道L上作直线运动的小车;2.与小车铰接在一起,并能在竖直平面内分别绕q,q点转动的下、上摆;3.驱动小车的直流力矩电机和转轮、钢丝等传动部分;4.使上、下摆稳定在垂直向上的平衡位置,且使小车稳定在轨道中心位置附近的控制器。
二级倒立摆

ux
(5)
带入参数值,系统的状态方程为:
x 0 0 0 1 0 0 0 2 0 0 0 0 0 x 0 0 86.69 21.62 1 0 40.31 39.45 2 x 1 0 0 0 0 y 0 1 0 0 0 1 2 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 x 0 0 1 0 1 2 0 u 0 x 1 6.64 0 1 0 2 0.08
通过如下公式可以求得综合误差E和综合误差率EC 表达式:
K1 K 2 Kr 0 K2 K2 K2 E EC f1 ( x) K r 0 0 0 K2 0 0 0.1 0.53 1 0 0 0.63 0.06 0 0 K1 K
二级倒立摆自动起 摆[标清版].mp4
20
x 1 0 0 2 u 0 0 x 0 0 1 2
模糊控制器的设计
二级倒立摆系统有6个状态变量,直接进行模糊控制器设计, 模糊控制规则会很多,而过多的控制规则,会使控制器的设计 和系统的实时性都难以达到要求,所以需要对状态变量进行适 当的处理,以减少模糊控制器输入变量,同时又能更好的控制 倒立摆系统。 根据各个状态变量的特点和作用,引入两个综合变量E和 EC,其中E表示综合误差(小车的位移 x 、上摆的摆角 1、下摆的 、上摆的角速 摆角 2),EC表示综合误差变化率(小车的速度 x )。 、下摆的角速度 x1 度 2 1
毕业设计-二级倒立摆建模

毕业设计-二级倒立摆建模四川理工学院毕业设计(论文)二级倒立摆系统建模与仿真学生:学号:专业:自动化班级:自动化指导教师:四川理工学院自动化与电子信息学院二O一一年六月摘要常规的PID控制从理论上可以控制二级倒立摆,但在实际中对PID控制器参数的整定为一难点。
本文针对二级倒立摆系统单输入三输出的不稳定系统,通过三回路PID控制方案,来完成对倒立摆的控制。
利用状态反馈极点配置的方法来对参数进行整定,解决PID参数整定的难点。
然后借助于MATLAB中的Simulink模块对所得的参数进行仿真,结果表明三回路PID控制是成功的,参数的有效性,也证实了这种参数整定方法简单实用。
并通过配置不同位置的极点,对其结果进行分析得到极点配置的最佳配置方案。
关键词:倒立摆;PID;状态反馈; MATLABABSTRACTDouble Inverted Pendulum System Modeling andSimulationConventional PID control theory to control the inverted pendulum, but in practice the parameters of PID controller tuning is a difficult. In this paper, double inverted pendulum system, the instability of single-input three-output system, through the three-loop PID control program to complete the inverted pendulum control.Pole placement using state feedback approach to setting the parameters to resolve the difficulties PID parameter tuning. With MATLAB and Simulink in the module parameters obtained from simulation results show that the three-loop PID control is successful, the effectiveness of the parameters, but also confirms this tuning method is simple and practical.Different locations through the pole configuration, the results were too extreme configuration of the best configuration.Key words:pendulum;PID control ;state feedback;MATLAB目录摘要............................................................. ABSTRACT. (I)第1章引言 01.1 倒立摆研究的目的及意义 01.2 倒立摆的发展史和研究现状 (1)本文的主要工作 (3)第2章倒立摆的建模 (4)2.1 二级倒立摆的简介及物理模型 (4)2.2 二级倒立摆计算机控制系统结构 (5)2.3 二级倒立摆的数学模型 (6)根据牛顿力学、刚体动力学列写二级倒立摆的数学模型 (7)第3章控制策略的选择 (13)3.1 MATLAB简介 (13)该系统的能控、能观及稳定性的分析 (17)系统的能控性 (17)系统能观性 (19)系统的稳定性 (19)3.3 确定控制策略 (20)3.4 控制器参数整定方法 (20)3.5 通过状态反馈极点配置法来整定参数 (22)第4章计算机仿真及结果分析 (25)4.1 Matlab下Simulink模块简介 (25)4.2 在Simulink下的仿真 (26)对仿真结果的分析 (34)第5章结束语 (36)致谢 (37)参考文献 (38)第1章引言1.1 倒立摆研究的目的及意义在控制理论发展的过程中, 一种理论的正确性及在实际应用中的可行性,往往需要一个典型对象来验证, 并比较各种控制理论之间的优劣, 倒立摆系统就是这样的一个可以将理论应用于实际的理想实验平台。
二级倒立摆模型

二级倒立摆模型1 系统数学模型在忽略空气阻力及各种摩擦力之后,可将倒立摆系统抽象成小车、匀质杆和质量块组成的系统。
利用拉格朗日方程推导倒立摆运动学方程,如下:),(),(),(...q q V q q T q q L -=其中,L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能。
拉格朗日方程由广义坐标i q 和L 表示为:i if q Lq L dt d =∂∂-∂∂.其中,i f n i ,,,2,1 =为系统沿该广义坐标方向上的外力,在本系统中,设系统的三个广义坐标分别为21,,θθx 。
由于在广义坐标21,θθ上均无外力作用,有以下等式成立:01.1=∂∂-∂∂θθLL dt d (1) 02.2=∂∂-∂∂θθLL dt d (2) 求解代数方程,表示成一下形式:),,,,,,(...2.1.211..1x x x f θθθθθ= (3)),,,,,,(...2.1.212..2x x x f θθθθθ= (4)取平衡位置时各变量初值为零)0,0,0,0,0,0,0(),,,,,,(...2.1.21=x x x θθθθ,将(3)(4)式在平衡位置进行泰勒级数展开,并线性化,)..17213112..1x K K K ++=θθθ (5))..27223122..2x K K K ++=θθθ (6)现在得到了两个线性微分方程,由于我们采用了加速度作为输入,因此还需要加上一个方程..x u = (7)取状态变量如下:.26.15.423121,,,,,θθθθ======x x x x x x x x 由(5) (6)(7)式得到状态空间方程如下:u K K x x x x x x K K K K x x x x x x ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡271765432123221311.6.5.4.3.2.11000000000000000001000000100000010002 线性二次型最优控制器的设计我们要设计一个线性二次型最优控制器,使得当给系统施加一个阶跃输入时,摆杆会摆动,然后仍然回到垂直位置,这里没有考虑小车位置。
直线二级倒立摆建模和控制综述

直线二级倒立摆的建模和控制综述西南科技大学自动化专业方向设计报告设计名称:直线二级倒立摆的建模和镇定控制姓名:学号:班级:指导教师:起止日期:1方向设计任务书学生班级:学生姓名:学号:设计名称:起止日期:指导教师:设计要求:(1)成立直线二级倒立摆系统的数学模型,并在垂直向上方向上(工作点邻近)获取线性化模型;(2)理解lqr(线性二次调理器)的基来源理,会利用matlab供给的lqr函数获取直线二级倒立摆线性化模型的lqr控制器;(3)利用matlab的simulink仿真环境,搭建倒立摆的控制系统,获取并剖析仿真结果;(4)撰写设计报告,达成辩论。
方向设计学诞辰记时间设计内容直线二级倒立摆的建模与镇定控制纲要(150-250字)倒立摆是一个典型的多变量、非线性、强耦合、欠驱动的自然不稳固系统,对倒立摆系统的控制研究,能反应控制过程中的镇定、非线性和随动等问题,所以常用于各样控制算法的研究。
并且对倒立摆系统的研究还有重要的工程背景,对机器人行走、火箭的姿态调整等都有重要的现实意义。
本文以直线二级倒立摆系统为模型,阐释了直线二级倒立摆的建模方法和镇定控制算法。
其次介绍了直线二级倒立摆系统的构造和参数,应用拉格朗日方程建模方法详尽推导了二级倒立摆的数学模型,并对系统的性能进行剖析。
接下来,本文要点研究了最优控制算法在直线二级倒立摆镇定控制中的应用;在介绍倒立摆系统的最优控制算法的基础上,设计了系统的最优控制器,剖析得出控制参数的选择规律;并且在 Simulink上达成仿真切验,察看控制系统性能。
要点词:倒立摆;建模;LQR;镇定控制Modeling and Balance Control of the Linear DoubleInverted PendulumAbstract:Invertedpendulumisatypicalmultivariable,nonliner,closedcoupledandquickmovement natural instable system.The process of control research can reflect many key problems incontroltheory,suchas theproblemoftranquilization,nonlinearity,followingand soon.Sotheinverted pendulum is commonly used for the study of many kinds of control theory. The research ofinverted pendulum also has important background of engineering, and has practical significance forthe Robot walk and Rocket-profile adjustment.In this paper, taking the linear double inverted pendulum system as the control model, reachingof the control system based on lagrange equation and optimal control algorithm. First of all, givingouttheresearchsignificanceand situationoftheinvertedpendulumsystem,and introducingthelineardoubleinvertedpendulummodelingmethodsandstabilizationcontroltheory.Secondly,introducingthestructureandparametersoftheinvertedpendulumsystem.Researchingoftheinverted pendulum mathematical model based on lagrange equation, and giving a detailed derivation,then having stability analysis of the system. Next, this paper studied the inverted pendulum system’soptimal control algorithm,and designedthe LQR controller based on it,then coming to the law ofselectionofcontrolthesimulationintheSimulinksoftware,observingtheperformance of the control system.Key words:inverted pendulum, modeling, LQR, balance control4一、设计目的和意义二、控制要求对直线二级倒立摆模型的物理特征做剖析,而后利用拉格朗日方程建模方法成立倒立摆的数学模型。
直线二级倒立摆系统MATLAB模型的建立与仿真

直线二级倒立摆系统模型的建立与仿真1 引言倒立摆是一个高阶次、非线性、快速、多变量、强藕合、不稳定的系统。
在控制理论发展过程中,倒立摆常常被做为典型的被控对象来验证某一理论的正确性,以及在实际应用中的可行性,通过对倒立摆引入一个适当的控制方法使之成为一个稳定系统,来检验控制方法对不稳定性、非线性和快速性系统的处理能力。
该控制方法在军工、航天、机器人等领域和一般工业过程中都有广泛应用。
本文主要讨论二级倒立摆系统模型的建立和仿真。
2二级倒立摆系统数学模型直线二级倒立摆系统是由直线运动模块和两级倒立摆组件组成。
主要包括导轨、小车和各级摆杆、编码器等元件。
由驱动电机给小车施加一个控制力,迫使小车在导轨上左右移动。
而小车的位移和各级摆杆角度由编码器测得。
倒立摆的控制目标是使倒立摆的摆杆能在有限长的导轨上快速的达到竖直向上的稳定状态,以实现系统的动态平衡,并且小车位移和摆杆角度的振荡幅度较小,系统具有一定的抗干扰能力。
系统简化后的直线二级倒立摆系统物理结构图如图2.1所示。
图1.二级倒立摆系统模型系统模型建立所用的各参数如下:应用Lagrange 方程建立的数学模型为012221221211121221222212212222cos (,)cos()cos cos()1121111121111m +m +m (m l +m L )cos m l H (m l +m L )cos J m l m L m l L m l m l L J m l θθθθθθθθθθ⎡⎤⎢⎥=++-⎢⎥⎢⎥-+⎣⎦.1011...1221212122.11222cos (,,,)0(0(112222222f m l +m L sin m l H f f m l L sin f m l L sin f f θθθθθθθθθθθθθ⎡⎤-•⎢⎥⎢⎥=--•+⎢⎥⎢⎥-•+-⎢⎥⎣⎦111()-)-) 312(,)h θθ= [0 11211()sin m l m L g θ+ 212sin m l g θ] T0h =[1 0 0]T()1121212121312022(,)(,,,),x x H H h h u θθθθθθθθθθθθ⎡⎤⎡⎤⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦3 倒立摆PID控制器系统PID控制是比例积分微分控制的简称。
二级倒立摆数学模型的建立

二级倒立摆数学模型的建立专业:自研-09姓名:刘文珍学号:2009Y01310126一、二级倒立摆系统的组成二级倒立摆主要由以下四部分组成:1.在有限长的轨道L上作直线运动的小车;2.与小车铰接在一起,并能在竖直平面内分别绕q,q点转动的下、上摆;3.驱动小车的直流力矩电机和转轮、钢丝等传动部分;4.使上、下摆稳定在垂直向上的平衡位置,且使小车稳定在轨道中心位置附近的控制器。
二级倒立摆的结构简图如图1的监督管理功能,如实时画面,数据采集等;数据采集卡安装在计算机内,用完成模/数、数/模转换;功率放大器用于电压和功率放大;电机是系统的执行元件;电位计是系统的测量元件,它分别检测小车相对于轨道中心点的相对位置、下摆相对于铅垂线的角位移、上摆相对于下摆延长线方向的角位移。
图1 倒立摆系统的计算机控制系统二级倒立摆系统的整套机械部件安装在一个钢架上,上面固定着导轨、电机底座和转轮等装置。
通过导轨支架安装好小车滑行的导轨,小车用电机和转轮通过传动钢丝实现运动。
2、结构参数通过实际物理测量,得到二级倒立摆系统的参数如下:小车的等效质量:M =1.0kg;小车与轨道间的滑动摩擦系数:b=5.0kg/s;下摆的质量:m=0.1481kg;下摆半长:1l =0.18m;下摆绕其重心的转动惯量:1j =0.00192kgm ; 上摆质量:2m =0.0998kg; 上摆半长:2l =0.24m;上摆绕其重心的转动惯量: 2j = 0.00182kgm ; 上、下摆重心之间的距离: 1L =0.29m;上、下摆之间的转动摩擦系数: 2F =0.0l 2kgm /s; 下摆和小车之间的转动摩擦系数:1F =0.012kgm /s; 电机及功率放大器的增益: u K =15Nt/V 。
3、Lagrange 方程介绍Lgarnage 方程为..11(1,2,...,)1i q d T T V DF i k dt q q i q q ⎛⎫⎪∂∂∂∂-++== ⎪∂∂ ⎪∂∂⎝⎭(1-1)式中T —系统的动能函数,.1q ,q ,—Lganarge 变量,分别成为广义坐标和广义速度Qi —作用于系统上的广义力 1(1,2,...,)i q VQi F i k q ∂=-+=∂,(1-2) 式中:V —系统的势能函数1Vq ∂-∂—有势力的广义力 i q F —非有势力的广义力将式(2-2)代入式(2-l)得.11(1,2,...,)1i q d T T VF i k dt q q q ⎛⎫⎪∂∂∂-+== ⎪∂∂ ⎪∂⎝⎭二、二级倒立摆数学模型的推导二级倒立摆是一个多变量、快速、非线性、强祸合、和绝对不稳定的系统,为了简化建立数学模型的过程,我们做了以下假设: 1.上摆、下摆都是一个均匀的刚体;2.力矩电机的输出驱动力与其输入电压成正比,且无滞后地直接作用在小车上;3.车与轨道间的摩擦力仅与小车的速度成正比,下摆与车绞接处的摩擦力仅与摆的角速度成正比,上、下摆绞接处的摩擦力仅与摆的角速度成正比;4.忽略电机的电感;5.忽略钢丝的弹性。
直线二级倒立摆的建模和控制

西南科技大学自动化专业方向设计报告设计名称:直线二级倒立摆的建模和镇定控制姓名:学号:班级:指导教师:起止日期:方向设计任务书学生班级:学生姓名:学号:设计名称:起止日期:指导教师:方向设计学生日志直线二级倒立摆的建模与镇定控制摘要(150-250字)倒立摆是一个典型的多变量、非线性、强耦合、欠驱动的自然不稳定系统,对倒立摆系统的控制研究,能反映控制过程中的镇定、非线性和随动等问题,因此常用于各种控制算法的研究。
而且对倒立摆系统的研究还有重要的工程背景,对机器人行走、火箭的姿态调整等都有重要的现实意义。
本文以直线二级倒立摆系统为模型,阐释了直线二级倒立摆的建模方法和镇定控制算法。
其次介绍了直线二级倒立摆系统的结构和参数,应用拉格朗日方程建模方法详细推导了二级倒立摆的数学模型,并对系统的性能进行分析。
接下来,本文重点研究了最优控制算法在直线二级倒立摆镇定控制中的应用;在介绍倒立摆系统的最优控制算法的基础上,设计了系统的最优控制器,分析得出控制参数的选择规律;并且在Simulink上完成仿真实验,观察控制系统性能。
关键词:倒立摆;建模;LQR;镇定控制Modeling and Balance Control of the Linear DoubleInverted PendulumAbstract:Inverted pendulum is a typical multivariable, nonliner, closed coupled and quick movement natural instable system.The process of control research can reflect many key problems in control theory, such as the problem of tranquilization, non linearity, following and so on. So the inverted pendulum is commonly used for the study of many kinds of control theory. The research of inverted pendulum also has important background of engineering, and has practical significance for the Robot walk and Rocket-profile adjustment.In this paper, taking the linear double inverted pendulum system as the control model, reaching of the control system based on lagrange equation and optimal control algorithm. First of all, giving out the research significance and situation of the inverted pendulum system,and introducing the linear double inverted pendulum modeling methods and stabilization control theory. Secondly, introducing the structure and parameters of the inverted pendulum system. Researching of the inverted pendulum mathematical model based on lagrange equation, and giving a detailed derivation, then having stability analysis of the system. Next, this paper studied the inverted pendulum system’s optimal control algorithm,and designed the LQR controller based on it,then coming to the law of selection of control parameters. Finishing the simulation in the Simulink software,observing the performance of the control system.Key words: inverted pendulum, modeling, LQR, balance control一、设计目的和意义二、控制要求对直线二级倒立摆模型的物理特性做分析,然后利用拉格朗日方程建模方法建立倒立摆的数学模型。
二阶倒立摆课程设计

二阶倒立摆课程设计一、课程目标知识目标:1. 让学生掌握二阶倒立摆的基本概念,理解其物理原理和数学模型;2. 使学生了解二阶倒立摆的控制方法,包括PID控制、状态空间控制等;3. 引导学生探讨二阶倒立摆系统的稳定性分析,理解平衡条件及其影响因素。
技能目标:1. 培养学生运用数学工具进行二阶倒立摆模型建立和求解的能力;2. 提高学生运用控制理论对二阶倒立摆进行设计和仿真实验的技能;3. 培养学生团队合作精神,提高解决实际问题的能力和创新意识。
情感态度价值观目标:1. 培养学生对物理和控制学科的兴趣,激发学习热情和探究精神;2. 引导学生关注我国在二阶倒立摆领域的研究成果,增强民族自豪感;3. 培养学生严谨的科学态度,认识到科学技术的实际应用价值。
课程性质:本课程为理科学科,涉及物理学、数学和控制理论等多个领域,具有较高的理论性和实践性。
学生特点:学生处于高年级阶段,具备一定的物理、数学和控制理论基础,具有较强的逻辑思维能力和动手实践能力。
教学要求:结合学生特点和课程性质,注重理论知识与实践操作相结合,提高学生的综合素质和能力。
通过本课程的学习,使学生能够达到上述课程目标,为后续相关课程和实际应用打下坚实基础。
二、教学内容1. 二阶倒立摆的基本概念及物理原理:介绍二阶倒立摆的定义、分类及在实际应用中的重要性;分析二阶倒立摆的动力学模型,探讨影响系统稳定性的因素。
关联教材章节:第五章“倒立摆控制系统”,第1节“倒立摆的基本概念和物理原理”。
2. 数学建模与求解:运用数学工具,如微分方程、状态空间方程等,对二阶倒立摆进行建模;结合实际案例,讲解建模过程及求解方法。
关联教材章节:第五章“倒立摆控制系统”,第2节“倒立摆的数学建模与求解”。
3. 控制方法及其应用:介绍PID控制、状态空间控制等常用的二阶倒立摆控制方法;分析各种控制方法的优缺点及适用场景。
关联教材章节:第五章“倒立摆控制系统”,第3节“倒立摆的控制方法及其应用”。
倒立摆研究报告(DOC)

基于LQR控制的二级倒立摆系统研究作者:牛娟031210308王晨琳031210307王鹤彬031210312 学院:自动化指导老师:王晶、陆宁云摘要倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统,是进行控制理论研究的典型实验平台。
本文采用最优控制的方法设计二级倒立摆系统的控制器。
首先简要介绍了倒立摆以及倒立摆的几种常见控制方法,着重介绍了最优控制理论,其次对二级倒立摆系统进行了数学建模,最后对线性二次型最优控制原理进行了分析并使用MATLAB进行了仿真。
关键词:二级倒立摆,最优控制目录一、绪论 (3)1.1、倒立摆系统简介 (3)1.2、倒立摆系统的控制算法 (3)1.3、小结 (4)二、直线倒立摆的建模 (4)2.1、直线二级倒立摆的建模 (4)2.2、直线二级倒立摆的定性分析 (6)三、基于MATLAB的LQR仿真 (9)3.1、最优控制(LQR)简介 (9)3.2、线性二次型最有调节器原理 (9)3.3、MATLAB仿真 (10)3.4、SIMULINK仿真 (11)四、结束语 (13)4.1、小结 (13)4.2、未解决问题展望 (13)五、附录 (13)一、绪论1.1、倒立摆系统简介倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统,是进行控制理论研究的典型实验平台。
许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等,都可以通过倒立摆系统实验直观的表现出来。
在控制理论发展的过程中,某种控制理论的正确性及可行性需要通过设计一个控制器去控制一个典型的控制对象去加以验证。
倒立摆系统正是这样一种比较典型的控制对象。
最简单的倒立摆可由一个可在水平轨道上自由移动的小车和倒置摆铰链组成。
倒立摆的种类繁多,分类方法也多种多样:按结构来分有直线倒立摆,环形倒立摆,平面倒立摆;按级数来分有一级摆,二级摆,三级摆乃至更高级摆;按运动轨道来分有水平轨道倒立摆,倾斜轨道倒立摆;按控制电机数目来分有单电机倒立摆,多电机倒立摆。
二级倒立摆的建模问题

目录摘要 ..................................................................................... 错误!未定义书签。
ABSTRACT ................................................................................ 错误!未定义书签。
第1章绪论 .. (1)1.1研究背景和意义 (1)1.2国内外研究现状 (2)1.3 模糊控制的简介 (3)1.4倒立摆的最优控制与模糊控制与神经网络系统的简要比较 (4)第2章控制方案 (6)2.1模糊控制方案 (6)2.2 PID方案 (7)2.3模糊控制与PID控制的比较 (8)第3章控制系统的设计 (9)3.1二级倒立摆数学模型的建立 (9)3.2二级倒立摆的最优状态反馈控制 (15)3.3融合函数的设计 (16)3.4模糊控制器的设计 (18)第4章控制仿真 (23)4.1二级倒立摆模糊控制的调试 (23)4.2二级倒立摆PID控制的调试 (26)4.3模糊控制与PID控制的比较 (28)第5章结论 (29)参考文献 (30)致谢 (32)第1章绪论1.1研究背景和意义1.1.1 研究倒立摆的工程背景20世纪60年代到现在以来,可以看到科学家们为了处理侦察卫星在摄像机的轻微抖动时等不利状况,并且摄像机的轻微抖动时等不利状况对摄像的图像质量产生的一些或小或大的影响,为了使摄像机能自动地保持摄像时摄像的图像质量稳定,并且能够消除摄像机摄像的震动。
尽管第一台机器人从制作出来问世至今已有三十年的历史,机器人的一些关键技术一直没有很好地被处理,可以看到就像机器人的行走的控制至今仍未能很好解决和得以很好的控制。
在看到通信卫星在预先计算好的轨道运行时必须要保持其稳定,并且要通信卫星在确定的位置上运行的同时,必须要保证通信卫星的稳定,从而使卫星天线的线能够恒定的指向地球。
二级倒立摆的建模与MATLAB仿真毕业论文

二级倒立摆的建模与MATLAB仿真摘要:本文根据牛顿力学原理,使用机理建模法对二级倒立摆系统进行了建模与仿真研究。
利用最优化控制理论,研究了线性二次型最优控制器对倒立摆系统进行了有效控制。
基于MATLAB程序的设计、仿真的运行,结果表明,二级倒立摆的数学建模法是切实可行的,而且十分可靠,同时利用LQR 控制器实现了对系统的控制,可以达到系统所需要的稳定性,鲁棒性。
关键词:二次型最优控制;二级倒立摆;MATLAB1 引言倒立摆系统是一个常用的、简单的、典型的可进行控制理论研究的实验平台,很多难以用常规实验研究的控制理论问题,都可以通过倒立摆系统来进行研究从而使这些抽象的控制理论问题,通过该系统可以直观的鲜明的显示出来。
所以倒立摆系统一直是控制领域的热点,并且在这些年来在不断的发展进步对控制理论的研究起到了重要作用。
倒立摆系统是一个典型的不稳定系统,具有多变量、强耦合、非线性等特点。
同时也是仿人类行走机器人和火箭发射飞行的过程调整和直升机飞行等实际运用控制对象的最简模型。
本文建立在牛顿力学定律的基础上,研究对象设置为二级倒立摆,对其进行数学建模,再使用二次型最优控制器(linear quadratic regulator,LQR)可以得到一个最优状态反馈的矩阵K,然后在通过对Q和R两个加权矩阵的严谨选取从而实现对二级倒立摆系统良好的自动控制。
2 二级倒立摆模型建立一个典型的二级倒立摆系统主要由机械部分和电气装置两部分组成。
机械装置的结构主要由小车、摆杆1、摆杆2及连接轴等组成,电气装置的主要结构是功率放大器、电动机、驱动电路、保护电路等。
其系统的结构如图1所示。
实验假设如下:(1)小车、摆杆1、摆杆2的材料性质都是刚体的。
(2)小车的驱动力和放大器的输出直接的,无滞后的作用于小车上。
(3)忽略实验中过程中出现的不可避免的各种摩擦力如库伦摩擦力等。
图1 二级倒立摆控制系统的结构二级倒立摆的参数设定如表1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二级倒立摆数学模型的建立专业:自研-09姓名:***学号:2009Y********一、二级倒立摆系统的组成二级倒立摆主要由以下四部分组成:1.在有限长的轨道L上作直线运动的小车;2.与小车铰接在一起,并能在竖直平面内分别绕q,q点转动的下、上摆;3.驱动小车的直流力矩电机和转轮、钢丝等传动部分;4.使上、下摆稳定在垂直向上的平衡位置,且使小车稳定在轨道中心位置附近的控制器。
二级倒立摆的结构简图如图1的监督管理功能,如实时画面,数据采集等;数据采集卡安装在计算机内,用完成模/数、数/模转换;功率放大器用于电压和功率放大;电机是系统的执行元件;电位计是系统的测量元件,它分别检测小车相对于轨道中心点的相对位置、下摆相对于铅垂线的角位移、上摆相对于下摆延长线方向的角位移。
图1 倒立摆系统的计算机控制系统二级倒立摆系统的整套机械部件安装在一个钢架上,上面固定着导轨、电机底座和转轮等装置。
通过导轨支架安装好小车滑行的导轨,小车用电机和转轮通过传动钢丝实现运动。
2、结构参数通过实际物理测量,得到二级倒立摆系统的参数如下:小车的等效质量:M =1.0kg;小车与轨道间的滑动摩擦系数:b=5.0kg/s;下摆的质量:m=0.1481kg;下摆半长:1l =0.18m;下摆绕其重心的转动惯量:1j =0.00192kgm ; 上摆质量:2m =0.0998kg; 上摆半长:2l =0.24m;上摆绕其重心的转动惯量: 2j = 0.00182kgm ; 上、下摆重心之间的距离: 1L =0.29m;上、下摆之间的转动摩擦系数: 2F =0.0l 2kgm /s; 下摆和小车之间的转动摩擦系数:1F =0.012kgm /s; 电机及功率放大器的增益: u K =15Nt/V 。
3、Lagrange 方程介绍Lgarnage 方程为..11(1,2,...,)1i q d T T V DF i k dt q q i q q ⎛⎫⎪∂∂∂∂-++== ⎪∂∂ ⎪∂∂⎝⎭(1-1)式中T —系统的动能函数,.1q ,q ,—Lganarge 变量,分别成为广义坐标和广义速度Qi —作用于系统上的广义力 1(1,2,...,)i q VQi F i k q ∂=-+=∂,(1-2) 式中:V —系统的势能函数1Vq ∂-∂—有势力的广义力 i q F —非有势力的广义力将式(2-2)代入式(2-l)得.11(1,2,...,)1i q d T T VF i k dt q q q ⎛⎫⎪∂∂∂-+== ⎪∂∂ ⎪∂⎝⎭二、二级倒立摆数学模型的推导二级倒立摆是一个多变量、快速、非线性、强祸合、和绝对不稳定的系统,为了简化建立数学模型的过程,我们做了以下假设: 1.上摆、下摆都是一个均匀的刚体;2.力矩电机的输出驱动力与其输入电压成正比,且无滞后地直接作用在小车上;3.车与轨道间的摩擦力仅与小车的速度成正比,下摆与车绞接处的摩擦力仅与摆的角速度成正比,上、下摆绞接处的摩擦力仅与摆的角速度成正比;4.忽略电机的电感;5.忽略钢丝的弹性。
在以上假设前提下,我们采用分析力学中的Lganarge 方程来建立系统的数学模型。
令:为水平导轨运动的位移,拭、氏分别为下摆和上摆偏移竖直方向的角度。
由于系统存在着摩擦力,属于一个耗散系统,因此式(2-3)部分应该加上耗能部分,对于同时受到保守力和耗散力作用的倒立摆系统的Lagrange 方程为:..11(1,2,...,)1i q d T T V DF i k dt q q i q q ⎛⎫⎪∂∂∂∂-++== ⎪∂∂ ⎪∂∂⎝⎭ 式中:i q —广义坐标,即r 、1θ、2θi q F —非有势广义力,当i q =r 时,i q F =0G U ,U 为控制量,0G 为增益常数,当i q =1θ、2θ时,i q F =0T 、V 、D —分别是系统的动能、势能和消耗能n i i T T ==∑、0n i i V V ==∑、0ni i D D ==∑ (1-5)式中:n —倒立摆的级数,这里n=2i T —小车和各级倒摆的动能i V —小车和各级倒摆的势能 i D —小车和各级倒摆的消耗能将上述各式i T ,i V ,i D (i=0,1,2)代入式(2-4),得二级倒立摆的数学模型为式(2-6)式是一个非线性向量微分方程。
考虑到系统工作时,是在平衡位置附近运动,可将式(2-6)在u=0的平衡位置r=1θ=2θ=.r =.1θ=.2θ=0附近线性化,以线性化后的方程来代替式(2-6)的非线性向量微分方程。
具体线性化是忽略二次以上的项(或因为1θ,2θ在5±。
以内,故sin θθ≈,cos 1θ≈),可求出关于dr ,d 1θ,d 2θ的线性化微分方程,而后将dr ,d 1θ,d 2θ改写成r ,1θ,2θ,便可得到系统的状态方程。
根据物理模型的实测数据,可求得平衡点处的常数阵:利用Matlab 中的求逆命令,可以解得1(0,0)M -阵所以,对式(2-6)进行线性化后,系统状态方程为:对于下摆有转角1θ时,取上摆的相对角位移为21θθ-,故令故式(2-7)可改写为定义状态向量x 为则由式(2-8)可得将物理模型的实测参数代入式(2-9),得到二级倒立摆的系数矩阵为由此可知,二级倒立摆系统的数学模型为.x Ax Bu y Cx ⎧⎪⎪⎨⎪⎪⎩=+= 式中:A=0 0 0 1.0000 0 0 0 0 0 0 1.0000 0 0 0 0 0 0 1.0000 0 -1.9600 0.0940 -4.8000 0.0040 -0.0040 0 46.1200 -25.0100 18.7600 -0.1300 0.2400 0 -51.0100 78.1600 -20.7500 0.2400 -0.5700 B=0 0 0 14.4137 -52.286462.2532 C=1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 系统状态图:首先,使用MATLAB ,判断系统的能控性矩阵是否为满秩。
程序如下:A=[0 0 0 1 0 0;0 0 0 0 1 0 ;0 0 0 0 0 1;0 -1.96 0.094 -4.8 0.004 -0.004;0 46.12 -25.01 18.76 -0.13 0.24;0 -51.01 78.16 -20.75 0.24 -0.57];B=[0 0 0 14.4137 -52.2864 62.2532];B1=B';C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];rct=rank(ctrb(A,B1))计算结果为:rct = 6根据判别系统能控性的定理,该系统的能控性矩阵满秩,所以该系统是能控的。
因为系统是能控的,所以,可以通过状态反馈来任意配置极点。
不失一般性,不妨将极点配置在s1=-6,s2=-6.5,s3=-7,s4=-7.5,s5=-8,s6=-8.5在MATLAB中输入程序:A=[0 0 0 1 0 0;0 0 0 0 1 0 ;0 0 0 0 0 1;0 -1.96 0.094 -4.8 0.004 -0.004;0 46.12 -25.01 18.76 -0.13 0.24;0 -51.01 78.16 -20.75 0.24 -0.57];B=[0 0 0 14.4137 -52.2864 62.2532];B1=B';P=[-6 -6.5 -7 -7.5 -8 -8.5 ];K=place(A,B1,P)计算结果为:K =4.8696 28.2425 36.0516 6.3136 7.83205.7267因此,求出状态反馈矩阵为K =4.8696 28.2425 36.0516 6.3136 7.83205.7267采用MATLAB/Simulink构造二级倒立摆状态反馈控制系统的仿真模型,如下图所示。
三、状态观测器实现状态反馈极点配置及其仿真首先,使用MATLAB,判断系统的能观性矩阵是否为满秩。
输入以下程序A=[0 0 0 1 0 0;0 0 0 0 1 0 ;0 0 0 0 0 1;0 -1.96 0.094 -4.8 0.004 -0.004;0 46.12 -25.01 18.76 -0.13 0.24;0 -51.01 78.16 -20.75 0.24 -0.57];B=[0 0 0 14.4137 -52.2864 62.2532];B1=B';C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];rob=rank(obsv(A,C))rob =6因为该系统的能观测性矩阵满秩,所以该系统是能观测的。
因为系统是能观测的,所以,可以设计状态观测器。
而系统又是能控的,因此可以通过状态观测器实现状态反馈。
设计状态观测器矩阵,使的特征值的实部均为负,且其绝对值要大于状态反馈所配置极点的绝对值。
通过仿真发现,这样才能保证状态观测器有足够快的收敛速度,才能够保证使用状态观测器所观测到的状态与原系统的状态充分接近。
不妨取状态观测器的特征值为:=---=-=-ssss1s-=s==,,256,,。
,20242123222345输入以下命令:A=[0 0 0 1 0 0;0 0 0 0 1 0 ;0 0 0 0 0 1;0 -1.96 0.094 -4.8 0.004 -0.004;0 46.12 -25.01 18.76 -0.13 0.24;0 -51.01 78.16 -20.75 0.24 -0.57];A1=A';C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];C1=C';P=[-20 -21 -22 -23 -24 -25];G1=place(A1,C1,P);G=G1'求出状态观测器矩阵为:G =38.2600 0.1197 -0.283617.7903 44.7264 0.7555-17.4652 0.6889 46.5137275.9610 1.1437 -5.5261690.8092 544.3198 -7.4808-704.7150 -33.5983 609.9059采用MATLAB/Simulink构造具有状态观测器的二级倒立摆状态反馈控制系统的仿真模型,如下图所示。
四、实验分析由两图可示,比较两个仿真结果,具有状态观测器的二级倒立摆状态反馈系统的控制效果和没有状态观测器的控制系统的控制效果是一样的。
可见,加状态观测器并不影响系统的输出。
