三角函数向量测试题
三角函数和平面向量专题练习2

北
B
的位置 C 处 (1) 求该船的行驶速度.
西
A
45° θ
C D
东
(2) 若该船不改变航行方向,判断它是否会进入警戒 水域,并说明理由.
P E Q
20 用 a, b, c 分别表示 ∆ABC 的三个内角 A, B, C 所对的边的边长, R 表示 ∆ABC 的外接圆半径 (1)如图在 O 以为圆心,半径为 2 的 O 中, BC , BA 分别是 O 的弦,其中 BC = 2, ∠ABC = 45° ,求 弦 AB 的长 (2)在 ∆ABC 中,若 ∠C 为钝角,求证: a 2 + b 2 ≤ 4 R 2 (3)给定三个正实数 a, b, R ,其中 a ≥ b ,问 a, b, R 满足怎样的关系是时,以 a, b 为边长,以 R 为外 接圆半径的 ∆ABC 不存在,存在一个,或存在两个(全等的 三角 形 算作同 一个 ), 在 ∆ABC 存 在的 情况 下 ,用 a, b, R 表 示c
uuu r uuur
1 2
16. 在三角形 ABC 中, 用 a, b, c 分别表示 ∆ABC 的三个内角 A, B, C 所对的边的边长,已知
∠B = 45° , b = 10, cos C = 2 5 5
(1)求边长 BC 的值 (2 若 AB 的中点为 D ,求中线 CD 的值.
2/8
π π 17. 已知函数 f ( x ) = 2 sin x + − 2 cos x, x ∈ , π 6 2
2 n 为偶数时, ○
f n (θ ) = sin n θ + cos n θ ,∴ f n′ (θ ) = n sin n −1 θ ⋅ cos θ − n cos n −1 θ sin θ = n sin θ cos θ ( sin n − 2 θ − cos n − 2 θ )
向量与三角函数专题

向量与三角函数一、解三角形例5.已知ABC △1,且sin sin A B C +=. (I )求边AB 的长;(II )若ABC △的面积为1sin 6C ,求角C 的度数.解:(I )由题意及正弦定理,得1AB BC AC ++=,BC AC +=,两式相减,得1AB =.(II )由ABC △的面积11sin sin 26BC AC C C = ,得13BC AC = , 由余弦定理,得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--== ,所以60C = .例6. 如图,在ABC ∆中,2AC =,1BC =,43cos =C .(1)求AB 的值;(2)求()C A +2sin 的值. 解答过程:(Ⅰ) 由余弦定理,得2222..cos AB AC BC AC BC C =+- 341221 2.4=+-⨯⨯⨯=那么,AB(Ⅱ)由3cos 4C =,且0,C π<<得sin C 由正弦定理,得,sin sin AB BC C A=解得sin sin BC C A AB==所以,cos A .由倍角公式sin 2sin 2cos A A A =⋅=, 且29cos 212sin 16A A =-=,故()sin 2sin 2cos cos 2sin A C A C A C +=+例7.在ABC △中,1tan 4A =,3tan 5B =. (Ⅰ)求角C 的大小;(Ⅱ)若AB,求BC 边的长.解:(Ⅰ)π()C A B =-+ ,1345tan tan()113145C A B +∴=-+=-=-- .又0πC << ,3π4C ∴=.(Ⅱ)由22sin 1tan cos 4sin cos 1A A A A A ⎧==⎪⎨⎪+=⎩,,且π02A ⎛⎫∈ ⎪⎝⎭,,得sin A =sin sin AB BC C A =,sin sin A BC AB C ∴== 二.求三角函数的定义域、值域或最值 典型例题例8.已知函数11()(sin cos )sin cos 22f x x x x x =+--,则()f x 的值域是( )A.[]1,1-B.⎡⎤⎢⎥⎣⎦C.⎡-⎢⎣⎦D.1,⎡-⎢⎣⎦)),,444, 1.,,,24f x x x x f x x f x A C D x f x πππππ+-∴==--=-=解法1:(当时(故选C.11解法2:当时()=知不可能.又由时(知选C.22例9. 设函数b a x f 、=)(.其中向量2)2π(R,),1,sin 1(),cos ,(=∈+==f x x b x m a 且. (Ⅰ)求实数m 的值;(Ⅱ)求函数)(x f 的最小值.解:(Ⅰ)()(1sin )cos f x m x x ==++a b ,πππ1sin cos 2222f m ⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭,得1m =. (Ⅱ)由(Ⅰ)得π()sin cos 114f x x x x ⎛⎫=++=++ ⎪⎝⎭,∴当πsin 14x ⎛⎫+=- ⎪⎝⎭时,()f x的最小值为1例10.已知函数1)4()cos x f x xπ-=, (Ⅰ)求()f x 的定义域;(Ⅱ)设α是第四象限的角,且4tan 3α=-,求()f α的值.解答过程:(Ⅰ) 由cos 0x≠得()2x k k Z ππ≠+∈.故()f x 的定义域为,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭, (Ⅱ) 因为43tan ,cos ,55αα=-=且第四象限的角, 所以43sin ,cos ,55αα=-=故()()21)4cos 122)22cos 1sin 2cos 2cos 2cos 2sin cos cos 2cos sin 14.5f πααααααααααααααα-==-+=-==-=例11设)0(cos sin )(>+=ωωωx b x a x f 的周期π=T ,最大值4)12(=πf , (1)求ω、a 、b 的值;(2)的值终边不共线,求、、的两根,为方程、、若)tan(0)(βαβαβα+=x f .解答过程:(1))x sin(b a )x (f 22ϕ+ω+=, π=∴T , 2=ω∴, 又 )x (f 的最大值4)12(f =π , 22b a 4+=∴ ① , 且 122cos b 122sin a 4π+π= ②, 由 ①、②解出 a=2 , b=3.(2) )3x 2sin(4x 2cos 32x 2sin 2)x (f π+=+=, 0)(f )(f =β=α∴,)32sin(4)32sin(4π+β=π+α∴,32k 232π+β+π=π+α∴, 或)32(k 232π+β-π+π=π+α, 即 β+π=αk (βα、 共线,故舍去) , 或 6k π+π=β+α,33)6k tan()tan(=π+π=β+α∴ )Z k (∈.例12.设函数2()sin cos f x x x x a ωωω=++(其中0,a R ω>∈),且()f x 的图象在y 轴右侧的第一个最高点的横坐标为6π.(I )求ω的值;(II )如果()f x 在区间5,36ππ⎡⎤-⎢⎥⎣⎦a 的值.解答过程:(Ⅰ)1()2sin 22f x x x a ωω=+sin(2)3x a πω=+, 依题意得 2632πππω⋅+=, 解得 12ω=.(Ⅱ)由(Ⅰ)知,()sin()3f x x a π=+,又当5,36x ππ⎡⎤∈-⎢⎥⎣⎦时,70,36x ππ⎡⎤+∈⎢⎥⎣⎦,故11sin()123x -≤+≤,从而()f x 在5[,]36ππ-上取得最小值12a -.因此,由题设知12a -故a =例13.已知函数R x x x x f ∈++=),2sin(sin )(π(Ⅰ)求)(x f 的最小正周期;(Ⅱ)求)(x f 的最大值和最小值; (Ⅲ)若43)(=αf ,求α2sin 的值.命题目的:本题考查利用三角函数的性质, 诱导公式、同角三角函数的关系式、两角和的公式,倍角公式等基本知识,考查运算和推理能力. 解答过程:)4sin(2cos sin )2sin(sin )(ππ+=+=++=x x x x x x f(Ⅰ))(x f 的最小正周期为ππ212==T ;(Ⅱ))(x f 的最大值为2和最小值2-;(Ⅲ)因为43)(=αf ,即37sin cos 2sin cos .416αααα+=⇒=-即 1672sin -=α. 三.三角函数的图象和性质 典型例题 例14.已知函数22()sin 2sin cos 3cos ,f x x x x x x R =++∈.求:(Ⅰ)求函数()f x 的最大值及取得最大值的自变量x 的集合; (Ⅱ)函数()f x 的单调增区间. 解答过程:(I )解法一: ()1cos 23(1cos 2)sin 222x f x x θ-+=++2sin 2cos 2x x =++2)4x π=+. ∴当2242x k πππ+=+,即()8x k k Z ππ=+∈时,()f x 取得最大值2因此,()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 解法二:222()(sin cos )sin 22cos f x x x x x =+++ 1sin 21cos 2x x =+++2)4x π=+.∴当2242x k πππ+=+,即()8x k k Z ππ=+∈时,()f x 取得最大值2因此,()f x 取得最大值的自变量x 的集合是,8x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭.(Ⅱ)解: ()2)4f x x π=+由题意得222()242k x k k Z πππππ-≤+≤+∈,即3()88k x k k Z ππππ-≤≤+∈.因此, ()f x 的单调增区间是()3,88k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.例15.(本小题满分12分) 已知函数2π()cos 12f x x ⎛⎫=+⎪⎝⎭,1()1sin 22g x x =+. (I )设0x x =是函数()y f x =图象的一条对称轴,求0()g x 的值. (II )求函数()()()h x f x g x =+的单调递增区间. 解:(I )由题设知1π()[1cos(2)]26f x x =++. 因为0x x =是函数()y f x =图象的一条对称轴,所以0π26x +πk =, 即0 π2π6x k =-(k ∈Z ). 所以0011π()1sin 21sin(π)226g x x k =+=+-.当k 为偶数时,01π13()1sin 12644g x ⎛⎫=+-=-= ⎪⎝⎭, 当k 为奇数时,01π15()1sin 12644g x =+=+=. (II )1π1()()()1cos 21sin 2262h x f x g x x x ⎡⎤⎛⎫=+=++++ ⎪⎢⎥⎝⎭⎣⎦1π3113cos 2sin 2sin 2262222x x x x ⎫⎡⎤⎛⎫=+++=++⎪ ⎪⎢⎥⎪⎝⎭⎣⎦⎝⎭1π3sin 2232x ⎛⎫=++ ⎪⎝⎭. 当πππ2π22π232k x k -++≤≤,即5ππππ1212k x k -+≤≤(k ∈Z )时, 函数1π3()sin 2232h x x ⎛⎫=++ ⎪⎝⎭是增函数, 故函数()h x 的单调递增区间是5ππππ1212k k ⎡⎤-+⎢⎥⎣⎦,(k ∈Z ) 例16.已知函数22()sin cos 2cos ,.f x x x x x x R =+∈ (I )求函数()f x 的最小正周期和单调增区间;(II )函数()f x 的图象可以由函数sin 2()y x x R =∈的图象经过怎样的变换得到?解答过程:(I)1cos 2()2(1cos 2)22x f x x x -=+++132cos 2223sin(2).62x x x π=++=++ ()f x ∴的最小正周期2.2T ππ== 由题意得222,,262k x k k Z πππππ-≤+≤+∈即 ,.36k x k k Z ππππ-≤≤+∈()f x ∴的单调增区间为,,.36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦(II )方法一:先把s i n 2y x =图象上所有点向左平移12π个单位长度,得到sin(2)6y x π=+的图象,再把所得图象上所有的点向上平移32个单位长度,就得到3s i n (2)62y x π=++的图象.方法二: 把sin 2y x =图象上所有的点按向量3(,)122a π=- 平移,就得到3sin(2)62y x π=++的图象.例17.已知函数2())2sin ()().612f x x x x R ππ=-+-∈(I )求函数()f x 的最小正周期;(II )求使函数()f x 取得最大值的x 集合.解答过程:(Ⅰ) f(x)=3sin(2x -π6)+1-cos2(x -π12) = 2[32sin2(x -π12)-12 cos2(x -π12)]+1 =2sin[2(x -π12)-π6]+1 = 2sin(2x -π3) +1 .∴ T=2π2 =π.(Ⅱ)当f(x)取最大值时, sin(2x -π3)=1,有 2x -π3 =2k π+π2 , 即x=k π+ 5π12 (k ∈Z) ∴所求x 的集合为{x ∈R|x= k π+ 5π12 , k ∈Z}. 四.平面向量、三角函数的图象和性质 典型例题例18.将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )A .sin()6y x π=+ B .sin()6y x π=-C .sin(2)3y x π=+ D .sin(2)3y x π=-解答过程:将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移,平移后的图象所对应的解析式为sin ()6y x πω=+,由图象知,73()1262πππω+=,所以2ω=,因此选C.例19.已知向量(sin ,1),(1,cos ),.22a b ππθθθ==-<<(Ⅰ)若a b ⊥,求θ;(Ⅱ)求a b +的最大值.解:(Ⅰ),sin cos 0a b θθ⊥若则+=,由此得 tan 1ππθθ=- (-<<),22所以 ;4πθ=-(Ⅱ) 由(sin ,1),(1,cos )(sin 1,1cos ),a b b b θθθθ== α+=++ α+= = =得当sin()1,,, 1.44a b a b ππθθ+=+=+时取得最大值即当时例20.已知,,A B C 是三角形ABC ∆三内角,向量((),cos ,sin m n A A =-=,且1m n ⋅=(Ⅰ)求角A ;(Ⅱ)若221sin 23cos sin BB B+=--,求tan B .解答过程:(Ⅰ)∵1m n ⋅=,∴(()cos ,sin 1A A -⋅= ,cos 1A A -=.12sin cos 12A A ⎛⎫⋅= ⎪ ⎪⎝⎭, 1sin 62A π⎛⎫-= ⎪⎝⎭. ∵50,666A A ππππ<<-<-<, ∴66A ππ-= . ∴3A π=.(Ⅱ)由题知2212sin cos 3cos sin B B B B+=--,整理得22sin sin cos 2cos 0B B B B --=∴cos 0B ≠ ∴2tan tan 20B B --=. ∴tan 2B =或tan 1B =-.而tan 1B =-使22cos sin 0B B -=,舍去. ∴tan 2B =.∴()tan tan C A B π=-+⎡⎤⎣⎦()tan A B =-+tan tan 1tan tan A B A B+=--=。
三角函数单招(大题)

三角函数解答题专项训练1.设向量a=(√3sinx,sinx),b=(cosx,sinx),x∈[0,π/2].(1)若∣a∣=∣b∣,求x的值;(2)设函数f(x)=a*b,求f(x)的最大值.2.已知函数f(x)=2sin(x-π/3).(1)写出函数f(x)的周期;(2)将函数f(x)图象上所有的点向左平移π/3个单位,得到函数g(x)的图象,写出函数g(x)的表达式,并判断函数g(x)的奇偶性.3.已知函数f(x)=sinx+√3 cosx-√3.(1)求f(x)的最小正周期;(2)求f(x)在区间[0,2π/3]上的最小值.4.在锐角△ABC 中,内角A 、B 、C 所对的边分别是a 、b 、c ,若C=45°,b=4√5,sinB= (1)求c 的值; (2)求sinA 的值.5.已知函数f (x )=sinx+√3cosx-√3.(1)求f (x )的最小正周期;(2)求f (x )在区间[0,2π/3]上的最小值.6. 已知函数f (x )=sinx+cosx ,x ∈R.(1)求f (x )的最小正周期和最大值;(2)函数f (x )的图象可由y=sinx 的图象经过怎样的变换得到?2√5 57.已知函数f(x)=2cos²x+√3sin2x-1;(1)求f(π/6)的值;(2)求函数f(x)的最小正周期和单调递增区间.8.已知函数f(x)=4cosx sin(x+π/6)-1.(1)求f(x)的最小正周期;(2)求f(x)在区间[-π/6,π/4]上的最大值和最小值.9.已知函数f(x)=2sinwxcoswx+cos2wx(w>0)的最小正周期为π.(1)求w的值;(2)求f(x)的单调递增区间.10.已知函数f (x )=cosx sin (x+π/3)-√3cos ²x+x ∈R. (1)求f (x )的最小正周期;(2)求f (x )在[-π/4,π/4]上的最大值和最小值.11.已知函数f (x )=√3sinx cosx-cos (2x+π/3)-cos ²x.(1)求f (x )的最小正周期、最值和单调区间.12.已知函数f (x )=sin ²x+√3sinx cosx+2cos ²x (x ∈R ).(1)求函数f (x )的最小正周期;(2)求函数的单调区间;(3)求函数图象的对称中心.√3 4。
向量和三角函数
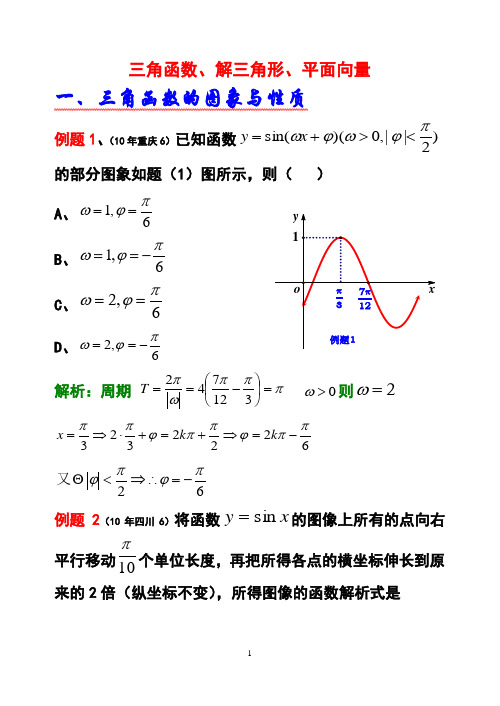
三角函数、解三角形、平面向量一、三角函数的图象与性质例题1、(10年重庆6)已知函数)2||,0)(sin(πϕωϕω<>+=x y的部分图象如题(1)图所示,则( ) A 、6,1πϕω==B 、6,1πϕω-==C 、6,2πϕω== D 、6,2πϕω-==解析:周期 πππωπ=⎪⎭⎫ ⎝⎛-==312742T 0>ω则2=ω6222323ππϕππϕππ-=⇒+=+⋅⇒=k k x62πϕπϕ-=⇒∴<又例题2(10年四川6)将函数x y sin =的图像上所有的点向右平行移动10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是(A )⎪⎭⎫ ⎝⎛-=102sin πx y (B )⎪⎭⎫ ⎝⎛-=52sin πx y(C )⎪⎭⎫ ⎝⎛-=1021sin πx y (D )⎪⎭⎫ ⎝⎛-=2021sin πx y 例题3(10年湖北)已知函数f(x)=cos ⎝ ⎛⎭⎪⎪⎫π3+x ·cos ⎝⎛⎭⎪⎪⎫π3-x ,g(x)=12sin 2x -14.(1)求函数f(x)的最小正周期;(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x 的集合. 解 (1)因为f(x)=cos ⎝ ⎛⎭⎪⎪⎫π3+x cos ⎝⎛⎭⎪⎪⎫π3-x =⎝ ⎛⎭⎪⎪⎫12cos x -32sin x ⎝ ⎛⎭⎪⎪⎫12cos x +32sin x =14cos 2x -34sin 2x =1+cos 2x 8-3-3cos 2x 8=12cos 2x -14, 所以f(x)的最小正周期为2π2=π.(2)h(x)=f(x)-g(x)=12cos 2x -12sin 2x =22cos ⎝⎛⎭⎪⎪⎫2x +π4, 当2x +π4=2k π(k ∈Z)时,h(x)取得最大值22.h(x)取得最大值时,对应的x 的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪x =kx -π8,k ∈Z试题分析 主要考查综合运用三角公式、三角函数图像和性质进行运算求解的能力.以三角函数的运算和性质为主线,着重对基础知识和基本方法的考查.题目难度不大,重视基础、强调应用.重点考查 (1)三角恒等变换公式.(2) B x A y ++=)sin(ϕω的性质和图像变化等基础知识. 主干知识:1.任意角的三角函数(1)设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么sin α=y ,cos α=x ,tan α=yx.(2)各象限角的三角函数值的符号:一全正,二正弦, 三正切,四余弦.2.诱导公式 απ±k 和απ±2 3.同角三角函数基本关系式sin 2α+cos 2α=1,tan α=sin αcos α(cos α≠0).4.正弦、余弦、正切函数的性质定义域 值域 图像 周期性 单调区间 对称中心 对称轴 最值考点分类题型一 三角函数的概念、诱导公式及基本关系式的 应用例题1、如图在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角α、β,它们的终边分别与单位圆交于A 、B 两点,已知A 、B 的横坐标分别为210、255.(1)求tan(α+β)的值;(2)求α+2β的值.分析 根据任意角三角函数的定义cos α=xr不难得到cos α、cos β的值,利用同角三角函数可求sin α、 sin β、tan α、tan β的值,进而利用和角公式求tan(α+β)的值.注意到第(2)问相当于“给值求角”问题,除注意到“角的变换”:α+2β=(α+β)+β外,还应注意该类问题求解的一般程序.解 (1)由已知条件及三角函数的定义可知, cos α=210,cos β=255.因为α为锐角,故sin α>0,从而sin α=1-cos 2α=7210.同理可得sin β=55.因此tan α=7,tan β=12.所以tan(α+β)=tan α+tan β1-tan αtan β=7+121-7×12=-3. (2)tan(α+2β)=tan[(α+β)+β]=tan(α+β)+tan β1-tan(α+β)tan β=-3+121-(-3)×12=-1,又0<α<π2,0<β<π2,故0<α+2β<3π2,从而由tan(α+2β)=-1得α+2β=3π4.本题考查三角函数的基本概念、三角函数的基本关系式、两角和的正切、二倍角的正切公式,考查考生的运算求解能力.根据三角函数的定义,本题所给的两个横坐标实际上就是α、β的余弦值,又由于这两个角都是锐角,由同角三角函数的关系式就可以求出这两个角的正切,剩下的问题就是代入公式计算了.例题2、 已知点P (sin 3π4,cos 3π4落在角θ的终边上,且θ∈[0,2π),则θ的值为 ( ) A.π4 B.3π4 C.5π4 D.7π4 解析 tan θ=cos 34πsin 34π=-cosπ4sin π4=-1,又sin 34π>0,cos 34π<0,∴θ为第四象限角且θ∈[0,2π),∴θ=7π4,故选D.题型二 三角函数的图象及函数y =A sin(ωx +φ)的解析式 例题1、函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的一段图象如图所示),求其解析式. 分析:先由图象求出函数的周期,从而求得ω的值,再由关键 点求φ,最后将(0,2)代入求A 的值 解 设函数的周期为T ,则34T =7π8-π8=34π,∴T =π,∴ω=2πT =2 又由2×π8+φ=π2,得φ=π4.∴函数解析式为y =A sin(2x +π4).又图象过点(0,2),∴A sin π4=2,∴22A =2,∴A =2.∴所求函数的解析式为y =2sin(2x +π4).分析提高 (1 )已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象求解析式时,常采用待定系数法,由图中的最高点、最低点或特殊点求A ;由函数的周期确定ω;由图象上的关键点确定φ.(2)求函数的周期时,注意以下规律:相邻的最高点与最低点的横坐标之差的绝对值为半个周期,最高点(或最低点)的横坐标与相邻零点差的绝对值为14个周期。
三角函数练习题及答案

三角函数练习题及答案一、填空题1.已知球O 的表面积为16π,点,,,A B C D 均在球O 的表面上,且,4ACB AB π∠=则四面体ABCD 体积的最大值为___________.2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,1a =,34A π=,若b c λ+有最大值,则实数λ的取值范围是_____.3.在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c .D 、E 是线段AB 上满足条件1()2CD CB CE =+,1()2CE CA CD =+的点,若2CD CE c λ⋅=,则当角C 为钝角时,λ的取值范围是______________4.通信卫星与经济、军事等密切关联,它在地球静止轨道上运行,地球静止轨道位于地球赤道所在平面,轨道高度为km h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球(球心为O ,半径为km r ),地球上一点A 的纬度是指OA 与赤道平面所成角的度数,点A 处的水平面是指过点A 且与OA 垂直的平面,在点A 处放置一个仰角为θ的地面接收天线(仰角是天线对准卫星时,天线与水平面的夹角),若点A 的纬度为北纬30,则tan θ________.5.在ABC 中,sin 2sin B C =,2BC =.则CA CB ⋅的取值范围为___________.(结果用区间表示)6.已知函数()()2sin 06f x x πωω⎛⎫=+> ⎪⎝⎭,若()f x 的图象关于直线3x π=对称,且在3,164ππ⎛⎫⎪⎝⎭上单调,则ω的最大值是______.7.关于函数())cos sin f x x x x =+①其表达式可写成()cos 26f x x π⎛⎫=+ ⎪⎝⎭;②直线12x π=-是曲线()y f x =的一条对称轴;③()f x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增;④存在0,2πα⎛⎫∈ ⎪⎝⎭使()()3f x f x αα+=+恒成立.其中正确的是______(填写正确的番号).8.如图,在边长为2的正方形ABCD 中,M ,N 分别为边BC ,CD 上的动点,以MN 为边作等边PMN ,使得点A ,P 位于直线MN 的两侧,则PN PB ⋅的最小值为______.9.已知直线y m =与函数3()sin (0)42f x x πωω⎛⎫=++> ⎪⎝⎭的图象相交,若自左至右的三个相.邻交点...A ,B ,C 满足2AB BC =,则实数m =______. 10.已知1OB →=,,A C 是以O 为圆心,220BA BC →→⋅=,设平面向量OA →与OB →的夹角为θ(π04θ≤≤),则平面向量OA →在BC →方向上的投影的取值范围是_____.二、单选题11.已知函数()|sin |(0)f x x ωω=>在区间,53ππ⎡⎤⎢⎥⎣⎦上单调递减,则实数ω的取值范围为( ) A .5,32⎡⎤⎢⎥⎣⎦B .30,2⎛⎤ ⎥⎝⎦C .8,33⎡⎤⎢⎥⎣⎦D .50,4⎛⎤ ⎥⎝⎦12.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭,3B π=,则a c +的取值范围是( ) A .33⎝ B .332⎛ ⎝C .33⎡⎤⎢⎥⎣ D .332⎡⎢⎣13.已知O 是三角形ABC 的外心,若()22AC ABAB AO AC AO m AO AB AC⋅+⋅=,且sin sin 3B C +=,则实数m 的最大值为( )A .3B .35C .75D .3214.已知函数()()sin f x x ωφ=+π0,02ωφ⎛⎫><< ⎪⎝⎭在π5π,88⎛⎫ ⎪⎝⎭上单调,且π3π088f f ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,则π2f ⎛⎫⎪⎝⎭的值为( ) A 22B .1C .1-D .22-15.已知F 是椭圆2221(1)x y a a+=>的左焦点,A 是该椭圆的右顶点,过点F 的直线l (不与x 轴重合)与该椭圆相交于点M ,N .记MAN α∠=,设该椭圆的离心率为e ,下列结论正确的是( ) A .当01e <<时,2πα<B .当202e <<时,2πα>C .当1222e <<时,23πα>D .当212e <<时,34πα> 16.如图,长方形ABCD 中,152AB =,1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14B .23C 151-D 51-17.在ABC 中,若22sin cos 1A B +=,则8cos AB BCBC A AC+的取值范围为( )A .)43,8⎡⎣B .)43,7⎡⎣C .()7,8D .(0,4318.设函数242,0()sin ,60x x x f x x x ⎧-+≥=⎨-≤<⎩,对于非负实数t ,函数()y f x t =-有四个零点1x ,2x ,3x ,4x .若1234x x x x <<<,则1234x x x x ++的取值范围中的整数个数为( )A .0B .1C .2D .319.已知1F ,2F 分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,过点1F 且垂直于x 轴的直线与双曲线交于A ,B 两点,若2ABF 是钝角三角形,则该双曲线离心率的取值范围是( ) A .(21,)+∞B .(12,)+∞C .(1,12)D .(31,)+∞20.在锐角ABC 中,若cos cos sin sin 3sin A C B C a c A+=3cos 2C C +=,则a b +的取值范围是( ) A .(6,23⎤⎦B .(0,43C .(23,43D .(6,43三、解答题21.若函数()y f x =的图像上存在两个不同的点关于y 轴对称,则称函数()y f x =图像上存在一对“偶点”.(1)写出函数()sin f x x =图像上一对“偶点”的坐标;(不需写出过程) (2)证明:函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”;(3)若函数()2()x h x e mx m =--∈R 图像上有且只有一对“偶点”,求m 的取值范围.22.已知函数()()()()2cos +2cos 02f x x x x πϕϕϕϕ⎛⎫=+++<< ⎪⎝⎭.(1)求()f x 的最小正周期;(2)若13f π⎛⎫= ⎪⎝⎭,求当()2f x =时自变量x 的取值集合.23.已知函数2()2sin cos ()f x x x x a a R =-++∈,且(0)f = (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围.24.已知(3cos ,sin ),(sin ,0),0a x x b x ωωωω==>,设()(),f x a b b k k R =+⋅+∈. (1)若()f x 图象中相邻两条对称轴间的距离不小于2π,求ω的取值范围; (2)若()f x 的最小正周期为π,且当,66x ππ⎡⎤∈-⎢⎥⎣⎦时,()f x 的最大值是12,求()f x 的解析式,并说明如何由sin y x =的图象变换得到()y f x =的图象.25.已知函数()2sin 2cos 3f x x a x =+-.(1)当1a =时,求该函数的最大值;(2)是否存在实数a ,使得该函数在闭区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为1?若存在,求出对应a的值;若不存在,试说明理由. 26.已知函数()sin 2coscos 2sin33f x x x ππ=+.(1)若对任意,63x ππ⎡⎤∈⎢⎥⎣⎦,都有4f x m π⎛⎫- ⎪⎝⎭成立,求实数m 的取值范围;(2)设函数()1226g x f x π⎛⎫=- ⎪⎝⎭()g x 在区间[],3ππ-内的所有零点之和.27.已知函数 2()sin 2cos 1f x x m x =--- [0,]2x π∈()1若()f x 的最小值为 - 3,求m 的值;()2当2m =时,若对任意 12,[0,]2x x π∈ 都有()()12124f x f x a -≤-恒成立,求实数a 的取值范围.28.已知函数())2sin cos 0f x x x x ωωωω=+>的最小正周期为π.将函数()y f x =的图象上各点的横坐标变为原来的4倍,纵坐标变为原来的2倍,得到函数()y g x =的图象.(1)求ω的值及函数()g x 的解析式; (2)求()g x 的单调递增区间及对称中心29.已知函数()()sin ,f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象如图所示:(1)求函数()f x 的解析式及其对称轴的方程;(2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,方程()23f x a =-有两个不等的实根12,x x ,求实数a 的取值范围,并求此时12x x +的值.30.已知函数()()()24sin sin cos sin cos sin 142x f x x x x x x π⎛⎫=+++-- ⎪⎝⎭.(1)求函数()f x 的最小正周期; (2)若函数()()()12122g x f x af x af x a π⎡⎤⎛⎫=+---- ⎪⎢⎥⎝⎭⎣⎦在,42ππ⎡⎤-⎢⎥⎣⎦的最大值为2,求实数a 的值.【参考答案】一、填空题1.3(21)22.22⎝ 3.12(,)369- 4.2rr h-+ 5.8,83⎛⎫ ⎪⎝⎭6.137.②③8.14-9.1或2##2或110.⎡⎢⎣⎦二、单选题 11.A 12.A 13.D 14.D 15.A 16.A 17.A 18.B 19.B 20.D 三、解答题21.(1)()(),0,0ππ-(2)见解析(3)()1,+∞ 【解析】(1)根据题意即正弦函数的性质即可直接求解;(2)要证:函数数()2x h x e mx =--图象上有且只有一对“偶点”,只需证:())()()y Q x g x g x ==--=在(0,2)上有且只有一个零点,结合导数及函数的性质即可证明;(3)由题意,问题可转化为函数()()y h x h x =--只有一个零点,结合函数的性质及导数可求. 【详解】(1)函数()sin f x x =图像上一对“偶点”的坐标为()(),0,0ππ-, (2)设()()()()()ln 2ln 22Q x g x g x x x x =--=+--+-, 因为()y Q x =的定义域为()2,2-,且()()Q x Q x -=-, 所以函数()y Q x =为奇函数,要证:函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”, 只需证:()y Q x =在()0,2上有且只有一个零点, 令()()222204x Q x x -'==-,得x =所以,函数()Q x 在(上为单调减函数,在)2上为单调增函数,(ln 30Q=+-<,4441122ln 40Q e e e ⎛⎫⎛⎫-=-+> ⎪ ⎪⎝⎭⎝⎭,所以函数()Q x 在41e ⎫-⎪⎭上有且只有一个零点,所以函数()ln(2)2g x x x =+-+图像上有且只有一对“偶点”,(3)设()()()2x xF x h x h x e e mx -=--=--,()00F =,因为()y F x =的定义域为R ,且()()F x F x -=-, 所以函数()y F x =为奇函数,因为函数()2()x h x e mx m =--∈R 图像上有且只有一对“偶点”, 所以函数()y F x =在()0,∞+有且只有一个零点, ()12x xF x e m e '=+-,()0,x ∈+∞, ①当1m 时,因为()220F x m '>-≥,所以函数()y F x =在()0,∞+上为单调增函数,所以()()00F x F >=, 所以函数()F x 在()0,∞+无零点,②当1m 时,由()212120x x xx xe me F x e m e e -+'=+-==,得:(0ln x m =,所以函数()y F x =在()00,x 上单调减函数,在()0,x +∞上单调增函数, 所以()()000F x F <=, 设()ln H x x x =-,()1xH x x-'=, 所以函数()H x 在()0,1上单调增函数,在()1,+∞上单调减函数, 所以()()110H x H ≤=-<,所以ln x x <,所以(ln ln 22m m m +<<,设()()211x m x e x x =-->,设()()2xM x m x e x '==-, 因为()220xM x e e '=->->,所以函数()M x 在()1,+∞单调增函数,所以()()120M x M e >=->,所以函数()m x 在()1,+∞单调增函数, 所以()()120m x m e >=->,所以当1x >时,21x e x >+, ()22222124140m m m F m e m e m e=-->-->, 因为函数()y F x =在()0,x +∞上单调增函数,所以函数()F x 在()0,2x m 上有且仅有一个1x ,使得()10F x =, 综上:m 的取值范围为()1,+∞. 【点睛】本题中综合考查了函数的性质及导数的综合应用,体现了分类讨论思想的应用,试题具有一定的综合性.22.(1)π;(2)12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭【解析】 【分析】(1)由辅助角公式可得()f x 2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭,再求周期即可;(2)由13f π⎛⎫= ⎪⎝⎭求出12πϕ=,再解方程2sin 2123x π⎛⎫++= ⎪⎝⎭即可.【详解】解:(1)()()()()2cos 2cos f x x x x ϕϕϕ=++++()()2cos21x x ϕϕ=++++2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭,则()f x 的最小正周期为2T ππω==.(2)因为13f π⎛⎫= ⎪⎝⎭,所以2sin 221136ππϕ⎛⎫⨯+++= ⎪⎝⎭,即()526k k Z πϕπ+=∈, 解得()5212k k Z ππϕ=-∈. 因为02πϕ<<,所以12πϕ=.因为()2f x =,所以2sin 2123x π⎛⎫++= ⎪⎝⎭,即1sin 232x π⎛⎫+= ⎪⎝⎭,则2236x k πππ+=+或()52236x k k Z πππ+=+∈, 解得12x k ππ=-+或()4x k k Z ππ=+∈.故当()2f x =时,自变量x 的取值集合为12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭.【点睛】本题考查了三角恒等变换,重点考查了解三角方程,属中档题.23.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】 【分析】(1)利用降次公式、辅助角公式化简()f x 表达式,利用(0)f =a 的值.(2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围. 【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭,[0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦,()f x 在[0,]π上有且只有一个零点,223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.24.(1)01ω<≤;(2)()sin 26f x x π⎛⎫=- ⎪⎝⎭;平移变换过程见解析.【解析】 【分析】(1)根据平面向量的坐标运算,表示出()f x 的解析式,结合辅助角公式化简三角函数式.结合相邻两条对称轴间的距离不小于2π及周期公式,即可求得ω的取值范围; (2)根据最小正周期,求得ω的值.代入解析式,结合正弦函数的图象、性质与()f x 的最大值是12,即可求得()f x 的解析式.再根据三角函数图象平移变换,即可描述变换过程.【详解】∵(3cos ,sin ),(sin ,0)a x x b x ωωω== ∴(3cos sin ,sin )a b x x x ωωω+=+∴2()()3sin cos sin f x a b b k x x x k ωωω=+⋅+=++1cos21122cos2222x x k x x k ωωωω-=++=-++ 1sin 262x k πω⎛⎫=-++ ⎪⎝⎭(1)由题意可知222T ππω=≥, ∴1ω≤ 又0>ω, ∴01ω<≤ (2)∵T πω=, ∴1ω=∴1()sin 262f x x k π⎛⎫=-++ ⎪⎝⎭∵,66x ππ⎡⎤∈-⎢⎥⎣⎦,∴2,626x πππ⎡⎤-∈-⎢⎥⎣⎦∴当266x ππ-=即6x π=时max 11()sin 16622f x f k k ππ⎛⎫==++=+= ⎪⎝⎭∴12k =-∴()sin 26f x x π⎛⎫=- ⎪⎝⎭将sin y x =图象上所有点向右平移6π个单位,得到sin 6y x π⎛⎫=- ⎪⎝⎭的图象;再将得到的图象上所有点的横坐标变为原来的12倍,纵坐标不变,得到sin 26y x π⎛⎫=- ⎪⎝⎭的图象(或将sin y x =图象上所有点的横坐标变为原来的12倍,纵坐标不变,得到sin 2y x =的图象;再将得到的图象上所有点向右平移12π个单位,得到sin 26y x π⎛⎫=- ⎪⎝⎭的图象) 【点睛】本题考查了正弦函数图像与性质的综合应用,根据最值求三角函数解析式,三角函数图象平移变换过程,属于中档题.25.(1)1-;(2)存在,且2a =. 【解析】 【分析】(1)将1a =代入函数()y f x =的解析式,得出()()2cos 11f x x =---,由1cos 1x -≤≤结合二次函数的基本性质可得出该函数的最大值;(2)换元[]cos 0,1t x =∈,将问题转化为二次函数()222t at g t -+-=在区间[]0,1上的最大值为1,然后分0a ≤、01a <<和1a ≥三种情况讨论,利用二次函数的基本性质求出函数()222t at g t -+-=在区间[]0,1上最大值,进而求得实数a 的值.【详解】(1)当1a =时,()()22sin 2cos 3cos 11f x x x x =+-=---,1cos 1x -≤≤,当cos 1x =时,该函数取得最大值,即()max 1f x =-;(2)()22sin 2cos 3cos 2cos 2x a x x a x f x =+-=-+-,当0,2x π⎡⎤∈⎢⎥⎣⎦时,设[]cos 0,1t x =∈,设()222t at g t -+-=,[]0,1t ∈,二次函数()y g t =的图象开口向下,对称轴为直线t a =.当0a ≤时,函数()y g t =在[]0,1上单调递减,所以0=t 时,()()max 021g t g ==-≠,0a ∴≤不符合题意;当1a ≥时,函数()y g t =在[]0,1上单调递增,所以1t =时,()()max 1231g t g a ==-=,2a ∴=满足1a ≥;当01a <<时,函数()y g t =在[]0,a 上单调递增,在(],1a 上单调递减, ∴当t a =时,()()2max 21g t g a a ==-=,a ∴=01a <<.综上,存在2a =符合题意. 【点睛】本题考查二次型余弦函数的最值,将问题转化为二次函数的最值来求解是解题的关键,第二问要对二次函数图象的对称轴与区间的位置关系进行分类讨论,结合二次函数的单调性求解,考查分类讨论思想的应用,属于中等题. 26.(1)1,2⎛⎤-∞ ⎥⎝⎦;(2)2π【解析】(1)首先根据两角和的正弦公式得到()sin 23f x x π⎛⎫=+ ⎪⎝⎭,从而得到4f x π⎛⎫- ⎪⎝⎭的解析式,根据正弦函数的性质求出其值域,从而得到参数的取值范围; (2)首先求出()g x 的解析式,根据正弦函数的对称性即可解答. 【详解】解:(1)因为()sin 2coscos 2sin33f x x x ππ=+()sin 23f x x π⎛⎫∴=+ ⎪⎝⎭, 所以sin 2sin 24436f x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.又,63x ππ⎡⎤∈⎢⎥⎣⎦,所以2,662x πππ⎡⎤-∈⎢⎥⎣⎦, 故1sin 2,162x π⎛⎫⎡⎤-∈ ⎪⎢⎥⎝⎭⎣⎦,即min 142f x π⎛⎫-= ⎪⎝⎭,12m, 所以实数m 的取值范围为1,2⎛⎤-∞ ⎥⎝⎦.(2)由(1)得()1122sin 22sin 26263g x f x x x πππ⎡⎤⎛⎫⎛⎫=-=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦令()0g x =,得sin x =sin x =[],3ππ-上有4个零点 这4个零点从小到大不妨设为1x ,2x ,3x ,4x ,则由对称性得1222x x π+=-,34322x x π+=, 从而所有零点和为12342x x x x π+++=. 【点睛】本题考查两角和的正弦公式的应用,三角函数的性质的应用,属于基础题. 27.(1)1m =;(2)13[,)8a ∈+∞【解析】 【分析】(1)将函数化为2()cos 2cos 2f x x m x =--,设cos [0,1]t x =∈,将函数转化为二次函数,利用二次函数在给定的闭区间上的最值问题的解法求解.(2) 对任意 12,[0,]2x x π∈ 都有()()12124f x f x a -≤-恒成立, 等价于12max1()()24f x f x a -≤-,然后求出函数()f x 的最值即可解决.【详解】(1)2()cos 2cos 2f x x m x =--,[0,]2x π∈令 cos [0,1]t x =∈, 设222()22()2g t t mt t m m =--=---, ①0m <,则min g(0)2()3g t ==-≠-,②01m ≤≤,则2min )3(2t m g =--=-,∴1m =± ∴1m =③1m ,则min g(1)21()3g m t ==--=-,∴1m =.(舍) 综上所述:1m =.(2)对任意12,[0,]2x x π∈都有()()12124f x f x a -≤-恒成立,等价于12max1()()24f x f x a -≤-,2m =,∴2g()(2)6t t =--,[0,1]t ∈max ()g(0)2f x ==-,min ()g(1)5f x ==-12max ()(25)()3f x f x =---=- ∴ 1234a -≥,∴ 138a ≥, 综上所述:13[,)8a ∈+∞.本题考查三角函数中的二次“型”的最值问题,和双参恒成立问题,属于中档题.28.(1)1ω=,()2sin()23x g x π=+;(2)单调递增区间为54,433k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈,对称中心为2(2,0)()3k k ππ-∈Z . 【解析】 【分析】(1)整理()f x 可得:()sin(2)3f x x πω=+,利用其最小正周期为π即可求得:1ω=,即可求得:()sin(2)3f x x π=+,再利用函数图象平移规律可得:()2sin()23x g x π=+,问题得解. (2)令222232x k k πππππ-≤+≤+,k Z ∈,解不等式即可求得()g x 的单调递增区间;令23x k ππ+=,k Z ∈,解方程即可求得()g x 的对称中心的横坐标,问题得解. 【详解】解:(1)1()2sin 2sin(2)23f x x x x πωωω=+=+, 由22ππω=,得1ω=. 所以()sin(2)3f x x π=+.于是()y g x =图象对应的解析式为()2sin()23x g x π=+.(2)由222232x k k πππππ-≤+≤+,k Z ∈得 54433k x k ππππ-≤≤+,k Z ∈ 所以函数()g x 的单调递增区间为54,433k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈. 由23x k ππ+=,解得22()3x k k ππ=-∈Z . 所以()g x 的对称中心为2(2,0)()3k k ππ-∈Z . 【点睛】本题主要考查了二倍角公式、两角和的正弦公式应用及三角函数性质,考查方程思想及转化能力、计算能力,属于中档题.29.(1)()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,()62k x k Z ππ=+∈;(2)522a ≤<,3π.【解析】(1)根据图像得A=2,利用412562T πππω=-=,求ω值,再利用6x π=时取到最大值可求φ,从而得到函数解析式,进而求得对称轴方程;(2)由0,2x π⎡⎤∈⎢⎥⎣⎦得72,666x πππ⎡⎤+∈⎢⎥⎣⎦,方程f (x )=2a ﹣3有两个不等实根转为f (x )的图象与直线y =2a ﹣3有两个不同的交点,从而可求得a 的取值范围,利用图像的性质可得12x x +的值. 【详解】(1)由图知,2,A =4156242=T ππππω=-=,解得ω=2,f(x)=2sin(2x+φ), 当6x π=时,函数取得最大值,可得2sin 226πϕ⎛⎫⨯+= ⎪⎝⎭,即sin 13πϕ⎛⎫+= ⎪⎝⎭,2,32k k Z ππϕπ+=+∈,解得2,6k k Z πϕπ=+∈ ,又(0,)2πϕ∈所以6π=ϕ, 故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,令262x k πππ+=+则()62k x k Z ππ=+∈, 所以()f x 的对称轴方程为()62k x k Z ππ=+∈; (2)70,2,2666x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦,所以方程()23f x a =-有两个不等实根时,()y f x =的图象与直线23y a =-有两个不同的交点,可得1232,a ≤-<522a ∴≤<, 当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()12f x f x =,有122266x x πππ+++=,故123x x π+=.【点睛】本题考查由y =A sin (ωx +φ)的部分图象确定函数解析式,考查函数y =A sin (ωx +φ)的图象及性质的综合应用,属于中档题. 30.(1) 2T π=;(2)2a =-或6a = 【解析】 【分析】(1)根据二倍角公式进行整理化简可得()2sin f x x =,从而可得最小正周期;(2)将()g x通过换元的方式变为21112y t at a =-+--,1t ≤;讨论对称轴的具体位置,分别求解最大值,从而建立方程求得a 的值. 【详解】(1)()2221cos sin cos sin 12f x x x x x π⎡⎤⎛⎫=-++-- ⎪⎢⎥⎝⎭⎣⎦()222sin sin 12sin 12sin x x x x =++--= ∴最小正周期2T π=(2)()1sin2sin cos 12g x a x a x x a =+---令sin cos x x t -=,则()22sin 21sin cos 1x x x t =--=-22221111122242a a y t at a t at a t a ⎛⎫∴=-+--=-+-=--+- ⎪⎝⎭sin cos 4t x x x π⎛⎫=-=- ⎪⎝⎭由42x ππ-≤≤得244x πππ-≤-≤1t ≤①当2a<a <-当t =max 122y a ⎫=--⎪⎭由1222a ⎫--=⎪⎭,解得()817a ==->-)②当12a≤,即2a -≤时 当2a t =时,2max 142a y a =- 由21242a a -=得2280a a --=,解得2a =-或4a =(舍去) ③当12a>,即2a >时 当1t =时,max 12a y =-,由122a-=,解得6a = 综上,2a =-或6a = 【点睛】本题考查正弦型函数最小正周期的求解、利用二次函数性质求解与三角函数有关的值域问题,解题关键是通过换元的方式将所求函数转化为二次函数的形式,再利用对称轴的位置进行讨论;易错点是忽略了换元后自变量的取值范围.。
三角函数练习题含答案

三角函数练习题含答案一、填空题1.在ABC 中,角A 、B 、C 的对边a 、b 、c 为三个连续偶数且2C A =,则b =__________.2.已知三棱锥S ABC -中,SA SB SC ==,ABC 是边长为4的正三角形,点E ,F 分别是SC ,BC 的中点,D 是AC 上的一点,且EF SD ⊥,若3FD =,则DE =___________. 3.已知函数()2sin()f x x ωφ=+(0>ω,||φπ<)的部分图象如图所示,()f x 的图象与y 轴的交点的坐标是(0,1),且关于点(,0)6π-对称,若()f x 在区间14(,)333ππ上单调,则ω的最大值是___________.4.在直角坐标系中,ABC 的顶点()cos ,sin A αα,()cos ,sin B ββ,432C ⎝,且ABC 的重心G 的坐标为232⎝,()cos αβ-=__________. 5.已知点A 为直线:3l y x =上一点,且A 位于第一象限,点()10,0B ,以AB 为直径的圆与l 交于点C (异于A ),若60CBA ∠≥,则点A 的横坐标的取值范围为___________.6.在ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,D 为边BC 上的一点,若6c =,32b =7sin BAD ∠=,2cos BAC ∠=,则AD =__________. 7.已知四棱锥P ABCD -的顶点均在球O 的球面上,底面ABCD 是正方形,23AB =120APB ∠=︒,当AD AP ⊥时,球O 的表面积为______.8.通信卫星与经济、军事等密切关联,它在地球静止轨道上运行,地球静止轨道位于地球赤道所在平面,轨道高度为km h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球(球心为O ,半径为km r ),地球上一点A 的纬度是指OA 与赤道平面所成角的度数,点A 处的水平面是指过点A 且与OA 垂直的平面,在点A 处放置一个仰角为θ的地面接收天线(仰角是天线对准卫星时,天线与水平面的夹角),若点A 的纬度为北纬30,则tan 3θ________.9.已知向量a 与b 的夹角为θ,27sin 7θ=,||4a b -=,向量,c a c b --的夹角为2π,||23c a -=,则a c ⋅的最大值是___________.10.函数ππ5sin (1510)55y x x ⎛⎫=+-≤≤ ⎪⎝⎭的图象与函数25(1)22x y x x +=++图象的所有交点的横坐标之和为___________.二、单选题11.已知函数()()sin cos sin cos 0f x x x x x ωωωωω=++->,则下列结论错误的是( )①1ω=时,函数()f x 图象关于π4x =对称;②函数()f x 的最小值为-2;③若函数()f x 在π,04⎡⎤-⎢⎥⎣⎦上单调递增,则(]03ω∈,;④1x ,2x 为两个不相等的实数,若()()124f x f x +=且12x x -的最小值为π,则2ω=. A .②③B .②④C .①③④D .②③④12.已知函数()|sin |(0)f x x ωω=>在区间,53ππ⎡⎤⎢⎥⎣⎦上单调递减,则实数ω的取值范围为( ) A .5,32⎡⎤⎢⎥⎣⎦B .30,2⎛⎤ ⎥⎝⎦C .8,33⎡⎤⎢⎥⎣⎦D .50,4⎛⎤ ⎥⎝⎦13.如图所示,已知△ABC ,D 是AB 的中点,沿直线CD 将△ACD 翻折成△ACD ',所成二面角A CD B '--的平面角为α,则( )A .A DB α'∠≤ B .A DB α'∠≥C .A CB α∠'≤D .A CB α'∠≥14.已知函数()sin 22cos f x x x =-,下列说法错误的是( ) A .函数()f x 是周期函数 B .6x π=是函数()f x 图象的一条对称轴C .函数()f x 的增区间为()72,266k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D .函数()f x 3315.已知函数()132,f x x x R =∈,若当02πθ≤≤时,(sin )(1)0f m f m θ+->恒成立,则实数m 的取值范围是( )A .0,1B .,0C .1,D .(),1-∞16.如图,将矩形纸片ABCD 折起一角落()EAF △得到EA F '△,记二面角A EF D '--的大小为π04θθ⎛⎫<< ⎪⎝⎭,直线A E ',A F '与平面BCD 所成角分别为α,β,则( ).A .αβθ+>B .αβθ+<C .π2αβ+>D .2αβθ+>17.如图,在正方体ABCD EFGH -中,P 在棱BC 上,BP x =,平行于BD 的直线l 在正方形EFGH 内,点E 到直线l 的距离记为d ,记二面角为A l P --为θ,已知初始状态下0x =,0d =,则( )A .当x 增大时,θ先增大后减小B .当x 增大时,θ先减小后增大C .当d 增大时,θ先增大后减小D .当d 增大时,θ先减小后增大18.()sin()(0)f x x ωφφ=+>的部分图象如图所示,设P 是图象的最高点,A ,B 是图象与x 轴的交点,若tan 2APB ∠=-,则ω的值为( )A .4π B .3π C .2π D .π19.设锐角ABC ∆的三个内角,,A B C 的对边分别为,,a b c 且1c =,2A C =,则ABC ∆周长的取值范围为( ) A .(0,22)+B .(0,33)+C .(22,33)++D .(22,33]++20.已知1sin ,sin ,sin ,222a x x b x ωωω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,其中0>ω,若函数1()2f x a b =⋅-在区间(,2)ππ内有零点,则实数ω的取值可能是( )A .18B .14C .12D .34三、解答题21.如图,在ABC ∆中,90,3,1ABC AB BC ︒∠===,P 为ABC ∆内一点,90BPC ︒∠=.(1)若32PC =,求PA ; (2)若120APB ︒∠=,求ABP ∆的面积S .22.如图,某景区内有一半圆形花圃,其直径AB 为6,O 是圆心,且OC ⊥AB .在OC 上有一座观赏亭Q ,其中∠AQC =23π,.计划在BC 上再建一座观赏亭P ,记∠POB =θ(0)2πθ<<.(1)当θ=3π时,求∠OPQ 的大小; (2)当∠OPQ 越大时,游客在观赏亭P 处的观赏效果越佳,求游客在观赏亭P 处的观赏效果最佳时,角θ的正弦值. 23.已知函数22cos 3sin 2f xxx a 的最小值为0.(1)求a 的值及函数()y f x =图象的对称中心;(2)若关于x 的方程()0f x m -=在区间70,6π⎡⎤⎢⎥⎣⎦上有三个不相等的实数根1x ,2x ,3x ,求m的取值范围及()123tan 2x x x ++的值.24.已知向量33cos ,sin 22x a x ⎛⎫= ⎪⎝⎭,cos ,sin 22x x b ⎛⎫- ⎪⎝=⎭,0,2x π⎡⎤∈⎢⎥⎣⎦.(1)用含x 的式子表示a b ⋅及a b +; (2)求函数的()f x a b a b =⋅-+值域. 25.已知函数()2sin cos cos2x x x x f =+. (1)求()f x 的最小正周期及单调递减区间; (2)求()f x 在区间0,4π⎡⎤⎢⎥⎣⎦上的最大值和最小值.26.函数()()sin tan f x x ω=,其中0ω≠. (1)讨论()f x 的奇偶性;(2)1ω=时,求证:()f x 的最小正周期是π;(3)()1.50,1.57ω∈,当函数()f x 的图像与()112g x x x ⎛⎫=+ ⎪⎝⎭的图像有交点时,求满足条件的ω的个数,说明理由.27.函数211()sin 2sin cos cos sin 222f x x x πϕϕϕ⎛⎫=⋅+⋅-+ ⎪⎝⎭,22ππϕ⎛⎫-<< ⎪⎝⎭其图像过定点1,64π⎛⎫⎪⎝⎭(1)求ϕ值;(2)将()y f x =的图像左移8π个单位后得到()y g x =,求()g x 在,44ππ⎡⎤-⎢⎥⎣⎦上的最大和最小值及此时对应的x 的取值是多少?28.已知(1,sin )a x =,(1,cos )b x =,(0,1)e =,且(cos sin )x x -∈. (1)若()//a e b +,求sin cos x x 的值;(2)设()()f x a b me a b =⋅+⋅-,m R ∈,若()f x 的最大值为12-,求实数m 的值.29.已知函数())2sin cos 0f x x x x ωωωω=+>的最小正周期为π.将函数()y f x =的图象上各点的横坐标变为原来的4倍,纵坐标变为原来的2倍,得到函数()y g x =的图象.(1)求ω的值及函数()g x 的解析式; (2)求()g x 的单调递增区间及对称中心30.设向量a =(2sin 2x cos 2xx ),b =(cos x ,sin x ),x ∈[-6π,3π],函数f (x )=2a •b .(1)若|a b |,求x 的值;(2)若f (x )-m m 的取值范围.【参考答案】一、填空题 1.1023.11 4.235.)1⎡++∞⎣6.47.28π 8.2rr h-+ 9.25 10.-7二、单选题 11.B 12.A 13.B 14.B 15.D 16.A 17.C18.C 19.C 20.D 三、解答题21.(12 【解析】 【分析】(1)求出12BP ==,,36CBP ABP ππ∠=∠=,ABP ∆中由余弦定理即可求得PA ;(2)设PBA α∠=,利用正弦定理表示出()sin120sin 60AB PB =︒︒-α,求得tan α=,利用面积公式即可得解. 【详解】(1)在ABC ∆中,90,1ABC AB BC ︒∠===,2AC =P 为ABC ∆内一点,90BPC ︒∠=,PC =,所以12BP =,CBP ∆中,由余弦定理得:2221cos 22BP BC PC CBP BP BC +-∠==⋅所以,36CBP ABP ππ∠=∠=ABP ∆中,由余弦定理得:AP==; (2)120APB ︒∠=,设0,,90,602PBA PBC PAB π⎛⎫∠=α∈∠=︒-α∠=︒-α ⎪⎝⎭,在Rt PBC ∆中,sin sin PB BC =⋅α=α, 在PBA ∆中,由正弦定理()sin120sin 60AB PB=︒︒-α,即()sin 2sin 60α=︒-α,sin sin α=α-α,所以tan α=sin PB α==ABP ∆的面积11sin 22S AB PB α=⋅==. 【点睛】此题考查解三角形,对正余弦定理的综合使用,涉及两角差的正弦公式以及同角三角函数关系的使用,综合性较强. 22.(1)6π.(2)sin θ=. 【解析】(1)设∠OPQ =α,在△POQ 中,用正弦定理sin sin OQ OPOPQ OQP=∠∠可得含α,θ的关系式,将其展开化简并整理后得tanαθ=3π代入得答案;(2)令f (θ)f (θ)的最大值,即此时的sin θ,由(1)可知tanα.【详解】(1)设∠OPQ =α,在△POQ 中,用正弦定理可得含α,θ的关系式. 因为∠AQC =23π,所以∠AQO =3π.又OA =OB =3,所以OQ在△OPQ 中,OQOP =3,∠POQ =2π-θ,设∠OPQ =α,则∠PQO =2π-α+θ. 由正弦定理,得3sin 2παθ⎛⎫-+ ⎪⎝⎭=cos (α-θ).展开并整理,得tanαθ∈0,2π⎛⎫⎪⎝⎭.此时当θ=3π时,tanα因为α∈(0,π),所以α=6π. 故当θ=3π时,∠OPQ =6π.(2)设f (θ)θ∈0,2π⎛⎫ ⎪⎝⎭.则f ′(θ)令f ′(θ)=0,得sinθθ0满足0sin θ则0cos θ=,即()0f θ===列表如下:2由(1)可知tanα=f (θ)>0,则0,2πα⎛⎫∈ ⎪⎝⎭, tanα单调递增则当tanαα也取得最大值.故游客在观赏亭P 处的观赏效果最佳时,sinθ 【点睛】本题考查三角函数和解三角形的实际应用,应优先建模,将实际问题转化为熟悉的数学问题,进而由正弦定理构建对应关系,还考查了利用导数求函数的最值,属于难题.23.(1)1,,2212k ππ⎛⎫-⎪⎝⎭,k Z ∈;(2)[)3,4, 【解析】(1)由题得()2sin 216f x x a π⎛⎫=+++ ⎪⎝⎭,求出a 的值即得函数()y f x =图象的对称中心;(2)作出函数()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象,求出123523x x x π++=即得解.【详解】(1)()cos 2212sin 216x x a x a f x π⎛⎫=++=+++ ⎪⎝⎭,由已知可得()2110a ⨯-++=,∴1a =,()2sin 226f x x π⎛⎫=++ ⎪⎝⎭,令26x k ππ+=可得()y f x =图象的对称中心为,2212k ππ⎛⎫- ⎪⎝⎭,k Z ∈. (2)()y f x =在70,6x π⎡⎤∈⎢⎥⎣⎦上的大致图象如图所示,由图可得[)3,4m ∈,所以123x x π+=,2343x x π+=,所以123523x x x π++=,所以()1235tan 2tan3x x x π++==【点睛】本题主要考查三角恒等变换和三角函数的图象和性质,考查三角函数图象的综合应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.24.(1)cos 2x a b ⋅=;2cos a b x +=,0,2x π⎡⎤∈⎢⎥⎣⎦(2)()3,12f x ⎡⎤∈--⎢⎥⎣⎦【解析】(1)根据平面向量数量积的坐标表示以及三角恒等变换公式可得a b ⋅,根据a b +=2||a b +可求得结果;(2)利用二倍角的余弦公式化为关于cos x 的二次函数可求得结果. 【详解】(1)因为向量33cos ,sin 22x x a ⎛⎫= ⎪⎝⎭,cos ,sin 22x x b ⎛⎫=- ⎪⎝⎭,0,2x π⎡⎤∈⎢⎥⎣⎦, 所以2233||cos sin 122x x a =+,22||cos sin 122x xb =+=, 所以333coscos sin sin cos()cos 2222222x a x x b x x xx -=+==⋅, ()2222212cos 2121cos 24cos a a b b x a b x x =+⋅+=++++==,2cos a b x +=,0,2x π⎡⎤∈⎢⎥⎣⎦;(2)()2cos22cos 2cos 2cos 1x x x f x x =-=--,又0,2x π⎡⎤∈⎢⎥⎣⎦,∴[]cos 0,1x ∈,()3,12f x ⎡⎤∈--⎢⎥⎣⎦.【点睛】本题考查了平面向量的数量积的坐标运算,考查了求平面向量的模,考查了二倍角的余弦公式,考查了整体换元化为二次函数求值域,属于基础题.25.(1)最小正周期π;单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈(2)最大值和最小值2和1. 【解析】(1)利用二倍角的正弦公式的逆用公式以及两角和的正弦公式的逆用公式化简得()24f x x π⎛⎫+ ⎪⎝⎭,再根据周期公式可得周期,利用正弦函数的递减区间可得()f x 的递减区间;(2)利用正弦函数的性质可求得结果.【详解】(1)因为()sin 2cos 224x f x x x π⎛⎫=+=+ ⎪⎝⎭. 所以()f x 的最小正周期22T ππ==. 由3222242k x k πππππ+≤+≤+,得588k x k ππππ+≤≤+, 所以()f x 的单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈. (2)因为0,4x π⎡⎤∈⎢⎥⎣⎦,所以32,444x πππ⎡⎤+∈⎢⎥⎣⎦.所以当242x ππ+=,即8x π= 当244x ππ+=或34π,即0x =或4x π=时,函数取得最小值1.所以()f x 在区间0,4⎡⎤⎢⎥⎣⎦π和1. 【点睛】本题考查了二倍角的正弦公式,考查了两角和的正弦公式,考查了正弦型函数的周期公式,考查了求三角函数的单调区间和最值,属于基础题.26.(1)奇函数;(2)见解析;(3)ω的个数为198个,见解析.【解析】(1)根据奇偶函数的定义进行判断即可;(2)根据最小正周期公式进行验证即可;(3)利用函数的图象和不等式的性质可以求出满足条件的ω的个数.【详解】(1)()sin[tan()]sin(tan )sin(tan )()f x x x x f x ωωω-=-=-=-=-,所以函数()f x 是奇函数;(2)()sin[tan()]sin(tan )()f x x x f x ππ+=+==,所以()f x 的最小正周期是π;(3)因为当0x >时,()111122g x x x ⎛⎫=+≥⨯ ⎪⎝⎭,(当且仅当1x =时取等号),所以当函数()f x 的图像与()112g x x x ⎛⎫=+ ⎪⎝⎭的图像有交点时,只能()sin tan 1x ω=,即tan 22k πωπ=+,因为(1.50, 1.57)ω∈,所以2(tan1.50,tan1.57)2k ππ+∈,因此1.99199.6k <<,2,3,4,,199k =⋯,因此满足条件的ω的个数为198个,当0x >时,也是一样的,因为两个函数是奇函数都关于原点对称,所以当函数()f x 的图像与()112g x x x ⎛⎫=+ ⎪⎝⎭的图像有交点时,满足条件的ω的个数为198. 【点睛】本题考查了函数奇偶性和周期性,考查了三角奇函数的性质,考查了基本不等式的应用,考查了数学运算能力.27.(1)0ϕ=(2)当4x π=时,min ()g x =;当8x π=-时,max 1()2g x = 【解析】【分析】 (1)先将函数表达式结合降幂公式化简可得()1cos(2)2f x x ϕ=-,结合函数过点1,64π⎛⎫ ⎪⎝⎭和,22ππϕ⎛⎫∈- ⎪⎝⎭即可求解具体ϕ值; (2)根据函数图像平移法则先求得1()cos 224g x x π⎛⎫=+ ⎪⎝⎭,由,44x ππ⎡⎤∈-⎢⎥⎣⎦求得32,444x πππ⎡⎤+∈-⎢⎥⎣⎦,再结合余弦函数性质即可求解 【详解】(1)11cos 21()sin 2sin cos cos 222x f x x ϕϕϕ+=⋅+⋅- 11sin 2sin cos 2cos 22x x ϕϕ=⋅+⋅ 1cos(2)2x ϕ=- 又图像过点1,64π⎛⎫ ⎪⎝⎭,11cos 423πϕ⎛⎫∴=- ⎪⎝⎭ 233k ππϕπ∴-=+或2()3k k Z ππ-+∈ 又,22ππϕ⎛⎫∈- ⎪⎝⎭,0ϕ∴= (2)由(1)知1()cos 22f x x =, 11()cos 2cos 22824g x x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭ 32,444x πππ⎡⎤+∈-⎢⎥⎣⎦当3244x ππ+=时,即4x π=时,min ()g x =当204x π+=时,即8x π=-时,max 1()2g x = 【点睛】本题考查三角函数表达式的化简求值,降幂公式的使用,两角差的余弦公式的逆用,在具体区间函数最值的求解,属于中档题28.(1)0 (2)32【解析】【分析】(1)通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+,移项、两边平方即可算出结果.(2)通过向量的运算,解出()()f x a b me a b =⋅+⋅-,再通过最大值根的分布,求出m 的值.【详解】(1)通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+,即2cos sin 1(cos sin )112sin cos 1sin cos 0x x x x x x x x -=⇒-=⇒-=⇒=故答案为0.(2)()1sin cos (sin cos )f x x x m x x =++-,设()cos sin x x t t ⎡-=∈⎣,22112sin cos sin cos 2t x x t x x --=⇒=,22113()()1222t g t f x mt t mt -==+-=--+,即213(),22g t t mt t ⎡=--+∈⎣的最大值为12-; ①当11m m -≤⇒≥-时,max 1313()(1)2222g x g m m ==--+=-⇒=(满足条件);②当11m m <-≤⇒<-时,222max 1311()()22222g x g m m m m =-=-++=-⇒=-(舍);③当m m -><max 131()22222g x g m ==-⨯-=-⇒=(舍) 故答案为32m =【点睛】 当式子中同时出现sin cos ,sin cos ,sin cos x x x x x x +-时,常常可以利用换元法,把sin cos x x 用sin cos ,sin cos x x x x +-进行表示,但计算过程中也要注意自变量的取值范围;二次函数最值一定要注意对称轴是否在规定区间范围内,再讨论最后的结果.29.(1)1ω=,()2sin()23x g x π=+;(2)单调递增区间为54,433k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈,对称中心为2(2,0)()3k k ππ-∈Z . 【解析】【分析】(1)整理()f x 可得:()sin(2)3f x x πω=+,利用其最小正周期为π即可求得:1ω=,即可求得:()sin(2)3f x x π=+,再利用函数图象平移规律可得:()2sin()23x g x π=+,问题得解.(2)令222232x k k πππππ-≤+≤+,k Z ∈,解不等式即可求得()g x 的单调递增区间;令23x k ππ+=,k Z ∈,解方程即可求得()g x 的对称中心的横坐标,问题得解. 【详解】解:(1)1()2sin 2sin(2)23f x x x x πωωω=+=+, 由22ππω=,得1ω=. 所以()sin(2)3f x x π=+. 于是()yg x =图象对应的解析式为()2sin()23x g x π=+. (2)由222232x k k πππππ-≤+≤+,k Z ∈得 54433k x k ππππ-≤≤+,k Z ∈ 所以函数()g x 的单调递增区间为54,433k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈. 由23x k ππ+=,解得22()3x k k ππ=-∈Z . 所以()g x 的对称中心为2(2,0)()3k k ππ-∈Z . 【点睛】本题主要考查了二倍角公式、两角和的正弦公式应用及三角函数性质,考查方程思想及转化能力、计算能力,属于中档题.30.(1)π4x =;(2)2⎤⎦. 【解析】【分析】(1)根据|a |=b |,利用化简函数化简解得x 的值;(2根据f (x )=2a •b .结合向量的坐标运算,根据x ∈[6π-,3π],求解范围,)﹣f (x )﹣m ≤m 的取值范围.【详解】解:(1)由|a b |, 可得222a b =;即4sin 2x =2(cos 2x +sin 2x ) 即sin 2x =12;∴sin x = ∵x ∈[-6π,3π], ∴x =4π(2)由函数f (x )=2a •b =2sin2x 2x=sin2x +1122-cos2x )=sin2x x (2x -3π)∵x ∈[-6π,3π], ∴2x -3π∈[-23π,3π],2≤2sin (2x -3π)要使f (x )-m则2m m ⎧-≤⎪⎨≥⎪⎩2m ≤故得m 的取值范围是2].【点睛】本题考查三角函数的化简能力和向量的运算,考查转化思想以及计算能力.。
高一数学三角函数试题

高一数学三角函数试题1.已知向量.(1)若,且,求角的值;(2)若,且,求的值.【答案】(1);(2)【解析】(1)根据向量垂直其数量积为0,可得到的关系式,从而得出的值,再根据角的范围得角的大小。
(2)根据数量积公式可得的关系式,用两角和差公式的逆用即化一公式将其化简为再根据角的范围找整体角的范围,从而可计算出的值。
用凑角的方法将写成的形式,用正弦的两角和公式展开计算即可。
(1)∵ , ∴ , 即 3分∴,又∴∴. 6分(2) 8分∴,又∵ , ∴, ∴ 10分∴. 12分【考点】1数量积公式;2两角和差公式。
2.如图,在中,已知,是上一点,,则【答案】【解析】由余弦定理得:,在三角形中,再由正弦定理得:【考点】正余弦定理综合3.已知,函数.(1)设,将函数表示为关于的函数,求的解析式和定义域;(2)对任意,不等式都成立,求实数的取值范围.【答案】(1),定义域为;(2)实数的取值范围是.【解析】(1)由恒等变换公式可求得,并可以表示出定义域;(2)由求出的取值范围,化简成形式,用函数单调性即可求出实数的取值范围.试题解析:(1)∴2分由可得4分∴6分定义域为 8分(2)∵∴10分∵恒成立∴恒成立化简得又∵∴ 12分令得∴在上为减函数14分∴∴ 16分【考点】恒等变换公式、恒成立问题.4.已知函数(1)用五点法画出它在一个周期内的闭区间上的图象;(2)求函数的单调增区间;(3)若,求的最大值和最小值.【答案】(1)(2)(3),【解析】(1)列表、作图 .4分6303(2)由得所以所以函数的单调增区间为 8分(3)因为所以,所以,所以当即时,当即时, -12分【考点】三角函数的性质点评:主要是考查了三角函数的图象与性质的求解运用,属于基础题。
5.已知函数(1)写出函数的单调递减区间;(2)设,的最小值是,最大值是,求实数的值.【答案】(1)(2)【解析】(1)为所求(2)【考点】三角函数的性质点评:主要是考查了三角函数的性质的运用,属于基础题。
三角函数与平面向量综合测试题

约稿:三角函数与平面向量综合测试题广东省珠海市斗门区第一中学 于发智 519100 jianghua20011628@一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,恰有..一项..是符合题目要求的。
1.下列函数中,周期为2π的是( ) A .sin2x y = B .sin 2y x = C .cos 4xy = D .cos 4y x = 2.已知命题:p x ∀∈R ,sin 1x ≤,则( ) A.:p x ⌝∃∈R ,sin 1x ≥ B.:p x ⌝∀∈R ,sin 1x ≥ C.:p x ⌝∃∈R ,sin 1x >D.:p x ⌝∀∈R ,sin 1x >3. 条件甲a =+θsin 1,条件乙a =+2cos2sin θθ,那么 ( )A .甲是乙的充分不必要条件B .甲是乙的充要条件C .甲是乙的必要不充分条件D .甲是乙的既不充分也不必要条件4.已知O 是ABC △所在平面内一点,D 为BC 边中点,且2OA OB OC ++=0,那么( )A.AO OD =B.2AO OD =C.3AO OD =D.2AO OD =5. 若函数f (x )=3sin21x , x ∈[0, 3π], 则函数f (x )的最大值是 ( ) A.21 B.32 C.22 D.23 6. (1+tan25°)(1+tan20°)的值是 ( ) A.-2 B.2 C.1 D.-1 7.α、β为锐角a =sin(βα+),b =ααcos sin +,则a 、b 之间关系为 ( )A .a >bB .b >aC .a =bD .不确定8. 下面有五个命题:①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =Z k k ∈π,2|.B ACD③在同一坐标系中,函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 3632sin(3的图象得到的图象向右平移x y x y =ππ+= ⑤函数.0)2sin(〕上是减函数,在〔ππ-=x y 其中真命题的序号是 ① ④ ((写出所有真命题的编号))9. )sin()(ϕω+=x A x f (A >0,ω>0)在x =1处取最大值,则 ( ) A .)1(-x f 一定是奇函数 B .)1(-x f 一定是偶函数 C .)1(+x f 一定是奇函数D .)1(+x f 一定是偶函数10. 使x y ωsin =(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( ) A .π25B .π45 C .πD .π2311、在直角坐标系xOy 中,,i j分别是与x 轴,y 轴平行的单位向量,若直角三角形ABC中,2AB i j =+ ,3AC i k j =+,则k 的可能值有 ( ) A 、1个 B 、2个 C 、3个 D 、4个12. 如图,l 1、l 2、l 3是同一平面内的三条平行直线,l 1与l 2间的距离是1, l 2与l 3间的距离是2,正三角形ABC 的三顶点分别在l 1、l 2、l 3上,则△ABC 的边长是 ( )(A )32 (B )364(C )4173 (D )3212二、填空题:本大题共4小题,每小题4分,共16分。
三角函数、平面向量单元测试题

A2 B C一 D一 . . 丢 .3 .
5 若 1 — 1 1 — 2, a b, c a。 . a1 , b1 c + 且 上 则
向 量 a与 b的 夹 角 为 (
A. 0 3 。 B. 。 60
c O,(n 1, (, ・ △ A o ) sO ) E o 则当 o B的面 s B i・ O 号]
c.一 2
D. ,
② 在 △ ABC 中 , c 一 9 。 则 lAC 若 O, l + lCB l 一 lAB l ; l 。 I l l
1 . 知 函 数 /( ) a i.— b o x( b为 1已 一 snr ; c s “、
③ 在 Z ABC 中 , l AC i+ l CB l>  ̄ l l l J
后 的 图 象 如 图 2所 示 , 则 新 图象 所 对 应 函 数 的 解
r 旁 ‘ \
| o\ j \/
一
芝 K 若 _
) .
厂 ) _ 1 + ’ ) 2・ a的 所 有 可 能 值 为 ( ( ( 一 4 则
A .1 B 1,一
l
维普资讯
l l AB . l 1
常数, ,∈R 在 一詈处取得最小值, n ) ≠0 则
其 中 真 命 题 的个 数 为 (
) .
D .3
P 5 P1
函 ,竿一 ) ( ) 数 一 ( 是 .
A. 函 数 且 它 的 图 象 关 于 点 ( , ) 称 偶 丌0 对
积 最 大 时 ,一 ( 日 ) ,
) .
C.1 0 2 。
1 一
D .1 0 5 。
6 将 函 数 — s  ̄x . i r ( > 0 的 图 象 按 向 量 a )
三角函数解三角形向量数列测试卷

三角函数、解三角形、向量、数列测试卷一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知(,3)a x =-, (3,1)b =, 且a b ⊥, 则x 等于 ( )A .-1B . 1C .9D .-92.已知ABC ∆中,31sin ,2,3===B AC AB .则=C ( )。
A. 30 B. 60 C. 30或 150 D. 60或 1203.已知1sin cos 3αα+=,则sin 2α=( ) A .21 B .21- C .89 D .89- 4. 在△ABC 中,若,3))((bc a c b c b a =-+++则A = ( ) A 090 B 060 C 0135 D 0150 5.已知等差数列{a n }满足a 2+a 4=4, a 3+a 5=10,则它的前10项的和S 10=( )A .138B .135C .95D .236. 化简10sin 1++10sin 1-,得到( )A -2sin5B -2cos5C 2sin5D 2cos57.等差数列{}n a 的前m 项和为30,前2m 项和为100,则它的前3m 项和是( )A.130B.170C.210D.2608.已知等比数列{}n a 的公比13q =-,则13572468a a a a a a a a ++++++等于( ) A.13- B.3- C.13 D.3 9.在△ABC 中,若)sin()sin(C B A C B A +-=-+,则△ABC 必是( )A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角 10.若{}n a 是等差数列,首项120032004200320040,0,.0a a a a a >+><,则使前n 项和0n S >成立的最大自然数n 是( )A .4005B .4006C .4007D .400二、填空题:本大题共5小题,每小题5分,共25分.11.若32)sin(-=-απ, 且)0,2(πα-∈, 则αtan 的值是____________. 12.在等比数列{a n }中,若a 9·a 11=4,则数列{n a 21log }前19项之和为_ __13.在△ABC 中,若=++=A c bc b a 则,22214.已知等比数列{a n }中,a 1+a 2=9,a 1a 2a 3=27,则{a n }的前n 项和是 。
人教版数学高二第一章三角函数单元测试精选(含答案)2

6
,
5 6
上单调递增
B.最小正周期是π
C.图象关于点
4
,
0
成中心对称
D.图象关于直线 x= 成轴对称
6
【来源】高中数学人教 A 版必修 4 第一章 三角函数 1.4.3 正切函数的性质与图象
【答案】B
9.已知函数
f(x)=3sin
ωx-
π 4
(0<ω<1),且
f
π 2
=0,则函数
)
A. 8
B. 8
C. 6
D. 6
【来源】福建省福州格致中学 2017-2018 学年高一下学期第四学段质量检测数学试题
【答案】C
23.如图,在棱长为 a 的正方体 ABCD A1B1C1D1 中,P 为 A1D1 的中点,Q 为 A1B1 上 任意一点, E , F 为 CD 上任意两点,且 EF 的长为定值,则下面的四个值中不为定
【来源】广东省揭阳市第三中学 2017-2018 学年高二上学期数学试题 1(必修 5 第一章)
【答案】D
16.若θ∈[ , ],sin2θ= 3 7 ,则 cosθ= ( )
42
8
3
A.
5
4
B.-
5
C. 7 4
3
D.
4
【来源】2017 秋人教 A 版高中数学必修四:学业质量标准检测 3
【答案】C
sin
பைடு நூலகம்
π 2
2 2cos2 (π θ) cos(-θ)
θ
-3
,则
f
17π 3
=_____.
【来源】2018-2019 学年高中数学(人教 A 版,必修 4)第一章《三角函数》测试题
三角函数、平面向量

三角函数与解三角形、平面向量(本卷满分150分,考试用时120分钟)一、选择题(本大题共 12小题,每小题 5分,共计 60分.在每小题给出的四个选项中,只有一项 是符合题目要求的)1.函数y =1-2sin 2 è ç æ ø÷ ö x - π 4 是 A .最小正周期为 π的偶函数 B .最小正周期为 π 的奇函数C .最小正周期为 π 2 的偶函数D .最小正周期为 π2的奇函数2.若函数 f (x )=sin ax + 3cos ax (a >0)的最小正周期为1,则它的图象的一个对称中心为A. è ç æ ø ÷ ö - 1 3 ,0B. è ç æ ø ÷ ö - π 3 ,0C. è ç æ ø÷ ö 1 3 ,0 D .(0,0) 3.已知实数a ,b 均不为零, a sin α+b cos α a cos α-b sin α =tan β,且 β-α= π 6 ,则 ba 等于A. 3B. 33C .- 3D .-334.设 a = è ç æ ø ÷ ö 3 2 ,sin α ,b = èç æ ø÷ ö cos α, 1 3 ,若 a ∥b ,则锐角 α 为A .30°B .45°C .60°D .75°5.在梯形 ABCD 中,AB ∥CD ,且|AB |=λ|DC |,设AB → =a ,AD → =b ,则AC →等于A .λa +bB .a +λb C. 1 λ a +b D .a + 1λb6.设函数 f (x )=sin è ç æ ø ÷ ö 2x + π 4 +cos è ç æ ø ÷ ö 2x + π 4 ,则 A .y =f (x )在 è ç æ ø ÷ ö 0, π 2 单调递增,其图象关于直线x = π 4 对称 B .y =f (x )在 è ç æ ø ÷ ö 0, π 2 单调递增,其图象关于直线 x = π 2 对称 C .y =f (x )在 è ç æ ø ÷ ö 0, π 2 单调递减,其图象关于直线 x = π 4 对称 D .y =f (x )在 è ç æ ø÷ ö 0, π 2 单调递减,其图象关于直线x = π 2 对称 7.下列命题中正确的是A .若 λa +μb =0,则 λ=μ=0B .若 a ∙b =0,则 a ∥bC .若 a ∥b ,则a 在 b 上的投影为|a |D .若 a ⊥b ,则 a ∙b =(a ∙b )28.在△ABC 中,sin 2 A ≤sin 2 B +sin 2C -sin B sin C ,则 A 的取值范围是A. è ç æ û ú ù 0, π 6B. ë ê é ø ÷ ö π 6 ,πC. è ç æ û ú ù 0, π 3D. ë ê é ø÷ ö π 3 ,π 9.函数 f (x )=sin (ωx +φ) è ç æ ø÷ ö |φ|< π 2 的最小正周期为 π,且其图象向左平移 π 6 个单位后得到的函数为奇 函数,则函数 f (x )的图象A .关于点 è ç æ ø ÷ ö π 12 ,0 对称B .关于直线x = 5π12 对称C .关于点 è ç æ ø÷ ö 5π12 ,0 对称 D .关于直线 x = π 12 对称 10.已知函数 f (x )=sin (2x +φ),其中 φ 为实数.若 f (x )≤ ï ï ï ï ï ï f è ç æ ø ÷ ö π 6 对 x ∈R 恒成立,且 f è ç æ ø÷ ö π 2 >f (π),则 f (x )的单调递增区间是A. ë ê é û ú ù k π- π 3 ,k π+ π 6 (k ∈Z )B. ë ê é ûú ù k π,k π+ π 2 (k ∈Z )C. ë ê é ûú ù k π+ π 6 ,k π+ 2π 3 (k ∈Z ) D. ë ê é ûú ù k π- π 2 ,k π (k ∈Z ) 11.设 ω>0,m >0,若函数 f (x )=m sin ωx 2 ∙cos ωx 2 在区间 ë ê é ûú ù - π 3 , π 4 上单调递增,则 ω 的取值范围 是A. è ç æ ø÷ ö 0, 2 3B. è ç æ ûú ù 0, 3 2C. ë ê é ø÷ ö 3 2,+∞ D .[1,+∞)12.在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,已知 b 2 =c (b +2c ),若 a = 6,cos A = 78,则△ABC 的面积等于 A. 17B. 15C.152D .3二、填空题(本大题共 4 小题,每小题 4 分,共计 16分.把答案填在题中的横线上)13.在△ABC 中,若 b =5,∠B = π 4 ,sin A = 13,则 a =________.14.已知向量 a 、b 满足(a +2b )∙(a -b )=-6,且|a |=1,|b |=2,则 a 与 b 的夹角为________. 15.在海岛 A 上有一座海拔 1 千米的山,山顶上有一个观察站,上午 11时,测得一轮船在岛的北 偏东 30°,俯角 30°的 B 处,到 11 时 10 分又测得该船在岛的北偏西 60°,俯角 60°的 C 处,则轮船航 行速度是________千米/小时.16.三角形 ABC 中,已知AB → ∙BC → +BC → ∙CA → +CA → ∙AB →=-6,且角 C 为直角,则角 C 的对边c 的长为__. 三、解答题(本大题共 6 小题,共 74分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(12分)已知向量 a = èç æ ø ÷ ö 1 2 , 3 2 ,b =(cos x ,sin x ),x ∈ è ç æ ø ÷ ö 0, π 2 . (1)若 a ∥b ,求 sin x 和 cos 2x 的值;(2)若 a ∙b =2cos è ç æ ø÷ ö 12k π+13π 6 +x (k ∈Z ),求 tan è ç æ ø ÷ ö x + 5π12 的值. 18.(12 分)如图,为了计算河岸边两景点B 与 C 的距离,由于地形的限制,需要在岸上选取A 和D 两个测量点.现测得 AD ⊥CD ,AD =100 m ,AB =140 m ,∠BDA =60°,∠BCD =135°,求两景点 B 与 C 之间的距离(假设 A ,B ,C ,D 在同一平面内,测量结果保留整数;参考数据: 2=1.414, 3= 1.732, 5=2.236).19.(12 分)已知 a =2(cos ωx ,cos ωx ),b =(cos ωx , 3sin ωx )(其中 0<ω<1),函数 f (x )=a ∙b ,若直线 x = π3是函数 f (x )图象的一条对称轴.(1)试求 ω 的值;(2)若函数 y =g (x )的图象是由 y =f (x )的图象的各点的横坐标伸长到原来的2 倍, 然后再向左平移2π3个单位长度得到,求y =g (x )的单调增区间.20.(12分)已知函数 f (x )=2sin è ç æ ø÷ ö 1 3 x - π 6 ,x ∈R . (1)求 f (0)的值;(2)设 α,β∈ ë ê é û ú ù 0, π 2 ,f è ç æ ø ÷ ö 3α+ π 2 = 1013,f (3β+2π)= 6 5 ,求 sin (α+β)的值. 21.(12分)在△ABC 中,内角 A ,B ,C 的对边分别为 a ,b ,c ,已知 cos A -2cos C cos B = 2c -ab.(1)求 sin C sin A的值;(2)若 cos B = 14,b =2,求△ABC 的面积S .22.(14分)已知向量 a =( 3sin 3x ,-y ),b =(m ,cos 3x -m )(m ∈R ),且 a +b =0.设 y =f (x ).(1)求 f (x )的表达式,并求函数 f (x )在 ëê é û ú ù π 18 , 2π 9 上图象最低点M 的坐标; (2)若对任意x ∈ ë ê é ûú ù 0, π 9 ,f (x )>t -9x +1 恒成立,求实数 t 的范围.。
高三数学三角与向量专题训练带解析

2015届高三数学三角与向量专题训练(带解析)2015届高三数学三角与向量专题训练(带解析)一、选择、填空题1、(2014广东高考)已知向量则下列向量中与成夹角的是A.(-1,1,0)B.(1,-1,0)C.(0,-1,1)D.(-1,0,1)2、(2012广东高考)若向量,,则()A.B.C.D.3、(2011广东高考)若向量满足∥且,则A.4B.3C.2D.04、(2014广东高考)在中,角所对应的边分别为,已知,则5、(广州市第六中学2015届高三上学期第一次质量检测)已知向量与的夹角为120°,且,若,且,则实数的值为()A.B.C.D.6、(广州市海珠区2015届高三摸底考试)已知菱形的边长为,,点分别在边上,.若,,则A.B.C.D.7、(广州市执信中学2015届高三上学期期中考试)在中,已知,则的面积是()A.B.C.或D.8、(惠州市2015届高三第二次调研考试)设向量,,则下列结论中正确的是()A.B.C.D.与垂直9、(江门市普通高中2015届高三调研测试)在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若∠A=75°,∠B=60°,c=10,则b=()A.5B.5C.10D.1010、(韶关市十校2015届高三10月联考)将函数的图象向左平移个单位,再向上平移1个单位,所得图象的函数解析式是()A.;B.;C.;D.11、(深圳市2015届高三上学期第一次五校联考)已知函数,当时,恒有成立,则实数的取值范围()A.B.C.D.12、(湛江市2015届高中毕业班调研测试)在△ABC中,边a、b所对的角分别为A、B,若cosA=﹣,B=,b=1,则a=.13、(肇庆市2015届高三10月质检)设,为非零向量,||=2||,两组向量,,,和,,,,均由2个和2个排列而成,若+++所有可能取值中的最小值为4||2,则与的夹角为()A.B.C.D.0二、解答题1、(2014广东高考)已知函数,且,(1)求的值;(2)若,,求。
《三角函数、平面向量》自测题

A
A一; 詈
C — ; . 3
B± ; —
D __ 4 =
) .
B 要;
D
b
4 .若 a ( ), sn a C S , d 的 取 值 范 围 是 ∈ 0, 且 i > O 则
A 4+ 4
c 4;
2 .若 P ( 6 与 Q( 6 口 分 别 是 角 、 终 边 上 的 一 n, ) 一 ,) J 9 点 , a = O, 角 a与 p 的 关 系 是 ( 且 b/ 则 =
A — a= 2 7 ( = 忌 c 忌∈ Z); =
) .
;
不 能 作 为 表 示 平 面 内 任 何 向 量 基 底 的 向 量 组 是
( ).
A C
① ; ② ;形 ABC 的 对 角 线 AC 上 的 动 点 ( 含 . D 不 江 苏 黄安 成 ( 级 教 师) 特 A、 , c) 则 A ( 等 于 ( + ) . ), 中 ∈ ( , ) 其 o1 ;
( ) .
A C
第 一象 限 ; 第 三象 限 ;
B D
D | 一 , ( ) ; 霞) L ( 其中 ∈ o ,
9 .若 a一 ( O , i ) 舀 ( , 1 , n+ b1 最 C S0 sn ,一 一 ) 1 2 的 大 、 小 值 分 别 为 M 、 , M - m一 ( 最 m 则 F
一
、
选 择 题 ( 题 5 分 , 60 分 ) 每 共
B ( + , ∈ o2 ; 赢) 其中A ( √) , - 2
高中数学三角函数与向量试题及详细答案

高中数学三角函数与向量试题及详细答案一.解答题(共30小题)1.设函数f(x)=sinxcosx﹣cos(x+π)cosx,(x∈R)(I)求f(x)的最小正周期;(II)若函数y=f(x)的图象按=(,)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,]上的最大值.2.设α∈R,f(x)=cosx(asinx﹣cosx)+cos2(﹣x)满足,求函数f(x)在上的最大值和最小值.3.已知函数,(Ⅰ)求f(x)的定义域与最小正周期;(Ⅱ)设,若,求α的大小.4.设函数f(θ)=,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.(Ⅰ)若点P的坐标为,求f(θ)的值;(Ⅱ)若点P(x,y)为平面区域Ω:上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.5.已知函数f(x)=(1+cotx)sin2x+msin(x+)sin(x﹣).(1)当m=0时,求f(x)在区间上的取值范围;(2)当tana=2时,,求m的值.6.已知tanα=a,(a>1),求的值.7.已知函数f(x)=cosx(sinx+cosx),x∈R.(1)请指出函数f(x)的奇偶性,并给予证明;(2)当时,求f(x)的取值范围.8.已知函数f(x)=sin2x+acos2x,a,a为常数,a∈R,且.(I)求函数f(x)的最小正周期.(Ⅱ)当时,求函数f(x)的最大值和最小值.9.已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点.(Ⅰ)求sin2α﹣tanα的值;(Ⅱ)若函数f(x)=cos(x﹣α)cosα﹣sin(x﹣α)sinα,求函数的最大值及对应的x的值.10.已知函数.(1)设ω>0为常数,若上是增函数,求ω的取值范围;(2)设集合,若A⊂B恒成立,求实数m的取值范围.11.已知函数f(x)=(Ⅰ)把f(x)解析式化为f(x)=Asin(ωx+ϕ)+b的形式,并用五点法作出函数f(x)在一个周期上的简图;(Ⅱ)计算f(1)+f(2)+…+f(2012)的值.12.已知α为锐角,且,函数,数列{a n}的首项.(1)求函数f(x)的表达式;(2)求证:a n+1>a n;(3)求证:.13.已知tan2θ=﹣,且3π<2θ<4π.求:(1)tanθ;(2).14.在平面直角坐标系xOy中,已知点A(0,﹣1),B点在直线y=﹣3上,M点满足∥,,=•,M点的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值.15.已知,①若向量.且∥,求f(x)的值;②在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且满足(2a﹣c)cosB=bcosC,求f(A)的取值范围.16.已知O是线段AB外一点,若,.(1)设点A1、A2是线段AB的三等分点,△OAA1、△OA1A2及△OA2B的重心依次为G1、G2、G3,试用向量、表示;(2)如果在线段AB上有若干个等分点,你能得到什么结论?请证明你的结论.17.已知向量=(1,2),=(cosα,sinα),设=+t(t为实数).(1)若,求当||取最小值时实数t的值;(2)若⊥,问:是否存在实数t,使得向量﹣和向量的夹角为,若存在,请求出t;若不存在,请说明理由.18.经过A(2,0),以(2cosθ﹣2,sinθ)为方向向量的直线与经过B(﹣2,0),以(2+2cosθ,sinθ)为方向向量的直线相交于点M(x,y),其中θ≠kπ.(I)求点M(x,y)的轨迹方程;(II)设(I)中轨迹为曲线C,,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求的取值范围.19.已知向量,,.(1)若,求向量、的夹角θ;(2)若,函数的最大值为,求实数λ的值.20.已知向量=(mcosα,msinα)(m≠0),=(﹣sinβ,cosβ.其中O为坐标原点.(I)若且m>0,求向量与的夹角;(II)当实数α,β变化时,求实数的最大值.21.已知中心在原点,长轴在x轴上的椭圆的一个顶点是点(0,),离心率为,左、右焦点分别为F1和F2.(1)求椭圆方程;(2)点M在椭圆上,求△MF1F2面积的最大值;(3)试探究椭圆上是否存在一点P,使,若存在,请求出点P的坐标;若不存在,请说明理由.22.已知△OFQ的面积为,且.(1)当时,求向量与的夹角θ的取值范围;(2)设,若以中心O为坐标原点,焦点F在x非负半轴上的双曲线经过点Q,当取得最小值时,求此双曲线的方程.23.在平行四边形ABCD中,设边AB、BC、CD的中点分别为E、F、G,设DF与AG、EG的交点分别为H、K,设=,=,试用、表示、.24.正方形ABCD的边长为1,记=(1)求作,(2)求|,|25.如图,平面内有三个向量,,,其中与的夹角为120°,与的夹角为30°.且||=1,||=1,||=2,若+,求λ+μ的值.26.例3.已知27.设动点M的坐标为(x,y)(x、y∈R),向量=(x﹣2,y),=(x+2,y),且|a|+|b|=8,(I)求动点M(x,y)的轨迹C的方程;(Ⅱ)过点N(0,2)作直线l与曲线C交于A、B两点,若(O为坐标原点),是否存在直线l,使得四边形OAPB为矩形,若存在,求出直线l的方程,若不存在,请说明理由.28.在福建省第14届运动会(2010•莆田)开幕式上,主会场中央有一块边长为a米的正方形地面全彩LED显示屏如图所示,点E、F分虽为BC、CD边上异于点C的动点,现在顶点A处有视角∠EAF设置为45°的摄像机,正录制形如△ECF的移动区域内表演的某个文艺节目,设DF=x米,BE=y米.(Ⅰ)试将y表示为x的函数;(Ⅱ)求证:△ECF周长p为定值;(Ⅲ)求△ECF面积S的最大值.29.如图所示,ABCD是一块边长为7米的正方形铁皮,其中A TN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是上一点.设∠TAP=θ,长方形PQCR的面积为S平方米.(1)求S关于θ的函数解析式;(2)设sinθ+cosθ=t,求S关于t的表达式以及S的最大值.30.如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4).赛道的后一段为折线段MNP,为保证参赛队员的安全,限定∠MNP=120°.(1)求实数A和ω的值以及M、P两点之间的距离;(2)连接MP,设∠NPM=θ,y=MN+NP,试求出用θ表示y的解析式;(3)(理科)应如何设计,才能使折线段MNP最长?(文科)求函数y的最大值.参考答案与试题解析一.解答题(共30小题)1.设函数f(x)=sinxcosx﹣cos(x+π)cosx,(x∈R)(I)求f(x)的最小正周期;(II)若函数y=f(x)的图象按=(,)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,]上的最大值.考点:三角函数的周期性及其求法;函数y=Asin(ωx+φ)的图象变换;三角函数的最值.专题:计算题;综合题.分析:(I)先利用诱导公式,二倍角公式与和角公式将函数解析式化简整理,然后利用周期公式可求得函数的最小正周期.(II)由(I)得函数y=f(x),利用函数图象的变换可得函数y=g(x)的解析式,通过探讨角的范围,即可的函数g(x)的最大值.解答:解:(I)∵f(x)=sinxcosx﹣cos(x+π)cosx=sinxcosx+cosxcosx=sin2x+cos2x+=sin(2x+)+∴f(x)的最小正周期T==π(II)∵函数y=f(x)的图象按=(,)平移后得到的函数y=g(x)的图象,∴g(x)=sin(2x+﹣)++=sin(2x﹣)+∵0<x≤∴<2x﹣≤,∴y=g(x)在(0,]上的最大值为:.点评:本题考查了三角函数的周期及其求法,函数图象的变换及三角函数的最值,各公式的熟练应用是解决问题的根本,体现了整体意识,是个中档题.2.设α∈R,f(x)=cosx(asinx﹣cosx)+cos2(﹣x)满足,求函数f(x)在上的最大值和最小值.考点:由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数的最值.专题:计算题.分析:利用二倍角公式化简函数f(x),然后,求出a的值,进一步化简为f(x)=2sin(2x ﹣),然后根据x的范围求出2x﹣,的范围,利用单调性求出函数的最大值和最小值.解答:解:f(x)=cosx(asinx﹣cosx)+cos2(﹣x)=asinxcosx﹣cos2x+sin2x=由得解得a=2所以f(x)=2sin(2x﹣),所以x∈[]时2x﹣,f(x)是增函数,所以x∈[]时2x﹣,f(x)是减函数,函数f(x)在上的最大值是:f()=2;又f()=,f()=;所以函数f(x)在上的最小值为:f()=;点评:本题是中档题,考查三角函数的化简,二倍角公式的应用,三角函数的求值,函数的单调性、最值,考查计算能力,常考题型.3.已知函数,(Ⅰ)求f(x)的定义域与最小正周期;(Ⅱ)设,若,求α的大小.考点:正切函数的周期性;同角三角函数基本关系的运用;二倍角的余弦;正切函数的定义域.专题:计算题.分析:(Ⅰ)利用正切函数的定义域求出函数的定义域,利用周期公式求出最小正周期;(Ⅱ)通过,化简表达式,结合α∈(0,),求出α的大小.解答:解:(Ⅰ)由2x+≠+kπ,k∈Z.所以x≠,k∈Z.所以f(x)的定义域为:f (x)的最小正周期为:.(Ⅱ)由得tan()=2cos2α,整理得因为α∈(0,),所以sinα+cosα≠0 因此(cosα﹣sinα)2=即sin2α=因为α∈(0,),所以α=点评:本题考查两角和的正弦函数、余弦函数、正切函数公式,同角三角函数的基本关系式,二倍角公式等基本知识,考查基本运算能力.4.设函数f(θ)=,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.(Ⅰ)若点P的坐标为,求f(θ)的值;(Ⅱ)若点P(x,y)为平面区域Ω:上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.考点:任意角的三角函数的定义;二元一次不等式(组)与平面区域;三角函数的最值.专题:综合题;压轴题;转化思想.分析:(I)由已知中函数f(θ)=,我们将点P的坐标代入函数解析式,即可求出结果.(II)画出满足约束条件的平面区域,数形结合易判断出θ角的取值范围,结合正弦型函数的性质我们即可求出函数f(θ)的最小值和最大值.解答:解(I)由点P的坐标和三角函数的定义可得:于是f(θ)===2(II)作出平面区域Ω(即感触区域ABC)如图所示其中A(1,0),B(1,1),C(0,1)于是0≤θ≤∴f(θ)==且故当,即时,f(θ)取得最大值2当,即θ=0时,f(θ)取得最小值1点评:本题主要考查三角函数、不等式等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想.5.已知函数f(x)=(1+cotx)sin2x+msin(x+)sin(x﹣).(1)当m=0时,求f(x)在区间上的取值范围;(2)当tana=2时,,求m的值.考点:弦切互化;同角三角函数间的基本关系.专题:综合题.分析:(1)把m=0代入到f(x)中,然后分别利用同角三角函数间的基本关系、二倍角的正弦、余弦函数公式以及特殊角的三角函数值把f(x)化为一个角的正弦函数,利用x的范围求出此正弦函数角的范围,根据角的范围,利用正弦函数的图象即可得到f(x)的值域;(2)把f(x)的解析式利用二倍角的正弦、余弦函数公式及积化和差公式化简得到关于sin2x和cos2x的式子,把x换成α,根据tanα的值,利用同角三角函数间的基本关系以及二倍角的正弦函数公式化简求出sin2α和cos2α的值,把sin2α和cos2α的值代入到f(α)=中得到关于m的方程,求出m的值即可.解答:解:(1)当m=0时,=,由已知,得sin(2x﹣)∈[﹣,1],从而得:f(x)的值域为.(2)因为=sin2x+sinxcosx+=+﹣=所以=①当tanα=2,得:,,代入①式,解得m=﹣2.点评:考查三角函数的化简、三角函数的图象和性质、已知三角函数值求值问题.依托三角函数化简,考查函数值域,作为基本的知识交汇问题,考查基本三角函数变换,属于中档题.6.已知tanα=a,(a>1),求的值.考点:两角和与差的正弦函数;弦切互化;二倍角的正切.专题:计算题.分析:利用两角和与差的正弦函数,以及二倍角的正切,化简,代入tanα=a,求出结果即可.解答:解:原式===.即:=.点评:本题是基础题,考查弦切互化,二倍角的正切,考查计算能力,常考题型.7.已知函数f(x)=cosx(sinx+cosx),x∈R.(1)请指出函数f(x)的奇偶性,并给予证明;(2)当时,求f(x)的取值范围.考点:两角和与差的正弦函数;二倍角的正弦;二倍角的余弦;正弦函数的单调性.专题:三角函数的图像与性质.分析:(1)先化简函数得出的表达式,通过f(﹣)≠±f(﹣),直接证明即可.(2)先得出,然后根据正弦函数的单调性求出取值范围.解答:解:(3分)(1)∵,∴f(x)是非奇非偶函数.(3分)注:本题可分别证明非奇或非偶函数,如∵f(0)=1≠0,∴f(x)不是奇函数.(2)由,得,.(4分)所以.即.(2分)点评:本题考查三角函数中的恒等变换应用,正弦函数的奇偶性的判断,考查计算能力.8.已知函数f(x)=sin2x+acos2x,a,a为常数,a∈R,且.(I)求函数f(x)的最小正周期.(Ⅱ)当时,求函数f(x)的最大值和最小值.考点:二倍角的余弦;两角和与差的正弦函数;正弦函数的定义域和值域.专题:三角函数的图像与性质.分析:(I)由,代入f(x)中即可求出a的值,然后把求出a的值代入然后把求出a的值代入f(x)中,然后利用二倍角的余弦函数公式及两角差的正弦函数公式和特殊角的三角函数值化为一个角的正弦函数,根据公式求出结果.(II)根据x的范围求出2x﹣的范围,根据正弦函数的图象求出sin(2x﹣)的值域即可得到f(x)的最值.解答:解:(Ⅰ)由已知得即,所以a=﹣2所以f(x)=sin2x﹣2cos2x=sin2x﹣cos2x﹣1=所以函数f(x)的最小正周期为π(Ⅱ)由,得则所以所以函数y=f(x)的最大值为;最小值为点评:本题三角函数周期的求法,又考查学生会求正弦函数的在某一范围内的最值以及会求正弦函数的值域.是一道综合题.9.已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点.(Ⅰ)求sin2α﹣tanα的值;(Ⅱ)若函数f(x)=cos(x﹣α)cosα﹣sin(x﹣α)sinα,求函数的最大值及对应的x的值.考点:两角和与差的正弦函数;任意角的三角函数的定义;同角三角函数间的基本关系.专题:三角函数的图像与性质.分析:(I)利用三角函数的定义求出sinα、cosα和tanα的值,利用两角和与差正弦公式化简sin2α﹣tanα并求出其值.(II)首先化简函数f(x),然后利用诱导公式以及两角和与差公式得出y=2sin(2x﹣)﹣1,进而求正弦函数的特点求出结果.解答:解:(Ⅰ)因为角α终边经过点,所以,,…(3分)(Ⅱ)∵f(x)=cos(x﹣α)cosα﹣sin(x﹣α)sinα=cosx,x∈R…(7分)∴y max=2﹣1=1,…(12分)此时,即…(13分)点评:此题考查了二倍角的正弦、三角函数定义、同角三角函数间的基本关系、诱导公式,以及两角和与差的正弦函数公式,熟练掌握公式是解本题的关键.10.已知函数.(1)设ω>0为常数,若上是增函数,求ω的取值范围;(2)设集合,若A⊂B恒成立,求实数m的取值范围.考点:二倍角的余弦;集合关系中的参数取值问题;二次函数的性质;正弦函数的单调性.专题:计算题.分析:(1)利用三角函数的降幂公式将化为f(x)=2sinx,从而f (ωx)=2sinωx,利用f(ωx)在[,]是增函数,可得到,从而可求ω的取值范围;(2)由于f(x)=2sinx,将化为sin2x﹣2msinx+m2+m﹣1>0,令sinx=t,则t2﹣2mt+m2+m﹣1>0,t∈[,1],记f(t)=t2﹣2mt+m2+m﹣1,问题转化为上式在t∈[,1]上恒成立问题,根据区间[,1]在对称轴t=m的左侧,右侧,对称轴穿过区间[,1]三种情况结合二次函数的单调性即可解决.解答:(本小题满分14分)解:(1)=2sinx(1+sinx)﹣2sin2x=2sinx.∵是增函数,∴,∴(2)=sin2x﹣2msinx+m2+m﹣1>0因为,设sinx=t,则t∈[,1]上式化为t2﹣2mt+m2+m﹣1>0由题意,上式在t∈[,1]上恒成立.记f(t)=t2﹣2mt+m2+m﹣1,这是一条开口向上抛物线,则或或解得:.点评:本题考查二倍角的余弦,二次函数的性质,难点在于转化与构造函数,利用f(t)=t2﹣2mt+m2+m﹣1>0恒成立,t∈[,1]来解决,属于难题.11.已知函数f(x)=(Ⅰ)把f(x)解析式化为f(x)=Asin(ωx+ϕ)+b的形式,并用五点法作出函数f(x)在一个周期上的简图;(Ⅱ)计算f(1)+f(2)+…+f(2012)的值.考点:二倍角的余弦;五点法作函数y=Asin(ωx+φ)的图象.专题:综合题.分析:(Ⅰ)利用倍角公式和诱导公式对函数解析式进行化简,再利用正弦函数的五个关键点进行列表、描点、连线;(Ⅱ)根据函数解析式先求出周期,再求出一个周期内的函数值的和,进而判断出2012与周期的关系,再求出式子和的值.解答:解:(Ⅰ)由题意知,列表:x 0 1 2 3 40 π2π1 2 1 0 1描点画图,如图所示:(Ⅱ)∵f(1)+f(2)+f(3)+f(4)=2+1+0+1=4,而y=f(x)的周期为4,且2012=4×503,∴f(1)+f(2)+…+f(2012)=4×503=2012.点评:本题是关于三角函数的综合题,涉及了倍角公式、诱导公式的应用,“五点作图法”的步骤,函数周期性的应用求式子的值,考查了分析、解决问题能力和作图能力.12.已知α为锐角,且,函数,数列{a n}的首项.(1)求函数f(x)的表达式;(2)求证:a n+1>a n;(3)求证:.考点:二倍角的正切;不等式比较大小;不等式的证明.专题:综合题.分析:(1)根据二倍角的正切函数公式,由tanα的值求出tan2α的值,根据特殊角的三角函数值以及α的范围即可求出2α的值,即可求出sin(2α+)的值,把求出的tan2α和sin2α的值代入f(x)中即可确定出f(x);(2)a n+1=f(a n),把a n代入(1)中求出的f(x)的解析式,移项后,根据a n2大于0,即可得证;(3)把a n代入(1)中求出的f(x)的解析式中化简后,求出,然后把等号右边的式子利用拆项相减的方法,得到,移项后得到,然后从n=1列举到n,抵消后得到所要证明的式子等于2﹣,根据题意分别求出a2和a3的值,根据(2)所证明的结论即可得证.解答:解:(1),又∵α为锐角,所以2α=,∴,则f(x)=x2+x;(2)∵a n+1=f(a n)=a n2+a n,∴a n+1﹣a n=a n2>0,∴a n+1>a n;(3)∵,且a1=,∴,则=,∵,,又n≥2时,∴a n+1>a n,∴a n+1≥a3>1,∴,∴.点评:此题考查学生灵活运用二倍角的正切函数公式化简求值,会利用不等式比较大小以及会进行不等式的证明,是一道综合题.13.已知tan2θ=﹣,且3π<2θ<4π.求:(1)tanθ;(2).考点:二倍角的正切.专题:计算题.分析:(1)由题意,可先判断角θ的取值范围,得出其是第四象限角从而确定出角的正切值的符号,再由正切的二倍角公式得到角的正切的方程,解此方程求出正切值;(2)由题意,先化简,再将tanθ=代入计算出答案.解答:解:(1)由题意3π<2θ<4π,得<θ<2π是第四象限角又tan2θ=﹣,∴=﹣,解得tanθ=(2)由题,将tanθ=代入得=点评:本题考查二倍角的正切,二倍角的余弦,同角三角函数的基本关系等,解题的关键是利用公式灵活变形,计算求值,本题中有一易错点,即没有判断角所在的象限,导致解出的正切值有两个答案,切记!三角函数化简求值题,公式较多,要注意选择公式使得解题的过程简捷.本题考查了利用公式变形计算的能力.14.在平面直角坐标系xOy中,已知点A(0,﹣1),B点在直线y=﹣3上,M点满足∥,,=•,M点的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值.考点:向量在几何中的应用;直线与圆锥曲线的综合问题.专题:计算题;综合题;函数思想;整体思想.分析:(Ⅰ)设M(x,y),由已知得B(x,﹣3),A(0,﹣1)并代入∥,,=•,即可求得M 点的轨迹C的方程;(Ⅱ)设P(x0,y0)为C上的点,求导,写出C在P点处的切线方程,利用点到直线的距离公式即可求得O点到l距离,然后利用基本不等式求出其最小值.解答:解:(Ⅰ)设M(x,y),由已知得B(x,﹣3),A(0,﹣1).所=(﹣x,﹣1﹣y),=(0,﹣3﹣y),=(x,﹣2).再由题意可知()•=0,即(﹣x,﹣4﹣2y)•(x,﹣2)=0.所以曲线C的方程式为y=﹣2.(Ⅱ)设P(x0,y0)为曲线C:y=﹣2上一点,因为y′=x,所以l的斜率为x0,因此直线l的方程为y﹣y0=x0(x﹣x0),即x0x﹣2y+2y0﹣x02=0.则o点到l的距离d=.又y0=﹣2,所以d==≥2,所以x02=0时取等号,所以O点到l距离的最小值为2.点评:此题是个中档题.考查向量与解析几何的交汇点命题及代入法求轨迹方程,以及导数的几何意义和点到直线的距离公式,综合性强,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.15.已知,①若向量.且∥,求f(x)的值;②在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且满足(2a﹣c)cosB=bcosC,求f(A)的取值范围.考点:平面向量的综合题.专题:计算题.分析:①利用向量共线的充要条件,可求x的值,从而可求f(x)的值;②利用余弦定理求出B的值,确定出<A+<π,然后求出函数f(A)的取值范围.解答:解:①由∥,得,∴或,∴x=2kπ+π或,∴②∵(2a﹣c)cosB=bcosC,由正弦定理得(2sinA﹣sinC)cosB=sinBcosC.∴2sinAcosB﹣cosBsinC=sinBcosC,∴2sinAcosB=sin(B+C),∵A+B+C=π,∴sin(B+C)=sinA,且sinA≠0,∴cosB=,B=,∴0<A<.∴<A+<π,0<sin(A+)≤1.又∵,∴故函数f(A)的取值范围是(0,2].点评:本题是中档题,考查三角函数的化简求值,考查向量共线的充要条件.16.已知O是线段AB外一点,若,.(1)设点A1、A2是线段AB的三等分点,△OAA1、△OA1A2及△OA2B的重心依次为G1、G2、G3,试用向量、表示;(2)如果在线段AB上有若干个等分点,你能得到什么结论?请证明你的结论.考点:向量在几何中的应用.专题:计算题.分析:(1)由题意画出图形由于点A1、A2是线段AB的三等分点,又由于△OAA1、△OA1A2及△OA2B的重心依次为G1、G2、G3,利用重心的性质及向量的三角形法则求得用向量、表示;(2)由题意若在线段AB上有若干个等分点,有(1)的证明过程及结论可以逐渐得到结论,并且利用向量的加法及减法得到证明过程.解答:解:(1)如图:点A1、A2是线段AB的三等分点,,同理可得:,,则==(2)层次1:设A1是AB的二等分点,则;;设A1、A2、A3是AB的四等分点,则;或设A1,A2,,A n﹣1是AB的n等分点,则,层次2:设A1,A2,,A n﹣1是AB的n等分点,,层次3:设A1,A2,,A n﹣1是AB的n等分点,则;证:===点评:此题考查了三角形重心的定义,向量的加法和减法,还考查了学生对于新问题逐渐分析并合理联想的能力.17.已知向量=(1,2),=(cosα,sinα),设=+t(t为实数).(1)若,求当||取最小值时实数t的值;(2)若⊥,问:是否存在实数t,使得向量﹣和向量的夹角为,若存在,请求出t;若不存在,请说明理由.考点:数量积表示两个向量的夹角;向量的模.专题:计算题.分析:(1)先把a=代入求出向量的坐标,再把转化为=,把所求结论以及已知条件代入得到关于实数t的二次函数,利用配方法求出的最小值以及实数t的值;(2)先利用向量垂直求出以及和()(),代入cos45°=,可得关于实数t的方程,解方程即可求出实数t.解答:解:(1)因为a=,所以=(),,则====所以当时,取到最小值,最小值为.(7分)(2)由条件得cos45°=,又因为==,==,()()=5﹣t,则有=,且t<5,整理得t2+5t﹣5=0,所以存在t=满足条件.(14分)点评:本题主要考查数量积表示两个向量的夹角以及向量的模.本题的易错点在于()()=5﹣t中的t<5,因为两个向量的夹角为锐角,所以向量的数量积为正得t<5.18.经过A(2,0),以(2cosθ﹣2,sinθ)为方向向量的直线与经过B(﹣2,0),以(2+2cosθ,sinθ)为方向向量的直线相交于点M(x,y),其中θ≠kπ.(I)求点M(x,y)的轨迹方程;(II)设(I)中轨迹为曲线C,,若曲线C内存在动点P,使得|PF1|、|OP|、|PF2|成等比数列(O为坐标原点),求的取值范围.考点:向量在几何中的应用;数列与解析几何的综合.专题:计算题.分析:(I)根据题意知,∥(2cosθ﹣2,sinθ),根据共线向量定理可得⇒(x﹣2)sinθ=y (2cosθ﹣2),同理(x+2)sinθ=y(2cosθ+2),两式相乘,即可得到点M(x,y)的轨迹方程;(II)设p(x0,y0)在曲线C内,得,再由|PF1|、|OP|、|PF2|成等比数列可得并代入求得,即可求得结果.解答:解:(I),(2﹣x)sinθ+y(2cosθ﹣2)=0⇒(x﹣2)sinθ=y(2cosθ﹣2)①同理(﹣2﹣x)sinθ+y(2cosθ+2)=0⇒(x+2)sinθ=y(2cosθ+2)②①×②得x2﹣4=﹣4y2即;(II)设p(x0,y0),则③化简得:④④代入③得点评:此题是个中档题.考查向量在几何中的应用,以及数列与解析几何的综合.同时考查学生灵活应用知识分析解决问题的能力.19.已知向量,,.(1)若,求向量、的夹角θ;(2)若,函数的最大值为,求实数λ的值.考点:数量积表示两个向量的夹角;数量积的坐标表达式;平面向量数量积的运算.专题:计算题;综合题.分析:(1)当时,求出向量、,利用数量积的坐标运算求出向量•,从而求出向量、的夹角θ;(2)向量,,代入函数,利用三角函数的诱导公式进行化简,转化为三角函数在定区间上的最值,即可求得结果.解答:解:(1)当时,,所以,因而;(2),,因为,所以,当λ>0时,,即,当λ<0时,,即,所以.点评:此题是个中档题.考查向量的数量积的坐标运算以及向量的夹角,和三角函数的诱导公式和三角函数在定区间上的最值等基础知识,同时也考查了学生灵活应用知识分析解决问题的能力.20.已知向量=(mcosα,msinα)(m≠0),=(﹣sinβ,cosβ.其中O为坐标原点.(I)若且m>0,求向量与的夹角;(II)当实数α,β变化时,求实数的最大值.考点:数量积表示两个向量的夹角;向量的模.专题:计算题;综合题.分析:(Ⅰ)设它们的夹角为θ,利用向量的数量积公式表示出cosθ,将已知条件代入,利用特殊角的三角函数值求出两个向量的夹角.(II)先将利用向量模的计算公式表示成,再利用三角函数的值域求出它的最大值即可.解答:解:(I)设它们的夹角为θ,则:=,故…(6分)(II)=…(10分)所以当m>0时,原式的最大值是m﹣1;当m<0时,原式的最大值是﹣m﹣1…(12分)点评:求向量的夹角问题,一般利用向量的数量积公式来解决;解决向量的模的最值问题,一般转化为函数的最值来解决.21.已知中心在原点,长轴在x轴上的椭圆的一个顶点是点(0,),离心率为,左、右焦点分别为F1和F2.(1)求椭圆方程;(2)点M在椭圆上,求△MF1F2面积的最大值;(3)试探究椭圆上是否存在一点P,使,若存在,请求出点P的坐标;若不存在,请说明理由.考点:向量在几何中的应用;椭圆的标准方程;椭圆的简单性质.专题:综合题;存在型;反证法.分析:(1)由题意设出椭圆标准方程,根据顶点的坐标和离心率得,根据a2=b2+c2求出a的值,即求出椭圆标准方程;(2)根据(1)求出的椭圆标准方程,求出点M纵坐标的范围,即求出三角形面积的最大值;(3)先假设存在点P满足条件,根据向量的数量积得,根据椭圆的焦距和椭圆的定义列出两个方程,求出的值,结合(2)中三角形面积的最大值,判断出是否存在点P.解答:解:(1)由题意设椭圆标准方程为.由已知得,.(2分)则,∴.解得a2=6(4分)∴所求椭圆方程为(5分)(2)令M(x1,y1),则(7分)∵点M在椭圆上,∴,故|y 1|的最大值为(8分)∴当时,的最大值为.(9分)(3)假设存在一点P,使,∵,∴,(10分)∴△PF1F2为直角三角形,∴|PF1|2+|PF2|2=|F1F2|2=4 ①(11分)又∵②(12分)∴②2﹣①,得2|PF1|•|PF2|=20,∴,(13分)即=5,由(1)得最大值为,故矛盾,∴不存在一点P,使.(14分)点评:本题考查了椭圆方程的求法以及椭圆的性质、向量数量积的几何意义,利用a、b、c、e几何意义和a2=b2+c2求出a和b的值,根据椭圆上点的坐标范围求出相应三角形的面积最值,即根据此范围判断点P是否存在,此题综合性强,涉及的知识多,考查了分析问题和解决问题的能力.22.已知△OFQ的面积为,且.(1)当时,求向量与的夹角θ的取值范围;(2)设,若以中心O为坐标原点,焦点F在x非负半轴上的双曲线经过点Q,当取得最小值时,求此双曲线的方程.考点:数量积表示两个向量的夹角;双曲线的标准方程.专题:计算题.分析:(1)利用两个向量的数量积的定义和三角形面积公式,推出tanθ的解析式,再根据m的范围,求得tanθ的范围,进而求得θ的取值范围.(2)设出双曲线的标准方程和点Q的坐标,有三角形的面积公式求出点Q的横坐标和纵坐标(用半焦距表示),用基本不等式求出||最小时点Q的坐标,从而得到双曲线方程中的待定系数.解答:解:(1)由已知得,∴tanθ=,∵<m<4,∴1<tanθ<4,∴<θ<arctan4.(2)设双曲线方程为﹣=1,(a>0,b>0),不妨设点Q的坐标为(m,n),n>0,则=(m﹣c,n),∵△OFQ的面积为||•n=2,∴n=.又由•=(c,0)•(m﹣c,n)=c(m﹣c)=(﹣1)c2,∴m=,||==≥,当且仅当c=4时,||有最小值,此时,点Q的坐标为(,),由此可得,解得,故所求的方程为:=1.点评:本题考查两个向量的数量积的定义,三角形的面积公式以及基本不等式的应用,用待定系数法求双曲线的方程.。
三角函数、平面向量、复数训练测试题

一致 掌 敦 掌 通 讯●蕙 0 年 月下半月 ● 第 月, 0 啪 职
.
魏 训练测试题
( A) . ( B) . ( c) 2 . ( D) .
中点 . E 作 F上 船 交 朋 于点 F. ( )证明 P ∥ 平面 E B; 1 A D
( A)一 2 ( . B)一 1 ( . C)3 ( . D)一 3 .
维普资讯
训练:试题魏 j i
5 .向量葫 : (,) 33 , = ( .)点 C满足I 一1o 。
=
I
有(
)
l则 1 1 , 菌 的取值范围是(
( A)E ,] 4 6.
B
CD 的距离相等 . 则动点 M 的轨迹
所形成_ 的曲线是(
( A)直 线 .
中点. ( )求异 面直线 A 与 B 成 的角 ; 1 B C 所 ( )求 MN 的长 } 2 ( )求 MN与底面 AB 3 C所成 的角.
( C)双 曲 线 . ( D)抛 物 线 . 二 、 空 题 填
三 、 答 题 解
选 择 题
1 .若 A、 B是锐角三角形 的两个 内角 , 则点 P(oB— cs
s A,i 一 1s 在 ( i s B 2 A) n n 0 )
( A)第一象限.
( C)第三象限.
( )第二 象限. B
( 第 四象 限. D)
I .如 图. 已 知 四 棱 锥 P —
3, ) 则 言与 的夹 角大 小 0 是
.
( 东省 邹城 市 实验 中学 2 3 O ) 万 兆峰 山 7 5 O
一
、
5 .等边 △A C 的边 长 为 a, D 是 BC边 上的 高 。 B A 沿 AD将 /A X BC折 成 直 二 面 角 则 点 A 到 BC 的距 离 是
三角函数向量解三角形练习题50套带答案

第四章三角函数练习一角的的概念的推广(一)要点1.正角、负角和零角:规定,一条射线绕它的端点按逆时针方向旋转形成的角为正角.按顺时针方向旋转形成的角为负角.射线没有旋转,形成零角.2.象限角:在平面直角坐标系中,使角的顶点与坐标原点重合,角的终边在x轴的非负半轴上,角的终边落在第几象限内,就称这个角是第几象限角.3. 轴上角:当角的终边落在坐标轴上时,就称之为轴上角,它不属于任何象限.同步练习1.给出命题:①-880是第四象限角;②2560是第三象限角;③4800是第二象限角;④-3000是第一象限角.其中正确的有别( )(A)1个(B)2个(C)3个(D)4个2.有下列四个角:⑴-2100,⑵-1900,⑶-6300,⑷12300其中第二象限的角为( )(A)⑴⑷(B)⑴⑶⑷(C)⑴⑵⑷(D)⑴⑵⑶⑷3.下列各组的两个角中,终边不重合的一组是( )(A) -210与6990(B) 1800与-5400(C) 900与9900(D) 1500与69004.时针的分针经过期2小时40分钟,它所转过的角是______度,这个角是第____象限角.5.在00~3600范围内,找出与下列各角终边相同的角,并判断它们是第几象限角或哪个轴上的角.⑴6900; ⑵5400; ⑶-2000; ⑷-4500.6.在平面直角坐标系中,作出下列各角,并指出它们是哪个象限的角.⑴-3300; ⑵-18300; ⑶-6300; ⑷9900.7.在[-1800, 12600]内,写出与1800角终边相同的所有角.练习二 角的概念的推广(二)要点1. 与角α终边相同的角的集合为{β|β=α+k ·3600,k ∈Z}.2. 第一象限角、锐角和小于900的角的区别与联系.1.下列命题中,正确的是 ( )(A)第一象限角必是锐角 (B)终边相同的角必相等(C)相等的角终边位置必相同 (D)不相等的角终边位置必不相同2. 以下四个命题:⑴小于900的角为锐角 ; ⑵钝角是第二象限角; ⑶第一象限角不一定是负角;⑷第二象限角必大于第一象限角.其中正确命题的个数是 ( ) (A)1 (B)2 (C) 3 (D)43. 角α的终边上一点的坐标是(2,-2),则角α的集合是________________.4. 与-20050终边相同且绝对值最小的角是________________.5. 写出与下列各角终边相同的角的集合,并把集合中适合不等式-3600≤α≤3600的元素α写出来.⑴ 600; ⑵ -834030/.6.写出下列角的集合:⑴终边在y 轴负半轴上的角;⑵终边在坐标轴上的角;⑶终边在第二、第四象限角平分线上的角;⑷终边在第三象限的角;⑸终边在第四象限的角. [思考与研究]若α是第一象限角,试确定2α、2α、3α所在的象限.练习三 弧度制 (一)要点1. 角度制与弧度制:这是两种不同的度量角的制度.角度制是以“度”为单位;弧度制是以“弧度”为单位. 2. 度与弧度的相互换算:10≈0.01745弧度, 1弧度≈57018/.3. 在同一个式子中,两种制度不能混用.如:与600终边相同的角的集合不能表示为{x|x=2k π+600,k ∈Z},正确的表示方法是x|x=2k π+3π,k ∈Z }或{ x|x=k ·3600 +600,k ∈Z } 同步练习1. 若α=-3.2,则角α的终边在 ( ) (A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限2.①4π, ② -45π,③419π,④-43π,其中终边相同的角是 ( )(A) ①和② (B) ②和③ (C) ③和④ (D) ①和④ 3. 若4π<α<6π,且与-32π角的终边相同,则α=_________. 4.正三角形,正四边形,正五边形, 正六边形, 正八边形, 正十边形, 正n 边形的一个内角的大小分别_____,____ ,_____,_____,_____,_____, ______.(用弧度表示) 5.把下列各角用另一种度量制表示. ⑴1350⑵ -67030/⑶2 ⑷-67π6. 将下列各数按从小到大的顺序排列.Sin40, sin21, sin300, sin17. 把下列各角化成2k π+α(0≤α<2π,)的形式, 并求出在(-2π,4π)内和它终边相同的角.(1)-316π; (2)-6750.8. 若角θ的终边与1680角的终边相同,求在[0,2π]内终边与3θ角的终边相同的角.练习四 弧度制(二)要点1. 弧长公式和扇形面积公式:弧长公式 L=|α|r 扇形面积公式 S=21Lr=21|α|r 2其中α是圆心角的弧度数,L 为圆心角α所对的弧长,r 为圆半径.2. 无论是角度制还是用弧度制,都能在角的集合与实数集之间建立起一一对应的关系,但用弧度制表示角时,容易找出与角对应的实数. 同步练习1.半径为5 cm 的圆中,弧长为415cm 的圆弧所对的圆心角等于 ( ) (A)145(B) 1350(C)π135 (D)π1452.将分针拨快10分钟,则分针转过的弧度数是 ( ) (A)3π (B)-3π (C) 6π (D)-6π 3. 半径为 4 的扇形,基它的周长等于弧所在的半圆周的长,则这个扇形的面积是_________.4. 已知一弧所对的圆周角为600,圆的半径为10cm,则此弧所在的弓形的面积等于___________.5. 已知扇形的周长为6cm,面积为2cm 2,求扇形圆心角的弧度数.6. 2弧度的圆心角所对的弦长为2,求这个圆心角所夹扇形的面积.7. 一条弦的长度等于其所在圆的半径r.(1) 求这条弦所在的劣弧长;(2) 求这条弦和劣弧所组成的弓形的面积.练习五 任意角的三角函数 (一)要点1. 三角函数是以角为自变量,以比值为函数值的函数.三角函数的定义域:sin α,cos α的定义域都是R,tan α的定义域是{α|α≠k π+2π, k ∈Z}. 2. 三角函数值在各个象限的符号:第一象限全正,第二象限只有正弦正,第三象限只有正切正,第四象限只有余弦正. 同步练习1.当α为第二象限角时ααsin |sin |-|cos |cos αα的值是 ( ) (A)-2 (B)0 (C)-1 (D)22.设角α的终边过点P(-3α,-4α),(α≠0),则sin α-cos α的值是 ( ) (A)51 (B)- 51 (C)- 51或 -57 (D) -51或51 3.在三角形ABC 中,若cosA ·tanB ·cotC<0,则这个三角形的的形状是_____. 4.设θ为第二象限角,其终边上一点为P(m,5),且cos α,则α的值为_______. 5.已知β的终边经过点P(m,-3)(m ≠0),且cos β=2m,求sin β,tan β的值.6.求cos 3π-tan 45π+43tan 26π+sin 611π+cos 267π-sin 23π的值.7.求函数y=xxsin 1tan +的定义域.练习六 任意角的三角函数(二)要点1. 终边相同角的同名三角函数值相等(公式一),利用这组公式可以将任意角的三角函数值化为00~3600(或0~2π)间的角的三角函数值. 2. 三角函数线都是有向线段、线段的方向表示三角函数值的正负,线段的长度表示三角函数值的绝对值.书写三角函数线时,要注意起点与与终点的次序. 同步练习 1.sin637π的值等于 ( ) (A)21 (B)23 (C)- 21(D) -232.设α、β是第二象限角,若sin α>sin β,则 ( )(A)tan α>tan β (B)cos α<cot β (C)cos α>cos β (D)sec α>sec β 3. 在下列各题中的_____处,填上适当的符号(>,=,<). ⑴sin1560·cos(-4400)_____0; ⑵cot(-817π)·sin(-34π)_______0;⑶5.1tan 4sin ____0;⑷sin320π·tan(-417π)·cos 27π______0. 4. 已知α∈(-π,π),且cos α>-23,则角α的取值范围是________. 5. 计算:(1) m 2sin(-6300)+n 2tan(-3150)-2mncos(-7200);(2) sin(-623π)+cos 713πtan4π-cos 313π.6. 在单位圆中,用阴影线表示满足条件的θ的终边的范围: (1)tan θ≥1 (2)cos θ<21 (3)-21<sin θ≤237. 设0<α<2π,利用单位圆中的三角函数线证明:sin α+cos α>1练习七 同角三角函数的基本关系式(一)要点同角三角函数的基本关系式:sin 2α+cos 2α=1,ααcos sin =tan α,tan α·cot α=1.(1)公式中应注意“同角”二字,如sin 2α+cos 2β=1就不恒成立.(2)注意α的范围,第二个关系式中α≠k π+2π(k ∈Z),第三个关系式中α≠2πk (k ∈Z).(3)对公式的的使用要做到顺用、逆用、变用、活用.同步练习1.下列各式正确的是 ( ) (A)sin 2300+cos 2600=1 (B)sin23π/cos 23π=tan 23π (C)tan2π·cot2π=1 (D)sin 220050+cos 220050=12.下列各式能成立的是 ( ) (A)sin α=cos α=21 (B)cos α=21且tan α=2 (C)sin α=21且tan α=33 (D)tan α=2且cot α=-213. 已知cos θ=31,,则1+tan 4θ=______. 4. 已知sin α+ sin 2α=1则cos 2α+cos 4α的值等于_________. 5. 已知sin α=-53,α是第四象限角,求cos α、tan α的值.6. 已知cot α=-3,求sin α、cos α的值.7. 已知cos α=m(|m|≤1),求tan α和sin α.练习八 同角三角函数的基本关系式(二)要点1. 化简三角函数式的一般要求是(1)能求出函数值的要求出函数值,函数种类尽可能的少;(2)要使化简后的式子项数最少,次数最低;(3)尽量化去含有根式的式子,尽可能的不含分母.2. 证明三角恒等式的实质是消除等式两边的差异,一般由繁到简,可采用:①左边⇒右边 ②右边⇒左边③左边-右边=0④分别从左右两边推出相同的结果. 同步练习1.化简02100sin 1-等于 ( )2.若tan α=a,且sin α=21aa +,则α是 ( )(A) 第一、二象限角 (B)第一、三象限角 (C)第一、四象限角 (D)第二、三象限角3. 化简sin 2α+sin 2β-sin 2αsin 2β+cos 2αcos 2β=____________4. 若tanx=3则xx22cos 1sin +的值是___________ 5. 化简下列各式: (1) ααcos 1cos 1-+-ααcos 1cos 1+-,其中α为第二象限角;(2)αααα2222tan sin tan sin -.6. 证明下列恒等式(1) cos α(αcos 2+tan α) (αcos 1-2tan α)=2cos α-3tan α (2) x x x x 2sin 2cos 2cos 2sin 2122--=xx2tan 12tan 1+-练习九 正余弦的诱导公式(一)要点1.公式二:sin(1800+α)=-sin α,cos(1800+α)=-cos α. 公式三: sin(-α)=-sin α, cos(-α)=cos α.2. 公式中的α是任意角,但在记忆时,可把α看作锐角,从而1800+α可看作第三象限角, -α可看作第四象限角. 同步练习1.下列等式中,恒成立的是 ( )(A) sin(1800+2000)=sin2000(B)cos(-α)=-cos α(C) cos(1800+2000)=-cos2000(D)sin(-α)=sin α 2.sin 2(π+α)-cos(π+α)cos(-α)+1的值是 ( )(A) 2sin 2α (B)0 (C)1 (D)2 3. 计算sin34πcos(-6π)tan(-45π)=_________.4. 化简sin 2(-α)tan α+cos 2(π+α)cot α-2 sin(π+α) cos(-α)=_____5. 求下列各三角函数值:(1) sin(-13200) (2) tan9450(3)cos655π(4)cot(-322π)6.(1)求值sin 2(-300) +sin 22250 +2sin2100 +cos 2(-450) ; (2)若sin(π+α)= 41,求[]1)cos(cos )cos(-++απααπ-)cos()cos()2cos()cos(απαπαπα-+++--值;(3) 已知sin(3π-α)= 31;求sin(6π+α),sin(310π-α)的值.7. 化简:)(cos )tan()2cot()cos()(sin 32πααππααππα++--++练习十 正余弦的诱导公式(二)要点1.公式四: sin(1800-α)=sin α,cos(1800-α)=-cos α.公式五sin(3600-α)=-sin α,cos(3600-α)=cos α.2.记忆公式时, 1800-α可看作第二象限角, 3600-α可看作第四象限角 同步练习 1.sin(-619π)的值是 ( ) (A)21 (B) -21(C)23 (D) -232.已知cos(π-x)=-21,23π<x<2π,则sin(2π-x)的值等于 ( ) (A)21(B)± 23 (C)23 (D) -233.计算:sin(-15600)cos9300+cos(-13800) sin(-14100)=_______. 4. 已知COS(6π+θ)= 33,则COS(65π-θ)=__________.5. 求值0200170cos 110cos 10cos 10sin 21---6. 已知cos(π-α)=-21,计算: (1) sin(2π-α); (2)cot[2)12(π+k +α](k ∈Z)7. 已知sin(α-π) =2cos(2π-α),求)sin()cos(3)2cos(5)sin(ααπαπαπ----+-的值数学家陈景润陈景润(1933~1996),中国数学家、中国科学院院士。
函数、三角函数、向量、数列综合测试二

函数、三角函数、向量、数列综合测试二一、选择题(本大题共12小题,每小题5分,共60分,)1.已知集合{2,1,0,1,2},{1,0,1},{0,1,2},U U A B C A B =--=-= 则=( )A .{-2}B .{0,1}C .{2}D .{0,1,2}2.已知复数21i z i=+,则z 2等于( )A .1-iB .-1+iC .-1-iD .1+i3.与函数)1lg(10-=x y 是同一函数的是( )A.1-=x yB.1-=x yC.112+-=x x y D.211⎪⎪⎭⎫ ⎝⎛--=x x y4.当1a >时,函数log a y x =和(1)y a x =-的图象只可能是( )5.设0.76a =,60.7b =,0.7log 6c =则a b c 、、的大小关系为( )A .b c a <<B .c b a <<C .c a b <<D .b a c << 6.已知向量(,3),(2,1)a x b a b =-=-⊥若,则x =( )A .32B .6C .-32D .-67.函数()sin(2)3f x y x π==-的图象的一条对称轴方程是( )A .12x π=B .6x π=C .512x π=D .3x π=8.将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( )A .22cos y x =B .22sin y x = C .)42sin(1π++=x y D .cos 2y x =9.在等差数列{}n a 中,n S 是其前n 项和,120112010,0a a =-=,则9797S S -= ( )A .2B .-2C .-1D .110.曲线3231y x x =-+在点(—1,—3)处的切线与坐标轴所围成的封闭图形的面积为( )A .2B .3C .4D .5 11.函数2()ln(2)f x x x=--的零点所在的大致区间是( )A .(1,2)B .(2,3)C .(3,4)D .(4,5)12.执行右图所示的程序框图,则输出的S 等于( ) A .254 B .255 C .511 D .512第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分。
三角函数、平面向量专题试题集

三角函数、平面向量专题试题集三角函数.平面向量专题试题集1. 函数的最小正周期为 ( A )A. B. C.8D.42. 已知函数的图象的一条对称轴方程为直线_=1,若将函数的图象向右平移b个单位后得到y=sin_的图象,则满足条件的b的值一定为( C )A.B. C.D.3. 在△ABC,为角A.B.C所对的三条边.(1)求时,t的取值范围;(2)化简(用(1)中t表示).(1)∵,∴△ABC为直角三角形,∴∠A+∠B= …………2分又…………4分∵ ∴, ∴…………6分(2)∵ ∴…………9分…………12分4. 已知向量a和b的夹角为60°,a = 3,b = 4,则(2a –b)·a等于 ( B )(A)15 (B)12 (C)6 (D)35. 已知.(Ⅰ)求cos的值;(Ⅱ)求满足sin(– _ ) – sin (+ _) + 2cos=的锐角_.解:(Ⅰ)因为,所以.(2分)所以=, (4分)由,所以.(6分)(Ⅱ)因为sin() – sin() + 2cos,所以, (8分)所以sin_=, (10分)因为_为锐角,所以.(12分)6. 下列函数中,最小正周期为,且图象关于直线对称的是( B )A. B.C. D.7. 若是纯虚数,则的值为 ( B )A.B.C.D.8. 已知向量上的一点(O为坐标原点),那么的最小值是( B )A.-16 B.-8 C.0 D.49. _年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为,大正方形的面积是1,小正方形的面积是的值等于( D )A.1 B.C.D.-10. 为锐角,为钝角,=.11. 已知a=1,b=,(1)若a//b,求a·b;(2)若a,b的夹角为135°,求a+b.解(1),①若,同向,则……3分②若,异向,则……3分(2)的夹角为135°,……2分……2分……2分12.已知函数(1)将的形式,并求其图象对称中心的横坐标;(2)如果△ABC的三边a.b.c成等比数列,且边b所对的角为_,试求_的范围及此时函数f(_)的值域.解:(1) ……3分由即对称中心的横坐标为……3分(2)由已知.……3分的值域为……2分综上所述, ……1分13. 设平面上的动向量a=(s,t),b=(-1,t2-k)其中s,t为不同时为0的两个实数,实数,满足a⊥b,(1)求函数关系式(2)若函数上是单调增函数,求证:;(3)对上述,存在正项数列,其中通项公式并证明.(1)解: ……3分(2)证明:成立, ……2分故; ……1分(3)故因为……4分事实上,……4分方法1:方法2:14. 如果函数的最小正周期是T,且当时取得最大值,那么( A )A. B. C. D.15. 在中,已知,那么一定是( B )A.直角三角形B.等腰三角形C.等腰直角三角形D.正三角形16. 已知,那么的值为,的值为.17. 若 , 且()⊥ ,则与的夹角是 ( B )(A)(B)(C)(D)18. 把y = sin_的图象向左平移个单位,得到函数y = sin的图象;再把所得图象上的所有点的横坐标伸长到原来的2倍,而纵坐标保持不变,得到函数的图象.19. 已知直线:_ – 2y + 3 = 0 ,那么直线的方向向量为(2,1)或等(注:只需写出一个正确答案即可);过点(1,1),并且的方向向量2与1满足1·= 0,则的方程为2_ + y – 3 = 0.20. 已知:tan= 2,求:(Ⅰ)tan的值;(Ⅱ)sin2的值.解:(Ⅰ)== 2,∴tan. (5分)(Ⅱ)解法一:sin2+sin2+ cos2= sin2+ sin2+ cos2– sin2= 2sincos+ cos2 (8分)= (11分)=.(13分)(Ⅱ)解法二:sin2+ sin2+ cos2= sin2+ sin2+ cos2– sin2= 2sincos+ cos2 (1)(8分)∵tan=,∴为第一象限或第三象限角.当为第一象限角时,sin=,cos=,代入(1)得2sincos+ cos2=; (10分)当为第三象限角时,sin=,cos=,代入(1)得2sincos+ cos2=. (12分)综上所述:sin2+ sin2+ cos2=.(13分)21. 已知常数a _gt; 0,向量,,经过定点A (0,–a )以+为方向向量的直线与经过定点B (0,a)以+ 2为方向向量的直线相交于点P,其中∈R.(Ⅰ)求点P的轨迹C的方程;(Ⅱ)若,过E (0,1)的直线l交曲线C于M.N两点,求的取值范围.解:(Ⅰ)设P点的坐标为(_,y),则,,又,故,.由题知向量与向量平行,故(y + a) = a_.又向量与向量平行,故y – a = 2.两方程联立消去参数,得点P (_,y)的轨迹方程是(y + a)(y – a)= 2a2_2,即y2 – a2 = 2a2_2.(6分)(Ⅱ)∵,故点P的轨迹方程为2y2 – 2_2= 1,此时点E (0,1)为双曲线的焦点.①若直线l的斜率不存在,其方程为_ = 0,l与双曲线交于.,此时. (8分)②若直线l的斜率存在,设其方程为y = k_ + 1,代入2y2 – 2_2= 1化简得2(k2 – 1) _2 + 4k_ + 1 = 0.∴直线l与双曲线交于两点,∴△=(4k)2 – 8 (k2 – 1) _gt; 0且k2 –1≠0.解得k≠±1.设两交点为M (_1,y1).N (_2,y2),则_1 + _2 =,_1_2 =. (10分)此时= _1_2 + k2_1_2= (k2 + 1) _1_2 =.当–1 _lt; k _lt; 1时,k2 – 1 _lt; 0,故≤;当k _gt; 1或k _lt; – 1时,k2 – 1 _gt; 0,故.综上所述,的取值范围是∪. (13分)22.23.24.25.26.27.28.29.30.31.32. 已知向量=(8, _),=(_,1),其中_>0,若(-2)∥(2+),则_的值为A.4B.8C.0D.2解:-2=(8-2_,_-2),2+=(16+_,_+1)由(-2)∥(2+),得(8-2_,_-2)=λ(16+_,_+1)即_THORN; _=4.选A33. 同时具有以下性质:〝①最小正周期实π;②图象关于直线_=对称;③在[-]上是增函数〞的一个函数是A.y=sin()B.y=cos(2_+)C.y=sin(2_-)D.y=cos(2_-)解:由性质①排除A,由性质②排除D,由性质③排除B,选C.34. 在△ABC中,已知sin2Asin2B=,tanAtanB=3,求角C.解:∵sin2Asin2B=,∴sinAsinBcosAcosB=……①……3’由A.B∈(0,π),知sinAsinB>0,∴cosAcosB>0又tanAtanB=3,即=3……②……6’由①②得:∴c osC=-cos(A+B)=-cosAcosB+sinAsinB=而C∈(0,π),∴C=.35. 如图,已知点P(3,0),点A.B分别在_轴负半轴和y轴上,且=0,,当点B在y轴上移动时,记点C的轨迹为E.(1)求曲线E的方程;(2)已知向量=(1,0),=(0,1),过点Q(1,0)且以向量+k(k∈R)为方向向量的直线l交曲线E于不同的两点M.N,若D(-1,0),且>0,求k的取值范围.解:(1)设A(a,0)(a<0),B(0,b),C(_,y)则=(_-a,y),=(a,-b),=(3,-b),∵=0,,∴……3’消去a.b得:y2=-4_∵a<0,∴_=3a<0故曲线E的方程为y2=-4_(_<0)……5’(2)设R(_,y)为直线l上一点,由条件知)即(_-1,y)=λ(1,k)∴,消去λ得l的方程为:y=k(_-1) ……7’由_THORN;k2_2-2(k2-2)_+k2=0 ……(_)∵直线l交曲线E与不同的两点M.N∴△>0 _THORN; -1<k<1……①……9’设M(_1,y1),N(_2,y2),则=(_1+1,y1),=(_2+1,y2)∵M.N在直线y=k(_-1)上,∴y1=k(_1-1),y2=k(_2-1)又由(_),有_1+_2=,_1_2=2∴=(_1+1)(_2+1)+y1y2=(_1+1)(_2+1)+k2(_1-1)(_2-1)=(k2+1)_1_2+(1-k2)(_1+_2)+k2+1=由条件知:>0 _THORN;k2>……②……12’由①②知:-1<k<-或<k<1.……13’36. 设集合,集合,则( A )A.中有3个元素 B.中有1个元素C.中有2个元素 D.37. 在△中,〝是〝〞的( C )A.充分非必要条件 B.必要非充分条件C.充要条件 D.既不充分也不必要条件38. 函数在下面哪个区间内是增函数( C )A.B.C. D.39. 函数的最小正周期为.40. 在三角形ABC中,设,,点在线段上,且,则用表示为.41. 将圆按向量平移得到圆,则的坐标为(-1,2);将抛物线按的相反向量平移后的曲线方程为.42. 已知向量,,,其中.(Ⅰ)当时,求值的集合;(Ⅱ)求的最大值.解:(Ⅰ)由,得,即.…………4分则,得.…………………………………5分∴为所求.…………………………………6分(Ⅱ),……………10分所以有最大值为3. (12)分。
三角函数和向量公式考试

1. 写出四个象限角的范围2. 写出弧长和扇形面积公式3. 把下列弧度化为角度,并写出正弦、余弦和正切值ππππππ2,,4,3,2,6 4. 写出同角三角函数的平方关系和商数关系 5.8.用cos α表示2sin 2α,2cos2α,2tan2α9.2tanα=αsin =asin10. sin α=2tan12tan22aa +,cos α= ,tan α=11.写出正弦、余弦定理公式,三角形面积公式(正弦定理) 12.已知向量b a 和,画出向量b a b a -+, (1)(3)13.向量a坐标为(11,γχ),向量b 坐标为(22,γχ),a b 坐标关系为 , a b ⋅= ,a b ⊥坐标关系b a +=(,),b a +=( , ),22b a +=( ,)()2b a +=,2a -2b=( , )14. 已知向量b a 和,cos b a ,=(),a b ⋅=()15. A 点坐标为(11,γχ)B 点坐标为(22,γχ),向量AB 的坐标为( , ),BA 的坐标为( , ) AB 的长度为( )16,.向量a 在b 方向上的投影为( )17.向量OA=λOB+μOC,则A ,B ,C 三点共线的充要条件是( ) 18.已知向量AB=(3,4),A 坐标(-2,-1)则B 点坐标为( )19.在三角形ABC 中,若a=2,b+c=7,cosB=41-,则B=( ) 20.已知θ为第二象限角,sin (θπ-)=2524,则cos 2θ=( )21. =--02010cos 270sin 322.复数bi a z +=,当a ,b 分别为何值时z 为实数,虚数,纯虚数,第三象限复数?它的共轭复数为?模为多少?23.复数bi a z +=1,di c z +=2,计算:21z z +,21z z -,21z z ⨯,21z z ÷24. i z θθsin cos +=,且122=+z z ,则=θ2sin ( )25.复数ia-+221为纯虚数,则a 为( ) 26.向量a =(1,θcos )与b =(-1,2θcos )垂直,则θ2cos 等于( )27. 0120的弧度为( ),0495的弧度为( ),π87的角度为( ),)311cos(π-=( )28.点P (ααcos ,tan )在第三象限,则角a 的终变在第( )象限 29.已知θsin =53,⎪⎭⎫⎝⎛∈ππθ,2,则θtan =( ),θcos =( ),θsin2=( ) 30.已知-sin θθcos =2,),0(π∈a ,则a tan =( ) 31.函数216sin x x y -+=的定义域为( ) 32.已知函数)(x f 的定义域为[]1,0,则)(cos x f 的定义域为( )33.函数)4(cos 2)(2π-=x x f -1是最小正周期为( )的( )填奇或偶函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一
(Ⅰ)卷
一、选择题(每小题5分,共60分)
1.下列各角中与︒90角终边相同的角为: ( ) A .
32π B .32π- C .π D .2
π
2.已知)1,2(=,)4,3(-=,则与的数量积为: ( )
A .)4,6(-
B .)5,1(-
C .2-
D .0
3.已知角α的终边经过点)4,3(P ,则角α的正弦值为: ( )
A .
43 B .3
4
C .53
D .5
4
4.已知角)2,0(πα∈,且2
1
sin =α,则αcos 的值为: ( )
A .3
B .
3
3
C .
2
3 D .
5
4 5.已知31)sin(=
-απ,则)2
cos(απ
+的值为: ( ) A .
31 B .3
1
- C .
3
2
2 D .3
2
2-
6.已知函数)421sin(2)(π
-=x x f ,(R x ∈)则)(x f 的最小正周期为:( )
A .π
B .2
π
C .π4
D .π2
7.计算:000043cos 13sin 13cos 43sin -的值等于: ( )
A .3
B .
23 C .2
2 D .
2
1
8.半径为πcm ,中心角为60o 的扇形的弧长为:
( )
A .cm 3π
B .
cm 3
2
π C .cm 32π
D .cm 3
22
π
93,42-=∙==b a +为: ( ) A .23 B .47
C .14
D .6
10.已知21tan -
=α,则α
ααα22cos sin cos sin 2-的值为: ( ) A .34 B .3
4- C .3 D .3-
11.已知函数x x x f cos sin )(+=,则)(x f 的最大值为: ( ) A .1 B .2
C .0
D .2
12.已知)1,(),2,1(x ==且)2(+∥)2(-,则x 为: ( ) A .2- B .2
C .
21 D .2
1
- 二,填空题(每小题5分,共20分)
13.已知5
3
cos -=α,且α为钝角,则=αtan
14.已知2tan =x ,则)24
tan(
x +π
=
15.已知)2,5(=,)1,2(-=,则在方向上的投影为: 16.已知βα,都是锐角,54sin =α,13
5
)cos(=+βα,则βsin =
河
( Ⅱ)卷
三、解答题(共6题,共70分)要求写出解答过程和步骤。
17.(10分)已知3
3
sin -=α,且α为第四象限的角,求αcos ,αtan 的值。
18.(12分)计算:0
420sin ·0
750
cos +)330sin(0-·)660cos(0-。
19.(12分)函数)sin()(ϕ+=wx A x f ,)2
,0,0(π
ϕ<
>>w A 的最小值为2-,其)(x f 图
像相邻的最高点与最低点的横坐标之差为π2,又)(x f 的图像经过点)1,0(,求函数)(x f 的解析式。
20.(12分)已知53sin =
α,),2(ππα∈ ,求)3
sin(π
α+的值。
21.(1243==且与的夹角为0
60++的值。
22.(12分)已知R x ∈,向量)1,cos (2x m =,)2sin 3,2(m x m -=,x f ∙=)(, 其中0>m 。
(1)求)(x f 的单调增区间; (2)当]2
,0[π
∈x 时,)(x f 的最大值为5,求m 的值。
河南
一:选择题:D C D C B C D B C A D C 二:填空题:
13. 34; 14.71-; 15.
558; 16.6516
三:解答题:
20.⎪⎭
⎫
⎝⎛∈=ππαα,2,53sin ,所以54cos -=α
所以αππαπαcos 3sin 3cos sin 3sin +=⎪⎭⎫ ⎝
⎛
+
10
3
4354232153-=
⎪⎭⎫ ⎝⎛-⋅+⋅=
21.=⋅→
→b a 0606=
372
=+→→
b a ,所以37=+→
→b a
132
=-→→
b a ,所以13=-→
→
b a
所以1337+=-++→
→
→
→
b a b a。
