9-第九章_层间应力解析
第九章第六节梁弯曲时的应力及强度计算(上课用)

m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以,在梁的横截面上一般
既有 正应力, 又有 剪应力
先观察下列各组图
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面,实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时,上面部分纵向纤维缩短,下面部分纵向纤维伸长,必 有一层纵向纤维既不伸长也不缩短,保持原来的长度,这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴,中性轴通过截面形心,是一条形心轴。 且与截面纵向对称轴y垂直,将截面分为受拉区及受压区。梁弯曲变形时, 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 )对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类:
(1)单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 (2)双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
(3)三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
梁的应力

ac
M
⑵、纵向线:由直线变为曲
线,且靠近上部的纤维缩短,
靠近下部的纤维伸长。
b
d
3、假设:
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线。
第九章 梁的应力
梁是由许多纵向纤维组成的
凹入一侧纤维缩短
突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变
z
A2 20120mm2 y2 80mm
yc
80 2010 120 2080 80 20 120 20
52mm
(2)求截面对中性轴z的惯性矩
Iz
Hale Waihona Puke 80 203 1280 20 422
y
201203 20120 282
12
7.64106 m4
第九章 梁的应力
横截面上应力分布
b
d2
c,m ax
h yt,max yc,max d1
oz y
Oz
y b
t,m ax
中性轴 z 不是横截面的对称轴时,其横截面上最大拉
应力值和最大压应力值为
t,m ax
My t ,m a x Iz
c,m ax
Myc ,m a x Iz
第九章 梁的应力
例 对于图示 T形截面梁,求横截面上的最大拉应力和最大压 应力.已知: I z 290 .6 10 8 m4
d
在弹性范围内, E E Ey ...... (2)
O
O1
A1
B1 x
y
第九章 梁的应力
应力的分布图:
9第九章 褶皱的成因分析

岩浆侵入穿刺/ 底劈构造
当岩浆上升, 侵入围 岩, 使上覆岩层发生 拱曲时, 则可形成岩 浆底辟/穿刺。
横弯褶皱之二 —同沉积褶皱
同沉积褶皱-岩层边 沉积边形成褶皱。
同沉积褶皱特征: 1)两翼产状倾角平 缓,总体为开阔褶皱; 2)岩层厚度背斜顶 薄,翼部厚;向斜核 部厚度大; 3)背斜顶部沉积物 为浅水粗粒物质,向 斜中心变细; 4)伴随滑塌断层。
(6)在厚层韧性岩层(如泥岩)夹薄层强 硬岩层(如石英砂岩)组成的岩系受到侧向顺 层挤压尚未发生褶皱时, 岩系先整体平行主 压应力方向压缩, 垂直主压应力方向伸长使 厚度略增; 在持续挤压下, 韧性厚岩层继续 压缩,而其间的薄层强岩层则形成一系列小 褶皱以适应压缩; 随着整个岩系在纵弯褶皱 作用下形成大型主褶皱, 这时强硬薄岩层中 的小褶皱整体地也随主褶皱而弯曲, 这些小 褶皱在枢纽部位仍保持对称式(M型), 在两 翼则变为不对称褶皱(左翼为Z型, 右翼为S 型) 。这一理论较为圆满地解释了层间小褶 皱不仅发育于大褶皱翼部, 也发育在大褶皱 的枢纽部位这一现象。
(4) 在侧向挤压力 作用下, 软岩层发生 强烈层内流动, 可产 生线理、劈理(兼有 变质作用)等小构造;
如果软岩层中夹有 脆性的薄层, 还可形 成构造透镜体。
纵弯褶皱中发育的劈理型式
可形成正扇形劈理、反扇形劈理、 轴面劈理和劈理折射等。
褶皱中劈理与层理关系的应用实例
利用劈理与层理关系判 断正常地层和倒转地层;
第一节 纵弯褶皱作用
1.纵弯褶皱作用的概念:
原始水平状态的岩层, 在受到侧向的顺层挤压力的作 用后发生褶皱弯曲叫做纵弯褶皱作用。
2. 单层岩层的纵弯褶皱作用:
在结构均一的单层板状材料侧面画上几排小圆,侧向挤 压使板状材料褶皱弯曲, 其面的小圆有以下情况:
9第九章 杆件变形及结构的位移计算

产生位移的原因 一般荷载——力的作用 广义荷载 温度变化 支座位移 制造误差
P
t
一般荷载
C C
温度变化
A
支座位移 B
B
B
制造误、位移计算的目的
⑴ 刚度要求 强度校核 结构设计计算应考虑的内容 稳定性验算 刚度验算 在工程上,吊车梁允许的挠度<1/600跨度; 房屋主梁允许挠度<1/350跨度。 高层建筑框架结构,风荷载作用下的最大位移<1/450高度, 最大层间位移<1/550层高; 地震作用下的最大位移<1/400高度; 最大层间位移<1/500层高。 ⑵ 超静定结构的计算基础 超静定结构必须考虑几何条件(位移约束或变形协调)方可求解。
1
B
C a-x
M =a x
横梁BC 竖柱CA
a
A
x
注意:负号表示位移 的方向与假设的单位 力的方向相反。 (4)求B点的线位移ΔB
§9-4 图乘法
刚架与梁的位移计算公式为:
MMds EI
在杆件数量多的情况下,不方便. 下面介绍 计算位移的图乘法.
梁和刚架位移计算公式
计算工作量很大,应用比较麻烦。一定条件下,上述积分计算可以简化。
ΔCV 2330 106 7.012mm 3 210 10 2 791.2
4m
–200
–200
5 8
3 8
5 8
3 8
5 8
杆件名称 A-C B-C D-E A-D C-D C-E
杆长l (m) 6 6 6 5 5 5
截面积A 轴力 FNP (cm2) (kN) 15.824 15.824 15.824 15.824 15.824 15.824 120 120 -120 -200 0 0
9-材料的变形与再结晶解析

(3) 弹性变形量随材料的不同而异。
对完全各向同性材料 υ= 0.25 对金属υ值约为0.33(或1/3)
当υ=0.25时,G=0.4E; 当υ=0.33时,G=0.375E , K=E/3(1-2υ) ≈E
弹性常数4个: E,G,υ,K 只要已知E和υ,就可求出G和K , 由于E易测,因此用的最多。
纳P—N力,其大小为:
τP-N = 2Gexp(-2пW/b)/(1-ν) τP-N与位错的宽度W 呈指数关系,滑移面间距d增大,w[=d /(1-ν)]增大, 或滑移方向上原子间距b减小,则τP-N下降,滑移阻
力小, 滑移容易进行。
刃位错的滑移示意图
刃位错的滑移模型
螺位错的滑移模型
2.孪生
根据拉伸试验研究表明,金属在外力作用下一般经历三个阶段:
弹性变形(elastic deformation) 塑性变形(plastic deformation) 断裂(fracture)
三、应力—应变曲线
原始曲线:载荷-伸长曲线 经过变换:应力-应变曲线
σp:比例极限
σe: 弹性极限
σs:屈服极限 σb: 强度极限
(1) 孪生变形过程 孪生变形是在切应力作用下,晶体的一部分沿一定晶面(孪晶面)
和一定方向(孪生方向)相对于另一部分作均匀的切变所产生的
变形。但是不同的层原子移动的距离也不同。
变形与未变形的两部分晶体构成镜面对称,合称为孪晶(twin)。
均匀切变区与未切变区的分界面成为孪晶界。
孪晶面(twining plane): 孪晶方向(twining direction):
② 每一种晶格类型的金属都有特定的滑移系,且滑移系数量不同。 如:fcc中有12个, bcc中有48个, hcp中有3个。
第9章 晶粒尺寸和微观应力测定-2012

(1) [A7.mdi] DX-1000 CSC 35kV/25mA Slit:1deg&1deg&0.2mm Monochromator: ON 1-2Theta, SCAN: 15.0/79.98/0.06/1(sec), Cu, I(max)=262231, 10-21-10 13:43
150
由于粉末多晶衍射仪使用的是多晶(粉末)样 品,因此,其衍射谱不是由一条一条的衍射线 组成,而是由具有一定宽度的衍射峰组成,每 个衍射峰下面都包含了一定的面积。如果把衍 射峰简单地看作是一个三角形,那么峰的面积 等于峰高乘以一半高处的宽度。这个半高处的 高度有个专门名词,称为“半高宽”,英文写 法是FWHM。如果采用的实验条件完全一样, 那么,测量不同样品在相同衍射角的衍射峰的 FWHM应当是相同的。这种由实验条件决定的 衍射峰宽度称为“仪器宽度”。仪器宽度并不 是一个常数,它随衍射角有变化。一般随衍射 角变化表示为抛物线形。
§9-2 仪器和实验条件的影响
多晶试样中,即使不存在微观应力,晶粒也不细小,测 得的衍射线也有一定的宽度b,这时衍射线的变宽,主 要是受X射线源的形状大小,不能完全聚焦的平板状试 样,试样安放时的轴偏离,试样的吸收和接收狭缝的大 小等影响。 怎样确定仪器本身造成的衍射线变宽呢?首先选择一个 标准样品(标准样品要求结构稳定、衍射峰分布合理、 晶粒尺寸1~5μ ),一般选用纯α -Al2O3粉或纯硅粉. 近年美国国家标准局推荐使用的标准物质为六硼化镧, 用此样品进行衍射,求出每一条衍射线的半高宽和对应 的2θ ,以2θ 为横坐标,半高宽为纵坐标,作工作曲线, 从工作曲线上可以得到任何2θ 所对应的仪器宽度b。
衍射线变宽
这样,我们知道了仪器本来有个线形宽, 由于晶块细化和微观应变的原因会导致线 形更宽。我们要计算晶粒尺寸或微观应变, 首先第一步应当从测量的宽度中扣除仪器 的宽度,得到晶粒细化或微观应变引起的 真实加宽。但是,这种线形加宽效应不是 简单的机械叠加,而是它们形成的卷积。 所以,我们得到一个样品的衍射谱以后, 首先要做的是从中解卷积,得到样品因为 晶粒细化或微观应变引起的加宽FW(S)。 这个解卷积的过程非常复杂。
第九章梁的弯曲应力

一、梁横截面上的正应力
横力 F 弯曲 A a F (+)
V图
纯弯曲 C l D
F
横力 弯曲 B
纯弯曲——梁弯曲变形
时,横截面上只有弯矩
F
a
F 而无剪力(M 0,V 0)。
F
(-)
横力弯曲——梁弯曲变形 时,横截面上既有弯矩又 有剪力(M 0,V 0)。
Fa
M图
(+) Fa
一、梁横截面上的正应力
* z
max
* Vmax Sz Vmax max * Izd ( I z Sz max )d
* 对于工字钢, I z Sz
max
可由型钢表中查得。
3.工字形截面梁的剪应力
V
三、梁的强度条件
1、弯曲正应力强度条件:
max
Mmax [ ] Wz
可解决工程中有关强度方面的三类问题:
3.在进行梁的强度计算时,需注意以下问题:
(1)对于细长梁的弯曲变形,正应力的强度条件是
主要的,剪应力的强度条件是次要的。但对于较粗的
短梁,当集中力较大时,截面上的剪力较大而弯矩较
小,或是薄壁截面梁时,也需要校核剪应力强度。 (2)正应力的最大值发生在横截面的上下边缘,该
正应力最大。
注意:
(3)梁在中性轴的两侧分别受拉或受压,正应力
的正负号(拉或压)可根据弯矩的正负及梁的变形状
态来确定。 (4)必须熟记矩形截面、圆形截面对中性轴的惯 性矩的计算式。
二、梁横截面上的剪(切)应力
1.剪(切)应力分布规律假设
V
A*
(1)各点处的剪(切)应力 都与剪力V方向一致; (2)横截面上距中性轴等距离各点处剪(切)应力大小 相等,即沿截面宽度为均匀分布。 (3)剪(切)应力大小沿截面高度按抛物线规律变化。
多高层建筑结构第九章

9.4 带错层的高层结构
1、带错层高层结构的形式
2、带错层高层结构应满足的要求
1、当房屋不同部位因功能不同而使用错层时,宜采用防震 缝划分为独立单元。错层两侧宜采用相近的结构体系。 2、错开的楼层应各自参加结构整体计算,不应归并为一层 计算。 3、错层处框架柱截面高度不应小于600mm,混凝土强度 等级不应低于C30,抗震等级提高一级,箍筋应全柱段 加密。 4、错层处平面外受力的剪力墙的截面厚度,非抗震设计时 不应小于200mm,抗震设计时不应小于250mm,抗 震等级应提高一级。混凝土的强度等级不应低于C30, 水平和竖向分布钢筋的配筋率,非抗震设计时不应小于 0.3%,抗震设计时不应小于0.5%。 5、错层结构错层处受力复杂,容易发生短柱受剪破坏,应 予加强。
● 刚性连接; ● 铰接连接; ● 滑动连接; ● 弹性连接。
22
刚性连接
铰接连接
23
滑动连接限位装置
24
橡胶垫支座
带阻尼器的橡胶垫支座
25
3、连体结构的计算
• 刚性连接的连接体楼板应进行受剪截面和承载 力验算。 • 刚性连接的连接体楼板较薄弱时,宜补充分塔 楼模型计算分析。
9.6 竖向体型收进结构
5、框支剪力墙转换梁上一层墙体不宜设边门洞,不宜在中柱 上方设门洞。 6、长矩形平面建筑中落地剪力墙的间距宜符合以下规定: 非抗震设计时:l ≤ 3B 且 l ≤ 36m。 抗震设计时: 底部为1~2层框支层时:l ≤2B 且 l ≤ 24m. 底部为3层及3层以上时: l ≤ 1.5B 且 l ≤ 20m. 7、落地剪力墙与相邻框支柱的距离,1~2层框支层时不宜 大于12m,3层及3层以上时不宜大于10m。 8、框支框架承担的地震倾覆力矩不应大于结构总倾覆力矩的 50%。 9、带托柱转换层的筒体结构,外围转换柱与内筒、核心筒的 间距不宜大于12m。
第9章_直梁

max
IZ 1.067106 ymax
M max 141 MN/m2 150MN/m2 WZ
故压板的强度足够
第九章 直梁弯曲
例9-8 一起重量原为 50kN 的吊车,其跨度l = 10.5m (如图),由 45a号工字钢制成。为发挥其潜力,现欲将 起重量提高到Q =70kN,试校核梁的强度;若强度不足, 再计算其可能承载的起重量。设梁的材料为 Q235钢, 许用应力[σ]=140MN/m2,电葫芦自重G = 15kN,梁
第九章 直梁弯曲
推断和假设
假设:(1) 梁在纯弯曲时,各横截 面始终保持为平面,并垂直于梁轴。
此即弯曲变形的平面假设。
(2) 纵向纤维之间没有相互挤压,每 根纵向纤维只受到简单拉伸或压缩。 中性层:从伸长到缩短区,中间必有一层纤维既不伸长也不缩短。这 一长度不变的过渡层称为中性层。 中性轴:中性层与横截面的交线 在纯弯曲的条件下,所有横截面仍保持平面,只是绕中性轴作 相对转动,横截面之间并无互相错动的变形,而每根纵向纤维 则处于简单的拉伸或压缩的受力状态。
Q max P M max Pl
Q O
x P
第九章 直梁弯曲
例9-3
一简支梁 AB ,受均布载荷 q 的作用,试作此梁的弯矩图。
解: 1、求支反力
由对称性知: ql FA FB 2
2、建立剪力方程和弯矩方程
ql Q = FA qx = qx (0 < x < 1) 2 qx2 qlx qx2 M = FA x = (0 ≤x < 1) 2 2 2
非对称弯曲:若梁不具有纵向对称面,或梁有纵向对称面上但 外力并不作用在纵向对称面内的弯曲。
第九章 直梁弯曲
工程力学 第九章 梁的应力及强度计算

1、矩形截面梁纯弯曲时的变形观察
现象:
(1)变形后各横向线仍为直线,只是相对旋转了一个角度,且与变形后的梁轴曲线保持垂直,即小矩形格仍为直角;
(2)梁表面的纵向直线均弯曲成弧线,而且,靠顶面的纵线缩短,靠底面的纵线拉长,而位于中间位置的纵线长度不变。
对剪应力的分布作如下假设:
(1)横截面上各点处剪应力均与剪力Q同向且平行;
(2)横截面上距中性轴等距离各点处剪应力大小相。
根据以上假设,可推导出剪应力计算公式:
式中:τ—横截面上距中性轴z距离为y处各点的剪应力;
Q—该截面上的剪力;
b—需求剪应力作用点处的截面宽度;
Iz—横截面对其中性轴的惯性矩;
Sz*—所求剪应力作用点处的横线以下(或以上)的截面积A*对中性轴的面积矩。
应力σ的正负号直接由弯矩M的正负来判断。M为正时,中性轴上部截面为压应力,下部为拉应力;M为负时,中性轴上部截面为拉应力,下部为压应力。
第二节 梁的正应力强度条件
一、弯曲正应力的强度条件
等直梁的最大弯曲正应力,发生在最大弯矩所在横截面上距中性轴最远的各点处,即
对于工程上的细长梁,强度的主要控制因素是弯曲正应力。为了保证梁能安全、正常地工作,必须使梁内最大正应力σmax不超过材料的许用应力[σ],故梁的正应力强度条件为:
圆形截面横梁截面上的最大竖向剪应力也都发生在中性轴上,沿中性轴均匀分布。
其它形状的截面上,一般地说,最大剪应力也出现在中性轴上各点。
结合书P161-162 例8-3进行详细讲解。
五、梁的剪应力强度校核
梁的剪应力强度条件为:
在梁的强度计算时,必须同时满足弯曲正应力强度条件和剪应力强度条件。但在一般情况下,满足了正应力强度条件后,剪应力强度都能满足,故通常只需按正应力条件进行计算。
9-4、基础地质学-第九章-地质构造(四)节理

2、张节理(右)
张节理是由张应力产生的破裂面,总体特征是: 短、小、粗糙不平,延伸不远,豆荚状、树枝状。
剪节理的特点:
①节理面产状较稳定,延伸较远; ②节理面平直光滑,有时留下的擦痕; ③如遇到砾石,一般切穿砾石; ④常呈共轭“X”型节理系; ⑤主剪裂面由羽状微裂面组成,微裂面与主 剪裂面交角一般为10°-15°,相当内摩擦角的 一半,其锐角指示本盘错动方向; ⑥尾端变化形式有三种: 折尾、菱形结环和 分叉。
(一)、与褶皱有关的节理
1、岩层在水平挤压作用下,首先发育了两组与挤压力(σ1) 斜交的剪节理和一组与挤压力(σ1)平行的张节理。
2、如水平压应力继续作用,形成纵弯褶皱,则在横剖 面上发育两组共轭剪节理(图上未画出)和两组张 节理:一组纵张节理(a),一组横张节理(c)。
(二)、与断层有关的节理
2、根据节理产状与褶皱轴向的关系划分
(1)纵节理:节理走向与褶皱轴向平行的节理; (2)横节理:节理走向与褶皱轴向直交的节理; (3)斜节理:节理走向与褶皱轴向斜交的节理。
(二)、成因分类
据节理的力学性质,可将节理分为剪节理和张节理两类。 1、剪节理(左) 剪节理是由剪应力产生的破裂面,总体特征是: 长、大、平直光滑,延伸稳定,常常呈“X”型;
2、张节理具体特征:
(1)产状不稳定,延伸不 远,单条节理多短而曲折,一 组节理有时呈侧列产出。 (2)节理面粗糙不平,无 擦痕; (3)张节理常常绕过砾石 和粗砂粒; (4)多开口,常被矿脉充 填,脉宽变化较大,脉壁不平 直;
(5)有时呈不规则的树枝状、网络状,有时也构成一定几 何形态,如追踪X型节理的锯齿状张节理,单列或共轭雁列 式张节理,以及放射状或同心圆状的组合形式;
由于构造作用的递进发展,会发生应力转向和变 化,常出现一种节理兼具两类力学性质特征或过渡 特征,早期形成的剪节理,在后期会被改造或叠加,发 生先剪后张或先张后剪等转化。
工程力学 第九章 梁的强度刚度计算

由结果知,梁的强度不满足要求。
返回 下一张 上一张
y2
z
例9-6 试为图示钢轨枕木选择矩形截面。已知矩形截面尺寸的比 例为b:h=3:4,枕木的弯曲许用正应力[]=15.6MPa,许用剪应力 P P 0 0 .2 m 1 .6 m []=1.7MPa,钢轨传给枕木的压力P=49KN。 .2 m
a
M D ya Iz
返回 下一张 上一张
10.7
第二节 梁横截面上的剪应力
一、矩形截面梁:
矩形截面剪应力计算公式: τ沿截面高度按抛物线规律变化:
2Iz 4
3
QS
* z
I zb
bh
4
τ m ax
2 3
y
h 2
, 0 ; y 0 , max
6 Qh 4 bh
校核梁的正应力强度。
解:(1) 内力及抗弯截面模量计算: MC=3.0KN.m; MD=-4.8KN.m
W1 W2
P1
A
a C a
P2
D
a B
y1
z
763 5 .2
146 . 7 cm
3
y1
z
763 8 .8
86 . 7 cm
3
4 .8 k N m
y2
(2)C截面的正应力强度校核:
4 Q 3 A1
max 2
Q A2
返回 下一张 上一张
例9-3 矩形截面简支梁如图,已知:l=2m,h=15cm,b=10cm, h1=3cm,q=3kN/m。试求A支座截面上K点的剪应力及该截面的最 b q 大剪应力。 解:1.求剪力:QA=3kN
工程力学 第9章 应力状态分析 习题及解析
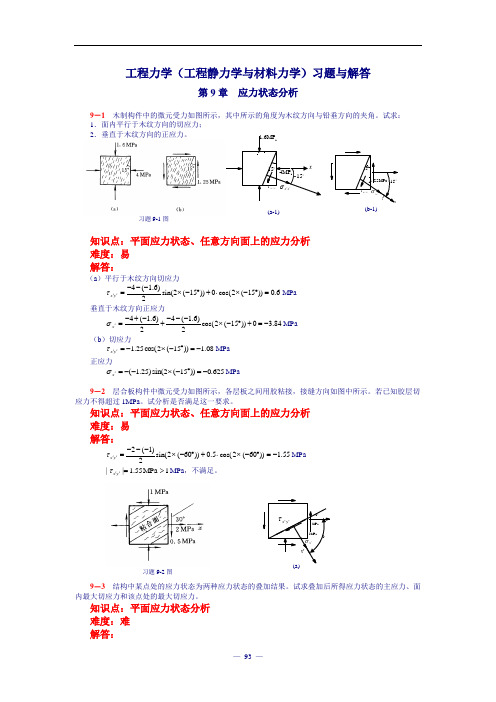
习题9-1图 x15-'x x'σy'x'τ 1.25MPa15 (b-1)15a 4MP15-y'x'τx'x'σa1.6MP x (a-1) 习题9-2图302MPa 0.5MPa-60x'σ'x ''y x τ 工程力学(工程静力学与材料力学)习题与解答第9章 应力状态分析9-1 木制构件中的微元受力如图所示,其中所示的角度为木纹方向与铅垂方向的夹角。
试求: 1.面内平行于木纹方向的切应力;2.垂直于木纹方向的正应力。
知识点:平面应力状态、任意方向面上的应力分析 难度:易 解答:(a )平行于木纹方向切应力6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa 垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa (b )切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9-2 层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。
若已知胶层切应力不得超过1MPa 。
试分析是否满足这一要求。
知识点:平面应力状态、任意方向面上的应力分析 难度:易 解答:55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ,不满足。
9-3 结构中某点处的应力状态为两种应力状态的叠加结果。
试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。
知识点:平面应力状态分析 难度:难 解答:习题9-2图yσxσxyτ=yσxσxyτx=yσxσxyτ=左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx y xy x 叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022cos 1022sin 022cos 3σθσσσθττσθσσσy y y x xy x x0)cos 1()cos 1( )22sin (4)22cos 122cos 3(21222cos 122cos 330020202021=⎩⎨⎧-+=-+--+±-++=⎭⎬⎫σσθσθσθσθθσθθσσ 面内最大切应力:θσσστcos 2021max=-='该点最大切应力:031max2cos 12σθσστ+=-=左微元0023))30(2sin()(ττσ=︒-⨯-='x ,0230τσσ-='-='x y ,2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x,0230τσσ-=''-=''x y ,2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ,03τσσσ-=''+'=y y y ,0=''+'=xyxy xy τττ 013τσ=,02=σ,033τσ-= 面内031max32||τσστ=-='xABOσOσαα(a)习题9-4图A60CB60100-x σxσyxτxyτ92MPa(a)习题9-5图该点031max 32||τσστ=-=叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点:5021002||||31max max=-=-=='σσττMPa9-4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上,其值为0σ。
第九章 管道内的流动

V32 2g
25
第九章 管道内的流动
可见局部损失与 V1 V3 2 成正比。上式也可以写为
hm
K1
V12 2g
K2
V32 2g
按A1截面速度计算的局部损失因数为
2
K1
1
A1 A2
按A3截面速度计算的局部损失因数为
K2
A2 A1
2 1
26
第九章 管道内的流动
当液体通过小直径管流入大面积水池时, A2>>A1, 管道出口损失为
直径管以降低沿程水力损失。
间有关系式
w
D 4
p* L
将上式代入沿程水力损失表示式,可得
hl
4W g
L D
(9-3)
沿程水力损失hf可视为直接由壁面切应力引起,基于这点, 通常将Δpl称作摩擦压降。
Q R4 p* D4 p* 8 L 128 L
摩擦压降Δpl=Δp*只是体积流量Q,流体粘度和管道几何参
数的函数。
7
第九章 管道内的流动
引用魏斯巴赫公式
p* f L 1 V 2
D2
pl
f
L D
1 V 2
2
(9-4)
将上式代入式(9-2),则沿程水力损失又可表示为
hl
f
L V2 D 2g
(9-5)
对于圆管层流
f 64 Re D
Re D
VD
(9-6)
即圆管内层流达西摩擦因数与以管径为特征长度的雷诺数
成反比。
8
第九章 管道内的流动
如果通过给定圆管的流量Q已知,则确定沿程损失 的计算直截了当,可依照下述步骤进行:
(1)计算雷诺数ReD= ρVD/ μ;
纤维—金属层合板层间应力分析

纤维—金属层合板层间应力分析作者:王昌昊,张驰,刘明强来源:《科技创新与生产力》 2012年第9期(1. 成都航空职业技术学院,四川成都 610100;2. 贵州航空发动机研究所,贵州贵阳550081)摘要:依据有限元方法,建立了纤维-金属层合板的有限元模型,有效模拟了金属层的弹塑性以及其层间的应力分布;分析了纤维-金属层合板的拉伸特性,与试验数值比较,证明了该有限元模型的准确性;从不同类型纤维-金属层合板的应力-应变曲线,得出结论:层合板在金属层进入塑性形变阶段后,强度下降较快且玻璃纤维层采用相同的铺排方式,有利于降低层间应力集中程度。
关键词:纤维-金属层合板;Glare层板;有限元方法;层间应力中图分类号:TB333 文献标志码:A DOI:10.3969/j.issn.1674-9146.2012.09.095玻璃纤维-铝合金层合板(简称Glare层板)是一种新型纤维-金属复合材料层板,是由铝合金薄片与预浸料薄片交替铺叠,然后热压成形的一类航空结构材料。
20世纪末,Vogelesang成功制成了Glare层板[1],克服了早期纤维-金属复合材料层板的不足,并在机身蒙皮等承载部件的制造中取得了广泛应用[2]。
纤维-金属复合材料层板结构的研发与制造,推动了其结构力学性能的理论分析和实验研究。
Chen等建立了分析其力学性能的理论模型[3],在此基础上,Wu等对拉伸载荷作用下层板的力学性能进行了验证[4]。
Akbar等研究了层板的断裂行为[5],Homan报道了层板的疲劳性质[6]。
在国内,赵祖虎、郭亚军以及廖建等也分别对层板的压缩性能、裂纹扩展性能和成形性进行了实验研究[7-8]。
众多的研究发现,纤维-金属层板受到外部激励时,其金属薄层会发生塑性屈服,若以弹性理论为基础,材料进入塑性阶段,结构即被视为失效。
但由于结构的内部应力分布是不均匀的,当高应力区域的材料达到弹性极限时,其他区域材料仍处于弹性范围内,结构并未失效。
9-第九章_层间应力详解

从单层的位移控制微分方程式(9.7)可知,它仅包含对y和z两 个坐标的偏微分,所以此模型属于准三维力学模型。由于在一 般情况下联立偏微分方程(9.7)得不到封闭解析解,因此就提 出了求解层间应力问题的一些方法,主要有:
①直接解法。它是利用解析法和数值法直接求解微分方程的边 值问题,包括复变函数解法、级数解法、摄动法和有限差分法 等。②变分解法。它是建立在变分原理基础上的近似解法,它 包括有限元法、瑞利—李兹法、伽辽金法等。③混合解法。它 是将直接解法与变分法结合起来求解问题,例如边界层法与瑞 利—李兹法的组合等。这些近似解法比较实用,但也存在一些 问题,主要是不能精确满足所有给定的边界条件和界面连续条 件,对于一边界值问题,若采用不同近似解法有时将得到不同 的结果。
不考虑体积力,并注意到所有应力分量与x无关,可把静力平衡 微分方程简化为
xy y
yz z
0
y y
yz z
0
yz
z
0
y z
(9.6)
把式(9.5)代入式(9.6)就得到用位移表示任意一个单层的平
衡微分方程为
2U
C66 y 2
C55
2U z 2
C26
2V y 2
C45
2V z 2
U y
y
C12 0
C2 2
V y
C23
W z
C26
U y
z
C13 0
C23
V y
C33
W z
C36
U y
(9.5a)
yz
C44
W y
V z
C45
U z
xz
C45
W y
V z
C55
U z
钢桥桥面铺装层间剪应力影响因素及简化计算_顾兴宇

第7卷 第3期2007年6月交通运输工程学报Journal of T raffic and Transportation EngineeringVo l .7 No .3Jun .2007收稿日期:2006-11-24基金项目:国家西部交通建设科技项目(200231800030)作者简介:顾兴宇(1976-),男,江苏泰兴人,东南大学副教授,工学博士,从事路面结构及材料研究。
文章编号:1671-1637(2007)03-0070-06钢桥桥面铺装层间剪应力影响因素及简化计算顾兴宇,吴一鸣(东南大学交通学院,江苏南京 210096)摘 要:为了减小钢桥桥面铺装层间剪应力,建立桥面系三维有限元计算模型,分析了不同荷位、钢板厚度、U 肋开口宽度、铺装厚度、铺装模量、层间接触条件以及轴载大小对铺装层间纵横向剪应力的影响,推导了实用的应力简化计算公式。
研究发现桥面板不均匀变形使得铺装层间剪应力远大于同条件下的路面结构;影响显著的因素依次为轴载大小、钢板厚度、U 肋开口宽度以及铺装参数;层间完全光滑有利于抗剪,但降低了桥面系整体刚度;控制重载,加强桥面系刚度与选择柔性层间粘结材料是减小层间剪应力的有效措施。
关键词:路面工程;钢桥面沥青铺装;有限元方法;纵横向剪应力;简化计算公式中图分类号:U443.33 文献标识码:AInfluence factors and simplified calculation of interbedded shearstress of asphalt paving on steel bridgeGu Xing -yu ,Wu Yi -ming(Scho ol of T ranspor tatio n ,Southeast Univ ersity ,N anjing 210096,Jiang su ,China )A bstract :In o rder to minish the interbedded shear stress of asphalt paving ,3-D finite elem ent model of bridg e deck w as se t up ,the influences o f load position ,steel deck thickness ,the open width of U shape rib ,asphalt thickness ,asphalt mo dulus ,contact condition and heav y lo ad on the lo ngitudinal -transverse shear stresses w ere analyzed ,and the sim plified calculatio n form ulaeof the stresses w ere concluded .It is pointed that the shear stre sses are m uch la rg er than that of road structure in sam e conditio n because of uneven defo rm ation ,the main influence factors in order are heavy load ,steel deck thickness ,the open width o f U shape rib and paving param eters ;com pletely smoo th state between asphalt concre te and steel deck low ers the who le stiffness of deck sy stem ,but benefits to resist shear stress ;co ntro lling heavy lo ads ,stiffening steel deck and selecting flexible interbedded sticking m aterials are effective metho d to reduce the shear stress between steel deck and asphalt paving .9tabs ,10fig s ,10refs .Key words :pavem ent engineering ;asphalt paving of steel bridge ;finite element m ethod ;longitudinal -transve rse shear stre sses ;sim plified calculation fo rm ula Author resume :Gu Xing -yu (1976-),male ,EngD ,associate professor ,+86-25-83795979,gux -ingy u1976@ .0 引 言中国大跨径钢桥常采用扁平流线型钢箱梁,桥面板厚度一般在12~14mm ,其柔性大,易挠曲,一般通过在桥面板底部设置纵向加劲肋及横向隔板来提高桥面板的整体承载能力,正交异性的结构特性对其上沥青铺装体系的性能提出了更高的要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图9.3 有限宽度 的层合板
在以xOy坐标面为对称的层合板中,任一个单层中可视为以z 轴为弹性主方向的单对称材料,其应力—应变关系可按角度铺 设单对称材料表达为
x C11 y C12 z C13 yz 0 xz 0 C16 xy
(9.1)
应变与位移的几何关系为
u x v y y w z z w v yz y z w u xz x z v u xy x y
x
(9.处于平面应力状态,不考虑层间应力 (面外应力)分量,层合板的应力分析比较简单。但无论是机械加载还是湿 热加载,层合板中都会产生层间应力,尤其是在板边缘附近层间应力分布复 杂,变化梯度大。层间应力往往引起层合板边缘脱黏,形成层间裂纹,造成 整个层合板的刚度和强度下降,使结构过早失效。经典层合板的理论不能完 全确定引起复合材料破坏的应力,它无法解决层间应力这类三维各向异性弹 性力学问题。本章主要介绍层合板产生层间应力的原因和基于弹性力学的一 些层间应力的分析方法。
图9.2 泊松耦合变形 协调引起层间剪应力 示意图
三、力矩平衡引起的层间正应力 [0/90]层合板中的y方向的正应力y1 和 y2 与层间剪应力zy 没有作用在同 一平面内,从而形成一个附加力矩,为了平衡该力矩必须产生层间正应力z。 已有的研究表明,该层间正应力z在层合板靠近自由边缘处可能达到无穷大, z 的分布特征是形成的力矩正好与y方向的正应力形成的力矩平衡。
图9.1 拉剪耦合变形协调 引起层间剪应力示意图
二、泊松耦合变形协调引起的层间剪应力
层间应力也会在正交铺设层合板中出现。设有一块[0/90]层合板承受有平 均轴向拉应力 x ,如图9.2所示。假如将0°单层和90°单层分别考虑,各自 只受有x方向的正应力 ,且沿x方向的变形相同。由于0°单层和90°单层在y 方向变形的泊松耦合效应不同,由式(3.12)可知0°单层沿y方向收缩较多, 90°单层沿y方向收缩较少。为了保证两单层黏层在一起后y方向变形协调一 致,就需要通过0°单层和90°单层相互施加y方向的力,将0°单层往外拉, 90°单层往里压,得到相同的y方向变形,这样就会在两板中产生沿y方向的 正应力y1(拉应力)和y2(压应力)。因为层合板两侧是自由边界,不能 提供沿y方向的作用力,所以两层中沿y方向的内力就只能由层间相互作用来 提供,这就形成了层间剪应力zy 。正交铺设层合板没有拉剪耦合相应,0° 单层和90°单层都不会出现面内剪切变形,因而没有剪切变形需要协调,各 层之间也不会出现协调剪切变形的层间剪应力zx 。
9.1 层间应力的定性分析 层合板一般由不同铺设方向的单层组成,各单层的弹性性能不同,受力 下的变形也不同。但是层合板中的各单层相互黏结成一体,层和层之间变形 相互制约和协调,于是在层间产生相应的正应力和剪应力,即层间应力。以 下通过对层合板和[0/90]层合板的拉剪耦合变形协调和泊松耦合变形协调分 析以及力矩平衡原理,解释层间应力产生的原因。
C12 C 22 C 23 0 0 C 26
C13 C 23 C 33 0 0 C 36
0 0 0 C 44 C 45 0
0 0 0 C 45 C55 0
C16 x C 26 y C36 z 0 yz 0 xz C 66 xy
z
y
z
zy
z
y
9.2 单向拉伸下对称层合板的弹性力学基本方程 考虑一个有限宽度的对称层合板,选取xOy坐标面为对称面,而 z轴为材料主轴,如图9.3所示。把层合板的每一个单层视为宏观 匀质的各向异性体,各个单层之间存在一个理想的物理非连续界 面。当在层合板的两端沿x方向承受均匀拉伸时,界面上产生层 间应力。一般情况下,界面上有层间正应力和切应力三个分量: z,zx,zy。因此对各个单层要从三维应力状态出发进行弹性 力学分析。
一、拉剪耦合变形协调引起的层间剪应力 一块材料和厚度相同的斜交铺设层合板,承受拉伸应力x,若将单 层分别考虑,各层除了有线应变x和y外,由于拉剪耦合效应的存在,还会 出现剪切应变xy,如图9.1所示。由式(3.26)可知,+和–层的 Q12 相等,因此两个相反方向铺层的正应变x,y相同,+和–层的 Q16
u 0 x U y, z v V y, z w W y, z
利用应变与位移的几何关系可得应变场为
x 0
V y W z z W yz y U xz z U xy y V z
相差一个负号,因此–层xy1与+层的xy2大小相等,方向相反。黏合在一起 的层合板的A16等于零,无拉剪耦合,层合板无剪切变形,因此层的剪切 变形必须相互协调为零。这一效果是通过各单层相互对对方施加剪应力来实现 的,又因为在层合板的自由边缘无剪力,因此只能靠层间剪切应力zx来提供。 同理,一块材料和厚度相同的斜交铺设层合板,只承受剪切应力xy,由 于剪拉耦合效应的存在,+和–层中会出现耦合线应变x和y,黏合在一起的 层合板无轴向变形,为协调轴向变形,在层间会产生层间剪切应力 zx和zy。
由于在层合板中各个单层的几何、弹性特性和受力形式沿 x方向都是均匀分布的,即不随x而变化,因此在层合板两端 承受均匀轴向拉伸作用力时,所有应力与x无关,应变也与x 无关。假设层合板各单层的任意点沿x方向的应变为常数,即
x 0
并设层合板中的其他应变分量与x无关。因此,各个铺层的位 移场可表示为
