(完整版)平行四边形的性质和判定练习题
平行四边形性质和判定习题(答案详细)
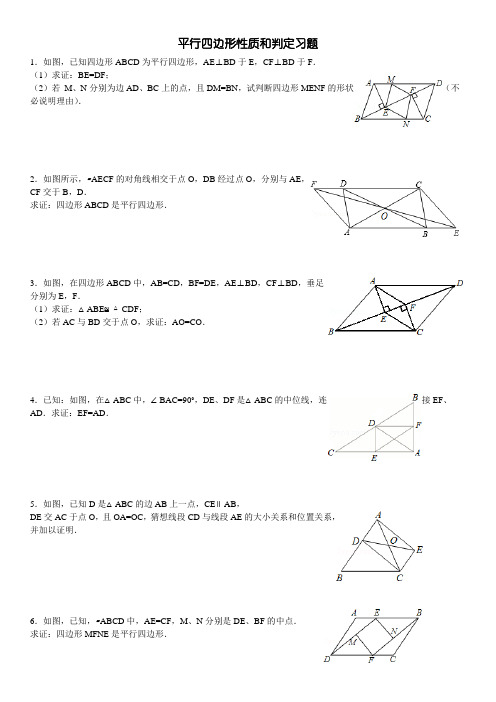
平行四边形性质和判定习题1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.8.在▱ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE.10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?11.如图:已知D、E、F分别是△ABC各边的中点,求证:AE与DF互相平分.12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分.14.如图:▱ABCD中,MN∥AC,试说明MQ=NP.15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2(1)求证:D是EC中点;(2)求FC的长.19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.20.如图,四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)请判断四边形EFGH的形状?并说明为什么;(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?21.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.22.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.23.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC 于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.24.如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE.探究:(1)请猜想与线段DE有关的三个结论;(2)请你利用图2,图3选择不同位置的点P按上述方法操作;(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图2或图3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案).25.在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有_________组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的两条直线有什么规律?26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2若存在,请求出所有满足条件的t的值;若不存在,请说明理由.27.已知平行四边形的三个顶点的坐标分别为O(0,0)、A(2,0)、B(1,1),则第四个顶点C的坐标是多少?28.已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF,且cm,,求平行四边形ABCD的面积.29.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣3,),B(﹣2,3),C(2,3),点D在第一象限.(1)求D点的坐标;(2)将平行四边形ABCD先向右平移个单位长度,再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?(3)求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积?30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.答案与评分标准1.如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).考点:平行四边形的判定与性质;全等三角形的判定与性质。
专题 平行四边形的性质和判定(原卷版)
八年级下册数学《第十八章 平行四边形》专题 平行四边形的性质与判定【例题1】如图,在平行四边形ABCD 中,CE 平分∠BCD ,交AB 于点E ,AE =3,EB =5,ED =4.则CE 的长是( )A .2√2B .6√2C .5√5D .4√5【变式1-1】如图,在平行四边形ABCD 中,AB =5,AD =7,AE 平分∠BAD 交BC 于点E ,作DG ⊥AE 于点G 并延长交BC 于点F ,则线段EF 的长为( )A .2B .52C .3D .2√6【变式1-2】如图,在▱ABCD 中,O 为对角线AC 与BD 的交点,AC ⊥AB ,E 为AD 的中点,并且OF ⊥BC ,∠D =53°,则∠FOE 的度数是( )A .143°B .127°C .53°D .37°【变式1-3】如图,将平行四边形OABC 放置在平面直角坐标系xOy 中,O 为坐标原点,若点C 的坐标是(1,3),点A 的坐标是(5,0),则点B 的坐标是( )A .(5,3)B .(4,3)C .(6,3)D .(8,1)【变式1-4】如图,在平行四边形ABCD 中P 是CD 边上一点,且AP 和BP 分别平分∠DAB 和∠CBA ,若AD =5,AP =8,则△APB 的周长是( )A.18B.24C.23D.14【变式1-5】如图,在平行四边形ABCD中,∠B=60°,AE平分∠BAD交BC于点E,若∠AED=80°,则∠ACE的度数是()A.30°B.35°C.40°D.45°【变式1-6】▱ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则边AB长的取值范围是()A.3≤AB≤4B.2<AB<14C.1<AB<7D.1≤AB≤7【变式1-7】在平行四边形ABCD中,∠A的角平分线把边BC分成长度为4和5的两条线段,则平行四边形ABCD的周长为()A.13或14B.26或28C.13D.无法确定【变式1-8】如图,▱ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.(1)求证:OE=OF;(2)若EF⊥AC,△BEC的周长是10,求▱ABCD的周长.【例题2】(2022•南京模拟)如图,在平行四边形ABCD中,E,F是对角线AC上的两点,且AE=EF =FC.(1)求证:DE∥BF;(2)若BE⊥BC,DE=6,求对角线AC的长.【变式2-1】(2022春•西吉县校级月考)如图.已知四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,求证:BE=DF.【变式2-2】(2022•泉山区校级三模)已知,如图,在平行四边形ABCD中,点E、F分别在AB、CD的延长线上,BE=DF,连接EF,分别交BC、AD于G、H.求证:EG=FH.【变式2-3】(2022秋•北碚区校级期末)如图,平行四边形ABCD中,CB=2AB,∠DCB的平分线交BA 的延长线于点F.(1)求证:DE=AE;(2)若∠DAF=70°,求∠BEA的度数.【变式2-4】(2022秋•道里区校级月考)在平行四边形ABCD中,点E在CD边上,点F在AB边上,连接AE、CF、DF、BE,∠DAE=∠BCF.(1)如图1,求证:DE=BF;(2)如图2,设AE交DF于点G,BE交CF于点H,连接GH,若E是CD边的中点,在不添加任何辅助线的情况下,请直接写出图中以G为顶点并且与△EHC全等的所有三角形.【变式2-5】(2021春•九龙坡区校级期中)在▱ABCD中,∠ABC=45°,过A作AE⊥CD于E,连接BE,延长EA至F,使CE=AF,连接DF.(1)求证:DF=BE;(2)若DF=√34,AD=3√2,求四边形ADEB的周长.【变式2-6】(2022春•济南期中)如图,将▱ABCD的边BC延长到点E,使BE=CD,连接AE交CD 于点F.(1)求证:AE平分∠BAD;(2)已知BC=CE=3,EF=4,FG⊥AB,求FG的长.【例题3】如图,平行四边形ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是()A.CE=AF B.BE=DF C.∠DAF=∠BCE D.AF∥CE【变式3-1】在下列条件中,能够判定一个四边形是平行四边形的有()①一组对边平行,另一组对边相等②一组对边平行,一条对角线平分另一条对角线③一组对边平行,一组对角相等④一组对角相等,一条对角线平分另一条对角线A.1个B.2个C.3个D.4个【变式3-2】下列条件能判定四边形ABCD是平行四边形的是()A.∠A=∠B,∠C=∠D B.AB=AD,BC=CDC.AB=CD,AD=BC D.AB∥CD,AD=BC【变式3-3】四边形ABCD中,对角线AC,BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB∥CD,∠BAD=∠BCD;③AO=CO,BO=DO;④AB∥CD,AD=BC.一定能判定四边形ABCD 是平行四边形的条件有()A.1组B.2组C.3组D.4组【变式3-4】如图,在△ABC中,D,F分别是AB,AC上的点,且DF∥BC.点E是射线DF上一点,若再添加下列其中一个条件后,不能判定四边形DBCE为平行四边形的是()A.∠ADE=∠E B.∠B=∠E C.DE=BC D.BD=CE【变式3-5】如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是()A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF【变式3-6】如图,在▱ABCD中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是(写出一个即可).【变式3-7】平行四边形ABCD中,E、F是对角线BD上不同的两点,写出一个能使四边形AECF一定为平行四边形的条件.(用题目中的已知字母表示)【例题4】(2021•江华县一模)如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.(1)求证:△ACD≌△CBF;(2)点D在线段BC上何处时,四边形CDEF是平行四边形且∠DEF=30°.【变式4-1】如图,点B、C、E、F在同一直线上,BE=CF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)四边形ABED是平行四边形.【变式4-2】如图所示,△ABC中,D是BC边上中点,AE是∠BAC的平分线,CE⊥AE,EF∥BC交AB于点F,求证:四边形BDEF是平行四边形.【变式4-3】(2021秋•海阳市期末)如图,在△ABC中,AD是BC边的中线,F是AC上一点,且满足2AF=CF,连接BF与AD相交于点E.若G为线段BF上一动点,试分析当点G在何位置时,四边形AFDG为平行四边形?【变式4-4】(2022春•顺义区校级月考)如图,四边形ABCD中,BD垂直平分AC,垂足为点F、E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.(1)求证:四边形ABDE是平行四边形;(2)如果DA平分∠BDE,AB=3,AD=4,求AC的长.【变式4-5】(2021春•西安期末)如图,在△AFC中,∠F AC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD,求证:四边形ABCD是平行四边形.【变式4-6】(2022春•礼泉县期末)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)求证:△AEF≌△BAC;(2)四边形ADFE是平行四边形吗?请说明理由.【例题5】如图,在▱ABCD 中,要在对角线BD 上找两点E 、F ,使A 、E 、C 、F 四点构成平行四边形,现有①,②,③,④四种方案,①只需要满足BE =DF ;②只需要满足AE ⊥BD ,CF ⊥BD ;③只需要满足AE ,CF 分别平分∠BAD ,∠BCD ,④只需要满足AE =CF .则对四种方案判断正确的是( )A .①②③B .①③④C .①②④D .②③④【变式5-1】如图,在▱ABCD 中,E 、F 分别为边AB 、DC 的中点,连接AF 、CE 、DE 、BF 、EF ,AF 与DE 交于点G ,CE 与BF 交于点H ,则图中共有平行四边形( )A .3个B .4个C .5个D .6个【变式5-2】如图,已知△ABC 是边长为6的等边三角形,点D 是线段BC 上的一个动点(点D 不与点B ,C 重合),△ADE 是以AD 为边的等边三角形,过点E 作BC 的平行线,分别交线段AB ,AC 于点F ,G ,连接BE 和CF .则下列结论中:①BE =CD ;②∠BDE =∠CAD ;③四边形BCGE 是平行四边形;④当CD =2时,S △AEF =23,其中正确的有( )A .4个B .3个C .2个D .1个【变式5-3】(2022春•南海区月考)如图,在▱ABCD 中,点E 是BC 边的中点,连接AE 并延长与DC的延长线交于F.(1)求证:四边形ABFC是平行四边形;(2)若AF平分∠BAD,∠D=60°,AD=8,求▱ABCD的面积.【变式5-4】(2022春•重庆月考)已知,如图,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.【变式5-5】(2022春•南湖区校级期中)如图,在平行四边形ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.(1)求证:四边形AFCE是平行四边形.(2)若AD=13cm,AE=12cm,AB=20cm,求四边形AFCE的面积.【变式5-6】(2021春•南昌期中)如图,点O是平行四边形ABCD对角线的交点,过点O的直线交AD,BC于P,Q两点,交BA,DC的延长线于M,N两点.(1)求证:AP=CQ;(2)连接DM,BN,求证:四边形BNDM是平行四边形.【变式5-7】(2022春•温州校级月考)在Rt△ABC中,∠ACB=90°,D是斜边AB上的一点,作DE ⊥BC,垂足为E,延长DE到F,连结CF,使∠A=∠F.(1)求证:四边形ADFC是平行四边形.(2)连接CD,若CD平分∠ADE,CF=10,CD=12,求四边形ADFC的面积.【变式5-8】(2022春•锦江区校级期中)如图,在等边△ABC中,D、E两点分别在边BC、AC上,BD =CE,以AD为边作等边△ADF,连接EF,CF.(1)求证:△CEF为等边三角形;(2)求证:四边形BDFE为平行四边形;(3)若AE=2,EF=4,求四边形BDFE的面积.。
(完整)平行四边形的性质练习题及答案-1

(完整)平行四边形的性质练习题及答案-1编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)平行四边形的性质练习题及答案-1)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)平行四边形的性质练习题及答案-1的全部内容。
平行四边形的性质一、课中强化(10分钟训练)1。
如图3,在平行四边形ABCD中,下列各式不一定正确的是( ) A。
∠1+∠2=180° B.∠2+∠3=180° C。
∠3+∠4=180° D.∠2+∠4=180°图3 图4 图52。
如图4,ABCD的周长为16 cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DC E的周长为( )A。
4 cm B。
6 cm C.8 cm D.10 cm3。
如图5,ABCD中,EF过对角线的交点O,如果AB=4 cm,AD=3 cm,OF=1 cm,则四边形BCFE的周长为__________________。
4。
如图6,已知在平行四边形ABCD中,AB=4 cm,AD=7 cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=_____________ cm。
图6 图75。
如图7,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF,求证:AE=CF。
6.如图8,在ABCD中,AE⊥BC于E,AF⊥CD于F,BE=2 cm,DF=3 cm,∠EAF=60°,试求CF的长。
图8二、课后巩固(30分钟训练)1。
ABCD中,∠A比∠B大20°,则∠C的度数为( )A。
60° B.80° C。
(完整版)平行四边形练习题及答案(DOC)

20.1平行四边形的判断一、选择题1 .四边形A BCD,从( 1)AB∥CD;( 2)AB=CD;( 3)BC∥AD;( 4) BC=AD这四个条件中任选两个,此中能使四边形ABCD是平行四边形的选法有()A .3种B.4种C.5种D.6种2.四边形的四条边长分别是a, b, c,d,此中 a,b 为一组对边边长, c,d?为另一组对边边长且知足a2+b2+c2+d2=2ab+2cd,则这个四边形是()A .随意四边形B.平行四边形C.对角线相等的四边形 D .对角线垂直的四边形3.以下说法正确的选项是()A.若一个四边形的一条对角线均分另一条对角线,则这个四边形是平行四边形B.对角线相互均分的四边形必定是平行四边形C.一组对边相等的四边形是平行四边形D.有两个角相等的四边形是平行四边形二、填空题4 .在□ ABCD中,点 E, F 分别是线段A D, BC上的两动点,点 E 从点 A 向 D 运动,点F从 C?向 B 运动,点 E 的速度边形.m与点F 的速度n 知足 _______关系时,四边形BFDE为平行四5.如图 1 所示,平行四边形ABCD中, E, F 分别为AD,BC边上的一点,连结EF,若再增添一个条件_______,就能够推出BE=DF.图1图26 .如图 2 所示, AO=OC,BD=16cm,则当 OB=_____cm时,四边形ABCD是平行四边形.三、解答题7.以下图,四边形 ABCD中,对角线 BD=4,一边长 AB=5,其他各边长用含有未知数 x 的代数式表示,且 AD⊥BD于点 D,BD⊥BC 于点 B.问:四边形 ABCD?是平行四边形吗?为什么?四、思虑题8.以下图,在□ABCD中, E,F 是对角线 AC上的两点,且 AF=CE,?则线段 DE?与 BF的长度相等吗?参照答案一、 1. B 点拨:可选择条件(1)(3)或(2)( 4)或( 1)( 2)或( 3)(4).故有 4 种选法.2. B 点拨: a2+b 2+c2+d2=2ab+2cd 即( a-b)2+( c-d )2=0,即( a-b )2=0 且( c-d )2=0.所以 a=b, c=d,即两组对边分别相等,所以四边形为平行四边形.3. B 点拨:娴熟掌握平行四边形的判断定理是解答这种题目的重点.二、 4.相等点拨:利用“一组对边平行且相等的四边形是平行四边形”来确立.5 .AE=CF 点拨:此题答案不唯一,只需增添的条件能使四边形EBFD?是平行四边形即可.6. 8 点拨:依据对角线相互均分的四边形为平行四边形来进行鉴别.三、 7.解:以下图,四边形ABCD是平行四边形.原因以下:在 Rt△BCD中,依据勾股定理,得BC2+BD 2=DC 2,即( x-5 )2+42=( x-3 )2,解得 x=8.所以 AD=11-8=3, BC=x-5=3, DC=x-3=8-3=5 ,所以 AD=BC, AB=DC.所以四边形ABCD是平行四边形.点拨:此题主要告诉的是线段的长度,故只需说明AD=BC, AB=DC即可,此题也可在Rt△ABD中求 x 的值.四、 8.解:线段DE与BF 的长度相等;连结BD交AC于O点,连结DF, BE,以下图.在ABCD中, DO=OB, AO=OC,又因为 AF=EC,所以 AF-AO=CE-OC,即 OF=OE,所以四边形 DEBF是平行四边形,所以DE=BF.点拨:此题若用三角形全等,也能够解答,但过程复杂,学了平行四边形性质后,要学会应用.20.2矩形的判断一、选择题1.矩形拥有而一般平行四边形不拥有的性质是()A.对角相等 B .对边相等 C .对角线相等 D .对角线相互垂直2.以下表达中能判断四边形是矩形的个数是()①对角线相互均分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线相互均分且相等的四边形.A . 1B. 2C. 3D. 43.以下命题中,正确的选项是()A.有一个角是直角的四边形是矩形B.三个角是直角的多边形是矩形C.两条对角线相互垂直且相等的四边形是矩形 D .有三个角是直角的四边形是矩形二、填空题4.如图 1 所示,矩形 ABCD中的两条对角线订交于点O,∠ AOD=120°, AB=4cm,则矩形的对角线的长为 _____.D E CF OA B图 1图 25.若四边形 ABCD的对角线 AC, BD相等,且相互均分于点 O,则四边形 ABCD?是_____ 形,若∠ AOB=60°,那么AB:AC=______.6.如图 2 所示,已知矩形ABCD周长为 24cm,对角线交于点O,OE⊥DC 于点 E,于点 F, OF-OE=2cm,则 AB=______, BC=______.三、解答题7.以下图,□ABCD的四个内角的均分线分别订交于E, F, G,H 两点,试说明四边形 EFGH是矩形.四、思虑题8.以下图,△ABC中, CE, CF分别均分∠ACB和它的邻补角∠ACD.AE⊥CE于 E,AF⊥CF 于F,直线EF分别交AB, AC于 M, N 两点,则四边形AECF是矩形吗?为何?参照答案一、 1. C点拨:A与B都是平行四边形的性质,而D是一般矩形与平行四边形都不具有的性质.2 .B点拨:③是矩形的判断定理;④中对角线相互均分的四边形是平行四边形,对角线相等的平行四边形是矩形,故④能判断矩形,应选B.3. D 点拨:选项 D 是矩形的判断定理.二、 4. 8cm5.矩; 1: 2 点拨:利用对角线相互均分来判断此四边形是平行四边形,再依据对角线相等来判断此平行四边形是矩形.由矩形的对角线相等且相互均分,?可知△ AOB 是等腰三角形,又因为∠ AOB=60°,所以AB=AO=1AC.26 . 8cm; 4cm三、 7.解:在□ABCD中,因为AD∥BC,所以∠ DAB+∠CBA=180°,又因为∠ HAB= 1∠DAB,∠ HBA=1∠CBA.22所以∠ HAB+∠HBA=90°,所以∠ H=90°.所以四边形EFGH是矩形.点拨:因为“两直线平行,同旁内角的均分线相互垂直”,所以很简单求出四边形EFGH 的四个角都是直角,从而求得四边形EFGH是矩形.四、 8.解:四边形AECF是矩形.原因:因为CE均分∠ ACB, ?CF?均分∠ ACD, ?所以∠ ACE=1∠ACB,∠ ACF=1∠ACD.所以∠ ECF=1(∠ ACB+∠ACD)=90°.222又因为 AE⊥CE,AF⊥CF, ?所以∠ AEC=∠AFC=90°,所以四边形AECF是矩形.点拨: ?此题是经过证四边形中三个角为直角得出结论.还能够经过证其为平行四边形,再证有一个角为直角得出结论.20.3菱形的判断一、选择题1.以下四边形中不必定为菱形的是()A .对角线相等的平行四边形B.每条对角线均分一组对角的四边形C.对角线相互垂直的平行四边形D.用两个全等的等边三角形拼成的四边形2.四个点 A, B, C,D 在同一平面内,从① AB∥CD;② AB=CD;③ AC⊥BD;④ AD=BC;5 个条件中任选三个,能使四边形ABCD是菱形的选法有().A .1种B.2种C.3种D.4种3 .菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是()A.8cm和 4 3 cm B.4cm和83 cm C.8cm和83 cm D.4cm和43 cm二、填空题4.如图 1 所示,已知□ABCD,AC,BD订交于点O,?增添一个条件使平行四边形为菱形,增添的条件为 ________.(只写出切合要求的一个即可)图1图25.如图 2 所示, D, E,F 分别是△ ABC 的边 BC, CA,AB 上的点,且 DE∥AB,DF∥CA,要使四边形 AFDE是菱形,则要增添的条件是 ________.(只写出切合要求的一个即可)6 .菱形 ABCD的周长为48cm,∠ BAD:∠ ABC=1:?2,?则 BD=?_____,?菱形的面积是______.7.在菱形ABCD中, AB=4, AB 边上的高DE垂直均分边AB,则 BD=_____,AC=_____.三、解答题8.以下图,在四边形ABCD中, AB∥CD, AB=CD=BC,四边形 ABCD是菱形吗? ?说明理由.四、思虑题9.如图,矩形 ABCD的对角线订交于点 O,PD∥AC,PC∥BD, PD,PC订交于点 P,四边形 PCOD是菱形吗?试说明原因.参照答案一、 1. A点拨:此题用清除法作答.2. D 点拨:依据菱形的判断方法判断,注意不要漏解.3. C点拨:以下图,若∠ ABC=60°,则△ ABC为等边三角形,?所以 AC=AB=1×32=8( cm), AO=1AC=4cm.42因为 AC⊥BD,在 Rt△AOB中,由勾股定理,得OB=2222AB OA8 4 =43(cm ?),所以 BD=2OB=8 3 cm.二、 4. AB=BC 点拨:还可增添AC⊥BD 或∠ ABD=∠CBD等.5.点 D 在∠ BAC的均分线上(或 AE=AF)26. 12cm; 723 cm点拨:以下图,过 D 作 DE⊥AB 于 E,因为 AD∥BC, ?所以∠ BAD+∠ABC=180°.又因为∠ BAD:∠A BC=1:2,所以∠ BAD=60°,因为 AB=AD,所以△ ABD 是等边三角形,所以BD=AD=12cm.所以 AE=6cm.在 Rt△AED 中,由勾股定理,得 AE 2+ED 2=AD 2, 62+ED 2=12 2,所以 ED 2=108 ,所以 ED=6 3 cm,所以S菱形ABCD=12×63=72 3 (cm2).7. 4;4 3点拨:以下图,因为DE垂直均分 AB,又因为 DA=AB,所以 DA=DB=4.所以△ ABD 是等边三角形,所以∠ BAD=60°,由已知可得AE=2.在 Rt△AED中,2222222?AE +DE=AD,即 2 +DE=4,所以 DE=12,所以 DE=2 3 ,因为1AC·BD=AB·DE,即1AC·4=4×2 3 ,所以AC=4 3 .22三、 8.解:四边形ABCD是菱形,因为四边形ABCD中, AB∥CD,且AB=CD,所以四边形ABCD是平行四边形,又因为AB=BC,所以Y ABCD是菱形.点拨:依据已知条件,不难得出四边形ABCD为平行四边形,又AB=BC,即一组邻边相等,由菱形的定义能够鉴别该四边形为菱形.四、 9.解:四边形PCOD是菱形.原因以下:因为 PD∥OC,PC∥OD, ?所以四边形P COD是平行四边形.又因为四边形ABCD是矩形,所以OC=OD,所以平行四边形PCOD是菱形.20.4正方形的判断一、选择题1.以下命题正确的选项是()A.两条对角线相互均分且相等的四边形是菱形B.两条对角线相互均分且垂直的四边形是矩形C.两条对角线相互垂直,均分且相等的四边形是正方形D.一组邻边相等的平行四边形是正方形2.矩形四条内角均分线能围成一个()A.平行四边形B.矩形C.菱形 D .正方形二、填空题3.已知点 D, E,F 分别是△ ABC 的边 AB, BC, CA的中点,连结 DE, EF, ?要使四边形ADEF是正方形,还需要增添条件_______.4.如图 1 所示,直线L 过正方形ABCD的极点 B,点 A, C 到直线 L?的距离分别是 1 和2,则正方形ABCD的边长是 _______.图1图2图35.如图 2 所示,四边形 ABCD是正方形,点 E 在 BC的延伸线上, BE=BD且 AB=2cm,则∠E的度数是 ______, BE 的长度为 ____.6.如图 3 所示,正方形 ABCD的边长为 4,E 为 BC上一点, BE=1,F?为 AB?上一点, AF=2,P 为 AC上一动点,则当 PF+PE取最小值时, PF+PE=______.三、解答题7.以下图,在 Rt△ABC中, CF为∠ ACB的均分线, FD⊥AC 于 D,FE⊥BC于点 E,试说明四边形 CDFE是正方形.BEF四、思虑题8.已知以下图,在正方形 ABCD中, E,F 分别是(1) AF 与 DE相等吗?为何?(2) AF 与 DE能否垂直?说明你的原因.C D A AB,BC边上的点,且 AE=BF,?请问:参照答案一、 1. C点拨:对角线相互均分的四边形是平行四边形,?对角线相互垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形必定是正方形,应选 C.2. D 点拨:由题意画出图形后,利用“一组邻边相等的矩形是正方形”来判断.二、 3.△ ABC是等腰直角三角形且∠ BAC=90°点拨:还可增添△ ABC 是等腰三角形且四边形ADEF是矩形或∠ BAC=90°且四边形ADEF 是菱形等条件.4.5点拨:察看图形易得两直角三角形全等,由全等三角形的性质和勾股定理得正方形的边长为 2212=5.5. 67. 5°; 2 2 cm点拨:因为BD是正方形ABCD的对角线,所以∠ DBC=45°, AD=?AB=2cm.在 Rt△BAD中,由勾股定理得 AD 2+AB 2=BD 2,即 22+22=BD 2,所以 BD=2 2 cm,所以 BE=BD=2 2( cm),又因为BE=BD,所以∠ E=∠EDB= 1(180°- 45°)=67. 5°.26.17点拨:以下图,作 F 对于AC的对称点G.连结EG交AC于P,则 PF+?PE=PG+PE=GE为最短.过 E 作 EH⊥AD.在 Rt△GHE中,HE=4,HG=AG-AH=AF-BE=1,所以 GE= 4212 = 17,?即 PF+PE= 17.三、 7.解:因为∠ FDC=∠FEC=∠BCD=90°,所以四边形CDFE是矩形,因为 CF?均分∠ ACB,FE⊥BC,FD⊥AC,所以FE=FD,所以矩形CDFE是正方形.点拨:此题先说明四边形是矩形,再求出有一组邻边相等,?还能够先说明其为菱形,再求其一个内角为90°.四、 8.解:( 1)相等.原因:在△ ADE 与△ BAF 中, AD=AB,∠ DAE=∠ABF=90°, AE=BF,所以△ ADE≌△ BAF( S. A. S.),所以 DE=AF.( 2) AF 与 DE垂直.原因:如图,设DE与 AF 订交于点O.因为△ ADE≌△ BAF, ?所以∠ AED=∠BFA.又因为∠ BFA+∠EAF=90°,所以∠ AEO+∠EAO=90°,所以∠ EOA=90°,所以DE⊥AF.20.5等腰梯形的判断1 A C 一、选择题.以下结论中,正确的选项是(.等腰梯形的两个底角相等.一组对边平行的四边形是梯形)BD.两个底角相等的梯形是等腰梯形.两条腰相等的梯形是等腰梯形2.以下图,等腰梯形ABCD的对角线 AC,BD订交于点O,则图中全等三角形有()A.2对B.3对C.4对D.5对3.课外活动课上, ?老师让同学们制作了一个对角线相互垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和起码为()A. 30 2 cm B.30cm C.60cm D.60 2 cm二、填空题4.等腰梯形上底,下底和腰分别为 4,?10,?5,?则梯形的高为 _____,?对角线为 ______.5.一个等腰梯形的上底长为5cm,下底长为 12cm,一个底角为 60°,则它的腰长为____cm,周长为 ______cm.6.在四边形 ABCD中, AD∥BC,但 AD≠BC,若使它成为等腰梯形,则需要增添的条件是__________ (填一个正确的条件即可).三、解答题7.以下图,AD是∠ BAC的均分线, DE∥AB, DE=AC,AD≠EC.求证: ?四边形 ADCE是等腰梯形.四、思虑题8.以下图,四边形ABCD中,有 AB=DC,∠ B=∠C,且AD<BC,四边形 ABCD是等腰梯形吗?为何?参照答案一、 1. D点拨:梯形的底角分为上底上的角和下底上的角,?所以在等腰梯形的性质和鉴别方法中一定重申同一底上的两个内角(?指上底上的两个内角或下底上的两个内角),不然就会出现错误,所以A, B 选项都不正确,而 C 选项中遗漏了限制条件此外一组对边不平行,若平行该四边形就形成了平行四边形了,所以应选D.2. B点拨:因为△ ABC≌△ DCB,△ BAD≌△ CDA,△ AOB≌△ DOC,所以共有 3 对全等的三角形.3. C点拨:设该等腰梯形对角线长为Lcm,因为两条对角线相互垂直,?所以梯形面积为122L =450,解得 L=30,所以所用竹条长度之和起码为2L=2× 30=60(cm).二、 4. 4:65点拨:以下图,连结BD,过 A,D 分别作 AE⊥BC,DF⊥BC,垂足分别为E, F.易知△ BAE≌△ CDF,在四边形 AEFD为矩形,所以BE=CF=3, AD=EF=4.在 Rt△CDF 中, FC2+DF 2=CD 2,即 32+DF 2=52,所以 DF=4 ,在 Rt △BFD 中, BF2+DF 2=BD 2,即 72+42=BD 2,所以 BD=65 .5. 7;31点拨:以下图,过点D作 DE∥AB 交 BC于 E.因为ABED是平行四边形.所以 BE=AD=5(cm), AB=DE.又因为 AB=CD,所以 DE=?DC,又因为∠ C=60°,所以△ DEC 是等边三角形,所以 DE=DC=EC=7( cm),所以周长为5+?12+7+7=31(cm).6. AB=CD(或∠ A=∠D,或∠ B=∠C,或 AC=BD,或∠ A+∠C=180°,或∠B+∠D=180°)三、 7.证明:因为 AB∥ED,所以∠ BAD=∠ADE.又因为 AD是∠ BAC的均分线,所以∠ BAD=∠CAD,所以∠ CAD=∠ADE,所以 OA=OD.又因为AC=DE,所以 AC-OA=DE-OD即 OC=OE, ?所以∠ OCE=∠OEC,又因为∠ AOD=∠COE,所以∠ CAD=∠OCE.所以AD∥CE,而 AD≠CE,故四边形ADCE是梯形.又因为∠ CAD=∠ADE, AD=DA, AC=DE,所以△ DAC≌△ ADE,所以DC=?AE,所以四边形ADCE是等腰梯形.点拨:证明一个四边形是等腰梯形时,应先证其是梯形尔后再证两腰相等或同一底上的两个角相等.四、 8.解:四边形ABCD是等腰梯形.原因:延伸BA, CD,订交于点 E,以下图,由∠ B=∠C,可得EB=EC.又 AB=DC,所以 EB-AB=EC-DC,即 AE=DE,所以∠ EAD=∠EDA.因为∠ E+∠EAD+∠EDA=180°,∠ E+∠B+∠C=180°,所以∠ EAD=∠B.故 AD∥BC. ?又 AD<BC,所以四边形 ABCD是梯形.又 AB=DC,所以四边形 ABCD是等腰梯形.点拨:由题意可知,只需推出AD∥BC,再由AD<BC便可知四边形ABCD为梯形,再由AB=DC,即可求得此四边形是等腰梯形,由∠ B=∠C联想到延伸 BA,CD,即可获得等腰三角形,从而使 AD∥BC.华东师大版数学八年级(下)第 20 章平行四边形的判断测试(答卷时间: 90 分钟,全卷满分: 100 分)姓名得分 ____________一、认认真真选,沉稳应战!(每题 3 分,共 30 分)1. 正方形拥有菱形不必定拥有的性质是()(A )对角线相互垂直(B)对角线相互均分(C)对角线相等(D)对角线均分一组对角2.如图 (1),EF 过矩形 ABCD 对角线的交点 O,且分别交 AB 、CD 于 E、 F,那么暗影部分的面积是矩形ABCD 的面积的()(A )A 111( D )3A5(B )( C)1043D E FFEB C D HB C(1)(2)(3)3.在梯形ABCD 中, AD ∥ BC ,那么 A : B : C : D 能够等于()( A)4:5:6:3(B)6:5:4:3(C)6:4:5:3(D)3:4:5:64.如图 (2) ,平行四边形ABCD 中,DE ⊥ AB 于 E,DF⊥ BC 于 F,若Y ABCD的周长为48,DE = 5, DF= 10,则Y ABCD的面积等于 ()( A)87.5(B)80(C)75(D)72.55. A 、 B、 C、 D 在同一平面内,从① AB∥CD;② AB=CD;③ BC∥AD;④ BC=AD这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有()( A)3种(B)4种(C)5种(D)6种6.如图 (3) ,D、E、F分别是VABC各边的中点,AH 是高,假如 ED5cm ,那么 HF的长为()( A ) 5cm(B)6cm(C)4cm(D)不可以确立7.如图( 4):E 是边长为 1 的正方形 ABCD 的对角线 BD 上一点,且 BE = BC, P 为 CE 上随意一点, PQ⊥BC 于点 Q, PR⊥ BE 于点 R,则 PQ+PR 的值是()2132( A )2(B)2(C)2(D)38.如图( 5),在梯形ABCD 中, AD ∥ BC , AB CD , C 60 ,BD均分ABC ,假如这个梯形的周长为30,则AB的长()( A)4( B)5(C)6( D)7A DA DERPB C( 5)B(4)Q C9.右图是一个利用四边形的不稳固性制作的菱形晾衣架.A B C 已知此中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉 A 、 B 之间的距离为20 3 cm,则∠1等于()1)( A)90°(B) 60°(C) 45°(D) 30°10.某校数学课外活动研究小组,在老师的指引下进一步研究了完整平方公式.联合实数的性质发现以下规律:对于随意正数a、 b,都有 a+b ≥ 2ab 建立.某同学在做一个面积为3600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来做对角线用的竹条至少需要准备xcm.则 x 的值是()(A) 1202(B) 602(C) 120(D) 60二、仔认真细填,记录自信!( 每题 2 分,共20 分)11.一个四边形四条边按序是a、b、c、d,且a2 b 2 c 2 d 22ac 2bd,则这个四边形是 _______________ .12.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB CD ;(2) AB∥CD ;(3)OA OC;(4)OB OD ;(5) AC ⊥ BD ;(6) AC 均分 BAD 这六个条件中,选用三个推出四边形ABCD是菱形.如( 1)( 2)( 5)ABCD 是菱形,再写出切合要求的两个:ABCD 是菱形;ABCD 是菱形.13. 如图,已知直线l 把 Y ABCD 分红两部分,要使这两部分的面积相等,直线l 所在地点需知足的条件是____________________. (只需填上一个你以为适合的条件)lA DB C(第 13 题)(第 16 题)14.梯形的上底长为 6cm ,过上底的一极点引一腰的平行线,与下底订交,所构成的三角形周长为 21cm ,那么梯形的周长为_________ cm。
(完整版)平行四边形的性质判定练习题

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
1、如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.3、平行四边形得周长为50cm ,两邻边之差为5cm,则长边是________ ,短边是__________.4、平行四边形ABCD 中,∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ .7、如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
平行四边形的性质与判定经典例题练习

平行四边形的性质与判定经典例题练习一、平行四边形的性质1. 定义:平行四边形是一种具有两对对边平行的四边形。
定义:平行四边形是一种具有两对对边平行的四边形。
2. 性质1:平行四边形的对边相等。
性质1:平行四边形的对边相等。
3. 性质2:平行四边形的对角线相等。
性质2:平行四边形的对角线相等。
4. 性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
5. 性质4:平行四边形的两组对边分别互相平行并且相互等长。
性质4:平行四边形的两组对边分别互相平行并且相互等长。
二、平行四边形的判定1. 判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
2. 判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
三、经典例题练1. 例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
2. 例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
3. 例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
- (a)根据对边平行和相等的判定方法,若AB = CD且AD与BC互相垂直,则四边形ABCD是平行四边形。
(完整版)平行四边形的性质习题(有答案)

平行四边形的性质测试题一、选择题(每题 3 分共 30 分)1.下边的性质中,平行四边形不必定具备的是()A.对角互补B.邻角互补C.对角相等D.内角和为 360°2.在中,∠ A:∠ B:∠ C:∠ D 的值能够是()A .1:2:3:4B .1:2:1:2C .1:1:2:2 D.1: 2:2:13.平行四边形的对角线和它的边能够构成全等三角形()A.3对B.4 对 C .5对D. 6 对A D 4.以下图,在中,对角线 AC、BD交于点 O,?以下式子中一O 定建立的是()B CA.AC⊥ BD B . OA=OC C. AC=BD D .AO=OD5.以下图,在中, AD=5,AB=3,AE均分∠ BAD交BC A D边于点 E,则线段 BE、 EC的长度分别为()BE C A .2和3 B.3和2 C .4和1 D .1和46.的两条对角线订交于点 O,已知 AB=8cm,BC=6cm,△AOB的周长是 18cm,那么△ AOD的周长是()A .14cmB .15cmC .16cmD .17cm7.平行四边形的一边等于14,它的对角线可能的取值是()A .8cm和 16cmB .10cm和 16cmC . 12cm和 16cmD . 20cm和 22cm 8.如图,在中,以下各式不必定正确的选项是()A.∠ 1+∠ 2=180° B .∠ 2+∠ 3=180C.∠ 3+∠ 4=180°D.∠ 2+∠4=180°9.如图,在中,∠ ACD=70°,AE⊥ BD于点E,则∠ ABE等于()A、20°B、25° C 、 30° D 、35°10.如图,在△ MBN中, BM=6,点 A、C、D 分别在 MB、NB、MN上,四边形 ABCD为平行四边形,∠NDC=∠ MDA,那么的周长是()二、填空题(每题 3 分共 18 分)11.在中,∠ A:∠ B=4:5,则∠ C=______.12.在中, AB:BC=1:2,周长为 18cm,则 AB=______cm,AD=_______cm.13.在中,∠A=30°,则∠ B=______,∠C=______,∠D=________.14.如图,已知:点 O是的对角线的交点, ?AC=?48mm,?BD=18mm,AD=16mm,那么△ OBC的周长等于 _______mm.15.如图,在中,E、F是对角线BD上两点,要使△ ADF≌△ CBE,还需增添一个条件是 ________.16.如图,在中,EF∥ AD,MN∥ AB,那么图中共有_______?个平行四边形.三、解答题17.已知:如图,在中,E、F是对角线AC?上的两点,AE=CF.BE与DF的大小有什么关系,并说明原因。
平行四边形的判定与性质

平行四边形的性质与判定一、平行四边形定义及其性质:1、两组对边分别平行的四边形是平行四边形,平行四边形对边平行且相等。
定义的几何语言表述 ∵ AB ∥CD AD ∥BC ∴四边形ABCD 是平行四边形 。
∵四边形ABCD 是平行四边形(或在 ABCD 中) ∴ AB=CD ,AD=BC 。
例题1、如图5,AD ∥BC ,AE ∥CD ,BD 平分∠ABC ,求证AB=CE2、平行四边形除了对边平行且相等外,其对角也相等。
∵四边形ABCD 是平行四边形(或在ABCD 中) ∴ ∠A=∠C ,∠B=∠D 。
例题2、在平行四边形ABCD 中,若∠A :∠B=2:3,求∠C 、∠D 的度数。
3、平行四边形的对角线互相平分。
例题3.已知O 是平行四边形ABCD 的对角线的交点,AC=24cm ,BD=38 cm ,AD= 28cm ,求三角形OBC 的周长。
5.如图,平行四边形ABCD 中,AC 交BD 于O ,AE ⊥BD 于E ,∠EAD=60°,AE=2cm,AC+BD=14cm, 求三角形BOC 的周长。
例题4:已知平行四边形ABCD ,AB=8cm ,BC=10cm,∠B=30°, 求平行四边形平行四边形ABCD 的面积。
对边分别平行 边 对边分别相等 对角线互相平分 平行四边形角 对角相等 邻角互补图(5)DCB AA B C D二、平行四边形的判定 方法一(定义法):两组对边分别平行的四边形的平边形。
几何语言表达定义法:∵AB ∥CD ,AD ∥BC ,∴四边形ABCD 是平行四边形方法二:两组对边分别相等的四边形是平行四边形。
∵AB=CD ,AD=BC ,∴四边形ABCD 是平行四边形 方法三:对角线互相平分的四边形是平行四边形。
∵OA=OC , OB= OD ∴四边形ABCD 是平行四边形 方法四:有一组对边平行且相等的四边形是平行四边形 ∵AB=CD ,AB ∥CD ,∴四边形ABCD 是平行四边形方法五:两组对角分别相等的四边形是平行四边形∵ ∠A =∠C ,∠B=∠D ,∴四边形ABCD 例1:已知:E 、F 分别为平行四边形ABCD 两边AD 、BC 的中点,连结BE 、DF 求证:2∠1∠=三、三角形中位线:三角形两边的中点连线线段(即中位线)与三角形的第三边平行,并且等于第三边的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初2017级寒假培训(八)A 层----平行四边形的性质与判定班级: 姓名:1.定义:两组对边互相平行的四边形叫做平行四边形,平行四边形ABCD 记作:□ 几何语言:,2.性质:平行四边形的对边平行且相等,对角相等,邻角互补,对角线互相平分;几何语言:∵ 四边形ABCD 是平行四边形∴AD ∥ BC, _________ (对边平行);AD=BC ,__________(对边相等);,_________(对角相等);…(邻角互补);, (对角线互相平分)。
平行四边形的判定:判定1.两组对边分别平行的四边形是平行四边形 判定2.两组对边分别相等的四边形是平行四边形 判定3.两组对角分别相等的四边形是平行四边形 判定4.对角线互相平分的四边形是平行四边形判定5.一组对边平行且相等的四边形是平行四边形; 几何语言判定1., 判定2.,判定3., 判定4. 判定5.,夯实基础:1.如图,将□的一边BC 延长至E ,若∠A =110°,则∠1=________.E2.如图,在□中,,则= °.3.在平行四边形ABCD 中,cm AB 6=,cm BC 8=,则平行四边形ABCD 的周长为 cm .4.如图,在□中,已知,平分交边于点,ABCD BC AD CD AB //,// 是平行四边形四边形ABCD ∴BCD BAC ∠=∠ 180=∠+∠ABC BAC OC OA =BC AD CD AB //,// 是平行四边形四边形ABCD ∴BC AD DC AB ==,是平行四边形四边形ABCD ∴BCD BAD ADC ABC ∠=∠∠=∠, 是平行四边形四边形ABCD ∴,,DO BO CO AO == 是平行四边形四边形ABCD ∴CD AB CD AB =,// 是平行四边形四边形ABCD ∴ABCD ABCD 120=∠A D ∠ABCD ,6,8CM AB CM AD ==DE ADC ∠BC E ABCDOA B CD 4 EA B C D 2 1A B C D则等于( )5.平行四边形中一边的长为10cm ,那么它的两条对角线的长度可以是( )6.在□ABCD 中,对角线AC ,BD 相交于点O ,若BD 与AC 的和为18cm , CD :DA=2:3,ΔAOB 的周长为13cm ,那么BC 的长为( ) A. 6cm B. 9cm C .3cm D .12cm7.如图,▱ABCD 中,AC 、BD 为对角线,BC=6,BC 边上的高为4,则阴影部分的面积为 .8.在下面给出的条件中,能判定四边形ABCD是平行四边形的是( )9.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( )10.点A ,B ,C ,D 在同一平面内,从①AB ∥CD ,②AB=CD ,③BC ∥AD ,④BC=AD 这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有( )种A .3B .4C .5D .68.如图,在平行四边形ABCD 中,若AB=6,AD=10,▱ABC 的平分线交AD 于点E ,交CD 的延长线于点F ,求DF 的长.9.已知:如图a ,的对角线、相交于点,过点与、分BE CM A 2.CM B 4.CM C 6.CM D 8.cm cm A 64.和cm cm B 3020.和cm cm C 86.和cm cm D 128.和CD AD BC AB A ==,.BC AD CD AB B =,//.D B CD AB C ∠=∠,//.D C B A D ∠=∠∠=∠,. 88,108,88.A 108,104,88.B 92,92,88.C 108,72,108.D ABCD AC BD O EF O AB CD DC B A别相交于点、.(1)求证:(2)若上题中的条件都不变,将EF 转动到图b 的位置,那么结论是否成立?若将EF 向两方延长与平行四边形的两对边的延长线分别相交(图c 和图d ),结论是否成立,说明你的理由.10.已知如图,O 为平行四边形ABCD 的对角线AC 的中点,EF 经过点O ,且与AB 交于E ,与CD 交于F ,求证:四边形AECF 是平行四边形。
E F .,,DF BE CF AE OF OE ===11.如图,在▱ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)试判断四边形AFCE是什么样的四边形,并证明你的结论.12.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.13..如图,已知四边形ABCD为平行四边形,AE▱BD于E,CF▱BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状.14..已知:如图,在梯形ABCD中,AD▱BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,▱B=60°,求DE的长.初2017级寒假培训(九)A 层----矩形的性质与判定班级: 姓名:定义:有一个角是直角的平行四边形叫做矩形矩形是特殊的平行四边形,所以,平行四边形的性质矩形都具备矩形的性质:性质1.对边平行且相等;性质2.矩形的四个角都是直角;性质3.矩形的对角线相等且互相平分。
几何语言: 性质1. 性质2. 性质矩形的判定:判定1.有一个角是直角的平行四边形是矩形;判定2.对角线相等的平行四边形是矩形;判定3.有三个角是直角的四边形是矩形; 几何语言: 判定1.,,判定2.,且判定3. 夯实基础:1.在下列图形性质中,矩形不一定具有的是( )A .对角线互相平分且相等B .四个角相等C .是轴对称图形D .对角线互相垂直平分 2.矩形具有而一般的平行四边形不一定具有的特征是( )。
A .对角相等 B. 对边相等 C .对角线相等 D. 对角线互相平分 3.如图,矩形ABCD 的对角线AC 、BD 相交于点O ,AB=3,∠AOD=120°,则AD 的长为( ) A .3B .3C .6D .34.如图,在矩形ABCD 中,对角线AC 、BD 交于点O ,以下说法错误的是( ) A .∠ABC=90° B .AC=BD C .OA=OB D .OA=AD3题图 4题图 5.判断一个四边形是矩形,下列条件正确的是( )A .对角线相等B .对角线垂直C .对角线互相平分且相等D .对角线互相垂直且相等。
BC AD DC AB BC AD DA AB ABCD ==∴,,//,//,矩形 ,ABCD 矩形 90=∠=∠=∠=∠∴ADC BCD ABC BAC DO BO CO AO BD AC ABCD ===,,,.3矩形 ABCD90=∠BAC 且是矩形四边形ABCD ∴ABCD ,BD AC =是矩形四边形ABCD ∴,90=∠=∠=∠BCD ABC BAC 是矩形四边形ABCD ∴ODCBA6.(A层)一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为 .6.(B层)矩形的两邻边分别为4㎝和3㎝,则其对角线为㎝,矩形面积为cm2.7.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是 .8.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.9.如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:(1)▱ABF▱▱DCE;(2)▱AOD是等腰三角形.10.已知:如图,平行四边形ABCD的四个内角的平分线分别相交于点E,F,G,H,求证:四边形EFGH是矩形。
11.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE▱AC交DC的延长线于点E.(1)求证:BD=BE;(2)若▱DBC=30°,BO=4,求四边形ABED的面积.12.如图,在▱ABCD中,DE▱AB,BF▱CD,垂足分别为E,F.(1)求证:▱ADE▱▱CBF;(2)求证:四边形BFDE为矩形.13.如图所示,四边形ABCD是平行四边形,AC、BD交于点O,▱1=▱2.(1)求证:四边形ABCD是矩形;(2)若▱BOC=120°,AB=4cm,求四边形ABCD的面积.14.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E,求证:四边形ADCE为矩形。
攻破动点问题:15.如图,在直角梯形ABCD中,AB∥C D,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC 方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.。
