瑞利衰落信道仿真 - 360文档中心

小尺度衰落信道中的瑞利衰落和莱斯衰落建模

图6.仿真的莱斯分布的概率密度函数(σ=1)
莱斯衰落信道仿真
• 脚本代码如下
莱斯衰落信道仿真
• 当然，也可以使用MATLAB自带的raylrnd或者random函数产生服从瑞利分布或莱斯分布的随机变量。
• raylrnd(σ,m,n) • random('rayl',σ,m,n) • random('rician',A,σ,m,n)
参考文献
• [1]赵勇洙等．MIMO-OFDM无线通信技术及MATLAB实现．电子工业出版社.2012.4
• [2]杨大成等．移动传播环境．机械工业出版社．2003,8 • [3]郭文斌等．通信原理--基于MATLAB的计算机仿真.北京邮电大学
出版社．2006.6 • [4]Proakis等．现代通信系统（MATLAB版）.电子工业出版
向量f，输出
瑞利衰落信道仿真
•通过该函数绘制的瑞利信道概率密度分布图（L=20000、σ2=1）
图5.仿真的瑞利分布的概率密度函数(σ=1)
莱斯衰落信道仿真
•存在强路径的LOS环境中，强路径不会有任何损耗，因此接收信号的幅度可以表示为：
X=A+W1+jW2 在NLOS环境下,A=0(K=0),莱斯分布退化为瑞利分布。
Clarke/Gans模型框图
• 图7.Clarke/Gans模型的框图
Clarke/Gans模型
• 图8.Clarke/Gans模型产生的时变信道
其他多径模型
• FWGN模型还包括改进频域FWGN模型以及时域FWGN模型。
• 其他多径模型还有：Jakes模型、基于射线信道模型、频率选择性衰落信道模型和SUI(斯坦福大学过渡)信道模型。

移动通信瑞利衰落信道建模及仿真

移动通信瑞利衰落信道建模及仿真信息与通信工程学院 09211123班 09212609 蒋砺思摘要：首先分析了移动信道的表述方法和衰落特性，针对瑞利衰落，给出了Clarke模型，并阐述了数学模型与物理模型之间的关系，详细分析了Jakes仿真方法，并用MATLAB进行了仿真，并在该信道上实现了OFDM仿真系统，仿真曲线表明结果正确，针对瑞利衰落的局限性，提出了采用Nakagami-m分布作为衰落信道物理模型，并给出了新颖的仿真方法。

关键词：信道模型；Rayleigh衰落；Clarke模型；Jakes仿真；Nakagami-m分布及仿真一．引言随着科学技术的不断进步和经济水平的逐渐提高，移动通信已成了我们日常生活中不可缺少的必备品。

然而，移动通信中的通话常常受到各种干扰导致话音质量的不稳定。

本文应用统计学及概率论相关知识对移动通信的信道进行建模仿真和详尽的分析。

先来谈谈移动通信的发展历史和发展趋势。

所谓通信就是指信息的传输、发射和接收。

人类通信史上革命性的变化是从电波作为信息载体（电信）开始的，近代电信的标志是电报的诞生。

为了满足人们随时随地甚至移动中通信的需求，移动通信便应运而生。

所谓移动通信是指通信的一方或双方处于移动中，其传播媒介是无线电波，现代移动通信以Maxwel1理论为基础，他奠定了电磁现象的基本规律；起源于Hertz的电磁辐射，他认识到电磁波和电磁能量是可以控制发射的，而Marconi无线电通信证实了电磁波携带信息的能力。

第二次世界大战结束后，开始了建立公用移动通信系统阶段。

这第一代移动通信系统最大缺点是采用模拟技术，频谱利用律低，容量小。

90年代初，各国又相继推出了GSM等第二代数字移动通信系统，其最大缺点是频谱利用率和容量仍然很低，不能经济的提供高速数据和多媒体业务，不能有效地支持Internet业务。

90年代中期以后，许多国家相继开始研究第三代移动通信系统，目前，我国及其他国家已开始了第四代移动通信的研究。

西南交通大学_通信工程实验_MATLAB实验_OFDM误码率仿真(衰落)

MATLAB 实验 OFDM 误码率仿真（衰落）
一、实验目的：
1、了解瑞利信道产生的原因及其特征。。 2、用 MATLAB 进行 OFDM 系统在瑞利信道下误码率分析。
二、实验原理： 1、OFDM 基本原理
OFDM （ Orthogonal Frequency Division Multiplexing ）正交频分复用，它是由多载波调制技术发展而来。其基本思想是把一路高速的数据流串并变换为 N 路的低速数据流再并行传输，因此数据流速度降为原来的 1/N，具有很强的抗多径衰落和抗脉冲干扰的能力，特别适合高速无线数据传输。OFDM 是一种子载波相混叠的多载波技术，但由于 OFDM 选择时域相互正交的子载波，他们在频域虽然相互混叠，却能在接收端被分离出来。 OFDM 信号频谱实际满足奈奎斯特准则即多个子载波之间不存在相互干扰。 OFDM 信号的基带形式
Ts=Tsym/N
x(t ) X [k ]exp j 2 f k (t Tsym
k 0
Nபைடு நூலகம்1
由于 OFDM 子载波之间满足正交性，因此可以采用离散傅立叶变换(DFT)表示信号。直接进行 IDFT/DFT 变换，算法复杂度为 O(N2) ，计算量非常大，但如果采用 IFFT/FFT 来实现，则算法复杂度降低为 O(N/2) (基 2 算法)，极大降低了 OFDM 系统的实现难度。图 1 为基带 OFDM 系统框图。
四、实验报告要求
1. 所有程序完整的源代码（.m 文件）以及注释。 2. 仿真结果。对于所有的图形结果（包括波形与仿真曲线等），将图形保存成.tif 或者.emf 的格式并插入 word 文档。
二进制信息
映射
s/p

瑞利信道衰减系数-概述说明以及解释

瑞利信道衰减系数-概述说明以及解释1.引言1.1 概述瑞利信道是一种常见的无线传输信道模型，其信号经过传输会受到一定程度的衰减影响。

瑞利信道衰减系数是用来描述信号在瑞利信道中衰减的程度的重要参数之一。

在无线通信系统中，了解和准确计算瑞利信道衰减系数对于系统设计和性能评估至关重要。

本文将围绕瑞利信道衰减系数展开详细讨论，包括其定义、计算方法以及影响因素等内容。

通过深入探讨瑞利信道衰减系数的相关知识，可以帮助读者更好地理解在实际通信系统中应用和优化瑞利信道的重要性。

1.2文章结构1.2 文章结构本文将首先介绍瑞利信道衰减系数的概念和定义，然后探讨影响瑞利信道衰减系数的因素，包括信号频率、传输距离、环境条件等。

接着将详细说明如何计算瑞利信道衰减系数，包括理论推导和实际计算方法。

最后，我们将总结瑞利信道衰减系数的重要性，并举例应用瑞利信道衰减系数的实际场景，展望未来的研究方向。

通过本文的阐述，读者将能够全面了解瑞利信道衰减系数在无线通信系统中的重要性和应用价值。

1.3 目的:本文旨在深入探讨瑞利信道衰减系数这一重要概念，阐明其在通信系统中的关键作用和影响因素。

通过详细介绍瑞利信道衰减系数的定义、计算方法以及实际应用场景，希望读者能够更加全面地了解该概念的重要性和实用性。

同时，本文也旨在对未来关于瑞利信道衰减系数的研究方向进行展望，为相关领域的进一步研究提供思路和启示。

通过本文的阐述，希望读者能够对瑞利信道衰减系数有一个全面深入的理解，为通信系统的设计和优化提供参考和指导。

2.正文2.1 什么是瑞利信道衰减系数瑞利信道衰减系数是描述在瑞利信道中信号传输衰减的重要参数。

瑞利信道是无线通信中常见的一种多路径衰落信道模型，其特点是接收端收到的信号是由多条不同路径的信号叠加而成的，这些信号经过不同的路径传播到达接收端，因此会受到多径效应的影响。

信号在传输过程中会出现衰减，其中瑞利信道衰减系数就是用来描述这种衰减情况的参数。

瑞利分布

瑞利分布信道M A T L A B 仿真一、瑞利衰落原理在陆地移动通信中，移动台往往受到各种障碍物和其他移动体的影响，以致到达移动台的信号是来自不同传播路径的信号之和。

而描述这样一种信道的常用信道模型便是瑞利衰落信道。

定义:由于信号进行多径传播达到接收点处的场强来自不同传播的路径，各条路径延时时间是不同的，而各个方向分量波的叠加，又产生了驻波场强，从而形成信号快衰落称为瑞利衰落。

瑞利衰落信道（Rayleighfadingchannel）是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，表现为“衰落”特性，并且多径衰落的信号包络服从瑞利分布。

由此，这种多径衰落也称为瑞利衰落。

这一信道模型能够描述由电离层和对流层反射的短波信道，以及建筑物密集的城市环境。

瑞利衰落只适用于从发射机到接收机不存在直射信号的情况，否则应使用莱斯衰落信道作为信道模型。

假设经反射（或散射）到达接收天线的信号为N 个幅值和相位均随机的且统计独立的信号之和。

信号振幅为r,相位为,则其包络概率密度函数为P(r)=2222rr e(r 0)相位概率密度函数为：P()=1/2（20）二、仿真原理（1）瑞利分布分析环境条件：通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路径（如视距传播路径），且存在大量反射波，到达接收天线的方向角随机的（（0~2π）均匀分布），各反射波的幅度和相位都统计独立。

幅度与相位的分布特性：包络r 服从瑞利分布，θ在0～2π内服从均匀分布。

瑞利分布的概率分布密度如图1所示：00.51 1.52 2.530.10.20.30.40.50.60.70.80.9图1瑞利分布的概率分布密度（2）多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k kk y t r t x t%%(1)其中,()k r t 复路径衰落，服从瑞利分布;k是多径时延。

多径衰落信道模型框图如图2所示：图2多径衰落信道模型框图（3）产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性，其振幅服从瑞利分布，即22()()()c s r t n t n t （2）上式中()()c s n t n t 、，分别为窄带高斯过程的同相和正交支路的基带信号。

一种瑞利衰落信道的高速仿真模型及DSP实现

线，可认为／（）间的互相关函数为零；／（）１ｔ之而１ｔ的自相关函数可表示为：
文献［］出了（）统计特性。其概率密３给￡的度函数和自相关函数为：
仅需要较少的低频正弦波分量以及简单的运算即可实现较高精度的信道建模；而可采用查表法并结合进
Ｔ３０６０ＭＳ２Ｃ２２定点数字信号处理器的高并行性和处理能力构造高速的仿真模型。关键词瑞利衰落信道确知性信道建模仿真模型
其中ｎ＝１２ … … ，、＝１２并取相位Ｏ，均匀分，，Ｎｉｉ，；ｉｎ
图１表示了确知性随机过程的直接实现。
其中（）零均值窄带实高斯噪声过程，差为ｔ为方
ｉ。对于二维各向同性的散射环境中的全向接收天
（）５
本文将对方法④ 进行介绍，涉及相应的ＤＰ并Ｓ
实现。作为理论基础，先将论述瑞利衰落信道的首基本特性和确知性瑞利过程的概念；次介绍用于其实现中的离散模型和对应的高速结构；后将描述最相应的ＤＰ实现，讨论其性能和实现复杂度。Ｓ并
瑞利过程（ａｌｉｒｃｓ）被用来描述在无ＲｙｇＰｏｅｓ常ｅｈ线传输中，发射机和接收机之间不存在直射路径当

瑞利衰落信道和高斯信道matlab

瑞利衰落信道和高斯信道是无线通信中常见的两种信道模型。

瑞利衰落信道适用于描述城市中的移动通信环境，而高斯信道则适用于描述开阔地带或者室内的通信环境。

本文将使用Matlab来分别模拟这两种信道，并对模拟结果进行分析和比较。

一、瑞利衰落信道模拟1. 利用Matlab中的rayleighchan函数可以模拟瑞利衰落信道。

该函数可以指定信道延迟配置、多径增益和相位等参数。

2. 我们需要生成随机的信号序列作为发送端的信号。

这里可以使用Matlab中的randn函数生成高斯白噪声信号作为发送端信号的模拟。

3. 接下来，我们需要创建一个瑞利衰落信道对象，并指定相应的参数。

这里可以设定信道延迟配置、多径增益和相位等参数，以便更好地模拟实际的信道环境。

4. 将发送端的信号通过瑞利衰落信道进行传输，即将信号与瑞利衰落信道对象进行卷积操作。

5. 我们可以通过Matlab中的plot函数绘制发送端和接收端信号的波形图以及信号经过瑞利衰落信道后的波形图，以便直观地观察信号经过信道传输后的变化。

二、高斯信道模拟1. 与瑞利衰落信道模拟类似，高斯信道的模拟同样可以使用Matlab 中的函数进行实现。

在高斯信道的模拟中，我们同样需要生成随机的信号序列作为发送端的信号。

2. 我们可以通过Matlab中的awgn函数为发送端信号添加高斯白噪声，模拟信号在传输过程中受到的噪声干扰。

3. 我们同样可以使用plot函数绘制发送端和接收端信号的波形图以及信号经过高斯信道后的波形图，以便观察信号传输过程中的噪声干扰对信号的影响。

三、模拟结果分析和比较对于瑞利衰落信道模拟结果和高斯信道模拟结果，我们可以进行一些分析和比较：1. 信号衰落特性：瑞利衰落信道模拟中，我们可以观察到信号在传输过程中呈现出快速衰落的特性，而高斯信道模拟中，信号的衰落速度相对较慢。

2. 噪声干扰：高斯信道模拟中，我们可以观察到添加了高斯白噪声对信号的影响，而在瑞利衰落信道模拟中，虽然也存在噪声干扰，但其影响相对较小。

瑞利衰落信道模型的研究与仿真

瑞利衰落信道模型的研究与仿真瑞利衰落信道模型的研究与仿真 matlab程序% written by Amir Sarrafzadeh (14Jan2008)% this function generates normalized rayleigh samples based on Inverse DFT% method as was proposed by David J. Young, and Norman C. Beaulieu% "The Generation of Correlated Rayleigh Random Variates by Inverse% Discrete Fourier Transform, "% Sample Use:% chan=genRayleighFading(512,ceil(10000/512),1e4,100);% chan=chan(1:10000);% where 10000=number of needed samples% parameters:% fftsize: size of fft which used% numBlocks: number of samples/fftsize% fs: sampling frequency(Hz)% fd: doppler shift(Hz)function [ outSignal ] = genRayleighFading( fftSize,numBlocks,fs,fd )numSamples=fftSize*numBlocks; %total number of samplesfM=fd/fs; %normalized doppler shiftNfM=fftSize*fM;kM=floor(NfM); %maximum freq of doppler filter in FFT samplesdoppFilter=[0,1./sqrt(2*sqrt(1-(((1:kM-1)./NfM).^2))),sqrt((kM/2)*((pi/2)-atan((kM-1)/sqrt(2*kM -1)))),...zeros(1,fftSize-2*kM-1),sqrt((kM/2)*((pi/2)-atan((kM-1)/sqrt(2*kM-1)))),1./sqrt(2*sqrt(1-(((kM-1:-1:1)./NfM).^2)))].';sigmaG=sqrt((2*2/(fftSize.^2))*sum(doppFilter.^2));gSamplesI=randn(numSamples,2); %i.i.d gaussian input samples (in phase)gSamplesQ=randn(numSamples,2); %i.i.d gaussian input samples (quadrature phase)gSamplesI=(1/sigmaG)*(gSamplesI(:,1)+1j*gSamplesI(:,2));gSamplesQ=(1/sigmaG)*(gSamplesQ(:,1)+1j*gSamplesQ(:,2));%filteringfilterSamples=kron(ones(numBlocks,1),doppFilter);gSamplesI=gSamplesI.*filterSamples;gSamplesQ=gSamplesQ.*filterSamples;freqSignal=gSamplesI-1j*gSamplesQ;freqSignal=reshape(freqSignal,fftSize,numBlocks); outSignal=ifft(freqSignal,fftSize);outSignal=abs(outSignal(:)); %Rayleigh distributed signal。

Rayleigh无线衰落信道的MATLAB仿真

通信原理课程设计汇报书课题名称Rayleigh 无线衰落信道的MATLAB 仿真姓名学号学院专业通信工程指导教师年月日※※※※※※※※※ ※※ ※※ ※※ ※※※※※※※※※通信工程专业通信原理课程设计Rayleigh无线衰落信道的MATLAB仿真1 设计目的〔1〕对瑞利信道的数学分析，得出瑞利信道的数学模型。

〔2〕利用MATLAB对瑞利无线衰落信道进行编程。

〔3〕针对服从瑞利分布的多径信道进行模拟仿真，加深对多径信道特性的了解。

〔4〕对仿真后的结果进行分析，得出瑞利无线衰落信道的特性。

2 设计思路无线衰落信道的MATLAB仿真：〔1〕分析出无线信道符合瑞利概率密度分布函数，写出数学表达式。

〔2〕建立多径衰落信道的根本模型。

〔3〕对符合瑞利信道的路径衰落进行分析，并利用MATLAB进行仿真。

3 设计过程3.1 方案论证3.1.1．瑞利信道环境与数学模型瑞利衰落信道〔Rayleigh fading channel〕是一种无线电信号传播环境的统计模型。

这种模型假设信号通过无线信道之后，其信号幅度是随机的，即“衰落〞，并且其包含服从瑞利分布。

瑞利衰落属于小尺寸的衰落效应，它总是叠加于如阴影、衰减等大尺度衰落效应上。

信道衰落的快慢与开展端和接收端的相对运动速度的大小有关，相对运动对导致接受信号的多普勒频移，一固定信号通过单径的瑞利衰落信道后，在1秒内的能量波动，这一瑞利衰落信道的多普勒频移最大分别为10Hz和100Hz，在GSM1800MHz的载波频率上，其相应的移动速度分别为约6千米每小时和60千米每小时。

特别需要注意的事信号“深衰落〞现象，此时信号能量的衰减到达数千倍，即30到40分贝。

瑞利衰落模型适用于描述建筑物密集的城镇中心地带的无线信道。

密集的建筑和其他物体使得无线设备的发射机和接收机之间没有直射路径，而且使得无线信号被衰减、反射、折射、衍射。

在曼哈顿的实验证明，当地的无线信道环境实在接近于瑞利衰落。

基于QAM调制的无线衰落信道的性能分析与仿真论文

*****************实践教学*****************兰州理工大学计算机与通信学院2013年秋季学期《通信系统综合训练》题目：基于QAM调制的无线衰落信道的性能分析与仿真专业班级：通信工程（1）班姓名：赵晓瑾学号：10250131指导教师：王惠琴成绩：摘要本次课程设计利用MATLAB软件对16QAM调制解调系统进行仿真,其中，信道采用瑞利衰落信道和高斯信道，调制方式为正交振幅调制方式，解调方式为相干解调方式。

并以此分析16QAM系统的信号经过的各个处理过程，由程序得到瑞利衰落信道下的系统误码率图，并与高斯信道下的误码率图进行对比。

矚慫润厲钐瘗睞枥庑赖。

关键词：16QAM;调制解调;瑞利信道;目录一、前言..................................................................................................................... 0聞創沟燴鐺險爱氇谴净。

二、16QAM调制解调系统基本原理............................................................................ 1残骛楼諍锩瀨濟溆塹籟。

2.1 调制及解调的相关概念............................................................................... 1酽锕极額閉镇桧猪訣锥。

2.2 16QAM调制系统.......................................................................................... 1彈贸摄尔霁毙攬砖卤庑。

2.2.1 16QAM系统的原理.......................................................................... 2謀荞抟箧飆鐸怼类蒋薔。

无线瑞利衰落信道建模

关键词：瑞利衰落；无线信道；仿真；ａｅＪｋｓ１信道建模研究的背景率谱Ｕ型分布。无线移动信道作为无线通信系统的重要组成部分，研究和开发的假设Ｅ和ｃ为实数，３式（可）首要工作就是要深＾理解无线信道本身的特ｌ考虑到风险和代价的因以表示为：生。素，前期方案设计通常采用仿真的方法模拟设计系统，因此需要建立信ｃｆ＝Ｃ（＋ｊ２（）１ｃ【道的仿真模型，进行信道仿真。其中：
Ｒ
ｃ）ｌ．Ｊ。ｌｃ。，，，２（（ｌ △△ ：）．＝ｘ
ｃ，，ｃ
，㈦
一
接收信号场强的统计挣于散射的，这正好与市区环境中无直视通将式（中Ｎ取有限值，４）并做一些变量替换，可化为：路的特点相吻合，因此广泛应用于市区环境的仿真中。０）（＋ｊ２）（＝ｆｃ（ｆ）ｆ（）６基站和移动台之间信号传播环境的主要特征是多径传播，即信号其中：（＝Ｅ∑ ｃ（ｒｏ目）ｅ）恕。０２ｆｔｃＱ＋ｒｓ￣ｓ并不仅仅来自一条直身路径，寸还包括由建筑物、树木等引起的反射、散射（ｆ）Ｅ∑ ｓ（ｆｔｓｇ）０ｉ￣ —ｃＯ＋ｎｒｏ２及绕射后的信号。由于电波通过各个路径的距离不同，反射波到达的时间也不同，相位就更不同。同相位的多个信号在接收端迭加，不同相迭加和ｑ，分别称作多普勒系数、？ｏ波到达角和多普勒相位。： — 五，，腰就加强，反相迭加就减弱。这样，接收信号的幅度将急剧变化，即产生了表示多普勒频率，在使用各种方法讨沦如何设计ｆ所有模型都可表ｆ时，１衰落。示为式（，６只是不同的模型对Ｃ）ｎ，的假设不同而已。和３平坦衰落信道模型的仿真模型现有的瑞利衰落信道仿真模型按ｃ和，是否随机变量，可分为４在现有的移动通信信道仿真模型中，大多数都是基于多个有色高大类：ａＣ和，目都是确定变量；斯随机过程来实现的。产生的方法主要有两类：一是滤波器成形法；二是基于正弦和理论来实现的。ｂＣ和是确定变量，．０都是随机变量；３．１正弦叠加法（ａｅ模型）Ｊｋｓｅ．ｃ是确定变量，，都是随机变量；ｄＣ和，都是随机变量；．ｎ由于正弦和理论是用有限个力权的正弦信号和来近似有色高斯过１１程，故式ｆ用）１）来近似均值为０方差为６的有色高斯过程０，。第（仿真模型中）１的多普勒系数，离散多普勒频率和多普勒相位为固定值，∽是时间ｔ的确定函数，故研究该类仿真模型的平／ｔ＝∑ ｃｃｓｒ．＋口）２）（ｏ（ｃｔ２ｆ（１）稳特陛和各态历经特性是没有任何意义的。然而我们可研究该类仿真模其中，Ｎ表示正弦波的数量，提多普勒系数，是离散多普勒频ｃ型的均值函数和自相关函数。由于（ｆ堤时间ｔ的确定函数，故这里的均率，是多普勒相位。０为了使可能接近（，ｆ必须使Ｎ））ｔ的概率密度值函数和自相关函数必须通过时间平均来得到。Ｃ和ｆ当ｎ为固定值时，函数和自相关函数与的概率密度函数和自相关函数尽可能吻合。式般认为它们为非０的固定值。（和式（别给出了，２）３盼（的概率密度函数和自相关函数。其中ｆ））的自相第２类仿真模型中的ｃ和ｆｎ为固定值，ｎ０为均匀分布于［２］０，的随关函数是使（）的多普勒功率谱符合Ｊｋｓａｅ功率谱而得到的。机变量。１一－寺）州（２）此类模型中（满足广义平稳特『和各态历经特ｌ。ｒ）生生当该类仿真模

matlab实现频域瑞利(Rayleigh)信道仿真

subplot(2,2,4)
plot(GaussN2);
title('频域复数高斯信号2');
xlabel('实部');
ylabel('虚部');
grid;
figure(5)
subplot(2,1,1)
plot(sqrt(SEf).*GaussN1);
title('高斯噪声与多普勒功率谱相乘1');
plot(Gauss_time2);
title('时域高斯信号2');
xlabel('N');
ylabel('V');
grid;
subplot(2,2,3)
plot(GaussN1);
title('频域复数高斯信号1');
xlabel('实部');
ylabel('虚部');
grid;
GaussN2=fft(Gauss_time2);
% 产生瑞利衰落信道
x = ifft(sqrt(SEf).*GaussN1);
y = ifft(sqrt(SEf).*GaussN2);
rayleigh_amp = sqrt(abs(x).^2+abs(y).^2);
rayleigh_db = 20*log10(rayleigh_amp); %用dB表示瑞利信号
figure(2);
plot(rayleigh_db);
% axis([0 140 -100 20]);
title('瑞利信号衰落');

matlab瑞利衰落信道仿真

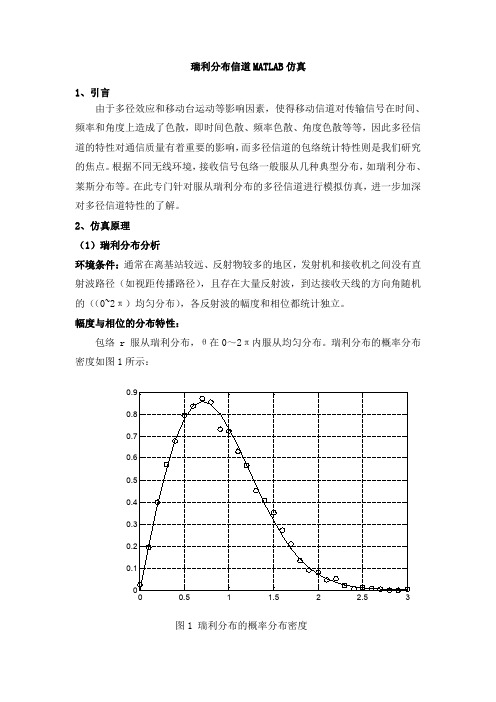
瑞利分布信道MATLAB仿真1、引言由于多径效应和移动台运动等影响因素，使得移动信道对传输信号在时间、频率和角度上造成了色散，即时间色散、频率色散、角度色散等等，因此多径信道的特性对通信质量有着重要的影响，而多径信道的包络统计特性则是我们研究的焦点。

根据不同无线环境，接收信号包络一般服从几种典型分布，如瑞利分布、莱斯分布等。

在此专门针对服从瑞利分布的多径信道进行模拟仿真，进一步加深对多径信道特性的了解。

2、仿真原理（1）瑞利分布分析环境条件：通常在离基站较远、反射物较多的地区，发射机和接收机之间没有直射波路径（如视距传播路径），且存在大量反射波，到达接收天线的方向角随机的（（0~2π）均匀分布），各反射波的幅度和相位都统计独立。

幅度与相位的分布特性：包络r服从瑞利分布，θ在0～2π内服从均匀分布。

瑞利分布的概率分布密度如图1所示：图1瑞利分布的概率分布密度（2）多径衰落信道基本模型离散多径衰落信道模型为()1()()()N t k k k yt r t x t τ==-∑ (1)其中,()k r t 复路径衰落，服从瑞利分布;k τ是多径时延。

多径衰落信道模型框图如图2所示：图2多径衰落信道模型框图（3）产生服从瑞利分布的路径衰落r(t)利用窄带高斯过程的特性，其振幅服从瑞利分布，即()r t =（2）上式中()()c s n t n t 、，分别为窄带高斯过程的同相和正交支路的基带信号。

3、仿真框架根据多径衰落信道模型（见图2），利用瑞利分布的路径衰落r(t)和多径延时参数k τ，我们可以得到多径信道的仿真框图，如图3所示；图3多径信道的仿真框图4、仿真结果（1）（1）多普勒滤波器的频响图4多普勒滤波器的频响（2）多普勒滤波器的统计特性图5多普勒滤波器的统计特性（3）信道的时域输入/输出波形图6信道的时域输入/输出波形5、仿真结果（2）（1）当终端移动速度为30km/h时，瑞利分布的包络如下图所示（2）当终端移动速度为100km/h时，瑞利分布的包络如下图所示三、仿真代码%main.mclc;LengthOfSignal=10240;%信号长度(最好大于两倍fc)fm=512;%最大多普勒频移fc=5120;%载波频率t=1:LengthOfSignal;%SignalInput=sin(t/100);SignalInput=sin(t/100)+cos(t/65);%信号输入delay=[03171109173251];power=[0-1-9-10-15-20];%dBy_in=[zeros(1,delay(6))SignalInput];%为时移补零y_out=zeros(1,LengthOfSignal);%用于信号输出for i=1:6Rayl;y_out=y_out+r.*y_in(delay(6)+1-delay(i):delay(6)+LengthOfSignal-delay (i))*10^(power(i)/20);end;figure(1);subplot(2,1,1);plot(SignalInput(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Input');subplot(2,1,2);plot(y_out(delay(6)+1:LengthOfSignal));%去除时延造成的空白信号title('Signal Output');figure(2);subplot(2,1,1);hist(r,256);title('Amplitude Distribution Of Rayleigh Signal')subplot(2,1,2);hist(angle(r0));title('Angle Distribution Of Rayleigh Signal');figure(3);plot(Sf1);title('The Frequency Response of Doppler Filter');%Rayl.mf=1:2*fm-1;%通频带长度y=0.5./((1-((f-fm)/fm).^2).^(1/2))/pi;%多普勒功率谱(基带)Sf=zeros(1,LengthOfSignal);Sf1=y;%多普勒滤波器的频响Sf(fc-fm+1:fc+fm-1)=y;%(把基带映射到载波频率)x1=randn(1,LengthOfSignal);x2=randn(1,LengthOfSignal);nc=ifft(fft(x1+i*x2).*sqrt(Sf));%同相分量x3=randn(1,LengthOfSignal);x4=randn(1,LengthOfSignal);ns=ifft(fft(x3+i*x4).*sqrt(Sf));%正交分量r0=(real(nc)+j*real(ns));%瑞利信号r=abs(r0);%瑞利信号幅值。

Rayleigh衰落信道的仿真模型_李子

文章编号:1009-3443(2004)02-0001-08Rayleigh 衰落信道的仿真模型李　子,　蔡跃明(解放军理工大学通信工程学院,江苏南京210007)摘　要:Rayleigh 衰落信道的仿真模型是许多信道仿真模型的基础。

用一个统一的表达式归纳和总结了各种Rayleigh 衰落信道仿真模型,根据表达式中参数的假设条件不同,将现有的仿真模型分为4类,分别讨论它们的均值、相关统计特性、平稳特性和各态历经特性。

通过对这些仿真模型的比较分析,可以看出,各态历经特性与相关特性的匹配是一对矛盾,不能同时满足。

在此基础上提出了一个高效的仿真模型应当满足的条件,这将有助于设计新的仿真模型。

关键词:信道模型;瑞利衰落;广义平稳;各态历经中图分类号:TN911.5文献标识码:ASimulation Models for R ayleigh Fading ChannelsL I Zi ,　CAI Yue -m ing(Instit ute o f Communications Engineering ,P L A U niv.of Sci.&T ech.,N anjing 210007,China)Abstract :Rayleigh fading channels are the fo unda tion of all cha nnel m odels.In this paper,sev eral kinds of the sim ula tion m odels of Rayleig h fading cha nnels by a uniform ex pression are sum mariv ed.Acco rding to the differences amo ng the a ssumed co ndition of the pa ram eters in the ex pression ,the simulatio n m odels fall into 4classes.Discussion is also made o f their m ean,cor relatio n,stationa ry and erg odicity.With the help of these discussio ns,it ca n be seen tha t the ergodicity and the fitting o f the sta tionary can 't exist simulta neously .Based on this ,some co nditio ns on an effectiv e channel m odel a re presented .And these conditions a re useful to desig n the new effectiv e channel m odels .Key words :channel m odel;Ray leigh fading;w ide-sense sta tio nary;ergodicity 收稿日期:2003-10-30.基金项目:江苏省自然科学基金资助项目(BK2003015).作者简介:李　子(1980-),男,硕士生. 无线通信系统的性能在很大程度上取决于无线信道。

实验二RICE信道模型仿真

实验二RICE信道模型仿真实验目的和要求1、学习移动通信系统信道概念；2、了解移动通信系统信道多径效应与瑞利分布；3、搭建RICE信道模型系统观察多径效应对移动通信性能的影响。

实验内容1、搭建RICE信道模型系统并完成调试。

2、绘制并分析各种情况下系统的BER曲线。

主要实验仪器与器材1.安装有System View软件的计算机实验指导多径效应多径效应移动体(如汽车)往来于建筑群与障碍物之间，其接收信号的强度，将由各直射波和反射波叠加合成。

多径效应会引起信号衰落。

各条路径的电长度会随时间而变化，故到达接收点的各分量场之间的相位关系也是随时间而变化的。

这些分量场的随机干涉，形成总的接收场的衰落。

各分量之间的相位关系对不同的频率是不同的。

因此，它们的干涉效果也因频率而异，这种特性称为频率选择性。

在宽带信号传输中，频率选择性可能表现明显，形成交调。

与此相应，由于不同路径有不同时延，同一时刻发出的信号因分别沿着不同路径而在接收点前后散开，而窄脉冲信号则前后重叠。

多径效应某些情况下满足瑞利分布。

瑞利分布一个均值为0，方差为σ2的平稳窄带高斯过程，其包络的一维分布是瑞利分布。

其表达式及概率密度如图所示。

瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。

两个正交高斯噪声信号之和的包络服从瑞利分布。

Rice衰落信道当多径扩展远远小于信号的符号周期时，衰落信道模型经常用于仿真通信系统在多径信道上的性能。

通常我们假设衰落过程相对于信号的符号速率要慢得多，因此我们可以精确地估计信号的相位。

所以我们只需考虑幅度衰落带来的影响，而不必关心相位的影响。

同时还假设符号间的衰落是相互独立的。

Rice衰落信道模型经常用于仿真一个因直射路径和多个散射路径共同产生的幅度衰落信道模型。

通常假设这些路径的延迟远远小于信号带宽的倒数，即延迟远小于符号宽度。

一个信号x(t)经过Rice信道后的输出y(t)可以表示为：这里z(t)是幅度衰落因式，它表示为：这里x1(t)和x2(t)是高斯随机变量N(0,σ),衰落信道的功率由以下条件归一化表示：A和σ的值由Rice衰落因子K决定。

基于Simulink的平坦瑞利衰落信道的建模与性能分析

基于Simulink的平坦瑞利衰落信道的建模与性能分析作者：陈凯曹海燕汤丽梅来源：《无线互联科技》2014年第05期摘要：该文利用Simulink建立了平坦瑞利衰落信道仿真模型，分别给出无信道编码和有信道编码两种情况下的建模仿真与性能。

信道编码采用卷积码，译码算法采用Viterbi译码。

仿真结果表明：在无信道编码情况下，由于深度衰落的影响，平坦瑞利衰落信道的误码性能与信噪比成线性关系，这与理论分析结果相一致。

而基于卷积码的平坦瑞利衰落信道的性能在高信噪比有明显改善，但低信噪比改善有限。

同时，仿真中给出不同的约束长度的卷积码，仿真表明卷积码的约束长度越长性能越好。

关键词：瑞利衰落信道；卷积码；维特比译码；误码性能在无线通信信道环境中，电磁波经过反射折射散射等多条路径传播到达接收机后，总信号的强度服从瑞利分布[1]。

同时由于接收机的移动及其他原因，信号强度和相位等特性又在起伏变化，这种无线电信号传播环境的统计模型称为瑞利衰落。

瑞利衰落能有效描述存在能够大量散射无线电信号的障碍物的无线传播环境。

若传播环境中存在足够多的散射，则冲激信号到达接收机后表现为大量统计独立的随机变量的叠加，根据中心极限定理，则这一无线信道的冲激响应将是一个高斯过程。

如果这一散射信道中不存在主要的信号分量，通常这一条件是指不存在直射信号（LoS），则这一过程的均值为0，且相位服从0到2π的均匀分布[2]。

即，信道响应的包络服从瑞利分布。

设随机变量R，于是其概率密度函数为：其中，。

其概率密度分布曲线如图1所示。

Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点。

基于以上优点，Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计[4]。

同时，有大量的第三方软件和硬件可应用于或被要求应用于Simulink。

瑞利衰落信道参数

瑞利衰落信道参数瑞利衰落是无线通信中常见的一种信道衰落模型，描述了信号在传输过程中遇到的衰落现象。

在无线通信中，信号在传输过程中会经历多次反射、散射和衍射等现象，导致信号强度的变化。

瑞利衰落信道参数是描述瑞利衰落特性的重要参数，对无线通信系统的设计和性能评估具有重要意义。

一、瑞利衰落信道参数的定义瑞利衰落信道参数包括衰落深度、衰落带宽和衰落速度三个方面。

1. 衰落深度（Fading Depth）：衰落深度是指信号在瑞利衰落信道中的幅度变化范围。

在瑞利衰落信道中，信号的幅度会随机地从强到弱或从弱到强变化，衰落深度是表示这种变化范围的参数。

2. 衰落带宽（Fading Bandwidth）：衰落带宽是指信号在瑞利衰落信道中的频率变化范围。

在瑞利衰落信道中，信号的频率会随机地从高频到低频或从低频到高频变化，衰落带宽是表示这种变化范围的参数。

3. 衰落速度（Fading Rate）：衰落速度是指信号在瑞利衰落信道中的变化速率。

在瑞利衰落信道中，信号的幅度和频率会随着时间的变化而变化，衰落速度是表示这种变化速率的参数。

二、瑞利衰落信道参数的影响因素瑞利衰落信道参数受到多种因素的影响，包括传输距离、传输环境、接收天线高度等。

1. 传输距离：传输距离是指信号从发送端到接收端的距离。

随着传输距离的增加，信号在传输过程中会经历更多的反射、散射和衍射现象，导致衰落深度增加，衰落带宽减小，衰落速度加快。

2. 传输环境：传输环境包括城市、农村、室内、室外等不同的环境条件。

不同的环境条件会导致信号的多径传播特性不同，进而影响瑞利衰落信道参数。

例如，在城市环境中，信号会经历更多的反射和散射，导致衰落深度增加，衰落带宽减小，衰落速度加快。

3. 接收天线高度：接收天线高度是指接收端天线距离地面的高度。

接收天线高度的增加会导致信号的多径传播路径增加，进一步影响瑞利衰落信道参数。

通常情况下，接收天线高度越高，瑞利衰落信道参数的变化范围越大。