自主设计实验8:最小生成树
课程设计-最小生成树
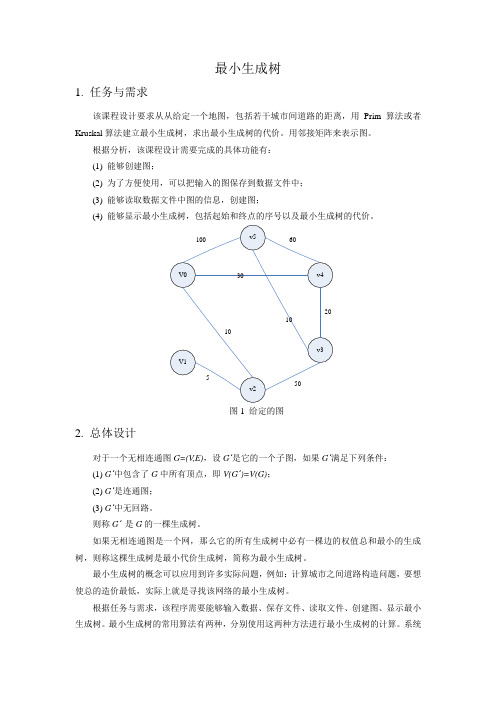
最小生成树1. 任务与需求该课程设计要求从从给定一个地图,包括若干城市间道路的距离,用Prim算法或者Kruskal算法建立最小生成树,求出最小生成树的代价。
用邻接矩阵来表示图。
根据分析,该课程设计需要完成的具体功能有:(1) 能够创建图;(2) 为了方便使用,可以把输入的图保存到数据文件中;(3) 能够读取数据文件中图的信息,创建图;(4) 能够显示最小生成树,包括起始和终点的序号以及最小生成树的代价。
图1 给定的图2. 总体设计对于一个无相连通图G=(V,E),设G’是它的一个子图,如果G’满足下列条件:(1) G’中包含了G中所有顶点,即V(G’)=V(G);(2) G’是连通图;(3) G’中无回路。
则称G’是G的一棵生成树。
如果无相连通图是一个网,那么它的所有生成树中必有一棵边的权值总和最小的生成树,则称这棵生成树是最小代价生成树,简称为最小生成树。
最小生成树的概念可以应用到许多实际问题,例如:计算城市之间道路构造问题,要想使总的造价最低,实际上就是寻找该网络的最小生成树。
根据任务与需求,该程序需要能够输入数据、保存文件、读取文件、创建图、显示最小生成树。
最小生成树的常用算法有两种,分别使用这两种方法进行最小生成树的计算。
系统功能模块如图:图2 系统功能模块图3. 详细设计3.1 最小生成树算法常见的两种构造最小生成树的算法是Prim算法和Kruskal算法。
1. Prim算法假设G=(V,E)为一网络,其中V为网络中的顶点集合,E为网络中的所有带权边集合。
设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,集合T存放G的最小生成树的边。
令集合U的初值为U={u0}(假设从u0出发),集合T的初值为T={}。
从所有u∈U,v∈V-U两个顶点构成的边中,选取具有最小权值的边(u,v),将顶点v加入集合U中,将边(u,v)加入集合T中。
如此不断重复,直到U=V时,最小生成树构造完毕,这时候集合T中包含了最小生成树的所有边。
最小生成树 实验报告

最小生成树实验报告最小生成树实验报告一、引言最小生成树是图论中的一个重要概念,它在实际问题中有着广泛的应用。
本次实验旨在通过编程实现最小生成树算法,并通过实验数据对算法进行分析和评估。
二、算法介绍最小生成树算法的目标是在给定的带权无向图中找到一棵生成树,使得树上所有边的权重之和最小。
本次实验我们选择了两种经典的最小生成树算法:Prim 算法和Kruskal算法。
1. Prim算法Prim算法是一种贪心算法,它从一个顶点开始,逐步扩展生成树的规模,直到包含所有顶点为止。
算法的具体步骤如下:(1)选择一个起始顶点,将其加入生成树中。
(2)从与生成树相邻的顶点中选择一个权重最小的边,将其加入生成树中。
(3)重复上述步骤,直到生成树包含所有顶点。
2. Kruskal算法Kruskal算法是一种基于并查集的贪心算法,它首先将图中的边按权重从小到大进行排序,然后逐个加入生成树中,直到生成树包含所有顶点为止。
算法的具体步骤如下:(1)将图中的边按权重从小到大进行排序。
(2)逐个加入边,如果该边的两个顶点不在同一个连通分量中,则将其加入生成树中。
(3)重复上述步骤,直到生成树包含所有顶点。
三、实验过程本次实验我们使用C++语言实现了Prim算法和Kruskal算法,并通过随机生成的图数据进行了测试。
1. Prim算法的实现我们首先使用邻接矩阵表示图的结构,然后利用优先队列来选择权重最小的边。
具体实现过程如下:(1)创建一个优先队列,用于存储生成树的候选边。
(2)选择一个起始顶点,将其加入生成树中。
(3)将与生成树相邻的顶点及其边加入优先队列。
(4)从优先队列中选择权重最小的边,将其加入生成树中,并更新优先队列。
(5)重复上述步骤,直到生成树包含所有顶点。
2. Kruskal算法的实现我们使用并查集来维护顶点之间的连通关系,通过排序后的边序列来逐个加入生成树中。
具体实现过程如下:(1)将图中的边按权重从小到大进行排序。
最小生成树 实验报告

最小生成树(Minimum Spanning Tree)实验报告1. 实验目的本实验旨在通过实践掌握最小生成树算法的基本原理和实现方法。
最小生成树是图论中的一个重要概念,用于解决具有权重的连通图的最优路径问题。
通过本实验,我们将学习如何使用最小生成树算法找到一棵连接图的所有节点且总权重最小的树。
2. 实验原理最小生成树是一个连通图的一种生成树,它的所有边的权重之和最小。
最小生成树的求解算法有多种,其中两种常用的算法是 Prim 算法和 Kruskal 算法。
2.1 Prim 算法Prim 算法是一种贪心算法,从一个节点开始,逐步扩展最小生成树的边。
具体步骤如下: 1. 选择一个起始节点作为最小生成树的根节点。
2. 在当前最小生成树的所有节点中选择一个与该树相连接的权重最小的边,将其加入最小生成树。
3. 将该节点标记为已访问。
4. 重复步骤 2 和步骤 3,直到所有节点都被访问。
2.2 Kruskal 算法Kruskal 算法也是一种贪心算法,通过不断选择权重最小的边来构建最小生成树。
具体步骤如下: 1. 对所有边按照权重进行排序。
2. 依次选择权重最小的边,如果该边的两个端点不在同一个连通分量中,则将该边加入最小生成树,并将这两个端点合并到同一个连通分量中。
3. 重复步骤 2,直到所有节点都在同一个连通分量中,即最小生成树构建完成。
3. 实验步骤本实验将使用 Prim 算法和 Kruskal 算法分别求解给定图的最小生成树。
3.1 数据准备首先,我们需要准备一个具有权重的连通图作为实验数据。
假设该图有 n 个节点和 m 条边,我们可以使用邻接矩阵或邻接表来表示这个图。
3.2 Prim 算法求解最小生成树1.首先,选择一个起始节点作为最小生成树的根节点,并将该节点标记为已访问。
2.初始化一个空的最小生成树,用于存储最终的结果。
3.重复以下步骤,直到所有节点都被访问:1.在当前最小生成树的所有节点中选择一个与该树相连接的权重最小的边,将其加入最小生成树。
写出最小生成树的构造过程

写出最小生成树的构造过程最小生成树(Minimum Spanning Tree,简称MST)是一个连通图上的生成树,它的边权重之和是所有可能生成树中最小的。
最小生成树在许多实际问题中有着广泛的应用,比如网络设计、电力输送、通信等领域。
下面我将为大家介绍最小生成树的构造过程。
一、Prim算法:Prim算法是一种贪心算法,它的基本思想是从一个顶点开始,逐渐扩展生成树,每一步选择一个与树相邻的权重最小的边,并将该边所指向的顶点加入树中。
具体的步骤如下:1.随机选择一个顶点作为起始点,将该顶点加入生成树。
2.在生成树中选择一个顶点v,寻找与v相邻的顶点中权重最小的边(u, v (u∈生成树,v∉生成树)),将该边加入生成树。
3.将顶点v加入生成树。
4.重复执行第2、3步,直到生成树中包含了所有的顶点。
在Prim算法中,我们需要用一个数组distance来记录各个顶点到生成树的最小距离(weight)。
在每一步中,通过更新distance数组的值,选择其中的最小值并将对应的顶点加入生成树。
二、Kruskal算法:Kruskal算法是一种基于边贪心策略的算法,其基本思想是将图中的所有边按照权重的非递减顺序排序,然后逐步加入生成树,直到生成树包含了所有的顶点。
具体的步骤如下:1.将图中的所有边按照权重的非递减顺序排序。
2.初始化一个空的生成树。
3.依次选择排好序的边,如果该边所连接的两个顶点不属于同一个连通分量,就将该边加入生成树。
如果加入该边之后,生成树中的边数等于顶点数减一,则结束算法。
4.重复执行第3步,直到生成树中的边数等于顶点数减一。
在Kruskal算法中,我们需要用一个数组parent来记录每个顶点所属的连通分量。
在每一步中,通过查找顶点的连通分量是否相同,判断是否可以加入生成树。
三、比较:Prim算法的时间复杂度为O(V^2),其中V为顶点数。
由于Prim算法需要维护一个数组distance,因此适用于稠密图,即顶点数较多的情况。
最小生成树算法实验报告

最小生成树算法实验报告【实验报告】最小生成树算法实验一、实验目的本次实验旨在研究最小生成树算法,通过对比不同的算法,并对实验结果进行分析,探索最小生成树算法的优劣势和适应场景。
二、实验过程1.算法介绍本次实验中我们将使用两种最小生成树算法:普里姆算法和克鲁斯卡尔算法。
- 普里姆算法(Prim算法):从一个顶点开始,不断在剩下的顶点中选择到当前已有的最小生成树的距离最小的边,将该边的另一个顶点加入树中,直到所有的顶点都加入树中。
- 克鲁斯卡尔算法(Kruskal算法):首先将所有边按照权值从小到大进行排序,然后以最小权值的边开始,依次选择权值最小且不会形成环路的边,直到找到n-1条边为止,其中n为顶点数。
2.实验步骤首先,我们使用Python语言实现了普里姆算法和克鲁斯卡尔算法。
然后,我们构造了一些测试用例,包括不同规模的图和不同权值分布的图。
最后,我们对实验结果进行对比分析。
三、实验结果1.测试用例设计我们设计了三个测试用例,分别为小规模图、中规模图和大规模图,具体如下:-小规模图:顶点数为5的图,权值随机分布。
-中规模图:顶点数为50的图,权值随机分布。
-大规模图:顶点数为100的图,权值随机分布。
2.实验结果分析我们的实验结果如下表所示:算法,小规模图,中规模图,大规模图:-------:,:------:,:------:,:------:普里姆算法,13,455,703从实验结果可以看出,对于小规模图和中规模图,普里姆算法的运行时间明显低于克鲁斯卡尔算法。
但是对于大规模图,克鲁斯卡尔算法的运行时间与普里姆算法的运行时间差距不大,甚至略小于普里姆算法。
这是因为克鲁斯卡尔算法中排序边的时间复杂度为O(ElogE),而普里姆算法中筛选最小距离的边的时间复杂度为O(V^2)。
综上所述,普里姆算法适用于较小规模的图,而克鲁斯卡尔算法适用于较大规模的图。
四、实验总结本次实验研究了最小生成树算法,通过对比实验结果,我们发现不同算法在不同规模的图上的表现有所差异。
最小生成树数据结构实验报告

摘要最小生成树是数据结构中图的一种重要应用,在图中对于n个顶点的连通网可以建立许多不同的生成树,最小生成树就是在所有生成树中总的权值最小的生成树。
本课程设计是以邻接矩阵作为图的存储结构,分别采用Prim和Kruskal算法求最小生成树。
Kruskal算法和Prim算法是求最小生成树的常用算法它们分别适用于稠密图和稀疏图。
最小生成树的应用非常的广,如矿井通风设计和改造最优化方面以及如何搭建最短的网络线缆, 构建造价最低的通讯网络等等一系列的应用。
关键词:最小生成树,邻接矩阵,Kruskal算法,Prim算法目录一、引言 (3)二、设计目的与任务 (4)2.1课程设计目的 (4)2.2课程设计的任务 (4)三、设计方案 (4)3.1需求分析 (4)3.2数据结构分析 (4)3.2.1抽象数据类型(ADT)如下 (4)3.2.2基本操作 (5)3.2.3存储结构 (5)3.3最小生成树的算法分析 (7)3.3.1主函数模块代码......................... 错误!未定义书签。
3.3.2邻接矩阵定义模块代码 (7)3.3.3创建链接矩阵模块代码 (7)3.3.4最小生成树Prim算法及代价模块代码...... 错误!未定义书签。
3.3.5最小生成树kruskal算法及代价模块代码 (8)四、调试分析与体会 (9)五、运行结果 (10)六、结论 (16)七、参考文献 (16)一、引言《数据结构》是计算机科学与技术专业和信息管理与信息系统专业的必修课之一,是一门综合性的专业基础课。
本课程较系统地介绍了软件设计中常用的数据结构以及相应的实现算法,如线性表、栈、队列、树和二叉树,图、检索和排序等,并对性能进行分析和比较,内容非常丰富。
本课程设计我们要解决的问题是图最小生成树问题。
要用到图的先相关数据结构和求最小生成树的两种数据结构算法普里姆算法和克鲁斯卡尔算法,以及储存图的边和点的邻接矩阵。
实验八 图的最小生成树

浙江大学城市学院实验报告课程名称数据结构与算法实验项目名称实验八图的最小生成树实验成绩指导老师(签名)日期1.一.实验目的和要求2.掌握图的最小生成树的概念。
3.掌握生成最小生成树的Prim算法(用邻接矩阵表示图)。
1、二.实验内容2、编写用邻接矩阵表示无向带权图时图的基本操作的实现函数, 主要包括:①初始化邻接矩阵表示的无向带权图 void InitMatrix(adjmatrix G); ②建立邻接矩阵表示的无向带权图 void CreateMatrix(adjmatrix G, int n) (即通过输入图的每条边建立图的邻接矩阵); ③输出邻接矩阵表示的无向带权图void PrintMatrix(adjmatrix G, int n) (即输出图的每条边)。
把邻接矩阵的结构定义以及这些基本操作实现函数存放在头文件Graph1.h 中。
3、编写生成最小生成树的Prim算法函数void Prim(adjmatrix G, edgset CT,int n)以及输出边集数组的函数void PrintEdge(edgeset CT, int n)。
编写测试程序(即主函数), 通过调用上述函数首先建立并输出无向带权图, 然后生成最小生成树并输出(即输出边集)。
要求: 把边集数组的结构定义、Prim算法函数、输出边集数组的函数PrintEdge 以及主函数存放在文件test8.cpp中。
测试数据如下:填写实验报告, 实验报告文件取名为report8.doc。
5.上传实验报告文件report8.doc与源程序文件test8.cpp及Graph1.h到Ftp服务器上自己的文件夹下。
三.函数的功能说明及算法思路函数: void InitMatrix(adjmatrix GA)功能: 初始化邻接矩阵表示的无向带权图函数: void CreateMatrix(adjmatrix GA,int n)功能: 建立邻接矩阵表示的无向带权图函数: void PrintMatrix(adjmatrix GA,int n)功能: 输出邻接矩阵表示的无向带权图函数: void Prim(adjmatrix GA,edgeset CT,int n)功能: 生成最小生成树思路:设从连通带权图G = { V, E }中的某一顶点u0 出发;选择与它关联的具有最小权值的边<u0, v>, 将其顶点加入到生成树的顶点集合U中;以后每一步从一个顶点在U中, 而另一个顶点在V-U中的各条边中选择权值最小的边<u, v>,把该顶点加入到集合U中;如此继续下去, 直到图中的所有顶点都加入到生成树顶点集合U中为止。
数据结构实验报告 最小生成树

实验报告六(数学学院08级4班080204015 余燕川)实验目的:通过对图的基本知识的学习, 掌握图的基本概念, 构造最小生成树, 在此基础上上机实践, 调试程序。
实验题目:对一个给定的图G(V, E), 构造最小生成树。
三、实验分析:1.假设网G(V, E)是连通的, 从顶点u出发构造G的最小生成树T, 开始时, 记T=(U, B), 其中U是T顶点集合, B是T的边集合;2、开始时U={u0 }( u0 ∈V)B=空,重复执行下述操作:在所有的u ∈U,V∈V-U组成的边(u,v)中找出一条权值最小的边(u0,v0)并入边集B中,同时将v0加入顶点集U,直到U=V为止, 此时T中必中必有n-1条边, 则T=(U, B)为G的最小生成树。
四、实验部骤:(1)构写程序的大体框架;(2)具体编写每个操作的程序;(3)程序的检查;(4)程序的调试;五、程序调试问题:输入顶点后, 边的信息输不进去;如下图:六、实验结果:输入顶点数为5, 边数为8, 顶点为v1,v2,v3,v4,v5;后面出现了问题。
七、实验程序:#define MAXSIZE 100#define max 10typedef char datatype;typedef struct{datatype vexs[MAXSIZE];int edges[MAXSIZE][MAXSIZE];int n,e;}graph;struct{char end;int len;}minedge[max];void Creatgraph(graph *ga){int i,j,k,w;printf("Please put the number of graph's vexs and edges:");scanf("%d,%d",&(ga->n),&(ga->e));printf("shu rui ding dian:\n");for(i=0;i<ga->n;i++)scanf("%2c\n",&(ga->vexs[i]));for(i=0;i<ga->n;i++)for(j=0;j<ga->n;j++)ga->edges[i][j]=100;for(k=0;k<ga->e;k++){printf("shu rui %d tiao bian de xu hao i,j and quan zhi w:",k+1);scanf("%d,%d,%d\n",&i,&j,&w);ga->edges[i][j]=w;ga->edges[j][i]=w;}}void prim(graph *g,char u){int v,k,j=0,min;for (v=1;v<=g->n;v++)if(v!=u){minedge[v].end=u;minedge[v].len=g->edges[v][u];}minedge[u].len=0;for(k=1;k<g->n;j++){min=minedge[k].len;v=j;}if(min==MAXSIZE){printf("error!");}printf("zui xiao sheng cheng shu:");printf("%d %d",v,minedge[v].end);minedge[v].len=-minedge[v].len; for(j=1;j<=g->n;j++)if(g->edges[j][v]<minedge[j].len) {minedge[j].len=g->edges[j][v]; minedge[j].end=v;}}void main(){int i,j;graph *g;g=(graph *)malloc(sizeof(graph)); Creatgraph(g);printf("Sheng cheng shu:\n"); prim(g,g->vexs[0]);}。
最小生成树实验报告

最小生成树实验报告最小生成树实验报告引言:最小生成树是图论中一个重要的概念,它在许多实际问题中都有广泛的应用。
本次实验旨在通过实际操作,深入理解最小生成树的概念、算法及其在实际问题中的应用。
本文将从实验的目的、实验过程、实验结果及分析等方面进行详细的论述。
实验目的:1. 理解最小生成树的概念及其在实际问题中的应用;2. 掌握最小生成树的两种常用算法:Prim算法和Kruskal算法;3. 通过实际操作,加深对最小生成树算法的理解。
实验过程:1. 实验环境的搭建:首先,我们需要在计算机上搭建一个图论实验环境。
选择一门编程语言,如Python,来实现最小生成树算法。
通过安装相应的开发环境和图论库,我们可以方便地进行实验。
2. 数据的准备:为了进行最小生成树的实验,我们需要准备一组具有权值的图数据。
可以通过手动输入或从文件中读取的方式获取数据。
确保数据的合理性和完整性,以便进行后续的实验操作。
3. Prim算法的实现:Prim算法是一种贪心算法,用于求解最小生成树。
在实验中,我们需要实现Prim算法,并将其应用于准备好的图数据上。
通过编程实现,我们可以得到Prim算法生成的最小生成树。
4. Kruskal算法的实现:Kruskal算法是另一种常用的最小生成树算法。
与Prim算法不同,Kruskal算法是一种基于边的贪心算法。
同样地,我们需要实现Kruskal算法,并将其应用于准备好的图数据上,以获得Kruskal算法生成的最小生成树。
实验结果与分析:通过实验,我们得到了Prim算法和Kruskal算法生成的最小生成树。
我们可以将这两个结果进行对比和分析,以进一步理解这两种算法的特点和应用场景。
首先,我们可以比较两个算法生成的最小生成树的权值。
通过计算权值的总和,我们可以确定哪个算法生成的最小生成树更优。
此外,我们还可以比较两个算法生成的最小生成树的结构,观察它们是否存在差异。
其次,我们可以分析两个算法的时间复杂度和空间复杂度。
最小生成树实验指导书.docx

实验1采用普里姆(prim)算法构造网络的最小生成树1、实验目的:深入理解最小生成树的概念,熟练掌握普里姆(prim)算法的工作过程,并通过定义合适的数据结构,釆用C语言程序实现。
2、实验内容:根据模板程序编制普里姆算法的程序,在计算机中进行调试,同时寻找两个结点大于6的网络,利用文件读入其邻接矩阵,运行程序。
记录运行结果,并把运行结果与手工生成的结果进行比较,验证程序的正解性。
要求从文本文件中读入网络的邻接矩阵。
3、实验原理①p rim算法的主要步骤②数据表示③算法实现细节4、实验步骤与实验结果①编写"im算法的C语言程序②输入计算机进行调试③准备两个顶点大于6的网络,把网络的邻接矩阵输入文本文件中,运行程序,记录程序的运行结果,根据结果画出最小生成树,并与手工生成的最小生成树进行比较。
实验结果:①画出网络图,写出相应的邻接矩阵②记录程序的运行结果,根据结果画出最小生成树并写出最小生成树的权值。
附录:程序模板#i nclude <std i o.h>/*定义一个结构体,用于记录一条边的始点与终点*/typedef struct pp{int p, q;} edge;i nt g [100] [100], u [100], v [100], vexnum;edge p[100] ;//用于记录最小生成树的各条边void input ()//读入图的邻接矩阵{i nt i, j, temp;FILE *fp;fp=fopen ("pp5. txt", " r");fscanf (fp,"%d",&vexnum);for (i=1;i<=vexnum;i++){printf(H\n n);for (j=1;j<=vexnum;j++){fscanf (fp, "%d", &temp);g[i] [jl=temp;pr i ntf (”%d ", temp);}}fclose (fp);}ma i n (){i nt i, j, k, m, n, ma, s=0;inputO;//输入数据for (ih ; iUvexnum; i++)//集合V中包含了所有顶点v[i]二 1 ;u[1]=1 ;v[1]=0;//第1个节点加入至集合U中,并从集合V中去掉for (i=1; i<=vexnum-1 ; i ++) //最多需vexnum-1 条边{〃以下找连接节点集U至节点集V的最小边ma=1000;//ma存放最小边的权值for (j=1;j<=i;j++)//集合U中的第j个节点,其编号为u[j],每次增加一个,共for (k=1;k<=vexnum;k++)/*v[k]!=0表示节点k在集合V中;g[u[j][k]>0表示有边*/ if(v[k] !=0&&ma>g[u[j]] [k]&&g[u[j]] [k]>0){ma二g[u[j]] [k] ;//保存最小边值m二u[j] ;//最小边的始点编号n二k;//最小边的终点编号}s=s+ma; // 求和u[i+1]=n;v[n]=0;//把找到最小边的终点编号从V中去掉,并加入至U中p[i]. p二m;p[i]. q二n;//保存最小边的始点编号与终点编号}printfC'\n H);for (i=1;i<=vexnum-1;i++)pr intf ("\n%d %d %d", p[i]. p, p[i]. q, g[p[i]. p] [p[i]. q]);printf("\nsum=%d\n\n",s);采用克鲁斯卡尔(kruskal)M法构造网络的最小生成树实验21、实验目的:深入理解最小生成树的概念,熟练掌握克鲁斯卡尔(kruskal)算法的工作过程,并通过定义合适的数据结构,采用C语言程序实现。
数据结构实验报告-最小生成树(精选5篇)

数据结构实验报告-最小生成树(精选5篇)第一篇:数据结构实验报告-最小生成树电子科技大学实验报告学生姓名:XXX 学号:20***指导教师:刘峤实验地点:信软楼306实验时间:5月17日一、实验室名称:软件实验室二、实验项目名称:数据结构与算法—图三、实验学时:4四、实验原理:Kruskal 算法是一种按照图中边的权值递增的顺序构造最小生成树的方法。
其基本思想是:设无向连通网为G=(V,E),令G 的最小生成树为T,其初态为T=(V,{}),即开始时,最小生成树T 由图G 中的n 个顶点构成,顶点之间没有一条边,这样T 中各顶点各自构成一个连通分量。
然后,按照边的权值由小到大的顺序,考察G 的边集E 中的各条边。
若被考察的边的两个顶点属于T 的两个不同的连通分量,则将此边作为最小生成树的边加入到T 中,同时把两个连通分量连接为一个连通分量;若被考察边的两个顶点属于同一个连通分量,则舍去此边,以免造成回路,如此下去,当T 中的连通分量个数为1 时,此连通分量便为G 的一棵最小生成树。
如教材153页的图4.21(a)所示,按照Kruskal 方法构造最小生成树的过程如图4.21 所示。
在构造过程中,按照网中边的权值由小到大的顺序,不断选取当前未被选取的边集中权值最小的边。
依据生成树的概念,n 个结点的生成树,有n-1 条边,故反复上述过程,直到选取了n-1 条边为止,就构成了一棵最小生成树。
五、实验目的:本实验通过实现最小生成树的算法,使学生理解图的数据结构存储表示,并能理解最小生成树Kruskal 算法。
通过练习,加强对算法的理解,提高编程能力。
六、实验内容:(1)假定每对顶点表示图的一条边,每条边对应一个权值;(2)输入每条边的顶点和权值;(3)输入每条边后,计算出最小生成树;(4)打印最小生成树边的顶点及权值。
七、实验器材(设备、元器件):八、数据结构及程序#include #include #include typedefstruct {intvex;intgno;}TVex,*TpVex;typedefstruct {intvhead, vtail;intwght;intflag;}TEdge,*TpEdge;typedef struct{TpVex VexList;TpEdge EdgeList;int nvex, nedge;}TGraph, *TpGraph;void begin(TpGraph G){ int i;for(i=1;i<=G->nvex;i++){G->VexList[i-1].gno=i;G->EdgeList[i-1].flag=0;} } int findmin(TpGraph G){ int i,j;int minwght=G->EdgeList[0].wght;for(i=0,j=-1;inedge;i++){ PC机一台,装有C/C++语言集成开发环境。
数据结构实验报告最小生成树

数据结构实验报告最小生成树实验目的:掌握最小生成树的概念和算法,培养分析和解决实际问题的能力。
实验内容:利用Kruskal算法求解带权无向连通图的最小生成树。
实验原理:最小生成树是指一个连通图的生成树,其中所有边的权值和最小。
最小生成树问题在图论中有着重要的应用,如网络设计、集成电路布线等领域。
本次实验使用Kruskal算法求解最小生成树。
Kruskal算法基于一个贪心的思想:每次选择权值最小的边,直到生成树中包含所有的节点。
具体算法如下:1.根据给定的连通图构造一个边的集合E,E中包含图中所有的边。
2.将E中的边按照权值从小到大排序。
3.依次遍历排序后的边,如果该边的两个节点不在同一个连通分量中,则选择该边,并将这两个节点合并到一个连通分量中。
4.重复第3步,直到生成树中包含所有的节点。
实验步骤及结果:1.根据给定的连通图构造边的集合E,并将E中的边按照权值从小到大排序。
2.初始化一个空的集合T作为最小生成树的边集合。
3.依次遍历排序后的边,如果该边的两个节点不在同一个连通分量中,则选择该边,并将这两个节点合并到一个连通分量中,同时将该边添加到集合T中。
4.重复第3步,直到生成树中包含所有的节点。
实验结果分析:通过Kruskal算法,可以得到带权无向连通图的最小生成树。
最小生成树具有多个优点,如能够保证连通、权值最小、无回路。
在实际应用中,最小生成树常常用于网络设计、集成电路布线等领域。
实验总结:通过本次实验,我掌握了最小生成树的概念和Kruskal算法的原理和实现方法。
实验中,我通过定义边的数据结构和构造边的集合,实现了Kruskal算法求解最小生成树。
通过实验,我深刻认识到数据结构在解决实际问题中的重要性和实用性。
最小生成树作为一种常用的图论算法,在实际应用中具有广泛的应用和重要的价值。
掌握了最小生成树的概念和算法,我相信能够在今后的学习和工作中更好地应用数据结构算法解决实际问题。
最小生成树实验报告

一、实验目的1. 通过上机程序,进一步加深对最小生成树的理解。
2. 掌握Kruskal算法。
3. 学会用程序解决离散数学中的问题。
4. 增强我们编写程序的能力。
二、实验内容求带权无向联通平面图的最小生成树三、实验环境我的实验依旧是在实验环境下完成的,而所设计的程序也在这个环境下通过了编译,运行和测试。
四、实验原理和实现过程利用Kruskal算法求最小生成树,原理如下:1.选取最小权边e1,置边数j 1.2.i=n-1结束,否则转c。
3.设已经选择的边为e1,e2,......,ei,在G中选取不同于e1,e2, (i)边,使{e1,e2,……,ei,ei+1}中无回路且ei+1是满足此条件的最小边。
4.i i+1,转b。
根据这个,还有以下思路:由G生成的最小生成树T所包含的边的集合1.按非降序权重将E中的边排序2.建立n个单元素集(每个顶点一个)3.最小生成树的边集合T初始为空4 .while |T|<n-15. 令e(x,y)为E中的下一条边6. if包含x的集合不是与包含y的集合不是同一个集合 then7. 将e(x,y)加入到T8. 将包含x的集合和包含y的集合合并9. end ifwhile五、实验源代码及分析#include<>struct Edge{int from, to, weight; rom); o);if(x!=y) rom, edge[k].to, edge[k].weight); rom, &edge[i].to, &edge[i].weight); eight>edge[j].weight){temp=edge[i];edge[i]=edge[j];edge[j]=temp;}printf("The minimum spanning tree is:\n");Kruskal(); //调用Kruskal算法return 0;}其中运用seek函数找出当前端点所在集合编号。
最小生成树构造过程

最小生成树构造过程嘿,朋友们!今天咱来唠唠最小生成树构造过程这个有意思的事儿。
你看啊,这最小生成树就像是搭积木,得找到最合适的那些“积木块”来搭出一个最稳固、最经济的结构。
想象一下,我们有好多好多的点和线,就像是一个复杂的迷宫。
那怎么开始呢?我们得从这些点和线里面找出最关键的那些。
这就好像你去超市买东西,得挑出性价比最高的商品一样。
我们从一个点开始,然后找和它相连的最短的那条边,这就是我们搭积木的第一块啦。
接着呢,我们再把这个边和它连接的点也算进来,继续找下一个最短的边。
这就好像是给我们的小结构添砖加瓦。
可不能随便找哦,得找最合适的,不然这“房子”可就盖歪啦!然后呢,一点一点地,我们把这些边都找出来,慢慢就搭成了一个完整的结构。
这过程中啊,有时候会有一些选择让人纠结,就好像你有两个都很喜欢的冰淇淋口味,不知道选哪个好。
但咱得坚定地选出那个最适合我们这个“小房子”的边呀。
比如说,有好几个边看起来都不错,长度都差不多,那可咋办呢?这时候就得靠咱的聪明才智啦,好好琢磨琢磨哪个对整个结构更有利。
这就跟你走迷宫一样,得选对路才能走到终点呀。
而且哦,这个过程中可不能马虎,要是一不小心选错了边,那可就麻烦啦。
就像盖房子,一块砖没放好,可能整座房子都不稳固了。
咱再想想,这最小生成树在生活中也有很多应用呢!比如规划交通路线,怎么让路线最短、最省钱;或者是网络布线,怎么让信号传输最顺畅、成本最低。
这可都是很实用的呀!哎呀,说了这么多,你们是不是对最小生成树构造过程有了更清楚的认识啦?总之呢,这就是一个很有趣、很有挑战性的事儿,就像一场刺激的冒险!希望你们也能在这个过程中找到乐趣,搭出属于你们自己的稳固“小房子”!。
最小生成树例题详解

最小生成树例题详解最小生成树(Minimum Spanning Tree,简称 MST)是一种图论中的算法,用于在一个加权连通图中找到一棵包含所有顶点且边权值之和最小的生成树。
下面是一个常见的最小生成树例题:给定一个由五只兔子和它们的家组成的奴隶图,如下图所示:```1 2 3 4 5/ / /6 7 8 9 10 11/ / /2 4 6 8 10 12```要求找到一棵包含所有顶点且边权值之和最小的生成树。
首先,我们需要遍历整个图,将每个节点的度数表示出来,度数等于该节点到其他节点的距离。
我们可以用度数最小的节点来代替这个节点。
接下来,我们需要计算每个节点到根节点的度数。
如果某个节点到根节点的度数大于等于它的度数,那么它就不是最小生成树的一部分,我们需要继续寻找。
最后,我们需要计算每个节点的边权值之和。
我们可以用度数最小的节点来代替这个节点,然后遍历该节点的邻居节点,计算它们的边权值之和。
以下是Python代码实现:```pythondef Minimum Spanning Tree(graph):# 遍历整个图,将每个节点的度数表示出来,度数最小为0for node in graph:度数 = [float(edge[node]) for edge ingraph.get_edges(node)]if度数[0] <= 0:return None# 找到最小生成树root = node = Nonefor node in graph.nodes():if root is None:if not any(edge[node] for edge in graph.get_edges(node)): root = nodebreakelse:# 度数最小的节点来代替该节点if not any(edge[node] for edge in graph.get_edges(node)): root = nodebreak# 计算该节点到根节点的度数度数 = [float(edge[node]) for edge ingraph.get_edges(node)]if度数[0] <= 0:return None# 找到连接到该节点的所有边neighbors = [node for edge in graph.get_edges(node) if edge[1] >= 0]# 计算该节点的边权值之和neighbors_sum = sum(度数)# 找到边权值之和最小的节点if neighbors_sum < neighbors_sum.min():root = nodebreakreturn root```在此算法中,我们使用了邻接表(neighbors table)来维护每个节点的邻居节点。
数据结构实验报告最小生成树参考模板

HUNAN UNIVERSITY 课程实习报告
题目:最小生成树
学生姓名:
学生学号:
专业班级:
指导老师:
完成日期:
一、需求分析
若要在n个城市之间建设通信网络,只需要架设n-1条线路即可。
如何以最低的经济代价建设这个通信网,是一个网的最小生成树问题
二、概要设计
抽象数据类型
用数组将边的距离及权值进行存储并排序。
算法的基本思想
构造生成树的网一定是无向网。
并设顶点数不超过30个,边权值为小于100的整数。
根据克鲁斯卡尔算法的特点,为便于选择选择权值小的边,存储结构不选用邻接矩阵和邻接表,而是可以用存储边(带权)的数组表示图。
程序的流程
程序由三个模块构成:
(1)从文件中读入图的信息。
(2)利用克鲁斯卡尔算法求网的最小生成树。
(3)以文本形式生成树中各条边以及他们的权值。
三、
四、详细设计
算法的具体步骤
先将用户的输入的顶点和边的数量,根据这些信息构建出图的结构,最后对边的权值进行排序。
输入和输出的格式
输入:
输入顶点和边的个数及顶点之间的权值。
输出:
输出最小生成树的序列。
五、测试结果
六、实验心得
实验的时候不是这个结果啊,可能是哪个环节出了错误,但是思想没有问题的,通过本次实验学会了用C++实现最小生成树。
友情提示:范文可能无法思考和涵盖全面,供参考!最好找专业人士起草或审核后使用,感谢您的下载!。
自主设计实验8:最小生成树

{
int g[max][max],n;
n=adjg(g);
printf("输入无向图的邻接矩阵:\n");
prg(g,n);
printf("最小生成树的构造:\n");
prim(g,n);
}
5、测试数据与实验结果
图5 测试数据及实验结果1
6、结果分析与实验体会
实验复习了图的存储方法和图的遍历方法,进一步掌握图的非线性特点,递归特性和动态特性,掌握最小生成树的求解算法。
在实验过程中,首先构建三个子程序分别为prim函数来实现最小树的生成,adjg函数来建立无向图, prg函数来输出无向图的邻接矩阵。
再建立主函数来调用三个子程序。
图是一种比树形结构更复杂的非线性结构。
在图形结构中,每个结点都可以有多个直接前驱何直接后继。
进一步掌握图的非线性特点、递归特点和动态特性。
掌握用prim函数来实现最小生成树的求解算法。
同时我充分了解到,程序的主要目的并不是多么的花哨,而是要让别人看的懂同时又便于计算机自身的运算和执行。
最小生成树问题的ampl实际案例

最小生成树问题的AMPL实际案例导言在图论中,最小生成树指的是在一个连接了所有节点的图中,找到一棵权重之和最小的树。
最小生成树问题被广泛应用于网络设计、电路布线、城市规划等领域。
AMPL(A Mathematical Programming Language)是一种用于数值分析和优化的高级建模语言。
本文将通过一个具体的案例,探讨如何使用AMPL解决最小生成树问题。
案例背景假设我们有一个城市网络,城市之间通过道路连接。
我们希望使用最小的成本来连接所有城市,以便人们可以在城市之间通行。
问题分析我们可以将城市网络表示为一个带权重的图,其中城市是节点,道路是边,道路的权重表示建造和维护道路的成本。
我们的目标是找到一个最小生成树,即在图中选择一些边,使得所有的城市都能够通过这些边连通,并且这些边的权重之和最小。
数学建模为了使用AMPL解决最小生成树问题,我们需要将问题建模成一个线性规划模型。
首先,我们定义一些变量: - x ij表示边(i,j)是否被选择,如果被选择则取值为1,否则取值为0。
- c ij表示边(i,j)的权重。
然后,我们需要定义一些约束条件: - 每个城市必须通过某条边连接到最小生成=1,其中j表示与城市i相连的边树中的其他城市。
对于每个城市i,我们有∑x ijj(i,j)。
- 最小生成树中不能形成环。
对于每个子集S,使得S中的城市通过(i,j)连≤|S|−1。
接到最小生成树中的其他城市,我们有∑x ij(i,j)⊆S最后,我们需要定义目标函数: - 目标函数是最小化边的权重之和。
我们有min∑c ijx ij。
i,jAMPL代码下面是用AMPL建模的代码:set Cities; # 定义城市集合param c{Cities, Cities} >= 0; # 定义边的权重矩阵var x{Cities, Cities} binary; # 是否选择边minimize Total_Cost: sum{i in Cities, j in Cities} c[i,j] * x[i,j];subject to Connectedness{i in Cities}:sum{j in Cities} x[i,j] = 1;subject to No_Cycles{S in subset(Cities)}:sum{(i,j) in (S cross S)} x[i,j] <= card(S) - 1;结果分析通过运行AMPL代码,我们可以得到最小生成树的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{
int g[max][max],n;
n=adjg(g);
printf("输入无向图的邻接矩阵:\n");
prg(g,n);
printf("最小生成树的构造:\n");
prim(g,n);
}
5、测试数据与实验结果
图5 测试数据及实验结果1
6、结果分析与实验体会
实验复习了图的存储方法和图的遍历方法,进一步掌握图的非线性特点,递归特性和动态特性,掌握最小生成树的求解算法。
在实验过程中,首先构建三个子程序分别为prim函数来实现最小树的生成,adjg函数来建立无向图, prg函数来输出无向图的邻接矩阵。
再建立主函数来调用三个子程序。
图是一种比树形结构更复杂的非线性结构。
在图形结构中,每个结点都可以有多个直接前驱何直接后继。
进一步掌握图的非线性特点、递归特点和动态特性。
掌握用prim函数来实现最小生成树的求解算法。
同时我充分了解到,程序的主要目的并不是多么的花哨,而是要让别人看的懂同时又便于计算机自身的运算和执行。
