九年级数学竞赛试题(无答案)

合集下载

九年级数学竞赛综合训练题(1)(含解答)-

九年级数学竞赛综合训练题(1)（满分120分，考试时间120分）学校班级姓名一、选择题:（每小题5分，共30分）1．过点P （-1，3）作直线，使它与两坐标轴围成的三角形面积为5，这样的直线可以作（）条（A ）4 （B ）3 （C ）2 （D ）1 2．方程13++x x －y=0的整数解有（）组（A ）1 （B ）2 （C ）3 （D ）4 3．如图，若将图（a ）的正方形剪成四块，恰能拼成图(b)的矩形，设a=1，则这个正方形的面积为（）（A ）2537+ （B ）253+（C ）251+ （D ）21(+)24．关于x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有5个整数解，则a 的取值范围是（）（A ）－6＜a ＜－211 （B ）－6≤a ＜－211 （C ）－6＜a ≤－211 （D ）－6≤a ≤－2115．已知四边形ABCD ，从下列条件：（1）AB ∥CD （2）BC ∥AD （3）AB ＝CD （4）BC ＝AD （5）∠A ＝∠C （6）∠B ＝∠D中任取其中两个，可以得出“四边形ABCD 是平行四边形”这一结论的情况有（）种（A ）4 （B ）9 （C ）13 （D ）15 6．已知x 、y 、z 都是实数，且x 2+y 2+z 2=1，则m=xy+yz+zx （）(A)只有最大值（B ）只有最小值（C ）既有最大值又有最小值（D ）既无最大值又无最小值二、填空题:（每小题5分，共30分）jab a b ⅠⅡⅢⅣⅣⅢⅡⅠ(b)(a)ba7．已知x=1313+-，y=1313-+, 则x 4+y 4等于 .8．甲、乙两商店某种铅笔标价都是1元，一天，让学生小王欲购这种铅笔，发现甲、乙两商店都让利优惠：甲店实行每买5枝送1枝（不足5枝不送）；乙店实行买4枝或4枝以上打8.5折，小王买了13枝这种铅笔，最少需要花元.9．若1≤p ≤20， 1≤q ≤10，且方程4x 2－px+q=0的两根均为奇数，则此方程的根为 . 10．在1、2、……，2003中有些正整数n ，使得x 2+x －n 能分解为两个整系数一次式的乘积，则这样的n 共有个.11．已知如图所示，∠MON=40°，P 为∠MON 内一点，A 为OM 上一点，B 为ON 上一点，则当△PAB 的周长取最小值时，∠APB 的度数为 .12．若关于x 的方程rx 2－(2r+7)x+r+7=0的根是正整数，则整数r 的值可以是 .三、解答题:（每小题15分，共60分）13．已知a 、b 、c满足方程组2848a b ab c +=⎧⎪⎨-+=⎪⎩, 试求方程bx 2+cx-a=0的根.PNMBOA14．已知两个二次函数y1 和y2，当x=a（a＞0）时，y1取得最大值5，且y2=25. 又y2的最小值为-2，y1+y2=x2+16x+13. 求a的值及二次函数y1、y2的解析式.15．如图所示，正方形ABCD的边长为1，点M、N分别在BC、CD上，使得△CMN的周长为2.求：（1）∠MAN的大小;（2）△MAN面积的最小值.ND CMAB16．如图所示，四边形ABCD 是矩形，甲、乙两人分别从A 、B 同时出发，沿矩形按逆时针方向前进，即按A →B →C →D →……顺序前进，已知甲的速度为每分钟65米，乙的速度为每分钟74米，问乙至少在跑第几圈时才有可能第一次追上甲？又乙至多在跑第几圈时一定能追上甲？请说明理由。

“学用杯”全国数学知识应用竞赛

第八届“学用杯”全国数学知识应用竞赛九年级初赛（B ）卷试题一、选择题（每小题6分，共30分）1．2008年8月1日，北京至天津最高时速高达350公里的城际高速铁路正式投入运行，大大缩短了北京至天津之间的交通出行时间，承载铁路运行的“和谐号”动车组装配工作的部分作业由机器人自动完成，这表明我国的机器人制作已经进入一个新的时代．现假设一工作流水线l 上，依次有a 、b 、c 、d 、e 五个性能相同的机器人在工作，如图1，机器人要从零件箱内取零件，若使机器人取零件时最省时间，零件箱需放在（）（A ）a 处（B ）b 、c 间（C ）c 处（D ）c 、d 间2．2008年我国南方发生重大雪灾，某村地处海拔1 020米，村里的电线断杆以及电杆倾斜多达23处，如图2所示就是一处电杆严重倾斜的情况，由于电线上缀满了冰，致使两个电杆都倾斜了26°，电线正好触及一棵高29.5米的大树，已知此树底部离右侧的电杆（电杆高40米，两杆之间距离为50米）20米远，那么此时，电线的最低处离地面约（）（A ）28.8米（B ）26.3米（C ）25.2米（D ）24.3米3．2008年5月12日，四川汶川发生里氏8.0级大地震，地震发生后，全国人民积极投入抗震救灾工作之中，图3为某军区空投物资用的某种降落伞及其轴截面示意图，△ABG 是等边三角形，C 、D 是以AB 为直径的半圆O 的两个三等分点，CG 、DG 分别交AB 于点E 、F ，现测得EO 的长为1.04m ，那么降落伞的直径AB 为（）（A ）6m （B ）6.24m （C）6.30m （D ）7.0m4．在一场赈灾演出中，根据需要必须用灯光照亮舞台中一个半径为2米的圆形区域，但由于当地条件简陋，当时没有这样的灯，舞台监督要求用另一种可照半径为1米的灯代替，那么至少需这样的代用灯（）（A ）5盏（B ）6盏（C ）7盏（D ）8盏5．2008年8月8日晚上8时，第29届奥运会开幕式在北京“鸟巢”举行，开幕式宏伟壮观，大气磅礴，给世人留下了深刻的印象，据悉，这部盛典的幕后工作者是中国航天人，他们使用了大量载人航天技术和火箭技术，给奥运场馆装上了“大脑”，实现“不同地域、不同场馆”的信息集成，以保证零失误，可想而知，其中的程序设计多么复杂．现在请同学们体会一个小小的程序设计．学校___________ 班级_____________ 姓名___________ 学号___________………………………………密…………封…………线…………内…………不…………得…………答…………题……………………如图4，若开始输入的x值为96，我们发现得到的结果为48，第2次得到的结果为24…，通过探索可知，第2 008次得到的结果为（）（A）8 （B）6 （C）3 （D）1二、填空题（每小题6分，共30分）6．数学家高斯在读小学二年级时，老师给出了这样一道题：1+2+3+…+100=？高斯很快做出了答案，他的计算方法是：1+2+3+…+100=（1+100）+（2+99）+（3+98）+…+（50+51）=50×101=5 050．根据此方法，试探究：有一堆堆放整齐的钢管其主（正）视图如图5所示，已知最下面一层有钢管50根，最上面一层有4根，则共有钢管根．7．《数书九章》中有一题目为：望故远近．内容如下：问敌军处北山下原，不知相去远近．乃于平地立一表（标杆），高四尺，人退表九百步（一步为五尺），遥望山原，适与表端参合（人目、标杆端和山脚三点共线）．人目高四尺八寸，欲知敌军相去几何（敌我之间的距离）．通过计算可知答案为：步．8．为了防止水土流失，合理利用和保护耕地，陈庄村在村里沙河两边植树造林，陈大叔栽植方式如图6（1），A、B、C、D组成菱形的形式，李伯伯的栽植方式如图6（2），A'、B'、C'、D'组成正方形的形式，你认为他们两位谁的栽植方式更好？．理由是：．9．图7（1）是某种台灯的示意图，AB可弯曲，根据测量，灯罩的截面△APQ是等腰直角三角形，此时很大一部分光照向远方而没有射在桌面上，若使AB绕转轴B顺时针转动θ，可使台灯的光更多地落在桌面上，如图7（2），现测得AC=30cm，且BC=2AB，灯心到桌面的距离A′M=25cm，则此时θ= ．若继续转动使AB与灯柱BC垂直，则此时台灯照在桌面上的最大面积为．10．某风景区山高AB为871.5米，为了游客的方便，景区设置了索道，如图8，索道路线为C→D→A，其中C是山脚，D是中转站．已知中转站D到山底的垂直高度为390.7米，∠ADE=37°，∠DCB=23°，缆车的速度为3.5米/秒，那么如果坐缆车上山，从山底到山顶大约需分钟．（精确到0.1分钟）三、解答题（第11、12、13题各15分，第14题20分，第15题25分，共90分）11．实践应用：2008年8月19日男子单杠决赛，第三个出场的是中国选手邹凯，他的一个直体360°抓杠非常的漂亮，最终得分是16.200分．第六个出场的是美国选手霍顿，霍顿的整套动作也非常漂亮，最终得分16.175分．以下是本次比赛前三名的成绩，请你根据下表分析选手最后得分是如何计算得出的？并举一例进行说明．12．动手操作：如图9，有一块矩形镀锌铁皮，长80cm ，宽30cm ．王师傅想把这块铁皮分割成6个矩形，把这6块铁皮作为6个面，焊接成一个长方体，如果不许添加材料，也不许浪费一点材料，该怎样分割呢？请你帮王师傅画出分割图形，并求出焊接成的长方体的体积．（至少提供两种方法）13．方案设计：某公司正在建厂房（平房），已知房檐离地面高4米，窗台高180厘米（窗高暂不考虑）．如果冬天太阳最低时，正午是31°，夏天太阳最高时，正午是78°，若你是一名建筑师，请你考虑房檐设计为多宽，才能正好在夏天使阳光进不了房子，而在冬天使阳光最大可能地照进屋里．写出你的方案并说明理由．14．实验探究：要把两直角边分别是30米和40米的Rt △ABC 菜地分成面积相等的两块，分给两菜农，且使分割线段尽量短．如图10，甲想到直角三角形斜边上中线可平分△ABC 的面积，于是作AB 边上的中线CD ，则ADC BDC S S =△△，此时1252CD AB ==（米）．乙认为CD 虽然平分△ABC 的面积，但不一定最短．问：（1）是否还有较短的分割线段满足题中的要求？写出你的方法与道理．（2）若将此Rt△ABC的菜地平均分给三户，使三户都能在河边AB上取水灌溉，又要使分割线段尽量的短，写出你的方法与道理．15．开放创新：一只乌鸦想喝到瓶子里的水，可是瓶子很高，口又小，里面的水也不多，怎么办？它把旁边的小石子一个又一个地衔起来，放到瓶子里，水面慢慢升高了，乌鸦喝到了水．这个故事同学们一定都知道，但对我们解数学题的有益启示却未必知道．如果题目所提供的信息少，难以入手，或按常规方法来解比较繁难，这时我们不妨向乌鸦学习，借些“石子”来帮我们解题．请看下面的例题：解析：此题对我们来说难度很大，好象无能为力，其实化简此式，可借方程为“石子”，设=．①x0，将①两边平方，得2222x=，即22x=．所以原式=在平时的学习中你是否用到过此方法来解决数学中的问题呢？请举一例．。

九年级第五届“睿达杯”初中数学能力竞赛一试试卷

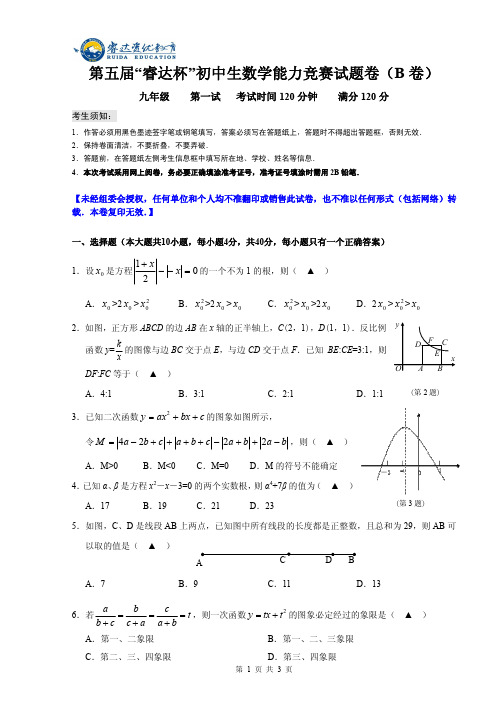
a b c t ，则一次函数 y tx t 2 的图象必定经过的象限是（ ▲ ） bc ca ab
B．第一、二、三象限 D．第三、四象限
第 1 页共 3 页
A．第一、二象限 C．第二、三、四象限
7．如图，平行四边形 ABCD 的面积为 1，点 E、F 分别是边 AB、BC 的中点，连 AF、CE 交于点 G，则四边形 AGCD 的面积 S四边形AGCD 等
第一试
考试时间 120 分钟
满分 120 分
【未经组委会授权，任何单位和个人均不准翻印或销售此试卷，也不准以任何形式（包括网络）转载．本卷复印无效．】一、选择题（本大题共10小题，每小题4分，共40分，每小题只有一个正确答案） 1．设 x0 是方程
1 x x 0 的一个不为 1 的根，则（ ▲ ） 2
x 3 y 3 38 17．（本题共 6 分）已知实数 x、y 满足条件求 xy 与 x 2 y 2 的值．， x y 2
已知立方和与立方差公式如下：
a 3 b 3 (a b )( a 2 ab b 2 ) ， a 3 b 3 (a b )( a 2 ab b 2 ) ．
第 3 页共 3 页
(第 3 题)
4．已知 α、 β 是方程 x2－x－3=0 的两个实数根，则 α4+7β 的值为（ ▲ A．17 B．19 C．21 D．23
5．如图，C、D 是线段 AB 上两点，已知图中所有线段的长度都是正整数，且总和为 29，则 AB 可以取的值是（ ▲ ） A A．7 6．若 B．9 C C．11 D B D．13
A
D F
C
G B
E
于（ A．

全国各地初中(九年级)数学竞赛《不等式》真题大全 (附答案)

全国初中（九年级））数学竞赛专题大全竞赛专题5 不等式一、单选题1．（2021·全国·九年级竞赛）若满足不等式871513n n k <<+的整数k 只有一个，则正整数n 的最大值为（）． A ．100B ．112C ．120D ．1502．（2021·全国·九年级竞赛）27234x x x ----有意义，则x 的取值范围是（）A ．4x >B ．7x ≥5x ≠C ．4x >且5x ≠D ．45x <<3．（2021·全国·九年级竞赛）某校初一运动队为了备战校运动会需要购置一批运动鞋．已知该运动队有20名同学，统计表如下表，由于不小心弄脏了统计表，下表中阴影部分的两个数据看不到．鞋码 38 394041 42 人数 532下列说法正确的是（）．A ．这组鞋码数据中的中位数是40，众数是39 B ．这组鞋码数据中的中位数与众数一定相等 C ．这组鞋码数据中的平均数p 满足3940p ≤≤ D ．以上说法都不对4．（2021·全国·九年级竞赛）如果不等式组9080x a x b -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的有序对(),a b 共有（）． A ．17个B ．64个C ．72个D ．81个5．（2021·全国·九年级竞赛）若不等式054ax ≤+≤的整数解是1，2，3，4，则a 的取值范围是（）． A ．54a -B ．1a <-C ．514a -≤<-D ．54a -6．（2021·全国·九年级竞赛）2009x y 且0x y <<，则满足此等式的不同整数对(,)x y 有（）对． A ．1B ．2C ．3D ．47．（2021·全国·九年级竞赛）有两个四位数，它们的差是534，它们平方数的末四位数相同．则较大的四位数有（）种可能．A ．1B ．2C ．3D ．48．（2021·全国·九年级竞赛）一个正方形纸片，用剪刀沿一条不过顶点的直线将其剪成两部分，拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分，又从得到的3部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分，……，如此下去，最后得到34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）． A ．2004B ．2005C ．2006D ．20079．（2021·全国·九年级竞赛）若正数a ，b ，c 满足不等式1126352351124c a b c a b c a b a c b ⎧<+<⎪⎪⎪<+<⎨⎪⎪<+<⎪⎩则a ，b ，c 的大小关系是（）A ．a b c <<B ．b c a <<C ．c a b <<D ．不确定10．（2021·全国·九年级竞赛）设114,,11(1)r a b c r r r r r r r ≥=-==++++的是（）． A ．a b c >> B ．b c a >> C ．c a b >> D ．c b a >>二、填空题11．（2021·全国·九年级竞赛）设a ，b 为正整数，且2537a b <<则b 取最小值时a b +=_____ 12．（2021·全国·九年级竞赛）已知实数x ，y 满足234x y -=且0,1x y ≥≤，则x y -的最大值是______，最小值是_______．13．（2021·全国·九年级竞赛）已知01a ≤≤，且满足122918303030a a a ⎡⎤⎡⎤⎡⎤++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ （[]x 表示不超过x 的最大整数），则[]10a 的值等于_______．14．（2021·全国·九年级竞赛）若化简2269x x x --+25x -，则满足条件是x 的取值围是_________．15．（2021·全国·九年级竞赛）[]x 表示不超过x 的最大整数（例如[]3.23=）．已知正整数n 小于2006，且362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦，则这样的n 有___________个． 16．（2021·全国·九年级竞赛）不等式2242x ax a +<的解是___________．17．（2021·全国·九年级竞赛）已知正整数m 和n 有大于1的最大公约数，并且满足3371m n +=，则mn =________．18．（2021·全国·九年级竞赛）长沙市某中学100名学生向某“希望学校”捐书1000本，其中任意10人捐书总数不超过190本，那么捐书最多的某同学最多能捐书_________本．19．（2021·全国·九年级竞赛）已知由小到大的10个正整数1210,,,a a a 的和是2000，那么5a 的最大值是_________，这时10a 的值应是_________．三、解答题20．（2021·全国·九年级竞赛）某宾馆底楼客房比二楼客房少5间，某旅游团有48人．若全部安排底楼，每间房间住4人，房间不够；每间住5人，则有房间没有住满5人．又若全部安排住2楼，每间住3人，房间不够；每间住4人，则有房间没有住满4人．问该宾馆底楼有多少间客房？21．（2021·全国·九年级竞赛）一座大楼有4部电梯，如果每部电梯可停靠三层（不一定连续三层，也不一定停最低层），对大楼中的任意两层，至少有一部电梯可在这两层停靠．问：这座大楼最多有几层22．（2021·全国·九年级竞赛）解方程22424x x x x ⎡⎤+-=⎢⎥⎣⎦．23．（2021·全国·九年级竞赛）证明：对任意实数x 及任意正整数n 有[][]121n x x x x nx n n n -⎡⎤⎡⎤⎡⎤+++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦．24．（2021·全国·九年级竞赛）已知01,01,01a b c <<<<<<，证明： ()()()1,1,1a b b c c a ---中至少有一个不大于14． 25．（2021·全国·九年级竞赛）设正数a ，b ，c ，x ，y ，x 满足a x b y c z k +=+=+=，证明；2ay bz cx k ++<． 26．（2021·全国·九年级竞赛）已知实数a ，b ，c 满足0,10a b c ac ++==，证明1110a b c++<．27．（2021·全国·九年级竞赛）下图是某单位职工年龄（取正整数）的频率分布图（每组可含最低年龄但不含最高值），根据图中提供的信息回答下列问题：（1）该厂共有多少职工?（2）年龄不小于38但小于44岁的职工人数占职工总人数的百分比是多少? （3）如果42岁的职工有4人，那么42岁以上的职工有多少人?（4）有人估计该单位职工的平均年龄在39岁与42岁之间，问这个估计正确吗?28．（2021·全国·九年级竞赛）某人到花店买花，他只有24元，打算买6支玫瑰和3支百合，但发现钱不够，只买了4支玫瑰和5支百合，这样还剩下2元多钱．请你算一算：2支玫瑰和3支百合哪个价格高？29．（2021·全国·九年级竞赛）1132x x -+ 30．（2021·全国·九年级竞赛）解不等式：2243414143x x x x x x x x +-->-++-- 31．（2021·全国·九年级竞赛）求满足下列条件的最小正整数n ，使得对这样的n ，有唯一的正整数k ，满足871513n n k <<+． 32．（2021·全国·九年级竞赛）解不等式： 2256154x x x x -+≤++．33．（2021·全国·九年级竞赛）解不等式21311x x x x -+>-+． 34．（2021·全国·九年级竞赛）如果二次不等式：28210ax ax ++<的解是71x -≤<-，求a 的值． 35．（2021·全国·九年级竞赛）某校参加全国数，理，化，计算机比赛的人数分别是20，16，x ，20人．已知这组数据的中位数和平均数相等，求这组数据的中位数．36．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6次、第7次，第8次，第9次射击中，分别得到9.0环、8.4环、8.1环、9.3环，他的前9次射击所得平均环数高于前5次射击所得平均环数，如果要使10次射击的平均环数超过8.8环，那么他第10次射击至少要得多少环?（每次射击环数精确到0.1环）37．（2021·全国·九年级竞赛）今有浓度为5%,8%,9%的甲、乙、丙三种盐水分别为60g,60g,47g ，现要配制成浓度为7%的盐水100g ．间甲盐水最多可用多少克?最少可用多少克?38．（2021·全国·九年级竞赛）求证：对任意的实数x ，y ，[2][2][][][]x y x x y y ++++．39．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6、第7、第8、第9次射击中，分别得了9.0环，8.4环，8.1环，9.3环，他的前9次射击所得环数的平均值高于前5次射击所得的平均环数．如果他要使10次射击的平均环数超过8.8环，那么他在第10次射击中最少要得多少环？（每次射击所得环数都精确到0.1环）40．（2021·全国·九年级竞赛）已知x ，y ，z 都是正数，证明：32()()()()()()x y x z y z y x z x z y +≤++++++．41．（2021·全国·九年级竞赛）某饮料厂生产A 、B 两种矿泉水，每天生产B 种矿泉水比A 种矿泉水多10吨，A 种矿泉水比B 种矿泉水每天多获利润2000元，其中A 种矿泉水每吨可获利润200元，B 种矿泉水每吨可获利润100元．（1）问：该厂每天生产A 种，B 种矿泉水各多少吨？（2）由于江水受到污染，市政府要求该厂每天必须多生产10吨矿泉水，该厂决定响应市政府的号召，在每天的利润不超过原利润的情况下不少于8000元，该厂每天生产A 种矿泉水最多多少吨？42．（2021·全国·九年级竞赛）要使不等式2320x x -+≤①与不等式2(1)(3)20m x m x -+--<②无公共解，求m 的取值范围．43．（2021·全国·九年级竞赛）已知三个非负数a ，b ，c ，满足325a b c ++=和231a b c +-=．若37m a b c =+-，求m 的最大值和最小值．44．（2021·全国·九年级竞赛）某班学生到公园进行活动，划船的有22人，乘电动车的有20人，乘过山车的有19人，既划船又乘电动车的有9人，既乘电动车又乘过山车的有6人，既划船又乘过山车的有8人，并且有4人没有参加上述3项活动中任何一项活动，问这个班学生人数的可能值是多少？竞赛专题5 不等式答案解析（竞赛真题强化训练）一、单选题1．（2021·全国·九年级竞赛）若满足不等式871513n n k <<+的整数k 只有一个，则正整数n 的最大值为（）． A ．100 B ．112C ．120D ．150【答案】B 【解析】【分析】【详解】由已知不等式得13156767,,787878n k k n nk n n +<<<<<<．因由已知条件，67n 与78n 之间只有唯一一个整数k ，所以76287n n-≤解得112n ≤．当112n =时，9698k ≤≤，存在唯一97k =，所以n 的最大值为112．故应选B ．2．（2021·全国·九年级竞赛）27234x x x ----有意义，则x 的取值范围是（）A ．4x >B ．7x ≥5x ≠C ．4x >且5x ≠D ．45x <<【答案】C 【解析】【分析】【详解】依题意得27077321544x x x x x x x x ⎧⎧-≥≤≥⎪⎪-≠⇒≠≠⎨⎨⎪⎪>>⎩⎩或且，4x ⇒>且5x ≠．故选C ．3．（2021·全国·九年级竞赛）某校初一运动队为了备战校运动会需要购置一批运动鞋．已知该运动队有20名同学，统计表如下表，由于不小心弄脏了统计表，下表中阴影部分的两个数据看不到．鞋码 38 39 40 41 42 人数 532下列说法正确的是（）．A ．这组鞋码数据中的中位数是40，众数是39 B ．这组鞋码数据中的中位数与众数一定相等 C ．这组鞋码数据中的平均数p 满足3940p ≤≤ D ．以上说法都不对【答案】C 【解析】【分析】【详解】设穿39码和40码的学生分别有x 人和y 人，则()2052310x y +=-++=．（1）若y x ≥，即穿40码的人数最多时，中位数和众数都等于40，故选A 错；（2）若5x y ==，则中位数1(3940)39.52=+=，众数为39和40，中位数不等于众数，故选B 错；（3）平均数[]13853940(10)41342239.75220xp x x =⨯++⨯-+⨯+⨯=-，且010x ≤≤，于是39.2539.75p <≤，满足3940p ≤≤，故选C 正确．所以应选C ．4．（2021·全国·九年级竞赛）如果不等式组9080x a x b -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的有序对(),a b 共有（）． A ．17个 B ．64个 C ．72个 D ．81个【答案】C 【解析】【分析】【详解】解因98ax b x ⎧≥⎪⎪⎨⎪<⎪⎩中x 的整数值仅为1，2，3，所以01,34,98a b <≤<≤即9a <≤， 2432b <≤，故a 可取1，2，…，9这9个值，b 可取25，26，…．32这8个值，所以有序对(),a b 有8972⨯=个．故选C ．5．（2021·全国·九年级竞赛）若不等式054ax ≤+≤的整数解是1，2，3，4，则a 的取值范围是（）． A ．54a -B ．1a <-C ．514a -≤<-D ．54a -【答案】C 【解析】【分析】【详解】解由054ax ≤+≤得51ax -≤≤-，且已知0x >，所以0a <，15ax a ≤-≤-．又不等式054ax ≤+≤的整数解是1，2，3，4，所以101a <-≤，且545a≤-<解得 1a ≤-且5114a -<-≤，故514a -≤<-，所以选C ．6．（2021·全国·九年级竞赛）2009x y 且0x y <<，则满足此等式的不同整数对(,)x y 有（）对． A ．1 B ．2 C ．3 D ．4【答案】C 【解析】【分析】【详解】选C ．理由：由20094941=⨯，得200941= 又0x y <<2009200941641241541341441===20094114761641025369656===因此，满足条件的整数对(,)x y 为(41,1476),(164,1025),(369,656)．共有3对．7．（2021·全国·九年级竞赛）有两个四位数，它们的差是534，它们平方数的末四位数相同．则较大的四位数有（）种可能． A ．1 B ．2C ．3D ．4【答案】C 【解析】【分析】【详解】理由：设较大的四位数为x ，较小的四位数为y ，则534x y -=， ① 且22x y -能被10000整除．而22()()x y x y x y -=+-2672()x y =⨯+，则x y +能被5000整除．令()5000x y k k ++=∈N ． ②由式①②解得2500267,2500267.x k y k =+⎧⎨=-⎩ 考虑到x ，y 均为四位数，于是，100025002679999,100025002679999,k k ≤+≤⎧⎨≤-≤⎩解得126755832500625k ≤≤． k 可取1，2或3．从而，x 可取的值有3个：2767，5267，7767．8．（2021·全国·九年级竞赛）一个正方形纸片，用剪刀沿一条不过顶点的直线将其剪成两部分，拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分，又从得到的3部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分，……，如此下去，最后得到34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）． A ．2004 B ．2005C ．2006D ．2007【答案】B 【解析】【分析】【详解】解（算两次方法）依题意，用剪刀沿不过顶点的直线剪成两部分时，所得各张多边形（包括三角形）的纸片的内角和增加了2180360⨯︒=︒，剪过k 刀后，可得(1)+k 个多边形，这些多边形的内角总和为360360(1)360k k ︒+⨯︒=+⨯︒．另一方面，因为这1k +个多边形中有34个为六十二边形，它们的内角总和为34(622)1802040180⨯-⨯=⨯︒︒，余下的多边形（包括三角形）有13433k k +-=-个，其内角总和至少为(33)180k -⨯︒，于是(1)3602040180(33)180k k +⨯︒≥⨯︒+-⨯︒，解得2005k ≥．其次，我们按如下方式剪2005刀时，可得到符合条件的结论．先从正方形剪下1个三角形和1个五边形，再将五边形剪成1个三角形和1个六边形，…，如此下去，剪了58刀后，得到1个六十二边形和58个三角形，取出其中33个三角形，每个各剪一刀，又可得到33个四边形和33个三角形，对这33个四边形，按上述方法各剪58刀，便得到33个六十二边形和3358⨯个三角形，于是共剪了583333582005++⨯=（刀），故选B ．9．（2021·全国·九年级竞赛）若正数a ，b ，c 满足不等式1126352351124c a b c a b c a b a c b ⎧<+<⎪⎪⎪<+<⎨⎪⎪<+<⎪⎩则a ，b ，c 的大小关系是（）A ．a b c <<B ．b c a <<C ．c a b <<D ．不确定【答案】B 【解析】【分析】【详解】解由已知条件及加法的单调性得1126352251124c c a b c c c a a a b c a a b b a b c b b ⎧+<++<+⎪⎪⎪+<++<+⎨⎪⎪+<++<+⎪⎩，即1736582371524c a b c c a a b c a b a b c b ⎧<++<⎪⎪⎪<++<⎨⎪⎪<++<⎪⎩①②③由①，②得17816176366c a b c a a a <++<=< （传递性），所以a c >．由①，③得7673222b a bc c c c <++<=< （传递性），所以b c <．可见，a ，b ，c 的大小关系是a c b >>，故选B ． 10．（2021·全国·九年级竞赛）设114,,11(1)r a b c r r r r r r r ≥=-==++++的是（）． A ．a b c >> B ．b c a >>C ．c a b >>D ．c b a >>【答案】D 【解析】【分析】【详解】解：因111221r r r ≥<+=+，故 ()(111a b r r r r r r =+<=+++， 1111r r r r c b r r r x +-+->=+⋅+．所以c b a >>．故选：D ．二、填空题11．（2021·全国·九年级竞赛）设a ，b 为正整数，且2537a b <<则b 取最小值时a b +=_____ 【答案】17 【解析】【分析】【详解】由已知条件得32,57a b b a >>．令32,57A a b B b a =-=-，则A ，B 均为正整数，解出52,737310a A B b A B =+=+≥+=．当1,1A B ==时等号成立，故b 的最小值为10，这时527a =+=，17a b +=．故应填17．12．（2021·全国·九年级竞赛）已知实数x ，y 满足234x y -=且0,1x y ≥≤，则x y -的最大值是______，最小值是_______．【答案】 4352【解析】【分析】【详解】 434370222y x ++≤=≤=．又243x y -=所以24433x x x y x -+-=-=．故当0x =时，x y -取最小值43；当72x =时，x y -取最大值175(4)322+=所以应填45,32．13．（2021·全国·九年级竞赛）已知01a ≤≤，且满足122918303030a a a ⎡⎤⎡⎤⎡⎤++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ （[]x 表示不超过x 的最大整数），则[]10a 的值等于_______．【答案】6 【解析】【分析】【详解】因122902303030a a a <+<+<<+<，所以1229,,,303030a a a ⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦每一个等于0或1．由题设知其中恰有18个等于1，所以12111213290,1303030303030a a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+==+=+=+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦于是111201,123030a a <+<≤+<，解得1183019,61063a a ≤<≤<所以[]106a =．故应填6． 14．（2021·全国·九年级竞赛）若化简2269x x x --+25x -，则满足条件是x 的取值围是_________．【答案】23x ≤≤ 【解析】【分析】【详解】由()2226923232(3)25x x x x x x x x x x --+=--=---=---=-，得2030x x -≥⎧⎨-≤⎩即23x ≤≤．故填23x ≤≤．15．（2021·全国·九年级竞赛）[]x 表示不超过x 的最大整数（例如[]3.23=）．已知正整数n 小于2006，且362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦，则这样的n 有___________个．【答案】334 【解析】【分析】【详解】解设[]6n m =则(01)6na a m =≤+<从而66n m a =+．当102a ≤<时， 22(021)3n m a a =+≤<，故23n m ⎡⎤=⎢⎥⎣⎦．于是由362n n n⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦得662332m a m m m a ++==+，从而0a =．此时(6204)06133n m m =<≤≤．当112a ≤<，223n m a =+由212222m m a m +≤+<+得213n m ⎡⎤=+⎢⎥⎣⎦代入 362n n n ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦得2133m m m a ++=+，得13a =，与112a ≤<矛盾，舍去．故所有的n 共有334个．16．（2021·全国·九年级竞赛）不等式2242x ax a +<的解是___________．【答案】67a a x -<<（当0a >时）；76a ax <<-（当0a <时）；无解（当0a =时）．【解析】【分析】【详解】解原不等式化为()()670x a x a +-<，方程()()670x a x a +-=的两根为6a -和7a．若0a >，则67a a -<不等式的解为67a ax -<<；若0a <，则76a a <-不等式的解为76a a x <<-；若0a =，则67a a-=，不等式无解．故应填：67a a x -<< （当0a >时）; 76a ax <<-（当0a <时）;无解（当0a =时）． 17．（2021·全国·九年级竞赛）已知正整数m 和n 有大于1的最大公约数，并且满足3371m n +=，则mn =________．【答案】196 【解析】【分析】【详解】理由：设k 是m ，n 的最大公约数，则m 和n 可以表示为,m ka n kb ==（1k >，a ，b 均为正整数）．于是，()3323()371753m n ka kb k k a b +=+=+==⨯．因为1k >且7与53都是质数，23232k a b k a k k +>≥>，所以7k =且2353k a b +=，即34953a b ⨯+=．由a ，b 是正整数，得1,4a b ==．所以7,28m n ==．故728196mn =⨯=．18．（2021·全国·九年级竞赛）长沙市某中学100名学生向某“希望学校”捐书1000本，其中任意10人捐书总数不超过190本，那么捐书最多的某同学最多能捐书_________本．【答案】109 【解析】【分析】【详解】设100名学生捐书数分别是12100,,,a a a ，不妨设其中100a 为最大，于是100101000a +=()129100a a a a +++++()101118100a a a a ++++()192027100a a a a +++++(91a +++)9299100a a a +++190190190≤+++111902090=⨯=，所以100109a ≤．另一方面，当12999a a a ====，100109a =时，满足题目要求，故捐书最多的人最多能捐书109本．19．（2021·全国·九年级竞赛）已知由小到大的10个正整数1210,,,a a a 的和是2000，那么5a 的最大值是_________，这时10a 的值应是_________．【答案】 329 335或334 【解析】【分析】【详解】要使10a 最大，必须1a ，2a ，3a ，4a 及6a ，7a ，8a ，9a ，10a 尽量小．又因为1210a a a <<<，且1a ，2a ，3a ，4a 的最小可能值依次为1，2，3，4，于是有2000123≥+++56104a a a ++++，即56101990a a a +++≤．又651a a ≥+，752a a ≥+，853a a ≥+，954a a ≥+，1055a a ≥+，故51990615a ≥+，51975132966a ≤=．又5a 为正整数，所以5329a ≤，于是6710a a a +++=199********-=．又761a a ≥+，862a a ≥+，963a a ≥+，1064a a ≥+，故65101661a +≤，616515a ≤=13305，且6a 为正整数，所以6330a ≤，而651330a a ≥+=，所以6330a =，要7a ，8a ，9a 最小得7331a =，8332a =，9333a =，这时101661a =-()6789335a a a a +++=．但如果取1a ，2a ，3a ，4a 依次为1，2，3，5，那么同样可得569,,,a a a 取上述值，这时10334a =．故应填5a 的最大值是329，这时10a 的值应是335或334．三、解答题20．（2021·全国·九年级竞赛）某宾馆底楼客房比二楼客房少5间，某旅游团有48人．若全部安排底楼，每间房间住4人，房间不够；每间住5人，则有房间没有住满5人．又若全部安排住2楼，每间住3人，房间不够；每间住4人，则有房间没有住满4人．问该宾馆底楼有多少间客房？【答案】宾馆的底楼有客房10间【解析】【分析】【详解】设底楼有x 间客房，则2楼有()5+x 间客房．简4485483(5)484(5)48x x x x <⎧⎪>⎪⎨+<⎪⎪+>⎩依题意可得不等式组解不等式组得9.611x <<．又x 为正整数，所以10x =．答：宾馆的底楼有客房10间．21．（2021·全国·九年级竞赛）一座大楼有4部电梯，如果每部电梯可停靠三层（不一定连续三层，也不一定停最低层），对大楼中的任意两层，至少有一部电梯可在这两层停靠．问：这座大楼最多有几层? 【答案】这座大楼最多有5层【解析】【分析】【详解】设大楼有n 层，则楼层对的个数为(1)2n n -每架电梯停3层，有3232⨯=个楼层对，所以(1)43,(1)242n n n n -⨯≥-≤，且n 为正整数，所以5n ≤．设置4部电梯使它们停靠的楼层分别为 ()()()()1,4,5,2,4,5,3,4,5,1,2,3满足题目要求，故这座大楼最多有5层．22．（2021·全国·九年级竞赛）解方程22424x x x x ⎡⎤+-=⎢⎥⎣⎦．【答案】4x =-或45【解析】【分析】【详解】原方程中显然0x ≠，故原方程可化为2241()2x x ⎡⎤+-=⎢⎥⎣⎦．又2222221()21()2()1x x x ⎡⎤⎡⎤⎡⎤+-=+-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，故原方程可化为224[()]1x x=+，所以4x 为整数，设4n x =（n 为整数），原方程又化为2[]14n n =+．于是2124n n n +≤<+，即222(12)2(12)440,2(13)2(12)4802(13)2(13)n n n n n n n n ⎧≤≥+⎧--≥⎪⇒≤≤⎨⎨--<<<⎩⎪⎩或或．2(12)2(13n <<）．又n 为整数，所以1n =-或5n =，故4x =-或4523．（2021·全国·九年级竞赛）证明：对任意实数x 及任意正整数n 有[][]121n x x x x nx n n n -⎡⎤⎡⎤⎡⎤+++++++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦．【答案】见解析【解析】【分析】【详解】设[]x x α=-，则01a ≤≤，于是存在小于n 的正整数r ，使1r rn nα-≤<故[][]1r rx x x n n-+<<+，故当0k n r ≤≤-时，[][][][]11r k r n rx x x x x n n n n--≤+≤+<++=-，故[](0)k x x k n r n ⎡⎤+=≤≤-⎢⎥⎣⎦当11n r k n -+≤≤-时，[][][][][]1111111r n r k r n r x x x x x x n n n n n n--+--+=++≤+<++=++<+，故[]1(11)k x x n r k n n ⎡⎤+=+-+≤≤-⎢⎥⎣⎦，于是[]1111[]()(n n r n r x x x x x x x n n n n n ---+⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+++++=++++++++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦[][]21)(1)(1)(1)[]1n r n x x n r x r x n x r n n -+-⎡⎤⎡⎤++++=-++-+=+-⎢⎥⎢⎥⎣⎦⎣⎦①．又因为[][]1n x r nx n x r +-≤≤+，所以[][]1nx n x r =+-②．由①及②便知要证等式成立．24．（2021·全国·九年级竞赛）已知01,01,01a b c <<<<<<，证明： ()()()1,1,1a b b c c a ---中至少有一个不大于14．【答案】见解析【解析】【分析】【详解】 (1)1(1)22a a a a +--≤=11(1)(1)22b bc c --≤三式平方后相乘得 31(1)(1)(1)()4a b b c c a -⋅-⋅-≤故()()()1,1,1a b b c c a ---中至少有一个不大于14．25．（2021·全国·九年级竞赛）设正数a ，b ，c ，x ，y ，x 满足a x b y c z k +=+=+=，证明； 2ay bz cx k ++<．【答案】见解析【解析】【分析】【详解】因3()()()()()()k a x b y c z abc xyz ay c z bz a x cx b y =+++=+++++++()()abc xyz k ay bz cx k ay bx cx =++++>++．又0k >，所以2ay bz cx k ++<．26．（2021·全国·九年级竞赛）已知实数a ，b ，c 满足0,10a b c ac ++==，证明1110a b c++<．【答案】见解析【解析】【分析】【详解】因10abc =，故a ，b ，c 都不为零．又2222()2()0a b c a b c ab bc ca ++=+++++=且2220a b c ++>，所以0ab bc ca ++<，于是1110bc ca ab a b c abc++++=<． 27．（2021·全国·九年级竞赛）下图是某单位职工年龄（取正整数）的频率分布图（每组可含最低年龄但不含最高值），根据图中提供的信息回答下列问题：（1）该厂共有多少职工?（2）年龄不小于38但小于44岁的职工人数占职工总人数的百分比是多少? （3）如果42岁的职工有4人，那么42岁以上的职工有多少人?（4）有人估计该单位职工的平均年龄在39岁与42岁之间，问这个估计正确吗? 【答案】（1）50；（2）60%；（3）15人；（4）正确【解析】【分析】【详解】（1）职工人数47911106350=++++++=；（2）年龄不小于38但小于44岁职工人数占职工总数的百分比为91110100%60%50++⨯=；（3）年龄在42岁以上职工人数()1063415=++-=（人）；（4）设该厂职工的年龄平均值为n ，则11(34436738940114210446463)199239.84395050n ≥⨯+⨯+⨯+⨯+⨯+⨯+⨯=⨯=>且11(36438740942114410466483)209241.84425050n <⨯+⨯+⨯+⨯+⨯+⨯+⨯=⨯=<，故所作的估计是正确的．28．（2021·全国·九年级竞赛）某人到花店买花，他只有24元，打算买6支玫瑰和3支百合，但发现钱不够，只买了4支玫瑰和5支百合，这样还剩下2元多钱．请你算一算：2支玫瑰和3支百合哪个价格高？【答案】2支玫瑰的价格高于3支百合的价格．【解析】【分析】【详解】解设玫瑰每支x 元，百合每支y 元，依题意得632445242x y x y +>⎧⎨+=-⎩①② 32⨯-⨯②①得918y <，故2y <． 53⨯-⨯①②得1854x >，故3x >．答：2支玫瑰的价格高于3支百合的价格．29．（2021·全国·九年级竞赛）1132x x -+ 【答案】8313x ---≤≤【解析】【分析】【详解】解首先，由1030x x -≥⎧⎨+≥⎩得31x -≤≤．1132x x -≥+① 数上式两边均非负（当31x -≤≤时），两边平方后，整理得 9843x x --≥+②于是980x --≥，即98x ≤-结合31x -≤≤得938x -≤≤-．并且②式两边平方，得2(98)16(3)x x ≥--+，整理得264128330x x ++≥．③因方程264128330x x ++=的两根为1,2831x -±= 所以③的解为831x --≤或831x -+≥结合938x -≤≤-得原不等式的解为8313x ---≤≤30．（2021·全国·九年级竞赛）解不等式：2243414143x x x x x x x x +-->-++-- 【答案】1144x -<<或364x -<<634x <【解析】【分析】【详解】解不等式两边乘以4，化简为5115(1)(1)(1)(1)43414143x x x x +-->+--++-- 移项、整理得22151169161x x ->--，移项、通分得2224(646)0(169)(161)x x x -<--，可化为222(646)(169)(161)0x x x ---<，即222139()()()0163216x x x ---<．如右图得2116x <或2393216x <<，解得1144x -<<或364x -<<634x <<31．（2021·全国·九年级竞赛）求满足下列条件的最小正整数n ，使得对这样的n ，有唯一的正整数k ，满足871513n n k <<+．【答案】15 【解析】【分析】【详解】因n ，k 为正整数，所以0,0n n k >+>．由题中不等式得151387n k n +>>，即1513187k n >+>所以7687k n >>，故76,87k n k n ><．令760,780A k n B n k =-≥=-≥，可解出87,76n A B k A B =+=+．又因为A ，B 均为正整数，1,1A B ≥≥，所以8715n ≥+=．当且仅当1,1A B ==时n 取最小值15，这时k 有唯一值716113⨯+⨯=．故所求n 的最小值为15．32．（2021·全国·九年级竞赛）解不等式： 2256154x x x x -+≤++．【答案】41x -≤<-或4x <-或15x ≥．【解析】【分析】【详解】解移项，通分整理得1020(1)(4)x x x -+≤++故得（Ⅰ） 1020(1)(4)0x x x -+≥⎧⎨++<⎩，或（Ⅱ）1020(1)(4)0x x x -+≤⎧⎨++>⎩．解（I ） 1541x x ⎧≤⎪⎨⎪-<<-⎩，∴41x -≤<-．解（Ⅰ）1541x x x ⎧≥⎪⎨⎪--⎩或∴4x <-或15x ≥．综上所述得，原不等式的解为41x -≤<-或4x <-或15x ≥．33．（2021·全国·九年级竞赛）解不等式21311x x x x -+>-+．【答案】1x <-或1x > 【解析】【分析】【详解】解移项通分得(21)(1)(3)(1)0(1)(1)x x x x x x -+-+->-+，即220(1)(1)x x x x -+>-+．因22172()024xx x，故上述不等式化为()()110,1x x x -+>∴<-或1x >. 34．（2021·全国·九年级竞赛）如果二次不等式：28210ax ax ++<的解是71x -≤<-，求a 的值．【答案】3a =【解析】【分析】【详解】解依题意，1,7--是方程28210ax ax ++=的两个根，且0a >，由韦达定理得 2(1)(7)a-⨯-=，所以3a =． 35．（2021·全国·九年级竞赛）某校参加全国数，理，化，计算机比赛的人数分别是20，16，x ，20人．已知这组数据的中位数和平均数相等，求这组数据的中位数．【答案】18或20．【解析】【分析】【详解】（1）当16x ≤时，平均数为564x x +=，中位数为2016182+=．由56184x+=，解得16x =，满足16x ≤；（2）当1620x ≤≤时，平均数564x x +=，中位数为202x +．由562042x x++=，解得16x =，不符合1620x <<；当20x ≥时，平均数为564x x +=，中位数为2020202+=．由56204x+=，解得24x =，符合20x ≥．因此，所求中位数为18或20．36．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6次、第7次，第8次，第9次射击中，分别得到9.0环、8.4环、8.1环、9.3环，他的前9次射击所得平均环数高于前5次射击所得平均环数，如果要使10次射击的平均环数超过8.8环，那么他第10次射击至少要得多少环?（每次射击环数精确到0.1环）【答案】第10次至少要射9.9环【解析】【分析】【详解】设前9次射击共得x 环，依题意得1(9.08.48.19.3)95x x -+++>，解得78.3x <，故78.30.178.2x ≤-=．依题目要求，第10次射击至少要达到的环数为()8.8100.178.29.9⨯+-=（环）．答：第10次至少要射9.9环37．（2021·全国·九年级竞赛）今有浓度为5%,8%,9%的甲、乙、丙三种盐水分别为60g,60g,47g ，现要配制成浓度为7%的盐水100g ．间甲盐水最多可用多少克?最少可用多少克? 【答案】甲种盐水最多可用49g ，最少可用35g 【解析】【分析】【详解】设3种盐水应分别取,,xg yg zg ，1005%8%9%1007%060060047x y z x y z x y z ++=⎧⎪++=⨯⎪⎪≤≤⎨⎪≤≤⎪≤≤⎪⎩，解得20043100y x z x =-⎧⎨=-⎩所以02004600310047x x ≤-≤⎧⎨≤-≤⎩，解得3549x ≤≤．答：甲种盐水最多可用40g ，最少可用35g ．38．（2021·全国·九年级竞赛）求证：对任意的实数x ，y ，[2][2][][][]x y x x y y ++++．【答案】见解析．【解析】【分析】【详解】设[],[]x x y y n αββ=+=+=+，其中0,1αβ≤<，m ，n 为整数．（1）若110,022αβ≤<≤<，则021,021,01αβαβ≤<≤<≤+<．这时有 [2][2][22][22]22x y m m m n αβ+=+++=+，[][][]x x y y +++[][()()][]m a m n n αββ=+++++++()22m m n n m n =+++=+，所以[2][2][][][]x y x x y y +=+++．（2）若111,122αβ≤<≤<，则122,122,12αβαβ≤<≤<≤+<．这时有 [2][2][22][22]2121x y m n m n αβ+=+++=+++222m n =++，[][][][][()()][]x x y y m m n n ααββ+++=+++++++()1221m m n n m n =++++=++．所以[2][2][][][]x y x x y y +>+++．（3）若110,122αβ≤<≤<（111,022αβ≤<≤<的情况类似），这时有021α≤<，13122,22βαβ≤<≤+<，这时有[2][2][22][22]221x y m a n m n β+=+++=++，[][][][()()]221x x y y m m n a n m n β+++=+++++++．综上所述，不论何种情况，都有[2][2][][][]x y x x y y +≤+++．39．（2021·全国·九年级竞赛）某个学生参加军训，进行打靶训练，必须射击10次，在第6、第7、第8、第9次射击中，分别得了9.0环，8.4环，8.1环，9.3环，他的前9次射击所得环数的平均值高于前5次射击所得的平均环数．如果他要使10次射击的平均环数超过8.8环，那么他在第10次射击中最少要得多少环？（每次射击所得环数都精确到0.1环）【答案】第10次最少要得9.9环．【解析】【分析】【详解】9．设前5次射击所得平均环数为a ，第10次击中x 环，依题意59.08.48.19.39a a ++++<， ① 59.08.48.19.38.810a x +++++<． ② 由①得8.7a <，从而558.70.143.4a ≤⨯-=．由②得8834.8553.243.49.8x a >--≥-=，所以9.9x ≥，即第10次最少要得9.9环．40．（2021·全国·九年级竞赛）已知x ，y ，z 都是正数，证明：32()()()()()()x y x z y z y x z x z y +≤++++++．【答案】见解析【解析】【分析】【详解】 (0,0)2a b ab a b +≥≥得 []()()()()11()2()()2()()x x y x z x x y x z x x x y x z x y x z x y x z +++++=⋅=+++++++①． 1()2()()y y y x y zy x y z ≤+++++②． 1()2()()z z z x z yz x z y ≤+++++③由①+②+③即得要证不等式． 41．（2021·全国·九年级竞赛）某饮料厂生产A 、B 两种矿泉水，每天生产B 种矿泉水比A 种矿泉水多10吨，A 种矿泉水比B 种矿泉水每天多获利润2000元，其中A 种矿泉水每吨可获利润200元，B 种矿泉水每吨可获利润100元．（1）问：该厂每天生产A 种，B 种矿泉水各多少吨？（2）由于江水受到污染，市政府要求该厂每天必须多生产10吨矿泉水，该厂决定响应市政府的号召，在每天的利润不超过原利润的情况下不少于8000元，该厂每天生产A 种矿泉水最多多少吨？【答案】（1）该厂每天生产A 种矿泉水30吨，B 种矿泉水40吨．（2）该厂每天最多生产A 种矿泉水20吨．【解析】【分析】【详解】解（1）设该厂每天生产A 种矿泉水x 吨，则该厂每天生产B 种矿泉水10x +吨，依题意得()200100102000x x -+=，解得30,1040x x =+=．（2）设该厂每天生产A 吨矿泉水y 吨，依题意得该厂每天共生产30401080++=吨矿泉水且()10000200100808000y y ≥+-≥，其中100002003010040=⨯+⨯为该厂原来每天获得的利润，解上述不等式得020y ≤≤．答：（1）该厂每天生产A 种矿泉水30吨，B 种矿泉水40吨．（2）该厂每天最多生产A 种矿泉水20吨．42．（2021·全国·九年级竞赛）要使不等式2320x x -+≤①与不等式2(1)(3)20m x m x -+--<②无公共解，求m 的取值范围．【答案】0m ≥【解析】【分析】【详解】解 ①化为()()120x x --<，故①的解为12x <<．②化为()()1210m x x ⎡⎤⎣⎦-+-<．③（1）当1m =，③为()210x -<，即1x <，符合题意．（2）当10m ->，即1m 时，③的解为211x m -<<-符合题意．（3）当10m -<，即1m <时，又分两种情形讨论：若211m <-，即1m <-时，③的解为21x m <-或1x >，不符合题意; 若211m >-，即1m >-时，③的解为1x <或21x m>-．要使①与②无公共解，必须221m ≥-即0m ≥，结合1m <得01m ≤<．综上所述，得到要使①与②无公共解，m 的取值范围是0m ≥．43．（2021·全国·九年级竞赛）已知三个非负数a ，b ，c ，满足325a b c ++=和231a b c +-=．若37m a b c =+-，求m 的最大值和最小值．【答案】m 的最大值为111-；m 的最小值为57- 【解析】【分析】【详解】解由325,231a b c a b c ++=+-=可解出73,711a c b c =-=-，于是()()37373711732m a b c c c c c =+-=-+--=-．由0,0,0a b c ≥≥≥得73071100c c c -≥⎧⎪-≥⎨⎪≥⎩解得37711c ≤≤．所以m 的最大值为71321111m =⨯-=-，m 的最小值为353277m =⨯-=-． 44．（2021·全国·九年级竞赛）某班学生到公园进行活动，划船的有22人，乘电动车的有20人，乘过山车的有19人，既划船又乘电动车的有9人，既乘电动车又乘过山车的有6人，既划船又乘过山车的有8人，并且有4人没有参加上述3项活动中任何一项活动，问这个班学生人数的可能值是多少？【答案】这个班的学生人数可能是42,43,44,45,46,47,48．【解析】【分析】【详解】解设3项活动都参加了的学生有n 人，于是由容斥原理I 知至少参加了一项活动人数为222019(968)38n n ++-+++=+．所以，这个班的学生人数为38442n n ++=+．另一方面参加了两项活动的学生人数分别是9,6,8，所以06n ≤≤，故424248n ≤+≤．综上所述，这个班的学生人数可能是42,43,44,45,46,47,48．。

九年级数学竞赛辅导系列讲座三方程练习(无答案) 试题

数学竞赛辅导系列讲座三 ——方程1、方程|3x|+|x －2|=4的解的个数是（）A 、0B 、1C 、2D 、32、以关于x ，y 的方程组32339mx y x my +=⎧⎨-=⎩的解为坐标的点（x ，y ）在第二象限，则符合条件的实数m 的范围是（）A 、m>19B 、m<－2C 、－2<m<19D 、－12<m<93、已知实数a>0，b>0，满足22012,2012a a b b +=+=，则a+b 的值是______．4、关于x 的方程22211axa a x -=+-的解为________． 5、已知p 是质数，且方程24440x px p +-=的两个根都是整数，则p=_____． 6、方程323652x x x y y ++=-+的整数解（x ，y ）的个数是（）A 、0B 、1C 、3D 、无数多个7、若a ，b 都是整数，方程220080ax bx +-=的两相异根都是质数，则3a+b 的值是（）A 、100B 、400C 、700D 、10008、对于实数x ，符合[x]表示不大于x 的最大整数，例如[3.14]=3，[－7.59]=-8，则关于x 的方程3747x +⎡⎤=⎢⎥⎣⎦的整数解有（）个 A 、4 B 、3 C 、2 D 、19、已知a ，b ，c ，d ，e ，f 满足1114,9,16,,,4916bcdef acdef abdef abcef abcdf abcde a b c d e f ======，则 (a+c+e)－(b+d+f)的值为________．10、方程||(1)0x x k --=有三个不相等的实根，则k 的取值范围是（）A 、－14<k<0B 、0<k<14C 、k>－14D 、k<1411、若整数m 使得方程220060x mx m -++=的根为非零整数，这样的整数m 的个数为________．12、设x 1，x 2是方程240x x +-=的两根，则3212510x x -+=（）A 、-29B 、-19C 、-15D 、-913、方程22332x xy y x y ++=-的非负整数解（x ，y ）的组数为（）A 、0B 、1C 、2D 、314、方程7[2][3]82x x x +=-的所有实数解为_____________． 15、对于实数u ，v ，定义一种运算“*”为：u*v=uv+v ，若关于x 的方程x*(a*x)=－ 14 有两个不同的实数根，则满足条件的实数a 的取值范围是____________．16、小王沿街匀速行走，发现每隔6分钟从背后驶过一辆18路公交车，每隔3分钟从迎面驶来一辆18路公交车，假设每辆18路公交车行驶速度一样，而且18路公交车总站每隔固定的时间发一辆车，那么发车间隔为几分钟？17、不定方程5x －14y=11的最小正整数解是____________．18、方程22[]30x x --=的解的个数是（）A 、1B 、2C 、3D 、419、已知t 是实数，若a ，b 是关于x 的一元二次方程2210x x t -+-=，的两个非负实根，则22(1)(1)a b --的最小值是________．20、已知m ，n 是二次方程2201270x x ++=的两根，那么22(20116)(20138)m m n n ++++等于（）A 、2004B 、2005C 、2006D 、200721、若实数x ，y ，z 满足方程组122232xyx y yzy z zxz x ⎧=⎪+⎪⎪=⎨+⎪⎪=⎪+⎩，则（） A 、x+2y+3z=0B 、7x+5y+2z=0C 、9x+6y+3z=0D 、10x+7y+z=022、已知实数a ，b ，c ，d ，且a ≠b ，c ≠d ，若关系式22222,2,4,4a ac b bc c ac d ad +=+=+=+=同时成立，则6a+2b+3c+2d=__________．23、方程组3322181x y z x y z +=-⎧⎨+=-⎩的正整数解（x ，y ，z ）为_____________． 24、方程222522007x xy y ++=的所有不同的整数解共有_______组．25、把三个连续的正整数a ，b ，c 按任意次序（次序不同视为不同组）填入□x 2+□x+□=0的三个方框中，作为一元二次方程的二次项系数，一次项系数和常数项，使得方程至少有一个整数根的a ，b ，c 有（）A 、不存在B 、有一组C 、有两组D 、多于两组26、已知a ，b ，c 为正数，关于x 的一元二次方程20ax bx c ++=有两个相等的实数根，则方程2(1)(2)(1)0a x b x c +++++=的根的情况是（）A 、没有实根B 、有两个相等的实根C 、有两个不等实根D 、根的情况不确定27、求方程232730x xy y -+=的正整数解．28、设x ，y ，z 是都不为零的相异实数，且满足等式y z z x x yy z x+++==，试证明：此等式的值不可能是实数． 29、解方程：222916(3)xx x +=-30、满足方程2221x y -=的所有质数解（即x ，y 都是质数的解）是_______． 31、若2222,x y m n x y m n +=++=+，求证：2012201220122012xymn+=+．32、已知a>0，且b>a+c ，证明方程20ax bx c ++=必有两个不同的实根． 33、解下列方程：（1）4322914920x x x x -+-+=（2）44(2)820x x +--= （3）222(231)(251)9x x x x x -+++=（4）222211114325671221x x x x x x x x +++=+++++++（5）2240119x x x x ⎛⎫⎛⎫+= ⎪ ⎪-+⎝⎭⎝⎭（6）1321121111x x x++=+++34、设a 为整数，使得关于x 的方程2(5)70ax a x a -+++=至少有一个有理根，试求方程所有可能的有理根．35、已知正整数a ，b ，c 满足a<b<c ，且ab+bc+ca=abc ，求所有可能符合条件的a ，b ，c ． 36、当a ，b 为何值时，方程2222(1)(3442)0x a x a ab b ++++++=有实根． 37、m 为有理数，试确定方程22443240x mx x m m k -++-+=的根为有理数．38、当12122()p p q q =+时，试证方程2110x p x q ++=和2220x p x q ++=中至少有一个方程有实根．39、周长为6，面积为整数的直角三角形是否存在？若不存在，请给出证明；若存在，请证明共有几个？40、若关于x 的方程2211k x kx x x x x+-=--只有一个解，求k 的值． 41、把最大正整数是31的连续31个正整数分成A ，B 两组，且10在A 组，如果把10从A 组移到B 组中，则A 组中的各数的平均数增加12 ，B 组中各数的平均数也增加12，问A 组中原有多少个数？42、已知a>2，b>2，试判断关于x 的方程2()0x a b x ab -++=与方程20x abx a b -++=有没有公共根，并说明理由．43、求所有的实数k ，使得关于x 的方程2(1)(1)0kx k x k +++-=的根都是整数． 44、设a ，b ，c 为互不相等的非零实数，求证三个方程22220,20,20ax bx c bx cx a cx ax b ++=++=++=不可能同时有两个相等实根．45、设△是整系数二次方程20ax bx c ++=的判别式，（1）4，5，6，7，8五个数值中，哪几个能作为判别式△的值？分别写出一个相应的二次方程；（2）请你从中导出一般规律——一切整数中怎样的整数值不能作为△的值，并给出理由．46．设a 、b 、c 、d 是正整数，a 、b 是方程()02=+--cd x c d x 的两个根．证明：存在边长是整数且面积为ab 的直角三角形．47、已知实数a 、b 、c 、d 互不相等，且.1111x ad d c c b b a =+=+=+=+试求x 的值．。

九上数学竞赛试题及答案

九上数学竞赛试题及答案九年级上学期数学竞赛试题一、选择题（每题3分，共15分）1. 下列哪个数是无理数？A. 3.1415926B. √2C. 0.33333D. π2. 如果一个直角三角形的两条直角边分别为3和4，那么斜边的长度是？A. 5B. 6C. 7D. 83. 一个数的立方根等于它本身，这个数可能是？A. 0B. 1C. -1D. 以上都是4. 一个二次方程ax² + bx + c = 0（a ≠ 0）的判别式是？A. b² - 4acB. b² + 4acC. a² + b² + c²D. a² - b² - c²5. 以下哪个代数式不是同类项？A. x³ + 2xB. 5x² - 3xC. 2x² - 3xD. x² + 5x二、填空题（每题3分，共15分）6. 如果一个数的平方等于81，那么这个数是________。

7. 一个数的相反数是-5，那么这个数是________。

8. 一个数的绝对值是5，那么这个数可能是________或________。

9. 一个多项式P(x) = x³ - 6x² + 11x - 6，P(1)的值是________。

10. 如果一个圆的半径是r，那么它的面积是________。

三、解答题（每题10分，共20分）11. 已知一个长方体的长、宽、高分别是a、b、c，求它的体积。

解：长方体的体积公式是V = abc，所以体积为abc。

12. 证明勾股定理：在一个直角三角形中，直角边的平方和等于斜边的平方。

证明：设直角三角形的直角边分别为a和b，斜边为c。

根据勾股定理，a² + b² = c²。

可以通过构造一个边长为a+b的正方形，将其分割成两个直角三角形和一个边长为c的正方形，从而证明a² +b² = c²。

人教版九年级数学上学期竞赛试卷及答案

人教版九年级数学上学期竞赛试卷及答案一、选择题（本题共计 12 小题，每题 3 分，共计36分，） 1. 在国庆节的一次同学聚会上，每人都向其他人赠送了一份小礼品，共互送110份小礼品，则参加聚会的同学有（） A.9人 B.10人 C.11人 D.12人 2. 三角形两边的长分别是12和16，第三边的长是一元二次方程x 2−32x +240=0的一个实数根，则该三角形的面积是( ) A.96 B.96或32√5 C.48 D.32√5 3. 方程(m −2)x 2−√3−mx +14=0有两个实数根，则m 的取值范围( ) A.m >52 B.m ≤52且m ≠2 ;C.m ≥3 D.m ≤3且m ≠2 4. a ，b ，c 为常数，且a ，c 互为相反数，则关于x 的方程ax 2+bx +c =0(a ≠0)根的情况( ) A.无实数根 B.有两个相等的实数根 C.有两个不相等的实数根 D.有一根为5 5. 把抛物线y =−2x 2+4的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是( ) A.y =−2(x −2)2+7 B.y =−2(x −2)2+1 C.y =−2(x +2)2+1 D.y =−2(x +2)2+7 6. 如图，已知二次函数y =ax 2+bx +c (a ≠0)图像过点(−1,0)，顶点为 (1,2)，则结论：①abc <0；②x =1时，函数的最大值是2；③a +2b +4c >0；④2a =−b ；⑤2c >3b ．其中正确的结论有( ) A.5个 B.4个 C.3个 D.2个7. 抛物线y =−3x 2−1是由抛物线y =−3(x +1)2+1怎样平移得到的（）A.左移1个单位上移2个单位B.右移1个单位上移2个单位学校：班级：姓名：准考证号：C.左移1个单位下移2个单位D.右移1个单位下移2个单位8. 如图，在Rt△ABC中，∠ABC=90∘，AB=2√3，BC=2，以AB的中点O为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为( )A.5√34−π2B.5√34+π2C.2√3−πD.4√3−π29. 如图，分别以等边三角形ABC的三个顶点为圆心，以其边长为半径画弧，得到的封闭图形是莱洛三角形，如果AB=2，那么此莱洛三角形（即阴影部分）的面积( )A.π+√3B.π−√3C.2π−2√3D.2π−√310. 如图，四边形ABCD内接于⊙O，若它的一个外角∠DCE=70∘，则∠BOD的度数是( )A.35∘B.70∘C.110∘D.140∘11. 从−2，3，4，5中随机选取一个数作为二次函数y=ax2中a的值，则抛物线开口向下的概率是( )A.1B.12C.14D.3412. 平移小菱形可以得到美丽的“中国结”图案，下面四个图案是小菱形平移后得到的类似“中国结”的图案，按图中规律，第20个图案中，小菱形的个数是( )A.800B.900C.1000D.1100二、填空题（本题共计4 小题，每题3 分，共计12分，）13. 国家统计局统计数据显示，我国快递业务收入逐年增加．2017年至2019年我国快递业务收入由5000亿元增加到7500亿元．设我国2017年至2019年快递业务收入的年平均增长率为x，则可列方程为________.14. 已知m是一元二次方程x2−x−2=0的一个根，则2020−m2+m的值为________.15. 明明和亮亮分别解同一道一元二次方程，明明把一次项系数看错了，解得方程的两个根分别为−3和5，亮亮把常数项看错了，解得两根为2和2，则原方程是________.16. 若实数p，q(p≠q)满足p2−5p+6=0，q2−5q+6=0，则1p2+1q2的值为________.三、解答题（本题共计7 小题，共计72分，）17.(10分) 解方程：(1)x2+4x−4=0；(2)3x(2x+1)=4x+2.18.(10分) 已知a，b是关于x的一元二次方程x2−2(m+1)x+m2+5=0的两实数根．(1)若(a−1)(b−1)=39，求m的值；(2)已知等腰△AOB的一边长为7，若a，b恰好是△AOB另外两边的边长，求这个三角形的周长．19.(11分) 某网店专售一品牌牙膏，其成本为22元/支，销售中发现，该商品每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系．(1)请求出y与x之间的函数关系式；(2)该品牌牙膏销售单价定为多少元时，每天销售利润最大？最大利润是多少元？(3)在武汉爆发“新型冠状病毒”疫情期间，该网店店主决定从每天获得的利润中抽出100元捐赠给武汉，为了保证捐款后每天剩余的利润不低于350元，市场监督管理局加大了对线上、线下商品销售的执法力度，对商品售价超过成本价的20%的商家进行处罚，请你给该网店店主提供一个合理化的销售单价范围．20.(10分) 嘉嘉同学用配方法推导二次函数y=ax2+bx+c(a≠0)的顶点坐标，她是这样做的：由于a≠0，解析式y=ax2+bx+c变形为y=a(x2+bax)+c，···························································第一步y=a[x2+ba x+(b2a)2−(b2a)2]+c，·······················第二步y=a(x+b2a )2−b24a+c，················································第三步y=a(x+b2a )2+b2−4ac4a．···········································第四步(1)嘉嘉的解法从第________步开始出现错误；事实上，抛物线y=ax2+ bx+c(a≠0)的顶点坐标是________.(2)用配方法求抛物线y=2x2−4x−3的顶点坐标和对称轴．21.(10分) 为了解我校落实新课改精神的情况，现以我校某班的同学参加课外活动的情况为样本，对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计，并绘制了如图所示的统计图．(1)参加音乐类活动的学生人数为________人，参加球类活动的人数的百分比为________；(2)请把图2（条形统计图）补充完整；(3)我校学生某年级共800人，则参加棋类活动的人数约为________；(4)该班参加舞蹈类活动的4位同学中，有1位男生（用E表示）和3位女生（分别用F，G，H表示），现准备从中选取两名同学组成舞伴，请用列表或画树状图的方法求恰好选中一男一女的概率．22.(10分) 如图，在△ABC中，∠C=90∘，以BC为直径的⊙O交AB于点D，E是AC中点．(1)求证：DE是⊙O的切线；(2)若AB=10,BC=6，连接CD，OE，交点为F，求OF的长．x2+c，且在函数值y=−4时，只有一个自23.(11分) 已知二次函数y=14变量x的值与其对应.(1)求c的值；(2)点M, N在该二次函数的图象上，记该二次函数图象的顶点为C，且∠MCN=90∘，求证：MN必过原点O；(3)将该二次函数图象落在直线l：x=t左侧部分沿着x轴翻折，其余部分图象保持不变，得到函数f的图象.问：是否存在实数t，使得函数f的图象位于直线l：x=t两侧的部分在y轴上的正投影没有重合部分？若存在，求t的取值范围；若不存在，说明理由.参考答案与试题解析一、选择题（本题共计12 小题，每题 3 分，共计36分）1.【答案】C【考点】由实际问题抽象出一元二次方程一元二次方程的应用——其他问题【解析】设参加聚会的有x名学生，根据“每人都向其他人赠送了一份小礼品，共互送110份小礼品”，列出关于x的一元二次方程，解之即可．【解答】解：设参加聚会的同学有x人，根据题意得：x(x−1)=110，解得x1=11，x2=−10(舍)，∴参加聚会的同学有11人.故选C.2.【答案】B【考点】解一元二次方程-因式分解法勾股定理等腰三角形的性质三角形的面积【解析】先求出一元二次方程x2−32x+240=0的实数根，再由三角形的三边关系判断出另一边的长度，由勾股定理的逆定理判断出三角形的性状，进而可得出结论．【解答】解：∵一元二次方程x2−32x+240=0,可化为(x−20)(x−12)=0，∴x1=20，x2=12，当x=12时，该三角形为以12为腰，16为底的等腰三角形，高∠=√122−82=4√5，则S=12×16×4√5=32√5；当x=20时，∵122+162=202，∴该三角形为以12和16为直角边，20为斜边的直角三角形．∴S=12×16×12=96．故选B.3.【答案】B【考点】一元二次方程的定义根的判别式二次根式有意义的条件【解析】根据一元二次方程的定义、二次根式有意义的条件和判别式的意义得到{m−2≠0 3−m≥0△=(−√3−m)2−4(m−2)×14≥0，然后解不等式组即可．【解答】解：根据题意，得{m−2≠0，3−m≥0，Δ=(−√3−m)2−4(m−2)×14≥0，解得m≤52且m≠2．故选B.4.【答案】C【考点】根的判别式【解析】直接利用判别式判断正负即可.【解答】解：由题意得：a=−c，则Δ=b2−4ac=b2+4a2.由于a≠0，所以Δ=b2−4ac=b2+4a2>0，所以方程必有两个不相等的实数根.故选C.5.【答案】D【考点】二次函数图象的平移规律【解析】根据抛物线图象平移规律：”左加右减“进行求解即可．【解答】解：根据抛物线图象平移规律：”左加右减，上加下减“可得，y=−2x2+4的图象向左平移2个单位，再向上平移3个单位，得到平移后抛物线的解析式为y=−2(x+2)2+4+3=−2(x+2)2+7.故选D．6.【答案】B【考点】二次函数图象与系数的关系二次函数的最值【解析】由抛物线的开口方向判断a与0的关系．由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【解答】解：①对称轴在y轴的右侧，则a，b异号，∴ab<0.由抛物线与y 轴的交点位于y 轴的正半轴，则c >0，∴ abc <0，故①正确；②∵抛物线的开口方向向下，顶点为(1,2)，∴x =1时，函数的最大值是2，故②正确；③当x =12时，y >0，即14a +12b +c >0， ∴a +2b +4c >0，故③正确；④∵抛物线的对称轴为直线x =−b 2a =1，∴2a =−b ，故④正确；⑤∵抛物线过点(−1,0)，∴a −b +c =0.∵ a =−12b ， ∴−12b −b +c =0， ∴2c =3b ，故⑤错误．综上所述，正确的结论有4个故选B ．7.【答案】D【考点】二次函数图象的平移规律【解析】此题暂无解析【解答】解：将抛物线y =−3(x +1)2+1向右移1个单位得到y =−3x 2+1，再向下移2个单位得到y =−3x 2−1.故选D .8.【答案】A【考点】扇形面积的计算解直角三角形求阴影部分的面积【解析】根据题意，作出合适的辅助线，即可求得DE 的长、∠DOB 的度数，然后根据图形可知阴影部分的面积是△ABC的面积减去△AOD的面积和扇形BOD的面积，从而可以解答本题．【解答】解：如图，连接OD，过点D作DE⊥AB于点E.∵在Rt△ABC中，∠ABC=90∘，AB=2√3，BC=2，则AC=4，AC=2BC，∴∠BAC=30∘，∴∠DOB=60∘.∵OD=12AB=√3，∴DE=32，∴阴影部分的面积是：2√3×22−√3×322−60×π×(√3)2360=5√34−π2.故选A.9.【答案】C【考点】扇形面积的计算等边三角形的性质三角形的面积【解析】图中三角形的面积是由三块相同的扇形叠加而成，其面积=三块扇形的面积相加，再减去两个等边三角形的面积，分别求出即可．【解答】解：过A作AD⊥BC于D，∵△ABC是等边三角形，∴AB=AC=BC=2，∠BAC=∠ABC=∠ACB=60∘，∵AD⊥BC，∴BD=CD=1，AD=√3BD=√3，∴△ABC的面积为12×BC×AD=12×2×√3=√3，S扇形BAC =60π×22360=23π，∴莱洛三角形的面积S=3×23π−2×√3=2π−2√3.故选C.10.【答案】D【考点】圆内接四边形的性质圆周角定理【解析】由圆内接四边形的外角等于它的内对角知，∠A＝∠DCE＝70∘，由圆周角定理知，∠BOD ＝2∠A＝140∘．【解答】解：∵四边形ABCD内接于⊙O，∴∠A+∠BCD=180∘，又∠BCD+∠DCE=180∘，∴∠A=∠DCE=70∘，∴∠BOD=2∠A=140∘．故选D.11.【答案】C【考点】二次函数图象与系数的关系概率公式【解析】根据抛物线的开口与系数的关系可知，当a<0时抛物线开口向下，在这一组数中只有−2为负数，所以当a=−2时抛物线开口向下，再根据概率公式解答即可．【解答】解：从−2，3，4，5四个数中，任意取一个数，有四种情况，满足抛物线开口向下的a值可以为−2，.∴该二次函数图象开口向下的概率是14故选C.12.【答案】A【考点】规律型：图形的变化类【解析】仔细观察图形发现第一个图形有2×12=2个小菱形；第二个图形有2×22=8个小菱形；第三个图形有2×32=18个小菱形；由此规律得到通项公式，然后代入n=20即可求得答案．【解答】解：∵第一个图形有2×12=2个小菱形；第二个图形有2×22=8个小菱形；第三个图形有2×32=18个小菱形；⋯以此类推，第n个图形有2n2个小菱形，∴第20个图形有2×202=800个小菱形.故选A.二、填空题（本题共计4 小题，每题 3 分，共计12分）13.【答案】5000(1+x)2=7500【考点】由实际问题抽象出一元二次方程【解析】根据题意可得等量关系：2017年的快递业务量×（1+增长率）2＝2019年的快递业务量，根据等量关系列出方程即可．【解答】解：根据题意，可列方程为5000(1+x)2=7500.故答案为：5000(1+x)2=7500.14.【答案】2018【考点】一元二次方程的解列代数式求值【解析】由方程根的定义把m的值代入可求得m2−m的值，代入可求得值．【解答】解：∵m是一元二次方程x2−x−2=0的一个根，∴m2−m−2=0，∴m2−m=2，∴2020−∠2+∠=2020−(∠2−∠)=2018.故答案为：2018.15.【答案】∠2−4∠−15=0【考点】根与系数的关系【解析】此题暂无解析【解答】解：设方程解析式为：∠2+∠∠+∠=0，由题意及根与系数的关系可得：−3×5=∠，−∠=2+2，故∠=−15，∠=−4，故答案为：∠2−4∠−15=0.16.【答案】1336【考点】解一元二次方程-因式分解法列代数式求值【解析】由题意得到实数∠， ∠是方程∠2−5∠+6=0的两个根，∠+∠=5，∠∠=6，代入1∠2+1∠2=∠2+∠2(∠∠)2=(∠+∠)2−2∠∠(∠∠)2即可. 【解答】解：∵ 实数∠， ∠(∠≠∠)满足∠2−5∠+6=0，∠2−5∠+6=0，∴ 解得∠=2或∠=3，∠=2或∠=3.∵实数∠， ∠不相等，∴ 1∠2+1∠2=122+132=1336. 故答案为：1336. 三、解答题（本题共计 7 小题，共计72分）17.【答案】解：(1)用公式法解：∠=1,∠=4,∠=−4，∴ ∠2−4∠∠=42−4×1×(−4)=32>0，∴ ∠=−∠±√∠2−4∠∠2∠=−4±√322×1=−2±2√2.(2)3∠(2∠+1)=2(2∠+1)，3∠(2∠+1)−2(2∠+1)=0，(3∠−2)(2∠+1)=0，3∠−2=0或2∠+1=0，∴ ∠1=23,∠2=−12. 【考点】解一元二次方程-公式法解一元二次方程-因式分解法【解析】此题暂无解析【解答】解：(1)用公式法解：∠=1,∠=4,∠=−4，∴ ∠2−4∠∠=42−4×1×(−4)=32>0，∴ ∠=−∠±√∠2−4∠∠2∠=−4±√322×1=−2±2√2.(2)3∠(2∠+1)=2(2∠+1)，3∠(2∠+1)−2(2∠+1)=0，(3∠−2)(2∠+1)=0，3∠−2=0或2∠+1=0，∴ ∠1=23,∠2=−12.18.【答案】解：(1)∵ ∠，∠是关于∠的一元二次方程∠2−2(∠+1)∠+∠2+5=0的两实数根， ∴ ∠+∠=2(∠+1)，∠∠=∠2+5，∴ (∠−1)(∠−1)=∠∠−(∠+∠)+1=∠2+5−2(∠+1)+1=39，解得∠=−5或∠=7，当∠=−5时，原方程无解，故舍去，∴ ∠=7．(2)①当7为底边时，此时方程∠2−2(∠+1)∠+∠2+5=0有两个相等的实数根， ∴ ∠=4(∠+1)2−4(∠2+5)=0，解得∠=2，∴ 方程变为∠2−6∠+9=0，解得∠=∠=3，∵ 3+3<7，∴ 不能构成三角形．②当7为腰时，设∠=7，代入方程得：49−14(∠+1)+∠2+5=0，解得：∠=10或4，当∠=10时，方程变为∠2−22∠+105=0，解得∠=7或15，∴∠=15，∵7+7<15，∴不能组成三角形；当∠=4时，方程变为∠2−10∠+21=0，解得∠=3或7，∴∠=3，∴此时三角形的周长为7+7+3=17．综上所述，三角形的周长为17.【考点】根与系数的关系根的判别式三角形三边关系等腰三角形的判定与性质【解析】无无【解答】解：(1)∵∠，∠是关于∠的一元二次方程∠2−2(∠+1)∠+∠2+5=0的两实数根，∴∠+∠=2(∠+1)，∠∠=∠2+5，∴(∠−1)(∠−1)=∠∠−(∠+∠)+1=∠2+5−2(∠+1)+1=39，解得∠=−5或∠=7，当∠=−5时，原方程无解，故舍去，∴∠=7．(2)①当7为底边时，此时方程∠2−2(∠+1)∠+∠2+5=0有两个相等的实数根，∴∠=4(∠+1)2−4(∠2+5)=0，解得∠=2，∴方程变为∠2−6∠+9=0，解得∠=∠=3，∵3+3<7，∴不能构成三角形．②当7为腰时，设∠=7，代入方程得：49−14(∠+1)+∠2+5=0，解得：∠=10或4，当∠=10时，方程变为∠2−22∠+105=0，解得∠=7或15，∴∠=15，∵7+7<15，∴不能组成三角形；当∠=4时，方程变为∠2−10∠+21=0，解得∠=3或7，∴∠=3，∴此时三角形的周长为7+7+3=17．综上所述，三角形的周长为17.19.【答案】解：(1)根据题意设∠=∠∠+∠(∠≠0)，将(30, 100)，(35, 50)代入得{30∠+∠=100, 35∠+∠=50,解得{∠=−10,∠=400,∴∠与∠之间的关系式为∠=−10∠+400.(2)设每天的利润为∠元，则∠=(∠−22)∠=(∠−22)(−10∠+400)=−10∠2+620∠−8800=−10(∠−31)2+810，∴销售单价定为31元时，每天最大利润为810元．(3)−10∠2+620∠−8800−100=350，解得∠=25或∠=37，结合图象和二次函数的特点得出25≤∠≤37，又∠≤22×(1+20%)，综上可得25≤∠≤26.4，∴按要求网店店主的销售单价范围为大于或等于25元且小于或等于26.4元．【考点】待定系数法求一次函数解析式二次函数的应用一元二次方程的应用一元一次不等式的实际应用【解析】（1）利用待定系数法求解可得；（2）设每天的利润为∠元，根据“总利润＝每支利润×每天销售量”得出函数解析式，配方成顶点式后利用二次函数的性质求解可得；（3）根据题意列出方程−10∠2+620∠−8800−100＝350，解之求出∠的值，再根据二次函数的性质得出25≤∠≤37，结合∠≤22×(1+20%)可得答案．【解答】解：(1)根据题意设∠=∠∠+∠(∠≠0)，将(30, 100)，(35, 50)代入得{30∠+∠=100,35∠+∠=50, 解得{∠=−10,∠=400,∴ ∠与∠之间的关系式为∠=−10∠+400.(2)设每天的利润为∠元，则∠=(∠−22)∠=(∠−22)(−10∠+400)=−10∠2+620∠−8800=−10(∠−31)2+810，∴ 销售单价定为31元时，每天最大利润为810元．(3)−10∠2+620∠−8800−100=350，解得∠=25或∠=37，结合图象和二次函数的特点得出25≤∠≤37，又∠≤22×(1+20%)，综上可得25≤∠≤26.4，∴ 按要求网店店主的销售单价范围为大于或等于25元且小于或等于26.4元． 20.【答案】四,(−∠2∠,4∠∠−∠24∠)(2)∵ ∠=2∠2−4∠−3=2(∠−1)2−5，∴ 抛物线的顶点坐标是(1,−5)，对称轴是直线∠=1.【考点】二次函数的三种形式解一元二次方程-配方法二次函数y=ax^2 、y=a （x-h ）^2+k (a≠0)的图象和性质【解析】(1)运用正确的方法把二次函数的解析式化成顶点式即可解答.(2)运用配方法，把函数的解析式化成顶点式，进一步可得抛物线的顶点坐标和对称轴.【解答】解：(1)∠=∠∠2+∠∠+∠变形为∠=∠(∠2+∠∠∠)+∠，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯第一步∠=∠[∠2+∠∠∠+(∠2∠)2−(∠2∠)2]+∠，⋯⋯第二步∠=∠(∠+∠2∠)2−∠24∠+∠，⋯⋯⋯⋯⋯⋯⋯⋯⋯第三步∠=∠(∠+∠2∠)2+4∠∠−∠24∠.⋯⋯⋯⋯⋯⋯⋯⋯第四步∴ 嘉嘉的解法从第四步开始出现错误；事实上抛物线∠=∠∠2+∠∠+∠(∠≠0)的顶点坐标是(−∠2∠,4∠∠−∠24∠).故答案为：四；(−∠2∠,4∠∠−∠24∠). (2)∵ ∠=2∠2−4∠−3=2(∠−1)2−5，∴ 抛物线的顶点坐标是(1,−5)，对称轴是直线∠=1. 21.【答案】7,30%(2)补全条形图如下：140(4)画树状图如下：共有12种情况，选中一男一女的有6种，则∠（选中一男一女）=612=12．【考点】扇形统计图条形统计图用样本估计总体列表法与树状图法【解析】（1）先根据绘画类人数及其百分比求得总人数，继而可得答案；（2）根据（1）中所求数据即可补全条形图；（3）总人数乘以棋类活动的百分比可得；（4）利用树状图法列举出所有可能的结果，然后利用概率公式即可求解．【解答】解：(1)本次调查的总人数为10÷25%=40（人），∴参加音乐类活动的学生人数为40×17.5%=7(人)，参加球类活动的人数的百分比为1240×100%=30%，故答案为：7；30%.(2)补全条形图如下：(3)我校学生某年级共800人，则参加棋类活动的人数约为800×740=140. 故答案为：140.(4)画树状图如下：共有12种情况，选中一男一女的有6种，则∠（选中一男一女）=612=12．22.【答案】(1)证明：连接∠∠，∠∠，如图，∵∠∠∠∠=90∘，∠∠为⊙∠直径，∴∠∠∠∠=∠∠∠∠=90∘.∠为∠∠中点，∴∠∠=∠∠=∠∠,∴∠∠∠∠=∠∠∠∠.又∵∠∠∠∠=∠∠∠∠，∴∠∠∠∠+∠∠∠∠=∠∠∠∠+∠∠∠∠=∠∠∠∠=90∘，即∠∠∠∠=90∘，∴∠∠是⊙∠的切线.(2)解：连接∠∠，交∠∠于点∠，如图，∵∠∠∠∠=90∘，∴∠∠为⊙∠的切线.∵∠∠是⊙∠的切线，∴∠∠平分∠∠∠∠,∴∠∠⊥∠∠，∠为∠∠的中点.∵点∠，∠别为∠∠，∠∠的中点，∴∠∠=12∠∠=12×10=5 .在∠∠△∠∠∠中，∠∠∠∠=90∘，∠∠=10，∠∠=6，由勾股定理得：∠∠=8.∵在∠∠△∠∠∠中，∠为∠∠的中点，∴∠∠=12∠∠=12×8=4.在∠∠△∠∠∠中，∠∠=12∠∠=12×6=3，在∠∠△∠∠∠中，∠∠=4，由勾股定理得：∠∠=5.由三角形的面积公式得：∠△∠∠∠=12×∠∠×∠∠=12×∠∠×∠∠,即4×3=5×∠∠,解得：∠∠=2.4 ,在∠∠△∠∠∠中，由勾股定理得：∠∠=√∠∠2−∠∠2=√32−2.42=1.8．【考点】切线的判定勾股定理切线的性质切线长定理【解析】（1）证明：连接∠∠，∠∠，∵∠∠∠∠=90∘，∠∠为⊙∠直径，∴∠∠∠∠=∠∠∠∠=90∘;∠为∠∠中点∴∠∠=∠∠=∠∠,∴∠∠∠∠=∠∠∠∠；又∵∠∠∠∠=∠∠∠∠∴∠∠∠∠+∠∠∠∠=∠∠∠∠+∠∠∠∠=∠∠∠∠=90∘∴∠∠是⊙∠的切线（2）解：连接∠∠，∵∠∠∠∠=90∘∴∠∠为⊙∠的切线，∵∠∠是⊙∠的切线，∴∠∠平分∠∠∠∠,∴∠∠⊥∠∠,∠为∠∠的中点，∵点∠、∠别为∠∠、∠∠的中点，∴∠∠=12∠∠=12×10=5 ,在∠∠△∠∠∠中，∠∠∠∠=90∘，∠∠=10．∠∠=6，由勾股定理得：∠∠=8，∵在∠∠△∠∠∠中，∠为∠∠的中点，∴∠∠=12∠∠=12×8=4,在∠∠△∠∠∠中，∠∠=12∠∠=12×6=3,∠∠−4，由勾股定理得：∠∠=5,由三角形的面积公式得：∠△∠∠∠=12×∠∠×∠∠=12×∠∠×∠∠,即4×3=5×∠∠,解得：∠∠=2.4 ,在∠∠△∠∠∠中，由勾股定理得：∠∠=√∠∠2−∠∠2=√32−2.42=1.8．【解答】(1)证明：连接∠∠，∠∠，如图，∵∠∠∠∠=90∘，∠∠为⊙∠直径，∴∠∠∠∠=∠∠∠∠=90∘.∠为∠∠中点，∴∠∠=∠∠=∠∠,∴∠∠∠∠=∠∠∠∠.又∵∠∠∠∠=∠∠∠∠，∴∠∠∠∠+∠∠∠∠=∠∠∠∠+∠∠∠∠=∠∠∠∠=90∘，即∠∠∠∠=90∘，∴∠∠是⊙∠的切线.(2)解：连接∠∠，交∠∠于点∠，如图，∵∠∠∠∠=90∘，∴∠∠为⊙∠的切线.∵∠∠是⊙∠的切线，∴∠∠平分∠∠∠∠,∴∠∠⊥∠∠，∠为∠∠的中点.∵点∠，∠别为∠∠，∠∠的中点，∴∠∠=12∠∠=12×10=5 .在∠∠△∠∠∠中，∠∠∠∠=90∘，∠∠=10，∠∠=6，由勾股定理得：∠∠=8.∵在∠∠△∠∠∠中，∠为∠∠的中点，∴∠∠=12∠∠=12×8=4.在∠∠△∠∠∠中，∠∠=12∠∠=12×6=3，在∠∠△∠∠∠中，∠∠=4，由勾股定理得：∠∠=5.由三角形的面积公式得：∠△∠∠∠=12×∠∠×∠∠=12×∠∠×∠∠,即4×3=5×∠∠,解得：∠∠=2.4 ,在∠∠△∠∠∠中，由勾股定理得：∠∠=√∠∠2−∠∠2=√32−2.42=1.8．23.【答案】(1)解：把∠=−4代入∠=14∠2+∠中，得∠2+4∠+16=0，∵此时只有一个自变量∠的值与其对应，∴∠=−4×(4∠+16)=0，解得∠=−4.(2)证明：设∠(∠1, ∠1)，∠(∠2, ∠2)，∠(0, −4)，∵∠∠∠∠=90∘，即∠∠⊥∠∠，∴∠∠∠⋅∠∠∠=−1，∴∠1+4∠1⋅∠2+4∠2=−1，消去∠得，∠1∠2=−16，设直线∠∠的方程为∠=∠1−∠2∠1−∠2∠+∠，代入(∠1, ∠1)，∠=14∠2−4，则有14∠12−4=14(∠12−∠22)∠1−∠2∠1+∠，1 4∠12=14∠12+14∠1∠2+∠+4，化简得0=−4+4+∠，即∠=0，∴∠∠的方程∠=∠1−∠2∠1−∠2∠过原点.(3)解：令∠=4，则4=14∠2−4，解得∠=±4√2，当∠>4√2时，画出图象如图：观察图象可知，无重合；当∠<−4√2时，画出图象如图：观察图象可知，无重合.∴∠的取值范围为∠<−4√2或∠>4√2. 【考点】二次函数的图象一次函数的应用函数的概念根的判别式【解析】此题暂无解析【解答】解：(1)把∠=−4代入∠=14∠2+∠中，得∠2+4∠+16=0，∵此时只有一个自变量∠的值与其对应，∴∠=−4×(4∠+16)=0，解得∠=−4.(2)证明：设∠(∠1, ∠1)，∠(∠2, ∠2)，∠(0, −4)，∵∠∠∠∠=90∘，即∠∠⊥∠∠，∴∠∠∠⋅∠∠∠=−1，∴∠1+4∠1⋅∠2+4∠2=−1，消去∠得，∠1∠2=−16，设直线∠∠的方程为∠=∠1−∠2∠1−∠2∠+∠，代入(∠1, ∠1)，∠=14∠2−4，则有14∠12−4=14(∠12−∠22)∠1−∠2∠1+∠，1 4∠12=14∠12+14∠1∠2+∠+4，化简得0=−4+4+∠，即∠=0，∴∠∠的方程∠=∠1−∠2∠1−∠2∠过原点.(3)解：令∠=4，则4=14∠2−4，解得∠=±4√2，当∠>4√2时，画出图象如图：观察图象可知，无重合；当∠<−4√2时，画出图象如图：观察图象可知，无重合.∴∠的取值范围为∠<−4√2或∠>4√2.。

全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案This manuscript was revised on November 28, 2020中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题（共5小题，每小题6分，共30分.）1（甲）．如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式22||()||a a b c a b c -++-++可以化简为（）．（A ）2c a - （B ）22a b - （C ）a - （D ）a 1（乙）．如果22a =-+11123a+++的值为（）．（A ）2- （B 2（C ）2 （D ）22（甲）．如果正比例函数y = ax （a ≠ 0）与反比例函数y =x b（b ≠0 ）的图象有两个交点，其中一个交点的坐标为（－3，－2），那么另一个交点的坐标为（）．（A ）（2，3）（B ）（3，－2）（C ）（－2，3）（D ）（3，2）2（乙）．在平面直角坐标系xOy 中，满足不等式x 2＋y 2≤2x ＋2y 的整数点坐标（x ，y ）的个数为（）．（A ）10 （B ）9 （C ）7 （D ）53（甲）．如果a b ，为给定的实数，且1a b <<，那么1121a a b a b ++++，，，这四个数据的平均数与中位数之差的绝对值是（）．（A ）1 （B ）214a - （C ）12（D ）143（乙）．如图，四边形ABCD 中，AC ，BD 是对角线，△ABC 是等边三角形．30ADC ∠=︒，AD = 3，BD = 5，则CD 的长为（）．（A ）23 （B ）4 （C ）52 （D ）OAB CED4（甲）．小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱数将是你的n 倍”；小玲对小倩说：“你若给我n 元，我的钱数将是你的2倍”，其中n 为正整数，则n 的可能值的个数是（）．（A ）1 （B ）2 （C ）3 （D ）44（乙）．如果关于x 的方程 20x px q p q --=（，是正整数）的正根小于3，那么这样的方程的个数是（）．（A ） 5 （B ） 6 （C ） 7 （D ） 85（甲）．一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，3，4，5，6．掷两次骰子，设其朝上的面上的两个数字之和除以4的余数分别是0，1，2，3的概率为0123p p p p ，，，，则0123p p p p ，，，中最大的是（）．（A ）0p （B ）1p （C ）2p （D ）3p5（乙）．黑板上写有111123100，　，，，　共100个数字．每次操作先从黑板上的数中选取2个数a b ，，然后删去a b ，，并在黑板上写上数a b ab ++，则经过99次操作后，黑板上剩下的数是（）．（A ）2012 （B ）101 （C ）100 （D ）99 二、填空题（共5小题，每小题6分，共30分） 6（甲）．按如图的程序进行操作，规定：程序运行从“输入一个值x ”到“结果是否>487”为一次操作. 如果操作进行四次才停止，那么x 的取值范围是 . 6（乙）.如果a ，b ，c 是正数，且满足9a b c ++=，111109a b b c c a ++=+++，那么a b cb c c a a b+++++的值为．7（甲）．如图，正方形ABCD 的边长为215，E ，F 分别是AB ，BC 的中点，AF 与DE ，DB 分别交于点M ，N ，则△DMN 的面积是 . 7（乙）.如图所示，点A 在半径为20的圆O 上，以OA为一条对角线作矩形OBAC ，设直线BC 交圆O 于D 、E 两点，xyO ECABD若12OC =，则线段CE 、BD 的长度差是。

浙教版-学年度九年级数学竞赛试卷1（含解析）

绝密★启用前浙教版2018-2019学年初三数学竞赛试卷1题号一二三总分得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）请点击修改第I卷的文字说明评卷人得分一．选择题（共8小题，4*8=32）1．若交换代数式中的任意两个字母，代数式不变，则称这个代数式为完全对称式，如a+b+c就是一个完全对称式．已知三个代数式：①a（b+c）+b（a+c）+c（a+b）；②a2bc+b2ac+c2ab；③a2+b2+c2﹣ab﹣bc﹣ac．其中是完全对称式的（）A．只有①②B．只有①③C．只有②③D．有①②③2．已知2x﹣3﹣2y＝0（x＞0），则的值是（）A．B．C．D．3．已知mn＜0且1﹣m＞1﹣n＞0＞n+m+1，那么n，m，，的大小关系是（）A．B．C．D．4．设x≥0，y≥0，2x+y＝6，则u＝4x2+3xy+y2﹣6x﹣3y的最大值是（）A．B．18 C．20 D．不存在5．x、y都是正数，且成反比例，当x增加a%时，y减少b%，则b的值为（）A．a B．C．D．6．如图，把正△ABC的外接圆对折，使点A与劣弧的中点M重合，若BC＝5，则折痕在△ABC内的部分DE的长为（）A．B．C．D．7．某寺院有甲、乙、丙三口铜钟．甲钟每4s敲响一声，乙钟每5s敲响一声，丙钟每6s敲响一声．新年到来时，三口钟同时敲响且同时停敲，某人共听到365声钟响．若在此期间，甲、乙、丙三口钟敲响的次数分别为x次、y次、z次，则x+y+z＝（）A．365 B．484 C．585 D．4658．记S n＝a1+a2+…+a n，令，称T n为a1，a2，…，a n这列数的“理想数”．已知a1，a2，…，a500的“理想数”为2004，那么8，a1，a2，…，a500的“理想数”为（）A．2004 B．2006 C．2008 D．2010第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明评卷人得分二．填空题（共6小题，4*6=24）9．已知不等式ax+3≥0的正整数解为1，2，3，则a的取值范围是．10．在一次剪纸活动中，小聪依次剪出6张正方形纸片拼成如图所示的图形，若小聪所拼得的图形中正方形①的面积为1，且正方形⑥与正方形③面积相等，那么正方形⑤的面积为．11．方程x2﹣4x+3a2﹣2＝O在区间[﹣1，1]上有实根．则实数a的取值范围是．12．设△ABC的重心为G，且AG＝6，BG＝8，CG＝10．则S△ABC＝．13．设二次函数y＝x2+2ax+（a＜0）的图象顶点为A，与x轴交点为B、C，当△ABC为等边三角形时，a的值为．14．如图，边长为1的正三角形ANB放置在边长为MN＝3，NP＝4的长方形MNPQ内，且NB在边NP上．若正三角形在长方形内沿着边NP、PQ、QM、MN翻转一圈后回到原来起始位置，则顶点A在翻转过程中形成轨迹的总长是（保留π）．评卷人得分三．解答题（共8小题，64分）15．（6分）现有长为150cm的铁丝，要截成n（n＞2）小段，每段的长为不小于1（cm）的整数．如果其中任意3小段都不能拼成三角形，试求n的最大值，此时有几种方法将该铁丝截成满足条件的n段．16．（6分）已知四边形ABCD两条对角线互相垂直，点O是对角线的交点，∠ACD＝60°，∠ABD ＝45°，点A到CD的距离是6，点D到AB的距离是8，求四边形ABCD的面积S．17．（6分）已知a、b、c满足方程组，试求方程bx2+cx﹣a＝0的根．18．如图所示，正方形ABCD的边长为1，点M、N分别在BC、CD上，使得△CMN的周长为2．求：（1）∠MAN的大小；（2）△MAN面积的最小值．19．（10分）如图所示，四边形ABCD是矩形，甲、乙两人分别从A、B同时出发，沿矩形按逆时针方向前进，即按A→B→C→D→…顺序前进，已知甲的速度为每分钟65米，乙的速度为每分钟74米，问乙至少在跑第几圈时才有可能第一次追上甲？又乙至多在跑第几圈时一定能追上甲？请说明理由．20．（10分）已知当﹣1＜x＜O时，二次函数y＝x2﹣4mx+3的值恒大于1，求m的取值范围．21．（12分）已知在矩形ABCD中，AB＝4，BC＝，O为BC上一点，BO＝，如图所示，以BC所在直线为x轴，O为坐标原点建立平面直角坐标系，M为线段OC上的一点．（1）若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P在矩形ABCD的一边上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标；（2）若将（1）中的点M的坐标改为（4，0），其它条件不变，如图②，那么符合条件的等腰三角形有几个？求出所有符合条件的点P的坐标；（3）若将（1）中的点M的坐标改为（5，0），其它条件不变，如图③，请直接写出符合条件的等腰三角形有几个．（不必求出点P的坐标）22．（14分）已知抛物线y＝ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2﹣10x+16＝0的两个根，且抛物线的对称轴是直线x＝﹣2．（1）求A、B、C三点的坐标；（2）求此抛物线的表达式；（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC 交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；（4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．参考答案与试题解析一．选择题（共8小题）1．若交换代数式中的任意两个字母，代数式不变，则称这个代数式为完全对称式，如a+b+c就是一个完全对称式．已知三个代数式：①a（b+c）+b（a+c）+c（a+b）；②a2bc+b2ac+c2ab；③a2+b2+c2﹣ab﹣bc﹣ac．其中是完全对称式的（）A．只有①②B．只有①③C．只有②③D．有①②③【分析】根据完全对称式的含义，把式子中任意两个字母交换，根据乘法的交换律和加法的交换律即可求出答案．【解答】解：根据完全对称式的含义：把a（b+c）+b（a+c）+c（a+b）中任意两个字母交换，如a 和c交换得到：c（b+a）+b（c+a）+a（c+b）＝a（b+c）+b（a+c）+c（a+b），交换其它的任意的两个字母也和原式相等，∴①正确；根据完全对称式的含义：把a2bc+b2ac+c2ab中任意两个字母交换，如b和c交换得到：a2cb+c2ab+b2ac ＝a2bc+b2ac+c2ab，交换其它的任意的两个字母也和原式相等∴②正确；根据完全对称式的含义：把a2+b2+c2﹣ab﹣bc﹣ac中任意两个字母交换，如b和a交换得到：b2+a2+c2﹣ba﹣ac﹣bc＝a2+b2+c2﹣ab﹣bc﹣ac，交换其它的任意的两个字母也和原式相等，∴③正确．故选：D．【点评】本题主要考查对对称式和轮换对称式的理解和掌握，能熟练地根据完全对称式的含义进行判断是解此题的关键．2．已知2x﹣3﹣2y＝0（x＞0），则的值是（）A．B．C．D．【分析】先把所给方程用十字相乘法因式分解，求出x，y之间的关系，然后代入分式化简求值．【解答】解：原方程得2（）﹣3﹣2＝0．令＝t，则方程变形为2t2﹣3t﹣2＝0，即（2t+1）（t﹣2）＝0，解得t1＝2，t2＝﹣（舍去），故＝4．将x＝4y代入分式，得＝．故选：D．【点评】本题考查的是用因式分解法解方程，求出x，y之间的关系，然后代入分式化简求值．3．已知mn＜0且1﹣m＞1﹣n＞0＞n+m+1，那么n，m，，的大小关系是（）A．B．C．D．【分析】根据条件设出符合条件的具体数值，根据负数小于一切正数，两个负数比较大小，两个负数绝对值大的反而小即可解答．【解答】解：∵mn＜0，∴m，n异号，由1﹣m＞1﹣n＞0＞n+m+1，可知m＜n，m+n＜﹣1，m＜0，0＜n＜1，|m|＞|n|，|m|＞2，假设符合条件的m＝﹣4，n＝0.2则＝5，n+＝0.2﹣＝﹣则﹣4＜﹣＜0.2＜5故m＜n+＜n＜．故选：D．【点评】此题主要考查了实数的大小的比较，解答此题的关键根据已知条件分析出n，m的符号，绝对值的大小，再设出符合条件的数值比较大小，以简化计算．4．设x≥0，y≥0，2x+y＝6，则u＝4x2+3xy+y2﹣6x﹣3y的最大值是（）A．B．18 C．20 D．不存在【分析】由2x+y＝6，得y＝6﹣2x，代入u＝4x2+3xy+y2﹣6x﹣3y，根据x≥0，y≥0，求出x的取值范围即可求出答案．【解答】解：由已知得：y＝6﹣2x，代入u＝4x2+3xy+y2﹣6x﹣3y，整理得：u＝2x2﹣6x+18，而x≥0，y＝6﹣2x≥0，则0≤x≤3，u＝2+18﹣，当x＝0或x＝3时，u取得最大值，u max＝18，故选：B．【点评】本题考查了二次函数的最值，难度不大，关键是先求出x的取值范围再根据配方法求最值．5．x、y都是正数，且成反比例，当x增加a%时，y减少b%，则b的值为（）A．a B．C．D．【分析】根据x、y都是正数，且成反比例，可设y＝，xy＝k，当x增加a%时，y减少b%，则（1+a%）x（1﹣b%）y＝k，继而即可得出答案．【解答】解：根据题意，可设y＝，则xy＝k①，当x增加a%时，y减少b%，则（1+a%）x（1﹣b%）y＝k②，将①和②式结合即：（1+a%）（1﹣b%）xy＝xy所以两边同乘：10000/xy可以得到：（100+a）（100﹣b）＝10000即100﹣b＝10000/（100+a）从而b＝＝＝可得：b＝．故选：C．【点评】本题考查反比例函数的定义，属于基础题，关键是根据题意设出x和y的关系式．6．如图，把正△ABC的外接圆对折，使点A与劣弧的中点M重合，若BC＝5，则折痕在△ABC内的部分DE的长为（）A．B．C．D．【分析】AM与DE交于点F，则F是△ABC的内心，同时又是重心，依据重心的性质即可得出AF 与AS的比值；再根据相似三角形的性质，对应边的比相等，即可求解．【解答】解：如图，连接AM，与DE、BC分别交于点F、点S，则点F是圆心，又是三角形的内心；∵点S是BC的中点，点F是DE的中点，则有DE∥BC，∴AF：AS＝DE：BC＝2：3，∴DE＝．故选：C．【点评】本题利用了圆的内接正三角形的内心到每个顶点的距离是等边三角形高的的性质，进行求解．7．某寺院有甲、乙、丙三口铜钟．甲钟每4s敲响一声，乙钟每5s敲响一声，丙钟每6s敲响一声．新年到来时，三口钟同时敲响且同时停敲，某人共听到365声钟响．若在此期间，甲、乙、丙三口钟敲响的次数分别为x次、y次、z次，则x+y+z＝（）A．365 B．484 C．585 D．465【分析】根据已知可以得出以一分钟为一个周期，甲钟响了15声，乙钟响了12声，丙钟响了10声，共响了37声，但人听到的只有28声，因有时是两钟或三钟同时敲响的．由题意知共敲了13分钟，即可求出x+y+z的值．【解答】解：由题意知：以一分钟为一个周期，设f（a1，a2．，an）表示60秒内同时听到隔a1，a2，．an秒敲钟的次数．则60秒内听到次数为f（4）+f（5）+f（6）﹣f（4，5）﹣f（5，6）﹣f（4，6）+f（4，5，6）＝15+12+10﹣3﹣5﹣2+1＝28．我们可以发现：甲钟响了15声，乙钟响了12声，丙钟响了10声，共响了37声，但人听到的只有28声，因有时是两钟或三钟同时敲响的．由题意知共敲了13分钟，x+y+z＝37×13+3＝484．故选：B．【点评】此题主要考查了整数问题的综合应用，根据已知得出以一分钟为周期得出人听到的只有28声是解决问题的关键．8．记S n＝a1+a2+…+a n，令，称T n为a1，a2，…，a n这列数的“理想数”．已知a1，a2，…，a500的“理想数”为2004，那么8，a1，a2，…，a500的“理想数”为（）A．2004 B．2006 C．2008 D．2010【分析】本题需先根据得出n×T n＝（S1+S2+…+S n），再根据a1，a2，…，a500的“理想数”为2004，得出T500的值，再设出新的理想数为T x，列出式子，把得数代入，即可求出结果．【解答】解：∵∴n×T n＝（S1+S2+…+S n）T500＝2004设新的理想数为T x501×T x＝8×501+500×T500T x＝（8×501+500×T500）÷501＝＝8+500×4＝2008故选：C．【点评】本题主要考查了有理数的混合运算，在解题时要根据题意找出关系是解题的关键．二．填空题（共6小题）9．已知不等式ax+3≥0的正整数解为1，2，3，则a的取值范围是﹣1≤a＜﹣．【分析】首先确定不等式组的解集，先利用含a的式子表示，根据整数解的个数就可以确定有哪些整数解，根据解的情况可以得到关于a的不等式，从而求出a的范围．注意当x的系数含有字母时要分情况讨论．【解答】解：不等式ax+3≥0的解集为：（1）a＞0时，x≥﹣，正整数解一定有无数个．故不满足条件．（2）a＝0时，无论x取何值，不等式恒成立；（3）当a＜0时，x≤﹣，则3≤﹣＜4，解得﹣1≤a＜﹣．故a的取值范围是﹣1≤a＜﹣．【点评】本题考查不等式的解法及整数解的确定．解不等式要用到不等式的性质：（1）不等式的两边加（或减）同一个数（或式子），不等号的方向不变；（2）不等式两边乘（或除以）同一个正数，不等号的方向不变；（3）不等式的两边乘（或除以）同一个负数，不等号的方向改变．当x的系数含有字母时要分情况讨论．10．在一次剪纸活动中，小聪依次剪出6张正方形纸片拼成如图所示的图形，若小聪所拼得的图形中正方形①的面积为1，且正方形⑥与正方形③面积相等，那么正方形⑤的面积为36．【分析】设正方形②的边长是x，则正方形③和正方形⑥的边长是x+1，正方形④的边长是x+1+1，正方形⑤的边长是x+1+1+1或x+1+x﹣1，从而建立方程求解．【解答】解：设正方形②的边长是x．结合图形，得x+1+1+1＝x+1+x﹣1，解得x＝3．则正方形⑤的边长是6，其面积是36．故答案为：36．【点评】此题主要是结合图形用两种不同的形式表示同一个正方形的边长，得到方程即可求解．11．方程x2﹣4x+3a2﹣2＝O在区间[﹣1，1]上有实根．则实数a的取值范围是﹣≤a≤．【分析】首先设f（x）＝x2﹣4x+3a2﹣2，由方程x2﹣4x+3a2﹣2＝O在区间[﹣1，1]上有实根，利用函数的性质，即可得f（﹣1）•f（1）＝（3a2+3）（3a2﹣5）≤0，然后解不等式即可求得答案．【解答】解：设f（x）＝x2﹣4x+3a2﹣2，∵方程x2﹣4x+3a2﹣2＝O在区间[﹣1，1]上有实根，∴f（﹣1）•f（1）＝（3a2+3）（3a2﹣5）≤0，∵3a2+3＞0，∴3a2﹣5≤0，∴a2≤，∴实数a的取值范围是﹣≤a≤．故答案为：﹣≤a≤．【点评】此题考查了一元二次方根的分布，函数的性质与一元二次不等式的解法．此题难度较大，解题的关键是掌握函数思想的应用．12．设△ABC的重心为G，且AG＝6，BG＝8，CG＝10．则S△ABC＝72．【分析】延长AG到G'，与BC相交于D，使DG＝DG′，则△BDG≌△CDG′，所以CG'＝BG＝8，根据重心的性质可求得DG＝DG′＝3，则GG'＝6，又CG＝10，所以△CGG'是直角三角形，并可求得其面积，从而得出△BGC的面积，即可求得△ABC的面积．【解答】解：延长AG到G'，与BC相交于D，使DG＝DG′，则△BDG≌△CDG′，∴CG'＝BG＝8，∵DG＝AG＝3，∴DG＝DG′＝3，∴GG'＝6，∵CG＝10，∴△CGG'是直角三角形，∴S△GBC＝S△CGG′＝×8×6＝24，∴S△ABC＝3S△GBC＝72．故选C．【点评】此题考查了三角形重心的性质与全等三角形的判定与性质，以及三角形面积问题的求解等知识．此题难度适中，解题时要注意数形结合思想的应用．13．设二次函数y＝x2+2ax+（a＜0）的图象顶点为A，与x轴交点为B、C，当△ABC为等边三角形时，a的值为﹣．【分析】根据已知的二次函数关系式，得出顶点坐标，用含x1、x2的式子表示出BC的长度；又利用BC在△ABC中与AD的关系，即可得出一个等式，解这个式子即可得出a的值（注意舍去不符合题意的值）．【解答】解：二次函数y＝x2+2ax+（a＜0）可得其顶点坐标为（﹣a，﹣），设抛物线与x轴的两个交点为B（x1，0）、C（x2，0）则x1+x2＝﹣2a，x1•x2＝，对称轴与x轴的交点为D，∴|BC|＝|x1﹣x2|＝＝﹣a，又△ABC为等边三角形，所以|AD|＝|BC|，即＝|BC|，代入即有a2+a＝0，所以a＝﹣或a＝0（舍去）．故答案为：﹣．【点评】本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和有关三角形的一些知识．在求的结果中要注意得出值的取舍问题．14．如图，边长为1的正三角形ANB放置在边长为MN＝3，NP＝4的长方形MNPQ内，且NB在边NP上．若正三角形在长方形内沿着边NP、PQ、QM、MN翻转一圈后回到原来起始位置，则顶点A在翻转过程中形成轨迹的总长是5π（保留π）．【分析】先根据旋转的性质，正三角形ANB旋转5圈，圆心角为7个120°和2个30°，半径为1的弧，代入公式计算即可．【解答】解：如图所示：l＝•π×1＝＝5π，故答案为5π．【点评】本题考查了旋转的性质，等边三角形的性质以及弧长的计算，是一道综合题，要认真分析题目中的条件是解题的关键．三．解答题（共8小题）15．现有长为150cm的铁丝，要截成n（n＞2）小段，每段的长为不小于1（cm）的整数．如果其中任意3小段都不能拼成三角形，试求n的最大值，此时有几种方法将该铁丝截成满足条件的n段．【分析】因n段之和为定值150cm，故欲n尽可能的大，必须每段的长度尽可能小，这样依题意可构造一个数列．【解答】解：因为n段之和为定值150（cm），故欲n尽可能的大，必须每段的长度尽可能的小．又由于每段的长度不小于1（cm），且任意3段都不能拼成三角形，因此这些小段的长度只可能分别是1，1，2，3，5，8，13，21，34，55，89，但1+1+2+…+34+55＝143＜150，1+1+2+…+34+55+89＝232＞150，故n的最大值为10．将长为150（cm）的铁丝分为满足条件的10段共有以下7种方式：1，1，2，3，5，8，13，21，34，62；1，1，2，3，5，8，13，21，35，61；1，1，2，3，5，8，13，21，36，60；1，1，2，3，5，8，13，21，37，59；1，1，2，3，5，8，13，22，35，60；1，1，2，3，5，8，13，22，36，59；1，1，2，3，5，8，14，22，36，58．【点评】本题考查了三角形三边关系．正确确定什么情况下n最大，是解决本题的关键；注意各个竖列之和为143，由于150﹣143＝7，故多余的7cm要加到数列的末几项上，而且使得任何三个不构成三角形，16．已知四边形ABCD两条对角线互相垂直，点O是对角线的交点，∠ACD＝60°，∠ABD＝45°，点A到CD的距离是6，点D到AB的距离是8，求四边形ABCD的面积S．【分析】过点A作CD的垂线，过点D作AB的垂线，取AC的中点G，连接EG，证出等边△CGE 和等腰直角△BFD，根据勾股定理求出AC和DB的长度，利用面积公式即可求出四边形ABCD的面积．【解答】解：过点A作CD的垂线，E是垂足，过点D作AB的垂线，F是垂足，取AC的中点G，连接EG，在Rt△ACE中，∠AEC＝90°，∴CG＝GE，又∵∠ACD＝60°，∴△GCE是等边三角形，∴CE＝CG＝，由勾股定理，得AC2＝CE2+AE2，∴，解得：，∵∠DFB＝90°，∠ABD＝45°，∴∠FBD＝∠FDB∴△FBD是等腰直角三角形，∴．∴四边形ABCD的面积S＝S△ABD+S△BCD，＝BD•AO+BD•CO，＝，＝．答：四边形ABCD的面积S是16．【点评】本题主要考查了面积与等积变换，等边三角形的性质和判定，含30°角的直角三角形，勾股定理，等腰直角三角形等知识点，正确作辅助线求出AC和BD的长是解此题的关键．17．已知a、b、c满足方程组，试求方程bx2+cx﹣a＝0的根．【分析】由已知a、b、c满足方程组，则a+b＝8，ab＝c2﹣c+48，可把a，b看成是方程y2﹣8y+c2﹣8c+48＝0的两根，然后求出a，b，c的值再进行求解即可．【解答】解：由题意可知，a+b＝8，ab＝c2﹣c+48，因此令a，b是方程y2﹣8y+c2﹣c+48＝0的两根，∴（y﹣4）2+（c﹣）2＝0，∴y＝4且c＝，即a＝b＝4，c＝，∴bx2+cx﹣a＝0可化为4x2+x﹣4＝0，即x2+x﹣1＝0，解得x1＝，x2＝，故方程根为：x1＝，x2＝．【点评】本题考查根与系数的关系，难度较大，关键是先构造方程，然后根据非负数的性质求出a，b，c的值后再进行求解．18．如图所示，正方形ABCD的边长为1，点M、N分别在BC、CD上，使得△CMN的周长为2．求：（1）∠MAN的大小；（2）△MAN面积的最小值．【分析】（1）延长CB至L，使BL＝DN，则Rt△ABL≌Rt△ADN，故AL＝AN，进而求证△AMN≌△AML，即可求得∠MAN＝∠MAL＝45°；（2）设CM＝x，CN＝y，MN＝z，根据x2+y2＝z2和x+y+z＝2，整理根据△＝4（z﹣2）2﹣32（1﹣z）≥0可以解题．【解答】解：（1）如图，延长CB至L，使BL＝DN，则Rt△ABL≌Rt△ADN，故AL＝AN，∠1＝∠2，∠NAL＝∠DAB＝90°又∵MN＝2﹣CN﹣CM＝DN+BM＝BL+BM＝ML∴△AMN≌△AML∴∠MAN＝∠MAL＝45°（2）设CM＝x，CN＝y，MN＝z，则x2+y2＝z2，∵x+y+z＝2，则x＝2﹣y﹣z于是（2﹣y﹣z）2+y2＝z2整理得2y2+（2z﹣4）y+（4﹣4z）＝0∴△＝4（z﹣2）2﹣32（1﹣z）≥0即（z+2+）（z+2﹣）≥0又∵z＞0∴z≥﹣2当且仅当x＝y＝2﹣时等号成立此时S△AMN＝S△AML＝ML•AB＝z因此，当z＝﹣2，x＝y＝2﹣时，S△AMN取到最小值为﹣1．【点评】本题考查了勾股定理在直角三角形中的运用，考查了正方形各边长相等，各内角为直角的性质，本题中求证△AMN≌△AML是解题的关键．19．如图所示，四边形ABCD是矩形，甲、乙两人分别从A、B同时出发，沿矩形按逆时针方向前进，即按A→B→C→D→…顺序前进，已知甲的速度为每分钟65米，乙的速度为每分钟74米，问乙至少在跑第几圈时才有可能第一次追上甲？又乙至多在跑第几圈时一定能追上甲？请说明理由．【分析】可设AD＝BC＝am，AB＝CD＝bm，求出乙第一次追上甲的时间是在出发后的分钟，从而求出乙第一次追上甲所走的路程．再设这时乙所走的圈数为p，可得p＝＝4+＝9﹣，求解即可．【解答】解：设AD＝BC＝am，AB＝CD＝bm，甲的速度为65m/min，乙的速度为74m/min．由题意得，乙的速度比甲快，所以乙第一次追上甲的时间是在出发后的分钟，乙第一次追上甲所走的路程为×74（米）设这时乙所走的圈数为p，则p＝＝4+＝9﹣从而得4＜p＜9，当38a+b＜9（a+b），即当a＜b时，＜1，所以乙至少在跑第五圈时，才能第一次追上甲，又∵当7a+44b＜9（a+b），即a＞b时，＜1，所以乙至多再跑第九圈时一定能追上甲．【点评】考查了分式方程的应用，本题是关于路程中的追及问题，得到乙所走的圈数与矩形的长与宽之间的关系是解题的关键．20．已知当﹣1＜x＜O时，二次函数y＝x2﹣4mx+3的值恒大于1，求m的取值范围．【分析】分别对①当抛物线的对称轴x＝2m≤﹣1时，②当抛物线的对称轴x＝2m≥0时，即m≥0时，③当抛物线的对称轴x＝2m在区间﹣1＜x＜0时，进行分析得出m的取值范围即可．【解答】解：二次函数y＝x2﹣4mx+3的图象是一条开口向上的抛物线，①当抛物线的对称轴x＝2m≤﹣1时，即m≤﹣，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要x＝﹣1，y＝1+4m+3＝4m+4≥1，解得：m≥﹣，∴﹣≤m≤﹣，②当抛物线的对称轴x＝2m≥0时，即m≥0时，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要m≥0即可；③当抛物线的对称轴x＝2m在区间﹣1＜x＜0时，∵﹣1＜2m＜0，∴﹣＜m＜0，此时，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要＞1即可，解得：﹣＜m＜，∴﹣＜m＜0，综上所述：m的取值范围是：m≥﹣．【点评】此题主要考查了二次函数的综合应用以及二次函数最值问题，利用对称轴取值范围进行分析是解决问题的关键．21．已知在矩形ABCD中，AB＝4，BC＝，O为BC上一点，BO＝，如图所示，以BC所在直线为x轴，O为坐标原点建立平面直角坐标系，M为线段OC上的一点．（1）若点M的坐标为（1，0），如图①，以OM为一边作等腰△OMP，使点P在矩形ABCD的一边上，则符合条件的等腰三角形有几个？请直接写出所有符合条件的点P的坐标；（2）若将（1）中的点M的坐标改为（4，0），其它条件不变，如图②，那么符合条件的等腰三角形有几个？求出所有符合条件的点P的坐标；（3）若将（1）中的点M的坐标改为（5，0），其它条件不变，如图③，请直接写出符合条件的等腰三角形有几个．（不必求出点P的坐标）【分析】（1）OM的长是1，小于矩形的宽，也小于OB的长，所以点P只能是OM的垂直平分线与AD的交点；（2）OM的长是4，等于矩形的宽，所以点P可以是过O、M的垂线与AD的交点，也可以是OM的垂直平分线与AD的交点，又OM的长大于OB的长，所以点P也可以在AB上；（3）OM的长是5，大于矩形的宽，所以点P可以在过O、M的垂线与AD的交点的两侧各一个，也可以是OM的垂直平分线与AD的交点，又OM的长大于OB的长也大于MC的长，所以点P也可以在AB和CD上，共有7个．【解答】解：（1）符合条件的等腰△OMP只有1个；点P的坐标为（，4）；（2）符合条件的等腰△OMP有4个．如图②，在△OP1M中，OP1＝OM＝4，在Rt△OBP1中，BO＝，BP1＝＝＝，∴P1（﹣，）；（5分）在Rt△OMP2中，OP2＝OM＝4，∴P2（0，4）；在△OMP3中，MP3＝OP3，∴点P3在OM的垂直平分线上，∵OM＝4，∴P3（2，4）；在Rt△OMP4中，OM＝MP4＝4，∴P4（4，4）；（3）若M（5，0），则符合条件的等腰三角形有7个．点P的位置如图③所示．【点评】根据OM的长与矩形的宽的大小确定点P的位置主要在AD边上的情况，需要注意的是当OM的长大于OB（或MC）时，点P也可以在AB（或CD）上的情况，学生容易忽视．22．已知抛物线y＝ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2﹣10x+16＝0的两个根，且抛物线的对称轴是直线x＝﹣2．（1）求A、B、C三点的坐标；（2）求此抛物线的表达式；（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC 交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；（4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．【分析】（1）先解一元二次方程，得到线段OB、OC的长，也就得到了点B、C两点坐标，根据抛物线的对称性可得点A坐标；（2）把A、B、C三点代入二次函数解析式就能求得二次函数解析式；（3）易得S△EFF＝S△BCE﹣S△BFE，只需利用平行得到三角形相似，求得EF长，进而利用相等角的正弦值求得△BEF中BE边上的高；（4）利用二次函数求出最值，进而求得点E坐标．OC垂直平分BE，那么EC＝BC，所求的三角形是等腰三角形．【解答】解：（1）解方程x2﹣10x+16＝0得x1＝2，x2＝8 （1分）∵点B在x轴的正半轴上，点C在y轴的正半轴上，且OB＜OC∴点B的坐标为（2，0），点C的坐标为（0，8）又∵抛物线y＝ax2+bx+c的对称轴是直线x＝﹣2∴由抛物线的对称性可得点A的坐标为（﹣6，0）（2分）（2）∵点C（0，8）在抛物线y＝ax2+bx+c的图象上∴c＝8，将A（﹣6，0）、B（2，0）代入表达式，得：解得∴所求抛物线的表达式为y＝﹣x2﹣x+8（5分）（3）依题意，AE＝m，则BE＝8﹣m，∵OA＝6，OC＝8，∴AC＝10∵EF∥AC∴△BEF∽△BAC∴＝，即＝∴EF＝（6分）过点F作FG⊥AB，垂足为G，则sin∠FEG＝sin∠CAB＝∴＝∴FG＝•＝8﹣m∴S＝S△BCE﹣S△BFE＝（8﹣m）×8﹣（8﹣m）（8﹣m）＝（8﹣m）（8﹣8+m）＝（8﹣m）m＝﹣m2+4m（8分）自变量m的取值范围是0＜m＜8 （9分）（4）存在．理由：∵S＝﹣m2+4m＝﹣（m﹣4）2+8且﹣＜0，∴当m＝4时，S有最大值，S最大值＝8 （10分）∵m＝4，∴点E的坐标为（﹣2，0）∴△BCE为等腰三角形．【点评】本题综合考查一元二次方程的解法；用待定系数法求二次函数解析式；以及求二次函数的最值等知识点．。

j初中九年级数学竞赛试题下载

j初中九年级数学竞赛试题下载一、选择题（每题3分，共15分）1. 下列哪个数是无理数？A. πB. 0.33333（无限循环）C. √2D. 1/32. 如果一个圆的半径是5，那么它的周长是多少？A. 10πB. 20πC. 30πD. 40π3. 以下哪个方程的解集是空集？A. x^2 + 4x + 4 = 0B. x^2 - 1 = 0C. x^2 + 2x + 1 = 0D. x^2 + 3x + 2 = 04. 一个数列的前三项为1, 1, 2，从第四项开始，每一项都是前三项的和。

这个数列的第10项是多少？A. 143B. 144C. 145D. 1465. 一个长方体的长、宽、高分别是2, 3, 4，那么它的对角线长度是多少？A. 5B. √29C. √35D. √41二、填空题（每题4分，共20分）6. 如果一个三角形的三边长分别为a, b, c，且满足a^2 + b^2 =c^2，那么这个三角形是_________三角形。

7. 一个数的立方根等于它本身，这个数可能是_________。

8. 将一个圆分成四个扇形，每个扇形的圆心角为90°，那么这四个扇形的面积之和等于_________。

9. 如果一个多项式f(x) = ax^3 + bx^2 + cx + d，且f(1) = 2，f(-1) = -2，那么a + c的值是_________。

10. 一个数列的前n项和为S(n)，如果S(3) = 9，S(5) = 25，那么S(4)的值是_________。

三、解答题（每题10分，共30分）11. 证明：对于任意实数x，等式e^x ≥ x + 1成立。

12. 给定一个等差数列，首项为a1，公差为d。

如果这个数列的前n 项和为S(n)，证明S(n) = na1 + n(n-1)d/2。

13. 一个直角三角形的两条直角边分别为6和8，求斜边的长度，并证明勾股定理。

四、综合题（每题15分，共20分）14. 有一个长方体，其长、宽、高分别是a, b, c。

2024全国初中数学重点高中自招竞赛试题精选精编(解析版)

专题分式学校:___________姓名：___________班级：___________考号：___________一、填空题1(2024·全国·八年级竞赛)如图，已知在△ABC 中，点D 、E 、F 分别为边AB 、BC 、AC 上的点，且AE 、BF 、CD 相交于点G ，如果AG GE +BG GF +CG GD =2014，那么AG GE ⋅BG GF ⋅CGGD的值为．【答案】2016【分析】本题主要考查了三角形面积的计算，分式化简求值，解题的关键是设S △ABG =a ，S △ACG =b ，S △BCG =c ，得出AG GE =a +b c ，BG GF =a +c b ，CG DG =b +c a ，根据AG GE +BG GF +CG GD=2014，得出a +b c +a +cb +b +c a =2014，将a +b c ⋅a +c b ⋅b +c a 化简为a +b c +a +c b +a +b c +2即可得出答案．【详解】解：设S △ABG =a ，S △ACG =b ，S △BCG =c ，则AG GE=S △ABG S △BEG =S △ACG S △CEG =S △ABG +S △ACG S △BEG +S △CEG =S △ABG +S △ACG S △BCG =a +bc ，同理可得：BG GF =a +c b ，CG DG=b +ca ，∵AG GE +BG GF +CG GD =2014，∴a +b c +a +c b +b +c a =2014，∴AG GE ⋅BG GF ⋅CG GD =a +b c ⋅a +c b⋅b +c a =a +b a +c b +c abc=a 2b +a 2c +abc +ac 2+ab 2+abc +b 2c +bc 2abc=a +b c +a +c b +a +b c +2=2014+2=2016．故答案为：2016．2(2024·全国·八年级竞赛)设a 、b 、c 是互不相等的实数，且a +4b=b +4c =c +4a ，则abc =．【答案】±8【分析】本题考查分式的化简求值，由a +4b =b +4c 可得bc =4b -c a -b ，同理可得ac =4c -a b -c，ab =4a -bc -a，由此三式相乘即可解答．【详解】解：∵a +4b=b +4c =c +4a ，∴a -b =4c -4b =4b -c bc ，b -c =4a -4c =4c -a ac ，c -a =4b -4a =4a -b ab ，∴bc =4b -c a -b ，ac =4c -a b -c，ab =4a -bc -a ，∴a 2b 2c 2=4(b -c )a -b ⋅4(c -a )b -c.4(a -b )c -a =64，∴abc =±8．故答案为：±8．3(2024·全国·八年级竞赛)已知6x 3+2x 2-8x -1x 2-1 x 2-2 =Ax +B x 2-1+Cx +Dx 2-2其中A 、B 、C 、D 为常数，则A ⋅B ⋅C ⋅D =．【答案】-24【分析】此题主要考查了分式的加减运算，先对Ax +B x 2-1+Cx +D x 2-2进行计算，然后根据题意列出关于A 、B 、C 、D 的方程组即可解决问题，解题的关键是熟练掌握分式的运算及法则的应用．【详解】解：6x 3+2x 2-8x -1x 2-1 x 2-2 =A +C x 3+B +D x 2-2A +C x -2B +D x 2-1 x 2-2 Ax +B x 2-1+Cx +Dx 2-2=Ax +B x 2-2 x 2-1 x 2-2 +Cx +D x 2-1 x 2-1 x 2-2=A +C x 3+B +D x 2-2A +C x -2B +Dx 2-1 x 2-2，∵6x 3+2x 2-8x -1x 2-1 x 2-2 =Ax +B x 2-1+Cx +D x 2-2，∴A +C =6，B +D =2，2A +C =8，2B +D =1，解得A =2，B =-1，C =4，D =3，∴A ⋅B ⋅C ⋅D =2×-1 ×4×3=-24，故答案为：-24．4(2024·全国·八年级竞赛)已知实数x ，y 满足条件1x -1y =2x +y ，则代数式y 2x -x2y=．【答案】1【分析】本题主要考查代数式求值，先将1x -1y =2x +y 变形为2xy =y -x y +x ，再把y 2x -x2y变形为y -x y +x2xy，然后代入计算即可．【详解】解：∵1x -1y =2x +y，∴2xy =y -x y +x ，∴y 2x -x 2y=y2-x2 2xy=y-xy+x2xy=y-xy+xy-xy+x=1，故答案为：1．5(2024·全国·七年级竞赛)已知实数a、b、c满足等式a2013=b2014=c2015，且2a+b-c=8050，则a-b+12c+1=．【答案】2014【分析】本题考查了分式的化简求值，代数式求值；解题的关键是令a2013=b2014=c2015=k求出a、b、c的值．令a2013=b2014=c2015=k，求得a=2013k，b=2014k，c=2015k，结合题意求出a、b、c的值，代入即可求解．【详解】解：设a2013=b2014=c2015=k，故a=2013k，b=2014k，c=2015k，则2a+b-c=2×2013k+2014k-2015k，即2×2013k+2014k-2015k=8050，解得：k=2；∴a=4026，b=4028，c=4030，∴a-b+12c+1=4026-4028+12×4030+1=2014．故答案为：2014．6(2024·全国·八年级竞赛)已知实数x、y、z满足下列等式：xyx+y =1b-1，yzy+z=1b，xzx+z=1b+1，那么代数式xyzxy+xz+yz的值为．【答案】1 6【分析】本题考查了分式的混合运算，熟练掌握分数的混合运算法则是解题的关键．根据分式的性质将分式适当变形后进行计算即可．【详解】由题意知xy、yz、xz都不为零，∴x+yxy=b-1 y+zyz=bx+zxz=b+1，即1x+1y=3 1y+1z=4 1x+1z=5，∴1x +1y +1z =6，即xy +yz +xz xyz =6，∴xyz xy +xz +yz =16．故答案为：16．7(2024·全国·八年级竞赛)已知三个数x ，y ，z 满足xy x +y =2015，yz y +z =43，zx z +x =-43，则xyzxy +yz +zx 的值为．【答案】4030【分析】本题考查分式的化简求值，灵活运用分式的运算法则是解答的关键．将所有分式的分子和分母颠倒位置，然后利用分式的混合运算法则化简求解即可．【详解】解：将所有分式的分子和分母颠倒位置，则由xy x +y =2015得x +y xy =1x +1y =120151 ，由yz y +z =43得y +z yz =1y +1z =342 ，由zx z +x =-43得x +z xz =1x +1z =-343 ，三式相加得21x +1y +1z=12015，则1x +1y +1z =xy +yz +zx xyz =12⋅12015=14030，∴xyzxy +yz +zx=4030．8(2024·全国·八年级竞赛)如图，将一张矩形卡片按图1所示的方式分成四块后，恰好能拼成图2所示的矩形，若S ①:S ③=1:5，则a :b =．【答案】2∶3【分析】本题主要考查了整式混合运算的应用，求比值，解题的关键是理解题意，根据S ①:S ③=1:5，得出S 矩形ABFE :S 矩形EFCD =1:5，求出AE ED=15，设AE =x ，则ED =5x ，得出a +b x +5x =b ⋅5x +5x ，求出3a =2b ，即可求出结果．【详解】解：如图所示，∵S ①:S ③=1:5，∴S 矩形ABFE :S 矩形EFCD =1:5，∴a +b ⋅AE a +b ⋅ED=15，∴AE ED=15，设AE =x ，则ED =5x ，∴a +b x +5x =b ⋅5x +5x ，整理得：3a =2b ，∴a :b =2:3．故答案为：2:3．9(2024·全国·八年级竞赛)对于正数x ，规定f x =x x +1，例如f 1 =11+1=12,f 2 =22+1=23,f 12 =1212+1=13，则f 12017 +f 12016 +⋯+f 12 +f 1 +f 2 +⋯+f 2016 +f 2017 =．【答案】40332【分析】本题考查代数式求值，分式的加法以及数字类规律探究，理解新定义函数的意义，掌握数字所呈现的规律是解决问题的关键．利用加法结合律以及探究所得规律得出答案．【详解】解：∵f x =xx +1，∴f x +f 1x =x x +1+1x1x+1=x x +1+1x +1=1，∴f 12017+f 12016 +⋯+f 12 +f 1 +f 2 +⋯+f 2016 +f 2017 =f 12017 +f 2017 +f 12016 +f 2016 +⋯+f 12 +f 2+f 1 =2016+11+1=40332．故答案为：40332．10(2024·全国·八年级竞赛)若x 为正数，且x -1x =3，则x x 2-x +1=．【答案】13+112【分析】先求出x 2+1x 2=11，再求出x +1x =13，最后整体代入x x 2-x +1=1x -1+1x进求解即可，此题考查了分式的运算和二次根式的运算，熟练掌握运算法则和灵活变形是解题的关键．【详解】解：∵x 为正数，且x -1x=3，∴x -1x 2=9，x +1x >0，即x 2+1x 2=11，∴x +1x 2=x 2+1x 2+2=13，∴x +1x =13，∴x x 2-x +1=1x -1+1x =113-1=13+112，故答案为：13+11211(2024·全国·八年级竞赛)已知x =2y +33y -2，则3x -2 3y -2 的值为．【答案】13【分析】本题考查了分式的混合运算，多项式乘以多项式，根据x 的值和题中式子即可求解，根据解题的关键是明确它们各自的计算方法．【详解】解：∵x =2y +33y -2，∴3x -2=6y +93y -2-2=6y +9-6y +43y -2=133y -2，∴3x -2 3y -2 =133y -2×3y -2 =13，故答案为：13．12(2024·全国·八年级竞赛)比较大小：22000+122001+1-22001+122002+10(填“>”、“=”或“<”)．【答案】>【分析】本题考查了实数的比较大小，异分母分式的运算．熟练掌握以上知识点并灵活运用是解题的关键．设a =22000，根据22000+122001+1-22001+122002+1=a +12a +1-2a +14a +1=a 8a 2+6a +1>0作答即可．【详解】解：设a =22000，∴22000+122001+1-22001+122002+1=a +12a +1-2a +14a +1=a 8a 2+6a +1>0，故答案为：>．13(2024·全国·八年级竞赛)已知11的小数部分为a ．则a 2-6a +9a 2+7a +12÷a -3a +4-aa +3=．【答案】-31111/-31111【分析】本题考查了分式的混合运算，无理数的估算，分母有理化，先根据分式的运算法则把所给代数式化简，再求出a 的值，然后代入化简后的结果计算即可．【详解】解：a 2-6a +9a 2+7a +12÷a -3a +4-aa +3=a -3 2a +3 a +4 ×a +4a -3-a a +3=a -3a +3-a a +3=-3a +3，∵3<11<4，∴11的整数部分3，∴a =11-3．∴-3a +3=-31111．故答案为：-31111．14(2024·全国·八年级竞赛)函数y =x -4-2-x -3x -5的自变量x 的取值范围是．【答案】x ≥3且x ≠4且x ≠5【分析】本题考查确定函数自变量取值范围．熟练掌握负整指数幂有意义的条件，二次根式有意义的条件，分式有意义的条件是解题的关键．根据题意得不等式组x -3≥0x -4≠0，x -5≠0求解即可．【详解】解：根据题意，得x -3≥0x -4≠0，x -5≠0∴x ≥3且x ≠4且x ≠5．故答案为：x ≥3且x ≠4且x ≠5．15(2024·全国·八年级竞赛)如果对于分式3x 2+4x +m，存在两个数使分式没有意义，则m 的取值范围是．【答案】m <4【分析】本题主要考查了分式有意义的条件、一元二次方程根的判别式等知识点，理解分式有意义的条件是解题的关键．由存在两个数使分式没有意义，则对于x 2+4x +m =0的判别式Δ>0，据此列不等式求解即可．【详解】解：∵分式3x 2+4x +m，存在两个数使分式没有意义，∴x 2+4x +m =0有两个解，∴Δ=42-4m >0，解得：m <4，∴当m <4时，存在两个实数使原式没有意义．故答案为m <4．二、单选题16(2024·全国·九年级竞赛)要使式子x +6x有意义，则x 的取值范围是()A.x ≥-6B.x ≠0C.x >6D.x ≥-6且x ≠0【答案】D【分析】本题主要考查了二次根式有意义的条件，分式有意义的条件．熟练掌握概念是解题的关键．分子上的二次根式要有意义，根号里面的式子为非负数，且分母不为零，分别求解满足条件的x 值．【详解】∵式子x +6x有意义，∴x +6≥0，x ≠0，∴x ≥-6且x ≠0．故选：D ．17(2024·全国·八年级竞赛)已知1x +1y =2，则2x +3xy +2y 3x -2xy +3y的值为()A.74B.72C.5D.12【答案】A【分析】本题考查分式的化简求值，根据1x +1y =2得x +y =2xy ，再将2x +3xy +2y 3x -2xy +3y的分子分母变形为含xy 的式子，即可解题．【详解】解：由1x +1y=2得x +y =2xy ，则2x +3xy +2y 3x -2xy +3y =2x +y +3xy 3x +y -2xy =7xy 4xy =74．故选：A ．18(2024·全国·八年级竞赛)已知实数x ，y 满足x +y =2，xy =-5，则xy +y x 的值为( )．A.65B.-145C.-65D.-45【答案】B【分析】本题考查了分式的化简求值，配方法，熟练掌握完全平方公式是解答本题的关键．先将xy +y x通分，然后将分子配方，并将分式化简成只含x +y ，xy 的代数式，最后将x +y ，xy 的值代入并计算即得答案．【详解】xy +y x =x 2+y 2xy=x 2+2xy +y 2-2xy xy=(x +y )2xy -2，当x +y =2，xy =-5时，原式=22-5-2=-145．故选B．19(2024·全国·八年级竞赛)若分式x-1x -2的值为正数，则x的取值范围是()A.1<x<2或x<-2B.x<-2或x>2C.-2<x<1或x>2D.-2<x<2【答案】C【分析】根据题意列出不等式组，解不等式组则可．此题考查分式的值，解不等式组，解题关键在于根据题意列出不等式组．【详解】解：∵分式x-1x -2的值为正数，∴x -2>0x-1>0或x -2<0x-1<0，解得：-2<x<1或x>2.故选：C．20(2024·全国·七年级竞赛)灰太狼在跑一段山路时，上山速度是80米/分，到达山顶后再下山，下山的速度是上山速度的3倍，如果上、下山的路程相同，那么灰太狼跑这段山路的平均速度是()A.160米/分B.140米/分C.60米/分D.120米/分【答案】D【分析】本题考查了分式乘除的应用，整式加减的应用，正确理解题中的数量关系是解答本题的关键，设上坡的路程为S，则上、下坡的总路程为2S，可逐步求得上下坡的总时间，最后利用平均速度等于上、下坡的总路程除以总时间，计算即得答案．【详解】设上坡的路程为S，则上、下坡的总路程为2S，上坡时间为S80，下坡时间为S80×3=S240，总时间为S80+S240=S60，所以平均速度为2S÷S60=120(米/分)．故选D．21(2024·全国·八年级竞赛)若xx2+x+1=15，则x2x4+x2+1=()A.5B.115C.4 D.14【答案】B【分析】本题考查分式的化简求值和完全平方公式，根据xx2+x+1=15得出x+1x=4，再将x2x4+x2+1变形为1x+1x2-1，将x+1x=4整体代入求值即可．【详解】解：∵xx2+x+1=1x+1x+1=15，∴x+1x=4，∴x2x4+x2+1=1x2+1x2+1=1x+1x2-1=142-1=115，故选B．22(2024·全国·八年级竞赛)若x2-3x+1=0，则x2x4+x2+1的值是( )．A.8B.110C.18D.14【答案】C【分析】本题考查了分式的混合运算，完全平方公式变形求值，换元法，由x2-3x+1=0得到x2+1x2=7，设x2x4+x2+1=A，得到1A=x2+1x2+1，代入即可求解，掌握完全平方公式是解题的关键．【详解】解：由x2-3x+1=0知x≠0，∴x+1x=3，∴x2+1x2=7，设x2x4+x2+1=A，则1A=x2+1x2+1=8，∴A=18，即x2x4+x2+1=18，故选：C．三、解答题23(2024·全国·九年级竞赛)若x-3x-2=13+2+1，求1-1x-2÷x-4+1x-2的值．【答案】3+2【分析】本题考查了分式的化简求值，涉及整体代入法；先化简分式，再由x-3x-2=13+2+1，得到x-2 x-3=3+2+1，变形为1+1x-3=3+2+1，即可求得1x-3的值．关键是由已知变形求得1x-3．【详解】解：1-1 x-2÷x-4+1x-2=x-3 x-2÷x2-6x+9x-2=x-3 x-2·x-2 x-3 2=1x-3；∵x-3 x-2=13+2+1，∴x-2x-3=3+2+1，∴1+1x-3=3+2+1，∴1x-3=3+2，即原式=3+2．24(2024·全国·九年级竞赛)已知实数a 满足a 2+2a -2016=0，求a 2-2a +1a 2+5a +4×a +4a 2-1-1a +1的值．【答案】-22017．【分析】此题考查了分式的化简求值，先把要求的式子进行计算，先进行因式分解，再把除法转化成乘法，然后进行约分，得到一个最简分式，最后把a 2+2a -2016=0进行配方，得到a +1 2=2017的值，再把它整体代入即可求出答案，解题的关键是熟练掌握分式化简的步骤．【详解】解：由a 2+2a -2016=0可得(a +1)2=2017，a 2-2a +1a 2+5a +4×a +4a 2-1-1a +1=(a -1)2a +1 a +4 ×a +4a -1 a +1-1a +1，=a -1(a +1)2-1a +1，=-2(a +1)2，=-22017．25(2024·全国·八年级竞赛)先化简，再求值：x 2-1x 2+x÷x +1x -2 ，其中x =2．【答案】1x -1，2+1【分析】本题考查了分式的混合运算以及分母有理化，解答时，先进行分式运算，再代入求值即可．【详解】解：x 2-1x 2+x÷x +1x -2 =x -1 x +1 x x +1 ÷x 2+1-2x x =x +1 x -1x x +1÷x -12x =x +1 x -1 x x +1 ⋅x x -1 2=1x -1，当x =2时，原式=12-1=2+1．26(2024·全国·八年级竞赛)如图1，有一个高为hcm 的瓶子，瓶中水面的高度为acm ，盖好瓶盖后倒置，这时瓶中水面的高度为bcm ，如图2，用代数式表示瓶中水的体积与瓶子容积之比；当a =9,b =15,h =21时，求出这个比值．【答案】a a +h -b ，35【分析】此题考查圆柱体体积的应用，解题的关键是理解掌握“转化”的思想方法在推导过程中的应用．根据“瓶子容积等于正放时水的体积加倒放时空白的体积”，即可列式；瓶子容积等于正放时水的体积加倒放时空白的体积，即底面积×9+底面积×21-15 ，也就是底面积×15；水的体积为底面积×9，即可得到答案．【详解】解：瓶子容积等于正放时水的体积加倒放时空白的体积，设瓶子的底面积为S ，即Sa +S h -b ；水的体积为Sa ，∴瓶中水的体积与瓶子容积之比为Sa Sa +S h -b=aa +h -b ，∵瓶子的容积=底面积×9+底面积×21-15 =底面积×15，水的体积=底面积×9，∴瓶中水的体积：瓶子容积=(底面积×9)：(底面积×15)=35，答：这个比值是35．27(2024·全国·八年级竞赛)(1)求证：1+1n 2+1(n +1)2=1+1n 2+n2；(2)计算：1+112+122+1+122+132+⋯+1+120162+120172．【答案】(1)证明见解析(2)201620162017【分析】本题主要考查了分式的化简求值，数字规律的运算；对于(1)，先将等式左边通分，再根据完全平方公式整理可得答案；对于(2)，先根据(1)整理得1+1n 2+1n +1 2=1+1n n +1 =1+1n -1n +1，再计算加减即可得出答案．【详解】(1)解：1+1n 2+1n +12=n 2n +1 2+n +1 2+n 2n 2n +1 2=n 2n +1 2+2n n +1 +1n 2n +1 2=n n +1 +1n n +12=1+1n 2+n2；(2)由(1)可知1+1n 2+1n +1 2=1+1n n +1=1+1n -1n +1，则原式=1+11-12+1+12-13+1+13-14+⋯+1+12016-12017=1×2016+1-12017=201620162017．28(2024·全国·八年级竞赛)(1)计算24×13-4×18×(2015-2016)0；(2)先化简，再求值：x 2-y 2x 2-2xy +y 2+xy -x÷y 2x 2-xy，其中x 、y 满足x +1+(y -3)2=0．【答案】(1)2(2)化简得：x y ；原式=33【分析】本题考查有理数的运算和分式的化简求值，熟练掌握二次根式的运算和正确化简分式是解题的关键，(1)根据二次根式的运算法则和零指数幂即可得到结果；(2)直接利用括号里面因式分解进行化简，再利用分式乘除运算法则化简，再根据二次根式、绝对值的性质得出x 、y 的值，进行代入求出答案．【详解】解：(1)原式=26×33-4×24×1=22-2=2；(2)原式=x -y x +y x -y2+x y -x ×x x -y y 2=x +y x -y -xx -y×x x -y y 2=yx -y ×x x -y y 2=x y．∵x +1+(y -3)2=0，∴x -1=0，y -3=0，∴x =1，y =3，故原式=x y =13=33．29(2024·全国·七年级竞赛)已知a 、b 、c 均为大于1的正整数，且1a <1b <1c ,1a +1b +1c -1abc为正整数．求a +b +c 的值．【答案】10【分析】本题考查异分母分式的加减，先得出1<1a +1b+1c <3c ，求出c =2，进而得出a =4或5，当a =4,b =3,c =2时，1a +1b +1c -1abc =2524(舍)．当a =5,b =3,c =2时，1a +1b +1c -1abc=1，进而可得出答案．【详解】解：因为1a +1b +1c -1abc 为正整数，且a 、b 、c 为大于1的正整数，1a <1b <1c ，所以1<1a +1b+1c <3c ，得1<c <3，所以c =2，∴1a +1b >1-1c =12，得12<1a +1b <2b ，所以c <b <4,∴b =3．∴1a >1-1b -1c =16，得b <a <6，所以a =4或5，当a =4,b =3,c =2时，1a +1b +1c -1abc =2524(舍)．当a =5,b =3,c =2时，1a +1b+1c -1abc=1，所以a +b +c =5+3+2=10．30(2024·全国·八年级竞赛)如果a 、b 、c 是不同的实数，且a 3+3a +15=b 3+3b +15=c 3+3c +15=0，求1a +1b+1c 的值．【答案】-15【分析】本题考查分式的求值，根据a 3+3a +15=b 3+3b +15=c 3+3c +15=0，得到a 、b 、c 都是方程x 3+3x +15=0的根，进而得到x 3+3x +15=x -a x -b x -c ，推出abc =-15，ab +bc +ac =3，即可得出1a +1b+1c 的值．解题的关键是得到x 3+3x +15=x -a x -b x -c ．【详解】解：1a +1b +1c =ac +bc +acabc，∵a 、b 、c 是不同的实数，且a 3+3a +15=b 3+3b +15=c 3+3c +15=0，∴a 、b 、c 都是方程x 3+3x +15=0的根．∴x 3+3x +15=x -a x -b x -c ，∴abc =-15，ab +bc +ac =3．∴1a +1b+1c =3-15=-15．31(2024·全国·八年级竞赛)求值：12+13+14+15+1⋯+12007+11+11+13+14+15+1⋯+【答案】1【分析】本题考查了繁分式的计算，设1+13+14+1⋯+12007=x ，变形计算即可．【详解】解：设1+13+14+1⋯+12007=x ，则原式=11+x +11+1x=11+x +x x +1=1+x1+x =1．32(2024·全国·八年级竞赛)设a ，b ，c 都是实数，若(a -2b +c )2+(a -2c +b )2+(b -2a +c )2=(a -b)2+(b-c)2+(c-a)2，求分式2ab2+7(2ab+6)2bc2+7(bc+3)的值．【答案】2【分析】本题主要考查了分式化简求值，解题的关键是熟练掌握分式的性质．设a-b=x,b-c=y,c-a =z，得出x2+y2+z2-2xy-2yz-2zx=0①，x+y+z2=x2+y2+z2+2xy+2yz+2zx=0②，由①+②得x2+y2+z2=0，求出x=y=z=0，则a=b=c，代入进行变形求值即可．【详解】解：设a-b=x,b-c=y,c-a=z，由已知得：(x-y)2+(y-z)2+(z-x)2=x2+y2+z2，故x2+y2+z2-2xy-2yz-2zx=0，①又x+y+z=a-b+b-c+c-a=0，故x+y+z2=x2+y2+z2+2xy+2yz+2zx=0，②①+②得x2+y2+z2=0，故x=y=z=0，则a=b=c，∴原式=22a3+7a2+32a3+7a2+3=2．。

初三数学竞赛试题及答案

初三数学竞赛试题及答案一、选择题1. 已知平面内一直线L的倾斜角为α，斜率为k，若点A(-1,2)在L 上，则直线L的方程为：A. y-2 = k(x+1)B. y+2 = k(x-1)C. y-2 = k(x-1)D. y+2 = k(x+1)答案：A2. 若函数f(x) = ax^2 + bx + c 是一个减函数，那么a, b, c的关系是：A. a > 0, b > 0, c > 0B. a > 0, b < 0, c < 0C. a < 0, b < 0, c < 0D. a < 0, b > 0, c > 0答案：D3. 已知等差数列{an}的公差为d，首项为a1，末项为an，且an =3a1，若a4 = 7，则d的值是：A. 1B. 2C. 3D. 4答案：B4. 在ΔABC中，∠A=60°，AC=2AB，则∠B的度数为：A. 40°B. 50°C. 60°D. 70°答案：D5. 若直角三角形的两直角边分别为3和4，求斜边的长度是：A. 5B. 6C. 7D. 8答案：A二、填空题1. 已知ABC是一个等边三角形，AB的边长为5，则三角形ABC 的面积为______。

答案：(25√3)/42. 若一组数据中50%的数据小于等于10，25%的数据大于15，中位数为12，则这组数据的总个数为______。

答案：83. 若甲数是乙数的8倍，且甲数减去乙数等于30，则甲数的绝对值为______。

答案：404. 已知某数的60%等于120，这个数是______。

答案：2005. 若甲数是乙数的1/5，乙数是丙数的1/3，则甲数与丙数之和的三倍为______。

答案：28三、解答题1. 一条细长导线的电阻率R为ρ，长度为l，截面积为A。

如果将导线的长度翻倍，截面积减半，则新的导线的电阻率是多少？答：R2. 已知函数f(x)满足f(x+1) = 2f(x) - 1，且f(2) = 3，求f(5)的值。

全国各地初中(九年级)数学竞赛《函数》真题大全 (附答案)

全国各地初中（9年级）数学竞赛专题大全竞赛专题6 函数一、单选题1．（2021·全国·九年级竞赛）2420x x y -+，则x y -的值为（）． A ．2B ．6C ．2或2-D ．6或6-2．（2021·全国·九年级竞赛）如图，两个反比例函数1k y x=和2ky x =在第一象限内的图象分别是1l 和2l ，设点P 在1l 上，PC x ⊥轴于点C ，交2l 于点,A PD y ⊥轴于点D ，交2l 于点B ，则四边形PAOB 的面积为（）．A ．12k k +B ．12k k -C ．12k kD ．21k k -3．（2021·全国·九年级竞赛）如右图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线交双曲线1y x=于点Q ，连接OQ ，当点P 向右运动时，Rt QOP 的面积（）．A ．逐渐增大B ．逐渐减小C ．保持不变D ．无法确定4．（2021·全国·九年级竞赛）设a ，b ，c 是ABC 三边的长，二次函数2()22b b y a x cx a =----在1x =取最小值83b -，则ABC 是（）A ．等腰三角形B ．锐角三角形C ．钝角三角形D ．直角三角形5．（2021·全国·九年级竞赛）若函数22(1)32y k x x k k =++++-的图象与x 轴交点的纵坐标为4-，则k 的值是（） A ．1-B ．2-C ．1-或2D ．1-或2-6．（2021·全国·九年级竞赛）设[]x 表示不超过实数x 的最大整数，{}[]x x x =-，则200983201083401783200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤+++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦（）． A ．249075 B ．250958 C ．174696 D ．2510007．（2021·全国·九年级竞赛）在实数范围内，设1988(2)(1)(2)(1)511111a a a a a x a a ⎡⎤--+--⎢⎥+=⎢⎥-⎢⎥+-⎣⎦，则x 的个位数字是（）． A ．1B ．2C ．4D ．68．（2021·全国·九年级竞赛）设抛物线24y x kx =++与x 轴有两个不同交点()()12,0,,0x x ，则下列结论中一定成立的是（）．A ．221217x x += B ．22128x x +=C ．221217x x +< D ．22128x x +>9．（2021·全国·九年级竞赛）设Rt ABC △的三个顶点A ，B ，C 均在抛物线2y x 上，并且斜边AB 平行于x 轴，若斜边上的高为h ，则（） A ．1h <B ．1h =C ．12h <<D ．2h >10．（2021·全国·九年级竞赛）设,n k 为正整数，12132(3)(1)4,(5)4,(7)4A n n A n A A n A +-+=++=++431(9)4,,(21)4,k k A n A A n k A -++=+++，已知1002005A =，则n 的值为（）．A ．1806B ．2005C ．3612D ．4100二、填空题11．（2021·全国·九年级竞赛）边长为整数的等腰三角形一腰上的中线将其周长分为1:2的两部分，那么所有这些等腰三角形中，面积最小的三角形的面积是_________． 12．（2021·全国·九年级竞赛）若0abc ≠，则||||||||a b c abca b c abc +++的最大值是________，最小值是__________． 13．（2021·全国·九年级竞赛）若0x >，则24411x x x y ++-+=的最大值是________．14．（2021·全国·九年级竞赛）设x 为正实数，则函数21y x x x=-+的最小值是______．15．（2021·全国·九年级竞赛）已知,a b 为抛物线()()2y x c x c d =----与x 轴交点的横坐标，a b <，则||||a c c b -+-的值为______．16．（2021·全国·九年级竞赛）设正ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上任意一点，PA PM 十的最大值和最小值分别记为s 和t ，则22s t -=_______． 17．（2021·全国·九年级竞赛）若2008个数122008,,,a a a 满足：12a =，2n a -1112008n n n a a a --⎛⎫+ ⎪⎝⎭102008+=，其中，2n =，3，…，2008．那么2008a 可能达到的最大值是_________．18．（2021·全国·九年级竞赛）设333199519961997,0x y z xyz ==>，且2223333199519961997199519961997x y z ++111x y z++=_______． 19．（2021·全国·九年级竞赛）如果代数式535ax bx cx ++-当2x =-时的值为7，那么当2x =时，该式的值是_________．20．（2021·全国·九年级竞赛）函数23||7y x x =-+的图象与函数22336y x x x x =-+-+的图象的交点个数是_______．21．（2021·全国·九年级竞赛）不论m 取任何实数，抛物线2221y x mx m m =+++-的顶点都在一条直线上，则这条直线的解析式是______．22．（2021·全国·九年级竞赛）如果一次函数y mx n =+与反比例函数3n x y x -=的图象相交于点1,22⎛⎫⎪⎝⎭，那么该直线与双曲线的另一个交点为________．23．（2021·全国·九年级竞赛）函数|1||2||3|y x x x =+++++，当x =_______时，y 有最小值，最小值等于_______．24．（2021·全国·九年级竞赛）当x 变化时，分式22365112x x x x ++++的最小值是_______．25．（2021·全国·九年级竞赛）代数式21133110x x +的最小值是_______．26．（2021·全国·九年级竞赛）已知a ，b 是正数，并且二次函数22y x ax b =++和22y x bx a =++的图象都与x 轴相交，则22a b +的最小值是________．三、解答题27．（2021·全国·九年级竞赛）在直径为5的圆内放入10个点，证明其中必有两点的距离小于2． 28．（2021·全国·九年级竞赛）试求1231997x x x x -+-+-++-的最小值．29．（2021·全国·九年级竞赛）当12x ≤≤2121x x x x +---30．（2021·全国·九年级竞赛）一幢33层的大楼里有一部电梯停在第一层，它一次最多容纳32人，而且只能在第2层至第33层中某一层停一次．对每个人来讲，他往下走一层楼感到1分不满意，往上走一层感到3分不满意．现有32个人在第一层，并且他们分别住在第2层至第33层的每一层，问：电梯停在哪一层，可以使得这32个人不满意的总分达到最小值？最小值是多少？（有些人可以不坐电梯直接从楼梯上楼） 31．（2021·全国·九年级竞赛）求函数22233x y x x +=++的最大值和最小值．32．（2021·全国·九年级竞赛）已知,,a b c 都是正整数，且抛物线2y ax bx c =++与x 轴有2个不同的交点A 和B ，若,A B 到原点的距离都小于1，求a b c ++的最小值．33．（2021·全国·九年级竞赛）求2221026249T x y z xy yz z =++---+的最小值．34．（2021·全国·九年级竞赛）在40与100之间任取一个实数x ，如果[]7x =，那么1610x ⎡=⎣的概率是多少?这是[]a 表示不超过a 的最大整数（要求答案写成最简分数的形式）．35．（2021·全国·九年级竞赛）如图，D E F 、、分别是ABC 的三边BC CA AB 、、上任意一点，证明：,,AEF BFD CDE △△△中至少有一个三角形的面积不大于ABC 的面积的四分之一．36．（2021·全国·九年级竞赛）某林场安排了7天的植树工作，从第二天起每天都比前一天增加5个植树的人，但从第二天起每人每天都比前一天少植5棵树，且同一天植树的人，植相同数量的树．若7天共植树9947棵，则植树最多的那天共植了多少棵？植树最少的那天，有多少人在植树？37．（2021·全国·九年级竞赛）一幢33层的大楼有一部电梯停在第一层，它一次最多能容纳32人，而且只能在第2层至第33层中某一层停一次．对于每个人来说他往下走一层楼梯感到1分不满意，往上走一层楼梯感到3分不满意．现在有32个人在第一层，并且他们分别在第2至第33层的每一层，问：电梯停在哪一层，可以使32人不满意的总分达到最小？最小值是多少？（有些人可以不坐电梯而直接从楼梯上楼）． 38．（2021·全国·九年级竞赛）已知正整数m ，n 17434m m n -+=，求n 的最大值． 39．（2021·全国·九年级竞赛）对于1,2,3,,i n =，有|| 1 i x <且有12||||||n x x x +++=122009||n x x x ++++．求正整数n 的最小值．40．（2021·全国·九年级竞赛）整数012010,,,x x x 满足条件：00x =，10|||1|x x =+，21|||1|x x =+，…，201020091x x =+，求122010x x x +++的最小值．41．（2021·全国·九年级竞赛）平面内给定一个方向l 和一个凸图形F ，其面积为()S F ，内接于F 且有一边平行于l 的所有三角形中面积最大的记为，其面积记()S ．求最大正实数c ，使对平面内任意给定的凸图形F ，都有()()S c S F ≥⋅．42．（2021·全国·九年级竞赛）已知x ，y ，z 是正数且1x y z ++=，比较149A x y z=++与36B =的大小，并问A 能否等于B ?43．（2021·全国·九年级竞赛）（1）证明：若x 取任意整数时，二次函数2y ax bx c =++总取整数值，那么2,,a a b c -都是整数；（2）写出上述命题的逆命题，并判断真假，且证明你的结论．44．（2021·全国·九年级竞赛）已知一次函数12y x =，二次函数221y x =+，是否存在二次函数23y ax bx c =++，其图象经过点(5,2)-，且对任意实数，这三个函数对应的函数值123,,y y y ，都有132y y y ≤≤成立？若存在，求出函数3y 的解析式；若不存在，请说明理由．45．（2021·全国·九年级竞赛）点(4,0),(0,3)A B 与点C 构成边长是3,4,5的直角三角形．如果点C 在反比例函数ky x=的图象上，求k 可能取到的一切值． 46．（2021·全国·九年级竞赛）已知一次函数y ax b =+的图象经过点(3,32),(3),(,2)A B C c c --，求222a b c ab bc ca ++---的值．47．（2021·全国·九年级竞赛）如图，在直角梯形OABC 中，//OA BC ，A ，B 两点的坐标分别是(13,0)A ，(11,12)B ，动点P ，Q 分别从O ，B 两点同时出发，点P 以每秒3个单位长的速度沿OA 方向运动，点Q 以每秒1个单位长的速度沿线段BC 运动，线段OB 与PQ 的交点为D ，过D 作//DE OA 交AB 于E ，射线QE 交x 轴于点F ，设P ，Q 运动的时间为t 秒．（1）当t 为何值时，以P A B Q 、、、为顶点的四边形是平行四边形，请写出推理过程．（2）设以P A E Q 、、、为顶点的图形面积为y ，求y 关于运动时间t 的函数关系式，并求出y 的最大值．（3）当t 为何值时，PQF △为等腰三角形？请写出推理过程．48．（2021·全国·九年级竞赛）已知抛物线21:34c y x x =--+和抛物线22:34c y x x =--相交于A ，B 两点，点P 在抛物线1c 上，且位于点A 与点B 之间；点Q 在抛物线2c 上，也位于点A 与点B 之间．（1）求线段AB 的长；（2）当//PQ y 轴时，求PQ 长度的最大值．49．（2021·全国·九年级竞赛）已知x ，y ，z 为实数，且满足2023x y z x y z +-=⎧⎨-+=⎩，求222x y z ++的最小值．50．（2021·全国·九年级竞赛）函数22(21)y x k x k =+-+的图象与x 轴的两个交点是否都在直线1x =的右侧，若是，请说明理由；若不一定，请求出两个交点在直线1x =的右侧时，k 的取值范围．竞赛专题6 函数答案解析一、单选题1．（2021·全国·九年级竞赛）2420x x y -+，则x y -的值为（）． A ．2 B ．6C ．2或2-D ．6或6-【答案】D 【解析】【分析】【详解】解：2420x x y -+，2420x x y -+=，240x -，20x y +=，即2,2x y x =±=-，于是()236x y x x x -=--==或6-．故选：D ．2．（2021·全国·九年级竞赛）如图，两个反比例函数1k y x=和2ky x =在第一象限内的图象分别是1l 和2l ，设点P 在1l 上，PC x ⊥轴于点C ，交2l 于点,A PD y ⊥轴于点D ，交2l 于点B ，则四边形PAOB 的面积为（）．A ．12k k +B ．12k k -C ．12k kD ．21k k -【答案】B 【解析】【分析】【详解】OACOBDPOOD PAOB S S SS=--长方形四边形．设(,),(,),(,)P a b A c d B e f ，则122,,ab k cd k ef k ===，所以12212111111222222PAOB S PC PD AC OC BD OD ab cd ef k k k k k =⨯-⨯⨯-⨯⨯=--=--=-四边形．故选：B ．3．（2021·全国·九年级竞赛）如右图，点P 是x 轴正半轴上一个动点，过点P 作x 轴的垂线交双曲线1y x=于点Q ，连接OQ ，当点P 向右运动时，Rt QOP 的面积（）．A ．逐渐增大B ．逐渐减小C ．保持不变D ．无法确定【答案】C 【解析】【分析】【详解】设(,)Q a b ，则,OP a PQ b ==，且1b a=，所以111222OPQS OP PQ ab =⨯⨯=⨯=．故选：C ．4．（2021·全国·九年级竞赛）设a ，b ，c 是ABC 三边的长，二次函数2()22b by a x cx a =----在1x =取最小值83b -，则ABC 是（）A ．等腰三角形B ．锐角三角形C ．钝角三角形D ．直角三角形【答案】D 【解析】【分析】【详解】解依题意可得2220,,42,231,2,52()52338()223ba b a a b c b c a a b c ABC b a c b c b b b a c a b⎧⎪->⎧⎪>⎧⎪⎪=⎪⎪-⎪⎪=⇒+=⇒⇒+=⇒⎨⎨⎨⎪⎪⎪-=⎪⎪⎪=⎩⎩⎪----=-⎪⎩是直角三角形．故应选D ．注：从前面的例题可以看出，解有关二次函数的最值问题，不仅要熟悉有关二次函数的性质，还要灵活运用相关的不等式知识、几何知识等，才能使问题得到顺利解决．5．（2021·全国·九年级竞赛）若函数22(1)32y k x x k k =++++-的图象与x 轴交点的纵坐标为4-，则k 的值是（） A ．1- B ．2-C ．1-或2D ．1-或2-【答案】B【分析】【详解】解因0x =时，4y =-代入函数关系得2432k k -=+-，即(1)(2)0k k ++=，所以1k =-或2k =-．故应选D ．注：本题中的函数可以是一次函数，也可以是二次函数．不能一开始就默认它是二次函数，约定10k +≠，从而错误地选择了B ．6．（2021·全国·九年级竞赛）设[]x 表示不超过实数x 的最大整数，{}[]x x x =-，则200983201083401783200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤+++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦（）． A ．249075 B ．250958 C ．174696 D ．251000【答案】A 【解析】【分析】【详解】原式(20090)83(20091)83(20092008)83200920092009+⨯+⨯+⨯⎡⎤⎡⎤⎡⎤=+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦083183200883838383200920092009⨯⨯⨯⎡⎤⎡⎤⎡⎤=++++++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦083183200883083183200883832009200920092009200920092009⨯⨯⨯⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯++++----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭83083183200883200983(122008)2009200920092009⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯++++----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭083183200883200983831004200920092009⨯⨯⨯⎧⎫⎧⎫⎧⎫=⨯+⨯----⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭．显然，2009与83互质，083,183,,200883⨯⨯⨯除以2009有2009个不同的余数．所以，08318320088301200810042009200920092009⨯⨯⨯+++⎧⎧⎫⎧⎫+++==⎨⎨⎬⎨⎬⎩⎩⎭⎩⎭．故原式200983831004100416674782328249075=⨯+⨯-=+=．7．（2021·全国·九年级竞赛）在实数范围内，设1988(2)(1)(2)(1)511111a a a a a x a a ⎡⎤--+--⎢⎥+=⎢⎥-⎢⎥+-⎣⎦，则x 的个位数字是（）． A ．1 B ．2C ．4D ．6【答案】D【分析】【详解】解：要使x 有意义，必须且只需(2)(1)0,(2)(1)0,(2)(1)0,1,110,21101a a a a a a a a a a a⎧--≥⎪⎧--=--≥⎪⎪⎪⇒≠⇒=-⎨⎨-≠⎪⎪≠⎩⎪+≠⎪-⎩．所以1988198********05(1)1()(2)(2)1611(1)12x ⨯⨯-+=+=-=-=--+，故x 的个位数字为6，故选：D ．8．（2021·全国·九年级竞赛）设抛物线24y x kx =++与x 轴有两个不同交点()()12,0,,0x x ，则下列结论中一定成立的是（）．A ．221217x x += B ．22128x x += C ．221217x x +< D ．22128x x +> 【答案】D 【解析】【分析】【详解】由2244016k k =-⨯>⇒>．又因1212,4x x k x x +=-=，所以()2222121212281688x x x x x x k +=+-=->-=．故选：D ．9．（2021·全国·九年级竞赛）设Rt ABC △的三个顶点A ，B ，C 均在抛物线2y x 上，并且斜边AB 平行于x 轴，若斜边上的高为h ，则（） A ．1h < B ．1h = C ．12h << D ．2h >【答案】B 【解析】【分析】【详解】解设A 的坐标为()2,a a ，点C 的坐标为()2,(|||| )c c c a <，则B 点的坐标为()2,a a -．由勾股定理可得()22222()AC a c a c =-+-，()22222()BC c a a c =++-，则22222(2)4AC BC AB a a +===，于是()()222222224a c a c a ++-=，即()22222a c a c -=-．由于22a c >，所以221a c -=，即斜边上的高h =（A 的纵坐标）-（C 的纵坐标）221a c =-=．注：（1）如图仅画出了0c a <<的情形，在其他情形下，计算是完全相同的．（2）设()()1122,,,A x y B x y ，利用勾股定理可得计算A 与B 的距离的公式为()()2222121AB x x y y =-+-．10．（2021·全国·九年级竞赛）设,n k 为正整数，12132(3)(1)4,(5)4,(7)4A n n A n A A n A +-+=++=++431(9)4,,(21)4,k k A n A A n k A -++=+++，已知1002005A =，则n 的值为（）．A ．1806B ．2005C ．3612D ．4100【答案】A 【解析】【分析】【详解】2221[(1)2][(1)2]4(1)24(1)1A n n n n n +++-+=+-++=+， 2222[(3)2][(3)2]4(3)24(3)3A n n n n n +++-+=+-+=+=+， 2223[(5)2][(5)2]4(5)24(5)5A n n n n n +++-++-+++，同理451007,9,,21001199200520051991806A n A n A n n n =+=+=+⨯-=+=⇒=-=．故选：A ．二、填空题11．（2021·全国·九年级竞赛）边长为整数的等腰三角形一腰上的中线将其周长分为1:2的两部分，那么所有这些等腰三角形中，面积最小的三角形的面积是_________． 37【解析】【分析】设等腰三角形的腰为x ，底为y ，周长被分为的两部分的长分别为n 和2n ，则222x x n x y n ⎧+=⎪⎪⎨⎪+=⎪⎩或222x x n x y n ⎧+=⎪⎪⎨⎪+=⎪⎩，解得25(,),33n n x y ⎛⎫= ⎪⎝⎭或4,33n n ⎛⎫ ⎪⎝⎭．因为25233n n ⨯<（此时不能够成三角形，舍去），所以4(,),33n n x y ⎛⎫= ⎪⎝⎭，其中n 是3的倍数．则三角形面积2221472336n n n S ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭．当0n ≥时，S 随着n 的增大而增大．所以3n =时．S 37 12．（2021·全国·九年级竞赛）若0abc ≠，则||||||||a b c abca b c abc +++的最大值是________，最小值是__________．【答案】 4 -4 【解析】【分析】【详解】因为1||a a =±，1||b b =±，1||c c =±，1||abc abc =±，所以44||||||a b ca b c -≤++≤．当a ，b ，c 全为正时等于4，当a ，b ，c 全为负时等于4-，故其最大值是4，最小值是4-． 13．（2021·全国·九年级竞赛）若0x >，则24411x x x y ++-+=的最大值是________．32 【解析】【分析】【详解】因0x >，244222441111111x x x x y xx x x ++++==++++-+22222211121232x x x x x x+⋅+⋅等号成立当且仅当221(0)x x x =>，即1x =，所以0x >时，1y 32y 3232=+ 故答案为：0x >时，1y 32y 3232=+ 14．（2021·全国·九年级竞赛）设x 为正实数，则函数21y x x x=-+的最小值是______．【答案】1【分析】【详解】 211(1)10211(0)y x x x x x x=-++-≥+⋅=>，等号当且仅当1x =且1x x =，即1x =时成立，故y 的最小值为1，故答案为：1．15．（2021·全国·九年级竞赛）已知,a b 为抛物线()()2y x c x c d =----与x 轴交点的横坐标，a b <，则||||a c c b -+-的值为______．【答案】b a - 【解析】【分析】【详解】依题意，该抛物线开口向上，又当x a =或b 时，0y =．当x c =时，20y =-<，所以a c b <<，故||||a c c b c a b c b a -+-=-+-=-．故答案为：b a -．16．（2021·全国·九年级竞赛）设正ABC 的边长为2，M 是AB 边上的中点，P 是BC 边上任意一点，PA PM 十的最大值和最小值分别记为s 和t ，则22s t -=_______．【答案】43 【解析】【分析】【详解】因为PA CA ≤，PM CM ≤，故当P 处于BC 边顶点C 这一极端位置时，PM PA 十取最大值，最大值为32s CM CA =+=．如图4-1，作正'A BC ，设'M 为'A B 的中点，则由'PBM PBM ≌得'PM PM ，于是''PA PM PA PM AM +=+≥．连'CM ，则'ACM ∠='ACB BCM ∠+∠=603090︒+︒=︒，所以'AM =22'AC CM +=222(3)7+'7PA AM PM +≥=A 、P 、'M 共线时等号成立，即PA AM +的最小值为7t =22s t -=22(32)(7)3-=4317．（2021·全国·九年级竞赛）若2008个数122008,,,a a a 满足：12a =，2n a -1112008n n n a a a --⎛⎫+ ⎪⎝⎭102008+=，其中，2n =，3，…，2008．那么2008a 可能达到的最大值是_________．【答案】200620082 【解析】【分析】【详解】依题意11102008n n nn a a a a --⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，12008n n a a -= ①或11n n a a -=② 于是连续两次第②类变换互相抵消，保持原数不变，并且当连续三次变换依次是“第①类变换，第②类变换，第①类变换”时，其效果相当为进行一次第②类变换，故从12a =出发变到2008a ，一共要经过2007次变换，相当于进行若干次第①类变换和至多2次第②类变换，并且第②类变换只有第一次、最后一次进行才可能使2008a 最大．其中以前2006次进行第①类变换，最后一次进行第②类变换时，2008a 达到最大值200620082．18．（2021·全国·九年级竞赛）设333199519961997,0x y z xyz ==>，且2223333199519961997199519961997x y z ++111x y z++=_______．【答案】1 【解析】【分析】【详解】解：因0xyz >，故3331995199619970x y z k ===>，则3331995,1996,1997k k k x y z ===， 3333333k k k k k kx y z x y z++，两端三次方得3111111()x y z x y z++=++．又0,0,0x y z >>>，所以1111x y z++=．故答案为：1．19．（2021·全国·九年级竞赛）如果代数式535ax bx cx ++-当2x =-时的值为7，那么当2x =时，该式的值是_________．【答案】17- 【解析】【分析】【详解】解：因为当2x =-时，535328257ax bx cx a b c ++-=----=，所以328212a b c +=-＋，于是当2x =时，5353282512517ax bx cx a b c ++-=++-=--=-．故答案为：17-．20．（2021·全国·九年级竞赛）函数23||7y x x =-+的图象与函数22336y x x x x =-+-+的图象的交点个数是_______．【答案】4 【解析】【分析】【详解】第一个函数化为2237(0),37(0),x x x y x x x ⎧++<=⎨-+≥⎩第二个函数化为26(03),266(03).x y x x x x ≤≤⎧=⎨-+⎩或分别作它们的图象知，它们共有4个交点．或者分别解方程组(22237,37,(0),00)2666y x x y x x x x y x x y ⎧=++=-+<≤≤⎨=-+=⎩及2237,(3)266y x x x y x x ⎧=-+>⎨=-+⎩，可得4个交点为(1111(985,6285,(35),6,(35),6,(313),82222A B C D ⎛⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎝⎭⎝⎭⎝⎭．故答案为：4．21．（2021·全国·九年级竞赛）不论m 取任何实数，抛物线2221y x mx m m =+++-的顶点都在一条直线上，则这条直线的解析式是______．【答案】1y x =-- 【解析】【分析】【详解】二次函数化为2()1y x m m =++-，得顶点坐标为,1,x m y m =-⎧⎨=-⎩消去m 得1y x =--．故答案为：1y x =--．22．（2021·全国·九年级竞赛）如果一次函数y mx n =+与反比例函数3n x y x -=的图象相交于点1,22⎛⎫⎪⎝⎭，那么该直线与双曲线的另一个交点为________．【答案】51,2⎛⎫-- ⎪⎝⎭【解析】【分析】【详解】将1,22x y ==代入,31y mx n ny x =+⎧⎪⎨=-⎪⎩得12,2261,m n n ⎧=+⎪⎨⎪=-⎩于是1,23.n m ⎧=⎪⎨⎪=⎩ 解方程13,2312y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩得1,22x y ⎧=⎪⎨⎪=⎩或1,5.2x y =-⎧⎪⎨=-⎪⎩故另一交点为51,2⎛⎫-- ⎪⎝⎭．故答案为：51,2⎛⎫-- ⎪⎝⎭．23．（2021·全国·九年级竞赛）函数|1||2||3|y x x x =+++++，当x =_______时，y 有最小值，最小值等于_______．【答案】 2- 2 【解析】【分析】【详解】解当3x ≤-时，(1)(2)(3)3(2)y x x x x =-+-+-+=-+；当32x -<≤-时，(1)(2)(3)y x x x x =-+-+++=-；当21x -<≤-时，(1)(2)(3)4y x x x x =-+++++=+；当1x >-时，(1)(2)(3)3(2)y x x x x =+++++=+．故|1||2||3|y x x x =+++++在(,2]-∞-上递减，在[2,)-+∞上递增，当2x =-时，y 取最小值2．故应填2,2-（如图）．注：①一般说来，对于含绝对值的一次函数，应分区间将绝对值符号去掉变成折线函数，再根据函数的增减性（一次项系数为正时递增，为负时递减）就不难得出所求函数的最大（或最小）值．如果作出其图象，那么其结果是一目了然的．②本题的一种简单解法是利用差的绝对值的几何意义来求解：因为||x a -表示数轴上坐标为x 的点P 到坐标为a 的点A 的距离，故|1||2||3|y x x x =+++++表示数轴上坐标为x 的点P 到坐标分别为1,2,3---的点,,A B C 的距离之和．显然当P 与B 重合时，即2x =-时，这个距离之和为最小，其最小值为线段AC 的长度|(1)(3)|2---=．又如，若要求|9||8||3||1||5||6|y x x x x x x =-+-+-++++++的最小值，则它等价于求数轴上坐标为x 的点P ，分别到坐标为9,8,3,1,5,6---的各点,,,,,A B C D E F 的距离之和的最小值．显然当P 在线段CD 上，即当13x -≤≤时，这个距离之和取最小值，并且最小值|9(6)||8(5)||3(1)|32AF BE CD =++=--+--+--=．24．（2021·全国·九年级竞赛）当x 变化时，分式22365112x x x x ++++的最小值是_______．【答案】4 【解析】【分析】【详解】解令22365112x x y x x ++=++，去分母整理得 2(6)(212)2100y x y x y -+-+-=．若6y =，则①化为20=，矛盾．故6y ≠．因为作为x 的方程①有实根x ，故()22(212)4(6)(210)410244(4)(6)0y y y y y y y =----=--+=---≥，即(4)(6)0y y --≤，解得46y ≤≤．而6y ≠，所以46y ≤<．4y =代入①可得1x =-，故当1x =-时，y 取最小值4．故应填4．注：例5~7中求最值的方法叫做判别式法．这是求函数最值的重要方法之一．但应该注意的是，化简整理为一个关于x 的二次方程后（其余数是变量y 的函数），对其二次项系数是否为零应进行讨论，只有在二次项系数不等于零的情形才能应用判别式法（若使二次项系数等于0的y 的值存在，则这个值也是函数y 可取到的值，在求最值时，应将这个值考虑在内进行讨论）．25．（2021·全国·九年级竞赛）代数式21133110x x +的最小值是_______．【答案】3223【解析】【分析】【详解】解设21133110y x x =+，则()222(110)1133y x x +=+，即22222032233113y xy x +=⨯+⨯．关于x 的方程222322322031130x yx y ⨯-+⨯-=有实根，所以 ()()222222(220)432233113411332230y y y =--⨯⨯⨯⨯-=⨯-⨯≥（因为22220432234113+⨯⨯=⨯），所以3223y ≥．当且仅当223x =y 取最小值3223 故应填322326．（2021·全国·九年级竞赛）已知a ，b 是正数，并且二次函数22y x ax b =++和22y x bx a =++的图象都与x 轴相交，则22a b +的最小值是________．【答案】20 【解析】【分析】【详解】解因两条抛物线都与x 轴相交，故其判别式218a b =-及22(2)4b a =-都不小于零，即22222280,8,8440a b a b a b a b b a b a⎧⎧-≥≥⎪⇒⇒+≥+⎨⎨-≥≥⎪⎩⎩．因,a b 都是正数，所以423(8)64644a b a a a ≥≥⇒≥⇒≥，及242b a b ≥≥⇒≥，所以22224220a b +≥+=，即22a b +的最小值为20．故应填20．注：本题中求最值的方法叫做放缩法，即根据题目条件，将各变量的值适当放缩为一个常数，从而求出其最值．三、解答题27．（2021·全国·九年级竞赛）在直径为5的圆内放入10个点，证明其中必有两点的距离小于2．【答案】见解析【解析】【分析】【详解】分析把圆等分为9个扇形显然不行（虽然必有一扇形内至少有2点，但不保证它们的距离小于2），因此，我们先作一个与已知圆同心的小圆（其直径必须小于2，但不能太小），然后将余下的圆环部分8等分．证明设O 是已知圆心，如图，以O 为圆心作半径为0.9的圆，再将余下的圆环8等分，于是将已知圆面分成了9个部分，由抽屉原理知其中必有一部分内至少有已知10点中的101129-⎡⎤+=⎢⎥⎣⎦点,M N ，若,M N 在小圆内，则220.9 1.82MN OC ≤=⨯=<．若,M N 同在一个扇面形内，则由余弦定理，有222cos45MN AC OC OA OC OA ≤+-⋅︒0.81 6.2520.9 2.50.7 3.912+-⨯⨯⨯<．从例2可以看出，分割图形制造“抽屉”时，可能不是将图形等分为几部分，而是要求分割的每一部分图形都具有所需要的性质（例2中每一部分图形内任意两点的距离都小于2），读者应用这种方法解题时，应该注意到这一点．28．（2021·全国·九年级竞赛）试求1231997x x x x -+-+-++-的最小值．【答案】997002．【解析】【分析】【详解】解：要求1219961997x x x x -+-+⋯+-+-的最小值，只要在数轴上找出x 所对应的点，使这点到1，2，3，…，1997所对应的点的距离之和最小即可．如图1-1所示，当999x =时，原式的值最小，最小值为999199929999989999999991000999100199919969991997-+-+⋯+--+-+-+⋯+-+-＋99899721012997998=++⋯++++++⋯++(9981)99822+⨯=⨯997002=．29．（2021·全国·九年级竞赛）当12x ≤≤2121x x x x +--- 【答案】21x -．【解析】【分析】【详解】解：令2121(12)A x x x x x +---≤≤，则 222212(21)21A x x x x x x =+-----22224422(2)x x x x x =--+=--()()22222241x x x x x =--=--=-，又0,12A x >≤≤，所以1A x =-30．（2021·全国·九年级竞赛）一幢33层的大楼里有一部电梯停在第一层，它一次最多容纳32人，而且只能在第2层至第33层中某一层停一次．对每个人来讲，他往下走一层楼感到1分不满意，往上走一层感到3分不满意．现有32个人在第一层，并且他们分别住在第2层至第33层的每一层，问：电梯停在哪一层，可以使得这32个人不满意的总分达到最小值？最小值是多少？（有些人可以不坐电梯直接从楼梯上楼）【答案】当电梯停在第27层时，不满意总分最小，最小值为316分【解析】【分析】【详解】解易知这32人恰好是从第2层到第33层各住1人．对于每个乘电梯上下楼的人，他所住的层数一定不小于直接上楼的人所住的层数（事实上，设住s 层的人乘电梯，而住第t 层的人直接上楼，s t <，则这2人不满意分数之和为3t ；若两人交换上楼方式，则2人不满意分数之和为33s t <，即不满意总分减小．设电梯停在第x 层，在第一层有y 人没有乘电梯而直接上楼，那么不满意总分为3[12(33)]3(12)[12(2)]S x y x y =+++-++++++++--，其中3[12(33)]x +++-是住在第1x +层至第33层的人（共33x -人）的不满意总分之和，3(12)y +++是直接从楼梯上楼的人（共y 人）的不满意总分之和，12(2)x y +++--是从第2y +层至第1x -层的人（共2x y --人）的不满意总分之和，于是331(33)(34)(1)(2)(1)222S x x y y x y x y =--+++----222102231684x xy x y y =--+++ 222(102)231684x y x y y =-++++()221021215180308648y x y y +⎛⎫=-+-+ ⎪⎝⎭22102152(6)31631648y x y +⎛⎫=-+-+≥ ⎪⎝⎭，且当27,6x y ==时，316S =．答：当电梯停在第27层时，不满意总分最小，最小值为316分．注：求含2个或2个以上变量的代数式的最大（小）值时，配方法是其中有效方法之一；另一种方法则是利用已有不等式将含有变量的代数式化为一个不大于（或不小于）一个常数c 的不等式，并能确定等号可以成立，则常数c 便是所求的最大值（或最小值）；第三种方法就是化为一元二次方程用判别式法（参看§5例4~7），等等．31．（2021·全国·九年级竞赛）求函数22233x y x x +=++的最大值和最小值．【答案】当2x =-时，y 取最小值2-；当0x =时，y 取最大值23，理由见解析．【解析】【分析】【详解】将原式整理为关于x 的方程：2(32)(32)0yx y x y +-+-=．若0y =，则1x =-，即0y =是函数的一个值；若0y ≠，则因关于x 的方程有实根，所以2(32)4(32)(32)(324)0y y y y y y =---=---≥，即(32)(2)0y y -+≤，解得223y -≤≤．由此可看出0y =即不是最大值也不是最小值．当2y =-时，由222233x x x +-=++，解得2x =-；当23y =时，由2222333x x x +=++，解得0x =．所以当2x =-时，y 取最小值2-；当0x =时，y 取最大值23．32．（2021·全国·九年级竞赛）已知,,a b c 都是正整数，且抛物线2y ax bx c =++与x 轴有2个不同的交点A 和B ，若,A B 到原点的距离都小于1，求a b c ++的最小值．【答案】11，见解析．【解析】【分析】【详解】设()()()1212,0,,0A x B x x x <，则1212120,0,00b x x ax x c x x a ⎧+=-<⎪⎪⇒<<⎨⎪⋅=>⎪⎩．又2402b ac b ac =->⇒>① 又因为121,1OA x OB x =<=<，故121210,101cx x x x c a a-<<-<<⇒=<⇒<．② 因0a >，抛物线开口向上，故1x =-时，0y a b c =-+>，得b a c <+．而,b a c +均为正整数，故1a c b +≥+，于是由①得21()1a c ac a c +>⇒>，由②1a c >，即1a c >，于是22(1)(11)4a c >≥+=，所以5a ≥．又22514b ac >⨯，所以5b ≥．取5,5,1a b c ===时，2551y x x =++满足题目条件，故a b c ++的最小值为55111++=． 33．（2021·全国·九年级竞赛）求2221026249T x y z xy yz z =++---+的最小值．【答案】5 【解析】【分析】【详解】解 ()()()22222692445T x xy y y yz z z z =-++-++-++222(3)()(2)55x y y z z =-+-+-+≥．当6,2x y z ===时，T 取最小值5．注：例2~3中求最值的方法是常用的配方法．34．（2021·全国·九年级竞赛）在40与100之间任取一个实数x ，如果[]7x =，那么1610x ⎡=⎣的概率是多少?这是[]a 表示不超过a 的最大整数（要求答案写成最简分数的形式）．【答案】780【解析】【分析】【详解】因[]7x =，故2278,78x x <≤≤≤．而要使[16]10x =，即22101611,2.5 2. 75,2.5 2.75x x x ≤≤≤，故所求概率22222.75 2.25 1.31257871580p -===-． 35．（2021·全国·九年级竞赛）如图，D E F 、、分别是ABC 的三边BC CA AB 、、上任意一点，证明：,,AEF BFD CDE △△△中至少有一个三角形的面积不大于ABC 的面积的四分之一．【答案】见解析【解析】【分析】【详解】证明记123,,,ABC AEF BFD CDE S S S S S S S S ====，于是11sin 21sin 2AE AF A S AE AFS AB ACAB AC A ⋅⋅⋅⋅==⋅⋅⋅⋅．同理32,S S BF BD CD CE S BA BC S CA CB⋅⋅==⋅⋅，所以1233222()()()S S S AF FB BD DC CE EA S AB BC CA ⋅⋅⋅⋅⋅=⋅⋅ 222222122264AF FB BD DC CE EA AB BC CA +++⎛⎫⎛⎫⎛⎫⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭≤=⋅⋅． 31234S S S S ．由平均值原理得123,,S S S 中必有一个不大于S4．即证． 36．（2021·全国·九年级竞赛）某林场安排了7天的植树工作，从第二天起每天都比前一天增加5个植树的人，但从第二天起每人每天都比前一天少植5棵树，且同一天植树的人，植相同数量的树．若7天共植树9947棵，则植树最多的那天共植了多少棵？植树最少的那天，有多少人在植树？【答案】植树最少的那天有54人或24人植树．【解析】【分析】【详解】设第4天有m 人植树，每人植树n 棵，则第4天共植树mn 棵；第3天有5m -人植树，每人植5n +棵，则第3天共植树(5)(5)m n -+棵．同理，第2天共植树(10)(10)m n -+棵；第1天共植树(15)(15)m n -+棵；第5天共植树(5)(5)m n +-棵；第6天共植树(10)(10)m n +-棵；第7天共植树(15)(15)m n +-棵．由七天共植树9947棵得(15)(15)(10)(10)m n m n -++-++(5)(5)(5)(5)m n mn m n -++++-(10)(10)m n ++-(15)(15)9947m n ++-=．化简得77009947mn -=，1521mn =．因221521313=⨯．又每天都有人植树，所以15m >，15n >，故39m n ==．因为第4天植树棵数为39391521⨯=，其他各天植树棵数为(39)(39)a a -+=21521a -（5a =，10或15），所以第4天植树最多，这一天共植树1521棵．当15a =时，2239a -的植树棵数最少．又当15a =时，植树人数为391554+=或391524-=，所以植树最少的那天有54人或24人植树． 37．（2021·全国·九年级竞赛）一幢33层的大楼有一部电梯停在第一层，它一次最多能容纳32人，而且只能在第2层至第33层中某一层停一次．对于每个人来说他往下走一层楼梯感到1分不满意，往上走一层楼梯感到3分不满意．现在有32个人在第一层，并且他们分别在第2至第33层的每一层，问：电梯停在哪一层，可以使32人不满意的总分达到最小？最小值是多少？（有些人可以不坐电梯而直接从楼梯上楼）．【答案】当电梯停在第27层时，这32人不满意的总分达到最小，最小值为316分．【解析】【分析】【详解】易知，这32人恰好是第2至第33层各住一人，对于每个乘电梯上、下梯的人，他所住的层数一定大于直接走楼梯上楼的人所住的层数．事实上，设住s 层的人乘电梯，而住第t 层的人直接走楼梯上楼，且s t <，交换两人上楼方式，其余人不变，则不满意总分不增．现分别证明如下：设电梯停在第x 层，①当x s t ≤<时，若住在第s 层的坐电梯，住第t 层的人直接走楼梯上楼，则这两者不满意总分为3(1)3()t s x -+-=3333t s x +--；交换两人上楼方式，则两者不满意总分为3(1)3()s t x -+-=3333t s x +--，两者相等；②当s x t <<时，若住s 层的人乘电梯，而住第t 层的人直接走楼梯上楼，则这两人不满意总分为3(1)()t x s -+-=33t x s +--；交换两人上楼方式，则这两者不满意总分为3(1)3()s t x -+-=3333t x s -+-，前者比后者多4()0x s ->；③当s t x <≤时，若住s 层的人乘电梯，住t 层的人直接走楼梯上楼，则这两者不满意总分为3(1)()t x s -+-=33t x s +--；交换两人上楼方式，则这两者的不满意总分为3(1)()s x t -+-=33s x t +--，前者比后者多4()0t s ->．今设电梯停在第x 层，设有y 人直接走楼梯上楼，则11y x +≤-，那么不满意总分为3(12)s y =+++3[12(33)]x ++++-[12(11)]x y ++++---3(1)3(33)(34)22y y x x +--=++(2)(1)2x y x y ----222102231684x xy x y y =--+++222(102)231684x y x y y =-++++=210224y x +⎡⎤-⎢⎥⎣⎦()211518030688y y +-+210224y x +⎛⎫=-+ ⎪⎝⎭215(6)3163168y +-+≥．当27x =，6y =时，316s =，所以，当电梯停在第27层时，这32人不满意的总分达到最小，最小值为316分．38．（2021·全国·九年级竞赛）已知正整数m ，n 17434m m n -+=，求n 的最大值．【答案】104 【解析】【分析】【详解】设70a m =-，104104a a n -+=，两边平方得22222104a a n +-=．令222104a b -=（b 为正整数），则2()()104a b a b -+=．由于-a b 与a b +同奇偶，即同为偶数，所以当2a b -=时，a b +取最大值52104⨯．这时，222()104n a b =+=为最大，所以n 的最大值为104． 39．（2021·全国·九年级竞赛）对于1,2,3,,i n =，有|| 1 i x <且有12||||||n x x x +++=122009||n x x x ++++．求正整数n 的最小值．【答案】正整数n 的最小值为2010．【解析】【分析】【详解】作整体估计如下：2009=1212||||||||n n x x x x x x +++-+++12||||||n x x x n ≤+++<，所以2010n ≥．当2010n =时，取121005x x x ===20092010=，10061007x x ===201020092010x =-，则||1i x <(1,2,,2010) i =且122010|||||x x x +++2009=+122010||x x x +++，满足题目条件，故所求n 的最小值为2010．40．（2021·全国·九年级竞赛）整数012010,,,x x x 满足条件：00x =，10|||1|x x =+，21|||1|x x =+，…，201020091x x =+，求122010x x x +++的最小值．【答案】122010x x x +++的最小值为7．【解析】【分析】【详解】由已知条件可得：2210021x x x =++，2221121x x x =++，…，2220102009200921x x x =++，各式相加整理后得22010x =()2001200922010x x x x +++++．又00x =，故有122010x x x +++=2201020101220102x x +-()220101120112x =+-．因122010x x x +++为整数，故()220101x +为奇数，又2243201045<<且2432011-=16214>=2452011-，所以122010x x x +++2145201172≥-=．。

【竞赛试题】2017年春季世界青少年奥林匹克数学竞赛(中国区)选拔赛初赛试卷★九年级试题

世界青少年奥林匹克数学竞赛(中国区)选拔赛考生须知:本卷考试时间90分钟,共120分,每题5分,不得使用计算工具或手机。

【竞赛试题】2017年春季世界青少年奥林匹克数学竞赛（中国区）选拔赛初赛试卷★九年级试题一.考试加分（5分）1.请选手认真仔细的在装订线外的内容，把自己的名字，年级，考号，辅导教师，家长手机的信息用正楷准确的填写好，符合要求加5分。

二．单项选择题（把字母填在横线上）2. 方程)25(11091981871761651541431321+=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯x的解是。

A. 21B. 21-C.0D. 1013. 已知三角形的三边长分别是5cm,12cm,13cm, 那么该三角形是三角形。

A. 锐角B.直角C.钝角D.不确定4.三角形三内角平分线的关系是。

A. 交于一点 B.互不相交 C.两两相交 D.不确定5. a 有若干本图书，b 借走一半加一本；剩下的书，c 借走一半加两本；再剩下的书，d 借走一半加3本；最后a 还有2本书。

a 原来有本书。

A. 50B. 55C.60D. 80 6. 方程33-x +195-x -82+x =0的解是。

A.1=x B. 2=x C.4=x D. 无解7. 一块草地长满了草，草每天还在匀速生长。

已知3头牛36天可把草吃光；5头牛20天可把草吃光。

现在要求12天把草吃光，需要头牛去吃。

A. 5B. 6C.8D. 108. 方程31535322=-+--x x x x 的解是=x 。

A. 1 B. 3 C.3 D. 49. 一项工程，甲、乙合做20天完成；如果单独完成全工程，甲比乙要多用9天。

甲单独做全工程需天。

（甲、乙独做的工作时间都是整天数）A. 20B. 30C.40D. 4510. 一只猴子吃一棵树上的桃子，第一天吃了树上桃子的101，以后八天分别吃了当天现有桃子的91，81，71，...，21，最后树上还剩下10个桃子。

人教版九年级数学上册竞赛试题及答案

人教版九年级数学上册竞赛试题及答案题号一二三四五总分得分（考试时间：90分钟，满分：120分）一、选择题。

（每小题4分，共32分）1. 某项工程估算总投资523亿元，用科学记数法表示正确的是（）。

A. 5.23×1010元B. 5.23×1011元C. 52.3×109元D. 0.523×1011元 2. 下面的图形可以折成一个正方体的盒子，折好后，与1相对的数是（）。

A. 5B. 6C. 4D. 33．不等式组⎪⎩⎪⎨⎧-≤-->-x x x x 32314315 的所有整数解的和是（）。

A. 1 B. 0 C. －1 D. －2 4. 弹簧的长度与所挂的物体的质量的关系为一次函数，如图所示，由图可知不挂物体时弹簧的长度是（）。

A. 6厘米B. 4厘米C. 5厘米D. 3厘米5．甲是乙现在年龄时，乙10岁，乙是甲现在年龄时，甲25岁，那么（）A ．甲比乙大5岁B ．甲比乙大10岁C ．乙比甲大10岁D ．乙比甲大5岁6．若142=++y xy x ，282=++x xy y ，则y x +的值为（）A ．－7B ．6C ．－7或6D ．－6或7 7．已知长方形的长为8，宽为4，将长方形沿一条对角线折起压平，如图所示，则重叠部分（阴影三角形）的面积是（） A ．10 B ．12 C ．14 D ．16 8．已知0≠abc ，并且p bac a c b c b a =+=+=+，那么直线p px y +=一定通过（） A ．第一、二象限 B ．第二、三象限 C ．第三、四象限 D ．第一、四象限二、填空题。

（每小题4分，共28分）9. 一个袋中装有12个红球，10个黑球，8个白球，每个球除颜色外都相同，从袋中摸出一个球，那么摸到黑球的概率为_______________。

10．化简：____________4821319125=+-.11．分解因式：______________________4123=-+x x x . 12．计算：______________)3(333)3(2032=---÷++--.13. 若关于x 、y 的二元一次方程组⎩⎨⎧-=+=-1872223a y x ay x 的解x ，y 的值互为相反数，则a 的值为_________.14. 已知m 、n 都是方程020*******=++x x 的根，则代数式＝______________.15. 如图，四边形ABCD 和BEFG 均为正方形，则________=DFAG. 三、解答题(每小题8分，共32分) 16．解方程：22412--=-x x17. 已知：点E ，F 分别是正方形ABCD 的边BC 上的一点，且∠EAF ＝45°，自E ，F 分别作AC 的垂线，垂足为P ，Q 。

九年级数学竞赛试题(满分100)

九年级数学竞赛试题（满分100）姓名：班级：成绩：一、选择题（''4832⨯=，每道题目只有一个正确选项）1.若||0a a +=+ ）A.1B.-1C.21a -D.12a -2.若方程2310x x --=的两根也是方程420x ax bx c +++=的根，则2a b c +-的值为（）A.-13B.-9C.6D.03.若三角形三边的长均能使代数式2918x x -+的值为0，则此三角形的周长是（）A.9或18B.12或15C.9或15或18D.9或12或15或184.已知2210m n mn m n +++-+=，则11m n+的值等于（） A.-1 B.0 C.1 D.25.若实数,a b 满足21202a ab b -++=，则a 的取值范围是（） A.2a ≤- B.4a ≥ C.2a ≤-或4a ≥ D.24a -≤≤6.如果方程210(0)x px p ++=>有实数根且它的两根之差是1，那么p 的值为（）A.2B.47.设12a -=，则5432322a a a a a a a+---+=-（） A.-1 B.1 C.-2 D.28.如图，在ABC 中，90ACB ∠=︒,20A ∠=︒，将ACB 绕点C 按逆时针方向旋转角α到'''A B C 的位置，'CA 交AB 于D ，则其中'A ,'B 分别是,A B 的对应点，B 在''A B 上，BDC ∠的度数为（）A.40︒B.45︒C.50︒D.60︒二、填空题（''4416⨯=，填写你认为最完美的答案）9.已知非零实数,a b 满足|24||2|42a b a -++=，则a b +等于 .10.已知222246140x y z x y z ++-+-+=，则x y z ++= .11.已知关于x 的方程2210x px ++=的两个实数根，一个小于1，另一个大于1，则实数p 的取值范围是 .12.已知方程210090x x a -+=有两个质数根，则常数a = .三、解答题（3大题，共'48，解答题需要详细的解题过程）13. 1)（62)（6分）已知方程2220132014201210x x -⨯-=的较大根是r ，方程22013201410x x -+=的较小根为s ，求r s -的值.14.已知关于x 的方程220x kx k n -++=有两个不相等的实数根12,x x ，且21212(2)8(2)150x x x x +-++=，请问：（1）（4分）求证：0n <；（2）（6分）试用k 的代数式表示1x ；（3）（6分）当3n =-时，求k 的值.15.已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF BD ⊥交BC 于F ，连结DF ，G 为DF 中点，连接,EG CG .（1）（6分）求证：EG CG =；（2）（10分）将BEF 绕点B 逆时针旋转45︒，如图二所示，取DF 中点G ，连接,EG CG ，问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由.（3）（4分）将图一中BEF 绕B 点旋转任意角度，如图三所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察，你还能得出什么结论？（只写结论，不需要证明）图一图二图三。

人教版九年级数学竞赛练习题之几何图形面积的计算(无答案)

人教版九年级数学竞赛练习之几何图形面积的计算（含答案）【例1】如图，△ABC 内三个三角形的面积分别为5，8，10，四边形AEFD 的面积为x ，则x ＝________.【例2】如图，在△ABC 中，已知BD 和CE 分别是两边上的中线，并且BD ⊥CE ，BD ＝4，CE ＝6，那么△ABC 的面积等于 ( )A ．12B ．14C ．16D ．18 解题思路：由中点想到三角形中位线，这样△ABC 与四边形BCDE 面积存在一定的关系.【例3】如图，依次延长四边形ABCD 的边AB ，BC ，CD ，DA 至E ，F ，G ，H ，使BE AB ＝CF BC ＝DG CD ＝AH DA＝m ，若S 四边形EFGH ＝2S 四边形ABCD ，求m 的值.【例4】如图，P ，Q 是矩形ABCD 的边BC 和CD 延长线上的两点，P A 与CQ 相交于点E ，且∠P AD＝∠QAD ，求证：S 矩形ABCD ＝S ∠APQ .例1图1085F ABCD E 例2图DABCE 例3图BC DEF G HA例4图EABPCD【例5】如图，在Rt ∠ABC 中，∠A ＝90°，AB ＝8，AC ＝6，若动点D 从点B 出发，沿线段BA 运动到点A 为止，移动速度为每秒2个单位长度. 过点D 作DE ∠BC 交AC 于点E ，设动点D 运动的时间为x 秒，AE 的长为y .(1) 求出y 关于x 的函数关系式，并写出自变量x 的取值范围；(2) 当x 为何值时，△BDE 的面积S 有最大值，最大值为多少？【例6】如图，设P 为∠ABC 内任意一点，直线AP ，BP ，CP 交BC ，CA ，AB 于点D ，E ，F . 求证：(1)PD AD ＋PE BE ＋PFCF＝1； (2)P A AD ＋PB BE ＋PC CF＝2A 级1．如图， ABCD 中，AE ∠BE ＝1∠2，S ∠AEF ＝6cm 2，则S ∠CDF 的值为________.2．如图，正六边形ABCDEF 的边长为23cm ，P 为正六边形内任一点，则点P 到各边距离之和为_______.例5图A BCDE例6图ABCDFE第1题图FAB CDE第2题图ABCF第3题图APD3．如图，P 是边长为8的正方形ABCD 外一点，PB ＝PC ，∠PBD 的面积等于48，则∠PBC 的面积为_____________.4．如图，已知∠BOF ，∠AOF ，∠BOD ，∠COE 的面积分别为30，40，35，84，则∠ABC 的面积为________. 5．如图，已知AD 是Rt ∠ABC 斜边BC 上的高，DE 是Rt ∠ADC 斜边上的高，如果DC ∠AD ＝1∠2， S ∠DCE ＝a ，那么S ∠ABC 等于 ( )A ．4aB ．9aC ．16aD ．25a6．如图，已知M 是 ABCD 边AB 的中点，CM 交BD 于点E ，则图中阴影部分面积与 ABCD 的面积之比为（）A ．16B ．14C ．13D ．5127．如图，在∠ABC 中，DE ∠BC ，DE 分别交AB ，AC 于点D ，E ，若S ∠ADE ＝2S ∠DCE ，则S ∠ADES ∠ABC等于( )A ．14B ．12C ．23D ．498．如图，∠ABC 是边长为6cm 的等边三角形，被一平行于BC 的矩形所截，AB 被截成三等分，则图中阴影部分面积面积为（）cm 2.A ．4B ．2 3C ．3 3D ．4 39．如图，平面上有两个边长相等的正方形ABCD 和 A ′B ′C ′D ′，且正方形A ′B ′C ′D ′的顶点A ′在正方形ABCD 的中心，当正方形A ′B ′C ′D ′绕A ′ 转动时，两个正方形重合部分的面积必然是一个定值. 这个结论对吗？证明你的判断.第4题图OA BCDEF 第5题图EDABC第6题图E ABCDM第7题图ABCD E 第8题图 HGF E B第9题图 A BCDA'C'D'10．如图，设凸四边形ABCD 的一组对边AB ，CD 的中点分别为K ，M .求证：S 四边形ABCD ＝S ∠ABM ＋S ∠DCK..11．如图1，AB ，CD 是两条线段，M 是AB 的中点，S ∠DMC ，S ∠DAC ，S ∠DBC 分别表示∠DMC ，∠DAC ，∠DBC 的面积，当AB ∠CD 时，有S ∠DMC ＝S ∠DAC ＋S ∠DBC2………..∠.(1) 如图2，若图1中AB 与CD 不平行时，∠式是否成立？请说明理由.(2) 如图3，若图1中AB 与CD 相交于点O 时，问S ∠DMC 与S ∠DAC 和S ∠DBC 有何相等关系？试证明你的结论.12．如图，在∠ABC 中，∠ACB ＝90°，∠ABC ＝30°，将∠ABC 绕顶点C 顺时针旋转，旋转角为θ（0°＜θ＜180°），得到∠A ′B ′C ′.(1) 如图1，当AB ∠CB ′时，设A ′B ′与CB 相交于点D ，证明：∠A ′CD 是等边三角形；(2) 如图2，连接A ′A ，B ′B ，设∠ACA ′和∠BCB ′的面积分别为S ∠ACA ′和S ∠BCB ′.求证：S ∠ACA ′∠S ∠BCB ′＝1∠3. (3) 如图3，设AC 的中点为E ，A ′B ′的中点为P ，AC ＝a ，连接EP ，当θ＝_____时，EP 长度最大，最大值是____________.图2图1图3O BCBA DCADCAMMM第10题图A BD K MB 级1．如图，A 在线段BG 上，ABCD 和DEFG 都是正方形，面积分别为7cm 2和11cm 2，则∠CDE 的面积等于___________cm 2.2．如图，P 为正方形ABCD 内一点，P A ＝PB ＝10，并且P 到CD 边的距离也等于10，那么正方形ABCD 的面积是_______________.3．如图，四边形ABCD 中，点E ，F 分别在BC ，DC 上，DF FC ＝1，CEBE ＝2，若∠ADF 的面积为m ，四边形AECF 的面积为n (n ＞m )，则四边形ABCD 的面积为___________.4．如图，图形ABCD 中，AB ∠CD ，AC 和BD 相交于点O ，若AC ＝5，BD ＝12，中位线长为132，∠AOB的面积为S 1，∠OCD 的面积为S 2，则S 1＋S 2＝_________.5．如图，分别延长∠ABC 的三边AB ，BC ，CA 至A ′，B ′，C ′，使得AA ′＝3AB ，BB ′＝3BC ，CC ′＝3AC ，若S ∠ABC ＝1，则S ∠A ′B ′C ′等于 ( ).A ．18B ．19C ．24D ．276．如图，若ABCD 是2×2的正方形，E 是AB 的中点，F 是BC 的中点，AF 与DE 相交于点I ，BD 和AF 相交于点H ，那么四边形BEIH 的面积是 ( )A ．13B ．52 C ．715 D ．815θθθ图2图1图3DA CB A'B'ACBA'B'A CB A'B'E P第1题图C BG D EFA第2题图ABCDP第3题图ABCD FE第4题图OA CB7．如图，矩形ABCD 中，E 是BC 上的一点，F 是CD 上的点，已知S ∠ABE ＝S ∠ADF ＝13S ABCD ，则S △AEF S △CEF的值等于 ( )A ．2B ．3C ．4D ．58．(1) 探究：如图1，在 ABCD 的形外分别作等腰直角三角形ABF 和等腰直角三角形ADE ，∠F AB ＝∠EAD ＝90°，连接AC ，EF. 在图中找一个与∠F AE 全等的三角形，并加以证明.(2) 应用：以 ABCD 的四条边为边，在其形外分别作正方形，如图2，连接EF ，GH ，IJ ，KL ，若 ABCD 的面积为5，则图中阴影部分四个三角形的面积之和为____________.9．如图，在梯形ABCD 中，AD ∠BC ，AB ＝AD ＝DC ＝2cm ，BC ＝4cm ，在等腰∠PQR 中，∠QPR ＝120°，底边QR ＝6cm ，点B ，C ，Q ，R 在同一条直线l 上，且C ，Q 两点重合，如果等腰∠PQR 以1cm/s 的速度沿直线l 箭头所示方向匀速运动，t 秒时梯形ABCD 与等腰∠PQR 重合部分的面积记为S cm 2.(1) 当t ＝4时，求S 的值；(2) 当4≤t ≤10时，求S 与t 的函数关系式，并求出S 的最大值.10．有一根直尺的短边长为2cm ，长边长为10cm ，还有一块锐角为45°的直角三角纸板，它的斜边长为12cm ，如图1将直尺的短边DE 放置与直角三角纸板的斜边AB 重合，且点D 与点A 重合将直尺沿AB 方向平移，如图2，设平移的长为x cm(0≤x ≤10)，直尺与三角形纸板重叠部分（图中阴影部分）的面积S cm 2.(1) 当x ＝0时，S ＝________，当10 x 时，S ＝________； (2) 当0＜x ≤4时，求S 关于x 的函数关系式；图1图2A DBCFE LK JIH GAD B CEF第5题图 A'B'C'A CB 第6题图 I HABC DEF 第7题图 A B CD EF第9题图ADP(3) 当4＜x ＜10时，求S 关于x 的函数关系式，并求出S 的最大值.11．如图，设H 是等腰三角形ABC 的三边上的高线的交点，在底边BC 保持不变的情况下，让顶点A 至底边BC 的距离变小（仍保持三角形为等腰三角形），这时HBC ABC S S ∆∆⋅的值变大、变小、还是不变?证明你的结论.12．(1) 请你在图1中作一条直线，使它将矩形ABCD 分成面积相等的两部分；(2) 如图2，点M 是矩形ABCD 内一定点，请你在图2中过点M 作一条直线，使它将矩形ABCD 分成面积相等的两部分；(3) 如图3，在平面直角坐标系中，直角梯形OBCD 是某市将要筹建的高新技术开发区用地示意图，其中DC ∠OB ，OB ＝6，BC ＝4，CD ＝4. 开发区综合服务管理委员会(其占地面积不计)设在点P (4，2)处. 为了方便驻区单位，准备过点P 修一条笔直的道路(路的宽不计)，并且使这条路所在的直线l 将直角梯形OBCD 分成面积相等的两部分. 你认为直线l 是否存在?若存在，求出直线l 的表达式；若不存在，请说明理由.图1图2FGFBC A BCEExy图1图2图3OC D DCBAMDCPB 第11题图 H DE F A。

1993第十届全国各地九年制义务教育初三数学竞赛试题及参考答案解析

1993第十届全国九年级义务教育初中中考数学联赛第一试一、选择题本题共有8个小题,每小题都给出了A.B.C.D 四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1261x x -+除以21x -的余式是() A.1 B.1- C.1x -D.1x +2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是() A.Ⅰ,Ⅱ都对 B.Ⅰ对,Ⅱ错 C.Ⅰ错,Ⅱ对 D.Ⅰ,Ⅱ都错 3.设x 是实数,|1||1|y x x =-++.下列四个结论: Ⅰ.y 没有最小值；Ⅱ.只有一个x 使y 取到最小值；Ⅲ.有有限多个x (不止一个)使y 取到最大值； Ⅳ.有无穷多个x 使y 取到最小值. 其中正确的是 A.Ⅰ B.Ⅱ C.Ⅲ D.Ⅳ 4.实数1x ,2x ,3x ,4x ,5x 满足方程组() 12312342345345145125.x x x a x x x a x x x a x x x a x x x a ++=⎧⎪++=⎪⎪++=⎨⎪++=⎪⎪++=⎩，，，，其中1a ,2a ,3a ,4a ,5a 是实常数,且12345a a a a a >>>>,则1x ,2x ,3x ,4x ,5x 的大小顺序是() A.1245x x x x >>>B.42135x x x x x >>>>C.31425x x x x x >>>>D.53142x x x x x >>>>5.不等式21(1)37x x x -<-<+的整数解的个解() A.等于4 B.小于4C.大于5D.等于56.在ABC △中,A ∠是钝角,O 是垂心,AO BC =,则cos()OBC OCB ∠+∠的值是()A.D.12-7.锐角三角形ABC 的三边是a ,b ,c ,它的外心到三边的距离分别为m ,n ,p ,那么::m n p 等于() A.111::a b cB.::a b cC.cos :cos :cos A B CD.sin :sin :sin A B C1-可以化简成() ED CB A OACnmp OB A)1)111二、填空题1.当x变化时,分式22365112x xx x++++的最小值是____________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有_______个小球.3.若方程22(1)(1)x x k--=有四个非零实根,且它们在数轴上对应的四个点等距排列,则k=_______.4.锐角三角形ABC中,ABC∠中,30A∠=︒.以BC边为直径作圆,与AB,AC分别交于D,E,连接DE,把三角形ABC分成三角形ADE与四边形BDEC,设它们的面积分别为1S,2S,则12:S S=__________.第二试一、设H是等腰三角形ABC垂心,在底边BC保持不变的情况下让顶点A至底边BC的距离变小,这时乘积ABC HBCS S⋅△△的值变小、变大,还是不变？证明你的结论.二、ABC△中,5BC=,12AC=,13AB=,在边AB,AC上分别取点D,E,使线段DE将ABC△分成面积相等的两部分.试求这样的线段DE的最小长度.三、已知方程20x bx c++=及20x cx b++=分别各有两个整数根1x,2x,及1x',2x',且12x x>,12x x''>.①求证:1x<,2x<,1x'<,2x'>.②求证:11b c b-+≤≤；③求b,c所有可能的值.1993第十届全国九年级义务教育初中中考数学联赛答案第一试一、选择题1.A【解析】直接利用整式除法比较繁琐,将原式变形得126661(1)1x x x x-+=-+,6242(1)(1)1x x x x=-+++∴所以余式为1.【点评】本题的关键是灵活利用立方差公式,将原来比较复杂的式子化简成需要的形式.2.B【解析】命题Ⅰ正确,证明如下:如图1,ABCDE为圆内接五边形,各内角相等,由A B∠=∠,知BCE CEA∠=∠于是BC EA=, ∴BC EA=,∴同理可证BC DE AB CD EA====,故ABCDE是正五边形.命题Ⅱ不正确,反例如下:如图6,ABCD为圆内接矩形90A B C D∠=∠=∠=∠=︒,AB CD=,BC DA=,但AB BC≠,显然,ABCD满足命题Ⅱ条件,但CEDBAHCBAAECBD不是正四边形.【点评】这道题不能想当然认为正四边形是对的,尽管正四边形我们比较熟悉,要经过分析得出结论.3.D 【解析】因为|1|x -,|1|x +分别表示数轴上的点x 到点和点1-的距离,因此,当11x -≤≤时,|1||1|2y x x =-++=；当1x <-时,|1||1|22|1|2y x x x =-++=++>； 1x >时,|1||1|22|1|2y x x x =-++=++>. 而在1-与1之间有无穷个实数x ,故有无穷多个x 使y 取到最小值.【点评】直接用分类讨论的方法也可以得到答案,但是用算式的几何意义这种方法计算更直观,而且也不容易出错.4.C【解析】给定方程组中的方程按顺序两两相减分别得1412x x a a -=-,2523x x a a -=-,3134x x a a -=-,4245x x a a -=-.∵12345a a a a a >>>>, ∴14x x >,25x x >,31x x >,42x x >,于是有31425x x x x x >>>>.【点评】这道题中方程组左边的项有一定规律,把方程两两相减就可以得出所需要的项,再利用所给的条件,比较一下就可以得出答案.5.A【解析】注意到2(2)(1)01(1)37(1)(6)0x x x x x x x -->-<-<+⇒+-<,(1)(6)016x x x +-<⇔-<<.于是原不等式的整数解是介于1-与6之间且不等于1,2的整数,即0,3,4,5四个整数.【点评】这道题主要要求出不等式的解集,题中给出的条件有一定的迷惑性,如果直接解这个不等式很难得出结果,所以考虑将原不等式化为两个一元二次不等式,再求它们的公共部分.6.A【解析】设ABC △的三条高AD ,BE ,CF 相交于点O .因ABC △为钝角三角形,故垂心O 在ABC △的外部(如图1)∵B ,D ,F ,O 四点共圆, 故12∠=∠又由题设OA BC =,知Rt Rt OAF BCF △≌△, ∴OF BF =,于是45BOF ∠=︒.而180135OBC OCB BOF ∠+∠=︒-∠=︒,∴cos()cos135OBC OCB ∠+∠=︒=.【点评】这道题关键是利用好OA BC =这个条件,因为初中范围内能计算出精确的三角函数值的不只有45︒,60︒这样的特殊角,观察后猜想45BOF ∠=︒,正好可利用到OA BC =这个条件,即可得出结论.7.C【解析】如图7,设O 是ABC △的外心,OA OB OC R ===,图 1DC BA1cos cos 2m BOC A R =∠=, ∴cos m R A =. 同理cos n R B =,cos p R C =.∴::cos :cos :cos m n p A B C =.【点评】 O 应为外心,所以我们画出三角形的外接圆帮助计算,容易发现m ,n ,p 的值都可以通过外接圆的半径来计算,再经过简单的推导即可得出结果.8.D【解析】原式111213333132219-⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭313131321321121⎡⎤⎛⎫⎢⎥+ ⎪⎢⎥⎝⎭==+=⎢⎥⎢⎥+⎢⎥⎣⎦.【点评】这个根式乍一看很复杂,我们观察后发现括号内的根式都是以9为分母的,所以考虑把19拿到括号外面来,再进行化简.这道题做的时候要细心,并且对于乘法公式能够灵活运用.二、填空题1.4【解析】 22222236561210226612422(1)112x x x x x x x x x x x ++++==-=-++++++++ ∴当1x =-时,公式取最小值4.【点评】这种题目一定要把分母或者分子中的一项变形成为不含末知数的项,这样只有分母或者分子变化,容易求最值.2.7【解析】设从左到右小盒里的球数为7,2a ,3a ,…,1993a .∵234730a a a +++=,234530a a a a +++= ∴57a =,同理913174119937k a a a a a +======L .【点评】根据已给出的条件显然不能求出所有盒子里面球的数目,而已知条件中给出了第一个盒子中球的数目,并且发现1993与1对于4同余,再根据四个相邻的盒里共有30个小球这个条件可得出结果.3.47【解析】设2x y =,原方程变为2540y y k -+-=,设此方程有根α,()x βαβ<<,则原方程的四个根为,由于它们的在数轴对应的四个点等距排列,(,故9βα=.12α=,92β=, 于是944k αβ-==,∴74k =. 【点评】直接计算这是一个4次方程,我们很难计算出结果,对于高次方程换元是我们最常用的方法,本题也不例外.4.3【解析】如图2,BC 为圆的直径,18090AEB BCE ∠=︒-∠=︒∵cos cos30AE A AB ==︒=又ADE ABC △∽△,∴AD AE AC AB =. 由此可知21sin 3214sin 2AED AEB AD AE AS AE S AB AB AC A ⋅⎛⎫=== ⎪⎝⎭⋅△△. 因而四边形DBCE 面积214ABC S S =△.12:3S S =.【点评】四边形的面积不好计算,为此我们考虑两个有公共角的三角形面积,这样它们的面积比就转化成为了边长乘积的比,便于计算.第二试一、【解析】解法一:不妨设角A 是锐角,连接AH 并延长交BC 于D 点,延长BH ,CH 分别交AC 于E ,交AB 于F ,如图2. ∵BHD AHE ∠=∠,∴HBD HAE ∠=∠.因为Rt Rt BDH ADC △≌△, ∴AC DC BD HD=. 又12BD DC BC ==, ∴214AD HD BD CD BC ⋅=⋅=.∴4111:2216ABC HBC S S BC AD BC HD BC ⎛⎫⎛⎫=⋅⨯⋅= ⎪ ⎪⎝⎭⎝⎭△△.当90A ∠︒≥时,同理可证上式也成立,由于BC 是不变的,所以当A 点至BC 的距离变小时,乘积ABC HBC S S ⋅△△保持不变.解法:作图3如解法1,再延长AD 至G ,使DG DH =,并分别连接BG ,GC .由HBD GBD △≌△, CBG CBH CAG ∠=∠=∠, 因而,A ,B ,G ,C 四点共圆,由相交弦定理, 得AD HD AD DG BD DC ⋅=⋅=⋅ 214BC =. 图 2F D E AC H G H F EDC B A 图 3因此,ABC HBC S S ⋅△△1122AD BC HD BC ⎛⎫⎛⎫=⋅⋅ ⎪⎪⎝⎭⎝⎭ 4116BC =. 由于BC 是不变的,所以当点A 至BC 的距离变小时,乘积ABC HBC S S ⋅△△保持不变.【点评】题目的已知条件中没有给出不等关系,所以容易猜想到结果是不变的,而三角形中只有底边BC是不变的,所以考虑将面积的乘积用BC 来表示.二、【解析】由于22251213==,知ABC △是直角三角形,如题图.1512302ABC S =⋅⋅=△,设AD x =,AE y =,由于1sin 2ADE S xy A =△15=,5sin 13A =,知78xy =. 由余弦定理知:22222cos ()2(1cos )DE x y xy A x y xy A =+-=-+-212()278113x y ⎛⎫=-+⨯⨯- ⎪⎝⎭2()1212x y =-+≥,当x y =时,上式的等号成立,此时DE =.【点评】求最值的几何问题我们可以用设未知数的方法来解,然后将已知的几何条件转化成为未知数的关系,最后用代数中常用的方法来求解.三、【解析】 1.假如10x >,同由12x x ,知20x >,对于已知两个方程用韦达定理得1212x x b x x ''+=-=-,这与已知120x x >,120x x ''>矛盾,因此,10x '<,20x '<. 同理10x '<,20x '<. 2.由韦达定理及10x <,20x <有 1212(1)1c b x x x x --=+++12(1)(1)0x x =++≥,所以1c b -≥.对于方程20x cx b ++=进行同样讨论,得 1b c -≥.综合以上结果,有 11b c b -+≤≤.3.根据2的结果可分下列情况讨论:①当1c b =+时,由韦达定理有12121x x x x =--+,从而12(1)(1)2x x ++=.由于1x ,2x 都是负整数,故121112x x +=-⎧⎨+=-⎩或121211x x +=-⎧⎨+=-⎩, 由此算出5b =,6c =.经检验5b =时,6c =符合题意.②当c b =时,有1212()x x x x =-+,从而12(1)(1)1x x ++=,因此122x x ==-,故4b c ==. 经检验4b c ==符合题意.③当1c b =-时,1b c ==对方程20x cx b +==作类似①讨论,得6b =,5c =. 综上所述得三组值: 56b c =⎧⎨=⎩,65b c =⎧⎨=⎩,44b c =⎧⎨=⎩. 【点评】这道题目比较繁琐,但是它分了三个问,这就给出了提示,我们做的时候要按照3问,依次解决,一定要注意利用上一问的结果.。