教师版2015届高考临门一脚

合集下载

2015高考语文“临门一脚”：考前叮嘱(考试指导)

A、认真读懂题干，利用好题干中包含的信息揭示。
所以读懂题干，有效地利用题干中的信息提示，方能回
答得全面。 B、查语境。把命题所涉及到的内容放回到原文中→找看是否有与之有并列或承接或递进等关系的语句、段
准相关的信息区，然后还要认真搜索相关信息区的前后，
落。
C、看赋分，配答案，一般来说，现代文阅读每题赋分
都在4分以上，这也决定了每个题目的答案要点一般不
可能只是一点。一般情况，4分题答案至少应有两点，6 分题答案至少应有三点。
如果命题人在作答处已标明(1)、(2)之类序号，则按序号答够要点。如果未标明序号，考生也应该心中有数，不可只答一点了事。如果题干中有“从不同角度”、
系上下文的翻译，远远比看完全文临做题时才翻译准确得多。一时不懂，不必着急，放一放先读下文，也许读了下文就自然能明白，也可到题目中去找答案。实在不懂也没什么，一般不会影响答题，没必要钻牛角尖，命题者不会在大多数考生读不懂的地方设题。
文言实词题
答题技巧：
• 代入法，联系上下文，将给出的词义带进原文，通顺就对，不通就错。
一、心态策略
高考是紧张、激烈的脑力劳动，需要考生全身心投入，且处于最佳状态，以保证每分钟都能积极思维。语文是第一堂考试，考试开始前，考生应像运动员竞赛前先做准备活动一样，摒弃与高考无关的一切杂念，排除种种可能在考场中分散注意力的因素，适当热身，提前进入“角色”。
考前指导
告诉自己： “我一直在努力，我很棒！高考必胜！”
四、答题技巧
1、拿到试卷（有题目的那张）先看作文题目，记住核心关键词，（看作文题目时，作文材料无论长短，都要用5－8分钟，这样才不至于审偏题。）因为潜意识会帮你构思的，在做其他题时突然想到的经典事例和名句马上在草稿纸上写下来，后面作文用得上的。

广东省湛江第一中学2015届高三语文下学期“临门一脚”试题(含解析)

广东省湛江第一中学2015届高三语文下学期“临门一脚”试题（含解析）本试卷共8页，满分为150分。

考试时间150分钟。

2015．05．25注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案；答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔或涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回。

一、本大题4小题，每小题3分，共12分。

1．下列词语中加点的字，每对读音都不相同的一组是A．联袂．/妩媚．沼．泽/迢．远慰藉．/狼藉．B．濒．危/摒．弃垂涎．/诞．生殷．红/殷．切C．裙裾．/拮据．聒．噪/恬．淡着．装/不着．边际D．绥．靖/骨髓．缄．默/信笺．裨．益/稗．官野史【答案】B考点：识记现代汉语普通话常用字的字音。

能力层级为识记A。

2．下面一段文字，加点的词语使用不恰当的一项是从南京市溧水区区委书记姜明，到建邺区区委书记冯亚军，短短数周，多名官员亦步亦．．．趋．，纷纷落马，中央反腐决心清晰可见。

叫好的同时也要警醒，决心能成就一时之效，完善制度方可长治久安．．．．，权力才不会．．．．。

治国先治吏，治吏必从严。

政府官员心怀敬畏，谨言慎行失范，民心才不会失散。

“只有让人民起来监督政府，政府才不敢松懈；只有人人起来负责，才不会人亡政息．．．．。

”A．亦步亦趋 B．长治久安 C．谨言慎行 D．人亡政息【答案】A【解析】试题分析：亦步亦趋：原意是说，你慢走我也慢走，你快走我也快走，比喻由于缺乏主张，或为了讨好，事事模仿或追随别人。

这与“贪官纷纷落马”的语境不符。

B．长治久安：治：太平；安：安定。

2015届物理临门一脚

2015届高考最后冲刺之——物理升华篇一、答题目标：1、一模在70分左右的同学在答题目标：注意做好选择题、34题实验题前几问以及35题前两问；2、一模在80分左右的同学在答题目标：立足突破选择题、34题、35题，并在36题（1）（2）问尽量拿分；3、一模在85分以上的同学在答题目标：在选择题、34题、35题和36题（1）（2）问要尽量拿满分，争取能突破36题第（3）问。

二、考查热点：1、选择题高频考点：（1）共点力的平衡（2）万有引力定律及其应用（3）静电场及其性质（4）交流电的表达式和图象（5）分子动理论（6）气体实验定律和热力学第一定律（7）近代物理：光电效应、原子结构、原子核（8）圆周运动和平抛运动【例1】如图所示，用质量不计的活塞在绝热汽缸内封闭一定质量的空气，在活塞上施加外力推动活塞，使气体体积减小，则上述过程中 A ．汽缸内气体温度不变 B ．汽缸内气体压强不变C ．汽缸内的气体向外界放出热量D ．外力做的功等于汽缸内气体内能的增量【例2】一定质量的气体在等温变化过程中（可视作理想气体），下列物理量中将发生变化的是A ．分子的平均动能 B. 单位体积内的分子数 C ．气体的压强 D . 分子总数【例3】下列说法正确的是A ．爱因斯坦提出了光子学说，成功解释了光电效应现象B ．核反应方程238 92U―→234 90Th ＋42He 属于裂变 C ．α粒子散射实验证明原子内是十分“空旷”的 D ．升高放射性物质的温度，可缩短其半衰期【例4】某静电场的电场线分布如图所示，P 、Q 为该电场中的两点，下列说法正确的是A ． P 点场强大于Q 点场强B ． P 点电势低于Q 点电势C ．将电子从P 点移动到Q 点，其电势能减少D ．将电子从P 点移动到Q 点，电场力做正功★【例5】如图所示，电源的电动势为E ，内阻r 忽略不计。

A 、B 是两个相同的小灯泡，L 是一个自感系数相当大的线圈。

武汉六中高三临门一脚考试

考点：分段函数在定义域上单调的条件.
6．选项 C 是求的是T 135101的值,答案选 C.
考点：算法与程序框图
[1 , 1) ，故答案为 C. 73
7．由函数 y sin ax b (a 0) 的图像可知周期 T 2 ，0 a 1，左图最小值属于
(1,0) ，可得 0 b 1 ，故函数 y loga (x b) 的图像单调递减，且向左平移，故选 C.
AB AD
AC
，
即
：
( AB )2 ( AD )2 2 AB AD ( 3 AC )2 ，化简得： 1
cos ABD 1 ，可得： ABD ，由面积公式知平行四边形的面积为：
2
3
S 2 (1 2 2sin ) 2 3 .
21．（本小题满分 14 分）函数 f (x) x a （ a 为常数）的图象过点 2 ,0．
x （1）求 a 的值；
（2）函数 g(x) lg[ f (x) 2x m] 在区间 2 ,3 上有意义，求实数 m 的取值范围；
（3）讨论关于 x 的方程 f (x) t 4x x2 （ t 为常数）的正根的个数.
9．由 sin A cosA
3 cosA 3 sin A
tan 5 6
可得：
sin A 3
cos A
tan 5 6
，
3
所以 tan A tan 5 所以 A 3 k , k Z ，
3
6
2
由于角 A 为三角形的内角所以 A ，所以 sinB C 1
2
10．因为 ABF2 为等边三角形，不妨设 AB BF2 AF2 m ， A 为双曲线上一点，
依题意，有 2(a3 2) a2 a4 ，代入 a2 a3 a4 28 ，可得 a3 8 ， 2 分

【历史】广东省湛江第一中学2015届高三“临门一脚”

广东省湛江第一中学2015届高三“临门一脚”12．周礼规定，天子三架编钟三面摆置，诸侯两架编钟两面摆置，大夫一架编钟一面摆置。

这表明西周时期A．分封制度瓦解 B．音乐教育普及 C．冶铁技术发达 D．等级制度森严13.以“六礼”为核心的传统婚礼，主要分为“纳采”、“问名”、“纳吉”、“纳征”、“请期”、“亲迎”六个阶段，整个过程形式繁琐，对家庭而言消耗巨大，但这种婚礼却在中国长期存在，究其原因有①小农经济的长期存在②结婚社会成本较高，有利于婚姻的稳定③加强专制皇权的需要④儒家思想的影响A、①②③④B、①②③C、①②④D、①③④14.春秋战国时期的百家争鸣为儒学的正统地位奠基，汉代董仲舒完成了儒学形态和内容的重大转折。

这种“转折”是指A．用法家思想来替代“仁义”学说 B．将儒学神学化并为君权辩护C．以“君权神授”否定“为政以德” D．确立“天理”体系取代“黄老之学15．《法国民法典》规定的“所有法国人都享有民事权利”的法律原则，正是罗马自然法思想与万民法追求的平等观念在新的历史条件下的继承与发展。

这充分反映了A．罗马法对近代欧洲国家立法、司法产生重大影响B．法国国民在法律上享有充分的民事权利C．民法典不断继承和发展罗马法的原则D．民法典是当今世界最完备的法律体系16.历史学家田玄认为：“辛亥革命没有从南方推进到北方，没有从长江流域推进到全国。

……形成革命运动沿海、沿江城市先进，内地和边疆城市落后；南方城市先进，北方城市落后（的状况）。

”这种“状况”说明A. 近代中国政治经济发展不平衡B. 革命的领导人多是南方人C. 南方人比北方人更有斗争精神D. 北方社会矛盾比南方缓和17．为“谋国民生活的安定与抵御外侮的国防能力的充实”，《请积极发展民营重工业以充实国力案》指出：“为从事经济建设应速完成重工业”，由“中央予以指导，令各省分别举办，以民营为主，或官民合办，以助成之。

”以上材料内容与下面哪一历史事件有关A．戊戌变法中“百日维新”法令B．北洋政府初期奖励实业政策C．国民经济建设运动D．“一五计划”优先发展重工业18．1958年，毛泽东曾把人民公社和巴黎公社相提并论，认为巴黎公社是世界上第一个公社，河南遂平的卫星公社是第二个公社。

2015届临门一脚

（非）金属元素的（非）金属性强弱判断
金属性强弱判断依据
1、金属单质与氧气反应的剧烈程度
非金属性强弱判断依据
1、单质与氢气反应生成气态氢化物的难易 2、单质与氢气反应生成气态氢化物的稳定性 3、最高价氧化物的水化物的酸性强弱 4、非金属间的置换反应５、非金属单质氧化性强弱
或非金属阴离子还原性的强弱
－－
7．在 O2、N2、CO2 等气体中均能燃烧的物质是 Mg。
提醒二
用途避免“张冠李戴”
1．Cl2、ClO2、NaClO 和漂白粉等可用于自来水的消毒杀菌，明矾可用作净水剂。 2．SO2 可用于工艺品的漂白，但不能用于食品漂白。 3．晶体硅可用作半导体材料、太阳能电池和硅合金。 4．SiO2 可用作制造光导纤维、光学仪器、电子部件和压电材料，石英还可用于制玻璃。 5．NaHCO3 可用于治疗胃酸过多，也可用于制造发酵粉。 6．Na2CO3 可用于制玻璃、造纸和食用碱。 7．AgBr 用作感光材料，AgI 用于人工降雨。 8．FeCl3 溶液可用作腐蚀印刷电路板。
三大基本营养物质
糖类油脂蛋白质
煤、石油和天然气是三种重要的化石燃料干馏直接煤液化间接气化天然有机高分子材料：蛋白质、淀粉、纤维素、天然橡胶
传统无机非金属：水泥、玻璃、陶瓷
原理原料石油炼制除去原油中的盐和水，减少脱水原油能耗及对设备的腐蚀。脱盐分馏
利用加热和冷凝，把石油分成不同沸点范围的产物。
提醒一
特征反应要记牢
1．在空气中迅速由无色变红棕色的气体只有 NO。 2．溶于水显碱性的气体只有 NH3。 3．在一定条件下能漂白有色物质的淡黄色粉末固体只有 Na2O2。 4．能与 NaOH 溶液反应产生氢气的金属只有 Al，非金属只有 Si。 5．可溶于氢氟酸的酸性氧化物只有 SiO2。 6．能与盐酸反应产生有刺激性气味的无色气体，且产生的气体能使品红溶液褪色，加热又恢复原色的，只有 SO2 3 和 HSO3 。

临门一脚：2015年四川高考理综物理查缺补漏试题

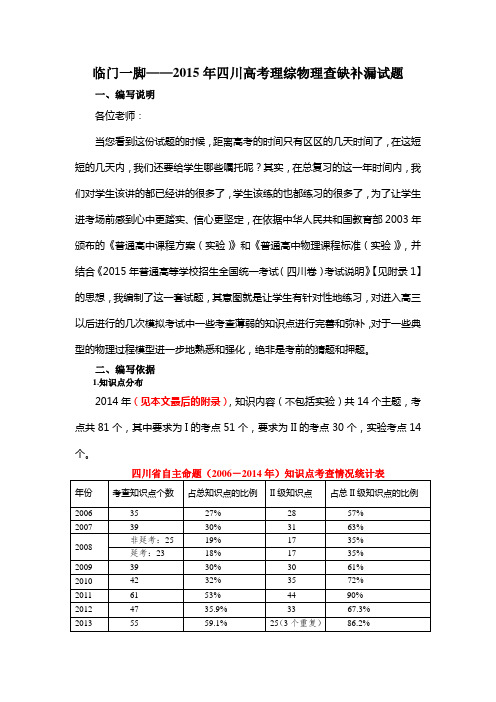
临门一脚——2015年四川高考理综物理查缺补漏试题一、编写说明各位老师：当您看到这份试题的时候，距离高考的时间只有区区的几天时间了，在这短短的几天内，我们还要给学生哪些嘱托呢？其实，在总复习的这一年时间内，我们对学生该讲的都已经讲的很多了，学生该练的也都练习的很多了，为了让学生进考场前感到心中更踏实、信心更坚定，在依据中华人民共和国教育部2003年颁布的《普通高中课程方案（实验）》和《普通高中物理课程标准（实验）》，并结合《2015年普通高等学校招生全国统一考试（四川卷）考试说明》【见附录1】的思想，我编制了这一套试题，其意图就是让学生有针对性地练习，对进入高三以后进行的几次模拟考试中一些考查薄弱的知识点进行完善和弥补，对于一些典型的物理过程模型进一步地熟悉和强化，绝非是考前的猜题和押题。

二、编写依据1.知识点分布2014年（见本文最后的附录），知识内容（不包括实验）共14个主题，考点共81个，其中要求为I的考点51个，要求为II的考点30个，实验考点14个。

从以上分析来看，四川试题考点较多，最近 3 年占了一半以上，且多数考题为综合题，往往一个试题考查多个知识点。

重点考查的知识点为：位移、速度和加速度；匀变速直线运动及其公式、图像；滑动摩擦力、动摩擦因数、静摩擦力；力的合成与分解；共点力的平衡；牛顿运动定律、牛顿运动定律的应用；运动的合成与分解；抛体运动；匀速圆周运动、角速度、线速度、向心力加速度；匀速圆周运动的向心力；功和功率；动能、动能定理；功能关系、机械能守恒定律及其应用；万有引力及其应用；电场强度、点电荷的场强；带电粒子在匀强电场中运动；欧姆定律；电阻的串联和并联；闭合电路欧姆定律；电功率、焦耳定律；安培力、安培力的方向；匀强磁场中的安培力；洛伦兹力和洛伦兹力的方向；洛伦兹力公式；带电粒子在匀强磁场中运动；法拉第电磁感应定律；楞次定律；横波的图像；波长、波速和频率（周期）的关系；光的折射定律。

2. 2015高考理数临门一脚---对学生

10 10 10 10 10 10 1000
1 4 16 61 EX 1 2 3 5 25 25 25
概率统计问题注意：细心阅读，认真审题；可套模型，不要错漏；书写表达，规范恰当；视应用题，最好写答。
（3）立体几何题：
占据着重要的地位，通过分析近几年的高考试题，可以发现高考对立体几何知识的考查已经突破了传统的模式，在命题风格上，正逐步由封闭向灵活、开放转变．近几年高考对立体几何的考查特点主要表现在以下几个方面：从命题形式来看，试题往往设计几个小问，往往以多面体为依托，第一小问考查线线、线面、面面的位置关系，后面几问考查空间角、空间距离、面积、体积等知识，其解题思路都是“作——证——算”，强调作图、证明和计算相结合．从内容上来看，主要考查：①空间直线和平面的各种位置关系的判定和性质；②角
A
6、函数的图像及性质：注意图像的变换、性质，给式判定图，给图判定式，等
B
7.平面向量----注意平行四边形法则和平面向量基本定理，及向量的运算及向量的夹角运算及模与数量积的关系
7.（2007四川）设A（a,1),B(2,b),C(4,5)，为坐标平面上三点，O为坐标原点，若
OA 与 OB 在 OC 方向上的投影相同，则a 与b满足的关系式为（ A）
cos 2 , sin
n1 S1 an S n S n 1 n 2
| AB | AB AB
a1 (1 q n ) ,q 1 sn 1 q na , q 1 1
2
E (a b) aE ( ) b
2 3
易错点
①曲线与方程的关系不明致错． ②曲线的性质与方程的特征对应致误． ③等价转化能力不够．

广东省广州市华南师大附中高考数学“临门一脚”试卷理(含解析)

广东省广州市华南师大附中2015届高考数学“临门一脚”试卷（理科）一、选择题（共5小题，每小题3分，满分15分）1．（3分）定义：分子为1且分母为正整数的分数称为单位分数．我们可以把1分拆为若干个不同的单位分数之和．如：1=++，1=+++，1=++++，…依此类推可得：1=++++++++++++，其中m≤n，m，n∈N*．设1≤x≤m，1≤y≤n，则的最小值为（）A．B．C．D．2．（3分）定义区间（a，b），[a，b），（a，b]，[a，b]的长度均为d=b﹣a，多个区间并集的长度为各区间长度之和，例如，（1，2）∪[3，5）的长度d=（2﹣1）+（5﹣3）=3．用[x]表示不超过x的最大整数，记{x}=x﹣[x]，其中x∈R．设f（x）=[x]{x}，g（x）=x﹣1，当0≤x≤k 时，不等式f（x）＜g（x）解集区间的长度为5，则k的值为（）A．6 B．7 C．8 D．93．（3分）设A是整数集的一个非空子集，对于k∈A，如果k﹣1∉A且k+1∉A，那么称k是A 的一个“孤立元”，给定S={1，2，3，4，5，6，7，8}，则S的3个元素构成的所有集合中，其元素都是“孤立元”的集合个数是（）A．6 B．15 C．20 D．254．（3分）在如图所示的空间直角坐标系O﹣xyz中，一个四面体的顶点坐标分别为（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出的编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为（）A．①和②B．③和①C．④和③D．④和②5．（3分）现安排甲、乙、丙、丁、戌5名同学参加上海世博会志愿者服务活动，每人从事翻译、导游、礼仪、司机四项工作之一，每项工作至少有一人参加．甲、乙不会开车但能从事其他三项工作，丙丁戌都能胜任四项工作，则不同安排方案的种数是（）A．152 B．126 C．90 D．54二、填空题（共3小题，每小题3分，满分9分）6．（3分）在平面直角坐标系xOy中，过点P（﹣5，a）作圆x2+y2﹣2ax+2y﹣1=0的两条切线，切点分别为M（x1，y1），N（x2，y2），且+=0，则实数a的值为．7．（3分）设（x﹣1）4（x+2）8=a0x12+a1x11+…+a n x+a12，则a2+a4+…+a12=．8．（3分）给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如图所示：由此推断，当n=6时，黑色正方形互不相邻的着色方案共有种，至少有两个黑色正方形相邻的着色方案共有种，（结果用数值表示）三、解答题（共15小题，满分122分）9．已知在△ABC中，角A，B，C所对的边分别为a，b，c，b（b﹣c）=（a﹣c）（a+c），且∠B为钝角．（Ⅰ）求角A的大小，并求出角C的范围；（Ⅱ）若a=，求b﹣c的取值范围．10．（12分）已知函数（x∈R）的图象经过点．（1）求函数f（x）的解析式；（2）设α，，，，求cos（α﹣β）的值．11．（12分）为备战2016年奥运会，甲、乙两位射击选手进行了强化训练，现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：甲：8.3，9.0，7.9，7.8，9.4，8.9，8.4，8.3；乙：9.2，9.5，8.0，7.5，8.2，8.1，9.0，8.5．（1）现要从中选派一人参见奥运会封闭集训，从统计学角度，你认为派哪位选手参加合理？简单说明理由；（2）若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8.5分的次数为ξ，求ξ的分布列及均值E（ξ）．12．如图，直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE=EB=，F为CE上的点，且BF⊥CE，G为AC中点．（Ⅰ）求证：AC⊥平面BGF；（Ⅱ）求二面角B﹣AC﹣E的平面角正弦的大小；（Ⅲ）求点D到平面ACE的距离．13．已知四棱锥P﹣ABCD的三视图如图所示，其中正（主）视图与侧（左）视为直角三角形，俯视图为正方形．（1）求四棱锥P﹣ABCD的体积；（2）若E是侧棱PA上的动点．问：不论点E在PA的任何位置上，是否都有BD⊥CE？请证明你的结论？（3）求二面角D﹣PA﹣B的余弦值．14．（14分）等边三角形ABC的边长为3，点D、E分别是边AB、AC上的点，且满足（如图1）．将△ADE沿DE折起到△A1DE的位置，使二面角A1﹣DE﹣B成直二面角，连结A1B、A1C （如图2）．（1）求证：A1D丄平面BCED；（2）在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB 的长；若不存在，请说明理由．15．（14分）已知数列{a n}是公比为的等比数列，数列{b n}满足a1=b1=1，且a n+12=，b n+1=1+，n∈N+，若c n=；（1）求证：数列{c n}是等差数列，并求出{c n}的通项公式；（2）记数列{c n}的前n项和为S n，若对于∀n∈N+，不等式a i≤k﹣恒成立，求实数k的取值范围．16．（14分）将数列{a n}中的所有项按每一行比上一行多一项的规则排成如下数表．记表中第一列数a1，a2，a4，a7，…构成的数列为{b n}，b1=a1=1．S n为数列{b n}的前n项和，且满足2b n=b n S n ﹣S n2（n≥2，n∈N*）．（1）证明数列{}是等差数列，并求数列{b n}的通项公式；（2）图中，若从第三行起，每一行中的数按从左到右的顺序构成等比数列，且公比为同一个正数．当a81=﹣时，求上表中第k（k≥3）行所有数的和．17．已知各项均为正数的数列{a n}的前n项和为S n，且4S n=a n2+2a n（n∈N*）．（1）求a1的值及数列{a n}的通项公式；（2）记数列{}的前n项和为T n，求证：T n＜（n∈N*）．18．已知圆C：（x﹣1）2+（y﹣1）2=2经过椭圆Γ：+=1（a＞b＞0）的右焦点F和上顶点B．（Ⅰ）求椭圆Γ的方程；（Ⅱ）过原点O的射线l与椭圆Γ在第一象限的交点为Q，与圆C的交点为P，M为OP的中点，求•的最大值．19．（14分）如图，已知点S（﹣2，0）和圆O：x2+y2=4，ST是圆O的直径，从左到右M、O和N依次是ST的四等分点，P（异于S，T）是圆O上的动点，PD⊥ST，交ST于D，=λ，直线PS与TE交于C，|CM|+|CN|为定值．（1）求点C的轨迹曲线Γ的方程及λ的值；（2）设n是过原点的直线，直线l与n垂直相交于Q点，l与轨迹Γ相交于A，B两点，且||=1．是否存在直线l，使•=1成立？若存在，求出直线l的方程；若不存在，请说明理由．20．（14分）如图，在平面直角坐标系xOy中，已知A，B，C是椭圆+=1（a＞b＞0）上不同的三点，A（3，），B（﹣3，﹣3），C在第三象限，线段BC的中点在直线OA上．（1）求椭圆的标准方程；（2）求点C的坐标；（3）设动点P在椭圆上（异于点A，B，C）且直线PB，PC分别交直线OA于M，N两点，证明•为定值并求出该定值．21．设函数f（x）=（1﹣ax）ln（x+1）﹣bx，其中a和b是实数，曲线y=f（x）恒与x轴相切于坐标原点．（1）求常数b的值；（2）当0≤x≤1时，关于x的不等式f（x）≥0恒成立，求实数a的取值范围；（3）求证：（）10000.4＜e＜（）1000.5．22．（14分）已知函数f（x）=2（a﹣1）ln（x﹣1）+x﹣（4a﹣2）lnx，其中实数a为常数．（Ⅰ）当a=2时，求函数f（x）的单调递减区间；（Ⅱ）设函数y=f（e x）有极大值点和极小值点分别为x1、x2，且x2﹣x1＞ln2，求a的取值范围．23．（14分）已知函数f（x）=x﹣xlnx，g（x）=f（x）﹣xf′（a），其中f′（a）表示函数f（x）在x=a处的导数，a为正常数．（1）求g（x）的单调区间；（2）对任意的正实数x1，x2，且x1＜x2，证明：（x2﹣x1）f′（x2）＜f（x2）﹣f（x1）＜（x2﹣x1）f′（x1）；（3）对任意的n∈N*，且n≥2，证明：．广东省广州市华南师大附中2015届高考数学“临门一脚”试卷（理科）参考答案与试题解析一、选择题（共5小题，每小题3分，满分15分）1．（3分）定义：分子为1且分母为正整数的分数称为单位分数．我们可以把1分拆为若干个不同的单位分数之和．如：1=++，1=+++，1=++++，…依此类推可得：1=++++++++++++，其中m≤n，m，n∈N*．设1≤x≤m，1≤y≤n，则的最小值为（）A．B．C．D．考点：归纳推理．专题：计算题；推理和证明．分析：由题意，m=13，n=4×5=20，则=1+，可得y=1，x=13时，取得最小值．解答：解：由题意，m=13，n=4×5=20，则=1+，∵1≤x≤m，1≤y≤n，∴y=1，x=13时，的最小值为，故选：C．点评：本题考查归纳推理，考查学生的计算能力，取得m，n的值是关键．2．（3分）定义区间（a，b），[a，b），（a，b]，[a，b]的长度均为d=b﹣a，多个区间并集的长度为各区间长度之和，例如，（1，2）∪[3，5）的长度d=（2﹣1）+（5﹣3）=3．用[x]表示不超过x的最大整数，记{x}=x﹣[x]，其中x∈R．设f（x）=[x]{x}，g（x）=x﹣1，当0≤x≤k 时，不等式f（x）＜g（x）解集区间的长度为5，则k的值为（）A．6 B．7 C．8 D．9考点：函数单调性的性质；函数的值域．专题：计算题；新定义．分析：先化简f（x）=[x]•{x}=[x]•（x﹣[x]）=[x]x﹣[x]2，再化简f（x）＜g（x），再分类讨论：①当x∈[0，1）时，②当x∈[1，2）时③当x∈[2，3）时，从而得出f（x）＜g（x）在0≤x≤k时的解集的长度，依题意即可求得k的值．解答：解：f（x）=[x]•{x}=[x]•（x﹣[x]）=[x]x﹣[x]2，g（x）=x﹣1，f（x）＜g（x）⇒[x]x﹣[x]2＜x﹣1即（[x]﹣1）x＜[x]2﹣1，当x∈[0，1）时，[x]=0，上式可化为x＞1，∴x∈∅；当x∈[1，2）时，[x]=1，上式可化为0＞0，∴x∈∅；当x∈[2，3）时，[x]=2，[x]﹣1＞0，上式可化为x＜[x]+1=3，∴当x∈[0，3）时，不等式f（x）＜g（x）解集区间的长度为d=3﹣2=1；同理可得，当x∈[3，4）时，不等式f（x）＜g（x）解集区间的长度为d=4﹣2=2；∵不等式f（x）＜g（x）解集区间的长度为5，∴k﹣2=5，∴k=7．故选B．点评：本题主要考查了抽象函数及其应用，同时考查了创新能力，以及分类讨论的思想和转化思想，属于中档题．3．（3分）设A是整数集的一个非空子集，对于k∈A，如果k﹣1∉A且k+1∉A，那么称k是A 的一个“孤立元”，给定S={1，2，3，4，5，6，7，8}，则S的3个元素构成的所有集合中，其元素都是“孤立元”的集合个数是（）A．6 B．15 C．20 D．25考点：分类加法计数原理；元素与集合关系的判断；排列、组合的实际应用．专题：集合；排列组合．分析：若集合S的子集的3个元素都是“孤立元”，则三元素两两不相邻，可采用间接法，即先不考虑相邻与否，算出S的所有三元素子集的个数，再从中去掉只有两个元素相邻和三个元素都相邻的三元素子集个数．解答：解：S的所有三元素子集共有个，三元素中只有两个相邻的有两类：一是若1、2，或7、8相邻，则只需再从与之不相邻的5个元素中任取一个，共有2=10个；二是若2、3或3、4或4、5或5、6或6、7相邻，则需从与之不相邻的四个元素中再任取一个，共5=20个；三元素都相邻的共有6个（即：123，234，345，456，567，678）；所以符合题意三元素子集共﹣10﹣20﹣6=20个．故选C点评：这个题以集合知识为载体，重点考查利用组合知识解决问题的能力．4．（3分）在如图所示的空间直角坐标系O﹣xyz中，一个四面体的顶点坐标分别为（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出的编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为（）A．①和②B．③和①C．④和③D．④和②考点：简单空间图形的三视图．专题：计算题；空间位置关系与距离．分析：在坐标系中，标出已知的四个点，根据三视图的画图规则，可得结论．解答：解：在坐标系中，标出已知的四个点，根据三视图的画图规则，可得三棱锥的正视图和俯视图分别为④②，故选：D．点评：本题考查三视图的画法，做到心中有图形，考查空间想象能力，是基础题．5．（3分）现安排甲、乙、丙、丁、戌5名同学参加上海世博会志愿者服务活动，每人从事翻译、导游、礼仪、司机四项工作之一，每项工作至少有一人参加．甲、乙不会开车但能从事其他三项工作，丙丁戌都能胜任四项工作，则不同安排方案的种数是（）A．152 B．126 C．90 D．54考点：排列、组合的实际应用．专题：计算题．分析：根据题意，按甲乙的分工情况不同分两种情况讨论，①甲乙一起参加除了开车的三项工作之一，②甲乙不同时参加一项工作；分别由排列、组合公式计算其情况数目，进而由分类计数的加法公式，计算可得答案．解答：解：根据题意，分情况讨论，①甲乙一起参加除了开车的三项工作之一：C31×A33=18种；②甲乙不同时参加一项工作，进而又分为2种小情况；1°丙、丁、戌三人中有两人承担同一份工作，有A32×C32×A22=3×2×3×2=36种；2°甲或乙与丙、丁、戌三人中的一人承担同一份工作：A32×C31×C21×A22=72种；由分类计数原理，可得共有18+36+72=126种，故选B．点评：本题考查排列、组合的综合运用，注意要根据题意，进而按一定顺序分情况讨论．二、填空题（共3小题，每小题3分，满分9分）6．（3分）在平面直角坐标系xOy中，过点P（﹣5，a）作圆x2+y2﹣2ax+2y﹣1=0的两条切线，切点分别为M（x1，y1），N（x2，y2），且+=0，则实数a的值为3或﹣2．考点：圆的切线方程．专题：计算题；直线与圆．分析：两者的和实质上是一个斜率与另一个斜率的倒数和，进而可得两斜率乘积为﹣1，可得P，Q，R，T共线，即可求出实数a的值．解答：解：设MN中点为Q（x0，y0），T（1，0），圆心R（a，﹣1），根据对称性，MN⊥PR，===，∵k MN=，+=0∴k MN•k TQ=﹣1，∴MN⊥TQ，∴P，Q，R，T共线，∴k PT=k RT，即，∴a2﹣a﹣6=0，∴a=3或﹣2．故答案为：3或﹣2．点评：本题考查实数a的值，考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．7．（3分）设（x﹣1）4（x+2）8=a0x12+a1x11+…+a n x+a12，则a2+a4+…+a12=7．考点：二项式系数的性质；二项式定理的应用．专题：计算题．分析：分别令x=1与x=﹣1即可求得a0+a2+a4+…+a12的值，而a0=1，从而可得答案．解答：解：∵（x﹣1）4（x+2）8=a0x12+a1x11+…+a11x+a12，∴当x=1时，a0+a1+a2+…+a12=0，①当x=﹣1时，a0﹣a1+a2﹣…﹣a11+a12=16，②①+②得：2（a0+a2+a4+…+a12）=16，∴a0+a2+a4+…+a12=8；又含x12项的系数为1，即a0=1，∴a2+a4+…+a12=7．故答案为：7．点评：本题考查二项式定理的应用，考查二项式系数的性质，突出赋值法的应用，属于中档题．8．（3分）给n个自上而下相连的正方形着黑色或白色．当n≤4时，在所有不同的着色方案中，黑色正方形互不相连的着色方案如图所示：由此推断，当n=6时，黑色正方形互不相邻的着色方案共有21种，至少有两个黑色正方形相邻的着色方案共有43种，（结果用数值表示）考点：归纳推理；计数原理的应用．专题：计算题；压轴题．分析：根据所给的涂色的方案，观测相互之间的方法数，得到规律，根据这个规律写出当n 取不同值时的结果数；利用给小正方形涂色的所有法数减去黑色正方形互不相邻的着色方案，得到结果．解答：解：由题意知当n=1时，有2种，当n=2时，有3种，当n=3时，有2+3=5种，当n=4时，有3+5=8种，当n=5时，有5+8=13种，当n=6时，有8+13=21种，当n=6时，黑色和白色的小正方形共有26种涂法，黑色正方形互不相邻的着色方案共有21种结果，∴至少有两个黑色正方形相邻的着色方案共有64﹣21=43种结果，故答案为：21；43点评：本题考查简单的排列组合及简单应用，考查观察规律，找出结果的过程，是一个比较麻烦的题目，当作为2015届高考题目比前几年的排列组合问题不难．三、解答题（共15小题，满分122分）9．已知在△ABC中，角A，B，C所对的边分别为a，b，c，b（b﹣c）=（a﹣c）（a+c），且∠B为钝角．（Ⅰ）求角A的大小，并求出角C的范围；（Ⅱ）若a=，求b﹣c的取值范围．考点：余弦定理；正弦定理．专题：解三角形．分析：（Ⅰ）把已知的等式变形，然后利用余弦定理求得cosA，再结合角A的范围求A，再由∠B为钝角可得C的范围；（Ⅱ）利用正弦定理得到b=sinB，c=sinC，代入b﹣c后利用辅助角公式化积，再由C的范围得答案．解答：解：（Ⅰ）由b（b﹣c）=（a﹣c）（a+c），得，得，于是．又A∈（0，π），∴A=∵B为钝角，于是A+C，又A=，∴；（Ⅱ）由正弦定理可知，，∴b=sinB，c=sinC．=，又0，，∴．点评：本题考查三角形的解法，考查了正弦定理和余弦定理的应用，训练了两角和与差的余弦公式，是中低档题．10．（12分）已知函数（x∈R）的图象经过点．（1）求函数f（x）的解析式；（2）设α，，，，求cos（α﹣β）的值．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；两角和与差的余弦函数．专题：计算题；三角函数的求值．分析：（1）由函数f（x）的解析式，代入点的坐标，解得a的值，从而可求函数f（x）的解析式．（2）由f（x）=可由解得sinα的值，利用三角函数恒等变换化简可得sinβ的值，结合范围，利用同角三角函数关系式可求cosα，cosβ的值，由两角和与差的余弦函数公式即可得解．解答：（本小题满分12分）解：（1）由函数f（x）的图象经过点，则．解得a=﹣1，因此．（2）==，∵，∴，∵，∴，又，∴，，∴．点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，两角和与差的余弦函数公式，同角三角函数关系式的应用，属于中档题．11．（12分）为备战2016年奥运会，甲、乙两位射击选手进行了强化训练，现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：甲：8.3，9.0，7.9，7.8，9.4，8.9，8.4，8.3；乙：9.2，9.5，8.0，7.5，8.2，8.1，9.0，8.5．（1）现要从中选派一人参见奥运会封闭集训，从统计学角度，你认为派哪位选手参加合理？简单说明理由；（2）若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8.5分的次数为ξ，求ξ的分布列及均值E（ξ）．考点：离散型随机变量的期望与方差；极差、方差与标准差；离散型随机变量及其分布列．专题：计算题；概率与统计．分析：（1）求平均数=8.5，=8.5；再求标准差S甲≈0.52，S乙≈0.64；从而确定；（2）对于乙射击选手，每次射击不低于8.5分的概率为，从而求ξ分布列及数学期望．解答：解：（1）==8.5，==8.5；S甲=≈0.52，S乙≈0.64；甲射击选手更稳定一些，故派甲选手参加合理．（2）对于乙射击选手，每次射击不低于8.5分的概率为，故ξ分布列为ξ 0 1 2 3P故E（ξ）=+×2+×3=．点评：本题考查了离散型随机变量的期望及分布列的求法，计算量比较大，属于中档题．12．如图，直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE=EB=，F为CE上的点，且BF⊥CE，G为AC中点．（Ⅰ）求证：AC⊥平面BGF；（Ⅱ）求二面角B﹣AC﹣E的平面角正弦的大小；（Ⅲ）求点D到平面ACE的距离．考点：二面角的平面角及求法；直线与平面垂直的判定；点、线、面间的距离计算．专题：空间位置关系与距离；空间角．分析：（1）证明CB⊥平面ABE．然后证明BF⊥AC．BG⊥AC．利用直线与平面垂直的判定定理证明AC⊥平面BGF．（2）连结BD交AC于G，连结FG，说明∠BGF是二面角B﹣AC﹣E的平面角，通过求解直角△BFG，得到二面角B﹣AC﹣E的平面角正弦值．（3）过点E作EO⊥AB交AB于点O，OE=1．利用V D﹣ACE=V E﹣ACD，求解点D到平面ACE的距离．解答：（1）证明：∵二面角DABE为直二面角，且CB⊥AB，∴CB⊥平面ABE．∴CB⊥AE．又∵AE=EB=，AB=2∴EB⊥AE．∴AE⊥平面BCE．∴BF⊥AE．又∵BF⊥CE．∴BF⊥平面ACE∴BF⊥AC．又∵BG⊥AC．∴AC⊥平面BGF；…（4分）（2）解：连结BD交AC于G，连结FG，∵正方形ABCD边长为2，∴BG⊥AC，BG=．∵BF⊥平面ACE，由三垂线定理的逆定理得FG⊥AC，∴∠BGF是二面角B﹣AC﹣E的平面角．…（6分）由（1）AE⊥平面BCE，又∵AE=EB，∴在等腰直角三角形AEB中，BE=．又∵直角△BCE中，，BF===，∴直角△BFG中，sin∠BGF===．∴二面角B﹣AC﹣E的平面角正弦值为：；…（10分）（3）解：过点E作EO⊥AB交AB于点O，OE=1．∵二面角D﹣AB﹣E为直二面角，∴EO⊥平面ABCD．设D到平面ACE的距离为h，∵V D﹣ACE=V E﹣ACD，∴=S△ACD•EO．…（12分）∵AE⊥平面BCE，∴AE⊥EC．∴h===．∴点D到平面ACE的距离为．…（14分）点评：本题考查二面角的平面角的求法，找出二面角的平面角是求解角的关键，同时考查点、线、面之间距离，考查几何体的体积的求法，直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．13．已知四棱锥P﹣ABCD的三视图如图所示，其中正（主）视图与侧（左）视为直角三角形，俯视图为正方形．（1）求四棱锥P﹣ABCD的体积；（2）若E是侧棱PA上的动点．问：不论点E在PA的任何位置上，是否都有BD⊥CE？请证明你的结论？（3）求二面角D﹣PA﹣B的余弦值．考点：由三视图求面积、体积；棱柱、棱锥、棱台的体积；与二面角有关的立体几何综合题．专题：计算题；转化思想．分析：（1）根据三视图的数据，结合三视图的特征直接求四棱锥P﹣ABCD的体积；（2）若E是侧棱PA上的动点．不论点E在PA的任何位置上，都有BD⊥CE，说明BD⊥平面PAC，都有CE⊂平面PAC，即可．（3）在平面DAP过点D作DF⊥PA于F，连接BF．说明∠DFB为二面角D﹣AP﹣B的平面角，在△DFB中，求二面角D﹣PA﹣B的余弦值．解答：解：（1）由三视图可知，四棱锥P﹣ABCD的底面是边长为1的正方形，侧棱PC⊥底面ABCD，且PC=2∴S正方形ABCD•PC=．（4分）（2）不论点E在何位置，都有BD⊥AE（5分）证明：连接AC，∵ABCD是正方形，∴BD⊥AC∵PC⊥底面ABCD，且BD⊂平面ABCD，∴BD⊥PC．（6分）又∵AC∩PC=C，∴BD⊥平面PAC（7分）∵不论点E在何位置，都有CE⊂平面PAC．∵不论点E在何位置，都有BD⊥CE．（9分）（3）在平面DAP过点D作DF⊥PA于F，连接BF∵，AD=AB=1，∴Rt△ADP≌Rt△ABP∴∠PAD=∠PAB，又AF=AF，AB=AD从而△ADF≌△ABF，∴BF⊥AP．∴∠DFB为二面角D﹣AP﹣B的平面角（12分）在Rt△ACP中，故在Rt△ADP中，．又，在△DFB中，由余弦定理得：．所以二面角D﹣PA﹣B的余弦值为．（14分）点评：本题是基础题，考查几何体的三视图，几何体的体积的求法，准确判断几何体的形状是解题的关键，同时注意：空间想象能力，逻辑思维能力的培养．14．（14分）等边三角形ABC的边长为3，点D、E分别是边AB、AC上的点，且满足（如图1）．将△ADE沿DE折起到△A1DE的位置，使二面角A1﹣DE﹣B成直二面角，连结A1B、A1C （如图2）．（1）求证：A1D丄平面BCED；（2）在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB 的长；若不存在，请说明理由．考点：用空间向量求直线与平面的夹角；直线与平面垂直的判定；直线与平面所成的角．专题：计算题；空间角；空间向量及应用．分析：（1）等边△ABC中，根据得到AD=1且AE=2，由余弦定理算出DE=，从而得到AD2+DE2=AE2，所以AD⊥DE．结合题意得平面A1DE⊥平面BCDE，利用面面垂直的性质定理，可证出A1D丄平面BCED；（2）作PH⊥BD于点H，连接A1H、A1P，由A1D丄平面BCED得A1D丄PH，所以PH⊥平面A1BD，可得∠PA1H是直线PA1与平面A1BD所成的角，即∠PA1H=60°．设PB=x（0≤x≤3），分别在Rt△BA1H、Rt△PA1H和Rt△DA1H中利用三角函数定义和勾股定理，建立等量关系得12+（2﹣x）2=（x）2，解之得x=，从而得到在BC上存在点P且当PB=时，直线PA1与平面A1BD所成的角为60°．解答：解：（1）∵正△ABC的边长为3，且==∴AD=1，AE=2，△ADE中，∠DAE=60°，由余弦定理，得DE==∵AD2+DE2=4=AE2，∴AD⊥DE．折叠后，仍有A1D⊥DE∵二面角A1﹣DE﹣B成直二面角，∴平面A1DE⊥平面BCDE又∵平面A1DE∩平面BCDE=DE，A1D⊂平面A1DE，A1D⊥DE∴A1D丄平面BCED；（2）假设在线段BC上存在点P，使直线PA1与平面A1BD所成的角为60°如图，作PH⊥BD于点H，连接A1H、A1P由（1）得A1D丄平面BCED，而PH⊂平面BCED所以A1D丄PH∵A1D、BD是平面A1BD内的相交直线，∴PH⊥平面A1BD由此可得∠PA1H是直线PA1与平面A1BD所成的角，即∠PA1H=60°设PB=x（0≤x≤3），则BH=PBcos60°=，PH=PBsin60°=x在Rt△PA1H中，∠PA1H=60°，所以A1H=，在Rt△DA1H中，A1D=1，DH=2﹣x由A1D2+DH2=A1H2，得12+（2﹣x）2=（x）2解之得x=，满足0≤x≤3符合题意所以在线段BC上存在点P，使直线PA1与平面A1BD所成的角为60°，此时PB=．点评：本题给出平面翻折问题，求证直线与平面垂直并探索了直线与平面所成角的问题，着重考查了线面垂直、面面垂直的判定与性质和直线与平面所成角的求法等知识，属于中档题．15．（14分）已知数列{a n}是公比为的等比数列，数列{b n}满足a1=b1=1，且a n+12=，b n+1=1+，n∈N+，若c n=；（1）求证：数列{c n}是等差数列，并求出{c n}的通项公式；（2）记数列{c n}的前n项和为S n，若对于∀n∈N+，不等式a i≤k﹣恒成立，求实数k的取值范围．考点：数列递推式；数列的求和．专题：等差数列与等比数列；不等式的解法及应用．分析：（1）把b n+1=1+右边通分后两边平方，与a n+12=两边作积即可证得数列{c n}是等差数列，由等差数列的通项公式求其通项公式；（2）求出数列{c n}的前n项和为S n，代入a i整理，利用错位相减法求其和，由不等式a i≤k﹣分离k后求得函数的最大值得答案．解答：（1）证明：递推关系可变形为：，（n∈N*），两式相乘得：（n∈N*），即c n+1=c n+1（n∈N*），又，∴．∴数列{c n}是首项为，公差为1的等差数列，故{c n}的通项公式：；（2）解：由（1）知道，，，∴a i=．记①②由①﹣②得：=．∴．∴，即对于任意的正整数n，不等式恒成立，∴k≥，当n=1时，．∴k的范围是[）．点评：本题考查数列递推式，考查了等差关系的确定，训练了错位相减法求数列的和，考查了数列的函数特性，属中高档题．16．（14分）将数列{a n}中的所有项按每一行比上一行多一项的规则排成如下数表．记表中第一列数a1，a2，a4，a7，…构成的数列为{b n}，b1=a1=1．S n为数列{b n}的前n项和，且满足2b n=b n S n ﹣S n2（n≥2，n∈N*）．（1）证明数列{}是等差数列，并求数列{b n}的通项公式；（2）图中，若从第三行起，每一行中的数按从左到右的顺序构成等比数列，且公比为同一个正数．当a81=﹣时，求上表中第k（k≥3）行所有数的和．考点：数列的求和；等差关系的确定．专题：综合题；等差数列与等比数列．分析：（1）由n≥2时，2b n=b n S n﹣S n2，得2（S n﹣S n﹣1）=（S n﹣S n﹣1）S n﹣=﹣S n S n﹣1，两边同除以S n S n﹣1整理后得，由此可知数列{}是等差数列，从而可求得S n，根据S n与b n的关系可求得b n；（2）设上表中从第三行起，每行中的数构成的等比数列的公比都为q，且q＞0．易判断a81所在的行和列，借助b n可求得公比q，再根据等比数列的求和公式可求得结果；解答：解：（1）由已知，当n≥2时，2b n=b n S n﹣S n2，又S n=b1+b2+b3+…+b n，∴2（S n﹣S n﹣1）=（S n﹣S n﹣1）S n﹣=﹣S n S n﹣1，∴，又S1=b1=a1=1．∴数列{}是首项为1，公差为的等差数列．∴，则．∴当n≥2时，b n=S n﹣S n﹣1==﹣，∴；（2）设上表中从第三行起，每行中的数构成的等比数列的公比都为q，且q＞0．∵1+2+…+12==78，∴表中第1行至第12行共含有数列{a n}的前78项，故a81在表中第13行第3列，∴．又，∴q=2．记表中第k（k≥3）行所有数的和为S n，则=﹣•=．点评：本题考查等差关系的确定、等比数列的通项公式及数列的求和，属中档题，考查学生分析问题解决问题的能力．17．已知各项均为正数的数列{a n}的前n项和为S n，且4S n=a n2+2a n（n∈N*）．（1）求a1的值及数列{a n}的通项公式；（2）记数列{}的前n项和为T n，求证：T n＜（n∈N*）．考点：数列的求和；数列递推式．专题：点列、递归数列与数学归纳法．分析：（1）通过4S n=a n2+2a n，令n=1可得首项，当n≥2时，利用4a n=a n2+2a n﹣（a n﹣12+2a n ﹣1）可得公差，进而可得结论；（Ⅱ）通过令n=1可得T1＜满足结论，当n≥2时，利用放缩法可得＜[•﹣•]，并项相加即得．解答：（1）解：当n=1时，4a1=4S1=+2a1，解得a1=2或a1=0（舍去）；当n≥2时，4S n=a n2+2a n，4S n﹣1=a n﹣12+2a n﹣1，相减得4a n=a n2+2a n﹣（a n﹣12+2a n﹣1），即a n2﹣a n﹣12=2（a n+a n﹣1），又a n＞0，∴a n+a n﹣1≠0，则a n﹣a n﹣1=2，∴数列{a n}是首项为2，公差为2的等差数列，∴a n=2n；（Ⅱ）证明：当n=1时，T1===＜；当n≥2时，==＜==•={+[﹣]}=[•﹣•]，∴T n＜+[﹣+﹣+…+•﹣•]=+（﹣•）＜+•=+=；综上，对任意n∈N*，均有T n＜成立．点评：本题考查求数列的通项、判断数列和的取值范围，注意解题方法的积累，属于中档题．18．已知圆C：（x﹣1）2+（y﹣1）2=2经过椭圆Γ：+=1（a＞b＞0）的右焦点F和上顶点B．（Ⅰ）求椭圆Γ的方程；（Ⅱ）过原点O的射线l与椭圆Γ在第一象限的交点为Q，与圆C的交点为P，M为OP的中点，求•的最大值．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线中的最值与范围问题．分析：（Ⅰ）在圆（x﹣1）2+（y﹣1）2=2中，令y=0，得F（2，0），令x=0，得B（0，2），由此能求出椭圆方程．（Ⅱ）设点Q（x0，y0），x0＞0，y0＞0，则==x0+y0，又，设b=x0+y0，与联立，得：，由此能求出的最大值．解答：解：（Ⅰ）在圆C：（x﹣1）2+（y﹣1）2=2中，令y=0，得F（2，0），即c=2，令x=0，得B（0，2），即b=2，∴a2=b2+c2=8，∴椭圆Γ的方程为：．（Ⅱ）设点Q（x0，y0），x0＞0，y0＞0，则==（1，1）•（x0，y0）=x0+y0，又，设b=x0+y0，与联立，得：，令△≥0，得16b2﹣12（12b2﹣8）≥0，解得﹣2．又点Q（x0，y0）在第一象限，∴当时，取最大值2．点评：本题考查直线、圆、椭圆、平面向量、分式函数等基础知识，考查直线与圆锥曲线的位置关系，考查运算求解能力、推理论证能力，考查数形结合、化归转化及函数与方程等数学思想．19．（14分）如图，已知点S（﹣2，0）和圆O：x2+y2=4，ST是圆O的直径，从左到右M、O和N依次是ST的四等分点，P（异于S，T）是圆O上的动点，PD⊥ST，交ST于D，=λ，直线PS与TE交于C，|CM|+|CN|为定值．（1）求点C的轨迹曲线Γ的方程及λ的值；（2）设n是过原点的直线，直线l与n垂直相交于Q点，l与轨迹Γ相交于A，B两点，且||=1．是否存在直线l，使•=1成立？若存在，求出直线l的方程；若不存在，请说明理由．考点：轨迹方程；直线与圆锥曲线的关系．专题：综合题；圆锥曲线的定义、性质与方程．分析：（1）设出点的坐标，得，根据|CM|+|CN|为定值，建立条件关系即可求λ的值及点C的轨迹曲线E的方程；（2）分类讨论，根据•=1，||=1，进行转化，将y=kx+m代入椭圆方程，利用x1x2+y1y2=0，即可得出结论．解答：解：（1）由题意，T（2，0），M（﹣1，0），N（1，0），设P（x0，y0），C（x，y），则E（x0，），直线PS与TE交于C，故x≠±2，①且，②①②相乘得，又点P是圆O上的动点，故，（4分）要使|CM|+|CN|为定值，则4﹣=1，解得λ=．此时（x≠±2）．即λ=时，点C的轨迹曲线E的方程为（x≠±2）．（2）设A，B两点的坐标分别为（x1，y1），（x2，y2），假设使•=1成立的直线l存在，（ⅰ）当l不垂直于x轴时，设l的方程为y=kx+m，由l与n垂直相交于Q点且||=1．得=1，即m2=k2+1∵•=1，||=1．∴•=（+）•（+）=0即x1x2+y1y2=0，将y=kx+m代入椭圆方程，得（3+4k2）x2+8kmx+（4m2﹣12）=0。

高2015届高考全国冲刺卷物理临门一脚

高2015届高考全国冲刺卷物理临门一脚第I卷（选择题，共42分）本卷共7小题．每题6分，共42分。

每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对得6分，选对但不全得3分，有选错的得0分1. 2013年度诺贝尔物理学奖授予了希格斯和恩格勒，以表彰他们对用来解释物质质量之谜的“上帝粒子”所做出的预测。

在物理学的发展过程中，许多物理学家的科学发现推动了人类历史的进步。

下列表述符合物理学史实的是A．开普勒认为只有在一定的条件下，弹簧的弹力才与弹簧的形变量成正比B．密立根最早通过实验比较准确的测定了电子的电量C．奥斯特发现了电磁感应现象，这和他坚信电和磁之间一定存在着联系的哲学思想是分不开的D．安培首先引入电场线和磁感线，极大地促进了他对电磁现象的研究2．关于光学现象，下列说法正确的是A．用光导纤维束传送图象信息，这是光的衍射的应用B．照相机的增透膜厚度通常为光在该薄膜介质中波长的1 4C．太阳光通过三棱镜形成彩色光谱，这是光的干涉的结果D．透过平行于日光灯的窄缝看正常发光的日光灯时能观察到彩色条纹，这是光的色散现象3．在水平长绳上的O点系着一个弹簧和小球组成的振动系统，小球振动的固有频率为2 Hz，在长绳丙端分别有一振源P、Q同时开始以相同振幅A上下振动了一段时间，某时刻两个振源在长绳上形成如图所示波形，两列波先后间隔一段时间经过弹簧振子所在位置，观察到小球先后出现了两次振动，小球第一次振动时起振方向向上，且振动并不显著，而小球第二次发生了共振现象，则下列说法错误的是A．PO的距离小于OQ的距离 B．由Q振源产生的波的波速接近4 m/s C．两列波相遇能产生稳定的干涉图样 D．绳上会出现振动位移大小为2A的点4．在如图所示的远距离输电电路中，升压变压器和降压变压器均视为理想变压器，发电厂的输出电压和输电线的电阻均不变。

当用电高峰期时，若发电厂将输出功率增加一倍，则下列说法中正确的有A．升压变压器的输出电压也增加一倍 B．降压变压器的输出电压也增加一倍C．输电线上损耗的功率也增加一倍 D．输电线上损耗的功率占总功率的比例也增加一倍5. 2013年12月2Fl1时30分，搭载月球车和着陆器的嫦娥三号月球探测器从西昌卫星发射中心升空，飞行约18min后，嫦娥三号进入如图所示的地月转移轨道AB，A为入口点，B 为出口点，嫦娥三号在B 点经过近月制动，进入距离月面h=100公里的环月圆轨道，其运行的周期为T ，然后择机在月球虹湾地区实行软着陆，展开月面巡视勘察。

广东省华南师大附中2015年高考语文临门一脚试题

2015届高三语文临门一脚系列训练之一语文基础、作文（1）训练一1．下列词语中加点的字，每对读音都不相同的一组是（）A．拱手／供述揭榜／劫难强行／强制B．湛蓝／斟酌憋闷／别扭量力／量刑C．杠杆／内讧舐犊／伺机螳臂当车／安步当车D．精粹／猝然稽查／畸形冠冕堂皇／张冠李戴2．下面语段中画线的词语，使用不恰当的一项是（）羊年的春节，派发微信红包成为让老百姓大快人心的问候新方式。

诚然，互联网红包的走俏和盛行捕捉到了大众的心理与趣味，却在一定程度上冲淡了传统节庆的味道，模糊了传统红包那份真挚祝福、祝愿的内涵，使得人与人之间多了小屏幕上的互动，少了现实中的交流。

其实，任何一种新民俗若不能稳固亲情，恐怕只会昙花一现。

A．大快人心B．诚然C．冲淡 D．昙花一现3．下列句子中，没有语病的一项是（）A．在“一带一路”国家战略影响下，未来5年，中国对外投资将超过5000亿美元以上，出境游客数量约5亿人次，周边国家以及丝绸之路沿线国家将率先受益。

B．亚洲基础设施投资银行不仅将经济增长动力引擎的基础设施建设，还会提高亚洲资本的利用效率及对区域发展的贡献水平。

C．2014“寻找最美乡村教师”活动继续围绕中国梦为主题开展，在推选出“最美乡村教师”的同时，特别增设一个团队奖，授予那些积极参与志愿支教的大学生团队。

D．李光耀是深谙东西方文化的政治家，他将东方的儒家文化和西方现代的法制、民主思想融合，创立了别具一格的新加坡发展模式。

4．依次填入下面一段文字横线处的词语，衔接最恰当的一组是（3分）没有怀疑，就没有创新。

，。

①就连怀疑本身也大可怀疑②因为在极端的怀疑主义者眼中③没有什么是确定无疑的④超出这个度，就会走向其反面⑤怀疑一切，和没有怀疑一样是不可取的⑥但是，怀疑也要不失理性和尺度A．⑥④⑤②①③B．⑥④②③①⑤C．②①⑥④⑤③D．③①②④③⑤训练二1．下列词语中加点的字，每对的读音都不相同的一项是（）A．妃嫔．／殡．葬龌．龊／优渥．强．人所难／强．颜欢笑B．掠．影／虐．待舐．犊／胼胝．安步当．车／螳臂当．车C．麻痹．／疲敝．肥膘．／飞镖．塞．责／塞．翁失马D．攻讦．／劫．难渎．职／疑窦．供．应／呈堂口供．2. 下面语段中加点的词语，使用恰当的一项是（）近日网上流传着香港的一份要求填上“草菅人命”形容警方才能得分的中文科测验卷。

2015高考历史临门一脚最后提能 15

2015高考历史临门一脚最后提能(十五)(时间：45分钟分值：100分)一、选择题(本大题共12小题，每小题5分，共60分，每小题只有一个正确选项) 1．(2015·江苏南通调研)某科学著作的序言中写道：“理性力学应当是研究任何力所引起的运动和产生任何运动的力的科学。

因此，本书被命名为自然哲学的数学原理。

”该著作提出的理论( )A．推动了欧洲启蒙运动的进程B．使人类对微观世界的认识取得突破C．为经典力学的创立奠定了基础D．弥补了牛顿力学认识宏观世界的不足解析据题干材料及所学知识可知，该理论是牛顿的经典力学，它的提出为欧洲启蒙运动奠定思想基础，故A项正确。

B项是量子论；C项是伽利略自由落体理论；D项是相对论，均排除。

答案 A2．(2015·福建泉州质检)1919年英国《泰晤士报》曾刊登标题文章——“科学革命”，两个副标题是“宇宙新理论”“牛顿观念的破产”。

据此判断，具有“科学革命”意义的理论是( )A．经典力学B．进化论C．量子论D．相对论解析据题干可判断，“科学革命”属于相对论研究的范畴，故D项正确。

“牛顿观念的破产”不符合经典力学主旨，排除A项；进化论属于生物学范畴，不符合题干意思，排除B项；量子论属于研究微观领域物理现象，排除C项。

答案 D3．(2015·山东淄博诊断)恩格斯曾这样评价一部著作：“至今还从来没有过这样大规模的证明自然界的历史发展的尝试，而且还做得这样成功。

”这是因为这部著作( ) A．从根本上否定了神创论B．摇撼了理学的理论基础C．建立起严密逻辑体系的近代科学D．在哲学上最终确立人的主体地位解析据题干材料及所学知识可知，这部著作是达尔文的《物种起源》。

《物种起源》从根本上否定了神创论，故A项正确；B项是王夫之的唯物论思想；C项是牛顿的《自然哲学的数学原理》；D项与古希腊的苏格拉底有关，故排除B、C、D三项。

答案 A4．(2015·天津河西质调)“科学革命是人认识客观世界的飞跃，技术革命是人改造客观世界技术的飞跃。

(临门一脚山东专用)2015年高考数学热点专题复习热点七圆锥曲线文

热点七圆锥曲线【考点精要】考点一. 椭圆及其标准方程。

椭圆的简单的几何性质，椭圆的参数方程的应用。

双曲线及其标准方程，抛物线的简单的几何性质及其标准方程。

如：设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F,且和y 轴交于点A,若△OAF(O 为坐标原点)的面积为4,则抛物线方程为( )A.24y x =±B.28y x =±C. 24y x =D.28y x =考点二. 直线与圆、椭圆、双曲线、抛物线的交点（向量的数量积）、截取的线段。

如：已知椭圆22:12x C y +=的右焦点为F,右准线l ，点A l ∈，线段AF 交C 于点B 。

若3FA FB =u r u r ,则AF uuu r=( )A. 2B. 2C. 3D.3考点三. 圆锥曲线的离心率。

一般考查两个方面：一是求离心率的值，另一个是根据题目条件求离心率的范围问题。

求解时或根据题意巧设参数，或利用直线与圆锥曲线的交点得到不等量关系进而求出离心率的范围。

如：已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12(,0),(,0)F c F c -，若双曲线上存在一点P 使caF PF F PF =∠∠1221sin sin ，则该双曲线的离心率的取值范围是 .考点四. 圆锥曲线的轨迹方程。

借助代数、几何、平面向量等求圆锥曲线的轨迹方程问题，一般运用代入法、交规法，参数法、设而不求法等。

如：已知抛物线C 的顶点坐标为原点，焦点在x 轴上，直线y=x 与抛物线C 交于A ，B 两点，若()2,2P 为AB 的中点，则抛物线C 的方程为。

24y x =考点五. 圆锥曲线的最值。

以圆锥曲线知识为依托，注重考查对称问题、最值问题、存在性问题等，这类问题入手点难，运算量大，题目往往涉及的知识多，层次复杂，多以大题出现。

巧点秒拨1. 直线与圆锥曲线有无公共点或有几个公共点的问题，实际上是研究它们的方程组成的方程组是否有实数解，或实数解的个数问题，此时要注意用好分类讨论和数形结合的思想方法.2. 当直线与圆锥曲线相交时，涉及弦长问题，常用“韦达定理法”设而不求计算弦长(即应用弦长公式)；涉及弦长的中点问题，常用“差分法”设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化.同时还应充分挖掘题目的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍.3. 求圆锥曲线中的最值问题解决方法一般有两种：一是几何法，特别是用圆锥曲线的定义和平面几何的有关结论来做非常巧妙；二是代数法，将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题，然后利用均值不等式、函数的单调性或三角函数的有界性等求最值。

【临门一脚】2015年语文高考热点专题复习实用类文本阅读

实用类文本阅读【考点精要】2015年语文科《考试说明》（新课标）对该考点的要求是：阅读评价中外实用类文本。

了解传记、新闻、报告、科普文章的文体基本特征和主要表现手法。

准确解读文本，筛选、整合信息。

分析思想内容、构成要素和语言特色，评价文本产生的社会功用，探讨文本反映的人生价值和时代精神。

它包括“分析综合（C）”“鉴赏评价（D）”和“探究（F）”三个层级，共有九条具体的测试要求。

巧点妙拨在传记文本的考查中，高频考点是筛选并整合文中信息；中频考点是对作品进行个性化阅读和有创意的解读，低频考点是鉴赏评价（D）中的欣赏作品的形象。

除人物传记外，新闻也是实用类文本阅读中考得频率较高的文体。

从考点上看，筛选并整合信息仍是100%的频率。

但这类文体在考点设计上较人物传记有所不同。

它更突出了对文体特点的考查。

比如说文章的结构特色、语言特色及修辞手法的运用。

对探究能力的考核也不含糊。

科普类文章从考查的考点看，除对重要概念含义的理解，对重点句子的内涵和作用的理解，筛选整合文中信息等传统考点的考查外，还涉及到对文中某个观点和看法的个性解读等。

报告是在调查事实的基础上对某个问题提出的看法总结。

报告的结构一般分为标题、导语、正文、结语、结尾几个部分。

导语和新闻的导语位置、功能等差不多。

高考题目至今还未涉及到这个体裁。

实用类文本的命题角度：1．关键性语句理解题。

对于这类题，应在整体感知文本的基础上进行局部的、有重点的阅读，理解，概括，归纳，瞻前顾后地根据其语段的“形”，深入领悟其语段的“意”。

提问方式：画横线的句子（或词语）在文中是什么意思？规范回答：该句子（词语）生动、具体（或形象、准确）地写出了＋对象＋效果。

2．句段作用（好处）类题目。

该类题目一般要从以下四个方面进行思考：句段的表层含意是什么，运用了什么手法，深层蕴涵是什么，对思想感情的表达有何作用。

提问方式：文中第几段写了什么内容，这样安排有什么好处？规范回答：该段运用了什么手法，写了什么内容，为下文写什么作铺垫（衬托），表达了作者怎样的思想感情。

2015高考点睛之临门一脚

2015高考点睛之临门一脚整理：赖启生一、语言表达简明、连贯、得体，准确、鲜明、生动1.下面是某毕业学生在春节给老师发的短信，其中有四处不得体，请找出并加以修改。

恩师无恙！毕业之后，学生垂念师恩。

我曾经是您的高足，现在也没让您失望！值此春节到来之际，谨祝恩师节日快乐，万事如意！以后还请恩师继续斧正我的不足，如有事需要学生效劳，我当鼎力相助！（1）将改为；（2）将改为；（3）将改为；（4）将改为；答案：（1）将“垂念”改为“常念”（2）将“高足”改为“得意门生”（3）将“斧正”改为“指出”（4）将“鼎力”改为“全力”（“垂念”指上对下挂念，也用做敬辞，指别人对自己挂念。

用在此处属谦敬不当。

“高足”犹言高才。

后常用为称呼别人的学生的敬词。

用在此处属谦敬不当。

“斧正”敬辞，用于请人改自己的文章。

用于此处属对象不当。

“鼎力”，敬辞，大力，用于请托或表示感谢时。

用在此处属谦敬不当）2.“过年亲友如相问，就说我在‘抢红包’。

”羊年春节，“抢红包”成为最热的话题之一。

长辈给晚辈发，老板给员工发，朋友、同学相互派发。

有的还玩起“红包接龙”，手气最佳的接着派发。

“抢红包”游戏大有旋风席卷之势。

与此同时，有关“抢红包”的争议也越来越大。

你如何看待春节期间的“抢红包”现象？请明确表态并阐明理由。

要求：①观点明确；②至少列出两条理由；③语言简明连贯。

答：答案：示例一：我觉得很好。

①无论是发红包，还是“抢红包”，都让参与者收获了前所未有的快乐。

②网络抢红包增强了新年的喜庆气氛，加强了人与人之间的交流。

③网络红包使人们从相对疏离的关系中获得收益，这种惊喜带来的幸福感让人感受到更广泛的关爱。

示例二：我觉得不好。

①淡了年味，让传统佳节成了“抢红包节”。

②冷了亲情，“抢红包”成了年轻人与中老年人的“新隔阂”。

③伤了身体，有人不分昼夜，机不离手，以致眼迷离、手抽筋。

（观点明确，言之成理即可）二、图文转换1.下面是从“实用新型外观设计”到“获得专利证”的过程示意图，请把这个过程写成一段话，要求内容完整，表述准确，语言连贯，不超过75个字。

高考数学临门一脚.docx

江苏省苏州市2015届高考数学临门一脚(满分160分时间 120分钟)一、填空题（本大题共14题，每小题5分，满分70分）1．已知全集R U =，集合{}0322>--=x x x A ，则=A C U ． 2．已知i 是虚数单位，a ∈R ．若复数22a ia i+-的虚部为1，则a ＝． 3．执行如图所示的程序框图，若输入p 的值是7，则输出S 的值是． 4．为了解1000名学生的学习情况，现采用系统抽样的方法从中抽取容量为40的样本，则抽样中分段的间隔为．5．已知),2(ππα∈，53sin =α，则)4tan(πα-的值等于． 6.在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝2A ，cos A ＝34，b ＝5，则△ABC 的面积为．7．已知圆锥底面半径与球的半径都是1cm ，如果圆锥的体积恰好也与球的体积相等，那么这个圆锥的母线长为 cm ．8．在△ABC 中，B (10，0)，直线BC 与圆Γ：x 2＋(y －5)2＝25相切，切点为线段BC 的中点．若△ABC 的重心恰好为圆Γ的圆心，则点A 的坐标为．9．已知函数()sin(2)(0)6f x x πωω=->在区间2π0,3⎛⎫⎪⎝⎭上单调递增，则ω的最大值为________．10．已知(A ，O 是原点，点P 的坐标为（x ，y ）满足条件0200y x y -≤-+≥⎨⎪≥⎪⎩，则||OAOP z OP ⋅=u u u r u u u r u u u r 的取值范围是________．11．已知两个不相等的平面向量，(0≠)满足||＝2，且与β－α的夹角为120°，则|α|的最大值是．12．已知双曲线22221(0,0)x y a b a b-=>>，两焦点为21,F F ，过2F 作x 轴的垂线交双曲线于B A ,两点，且1ABF ∆内切圆的半径为a ，则此双曲线的离心率为 .P F EDCBA 13．设有一个4⨯4网格，其各个最小的正方形的边长为4cm ，现用直径为2cm 的硬币投掷到此网格上，设每次投掷都落在最大的正方形内或与最大的正方形有公共点，则硬币落下后完全在最大的正方形内的概率．14．已知函数()y f x =满足对于任意的0x >恒有(3)3()f x f x =成立，当13x ≤≤时，()12f x x =--，则集合{}()(33)x f x f =中最小的元素为．二、解答题（本大题共6题,满分90分）15．(本题满分14分)在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且()f A =2cossin()22A A π-22sin cos 22A A+-．（1）求函数()f A 的最大值；（2）若()0,,12f A C a 5π===b 的值． 16．（本题满分14分）如图,在四棱锥P ABCD -中，底面ABCD 是正方形，侧面PAD ⊥底面ABCD，且22PA PD AD ===，E 、F 分别为PC 、BD 的中点．（1）求证：//EF 平面PAD ；（2）求三棱锥P BCD -的体积；（3）在线段AB 上是否存在点,G 使得CD EFG ⊥平面？说明理由．17．（本题满分14分）为了制作广告牌，需在如图所示的铁片上切割出一个直角梯形，已知铁片由两部分组成，半径为1的半圆O 及等腰直角三角形EFH ，其中FE FH ⊥．为裁剪出面积尽可能大的梯形铁片ABCD （不计损耗），将点A ，B 放在弧EF 上，点C 、D 放在斜边EH 上，且////AD BC HF ，设AOE θ∠=. （1）求梯形铁片ABCD 的面积S 关于θ的函数关系式；（2）试确定θ的值，使得梯形铁片ABCD 的面积S 最大，并求出最大值．18．（本题满分16分）已知椭圆)0(1:22221>>=+b a by a x C 的离心率为33，直线2:+=x y l 与以原点为圆心、椭圆1C 的短半轴长为半径的圆相切．（1）求椭圆1C 的方程；（2）设椭圆1C 的左焦点为1F ，右焦点为2F ，直线1l 过点1F 且垂直于椭圆的长轴，动直线2l 垂直于直线1l ，垂足为点P ，线段2PF 的垂直平分线交2l 于点M ，求点M 的轨迹2C 的方程；（3）设2C 与x 轴交于点Q ，不同的两点S R ,在2C 上，且满足0=⋅，求||的取值范围．19．（本题满分16分）已知函数2()ln f x ax x=+(a ∈R )．（1）当12a =时，求f (x )在区间[]1,e 上的最大值和最小值；（2）如果函数12(),(),()g x f x f x ，在公共定义域D 上，满足)()()(21x f x g x f <<，那么就称)(x g 为)x (f ),x (f 21的“活动函数”；已知函数2221211()()2(1)ln ,()222f x a x ax a x f x x ax =-++-=+．若在区间()1+∞，上，函数()f x 是12(),()f x f x 的“活动函数”，求a 的取值范围． 20．(本题满分16分) 已知数列}{n a ，}{n b 对任意的正整数*∈N n ，都有12123121b a b a b a b a b a n n n n n +++++---Λ221--=+n n 成立．（1）若}{n a 是等差数列，且首项和公差相等，求证：}{n b 是等比数列；（2）若}{n a 是等差数列，且}{n b 是等比数列，求证：12-⋅=n n n n b a ．参考答案1．]3,1[-；2;3.646317;8.(0，15) 或 (－8，－1);9.21;10．[]3,3-;13.196320π+;14. 15.15.（1）22()2cossin sin cos 2222A A A A f A =+-sin cos )4A A A π=-=-. 因为0A <<π，所以444A ππ3π-<-<.则所以当42A ππ-=，即34A π=时，()f A.（2）由题意知())04f A A π=-=，所以sin()04A π-=．又知444A ππ3π-<-<，所以04A π-=，则4A π=.因为12C 5π=，所以712A B π+=，则3B π=.由sin sin a b A B =得，sinsin 33sin sin 4a Bb A π===π．ABCDEFPOG16.（1）证明：连结AC BD F =I ，ABCD 为正方形，F 为AC 中点，E 为PC 中点， ∴在CPA ∆中，EF //PA ，且PA ⊂平面PAD ，EF ⊄平面PAD ，∴//EF PAD 平面；（2）解：如图，取AD 的中点O ，连结OP ， ∵PA PD =，∴PO AD ⊥， ∵侧面PAD ⊥底面ABCD ，PAD ABCD AD ⋂=平面平面，∴PO ABCD ⊥平面，又2,2PA PD AD ===所以PAD ∆是等腰直角三角形，且12AD PO AD === 在正方形 ABCD中，11422BCD ABCDS S ==⨯=V 正方形，11433P BCD BCD V S PO -∆==⨯=g （3）存在点G 满足条件，理由如下：设点G 为AB 中点，连接,.EG FG 由F 为BD 的中点，所以FG //AD ，由（1）得EF //PA ，且,,FG EF F AD PA A ⋂=⋂= 所以EFG PAD 平面//平面，∵侧面PAD ⊥底面ABCD ，PAD ABCD AD ⋂=平面平面， CD AD ⊥，CD PAD ∴⊥平面，所以CD EFG ⊥平面，所以AB 的中点G 为满足条件的点．17. 解：（1）连接OB ，根据对称性可得AOE BOF θ∠=∠=且1OA OB ==，所以1cos sin AD θθ=-+，1cos sin BC θθ=++，2cos AB θ=……………4分所以()2(1sin )cos 2AD BC AB S θθ+⋅==+，其中02πθ<<.……………7分（2）记()2(1sin )cos ,02f πθθθθ=+<<，22'()2(cos sin sin )f θθθθ=--=2(2sin 1)(sin 1)(0)2πθθθ--+<<.………10分当06πθ<<时，'()0f θ>，当62ππθ<<时，'()0f θ<所以min ()()6f f πθ==，即6πθ=时，max S =14分 18. 解：（1）由33=e 得2232b a =，又由直线2:+=x y l 与圆222b y x =+相切，得2=b ，3=a ，∴椭圆1C 的方程为：12322=+y x . 4分（2）由2MF MP =得动点M 的轨迹是以1:1-=x l 为准线，2F 为焦点的抛物线，∴点M 的轨迹2C 的方程为x y 42=. 8分（3）)0,0(Q ，设),4(),,4(222121y y S y y R ， ∴),4(),,4(122122121y y y y y y --==，由0=⋅，得0)(16)(121212221=-+-y y y y y y ，∵21y y ≠ ∴化简得11216y y y --=， 10分 ∴6432256232256212122=+≥++=y y y (当且仅当41±=y 时等号成立)， ∵64)8(41)4(||22222222-+=+=y y y ，又∵6422≥y ，∴当6422=y ，即82±=y 时58||min =， ∴||的取值范围是),58[+∞ 16分 19.解：（1）当12a =时，21()ln 2f x x x =+Q ， 211()x f x x x x+'∴=+=；对于[]1,x e ∈，有()0f x '>， ∴()f x 在区间[1, e]上为增函数，∴2max ()()12e f x f e ==+，min 1()(1)2f x f ==.（2）①在区间（1，+∞）上，函数()f x 是12(),()f x f x 的“活动函数”，则12()()()f x f x f x <<，令221()()()()2ln 2p x f x f x a x ax x =-=--+<0，对(1,)x ∈+∞恒成立，且1()()()h x f x f x =-=2212ln 2x ax a x -+-<0对(1,)x ∈+∞恒成立， ∵21(21)21(1)[(21)1]()(21)2a x ax x a x p x a x a x x x--+---'=--+==(*) 1）若12a >，令()0p x '=，得极值点11x =，2121x a =-，当211x x >=，即112a <<时，在（2x ，+∞)上有()0p x '>，此时)(x p 在区间(2x ，+∞)上是增函数，并且在该区间上有()p x ∈(2()p x ，+∞)，不合题意；当211x x <=，即1a ≥时，同理可知，)(x p 在区间(1，+∞)上，有)(x p ∈()1(p ，+∞)，也不合题意； 2）若12a ≤，则有210a -≤，此时在区间(1，+∞)上恒有()0p x '<，从而)(x p 在区间(1，+∞)上是减函数；要使0)(<x p 在此区间上恒成立，只须满足1(1)02p a =--≤12a ⇒≥-，所以21-≤a ≤21. 又因为2()2a h x x a x '=-+-=2222()x ax a x a x x-+---=<0, ()h x 在(1, +∞)上为减函数， 1()(1)202h x h a ∴<=-+≤， 14a ∴≤. 综合可知a 的范围是11,24⎡⎤-⎢⎥⎣⎦.。

高三物理“临门一脚”试题(含解析)-人教版高三全册物理试题

广东省湛江第一中学2015届高三“临门一脚〞物理试题13.【题文】鱼在水中沿直线水平向左加速游动过程中，水对鱼的作用力方向合理的是A B C D【答案】D【解析】此题主要考查牛顿运动定律以与力的合成与分解；鱼受到竖直向下的重力，且具有向左的加速度，因此所受水的力向左上方，这样竖直方向分力与重力平衡，水平方向分力提供加速度，应当选项D正确。

【题型】单项选择题【备注】【完毕】14.【题文】如下列图，气垫床是一种可以注入空气的床垫，睡在气垫床上可以让肌肉得到放松，是不少人舒缓神经的不错选择。

当人从床上起身下床时，假设床垫内气体与外界无热交换，且密封性良好，如此有关床垫内气体如下说法正确的答案是A.体积增大，内能增大B.体积减小，压强减小C.对外界做负功，分子平均动能增大D.对外界做正功，压强减小【答案】D【解析】此题主要考查分子动理论；当人起身下床后，内部气体所受压力减小，体积变大，对外做正功，内能减小，分子平均动能减小，压强减小，应当选项D正确。

【题型】单项选择题【备注】【完毕】15.【题文】如下说法正确的答案是A、α衰变过程中放出的α射线是氦原子B、波尔理论的假设之一是原子能量是具有连续性C.当分子间的引力和斥力平衡时，分子势能最小D、飘浮在热菜汤外表上的油滴，从上面观察是圆形的，是因为油滴液体呈各向同性的缘故【答案】C【解析】此题主要考查衰变、分子动理论以与波尔理论；选项A，α衰变过程中放出的α射线是氦原子核，选项A错误；选项B，波尔理论的假设之一是原子能量是具有不连续性，选项B错误；选项C，当分子间的引力和斥力平衡时，无论二者是靠近还是远离分子都会做负功，使得分子势能增大，故平衡时分子势能最小，选项C正确；选项D，飘浮在热菜汤外表上的油滴，从上面观察是圆形的，是因为外表张力的原因，选项D错误；此题正确选项为C。

【题型】单项选择题【备注】【完毕】16.【题文】如下列图，轻质弹簧的劲度系数为k，小球重G，平衡时小球在A处，今用力F压小球至B处，使弹簧再缩短x，如此如下说法正确的答案是A、此时弹簧的弹力大小为kxB.此时弹簧的弹力大小为kx＋GC.将力F撤去的瞬间，小球处于平衡状态D.将力F撤去以后，小球的机械能守恒【答案】B【解析】此题主要考查弹力以与共点力平衡条件；选项A，既然在A处平衡，即重力等于弹力，如此B处压缩量增大，弹力大于重力，应当选项A错误；选项B，在A处有弹力等于重力，在B处弹力增大了kx，即弹力为kx+G,选项B正确；选项C,撤去F后，弹力大于重力，小球所受合力向上，应当选项C错误；选项D，撤去F后，对小球合弹簧的系统机械能守恒，应当选项D错误；此题正确选项为B。