中考数学:锐角三角函数试题解析
2023年中考数学二轮复习之锐角三角函数(含解析)
2023年中考数学二轮复习之锐角三角函数一.选择题(共10小题)1.(2022秋•余姚市期末)在Rt△ABC中,∠C=90°,AC=4,AB=5,则cos A的值为( )A.B.C.D.2.(2022秋•未央区期末)2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习.如图,某滑雪斜坡的坡角为28°,一位同学乘滑雪板沿斜坡下滑了100米,则该同学在竖直方向上下降的高度为( )A.100sin28°B.100cos28°C.D.3.(2022秋•兴县期末)如图是由边长为1的小正方形组成的网格图,点A,B,C都在小正方形的顶点处,则∠BAC的余弦值是( )A.B.2C.D.4.(2022秋•临平区期末)sin45°的值是( )A.1B.C.D.5.(2022秋•叙州区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.如果AD =8,BD=4,那么tan B的值是( )A.B.C.D.6.(2023•碑林区校级模拟)如图,AD是△ABC的高,AB=4,∠BAD=60°,tan∠CAD=,则BC的长为( )A.+1B.2+2C.2+1D.+4 7.(2022秋•未央区期末)如图,在中Rt△ABC,∠C=90°,AB=13,AC=5,下列结论中,正确的是( )A.tan B=B.tan A=C.sin A=D.cos B=8.(2022秋•永春县期末)如图是某商场自动扶梯的示意图,自动扶梯AB的坡角(∠BAC)为30.5°,乘客从扶梯底端升到顶端上升的高度BC为5米,则自动扶梯AB的长为( )A.5tan30.5°米B.5sin30.5°米C.米D.米9.(2022秋•永春县期末)如图,在网格中,点A,B,C都在格点上,则∠CAB的正弦值是( )A.B.C.D.2 10.(2023•市北区开学)如图,在△ACB中,∠C=90°,sin B=,若AC=6,则BC的长为( )A.8B.12C.D.二.填空题(共8小题)11.(2022秋•遂川县期末)计算:2tan45°= .12.(2023•蕉岭县校级开学)在△ABC中,已知AB=5,BC=6,∠B=30°,那么S△ABC 为 .13.(2022秋•抚州期末)如图,在网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 .14.(2022秋•兴隆县期末)已知:如图,△ABC中,AC=10,,,则AB = .15.(2022秋•晋江市期末)如图,河堤横断面迎水坡AC的坡度i=1:2,若垂直高度AB=15米,则迎水坡AC的长度为 米.16.(2022秋•峄城区期末)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角∠DPC =30°,已知窗户的高度,窗台的高度CF=1m,窗外水平遮阳篷的宽AD=0.8m,则CP 的长度为 (结果精确到0.1m).17.(2022秋•兴县期末)无人机是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机,在跟踪、定位、遥测、数据传输等方面发挥着重要作用,在如图所示的某次测量中,无人机在小山上方的A处,测得小山两端B,C的俯角分别是45°和30°,此时无人机距直线BC的垂直距离是200米,则小山两端B,C之间的直线距离是 米(结果保留准确值).18.(2022秋•遂川县期末)如图,一个斜坡AB长130m,斜坡与水平地面夹角∠ABC的正切值为,坡顶A离水平地面的距离AC为 m.三.解答题(共3小题)19.(2022秋•余姚市期末)消防车是救援火灾的主要装备.图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC(20米≤AC≤30米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角∠CAE(90°≤∠CAE≤150°),转动点A距离地面的高度AE为3米.(1)当起重臂AC的长为24米,张角∠CAE=120°时,求云梯消防车最高点C距离地面的高度CF.(2)某日一栋大楼突发火灾,着火点距离地面的高度为26米,问该消防车在这栋楼下能否实施有效救援?请说明理由.(参考数据:≈1.7)(提示:当起重臂AC伸到最长且张角∠CAE最大时,云梯顶端C可以达到最大高度.)20.(2022秋•未央区期末)夏秋季节,许多露营爱好者晚间会在湖边露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处(EF⊥BF),使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,幕布宽AC=AD=2m,CD⊥AB于点O,支杆AB与树干EF的横向距离BF=2.2m.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)(1)天晴时打开“天幕”,若∠CAE=140°,求遮阳宽度CD.(2)下雨时收拢“天幕”,∠CAE由140°减小到90°,求点E下降的高度.21.(2022秋•未央区期末)如图,在△ABC中,AB=13,AC=15,sin C=.(1)求BC的长.(2)求tan B的值.2023年中考数学二轮复习之锐角三角函数参考答案与试题解析一.选择题(共10小题)1.(2022秋•余姚市期末)在Rt△ABC中,∠C=90°,AC=4,AB=5,则cos A的值为( )A.B.C.D.【考点】锐角三角函数的定义.【专题】等腰三角形与直角三角形;推理能力.【分析】根据题意画出图,再根据余弦的定义计算即可.【解答】解:根据题意画出图如图所示:∵∠C=90°,AC=4,AB=5,∴.故选:C.【点评】本题考查的是锐角三角函数的定义,掌握锐角A的邻边与斜边的比叫做∠A的余弦是解题的关键.2.(2022秋•未央区期末)2022年2月4日在北京举办了第24届冬季奥运会,很多学校都开展冰雪项目学习.如图,某滑雪斜坡的坡角为28°,一位同学乘滑雪板沿斜坡下滑了100米,则该同学在竖直方向上下降的高度为( )A.100sin28°B.100cos28°C.D.【考点】解直角三角形的应用﹣坡度坡角问题.【专题】解直角三角形及其应用;应用意识.【分析】根据三角函数定义进行解答即可.【解答】解:∵滑雪斜坡的坡角为28°,一位同学乘滑雪板沿斜坡下滑了100米,∴该同学在竖直方向上下降的高度为100sin28°,故A正确.故选:A.【点评】本题主要考查了三角函数定义,熟练掌握正弦函数的定义,是解题的关键.3.(2022秋•兴县期末)如图是由边长为1的小正方形组成的网格图,点A,B,C都在小正方形的顶点处,则∠BAC的余弦值是( )A.B.2C.D.【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】先根据勾股定理求出三角形三边的长,得出∠ACB=90°,再根据求解.【解答】解:∵,,,∴BC2+AC2=AB2,∴∠ACB=90°,∴.故选:D.【点评】本题考查勾股定理和三角函数,解题的关键是证明∠ACB=90°.4.(2022秋•临平区期末)sin45°的值是( )A.1B.C.D.【考点】特殊角的三角函数值.【专题】解直角三角形及其应用;应用意识.【分析】直接根据特殊角的三角函数值进行解答即可.【解答】解:由特殊角的三角函数值可知,sin45°=.故选:C.【点评】本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.5.(2022秋•叙州区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.如果AD =8,BD=4,那么tan B的值是( )A.B.C.D.【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】根据相似三角形的判定和性质可以求得CD的长,然后即可求得tan B的值.【解答】解:∵CD⊥AB,∴∠ADC=∠CDB=90°,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵∠ACD+∠A=90°,∴∠A=∠DCB,∴△ACD∽△CBD,∴,∵AD=8,BD=4,∴,解得CD=4,∴tan B===,故选:D.【点评】本题考查解直角三角形,解答本题的关键是明确题意,求出CD的值.6.(2023•碑林区校级模拟)如图,AD是△ABC的高,AB=4,∠BAD=60°,tan∠CAD=,则BC的长为( )A.+1B.2+2C.2+1D.+4【考点】解直角三角形;含30度角的直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】先在Rt△ABD中,利用60°的余弦和正弦求出AD=2,BD=2,再在Rt△ACD中,利用正切的定义求出CD,然后计算BD+CD即可.【解答】解:∵AD是△ABC的高,∴∠ADB=∠ADC=90°,在Rt△ABD中,cos∠BAD=,sin∠BAD=,∴cos60°=,sin60°=,∴AD=4cos60°=4×=2,BD=4sin60°=4×=2,在Rt△ADC中,tan∠CAD=,∴=,解得CD=1,∴BC=BD+CD=2+1.故选:C.【点评】本题考查了解直角三角形:灵活运用勾股定理和锐角三角函数的定义是解决问题的关键.7.(2022秋•未央区期末)如图,在中Rt△ABC,∠C=90°,AB=13,AC=5,下列结论中,正确的是( )A.tan B=B.tan A=C.sin A=D.cos B=【考点】锐角三角函数的定义.【专题】解直角三角形及其应用;运算能力.【分析】首先利用勾股定理求得BC,再根据各三角函数的定义,即可一一判定.【解答】解:∵在中Rt△ABC,∠C=90°,AB=13,AC=5,∴,∴,,,,故选:C.【点评】本题考查了勾股定理,三角函数的定义,熟练掌握和运用各三角函数的定义是解决本题的关键.8.(2022秋•永春县期末)如图是某商场自动扶梯的示意图,自动扶梯AB的坡角(∠BAC)为30.5°,乘客从扶梯底端升到顶端上升的高度BC为5米,则自动扶梯AB的长为( )A.5tan30.5°米B.5sin30.5°米C.米D.米【考点】解直角三角形的应用﹣坡度坡角问题.【专题】解直角三角形及其应用;运算能力;推理能力.【分析】根据正弦的定义计算,则得到答案.【解答】解:在Rt△ABC中,sin A=,则AB==米.故选:C.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握正弦的定义是解题的关键.9.(2022秋•永春县期末)如图,在网格中,点A,B,C都在格点上,则∠CAB的正弦值是( )A.B.C.D.2【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】连接CD,先利用勾股定理的逆定理证明△ACD是直角三角形,从而可得∠ADC =90°,然后在Rt△ADC中,利用锐角三角函数的定义,进行计算即可解答.【解答】解:如图:连接CD,由题意得:AC2=12+32=10,CD2=12+12=2,AD2=22+22=8,∴AD2+CD2=AC2,∴△ACD是直角三角形,∴∠ADC=90°,在Rt△ADC中,CD=,AC=,∴sin∠CAD===,故选:A.【点评】本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.10.(2023•市北区开学)如图,在△ACB中,∠C=90°,sin B=,若AC=6,则BC的长为( )A.8B.12C.D.【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】根据锐角三角函数的边角间关系,先求出AB,再利用勾股定理求出BC.【解答】解:在Rt△ACB中,sin B===0.5,∴AB=12.∴BC===6.故选:C.【点评】本题考查了解直角三角形.掌握直角三角形的边角间关系是解决本题的关键.二.填空题(共8小题)11.(2022秋•遂川县期末)计算:2tan45°= 2 .【考点】特殊角的三角函数值.【专题】实数;运算能力.【分析】代入45°的正切值计算即可.【解答】解:2tan45°=2×1=2.故答案为:2.【点评】本题考查了特殊角的三角函数值,熟记特殊角的三角函数值是解答本题的关键.12.(2023•蕉岭县校级开学)在△ABC中,已知AB=5,BC=6,∠B=30°,那么S△ABC 为 7.5 .【考点】解直角三角形;勾股定理.【专题】三角形;推理能力.【分析】作AD⊥BC于D,由直角三角形的性质得出AD=AB=2.5,由三角形面积公式即可得出答案.【解答】解:作AD⊥BC于D,如图所示:则∠ADB=90°,∵∠B=30°,∴AD=AB=2.5,∴S△ABC=BC×AD=×6×2.5=7.5.故答案为:7.5.【点评】本题考查了含30°角的直角三角形的性质、三角形面积,熟练掌握含30°角的直角三角形的性质是解题的关键.13.(2022秋•抚州期末)如图,在网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 3 .【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】连接格点D,根据勾股定理求出AB、AC的长度,根据等腰三角形的性质,可得,最后根据勾股定理求出AD,再根据正切的定义求解即可.【解答】解:连接格点D,如图所示,∵AB2=52+52=50,AC2=12+72=50,BD2=12+22=5,AD2=32+62=45,∴AB=AC,AB2=AD2+BD2,∴AD⊥BD,∵,∴,根据勾股定理可得:,∴,故答案为:3.【点评】本题主要考查了勾股定理,等腰三角形的判定和性质,求已知角的正切值,解题的关键是正确作出辅助线,构造直角三角形.14.(2022秋•兴隆县期末)已知:如图,△ABC中,AC=10,,,则AB = 24 .【考点】解直角三角形.【专题】解直角三角形及其应用;运算能力.【分析】过A作AD垂直于BC,交BC于点D,在Rt△ACD中,由AC与sin C的值,利用正弦函数定义求出AD的长,在Rt△ABD中,由AD与sin B的值,利用正弦函数定义即可求出AB的长.【解答】解:作AD⊥BC于D点,如图所示,在Rt△ADC中,AC=10,sin C=,∴AD=AC sin C=10×=8,在Rt△ABD中,sin B=,AD=8,则AB===24.故答案为:24.【点评】本题考查了解直角三角形,正确添加辅助线AD构建直角三角形、熟练掌握三角函数的定义是解题的关键.15.(2022秋•晋江市期末)如图,河堤横断面迎水坡AC的坡度i=1:2,若垂直高度AB=15米,则迎水坡AC的长度为 米.【考点】解直角三角形的应用﹣坡度坡角问题.【专题】解直角三角形及其应用;应用意识.【分析】直接利用坡度的定义得出,进而利用坡度的定义以及勾股定理得出答案.【解答】解:∵河堤横断面迎水坡AC的坡度i=1:2,垂直高度AB=15米,=,解得BC=30,则AC===(米).故答案为:.【点评】此题主要考查了解直角三角形的应用,正确掌握坡度的定义是解题关键.16.(2022秋•峄城区期末)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角∠DPC =30°,已知窗户的高度,窗台的高度CF=1m,窗外水平遮阳篷的宽AD=0.8m,则CP 的长度为 4.4m (结果精确到0.1m).【考点】解直角三角形的应用.【专题】解直角三角形及其应用;运算能力;应用意识.【分析】根据题意可得AD∥CP,从而得到∠ADB=30°,利用锐角三角函数可得AB=AD×tan∠ADB=≈0.46m,从而得到BC=AF+CF﹣AB=2.54m,即可求解.【解答】解:根据题意得:AD∥CP,∵∠DPC=30°,∴∠ADB=30°,∵AD=0.8m,∴AB=AD×tan∠ADB=0.8×≈0.46(m),∵AF=2m,CF=1m,∴BC=AF+CF﹣AB=2.54m,∴CP==≈4.4(m),即CP的长度为4.4m.故答案为:4.4m.【点评】本题主要考查了解直角三角形、平行线的性质,熟练掌握锐角三角函数是解题的关键.17.(2022秋•兴县期末)无人机是利用无线电遥控设备和自备的程序控制装置操纵的不载人飞机,在跟踪、定位、遥测、数据传输等方面发挥着重要作用,在如图所示的某次测量中,无人机在小山上方的A处,测得小山两端B,C的俯角分别是45°和30°,此时无人机距直线BC的垂直距离是200米,则小山两端B,C之间的直线距离是 米(结果保留准确值).【考点】解直角三角形的应用﹣仰角俯角问题.【专题】解直角三角形及其应用;运算能力;推理能力.【分析】先作AD⊥BC于D,分别求出BD和CD,再相加即可.【解答】解:如图,作AD⊥BC于D,则AD=200米,∵∠EAB=45°,∠FAC=30°,∴∠DAB=45°,∠DAC=60°,∴BD=AD⋅tan45°=200×1=200(米),(米),∴米,故答案为:.【点评】本题考查了解直角三角形的应用,解题关键是读懂题意,构造直角三角形求解.18.(2022秋•遂川县期末)如图,一个斜坡AB长130m,斜坡与水平地面夹角∠ABC的正切值为,坡顶A离水平地面的距离AC为 50 m.【考点】解直角三角形的应用﹣坡度坡角问题.【专题】等腰三角形与直角三角形;推理能力.【分析】根据正切的定义设AC=5x,BC=12x,利用勾股定理列方程求出x,从而可得AC.【解答】解:由题意可得:AB=130,,∴设AC=5xm,BC=12xm,∴AC2+BC2=AB2,即(5x)2+(12x)2=1302,解得:x=10或x=﹣10(舍去),∴AC=5×10=50(m),故答案为:50.【点评】本题考查解直角三角形的应用,勾股定理,解题的关键是掌握正切的定义.三.解答题(共3小题)19.(2022秋•余姚市期末)消防车是救援火灾的主要装备.图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC(20米≤AC≤30米)是可伸缩的,且起重臂AC可绕点A在一定范围内上下转动,张角∠CAE(90°≤∠CAE≤150°),转动点A距离地面的高度AE为3米.(1)当起重臂AC的长为24米,张角∠CAE=120°时,求云梯消防车最高点C距离地面的高度CF.(2)某日一栋大楼突发火灾,着火点距离地面的高度为26米,问该消防车在这栋楼下能否实施有效救援?请说明理由.(参考数据:≈1.7)(提示:当起重臂AC伸到最长且张角∠CAE最大时,云梯顶端C可以达到最大高度.)【考点】解直角三角形的应用.【专题】解直角三角形及其应用;应用意识.【分析】(1)过点A作AG⊥CF,垂足为F.先在Rt△AGC中求出CG,再利用直角三角形的边角间关系求出CF;(2)先计算当AC长30米且∠CAE=150°时救援的高度,再判断该消防车能否实施有效救援.【解答】解:(1)作AG⊥CF于点G,由题意,得AE⊥BD,CF⊥BD,∴四边形AEFG是矩形,∴AE=FG=3(米),∠GAE=90°.∵∠CAE=120°,∴∠CAG=∠CAE﹣∠GAE=30°.在Rt△CAG中,,∴(米),∴CF=CG+GF=12+3=15(米).答:云梯消防梯最高点C距离地面的高度CF为15米(2)当AC=30米,∠CAE=150°时,云梯顶端C可以达到最大高度则有GF=AE=3米,∠CAG=∠CAE﹣∠GAE=60°,在Rt△CAG中,,∴(米),∴(米)>26(米).答:该消防车在这栋楼下能实施有效救援.【点评】本题考查解直角三角形的实际应用,在抽象图中找到直角三角形、熟记锐角三角函数的定义及特殊角的三角函数值是本题的解题关键.20.(2022秋•未央区期末)夏秋季节,许多露营爱好者晚间会在湖边露营,为遮阳和防雨会搭建一种“天幕”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AB,用绳子拉直AD后系在树干EF上的点E处(EF⊥BF),使得A,D,E在一条直线上,通过调节点E的高度可控制“天幕”的开合,幕布宽AC=AD=2m,CD⊥AB于点O,支杆AB与树干EF的横向距离BF=2.2m.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)(1)天晴时打开“天幕”,若∠CAE=140°,求遮阳宽度CD.(2)下雨时收拢“天幕”,∠CAE由140°减小到90°,求点E下降的高度.【考点】解直角三角形的应用;轴对称图形.【专题】解直角三角形及其应用;应用意识.【分析】(1)根据在Rt△AOD中,,先算出OD的长,再根据AD=2OD 即可得到答案;(2)过点E作EH⊥AB于H,在Rt△AHE中,,得,当∠CAE=140°时和当∠CAE=90°时,分别求出AH的值,作差即可得到答案.【解答】解:(1)∵∠CAE=140°,AC=AD,AO⊥CD,∴,CD=2DO,在Rt△AOD中,,即,解得:OD≈1.88m,∴CD=2OD≈3.76m,答:遮阳宽度CD约为3.76m;(2)如图,过点E作EH⊥AB于H,∴∠BHE=90°,∵AB⊥BF,EF⊥BF,∴∠ABF=∠EFB=90°,∴∠ABF=∠EFB=∠BHE=90°,∴EH=BF=2.2m,在Rt△AHE中,,∴,当∠CAE=140°时,∠EAO=70°,m,当∠CAE=90°时,∠EAO=45°,AH=2.2m,2.2﹣0.8=1.4m,答:点E下降的高度为1.4m.【点评】本题考查了锐角三角函数,矩形的判定和性质,熟练应用锐角三角函数是解本题的关键.21.(2022秋•未央区期末)如图,在△ABC中,AB=13,AC=15,sin C=.(1)求BC的长.(2)求tan B的值.【考点】解直角三角形.【专题】解直角三角形及其应用;推理能力.【分析】(1)过点A作BC边上的垂线,垂足为D.利用三角函数求出AD,根据勾股定理求出CD,BD即可;(2)根据公式直接计算可得.【解答】解:(1)如图,过点A作BC边上的垂线,垂足为D.在Rt△ADC中,,∴.由勾股定理,得,,∴BC=BD+CD=14.(2)在Rt△ABD中,.【点评】此题考查了锐角三角函数,勾股定理,熟记各三角函数的计算公式是解题的关键.考点卡片1.含30度角的直角三角形(1)含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.(2)此结论是由等边三角形的性质推出,体现了直角三角形的性质,它在解直角三角形的相关问题中常用来求边的长度和角的度数.(3)注意:①该性质是直角三角形中含有特殊度数的角(30°)的特殊定理,非直角三角形或一般直角三角形不能应用;②应用时,要注意找准30°的角所对的直角边,点明斜边.2.勾股定理(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.(2)勾股定理应用的前提条件是在直角三角形中.(3)勾股定理公式a2+b2=c2的变形有:a=,b=及c=.(4)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.3.轴对称图形(1)轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.(2)轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.(3)常见的轴对称图形:等腰三角形,矩形,正方形,等腰梯形,圆等等.4.锐角三角函数的定义在Rt△ABC中,∠C=90°.(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sin A.即sin A=∠A的对边除以斜边=.(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cos A.即cos A=∠A的邻边除以斜边=.(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tan A.即tan A=∠A的对边除以∠A的邻边=.(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.5.特殊角的三角函数值(1)特指30°、45°、60°角的各种三角函数值.sin30°=;cos30°=;tan30°=;sin45°=;cos45°=;tan45°=1;sin60°=;cos60°=;tan60°=;(2)应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.(3)特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.6.解直角三角形(1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.(2)解直角三角形要用到的关系①锐角、直角之间的关系:∠A+∠B=90°;②三边之间的关系:a2+b2=c2;③边角之间的关系:sin A==,cos A==,tan A==.(a,b,c分别是∠A、∠B、∠C的对边)7.解直角三角形的应用(1)通过解直角三角形能解决实际问题中的很多有关测量问.如:测不易直接测量的物体的高度、测河宽等,关键在于构造出直角三角形,通过测量角的度数和测量边的长度,计算出所要求的物体的高度或长度.(2)解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.8.解直角三角形的应用-坡度坡角问题(1)坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.(2)把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h/l=tanα.(3)在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.应用领域:①测量领域;②航空领域③航海领域:④工程领域等.9.解直角三角形的应用-仰角俯角问题(1)概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.(2)解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.。
中考数学-锐角三角函数(解析版)

知识点一:锐角三角函数 1.三角函数定义 在 Rt△ABC 中,若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
(1)平方关系: sin2 Acos2 A1
(1)三边之间的关系为 a2 b2 c2 (勾股定理)
(2)锐角之间的关系为∠A+∠B=90°
(3)30°角所对直角边等于斜边的一半。
(4)直角三角形斜边上的中线等于斜边的一半。
(5)边角之间的关系为:(三角函数定义)
2.其他有关公式
(1)
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
(2)Rt△面积公式:
S
1 2
ab
1 2
ch
(3)直角三角形外接圆的半径
R c 2
,内切圆半径
r abc 2
结论:直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母 i 表示,即 i h . l
见问题,这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型,要善于把实际问题的数量关系转化为解直角三角形的问题.在 解直角三角形的过程中,常会遇到近似计算,应根据题目要求的精确度定答案.
中考数学频考点突破--锐角三角函数

中考数学频考点突破--锐角三角函数1.教育部颁布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B 处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:√3,AB=10米,AE=21米(测角器的高度忽略不计,结果精确到0.1米,参考数据:√2≈1.41,√3≈1.73,sin53°≈45,cos53°≈35,tan53°≈43)(1)求点B距水平地面AE的高度;(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.2.如图,AD是△ABC的中线,tanB= 13,cosC= √22,AC= √2.求:(1)BC的长;(2)sin△ADC的值.3.如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.(1)若轮船照此速度与航向航向,何时到达海岸线?(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:√2≈1.4,√3≈1.7)4.如图,AB是△O的直径,PA切△O于点A,PO交△O于点C,连接BC,△P=△B.(1)求△P的度数;(2)连接PB,若△O的半径为a,写出求△PBC面积的思路.5.如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC= 30m,现需了解甲楼对乙楼的采光的影响情况.(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(答案可用根号表示);(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?6.化简:(1)√9 ﹣( 12 )0+2sin30°(2)x+1x−1﹣ xx+1 .7.如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD ),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿坡面AB 向上走到B 处测得宣传牌顶部C 的仰角为45°.已知山坡AB 的坡度为i=1: √3 ,AB=10米,AE=15米.(i=1: √3 是指坡面的铅直高度BH 与水平宽度AH 的比)(1)求点B 距水平而AE 的高度BH ; (2)求宣传牌CD 的高度.(结果精确到0.1米.参考数据: √2 ≈1.414, √3 ≈1.732)8.如图, AB 为 ⊙O 直径,D 为 ⊙O 上一点, BC ⊥CD 于点C ,交 ⊙O 于点E , CD 与 BA 的延长线交于点F , BD 平分 ∠ABC .(1)求证: CD 是 ⊙O 的切线;(2)若 AB =10,CE =1 ,求 CD 和 DF 的长.9.如图,已知△O 是以AB 为直径的△ABC 的外接圆,过点A 作△O 的切线交OC 的延长线于点D ,交BC 的延长线于点E.(1)求证:△DAC=△DCE;(2)若AB=2,sin△D= 13,求AE的长.10.校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使△CAD=30 °,△CBD=60 °.(1)求AB的长(精确到0.1米,参考数据:√3≈1.73,√2≈1.41);(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.11.如图,PA,PB是△O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin△APC= 513.(1)求△O的半径;(2)求弦AB的长.12.根据题意解答(1)计算:|﹣√2|+(π﹣3)0+(12)﹣1﹣2cos45°(2)若关于x的一元二次方程x2+(k+3)x+k=0的一个根是﹣2,求方程的另一个根.13.如图,四边形ABCD内接于△O,点O在AB上,BC=CD,过点C作△O的切线,分别交AB,AD的延长线于点E,F.(1)求证:AF△EF;(2)若cos△DAB=34,BE=1,则线段AD的长是.14.如图,在Rt△ABC中,△C=90°,AC=8,sin A= 3 5(1)求AB的长;(2)若点E在Rt△ABC的直角边上,点F在斜边AB上,当△CFE△△ABC时,求CE的长.15.如图海中有一灯塔P,它的周围8海里内有暗礁,海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东58°方向上,航行40分钟到达B处,测得灯塔P 在北偏东26°方向上.(1)求灯塔P到点B的距离;(2)如果海轮不改变航线由B继续向东航行,通过计算估计海轮有没有触礁的危险?16.“低碳环保,你我同行”.近两年,南京市区的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD△AE于点D,座杆CE=15cm,且△EAB=75°.(1)求AD的长;(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)答案解析部分1.【答案】(1)解:过B作BG⊥DE于G,BH⊥AE于H,Rt△ABH中,i=tan∠BAH=√3,∴∠BAH=30°,∴BH=12AB=5米∴点B距水平地面AE的距离为5米.(2)解:由(1)得:BH=5,AH=5√3,∵BG⊥DE于G,BH⊥AE于H,△AED=90°,∴四边形BHEG是矩形,∴BG=HE即BG=AH+AE=5√3+21,在Rt△BGC中,∠CBG=45°,∴CG=BG=5√3+21.在Rt△ADE中,∠DAE=53°,AE=21,∴DE=AEtan53°=43AE=43×21=28.∴CD=CG+GE−DE=26+5√3−28≈6.7m<7m.答:广告牌CD高符合要求.【知识点】解直角三角形的应用【解析】【分析】(1)过B作BG△DE于G,BH△AE于H,根据坡度可得△BAH=30°,然后根据含30°角的直角三角形的性质就可得到BH;(2)由(1)得BH=5,AH=5√3,易得四边形BHEG是矩形,则BG=HE,求出BG,进而得到CG,在Rt△ADE中,应用三角函数的概念可得DE,进而可求得CD. 2.【答案】(1)解:过点A作AE△BC于点E,∵cosC= √22,在Rt△ACE中,CE=AC•cosC=1,∴AE=CE=1,在Rt△ABE中,tanB= 13,即AEBE=13,∴BE=3AE=3,∴BC=BE+CE=4(2)解:∵AD是△ABC的中线,∴CD= 12BC=2,∴DE=CD﹣CE=1,∵AE△BC,DE=AE,∴△ADC=45°,∴sin△ADC= √22.【知识点】解直角三角形【解析】【分析】(1)过点A作AE△BC于点E,根据cosC= √22,求出△C=45°,求出AE=CE=1,根据tanB= 13,求出BE的长即可;(2)根据AD是△ABC的中线,求出BD的长,得到DE的长,得到答案.3.【答案】(1)解:延长AB交海岸线l于点D,过点B作BE△海岸线l于点E,过点A作AF△l于F,如图所示.∵△BEC=△AFC=90°,△EBC=60°,△CAF=30°,∴△ECB=30°,△ACF=60°,∴△BCA=90°,∵BC=12,AB=36× 4060=24,∴AB=2BC,∴△BAC=30°,△ABC=60°,∵△ABC=△BDC+△BCD=60°,∴△BDC=△BCD=30°,∴BD=BC=12,∴时间t= 1236=13小时=20分钟,∴轮船照此速度与航向航向,上午11:00到达海岸线(2)∵BD=BC,BE△CD,在Rt△BEC中,∵BC=12,△BCE=30°,∴BE=6,EC=6 √3≈10.2,∴CD=20.4,∵20<20.4<21.5,∴轮船不改变航向,轮船可以停靠在码头.【知识点】解直角三角形的应用﹣方向角问题【解析】【分析】(1)延长AB交海岸线l于点D,过点B作BE△海岸线l于点E,过点A作AF△l于F,首先证明△ABC是直角三角形,再证明△BAC=30°,再求出BD的长即可角问题.(2)求出CD的长度,和CN、CM比较即可解决问题.本题考查方向角、解直角三角形等知识,解题的关键是添加辅助线构造直角三角形,由数量关系推出△BAC=30°,属于中考常考题型.4.【答案】(1)解:∵PA切△O于点A,∴PA△AB,∴△P+△POA=90°.∵△POA=△B+△OCB,∴△P+△B+△OCB=90°,∵OB=OC,∴△B=△OCB.又∵△P=△B,∴△P=△B=△OCB.∴△P=30°;(2)解:∵在Rt△PAO中,△APO=30°,OA=a,∴PA= √3AO=√3a,∴△PBC面积是12PA×AB= 12× √3a×(a+a)= √3a2【知识点】切线的性质;解直角三角形【解析】【分析】(1)根据切线的性质求出△PAB=90°,求出△P=△B=△OCB,即可得出答案;(2)解直角三角形求出AP,根据三角形面积公式求出即可.5.【答案】(1)解:如图,延长OB交DC于E,作EF⊥AB,交AB于F,在 RtΔBEF 中,∵EF =AC =30m , ∠FEB =30∘ , ∴BE =2BF设 BF =x ,则 BE =2x ,根据勾股定理知, BE 2=BF 2+EF 2 , ∴(2x)2=x 2+302 ,∴x =±10√3 ,(负值舍去), x =10√3 因此, EC =30−10√3(m)(2)解:当甲幢楼的影子刚好落在点 C 处时, ΔABC 为等腰三角形, 因此,当太阳光与水平线夹角为 45∘ 时,甲楼的影子刚才不落在乙楼的墙上【知识点】解直角三角形的应用【解析】【分析】(1)如图所示作出辅助线,在 RtΔBEF 中运用勾股定理列出方程解答即可;(2)当甲幢楼的影子刚好落在点 C 处时,可得 ΔABC 为等腰三角形,从而得出太阳光与水平线夹角.6.【答案】(1)解:原式=3﹣1+2× 12=3﹣1+1 =3(2)解:原式= (x+1)2(x+1)(x−1) ﹣ x(x−1)(x+1)(x−1) = x 2+2x+1−x 2+x (x+1)(x−1)= 3x+1(x+1)(x−1)【知识点】实数的运算;分式的加减法;0指数幂的运算性质;特殊角的三角函数值 【解析】【分析】(1)由二次根式的化简、零指数幂的性质以及特殊角的三角函数值,即可将原式化简,继而求得答案;(2)首先通分,然后利用同分母的分式相加减的运算法则求解即可,注意运算结果需化为最简.7.【答案】(1)解:在Rt△ABH 中, ∵tan△BAH= BH AH =i= 1√3 = √33. ∴△BAH=30°,∴BH=AB .sin△BAH=10.sin30°=10× 12=5.答:点B 距水平面AE 的高度BH 是5米;(2)解:在Rt△ABH中,AH=AB.cos△BAH=10.cos30°=5 √3,在Rt△ADE中,tan△DAE= DE AE,即tan60°= DE15,∴DE=15 √3,如图,过点B作BF△CE,垂足为F,∴BF=AH+AE=5 √3+15,DF=DE﹣EF=DE﹣BH=15 √3﹣5,在Rt△BCF中,△C=90°﹣△CBF=90°﹣45°=45°,∴△C=△CBF=45°,∴CF=BF=5 √3+15,∴CD=CF﹣DF=5 √3+15﹣(15 √3﹣5)=20﹣10 √3≈20﹣10×1.732≈2.7(米),答:广告牌CD的高度约为2.7米.【知识点】解直角三角形的应用﹣仰角俯角问题【解析】【分析】(1)在Rt△ABH中,由tan△BAH= BHAH=i=1√3= √33.得到△BAH=30°,于是得到结果BH=AB.sin△BAH=10.sin30°=10× 12=5;(2)在Rt△ABH中,AH=AB.cos△BAH=10.cos30°=5 √3,在Rt△ADE中,tan△DAE=DEAE,即tan60°= DE15,得到DE=15 √3,如图,过点B作BF△CE,垂足为F,求出BF=AH+AE=5 √3+15,于是得到DF=DE﹣EF=DE﹣BH=15 √3﹣5,在Rt△BCF 中,△C=90°﹣△CBF=90°﹣45°=45°,求得△C=△CBF=45°,得出CF=BF=5 √3+15,即可求得结果.8.【答案】(1)证明:如图,连接OD,则OB=OD,∴∠OBD=∠ODB,∵BD平分∠ABC,∴∠OBD=∠CBD,∴∠ODB=∠CBD,∴OD//BC,∵BC⊥CD,∴OD⊥CD,又∵OD是⊙O的半径,∴CD是⊙O的切线;(2)解:如图,连接OD,OE,DE,过点D作DG⊥OE于点G,∵AB=10,∴OD=OE=12AB=5,∴∠ODE=∠OED,∵OD//BC,∴∠ODE=∠CED,∴∠OED=∠CED,∵DG⊥OE,BC⊥CD,∴CD=GD(角平分线的性质),在Rt△DEG和Rt△DEC中,{GD=CDDE=DE,∴Rt△DEG≅Rt△DEC(HL),∴GE=CE=1,∴OG=OE−GE=4,在Rt△ODG中,GD=√OD2−OG2=√52−42=3,∴CD=GD=3,由圆周角定理得:∠FOE=2∠ABC,即∠FOD+∠DOE=2∠ABC,∵OD//BC,∴∠FOD=∠ABC,∴∠FOD+∠DOE=2∠FOD,解得∠FOD=∠DOE,在Rt△ODG中,tan∠DOE=GDOG=34,∴tan∠FOD=tan∠DOE=34,在Rt△DOF中,DF=OD⋅tan∠FOD=5×34=154.【知识点】直角三角形全等的判定(HL);角平分线的性质;圆周角定理;切线的判定;解直角三角形【解析】【分析】(1)连接OD,根据等腰三角形的性质及角平分线的定义可得∠ODB=∠CBD,可证OD//BC,利用平行线的性质可得OD⊥CD,根据切线的判定定理即证;(2)连接OD,OE,DE,过点D作DG⊥OE于点G,先求出OD=OE=12AB=5,证明Rt△DEG≅Rt△DEC(HL),可得GE=CE=1,从而求出OG=OE−GE=4,在Rt△ODG中利用勾股定理求出GD=3,由角平分线的性质可得CD=GD=3,由圆周角定理及平行线的性质可求出∠FOD=∠DOE,从而可得tan∠FOD=tan∠DOE=GD OG=34,利用DF=OD⋅tan∠FOD求出结论即可.9.【答案】(1)解:∵AD是圆O的切线,∴△DAB=90°. ∵AB是圆O的直径,∴△ACB=90°.∵△DAC+△CAB=90°,△CAB+△ABC=90°,∴△DAC=△B.∵OC=OB,∴△B=△OCB.又∵△DCE=△OCB,∴△DAC=△DCE.(2)解:∵AB=2,∴AO=1.∵sin△D= 13,∴OD=3,DC=2.在Rt△DAO中,由勾股定理得AD= √OD2−OA2= 2√2.∵△DAC=△DCE,△D=△D,∴△DEC△△DCA,∴DCAD=DEDC,即2√2=ED2.解得:DE= √2,∴AE=AD﹣DE= √2.【知识点】圆周角定理;切线的性质;相似三角形的判定与性质;锐角三角函数的定义【解析】【分析】(1)由切线的性质可知△DAB=90°,由直角所对的圆周为90°可知△ACB=90°,根据同角的余角相等可知△DAC=△B,然后由等腰三角形的性质可知△B=△OCB,由对顶角的性质可知△DCE=△OCB,故此可知△DAC=△DCE;(2)题意可知AO=1,OD=3,DC=2,由勾股定理可知AD= 2√2,由△DAC=△DCE,△D=△D 可知△DEC△△DCA,故此可得到DC2=DE•AD,故此可求得DE= √2,于是可求得AE= √2.10.【答案】(1)解:由题意得,在Rt△ADC中,AD=CDtan30°=√33=21√3,在Rt△BDC中,BD=CDtan60°=√3=7√3,∴AB=AD-BD= 21√3−7√3=14√3≈14×1.73=24.22≈24.2(米).(2)解:∵汽车从A到B用时2秒,∴速度为24.2÷2=12.1(米/秒),∵12.1米/秒=43.56千米/小时,∴该车速度为43.56千米/小时.∵43.56千米/小时大于40千米/小时,∴此校车在AB路段超速.【知识点】解直角三角形的应用【解析】【分析】(1)分别再Rt△ADC和Rt△BDC中,利用正切函数,即可求出AD 与BD的长,从而求出AB的长;(2)由从A到B用时2秒,即可求得这辆车的速度,比较与40千米每小时的大小即可确定是否超速。
2024年人教版九年级数学中考专题训练:锐角三角函数(含解析)

2024年人教版九年级数学中考专题训练:锐角三角函数1.如图,在数学综合实践活动课上,两名同学要测量小河对岸大树BC 的高度,甲同学在点A 测得大树顶端B 的仰角为45°,乙同学从A 点出发沿斜坡走米到达斜坡上点D ,在此处测得树顶端点B 的仰角为26.7°,且斜坡AF 的坡度为1:2.(1)求乙同学从点A 到点D 的过程中上升的高度;(2)依据他们测量的数据求出大树BC 的高度.(参考数据:sin26.7°≈0.45,cos26.7°≈0.89,tan26.7°≈0.50)2.如图,在中,D 是上一点,,以为直径的经过点C ,交于点E ,过点E 作的切线交于点F.(1)求证:.(2)若,,求的长.3.如图1,在△ABC 中,AD ⊥BC 于点D ,正方形PQMN 的边QM 在BC 上,顶点P ,N 分别在AB ,AC 上,BC=a ,AD=h .(1)求正方形PQMN 的边长(用a 和h 的代数式表示);ABC BC BD AD =AD O AB O BD EF BC ⊥5CD =2tan 3B =DF(2)如图2,在△ABC 中,在AB 上任取一点P',画正方形P'Q'M'N',使Q',M'在BC 边上,N'在△ABC 内,连接BN 并延长交AC 于点N ,画NM BC 于点M ,画NP ⊥NM 交AB 于点P ,再画PQ ⊥BC 于点Q ,得到四边形PQMN ,证明四边形PQMN 是正方形;(3)在(2)中的线段BN 该线上截取NE=NM 连接EQ ,EM (如图3),当∠QEM=90°时,求线段BN 的长(用a ,h 表示)4.如图,在直角坐标系中有,O 为坐标原点,,,将此三角形绕原点O 顺时针旋转,得到,二次函数的图象刚好经过A ,B ,C 三点.(1)求二次函数的解析式及顶点P 的坐标;(2)过定点Q 的直线与二次函数图象相交于M ,N 两点.①若,求k 的值;②证明:无论k 为何值,恒为直角三角形.5.如图,四边形ABCD 内接于,的半径为4,,对角线AC 、BD 相交于点P.过点P 分别作于点E ,于点F.(1)求证:四边形为正方形;(2)若,求正方形的边长;(3)设PC 的长为x ,图中阴影部分的面积为y ,求y 与x 之间的函数关系式,并写出y 的最大值.6.如图,已知一次函数的图象经过,两点,且与轴交于点,二次函数的图象经过点,,连接.Rt AOB ()03A ,()10B -,90︒Rt COD 2y ax bx c =++3l y kx k =-+:2PMN S = PMN O O 90ADC AB BC ∠=︒=,PE AD ⊥PF CD ⊥DEPF 2AD CD=DEPF 1y kx m =+()15A --,()04B -,x C 224y ax bx =++A C OA(1)求一次函数和二次函数的解析式.(2)求的正弦值.(3)在点右侧的轴上是否存在一点,使得与相似?若存在,求出点的坐标;若不存在,请说明理由.7.如图1,在四边形ABCD 中,AC 交BD 于点E ,△ADE 为等边三角形.(1)若点E 为BD 的中点,AD =4,CD =5,求△BCE 的面积;(2)如图2,若BC =CD ,点F 为CD 的中点,求证:AB =2AF ;(3)如图3,若AB ∥CD ,∠BAD =90°,点P 为四边形ABCD 内一点,且∠APD =90°,连接BP ,取BP 的中点Q ,连接CQ.当AB =,AD =,tan ∠ABC =2时,求CQ 的最小值.8.如图1,在矩形中,,.P ,Q 分别是,上的动点,且满足,E 是射线上一点,,设,.OAB ∠C x D BCD OAB D ABCD 4AB =30ACB ∠=︒AC CD 35DQ CP =AD AP EP =DQ x =AP y =(1)求y 关于x 的函数表达式.(2)当中有一条边与垂直时,求的长.(3)如图2,当点Q 运动到点C 时,点P 运动到点F.连结,以,为边作.①当所在直线经过点D 时,求的面积;②当点G 在的内部(不含边界)时,直接写出x 的取值范围.9.等边中,是中线,一个以点D 为顶点的30°角绕点D 旋转,使角的两边分别与,的延长线相交于点E ,F .交于点M ,交于点N .(1)如图①,若,求证:.(2)如图②,在绕点D 旋转的过程中:①探究三条线段,,之间的数量关系,并说明理由;②若,,求的长.10. 在平面直角坐标系中,对于和点不与点重合给出如下定义:若边,上分别存在点,点,使得点与点关于直线对称,则称点为的“翻折点”.(1)已知,若点与点重合,点与点重合,直接写出的“翻折点”的坐标;是线段上一动点,当是的“翻折点”时,求长的取值范围;PQE AC DQ FQ FQ PQ PQFG GF PQFG ABC ABC CD AC BC DF AC DE BC CE CF =DE DF =EDF ∠CD CE CF 6CE =2CF =DM xOy OAB (P O )OA OB M N O P MN P OAB ()30A,(0.B ①M A N B OAB P ②AB P OAB AP(2)直线与轴,轴分别交于,两点,若存在以直线为对称轴,且斜边长为的等腰直角三角形,使得该三角形边上任意一点都为的“翻折点”,直接写出的取值范围.11. 如图,在中,边绕点顺时针旋转得到线段,边绕点逆时针旋转得到线段,连接,点是的中点.(1)以点为对称中心,作点关于点的对称点,连接,.依题意补全图形,并证明;求证:;(2)若,且于,直接写出用等式表示的与的数量关系.12.如图1,菱形的边长为,,,分别在边,上,,,点从点出发,沿折线以的速度向点匀速运动不与点 C 重合 ;的外接圆与相交于点,连接交于点设点的运动时间为ts.(1) ;(2)若与相切,判断与的位置关系;求的长;(3)如图3,当点在上运动时,求的最大值,并判断此时与的位置关系; (4)若点在的内部,直接写出的取值范围.13.如图,已知菱形ABCD , E 为对角线AC 上一点.3(0)4y x b b =-+>x y A B AB 2OAB b ABC AB B α(0α180)︒<<︒BD AC C 180α︒-CE DE F DE F C F G BG DG ①AC DG =②DGB ACB ∠=∠α60=︒FH BC ⊥H FH BC ABCD 12cm B 60∠=︒M N AB CD.AM 3cm =DN 4cm =P M MB BC -1cm /s C ()APC O CD E PE AC F.P APE ∠=︒O AD ①O CD ② APCP BC CF PE AC N O t(1)[建立模型]如图1,连结BE,DE.求证:∠EBC=∠EDC.(2)[模型应用]如图2,F是DE延长线上一点,∠EBF=∠ABC,EF交AB于点G.①判断△FBG的形状,并说明理由.②若G为AB的中点,且AB=4,∠ABC=60°,求AF的长.(3)[模型迁移]F是DE延长线上一点,∠EBF=∠ABC,EF交射线AB于点G,且sin∠BAC=,BF//AC.求的值. 14.小明家住在某小区一楼,购房时开发商赠送了一个露天活动场所,现小明在活动场所正对的墙上安装了一个遮阳棚,经测量,安装遮阳棚的那面墙高,安装的遮阳棚展开后可以使正午时刻房前能有宽的阴影处以供纳凉.已知正午时刻太阳光与水平地面的夹角为,安装好的遮阳篷与水平面的夹角为,如下右图为侧面示意图.(参考数据:,,,,,)(1)据研究,当一个人从遮阳棚进出时,如果遮阳棚外端(即图中点C)到地面的距离小于时,则人进出时总会觉得没有安全感,就会不自觉的低下头或者用手护着头,请你通过计算,判断此遮阳棚是否使得人进出时具有安全感?(2)请计算此遮阳棚延展后的长度(即的长度).(结果精确到)15.数学兴趣小组在探究圆中图形的性质时,用到了半径是6的若干圆形纸片.45ABBG BC AB3m2m()AD63.4︒BC10︒100.17sin︒≈100.98cos︒≈100.18tan︒≈63.40.89sin︒≈63.40.45cos︒≈63.4 2.00tan︒≈2.3mBC0.1m(1)如图1,一张圆形纸片,圆心为O ,圆上有一点A ,折叠圆形纸片使得A 点落在圆心O 上,折痕交于B 、C 两点,求的度数.(2)把一张圆形纸片对折再对折后得到如图扇形,点M 是弧上一动点.①如图2,当点M 是弧中点时,在线段、上各找一点E 、F ,使得是等边三角形.试用尺规作出,不证明,但简要说明作法,保留作图痕迹.②在①的条件下,取的内心N ,则 .③如图3,当M 在弧上三等分点S 、T 之间(包括S 、T 两点)运动时,经过兴趣小组探究都可以作出一个是等边三角形,取的内心N ,请问的长度是否变化.如变化,请说明理由;如不变,请求出的长度.16.已知二次函数的图像与轴交于点,且经过点和点.(1)请直接写出,的值;(2)直线交轴于点,点是二次函数图像上位于直线下方的动点,过点作直线的垂线,垂足为.①求的最大值;②若中有一个内角是的两倍,求点的横坐标.17.如图1,在平面直角坐标系中,Rt △OAB 的直角边OA 在y 轴的正半轴上,且OA =6,斜边OB =10,点P 为线段AB 上一动点.O BAC ∠PQ PQ OP OQ EFM EFM EFM ON =PQ EFM EFM ONON )2y x bx c =++yA (4B(C -b c BC y DE )2y x bx c =++AB E AB F EF AEF ABC ∠E(1)请直接写出点B 的坐标;(2)若动点P 满足∠POB =45°,求此时点P 的坐标;(3)如图2,若点E 为线段OB 的中点,连接PE ,以PE 为折痕,在平面内将△APE 折叠,点A 的对应点为A′,当PA′⊥OB 时,求此时点P 的坐标;18.如图,在菱形中,对角线相交于点O ,,.动点P 从点A 出发,沿方向匀速运动,速度为;同时,动点Q 从点A 出发,沿方向匀速运动,速度为.以为邻边的平行四边形的边与交于点E .设运动时间为,解答下列问题:(1)当点M 在上时,求t 的值;(2)连接.设的面积为,求S 与t 的函数关系式和S 的最大值;(3)是否存在某一时刻t ,使点B 在的平分线上?若存在,求出t 的值;若不存在,请说明理由.19.在矩形中,点E 为射线上一动点,连接.ABCD AC BD ,10cm AB=BD =AB 1cm /s AD 2cm /s AP AQ ,APMQ PM AC ()()s 05t t <≤BD BE PEB ()2cm S PEC ∠ABCD BC AE(1)当点E 在边上时,将沿翻折,使点B 恰好落在对角线上点F 处,交于点G .①如图1,若,求的度数;②如图2,当,且时,求的长.(2)在②所得矩形中,将矩形沿进行翻折,点C 的对应点为C ′,当点E ,C ′,D 三点共线时,求的长.20.如图,在矩形ABCD 中,AB=2,BC=4,点E 在直线AB 上,连结DE ,过点A 作AF ⊥DE 交直线BC 于点F ,以AE 、AF 为邻边作平行四边形AEGF.直线DG 交直线AB 于点H.(1)当点E 在线段AB 上时,求证:△ABF ∽△DAE.(2)当AE=2时,求EH 的长.(3)在点E 的运动过程中,是否存在某一位置,使得△EGH 为等腰三角形.若存在,求AE 的长.21.如图1,等边三角形纸片中,,点D 在边上(不与点B 、C 重合),,点E 在边上,将沿折叠得到(其中点C ′是点C 的对应点).BC ABE AE BD AEBD BC =AFD ∠=4AB EF EC =BC ABCD ABCD AE BE ABC 12AB =BC 4CD =AC CDE DE 'C DE(1)当点C ′落在上时,依题意补全图2,并指出C ′D 与的位置关系;(2)如图3,当点C ′落到的平分线上时,判断四边形CDC ′E 的形状并说明理由;(3)当点C ′到的距离最小时,求的长;(4)当A ,C ′,D 三点共线时,直接写出∠AEC ′的余弦值.22.如图,四边形是菱形,其中,点E 在对角线上,点F 在射线上运动,连接,作,交直线于点G.(1)在线段上取一点T ,使,①求证:;②求证:;(2)图中,.①点F 在线段上,求周长的最大值和最小值;②记点F 关于直线的轴对称点为点N.若点N 落在的内部(不含边界),求的取值范围.AC AB ACB ∠AB CE ABCD 60ABC ∠=︒AC CB EF 60FEG ∠=︒DC BC CE CT =FET GEC ∠=∠FT CG =7AB =1AE =BC EFG AB EDC ∠CF答案解析部分1.【答案】(1)解:作DH ⊥AE 于H ,如图所示:在Rt △ADH中,∵,∴AH =2DH ,∵AH 2+DH2=AD 2,∴(2DH )2+DH 2=()2,∴DH =6(米).答:乙同学从点A 到点D 的过程中,他上升的高度为6米;(2)解:如图所示:过点D 作DG ⊥BC 于点G ,设BC =x 米,在Rt △ABC 中,∠BAC =45°,∴AC =BC =x ,由(1)得AH =2DH =12,在矩形DGCH 中,DH =CG =6,DG =CH =AH+AC =x+12,在Rt △BDG 中,BG =BC-CG =BC-DH =x-6,∵tan ∠BDG =,∴,解得:x≈24,12DH AH =BG DG626.70.512x tan x -=︒≈+答:大树的高度约为24米.【解析】【分析】(1)作DH ⊥AE 于H ,利用勾股定理可得AH 2+DH 2=AD 2,再结合AH =2DH ,可得(2DH )2+DH 2=(2,最后求出DH=6即可;(2)过点D 作DG ⊥BC 于点G ,设BC =x 米,则DH =CG =6,DG =CH =AH+AC =x+12,BG =BC-CG =BC-DH =x-6,再结合tan ∠BDG =, 可得,最后求出x 的值即可。
2023 数学浙教版新中考 考点29锐角三角函数(解析版)

考点29锐角三角函数考点总结1.锐角三角函数的意义:如图,在Rt △ABC 中,设∠C =90°,∠α为Rt △ABC 的一个锐角,则: ∠α的正弦sin α=∠α的对边斜边;∠α的余弦cos α=∠α的邻边斜边;∠α的正切tan α=∠α的对边∠α的邻边2.同角三角函数之间的关系: sin 2A +cos 2A = 1 ,tan A =s inA cos A .3.互余两角三角函数之间的关系:(1)sin α=cos (90°-α),cos α=sin (90°-α). (2)tan α·tan (90°-α)=1.(3)锐角的正弦值或正切值随着角度的增大而增大,锐角的余弦值随着角度的增大而减小.(4)对于锐角A 有0<sin A <1,0<cos A <1,tan A >0. 4.特殊的三角函数值:5.如图,直角三角形的三条边与三个角这六个元素中,有如下的关系:(1)三边的关系(勾股定理):a 2+b 2=c 2. (2)两锐角间的关系:∠A +∠B =90°. (3)边与角的关系:sin A =cos B =a c, cos A =sin B =b c ,tan A =a b ,tan B =b a.6.直角三角形的边角关系在现实生活中有着广泛的应用,它经常涉及测量、工程、航海、航空等,其中包括了一些概念,一定要根据题意理解其中的含义才能正确解题. (1)仰角:向上看时,视线与水平线的夹角,如图.(2)俯角:向下看时,视线与水平线的夹角, (3)坡角:坡面与水平面的夹角.(4)坡度:坡面的铅直高度与水平宽度的比叫做坡度(或坡比),一般情况下,我们用h 表示坡的铅直高度,用l 表示坡的水平宽度,用i 表示坡度,即i =hl=tan α,显然,坡度越大,坡角就越大,坡面也就越陡,如图.(5)方向角:指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角,如图324.真题演练一、单选题1.(2021·浙江台州·中考真题)如图,将长、宽分别为12cm ,3cm 的长方形纸片分别沿AB ,AC 折叠,点M ,N 恰好重合于点P .若∠α=60°,则折叠后的图案(阴影部分)面积为( )A .(36-cm 2B .(36-cm 2C .24 cm 2D .36 cm 2【答案】A 【分析】过点C 作CF MN ⊥,过点B 作BE MN ⊥,根据折叠的性质求出60PAC α∠=∠=︒,30EAB PAB ∠=∠=︒,分别解直角三角形求出AB 和AC 的长度,即可求解.【详解】解:如图,过点C 作CF MN ⊥,过点B 作BE MN ⊥,∵长方形纸片分别沿AB ,AC 折叠,点M ,N 恰好重合于点P , ∵60PAC α∠=∠=︒, ∵30EAB PAB ∠=∠=︒,∵90BAC ∠=︒,6cm sin BE AB EAB ==∠,sin CFAC α==,∵12ABCSAB AC =⋅=∵(212336cm ABCS S S=-=⨯-=-阴矩形,故选:A .2.(2021·浙江金华·中考真题)如图是一架人字梯,已知2AB AC ==米,AC 与地面BC 的夹角为α,则两梯脚之间的距离BC 为( )A .4cos α米B .4sin α米C .4tan α米D .4cos α米 【答案】A 【分析】根据等腰三角形的性质得到12BD DC BC ==,根据余弦的定义即可,得到答案. 【详解】过点A 作AD BC ⊥,如图所示:∵AB AC =,AD BC ⊥, ∵BD DC =, ∵DCco ACα=, ∵cos 2cos DC AC αα=⋅=, ∵24cos BC DC α==, 故选:A .3.(2021·浙江温州·中考真题)图1是第七届国际数学教育大会(ICME )的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若1AB BC ==.AOB α∠=,则2OC 的值为( )A .211sin α+ B .2sin 1α+ C .211cos α+ D .2cos 1α+【答案】A 【分析】根据勾股定理和三角函数求解. 【详解】∵在Rt OAB 中,AOB α∠=,1AB = ∵1=sin sin AB OB αα= 在Rt OBC 中,1BC =,2222221111sin sin OC OB BC αα⎛⎫=+=+=+ ⎪⎝⎭故选:A .4.(2021·浙江·中考真题)如图,已知在矩形ABCD 中,1,AB BC ==P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .π+C D .2π【答案】B 【分析】先判断出点Q 在以BC 为直径的圆弧上运动,再判断出点C 1在以B 为圆心,BC 为直径的圆弧上运动,找到当点P 与点A 重合时,点P 与点D 重合时,点C 1运动的位置,利用扇形的面积公式及三角形的面积公式求解即可. 【详解】解:设BP 与CC 1相交于Q ,则∵BQC =90°,∵当点P 在线段AD 运动时,点Q 在以BC 为直径的圆弧上运动, 延长CB 到E ,使BE =BC ,连接EC , ∵C 、C 1关于PB 对称, ∵∵EC 1C =∵BQC =90°,∵点C 1在以B 为圆心,BC 为直径的圆弧上运动, 当点P 与点A 重合时,点C 1与点E 重合, 当点P 与点D 重合时,点C 1与点F 重合,此时,tanPC AB PBC BC BC ∠=== ∵∵PBC =30°,∵∵FBP =∵PBC =30°,CQ =12BC =BQ 32=,∵∵FBE =180°-30°-30°=120°,11322BCFS CC BQ =⨯==线段1CC 扫过的区域的面积是2120360BCFSππ⨯+=故选:B .5.(2021·浙江丽水·中考真题)如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A .tan OE m α=⋅B .2sin CD m α=⋅C .cos AE m α=⋅D .2sin CODSm α=⋅【答案】B 【分析】根据垂径定理、锐角三角函数的定义进行判断即可解答. 【详解】解:∵AB 是O 的直径,弦CD OA ⊥于点E , ∵12DE CD =在Rt EDO ∆中,OD m =,AOD α∠=∠ ∵tan =DEOEα ∵=tan 2tan DE CDOE αα=,故选项A 错误,不符合题意; 又sin DEODα=∵sin DE OD α=∵22sin CD DE m α==,故选项B 正确,符合题意; 又cos OEODα=∵cos cos OE OD m αα== ∵AO DO m ==∵cos AE AO OE m m α=-=-,故选项C 错误,不符合题意; ∵2sin CD m α=,cos OE m α=∵2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=,故选项D 错误,不符合题意; 故选B .6.(2021·浙江宁波·中考真题)如图,在ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,BD =E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D 【答案】C 【分析】根据条件可知∵ABD 为等腰直角三角形,则BD =AD ,∵ADC 是30°、60°的直角三角形,可求出AC 长,再根据中位线定理可知EF =2AC。
备战中考数学综合题专题复习【锐角三角函数】专题解析附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定3.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(215-+;(3758+【解析】试题分析:(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ; (2)∵∠A=∠ABD=36°, ∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1, ∵△ABC ∽△BCD ,∴AB BC BD CD =,即111x x +=, 整理得:x 2+x-1=0,解得:x 1=15-+,x 2=15--(负值,舍去),则x=15-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=151514151AE AB -+++==-++ 在Rt △BCE 中,cosC=cos72°=1515414EC BC -+-+==, 则cos36°-cos72°=51+=15-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.6.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB=45°,∵EG⊥AC,∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC , ∴∠GEC =∠GCE =45°, ∴∠BEG =∠GCF =135°, 由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ), ∴BG =GF ,∵G 在正方形ABCD 对角线上, ∴BG =DG , ∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°, ∴∠CGF+∠AGB =90°, ∴∠AGD+∠CGF =90°, ∴∠DGF =90°, ∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示, 在Rt △ADG 中, ∵∠DAC =45°, ∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°, ∴GH 33236,∴DG =2GH =6, ∴DF 2DG =3 在Rt △DCF 中,CF ()22436-3∴BE =CF =3.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.7.在Rt△ABC中,∠ACB=90°,AB=7,AC=2,过点B作直线m∥AC,将△ABC绕点C 顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分別交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在C A′,CB′的延长线上时,试探究四边形PA'B′Q的面积是否存在最小值.若存在,求出四边形PA′B′Q的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ=72;(3)存在,S四边形PA'B′Q=33【解析】【分析】(1)由旋转可得:AC=A'C=2,进而得到BC3=∠A'BC=90°,可得cos∠A'CB3'BCA C==∠A'CB=30°,∠ACA'=60°;(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB3=32=,依据tan∠Q=tan∠A32=BQ=BC3=2,进而得出PQ=PB+BQ72=;(3)依据S四边形PA'B'Q=S△PCQ﹣S△A'CB'=S△PCQ3-S四边形PA'B'Q最小,即S△PCQ最小,而S△PCQ12=PQ×BC3=,利用几何法即可得到S△PCQ的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB 7=,AC =2,∴BC 3=. ∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 3'BC A C ==,∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A 3=,∴PB 3=BC 32=. ∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A 3=,∴BQ =BC 3⨯=2,∴PQ =PB +BQ 72=; (3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ 3-,∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC 3=PQ , 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min 3=,PQ min =23,∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =33-;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.8.在Rt △ABC 中,∠ACB =90°,CD 是AB 边的中线,DE ⊥BC 于E ,连结CD ,点P 在射线CB 上(与B ,C 不重合)(1)如果∠A =30°,①如图1,∠DCB 等于多少度;②如图2,点P 在线段CB 上,连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,补全图2猜想CP 、BF 之间的数量关系,并证明你的结论;(2)如图3,若点P 在线段CB 的延长线上,且∠A =α(0°<α<90°),连结DP ,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB=∠CDP,在△DCP和△DBF中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.9.如图,正方形ABCD+1,对角线AC 、BD 相交于点O ,AE 平分∠BAC 分别交BC 、BD 于E 、F ,(1)求证:△ABF ∽△ACE ;(2)求tan ∠BAE 的值;(3)在线段AC 上找一点P ,使得PE+PF 最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt△ABE中,∵∠ABE=90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •(2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.10.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
中考数学锐角三角函数-经典压轴题附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.如图,某无人机于空中A处探测到目标B、D的俯角分别是30。
、60。
,此时无人机的飞行高度AC为60m,随后无人机从A处继续水平飞行30 m到达A *处.(1)求A、B之间的距离(2)求从无人机/V上看目标D的俯角的正切值.【答案】(1) 120米;(2) ML5【解析】【分析】(1) 解直角三角形即可得到结论:(2) 过川作A'E丄BC交BC的延长线于E,连接A'D,于是得到4E = AC = 60, CE = AA' = 30 JJ,在Rt^ABC中,求得DC=2^AC=2O V3»然后根据三角函数的泄义即可得到结论.【详解】解:(1)由题意得:Z ABD=30% Z ADC=60%在RtA ABC 中,AC=60m,60AC・・・AB二- =1 =120 (m)sin 30°-2(2)过A作A'E丄BC交BC的延长线于E,连接A'D,则A'E = AC = 60, CE = A4* = 30 VJ ,在RtA ABC 中.AC=60m, Z ADC二60°,DC= —AC=203・・・DE=50DE 50>/3 5答:从无人机/T上看目标D的俯角的正切值是2 JLBDC E【点睛】本题考查了解直角三角形的应用,添加辅助线建立直角三角形是解题的关键.2.已知:如图,在四边形 ABCD 中,ABII CD, Z ACB =90°, AB=10cm, BC=8cm, OD 垂 直平分A C.点P 从点B 出发,沿BA 方向匀速运动,速度为lcm/s :同时,点Q 从点D 岀 发,沿DC 方向匀速运动,速度为lcm/s :当一个点停I 上运动,另一个点也停止运动.过点 P 作PE 丄AB,交BC 于点E,过点Q 作QFII AC,分别交AD, 0D 于点F, G.连接OP, EG.设运动时间为t (s ) (0<t<5),解答下列问题:(1)当t 为何值时,点E 在BAC 的平分线上?(2 )设四边形PEGO 的而积为S (cm 2),求S 与t 的函数关系式:(3) 在运动过程中,是否存在某一时刻t,使四边形PEGO 的面积最大?若存在,求出t 的值:若不存在,请说明理由:(4) 连接OE, 0Q,在运动过程中,是否存在某一时刻t,使0E 丄0Q?若存在,求出t 的值:若不存在,请说明理由.【解析】【分析】(1)当点E 在Z BAC 的平分线上时,因为EP 丄AB, EC 丄AC,可得PE=EC,由此构建方程 即可解决问题・(2 )根据 S 以边形OPEG =S A OEG +S A OPE =S A OEG +(S A OPC +S A PCE -S A OEC )构建函数关系式即可・ (3) 利用二次函数的性质解决问题即可. Ec(4) 证明ZEOC 二ZQOG,可得tanZ EOC=tanZ QOG>推出一 =—,由此构建方程即 可解决问题.OC OG *四边形PEGO 取得最大值:(4) t =—时,OE 丄•【详解】(1)在 RtA ABC 中,•/ Z ACB=90% AB=10cm, BC=8cm, .•・ AC 二 J]。
中考数学锐角三角函数-经典压轴题附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题) 1.如图,某无人机于空中A 处探测到目标B D 、的俯角分别是30、60︒︒,此时无人机的飞行高度AC 为60m ,随后无人机从A 处继续水平飞行303m 到达'A 处.(1)求之间的距离(2)求从无人机'A 上看目标的俯角的正切值. 【答案】(1)120米;(223. 【解析】 【分析】(1)解直角三角形即可得到结论;(2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D ,于是得到'60A E AC ==,'30CE AA ==3Rt △ABC 中,求得33,然后根据三角函数的定义即可得到结论. 【详解】解:(1)由题意得:∠ABD=30°,∠ADC=60°, 在Rt △ABC 中,AC=60m ,∴AB=sin 30AC︒=6012=120(m )(2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D , 则'60A E AC ==, '30CE AA ==3在Rt △ABC 中, AC=60m ,∠ADC=60°,∴33∴3∴tan ∠A 'A D= tan ∠'A DC='A E DE 503235答:从无人机'A 上看目标D 235【点睛】本题考查了解直角三角形的应用,添加辅助线建立直角三角形是解题的关键.2.已知:如图,在四边形 ABCD 中, AB ∥CD , ∠ACB =90°, AB=10cm , BC=8cm , OD 垂直平分 A C .点 P 从点 B 出发,沿 BA 方向匀速运动,速度为 1cm/s ;同时,点 Q 从点 D 出发,沿 DC 方向匀速运动,速度为 1cm/s ;当一个点停止运动,另一个点也停止运动.过点 P 作 PE ⊥AB ,交 BC 于点 E ,过点 Q 作 QF ∥AC ,分别交 AD , OD 于点 F , G .连接 OP ,EG .设运动时间为 t ( s )(0<t <5) ,解答下列问题: (1)当 t 为何值时,点 E 在BAC 的平分线上?(2)设四边形 PEGO 的面积为 S(cm 2) ,求 S 与 t 的函数关系式;(3)在运动过程中,是否存在某一时刻 t ,使四边形 PEGO 的面积最大?若存在,求出t 的值;若不存在,请说明理由;(4)连接 OE , OQ ,在运动过程中,是否存在某一时刻 t ,使 OE ⊥OQ ?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)4s t =;(2)PEGO S 四边形2315688t t =-++ ,(05)t <<;(3)52t =时,PEGO S 四边形取得最大值;(4)165t =时,OE OQ ⊥. 【解析】 【分析】(1)当点E 在∠BAC 的平分线上时,因为EP ⊥AB ,EC ⊥AC ,可得PE=EC ,由此构建方程即可解决问题.(2)根据S 四边形OPEG =S △OEG +S △OPE =S △OEG +(S △OPC +S △PCE -S △OEC )构建函数关系式即可. (3)利用二次函数的性质解决问题即可.(4)证明∠EOC=∠QOG ,可得tan ∠EOC=tan ∠QOG ,推出EC GQOC OG=,由此构建方程即可解决问题.【详解】(1)在Rt △ABC 中,∵∠ACB=90°,AB=10cm ,BC=8cm , ∴AC=22108-=6(cm ), ∵OD 垂直平分线段AC , ∴OC=OA=3(cm ),∠DOC=90°, ∵CD ∥AB , ∴∠BAC=∠DCO , ∵∠DOC=∠ACB , ∴△DOC ∽△BCA , ∴AC AB BCOC CD OD==, ∴61083CD OD==, ∴CD=5(cm ),OD=4(cm ), ∵PB=t ,PE ⊥AB , 易知:PE=34t ,BE=54t ,当点E 在∠BAC 的平分线上时, ∵EP ⊥AB ,EC ⊥AC , ∴PE=EC ,∴34t=8-54t ,∴t=4.∴当t 为4秒时,点E 在∠BAC 的平分线上. (2)如图,连接OE ,PC .S 四边形OPEG =S △OEG +S △OPE =S △OEG +(S △OPC +S △PCE -S △OEC ) =1414153154338838252524524t t t t t ⎡⎛⎫⎛⎫⎛⎫⎛⎫⨯-⨯+⨯⨯-+⨯-⨯-⨯⨯- ⎪ ⎪ ⎪ ⎪⎢⎝⎭⎝⎭⎝⎭⎝⎭⎣ =281516(05)33t t t -++<<. (3)存在.∵28568(05)323S t t⎛⎫=--+<<⎪⎝⎭,∴t=52时,四边形OPEG的面积最大,最大值为683.(4)存在.如图,连接OQ.∵OE⊥OQ,∴∠EOC+∠QOC=90°,∵∠QOC+∠QOG=90°,∴∠EOC=∠QOG,∴tan∠EOC=tan∠QOG,∴EC GQOC OG=,∴358544345ttt -=-,整理得:5t2-66t+160=0,解得165t=或10(舍弃)∴当165t=秒时,OE⊥OQ.【点睛】本题属于四边形综合题,考查了解直角三角形,相似三角形的判定和性质,锐角三角函数,多边形的面积等知识,解题的关键是学会利用参数构建方程解决问题.3.如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,2 1.4142≈.【答案】塔高AB约为32.99米.【解析】【分析】过点D 作DH ⊥AB ,垂足为点H ,设AB =x ,则 AH =x ﹣3,解直角三角形即可得到结论. 【详解】解:过点D 作DH ⊥AB ,垂足为点H .由题意,得 HB = CD = 3,EC = 15,HD = BC ,∠ABC =∠AHD = 90°, ∠ADH = 32°.设AB = x ,则 AH = x – 3.在Rt △ABE 中,由 ∠AEB = 45°,得 tan tan451ABAEB EB∠=︒==. ∴ EB = AB = x .∴ HD = BC = BE + EC = x + 15. 在Rt △AHD 中,由 ∠AHD = 90°,得 tan AHADH HD∠=. 即得 3tan3215x x -︒=+. 解得 15tan32332.991tan32x ⋅︒+=≈-︒.∴ 塔高AB 约为32.99米. 【点睛】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.4.水库大坝截面的迎水坡坡比(DE 与AE 的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米. 【解析】试题分析:先根据两个坡比求出AE 和BF 的长,然后利用勾股定理求出AD 和BC ,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC ,梯形的面积公式可得出答案. 试题解析:∵迎水坡坡比(DE 与AE 的长度之比)为1:0.6,DE=30m , ∴AE=18米,在RT△ADE中,AD=22DE AE+=634米∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,BC=22CF BF+=305米,∴周长=DC+AD+AE+EF+BF+BC=634+10+305+88=(634+305+98)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(634+305+98)米,面积是1470平方米.5.如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段BC上,点Q在线段AB上,且PQ=BQ,延长QP交射线AC于点D.(1)求证:QA=QD;(2)设∠BAP=α,当2tanα是正整数时,求PC的长;(3)作点Q关于AC的对称点Q′,连结QQ′,AQ′,DQ′,延长BC交线段DQ′于点E,连结AE,QQ′分别与AP,AE交于点M,N(如图2所示).若存在常数k,满足k•MN=PE•QQ′,求k的值.【答案】(1)证明见解析(2)PC的长为37或32(3)8【解析】【分析】(1)由等腰三角形的性质得出∠B=∠BPQ=∠CPD,由直角三角形的性质得出∠BAC=∠D,即可得出结论;(2)过点P作PH⊥AB于H,设PH=3x,BH=4x,BP=5x,由题意知tanα=1或12,当tanα=1时,HA=PH=3x,与勾股定理得出3x+4x=5,解得x=57,即可求出PC长;当tanα=12时,HA=2PH﹣6x,得出6x+4x=5,解得x=12,即可求出PC长;(3)设QQ′与AD交于点O,由轴对称的性质得出AQ′=AQ=DQ=DQ′,得出四边形AQDQ′是菱形,由菱形的性质得出QQ′⊥AD,AO=12AD,证出四边形BEQ'Q是平行四边形,得出QQ′=BE,设CD=3m,则PC=4m,AD=3+3m,即QQ′﹣BE=4m+4,PE=8m,由三角函数得出MOAO=tan∠PAC=PCAC,即可得出结果.【详解】(1)证明:∵PQ=BQ,∴∠B=∠BPQ=∠CPD,∵∠ACB=∠PCD=90°,∴∠A+∠BAC=90°,∠D+∠CPD=90°,∴∠BAC=∠D,∴QA=QD;(2)解:过点P作PH⊥AB于H,如图1所示:设PH=3x,BH=4x,BP=5x,由题意得:tan∠BAC=43,∠BAP<∠BAC,∴2tanα是正整数时,tanα=1或12,当tanα=1时,HA=PH=3x,∴3x+4x5,∴x=57,即PC=4﹣5x=37;当tanα=12时,HA=2PH﹣6x,∴6x+4x=5,∴x=12,即PC=4﹣5x=32;综上所述,PC的长为37或32;(3)解:设QQ′与AD交于点O,如图2所示:由轴对称的性质得:AQ′=AQ=DQ=DQ′,∴四边形AQDQ′是菱形,∴QQ′⊥AD,AO=12AD,∵BC⊥AC,∴QQ′∥BE,∵BQ∥EQ′,∴四边形BEQ'Q 是平行四边形, ∴QQ′=BE ,设CD =3m ,则PC =4m ,AD =3+3m , 即QQ′﹣BE =4m+4,PE =8m , ∵MO AO =tan ∠PAC =PCAC, ∴332MOm +=43m,即MN =2MO =4m (1+m ), ∴k =PE QQ MN′=8(44)4(1)m m m m ++=8.【点睛】本题是三角形综合题目,考查了等腰三角形的性质与判定、三角函数、勾股定理、菱形的判定与性质、平行线的性质以及分类讨论等知识;本题综合性强,熟练掌握等腰三角形的判定与性质,灵活运用三角函数是解题关键.6.如图,△ABC 中,AC =BC =10,cosC =35,点P 是AC 边上一动点(不与点A 、C 重合),以PA 长为半径的⊙P 与边AB 的另一个交点为D ,过点D 作DE ⊥CB 于点E . (1)当⊙P 与边BC 相切时,求⊙P 的半径.(2)连接BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围.(3)在(2)的条件下,当以PE 长为直径的⊙Q 与⊙P 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409R=;(2)25880320xy x xx=-++;(3)50105-.【解析】【分析】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,即可求解;(2)首先证明PD∥BE,则EB BFPD PF=,即:2024588x yxxxy-+--=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=EP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH =ACsinC =8,同理可得:CH =6,HA =4,AB =45,则:tan ∠CAB =2, BP =228+(4)x -=2880x x -+,DA =255x ,则BD =45﹣255x , 如下图所示,PA =PD ,∴∠PAD =∠CAB =∠CBA =β,tanβ=2,则cosβ5,sinβ5, EB =BDcosβ=(525x )5=4﹣25x ,∴PD ∥BE ,∴EB BFPD PF=,即:2024588x y x xx -+--=,整理得:y 25xx 8x 803x 20-++(3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG =PQ ,即两个圆的半径相等,则两圆另外一个交点为D , GD 为相交所得的公共弦, ∵点Q 是弧GD 的中点, ∴DG ⊥EP , ∵AG 是圆P 的直径, ∴∠GDA =90°, ∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形, ∴AG =EP =BD ,∴AB =DB+AD =AG+AD =5 设圆的半径为r ,在△ADG 中,AD =2rcosβ5DG 5AG =2r ,5=52r 51+, 则:DG 550﹣5相交所得的公共弦的长为50﹣5 【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.7.如图,在ABC △中,10AC BC ==,3cos 5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P与边BC相切时,求P的半径;()2联结BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围;()3在()2的条件下,当以PE长为直径的Q与P相交于AC边上的点G时,求相交所得的公共弦的长.【答案】(1)409;(2)()25880010320x x xy xx-+=<<+;(3)1025-【解析】【分析】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=R10R-=45,即可求解;(2)PD∥BE,则EBPD=BFPF,即:2248805x x x yx y--+-=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=GP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=35,sinC=HP CP =R 10R -=45,解得:R=409; (2)在△ABC 中,AC=BC=10,cosC=35, 设AP=PD=x ,∠A=∠ABC=β,过点B 作BH ⊥AC ,则BH=ACsinC=8, 同理可得:CH=6,HA=4,AB=45,则:tan ∠CAB=2BP=()2284x +-=2880x x -+, DA=255x ,则BD=45-255x ,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则55EB=BDcosβ=(555x )525x ,∴PD ∥BE ,∴EB PD =BFPF,即:2248805x x x y xy--+=,整理得:y=)2x 8x 800x 103x 20-+<<+;(3)以EP 为直径作圆Q 如下图所示,两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,∵点Q时弧GD的中点,∴DG⊥EP,∵AG是圆P的直径,∴∠GDA=90°,∴EP∥BD,由(2)知,PD∥BC,∴四边形PDBE为平行四边形,∴AG=EP=BD,∴5设圆的半径为r,在△ADG中,55AG=2r,5551,则:55相交所得的公共弦的长为5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.8.如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C 处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km3,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)【答案】20.9km 【解析】分析:根据题意,构造直角三角和相似三角形的数学模型,利用相似三角形的判定与性质和解直角三角形即可. 详解:如图,在Rt △BDF 中,∵∠DBF=60°,BD=4km ,∴BF=cos 60BD=8km ,∵AB=20km , ∴AF=12km ,∵∠AEB=∠BDF ,∠AFE=∠BFD , ∴△AEF ∽△BDF ,∴AE BDAF BF , ∴AE=6km ,在Rt △AEF 中,CE=AE•tan74°≈20.9km . 故这艘轮船的航行路程CE 的长度是20.9km .点睛:本题考查相似三角形,掌握相似三角形的概念,会根据条件判断两个三角形相似.9.如图,湿地景区岸边有三个观景台、、.已知米,米,点位于点的南偏西方向,点位于点的南偏东方向.(1)求的面积;(2)景区规划在线段的中点处修建一个湖心亭,并修建观景栈道.试求、间的距离.(结果精确到米)(参考数据:,,,,,,)【答案】(1)560000(2)565.6【解析】试题分析:(1)过点作交的延长线于点,,然后根据直角三角形的内角和求出∠CAE,再根据正弦的性质求出CE的长,从而得到△ABC的面积;(2)连接,过点作,垂足为点,则.然后根据中点的性质和余弦值求出BE、AE的长,再根据勾股定理求解即可.试题解析:(1)过点作交的延长线于点,在中,,所以米.所以(平方米).(2)连接,过点作,垂足为点,则.因为是中点,所以米,且为中点,米,所以米.所以米,由勾股定理得,米.答:、间的距离为米.考点:解直角三角形10.已知Rt△ABC,∠A=90°,BC=10,以BC为边向下作矩形BCDE,连AE交BC于F.(1)如图1,当AB=AC,且sin∠BEF=35时,求BFCF的值;(2)如图2,当tan∠ABC=12时,过D作DH⊥AE于H,求EH EA⋅的值;(3)如图3,连AD交BC于G,当2FG BF CG=⋅时,求矩形BCDE的面积【答案】(1)17;(2)80;(3)100. 【解析】 【分析】(1)过A 作AK ⊥BC 于K ,根据sin ∠BEF=35得出35FK AK =,设FK =3a ,AK =5a ,可求得BF =a ,故17BF CF =;(2)过A 作AK ⊥BC 于K ,延长AK 交ED 于G ,则AG ⊥ED ,得△EGA ∽△EHD ,利用相似三角形的性质即可求出;(3)延长AB 、ED 交于K ,延长AC 、ED 交于T ,根据相似三角形的性质可求出BE =ED ,故可求出矩形的面积. 【详解】解:(1)过A 作AK ⊥BC 于K , ∵sin ∠BEF =35,sin ∠FAK =35, ∴35FK AK =, 设FK =3a ,AK =5a , ∴AK =4a ,∵AB =AC ,∠BAC =90°, ∴BK =CK =4a , ∴BF =a , 又∵CF =7a , ∴17BF CF = (2)过A 作AK ⊥BC 于K ,延长AK 交ED 于G ,则AG ⊥ED , ∵∠AGE =∠DHE =90°, ∴△EGA ∽△EHD , ∴EH EDEG EA=, ∴·EH EA EG ED ⋅=,其中EG =BK , ∵BC =10,tan ∠ABC =12,cos ∠ABC =25, ∴BA =BC · cos ∠ABC =205, BK= BA·cos ∠ABC =202855⨯= ∴EG =8,另一方面:ED =BC =10, ∴EH ·EA =80(3)延长AB 、ED 交于K ,延长AC 、ED 交于T , ∵BC ∥KT , BF AF FG KE AE ED==, ∴BF KE FG DE =,同理:FG EDCG DT= ∵FG 2= BF ·CG ∴BF FGFG CG=, ∴ED 2= KE ·DT ∴KE EDDE DT= , 又∵△KEB ∽△CDT ,∴KE CDBE DT=, ∴KE ·DT =BE 2, ∴BE 2=ED 2 ∴ BE =ED∴1010100BCDE S =⨯=矩形【点睛】此题主要考查相似三角形的判定与性质,解题的关键根据题意作出辅助线再进行求解.。
2023年九年级中考数学一轮复习:锐角三角函数(含答案)
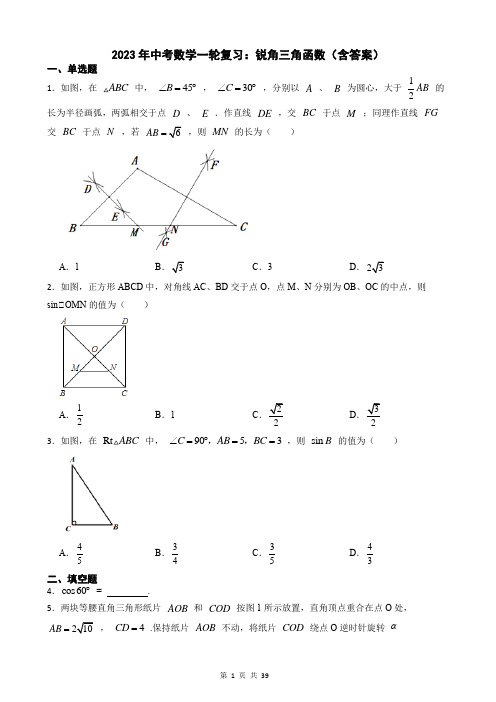
2023年中考数学一轮复习:锐角三角函数(含答案)一、单选题1.如图,在ABC 中, 45B ∠=︒ , 30C ∠=︒ ,分别以 A 、 B 为圆心,大于12AB 的长为半径画弧,两弧相交于点 D 、 E .作直线 DE ,交 BC 于点 M ;同理作直线 FG 交 BC 于点 N ,若 6AB = ,则 MN 的长为( )A .1B 3C .3D .232.如图,正方形ABCD 中,对角线AC 、BD 交于点O ,点M 、N 分别为OB 、OC 的中点,则sin∠OMN 的值为( )A .12B .1C .2 D 33.如图,在 Rt ABC 中, 9053C AB BC ∠=︒==,, ,则 sin B 的值为( )A .45B .34C .35D .43二、填空题4.cos60︒ = .5.两块等腰直角三角形纸片 AOB 和 COD 按图1所示放置,直角顶点重合在点O 处,210AB = , 4CD = .保持纸片 AOB 不动,将纸片 COD 绕点O 逆时针旋转 α()090α<<︒ .当BD 与 CD 在同一直线上(如图2)时, α 的正切值等于 .6.在 ABC ∆ 中, 903016ACB A AB ︒︒∠=∠==,, ,点 P 是斜边 AB 上一点,过点 P 作PQ AB ⊥ ,垂足为 P ,交边 AC (或边 CB )于点 Q ,设 AP x = ,当 APQ ∆ 的面积为 3时, x 的值为 .三、综合题7.如图,在直角三角形ABC 中,∠C =90°,∠A =30°,AC =4,将∠ABC 绕点A 逆时针旋转60°,使点B 落在点E 处,点C 落在点D 处.P 、Q 分别为线段AC 、AD 上的两个动点,且AQ =2PC ,连接PQ 交线段AE 于点M .(1)AQ = ,∠APQ 为等边三角形;(2)是否存在点Q ,使得∠AQM 、∠APQ 和∠APM 这三个三角形中一定有两个三角形相似?若存在请求出AQ 的长;若不存在请说明理由; (3)AQ = ,B 、P 、Q 三点共线.8.(1)计算:3tan30°-(cos60°)-1+8 cos45°+()1tan 60-︒(2)先化简,再求代数式 221(1)122x x x --÷++ 的值,其中x=4cos30°-tan45° 9.如图,AB 是∠O 的直径,点P 在∠O 上,且PA =PB ,点M 是∠O 外一点,MB 与∠O 相切于点B ,连接OM ,过点A 作AC OM 交∠O 于点C ,连接BC 交OM 于点D .(1)求证:MC是∠O的切线;(2)若152OB=,12BC=,连接PC,求PC的长.10.如图,在∠ABC中,过点C作CD//AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.(1)求证:四边形AFCD是平行四边形;(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.11.如图,∠ABC内接于∠O,AB是∠O的直径,∠O的切线AP与OC的延长线相交于点P,∠P=∠BCO.(1)求证:AC=PC;(2)若AB=6 3,求AP的长.12.(12744 sin603233-︒-(2)先化简,再求值:342111xxx x-⎛⎫+-÷⎪--⎝⎭,其中22x=.13.如图,以AB为直径作O,过点A作O的切线AC,连接BC,交O于点D,点E是BC边的中点,连结AE.(1)求证: 2AEB C ∠=∠ ; (2)若 5AB = , 3cos 5B =,求 DE 的长. 14.(1)计算: 2cos 45sin 30tan 45︒︒︒+⋅ . (2)求二次函数 21212y x x =++ 图象的顶点坐标. 15. 如图,直线y =-x +b 与反比例函数 3y x=-的图象相交于点A (a ,3),且与x 轴相交于点B .(1) 求a 、b 的值;(2) 若点P 在x 轴上,且∠AOP 的面积是∠AOB 的面积的12,求点P 的坐标. 16.如图, PA 、 PB 为O 的切线,A 、B 为切点,点C 为半圆弧的中点,连 AC 交 PO于E 点.(1)求证: PB PE = ; (2)若 3tan 5CPO ∠=,求 sin PAC ∠ 的值. 17.(120313213(202248)64---⨯--().(2)先化简,再求值:2243()22ab a ba b a b b a a b---⨯÷+-+,代入你喜欢的a ,b 值求结果. 18.矩形AOBC 中,OB =4,OA =3,分别以OB ,OA 所在直线为x 轴,y 轴,建立如图所示的平面直角坐标系,F 是BC 边上一个动点(不与B ,C 重合),过点F 的反比例函数 ky x= (k >0)的图象与边AC 交于点E.(1)当点F 为边BC 的中点时,求点E 的坐标; (2)连接EF ,求∠EFC 的正切值.19.如图1,已知矩形ABCD 中,AB=6,BC=8,O 是对角线AC 的中点,点E 从A 点沿AB 向点B运动,运动过程中连接OE ,过O 作OF∠OE 交BC 于F ,连接EF ,(1)当点E 与点A 重合时,如图2,求 tan OEF ∠ 的值;(2)运动过程中, tan OEF ∠ 的值是否与(1)中所求的值保持不变,并说明理由; (3)当EF 平分∠OEB 时,求AE 的长.20.如图1,已知二次函数()20y ax bx c a =++>的图象与x 轴交于点()10A -,、()20B ,,与y 轴交于点C ,且2tan OAC ∠=.(1)求二次函数的解析式;(2)如图2,过点C 作CD x 轴交二次函数图象于点D ,P 是二次函数图象上异于点D 的一个动点,连接PB 、PC ,若PBCBCDSS=,求点P 的坐标;(3)如图3,若点P 是二次函数图象上位于BC 下方的一个动点,连接OP 交BC 于点Q.设点P 的横坐标为t ,试用含t 的代数式表示PQ OQ 的值,并求PQOQ的最大值. 21.如图1,四边形 ABCD 内接于O , BD 为直径, AD 上存在点E ,满足AE CD = ,连结 BE 并延长交 CD 的延长线于点F , BE 与 AD 交于点G.(1)若 DBC α∠= ,请用含 α 的代数式表列 AGB ∠ . (2)如图2,连结 ,CE CE BG = .求证; EF DG = . (3)如图3,在(2)的条件下,连结 CG , 2AG = . ①若 3tan 2ADB ∠=,求 FGD 的周长. ②求 CG 的最小值.22.如图,直线364y x =+分别与x 轴、y 轴交于点A 、B ,点C 为线段AB 上一动点(不与A 、B 重合),以C 为顶点作OCD OAB ∠=∠,射线CD 交线段OB 于点D ,将射线OC 绕点O 顺时针旋转90︒交射线CD 于点E ,连接BE .(1)证明:CD ODDB DE=;(用图1) (2)当BDE 为直角三角形时,求DE 的长度;(用图2) (3)点A 关于射线OC 的对称点为F ,求BF 的最小值.(用图3)23.如图,在二次函数 2221y x mx m =-+++ (m 是常数,且 0m > )的图象与x 轴交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D.其对称轴与线段BC 交于点E ,与x 轴交于点F.连接AC ,BD.(1)求A ,B ,C 三点的坐标(用数字或含m 的式子表示),并求 OBC ∠ 的度数; (2)若 ACO CBD ∠=∠ ,求m 的值;(3)若在第四象限内二次函数 2221y x mx m =-+++ (m 是常数,且 0m > )的图象上,始终存在一点P ,使得 75ACP ∠=︒ ,请结合函数的图象,直接写出m 的取值范围.24.如图,已知 AB 是O 的直径,点 E 是O 上异于 A , B 的点,点 F 是 EB 的中点,连接 AE , AF , BF ,过点 F 作 FC AE ⊥ 交 AE 的延长线于点 C ,交 AB 的延长线于点 D , ADC ∠ 的平分线 DG 交 AF 于点 G ,交 FB 于点 H .(1)求证: CD 是 O 的切线;(2)求 sin FHG ∠ 的值; (3)若 GH 42=, HB 2= ,求 O 的直径.25.如图,在平面直角坐标系中,二次函数 ()240y ax bx a =++≠ 的图象经过 ()3,0A - ,()4,0B 两点,且与 y 轴交于点 C .点 D 为 x 轴负半轴上一点,且 BC BD = ,点 P ,Q 分别在线段 AB 和 CA 上.(1)求这个二次函数的表达式.(2)若线段 PQ 被 CD 垂直平分,求 AP 的长. (3)在第一象限的这个二次函数的图象上取一点 G ,使得 GCBGCASS= ,再在这个二次函数的图象上取一点 E (不与点 A , B , C 重合),使得 45GBE ∠=︒ ,求点 E 的坐标.参考答案1.【答案】A【解析】【解答】如解图,连接AM、AN,由作法可知,DE、FG分别为线段AB、AC的垂直平分线,∴AM=BM,AN=CN.∵∠B=45°,∠C=30°,∴∠BAM=45°,∠CAN=30°.∴∠AMB=∠AMC=90°.∴∠MAN=90°−∠C−∠CAN=30°.∵AB= 6,∴AM= 3,∴MN=AM·tan30°=1,故答案为:A.【分析】利用线段垂直平分线的性质得到AM=BM,AN=CN,∠BAM=45°,∠CAN=30°.求得∠MAN=90°−∠C−∠CAN=30°,利用特殊角的三角函数值即可求解。
中考数学第四章 三角形 第七节 锐角三角函数与解直角三角形

所以EF=BE+BF=6+4.8=10.8,
1
1
1
1
所以S四边形ABCD=AE×EF- AE×BE- BF×FC=8×10.8- ×8×6- ×4.8×
2
2
2
2
3.6=53.76.
故零件的截面面积约为53.76 cm2.
前往
考点
ห้องสมุดไป่ตู้方法
a2+⑨
两锐角间
的关系
∠A+∠B=⑩
b2 =c2(勾股定理)
sin A=cos
边角
关系
B= ;
cos A=sin B=⑪
tan A=⑫
tan B=⑬
面积关系
90°
S△ABC=⑭
;
;
ab
1
= ch
2
前往
考点
方法
真题
考点
考点4 解直角三角形的实际应用
1.仰角、俯角:如图,在同一铅垂面内视线和水平线的夹角中,视线在
∠ABC,∴AC=BC=12 n mile,∴AF=ACsin 60°=
12×
3
=6
2
3≈10.4(n mile).
答图
前往
考点
方法
真题
方法
考法2
解直角三角形的实际应用
提分特训
3.[2021安徽中考]学生到工厂劳动实践,学习制作机械零件.零件的截面
如图所示(阴影部分).已知四边形AEFD为矩形,点B,C分别在EF,DF上,
【解析】由题易得,AC=AB= 22 + 42 =2 5,BC= 22 + 22 =2 2.如
中考数学:锐角三角函数试卷解析

中考数学:锐角三角函数试卷解析一、选择题1.(2021四川巴中,第8题3分)在Rt△ABC中,C=90,sinA=1/2,则t anB的值为()A.1B.3C.1/2D.2考点:锐角三角函数.分析:依照题意作出直角△ABC,然后依照sinA=,设一条直角边BC 为5x,斜边AB为13x,依照勾股定理求出另一条直角边AC的长度,然后依照三角函数的定义可求出tanB.解答:∵sinA=,设BC=5x,AB=13x,则AC==12x,故tanB==.故选D.点评:本题考查了互余两角三角函数的关系,属于基础题,解题的关键是把握三角函数的定义和勾股定理的运用.2.(2021山东威海,第8题3分)如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则AOB的正弦值是()A.1B.1/2C.3/5D.2/3考点:锐角三角函数的定义;三角形的面积;勾股定理分析:作ACOB于点C,利用勾股定理求得AC和AB的长,依照正弦的定义即可求解.解答:解:作ACOB于点C.则AC=AB===2,则sinAOB===.故选D.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.3.(2021四川凉山州,第10题,4分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则C的度数是()A.45B.60C.75D.105考点:专门角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方;三角形内角和定理分析:依照非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,依照三角形的内角和定理可得出C的度数.解答:解:由题意,得cosA=,tanB=1,A=60,B=45,C=180﹣A﹣B=180﹣60﹣45=75.故选:C.点评:此题考查了专门角的三角形函数值及绝对值、偶次方的非负性,属于基础题,关键是熟记一些专门角的三角形函数值,也要注意运用三角形的内角和定理.4.(2021甘肃兰州,第5题4分)如图,在Rt△ABC中,C=90,BC=3,A C=4,那么cosA的值等于()A.1/2B.3/5C.2D.1/5考点:锐角三角函数的定义;勾股定理.分析:第一运用勾股定理求出斜边的长度,再利用锐角三角函数的定义求解.解答:解:∵在Rt△ABC中,C=90,AC=4,BC=3,AB=.cosA=,故选:D.点评:本题要紧考查了锐角三角函数的定义:在直角三角形中,锐角的余弦为邻边比斜边.5.(2021广州,第3题3分)如图1,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则().(A)(B)(C)(D)【考点】正切的定义.【分析】.【答案】D6.(2021浙江金华,第6题4分)如图,点A(t,3)在第一象限,OA与x 轴所夹的锐角为,则t的值是【】A.1B.1.5C.2D.3【答案】C.【解析】7.(2021滨州,第11题3分)在Rt△ACB中,C=90,AB=10,sinA=,c osA=,tanA=,则BC的长为()A.6B.7.5C.8D.12.5考点:解直角三角形分析:依照三角函数的定义来解决,由sinA==,得到BC==.解答:解:∵C=90AB=10,sinA=,BC=AB=10=6.故选A.点评:本题考查了解直角三角形和勾股定理的应用,注意:在Rt△AC B中,C=90,则sinA=,cosA=,tanA=.8.(2021扬州,第7题,3分)如图,已知AOB=60,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=()A.3B.4C.5D.6(第1题图)考点:含30度角的直角三角形;等腰三角形的性质分析:过P作PDOB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN 中点,依照MN求出MD的长,由OD﹣MD即可求出OM的长.解答:解:过P作PDOB,交OB于点D,在Rt△OPD中,cos60==,OP=12,OD=6,∵PM=PN,PDMN,MN=2,MD=ND=MN=1,OM=OD﹣MD=6﹣1=5.故选C.点评:此题考查了含30度直角三角形的性质,等腰三角形的性质,熟练把握直角三角形的性质是解本题的关键.9.(2021四川自贡,第10题4分)如图,在半径为1的⊙O中,AOB=4 5,则sinC的值为()A.1B.1/2C.2D.3考点:圆周角定理;勾股定理;锐角三角函数的定义专题:压轴题.分析:第一过点A作ADOB于点D,由在Rt△AOD中,AOB=45,可求得AD与OD的长,继而可得BD的长,然后由勾股定理求得AB的长,继而可求得sinC的值.解答:解:过点A作ADOB于点D,∵在Rt△AOD中,AOB=45,OD=AD=OAcos45=1=,BD=OB﹣OD=1﹣,AB==,∵AC是⊙O的直径,ABC=90,AC=2,sinC=.故选B.点评:此题考查了圆周角定理、三角函数以及勾股定理.此题难度适中,注意把握辅助线的作法,注意数形结合思想的应用.10.(2021浙江湖州,第6题3分)如图,已知Rt△ABC中,C=90,AC =4,tanA=,则BC的长是()A.2B.8C.2D.4分析:依照锐角三角函数定义得出tanA=,代入求出即可.解:∵tanA==,AC=4,BC=2,故选A.点评:本题考查了锐角三角函数定义的应用,注意:在Rt△ACB中,C=90,sinA=,cosA=,tanA=.11.(2021广西来宾,第17题3分)如图,Rt△ABC中,C=90,B=30,BC=6,则AB的长为4考点:解直角三角形.分析:依照cosB=及专门角的三角函数值解题.解答:解:∵cosB=,即cos30=,AB===4.故答案为:4.点评:本题考查了三角函数的定义及专门角的三角函数值,是基础知识,需要熟练把握.12.(2021年贵州安顺,第9题3分)如图,在Rt△ABC中,C=90,A= 30,E为AB上一点且AE:EB=4:1,EFAC于F,连接FB,则tanCFB的值等于()A.30B.45C.60D.15考点:锐角三角函数的定义..分析:tanCFB的值确实是直角△BCF中,BC与CF的比值,设BC=x,则BC与CF就能够用x表示出来.就能够求解.解答:解:依照题意:在Rt△ABC中,C=90,A=30,∵EFAC,EF∥BC,∵AE:EB=4:1,=5,设AB=2x,则BC=x,AC=x.在Rt△CFB中有CF=x,BC=x.则tanCFB==.故选C.点评:本题考查锐角三角函数的概念:在直角三角形中,正弦等于对比斜;余弦等于邻边比斜边;正切等于对边比邻边.13.(2021年广东汕尾,第7题4分)在Rt△ABC中,C=90,若sinA=,则cosB的值是()A.1B.3C.2D.-1分析:依照互余两角的三角函数关系进行解答.解:∵C=90,B=90,cosB=sinA,∵sinA=,cosB=.故选B.点评:本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.14.(2021毕节地区,第15题3分)如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.已知cosACD=,BC =4,则AC的长为()A.1B.4C.3D.2考点:圆周角定理;解直角三角形分析:由以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.易得ACD=B,又由cosACD=,BC=4,即可求得答案.解答:解:∵AB为直径,ACB=90,ACD+BCD=90,∵CDAB,BCD+B=90,ACD,∵cosACD=,cosB=,tanB=,∵BC=4,tanB===,AC=.故选D.点评:此题考查了圆周角定理以及三角函数的性质.此题难度适中,注意把握数形结合思想的应用.15.(2021年天津市,第2题3分)cos60的值等于()A.1/2B.1C.3D.5点:专门角的三角函数值.分析:依照专门角的三角函数值解题即可.解答:解:cos60=.故选A.点评:本题考查专门角的三角函数值,准确把握专门角的函数值是解题关键.二、填空题1.(2021年贵州黔东南11.(4分))cos60=.考点:专门角的三角函数值.分析:依照专门角的三角函数值运算.解答:解:cos60=.点评:本题考查专门角三角函数值的运算,专门角三角函数值运算在中考中经常显现,要把握专门角度的三角函数值.2.(2021江苏苏州,第15题3分)如图,在△ABC中,AB=AC=5,BC=8.若BPC=BAC,则tanBPC=.考点:锐角三角函数的定义;等腰三角形的性质;勾股定理分析:先过点A作AEBC于点E,求得BAE=BAC,故BPC=BAE.再在Rt△BAE中,由勾股定理得AE的长,利用锐角三角函数的定义,求得tanBPC=tanBAE=.解答:解:过点A作AEBC于点E,∵AB=AC=5,BE=BC=8=4,BAE=BAC,∵BPC=BAC,BPC=BAE.在Rt△BAE中,由勾股定理得AE=,tanBPC=tanBAE=.故答案为:.点评:求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.3.(2021四川内江,第23题,6分)如图,AOB=30,OP平分AOB,P COB于点C.若OC=2,则PC的长是.考点:含30度角的直角三角形;勾股定理;矩形的判定与性质.专题:运算题.分析:延长CP,与OA交于点Q,过P作PDOA,利用角平分线定理得到PD=PC,在直角三角形OQC中,利用锐角三角函数定义求出QC的长,在直角三角形QDP中,利用锐角三角函数定义表示出PQ,由QP+PC=QC,求出PC的长即可.解答:解:延长CP,与OA交于点Q,过P作PDOA,∵OP平分AOB,PDOA,PCOB,PD=PC,在Rt△QOC中,AOB=30,OC=2,QC=OCtan30=2=,APD=30,在Rt△QPD中,cos30==,即PQ=DP=PC,QC=PQ+PC,即PC+PC=,解得:PC=.故答案为:点评:此题考查了含30度直角三角形的性质,锐角三角函数定义,熟练把握直角三角形的性质是解本题的关键.4.(2021四川宜宾,第16题,3分)规定:sin(﹣x)=﹣sinx,cos(﹣x)=co sx,sin(x+y)=sinxcosy+cosxsiny.据此判定下列等式成立的是②③④(写出所有正确的序号)①cos(﹣60②sin75③sin2x=2sinx④sin(x﹣y)=sinxcosy﹣cosxsiny.考点:锐角三角函数的定义;专门角的三角函数值.专题:新定义.分析:依照已知中的定义以及专门角的三角函数值即可判定.解答:解:①cos(﹣60)=cos60=,命题错误;②sin75=sin(30+45)=sin30cos45+cos30sin45=+=+=,命题正确;③sin2x=sinxcosx+cosxsinx═2sinxcosx,故命题正确;④sin(x﹣y)=sinxcos(﹣y)+cosxsin(﹣y)=sinxcosy﹣cosxsiny,命题正确.故答案是:②③④.点评:本题考查锐角三角函数以及专门角的三角函数值,正确明白得题目中的定义是关键.5.(2021甘肃白银、临夏,第15题4分)△ABC中,A、B差不多上锐角,若sinA=,cosB=,则C=.考点:专门角的三角函数值;三角形内角和定理.分析:先依照专门角的三角函数值求出A、B的度数,再依照三角形内角和定理求出C即可作出判定.解答:解:∵△ABC中,A、B差不多上锐角sinA=,cosB=,B=60.C=180﹣A﹣B=180﹣60﹣60=60.故答案为:60.点评:本题考查的是专门角的三角函数值及三角形内角和定理,比较简单.6.(2021广西贺州,第18题3分)网格中的每个小正方形的边长差不多上1,△ABC每个顶点都在网格的交点处,则sinA=.考点:锐角三角函数的定义;三角形的面积;勾股定理.分析:依照正弦是角的对边比斜边,可得答案.解答:解:如图,作ADBC于D,CEAB于E,由勾股定理得AB=AC=2,BC=2,AD=3,由BCAD=ABCE,观看内容的选择,我本着先静后动,由近及远的原则,有目的、有打算的先安排与幼儿生活接近的,能明白得的观看内容。
人教初中数学《锐角三角函数及解直---角三角形》中考真题详解课件PPT(47页)全文

不改变斜坡高度的情况下,把坡角降为15°.
(1)求该斜坡的高度BD;
(2)求斜坡新起点C与原起点A之间的距离.(假设图中C,A,D三点共线)
1
2
3
4
5
ቤተ መጻሕፍቲ ባይዱ
6
7
8
9
10
11
12
13
解:(1)∵∠BAD=30°,BD⊥AD,AB=20 m,
的高度,在距离百货大楼30 m的A处用仪器测得∠DAC=30°;向百货
大楼的方向走10 m,到达B处时,测得∠EBC=48°,仪器高度忽略不计,
求广告牌ED的高度.(结果保留小数点后一位)(参考数据: 3≈1.732,
sin 48°≈0.743,cos 48°≈0.669,tan 48°≈1.111)
0.77,tan 40°≈0.84)
(1)连接DE,求线段DE的长;
(2)求点A,B之间的距离.
14
15
16
17
18
解:(1)如图1,过点C作CF⊥DE于点F,
∵CD=CE,
∴DF=EF,CF平分∠DCE.
∴∠DCF=∠ECF=20°,
∴DF=CD·sin 20°≈5×0.34=1.7,
∴DE=2DF=3.4 cm;
过纪念园.试通过计算加以说明.(参考数据: 3≈1.73, 2≈1.41)
1
2
3
4
5
6
7
8
9
10
11
12
13
解:不穿过,理由如下:
如图,过点A作AD⊥BC,交BC于点D,
根据题意可知∠ACD=45°,∠ABD=30°.
中考数学锐角三角函数-经典压轴题及答案解析

中考数学锐角三角函数-经典压轴题及答案解析一、锐角三角函数1.如图,海上观察哨所B 位于观察哨所A 正北方向,距离为25海里.在某时刻,哨所A 与哨所B 同时发现一走私船,其位置C 位于哨所A 北偏东53°的方向上,位于哨所B 南偏东37°的方向上.(1)求观察哨所A 与走私船所在的位置C 的距离;(2)若观察哨所A 发现走私船从C 处以16海里/小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东76°的方向前去拦截.求缉私艇的速度为多少时,恰好在D 处成功拦截.(结果保留根号)(参考数据:sin37°=cos53°≈,cos37 =sin53°≈去,tan37°≈2,tan76°≈)【答案】(1)观察哨所A 与走私船所在的位置C 的距离为15海里;(2)当缉私艇以每小时617D 处成功拦截. 【解析】 【分析】(1)先根据三角形内角和定理求出∠ACB =90°,再解Rt △ABC ,利用正弦函数定义得出AC 即可;(2)过点C 作CM ⊥AB 于点M ,易知,D 、C 、M 在一条直线上.解Rt △AMC ,求出CM 、AM .解Rt △AMD 中,求出DM 、AD ,得出CD .设缉私艇的速度为x 海里/小时,根据走私船行驶CD 所用的时间等于缉私艇行驶AD 所用的时间列出方程,解方程即可. 【详解】(1)在ABC △中,180180375390ACB B BAC ︒︒︒︒︒∠=-∠-∠=--=. 在Rt ABC V 中,sin AC B AB =,所以3sin 3725155AC AB ︒=⋅=⨯=(海里). 答:观察哨所A 与走私船所在的位置C 的距离为15海里.(2)过点C 作CM AB ⊥,垂足为M ,由题意易知,D C M 、、在一条直线上. 在Rt ACM V 中,4sin 15125CM AC CAM =⋅∠=⨯=,3cos 1595AM AC CAM =⋅∠=⨯=.在Rt ADM △中,tan MDDAM AM∠=,所以tan 7636MD AM ︒=⋅=. 所以222293691724AD AM MD CD MD MC =+=+==-=,.设缉私艇的速度为v海里/小时,则有2491716=,解得617v=.经检验,617v=是原方程的解.答:当缉私艇以每小时617海里的速度行驶时,恰好在D处成功拦截.【点睛】此题考查了解直角三角形的应用﹣方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.2.小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C ⊥OA 于C ,OA=OB=24cm , ∴sin ∠CAO′=,∴∠CAO′=30°;(2)过点B 作BD ⊥AO 交AO 的延长线于D ,∵sin ∠BOD=,∴BD=OBsin ∠BOD ,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin ∠BOD=24×=12,∵O′C ⊥OA ,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°, ∴O′B′+O′C ﹣BD=24+12﹣12=36﹣12, ∴显示屏的顶部B′比原来升高了(36﹣12)cm ;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°, 理由:∵显示屏O′B 与水平线的夹角仍保持120°, ∴∠EO′F=120°, ∴∠FO′A=∠CAO′=30°, ∵∠AO′B′=120°, ∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.3.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知1tan 1.082θ=,2tan 0.412θ=.如果安装工人确定支架AB 高为25cm ,求支架CD 的高(结果精确到1cm)?【答案】【解析】于F,根据锐角三角函数的定义用θ1、θ2表示出DF、EF的值,又可证过A作AF CD四边形ABCE为平行四边形,故有EC=AB=25cm,再再根据DC=DE+EC进行解答即可.4.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(3=1.7).【答案】32.4米.【解析】试题分析:首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造关系式求解.试题解析:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°.∵AB⊥AC,CD⊥AC,∴四边形ABEC为矩形,∴CE=AB=12m,在Rt△CBE中,cot∠CBE=BE CE,∴BE=CE•cot30°=12×3=123,在Rt△BDE中,由∠DBE=45°,得DE=BE=123.∴CD=CE+DE=12(3+1)≈32.4.答:楼房CD的高度约为32.4m.考点:解直角三角形的应用——仰角俯角问题.5.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G,连接AG交CD于K.(1)求证:KE=GE;(2)若KG2=KD•GE,试判断AC与EF的位置关系,并说明理由;(3)在(2)的条件下,若sinE=,AK=,求FG的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.6.在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH、PH.(1)若点P在线CD上,如图1,①依题意补全图1;②判断AH与PH的数量关系与位置关系并加以证明;(2)若点P在线CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)【答案】(1)①如图;②AH=PH,AH⊥PH.证明见解析(2)或【解析】试题分析:(1)①如图(1);②(1)法一:轴对称作法,判断:AH=PH,AH⊥PH.连接CH,根据正方形的每条对角线平分一组对角得:△DHQ等腰Rt△,根据平移的性质得DP=CQ,证得△HDP≌△△HQC,全等三角形的对应边相等得PH=CH,等边对等角得∠HPC=∠HCP,再结合BD是正方形的对称轴得出∠AHP=180°-∠ADP=90°,∴AH=PH且AH⊥PH.四点共圆作法,同上得:∠HPC=∠DAH,∴A、D、P、H共向,∴∠AHP=90°,∠APH=∠ADH=45°,∴△APH等腰Rt△.(2)轴对称作法同(1)作HR⊥PC于R,∵∠AHQ=152°,∴∠AHB=62°,∴∠DAH=17°∴∠DCH=17°.设DP=x,则.由代入HR,CR解方程即可得出x的值. 四点共圆作法,A、H、D、P共向,∴∠APD=∠AHB=62°,∴.试题解析:(1)①法一:轴对称作法,判断:AH=PH,AH⊥PH证:连接CH,得:△DHQ等腰Rt△,又∵DP=CQ,∴△HDP≌△△HQC,∴PH=CH,∠HPC=∠HCPBD为正方形ABCD对称轴,∴AH=CH,∠DAH=∠HCP,∴AH=PH,∠DAH=∠HPC,∴∠AHP=180°-∠ADP=90°,∴AH=PH且AH⊥PH.法二:四点共圆作法,同上得:∠HPC=∠DAH,∴A、D、P、H共向,∴∠AHP=90°,∠APH=∠ADH=45°,∴△APH等腰Rt△.(2)法一:轴对称作法考虑△DHQ等腰Rt△,PD=CQ,作HR⊥PC于R,∵∠AHQ=152°,∴∠AHB=62°,∴∠DAH=17°∴∠DCH=17°.设DP=x,则.由得:,∴.即PD=法二:四点共向作法,A、H、D、P共向,∴∠APD=∠AHB=62°,∴.考点:全等三角形的判定;解直角三角形;正方形的性质;死电脑共圆7.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.8.如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.(1)求菱形ABCD的周长;(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.【答案】解:(1)在菱形ABCD中,∵AC⊥BD,AC=80,BD=60,∴。
中考数学专题复习10锐角三角函数及其运用(解析版)

锐角三角函数及其运用复习考点攻略考点一 锐角三角函数1. 锐角三角函数的定义:在Rt △ABC 中.∠C =90°.AB =c .BC =a .AC =b .正弦:sin A =∠的对边=斜边A ac ;余弦:cos A =∠的邻边=斜边A bc;正切:tanA =∠的对边=邻边A ab.【注意】根据定义求三角函数值时.一定要根据题目图形来理解.严格按照三角函数的定义求解.有时需要通过辅助线来构造直角三角形.2【例2】A .BCD .1【答案】C 【解析】把sin45°=代入原式得:原式=2×.故选C . 考点三 解直角三角形1.在直角三角形中.求直角三角形所有未知元素的过程叫做解直角三角形. 2.解直角三角形的常用关系: 在Rt △ABC 中.∠C =90°.则: (1)三边关系:a 2+b 2=c 2; (2)两锐角关系:∠A +∠B =90°; (3)边与角关系:sin A =cos B =a c .cos A =sin B =b c .tan A =ab; (4)sin 2A +cos 2A =1.3.科学选择解直角三角形的方法口诀: 已知斜边求直边.正弦、余弦很方便; 已知直边求直边.理所当然用正切; 已知两边求一边.勾股定理最方便; 已知两边求一角.函数关系要记牢; 已知锐角求锐角.互余关系不能少; 已知直边求斜边.用除还需正余弦.【例3】如图.我市在建高铁的某段路基横断面为梯形ABCD .DC ∥AB ,BC 长为6米.坡角β为45°.AD 的坡角α为30°.则AD 的长为 ________ 米 (结果保留根号)2sin 222【答案】62【解析】解:过C 作CE ⊥AB 于E.DF ⊥AB 于F.可得矩形CEFD 和Rt △CEB 与Rt △DFA. ∵BC=6.∴CE=2sin 456322BC ︒=⨯=.∴DF=CE=32.∴62sin 30DF AD ==︒.故答案为:62.【例4】如图.大海中有A 和B 两个岛屿.为测量它们之间的距离.在海岸线PQ 上点E 处测得74AEP =︒∠.30BEQ =︒∠;在点F 处测得60AFP =︒∠.60BFQ =︒∠.1km EF =.⑴ 判断AB 、AE 的数量关系.并说明理由⑵ 求两个岛屿A 和B 之间的距离(结果精确到0.1km ).(参考数据:3 1.73≈. sin740.96︒≈.cos740.28︒≈.tan74 3.49︒≈.sin760.97︒≈.cos760.24︒≈)【答案】(1)见解析;(2)3.6km【解析】(1)相等.证明:∵30BEQ =︒∠.60BFQ =︒∠.∴30EBF =︒∠.EF BF =.又∵60AFP =︒∠.∴60BFA =︒∠.在AEF △与ABF △中.EF BF =.AFE AFB =∠∠.AF AF =. ∴AEF ABF △≌∠.∴AB AE =. (2)作AH PQ ⊥.垂足为H .设AE x =.则sin74AH x =︒.cos74HE x =︒.cos741HF x =︒+.Rt AHF △中.tan60AH HF =⋅︒.∴()cos74cos741tan 60x x ︒=︒+⋅︒.即()0.960.281 1.73x x =+⨯. ∴ 3.6x ≈.即 3.6km AB ≈.考点四 锐角三角函数的应用1.仰角和俯角:仰角:在视线与水平线所成的角中.视线在水平线上方的角叫做仰角. 俯角:在视线与水平线所成的角中.视线在水平线下方的角叫做俯角. 2.坡度和坡角坡度:坡面的铅直高度h 和水平宽度l 的比叫做坡面的坡度(或坡比).记作i =h l. 坡角:坡面与水平面的夹角叫做坡角.记作α.i =tan α. 坡度越大.α角越大.坡面越陡. 3.方向角(或方位角)指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角.4.解直角三角形中“双直角三角形”的基本模型:5.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语.根据题意画出图形.建立数学模型;(2)将条件转化为几何图形中的边、角或它们之间的关系.把实际问题转化为解直角三角形问题;(3)选择合适的边角关系式.使运算简便、准确;(4)得出数学问题的答案并检验答案是否符合实际意义.从而得到问题的解.6.解直角三角形应用题应注意的问题:(1)分析题意.根据已知条件画出它的平面或截面示意图.分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义;(2)找出要求解的直角三角形.有些图形虽然不是直角三角形.但可添加适当的辅助线.把它们分割成一些直角三角形和矩形(包括正方形);(3)根据已知条件.选择合适的边角关系式解直角三角形;(4)按照题目中已知数据的精确度进行近似计算.检验是否符合实际.并按题目要求的精确度取近似值.注明单位.【例5】如图.一名滑雪爱好者先从山脚下A处沿登山步道走到点B处.再沿索道乘坐缆车到达顶部C.已知在点A处观测点C.得仰角为35°.且A.B的水平距离AE=1000米.索道BC 的坡度i=1:1.长度为2600米.求山的高度(即点C到AE的距离)(参考数据:sin35°≈0.57.cos35°≈0.82.tan35°≈0.70.≈1.41.结果保留整数)【答案】1983米【解析】:如图.作CD⊥AE于点D.BF⊥CD于点F.又∵BE⊥AD.∴四边形BEDF是矩形.在Rt△BCF中.∵BC的坡度i=1:1.∴∠CBF=45°.∵BC=2600米.∴米.∴米.∵A.B的水平距离AE=1000米.∴米.∵∠CAD=35°.∴(米).答:山高CD约为1983米.【例6】如图.一艘海轮位于灯塔P的南偏东30°方向.距离灯塔100海里的A处.它计划沿正北方向航行.去往位于灯塔P的北偏东45°方向上的B处.(1)问B处距离灯塔P有多远?(结果精确到0.1海里)(2)假设有一圆形暗礁区域.它的圆心位于射线PB上.距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里.进入这个区域.就有触礁的危险.请判断海轮到达B处是否有触礁的危险?如果海伦从B处继续向正北方向航行.是否有触礁的危险?并说明理由.(参考数据:≈1.414.≈1.732)【答案】(1)71海里;(2)见解析【解析】解:(1)过点P作PD⊥AB于点D.依题意可知.P A=100.∠APD=60°.∠BPD=45°.∴∠A=30°.∴PD=50.在△PBD中.BD=PD=50.∴PB =50≈71.答:B 处距离灯塔P 约71海里.(2)依题意知:OP =150.OB =150﹣71=79>60. ∴海轮到达B 处没有触礁的危险.海伦从B 处继续向正北方向航行.有触礁的危险.第一部分 选择题一、选择题(本题有10小题.每题3分.共30分)1. 比萨斜塔是意大利的著名建筑.其示意图如图所示.设塔顶中心点为点B .塔身中心线AB 与垂直中心线AC 的夹角为A ∠.过点B 向垂直中心线AC 引垂线.垂足为点D .通过测量可得AB 、BD 、AD 的长度.利用测量所得的数据计算A ∠的三角函数值.进而可求A ∠的大小.下列关系式正确的是( )A .sin BDA AB= B .cos ABA AD=C .tan ADA BD=D .sin ADA AB=【答案】A【解析】由题可知.△ABD 是直角三角形.90BDA ∠=︒.sin BD A AB ∴=.cos AD A AB=,tan BDA AD =.∴选项B 、C 、D 都是错误的.故答案选A . 2. 如图.在ABC 中.∠C =90°.设∠A .∠B .∠C 所对的边分别为a .b .c .则( )A .c =b sinB B .b =c sin BC .a =b tan BD .b =c tan B【答案】B【解析】∵Rt ABC 中.90C ∠=︒.A ∠、B 、C ∠所对的边分别为a 、b 、c ∴sin bB c=.即sin b c B =.则A 选项不成立.B 选项成立 tan bB a=.即tan b a B =.则C 、D 选项均不成立故选:B . 3. 已知α是锐角.sin α=cos60°.则α等于( ) A .30° B .45°C .60°D .不能确定4. 若∠A 是锐角.且sinA= 3.则( )A. 0°<∠A<30°B. 30°<∠A<45°C. 45°<∠A<60°D. 60°<∠A<90° 【答案】 A【解析】∵sin0°=0.sinα= 13.sin30°= 12.又0< 13< 12.∴0°<α<30°. 故答案为:A .5. 点(-sin60°.cos60°)关于y 轴对称的点的坐标是( )A. (√32.12) B. (-√32.12) C. (-√32.-12) D. (- 12.- 32)【答案】 A 【解析】∵sin60°=√32.cos60°=12.∴(-sin60°.cos60°)=(-√32. 12).关于y 轴对称点的坐标是( √32.12).故答案为:A .6. 在Rt △ABC 中.∠C =90°.BC =5.AC =12.则sinB 的值是( )A .512B .125C .513D .1213【答案】D【解析】解:如图所示:∵∠C =90°.BC =5.AC =12.∴13AB =. ∴12sin 13AC B AB ==.故选:D .7. 如图.某停车场入口的栏杆AB.从水平位置绕点O 旋转到A′B′的位置.已知AO 的长为4米.若栏杆的旋转角∠AOA′=α.则栏杆A 端升高的高度为( ) A .米 B .4sinα米 C .米 D .4cosα米【答案】B【解析】 解:如答图.过点A′作A′C ⊥AB 于点C .在Rt △OCA′.sinα=.所以A′C =A′O ·sinα.由题意得A′O =AO =4.所以A′C =4sinα.因此本题选B .8. 菱形ABCD 的对角线AC =10cm.BD =6cm.那么tan为( )【解析】如图.由题意得.AO ⊥BO .AO =AC =5cm.BO =BD =3cm. 4sin α4cos αA CA O''2B1212则tan=tan ∠OBA .故选A.9. 如图.AB 是圆锥的母线.BC 为底面直径.已知BC =6 cm.圆锥的侧面积为15π cm 2 . 则sin∠ABC 的值为 ( )A.34B.35C.45 D. 53【答案】 C【解析】解:设圆锥的母线长为R.由题意得: 15π=π6R.解得:R=5. ∴圆锥的高为4. ∴.故答案为:C.10. 如图.四边形ABCD 是一张平行四边形纸片.其高2cm AG =.底边6cm BC .45B ∠=︒.沿虚线EF 将纸片剪成两个全等的梯形.若30BEF ∠=︒.则AF 的长为( )2B53AO BO ==A .1cm B.cm 3C.3)cm - D.(2-【答案】D【解析】如图所示.过点F 作FM BC ⊥交BC 于点M.∵AG BC ⊥.45B ∠=︒.AG=2.∴BG=FM=2.AF=GM.令AF=x. ∵两个梯形全等.∴AF=GM=EC=x.又∵30BEF ∠=︒.∴2=tan 30FMME =︒.∴ME =.又∵BC=6.∴26BC BG GM ME EC x x =+++=+++=.∴2x =-D .第二部分 填空题二、填空题(本题有6小题.每题4分.共24分)11..若tan (α–15°)= .则锐角α的度数是________.【答案】 75°【解析】【解答】由tan(α−15°)= √3.得 α−15°=60°. 解得α=75°. 故答案为:75°12.如图.在Rt △ABC 中.∠C =90°.BC =12.tan A =.则sin B =___________.125【答案】【解析】在Rt △ABC 中.∠C =90°.BC =12.tan A =.得.即. ∴AC =5.由勾股定理.得AB.所以sin B =. 故答案为:.13. 如图.A.B.C 是O上的三点.若OBC ∆是等边三角形.则cos A ∠=___________.【解析】解:∵△OBC 是等边三角形∴∠COB=60° ∴∠A=12COB ∠=30°∴cos cos30A ∠= 14. 如图是某商场营业大厅自动扶梯示意图.自动扶梯AB 的倾斜角为30.在自动扶梯下方地面C 处测得扶梯顶端B 的仰角为60︒.A 、C 之间的距离为4m . 则自动扶梯的垂直高度BD =_________m .(结果保留根号)【答案】【解析】∵∠BAC+∠ABC=∠BCD=60°.∠BAC=30°. ∴∠ABC=30°.∴∠ABC=∠BAC.∴BC=AC=4. 在Rt △BCD 中.BD=BCsin60°=4×2=故答案为: 513125125BC AC =12125AC =513AC AB =51315. 如图所示.在四边形ABCD 中.90B ∠=︒.2AB =.8CD =.连接AC .AC CD ⊥.若1sin 3ACB ∠=.则AD 长度是_________.【答案】10【解析】解:在Rt ABC 中.∵12,sin 3AB AB ACB AC =∠==.∴1263AC =÷=.在Rt ADC 中.AD ==10=.故答案为:10.16. 如图.某校教学楼后面紧邻着一个山坡.坡上面是一块平地.//,BC AD BE AD ⊥.斜坡AB 长26m .斜坡AB 的坡比为12∶5.为了减缓坡面.防止山体滑坡.学校决定对该斜坡进行改造.经地质人员勘测.当坡角不超过50°时.可确保山体不滑坡.如果改造时保持坡脚A 不动.则坡顶B 沿BC 至少向右移________m 时.才能确保山体不滑坡.(取tan50 1.2︒=)【答案】10【解析】解:如图.设点B 沿BC 向右移动至点H.使得∠HAD=50°.过点H 作HF ⊥AD 于点F.∵AB=26.斜坡AB 的坡比为12∶5.则设BE=12a.AE=5a.∴()()22212526a a +=.解得:a=2.∴BE=24.AE=10.∴HF=BE=24.∵∠HAF=50°.则24tan50 1.2HFAF AF︒===.解得:AF=20.∴BH=EF=20-10=10.故坡顶B沿BC至少向右移10m时.才能确保山体不滑坡.故答案为:10.第三部分解答题二、解答题(本题有7小题.共46分)17. 如图.在ABC中.90,tanC A ABC∠==∠的平分线BD交AC于点.D CD=AB的长?【答案】6【解析】解:在Rt ABC中.90,3C tanA∠==30,60,A ABC∴∠=∠=BD是ABC∠的平分线.30,CBD ABD∴∠=∠=︒又3,CD=330CDBCtan∴==.在Rt ABC中.90,30∠=︒∠=︒C A.630BCABsin∴==︒.故答案为:6.18. 已知:如图.在菱形ABCD中.AE⊥BC.垂足为E.对角线BD=8.tan∠CBD=.(1)求边AB的长;(2)求cos∠BAE的值.12【答案】(1)2√5 ;(2)35【解析】(1)连接AC .AC 与BD 相交于点O .∵四边形ABCD 是菱形.∴AC ⊥BD .BO =BD =4. ∵Rt △BOC 中.tan ∠CBD ==.∴OC =2. ∴AB =BC(2)∵AE ⊥BC.∴S 菱形ABCD =BC ·AE=BD ·AC . ∵AC=2OC =4.∴=×8×4.∴AE =.∴BE. ∴cos ∠ABE ==.19. 如图.小明利用学到的数学知识测量大桥主架在水面以上的高度AB .在观测点C 处测得大桥主架顶端A 的仰角为30°.测得大桥主架与水面交汇点B 的俯角为14°.观测点与大桥主架的水平距离CM 为60米.且AB 垂直于桥面.(点,,,A B C M 在同一平面内)12OC OB 1212125BE AB 35(1)求大桥主架在桥面以上的高度AM ;(结果保留根号)(2)求大桥主架在水面以上的高度AB .(结果精确到1米)(参考数据sin140.24,cos140.97,tan14 1.73︒︒︒≈≈≈≈)【答案】(1)大桥主架在桥面以上的高度AM 为(2)大桥主架在水面以上的高度AB 约为50米.【解析】解:(1)AB 垂直于桥面90︒∴∠=∠=AMC BMC在Rt AMC △中.60,30︒=∠=CM ACMtan ∠=AM ACM CM tan 30603︒∴=⋅=⨯=AM CM (米)答:大桥主架在桥面以上的高度AM 为(2)在Rt BMC △中.60,14︒=∠=CM BCMtan ∠=MBBCM CMtan14600.2515︒∴=⋅=⨯≈MB CM=+AB AM MB 1550∴≈+≈AB (米)答:大桥主架在水面以上的高度AB 约为50米.20. 如图.某船向正东航行.在A 处望见海岛C 在北偏东60°.前进6海里到B 点.此时测得海岛C 在北偏东45°.已知在该岛周围6海里内有暗礁.问船继续向正东航行.有触礁的危险吗?【答案】见解析【解析】 解:如图.过点C 作CD ⊥AB 于点D.∵∠CAD=90°-60°=30°.∠CBD=90°-45°=45°.∴BD=CD.设CD=x.∴AD=AB+6=6+x.在Rt△CAD中.tan∠CAD=CD AD.∴√33= xx+6.3x=6 √3+ √3x.(3-√3)x=6 √3.解得x=3 √3+3>6.答:若船继续向东航行.无触礁危险。
2024年中考数学总复习:锐角三角形函数(附答案解析)

一.选择题(共25小题)
1.若用我们数学课本上采用的科学计算器计算tan35°12',按键顺序正确的是( )
A.
Байду номын сангаасB.
C.
D.
2.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,下列结论正确的是( )
A.sinC B.sinC C.sinC D.sinC
A. 海里B. 海里C.40海里D. 海里
6.tan45°的值等于( )
A. B. C.1D.
7.已知sina ,那么锐角a的取值范围是( )
A.60°<a<90°B.0°<a<60°C.45°<a<90°D.0°<a<30°
8.如图,在“庆国庆,手拉手”活动中,某小组从营地A出发,沿北偏东53°方向走了1200m到达B点,然后再沿北偏西37°方向走了500m到达目的地C点,此时A,C两点之间的距离为( )
A.15+5 B.10+5 C.10 5 D.15+5
18.一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为( )
A.700米B.10 米C.2 米D.4 米
19.在Rt△ABC中,∠B=90°,如果∠A=α,BC=α.那么AC的长是( )
A.α•tanαB.α•tanαα•cotα
A.900mB.900 mC.900 mD.1800m
24.在Rt△ABC中,∠C=90°,BC=1,AC ,那么tanB的值是( )
A. B. C. D.
25.图1是一款平板电脑支架,由托板、支撑板和底座构成.工作时,可将平板电脑吸附在托板上,底座放置在桌面上.图2是其侧面结构示意图,已知托板AB长200mm,支撑板CB长80mm,当∠ABC=130°,∠BCD=70°时,则托板顶点A到底座CD所在平面的距离为( )(结果精确到1mm).
2023年中考数学一轮复习:锐角三角函数

2023年中考数学一轮复习:锐角三角函数一、单选题1.如图,一座厂房屋顶人字架的跨度12AC =m ,上弦AB BC =,25BAC ∠=︒.若用科学计算器求上弦AB 的长,则下列按键顺序正确的是( )A .1225cos ÷=B .625cos ÷=C .625tan ÷=D .625sin ÷=2.如图,一块矩形木板ABCD 斜靠在墙边(OC⊥OB ,点A ,B ,C ,D ,O 在同一平面内) 。
已知AB=a ,AD=b ,⊥BCO=θ,则点A 到OC 的距离等于( )A .asinθ+bsinθB .acosθ+bcosθC .asinθ+bcosθD .acosθ+bsinθ3.如图,在⊥ ABC 中,⊥C =90°,以OA 为半径的半圆经过Rt ⊥ABC 的顶点B ,交直角边AC 于点E ,且B ,E 是半圆的三等分点,弧BE 的长为43π,则图中阴影部分的面积为( )A .38π B .83π C .38πD .83π二、填空题4.在 Rt ABC 中, 90ACB ∠=︒ , 6BC = , 3sin 5A =,则 AB = . 5.计算: ()0212014()2sin 6012π----︒+= .6452sin 60︒-︒= .三、综合题7.如图,在⊥ABC 中,AB=AC ,以AC 边为直径作O 交BC 边于点D ,过点D 作DE⊥AB 于点E ,ED 、AC 的延长线交于点F.(1)求证:EF 是O 的切线;(2)若EB=6,且sin⊥CFD=35,求O 的半径.8.如图,四边形ABCD 是平行四边形,延长AD 至点E ,使DE =AD ,连接BD 、CE.(1)求证:四边形BCED 是平行四边形;(2)若DA =DB =4,cosA =14,求点B 到点E 的距离. 9.(1)计算:02012460sin ⨯︒(2)求代数式的值:2222(2)42x x x x x x -÷++-+,其中12x =.10.测量计算是日常生活中常见的问题,如图,建筑物BC 的屋顶有一根旗杆AB ,从地面上D 点处观测旗杆顶点A 的仰角为50°,观测旗杆底部B 点的仰角为45°(参考数据:sin50°≈0.8,tan50°≈1.2).(1)若已知CD =20米,求建筑物BC 的高度; (2)若已知旗杆的高度AB =5米,求建筑物BC 的高度.11.随着精准扶贫政策的落地实施,小亮家所在的村落进行了整村搬迁,小亮同家人一起告别了祖辈们世代居住的窑洞,搬进了宽敞明亮的新房.他家的新房全部安装的是内倒式窗户.为帮助家人确定窗边家具摆放位置,小亮想要知道开启窗扇时,窗扇顶端向屋内移动的水平距离.如图,小亮测得窗扇高度AB=80cm,开启时的最大张角⊥A=22.5°,窗扇开启后的位置为AB'.(1)请根据这些数据帮助小亮计算开启窗扇时,窗扇顶端向屋内移动的最大水平距离(不考虑窗扇的厚度,参考数据sin22.5°≈0.38,cos22.5°≈0.92,tan22.5°≈0.41);(2)小亮的爸爸说:“咱家安装窗户总共花了4800元,隔壁小明家安装的是平移式窗户,他家窗户总面积比咱家多3平方米,但他家总共才花了3680元,咱家安装的这种内倒式窗户每平方米的价格是小明家安装的平移式窗户每平方米价格的1.5倍.”请你根据以上信息求出小亮家安装的这种内倒式窗户每平方米多少元?12.有两张完全重合的矩形纸片,将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD,MF,若BD=16cm,⊥ADB=30°.(1)试探究线段BD 与线段MF的数量关系和位置关系,并说明理由;(2)把⊥BCD 与⊥MEF 剪去,将⊥ABD绕点A顺时针旋转得⊥AB1D1,边AD1交FM 于点K(如图2),设旋转角为β(0°<β<90°),当⊥AFK 为等腰三角形时,求β的度数;(3)若将⊥AFM沿AB方向平移得到⊥A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP⊥AB时,求平移的距离.13.如图,在⊥ABC中,以BC为直径的⊥O交AC于点D,点E在⊥O上,且BD DE=,连接BE交AC于点F,已知BA=BF.(1)求证:AB是⊥O的切线;(2)若AF=6,35ABAC=,求⊥O的直径.14.如图,在⊥O中,C,D是直径AB上的两点,且AC=BD,EG⊥AB,FH⊥AB,交AB于C、D,点E,G,F,H在⊥O上.(1)若EG=8,AC=2,求⊥O半径;(2)求证:AE=BF;(3)若C,D分别为OA,OB的中点,则AE=EF=FB成立吗?请说明理由.15.如图,某天然气公司的主输气管道途经A小区,继续沿A小区的北偏东60°方向往前铺设,测绘员在A 处测得另一个需要安装天然气的M小区位于北偏东30°方向,测绘员从A处出发,沿主输气管道步行到达C 处,此时测得M小区位于北偏西60°方向.(1)求⊥AMC与⊥ACM度数.(2)现要在主输气管道AC上选择一个支管道连接点N,使从N处到M小区铺设的管道最短,且AC=2000米,求A小区与支管道连接点N的距离.16.在平面直角坐标系中,一次函数()0y ax b a=+≠的图形与反比例函数()0ky kx=≠的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH y⊥轴,垂足为H,3OH=,4tan3AOH∠=,点B的坐标为()2m-,.(1)求 AHO 的周长;(2)求该反比例函数和一次函数的解析式;(3)写出不等式 kax b x+≥ 的解集.17.(1)计算: ()(04116tan 303--+︒-- ;(2)已知 ()223400x xy y y --=≠ ,试求代数式2x yx y-+ 的值. 18.如图,ABCD 中,点E ,F 分别在BC ,AD 上,BE=DF ,连结AE ,CF 。
中考数学培优 易错 难题(含解析)之锐角三角函数附详细答案

中考数学培优 易错 难题(含解析)之锐角三角函数附详细答案一、锐角三角函数1.如图,山坡上有一棵树AB ,树底部B 点到山脚C 点的距离BC 为63米,山坡的坡角为30°.小宁在山脚的平地F 处测量这棵树的高,点C 到测角仪EF 的水平距离CF=1米,从E 处测得树顶部A 的仰角为45°,树底部B 的仰角为20°,求树AB 的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)【答案】6.4米 【解析】解:∵底部B 点到山脚C 点的距离BC 为6 3 米,山坡的坡角为30°. ∴DC=BC•cos30°=3639=⨯=米, ∵CF=1米, ∴DC=9+1=10米, ∴GE=10米, ∵∠AEG=45°, ∴AG=EG=10米, 在直角三角形BGF 中, BG=GF•tan20°=10×0.36=3.6米, ∴AB=AG-BG=10-3.6=6.4米, 答:树高约为6.4米首先在直角三角形BDC 中求得DC 的长,然后求得DF 的长,进而求得GF 的长,然后在直角三角形BGF 中即可求得BG 的长,从而求得树高2.如图,某无人机于空中A 处探测到目标B D 、的俯角分别是30、60︒︒,此时无人机的飞行高度AC 为60m ,随后无人机从A 处继续水平飞行303m 到达'A 处.(1)求之间的距离(2)求从无人机'A 上看目标的俯角的正切值.【答案】(1)120米;(2)235. 【解析】 【分析】(1)解直角三角形即可得到结论;(2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D ,于是得到'60A E AC ==,'30CE AA ==3,在Rt △ABC 中,求得DC=33AC=203,然后根据三角函数的定义即可得到结论. 【详解】解:(1)由题意得:∠ABD=30°,∠ADC=60°, 在Rt △ABC 中,AC=60m ,∴AB=sin 30AC︒=6012=120(m )(2)过'A 作'A E BC ⊥交BC 的延长线于E ,连接'A D , 则'60A E AC ==, '30CE AA ==3,在Rt △ABC 中, AC=60m ,∠ADC=60°,∴DC=3AC=203∴DE=503∴tan ∠A 'A D= tan ∠'A DC='A E DE =503=235答:从无人机'A 上看目标D 的俯角的正切值是235.【点睛】本题考查了解直角三角形的应用,添加辅助线建立直角三角形是解题的关键.3.小红将笔记本电脑水平放置在桌子上,显示屏OB 与底板OA 所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO '后,电脑转到AO 'B '位置(如图3),侧面示意图为图4.已知OA=OB=24cm ,O 'C ⊥OA 于点C ,O 'C=12cm .(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【解析】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,∴sin∠CAO′=,∴∠CAO′=30°;(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×=12,∵O′C⊥OA,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,∴O′B′+O′C﹣BD=24+12﹣12=36﹣12,∴显示屏的顶部B′比原来升高了(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,理由:∵显示屏O′B与水平线的夹角仍保持120°,∴∠EO′F=120°,∴∠FO′A=∠CAO′=30°,∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.4.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.5.如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)【答案】(1)证明见解析;(2);(3).【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.(2)由AC=2BC,设,应用勾股定理即可求得BC,AC的长,则由AC=2BC得,由△ACE∽△ABC可求得AE,CE的长,由可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得,即可求得PD的长.(3)连接BP,BD,AD,根据圆的对称性,可得,由角的转换可得,由△AGP∽△DGB可得,由△AGD∽△PGB可得,两式相乘可得结果.试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.又∵∠PAC=∠PDC,∴△PAC∽△PDF.(2)连接BP,设,∵∠ACB=90°,AB=5,∴.∴.∵△ACE∽△ABC,∴,即. ∴.∵AB⊥CD,∴.如图,连接BP,∵,∴△APB是等腰直角三角形. ∴∠PAB=45°,.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由(1)△PAC∽△PDF得,即.∴PD的长为.(3)如图,连接BP,BD,AD,∵AC=2BC,∴根据圆的对称性,得AD=2DB,即.∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.∵,∴.∵△AGP∽△DGB,∴.∵△AGD∽△PGB,∴.∴,即.∵,∴.∴与之间的函数关系式为.考点:1.单动点问题;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质;6.垂径定理;7.锐角三角函数定义;8.由实际问题列函数关系式.6.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.7.(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)CD AB,动点P、Q分别在线段OC、CD已知:如图,AB是半圆O的直径,弦//,AP的延长线与射线OQ相交于点E、与弦CD相交于点F(点F与上,且DQ OP点C 、D 不重合),20AB =,4cos 5AOC ∠=.设OP x =,CPF ∆的面积为y .(1)求证:AP OQ =;(2)求y 关于x 的函数关系式,并写出它的定义域; (3)当OPE ∆是直角三角形时,求线段OP 的长.【答案】(1)证明见解析;(2)236030050(10)13x x y x x -+=<<;(3)8OP =【解析】 【分析】(1)证明线段相等的方法之一是证明三角形全等,通过分析已知条件,OP DQ =,联结OD 后还有OA DO =,再结合要证明的结论AP OQ =,则可肯定需证明三角形全等,寻找已知对应边的夹角,即POA QDO ∠=∠即可;(2)根据PFC ∆∽PAO ∆,将面积转化为相似三角形对应边之比的平方来求;(3)分成三种情况讨论,充分利用已知条件4cos 5AOC ∠=、以及(1)(2)中已证的结论,注意要对不符合(2)中定义域的答案舍去. 【详解】(1)联结OD ,∵OC OD =, ∴OCD ODC ∠=∠, ∵//CD AB , ∴OCD COA ∠=∠, ∴POA QDO ∠=∠. 在AOP ∆和ODQ ∆中,{OP DQPOA QDO OA DO=∠=∠=, ∴AOP ∆≌ODQ ∆, ∴AP OQ =;(2)作PH OA ⊥,交OA 于H , ∵4cos 5AOC ∠=,∴4455OH OP x ==,35PH x =, ∴132AOP S AO PH x ∆=⋅=. ∵//CD AB , ∴PFC ∆∽PAO ∆, ∴2210()()AOPy CP x S OP x∆-==, ∴2360300x x y x-+=,当F 与点D 重合时,∵42cos 210165CD OC OCD =⋅∠=⨯⨯=, ∴101016x x =-,解得5013x =, ∴2360300x x y x-+=50(10)13x <<; (3)①当90OPE ∠=o 时,90OPA ∠=o , ∴4cos 1085OP OA AOC =⋅∠=⨯=; ②当90POE ∠=o 时,1010254cos cos 25OC CQ QCO AOC ====∠∠,∴252OP DQ CD CQ CD ==-=-2571622=-=, ∵501013OP <<, ∴72OP =(舍去); ③当90PEO ∠=o 时,∵//CD AB , ∴AOQ DQO ∠=∠, ∵AOP ∆≌ODQ ∆, ∴DQO APO ∠=∠, ∴AOQ APO ∠=∠,∴90AEO AOP ∠=∠=o ,此时弦CD 不存在,故这种情况不符合题意,舍去; 综上,线段OP 的长为8.8.如图,已知正方形在直角坐标系中,点分别在轴、轴的正半轴上,点在坐标原点.等腰直角三角板的直角顶点在原点,分别在上,且将三角板绕点逆时针旋转至的位置,连结(1)求证:(2)若三角板绕点逆时针旋转一周,是否存在某一位置,使得若存在,请求出此时点的坐标;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,或【解析】(1)证明:∵四边形为正方形,∴∵三角板是等腰直角三角形,∴又三角板绕点逆时针旋转至的位置时,∴···························· 3分(2)存在.································· 4分∵∴过点与平行的直线有且只有一条,并与垂直,又当三角板绕点逆时针旋转一周时,则点在以为圆心,以为半径的圆上,························ 5分∴过点与垂直的直线必是圆的切线,又点是圆外一点,过点与圆相切的直线有且只有2条,不妨设为和此时,点分别在点和点,满足·························· 7分当切点在第二象限时,点在第一象限,在直角三角形中,∴∴∴点的横坐标为:点的纵坐标为:∴点的坐标为··························· 9分当切点在第一象限时,点在第四象限,同理可求:点的坐标为综上所述,三角板绕点逆时针旋转一周,存在两个位置,使得此时点的坐标为或································ 11分(1)根据旋转的性质找到相等的线段,根据SAS定理证明;(2)由于△OEF是等腰Rt△,若OE∥CF,那么CF必与OF垂直;在旋转过程中,E、F的轨迹是以O为圆心,OE(或OF)长为半径的圆,若CF⊥OF,那么CF必为⊙O的切线,且切点为F;可过C作⊙O的切线,那么这两个切点都符合F点的要求,因此对应的E点也有两个;在Rt△OFC中,OF=2,OC=OA=4,可证得∠FCO=30°,即∠EOC=30°,已知了OE 的长,通过解直角三角形,不难得到E点的坐标,由此得解.9.如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.(1)求证:∠EPD=∠EDO;(2)若PC=3,tan∠PDA=34,求OE的长.【答案】(1)见解析;(25.【解析】【分析】(1)由切线的性质即可得证.(2)连接OC,利用tan∠PDA=34,可求出CD=2,进而求得OC=32,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.【详解】(1)证明:∵PA,PC与⊙O分别相切于点A,C,∴∠APO=∠CPO, PA⊥AO,∵DE⊥PO,∴∠PAO=∠E=90°,∵∠AOP=∠EOD,∴∠APO=∠EDO,∴∠EPD=∠EDO.(2)连接OC,∴PA=PC=3,∵tan∠PDA=34,∴在Rt△PAD中,AD=4,PD=22PA AD+=5,∴CD=PD-PC=5-3=2,∵tan∠PDA=34,∴在Rt△OCD中,OC=32,OD=22OC CD+=52,∵∠EPD=∠ODE,∠OCP=∠E=90°,∴△OED∽△DEP,∴PDDO =PEDE=DEOE=2,∴DE=2OE,在Rt△OED中,OE2+DE2=OD2,即5OE2=252⎛⎫⎪⎝⎭=254,∴OE=5.【点睛】本题考查了切线的性质;锐角三角函数;勾股定理和相似三角形的判定与性质,充分利用tan∠PDA=34,得线段的长是解题关键.10.如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD=12,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.(1)求B,D两点的坐标;(2)当点E在线段OB上运动时,求∠HDA的大小;(3)以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.【答案】(1)B(4,4),D(4,2);(2)45°;(3)存在,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216,77⎛⎫⎪ ⎪⎝⎭或16421642--⎝⎭,理由见解析【解析】【分析】(1)由正方形性质知AB=OA=4,∠OAB=90°,据此得B(4,4),再由tan∠AOD= 12得AD=12OA=2,据此可得点D坐标;(2)由1tan2GFGOFOF∠==知GF=12OF,再由∠AOB=∠ABO=45°知OF=EF,即GF=12EF,根据GH∥x轴知H为AE的中点,结合D为AB的中点知DH是△ABE的中位线,即HD∥BE,据此可得答案;(3)分⊙G与对角线OB和对角线AC相切两种情况,设PG=x,结合题意建立关于x的方程求解可得.【详解】解:(1)∵A(4,0),∴OA=4,∵四边形OABC为正方形,∴AB=OA=4,∠OAB=90°,∴B(4,4),在Rt△OAD中,∠OAD=90°,∵tan∠AOD=12,∴AD=12OA=12×4=2,∴D(4,2);(2)如图1,在Rt△OFG中,∠OFG=90°∴tan∠GOF=GFOF =12,即GF=12OF,∵四边形OABC为正方形,∴∠AOB=∠ABO=45°,∴OF=EF,∴GF=12EF,∴G为EF的中点,∵GH∥x轴交AE于H,∴H为AE的中点,∵B(4,4),D(4,2),∴D为AB的中点,∴DH是△ABE的中位线,∴HD∥BE,∴∠HDA=∠ABO=45°.(3)①若⊙G与对角线OB相切,如图2,当点E在线段OB上时,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG=2x,OF=EF=22x,∵OA=4,∴AF=4﹣22x,∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,∴GH=12AF=12×(4﹣22x)=2﹣2x,则x=2﹣2x,解得:x=22﹣2,∴E(8﹣42,8﹣42),如图3,当点E在线段OB的延长线上时,x2x﹣2,解得:x=2∴E(2,2②若⊙G与对角线AC相切,如图4,当点E在线段BM上时,对角线AC,OB相交于点M,过点G 作GP ⊥OB 于点P ,设PG =x ,可得PE =x , EG =FG =2x , OF =EF =22x , ∵OA =4, ∴AF =4﹣22x ,∵G 为EF 的中点,H 为AE 的中点, ∴GH 为△AFE 的中位线, ∴GH =12AF =12×(4﹣22x )=2﹣2x , 过点G 作GQ ⊥AC 于点Q ,则GQ =PM =3x ﹣22, ∴3x ﹣22=2﹣2x , ∴4227x +=, ∴42164216,E ⎛⎫++ ⎪ ⎪⎝⎭; 如图5,当点E 在线段OM 上时,GQ =PM =23x ,则23x =22, 解得4227x =,∴16421642,E ⎛⎫-- ⎪⎪⎝⎭; 如图6,当点E 在线段OB 的延长线上时,3x ﹣22x ﹣2, 解得:4227x =(舍去); 综上所述,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216,77⎛⎫ ⎪ ⎪⎝⎭或16421642,77⎛-- ⎝⎭. 【点睛】本题是圆的综合问题,解题的关键是掌握正方形和直角三角形的性质、正切函数的定义、三角形中位线定理及分类讨论思想的运用.11.如图,在平面直角坐标系中,菱形ABCD 的边AB 在x 轴上,点B 坐标(﹣6,0),点C 在y 轴正半轴上,且cos B =35,动点P 从点C 出发,以每秒一个单位长度的速度向D 点移动(P 点到达D 点时停止运动),移动时间为t 秒,过点P 作平行于y 轴的直线l 与菱形的其它边交于点Q . (1)求点D 坐标;(2)求△OPQ 的面积S 关于t 的函数关系式,并求出S 的最大值; (3)在直线l 移动过程中,是否存在t 值,使S =320ABCD S 菱形?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)点D 的坐标为(10,8).(2)S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…,S 的最大值为503.(3)3或7. 【解析】 【分析】(1)在Rt △BOC 中,求BC,OC,根据菱形性质再求D 的坐标;(2)分两种情况分析:①当0≤t ≤4时和②当4<t ≤10时,根据面积公式列出解析式,再求函数的最值;(3)分两种情况分析:当0≤t ≤4时,4t =12,;当4<t ≤10时,22201233t t -+= 【详解】解:(1)在Rt △BOC 中,∠BOC =90°,OB =6,cos B =35, 10cos OBBC B∴== 228OC BC OB ∴=-=∵四边形ABCD 为菱形,CD ∥x 轴, ∴点D 的坐标为(10,8).(2)∵AB =BC =10,点B 的坐标为(﹣6,0), ∴点A 的坐标为(4,0). 分两种情况考虑,如图1所示.①当0≤t ≤4时,PQ =OC =8,OQ =t ,∴S =12PQ •OQ =4t ,∵4>0,∴当t =4时,S 取得最大值,最大值为16;②当4<t ≤10时,设直线AD 的解析式为y =kx +b (k ≠0), 将A (4,0),D (10,8)代入y =kx +b ,得:4k b 010k b 8+=⎧⎨+=⎩,解得:4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩,∴直线AD 的解析式为41633y x =-. 当x =t 时,41633y t =-, 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<Q ∴当t =5时,S 取得最大值,最大值为503. 综上所述:S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…,S 的最大值为503.(3)S 菱形ABCD =AB •OC =80. 当0≤t ≤4时,4t =12, 解得:t =3; 当4<t ≤10时,222033t t -+=12, 解得:t 1=5﹣7(舍去),t 2=5+ 7. 综上所述:在直线l 移动过程中,存在t 值,使S =320ABCD S 菱形,t 的值为3或5+7.【点睛】考核知识点:一次函数和二次函数的最值问题.数形结合,分类讨论是关键.12.超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路(直线AO )的距离为120米的点P 处.这时,一辆小轿车由西向东匀速行驶,测得此车从A 处行驶到B 处所用的时间为5秒且∠APO =60°,∠BPO =45°. (1)求A 、B 之间的路程;(2)请判断此车是否超过了万丰路每小时65千米的限制速度?请说明理由.(参考数据:2 1.414,3 1.73≈≈).【答案】【小题1】73.2【小题2】超过限制速度.【解析】解:(1)100(31)AB =-73.2 (米).…6分 (2) 此车制速度v==18.3米/秒13.如图①,在菱形ABCD 中,60B ︒∠= ,4AB =.点P 从点A 出发以每秒2个单位的速度沿边AD 向终点D 运动,过点P 作PQ AC ⊥交边AB 于点Q ,过点P 向上作//PN AC ,且3PN PQ =,以PN 、PQ 为边作矩形PQMN .设点P 的运动时间为t (秒),矩形PQMN 与菱形ABCD 重叠部分图形的面积为S .(1)用含t 的代数式表示线段PQ 的长.(2)当点M 落在边BC 上时,求t 的值.(3)当0t 1<<时,求S 与t 之间的函数关系式,(4)如图②,若点O 是AC 的中点,作直线OM .当直线OM 将矩形PQMN 分成两部分图形的面积比为12:时,直接写出t 的值【答案】(1)23PQ t =;(2)45;(3)2193403163t t -+-;(4) 23t = 或87t = . 【解析】【分析】(1)由菱形性质得∠D=∠B=60°,AD=AB=CD=4,△ACD 是等边三角形,证出△APQ 是等腰三角形,得出PF=QF,PF=P A•sin60°=3t,即可得出结果;(2)当点M落在边BC上时,由题意得:△PDN是等边三角形,得出PD=PN,由已知得PN=3PQ=3t,得出PD=3t,由题意得出方程,解方程即可;(3)当0<t≤45时,PQ=23t,PN=3PQ=3t,S=矩形PQMN的面积=PQ×PN,即可得出结果;当45<t<1时,△PDN是等边三角形,得出PE=PD=AD-PA=4-2t,∠FEN=∠PED=60°,得出NE=PN-PE=5t-4,FN=3NE=3(5t-4),S=矩形PQMN的面积-2△EFN的面积,即可得出结果;(4)分两种情况:当0<t≤45时,△ACD是等边三角形,AC=AD=4,得出OA=2,OG是△MNH的中位线,得出OG=4t-2,NH=2OG=8t-4,由面积关系得出方程,解方程即可;当45<t≤2时,由平行线得出△OEF∽△MEQ,得出EF OFEQ MQ=,即233ttEF t-=+,解得EF=2332t t-,得出EQ=23323t tt-+,由三角形面积关系得出方程,解方程即可.【详解】(1)∵在菱形ABCD中,∠B=60°,∴∠D=∠B=60°,AD=AB=CD=4,△ACD是等边三角形,∴∠CAD=60°,∵PQ⊥AC,∴△APQ是等腰三角形,∴PF=QF,PF=PA•sin60°=2t×32=3t,∴PQ=23t;(2)当点M落在边BC上时,如图2所示:由题意得:△PDN是等边三角形,∴PD=PN,∵333t=3t,∴PD=3t,∵PA+PD=AD,即2t+3t=4,解得:t=45.(3)当0<t≤45时,如图1所示:PQ=23t,PN=3PQ=3×23t=3t,S=矩形PQMN的面积=PQ×PN=23t×3t=63t2;当45<t<1时,如图3所示:∵△PDN是等边三角形,∴PE=PD=AD-PA=4-2t,∠FEN=∠PED=60°,∴NE=PN-PE=3t-(4-2t)=5t-4,∴335t-4),∴S=矩形PQMN的面积-2△EFN的面积32-2×1235t-4)2=-19t233,即S=-19t233(4)分两种情况:当0<t≤45时,如图4所示:∵△ACD 是等边三角形,∴AC=AD=4,∵O 是AC 的中点,∴OA=2,OG 是△MNH 的中位线,∴OG=3t-(2-t )=4t-2,NH=2OG=8t-4,∴△MNH 的面积=12MN×NH=12×23t×(8t-4)=13×63t 2, 解得:t=23; 当45<t≤2时,如图5所示:∵AC ∥QM ,∴△OEF ∽△MEQ ,∴EF OF EQ MQ =233t t EF t-=+, 解得:2332t t -, ∴23323t t t - ∴△MEQ 的面积=12×3t×23323t t t -+=1332, 解得:t=87; 综上所述,当直线OM 将矩形PQMN 分成两部分图形的面积比为1:2时,t 的值为23或87.【点睛】本题是四边形综合题目,考查了菱形的性质、矩形的性质、等边三角形的判定与性质、勾股定理、相似三角形的判定与性质、三角形中位线定理等知识;本题综合性强,难度较大,熟练掌握菱形和矩形的性质,综合运用知识,进行分类讨论是解题的关键.14.已知:如图,在Rt △ABO 中,∠B =90°,∠OAB =30°,OA =3.以点O 为原点,斜边OA 所在直线为x 轴,建立平面直角坐标系,以点P (4,0)为圆心,PA 长为半径画圆,⊙P 与x 轴的另一交点为N ,点M 在⊙P 上,且满足∠MPN =60°.⊙P 以每秒1个单位长度的速度沿x 轴向左运动,设运动时间为ts ,解答下列问题:(发现)(1)MN n的长度为多少;(2)当t =2s 时,求扇形MPN (阴影部分)与Rt △ABO 重叠部分的面积.(探究)当⊙P 和△ABO 的边所在的直线相切时,求点P 的坐标.(拓展)当MN n 与Rt △ABO 的边有两个交点时,请你直接写出t 的取值范围.【答案】【发现】(1)MN n 的长度为π3;(2)重叠部分的面积为38;【探究】:点P 的坐标为10(,);或23 0)或23 0();【拓展】t 的取值范围是23t ≤<或45t ≤<,理由见解析.【解析】【分析】发现:(1)先确定出扇形半径,进而用弧长公式即可得出结论;(2)先求出PA =1,进而求出PQ ,即可用面积公式得出结论;探究:分圆和直线AB 和直线OB 相切,利用三角函数即可得出结论;拓展:先找出·MN和直角三角形的两边有两个交点时的分界点,即可得出结论. 【详解】[发现](1)∵P (4,0),∴OP =4.∵OA =3,∴AP =1,∴·MN 的长度为6011803ππ⨯=. 故答案为3π; (2)设⊙P 半径为r ,则有r =4﹣3=1,当t =2时,如图1,点N 与点A 重合,∴PA =r =1,设MP 与AB 相交于点Q .在Rt △ABO 中,∵∠OAB =30°,∠MPN =60°.∵∠PQA =90°,∴PQ 12=PA 12=,∴AQ =AP ×cos30°32=,∴S 重叠部分=S △APQ 12=PQ ×AQ 38=. 即重叠部分的面积为38. [探究]①如图2,当⊙P 与直线AB 相切于点C 时,连接PC ,则有PC ⊥AB ,PC =r =1. ∵∠OAB =30°,∴AP =2,∴OP =OA ﹣AP =3﹣2=1;∴点P 的坐标为(1,0);②如图3,当⊙P 与直线OB 相切于点D 时,连接PD ,则有PD ⊥OB ,PD =r =1,∴PD ∥AB ,∴∠OPD =∠OAB =30°,∴cos ∠OPD PD OP =,∴OP 12330cos ==︒,∴点P 的坐标为(23,0); ③如图4,当⊙P 与直线OB 相切于点E 时,连接PE ,则有PE ⊥OB ,同②可得:OP 23=; ∴点P 的坐标为(23-,0);[拓展]t 的取值范围是2<t ≤3,4≤t <5,理由:如图5,当点N 运动到与点A 重合时,·MN与Rt △ABO 的边有一个公共点,此时t =2; 当t >2,直到⊙P 运动到与AB 相切时,由探究①得:OP =1,∴t 411-==3,·MN 与Rt △ABO 的边有两个公共点,∴2<t ≤3.如图6,当⊙P运动到PM与OB重合时,·MN与Rt△ABO的边有两个公共点,此时t=4;直到⊙P运动到点N与点O重合时,·MN与Rt△ABO的边有一个公共点,此时t=5;∴4≤t<5,即:t的取值范围是2<t≤3,4≤t<5.【点睛】本题是圆的综合题,主要考查了弧长公式,切线的性质,锐角三角函数,三角形面积公式,作出图形是解答本题的关键.15.如图,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.(1)求证:四边形AGDH为菱形;(2)若EF=y,求y关于x的函数关系式;(3)连结OF,CG.①若△AOF为等腰三角形,求⊙O的面积;②若BC=3,则30CG+9=______.(直接写出答案).【答案】(1)证明见解析;(2)y=18x2(x>0);(3)①163π或8π或(17+2)π;21.【解析】【分析】(1)根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可;(2)只要证明△AEF∽△ACB,可得AE EFAC BC解决问题;(3)①分三种情形分别求解即可解决问题;②只要证明△CFG∽△HFA,可得GFAF=CGAH,求出相应的线段即可解决问题;【详解】(1)证明:∵GH垂直平分线段AD,∴HA=HD,GA=GD,∵AB是直径,AB⊥GH,∴EG=EH,∴DG=DH,∴AG=DG=DH=AH,∴四边形AGDH是菱形.(2)解:∵AB是直径,∴∠ACB=90°,∵AE⊥EF,∴∠AEF=∠ACB=90°,∵∠EAF=∠CAB,∴△AEF∽△ACB,∴AE EF AC BC=,∴124x yx=,∴y=18x2(x>0).(3)①解:如图1中,连接DF.∵GH垂直平分线段AD,∴FA=FD,∴当点D与O重合时,△AOF是等腰三角形,此时AB=2BC,∠CAB=30°,∴AB=833,∴⊙O的面积为163π.如图2中,当AF=AO时,∵AB =22AC BC +=216x +,∴OA =216x +, ∵AF =22EF AE +=2221182x ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭, ∴216x +=2221182x ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭, 解得x =4(负根已经舍弃),∴AB =42,∴⊙O 的面积为8π.如图2﹣1中,当点C 与点F 重合时,设AE =x ,则BC =AD =2x ,AB =2164x +,∵△ACE ∽△ABC ,∴AC 2=AE•AB ,∴16=2164x +解得x 2=17﹣2(负根已经舍弃),∴AB 2=16+4x 2=17+8,∴⊙O 的面积=π•14•AB 2=(17+2)π综上所述,满足条件的⊙O的面积为163π或8π或(217+2)π;②如图3中,连接CG.∵AC=4,BC=3,∠ACB=90°,∴AB=5,∴OH=OA=52,∴AE=32,∴OE=OA﹣AE=1,∴EG=EH2512⎛⎫-⎪⎝⎭212,∵EF=18x2=98,∴FG=212﹣98,AF22AE EF+158,AH22AE EH+302,∵∠CFG=∠AFH,∠FCG=∠AHF,∴△CFG∽△HFA,∴GF CGAF AH=,∴219281530 8-=∴CG=705﹣33010,∴30=21.故答案为21【点睛】本题考查圆综合题、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质、菱形的判定和性质、勾股定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用分类讨论的思想思考问题.。
中考数学压轴题专题锐角三角函数的经典综合题及答案

中考数学压轴题专题锐角三角函数的经典综合题及答案一、锐角三角函数1.如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为63米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)【答案】6.4米【解析】解:∵底部B点到山脚C点的距离BC为6 3 米,山坡的坡角为30°.∴DC=BC•cos30°=3==米,639∵CF=1米,∴DC=9+1=10米,∴GE=10米,∵∠AEG=45°,∴AG=EG=10米,在直角三角形BGF中,BG=GF•tan20°=10×0.36=3.6米,∴AB=AG-BG=10-3.6=6.4米,答:树高约为6.4米首先在直角三角形BDC中求得DC的长,然后求得DF的长,进而求得GF的长,然后在直角三角形BGF中即可求得BG的长,从而求得树高2.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.3.已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=3,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)如图3,若k=3,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.【答案】(1)45°;(2)(1)中结论不成立,理由见解析;(3)(2)中结论成立,理由见解析.【解析】分析:(1)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE≌△ACD,得出EF=AD=BF,再判断出∠EFB=90°,即可得出结论;(2)先判断出四边形ADBF 是平行四边形,得出BD=AF ,BF=AD ,进而判断出△FAE ∽△ACD ,再判断出∠EFB=90°,即可得出结论;(3)先判断出四边形ADBF 是平行四边形,得出BD=AF ,BF=AD ,进而判断出△ACD ∽△HEA ,再判断出∠EFB=90°,即可得出结论;详解:(1)如图1,过点A 作AF ∥CB ,过点B 作BF ∥AD 相交于F ,连接EF ,∴∠FBE=∠APE ,∠FAC=∠C=90°,四边形ADBF 是平行四边形, ∴BD=AF ,BF=AD . ∵AC=BD ,CD=AE , ∴AF=AC . ∵∠FAC=∠C=90°, ∴△FAE ≌△ACD ,∴EF=AD=BF ,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°, ∴∠FEA+∠CAD=90°=∠EHD . ∵AD ∥BF , ∴∠EFB=90°. ∵EF=BF , ∴∠FBE=45°, ∴∠APE=45°.(2)(1)中结论不成立,理由如下:如图2,过点A 作AF ∥CB ,过点B 作BF ∥AD 相交于F ,连接EF ,∴∠FBE=∠APE ,∠FAC=∠C=90°,四边形ADBF 是平行四边形, ∴BD=AF ,BF=AD . ∵3BD ,3AE , ∴3AC CDBD AE==.∵BD=AF ,∴3AC CDAF AE==. ∵∠FAC=∠C=90°, ∴△FAE ∽△ACD ,∴3AC AD BFAF EF EF ===,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EMD . ∵AD ∥BF , ∴∠EFB=90°.在Rt △EFB 中,tan ∠FBE=3EF BF =, ∴∠FBE=30°, ∴∠APE=30°,(3)(2)中结论成立,如图3,作EH ∥CD ,DH ∥BE ,EH ,DH 相交于H ,连接AH ,∴∠APE=∠ADH ,∠HEC=∠C=90°,四边形EBDH 是平行四边形, ∴BE=DH ,EH=BD . ∵3BD ,3AE ,∴3AC CDBD AE==. ∵∠HEA=∠C=90°, ∴△ACD ∽△HEA ,∴3AD ACAH EH==∠ADC=∠HAE . ∵∠CAD+∠ADC=90°, ∴∠HAE+∠CAD=90°, ∴∠HAD=90°.在Rt △DAH 中,tan ∠ADH=3AHAD= ∴∠ADH=30°, ∴∠APE=30°.点睛:此题是三角形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,构造全等三角形和相似三角形的判定和性质.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米.【解析】试题分析:先根据两个坡比求出AE和BF的长,然后利用勾股定理求出AD和BC,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC,梯形的面积公式可得出答案.试题解析:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,∴AE=18米,在RT△ADE中,22+34DE AE∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,22CF BF+5∴周长345(345)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(634+305+98)米,面积是1470平方米.6.如图,AB是⊙O的直径,E是⊙O上一点,C在AB的延长线上,AD⊥CE交CE的延长线于点D,且AE平分∠DAC.(1)求证:CD是⊙O的切线;(2)若AB=6,∠ABE=60°,求AD的长.【答案】(1)详见解析;(2)9 2【解析】【分析】(1)利用角平分线的性质得到∠OAE=∠DAE,再利用半径相等得∠AEO=∠OAE,等量代换即可推出OE∥AD,即可解题,(2)根据30°的三角函数值分别在Rt△ABE中,AE=AB·cos30°,在Rt△ADE中,AD=cos30°×AE即可解题.【详解】证明:如图,连接OE,∵AE平分∠DAC,∴∠OAE=∠DAE.∵OA=OE,∴∠AEO=∠OAE.∴∠AEO=∠DAE.∴OE∥AD.∵DC⊥AC,∴OE⊥DC.∴CD是⊙O的切线.(2)解:∵AB是直径,∴∠AEB=90°,∠ABE=60°.∴∠EAB=30°,在Rt△ABE中,AE=AB·cos30°=6×32=33,在Rt△ADE中,∠DAE=∠BAE=30°,∴AD=cos30°×AE=3×33=9 2 .【点睛】本题考查了特殊的三角函数值的应用,切线的证明,中等难度,利用特殊的三角函数表示出所求线段是解题关键.7.在△ABC中,∠B=45°,∠C=30°,点D是边BC上一点,连接AD,将线段AD绕点A 逆时针旋转90°,得到线段AE,连接DE.(1)如图①,当点E落在边BA的延长线上时,∠EDC=度(直接填空);(2)如图②,当点E落在边AC上时,求证:BD=12 EC;(3)当AB=22,且点E到AC的距离等于3﹣1时,直接写出tan∠CAE的值.【答案】(1)90;(2)详见解析;(3)633 tan EAC-∠=【解析】【分析】(1)利用三角形的外角的性质即可解决问题;(2)如图2中,作PA⊥AB交BC于P,连接PE.只要证明△BAD≌△PAE(SAS),提出BD=PE,再证明EC=2PE即可;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,可得EP3,EH=2PH=2x,由此FH=31,CF=33,由△BAD≌△PAE,得BD=EP3x,AE=AD,在Rt△ABG中, AG=GB=2,在Rt△AGC中,AC=2AG=4,故AE2=AD2=AF2+EF2,由勾股定理得AF=3tan∠EAF=23tan∠EAC=6-33【详解】(1)如图1中,∵∠EDC=∠B+∠BED,∠B=∠BED=45°,∴∠EDC=90°,故答案为90;(2)如图2中,作PA⊥AB交BC于P,连接PE.∵∠DAE=∠BAP=90°,∴∠BAD=∠PAE,∵∠B=45°,∴∠B=∠APB=45°,∴AB=AP,∵AD=AE,∴△BAD≌△PAE(SAS),∴BD=PE,∠APE=∠B=45°,∴∠EPD=∠EPC=90°,∵∠C=30°,∴EC=2PE=2BD;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,∵∠EPH=90°,∠EHP=60°,∴EP3,EH=2PH=2x,∴FH=31,CF3FH=33∵△BAD≌△PAE,∴BD=EP3,AE=AD,在Rt△ABG中,∵AB=2∴AG=GB=2,在Rt△AGC中,AC=2AG=4,∵AE2=AD2=AF2+EF2,∴22+(23)231)2+(4﹣3﹣32,整理得:9x2﹣12x=0,解得x=43(舍弃)或0∴PH=0,此时E,P,H共点,∴AF=3∴tan∠EAF=EFAF 331+=23根据对称性可知当点E在AC的上方时,同法可得tan∠EAC 6-33.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.如图,在▱ABCD中,AC与BD交于点O,AC⊥BC于点C,将△ABC沿AC翻折得到△AEC,连接DE.(1)求证:四边形ACED是矩形;(2)若AC=4,BC=3,求sin∠ABD的值.【答案】(1)证明见解析(2)613 【解析】【分析】 (1)根据▱ABCD 中,AC ⊥BC ,而△ABC ≌△AEC ,不难证明;(2)依据已知条件,在△ABD 或△AOC 作垂线AF 或OF ,求出相应边的长度,即可求出∠ABD 的正弦值.【详解】(1)证明:∵将△ABC 沿AC 翻折得到△AEC ,∴BC =CE ,AC ⊥CE ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴AD =CE ,AD ∥CE , ∴四边形ACED 是平行四边形,∵AC ⊥CE ,∴四边形ACED 是矩形.(2)解:方法一、如图1所示,过点A 作AF ⊥BD 于点F ,∵BE =2BC =2×3=6,DE =AC =4,∴在Rt △BDE 中,2222BD BE DE 64213=+=+=∵S △BDE =12×DE•AD =12AF•BD , ∴AF 61313213=, ∵Rt △ABC 中,AB 2234+5,∴Rt △ABF 中,sin ∠ABF =sin ∠ABD =6136135AF AB ==方法二、如图2所示,过点O 作OF ⊥AB 于点F ,同理可得,OB =1132BD = ∵S △AOB =11OF AB OA BC 22⋅=⋅,∴OF =23655⨯=, ∵在Rt △BOF 中, sin ∠FBO =0661365513F OB ==, ∴sin ∠ABD =61365.【点睛】本题考查直角三角形翻折变化后所得图形的性质,矩形的判定和性质,平行四边形的性质和解直角三角形求线段的长度,关键是正确添加辅助线和三角形面积的计算公式求出sin ∠ABD .9.在Rt △ABC 中,∠ACB=90°,AB=7,AC=2,过点B 作直线m ∥AC ,将△ABC 绕点C 顺时针旋转得到△A′B′C(点A ,B 的对应点分别为A',B′),射线CA′,CB′分別交直线m 于点P ,Q .(1)如图1,当P 与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC 的交点为M ,当M 为A′B′的中点时,求线段PQ 的长;(3)在旋转过程中,当点P ,Q 分别在CA′,CB′的延长线上时,试探究四边形PA'B′Q 的面积是否存在最小值.若存在,求出四边形PA′B′Q 的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ =72;(3)存在,S 四边形PA 'B ′Q =3【解析】【分析】(1)由旋转可得:AC =A 'C =2,进而得到BC =∠A 'BC =90°,可得cos ∠A 'CB 'BC A C ==∠A 'CB =30°,∠ACA '=60°;(2)根据M 为A 'B '的中点,即可得出∠A =∠A 'CM ,进而得到PB =32=,依据tan ∠Q =tan ∠A2=BQ =BC =2,进而得出PQ =PB +BQ 72=;(3)依据S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ S 四边形PA 'B 'Q 最小,即S △PCQ 最小,而S △PCQ 12=PQ ×BC =,利用几何法即可得到S △PCQ 的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB=AC =2,∴BC =∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 'BC A C ==∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A =∴PB =32=.∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A2=,∴BQ =BC =2,∴PQ =PB +BQ 72=;(3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ ∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC =, 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min =PQ min ∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =3;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.10.已知:如图,直线y=-x+12分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.(1)求AE的长及sin∠BEC的值;(2)求△CDE的面积.【答案】(1)2,sin∠BEC=35;(2)754【解析】【分析】(1)如图,作CF⊥BE于F点,由函数解析式可得点B,点A坐标,继而可得∠A=∠B=45°,再根据中点的定义以及等腰直角三角形的性质可得OC=BC=6,2,设AE=CE=x,则222-x,在Rt△CEF中,利用勾股定理求出x 的值即可求得答案;(2)如图,过点E作EM⊥OA于点M,根据三角形面积公式则可得S△CDE=S△AED=2,设AD=y,则CD=y,OD=12-y,在Rt△OCD中,利用勾股定理求出y,继而可求得答案.【详解】(1)如图,作CF⊥BE于F点,由函数解析式可得点B(0,12),点A(12,0),∠A=∠B=45°,又∵点C是OB中点,∴OC=BC=6,CF=BF=32,设AE=CE=x,则EF=AB-BF-AE=122-32-x=92-x,在Rt△CEF中,CE2=CF2+EF2,即x2=(92-x)2+(32)2,解得:x=52,故可得sin∠BEC=35CFCE,AE=52;(2)如图,过点E作EM⊥OA于点M,则S△CDE=S△AED=12AD•EM=12AD×AEsin∠EAM=12AD•AE×sin45°=24AD×AE,设AD=y,则CD=y,OD=12-y,在Rt△OCD中,OC2+OD2=CD2,即62+(12-y)2=y2,解得:y=152,即AD=152,故S△CDE=S△AED=24AD×AE=754.【点睛】本题考查了解直角三角形的应用,涉及了勾股定理、折叠的性质、三角形面积、一次函数的性质等知识,综合性较强,正确添加辅助线、熟练应用相关知识是解题的关键.11.在Rt△ABC中,∠ACB=90°,CD是AB边的中线,DE⊥BC于E,连结CD,点P在射线CB上(与B,C不重合)(1)如果∠A=30°,①如图1,∠DCB等于多少度;②如图2,点P在线段CB上,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,补全图2猜想CP、BF之间的数量关系,并证明你的结论;(2)如图3,若点P在线段CB 的延长线上,且∠A=α(0°<α<90°),连结DP,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB =∠CDP ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.12.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C 处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D 处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).【答案】拦截点D处到公路的距离是(500+500)米.【解析】试题分析:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.解Rt△BCE,求出BE=BC=×1000=500米;解Rt△CDF,求出CF=CD=500米,则DA=BE+CF=(500+500)米.试题解析:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF.在Rt△BCE中,∵∠E=90°,∠CBE=60°,∴∠BCE=30°,∴BE=BC=×1000=500米;在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=BC=1000米,∴CF=CD=500米,∴DA=BE+CF=(500+500)米,故拦截点D处到公路的距离是(500+500)米.考点:解直角三角形的应用-方向角问题.13.如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P 处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)(测倾器的高度忽略不计,参考数据:tan53°≈43,tan63.4°≈2)【答案】(1)此人所在P的铅直高度约为14.3米;(2)从P到点B的路程约为127.1米【解析】分析:(1)过P作PF⊥BD于F,作PE⊥AB于E,设PF=5x,在Rt△ABC中求出AB,用含x 的式子表示出AE,EP,由tan∠APE,求得x即可;(2)在Rt△CPF中,求出CP的长.详解:过P作PF⊥BD于F,作PE⊥AB于E,∵斜坡的坡度i=5:12,设PF=5x,CF=12x,∵四边形BFPE为矩形,∴BF=PEPF=BE.在RT△ABC中,BC=90,tan∠ACB=AB BC,∴AB=tan63.4°×BC≈2×90=180,∴AE=AB-BE=AB-PF=180-5x,EP=BC+CF≈90+120x.在RT△AEP中,tan∠APE=1805490123 AE xEP x-≈=+,∴x=207,∴PF=5x=10014.37≈.答:此人所在P的铅直高度约为14.3米.由(1)得CP=13x,∴CP=13×207≈37.1,BC+CP=90+37.1=127.1.答:从P到点B的路程约为127.1米.点睛:本题考查了解直角三角形的应用,关键是正确的画出与实际问题相符合的几何图形,找出图形中的相关线段或角的实际意义及所要解决的问题,构造直角三角形,用勾股定理或三角函数求相应的线段长.14.如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD 相交于点E(点E与点C、D不重合),设OM=m.(1)求DE的长(用含m的代数式表示);(2)令弦CD所对的圆心角为α,且sin4 =25α.①若△DEM的面积为S,求S关于m的函数关系式,并求出m的取值范围;②若动点N在CD上,且CN=OM,射线BM与射线ON相交于点F,当∠OMF=90°时,求DE的长.【答案】(1)DE=10010mm-;(2)①S=2360300m mm-+,(5013<m<10),②DE=5 2 .【解析】【分析】(1)由CD∥AB知△DEM∽△OBM,可得DE DMOB OM=,据此可得;(2)①连接OC 、作OP ⊥CD 、MQ ⊥CD ,由OC =OD 、OP ⊥CD 知∠DOP =12∠COD ,据此可得sin ∠DOP =sin ∠DMQ =45、sin ∠ODP =35,继而由OM =m 、OD =10得QM =DM sin ∠ODP =35(10﹣m ),根据三角形的面积公式即可得;如图2,先求得PD =8、CD =16,证△CDM ∽△BOM 得CD DM BO OM =,求得OM =5013,据此可得m 的取值范围; ②如图3,由BM =OB sin ∠BOM =10×35=6,可得OM =8,根据(1)所求结果可得答案. 【详解】(1)∵CD ∥AB , ∴△DEM ∽△OBM ,∴DE DM OB OM =,即1010DE m m-=, ∴DE =10010m m -; (2)①如图1,连接OC 、作OP ⊥CD 于点P ,作MQ ⊥CD 于点Q ,∵OC =OD 、OP ⊥CD ,∴∠DOP =12∠COD , ∵sin 2α=45, ∴sin ∠DOP =sin ∠DMQ =45,sin ∠ODP =35, ∵OM =m 、OD =10,∴DM =10﹣m ,∴QM =DM sin ∠ODP =35(10﹣m ), 则S △DEM =12DE •MQ =12×10010m m -×35(10﹣m )=2360300m m m-+, 如图2,∵PD =OD sin ∠DOP =10×45=8, ∴CD =16,∵CD ∥AB ,∴△CDM ∽△BOM ,∴CD DM BO OM =,即1610=10OM OM-, 解得:OM =5013, ∴5013<m <10, ∴S =2360300m m m-+,(5013<m <10). ②当∠OMF =90°时,如图3,则∠BMO =90°,在Rt △BOM 中,BM =OB sin ∠BOM =10×35=6, 则OM =8,由(1)得DE =100108582-⨯=. 【点睛】本题主要考查圆的综合题,解题的关键是熟练掌握圆的有关性质、相似三角形的判定与性质及解直角三角形的能力.15.小明坐于堤边垂钓,如图①,河堤AC的坡角为30°,AC长米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
中考数学与锐角三角函数有关的压轴题附答案

中考数学与锐角三角函数有关的压轴题附答案一、锐角三角函数1.下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)【答案】2.5m.【解析】试题分析:设DF=x,在Rt△DFC中,可得CF=DF=x,则BF=4-x,根据线段的和差可得AN=5-x,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,利用∠EAB的正切值解得x的值.试题解析:解:设DF=,在Rt△DFC中,∠CDF=,∴CF=tan·DF=,又∵CB=4,∴BF=4-,∵AB=6,DE=1,BM= DF=,∴AN=5-,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,EN=4-,AN=5-,tan==0.60,解得=2.5,答:DM和BC的水平距离BM为2.5米.考点:解直角三角形.2.如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.(1)求证:∠AEC=90°;(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;(3)若DC=2,求DH的长.【答案】(1)证明见解析;(2)四边形AOCD为菱形;(3)DH=2.【解析】试题分析:(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;(2)四边形AOCD为菱形.由(1)得,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=,求得DH的长.试题解析:(1)连接OC,∵EC与⊙O切点C,∴OC⊥EC,∴∠OCE=90°,∵点CD是半圆O的三等分点,∴,∴∠DAC=∠CAB,∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,∴AE∥OC(内错角相等,两直线平行)∴∠AEC+∠OCE=180°,∴∠AEC=90°;(2)四边形AOCD为菱形.理由是:∵,∴∠DCA=∠CAB,∴CD∥OA,又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC,∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.∵四边形AOCD为菱形,∴OA=AD=DC=2,∵OA=OD,∴OA=OD=AD=2,∴△OAD是等边三角形,∴∠AOD=60°,∵DH⊥AB于点F,AB为直径,∴DH=2DF,在Rt△OFD中,sin∠AOD=,∴DF=ODsin∠AOD=2sin60°=,∴DH=2DF=2.考点:1.切线的性质2.等边三角形的判定与性质3.菱形的判定与性质4.解直角三角形.3.如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;(2)求证:BC2=2CD•OE;(3)若314cos,53BAD BE∠==,求OE的长.【答案】(1)DE为⊙O的切线,理由见解析;(2)证明见解析;(3)OE =356.【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.试题解析:(1)DE为⊙O的切线,理由如下:连接OD,BD,∵AB为⊙O的直径,∴∠ADB=90°,在Rt△BDC中,E为斜边BC的中点,∴CE=DE=BE=BC,∴∠C=∠CDE,∵OA=OD,∴∠A=∠ADO,∵∠ABC=90°,∴∠C+∠A=90°,∴∠ADO+∠CDE=90°,∴∠ODE=90°,∴DE⊥OD,又OD为圆的半径,∴DE为⊙O的切线;(2)∵E是BC的中点,O点是AB的中点,∴OE是△ABC的中位线,∴AC=2OE,∵∠C=∠C,∠ABC=∠BDC,∴△ABC∽△BDC,∴,即BC2=AC•CD.∴BC2=2CD•OE;(3)解:∵cos∠BAD=,∴sin∠BAC=,又∵BE=,E是BC的中点,即BC=,∴AC=.又∵AC=2OE,∴OE=AC=.考点:1、切线的判定;2、相似三角形的判定与性质;3、三角函数4.如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点F.(1)求证:DF⊥AC;(2)若∠ABC=30°,求tan∠BCO的值.3【答案】(1)证明见解析; (2) tan∠【解析】试题分析:(1)连接OD,根据三角形的中位线定理可求出OD∥AC,根据切线的性质可证明DE⊥OD,进而得证.(2)过O作OF⊥BD,根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长,根据三角函数的定义求解.试题解析:证明:连接OD∵DE为⊙O的切线, ∴OD⊥DE ∵O为AB中点, D为BC的中点∴OD‖AC∴DE⊥AC(2)过O作OF⊥BD,则BF=FD在Rt△BFO中,∠ABC=30°∴OF=12OB, BF=3OB∵BD=DC, BF=FD,∴FC=3BF=33OB在Rt△OFC中,tan∠BCO=13233OBOFFCOB==.点睛:此题主要考查了三角形中位线定理及切线的性质与判定、三角函数的定义等知识点,有一定的综合性,根据已知得出OF=12OB,BF=3OB,FC=3BF=33OB是解题关键.5.如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).(1)若△BDE是以BE为底的等腰三角形,求t的值;(2)若△BDE为直角三角形,求t的值;(3)当S△BCE≤92时,所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=23【答案】(1)332;(23秒或3秒;(3)6﹣3【解析】【分析】(1)如图1,先由勾股定理求得AB的长,根据点A、E关于直线CD的对称,得CD垂直平分AE,根据线段垂直平分线的性质得:AD=DE,所以AD=DE=BD,由3,可得t的值;(2)分两种情况:①当∠DEB=90°时,如图2,连接AE,根据t的值;②当∠EDB=90°时,如图3,根据△AGC≌△EGD,得AC=DE,由AC∥ED,得四边形CAED 是平行四边形,所以AD=CE=3,即t=3;(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化,①当△BCE在BC的下方时,②当△BCE在BC的上方时,分别计算当高为3时对应的t的值即可得结论.【详解】解:(1)如图1,连接AE,由题意得:AD=t,∵∠CAB=90°,∠CBA=30°,∴BC=2AC=6,∴∵点A、E关于直线CD的对称,∴CD垂直平分AE,∴AD=DE,∵△BDE是以BE为底的等腰三角形,∴DE=BD,∴AD=BD,∴;(2)△BDE为直角三角形时,分两种情况:①当∠DEB=90°时,如图2,连接AE,∵CD垂直平分AE,∴AD=DE=t,∵∠B=30°,∴BD=2DE=2t,∴∴②当∠EDB=90°时,如图3,连接CE,∵CD垂直平分AE,∴CE=CA=3,∵∠CAD=∠EDB=90°,∴AC∥ED,∴∠CAG=∠GED,∵AG=EG,∠CGA=∠EGD,∴△AGC≌△EGD,∴AC=DE,∵AC∥ED,∴四边形CAED是平行四边形,∴AD=CE=3,即t=3;综上所述,△BDE为直角三角形时,t的值为3秒或3秒;(3)△BCE中,由对称得:AC=CE=3,所以点D在运动过程中,CE的长不变,所以△BCE 面积的变化取决于以CE作底边时,对应高的大小变化,①当△BCE在BC的下方时,过B作BH⊥CE,交CE的延长线于H,如图4,当AC=BH=3时,此时S△BCE=12AE•B H=12×3×3=92,易得△ACG≌△HBG,∴CG=BG,∴∠ABC=∠BCG=30°,∴∠ACE=60°﹣30°=30°,∵AC=CE,AD=DE,DC=DC,∴△ACD≌△ECD,∴∠ACD=∠DCE=15°,tan∠ACD=tan15°=t3=2﹣3,∴t=6﹣33,由图形可知:0<t<6﹣33时,△BCE的BH越来越小,则面积越来越小,②当△BCE在BC的上方时,如图3,CE=ED=3,且CE⊥ED,此时S△BCE=12CE•DE=12×3×3=92,此时t=3,综上所述,当S△BCE≤92时,t的取值范围是6﹣33≤t≤3.【点睛】本题考查三角形综合题、平行四边形的判定和性质、直角三角形的性质、三角形的面积问题、轴对称等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会寻找特殊点解决问题,属于中考压轴题.6.如图,在平面直角坐标系xOy中,点P是⊙C外一点,连接CP交⊙C于点Q,点P关于点Q的对称点为P′,当点P′在线段CQ上时,称点P为⊙C“友好点”.已知A(1,0),B(0,2),C(3,3)(1)当⊙O的半径为1时,①点A,B,C中是⊙O“友好点”的是;②已知点M在直线y=﹣3x+2 上,且点M是⊙O“友好点”,求点M的横坐标m的取值范围;(2)已知点D(23,0),连接BC,BD,CD,⊙T的圆心为T(t,﹣1),半径为1,若在△BCD 上存在一点N,使点N是⊙T“友好点”,求圆心T的横坐标t的取值范围.【答案】(1)①B;②0≤m3(2)﹣3t<3【解析】【分析】(1))①根据“友好点”的定义,OB=<2r=2,所以点B是⊙O“友好点”;②设M(m,﹣33m+2 ),根据“友好点”的定义,OM223222m m⎛⎫+-+≤⎪⎪⎝⎭,由此求解即可;(2)B(0,2),C(3,3),D(23,0),⊙T的圆心为T(t,﹣1),点N是⊙T“友好点”,NT≤2r=2,所以点N只能在线段BD上运动,过点T作TN⊥BD于N,作TH∥y轴,与BD交于点H.易知∠BDO=30°,∠OBD=60°,NT=3HT,直线BD:y=﹣3x+2,可知H(t,﹣3t+2),继而可得NT=﹣12t+33,由此可得关于t的不等式,解出t的范围即可.【详解】(1)①∵r=1,∴根据“友好点”的定义,OB=<2r=2,∴点B是⊙O“友好点”,∵OC=2233+=32>2r=2,∴点C不是⊙O“友好点”,A(1,0)在⊙O上,不是⊙O“友好点”,故答案为B;②如图,设M(m 3+2 ),根据“友好点”的定义,∴OM223222m m⎛⎫+-+≤⎪⎪⎝⎭,整理,得2m2﹣3≤0,解得0≤m3∴点M的横坐标m的取值范围:0≤m3;(2)∵B(0,2),C(3,3),D30),⊙T的圆心为T(t,﹣1),点N是⊙T“友好点”,∴NT≤2r=2,∴点N只能在线段BD上运动,过点T作TN⊥BD于N,作TH∥y轴,与BD交于点H.∵tan ∠BDO =3323OB OD ==∴∠BDO=30°, ∴∠OBD =60°, ∴∠THN=∠OBD=60°, ∴NT =HT•sin ∠3, ∵B (0,2),D 30), ∴直线BD :y 3+2, ∵H 点BD 上, ∵H (t ,﹣33t +2), ∴HT 3+2﹣(﹣1)3+3, ∴NT 333+3)=﹣12t 33∴﹣12t +332≤2, ∴t ≥﹣3当H 与点D 重合时,点T 的横坐标等于点D 的横坐标,即t =3, 此时点N 不是“友好点”, ∴t <3故圆心T 的横坐标t 的取值范围:﹣3t <3 【点睛】本题是圆的综合题,正确理解“友好点”的意义,熟练运用相似三角形的性质与特殊三角函数是解题的关键.7.如图,在矩形ABCD 中,AB =6cm ,AD =8cm ,连接BD ,将△ABD 绕B 点作顺时针方向旋转得到△A ′B ′D ′(B ′与B 重合),且点D ′刚好落在BC 的延长上,A ′D ′与CD 相交于点E . (1)求矩形ABCD 与△A ′B ′D ′重叠部分(如图1中阴影部分A ′B ′CE )的面积;(2)将△A ′B ′D ′以每秒2cm 的速度沿直线BC 向右平移,如图2,当B ′移动到C 点时停止移动.设矩形ABCD 与△A ′B ′D ′重叠部分的面积为y ,移动的时间为x ,请你直接写出y 关于x 的函数关系式,并指出自变量x 的取值范围;(3)在(2)的平移过程中,是否存在这样的时间x ,使得△AA ′B ′成为等腰三角形?若存在,请你直接写出对应的x 的值,若不存在,请你说明理由.【答案】(1)452;(2)详见解析;(3)使得△AA ′B ′成为等腰三角形的x 的值有:0秒、32 669-. 【解析】 【分析】(1)根据旋转的性质可知B ′D ′=BD =10,CD ′=B ′D ′﹣BC =2,由tan ∠B ′D ′A ′='''''=A B CE A D CD 可求出CE ,即可计算△CED ′的面积,S ABCE =S ABD ′﹣S CED ′; (2)分类讨论,当0≤x ≤115时和当115<x ≤4时,分别列出函数表达式; (3)分类讨论,当AB ′=A ′B ′时;当AA ′=A ′B ′时;当AB ′=AA ′时,根据勾股定理列方程即可. 【详解】解:(1)∵AB =6cm ,AD =8cm , ∴BD =10cm ,根据旋转的性质可知B ′D ′=BD =10cm ,CD ′=B ′D ′﹣BC =2cm , ∵tan ∠B ′D ′A ′='''''=A B CE A D CD ∴682=CE ∴CE =32cm ,∴S ABCE =S ABD ′﹣S CED ′=8634522222⨯-⨯÷=(cm 2); (2)①当0≤x <115时,CD ′=2x +2,CE =32(x +1), ∴S △CD ′E =32x 2+3x +32, ∴y =12×6×8﹣32x 2﹣3x ﹣32=﹣32x 2﹣3x +452; ②当115≤x ≤4时,B ′C =8﹣2x ,CE =43(8﹣2x ) ∴()214y 8223x =⨯-=83x 2﹣643x +1283. (3)①如图1,当AB ′=A ′B ′时,x =0秒;②如图2,当AA ′=A ′B ′时,A ′N =BM =BB ′+B ′M =2x +185,A ′M =NB =245, ∵AN 2+A ′N 2=36, ∴(6﹣245)2+(2x +185)2=36, 解得:x =6695-,x =6695--(舍去); ③如图2,当AB ′=AA ′时,A ′N =BM =BB ′+B ′M =2x +185,A ′M =NB =245, ∵AB 2+BB ′2=AN 2+A ′N 2 ∴36+4x 2=(6﹣245)2+(2x +185)2 解得:x =32. 综上所述,使得△AA ′B ′成为等腰三角形的x 的值有:0秒、32秒、6695-.【点睛】本题主要考查了图形的平移变换和旋转变换,能够数形结合,运用分类讨论的思想方法全面的分析问题,思考问题是解决问题的关键.8.阅读下面材料:观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,过A 作AD ⊥BC 于D (如图),则sin B =AD c ,sin C =ADb,即AD =c sin B ,AD =b sin C ,于是c sin B =b sin C ,即sin sin b c B C = .同理有:sin sin c aC A=,sin sin a b A B=,所以sin sin sin a b cA B C ==. 即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC 中,∠B =75°,∠C =45°,BC =60,则AB = ;(2)如图,一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B 处,此时又测得灯塔A 在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A 的距离AB . (3)在(2)的条件下,试求75°的正弦值.(结果保留根号)【答案】(1)6;(2)6海里;(36+2【解析】 【分析】(1)根据材料:在一个三角形中,各边和它所对角的正弦的比相等,写出比例关系,代入数值即可求得AB的值.(2)此题可先由速度和时间求出BC的距离,再由各方向角得出∠A的角度,过B作BM⊥AC于M,求出∠MBC=30°,求出MC,由勾股定理求出BM,求出AM、BM的长,由勾股定理求出AB即可;(3)在三角形ABC中,∠A=45,∠ABC=75,∠ACB=60,过点C作AC的垂线BD,构造直角三角形ABD,BCD,在直角三角形ABD中可求出AD的长,进而可求出sin75°的值.【详解】解:(1)在△ABC中,∠B=75°,∠C=45°,BC=60,则∠A=60°,∵ABsinC =sinBCA,∴45ABsin o=60sin60o,即22=3,解得:AB=206.(2)如图,依题意:BC=60×0.5=30(海里)∵CD∥BE,∴∠DCB+∠CBE=180°∵∠DCB=30°,∴∠CBE=150°∵∠ABE=75°.∴∠ABC=75°,∴∠A=45°,在△ABC中,sinABACB∠=BCsin A∠即60?ABsin=3045?sin,解之得:6.答:货轮距灯塔的距离AB=156海里.(3)过点B作AC的垂线BM,垂足为M.在直角三角形ABM中,∠A=45°,AB=156,所以AM=153,在直角三角形BDC中,∠BCM=60°,BC=30°,可求得CM=15,所以AC=153+15,由题意得,1531575sin+o=15660sin o,sin75°=6+24.【点睛】本题考查方向角的含义,三角形的内角和定理,含30度角的直角三角形,等腰三角形的性质和判定等知识点,解题关键是熟练掌握解直角三角形方法.9.如图,公路AB为东西走向,在点A北偏东36.5︒方向上,距离5千米处是村庄M,在点A北偏东53.5︒方向上,距离10千米处是村庄N;要在公路AB旁修建一个土特产收购站P(取点P在AB上),使得M,N两村庄到P站的距离之和最短,请在图中作出P的位置(不写作法)并计算:(1)M,N两村庄之间的距离;(2)P到M、N距离之和的最小值.(参考数据:sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75计算结果保留根号.)【答案】(1) M,N29千米;(2) 村庄M、N到P站的最短距离和是5【解析】【分析】(1)作N关于AB的对称点N'与AB交于E,连结MN’与AB交于P,则P为土特产收购站的位置.求出DN,DM,利用勾股定理即可解决问题.(2)由题意可知,M、N到AB上点P的距离之和最短长度就是MN′的长.【详解】解:作N关于AB的对称点N'与AB交于E,连结MN’与AB交于P,则P为土特产收购站的位置.(1)在Rt△ANE中,AN=10,∠NAB=36.5°∴NE=AN•sin∠NAB=10•sin36.5°=6,AE=AN•cos∠NAB=10•cos36.5°=8,过M作MC⊥AB于点C,在Rt△MAC中,AM=5,∠MAB=53.5°∴AC=MA•sin∠AMB=MA•sin36.5°=3,MC=MA•cos∠AMC=MA•cos36.5°=4,过点M作MD⊥NE于点D,在Rt△MND中,MD=AE-AC=5,ND=NE-MC=2,∴MN22+2952即M,N29(2)由题意可知,M、N到AB上点P的距离之和最短长度就是MN′的长.DN′=10,MD=5,在Rt△MDN′中,由勾股定理,得MN22+5510∴村庄M、N到P站的最短距离和是5【点睛】本题考查解直角三角形,轴对称变换等知识,解题的关键是熟练掌握基本知识,学会添加常用辅助线,构造直角三角形解决问题.10.如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段BC上,点Q在线段AB上,且PQ=BQ,延长QP交射线AC于点D.(1)求证:QA=QD;(2)设∠BAP=α,当2tanα是正整数时,求PC的长;(3)作点Q关于AC的对称点Q′,连结QQ′,AQ′,DQ′,延长BC交线段DQ′于点E,连结AE,QQ′分别与AP,AE交于点M,N(如图2所示).若存在常数k,满足k•MN=PE•QQ′,求k的值.【答案】(1)证明见解析(2)PC的长为37或32(3)8【解析】【分析】(1)由等腰三角形的性质得出∠B=∠BPQ=∠CPD,由直角三角形的性质得出∠BAC=∠D,即可得出结论;(2)过点P作PH⊥AB于H,设PH=3x,BH=4x,BP=5x,由题意知tanα=1或12,当tanα=1时,HA=PH=3x,与勾股定理得出3x+4x=5,解得x=57,即可求出PC长;当tanα=12时,HA=2PH﹣6x,得出6x+4x=5,解得x=12,即可求出PC长;(3)设QQ′与AD交于点O,由轴对称的性质得出AQ′=AQ=DQ=DQ′,得出四边形AQDQ′是菱形,由菱形的性质得出QQ′⊥AD,AO=12AD,证出四边形BEQ'Q是平行四边形,得出QQ′=BE,设CD=3m,则PC=4m,AD=3+3m,即QQ′﹣BE=4m+4,PE=8m,由三角函数得出MOAO=tan∠PAC=PCAC,即可得出结果.【详解】(1)证明:∵PQ=BQ,∴∠B=∠BPQ=∠CPD,∵∠ACB=∠PCD=90°,∴∠A+∠BAC=90°,∠D+∠CPD=90°,∴∠BAC=∠D,∴QA=QD;(2)解:过点P作PH⊥AB于H,如图1所示:设PH =3x ,BH =4x ,BP =5x , 由题意得:tan ∠BAC =43,∠BAP <∠BAC , ∴2tanα是正整数时,tanα=1或12, 当tanα=1时,HA =PH =3x , ∴3x+4x5, ∴x =57, 即PC =4﹣5x =37; 当tanα=12时,HA =2PH ﹣6x , ∴6x+4x =5,∴x =12, 即PC =4﹣5x =32; 综上所述,PC 的长为37或32; (3)解:设QQ′与AD 交于点O ,如图2所示: 由轴对称的性质得:AQ′=AQ =DQ =DQ′, ∴四边形AQDQ′是菱形, ∴QQ′⊥AD ,AO =12AD , ∵BC ⊥AC , ∴QQ′∥BE , ∵BQ ∥EQ′,∴四边形BEQ'Q 是平行四边形, ∴QQ′=BE ,设CD =3m ,则PC =4m ,AD =3+3m , 即QQ′﹣BE =4m+4,PE =8m , ∵MO AO =tan ∠PAC =PCAC, ∴332MOm +=43m,即MN =2MO =4m (1+m ),∴k =PE QQ MNg ′=8(44)4(1)m m m m ++=8.【点睛】本题是三角形综合题目,考查了等腰三角形的性质与判定、三角函数、勾股定理、菱形的判定与性质、平行线的性质以及分类讨论等知识;本题综合性强,熟练掌握等腰三角形的判定与性质,灵活运用三角函数是解题关键.11.如图,在ABC △中,10AC BC ==,3cos 5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P e 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P e 与边BC 相切时,求P e 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q e 与P e 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】 【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HP CP =R 10R -=45,即可求解;(2)PD∥BE,则EBPD=BFPF,即:2248805x x x yx y--+-=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=GP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=35,sinC=HPCP=R10R-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH=ACsinC=8,同理可得:CH=6,HA=4,5tan∠()2284x+-2880x x-+25,则525,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β, tanβ=2,则cosβ=5,sinβ=5, EB=BDcosβ=(45-25x )×5=4-25x ,∴PD ∥BE ,∴EB PD =BFPF,即:2248805x x x y x--+-=,整理得:y=()25x x 8x 800x 103x 20-+<<+;(3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG=PQ ,即两个圆的半径相等,则两圆另外一个交点为D ,GD 为相交所得的公共弦, ∵点Q 时弧GD 的中点, ∴DG ⊥EP , ∵AG 是圆P 的直径, ∴∠GDA=90°, ∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形, ∴AG=EP=BD ,∴5设圆的半径为r,在△ADG中,AD=2rcosβ=5,DG=5,AG=2r,5+2r=45,解得:2r=51,则:DG=5=10-25,相交所得的公共弦的长为10-25.【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.12.已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.(1)如图1,求证:KE=GE;(2)如图2,连接CABG,若∠FGB=12∠ACH,求证:CA∥FE;(3)如图3,在(2)的条件下,连接CG交AB于点N,若sin E=35,AK=10,求CN的长.【答案】(1)证明见解析;(2)△EAD是等腰三角形.证明见解析;(32010 13【解析】试题分析:(1)连接OG,则由已知易得∠OGE=∠AHK=90°,由OG=OA可得∠AGO=∠OAG,从而可得∠KGE=∠AKH=∠EKG,这样即可得到KE=GE;(2)设∠FGB=α,由AB是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE可得∠EKG=90°-α,这样在△GKE中可得∠E=2α,由∠FGB=12∠ACH可得∠ACH=2α,这样可得∠E=∠ACH,由此即可得到CA∥EF;(3)如下图2,作NP⊥AC于P,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,AK=10a ,结合AK=10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α, ∵∠FGB=12∠ACH ,∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a ,则4a =,tan ∠CAH=43CH AH =, ∵CA ∥FE , ∴∠CAK=∠AGE , ∵∠AGE=∠AKH , ∴∠CAK=∠AKH ,∴AC=CK=5a ,HK=CK ﹣CH=4a ,tan ∠AKH=AHHK=3,=, ∵∴=∴a=1.AC=5, ∵∠BHD=∠AGB=90°, ∴∠BHD+∠AGB=180°,在四边形BGKH 中,∠BHD+∠HKG+∠AGB+∠ABG=360°, ∴∠ABG+∠HKG=180°, ∵∠AKH+∠HKG=180°, ∴∠AKH=∠ABG , ∵∠ACN=∠ABG , ∴∠AKH=∠ACN , ∴tan ∠AKH=tan ∠ACN=3, ∵NP ⊥AC 于P , ∴∠APN=∠CPN=90°, 在Rt △APN 中,tan ∠CAH=43PN AP =,设PN=12b ,则AP=9b , 在Rt △CPN 中,tan ∠ACN=PNCP=3, ∴CP=4b , ∴AC=AP+CP=13b , ∵AC=5, ∴13b=5, ∴b=513,∴CN=22PN CP+=410b⋅=2010 13.13.抛物线y=ax²+bx+4(a≠0)过点A(1, ﹣1),B(5, ﹣1),与y轴交于点C.(1)求抛物线表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC下方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,①求点P坐标;②过此二点的直线交y轴于F, 此直线上一动点G,当GB+2GF2最小时,求点G坐标.(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值【答案】(1)y=x²﹣6x+4(2)①P(2, -4)或P(3, -5) ②G(0, -2)(3)313【解析】【分析】(1)把点A(1,-1),B(5,-1)代入抛物线y=ax2+bx+4解析式,即可得出抛物线的表达式;(2)①如图,连接PC,过点P作y轴的平行线交直线BC于R,可求得直线BC的解析式为:y=-x+4,设点P(t,t2-6t+4),R(t,-t+4),因为▱CBPQ的面积为30,所以S△PBC=1 2×(−t+4−t2+6t−4)×5=15,解得t的值,即可得出点P的坐标;②当点P为(2,-4)时,求得直线QP的解析式为:y=-x-2,得F(0,-2),∠GOR=45°,因为2GF=GB+GR,所以当G于F重合时,GB+GR最小,即可得出点G的坐标;当点P为(3,-5)时,同理可求;(3)先用面积法求出sin∠ACB=213,tan∠ACB=23,在Rt△ABE中,求得圆的直径,因为MB⊥NB,可得∠N=∠AEB=∠ACB,因为tanN=MBBN=23,所以BN=32MB,当MB为直径时,BN的长度最大.【详解】(1) 解:(1)∵抛物线y=ax2+bx+4(a≠0)过点A(1,-1),B(5,-1),∴1412554a ba b-++⎧⎨-++⎩=,=解得16ab⎧⎨-⎩=,=∴抛物线表达式为y=x²﹣6x+4.(2)①如图,连接PC,过点P作y轴的平行线交直线BC于R,设直线BC的解析式为y=kx+m,∵B(5,-1),C(0,4),∴154k mm-+⎧⎨⎩==,解得14km=,=-⎧⎨⎩∴直线BC的解析式为:y=-x+4,设点P(t,t2-6t+4),R(t,-t+4),∵▱CBPQ的面积为30,∴S△PBC=12×(−t+4−t2+6t−4)×5=15,解得t=2或t=3,当t=2时,y=-4当t=3时,y=-5,∴点P坐标为(2,-4)或(3,-5);②当点P为(2,-4)时,∵直线BC解析式为:y=-x+4, QP∥BC,设直线QP的解析式为:y=-x+n,将点P代入,得-4=-2+n,n=-2,∴直线QP的解析式为:y=-x-2,∴F(0,-2),∠GOR=45°,∴GB+22GF=GB+GR当G于F重合时,GB+GR最小,此时点G的坐标为(0,-2),同理,当点P为(3,-5)时,直线QP的解析式为:y=-x-2,同理可得点G的坐标为(0,-2),(3) )∵A(1,-1),B(5,-1)C(0,4),∴AC=26,BC=52,∵S△ABC=12AC×BCsin∠ACB=12AB×5,∴sin∠ACB=21313,tan∠ACB=23,∵AE为直径,AB=4,∴∠ABE=90°,∵sin∠AEB=sin∠ACB=213=4AE,∴AE=213,∵MB⊥NB,∠NMB=∠EAB,∴∠N=∠AEB=∠ACB,∴tanN=MBBN =23,∴BN=32MB,当MB为直径时,BN的长度最大,为313.【点睛】题考查用到待定系数法求二次函数解析式和一次函数解析式,圆周角定理,锐角三角函数定义,平行四边形性质.解决(3)问的关键是找到BN与BM之间的数量关系.14.如图,正方形ABCD2+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,(1)求证:△ABF∽△ACE;(2)求tan∠BAE的值;(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为22.【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt △ABE 中,∵∠ABE =90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =2, ∵AC =22AB BC +=2+2, ∴OA =OC =OB =12AC =222+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =22+ •(2﹣1)=2, ∴HM =OH+OM =22+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+.. 【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.15.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019中考数学:锐角三角函数试题解析一、选择题1.(2019四川巴中,第8题3分)在Rt△ABC中,C=90,,则tanB的值为()考点:锐角三角函数.分析:根据题意作出直角△ABC,然后根据sinA=,设一条直角边BC为5x,斜边AB为13x,根据勾股定理求出另一条直角边AC的长度,然后根据三角函数的定义可求出tanB.解答:∵sinA=,设BC=5x,AB=13x,则AC==12x,故tanB==.故选D.点评:本题考查了互余两角三角函数的关系,属于基础题,解题的关键是掌握三角函数的定义和勾股定理的运用.2.(2019山东威海,第8题3分)如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则AOB的正弦值是()考点:锐角三角函数的定义;三角形的面积;勾股定理分析:作ACOB于点C,利用勾股定理求得AC和AB的长,根据正弦的定义即可求解.解答:解:作ACOB于点C.则AC=AB===2,则sinAOB===.故选D.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.3.(2019四川凉山州,第10题,4分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则C的度数是()A.45B.60C.75D.105考点:特殊角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方;三角形内角和定理分析:根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出C的度数.解答:解:由题意,得cosA=,tanB=1,A=60,B=45,C=180﹣A﹣B=180﹣60﹣45=75.故选:C.点评:此题考查了特殊角的三角形函数值及绝对值、偶次方的非负性,属于基础题,关键是熟记一些特殊角的三角形函数值,也要注意运用三角形的内角和定理.4.(2019甘肃兰州,第5题4分)如图,在Rt△ABC中,C=90,BC=3,AC=4,那么cosA的值等于()考点:锐角三角函数的定义;勾股定理.分析:首先运用勾股定理求出斜边的长度,再利用锐角三角函数的定义求解.解答:解:∵在Rt△ABC中,C=90,AC=4,BC=3,AB=.cosA=,故选:D.点评:本题主要考查了锐角三角函数的定义:在直角三角形中,锐角的余弦为邻边比斜边.5.(2019广州,第3题3分)如图1,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则().(A)(B)(C)(D)【考点】正切的定义.【分析】.【答案】D6.(2019浙江金华,第6题4分)如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为,则t的值是【】A.1B.1.5C.2D.3【答案】C.【解析】7.(2019滨州,第11题3分)在Rt△ACB中,C=90,AB=10,sinA=,cosA=,tanA=,则BC的长为()A.6B.7.5C.8D.12.5考点:解直角三角形分析:根据三角函数的定义来解决,由sinA==,得到BC==.解答:解:∵C=90AB=10,sinA=,BC=AB=10=6.故选A.点评:本题考查了解直角三角形和勾股定理的应用,注意:在Rt△ACB 中,C=90,则sinA=,cosA=,tanA=.8.(2019扬州,第7题,3分)如图,已知AOB=60,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=()A.3 B.4 C.5 D.6(第1题图)考点:含30度角的直角三角形;等腰三角形的性质分析:过P作PDOB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD﹣MD即可求出OM的长.解答:解:过P作PDOB,交OB于点D,在Rt△OPD中,cos60==,OP=12,OD=6,∵PM=PN,PDMN,MN=2,MD=ND=MN=1,OM=OD﹣MD=6﹣1=5.故选C.点评:此题考查了含30度直角三角形的性质,等腰三角形的性质,熟练掌握直角三角形的性质是解本题的关键.9.(2019四川自贡,第10题4分)如图,在半径为1的⊙O中,AOB=45,则sinC的值为()考点:圆周角定理;勾股定理;锐角三角函数的定义专题:压轴题.分析:首先过点A作ADOB于点D,由在Rt△AOD中,AOB=45,可求得AD与OD的长,继而可得BD的长,然后由勾股定理求得AB的长,继而可求得sinC的值.解答:解:过点A作ADOB于点D,∵在Rt△AOD中,AOB=45,OD=AD=OAcos45=1=,BD=OB﹣OD=1﹣,AB==,∵AC是⊙O的直径,ABC=90,AC=2,sinC=.故选B.点评:此题考查了圆周角定理、三角函数以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.10.(2019浙江湖州,第6题3分)如图,已知Rt△ABC中,C=90,AC=4,tanA=,则BC的长是()A.2B.8C.2D.4分析:根据锐角三角函数定义得出tanA=,代入求出即可.解:∵tanA==,AC=4,BC=2,故选A.点评:本题考查了锐角三角函数定义的应用,注意:在Rt△ACB中,C=90,sinA=,cosA=,tanA=.11.(2019广西来宾,第17题3分)如图,Rt△ABC中,C=90,B=30,BC=6,则AB的长为4考点:解直角三角形.分析:根据cosB=及特殊角的三角函数值解题.解答:解:∵cosB=,即cos30=,AB===4.故答案为:4.点评:本题考查了三角函数的定义及特殊角的三角函数值,是基础知识,需要熟练掌握.12.(2019年贵州安顺,第9题3分)如图,在Rt△ABC中,C=90,A=30,E 为AB上一点且AE:EB=4:1,EFAC于F,连接FB,则tanCFB的值等于()A.30B.45C.60D.15考点:锐角三角函数的定义..分析:tanCFB的值就是直角△BCF中,BC与CF的比值,设BC=x,则BC与CF就可以用x表示出来.就可以求解.解答:解:根据题意:在Rt△ABC中,C=90,A=30,∵EFAC,EF∥BC,∵AE:EB=4:1,=5,设AB=2x,则BC=x,AC=x.在Rt△CFB中有CF=x,BC=x.则tanCFB==.故选C.点评:本题考查锐角三角函数的概念:在直角三角形中,正弦等于对比斜;余弦等于邻边比斜边;正切等于对边比邻边.13.(2019年广东汕尾,第7题4分)在Rt△ABC中,C=90,若sinA=,则cosB的值是()A.1B.3C.2D.-1分析:根据互余两角的三角函数关系进行解答.解:∵C=90,B=90,cosB=sinA,∵sinA=,cosB=.故选B.点评:本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.14.(2019毕节地区,第15题3分)如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.已知cosACD=,BC=4,则AC的长为()A.1B.4C.3D.2考点:圆周角定理;解直角三角形分析:由以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.易得ACD=B,又由cosACD=,BC=4,即可求得答案.解答:解:∵AB为直径,ACB=90,ACD+BCD=90,∵CDAB,BCD+B=90,ACD,∵cosACD=,cosB=,tanB=,∵BC=4,tanB===,AC=.故选D.点评:此题考查了圆周角定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.15.(2019年天津市,第2题3分)cos60的值等于()点:特殊角的三角函数值.分析:根据特殊角的三角函数值解题即可.解答:解:cos60=.故选A.点评:本题考查特殊角的三角函数值,准确掌握特殊角的函数值是解题关键.二、填空题1.(2019年贵州黔东南11.(4分))cos60=.考点:特殊角的三角函数值.分析:根据特殊角的三角函数值计算.解答:解:cos60=.点评:本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,要掌握特殊角度的三角函数值.2.(2019江苏苏州,第15题3分)如图,在△ABC中,AB=AC=5,BC=8.若BPC=BAC,则tanBPC=.考点:锐角三角函数的定义;等腰三角形的性质;勾股定理分析:先过点A作AEBC于点E,求得BAE=BAC,故BPC=BAE.再在Rt△BAE中,由勾股定理得AE 的长,利用锐角三角函数的定义,求得tanBPC=tanBAE=.解答:解:过点A作AEBC于点E,∵AB=AC=5,BE=BC=8=4,BAE=BAC,∵BPC=BAC,BPC=BAE.在Rt△BAE中,由勾股定理得AE=,tanBPC=tanBAE=.故答案为:.点评:求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.3.(2019四川内江,第23题,6分)如图,AOB=30,OP平分AOB,PCOB于点C.若OC=2,则PC的长是.考点:含30度角的直角三角形;勾股定理;矩形的判定与性质.专题:计算题.分析:延长CP,与OA交于点Q,过P作PDOA,利用角平分线定理得到PD=PC,在直角三角形OQC中,利用锐角三角函数定义求出QC的长,在直角三角形QDP中,利用锐角三角函数定义表示出PQ,由QP+PC=QC,求出PC的长即可.解答:解:延长CP,与OA交于点Q,过P作PDOA,∵OP平分AOB,PDOA,PCOB,PD=PC,在Rt△QOC中,AOB=30,OC=2,QC=OCtan30=2=,APD=30,在Rt△QPD中,cos30==,即PQ=DP=PC,QC=PQ+PC,即PC+PC=,解得:PC=.故答案为:点评:此题考查了含30度直角三角形的性质,锐角三角函数定义,熟练掌握直角三角形的性质是解本题的关键.4.(2019四川宜宾,第16题,3分)规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.据此判断下列等式成立的是②③④(写出所有正确的序号)①cos(﹣60②sin75③sin2x=2sinx④sin(x﹣y)=sinxcosy﹣cosxsiny.考点:锐角三角函数的定义;特殊角的三角函数值.专题:新定义.分析:根据已知中的定义以及特殊角的三角函数值即可判断.解答:解:①cos(﹣60)=cos60=,命题错误;②sin75=sin(30+45)=sin30cos45+cos30sin45=+=+=,命题正确;③sin2x=sinxcosx+cosxsinx═2sinxcosx,故命题正确;④sin(x﹣y)=sinxcos(﹣y)+cosxsin(﹣y)=sinxcosy﹣cosxsiny,命题正确.故答案是:②③④.点评:本题考查锐角三角函数以及特殊角的三角函数值,正确理解题目中的定义是关键.5.(2019甘肃白银、临夏,第15题4分)△ABC中,A、B都是锐角,若sinA=,cosB=,则C=.考点:特殊角的三角函数值;三角形内角和定理.分析:先根据特殊角的三角函数值求出A、B的度数,再根据三角形内角和定理求出C即可作出判断.解答:解:∵△ABC中,A、B都是锐角sinA=,cosB=,B=60.C=180﹣A﹣B=180﹣60﹣60=60.故答案为:60.点评:本题考查的是特殊角的三角函数值及三角形内角和定理,比较简单.6.(2019广西贺州,第18题3分)网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA=.考点:锐角三角函数的定义;三角形的面积;勾股定理.分析:根据正弦是角的对边比斜边,可得答案.解答:解:如图,作ADBC于D,CEAB于E,由勾股定理得AB=AC=2,BC=2,AD=3,由BCAD=ABCE,即CE==,sinA===,故答案为:.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.。
