通过概率基础理论研究证券组合风险
2023年基金从业资格证之证券投资基金基础知识押题练习试卷A卷附答案

2023年基金从业资格证之证券投资基金基础知识押题练习试卷A卷附答案单选题(共30题)1、下列关于资本结构和债权资本的说法错误的是()。
A.资本结构是指企业资本总额中各种资本的构成比例。
最基本的资本结构是债权资本和权益资本的比例,通常用债务股权比率或资产负债率表示B.一个公司的总资本是1 000万元,其中有300万元的债权资本和700万元的权益资本,那么该公司的资本结构即包含30%的债务和70%的权益,该公司的资产负债率是30%C.有负债的公司被称为杠杆公司,一个拥有100%权益资本的公司被称为完全杠杆公司,因为它没有债权资本D.债权资本是通过借债方式筹集的资本,公司向债权人(如银行、债券持有人及供应商等)借入资金,定期向他们支付利息【答案】 C2、证券登记结算机构的职能不包括()A.制定交易规则,维护交易秩序B.证券持有人名册登记及权益登记C.证券账户、结算账户的设立和管理D.证券和资金的清算交收及相关管理【答案】 A3、下列选项中属于显性成本的是()。
A.机会成本B.佣金C.市场冲击D.买卖价差【答案】 B4、下列关于基金资产估值,表述错误的是()。
A.基金管理人进行基金估值时,可参考估值工作小组的意见,但不能免除其估值责任B.基金管理人每个工作日对基金资产估值C.基金资产估值的责任人是基金托管人D.基金托管人按基金合同规定,对管理人计算的基金份额净值进行复核【答案】 C5、以下属于中国证券业协会公布的第一批具有协会会员资格的基金评价机构的是()。
A.Ⅰ、Ⅱ、Ⅲ、ⅣB.Ⅰ、Ⅱ、ⅢC.Ⅰ、Ⅱ、ⅣD.Ⅰ、Ⅲ、Ⅳ【答案】 C6、一般票据的贴现不超过(),贴现期从贴现日起计算至票据到期日。
A.5个月B.6个月C.1年D.2年【答案】 B7、下列关于资本资产定价模型的说法错误的是()。
A.本资产定价模型(CAPM)以马可维茨证券组合理论为基础,研究如果投资者都按照分散化的理念去投资,最终证券市场达到均衡时,价格和收益率如何决定的问题B.资本资产定价模型认为只有证券或证券组合的系统性风险才能获得收益补偿,其非系统性风险将得不到收益补偿C.现实中并不是所有的投资者都能够持有充分分散化的投资组合,这也是造成CAPM不能够完全预测股票收益的一个重要原因D.投资者要想获得更高的报酬,必须承担更高的系统性风险;承担额外的非系统性风险将会给投资者带来收益【答案】 D8、从2012年6月1日起,上海证券交易所A股交易过户费的收费标准调整为按成交面额的()向买卖双方投资者分别收取。
组合风险与收益

(一)个别证券资产(股票)的β系数
•股票投资组合重要的该组合总的风险大小,而不是每一种 股票个别风险的大小。当考虑是否在已有的股票投资组合 中加入新股票时,重点也是这一股票对资产组合总风险的 贡献大小,而不是其个别风险的大小 •每一种股票对风险充分分散的资产组合(证券市场上所有 股票的组合)的总风险(系统风险)的贡献,可以用β系数 来衡量。β系数反映了个别股票收益的变化与证券市场上全 部股票平均收益变化的关联程度。也就是相对于市场上所 有股票的平均风险水平来说,一种股票所含系统风险的大 小。
图3—7 某一时期两种资产收益之间的相互关系
表3—3
两种完全负相关股票组合的收益与风险
图3—8两种完全负相关股票的收益与风险
图3—9两种不完全负相关资产组合的风险分散效果
(二)多项资产组合的风险与收益 E(Rp)=∑WiRi 公式(3—14)
σp=√ ∑Wi2σi2+2∑∑WiWjσiσjρij
•例题(略)由例子可以得到的结论是:两种资产的投 资组合,只要ρAB<1,即两种资产的收益不完全正相关, 组合的标准差就会小于这两种资产各自标准差的加权平 均数,也就是说,就可以抵消掉一些风险,这就是“投 资组合的多元化效应”。 •在证券市场上,大部分股票是正相关的,但属于不完 全正相关。根据资产组合标准差的计算原理,投资者可 以通过不完全正相关的资产组合来降低投资风险。
•一般是以一些代表性的股票指数作为市场投资组合,再 根据股票指数中个别股票的收益率来估计市场投资组合的 收益率。美国是以标准普尔500家股票价格指数作为市场 投资组合。图3—8就是一个个股的超额期望收益率与市场 组合的超额期望收益相比较的例子。(超额期望收益率 =期望收益率-无风险收益率,超额收益率就是风险报酬率) •其中特征线的斜率就是β系数,它反映了个股超额收益率 的变化相当于市场组合的超额收益率 变化的程度。
证券投资组合研究

本科生实践教学活动周实践教学成果成果形式:论文成果名称:证券投资组合模型研究学生姓名:目录一类证券投资组合模型研究 (2)序言 (1)一、证券投资组合模型的发展现状 (1)二、证券投资组合理论概述 (3)三、CEVaR风险度量的理论建构 (3)(一)证券投资组合中熵风险度量的引入 (3)(二)证券投资组合的 CVaR 风险度量的引入 (4)(三)CEVaR 风险度量方法的提出 (5)四、CEVaR模型在证券投资组合中的实证研究 (5)(一)证券投资组合的CEVaR模型 (5)(二)数据的选取与处理 (6)结论 (10)参考文献 (11)一类证券投资组合模型研究研究背景:证券市场是一个高风险市场。
为了分散风险并获得最大收益,许多投资者将多种证券组合在一起进行投资,使得证券投资组合的研究成为金融界面临的重要课题之一。
Markowitz 以证券收益率的方差作为组合证券风险的度量,开辟了金融定量分析的时代,在度量风险的基础上建立了组合投资决策模型。
关键字:证券投资组合;风险;熵;CVaR 度量;CEVaR 模型序言随着经济全球化、金融一体化进程的加快,各国金融市场的开放程度不断加深、金融市场之间的联系进一步加强。
资本在全球范围内大量、快速和自由流动以及全球金融市场之间的价格协同运动使得任何地区的金融市场的局部波动都会迅速波及、传染、放大到其他市场。
金融业的激烈竞争导致了金融创新的浪潮,并由此引发了政府对金融业的放松管制,反过来又加剧了市场竞争,为以衍生金融产品为核心的金融创新提供了内在的动机和良好的环境,这一螺旋式的过程导致金融市场的不确定性和波动性增大;信息技术、现代金融理论和金融工程技术的突破性发展,提高了国际金融市场中资金和信息的流通效率,提高了对复杂金融产品和交易的准确定价能力,从而导致金融市场的交易品种、交易量和交易速度的爆发性增长,金融市场的复杂性和不稳定性大大提高;同时,为了规避风险、提高竞争力、逃避管制而展开的金融创新活动,在放松管制和技术进步的刺激下异常活跃,导致高风险的衍生金融工具飞速增长,这使金融风险得到有效的分散和转移的同时又成为金融市场风险新的来源。
均值-CVaR模型在正态条件下风险资产组合的研究

准差满足:
, 显然,均值 - 边界等价于均值
- 方差边界的一个变换。 定理 1 组合 属于均值 -
边界 组合 属于均值 - 方差
边界。 定理 2 风险证券的预期回报率服从正态分布,
组合
它是关于 的非增,右连续函数,
在相应的概率置信
度
下,损失 VaR 和 CVaR 分
,
因为,
,
,
关键词:均值 -CVaR 模型;金融资产;正态分布
一、引言
风险价值(Value at Risk ,简称 VaR),是一种风险管理与控
制的新工具,是指在正常的市场条件下和给定的置信水平上,在给
定的持有期内,投资组合或资产所面临的潜在最大损失,其数学表
达式为:
,其中 表示组合在持有期内 的价值
变动量, 表示指定概率分布的分位数。VaR 最大的优点就是其定
Conditional Value at-Risk[J].Joumal of Risk,2000,2:21-24. [3]R. Tyrrell,Rockafellar and Stanislav Uryasev. Conditional
value-at-Risk for general loss distributions [J]. Jourmal of Banking & Finance,2002,26:1443-1471.
量标准化,从而营造了一个统一的框架,把金融机构所有资产组合
的风险量化为一个简单的数字,VaR 的概念虽然简单,但 VaR 方法
在原理和统计估计方面存在一定局限性,如 VaR 的计算结果不稳
定;VaR 不满足次可加性,所以不是一致风险度量;VaR 不满足凸
性,VaR 对证券投资组合进行优化时可能存在多个极值,局部最优
证券投资组合风险管理

R
B
1
1
O
12
一、证券收益率和风险的测度
(三)三个证券组合的收益率和风险的测度
1、三个证券组合的预期收益率的 R P 测度
R PX 1R 1X 2R 2X 3R 3 式中,Xi是第i个证券在证券组合中所占的比重,R i 是第i个 证券的预期收益率,i=1,2,3。 2、三个证券组合风险的测度
22
不同风险厌恶水平的无差异曲线
E(RP)
I1 I2 I3
E(RP)
I1 I2
I3
E(RP)
P
P
I1
I2 I3
P
23
二、现代投资组合理论
(三)现代投资组合理论的均值方差分析
两资产构成的投资组合的风险——收益状况
保持资产的相关系数 不变而改变两项资产 的权数,将得到一系 列组合:其轨迹类似 于椭圆弧线。
r(Dt Pt Pt1)10% 0 Pt1
5
一、证券收益率和风险的测度
(一)单个证券收益率和风险的测度
1、单个证券收益的测度
(3)风险证券期望收益率的测度
风险证券的收益率通常用统计学中的期望值来
表示:
n
R RiPi i1
式中,Ri是证券第i情况下的收益率,Pi是i种 情况下的概率
6
一、证券收益率和风险的测度
(二)两个证券组合收益率和风险的测度 3、两个证券收益率、风险和相关系数之间的关系
2 P X 2 A 2 A X 2 B 2 B 2 X A X B AA B B
当ρAB=-1时, 表示证券A、B收益变动完全负相关; 当ρAB=+1时, 表示证券A、B完全正相关 当ρAB=0时, 表示完全不相关 当0<ρAB<1时, 表示正相关 当-1<ρAB<0时,表示负相关
证券投资学(第五版)第10章 证券组合管理

6 什么叫卖空?如果你有本金1 000元,卖空股票A 并将收入的500元连同本金全部投资于股票B,那 么在你的资产组合中A、B的权数各是多少?
7 如果两项资产完全正相关,是否能把它们组成一 个方差为零的资产组合?
8 如果股票A和股票B的协方差为正值,当股票A的 实际收益大于其预期收益时,你对股票B会有什 么样的预期?
(3)什么样的事件可以造成资产实际收益对回归线的 偏离?哪个符号可以反映这种偏离?
13 利用β值进行投资决策时需注意什么问题?
14 卖空限制对资产组合管理有什么影响?
三. 计算题
1.一个投资者筛选出2种风险资产作为其投资目标。资产的
具体情况如下:
E(R) σ
资产A 15%
30%
资产B 10%
22%
2 制定组合管理政策:包括规定投资范围和考 虑客户要求和市场监管机构的限制。
3 构建证券组合:取决于组合管理者的投资策 略(积极进取型投资策略、消极保守型投资策略 和混合型投资策略)。
4 修订证券组合资产结构:剔除或增加证券。
5 证券组合资产的业绩评估。
5.现代组合理论的形成与发展
1. 现代组合理论最早是由美国著名经济学家哈 里·马科维茨于1952年系统提出。
9 为什么大多数金融资产都呈不完全正相关关系? 试分别举一个资产收益高度正相关和高度负相关 的例子。
10 请分析资产的数量与资产组合风险的关系。
11 什么是系统风险和非系统风险?
12 根据单一指数模型的假设,资产 I 的收益率可表 示如下:
ri=ai+βirm+εi
(1)式中各符号分别代表什么?
(2)宏观因素对这一模型会有什么影响?哪个符号可 以反映这种影响的大小?
6-1证券投资组合理论

现资产收益最大化,或者是要在资产收益一定的条件 下实现风险的最小化。
无差异曲线是用来表示两种商品或两组商品的不同数
量的组合对消费者所提供的效用是相同的,无差异曲 线符合这样一个要求:如果听任消费者对曲线上的点 作选择,那么,所有的点对他都是同样可取的,因为 任一点所代表的组合给他所带来的满足都是无差异的。
投资情况下的无差异曲线
有效集与可行集
证券投资组合管理
证券投资收益的概念
证券投资收益是投资者在购买、持有和出售
某种有价证券的过程中所获得的各种投资回 报与投入本金之差额。
证券 持有收益
证券 交易收益
证券 投资 收益
证券投资风险
证券投资风险也被称为金融风险,是指投资者在证券
投资过程中遭受损失或达不到预期收益率的可能性。
证券投资风险分为两类,即经济风险与心理风险。证
收益是这些证券收益的加权平均数,但是其风险不是 这些证券风险的加权平均风险,投资组合能降低非系 统性风险。
人们进行投资,本质上是在不确定性的收益和风险中
进行选择。投资组合理论用均值—方差来刻画这两个 关键因素。所谓均值,是指投资组合的期望收益率, 它是单只证券的期望收益率的加权平均,权重为相应 的投资比例。当然,股票的收益包括分红派息和资本 增值两部分。所谓方差,是指投资组合的收益率的方 差。我们把收益率的标准差称为波动率,它刻画了投 资组合的风险。
协方差的计算
COVAB Pi (rA ErA )(rB ErB )
i 1 n
Cov
A
A
AB
—证券A与证券B的协方差
r ,r
Pt
B —证券A与证券B的各种可能收益率
证券投资组合的概率准则模型研究

第2 1卷第 4期 20 0 8年 8月
常 州 工 学 院 学 报 r
J u a f Ch n z o n t u e o e h o o y o r lo a g h u I s tt fT c n l g n i
VO . No. 1 21 4 Au 2 08 g. 0
O 引言
证券投资是在不确定条件下进行的一种风险 投资。任何的收益都不可避免地伴随着一定的风 险, 为了获得稳定 的收益, 投资者一般将资金按一
定 比例同时投资 于若 干种证券 以分散 较大 的风 险 , 从而形 成证券 投 资组合 。投 资者 所 关 心 的问题 是
准则决策与授资组合有效边界的关系。文章主要
=
~
Ⅳ( 1 , 0,) 目标 函数 变为
X‘ VX
√xI X V
=
s £ X . . I: 1
率准则下以实现预期收益的概率作为 目 函数的 标
投资组合的决策模型 , 并认为概率准则模型考虑 了 投资者的非理性行为; 文献[ ] 4 进一步探讨了概率
收 稿 日期 :0 8~ 6—2 20 O 3
为协方差矩阵 , 则投资组合 的收益率 R = T 。 X R~
基金项 目:山东省教育厅人文社会科 学研究项 目, 目编号 :0 Y 9—1 项 S 7 D0 。
的投资比例向量, 其中 为投资于第 i 种证券的资
金 比例 , 满 足 j=l其 中 j=( , , ,)。 且 , 1 l… 1 , 此 时投资组合 的收益 率 R = R。设 投 资者 预 置 的 XT 基 准收益率 为 R , 。则在允许 卖 空 的市 场 环境 中 , 可 建立如下概率 准则模型 : J
证券投资学之证券投资组合管理基础

关于资本市场的假设:
1.资本市场是有效的。证券的价格反映了 其内在价值;市场无摩擦,不存在税收 和佣金、保证金、买卖差价等交易成本。
2.资本市场上证券有风险,收益都服从正 态分布,不同证券之间有一定的相关性。
3.资本市场上证券无限可分,可买任意小 数量的股票、债券;且任何证券的购买 不影响市场价格,即资本市场的供给具 有无限弹性。
第一类风险是与市场的整体运动相关联的。 这类风险因其来源于宏观因素变化对市场 整体的影响,因而亦称之为“宏观风险”。 前面提及的市场风险、贬值风险、利率风 险、汇率风险和政治风险均属此类。我们 称之为系统风险。
第二类风险则基本上只同某个具体的股票、 债券相关联。这种风险来自于企业内部的 微观因素,因而亦称之为“微观风险”。 前面提到的偶然事件风险、破产风险、流 通性风险、违约风险等均属此类。我们称 之为非系统风险。
二、投资组合的基本类型
通常,以组合的投资目标为标准: 1.收入型 2.增长型 3.收入和增长混合型
4.货币市场型 5.国际型 6.指数化型 7.避税型
三、传统证券组合管理理论
传统的证券组合管理依靠非数量化的方 法,即基础分析和技术分析来选择证券, 构建和调整证券组合。
传统证券组合管理理论构建投资组合主要 包括以下几个步骤:
少,但风险的减少达到一个极限就不会再减少
了。
一般来说,代表不同风险特征性的证券数目达
到20种以上时,风险的分散就相当的充分了。
(四)证券相关性与投资组合的风险
1.证券组合中各单个证券预期收益存在着正相 关时,如属完全正相关,则这些证券的组合 不会产生任何的风险分散效应;它们之间正 相关的程度越小,则其组合可产生的分散效 应越大。
第10章--证券组合管理概述分析

调整风险资产和无风险资产的比例,同时
略
不放弃资产升值潜力的一种动态调整策略
战
术
性
根据资本市场环境及经济条件对资 Nhomakorabea产
资产配置状态进行动态调整,从而增
配
置
加投资组合价值的积极战略
策
略
资产配置策略的特征比较
资产配置 策略
买入并持 有
恒定混合
市场变动时
市场环境与收益
的行动方向 适合的 市场
趋势 无趋势
不行动
自下而上: 通过基本分析的方法,来预测股票的未来收益, 根据股票所处的行业及其他一些参数确定股票的内在 价值
代表人物: 沃伦·巴非特 (Warren Buffet) 彼得·林奇 (Peter Lynch)
积极投资策略构筑投资组合的方式
自上而下: 对宏观经济的环境进行评估,预测近期经济前景, 决定资金在资本市场不同部分之间的分配
• 资本资产定价模型最早是由夏普 (Sharpe)、林特(Lintner)和莫森 (Mossin)根据马科威茨(Markowitz)最 有资产组合选择的思想分别独立的提出的, 经过几十年的发展,已经产生了多种多样 的资本资产定价模型,有些学者还创新出 套利定价理论,从而形成了资本市场均衡 理论体系。
• 1.所有资产都是可以在市场上买卖的,即这是一 个高度市场化的经济。
• 2.资本市场是完美无缺的,不存在摩擦。具体体 现在:所有资产都是无限可分的,即资产的任何 一部分都是可以单独买卖的;所有投资者都是随 行逐市者,任何人的买卖行为都不能影响市场价 格,即资产价格由市场决定;没有交易成本和税 收,或者说,这些问题不影响投资决策;对借入 和卖出数量没有限制,也没有保证金要求;所有 投资者都可以无偿获取信息,并掌握同样的信息。
(整理)第5章投资组合
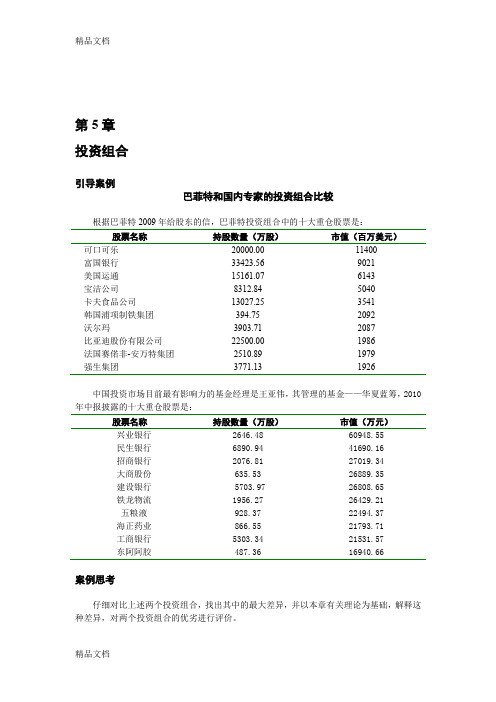
第5章投资组合引导案例巴菲特和国内专家的投资组合比较根据巴菲特2009年给股东的信,巴菲特投资组合中的十大重仓股票是:股票名称持股数量(万股)市值(百万美元)可口可乐富国银行美国运通宝洁公司卡夫食品公司韩国浦项制铁集团沃尔玛比亚迪股份有限公司法国赛偌非-安万特集团强生集团20000.0033423.5615161.078312.8413027.25394.753903.7122500.002510.893771.1311400902161435040354120922087198619791926中国投资市场目前最有影响力的基金经理是王亚伟,其管理的基金——华夏蓝筹,2010年中报披露的十大重仓股票是:股票名称持股数量(万股)市值(万元)兴业银行民生银行招商银行大商股份建设银行铁龙物流五粮液海正药业工商银行东阿阿胶2646.486890.942076.81635.535703.971956.27928.37866.555303.34487.3660948.5541690.1627019.3426889.3526808.6526429.2122494.3721793.7121531.5716940.66案例思考仔细对比上述两个投资组合,找出其中的最大差异,并以本章有关理论为基础,解释这种差异,对两个投资组合的优劣进行评价。
投资组合(portfolio)是指将资金配置在一种以上的证券上,获取在风险可控下最大化回报的投资方式。
本章将从理论上分析,投资组合降低风险、提高收益的机制,如何构建最优化的投资组合等问题。
5.1 两种证券组合的收益和风险两种证券构成的投资组合,是最简单的投资组合形式,是分析三种以上证券组合的基础。
假设有两种证券A S 、B S ,投资者将资金按照A X 、B X 的比例构建证券组合,则该证券组合的收益率可以表示为:P A A B B R X R X R =+上式中A X +B X =1,且A X 、B X 可以是正数也可以是负数,负数表示卖空该股票,实际上就是借钱买另外一只股票。
组合证券的投资风险分析

组合证券的投资风险分析傅仙发(湄洲湾职业技术学院,福建莆曰351254)摘要:本文主要根据M ar kow i t z理论,研究组合证券的总风险大小。
关键词:组合证券:投资风险:H ar koW l tz理论:投资组合1引言‘随着中国经济的日益增强和证券市场的不断完善,越来越多的人把他们闲散的资金投到证券市场中。
在众多基础分析和技术分析的结果下,如何衡量风险,如何选择投资组合才是最优,是现在投资者所注重的重要问题。
1952年,美国人H.M.M ar kow i t z提出了一个创新理论一投资组合理论。
M ar kow i t z的现代投资组合理论,提出了用均值衡量投资组合的收益;用方差衡量该投资组合的风险的原则,并据此建立了一套用于分析和选择最优投资组合数学方法和模型。
本文正是利用数学知识和M ar kow i t z理论中的模型对风险进行衡量。
2组合证券投资的风险2.1证券投资风险的概念投资者从事证券投资的目的,主要在于获取适当的预期收益。
但是在证券投资过程中,投资者的行为结果与他们的预期有一定的偏差,这种偏差(不确定因素)就称为证券投资的风险。
2.2证券投资风险的类别证券投资风险,按其影响范围和能否避免可分为系统性风险和非系统性风险两类。
系统性风险是指某种对市场上所有的证券都会带来损失可能性的风险。
如:重大政治变动,政府有关政策的出台等等。
非系统性风险指对市场上某一单个或几个证券造成损失的可能性的风险。
如:某一企业的经营状况恶化,市场供求关系的变化等等。
由于这不是本文研究的重点,故不详细分析。
2.3组合证券的投资风险在证券市场中,收益与风险是并存的。
而且通常是收益越大,风险也越大;反之亦然。
所以投资者追求的只能是,在一定风险下收益最大的投资决策或在一定收益下风险最小的投资决策或收益与风险按一定的比例组合最优的投资决策。
不管是哪一种决策都必须考虑投资的风险因素。
证券投资的风险不能消除,不能避免,但可以降低。
证券投资学第八章证券组合管理理论

B
即ρAB=0,则:
不相关情形下的组合线。
(一)证券组合的可行域 1、两种证券组合的可行域 (3)不相关情形下的组合线。 由上述方程确定的σP与E(rP)的曲线是一条经过A和B的 双曲线。
E(rp)
(σp)
0
A
B
C
·
·
·
·
证券组合的可行域 两种证券组合的可行域 不相关情形下的组合线。 为了得到方差最小的证券组合,对方程 求极小值可得: 以及组合的最小方差:
协方差 协方差是刻划二维随机向量中两个分量取值间的相互关系的数值。 协方差被用于揭示资产组合两种证券未来可能收益率之间的相互关系。
协方差 其中:
相关系数 相关系数是反映两个随机变量的概率分布之间的相互关系。 相关系数可用以衡量两种证券收益率的相关程度。 相关系数是标准化的计量单位,取值在±1之间。
D
F
A
B
C
E(rp)
(σp)
0
(一)证券组合的可行域 2、多种证券组合的可行域 一般而言,当由多种证券(不少于3种)构成证券组合时, 组合可行域是所有合法证券组合构成的E—σ坐标系中的一个 区域,其形状如下图。
E(rp)
(σp)
0
0
E(rp)
(一)证券组合的可行域 2、多种证组合的可行域 允许卖空时:
(σp)
(一)证券组合的可行域 2、多种证券组合的可行域 可行域的形状依赖于可供选择的单个证券的特征E(ri)和 σi以及它们收益率之间的相互关系ρij,还依赖于投资组合中 权数的约束。 可行域满足一个共同的特点:左边界必然向外凸或呈线性,即不会出现凹陷。
(二)证券组合的有效边界 同时满足以下两个条件的一组证券组合,称为有效组合: 如果两种证券组合具有相同的收益率方差和不同期望收益率,即 ,而 ,且 ,那么投资者选择期望收益率高的组合,即A。 如果两种证券组合具有相同的期望收益率和不同的收益率方差,即 ,而 , 且 ,那么投资者选择方差较小的组合,即A。 这种选择原则,我们称为投资者的共同偏好规则。
谈谈对证券投资组合的看法

谈谈对证券投资组合的看法
证券投资组合是指投资者将资金分散投资于多种证券资产,以实现风险和收益的平衡。
以下是对证券投资组合的几点看法:
优点:
1. 分散风险:证券投资组合通过将资金分散投资于不同的证券,降低了单一证券的风险,从而实现了风险分散。
2. 实现收益最大化:投资者可以根据自身的风险承受能力和收益预期,选择适合自己的证券投资组合,从而实现收益最大化。
3. 提高投资效率:通过科学的证券投资组合管理,投资者可以更加有效地管理自己的投资,提高投资效率。
缺点:
1. 管理难度大:证券投资组合包含多种证券资产,管理难度较大,需要投资者具备较高的投资管理和风险控制能力。
2. 信息披露不充分:证券市场信息披露不充分,投资者难以全面了解证券的质量和风险,增加了投资风险。
3. 市场波动影响大:证券市场波动较大,投资者可能会面临较大的市场风险和流动性风险。
综上所述,证券投资组合既有优点也有缺点。
投资者应该根据自己的实际情况和投资目标,选择适合自己的证券投资组合,并加强风险管理,以实现长期稳定的投资回报。
证券投资组合理论与方法

2.在坐标系中,越是位于西北方向的无差异曲线上的证券组
合越为投资者所偏好。
2021/4/22
图7 .12 无差异曲线的特点
回本章2目1 录
三、有效边界的确定
(一)有效边界的概念
在风险和收益的权衡中,投资者必然采取如下策略:
(1)在风险相同的条件下,选择期望收益最大的证券;
(2)在期望收益相同的条件下,选择风险最小的证券。
着相关关系为-1的线段上进行运动,当运动至G点
时, p 0,此时的证券甲的比例为 B /A B ,过了G点,风
险又逐步回升。AG和GB上的点风险相同,但是存在着
期望值不同的对应的两个点,如L点和M点,这也表明
A点沿着GB运动比AG为优。
结论:从以上分析可知,组合证券沿着所有线段
运动都是可以的,但存在着一些比其他效应为优的线
假设三种证券A、B、C,可以求得 关于 的函数:
XB XA
【例X B7.3】EE三RRCC种股EE票RRB的p 收益EE率RRCA、方EE差RRCB、协X 方A 差等数据如
表7.7所示。
表7.7 三种股票的收益率、方差、协方差数据
收益率
方差 协方差
A
B
C
5%
10% 15%
0.50
0.46
0.53
1、两种股票组合效应图示及其分析(续)
A、B点分别表示证券甲和乙的比例为100%,这里的三条直线
AB、AG、GB分别表示相关系数为+1和-1时,证券甲和证券乙分别
在组合证券中所占的比例,曲线AB是一条双曲线,表示 时的
证券甲和证券乙所占的比例。
RAB 0
(1)线段AB,相关系数=+1,一揽子证券未产生组合效应。
证券投资学5证券投资组合理论

布的良好效果,请言简意赅地阐述您的观点。
三项资产组合的效率前沿 方差为:
ABCE(aRAbRBCRC) 0.334.6%+0.338.60%+0.3416%
=9.765%
若
将
,相关系数
Var(aRA bRB CRC)
的资产C引入组合 AB中,
0.332 0.05622+0.332 0.06332+0.342 0.0752
有无风险资产组合的效率前沿
(一)无风险资产的定义
第二节 证券资产组合的效率前沿
(二)允许无风险资产下的投资组合
一.投资于一种无风险资产和一种风险资产的情形
为了考察无风险贷款对有效集的影响,我们首先要分析由一种无风险资产和一种风险资产组 成的投资组合的预期收益率和风险。
假设风险资产和无风险资产在投资组合中的比例分别为X1和X2,它们的预期收益率分别
1
p
这样,我们可以算出该组合的预期收益率为: 我们可以算出改组合的标准差为: 由上式可得: 代入一式
第二节 证券资产组合的效率前沿
在图中,A点表示无风险资产,B点
表示风险资产,由这两种资产构成的投资组
合的预期收益率和风险一定落在A、B这个
RP
线段上,因此AB连线可以称为资产配置线。 B
由于A、B线段上的组合均是可行的,
率最高。
E(R)
C
比如,相对于区域中的L点,组合N与他的
F
期望收益率相同,但风险却低得多,组合F与L的风
NL
险大小相同,但期望收益率相同。
E
B
A
因此,现在投资者只会在NF之间选择,不
σ
必估计到L的存在
第二节 证 券资产组合 的效率前沿
《经济数学基础》答案

第17题: 下面哪一个可以用泊松分布来衡量( B)。
A一个班学生们的身高B一段道路上碰到坑的次数C投掷硬币时遇到正面朝上的概率D某稀有金属的半衰期长短第18题: 线性回归方法是做出这样一条直线,使得它与坐标系中具有一定线性关系的各点的( C)为最小。
A水平距离的平方和B垂直距离的和C垂直距离的平方和D垂直距离的平方第19题: 当两变量的相关系数接近相关系数的最小取值-1时,表示这两个随机变量之间( B)。
A几乎没有什么相关性B近乎完全负相关C近乎完全正相关D可以直接用一个变量代替另一个第20题: 关于概率,下列说法正确的是( ABC)。
A是度量某一事件发生的可能性的方法B概率分布是不确定事件发生的可能性的一种数学模型C值介于0和1之间D所有未发生的事件的概率值一定比1小第21题: 下列哪些方面需要用到概率知识分析其不确定性( ABC )。
A外汇走势B不良贷款率预测C证卷走势D税收确认第22题: 什么样的情况下,可以应用古典概率或先验概率方法( BD )。
A不确定有什么样的结果空间B不确定结果的范围是已知的C不确定结果发生的概率不一样D不确定结果具有等可能性第23题: 关于协方差,下列说法正确的有( ABD )。
A协方差体现的两个随机变量随机变动时的相关程度B如果P=1,则I 和n有完全的正线性相关关系C方差越大,协方差越大D Cov(x,η)=E(X-EX)( η-Eη)第24题: 关于中位数,下列理解错误的有( BC )。
A当所获得的数据资料呈偏态分布时,中位数的代表性优于算术平均数B当观测值个数为偶数时,(n+1)/2位置的观测值,即X(n+1)/2为中位数C当观测值个数为偶数时,(n+1)/2位置的观测值,X(n+1)/2为中位数D将资料内所有观测值从小到大一次排列,位于中间的那个观测值,称为中位数第25题: 线性回归时,在各点的坐标为已知的前提下,要获得回归直线的方程就是要确定该直线的( BD )。
投资组合的风险与报酬重点

第07 讲投资组合的风险与酬劳知识点投资组合的风险与酬劳〔一〕投资组合理论1.投资组合的收益是组合内各证券收益以其投资比重为权数的加权平均数。
(提示)某证券的期望酬劳率是该证券全部可能的酬劳率的加权平均数,其权数为出现的概率。
——参见“预期值〞2.投资组合的风险〔指整体风险即标准差〕通常小于组合内各证券风险〔即标准差〕的加权平均数,投资组合能分散〔或者说降低〕风险。
(提示)一般情况下,对投资组合来说,以各种证券在组合中的投资比重为权数的“加权平均〞代表“没有分散〞效应。
具体来说:投资组合的收益等于组合内各证券的收益的加权平均值,说明投资组合没有分散收益。
投资组合的标准差〔即风险〕小于组合内各证券的标准差〔即风险〕的加权平均值,说明投资组合能分散〔或者说降低〕风险。
(例如)某投资组合由 10 种股piao组成。
这 10 种股piao的期望酬劳率均为 10%;标准差均为 5%。
由于组合的期望酬劳率是组合内各股piao的期望酬劳率的加权平均值,显然无论如何安排 10 种股piao的投资比重,权数〔投资比重〕之和始终为 1,因此组合的期望酬劳率始终是 10%不变。
但是组合的标准差通常小于组合内各股piao的标准差的加权平均值〔5%〕,因此组合能够在不分散收益的前提下分散风险。
〔二〕证券酬劳率之间的相关性〔共同变动程度〕与风险分散1.衡量两种证券酬劳率之间相关性的指标(1)相关系数——衡量相关性的相对数指标①公式②取值范围:-1≤相关系数≤1〔通常:0<相关系数<1〕(2)协方差——衡量相关性的绝对数指标①公式:σ AB=r AB·σ A·σ B②协方差的正负方向与相关系数一致③ 某证券与其本身的协方差等于该证券的方差2.证券酬劳率的相关性与风险分散的关系(例如)假设某投资组合由 A 汽车公司和 B 石油公司的股piao组成,投资比重各为 50%,两支股piao的酬劳率均受到原油市场价格变动的影响,有关情况如下:完全负相关,所构成的投资组合,期望酬劳率不变,而标准差〔风险〕为 0。
失真风险度量

中国科学技术大学硕士学位论文失真风险度量姓名:贾佳申请学位级别:硕士专业:概率论与数理统计指导教师:胡太忠20090501失真风险度量作者:贾佳学位授予单位:中国科学技术大学1.学位论文刘俊山基于风险测度理论的证券投资组合优化研究2007首先,本文分别讨论了一致风险测度理论、谱风险测度理论、失真风险测度理论和随机占优一致风险测度理论等风险度量评价理论,在这些理论框架内讨论和比较了标准差、平均绝对离差、下偏位矩、基尼均差、VaR以及CVaR等风险度量。
结果显示,CVaR在理论性质上优于其他风险度量,表现在:1) CVaR满足子可加性,属于一致风险度量;2) CVaR是二阶随机占优一致风险度量;3)CVaR既属于谱风险度量又属于失真风险度量,虽然性质不够完美,但依然优于其他风险度量指标。
其次,本文讨论了投资组合优化模型,认为一个“好”的投资组合优化模型既应理论性质完美,又应易于求解、扩展与实施。
通常,风险度量的性质决定了模型的性质,因此应优先考虑基于CVaR的投资组合优化模型(以下简称CVaR模型),理由如下:1)CVaR承认分散化效应;2)CVaR模型给出的最优解是二阶随机占优有效的;3)CVaR模型通常是凸的,可有效避免多重极值问题:4)在有限情景下,CVaR模型可归结为线性规划问题,因而易于求解与扩展,适合于求解大规模投资组合优化问题;5)CVaR为下行风险度量,适合于求解包含期权等衍生品的投资组合优化问题。
再次,本文详细讨论了CVaR以及CVaR模型,构建了基于短期CVaR约束的长期CVaR模型,并利用由滤波历史模拟法产生的收益率情景对模型做了实证模拟。
对于基金公司等机构投资者而言,基于短期CVaR约束的长期CVaR模型具有一定的实用价值。
通过该模型,基金公司可在控制组合短期风险的条件下使得长期均值-CVaR关系达最优,从而在不改变长期投资目标的情况下降低因市场下滑带来的赎回风险等短期风险。
证券投资分析

证券投资分析证券投资分析指的是对证券市场上的股票、债券、期货等金融工具进行系统的分析和评估,以便替投资者选择最佳的投资策略。
随着金融市场的不断发展和国家政策的支持,证券投资成为了各类投资人的选择,而对于证券投资的分析,是正确决策的基础。
一、证券投资的基本知识1. 股票股票是公司发行的证明持有者在该公司享有所有权和分配权利的股份凭证。
股票的收益主要来源于股息和资本收益。
股票与公司的业绩、市场风险等有关,是风险较大的投资方式。
2. 债券债券是债务人发行的债权凭证,是从发行人处借入资金并承诺还本付息的凭证。
债券的收益主要来源于固定的利息,是风险较小的投资方式。
3. 期货期货是在期货交易所交易的、未来交割的标准化合约,主要包括农产品、能源、金属、金融等品种,期货的收益主要来源于升水或贴水。
二、证券投资分析的要点1. 基本面分析基本面分析是对上市公司的财务状况、业务发展情况、经营管理、产业政策等进行分析的方法。
通过对基本面的分析,可以判断一家公司的价值,从而决定是否持有或卖出该公司的股票。
2. 技术面分析技术面分析是通过对证券价格、成交量、市场情绪等的图表分析,以判断市场趋势、支撑和阻力位、买卖信号等,从而决定证券的买入和卖出时机。
3. 行业分析行业分析是对所处行业发展趋势、市场份额、产业链布局、政策环境等的分析,从中寻找优秀企业进行投资。
对于投资者来说,选择正确的行业极其重要,尤其是未来前景看好的行业,投资回报率可能会比行业平均水平更高。
三、如何进行证券投资分析1. 宏观经济环境的分析经济政策、货币政策、利率政策、财政政策、经济周期等对证券市场的影响非常重要,因此了解经济环境对证券的影响,可以更好地把握市场的走向。
2. 公司财务报表的分析公司财务报表包括资产负债表、现金流量表、利润表等,是进行基本面分析的重要依据。
通过对公司财务报表的分析,可以了解公司的财务状况、盈利能力、发展潜力等。
3. 技术面的分析技术面分析主要包括K线图、均线、MACD、RSI等分析方法,通过这些技术指标的分析可以更好地把握市场变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
引言
证券市场价格的波动主要是受市场供应和需求等基本因素的影响,任何减少供应和资金增加的因素,将导致价格是上涨的的变化,反之,任何增加供应或减少资金流入的因素,将导致价格下跌。
然而,随着现代经济的发展,一些非供求因素也对市场价格的变化起到越来越大的作用,这就使投资市场变得更加复杂。
更加难以预料。
这一切不确定性使得怎样在金融市场尤其是证券市场中在保证一定收益的同时尽可能地减少风险成为了投资者以及金融学家主要讨论的一个问题。
在过去几百年的金融市场发展过程中,人们发现,投资者手中持有多种不同风险的证券,可以减轻所遇风险带来的损失。
对于投资若干种不同风险与收益的证券形成的证券组,称为证券投资组合。
在传统的投资分析中,大都以定性的方法来说明证券投资组合的收益和风险,本文就证券投资组合的概率统计原理作简要探讨,使投资者从定量的方法上对证券投资组合能减轻所遇风险带来的损失有深刻的了解。
并介绍多种证券投资组合方案的选择及如何在多种证券中选出几种进行投资组合。
一、证券投资组合理论简介
证券投资组合理论是由美国经济学家哈里·马柯威茨等人建立的,其主要内容是在投资者为追求高的投资预期收益,并希望尽可能躲避风险的前提下,阐述了一整套理论框架,并运用一套数理统计方法,以解决如何最有效地分散组合证券风险,求得最大收益。
其立论是,人们在任何投资预期收益上,宁愿证券组合的风险承受是最小的,而在任何既定的投资风险上,要追求投资预期收益的最大化。
均值方差理论奠定了证券组合理论的基本框架,通过风险测量较为准确地计算出投资者收益和成本遭受损失的可能性大小,在此基础上,经过许多学者的不断完善和发展,证券组合理论逐渐形成。
特别是概率论在证券组合理论中关于风险与收益的计量中起到了不可忽视的作用。
二、证券组合收益与风险的计算
证券投资中,假定对证券A投资100元,收益的概率分布为:负收益(即损
此它们的平均收益(期望值)都是:
收益的风险(方差)都是
假定A,B两种证券不相关,即相关系数ρAB=0。
如果有资金100元,50元投资于证券A,50元投资于证券B,这种投资组合相当于A和B的一个线性组
合
由期望收益与收益的风险(方差)公式得:
得它们的收益期望值为:
风险(方差)为:
从上述结果我们看到一个重要结论:组合证券的收益不变,而风险比原来的风险减小了。
三、证券投资组合方案的选择
多种证券投资组合的原则是,组合期望收益愈大愈好,组合标准差越小越好。
即如果说选择证券A优于选择证券B,那么下列不等式中有且至少有一个不等式成立:
但在同一证券市场中,一般的情形是:一种证券的平均收益愈大,收益的方差(风险)也愈大。
因此,上述选择的准则似乎没有什么实用价值,然而,考虑到均值和方差之间的抵换作用,就可以发现它的潜在价值。
什么是抵换作用呢?看下面的例子:假如证券A和证券B的标准差及均值分别是(0.2,0.2)和(0.3,0.1)。
若按比例χA,(1-χA),(其中0≤χA≤1)购买证券A和B,这种证券组合的平均收益将是:
E(AB)=χAEA+(1-χA)EB
方差为:
假定:ρAB=0.2,按不同的χA(7个)可得7个投资方案的期望收益和标
把这七个投资方案绘入以χA为横坐标,σ为纵坐标的坐标系中,得到一条曲线,事实上,此曲线就是当χA在(0,1)区间上连续变化时,所得的曲线,称为A、B组合的有效前沿,投资者可根据自己的偏好,在有效前沿上选择投资。
对于不同的ρAB,可得到不同的曲线,也就是可以得到不同的有效前沿,从而决定资金的分配比例。
具体选择投资组合时,也可以把投资人的无差别区线绘入χA,σ坐标系中,在无差别曲线与有效前沿相切处的投资组合为最优方案,这里不作详细讨论。
四、相关系数对证券组合风险的影响
相关系数是反映两个随机变量之间共同变动程度的相关关系数量的表示。
对证券组合来说,相关系数可以反映一组证券中,每两组证券之间的期望收益作同方向运动或反方向运动的程度。
相关系数的绝对值小于等于1,即-1≤ρ≤1,当0<ρ≤1时,称为正相关,表示两种证券的收益作同方向运动,即一种证券的收益增加或减小,另一种证券的收益也增加或减小。
ρ越接近于1,一种证券收益增减值与另一种证券的收益增减值越接近。
组合期望收益在两种证券的收益之间是同一趋势波动。
这个结果意味着投资组合并不收到降低风险的效果。
当ρ=0时表示一种证券的期望收益的变动,对另一种证券收益丝毫不产生影响。
这个组合结果,意味着可能降低部分风险,也可能不能降低风险。
当-1≤ρ<0,称为负相关,表示两种证券的收益作反方向运动。
即一种证券的期望收益增加或减小,另一种证券的收益则减小或增加,这种证券组合期望收益变化较为平缓。
取得了降低风险的效果。
可见,在多种证券中,要选几种证券进行组合投资,应选相关度较低的证券组合,比如说不同行业类型的证券;不同市场中的证券;不同种类的资产,等等。
在理论中我们假设存在不相关、甚至负相关的证券。
但在经验中我们几乎找不到不相关或负相关的证券。
以美国股票市场为例,股票收益率之间的相关系数多数介于0.5-0.6之间。
因此,分散投资降低组合风险可能达不到理论预期效果,但是为了尽可能地降低组合的风险,我们在投资过程中应该尽量选择相关度较低的证券进行资产组合。
