2015年春季新版苏科版八年级数学下学期周周练习试卷112

合集下载

2015年春季新版苏科版八年级数学下学期周周练习试卷72

泗洪育才实验学校八年级数学第一次周测试卷（满分：100分时间：80分钟）班级姓名学号得分一、选择题（每小题3分，共24分）1．下列调查工作需采用的普查方式的是（）A ．环保部门对淮河某段水域的水污染情况的调查B ．电视台对正在播出的某电视节目收视率的调查C ．质检部门对各厂家生产的电池使用寿命的调查D ．企业在给职工做工作服前进行的尺寸大小的调查2．要反映宿迁市一周内每天的最高气温的变化情况，宜采用（）A ．条形统计图B ．扇形统计图C ．折线统计图D ．频数分布直方图3．为了了解某县八年级学生的体重情况，从中抽取了200名学生进行体重测试 .在这个问题中，下列说法错误的是（）A ．全县八年级学生的体重是总体。

B ．200名学生的体重是一个样本。

C ．每个学生的体重是一个个体。

D ．200名学生的体重是总体4．对某班40同学的一次数学成绩进行统计，适当分组后80～90分这个分数段的划记人数为“正”，那么此班在这个分数段的人数占全班人数的百分比是（）A ．20%B ．40%C ．8%D ．25%5．在整理数据5，5，3，■，2，，4时，■处的数据看不清，但从扇形统计图的答案上发现数据5的圆心角是1800，则■处的数据是（）A ．2B ．3C ．4D ．56．下图是某厂2007年各季度产值统计图（单位：万元）：则下列说法正确的是（）A ．四季度中，每季度生产总值有增有减B ．四季度中，前三个季度的生产总值增长较快C ．四季度中，各季度的生产总值变化一样D ．第四季度生产总值增长最快7第二季度比第一季度增长8．如图的两个统计图，女生人数多的学校是（）A ．甲校B ．校C ．甲、乙两校女生人数一样多D ．无法确定二、填空题（每题3分，共24分） 7题第8题9．某中学要了解初二学生的视力情况，在全校初二年级中抽取了25名学生进行检测，在这个问题中，总体是 _________ ，样本是 _________ ．样本容量是．10．常用统计图的类型有： _________ 、 _________ 、 _________ ．11．在对25个数据进行整理的频数分布表中，各组的频数之和等于______，各组的频率之和等于__________．12．某中学数学教研组有25名教师，将他们按年龄分组，在38~45岁组内的教师有8名教师，那么这个小组的频率是．13．某图书馆有A 、B 、C 三类图书，它的扇形统计图如图所示，那么（1）A 类图书所占百分比为 %；（2）若B 类图书有420万册，则C 类图书有___ 册．A 类书有册。

苏科版2014-2015学年度第二学期期末考试八年级数学试题(二)

苏科版2014-2015学年度第二学期期末考试八年级数学模拟试题（二）（满分：150分时间：120分钟）一、选择题：（每小题3分，共30分，）1．下列调查适合普查的是A ．夏季冷饮市场上冰淇淋的质量B ．某本书中某页的印刷错误C ．公民保护环境的意识D ．某批灯泡的使用寿命2．下列事件是随机事件的是A ．没有水分，种子发芽B ．367人中至少有2人的生日相同C ．在标准气压下，－1℃冰融化D ．小瑛买了一张彩票获得500万大奖 3．下列是中心对称图形的是4．下列各式成立的是A ．()23434+=+B ．223434+=+C ．21122⎛⎫-=± ⎪⎝⎭D ．21122⎛⎫-=- ⎪⎝⎭ 5．下列分式中，属于最简分式的是A ．42xB ．221x x +C ．211x x --D ．11x x -- 6．在反比例函数2k y x-=图象的每个象限内，y 随x 的增大而减少，则k 值可以是 A ．3B ．2C ．1D ．－1 7．如图，在等腰梯形ABCD 中，AD ∥B C ，AB ＝AD ＝DC ，∠B ＝60°，DE//AB ，梯形ABCD 的周长等于20 cm ，则DE 等于A ．6 cmB ．5 cmC ．4 cmD ．3 cm8．如图，将矩形ABCD 绕点A 顺时针旋转到矩形AB'C'D'的位置，旋转角为α（0°<α<90°）．若∠1＝112°，则∠α的大小是A ．68°B ．20°C ．28°D ．22°9．已知m 是2的小数部分，则2212m m +-的值是 A ．0 B ．1 C ．2 D ．310．如图，正方形ABCD 内有两点E 、F 满足AE ＝4，EF ＝FC ＝12，AE ⊥EF ，CF ⊥EF ，则正方形ABCD 的边长为A ．252B ．102C ．20D ．202 二、填空题：(本大题共8小题，每小题4分，共32分，把答案直接填在答题卷相对应的位置上)11．当x 等于时，分式223x x --无意义．12．化简82-的结果是 ▲13．向如图所示的正三角形区域扔沙包（区域中每一个小正三角形除颜色外完全相同），假设沙包击中每一个小三角形是等可能的，扔沙包1次击中阴影区域的概率等于 ▲ ．14．反比例函数y ＝k x的图象过点P(2,6)，那么k 的值是． 15．化简113232+-+＝． 16．若a <1，化简()211a --的结果为． 17．设a >b >0．a 2＋b 2＝4ab ，则22a b ab -的值等于．18．如图，已知双曲线y ＝k x(k>0)经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若△OBC 的面积为3，则k ＝ ▲ ．三、解答题：(共88分，）19．化简与计算（本题满分24分，每小题6分） (1)114224÷； (2)()2312603a b b b ⎛⎫∙-≥ ⎪⎝⎭ (3)、10112()32(3)2π-+----; (4) 22)232(1)-2(2÷--;20．（本题满分12分，每小题6分）解下列方程：(1)30201x x =+ (2)11322x x x-=---21．（本题满分8分）先化简，再求值：2111211x x x x x x +⎛⎫+÷⎪--+-⎝⎭，其中x ＝21+．22．（本题满分12分）今年某中学到“格林乡村公园”植树，已知该中学离公园约15km ，部分学生骑自行车出发40分钟后，其余学生乘汽车出发，汽车速度是自行车速度的3倍，全体学生同时到达，设自行车的速度为v km/h ．(1)用v 分别表示自行车和汽车从学校到公园所用的时间；(2)求v 的值； (3)植树活动完成后，由于学生比较劳累，骑自行车的学生的速度变为原来的23，汽车速度不变，为了使两批学生同时到达学校，那么骑自行的学生应该提前多少时间出发．23．（本题满分10分）某校为了提高学生的身体素质，每年都举行“冬季三项比赛”，要求每位同学都从“跳绳、踢毽子、长跑”三个项目中选取一个项目参加比赛．为了便于学校安排场地，体育组老师随机抽取了部分学生，对他们报名情况进行调查，并根据调查收集的数据绘制了如下两幅不完整的统计图：根据上述信息，解答下列问题：(1)将两幅统计图补充完整；(2)抽取的学生人数为 ▲ ；(3)若该校有1200名学生，试计算抽取的比例，并估计该校中选择“长跑”的人数．24．（本题满分10分）如图，在矩形ABCD中，点E在AD上，且EC平分∠BED．(1)△BEC是否为等腰三角形？请给出证明；(2)若AB＝1，∠ABE＝45°，求矩形的面积．25．（本题满分12分）某种商品上市之初采用了大量的广告宣传，其销售量与上市的天数之间成正比，当广告停止后，销售量与上市的天数之间成反比（如图所示），现己知上市30天时，当日销售量为120万件．(1)写出该商品上市以后销售量y（万件）与时间x（天数）之间的表达式；(2)求上市至第100天（含第100天），日销售量在36万件以下（不含36万件）的天数；(3)广告合同约定，当销售量不低于100万件，并且持续天数不少于12天时，广告设计师就可以拿到“特殊贡献奖”，问题本次广告策划，设计师能否拿到“特殊贡献奖”？（说明：天数可以为小数，如3.14天等．）。

苏科版使用地区2015年八年级第二学期学期调查数学试卷

二、填空题：（本大题共 8 小题，每题 3 分，共 24 分）
11．调查市场上某种食品的色素含量是否符合国家标准，这种调查适用或者“抽样调查” ）
12．某中学要了解八年级学生的视力情况，在全校八年级中抽取了 30 名学生进行检测，在这个问题中，总体是 ______ ___ ，样本是 _________ ．，∠D＝．
5．下列事件是必然发生事件的是„„„„„„„„„„„„„„„„„„„„„（） A．打开电视机，正在转播足球比赛； B．小麦的亩产量一定为 1500 千克； C．在只装有 5 个红球的袋中摸出 1 球，是红球； D．农历十五的晚上一定能看到圆月； 6．如图，直线 l 是一条河，P，Q 是两个村庄．计划在 l 上的某处修建一个水泵站 M，向 P， Q 两地供水．现有如下四种铺设方案（图中实线表示铺设的管道），则所需管道最短的是„„ （）
A．1 个
B．2 个
C．3 个
D．4 个
3．如图是一个风筝设计图，其主体部分（四边形 ABCD）关于 BD 所在的直线对称，AC 与 BD 相交于点 O，且 AB≠AD，则下列判断不正确的是„„„„„„„„„„„„„„„„„ （） A．△ABD≌△CBD B．△ABC 是等边三角形 C．△AOB≌△COB D．△AOD≌△COD 4．已知：一次函数 y＝(a－1)x＋b 的图象如图所示，那么 a 的取值范围是„„„„„„„„ （） A．a＞1 B．a＜1 C．a＞0 D．a＜0
．（填“普查”
13．在平行四边形 ABCD 中，∠B+∠D＝200o, 则∠A＝
14．点 A（－3，4）关于原点对称的点的坐标为______________． 15．函数 y＝kx＋b（k≠0）的图象平行于直线 y＝2x＋3，且交 y 轴于点（0，－1），则其函数表达式是． 16．如图，已知函数 y1＝2x－1 和 y2＝x－3 的图像交于点 P(－2，－5)，则根据图像可得不等式 y1＞y2 的解集是． 17．如图，在△ABC 中，∠BAC=90°,AB=6，AC=8，点 P 是 BC 边上任意一点（B、C 除外）PD ⊥AB 于点 E，PF⊥AC 于点 F，连接 EF,则 EF 的最小值为． 18．如图，在 Rt△ABC 中，∠ACB＝90°，AB＝5cm，BC＝4cm．动点 D 从点 A 出发，以每秒 1cm 的速度沿射线 AC 运动，当 t＝时，△ABD 为等腰三角形．

2015～2016学年苏科版初二数学第二学期期末测试卷有答案

2015～2016学年第二学期初二数学期末试卷一.选择题（共10小题，每小题3分，共30分） 1．（2015•重庆）下列调查中，最适宜采用全面调查方式（普查）的是……………………（） A ．对重庆市中学生每天学习所用时间的调查；B ．对全国中学生心理健康现状的调查； C ．对某班学生进行6月5日是“世界环境日”知晓情况的调查； D ．对重庆市初中学生课外阅读量的调查；2．下列标识中，既是轴对称图形，又是中心对称图形的是…………………………（）A ．B ．C ．D ．3．分式的值为0，则…………………………………………………………（）A ． x=﹣2B ． x=±2C ． x=2D ． x=0 4．若反比例函数图象经过点（﹣1，6），则此函数图象也经过的点是………………（） A ．（6，1） B ．（3，2） C ．（2，3） D ．（﹣3，2）5．（）A B C D 6．下列等式一定成立的是……………………………………………………………（）A =B =；C 3±；D ．；7．（2015•巴中）下列说法中正确的是………………………………………………（） A ．“打开电视，正在播放新闻节目”是必然事件B ．“抛一枚硬币，正面向上的概率为12”表示每抛两次就有一次正面朝上； C ．“抛一枚均匀的正方体骰子，朝上的点数是6的概率为16”表示随着抛掷次数的增加，“抛出朝上的点数是6”这一事件发生的频率稳定在16附近；D ．为了解某种节能灯的使用寿命，选择全面调查； 8．函数y=kx+1与函数ky x=在同一坐标系中的大致图象是……………………（）A ．B ．C ．D ．9．如图，正比例函数1y 与反比例函数2y 相交于点E （﹣1，2），若1y ＞2y ＞0，则x 的取值范围是（）A ． x ＜﹣1；B ． ﹣1＜x ＜0；C ． x ＞1；D ． 0＜x ＜1；10.如图，已知四边形OABC 是菱形，CD ⊥x 轴，垂足为D ，函数4y x=的图象经过点C ，且与AB 交于点E ．若OD=2，则△OCE 的面积为………………………………………………（） A ．2B ．4C．D．二.填空题（共8小题，每小题3分，共24分） 111= ；12．一个口袋中装有4个白色球，1个红色球，7个黄色球，搅匀后随机从袋中摸出1个球是黄色球的概率是． 13．若双曲线21k y x-=的图象经过第二、四象限，则k 的取值范围是． 14()210n +=，则m n -的值为． 15．若关于x 的方程2111x m x x ++=--产生增根，则m = ． 16．如图，▱ABCD 的对角线AC ，BD 相交于点O ，点E ，F 分别是线段AO ，BO 的中点．若AC+BD=24厘米，△OAB 的周长是18厘米，则EF= 厘米． 17．如图，矩形ABCD 的对角线AC 、BD 相交于点O ，∠AOB=120°，CE ∥BD ，DE ∥AC ，若AD=4，则四边形CODE 的周长．18．如图，已知点A 是双曲线y =3x在第一象限上的一动点，连接AO ，以OA 为一边作等腰直角三角形AOB (∠AOB =90°)，点B 在第四象限，随着点A 的运动，点B 的位置也不断的变化，但始终在一函数图像上运动，则这个函数关系式为．第10题图第9题图第17题图第16题图第18题图三.解答题（共10小题，共76分） 19．计算：（1）（2）22111121x x x x x x x ++⎛⎫+÷ ⎪---+⎝⎭；20．解方程：（1）=（2）= ﹣3．21．先化简，再求值：221a b a b a b⎛⎫-÷⎪--⎝⎭，其中1a ，1b =．22．如图，平行四边形ABCD 中，EF 过AC 的中点O ，与边AD 、BC 分别相交于点E 、F ．（1）试判断四边形AECF 的形状，并说明理由．（2）若EF ⊥AC ，试判断四边形AECF 的形状，并说明理由．（3）请添加一个EF 与AC 满足的条件，使四边形AECF 是矩形，并说明理由．23. 如图，平行四边形ABCD 放置在平面直角坐标系A （-2，0）、B （6，0），D （0，3），反比例函数的图象经过点C ．（1）求点C 的坐标和反比例函数的解析式；（2）将四边形ABCD 向上平移m 个单位后，使点B 恰好落在双曲线上，求m 的值．24．（2015•岳阳）某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项）．根据调（1）频数分布表中的m= ，n= ；（2）在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为；（3）从选择“篮球”选项的30名学生中，随机抽取3名学生作为代表进行投篮测试，则其中某位学生被选中的概率是．25．如图，已知反比例函数1ky x=和一次函数2y ax b =+的图象相交于点A 和点D ，且点A 的横坐标为1，点D 的纵坐标为-1．过点A 作AB ⊥x 轴于点B ，△AOB 的面积为1．（1）求反比例函数和一次函数的解析式．（2）若一次函数2y ax b =+的图象与x 轴相交于点C ，求∠ACO 的度数．（3）结合图象直接写出：当12y y >时，x 的取值范围．26.（2015•济南）济南与北京两地相距480km ，乘坐高铁列车比乘坐普通快车能提前4h 到达，已知高铁列车的平均行驶速度是普通快车的3倍，求高铁列车的平均行驶速度．27．如图1，在平面直角坐标系中，等腰Rt △AOB 的斜边OB 在x 轴上，直线y=3x-4经过等腰Rt △AOB 的直角顶点A ，交y 轴于C 点，双曲线ky x=（x ＞0）也恰好经过点A ．（1）求k 的值；（2）如图2，过O 点作OD ⊥AC 于D 点，求22CD AD -的值；（3）如图3，点P 为x 轴上一动点．在（1）中的双曲线上是否存在一点Q ，使得△PAQ 是以点A 为直角顶点的等腰三角形．若存在，求出点P 、点Q 的坐标，若不存在，请说明理由．28. 如图，已知四边形ABCD 是平行四边形，AC 为对角线，∠DAC=30°，∠ACD=90°，AD=8，点M 为AC 的中点，动点E 从点C 出发以每秒1个单位的速度运动到点B 停止，连接EM 并延长交AD 于点F ，设点E 的运动时间为t 秒．（1）求四边形ABCD 的面积；（2）当∠EMC=90°时，判断四边形DCEF的形状，并说明理由；（3）连接BM，点E在运动过程中是否能使△BEM为等腰三角形？如果能，求出t；如果不能，请说明理由．参考答案一、选择题：1.C ；2.A；3.C；4.C；5.D；6.B；7.C；8.A；9.A；10.C；二、填空题：1；12. 712；13. 12k <；14.2；15.2；16.3；17.16；18. 3y x=；三、解答题：19.（13；（2）1x -； 20.（1）3x =-；（2）2x =；21. a b +=22. 解：（1）四边形AECF 的形状是平行四边形，理由是：∵平行四边形ABCD ，∴AD ∥BC ，∴∠DAO=∠ACF ，∠AEO=∠CFO ， ∵EF 过AC 的中点O ，∴OA=OC ，在△AEO 和△CFO 中∠EAO ＝∠OCF ，∠AEO ＝∠CFO ，OA ＝OC ，∴△AEO ≌△CFO ， ∴OE=OF ，∵OA=CO ，∴四边形AECF 是平行四边形，（2）四边形AECF 是菱形，理由是：由（1）知四边形AECF 是平行四边形， ∵EF ⊥AC ；∴四边形AECF 是菱形．（3）添加条件：EF=AC ，理由是：由（1）知四边形AECF 是平行四边形， ∵EF=AC ，∴四边形AECF 是矩形．23.（1）C （8，3），24y x=；（2）4m =；24.（1）24，0.3；（2）108°；（3）110；25.（1）12y x=，21y x =+；（2）45°；（3）2x <- 或01x <<；26.240； 27. 解：（1）过点A 分别作AM ⊥y 轴于M 点，AN ⊥x 轴于N 点，△AOB 是等腰直角三角形，∴AM=AN ．∴可设点A 的坐标为（a ，a ），点A 在直线y=3x-4上，∴a=3a-4，解得a=2，则点A 的坐标为（2，2）．将点A （2，2）代入反比例函数的解析式为ky x=，求得k=4．则反比例函数的解析式为4y x =．（2）点A 的坐标为（2，2），在Rt △AMO 中，222AO AM MO =+=4+4=8． ∵直线AC 的解析式为y=3x-4，则点C 的坐标为（0，-4），OC=4．在Rt △COD 中，222OC OD CD =+（1）；在Rt △AOD 中，222AO AD OD =+（2）；（1）-（2），得2222CD AD OC OA -=-=16-8=8．（3）双曲线上是存在一点Q （4，1），使得△PAQ 是等腰直角三角形．过B 作BQ ⊥x 轴交双曲线于Q 点，连接AQ ，过A 点作AP ⊥AQ 交x 轴于P 点，则△APQ 为所求作的等腰直角三角形．在△AOP 与△ABQ 中，∠OAB-∠PAB=∠PAQ-∠PAB ，∴∠OAP=∠BAQ ，AO=BA ，∠AOP=∠ABQ=45°，∴△AOP ≌△ABQ （ASA ），∴AP=AQ ，∴△APQ 是所求的等腰直角三角形．∵B （4，0），点Q 在双曲线4y x=上，∴Q （4，1），则OP=BQ=1．则点P 、Q 的坐标分别为（1，0）、（4，1）．28. 解：（1）（2）如图1，当∠EMC=90°时，四边形DCEF 是菱形．∵∠EMC=∠ACD=90°，∴DC ∥EF ．∵BC ∥AD ，∴四边形DCEF 是平行四边形，∠BCA=∠DAC ．由（1）可知：CD=4，AC=∵点M 为AC 的中点，∴CM= Rt △EMC 中，∠CME=90°，∠BCA=30°．∴CE=2ME ，可得(()2222ME +=，解得：ME=2．∴CE=2ME=4．∴CE=DC ．又∵四边形DCEF 是平行四边形， ∴四边形DCEF 是菱形．（3）点E 在运动过程中能使△BEM 为等腰三角形．理由：如图2，过点B 作BG ⊥AD 与点G ，过点E 作EH ⊥AD 于点H ，连接DM ． ∵DC ∥AB ，∠ACD=90°，∴∠CAB=90°．∴∠BAG=180°-30°-90°=60°．∴∠ABG=30°．∴AG=12AB=2，BG=∵点E 的运动速度为每秒1个单位，运动时间为t 秒， ∴CE=t ，BE=8-t ．在△CEM 和△AFM 中∠BCM ＝∠MAF,MC ＝AM,∠CME ＝∠AMF,∴△CEM ≌△AFM ．∴ME=MF ，CE=AF=t ．∴HF=HG-AF-AG=BE-AF-AG=8-t-2-t=6-2t ．∵EH=BG= Rt △EHF 中，ME=12=∵M 为平行四边形ABCD 对角线AC 的中点，∴D ，M ，B 共线，且DM=BM ．∵在Rt △DBG 中，DG=AD+AG=10，BG=BM=12⨯=要使△BEM 为等腰三角形，应分以下三种情况：当EB=EM 时，有()()221812624t t ⎡⎤-=+-⎣⎦，解得：t=5.2．当EB=BM 时，有8-t=t=8-当EM=BM 时，由题意可知点E 与点B 重合，此时点B 、E 、M 不构成三角形．综上所述，当t=5.2或t=8-时，△BEM 为等腰三角形．。

2015年春季新版苏科版八年级数学下学期周周练习试卷128

江苏省张家港市第一中学2013-2014学年八年级数学下学期测试题（第五周双休日作业）班级姓名学号1.能够找到一点，使该点到各边距离都相等的图形为（） ①平行四边形 ②菱形 ③矩形 ④正方形A ．①与②B ．②与③C ．②与④D ．③与④2.矩形、菱形、正方形都具有的性质是 ( ) A ．每一条对角线平分一组对角 B ．对角线相等 C ．对角线互相平分 D ．对角线互相垂直3.．在菱形ABCD 中，对角线AC 、BD 相交于点O ，E 为AB 的中点，且OE=a ，则菱形 ABCD 的周长为 A ．16a B ．12a C ．8a D ．4a ( )4.如图，E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE=DF ，AE 、BF 相交于点O ，下列结论：①AE=BF ；②AE ⊥BF ；③AO=OE ；④S △AOB =S 四边OEDF ，其中错误的有 A ．1个 B ．2个 C ．3个 D ．4个（）5.如图，直线AB 交y 轴于点C ，与双曲线1y x=(k ＜0)交于A 、B 两点，P 是线段AB 上的点(不与A 、B 重合)，Q 为线段BC 上的点(不与B 、C 重合)，过点A 、P 、Q 分别向x 轴作垂线，垂足分别为D 、E 、F ，连结OA 、OP 、OQ ，设△AOD 的面积为S 1、△POE 的面积为S 2、△QOF 的面积为S 3，则有（） A ．S 1＜S 2＜S 3 B ．S 3＜S 1＜S 2 C ．S 3＜S 2＜S 1 D ．S 1、S 2、S 3 相等 6.如图，已知点A是一次函数y =的图象与反比例函数ky x =点，AB ⊥x 轴于点B ，点C 在x轴的负半轴上，且OA=OC ，△AOB的面积为2，则AC的长为 A B ．．．4 （）7.反比例函数3k y x-=图象的每一支曲线上，y 都随x 的增大而减小，则k 的取值范围是（）A ．k ＞3 B ．k ＞0 C ．k ＜3 D ． k ＜08、在反比例函数y=x2的图象中，阴影部分的面积不等于2的是（）9.如果函数122--=m x m y 是反比例函数，则=m （） A、0 B 、10.如果一个平行四边形的对角线长分别为8和6，那么这个平行四边形的边长m 的取值范围是__________．11.在菱形ABCD 中，∠A=60°，对角线BD=8，则菱形ABCD 的周长等于________．ABCDPFEDCBA12.方形ABCD 中，P 为AB 的中点，BE ⊥PD 的延长线于点E,连结AE 、BE 、FA ⊥AE 交DP 于点F ，连结BF,FC.下列结论：①△ABE ≌△ADF ； ②FB=AB ；③CF ⊥DP ；④FC=EF 其中正确的是13.如图，A 、B 是双曲线y=kx (k>0)上的点，A 、B 两点的横坐标分别是a 、2a ，线段AB 的延长线交x 轴于点C ，若AOC S =6．则k=__________．14.如图，若点A 在反比例函数(0)ky k x=≠的图象上， AM x ⊥轴于点M ，AMO △的面积为4，则k = ．15.如图，点A(m ，0)，B(0，n)，直线AB 与反比例函数m y x=的图象交于C 、D 两点．若S △AOD =S △COD =S △COB ，则n 的值为16.若m ＜－1，则下列函数：①x my =;② y =－mx+1; ③y = mx; ④ y =(m + 1)x 中，y 随x 增大而增大的是___________（填序号）。

2015年春季新版苏科版八年级数学下学期周周练习试卷122

江苏省张家港市第一中学2013-2014学年八年级数学下学期测试题（第十二周双休作业）班级姓名学号1．为了了解2014年我市八年级学生学业水平考试的数学成绩，从中随机抽取1000名学生的数学成绩，下列说法正确的是( )A ．2014年我市八年级学生是总体B ．每一名八年级学生是个体C ．1000名八年级学生是总体的一个样本D ．样本容量是10002．下列事件中，属于随机事件的是( )A ．从装有黑球、白球的袋里摸出红球B ．抛出的篮球会下落C ．367人中有2人是同月同日出生D ．买1张彩票，中500万大奖3．如果把223y x y-中的x 和y 都扩大5倍，那么分式的值( ) A ．扩大5倍 B ．不变C ．缩小5倍D ．扩大4倍 4．在下列命题中，正确的是( )A ．一组对边平行的四边形是平行四边形B ．有一个角是直角的四边形是矩形C ．有一组邻边相等的平行四边形是菱形D ．对角线互相垂直平分的四边形是正方形5．为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等，如果设第一次捐款人数为x 人，那么方程是( ) A ．4800500020x x =- B ．4800500020x x =+ C ．4800500020x x =- D ．4800500020x x=+ 6．若23a b =，则2a b a b +=- ． 7．若分式1x x -有意义，则x 的范围是．8．如果分式2424a a --的值为零，那么a 的值为． 9．若关于x 的方程111m x x x ----＝0有增根，则m = ．10．有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面，则钥匙藏在黑色瓷砖下面的概率是．11．如图，□ABCD 的周长为36，对角线AC ，BD 相交于点O ．点E 是CD 的中点，BD ＝12，则△DOE 的周长为．12．如图，已知菱形ABCD 的对角线AC ，BD 的长分别为6cm 、8cm ，AE ⊥BC 于点E ，则AE 的长是 cm ．13．如图，菱形纸片ABCD 中，∠A ＝60°，折叠菱形纸片ABCD ，使点C 落在DP (P 为AB 中点)所在的直线上，得到经过点D 的折痕DE ．则∠DEC 的大小为．14．如图，点E 、F 、G 、H 分别是四边形ABCD 中AD 、BD 、BC 、CA 的中点，当四边形ABCD的边至少满足条件时，四边形EFGH 是菱形．15．计算：(1)222b a ab a b a b b a +--+- (2)265222x x x x -⎛⎫÷-- ⎪--⎝⎭16、解方程：(1)1132422x x +=-- (2)214111x x x +-=--17．先化简：2344111x x x x x -+⎛⎫-+÷ ⎪++⎝⎭，然后从一1≤x ≤2中选一个合适的整数作为x 的值代入求值．18．计算：⎝ ∙19．若x、y是实数，且12，求11yy--的值．20．某校一课外活动小组为了解学生最喜欢的球类运动情况，随机抽查本校九年级的200名学生，调查的结果如图所示．请根据该扇形统计图解答以下问题：（1）求图中的x的值；（2）求最喜欢乒乓球运动的学生人数；（3）若由3名最喜欢篮球运动的学生，1名最喜欢乒乓球运动的学生，1名最喜欢足球运动的学生组队外出参加一次联谊活动．欲从中选出2人担任组长（不分正副），通过画树状图或列表列举所有可能情况，并求2人均是最喜欢篮球运动的学生的概率．21．甲、乙两地相距360千米，新修的高速公路开通后，在甲乙两地之间行驶的长途客运车车速提高了50%，而从甲地到乙地的时间缩短了2小时，试求原来的车速．22．已知关于x的分式方程21ax+-＝1的解是非负数，求a的取值范围．23．如图，将□ABCD的对角线BD向两个方向延长至点E和点F，使BE＝DF，求证：四边形AECF是平行四边形．24．已知：如图，在矩形ABCD中，M，N分别是边AD、BC的中点．E，F分别是线段BM，CM的中点．(1)求证：△ABM≌△DCM；(2)判断四边形MENF是什么特殊四边形，并证明你的结论；(3)当AD：AB＝_______时，四边形MENF是正方形（只写结论，不需证明）25．如图，在平面直角坐标系中，已知四边形ABCD为菱形，且A(0，3)、B（－4，0）．(1)求过点C的反比例函数的表达式；(2)若P是(1)中所求函数图像上一点，以P、O、A为顶点的三角形面积与△COD的面积相等，求点P的坐标．26．如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE(1)求证：CE＝CF；(2)若G在AD上，且∠GCE＝45°，求证：GE＝BE＋GD；(3)在(2)条件下，若BC＝12，BE＝4，求EG的长．。

苏科版八年级数学下册周检1

陆集中学2015年春学期八年级数学第六周周检试卷4.12班级_______姓名___________得分_____________一、填空（每空2分） 1.用分式填空：①小明t 小时走了s 千米的路，则小明的速度是＿＿＿＿千米/时； ②a 千克盐溶于b 千克水，所得盐水的含盐量是＿＿＿＿；③某食堂有煤m 吨，原计划每天烧煤a 吨，现每天节约用煤b （a b <）吨，则这批煤可比原计划多烧________天.④一货车送货上山，上山速度为x 千米/时，下山速度为y 千米/时，则该货车的平均速度为＿＿＿＿千米/时.⑤小明参加打靶比赛,有a 次打了m 环,b 次打了n 环,则此次打靶的平均成绩是________； ⑥一箱苹果售价p 元，总重m 千克，箱重n 千克，则每千克苹果的售价是______元；2.在x 3-、y x 、22732xy y x -、x 81-、y +53、5y x -、πy x +3中，是分式的有_______________________；3.()()23+÷-m m 写成分式为____________，且当m ≠_____时分式有意义；4.当x________时，分式521--x x无意义，当x________时，分式的值为1； 5.当x= 时，分式112--x x 的值是0。

6、分式和的最简公分母是__________．6x 2y 54xy 37、21()()2()x x xy y x ==-- 8、若32=n m ，则=-+n m n m ；若313=-x y x ，则=y x .二、选择（每题3分） 9.下列各式①x 2，②5y x +，③a -21，④1-πx 中，是分式的有 ( ) A ①②. B.③④ C.①③ D.①②③④ 10. 当x=-2时,分式①32--x x ，②22+-x x ，③()()()()3232--++x x x x ，④()()()()3232-+++x x x x 中有意义的有 ( ) A.只有① B.只有④ C.①③ D.②④ 11.若分式x231-的值为正数，则x 的取值应是 ( ) A.0>x ， B.23=x C. 23<x D.x 为任意实数 12.要使xyyx +有意义，则下列说法中正确的是 ( ) A.x 、y 全不为零; B.0=x 或0=y ; C.x 、y 不全为零; D. x 、y 全为零 13.当x 为任意实数时，下列分式中，一定有意义的是 ( )A.21x x - B.112-+x x C.112+-x x D.21+-x x14.如果分式212-+-x x x 的值为0，那么x 的值是( )A.±1B.1C.-2D.-115、分式n m a--与下列分式相等的是（） A .n m a - B. n m a +- C. n m a + D. am n-+16、已知0≠x ，xx x 31211++等于（）、 A 、x 21 B 、x 61 C 、x 65 D 、x611三、解答题（共42分）17..当x 取什么值时，下列分式的值为零？（每题3分，共6分）（1）77--x x ；（2）362--x x .18、约分：（每题3分，共18分）（1（2（3）232636yz z xy - （4（5）2224m m m +- （6） 44422-+-a a a19、通分：（每题3分，共18分）（1）231x ，xy 125；（2）xy c z xy x y 34,65,222；（3）x x +21，xx -21.；（4）x x +21，1212++-x x ；（5）2142,,242x x x x+--；（6）32)(,)(x y x y x x y --；初中数学试卷。

江苏省连云港2015-2016学年八年级数学下册第2周周测试题

广东省揭阳市普宁华侨管理区中学2015-2016学年八年级数学下学期第一次月考试题一、选择题（共10题，每小题3分，共30分）1. 下列条件中能判定△ ABCDEF的是（）A. AB = DE , BC = EF ,Z A =Z DB.Z A =Z D,Z B =/ E,Z C=Z FC. AC = DF ,Z B=Z F, AB = DE D . Z B=Z E ,Z C =/ F, AC = DF2. 下列命题中正确的是（）A .有两条边相等的两个等腰三角形全等B .两腰对应相等的两个等腰三角形全等C .两角对应相等的两个等腰三角形全等D .一边对应相等的两个等边三角形全等3. 对“等角对等边”这句话的理解，正确的是（）A .只要两个角相等，那么它们所对的边也相等B. 在两个三角形中，如果有两个角相等，那么它们所对的边也相等C .在一个三角形中，如果有两个角相等，那么它们所对的边也等AD. 以上说法都是正确的4. 已知，如图1,在厶ABC中，OB和OC分别平分Z ABC和ZACB,过O 作DE // BC,分别交AB、AC 于点D、E，若BD+CE=5,则线段DE的长为（）B. 6图1图1C . -2x ：： -2 yD . -3x 6-3y 65.已知：在△ ABC 中，AB 半AC ,求证：/ B ^Z C .若用反证法来证明这个结论，可以假设（）Z B =Z C关系为7.以下各组数为三角形的三条边长，其中能作成直角三角形的是A . 2, 3, 4B . 4, 5, 6C . 1, 2 , 3D . 2, 2 , 48.函数y = kx + b （k 、b 为常数，k = 0）的图象如图3所示，则关于 x 的不等式kx+b>0的解集为（）.A . x>0B . x<0图3C . x<2D . x>29.已知x y ，则下列不等式不成立的是 A . x -6 y -6 B . 3x 3yB . AB = BC6.如图2,A ABC 与厶BDE 都是等边三角形, 不动，将△ BDC 绕B 点旋转，则在旋转过程中,AE 与CD 的大小A . AE = CDB . AE>CDC AEVCD D .无法确定).AB<BD .若△ ABC15 如果 1VXV2，贝卩（x -1）（x -2） 0.（填写“ >”、“V ”10.如图4所示，一次函数y=kx + b （ k 、b 为常数，且k-0）与正比例函数y = ax （a 为常数，且a = 0）相交于点P ,则不等式kx+b>ax 的解集是（）二、填空题（共6题，每小题4分，共24 分）11.已知：如图5, AB = AC , FD 丄BC 于D , DE 丄AB 于E ,若/和为12cm,那么斜边长为 ___________ 13如图6, ED ABC 的AC 边的垂直平分线，且 AB=5cm ,ABCE 的周长为8cm ,则BC = _________ 14如图7,在厶ABC 中，/ C = 90°,/ B = 15°, AB 的垂直平分线交BC 于D ，交AB 于E ,若DB = 10cm ,则AC = ____________ ・AFD = 145° 则/12在直角三角形中，如果一个锐角为 30 °,而斜边与较小直角边的图4D . x<2图5或“=”16已知点P ( m —3 , m + 1)在第一象限，则m的取值范围是__________________ .三、解答题(4X2 + 6 + 10 + 8 + 8 + 5 + 6 + 6 + 9=) r 2—x+5>1-x17(1)解不等式组,并写出它的非负整数解。

苏科版八年级(下)数学周周练(11)及答案

八年级数学(下)周周练11（10.4-10.5）一、选择题1．下列命题：①三边对应成比例的两个三角形相似；②两边对应成比例且一个角对应相等的两个三角形相似；③一个锐角对应相等的两个直角三角形相似；④有一个角对应相等的两个等腰三角形相似，其中正确的是( ) A．①③B．①④C．①②④D．①③④2．下列命题错误的是( ) A．两角对应相等的两个三角形相似B．两边对应成比例的两个三角形相似C．两边对应成比例且夹角相等的两个三角形相似D．三边对应成比例的两个三角形相似3．如图，E是□ABCD的边BC延长线上的一点，连接AE交CD于点F，则图中共有相似三角形( )A．1对B．2 对C．3对D．4对4．如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3、4和x，那么x的值( ) A．只有1个B．可以有2个C．有2个以上但有限D．有无数个5．已知四边形ABCD∽四边形A′B′C′D′．四边形ABCD与四边形A′B′C′D′的周长分别为24、36，则它们的对角线AC与A′C′的比为( )A．2：3 B．3：2 C．4：9 D．9：46．如图，大正方形是由边长为1的小正方形组成的，则下列图形中的三角形(阴影部分) 与△ABC相似的是( )7．如图，在钝角△ABC中，AB=6 cm，AC=12 cm，动点D从点A出发到点B止．动点E从点C出发到点A止．点D运动的速度为1 cm／s，点E运动的速度为2 cm／s．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时．运动的时间是( )A．3 s或4．8 s B．3 s C．4．5 s D．4．5 s或4．8 s8．如图，在Rt△ABC内有边长分别为a、b、c的三个正方形，则a、b、c满足的关系式是( )A．b=a+c B．b=ac C．b2=a2+c2 D．b=2a=2c二、填空题9．下列命题：①有一对锐角相等的两个直角三角形相似；②所有的等腰三角形都相似； ③全等的三角形一定相似；④所有的等边三角形都相似，其中是真命题的有______(写出正确答案的序号)．10．如图，在△ABC 中，若∠AEB=∠ADC ，则图中共有相似三角形_________对．11．两个相似多边形的面积之比为9：25，且这两个多边形的周长之和为160 cm ，则其中较大多边形的周长为_________cm ．12．如图，D 、E 分别是△ABC 的边AB 、AC 上的点，DE ∥BC ，2AD DB =，若S △ABC 的面积为9，则四边形DBCE 的面积为_________．13．如图，在□ABCD 中，E 是边BC 上的点，AE 交BD 于点F ，如果23BE BC =，那么BF FD=__________． 14．如图，D 、E 两点分别在△ABC 的边AB 、AC 上，DE 与BC 不平行，当_________(写出一个即可)时，△AD E ∽△ACB ．15．如图，A B ⊥BD ，ED ⊥BD ，C 是线段BD 的中点，且AC ⊥CE ，ED=1，BD=4，那么 AB=_________．16．在△ABC 中，AB=16，AC=12，点D 在AB 上，且AD=4，若要在AC 上找一点E ，使△ADE 与原三角形相似，那么AE=__________．17．在Rt △ABC 中，∠C=90°，CD ⊥AB 于点D ，BC=3，AB=5，则其中的一对相似三角形是___________和__________．它们的面积比为___________．18．如图，电影胶片上每一个图片的规格为3．5 cm ×3．5 cm ，放映屏幕的规格为2 m × 2 m ，如果放映机的光源S 距胶片20 cm ．那么光源S 距屏幕_________米时，放映的图像刚好不满整个屏幕．三、解答题19．如图，E是矩形ABCD的边CD上的一点，BF⊥AE于点F．试说明：△ABF∽△EAD．20．如图，在△ABC中，∠C=90°，在AB边上取一点D，使BD=BC，过点D作DE⊥AB交AC于点E，AC=8，BC=6．求DE的长．21．如图，在等边△CDE中，A、B分别是ED、DF延长线上的两个动点，线段DE、AD与EB之间满足关系：DE2=AD·EB．试求∠ACB的度数．22．(9分)如图，在□ABCD中，E是CD延长线上的一点，BE与AD交于点F，1 2DE CD．(1)△ABF与△CEB相似吗?为什么?(2)若△DEF的面积为2，求□ABCD的面积．23．如图，在△ABC和△DEF中，∠A=∠D=90°，AB=DE=3，AC=2DF=4．(1)这两个三角形是否相似?请说明理由．(2)能否分别过点A、D在这两个三角形中各作一条辅助线，使△ABC分割成的两个三角形与△DEF分割成的两个三角形分别对应相似?证明你的结论．24．在等腰△ABC中，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕点P旋转．(1)如图(1)，当三角板的两边分别交AB、AC于点E、F时，△BPE与△CFP相似吗?为什么?(2)将三角板绕点P旋转到图(2)的情形时，三角板的两边分别交BA的延长线、边AC于点E、F．①△BPE与△CFP还相似吗(只需写出结论)?②连接EF，△BPE与△PFE是否相似?请说明理由．参考答案一、1．A 2．B 3．C 4．B 5．A 6．A 7．A 8．A二、9．①③④ 10．2 11．100 12．5 13．23 14．∠ADE=∠ACB(或∠AED=∠ABC 或AD AE AC AB =) 15．4 16．3或16317．△BCD △CAD 9：16(或△BCD △BAC 9：25或△CAD △BAC 16：25) 18．807三、19．因为四边形ABCD 是矩形，AB ∥CD ，∠D=90°，所以∠BAF=∠AED ．因为BF ⊥AE ，所以∠AFB=90°．所以∠AFB=∠D ．所以△AB F ～△EAD 20．因为在△ABC 中，∠C=90°，AC=8，BC=6，所以2210AB AC BC =+=．又因为BD=BC=6，所以AD=AB －BD=4．因为DE ⊥A B ，所以∠ADE=∠C=90°．又因为∠A=∠A ，所以△AE D ～△ABC ．所以DE AD BC AC =．所以4638AD DE BC AC ==⨯= 21．因为△CDE 为等边三角形，所以∠CDE=∠CED=∠DCE=60°．CD=CE=DE ．所以∠ADC=∠BEC=120°．因为DE 2=AD ·EB ，所以DE EB AD ED =，即DC EB AD EC =．所以△ACD ∽△CBE ．所以∠ACD=∠B ．又因为∠ACB=∠ECD+∠ACD+∠ECB ，所以∠ACB=∠B+∠ECB+∠ECD=∠CED+∠ECD=60°+60°=120°．即∠ACB 的度数为120° 22．(1)因为四边形ABCD 是平行四边形，所以∠A=∠C ，AB ∥CD ．所以∠ABF=∠CEB ．所以△AB F ∽△CEB (2)因为四边形ABCD 是平行四边形，所以AD ∥BC ，ABCD ．所以△DEF ∽△CEB ，△DEF ∽△ABF ．因为12DE CD =，所以219DEF CEB S DE S EC ∆∆⎛⎫== ⎪⎝⎭，214DEF ABF S DE S AB ∆∆⎛⎫== ⎪⎝⎭．因为S △DEF =2，所以S △CEB =18，S △ABF =8．所以S 四边形BCDF =S △CEB －S △DEF =16．所以S 四边形ABCD =S 四边形BCDF +S △ABF =16+8=24 23．(1)不相似．因为在Rt △BAC 中，∠A=90°，AB=3，AC=4；在Rt △EDF 中，∠D=90°，DE=3，DF=2．所以1AB DE =，2AC DF =．所以AB AC DE DF ≠．同理AB AC DF DE≠．所以Rt △BAC 与Rt △EDF 不相似 (2)能作如图所示的辅助线进行分割．具体作法；作∠BAM=∠E ，交BC 于点M ；作∠ND E=∠B ，交EF 于点N ．由作法和已知条件可知△BAM ≌△DEN ．因为∠BAM=∠E ，∠NDE=∠B ，∠AMC=∠BAM+∠B ，∠FND=∠E+∠NDE ，所以∠AMC =∠FND ．因为∠FDN=90°－∠NDE ，∠C=90°－∠B ，所以∠FDN=∠C ．所以△AM C ∽△FND24．(1)在△ABC中，∠BAC=120°，AB=AC，所以∠B=∠C=30°．因为∠B+∠BPE+∠BEP=180°，所以∠BPE+∠BEF=150°．因为∠EPF=30°．∠BPE+∠EPF+∠CPF=180°，所以∠BPE+∠CPF=150°．所以∠BEP=∠CPF．所以△BP E∽△CFP(两角对应相等的两个三角形相似) (2)①△BPE∽△CFP ②△BPE与△PFE相似．同(1)可证△BP E∽△CFP，得CP PFBE PE=．而CP=BP，因此BP PFBE PE=．又因为∠EBP=∠EPF．所以△BP E∽△PFE(两边对应成比例且夹角相等的两个三角形相似)。

2015年春季新版苏科版八年级数学下学期周周练习试卷102

宜陵镇中八年级数学周周练（6）一分式的概念在x 3-、y x 、22732xy y x -、x 81-、y +53、5y x -、πy x +3中，是整式的有___________________________，是分式的有_______________________；二 .分式中字母的取值（1）当x___________时，分式51-x 有意义；当x________时，分式521--x x 无意义，（2）当x 为任意实数时，下列分式中，一定有意义的是 ( ) A.21x x - B.112-+x x C.112+-x x D.21+-x x（3）函数x xy 21-=中自变量x 的取值范围是：A 、x ≤21且x ≠0 B 、x 21->且x ≠0 C 、x ≠0 D 、x 21<且x ≠0例题若分式112+-x x 的值为0，则x 的取值为（）A 、1=xB 、1-=xC 、1±=xD 、无法确定练习如果分式212-+-x x x 的值为0，那么x 的值是________例题若关于x 的方程112=-+x ax 的解为正数，求a 的取值范围？练习已知关于x 的方程322=-+x mx 的解是正数，求m 的取值范围？三分式的性质：如果把223yx y -中的x 和y 都扩大5倍，那么分式的值（）A 、扩大5倍B 、不变C 、缩小5倍D 、扩大4倍例题请从下列三个代数式中任选两个构成一个分式，并化简该分式ｘ2－4ｘｙ＋4ｙ2 ｘ2－4ｙ2 ｘ－2ｙ练习 1.1211222+++÷--x x x x x2.有这样一道题：“计算：2222111x x x x x x x-+-÷--+的值，其中2007x =”，某同学把2007x =错抄成2008x =，但它的结果与正确答案相同，你说这是怎么回事？四最简公分母 xyzx y xy 61,4,13-的最简公分母是_____。

苏科版八年级数学下册周检.docx

初中数学试卷桑水出品八年级周检试卷班级___________ _姓名_____________一、选择题（3分×8=24分） 1、下列各式：π8,11,5,21,7,322xx y x b a a -++中，分式有（） A 、1个 B 、2个 C 、3个 D 、4个2、若分式112+-x x 的值为0，则x 的取值为（）A 、1=xB 、1-=xC 、1±=xD 、无法确定 3、如果把分式yx x+2中的x 和y 都扩大3倍，那么分式的值（） A 、扩大3倍 B 、缩小3倍 C 、缩小6倍 D 、不变 4、下列约分结果正确的是（）A 、yzz y x yz x 1281282222=B 、y x y x y x -=--22C 、11122+-=--+-m m m m D 、b a m b m a =++ 5、计算：xy yy x x 222-+-，结果为（） A 、1 B 、-1 C 、y x +2 D 、y x + 6、把分式方程12121=----xxx 的两边同时乘以()2-x 约去分母得（） A.()111=--x B.()111=-+x C.()211-=--x x D.()211-=-+x x 7、如果方程333-=-x mx x 有增根，那么m 的值为（） A.0 B.-1 C.3 D.18、若xy y x =+，则yx 11+的值为（）A 、0B 、1C 、-1D 、2二、填空题（2分×11=22分） 9、当x 时，分式31-+x x 有意义，当x 时，分式32-x x无意义。

10、xyzx y xy 61,4,13-的最简公分母是。

11、计算：=•c b a a bc 222 ；=÷23342yxy x ；12、计算：=-b aa b 32 ；=--+y x y x 12 。

13、已知113xy-=，则代数式21422x xy yx xy y----的值为_________．14、一件工作，甲单独做a 小时完成，乙单独做b 小时完成，则甲、乙合作小时完成。

苏科版八年级(下)数学周周练(13)及答案

八年级数学(下)周周练12(10.6-10.7)一、选择1．如图，两个三角形是位似图形，那么它们的位似中心是( ) A．点P B．点O C．点M D．点N2．在一个晴朗的上午，小丽拿着一块矩形木板在阳光下做投影实验，矩形木板在地面上形成的投影不可能是( )3．某同学的身高为1．6米，某一时刻他在阳光下的影长为1．2米，同一时刻与他相邻的一棵树的影长为3．6米，则这棵树的高度为( ) A．5．3米B．4．8米C．4．0米D．2．7米4．如图是小明设计的用手电来测量某古城墙高度的示意图．在点P处放一个水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知A B⊥BD，CD⊥BD，且测得AB=1．2米，BP=1．8米，PD=12米，那么该古城墙的高度是( ) A．6米B．8米C．18米D．24米5．如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，则下列结论不正确的是( ) A．四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2：3C．四边形ABCD与四边形AEFG的周长比是2：3D．四边形ABCD与四边形AEFG的面积比是4：96．如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是( )A ．1：6B ．1：5C ．1：4D ．1：27．如图，在斜坡的顶部有一座铁塔AB ，B 是CD 的中点，CD 是水平的，在阳光的照射下，塔影DE 留在坡面上．已知铁塔底座宽CD=12 m ，塔影长DE=18 m ，小明和小华的身高都是1．6 m ，同一时刻，小明站在点E 处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2 m 和1 m ，那么塔高AB 为 ( )A ．24 mB ．22 mC ．20 mD ．18 m8．如图，相邻两根电杆都用钢索在地面上固定，一根电杆钢索系在离地面4米处，另一根电杆钢索系在离地面6米处，则中间两根钢索相交处点P 离地面 ( )A ．2．4米B ．2．8米C ．3米D ．高度不能确定二、填空9．如图，课堂上小亮站起来回答数学老师提出的问题，那么数学老师观察小亮身后的盲区是_________．10．如图，用放大镜将图形放大，应属于_________(填“对称变换”、“平移变换”、“旋转变换”或“相似变换”)．11．在平面直角坐标系中，已知A(6，3)、B(6，0)两点，以坐标原点O 为位似中心，相似比为13，把线段AB 缩小后得到线段A ′B ′，则A ′B ′的长度等于________． 12．如图是农村一个古老的捣碎器，支撑柱AB 的高为0．3米，踏板DE 长为1．6米，支撑点A 到踏脚D 的距离为0．6米．现在踏脚着地，则捣头点E 上升了________米．13．如图，小明将长梯AB 斜靠在墙上，测得梯脚B 与墙脚C 的距离为1．6 m ，梯上的点D 与墙的距离DE 为1．4 m ，BD 长0．55 m ，我们可以应用学过的知识求得该梯子的长为_________m ．14．如图，阳光通过窗口照到室内，在地面上留下1．6 m 宽的亮区DE ，已知亮区一边到窗下的墙脚距离CE=3．6 m ，窗高AB=1．2 m ，那么窗口底边离地面的高度BC=________m．15．如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36 cm，那么它在暗盒中所成的像CD的高度应为________cm．16．如图，一个落地晾衣架两撑杆的公共点为O，OA=75 cm，OD=50 cm．若撑杆下端点A、B所在直线平行于上端点C、D所在直线，且AB=90 cm，则CD=_______cm．17．如图，△ABC的三个顶点的坐标分别为A(0，2)、B(3，3)、C(2，1)．以点B为位似中心，画出与△ABC相似的三角形(在点B同侧)，且相似比为3，则点A的对应点的坐标是_________．18．如图，在正方形ABCD和正方形OEFG中，点A和点F的坐标分别为(3，2)、(－1，－1)，则这两个正方形的位似中心的坐标是___________．三、解答题19．(8分)如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出△OAB的一个位似图形，使两个图形以点O为位似中心，且所画图形与△OAB的位似比为2：1．20．(8分)如图，△ABC与△A′B′C′是位似图形，且位似比是1：2．(1)在图中画出位似中心点O．(2)若AB=2 cm，则A′B′的长为多少?21．(9分)如图，A、B两点被池塘隔开，为了测量A、B之间的距离，王刚同学采用了如下的方法解决问题：在AB外任选一点C，连接AC、BC，再分别取其三等分点M、N，量得MN=38 m，即知道了A、B之间的距离，你知道王刚同学是怎样求得结果的吗?请求出A、B之间的距离．22．(9分)如图，晚上小亮在广场上乘凉，图中线段AB表示站在广场上的小亮，线段PO 表示直立在广场上的灯杆，点P表示照明灯．(1)请你在图中画出小亮在照明灯(P)照射下的影子．(2)已知灯杆高PO=12 m，小亮的身高AB=1．6 m，小亮与灯杆的距离BO=13 m，请求出小亮影子的长度．23．(11分)如图，路灯(点P)距地面8米，身高1．6米的小明从距路灯的底部(点O)20 米的点A?沿AO所在的直线行走14米到点B时，身影的长度是变长了还是变短了?变长或变短了多少米?24．(11分)亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M、颖颖的头顶B及亮亮的眼睛A恰在一条直线上时，两人分别标定自己的位置C、D．然后测出两人之间的距离CD=1．25 m，颖颖与楼之间的距离DN=30 m(C、D、N在同一条直线上)，颖颖的身高BD=1．6 m，亮亮蹲地观测时眼睛到地面的距离AC=0．8 m．你能根据以上测量的数据帮助他们求出住宅楼的高度吗?参考答案一、1．A 2．A 3．B 4．B 5．B 6．C 7．A 8．A二、9．△ABE 10．相似变换11．1 12．0．8 13．4．4 14．1．5 15．16 16．60 17．(－6，0) 18．(1，0)或(－5，－2)三、19．如图所示20．(1)连接BB ′、CC ′，它们的交点即为位似中心O (2)A ′B ′的长为4 cm21．A 、B 之间的距离是114 m22．(1)连接PA 并延长交OB 的延长线于点C ，线段BC 就是小亮在照明灯(P)照射下的影子 (2)在△CAB 和△CPO 中，因为∠C =∠C ，∠ABC=∠POC=90°，所以△CA B ∽△CPO ．所以AB CB PO CO =，即1.61213CB BC=+．所以BC=2，即小亮影子的长度为2 m 23．小明身影的长度变短了3．5米 24．过点A 作CN 的平行线交BD 于点E ，交MN 于点F ．由已知可得FN=ED=AC=0．8m ，AE=CD=1．25m ，EF=DN=30 m ，∠AEB=∠AFM=90°．又因为∠BAE=∠MA F ，所以△AB E ∽△AMF ．所以BE AE MF AF =，即1.60.8 1.251.2530MF -=+．解得MF=20m ．所以MN=MF+FN=20+0．8=20．8(m)．所以住宅楼的高度为20．8 m。

苏科版八年级下数学周周练试卷

八年级数学周周练0505一、选择题：1. 已知点M 将线段AB 黄金分割(AM ＞BM)，则下列各式中不正确的是（） A. AM ∶BM=AB ∶AM B. AM=215-AB C. BM=215-AB D. AM ≈0.618AB 2. 下列四个三角形，与左图中的三角形相似的是（）3.直线AB 与平行四边形MNPQ 的四边所在直线分别交于A 、B 、C 、D ，则图中的相似三角形有（） A.4对 B.5对 C.6对 D.7对4.如图,在平行四边形ABCD 中,O 1、O 2、O 3分别是对角线BD 上的三点，且BO 1=O 1O 2=O 2O 3=O 3D ，连接AO 1并延长交BC 于点E ，连接EO 3并延长交AD 于点F ，则AD ：DF 等于（）A. 19:2 B. 9:1 C.8:1 D. 7:15. 如图,在△ABC 中，P 为AB 上一点，则下列条件中(1)∠ACP=∠B ；(2)∠APC=∠ACB ；(3)AC 2=AP •AB ； (4)AB •CP=AP •CB ，其中使△APC 和△ACB 相似的条件有（）A 、1个 B 、2个 C 、3个 D 、4个二、填空题：1.在比例尺为1∶400000的中国地图上，量得A 、B 两地相距15厘米，那么A 、B 两地的实际距离是千米．2.已知：点P 是线段AB 的黄金分割点，且AB=10cm ，则线段AP 的长度是 cm.(精确到0.1cm)3.将三角形纸片△ABC 按如图所示的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF 。

已知AB ＝AC ＝8，BC ＝10，若以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是______________.4.如图，一次函数y ax b =+的图象与x 轴，y 轴交于A 、B 两点，与反比例函数ky x=的图象相交于C 、D 两点，分别过C 、D 两点作y 轴、x 轴的垂线，垂足为E 、F ，连接CF 、DE ．有下列四个结论：①AC BD =；②△DCE≌△CDF；③△CEF 与△DEF 的面积相等；④△AOB∽△FOE．其中正确的结论是．（把你认为正确结论的序号都填上）5.已知a 、b 、c 三条线段，其中2,8a c ==，若线段b 是线段a 、c 的比例中项，则b ＝。

苏科版八年级(下)数学周周练(13)及答案

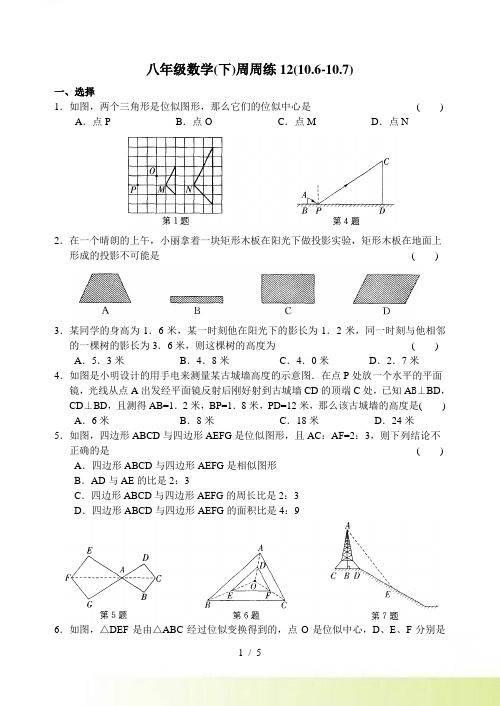
八年级数学(下)周周练12(10.6-10.7)一、选择1．如图，两个三角形是位似图形，那么它们的位似中心是( ) A．点P B．点O C．点M D．点N2．在一个晴朗的上午，小丽拿着一块矩形木板在阳光下做投影实验，矩形木板在地面上形成的投影不可能是( )3．某同学的身高为1．6米，某一时刻他在阳光下的影长为1．2米，同一时刻与他相邻的一棵树的影长为3．6米，则这棵树的高度为( ) A．5．3米B．4．8米C．4．0米D．2．7米4．如图是小明设计的用手电来测量某古城墙高度的示意图．在点P处放一个水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知A B⊥BD，CD⊥BD，且测得AB=1．2米，BP=1．8米，PD=12米，那么该古城墙的高度是( ) A．6米B．8米C．18米D．24米5．如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，则下列结论不正确的是( ) A．四边形ABCD与四边形AEFG是相似图形B．AD与AE的比是2：3C．四边形ABCD与四边形AEFG的周长比是2：3D．四边形ABCD与四边形AEFG的面积比是4：96．如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是( ) A．1：6 B．1：5 C．1：4 D．1：27．如图，在斜坡的顶部有一座铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是1．6 m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2 m和1 m，那么塔高AB为( ) A．24 m B．22 m C．20 m D．18 m8．如图，相邻两根电杆都用钢索在地面上固定，一根电杆钢索系在离地面4米处，另一根电杆钢索系在离地面6米处，则中间两根钢索相交处点P离地面( )A．2．4米B．2．8米C．3米D．高度不能确定二、填空9．如图，课堂上小亮站起来回答数学老师提出的问题，那么数学老师观察小亮身后的盲区是_________．10．如图，用放大镜将图形放大，应属于_________(填“对称变换”、“平移变换”、“旋转变换”或“相似变换”)．11．在平面直角坐标系中，已知A(6，3)、B(6，0)两点，以坐标原点O为位似中心，相似比为13，把线段AB缩小后得到线段A′B′，则A′B′的长度等于________．12．如图是农村一个古老的捣碎器，支撑柱AB的高为0．3米，踏板DE长为1．6米，支撑点A到踏脚D的距离为0．6米．现在踏脚着地，则捣头点E上升了________米．13．如图，小明将长梯AB斜靠在墙上，测得梯脚B与墙脚C的距离为1．6 m，梯上的点D与墙的距离DE为1．4 m，BD长0．55 m，我们可以应用学过的知识求得该梯子的长为_________m．14．如图，阳光通过窗口照到室内，在地面上留下1．6 m宽的亮区DE，已知亮区一边到窗下的墙脚距离CE=3．6 m，窗高AB=1．2 m，那么窗口底边离地面的高度BC=________m．15．如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36 cm，那么它在暗盒中所成的像CD的高度应为________cm．16．如图，一个落地晾衣架两撑杆的公共点为O，OA=75 cm，OD=50 cm．若撑杆下端点A、B所在直线平行于上端点C、D所在直线，且AB=90 cm，则CD=_______cm．17．如图，△ABC的三个顶点的坐标分别为A(0，2)、B(3，3)、C(2，1)．以点B为位似中心，画出与△ABC相似的三角形(在点B同侧)，且相似比为3，则点A的对应点的坐标是_________．18．如图，在正方形ABCD和正方形OEFG中，点A和点F的坐标分别为(3，2)、(－1，－1)，则这两个正方形的位似中心的坐标是___________．三、解答题19．(8分)如图，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出△OAB的一个位似图形，使两个图形以点O为位似中心，且所画图形与△OAB的位似比为2：1．20．(8分)如图，△ABC与△A′B′C′是位似图形，且位似比是1：2．(1)在图中画出位似中心点O．(2)若AB=2 cm，则A′B′的长为多少?21．(9分)如图，A、B两点被池塘隔开，为了测量A、B之间的距离，王刚同学采用了如下的方法解决问题：在AB外任选一点C，连接AC、BC，再分别取其三等分点M、N，量得MN=38 m，即知道了A、B之间的距离，你知道王刚同学是怎样求得结果的吗?请求出A、B之间的距离．22．(9分)如图，晚上小亮在广场上乘凉，图中线段AB表示站在广场上的小亮，线段PO 表示直立在广场上的灯杆，点P表示照明灯．(1)请你在图中画出小亮在照明灯(P)照射下的影子．(2)已知灯杆高PO=12 m，小亮的身高AB=1．6 m，小亮与灯杆的距离BO=13 m，请求出小亮影子的长度．23．(11分)如图，路灯(点P)距地面8米，身高1．6米的小明从距路灯的底部(点O)20 米的点A?沿AO所在的直线行走14米到点B时，身影的长度是变长了还是变短了?变长或变短了多少米?24．(11分)亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M、颖颖的头顶B及亮亮的眼睛A恰在一条直线上时，两人分别标定自己的位置C、D．然后测出两人之间的距离CD=1．25 m，颖颖与楼之间的距离DN=30 m(C、D、N在同一条直线上)，颖颖的身高BD=1．6 m，亮亮蹲地观测时眼睛到地面的距离AC=0．8 m．你能根据以上测量的数据帮助他们求出住宅楼的高度吗?参考答案一、1．A 2．A 3．B 4．B 5．B 6．C 7．A 8．A二、9．△ABE 10．相似变换 11．1 12．0．8 13．4．4 14．1．5 15．16 16．6017．(－6，0) 18．(1，0)或(－5，－2)三、19．如图所示20．(1)连接BB ′、CC ′，它们的交点即为位似中心O (2)A ′B ′的长为4 cm21．A 、B 之间的距离是114 m22．(1)连接PA 并延长交OB 的延长线于点C ，线段BC 就是小亮在照明灯(P)照射下的影子 (2)在△CAB 和△CPO 中，因为∠C =∠C ，∠ABC=∠POC=90°，所以△CA B ∽△CPO ．所以AB CB PO CO =，即1.61213CB BC=+．所以BC=2，即小亮影子的长度为2 m 23．小明身影的长度变短了3．5米 24．过点A 作CN 的平行线交BD 于点E ，交MN 于点F ．由已知可得FN=ED=AC=0．8m ，AE=CD=1．25m ，EF=DN=30 m ，∠AEB=∠AFM=90°．又因为∠BAE=∠MA F ，所以△AB E ∽△AMF ．所以BE AE MF AF =，即1.60.8 1.251.2530MF -=+．解得MF=20m ．所以MN=MF+FN=20+0．8=20．8(m)．所以住宅楼的高度为20．8 m。

2015年春季新版苏科版八年级数学下学期周周练习试卷112

2015年春季新版苏科版八年级数学下学期周周练习试卷72

苏科版2014-2015学年度第二学期期末考试八年级数学试题(二)

苏科版使用地区2015年八年级第二学期学期调查数学试卷

2015～2016学年苏科版初二数学第二学期期末测试卷 有答案

2015年春季新版苏科版八年级数学下学期周周练习试卷128

2015年春季新版苏科版八年级数学下学期周周练习试卷122

苏科版八年级数学下册周检1

江苏省连云港2015-2016学年八年级数学下册第2周周测试题

苏科版八年级(下)数学周周练(11)及答案

2015年春季新版苏科版八年级数学下学期周周练习试卷102

苏科版八年级数学下册周检.docx

最新苏科版2015-2016学年八年级册第二学期期末测试题及答案

苏科版八年级(下)数学周周练(13)及答案

苏科版八年级下数学周周练试卷

苏科版八年级(下)数学周周练(13)及答案

2015～2016学年苏科版初二数学第二学期期末测试卷有答案