现代控制理论第5章
现代控制理论知到章节答案智慧树2023年哈尔滨工程大学

现代控制理论知到章节测试答案智慧树2023年最新哈尔滨工程大学绪论单元测试1.经典控制理论以单变量线性定常系统作为主要的研究对象,以时域法作为研究控制系统动态特性的主要方法。
参考答案:错2.1892年俄国数学家李亚普诺夫发表了论文《运动稳定性的一般问题》,用严格的数学分析方法全面地论述了稳定性问题。
参考答案:对3.现代控制理论以多变量线性系统和非线性系统作为研究对象,以时域法,特别是状态空间方法作为主要的研究方法。
参考答案:对4.研究系统控制的一个首要前提是建立系统的数学模型,线性系统的数学模型主要有两种形式,即时间域模型和频率域模型。
参考答案:对5.下述描述中哪些作为现代控制理论形成的标志()。
参考答案:最优控制中的Pontriagin极大值原理和Bellman动态规划;用于系统的整个描述、分析和设计过程的状态空间方法;随机系统理论中的Kalman滤波技术第一章测试1.输入输出描述是描述系统输入变量和输出变量关系的模型。
参考答案:对2.状态空间描述能完全表征系统的一切动力学特征。
参考答案:对3.系统的状态是指能够完全表征系统时间域行为的一个最小内部变量组。
参考答案:对4.系统的状态空间描述是唯一的。
参考答案:错5.坐标变换是指将系统在状态空间的一个基底上的表征,化为另一个基底上的表征。
参考答案:对6.当状态空间描述中的A矩阵有相同的特征值时,一定不能将其化成对角规范形。
参考答案:错7.并联组合系统的传递函数矩阵为各并联子系统的传递函数矩阵之和。
参考答案:对8.若两个子系统输出向量的维数相同,则可实现反馈连接。
参考答案:错9.线性定常系统线性非奇异变换后()。
参考答案:系统的特征值不变10.考虑如图所示的串联组合系统,下列论述正确的是()。
参考答案:串联组合后系统的状态方程为第二章测试1.一般线性系统状态方程的解由两部分组成,第一部分反映系统初态的影响,第二部分反映系统输入对状态的影响。
参考答案:对2.零初态响应指系统初始状态为零时,由系统输入单独作用所引起的运动。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Prepared on 22 November 2020《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解:()()22232321s s s s s s s++ =++ ? ?D S N S ; ()3r 2,1,2E -:223381s s s s s s ??++ ?-- ? ???;()3r 2,3,3E :223051s s s s s ??++ ?- ? ???;()3r 1,3,2E s --:01051s s ?? ?- ? ;()3r 2,1,5E s -:01001s ?? ?;()3r 3,1,1E -:01000s ?? ? ? ???;()1r 2,3E :01000s ?? ? ? ???;()1r 1,2E :00100s ?? ?;所以⼀个gcrd 为001s ??;取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ,根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ,根据C-H 有限项展开法求解转移矩阵t A e 。
解:(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -,得1,233,1λλ== 对1,23λ=,可以计算1,2()2rank λ=A I -,所以该特征值的⼏何重数为1。
现代控制理论课后答案

前言
本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答,可帮助同学学习和理解教材的内容。由于习题数量较多,难易程度不同,虽然主要对象是研究型大学自动化专业本科学生,但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答;第4、7 章由井元伟教授组织编选和解答,第1、2章由郑艳副教授组织编选和解答。
+
若取 ,则有
(2)解 由(1)知
取 ,则有
若取 ,则有 ,
3.11 求下列系统在输入作用为:① 脉冲函数;② 单位阶跃函数;③ 单位斜坡函数下的状态响应。
(1)
(2)
图P2.2
解 这是一个物理系统,采用机理分析法求状态空间表达式会更为方便。令 为输入量,即 , , 的位移量 , 为输出量,
选择状态变量 , = , = , 。
根据牛顿定律对 有:
对 有:
经整理得:
状态方程为:
输出方程为:
写成矩阵形式为:
2.5 系统的结构如图P2.5所示。以图中所标记的 、 、 作为状态变量,推导其状态空间表达式。其中, 、 分别为系统的输入、输出, 、 、 均为标量。
图P2.5系统结构图
解 图P2.5给出了由积分器、放大器及加法器所描述的系统结构图,且图中每个积分器的输出即为状态变量,这种图形称为系统状态变量图。状态变量图即描述了系统状态变量之间的关系,又说明了状态变量的物理意义。由状态变量图可直接求得系统的状态空间表达式。
(2) 解 由已知得:
,
令: ,
得:
状态变量图如下:
现代控制理论(17-21讲:第5章知识点)

0
试分析系统的稳定性。
解:(1)由 x(t ) 0 , 求得 xe = 0 是系统唯一平衡状态;
(2)选择Lyapunov函数为 1
2 2
二次型函数,是正定的; d 2 2 2 (3) V (x) ( x1 x2 ) 2 x1 x1 2 x2 x 2 2 x2 dt 故V(x)的导数是半负定的; (4)由:
(1) V(x)是正定的; (2) V ( x )是负定的;
则在状态空间坐标原点处的平衡状态是渐近稳定的。此时, 如果随着||x||→∞,V(x) →∞,那么在原点处的平衡状态是大 范围渐近稳定的。
2 2 例1:设系统的状态方程为: x1 x2 ax1 ( x1 x2 ) 其中:a为非零正常数。试 2 x2 x1 ax2 ( x12 x2 ) 分析系统的稳定性。
(2) V ( x ) 是半负定的; (3) 对于任意初始时刻t0时的任意状态x0≠0, 在t≥t0时,除了在 x=0时,有 V ( x) 0 外,V ( x )不恒等于零,则系统在平衡状 态是渐近稳定的。如果随着||x||→∞,V(x) →∞,那么在原 点处的平衡状态是大范围渐近稳定的。 在应用定理二时,注意以下两种情况: (1)极限环的情况。稳定, 但不是渐近稳定;
(1) V(x)在原点的某一邻域内是正定的; (2) V ( x ) 在同样的邻域内也是正定的;
那么系统在原点处的平衡状态是不稳定的。(注意:此地 V(x)的导数也可半正定,但有V(x)的导数不恒为零。)
例3:设时变系统的状态方程为: x1 x1 sin 2 t x2et x 2 x1et x2 cos 2 t 分析系统的稳定性。 解:(1) 显然 xe = 0 是系统平衡状态; (2)选择V(x)为:
《现代控制理论》第三版_.习题答案

1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
现代控制理论基础_周军_第五章状态反馈与状态观测器
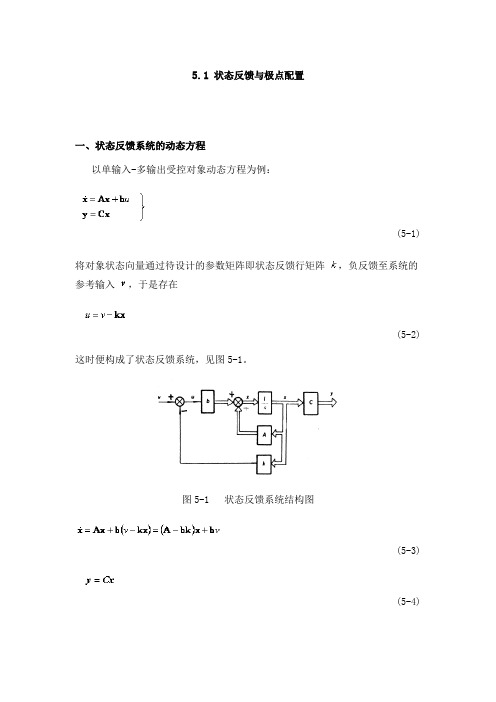
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
《现代控制理论基础》第2版 现代控制理论基础_上海交通大学_施颂椒等_PPT_第5章

① 定义 有理函数 g(s) 当s 时,
② g(假)设
常n数(s〔) d(s) g(s)〕, 就称为正那么有理函数。
③ g假( 设)那么有理函数。
④
假g(设) 〔 n(s)d(s)
g(〕s) , 就是 非正那么有理函数。
有理函数阵 G (s) 假设G() 0 ,那G (s么) 是严格正那么有理函数阵〔其每个元均为
G (s) C (sI A )1BD
那么(称A,B,C,D) 是G (s) 的一个实现。
•实现研究的问题
⑴ G (s)可实现为 (A,B,C,D) 的条件问题 ⑵ G (s) 实现的方法
〔5-1〕
•最小实现
如果 (A,B,C,D)是G (s) 的一个实现,那么其所有等价系统也都是其 实现 。 G (s) 可有不同维数的实现,其中维数最小的实现称为最小实 现。它描述了系统的既能控又能观的局部。通常要求的实现 为最小实现。
s 1 s4 s(s1) (s1)s(3) (s1)s(3)
s
1
3
s(s 1 )s( 2 ) (s 1 )s( 2 )s( 3 ) s(s 1 )s( 2 )s( 3 )
G (s) 的特征多项式为:s(s1)s(2)s(3),deG g(s)4。
⑵ G (s) 可实现为 (A,B,C,D) 的条件
③ 非正那么传递函数〔G() 〕,也存在实现,其实现具有
④ 如下形式
Ex(t)A(xt)Bu(t) y(t)Cx(t)Du(t)
〔5-9〕
式中 E为奇异阵。这种形式的系统称为广义系统,或奇异 系统。(本书不予讨论,在专门文献中研究)
5.2.2 最小实现的性质
如果将例〔5-5〕的传递函数阵写成
G ( s ) G 1 ( s )G 2 ( s )
第5章现代控制理论之系统运动的稳定性分析

由稳定性定义知,球域S(δ) 限制着初始状态x0的取值,球域
S(ε)规定了系统自由运动响应 xt xt; x0的, t0边 界。
简单地说:1.如果 x t; x0, t0 有界,则称 xe 稳定;
2.如果 x t; x0, t0 不仅有界,而且当t→∞时收敛于原点,则
5.1.1 平衡状态
李雅普诺夫关于稳定性的研究均针对平衡状态而言。
1. 平衡状态的定义
设系统状态方程为: x f x,t , x Rn
若对所有t ,状态 x 满足 x 0 ,则称该状态x为平衡状
态,记为xe。故有下式成立:f xe ,t 0
由平衡状态在状态空间中所确定的点,称为平衡点。
2.平衡状态的求法
由定义,平衡状态将包含在 f x,t 这样0 一个代数方程组
中。
对于线性定常系统 x A,x其平衡状态为 xe 应满足代数
方程 。Ax 0
只有坐标原点处是线性系统的平衡状态点。
对于非线性系统,方程 方程而定。
如:
x1 x2
x1 x1
x2
x
3 2
f x的,t 解 可0 能有多个,视系统
稳定性是系统的重要特性,是系统正常工作的必要条件。
稳定性是指系统在平衡状态下受到扰动后,系统自由运动 的性质。因此,系统的稳定性是相对于系统的平衡状态而 言的。它描述初始条件下系统方程是否具有收敛性,而不 考虑输入作用。
1. 线性系统的稳定性只取决于系统的结构和参数,与系统 初始条件及外作用无关; 2. 非线性系统的稳定性既取决于系统的结构和参数,也与 系统初始条件及外作用有关;
当稳定性与 t0 的选择无关时,称一致全局渐近稳定。
现代控制理论课后答案(俞立)第五章
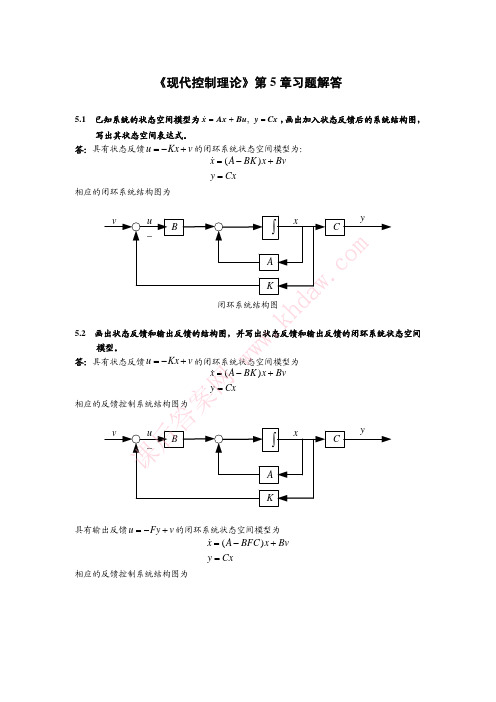
《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ,画出加入状态反馈后的系统结构图,写出其状态空间表达式。
答:具有状态反馈的闭环系统状态空间模型为:u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图,并写出状态反馈和输出反馈的闭环系统状态空间模型。
答:具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响?输出反馈对系统能控性和能观性的影响如何?答:状态反馈不改变系统的能控性,但不一定能保持系统的能观性。
输出反馈不改变系统的能控性和能观性。
5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。
答:加入状态反馈后得到闭环系统K S ,其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推,总可以写成的线性组合。
因此,存在一个适当非奇异的矩阵U ,使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得:若rank([,])c A B n Γ=,即有个线性无关的列向量,则n [(),]cK A BK B Γ−也有个线性无关的列向量,故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。
现代控制理论第版课后习题答案

现代控制理论第版课后习题答案Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下: 系统的状态方程如下: 令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:1-4 两输入1u ,2u ,两输出1y ,2y 的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示: 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令..3.21y x y x y x ===,,,则有相应的模拟结构图如下: 1-6 (2)已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++= 1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘(1) 画出其模拟结构图 (2) 求系统的传递函数 解:(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量(3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解:A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得:3,2,1321-=-=-=λλλ当11-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得: 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P(或令111-=p ,得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ) 当21-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得: 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1423222122p p p P(或令112=p ,得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P )当31-=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得: 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解:A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P当32=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P当13=λ时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--332313332313311201214p p p p p p 解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解:(1)串联联结 (2)并联联结1-11 (第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材) 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数 解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u 的系数b(即控制列阵)为(1)⎥⎦⎤⎢⎣⎡=11b解法1: 解法2:求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
江苏大学线性系统理论(现代控制理论)考试必备--第5章

望的闭环系统特征多项式
* n 1 * 1 * * ( s) ( s i* ) s n an s a s a 1 1 0 i 0 n
第5章 状态反馈
江苏大学电气学院
第3步:写出通过非奇异变换 x Px 将(A,b)化成能控
第5章 状态反馈
江苏大学电气学院
系统经输出反馈后,其系统矩阵变成了 A -BFC ,此处 FC的相当于状态反馈中的K。可见,选择 F 也可以改变系
统矩阵的值使系统特征根位置发生改变。
虽然状态反馈和输出反馈都可改变系统矩阵,但两者 是有区别的。状态变量包含了系统所有的运动信息,而系
统输出量是状态变量的线性组合。当输出矩阵 C 为单位矩
变成了一个单输入能控系统 ( A BK, bi ) 。 利用这一结论,在随后的多输入系统状态反馈极点 配置相关的结论证明中,可以方便地将多输入能控系统 变成单输入系统来讨论,从而利用单输入系统的极点配 置的相关结论。
第5章 状态反馈
江苏大学电气学院
5.3 系统的极点配置
一. 极点配置的概念
由前面的讨论可知,状态反馈使原系统的系统矩阵由 A变成了A-BK,通过选择不同的反馈增益矩阵 K ,可改 变系统的特征值。后面将看到,当系统完全能控且完全能 观时,系统的特征值也就是闭环传递函数矩阵的极点 。 由经典控制理论可知,闭环系统传统意义上的一些主
1.状态反馈与输出反馈的概念 2.反馈对能控性和能观性的影响 3.系统与输出反馈的极点配置 4.状态反馈的解耦
第5章 状态反馈
江苏大学电气学院
5.1 状态反馈与输出反馈的概念
经典控制理论以输出量作为反馈量,使系统得以稳定 或使系统性能指标得到改善。在系统的状态空间描述中,
现代控制理论

5.1.2 输出反馈
设线性定常系统为
Ax Bu x y Cx Du
其输入u ,状态变量 x,输出量y 的维数分别是r,n,m 状态反馈控制律 u Fv Hy
F输入变换阵
D
H输出反馈阵
+ +
v
+
F
u
B
+ +
∫
A
x
C
y
H
u Fv Hy Fv H (Cx Du )
0 0 0 s 3 18s 2 72s det(sI A) 1 s 6 0 1 s 12 0
a 0= 0,a1= 72,a2=18
5.2.1状态反馈极点配置
计算由期望闭环极点组决定的特征多项式
3 2 f ( s) ( s * ) ( s 2 )( s 1 j )( s 1 j ) s 4 s 6s 4 i * i 1 3
性能指标的类型
性能指标实质上是对所要综合的控制系统在运动过程行为 上的一种规定。
非优化型性能指标 (不等式型) 优化性型能指标 (极值型)
(1)镇定问题 (2)极点配置 (3)解耦控制 (4)跟踪问题
J (u()) ( x T Qx uT Ru)dt
0
5.1 反馈控制系统的基本结构
0 1 0 0 0 0 1 0 A bc K 0 0 0 0 1 (an 1 kn 1 ) (a0 k0 ) (a1 k1 )
sI ( Ac bc K ) s n ( an 1 kn 1 ) s n 1 ( a1 k1 ) s ( a0 k0 )
现代控制理论习题集

《现代控制理论》习题第一章 控制系统的状态空间模型1.1 考虑以下系统的传递函数:656)()(2+++=s s s s U s Y试求该系统状态空间表达式的能控标准形和可观测标准形。
1.2 考虑下列单输入单输出系统:u y y yy 66116=+++试求该系统状态空间表达式的对角线标准形。
1.3 考虑由下式定义的系统:Cxy Bu Ax x=+=式中]11[,213421=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C B A ,--试将该系统的状态空间表达式变换为能控标准形。
1.4 考虑由下式定义的系统:Cxy Bu Ax x=+=式中]011[,10030021101=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C B A ,--试求其传递函数Y(s)/U(s)。
1.5 考虑下列矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001100001000010A试求矩阵A 的特征值λ1,λ2,λ3 和λ4。
再求变换矩阵P ,使得),,,(diag 43211λλλλ=-AP P第二章 状态方程的解2.1 用三种方法计算下列矩阵A 的矩阵指数函数At e 。
1) ⎥⎦⎤⎢⎣⎡--=5160A; 2) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6116100010A2.2 计算下列矩阵的矩阵指数函数At e 。
1) ⎥⎦⎤⎢⎣⎡=0010A ; 2) ⎥⎦⎤⎢⎣⎡=1002--A ; 3) ⎥⎦⎤⎢⎣⎡-=0110A ; 4) ⎥⎦⎤⎢⎣⎡=1021A5) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=200010011A ; 6) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=210010001A ; 7) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000100010A2.2 给定线性定常系统Ax x=式中⎥⎦⎤⎢⎣⎡--=2310A且初始条件为⎥⎦⎤⎢⎣⎡-=11)0(x试求该齐次状态方程的解x (t )。
2.4 已知系统方程如下[]xy u x x 11015610-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=求输入和初值为以下值时的状态响应和输出响应。
《现代控制理论》刘豹著(第版)课后习题答案

《现代控制理论》刘豹著(第3版)课后习题答案《现代控制理论》刘豹著(第3版)课后习题答案第一章习题答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:令,则所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻上的电压作为输出量的输出方程。
解:由图,令,输出量有电路原理可知:既得写成矢量矩阵形式为:1-3参考例子1-3(P19).1-4两输入,,两输出,的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令,则有相应的模拟结构图如下:1-6(2)已知系统传递函数,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:1-7给定下列状态空间表达式‘(1)画出其模拟结构图(2)求系统的传递函数解:(2)1-8求下列矩阵的特征矢量(3)解:A的特征方程解之得:当时,解得:令得(或令,得)当时,解得:令得(或令,得)当时,解得:令得1-9将下列状态空间表达式化成约旦标准型(并联分解)(2)解:A的特征方程当时,解之得令得当时,解之得令得当时,解之得令得约旦标准型1-10已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:(1)串联联结(2)并联联结1-11(第3版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11(第2版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-12已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为(1)解法1:解法2:求T,使得得所以所以,状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数。
现代控制理论-09(第5章状态反馈控制器设计)

期望的闭环特征多项式
(λ − λ1 )(λ − λ 2 )(λ − λ3 ) = λ3 + b2 λ2 + b1 λ + b0
要实现极点配置,须
λ3 + (a 2 + k 2 )λ2 + (a1 + k1 )λ + a 0 + k 0 = λ3 + b2 λ2 + b1λ + b0
a 0 + k 0 = b0 a1 + k1 = b1 a 2 + k 2 = b2
− 设计一个状态反馈控制器,使得闭环极点是-2, 1 ± j
解
确定能控标准型实现
1 0⎤ ⎡0 ⎡0 ⎤ x = ⎢0 0 1⎥ x + ⎢0⎥u ⎢ ⎥ ⎢ ⎥ ⎢0 − 2 − 3⎥ ⎢1⎥ ⎣ ⎦ ⎣ ⎦ y = [10 0 0]x
状态反馈控制器 u = − Kx ,K = [k1 k 2 k3 ] 闭环多项式:det[λI − ( A − BK )] = λ3 + (3 + k 3 )λ2 + (2 + k 2 )λ + k1 期望多项式: (λ + 2)(λ + 1 − j)(λ + 1 + j) = λ3 + 4λ2 + 6λ + 4
问题:对一般状态空间模型,如何解极点配置问题? 思路:考虑能控状态空间模型 将能控状态空间模型等价地转化为能控标准型 如何从能控标准型模型的解导出一般模型的极 点配置控制器。
系统模型
x = Ax + Bu
~ TAT −1 = A, ~ TB = B
0 ⎤ 0 ⎥ ⎥ ⎥, ⎥ 1 ⎥ − an−1 ⎥ ⎦ ⎡0 ⎤ ⎢0 ⎥ ~ ⎢ ⎥ B=⎢ ⎥ ⎢ ⎥ ⎢0 ⎥ ⎢1⎥ ⎣ ⎦
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 Lyapunov稳定性分析和二次型最优控制5.1 概述本章首先讨论Lyapunov稳定性分析,然后介绍线性二次型最优控制问题。
我们将使用Lyapunov稳定性方法作为线性二次型最优控制系统设计的基础。
应用于线性定常系统的稳定性分析方法很多。
然而,对于非线性系统和线性时变系统,这些稳定性分析方法实现起来可能非常困难,甚至是不可能的。
Lyapunov稳定性分析是解决非线性系统稳定性问题的一般方法。
虽然在非线性系统的稳定性问题中,Lyapunov稳定性分析方法具有基础性的地位,但在具体确定许多非线性系统的稳定性时,却并不是直截了当的。
技巧和经验在解决非线性问题时显得非常重要。
在本章中,对于实际非线性系统的稳定性分析仅限于几种简单的情况。
本章5.1节为概述。
5.2节介绍Lyapunov意义下的稳定性定义。
5.3节给出Lyapunov稳定性定理,并将其应用于非线性系统的稳定性分析。
5.4节讨论线性定常系统的Lyapunov稳定性分析。
5.5节给出模型参考控制系统,首先用公式表示Lyapunov稳定性条件,然后在这些条件的限制下设计系统。
5.6节讨论线性二次型最优控制系统,将采用Lyapunov稳定性方程导出线性二次型最优控制的条件。
5.7节给出线性二次型最优控制问题的MATLAB解法。
5.2 Lyapunov意义下的稳定性问题对于一个给定的控制系统,稳定性分析通常是最重要的。
如果系统是线性定常的,那么有许多稳定性判据,如Routh-Hurwitz稳定性判据和Nyquist稳定性判据等可资利用。
然而,如果系统是非线性的,或是线性时变的,则上述稳定性判据就将不再适用。
本节所要介绍的Lyapunov第二法(也称Lyapunov直接法)是确定非线性系统和线性时变系统的最一般的方法。
当然,这种方法也可适用于线性定常系统的稳定性分析。
此外,它还可应用于线性二次型最优控制问题。
5.2.1 平衡状态、给定运动与扰动方程之原点考虑如下非线性系统),(t x f x = (5.1)式中x 为n 维状态向量,),(t x f 是变量x 1,x 2,…,x n 和t 的n 维向量函数。
假设在给定的初始条件下,式(5.1)有唯一解),;(00t x t Φ。
当t =t o 时,0x x =。
于是0000),;(x t x t =Φ在式(5.1)的系统中,总存在0),(≡t x f e , 对所有t (5.2) 则称e x 为系统的平衡状态或平衡点。
如果系统是线性定常的,也就是说Ax t x f =),(,则当A 为非奇异矩阵时,系统存在一个唯一的平衡状态;当A 为奇异矩阵时,系统将存在无穷多个平衡状态。
对于非线性系统,可有一个或多个平衡状态,这些状态对应于系统的常值解(对所有t ,总存在e x x =)。
平衡状态的确定不包括式(5.1)的系统微分方程的解,只涉及式(5.2)的解。
任意一个孤立的平衡状态(即彼此孤立的平衡状态)或给定运动)(t g x =都可通过坐标变换,统一化为扰动方程),~(~~t x f x = 之坐标原点,即0),0(=t f 或0=e x 。
在本章中,除非特别申明,我们将仅讨论扰动方程关于原点(0=e x )处之平衡状态的稳定性问题。
这种“原点稳定性问题”由于使问题得到极大简化,而不会丧失一般性,从而为稳定性理论的建立奠定了坚实的基础,这是Lyapunov 的一个重要贡献。
5.2.2 Lyapunov 意义下的稳定性定义下面首先给出Lyapunov 意义下的稳定性定义,然后回顾某些必要的数学基础,以便在下一小节具体给出Lyapunov 稳定性定理。
定义5.1 (Lyapunov 意义下的稳定) 设系统),(t x f x= ,0),(≡t x f e 之平衡状态0=e x 的H 邻域为H x x e ≤-其中,0>H ,⋅为向量的2范数或欧几里德范数,即2/12222211])()()[(ne n e e e x x x x x x x x -++-+-=-类似地,也可以相应定义球域S (ε)和S (δ)。
在H 邻域内,若对于任意给定的H <<ε0,均有(1) 如果对应于每一个S (ε),存在一个S (δ),使得当t 趋于无穷时,始于S (δ)的轨迹不脱离S (ε),则式(5.1)系统之平衡状态0=e x 称为在Lyapunov意义下是稳定的。
一般地,实数δ与ε有关,通常也与t 0有关。
如果δ 与t 0无关,则此时平衡状态0=e x 称为一致稳定的平衡状态。
以上定义意味着:首先选择一个域S (ε),对应于每一个S (ε),必存在一个域S (δ),使得当t 趋于无穷时,始于S (δ)的轨迹总不脱离域S (ε)。
(2) 如果平衡状态0=e x ,在Lyapunov 意义下是稳定的,并且始于域S (δ)的任一条轨迹,当时间t 趋于无穷时,都不脱离S (ε),且收敛于0=e x ,则称式(5.1)系统之平衡状态0=e x 为渐近稳定的,其中球域S (δ)被称为平衡状态0=e x 的吸引域。
实际上,渐近稳定性比纯稳定性更重要。
考虑到非线性系统的渐近稳定性是一个局部概念,所以简单地确定渐近稳定性并不意味着系统能正常工作。
通常有必要确定渐近稳定性的最大范围或吸引域。
它是发生渐近稳定轨迹的那部分状态空间。
换句话说,发生于吸引域内的每一个轨迹都是渐近稳定的。
(3) 对所有的状态(状态空间中的所有点),如果由这些状态出发的轨迹都保持渐近稳定性,则平衡状态0=e x 称为大范围渐近稳定。
或者说,如果式(5.1)系统之平衡状态0=e x 渐近稳定的吸引域为整个状态空间,则称此时系统的平衡状态0=e x 为大范围渐近稳定的。
显然,大范围渐近稳定的必要条件是在整个状态空间中只有一个平衡状态。
在控制工程问题中,总希望系统具有大范围渐近稳定的特性。
如果平衡状态不是大范围渐近稳定的,那么问题就转化为确定渐近稳定的最大范围或吸引域,这通常非常困难。
然而,对所有的实际问题,如能确定一个足够大的渐近稳定的吸引域,以致扰动不会超过它就可以了。
(4) 如果对于某个实数ε>0和任一个实数δ >0,不管这两个实数多么小,在S (δ)内总存在一个状态0x ,使得始于这一状态的轨迹最终会脱离开S (ε),那么平衡状态0=e x 称为不稳定的。
图 5.1(a )、(b)和(c)分别表示平衡状态及对应于稳定性、渐近稳定性和不稳定性的典型轨迹。
在图5.1(a)、(b)和(c)中,域S (δ)制约着初始状态0x ,而域S (ε)是起始于0x 的轨迹的边界。
注意,由于上述定义不能详细地说明可容许初始条件的精确吸引域,因而除非S (ε)对应于整个状态平面,否则这些定义只能应用于平衡状态的邻域。
此外,在图5.1(c )中,轨迹离开了S (ε),这说明平衡状态是不稳定的。
然而却不能说明轨迹将趋于无穷远处,这是因为轨迹还可能趋于在S (ε)外的某个极限环(如果线性定常系统是不稳定的,则在不稳定平衡状态附近出发的轨迹将趋于无穷远。
但在非线性系统中,这一结论并不一定正确)。
图5.1 (a )稳定平衡状态及一条典型轨迹(b )渐近稳定平衡状态及一条典型轨迹(c )不稳定平衡状态及一条典型轨迹上述各定义的内容,对于理解本章介绍的线性和非线性系统的稳定性分析,是最低限度的要求。
注意,这些定义不是确定平衡状态稳定性概念的唯一方法。
实际上,在其他文献中还有另外的定义。
对于线性系统,渐近稳定等价于大范围渐近稳定。
但对于非线性系统,一般只考虑吸引区为有限的定范围的渐近稳定。
最后指出,在经典控制理论中,我们已经学过稳定性概念,它与Lyapunov意义下的稳定性概念是有一定的区别的,例如,在经典控制理论中只有渐近稳定的系统才称为稳定的系统。
在Lyapunov 意义下是稳定的,但却不是渐近稳定的系统,则叫做不稳定系统。
两者的区别与联系如下表所示。
5.2.3 预备知识1、纯量函数的正定性如果对所有在域Ω中的非零状态0≠x ,有0)(>x V ,且在x = 0处有)0(V =0,则在域Ω(域Ω包含状态空间的原点)内的纯量函数)(x V 称为正定函数。
如果时变函数),(t x V 由一个定常的正定函数作为下限,即存在一个正定函数)(x V ,使得)(),(x V t x V >, 对所有0t t ≥ 0),0(=t V , 对所有0t t ≥则称时变函数),(t x V 在域Ω(Ω包含状态空间原点)内是正定的。
2、纯量函数的负定性如果 -)(x V 是正定函数,则纯量函数)(x V 称为负定函数。
3、纯量函数的正半定形如果纯量函数)(x V 除了原点以及某些状态等于零外,在域Ω内的所有状态都是正定的,则)(x V 称为正半定纯量函数。
4、纯量函数的负半定性如果 -)(x V 是正半定函数,则纯量函数)(x V 称为负半定函数。
5、纯量函数的不定性如果在域Ω内,不论域Ω多么小,)(x V 既可为正值,也可为负值时,纯量函数)(x V 称为不定的纯量函数。
------------------------------------------------------------------[例5.1] 本例给出按照以上分类的几种纯量函数。
假设x 为二维向量。
1、22212)(x x x V += 正定的2、221)()(x x x V += 正半定的3、22121)23()(x x x x V +--=负定的 4、2221)x x x x V +=( 不定的 5、 正定的 ------------------------------------------------------------------6、二次型建立在Lyapunov 第二法基础上的稳定性分析中,有一类纯量函数起着很重要的作用,即二次型函数。
例如,注意,这里的x 为实向量,P 为实对称矩称。
7、复二次型或Hermite 型如果x 是n 维复向量,P 为Hermite 矩阵,则该复二次型函数称为Hermite 型函数。
例如22222112x x x x V ++=)(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==n nn n n n n n T x x x p p p p p p p p p x x x Px x x V2121222211121121][)(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==n nn n nn n n H x x x p p p p p p p p p x x x Px x x V 2121222211121121][)(在状态空间的稳定性分析中,经常使用Hermite 型,而不使用二次型,这是因为Hermite 型比二次型更具一般性(对于实向量x 和实对称矩阵P ,Hermite 型Px x H 等于二次型Px x T )。
