北京八中2016-2017学年七年级(上)期中数学试卷(解析版)
新北师大版七年级(上)期中考试数学试题(含答案) (82)

2015-2016学年七年级上学期期中联考数学试题一、选择题:(每小题3分,共36分,请把答案涂在答题卡上) 1.如右图,直角三角形绕直线 l 旋转一周,得到的立体图形是( )A .B .C .D .2. 2-的绝对值是( )A .2B .2-C . 21D . 21-3.计算23-的结果是( ) A .9 B .9-C .6D . 6-4.钓鱼岛周围海域面积约为170000平方千米,170000用科学记数法表示为( ) A .3107.1⨯ B .4107.1⨯C .41017⨯D . 5107.1⨯5.如图,将4×3的网格图剪去5个小正方形后,图中还剩下7个小正方形,为了使余下的部分(小正方形之间至少要有一条边相连)恰好能折成一个正方体,需要再剪去1个小正方形,则应剪去的小正方形的编号是( ) A .7 B .6C .5D .46.下列各组数中,结果相等的是( )A .()2211--与 B .332233⎛⎫ ⎪⎝⎭与 C .()22----与 D .()3333--与7.下列各式计算正确的是( ) A .253a b ab -+=B .266a a a +=C .22422m n mn mn -=D .222352ab b a ab -=-8.刘谦的魔术表演风靡全国,小明同学也学起了刘谦发明了一个魔术盒,当任意有理数对),(b a 进入其中时,会得到一个新的有理数:12--b a .例如把(3,-2)放入其中,就会得到32-(-2)-1=10.现将有理数对(-1,-2)放入其中,则会得到( ) A .0 B . 2 C .4- D . 2-9.下列说法中正确的有( )①若两数的差是正数,则这两个数都是正数; ②任何数的绝对值一定是正数;③零减去任何一个有理数,其差是该数的相反数;④在数轴上与原点距离越远的点表示的数越大.⑤正数的倒数是正数,负数的倒数是负数,任何数都有倒数. A .0个B . 1个C .2个D . 3个10. 若x 表示一个两位数,把数字3放在x 的左边,组成一个三位数是( ) A .x 3B .x +⨯1003C .3100+xD .310+x11.长方形的一边长等于y x 23+,另一边长比它长y x -,这个长方形的周长是( ) A .y x +4 B .y x 212+ C .y x 28+ D . y x 614+12.已知当1=x 时,代数式4323++bx ax 值为6,那么当1-=x 时,代数式4323++bx ax 值为( )A. 2B. 3C. -4D.-5二、填空题:(请将答案填在答题卡上,注意看清题号.每空3分,共12分) 13.比较大小: 3____2--14.今年元月份姜老师到银行开户,存入6000元钱,以后的每月根据收入情况存入一笔钱,下表为姜老师从2月份到7月份的存款情况:(超出上月记为正)根据记录,从2月份至7月份中 月份存入的钱最多。
北京八中初一上期中数学(含解析)

2014年北京八中初一(上)期中数学试卷一、选择题(每小题所给4个选项中只有一个符合要求,每小题3分,共30分)1.在(8)--,7--,0-,22()3-这四个数中,负数有( ). A .1个 B .2个 C .3个 D .4个2.甲、乙、丙三地的海拔高度分别为50米,5-米和15-米,那么最髙的地方比最低的地方高( ).A .35米B .25米C .55米D .65米3.下列说法正确的是( ).A .一个数前面加上“-”号这个数就是负数B .非负数就是正数C .正数和负数统称为有理数D .0既不是正数也不是负数4.若a 、b 互为相反数,那么( ).A .0ab <B .22a b =-C .33a b =D .a b =5.已知两个有理数的和比其中任何一个加数都小,那么一定是( ).A .这两个有理数同为正数B .这两个有理数同为负数C .这两个有理数异号D .这两个有理数中有一个为零6.下面运算正确的是( ).A .336ab ac abc +=B .22440a b b a -=C .224279x x x +=D .22232y y y -=7.设x 为有理数,若x x >,则( ).A .x 为正数B .x 为负数C .x 为非正数D .x 为非负数8.下列各式正确的是( ).A .1(1)()a b c a b c +++=---+B .222()2a a b c a a b c --+=--+C .27(27)a b c a b c -+=--D .()()a b c d a d b c -+-=--+9.已知代数式2346x x -+的值为9,则2686x x -+的值为( ).A .9B .7C .18D .1210.已知:数a ,b ,c 在数轴上的对应点如图所示,化简3a b c c a +----的值是().A .4b c --B .4b c +C .2b c -+D .24a b c +-O a b c。
2016-2017学年北京师大附中七年级(上)期中数学试卷

2016-2017学年北京师大附中七年级(上)期中数学试卷一、选择题(本大题共10道小题,每小题3分,共30分)1.(3分)﹣的相反数是()A.﹣8 B.C.0.8 D.82.(3分)神州十一号飞船成功飞向浩瀚宇宙,并在距地面约390000米的轨道上与天宫二号交会对接.将390000用科学记数法表示应为()A.3.9×104B.3.9×105C.39×104D.0.39×1063.(3分)下列各对数中,相等的一对数是()A.(﹣2)3与﹣23B.﹣22与(﹣2)2C.﹣(﹣3)与﹣|﹣3|D.与()24.(3分)下列说法中正确的是()A.是单项式B.﹣πx 的系数为﹣1C.﹣5不是单项式D.﹣5a2b 的次数是35.(3分)下列计算正确的是()A.x2y﹣2xy2=﹣x2y B.2a+3b=5abC.a3+a2=a5 D.﹣3ab﹣3ab=﹣6ab6.(3分)已知﹣2m6n与5m2x n y是的和是单项式,则()A.x=2,y=1 B.x=3,y=1 C.x=,y=1 D.x=1,y=37.(3分)关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是()A.这个多项式是五次四项式B.四次项的系数是7C.常数项是1D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+18.(3分)下列方程中,是一元一次方程的是()A.=3 B.x2+1=5 C.x=0 D.x+2y=39.(3分)已知ax=ay,下列等式变形不一定成立的是()A.b+ax=b+ay B.x=yC.x﹣ax=x﹣ay D.=10.(3分)如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P 与R之间,若|a|+|b|=3,则原点是()A.M或R B.N或P C.M或N D.P或R二、填空题(本大题共10道小题,每小题2分,共20分)11.(2分)比较大小:.12.(2分)1.9583≈(精确到百分位).13.(2分)若(a﹣1)2+|b+2|=0,则a﹣b﹣1=.14.(2分)设甲数为x,乙数比甲数的3倍少6,则乙数表示为.15.(2分)若a,b互为倒数,c,d互为相反数,则﹣c﹣d=.16.(2分)数轴上表示点A的数是最大的负整数,则与点A相距3个单位长度的点表示的数是.17.(2分)阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书本.18.(2分)如果方程ax|a+1|+3=0是关于x的一元一次方程,则a的值为.19.(2分)若方程2x+1=﹣1的解也是关于x的方程1﹣2(x﹣a)=2的解,则a 的值为.20.(2分)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是.三.计算题(本大题共4道小题,每小题20分,共20分)21.(20分)计算题(1)﹣2﹣1+(﹣16)﹣(﹣13);(2)25÷5×(﹣)÷(﹣);(3)(﹣+)×(﹣18);(4)﹣42+1÷|﹣|×(﹣2)2.四.化简求值题(本大题共2道小题,每小题4分,共8分)25.(4分)化简:﹣2x2﹣5x+3﹣3x2+6x﹣1.26.(4分)先化简,后求值:3(a2﹣ab+7)﹣2(3ab﹣a2+1)+3,其中a=2,b=.五.解方程(本大题共2道小题,每小题10分,共10分)27.(10分)解方程(1)4(2x﹣1)﹣3(5x+1)=14;(2)﹣=2.六.解答题(本大题共3道小题,每小题4分,共12分)29.(4分)有理数a,b在数轴上的对应点位置如图所示,且|a|=|c|.(1)用“<”连接这四个数:0,a,b,c;(2)化简:|a+b|﹣2|a|﹣|b+c|.30.(4分)已知:2x﹣y=5,求﹣2(y﹣2x)2+3y﹣6x的值.31.(4分)将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=,S2=;(2)求a,b满足的关系式,写出推导过程.七.附加题(本大题共20分,第32,33小题各6分,第34小题8分)32.(6分)填空题:(请将结果直接写在横线上)定义新运算“⊕”,对于任意有理数a,b有a⊕b=,(1)4(2⊕5)=.(2)方程4⊕x=5的解是.(3)若A=x2+2xy+y2,B=x2﹣2xy+y2,则(A⊕B)+(B⊕A)=.33.(6分)探究题:定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[﹣π]=﹣4.(1)如果[a]=﹣2,那么a可以是A.﹣15 B.﹣2.5 C.﹣3.5 D.﹣4.5(2)如果[]=3,则整数x=.(3)如果[﹣1.6﹣[]]=﹣3,满足这个方程的整数x共有个.34.(8分)阅读理解题:对于任意由0,1组成的一列数.将原有的每个1变成01,并将每个原有的0变成10称为一次变换.如101经过一次变换成为011001.请你经过思考、操作回答下列问题:(1)将11变换两次后得到;(2)若100101101001是由某数列两次变换后得到.则这个数列是;(3)一个10项的数列经过两次变换后至少有多少对两个连续相等的数对(即1100)?请证明你的结论;(4)01经过10次操作后连续两项都是0的数对个数有个.2016-2017学年北京师大附中七年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共10道小题,每小题3分,共30分)1.(3分)(2014•南宁校级一模)﹣的相反数是()A.﹣8 B.C.0.8 D.8【解答】解:﹣的相反数是.故选B.2.(3分)(2016秋•郴州期末)神州十一号飞船成功飞向浩瀚宇宙,并在距地面约390000米的轨道上与天宫二号交会对接.将390000用科学记数法表示应为()A.3.9×104B.3.9×105C.39×104D.0.39×106【解答】解:390 000=3.9×105,故选:B.3.(3分)(2016秋•西城区校级期中)下列各对数中,相等的一对数是()A.(﹣2)3与﹣23B.﹣22与(﹣2)2C.﹣(﹣3)与﹣|﹣3|D.与()2【解答】解:∵(﹣2)3=﹣8,﹣23=﹣8,∴(﹣2)3=﹣23,∴选项A正确.∵﹣22=﹣4,(﹣2)2=4,∴﹣22≠(﹣2)2,∴选项B不正确.∵﹣(﹣3)=3,﹣|﹣3|=﹣3,∴﹣(﹣3)≠﹣|﹣3|,∴选项C不正确.∵=,()2=,∴≠()2,∴选项D不正确.故选:A.4.(3分)(2016秋•西城区校级期中)下列说法中正确的是()A.是单项式B.﹣πx 的系数为﹣1C.﹣5不是单项式D.﹣5a2b 的次数是3【解答】解:(A)时多项式,故A错误;(B)﹣πx 的系数为﹣π,故B错误;(C)﹣5是单项式,故C错误;故选(D)5.(3分)(2015秋•常熟市期中)下列计算正确的是()A.x2y﹣2xy2=﹣x2y B.2a+3b=5abC.a3+a2=a5 D.﹣3ab﹣3ab=﹣6ab【解答】解:A、x2y和﹣2xy2不是同类项,不能合并,故本选项错误;B、2a和3b不是同类项,不能合并,故本选项错误;C、a3和a2不是同类项,不能合并,而a3•a2=a5,故本选项错误;D、﹣3ab﹣3ab=﹣6ab,故本选项正确;故选D.6.(3分)(2016秋•西城区校级期中)已知﹣2m6n与5m2x n y是的和是单项式,则()A.x=2,y=1 B.x=3,y=1 C.x=,y=1 D.x=1,y=3【解答】解:由题意,得2x=6,y=1,解得x=3,y=1,故选:B.7.(3分)(2016秋•郴州期末)关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是()A.这个多项式是五次四项式B.四次项的系数是7C.常数项是1D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1【解答】解:该多项式四次项是﹣7xy3,其系数为﹣7,故选(B)8.(3分)(2016秋•宁江区期末)下列方程中,是一元一次方程的是()A.=3 B.x2+1=5 C.x=0 D.x+2y=3【解答】解:A、不是一元一次方程,故此选项错误;B、不是一元一次方程,故此选项错误;C、是一元一次方程,故此选项正确;D、不是一元一次方程,故此选项错误;故选:C.9.(3分)(2016秋•西城区校级期中)已知ax=ay,下列等式变形不一定成立的是()A.b+ax=b+ay B.x=yC.x﹣ax=x﹣ay D.=【解答】解:A、两边都加b,结果不变,故A不符合题意;B、a=0时两边都除以a,无意义,故B符合题意;C、两边都乘以﹣1,都加x,结果不变,故C不符合题意;D、两边都除以同一个不为零的整式结果不变,故D不符合题意;故选:B.10.(3分)(2007•佛山)如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是()A.M或R B.N或P C.M或N D.P或R【解答】解:∵MN=NP=PR=1,∴|MN|=|NP|=|PR|=1,∴|MR|=3;①当原点在N或P点时,|a|+|b|<3,又因为|a|+|b|=3,所以,原点不可能在N或P点;②当原点在M、R时且|Ma|=|bR|时,|a|+|b|=3;综上所述,此原点应是在M或R点.故选A.二、填空题(本大题共10道小题,每小题2分,共20分)11.(2分)(2007•漳州质检)比较大小:>.【解答】解:∵|﹣|==,|﹣|==,而<,∴﹣>﹣.故答案为:>.12.(2分)(2016秋•西城区校级期中)1.9583≈ 1.96(精确到百分位).【解答】解:1.9583≈1.96(精确到百分位)故答案为1.96.13.(2分)(2016秋•西城区校级期中)若(a﹣1)2+|b+2|=0,则a﹣b﹣1=2.【解答】解:由题意得,a﹣1=0,b=2=0,解得,a=1,b=﹣2,则a﹣b﹣1=1+2﹣1=2,故答案为:2.14.(2分)(2016秋•西城区校级期中)设甲数为x,乙数比甲数的3倍少6,则乙数表示为3x﹣6.【解答】解:乙数表示为3x﹣6;故答案为:3x﹣615.(2分)(2016秋•西城区校级期中)若a,b互为倒数,c,d互为相反数,则﹣c﹣d=.【解答】解:∵a,b互为倒数,c,d互为相反数,∴ab=1,c+d=0.∴原式=﹣0=.故答案为:.16.(2分)(2016秋•西城区校级期中)数轴上表示点A的数是最大的负整数,则与点A相距3个单位长度的点表示的数是2或﹣4.【解答】解:∵点A的数是最大的负整数,∴点A表示数﹣1,∴在点A左侧,与点A相距3个单位长度的点表示的数是﹣1﹣3=﹣4,在点A右侧,与点A相距3个单位长度的点表示的数是﹣1+3=2,故答案为:2或﹣4.17.(2分)(2016秋•宁江区期末)阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书19本.【解答】解:20﹣3+1﹣1+2=19(本)故答案为:1918.(2分)(2016秋•西城区校级期中)如果方程ax|a+1|+3=0是关于x的一元一次方程,则a的值为﹣2.【解答】解:∵方程ax|a+1|+3=0是关于x的一元一次方程,∴|a+1|=1且a≠0,解得a=﹣2.故答案是:﹣2.19.(2分)(2016秋•郴州期末)若方程2x+1=﹣1的解也是关于x的方程1﹣2(x﹣a)=2的解,则a的值为﹣.【解答】解:方程2x+1=﹣1,解得:x=﹣1,代入方程得:1+2+2a=2,解得:a=﹣,故答案为:﹣20.(2分)(2011•肇庆)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是n2+2n.【解答】解:第一个是1×3,第二个是2×4,第三个是3×5,…第n个是nx(n+2)=n2+2n故答案为:n2+2n.三.计算题(本大题共4道小题,每小题20分,共20分)21.(20分)(2016秋•西城区校级期中)计算题(1)﹣2﹣1+(﹣16)﹣(﹣13);(2)25÷5×(﹣)÷(﹣);(3)(﹣+)×(﹣18);(4)﹣42+1÷|﹣|×(﹣2)2.【解答】解:(1)原式=﹣2﹣1﹣16+13=﹣6;(2)原式=25×××=;(3)原式=﹣14+15﹣5=﹣4;(4)原式=﹣16+××=﹣16+=﹣14.四.化简求值题(本大题共2道小题,每小题4分,共8分)25.(4分)(2016秋•西城区校级期中)化简:﹣2x2﹣5x+3﹣3x2+6x﹣1.【解答】解:原式=(﹣2﹣3)x2+(﹣5+6)x+(3﹣1)=﹣5x2+x+226.(4分)(2016秋•西城区校级期中)先化简,后求值:3(a2﹣ab+7)﹣2(3ab ﹣a2+1)+3,其中a=2,b=.【解答】解:原式=3a2﹣3ab+21﹣6ab+2a2﹣2+3=5a2﹣9ab+22,当a=2,b=时,原式=20﹣6+22=36.五.解方程(本大题共2道小题,每小题10分,共10分)27.(10分)(2016秋•西城区校级期中)解方程(1)4(2x﹣1)﹣3(5x+1)=14;(2)﹣=2.【解答】解:(1)去括号得:8x﹣4﹣15x﹣3=14,移项合并得:﹣7x=21,解得:x=﹣3;(2)去分母得:3(x+2)﹣2(2x﹣3)=24,去括号得:3x+6﹣4x+6=24,移项合并得:﹣x=12,解得:x=﹣12.六.解答题(本大题共3道小题,每小题4分,共12分)29.(4分)(2016秋•西城区校级期中)有理数a,b在数轴上的对应点位置如图所示,且|a|=|c|.(1)用“<”连接这四个数:0,a,b,c;(2)化简:|a+b|﹣2|a|﹣|b+c|.【解答】解:(1)根据数轴得:b<a<0<c;(2)由图可知:a<0,a+b<0,b+c<0,a与c互为相反数,即a+c=0,∴原式=﹣a﹣b+2a+b+c=a+c=0.30.(4分)(2016秋•西城区校级期中)已知:2x﹣y=5,求﹣2(y﹣2x)2+3y﹣6x的值.【解答】解:原式=﹣2(y﹣2x)2﹣3(2x﹣y)∵2x﹣y=5,∴原式=﹣2×52﹣3×5=﹣65.31.(4分)(2016秋•西城区校级期中)将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=a(x+a),S2=4b(x+2b);(2)求a,b满足的关系式,写出推导过程.【解答】解:(1)S1=a(x+a),S2=4b(x+2b),故答案为:a(x+a),4b(x+2b),(2)由(1)知:S1=a(x+a),S2=4b(x+2b),∴S1﹣S2=a(x+a)﹣4b(x+2b)=ax+a2﹣4bx﹣8b2=(a﹣4b)x+a2﹣8b2,∵S1与S2的差总保持不变,∴a﹣4b=0.∴a=4b.七.附加题(本大题共20分,第32,33小题各6分,第34小题8分)32.(6分)(2016秋•西城区校级期中)填空题:(请将结果直接写在横线上)定义新运算“⊕”,对于任意有理数a,b有a⊕b=,(1)4(2⊕5)=34.(2)方程4⊕x=5的解是x=2.(3)若A=x2+2xy+y2,B=x2﹣2xy+y2,则(A⊕B)+(B⊕A)=4x2+4y2.【解答】解:(1)∵2⊕5==,∴4(2⊕5)=4×=34.故答案为34;(2)4⊕x=,解方程=5,得x=2,故答案为x=2;(3)∵A=x2+2xy+y2,B=x2﹣2xy+y2,∴(A⊕B)==2x2﹣2xy+2y2,(B⊕A)==2x2+2xy+2y2,∴(A⊕B)+(B⊕A)=4x2+4y2.故答案为4x2+4y2.33.(6分)(2016秋•西城区校级期中)探究题:定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[﹣π]=﹣4.(1)如果[a]=﹣2,那么a可以是AA.﹣15 B.﹣2.5 C.﹣3.5 D.﹣4.5(2)如果[]=3,则整数x=5或6.(3)如果[﹣1.6﹣[]]=﹣3,满足这个方程的整数x共有12个.【解答】解:(1)根据题意知,[a]=﹣2表示不超过a的最大整数,∴a可以是﹣15,故选:A;(2)根据题意得3≤<4,解得:5≤x<7,则整数x=5或6,故答案为:5或6;(3)令[]=y,则原方程可变形为[﹣1.6﹣y]=﹣3,∴﹣3≤﹣1.6﹣y<﹣2,解得:2.4<y≤8.4,则y可取的整数有3、4、5、6、7、8,若y=3,则3≤<4,解得:5≤x<7,其整数解有5、6;若y=4,则4≤<5,解得:7≤x<9,其整数解有7、8;若y=5,则5≤<6,解得:9≤x<11,其整数解有9、10;若y=6,则6≤<7,解得:11≤x<13,其整数解有11、12;若y=7,则7≤<8,解得:13≤x<15,其整数解有13、14;若y=8,则8≤<9,解得:15≤x<17,其整数解有15、16;∴满足这个方程的整数x共有12个,故答案为:12.34.(8分)(2016秋•西城区校级期中)阅读理解题:对于任意由0,1组成的一列数.将原有的每个1变成01,并将每个原有的0变成10称为一次变换.如101经过一次变换成为011001.请你经过思考、操作回答下列问题:(1)将11变换两次后得到10011001;(2)若100101101001是由某数列两次变换后得到.则这个数列是101;(3)一个10项的数列经过两次变换后至少有多少对两个连续相等的数对(即1100)?请证明你的结论;(4)01经过10次操作后连续两项都是0的数对个数有341个.【解答】解:(1)将11一次変换得0101,再次变换得10011001,故答案为:10011001;(2)100101101001一次変换的原数是011001,再次变换的原数是101,故答案为:101;(3)经过两次变换后至少有10对两个连续相等的数对,∵0经过两次变换后得到0110,1经过两次变换后得到1001,∴10项的数列至少有10对连续相等的数对,又∵010*******经过两次变换后得到0110100101101001…恰有10对连续相等的数对,∴一个10项的数列经过两次变换后至少有10对两个连续相等的数对;(4)记数列01为A0,k次变换后数列为A k,连续两项都是0的数对个数为l k,设A k中有b k个01数对,A k+1中的00数对只能由A k中的01数对得到,∴l k=b k,A k+1中的01数对有2种产生途径:①由A k中的1得到;②由A k中的+100得到;根据题意知,A k中的0和1的个数总是相等,且共有2k+1个,=l k+2k,∴b k+1=l k+2k,∴l k+2由A0:0、1可得A1:1、0、0、1,A2:0、1、1、0、1、0、0、1,∴l1=1、l2=2,当k≥3时,若k为偶数,l k=l k﹣2+2k﹣2、l k﹣2=l k﹣4+2k﹣4、…、l4=l2+22,上述各式相加可得l k=1+22+24+…+2k﹣2==(2k﹣1),经检验,k=2时也满足l k=(2k﹣1),∴当k=10时,l10=(210﹣1)=341,故答案为:341.。
北京XX附中2016-2017学年七年级上期中数学试卷含答案解析

第 5 页(共 21 页)
4.下列说法中正确的是( ) A. 是单项式 B.﹣ππ 的系数为﹣1 C.﹣3 不是单项式 D.﹣3a2b 的次数是 3 5.下列计算正确的是( ) A.x2y﹣2πy2=﹣π2y B.2a+3b=5ab C.a3+a2 =5a 6.已知﹣2mD6.n﹣与3ab5﹣m3a2xbn=﹣6ab
B.x=3y,是y的=和1 是单C.项x式=,则,(y=1 )D.x=1,y=3 A.x=2,y=1 2y﹣2π3y2﹣ππy3+1,下列说法错误的是( ) A.这个多项式是五次四项式 7.关于多项式 0.3x B.四次项的系数是 7 C.常数项是 1 D.按 y 降幂排列为﹣ππy3﹣2π3y2+0.3x2y+1 8.下列方程中,是一元一次方程的是( ) A. =3 B.x2+1=5 C.x=0 D. x+2y=3 9.已知 ax=ay,下列等式变形不一定成立的是( ) A.b+ax=b+ay B.x=y
2016-2017 学年北京 X附X中七年级(上)期中数学试卷
一、选择题(本大题共 10 道小题,每小题 3 分,共 30 分) 1.﹣ 的相反数是( )
A.﹣8 B. C.0.8 D.8 2.神州十一号飞船成功飞向浩瀚宇宙,并在距地面约 390000 米的轨道上与天 宫二号交会对接.将 390000 用科学记数法表示应为( ) A.3.9×104B.3.9×105C.39×104 D.0.39×106 3.下列各对数中,相等的一对数是( ) A.(﹣2)3 与﹣23B.﹣22 与(﹣2)2 C.﹣(﹣3)与﹣|﹣3| D. 与( )2
北京市XX中学2016-2017学年度七年级上数学期中试卷含答案

北京市XX 中学2016-2017学年度七年级数学期中测试 2016年11月一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的。
1、某市2013年元旦的最高气温为2℃,最低气温为-8℃,这天的最高气温比最低气温高( )A .-10℃B .-6℃C .6℃D .10℃2、地球与太阳之间的距离约为149600000千米,将149600000用科学记数法表示应为( ).A .5101496⨯B .71096.14⨯C .810496.1⨯D .9101496.0⨯ 3、下列式子中,正确的是 ( ) A .0<-21 B .54<76- C .89> 98 D .4->3- 4、下列式子的变形中,正确的是( )A . 由6+x =10得x =10+6B . 由3x +5=4x 得3x -4x =-5C . 由8x =4-3x 得8x -3x =4D . 由2(x -1)= 3得2x -1=3 5、下列各式中运算正确的是( )A . 43m m -=B . 220a b ab -=C . 33323a a a -=D . 2xy xy xy -=- 6、若0)3-(22=++y x ,则=yx( )A . -8B . -6C . 6D . 87、今年哥哥的年龄是妹妹年龄的2倍,四年前哥哥的年龄是妹妹年龄的3倍,如果设妹妹今年x 岁,可列方程为( )A .2x+4=3(x-4)B .2x-4=3(x-4)C .2x=3(x-4)D .2x-4=3x8、已知代数式-2.5x a+b y a-1与3x 2y 是同类项,则a-b 的值为( )A.2B.0C. 2-D.19、表示x 、y 两数的点在x 轴上的位置如图所示,则x y 1x -+-等于( )A .y -1B .x y 21-+C .x y 21--D .2x -y -110、如图,M N P R ,,,分别是数轴上四个整数所对应的点,其中有一点是原点,并且1MN NP PR ===.数a 对应的点在M 与N 之间,数b 对应的点在P 与R 之间,若3a b +=,则原点可能是( )A .M 或RB .N 或PC .M 或ND .P 或R二、填空题(本题共16分,每小题2分) 11、31-的倒数是 . 12、某商店上月收入为a 元,本月的收入比上月的2倍还多10元,本月的收入是 元.13、若关于x 的一元一次方程23=+x ax 的解是1=x ,则a = . 14、化简3()()2()m n m n m n ---+-的结果是 . 15、当x = 时,代数式534x +的值为2. 16、若代数式2x 2+3y +7的值为8,那么代数式6x 2+9y +8的值为 . 17、定义运算“∆”,对于两个有理数a ,b ,有a ∆b =ab -(a +b ),例如:-3∆2=516)23(23-=+-=+--⨯-,则[]4)1()1(∆-∆-m =___ __. 18、有一列式子,按一定规律排列成-2a 2,4a 5,-8a 10,16a 17,-32a 26,……,第n 个式子为 (n 为正整数).三、解答题(本题共40分,每小题4分)19、计算:(1)23-17-(-7)+(-16) (2) )32(176)211(652-÷⨯-⨯ (3) 2111()()941836-+÷- (4)-72 + 2 ⨯ (-3)2 + (-6) ÷ (-21)3ab x20、化简:(1)3x 2-y 2-3x 2-5y +x 2-5y +y 2 (2) 22123(2)33x y x y --+() 21、求abc c a c a abc b a b a 3431323212222-⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛----的值, 其中a = -1, b = -3, c = 1.22、解方程:(1)90.55.14--=-x x x (2)2(10)6x x x -+=(3)+221=132x x --四、解答题(本题共14分,其中23题4分,24、25每题5分)23、某日,司机小张作为志愿者在东西向的公路上免费接送游客。
2016-2017学年北京七中七年级(上)期中数学试卷

2016-2017学年北京七中七年级(上)期中数学试卷一、选择题(每题3分,共30分)1.如果零上5∘C记作+5∘C,那么零下5∘C记作()A.−5B.−10C.−10∘CD.−5∘C2.以下4个有理数中,最小的是()A.−1B.1C.−2D.03.龙庆峡冰灯于2016年1月中旬接待游客.今年的龙庆峡冰灯以奥运五环、冬奥会运动项目等奥运元素为题材,分为彩灯区、娱乐区、冰展区,总面积达到200 000平方米.将200 000用科学记数法表示应为()A.20×104B.0.20×106C.2.0×106D.2.0×1054.如图,数轴上有A,B,C,D四个点,其中表示互为相反数的点是()A.点A与点BB.点B与点CC.点B与点DD.点A与点D5.如果a是有理数,下列各式一定为正数的()A.aB.a+1C.|a|D.a2+16.下列式子中,是单项式的是()A.−12x3yz2 B.x+y C.−m2−n2 D.12x7.下列计算正确的是()A.3a+b=3abB.3a−a=2C.2a3+3a2=5a5D.−a2b+2a2b=a2b8.−(a−b+c)去括号的结果是()A.−a+b−cB.−a−b+cC.−a+b+cD.a+b−c9.现有五种说法:①−a表示负数;②绝对值最小的有理数是0;③3×102x2y是5次单项式;④x−y5是多项式.其中正确的是()A.①③B.②④C.②③D.①④10.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则100!98!的值为()A.5049B.99!C.9900D.2!二、填空题(每题2分,共20分)11.根据要求,用四舍五入法取下列各数的近似数:1.4149≈________(精确到千分位)12.用代数式表示“a的3倍与b的差“是________.13.比较大小:−1________−13.14.化简:−(−5)=________,−|−5|=________.15.若a2m b3和−7a2b3是同类项,则m值为________.16.任意写一个含有字母a、b的三次二项式,常数项为−9,________.17.若|x−3|+(y−2)2=0,则y−x=________.18.已知:(m−2)x−1=0是关于x的一元一次方程,则m________.19.若a2+ab=5,ab+b2=4,则a2+2ab+b2的值为________.20.如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第一次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,点A4表示的数是________,如果点A n与原点的距离不小于20,那么n的最小值是________.三、解答题(共50分)21.计算(1)12−7+18−15(2)1÷(−2)×(−13)(3)(1−1+1)×(−48)(4)−24+(−5)2÷(−11 4 )22.化简(1)5x2+x+3+4x−8x2−2(2)(2x3−3x2−3)−(−x3+4x2)(3)3 (x2−5x+1)−2 (3x−6+x2)23.先化简,再求值(1)4x−x2+2x3−(3x2+x+2x3),其中x=3.(2)4x2−xy−(43y2+2x2)+2(3xy−13y2),其中x=5,y=12.24.解方程(1)−2x=4(2)x−10=7(3)x+13=5x+37(4)3x−x=−12+1.25.有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:回答下列问题:(1)这8筐白菜中,最接近25千克的那筐白菜为________千克;(2)以每筐25千克为标准,这8筐白菜总计超过多少千克或不足多少千克?(3)若白菜每千克售价2.6元,则出售这8筐白菜可卖多少元?26.某学校初一年级参加社会实践课,报名第一门课的有x人,第二门课的人数比第一门课的45少20人,现在需要从报名第二门课的人中调出10人学习第一门课,那么:(1)报两门课的共有多少人?(2)调动后,报名第一门课的人数为________人,第二门课人数为________人.(3)调动后,报名第一门课比报名第二门课多多少人?计算出代数式后,请选择一个你觉得合适的x的值代入,并求出具体的人数.四、附加题(每题4分,共20分)27.下面的图表是我国数学家发明的“杨辉三角”,此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律.请你观察,并根据此规律写出:(a+b)7的展开式共有________项,(a+b)n的展开式共有________项,各项的系数和是________.28.规定“*”表示一种运算,且a∗b=a−2bab ,则3∗(4∗12)的值是________.29.已知当x=2时,代数式ax3−bx+1的值为−17,求当x=−1时,代数式12ax−3bx3−5的值是多少?30.已知|a+2|=−b2,求:2a+3b2a−3b+2002b的值?31.阅读下面材料并解决有关问题:我们知道:|x|=x(x>0)0(x=0)−x(x<0).现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x−2|时,可令x+1=0和x−2=0,分别求得x=−1,x=2(称−1,2分别为|x+1|与|x−2|的零点值).在实数范围内,零点值x=−1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:①x<−1;②−1≤x<2;③x≥2.从而化简代数式|x+1|+|x−2|可分以下3种情况:①当x<−1时,原式=−(x+1)−(x−2)=−2x+1;②当−1≤x<2时,原式=x+1−(x−2)=3;③当x≥2时,原式=x+1+x−2=2x−1.综上讨论,原式=−2x+1(x<−1) 3(−1≤x<2)2x−1(x≥2).通过以上阅读,请你解决以下问题:(1)化简代数式|x+2|+|x−4|.(2)求|x−1|−4|x+1|的最大值.。
北京市 七年级(上)期中数学试卷 (含答案)

七年级(上)期中数学试卷一、选择题(本大题共10小题,共30.0分)1.-2的相反数是()A. B. C. D. 22.在-,0,,-1这四个数中,最小的数是()A. B. 0 C. D.3.有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是()A. B. C. D.4.A、B两地相距6980000m,用科学记数法表示为()m.A. B. C. D.5.下面各式中,与-2xy2是同类项的是()A. B. C. D.6.一个长方形的一边长是2a+3b,另一边的长是a+b,则这个长方形的周长是()A. B. C. D.7.下列代数式书写规范的是()A. B. C. ax3 D.8.关于多项式x5-3x2-7,下列说法正确的是()A. 最高次项是5B. 二次项系数是3C. 常数项是7D. 是五次三项式9.在代数式:,3m-3,-22,-,2πb2中,单项式的个数有()A. 1个B. 2个C. 3个D. 4个10.如果x是最大的负整数,y绝对值最小的整数,则-x2016+y的值是()A. B. C. 1 D. 2016二、填空题(本大题共10小题,共20.0分)11.的绝对值是______ ,的倒数是______ .12.在数轴上,若点P表示-2,则距P点3个单位长的点表示的数是______ .13.单项式-5πab2的系数是______ ,次数是______ .14.如图是一数值转换机,若输入的x为-1,则输出的结果为______ .15.绝对值小于3的所有整数的和是______ .16.数轴上表示数-5和表示-14的两点之间的距离是______ .17.在数4.3,-,|0|,-(-),-|-3|,-(+5)中,______ 是正数.18.已知|a|=2,|b|=5,且ab<0,那么a+b的值为______ .19.如果有|x-3|+(y+4)2=0,则x= ______ ,y x= ______ .20.现规定一种新的运算“*”:a*b=a b,如3*2=32=9,则()*3= ______ .三、解答题(本大题共13小题,共66.0分)21.把下面的有理数填在相应的大括号里:(★友情提示:将各数用逗号分开)15,,0,-30,0.15,-128,,+20,-2.6正数集合﹛______﹜负数集合﹛______﹜整数集合﹛______﹜分数集合﹛______﹜22.计算:28-37-3+52.23.计算:(-+)÷(-)24.计算(-4)×(-9)+(-)-23.25.化简:3x2-3+x-2x2+5.26.化简(5a-3a2+1)-(4a3-3a2).27.观察图形,写出一个与阴影面积有关的代数恒等式.28.(1)在数轴上表示下列各数,(2)用“<”连接:-3.5,,-1,4,0,2.5.29.先化简,再求值:5(a2b-ab2)-(ab2+5a2b),其中a=1,b=-2.30.10盒火柴如果以每盒100根为准,超过的根数记作正数,不足的根数记作负数,每盒数据记录如下:+3,+2,0,-1,-2,-3,-2,+3,-2,-2.求:这10盒火柴共有多少根.31.已知有理数a,b,c在数轴上的位置如图所示,(1)用<,>,=填空:a+c ______ 0,c-b ______ 0,b+a ______ 0,abc ______ 0;(2)化简:|a+c|+|c-b|-|b+a|.32.阅读下列解题过程,然后答题:已知如果两个数互为相反数,则这两个数的和为0,例如,若x和y互为相反数,则必有x+y=0.(1)已知:|a|+a=0,求a的取值范围.(2)已知:|a-1|+(a-1)=0,求a的取值范围.33.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.(1)根据上面的规律,写出(a+b)5的展开式.(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.答案和解析1.【答案】D【解析】解:-2的相反数是2,故选:D.根据相反数的定义:只有符号不同的两个数叫做互为相反数即可得到答案.此题主要考查了相反数,关键是掌握相反数的定义.2.【答案】D【解析】解:根据有理数大小比较的法则,可得-1<-,所以在-,0,,-1这四个数中,最小的数是-1.故选:D.有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.3.【答案】D【解析】解:∵从数轴可知:b<0<a,|b|>|a|,∴A错误;B错误;∵a>0,b<0,∴ab<0,∴C错误;∵b<0<a,|b|>|a|,∴a-b>0,a+b<0,∴a-b>a+b,∴D正确;故选D.数轴可知b<0<a,|b|>|a|,求出ab<0,a-b>0,a+b<0,根据以上结论判断即可.本题考查了数轴,有理数的乘法、加法、减法等知识点的应用,关键是能根据数轴得出b<0<a,|b|>|a|.4.【答案】D【解析】解:6980000=6.98×106,故选:D.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.【答案】A【解析】解:由题意,得y2x与-2xy2是同类项,故选:A.根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,可得答案.本题考查同类项的定义,同类项定义中的两个“相同”:所含字母相同;相同字母的指数相同,是易混点,还有注意同类项定义中隐含的两个“无关”:①与字母的顺序无关;②与系数无关.6.【答案】B【解析】解:周长=2(2a+3b+a+b)=6a+8b.故选B.长方形的周长等于四边之和,由此可得出答案.本题考查有理数的加减运算,比较简单,注意长方形的周长可表示为2(长加宽).7.【答案】A【解析】解:选项A正确,B正确的书写格式是b,C正确的书写格式是3ax,D正确的书写格式是.故选A.根据代数式的书写要求判断各项即可得出正确答案.代数式的书写要求:(1)在代数式中出现的乘号,通常简写成“•”或者省略不写;(2)数字与字母相乘时,数字要写在字母的前面;(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.8.【答案】D【解析】解:A、多项式x5-3x2-7的最高次项是x5,故本选项错误;B、多项式x5-3x2-7的二次项系数是-3,故本选项错误;C、多项式x5-3x2-7的常数项是-7,故本选项错误;D、多项式x5-3x2-7是五次三项式,故本选项正确.故选:D.根据多项式的项和次数的定义,确定各个项和各个项的系数,注意要带有符号.本题考查与多项式相关的概念,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.9.【答案】C【解析】解:-22,-,2πb2中是单项式;是分式;3m-3是多项式.故选C.根据单项式的定义进行解答即可.本题考查的是单项式,熟知数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式是解答此题的关键.10.【答案】B【解析】解:∵x是最大的负整数,y绝对值最小的整数,∴x=-1,y=0,∴-x2016+y=-(-1)2016=-1.故选B.由于x是最大的负整数,y绝对值最小的整数,由此可以分别确定x=-1,y=0,把它们代入所求代数式计算即可求解.此题主要考查了有理数的混合运算,解题的关键是根据最大的负整数,绝对值最小的整数的性质确定x、y的值,然后代入所求代数式即可解决问题.11.【答案】;【解析】解:-的绝对值为,1的倒数为.故答案为:,.根据绝对值、倒数,即可解答.本题考查了绝对值、倒数,解决本题的关键是熟记绝对值、倒数的定义.12.【答案】-5或1【解析】解:设距P点3个单位长的点表示的数是x,则|x+2|=3,当x+2≥0时,原式可化为:x+2=3,解得x=1;当x+2<0时,原式可化为:-x-2=3,解得x=-5.故答案为:-5或1.设距P点3个单位长的点表示的数是x,则|x+2|=3,求出x的值即可.本题考查的是数轴,熟知数轴上两点间的距离公式是解答此题的关键.13.【答案】-5π;3【解析】解:单项式-5πab2的系数是-5π,次数是3.故答案为:-5π,3.根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.此题考查了单项式,确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.14.【答案】9【解析】解:(-1-2)×(-3)=(-3)×(-3)=9.故答案为:9.根据运算规则:先-2,再×(-3),进行计算即可求解.此题主要考察根据运算规则列式计算,读懂题中的运算规则,并准确代入求值是解题的关键.15.【答案】0【解析】解:根据绝对值的意义得绝对值小于3的所有整数为0,±1,±2.所以0+1-1+2-2=0.故答案为:0.绝对值的意义:一个数的绝对值表示数轴上对应的点到原点的距离.互为相反数的两个数的和为0.依此即可求解.此题考查了绝对值的意义,并能熟练运用到实际当中.16.【答案】9【解析】解:|-5-(-14)|=9.数轴上两点之间的距离等于这两点的数的差的绝对值,即较大的数减去较小的数.考查了数轴上两点之间的距离的计算方法.17.【答案】4.3,-(-)【解析】解:在数4.3,-,|0|,-(-)=,-|-3|=-3,-(+5)=-5中,4.3,-(-)是正数.故答案为:4.3,-(-).首先将各数化简,再根据正数的定义可得结果.本题主要考查了有理数的定义,熟练掌握有理数的分类是解答此题的关键.18.【答案】3或-3【解析】解:①a>0,b<0,则a=2,b=-5,a+b=-3;②a<0,b>0,则a=-2,b=5,a+b=3.故填3或-3.根据题意可得a和b异号,分情况讨论①a>0,b<0;②a<0,b>0.本题考查有理数的加法,注意讨论a和b的取值范围得出a和b的值是关键.19.【答案】3;-64【解析】解:由题意得,x-3=0,y+4=0,解得,x=3,y=-4,则y x=-64,故答案为:3;-64.根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.20.【答案】【解析】解:∵a*b=a b,3*2=32=9,∴()*3=(-)3=-.故答案为:-.根据题中所给出的运算方法列出乘方的式子,再根据乘方的运算法则进行计算即可.本题考查的是有理数的混合运算,熟知数的乘方法则是解答此题的关键.21.【答案】15,0.15,,+20;,-30,-128,-2.6;15,0,-30,-128,+20;,0.15,,-2.6【解析】解:正数集合﹛15,0.15,,+20,﹜负数集合﹛,-30,-128,-2.6,﹜整数集合﹛15,0,-30,-128,+20,﹜分数集合﹛,0.15,,-2.6,﹜按照有理数的分类填写:有理数.认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.22.【答案】解:28-37-3+52,=28+52-37-3,=80-40,=40.【解析】先根据加法交换律将同号数相加,再把两个异号数相加.本题是有理数的加减混合运算,可以看作是省略加号的加法,注意运用简便算法进行计算.23.【答案】解:原式=(-+)×(-36),=×(-36)-×(-36)+×(-36),=-8+9-2,=-1.【解析】首先根据除以一个不为0的数等于乘以这个数的倒数可得(-+)×(-36),再用乘法分配律计算即可.此题主要考查了有理数的除法,关键是掌握有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.24.【答案】解:(-4)×(-9)+(-)-23=36+(-)-8=27.【解析】根据有理数的乘法和加减法可以解答本题.本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.25.【答案】解:3x2-3+x-2x2+5=(3x2-2x2)+x+(5-3)=x2+x+2.【解析】首先找出同类项,进而合并同类项得出答案.此题主要考查了合并同类项,正确找出同类项是解题关键.26.【答案】解:(5a-3a2+1)-(4a3-3a2)=5a-3a2+1-4a3+3a2=-4a3+5a+1.【解析】先去括号,然后合并同类项即可解答本题.本题考查整式的加减,解题的关键是明确整式的加减的计算方法,注意去括号后,各项内的符号是否变号.27.【答案】解:阴影部分的面积可表示为:a2-b2或(a+b)(a-b),∴a2-b2=(a+b)(a-b).【解析】分别利用不同的方法表示出阴影部分的面积,得到恒等式.本题考查的是平方差公式的几何背景,掌握平方差公式、矩形的面积公式是解题的关键.28.【答案】解:(1)如图所示:(2)-3.5<-1<0<<2.5<4【解析】在数轴上表示各数,数轴上各数从左往右的顺序,就是各数从小到大的顺序.本题考查了用数轴表示有理数和有理数的大小比较.数轴上各数从左往右的顺序就是各数从小到大的顺序.29.【答案】解:原式=5a2b-5ab2-ab2-5a2b=-6ab2,∴当a=1,b=-2时,∴原式=-6×1×4=-24【解析】先将原式化简,然后将a与b的值代入即可求出答案.本题考查整式运算,涉及代入求值.30.【答案】解:先求超过的根数:(+3)+(+2)+0+(-1)+(-2)+(-3)+(-2)+(+3)+(-2)+(-2)=-4;则10盒火柴的总数量为:100×10-4=996(根).答:10盒火柴共有996根.【解析】首先审清题意,明确“正”和“负”所表示的意义;然后根据每盒的数据记录求出超过的根数,进而可求得10盒火柴的总数量.解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.31.【答案】<;>;<;>【解析】解:(1)根据数轴可知:a<b<0<c,且|c|<|b|<|a|,∴a+c<0,c-b>0,b+a<0,abc>0,故答案为:<,>,<,>;(2)原式=-(a+c)+(c-b)+(b+a)=-a-c+c-b+b+a=0.(1)根据数轴,判断出a,b,c的取值范围,进而求解;(2)根据绝对值的性质,去绝对值号,合并同类项即可.本题主要考查数轴、绝对值、整式的加减等知识的综合运用,解决此题的关键是能够根据数轴上的信息,判断出a,b,c等字母的取值范围,同时解决此题时也要注意绝对值性质的运用.32.【答案】解:(1)∵|a|≥0,|a|+a=0,∴a≤0;(2)∵|a-1|≥0,∴a-1≤0,解得a≤1.【解析】(1)根据绝对值的性质可得出|a|≥0,再由相反数的定义即可得出结论;(2)根据绝对值的性质可得出|a-1|≥0,再由相反数的定义即可得出结论.本题考查的是有理数的加法,熟知相反数的定义是解答此题的关键.33.【答案】解:(1)如图,则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(2)25-5×24+10×23-10×22+5×2-1.=25+5×24×(-1)+10×23×(-1)2+10×22×(-1)3+5×2×(-1)4+(-1)5.=(2-1)5,=1.【解析】(1)直接根据图示规律写出图中的数字,再写出(a+b)5的展开式;(2)发现这一组式子中是2与-1的和的5次幂,由(1)中的结论得:25-5×24+10×23-10×22+5×2-1=(2-1)5,计算出结果.本题考查了完全式的n次方,也是数字类的规律题,首先根据图形中数字找出对应的规律,再表示展开式:对应(a+b)n中,相同字母a的指数是从高到低,相同字母b的指数是从低到高.。
北京市XX中学2016—2017学年初一上期中质量检测数学试卷含答案

初一数学 共4页 第1页北京市XX 中学2016—2017第一学期期中质量检测初 一 数 学(每小题的四个选项中,只有一个是符合题目要求的.请将你认为符合要求的一3分,共30分) 如果a 与3互为倒数,那么a 是( ). A. 3- B. 3 C. 13- D. 13 .三峡工程是具有防洪、发电、航运、供水等巨大综合利用效益的特大型水利水电工程,22 150 000 0003m ,这个数用科学记数法表示为( ). A .83221.510m ⨯ B .9322.1510m ⨯ C .1032.21510m ⨯ D .1132.21510m ⨯ .下列单项式中,与2a b 是同类项的是( ). A. 22a b B. 22a b C. 2ab D. 3ab 在22-,2)2(-,)2(--,2--,0-中,负数的个数是( ). A .1个 B. 2个 C. 3个 D. 4个 化简16(0.5)x --的结果是( ). A .160.5x -- B. 16+0.5x - C .168x - D .16+8x - 运用等式性质进行变形, 正确的是 ( ). A. 如果b a =, 那么c b c a -=+ B. 如果c b c a =, 那么b a = C. 如果b a =, 那么c b c a = D. 如果a a 32=, 那么3=a 若0x =是关于x 的方程23=1x n -的解.则n =( ). A.31 B. 3C.31-D.3- .有理数a b ,在数轴上的位置如图所示,则下列结论中,错误..的是( ). .b a <<0B . b a > .b a >- D . b a a b +<-初一数学 共4页 第4页9.式子31+-x 取最小值时,x 等于( ).A.1B.2C.3D. 010. 在如图的2016年11月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( ).A .27B .51C .69D .72二、 填空题(每题2分,共16分)11. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示 .12. 如果12a =,3b =-,那么代数式2a b +的值为 . 13. 多项式7324223173+--xy y x y x , 按y 的降幂排列为_____________________________. 14.多项式223368x kxy y xy --+-不含xy 项,则k = .15.3+a 与1互为相反数,那么a = .16. 在数轴上,若点P 表示-2,则距P 点5个单位长度的点表示的数是 .17. 已知23x y -=,那么代数式324x y -+的值是 .18. a >0,b <0且a +b <0,用“<”连结a ,b , -a , -b , a -b 为:_____________________.三、解答题(第19至30题,每题4分,31,32每题3分,共54分)计算下列各题:19.)125(41)32(12125.0-+--++ . 20.)49(944-⨯÷-.初一数学 共4页 第1页.5]24)436183(411[÷⨯-+-. 22. 1.0)8.2(2)3(34)2(23÷---⨯+- . 化简 222423a ab ab a +-+-. 24.化简:()22432a b b a +--+. 化简求值:]2)43(37[322x x x x ---- ,其中1x =-. .解方程:4587+=-x x . 27.解方程:)5.0(4107+-=-x x . .解方程:132321=+--x x . .某中学七年级A 班有40人,某次活动中分为四组,第一组有a 人,第二组比第一组的一6人,第三组的人数等于前两组人数的和. 1) 第二组的人数; 2) 第三组的人数; 3) 第四组的人数; 4) 找一个你喜欢的数作为的a 值,求出此时第四组的人数. 若a - b = 2, a - c = 1,求(2a - b - c )2 + (c -b )2的值.初一数学 共4页 第4页31.观察图形,利用图形面积关系用写出一个代数恒等式.32. 观察下列式子,定义一种新运算:734131=+⨯=⊗; 11143)1(3=-⨯=-⊗;2444545=+⨯=⊗; 4(3)44319-⊗-=-⨯-=-;(1)请你想一想: =⊗b a ; (用含a 、b 的代数式表示)(2)如果b a ≠,那么b a ⊗ a b ⊗ (填 “=”或 “≠ ”);(3)如果a a ⊗=-⊗3)6(,请求出a 的值.初一数学 共4页 第1页北京市XX 中学2016—2017学年度第一学期期中质量检测初 一 数 学 答案每小题3分,共30分)2.C.3.A.4.B.5.D.6.B.7.C.8.D.9.A. 10.D.(每题2分,共16分)支出80元; 12. -2; 13.342271732;3xy x y x y --++ 14.;2=k 15.;4-=a或3; 17. -3; 18.;b a b a a b -<-<<-<.解答题(19-30,每题4分,31,32每题3分,共54分).)125(41)32(12125.0-+--++ =)32()125(1214141-+-++-=32(31(-+- ………………………………………2分=1-. ………………………………………4分49(944-⨯÷- =49494⨯⨯+ ………………………………………2分 =481. ………………………………………4分5]24)436183(411[÷⨯-+-=5)]244324612483(411[÷⨯-⨯+⨯-=5)]1849(411[÷-+-初一数学 共4页 第4页=51)]5(45[⨯-- ………………………………………2分 =141+ =411 . ………………………………………4分 22. 1.0)8.2(2)3(34)2(23÷---⨯+- =49-8++2832⨯………………………………3分 =26 ………………………………4分23. 222423a ab ab a +-+-=ab a )42()23(2-++-=ab a 22--………………………………………4分24. ()22432a b b a +--+=22432a b b a +-+-=2 3.a +………………………………………4分25.]2)43(37[322x x x x ----=]21297[322x x x x -+--22212973x x x x +-+-==91952+-x x ………………………………………3分当1-=x 时,原式=.339)1(19)1(52=+-⨯--⨯ ………………………………………4分26.4587+=-x x7548x x -=+212x =6.x =………………………………………4分 27.)5.0(4107+-=-x x初一数学 共4页 第1页24107--=-x x …………………………………1分 72104+-=+x x155=x ………………………………………3分 3=x . ………………………………………4分132321=+--x x 6)23(2)1(3=+--x x …………………………………1分 64633=---x x 63643++=-x x 15=-x …………………………………3分 15-=x . …………………………………4分 解:第二组人数(6)2a +人;………………………………1分 第三组人数(36)2a +人;………………………………2分 第四组人数(28-3)a 人;………………………………3分 a 可以取2,4,6,8,第四组的人数分别为22,16,10,4人……………………4分 (只写出一组即可) 解:由题意,,1,32=-=--b c c b a …………………………………3分 =10. …………………………………4分 22()();a b a b a b -=+-…………………………………3分,(只要符合图形题意即可) (1)4;a b +………………………………1分 (2)≠;………………………………2分 (3)46=12;6;a a a -+=………………………………3分。
2016—2017学年北师大初一上期中考试数学试卷含答案

得到分割成的
三 、解答题(共 80 分) 21 计算或化简( 24 分)
( 1) 3 ( 2) 3 ( 5) 0
(2)
16
3
1
-2 - -
-4
8
( 3) ( 2a2-1+2a) -( a- 1+ a2) .
(4) 8a 2b 2 5a 2b
22、( 8 分)画出数轴,把下列各组数分别在数轴上表示出来,并用“<”连接
C.
5
3、下列图形经过折叠不能围成棱柱的是 ( )
5
D.
5
座
……
……
……
场
………………
考
线… A
B
C
D
…… ……
4、绝对值等于 8 的是 (
)
……
A. 8
B.
8
C.8 或 8
D. 不能确定
场 考
…… …线
5、数轴上与 O的距离等于 2 个单位的点表示的数是
(
)
……
A.0 和 2
B. -1 和 2 C.
1234567
日期 (日)
27、( 12 分) 张叔叔在南涧“龙凤丽都”房地产公司买了一套经济适用房,他 准备将地面铺上地砖, 这套住宅的建筑平面图 (由四个长方形组成) 如图所示(图 中长度单位:米),解答下列问题:
(1)用代数式表示这所住宅的总面积。 ( 6 分)
( 2)若铺 1 平方米地砖平均费用 120 元,求当 x=6 时,这套住宅铺地砖总 费用为多少元?( 6 分)
…
2016— 2017学年第一学期期中考试
…
…
…
初二数学试卷答题卡
…
…
… 一、选择题(每小题 4分,共 40分)
2016_2017学年七年级数学上学期期中试卷(含解析)北师大版

七年级(上)期中数学试卷一、选择题(共10小题,每小题3分,满分30分)1.一个有理数的倒数是它本身,这个数是()A.0 B.1 C.﹣1 D.1或﹣12.数a,b在数轴上的位置如图所示,则a+b是()A.正数 B.零C.负数 D.都有可能3.下列各题运算正确的是()A.3x+3y=6xy B.x+x=x2C.﹣9y2+16y2=7 D.9a2b﹣9a2b=04.一个棱柱有12条棱,那么它的底面一定是()A.十八边形 B.六边形C.四边形D.八边形5.如图所示,陀螺是由下面哪两个几何体组合而成的()A.长方体和圆锥 B.长方形和三角形C.圆和三角形D.圆柱和圆锥6.一个数是9,另一个数比9的相反数大2,那么这两个数的和为()A.2 B.﹣2 C.20 D.﹣207.在下列各组中,是同类项的是()A.9a2x和9a2B.a2和2a C.2a2b和3ab2D.4x2y和﹣yx28.已知代数式x+2y的值是3,则代数式2x+4y+1的值是()A.1 B.4 C.7 D.不能确定9.用代数式表示a、b两数的和与a、b两数的差的积是()A.(a+b)(a﹣b)B.(a+b)•a﹣b C.a•(a+b)﹣b D.(a+b)﹣ab10.若a、b互为相反数,c为最大的负整数,d的倒数等于它本身,则2a+2b﹣cd的值是()A.1 B.﹣2 C.﹣1 D.1或﹣1二、填空题11.绝对值小于4的整数有个,它们的和是,积是.12.主视图、俯视图和左视图都是正方形的几何体是13.圆锥有个面,它的侧面展开图是.14.若3a m b2与ab n是同类项,则m= ,n= .15.﹣1的倒数是,相反数是绝对值是.16.在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作.17.比较大小:﹣π﹣3.14(选填“>”、“=”、“<”).18.用一个平面去截长方体,截面是平行四边形(填“可能”或“不可能”).19.按规律填空:a,﹣2a2,3a3,﹣4a4,,.20.若|x+2|+(y﹣1)2=0,则x= ,y= .三、计算题:21.计算:(1)﹣1+﹣+;(2)(﹣2)÷×(﹣3);(3)﹣24×(﹣+﹣);(4)﹣5﹣(﹣11)+2﹣(﹣).四、解答题(共40分)22.如图所示的几何体是由5个相同的正方体搭成的,请画出它的主视图、左视图和俯视图.23.合并同类项:2a3b﹣a3b﹣a2b+a2b﹣ab2.24.先化简,再求值:3(x﹣y)﹣2(x+y)+2,其中x=﹣1,.25.某储蓄所,某日办理了7项储蓄业务:取出9.6万元,存入5万元,取出7万元,存入12万元,存入22万元,取出10.25万元,取出2.4万元,求储蓄所该日现金增加多少万元?26.用棋子摆出下列一组图形:(1)填写下表:(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?2016-2017学年甘肃省张掖市高台县南华中学七年级(上)期中数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.一个有理数的倒数是它本身,这个数是()A.0 B.1 C.﹣1 D.1或﹣1【考点】倒数.【专题】常规题型.【分析】根据倒数的定义可知如果一个数的倒数等于它本身,则这个数是±1.【解答】解:如果一个数的倒数等于它本身,则这个数是±1,故选:D.【点评】此题考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.要求掌握并熟练运用.尤其是±1这两个特殊的数字.2.数a,b在数轴上的位置如图所示,则a+b是()A.正数 B.零C.负数 D.都有可能【考点】数轴;有理数的加法.【专题】数形结合.【分析】首先根据数轴发现a,b异号,再进一步比较其绝对值的大小,然后根据有理数的加法运算法则确定结果的符号.异号两数相加,取绝对值较大的加数的符号.【解答】解:由图,可知:a<0,b>0,|a|>|b|.则a+b<0.故选:C.【点评】本题结合数轴,主要考查了有理数的加法法则,体现了数形结合的思想.3.下列各题运算正确的是()A.3x+3y=6xy B.x+x=x2C.﹣9y2+16y2=7 D.9a2b﹣9a2b=0【考点】合并同类项.【分析】根据同类项的定义及合并同类项法则解答.【解答】解:A、3x+3y不是同类项,不能合并,故A错误;B、x+x=2x≠x2,故B错误;C、﹣9y2+16y2=7y2≠7,故C错误;D、9a2b﹣9a2b=0,故D正确.故选:D.【点评】本题考查的知识点为:同类项的定义:所含字母相同,相同字母的指数相同;合并同类项的方法:字母和字母的指数不变,只把系数相加减;不是同类项的一定不能合并.4.一个棱柱有12条棱,那么它的底面一定是()A.十八边形 B.六边形C.四边形D.八边形【考点】认识立体图形.【分析】依据n棱柱有3n条棱进行求解即可.【解答】解:设该棱柱为n棱柱.根据题意得:3n=12.解得:n=4.所以该棱柱为4棱柱.故选:C.【点评】本题主要考查的是认识立体图形,掌握棱柱的棱的条数和棱柱的底面的边数之间的关系是解题的关键.5.如图所示,陀螺是由下面哪两个几何体组合而成的()A.长方体和圆锥 B.长方形和三角形C.圆和三角形D.圆柱和圆锥【考点】认识立体图形.【分析】根据立体图形的概念和定义对图进行分析知:该图上部分是圆柱,下部分是圆锥.【解答】解:由组成几何体的特征知,上面是圆柱,下面是圆锥.【点评】本题考查的圆柱和圆锥的定义,关键点在于理解圆柱和圆锥的特征.6.一个数是9,另一个数比9的相反数大2,那么这两个数的和为()A.2 B.﹣2 C.20 D.﹣20【考点】有理数的加法.【分析】首先确定另一个数比9的相反数大2为﹣9+2=﹣7,然后计算两数的和即可.【解答】解:设一个数为a,另一个数为b,由题意得a=9,b=﹣9+2=﹣7,则a+b=9+(﹣7)=2.故选A.【点评】本题主要考查代数式求值,解题的关键在于根据题意求得另一个数的值.7.在下列各组中,是同类项的是()A.9a2x和9a2B.a2和2a C.2a2b和3ab2D.4x2y和﹣yx2【考点】同类项.【分析】根据同类项的概念求解.【解答】解:A、9a2x和9a2字母不同,不是同类项,故本选项错误;B、a2和2a字母相同,指数不同,故本选项错误;C、2a2b和3ab2字母相同,指数不同,故本选项错误;D、4x2y和﹣yx2字母相同,指数相同,故本选项正确.故选D.【点评】本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.8.已知代数式x+2y的值是3,则代数式2x+4y+1的值是()A.1 B.4 C.7 D.不能确定【考点】代数式求值.【分析】把x+2y看作一个整体并把所求代数式整理成已知条件的形式,然后计算即可得解.【解答】解:∵x+2y=3,∴2x+4y+1=2(x+2y)+1,=2×3+1,=6+1,=7.【点评】本题考查了代数式求值,整体思想的利用是解题的关键.9.用代数式表示a、b两数的和与a、b两数的差的积是()A.(a+b)(a﹣b)B.(a+b)•a﹣b C.a•(a+b)﹣b D.(a+b)﹣ab【考点】列代数式.【分析】根据题意列出代数式即可.【解答】解:a、b两数的和与a、b两数的差的积为(a+b)(a﹣b),故选A【点评】本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.列代数式时,要先认真审题,抓住关键词语,仔细辩析词义;分清数量关系;规范书写格式.10.若a、b互为相反数,c为最大的负整数,d的倒数等于它本身,则2a+2b﹣cd的值是()A.1 B.﹣2 C.﹣1 D.1或﹣1【考点】代数式求值;有理数;相反数;倒数.【分析】根据相反数,最大的负整数为﹣1,以及倒数的定义求出a+b,cd的值,即可求出原式的值.【解答】解:根据题意得:a+b=0,c=﹣1,d=1或﹣1,则原式=2(a+b)﹣cd=1或﹣1.故选D【点评】此题考查了代数式求值,相反数,倒数,以及有理数,熟练掌握各自的定义是解本题的关键.二、填空题11.绝对值小于4的整数有7 个,它们的和是0 ,积是0 .【考点】绝对值;有理数的加法;有理数的乘法.【专题】计算题.【分析】根据题意可以直接求出绝对值小于4的整数,然后再求出它们的积和它们的和即可.【解答】解:绝对值小于4的整数有1、2、3、0、﹣1、﹣2、﹣3共7个,它们的和=1+2+3+0﹣1﹣2﹣3=0,它们的积=1×2×3×0×(﹣1)×(﹣2)×(﹣3)=0.故答案为7、0、0.【点评】本题考查了绝对值、有理数的加法以及有理数的乘方,此题比较简单,易于掌握.12.主视图、俯视图和左视图都是正方形的几何体是正方体【考点】由三视图判断几何体.【分析】找到从正面、左面和上面看得到的图形是正方形的几何体即可.【解答】解:∵主视图和左视图都是正方形,∴此几何体为柱体,∵俯视图是一个正方形,∴此几何体为正方体.【点评】用到的知识点为:三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个试图确定其具体形状.13.圆锥有二个面,它的侧面展开图是扇形.【考点】几何体的展开图;认识立体图形.【分析】根据圆锥的概念和特性即可求解.【解答】解:圆锥有二个面组成,它的侧面展开图是扇形.故答案为:二,扇形.【点评】本题考查几何体的面的组成情况和立体图形的侧面展开图的特征,属于基础题型.14.若3a m b2与ab n是同类项,则m= 1 ,n= 2 .【考点】同类项.【专题】计算题.【分析】根据同类项的定义:所含字母相同,相同字母的指数相同即可得出答案.【解答】解:∵3a m b2与是同类项,∴m=1,n=2.故答案为:1,2.【点评】本题考查同类项的知识,注意同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.15.﹣1的倒数是﹣,相反数是1绝对值是1.【考点】倒数;相反数;绝对值.【分析】利用绝对值、倒数、相反数的定义进而求出即可.【解答】解:﹣1的倒数是:﹣,相反数是:1;绝对值是:1;故答案为:﹣;1;1.【点评】此题主要考查了绝对值、倒数、相反数的定义,正确把握定义是解题关键.16.在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作﹣0.15米.【考点】正数和负数.【专题】应用题.【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.以4.00米为标准,因为超过这个标准记为正数,所以3.85米,不足这个标准记为负数,又4.00﹣3.85=0.15,故记作﹣0.15米.【解答】解:“正”和“负”相对,所以在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作﹣0.15.【点评】解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.17.比较大小:﹣π<﹣3.14(选填“>”、“=”、“<”).【考点】实数大小比较.【分析】先比较π和3.14的大小,再根据“两个负数,绝对值大的反而小”即可比较﹣π<﹣3.14的大小.【解答】解:因为π是无理数所以π>3.14,故﹣π<﹣3.14.故填空答案:<.【点评】此题主要考查了实数的大小的比较,实数大小比较法则:(1)正数大于0,0大于负数,正数大于负数;(2)两个负数,绝对值大的反而小.18.用一个平面去截长方体,截面可能是平行四边形(填“可能”或“不可能”).【考点】截一个几何体.【分析】让截面不垂直于长方体,又经过长方体的4个面,动手操作可得到答案.【解答】解:当截面不垂直于长方体,又经过长方体的4个面时,得到截面为四边形,对边平行且相等,为平行四边形.【点评】解决本题的关键是理解截面经过几个面,得到的截面形状就是几边形;经过面相同,从不同的位置截取得到的多边形的形状也不相同.19.按规律填空:a,﹣2a2,3a3,﹣4a4,5a5,﹣6a6.【考点】单项式.【专题】规律型.【分析】根据题中给出的规律可知,偶数项的系数是负数,奇数项的系数时正数,而且系数的绝对值和指数是按1、2、3…进行变化.【解答】解:故答案为:5a5;﹣6a6;【点评】本题考查数字规律,属于基础题型.20.若|x+2|+(y﹣1)2=0,则x= ﹣2 ,y= 1 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出算式,求出x、y的值即可.【解答】解:由题意得,x+2=0,y﹣1=0,解得,x=﹣2,y=1,故答案为:﹣2;1.【点评】本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.三、计算题:21.(20分)(2016秋•高台县校级期中)计算:(1)﹣1+﹣+;(2)(﹣2)÷×(﹣3);(3)﹣24×(﹣+﹣);(4)﹣5﹣(﹣11)+2﹣(﹣).【考点】有理数的混合运算.【专题】计算题;实数.【分析】(1)原式通分并利用同分母分数的加减法则计算即可得到结果;(2)原式从左到右依次计算即可得到结果;(3)原式利用乘法分配律计算即可得到结果;(4)原式利用减法法则变形计算,即可得到结果.【解答】解:(1)原式=﹣1+﹣+=﹣;(2)原式=2×3×3=18;(3)原式=20﹣9+2=13;(4)原式=﹣5+11+2+=6+3=9.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.四、解答题(共40分)22.如图所示的几何体是由5个相同的正方体搭成的,请画出它的主视图、左视图和俯视图.【考点】作图-三视图.【分析】主视图有3列,每列小正方形数目分别为2,1,1;左视图有2列,每列小正方形数目分别为1,2;俯视图有3列,每行小正方形数目分别为2,1,1.【解答】解:如图所示:.【点评】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.23.合并同类项:2a3b﹣a3b﹣a2b+a2b﹣ab2.【考点】合并同类项.【分析】这个式子的运算是合并同类项的问题,根据合并同类项的法则,即系数相加作为系数,字母和字母的指数不变.【解答】解:=(2﹣)a3b+(﹣1+)a2b﹣ab2=a3b﹣a2b﹣ab2【点评】本题主要考查合并同类项的法则.即系数相加作为系数,字母和字母的指数不变.24.先化简,再求值:3(x﹣y)﹣2(x+y)+2,其中x=﹣1,.【考点】整式的加减—化简求值.【分析】先把原式去括号,再合并同类项,然后把x、y的值代入即可.【解答】解:3(x﹣y)﹣2(x+y)+2=3x﹣3y﹣2x﹣2y+3=x﹣5y+2,∵x=﹣1,.,∴x﹣5y+2=﹣1﹣5×+2=﹣.【点评】本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点25.某储蓄所,某日办理了7项储蓄业务:取出9.6万元,存入5万元,取出7万元,存入12万元,存入22万元,取出10.25万元,取出2.4万元,求储蓄所该日现金增加多少万元?【考点】有理数的减法;有理数的加法.【专题】计算题.【分析】根据有理数的加法、有理数的减法的运算方法,用3次一共存入的钱数减去4次一共支出的钱数,求出储蓄所该日现金增加多少万元即可.【解答】解:(5+12+22)﹣(9.6+7+10.25+2.4)=39﹣29.25=9.75(万元)答:储蓄所该日现金增加9.75万元.【点评】此题主要考查了有理数的加法、有理数的减法,要熟练掌握,解答此题的关键是要明确:(1)同号相加,取相同符号,并把绝对值相加.(2)绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.(3)减去一个数,等于加上这个数的相反数.26.用棋子摆出下列一组图形:(1)填写下表:(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?【考点】规律型:图形的变化类;列代数式.【专题】规律型.【分析】观察图形,发现(1)中是6个棋子.后边依次多3个棋子.根据这一规律即可解决下列问题.【解答】解:(1)如图所示:(2)依题意可得当摆到第n个图形时棋子的枚数应为:6+3(n﹣1)=6+3n﹣3=3n+3;(3)由上题可知此时3n+3=99,∴n=32.答:第32个图形共有99枚棋子.【点评】本题考查了规律型:图形的变化.解题注意根据图形发现规律,并用字母表示.然后根据条件代入计算.。
北京七中2016-2017学年八年级(上)期中数学试卷(解析版)

2016-2017学年北京七中八年级(上)期中数学试卷一.选择题(每题3分,共30分)1.若x、y互为倒数,则下列等式正确的是()A.x=﹣y B.xy=﹣1 C.x= D.y=±2.下列计算中正确的是()A.a2+b3=2a5B.a4÷a=a4C.a2•a4=a8 D.(﹣a2)3=﹣a63.在代数式x,,xy2,,,x2﹣x 中,分式共有()A.2个 B.3个 C.4个 D.5个4.因式分解的结果是(x﹣3)(x﹣4)的多项式是()A.x2﹣7x﹣12 B.x2+7x+12 C.x2﹣7x+12 D.x2+7x﹣125.如果把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.缩小3倍C.缩小6倍D.不变6.能确定△ABC≌△DEF的条件是()A.AB=DE,BC=EF,∠A=∠E B.AB=DE,BC=EF,∠C=∠EC.∠A=∠E,AB=EF,∠B=∠D D.∠A=∠D,AB=DE,∠B=∠E7.下列分式为最简分式的是()A. B.C.D.8.下列各式能用完全平方公式分解因式的是()A.x2﹣6x+9 B.1+x2 C.x+2xy+1 D.x2+2x﹣19.下列各式中,不能用平方差公式分解因式的是()A.y2﹣49x2B.﹣x4C.﹣m4﹣n2D.(p+q)2﹣910.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲B.乙C.丙D.乙与丙二.填空题(每题2分,共20分)11.当x=时,分式无意义.12.当x满足时,(x﹣4)0=1.13.分解因式:x2﹣16=.14.①=②=.15.一种细菌半径为0.000432米,用科学记数法表示为米.16.把下列三个数:6﹣1、(﹣2)0、(﹣2)3按从小到大的顺序排列为.17.如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件时,就可得到△ABC≌△FED.(只需填写一个即可)18.分式与的最简公分母是.19.加工一批产品m件,原计划a天完成,今需要提前b天完成,则每天应生产件产品.20.若|a﹣2|+2b2﹣4b+2=0,则a=,b=.三.简答题:(每小题6分,本题共35分)21.计算:①(﹣)2﹣(﹣)3÷(﹣a2b)2②+﹣.22.请先将下式化简,再选择一个你喜欢又使原式有意义的数代入求值.()÷.23.已知:如图,△RPQ中,RP=RQ,M为PQ的中点.求证:RM平分∠PRQ.证明:∵M为PQ的中点(已知),∴=()在△和△中,∴≌()∴∠PRM=()即RM平分∠PRQ.24.已知:如图,PM=PN,∠M=∠N.求证:AM=BN.证明:在△与△中,∴△≌△.∴PA=.∵PM=PN,∴PM﹣=PN﹣.即AM=.25.解方程:(1)=+(2)=﹣1.四.简答题:(每小题3分,本题共15分)26.作图题:请用尺规作图作出以下图形:(1)画一个与已知角相等的角.(请把图作在如图方框内,请保留作图痕迹)作法:①以点O为圆心,为半径画弧,分别交OA,OB于.②画射线EM,以点为圆心,为半径画弧,交EM于.③以点为圆心,为半径画弧,与第二步所画弧相交于点.④过点画射线,则.所作的两个角相等的依据是:.27.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:EF∥CD.28.甲、乙两地相距50km,A骑自行车,B乘汽车,同时从甲城出发去乙城,已知汽车的速度是自行车速度的2.5倍,B中途休息了0.5小时还比A早到2小时,求自行车和汽车的速度.29.已知:如图,点D是△ABC的BC边上的中点.作图:连接AD;延长AD至E,使DE=AD;连接BE;求证:AC∥BE.30.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE ⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.五、解答题(共3小题,满分0分)31.如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P 点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为.32.当m,关于x的方程+=无解.33.在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生密码,方便记忆.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,取x=10,y=10时,用上述方法产生的密码是:(写出一个即可).2016-2017学年北京七中八年级(上)期中数学试卷参考答案与试题解析一.选择题(每题3分,共30分)1.若x、y互为倒数,则下列等式正确的是()A.x=﹣y B.xy=﹣1 C.x= D.y=±【考点】倒数.【分析】根据倒数的定义可知xy=1,然后进行变形即可.【解答】解:由倒数的定义可知:xy=1,则x=.故选:C.2.下列计算中正确的是()A.a2+b3=2a5B.a4÷a=a4C.a2•a4=a8 D.(﹣a2)3=﹣a6【考点】同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.【分析】根据合并同类项,可判断A;根据同底数幂的除法,可判断B;根据同底数幂的乘法,可判断C;根据积的乘方,可判断D.【解答】解:A、不是同类项不能合并,故A错误;B、同底数幂的除法底数不变指数相减,故B错误;C、同底数幂的乘法底数不变指数相加,故C错误;D、积的乘方等于乘方的积,故D正确;故选:D.3.在代数式x,,xy2,,,x2﹣x 中,分式共有()A.2个 B.3个 C.4个 D.5个【考点】分式的定义.【分析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.【解答】解:在代数式x,,xy2,,,x2﹣x 中,分式有,,,共有3个.故选:B.4.因式分解的结果是(x﹣3)(x﹣4)的多项式是()A.x2﹣7x﹣12 B.x2+7x+12 C.x2﹣7x+12 D.x2+7x﹣12【考点】因式分解-十字相乘法等.【分析】直接将各选项分解因式得出答案.【解答】解:A、x2﹣7x﹣12,无法分解因式,故此选项错误;B、x2+7x+12=(x+3)(x+4),不合题意,故此选项错误;C、x2﹣7x+12=(x﹣3)(x﹣4),正确;D、x2+7x﹣12,无法分解因式,故此选项错误.故选:C.5.如果把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.缩小3倍C.缩小6倍D.不变【考点】分式的基本性质.【分析】要解此题,可以将x,y用3x,3y代入、化简,跟原式对比.【解答】解:将x,y用3x,3y代入中可得=,∴分式的值不变.故选D.6.能确定△ABC≌△DEF的条件是()A.AB=DE,BC=EF,∠A=∠E B.AB=DE,BC=EF,∠C=∠EC.∠A=∠E,AB=EF,∠B=∠D D.∠A=∠D,AB=DE,∠B=∠E【考点】全等三角形的判定.【分析】从选项提供的已知条件开始思考,结合全等三角形的判定方法,与之符合的能够判定全等,不符合的不全等,本题中,D符合ASA,能确定△ABC≌△DEF,其它则不能确定△ABC≌△DEF.【解答】解:A、AB=DE,BC=EF,∠A=∠E,符合SSA,不能判断三角形全等;B、AB=DE,BC=EF,∠C=∠E,符合SSA,不能判断三角形全等;C、∠A=∠E,AB=EF,∠B=∠D,AB、EF不是对应边,不能判断三角形全等;D、当∠A=∠D,AB=DE,∠B=∠E,符合ASA,所以△ABC≌△DEF.故选D.7.下列分式为最简分式的是()A. B. C.D.【考点】最简分式.【分析】最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.【解答】解:A、,故本选项错误;B、,故本选项错误;C、,故本选项错误;D、分子、分母都不能再分解,且不能约分,是最简分式.故本选项正确;故选D8.下列各式能用完全平方公式分解因式的是()A.x2﹣6x+9 B.1+x2 C.x+2xy+1 D.x2+2x﹣1【考点】因式分解-运用公式法.【分析】利用完平方公式分解因式进而得出答案.【解答】解:A、x2﹣6x+9=(x﹣3)2,可以用完平方公式分解因式,故此选项正确;B、1+x2,不可以分解因式,故此选项错误;C、x+2xy+1,不可以分解因式,故此选项错误;D、x2+2x﹣1,不可以分解因式,故此选项错误;故选:A.9.下列各式中,不能用平方差公式分解因式的是()A.y2﹣49x2B.﹣x4C.﹣m4﹣n2D.(p+q)2﹣9【考点】因式分解-运用公式法.【分析】分别利用平方差公式分解因式进而得出答案.【解答】解:A、y2﹣49x2=(y+7x)(y﹣7x),可以用平方差公式分解因式,故此选项错误;B、﹣x4=(+x2)(﹣x2),可以用平方差公式分解因式,故此选项错误;C、﹣m4﹣n2,不可以用平方差公式分解因式,故此选项正确;D、(p+q)2﹣9=(p+q+3)(p+q﹣3),可以用平方差公式分解因式,故此选项错误;故选:C.10.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲B.乙C.丙D.乙与丙【考点】全等三角形的判定.【分析】首先观察图形,然后根据三角形全等的判定方法(AAS与SAS),即可求得答案.【解答】解:如图:在△ABC和△MNK中,,∴△ABC≌△MNK(AAS);在△ABC和△HIG中,,∴△ABC≌△HIG(SAS).∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙或丙.故选D.二.填空题(每题2分,共20分)11.当x=时,分式无意义.【考点】分式有意义的条件.【分析】根据分式无意义的条件可得3x﹣1=0,再解即可.【解答】解:由题意得:3x﹣1=0,解得:x=,故答案为:.12.当x满足x≠4时,(x﹣4)0=1.【考点】零指数幂.【分析】根据菲零的零次幂等于1,可得答案.【解答】解:由题意,得x﹣4≠0.解得x≠4,故答案为:x≠4.13.分解因式:x2﹣16=(x﹣4)(x+4).【考点】因式分解-运用公式法.【分析】运用平方差公式分解因式的式子特点:两项平方项,符号相反.直接运用平方差公式分解即可.a2﹣b2=(a+b)(a﹣b).【解答】解:x2﹣16=(x+4)(x﹣4).14.①=②=.【考点】分式的基本性质.【分析】根据分式的分子分母都乘以(或除以)同一个不为零整式,分式的值不变,可得答案.【解答】解:①=,②=,故答案为:5y,2﹣x.15.一种细菌半径为0.000432米,用科学记数法表示为 4.32×10﹣4米.【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000432=4.32×10﹣4,故答案为:4.32×10﹣4.16.把下列三个数:6﹣1、(﹣2)0、(﹣2)3按从小到大的顺序排列为(﹣2)3<6﹣1<(﹣2)0.【考点】有理数大小比较;零指数幂;负整数指数幂.【分析】先求出每个式子的值,再比较即可.【解答】解:∵6﹣1=,(﹣2)0=1,(﹣2)3,=﹣8,∴(﹣2)3<6﹣1<(﹣2)0,故答案为:(﹣2)3<6﹣1<(﹣2)0.17.如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件BC=ED或∠A=∠F或AB∥EF时,就可得到△ABC≌△FED.(只需填写一个即可)【考点】全等三角形的判定.【分析】要得到△ABC≌△FED,现有条件为两边分别对应相等,找到全等已经具备的条件,根据全等的判定方法选择另一条件即可得等答案.【解答】解:AD=FC⇒AC=FD,又AB=EF,加BC=DE就可以用SSS判定△ABC≌△FED;加∠A=∠F或AB∥EF就可以用SAS判定△ABC≌△FED.故答案为:BC=ED或∠A=∠F或AB∥EF.18.分式与的最简公分母是9ab2c2.【考点】最简公分母.【分析】确定最简公分母的方法是:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.【解答】解:分式与的分母分别是3b2c、9ac2,故最简公分母是9ab2c2.故答案为9ab2c2.19.加工一批产品m件,原计划a天完成,今需要提前b天完成,则每天应生产件产品.【考点】列代数式(分式).【分析】原计划a天完成,今需要提前b天完成,则实际用a﹣b天,利用总产品数除以实际的天数即可求解.【解答】解:原计划a天完成,今需要提前b天完成,则实际用a﹣b天,则每天应生产件产品.故答案是:.20.若|a﹣2|+2b2﹣4b+2=0,则a=2,b=1.【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】先利用完全平方公式整理,再根据非负数的性质列方程求解即可得到a、b的值.【解答】解:|a﹣2|+2(b2﹣2b+1)=0,|a﹣2|+2(b﹣1)2=0,所以,a﹣2=0,b﹣1=0,所以,a=2,b=1.故答案为:2;1.三.简答题:(每小题6分,本题共35分)21.计算:①(﹣)2﹣(﹣)3÷(﹣a2b)2②+﹣.【考点】分式的混合运算.【分析】结合分式混合运算的运算法则进行求解即可.【解答】解:①原式=﹣(﹣)÷a4b2=﹣(﹣)×=﹣(﹣)=.②原式=﹣﹣===﹣1.22.请先将下式化简,再选择一个你喜欢又使原式有意义的数代入求值.()÷.【考点】分式的化简求值.【分析】先化简题目中的式子,然后选取合适的x的值代入即可解答本题,注意x不能取1,﹣1.【解答】解:()÷==,当a=0时,原式==0.23.已知:如图,△RPQ中,RP=RQ,M为PQ的中点.求证:RM平分∠PRQ.证明:∵M为PQ的中点(已知),∴PM=QM(线段中点的定义)在△RPM和△RQM中,∴△RPM≌△RQM(SSS)∴∠PRM=∠QRM(两三角形全等,对应角相等)即RM平分∠PRQ.【考点】全等三角形的判定与性质.【分析】先根据M为PQ的中点得出PM=QM,再由SSS定理得出△PRM≌△QRM,由全等三角形的性质即可得出结论.【解答】证明:∵M为PQ的中点(已知),∴PM=QM(线段中点的定义)在△PRM和△QRM中,,∴△PRM≌△QRM(SSS)∴∠PRM=∠QRM(两三角形全等,对应角相等)即RM平分∠PRQ.故答案为:QM,线段中点的定义,,△PRM,△QRM,(SSS),∠QRM,(两三角形全等,对应角相等).24.已知:如图,PM=PN,∠M=∠N.求证:AM=BN.证明:在△PAN与△PBM中,∴△PAN≌△PBM.∴PA=PB.∵PM=PN已知,∴PM﹣PA=PN﹣PB.即AM=BN.【考点】全等三角形的判定与性质.【分析】欲证明AM=AN,因为PM=PN,只要证明PA=PB即可,只要证明△PAN ≌△PBM.【解答】证明:在△PAN和△PBM中,,∴△PAN≌△PBM(ASA)∴PA=PB(全等三角形对应边相等)∵PM=PN(已知)∴PM﹣PA=PN﹣PB,即AM=BN.故答案分别为:PB,△PAN,△PBM,PAN.PBM,P,P,公共角,PM,PN,已知,N,M,已知,PAN,PBM,ASA,PB,全等三角形对应边相等,已知,PA,PB,BN.25.解方程:(1)=+(2)=﹣1.【考点】解分式方程.【分析】(1)首先方程的两边同乘以最简公分母2(x+3),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.(2)首先方程的两边同乘以最简公分母6(m﹣2),把分式方程转化为整式方程,再求解即可,最后要把求得的m的值代入到最简公分母进行检验.【解答】解:(1)=+,方程两边同乘以最简公分母2(x+3)得:2(2﹣x)=x+3+2,解得:x=﹣,检验:把x=﹣代入2(x+3)得:2×(﹣+3)≠0,故原方程的解为x=﹣.(2)=﹣1,方程两边同乘以最简公分母6(m﹣2)得:3(5m﹣4)=2(2m+5)﹣6(m﹣2),解得:m=2,检验:把m=2代入6(m﹣2)得:6×(2﹣2)=0,故原方程无解.四.简答题:(每小题3分,本题共15分)26.作图题:请用尺规作图作出以下图形:(1)画一个与已知角相等的角.(请把图作在如图方框内,请保留作图痕迹)作法:①以点O为圆心,CD为半径画弧,分别交OA,OB于C,D.②画射线EM,以点E为圆心,CD为半径画弧,交EM于F.③以点F为圆心,大于CD的长为半径画弧,与第二步所画弧相交于点G.④过点G画射线,则∠MEN.所作的两个角相等的依据是:三角形全等的判定定理SSS.【考点】作图—基本作图.【分析】根据作一个角等于已知角的方法即可得到结论.【解答】作法:①以点O为圆心,CD为半径画弧,分别交OA,OB于C,D.②画射线EM,以点E为圆心,CD为半径画弧,交EM于F.③以点F为圆心,大于CD的长为半径画弧,与第二步所画弧相交于点G.④过点G画射线,则∠MEN即为所求.所作的两个角相等的依据是:三角形全等的判定定理SSS.故答案为:CD,C,D,E,CD,F,F,大于CD的长,G,G,∠MEN,三角形全等的判定定理SSS.27.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:EF∥CD.【考点】全等三角形的判定与性质;平行线的判定与性质.【分析】由于AE∥BC,根据平行线的性质可得∠A=∠B,又AD=BF,根据等式性质可得AF=BD,再结合AE=BC,利用SAS可证△AEF≌△BCD,于是∠AFE=∠BDC,那么EF∥CD.【解答】证明:∵AE∥BC,∴∠A=∠B,∵AD=BF,∴AD+DF=BF+DF,∴AF=BD,在△AEF和△BCD中,,∴△AEF≌△BCD,∴∠AFE=∠BDC,∴EF∥CD.28.甲、乙两地相距50km,A骑自行车,B乘汽车,同时从甲城出发去乙城,已知汽车的速度是自行车速度的2.5倍,B中途休息了0.5小时还比A早到2小时,求自行车和汽车的速度.【考点】分式方程的应用.【分析】设自行车的速度是x千米/小时,汽车的速度是2.5x千米/小时,根据甲、乙两地相距50千米,A骑自行车由甲地往乙地出发,2小时30分钟后,B骑摩托车也由甲地前往乙地,结果两人同时到达乙地,可列方程求解.【解答】解:设自行车的速度是x千米/小时,B的速度是2.5x千米/小时,﹣0.5﹣2=,解得x=12,经检验x=12是分式方程的解.12×2.5=30.答自行车的速度是12千米/小时,汽车的速度是30千米/小时.29.已知:如图,点D是△ABC的BC边上的中点.作图:连接AD;延长AD至E,使DE=AD;连接BE;求证:AC∥BE.【考点】全等三角形的判定与性质.【分析】首先画出图形,利用SAS证得△ACD≌△EBD,得出∠CAE=∠E,证得AC∥BE.【解答】证明:如图,∵点D是△ABC的BC边上的中点,∴BD=CD,在△ACD和△EBD中,,∴△ACD≌△EBD(SAS),∴∠CAE=∠E,∴AC∥BE.30.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE ⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.【考点】全等三角形的判定与性质.【分析】(1)直角三角形中斜边对应相等,即可证明全等,再由线段对应相等,得出②中结论;(2)由图可知,△ADC与△CEB仍全等,但线段的关系已发生改变.【解答】(1)证明:①∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,∴∠DAC=∠BCE.又AC=BC,∠ADC=∠BEC=90°,∴△ADC≌△CEB.②∵△ADC≌△CEB,∴CD=BE,AD=CE.∴DE=CE+CD=AD+BE.(2)△ADC≌△CEB成立,DE=AD+BE.不成立,此时应有DE=AD﹣BE.证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,∴∠DAC=∠BCE.又AC=BC,∠ADC=∠BEC=90°,∴△ADC≌△CEB.∴CD=BE,AD=CE.∴DE=AD﹣BE.五、解答题(共3小题,满分0分)31.如图,有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P 点在AC上,Q点在过A点且垂直于AC的射线AM上运动.当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.【考点】勾股定理;全等三角形的性质.【分析】分情况讨论:①Rt△APQ≌Rt△CBA,此时AQ=AC=10cm,②Rt△QAP≌Rt△BCA,此时AQ=BC=5cm.【解答】解:根据三角形全等的判定方法HL可知:①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,,∴Rt△ABC≌Rt△QPA(HL),即AQ=AC=10cm;②当P运动到与C点重合时,AP=AC,在Rt△ABC与Rt△QPA中,,∴Rt△QAP≌Rt△BCA(HL),即AQ=BC=5cm,综上所述,当△ABC和△APQ全等时,点Q到点A的距离为10cm或5cm.故答案为10cm或5cm.32.当m=1或6或﹣4,关于x的方程+=无解.【考点】分式方程的解.【分析】分式方程无解,即化成整式方程时无解,或者求得的x能令最简公分母为0,据此进行解答.【解答】解:方程两边都乘(x+2)(x﹣2)得,2(x+2)+mx=3(x﹣2),整理得,(m﹣1)x=﹣10,当整式方程无解时,m﹣1=0即m=1,当分式方程无解时:①x+2=0,即x=﹣2时,方程无解,则﹣2(m﹣1)=﹣10,解得m=6;②x﹣2=0,即x=2时,方程无解,则2(m﹣1)=﹣10,解得m=﹣4,所以m=1或6或﹣4时,原方程无解.故答案为:=1或6或﹣4.33.在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生密码,方便记忆.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,取x=10,y=10时,用上述方法产生的密码是:103010(写出一个即可).【考点】因式分解的应用.【分析】把所求的代数式分解因式后整理成条件中所给出的代数式的形式,然后整体代入即可.【解答】解:4x3﹣xy2=x(4x2﹣y2)=x(2x+y)(2x﹣y),当x=10,y=10时,x=10;2x+y=30;2x﹣y=10,用上述方法产生的密码是:103010.故答案为103010.2017年2月11日。
2017-2018北京八中初一第一学期数学期中试卷 pdf版

出生后的天数,由图可知,孩子自出生后的天数是
天.
第 19 题
第 20 题
北京八中 20172018 学年度第一学期期中练习题
三、计算题(共 32 分) 21.计算下列各式 (每题 3 分)
(1) (5) (7)
(2) 5 8 24 3
(3) 0.25 ( 3) (1 1)
须 2.在试卷和答题纸上准确填写班级、姓名、学号。 知 3.答案一律填写在答题纸上,在试卷上作答无效。
4.考试结束,将试卷和答题纸一并交回。
一、选择题(每小题所给 4 个选项中只有一个符合要求,每小题 3 分,共 30 分)
1.-4 的相反数是
A. 1 4
B. 1 4
C.4
D.-4
2.计算 -2×3 结果正确的是
A.6
B.-6
C.5
D.-5
3 . 2016 年 春 节 假 期 期 间 , 我 市 接 待 旅 游 总 人 数 达 到 9 186 000 人 次 , 比 去 年 同 期 增 长
1.9%.将 9 186 000 用科学计数法表示应为
A.9186×103
B.9.186×105
C.9.186×106
D.9.186×107
7
5
(4) 36(1 1 3) 964
(5)1
1 2
1
1
2 3
4
(6) 23
1
0.5
1 3
2
32
22.合并同类项 (每题 3 分)
(1) 1 x2 y3 7 x2 y3
北京XX附中2016-2017学年七年级上期中数学试卷(有答案)-(新课标人教版)AKwnlU

2016-2017学年北京XX附中七年级(上)期中数学试卷一、选择题(本大题共10道小题,每小题3分,共30分)1.﹣的相反数是()A.﹣8 B.C.0.8 D.82.神州十一号飞船成功飞向浩瀚宇宙,并在距地面约390000米的轨道上与天宫二号交会对接.将390000用科学记数法表示应为()A.3.9×104B.3.9×105C.39×104D.0.39×1063.下列各对数中,相等的一对数是()A.(﹣2)3与﹣23B.﹣22与(﹣2)2C.﹣(﹣3)与﹣|﹣3|D.与()24.下列说法中正确的是()A.是单项式B.﹣πx 的系数为﹣1C.﹣5不是单项式D.﹣5a2b 的次数是35.下列计算正确的是()A.x2y﹣2xy2=﹣x2y B.2a+3b=5abC.a3+a2=a5 D.﹣3ab﹣3ab=﹣6ab6.已知﹣2m6n与5m2x n y是的和是单项式,则()A.x=2,y=1 B.x=3,y=1 C.x=,y=1 D.x=1,y=37.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是()A.这个多项式是五次四项式B.四次项的系数是7C.常数项是1D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+18.下列方程中,是一元一次方程的是()A.=3 B.x2+1=5 C.x=0 D.x+2y=39.已知ax=ay,下列等式变形不一定成立的是()A.b+ax=b+ay B.x=yC.x﹣ax=x﹣ay D.=10.如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是()A.M或R B.N或P C.M或N D.P或R二、填空题(本大题共10道小题,每小题2分,共20分)11.比较大小:.12.1.9583≈(精确到百分位).13.若(a﹣1)2+|b+2|=0,则a﹣b﹣1=.14.设甲数为x,乙数比甲数的3倍少6,则乙数表示为.15.若a,b互为倒数,c,d互为相反数,则﹣c﹣d=.16.数轴上表示点A的数是最大的负整数,则与点A相距3个单位长度的点表示的数是.17.阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书本.18.如果方程ax|a+1|+3=0是关于x的一元一次方程,则a的值为.19.若方程2x+1=﹣1的解也是关于x的方程1﹣2(x﹣a)=2的解,则a的值为.20.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是.三.计算题(本大题共4道小题,每小题20分,共20分)21.计算题(1)﹣2﹣1+(﹣16)﹣(﹣13);(2)25÷5×(﹣)÷(﹣);(3)(﹣+)×(﹣18);(4)﹣42+1÷|﹣|×(﹣2)2.四.化简求值题(本大题共2道小题,每小题4分,共8分)25.化简:﹣2x2﹣5x+3﹣3x2+6x﹣1.26.先化简,后求值:3(a2﹣ab+7)﹣2(3ab﹣a2+1)+3,其中a=2,b=.五.解方程(本大题共2道小题,每小题10分,共10分)27.解方程(1)4(2x﹣1)﹣3(5x+1)=14;(2)﹣=2.六.解答题(本大题共3道小题,每小题4分,共12分)29.有理数a,b在数轴上的对应点位置如图所示,且|a|=|c|.(1)用“<”连接这四个数:0,a,b,c;(2)化简:|a+b|﹣2|a|﹣|b+c|.30.已知:2x﹣y=5,求﹣2(y﹣2x)2+3y﹣6x的值.31.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=,S2=;(2)求a,b满足的关系式,写出推导过程.七.附加题(本大题共20分,第32,33小题各6分,第34小题8分)32.填空题:(请将结果直接写在横线上)定义新运算“⊕”,对于任意有理数a,b有a⊕b=,(1)4(2⊕5)=.(2)方程4⊕x=5的解是.(3)若A=x2+2xy+y2,B=x2﹣2xy+y2,则(A⊕B)+(B⊕A)=.33.探究题:定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[﹣π]=﹣4.(1)如果[a]=﹣2,那么a可以是A.﹣15 B.﹣2.5 C.﹣3.5 D.﹣4.5(2)如果[]=3,则整数x=.(3)如果[﹣1.6﹣ []]=﹣3,满足这个方程的整数x共有个.34.阅读理解题:对于任意由0,1组成的一列数.将原有的每个1变成01,并将每个原有的0变成10称为一次变换.如101经过一次变换成为011001.请你经过思考、操作回答下列问题:(1)将11变换两次后得到;(2)若100101101001是由某数列两次变换后得到.则这个数列是;(3)一个10项的数列经过两次变换后至少有多少对两个连续相等的数对(即1100)?请证明你的结论;(4)01经过10次操作后连续两项都是0的数对个数有个.2016-2017学年北京XX附中七年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共10道小题,每小题3分,共30分)1.﹣的相反数是()A.﹣8 B.C.0.8 D.8【考点】14:相反数.【分析】根据只有符号不同的两数叫做互为相反数解答.【解答】解:﹣的相反数是.故选B.2.神州十一号飞船成功飞向浩瀚宇宙,并在距地面约390000米的轨道上与天宫二号交会对接.将390000用科学记数法表示应为()A.3.9×104B.3.9×105C.39×104D.0.39×106【考点】1I:科学记数法—表示较大的数.【分析】数据绝对值大于10或小于1时科学记数法的表示形式为a×10n的形式.其中1≤|a|<10,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n 是负数.【解答】解:390 000=3.9×105,故选:B.3.下列各对数中,相等的一对数是()A.(﹣2)3与﹣23B.﹣22与(﹣2)2C.﹣(﹣3)与﹣|﹣3|D.与()2【考点】1E:有理数的乘方;14:相反数;15:绝对值.【分析】根据有理数的乘方的运算方法,相反数的含义和求法,以及绝对值的含义和求法,逐项判断即可.【解答】解:∵(﹣2)3=﹣8,﹣23=﹣8,∴(﹣2)3=﹣23,∴选项A正确.∵﹣22=﹣4,(﹣2)2=4,∴﹣22≠(﹣2)2,∴选项B不正确.∵﹣(﹣3)=3,﹣|﹣3|=﹣3,∴﹣(﹣3)≠﹣|﹣3|,∴选项C不正确.∵=,()2=,∴≠()2,∴选项D不正确.故选:A.4.下列说法中正确的是()A.是单项式B.﹣πx 的系数为﹣1C.﹣5不是单项式D.﹣5a2b 的次数是3【考点】42:单项式.【分析】根据单项式与多项式的概念即可判断.【解答】解:(A)时多项式,故A错误;(B)﹣πx 的系数为﹣π,故B错误;(C)﹣5是单项式,故C错误;故选(D)5.下列计算正确的是()A.x2y﹣2xy2=﹣x2y B.2a+3b=5abC.a3+a2=a5 D.﹣3ab﹣3ab=﹣6ab【考点】35:合并同类项.【分析】先判断是否是同类项,再按合并同类项的法则合并即可.【解答】解:A、x2y和﹣2xy2不是同类项,不能合并,故本选项错误;B、2a和3b不是同类项,不能合并,故本选项错误;C、a3和a2不是同类项,不能合并,而a3•a2=a5,故本选项错误;D、﹣3ab﹣3ab=﹣6ab,故本选项正确;故选D.6.已知﹣2m6n与5m2x n y是的和是单项式,则()A.x=2,y=1 B.x=3,y=1 C.x=,y=1 D.x=1,y=3【考点】35:合并同类项.【分析】根据合并同类项的法则把系数相加即可.【解答】解:由题意,得2x=6,y=1,解得x=3,y=1,故选:B.7.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是()A.这个多项式是五次四项式B.四次项的系数是7C.常数项是1D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1【考点】43:多项式.【分析】根据多项式的概念即可求出答案.【解答】解:该多项式四次项是﹣7xy3,其系数为﹣7,故选(B)8.下列方程中,是一元一次方程的是()A.=3 B.x2+1=5 C.x=0 D.x+2y=3【考点】84:一元一次方程的定义.【分析】根据只含有一个未知数(元),且未知数的次数是1,这样的方程叫一元一次方程进行分析即可.【解答】解:A、不是一元一次方程,故此选项错误;B、不是一元一次方程,故此选项错误;C、是一元一次方程,故此选项正确;D、不是一元一次方程,故此选项错误;故选:C.9.已知ax=ay,下列等式变形不一定成立的是()A.b+ax=b+ay B.x=yC.x﹣ax=x﹣ay D.=【考点】83:等式的性质.【分析】根据等式的性质,可得答案.【解答】解:A、两边都加b,结果不变,故A不符合题意;B、a=0时两边都除以a,无意义,故B符合题意;C、两边都乘以﹣1,都加x,结果不变,故C不符合题意;D、两边都除以同一个不为零的整式结果不变,故D不符合题意;故选:B.10.如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是()A.M或R B.N或P C.M或N D.P或R【考点】15:绝对值;13:数轴.【分析】先利用数轴特点确定a,b的关系从而求出a,b的值,确定原点.【解答】解:∵MN=NP=PR=1,∴|MN|=|NP|=|PR|=1,∴|MR|=3;①当原点在N或P点时,|a|+|b|<3,又因为|a|+|b|=3,所以,原点不可能在N或P点;②当原点在M、R时且|Ma|=|bR|时,|a|+|b|=3;综上所述,此原点应是在M或R点.故选A.二、填空题(本大题共10道小题,每小题2分,共20分)11.比较大小:>.【考点】18:有理数大小比较.【分析】先计算|﹣|==,|﹣|==,然后根据负数的绝对值越大,这个数反而越小即可得到它们的关系关系.【解答】解:∵|﹣|==,|﹣|==,而<,∴﹣>﹣.故答案为:>.12.1.9583≈ 1.96(精确到百分位).【考点】1H:近似数和有效数字.【分析】根据近似数的精确度求解.【解答】解:1.9583≈1.96(精确到百分位)故答案为1.96.13.若(a﹣1)2+|b+2|=0,则a﹣b﹣1=2.【考点】1F:非负数的性质:偶次方;16:非负数的性质:绝对值.【分析】根据非负数的性质列出算式,求出a、b的值,计算即可.【解答】解:由题意得,a﹣1=0,b=2=0,解得,a=1,b=﹣2,则a﹣b﹣1=1+2﹣1=2,故答案为:2.14.设甲数为x,乙数比甲数的3倍少6,则乙数表示为3x﹣6.【考点】32:列代数式.【分析】根据题意列出代数式解答即可.【解答】解:乙数表示为3x﹣6;故答案为:3x﹣615.若a,b互为倒数,c,d互为相反数,则﹣c﹣d=.【考点】33:代数式求值.【分析】依据倒数的定义得到ab=1,依据相反数的性质得到c+d=0,然后代入求解即可.【解答】解:∵a,b互为倒数,c,d互为相反数,∴ab=1,c+d=0.∴原式=﹣0=.故答案为:.16.数轴上表示点A的数是最大的负整数,则与点A相距3个单位长度的点表示的数是2或﹣4.【考点】13:数轴.【分析】由点A的数是最大的负整数知点A表示数﹣1,再分点A左侧和点A右侧两种情况可得与点A相距3个单位长度的点表示的数.【解答】解:∵点A的数是最大的负整数,∴点A表示数﹣1,∴在点A左侧,与点A相距3个单位长度的点表示的数是﹣1﹣3=﹣4,在点A右侧,与点A相距3个单位长度的点表示的数是﹣1+3=2,故答案为:2或﹣4.17.阅览室某一书架上原有图书20本,规定每天归还图书为正,借出图书为负,经过两天借阅情况如下:(﹣3,+1),(﹣1,+2),则该书架上现有图书19本.【考点】11:正数和负数.【分析】(﹣3,+1)表示借出3本归还1本,求出20与借出归还的和就是该书架上现有图书的本数,【解答】解:20﹣3+1﹣1+2=19(本)故答案为:1918.如果方程ax|a+1|+3=0是关于x的一元一次方程,则a的值为﹣2.【考点】84:一元一次方程的定义.【分析】根据一元一次方程的定义得到|a+1|=1且a≠0,据此求得a的值.【解答】解:∵方程ax|a+1|+3=0是关于x的一元一次方程,∴|a+1|=1且a≠0,解得a=﹣2.故答案是:﹣2.19.若方程2x+1=﹣1的解也是关于x的方程1﹣2(x﹣a)=2的解,则a的值为﹣.【考点】85:一元一次方程的解.【分析】求出第一个方程的解得到x的值,代入第二个方程计算即可求出a的值.【解答】解:方程2x+1=﹣1,解得:x=﹣1,代入方程得:1+2+2a=2,解得:a=﹣,故答案为:﹣20.如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是n2+2n.【考点】L1:多边形.【分析】第1个图形是2×3﹣3,第2个图形是3×4﹣4,第3个图形是4×5﹣5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)﹣(n+2)=n2+2n.【解答】解:第n个图形需要黑色棋子的个数是n2+2n.故答案为:n2+2n.三.计算题(本大题共4道小题,每小题20分,共20分)21.计算题(1)﹣2﹣1+(﹣16)﹣(﹣13);(2)25÷5×(﹣)÷(﹣);(3)(﹣+)×(﹣18);(4)﹣42+1÷|﹣|×(﹣2)2.【考点】1G:有理数的混合运算.【分析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式从左到右依次计算即可得到结果;(3)原式利用乘法分配律计算即可得到结果;(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣2﹣1﹣16+13=﹣6;(2)原式=25×××=;(3)原式=﹣14+15﹣5=﹣4;(4)原式=﹣16+××=﹣16+=﹣14.四.化简求值题(本大题共2道小题,每小题4分,共8分)25.化简:﹣2x2﹣5x+3﹣3x2+6x﹣1.【考点】35:合并同类项.【分析】根据合并同类项的法则即可求出答案.【解答】解:原式=(﹣2﹣3)x2+(﹣5+6)x+(3﹣1)=﹣5x2+x+226.先化简,后求值:3(a2﹣ab+7)﹣2(3ab﹣a2+1)+3,其中a=2,b=.【考点】45:整式的加减—化简求值.【分析】原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=3a2﹣3ab+21﹣6ab+2a2﹣2+3=5a2﹣9ab+22,当a=2,b=时,原式=20﹣6+22=36.五.解方程(本大题共2道小题,每小题10分,共10分)27.解方程(1)4(2x﹣1)﹣3(5x+1)=14;(2)﹣=2.【考点】86:解一元一次方程.【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.【解答】解:(1)去括号得:8x﹣4﹣15x﹣3=14,移项合并得:﹣7x=21,解得:x=﹣3;(2)去分母得:3(x+2)﹣2(2x﹣3)=24,去括号得:3x+6﹣4x+6=24,移项合并得:﹣x=12,解得:x=﹣12.六.解答题(本大题共3道小题,每小题4分,共12分)29.有理数a,b在数轴上的对应点位置如图所示,且|a|=|c|.(1)用“<”连接这四个数:0,a,b,c;(2)化简:|a+b|﹣2|a|﹣|b+c|.【考点】44:整式的加减;13:数轴;15:绝对值.【分析】(1)根据数轴上点的位置判断即可;(2)判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.【解答】解:(1)根据数轴得:b<a<0<c;(2)由图可知:a<0,a+b<0,b+c<0,a与c互为相反数,即a+c=0,∴原式=﹣a﹣b+2a+b+c=a+c=0.30.已知:2x﹣y=5,求﹣2(y﹣2x)2+3y﹣6x的值.【考点】33:代数式求值.【分析】把2x﹣y=5整体代入代数式求得答案即可.【解答】解:原式=﹣2(y﹣2x)2﹣3(2x﹣y)∵2x﹣y=5,∴原式=﹣2×52﹣3×5=﹣65.31.将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,求a,b满足的关系式.(1)为解决上述问题,如图3,小明设EF=x,则可以表示出S1=a(x+a),S2=4b(x+2b);(2)求a,b满足的关系式,写出推导过程.【考点】32:列代数式.【分析】(1)根据题意得出面积即可;(2)表示出左上角与右下角部分的面积,求出它们的差,根据它们的差与BC无关即可求出a 与b的关系式.【解答】解:(1)S1=a(x+a),S2=4b(x+2b),故答案为:a(x+a),4b(x+2b),(2)由(1)知:S1=a(x+a),S2=4b(x+2b),∴S1﹣S2=a(x+a)﹣4b(x+2b)=ax+a2﹣4bx﹣8b2=(a﹣4b)x+a2﹣8b2,∵S1与S2的差总保持不变,∴a﹣4b=0.∴a=4b.七.附加题(本大题共20分,第32,33小题各6分,第34小题8分)32.填空题:(请将结果直接写在横线上)定义新运算“⊕”,对于任意有理数a,b有a⊕b=,(1)4(2⊕5)=34.(2)方程4⊕x=5的解是x=2.(3)若A=x2+2xy+y2,B=x2﹣2xy+y2,则(A⊕B)+(B⊕A)=4x2+4y2.【考点】1G:有理数的混合运算.【分析】(1)由题目中给出的运算方法,先算2⊕5,再算4(2⊕5)即可;(2)由题目中给出的运算方法,得出4⊕x=,解方程=5即可;(3)由题目中给出的运算方法,先求出(A⊕B)与(B⊕A),再相加即可.【解答】解:(1)∵2⊕5==,∴4(2⊕5)=4×=34.故答案为34;(2)4⊕x=,解方程=5,得x=2,故答案为x=2;(3)∵A=x2+2xy+y2,B=x2﹣2xy+y2,∴(A⊕B)==2x2﹣2xy+2y2,(B⊕A)==2x2+2xy+2y2,∴(A⊕B)+(B⊕A)=4x2+4y2.故答案为4x2+4y2.33.探究题:定义:对于实数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[﹣π]=﹣4.(1)如果[a]=﹣2,那么a可以是AA.﹣15 B.﹣2.5 C.﹣3.5 D.﹣4.5(2)如果[]=3,则整数x=5或6.(3)如果[﹣1.6﹣ []]=﹣3,满足这个方程的整数x共有12个.【考点】CB:解一元一次不等式组;2A:实数大小比较.【分析】(1)根据新定义解答即可得;(2)由新定义得出3≤<4,解之可得答案;(3)令[]=y,得[﹣1.6﹣y]=﹣3,即﹣3≤﹣1.6﹣y<﹣2,解之得出整数y的值,从而有[]=3、4、5、6、7、8,再进一步求解可得.【解答】解:(1)根据题意知,[a]=﹣2表示不超过a的最大整数,∴a可以是﹣15,故选:A;(2)根据题意得3≤<4,解得:5≤x<7,则整数x=5或6,故答案为:5或6;(3)令[]=y,则原方程可变形为[﹣1.6﹣y]=﹣3,∴﹣3≤﹣1.6﹣y<﹣2,解得:2.4<y≤8.4,则y可取的整数有3、4、5、6、7、8,若y=3,则3≤<4,解得:5≤x<7,其整数解有5、6;若y=4,则4≤<5,解得:7≤x<9,其整数解有7、8;若y=5,则5≤<6,解得:9≤x<11,其整数解有9、10;若y=6,则6≤<7,解得:11≤x<13,其整数解有11、12;若y=7,则7≤<8,解得:13≤x<15,其整数解有13、14;若y=8,则8≤<9,解得:15≤x<17,其整数解有15、16;∴满足这个方程的整数x共有12个,故答案为:12.34.阅读理解题:对于任意由0,1组成的一列数.将原有的每个1变成01,并将每个原有的0变成10称为一次变换.如101经过一次变换成为011001.请你经过思考、操作回答下列问题:(1)将11变换两次后得到10011001;(2)若100101101001是由某数列两次变换后得到.则这个数列是101;(3)一个10项的数列经过两次变换后至少有多少对两个连续相等的数对(即1100)?请证明你的结论;(4)01经过10次操作后连续两项都是0的数对个数有341个.【考点】1G:有理数的混合运算.【分析】(1)根据变换规则解答即可得;(2)逆用变换规则,反向推理可得答案;(3)由0经过两次变换后得到0110、1经过两次变换后得到1001知10项的数列至少有10对连续相等的数对,根据010*******经过两次变换后得到0110100101101001…恰有10对连续相等的数对,得出答案;(4)记数列01为A0,k次变换后数列为A k,连续两项都是0的数对个数为l k,设A k中有b k个01数对,A k+1中的00数对只能由A k中的01数对得到,可得l k+1=b k,A k+1中的01数对有2种产生途径:①由A k中的1得到;②由A k中的00得,由此得出k为偶数时,l k关于k的函数表达式,将k=10代入即可得.【解答】解:(1)将11一次変换得0101,再次变换得10011001,故答案为:10011001;(2)100101101001一次変换的原数是011001,再次变换的原数是101,故答案为:101;(3)经过两次变换后至少有10对两个连续相等的数对,∵0经过两次变换后得到0110,1经过两次变换后得到1001,∴10项的数列至少有10对连续相等的数对,又∵010*******经过两次变换后得到0110100101101001…恰有10对连续相等的数对,∴一个10项的数列经过两次变换后至少有10对两个连续相等的数对;(4)记数列01为A0,k次变换后数列为A k,连续两项都是0的数对个数为l k,设A k中有b k个01数对,A k+1中的00数对只能由A k中的01数对得到,∴l k+1=b k,A k+1中的01数对有2种产生途径:①由A k中的1得到;②由A k中的00得到;根据题意知,A k中的0和1的个数总是相等,且共有2k+1个,∴b k+1=l k+2k,∴l k+2=l k+2k,由A0:0、1可得A1:1、0、0、1,A2:0、1、1、0、1、0、0、1,∴l1=1、l2=2,当k≥3时,若k为偶数,l k=l k﹣2+2k﹣2、l k﹣2=l k﹣4+2k﹣4、…、l4=l2+22,上述各式相加可得l k=1+22+24+…+2k﹣2==(2k﹣1),经检验,k=2时也满足l k=(2k﹣1),∴当k=10时,l10==341,故答案为:341.2017年5月19日。
北京八中2016-2017学年度第二学期期中考试初一数学试题及答案
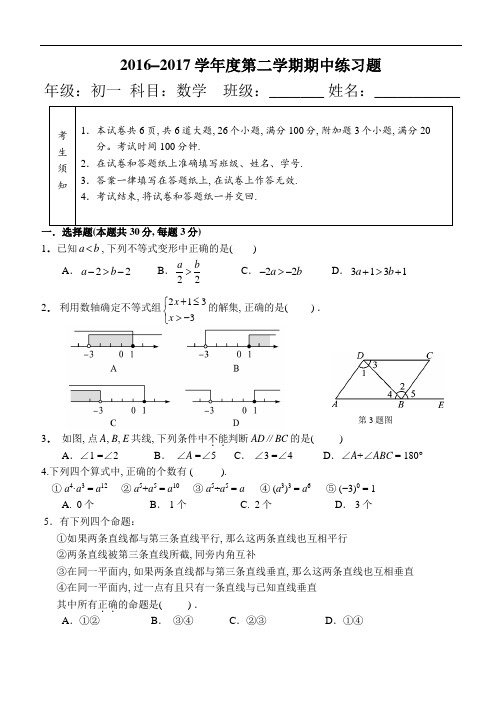
2016-2017学年度第二学期期中练习题年级:初一 科目:数学 班级:_______ 姓名:___________1.已知b a <, 下列不等式变形中正确的是( )A .22->-b aB .22ba > C .b a 22->- D .1313+>+b a 2. 利用数轴确定不等式组2133x x +≤⎧⎨>-⎩的解集, 正确的是( ) .3. 如图, 点A , B , E 共线, 下列条件中不.能.判断AD ∥BC 的是( ) A .∠1 =∠2 B . ∠A =∠5 C . ∠3 =∠4 D .∠A +∠ABC = 180° 4.下列四个算式中, 正确的个数有 ( ).① a 4·a 3 = a 12 ② a 5+a 5 = a 10 ③ a 5÷a 5 = a ④ (a 3)3 = a 6 ⑤ (−3)0 = 1A. 0个 B . 1个 C. 2个 D . 3个 5.有下列四个命题:①如果两条直线都与第三条直线平行, 那么这两条直线也互相平行 ②两条直线被第三条直线所截, 同旁内角互补③在同一平面内, 如果两条直线都与第三条直线垂直, 那么这两条直线也互相垂直 ④在同一平面内, 过一点有且只有一条直线与已知直线垂直其中所有正确..的命题是( ) . A .①② B . ③④ C .②③ D .①④第3题图6.下列各多项式相乘, 可以用平方差公式的有( )① (−2ab +5x ) (5x +2ab ) ② (ax − y ) ( −ax − y ) ③ (−ab − c ) (ab − c ) ④ (m +n ) ( −m − n ) A .4个B .3个C .2个D .1个7.如图是某公园里一处长方形风景欣赏区ABCD , AB 长50米, BC 宽25米, 为方便游人观赏, 公园特意修建了如图所示的小路(图中非阴影部分) , 小路的宽均为1米, 则小明沿着小路的中间行走的路线(图中虚线) 长为( )A .100米B .99米C .98米D .74米 8.如图所示的图形面积由以下哪个公式表示( )A . a 2 − b 2 = (a − b ) (a +b )B .(a − b )2 = a 2 − 2ab +b 2C .(a +b )2 = a 2+2ab +b 2D . a 2+ab = a (a +b )第7题图 第8题图 第9题图 9.如图, 把一块含有45°角的直角三角板的两个顶点放在直尺的对边上, 如果∠1=20°, 那么∠2等于 ( )A .30° B.25° C.20° D.15° 10.如图, 点E 在CA 延长线上, DE 、AB 交于F , 且∠BDE =∠AEF , ∠B =∠C ,∠EFA 比∠FDC 的余角小10°, P 为线段DC 上一动点,Q 为PC 上一点, 且满足∠FQP =∠QFP , FM 为∠EFP 的平分线. 则下列结论:① AB ∥CD ; ②FQ 平分∠AFP ; ③∠B +∠E =140°; ④∠QFM 的角度为定值. 其中正确结论有( ) 个 A .1 B .2 C .3 D .4二.填空题(本题共24分, 每题3分) 11.计算:()232m = .12.把命题“同角的余角相等”写成“如果…, 那么…” 的形式为 . 13.若x 2+2ax +16是一个完全平方式, 则a =______. 14. 生活中, 将一个宽度相等的纸条按图5所示折叠一下,如果∠1 =140º, 那么∠2 = .C第10题图第14题图15.如果x 4= 2, y 4= 3, 那么y x 222+= .老师说:“小明的作法正确.”请回答:小明的作图依据是 .17. 如图, B 点在A 点的北偏西30︒方向, 距A 点100米, C 点在B 点的北偏东60︒, ∠ACB = 40︒. (1)A 点在C 点的南偏西 度; (2) A 点到直线BC 的距离为 米.18.如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1)若不等式组⎪⎩⎪⎨⎧+->+<-231121x x x 的一个关联方程的解是整数,则这个关联方程可以是 ; (写出一个即可) (2)在方程①013=-x , ②0132=+x , ③()513-=+-x x 中, 不等式组⎩⎨⎧+->-->+-21352x x x x 的 关联方程是 ; (填序号)(3) 若方程x x 23=-, ⎪⎭⎫ ⎝⎛+=+2123x x 都是关于x 的不等式组⎩⎨⎧≤--<m x m x x 22 的关联方程,则m 的取值范围 .三.计算题(本题共18分, 19题9分, 20题5分, 21题4分)19. (1)()()y x y x 4332-- (2) 102⨯98 (3) ()()b ab a a ⋅-⋅⋅-2321320.解不等式组()⎪⎩⎪⎨⎧-<-+≤+37510714x x x x 把解集在数轴上表示出来, 并求出所有非负整数解.21.先化简, 再求值:()()()()151313122-+-+--x x x x x , 其中x = −2.第17题图C四.证明题(本题共10分, 每题5分)22.如图, ADC ABC ∠=∠, BF 、DE 分别平分ABC ∠与ADC ∠, 且∠1 =∠3.求证:AB ∥DC .请根据条件进行推理, 得出结论, 并在括号内注明理由. 证明:∵ BF 、DE 分别平分ABC ∠与ADC ∠,∴ ABC ∠=∠211, ADC ∠=∠212.(________________)∵ ∠ABC =∠ADC ,∴ ∠_____________=∠______________. ∵ ∠1 =∠3,∴ ∠2 =_______.(__________________) ∴ AB ∥CD .(________________________)23. 如图, EF //AD , ∠1 =∠2, ∠BAC = 70°. 求∠AGD . 解:五.作图题:(不写作法,保留作图痕迹,6分) 24.如图, 直线AB 、CD 相交于点O , P 是CD 上一点, (1) 过点P 画PE ⊥AB 于E(2) 过点P 画PF ⊥CD , 与AB 相交于点F(3) 将线段PF 、PE 、FO 从小到大排列为____________,这样排列的依据是______________________________.六.解答题(本题共12分, 每题6分)25. 某学校将周三“阳光体育”项目定为跳绳活动, 为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的两倍多4元, 且购买2条长跳绳与购买5条短跳绳的费用相同. (1)两种跳绳的单价各是多少元?(2)若该学校准备用不超过2000元的现金购买200条长、短跳绳, 且短跳绳的条数不超过长跳绳的6倍, 问学校有几种购买方案可供选择?321AEBDFCB26.阅读学习:数学中有很多恒等式可以用图形的面积来得到.如图1, 可以求出阴影部分的面积是a 2−b 2; 如图2, 若将阴影部分裁剪下来, 重新拼成一个矩形, 它的长是a +b , 宽是 a −b , 比较图1、图2阴影部分的面积, 可以得到恒等式()()22b a b a b a -=-+.(1) 观察图3, 请你写出2b a +, 2b a -, ab 之间的一个恒等式_________________. (2) 观察图4, 请写出图4所表示的代数恒等式:______________________________. (3) 现有若干块长方形和正方形硬纸片如图5所示.请你用拼图的方法推出一个恒等式2222)(b ab a b a ++=+, 仿照图4画出你的拼图并标出相关数据.附加题(本题共20分)1.我国古代《易经》一书中记载, 远古时期, 人们通过在绳子上打结来记录数量, 即“结绳计数”.如图, 一位母亲在从右到左依次排列的绳子上打结, 满七进一, 用来记录孩子自出生后的天数, 由图可知, 孩子自出生后的天数是 天.2.先阅读短文, 然后回答短文后面所给出的问题:对于三个数c b a 、、的平均数, 最小的数都可以给出符号来表示, 我们规定{}c b a M ,,表示c b a ,,这三个数的平均数, {}c b a ,,m in 表示c b a ,,这三个数中最小的数, {}c b a ,,m ax 表示 c b a ,,这三个数中最大的数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年北京八中七年级(上)期中数学试卷一、选择题(每小题所给4个选项中只有一个符合要求,每小题3分,共30分)1.零上3℃记作+3℃,那么零下5℃记作()A.﹣5 B.﹣10 C.﹣5℃D.﹣10℃2.2016年春节假期期间,我市接待旅游总人数达到9 186 000人次,比去边同期增长1.9%,将9 186 000用科学记数法表示应为()A.9186×103B.9.186×105C.9.186×106D.9.186×1073.方程3﹣2x=﹣1的解为()A.x=1 B.x=2 C.x=3 D.x=44.下列各组式子中的两个单项式是同类项的是()A.2x3与3x2B.12ax与8bx C.x4与a4D.23与﹣35.下列说法正确的是()①任何一个有理数的平方都是正数②任何一个有理数的绝对值都是非负数③0既不是正数也不是负数④符号不同的两个数是互为相反数的.A.①④B.②③C.③④D.②④6.在数轴上,与表示数﹣1的点的距离是3的点表示的数是()A.2 B.﹣4 C.±3 D.2或﹣47.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b8.有理数﹣32,(﹣3)2,|﹣33|,按从小到大的顺序排列是()A.<﹣32<(﹣3)2<|﹣33|B.|﹣33|<﹣32<<(﹣3)2C.﹣32<<(﹣3)2<|﹣33|D.<﹣32<|﹣33|<(﹣3)29.数a、b、c在数轴上对应的位置如图,化简|a+b|﹣|c﹣b|的结果()A.a+c B.c﹣a C.﹣c﹣a D.a+2b﹣c10.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则的值为()A.B.99! C.9900 D.2!二、填空题(每小题2分,共20分)11.﹣的系数是,次数是.12.用四舍五入法取近似数,1.895精确到百分位后是.13.多项式3x2y﹣7x4y2﹣xy3+27是次项式,最高次项是,按y的升幂排列为.14.若x=﹣3是方程3(x﹣a)=7的解,则a=.15.若a、b互为相反数,c、d互为倒数,则2﹣(a+b)+(﹣3cd)=.16.已知(a﹣2)2+|b+3|=0,则a﹣b=.17.用“☆”定义一种新运算:对于任意有理数a、b,都有a☆b=ab+a2,则(﹣3)☆2=.18.某地对居民用电的收费标准为:每月如果不超过100度,那么每度电价按a 元收费,如果超过100度,超出部分电价按b元收费,某户居民一个月用电160度,该户居民这个月应交纳电费是元(用含a、b的代数式表示).19.若代数式x2+x+3的值为5,则代数式﹣x2﹣x+7的值是.20.如图,一个数表有7行7列,设a ij表示第i行第j列上的数(其中i=1,2,3,…,j=1,2,3,…,)例如:第5行第3列上的数a53=7,则:(1)(a23﹣a22)+(a52﹣a53)=;(2)此数表中的四个数a np,a nk,a mp,a mk,满足(a np﹣a nk)+(a mk﹣a mp)=.三、计算题(21题每题3分,22题每题5分,23题4分,24题每题4分,共40分).21.计算:(1)23﹣17﹣(﹣7)+(﹣16)(2)(﹣)÷×(﹣1.5)(3)(+﹣)×(﹣36)(4)(3+)﹣3(1﹣|﹣1|)+(5)56÷(+﹣)(6)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].22.计算:(1)3a2﹣2a+4a2﹣7a(2)(3x+1)﹣2(2x2﹣5x+1)﹣3x2.23.先化简,再求值5(3a2b﹣ab2)﹣(ab2+3a2b)+2ab2,其中a=,b=﹣3.24.解方程:(1)﹣4(1﹣)=3(﹣1+x);(2)=1﹣.四、探究题(25题5分,26题5分,共10分)25.阅读下列材料,并解决后面的问题.材料:一般地,n个相同的因数a相乘:记为a n.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).问题:(1)计算以下各对数的值:log24=;log216=;log264=.(2)观察(1)中三数4、16、64之间满足怎样的关系式,然后利用4、16、64之间的数量关系猜想log24、log216、log264之间又满足怎样的关系式?答:log24、log216、log264关系式为.(3)由(2)的结果,请你能归纳出:log a M+log a N=(a>0且a≠1,M>0,N>0).26.认真完成下列题:(1)当a=,b=时,分别求代数式①a2﹣2ab+b2,②(a﹣b)2的值.(2)当a=5,b=3时,分别求代数式①a2﹣2ab+b2,②(a﹣b)2的值.(3)观察(1)(2)中代数式的值,a2﹣2ab+b2与(a﹣b)2有何关系?(4)利用你发现的规律,求135.72﹣2×135.7×35.7+35.72的值.五、附加题(共10分.计入总分,但总分不超过100分.)27.如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,(1)用含x的代数式表示CM=cm,DM=cm.(2)若DC=10cm,x的值为cm.28.你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.(1)阅读下列材料:问题:利用一元一次方程将0.化成分数.解:设0.=x.方程两边都乘以10,可得10×0.=10x.由0.=0.777…,可知10×0.=7.777…=7+0.,即7+x=10x.(请你体会将方程两边都乘以10起到的作用)可解得x=,即0.=.填空:将0.写成分数形式为.(2)请你仿照上述方法把下列两个小数化成分数,要求写出利用一元一次方程进行解答的过程:①0.;②0.43.29.有这样一个数字游戏:将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x代表的数字是,此时按游戏规则填写空格,所有可能出现的结果共有种.2016-2017学年北京八中七年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题所给4个选项中只有一个符合要求,每小题3分,共30分)1.零上3℃记作+3℃,那么零下5℃记作()A.﹣5 B.﹣10 C.﹣5℃D.﹣10℃【考点】正数和负数.【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答.【解答】解:零上3℃记作+3℃,那么零下5℃记作﹣5℃.故选C.2.2016年春节假期期间,我市接待旅游总人数达到9 186 000人次,比去边同期增长1.9%,将9 186 000用科学记数法表示应为()A.9186×103B.9.186×105C.9.186×106D.9.186×107【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n 是负数.【解答】解:9 186 000=9.186×106,故选:C.3.方程3﹣2x=﹣1的解为()A.x=1 B.x=2 C.x=3 D.x=4【考点】解一元一次方程.【分析】根据解方程步骤移项、合并同类项以及系数化为1即可求出方程的解.【解答】解:移项得:﹣2x=﹣1﹣3,合并同类项得:﹣2x=﹣4,系数化为1得:x=2,故选B.4.下列各组式子中的两个单项式是同类项的是()A.2x3与3x2B.12ax与8bx C.x4与a4D.23与﹣3【考点】同类项.【分析】根据同类项的概念即可求出答案.【解答】解:同类项是指具有相同的字母,且相同字母的指数要相同,常数也是同类项,故选(D)5.下列说法正确的是()①任何一个有理数的平方都是正数②任何一个有理数的绝对值都是非负数③0既不是正数也不是负数④符号不同的两个数是互为相反数的.A.①④B.②③C.③④D.②④【考点】有理数;相反数;绝对值.【分析】根据有理数的定义和特点,绝对值、相反数的定义及性质,对选项进行一一分析,排除错误答案.【解答】解:①任何一个有理数的平方都不是负数,错误;②任何一个有理数的绝对值都是非负数,正确;③0既不是正数也不是负数,正确;④只有符号不同的两个数是互为相反数的,错误;故选B6.在数轴上,与表示数﹣1的点的距离是3的点表示的数是()A.2 B.﹣4 C.±3 D.2或﹣4【考点】数轴.【分析】此题可借助数轴用数形结合的方法求解.在数轴上,与表示数﹣1的点的距离是3的点有两个,分别位于与表示数﹣1的点的左右两边.【解答】解:在数轴上,与表示数﹣1的点的距离是3的点表示的数有两个:﹣1﹣3=﹣4;﹣1+3=2.故选:D.7.下列计算正确的是()A.3a+b=3ab B.3a﹣a=2C.2a3+3a2=5a5D.﹣a2b+2a2b=a2b【考点】合并同类项.【分析】本题考查同类项的概念,含有相同的字母,并且相同字母的指数相同,是同类项的两项可以合并,否则不能合并.合并同类项的法则是系数相加作为系数,字母和字母的指数不变.【解答】解:A、3a与b不是同类项,不能合并.错误;B、3a﹣a=2a.错误;C、2a3与3a2不是同类项,不能合并.错误;D、﹣a2b+2a2b=a2b.正确.故选D.8.有理数﹣32,(﹣3)2,|﹣33|,按从小到大的顺序排列是()A.<﹣32<(﹣3)2<|﹣33|B.|﹣33|<﹣32<<(﹣3)2C.﹣32<<(﹣3)2<|﹣33|D.<﹣32<|﹣33|<(﹣3)2【考点】有理数大小比较.【分析】先根据乘方的意义得到﹣32=﹣9,(﹣3)2,=9,|﹣33|=|﹣27|=27,由|﹣9|=9,|﹣|=得到﹣9<﹣,则所给四个数的大小关系为﹣32<<(﹣3)2<|﹣33|.【解答】解:﹣32=﹣9,(﹣3)2,=9,|﹣33|=|﹣27|=27,∵|﹣9|=9,|﹣|=,∴﹣9<﹣,∴有理数﹣32,(﹣3)2,|﹣33|,按从小到大的顺序排列为﹣32<<(﹣3)2<|﹣33|.故选C.9.数a、b、c在数轴上对应的位置如图,化简|a+b|﹣|c﹣b|的结果()A.a+c B.c﹣a C.﹣c﹣a D.a+2b﹣c【考点】整式的加减;数轴;绝对值.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简即可得到结果.【解答】解:根据题意得:b<a<0<c,∴a+b<0,c﹣b>0,则原式=﹣a﹣b﹣c+b=﹣a﹣c,故选C10.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则的值为()A.B.99! C.9900 D.2!【考点】有理数的混合运算.【分析】由题目中的规定可知100!=100×99×98×...×1,98!=98×97× (1)然后计算的值.【解答】解:∵100!=100×99×98×...×1,98!=98×97× (1)所以=100×99=9900.故选:C.二、填空题(每小题2分,共20分)11.﹣的系数是﹣,次数是2.【考点】单项式.【分析】根据单项式的系数与次数的定义解答.【解答】解:﹣的系数是﹣,次数是2.故答案为﹣,2.12.用四舍五入法取近似数,1.895精确到百分位后是 1.9.【考点】近似数和有效数字.【分析】把千分位上的数字进行四舍五入即可.【解答】解:1.895≈1.90(精确到百分位).故答案为1.90.13.多项式3x2y﹣7x4y2﹣xy3+27是六次四项式,最高次项是﹣7x4y2,按y的升幂排列为27+3x2y﹣xy3﹣7x4y2.【考点】多项式.【分析】找出多项式中最高次项即可;找出最高项的次数即可的答案;再按照y 升幂排列即可.【解答】解:多项式3x2y﹣7x4y2﹣xy3+27的最高次项是﹣7x4y2;最高次项的次数是6,故是六次四项式,把多项式按字母y的升幂排列为27+3x2y﹣xy3﹣7x4y2,故答案为:六,四;﹣7x4y2;27+3x2y﹣xy3﹣7x4y2.14.若x=﹣3是方程3(x﹣a)=7的解,则a=﹣.【考点】方程的解.【分析】使方程左右两边的值相等的未知数的值是该方程的解.若x=﹣3是方程3(x﹣a)=7的解,把x=﹣3代入方程就得到一个关于a的方程,就可以求出a的值.【解答】解:根据题意得:3(﹣3﹣a)=7解得:a=﹣.15.若a、b互为相反数,c、d互为倒数,则2﹣(a+b)+(﹣3cd)=﹣1.【考点】代数式求值.【分析】a、b互为相反数,则a+b=0;c、d互为倒数,则cd=1,然后把它们代入,即可求出代数式2﹣(a+b)+(﹣3cd)的值.【解答】解:∵a、b互为相反数,∴a+b=0,∵c、d互为倒数,∴cd=1,∴2﹣(a+b)+(﹣3cd)=2﹣3=﹣1.故答案为﹣1.16.已知(a﹣2)2+|b+3|=0,则a﹣b=5.【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.【解答】解:根据题意得,a﹣2=0,b+3=0,解得a=2,b=﹣3,所以,a﹣b=2﹣(﹣3)=2+3=5.故答案为:5.17.用“☆”定义一种新运算:对于任意有理数a、b,都有a☆b=ab+a2,则(﹣3)☆2=3.【考点】有理数的混合运算.【分析】由题目中给出的运算方法,即可推出原式=﹣3×2+22,通过计算即可推出结果.【解答】解:(﹣3)☆2=﹣3×2+(﹣3)2=﹣6+9=3.故答案为:3.18.某地对居民用电的收费标准为:每月如果不超过100度,那么每度电价按a 元收费,如果超过100度,超出部分电价按b元收费,某户居民一个月用电160度,该户居民这个月应交纳电费是元(用含a、b的代数式表示).【考点】列代数式.【分析】根据题意可以用代数式表示出该户居民这个月应交的电费,本题得以解决.【解答】解:由题意可得,某户居民一个月用电160度,该户居民这个月应交纳电费是:100a+b=(元),故答案为:.19.若代数式x2+x+3的值为5,则代数式﹣x2﹣x+7的值是4.【考点】代数式求值.【分析】原式前两项提取公因式变形后,将已知代数式变形后代入计算即可求出值.【解答】解:∵x2+x+3=5,即x2+x=2,∴原式=﹣(x2+x)+7=﹣3+7=4,故答案为:420.如图,一个数表有7行7列,设a ij表示第i行第j列上的数(其中i=1,2,3,…,j=1,2,3,…,)例如:第5行第3列上的数a53=7,则:(1)(a23﹣a22)+(a52﹣a53)=0;(2)此数表中的四个数a np,a nk,a mp,a mk,满足(a np﹣a nk)+(a mk﹣a mp)=0.【考点】规律型:数字的变化类.【分析】(1)根据题意,观察数表可得a23=4,a32=3,a52=6,a53=7代入即可求解;(2)观察可知每行中的第p列和第k列的差是相等的,从而可得(a np﹣a nk)与(a mk﹣a mp)互为相反数.【解答】解:(1)∵a23=4,a22=3,a52=6,a53=7∴(a23﹣a22)+(a52﹣a53)=1﹣1=0;(2)∵每行中的第p列和第k列的差是相等的(如(1))∴(a np﹣a nk)与(a mk﹣a mp)互为相反数∴(a np﹣a nk)+(a mk﹣a mp)=0.三、计算题(21题每题3分,22题每题5分,23题4分,24题每题4分,共40分).21.计算:(1)23﹣17﹣(﹣7)+(﹣16)(2)(﹣)÷×(﹣1.5)(3)(+﹣)×(﹣36)(4)(3+)﹣3(1﹣|﹣1|)+(5)56÷(+﹣)(6)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2].【考点】有理数的混合运算.【分析】(1)根据有理数的加减法可以解答本题;(2)根据有理数的乘除法可以解答本题;(3)根据乘法分配律可以解答本题;(4)根据有理数的加减法可以解答本题;(5)根据有理数的加减法和除法可以解答本题;(6)根据有理数的加减法和乘法可以解答本题.【解答】解:(1)23﹣17﹣(﹣7)+(﹣16)=23+(﹣17)+7+(﹣16)=﹣3;(2)(﹣)÷×(﹣1.5)==;(3)(+﹣)×(﹣36)==(﹣4)+(﹣24)+6=﹣22;(4)(3+)﹣3(1﹣|﹣1|)+====3.5;(5)56÷(+﹣)=56÷(﹣)=56×(﹣)=﹣;(6)﹣14﹣(1﹣0.5)××[2﹣(﹣3)2]=﹣14﹣==.22.计算:(1)3a2﹣2a+4a2﹣7a(2)(3x+1)﹣2(2x2﹣5x+1)﹣3x2.【考点】整式的加减.【分析】(1)原式合并同类项即可得到结果;(2)原式去括号合并即可得到结果.【解答】解:(1)原式=7a2﹣9a;(2)原式=3x+1﹣4x2+10x﹣2﹣3x2=﹣7x2+13x﹣1.23.先化简,再求值5(3a2b﹣ab2)﹣(ab2+3a2b)+2ab2,其中a=,b=﹣3.【考点】整式的加减—化简求值.【分析】原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=15a2b﹣5ab2﹣ab2﹣3a2b+2ab2=12a2b﹣4ab2,把a=,b=﹣3代入得:原式=﹣9﹣18=﹣27.24.解方程:(1)﹣4(1﹣)=3(﹣1+x);(2)=1﹣.【考点】解一元一次方程.【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程去分母,去括号,移项合并,把y系数化为1,即可求出解.【解答】解:(1)去括号得:﹣4+2x=﹣3+3x,移项合并得:x=﹣1;(2)去分母得:2y﹣2=6﹣3y﹣3,移项合并得:5y=5,解得:y=1.四、探究题(25题5分,26题5分,共10分)25.阅读下列材料,并解决后面的问题.材料:一般地,n个相同的因数a相乘:记为a n.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为log a b(即log a b=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).问题:(1)计算以下各对数的值:log24=2;log216=4;log264=6.(2)观察(1)中三数4、16、64之间满足怎样的关系式,然后利用4、16、64之间的数量关系猜想log24、log216、log264之间又满足怎样的关系式?答:log24、log216、log264关系式为log24+log216=log264.(3)由(2)的结果,请你能归纳出:log a M+log a N=log a M+log a N=log a MN(a >0且a≠1,M>0,N>0).【考点】规律型:数字的变化类.【分析】(1)根据对数的定义求解;(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;(3)首先可设log a M=b1,log a N=b2,再根据幂的运算法则:a n•a m=a n+m以及对数的含义,得出结论:log a M+log a N=log a MN.【解答】解:(1)∵22=4,24=16,26=64,∴log24=2;log216=4;log264=6,故答案为:2,4,6;(2)由(1)知,∵2+4=6,∴log24+log216=log264=log2(4×16),故答案为:log24+log216=log264;(3)设log a M=x,log a N=y,则a x=M,a y=N,∴MN=a x•a y=a x+y,∴x+y=log a MN,即log a M+log a N=log a MN故答案为:log a M+log a N=log a MN.26.认真完成下列题:(1)当a=,b=时,分别求代数式①a2﹣2ab+b2,②(a﹣b)2的值.(2)当a=5,b=3时,分别求代数式①a2﹣2ab+b2,②(a﹣b)2的值.(3)观察(1)(2)中代数式的值,a2﹣2ab+b2与(a﹣b)2有何关系?(4)利用你发现的规律,求135.72﹣2×135.7×35.7+35.72的值.【考点】代数式求值.【分析】(1)把a与b的值分别代入两式计算即可得到结果;(2)把a与b的值分别代入两式计算即可得到结果;(3)观察(1)与(2),得到两式关系即可;(4)利用得出的关系将原式变形,计算即可得到结果.【解答】解:(1)当a=,b=时,①原式=﹣+=,②原式=(﹣)2=;(2)当a=5,b=3时,①原式=25﹣30+9=4,②原式=(5﹣3)2=4;(3)a2﹣2ab+b2=(a﹣b)2;(4)原式=2=1002=10000.五、附加题(共10分.计入总分,但总分不超过100分.)27.如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,(1)用含x的代数式表示CM=(x+2)cm,DM=(2x+2)cm.(2)若DC=10cm,x的值为2cm.【考点】列代数式.【分析】延长EK、FK得到正方形GKNH,(1)利用正方形的性质与线段的和差关系,用含x的代数式表示出CM、DM.(2)利用DC与DM、CM的关系列出方程,求出x.【解答】解:延长EK、FH交于点N.则四边形GKNH是边长为2的正方形(1)CM=GH+BF=(x+2)cm,DM=MK=MG﹣KG=2CM﹣GK=2(x+2)﹣2=(2x+2)cm;(2)DC=DM+MC∵DM=(2x+2)cm,MC=(x+2)cm若DC=10cm则2x+2+x+2=10解得:x=2.故答案为:(1)x+2,2x+2,(2)2.28.你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.(1)阅读下列材料:问题:利用一元一次方程将0.化成分数.解:设0.=x.方程两边都乘以10,可得10×0.=10x.由0.=0.777…,可知10×0.=7.777…=7+0.,即7+x=10x.(请你体会将方程两边都乘以10起到的作用)可解得x=,即0.=.填空:将0.写成分数形式为.(2)请你仿照上述方法把下列两个小数化成分数,要求写出利用一元一次方程进行解答的过程:①0.;②0.43.【考点】一元一次方程的应用.【分析】(1)根据0.转化分数的方法,设0.=x,仿照例题的解法即可得出结论;(2)①根据0.转化分数的方法,设0.=x,仿照例题的解法(×10换成×100)即可得出结论;②根据0.转化分数的方法,设0.43=x,仿照例题的解法即可得出结论.【解答】解:(1)设0.=x.方程两边都乘以10,可得10×0.=10x.由0.=0.444…,可知10×0.=4.444…=4+0.,即4+x=10x.解得:x=,即0.=.故答案为:.(2)①设0.=x.方程两边都乘以100,可得100×0.=100x.由0.=0.7373…,可知100×0.=73.7373…=73+0.,即73+x=100x.解得:x=,即0.=.②设0.43=x.方程两边都乘以10,可得10×0.43=10x.由0.43=0.43222…,可知10×0.43=4.3222…=3.89+0.43,即3.89+x=10x.解得:x=,即0.43=.29.有这样一个数字游戏:将1,2,3,4,5,6,7,8,9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字3和4固定在图中所示的位置时,x代表的数字是2,此时按游戏规则填写空格,所有可能出现的结果共有6种.【考点】规律型:数字的变化类.【分析】每一行从左到右、每一列从上到下分别依次增大,1、2、9只有一种填法,5只能填右上角或左下角,有2种方法,5之后与之相邻的空格可填6、7、8任意一个,有3种选择;余下的两个数字按从小到大只有一种方法,根据分步计数原理可得结果.【解答】解:根据题意知,x<4且x≠3,则x=2或x=1,∵x前面的数要比x小,∴x=2,∵每一行从左到右、每一列从上到下分别依次增大,∴9只能填在右下角,5只能填右上角或左下角,5之后与之相邻的空格可填6、7、8任意一个,余下的两个数字按从小到大只有一种方法,∴共有2×3=6种结果,故答案为:2,6.2017年3月11日。
